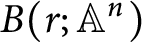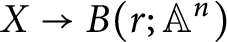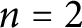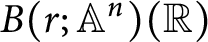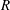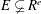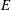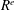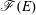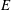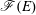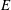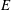Refine search
Actions for selected content:
5 results
Classifying spaces for étale algebras with generators
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 30 March 2020, pp. 854-874
- Print publication:
- June 2021
-
- Article
- Export citation
On Special Fiber Rings of Modules
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 09 January 2019, pp. 225-242
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
NOETHERIAN SPECTRUM ON RINGS AND MODULES
-
- Journal:
- Glasgow Mathematical Journal / Volume 53 / Issue 3 / September 2011
- Published online by Cambridge University Press:
- 01 August 2011, pp. 707-715
- Print publication:
- September 2011
-
- Article
-
- You have access
- Export citation
A Gorenstein Ring with Larger Dilworth Number than Sperner Number
-
- Journal:
- Canadian Mathematical Bulletin / Volume 43 / Issue 1 / 01 March 2000
- Published online by Cambridge University Press:
- 20 November 2018, pp. 100-104
- Print publication:
- 01 March 2000
-
- Article
-
- You have access
- Export citation
One-Dimensional Monoid Rings with n-Generated Ideals
-
- Journal:
- Canadian Mathematical Bulletin / Volume 36 / Issue 3 / 01 September 1993
- Published online by Cambridge University Press:
- 20 November 2018, pp. 344-350
- Print publication:
- 01 September 1993
-
- Article
-
- You have access
- Export citation