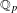Refine search
Actions for selected content:
2 results
VARIÉTÉS DE KISIN STRATIFIÉES ET DÉFORMATIONS POTENTIELLEMENT BARSOTTI-TATE
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 5 / November 2018
- Published online by Cambridge University Press:
- 08 September 2016, pp. 1019-1064
- Print publication:
- November 2018
-
- Article
- Export citation
Well Ramified Extensions of Complete Discrete Valuation Fields with Applications to the Kato Conductor
-
- Journal:
- Canadian Journal of Mathematics / Volume 52 / Issue 6 / 01 December 2000
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1269-1309
- Print publication:
- 01 December 2000
-
- Article
-
- You have access
- Export citation