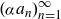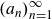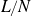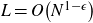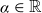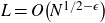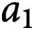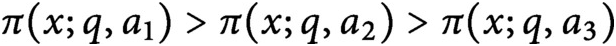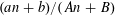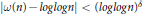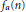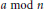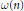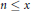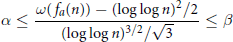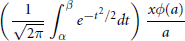Refine search
Actions for selected content:
9 results
Almost sure upper bound for a model problem for multiplicative chaos in number theory
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 1 / July 2025
- Published online by Cambridge University Press:
- 13 May 2025, pp. 29-44
- Print publication:
- July 2025
-
- Article
- Export citation
On inhomogeneous Poissonian pair correlations
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 1 / July 2025
- Published online by Cambridge University Press:
- 13 May 2025, pp. 17-27
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Intermediate-scale statistics for real-valued lacunary sequences
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 2 / September 2023
- Published online by Cambridge University Press:
- 11 April 2023, pp. 303-318
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the distribution of the digits of quotients of integers and primes
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 11 May 2021, pp. 279-295
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Densities in certain three-way prime number races
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 12 October 2020, pp. 232-265
- Print publication:
- February 2022
-
- Article
- Export citation
HARMONIC ANALYSIS ON THE POSITIVE RATIONALS. DETERMINATION OF THE GROUP GENERATED BY THE RATIOS
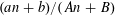 $(an+b)/(An+B)$
$(an+b)/(An+B)$
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 919-943
- Print publication:
- 2017
-
- Article
- Export citation
Spacings Between Integers Having Typically Many Prime Factors
-
- Journal:
- Canadian Mathematical Bulletin / Volume 53 / Issue 1 / 01 March 2010
- Published online by Cambridge University Press:
- 20 November 2018, pp. 102-117
- Print publication:
- 01 March 2010
-
- Article
-
- You have access
- Export citation
From uniform distributions to Benford's law
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 4 / December 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1203-1210
- Print publication:
- December 2004
-
- Article
- Export citation
Non-Abelian Generalizations of the Erdős-Kac Theorem
-
- Journal:
- Canadian Journal of Mathematics / Volume 56 / Issue 2 / 01 April 2004
- Published online by Cambridge University Press:
- 20 November 2018, pp. 356-372
- Print publication:
- 01 April 2004
-
- Article
-
- You have access
- Export citation