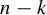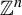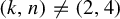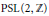Refine search
Actions for selected content:
2 results
Equidistribution of rational subspaces and their shapes
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 8 / August 2024
- Published online by Cambridge University Press:
- 10 November 2023, pp. 2009-2062
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Perfect Non-Extremal Riemann Surfaces
-
- Journal:
- Canadian Mathematical Bulletin / Volume 43 / Issue 1 / 01 March 2000
- Published online by Cambridge University Press:
- 20 November 2018, pp. 115-125
- Print publication:
- 01 March 2000
-
- Article
-
- You have access
- Export citation