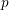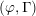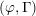3 results
Paraboline variation over
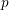 $p$-adic families of
$p$-adic families of 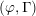 $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$-modules
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$-modules
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 19 January 2017, pp. 132-174
- Print publication:
- January 2017
-
- Article
- Export citation
Galois representations associated to holomorphic limits of discrete series
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 2 / February 2014
- Published online by Cambridge University Press:
- 26 November 2013, pp. 191-228
- Print publication:
- February 2014
-
- Article
- Export citation
Theta constants associated to coverings of P1 branching at eight points
-
- Journal:
- Compositio Mathematica / Volume 140 / Issue 5 / September 2004
- Published online by Cambridge University Press:
- 04 December 2007, pp. 1277-1301
- Print publication:
- September 2004
-
- Article
-
- You have access
- Export citation