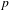 $p$-ADIC
$p$-ADIC  $L$-FUNCTIONS FOR ORDINARY FAMILIES ON SYMPLECTIC GROUPS
$L$-FUNCTIONS FOR ORDINARY FAMILIES ON SYMPLECTIC GROUPS
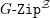 $G\text{-}\mathtt{Zip}^{{\mathcal{Z}}}$-schemes
$G\text{-}\mathtt{Zip}^{{\mathcal{Z}}}$-schemes
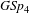 $\mathit{GSp}_{4}$ AND ITS APPLICATIONS
$\mathit{GSp}_{4}$ AND ITS APPLICATIONS