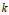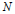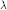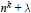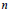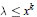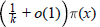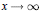Refine search
Actions for selected content:
1 results
Sequences with Translates Containing Many Primes
-
- Journal:
- Canadian Mathematical Bulletin / Volume 41 / Issue 1 / 01 March 1998
- Published online by Cambridge University Press:
- 20 November 2018, pp. 15-19
- Print publication:
- 01 March 1998
-
- Article
-
- You have access
- Export citation
-
Garrison [3], Forman [2], and Abel and Siebert [1] showed that for all positive integers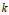
$k$ and 
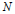$N$ , there exists a positive integer 
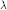$\lambda $ such that 
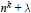${{n}^{k}}\,+\,\lambda $ is prime for at least 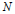$N$ positive integers 
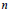$n$ . In other words, there exists 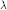$\lambda $ such that 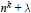${{n}^{k}}\,+\,\lambda $ , represents at least 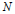$N$ primes.We give a quantitative version of this result.We show that there exists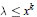
$\lambda \le {{x}^{k}}$ such that 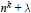${{n}^{k}}\,+\,\lambda $ , 1 ≤ n ≤ x, represents at least 
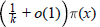$\left( \frac{1}{k}\,+\,o\left( 1 \right) \right)\,\pi \left( x \right)$ primes, as 
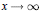$x\to \infty $ . We also give some related results.
