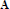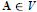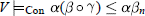Refine search
Actions for selected content:
14 results
RINGS WITH COMMON DIVISION, COMMON MEADOWS AND THEIR CONDITIONAL EQUATIONAL THEORIES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 23 December 2024, pp. 1-31
-
- Article
- Export citation
SEMIRING AND INVOLUTION IDENTITIES OF POWER GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 115 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 17 January 2023, pp. 354-374
- Print publication:
- December 2023
-
- Article
- Export citation
ON EQUATIONAL COMPLETENESS THEOREMS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 13 September 2021, pp. 1522-1575
- Print publication:
- December 2022
-
- Article
- Export citation
THE POSET OF ALL LOGICS II: LEIBNIZ CLASSES AND HIERARCHY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 10 June 2021, pp. 324-362
- Print publication:
- March 2023
-
- Article
- Export citation
THE POSET OF ALL LOGICS I: INTERPRETATIONS AND LATTICE STRUCTURE
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 10 June 2021, pp. 935-964
- Print publication:
- September 2021
-
- Article
- Export citation
MALTSEV CONDITIONS FOR GENERAL CONGRUENCE MEET-SEMIDISTRIBUTIVE ALGEBRAS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 01 February 2021, pp. 1432-1451
- Print publication:
- December 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GROWTH RATES OF ALGEBRAS, I: POINTED CUBE TERMS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 101 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 22 January 2016, pp. 56-94
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
THE CONSTRAINT SATISFACTION PROBLEM AND UNIVERSALALGEBRA
-
- Journal:
- Bulletin of Symbolic Logic / Volume 21 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 15 September 2015, pp. 319-337
- Print publication:
- September 2015
-
- Article
- Export citation
SUPERNILPOTENCE PREVENTS DUALIZABILITY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 96 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 30 September 2013, pp. 1-24
- Print publication:
- February 2014
-
- Article
-
- You have access
- Export citation
Finitely Related Algebras in CongruenceDistributive Varieties Have Near UnanimityTerms
-
- Journal:
- Canadian Journal of Mathematics / Volume 65 / Issue 1 / 01 February 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 3-21
- Print publication:
- 01 February 2013
-
- Article
-
- You have access
- Export citation
A Subalgebra Intersection Property for Congruence Distributive Varieties
-
- Journal:
- Canadian Journal of Mathematics / Volume 61 / Issue 2 / 01 April 2009
- Published online by Cambridge University Press:
- 20 November 2018, pp. 451-464
- Print publication:
- 01 April 2009
-
- Article
-
- You have access
- Export citation
A Characterization of Varieties with a Difference Term, II: Neutral = Meet Semi-Distributive
-
- Journal:
- Canadian Mathematical Bulletin / Volume 41 / Issue 3 / 01 September 1998
- Published online by Cambridge University Press:
- 20 November 2018, pp. 318-327
- Print publication:
- 01 September 1998
-
- Article
-
- You have access
- Export citation
A Characterization of Varieties with a Difference Term
-
- Journal:
- Canadian Mathematical Bulletin / Volume 39 / Issue 3 / 01 September 1996
- Published online by Cambridge University Press:
- 20 November 2018, pp. 308-315
- Print publication:
- 01 September 1996
-
- Article
-
- You have access
- Export citation
Inherently Nonfinitely Based Solvable Algebras
-
- Journal:
- Canadian Mathematical Bulletin / Volume 37 / Issue 4 / 01 December 1994
- Published online by Cambridge University Press:
- 20 November 2018, pp. 514-521
- Print publication:
- 01 December 1994
-
- Article
-
- You have access
- Export citation