Refine search
Actions for selected content:
4 results
CHARACTERIZATION OF PROJECTIVE QUANTALES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 08 January 2016, pp. 403-420
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
Transferring Optimal Dualities: Theory and Practice
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 74 / Issue 3 / June 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 393-420
- Print publication:
- June 2003
-
- Article
-
- You have access
- Export citation
Atoms, Primes and Implicative Lattices
-
- Journal:
- Canadian Mathematical Bulletin / Volume 27 / Issue 3 / 01 September 1984
- Published online by Cambridge University Press:
- 20 November 2018, pp. 279-285
- Print publication:
- 01 September 1984
-
- Article
-
- You have access
- Export citation
0-Distributive and P-Uniform Semilattices
-
- Journal:
- Canadian Mathematical Bulletin / Volume 25 / Issue 3 / 01 September 1982
- Published online by Cambridge University Press:
- 20 November 2018, pp. 317-324
- Print publication:
- 01 September 1982
-
- Article
-
- You have access
- Export citation
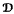 generated by a finite algebra
generated by a finite algebra 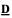 and assume that
and assume that 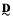 yields a natural duality on
yields a natural duality on 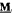 , which is also optimal modulo endormorphisms, for any finite algebra
, which is also optimal modulo endormorphisms, for any finite algebra 