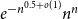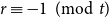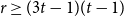Refine search
Actions for selected content:
6 results
On the size of maximal intersecting families
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 08 September 2023, pp. 32-49
-
- Article
- Export citation
Complete subgraphs in a multipartite graph
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 13 June 2022, pp. 1092-1101
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Full rainbow matchings in graphs and hypergraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 5 / September 2021
- Published online by Cambridge University Press:
- 20 January 2021, pp. 762-780
-
- Article
- Export citation
Pseudorandom hypergraph matchings
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 6 / November 2020
- Published online by Cambridge University Press:
- 22 July 2020, pp. 868-885
-
- Article
- Export citation
A Stability Theorem for Matchings in Tripartite 3-Graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 5 / September 2018
- Published online by Cambridge University Press:
- 02 April 2018, pp. 774-793
-
- Article
- Export citation
INFINITE MATROIDAL VERSION OF HALL'S MATCHING THEOREM
-
- Journal:
- Journal of the London Mathematical Society / Volume 71 / Issue 3 / June 2005
- Published online by Cambridge University Press:
- 24 May 2005, pp. 563-578
- Print publication:
- June 2005
-
- Article
- Export citation