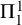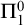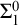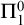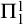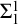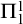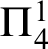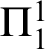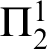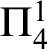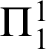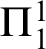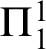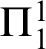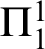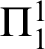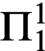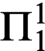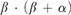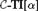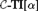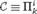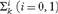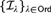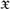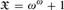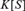12 results
Functorial Fast-Growing Hierarchies
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 26 January 2024, e15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
WEAK WELL ORDERS AND FRAÏSSÉ’S CONJECTURE
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 27 September 2023, pp. 1-16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
AN INCOMPLETENESS THEOREM VIA ORDINAL ANALYSIS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 12 September 2022, pp. 80-96
- Print publication:
- March 2024
-
- Article
-
- You have access
- HTML
- Export citation
COMPUTABLE REDUCIBILITY OF EQUIVALENCE RELATIONS AND AN EFFECTIVE JUMP OPERATOR
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 13 June 2022, pp. 540-561
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GOODSTEIN SEQUENCES BASED ON A PARAMETRIZED ACKERMANN–PÉTER FUNCTION
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 27 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 02 July 2021, pp. 168-186
- Print publication:
- June 2021
-
- Article
- Export citation
WELL ORDERING PRINCIPLES AND
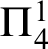 ${\Pi }^{1}_{4}$
-STATEMENTS: A PILOT STUDY
${\Pi }^{1}_{4}$
-STATEMENTS: A PILOT STUDY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 16 February 2021, pp. 709-745
- Print publication:
- June 2021
-
- Article
- Export citation
REFLECTION RANKS AND ORDINAL ANALYSIS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 10 July 2020, pp. 1350-1384
- Print publication:
- December 2021
-
- Article
- Export citation
HOW STRONG ARE SINGLE FIXED POINTS OF NORMAL FUNCTIONS?
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 20 July 2020, pp. 709-732
- Print publication:
- June 2020
-
- Article
- Export citation
PREDICATIVE COLLAPSING PRINCIPLES
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 09 December 2019, pp. 511-530
- Print publication:
- March 2020
-
- Article
- Export citation
A NOTE ON PREDICATIVE ORDINAL ANALYSIS I: ITERATED COMPREHENSION AND TRANSFINITE INDUCTION
-
- Journal:
- The Journal of Symbolic Logic / Volume 84 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 13 February 2019, pp. 226-265
- Print publication:
- March 2019
-
- Article
- Export citation
STRONG COMPLETENESS OF PROVABILITY LOGIC FOR ORDINAL SPACES
-
- Journal:
- The Journal of Symbolic Logic / Volume 82 / Issue 2 / June 2017
- Published online by Cambridge University Press:
- 19 June 2017, pp. 608-628
- Print publication:
- June 2017
-
- Article
- Export citation
REVERSE MATHEMATICS, YOUNG DIAGRAMS, AND THE ASCENDING CHAIN CONDITION
-
- Journal:
- The Journal of Symbolic Logic / Volume 82 / Issue 2 / June 2017
- Published online by Cambridge University Press:
- 19 June 2017, pp. 576-589
- Print publication:
- June 2017
-
- Article
- Export citation