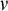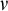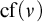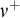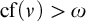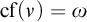1 Introduction
We study stationary reflection at successors of singular cardinals and its connection with cardinal arithmetic. We start by recalling some basic definitions. For an ordinal
![]() $\delta $
and a set
$\delta $
and a set
![]() $S \subseteq \delta $
, we say that S is stationary if it meets every closed and unbounded subset of
$S \subseteq \delta $
, we say that S is stationary if it meets every closed and unbounded subset of
![]() $\delta $
. If
$\delta $
. If
![]() $\{S_i \mid i \in I\}$
is a collection of stationary subsets of a regular cardinal
$\{S_i \mid i \in I\}$
is a collection of stationary subsets of a regular cardinal
![]() $\kappa $
, then we say that
$\kappa $
, then we say that
![]() $\{S_i \mid i \in I\}$
reflects simultaneously if there is an ordinal
$\{S_i \mid i \in I\}$
reflects simultaneously if there is an ordinal
![]() $\delta $
such that
$\delta $
such that
![]() $S_i \cap \delta $
is stationary for all
$S_i \cap \delta $
is stationary for all
![]() $i \in I$
.
$i \in I$
.
The consistency of stationary reflection at the successor of singular cardinal is already complex in the context of the generalized continuum hypothesis (GCH). A theorem of Magidor [Reference Magidor14] shows that it is consistent relative to the existence of infinitely many supercompact cardinals that every finite collection of stationary subsets of
![]() $\aleph _{\omega +1}$
reflects. Recently, the second and third authors [Reference Hayut and Unger13] were able to show the same result from an assumption below the existence of a cardinal
$\aleph _{\omega +1}$
reflects. Recently, the second and third authors [Reference Hayut and Unger13] were able to show the same result from an assumption below the existence of a cardinal
![]() $\kappa $
which is
$\kappa $
which is
![]() $\kappa ^{+}$
-supercompact. Both of these models satisfy GCH. Combining stationary reflection at the successor of a singular cardinal with the failure of
$\kappa ^{+}$
-supercompact. Both of these models satisfy GCH. Combining stationary reflection at the successor of a singular cardinal with the failure of
![]() $\operatorname {\mathrm {SCH}}$
presents additional difficulties.
$\operatorname {\mathrm {SCH}}$
presents additional difficulties.
For a singular cardinal
![]() $\nu $
, the singular cardinal hypothesis (
$\nu $
, the singular cardinal hypothesis (
![]() $\operatorname {\mathrm {SCH}}$
) at
$\operatorname {\mathrm {SCH}}$
) at
![]() $\nu $
is the assertion that if
$\nu $
is the assertion that if
![]() $\nu $
is strong limit, then
$\nu $
is strong limit, then
![]() $2^\nu = \nu ^{+}$
. The failure of the singular cardinal hypothesis at a singular cardinal
$2^\nu = \nu ^{+}$
. The failure of the singular cardinal hypothesis at a singular cardinal
![]() $\nu $
is known to imply the existence of many nonreflecting objects. For instance, Foreman and Todorcevic [Reference Foreman and Todorcevic4] have shown that the failure of the singular cardinal hypothesis at
$\nu $
is known to imply the existence of many nonreflecting objects. For instance, Foreman and Todorcevic [Reference Foreman and Todorcevic4] have shown that the failure of the singular cardinal hypothesis at
![]() $\nu $
implies that there are two stationary subsets of
$\nu $
implies that there are two stationary subsets of
![]() $[\nu ^{+}]^\omega $
which do not reflect simultaneously. This was improved by Shelah [Reference Shelah22] to obtain a single stationary subset of
$[\nu ^{+}]^\omega $
which do not reflect simultaneously. This was improved by Shelah [Reference Shelah22] to obtain a single stationary subset of
![]() $[\nu ^{+}]^\omega $
which does not reflect. Reflection for stationary subsets of
$[\nu ^{+}]^\omega $
which does not reflect. Reflection for stationary subsets of
![]() $[\nu ^{+}]^\omega $
has a different character than reflection for stationary subsets of ordinals.
$[\nu ^{+}]^\omega $
has a different character than reflection for stationary subsets of ordinals.
In [Reference Poveda, Rinot and Sinapova19, Corollary 5.4], Poveda, Rinot, and Sinapova showed that the failure of
![]() $\operatorname {\mathrm {SCH}}$
at cardinal
$\operatorname {\mathrm {SCH}}$
at cardinal
![]() $\nu $
implies the failure of simultaneous reflection for collections of
$\nu $
implies the failure of simultaneous reflection for collections of
![]() $\operatorname {\mathrm {cf}}\, (\nu )$
many stationary subsets of
$\operatorname {\mathrm {cf}}\, (\nu )$
many stationary subsets of
![]() $\nu ^{+}$
. In his PhD thesis from 2005, Sharon [Reference Sharon21] proved that relative to the existence of infinitely many supercompact cardinals it is consistent that there is a singular cardinal
$\nu ^{+}$
. In his PhD thesis from 2005, Sharon [Reference Sharon21] proved that relative to the existence of infinitely many supercompact cardinals it is consistent that there is a singular cardinal
![]() $\nu $
of cofinality
$\nu $
of cofinality
![]() $\omega $
such that
$\omega $
such that
![]() $\operatorname {\mathrm {SCH}}$
fails at
$\operatorname {\mathrm {SCH}}$
fails at
![]() $\nu $
and every stationary subset of
$\nu $
and every stationary subset of
![]() $\nu ^{+}$
reflects. Sharon’s method is a tour de force construction, which builds on Gitik’s long extenders forcing [Reference Gitik6] for
$\nu ^{+}$
reflects. Sharon’s method is a tour de force construction, which builds on Gitik’s long extenders forcing [Reference Gitik6] for
![]() $\omega $
-sequence of hypermeasurable cardinals. As such, the construction does not extend to singular cardinals of uncountable cofinalities, and the question of whether the failure of
$\omega $
-sequence of hypermeasurable cardinals. As such, the construction does not extend to singular cardinals of uncountable cofinalities, and the question of whether the failure of
![]() $\operatorname {\mathrm {SCH}}$
at singular
$\operatorname {\mathrm {SCH}}$
at singular
![]() $\kappa $
of uncountable cofinality together with stationary reflection at
$\kappa $
of uncountable cofinality together with stationary reflection at
![]() $\kappa ^{+}$
is at all consistent.
$\kappa ^{+}$
is at all consistent.
This paper follows a study by the authors on stationary reflection at successors of singular cardinals at which
![]() $\operatorname {\mathrm {SCH}}$
fails. This study was prompted by two other recent studies. First, the work of second and third authors in [Reference Hayut and Unger13] on stationary reflection in Prikry forcing extensions from subcompactness assumptions. The arguments of [Reference Hayut and Unger13] show how to examine the stationary reflection in the extension by Prikry type forcing by studying suitable iterated ultrapowers of V. This approach and method has been highly effective in our situation and we follow it here. The second study is Gitik’s recent work [Reference Gitik8] for blowing up the power of a singular cardinal using a Mitchell order increasing sequence of overlapping extenders. The new forcing machinery of [Reference Gitik8] gives new models combining the failure of
$\operatorname {\mathrm {SCH}}$
fails. This study was prompted by two other recent studies. First, the work of second and third authors in [Reference Hayut and Unger13] on stationary reflection in Prikry forcing extensions from subcompactness assumptions. The arguments of [Reference Hayut and Unger13] show how to examine the stationary reflection in the extension by Prikry type forcing by studying suitable iterated ultrapowers of V. This approach and method has been highly effective in our situation and we follow it here. The second study is Gitik’s recent work [Reference Gitik8] for blowing up the power of a singular cardinal using a Mitchell order increasing sequence of overlapping extenders. The new forcing machinery of [Reference Gitik8] gives new models combining the failure of
![]() $\operatorname {\mathrm {SCH}}$
with reflection properties at successors of singulars. Moreover the arguments are uniform in the choice of cofinality. For example, Gitik has shown that in a related model the tree property holds at
$\operatorname {\mathrm {SCH}}$
with reflection properties at successors of singulars. Moreover the arguments are uniform in the choice of cofinality. For example, Gitik has shown that in a related model the tree property holds at
![]() $\kappa ^{+}$
[Reference Gitik7] and that for all
$\kappa ^{+}$
[Reference Gitik7] and that for all
![]() $\delta < \kappa $
there is a stationary subset of
$\delta < \kappa $
there is a stationary subset of
![]() $\kappa ^{+}$
of ordinals of cofinality greater than
$\kappa ^{+}$
of ordinals of cofinality greater than
![]() $\delta $
which is not a member of
$\delta $
which is not a member of
![]() $I[\kappa ^{+}]$
[Reference Gitik9].
$I[\kappa ^{+}]$
[Reference Gitik9].
Our first main theorem shows how to construct a model in which there is a singular cardinal
![]() $\nu $
such that stationary reflection holds at
$\nu $
such that stationary reflection holds at
![]() $\nu^+$
, SCH fails at
$\nu^+$
, SCH fails at
![]() $\nu $
and the cofinality of
$\nu $
and the cofinality of
![]() $\nu $
can be chosen in advance.
$\nu $
can be chosen in advance.
Theorem 1.1. Let
![]() $\eta < \lambda $
be regular cardinals. Suppose that there is an increasing sequence of cardinals
$\eta < \lambda $
be regular cardinals. Suppose that there is an increasing sequence of cardinals
![]() $\langle \kappa _\alpha \mid \alpha < \eta \rangle $
with:
$\langle \kappa _\alpha \mid \alpha < \eta \rangle $
with:
-
(1)
 $\eta < \kappa _0$
,
$\eta < \kappa _0$
, -
(2) for each
 $\alpha < \eta $
,
$\alpha < \eta $
,
 $\kappa _\alpha $
carries a
$\kappa _\alpha $
carries a
 $(\kappa _\alpha ,\lambda )$
-extender
$(\kappa _\alpha ,\lambda )$
-extender
 $E_\alpha $
and there is a supercompact cardinal between
$E_\alpha $
and there is a supercompact cardinal between
 $\sup _{\beta <\alpha }\kappa _\beta $
and
$\sup _{\beta <\alpha }\kappa _\beta $
and
 $\kappa _\alpha $
, and
$\kappa _\alpha $
, and -
(3) the sequence
 $\langle E_{\alpha } \mid \alpha < \eta \rangle $
is Mitchell order increasing and coherent.
$\langle E_{\alpha } \mid \alpha < \eta \rangle $
is Mitchell order increasing and coherent.
Then, there is a cardinal and cofinality preserving extension in which, setting
![]() $\kappa = \sup _{\alpha < \eta }\kappa _\alpha $
,
$\kappa = \sup _{\alpha < \eta }\kappa _\alpha $
,
![]() $2^{\kappa } = \lambda $
and every collection of fewer than
$2^{\kappa } = \lambda $
and every collection of fewer than
![]() $\eta $
stationary subsets of
$\eta $
stationary subsets of
![]() $\kappa ^{+}$
reflects.Footnote
1
$\kappa ^{+}$
reflects.Footnote
1
We have the following improvement of Gitik’s result about
![]() $I[\kappa ^{+}]$
.
$I[\kappa ^{+}]$
.
Theorem 1.2. Let
![]() $\langle \kappa _\alpha \mid \alpha < \eta \rangle $
be as in Theorem 1.1 with the exception that we only assume there is a single supercompact cardinal
$\langle \kappa _\alpha \mid \alpha < \eta \rangle $
be as in Theorem 1.1 with the exception that we only assume there is a single supercompact cardinal
![]() $\theta <\kappa _0$
. There is a cardinal and cofinality preserving extension in which setting
$\theta <\kappa _0$
. There is a cardinal and cofinality preserving extension in which setting
![]() $\kappa = \sup _{\alpha <\eta }\kappa _\alpha $
, we have that
$\kappa = \sup _{\alpha <\eta }\kappa _\alpha $
, we have that
![]() $\kappa $
is strong limit,
$\kappa $
is strong limit,
![]() $2^\kappa =\lambda $
and there is a scale of length
$2^\kappa =\lambda $
and there is a scale of length
![]() $\kappa ^{+}$
such that the set of nongood points of cofinality less than
$\kappa ^{+}$
such that the set of nongood points of cofinality less than
![]() $\theta $
is stationary.
$\theta $
is stationary.
After a suitable preparation, the extension is obtained using the same forcing as in Theorem 1.1. Standard arguments show that in this model, the set of nongood points is stationary in cofinalities that are arbitrarily high below
![]() $\theta $
. Further, the same argument shows that we can take
$\theta $
. Further, the same argument shows that we can take
![]() $\theta $
between
$\theta $
between
![]() $\sup _{\alpha <\beta }\kappa _\alpha $
and
$\sup _{\alpha <\beta }\kappa _\alpha $
and
![]() $\kappa _\beta $
and reach the same conclusion.
$\kappa _\beta $
and reach the same conclusion.
These two results continue a long line of research about the interaction between the failure of the singular cardinal hypothesis and weak square-like principles [Reference Gitik and Sharon11, Reference Neeman18, Reference Sinapova23–Reference Sinapova and Unger26].
We do not know whether these results can also be obtained at small singular cardinals of uncountable cofinalities. For concreteness we suggest the following question.
Question 1.3. Is it consistent that
![]() $\operatorname {\mathrm {SCH}}$
fails
$\operatorname {\mathrm {SCH}}$
fails
![]() $\aleph _{\omega _1}$
and every stationary subset of
$\aleph _{\omega _1}$
and every stationary subset of
![]() $\aleph _{\omega _1+1}$
reflects?
$\aleph _{\omega _1+1}$
reflects?
We also give another model for stationary reflection at
![]() $\nu ^{+}$
where
$\nu ^{+}$
where
![]() $\nu $
is a singular cardinal of cofinality
$\nu $
is a singular cardinal of cofinality
![]() $\omega $
where the singular cardinal hypothesis fails. This construction replaces the supercompactness assumption in Sharon’s result and Theorem 1.1 with the weaker one of subcompactness together with hypermeasurability.
$\omega $
where the singular cardinal hypothesis fails. This construction replaces the supercompactness assumption in Sharon’s result and Theorem 1.1 with the weaker one of subcompactness together with hypermeasurability.
Theorem 1.4. Suppose that
![]() $\kappa $
is
$\kappa $
is
![]() $\kappa ^{+}$
-
$\kappa ^{+}$
-
![]() $\Pi _1^1$
-subcompact and carries a
$\Pi _1^1$
-subcompact and carries a
![]() $(\kappa ,\kappa ^{++})$
-extender. There is a forcing extension in which
$(\kappa ,\kappa ^{++})$
-extender. There is a forcing extension in which
![]() $\kappa $
is singular strong limit of cofinality
$\kappa $
is singular strong limit of cofinality
![]() $\omega $
,
$\omega $
,
![]() $2^\kappa =\kappa ^{++}$
and every finite collection of stationary subsets of
$2^\kappa =\kappa ^{++}$
and every finite collection of stationary subsets of
![]() $\kappa ^{+}$
reflects simultaneously.
$\kappa ^{+}$
reflects simultaneously.
In Theorem 6.22, we will also show how to collapse cardinals and make
![]() $\kappa $
in Theorem 1.4 to be
$\kappa $
in Theorem 1.4 to be
![]() $\aleph _{\omega }$
.Footnote
2
$\aleph _{\omega }$
.Footnote
2
The construction and proof follows the lines of the second and third authors’ paper [Reference Hayut and Unger13], and the work of Merimovich [Reference Merimovich15] on generating generics for extender based forcing over iterated ultrapowers. The large cardinal assumption in the theorem is the natural combination of the assumption from [Reference Hayut and Unger13] and an assumption sufficient to get the failure of
![]() $\operatorname {\mathrm {SCH}}$
by extender based forcing. Unfortunately, we are unable to adapt the argument from the previous theorem to a singular cardinal of uncountable cofinality. We ask:
$\operatorname {\mathrm {SCH}}$
by extender based forcing. Unfortunately, we are unable to adapt the argument from the previous theorem to a singular cardinal of uncountable cofinality. We ask:
Question 1.5. It is possible to obtain the result of Theorem 1.1 without any supercompactness assumptions? Namely, is it possible to start with a single partially supercompact cardinal
![]() $\kappa $
and force
$\kappa $
and force
![]() $\kappa $
to be a strong limit singular of uncountable cofinality such that every stationary subset of
$\kappa $
to be a strong limit singular of uncountable cofinality such that every stationary subset of
![]() $\kappa ^{+}$
reflects? Is it possible to obtain that together with the failure of
$\kappa ^{+}$
reflects? Is it possible to obtain that together with the failure of
![]() $\operatorname {\mathrm {SCH}}$
at
$\operatorname {\mathrm {SCH}}$
at
![]() $\kappa $
?
$\kappa $
?
The paper is organized as follows. In Section 2, we define Gitik’s forcing from [Reference Gitik8], which will be used in our main theorem. In Section 3, we prove that in mild generic extensions of V we can find a generic for Gitik’s forcing over a suitable iterated ultrapower. In Section 4, we give the proof of the main theorem by arguing that stationary reflection holds in the generic extension of the iterated ultrapower constructed in the previous section. In Section 5, we prove Theorem 1.2. In Section 6, we give the proof of Theorem 1.4 and its variation for
![]() $\aleph _\omega $
.
$\aleph _\omega $
.
2 Gitik’s forcing
In this section we give a presentation of Gitik’s forcing [Reference Gitik8] for blowing up the power of a singular cardinal with a Mitchell order increasing sequence of extenders.
Let us start with the following definitions:
Definition 2.1. Let
![]() $E_0, E_1$
be
$E_0, E_1$
be
![]() $(\kappa _0, \lambda _0)$
and
$(\kappa _0, \lambda _0)$
and
![]() $(\kappa _1, \lambda _1)$
-extenders respectively. We say that
$(\kappa _1, \lambda _1)$
-extenders respectively. We say that
![]() $E_0$
is less than
$E_0$
is less than
![]() $E_1$
in the Mitchell order, or
$E_1$
in the Mitchell order, or
![]() $E_0 \trianglelefteq E_1$
, if
$E_0 \trianglelefteq E_1$
, if
![]() $E_0 \in \operatorname {Ult}(V, E_1)$
. We say that
$E_0 \in \operatorname {Ult}(V, E_1)$
. We say that
![]() $E_0$
coheres with
$E_0$
coheres with
![]() $E_1$
if
$E_1$
if
![]() $j_{E_1}(E_0) \restriction \lambda _0 = E_0$
.
$j_{E_1}(E_0) \restriction \lambda _0 = E_0$
.
The existence of a long Mitchell increasing and pairwise coherent sequence of extenders
![]() $E_i$
, where
$E_i$
, where
![]() $E_i$
is a
$E_i$
is a
![]() $(\kappa _i, \lambda )$
-extender, follows from the existence of superstrong cardinal or even weaker large cardinal axioms.
$(\kappa _i, \lambda )$
-extender, follows from the existence of superstrong cardinal or even weaker large cardinal axioms.
Before we begin with the definition of the forcing, let us show a few basic facts about extenders and Mitchell order. We recall the notion of width from [Reference Cummings2].
Definition 2.2. Let
![]() $k\colon M \to N$
be an elementary embedding between transitive models of set theory and let
$k\colon M \to N$
be an elementary embedding between transitive models of set theory and let
![]() $\mu $
be an ordinal. We say the embedding k has width
$\mu $
be an ordinal. We say the embedding k has width
![]() ${\leq}\mu $
if every element of N is of the form
${\leq}\mu $
if every element of N is of the form
![]() $k(f)(a)$
for some
$k(f)(a)$
for some
![]() $f \in M$
and
$f \in M$
and
![]() $a \in N$
such that
$a \in N$
such that
![]() $M \models \vert \operatorname {\mathrm {dom}}(f)\vert \leq \mu $
.
$M \models \vert \operatorname {\mathrm {dom}}(f)\vert \leq \mu $
.
Lemma 2.3. Let E be a
![]() $(\kappa ,\lambda )$
-extender and let
$(\kappa ,\lambda )$
-extender and let
![]() $\leq _E$
be the Rudin–Keisler order of the extender E. Let
$\leq _E$
be the Rudin–Keisler order of the extender E. Let
![]() $k\colon V \to M$
be an elementary embedding with width
$k\colon V \to M$
be an elementary embedding with width
![]() ${\leq}\kappa $
. Then the set
${\leq}\kappa $
. Then the set
![]() $k " \operatorname {\mathrm {dom}} E$
is
$k " \operatorname {\mathrm {dom}} E$
is
![]() $\leq _{k(E)}$
-cofinal in
$\leq _{k(E)}$
-cofinal in
![]() $\operatorname {\mathrm {dom}} k(E)$
.
$\operatorname {\mathrm {dom}} k(E)$
.
Proof By [Reference Gitik6], the Rudin–Keisler order
![]() $\leq _E$
is
$\leq _E$
is
![]() $\kappa ^{+}$
-directed.
$\kappa ^{+}$
-directed.
Let
![]() $a \in \operatorname {\mathrm {dom}} k(E)$
. Then, by the definition of width, there is a function
$a \in \operatorname {\mathrm {dom}} k(E)$
. Then, by the definition of width, there is a function
![]() $f\colon \kappa \to \operatorname {\mathrm {dom}} E$
and some generator b such that
$f\colon \kappa \to \operatorname {\mathrm {dom}} E$
and some generator b such that
![]() $k(f)(b) = a$
. Let
$k(f)(b) = a$
. Let
![]() $a'$
be a
$a'$
be a
![]() $\leq _E$
upper bound of the image of f. Then, clearly,
$\leq _E$
upper bound of the image of f. Then, clearly,
![]() $k(a')$
is
$k(a')$
is
![]() $\leq _{k(E)}$
above a.
$\leq _{k(E)}$
above a.
Lemma 2.4. Let
![]() $E_0$
be a
$E_0$
be a
![]() $(\kappa _0, \lambda )$
-extender and let
$(\kappa _0, \lambda )$
-extender and let
![]() $E_1$
be a
$E_1$
be a
![]() $(\kappa _1,\lambda )$
-extender, where
$(\kappa _1,\lambda )$
-extender, where
![]() $\kappa _0 \leq \kappa _1$
. Let us assume that
$\kappa _0 \leq \kappa _1$
. Let us assume that
![]() $E_0 \trianglelefteq E_1$
. Then the following diagram commutes:
$E_0 \trianglelefteq E_1$
. Then the following diagram commutes:

where each arrow represents the ultrapower map using the indicated extender.
Proof First, since
![]() $E_0\in M_1$
, all maps are internally defined and in particular, all models are well founded.
$E_0\in M_1$
, all maps are internally defined and in particular, all models are well founded.
Moreover,
In order to verify this, it is sufficient to show that those maps are the same on sets of ordinals. First, let us verify that they agree of the ordinals. Indeed, let us consider the class:
ordered using the extender
![]() $E_0$
:
$E_0$
:
Using the combinatorial definition of the extender ultrapower, we conclude that
![]() $M_1$
can compute this order correctly, and in particular, it computes correctly the ordertype of the elements below any constant function, or indeed below any element of the form
$M_1$
can compute this order correctly, and in particular, it computes correctly the ordertype of the elements below any constant function, or indeed below any element of the form
![]() $[f,a]$
that represents an ordinal. Indeed, as the ultrapower by
$[f,a]$
that represents an ordinal. Indeed, as the ultrapower by
![]() $E_1$
is closed under
$E_1$
is closed under
![]() $\kappa _0$
-sequences, it contains the above class. Since
$\kappa _0$
-sequences, it contains the above class. Since
![]() $E_0 \trianglelefteq E_1$
,
$E_0 \trianglelefteq E_1$
,
![]() $M_1$
contains the relevant measures and Rudin–Keisler projections.
$M_1$
contains the relevant measures and Rudin–Keisler projections.
For an arbitrary set of ordinals, y, one can easily compute whether
![]() $[f,a] \in [c_y, \{\kappa_0\}]$
using the combinatorial information of the extender.
$[f,a] \in [c_y, \{\kappa_0\}]$
using the combinatorial information of the extender.
Let us consider an element of
![]() $\operatorname {Ult}(M_1, E_0)$
. By the definition, it has the form:
$\operatorname {Ult}(M_1, E_0)$
. By the definition, it has the form:
![]() $x = j_{E_0}(g)(a_0)$
where
$x = j_{E_0}(g)(a_0)$
where
![]() $g\colon \kappa _0^{<\omega } \to M_1$
. Going backwards, we can find a function in V, f, and a generator
$g\colon \kappa _0^{<\omega } \to M_1$
. Going backwards, we can find a function in V, f, and a generator
![]() $a_1$
such that for every z,
$a_1$
such that for every z,
![]() $j_{E_1}(f)(z, a_1) = g(y)$
and therefore
$j_{E_1}(f)(z, a_1) = g(y)$
and therefore
This element in obviously in
![]() $\operatorname {Ult}(M_0, j_{E_0}(E_1))$
.
$\operatorname {Ult}(M_0, j_{E_0}(E_1))$
.
On the other hand, if
![]() $y \in \operatorname {Ult}(M_0, j_{E_0}(E_1))$
then there is some generator
$y \in \operatorname {Ult}(M_0, j_{E_0}(E_1))$
then there is some generator
![]() $a_1^{\prime } \in \operatorname {\mathrm {dom}} j_{E_0}(E_1)$
and a function g such that
$a_1^{\prime } \in \operatorname {\mathrm {dom}} j_{E_0}(E_1)$
and a function g such that
![]() $y = j_{j_{E_0}(E_1)}(g)(a_1^{\prime })$
. By Lemma 2.3, we may assume that
$y = j_{j_{E_0}(E_1)}(g)(a_1^{\prime })$
. By Lemma 2.3, we may assume that
![]() $a_1^{\prime } = j_{E_0}(a_1)$
. Let f be a function in V and let
$a_1^{\prime } = j_{E_0}(a_1)$
. Let f be a function in V and let
![]() $a_0$
be some generator such that
$a_0$
be some generator such that
![]() $g = j_{E_0}(f)(a_0)$
, then we have
$g = j_{E_0}(f)(a_0)$
, then we have
 $$\begin{align*}\begin{matrix} y & = & j_{j_{E_0}(E_1)}\left(j_{E_0}(f)(a_0, - )\right)(j_{E_0}(a_1)) \\ & = & j_{j_{E_0}(E_1)}\left(j_{E_0}\left(f(-, a_1)\right)(a_0)\right) \\ & = & j_{E_0}\big(j_{E_1}(f)( - , a_1)\big)(a_0), \end{matrix} \end{align*}$$
$$\begin{align*}\begin{matrix} y & = & j_{j_{E_0}(E_1)}\left(j_{E_0}(f)(a_0, - )\right)(j_{E_0}(a_1)) \\ & = & j_{j_{E_0}(E_1)}\left(j_{E_0}\left(f(-, a_1)\right)(a_0)\right) \\ & = & j_{E_0}\big(j_{E_1}(f)( - , a_1)\big)(a_0), \end{matrix} \end{align*}$$
as wanted.
Let
![]() $\langle \kappa _\alpha \mid \alpha < \eta \rangle $
be a sequence of cardinals as in Theorem 1.1. Following Merimovich (see for example [Reference Merimovich15]), we can assume that the extenders
$\langle \kappa _\alpha \mid \alpha < \eta \rangle $
be a sequence of cardinals as in Theorem 1.1. Following Merimovich (see for example [Reference Merimovich15]), we can assume that the extenders
![]() $E_\alpha $
are of the form
$E_\alpha $
are of the form
![]() $\langle E_\alpha (d) \mid d \in [\lambda ]^{\kappa _\alpha } \rangle $
where for
$\langle E_\alpha (d) \mid d \in [\lambda ]^{\kappa _\alpha } \rangle $
where for
![]() $X \subseteq \{f\mid \operatorname {\mathrm {dom}} f \subseteq d,\, \operatorname {\mathrm {range}} f \subseteq \kappa _\alpha ,\, |f| < \kappa _\alpha \}$
,
$X \subseteq \{f\mid \operatorname {\mathrm {dom}} f \subseteq d,\, \operatorname {\mathrm {range}} f \subseteq \kappa _\alpha ,\, |f| < \kappa _\alpha \}$
,
![]() $X \in E_\alpha (d)$
if and only if
$X \in E_\alpha (d)$
if and only if
![]() $\{ (j_{E_\alpha }(\xi ),\xi ) \mid \xi \in d \} \in j_{E_\alpha }(X)$
.
$\{ (j_{E_\alpha }(\xi ),\xi ) \mid \xi \in d \} \in j_{E_\alpha }(X)$
.
For
![]() $d\in [\lambda ]^{\kappa _\alpha }$
with
$d\in [\lambda ]^{\kappa _\alpha }$
with
![]() $\kappa _\alpha \in d$
, it is easy to see that the measure
$\kappa _\alpha \in d$
, it is easy to see that the measure
![]() $E_\alpha (d)$
concentrates on a set of order preserving functions
$E_\alpha (d)$
concentrates on a set of order preserving functions
![]() $\nu $
with
$\nu $
with
![]() $\kappa \in \operatorname {\mathrm {dom}}(\nu )$
. So we may assume that the elements of every measure one set mentioned below are of this form. We also fix functions
$\kappa \in \operatorname {\mathrm {dom}}(\nu )$
. So we may assume that the elements of every measure one set mentioned below are of this form. We also fix functions
![]() $\langle \ell _\alpha \mid \alpha < \eta \rangle $
so that for every
$\langle \ell _\alpha \mid \alpha < \eta \rangle $
so that for every
![]() $\alpha < \eta $
,
$\alpha < \eta $
,
![]() $j_{E_\alpha }(\ell _\alpha )(\kappa _\alpha ) = \lambda $
. The existence of such functions can always be arranged by a simple preparatory forcing.
$j_{E_\alpha }(\ell _\alpha )(\kappa _\alpha ) = \lambda $
. The existence of such functions can always be arranged by a simple preparatory forcing.
Using the set
![]() $d \in [\lambda ]^{\kappa _\alpha }$
to index the extenders
$d \in [\lambda ]^{\kappa _\alpha }$
to index the extenders
![]() $E_\alpha $
has the advantage that the projection maps from
$E_\alpha $
has the advantage that the projection maps from
![]() $E_\alpha (d')$
and
$E_\alpha (d')$
and
![]() $E_\alpha (d)$
for
$E_\alpha (d)$
for
![]() $d \subseteq d'$
can be made very explicit. The measure
$d \subseteq d'$
can be made very explicit. The measure
![]() $E_\alpha (d^{\prime })$
concentrates on partial functions from
$E_\alpha (d^{\prime })$
concentrates on partial functions from
![]() $d'$
to
$d'$
to
![]() $\kappa _\alpha $
with domain smaller than
$\kappa _\alpha $
with domain smaller than
![]() $\kappa _\alpha $
. Thus, the map
$\kappa _\alpha $
. Thus, the map
![]() $\nu \to \nu \restriction d$
is a projection from
$\nu \to \nu \restriction d$
is a projection from
![]() $E_\alpha (d^{\prime })$
to
$E_\alpha (d^{\prime })$
to
![]() $E_\alpha (d)$
.
$E_\alpha (d)$
.
For every two cardinals
![]() $\mu < \lambda $
, let
$\mu < \lambda $
, let
![]() $\mathcal {A}(\lambda ,\mu )$
be the poset consisting of partial functions
$\mathcal {A}(\lambda ,\mu )$
be the poset consisting of partial functions
![]() $f \colon \lambda \to \mu $
with
$f \colon \lambda \to \mu $
with
![]() $|f| \leq \mu $
and
$|f| \leq \mu $
and
![]() $\mu \in \operatorname {\mathrm {dom}}(f)$
. Therefore
$\mu \in \operatorname {\mathrm {dom}}(f)$
. Therefore
![]() $\mathcal {A}(\lambda ,\mu )$
is isomorphic to Cohen forcing for adding
$\mathcal {A}(\lambda ,\mu )$
is isomorphic to Cohen forcing for adding
![]() $\lambda $
many subsets of
$\lambda $
many subsets of
![]() $\mu ^{+}$
.
$\mu ^{+}$
.
We let
![]() $\mathbb {P}$
be Gitik’s forcing from [Reference Gitik8] defined from the sequence of extenders
$\mathbb {P}$
be Gitik’s forcing from [Reference Gitik8] defined from the sequence of extenders
![]() $\langle E_\alpha \mid \alpha < \eta \rangle $
. We give a compact description of the forcing. A condition
$\langle E_\alpha \mid \alpha < \eta \rangle $
. We give a compact description of the forcing. A condition
![]() $p \in \mathbb {P}$
is a sequence
$p \in \mathbb {P}$
is a sequence
![]() $\langle p_\alpha \mid \alpha < \eta \rangle $
such that there is a finite set
$\langle p_\alpha \mid \alpha < \eta \rangle $
such that there is a finite set
![]() $s^p \subseteq \eta $
such that for each
$s^p \subseteq \eta $
such that for each
![]() $\alpha < \eta $
,
$\alpha < \eta $
,
![]() $p_\alpha = (f_\alpha ,\lambda _\alpha )$
if
$p_\alpha = (f_\alpha ,\lambda _\alpha )$
if
![]() $\alpha \in s^p$
, and
$\alpha \in s^p$
, and
![]() $p_\alpha = (f_\alpha ,A_\alpha )$
otherwise, and the following conditions hold.
$p_\alpha = (f_\alpha ,A_\alpha )$
otherwise, and the following conditions hold.
-
(1)
 $f_\alpha \in \mathcal {A}(\lambda _{\alpha ^*},\kappa _\alpha )$
where
$f_\alpha \in \mathcal {A}(\lambda _{\alpha ^*},\kappa _\alpha )$
where
 $\alpha ^*$
is the next element of
$\alpha ^*$
is the next element of
 $s^p$
above
$s^p$
above
 $\alpha $
if it exists and
$\alpha $
if it exists and
 $f_\alpha \in \mathcal {A}(\lambda ,\kappa _\alpha )$
otherwise.
$f_\alpha \in \mathcal {A}(\lambda ,\kappa _\alpha )$
otherwise. -
(2) For all
 $\alpha \in s^p$
,
$\alpha \in s^p$
,
 $\lambda _\alpha $
is a cardinal and
$\lambda _\alpha $
is a cardinal and
 $\sup _{\beta < \alpha }\kappa _\beta < \lambda _\alpha < \kappa _\alpha $
.
$\sup _{\beta < \alpha }\kappa _\beta < \lambda _\alpha < \kappa _\alpha $
. -
(3) For all
 $\alpha \in \eta \setminus s^p$
, if
$\alpha \in \eta \setminus s^p$
, if
 $\alpha> \max (s^p)$
, then
$\alpha> \max (s^p)$
, then
 $A_\alpha \in E_\alpha (\operatorname {\mathrm {dom}}(f_\alpha ))$
, otherwise if
$A_\alpha \in E_\alpha (\operatorname {\mathrm {dom}}(f_\alpha ))$
, otherwise if
 $\alpha ^*$
is the least element of
$\alpha ^*$
is the least element of
 $s^p$
above
$s^p$
above
 $\alpha $
, then
$\alpha $
, then
 $A_\alpha \in E_\alpha (\operatorname {\mathrm {dom}}(f_\alpha ))$
.
$A_\alpha \in E_\alpha (\operatorname {\mathrm {dom}}(f_\alpha ))$
. -
(4) For
 $\alpha \notin s^p$
,
$\alpha \notin s^p$
,
 $f_\alpha ^p(\kappa _\alpha ) =0$
.Footnote
3
$f_\alpha ^p(\kappa _\alpha ) =0$
.Footnote
3
-
(5) The sequence
 $\langle \operatorname {\mathrm {dom}}(f_\alpha ) \mid \alpha < \eta \rangle $
is increasing.
$\langle \operatorname {\mathrm {dom}}(f_\alpha ) \mid \alpha < \eta \rangle $
is increasing.
We adopt the convention of adding a superscript
![]() $f_\alpha ^p$
,
$f_\alpha ^p$
,
![]() $A_\alpha ^p$
, etc. to indicate that each component belongs to p. When the value of
$A_\alpha ^p$
, etc. to indicate that each component belongs to p. When the value of
![]() $\lambda _{\alpha ^{*}}$
might behave non-trivially, we will add it as a third coordinate to the pairs
$\lambda _{\alpha ^{*}}$
might behave non-trivially, we will add it as a third coordinate to the pairs
![]() $p_\alpha $
, where
$p_\alpha $
, where
![]() $\alpha \notin s^p$
. We call
$\alpha \notin s^p$
. We call
![]() $\eta \setminus s^p$
the pure part of p and
$\eta \setminus s^p$
the pure part of p and
![]() $s^p$
the non-pure part of p.
$s^p$
the non-pure part of p.
We briefly sketch the notion of extension. A condition p is a direct extension of q if
![]() $s^p = s^q$
and for all
$s^p = s^q$
and for all
![]() $\alpha $
,
$\alpha $
,
![]() $f_\alpha ^p$
is stronger than
$f_\alpha ^p$
is stronger than
![]() $f_\alpha ^q$
and
$f_\alpha ^q$
and
![]() $A_\alpha ^p$
projects to a subset of
$A_\alpha ^p$
projects to a subset of
![]() $A_\alpha ^q$
using the natural Rudin–Keisler projection from
$A_\alpha ^q$
using the natural Rudin–Keisler projection from
![]() $E_\alpha (\operatorname {\mathrm {dom}} f_\alpha ^p)$
to
$E_\alpha (\operatorname {\mathrm {dom}} f_\alpha ^p)$
to
![]() $E_\alpha (\operatorname {\mathrm {dom}} f_\alpha ^q)$
.
$E_\alpha (\operatorname {\mathrm {dom}} f_\alpha ^q)$
.
Let us describe now the one point extension. Suppose that
![]() $\nu \in A_\beta ^p$
. We let
$\nu \in A_\beta ^p$
. We let
![]() $q = p \frown \nu $
be the condition with
$q = p \frown \nu $
be the condition with
![]() $s^q = s^p \cup \{\beta \}$
and the following.
$s^q = s^p \cup \{\beta \}$
and the following.
-
(1)
 $f_\beta ^q = f_\beta ^p {}^\frown \nu $
is the overwriting of
$f_\beta ^q = f_\beta ^p {}^\frown \nu $
is the overwriting of
 $f_\beta ^p$
by
$f_\beta ^p$
by
 $\nu $
, that is,
$\nu $
, that is,  $$\begin{align*}(f_\beta^p{}^\frown \nu)(\tau) = \begin{cases} \nu(\tau), \mbox{ if } \tau \in \operatorname{\mathrm{dom}}(\nu),\\ f^p_\beta(\tau), \mbox{ otherwise. } \end{cases} \end{align*}$$
$$\begin{align*}(f_\beta^p{}^\frown \nu)(\tau) = \begin{cases} \nu(\tau), \mbox{ if } \tau \in \operatorname{\mathrm{dom}}(\nu),\\ f^p_\beta(\tau), \mbox{ otherwise. } \end{cases} \end{align*}$$
-
(2)
 $\lambda _\beta ^q = \ell _\beta (\nu (\kappa _\beta ))$
.
$\lambda _\beta ^q = \ell _\beta (\nu (\kappa _\beta ))$
. -
(3) For
 $\alpha \in [\max (s^p) \cap \beta ,\beta )$
,
$\alpha \in [\max (s^p) \cap \beta ,\beta )$
,
 $f_\alpha ^q = f_\alpha ^p \circ \nu ^{-1}$
and
$f_\alpha ^q = f_\alpha ^p \circ \nu ^{-1}$
and
 $A_\alpha ^q = \{ \xi \circ \nu ^{-1} \mid \xi \in A_\alpha ^p \}$
if applicable.
$A_\alpha ^q = \{ \xi \circ \nu ^{-1} \mid \xi \in A_\alpha ^p \}$
if applicable.
The following analysis of dense open sets of
![]() $\mathbb {P}$
was established in [Reference Gitik8].
$\mathbb {P}$
was established in [Reference Gitik8].
Lemma 2.5. For every condition
![]() $p \in \mathbb {P}$
and dense open set
$p \in \mathbb {P}$
and dense open set
![]() $D \subseteq \mathbb {P}$
, there are
$D \subseteq \mathbb {P}$
, there are
![]() $p^* \geq ^* p$
and a finite subset
$p^* \geq ^* p$
and a finite subset
![]() $\{ \alpha _0, \dots , \alpha _{m-1}\}$
of the pure part of p, such that for every sequence
$\{ \alpha _0, \dots , \alpha _{m-1}\}$
of the pure part of p, such that for every sequence
![]() $\vec {\nu } = \langle \nu _{\alpha _0},\dots , \nu _{\alpha _{m-1}}\rangle \in \prod _{i< m} A^{p^*}_{\alpha _i}$
,
$\vec {\nu } = \langle \nu _{\alpha _0},\dots , \nu _{\alpha _{m-1}}\rangle \in \prod _{i< m} A^{p^*}_{\alpha _i}$
,
![]() $p^* {}^\frown \vec {\nu } \in D$
.
$p^* {}^\frown \vec {\nu } \in D$
.
For limit
![]() $\delta \leq \eta $
, we define
$\delta \leq \eta $
, we define
![]() $\bar {\kappa }_\delta = \sup _{\alpha <\delta }\kappa _\alpha $
. Gitik used the previous lemma to prove:
$\bar {\kappa }_\delta = \sup _{\alpha <\delta }\kappa _\alpha $
. Gitik used the previous lemma to prove:
Theorem 2.6. In the generic extension by
![]() $\mathbb {P}$
, cardinals and cofinalities are preserved and for every limit
$\mathbb {P}$
, cardinals and cofinalities are preserved and for every limit
![]() $\delta \leq \eta $
, the singular cardinal hypothesis fails at
$\delta \leq \eta $
, the singular cardinal hypothesis fails at
![]() $\bar {\kappa }_\delta $
.
$\bar {\kappa }_\delta $
.
For use later, we define
![]() $\vec {\mathcal {A}}$
to be the full-support product
$\vec {\mathcal {A}}$
to be the full-support product
![]() $\prod _{\alpha < \eta } \mathcal {A}(\lambda ,\kappa _\alpha )$
, and similarly, for each
$\prod _{\alpha < \eta } \mathcal {A}(\lambda ,\kappa _\alpha )$
, and similarly, for each
![]() $\beta < \eta $
,
$\beta < \eta $
,
![]() $\vec {\mathcal {A}}_{\geq \beta } = \prod _{\beta \leq \alpha < \eta } \mathcal {A}(\lambda ,\kappa _\alpha )$
. We aim to show that if
$\vec {\mathcal {A}}_{\geq \beta } = \prod _{\beta \leq \alpha < \eta } \mathcal {A}(\lambda ,\kappa _\alpha )$
. We aim to show that if
![]() $\vec {H} = \langle H(\alpha ) \mid \alpha < \eta \rangle $
is
$\vec {H} = \langle H(\alpha ) \mid \alpha < \eta \rangle $
is
![]() $\vec {\mathcal {A}}$
generic over V, then there is a generic for the image of
$\vec {\mathcal {A}}$
generic over V, then there is a generic for the image of
![]() $\mathbb {P}$
in a suitable iterated ultrapower.
$\mathbb {P}$
in a suitable iterated ultrapower.
3 The iterated ultrapower
 $M_{\eta }$
and the generic filter
$M_{\eta }$
and the generic filter
 $G^*$
$G^*$
We consider the following iterated ultrapower
by the extenders in
![]() $\vec {E}$
. The iteration is defined by induction of
$\vec {E}$
. The iteration is defined by induction of
![]() $\alpha $
. Let
$\alpha $
. Let
![]() $M_0 = V$
. For every
$M_0 = V$
. For every
![]() $\alpha < \eta $
, given that
$\alpha < \eta $
, given that
![]() $j_{0,\alpha } \colon M_0 \to M_\alpha $
has been defined, we take
$j_{0,\alpha } \colon M_0 \to M_\alpha $
has been defined, we take
![]() $E^\alpha _\alpha = j_{0,\alpha }(E_\alpha )$
, and set
$E^\alpha _\alpha = j_{0,\alpha }(E_\alpha )$
, and set
![]() $j_{\alpha ,\alpha +1} \colon M_\alpha \to M_{\alpha +1} \cong \operatorname {Ult}(M_\alpha ,E_{\alpha }^\alpha )$
. At limit stage
$j_{\alpha ,\alpha +1} \colon M_\alpha \to M_{\alpha +1} \cong \operatorname {Ult}(M_\alpha ,E_{\alpha }^\alpha )$
. At limit stage
![]() $\delta \leq \eta $
we take
$\delta \leq \eta $
we take
![]() $M_\delta $
to be the direct limit of the system
$M_\delta $
to be the direct limit of the system
![]() ${\langle } M_\alpha ,j_{\alpha ,\beta } \colon \alpha \leq \beta <\delta {\rangle }$
, and
${\langle } M_\alpha ,j_{\alpha ,\beta } \colon \alpha \leq \beta <\delta {\rangle }$
, and
![]() $j_{\alpha , \delta }$
to be the limit maps.
$j_{\alpha , \delta }$
to be the limit maps.
For every
![]() $\beta \leq \eta $
, we shall abbreviate and write
$\beta \leq \eta $
, we shall abbreviate and write
![]() $j_\beta $
for
$j_\beta $
for
![]() $j_{0,\beta }$
. For a given
$j_{0,\beta }$
. For a given
![]() $\beta \leq \eta $
we shall denote
$\beta \leq \eta $
we shall denote
![]() $j_{\beta }(\kappa _\alpha ), j_{\beta }(E_\alpha )$
,
$j_{\beta }(\kappa _\alpha ), j_{\beta }(E_\alpha )$
,
![]() $j_{\beta }(\lambda )$
by
$j_{\beta }(\lambda )$
by
![]() $\kappa _\alpha ^\beta $
,
$\kappa _\alpha ^\beta $
,
![]() $E_\alpha ^\beta $
, and
$E_\alpha ^\beta $
, and
![]() $\lambda ^\beta $
respectively. Similarly, we will denote
$\lambda ^\beta $
respectively. Similarly, we will denote
![]() $j_{\beta }(x) = x^\beta $
for objects
$j_{\beta }(x) = x^\beta $
for objects
![]() $x \in V$
whose images along the iteration will be significant for our construction.
$x \in V$
whose images along the iteration will be significant for our construction.
Lemma 3.1. Let
![]() $\beta \leq \eta $
. For every
$\beta \leq \eta $
. For every
![]() $x \in M_{\beta }$
there are
$x \in M_{\beta }$
there are
![]() $\beta _0< \beta _1 < \dots < \beta _{l-1}$
below
$\beta _0< \beta _1 < \dots < \beta _{l-1}$
below
![]() $\beta $
, ordinals
$\beta $
, ordinals
![]() $\tau _0,\dots ,\tau _{l-1}$
below
$\tau _0,\dots ,\tau _{l-1}$
below
![]() $\lambda $
, and
$\lambda $
, and
![]() $f \colon \prod _{i < l} \kappa _{\beta _i} \to V$
, such that
$f \colon \prod _{i < l} \kappa _{\beta _i} \to V$
, such that
Proof It is immediate from the definition of the iteration that for every
![]() $x \in M_\beta $
there are
$x \in M_\beta $
there are
![]() $\beta _0 < \dots < \beta _{l-1}$
below
$\beta _0 < \dots < \beta _{l-1}$
below
![]() $\beta $
, finite subsets of ordinals
$\beta $
, finite subsets of ordinals
![]() $a_0,\dots , a_{l-1}$
, with each
$a_0,\dots , a_{l-1}$
, with each
![]() $a_i \in [\lambda ^{\beta _i}]^{<\omega }$
a generator of
$a_i \in [\lambda ^{\beta _i}]^{<\omega }$
a generator of
![]() $E_{\beta _i}^{\beta _i}$
, and a function
$E_{\beta _i}^{\beta _i}$
, and a function
![]() $g \colon \prod _{i < l} \kappa _{\beta _i}^{<\omega } \to V$
so that
$g \colon \prod _{i < l} \kappa _{\beta _i}^{<\omega } \to V$
so that
Note that for each
![]() $i < l$
,
$i < l$
,
![]() $j_{\beta _i+1,\beta }(a_i) = a_i$
, because
$j_{\beta _i+1,\beta }(a_i) = a_i$
, because
It follows that
We may further assume that each
![]() $a_i < \lambda ^{\beta _i}$
is an ordinal. Finally, we claim that we may replace each
$a_i < \lambda ^{\beta _i}$
is an ordinal. Finally, we claim that we may replace each
![]() $a_i$
with an ordinal of the form
$a_i$
with an ordinal of the form
![]() $j_{\beta _i}(\tau _i)$
, for some
$j_{\beta _i}(\tau _i)$
, for some
![]() $\tau _i < \lambda $
. By Lemma 2.3, in
$\tau _i < \lambda $
. By Lemma 2.3, in
![]() $M_{\beta _i}$
, the extender
$M_{\beta _i}$
, the extender
![]() $E_{\beta _i}^{\beta _i} = j_{\beta _i}(E_{\beta _i})$
is generated by a subset of its measures, which are of the form
$E_{\beta _i}^{\beta _i} = j_{\beta _i}(E_{\beta _i})$
is generated by a subset of its measures, which are of the form
![]() $j_{\beta _i}(E_{\beta _i}(\tau _i)) = E_{\beta _i}^{\beta _i}(j_{\beta _i}(\tau _i))$
. Namely, for every
$j_{\beta _i}(E_{\beta _i}(\tau _i)) = E_{\beta _i}^{\beta _i}(j_{\beta _i}(\tau _i))$
. Namely, for every
![]() $a_i \in \lambda ^{\beta _i}$
there exists some
$a_i \in \lambda ^{\beta _i}$
there exists some
![]() $\tau _i \in \lambda $
such that
$\tau _i \in \lambda $
such that
![]() $a_i \leq ^{RK}_{E_{\beta _i}^{\beta _i}} j_{\beta _i}(\tau _i)$
.
$a_i \leq ^{RK}_{E_{\beta _i}^{\beta _i}} j_{\beta _i}(\tau _i)$
.
In particular
The claim follows.
Having defined the iterated ultrapower
![]() $M_{\eta }$
we proceed to introduce relevant conditions in
$M_{\eta }$
we proceed to introduce relevant conditions in
![]() $j_{\eta }(\mathbb {P})$
. Let
$j_{\eta }(\mathbb {P})$
. Let
![]() $p = {\langle } p_\alpha \mid \alpha < \eta {\rangle }$
be a pure condition in
$p = {\langle } p_\alpha \mid \alpha < \eta {\rangle }$
be a pure condition in
![]() $\mathbb {P}$
, that is, a condition with
$\mathbb {P}$
, that is, a condition with
![]() $s^p = \emptyset $
. For every
$s^p = \emptyset $
. For every
![]() $\alpha < \eta $
, we set
$\alpha < \eta $
, we set
![]() $p_\alpha = \langle f_\alpha ,A_\alpha ,\lambda \rangle $
, where
$p_\alpha = \langle f_\alpha ,A_\alpha ,\lambda \rangle $
, where
![]() $f_\alpha \in A(\lambda ,\kappa _\alpha )$
and
$f_\alpha \in A(\lambda ,\kappa _\alpha )$
and
![]() $A_\alpha \in E_\alpha (d_\alpha )$
where
$A_\alpha \in E_\alpha (d_\alpha )$
where
![]() $d_\alpha = \operatorname {\mathrm {dom}}(f_\alpha ) \in [\lambda ]^{\leq \kappa _\alpha }$
.
$d_\alpha = \operatorname {\mathrm {dom}}(f_\alpha ) \in [\lambda ]^{\leq \kappa _\alpha }$
.
Since
![]() $j_{\alpha ,\alpha +1} = j^{M_\alpha }_{E_\alpha ^\alpha }$
it follows that the function
$j_{\alpha ,\alpha +1} = j^{M_\alpha }_{E_\alpha ^\alpha }$
it follows that the function
belongs to
![]() $j_{\alpha ,\alpha +1}(A^\alpha _\alpha ) = A^{\alpha +1}_\alpha $
, which is the measure one set of the
$j_{\alpha ,\alpha +1}(A^\alpha _\alpha ) = A^{\alpha +1}_\alpha $
, which is the measure one set of the
![]() $\alpha $
-th component of
$\alpha $
-th component of
![]() $j_{\alpha +1}(p)$
. By applying
$j_{\alpha +1}(p)$
. By applying
![]() $j_{\alpha +1,\eta }$
to
$j_{\alpha +1,\eta }$
to
![]() $j_{\alpha +1}(p)$
, we conclude that the function
$j_{\alpha +1}(p)$
, we conclude that the function
belongs to
![]() $j_{\eta }(A_\alpha )$
, and thus
$j_{\eta }(A_\alpha )$
, and thus
![]() $j_{\eta }(p)$
has an one point extension at the
$j_{\eta }(p)$
has an one point extension at the
![]() $\alpha $
-th coordinate of the form
$\alpha $
-th coordinate of the form
It is clear that for every finite sequence
![]() $\alpha _0 < \dots < \alpha _{m-1}$
of ordinals below
$\alpha _0 < \dots < \alpha _{m-1}$
of ordinals below
![]() $\eta $
, and pure condition
$\eta $
, and pure condition
![]() $p \in \mathbb {P}$
, we have
$p \in \mathbb {P}$
, we have
![]() $j_{\eta }(p) {}^\frown {\langle } \nu ^{p^{\alpha _0}}_{\alpha _0,\eta }, \nu ^{p^{\alpha _1}}_{\alpha _1,\eta }, \dots , \nu ^{p^{\alpha _{m-1}}}_{\alpha _{m-1},\eta }{\rangle }$
is an extension of
$j_{\eta }(p) {}^\frown {\langle } \nu ^{p^{\alpha _0}}_{\alpha _0,\eta }, \nu ^{p^{\alpha _1}}_{\alpha _1,\eta }, \dots , \nu ^{p^{\alpha _{m-1}}}_{\alpha _{m-1},\eta }{\rangle }$
is an extension of
![]() $j_{\eta }(p)$
in
$j_{\eta }(p)$
in
![]() $j_{\eta }(\mathbb {P})$
. It is also clear that if
$j_{\eta }(\mathbb {P})$
. It is also clear that if
![]() $p,q \in \mathbb {P}$
are two pure conditions so that for all
$p,q \in \mathbb {P}$
are two pure conditions so that for all
![]() $\alpha < \eta $
,
$\alpha < \eta $
,
![]() $f_\alpha ^p,f_\alpha ^q$
are compatible, then for every two sequences
$f_\alpha ^p,f_\alpha ^q$
are compatible, then for every two sequences
![]() $\alpha _0 < \dots < \alpha _{m-1}$
and
$\alpha _0 < \dots < \alpha _{m-1}$
and
![]() $\beta _0 < \dots < \beta _{l-1}$
of ordinals below
$\beta _0 < \dots < \beta _{l-1}$
of ordinals below
![]() $\eta $
, the conditions
$\eta $
, the conditions
and
are compatible in
![]() $j_{\eta }(\mathbb {P})$
. We remark that in the assumption that the sequence of extenders
$j_{\eta }(\mathbb {P})$
. We remark that in the assumption that the sequence of extenders
![]() ${\langle } E_\alpha \mid \alpha < \eta {\rangle }$
is Mitchell order increasing is used in order to be able to permute the order in which the extensions are done, using a sequence of applications of Lemma 2.4.
${\langle } E_\alpha \mid \alpha < \eta {\rangle }$
is Mitchell order increasing is used in order to be able to permute the order in which the extensions are done, using a sequence of applications of Lemma 2.4.
Fix
![]() $\vec {H} = {\langle } H(\alpha ) \mid \alpha < \eta {\rangle }$
a V-generic for
$\vec {H} = {\langle } H(\alpha ) \mid \alpha < \eta {\rangle }$
a V-generic for
![]() $\vec {\mathcal {A}} = \prod _{\alpha < \eta } \mathcal {A}(\lambda ,\kappa _\alpha )$
.
$\vec {\mathcal {A}} = \prod _{\alpha < \eta } \mathcal {A}(\lambda ,\kappa _\alpha )$
.
Definition 3.2. Define
![]() $G^* \subset j_{\eta }(\mathbb {P})$
to be the filter generated by all conditions
$G^* \subset j_{\eta }(\mathbb {P})$
to be the filter generated by all conditions
where
![]() $p \in \mathbb {P}$
satisfy that
$p \in \mathbb {P}$
satisfy that
![]() $f^p_\alpha \in H(\alpha )$
for all
$f^p_\alpha \in H(\alpha )$
for all
![]() $\alpha < \eta $
,
$\alpha < \eta $
,
![]() $m < \omega $
, and
$m < \omega $
, and
![]() $\alpha _0 < \dots < \alpha _{m-1}$
are ordinals below
$\alpha _0 < \dots < \alpha _{m-1}$
are ordinals below
![]() $\eta $
.
$\eta $
.
Our first goal is to prove that
![]() $G^*$
generates a
$G^*$
generates a
![]() $j_{\eta }(\mathbb {P})$
generic filter over
$j_{\eta }(\mathbb {P})$
generic filter over
![]() $M_{\eta }$
.
$M_{\eta }$
.
Proposition 3.3.
![]() $G^*_{\eta }$
is
$G^*_{\eta }$
is
![]() $j_{\eta }(\mathbb {P})$
generic over
$j_{\eta }(\mathbb {P})$
generic over
![]() $M_{\eta }$
.
$M_{\eta }$
.
Before moving to the proof of the proposition, we discuss finite subiterates of
![]() $M_{\eta }$
.
$M_{\eta }$
.
3.1 Finite sub-iterations
 $N^F$
$N^F$
The model
![]() $M_{\eta }$
can be seen as a directed limit of all its finite subiterates,
$M_{\eta }$
can be seen as a directed limit of all its finite subiterates,
![]() $N^F$
,
$N^F$
,
![]() $F \in [\eta ]^{<\omega }$
. Given a finite set
$F \in [\eta ]^{<\omega }$
. Given a finite set
![]() $F = \{ \beta _0,\dots ,\beta _{l-1} \} \in [\eta ]^{<\omega }$
, we define its associated iteration
$F = \{ \beta _0,\dots ,\beta _{l-1} \} \in [\eta ]^{<\omega }$
, we define its associated iteration
![]() $\langle N^F_{i}, i^F_{m,n} \mid m \leq n \leq l\rangle $
by
$\langle N^F_{i}, i^F_{m,n} \mid m \leq n \leq l\rangle $
by
![]() $N^F_0 = V$
, and
$N^F_0 = V$
, and
![]() $i^F_{n,n+1} \colon N^F_n \to N^F_{n+1} \cong \operatorname {Ult}(N^F_{n}, i^F_n(E_{\beta _{n}}))$
. Since for the moment we handle a single finite set at a time, we will suppress the mention of the finite set F and refer only to the iteration as
$i^F_{n,n+1} \colon N^F_n \to N^F_{n+1} \cong \operatorname {Ult}(N^F_{n}, i^F_n(E_{\beta _{n}}))$
. Since for the moment we handle a single finite set at a time, we will suppress the mention of the finite set F and refer only to the iteration as
![]() $i_{m,n}\colon N_m \to N_n$
for
$i_{m,n}\colon N_m \to N_n$
for
![]() $m \leq n \leq l$
and as usual we set
$m \leq n \leq l$
and as usual we set
![]() $i_n = i_{0,n}$
for
$i_n = i_{0,n}$
for
![]() $n \leq l$
.
$n \leq l$
.
The proof of Lemma 3.1 shows that the elements of
![]() $N_l$
are of the form
$N_l$
are of the form
![]() $i_l(f)\left (\tau _0, i_{1}(\tau _1), \dots , i_{l-1}(\tau _{l-1})\right )$
. Let
$i_l(f)\left (\tau _0, i_{1}(\tau _1), \dots , i_{l-1}(\tau _{l-1})\right )$
. Let
![]() $k\colon N_l \to M_{\eta }$
be the usual factor map defined by
$k\colon N_l \to M_{\eta }$
be the usual factor map defined by
It is routine to verify that k is well defined, elementary, and
![]() $j_{\eta } = k \circ i_l$
.
$j_{\eta } = k \circ i_l$
.
Moreover, following this explicit description of k, it is straightforward to verify that
![]() $k : N_l \to M_{\eta }$
is the resulting iterated ultrapower limit embedding, associated with the iteration of
$k : N_l \to M_{\eta }$
is the resulting iterated ultrapower limit embedding, associated with the iteration of
![]() $N_l$
by the sequence
$N_l$
by the sequence
where
![]() $n_\alpha $
is the minimal
$n_\alpha $
is the minimal
![]() $n < l$
for which
$n < l$
for which
![]() $\beta _n \geq \alpha $
, if exists, and
$\beta _n \geq \alpha $
, if exists, and
![]() $n_\alpha = l$
otherwise. This again uses the Mitchell order assumption of the sequence of extenders in order to get the desired commutativity.
$n_\alpha = l$
otherwise. This again uses the Mitchell order assumption of the sequence of extenders in order to get the desired commutativity.
Next, we observe that our assignment of generators
![]() $\nu ^{p^\alpha }_{\alpha ,\eta }$
,
$\nu ^{p^\alpha }_{\alpha ,\eta }$
,
![]() $\alpha < \eta $
, to
$\alpha < \eta $
, to
![]() $j_{\eta }(p)$
of conditions
$j_{\eta }(p)$
of conditions
![]() $p \in \mathbb {P}$
, in Definition 3.2, can be defined at the level of the finite subiterates.
$p \in \mathbb {P}$
, in Definition 3.2, can be defined at the level of the finite subiterates.
Indeed, for a condition
![]() $p \in \mathbb {P}$
,
$p \in \mathbb {P}$
,
![]() $n < l$
, we temporarily define
$n < l$
, we temporarily define
where
![]() $d = \operatorname {\mathrm {dom}}(f^{i_n(p)})_{\beta _n}$
. We let
$d = \operatorname {\mathrm {dom}}(f^{i_n(p)})_{\beta _n}$
. We let
![]() $\nu ^{i_n(p)}_{n,l} = i_{n+1,l}(\nu ^{i_n(p)}_{n,n+1})$
be the natural push forward to
$\nu ^{i_n(p)}_{n,l} = i_{n+1,l}(\nu ^{i_n(p)}_{n,n+1})$
be the natural push forward to
![]() $N_l$
. As with the conditions
$N_l$
. As with the conditions
![]() $j_{\eta }(p)$
, we have that
$j_{\eta }(p)$
, we have that
is a valid extension of
![]() $i_l(p)$
in
$i_l(p)$
in
![]() $i_l(\mathbb {P})$
.
$i_l(\mathbb {P})$
.
To record this definition (which depends on F), we make a few permanent definitions which explicitly mention F as well as objects from the discussion above:
Definition 3.4. Fix
![]() $i^F = i_l$
and
$i^F = i_l$
and
![]() $k^F=k$
and the model
$k^F=k$
and the model
![]() $N^F = N_l$
. Denote the condition defined above by
$N^F = N_l$
. Denote the condition defined above by
![]() $i^F(p) {}^\frown \vec {\nu }^{p,F}$
and refer to it as the natural non-pure extension of
$i^F(p) {}^\frown \vec {\nu }^{p,F}$
and refer to it as the natural non-pure extension of
![]() $i^F(p)$
.
$i^F(p)$
.
Using the description of
![]() $k^F \colon N^F \to M_{\eta }$
, it is straightforward to apply Łoś’s Theorem and show that
$k^F \colon N^F \to M_{\eta }$
, it is straightforward to apply Łoś’s Theorem and show that
![]() $k^F(\vec {\nu }^{p,F}) = {\langle } \nu ^{p^{\beta _n}}_{\beta _n,\eta }\mid n < l {\rangle }$
. We conclude that
$k^F(\vec {\nu }^{p,F}) = {\langle } \nu ^{p^{\beta _n}}_{\beta _n,\eta }\mid n < l {\rangle }$
. We conclude that
Finally, we note that the forcing
![]() $\vec {\mathcal {A}} = \prod _{\alpha < \eta }\mathcal {A}(\lambda ,\kappa _\alpha )$
has a natural factorization, associated with F. Setting
$\vec {\mathcal {A}} = \prod _{\alpha < \eta }\mathcal {A}(\lambda ,\kappa _\alpha )$
has a natural factorization, associated with F. Setting
![]() $\beta _{-1} = 0$
and
$\beta _{-1} = 0$
and
![]() $\beta _l = \eta $
, we have
$\beta _l = \eta $
, we have
 $$\begin{align*}\vec{\mathcal{A}} = \prod_{n \leq l}\vec{\mathcal{A}}\restriction{[\beta_{n-1},\beta_{n})},\end{align*}$$
$$\begin{align*}\vec{\mathcal{A}} = \prod_{n \leq l}\vec{\mathcal{A}}\restriction{[\beta_{n-1},\beta_{n})},\end{align*}$$
where for each
![]() $n \leq l$
,
$n \leq l$
,
 $$\begin{align*}\vec{\mathcal{A}}\restriction{[\beta_{n-1},\beta_{n})} = \prod_{\beta_{n-1} \leq \alpha < \beta_n} \mathcal{A}(\lambda,\kappa_\alpha).\end{align*}$$
$$\begin{align*}\vec{\mathcal{A}}\restriction{[\beta_{n-1},\beta_{n})} = \prod_{\beta_{n-1} \leq \alpha < \beta_n} \mathcal{A}(\lambda,\kappa_\alpha).\end{align*}$$
For each
![]() $0\leq n \leq l$
, we define
$0\leq n \leq l$
, we define
and denote the resulting product by
![]() $\vec {\mathcal {A}}^F = \prod _{n \leq l} \vec {\mathcal {A}}^F_n$
. Suppose that
$\vec {\mathcal {A}}^F = \prod _{n \leq l} \vec {\mathcal {A}}^F_n$
. Suppose that
![]() $\vec {H} \subseteq \vec {\mathcal {A}}$
is a V-generic filter. For each
$\vec {H} \subseteq \vec {\mathcal {A}}$
is a V-generic filter. For each
![]() $n \leq l$
, the fact
$n \leq l$
, the fact
![]() $\vec {\mathcal {A}}\restriction {[\beta _{n-1},\beta _{n})}$
is a
$\vec {\mathcal {A}}\restriction {[\beta _{n-1},\beta _{n})}$
is a
![]() $\kappa _{\beta _{n-1}}^{+}$
-closed forcing guarantees that
$\kappa _{\beta _{n-1}}^{+}$
-closed forcing guarantees that
![]() $i_n"\vec {H}\restriction {[\beta _{n-1},\beta _{n})}) \subseteq \vec {\mathcal {A}}^F_n$
forms a generic filter over
$i_n"\vec {H}\restriction {[\beta _{n-1},\beta _{n})}) \subseteq \vec {\mathcal {A}}^F_n$
forms a generic filter over
![]() $N_n$
, hence also
$N_n$
, hence also
![]() $N_l=N^F$
.Footnote
4
For each n, we denote the resulting
$N_l=N^F$
.Footnote
4
For each n, we denote the resulting
![]() $N_l$
generic for
$N_l$
generic for
![]() $\vec {\mathcal {A}}^F_n$
by
$\vec {\mathcal {A}}^F_n$
by
![]() $\vec {J}^F_n$
.
$\vec {J}^F_n$
.
This is the crucial part: the main effect of taking a non-pure extension of a condition is the reflection of its Cohen part downwards. This reflection is exactly moving from
![]() $\vec {H}$
to
$\vec {H}$
to
![]() $\vec {J}^F_n$
.
$\vec {J}^F_n$
.
It is clear that the product
![]() $\prod _{0 \leq n \leq l} \vec {J}^F_n$
is
$\prod _{0 \leq n \leq l} \vec {J}^F_n$
is
![]() $\vec {\mathcal {A}}^F$
generic over
$\vec {\mathcal {A}}^F$
generic over
![]() $N_l$
. We note that for each pure
$N_l$
. We note that for each pure
![]() $p \in \mathbb {P}$
with
$p \in \mathbb {P}$
with
![]() $\vec {f}^p \in \vec {H}$
, if
$\vec {f}^p \in \vec {H}$
, if
![]() $\vec {f}$
is the Cohen part of the natural non-pure extension of
$\vec {f}$
is the Cohen part of the natural non-pure extension of
![]() $i^F(p)$
, then
$i^F(p)$
, then
![]() $\vec {f} \in \vec {\mathcal {A}}^F$
. Moreover the collection of such
$\vec {f} \in \vec {\mathcal {A}}^F$
. Moreover the collection of such
![]() $\vec {f}$
forms an
$\vec {f}$
forms an
![]() $\vec {\mathcal {A}}^F$
-generic filter over
$\vec {\mathcal {A}}^F$
-generic filter over
![]() $N^F$
which is obtained by modifying
$N^F$
which is obtained by modifying
![]() $\prod _{0 \leq n \leq l} \vec {J}^F_n$
on the coordinates
$\prod _{0 \leq n \leq l} \vec {J}^F_n$
on the coordinates
![]() $\beta _n$
for
$\beta _n$
for
![]() $n<l$
by taking the natural non-pure extensions of
$n<l$
by taking the natural non-pure extensions of
![]() $i^F(p)$
for
$i^F(p)$
for
![]() $p\in \vec {J}^F$
(see Definition 3.4).
$p\in \vec {J}^F$
(see Definition 3.4).
For each individual modified filter, its genericity follows from Woodin’s surgery argument [Reference Gitik5].Footnote
5
The fact that the product remains generic follows by induction on n from applications of Easton’s lemma, using the chain condition of the forcing notions with smaller indexes and the closure of the components with larger indexes. We denote by
![]() $\vec {H}^F$
the resulting
$\vec {H}^F$
the resulting
![]() $N^F$
-generic filter over
$N^F$
-generic filter over
![]() $\vec {\mathcal {A}}^F$
.
$\vec {\mathcal {A}}^F$
.
Remark 3.5.
![]() $G^*$
can be constructed in
$G^*$
can be constructed in
![]() $N^F[\vec {H}^F]$
in the same way that it was constructed in V using the fact that
$N^F[\vec {H}^F]$
in the same way that it was constructed in V using the fact that
![]() $M_\eta $
can be described as an iterated ultrapower of
$M_\eta $
can be described as an iterated ultrapower of
![]() $N^F$
and starting with conditions q such that
$N^F$
and starting with conditions q such that
![]() $s^q=F$
and
$s^q=F$
and
![]() $\vec {f}^q \in \vec {H}^F$
.
$\vec {f}^q \in \vec {H}^F$
.
We turn to the proof of Proposition 3.3.
Proof It is clear that
![]() $G^* \subseteq j_{\eta }(\mathbb {P})$
is a filter. We verify that
$G^* \subseteq j_{\eta }(\mathbb {P})$
is a filter. We verify that
![]() $G^*$
meets every dense open set
$G^*$
meets every dense open set
![]() $D \subseteq j_{\eta }(\mathbb {P})$
in
$D \subseteq j_{\eta }(\mathbb {P})$
in
![]() $M_{\eta }$
. Since
$M_{\eta }$
. Since
![]() $M_\eta $
is the direct limit of its finite subiterates. There are
$M_\eta $
is the direct limit of its finite subiterates. There are
![]() $F = \{\beta _0, \dots \beta _{l-1}\} \in [\eta ]^{<\omega }$
and
$F = \{\beta _0, \dots \beta _{l-1}\} \in [\eta ]^{<\omega }$
and
![]() $\bar {D}$
such that
$\bar {D}$
such that
![]() $k^F(\bar {D}) = D$
.
$k^F(\bar {D}) = D$
.
Let
![]() $p'$
be the natural non-pure extension of
$p'$
be the natural non-pure extension of
![]() $i^F(p)$
for some p with
$i^F(p)$
for some p with
![]() $\vec {f}^p \in \vec {H}$
. Now by its definition
$\vec {f}^p \in \vec {H}$
. Now by its definition
![]() $\vec {f}^{p'} \in \vec {H}^F$
. Appealing to Lemma 2.5 and the genericity of
$\vec {f}^{p'} \in \vec {H}^F$
. Appealing to Lemma 2.5 and the genericity of
![]() $\vec {H}^F$
, we conclude that there exists a direct extension
$\vec {H}^F$
, we conclude that there exists a direct extension
![]() $p^* \geq ^* p'$
, with
$p^* \geq ^* p'$
, with
![]() ${\langle } f^{p^*}_\alpha \mid \alpha <\eta {\rangle } \in \vec {H}^F$
and a finite set
${\langle } f^{p^*}_\alpha \mid \alpha <\eta {\rangle } \in \vec {H}^F$
and a finite set
![]() $\{ \alpha _0,\dots ,\alpha _{m-1}\} \subset (\eta \setminus F)$
, such that
$\{ \alpha _0,\dots ,\alpha _{m-1}\} \subset (\eta \setminus F)$
, such that
![]() $p^* {}^\frown \vec {\nu } \in \bar {D}$
for every
$p^* {}^\frown \vec {\nu } \in \bar {D}$
for every
![]() $\vec {\nu } = \langle \nu _{\alpha _0},\dots , \nu _{\alpha _{m-1}}\rangle \in \prod _{i<m} A^{p^*}_{\alpha _i}$
. By the elementarity of
$\vec {\nu } = \langle \nu _{\alpha _0},\dots , \nu _{\alpha _{m-1}}\rangle \in \prod _{i<m} A^{p^*}_{\alpha _i}$
. By the elementarity of
![]() $k^F$
,
$k^F$
,
![]() $k^F(p^*) {}^\frown \vec {\nu } \in D$
for every
$k^F(p^*) {}^\frown \vec {\nu } \in D$
for every
![]() $\vec {\nu } \in \prod _{i<m} k^F(A^{p^*})_{\alpha _i}$
.
$\vec {\nu } \in \prod _{i<m} k^F(A^{p^*})_{\alpha _i}$
.
In particular,
It remains to verify that the last condition belongs to
![]() $G^*$
. This is immediate from Remark 3.5 and the fact that
$G^*$
. This is immediate from Remark 3.5 and the fact that
![]() $\vec {f}^{p^*} \in \vec {H}^F$
.
$\vec {f}^{p^*} \in \vec {H}^F$
.
Proposition 3.6.
![]() $M_{\eta }[G^*]$
is closed under
$M_{\eta }[G^*]$
is closed under
![]() $\kappa _0 = \mathop {\mathrm {crit}}(j_{\eta })$
sequences of its elements in
$\kappa _0 = \mathop {\mathrm {crit}}(j_{\eta })$
sequences of its elements in
![]() $V[\vec {H}]$
.
$V[\vec {H}]$
.
Proof Let
![]() ${\langle } x_\mu \mid \mu < \kappa _0{\rangle }$
be a sequence of elements in
${\langle } x_\mu \mid \mu < \kappa _0{\rangle }$
be a sequence of elements in
![]() $M_{\eta }[G^*]$
. Since
$M_{\eta }[G^*]$
. Since
![]() $M_\eta [G^*]$
is a model of
$M_\eta [G^*]$
is a model of
![]() $\mathrm {ZFC}$
, we may assume that all
$\mathrm {ZFC}$
, we may assume that all
![]() $x_\mu $
are ordinals. By Lemma 3.1, for each
$x_\mu $
are ordinals. By Lemma 3.1, for each
![]() $x_\mu $
is of the form
$x_\mu $
is of the form
for some finite sequences
![]() $\beta ^\mu _0 < \dots , \beta ^\mu _{l^\mu -1} < \eta $
and
$\beta ^\mu _0 < \dots , \beta ^\mu _{l^\mu -1} < \eta $
and
![]() $\tau ^\mu _0, \dots , \tau ^\mu _{l^\mu -1} < \lambda $
. Moreover, since the Rudin–Keisler order
$\tau ^\mu _0, \dots , \tau ^\mu _{l^\mu -1} < \lambda $
. Moreover, since the Rudin–Keisler order
![]() $\leq ^{RK}_{E_{\beta ^\mu _i}}$
is
$\leq ^{RK}_{E_{\beta ^\mu _i}}$
is
![]() $\kappa _0^{+}$
-directed, we may assume that there exists some
$\kappa _0^{+}$
-directed, we may assume that there exists some
![]() $\tau ^* < \lambda $
such that
$\tau ^* < \lambda $
such that
![]() $\tau ^\mu _i = \tau ^*$
for all
$\tau ^\mu _i = \tau ^*$
for all
![]() $\mu < \kappa _0$
and
$\mu < \kappa _0$
and
![]() $i<l^\mu $
. Hence for
$i<l^\mu $
. Hence for
![]() ${\langle } x_\mu \mid \mu < \kappa _0{\rangle }$
to be a member of
${\langle } x_\mu \mid \mu < \kappa _0{\rangle }$
to be a member of
![]() $M_{\eta }[G^*]$
, it suffices to verify that the sequences
$M_{\eta }[G^*]$
, it suffices to verify that the sequences
![]() $\langle j_{\eta }(g_\mu ) \mid \mu < \kappa _0\rangle $
and
$\langle j_{\eta }(g_\mu ) \mid \mu < \kappa _0\rangle $
and
![]() ${\langle } j_{\alpha }(\tau ^*) \mid \alpha < \eta {\rangle }$
belong to
${\langle } j_{\alpha }(\tau ^*) \mid \alpha < \eta {\rangle }$
belong to
![]() $M_{\eta }[G^*]$
.
$M_{\eta }[G^*]$
.
The first sequence already belongs to
![]() $M_{\eta }$
as
$M_{\eta }$
as
![]() $\mathop {\mathrm {crit}}(j_{\eta }) = \kappa _0$
implies that it is just
$\mathop {\mathrm {crit}}(j_{\eta }) = \kappa _0$
implies that it is just
![]() $j_{\eta }(\vec {g})\restriction \kappa _0$
. The latter sequence
$j_{\eta }(\vec {g})\restriction \kappa _0$
. The latter sequence
![]() $\langle j_{\alpha }(\tau ^*) \mid \alpha < \eta \rangle $
can be recovered from
$\langle j_{\alpha }(\tau ^*) \mid \alpha < \eta \rangle $
can be recovered from
![]() $G^*$
as follows. It follows from a simple density argument that for every
$G^*$
as follows. It follows from a simple density argument that for every
![]() $\alpha < \eta $
, there exists some
$\alpha < \eta $
, there exists some
![]() $q \in G^*$
such that:
$q \in G^*$
such that:
-
(1)
 $\alpha $
is a non-pure coordinate of q, and
$\alpha $
is a non-pure coordinate of q, and -
(2)
 $j_{\eta }(\tau ^*) \in \operatorname {\mathrm {dom}}(f^q_\alpha )$
.
$j_{\eta }(\tau ^*) \in \operatorname {\mathrm {dom}}(f^q_\alpha )$
.
It is also clear that two conditions
![]() $q,q' \in G^*$
of this form must satisfy
$q,q' \in G^*$
of this form must satisfy
![]() $f^{q}_\alpha (j_{\eta }(\tau ^*)) = f^{q'}_\alpha (j_{\eta }(\tau ^*))$
. We may therefore define in
$f^{q}_\alpha (j_{\eta }(\tau ^*)) = f^{q'}_\alpha (j_{\eta }(\tau ^*))$
. We may therefore define in
![]() $M_{\eta }[G^*]$
a function
$M_{\eta }[G^*]$
a function
![]() $t_{j_{\eta }(\tau ^*)} \colon \eta \to \lambda ^{\eta }$
by
$t_{j_{\eta }(\tau ^*)} \colon \eta \to \lambda ^{\eta }$
by
![]() $t_{j_{\eta }(\tau ^*)}(\alpha ) = f^{q}_\alpha (j_{\eta }(\tau ^*))$
for some condition
$t_{j_{\eta }(\tau ^*)}(\alpha ) = f^{q}_\alpha (j_{\eta }(\tau ^*))$
for some condition
![]() $q \in G^*$
as above. We claim that
$q \in G^*$
as above. We claim that
![]() $t_{j_{\eta }(\tau ^*)}(\alpha ) = j_{\alpha }(\tau ^*)$
for all
$t_{j_{\eta }(\tau ^*)}(\alpha ) = j_{\alpha }(\tau ^*)$
for all
![]() $\alpha < \eta $
. Indeed, for every
$\alpha < \eta $
. Indeed, for every
![]() $\alpha < \eta $
, there exists a condition
$\alpha < \eta $
, there exists a condition
![]() $p \in \mathbb {P}$
with
$p \in \mathbb {P}$
with
![]() ${\langle } f^p_\alpha \mid \alpha < \eta {\rangle } \in \vec {H}$
so that
${\langle } f^p_\alpha \mid \alpha < \eta {\rangle } \in \vec {H}$
so that
![]() $\tau ^* \in \operatorname {\mathrm {dom}}(f^p_\alpha )$
, and clearly, the condition
$\tau ^* \in \operatorname {\mathrm {dom}}(f^p_\alpha )$
, and clearly, the condition
![]() $q = j_{\eta }(p) {}^\frown \langle \nu ^{p^\alpha }_{\alpha ,\eta }\rangle \in G^*$
has
$q = j_{\eta }(p) {}^\frown \langle \nu ^{p^\alpha }_{\alpha ,\eta }\rangle \in G^*$
has
![]() $j_{\eta }(\tau ^*) \in \operatorname {\mathrm {dom}}(f^q_\alpha )$
. But
$j_{\eta }(\tau ^*) \in \operatorname {\mathrm {dom}}(f^q_\alpha )$
. But
![]() $j_{\eta }(\tau ^*) \in \operatorname {\mathrm {dom}}(\nu ^{p^\alpha }_{\alpha ,\eta }) = j_{\alpha +1,\eta }"j_{\alpha }(\operatorname {\mathrm {dom}}(f^p_\alpha ))$
and
$j_{\eta }(\tau ^*) \in \operatorname {\mathrm {dom}}(\nu ^{p^\alpha }_{\alpha ,\eta }) = j_{\alpha +1,\eta }"j_{\alpha }(\operatorname {\mathrm {dom}}(f^p_\alpha ))$
and
![]() $\nu ^{p^\alpha }_{\alpha ,\eta } = (j_{\alpha ,\eta }\restriction d_\alpha ^\alpha )^{-1}$
; thus, it follows that
$\nu ^{p^\alpha }_{\alpha ,\eta } = (j_{\alpha ,\eta }\restriction d_\alpha ^\alpha )^{-1}$
; thus, it follows that
Fix some ordinal
![]() $\beta < \eta $
. The forcing
$\beta < \eta $
. The forcing
![]() $\vec {\mathcal {A}}$
naturally breaks into the product
$\vec {\mathcal {A}}$
naturally breaks into the product
![]() ${\vec {\mathcal {A}}\restriction \beta \times \vec {\mathcal {A}}_{\geq \beta }}$
, and we observe that:
${\vec {\mathcal {A}}\restriction \beta \times \vec {\mathcal {A}}_{\geq \beta }}$
, and we observe that:
-
(1) The latter part
 $\vec {\mathcal {A}}_{\geq \beta }$
is
$\vec {\mathcal {A}}_{\geq \beta }$
is
 $\kappa _\beta ^{+}$
-closed. Therefore, if
$\kappa _\beta ^{+}$
-closed. Therefore, if
 $\vec {H}_{\geq \beta } \subset \vec {\mathcal {A}}_{\geq \beta }$
is V-generic, then by [Reference Cummings2, Proposition 15.1] its pointwise image
$\vec {H}_{\geq \beta } \subset \vec {\mathcal {A}}_{\geq \beta }$
is V-generic, then by [Reference Cummings2, Proposition 15.1] its pointwise image
 $j_{\beta }"\vec {H}_{\geq \beta }$
generates an
$j_{\beta }"\vec {H}_{\geq \beta }$
generates an
 $M_{\beta }$
generic filter for the forcing We denote this generic by
$M_{\beta }$
generic filter for the forcing We denote this generic by $$\begin{align*}j_{\beta}(\vec{\mathcal{A}}_{\geq \beta}) = \prod_{\beta \leq \alpha < \eta} \mathcal{A}(\lambda^\beta,\kappa_\alpha^\beta)^{M_\beta}.\end{align*}$$
$$\begin{align*}j_{\beta}(\vec{\mathcal{A}}_{\geq \beta}) = \prod_{\beta \leq \alpha < \eta} \mathcal{A}(\lambda^\beta,\kappa_\alpha^\beta)^{M_\beta}.\end{align*}$$
 $\vec {H}^{\beta }_{\geq \beta }$
.
$\vec {H}^{\beta }_{\geq \beta }$
.
-
(2) Using the same arguments as above, a V-generic filter
 $\vec {H}_\beta \subset \vec {\mathcal {A}}\restriction \beta $
generates an
$\vec {H}_\beta \subset \vec {\mathcal {A}}\restriction \beta $
generates an
 $M_\beta $
-generic filter
$M_\beta $
-generic filter
 $G^*_\beta $
for the
$G^*_\beta $
for the
 $j_{\beta }(\mathbb {P}_{\vec {E}\restriction \beta })$
.
$j_{\beta }(\mathbb {P}_{\vec {E}\restriction \beta })$
.
We conclude that in the model
![]() $V[\vec {H}]$
, we can form the generic extension
$V[\vec {H}]$
, we can form the generic extension
![]() $M_\beta [G^*_\beta \times \vec {H}^\beta _{\geq \beta }]$
of
$M_\beta [G^*_\beta \times \vec {H}^\beta _{\geq \beta }]$
of
![]() $M_\beta $
, with respect to the product
$M_\beta $
, with respect to the product
![]() $j_{\beta }(\mathbb {P}_{\vec {E}\restriction \beta }) \times j_{\beta }(\vec {\mathcal {A}}_{\geq \beta })$
.
$j_{\beta }(\mathbb {P}_{\vec {E}\restriction \beta }) \times j_{\beta }(\vec {\mathcal {A}}_{\geq \beta })$
.
We have the following.
Proposition 3.7. For each
![]() $\beta < \eta $
, the model
$\beta < \eta $
, the model
![]() $M_{\beta }[G^*_\beta \times \vec {H}^\beta _{\geq \beta }]$
can compute
$M_{\beta }[G^*_\beta \times \vec {H}^\beta _{\geq \beta }]$
can compute
![]() $M_{\eta }[G^*_{\eta }]$
and therefore
$M_{\eta }[G^*_{\eta }]$
and therefore
 $$\begin{align*}\bigcap_{\beta<\eta}M_\beta[G^*_\beta\times \vec{H}^\beta_{\geq\beta}] \supseteq M_\eta[G^*].\end{align*}$$
$$\begin{align*}\bigcap_{\beta<\eta}M_\beta[G^*_\beta\times \vec{H}^\beta_{\geq\beta}] \supseteq M_\eta[G^*].\end{align*}$$
It seems likely that equality holds,
![]() $\bigcap _{\beta <\eta }M_\beta [G^*_\beta \times \vec {H}^\beta _{\geq \beta }] = M_\eta [G^*]$
, but we will not need that in our argument.
$\bigcap _{\beta <\eta }M_\beta [G^*_\beta \times \vec {H}^\beta _{\geq \beta }] = M_\eta [G^*]$
, but we will not need that in our argument.
4 Stationary reflection in
 $M_\eta [G^*_\eta ]$
$M_\eta [G^*_\eta ]$
We assume that for every
![]() $\alpha < \eta $
, there is a Laver indestructible supercompact cardinal
$\alpha < \eta $
, there is a Laver indestructible supercompact cardinal
![]() $\theta _\alpha $
such that
$\theta _\alpha $
such that
![]() $\sup _{\beta <\alpha } \kappa _\beta < \theta _\alpha < \kappa _\alpha $
.
$\sup _{\beta <\alpha } \kappa _\beta < \theta _\alpha < \kappa _\alpha $
.
We prove the following which completes the proof of Theorem 1.1.
Theorem 4.1. In
![]() $M_{\eta }[G^*]$
, every collection of fewer than
$M_{\eta }[G^*]$
, every collection of fewer than
![]() $\eta $
many stationary subsets of
$\eta $
many stationary subsets of
![]() $j_{\eta }(\bar {\kappa }_{\eta }^{+})$
reflects.
$j_{\eta }(\bar {\kappa }_{\eta }^{+})$
reflects.
We start by proving a stationary reflection fact that will be used as an intermediate step in the proof.
Claim 4.2. For every
![]() $\alpha <\eta $
, every collection of fewer than
$\alpha <\eta $
, every collection of fewer than
![]() $\eta $
many stationary subsets of
$\eta $
many stationary subsets of
![]() $j_{\alpha }(\bar {\kappa }_{\eta }^{+})$
with cofinalities bounded by
$j_{\alpha }(\bar {\kappa }_{\eta }^{+})$
with cofinalities bounded by
![]() $\sup _{\beta <\alpha }\kappa _{\beta }^\alpha $
reflects in
$\sup _{\beta <\alpha }\kappa _{\beta }^\alpha $
reflects in
![]() $M_{\alpha }[G^*_\alpha \times \vec {H}^\alpha _{\geq \alpha }]$
.
$M_{\alpha }[G^*_\alpha \times \vec {H}^\alpha _{\geq \alpha }]$
.
Proof Let
![]() $T_i$
for
$T_i$
for
![]() $i<\mu $
be such a collection of stationary sets. By elementarity,
$i<\mu $
be such a collection of stationary sets. By elementarity,
![]() $j_\alpha (\theta _\alpha )$
is an indestructible supercompact cardinal between
$j_\alpha (\theta _\alpha )$
is an indestructible supercompact cardinal between
![]() $\sup _{\beta <\alpha }\kappa ^\alpha _\beta $
and
$\sup _{\beta <\alpha }\kappa ^\alpha _\beta $
and
![]() $\kappa _\alpha ^\alpha $
. Recall that
$\kappa _\alpha ^\alpha $
. Recall that
![]() $\vec {H}^\alpha _{\geq \alpha }$
is generic for
$\vec {H}^\alpha _{\geq \alpha }$
is generic for
![]() $(\kappa _\alpha ^\alpha )^{+}$
-directed closed forcing. By the indestructibility of
$(\kappa _\alpha ^\alpha )^{+}$
-directed closed forcing. By the indestructibility of
![]() $j_\alpha (\theta _\alpha )$
, there is a
$j_\alpha (\theta _\alpha )$
, there is a
![]() $j_\alpha (\bar {\kappa }_{\eta }^{+})$
-supercompact embedding
$j_\alpha (\bar {\kappa }_{\eta }^{+})$
-supercompact embedding
![]() $k\colon M_{\alpha }[\vec {H}^\alpha _{\geq \alpha }] \to N$
. Further,
$k\colon M_{\alpha }[\vec {H}^\alpha _{\geq \alpha }] \to N$
. Further,
![]() $G^*_\alpha $
is generic for
$G^*_\alpha $
is generic for
![]() $j_\alpha (\bar {\kappa }_\alpha ^{++})$
-cc forcing and
$j_\alpha (\bar {\kappa }_\alpha ^{++})$
-cc forcing and
![]() $j_{\alpha }(\bar {\kappa }_\alpha ^{++}) < j_\alpha (\theta _\alpha )$
. By standard arguments, we can extend k to include
$j_{\alpha }(\bar {\kappa }_\alpha ^{++}) < j_\alpha (\theta _\alpha )$
. By standard arguments, we can extend k to include
![]() $M_\alpha [G^*_\alpha \times \vec {H}^\alpha _{\geq \alpha }]$
in the extension by a
$M_\alpha [G^*_\alpha \times \vec {H}^\alpha _{\geq \alpha }]$
in the extension by a
![]() $j_{\alpha }(\bar {\kappa }_\alpha ^{++})$
-cc forcing. Each
$j_{\alpha }(\bar {\kappa }_\alpha ^{++})$
-cc forcing. Each
![]() $T_i$
remains stationary in this extension, so
$T_i$
remains stationary in this extension, so
![]() $\{k(T_i) \mid i < \mu \}$
reflects at
$\{k(T_i) \mid i < \mu \}$
reflects at
![]() $\sup k"j_\alpha (\bar {\kappa }_{\eta }^{+})$
. It follows that
$\sup k"j_\alpha (\bar {\kappa }_{\eta }^{+})$
. It follows that
![]() $\{T_i \mid i < \mu \}$
reflects in
$\{T_i \mid i < \mu \}$
reflects in
![]() $M_\alpha [G^*_\alpha \times \vec {H}^\alpha _{\geq \alpha }]$
.
$M_\alpha [G^*_\alpha \times \vec {H}^\alpha _{\geq \alpha }]$
.
We begin the proof of Theorem 4.1. Suppose that for each
![]() $i<\mu $
,
$i<\mu $
,
![]() $S_i \in M_{\eta }[G^*]$
is a stationary subset of
$S_i \in M_{\eta }[G^*]$
is a stationary subset of
![]() $j_{\eta }(\bar {\kappa }_{\eta }^{+})$
. We can assume that for all i, the cofinality of each ordinal in
$j_{\eta }(\bar {\kappa }_{\eta }^{+})$
. We can assume that for all i, the cofinality of each ordinal in
![]() $S_i$
is some fixed
$S_i$
is some fixed
![]() $\gamma _i$
. It follows that there is some
$\gamma _i$
. It follows that there is some
![]() $\bar {\alpha }<\eta $
such that
$\bar {\alpha }<\eta $
such that
![]() $\sup _{i<\mu } \gamma _i < \sup _{\beta <\bar {\alpha }}\kappa _{\beta }^{\bar {\alpha }}$
. For each
$\sup _{i<\mu } \gamma _i < \sup _{\beta <\bar {\alpha }}\kappa _{\beta }^{\bar {\alpha }}$
. For each
![]() $\alpha $
in the interval
$\alpha $
in the interval
![]() $[\bar {\alpha },\eta )$
, let
$[\bar {\alpha },\eta )$
, let
![]() $T_i^\alpha = \{ \delta < j_\alpha (\bar {\kappa }_{\eta }^{+}) \mid j_{\alpha ,\eta }(\delta ) \in S_i\}$
.
$T_i^\alpha = \{ \delta < j_\alpha (\bar {\kappa }_{\eta }^{+}) \mid j_{\alpha ,\eta }(\delta ) \in S_i\}$
.
Claim 4.3. For
![]() $\alpha \geq \bar {\alpha }$
, if
$\alpha \geq \bar {\alpha }$
, if
![]() $\{T_i^{\alpha } \mid i<\mu \}$
reflects at an ordinal of cofinality less than
$\{T_i^{\alpha } \mid i<\mu \}$
reflects at an ordinal of cofinality less than
![]() $\kappa _\alpha ^\alpha $
in
$\kappa _\alpha ^\alpha $
in
![]() $M_\alpha [G_\alpha ^* \times \vec {H}^\alpha _{\geq \alpha }]$
, then
$M_\alpha [G_\alpha ^* \times \vec {H}^\alpha _{\geq \alpha }]$
, then
![]() $\{S_i \mid i<\mu \}$
reflects in
$\{S_i \mid i<\mu \}$
reflects in
![]() $M_{\eta }[G^*]$
.
$M_{\eta }[G^*]$
.
Proof Let
![]() $\delta < j_\alpha (\bar {\kappa }_{\eta }^{+})$
with
$\delta < j_\alpha (\bar {\kappa }_{\eta }^{+})$
with
![]() $\operatorname {\mathrm {cf}}(\delta ) < \kappa _\alpha ^\alpha $
be a common reflection point of the collection
$\operatorname {\mathrm {cf}}(\delta ) < \kappa _\alpha ^\alpha $
be a common reflection point of the collection
![]() $\{T_i^\alpha \mid i<\mu \}$
. We claim that each
$\{T_i^\alpha \mid i<\mu \}$
. We claim that each
![]() $S_i$
reflects at
$S_i$
reflects at
![]() $j_{\alpha ,\eta }(\delta )$
. Let
$j_{\alpha ,\eta }(\delta )$
. Let
![]() $D \subseteq j_{\alpha ,\eta }(\delta )$
be club in
$D \subseteq j_{\alpha ,\eta }(\delta )$
be club in
![]() $M_{\eta }[G^*]$
, of order type
$M_{\eta }[G^*]$
, of order type
![]() $\operatorname {\mathrm {cf}}(\delta ) = \operatorname {\mathrm {cf}}(j_{\alpha ,\eta }(\delta ))$
.
$\operatorname {\mathrm {cf}}(\delta ) = \operatorname {\mathrm {cf}}(j_{\alpha ,\eta }(\delta ))$
.
Since
![]() $\mathop {\mathrm {crit}}{j_{\alpha ,\eta }}> \operatorname {\mathrm {cf}}(\delta )$
,
$\mathop {\mathrm {crit}}{j_{\alpha ,\eta }}> \operatorname {\mathrm {cf}}(\delta )$
,
![]() $j_{\alpha ,\eta }$
is continuous at
$j_{\alpha ,\eta }$
is continuous at
![]() $\delta $
and
$\delta $
and
![]() $E = \{\gamma < \delta \mid j_{\alpha ,\eta }(\gamma ) \in D \}$
is a club in
$E = \{\gamma < \delta \mid j_{\alpha ,\eta }(\gamma ) \in D \}$
is a club in
![]() $\delta $
. Note that
$\delta $
. Note that
![]() $E \in M_{\alpha }[G^*_\alpha \times \vec {H}^{\alpha }_{\geq \alpha }]$
. Since
$E \in M_{\alpha }[G^*_\alpha \times \vec {H}^{\alpha }_{\geq \alpha }]$
. Since
![]() $T_i^\alpha $
reflects at
$T_i^\alpha $
reflects at
![]() $\delta $
,
$\delta $
,
![]() $T_i^\alpha \cap E \neq \emptyset $
and hence
$T_i^\alpha \cap E \neq \emptyset $
and hence
![]() $S_i \cap D \neq \emptyset $
.
$S_i \cap D \neq \emptyset $
.
Combining the previous two claims if for some
![]() $\alpha \geq \bar {\alpha }$
,
$\alpha \geq \bar {\alpha }$
,
![]() $\{T_i^\alpha \mid i < \mu \}$
consists of stationary sets, then
$\{T_i^\alpha \mid i < \mu \}$
consists of stationary sets, then
![]() $\{S_i \mid i<\mu \}$
reflects. So we assume for a contradiction that for each
$\{S_i \mid i<\mu \}$
reflects. So we assume for a contradiction that for each
![]() $\alpha {\kern-1pt}\geq{\kern-1pt} \bar {\alpha }$
, there are
$\alpha {\kern-1pt}\geq{\kern-1pt} \bar {\alpha }$
, there are
![]() $i_\alpha {\kern-1pt}<{\kern-1pt}\mu $
and a club
$i_\alpha {\kern-1pt}<{\kern-1pt}\mu $
and a club
![]() $C_\alpha {\kern-1pt}\in{\kern-1pt} M_\alpha [G_\alpha ^* {\kern-1pt}\times{\kern-1pt} \vec {H}^\alpha _{\geq \alpha }]$
such that
$C_\alpha {\kern-1pt}\in{\kern-1pt} M_\alpha [G_\alpha ^* {\kern-1pt}\times{\kern-1pt} \vec {H}^\alpha _{\geq \alpha }]$
such that
![]() $T_{i_\alpha }^\alpha \cap C_\alpha = \emptyset $
. We fix
$T_{i_\alpha }^\alpha \cap C_\alpha = \emptyset $
. We fix
![]() $J \subseteq \eta $
unbounded and
$J \subseteq \eta $
unbounded and
![]() $i^*<\mu $
such that for all
$i^*<\mu $
such that for all
![]() $\alpha \in J$
,
$\alpha \in J$
,
![]() $i_\alpha = i^*$
.
$i_\alpha = i^*$
.
Let
![]() $I_\eta $
be the ideal of bounded subsets of
$I_\eta $
be the ideal of bounded subsets of
![]() $\eta $
. For
$\eta $
. For
![]() $\alpha \leq \eta $
, let
$\alpha \leq \eta $
, let
![]() $\vec {H}^\alpha /I_\eta $
be the generic for
$\vec {H}^\alpha /I_\eta $
be the generic for
![]() $j_\alpha (\vec {\mathbb {A}})/I_\eta $
derived from
$j_\alpha (\vec {\mathbb {A}})/I_\eta $
derived from
![]() $j_\alpha "\vec {H}$
. Recall that
$j_\alpha "\vec {H}$
. Recall that
![]() $\vec {H}$
is generic for
$\vec {H}$
is generic for
![]() $\vec {\mathbb {A}}$
which is a product of Cohen posets, so this makes sense.
$\vec {\mathbb {A}}$
which is a product of Cohen posets, so this makes sense.
Claim 4.4. For
![]() $\alpha \geq \bar {\alpha }$
, there is a club subset of
$\alpha \geq \bar {\alpha }$
, there is a club subset of
![]() $C_\alpha $
in
$C_\alpha $
in
![]() $M_\alpha [\vec {H}^\alpha /I_\eta ]$
.
$M_\alpha [\vec {H}^\alpha /I_\eta ]$
.
Proof We start by showing that for all
![]() $\beta> \alpha $
below
$\beta> \alpha $
below
![]() $\eta $
there is a club subset of
$\eta $
there is a club subset of
![]() $C_\alpha $
in
$C_\alpha $
in
![]() $M_{\alpha }[\vec {H}^\alpha \restriction [\beta , \eta )]$
.
$M_{\alpha }[\vec {H}^\alpha \restriction [\beta , \eta )]$
.
To see this, note that
![]() $M_\alpha [G^*_\alpha \times \vec {H}^\alpha _{\geq \alpha }]$
is
$M_\alpha [G^*_\alpha \times \vec {H}^\alpha _{\geq \alpha }]$
is
![]() $(\bar {\kappa }^\alpha _\beta )^{++}$
-cc extension of
$(\bar {\kappa }^\alpha _\beta )^{++}$
-cc extension of
![]() $M_\alpha [\vec {H}^\alpha \upharpoonright [\beta ,\eta )]$
and
$M_\alpha [\vec {H}^\alpha \upharpoonright [\beta ,\eta )]$
and
![]() $\bar {\kappa }_\beta ^\alpha <j_\alpha (\bar {\kappa }_{\eta })$
. Indeed, this forcing decomposes into a part contributing
$\bar {\kappa }_\beta ^\alpha <j_\alpha (\bar {\kappa }_{\eta })$
. Indeed, this forcing decomposes into a part contributing
![]() $G^*_\alpha $
which have small cardinality and the product of forcing notions
$G^*_\alpha $
which have small cardinality and the product of forcing notions
![]() $j_{\alpha }(\mathcal {A}(\lambda , \kappa _\gamma ))$
for
$j_{\alpha }(\mathcal {A}(\lambda , \kappa _\gamma ))$
for
![]() $\gamma < \beta $
, whose product has
$\gamma < \beta $
, whose product has
![]() $(\bar \kappa _\beta ^\alpha )^{++}$
-cc. For the moment we let
$(\bar \kappa _\beta ^\alpha )^{++}$
-cc. For the moment we let
![]() $\mathbb {Q}_\beta $
denote the
$\mathbb {Q}_\beta $
denote the
![]() $(\bar {\kappa }^\alpha _\beta )^{++}$
-cc poset used in order to move from
$(\bar {\kappa }^\alpha _\beta )^{++}$
-cc poset used in order to move from
![]() $M_\alpha [\vec {H}^\alpha \restriction [\beta ,\eta )]$
to
$M_\alpha [\vec {H}^\alpha \restriction [\beta ,\eta )]$
to
![]() $M_\alpha [G_\alpha ^* \times \vec {H}^\alpha _{\geq \alpha }]$
.
$M_\alpha [G_\alpha ^* \times \vec {H}^\alpha _{\geq \alpha }]$
.
We set take
![]() $C_{\alpha ,\beta }$
to be the set of closure points of the function assigning each
$C_{\alpha ,\beta }$
to be the set of closure points of the function assigning each
![]() $\gamma $
to the supremum of the set
$\gamma $
to the supremum of the set
as computed in the model
![]() $M_\alpha [\vec {H}^\alpha \upharpoonright [\beta ,\eta )]$
. Clearly this is a club. Further if
$M_\alpha [\vec {H}^\alpha \upharpoonright [\beta ,\eta )]$
. Clearly this is a club. Further if
![]() $\beta < \beta '$
, then
$\beta < \beta '$
, then
![]() $C_{\alpha ,\beta '} \subseteq C_{\alpha ,\beta }$
.
$C_{\alpha ,\beta '} \subseteq C_{\alpha ,\beta }$
.
Since the clubs are decreasing,
![]() $\bigcap _{\beta> \alpha } C_{\alpha ,\beta }$
is definable in
$\bigcap _{\beta> \alpha } C_{\alpha ,\beta }$
is definable in
![]() $M_\alpha [\vec {H}^\alpha /I_\eta ]$
as the set of ordinals
$M_\alpha [\vec {H}^\alpha /I_\eta ]$
as the set of ordinals
![]() $\gamma $
such that for some condition
$\gamma $
such that for some condition
![]() $\vec {a} \in j_\alpha (\vec {\mathbb {A}})$
,
$\vec {a} \in j_\alpha (\vec {\mathbb {A}})$
,
![]() $\vec {a}/I_\eta \in \vec {H}^\alpha / I_\eta $
and for all sufficiently large
$\vec {a}/I_\eta \in \vec {H}^\alpha / I_\eta $
and for all sufficiently large
![]() $\beta $
,
$\beta $
,
![]() $\vec {a} \upharpoonright [\beta ,\eta )$
forces
$\vec {a} \upharpoonright [\beta ,\eta )$
forces
![]() $\gamma \in C_{\alpha ,\beta }$
. So
$\gamma \in C_{\alpha ,\beta }$
. So
![]() $\bigcap _{\beta>\alpha }C_{\alpha ,\beta }$
is as required for the claim.
$\bigcap _{\beta>\alpha }C_{\alpha ,\beta }$
is as required for the claim.
Let
![]() $\dot {D}_\alpha $
be an
$\dot {D}_\alpha $
be an
![]() $\vec {H}^\alpha /I_\eta $
-name for the club from the previous lemma.
$\vec {H}^\alpha /I_\eta $
-name for the club from the previous lemma.
Lemma 4.5.
![]() $\vec {H}^{\eta }/I_\eta \in M_{\eta }[G^*]$
.
$\vec {H}^{\eta }/I_\eta \in M_{\eta }[G^*]$
.
Proof Let
![]() $p \in j_\eta(\vec{\mathbb{A}})$
. We will show how to decide in
$p \in j_\eta(\vec{\mathbb{A}})$
. We will show how to decide in
![]() $M_\eta [G^*]$
whether
$M_\eta [G^*]$
whether
![]() $p \in \vec {H}^\eta /I_\eta $
or not.
$p \in \vec {H}^\eta /I_\eta $
or not.
Now, fix
![]() $q \in G^*$
with
$q \in G^*$
with
![]() $\operatorname {\mathrm {dom}} q(\alpha ) \supseteq \operatorname {\mathrm {dom}} p(\alpha )$
. Let us claim that
$\operatorname {\mathrm {dom}} q(\alpha ) \supseteq \operatorname {\mathrm {dom}} p(\alpha )$
. Let us claim that
![]() $p \in \vec {H}/I_\eta $
if and only if there is
$p \in \vec {H}/I_\eta $
if and only if there is
![]() $\beta $
such that
$\beta $
such that
![]() $f^q(\gamma )\supseteq p(\gamma )$
for all
$f^q(\gamma )\supseteq p(\gamma )$
for all
![]() $\gamma \in [\beta , \eta )$
.
$\gamma \in [\beta , \eta )$
.
Indeed, without loss of generality,
![]() $q = j_\eta (\bar {q}) ^\smallfrown \langle \nu _0,\dots , \nu _{m-1}\rangle $
for
$q = j_\eta (\bar {q}) ^\smallfrown \langle \nu _0,\dots , \nu _{m-1}\rangle $
for
![]() $\bar {q} \in \vec {H}$
and
$\bar {q} \in \vec {H}$
and
![]() $\nu _0,\dots , \nu _{m-1}$
generators.
$\nu _0,\dots , \nu _{m-1}$
generators.
Thus, for every
![]() $\beta $
which is larger than the index of the measures of
$\beta $
which is larger than the index of the measures of
![]() $\nu _0,\dots ,\nu _{m-1}\ f^{\bar {q}(\beta )} \in H(\beta )$
and thus after applying
$\nu _0,\dots ,\nu _{m-1}\ f^{\bar {q}(\beta )} \in H(\beta )$
and thus after applying
![]() $j_\eta $
we conclude that the condition which is defined by
$j_\eta $
we conclude that the condition which is defined by
![]() $\langle f^q(\gamma ) \mid \beta \leq \gamma < \eta \rangle $
belongs to
$\langle f^q(\gamma ) \mid \beta \leq \gamma < \eta \rangle $
belongs to
![]() $\vec {H}^\eta \restriction [\beta ,\eta )$
. Since it is compatible with p,
$\vec {H}^\eta \restriction [\beta ,\eta )$
. Since it is compatible with p,
![]() $p \in \vec {H}^\eta /I_\eta $
.
$p \in \vec {H}^\eta /I_\eta $
.
In the other direction, one can take
![]() $\beta $
large enough so that
$\beta $
large enough so that
![]() $p \restriction [\beta ,\eta ) \in \vec {H}^\eta \restriction [\beta ,\eta )$
and then
$p \restriction [\beta ,\eta ) \in \vec {H}^\eta \restriction [\beta ,\eta )$
and then
![]() $p \restriction [\beta ,\eta )$
is the Cohen part of a condition in
$p \restriction [\beta ,\eta )$
is the Cohen part of a condition in
![]() $G^*$
.
$G^*$
.
Claim 4.6.
![]() $\langle j_{\alpha ,\eta }(\dot {D}_\alpha )_{\vec {H}^{\eta }/I_\eta } \mid \bar {\alpha } \leq \alpha < \eta \rangle \in M_{\eta }[G^*]$
.
$\langle j_{\alpha ,\eta }(\dot {D}_\alpha )_{\vec {H}^{\eta }/I_\eta } \mid \bar {\alpha } \leq \alpha < \eta \rangle \in M_{\eta }[G^*]$
.
Proof By the previous lemma,
![]() $\vec {H}^{\eta }/I_\eta \in M_{\eta }[G^*]$
. Further by Proposition 3.6,
$\vec {H}^{\eta }/I_\eta \in M_{\eta }[G^*]$
. Further by Proposition 3.6,
![]() $M_{\eta }[G^*]$
is closed under
$M_{\eta }[G^*]$
is closed under
![]() $\eta $
-sequences. So the sequence of names for clubs
$\eta $
-sequences. So the sequence of names for clubs
![]() $\langle j_{\alpha ,\eta }(\dot {D}_\alpha ) \mid \alpha < \eta \rangle \in M_{\eta }[G^*]$
.
$\langle j_{\alpha ,\eta }(\dot {D}_\alpha ) \mid \alpha < \eta \rangle \in M_{\eta }[G^*]$
.
To get a contradiction it is enough to show that
![]() $\bigcap _{\bar {\alpha } \leq \alpha <\eta } j_{\alpha }(\dot {D}_\alpha )_{\vec {H}^{\eta }/I_\eta } \cap S_{i^*} = \emptyset $
. Suppose that there is some
$\bigcap _{\bar {\alpha } \leq \alpha <\eta } j_{\alpha }(\dot {D}_\alpha )_{\vec {H}^{\eta }/I_\eta } \cap S_{i^*} = \emptyset $
. Suppose that there is some
![]() $\delta $
in the intersection. We can find some
$\delta $
in the intersection. We can find some
![]() $\alpha \in J$
and
$\alpha \in J$
and
![]() $\bar {\delta }$
such that
$\bar {\delta }$
such that
![]() $j_{\alpha ,\eta }(\bar {\delta }) = \delta $
. However, by the definitions of
$j_{\alpha ,\eta }(\bar {\delta }) = \delta $
. However, by the definitions of
![]() $D_\alpha $
and
$D_\alpha $
and
![]() $T_{i^*}^\alpha $
, we must have that
$T_{i^*}^\alpha $
, we must have that
![]() $\bar {\delta } \in C_\alpha \cap T_{i^*}^\alpha $
, a contradiction.
$\bar {\delta } \in C_\alpha \cap T_{i^*}^\alpha $
, a contradiction.
This completes the proof of Theorem 1.1.
5 Bad scales
In this section we give the proof of Theorem 1.2. For this theorem we work with the forcing
![]() $\mathbb {P}$
as before and assume that there is an indestructibly supercompact cardinal
$\mathbb {P}$
as before and assume that there is an indestructibly supercompact cardinal
![]() $\theta < \kappa _0$
. Working in V, let
$\theta < \kappa _0$
. Working in V, let
![]() $\vec {f}$
be a scale of length
$\vec {f}$
be a scale of length
![]() $\bar {\kappa }_\eta ^{+}$
in
$\bar {\kappa }_\eta ^{+}$
in
![]() $\prod _{\alpha <\eta }\kappa _\alpha ^{+}$
. As before let
$\prod _{\alpha <\eta }\kappa _\alpha ^{+}$
. As before let
![]() $\vec {H}$
be generic for
$\vec {H}$
be generic for
![]() $\vec {\mathcal {A}}$
over V and let
$\vec {\mathcal {A}}$
over V and let
![]() $G^*$
be the
$G^*$
be the
![]() $j_\eta (\mathbb {P})$
generic over
$j_\eta (\mathbb {P})$
generic over
![]() $M_\eta $
defined above.
$M_\eta $
defined above.
Lemma 5.1. In
![]() $M_\eta [G^*]$
,
$M_\eta [G^*]$
,
![]() $j_\eta (\vec {f})$
is a scale of length
$j_\eta (\vec {f})$
is a scale of length
![]() $j_\eta (\bar {\kappa }_\eta ^{+})$
in
$j_\eta (\bar {\kappa }_\eta ^{+})$
in
![]() $\prod _{\alpha <\eta }j(\kappa _\alpha )^{+}$
.
$\prod _{\alpha <\eta }j(\kappa _\alpha )^{+}$
.
Proof Let
![]() $g \in \left (\prod _{\alpha <\eta }j(\kappa _\alpha )^{+} \right )\cap M_\eta [G^*]$
. Clearly
$g \in \left (\prod _{\alpha <\eta }j(\kappa _\alpha )^{+} \right )\cap M_\eta [G^*]$
. Clearly
![]() $g \in V[\vec {H}]$
. Since each
$g \in V[\vec {H}]$
. Since each
![]() $\kappa _\alpha ^{+}$
is a continuity point of
$\kappa _\alpha ^{+}$
is a continuity point of
![]() $j_\eta $
, we can find an ordinal
$j_\eta $
, we can find an ordinal
![]() $\gamma _\alpha <\kappa _\alpha ^{+}$
such that
$\gamma _\alpha <\kappa _\alpha ^{+}$
such that
![]() $j_\eta (\gamma _\alpha )>g(\alpha )$
.
$j_\eta (\gamma _\alpha )>g(\alpha )$
.
By the distributivity of
![]() $\vec {\mathbb {A}}$
, the sequence
$\vec {\mathbb {A}}$
, the sequence
![]() $\tilde {g} = \langle \gamma _\alpha \mid \alpha < \eta \rangle $
belongs to V. Pick (in V) an ordinal
$\tilde {g} = \langle \gamma _\alpha \mid \alpha < \eta \rangle $
belongs to V. Pick (in V) an ordinal
![]() $\zeta $
such that
$\zeta $
such that
![]() $f_\zeta $
dominates
$f_\zeta $
dominates
![]() $\tilde {g}$
. Then,
$\tilde {g}$
. Then,
![]() $j_\eta (f_\zeta ) = j_\eta (f)_{j_\eta (\zeta )}$
dominates g.
$j_\eta (f_\zeta ) = j_\eta (f)_{j_\eta (\zeta )}$
dominates g.
Lemma 5.2. For
![]() $\delta <\kappa _\eta ^{+}$
with
$\delta <\kappa _\eta ^{+}$
with
![]() $\eta < \operatorname {\mathrm {cf}}(\delta )<\kappa _0$
, if
$\eta < \operatorname {\mathrm {cf}}(\delta )<\kappa _0$
, if
![]() $j_\eta (\delta )$
is a good point for
$j_\eta (\delta )$
is a good point for
![]() $j(\vec {f})$
in
$j(\vec {f})$
in
![]() $M_\eta [G^*]$
, then
$M_\eta [G^*]$
, then
![]() $\delta $
is a good point for
$\delta $
is a good point for
![]() $\vec {f}$
in
$\vec {f}$
in
![]() $V[\vec {H}]$
.
$V[\vec {H}]$
.
Proof Suppose that
![]() $A \subseteq j_\eta (\delta )$
and
$A \subseteq j_\eta (\delta )$
and
![]() $\alpha ^* < \eta $
witness that
$\alpha ^* < \eta $
witness that
![]() $j_\eta (\delta )$
is good for
$j_\eta (\delta )$
is good for
![]() $\vec {f}$
in
$\vec {f}$
in
![]() $M_\eta [G^*]$
. Note that
$M_\eta [G^*]$
. Note that
![]() $j_\eta "\delta $
is cofinal in
$j_\eta "\delta $
is cofinal in
![]() $j(\delta )$
. By thinning A if necessary we let
$j(\delta )$
. By thinning A if necessary we let
![]() $B \subseteq j_\eta "\delta $
be an unbounded set such that each element
$B \subseteq j_\eta "\delta $
be an unbounded set such that each element
![]() $\gamma \in B$
has a greatest element of A less than or equal to it. For each
$\gamma \in B$
has a greatest element of A less than or equal to it. For each
![]() $\gamma $
in B, let
$\gamma $
in B, let
![]() $\alpha _\gamma $
be such that for all
$\alpha _\gamma $
be such that for all
![]() $\alpha \geq \alpha _\gamma $
,
$\alpha \geq \alpha _\gamma $
,
Let
![]() $B'$
be an unbounded subset of B on which
$B'$
be an unbounded subset of B on which
![]() $\alpha _\gamma $
is fixed. Then
$\alpha _\gamma $
is fixed. Then
![]() $B'$
witnesses that
$B'$
witnesses that
![]() $j_\eta (\delta )$
is good. Since
$j_\eta (\delta )$
is good. Since
![]() $B' \subseteq j_\eta "\delta $
, we have that
$B' \subseteq j_\eta "\delta $
, we have that
![]() $\{ \gamma < \delta \mid j_\eta (\gamma ) \in B' \}$
witnesses that
$\{ \gamma < \delta \mid j_\eta (\gamma ) \in B' \}$
witnesses that
![]() $\delta $
is good for
$\delta $
is good for
![]() $\vec {f}$
in
$\vec {f}$
in
![]() $V[\vec {H}]$
.
$V[\vec {H}]$
.
In
![]() $V[\vec {H}]$
, let
$V[\vec {H}]$
, let
![]() $S = \{ \delta < \bar {\kappa }_\eta ^{+} \mid \delta $
is nongood for
$S = \{ \delta < \bar {\kappa }_\eta ^{+} \mid \delta $
is nongood for
![]() $\vec {f}$
and
$\vec {f}$
and
![]() $\eta < \operatorname {\mathrm {cf}}(\delta ) < \theta \}$
. We claim that S is stationary. Let
$\eta < \operatorname {\mathrm {cf}}(\delta ) < \theta \}$
. We claim that S is stationary. Let
![]() $k\colon V[\vec {H}] \to N$
be an elementary embedding witnessing that
$k\colon V[\vec {H}] \to N$
be an elementary embedding witnessing that
![]() $\theta $
is
$\theta $
is
![]() $\bar {\kappa }_\eta ^{+}$
-supercompact in
$\bar {\kappa }_\eta ^{+}$
-supercompact in
![]() $V[\vec {H}]$
. Standard arguments show that
$V[\vec {H}]$
. Standard arguments show that
![]() $\sup k"\bar {\kappa }_\eta ^{+}$
is a nongood point for
$\sup k"\bar {\kappa }_\eta ^{+}$
is a nongood point for
![]() $k(\vec {f})$
. It follows that S is stationary, since
$k(\vec {f})$
. It follows that S is stationary, since
![]() $\sup k"\bar {\kappa }_\eta ^{+} \in k(C)$
every club
$\sup k"\bar {\kappa }_\eta ^{+} \in k(C)$
every club
![]() $C \subseteq \bar {\kappa }_\eta ^{+}$
in
$C \subseteq \bar {\kappa }_\eta ^{+}$
in
![]() $V[\vec {H}]$
.
$V[\vec {H}]$
.
Now suppose that in
![]() $M_\eta [G^*]$
, there is a club D of good points for
$M_\eta [G^*]$
, there is a club D of good points for
![]() $j_\eta (\vec {f})$
. In
$j_\eta (\vec {f})$
. In
![]() $V[\vec {H}]$
, let
$V[\vec {H}]$
, let
![]() $C = \{ \delta < \bar {\kappa }_\eta ^{+} \mid j_\eta (\delta ) \in D \}$
. By the previous lemma, C is a
$C = \{ \delta < \bar {\kappa }_\eta ^{+} \mid j_\eta (\delta ) \in D \}$
. By the previous lemma, C is a
![]() $<\ \kappa _0$
-club consisting of good points for
$<\ \kappa _0$
-club consisting of good points for
![]() $\vec {f}$
. However,
$\vec {f}$
. However,
![]() $S \cap C$
is nonempty, a contradiction.
$S \cap C$
is nonempty, a contradiction.
6 Countable cofinality
Our goal in this section is to show that given the assumptions of Theorem 1.4, there exists a forcing extension which adds a generic filter for the extender based Prikry forcing by a
![]() $(\kappa ,\kappa ^{++})$
-extender (in particular, forces
$(\kappa ,\kappa ^{++})$
-extender (in particular, forces
![]() $\operatorname {\mathrm {cf}}(\kappa ) = \omega $
and
$\operatorname {\mathrm {cf}}(\kappa ) = \omega $
and
![]() $2^\kappa = \kappa ^{++}$
) and satisfies that every stationary subset of
$2^\kappa = \kappa ^{++}$
) and satisfies that every stationary subset of
![]() $\kappa ^{+}$
reflects.
$\kappa ^{+}$
reflects.
A necessary step for obtaining the latter is to add a club
![]() $D \subseteq \kappa ^{+}$
disjoint from
$D \subseteq \kappa ^{+}$
disjoint from
![]() $S^{\kappa ^{+}}_{\kappa }$
, the set of ordinals
$S^{\kappa ^{+}}_{\kappa }$
, the set of ordinals
![]() $\alpha < \kappa ^{+}$
of cofinality
$\alpha < \kappa ^{+}$
of cofinality
![]() $\kappa $
in the ground model. In [Reference Hayut and Unger13], the second and third authors address the situation for adding a single Prikry sequence to
$\kappa $
in the ground model. In [Reference Hayut and Unger13], the second and third authors address the situation for adding a single Prikry sequence to
![]() $\kappa $
. It is shown that under the subcompactness assumption of
$\kappa $
. It is shown that under the subcompactness assumption of
![]() $\kappa $
, there is a Prikry-type forcing which both singularizes
$\kappa $
, there is a Prikry-type forcing which both singularizes
![]() $\kappa $
and adds a club D as above, without generating new nonreflecting stationary sets.
$\kappa $
and adds a club D as above, without generating new nonreflecting stationary sets.
An additional remarkable aspect of the argument of [Reference Hayut and Unger13] is that it presents a fertile framework in which the arguments address an extension
![]() $N_\omega [\mathcal {H}]$
of an iterated ultrapower
$N_\omega [\mathcal {H}]$
of an iterated ultrapower
![]() $N_\omega $
of V, and assert directly that stationary reflection holds in
$N_\omega $
of V, and assert directly that stationary reflection holds in
![]() $N_{\omega }[\mathcal {H}]$
without having to specify the poset by which
$N_{\omega }[\mathcal {H}]$
without having to specify the poset by which
![]() $\mathcal {H}$
is added.
$\mathcal {H}$
is added.
Let us briefly describe the key ingredients of the construction of [Reference Hayut and Unger13], to serve as a reference for our arguments in the context of the failure of SCH. In [Reference Hayut and Unger13], one starts from a normal measure U on
![]() $\kappa $
in V, and consider the
$\kappa $
in V, and consider the
![]() $\omega $
-iterated ultrapower by U, given by
$\omega $
-iterated ultrapower by U, given by
and the direct limit embedding
![]() $i_{\omega } \colon V \to N_\omega $
. It is well known that the sequence of critical points
$i_{\omega } \colon V \to N_\omega $
. It is well known that the sequence of critical points
![]() ${\langle } \kappa _n \mid n < \omega {\rangle }$
,
${\langle } \kappa _n \mid n < \omega {\rangle }$
,
![]() $\kappa _{n+1} = i_{n,n+1}(\kappa _{n})$
is Prikry generic over
$\kappa _{n+1} = i_{n,n+1}(\kappa _{n})$
is Prikry generic over
![]() $N_\omega $
and that
$N_\omega $
and that
![]() $N_{\omega }[{\langle } \kappa _n \mid n<\omega {\rangle }] = \bigcap _n N_n$
[Reference Bukovský1, Reference Dehornoy3].
$N_{\omega }[{\langle } \kappa _n \mid n<\omega {\rangle }] = \bigcap _n N_n$
[Reference Bukovský1, Reference Dehornoy3].
Let
![]() $\mathbb {Q}$
be the Prikry name for the forcing for adding a disjoint club from
$\mathbb {Q}$
be the Prikry name for the forcing for adding a disjoint club from
![]() $(S^{\kappa ^{+}}_\kappa )^V = \kappa ^{+} \cap \operatorname {\mathrm {Cof}}^V(\kappa )$
. The forcing
$(S^{\kappa ^{+}}_\kappa )^V = \kappa ^{+} \cap \operatorname {\mathrm {Cof}}^V(\kappa )$
. The forcing
![]() $\mathbb {Q}_{\omega } = i_\omega (\mathbb {Q})^{{\langle } \kappa _n \mid n < \omega {\rangle }} \in N_\omega [{{\langle } \kappa _n \mid n < \omega {\rangle }}]$
is isomorphic to the forcing for adding a
$\mathbb {Q}_{\omega } = i_\omega (\mathbb {Q})^{{\langle } \kappa _n \mid n < \omega {\rangle }} \in N_\omega [{{\langle } \kappa _n \mid n < \omega {\rangle }}]$
is isomorphic to the forcing for adding a
![]() $\kappa ^{+}$
-Cohen set over V, and likewise, to adding a
$\kappa ^{+}$
-Cohen set over V, and likewise, to adding a
![]() $\kappa _n^{+}$
-Cohen set over
$\kappa _n^{+}$
-Cohen set over
![]() $N_n$
, for each
$N_n$
, for each
![]() $n < \omega $
.
$n < \omega $
.
Moreover, taking a
![]() $\mathbb {Q}_{\omega }$
-generic filter
$\mathbb {Q}_{\omega }$
-generic filter
![]() $H $
over V, we have that both H and
$H $
over V, we have that both H and
![]() $i_{0,1}"H $
generate mutually generic filters over
$i_{0,1}"H $
generate mutually generic filters over
![]() $N_1$
for
$N_1$
for
![]() $i_1(\mathbb {Q}_\omega ) = \mathbb {Q}_\omega $
. More generally, for each n, the sequence
$i_1(\mathbb {Q}_\omega ) = \mathbb {Q}_\omega $
. More generally, for each n, the sequence
![]() $H^n_0, \dots , H^n_n$
, where each
$H^n_0, \dots , H^n_n$
, where each
![]() $H^n_k$
is generated by
$H^n_k$
is generated by
![]() $i_{k,n}"H \subset i_n(\mathbb {Q}_\omega ) = \mathbb {Q}_\omega $
for
$i_{k,n}"H \subset i_n(\mathbb {Q}_\omega ) = \mathbb {Q}_\omega $
for
![]() $1 \leq k \leq n$
, are mutually generic filters for
$1 \leq k \leq n$
, are mutually generic filters for
![]() $\mathbb {Q}_\omega $
over
$\mathbb {Q}_\omega $
over
![]() $N_n$
. With this choice of “shifts” of H, we obtain that for each
$N_n$
. With this choice of “shifts” of H, we obtain that for each
![]() $n < k$
, the standard iterated ultrapower map
$n < k$
, the standard iterated ultrapower map
![]() $i_{n,k} \colon N_n \to N_k$
extends to
$i_{n,k} \colon N_n \to N_k$
extends to
![]() $i_{n,k}^* \colon N_n[{\langle } H^n_0,\dots , H^n_n {\rangle }] \to N_k[ {\langle } H^{k}_0, \dots , H^{k}_n{\rangle }] \subseteq N_k[ {\langle } H^{k}_0, \dots , H^{k}_k{\rangle }]$
. For each n, the sequence
$i_{n,k}^* \colon N_n[{\langle } H^n_0,\dots , H^n_n {\rangle }] \to N_k[ {\langle } H^{k}_0, \dots , H^{k}_n{\rangle }] \subseteq N_k[ {\langle } H^{k}_0, \dots , H^{k}_k{\rangle }]$
. For each n, the sequence
![]() ${\langle } H^n_0, \dots , H^n_n {\rangle }$
is denoted by
${\langle } H^n_0, \dots , H^n_n {\rangle }$
is denoted by
![]() $\mathcal {H}_n$
. The final extension
$\mathcal {H}_n$
. The final extension
![]() $N_\omega [\mathcal {H}]$
of
$N_\omega [\mathcal {H}]$
of
![]() $N_\omega $
is given by the sequence
$N_\omega $
is given by the sequence
![]() $\mathcal {H} = {\langle } H_n^\omega \mid n < \omega {\rangle }$
, where
$\mathcal {H} = {\langle } H_n^\omega \mid n < \omega {\rangle }$
, where
![]() $H_n^\omega $
is the filter generated by
$H_n^\omega $
is the filter generated by
![]() $i_{n,\omega }"H$
, which achieves the critical equality
$i_{n,\omega }"H$
, which achieves the critical equality
From this equality it follows at once that:
-
(1)
 $N_\omega [\mathcal {H}]$
is closed under its
$N_\omega [\mathcal {H}]$
is closed under its
 $\kappa $
-sequences;
$\kappa $
-sequences; -
(2)
 $\kappa _\omega = i_\omega (\kappa )$
is singular in
$\kappa _\omega = i_\omega (\kappa )$
is singular in
 $N_\omega [\mathcal {H}]$
, as
$N_\omega [\mathcal {H}]$
, as
 ${\langle } \kappa _n \mid n<\omega {\rangle }$
belongs to each
${\langle } \kappa _n \mid n<\omega {\rangle }$
belongs to each
 $N_n[\mathcal {H}_n]$
; and
$N_n[\mathcal {H}_n]$
; and -
(3)
 $H \in N_\omega [\mathcal {H}]$
, as
$H \in N_\omega [\mathcal {H}]$
, as
 $H = H^n_n$
for all
$H = H^n_n$
for all
 $n < \omega $
.
$n < \omega $
.
Therefore every stationary subset S of
![]() $\kappa _\omega ^{+}$
in
$\kappa _\omega ^{+}$
in
![]() $N_\omega [\mathcal {H}]$
can be assumed to concentrate at some cofinality
$N_\omega [\mathcal {H}]$
can be assumed to concentrate at some cofinality
![]() $\rho < \kappa _\omega $
. Say for simplicity that
$\rho < \kappa _\omega $
. Say for simplicity that
![]() $\rho < \kappa _0$
, one shows that S reflects in
$\rho < \kappa _0$
, one shows that S reflects in
![]() $N_\omega [\mathcal {H}]$
by examining its pull backs
$N_\omega [\mathcal {H}]$
by examining its pull backs
![]() $S_n = i_{n,\omega }^{-1}(S) \subseteq \kappa _n^{+}$
. If we have that
$S_n = i_{n,\omega }^{-1}(S) \subseteq \kappa _n^{+}$
. If we have that
![]() $\kappa _n = i_n(\kappa )$
is
$\kappa _n = i_n(\kappa )$
is
![]() $\Pi ^1_1$
-subcompact in the Cohen extension
$\Pi ^1_1$
-subcompact in the Cohen extension
![]() $N_n[\mathcal {H}_n]$
of
$N_n[\mathcal {H}_n]$
of
![]() $N_n$
, then we have that if
$N_n$
, then we have that if
![]() $S_n$
is stationary then it must reflect at some
$S_n$
is stationary then it must reflect at some
![]() $\delta < \kappa _n^{+}$
of cofinality
$\delta < \kappa _n^{+}$
of cofinality
![]() $\delta <\kappa _n$
. Using
$\delta <\kappa _n$
. Using
![]() $i_{n,\omega }$
, we conclude from this that S reflects at
$i_{n,\omega }$
, we conclude from this that S reflects at
![]() $i_{n,\omega }(\delta )$
in
$i_{n,\omega }(\delta )$
in
![]() $N_\omega [\mathcal {H}]$
.
$N_\omega [\mathcal {H}]$
.
To rule out the other option, of having all
![]() $S_n \subseteq \kappa _n^{+}$
being nonstationary in
$S_n \subseteq \kappa _n^{+}$
being nonstationary in
![]() $N_n[\mathcal {H}_n]$
, one takes witnessing disjoint clubs
$N_n[\mathcal {H}_n]$
, one takes witnessing disjoint clubs
![]() $C_n \subseteq \kappa _n^{+}$
and uses the fact that for each
$C_n \subseteq \kappa _n^{+}$
and uses the fact that for each
![]() $n < \omega $
,
$n < \omega $
,
![]() $i_{n,\omega } \colon N_n \to N_\omega $
extends to
$i_{n,\omega } \colon N_n \to N_\omega $
extends to
![]() $i_{n,\omega }^* \colon N_n[\mathcal {H}_n] \to N_\omega [ i_{n,\omega }"\mathcal {H}_n] \subset N_{\omega }[\mathcal {H}]$
. This allows us to show that the club
$i_{n,\omega }^* \colon N_n[\mathcal {H}_n] \to N_\omega [ i_{n,\omega }"\mathcal {H}_n] \subset N_{\omega }[\mathcal {H}]$
. This allows us to show that the club
![]() $D_n = i_{n,\omega }^*(C_n) \subseteq \kappa _\omega ^{+}$
belongs to
$D_n = i_{n,\omega }^*(C_n) \subseteq \kappa _\omega ^{+}$
belongs to
![]() $N_\omega [\mathcal {H}]$
for each n. Since
$N_\omega [\mathcal {H}]$
for each n. Since
![]() $N_\omega [\mathcal {H}]$
is closed under its
$N_\omega [\mathcal {H}]$
is closed under its
![]() $\kappa $
sequences, it computes
$\kappa $
sequences, it computes
![]() ${\langle } D_n \mid n < \omega {\rangle }$
correctly and thus also
${\langle } D_n \mid n < \omega {\rangle }$
correctly and thus also
![]() $D = \bigcap _n D_n$
, that would have to be disjoint from S, a contradiction.
$D = \bigcap _n D_n$
, that would have to be disjoint from S, a contradiction.
We turn now to the new construction and prove Theorem 1.4. Let
![]() $V'$
be a model which contains a
$V'$
be a model which contains a
![]() $\kappa ^{+}$
-
$\kappa ^{+}$
-
![]() $\Pi ^1_1$
-subcompact cardinal
$\Pi ^1_1$
-subcompact cardinal
![]() $\kappa $
, which also carries a
$\kappa $
, which also carries a
![]() $(\kappa ,\kappa ^{++})$
-extender.
$(\kappa ,\kappa ^{++})$
-extender.
Recall that
![]() $\kappa $
is
$\kappa $
is
![]() $\kappa ^{+}$
-
$\kappa ^{+}$
-
![]() $\Pi ^1_1$
-subcompact if for every set
$\Pi ^1_1$
-subcompact if for every set
![]() $A \subseteq H(\kappa ^{+})$
and every
$A \subseteq H(\kappa ^{+})$
and every
![]() $\Pi ^1_1$
-statement
$\Pi ^1_1$
-statement
![]() $\Phi $
such that
$\Phi $
such that
![]() ${\langle } H(\kappa ^{+}), \in ,A\rangle \models \Phi $
, there are
${\langle } H(\kappa ^{+}), \in ,A\rangle \models \Phi $
, there are
![]() $\rho < \kappa $
,
$\rho < \kappa $
,
![]() $B \subseteq H(\rho ^{+})$
, and an elementary embedding
$B \subseteq H(\rho ^{+})$
, and an elementary embedding
![]() $j \colon {\langle } H(\rho ^{+}), \in ,B\rangle \to {\langle } H(\kappa ^{+}), \in ,A{\rangle }$
with
$j \colon {\langle } H(\rho ^{+}), \in ,B\rangle \to {\langle } H(\kappa ^{+}), \in ,A{\rangle }$
with
![]() $cp(j) = \rho $
, such that
$cp(j) = \rho $
, such that
![]() ${\langle } H(\rho ^{+}), \in ,B\rangle \models \Phi $
.
${\langle } H(\rho ^{+}), \in ,B\rangle \models \Phi $
.
Let V be obtained from
![]() $V'$
by an Easton-support iteration of products
$V'$
by an Easton-support iteration of products
![]() $\mathop {\mathrm {Add}}(\alpha ^{+},\alpha ^{++})$
for inaccessible
$\mathop {\mathrm {Add}}(\alpha ^{+},\alpha ^{++})$
for inaccessible
![]() $\alpha \leq \kappa $
.
$\alpha \leq \kappa $
.
By [Reference Hayut and Unger13, Lemma 42],
![]() $\kappa $
remains
$\kappa $
remains
![]() $\kappa ^{+}$
-
$\kappa ^{+}$
-
![]() $\Pi _1^1$
-subcompact in V and even in a further extension by
$\Pi _1^1$
-subcompact in V and even in a further extension by
![]() $\mathop {\mathrm {Add}}(\kappa ^{+},\kappa ^{++})$
. Moreover, by standard arguments it is routine to verify that
$\mathop {\mathrm {Add}}(\kappa ^{+},\kappa ^{++})$
. Moreover, by standard arguments it is routine to verify that
![]() $\kappa $
still carries a
$\kappa $
still carries a
![]() $(\kappa ,\kappa ^{++})$
-extender in V. We note that as a consequence of
$(\kappa ,\kappa ^{++})$
-extender in V. We note that as a consequence of
![]() $\kappa ^{+}$
-
$\kappa ^{+}$
-
![]() $\Pi _1^1$
-subcompactness in V, simultaneous reflection holds for collections of fewer than
$\Pi _1^1$
-subcompactness in V, simultaneous reflection holds for collections of fewer than
![]() $\kappa $
many stationary subsets of
$\kappa $
many stationary subsets of
![]() $S^{\kappa ^{+}}_{<\kappa }$
. Further this property is indestructible under
$S^{\kappa ^{+}}_{<\kappa }$
. Further this property is indestructible under
![]() $\mathop {\mathrm {Add}}(\kappa ^{+},\kappa ^{++})$
.
$\mathop {\mathrm {Add}}(\kappa ^{+},\kappa ^{++})$
.
Working in V, let E be a
![]() $(\kappa ,\kappa ^{++})$
-extender. Let
$(\kappa ,\kappa ^{++})$
-extender. Let
be the iteration by E and let
be the iteration by the normal measure
![]() $E_\kappa $
where
$E_\kappa $
where
![]() $V = M_0 = N_0$
. We write
$V = M_0 = N_0$
. We write
![]() $j_n$
for
$j_n$
for
![]() $j_{0,n}$
and
$j_{0,n}$
and
![]() $i_n$
for
$i_n$
for
![]() $i_{0,n}$
.
$i_{0,n}$
.
We describe a generic extension of
![]() $M_\omega $
in which
$M_\omega $
in which
![]() $j_\omega (\kappa ^{+})$
satisfies the conclusion of the theorem. It follows by elementarity that there is such an extension of V. We are able to isolate the forcing used, but this is not required in the proof.
$j_\omega (\kappa ^{+})$
satisfies the conclusion of the theorem. It follows by elementarity that there is such an extension of V. We are able to isolate the forcing used, but this is not required in the proof.
We start by constructing a generic object for
![]() $j_\omega (\mathbb {P}_E)$
over
$j_\omega (\mathbb {P}_E)$
over
![]() $M_\omega $
, where
$M_\omega $
, where
![]() $\mathbb {P}_E$
is the extender based forcing of Merimovich. Although for the most part, we will refer to Merimovich’s arguments in [Reference Merimovich15], our presentation follows a more up-do-date presentation of the forcing, given by Merimovich in [Reference Merimovich16, Section 2].
$\mathbb {P}_E$
is the extender based forcing of Merimovich. Although for the most part, we will refer to Merimovich’s arguments in [Reference Merimovich15], our presentation follows a more up-do-date presentation of the forcing, given by Merimovich in [Reference Merimovich16, Section 2].
We recall that conditions
![]() $p \in \mathbb {P}_E$
are pairs of the form
$p \in \mathbb {P}_E$
are pairs of the form
![]() $p = {\langle } f, T{\rangle }$
, where
$p = {\langle } f, T{\rangle }$
, where
![]() $f \colon d \to [\kappa ]^{<\omega }$
is a partial function from
$f \colon d \to [\kappa ]^{<\omega }$
is a partial function from
![]() $\kappa ^{++}$
to
$\kappa ^{++}$
to
![]() $[\kappa ]^{<\omega }$
with domain
$[\kappa ]^{<\omega }$
with domain
![]() $d \in [\kappa ^{++}]^{\leq \kappa }$
with
$d \in [\kappa ^{++}]^{\leq \kappa }$
with
![]() $\kappa \in d$
, and T is tree of height
$\kappa \in d$
, and T is tree of height
![]() $\omega $
, whose splitting sets are all measure one with respect to a measure
$\omega $
, whose splitting sets are all measure one with respect to a measure
![]() $E(d)$
on
$E(d)$
on
![]() $V_\kappa $
, derived from the extender E. The generator of
$V_\kappa $
, derived from the extender E. The generator of
![]() $E(d)$
is the function
$E(d)$
is the function
![]() $\operatorname {\mathrm {mc}}(d) = \{ {\langle } j(\alpha ), \alpha {\rangle } \mid \alpha \in d\}$
. Therefore, a typical node in the tree is an increasing sequence of functions
$\operatorname {\mathrm {mc}}(d) = \{ {\langle } j(\alpha ), \alpha {\rangle } \mid \alpha \in d\}$
. Therefore, a typical node in the tree is an increasing sequence of functions
![]() ${\langle } \nu _0,\dots ,\nu _{k-1}{\rangle }$
where each
${\langle } \nu _0,\dots ,\nu _{k-1}{\rangle }$
where each
![]() $\nu _i$
is a partial, order preserving function
$\nu _i$
is a partial, order preserving function
![]() $\nu _i \colon \operatorname {\mathrm {dom}}(\nu _i) \to \kappa $
, with
$\nu _i \colon \operatorname {\mathrm {dom}}(\nu _i) \to \kappa $
, with
![]() $\kappa \in \operatorname {\mathrm {dom}}(\nu _i)$
and
$\kappa \in \operatorname {\mathrm {dom}}(\nu _i)$
and
![]() $|\nu _i| = \nu _i(\kappa )$
. The sequence
$|\nu _i| = \nu _i(\kappa )$
. The sequence
![]() ${\langle } \nu _0,\dots , \nu _{k-1}{\rangle }$
is increasing in the sense that
${\langle } \nu _0,\dots , \nu _{k-1}{\rangle }$
is increasing in the sense that
![]() $\nu _i(\kappa ) < \nu _{i+1}(\kappa )$
for all i. When extending conditions
$\nu _i(\kappa ) < \nu _{i+1}(\kappa )$
for all i. When extending conditions
![]() $p = {\langle } f, T{\rangle } \in \mathbb {P}_E$
we are allowed to:
$p = {\langle } f, T{\rangle } \in \mathbb {P}_E$
we are allowed to:
-
(i) extend f in as Cohen conditions (namely, add points
 $\gamma < \kappa ^{++}$
to
$\gamma < \kappa ^{++}$
to
 $\operatorname {\mathrm {dom}}(f)$
and arbitrarily choose
$\operatorname {\mathrm {dom}}(f)$
and arbitrarily choose
 $f(\gamma ) \in [\kappa ]^{<\omega }$
), and modify the tree parts;
$f(\gamma ) \in [\kappa ]^{<\omega }$
), and modify the tree parts; -
(ii) shrink the tree T; and
-
(iii) choose a point
 ${\langle } \nu {\rangle } \in \operatorname {\mathrm {succ}}_{\emptyset }(T)$
to extend
${\langle } \nu {\rangle } \in \operatorname {\mathrm {succ}}_{\emptyset }(T)$
to extend
 $p = {\langle } f,T{\rangle }$
to
$p = {\langle } f,T{\rangle }$
to
 $p_{{\langle } \nu {\rangle }} = {\langle } f_{{\langle } \nu {\rangle }}, T_{{\langle } \nu {\rangle }}{\rangle }$
, where
$p_{{\langle } \nu {\rangle }} = {\langle } f_{{\langle } \nu {\rangle }}, T_{{\langle } \nu {\rangle }}{\rangle }$
, where
 $f_{{\langle } \nu {\rangle }}$
is defined by
$f_{{\langle } \nu {\rangle }}$
is defined by
 $\operatorname {\mathrm {dom}}(f_{{\langle } \nu {\rangle }}) = \operatorname {\mathrm {dom}}(f)$
and
$\operatorname {\mathrm {dom}}(f_{{\langle } \nu {\rangle }}) = \operatorname {\mathrm {dom}}(f)$
and  $$ \begin{align*} f_{{\langle} \nu {\rangle}}(\alpha) = \begin{cases} f(\alpha) \cup \{\nu(\alpha)\}, &\mbox{if } \alpha \in \operatorname{\mathrm{dom}}(\nu) \text{ and } \nu(\alpha)> \max(f(\alpha)),\\ f(\alpha), &\mbox{otherwise. } \end{cases} \end{align*} $$
$$ \begin{align*} f_{{\langle} \nu {\rangle}}(\alpha) = \begin{cases} f(\alpha) \cup \{\nu(\alpha)\}, &\mbox{if } \alpha \in \operatorname{\mathrm{dom}}(\nu) \text{ and } \nu(\alpha)> \max(f(\alpha)),\\ f(\alpha), &\mbox{otherwise. } \end{cases} \end{align*} $$
Any extension of p is obtained by finite combination of (i)–(iii), and the direct extensions of p are those which are obtained by (i) and (ii). The poset
![]() $\mathbb {P}_E^*$
is the suborder of
$\mathbb {P}_E^*$
is the suborder of
![]() $\mathbb {P}_E$
whose extension consists only of the Cohen type extension (i). Clearly,
$\mathbb {P}_E$
whose extension consists only of the Cohen type extension (i). Clearly,
![]() $\mathbb {P}_E^*$
is isomorphic to
$\mathbb {P}_E^*$
is isomorphic to
![]() $\mathop {\mathrm {Add}}(\kappa ^{+},\kappa ^{++})$
.
$\mathop {\mathrm {Add}}(\kappa ^{+},\kappa ^{++})$
.
We turn to describe the construction of a
![]() $j_\omega (\mathbb {P}_E)$
generic following [Reference Merimovich15]. Let
$j_\omega (\mathbb {P}_E)$
generic following [Reference Merimovich15]. Let
![]() $G_0$
be
$G_0$
be
![]() $\mathbb {P}_E^*$
generic. We work by induction to define
$\mathbb {P}_E^*$
generic. We work by induction to define
![]() $G_n$
for
$G_n$
for
![]() $n < \omega $
. Suppose that we have defined
$n < \omega $
. Suppose that we have defined
![]() $G_n \subseteq j_n(\mathbb {P}_E^*)$
for some
$G_n \subseteq j_n(\mathbb {P}_E^*)$
for some
![]() $n<\omega $
. First, let
$n<\omega $
. First, let
![]() $G_{n+1}'$
be the closure of the set
$G_{n+1}'$
be the closure of the set
![]() $j_{n,n+1}"G_n$
. Then, we take
$j_{n,n+1}"G_n$
. Then, we take
![]() $G_{n+1}$
to be obtained from
$G_{n+1}$
to be obtained from
![]() $G_{n+1}'$
by adding the ordinal
$G_{n+1}'$
by adding the ordinal
![]() $\alpha $
to
$\alpha $
to
![]() $G_{n+1}'$
at coordinate
$G_{n+1}'$
at coordinate
![]() $j_{n,n+1}(\alpha )$
, for all
$j_{n,n+1}(\alpha )$
, for all
![]() $\alpha < j_n(\kappa ^{++})$
.
$\alpha < j_n(\kappa ^{++})$
.
Claim 6.1.
![]() $G_{n+1}$
is
$G_{n+1}$
is
![]() $M_{n+1}$
-generic for
$M_{n+1}$
-generic for
![]() $j_{n+1}(\mathbb {P}_E^*)$
.
$j_{n+1}(\mathbb {P}_E^*)$
.
Proof This is a straightforward application of Woodin’s surgery argument [Reference Gitik5], so we only sketch the proof. Let D be a dense open subset of
![]() $j_{n+1}(\mathbb {P}_E^*)$
. Let E be the set of all f in D such that all
$j_{n+1}(\mathbb {P}_E^*)$
. Let E be the set of all f in D such that all
![]() $j_{n}(\kappa )$
sized modifications of f are in D. E is dense using the closure of
$j_{n}(\kappa )$
sized modifications of f are in D. E is dense using the closure of
![]() $j_{n+1}(\mathbb {P}_E^*)$
. Now the fact that
$j_{n+1}(\mathbb {P}_E^*)$
. Now the fact that
![]() $G_{n+1}'$
meets E implies that
$G_{n+1}'$
meets E implies that
![]() $G_{n+1}$
meets D, since each condition in
$G_{n+1}$
meets D, since each condition in
![]() $G_{n+1}$
is a
$G_{n+1}$
is a
![]() $j_n(\kappa )$
sized modification of one in
$j_n(\kappa )$
sized modification of one in
![]() $G_{n+1}'$
.
$G_{n+1}'$
.
We make a few remarks.
Remark 6.2. For each n,
![]() $G_{n}$
can be obtained directly from the upwards closure of
$G_{n}$
can be obtained directly from the upwards closure of
![]() $j_n"G_0$
by combining the alterations used in construction of
$j_n"G_0$
by combining the alterations used in construction of
![]() $G_i$
for
$G_i$
for
![]() $i<n$
.
$i<n$
.
Since the proof of the previous claim can be repeated in any suitably closed forcing extension, we have the following.
Remark 6.3. If H is generic for
![]() $j_n(\kappa ^{+})$
-closed forcing and mutually generic to the upwards closure of
$j_n(\kappa ^{+})$
-closed forcing and mutually generic to the upwards closure of
![]() $j_n"G_0$
, then H and
$j_n"G_0$
, then H and
![]() $G_n$
are mutually generic.
$G_n$
are mutually generic.
Let
![]() $G_\omega $
be the
$G_\omega $
be the
![]() $j_\omega (\mathbb {P}_E)$
-generic obtained from
$j_\omega (\mathbb {P}_E)$
-generic obtained from
![]() $G_0$
as in [Reference Merimovich15].
$G_0$
as in [Reference Merimovich15].
Claim 6.4.
![]() $M_\omega [G_\omega ]$
is closed under
$M_\omega [G_\omega ]$
is closed under
![]() $\kappa $
-sequences.
$\kappa $
-sequences.
Proof It is enough to show that
![]() $M_\omega [G_\omega ]$
is closed under
$M_\omega [G_\omega ]$
is closed under
![]() $\kappa $
-sequences of ordinals. Let
$\kappa $
-sequences of ordinals. Let
![]() ${\langle } \gamma _\delta \mid \delta < \kappa {\rangle }$
be a sequence of ordinals. We can assume that each
${\langle } \gamma _\delta \mid \delta < \kappa {\rangle }$
be a sequence of ordinals. We can assume that each
![]() $\gamma _\delta $
is of the form
$\gamma _\delta $
is of the form
![]() $j_\omega (g_\delta )(\alpha _\delta , j(\alpha _\delta ),\dots j_{n_\delta -1}(\alpha _\delta ))$
for some
$j_\omega (g_\delta )(\alpha _\delta , j(\alpha _\delta ),\dots j_{n_\delta -1}(\alpha _\delta ))$
for some
![]() $g_\delta \colon [\kappa ]^{n_\delta } \to \kappa ^{++}$
and
$g_\delta \colon [\kappa ]^{n_\delta } \to \kappa ^{++}$
and
![]() $\alpha _\delta <\kappa ^{++}$
. We refer the reader to [Reference Merimovich15, Corollary 2.6] for a proof. Since
$\alpha _\delta <\kappa ^{++}$
. We refer the reader to [Reference Merimovich15, Corollary 2.6] for a proof. Since
![]() ${\langle } j_\omega (g_\delta ) \mid \delta < \kappa {\rangle } = j_\omega ({\langle } g_\delta \mid \delta <\kappa {\rangle })\restriction \kappa \in M_\omega $
, it is enough to show that
${\langle } j_\omega (g_\delta ) \mid \delta < \kappa {\rangle } = j_\omega ({\langle } g_\delta \mid \delta <\kappa {\rangle })\restriction \kappa \in M_\omega $
, it is enough to show that
![]() ${\langle } (\alpha _\delta , \dots j_{n_\delta -1}(\alpha _\delta )) \mid \delta < \kappa {\rangle } \in M_\omega [G_\omega ]$
. To see this note that
${\langle } (\alpha _\delta , \dots j_{n_\delta -1}(\alpha _\delta )) \mid \delta < \kappa {\rangle } \in M_\omega [G_\omega ]$
. To see this note that
![]() $\{\alpha _\delta \mid \delta < \kappa \} = \operatorname {\mathrm {dom}}(f)$
for some
$\{\alpha _\delta \mid \delta < \kappa \} = \operatorname {\mathrm {dom}}(f)$
for some
![]() $f \in G_0$
and that the sequence
$f \in G_0$
and that the sequence
![]() $f(\alpha _\delta ) \frown (\alpha _\delta , \dots j_{n_\delta -1}(\alpha _\delta ))$
is an initial segment of the
$f(\alpha _\delta ) \frown (\alpha _\delta , \dots j_{n_\delta -1}(\alpha _\delta ))$
is an initial segment of the
![]() $\omega $
-sequence with index
$\omega $
-sequence with index
![]() $j_\omega (\alpha _\delta )$
in
$j_\omega (\alpha _\delta )$
in
![]() $G_\omega $
. This is enough to compute
$G_\omega $
. This is enough to compute
![]() ${\langle } (\alpha _\delta , \dots j_{n_\delta -1}(\alpha _\delta )) \mid \delta < \kappa {\rangle }$
, since
${\langle } (\alpha _\delta , \dots j_{n_\delta -1}(\alpha _\delta )) \mid \delta < \kappa {\rangle }$
, since
![]() $j_\omega "f \in M_\omega $
.
$j_\omega "f \in M_\omega $
.
The following lemma is proved in [Reference Hayut12, Section 4].
Lemma 6.5.
![]() $\bigcap _{n<\omega } M_n[G_n] = M_\omega [G_\omega ]$
.
$\bigcap _{n<\omega } M_n[G_n] = M_\omega [G_\omega ]$
.
Since we will need to prove a stronger version ahead, let us sketch the proof of this lemma.
Proof First, the inclusion
![]() $\bigcap _{n<\omega } M_n[G_n] \supseteq M_\omega [G_\omega ]$
is clear.
$\bigcap _{n<\omega } M_n[G_n] \supseteq M_\omega [G_\omega ]$
is clear.
As in the case of the standard Bukovský–Dehornoy Theorem, in order to prove the other direction we would like to take a set of ordinals
![]() $X \in M_\omega [G_\omega ]$
and consider the sets
$X \in M_\omega [G_\omega ]$
and consider the sets
Note that the filter generated by
![]() $j_{n,\omega }" G_n$
is not a member of
$j_{n,\omega }" G_n$
is not a member of
![]() $M_\omega [G_\omega ]$
and thus we must be more careful about the way we push
$M_\omega [G_\omega ]$
and thus we must be more careful about the way we push
![]() $Y_n$
into
$Y_n$
into
![]() $M_\omega [G_\omega ]$
.
$M_\omega [G_\omega ]$
.
Let us pick for each n a name
![]() $\dot {y}_n \in M_n$
for
$\dot {y}_n \in M_n$
for
![]() $Y_n$
. As the sequence of names
$Y_n$
. As the sequence of names
![]() $\langle j_{n,\omega }(\dot {y}_n)\mid n < \omega \rangle $
is a member of
$\langle j_{n,\omega }(\dot {y}_n)\mid n < \omega \rangle $
is a member of
![]() $M_\omega [G_\omega ]$
(using its closure under countable sequence), we must verify that we can evaluate correctly, without access to the filters
$M_\omega [G_\omega ]$
(using its closure under countable sequence), we must verify that we can evaluate correctly, without access to the filters
![]() $j_{n,\omega }(G_n)$
, whether an ordinal
$j_{n,\omega }(G_n)$
, whether an ordinal
![]() $\gamma $
belongs to a tail of sets
$\gamma $
belongs to a tail of sets
![]() $j_{n,\omega }(\dot {y}_n)_{j_{n,\omega }(G_n)}$
.
$j_{n,\omega }(\dot {y}_n)_{j_{n,\omega }(G_n)}$
.
This is done using Merimovich’s genericity criteria [Reference Merimovich17]. Indeed, for
![]() $a \subseteq j_{\omega }(\kappa ^{++})$
set of ordinals of cardinality
$a \subseteq j_{\omega }(\kappa ^{++})$
set of ordinals of cardinality
![]() $j_{\omega }(\kappa )$
, which is the set of ordinals of an elementary substructure of a sufficiently large initial segment of
$j_{\omega }(\kappa )$
, which is the set of ordinals of an elementary substructure of a sufficiently large initial segment of
![]() $M_\omega $
, one can consider a tree Prikry type forcing using
$M_\omega $
, one can consider a tree Prikry type forcing using
![]() $j_\omega (E)(a)$
, and verify that there is a generic sequence
$j_\omega (E)(a)$
, and verify that there is a generic sequence
![]() $\langle t_n \mid n < \omega \rangle $
for it in
$\langle t_n \mid n < \omega \rangle $
for it in
![]() $M_\omega [G_\omega ]$
such that,
$M_\omega [G_\omega ]$
such that,
![]() $\exists q \in j_\omega (\mathbb {P}_E^*)$
such that for all n,
$\exists q \in j_\omega (\mathbb {P}_E^*)$
such that for all n,
![]() $q^\smallfrown \langle t_0,\dots , t_{n-1}\rangle \in G_\omega $
. Moreover, this sequence is unique up to shifts and finite modifications (see [Reference Merimovich17, Lemma 3.4])—which is the crux of this argument.
$q^\smallfrown \langle t_0,\dots , t_{n-1}\rangle \in G_\omega $
. Moreover, this sequence is unique up to shifts and finite modifications (see [Reference Merimovich17, Lemma 3.4])—which is the crux of this argument.
As
![]() $j_{\omega }(\kappa ) \in a$
and we may assume that the Prikry sequence at this coordinate is the standard one, one can fix the shift and identify the sequence
$j_{\omega }(\kappa ) \in a$
and we may assume that the Prikry sequence at this coordinate is the standard one, one can fix the shift and identify the sequence
![]() $\langle j_{\omega }(p)^\smallfrown \langle \nu _0, \dots , \nu _{n-1}\rangle \mid n < \omega \rangle $
up to a finite error.
$\langle j_{\omega }(p)^\smallfrown \langle \nu _0, \dots , \nu _{n-1}\rangle \mid n < \omega \rangle $
up to a finite error.
In particular, by taking a to be large enough, we conclude that there is
![]() $p \in G_0$
such that for all large n,
$p \in G_0$
such that for all large n,
if and only if
![]() $\gamma \in X$
.
$\gamma \in X$
.
Therefore,
![]() $\gamma \in X$
if and only if there is a condition
$\gamma \in X$
if and only if there is a condition
![]() $q\in G_\omega $
with large domain a and a Prikry generic
$q\in G_\omega $
with large domain a and a Prikry generic
![]() $\langle t_n \mid n < \omega \rangle $
such that the length of
$\langle t_n \mid n < \omega \rangle $
such that the length of
![]() $q(j_\omega (\kappa ))$
is zero and for all large n
$q(j_\omega (\kappa ))$
is zero and for all large n
We are now ready to describe the generic extension of
![]() $M_\omega $
. We recall some of the basic ideas from [Reference Hayut and Unger13]. Let
$M_\omega $
. We recall some of the basic ideas from [Reference Hayut and Unger13]. Let
![]() $\dot {\mathbb {Q}}$
be the canonical name in the Prikry forcing defined from
$\dot {\mathbb {Q}}$
be the canonical name in the Prikry forcing defined from
![]() $E_\kappa $
for the poset to shoot a club disjoint from the set of
$E_\kappa $
for the poset to shoot a club disjoint from the set of
![]() $\alpha < \kappa ^{+}$
such that
$\alpha < \kappa ^{+}$
such that
![]() $\operatorname {\mathrm {cf}}^V(\alpha ) = \kappa $
. Let
$\operatorname {\mathrm {cf}}^V(\alpha ) = \kappa $
. Let
![]() $\mathbb {Q}_\omega $
be the forcing
$\mathbb {Q}_\omega $
be the forcing
![]() $i_\omega (\dot {\mathbb {Q}})$
as interpreted by the critical sequence
$i_\omega (\dot {\mathbb {Q}})$
as interpreted by the critical sequence
![]() $\langle i_n(\kappa ) \mid n<\omega \rangle $
. By the argument following Claim 39 of [Reference Hayut and Unger13],
$\langle i_n(\kappa ) \mid n<\omega \rangle $
. By the argument following Claim 39 of [Reference Hayut and Unger13],
![]() $\mathbb {Q}_\omega $
is equivalent to the forcing
$\mathbb {Q}_\omega $
is equivalent to the forcing
![]() $\mathop {\mathrm {Add}}(\kappa ^{+},1)$
in V. In fact, for every
$\mathop {\mathrm {Add}}(\kappa ^{+},1)$
in V. In fact, for every
![]() $n<\omega $
, in
$n<\omega $
, in
![]() $N_n$
it is equivalent to
$N_n$
it is equivalent to
![]() $\mathop {\mathrm {Add}}(i_n(\kappa ^{+}),1)$
.
$\mathop {\mathrm {Add}}(i_n(\kappa ^{+}),1)$
.
Let
![]() $k_n\colon N_n \to M_n$
be the natural embedding given by
$k_n\colon N_n \to M_n$
be the natural embedding given by
We discussed the notion of a width of an elementary embedding in the previous section. We recall a fundamental result concerning lifting embeddings and their widths (see [Reference Cummings2]).
Lemma 6.6. Suppose that
![]() $k \colon N \to M$
has width
$k \colon N \to M$
has width
![]() $\mu $
,
$\mu $
,
![]() $\mathbb {Q} \in N$
is a
$\mathbb {Q} \in N$
is a
![]() $\mu ^{+}$
-distributive forcing, and
$\mu ^{+}$
-distributive forcing, and
![]() $H \subseteq \mathbb {Q}$
is generic over N, then
$H \subseteq \mathbb {Q}$
is generic over N, then
![]() $k"H \subset k(\mathbb {Q})$
generates a generic filter
$k"H \subset k(\mathbb {Q})$
generates a generic filter
![]() ${\langle } k"H {\rangle }$
for M.
${\langle } k"H {\rangle }$
for M.
Claim 6.7. For all
![]() $1\leq n<\omega $
,
$1\leq n<\omega $
,
![]() $k_n$
has width
$k_n$
has width
![]() $\leq (i_{n-1}(\kappa )^{++})^{N_n}$
.
$\leq (i_{n-1}(\kappa )^{++})^{N_n}$
.
Proof Let
![]() $x = j_n(g)(\alpha ,j(\alpha ), \dots j_{n-1}(\alpha ))$
be an element of
$x = j_n(g)(\alpha ,j(\alpha ), \dots j_{n-1}(\alpha ))$
be an element of
![]() $M_n$
,
$M_n$
,
![]() $g\colon [\kappa ]^n \to V$
and
$g\colon [\kappa ]^n \to V$
and
![]() $\alpha < \kappa ^{++}$
. Consider
$\alpha < \kappa ^{++}$
. Consider
![]() $h = i_n(g) \restriction (i_{n-1}(\kappa )^{++})^{N_n}$
. Then
$h = i_n(g) \restriction (i_{n-1}(\kappa )^{++})^{N_n}$
. Then
Indeed, the domain of
![]() $k(h)$
is large enough for this evaluation to make sense.
$k(h)$
is large enough for this evaluation to make sense.
We are now ready to define the analogs of
![]() $\mathcal {H}$
and
$\mathcal {H}$
and
![]() $\mathcal {H}_n$
for our situation. Recall that for subset X of some poset, we write
$\mathcal {H}_n$
for our situation. Recall that for subset X of some poset, we write
![]() $< X>$
for the upwards closure in that poset. It will be clear from the context which poset we are working with, when taking this upwards closure.
$< X>$
for the upwards closure in that poset. It will be clear from the context which poset we are working with, when taking this upwards closure.
Let H be generic for
![]() $\mathbb {Q}_\omega $
over
$\mathbb {Q}_\omega $
over
![]() $V[G_0]$
and recall that
$V[G_0]$
and recall that
![]() $\mathbb {Q}_\omega = i_n(\mathbb {Q}_\omega )$
is also a member of
$\mathbb {Q}_\omega = i_n(\mathbb {Q}_\omega )$
is also a member of
![]() $N_n$
for every n, and is
$N_n$
for every n, and is
![]() $i_n(\kappa ^{+})$
-closed. We note that clearly,
$i_n(\kappa ^{+})$
-closed. We note that clearly,
![]() $i_n(\kappa^+) \geq (i_{n-1}(\kappa)^{++})^{N_n} \geq \text{width}(k_n)$
.
$i_n(\kappa^+) \geq (i_{n-1}(\kappa)^{++})^{N_n} \geq \text{width}(k_n)$
.
Let
and
Note that
![]() $\mathcal {H}_n$
is a subset of
$\mathcal {H}_n$
is a subset of
![]() $\prod _{m \leq n} j_{m,n}(k_m(\mathbb {Q}_\omega ))$
. We do not yet know that it is generic.
$\prod _{m \leq n} j_{m,n}(k_m(\mathbb {Q}_\omega ))$
. We do not yet know that it is generic.
We prove a sequence of claims about
![]() $\mathcal {H}_n$
and
$\mathcal {H}_n$
and
![]() $\mathcal {H}$
. The first is straightforward.
$\mathcal {H}$
. The first is straightforward.
Claim 6.8. For all
![]() $n<\omega $
,
$n<\omega $
,
Let
![]() $\bar {\mathcal {H}}_n = \langle {<} i_{m,n}"H{>} \mid m \leq n \rangle $
.
$\bar {\mathcal {H}}_n = \langle {<} i_{m,n}"H{>} \mid m \leq n \rangle $
.
Claim 6.9.
![]() $\mathcal {H}_n = {<} k_n " \bar {\mathcal {H}}_n{>}$
.
$\mathcal {H}_n = {<} k_n " \bar {\mathcal {H}}_n{>}$
.
This is immediate from the following. For
![]() $m \leq n$
, we have
$m \leq n$
, we have
since
![]() $k_n \circ i_{m,n} = j_{m,n} \circ k_m$
. In particular, since
$k_n \circ i_{m,n} = j_{m,n} \circ k_m$
. In particular, since
![]() $\bar {\mathcal {H}}_n$
is generic for
$\bar {\mathcal {H}}_n$
is generic for
![]() $i_n(\kappa ^{+})$
-closed forcing over
$i_n(\kappa ^{+})$
-closed forcing over
![]() $N_n$
and
$N_n$
and
![]() $k_n$
has width less than
$k_n$
has width less than
![]() $i_n(\kappa )$
,
$i_n(\kappa )$
,
![]() $\mathcal {H}_n$
is generic over
$\mathcal {H}_n$
is generic over
![]() $M_n$
.
$M_n$
.
Claim 6.10.
![]() $\mathcal {H}_n$
is mutually generic with
$\mathcal {H}_n$
is mutually generic with
![]() $G_n$
over
$G_n$
over
![]() $M_n$
.
$M_n$
.
Proof Since
![]() $G_0$
and H are mutually generic over V, we can repeat the argument from Claim 18 of [Reference Hayut and Unger13] to see that
$G_0$
and H are mutually generic over V, we can repeat the argument from Claim 18 of [Reference Hayut and Unger13] to see that
![]() $\bar {\mathcal {H}}_n$
is generic over the model
$\bar {\mathcal {H}}_n$
is generic over the model
![]() $N_n[{<}i_n"G_0{>}]$
. By the previous claim,
$N_n[{<}i_n"G_0{>}]$
. By the previous claim,
![]() ${<}j_n"G_0{>}$
and
${<}j_n"G_0{>}$
and
![]() $\mathcal {H}_n$
are mutually generic over
$\mathcal {H}_n$
are mutually generic over
![]() $M_n$
. By Remark 6.3,
$M_n$
. By Remark 6.3,
![]() $\mathcal {H}_n$
is mutually generic with
$\mathcal {H}_n$
is mutually generic with
![]() $G_n$
.
$G_n$
.
Lemma 6.11.
![]() $M_\omega [G_\omega ][\mathcal {H}]$
is closed under
$M_\omega [G_\omega ][\mathcal {H}]$
is closed under
![]() $\kappa $
-sequences.
$\kappa $
-sequences.
Proof It is enough to show that every
![]() $\kappa $
-sequence of ordinals from the larger model
$\kappa $
-sequence of ordinals from the larger model
![]() $M_\omega [G_\omega ][\mathcal {H}]$
is in
$M_\omega [G_\omega ][\mathcal {H}]$
is in
![]() $M_\omega [G_\omega ]$
. Let
$M_\omega [G_\omega ]$
. Let
![]() $\vec {\alpha }$
be such a sequence. By construction,
$\vec {\alpha }$
be such a sequence. By construction,
![]() $\vec {\alpha } \in V[G_0][H]$
and hence in
$\vec {\alpha } \in V[G_0][H]$
and hence in
![]() $V[G_0]$
. However,
$V[G_0]$
. However,
![]() $M_\omega [G_\omega ]$
is closed under
$M_\omega [G_\omega ]$
is closed under
![]() $\kappa $
-sequences in
$\kappa $
-sequences in
![]() $V[G_0]$
, so
$V[G_0]$
, so
![]() $\vec {\alpha } \in M_\omega [G_\omega ]$
, as required.
$\vec {\alpha } \in M_\omega [G_\omega ]$
, as required.
Lemma 6.12.
![]() $\bigcap _{n<\omega }M_n[G_n][\mathcal {H}_n] = M_\omega [G_\omega ][\mathcal {H}]$
.
$\bigcap _{n<\omega }M_n[G_n][\mathcal {H}_n] = M_\omega [G_\omega ][\mathcal {H}]$
.
Proof The proof is similar to the proof of Lemma 6.5. First, note that the embedding
![]() $j_{n,\omega }\colon M_n \to M_\omega $
lifts to an elementary embedding
$j_{n,\omega }\colon M_n \to M_\omega $
lifts to an elementary embedding
and
![]() $M_\omega [{<}j_{n,\omega }"\mathcal {H}_n{>}] \subseteq M_{\omega }[\mathcal {H}]$
. Further, the construction of
$M_\omega [{<}j_{n,\omega }"\mathcal {H}_n{>}] \subseteq M_{\omega }[\mathcal {H}]$
. Further, the construction of
![]() $G_\omega $
is the same whether we start in
$G_\omega $
is the same whether we start in
![]() $M_n$
or
$M_n$
or
![]() $M_n[\mathcal {H}_n]$
.
$M_n[\mathcal {H}_n]$
.
It is immediate that
![]() $\bigcap _{n<\omega }M_n[G_n][\mathcal {H}_n] \supseteq M_\omega [G_\omega ][\mathcal {H}]$
. For the other inclusion, we work as before and suppose that
$\bigcap _{n<\omega }M_n[G_n][\mathcal {H}_n] \supseteq M_\omega [G_\omega ][\mathcal {H}]$
. For the other inclusion, we work as before and suppose that
![]() $x \in \bigcap _{n<\omega }M_n[G_n][\mathcal {H}_n]$
is a set of ordinals. For each n, we can define
$x \in \bigcap _{n<\omega }M_n[G_n][\mathcal {H}_n]$
is a set of ordinals. For each n, we can define
![]() $y_n = \{ \gamma \mid j_{n,\omega }(\gamma ) \in x \}$
. Continuing as before, but working in
$y_n = \{ \gamma \mid j_{n,\omega }(\gamma ) \in x \}$
. Continuing as before, but working in
![]() $M_n[\mathcal {H}_n]$
, we have that
$M_n[\mathcal {H}_n]$
, we have that
![]() $y_n = \dot {y}_n^{G_n}$
for some name
$y_n = \dot {y}_n^{G_n}$
for some name
![]() $\dot {y}_n$
.
$\dot {y}_n$
.
By the previous lemma,
![]() $M_\omega [G_\omega ][\mathcal {H}]$
has the sequence
$M_\omega [G_\omega ][\mathcal {H}]$
has the sequence
![]() ${\langle } j^*_{n,\omega }(\dot {x}_n^*) \mid n<\omega {\rangle }$
. As in the proof of Lemma 6.5, we will now argue that for every suitable set of ordinals
${\langle } j^*_{n,\omega }(\dot {x}_n^*) \mid n<\omega {\rangle }$
. As in the proof of Lemma 6.5, we will now argue that for every suitable set of ordinals
![]() $a \subseteq j_\omega (\kappa ^{++})$
of cardinality
$a \subseteq j_\omega (\kappa ^{++})$
of cardinality
![]() $j_\omega (\kappa )$
, there is a unique (up to finite shift and finite modification) sequence
$j_\omega (\kappa )$
, there is a unique (up to finite shift and finite modification) sequence
![]() $\langle t_n \mid n < \omega \rangle $
which is generic for the Prikry forcing for the measure
$\langle t_n \mid n < \omega \rangle $
which is generic for the Prikry forcing for the measure
![]() $j_\omega (E)(a)$
and satisfies that
$j_\omega (E)(a)$
and satisfies that
![]() $q ^\smallfrown \langle t_n \mid n < \omega \rangle \in G_\omega $
for all n.
$q ^\smallfrown \langle t_n \mid n < \omega \rangle \in G_\omega $
for all n.
Since there is
![]() $p\in G$
such that for
$p\in G$
such that for
![]() $j_{\omega }(p)$
the sequence
$j_{\omega }(p)$
the sequence
![]() $\langle \nu _n \restriction a \mid n < \omega \rangle $
will be generic for the corresponding forcing, we conclude (by uniqueness) that for every such sequence, for all large n,
$\langle \nu _n \restriction a \mid n < \omega \rangle $
will be generic for the corresponding forcing, we conclude (by uniqueness) that for every such sequence, for all large n,
assume that the length of q at
![]() $j_{\omega }(\kappa )$
is zero, so there is no shift relative to the indexing of the
$j_{\omega }(\kappa )$
is zero, so there is no shift relative to the indexing of the
![]() $G_n$
-s.
$G_n$
-s.
For each ordinal
![]() $\gamma $
one can take a large enough so that for all n, the truth value of
$\gamma $
one can take a large enough so that for all n, the truth value of
![]() $\gamma \in j_{n,\omega }(\dot {y}_n)$
is decided by
$\gamma \in j_{n,\omega }(\dot {y}_n)$
is decided by
![]() $q ^\smallfrown \langle t_i \mid i < n\rangle $
. Therefore,
$q ^\smallfrown \langle t_i \mid i < n\rangle $
. Therefore,
![]() $\gamma \in x$
if and only if there is
$\gamma \in x$
if and only if there is
![]() $q \in G_\omega $
and
$q \in G_\omega $
and
![]() $\langle t_n \mid n < \omega \rangle $
Prikry generic for
$\langle t_n \mid n < \omega \rangle $
Prikry generic for
![]() $\operatorname {\mathrm {dom}} q$
as above such that for all large n,
$\operatorname {\mathrm {dom}} q$
as above such that for all large n,
Let
![]() $k_\omega \colon N_\omega \to M_\omega $
be the natural elementary embedding. Note that
$k_\omega \colon N_\omega \to M_\omega $
be the natural elementary embedding. Note that
![]() $k_\omega $
naturally extends to an embedding between the two Prikry generic extensions,
$k_\omega $
naturally extends to an embedding between the two Prikry generic extensions,
Similarly, for each
![]() $n<\omega $
we define
$n<\omega $
we define
![]() $W_{n,\omega }$
to be the limit ultrapower obtained by starting in
$W_{n,\omega }$
to be the limit ultrapower obtained by starting in
![]() $M_n$
and iterating the measure
$M_n$
and iterating the measure
![]() $j_n(E_\kappa )$
, the normal measure of
$j_n(E_\kappa )$
, the normal measure of
![]() $j_n(E)$
. As with
$j_n(E)$
. As with
![]() $N_\omega $
, denote the critical points of the iteration by
$N_\omega $
, denote the critical points of the iteration by
![]() $j_n(E_\kappa )$
and its images by
$j_n(E_\kappa )$
and its images by
![]() ${\langle } \kappa ^n_m {\rangle }_{m<\omega }$
, and let
${\langle } \kappa ^n_m {\rangle }_{m<\omega }$
, and let
![]() $i^n_\omega \colon V \to W_{n,\omega }$
denote the composition of the finite ultrapower map
$i^n_\omega \colon V \to W_{n,\omega }$
denote the composition of the finite ultrapower map
![]() $j \colon V \to M_n$
with the latter infinite iteration map by the normal measures. Therefore elements
$j \colon V \to M_n$
with the latter infinite iteration map by the normal measures. Therefore elements
![]() $y_n \in W_{n,\omega }$
are of the form
$y_n \in W_{n,\omega }$
are of the form
![]() $i^n_\omega (f)(\alpha _0,\dots ,\alpha _{n-1},\kappa ^n_0,\dots ,\kappa ^n_{m-1})$
for some
$i^n_\omega (f)(\alpha _0,\dots ,\alpha _{n-1},\kappa ^n_0,\dots ,\kappa ^n_{m-1})$
for some
![]() $n,m < \omega $
,
$n,m < \omega $
,
![]() $f \colon \kappa ^{n+m} \to V$
in V, and
$f \colon \kappa ^{n+m} \to V$
in V, and
![]() $\alpha _{\ell } \in j_{\ell }(\kappa ^{++})$
for each
$\alpha _{\ell } \in j_{\ell }(\kappa ^{++})$
for each
![]() $\ell < n$
.
$\ell < n$
.
The structures
![]() $W_{n,\omega }$
are naturally connected via maps
$W_{n,\omega }$
are naturally connected via maps
![]() $k_{n,r} \colon W_{n,\omega } \to W_{r,\omega }$
for
$k_{n,r} \colon W_{n,\omega } \to W_{r,\omega }$
for
![]() $n \leq r < \omega $
, given by
$n \leq r < \omega $
, given by
It is straightforward to verify that the limit of the directed system
is
![]() $M_\omega $
, and the direct limit maps
$M_\omega $
, and the direct limit maps
![]() $k_{n,\omega } \colon W_{n,\omega } \to M_\omega $
, which are defined by
$k_{n,\omega } \colon W_{n,\omega } \to M_\omega $
, which are defined by
naturally extend to the generic extensions by the suitable Prikry sequences. Indeed, denote
![]() $W_{n,\omega }[{\langle } j_m(\kappa ) \mid m<n {\rangle } {}^\frown {\langle } i_m(j_n(\kappa )) \mid m < \omega {\rangle }]$
by
$W_{n,\omega }[{\langle } j_m(\kappa ) \mid m<n {\rangle } {}^\frown {\langle } i_m(j_n(\kappa )) \mid m < \omega {\rangle }]$
by
![]() $W^*_{n,\omega }$
, for each
$W^*_{n,\omega }$
, for each
![]() $n <\omega $
. Then
$n <\omega $
. Then
![]() $k_{n,\omega }$
lifts to
$k_{n,\omega }$
lifts to
Finally, we note that the following implies that
![]() $M_\omega [{\langle } j_m(\kappa ) \mid m < \omega {\rangle }]$
is the direct limit of the system of Prikry generic extensions
$M_\omega [{\langle } j_m(\kappa ) \mid m < \omega {\rangle }]$
is the direct limit of the system of Prikry generic extensions
Claim 6.13.
![]() ${<}k^*_\omega "H{>} \in M_\omega [G_\omega ][\mathcal {H}]$
is generic for
${<}k^*_\omega "H{>} \in M_\omega [G_\omega ][\mathcal {H}]$
is generic for
![]() $j_\omega (\dot {\mathbb {Q}})^{{\langle } j_n(\kappa ) \mid n<\omega {\rangle }}$
over
$j_\omega (\dot {\mathbb {Q}})^{{\langle } j_n(\kappa ) \mid n<\omega {\rangle }}$
over
![]() $M_\omega [{\langle } j_n(\kappa )\mid n<\omega {\rangle }]$
.
$M_\omega [{\langle } j_n(\kappa )\mid n<\omega {\rangle }]$
.
Proof Let
![]() $D \in M_\omega [{\langle } j_n(\kappa ) \mid n < \omega {\rangle }]$
be a dense open subset of the forcing
$D \in M_\omega [{\langle } j_n(\kappa ) \mid n < \omega {\rangle }]$
be a dense open subset of the forcing
![]() $j_\omega (\dot {\mathbb {Q}})^{{\langle } j_n(\kappa ) \mid n <\omega {\rangle }}$
. Then there are
$j_\omega (\dot {\mathbb {Q}})^{{\langle } j_n(\kappa ) \mid n <\omega {\rangle }}$
. Then there are
![]() $n<\omega $
and
$n<\omega $
and
![]() $\bar {D} \in W_{n,\omega }^*$
such that
$\bar {D} \in W_{n,\omega }^*$
such that
![]() $k^*_{n,\omega }(\bar {D}) = D$
. It follows from our arguments above that
$k^*_{n,\omega }(\bar {D}) = D$
. It follows from our arguments above that
![]() $<k_n"H>$
is generic for
$<k_n"H>$
is generic for
![]() $k_n(\mathbb {Q}_\omega )$
over
$k_n(\mathbb {Q}_\omega )$
over
![]() $M_n$
. Now
$M_n$
. Now
![]() $k_{n}(\mathbb {Q}_\omega ) \in W_{n,\omega }^*$
and
$k_{n}(\mathbb {Q}_\omega ) \in W_{n,\omega }^*$
and
![]() $\bar {D}$
is a dense subset of it. So
$\bar {D}$
is a dense subset of it. So
![]() $<k_{n}"H>\cap \bar {D}$
is nonempty. Let
$<k_{n}"H>\cap \bar {D}$
is nonempty. Let
![]() $q \in H$
be such that
$q \in H$
be such that
![]() $k_{n}(q) \in \bar {D}$
. It follows that
$k_{n}(q) \in \bar {D}$
. It follows that
![]() $k^*_\omega (q) = k^*_{n,\omega }(k^*_n(q)) \in D$
. So we have shown that
$k^*_\omega (q) = k^*_{n,\omega }(k^*_n(q)) \in D$
. So we have shown that
![]() $<k^*_\omega "H>$
is generic over
$<k^*_\omega "H>$
is generic over
![]() $M_\omega [{\langle } j_n(\kappa ) \mid n <\omega {\rangle }]$
. It remains to show that it is a member of
$M_\omega [{\langle } j_n(\kappa ) \mid n <\omega {\rangle }]$
. It remains to show that it is a member of
![]() $M_\omega [G_\omega ][\mathcal {H}]$
. Since
$M_\omega [G_\omega ][\mathcal {H}]$
. Since
![]() $<k^*_\omega "H>= <k^*_{n,\omega }"<k^*_n"H>>$
, we have that
$<k^*_\omega "H>= <k^*_{n,\omega }"<k^*_n"H>>$
, we have that
![]() $<k^*_\omega "H>\in M_n[\mathcal {H}_n]$
for all
$<k^*_\omega "H>\in M_n[\mathcal {H}_n]$
for all
![]() $n<\omega $
. By Claim 6.12, it follows that
$n<\omega $
. By Claim 6.12, it follows that
![]() $<k^*_\omega "H>\in M_\omega [G_\omega ][\mathcal {H}]$
.
$<k^*_\omega "H>\in M_\omega [G_\omega ][\mathcal {H}]$
.
To complete the proof of Theorem 1.4 we need a finer control of the relationship between
![]() $\mathbb {P}$
and
$\mathbb {P}$
and
![]() $\mathbb {P}^*$
names. To this end we make some definitions.
$\mathbb {P}^*$
names. To this end we make some definitions.
Definition 6.14. Let
![]() $f \in \mathbb {P}^*$
,
$f \in \mathbb {P}^*$
,
![]() $\alpha $
be an ordinal and let
$\alpha $
be an ordinal and let
![]() $\dot {C}$
be a
$\dot {C}$
be a
![]() $\mathbb {P}^*$
-name for a club subset of
$\mathbb {P}^*$
-name for a club subset of
![]() $\kappa ^{+}$
. We say that f stably forces
$\kappa ^{+}$
. We say that f stably forces
![]() $\check {\alpha } \in \dot {C}$
(
$\check {\alpha } \in \dot {C}$
(
![]() $f \Vdash ^s_{\mathbb {P}^*} \check {\alpha } \in \dot {C}$
) if every alteration of f on fewer than
$f \Vdash ^s_{\mathbb {P}^*} \check {\alpha } \in \dot {C}$
) if every alteration of f on fewer than
![]() $\kappa $
many coordinates forces
$\kappa $
many coordinates forces
![]() $\check {\alpha } \in \dot {C}$
.
$\check {\alpha } \in \dot {C}$
.
We have the following straightforward claims.
Claim 6.15. If g extends f in
![]() $\mathbb {P}^*$
and
$\mathbb {P}^*$
and
![]() $f \Vdash ^s \check {\alpha } \in \dot {C}$
, then
$f \Vdash ^s \check {\alpha } \in \dot {C}$
, then
![]() $g \Vdash ^s \check {\alpha } \in \dot {C}$
.
$g \Vdash ^s \check {\alpha } \in \dot {C}$
.
Claim 6.16. If
![]() $f \Vdash ^s \check {\alpha } \in \dot {C}$
, then for every finite sequence
$f \Vdash ^s \check {\alpha } \in \dot {C}$
, then for every finite sequence
![]() $\vec {\nu }$
from some tree associated with f,
$\vec {\nu }$
from some tree associated with f,
![]() $f \frown \vec {\nu } \Vdash ^s \check {\alpha } \in \dot {C}$
. If in addition
$f \frown \vec {\nu } \Vdash ^s \check {\alpha } \in \dot {C}$
. If in addition
![]() $f = f' \frown \vec {\nu }$
for some finite sequence
$f = f' \frown \vec {\nu }$
for some finite sequence
![]() $\vec {\nu }$
, then
$\vec {\nu }$
, then
![]() $f' \Vdash ^s \check {\alpha } \in \dot {C}$
.
$f' \Vdash ^s \check {\alpha } \in \dot {C}$
.
We define
![]() $\dot {C}^s = \{ (\check {\alpha },f) \mid f \Vdash ^s \check {\alpha } \in \dot {C} \}$
. Clearly it is forced that
$\dot {C}^s = \{ (\check {\alpha },f) \mid f \Vdash ^s \check {\alpha } \in \dot {C} \}$
. Clearly it is forced that
![]() $\dot {C}^s \subseteq \dot {C}$
. It is also straightforward to see that
$\dot {C}^s \subseteq \dot {C}$
. It is also straightforward to see that
![]() $\dot {C}^s$
is forced to be closed.
$\dot {C}^s$
is forced to be closed.
Claim 6.17.
![]() $\dot {C}^s$
is forced to be unbounded in
$\dot {C}^s$
is forced to be unbounded in
![]() $\kappa ^{+}$
.
$\kappa ^{+}$
.
Proof Fix some
![]() $f \in \mathbb {P}^*$
and
$f \in \mathbb {P}^*$
and
![]() $\alpha _0< \kappa ^{+}$
. Take some sufficiently large
$\alpha _0< \kappa ^{+}$
. Take some sufficiently large
![]() $\theta $
and some
$\theta $
and some
![]() $N \prec H_\theta $
of size
$N \prec H_\theta $
of size
![]() $\kappa $
such that
$\kappa $
such that
![]() $\mathbb {P}^*,f,\dot {C},\alpha _0 \in N$
and
$\mathbb {P}^*,f,\dot {C},\alpha _0 \in N$
and
![]() ${}^{<\kappa }N \subseteq N$
. Since
${}^{<\kappa }N \subseteq N$
. Since
![]() $\mathbb {P}^*$
is
$\mathbb {P}^*$
is
![]() $\kappa ^{+}$
-closed we can find a
$\kappa ^{+}$
-closed we can find a
![]() $(\mathbb {P}^*,N)$
-generic condition
$(\mathbb {P}^*,N)$
-generic condition
![]() $f^* \geq f$
with
$f^* \geq f$
with
![]() $\operatorname {\mathrm {dom}}(f^*) = N \cap \kappa ^{++}$
. Let
$\operatorname {\mathrm {dom}}(f^*) = N \cap \kappa ^{++}$
. Let
![]() $\alpha = \sup (N \cap \kappa ^{++})$
.
$\alpha = \sup (N \cap \kappa ^{++})$
.
Let
![]() $f'$
be any condition obtained by altering
$f'$
be any condition obtained by altering
![]() $f^*$
on a set of size less than
$f^*$
on a set of size less than
![]() $\kappa $
. Since
$\kappa $
. Since
![]() ${}^{<\kappa }N \subseteq N$
, the alteration is a member of N. Hence a standard argument shows that
${}^{<\kappa }N \subseteq N$
, the alteration is a member of N. Hence a standard argument shows that
![]() $f'$
is also
$f'$
is also
![]() $(\mathbb {P}^*,N)$
-generic and so
$(\mathbb {P}^*,N)$
-generic and so
![]() $f' \Vdash \check {\alpha } \in \dot {C}$
.
$f' \Vdash \check {\alpha } \in \dot {C}$
.
The name
![]() $\dot {C}^s$
behaves well when translated to a
$\dot {C}^s$
behaves well when translated to a
![]() $\mathbb {P}$
-name. Let
$\mathbb {P}$
-name. Let
Claim 6.18.
![]() $\dot {E}$
is forced by
$\dot {E}$
is forced by
![]() $\mathbb {P}$
to be a club subset of
$\mathbb {P}$
to be a club subset of
![]() $\kappa ^{+}$
.
$\kappa ^{+}$
.
Proof By the arguments of Claim 6.17,
![]() $\dot {E}$
is unbounded. Let us show first that
$\dot {E}$
is unbounded. Let us show first that
![]() $\dot {E}$
is forces to be closed.
$\dot {E}$
is forces to be closed.
Let
![]() $p = {\langle } f, T{\rangle }$
be a condition that forces that
$p = {\langle } f, T{\rangle }$
be a condition that forces that
![]() $\delta $
is an accumulation point of
$\delta $
is an accumulation point of
![]() $\dot {E}$
. Therefore, for every
$\dot {E}$
. Therefore, for every
![]() $\alpha < \delta $
there are
$\alpha < \delta $
there are
![]() $\vec {\nu } = {\langle } \nu _0,\dots ,\nu _{n-1}{\rangle } \in T$
,
$\vec {\nu } = {\langle } \nu _0,\dots ,\nu _{n-1}{\rangle } \in T$
,
![]() $p' = {\langle } f' , T'{\rangle } \leq ^* p {}^\frown \vec {\nu }$
, and
$p' = {\langle } f' , T'{\rangle } \leq ^* p {}^\frown \vec {\nu }$
, and
![]() $\gamma < \delta $
such that
$\gamma < \delta $
such that
![]() $f' \Vdash ^s \gamma \in \dot {C}$
. Clearly,
$f' \Vdash ^s \gamma \in \dot {C}$
. Clearly,
![]() $f'$
is a Cohen extension of
$f'$
is a Cohen extension of
![]() $f {}^\frown \vec {\nu }$
. Denote by
$f {}^\frown \vec {\nu }$
. Denote by
![]() $f^*$
the Cohen extension of f for which
$f^*$
the Cohen extension of f for which
![]() $f' = f^* {}^\frown \vec {\nu }$
. Since
$f' = f^* {}^\frown \vec {\nu }$
. Since
![]() $f' \Vdash ^s \gamma \in \dot {C}$
,
$f' \Vdash ^s \gamma \in \dot {C}$
,
![]() $f^* \Vdash ^s \gamma \in \dot {C}$
as well. It follows that the condition
$f^* \Vdash ^s \gamma \in \dot {C}$
as well. It follows that the condition
![]() $p^* = {\langle } f^*,T^*{\rangle }$
,
$p^* = {\langle } f^*,T^*{\rangle }$
,
![]() $T^* = \pi _{\operatorname {\mathrm {dom}}(f^*),\operatorname {\mathrm {dom}}(f)}^{-1}(T)$
is a direct extension of p and forces “
$T^* = \pi _{\operatorname {\mathrm {dom}}(f^*),\operatorname {\mathrm {dom}}(f)}^{-1}(T)$
is a direct extension of p and forces “
![]() $\check {\gamma } \in \dot {E}$
”.
$\check {\gamma } \in \dot {E}$
”.
Using the fact that the Cohen extension order on the function f is
![]() $\kappa ^{+}$
-closed and
$\kappa ^{+}$
-closed and
![]() $\operatorname {\mathrm {cf}}(\delta ) \leq \kappa $
, we can repeat this process and construct a sequence of Cohen extensions
$\operatorname {\mathrm {cf}}(\delta ) \leq \kappa $
, we can repeat this process and construct a sequence of Cohen extensions
![]() ${\langle } f_i \mid i \leq \operatorname {\mathrm {cf}}(\delta ){\rangle }$
of f, and an increasing sequence
${\langle } f_i \mid i \leq \operatorname {\mathrm {cf}}(\delta ){\rangle }$
of f, and an increasing sequence
![]() ${\langle } \gamma _i \mid i < \operatorname {\mathrm {cf}}(\delta ){\rangle }$
cofinal in
${\langle } \gamma _i \mid i < \operatorname {\mathrm {cf}}(\delta ){\rangle }$
cofinal in
![]() $\delta $
, such that
$\delta $
, such that
![]() $f_i \Vdash ^s \check {\gamma _i} \in \dot {C}$
. Let
$f_i \Vdash ^s \check {\gamma _i} \in \dot {C}$
. Let
![]() $\bar {f} = f_{\operatorname {\mathrm {cf}}(\delta )}$
. Since
$\bar {f} = f_{\operatorname {\mathrm {cf}}(\delta )}$
. Since
![]() $\dot {C}$
is a Cohen name of a club,
$\dot {C}$
is a Cohen name of a club,
![]() $\bar {f} \Vdash ^s \check {\delta } \in \dot {C}$
. Setting
$\bar {f} \Vdash ^s \check {\delta } \in \dot {C}$
. Setting
![]() $\bar {T} = \pi _{\operatorname {\mathrm {dom}}(\bar {f}),\operatorname {\mathrm {dom}}(f)}^{-1}(T)$
and
$\bar {T} = \pi _{\operatorname {\mathrm {dom}}(\bar {f}),\operatorname {\mathrm {dom}}(f)}^{-1}(T)$
and
![]() $\bar {p} = {\langle } \bar {f},\bar {T}{\rangle }$
, we have that
$\bar {p} = {\langle } \bar {f},\bar {T}{\rangle }$
, we have that
![]() $\bar {p}$
is a direct extension of p, and forces
$\bar {p}$
is a direct extension of p, and forces
![]() $\check {\delta } \in \dot {E}$
.
$\check {\delta } \in \dot {E}$
.
Remark 6.19. The proofs of the previous two claims work for any
![]() $\mathbb {P}^*$
-name for a club
$\mathbb {P}^*$
-name for a club
![]() $\dot {C}$
in any
$\dot {C}$
in any
![]() $\kappa ^{+}$
-closed generic extension.
$\kappa ^{+}$
-closed generic extension.
We are now ready to finish the proof of Theorem 1.4.
Claim 6.20. In
![]() $M_\omega [G_\omega ][\mathcal {H}]$
, every finite collection of stationary subsets of
$M_\omega [G_\omega ][\mathcal {H}]$
, every finite collection of stationary subsets of
![]() $j_\omega (\kappa ^{+})$
reflects at a common point.
$j_\omega (\kappa ^{+})$
reflects at a common point.
Proof Let
![]() $S_i$
for
$S_i$
for
![]() $i < m$
be a sequence of stationary sets in
$i < m$
be a sequence of stationary sets in
![]() $M_\omega [G_\omega ][\mathcal {H}]$
. By Claim 6.13,
$M_\omega [G_\omega ][\mathcal {H}]$
. By Claim 6.13,
![]() ${<}k_\omega "H{>}$
is a club in
${<}k_\omega "H{>}$
is a club in
![]() $j_\omega (\kappa ^{+})$
disjoint from
$j_\omega (\kappa ^{+})$
disjoint from
![]() $S_{j_\omega (\kappa )}^{j_\omega (\kappa ^{+})}$
as computed in
$S_{j_\omega (\kappa )}^{j_\omega (\kappa ^{+})}$
as computed in
![]() $M_\omega $
and
$M_\omega $
and
![]() ${<}k_\omega "H{>} \in M_\omega [G_\omega ][\mathcal {H}]$
. So we can assume that each
${<}k_\omega "H{>} \in M_\omega [G_\omega ][\mathcal {H}]$
. So we can assume that each
![]() $S_i$
concentrates on a fixed cofinality below
$S_i$
concentrates on a fixed cofinality below
![]() $j_\omega (\kappa )$
. For simplicity we assume that the cofinalities of the
$j_\omega (\kappa )$
. For simplicity we assume that the cofinalities of the
![]() $S_i$
are bounded below
$S_i$
are bounded below
![]() $\kappa $
.
$\kappa $
.
Let
![]() $T_n^i$
be the set of
$T_n^i$
be the set of
![]() $\alpha $
such that
$\alpha $
such that
![]() $j_{n,\omega }(\alpha ) \in S_i$
. For a fixed
$j_{n,\omega }(\alpha ) \in S_i$
. For a fixed
![]() $n<\omega $
,
$n<\omega $
,
![]() $T_n^i$
for
$T_n^i$
for
![]() $i < m$
is definable in
$i < m$
is definable in
![]() $M_n[G_n][\mathcal {H}_n]$
. By the indestructibility of stationary reflection at
$M_n[G_n][\mathcal {H}_n]$
. By the indestructibility of stationary reflection at
![]() $j_n(\kappa ^{+})$
in
$j_n(\kappa ^{+})$
in
![]() $M_n$
, if each
$M_n$
, if each
![]() $T_n^i$
for
$T_n^i$
for
![]() $i < m$
is stationary, then they reflect at a common point. Suppose that
$i < m$
is stationary, then they reflect at a common point. Suppose that
![]() $\delta $
is this common reflection point. Then there are sets
$\delta $
is this common reflection point. Then there are sets
![]() $A_i\in M_n$
for
$A_i\in M_n$
for
![]() $i <k$
with
$i <k$
with
![]() $\mathop {\mathrm {ot}}(A)=\operatorname {\mathrm {cf}}(\delta )$
such that
$\mathop {\mathrm {ot}}(A)=\operatorname {\mathrm {cf}}(\delta )$
such that
![]() $A_i$
is stationary in
$A_i$
is stationary in
![]() $\delta $
and
$\delta $
and
![]() $A_i \subseteq T_n^i$
. It follows that for each
$A_i \subseteq T_n^i$
. It follows that for each
![]() $i<m$
,
$i<m$
,
![]() $j_{n,\omega }(A_i) = j_{n,\omega }"A_i \subseteq S_i$
and hence the collection of
$j_{n,\omega }(A_i) = j_{n,\omega }"A_i \subseteq S_i$
and hence the collection of
![]() $S_i$
reflect at
$S_i$
reflect at
![]() $j(\delta )$
.
$j(\delta )$
.
We assume for the sake of a contradiction that for each
![]() $n<\omega $
at least one of the
$n<\omega $
at least one of the
![]() $T_n^i$
is nonstationary. Let
$T_n^i$
is nonstationary. Let
![]() $\dot {C}_n$
be a name whose interpretation by
$\dot {C}_n$
be a name whose interpretation by
![]() $G_n$
and
$G_n$
and
![]() $\mathcal {H}_n$
,
$\mathcal {H}_n$
,
![]() $C_n$
, is a club disjoint from some
$C_n$
, is a club disjoint from some
![]() $T_n^{i_n}$
. By the arguments above and Remark 6.19, we can work in
$T_n^{i_n}$
. By the arguments above and Remark 6.19, we can work in
![]() $M_n[\mathcal {H}_n]$
and translate
$M_n[\mathcal {H}_n]$
and translate
![]() $\dot {C}_n$
to a
$\dot {C}_n$
to a
![]() $j_n(\mathbb {P})$
-name
$j_n(\mathbb {P})$
-name
![]() $\dot {E}_n$
for a club subset of
$\dot {E}_n$
for a club subset of
![]() $j_n(\kappa ^{+})$
. By the construction of
$j_n(\kappa ^{+})$
. By the construction of
![]() $\dot {E}_n$
, we have that for
$\dot {E}_n$
, we have that for
![]() $\alpha < j_n(\kappa ^{+})$
,
$\alpha < j_n(\kappa ^{+})$
,
![]() $j_{n,\omega }(\alpha )$
is in
$j_{n,\omega }(\alpha )$
is in
![]() $j_{n,\omega }(\dot {E}_n)^{G_\omega }$
if and only if it is in
$j_{n,\omega }(\dot {E}_n)^{G_\omega }$
if and only if it is in
![]() $j_{n,\omega }(\dot {C}_n)^{{<}j_{n,\omega }"G_n{>}}$
.
$j_{n,\omega }(\dot {C}_n)^{{<}j_{n,\omega }"G_n{>}}$
.
By the closure of
![]() $M_\omega [G_\omega ]$
under
$M_\omega [G_\omega ]$
under
![]() $\omega $
-sequences,
$\omega $
-sequences,
![]() $\langle j_{n,\omega }(\dot {E}_n) \mid n<\omega \rangle $
is in
$\langle j_{n,\omega }(\dot {E}_n) \mid n<\omega \rangle $
is in
![]() $M_\omega [G_\omega ]$
. Hence we can interpret it using
$M_\omega [G_\omega ]$
. Hence we can interpret it using
![]() $G_{\omega }$
and
$G_{\omega }$
and
![]() $j_{n,\omega }"\mathcal {H}_n$
. Let
$j_{n,\omega }"\mathcal {H}_n$
. Let
![]() $D_n$
denote the resulting club. Let
$D_n$
denote the resulting club. Let
![]() $i^*<m$
be such that
$i^*<m$
be such that
![]() $i^* = i_n$
for infinitely many n. We claim that
$i^* = i_n$
for infinitely many n. We claim that
![]() $\bigcap _{n<\omega }D_n$
is disjoint from
$\bigcap _{n<\omega }D_n$
is disjoint from
![]() $S_{i^*}$
. Otherwise, we have
$S_{i^*}$
. Otherwise, we have
![]() $j_{n,\omega }(\alpha ) \in D_n \cap S_{i^*}$
for some n such that
$j_{n,\omega }(\alpha ) \in D_n \cap S_{i^*}$
for some n such that
![]() $i^* = i_n$
. It follows that
$i^* = i_n$
. It follows that
![]() $\alpha \in C_n \cap T_n^{i_n}$
, a contradiction.
$\alpha \in C_n \cap T_n^{i_n}$
, a contradiction.
6.1 Down to
 $\aleph _{\omega }$
$\aleph _{\omega }$
In the paper [Reference Poveda, Rinot and Sinapova20] it is shown that it is consistent relative to infinitely many supercompact cardinals, that stationary reflection at
![]() $\aleph _{\omega +1}$
together with the failure of
$\aleph _{\omega +1}$
together with the failure of
![]() $\operatorname {\mathrm {SCH}}$
at
$\operatorname {\mathrm {SCH}}$
at
![]() $\aleph _{\omega }$
.
$\aleph _{\omega }$
.
Let us show how to obtain the same result in our case, starting with the assumption of
![]() $\kappa ^{+}$
-
$\kappa ^{+}$
-
![]() $\Pi ^1_1$
-subcompact that carries a
$\Pi ^1_1$
-subcompact that carries a
![]() $(\kappa ,\kappa ^{++})$
-extender, as in the previous part.
$(\kappa ,\kappa ^{++})$
-extender, as in the previous part.
Theorem 6.21. Let
![]() $\kappa $
be a
$\kappa $
be a
![]() $\kappa ^{+}$
-
$\kappa ^{+}$
-
![]() $\Pi ^1_1$
-subcompact cardinal and let us assume that it carries a
$\Pi ^1_1$
-subcompact cardinal and let us assume that it carries a
![]() $(\kappa ,\kappa ^{++})$
-extender. Then, there is a forcing extension in which
$(\kappa ,\kappa ^{++})$
-extender. Then, there is a forcing extension in which
![]() $\kappa =\aleph _\omega $
,
$\kappa =\aleph _\omega $
,
![]() $2^{\aleph _{\omega }} = \aleph _{\omega +2}$
,
$2^{\aleph _{\omega }} = \aleph _{\omega +2}$
,
![]() $\operatorname {\mathrm {GCH}}$
holds below
$\operatorname {\mathrm {GCH}}$
holds below
![]() $\aleph _{\omega }$
and every finite collection of stationary subsets of
$\aleph _{\omega }$
and every finite collection of stationary subsets of
![]() $\aleph _{\omega +1}$
reflects simultaneously.
$\aleph _{\omega +1}$
reflects simultaneously.
The proof of this theorem is essentially the same as the proof of Theorem 1.4. We follow the argument as in the previous subsection and explain the differences.
Let us prepare the universe so that
![]() $\operatorname {\mathrm {GCH}}$
holds and the subcompactness of
$\operatorname {\mathrm {GCH}}$
holds and the subcompactness of
![]() $\kappa $
is indestructible under Cohen forcing
$\kappa $
is indestructible under Cohen forcing
![]() $\mathop {\mathrm {Add}}(\kappa ^{+},\kappa ^{++})$
. Let
$\mathop {\mathrm {Add}}(\kappa ^{+},\kappa ^{++})$
. Let
![]() $j_E \colon V \to M_1$
be the extender ultrapower embedding. Let us assume moreover that the approachability ideal is always maximal. Namely, for every regular uncountable cardinal
$j_E \colon V \to M_1$
be the extender ultrapower embedding. Let us assume moreover that the approachability ideal is always maximal. Namely, for every regular uncountable cardinal
![]() $\rho $
,
$\rho $
,
![]() $\rho \in I[\rho ]$
$\rho \in I[\rho ]$
We define the iterations
![]() $\langle j_{n,m} \colon M_n\to M_m \mid n < m \leq \omega \rangle $
, and
$\langle j_{n,m} \colon M_n\to M_m \mid n < m \leq \omega \rangle $
, and
![]() $\langle \iota _{n,m} \colon N_n \to N_m \mid n < m \leq \omega \rangle $
as before.
$\langle \iota _{n,m} \colon N_n \to N_m \mid n < m \leq \omega \rangle $
as before.
By standard arguments (see for example [Reference Cummings2, Lemma 8.5 and Proposition 15.1], and use Claim 6.7 for the computation of the width), there is an
![]() $M_1$
-generic filter
$M_1$
-generic filter
![]() $K\subseteq \operatorname {Col}(\kappa ^{+3}, <j_E(\kappa ))$
. Moreover, by elementarity for every n, the filter
$K\subseteq \operatorname {Col}(\kappa ^{+3}, <j_E(\kappa ))$
. Moreover, by elementarity for every n, the filter
![]() $j_n(K)$
is
$j_n(K)$
is
![]() $M_{n+1}$
-generic. Fix
$M_{n+1}$
-generic. Fix
![]() $K_0 \subseteq \operatorname {Col}(\omega _4, <\kappa )$
a V-generic and let
$K_0 \subseteq \operatorname {Col}(\omega _4, <\kappa )$
a V-generic and let
Let us define the filters
![]() $G_n, \mathcal {H}_n$
and the models
$G_n, \mathcal {H}_n$
and the models
![]() $M_n$
for
$M_n$
for
![]() $n \leq \omega $
exactly as before and let us consider the model
$n \leq \omega $
exactly as before and let us consider the model
![]() $M_{\omega }[G_\omega ][\mathcal {H}][\mathcal {K}]$
. Let
$M_{\omega }[G_\omega ][\mathcal {H}][\mathcal {K}]$
. Let
![]() $K_n = \mathcal {K} \restriction n + 1$
.
$K_n = \mathcal {K} \restriction n + 1$
.
In [Reference Hayut12], it is shown that the parallel of Lemma 6.5, namely
![]() $M_\omega [G_\omega ][\mathcal {K}] = \bigcap M_n[G_n][K_n]$
, holds.
$M_\omega [G_\omega ][\mathcal {K}] = \bigcap M_n[G_n][K_n]$
, holds.
The next point in the proof in which we need to modify the argument slightly is Lemma 6.12, in which we need to show
As there are elementary embeddings
the argument of [Reference Hayut12] for extender-based Prikry forcing with interleaved collapses works without further modifications.
The claims for the existence of a generic for the forcing that shoots a club disjoint from
![]() $j_\omega (S^{\kappa ^{+}}_{\kappa })$
, Claim 6.13, remains the same. We are now ready for the proof of the main theorem of this subsection.
$j_\omega (S^{\kappa ^{+}}_{\kappa })$
, Claim 6.13, remains the same. We are now ready for the proof of the main theorem of this subsection.
Theorem 6.22. In
![]() $M_{\omega }[G_\omega ][\mathcal {H}][\mathcal {K}]\ \operatorname {\mathrm {SCH}}$
fails at
$M_{\omega }[G_\omega ][\mathcal {H}][\mathcal {K}]\ \operatorname {\mathrm {SCH}}$
fails at
![]() $j_{\omega }(\kappa )$
which is
$j_{\omega }(\kappa )$
which is
![]() $\aleph _{\omega }$
and every finite collection of stationary subsets of
$\aleph _{\omega }$
and every finite collection of stationary subsets of
![]() $j_{\omega }(\kappa ^{+})$
reflects simultaneously.
$j_{\omega }(\kappa ^{+})$
reflects simultaneously.
Proof Let us verify first that the only cardinals which are collapsed are the cardinals in the intervals
![]() $[\omega _4, \kappa ) \cup [\kappa ^{+3}, j_1(\kappa )) \cup \cdots [j_n(\kappa ^{+3}), j_{n+1}(\kappa )) \cup \cdots $
.
$[\omega _4, \kappa ) \cup [\kappa ^{+3}, j_1(\kappa )) \cup \cdots [j_n(\kappa ^{+3}), j_{n+1}(\kappa )) \cup \cdots $
.
As mentioned above,
and in particular, every
![]() $M_\omega $
-cardinal below
$M_\omega $
-cardinal below
![]() $j_\omega (\kappa )$
which is collapsed in the extension must be collapsed in
$j_\omega (\kappa )$
which is collapsed in the extension must be collapsed in
![]() $M_{n}[G_n][\mathcal {H}_n][K_n]$
for all large n. For cardinals above
$M_{n}[G_n][\mathcal {H}_n][K_n]$
for all large n. For cardinals above
![]() $j_{\omega }(\kappa )$
one can use the continuity of the elementary embeddings in order to show that they do not change cofinality. Therefore, the arguments for the failure of
$j_{\omega }(\kappa )$
one can use the continuity of the elementary embeddings in order to show that they do not change cofinality. Therefore, the arguments for the failure of
![]() $\operatorname {\mathrm {SCH}}$
remains the same.
$\operatorname {\mathrm {SCH}}$
remains the same.
Let us prove the stationary reflection. For simplicity, let us show that every stationary subset of
![]() $j_\omega (\kappa ^{+})$
reflects in this model. The general case is similar.
$j_\omega (\kappa ^{+})$
reflects in this model. The general case is similar.
There are two components in the proof which are slightly different: First, given a stationary set
![]() $S \in M_{\omega }[G_\omega ][\mathcal {H}][\mathcal {K}]$
, one can pull it to a set
$S \in M_{\omega }[G_\omega ][\mathcal {H}][\mathcal {K}]$
, one can pull it to a set
![]() $T_n \in M_n[G_n][\mathcal {H}_n][K_n]$
exactly as before and check whether it is stationary there. Note that the forcing adding
$T_n \in M_n[G_n][\mathcal {H}_n][K_n]$
exactly as before and check whether it is stationary there. Note that the forcing adding
![]() $K_n$
is of cardinality
$K_n$
is of cardinality
![]() $j_n(\kappa )$
. So, if
$j_n(\kappa )$
. So, if
![]() $T_n$
is stationary in
$T_n$
is stationary in
![]() $M_n[G_n][\mathcal {H}_n][K_n]$
then there is a single condition
$M_n[G_n][\mathcal {H}_n][K_n]$
then there is a single condition
![]() $q \in K_n$
and stationary set
$q \in K_n$
and stationary set
![]() $T^{\prime }_n \in M_n[G_n][\mathcal {H}_n]$
such that
$T^{\prime }_n \in M_n[G_n][\mathcal {H}_n]$
such that
![]() $q \Vdash T^{\prime }_n \subseteq T_n$
.
$q \Vdash T^{\prime }_n \subseteq T_n$
.
Then, by the
![]() $j_n(\kappa ^{+})$
-subcompactness of
$j_n(\kappa ^{+})$
-subcompactness of
![]() $j_n(\kappa )$
in
$j_n(\kappa )$
in
![]() $M_n[G_n][\mathcal {H}_n]$
one can conclude that
$M_n[G_n][\mathcal {H}_n]$
one can conclude that
![]() $T_n^{\prime }$
has a reflection point
$T_n^{\prime }$
has a reflection point
![]() $\delta $
of cofinality
$\delta $
of cofinality
![]() $<j_n(\kappa )$
and above
$<j_n(\kappa )$
and above
![]() $j_{n-1}(\kappa )^{+++}$
(see [Reference Hayut and Unger13] for details). This is where the assumption about the approachability plays a role: we conclude that this stationary subset of
$j_{n-1}(\kappa )^{+++}$
(see [Reference Hayut and Unger13] for details). This is where the assumption about the approachability plays a role: we conclude that this stationary subset of
![]() $\delta $
remains stationary in
$\delta $
remains stationary in
![]() $M_n[G_n][\mathcal {H}_n][\mathcal K_n]$
. So, there is a stationary subset of
$M_n[G_n][\mathcal {H}_n][\mathcal K_n]$
. So, there is a stationary subset of
![]() $\delta $
of order type
$\delta $
of order type
![]() $\operatorname {\mathrm {cf}} \delta $
in
$\operatorname {\mathrm {cf}} \delta $
in
![]() $M_n$
,
$M_n$
,
![]() $T_n^{\prime \prime }\subseteq T_n \cap \delta $
. Since
$T_n^{\prime \prime }\subseteq T_n \cap \delta $
. Since
![]() $j_{n,\omega }(T_n^{\prime \prime }) = j_{n,\omega } \text { " } T_n^{\prime \prime }$
, we conclude that
$j_{n,\omega }(T_n^{\prime \prime }) = j_{n,\omega } \text { " } T_n^{\prime \prime }$
, we conclude that
![]() $M_{\omega }[G_\omega ][\mathcal {H}][K_n]\models j_{n,\omega }(T_n^{\prime \prime }) \subseteq S$
.
$M_{\omega }[G_\omega ][\mathcal {H}][K_n]\models j_{n,\omega }(T_n^{\prime \prime }) \subseteq S$
.
By downwards absoluteness of stationarity and continuity of the embedding
![]() $j_{n,\omega }$
,
$j_{n,\omega }$
,
![]() $j_{n,\omega }(T_n^{\prime \prime })$
is stationary at
$j_{n,\omega }(T_n^{\prime \prime })$
is stationary at
![]() $j_{n,\omega }(\delta )$
in
$j_{n,\omega }(\delta )$
in
![]() $M_{\omega }[G_\omega ][\mathcal {H}][K_n]$
and thus S reflects at
$M_{\omega }[G_\omega ][\mathcal {H}][K_n]$
and thus S reflects at
![]() $j_{n,\omega }(\delta )$
in this model.
$j_{n,\omega }(\delta )$
in this model.
To summarize, if there is n such that
![]() $T_n$
is stationary, then S reflects in
$T_n$
is stationary, then S reflects in
![]() $M_\omega [G_\omega ][\mathcal {H}][\mathcal {K}]$
.
$M_\omega [G_\omega ][\mathcal {H}][\mathcal {K}]$
.
Otherwise, for all n,
![]() $T_n$
is non-stationary. In this case, for each n there is a club name for a club
$T_n$
is non-stationary. In this case, for each n there is a club name for a club
![]() $\dot {C}_n$
disjoint from
$\dot {C}_n$
disjoint from
![]() $T_n$
and we would like to push them (or subclubs of them) to
$T_n$
and we would like to push them (or subclubs of them) to
![]() $M_{\omega }[G_\omega ][\mathcal {H}][\mathcal {K}]$
.
$M_{\omega }[G_\omega ][\mathcal {H}][\mathcal {K}]$
.
For every n, the forcing introducing
![]() $K_n$
is
$K_n$
is
![]() $j_n(\kappa )$
-cc, and therefore, for every club
$j_n(\kappa )$
-cc, and therefore, for every club
![]() $C_n \in M_n[G_n][\mathcal {H}_n][K_n]$
there is a subclub
$C_n \in M_n[G_n][\mathcal {H}_n][K_n]$
there is a subclub
![]() $C^{\prime }_n \in M_n[G_n][\mathcal {H}_n]$
. We are now in exactly the same situation of the proof of Theorem 1.4: we obtain for each n a stable name
$C^{\prime }_n \in M_n[G_n][\mathcal {H}_n]$
. We are now in exactly the same situation of the proof of Theorem 1.4: we obtain for each n a stable name
![]() $\dot {E}_n$
which is forced to be a subclub of
$\dot {E}_n$
which is forced to be a subclub of
![]() $C^{\prime }_n$
and thus there is in
$C^{\prime }_n$
and thus there is in
![]() $M_{\omega }[G_\omega ][\mathcal {H}]$
a subclub of the set
$M_{\omega }[G_\omega ][\mathcal {H}]$
a subclub of the set
![]() $\bigcap j_{n,\omega }(\dot {E}_n)$
which is forced to be disjoint from S.
$\bigcap j_{n,\omega }(\dot {E}_n)$
which is forced to be disjoint from S.
Remark 6.23. The same method can be used to obtain arbitrary finite gap in the failure of
![]() $\operatorname {\mathrm {SCH}}$
.
$\operatorname {\mathrm {SCH}}$
.
Funding
The first author was partially supported by the Israel Science Foundation Grant 1832/19. The second author was partially supported by the FWF Lise Meitner Grant 2650-N35 and the Israel Science Foundation Grant 1967/21. The third author was partially supported by the NSF grant DMS-1700425 and an NSERC Discovery grant.