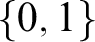1 Overview
It is a common assumption in formal epistemology that an agent’s beliefs can be represented by (or even identified with) a credence function
![]() $cr$
, which assigns to each proposition A a number
$cr$
, which assigns to each proposition A a number
![]() $cr(A) \in \mathbb {R}$
, interpreted as the agent’s degree of belief in that proposition. On this foundation is built the position known as probabilism; the claim that, in order to be rational, an agent’s credence function must be a probability distribution. In other words, supporters of probabilism see the probability axioms as epistemic norms that all rational agents should respect.Footnote
1
$cr(A) \in \mathbb {R}$
, interpreted as the agent’s degree of belief in that proposition. On this foundation is built the position known as probabilism; the claim that, in order to be rational, an agent’s credence function must be a probability distribution. In other words, supporters of probabilism see the probability axioms as epistemic norms that all rational agents should respect.Footnote
1
One way to argue for probabilism is to show that probabilistic credences are in some way more epistemically valuable than non-probabilistic ones. Many arguments to this effect assume that the fundamental value of credences is their accuracy, which intuitively reflects how closely they align with the truth. The concept of accuracy is made precise by introducing inaccuracy measures, functions
![]() $I(cr, w)$
which assign a penalty to the credence
$I(cr, w)$
which assign a penalty to the credence
![]() $cr$
for each state of the world w. These measures are then used to show that a rational agent who values accuracy ought to have probabilistic credences.
$cr$
for each state of the world w. These measures are then used to show that a rational agent who values accuracy ought to have probabilistic credences.
Clearly, a great deal of an accuracy argument’s strength rests on what we take to be a reasonable accuracy measure. This will be a main theme in this essay, which aims to generalize an accuracy argument due to Lindley. Lindley’s argument makes remarkably weak assumptions on what should count as a reasonable accuracy measure; because of this, it leads to a weaker set of rationality norms than probabilism proper, one that has a number of interesting philosophical ramifications.
The generalization I pursue involves the logical setting of the argument. Like most accuracy arguments in the literature, Lindley’s assumes that sentences are either true or false, and that logical consequence is defined in the classical way. Although [Reference Williams20] has generalized an argument due to Joyce [Reference Joyce6] to a broad class of non-classical settings, this generalization relies on Joyce’s specific assumptions on what counts as an accuracy measure, and thus cannot be applied to Lindley’s argument. I will proceed in a fundamentally different way to extend Lindley’s argument to some of the non-classical settings discussed by Williams.
I will start in Section 2 by introducing probabilism as an epistemological position, and accuracy arguments as a way to justify it. Section 3 is an overview of Lindley’s accuracy argument, with particular attention devoted to spelling out its assumptions and philosophical consequences. The remainder of the paper contains my generalisation of Lindley’s argument. Section 4 prepares the ground by making precise the non-classical settings which I will be working with, and the non-classical probability axioms I will be justifying as rational norms for credences. In Section 5 prove the main result: rational agents are required to have credences whose transforms obey the non-classical probability axioms, if they want to avoid accuracy-domination. Section 6 discusses the problem of a converse result, and shows that, for a class of reasonable inaccuracy measures, having a probabilistic transform is sufficient to avoid accuracy-domination. Some open problems are briefly outlined in Section 7, and Section 8 concludes the essay with a summary of its main results.
2 Probabilism and accuracy
Let’s start by introducing some notation. We consider an agent who has beliefs towards a set of sentences
![]() $\mathcal {F}$
in a finite propositional language
$\mathcal {F}$
in a finite propositional language
![]() $\mathcal {L}$
, which includes the standard connectives
$\mathcal {L}$
, which includes the standard connectives
![]() $\land , \lor , \lnot $
. We assume
$\land , \lor , \lnot $
. We assume
![]() $\mathcal {F}$
to be closed under
$\mathcal {F}$
to be closed under
![]() $\land , \lor , \lnot $
. For the moment, we restrict ourselves to the classical case, and assume that each sentence in
$\land , \lor , \lnot $
. For the moment, we restrict ourselves to the classical case, and assume that each sentence in
![]() $\mathcal {L}$
must be either true or false (this assumption will be abandoned in later sections). We denote this by taking
$\mathcal {L}$
must be either true or false (this assumption will be abandoned in later sections). We denote this by taking
![]() $S = \{true, false\}$
as our set of truth-statuses. We will consider a finite set W of functions
$S = \{true, false\}$
as our set of truth-statuses. We will consider a finite set W of functions
![]() $w : \mathcal {F} \to S$
satisfying the classical truth conditions (e.g.,
$w : \mathcal {F} \to S$
satisfying the classical truth conditions (e.g.,
![]() $w(A) = true$
iff
$w(A) = true$
iff
![]() $w(\lnot A) = false$
). Each
$w(\lnot A) = false$
). Each
![]() $w \in W$
is a classically possible world. The agent’s beliefs are modeled by credence functions
$w \in W$
is a classically possible world. The agent’s beliefs are modeled by credence functions
![]() $cr : \mathcal {F} \to \mathbb {R}$
, with
$cr : \mathcal {F} \to \mathbb {R}$
, with
![]() $cr(A)$
being interpreted as the agent’s degree of belief in A. We denote by
$cr(A)$
being interpreted as the agent’s degree of belief in A. We denote by
![]() $Cred$
the set of all credence functions defined over
$Cred$
the set of all credence functions defined over
![]() $\mathcal {F}$
.
$\mathcal {F}$
.
A popular way to argue for probabilism starts from the idea that the fundamental epistemic virtue of a credence is its accuracy. Accuracy is taken to be a gradational concept: one is more accurate at a world w the higher one’s degree of belief in the sentences that are true at w, and the lower one’s degree of belief in the sentences that are false at w. It is normally assumed that credence
![]() $0$
represents complete lack of belief, and that credence
$0$
represents complete lack of belief, and that credence
![]() $1$
represents the maximum degree of belief the agent can have; thus the function
$1$
represents the maximum degree of belief the agent can have; thus the function
![]() defined by:
defined by:

will be the most accurate credence at world w.Footnote
2
We can think of
![]() as providing an aim for belief at world w, in the sense that it is the credence of an ideal agent who knows the truth or falsity of every proposition, and thus will assign maximum belief to all truths, and minimum belief to all falsities [Reference Williams20]. I refer to the value
as providing an aim for belief at world w, in the sense that it is the credence of an ideal agent who knows the truth or falsity of every proposition, and thus will assign maximum belief to all truths, and minimum belief to all falsities [Reference Williams20]. I refer to the value
![]() as the truth-value of A at world w.
as the truth-value of A at world w.
Most accuracy arguments for probabilism follow the same three-step structure.
-
1. A function (or class of functions)
 $I : Cred \times W \to \mathbb {R}$
is defined, such that
$I : Cred \times W \to \mathbb {R}$
is defined, such that
 $I(cr, w)$
is a reasonable measure of how accurate the credence function
$I(cr, w)$
is a reasonable measure of how accurate the credence function
 $cr$
is at world w (i.e., how “close” it is to the ideal credence
$cr$
is at world w (i.e., how “close” it is to the ideal credence
 ). Whether I assigns higher values to more accurate credences and lower values to less accurate ones, or vice versa, is just a matter of convention. Throughout this paper we will assume that the higher the value
). Whether I assigns higher values to more accurate credences and lower values to less accurate ones, or vice versa, is just a matter of convention. Throughout this paper we will assume that the higher the value
 $I(cr, w)$
, the more inaccurate the credence
$I(cr, w)$
, the more inaccurate the credence
 $cr$
is at world w. This way, the function I will act as a kind of distance between the agent’s beliefs and the ideal credence. I will write
$cr$
is at world w. This way, the function I will act as a kind of distance between the agent’s beliefs and the ideal credence. I will write
 $I_{\mathcal {G}}$
to denote the inaccuracy of a credence
$I_{\mathcal {G}}$
to denote the inaccuracy of a credence
 $cr$
on a subset
$cr$
on a subset
 $\mathcal {G}$
of
$\mathcal {G}$
of
 $\mathcal {F}$
.
$\mathcal {F}$
. -
2. As a second step, the accuracy measure I is used to define one or more rationality requirements. For example, we may think that an agent with credence function
 $cr$
is not rational if there is another credence function
$cr$
is not rational if there is another credence function
 $cr'$
that is more accurate than
$cr'$
that is more accurate than
 $cr$
in every possible world. This is known as the Non-Dominance requirement.
$cr$
in every possible world. This is known as the Non-Dominance requirement. -
3. Finally, a theorem proves that in order for an agent’s credence to be rational according to the specified measure and requirement, it must be probabilistic.
A classical example of accuracy argument is due to Joyce [Reference Joyce6], who takes advantage of an earlier theorem proven by De Finetti [Reference De Finetti2]. Following the above schema, Joyce begins by laying down some conditions to establish what functions can be considered appropriate measures of accuracy. Then, the Non-Dominance criterion is introduced as a way of discriminating between rational and irrational credences. Finally, Joyce proves the following result:
-
• Accuracy Theorem: When evaluating credences with an acceptable accuracy measure I, every non-probabilistic credence
 $cr$
is accuracy-dominated by a probabilistic
$cr$
is accuracy-dominated by a probabilistic
 $cr'$
, meaning that
$cr'$
, meaning that
 $cr'$
is more accurate than
$cr'$
is more accurate than
 $cr$
in each world. More formally: (2)for every possible world
$cr$
in each world. More formally: (2)for every possible world $$ \begin{align} I(cr', w) < I(cr, w) \end{align} $$
$$ \begin{align} I(cr', w) < I(cr, w) \end{align} $$
 $w \in W$
.
$w \in W$
.
Putting the pieces together, we deduce that the credence function
![]() $cr$
of a rational agent must be probabilistic, for otherwise there would be some other credence function
$cr$
of a rational agent must be probabilistic, for otherwise there would be some other credence function
![]() $cr'$
which is more accurate than
$cr'$
which is more accurate than
![]() $cr$
no matter what, and this we regard as a failure of rationality on the part of the agent.
$cr$
no matter what, and this we regard as a failure of rationality on the part of the agent.
Most of the criticism of Joyce’s argument is directed towards its assumptions, rather than towards the theorem that contains the argument’s deductive step. In particular, the following have been questioned:
-
(i) The assumption that the rationality of an agent’s beliefs depends on how accurate her credence is with regards to the actual world.
-
(ii) The assumption that a rational credence function should not be accuracy-dominated (Non-Dominance).
-
(iii) Assumptions on what counts as an acceptable accuracy measure.
Critics of (i) argue that accuracy is not the only criterion required to define rationality. Other properties of an agent’s beliefs, such as the degree by which they are supported by evidence, or their behavioural implications, might be just as (if not more) important for the agent’s epistemic profile. Furthermore, these other virtues might trade-off with accuracy, so that pursuing the one requires implies giving up the other [Reference Carr1]. A serious answer to this objection goes beyond the scope of this essay, and has already been discussed at length by others.Footnote
3
However, I hope that even a sceptical reader will agree that there are at least some contexts in which credal accuracy is the most important epistemic desideratum—think for example of a meteorologist making weather predictions, or a computer program making economic forecasts. The sceptic can read the present discussion as limited in scope to those contexts. After settling on (i), (ii) is fairly uncontroversial: if all we care about is accuracy, and
![]() $cr'$
is more accurate than
$cr'$
is more accurate than
![]() $cr$
no matter what, then there’s no reason why we should hold the latter instead of the former. On the other hand, Joyce’s assumptions on (iii) what counts as an acceptable accuracy measure are not trivial, and they have sparked considerable debate [Reference Maher10].Footnote
4
$cr$
no matter what, then there’s no reason why we should hold the latter instead of the former. On the other hand, Joyce’s assumptions on (iii) what counts as an acceptable accuracy measure are not trivial, and they have sparked considerable debate [Reference Maher10].Footnote
4
Given the above discussion, it is natural to ask ourselves whether it’s possible to justify probabilism with a different set of conditions on what an appropriate measure of accuracy should be like. Many justifications of probabilism rely on a specific class of measures of inaccuracy, which are called strictly proper [Reference Joyce7, Reference Pettigrew14, Reference Predd, Seiringer, Lieb, Osherson, Poor and Kulkarni15].
Definition 2.1 ((Strictly) proper inaccuracy measure)
Let W be a finite set of worlds mapping sentences in
![]() $\mathcal {F}$
into
$\mathcal {F}$
into
![]() $\{true, false\}$
. Then I is proper iff for every probability function p and every finite subset
$\{true, false\}$
. Then I is proper iff for every probability function p and every finite subset
![]() $\mathcal {G} \subseteq \mathcal {F}$
, the expected score
$\mathcal {G} \subseteq \mathcal {F}$
, the expected score
 $$ \begin{align} Exp_p[I_{\mathcal{G}}(cr, \cdot)] = \sum_{w \in W} p(\{w\})I_{\mathcal{G}}(cr, w), \end{align} $$
$$ \begin{align} Exp_p[I_{\mathcal{G}}(cr, \cdot)] = \sum_{w \in W} p(\{w\})I_{\mathcal{G}}(cr, w), \end{align} $$
taken as a function of
![]() $cr$
for fixed p, is minimized when
$cr$
for fixed p, is minimized when
![]() $cr = p$
. Furthermore, if
$cr = p$
. Furthermore, if
![]() $cr = p$
uniquely minimises this function
$cr = p$
uniquely minimises this function
![]() $($
on all finite
$($
on all finite
![]() $\mathcal {G}$
’s
$\mathcal {G}$
’s
![]() $)$
, we say that I is strictly proper.Footnote
5
$)$
, we say that I is strictly proper.Footnote
5
Intuitively, the above definition requires that the inaccuracy measure I make all probabilistic credences immodest, in the sense that an agent whose beliefs are represented by such a credence would expect her own beliefs to be more accurate than any other. By arguing that these rules provide reasonable measures of epistemic accuracy, and assuming Non-Dominance to be a rationality requirement, it’s possible to show that all rational credences respect the probability axioms.
Lindley [Reference Lindley9] also evaluates an agent’s beliefs in terms of their accuracy, and takes Non-Dominance to be a requirement for rational credences. However, he considers a class of reasonable accuracy measures other than the class of proper ones. This difference in his assumptions leads him to a weaker conclusion. Avoiding accuracy-domination does not require credences to be probabilistic; instead, Lindley argues, it merely requires that they can be transformed into probabilistic functions by a canonical transform. In other words, although Lindley’s undemanding assumptions are not sufficient to justify full-blown probabilism, the rational credences they characterise all share some probabilistic structure. The details and philosophical significance of this result will be discussed in more detail in the next section.
3 Lindley’s argument
I will now go over Lindley’s accuracy argument. I begin with an overview of the formal result, and then discuss its philosophical consequences. The result is presented with the notation introduced in the previous section, in order to simplify the extension to non-classical settings in following sections.
Like Joyce, Lindley begins with assumptions that establish what kind of measure of inaccuracy should be considered reasonable, and what it means for a credence function to be rational according to such a measure.
-
(a) Score assumption: if
 $cr$
is a credence function defined over
$cr$
is a credence function defined over
 $\mathcal {F}$
, f is a score function, and
$\mathcal {F}$
, f is a score function, and
 $\mathcal {G}$
is a subset of
$\mathcal {G}$
is a subset of
 $\mathcal {F}$
, then the total inaccuracy of
$\mathcal {F}$
, then the total inaccuracy of
 $cr$
at world w over
$cr$
at world w over
 $\mathcal {G}$
is given by
$\mathcal {G}$
is given by
 . I will abuse the notation and use the symbol f to denote both the local score function and the global inaccuracy measure defined by that score function. So the score assumption can be written as: (4)Note that the inaccuracy of
. I will abuse the notation and use the symbol f to denote both the local score function and the global inaccuracy measure defined by that score function. So the score assumption can be written as: (4)Note that the inaccuracy of
 $cr$
over an infinite
$cr$
over an infinite
 $\mathcal {G}$
may be infinite, so the range of
$\mathcal {G}$
may be infinite, so the range of
 $I_{\mathcal {G}}$
is the extended real numbers.
$I_{\mathcal {G}}$
is the extended real numbers.
-
(b) Admissibility assumption: We say an agent’s credence
 $cr: \mathcal {F} \to \mathbb {R}$
is accuracy-dominated on a finite subset
$cr: \mathcal {F} \to \mathbb {R}$
is accuracy-dominated on a finite subset
 $\mathcal {G} \subset \mathcal {F}$
(according to the inaccuracy measure f) iff there is some other credence function
$\mathcal {G} \subset \mathcal {F}$
(according to the inaccuracy measure f) iff there is some other credence function
 $cr'$
such that: (5)for all possible worlds
$cr'$
such that: (5)for all possible worlds
 $w \in W$
, with some worlds in which the inequality is strict. This means that
$w \in W$
, with some worlds in which the inequality is strict. This means that
 $cr$
is never more accurate than some other
$cr$
is never more accurate than some other
 $cr'$
on
$cr'$
on
 $\mathcal {G}$
, no matter what world is the case, and in some worlds
$\mathcal {G}$
, no matter what world is the case, and in some worlds
 $cr'$
is more accurate than
$cr'$
is more accurate than
 $cr$
. We say
$cr$
. We say
 $cr$
is accuracy-dominated (according to f) if it is accuracy-dominated on some finite
$cr$
is accuracy-dominated (according to f) if it is accuracy-dominated on some finite
 $\mathcal {G} \subset \mathcal {F}$
. We then introduce the following rationality criterion: a credence
$\mathcal {G} \subset \mathcal {F}$
. We then introduce the following rationality criterion: a credence
 $cr$
is rationally admissible according to an inaccuracy measure f only if it is not accuracy-dominated according to that f (Non-Dominance).
$cr$
is rationally admissible according to an inaccuracy measure f only if it is not accuracy-dominated according to that f (Non-Dominance).
-
(c) Origin and Scale assumption: There are two distinct values
 $x_F, x_T \in \mathbb {R}$
with
$x_F, x_T \in \mathbb {R}$
with
 $x_F < x_T$
, such that:
$x_F < x_T$
, such that:-
•
 $x_F$
is the only rationally admissible value for
$x_F$
is the only rationally admissible value for
 $cr(A)$
if A is false in all possible worlds
$cr(A)$
if A is false in all possible worlds
 $w \in W$
.
$w \in W$
. -
•
 $x_T$
is the only rationally admissible value for
$x_T$
is the only rationally admissible value for
 $cr(A)$
if A is true in all possible worlds
$cr(A)$
if A is true in all possible worlds
 $w \in W$
.
$w \in W$
.
In Lindley’s argument, the credence values
 $x_F, x_T$
represent the agent’s certainty in the falsity/truth of a proposition, respectively.
$x_F, x_T$
represent the agent’s certainty in the falsity/truth of a proposition, respectively. -
-
(d) Regularity assumptions: The credence
 $cr$
can assume all values in a closed, bounded interval
$cr$
can assume all values in a closed, bounded interval
 $J \subset \mathbb {R}$
. There exists the derivative
$J \subset \mathbb {R}$
. There exists the derivative
 $f'(x, y)$
of
$f'(x, y)$
of
 $f(x, y)$
with respect to
$f(x, y)$
with respect to
 $x \in J$
. This derivative is continuous in x for each y and, for both
$x \in J$
. This derivative is continuous in x for each y and, for both
 $y = 0$
and
$y = 0$
and
 $y = 1$
, is zero at no more than one point. Also
$y = 1$
, is zero at no more than one point. Also
 $x_F$
and
$x_F$
and
 $x_T$
are interior points of J.
$x_T$
are interior points of J.
Lindley’s assumptions are too weak to imply that all rational credences be probabilistic. Instead they imply that a rational credence’s canonical transform must respect the probability axioms. For each inaccuracy measure f, this transform is obtained by composing the agent’s credence with the function
![]() $P_f: \mathbb {R} \to \mathbb {R}$
defined as:
$P_f: \mathbb {R} \to \mathbb {R}$
defined as:
 $$ \begin{align} P_f(x) := \frac{f'(x, 0)}{f'(x,0) - f'(x, 1)}. \end{align} $$
$$ \begin{align} P_f(x) := \frac{f'(x, 0)}{f'(x,0) - f'(x, 1)}. \end{align} $$
Lindley’s proof is then developed via three main lemmas, each showing that
![]() $P_f \circ cr$
respects one of the probability axioms. The axioms are taken to be:
$P_f \circ cr$
respects one of the probability axioms. The axioms are taken to be:
After proving the lemmas, the following theorem can be derived straightforwardly:
Theorem 3.2 (Lindley [Reference Lindley9])
Under the assumptions
![]() $(a--d)$
listed above, if
$(a--d)$
listed above, if
![]() $cr:\mathcal {F}\to \mathbb {R}$
is admissible according to a reasonable inaccuracy measure f (i.e.,
$cr:\mathcal {F}\to \mathbb {R}$
is admissible according to a reasonable inaccuracy measure f (i.e.,
![]() $cr$
is not accuracy-dominated under f), and if
$cr$
is not accuracy-dominated under f), and if
![]() $P_f$
is the canonical transform defined as in (6), then the composite function
$P_f$
is the canonical transform defined as in (6), then the composite function
![]() $(P_f \circ cr): \mathcal {F} \to R$
obeys the probability axioms (A1)–(A3).
$(P_f \circ cr): \mathcal {F} \to R$
obeys the probability axioms (A1)–(A3).
To better understand the nature of Lindley’s conclusions, it will be useful to discuss the assumptions he makes about the inaccuracy measures. In particular, we will compare the kind of measures of accuracy he considers reasonable to the (strictly) proper measures which are commonly used in accuracy arguments for probabilism. Assumption (a) demands that the total inaccuracy of a credence
![]() $cr$
over
$cr$
over
![]() $\mathcal {G}$
is simply the sum of the scores
$\mathcal {G}$
is simply the sum of the scores
![]() on each
on each
![]() $A \in \mathcal {G}$
. This is also commonly assumed for proper inaccuracy measures, which are usually defined as sums of proper scoring rules. Assumption (c) reflects the fact that the rational credence values
$A \in \mathcal {G}$
. This is also commonly assumed for proper inaccuracy measures, which are usually defined as sums of proper scoring rules. Assumption (c) reflects the fact that the rational credence values
![]() $cr(\top ) = 1$
for a tautology, and
$cr(\top ) = 1$
for a tautology, and
![]() $cr(\bot ) = 0$
for a contradiction, are conventional. This level of generality can also be achieved by proper inaccuracy measures. In his reply to Howson, Joyce [Reference Joyce8] shows that we can adapt these measures so that any two values may be used as the endpoints of a rational credal scale. By doing so we derive a different form of probabilism, where the usual probability axioms are substituted by “scale-invariant” formulations. Assumption (d) mainly requires the score functions to be smooth. This guarantees that if the credence
$cr(\bot ) = 0$
for a contradiction, are conventional. This level of generality can also be achieved by proper inaccuracy measures. In his reply to Howson, Joyce [Reference Joyce8] shows that we can adapt these measures so that any two values may be used as the endpoints of a rational credal scale. By doing so we derive a different form of probabilism, where the usual probability axioms are substituted by “scale-invariant” formulations. Assumption (d) mainly requires the score functions to be smooth. This guarantees that if the credence
![]() $cr(A)$
is very close to
$cr(A)$
is very close to
![]() $cr'(A)$
, the respective scores will be close as well. It also adds some further technical conditions, some of which can be weakened (see [Reference Lindley9]).
$cr'(A)$
, the respective scores will be close as well. It also adds some further technical conditions, some of which can be weakened (see [Reference Lindley9]).
If we restrict ourselves to smooth inaccuracy measures in the sense of (d), then the measures Lindley finds reasonable are a strictly larger class than the proper ones. Indeed, Lindley points out that, among the inaccuracy measures he considers, the proper ones are those that “lead[] directly to a probability” [Reference Lindley9, p. 7]. By this he means that the transform
![]() $P_f$
defined from a proper inaccuracy measure f is simply the identity function, so
$P_f$
defined from a proper inaccuracy measure f is simply the identity function, so
![]() $P_f \circ cr = cr$
for each
$P_f \circ cr = cr$
for each
![]() $cr \in Cred$
. As a consequence of this, for a credence
$cr \in Cred$
. As a consequence of this, for a credence
![]() $cr$
to be non-dominated under a proper measure of inaccuracy,
$cr$
to be non-dominated under a proper measure of inaccuracy,
![]() $cr$
must itself be probabilistic, regardless of whether we define probability by means of the standard or “scale-invariant” axioms. Under Lindley’s more general assumptions, on the other hand, it might be that a non-probabilistic
$cr$
must itself be probabilistic, regardless of whether we define probability by means of the standard or “scale-invariant” axioms. Under Lindley’s more general assumptions, on the other hand, it might be that a non-probabilistic
![]() $cr$
is non-dominated under f (when f is not proper). In this case, the transform
$cr$
is non-dominated under f (when f is not proper). In this case, the transform
![]() $P_f \circ cr$
produces a different credence
$P_f \circ cr$
produces a different credence
![]() $cr'$
, which Theorem 3.2 ensures is probabilistic, again with either standard or “scale-invariant” fomulations of the axioms.Footnote
6
$cr'$
, which Theorem 3.2 ensures is probabilistic, again with either standard or “scale-invariant” fomulations of the axioms.Footnote
6
Titelbaum [Reference Titelbaum17] suggests that Lindley’s conclusions can be interpreted in different ways depending on one’s position with regards to the numerical representation of beliefs. On one hand, if we think all that matters to an epistemologist are qualitative statements like “Sally believes A more than B,” then quantifying the agent’s beliefs with real numbers is a useful modeling technique, but nothing more than that. Since different credence functions corresponding to the same probability distribution are ordinally equivalent, according to this view they are just different ways to represent the same beliefs. Every rational credence is then either probabilistic, or, by Lindley’s theorem, epistemically equivalent to a probabilistic one.
On the other hand, we may think that numeric representations capture some deeper facts about belief, facts that cannot always be expressed by mere qualitative judgements. In this case, there can be a real difference between ordinally equivalent credence functions, and in particular between a credence function and its probabilistic transform. So the result takes a more negative light, showing just how demanding our assumptions have to be in order to induce full-blown probabilism. This double relevance of Lindley’s argument makes it an interesting target for generalization, which will be the subject of the next section.
4 Non-classical generalisation: the set-up
This section lays the groundwork for the generalization of Lindley’s accuracy argument in Section 5 First of all, I specify the family of non-classical logics to which my generalised result applies, and then list some of them. I show that Lindley’s proof of Theorem 3.2 does not extend to these settings in general, and explain why this has to do with the axiomatisation of probability he is working with. Secondly, I clarify what my generalised result establishes by presenting an alternative version of the probability axioms, due to Paris [Reference Paris, De Cooman, Fine and Seidenfeld12], which characterises closed convex combinations of truth-values in the non-classical settings under consideration.
This setup closely follows the one used by Williams in his generalization of Joyce’s accuracy argument. To prove his accuracy theorem, Joyce [Reference Joyce6] uses the fact that probability functions are convex combinations of the ideal credences induced by each (classically) possible world, which I denoted earlier by
![]() . In his generalization, Williams [Reference Williams19, Reference Williams20] takes advantage of the fact that the concept of convex combination can be easily extended to the non-classical case. More precisely: if the truth-status of a sentence A at world w is
. In his generalization, Williams [Reference Williams19, Reference Williams20] takes advantage of the fact that the concept of convex combination can be easily extended to the non-classical case. More precisely: if the truth-status of a sentence A at world w is
![]() $w(A)$
, Williams interprets the truth-value
$w(A)$
, Williams interprets the truth-value
![]() as the ideal belief of an agent towards A, if w is the case. Then nonclassical probabilities end up being convex combinations of the functions
as the ideal belief of an agent towards A, if w is the case. Then nonclassical probabilities end up being convex combinations of the functions
![]() induced by each non-classical possible world.
induced by each non-classical possible world.
Unlike Joyce, however, Lindley does not rely on a concept like that of convex combinations which can be so readily generalized. In order to transfer Lindley’s argument to the non-classical case, I will need to adjust some of his assumptions and proofs in Section 5 My conclusion will also be different; whereas Williams vindicates full-blown non-classical probabilism, I aim to justify its weaker version, analogous to that justified by Lindley: in a number of non-classical settings, all rational credence functions can be canonically transformed into functions that respect Paris’s generalised probablity axioms.
We are interested in generalising Lindley’s argument to non-classical logics with truth-values in
![]() $\{0, 1\}$
. We do not impose any restrictions on the set S of truth-statuses of these logics, but we do require that the truth-value assignment functions
$\{0, 1\}$
. We do not impose any restrictions on the set S of truth-statuses of these logics, but we do require that the truth-value assignment functions
![]() of each possible world
of each possible world
![]() $w \in W$
satisfy the following:
$w \in W$
satisfy the following:
Since we interpret truth-values as aims for belief, the above conditions concern the ways an ideal agent’s degree of belief in a composite propositions is constrained by her degree of belief in its components. The classical setting with its usual truth-value assignment clearly satisfies both conditions, and so we include it as a particular case of the more general non-classical pattern. But many non-classical settings also fall within this family. Here I list some of them, again following Williams [Reference Williams20] in their definitionFootnote 7 :
-
• Classical:
-
–
 $S := \{true, false\}. $
$S := \{true, false\}. $
-
– The truth-value mapping
 is defined by:
is defined by: 
-
–
 $\land , \lnot $
follow their usual classical truth tables.
$\land , \lnot $
follow their usual classical truth tables.
-
-
• LP Gluts:
-
–
 $S := \{true, both, false\} $
$S := \{true, both, false\} $
-
– The truth-value mapping
 is defined by:
is defined by: 
-
– The connectives
 $\land , \lnot $
follow the rules:
$\land , \lnot $
follow the rules:  $$ \begin{align*}w(A \land B) = \begin{cases} true, & \text{if} \;\, w(A) = true \; \text{and} \; w(B) = true, \\ false, & \text{if} \;\, w(A) = false \; \text{or} \; w(B) = false, \\ both, & \text{otherwise}. \end{cases}\end{align*} $$
$$ \begin{align*}w(A \land B) = \begin{cases} true, & \text{if} \;\, w(A) = true \; \text{and} \; w(B) = true, \\ false, & \text{if} \;\, w(A) = false \; \text{or} \; w(B) = false, \\ both, & \text{otherwise}. \end{cases}\end{align*} $$
 $$ \begin{align*}w(\lnot A) = \begin{cases} true, & \text{if} \;\, w(A) = false, \\ false, & \text{if} \;\, w(A) = true, \\ both, & \text{if} \;\, w(A) = both. \end{cases}\end{align*} $$
$$ \begin{align*}w(\lnot A) = \begin{cases} true, & \text{if} \;\, w(A) = false, \\ false, & \text{if} \;\, w(A) = true, \\ both, & \text{if} \;\, w(A) = both. \end{cases}\end{align*} $$
-
-
• Kleene gaps: (see Appendix)
-
• Intuitionism: (see Appendix)
-
• Fuzzy Gaps (finite or infinite): (see Appendix)
Lindley’s proof does not apply in general to these logical settings. To show this, I take as an example Lindley’s proof of (A2), showing how it breaks in the case of LP Gluts. This is also a nice way to introduce Lindley’s proof strategy, which I will adapt later in this section.
Proposition 4.3 (Lindley’s Lemma 2 [Reference Lindley9])
Under the assumptions (a-d) listed in Section 3, if the credence
![]() $cr: \mathcal {F} \to \mathbb {R}$
is not accuracy-dominated according to a reasonable inaccuracy measure f, then for all
$cr: \mathcal {F} \to \mathbb {R}$
is not accuracy-dominated according to a reasonable inaccuracy measure f, then for all
![]() $A \in \mathcal {F}$
:
$A \in \mathcal {F}$
:
Proof.
Classical case: Assume
![]() $cr$
is not accuracy-dominated for some inaccuracy measure f. There can be only two distinct (classically) possible worlds
$cr$
is not accuracy-dominated for some inaccuracy measure f. There can be only two distinct (classically) possible worlds
![]() $w_1, w_2$
with:
$w_1, w_2$
with:
![]() $w_1(A) = true$
,
$w_1(A) = true$
,
![]() $w_1(\lnot A) = false$
and
$w_1(\lnot A) = false$
and
![]() $w_2(A) = false$
,
$w_2(A) = false$
,
![]() $w_2(\lnot A) = true$
. Let
$w_2(\lnot A) = true$
. Let
![]() $x := cr(A)$
and
$x := cr(A)$
and
![]() $y := cr(\lnot A)$
. Then from the Score assumption (a) we know that the total inaccuracy in the two possible cases is:
$y := cr(\lnot A)$
. Then from the Score assumption (a) we know that the total inaccuracy in the two possible cases is:
Now we move from
![]() $cr$
to a new credence distribution
$cr$
to a new credence distribution
![]() $cr'$
such that:
$cr'$
such that:
with
![]() $h,k \in \mathbb {R}$
. You can think of this as nudging our credence in A by some small quantity h, nudging our credence in
$h,k \in \mathbb {R}$
. You can think of this as nudging our credence in A by some small quantity h, nudging our credence in
![]() $\lnot A$
by some small quantity k, and leaving unchanged our credence in all other sentences in
$\lnot A$
by some small quantity k, and leaving unchanged our credence in all other sentences in
![]() $\mathcal {F}$
. The idea is that, since
$\mathcal {F}$
. The idea is that, since
![]() $cr$
is not accuracy-dominated, it should not be possible to decrease our total inaccuracy in every world by means of this sort of nudging.
$cr$
is not accuracy-dominated, it should not be possible to decrease our total inaccuracy in every world by means of this sort of nudging.
By Score assumption (a) we have that the total inaccuracy of an agent is the sum of the scores she obtains on each sentence, and since
![]() $cr$
and
$cr$
and
![]() $cr'$
agree on all sentences except for A and
$cr'$
agree on all sentences except for A and
![]() $\lnot A$
, the difference in total inaccuracy between these two credences will amount to the difference in their scores on A and
$\lnot A$
, the difference in total inaccuracy between these two credences will amount to the difference in their scores on A and
![]() $\lnot A$
:
$\lnot A$
:
Thinking of
![]() $f(x, 1)$
and
$f(x, 1)$
and
![]() $f(x, 0)$
as functions of a single variable x, for small
$f(x, 0)$
as functions of a single variable x, for small
![]() $h, k$
we can rewrite this shift in accuracy in terms of the derivative of f:
$h, k$
we can rewrite this shift in accuracy in terms of the derivative of f:
If we equate these two expressions to small, selected negative values, we get a system of two linear equations in unknowns
![]() $h,k$
, one for each distinct possible world. If this system had a solution, then defining
$h,k$
, one for each distinct possible world. If this system had a solution, then defining
![]() $cr'$
as above would make it more accurate than
$cr'$
as above would make it more accurate than
![]() $cr$
over the set
$cr$
over the set
![]() $\{A, \lnot A\}$
in all possible worlds, but this would contradict the assumption that
$\{A, \lnot A\}$
in all possible worlds, but this would contradict the assumption that
![]() $cr$
is not accuracy-dominated. So the system must not have a solution, that is, its determinant must be equal to zero.Footnote
8
This happens when:
$cr$
is not accuracy-dominated. So the system must not have a solution, that is, its determinant must be equal to zero.Footnote
8
This happens when:
We now expand the sum
![]() $P_f(x) + P_f(y)$
using the transform’s definition in (6):
$P_f(x) + P_f(y)$
using the transform’s definition in (6):
 $$ \begin{align} \,\,&\,\,\,\,\, P_f(x) + P_f(y) = \frac{f'(x, 0)}{f'(x,0) - f'(x, 1)} + \frac{f'(y, 0)}{f'(y,0) - f'(y, 1)}, \end{align} $$
$$ \begin{align} \,\,&\,\,\,\,\, P_f(x) + P_f(y) = \frac{f'(x, 0)}{f'(x,0) - f'(x, 1)} + \frac{f'(y, 0)}{f'(y,0) - f'(y, 1)}, \end{align} $$
 $$ \begin{align} &\,\,\,= \frac{f'(x,0)f'(y,0) - f'(x,0)f'(y,1) - f'(x,1)f'(y,0) +f'(x,0)f'(y,0)}{f'(x,0)f'(y,0) - f'(x,0)f'(y,1) - f'(x,1)f'(y,0) + f'(x,1)f'(y,1)}. \end{align} $$
$$ \begin{align} &\,\,\,= \frac{f'(x,0)f'(y,0) - f'(x,0)f'(y,1) - f'(x,1)f'(y,0) +f'(x,0)f'(y,0)}{f'(x,0)f'(y,0) - f'(x,0)f'(y,1) - f'(x,1)f'(y,0) + f'(x,1)f'(y,1)}. \end{align} $$
So by (18) we have
![]() $P_f(x) + P_f(y) = 1$
, that is,
$P_f(x) + P_f(y) = 1$
, that is,
as needed.Footnote 9
LP Case: Here there are three distinct possible worlds
![]() $w_1,w_2,w_3$
with:
$w_1,w_2,w_3$
with:
![]() $w_1(A)= true$
,
$w_1(A)= true$
,
![]() $w_1(\lnot A)= false$
,
$w_1(\lnot A)= false$
,
![]() $w_2(A) = false$
,
$w_2(A) = false$
,
![]() $w_2(\lnot A) = true$
,
$w_2(\lnot A) = true$
,
![]() $w_3(A) = both$
,
$w_3(A) = both$
,
![]() $w_3(\lnot A) = both$
. So by replicating the procedure above, in our move from
$w_3(\lnot A) = both$
. So by replicating the procedure above, in our move from
![]() $cr$
to
$cr$
to
![]() $cr'$
we get the following variation in accuracy in the three possible cases:
$cr'$
we get the following variation in accuracy in the three possible cases:
since
![]() when
when
![]() $w(A) = both$
in LP Gluts. At this point, if we attempt to equate these expressions to some selected negative values as above, we obtain a system of three linear equations in unknowns
$w(A) = both$
in LP Gluts. At this point, if we attempt to equate these expressions to some selected negative values as above, we obtain a system of three linear equations in unknowns
![]() $h,k$
, which does not have a solution in general.
$h,k$
, which does not have a solution in general.
The reason why Lindley’s proof does not immediately extend to non-classical settings is that the very probability axioms he is trying to justify contain implicit references to classical logical notions. For example, the definition of tautology is dependent on the notion of logical consequence: A is a tautology if and only if
![]() $\models A$
, where the double turnstile denotes the classical logical consequence. Axiom (P2) says that
$\models A$
, where the double turnstile denotes the classical logical consequence. Axiom (P2) says that
![]() $(A \lor \lnot A)$
, which is a classical tautology, ought to be believed with credence 1. However there are logical settings in which it might be reasonable to be less than certain about the truth of
$(A \lor \lnot A)$
, which is a classical tautology, ought to be believed with credence 1. However there are logical settings in which it might be reasonable to be less than certain about the truth of
![]() $(A \lor \lnot A)$
. In a treatment of scientific confirmation, for instance, it might be appropriate to have low belief in both A and
$(A \lor \lnot A)$
. In a treatment of scientific confirmation, for instance, it might be appropriate to have low belief in both A and
![]() $\lnot A$
, and to not be certain of their disjunction, if neither has received any supporting evidence [Reference Weatherson18].
$\lnot A$
, and to not be certain of their disjunction, if neither has received any supporting evidence [Reference Weatherson18].
If we want to extend Lindley’s argument, we must first understand what probabilism would look like in a non-classical setting. To this purpose we introduce Paris’s axioms [Reference Paris, De Cooman, Fine and Seidenfeld12]:
 $$ \begin{align} \begin{aligned} \models A \implies P(A) = 1, \\ A \models \implies P(A) = 0, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \models A \implies P(A) = 1, \\ A \models \implies P(A) = 0, \end{aligned} \end{align} $$
Note that this axiomatisation of probability makes explicit reference to a notion of logical consequence. When we restrict ourselves to classical logic this notion is uniquely defined, but many definitions are possible in non-classical contexts. The conclusion of my generalised accuracy argument will be that Paris’s axioms provide epistemic norms for a number of non-classical settings when logical consequence is given a no-drop characterization. This is defined as follows:
Definition 4.4 (No-drop logical consequence)
This point highlights another perspective from which to consider the generalisation of Lindley’s accuracy argument presented in this essay. As noted by Williams [Reference Williams20], the ability to support (some form of) probabilism might offer a reason to prefer the no-drop characterization of logical consequence over its alternatives, opening up an interesting connection between our epistemology and the underlying semantic theory.
Before we move on, it’s worth pointing out an important difference between Lindley’s result and what we are trying to prove. Lindley’s original argument considers conditional credences as the fundamental expression of the uncertainty of an agent. This reflects a stance in the philosophy of probability that sees conditional probability as the fundamental notion, and derives unconditional probability from it. In contrast to this view, many textbooks on probability theory, but also many philosophical treatments, take unconditional judgements as primitive and interpret axiom (A3) as a definition of conditional probability (see [Reference Easwaran, Bandyopadhyay and Forster4, Reference Hájek5] for some discussion of these two positions). While I will not go over the details of this debate here, I want to point out that, unlike Lindley’s, my argument will be limited to agents expressing unconditional beliefs. This is not because I consider unconditional belief to be more fundamental in any way, but because the relationship between conditional and unconditional probabilities in a non-classical setting is not at all straightforward. A number of different approaches are available for specifying it [Reference Williams21], and they can lead to fairly different results. Thus I will restrict myself to the simpler unconditional case. Indeed, Paris’s (P1)–(P3), which I try to justify here, do not make any reference to conditional probability. Thus my goal is not to extend Lindley’s result itself, but rather to generalize his argument strategy in order to prove a weaker result in a number of non-classical settings.
5 Non-classical generalisation: the necessary condition
It’s time to start working on our generalization of Theorem 3.2. As mentioned in the previous section, in order to transfer the argument to a non-classical setting, we need to adapt some of its assumptions. The obvious place to start is the origin and scale assumption (c): unlike in the classical case, we don’t have a perfect correspondence between truth-statuses and truth-values anymore, so we must further specify the role of truth-values as ideal aims for belief.
-
(c *) Origin and Scale assumption There are two distinct values,
 $x_0, x_1 \in \mathbb {R}$
with
$x_0, x_1 \in \mathbb {R}$
with
 $x_0 < x_1$
, such that:
$x_0 < x_1$
, such that:-
•
 $x_0$
uniquely minimises
$x_0$
uniquely minimises
 $f(x, 0)$
.
$f(x, 0)$
. -
•
 $x_1$
uniquely minimises
$x_1$
uniquely minimises
 $f(x, 1)$
.
$f(x, 1)$
.
-
This new formulation differs from the original in two ways. First, we use the names
![]() $x_0, x_1$
for our admissible values instead of
$x_0, x_1$
for our admissible values instead of
![]() $x_T, x_F$
. This is because they do not really correspond to a sentence’s truth status, but rather to the ideal belief the agent should have in it. Secondly, the way these values are defined is different. Notice that if we define
$x_T, x_F$
. This is because they do not really correspond to a sentence’s truth status, but rather to the ideal belief the agent should have in it. Secondly, the way these values are defined is different. Notice that if we define
![]() $x_0$
as in (c), it must be that
$x_0$
as in (c), it must be that
![]() $f(x, 0)$
is uniquely minimised at
$f(x, 0)$
is uniquely minimised at
![]() $x_0$
. If that were not the case, then having credence
$x_0$
. If that were not the case, then having credence
![]() $cr(A) = x_F$
when
$cr(A) = x_F$
when
![]() in every possible world would make one accuracy-dominated, and thus
in every possible world would make one accuracy-dominated, and thus
![]() $x_F$
would be inadmissible, contradicting our assumption (similarly for
$x_F$
would be inadmissible, contradicting our assumption (similarly for
![]() $x_T$
). But in the non-classical case, we might be working in a logic for which there is no
$x_T$
). But in the non-classical case, we might be working in a logic for which there is no
![]() $A \in \mathcal {F}$
such that
$A \in \mathcal {F}$
such that
![]() for all possible worlds, in which case the previous formulation of the assumption would hold vacuously. Thus we must directly assume that
for all possible worlds, in which case the previous formulation of the assumption would hold vacuously. Thus we must directly assume that
![]() $x_0$
uniquely minimises
$x_0$
uniquely minimises
![]() $f(x, 0)$
(and similarly for
$f(x, 0)$
(and similarly for
![]() $x_1$
).
$x_1$
).
We begin our generalisation by proving an analogue of Lindley [Reference Lindley9]’s Lemma 1.
Lemma 5.5. Under the assumptions
![]() $(a)$
,
$(a)$
,
![]() $(b)$
, and
$(b)$
, and
![]() $(d)$
listed in Section 3 and the assumption
$(d)$
listed in Section 3 and the assumption
![]() $(c^{*})$
above, if the credence function
$(c^{*})$
above, if the credence function
![]() $cr: \mathcal {F} \to \mathbb {R}$
is not accuracy-dominated under a reasonable inaccuracy measure f, then:
$cr: \mathcal {F} \to \mathbb {R}$
is not accuracy-dominated under a reasonable inaccuracy measure f, then:
-
1. For all
 $A \in \mathcal {F}$
,
$A \in \mathcal {F}$
,
 $cr(A) \in [x_0, x_1]$
.
$cr(A) \in [x_0, x_1]$
. -
2. The function
 $P_f: \mathbb {R} \to \mathbb {R}$
defined as in (6), takes values in
$P_f: \mathbb {R} \to \mathbb {R}$
defined as in (6), takes values in
 $[0,1]$
for
$[0,1]$
for
 $x \in [x_0, x_1]$
.
$x \in [x_0, x_1]$
. -
3.
 $P_f(x)$
is continuous in
$P_f(x)$
is continuous in
 $[x_0, x_1]$
, with
$[x_0, x_1]$
, with
 $P(x_0)=0$
and
$P(x_0)=0$
and
 $P(x_1)=1$
.
$P(x_1)=1$
.
Proof. The proof follows the original one [Reference Lindley9]. Assume
![]() $cr$
is not accuracy-dominated according to inaccuracy measure f. Let
$cr$
is not accuracy-dominated according to inaccuracy measure f. Let
![]() $A \in \mathcal {F}$
, and let
$A \in \mathcal {F}$
, and let
![]() $x := cr(A)$
. By regularity assumptions we know:
$x := cr(A)$
. By regularity assumptions we know:
If we had
![]() $x> x_1$
then both derivatives
$x> x_1$
then both derivatives
![]() $f'(x, 0), f'(x, 1)$
would be positive, and so moving to a credence
$f'(x, 0), f'(x, 1)$
would be positive, and so moving to a credence
![]() $cr'$
with
$cr'$
with
![]() $cr'(A) = cr(A) - h = x-h$
for some small positive h would guarantee a reduction of inaccuracy. But this contradicts our assumption that
$cr'(A) = cr(A) - h = x-h$
for some small positive h would guarantee a reduction of inaccuracy. But this contradicts our assumption that
![]() $cr$
is not accuracy-dominated. Likewise for
$cr$
is not accuracy-dominated. Likewise for
![]() $x < x_0$
. So we have proven the first point.
$x < x_0$
. So we have proven the first point.
Consider now the case where
![]() $x \in [x_0, x_1]$
. Decreasing the value of x will decrease
$x \in [x_0, x_1]$
. Decreasing the value of x will decrease
![]() $f(x, 0)$
(i.e., we get “closer” to the ideal belief when A has truth-value 0) but increase
$f(x, 0)$
(i.e., we get “closer” to the ideal belief when A has truth-value 0) but increase
![]() $f(x, 1)$
(i.e., we get “further away” from the ideal belief when A has truth-value 1), and vice versa when the value of x increases. We can now see from
$f(x, 1)$
(i.e., we get “further away” from the ideal belief when A has truth-value 1), and vice versa when the value of x increases. We can now see from
![]() $P_f$
’s definition that
$P_f$
’s definition that
![]() $P_f(x) \in [0, 1]$
, so the second point holds. Also, from the continuity of
$P_f(x) \in [0, 1]$
, so the second point holds. Also, from the continuity of
![]() $f'(x,y)$
, we have that
$f'(x,y)$
, we have that
![]() $P_f$
is continuous for all non-dominated degrees of belief
$P_f$
is continuous for all non-dominated degrees of belief
![]() $x \in [x_0, x_1]$
, and:
$x \in [x_0, x_1]$
, and:
 $$ \begin{align} P_f(x_0) &= \frac{f'(x_0, 0)}{f'(x_0,0) - f'(x_0, 1)}, \end{align} $$
$$ \begin{align} P_f(x_0) &= \frac{f'(x_0, 0)}{f'(x_0,0) - f'(x_0, 1)}, \end{align} $$
 $$ \begin{align} & \kern-1pt = \frac{0}{0 - f'(x_0, 1)}, \end{align} $$
$$ \begin{align} & \kern-1pt = \frac{0}{0 - f'(x_0, 1)}, \end{align} $$
and, similarly,
![]() $P_f(x_1) = 1$
. This proves the third point.
$P_f(x_1) = 1$
. This proves the third point.
From Lemma 5.5 we obtain that
![]() $P_f \circ cr$
respects (P1). We prove now that (P3) is also satisfied, employing a similar strategy to that used by Lindley for his Lemma 2. In the proof we will use the LP Gluts case as an example, and explain how analogous proofs can be constructed for the other settings under consideration.
$P_f \circ cr$
respects (P1). We prove now that (P3) is also satisfied, employing a similar strategy to that used by Lindley for his Lemma 2. In the proof we will use the LP Gluts case as an example, and explain how analogous proofs can be constructed for the other settings under consideration.
Lemma 5.6. Under the assumptions
![]() $(a)$
,
$(a)$
,
![]() $(b)$
, and
$(b)$
, and
![]() $(d)$
listed in Section 3 and the assumption
$(d)$
listed in Section 3 and the assumption
![]() $(c^{*})$
above, if the credence function
$(c^{*})$
above, if the credence function
![]() $cr: \mathcal {F} \to \mathbb {R}$
is not accuracy-dominated under a reasonable inaccuracy measure f, then for any
$cr: \mathcal {F} \to \mathbb {R}$
is not accuracy-dominated under a reasonable inaccuracy measure f, then for any
![]() $A, B \in \mathcal {F}$
:
$A, B \in \mathcal {F}$
:
Proof. Assume the credence function
![]() $cr$
is not accuracy-dominated under the inaccuracy measure f. Let
$cr$
is not accuracy-dominated under the inaccuracy measure f. Let
![]() $A,B \in \mathcal {F}$
and let
$A,B \in \mathcal {F}$
and let
![]() $x := cr(A), y := cr(B), p := cr(A \land B), s := cr(A \lor B)$
. We want to prove that
$x := cr(A), y := cr(B), p := cr(A \land B), s := cr(A \lor B)$
. We want to prove that
Applying the Definition (6) of
![]() $P_f$
and moving all the terms to the left-hand side, this becomes:
$P_f$
and moving all the terms to the left-hand side, this becomes:
 $$ \begin{align} \frac{f'(x,0)}{f'(x, 0) - f'(x, 1)} \kern1.2pt{+}\kern1.2pt \frac{f'(y,0)}{f'(y, 0) - f'(y, 1)} \kern1.2pt{-}\kern1.2pt \frac{f'(p,0)}{f'(p, 0) - f'(p, 1)} \kern1.2pt{-}\kern1.2pt \frac{f'(s,0)}{f'(s, 0) - f'(s, 1)} \kern1.2pt{=}\kern1.2pt 0. \end{align} $$
$$ \begin{align} \frac{f'(x,0)}{f'(x, 0) - f'(x, 1)} \kern1.2pt{+}\kern1.2pt \frac{f'(y,0)}{f'(y, 0) - f'(y, 1)} \kern1.2pt{-}\kern1.2pt \frac{f'(p,0)}{f'(p, 0) - f'(p, 1)} \kern1.2pt{-}\kern1.2pt \frac{f'(s,0)}{f'(s, 0) - f'(s, 1)} \kern1.2pt{=}\kern1.2pt 0. \end{align} $$
The expression on the left-hand side can be simplified to have a common denominator. Let
![]() $\phi $
be the numerator of the resulting fraction. Ultimately, then, we need to prove:
$\phi $
be the numerator of the resulting fraction. Ultimately, then, we need to prove:
Now in the case of LP Gluts, we have at most nine distinct possible worlds. These are:
 $$ \begin{align*} \begin{array}{ccccc}\hline {{{\rm World}}} & {{{\rm A}}} & {{{\rm B}}} & {{{\rm A \land B}}} & {{{\rm A \lor B}}}\\ \hline w_1 & true & true & true & true \\ w_2 & true & both & both & true \\ w_3 & true & false & false & true \\ w_4 & both & true & both & true \\ w_5 & both & both & both & both \\ w_6 & both & false & false & both \\ w_7 & false & true & false & true \\ w_8 & false & both & false & both \\ w_9 & false & false & false & false \\ \hline \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{ccccc}\hline {{{\rm World}}} & {{{\rm A}}} & {{{\rm B}}} & {{{\rm A \land B}}} & {{{\rm A \lor B}}}\\ \hline w_1 & true & true & true & true \\ w_2 & true & both & both & true \\ w_3 & true & false & false & true \\ w_4 & both & true & both & true \\ w_5 & both & both & both & both \\ w_6 & both & false & false & both \\ w_7 & false & true & false & true \\ w_8 & false & both & false & both \\ w_9 & false & false & false & false \\ \hline \end{array} \end{align*} $$
which lead to the following inaccuracy for each possible case (note that
![]() ):
):
Consider the change from credence
![]() $cr$
to a new credence
$cr$
to a new credence
![]() $cr'$
such that:
$cr'$
such that:
 $$ \begin{align*} \begin{cases} cr'(A) = cr(A) + d_1 = x + d_1, \\ cr'(B) = cr(B) + d_2 = y + d_2, \\ cr'(A \land B) = cr(A \land B) + d_3 = p + d_3, \\ cr'(A \lor B) = cr(A \lor B) + d_4 = s + d_4. \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} cr'(A) = cr(A) + d_1 = x + d_1, \\ cr'(B) = cr(B) + d_2 = y + d_2, \\ cr'(A \land B) = cr(A \land B) + d_3 = p + d_3, \\ cr'(A \lor B) = cr(A \lor B) + d_4 = s + d_4. \end{cases} \end{align*} $$
This leads to a corresponding change in the accuracy for each possible case:
Again we can equate these expressions to small, selected negative values, and obtain a linear system in unknowns
![]() $d_1, d_2, d_3, d_4$
.
$d_1, d_2, d_3, d_4$
.
However, notice that many of the system’s equations are repeated. This is no coincidence: we assumed that the truth-value assignment
![]() respects (TV1) and (TV2), which means that the truth-values of A and B are jointly sufficient to determine the truth-values of
respects (TV1) and (TV2), which means that the truth-values of A and B are jointly sufficient to determine the truth-values of
![]() $A \land B$
and
$A \land B$
and
![]() $A \lor B$
. So for any two worlds
$A \lor B$
. So for any two worlds
![]() $w_1, w_2$
such that:
$w_1, w_2$
such that:
the two expressions:
will be identical, and will produce identical inequalities in our linear system. Because we restrict the truth-values of sentences to the two values
![]() $\{0,1\}$
, once we get rid of duplicates we will have at most four equalities in our linear system, regardless of which non-classical setting we are working with.
$\{0,1\}$
, once we get rid of duplicates we will have at most four equalities in our linear system, regardless of which non-classical setting we are working with.
This gives us a system of four linear equations in four unknowns.
Since we assumed that
![]() $cr$
is not accuracy-dominated under f, this system cannot have a solution, since in that case the shift to
$cr$
is not accuracy-dominated under f, this system cannot have a solution, since in that case the shift to
![]() $cr'$
would reduce inaccuracy in every possible world. So the system’s determinant must be equal to zero. But the determinant is precisely the expression
$cr'$
would reduce inaccuracy in every possible world. So the system’s determinant must be equal to zero. But the determinant is precisely the expression
![]() $\phi $
obtained in the first part of the proof. We conclude that
$\phi $
obtained in the first part of the proof. We conclude that
![]() $\phi = 0$
, and therefore
$\phi = 0$
, and therefore
![]() $P_f(x) + P_f(y) = P_f(p) + P_f(s)$
as needed (boundary cases are discussed in the Appendix).
$P_f(x) + P_f(y) = P_f(p) + P_f(s)$
as needed (boundary cases are discussed in the Appendix).
Note how in the proof above each equation of the reduced
![]() $4\times 4$
system corresponds to one of the four possible classical worlds. Indeed, the result holds for the classical setting as a particular case of the more general non-classical,
$4\times 4$
system corresponds to one of the four possible classical worlds. Indeed, the result holds for the classical setting as a particular case of the more general non-classical,
![]() $\{0,1\}$
-valued one. In order to prove that (P2) also holds for the transform, we apply a similar technique, with the key difference that we are dealing with inequalities rather than with equations. Again, the the proof for LP Gluts is shown as an example of the general strategy.
$\{0,1\}$
-valued one. In order to prove that (P2) also holds for the transform, we apply a similar technique, with the key difference that we are dealing with inequalities rather than with equations. Again, the the proof for LP Gluts is shown as an example of the general strategy.
Lemma 5.7. Under the assumptions
![]() $(a)$
,
$(a)$
,
![]() $(b)$
, and
$(b)$
, and
![]() $(d)$
listed in Section 3 and the assumption
$(d)$
listed in Section 3 and the assumption
![]() $(c^{*})$
above, if the credence
$(c^{*})$
above, if the credence
![]() $cr: \mathcal {F} \to \mathbb {R}$
is not accuracy-dominated according to an acceptable inaccuracy score f, then for any
$cr: \mathcal {F} \to \mathbb {R}$
is not accuracy-dominated according to an acceptable inaccuracy score f, then for any
![]() $A, B \in \mathcal {F}$
:
$A, B \in \mathcal {F}$
:
Proof. Let
![]() $x := cr(A)$
and
$x := cr(A)$
and
![]() $y := cr(B)$
, and we know that
$y := cr(B)$
, and we know that
![]() $A \models B$
. Since
$A \models B$
. Since
![]() $cr$
is admissible, Lemma 5.5 tells us that
$cr$
is admissible, Lemma 5.5 tells us that
![]() $x, y \in [x_0, x_1]$
. First consider the case where
$x, y \in [x_0, x_1]$
. First consider the case where
![]() $x = x_1$
. This value is admissible only when
$x = x_1$
. This value is admissible only when
![]() for all possible worlds w. Furthermore, from Lemma 5.5 we have that
for all possible worlds w. Furthermore, from Lemma 5.5 we have that
![]() $P_f(x) = P_f(x_1) = 1$
. We know from the no-drop characterization of
$P_f(x) = P_f(x_1) = 1$
. We know from the no-drop characterization of
![]() $\models $
that
$\models $
that
![]() $A \models B$
iff
$A \models B$
iff
![]() for all
for all
![]() $w \in W$
. Therefore it must be that
$w \in W$
. Therefore it must be that
![]() for all possible w in the current non-classical interpretation. But then the only admissible value for y is
for all possible w in the current non-classical interpretation. But then the only admissible value for y is
![]() $x_1$
and
$x_1$
and
![]() $P_f(y) = P_f(x_1) = 1$
. So:
$P_f(y) = P_f(x_1) = 1$
. So:
as needed.
In the case where
![]() $x = x_0$
, we have from Lemma 5.5 that
$x = x_0$
, we have from Lemma 5.5 that
![]() $P(x)=0$
, and since in the same lemma we proved that
$P(x)=0$
, and since in the same lemma we proved that
![]() $P_f(y) \in [0,1]$
for all admissible y, it clearly holds that
$P_f(y) \in [0,1]$
for all admissible y, it clearly holds that
![]() $P(x) \leq P(y)$
. Footnote
10
$P(x) \leq P(y)$
. Footnote
10
Consider now the case where
![]() $x, y \in (x_0, x_1)$
. We want to prove that
$x, y \in (x_0, x_1)$
. We want to prove that
![]() $P_f(x) \leq P_f(y)$
, which by definition of
$P_f(x) \leq P_f(y)$
, which by definition of
![]() $P_f$
means:
$P_f$
means:
 $$ \begin{align} \frac{f'(x, 0)}{f'(x,0) - f'(x, 1)} \leq \frac{f'(y, 0)}{f'(y,0) - f'(y, 1)}, \end{align} $$
$$ \begin{align} \frac{f'(x, 0)}{f'(x,0) - f'(x, 1)} \leq \frac{f'(y, 0)}{f'(y,0) - f'(y, 1)}, \end{align} $$
since the denominators are both positive and greater than
![]() $0$
we can simplify to:
$0$
we can simplify to:
this inequality is what we are going prove.
We know that
![]() $A \models B$
, so in the case of LP Gluts we have at most seven possible worlds:
$A \models B$
, so in the case of LP Gluts we have at most seven possible worlds:

For
![]() $i = 1, \ldots ,7$
the total inaccuracy at world
$i = 1, \ldots ,7$
the total inaccuracy at world
![]() $w_i$
is given by:
$w_i$
is given by:
As in the previous proof, consider the change in the total inaccuracy when we move from
![]() $cr$
to
$cr$
to
![]() $cr'$
by changing the credence in
$cr'$
by changing the credence in
![]() $A, B$
of small quantities
$A, B$
of small quantities
![]() $h, k$
respectively. By imposing that this inaccuracy change be less then zero we obtain a system of seven inequalities. Once again, we see that some of these inequalities are duplicates. Regardless of which one of the non-classical settings under consideration we are working on, we are forced to assign truth-values in
$h, k$
respectively. By imposing that this inaccuracy change be less then zero we obtain a system of seven inequalities. Once again, we see that some of these inequalities are duplicates. Regardless of which one of the non-classical settings under consideration we are working on, we are forced to assign truth-values in
![]() $\{0,1\}$
to A and B, and because of the no-drop characterization of logical consequence, a world where
$\{0,1\}$
to A and B, and because of the no-drop characterization of logical consequence, a world where
and
is not possible. So we always obtain a system of at most three inequalities:
 $$ \begin{align} \begin{cases} k f'(x, 0) + h f'(y, 0) < 0,\\ k f'(x, 0) + h f'(y, 1) < 0,\\ k f'(x, 1) + h f'(y, 1) < 0. \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} k f'(x, 0) + h f'(y, 0) < 0,\\ k f'(x, 0) + h f'(y, 1) < 0,\\ k f'(x, 1) + h f'(y, 1) < 0. \end{cases} \end{align} $$
Since by regularity assumptions
![]() $f'(y, 0)> 0$
for all
$f'(y, 0)> 0$
for all
![]() $y \in (x_0,x_1)$
, the first inequality becomes:
$y \in (x_0,x_1)$
, the first inequality becomes:
 $$ \begin{align} h < -k \frac{f'(x, 0)}{f'(y, 0)}, \end{align} $$
$$ \begin{align} h < -k \frac{f'(x, 0)}{f'(y, 0)}, \end{align} $$
and the angular coefficient of the corresponding equation is negative, because
![]() $f'(x, 0)> 0$
. Similarly, the second inequality becomes:
$f'(x, 0)> 0$
. Similarly, the second inequality becomes:
 $$ \begin{align} h> -k \frac{f'(x, 0)}{f'(y, 1)}, \end{align} $$
$$ \begin{align} h> -k \frac{f'(x, 0)}{f'(y, 1)}, \end{align} $$
where
![]() ${f'(y, 1)} < 0$
and so the corresponding angular coefficient is positive. Figure A.1 in the Appendix shows the space of the solutions of these two inequalities. The third inequality becomes:
${f'(y, 1)} < 0$
and so the corresponding angular coefficient is positive. Figure A.1 in the Appendix shows the space of the solutions of these two inequalities. The third inequality becomes:
 $$ \begin{align} h> -k \frac{f'(x, 1)}{f'(y, 1)}, \end{align} $$
$$ \begin{align} h> -k \frac{f'(x, 1)}{f'(y, 1)}, \end{align} $$
and the corresponding equation has negative angular coefficient. The space of the solutions of the system is the one highlighted in Figure A.2 in the Appendix.
If this system had a solution, then changing from
![]() $cr$
to
$cr$
to
![]() $cr'$
would guarantee us greater accuracy no matter what, which is absurd because
$cr'$
would guarantee us greater accuracy no matter what, which is absurd because
![]() $cr$
is assumed to not be accuracy-dominated. So the space of solutions must be empty, which happens when:
$cr$
is assumed to not be accuracy-dominated. So the space of solutions must be empty, which happens when:
 $$ \begin{align} - \frac{f'(x, 1)}{f'(y, 1)} \leq - \frac{f'(x, 0)}{f'(y, 0)}, \end{align} $$
$$ \begin{align} - \frac{f'(x, 1)}{f'(y, 1)} \leq - \frac{f'(x, 0)}{f'(y, 0)}, \end{align} $$
that is, when:
This is exactly the inequality we needed to prove.
Combining the three lemmas above, we get a result analogous to Lindley’s Theorem 1 [Reference Lindley9]:
Theorem 5.8. Under the assumptions
![]() $(a)$
,
$(a)$
,
![]() $(b)$
, and
$(b)$
, and
![]() $(d)$
listed in Section 3 and the assumption
$(d)$
listed in Section 3 and the assumption
![]() $(c^{*})$
above, if
$(c^{*})$
above, if
![]() $cr: \mathcal {F} \to \mathbb {R}$
is not accuracy-dominated according to a reasonable inaccuracy measure f, then the transform
$cr: \mathcal {F} \to \mathbb {R}$
is not accuracy-dominated according to a reasonable inaccuracy measure f, then the transform
![]() $(P_f \circ cr): \mathcal {F} \to \mathbb {R}$
, where
$(P_f \circ cr): \mathcal {F} \to \mathbb {R}$
, where
![]() $P_f$
is defined as in (6), obeys Paris’s probability axioms (P1)–(P3).
$P_f$
is defined as in (6), obeys Paris’s probability axioms (P1)–(P3).
This result, together with our assumption (Non-Dominance) that avoiding accuracy-domination is a necessary requirement for rationality, shows that all rational credences must have a probabilistic transform in the logical settings under discussion.
6 Sufficient conditions
Let us take a moment to look back at the main result of the previous section, Theorem 5.8 It has the typical form of the accuracy theorems discussed in Section 2: starting from some assumptions on what counts as a reasonable measure of inaccuracy, we have shown that in order to avoid accuracy-domination, a credence’s transform must respect Paris’s probability axioms (P1)–(P3). If we take Non-Dominance as a rationality requirement for credences, we can then conclude that having a probabilistic transform is a necessary condition for rationality.
It is natural to ask at this point whether the probability axioms also provide a sufficient condition for rationality. If we pose the question in this form, however, the answer will have to be no. There are plenty of cases where holding a certain credence whose canonical transform is probabilistic makes one irrational. We don’t need to move to non-classical logics to find examples of this. Imagine you have an urn in front of you, which you know contains five red balls and five black balls. You extract a ball from the urn after it has been shaken. We would like to say that, if you are rational, then
![]() $P_f$
should transform your credence into a probability that assigns value 1/2 to the sentence “the next extracted ball will be red.” Any other credence, whether it has probabilistic transform or not, seems irrational in this case, as it would go against your evidence.
$P_f$
should transform your credence into a probability that assigns value 1/2 to the sentence “the next extracted ball will be red.” Any other credence, whether it has probabilistic transform or not, seems irrational in this case, as it would go against your evidence.
So we must reformulate our question. What we want to ask is: is having a credence whose transform respects the probability axioms a sufficient condition for avoiding the kind of irrationality that follows from a violation of Non-Dominance? In other words, is every
![]() $cr$
with a probabilistic transform safe from accuracy-domination?
$cr$
with a probabilistic transform safe from accuracy-domination?
We can think of the question above as a sanity check on the assumptions we used to prove our accuracy theorem. If it turns out that some intuitively reasonable credences with probabilistic transforms are accuracy-dominated, we should probably conclude that our measures of inaccuracy are inadequate, or that the Non-dominance requirement is too demanding. Joyce [Reference Joyce7] seems to view the question in this way when he discusses it in the context of his own accuracy argument for probabilism, in the classical setting. Indeed, he responds by arguing that no inaccuracy measure can be reasonable if it makes some probabilistic credence accuracy-dominated, and defines his measures of inaccuracy accordingly. But the fundamental problem is only pushed back by this answer. A new question arises: why should we require our measures of inaccuracy to protect probabilities from domination, and not some other class of credences?
Although Joyce [Reference Joyce7] does attempt to answer this second question, I will not spend more time on his reply here. Instead, I want to look at how this same problem affects arguments for non-classical versions of probabilism. Here Joyce’s reply sounds much less appealing: compared to the classical case, there is even less of a consensus that any class of credences is so intuitively rational that we ought to tailor our inaccuracy measures around it. Perhaps this is the reason why Williams [Reference Williams20] seems unwilling to pursue this strategy in his generalisation of Joyce’s argument. Instead, he responds to the overdemandingness problem by trying to contain the damage it may cause. It would be fatal for his argument if it turned out that every reasonable inaccuracy measure made some (non-classically) probabilistic credences accuracy-dominated. Luckily, Williams is able to show that this is not the case by showing that there is an inaccuracy measure, known as the Brier score, under which all (non-classical) probabilities are safe from accuracy-domination.Footnote 11
I want to extend this result and show that, for a class of inaccuracy measures that respect the assumptions of Theorem 5.8, all credences whose transformed is probabilistic are safe from accuracy-domination. Interestingly, this class contains many proper scoring rules, including the Brier score, while still being strictly smaller than the class of all inaccuracy measures which we consider reasonable. Once again, this result is the generalization of a theorem due to Lindley [Reference Lindley9].
We start by defining the class of rules for which we will prove that credences with a probabilistic transform avoid accuracy-domination.
Definition 6.9. (Single-valued score)
An inaccuracy measure f is single-valued iff for every
![]() $p \in [0,1]$
the equation:
$p \in [0,1]$
the equation:
in unknown x has a unique solution.
In proving our result we rely on the following theorem by Paris [Reference Paris, De Cooman, Fine and Seidenfeld12]. We only report the theorem’s statement here, adapting its notation to the present context.
Theorem 6.10 (Paris [Reference Paris, De Cooman, Fine and Seidenfeld12])
Assume we are in a logical setting such that:
-
1. The set of truth-values is
 $\{0,1\}$
.
$\{0,1\}$
. -
2.
 $\models $
is given the no-drop characterization (25).
$\models $
is given the no-drop characterization (25). -
3. For each possible world
 $w \in W$
, the corresponding truth-value assignment function
$w \in W$
, the corresponding truth-value assignment function
 satisfies (TV1) and (TV2).
satisfies (TV1) and (TV2).
Let
![]() $P : \mathcal {F} \to \mathbb {R}$
. Then P obeys Paris’s probability axioms (P1)–(P3) on
$P : \mathcal {F} \to \mathbb {R}$
. Then P obeys Paris’s probability axioms (P1)–(P3) on
![]() $\mathcal {F}$
if and only if, for every finite subset
$\mathcal {F}$
if and only if, for every finite subset
![]() $\mathcal {G} \subseteq \mathcal {F}$
, we have that
$\mathcal {G} \subseteq \mathcal {F}$
, we have that
![]() $P \restriction \mathcal {G}$
is a convex combination of the set of restricted truth-value assignments
$P \restriction \mathcal {G}$
is a convex combination of the set of restricted truth-value assignments
![]() .
.
Since we have been restricting ourselves to the logical settings that satisfy the assumptions of Theorem 6.10, we can use it to prove the following result.
Theorem 6.11. Under the assumptions
![]() $(a)$
,
$(a)$
,
![]() $(b)$
, and
$(b)$
, and
![]() $(d)$
listed in Section 3 and the assumption
$(d)$
listed in Section 3 and the assumption
![]() $(c^{*})$
in Section 4, let f be a reasonable single-valued scoring rule and
$(c^{*})$
in Section 4, let f be a reasonable single-valued scoring rule and
![]() $cr$
a credence such that its canonical transform
$cr$
a credence such that its canonical transform
![]() $P_f \circ cr$
obeys Paris’s probability axioms (P1)–(P3). Then
$P_f \circ cr$
obeys Paris’s probability axioms (P1)–(P3). Then
![]() $cr$
is not accuracy-dominated on any finite set
$cr$
is not accuracy-dominated on any finite set
![]() $\mathcal {G} \subseteq \mathcal {F}$
when accuracy is measured according to f.
$\mathcal {G} \subseteq \mathcal {F}$
when accuracy is measured according to f.
Proof. Assume f is single-valued, and assume
![]() $P = P_f \circ cr$
respects (P1)–(P3). Let
$P = P_f \circ cr$
respects (P1)–(P3). Let
![]() $\mathcal {G} \subseteq \mathcal {F}$
be a finite set of sentences. Then by Paris’s Theorem 6.10 we know that
$\mathcal {G} \subseteq \mathcal {F}$
be a finite set of sentences. Then by Paris’s Theorem 6.10 we know that
![]() $P \restriction \mathcal {G}$
can be written as a convex combination of the set of restricted valuations
$P \restriction \mathcal {G}$
can be written as a convex combination of the set of restricted valuations
![]() , that is:
, that is:

where
![]() is the set of restricted valuations, and
is the set of restricted valuations, and
![]() $\lambda _i \geq 0$
for all
$\lambda _i \geq 0$
for all
![]() $i = 1, \ldots , n$
. We can think of the
$i = 1, \ldots , n$
. We can think of the
![]() $\lambda _i$
as defining a standard probability function
$\lambda _i$
as defining a standard probability function
![]() $\Pi $
over a possibility space consisting of the worlds
$\Pi $
over a possibility space consisting of the worlds
![]() $\{w_1, \ldots , w_n\}$
Footnote
12
:
$\{w_1, \ldots , w_n\}$
Footnote
12
:
It then makes sense to ask for the expected score of assigning credence x to A according to
![]() $\Pi $
. This quantity is given by:
$\Pi $
. This quantity is given by:
where A is used as an indicator variable over
![]() $\{w_1, \ldots , w_n\}$
. Because of our regularity assumptions, we know that
$\{w_1, \ldots , w_n\}$
. Because of our regularity assumptions, we know that
![]() $Exp_{\Pi }[f(x, A)]$
is continuous as a function of x in
$Exp_{\Pi }[f(x, A)]$
is continuous as a function of x in
![]() $[x_0, x_1]$
, and its derivative is positive for
$[x_0, x_1]$
, and its derivative is positive for
![]() $x> x_T$
and negative for
$x> x_T$
and negative for
![]() $x < x_0$
. So
$x < x_0$
. So
![]() $Exp_{\Pi }[f(x, A)]$
must have some minimum in
$Exp_{\Pi }[f(x, A)]$
must have some minimum in
![]() $[x_0, x_1]$
, which we can find by looking at its derivative:
$[x_0, x_1]$
, which we can find by looking at its derivative:
 $$ \begin{align} & \,\, = \left(\sum_{i :\,\, w_i(A) = 1} \lambda_i\right) f'(x, 1) + \left(1 - \left(\sum_{i :\,\, w_i(A) = 1} \lambda_i\right)\right) f'(x, 0). \end{align} $$
$$ \begin{align} & \,\, = \left(\sum_{i :\,\, w_i(A) = 1} \lambda_i\right) f'(x, 1) + \left(1 - \left(\sum_{i :\,\, w_i(A) = 1} \lambda_i\right)\right) f'(x, 0). \end{align} $$
This derivative equals zero just in case
 $$ \begin{align*} \sum_{i :\,\, w_i(A) = 1} \lambda_i = \frac{f'(x, 0)}{f'(x,0) - f'(x, 1)}, \end{align*} $$
$$ \begin{align*} \sum_{i :\,\, w_i(A) = 1} \lambda_i = \frac{f'(x, 0)}{f'(x,0) - f'(x, 1)}, \end{align*} $$
that is, just in case
![]() $P(A) = P_f(x)$
. But as f is single-valued, this is true for exactly one x, since
$P(A) = P_f(x)$
. But as f is single-valued, this is true for exactly one x, since
![]() $P_f(x) \in [0,1]$
whenever
$P_f(x) \in [0,1]$
whenever
![]() $x \in [x_0, x_1]$
by Lemma 5.5. We conclude that
$x \in [x_0, x_1]$
by Lemma 5.5. We conclude that
![]() $x = cr(A)$
uniquely minimizes expected score according to
$x = cr(A)$
uniquely minimizes expected score according to
![]() $\Pi $
on each
$\Pi $
on each
![]() $A \in \mathcal {G}$
.
$A \in \mathcal {G}$
.
Now assume by way of contradiction that
![]() $cr \restriction \mathcal {G}$
is accuracy-dominated on
$cr \restriction \mathcal {G}$
is accuracy-dominated on
![]() $\mathcal {G}$
by some other function
$\mathcal {G}$
by some other function
![]() $cr'$
. So the inequality:
$cr'$
. So the inequality:
holds on each
![]() $w_i$
, and is strict for at least one i. But then the inequality must also hold for
$w_i$
, and is strict for at least one i. But then the inequality must also hold for
![]() $\Pi $
’s expectations of these scores; that is, thinking of
$\Pi $
’s expectations of these scores; that is, thinking of
![]() $f(cr, w)$
and
$f(cr, w)$
and
![]() $f(cr', w)$
as random variables over
$f(cr', w)$
as random variables over
![]() $\{w_1, \ldots , w_n\}$
:
$\{w_1, \ldots , w_n\}$
:

where
![]() $\mathcal {G} = \{A_1, \ldots , A_m\}$
. We can swap the order of the sums to obtain:
$\mathcal {G} = \{A_1, \ldots , A_m\}$
. We can swap the order of the sums to obtain:

We can remove from the above inequality all terms associated to the
![]() $A_j$
’s for which
$A_j$
’s for which
![]() $cr(A_j) = cr'(A_j)$
, since they will be equal on both sides. Then for the inequality to hold, it must be that for at least one of the remaining
$cr(A_j) = cr'(A_j)$
, since they will be equal on both sides. Then for the inequality to hold, it must be that for at least one of the remaining
![]() $A_j$
we have:
$A_j$
we have:

but this is a contradiction, given that
![]() $cr(A)$
uniquely minimizes expected score according to
$cr(A)$
uniquely minimizes expected score according to
![]() $\Pi $
on each
$\Pi $
on each
![]() $A \in \mathcal {G}$
.
$A \in \mathcal {G}$
.
This theorem shows that, in the non-classical settings we have been working with, single-valued inaccuracy scores make all credences whose canonical transform respects (P1)–(P3) safe from domination. It’s easy to see that all proper inaccuracy measures which respect our regularity assumptions are single-valued, given that when f is proper in the sense of Definition 2.1,
![]() $P_f$
is just the identity function. Although we cannot dispel the worry that, under some reasonable inaccuracy measures, some credences whose transform is probabilistic are accuracy-dominated, we have at least shown that for a large class of these measures (which includes all those that are proper) this does not happen.
$P_f$
is just the identity function. Although we cannot dispel the worry that, under some reasonable inaccuracy measures, some credences whose transform is probabilistic are accuracy-dominated, we have at least shown that for a large class of these measures (which includes all those that are proper) this does not happen.
7 Some open questions
A number of non-classical logics have not been discussed in this paper. This is because the generalization of Lindley’s argument, if it is possible, is not as straightforward in these settings. I will not provide such a generalization in this paper. But I want to use this section to discuss the kind of additional adjustments that such a task might require, and highlight the difficulties it presents.
An example of a logical setting whose truth-values are
![]() $\{0,1\}$
but the conditions (TV1) and (TV2) are not satisfied is the Gap Supervaluation one (see Appendix for a definition). Here the three axioms (P1)–(P3) do not characterize closed convex combinations of truth-value distributions. Paris [Reference Paris, De Cooman, Fine and Seidenfeld12] shows that in this case the axioms should be:
$\{0,1\}$
but the conditions (TV1) and (TV2) are not satisfied is the Gap Supervaluation one (see Appendix for a definition). Here the three axioms (P1)–(P3) do not characterize closed convex combinations of truth-value distributions. Paris [Reference Paris, De Cooman, Fine and Seidenfeld12] shows that in this case the axioms should be:
 $$ \begin{align} \begin{split} \models A \implies P(A) = 1, \\ A \models \implies P(A) = 0, \end{split} \end{align} $$
$$ \begin{align} \begin{split} \models A \implies P(A) = 1, \\ A \models \implies P(A) = 0, \end{split} \end{align} $$
 $$ \begin{align} P\left(\bigvee_{i=1}^{m}A_i\right) = \sum_S(-1)^{|S|-1} P\left(\bigwedge_{i \in S} A_i\right), \end{align} $$
$$ \begin{align} P\left(\bigvee_{i=1}^{m}A_i\right) = \sum_S(-1)^{|S|-1} P\left(\bigwedge_{i \in S} A_i\right), \end{align} $$
where
![]() $A, B, A_1, \ldots , A_m \in \mathcal {F}$
, and S ranges over the non-empty subsets of
$A, B, A_1, \ldots , A_m \in \mathcal {F}$
, and S ranges over the non-empty subsets of
![]() $\{1,2, \ldots , m\}$
. And even this result holds only for specific languages, as Williams [Reference Williams20] notes. In supervaluation settings, more sophisticated axioms seem necessary in order to account for variation in the expressive power of the language.
$\{1,2, \ldots , m\}$
. And even this result holds only for specific languages, as Williams [Reference Williams20] notes. In supervaluation settings, more sophisticated axioms seem necessary in order to account for variation in the expressive power of the language.
Other logical settings, such as the Finite and Infinite Fuzzy (see Appendix for their definition) violate our assumptions by having truth-values outside of
![]() $\{0,1\}$
. Here the axioms (P1)–(P3) do pick out closed convex combinations of truth values [Reference Di Nola, Georgescu, Lettieri, Dubois, Prade and Klement3, Reference Mundici11]. However, extending Lindley’s argument to non-classical settings with truth values beyond
$\{0,1\}$
. Here the axioms (P1)–(P3) do pick out closed convex combinations of truth values [Reference Di Nola, Georgescu, Lettieri, Dubois, Prade and Klement3, Reference Mundici11]. However, extending Lindley’s argument to non-classical settings with truth values beyond
![]() $\{0,1\}$
requires a more radical modification of his inaccuracy measures.
$\{0,1\}$
requires a more radical modification of his inaccuracy measures.
The origin and score assumption (c) needs additional credence values to represent the certainty of a proposition being in any of the different truth statuses. For example, in a Finite Fuzzy setting with truth statuses
![]() $S = \{0, 1/n, 2/n, \ldots , (n-1)/n, 1\}$
we need values
$S = \{0, 1/n, 2/n, \ldots , (n-1)/n, 1\}$
we need values
![]() $x_0, x_{1/n}, \ldots , x_{((n-1)/n)}, x_1$
so that
$x_0, x_{1/n}, \ldots , x_{((n-1)/n)}, x_1$
so that
![]() $x_i$
is the only admissible value for
$x_i$
is the only admissible value for
![]() $cr(p)$
when
$cr(p)$
when
![]() for all
for all
![]() $w \in W$
. New questions arise concerning these additional values, and how they should be distributed: should there be a requirement that
$w \in W$
. New questions arise concerning these additional values, and how they should be distributed: should there be a requirement that
![]() $x_{1/2}$
be equidistant from
$x_{1/2}$
be equidistant from
![]() $x_0$
and
$x_0$
and
![]() $x_1$
, or can it be placed anywhere between them, as long as it is greater than
$x_1$
, or can it be placed anywhere between them, as long as it is greater than
![]() $x_{1/4}$
and lower than
$x_{1/4}$
and lower than
![]() $x_{3/4}$
? The fact that
$x_{3/4}$
? The fact that
![]() $x_0, x_1$
should maintain a special status is suggested by their role in the first axiom.
$x_0, x_1$
should maintain a special status is suggested by their role in the first axiom.
The regularity (d) assumptions and, more importantly, the definition of
![]() $P_f$
(6), should also be adapted to take the new truth-values into account. In fact, the value of the original transform depends only on the derivatives
$P_f$
(6), should also be adapted to take the new truth-values into account. In fact, the value of the original transform depends only on the derivatives
![]() $f'(x, 0), f'(x, 1)$
, which does not seem right in this context. Whether it’s possible to generalize the definition of
$f'(x, 0), f'(x, 1)$
, which does not seem right in this context. Whether it’s possible to generalize the definition of
![]() $P_f$
to include more than two truth-values, and what this generalization would look like, remain open questions.
$P_f$
to include more than two truth-values, and what this generalization would look like, remain open questions.
8 Conclusion
Philosophers have argued for probabilism in many ways. Among them, accuracy-based arguments provide some of the most interesting justifications, but their assumptions are not at all uncontroversial. Thus it is interesting to explore how much we can relax these assumptions, while still deriving from them some meaningful epistemic norms. Lindley’s argument answers this question differently depending on one’s position regarding the nature of credence. Those who see credences as a mere convention for discussing human beliefs and who do not distinguish between structurally similar credence functions, will find that Lindley’s assumptions are sufficient to derive probabilism as they intend it. Those who maintain that, on the contrary, numeric representations capture some key features of belief, will have to face just how strong of a foundation is needed to support full-blown probabilism.
In this paper I have adapted Lindley’s argument for probabilism as a necessary condition for rationality to a number of unconditional, non-classical settings that were excluded from the original result. I have also specified a class of inaccuracy measures for which Lindley’s version of probabilism is sufficient to avoid accuracy-domination. These generalisations are relevant for three main reasons. First, they allow to justify probabilism as a theory of rationality for all fields of research where it might be appropriate to step outside the boundaries of classical logic. Secondly, they might give philosophers in these fields some reason to prefer a no-drop characterisation of non-classical logical consequence, since this is fruitfully connected with probabilistic epistemology. Lastly, they highlight a strong connection between our measures of inaccuracy and the underlying logic. This connection is visible in the way Lindley’s origin and score assumption was adapted to the
![]() $\{0,1\}$
-valued non-classical case, and in the issues caused by the multiplicity of truth values in the supervaluational and fuzzy settings. It remains to be seen whether Lindley’s argument can be generalised to multi-valued settings of this kind, and whether it can support (some form of) conditional probability in the non-classical case. This paper may be considered as a starting point for future work on this topic.
$\{0,1\}$
-valued non-classical case, and in the issues caused by the multiplicity of truth values in the supervaluational and fuzzy settings. It remains to be seen whether Lindley’s argument can be generalised to multi-valued settings of this kind, and whether it can support (some form of) conditional probability in the non-classical case. This paper may be considered as a starting point for future work on this topic.
A Appendix
1.1 Figures

Fig. A.1 Solutions of the first two inequalities. In this example
![]() $x = 0.6, y = 0.4$
, and f is the Brier score (MATLAB figure).
$x = 0.6, y = 0.4$
, and f is the Brier score (MATLAB figure).

Fig. A.2 Solutions of the whole system. In this example
![]() $x = 0.6, y = 0.4$
, and f is the Brier score (MATLAB figure).
$x = 0.6, y = 0.4$
, and f is the Brier score (MATLAB figure).
1.2 Proof of Lemma 5.6—Boundary cases
The proof above doesn’t work for boundary cases, for example when
![]() in all possible worlds. This is because
in all possible worlds. This is because
![]() $cr(A) = x = x_1$
in this case, so by defining
$cr(A) = x = x_1$
in this case, so by defining
![]() $cr'(A) = x + d_1$
we might go outside the interval
$cr'(A) = x + d_1$
we might go outside the interval
![]() $[x_0, x_1]$
of admissible values (first point of Lemma 5.5). Let’s once again take the LP Gluts setting as an example for our proof.
$[x_0, x_1]$
of admissible values (first point of Lemma 5.5). Let’s once again take the LP Gluts setting as an example for our proof.
In this case, the possible worlds are limited to the following:
 $$ \begin{align*} \begin{array}{ccccc} \hline {{{\rm World}}} & {{{\rm A}}} & {{{\rm B}}} & {{{\rm A \land B}}} & {{{\rm A \lor B}}}\\ \hline w_1 & true & true & true & true\\ w_2 & true & both & both & true\\ w_3 & true & false & false & true\\ w_4 & both & true & both & true\\ w_5 & both & both & both & both\\ w_6 & both & false & false & both\\ \hline \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{ccccc} \hline {{{\rm World}}} & {{{\rm A}}} & {{{\rm B}}} & {{{\rm A \land B}}} & {{{\rm A \lor B}}}\\ \hline w_1 & true & true & true & true\\ w_2 & true & both & both & true\\ w_3 & true & false & false & true\\ w_4 & both & true & both & true\\ w_5 & both & both & both & both\\ w_6 & both & false & false & both\\ \hline \end{array} \end{align*} $$
Giving rise to the following inaccuracy measures:
But since we know
![]() $x=x_1$
, by origin and scale assumptions we have
$x=x_1$
, by origin and scale assumptions we have
![]() $f'(x, 1)=0$
. And not only that, because the fact that
$f'(x, 1)=0$
. And not only that, because the fact that
![]() in all these worlds means that for
in all these worlds means that for
![]() $cr$
to be acceptable it must be
$cr$
to be acceptable it must be
![]() $cr(A \lor B) = s = x_1$
. Thus any admissible
$cr(A \lor B) = s = x_1$
. Thus any admissible
![]() $cr'$
must be defined as follows:
$cr'$
must be defined as follows:
 $$ \begin{align*}\begin{cases} cr'(A) = cr(A) = x = x_1, \\ cr'(B) = cr(B) + d_2 = y + d_2, \\ cr'(A \land B) = cr(A \land B) + d_3 = p + d_3, \\ cr'(A \lor B) = cr(A \lor B) = s = x_1, \end{cases} \end{align*} $$
$$ \begin{align*}\begin{cases} cr'(A) = cr(A) = x = x_1, \\ cr'(B) = cr(B) + d_2 = y + d_2, \\ cr'(A \land B) = cr(A \land B) + d_3 = p + d_3, \\ cr'(A \lor B) = cr(A \lor B) = s = x_1, \end{cases} \end{align*} $$
for some
![]() $d_2,d_3 \in \mathbb {R}$
.
$d_2,d_3 \in \mathbb {R}$
.
Proceeding as in the main proof, we obtain the following variation of accuracy in moving from
![]() $cr$
to
$cr$
to
![]() $cr'$
:
$cr'$
:
And through the same reasoning we find that to avoid accuracy domination it must be:
This is equivalent to:
But by Lemma 5.5 we know
![]() $P(x) = 1 = P(s)$
in this case. Combining this with (A.14) we get
$P(x) = 1 = P(s)$
in this case. Combining this with (A.14) we get
![]() $P(x) + P(y) = P(p) + P(s)$
as needed. Other boundary cases are dealt with similarly.
$P(x) + P(y) = P(p) + P(s)$
as needed. Other boundary cases are dealt with similarly.
1.3 Other non-classical settings
Here are defined the nonclassical settings mentioned in Sections 4 and 7. The definitions follow those in Williams [Reference Williams20].
-
• Kleene gaps:
-
–
 $S := \{\text {true, neither, false}\}. $
$S := \{\text {true, neither, false}\}. $
-
– The truth-value mapping
 is defined by:
is defined by: 
-
– The connectives
 $\land , \lnot $
follow the rules:
$\land , \lnot $
follow the rules:  $$ \begin{align*}w(A \land B) = \begin{cases} \text{true,} \qquad \text{if} \; w(A) = \text{true} \; \text{and} \; w(B) = \text{true}, \\ \text{false,} \qquad \text{if} \; w(A) = \text{false} \; \text{or} \; w(B) = \text{false}, \\ \text{neither,} \qquad \text{otherwise}. \end{cases}\end{align*} $$
$$ \begin{align*}w(A \land B) = \begin{cases} \text{true,} \qquad \text{if} \; w(A) = \text{true} \; \text{and} \; w(B) = \text{true}, \\ \text{false,} \qquad \text{if} \; w(A) = \text{false} \; \text{or} \; w(B) = \text{false}, \\ \text{neither,} \qquad \text{otherwise}. \end{cases}\end{align*} $$
 $$ \begin{align*}w(\lnot A) = \begin{cases} \text{true,} \qquad \text{if} \; w(A) = \text{false}, \\ \text{false,} \qquad \text{if} \; w(A) = \text{true}, \\ \text{neither,} \qquad \text{if} \; w(A) = \text{neither}. \end{cases}\end{align*} $$
$$ \begin{align*}w(\lnot A) = \begin{cases} \text{true,} \qquad \text{if} \; w(A) = \text{false}, \\ \text{false,} \qquad \text{if} \; w(A) = \text{true}, \\ \text{neither,} \qquad \text{if} \; w(A) = \text{neither}. \end{cases}\end{align*} $$
-
-
• Intuitionism See Williams’ paper [Reference Williams20, pp. 518–519].
-
• Finite Fuzzy
-
– For some choice of n,
 $S = \{m/n : m \in \mathbb {N} \,\, \text {and} \, \,0 \leq m \leq n\}.$
$S = \{m/n : m \in \mathbb {N} \,\, \text {and} \, \,0 \leq m \leq n\}.$
-
– The truth-value mapping
 is defined by:
is defined by:

-
– The connectives
 $\land , \lor , \lnot , \to $
follow the rules:
$\land , \lor , \lnot , \to $
follow the rules:  $$ \begin{align*}w(A \land B) = min(w(A),w(B)),\end{align*} $$
$$ \begin{align*}w(A \land B) = min(w(A),w(B)),\end{align*} $$
 $$ \begin{align*}w(A \lor B) = max(w(A),w(B)),\end{align*} $$
$$ \begin{align*}w(A \lor B) = max(w(A),w(B)),\end{align*} $$
 $$ \begin{align*}w(\lnot A) = 1- w(A),\end{align*} $$
$$ \begin{align*}w(\lnot A) = 1- w(A),\end{align*} $$
 $$ \begin{align*}w(A \to B) = \begin{cases} 1-(w(A)-w(B)), \qquad \text{if} \; w(A) \geq w(B), \\ 1, \qquad \text{otherwise.} \end{cases}\end{align*} $$
$$ \begin{align*}w(A \to B) = \begin{cases} 1-(w(A)-w(B)), \qquad \text{if} \; w(A) \geq w(B), \\ 1, \qquad \text{otherwise.} \end{cases}\end{align*} $$
-
-
• Infinite Fuzzy Like Finite Fuzzy but
 $S = [0,1]$
.
$S = [0,1]$
. -
• Supervaluations:
-
–
 $S := \{f: D \to \{true, false\}\}$
where D is a set of delineations (see [Reference Williams20, p. 518]).
$S := \{f: D \to \{true, false\}\}$
where D is a set of delineations (see [Reference Williams20, p. 518]). -
– The truth-value mapping
 is defined by:
is defined by: 
-
– The connectives
 $\land , \lnot $
follow the rules:
$\land , \lnot $
follow the rules:  $$ \begin{align*}w(A \land B)(x) = \begin{cases} \text{true,} \qquad \text{if} \; w(A)(x) = \text{true} \; \text{and} \; w(B)(x) = \text{true}, \\ \text{false,} \qquad \!\text{otherwise}. \end{cases}\end{align*} $$
$$ \begin{align*}w(A \land B)(x) = \begin{cases} \text{true,} \qquad \text{if} \; w(A)(x) = \text{true} \; \text{and} \; w(B)(x) = \text{true}, \\ \text{false,} \qquad \!\text{otherwise}. \end{cases}\end{align*} $$
 $$ \begin{align*}w(\lnot A)(x) = \begin{cases} \text{true,} \qquad \text{if} \; w(A)(x) = \text{false}, \\ \text{false,} \qquad\! \text{otherwise}. \end{cases}\end{align*} $$
$$ \begin{align*}w(\lnot A)(x) = \begin{cases} \text{true,} \qquad \text{if} \; w(A)(x) = \text{false}, \\ \text{false,} \qquad\! \text{otherwise}. \end{cases}\end{align*} $$
-
-
• Degree Supervaluations
-
– S defined as above.
-
– The truth-value mapping
 is defined by:
is defined by: 
-
– The connectives
 $\land , \lnot $
are defined as above.
$\land , \lnot $
are defined as above.
-
-
• Finite Fuzzy gaps: Like Finite Fuzzy, but
 if
if
 $w(A) = 1$
,
$w(A) = 1$
,
 otherwise.
otherwise. -
• Infinite Fuzzy gaps: Like Infinite Fuzzy, but
 if
if
 $w(A) = 1$
,
$w(A) = 1$
,
 otherwise.
otherwise.