1. Introduction
In models of representative democracy, voters typically select candidates based on their policy proposals. However, prior literature often analyzes election outcomes in isolation, implying that voters’ decisions in one election are influenced solely by the policies presented in that specific contest. In practice, many countries conduct multiple elections concurrently. For instance, the USA holds its presidential, congressional, and gubernatorial elections on the second Tuesday of November. Similarly, Brazil conducts its general elections for the presidency, National Congress members, and state governors every four years. Taiwan, until a 2012 reform, staggered its presidential and legislative elections, but now these occur simultaneously.
Empirical evidence highlights the interplay between concurrent elections. A notable instance is the “coattail effect” in the USA, where the popularity of a presidential candidate might sway votes in favor of same-party candidates in legislative elections (Miller, Reference Miller1955; Ferejohn and Calvert, Reference Ferejohn and Calvert1984; Campbell, Reference Campbell1986; Campbell and Sumners, Reference Campbell and Sumners1990; Mondak, Reference Mondak1990, Reference Mondak1993). These simultaneous elections demonstrate mutual influence. While an upper-level election, such as a presidential election, can affect a more localized election, the reverse can also occur. Research by Wang et al. (Reference Wang, Weng and Wang2018) found that in Taiwan, fielding a popular candidate in a local election can enhance the party's vote share in the national election. In an interesting observation, Fukumoto and Miwa (Reference Fukumoto and Miwa2018) noted that in Japan, a national candidate sharing a surname with a local district candidate secured a vote share 69 percent greater in that specific district than elsewhere. This suggests that a local candidate's surname can elevate the national candidate's visibility. Such findings underscore the intricate interrelationships between different election levels. However, understanding the dynamics and repercussions of these interactions on policy formation and voter behavior is still unclear. This study addresses these gaps by introducing a simple theoretical model to assess how simultaneous elections shape policy decisions.
The baseline model assumes that two parties, left and right, are competing in two simultaneous elections within a single district. Each party sends two candidates to each election, and these candidates are policy motivated and choose their positions accordingly. Voters cast two votes, one for each election. A voter's utility from one election is determined by the policy proposals chosen by the candidates in that election and is also influenced by the policy positions taken in the other election, reflecting the interaction between the two elections. The equilibrium result indicates that candidates choose more divergent positions in both elections compared to the classic Calvert–Wittman model (Wittman, Reference Wittman1977, Reference Wittman1983; Calvert, Reference Calvert1985). This is because voters’ decisions in one election are also affected by the policy positions in another election through their utility functions. This interaction effect between the elections allows candidates in one election to leverage the policy positions taken by their co-partisan candidates in the other election to pursue their ideal positions.
Our model draws inspiration from real-world observations. When a voter considers supporting a candidate in a local election, the national policy of that candidate's party also weighs on their decision-making. For example, policy decisions by Donald Trump during his presidential campaign could negatively affect moderate Republican candidates, such as Senator Susan Collins from Maine. On the other hand, candidates in conservative districts vying for local elections might actively pursue Trump's endorsement. This dynamic implies that voters derive utility not just from the instrumental benefits tied to electoral outcomes but also from an expressive value attached to their ballots, whereby, in local elections, voters may derive satisfaction from supporting a national candidate whose position they appreciate (Brennan and Hamlin, Reference Brennan and Hamlin1998; Schuessler, Reference Schuessler2000; Brennan, Reference Brennan2008; Hamlin and Jennings, Reference Hamlin and Jennings2011, Reference Hamlin and Jennings2018). Similarly, Krasa and Polborn (Reference Krasa and Polborn2018) posit that a voter's choice in a local legislative election can be shaped by both local and national policies. Our model reveals that within a single election, not only does a candidate's policy influence voter decisions, but the policy choices of their co-partisan candidates in other elections might also sway voter preferences.
The baseline model provides a foundation for broadening the analysis to various scenarios, including multidistrict elections. Within this streamlined election framework, a national-level election, such as a presidential race, and multidistrict local elections, akin to legislative elections, occur simultaneously. Equilibrium results suggest that national election candidates adopt positions mirroring those in the single-district baseline model. In contrast, local election candidates exhibit more polarized stances. For instance, in districts leaning left, the left-wing candidate can leverage the national-level election's influence to adopt a more leftward extremist position, sidestepping the local median voter's preferences. Conversely, the right-wing contender may feel compelled to inch leftward, counterbalancing the national election's unfavorable impact within this left-skewed district. Analogously, in right-leaning territories, both candidates veer further right. Consequently, all candidates diverge from the stance of the national median voter.
Examining the interactions within multidistrict elections provides insights into potential coordination and strategy among various candidates. The initial scenario we delve into is candidate selection. A national election's impact may alter local candidates’ inclinations to run. Given that the interaction effect prompts more polarized policy choices in local elections, would-be candidates with moderate views might anticipate reduced benefits from contesting. Therefore, they are more likely to be replaced by those with more extreme positions. For context, during Donald Trump's presidency in the 2020 election season, 36 representatives—of which 26 were Republicans—publicly stated their decisions not to seek reelection. This figure exceeds the average from the preceding 14 cycles and is only surpassed by the 2018 election.Footnote 1 Additionally, candidates endorsed by Trump secured victories in 97 percent of Republican primary elections and 78 percent of general elections in 2020.Footnote 2
The paper proceeds as follows: in Section 2, we discuss the related literature. In Section 3, we develop the baseline model and analyze its equilibrium result. In Section 4, we extend the model to multidistrict elections. Section 5 concludes.
2. Literature review
Few theoretical studies have focused on simultaneous elections. Alesina and Rosenthal (Reference Alesina and Rosenthal1996) develop a simultaneous election model wherein the presidential election is determined by majority rule, while the legislative election is based on proportional representation. The policy outcome in this model emerges as a compromise between the president and the legislature. Halberstam and Montagnes (Reference Halberstam and Montagnes2015) find that senators elected in presidential elections are more ideologically extreme than those elected in midterm elections. They explain this phenomenon as a spillover effect from the information asymmetry perspective. Our study directly models the interaction effect among different elections.
Our baseline model setup follows the electoral competition model, in which candidates are policy motivated to create policy divergence in equilibrium (Wittman, Reference Wittman1983; Calvert, Reference Calvert1985; Londregan and Romer, Reference Londregan and Romer1993). With respect to the interaction between the voter's utility functions, our model setup is close to the expressive voting model, in which people cast their vote not only to increase the odds for one or another policy, but also to express themselves in elections (see Hamlin and Jennings, Reference Hamlin and Jennings2011, Reference Hamlin and Jennings2018, for an overview). Studies suggest that participating in an election yields expressive benefits for voters. This could be a driving force behind voters’ motivation to vote, and they may also abstain from voting without feeling a need to be expressive. Expressive voting not only affects voter turnout, but it may also influence how people cast their votes. Callander and Wilson (Reference Callander and Wilson2006) and Callander and Wilson (Reference Callander and Wilson2008) develop a context-dependent voting model where a voter's choice between two candidates is influenced by both the candidates’ policy positions and the positions of other candidates in the set. Additionally, they discover that voters develop a preference for policy ambiguity, leading candidates to prefer offering ambiguous platforms. Furthermore, Howell et al. (Reference Howell, Krasa and Polborn2022) integrate the psychological costs associated with deviating from one's preferred policy and the psychological benefits of opposing an out-group into the standard electoral model's policy concerns.
Our model also contributes to the literature on multidistrict elections. Austen-Smith (Reference Austen-Smith1984) examines a multidistrict competition in which each candidate chooses their individual position in the district and the party's platform is the aggregate of its candidates’ positions. Snyder (Reference Snyder1994) and Ansolabehere et al. (Reference Ansolabehere, Leblanc and Snyder2012) explore scenarios in which a party's platform for legislative elections is not a uniform decision across all its candidates. Instead, the party's stance is collectively determined by legislators belonging to the same party. Polborn and Snyder (Reference Polborn and Snyder2017) examine a scenario where national party positions are decided by the median legislators of the parties, and voters also take into account the local candidate's valence. They suggest that party polarization increases as the uncertainty of the election and voters’ preference for valence decrease. Bernhardt et al. (Reference Bernhardt, Buisseret and Hidir2020) examine multidistrict elections involving two parties, where the focus is not only on winning a majority but also on seat shares. They explore scenarios where one party holds a valence advantage and characterizes the equilibrium strategies of both parties under various magnitudes of this advantage. Callander (Reference Callander2005) analyzes a situation in which two parties choose national policies with respect to which, in response, local candidates make their entry decisions.
Similar to our model, Eyster and Kittsteiner (Reference Eyster and Kittsteiner2007) investigate a two-tiered election, in which two parties choose their national platforms, while individual candidates select their local policy positions, bearing in mind the cost of deviating from their party's national stance. Their findings suggest that while this competition tends to bring candidates closer together, it simultaneously drives the parties further apart. Our model is closer to that of Krasa and Polborn (Reference Krasa and Polborn2018), in which local election candidates choose their own positions, and voters’ decisions depend on both local and national policy positions. In contrast, in this study the national policy is defined as the policy position chosen by national-level election candidates.
In our study, the influence of one candidate's policy position in one election on their co-partisan candidate in another election can also be explained as a party “valence.” This setup is similar to a recent discussion that parties may endogenously increase their valence in the campaign (e.g., Meirowitz, Reference Meirowitz2008; Ashworth and Bueno de Mesquita, Reference Ashworth and Bueno de Mesquita2009; Hirsch, Reference Hirsch2023). In contrast, in our model, the valence is not endogenously chosen by the candidates themselves but instead arises from another election.
3. Baseline model
3.1. Model setup
Two parties, L and R, compete in two simultaneous elections, A and B. In election A, candidate L A represents party L and candidate R A represents party R. Meanwhile, in election B, candidates L B and R B represent parties L and R, respectively.
We focus on the case of a one-dimensional policy (ideology) space, which we assume to be the entire real number line, for simplicity. All candidates have the same strategy space. One candidate from party j chooses a position $x^k_j\in {\opf R}$![]() for election k, with j ∈ {L, R} and k ∈ {A, B}. The policy space represents the general policy position that combines all specific policies, so we do not distinguish the policy space in different elections. For example, the policy space may represent a general liberal or conservative ideological position chosen by candidates in the national-level election A, as well as the similar liberal or conservative position in a local election B. All candidates are policy motivated, and those from the same party share the same ideal position as the party. The ideal policy position of party L is −1, while that of party R is 1.
for election k, with j ∈ {L, R} and k ∈ {A, B}. The policy space represents the general policy position that combines all specific policies, so we do not distinguish the policy space in different elections. For example, the policy space may represent a general liberal or conservative ideological position chosen by candidates in the national-level election A, as well as the similar liberal or conservative position in a local election B. All candidates are policy motivated, and those from the same party share the same ideal position as the party. The ideal policy position of party L is −1, while that of party R is 1.
There is a continuum of voters, indexed by i, each with unique ideal position $x_i\in {\opf R}$![]() . The distribution of ideal positions is continuous and there is a unique median ideal position x m. However, x m cannot be observed by candidates, who share common knowledge that the median voter's position is uniformly distributed in an interval [μ − α, μ + α] with $\mu \in {\opf R}$
. The distribution of ideal positions is continuous and there is a unique median ideal position x m. However, x m cannot be observed by candidates, who share common knowledge that the median voter's position is uniformly distributed in an interval [μ − α, μ + α] with $\mu \in {\opf R}$![]() and α > 0. Voters have Euclidean preferences over policy. In election A, the utility of a voter with ideal position x i from voting for candidate j A is
and α > 0. Voters have Euclidean preferences over policy. In election A, the utility of a voter with ideal position x i from voting for candidate j A is
In election B, the voter's utility from voting for candidate j B is
with j ∈ {L, R}. Constants β and γ represent the interaction of the two elections. We further assume 0 < γ < β, which means that upper-level election A has a larger influence on lower-level election B than vice versa, and −1 < μ − (1 + β)α < μ + (1 + β)α < 1 to guarantee an interior solution.
In election k, the voter's utility function $u^{j^k}_i$![]() has two parts. The first, $-\vert x_i-x^k_j\vert$
has two parts. The first, $-\vert x_i-x^k_j\vert$![]() , is a standard setup that measures the voter's utility from the policy proposal $x^k_j$
, is a standard setup that measures the voter's utility from the policy proposal $x^k_j$![]() . The second part, $-\vert x_i-x^{-k}_j\vert$
. The second part, $-\vert x_i-x^{-k}_j\vert$![]() , represents the influence of another election on this voter in this election. In other words, the voter also cares about j k's co-partisan candidate's policy in another election.
, represents the influence of another election on this voter in this election. In other words, the voter also cares about j k's co-partisan candidate's policy in another election.
Different from voters’ utility, which directly reflects the interaction of the two elections, candidates are assumed to be rational and selfish, and care only about their own elections rather than the result in another election (an extension that candidates also consider the policy outcome from another election is discussed in Section B.1 of the Appendix, and potential coordination among candidates is discussed in Section B.2).
In each election, the candidate who obtains the majority vote wins the election. In election k, candidate j k chooses policy $x^k_j$![]() to solve the following problem:
to solve the following problem:
where $\pi ^k_j$![]() is the probability that candidate j k wins the election, I j is this candidate's ideal position with I j ∈ { − 1, 1}, and $x^k_{-j}$
is the probability that candidate j k wins the election, I j is this candidate's ideal position with I j ∈ { − 1, 1}, and $x^k_{-j}$![]() is their opponent's policy choice in the election.
is their opponent's policy choice in the election.
3.1.1. Equilibrium concept
In election k, two candidates simultaneously choose their policy positions. A candidate's strategy is a mapping from { − 1, 1} to ${\opf R}$![]() to maximize Equation 3. After observing all candidates’ policy positions in both elections A and B, each voter casts two votes. For election k, a voter's strategy is a mapping from ${\opf R}$
to maximize Equation 3. After observing all candidates’ policy positions in both elections A and B, each voter casts two votes. For election k, a voter's strategy is a mapping from ${\opf R}$![]() to {L, R} to maximize her utility function defined in Equations 1 and 2. We focus on pure strategy Nash equilibrium.
to {L, R} to maximize her utility function defined in Equations 1 and 2. We focus on pure strategy Nash equilibrium.
3.1.2. Model discussion
The utility function of voters defined in Equations 1 and 2 depends on the candidates’ positions in that election as well as the positions of candidates in another election. Unlike the traditional voters’ utility (Wittman, Reference Wittman1983; Calvert, Reference Calvert1985) that represents the payoff from the policy outcome of the election result, our utility function tries to capture the factors that may influence the voting decision when voters cast their votes.
This model setup is related to expressive voting. Expressive voting emphasizes the intrinsic rewards of the voting process, rather than the election outcome. Voters may find value in expressing their views, affirming their identities, aligning with candidates or parties, adhering to moral principles, or other factors related to the act of voting for a chosen option, irrespective of the final election outcome (Hamlin and Jennings, Reference Hamlin and Jennings2011, Reference Hamlin and Jennings2018).
There are various explanations and evidence supporting the presence of expressive factors in voting behavior, which differ from instrumental accounts (Hamlin and Jennings, Reference Hamlin and Jennings2018). Our model closely resembles one in which expressive choices are linked to identifying with parties, candidates, or political positions, as described in Brennan and Hamlin (Reference Brennan and Hamlin1998). Specifically, in Brennan and Hamlin (Reference Brennan and Hamlin1998), two candidates compete on a policy issue, representing the instrumental account. For this account, a voter prefers the candidate whose policy position is closest to her ideal position. Meanwhile, voters also consider the expressive domain, which may represent a candidate's party affiliation or the party's political position/ideology. They argue that “voters will be more likely to vote for parties/representatives/policies that are closer to their expressive ideal.”
In our model, the policy positions proposed by candidates in an election can be treated as the instrumental account, and the influence from another election can be considered the expressive account. For example, in a local election B, a voter's instrumental account will prefer the local policy position $x^B_j$![]() that is close to her ideal point. Meanwhile, the candidates’ party position comes from their national leaders’ policy positions $x^A_j$
that is close to her ideal point. Meanwhile, the candidates’ party position comes from their national leaders’ policy positions $x^A_j$![]() in election A, which affects voters’ decisions through local candidates’ party affiliation. For the expressive account, a voter will also prefer the local candidate whose national party leader's position is closer to her ideal position x i, and this expressive account is weighted β in the voter's decision in election B.
in election A, which affects voters’ decisions through local candidates’ party affiliation. For the expressive account, a voter will also prefer the local candidate whose national party leader's position is closer to her ideal position x i, and this expressive account is weighted β in the voter's decision in election B.
The interaction among simultaneous elections can also be explained through cognitive heuristics, drawing on contemporary cognitive theories about information processing and decision-making as applied by Mondak (Reference Mondak1990, Reference Mondak1993) and Mondak and McCurley (Reference Mondak and McCurley1994). In the unpredictable environment of elections, voters cannot be certain which candidate is the optimal choice; they can only estimate which candidate might perform better. Heuristic judgment principles focus on cues or contextual elements that may not be directly related to the central issue. According to Mondak and McCurley (Reference Mondak and McCurley1994), the cognitive process involves a sequence where a voter's approval of a president's stance on an issue leads to support for related issues backed by the president, thus affecting their choices in congressional elections. Presidential candidates thus act as informational cues for voters in congressional races, fostering a perceived linkage between presidential and congressional elections. This perception allows voters to evaluate presidential candidates and draw conclusions about their affiliations with local candidates.
From this framework, in one election, such as the lower level election B, $-\vert x_i-x^B_j\vert$![]() is the direct utility voter i derives from party j's candidate's policy proposal, meanwhile $-\vert x_i-x^A_j\vert$
is the direct utility voter i derives from party j's candidate's policy proposal, meanwhile $-\vert x_i-x^A_j\vert$![]() reflects the cue i used to infer the connection and affiliation between same party candidates. For example, Donald Trump's policy choices in the presidential election might represent the Republican Party's national stance. When voters make choices in local elections, their preference for Trump's policy position becomes the cue for them to justify the local elections. Consequently, this heuristic judgment might influence their decisions regarding other Republican candidates in local elections.
reflects the cue i used to infer the connection and affiliation between same party candidates. For example, Donald Trump's policy choices in the presidential election might represent the Republican Party's national stance. When voters make choices in local elections, their preference for Trump's policy position becomes the cue for them to justify the local elections. Consequently, this heuristic judgment might influence their decisions regarding other Republican candidates in local elections.
Another interpretation of the influence of simultaneous elections is endogenized party valence. While a voter can derive utility from a local candidate's policy, the candidate's party affiliation can further influence this utility. In our model, this valence could arise from the policy positions taken in the national election. Considering a local election B in a left-leaning district, where the local median voter's position significantly diverges from the national median voter's position, the policy positions in the national election A will establish the valence $\tau \equiv \beta \vert x^A_L-x^A_R\vert$![]() for the local election (τ is derived from Equations 1 and 2). Specifically, in election B, voter i's utility from voting for party L's candidate and party R's candidate can be rewritten as $-\vert x_i-x^A_L\vert + \tau$
for the local election (τ is derived from Equations 1 and 2). Specifically, in election B, voter i's utility from voting for party L's candidate and party R's candidate can be rewritten as $-\vert x_i-x^A_L\vert + \tau$![]() and $-\vert x_i-x^A_R\vert$
and $-\vert x_i-x^A_R\vert$![]() .Footnote 3 This aligns with the literature on party valence (e.g., Ashworth and Bueno de Mesquita, Reference Ashworth and Bueno de Mesquita2009).
.Footnote 3 This aligns with the literature on party valence (e.g., Ashworth and Bueno de Mesquita, Reference Ashworth and Bueno de Mesquita2009).
Our utility functional form is similar to the model presented by Krasa and Polborn (Reference Krasa and Polborn2018), wherein a voter's utility hinges on both local and national policy positions.Footnote 4 In our model, we choose a linear functional form for its simplicity (e.g., Gehlbach, Reference Gehlbach2021, 6; Howell et al., Reference Howell, Krasa and Polborn2022), although our main findings do not depend on the adoption of this specific functional form.Footnote 5 The interaction term is modeled as the distance between the voter's ideal position and the policy position from another election, rather than the distance between two same-party candidates’ policy positions. This setup avoids the implausible situation in which the interaction term between two conservative candidates provides a higher utility to a liberal voter than that between two liberal candidates.Footnote 6
Similar to the model concerning policy-motivated candidates (e.g., Krasa and Polborn, Reference Krasa and Polborn2018), the utility function of electoral candidates in our framework is solely derived from policy proposals of their own elections, without considering the potential influence from other elections.Footnote 7 This divergence in the utilities of voters and candidates stems from the different nature of decisions they encounter within the varied environments of the electoral context.
As previously discussed, voters are tasked with selecting a candidate to support, and their utility function aims to encapsulate the various factors that influence this decision at the ballot box. Given that voters are not entirely certain about which candidate would best serve their interests, information from other elections can act as valuable cues, enabling voters to better gauge the candidates and the feasibility of their policy proposals. Conversely, the primary task of candidates is to select their policy proposals before the elections, which may enhance their chances of winning and subsequently enable them to derive utility from the policy outcomes. Generally, electoral candidates have a thorough understanding of the policies they advocate for. In other words, while policies in other elections may influence the likelihood of winning their own election or even the implementation of their chosen policy in the future, candidates do not require this information to comprehend the payoff they can derive from their self-selected policy.
3.2. Equilibrium
In each election, we need to find the indifference point at which the voter is indifferent between the two candidates. The indifferent voter's position in election A is $x^{\ast A} = ( 1/( 1 + \gamma ) ) ( ( x^A_L + x^A_R) /2) + ( \gamma /( 1 + \gamma ) ) ( ( x^B_L + x^B_R) /2)$![]() , which is the weighted average of the midpoints of the policy choices in two elections: $( x^A_L + x^A_R) /2$
, which is the weighted average of the midpoints of the policy choices in two elections: $( x^A_L + x^A_R) /2$![]() in election A and $( x^B_L + x^B_R) /2$
in election A and $( x^B_L + x^B_R) /2$![]() in election B. This expression indicates that the candidates in one election need to consider how to balance the impact of another election. For instance, if γ is small, it means that voters’ decisions in election A are largely determined by the policy proposals in election A itself. Meanwhile, when β is large, voters’ decisions in election B are largely influenced by the policy proposals from election A. The probability that candidate L A wins the election is $\pi ^A_L = P( x_m\leq x^{\ast A})$
in election B. This expression indicates that the candidates in one election need to consider how to balance the impact of another election. For instance, if γ is small, it means that voters’ decisions in election A are largely determined by the policy proposals in election A itself. Meanwhile, when β is large, voters’ decisions in election B are largely influenced by the policy proposals from election A. The probability that candidate L A wins the election is $\pi ^A_L = P( x_m\leq x^{\ast A})$![]() . If we plug $\pi ^A_L$
. If we plug $\pi ^A_L$![]() into the candidate's problem in Equation 3 and use the first order condition, we can solve $x^A_L = ( 1 + \gamma ) ( \mu -\alpha ) -\gamma [ ( x^B_L + x^B_R) /2]$
into the candidate's problem in Equation 3 and use the first order condition, we can solve $x^A_L = ( 1 + \gamma ) ( \mu -\alpha ) -\gamma [ ( x^B_L + x^B_R) /2]$![]() and $x^A_R = ( 1 + \gamma ) ( \mu + \alpha ) -\gamma [ ( x^B_L + x^B_R) /2]$
and $x^A_R = ( 1 + \gamma ) ( \mu + \alpha ) -\gamma [ ( x^B_L + x^B_R) /2]$![]() . The policy choice in election B can be solved in a similar way. Combining the equations, the equilibrium strategies are summarized as follows:
. The policy choice in election B can be solved in a similar way. Combining the equations, the equilibrium strategies are summarized as follows:
Proposition 1: There exists a unique pure strategy Nash equilibrium:
In election A :
In election B :
(Proofs are given in the online Appendices.)
The classic Calvert–Wittman model assumes no interaction between the two elections (i.e., β = γ = 0). In this case, candidates from party L choose the optimal policy μ − α in both elections, and their opponents from party R choose μ + α. Proposition 1 retains some properties of the classic model: policy choices are divergent, each candidate has a 50 percent chance of winning their own election, and candidates from party L have expected utility −1 − μ, while those from party R have expected utility −1 + μ. However, this proposition also suggests that the interaction effect leads to more polarized policy choices than in the classic model. Figure 1 illustrates that each chosen policy position moves toward the candidate's ideal position, even without coordination among candidates. This is because the interaction term in the voter's utility function transmits the influence of one election to another, and the same-party candidate in another election creates a party valence, causing the candidate in one election to focus more on their ideal policy than pandering to the median voter. Like the classic model, the proposition implies that the midpoints of policy choices in both elections are μ, which is also the indifference point of the two elections. Furthermore, the upper-level election (election A) has a stronger impact on the lower-level election (γ < β) than the other way around. Therefore, candidates in the lower-level election (election B) may choose more polarized policies than their same-party candidates in the upper-level election. In other words, candidates at the national level may choose policies closer to the median voter's position, while candidates in the local election can leverage the impact of the national election to choose more extreme positions.

Figure 1. Equilibrium positions in the baseline model.
4. Multidistrict elections
4.1. Model and equilibrium
In this section, we expand the baseline model to multidistrict elections. A polity has an odd number 2N + 1 districts with an equal population in each district. Two parties, L and R, compete in two types of elections that are running simultaneously. The lower-level election B, which can be viewed as the legislative election, consists of 2N + 1 separate local elections B ≡ {B k|k = 1, …, 2N + 1}. In each district k, candidate L k from party L chooses policy position $x^k_L\in {\opf R}$![]() , and candidate R k from party R chooses $x^k_R\in {\opf R}$
, and candidate R k from party R chooses $x^k_R\in {\opf R}$![]() . Local voters in k elect one candidate using plurality rule.
. Local voters in k elect one candidate using plurality rule.
The upper-level election A, which can be considered as the presidential election, is held in all districts. Party L's candidate L A chooses a policy position $x^A_L\in {\opf R}$![]() , and party R's candidate R A chooses a policy position $x^A_R\in {\opf R}$
, and party R's candidate R A chooses a policy position $x^A_R\in {\opf R}$![]() . For simplicity, we assume that the candidate who wins more districts wins election A, and the plurality rule is adopted in each district. This setup is similar to the Electoral College system in the USA.Footnote 8
. For simplicity, we assume that the candidate who wins more districts wins election A, and the plurality rule is adopted in each district. This setup is similar to the Electoral College system in the USA.Footnote 8
The local median voter's position $x^k_{m}$![]() in district k cannot be observed by any candidate, but it is publicly known that $x^k_{m}$
in district k cannot be observed by any candidate, but it is publicly known that $x^k_{m}$![]() is uniformly distributed in an interval [μ k − α, μ k + α] with μ k ∈ R. The expected the median vote's position in the Nth district (the central district) is denoted as $\bar {\mu }\equiv \mu ^N$
is uniformly distributed in an interval [μ k − α, μ k + α] with μ k ∈ R. The expected the median vote's position in the Nth district (the central district) is denoted as $\bar {\mu }\equiv \mu ^N$![]() , and all μ ks have the same adjacent distance (i.e., μ k − μ k−1 = d > 0).
, and all μ ks have the same adjacent distance (i.e., μ k − μ k−1 = d > 0).
In election A, candidates from parties R and L have ideal positions of −1 and 1, respectively. In election B k, the candidate from the left party has the ideal position $I^k_L\equiv \mu ^k-v^k$![]() ; the candidate from the right party has the ideal position $I^k_R\equiv \mu ^k + v^k$
; the candidate from the right party has the ideal position $I^k_R\equiv \mu ^k + v^k$![]() , with v k > (1 + β(1 + γ))α.
, with v k > (1 + β(1 + γ))α.
In district k, each voter casts two votes on a ballot, one for election A and another for election B k. In election A, the utility of a voter with ideal position $x^k_i$![]() from voting for the candidate from party j ∈ {L, R} is
from voting for the candidate from party j ∈ {L, R} is
In election B k, voter i's utility from voting for the candidate from party j ∈ {L, R} is
For simplicity, we also make the following assumptions:
Assumption 1: β(1 + γ) < 1.
Assumption 2: (2 + γ)α < d.
Assumption 1 states that the interaction effects of two different elections have an upper bound. This assumption, combined with γ < β, implies that the influence of one election on another cannot exceed the effect of the policy competition itself. Assumption 2 sets up a lower bound for the distance of the expected median voter's positions in two adjacent districts. This assumption rules out spillover effects between two adjacent districts.
In election A, the Nth district, characterized by the median voter's expected position $\bar {\mu }$![]() , serves as the pivotal district. This pivotal role arises because districts are equally distributed on both sides of the Nth district, and assumption 2 ensures that the median voter positions in each district do not overlap. Consequently, policy positions selected by candidates in other districts do not affect the voting decisions in the Nth district. Therefore, candidates in election A need only focus on choosing the appropriate policy positions in this district while considering the interaction effect from its local election.
, serves as the pivotal district. This pivotal role arises because districts are equally distributed on both sides of the Nth district, and assumption 2 ensures that the median voter positions in each district do not overlap. Consequently, policy positions selected by candidates in other districts do not affect the voting decisions in the Nth district. Therefore, candidates in election A need only focus on choosing the appropriate policy positions in this district while considering the interaction effect from its local election.
In the lower-level election, the impact of election A can have varying effects on different districts. In the pivotal district with an expected median voter's position of $\bar {\mu }$![]() , policy choices in election A are on opposite sides of this position. This implies that the indifference point of election B N is $( 1/( 1 + \beta ) ) ( ( x^{N}_L + x^{N}_R) /2) + ( \beta /( 1 + \beta ) ) ( ( x^A_L + x^A_R) /2)$
, policy choices in election A are on opposite sides of this position. This implies that the indifference point of election B N is $( 1/( 1 + \beta ) ) ( ( x^{N}_L + x^{N}_R) /2) + ( \beta /( 1 + \beta ) ) ( ( x^A_L + x^A_R) /2)$![]() . Therefore, the policy choices in this local election should be the same as those in the baseline model. For a left-leaning district, the policy choices in election A lie to the right of the district's expected median voter's position, and hence the indifference point of election B k with $\mu ^k< \bar {\mu }$
. Therefore, the policy choices in this local election should be the same as those in the baseline model. For a left-leaning district, the policy choices in election A lie to the right of the district's expected median voter's position, and hence the indifference point of election B k with $\mu ^k< \bar {\mu }$![]() should be $( ( x^{k}_L + x^{k}_R) /2) +( \beta ( x^A_R-x^A_L) /2)$
should be $( ( x^{k}_L + x^{k}_R) /2) +( \beta ( x^A_R-x^A_L) /2)$![]() . Similarly, for a district on the right with $\mu ^k> \bar {\mu }$
. Similarly, for a district on the right with $\mu ^k> \bar {\mu }$![]() , the indifference point is $( ( x^{k}_L + x^{k}_R) /2) -( \beta ( x^A_R-x^A_L) /2)$
, the indifference point is $( ( x^{k}_L + x^{k}_R) /2) -( \beta ( x^A_R-x^A_L) /2)$![]() . These indifference points indicate that policy choices in election A have different influences on left- and right-leaning districts. Consequently, these heterogeneous effects may lead to more biased policy choices for candidates in local elections. The equilibrium strategies are summarized as follows:
. These indifference points indicate that policy choices in election A have different influences on left- and right-leaning districts. Consequently, these heterogeneous effects may lead to more biased policy choices for candidates in local elections. The equilibrium strategies are summarized as follows:
Proposition 2: There exists a unique Nash equilibrium such that
• in election A:
$$x^A_L = \bar{\mu}-( 1 + \gamma) \alpha,\; \quad x^A_R = \bar{\mu} + ( 1 + \gamma) \alpha;\;$$
• in election B k :
◦ when $\mu ^k = \bar {\mu },\;$
 $$x^k_L = \bar{\mu}-( 1 + \beta) \alpha,\; \quad x^k_R = \bar{\mu} + ( 1 + \beta) \alpha;\;$$
$$x^k_L = \bar{\mu}-( 1 + \beta) \alpha,\; \quad x^k_R = \bar{\mu} + ( 1 + \beta) \alpha;\;$$
◦ when $\mu ^k< \bar {\mu },\;$
 $$x^k_L = \mu^k-\alpha-\beta( 1 + \gamma) \alpha,\; \quad x^k_R = \mu^k + \alpha-\beta( 1 + \gamma) \alpha;\;$$
$$x^k_L = \mu^k-\alpha-\beta( 1 + \gamma) \alpha,\; \quad x^k_R = \mu^k + \alpha-\beta( 1 + \gamma) \alpha;\;$$
◦ when $\mu ^k> \bar {\mu },\;$
 $$x^k_L = \mu^k-\alpha + \beta( 1 + \gamma) \alpha,\; \quad x^k_R = \mu^k + \alpha + \beta( 1 + \gamma) \alpha.$$
$$x^k_L = \mu^k-\alpha + \beta( 1 + \gamma) \alpha,\; \quad x^k_R = \mu^k + \alpha + \beta( 1 + \gamma) \alpha.$$
Part 1 of Proposition 2 shows that candidates in election A choose policy positions similar to those in the baseline model (Figure 2). This is because candidates in the upper-level election focus solely on securing victory in the central district. For the lower-level election B, candidates face one of three distinct scenarios. In the central district N, candidates in B N make the same decision as in the baseline model. For districts on the left side with $\mu ^k< \bar {\mu }$![]() , policy choices for both parties are more biased toward candidate L k's ideal position. Specifically, for these districts, the policy choices in election A are on the right of their expected local median voters’ positions, and thus the influence from election A creates an advantage for candidates from party L in the local elections. As a consequence, these candidates can choose positions further toward their ideal positions by αβγ unit than the candidate in the central district. Meanwhile, to offset party L's advantage in these districts, their opponents in party R have to follow this trend by shifting in an equally unfavorable direction. This effect can also be observed in right-leaning districts with $\mu ^k> \bar {\mu }$
, policy choices for both parties are more biased toward candidate L k's ideal position. Specifically, for these districts, the policy choices in election A are on the right of their expected local median voters’ positions, and thus the influence from election A creates an advantage for candidates from party L in the local elections. As a consequence, these candidates can choose positions further toward their ideal positions by αβγ unit than the candidate in the central district. Meanwhile, to offset party L's advantage in these districts, their opponents in party R have to follow this trend by shifting in an equally unfavorable direction. This effect can also be observed in right-leaning districts with $\mu ^k> \bar {\mu }$![]() in the opposite direction.
in the opposite direction.
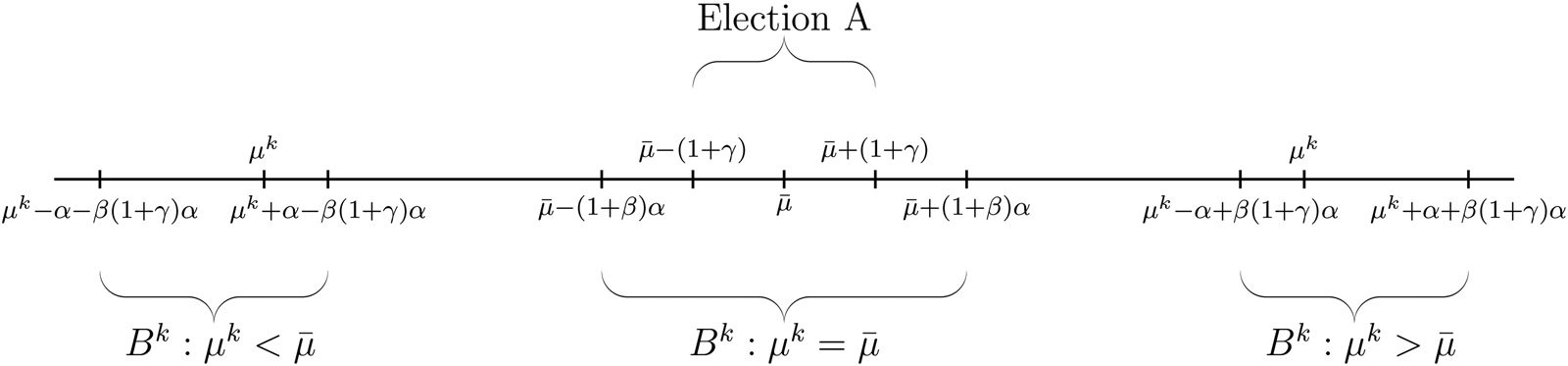
Figure 2. Equilibrium positions in multidistrict elections.
By comparing the policy choices in local elections, we find that all candidates choose more polarized positions than in the classic model without the interaction effect. In the central district, the national election has an effect equivalent to that of two candidates in the local election; therefore, their equilibrium positions are still symmetric around the local median voter's position. However, in districts with more biased ideologies ($\mu ^k< \bar {\mu }$![]() or $\mu ^k> \bar {\mu }$
or $\mu ^k> \bar {\mu }$![]() ), the national election generates different influences for the two candidates, favoring only the candidate with the more extreme ideal position (i.e., the right-party candidates in right-leaning districts or the left-party candidates in the left-leaning districts). Consequently, candidates in ideologically skewed districts choose more extreme policies compared to those in more centrist districts.
), the national election generates different influences for the two candidates, favoring only the candidate with the more extreme ideal position (i.e., the right-party candidates in right-leaning districts or the left-party candidates in the left-leaning districts). Consequently, candidates in ideologically skewed districts choose more extreme policies compared to those in more centrist districts.
4.2. Candidate selection
In the previous sections, we assume fixed candidates and ideal positions in the model. In this section, we consider how different elections may interact and affect candidate selection in multidistrict elections, specifically in local election B.Footnote 9 Here, we focus on party L's candidate selection process for local election B k. Party L has a pool of Q potential candidates, and the qth candidate's ideal position is $\mu ^k-q\bar {v}$![]() , where $\bar {v}$
, where $\bar {v}$![]() is a constant that measures the ideological distance between any two adjacent candidates. Similarly, party R also has a pool of Q potential candidates, and its qth candidate's ideal position is $\mu ^k + q\bar {v}$
is a constant that measures the ideological distance between any two adjacent candidates. Similarly, party R also has a pool of Q potential candidates, and its qth candidate's ideal position is $\mu ^k + q\bar {v}$![]() .
.
Before the general election, each potential candidate may decide whether to participate in the primary election without any cost.Footnote 10 After that, for simplicity, we assume that the party randomly chooses one candidate from those who participated in the primary election to compete in election B k. Any potential candidate who does not participate in the general election has a default payoff of −w.Footnote 11 The model setup for the general election is the same as that in Section 4.1. To guarantee that the set of the selected candidates is not trivial, we make the following assumption:
Assumption 3: $\bar {v}< w< ( Q + 1) \bar {v}-\alpha ( 1 + \gamma ) \beta$![]() .
.
Any candidate from party L prefers to enter the election if and only if their expected payoff from the election is not less than −w. Since the expected payoff from the election increases with candidates’ ideal positions, a threshold exists to select the candidate for the party. A similar result can also be found for party R.
Proposition 3: In election B k,
• when $\mu ^k = \bar {\mu },\;$
 a candidate in party L prefers to participate in the election if her ideal position is in $[ \mu ^k-w,\; \, \mu ^k-\bar {v}]$
a candidate in party L prefers to participate in the election if her ideal position is in $[ \mu ^k-w,\; \, \mu ^k-\bar {v}]$ ; and a candidate from party R prefers to participate in the election if her ideal position is in $[ \mu ^k + \bar {v},\; \, \mu ^k + w]$
; and a candidate from party R prefers to participate in the election if her ideal position is in $[ \mu ^k + \bar {v},\; \, \mu ^k + w]$ ;
;• when $\mu ^k< \bar {\mu },\;$
 a candidate in party L prefers to participate in the election if her ideal position is in $[ \mu ^k-w-\beta ( 1 + \gamma ) \alpha ,\; \, \mu ^k-\bar {v}]$
a candidate in party L prefers to participate in the election if her ideal position is in $[ \mu ^k-w-\beta ( 1 + \gamma ) \alpha ,\; \, \mu ^k-\bar {v}]$ ; a candidate from party R prefers to participate in the election if her ideal position is in $[ \mu ^k + \bar {v},\; \, \mu ^k + w-\beta ( 1 + \gamma ) \alpha ]$
; a candidate from party R prefers to participate in the election if her ideal position is in $[ \mu ^k + \bar {v},\; \, \mu ^k + w-\beta ( 1 + \gamma ) \alpha ]$ ;
;• when $\mu ^k> \bar {\mu },\;$
 a candidate in party L prefers to participate in the election if her ideal position is in $[ \mu ^k-w + \beta ( 1 + \gamma ) \alpha ,\; \, \mu ^k-\bar {v}]$
a candidate in party L prefers to participate in the election if her ideal position is in $[ \mu ^k-w + \beta ( 1 + \gamma ) \alpha ,\; \, \mu ^k-\bar {v}]$ ; a candidate from party R prefers to participate in the election if her ideal position is in $[ \mu ^k + \bar {v},\; \, \mu ^k + w + \beta ( 1 + \gamma ) \alpha ]$
; a candidate from party R prefers to participate in the election if her ideal position is in $[ \mu ^k + \bar {v},\; \, \mu ^k + w + \beta ( 1 + \gamma ) \alpha ]$ .
.
When there is no interaction between elections (γ = 0), it is easy to calculate that parties L and R should respectively select candidates with ideal positions in $[ \mu ^k-w,\; \, \mu ^k-\bar {v}]$![]() and $[ \mu ^k + \bar {v},\; \, \mu ^k + w]$
and $[ \mu ^k + \bar {v},\; \, \mu ^k + w]$![]() in each district, except for the central one. However, Proposition 3 demonstrates that only the central district remains unaffected when accounting for interaction effects. This is because candidate policies are symmetric around the central district's median voter, and this symmetry does not impact expected payoffs.
in each district, except for the central one. However, Proposition 3 demonstrates that only the central district remains unaffected when accounting for interaction effects. This is because candidate policies are symmetric around the central district's median voter, and this symmetry does not impact expected payoffs.
On the other hand, in a left-leaning district (part 2 of Proposition 3), both candidates’ policy positions are biased toward the local median voter's left side (Proposition 2). This boosts the expected payoffs for left-party candidates while harming those for right-party candidates. As a result, more extreme party L candidates are likely to participate, shifting their average ideal position further left. Conversely, more moderate party R candidates may drop out, and the average ideal position of remaining competitors shifts leftward too. This effect is observed in right-leaning districts as well (part 3 of Proposition 3).
In summary, election interactions can polarize policy choices on the local level and lead to the selection of more extreme candidates, ultimately resulting in greater polarization from a national perspective. In Appendix B, we explore additional extensions of the model to further discuss potential coordination and manipulation strategies among candidates in elections.
5. Conclusion
In this study, we delve into the nuanced dynamics of simultaneous elections, revealing the interplay between electoral competitions and the strategic positioning of candidates across multiple elections. Employing a model grounded in voters’ utility functions, our investigation illuminates how decisions in one election are intricately linked to outcomes and strategies in others, allowing us to explore the broader implications of election interactions.
In the baseline model, two parties compete in two elections within a single district. We introduce a new perspective on voters’ utility functions, determined by the policy proposals chosen by the candidates in that election and influenced by the policy positions taken in the other election, reflecting the interaction between the two elections. We find that candidates in both elections tend to adopt more extreme positions than those predicted by the Calvert–Wittman model. This behavior arises because they leverage their co-partisan candidates’ positions in the other election to pursue their preferred positions.
The extension of our model to include multidistrict elections further enriches our understanding of the electoral landscape. In this context, we observe that candidates in districts with pronounced ideological leanings are more likely to diverge from the median voter's position at the national level. Moreover, examining the interactions within multidistrict elections provides insights into potential coordination and strategy among various candidates, such as candidate selection. Since the interaction effect prompts more polarized policy choices in local elections, candidates with moderate views might anticipate reduced benefits from contesting. Consequently, they are more likely to be replaced by those with more extreme positions.
Acknowledgements
I would like to thank Tiberiu Dragu, Catherine Hafer, Alex Hirsch, Dimitri Landa, Nicola Persico, Carlo Prato, Alastair Smith, Stephane Wolton, and the workshop and conference participants at the LSE-NYU PSPE conference and the APSA annual conference for their insightful comments and suggestions. I also extend our gratitude to Ken Shotts (the handling editor) and two anonymous referees for their constructive feedback, which significantly improved the paper during the review process.
Supplementary material
The supplementary material for this article can be found at https://doi.org/10.1017/psrm.2024.66.



