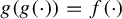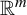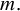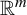1 Introduction
Given a map
![]() $f: X \to X$
on a non-empty set X and a positive integer n, an iterative root of order n (or simply
$f: X \to X$
on a non-empty set X and a positive integer n, an iterative root of order n (or simply
![]() $n{\mathrm{th}}$
root) of f is a map
$n{\mathrm{th}}$
root) of f is a map
![]() $g: X\to X$
such that
$g: X\to X$
such that
where for each non-negative integer k,
![]() $g^{k}$
denote the
$g^{k}$
denote the
![]() $k{\mathrm{th}}$
order iterate of g defined recursively by
$k{\mathrm{th}}$
order iterate of g defined recursively by
![]() $g^{0}=\text {id}$
, the identity map on X, and
$g^{0}=\text {id}$
, the identity map on X, and
![]() $g^{k}=g\circ g^{k-1}$
. For
$g^{k}=g\circ g^{k-1}$
. For
![]() $n=2$
, a solution of equation (1.1) is called an iterative square root (or simply a square root) of f. The iterative root problem (1.1), which is closely related to the embedding flow problem [Reference Fort13, Reference Kuczma22, Reference Zdun53], the invariant curve problem [Reference Kuczma, Choczewski and Ger24], and linearization [Reference Bogatyi9], is of particular interest [Reference Baron and Jarczyk4, Reference Bödewadt8, Reference Kuczma22, Reference Targonski47, Reference Targonski48, Reference Zdun and Solarz54] both in the theory of the functional equations and in that of dynamical systems, and has applications in statistics, signal processing, computer graphics, and information techniques [Reference Iannella and Kindermann16, Reference Kindermann, Omori and Usui19, Reference Martin38]. Since the initial works of Babbage [Reference Babbage3], Abel [Reference Abel1], and Königs [Reference Königs20], various researchers have paid increasing attention to the iterative root problem, and many advances have been made on its solutions for various classes of maps, e.g. continuous maps on intervals and in particular those which are piecewise monotone [Reference Blokh, Coven, Misiurewicz and Nitecki6, Reference Kuczma21, Reference Li, Yang and Zhang28, Reference Li and Zhang30–Reference Liu, Li and Zhang34, Reference Liu and Zhang36, Reference Liu and Zhang37, Reference Zhang and Zhang57, Reference Zhang59], continuous complex maps [Reference Rice, Schweizer and Sklar40, Reference Solarz45, Reference Solarz46, Reference Zdun52], series and transseries [Reference Edgar12], continuous maps on planes and
$n=2$
, a solution of equation (1.1) is called an iterative square root (or simply a square root) of f. The iterative root problem (1.1), which is closely related to the embedding flow problem [Reference Fort13, Reference Kuczma22, Reference Zdun53], the invariant curve problem [Reference Kuczma, Choczewski and Ger24], and linearization [Reference Bogatyi9], is of particular interest [Reference Baron and Jarczyk4, Reference Bödewadt8, Reference Kuczma22, Reference Targonski47, Reference Targonski48, Reference Zdun and Solarz54] both in the theory of the functional equations and in that of dynamical systems, and has applications in statistics, signal processing, computer graphics, and information techniques [Reference Iannella and Kindermann16, Reference Kindermann, Omori and Usui19, Reference Martin38]. Since the initial works of Babbage [Reference Babbage3], Abel [Reference Abel1], and Königs [Reference Königs20], various researchers have paid increasing attention to the iterative root problem, and many advances have been made on its solutions for various classes of maps, e.g. continuous maps on intervals and in particular those which are piecewise monotone [Reference Blokh, Coven, Misiurewicz and Nitecki6, Reference Kuczma21, Reference Li, Yang and Zhang28, Reference Li and Zhang30–Reference Liu, Li and Zhang34, Reference Liu and Zhang36, Reference Liu and Zhang37, Reference Zhang and Zhang57, Reference Zhang59], continuous complex maps [Reference Rice, Schweizer and Sklar40, Reference Solarz45, Reference Solarz46, Reference Zdun52], series and transseries [Reference Edgar12], continuous maps on planes and
![]() $\mathbb {R}^{m}$
[Reference Leśniak25, Reference Leśniak26, Reference Narayaninsamy39, Reference Yu, Li and Liu51], and set-valued maps [Reference Jarczyk and Zhang18, Reference Li, Jarczyk, Jarczyk and Zhang27, Reference Li and Zhang29, Reference Liu, Li and Zhang35]. In particular, various properties of the iterative roots have also been studied, see for instance, approximation [Reference Zhang and Zhang60], stability [Reference Xu and Zhang50, Reference Zhang, Zeng, Jarczyk and Zhang58], differentiability [Reference Kuczma23, Reference Zdun and Zhang55, Reference Zhang56], and category and measure [Reference Blokh7, Reference Simon41].
$\mathbb {R}^{m}$
[Reference Leśniak25, Reference Leśniak26, Reference Narayaninsamy39, Reference Yu, Li and Liu51], and set-valued maps [Reference Jarczyk and Zhang18, Reference Li, Jarczyk, Jarczyk and Zhang27, Reference Li and Zhang29, Reference Liu, Li and Zhang35]. In particular, various properties of the iterative roots have also been studied, see for instance, approximation [Reference Zhang and Zhang60], stability [Reference Xu and Zhang50, Reference Zhang, Zeng, Jarczyk and Zhang58], differentiability [Reference Kuczma23, Reference Zdun and Zhang55, Reference Zhang56], and category and measure [Reference Blokh7, Reference Simon41].
Given a topological space X, let
![]() $\mathcal {C}(X)$
denote the set of all continuous self-maps of X. For each positive integer n, let
$\mathcal {C}(X)$
denote the set of all continuous self-maps of X. For each positive integer n, let
![]() $\mathcal {W}(n;X):=\{f^{n}: f\in \mathcal {C}(X)\}$
, the set of
$\mathcal {W}(n;X):=\{f^{n}: f\in \mathcal {C}(X)\}$
, the set of
![]() $n{\mathrm{th}}$
iterates of all the maps in
$n{\mathrm{th}}$
iterates of all the maps in
![]() $\mathcal {C}(X)$
, and
$\mathcal {C}(X)$
, and
![]() $\mathcal {W}(X):=\bigcup _{n=2}^{\infty } \mathcal {W}(n;X)$
. Then it is interesting to ask how big these spaces are inside
$\mathcal {W}(X):=\bigcup _{n=2}^{\infty } \mathcal {W}(n;X)$
. Then it is interesting to ask how big these spaces are inside
![]() $\mathcal {C}(X).$
We need a metric or topology on
$\mathcal {C}(X).$
We need a metric or topology on
![]() ${\mathcal C}(X)$
to make this question more precise.
${\mathcal C}(X)$
to make this question more precise.
Let X be a compact metric space with metric d. Then it is natural to have the supremum metric (or uniform metric)
on
![]() $C(X)$
, and this is our convention unless mentioned otherwise. Humke and Laczkovich considered the above question when
$C(X)$
, and this is our convention unless mentioned otherwise. Humke and Laczkovich considered the above question when
![]() $X=[0,1]$
with the usual metric
$X=[0,1]$
with the usual metric
![]() $d(x,y)=|x-y|.$
This paper is heavily motivated by their results. They proved in [Reference Humke and Laczkovich14, Reference Humke and Laczkovich15] that
$d(x,y)=|x-y|.$
This paper is heavily motivated by their results. They proved in [Reference Humke and Laczkovich14, Reference Humke and Laczkovich15] that
![]() $\mathcal {W}(2;[0,1])$
is not dense in
$\mathcal {W}(2;[0,1])$
is not dense in
![]() $\mathcal {C}([0,1])$
,
$\mathcal {C}([0,1])$
,
![]() $\mathcal {W}(2;[0,1])$
contains no balls of
$\mathcal {W}(2;[0,1])$
contains no balls of
![]() $\mathcal {C}([0,1])$
(that is, its complement
$\mathcal {C}([0,1])$
(that is, its complement
![]() $(\mathcal {W}(2;[0,1]))^{c}$
is dense in
$(\mathcal {W}(2;[0,1]))^{c}$
is dense in
![]() $\mathcal {C}([0,1])$
), and
$\mathcal {C}([0,1])$
), and
![]() $\mathcal {W}(n;[0,1])$
is an analytic non-Borel subset of
$\mathcal {W}(n;[0,1])$
is an analytic non-Borel subset of
![]() $\mathcal {C}([0,1])$
for
$\mathcal {C}([0,1])$
for
![]() $n\ge 2$
. Simon proved in [Reference Simon42–Reference Simon44] that
$n\ge 2$
. Simon proved in [Reference Simon42–Reference Simon44] that
![]() $\mathcal {W}(2;[0,1])$
is nowhere dense in
$\mathcal {W}(2;[0,1])$
is nowhere dense in
![]() $\mathcal {C}([0,1])$
and
$\mathcal {C}([0,1])$
and
![]() $\mathcal {W}([0,1])$
is not dense in
$\mathcal {W}([0,1])$
is not dense in
![]() $\mathcal {C}([0,1])$
. Subsequently, nowhere denseness of
$\mathcal {C}([0,1])$
. Subsequently, nowhere denseness of
![]() $\mathcal {W}([0,1])$
in
$\mathcal {W}([0,1])$
in
![]() ${\mathcal C}([0,1])$
was proved by Blokh [Reference Blokh7] using a method different from that of Humke-Laczkovich and Simon.
${\mathcal C}([0,1])$
was proved by Blokh [Reference Blokh7] using a method different from that of Humke-Laczkovich and Simon.
It is seen that the majority of papers on iterative roots of functions are restricted to continuous self-maps on intervals of the real line. This is not surprising because the setup is simpler to deal with. It has several advantages, including the intermediate value theorem, monotonicity of bijections, and so on. Extending these results to higher dimensions or more generic topological spaces is generally complex. We develop a new approach (see Theorem 2.4) to determine the non-existence of square roots of self-maps on arbitrary sets in §2. This approach can be used effectively to construct continuous self-maps on a wide range of topological spaces, which do not even have discontinuous square roots. We demonstrate the procedure in §3 by showing that the continuous self-maps without square roots are dense in the space of all continuous self-maps of the unit cube in
![]() ${\mathbb R}^{m}$
for the supremum metric
${\mathbb R}^{m}$
for the supremum metric
![]() $\rho $
(see Theorem 3.8). This is a significant generalization of a similar result in [Reference Humke and Laczkovich15] (Corollary 5, p. 362) for intervals of the real line. We believe that the most significant contribution of this article is the method itself. The scheme can be used in various other settings. We demonstrate this claim in §4 by proving that the continuous self-maps without square roots are dense in the space of all continuous self-maps of
$\rho $
(see Theorem 3.8). This is a significant generalization of a similar result in [Reference Humke and Laczkovich15] (Corollary 5, p. 362) for intervals of the real line. We believe that the most significant contribution of this article is the method itself. The scheme can be used in various other settings. We demonstrate this claim in §4 by proving that the continuous self-maps without square roots are dense in the space of all continuous self-maps of
![]() ${\mathbb R}^{m}$
for the compact-open topology (see Theorem 4.3).
${\mathbb R}^{m}$
for the compact-open topology (see Theorem 4.3).
The outline of the paper is as follows. In §2, we study iterates and orbits of self-maps on arbitrary sets (without any topology). Isaacs conducted a detailed investigation on the fractional iterates of such functions in [Reference Isaacs17]. Here we discuss some of the basic aspects of such an approach. The main new result is Theorem 2.4, which presents a variety of cases in which we can be certain that the given function does not admit any iterative square root. This will be our principal tool in §§3 and 4. Section 2 also contains some background material and new results on fractional iterates of continuous self-maps on general topological spaces. In particular, Theorem 2.6 shows that in some cases, the problem of the non-existence of iterative roots of continuous maps can be reduced to elementary combinatorics.
In §3, we study iterative square roots of continuous self-maps on the unit cube
![]() $I^{m}$
in
$I^{m}$
in
![]() ${\mathbb R}^{m}.$
We find it convenient to triangulate
${\mathbb R}^{m}.$
We find it convenient to triangulate
![]() $I^{m}$
and sew together affine linear maps piece by piece. For this purpose, we use some fundamental notions and notation from the theory of simplicial complexes. Given any continuous self-map on
$I^{m}$
and sew together affine linear maps piece by piece. For this purpose, we use some fundamental notions and notation from the theory of simplicial complexes. Given any continuous self-map on
![]() $I^{m}$
, we approximate it with a piecewise affine linear map, and in turn close to any such map, we find another piecewise affine linear map with no square roots (see Theorem 3.8). This is the main result of this section. In contrast, we also show that any continuous self-map on
$I^{m}$
, we approximate it with a piecewise affine linear map, and in turn close to any such map, we find another piecewise affine linear map with no square roots (see Theorem 3.8). This is the main result of this section. In contrast, we also show that any continuous self-map on
![]() $I^{m}$
with a fixed point on the boundary can be approximated by iterative squares of continuous self-maps (see Theorem 3.9). A simple example shows that fixed points on the boundary are not required for such approximations.
$I^{m}$
with a fixed point on the boundary can be approximated by iterative squares of continuous self-maps (see Theorem 3.9). A simple example shows that fixed points on the boundary are not required for such approximations.
In §4, we analyze continuous self-maps on
![]() ${\mathbb R}^{m}$
. As in §3, we prove that the continuous self-maps with no square roots are dense in the space of all continuous self-maps in a suitable topology, namely the compact-open topology (see Theorem 4.3). Finally, in §5, we prove that the squares of continuous self-maps are
${\mathbb R}^{m}$
. As in §3, we prove that the continuous self-maps with no square roots are dense in the space of all continuous self-maps in a suitable topology, namely the compact-open topology (see Theorem 4.3). Finally, in §5, we prove that the squares of continuous self-maps are
![]() $L^{p}$
dense in the space of all continuous self-maps on
$L^{p}$
dense in the space of all continuous self-maps on
![]() $I^{m}$
, generalizing a result of [Reference Humke and Laczkovich15] to higher dimensions.
$I^{m}$
, generalizing a result of [Reference Humke and Laczkovich15] to higher dimensions.
2 Functions on arbitrary sets and general topological spaces
In this section, we study iterative roots of self-maps on arbitrary sets and continuous self-maps on general topological spaces. First, we consider X to be a non-empty set with no predefined topology, and prove some new results on the existence and non-existence of iterative square roots of maps in
![]() $\mathcal {F}(X)$
, the set of all self-maps on X. Surprisingly, some of these results are useful even when X has a topology and we seek for roots inside
$\mathcal {F}(X)$
, the set of all self-maps on X. Surprisingly, some of these results are useful even when X has a topology and we seek for roots inside
![]() ${\mathcal C}(X)$
, the space of all continuous self-maps on X.
${\mathcal C}(X)$
, the space of all continuous self-maps on X.
Henceforth, let
![]() ${\mathbb Z}_{+}$
denote the set
${\mathbb Z}_{+}$
denote the set
![]() $\{0,1,2,\ldots \}$
of non-negative integers, and for each
$\{0,1,2,\ldots \}$
of non-negative integers, and for each
![]() $f\in \mathcal {F}(X)$
and
$f\in \mathcal {F}(X)$
and
![]() $A\subseteq X$
, let
$A\subseteq X$
, let
![]() $R(f)$
denote the range of f and
$R(f)$
denote the range of f and
![]() $f|_{A}$
the restriction of f to A. Given an
$f|_{A}$
the restriction of f to A. Given an
![]() $f\in \mathcal {F}(X)$
, we define its graph as the directed graph
$f\in \mathcal {F}(X)$
, we define its graph as the directed graph
![]() $G= (X, E)$
, whose vertex set is X and the edge set is
$G= (X, E)$
, whose vertex set is X and the edge set is
![]() $E=\{(x, f(x)): x\in X \}$
. In other words, we are looking at the same mathematical structure from a different viewpoint. This allows us to borrow some notions from graph theory. To begin, consider the connected components of G in the context of graph theory. We call C a connected component of X if it is the vertex set of some connected component of the graph of f. Observe that a pair of vertices x and y are in the same connected component
$E=\{(x, f(x)): x\in X \}$
. In other words, we are looking at the same mathematical structure from a different viewpoint. This allows us to borrow some notions from graph theory. To begin, consider the connected components of G in the context of graph theory. We call C a connected component of X if it is the vertex set of some connected component of the graph of f. Observe that a pair of vertices x and y are in the same connected component
![]() $C\subseteq X$
if and only if there exist
$C\subseteq X$
if and only if there exist
![]() $m,n \in {\mathbb Z}_{+}$
such that
$m,n \in {\mathbb Z}_{+}$
such that
![]() $f^{m}(x)=f^{n}(y).$
The connected component of X containing x is called the orbit of x under f, and is denoted by
$f^{m}(x)=f^{n}(y).$
The connected component of X containing x is called the orbit of x under f, and is denoted by
![]() $O_{f}(x)$
. An extensive analysis of iterative square roots of functions in
$O_{f}(x)$
. An extensive analysis of iterative square roots of functions in
![]() $\mathcal {F}(X)$
can be found in [Reference Isaacs17]. In what follows, we analyze them in some special cases and present all the results needed for our further discussions.
$\mathcal {F}(X)$
can be found in [Reference Isaacs17]. In what follows, we analyze them in some special cases and present all the results needed for our further discussions.
Let
![]() $f\in \mathcal {F}(X)$
, and
$f\in \mathcal {F}(X)$
, and
![]() $G_{1}$
and
$G_{1}$
and
![]() $G_{2}$
be two connected components of the graph G of f. An isomorphism of
$G_{2}$
be two connected components of the graph G of f. An isomorphism of
![]() $G_{1}$
and
$G_{1}$
and
![]() $G_{2}$
is a bijective function
$G_{2}$
is a bijective function
![]() $\phi :C_{1} \to C_{2}$
between the vertex sets of
$\phi :C_{1} \to C_{2}$
between the vertex sets of
![]() $G_{1}$
and
$G_{1}$
and
![]() $G_{2}$
such that any two vertices x and y are adjacent in
$G_{2}$
such that any two vertices x and y are adjacent in
![]() $G_{1}$
if and only if
$G_{1}$
if and only if
![]() $\phi (x)$
and
$\phi (x)$
and
![]() $\phi (y)$
are adjacent in
$\phi (y)$
are adjacent in
![]() $G_{2}$
. By the definition of graphs, this means that
$G_{2}$
. By the definition of graphs, this means that
![]() $y=f(x)$
if and only if
$y=f(x)$
if and only if
![]() $\phi (y)= f(\phi (x)).$
In other words,
$\phi (y)= f(\phi (x)).$
In other words,
![]() $G_{2}$
is isomorphic to
$G_{2}$
is isomorphic to
![]() $G_{1}$
if and only if there exists a bijective function
$G_{1}$
if and only if there exists a bijective function
![]() $\phi :C_{1}\to C_{2}$
such that
$\phi :C_{1}\to C_{2}$
such that
![]() $\phi \circ f= f\circ \phi .$
$\phi \circ f= f\circ \phi .$
Proposition 2.1. Let
![]() $f\in \mathcal {F}(X)$
be such that the graph of f has exactly two isomorphic connected components. Then f has an iterative square root in
$f\in \mathcal {F}(X)$
be such that the graph of f has exactly two isomorphic connected components. Then f has an iterative square root in
![]() $\mathcal {F}(X)$
.
$\mathcal {F}(X)$
.
Proof. Let
![]() $C_{1}$
and
$C_{1}$
and
![]() $C_{2}$
be the two isomorphic connected components of X corresponding to those of the graph of f. Then
$C_{2}$
be the two isomorphic connected components of X corresponding to those of the graph of f. Then
![]() $X=C_{1}\cup C_{2}, C_{1}\cap C_{2}=\emptyset $
, and as indicated above, there exists a bijective function
$X=C_{1}\cup C_{2}, C_{1}\cap C_{2}=\emptyset $
, and as indicated above, there exists a bijective function
![]() $\phi :C_{1}\to C_{2}$
such that
$\phi :C_{1}\to C_{2}$
such that
![]() $\phi \circ f= f\circ \phi $
. Define a map
$\phi \circ f= f\circ \phi $
. Define a map
![]() $g:X\to X$
by
$g:X\to X$
by
 $$ \begin{align*} g(x) = \begin{cases} \phi(x)& \mbox{if}~x\in C_{1},\\ f\circ \phi^{-1}(x)& \mbox{if}~x\in C_{2}.\end{cases} \end{align*} $$
$$ \begin{align*} g(x) = \begin{cases} \phi(x)& \mbox{if}~x\in C_{1},\\ f\circ \phi^{-1}(x)& \mbox{if}~x\in C_{2}.\end{cases} \end{align*} $$
Now, we have
![]() $g(x)=\phi (x)\in C_{2}$
for each
$g(x)=\phi (x)\in C_{2}$
for each
![]() $x\in C_{1}$
, implying that
$x\in C_{1}$
, implying that
![]() $g^{2}(x)= f\circ \phi ^{-1}\circ \phi (x)= f(x)$
. Similarly, we have
$g^{2}(x)= f\circ \phi ^{-1}\circ \phi (x)= f(x)$
. Similarly, we have
![]() $g(x)=f\circ \phi ^{-1}(x) \in C_{1}$
for each
$g(x)=f\circ \phi ^{-1}(x) \in C_{1}$
for each
![]() $x\in C_{2}$
, and so
$x\in C_{2}$
, and so
![]() $g^{2}(x)= \phi \circ f\circ \phi ^{-1}(x)= f(x)$
. Therefore, g is an iterative square root of f on X.
$g^{2}(x)= \phi \circ f\circ \phi ^{-1}(x)= f(x)$
. Therefore, g is an iterative square root of f on X.
The above proposition leads to the following result, where a fixed point x of f is said to be isolated if there is no
![]() $y\ne x$
in X such that
$y\ne x$
in X such that
![]() $f(y)=x$
. By convention, the empty set and all infinite sets are assumed to have an even number of elements here and elsewhere.
$f(y)=x$
. By convention, the empty set and all infinite sets are assumed to have an even number of elements here and elsewhere.
Theorem 2.2. Let
![]() $f\in \mathcal {F}(X)$
be such that excluding isolated fixed points of f, the number of isomorphic copies is even for each connected component of the graph of f. Then f has an iterative square root in
$f\in \mathcal {F}(X)$
be such that excluding isolated fixed points of f, the number of isomorphic copies is even for each connected component of the graph of f. Then f has an iterative square root in
![]() $\mathcal {F}(X)$
.
$\mathcal {F}(X)$
.
Proof. Let
![]() $g:X\to X$
be a map defined as
$g:X\to X$
be a map defined as
![]() $g(x)=x$
for isolated fixed points
$g(x)=x$
for isolated fixed points
![]() $x\in X$
of f and g as in the previous proposition on the union of pairs of connected components of X corresponding to pairs of isomorphic copies of those of the graph of f. Since there are an even number of connected components, we can pair them, and the result follows from the previous proposition.
$x\in X$
of f and g as in the previous proposition on the union of pairs of connected components of X corresponding to pairs of isomorphic copies of those of the graph of f. Since there are an even number of connected components, we can pair them, and the result follows from the previous proposition.
The above results are given for general
![]() $f\in \mathcal {F}(X)$
. If we restrict ourselves to injective maps, we can describe the functions with square roots transparently, as seen below. To make our thoughts more concrete, we borrow some ideas and terminologies from [Reference Bhat, De and Rakshit5]. Note that given an injective map
$f\in \mathcal {F}(X)$
. If we restrict ourselves to injective maps, we can describe the functions with square roots transparently, as seen below. To make our thoughts more concrete, we borrow some ideas and terminologies from [Reference Bhat, De and Rakshit5]. Note that given an injective map
![]() $f\in \mathcal {F}(X)$
, any two points
$f\in \mathcal {F}(X)$
, any two points
![]() $x, y \in X$
are in the same orbit under f if and only if there exists an
$x, y \in X$
are in the same orbit under f if and only if there exists an
![]() $n\in {\mathbb Z}_{+}$
such that either
$n\in {\mathbb Z}_{+}$
such that either
![]() $y=f^{n}(x)$
or
$y=f^{n}(x)$
or
![]() $x=f^{n}(y).$
Indeed, an orbit under f has one of the following forms for some
$x=f^{n}(y).$
Indeed, an orbit under f has one of the following forms for some
![]() $x\in X$
:
$x\in X$
:
-
(i)
 $\{x, f(x), f^{2}(x), \ldots ,f^{d-1}(x)\}$
for some
$\{x, f(x), f^{2}(x), \ldots ,f^{d-1}(x)\}$
for some
 $d\in \mathbb {N}$
with
$d\in \mathbb {N}$
with
 $f^{d}(x)=x$
;
$f^{d}(x)=x$
; -
(ii)
 $\{x, f(x), f^{2}(x), \ldots \}$
with
$\{x, f(x), f^{2}(x), \ldots \}$
with
 $x\notin R(f)$
;
$x\notin R(f)$
; -
(iii)
 $\{\ldots ,f^{-2}(x), f^{-1}(x), x, f(x), f^{2}(x), \ldots \}$
.
$\{\ldots ,f^{-2}(x), f^{-1}(x), x, f(x), f^{2}(x), \ldots \}$
.
Therefore, it follows that an injective map
![]() $f\in \mathcal {F}(X)$
with exactly one orbit
$f\in \mathcal {F}(X)$
with exactly one orbit
![]() $O_{f}(x)$
for some
$O_{f}(x)$
for some
![]() $x\in X$
is in bijective correspondence with precisely one of the following maps (see [Reference Bhat, De and Rakshit5]).
$x\in X$
is in bijective correspondence with precisely one of the following maps (see [Reference Bhat, De and Rakshit5]).
-
(a) Cyclic permutations: For
 $d\in {\mathbb N}$
, consider
$d\in {\mathbb N}$
, consider
 ${\mathbb Z}_{d} =\{0, 1, 2, \ldots , d-1\}$
with addition modulo
${\mathbb Z}_{d} =\{0, 1, 2, \ldots , d-1\}$
with addition modulo
 $d.$
Define
$d.$
Define
 $s_{d}: {\mathbb Z}_{d}\to {\mathbb Z}_{d}$
by
$s_{d}: {\mathbb Z}_{d}\to {\mathbb Z}_{d}$
by
 $s_{d}(k)=k+1~(\mbox {mod}~d)$
. Note that
$s_{d}(k)=k+1~(\mbox {mod}~d)$
. Note that
 ${\mathbb Z}_{1}=\{0\}$
and
${\mathbb Z}_{1}=\{0\}$
and
 $s_{1}(0)=0$
. Then
$s_{1}(0)=0$
. Then
 $s_{d}$
is bijective and has exactly one orbit.
$s_{d}$
is bijective and has exactly one orbit. -
(b) Unilateral translation/shift: Define
 $s_{+}: {\mathbb Z}_{+}\to {\mathbb Z}_{+}$
by
$s_{+}: {\mathbb Z}_{+}\to {\mathbb Z}_{+}$
by
 $s_{+}(k)=k+1.$
Then
$s_{+}(k)=k+1.$
Then
 $s_{+}$
is a shift with a single orbit.
$s_{+}$
is a shift with a single orbit. -
(c) Bilateral translation: Define
 $s: {\mathbb Z}\to {\mathbb Z}$
by
$s: {\mathbb Z}\to {\mathbb Z}$
by
 $s(k)=k+1$
. Then s is bijective and has exactly one orbit.
$s(k)=k+1$
. Then s is bijective and has exactly one orbit.
More precisely, if
![]() $f\in \mathcal {F}(X)$
has exactly one orbit
$f\in \mathcal {F}(X)$
has exactly one orbit
![]() $O_{f}(x)$
, then there exists a bijective function
$O_{f}(x)$
, then there exists a bijective function
![]() $\phi : O_{f}(x)\to Z$
defined by
$\phi : O_{f}(x)\to Z$
defined by
![]() $\phi (f^{k}(x))=k$
, where Z is
$\phi (f^{k}(x))=k$
, where Z is
![]() $\mathbb {Z}_{d}$
(for some
$\mathbb {Z}_{d}$
(for some
![]() $d\in \mathbb {N}$
),
$d\in \mathbb {N}$
),
![]() $\mathbb {Z}_{+}$
or
$\mathbb {Z}_{+}$
or
![]() $\mathbb {Z}$
according as
$\mathbb {Z}$
according as
![]() $O_{f}(x)$
has the form (i), (ii) or (iii), respectively. Consider any arbitrary non-empty sets
$O_{f}(x)$
has the form (i), (ii) or (iii), respectively. Consider any arbitrary non-empty sets
![]() $M_{d}$
,
$M_{d}$
,
![]() $M_{+}$
and
$M_{+}$
and
![]() $M.$
We define
$M.$
We define
![]() $1_{M_{d}}\times s_{d}: M_{d}\times {\mathbb Z}_{d}\to M_{d}\times {\mathbb Z}_{d}$
by
$1_{M_{d}}\times s_{d}: M_{d}\times {\mathbb Z}_{d}\to M_{d}\times {\mathbb Z}_{d}$
by
called the d-cyclic permutation with multiplicity
![]() $M_{d}$
for each
$M_{d}$
for each
![]() $d\in \mathbb {N}$
. Similarly, we define
$d\in \mathbb {N}$
. Similarly, we define
![]() $1_{M_{+}}\times s_{+}:M_{+}\times \mathbb {Z}_{+}\to M_{+}\times \mathbb {Z}_{+}$
and
$1_{M_{+}}\times s_{+}:M_{+}\times \mathbb {Z}_{+}\to M_{+}\times \mathbb {Z}_{+}$
and
![]() $1_{M}\times s:M\times \mathbb {Z}\to M\times \mathbb {Z}$
by
$1_{M}\times s:M\times \mathbb {Z}\to M\times \mathbb {Z}$
by
called the unilateral shift with multiplicity
![]() $M_{+}$
and the bilateral translation with multiplicity M, respectively. Then, given any injective map
$M_{+}$
and the bilateral translation with multiplicity M, respectively. Then, given any injective map
![]() $f\in \mathcal {F}(X)$
, decomposing
$f\in \mathcal {F}(X)$
, decomposing
![]() $X=\bigsqcup _{x\in X} O_{f}(x)$
into orbits under f, we see that
$X=\bigsqcup _{x\in X} O_{f}(x)$
into orbits under f, we see that
![]() $(X,f)$
is in bijective correspondence with
$(X,f)$
is in bijective correspondence with
![]() $(Y,\tilde {f})$
, where
$(Y,\tilde {f})$
, where
![]() $Y= \bigsqcup _{d\in {\mathbb N}}(M_{d}\times {\mathbb Z}_{d})\bigsqcup (M_{+}\times {\mathbb Z}_{+})\bigsqcup (M\times {\mathbb Z})$
for some suitable multiplicity spaces
$Y= \bigsqcup _{d\in {\mathbb N}}(M_{d}\times {\mathbb Z}_{d})\bigsqcup (M_{+}\times {\mathbb Z}_{+})\bigsqcup (M\times {\mathbb Z})$
for some suitable multiplicity spaces
![]() $M_{d}$
,
$M_{d}$
,
![]() $M_{+}$
and M (some of these sets may be absent in the union), and
$M_{+}$
and M (some of these sets may be absent in the union), and
![]() $\tilde {f}$
is
$\tilde {f}$
is
![]() $1_{M_{d}}\times s_{d}$
,
$1_{M_{d}}\times s_{d}$
,
![]() $1_{M_{+}}\times s_{+}$
and
$1_{M_{+}}\times s_{+}$
and
![]() $1_{M}\times s$
on
$1_{M}\times s$
on
![]() $M_{d}\times {\mathbb Z}_{d}$
,
$M_{d}\times {\mathbb Z}_{d}$
,
![]() $M_{+}\times {\mathbb Z}_{+}$
and
$M_{+}\times {\mathbb Z}_{+}$
and
![]() $M\times {\mathbb Z}$
, respectively. Furthermore, the cardinalities of these multiplicity spaces are uniquely determined. We call
$M\times {\mathbb Z}$
, respectively. Furthermore, the cardinalities of these multiplicity spaces are uniquely determined. We call
![]() $(m_{1}, m_{2}, \ldots , m_{+},m)$
as the multiplicity sequence of f, where
$(m_{1}, m_{2}, \ldots , m_{+},m)$
as the multiplicity sequence of f, where
![]() $m_{d}$
,
$m_{d}$
,
![]() $m_{+}$
and m are the cardinalities of
$m_{+}$
and m are the cardinalities of
![]() $M_{d}$
(for
$M_{d}$
(for
![]() $d\in {\mathbb N}$
),
$d\in {\mathbb N}$
),
![]() $M_{+}$
and M, respectively.
$M_{+}$
and M, respectively.
Theorem 2.3. Let
![]() $f\in \mathcal {F}(X)$
be an injective map. Then f has an iterative square root in
$f\in \mathcal {F}(X)$
be an injective map. Then f has an iterative square root in
![]() $\mathcal {F}(X)$
if and only if the multiplicity sequence
$\mathcal {F}(X)$
if and only if the multiplicity sequence
![]() $(m_{1}, m_{2}, \ldots , m_{+},m)$
of f satisfies that
$(m_{1}, m_{2}, \ldots , m_{+},m)$
of f satisfies that
![]() $m_{d}$
with d even,
$m_{d}$
with d even,
![]() $m_{+}$
and m are even (
$m_{+}$
and m are even (
![]() $0$
and infinity allowed).
$0$
and infinity allowed).
Proof. Let
![]() $f\in \mathcal {F}(X)$
be an injective map and
$f\in \mathcal {F}(X)$
be an injective map and
![]() $(m_{1}, m_{2}, \ldots , m_{+},m)$
be the multiplicity sequence of f. Suppose that
$(m_{1}, m_{2}, \ldots , m_{+},m)$
be the multiplicity sequence of f. Suppose that
![]() $f=g^{2}$
for some
$f=g^{2}$
for some
![]() $g\in \mathcal {F}(X)$
. Then, clearly g is an injective map on X, and therefore we can associate a multiplicity sequence
$g\in \mathcal {F}(X)$
. Then, clearly g is an injective map on X, and therefore we can associate a multiplicity sequence
![]() $(m_{1}^{\prime }, m_{2}^{\prime }, \ldots , m_{+}^{\prime },m^{\prime })$
for g. Further, it is easily seen that an orbit under g corresponding to a cyclic permutation on
$(m_{1}^{\prime }, m_{2}^{\prime }, \ldots , m_{+}^{\prime },m^{\prime })$
for g. Further, it is easily seen that an orbit under g corresponding to a cyclic permutation on
![]() ${\mathbb Z}_{d}$
gives rise to two orbits (respectively a unique orbit) under
${\mathbb Z}_{d}$
gives rise to two orbits (respectively a unique orbit) under
![]() $g^{2}$
corresponding to cyclic permutation on
$g^{2}$
corresponding to cyclic permutation on
![]() ${\mathbb Z}_{ {d}/{2}}$
(respectively on
${\mathbb Z}_{ {d}/{2}}$
(respectively on
![]() $\mathbb {Z}_{d}$
) whenever d is even (respectively odd). Similarly, an orbit under g corresponding to the unilateral shift on
$\mathbb {Z}_{d}$
) whenever d is even (respectively odd). Similarly, an orbit under g corresponding to the unilateral shift on
![]() ${\mathbb Z}_{+}$
(respectively the bilateral translation on
${\mathbb Z}_{+}$
(respectively the bilateral translation on
![]() $\mathbb {Z}$
) gives rise to two orbits under
$\mathbb {Z}$
) gives rise to two orbits under
![]() $g^{2}$
corresponding to the unilateral shift on
$g^{2}$
corresponding to the unilateral shift on
![]() ${\mathbb Z}_{+}$
(respectively the bilateral translation on
${\mathbb Z}_{+}$
(respectively the bilateral translation on
![]() $\mathbb {Z}$
). Therefore, the multiplicity sequence of
$\mathbb {Z}$
). Therefore, the multiplicity sequence of
![]() $g^{2}$
is
$g^{2}$
is
![]() $(m_{1}^{\prime }+2m_{2}^{\prime }, 2m_{4}^{\prime }, m_{3}^{\prime }+2m_{6}^{\prime }, 2m_{8}^{\prime }, m_{5}^{\prime }+2m_{10}^{\prime }, 2m_{12}^{\prime }, \ldots , 2m_{+}^{\prime }, 2m^{\prime })$
. Consequently, we must have
$(m_{1}^{\prime }+2m_{2}^{\prime }, 2m_{4}^{\prime }, m_{3}^{\prime }+2m_{6}^{\prime }, 2m_{8}^{\prime }, m_{5}^{\prime }+2m_{10}^{\prime }, 2m_{12}^{\prime }, \ldots , 2m_{+}^{\prime }, 2m^{\prime })$
. Consequently, we must have
![]() $m_{+}=2m_{+}^{\prime }$
,
$m_{+}=2m_{+}^{\prime }$
,
![]() $m=2m^{\prime }$
, and
$m=2m^{\prime }$
, and
 $$ \begin{align*} m_{d} = \begin{cases} m_{d}^{\prime}+2m_{2d}^{\prime}&\mbox{if }d\text{ is odd},\\ 2m_{2d}^{\prime}& \mbox{if } d \text{ is even},\end{cases} \end{align*} $$
$$ \begin{align*} m_{d} = \begin{cases} m_{d}^{\prime}+2m_{2d}^{\prime}&\mbox{if }d\text{ is odd},\\ 2m_{2d}^{\prime}& \mbox{if } d \text{ is even},\end{cases} \end{align*} $$
and hence
![]() $m_{d}$
for d even,
$m_{d}$
for d even,
![]() $m_{+}$
and m are even.
$m_{+}$
and m are even.
Conversely, suppose that the multiplicity sequence
![]() $(m_{1}, m_{2}, \ldots , m_{+}, m)$
of f satisfies that
$(m_{1}, m_{2}, \ldots , m_{+}, m)$
of f satisfies that
![]() $m_{d}$
for d even,
$m_{d}$
for d even,
![]() $m_{+}$
and m are even. Then X can be decomposed into orbits under f as
$m_{+}$
and m are even. Then X can be decomposed into orbits under f as
![]() $X=\bigsqcup _{x\in X} O_{f}(x)$
and
$X=\bigsqcup _{x\in X} O_{f}(x)$
and
![]() $(X,f)$
is in bijective correspondence with
$(X,f)$
is in bijective correspondence with
![]() $(Y,\tilde {f})$
, where
$(Y,\tilde {f})$
, where
![]() $Y= \bigsqcup _{d\in {\mathbb N}}(M_{d}\times {\mathbb Z}_{d})\bigsqcup (M_{+}\times {\mathbb Z}_{+})\bigsqcup (M\times {\mathbb Z})$
such that:
$Y= \bigsqcup _{d\in {\mathbb N}}(M_{d}\times {\mathbb Z}_{d})\bigsqcup (M_{+}\times {\mathbb Z}_{+})\bigsqcup (M\times {\mathbb Z})$
such that:
-
• each orbit
 $O_{f}(x)$
in X under f has one of the above-mentioned forms (i), (ii) or (iii);
$O_{f}(x)$
in X under f has one of the above-mentioned forms (i), (ii) or (iii); -
• the cardinalities of multiplicity spaces
 $M_{d}$
(for all
$M_{d}$
(for all
 $d\in \mathbb {N}$
),
$d\in \mathbb {N}$
),
 $M_{+}$
and M are
$M_{+}$
and M are
 $m_{d}$
,
$m_{d}$
,
 $m_{+}$
and m, respectively; and
$m_{+}$
and m, respectively; and -
•
 $\tilde {f}$
is
$\tilde {f}$
is
 $1_{M_{d}}\times s_{d}$
,
$1_{M_{d}}\times s_{d}$
,
 $1_{M_{+}}\times s_{+}$
and
$1_{M_{+}}\times s_{+}$
and
 $1_{M}\times s$
on
$1_{M}\times s$
on
 $M_{d}\times {\mathbb Z}_{d}$
,
$M_{d}\times {\mathbb Z}_{d}$
,
 $M_{+}\times {\mathbb Z}_{+}$
and
$M_{+}\times {\mathbb Z}_{+}$
and
 $M\times {\mathbb Z}$
, respectively.
$M\times {\mathbb Z}$
, respectively.
Now, define a map
![]() $g:X\to X$
as follows. If
$g:X\to X$
as follows. If
![]() $d\in \mathbb {N}$
is odd, then for each of the orbits
$d\in \mathbb {N}$
is odd, then for each of the orbits
![]() $O_{f}(x)=\{x,f(x),f^{2}(x),\ldots , f^{d-1}(x)\}$
corresponding to the cyclic permutation on
$O_{f}(x)=\{x,f(x),f^{2}(x),\ldots , f^{d-1}(x)\}$
corresponding to the cyclic permutation on
![]() ${\mathbb Z}_{d}$
, define
${\mathbb Z}_{d}$
, define
for all
![]() $0\le l\le d-1$
. Then,
$0\le l\le d-1$
. Then,
for all
![]() $0\le l\le d-1$
, implying that
$0\le l\le d-1$
, implying that
![]() $g^{2}=f$
on
$g^{2}=f$
on
![]() $O_{f}(x)$
. If
$O_{f}(x)$
. If
![]() $d\in \mathbb {N}$
is even, then as
$d\in \mathbb {N}$
is even, then as
![]() $m_{d}$
is even, by pairing any two distinct orbits
$m_{d}$
is even, by pairing any two distinct orbits
![]() $O_{f}(x)=\{x,f(x),f^{2}(x),\ldots , f^{d-1}(x)\}$
and
$O_{f}(x)=\{x,f(x),f^{2}(x),\ldots , f^{d-1}(x)\}$
and
![]() $O_{f}(y)=\{y,f(y),f^{2}(y),\ldots , f^{d-1}(y)\}$
corresponding to the cyclic permutation on
$O_{f}(y)=\{y,f(y),f^{2}(y),\ldots , f^{d-1}(y)\}$
corresponding to the cyclic permutation on
![]() ${\mathbb Z}_{d}$
, define g on
${\mathbb Z}_{d}$
, define g on
![]() $O_{f}(x)\cup O_{f}(y)$
by
$O_{f}(x)\cup O_{f}(y)$
by
 $$ \begin{align*} g(z) = \begin{cases} \phi(z)& \mbox{if}~z\in O_{f}(x),\\ f\circ \phi^{-1}(z)& \mbox{if}~z\in O_{f}(y),\end{cases} \end{align*} $$
$$ \begin{align*} g(z) = \begin{cases} \phi(z)& \mbox{if}~z\in O_{f}(x),\\ f\circ \phi^{-1}(z)& \mbox{if}~z\in O_{f}(y),\end{cases} \end{align*} $$
where
![]() $\phi :O_{f}(x)\to O_{f}(y)$
is a bijective function such that
$\phi :O_{f}(x)\to O_{f}(y)$
is a bijective function such that
![]() $\phi \circ f= f\circ \phi $
. Then, by a similar argument as in Proposition 2.1, it follows that
$\phi \circ f= f\circ \phi $
. Then, by a similar argument as in Proposition 2.1, it follows that
![]() $g^{2}=f$
on
$g^{2}=f$
on
![]() $O_{f}(x)\cup O_{f}(y)$
. Since
$O_{f}(x)\cup O_{f}(y)$
. Since
![]() $m_{+}$
(respectively m) is even, g can be defined similarly on the union
$m_{+}$
(respectively m) is even, g can be defined similarly on the union
![]() $O_{f}(x)\cup O_{f}(y)$
of each pair of distinct orbits
$O_{f}(x)\cup O_{f}(y)$
of each pair of distinct orbits
![]() $O_{f}(x)$
and
$O_{f}(x)$
and
![]() $O_{f}(y)$
corresponding to the unilateral shift on
$O_{f}(y)$
corresponding to the unilateral shift on
![]() ${\mathbb Z}_{+}$
(respectively the bilateral translation on
${\mathbb Z}_{+}$
(respectively the bilateral translation on
![]() $\mathbb {Z}$
) such that
$\mathbb {Z}$
) such that
![]() $g^{2}=f$
on
$g^{2}=f$
on
![]() $O_{f}(x)\cup O_{f}(y)$
. Therefore, f has a square root in
$O_{f}(x)\cup O_{f}(y)$
. Therefore, f has a square root in
![]() $\mathcal {F}(X)$
.
$\mathcal {F}(X)$
.
For each
![]() $f\in \mathcal {F}(X)$
and
$f\in \mathcal {F}(X)$
and
![]() $x\in X$
, let
$x\in X$
, let
![]() $f^{-1}(x)$
and
$f^{-1}(x)$
and
![]() $f^{-2}(x)$
denote the usual inverse images defined by
$f^{-2}(x)$
denote the usual inverse images defined by
![]() $f^{-1}(x)=\{y\in X: f(y)=x\}$
and
$f^{-1}(x)=\{y\in X: f(y)=x\}$
and
![]() $f^{-2}(x)=\{y\in X: f^{2}(y)=x\}$
. Further, for each set A, let
$f^{-2}(x)=\{y\in X: f^{2}(y)=x\}$
. Further, for each set A, let
![]() $\# A$
denote the number of elements or the cardinality of A. So far, we have studied various conditions under which maps in
$\# A$
denote the number of elements or the cardinality of A. So far, we have studied various conditions under which maps in
![]() $\mathcal {F}(X)$
have square roots. We now have some instances in which they have no square roots. The following result is very useful for constructing functions without square roots in the next two sections.
$\mathcal {F}(X)$
have square roots. We now have some instances in which they have no square roots. The following result is very useful for constructing functions without square roots in the next two sections.
Theorem 2.4. Let
![]() $f\in \mathcal {F}(X)$
be such that
$f\in \mathcal {F}(X)$
be such that
![]() $f(x_{0})\ne x_{0}$
for some
$f(x_{0})\ne x_{0}$
for some
![]() $x_{0}\in X$
. Then f has no iterative square roots in
$x_{0}\in X$
. Then f has no iterative square roots in
![]() $\mathcal {F}(X)$
in the following cases:
$\mathcal {F}(X)$
in the following cases:
Case (i):
![]() $\# f^{-2}(x_{0})>1$
, and
$\# f^{-2}(x_{0})>1$
, and
![]() $\# f^{-1}(x)\leq 1$
for all
$\# f^{-1}(x)\leq 1$
for all
![]() $x\neq x_{0}$
;
$x\neq x_{0}$
;
Case (ii):
![]() $ f^{-2}(x_{0})$
is infinite, and
$ f^{-2}(x_{0})$
is infinite, and
![]() $ f^{-1}(x)$
is finite for all
$ f^{-1}(x)$
is finite for all
![]() $x\ne x_{0}$
;
$x\ne x_{0}$
;
Case (iii):
![]() $f^{-2}(x_{0})$
is uncountable, and
$f^{-2}(x_{0})$
is uncountable, and
![]() $f^{-1}(x)$
is countable for all
$f^{-1}(x)$
is countable for all
![]() $x\ne x_{0}$
.
$x\ne x_{0}$
.
Proof. Suppose that
![]() $f=g^{2}$
for some
$f=g^{2}$
for some
![]() $g\in \mathcal {F}(X)$
. Consider the action of g on various subsets of X around
$g\in \mathcal {F}(X)$
. Consider the action of g on various subsets of X around
![]() $x_{0}$
:
$x_{0}$
:
where
![]() $y_{0}=g(x_{0})$
,
$y_{0}=g(x_{0})$
,
![]() $A_{-1} =f^{-1}(x_{0})$
,
$A_{-1} =f^{-1}(x_{0})$
,
![]() $A_{-2} =f^{-2}(x_{0})$
,
$A_{-2} =f^{-2}(x_{0})$
,
![]() $B_{-1}=g(A_{-1})$
and
$B_{-1}=g(A_{-1})$
and
![]() $B_{-2}=g(A_{-2})$
. Let
$B_{-2}=g(A_{-2})$
. Let
![]() $\tilde {A}_{-1}=f(A_{-2})$
and
$\tilde {A}_{-1}=f(A_{-2})$
and
![]() $\tilde {B}_{-1}=g(\tilde {A}_{-1})$
. Then
$\tilde {B}_{-1}=g(\tilde {A}_{-1})$
. Then
![]() $\tilde {A}_{-1}\subseteq A_{-1}$
,
$\tilde {A}_{-1}\subseteq A_{-1}$
,
![]() $\tilde {B}_{-1}\subseteq B_{-1}\subseteq g^{-1}(x_{0})$
and
$\tilde {B}_{-1}\subseteq B_{-1}\subseteq g^{-1}(x_{0})$
and
![]() $B_{-2}\subseteq g^{-1}(A_{-1})$
. Also, since
$B_{-2}\subseteq g^{-1}(A_{-1})$
. Also, since
![]() $f(x_{0})\ne x_{0}$
, we have
$f(x_{0})\ne x_{0}$
, we have
![]() $y_{0}\neq x_{0}$
,
$y_{0}\neq x_{0}$
,
![]() $x_{0} \notin A_{-1}$
and
$x_{0} \notin A_{-1}$
and
![]() $x_{0}\notin B_{-1}$
.
$x_{0}\notin B_{-1}$
.
Case (i): Since
![]() $x_{0}\notin A_{-1}$
and
$x_{0}\notin A_{-1}$
and
![]() $\tilde {A}_{-1}\subseteq A_{-1}$
, we have
$\tilde {A}_{-1}\subseteq A_{-1}$
, we have
![]() $\#f^{-1}(x)\leq 1$
for all
$\#f^{-1}(x)\leq 1$
for all
![]() $x\in \tilde {A}_{-1}$
. Therefore, as
$x\in \tilde {A}_{-1}$
. Therefore, as
![]() $A_{-2}\subseteq \bigcup _{x\in \tilde {A}_{-1}}f^{-1}(x)$
and
$A_{-2}\subseteq \bigcup _{x\in \tilde {A}_{-1}}f^{-1}(x)$
and
![]() $\#A_{-2}>1$
, it follows that
$\#A_{-2}>1$
, it follows that
![]() $\#\tilde {A}_{-1}>1$
.
$\#\tilde {A}_{-1}>1$
.
However, since
![]() $y_{0}\ne x_{0}$
, we have
$y_{0}\ne x_{0}$
, we have
![]() $\#f^{-1}(y_{0})\le 1$
. This implies that
$\#f^{-1}(y_{0})\le 1$
. This implies that
![]() $\#\tilde {B}_{-1}=1$
, because
$\#\tilde {B}_{-1}=1$
, because
![]() $\tilde {B}_{-1}\ne \emptyset $
and
$\tilde {B}_{-1}\ne \emptyset $
and
![]() $\tilde {B}_{-1}\subseteq B_{-1}\subseteq f^{-1}(y_{0})$
. Therefore, as
$\tilde {B}_{-1}\subseteq B_{-1}\subseteq f^{-1}(y_{0})$
. Therefore, as
![]() $x_{0}\notin \tilde {B}_{-1}$
, we get that
$x_{0}\notin \tilde {B}_{-1}$
, we get that
![]() $\#f^{-1}(\tilde {B}_{-1})=1$
. Consequently,
$\#f^{-1}(\tilde {B}_{-1})=1$
. Consequently,
![]() $\#B_{-2}=1$
, implying that
$\#B_{-2}=1$
, implying that
![]() $\#\tilde {A}_{-1}=\#f(A_{-2})= \#g(B_{-2})=1$
. This contradicts an earlier conclusion. Hence, f has no square roots in
$\#\tilde {A}_{-1}=\#f(A_{-2})= \#g(B_{-2})=1$
. This contradicts an earlier conclusion. Hence, f has no square roots in
![]() $\mathcal {F}(X)$
.
$\mathcal {F}(X)$
.
Case (ii): Since
![]() $x_{0}\notin A_{-1}$
and
$x_{0}\notin A_{-1}$
and
![]() $\tilde {A}_{-1}\subseteq A_{-1}$
, we see that
$\tilde {A}_{-1}\subseteq A_{-1}$
, we see that
![]() $f^{-1}(x)$
is finite for all
$f^{-1}(x)$
is finite for all
![]() $x\in \tilde {A}_{-1}$
. Therefore, as
$x\in \tilde {A}_{-1}$
. Therefore, as
![]() $A_{-2}\subseteq \bigcup _{x\in \tilde {A}_{-1}}f^{-1}(x)$
and
$A_{-2}\subseteq \bigcup _{x\in \tilde {A}_{-1}}f^{-1}(x)$
and
![]() $A_{-2}$
is infinite, it follows that
$A_{-2}$
is infinite, it follows that
![]() $\tilde {A}_{-1}$
is infinite.
$\tilde {A}_{-1}$
is infinite.
However, since
![]() $y_{0}\ne x_{0}$
, we have that
$y_{0}\ne x_{0}$
, we have that
![]() $f^{-1}(y_{0})$
is finite. This implies that
$f^{-1}(y_{0})$
is finite. This implies that
![]() $\tilde {B}_{-1}$
is finite, because
$\tilde {B}_{-1}$
is finite, because
![]() $\tilde {B}_{-1} \subseteq B_{-1}\subseteq f^{-1}(y_{0})$
. Also, as
$\tilde {B}_{-1} \subseteq B_{-1}\subseteq f^{-1}(y_{0})$
. Also, as
![]() $x_{0}\notin B_{-1}$
and
$x_{0}\notin B_{-1}$
and
![]() $\tilde {B}_{-1} \subseteq B_{-1}$
, we see that
$\tilde {B}_{-1} \subseteq B_{-1}$
, we see that
![]() $f^{-1}(x)$
is finite for all
$f^{-1}(x)$
is finite for all
![]() $x\in \tilde {B}_{-1}$
. Then it follows that
$x\in \tilde {B}_{-1}$
. Then it follows that
![]() $f^{-1}(\tilde {B}_{-1})$
is finite. Consequently,
$f^{-1}(\tilde {B}_{-1})$
is finite. Consequently,
![]() $B_{-2}$
is finite, implying that
$B_{-2}$
is finite, implying that
![]() $\tilde {A}_{-1}=f(A_{-2})= g(B_{-2})$
is finite. This contradicts the conclusion of the previous paragraph. Hence, f has no square roots in
$\tilde {A}_{-1}=f(A_{-2})= g(B_{-2})$
is finite. This contradicts the conclusion of the previous paragraph. Hence, f has no square roots in
![]() $\mathcal {F}(X)$
.
$\mathcal {F}(X)$
.
Case (iii): The proof of Case (ii) repeatedly uses the fact that a finite union of finite sets is finite. The proof for this case is similar, using the result that a countable union of countable sets is countable.
It is worth noting that
![]() $f^{-2}$
in the previous theorem cannot be replaced by
$f^{-2}$
in the previous theorem cannot be replaced by
![]() $f^{-1}$
, as seen from the following.
$f^{-1}$
, as seen from the following.
Example 2.5. Consider the continuous map
![]() $f:[0,1]\to [0,1]$
defined by
$f:[0,1]\to [0,1]$
defined by
 $$ \begin{align*} f(x)= \begin{cases} \dfrac{3}{4}& \text{if } 0\leq x\leq \dfrac{1}{2},\\[6pt] \dfrac{5}{8}+\dfrac{x}{4}& \text{if } \dfrac{1}{2}< x\leq 1.\end{cases} \end{align*} $$
$$ \begin{align*} f(x)= \begin{cases} \dfrac{3}{4}& \text{if } 0\leq x\leq \dfrac{1}{2},\\[6pt] \dfrac{5}{8}+\dfrac{x}{4}& \text{if } \dfrac{1}{2}< x\leq 1.\end{cases} \end{align*} $$
Then
![]() $f(\tfrac 34)\neq \tfrac 34$
,
$f(\tfrac 34)\neq \tfrac 34$
,
![]() $f^{-1}(\tfrac 34)$
is uncountable and
$f^{-1}(\tfrac 34)$
is uncountable and
![]() $f^{-1}(x)$
is finite for all
$f^{-1}(x)$
is finite for all
![]() $x\neq \tfrac 34.$
However, f has a square root
$x\neq \tfrac 34.$
However, f has a square root
 $$ \begin{align*} g(x)= \begin{cases} 1& \text{if } 0\leq x\leq \dfrac{1}{2},\\ \dfrac{5}{4}-\dfrac{x}{2}&\text{if } \dfrac{1}{2}< x\leq 1,\end{cases} \end{align*} $$
$$ \begin{align*} g(x)= \begin{cases} 1& \text{if } 0\leq x\leq \dfrac{1}{2},\\ \dfrac{5}{4}-\dfrac{x}{2}&\text{if } \dfrac{1}{2}< x\leq 1,\end{cases} \end{align*} $$
on
![]() $[0,1]$
that is even continuous.
$[0,1]$
that is even continuous.
The above results are given for an arbitrary set X. In the rest of the section and those that follow, we consider X to be a topological space or a specific metric space and study continuous roots of continuous self-maps on X. It is useful to have some notation in this context. Recall that for a topological space X, the space of all continuous self-maps of X is denoted by
![]() $\mathcal {C}(X)$
. For each
$\mathcal {C}(X)$
. For each
![]() $A\subseteq X$
, let
$A\subseteq X$
, let
![]() $A^{0}$
denote the interior of A,
$A^{0}$
denote the interior of A,
![]() $\overline {A}$
the closure of A and
$\overline {A}$
the closure of A and
![]() $\partial A$
the boundary of A. In particular, if X is a metric space equipped with metric d, then for each
$\partial A$
the boundary of A. In particular, if X is a metric space equipped with metric d, then for each
![]() $x\in X$
and
$x\in X$
and
![]() $\epsilon>0$
, let
$\epsilon>0$
, let
![]() $B_{\epsilon }(x):=\{y\in X: d(x,y)<\epsilon \}$
, the open ball in X around x of radius
$B_{\epsilon }(x):=\{y\in X: d(x,y)<\epsilon \}$
, the open ball in X around x of radius
![]() $\epsilon $
. For any index set
$\epsilon $
. For any index set
![]() $\Lambda $
, let
$\Lambda $
, let
![]() $S_{\Lambda }$
denote the group of all permutations (bijections) on
$S_{\Lambda }$
denote the group of all permutations (bijections) on
![]() $\Lambda $
, and for convenience, we denote
$\Lambda $
, and for convenience, we denote
![]() $S_{\Lambda }$
by
$S_{\Lambda }$
by
![]() $S_{k}$
when
$S_{k}$
when
![]() $\Lambda =\{1,2,\ldots , k\}$
.
$\Lambda =\{1,2,\ldots , k\}$
.
We motivate the next theorem through two examples. The map
![]() $f_{1}(x)=1-x$
on the unit interval
$f_{1}(x)=1-x$
on the unit interval
![]() $[0,1]$
as an element of
$[0,1]$
as an element of
![]() ${\mathcal C}([0,1])$
, with
${\mathcal C}([0,1])$
, with
![]() $[0,1]$
in the usual metric induced by
$[0,1]$
in the usual metric induced by
![]() $|\cdot |$
, has no continuous square roots on
$|\cdot |$
, has no continuous square roots on
![]() $[0,1]$
(see [Reference Kuczma, Choczewski and Ger24, pp. 425–426]). However, the map
$[0,1]$
(see [Reference Kuczma, Choczewski and Ger24, pp. 425–426]). However, the map
![]() $f_{2}(x,y) = (1-x, 1-y)$
on
$f_{2}(x,y) = (1-x, 1-y)$
on
![]() $[0,1]\times [0,1]$
as an element of
$[0,1]\times [0,1]$
as an element of
![]() ${\mathcal C}([0,1]\times [0,1])$
, where
${\mathcal C}([0,1]\times [0,1])$
, where
![]() $[0,1]\times [0,1]$
has the metric induced by the norm
$[0,1]\times [0,1]$
has the metric induced by the norm
![]() $\|(x,y)\|_{\infty }:=\max \{|x|,|y|\}$
, has a continuous square root
$\|(x,y)\|_{\infty }:=\max \{|x|,|y|\}$
, has a continuous square root
![]() $g(x,y)= (y,1-x)$
on
$g(x,y)= (y,1-x)$
on
![]() $[0,1]\times [0,1]$
. The reason for these contrasting conclusions can be detected by observing the fixed points of these maps.
$[0,1]\times [0,1]$
. The reason for these contrasting conclusions can be detected by observing the fixed points of these maps.
Let f be a continuous self-map on a topological space X and Y a non-empty subset of X invariant under f, that is,
![]() $f(Y)\subseteq Y$
. Then it is clear that if x and
$f(Y)\subseteq Y$
. Then it is clear that if x and
![]() $x^{\prime }$
are path-connected in Y, then so are
$x^{\prime }$
are path-connected in Y, then so are
![]() $f(x)$
and
$f(x)$
and
![]() $f(x^{\prime })$
. Therefore, if
$f(x^{\prime })$
. Therefore, if
![]() $Y=\bigcup _{\alpha \in \Lambda }Y_{\alpha }$
is the decomposition of Y into its path components for some index set
$Y=\bigcup _{\alpha \in \Lambda }Y_{\alpha }$
is the decomposition of Y into its path components for some index set
![]() $\Lambda $
, then there exists a unique map
$\Lambda $
, then there exists a unique map
![]() $\sigma _{f,Y}: \Lambda \to \Lambda $
such that
$\sigma _{f,Y}: \Lambda \to \Lambda $
such that
![]() $f(x)\in Y_{\beta }$
whenever
$f(x)\in Y_{\beta }$
whenever
![]() $x\in Y_{\alpha }$
and
$x\in Y_{\alpha }$
and
![]() $\sigma _{f,Y}(\alpha )=\beta $
(note that y and
$\sigma _{f,Y}(\alpha )=\beta $
(note that y and
![]() $y^{\prime }$
are path-connected in Y if and only if there exists an
$y^{\prime }$
are path-connected in Y if and only if there exists an
![]() $\alpha \in \Lambda $
such that
$\alpha \in \Lambda $
such that
![]() $y,y^{\prime }\in Y_{\alpha }$
). We call
$y,y^{\prime }\in Y_{\alpha }$
). We call
![]() $\sigma _{f,Y}$
as the map induced by the map f and the invariant set Y. Let
$\sigma _{f,Y}$
as the map induced by the map f and the invariant set Y. Let
![]() $F(f):=\{x\in X: f(x)=x\}$
, the set of all fixed points of f in X, and
$F(f):=\{x\in X: f(x)=x\}$
, the set of all fixed points of f in X, and
![]() $E(f):= R(f)\setminus F(f)$
, the complement of
$E(f):= R(f)\setminus F(f)$
, the complement of
![]() $F(f)$
in
$F(f)$
in
![]() $R(f)$
.
$R(f)$
.
Theorem 2.6. Let
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
![]() $f\in {\mathcal C}(X)$
be such that
$f\in {\mathcal C}(X)$
be such that
![]() $E(f)$
is invariant under f. If
$E(f)$
is invariant under f. If
![]() $f=g^{n}$
for some
$f=g^{n}$
for some
![]() $g\in {\mathcal C}(X)$
, then
$g\in {\mathcal C}(X)$
, then
![]() $E(f)$
is invariant under g and the induced maps satisfy that
$E(f)$
is invariant under g and the induced maps satisfy that
![]() $\sigma _{f,E(f)} = \sigma _{g, E(f)}^{n}$
. In other words, if
$\sigma _{f,E(f)} = \sigma _{g, E(f)}^{n}$
. In other words, if
![]() $\sigma _{f, E(f)}$
has no
$\sigma _{f, E(f)}$
has no
![]() $n{\mathrm{th}}$
roots, then f also has no continuous
$n{\mathrm{th}}$
roots, then f also has no continuous
![]() $n{\mathrm{th}}$
roots on X.
$n{\mathrm{th}}$
roots on X.
Proof. Let
![]() $E(f)=\bigcup _{\alpha \in \Lambda }Y_{\alpha }$
be the decomposition of
$E(f)=\bigcup _{\alpha \in \Lambda }Y_{\alpha }$
be the decomposition of
![]() $E(f)$
into its path components for some index set
$E(f)$
into its path components for some index set
![]() $\Lambda $
. The case
$\Lambda $
. The case
![]() $n=1$
is trivial. So, let
$n=1$
is trivial. So, let
![]() $n>1$
, and consider an arbitrary
$n>1$
, and consider an arbitrary
![]() $x\in E(f)$
. Then
$x\in E(f)$
. Then
![]() $x=f(x^{\prime })$
for some
$x=f(x^{\prime })$
for some
![]() $x^{\prime }\in X$
. Clearly,
$x^{\prime }\in X$
. Clearly,
![]() $g(x)\in R(f)$
, because
$g(x)\in R(f)$
, because
![]() $g(x)= g(f(x^{\prime }))= g(g^{n}(x^{\prime }))=g^{n}(g(x^{\prime }))= f(g(x^{\prime }))$
. Also, if
$g(x)= g(f(x^{\prime }))= g(g^{n}(x^{\prime }))=g^{n}(g(x^{\prime }))= f(g(x^{\prime }))$
. Also, if
![]() $g(x)\in F(f)$
, then
$g(x)\in F(f)$
, then
![]() $g(x)=f(g(x))= g^{n}(g(x))=g(f(x))$
, implying that
$g(x)=f(g(x))= g^{n}(g(x))=g(f(x))$
, implying that
![]() $f(x)=g^{n}(x)=g^{n}(f(x))=f^{2}(x)$
, that is,
$f(x)=g^{n}(x)=g^{n}(f(x))=f^{2}(x)$
, that is,
![]() $f(x)$
is a fixed point of f. This contradicts the hypothesis that
$f(x)$
is a fixed point of f. This contradicts the hypothesis that
![]() $E(f)$
is invariant under f. Therefore,
$E(f)$
is invariant under f. Therefore,
![]() $g(x)\in E(f)$
.
$g(x)\in E(f)$
.
The equality
![]() $\sigma _{f,E(f)}= \sigma _{g, E(f)}^{n}$
follows from the definitions of
$\sigma _{f,E(f)}= \sigma _{g, E(f)}^{n}$
follows from the definitions of
![]() $\sigma _{f,E(f)}$
and
$\sigma _{f,E(f)}$
and
![]() $\sigma _{g,E(f)}$
, and the relation
$\sigma _{g,E(f)}$
, and the relation
![]() $f=g^{n}.$
$f=g^{n}.$
In the remainder of this section, we illustrate Theorem 2.6 through some simple examples. Remark that
![]() $\sigma \in S_{k}$
, the group of permutation of k elements, has a square root if and only if the number of even cycles of
$\sigma \in S_{k}$
, the group of permutation of k elements, has a square root if and only if the number of even cycles of
![]() $\sigma $
is even. More generally,
$\sigma $
is even. More generally,
![]() $\sigma \in S_{k}$
has an
$\sigma \in S_{k}$
has an
![]() $n{\mathrm{th}}$
root if and only if for every
$n{\mathrm{th}}$
root if and only if for every
![]() $m = 1,2, \ldots,$
it is true that the number of m-cycles that
$m = 1,2, \ldots,$
it is true that the number of m-cycles that
![]() $\sigma $
has is a multiple of
$\sigma $
has is a multiple of
![]() $((m,n))$
, where
$((m,n))$
, where
![]() $((m,n)):=\prod _{p|m}^{}p^{e(p,n)}$
,
$((m,n)):=\prod _{p|m}^{}p^{e(p,n)}$
,
![]() $e(p,n)$
being the highest power of p dividing n (see [Reference Wilf49, pp. 155–158]).
$e(p,n)$
being the highest power of p dividing n (see [Reference Wilf49, pp. 155–158]).
Corollary 2.7. Let
![]() $a<b$
be real numbers and
$a<b$
be real numbers and
![]() $f\in \mathcal {C}([a,b])$
be such that
$f\in \mathcal {C}([a,b])$
be such that
![]() $f|_{R(f)}$
is a non-constant strictly decreasing map. Then f has no iterative roots of even orders in
$f|_{R(f)}$
is a non-constant strictly decreasing map. Then f has no iterative roots of even orders in
![]() $\mathcal {C}([a,b])$
.
$\mathcal {C}([a,b])$
.
Proof. Since
![]() $f:[a,b]\to [a,b]$
is a non-constant strictly decreasing continuous map, we see that
$f:[a,b]\to [a,b]$
is a non-constant strictly decreasing continuous map, we see that
![]() $R(f)$
is a compact interval
$R(f)$
is a compact interval
![]() $[c,d]$
in
$[c,d]$
in
![]() $\mathbb {R}$
for some
$\mathbb {R}$
for some
![]() $c<d$
in
$c<d$
in
![]() $[a,b]$
and f has a unique fixed point
$[a,b]$
and f has a unique fixed point
![]() $x_0$
in
$x_0$
in
![]() $(c, d)$
. Also,
$(c, d)$
. Also,
![]() $E(f)=[c,x_0)\cup (x_0, d]$
is the decomposition of
$E(f)=[c,x_0)\cup (x_0, d]$
is the decomposition of
![]() $E(f)$
into path components and
$E(f)$
into path components and
![]() $\sigma :=\sigma _{f, E(f)}$
is the transposition of the two-point set
$\sigma :=\sigma _{f, E(f)}$
is the transposition of the two-point set
![]() $S_{2}$
. Since
$S_{2}$
. Since
![]() $\sigma $
has no iterative roots of even orders in
$\sigma $
has no iterative roots of even orders in
![]() $S_{2}$
, it follows from Theorem 2.6 that f has no iterative roots of even orders in
$S_{2}$
, it follows from Theorem 2.6 that f has no iterative roots of even orders in
![]() $\mathcal {C}([a,b])$
.
$\mathcal {C}([a,b])$
.
Example 2.8. Consider
![]() $[0,1]\times [0,1]$
in the topology induced by the norm
$[0,1]\times [0,1]$
in the topology induced by the norm
![]() $\|(x,y)\|_{\infty }:=\max \{|x|,|y|\}$
, and let
$\|(x,y)\|_{\infty }:=\max \{|x|,|y|\}$
, and let
![]() $f_{1}, f_{2}$
be the continuous maps on
$f_{1}, f_{2}$
be the continuous maps on
![]() $[0,1]\times [0,1]$
defined by
$[0,1]\times [0,1]$
defined by
![]() $f_{1}(x,y)=(1-x, 0)$
and
$f_{1}(x,y)=(1-x, 0)$
and
![]() $f_{2}(x,y)=(y,x)$
. Then Theorem 2.6 is applicable to
$f_{2}(x,y)=(y,x)$
. Then Theorem 2.6 is applicable to
![]() $f_{1}$
and
$f_{1}$
and
![]() $f_{2}$
with
$f_{2}$
with
 $$ \begin{align*}E(f_{1})&= \big\{(x,0): 0\le x<\tfrac{1}{2}\big\}\cup \big\{(x,0):\tfrac{1}{2}<x\le 1\big\};\\ E(f_{2})&= \{ (x,y): 0\leq x<y\leq 1\}\cup \{(x,y): 0\leq y<x\leq 1\}.\end{align*} $$
$$ \begin{align*}E(f_{1})&= \big\{(x,0): 0\le x<\tfrac{1}{2}\big\}\cup \big\{(x,0):\tfrac{1}{2}<x\le 1\big\};\\ E(f_{2})&= \{ (x,y): 0\leq x<y\leq 1\}\cup \{(x,y): 0\leq y<x\leq 1\}.\end{align*} $$
It follows that both
![]() $f_{1}$
and
$f_{1}$
and
![]() $f_{2}$
have no iterative roots of even orders in
$f_{2}$
have no iterative roots of even orders in
![]() $\mathcal {C}([0,1]\times [0,1])$
.
$\mathcal {C}([0,1]\times [0,1])$
.
3 Continuous functions on the unit cube in
 ${\mathbb R}^{m}$
${\mathbb R}^{m}$
As seen in §1, much literature is available on iterative square roots of functions on compact real intervals. In this section, we extend some of the results in [Reference Humke and Laczkovich15] to the unit cube
considered in the metric induced by the norm
where
![]() $I:=[0,1]$
. In studying iterative roots of continuous maps on intervals, one observes that it becomes essential to look at piecewise linear maps. Here we study their analogs in higher dimensions. It is convenient to have the following elementary notions and notation from the theory of simplicial complexes to present our proofs.
$I:=[0,1]$
. In studying iterative roots of continuous maps on intervals, one observes that it becomes essential to look at piecewise linear maps. Here we study their analogs in higher dimensions. It is convenient to have the following elementary notions and notation from the theory of simplicial complexes to present our proofs.
As defined in [Reference Deo10], a set
![]() $S=\{x_{0}, x_{1}, \ldots , x_{k}\}$
in
$S=\{x_{0}, x_{1}, \ldots , x_{k}\}$
in
![]() $\mathbb {R}^{m}$
, where
$\mathbb {R}^{m}$
, where
![]() $k\ge 1$
, is said to be geometrically independent if the set
$k\ge 1$
, is said to be geometrically independent if the set
![]() $\{x_{1}-x_{0}, x_{2}-x_{0}, \ldots , x_{k}-x_{0}\}$
is linearly independent in
$\{x_{1}-x_{0}, x_{2}-x_{0}, \ldots , x_{k}-x_{0}\}$
is linearly independent in
![]() $\mathbb {R}^{m}$
. Equivalently, S is geometrically independent if and only if for arbitrary reals
$\mathbb {R}^{m}$
. Equivalently, S is geometrically independent if and only if for arbitrary reals
![]() $\alpha _{i}$
, the equalities
$\alpha _{i}$
, the equalities
![]() $\sum _{i=0}^{k}\alpha _{i}x_{i}=0$
and
$\sum _{i=0}^{k}\alpha _{i}x_{i}=0$
and
![]() $\sum _{i=0}^{k}\alpha _{i}=0$
imply that
$\sum _{i=0}^{k}\alpha _{i}=0$
imply that
![]() $\alpha _{i}=0$
for all
$\alpha _{i}=0$
for all
![]() $0\le i\le k$
. A set having only one point is assumed to be geometrically independent. If S is geometrically independent, then there exists a unique k-dimensional hyperplane which passes through all the points of S and each point x on this hyperplane can be expressed uniquely as
$0\le i\le k$
. A set having only one point is assumed to be geometrically independent. If S is geometrically independent, then there exists a unique k-dimensional hyperplane which passes through all the points of S and each point x on this hyperplane can be expressed uniquely as
![]() $x=\sum _{i=0}^{k}\alpha _{i}x_{i}$
such that
$x=\sum _{i=0}^{k}\alpha _{i}x_{i}$
such that
![]() $\sum _{i=0}^{k}\alpha _{i}=1$
. The real numbers
$\sum _{i=0}^{k}\alpha _{i}=1$
. The real numbers
![]() $\alpha _{0}, \alpha _{1}, \ldots , \alpha _{k}$
, which are uniquely determined by S, are called the barycentric coordinates of the point x with respect to the set S.
$\alpha _{0}, \alpha _{1}, \ldots , \alpha _{k}$
, which are uniquely determined by S, are called the barycentric coordinates of the point x with respect to the set S.
Let
![]() $S=\{x_{0}, x_{1}, \ldots , x_{k}\}$
be a geometrically independent set in
$S=\{x_{0}, x_{1}, \ldots , x_{k}\}$
be a geometrically independent set in
![]() $\mathbb {R}^{m}$
, where
$\mathbb {R}^{m}$
, where
![]() $0\leq k\leq m$
. Then the k-dimensional geometric simplex or k-simplex spanned by S, denoted by
$0\leq k\leq m$
. Then the k-dimensional geometric simplex or k-simplex spanned by S, denoted by
![]() $\sigma $
, is defined as the set of all points
$\sigma $
, is defined as the set of all points
![]() $x\in \mathbb {R}^{m}$
such that
$x\in \mathbb {R}^{m}$
such that
![]() $x=\sum _{i=0}^{k}\alpha _{i}x_{i}$
, where
$x=\sum _{i=0}^{k}\alpha _{i}x_{i}$
, where
![]() $\sum _{i=0}^{k}\alpha _{i}=1$
and
$\sum _{i=0}^{k}\alpha _{i}=1$
and
![]() $\alpha _{i}\ge 0$
for all
$\alpha _{i}\ge 0$
for all
![]() $0\le i \le k$
. Equivalently,
$0\le i \le k$
. Equivalently,
![]() $\sigma $
is the convex hull of S. The points
$\sigma $
is the convex hull of S. The points
![]() $x_{0}, x_{1}, \ldots , x_{k}$
are called the vertices of
$x_{0}, x_{1}, \ldots , x_{k}$
are called the vertices of
![]() $\sigma $
, and we usually write
$\sigma $
, and we usually write
![]() $\sigma =\langle x_{0}, x_{1}, \ldots , x_{k}\rangle $
to indicate that
$\sigma =\langle x_{0}, x_{1}, \ldots , x_{k}\rangle $
to indicate that
![]() $\sigma $
is the k-simplex with vertices
$\sigma $
is the k-simplex with vertices
![]() $x_{0}, x_{1}, \ldots , x_{k}$
. If
$x_{0}, x_{1}, \ldots , x_{k}$
. If
![]() $\sigma =\langle x_{0}, x_{1}, \ldots , x_{k}\rangle $
is a k-simplex, then the set of those points of
$\sigma =\langle x_{0}, x_{1}, \ldots , x_{k}\rangle $
is a k-simplex, then the set of those points of
![]() $\sigma $
for which all barycentric coordinates are strictly positive, is called the open k-simplex
$\sigma $
for which all barycentric coordinates are strictly positive, is called the open k-simplex
![]() $\sigma $
(or the interior of
$\sigma $
(or the interior of
![]() $\sigma $
), and is denoted by
$\sigma $
), and is denoted by
![]() $\sigma ^{0}$
. If
$\sigma ^{0}$
. If
![]() $\sigma $
is a p-simplex and
$\sigma $
is a p-simplex and
![]() $\tau $
is a q-simplex in
$\tau $
is a q-simplex in
![]() $\mathbb {R}^{m}$
such that
$\mathbb {R}^{m}$
such that
![]() $0\le p\le q \le m$
, then we say that
$0\le p\le q \le m$
, then we say that
![]() $\sigma $
is a p-dimensional face (or simply a p-simplex) of
$\sigma $
is a p-dimensional face (or simply a p-simplex) of
![]() $\tau $
if each vertex of
$\tau $
if each vertex of
![]() $\sigma $
is also a vertex of
$\sigma $
is also a vertex of
![]() $\tau $
. If
$\tau $
. If
![]() $\sigma $
is a face of
$\sigma $
is a face of
![]() $\tau $
with
$\tau $
with
![]() $p<q$
, then
$p<q$
, then
![]() $\sigma $
is called a proper face of
$\sigma $
is called a proper face of
![]() $\tau $
. Any zero-dimensional face of a simplex is simply a vertex of the simplex and a one-dimensional face of a simplex is usually called an edge of that simplex.
$\tau $
. Any zero-dimensional face of a simplex is simply a vertex of the simplex and a one-dimensional face of a simplex is usually called an edge of that simplex.
A finite (respectively countable) simplicial complex
![]() $\mathcal {K}$
is a finite (respectively countable) collection of simplices of
$\mathcal {K}$
is a finite (respectively countable) collection of simplices of
![]() $\mathbb {R}^{m}$
satisfying the following conditions: (i) If
$\mathbb {R}^{m}$
satisfying the following conditions: (i) If
![]() $\sigma \in \mathcal {K}$
, then all the faces of
$\sigma \in \mathcal {K}$
, then all the faces of
![]() $\sigma $
are in
$\sigma $
are in
![]() $\mathcal {K}$
; (ii) If
$\mathcal {K}$
; (ii) If
![]() $\sigma , \tau \in \mathcal {K}$
, then either
$\sigma , \tau \in \mathcal {K}$
, then either
![]() $\sigma \cap \tau =\emptyset $
or
$\sigma \cap \tau =\emptyset $
or
![]() $\sigma \cap \tau $
is a common face of both
$\sigma \cap \tau $
is a common face of both
![]() $\sigma $
and
$\sigma $
and
![]() $\tau $
. Let
$\tau $
. Let
![]() $\mathcal {K}$
be a finite simplicial complex and
$\mathcal {K}$
be a finite simplicial complex and
![]() $|\mathcal {K}|=\bigcup _{\sigma \in \mathcal {K}}\sigma $
be the union of all simplices of
$|\mathcal {K}|=\bigcup _{\sigma \in \mathcal {K}}\sigma $
be the union of all simplices of
![]() $\mathcal {K}$
. Then
$\mathcal {K}$
. Then
![]() $|\mathcal {K}|$
is a topological space with the topology inherited from
$|\mathcal {K}|$
is a topological space with the topology inherited from
![]() $\mathbb {R}^{m}$
. The space
$\mathbb {R}^{m}$
. The space
![]() $|\mathcal {K}|$
is called the geometric carrier of
$|\mathcal {K}|$
is called the geometric carrier of
![]() $\mathcal {K}$
. A topological subspace of
$\mathcal {K}$
. A topological subspace of
![]() $\mathbb {R}^{m}$
, which is the geometric carrier of some finite simplicial complex, is called a rectilinear polyhedron. A topological space X is said to be a polyhedron if there exists a finite simplicial complex
$\mathbb {R}^{m}$
, which is the geometric carrier of some finite simplicial complex, is called a rectilinear polyhedron. A topological space X is said to be a polyhedron if there exists a finite simplicial complex
![]() $\mathcal {K}$
such that
$\mathcal {K}$
such that
![]() $|\mathcal {K}|$
is homeomorphic to X. In this case, the space X is said to be triangulable and
$|\mathcal {K}|$
is homeomorphic to X. In this case, the space X is said to be triangulable and
![]() $\mathcal {K}$
is called a triangulation of X. A space X is said to be countably triangulable if there exists a countable triangulation of X, that is, there exists a countable simplicial complex
$\mathcal {K}$
is called a triangulation of X. A space X is said to be countably triangulable if there exists a countable triangulation of X, that is, there exists a countable simplicial complex
![]() $\mathcal {K}$
of simplices of
$\mathcal {K}$
of simplices of
![]() $\mathbb {R}^{m}$
such that its geometric carrier
$\mathbb {R}^{m}$
such that its geometric carrier
![]() $|\mathcal {K}|$
is homeomorphic to X. Further, we do not distinguish between X and its geometric carrier
$|\mathcal {K}|$
is homeomorphic to X. Further, we do not distinguish between X and its geometric carrier
![]() $|\mathcal {K}|$
whenever
$|\mathcal {K}|$
whenever
![]() $X=|\mathcal {K}|$
for some (finite or countable) triangulation
$X=|\mathcal {K}|$
for some (finite or countable) triangulation
![]() $\mathcal {K}$
of X, because in that case, we always consider the identity map id to be the homeomorphism between
$\mathcal {K}$
of X, because in that case, we always consider the identity map id to be the homeomorphism between
![]() $|\mathcal {K}|$
and X.
$|\mathcal {K}|$
and X.
If
![]() $\sigma =\langle x_{0}, x_{1}, \ldots , x_{k}\rangle $
is a k-simplex in
$\sigma =\langle x_{0}, x_{1}, \ldots , x_{k}\rangle $
is a k-simplex in
![]() $\mathbb {R}^{m}$
, then the point
$\mathbb {R}^{m}$
, then the point
![]() $\sum _{i=0}^{k}({1}/({k+1}))x_{i}$
is called the barycenter of
$\sum _{i=0}^{k}({1}/({k+1}))x_{i}$
is called the barycenter of
![]() $\sigma $
and is denoted by
$\sigma $
and is denoted by
![]() $\dot {\sigma }$
. In other words, barycenter of
$\dot {\sigma }$
. In other words, barycenter of
![]() $\sigma $
is that point of
$\sigma $
is that point of
![]() $\sigma $
whose barycentric coordinates, with respect to each of the vertices of
$\sigma $
whose barycentric coordinates, with respect to each of the vertices of
![]() $\sigma $
, are equal. Given a simplicial complex
$\sigma $
, are equal. Given a simplicial complex
![]() $\mathcal {K}$
, let
$\mathcal {K}$
, let
![]() $\mathcal {K}^{(1)}$
be a simplicial complex whose vertices are barycenters of all simplices of
$\mathcal {K}^{(1)}$
be a simplicial complex whose vertices are barycenters of all simplices of
![]() $\mathcal {K}$
, and for any distinct simplices
$\mathcal {K}$
, and for any distinct simplices
![]() $\sigma _{1}, \sigma _{2}, \ldots , \sigma _{k}$
of
$\sigma _{1}, \sigma _{2}, \ldots , \sigma _{k}$
of
![]() $\mathcal {K}$
,
$\mathcal {K}$
,
![]() $\langle \dot {\sigma _{1}}, \dot {\sigma _{2}}, \ldots , \dot {\sigma _{k}}\rangle $
is a simplex of
$\langle \dot {\sigma _{1}}, \dot {\sigma _{2}}, \ldots , \dot {\sigma _{k}}\rangle $
is a simplex of
![]() $\mathcal {K}^{(1)}$
if and only if
$\mathcal {K}^{(1)}$
if and only if
![]() $\sigma _{i}$
is a face of
$\sigma _{i}$
is a face of
![]() $\sigma _{i+1}$
for
$\sigma _{i+1}$
for
![]() $i=0, 1,\ldots , k-1$
. Then
$i=0, 1,\ldots , k-1$
. Then
![]() $\mathcal {K}^{(1)}$
is a simplicial complex and is called the first barycentric subdivision of
$\mathcal {K}^{(1)}$
is a simplicial complex and is called the first barycentric subdivision of
![]() $\mathcal {K}$
. By induction, we define the
$\mathcal {K}$
. By induction, we define the
![]() $l{\mathrm{th}}$
barycentric subdivision
$l{\mathrm{th}}$
barycentric subdivision
![]() $\mathcal {K}^{(l)}$
of
$\mathcal {K}^{(l)}$
of
![]() $\mathcal {K}$
to be the first barycentric subdivision of
$\mathcal {K}$
to be the first barycentric subdivision of
![]() $\mathcal {K}^{(l-1)}$
for each
$\mathcal {K}^{(l-1)}$
for each
![]() $l>1$
. We also put
$l>1$
. We also put
![]() $\mathcal {K}^{(0)}=\mathcal {K}$
for convenience. For a simplicial complex
$\mathcal {K}^{(0)}=\mathcal {K}$
for convenience. For a simplicial complex
![]() $\mathcal {K}$
, we define the mesh of
$\mathcal {K}$
, we define the mesh of
![]() $\mathcal {K}$
, denoted by
$\mathcal {K}$
, denoted by
![]() $\mbox {mesh}(\mathcal {K})$
, as
$\mbox {mesh}(\mathcal {K})$
, as
where
![]() $\mbox {diam}(\sigma )$
denote the diameter of
$\mbox {diam}(\sigma )$
denote the diameter of
![]() $\sigma $
. Then
$\sigma $
. Then
![]() $\lim \nolimits _{l\to \infty }\mbox {mesh}(\mathcal {K}^{(l)})=0$
for every non-empty simplicial complex
$\lim \nolimits _{l\to \infty }\mbox {mesh}(\mathcal {K}^{(l)})=0$
for every non-empty simplicial complex
![]() $\mathcal {K}$
.
$\mathcal {K}$
.
An
![]() $f\in \mathcal {F}(\mathbb {R}^{m})$
is said to be affine linear if
$f\in \mathcal {F}(\mathbb {R}^{m})$
is said to be affine linear if
![]() $f(\cdot )=T(\cdot )+z$
for some linear map
$f(\cdot )=T(\cdot )+z$
for some linear map
![]() $T\in \mathcal {F}(\mathbb {R}^{m})$
and
$T\in \mathcal {F}(\mathbb {R}^{m})$
and
![]() $z\in \mathbb {R}^{m}$
. Clearly, each affine linear map on
$z\in \mathbb {R}^{m}$
. Clearly, each affine linear map on
![]() $\mathbb {R}^{m}$
is continuous. An affine linear map f is said to be of full rank if the associated linear map T is invertible. Note that full rank affine linear maps are open maps, that is, they map open sets to open sets. They also map geometrically independent sets to geometrically independent sets. We sew affine linear maps on simplices piece by piece to get many continuous maps on
$\mathbb {R}^{m}$
is continuous. An affine linear map f is said to be of full rank if the associated linear map T is invertible. Note that full rank affine linear maps are open maps, that is, they map open sets to open sets. They also map geometrically independent sets to geometrically independent sets. We sew affine linear maps on simplices piece by piece to get many continuous maps on
![]() $\mathbb {R}^{m}$
.
$\mathbb {R}^{m}$
.
An
![]() ${\mathbb R}^{m}$
-valued function f on a subset X of
${\mathbb R}^{m}$
-valued function f on a subset X of
![]() ${\mathbb R}^{m}$
is said to be piecewise affine linear (respectively countably piecewise affine linear) if
${\mathbb R}^{m}$
is said to be piecewise affine linear (respectively countably piecewise affine linear) if
![]() $X=|\mathcal {K}\kern2pt|$
for some finite (respectively countable) simplicial complex
$X=|\mathcal {K}\kern2pt|$
for some finite (respectively countable) simplicial complex
![]() $\mathcal {K}$
of simplices of
$\mathcal {K}$
of simplices of
![]() $\mathbb {R}^{m}$
and
$\mathbb {R}^{m}$
and
![]() $f|_{\sigma }$
is the restriction of some affine linear map
$f|_{\sigma }$
is the restriction of some affine linear map
![]() $\phi _{\sigma }$
on
$\phi _{\sigma }$
on
![]() $\mathbb {R}^{m}$
to
$\mathbb {R}^{m}$
to
![]() $\sigma $
for every
$\sigma $
for every
![]() $\sigma \in \mathcal {K}$
. In this case, we say that f is supported by the simplicial complex
$\sigma \in \mathcal {K}$
. In this case, we say that f is supported by the simplicial complex
![]() ${\mathcal K}.$
${\mathcal K}.$
Here is a basic construction of piecewise affine linear maps that we use repetitively. Let
![]() $\mathcal {K}$
be a simplicial complex in
$\mathcal {K}$
be a simplicial complex in
![]() $\mathbb {R}^{m}$
and
$\mathbb {R}^{m}$
and
![]() $U=\{x_{0}, x_{1}, \ldots \}$
be its set of vertices ordered in some arbitrary way. Let
$U=\{x_{0}, x_{1}, \ldots \}$
be its set of vertices ordered in some arbitrary way. Let
![]() $V=\{y_{0}, y_{1}, \ldots \}$
be an ordered set of points in
$V=\{y_{0}, y_{1}, \ldots \}$
be an ordered set of points in
![]() ${\mathbb R}^{m}$
. Then we can define a
${\mathbb R}^{m}$
. Then we can define a
![]() ${\mathbb R}^{m}$
-valued function
${\mathbb R}^{m}$
-valued function
![]() $f_{U,V}$
on
$f_{U,V}$
on
![]() $|\mathcal {K}|$
satisfying
$|\mathcal {K}|$
satisfying
![]() $f_{U,V}(x_{j})=y_{j}$
for all
$f_{U,V}(x_{j})=y_{j}$
for all
![]() $j\in \mathbb {Z}_{+}$
as follows: If
$j\in \mathbb {Z}_{+}$
as follows: If
![]() $x\in |\mathcal {K}|$
, then x is in the interior of a unique k-simplex
$x\in |\mathcal {K}|$
, then x is in the interior of a unique k-simplex
![]() $\langle x_{i_{0}}, x_{i_{1}}, \ldots , x_{i_{k}}\rangle $
in
$\langle x_{i_{0}}, x_{i_{1}}, \ldots , x_{i_{k}}\rangle $
in
![]() $\mathcal {K}$
for some
$\mathcal {K}$
for some
![]() $0\le k\le m$
. We write
$0\le k\le m$
. We write
![]() $x=\sum _{j=0}^{k}\alpha _{i_{j}}x_{i_{j}}$
with
$x=\sum _{j=0}^{k}\alpha _{i_{j}}x_{i_{j}}$
with
![]() $\sum _{j=0}^{k}\alpha _{i_{j}}=1$
and define
$\sum _{j=0}^{k}\alpha _{i_{j}}=1$
and define
 $$ \begin{align} f_{U,V}(x)=\sum_{j=0}^{k}\alpha_{i_{j}}y_{i_{j}}. \end{align} $$
$$ \begin{align} f_{U,V}(x)=\sum_{j=0}^{k}\alpha_{i_{j}}y_{i_{j}}. \end{align} $$
Clearly,
![]() $f_{U,V}$
is a continuous piecewise affine linear map on
$f_{U,V}$
is a continuous piecewise affine linear map on
![]() $|\mathcal {K}|$
satisfying that
$|\mathcal {K}|$
satisfying that
![]() $f_{U,V}(x_{j})=y_{j}$
for every
$f_{U,V}(x_{j})=y_{j}$
for every
![]() $j\in \mathbb {Z}_{+}$
. Furthermore, if
$j\in \mathbb {Z}_{+}$
. Furthermore, if
![]() $|{\mathcal K}|$
is convex and
$|{\mathcal K}|$
is convex and
![]() $y_{j}\in |\mathcal {K}|$
for every j, then
$y_{j}\in |\mathcal {K}|$
for every j, then
![]() $f_{U,V}$
is a self-map of
$f_{U,V}$
is a self-map of
![]() $|{\mathcal K}|.$
$|{\mathcal K}|.$
Lemma 3.1. Let
![]() ${\mathcal K}$
and
${\mathcal K}$
and
![]() $f_{U,V}$
be as described above.
$f_{U,V}$
be as described above.
-
(i) If
 $\sigma =\langle x_{i_{0}}, x_{i_{1}}, \ldots , x_{i_{k}}\rangle $
is a k-simplex in
$\sigma =\langle x_{i_{0}}, x_{i_{1}}, \ldots , x_{i_{k}}\rangle $
is a k-simplex in
 $\mathcal {K}$
and
$\mathcal {K}$
and
 $\{y_{i_{0}}, y_{i_{1}}, \ldots , y_{i_{k}}\}$
is geometrically independent in
$\{y_{i_{0}}, y_{i_{1}}, \ldots , y_{i_{k}}\}$
is geometrically independent in
 ${\mathbb R}^{m}$
, then
${\mathbb R}^{m}$
, then
 $f_{U,V}|_{\sigma }$
is injective and
$f_{U,V}|_{\sigma }$
is injective and
 $f_{U,V}(\sigma )^{0}=f_{U,V}(\sigma ^{0})$
.
$f_{U,V}(\sigma )^{0}=f_{U,V}(\sigma ^{0})$
. -
(ii) If
 $V=\{y_{0}, y_{1}, \ldots \}$
and
$V=\{y_{0}, y_{1}, \ldots \}$
and
 $W=\{z_{0}, z_{1}, \ldots \}$
are ordered sets in
$W=\{z_{0}, z_{1}, \ldots \}$
are ordered sets in
 $|\mathcal {K}|$
such that
$|\mathcal {K}|$
such that
 $\|y_{j}-z_{j}\|_{\infty }\le \eta $
for all
$\|y_{j}-z_{j}\|_{\infty }\le \eta $
for all
 $j\in \mathbb {Z}_{+}$
, where
$j\in \mathbb {Z}_{+}$
, where
 $\eta>0$
, then
$\eta>0$
, then
 $\|f_{U,V}(x)-f_{U,W}(x)\|_{\infty }\le \eta $
for all
$\|f_{U,V}(x)-f_{U,W}(x)\|_{\infty }\le \eta $
for all
 $x\in |\mathcal {K}|$
.
$x\in |\mathcal {K}|$
.
Proof. The result (i) is trivial. For each
![]() $x\in |\mathcal {K}|$
, by equation (3.2) we have
$x\in |\mathcal {K}|$
, by equation (3.2) we have
 $$ \begin{align*} \|f_{U,V}(x)-f_{U,W}(x)\|_{\infty}\le \sum_{j=0}^{k}\alpha_{i_{j}}\|y_{i_{j}}-z_{i_{j}}\|_{\infty}\le \eta, \end{align*} $$
$$ \begin{align*} \|f_{U,V}(x)-f_{U,W}(x)\|_{\infty}\le \sum_{j=0}^{k}\alpha_{i_{j}}\|y_{i_{j}}-z_{i_{j}}\|_{\infty}\le \eta, \end{align*} $$
proving result (ii).
Lemma 3.2. If
![]() $f\in \mathcal {F}(\mathbb {R}^{m})$
is an affine linear map such that
$f\in \mathcal {F}(\mathbb {R}^{m})$
is an affine linear map such that
![]() $f|_{S}=0$
for a geometrically independent set
$f|_{S}=0$
for a geometrically independent set
![]() $S=\{x_{0}, x_{1}, \ldots , x_{m}\}$
of
$S=\{x_{0}, x_{1}, \ldots , x_{m}\}$
of
![]() $\mathbb {R}^{m}$
, then
$\mathbb {R}^{m}$
, then
![]() $f=0$
on
$f=0$
on
![]() $\mathbb {R}^{m}$
.
$\mathbb {R}^{m}$
.
Proof. Let
![]() $f(\cdot )=T(\cdot ) +z$
for some
$f(\cdot )=T(\cdot ) +z$
for some
![]() $z\in \mathbb {R}^{m}$
and a linear map
$z\in \mathbb {R}^{m}$
and a linear map
![]() $T\in \mathcal {F}(\mathbb {R}^{m})$
. Since S is geometrically independent, we have
$T\in \mathcal {F}(\mathbb {R}^{m})$
. Since S is geometrically independent, we have
![]() $B=\{x_{1}-x_{0}, x_{2}-x_{0}, \ldots , x_{m}-x_{0}\}$
is linearly independent, and therefore it is a Hamel basis for
$B=\{x_{1}-x_{0}, x_{2}-x_{0}, \ldots , x_{m}-x_{0}\}$
is linearly independent, and therefore it is a Hamel basis for
![]() $\mathbb {R}^{m}$
. To prove
$\mathbb {R}^{m}$
. To prove
![]() $f= 0$
, consider an arbitrary
$f= 0$
, consider an arbitrary
![]() $x\in \mathbb {R}^{m}$
. Then
$x\in \mathbb {R}^{m}$
. Then
![]() $x=\sum _{j=1}^{m}\alpha _{j}(x_{j}-x_{0})$
for some
$x=\sum _{j=1}^{m}\alpha _{j}(x_{j}-x_{0})$
for some
![]() $\alpha _{1}, \alpha _{2}, \ldots , \alpha _{m}\in \mathbb {R}$
, implying that
$\alpha _{1}, \alpha _{2}, \ldots , \alpha _{m}\in \mathbb {R}$
, implying that
 $$ \begin{align*} f(x)&=T\bigg(\sum_{j=1}^{m}\alpha_{j}(x_{j}-x_{0})\bigg)+z\\ &=\sum_{j=1}^{m}\alpha_{j}T(x_{j})-\sum_{j=1}^{m}\alpha_{j}T(x_{0})+z\\ &=\sum_{j=1}^{m}\alpha_{j}(-z)-\sum_{j=1}^{m}\alpha_{j}(-z)+z=z. \end{align*} $$
$$ \begin{align*} f(x)&=T\bigg(\sum_{j=1}^{m}\alpha_{j}(x_{j}-x_{0})\bigg)+z\\ &=\sum_{j=1}^{m}\alpha_{j}T(x_{j})-\sum_{j=1}^{m}\alpha_{j}T(x_{0})+z\\ &=\sum_{j=1}^{m}\alpha_{j}(-z)-\sum_{j=1}^{m}\alpha_{j}(-z)+z=z. \end{align*} $$
In particular,
![]() $f(x_{0})=z$
, and therefore we get that
$f(x_{0})=z$
, and therefore we get that
![]() $z=0$
. Hence,
$z=0$
. Hence,
![]() $f=0$
on
$f=0$
on
![]() $\mathbb {R}^{m}$
.
$\mathbb {R}^{m}$
.
Using the above lemma, we can deduce the following result on the uniqueness of affine linear maps.
Corollary 3.3. If
![]() $f_{1}, f_{2} \in \mathcal {F}(\mathbb {R}^{m})$
are affine linear maps such that
$f_{1}, f_{2} \in \mathcal {F}(\mathbb {R}^{m})$
are affine linear maps such that
![]() $f_{1}|_{\sigma }= f_{2}|_{\sigma }$
for some m-simplex
$f_{1}|_{\sigma }= f_{2}|_{\sigma }$
for some m-simplex
![]() $\sigma \in \mathcal {K}$
, then
$\sigma \in \mathcal {K}$
, then
![]() $f_{1}=f_{2}$
on
$f_{1}=f_{2}$
on
![]() $\mathbb {R}^{m}$
. Consequently, if
$\mathbb {R}^{m}$
. Consequently, if
![]() $f_{1}|_{U}=f_{2}|_{U}$
for some open subset U of
$f_{1}|_{U}=f_{2}|_{U}$
for some open subset U of
![]() $\mathbb {R}^{m}$
, then
$\mathbb {R}^{m}$
, then
![]() $f_{1}=f_{2}$
on
$f_{1}=f_{2}$
on
![]() $\mathbb {R}^{m}.$
$\mathbb {R}^{m}.$
Proof. Follows from the above lemma, because
![]() $f_{1}-f_{2}$
is an affine linear map on
$f_{1}-f_{2}$
is an affine linear map on
![]() $\mathbb {R}^{m}$
that vanishes on the geometrically independent set of all vertices of
$\mathbb {R}^{m}$
that vanishes on the geometrically independent set of all vertices of
![]() $\sigma $
.
$\sigma $
.
Corollary 3.4. Let
![]() $f \in \mathcal {F}(\mathbb {R}^{m})$
be an affine linear map and
$f \in \mathcal {F}(\mathbb {R}^{m})$
be an affine linear map and
![]() $\sigma $
be an m-simplex in
$\sigma $
be an m-simplex in
![]() $\mathbb {R}^{m}$
with vertices
$\mathbb {R}^{m}$
with vertices
![]() $x_{0}, x_{1}, \ldots , x_{m}$
such that
$x_{0}, x_{1}, \ldots , x_{m}$
such that
![]() $y_{0}, y_{1}, \ldots , y_{m}$
are geometrically independent in
$y_{0}, y_{1}, \ldots , y_{m}$
are geometrically independent in
![]() $\mathbb {R}^{m}$
, where
$\mathbb {R}^{m}$
, where
![]() $y_{j}=f(x_{j})$
for all
$y_{j}=f(x_{j})$
for all
![]() $0\leq j\leq m$
. Then the following statements are true.
$0\leq j\leq m$
. Then the following statements are true.
-
(i)
 $f(U)$
is open for every open set U in the interior of
$f(U)$
is open for every open set U in the interior of
 $\sigma $
.
$\sigma $
. -
(ii) f maps geometrically independent subsets of
 ${\mathbb R}^{m}$
to geometrically independent subsets.
${\mathbb R}^{m}$
to geometrically independent subsets. -
(iii) If
 $y_{j}\neq x_{j}$
for some
$y_{j}\neq x_{j}$
for some
 $0\le j\le m$
and
$0\le j\le m$
and
 $\{v_{0}, v_{1}, \ldots , v_{m}\}$
is a geometrically independent subset of
$\{v_{0}, v_{1}, \ldots , v_{m}\}$
is a geometrically independent subset of
 $\sigma $
, then there exists at least one j such that
$\sigma $
, then there exists at least one j such that
 $f(v_{j})\neq v_{j}$
.
$f(v_{j})\neq v_{j}$
.
Proof. Results (i) and (ii) are trivially true, because geometric independence of
![]() $\{y_{0}, y_{1}, \ldots , y_{m}\}$
implies that f is of full rank. If
$\{y_{0}, y_{1}, \ldots , y_{m}\}$
implies that f is of full rank. If
![]() $f(v_{j})=v_{j}$
for all
$f(v_{j})=v_{j}$
for all
![]() $0\le j\le m$
, then
$0\le j\le m$
, then
![]() $f=\text {id}$
on
$f=\text {id}$
on
![]() $\mathbb {R}^{m}$
, implying that
$\mathbb {R}^{m}$
, implying that
![]() $y_j=f(x_j)=x_j$
for all
$y_j=f(x_j)=x_j$
for all
![]() $0\le j\le m$
. Therefore, (iii) follows.
$0\le j\le m$
. Therefore, (iii) follows.
For each subset S of
![]() $\mathbb {R}^{m}$
, let
$\mathbb {R}^{m}$
, let
 $$ \begin{align*} \textrm{Aff}(S):=\bigg\{\sum_{j=1}^{l}\alpha_{j}x_{j}: x_{j}\in S~\text{for}~1\le j\le l~\text{and}~\sum_{j=1}^{l}\alpha_{j}=1\bigg\} \end{align*} $$
$$ \begin{align*} \textrm{Aff}(S):=\bigg\{\sum_{j=1}^{l}\alpha_{j}x_{j}: x_{j}\in S~\text{for}~1\le j\le l~\text{and}~\sum_{j=1}^{l}\alpha_{j}=1\bigg\} \end{align*} $$
and
 $$ \begin{align*} \textrm{Aff}_{0}(S):=\bigg\{\sum_{j=1}^{l}\alpha_{j}x_{j}: x_{j}\in S~\text{for}~1\le j\le l~\text{and}~\sum_{j=1}^{l}\alpha_{j}=0\bigg\}. \end{align*} $$
$$ \begin{align*} \textrm{Aff}_{0}(S):=\bigg\{\sum_{j=1}^{l}\alpha_{j}x_{j}: x_{j}\in S~\text{for}~1\le j\le l~\text{and}~\sum_{j=1}^{l}\alpha_{j}=0\bigg\}. \end{align*} $$
Then
![]() $\text {Aff}_{0}(S)$
is a vector subspace of
$\text {Aff}_{0}(S)$
is a vector subspace of
![]() $\mathbb {R}^{m}$
and
$\mathbb {R}^{m}$
and
![]() $\text {Aff}(S)=\text {Aff}_{0}(S)+x$
for some
$\text {Aff}(S)=\text {Aff}_{0}(S)+x$
for some
![]() $x\in S$
, where
$x\in S$
, where
![]() $\text { Aff}_{0}(S)+x:=\{y+x:y\in \text {Aff}_{0}(S)\}$
. We say that
$\text { Aff}_{0}(S)+x:=\{y+x:y\in \text {Aff}_{0}(S)\}$
. We say that
![]() $\text {Aff}(S)$
has dimension k, written as
$\text {Aff}(S)$
has dimension k, written as
![]() $dim(\text {Aff}(S))=k$
, if
$dim(\text {Aff}(S))=k$
, if
![]() $\text {Aff}_{0}(S)$
is a k-dimensional vector subspace of
$\text {Aff}_{0}(S)$
is a k-dimensional vector subspace of
![]() $\mathbb {R}^{m}$
. A point
$\mathbb {R}^{m}$
. A point
![]() $z\in \mathbb {R}^{m}$
is said to be geometrically independent of S if
$z\in \mathbb {R}^{m}$
is said to be geometrically independent of S if
![]() $z\notin \text {Aff}(S)$
. Then it is clear that z is geometrically independent of S if and only if
$z\notin \text {Aff}(S)$
. Then it is clear that z is geometrically independent of S if and only if
![]() $0$
is geometrically independent of
$0$
is geometrically independent of
![]() $S-z$
.
$S-z$
.
Lemma 3.5. Let S be a countable subset of
![]() $\mathbb {R}^{m}$
. Then for each
$\mathbb {R}^{m}$
. Then for each
![]() $z\in \mathbb {R}^{m}$
and
$z\in \mathbb {R}^{m}$
and
![]() $\zeta>0$
, there exists a
$\zeta>0$
, there exists a
![]() $y\in B_{\zeta }(z)$
such that y is geometrically independent of Z for all subsets Z of S such that
$y\in B_{\zeta }(z)$
such that y is geometrically independent of Z for all subsets Z of S such that
![]() $\#Z\le m$
.
$\#Z\le m$
.
Proof. Since
![]() $dim(\text {Aff}(Z))\le m-1$
, clearly
$dim(\text {Aff}(Z))\le m-1$
, clearly
![]() $\text {Aff}(Z)\bigcap \overline{B_{\zeta/2}(z)}$
is a nowhere dense subset of the complete metric space
$\text {Aff}(Z)\bigcap \overline{B_{\zeta/2}(z)}$
is a nowhere dense subset of the complete metric space
![]() $\overline{B_{\zeta/2}(z)}$
for each subset Z of S such that
$\overline{B_{\zeta/2}(z)}$
for each subset Z of S such that
![]() $\#Z\le m$
. Therefore, by the Baire category theorem, we have
$\#Z\le m$
. Therefore, by the Baire category theorem, we have
 $$ \begin{align*} \overline{B_{\zeta/2}(z)}\ne \bigcup\bigg(\textrm{Aff}(Z)\bigcap \overline{B_{\zeta/2}(z)}\bigg), \end{align*} $$
$$ \begin{align*} \overline{B_{\zeta/2}(z)}\ne \bigcup\bigg(\textrm{Aff}(Z)\bigcap \overline{B_{\zeta/2}(z)}\bigg), \end{align*} $$
where the union is taken over all subsets Z of S such that
![]() $\#Z\le m$
. Hence, there exists a
$\#Z\le m$
. Hence, there exists a
![]() $y\in \overline{B_{\zeta/2}(z)}$
such that y is geometrically independent of Z for all subsets Z of S such that
$y\in \overline{B_{\zeta/2}(z)}$
such that y is geometrically independent of Z for all subsets Z of S such that
![]() $\#Z\le m$
. Since
$\#Z\le m$
. Since
![]() $\overline{B_{\zeta/2}(z)}\subseteq B_{\zeta }(z)$
, the result follows.
$\overline{B_{\zeta/2}(z)}\subseteq B_{\zeta }(z)$
, the result follows.
Lemma 3.6. Let
![]() $z_{1}, z_{2}, \ldots $
be a sequence of points in
$z_{1}, z_{2}, \ldots $
be a sequence of points in
![]() $\mathbb {R}^{m}$
and
$\mathbb {R}^{m}$
and
![]() $\zeta _{1}, \zeta _{2}, \ldots $
be a sequence of positive reals. Then there exists a sequence
$\zeta _{1}, \zeta _{2}, \ldots $
be a sequence of positive reals. Then there exists a sequence
![]() $y_{1}, y_{2}, \ldots $
in
$y_{1}, y_{2}, \ldots $
in
![]() $\mathbb {R}^{m}$
such that
$\mathbb {R}^{m}$
such that
![]() $y_{j}\in B_{\zeta _{j}}(z_{j})$
for each
$y_{j}\in B_{\zeta _{j}}(z_{j})$
for each
![]() $j\in \mathbb {N}$
and every subset Z of
$j\in \mathbb {N}$
and every subset Z of
![]() $S=\{y_{1}, y_{2}, \ldots \}$
where
$S=\{y_{1}, y_{2}, \ldots \}$
where
![]() $\#Z\le m+1$
is geometrically independent.
$\#Z\le m+1$
is geometrically independent.
Proof. Given
![]() $z_{1}\in \mathbb {R}^{m}$
and
$z_{1}\in \mathbb {R}^{m}$
and
![]() $\zeta _{1}>0$
, consider any
$\zeta _{1}>0$
, consider any
![]() $y_{1}\in B_{\zeta _{1}}(z_{1})$
such that
$y_{1}\in B_{\zeta _{1}}(z_{1})$
such that
![]() $y_{1}\ne z_{1}$
. Then clearly any subset Z of
$y_{1}\ne z_{1}$
. Then clearly any subset Z of
![]() $S_{1}=\{y_{1}\}$
with
$S_{1}=\{y_{1}\}$
with
![]() $\#Z\le m+1$
is geometrically independent. Next, by induction, suppose that
$\#Z\le m+1$
is geometrically independent. Next, by induction, suppose that
![]() $k>1$
, and there exist
$k>1$
, and there exist
![]() $y_{1}, y_{2}, \ldots , y_{k} \in \mathbb {R}^{m}$
with
$y_{1}, y_{2}, \ldots , y_{k} \in \mathbb {R}^{m}$
with
![]() $y_{j}\in B_{\zeta _{j}}(z_{j})$
for
$y_{j}\in B_{\zeta _{j}}(z_{j})$
for
![]() $1\le j\le k$
such that Z is geometrically independent for all subsets Z of
$1\le j\le k$
such that Z is geometrically independent for all subsets Z of
![]() $S_{k}=\{y_{1}, y_{2}, \ldots , y_{k}\}$
with
$S_{k}=\{y_{1}, y_{2}, \ldots , y_{k}\}$
with
![]() $\#Z\le m+1$
. Then by Lemma 3.5, there exists
$\#Z\le m+1$
. Then by Lemma 3.5, there exists
![]() $y_{k+1}\in B_{\zeta _{k+1}}(z_{k+1})$
such that
$y_{k+1}\in B_{\zeta _{k+1}}(z_{k+1})$
such that
![]() $y_{k+1}$
is geometrically independent of Z for all subsets Z of
$y_{k+1}$
is geometrically independent of Z for all subsets Z of
![]() $S_{k}$
such that
$S_{k}$
such that
![]() $\#Z\le m$
. This implies that Z is geometrically independent for all subsets Z of
$\#Z\le m$
. This implies that Z is geometrically independent for all subsets Z of
![]() $S_{k+1}=\{y_1, y_2, \ldots, y_{k+1}\}$
such that
$S_{k+1}=\{y_1, y_2, \ldots, y_{k+1}\}$
such that
![]() $\#Z\le m+1$
, proving the result for
$\#Z\le m+1$
, proving the result for
![]() $k+1$
. Thus, continuing the above process, we get a sequence
$k+1$
. Thus, continuing the above process, we get a sequence
![]() $y_{1}, y_{2}, \ldots $
in
$y_{1}, y_{2}, \ldots $
in
![]() $\mathbb {R}^{m}$
such that
$\mathbb {R}^{m}$
such that
![]() $y_{j}\in B_{\zeta _{j}}(z_{j})$
for each
$y_{j}\in B_{\zeta _{j}}(z_{j})$
for each
![]() $j\in \mathbb {N}$
satisfying the desired property.
$j\in \mathbb {N}$
satisfying the desired property.
In addition to the above notions and results on simplicial complexes, we need the following lemma to prove our results.
Lemma 3.7. Let X be a metric space with metric d and
![]() $f\in \mathcal {C}(X)$
. If
$f\in \mathcal {C}(X)$
. If
![]() $x\in X$
is not a fixed point of f, then there exists an open set V in X containing x such that
$x\in X$
is not a fixed point of f, then there exists an open set V in X containing x such that
![]() $f^{-1}(V)\cap V=\emptyset $
and
$f^{-1}(V)\cap V=\emptyset $
and
![]() $f(V)\cap V=\emptyset $
.
$f(V)\cap V=\emptyset $
.
Proof. Let
![]() $\epsilon =d(x,f(x))$
. Since
$\epsilon =d(x,f(x))$
. Since
![]() $f(x)\ne x$
, clearly
$f(x)\ne x$
, clearly
![]() $\epsilon>0$
. Since f is continuous at x, there exists a
$\epsilon>0$
. Since f is continuous at x, there exists a
![]() $\delta>0$
with
$\delta>0$
with
![]() $\delta <{\epsilon }/{4}$
such that
$\delta <{\epsilon }/{4}$
such that
Let
![]() $V:=B_{{\delta }/{2}}(x)$
.
$V:=B_{{\delta }/{2}}(x)$
.
Claim.
![]() $f^{-1}(V)\cap V=\emptyset $
and
$f^{-1}(V)\cap V=\emptyset $
and
![]() $f(V)\cap V=\emptyset $
.
$f(V)\cap V=\emptyset $
.
Suppose that
![]() $y\in f^{-1}(V)\cap V$
. Then
$y\in f^{-1}(V)\cap V$
. Then
![]() $f(y)\in V$
, implying that
$f(y)\in V$
, implying that
![]() $d(y, f(y))\le d(y,x)+d(x,f(y))<\delta $
. Also, by equation (3.3), we have
$d(y, f(y))\le d(y,x)+d(x,f(y))<\delta $
. Also, by equation (3.3), we have
![]() $d(f(x), f(y))<{\epsilon }/{4}$
. Therefore,
$d(f(x), f(y))<{\epsilon }/{4}$
. Therefore,
![]() $\epsilon =d(x, f(x))\le d(x, y)+d(y, f(y))+d(f(y), f(x))<{3\epsilon }/{4}$
is a contradiction. Next, suppose that
$\epsilon =d(x, f(x))\le d(x, y)+d(y, f(y))+d(f(y), f(x))<{3\epsilon }/{4}$
is a contradiction. Next, suppose that
![]() $y\in f(V)\cap V$
. Then
$y\in f(V)\cap V$
. Then
![]() $y=f(z)$
for some
$y=f(z)$
for some
![]() $z\in V$
. Therefore, by equation (3.3), we have
$z\in V$
. Therefore, by equation (3.3), we have
![]() $d(f(x), y)<{\epsilon }/{4}$
, implying that
$d(f(x), y)<{\epsilon }/{4}$
, implying that
![]() $\epsilon =d(x, f(x))\le d(x, y)+d(y, f(x))<{\epsilon }/{2}$
, which is a contradiction. Thus the claim holds, and the result follows.
$\epsilon =d(x, f(x))\le d(x, y)+d(y, f(x))<{\epsilon }/{2}$
, which is a contradiction. Thus the claim holds, and the result follows.
Having the above machinery, we are ready to prove our desired results.
Theorem 3.8. If
![]() $h\in \mathcal {C}(I^{m})$
, then for each
$h\in \mathcal {C}(I^{m})$
, then for each
![]() $\epsilon>0$
the ball
$\epsilon>0$
the ball
![]() $B_{\epsilon }(h)$
of radius
$B_{\epsilon }(h)$
of radius
![]() $\epsilon $
around h contains a map f having no (even discontinuous) iterative square roots on
$\epsilon $
around h contains a map f having no (even discontinuous) iterative square roots on
![]() $I^{m}$
. In particular,
$I^{m}$
. In particular,
![]() $\mathcal {W}(2;I^{m})$
does not contain any ball of
$\mathcal {W}(2;I^{m})$
does not contain any ball of
![]() $\mathcal {C}(I^{m})$
.
$\mathcal {C}(I^{m})$
.
Proof. Let
![]() $h\in \mathcal {C}(I^{m})$
and
$h\in \mathcal {C}(I^{m})$
and
![]() $\epsilon>0$
be arbitrary. Our strategy to prove the existence of an
$\epsilon>0$
be arbitrary. Our strategy to prove the existence of an
![]() $f\in B_{\epsilon }(h)$
with no square roots is to make use of Theorem 2.4, and we construct this f in a few steps.
$f\in B_{\epsilon }(h)$
with no square roots is to make use of Theorem 2.4, and we construct this f in a few steps.
Step 1: Construct a piecewise affine linear map
![]() $f_{0}\in B_{\epsilon }(h)$
supported by some suitable triangulation
$f_{0}\in B_{\epsilon }(h)$
supported by some suitable triangulation
![]() $\mathcal {K}$
of
$\mathcal {K}$
of
![]() $I^{m}$
. Since h is uniformly continuous on
$I^{m}$
. Since h is uniformly continuous on
![]() $I^{m}$
, there exists a
$I^{m}$
, there exists a
![]() $\delta>0$
such that
$\delta>0$
such that
Being a polyhedron,
![]() $I^{m}$
is triangulable. Consider a triangulation
$I^{m}$
is triangulable. Consider a triangulation
![]() $\mathcal {K}$
of
$\mathcal {K}$
of
![]() $I^{m}$
with vertices
$I^{m}$
with vertices
![]() $x_{0}, x_{1}, x_{2}, \ldots , x_{r}$
such that
$x_{0}, x_{1}, x_{2}, \ldots , x_{r}$
such that
![]() $\|x_{i_{0}}-x_{i_{1}}\|_{\infty }<{\delta }/{4}$
for all
$\|x_{i_{0}}-x_{i_{1}}\|_{\infty }<{\delta }/{4}$
for all
![]() $2$
-simplex
$2$
-simplex
![]() $\langle x_{i_{0}},x_{i_{1}}\rangle $
of
$\langle x_{i_{0}},x_{i_{1}}\rangle $
of
![]() $\sigma $
and for all m-simplex
$\sigma $
and for all m-simplex
![]() $\sigma \in \mathcal {K}$
. Choose
$\sigma \in \mathcal {K}$
. Choose
![]() $y_{0}, y_{1}, y_{2},\ldots , y_{r} \in I^{m}$
inductively such that
$y_{0}, y_{1}, y_{2},\ldots , y_{r} \in I^{m}$
inductively such that
![]() $y_{j}\ne x_{j}$
and
$y_{j}\ne x_{j}$
and
and
![]() $\{y_{i_{0}}, y_{i_{1}}, \ldots , y_{i_{m}}\}$
is geometrically independent whenever
$\{y_{i_{0}}, y_{i_{1}}, \ldots , y_{i_{m}}\}$
is geometrically independent whenever
![]() $\langle x_{i_{0}}, x_{i_{1}},\ldots , x_{i_{m}}\rangle \in \mathcal {K}$
for
$\langle x_{i_{0}}, x_{i_{1}},\ldots , x_{i_{m}}\rangle \in \mathcal {K}$
for
![]() $0\le i_{0}, i_{1}, \ldots , i_{m}\le r$
. This is possible by Lemma 3.6. Here, while choosing points
$0\le i_{0}, i_{1}, \ldots , i_{m}\le r$
. This is possible by Lemma 3.6. Here, while choosing points
![]() $y_{j}$
with
$y_{j}$
with
![]() $y_{j}\in B_{ {\epsilon }/{20} }(h(x_{j}))$
for
$y_{j}\in B_{ {\epsilon }/{20} }(h(x_{j}))$
for
![]() $0\le j\le r$
satisfying the geometric independence condition, we have some additional restrictions to fulfill, viz.
$0\le j\le r$
satisfying the geometric independence condition, we have some additional restrictions to fulfill, viz.
![]() $y_{j}\neq x_{j}$
and
$y_{j}\neq x_{j}$
and
![]() $y_{j}\in I^{m}$
for all
$y_{j}\in I^{m}$
for all
![]() $0\le j\le r$
. However, the Baire category theorem provides this flexibility as there are plenty of vectors to choose from. Then,
$0\le j\le r$
. However, the Baire category theorem provides this flexibility as there are plenty of vectors to choose from. Then,
 $$ \begin{align} \|y_{i_{0}}-y_{i_{1}}\|_{\infty}&\le \|y_{i_{0}}-h(x_{i_{0}})\|_{\infty}+\|h(x_{i_{0}})-h(x_{i_{1}})\|_{\infty}+ \|h(x_{i_{1}})-y_{i_{1}}\|_{\infty}\nonumber \\ &< \frac{\epsilon}{20}+\frac{\epsilon }{10}+\frac{\epsilon }{20}=\frac{\epsilon }{5} \end{align} $$
$$ \begin{align} \|y_{i_{0}}-y_{i_{1}}\|_{\infty}&\le \|y_{i_{0}}-h(x_{i_{0}})\|_{\infty}+\|h(x_{i_{0}})-h(x_{i_{1}})\|_{\infty}+ \|h(x_{i_{1}})-y_{i_{1}}\|_{\infty}\nonumber \\ &< \frac{\epsilon}{20}+\frac{\epsilon }{10}+\frac{\epsilon }{20}=\frac{\epsilon }{5} \end{align} $$
whenever
![]() $\langle x_{i_{0}},x_{i_{1}}\rangle $
is a
$\langle x_{i_{0}},x_{i_{1}}\rangle $
is a
![]() $2$
-simplex of
$2$
-simplex of
![]() $\sigma $
for all m-simplex
$\sigma $
for all m-simplex
![]() $\sigma \in \mathcal {K}$
. Let
$\sigma \in \mathcal {K}$
. Let
![]() $f_{0}:|\mathcal {K}|=I^{m} \to I^{m}$
be the map
$f_{0}:|\mathcal {K}|=I^{m} \to I^{m}$
be the map
![]() $f_{U, V}$
defined as in equation (3.2), where U and V are the ordered sets
$f_{U, V}$
defined as in equation (3.2), where U and V are the ordered sets
![]() $\{x_{0}, x_{1}, \ldots , x_{r}\}$
and
$\{x_{0}, x_{1}, \ldots , x_{r}\}$
and
![]() $\{y_{0}, y_{1}, \ldots , y_{r}\}$
, respectively. Then
$\{y_{0}, y_{1}, \ldots , y_{r}\}$
, respectively. Then
![]() $f_{0}$
is a continuous piecewise affine linear self-map of
$f_{0}$
is a continuous piecewise affine linear self-map of
![]() $I^{m}$
satisfying that
$I^{m}$
satisfying that
![]() $f_{0}(x_{j})=y_{j}$
for all
$f_{0}(x_{j})=y_{j}$
for all
![]() $0\le j\le r$
. Also, by using result (i) of Lemma 3.1, we have
$0\le j\le r$
. Also, by using result (i) of Lemma 3.1, we have
![]() $R(f_{0})^{0}\ne \emptyset $
and
$R(f_{0})^{0}\ne \emptyset $
and
![]() $f_{0}|_{\sigma }$
is injective for all
$f_{0}|_{\sigma }$
is injective for all
![]() $\sigma \in \mathcal {K}$
. Further, from equation (3.6) we have
$\sigma \in \mathcal {K}$
. Further, from equation (3.6) we have
Claim.
![]() $\rho (f_{0},h)<{\epsilon }/{6}$
.
$\rho (f_{0},h)<{\epsilon }/{6}$
.
Consider an arbitrary
![]() $x\in I^{m}$
. Then x is in the interior of some unique k-simplex
$x\in I^{m}$
. Then x is in the interior of some unique k-simplex
![]() $\langle x_{i_{0}}, x_{i_{1}}, \ldots , x_{i_{k}}\rangle $
in
$\langle x_{i_{0}}, x_{i_{1}}, \ldots , x_{i_{k}}\rangle $
in
![]() $\mathcal {K}$
for some
$\mathcal {K}$
for some
![]() $0\le k\le m$
. Let
$0\le k\le m$
. Let
![]() $x=\sum _{j=0}^{k}\alpha _{i_{j}}x_{i_{j}}$
with
$x=\sum _{j=0}^{k}\alpha _{i_{j}}x_{i_{j}}$
with
![]() $\sum _{j=0}^{k}\alpha _{i_{j}}=1$
. Then by equations (3.4) and (3.5), we have
$\sum _{j=0}^{k}\alpha _{i_{j}}=1$
. Then by equations (3.4) and (3.5), we have
 $$ \begin{align} \|f_{0}(x)-h(x)\|_{\infty}&=\bigg\|\sum_{j=0}^{k}\alpha_{i_{j}}y_{i_{j}}-\sum_{j=0}^{k}\alpha_{i_{j}}h(x)\bigg\|_{\infty} \nonumber\\ &\le \sum_{j=0}^{k}\alpha_{i_{j}}\{\|y_{i_{j}}-h(x_{i_{j}})\|_{\infty}+\|h(x_{i_{j}})-h(x)\|_{\infty}\}\nonumber\\ &< \frac{\epsilon }{20}+\frac{\epsilon }{10}\nonumber\\ &<\frac{\epsilon}{6}, \end{align} $$
$$ \begin{align} \|f_{0}(x)-h(x)\|_{\infty}&=\bigg\|\sum_{j=0}^{k}\alpha_{i_{j}}y_{i_{j}}-\sum_{j=0}^{k}\alpha_{i_{j}}h(x)\bigg\|_{\infty} \nonumber\\ &\le \sum_{j=0}^{k}\alpha_{i_{j}}\{\|y_{i_{j}}-h(x_{i_{j}})\|_{\infty}+\|h(x_{i_{j}})-h(x)\|_{\infty}\}\nonumber\\ &< \frac{\epsilon }{20}+\frac{\epsilon }{10}\nonumber\\ &<\frac{\epsilon}{6}, \end{align} $$
since
![]() $\|x-x_{i_{j}}\|_{\infty }\le \mbox {diam}(\langle x_{i_{0}}, x_{i_{1}}, \ldots , x_{i_{k}}\rangle )<{\delta }/{4}$
for
$\|x-x_{i_{j}}\|_{\infty }\le \mbox {diam}(\langle x_{i_{0}}, x_{i_{1}}, \ldots , x_{i_{k}}\rangle )<{\delta }/{4}$
for
![]() $0\le j\le k$
. This proves the claim and Step 1 follows.
$0\le j\le k$
. This proves the claim and Step 1 follows.
Step 2: Obtain an m-simplex
![]() $\Delta \in \mathcal {K} $
containing a non-empty open set
$\Delta \in \mathcal {K} $
containing a non-empty open set
![]() $Y\subseteq \Delta ^{0}\cap R(f_{0})^{0}$
such that
$Y\subseteq \Delta ^{0}\cap R(f_{0})^{0}$
such that
![]() $f_{0}(Y)\subseteq \Delta _{1}^{0}$
for some m-simplex
$f_{0}(Y)\subseteq \Delta _{1}^{0}$
for some m-simplex
![]() $\Delta _{1}$
in
$\Delta _{1}$
in
![]() ${\mathcal K}.$
Consider any m-simplex
${\mathcal K}.$
Consider any m-simplex
![]() $\sigma =\langle x_{i_{0}}, x_{i_{1}},\ldots , x_{i_{m}}\rangle $
in
$\sigma =\langle x_{i_{0}}, x_{i_{1}},\ldots , x_{i_{m}}\rangle $
in
![]() $\mathcal {K}$
. Since
$\mathcal {K}$
. Since
![]() $\{y_{i_{0}}, y_{i_{1}},\ldots , y_{i_{m}}\}$
is geometrically independent by construction, we have
$\{y_{i_{0}}, y_{i_{1}},\ldots , y_{i_{m}}\}$
is geometrically independent by construction, we have
![]() $f_{0}(Z)$
is open in
$f_{0}(Z)$
is open in
![]() $I^{m}$
for each open set Z in
$I^{m}$
for each open set Z in
![]() $\sigma ^{0}$
. Choose a non-empty open subset
$\sigma ^{0}$
. Choose a non-empty open subset
![]() $Y_{0}$
of
$Y_{0}$
of
![]() $f_0(\sigma )^{0}$
so small that
$f_0(\sigma )^{0}$
so small that
![]() $Y_{0}\subseteq \Delta ^{0}$
for some m-simplex
$Y_{0}\subseteq \Delta ^{0}$
for some m-simplex
![]() $\Delta \in \mathcal {K}$
. Then
$\Delta \in \mathcal {K}$
. Then
![]() $f_{0}(Y_{0})$
has non-empty interior. Again, choose a sufficiently small non-empty open subset Y of
$f_{0}(Y_{0})$
has non-empty interior. Again, choose a sufficiently small non-empty open subset Y of
![]() $Y_{0}$
such that
$Y_{0}$
such that
![]() $f_{0}(Y)\subseteq \Delta _{1}$
for some m-simplex
$f_{0}(Y)\subseteq \Delta _{1}$
for some m-simplex
![]() $\Delta _{1}\in {\mathcal K}.$
This completes the proof of Step 2.
$\Delta _{1}\in {\mathcal K}.$
This completes the proof of Step 2.
Step 3: Show that there exists a barycentric subdivision
![]() $\mathcal {K}^{(s)}$
of
$\mathcal {K}^{(s)}$
of
![]() $\mathcal {K}$
for some
$\mathcal {K}$
for some
![]() $s \in \mathbb {N}$
with an m-simplex
$s \in \mathbb {N}$
with an m-simplex
![]() $\sigma _{0}\in \mathcal {K}^{(s)}$
such that
$\sigma _{0}\in \mathcal {K}^{(s)}$
such that
![]() $\sigma _{0}\subseteq Y$
, and
$\sigma _{0}\subseteq Y$
, and
![]() $f_{0}^{-1}(\sigma _{0})\cap \sigma =\emptyset $
and
$f_{0}^{-1}(\sigma _{0})\cap \sigma =\emptyset $
and
![]() $f_{0}(\sigma _{0})\cap \sigma =\emptyset $
for all
$f_{0}(\sigma _{0})\cap \sigma =\emptyset $
for all
![]() $\sigma \in \mathcal {K}^{(s)}$
with
$\sigma \in \mathcal {K}^{(s)}$
with
![]() $\sigma \cap \sigma _{0}\ne \emptyset $
. Since
$\sigma \cap \sigma _{0}\ne \emptyset $
. Since
![]() $y_{j}\neq x_{j}$
for all
$y_{j}\neq x_{j}$
for all
![]() $0\le j\le r$
, by Corollary 3.4, we have
$0\le j\le r$
, by Corollary 3.4, we have
![]() $f_{0}(z_{0})\ne z_{0}$
for some
$f_{0}(z_{0})\ne z_{0}$
for some
![]() $z_{0}\in Y$
. Choose an open set
$z_{0}\in Y$
. Choose an open set
![]() $W_0$
in
$W_0$
in
![]() $I^{m}$
such that
$I^{m}$
such that
![]() $z_{0}\in W_0\subseteq Y$
and
$z_{0}\in W_0\subseteq Y$
and
![]() $f_{0}(x)\ne x$
for all
$f_{0}(x)\ne x$
for all
![]() $x\in W_0$
. Then using Lemma 3.7, we get an open set W in
$x\in W_0$
. Then using Lemma 3.7, we get an open set W in
![]() $I^{m}$
with
$I^{m}$
with
![]() $z_{0}\in W\subseteq W_0$
such that
$z_{0}\in W\subseteq W_0$
such that
![]() $f_{0}^{-1}(W)\cap W=\emptyset $
and
$f_{0}^{-1}(W)\cap W=\emptyset $
and
![]() $f_{0}(W)\cap W=\emptyset $
. Perform a barycentric subdivision of
$f_{0}(W)\cap W=\emptyset $
. Perform a barycentric subdivision of
![]() $\mathcal {K}$
of order s so large that W contains an m-simplex
$\mathcal {K}$
of order s so large that W contains an m-simplex
![]() $\sigma _{0}\in \mathcal {K}^{(s)}$
and all m-simplices
$\sigma _{0}\in \mathcal {K}^{(s)}$
and all m-simplices
![]() $\sigma \in \mathcal {K}^{(s)}$
adjacent to it, that is,
$\sigma \in \mathcal {K}^{(s)}$
adjacent to it, that is,
![]() $\sigma \subseteq W$
for all m-simplices
$\sigma \subseteq W$
for all m-simplices
![]() $\sigma \in \mathcal {K}^{(s)}$
such that
$\sigma \in \mathcal {K}^{(s)}$
such that
![]() $\sigma \cap \sigma _{0}\ne \emptyset $
. Since
$\sigma \cap \sigma _{0}\ne \emptyset $
. Since
![]() $\lim \nolimits _{l\to \infty }\mbox {mesh}(\mathcal {K}^{\kern2pt(l)})=0$
, it is possible to obtain such a subdivision of
$\lim \nolimits _{l\to \infty }\mbox {mesh}(\mathcal {K}^{\kern2pt(l)})=0$
, it is possible to obtain such a subdivision of
![]() $\mathcal {K}$
. This completes the proof of Step 3.
$\mathcal {K}$
. This completes the proof of Step 3.
Step 4: Modify
![]() $f_{0}$
slightly to get a new piecewise affine linear map
$f_{0}$
slightly to get a new piecewise affine linear map
![]() $f\in B_{\epsilon } (h)$
that is constant on
$f\in B_{\epsilon } (h)$
that is constant on
![]() $\sigma {}_{0}.$
To retain continuity, when we modify
$\sigma {}_{0}.$
To retain continuity, when we modify
![]() $f_{0}$
on
$f_{0}$
on
![]() $\sigma _{0}$
, we must also modify it on all m-simplices in
$\sigma _{0}$
, we must also modify it on all m-simplices in
![]() $\mathcal {K}^{\kern2pt(s)}$
adjacent to it. Let
$\mathcal {K}^{\kern2pt(s)}$
adjacent to it. Let
![]() $A:=\bigcup _{j=0}^{p}\sigma _{j}$
, where
$A:=\bigcup _{j=0}^{p}\sigma _{j}$
, where
![]() $\sigma _{j}$
is precisely an m-simplex in
$\sigma _{j}$
is precisely an m-simplex in
![]() $\mathcal {K}^{\kern2pt(s)}$
such that
$\mathcal {K}^{\kern2pt(s)}$
such that
![]() $\sigma _{j}\cap \sigma _{0}\ne \emptyset $
for all
$\sigma _{j}\cap \sigma _{0}\ne \emptyset $
for all
![]() $0\le j\le p$
. Then, it is clear that
$0\le j\le p$
. Then, it is clear that
![]() $A\subseteq W\subseteq \Delta {}^{0}$
.
$A\subseteq W\subseteq \Delta {}^{0}$
.
Let the vertices of
![]() $\sigma _{0}$
be
$\sigma _{0}$
be
![]() $u_{0},\ldots , u_{m-1}$
and
$u_{0},\ldots , u_{m-1}$
and
![]() $u_{m}$
, and let
$u_{m}$
, and let
![]() $v_{j}:=f_{0}(u_{j})$
for all
$v_{j}:=f_{0}(u_{j})$
for all
![]() $0\le j \le m$
. Then
$0\le j \le m$
. Then
![]() $v_{j}\ne u_{j}$
for all
$v_{j}\ne u_{j}$
for all
![]() $0\le j\le m$
, because
$0\le j\le m$
, because
![]() $u_{j}\in W$
for all
$u_{j}\in W$
for all
![]() $0\le j\le m$
and
$0\le j\le m$
and
![]() $f_{0}(W)\cap W=\emptyset $
. Also, since
$f_{0}(W)\cap W=\emptyset $
. Also, since
![]() $u_{0}, u_{1}, \ldots , u_{m}$
are geometrically independent vectors in
$u_{0}, u_{1}, \ldots , u_{m}$
are geometrically independent vectors in
![]() $\Delta $
, by result (ii) of Corollary 3.4, we see that
$\Delta $
, by result (ii) of Corollary 3.4, we see that
![]() $v_0, v_1,\ldots,v_m$
are geometrically independent. Further, they are all contained in the interior of a single simplex
$v_0, v_1,\ldots,v_m$
are geometrically independent. Further, they are all contained in the interior of a single simplex
![]() $\Delta _{1}$
of
$\Delta _{1}$
of
![]() $\mathcal {K}$
by Step 2. Hence, by result (iii) of Corollary 3.4, it follows that
$\mathcal {K}$
by Step 2. Hence, by result (iii) of Corollary 3.4, it follows that
![]() $f_{0}(v_{j})\neq v_{j}$
for some
$f_{0}(v_{j})\neq v_{j}$
for some
![]() $0\le j\le m$
. Without loss of generality, we assume that
$0\le j\le m$
. Without loss of generality, we assume that
![]() $f_{0}(v_{0})\neq v_{0}.$
$f_{0}(v_{0})\neq v_{0}.$
Extend
![]() $\{u_{0}, \ldots , u_{m}\}$
to
$\{u_{0}, \ldots , u_{m}\}$
to
![]() $\{u_{0}, \ldots , u_{k_0}\}$
with
$\{u_{0}, \ldots , u_{k_0}\}$
with
![]() $k_0 > m$
to include the vertices of all the simplices of
$k_0 > m$
to include the vertices of all the simplices of
![]() ${\mathcal K}^{(s)}$
, and let
${\mathcal K}^{(s)}$
, and let
![]() $v_{j}:= f_{0}(u_{j})$
for all
$v_{j}:= f_{0}(u_{j})$
for all
![]() $0\leq j\leq k_0$
. Now, define f by
$0\leq j\leq k_0$
. Now, define f by
 $$ \begin{align*} f(u_{j}) = \begin{cases} v_{0}&\text{if } 0\leq j\leq m,\\ v_{j}&\text{if } m<j\leq k_0,\end{cases} \end{align*} $$
$$ \begin{align*} f(u_{j}) = \begin{cases} v_{0}&\text{if } 0\leq j\leq m,\\ v_{j}&\text{if } m<j\leq k_0,\end{cases} \end{align*} $$
and extend it piecewise affine linearly to the whole of
![]() $|{\mathcal K}^{(s)}|= I^{m}$
. Then
$|{\mathcal K}^{(s)}|= I^{m}$
. Then
![]() $f_{0}$
is modified only on A and
$f_{0}$
is modified only on A and
![]() $f(x)=v_{0}$
for all
$f(x)=v_{0}$
for all
![]() $x\in \sigma _{0}$
.
$x\in \sigma _{0}$
.
Consider an arbitrary
![]() $x\in A$
. Then
$x\in A$
. Then
![]() $x\in \sigma _{j}$
for some
$x\in \sigma _{j}$
for some
![]() $0\le j\le p$
. Let
$0\le j\le p$
. Let
![]() $\sigma _{j}=\langle u_{j_{0}}, u_{j_{1}}, \ldots , u_{j_{m}}\rangle $
and
$\sigma _{j}=\langle u_{j_{0}}, u_{j_{1}}, \ldots , u_{j_{m}}\rangle $
and
![]() $x=\sum _{i=0}^{m}\alpha _{j_{i}}u_{j_{i}}$
with
$x=\sum _{i=0}^{m}\alpha _{j_{i}}u_{j_{i}}$
with
![]() $\sum _{i=0}^{m}\alpha _{j_{i}}=1$
. Then by equation (3.7), we have
$\sum _{i=0}^{m}\alpha _{j_{i}}=1$
. Then by equation (3.7), we have
 $$ \begin{align*} \|f(x)-f_{0}(x)\|_{\infty}\le \sum_{i=0}^{m}\alpha_{j_{i}}\|f(u_{j_{i}})-f_{0}(u_{j_{i}})\|_{\infty} \le \sum_{i=0}^{m}\alpha_{j_{i}}\mbox{diam}(f_0(\Delta)) < \frac{\epsilon}{5}, \end{align*} $$
$$ \begin{align*} \|f(x)-f_{0}(x)\|_{\infty}\le \sum_{i=0}^{m}\alpha_{j_{i}}\|f(u_{j_{i}})-f_{0}(u_{j_{i}})\|_{\infty} \le \sum_{i=0}^{m}\alpha_{j_{i}}\mbox{diam}(f_0(\Delta)) < \frac{\epsilon}{5}, \end{align*} $$
implying by equation (3.8) that
Therefore,
![]() $f\in B_{\epsilon }(h)$
and the proof of Step 4 is completed.
$f\in B_{\epsilon }(h)$
and the proof of Step 4 is completed.
Step 5. Prove that f has no square roots in
![]() $\mathcal {C}(I^{m})$
. Since
$\mathcal {C}(I^{m})$
. Since
![]() $A\subseteq W$
,
$A\subseteq W$
,
![]() $f=f_{0}$
on
$f=f_{0}$
on
![]() $A^{c}$
, and
$A^{c}$
, and
![]() $f_{0}(W)\cap W=\emptyset $
, we see that
$f_{0}(W)\cap W=\emptyset $
, we see that
![]() $f(v_{0})\neq v_{0}$
. Also, by Step 3, we have
$f(v_{0})\neq v_{0}$
. Also, by Step 3, we have
![]() $f_{0}^{-1}(\sigma _{0})\cap \sigma =\emptyset $
for all
$f_{0}^{-1}(\sigma _{0})\cap \sigma =\emptyset $
for all
![]() $\sigma \in {\mathcal K}^{(s)}$
with
$\sigma \in {\mathcal K}^{(s)}$
with
![]() $\sigma \cap \sigma _{0}\neq \emptyset $
, implying that
$\sigma \cap \sigma _{0}\neq \emptyset $
, implying that
![]() $f=f_{0}$
on
$f=f_{0}$
on
![]() $f_{0}^{-1}(\sigma _{0})$
. Further,
$f_{0}^{-1}(\sigma _{0})$
. Further,
![]() $f_{0}^{-1}(\sigma _{0})$
is infinite, since
$f_{0}^{-1}(\sigma _{0})$
is infinite, since
![]() $\sigma _{0}$
is infinite and
$\sigma _{0}$
is infinite and
![]() $\sigma _{0}\subseteq R(f_{0})^{0}$
. Therefore, as
$\sigma _{0}\subseteq R(f_{0})^{0}$
. Therefore, as
![]() $f^{-2}(v_{0})\supseteq f^{-1}(f^{-1}(v_{0}))\supseteq f^{-1}(\sigma {}_{0})\supseteq f_{0}^{-1}(\sigma _{0})$
, it follows that
$f^{-2}(v_{0})\supseteq f^{-1}(f^{-1}(v_{0}))\supseteq f^{-1}(\sigma {}_{0})\supseteq f_{0}^{-1}(\sigma _{0})$
, it follows that
![]() $f^{-2}(v_{0})$
is infinite. Moreover,
$f^{-2}(v_{0})$
is infinite. Moreover,
![]() $f|_{\sigma }$
is injective for every
$f|_{\sigma }$
is injective for every
![]() $\sigma \in \mathcal {K}^{\kern2pt(s)}$
with
$\sigma \in \mathcal {K}^{\kern2pt(s)}$
with
![]() $\sigma \neq \sigma _{0}$
by result (i) of Lemma 3.1, and hence
$\sigma \neq \sigma _{0}$
by result (i) of Lemma 3.1, and hence
![]() $f^{-1}(x)$
is finite for all
$f^{-1}(x)$
is finite for all
![]() $x\ne v_{0}$
in
$x\ne v_{0}$
in
![]() $I^{m}$
. Thus, f satisfies the conditions of Case (ii) of Theorem 2.4, proving that it has no square roots in
$I^{m}$
. Thus, f satisfies the conditions of Case (ii) of Theorem 2.4, proving that it has no square roots in
![]() $\mathcal {C}(I^{m})$
.
$\mathcal {C}(I^{m})$
.
Theorem 3.9. Let
![]() $h\in \mathcal {C}(I^{m})$
be such that
$h\in \mathcal {C}(I^{m})$
be such that
![]() $h(x_{0})=x_{0}$
for some
$h(x_{0})=x_{0}$
for some
![]() $x_{0} \in \partial I^{m}$
. Then for each
$x_{0} \in \partial I^{m}$
. Then for each
![]() $\epsilon>0$
, the ball
$\epsilon>0$
, the ball
![]() $B_{\epsilon }(h)$
of radius
$B_{\epsilon }(h)$
of radius
![]() $\epsilon $
around h contains a map f having a continuous iterative square root on
$\epsilon $
around h contains a map f having a continuous iterative square root on
![]() $I^{m}$
. In other words, the closure of
$I^{m}$
. In other words, the closure of
![]() $\mathcal {W}(2;I^{m})$
contains all maps in
$\mathcal {W}(2;I^{m})$
contains all maps in
![]() $\mathcal {C}(I^{m})$
that have a fixed point on the boundary of
$\mathcal {C}(I^{m})$
that have a fixed point on the boundary of
![]() $I^{m}$
.
$I^{m}$
.
Proof. Let
![]() $h\in \mathcal {C}(I^{m})$
be such that
$h\in \mathcal {C}(I^{m})$
be such that
![]() $h(x_{0})=x_{0}$
for some
$h(x_{0})=x_{0}$
for some
![]() $x_{0}\in \partial I^{m}$
. In view of Step 1 of Theorem 3.8, without loss of generality, we assume that h is piecewise affine linear on
$x_{0}\in \partial I^{m}$
. In view of Step 1 of Theorem 3.8, without loss of generality, we assume that h is piecewise affine linear on
![]() $I^{m}$
. Since h is uniformly continuous on
$I^{m}$
. Since h is uniformly continuous on
![]() $I^{m}$
, there is a
$I^{m}$
, there is a
![]() $\delta $
with
$\delta $
with
![]() $0<\delta <{\epsilon }/{4}$
such that
$0<\delta <{\epsilon }/{4}$
such that
Consider a triangulation
![]() $\mathcal {K}$
of
$\mathcal {K}$
of
![]() $I^{m}$
with vertices
$I^{m}$
with vertices
![]() $x_{0}, x_{1}, x_{2},\ldots , x_{r}$
such that
$x_{0}, x_{1}, x_{2},\ldots , x_{r}$
such that
![]() $\|x_{i_{0}}-x_{i_{1}}\|_{\infty }<{\delta }/{4}$
for all
$\|x_{i_{0}}-x_{i_{1}}\|_{\infty }<{\delta }/{4}$
for all
![]() $2$
-simplices
$2$
-simplices
![]() $\langle x_{i_{0}},x_{i_{1}}\rangle $
of
$\langle x_{i_{0}},x_{i_{1}}\rangle $
of
![]() $\sigma $
and for all m-simplex
$\sigma $
and for all m-simplex
![]() $\sigma \in \mathcal {K}$
. Let
$\sigma \in \mathcal {K}$
. Let
![]() $y_{j}:=h(x_{j})$
for all
$y_{j}:=h(x_{j})$
for all
![]() $0\le j \le r$
and
$0\le j \le r$
and
![]() $\sigma _{0}=\langle x_{0}, x_{1}, \ldots , x_{m}\rangle $
be an m-simplex in
$\sigma _{0}=\langle x_{0}, x_{1}, \ldots , x_{m}\rangle $
be an m-simplex in
![]() $\mathcal {K}$
having
$\mathcal {K}$
having
![]() $x_{0}$
as a vertex. Let
$x_{0}$
as a vertex. Let
![]() $\phi :I^{m} \to I^{m}$
be a homeomorphism such that
$\phi :I^{m} \to I^{m}$
be a homeomorphism such that
![]() $\phi (\sigma _{0})=\overline {I^{m}\setminus \sigma _{0}}$
,
$\phi (\sigma _{0})=\overline {I^{m}\setminus \sigma _{0}}$
,
![]() $\phi (\overline {I^{m}\setminus \sigma _{0}})= \sigma _{0}$
,
$\phi (\overline {I^{m}\setminus \sigma _{0}})= \sigma _{0}$
,
![]() $\phi =\text {id}$
on
$\phi =\text {id}$
on
![]() $\partial \sigma _{0}\bigcap \partial (I^{m}\setminus \sigma _{0})$
, and
$\partial \sigma _{0}\bigcap \partial (I^{m}\setminus \sigma _{0})$
, and
![]() $\phi ^{2}=\text {id}$
on
$\phi ^{2}=\text {id}$
on
![]() $I^{m}$
. This is where we use the assumption that
$I^{m}$
. This is where we use the assumption that
![]() $x_{0}$
is on the boundary of
$x_{0}$
is on the boundary of
![]() $I^{m}.$
Indeed, a little thought shows that there exists a piecewise affine linear map
$I^{m}.$
Indeed, a little thought shows that there exists a piecewise affine linear map
![]() $\phi $
that satisfies these conditions. Define a function
$\phi $
that satisfies these conditions. Define a function
![]() $f_{1}$
by
$f_{1}$
by
 $$ \begin{align*} f_{1}(x_{j}) = \begin{cases} x_{j}&\text{if } x_{j}\in \sigma_{0},\\ x_{1}&\text{if } x_{j}\notin \sigma_{0} \text{ and } y_{j}\in \sigma_{0}^{0},\\ y_{j}&\text{if } x_{j}\notin \sigma_{0} \text{ and } y_{j}\notin \sigma_{0}^{0}, \end{cases} \end{align*} $$
$$ \begin{align*} f_{1}(x_{j}) = \begin{cases} x_{j}&\text{if } x_{j}\in \sigma_{0},\\ x_{1}&\text{if } x_{j}\notin \sigma_{0} \text{ and } y_{j}\in \sigma_{0}^{0},\\ y_{j}&\text{if } x_{j}\notin \sigma_{0} \text{ and } y_{j}\notin \sigma_{0}^{0}, \end{cases} \end{align*} $$
and extend it piecewise affine linearly to the whole of
![]() $|{\mathcal K}|= I^{m}$
. Then
$|{\mathcal K}|= I^{m}$
. Then
![]() $f_{1}\in \mathcal {C}(I^{m})$
such that
$f_{1}\in \mathcal {C}(I^{m})$
such that
![]() $f_{1}|_{\sigma _{0}}=\text {id}$
and
$f_{1}|_{\sigma _{0}}=\text {id}$
and
![]() $f_{1}(\overline {I^{m}\setminus \sigma _{0}})\subseteq \overline {I^{m}\setminus \sigma _{0}}$
.
$f_{1}(\overline {I^{m}\setminus \sigma _{0}})\subseteq \overline {I^{m}\setminus \sigma _{0}}$
.
Claim.
![]() $\rho (f_{1},h)<\epsilon $
.
$\rho (f_{1},h)<\epsilon $
.
Let
![]() $x\in I^{m}$
be arbitrary. If
$x\in I^{m}$
be arbitrary. If
![]() $x\in \sigma _{0}$
, then there exist non-negative reals
$x\in \sigma _{0}$
, then there exist non-negative reals
![]() $\alpha _{0}, \alpha _{1}, \ldots , \alpha _{m}$
with
$\alpha _{0}, \alpha _{1}, \ldots , \alpha _{m}$
with
![]() $\sum _{j=0}^{m}\alpha _{j}=1$
such that
$\sum _{j=0}^{m}\alpha _{j}=1$
such that
![]() $x=\sum _{j=0}^{m}\alpha _{j}x_{j}$
, implying by equation (3.9) that
$x=\sum _{j=0}^{m}\alpha _{j}x_{j}$
, implying by equation (3.9) that
 $$ \begin{align*} \|f_{1}(x)-h(x)\|_{\infty}&=\bigg\|\sum_{j=0}^{m}\alpha_{j}f_{1}(x_{j})-\sum_{j=0}^{m}\alpha_{j}h(x_{j})\bigg\|_{\infty} \\ &\le \sum_{j=0}^{m}\alpha_{j}\{\|x_{j}-x_{0}\|_{\infty}+\|h(x_{0})-h(x_{j})\|_{\infty}\}\\ &< \frac{\epsilon }{4}+\frac{\epsilon }{4}=\frac{\epsilon}{2}, \end{align*} $$
$$ \begin{align*} \|f_{1}(x)-h(x)\|_{\infty}&=\bigg\|\sum_{j=0}^{m}\alpha_{j}f_{1}(x_{j})-\sum_{j=0}^{m}\alpha_{j}h(x_{j})\bigg\|_{\infty} \\ &\le \sum_{j=0}^{m}\alpha_{j}\{\|x_{j}-x_{0}\|_{\infty}+\|h(x_{0})-h(x_{j})\|_{\infty}\}\\ &< \frac{\epsilon }{4}+\frac{\epsilon }{4}=\frac{\epsilon}{2}, \end{align*} $$
since
![]() $\|x_{j}-x_{0}\|_{\infty } \le \mbox {diam}(\sigma _{0})<\delta <{\epsilon }/{4}$
for all
$\|x_{j}-x_{0}\|_{\infty } \le \mbox {diam}(\sigma _{0})<\delta <{\epsilon }/{4}$
for all
![]() $0\le j\le m$
. If
$0\le j\le m$
. If
![]() $x\notin \sigma _{0}$
, then there exists a
$x\notin \sigma _{0}$
, then there exists a
![]() $\sigma =\langle x_{i_{0}}, x_{i_{1}},\ldots , x_{i_{m}}\rangle \in \mathcal {K} \text{ with } \sigma \ne \sigma_0$
such that
$\sigma =\langle x_{i_{0}}, x_{i_{1}},\ldots , x_{i_{m}}\rangle \in \mathcal {K} \text{ with } \sigma \ne \sigma_0$
such that
![]() $x\in \sigma $
. Let
$x\in \sigma $
. Let
![]() $x=\sum _{j=0}^{m}\alpha _{i_{j}}x_{i_{j}}$
, where
$x=\sum _{j=0}^{m}\alpha _{i_{j}}x_{i_{j}}$
, where
![]() $\alpha _{i_{0}}, \alpha _{i_{1}}, \ldots , \alpha _{i_{m}}$
are non-negative and
$\alpha _{i_{0}}, \alpha _{i_{1}}, \ldots , \alpha _{i_{m}}$
are non-negative and
![]() $\sum _{j=0}^{m}\alpha _{i_{j}}=1$
. Then by using equation (3.9), we have
$\sum _{j=0}^{m}\alpha _{i_{j}}=1$
. Then by using equation (3.9), we have
 $$ \begin{align*} \|f_{1}(x)-h(x)\|_{\infty}&=\bigg\|\sum_{j=0}^{m}\alpha_{i_{j}}f_{1}(x_{i_{j}})-\sum_{j=0}^{m}\alpha_{i_{j}}h(x_{i_{j}})\bigg\|_{\infty} \le \sum_{j=0}^{m}\alpha_{i_{j}}\|f_{1}(x_{i_{j}})-y_{i_{j}}\|_{\infty}\\&=\sum_{\substack{0\le j\le m\\x_{i_{j}}\in \sigma_{0}}}^{}\alpha_{i_{j}}\|f_{1}(x_{i_{j}})-y_{i_{j}}\|_{\infty}+ \sum_{\substack{0\le j\le m\\ x_{i_{j}}\notin \sigma_{0}~\text{and}~ y_{i_{j}}\in \sigma_{0}^{0}} }^{}\alpha_{i_{j}}\|f_{1}(x_{i_{j}})-y_{i_{j}}\|_{\infty}\\& \quad +\sum_{\substack{0\le j\le m\\ x_{i_{j}}\notin \sigma_{0}~\text{and}~ y_{i_{j}}\notin \sigma_{0}^{0}}}^{}\alpha_{i_{j}}\|f_{1}(x_{i_{j}})-y_{i_{j}}\|_{\infty}\\& \le \sum_{\substack{0\le j\le m\\x_{i_{j}}\in \sigma_{0}}}^{}\alpha_{i_{j}}\|x_{i_{j}}-y_{i_{j}}\|_{\infty}+ \sum_{\substack{0\le j\le m\\ x_{i_{j}}\notin \sigma_{0}~\text{and}~ y_{i_{j}}\in \sigma_{0}^{0}} }^{}\alpha_{i_{j}}\|x_{1}-y_{i_{j}}\|_{\infty}\\& \quad +\sum_{\substack{0\le j\le m\\ x_{i_{j}}\notin \sigma_{0}~\text{and}~ y_{i_{j}}\notin \sigma_{0}^{0}}}^{}\alpha_{i_{j}}\|y_{i_{j}}-y_{i_{j}}\|_{\infty} \\&\le \sum_{\substack{0\le j\le m\\x_{i_{j}}\in \sigma_{0}}}^{}\alpha_{i_{j}}\{\|x_{i_{j}}-x_{0}\|_{\infty}+\|h(x_{0})-h(x_{i_{j}})\|_{\infty}\}\\& \quad + \sum_{\substack{0\le j\le m\\ x_{i_{j}}\notin \sigma_{0}~\text{and}~ y_{i_{j}}\in \sigma_{0}^{0}} }^{}\alpha_{i_{j}}\|x_{1}-y_{i_{j}}\|_{\infty} < \frac{\epsilon}{4}+\frac{\epsilon}{4}+\frac{\epsilon}{4}=\frac{3\epsilon}{4}, \end{align*} $$
$$ \begin{align*} \|f_{1}(x)-h(x)\|_{\infty}&=\bigg\|\sum_{j=0}^{m}\alpha_{i_{j}}f_{1}(x_{i_{j}})-\sum_{j=0}^{m}\alpha_{i_{j}}h(x_{i_{j}})\bigg\|_{\infty} \le \sum_{j=0}^{m}\alpha_{i_{j}}\|f_{1}(x_{i_{j}})-y_{i_{j}}\|_{\infty}\\&=\sum_{\substack{0\le j\le m\\x_{i_{j}}\in \sigma_{0}}}^{}\alpha_{i_{j}}\|f_{1}(x_{i_{j}})-y_{i_{j}}\|_{\infty}+ \sum_{\substack{0\le j\le m\\ x_{i_{j}}\notin \sigma_{0}~\text{and}~ y_{i_{j}}\in \sigma_{0}^{0}} }^{}\alpha_{i_{j}}\|f_{1}(x_{i_{j}})-y_{i_{j}}\|_{\infty}\\& \quad +\sum_{\substack{0\le j\le m\\ x_{i_{j}}\notin \sigma_{0}~\text{and}~ y_{i_{j}}\notin \sigma_{0}^{0}}}^{}\alpha_{i_{j}}\|f_{1}(x_{i_{j}})-y_{i_{j}}\|_{\infty}\\& \le \sum_{\substack{0\le j\le m\\x_{i_{j}}\in \sigma_{0}}}^{}\alpha_{i_{j}}\|x_{i_{j}}-y_{i_{j}}\|_{\infty}+ \sum_{\substack{0\le j\le m\\ x_{i_{j}}\notin \sigma_{0}~\text{and}~ y_{i_{j}}\in \sigma_{0}^{0}} }^{}\alpha_{i_{j}}\|x_{1}-y_{i_{j}}\|_{\infty}\\& \quad +\sum_{\substack{0\le j\le m\\ x_{i_{j}}\notin \sigma_{0}~\text{and}~ y_{i_{j}}\notin \sigma_{0}^{0}}}^{}\alpha_{i_{j}}\|y_{i_{j}}-y_{i_{j}}\|_{\infty} \\&\le \sum_{\substack{0\le j\le m\\x_{i_{j}}\in \sigma_{0}}}^{}\alpha_{i_{j}}\{\|x_{i_{j}}-x_{0}\|_{\infty}+\|h(x_{0})-h(x_{i_{j}})\|_{\infty}\}\\& \quad + \sum_{\substack{0\le j\le m\\ x_{i_{j}}\notin \sigma_{0}~\text{and}~ y_{i_{j}}\in \sigma_{0}^{0}} }^{}\alpha_{i_{j}}\|x_{1}-y_{i_{j}}\|_{\infty} < \frac{\epsilon}{4}+\frac{\epsilon}{4}+\frac{\epsilon}{4}=\frac{3\epsilon}{4}, \end{align*} $$
since
![]() $\|x_{i_{j}}-x_{0}\|_{\infty } \le \mbox {diam}(\sigma _{0})<\delta <{\epsilon }/{4}$
for all
$\|x_{i_{j}}-x_{0}\|_{\infty } \le \mbox {diam}(\sigma _{0})<\delta <{\epsilon }/{4}$
for all
![]() $0\le j\le m$
such that
$0\le j\le m$
such that
![]() $x_{i_{j}}\in \sigma _{0}$
, and
$x_{i_{j}}\in \sigma _{0}$
, and
![]() $\|x_{1}-y_{i_{j}}\|_{\infty } \le \mbox {diam}(\sigma _{0})<\delta <{\epsilon }/{4}$
for all
$\|x_{1}-y_{i_{j}}\|_{\infty } \le \mbox {diam}(\sigma _{0})<\delta <{\epsilon }/{4}$
for all
![]() $0\le j\le m$
such that
$0\le j\le m$
such that
![]() $x_{i_{j}}\notin \sigma _{0}$
and
$x_{i_{j}}\notin \sigma _{0}$
and
![]() $y_{i_{j}}\in \sigma _{0}^{0}$
. This proves the claim.
$y_{i_{j}}\in \sigma _{0}^{0}$
. This proves the claim.
Now, define a map
![]() $f:I^{m}\to I^{m}$
by
$f:I^{m}\to I^{m}$
by
 $$ \begin{align*} f(x) = \begin{cases} f_{1}\circ \phi(x)&\text{if } x\in \sigma_{0},\\ \phi(x)&\text{if } x\notin \sigma_{0}. \end{cases} \end{align*} $$
$$ \begin{align*} f(x) = \begin{cases} f_{1}\circ \phi(x)&\text{if } x\in \sigma_{0},\\ \phi(x)&\text{if } x\notin \sigma_{0}. \end{cases} \end{align*} $$
Since
![]() $f_{1} \circ \phi (x)=x=\phi (x)$
for all
$f_{1} \circ \phi (x)=x=\phi (x)$
for all
![]() $x\in \partial \sigma _{0}\bigcap \partial (I^{m}\setminus \sigma _{0})$
, clearly f is continuous on
$x\in \partial \sigma _{0}\bigcap \partial (I^{m}\setminus \sigma _{0})$
, clearly f is continuous on
![]() $I^{m}$
. We prove that
$I^{m}$
. We prove that
![]() $\rho (f^{2},h)<\epsilon $
. Consider an arbitrary
$\rho (f^{2},h)<\epsilon $
. Consider an arbitrary
![]() $x\in I^{m}$
. If
$x\in I^{m}$
. If
![]() $x\in \sigma _{0}$
, then
$x\in \sigma _{0}$
, then
![]() $f(x)\in \overline {I^{m}\setminus \sigma _{0}}$
, because
$f(x)\in \overline {I^{m}\setminus \sigma _{0}}$
, because
![]() $\phi (x)\in \overline {I^{m}\setminus \sigma _{0}}$
and
$\phi (x)\in \overline {I^{m}\setminus \sigma _{0}}$
and
![]() $f_{1}(\overline {I^{m}\setminus \sigma _{0}})\subseteq \overline {I^{m}\setminus \sigma _{0}}$
. Therefore,
$f_{1}(\overline {I^{m}\setminus \sigma _{0}})\subseteq \overline {I^{m}\setminus \sigma _{0}}$
. Therefore,
![]() $f^{2}(x)\in \sigma _{0}$
, implying by equation (3.9) that
$f^{2}(x)\in \sigma _{0}$
, implying by equation (3.9) that
since
![]() $\|f^{2}(x)-x_{0}\|_{\infty }\le \mbox {diam}(\sigma _{0})<\delta <{\epsilon }/{4}$
. If
$\|f^{2}(x)-x_{0}\|_{\infty }\le \mbox {diam}(\sigma _{0})<\delta <{\epsilon }/{4}$
. If
![]() $x\notin \sigma _{0}$
, then
$x\notin \sigma _{0}$
, then
![]() $f^{2}(x)=f_{1}(x)$
, and therefore
$f^{2}(x)=f_{1}(x)$
, and therefore
![]() $\|f^{2}(x)-h(x)\|_{\infty } = \|f_{1}(x)-h(x)\|_{\infty }<{3\epsilon }/{4}$
. This completes the proof.
$\|f^{2}(x)-h(x)\|_{\infty } = \|f_{1}(x)-h(x)\|_{\infty }<{3\epsilon }/{4}$
. This completes the proof.
Now it is a natural question to ask what happens if all the fixed points of the map are in the interior of
![]() $I^{m}$
. Theorem 10 of [Reference Humke and Laczkovich15, p. 364] shows that the map
$I^{m}$
. Theorem 10 of [Reference Humke and Laczkovich15, p. 364] shows that the map
![]() $f(x)=1-x$
on the unit interval
$f(x)=1-x$
on the unit interval
![]() $[0,1]$
, with only
$[0,1]$
, with only
![]() $x=\tfrac 12$
as the fixed point, cannot be approximated by squares of continuous maps. In contrast, we have the following.
$x=\tfrac 12$
as the fixed point, cannot be approximated by squares of continuous maps. In contrast, we have the following.
Example 3.10. In this example we show that, despite having no continuous square roots, the map
![]() $f:I^{2}\to I^{2}$
defined by
$f:I^{2}\to I^{2}$
defined by
having an interior point
![]() $(x,y)=(\tfrac 12,\tfrac 12)$
as the unique fixed point can be approximated by squares of continuous maps on
$(x,y)=(\tfrac 12,\tfrac 12)$
as the unique fixed point can be approximated by squares of continuous maps on
![]() $I^{2}$
. To prove that f has no continuous square roots, on the contrary, assume that
$I^{2}$
. To prove that f has no continuous square roots, on the contrary, assume that
![]() $f=g^{2}$
for some
$f=g^{2}$
for some
![]() $g\in \mathcal {C}(I^{2})$
. Since
$g\in \mathcal {C}(I^{2})$
. Since
![]() $(1-x, \tfrac 12) \in R(g)$
, there exists
$(1-x, \tfrac 12) \in R(g)$
, there exists
![]() $(f_{1}(x), f_{2}(x)) \in I^{2}$
such that
$(f_{1}(x), f_{2}(x)) \in I^{2}$
such that
![]() $g(f_{1}(x), f_{2}(x))=(1-x, \tfrac 12)$
for each
$g(f_{1}(x), f_{2}(x))=(1-x, \tfrac 12)$
for each
![]() $x\in I$
. Then
$x\in I$
. Then
implying that
Therefore,
and hence
![]() $f_{1}^{2}(x)=1-x$
for all
$f_{1}^{2}(x)=1-x$
for all
![]() $x\in I$
. Also, from equation (3.10), it follows that
$x\in I$
. Also, from equation (3.10), it follows that
![]() $f_{1}$
is continuous on I. Thus, the map
$f_{1}$
is continuous on I. Thus, the map
![]() $x\mapsto 1-x$
has a continuous square root on I, a contradiction to Corollary 2.7. Hence, f has no continuous square roots on
$x\mapsto 1-x$
has a continuous square root on I, a contradiction to Corollary 2.7. Hence, f has no continuous square roots on
![]() $I^{2}$
.
$I^{2}$
.
Now, to prove that f can be approximated by squares of continuous maps, consider an arbitrary
![]() $\epsilon>0$
. Without loss of generality, we assume that
$\epsilon>0$
. Without loss of generality, we assume that
![]() $\epsilon <\tfrac 12.$
The idea is to compress
$\epsilon <\tfrac 12.$
The idea is to compress
![]() $I^{2}$
to the small strip
$I^{2}$
to the small strip
![]() $I\times [\tfrac 12-{\epsilon }/{2}, \tfrac 12+{\epsilon }/{2}]$
and then rotate this strip ninety degrees clockwise with a suitable scaling to stay within the strip. More explicitly, let
$I\times [\tfrac 12-{\epsilon }/{2}, \tfrac 12+{\epsilon }/{2}]$
and then rotate this strip ninety degrees clockwise with a suitable scaling to stay within the strip. More explicitly, let
![]() $g:I^{2}\to I\times [\tfrac 12-{\epsilon }/{2}, \tfrac 12+{\epsilon }/{2}]$
be defined by
$g:I^{2}\to I\times [\tfrac 12-{\epsilon }/{2}, \tfrac 12+{\epsilon }/{2}]$
be defined by
![]() $g=g_{1}\circ g_{2}$
, where
$g=g_{1}\circ g_{2}$
, where
![]() $g_{1}:I\times [\tfrac 12-{\epsilon }/{2}, \tfrac 12+{\epsilon }/{2}] \to I\times [\tfrac 12-{\epsilon }/{2}, \tfrac 12+{\epsilon }/{2}]$
and
$g_{1}:I\times [\tfrac 12-{\epsilon }/{2}, \tfrac 12+{\epsilon }/{2}] \to I\times [\tfrac 12-{\epsilon }/{2}, \tfrac 12+{\epsilon }/{2}]$
and
![]() $g_{2}: I^{2}\to I\times [\tfrac 12-{\epsilon }/{2}, \tfrac 12+{\epsilon }/{2}]$
are given by
$g_{2}: I^{2}\to I\times [\tfrac 12-{\epsilon }/{2}, \tfrac 12+{\epsilon }/{2}]$
are given by
 $$ \begin{align*} g_{1}(x,y) = \bigg(\dfrac{\epsilon-1}{2\epsilon}, \dfrac{\epsilon+1}{2}\bigg)+(x,y)\left(\begin{array}{cc} 0&-\epsilon \\ \dfrac{1}{\epsilon} &0 \end{array}\right)=\bigg(\dfrac{1}{2}+\dfrac{2y-1}{2\epsilon}, \dfrac{1}{2}- \dfrac{\epsilon(2x-1)}{2}\bigg) \end{align*} $$
$$ \begin{align*} g_{1}(x,y) = \bigg(\dfrac{\epsilon-1}{2\epsilon}, \dfrac{\epsilon+1}{2}\bigg)+(x,y)\left(\begin{array}{cc} 0&-\epsilon \\ \dfrac{1}{\epsilon} &0 \end{array}\right)=\bigg(\dfrac{1}{2}+\dfrac{2y-1}{2\epsilon}, \dfrac{1}{2}- \dfrac{\epsilon(2x-1)}{2}\bigg) \end{align*} $$
and
 $$ \begin{align*} g_{2}(x,y) = \begin{cases} \bigg(x, \dfrac{1}{2}-\dfrac{\epsilon}{2}\bigg)&\text{if } (x,y)\in I\times \bigg[0, \dfrac{1}{2}-\dfrac{\epsilon}{2}\bigg],\\[10pt] (x, y)&\text{if } (x,y)\in I\times \bigg[\dfrac{1}{2}-\dfrac{\epsilon}{2},\dfrac{1}{2}+\dfrac{\epsilon}{2}\bigg],\\[10pt] \bigg(x, \dfrac{1}{2}+\dfrac{\epsilon}{2}\bigg)&\text{if } (x,y)\in I\times \bigg[ \dfrac{1}{2}+\dfrac{\epsilon}{2},1\bigg]. \end{cases} \end{align*} $$
$$ \begin{align*} g_{2}(x,y) = \begin{cases} \bigg(x, \dfrac{1}{2}-\dfrac{\epsilon}{2}\bigg)&\text{if } (x,y)\in I\times \bigg[0, \dfrac{1}{2}-\dfrac{\epsilon}{2}\bigg],\\[10pt] (x, y)&\text{if } (x,y)\in I\times \bigg[\dfrac{1}{2}-\dfrac{\epsilon}{2},\dfrac{1}{2}+\dfrac{\epsilon}{2}\bigg],\\[10pt] \bigg(x, \dfrac{1}{2}+\dfrac{\epsilon}{2}\bigg)&\text{if } (x,y)\in I\times \bigg[ \dfrac{1}{2}+\dfrac{\epsilon}{2},1\bigg]. \end{cases} \end{align*} $$
Then g is continuous on
![]() $I^{2}$
such that
$I^{2}$
such that
 $$ \begin{align*} g^{2}(x,y) = \begin{cases} \bigg(1-x, \dfrac{1}{2}+\dfrac{\epsilon}{2}\bigg)&\text{if } (x,y)\in I\times \bigg[0, \dfrac{1}{2}-\dfrac{\epsilon}{2}\bigg],\\[10pt] (1-x, 1-y)&\text{if } (x,y)\in I\times \bigg[\dfrac{1}{2}-\dfrac{\epsilon}{2},\dfrac{1}{2}+\dfrac{\epsilon}{2}\bigg],\\[10pt] \bigg(1-x, \dfrac{1}{2}-\dfrac{\epsilon}{2}\bigg)&\text{if } (x,y)\in I\times \bigg[ \dfrac{1}{2}+\dfrac{\epsilon}{2},1\bigg], \end{cases} \end{align*} $$
$$ \begin{align*} g^{2}(x,y) = \begin{cases} \bigg(1-x, \dfrac{1}{2}+\dfrac{\epsilon}{2}\bigg)&\text{if } (x,y)\in I\times \bigg[0, \dfrac{1}{2}-\dfrac{\epsilon}{2}\bigg],\\[10pt] (1-x, 1-y)&\text{if } (x,y)\in I\times \bigg[\dfrac{1}{2}-\dfrac{\epsilon}{2},\dfrac{1}{2}+\dfrac{\epsilon}{2}\bigg],\\[10pt] \bigg(1-x, \dfrac{1}{2}-\dfrac{\epsilon}{2}\bigg)&\text{if } (x,y)\in I\times \bigg[ \dfrac{1}{2}+\dfrac{\epsilon}{2},1\bigg], \end{cases} \end{align*} $$
and it can be easily verified that
![]() $\rho (f,g^{2})<\epsilon $
.
$\rho (f,g^{2})<\epsilon $
.
4 Continuous functions on
 $\mathbb {R}^{m}$
$\mathbb {R}^{m}$
Consider
![]() $\mathbb {R}^{m}$
in the metric induced by the norm
$\mathbb {R}^{m}$
in the metric induced by the norm
![]() $\|\cdot \|_{\infty }$
defined as in equation (3.1). Since it is a locally compact separable metric space, by Corollary 7.1 of [Reference Arens2], the compact-open topology on
$\|\cdot \|_{\infty }$
defined as in equation (3.1). Since it is a locally compact separable metric space, by Corollary 7.1 of [Reference Arens2], the compact-open topology on
![]() $\mathcal {C}(\mathbb {R}^{m})$
is metrizable with the metric D given by
$\mathcal {C}(\mathbb {R}^{m})$
is metrizable with the metric D given by
such that
 $$ \begin{align*} \mu_{j}(f,g)&=\min\bigg\{\frac{1}{2^{j}}, \rho_{j}(f,g)\bigg\}\quad \text{for all } j\in \mathbb{N},\\[6pt] \rho_{j}(f,g)&=\sup \{\|f(x)-g(x)\|_{\infty}: x\in M_{j}\}\quad \text{for all } j\in \mathbb{N}, \end{align*} $$
$$ \begin{align*} \mu_{j}(f,g)&=\min\bigg\{\frac{1}{2^{j}}, \rho_{j}(f,g)\bigg\}\quad \text{for all } j\in \mathbb{N},\\[6pt] \rho_{j}(f,g)&=\sup \{\|f(x)-g(x)\|_{\infty}: x\in M_{j}\}\quad \text{for all } j\in \mathbb{N}, \end{align*} $$
where
![]() $(M_{j})_{j\in \mathbb {N}}$
is a sequence of compact sets in
$(M_{j})_{j\in \mathbb {N}}$
is a sequence of compact sets in
![]() $\mathbb {R}^{m}$
satisfying that
$\mathbb {R}^{m}$
satisfying that
![]() $\mathbb {R}^{m}=\bigcup _{j=1}^{\infty }M_{j}$
, and if M is any compact subset of
$\mathbb {R}^{m}=\bigcup _{j=1}^{\infty }M_{j}$
, and if M is any compact subset of
![]() $\mathbb {R}^{m}$
, then
$\mathbb {R}^{m}$
, then
![]() $M\subseteq \bigcup _{i=1}^{k}M_{m_{i}}$
for some finitely many
$M\subseteq \bigcup _{i=1}^{k}M_{m_{i}}$
for some finitely many
![]() $M_{m_{1}}, M_{m_{2}}, \ldots , M_{m_{k}}$
. For convenience, we assume that
$M_{m_{1}}, M_{m_{2}}, \ldots , M_{m_{k}}$
. For convenience, we assume that
![]() $M_{j}$
is an m-simplex of
$M_{j}$
is an m-simplex of
![]() ${\mathbb R}^{m}$
for each
${\mathbb R}^{m}$
for each
![]() $j\in \mathbb {N}$
, and either
$j\in \mathbb {N}$
, and either
![]() $M_{i}\cap M_{j}=\emptyset $
or
$M_{i}\cap M_{j}=\emptyset $
or
![]() $M_{i}\cap M_{j}$
is a common face of both
$M_{i}\cap M_{j}$
is a common face of both
![]() $M_{i}$
and
$M_{i}$
and
![]() $M_{j}$
for all
$M_{j}$
for all
![]() $i,j\in \mathbb {N}$
. Considering all the faces
$i,j\in \mathbb {N}$
. Considering all the faces
![]() $M_{j}$
for all
$M_{j}$
for all
![]() $j\in \mathbb {N}$
, we get a countable triangulation of
$j\in \mathbb {N}$
, we get a countable triangulation of
![]() ${\mathbb R}^{m}.$
Throughout this section, we fix one such triangulation of
${\mathbb R}^{m}.$
Throughout this section, we fix one such triangulation of
![]() ${\mathbb R}^{m}.$
${\mathbb R}^{m}.$
Lemma 4.1. Let
![]() $\sigma =\langle x_{0}, x_{1}, \ldots , x_{m}\rangle $
be an m-simplex of
$\sigma =\langle x_{0}, x_{1}, \ldots , x_{m}\rangle $
be an m-simplex of
![]() $\mathbb {R}^{m}$
and
$\mathbb {R}^{m}$
and
![]() $z\in \sigma $
be such that
$z\in \sigma $
be such that
![]() $z\ne x_{j}$
for all
$z\ne x_{j}$
for all
![]() $0\le j\le m$
. Then there exists a simplicial complex
$0\le j\le m$
. Then there exists a simplicial complex
![]() $\mathcal {L}_{\sigma }$
with the set of vertices
$\mathcal {L}_{\sigma }$
with the set of vertices
![]() $\{x_{0}, x_{1}, \ldots , x_{m}, z\}$
such that
$\{x_{0}, x_{1}, \ldots , x_{m}, z\}$
such that
![]() $| \mathcal {L}_{\sigma }| =\sigma $
. In other words, every m-simplex of
$| \mathcal {L}_{\sigma }| =\sigma $
. In other words, every m-simplex of
![]() $\mathbb {R}^{m}$
can be triangulated to have a desired point as an extra vertex.
$\mathbb {R}^{m}$
can be triangulated to have a desired point as an extra vertex.
Proof. Without loss of generality, we assume that
![]() $z\in \langle x_{0}, x_{1}, \ldots , x_{k}\rangle ^{0}$
for some
$z\in \langle x_{0}, x_{1}, \ldots , x_{k}\rangle ^{0}$
for some
![]() $1\le k \le m$
, say
$1\le k \le m$
, say
![]() $z=\sum _{j=0}^{k}\alpha _{j}x_{j}$
for some strictly positive real numbers
$z=\sum _{j=0}^{k}\alpha _{j}x_{j}$
for some strictly positive real numbers
![]() $\alpha _{j}$
such that
$\alpha _{j}$
such that
![]() $\sum _{j=0}^{k}\alpha _{j}=1$
. Then
$\sum _{j=0}^{k}\alpha _{j}=1$
. Then
![]() $V_{i}:=\{x_{0}, x_{1},\ldots , x_{i-1}, z, x_{i+1},\ldots , x_{m}\}$
is geometrically independent for all
$V_{i}:=\{x_{0}, x_{1},\ldots , x_{i-1}, z, x_{i+1},\ldots , x_{m}\}$
is geometrically independent for all
![]() $0\le i\le k$
. In fact, for a fixed
$0\le i\le k$
. In fact, for a fixed
![]() $0\le i\le k$
, if the real numbers
$0\le i\le k$
, if the real numbers
![]() $\beta _{j}$
are arbitrary such that
$\beta _{j}$
are arbitrary such that
![]() $\sum _{j=0}^{m}\beta _{j}=0$
and
$\sum _{j=0}^{m}\beta _{j}=0$
and
 $$ \begin{align*}\sum\limits_{\substack{0\le j \le m\\ j\ne i}}^{}\beta_{j}x_{j}+\beta_{i}z=0,\end{align*} $$
$$ \begin{align*}\sum\limits_{\substack{0\le j \le m\\ j\ne i}}^{}\beta_{j}x_{j}+\beta_{i}z=0,\end{align*} $$
then
 $$ \begin{align*} \sum_{\substack{0\le j \le k\\ j\ne i}}^{}(\beta_{j}+\beta_{i}\alpha_{j})x_{j}+\beta_{i}\alpha_{i}x_{i}+\sum_{k< j \le m}^{}\beta_{j}x_{j}=0, \end{align*} $$
$$ \begin{align*} \sum_{\substack{0\le j \le k\\ j\ne i}}^{}(\beta_{j}+\beta_{i}\alpha_{j})x_{j}+\beta_{i}\alpha_{i}x_{i}+\sum_{k< j \le m}^{}\beta_{j}x_{j}=0, \end{align*} $$
and therefore by geometric independence of
![]() $\{x_{0}, x_{1}, \ldots , x_{m}\}$
, we have
$\{x_{0}, x_{1}, \ldots , x_{m}\}$
, we have
![]() $\beta _{j}+\beta _{i}\alpha _{j}=\beta _{i}\alpha _{i}=0$
for all
$\beta _{j}+\beta _{i}\alpha _{j}=\beta _{i}\alpha _{i}=0$
for all
![]() $0\le j\le k$
with
$0\le j\le k$
with
![]() $j\ne i$
, and
$j\ne i$
, and
![]() $\beta _{j}=0$
for all
$\beta _{j}=0$
for all
![]() $k<j\le m$
. This implies that
$k<j\le m$
. This implies that
![]() $\beta _{j}=0$
for all
$\beta _{j}=0$
for all
![]() $0\le j\le m$
, since
$0\le j\le m$
, since
![]() $\alpha _{i}>0$
.
$\alpha _{i}>0$
.
Now, let
![]() $\sigma _{i}:= \langle x_{0}, x_{1}, \ldots , x_{i-1}, z, x_{i+1}, \ldots x_{m}\rangle $
and
$\sigma _{i}:= \langle x_{0}, x_{1}, \ldots , x_{i-1}, z, x_{i+1}, \ldots x_{m}\rangle $
and
![]() ${\mathcal L}_{i}$
be the simplicial complex of all faces of
${\mathcal L}_{i}$
be the simplicial complex of all faces of
![]() $\sigma _{i}$
for all
$\sigma _{i}$
for all
![]() $0\le i\le k$
.
$0\le i\le k$
.
Claim.
![]() ${\mathcal L}_{\sigma }= \bigcup {}_{i=0}^{k}{\mathcal L}_{i}$
is a triangulation of
${\mathcal L}_{\sigma }= \bigcup {}_{i=0}^{k}{\mathcal L}_{i}$
is a triangulation of
![]() $\sigma $
with the set of vertices
$\sigma $
with the set of vertices
![]() $\{x_{0}, x_{1}, \ldots , x_{m}, z\}$
.
$\{x_{0}, x_{1}, \ldots , x_{m}, z\}$
.
Clearly,
![]() $\mathcal {L}_{\sigma }$
is a collection of simplices of
$\mathcal {L}_{\sigma }$
is a collection of simplices of
![]() $\mathbb {R}^{m}$
with
$\mathbb {R}^{m}$
with
![]() $\{x_{0}, x_{1}, \ldots , x_{m}, z\}$
as its set of vertices. To show that it is a simplicial complex, consider an arbitrary
$\{x_{0}, x_{1}, \ldots , x_{m}, z\}$
as its set of vertices. To show that it is a simplicial complex, consider an arbitrary
![]() $\unicode{x3bb} \in \mathcal {L}_{\sigma }$
. Then
$\unicode{x3bb} \in \mathcal {L}_{\sigma }$
. Then
![]() $\unicode{x3bb} \in \mathcal {L}_{i}$
for some
$\unicode{x3bb} \in \mathcal {L}_{i}$
for some
![]() $0\le i\le k$
, implying that
$0\le i\le k$
, implying that
![]() $\kappa \in \mathcal {L}_{i}\subseteq \mathcal {L}_{\sigma }$
whenever
$\kappa \in \mathcal {L}_{i}\subseteq \mathcal {L}_{\sigma }$
whenever
![]() $\kappa $
is a face of
$\kappa $
is a face of
![]() $\unicode{x3bb} $
, because
$\unicode{x3bb} $
, because
![]() $\mathcal {L}_{i}$
is a simplicial complex. Next, consider any two simplices
$\mathcal {L}_{i}$
is a simplicial complex. Next, consider any two simplices
![]() $\unicode{x3bb} , \eta \in \mathcal {L}_{\sigma }$
. If
$\unicode{x3bb} , \eta \in \mathcal {L}_{\sigma }$
. If
![]() $\unicode{x3bb} , \eta \in \mathcal {L}_{i}$
for the same
$\unicode{x3bb} , \eta \in \mathcal {L}_{i}$
for the same
![]() $i\in \{0,1,\ldots ,k\}$
, then clearly
$i\in \{0,1,\ldots ,k\}$
, then clearly
![]() $\unicode{x3bb} \cap \eta $
is either empty or a common face of both
$\unicode{x3bb} \cap \eta $
is either empty or a common face of both
![]() $\unicode{x3bb} $
and
$\unicode{x3bb} $
and
![]() $\eta $
, because
$\eta $
, because
![]() $\mathcal {L}_{i}$
is a simplicial complex. So, let
$\mathcal {L}_{i}$
is a simplicial complex. So, let
![]() $\unicode{x3bb} \cap \eta \ne \emptyset $
, and suppose that
$\unicode{x3bb} \cap \eta \ne \emptyset $
, and suppose that
![]() $\unicode{x3bb} \in \mathcal {L}_{i}$
and
$\unicode{x3bb} \in \mathcal {L}_{i}$
and
![]() $\eta \in \mathcal {L}_{j}$
for some
$\eta \in \mathcal {L}_{j}$
for some
![]() $i\ne j$
, where
$i\ne j$
, where
![]() $0\le i, j\le k$
. Further, assume that
$0\le i, j\le k$
. Further, assume that
![]() $\unicode{x3bb} $
and
$\unicode{x3bb} $
and
![]() $\eta $
are s and t dimensional, respectively, for some
$\eta $
are s and t dimensional, respectively, for some
![]() $0\le s,t\le m$
. Then it is easily seen
$0\le s,t\le m$
. Then it is easily seen
![]() $\unicode{x3bb} \cap \eta $
is the l-simplex with vertex set
$\unicode{x3bb} \cap \eta $
is the l-simplex with vertex set
![]() $V_{i}\cap V_{j}$
, where
$V_{i}\cap V_{j}$
, where
![]() $l=\#(V_{i}\cap V_{j})-1$
. This implies that
$l=\#(V_{i}\cap V_{j})-1$
. This implies that
![]() $\unicode{x3bb} \cap \eta \in \mathcal {L}_{i}\cap \mathcal {L}_{j}$
, and therefore it is a common face of both
$\unicode{x3bb} \cap \eta \in \mathcal {L}_{i}\cap \mathcal {L}_{j}$
, and therefore it is a common face of both
![]() $\unicode{x3bb} $
and
$\unicode{x3bb} $
and
![]() $\eta $
. Hence,
$\eta $
. Hence,
![]() $\mathcal {L}_{\sigma }$
is a simplicial complex.
$\mathcal {L}_{\sigma }$
is a simplicial complex.
Now, to prove that
![]() $\mathcal {L}_{\sigma }$
is a triangulation of
$\mathcal {L}_{\sigma }$
is a triangulation of
![]() $\sigma $
, consider an arbitrary
$\sigma $
, consider an arbitrary
![]() $x\in \sigma $
. Then
$x\in \sigma $
. Then
![]() $x\in \unicode{x3bb} :=\langle x_{i_{0}}, x_{i_{1}}, \ldots , x_{i_{s}}\rangle $
for some s-dimensional face
$x\in \unicode{x3bb} :=\langle x_{i_{0}}, x_{i_{1}}, \ldots , x_{i_{s}}\rangle $
for some s-dimensional face
![]() $\unicode{x3bb} $
of
$\unicode{x3bb} $
of
![]() $\sigma $
, where
$\sigma $
, where
![]() $0\le s\le m$
. If
$0\le s\le m$
. If
![]() $\unicode{x3bb} \in \mathcal {L}_{i}$
for some
$\unicode{x3bb} \in \mathcal {L}_{i}$
for some
![]() $0\le i\le k$
, then clearly
$0\le i\le k$
, then clearly
![]() $x\in |\mathcal {L}_{i}|\subseteq |\mathcal {L}_{\sigma }|$
. If
$x\in |\mathcal {L}_{i}|\subseteq |\mathcal {L}_{\sigma }|$
. If
![]() $\unicode{x3bb} \notin \mathcal {L}_{i}$
for all
$\unicode{x3bb} \notin \mathcal {L}_{i}$
for all
![]() $0\le i\le k$
, then there exist at least two
$0\le i\le k$
, then there exist at least two
![]() $i\in \{0, 1, \ldots , k\}$
such that
$i\in \{0, 1, \ldots , k\}$
such that
![]() $(V_{\unicode{x3bb} }\!\setminus \! \{z\})\cap (V_{i}\!\setminus \!\{z\})\ne \emptyset $
, where
$(V_{\unicode{x3bb} }\!\setminus \! \{z\})\cap (V_{i}\!\setminus \!\{z\})\ne \emptyset $
, where
![]() $V_{\unicode{x3bb} }=\{x_{i_{0}}, x_{i_{1}}, \ldots , x_{i_{s}}\}$
. This implies that
$V_{\unicode{x3bb} }=\{x_{i_{0}}, x_{i_{1}}, \ldots , x_{i_{s}}\}$
. This implies that
![]() $x\in \unicode{x3bb} \subseteq \bigcup _{i\in \Gamma }|\mathcal {L}_{i}|\subseteq |\mathcal {L}_{\sigma }|$
, where
$x\in \unicode{x3bb} \subseteq \bigcup _{i\in \Gamma }|\mathcal {L}_{i}|\subseteq |\mathcal {L}_{\sigma }|$
, where
![]() $\Gamma :=\{i: 0\le i\le k~\text {and}~(V_{\unicode{x3bb} }\!\setminus \!\{z\})\cap (V_{i}\setminus \{z\})\ne \emptyset \}$
. Thus the claim holds and result follows.
$\Gamma :=\{i: 0\le i\le k~\text {and}~(V_{\unicode{x3bb} }\!\setminus \!\{z\})\cap (V_{i}\setminus \{z\})\ne \emptyset \}$
. Thus the claim holds and result follows.
Lemma 4.2. Let
![]() $\mathbb {R}^{m}=\bigcup _{j=1}^{\infty }M_{j}$
be the decomposition of
$\mathbb {R}^{m}=\bigcup _{j=1}^{\infty }M_{j}$
be the decomposition of
![]() $\mathbb {R}^{m}$
fixed above, and let
$\mathbb {R}^{m}$
fixed above, and let
![]() $\delta _{1}, \delta _{2}, \ldots $
be a sequence of positive real numbers. Then there exists a countable triangulation
$\delta _{1}, \delta _{2}, \ldots $
be a sequence of positive real numbers. Then there exists a countable triangulation
![]() $\mathcal {K}= \bigcup _{j=1}^{\infty }{\mathcal K}_{j}$
of
$\mathcal {K}= \bigcup _{j=1}^{\infty }{\mathcal K}_{j}$
of
![]() $\mathbb {R}^{m}$
such that
$\mathbb {R}^{m}$
such that
![]() ${\mathcal K}_{j}$
is a triangulation of
${\mathcal K}_{j}$
is a triangulation of
![]() $M_{j}$
and
$M_{j}$
and
![]() $\mbox {diam}(\sigma )<\delta _{j}$
for all
$\mbox {diam}(\sigma )<\delta _{j}$
for all
![]() $\sigma \in {\mathcal {K}_{j}}$
and
$\sigma \in {\mathcal {K}_{j}}$
and
![]() $j\in \mathbb {N}$
.
$j\in \mathbb {N}$
.
Proof. Perform a barycentric subdivision of the m-simplex
![]() $M_{j}$
of sufficient order to get a simplicial complex
$M_{j}$
of sufficient order to get a simplicial complex
![]() $\mathcal {L}_{j}$
such that
$\mathcal {L}_{j}$
such that
![]() $\mbox {diam}(\sigma )<\delta _{j}$
for all
$\mbox {diam}(\sigma )<\delta _{j}$
for all
![]() $\sigma \in \mathcal {L}_{j}$
and
$\sigma \in \mathcal {L}_{j}$
and
![]() $j\in \mathbb {N}$
. Then
$j\in \mathbb {N}$
. Then
![]() $\mathcal {L}:=\bigcup _{j=1}^{\infty }\mathcal {L}_{j}$
is not necessarily a simplicial complex, and therefore need not be a countable triangulation of
$\mathcal {L}:=\bigcup _{j=1}^{\infty }\mathcal {L}_{j}$
is not necessarily a simplicial complex, and therefore need not be a countable triangulation of
![]() $\mathbb {R}^{m}$
, as neighboring m-simplices
$\mathbb {R}^{m}$
, as neighboring m-simplices
![]() $M_{j}$
might have undergone barycentric subdivisions of different orders. Let
$M_{j}$
might have undergone barycentric subdivisions of different orders. Let
![]() $\{\sigma _{1}, \sigma _{2}, \ldots \}$
be the collection of all m-simplices in
$\{\sigma _{1}, \sigma _{2}, \ldots \}$
be the collection of all m-simplices in
![]() $\mathcal {L}$
and V be the set of vertices of all simplices in
$\mathcal {L}$
and V be the set of vertices of all simplices in
![]() $\mathcal {L}$
. Observe that V may contain some points of
$\mathcal {L}$
. Observe that V may contain some points of
![]() $\sigma _{i}$
that are not its vertices for each
$\sigma _{i}$
that are not its vertices for each
![]() $i\in \mathbb {N}$
due to the barycentric subdivision of its neighboring m-simplices. However, there are at most finitely many such points of each
$i\in \mathbb {N}$
due to the barycentric subdivision of its neighboring m-simplices. However, there are at most finitely many such points of each
![]() $\sigma _{i}$
, since every compact subset of
$\sigma _{i}$
, since every compact subset of
![]() ${\mathbb R}^{m}$
is contained in a finite union of m-simplices
${\mathbb R}^{m}$
is contained in a finite union of m-simplices
![]() $M_{j}$
. Now, using Lemma 4.1, we refine
$M_{j}$
. Now, using Lemma 4.1, we refine
![]() $\sigma _{1}$
inductively so that we have a triangulation of
$\sigma _{1}$
inductively so that we have a triangulation of
![]() $\sigma _{1}$
, which includes all these points as vertices. Next, we consider
$\sigma _{1}$
, which includes all these points as vertices. Next, we consider
![]() $\sigma _{2}$
and repeat the same procedure. Note that these refinements add new simplices but do not increase the number of vertices. So, the refinement of
$\sigma _{2}$
and repeat the same procedure. Note that these refinements add new simplices but do not increase the number of vertices. So, the refinement of
![]() $\sigma _{2}$
does not disturb that of
$\sigma _{2}$
does not disturb that of
![]() $\sigma _{1}$
done before. Continuing in this way, we obtain a triangulation
$\sigma _{1}$
done before. Continuing in this way, we obtain a triangulation
![]() $\mathcal {K}_{j}$
of
$\mathcal {K}_{j}$
of
![]() $M_{j}$
for each
$M_{j}$
for each
![]() $j\in \mathbb {N}$
so that
$j\in \mathbb {N}$
so that
![]() $\mathcal {K}=\bigcup _{j=1}^{\infty }\mathcal {K}_{j}$
is a countable triangulation of
$\mathcal {K}=\bigcup _{j=1}^{\infty }\mathcal {K}_{j}$
is a countable triangulation of
![]() ${\mathbb R}^{m}$
with the set of vertices
${\mathbb R}^{m}$
with the set of vertices
![]() $V$
. This completes the proof.
$V$
. This completes the proof.
Having the above lemmas, we are ready to prove our desired result.
Theorem 4.3. If
![]() $h\in \mathcal {C}(\mathbb {R}^{m})$
, then for each
$h\in \mathcal {C}(\mathbb {R}^{m})$
, then for each
![]() $\epsilon>0$
, the ball
$\epsilon>0$
, the ball
![]() $B_{\epsilon }(h)$
of radius
$B_{\epsilon }(h)$
of radius
![]() $\epsilon $
around h contains a map f having no (even discontinuous) iterative square roots on
$\epsilon $
around h contains a map f having no (even discontinuous) iterative square roots on
![]() $\mathbb {R}^{m}$
. In particular,
$\mathbb {R}^{m}$
. In particular,
![]() $\mathcal {W}(2;\mathbb {R}^{m})$
does not contain any ball of
$\mathcal {W}(2;\mathbb {R}^{m})$
does not contain any ball of
![]() $\mathcal {C}(\mathbb {R}^{m})$
.
$\mathcal {C}(\mathbb {R}^{m})$
.
Proof. Let
![]() $h\in \mathcal {C}(\mathbb {R}^{m})$
and
$h\in \mathcal {C}(\mathbb {R}^{m})$
and
![]() $\epsilon>0$
be arbitrary. Our strategy to prove the existence of an
$\epsilon>0$
be arbitrary. Our strategy to prove the existence of an
![]() $f\in B_{\epsilon }(h)$
with no square roots is to make use of Theorem 2.4, and we construct this f in a few steps as done in Theorem 3.8.
$f\in B_{\epsilon }(h)$
with no square roots is to make use of Theorem 2.4, and we construct this f in a few steps as done in Theorem 3.8.
Step 1: Construct a piecewise affine linear map
![]() $f_{0}\in B_{\epsilon }(h)$
supported by some suitable triangulation
$f_{0}\in B_{\epsilon }(h)$
supported by some suitable triangulation
![]() $\mathcal {K}$
of
$\mathcal {K}$
of
![]() $\mathbb {R}^{m}$
. Consider the decomposition
$\mathbb {R}^{m}$
. Consider the decomposition
![]() $\mathbb {R}^{m}=\bigcup _{j=1}^{\infty }M_{j}$
of
$\mathbb {R}^{m}=\bigcup _{j=1}^{\infty }M_{j}$
of
![]() $\mathbb {R}^{m}$
fixed above. Since
$\mathbb {R}^{m}$
fixed above. Since
![]() $h|_{M_{j}}$
is uniformly continuous, there exists a
$h|_{M_{j}}$
is uniformly continuous, there exists a
![]() $\delta _{j}>0$
such that
$\delta _{j}>0$
such that
for each
![]() $j\in \mathbb {N}$
. Also, by Lemma 4.2, there exists a triangulation
$j\in \mathbb {N}$
. Also, by Lemma 4.2, there exists a triangulation
![]() ${\mathcal {K}}$
of
${\mathcal {K}}$
of
![]() $\mathbb {R}^{m}$
such that
$\mathbb {R}^{m}$
such that
![]() $\mbox {diam}(\sigma )<{\delta _{j}}/{4}$
for all m-simplex
$\mbox {diam}(\sigma )<{\delta _{j}}/{4}$
for all m-simplex
![]() $\sigma \in {\mathcal {K}}$
contained in
$\sigma \in {\mathcal {K}}$
contained in
![]() $M_{j}$
and for all
$M_{j}$
and for all
![]() $j\in \mathbb {N}$
.
$j\in \mathbb {N}$
.
Let
![]() $x_{0}, x_{1}, \ldots $
be the vertices of
$x_{0}, x_{1}, \ldots $
be the vertices of
![]() ${\mathcal K} .$
Choose
${\mathcal K} .$
Choose
![]() $y_0,y_1,\ldots$
in
$y_0,y_1,\ldots$
in
![]() $\mathbb {R}^{m}$
inductively such that
$\mathbb {R}^{m}$
inductively such that
![]() $y_{j}\ne x_{j}$
and
$y_{j}\ne x_{j}$
and
and
![]() $\{y_{i_{0}}, y_{i_{1}}, \ldots , y_{i_{m}}\}$
is geometrically independent whenever
$\{y_{i_{0}}, y_{i_{1}}, \ldots , y_{i_{m}}\}$
is geometrically independent whenever
![]() $\langle x_{i_{0}}, x_{i_{1}},\ldots , x_{i_{m}}\rangle \in {\mathcal {K}}$
for
$\langle x_{i_{0}}, x_{i_{1}},\ldots , x_{i_{m}}\rangle \in {\mathcal {K}}$
for
![]() $i_{0}, i_{1}, \ldots , i_{m}\in \mathbb {Z}_{+}$
. This is possible by Lemma 3.6. Here, while choosing points
$i_{0}, i_{1}, \ldots , i_{m}\in \mathbb {Z}_{+}$
. This is possible by Lemma 3.6. Here, while choosing points
![]() $y_{j}$
using Baire Category theorem with
$y_{j}$
using Baire Category theorem with
![]() $y_{j}\in B_{ {\epsilon }/{2^{j+6}} }(h(x_{j}))$
for all
$y_{j}\in B_{ {\epsilon }/{2^{j+6}} }(h(x_{j}))$
for all
![]() $j\in \mathbb {Z}_{+}$
, satisfying the geometric independence condition, it is also possible to ensure that
$j\in \mathbb {Z}_{+}$
, satisfying the geometric independence condition, it is also possible to ensure that
![]() $y_{j}\neq x_{j}$
for all
$y_{j}\neq x_{j}$
for all
![]() $j\in \mathbb {Z}_{+}$
. Then, for each
$j\in \mathbb {Z}_{+}$
. Then, for each
![]() $j\in \mathbb {N}$
, we have
$j\in \mathbb {N}$
, we have
 $$ \begin{align} \|y_{i_{0}}-y_{i_{1}}\|_{\infty}&\le \|y_{i_{0}}-h(x_{i_{0}})\|_{\infty}+\|h(x_{i_{0}})-h(x_{i_{1}})\|_{\infty}+ \|h(x_{i_{1}})-y_{i_{1}}\|_{\infty}\nonumber \\ &< \frac{\epsilon }{2^{j+5}}+2\frac{\epsilon }{2^{j+6}}=\frac{\epsilon }{2^{j+4}}, \end{align} $$
$$ \begin{align} \|y_{i_{0}}-y_{i_{1}}\|_{\infty}&\le \|y_{i_{0}}-h(x_{i_{0}})\|_{\infty}+\|h(x_{i_{0}})-h(x_{i_{1}})\|_{\infty}+ \|h(x_{i_{1}})-y_{i_{1}}\|_{\infty}\nonumber \\ &< \frac{\epsilon }{2^{j+5}}+2\frac{\epsilon }{2^{j+6}}=\frac{\epsilon }{2^{j+4}}, \end{align} $$
whenever
![]() $\langle x_{i_{0}},x_{i_{1}}\rangle $
is a
$\langle x_{i_{0}},x_{i_{1}}\rangle $
is a
![]() $2$
-simplex of
$2$
-simplex of
![]() $\sigma $
for all m-simplex
$\sigma $
for all m-simplex
![]() $\sigma \in {\mathcal {K}}$
contained in
$\sigma \in {\mathcal {K}}$
contained in
![]() $M_{j}$
. Let
$M_{j}$
. Let
![]() $f_{0}:|{\mathcal {K}}|=\mathbb {R}^{m} \to \mathbb {R}^{m}$
be the map
$f_{0}:|{\mathcal {K}}|=\mathbb {R}^{m} \to \mathbb {R}^{m}$
be the map
![]() $f_{U, V}$
defined as in equation (3.2), where U and V are the ordered sets
$f_{U, V}$
defined as in equation (3.2), where U and V are the ordered sets
![]() $\{x_{0}, x_{1}, \ldots \}$
and
$\{x_{0}, x_{1}, \ldots \}$
and
![]() $\{y_{0}, y_{1}, \ldots \}$
, respectively. Then
$\{y_{0}, y_{1}, \ldots \}$
, respectively. Then
![]() $f_{0}$
is a continuous piecewise affine linear self-map of
$f_{0}$
is a continuous piecewise affine linear self-map of
![]() $\mathbb {R}^{m}$
satisfying that
$\mathbb {R}^{m}$
satisfying that
![]() $f_{0}(x_{j})=y_{j}$
for all
$f_{0}(x_{j})=y_{j}$
for all
![]() $j\in \mathbb {Z}_{+}$
. Also, by using result (i) of Lemma 3.1, we have
$j\in \mathbb {Z}_{+}$
. Also, by using result (i) of Lemma 3.1, we have
![]() $R(f_{0})^{0}\ne \emptyset $
, and
$R(f_{0})^{0}\ne \emptyset $
, and
![]() $f_{0}|_{\sigma }$
is injective for all
$f_{0}|_{\sigma }$
is injective for all
![]() $\sigma \in {\mathcal {K}}$
contained in
$\sigma \in {\mathcal {K}}$
contained in
![]() $M_{j}$
for all
$M_{j}$
for all
![]() $j\in \mathbb {N}$
. Further, from equation (4.3) we have
$j\in \mathbb {N}$
. Further, from equation (4.3) we have
Claim.
![]() $D(f_{0},h)<{\epsilon }/{4}$
.
$D(f_{0},h)<{\epsilon }/{4}$
.
Consider arbitrary
![]() $j\in \mathbb {N}$
and
$j\in \mathbb {N}$
and
![]() $x\in M_{j}$
. Then x is in the interior of a unique k-simplex
$x\in M_{j}$
. Then x is in the interior of a unique k-simplex
![]() $\langle x_{i_{0}}, x_{i_{1}}, \ldots , x_{i_{k}}\rangle $
in
$\langle x_{i_{0}}, x_{i_{1}}, \ldots , x_{i_{k}}\rangle $
in
![]() ${\mathcal {K}}$
contained in
${\mathcal {K}}$
contained in
![]() $M_j$
for some
$M_j$
for some
![]() $0\le k\le m$
. Let
$0\le k\le m$
. Let
![]() $x=\sum _{j=0}^{k}\alpha _{i_{j}}x_{i_{j}}$
with
$x=\sum _{j=0}^{k}\alpha _{i_{j}}x_{i_{j}}$
with
![]() $\sum _{j=0}^{k}\alpha _{i_{j}}=1$
. Then by equations (4.1) and (4.2), we have
$\sum _{j=0}^{k}\alpha _{i_{j}}=1$
. Then by equations (4.1) and (4.2), we have
 $$ \begin{align} \|f_{0}(x)-h(x)\|_{\infty}&=\bigg\|\sum_{j=0}^{k}\alpha_{i_{j}}y_{i_{j}}-\sum_{j=0}^{k}\alpha_{i_{j}}h(x)\bigg\|_{\infty} \nonumber\\ &\le \sum_{j=0}^{k}\alpha_{i_{j}}\{\|y_{i_{j}}-h(x_{i_{j}})\|_{\infty}+\|h(x_{i_{j}})-h(x)\|_{\infty}\}\nonumber\\ &< \frac{\epsilon}{2^{j+6}}+\frac{\epsilon}{2^{j+5}}\nonumber \\ &< \frac{\epsilon}{2^{j+4}}, \end{align} $$
$$ \begin{align} \|f_{0}(x)-h(x)\|_{\infty}&=\bigg\|\sum_{j=0}^{k}\alpha_{i_{j}}y_{i_{j}}-\sum_{j=0}^{k}\alpha_{i_{j}}h(x)\bigg\|_{\infty} \nonumber\\ &\le \sum_{j=0}^{k}\alpha_{i_{j}}\{\|y_{i_{j}}-h(x_{i_{j}})\|_{\infty}+\|h(x_{i_{j}})-h(x)\|_{\infty}\}\nonumber\\ &< \frac{\epsilon}{2^{j+6}}+\frac{\epsilon}{2^{j+5}}\nonumber \\ &< \frac{\epsilon}{2^{j+4}}, \end{align} $$
since
![]() $\|x-x_{i_{j}}\|_{\infty }\le \mbox {diam}(\langle x_{i_{0}}, x_{i_{1}}, \ldots , x_{i_{k}}\rangle )<\delta _{j}$
for all
$\|x-x_{i_{j}}\|_{\infty }\le \mbox {diam}(\langle x_{i_{0}}, x_{i_{1}}, \ldots , x_{i_{k}}\rangle )<\delta _{j}$
for all
![]() $0\le j\le k$
. Therefore,
$0\le j\le k$
. Therefore,
![]() $\rho _{j}(f_{0}, h) \le {\epsilon }/{2^{j+4}}<{\epsilon }/{2^{j+2}}$
for all
$\rho _{j}(f_{0}, h) \le {\epsilon }/{2^{j+4}}<{\epsilon }/{2^{j+2}}$
for all
![]() $j\in \mathbb {N}$
, implying that
$j\in \mathbb {N}$
, implying that
![]() $D(f_{0}, h)< \sum _{j=1}^{\infty }({\epsilon }/{2^{j+2}})={\epsilon }/{4}$
.
$D(f_{0}, h)< \sum _{j=1}^{\infty }({\epsilon }/{2^{j+2}})={\epsilon }/{4}$
.
Step 2: Obtain an m-simplex
![]() $\Delta \in {\mathcal {K}}$
contained in
$\Delta \in {\mathcal {K}}$
contained in
![]() $M_{r}$
for some
$M_{r}$
for some
![]() $r\in \mathbb {N}$
containing a non-empty open set
$r\in \mathbb {N}$
containing a non-empty open set
![]() $Y\subseteq \Delta ^{0}\cap R(f_{0})^{0}$
such that
$Y\subseteq \Delta ^{0}\cap R(f_{0})^{0}$
such that
![]() $f_{0}(Y)\subseteq \Delta _{1}^{0}$
for some m-simplex
$f_{0}(Y)\subseteq \Delta _{1}^{0}$
for some m-simplex
![]() $\Delta _{1}$
in
$\Delta _{1}$
in
![]() ${\mathcal K}$
. Consider any m-simplex
${\mathcal K}$
. Consider any m-simplex
![]() $\sigma =\langle x_{i_{0}}, x_{i_{1}},\ldots , x_{i_{m}}\rangle $
in
$\sigma =\langle x_{i_{0}}, x_{i_{1}},\ldots , x_{i_{m}}\rangle $
in
![]() $\mathcal {K}$
. Since
$\mathcal {K}$
. Since
![]() $\{y_{i_{0}}, y_{i_{1}},\ldots , y_{i_{m}}\}$
is geometrically independent by construction, we have
$\{y_{i_{0}}, y_{i_{1}},\ldots , y_{i_{m}}\}$
is geometrically independent by construction, we have
![]() $f_{0}(Z)$
is open in
$f_{0}(Z)$
is open in
![]() $\mathbb {R}^{m}$
for each open subset Z of
$\mathbb {R}^{m}$
for each open subset Z of
![]() $\sigma ^{0}$
. Choose a sufficiently small non-empty open subset
$\sigma ^{0}$
. Choose a sufficiently small non-empty open subset
![]() $Y_{0}$
of
$Y_{0}$
of
![]() $f_0(\sigma )^{0}$
such that
$f_0(\sigma )^{0}$
such that
![]() $Y_{0}\subseteq \Delta ^{0}$
for some m-simplex
$Y_{0}\subseteq \Delta ^{0}$
for some m-simplex
![]() $\Delta \in \mathcal {K}$
contained in
$\Delta \in \mathcal {K}$
contained in
![]() $M_r$
for some
$M_r$
for some
![]() $r \in \mathbb{N}$
. Then
$r \in \mathbb{N}$
. Then
![]() $f_{0}(Y_{0})$
has non-empty interior. Again, choose a non-empty open subset Y of
$f_{0}(Y_{0})$
has non-empty interior. Again, choose a non-empty open subset Y of
![]() $Y_{0}$
so small that
$Y_{0}$
so small that
![]() $f_{0}(Y)\subseteq \Delta _{1}$
for some m-simplex
$f_{0}(Y)\subseteq \Delta _{1}$
for some m-simplex
![]() $\Delta _{1}\in {\mathcal K}.$
This completes the proof of Step 2.
$\Delta _{1}\in {\mathcal K}.$
This completes the proof of Step 2.
Step 3: Show that there exists a barycentric subdivision
![]() $\mathcal {K}^{\kern2pt(s)}$
of
$\mathcal {K}^{\kern2pt(s)}$
of
![]() ${\mathcal {K}}$
for some
${\mathcal {K}}$
for some
![]() $s \in \mathbb {N}$
with an m-simplex
$s \in \mathbb {N}$
with an m-simplex
![]() $\sigma _{0}\in \mathcal {K}^{\kern2pt(s)}$
such that
$\sigma _{0}\in \mathcal {K}^{\kern2pt(s)}$
such that
![]() $\sigma _{0}\subseteq Y$
, and
$\sigma _{0}\subseteq Y$
, and
![]() $f_{0}^{-1}(\sigma _{0})\cap \sigma =\emptyset $
and
$f_{0}^{-1}(\sigma _{0})\cap \sigma =\emptyset $
and
![]() $f_{0}(\sigma _{0})\cap \sigma =\emptyset $
for all
$f_{0}(\sigma _{0})\cap \sigma =\emptyset $
for all
![]() $\sigma \in \mathcal {K}^{\kern2pt(s)}$
with
$\sigma \in \mathcal {K}^{\kern2pt(s)}$
with
![]() $\sigma \cap \sigma _{0}\ne \emptyset $
. The proof is similar to that of Step 3 of Theorem 3.8.
$\sigma \cap \sigma _{0}\ne \emptyset $
. The proof is similar to that of Step 3 of Theorem 3.8.
Step 4: Modify
![]() $f_{0}$
slightly to get a new piecewise affine linear map
$f_{0}$
slightly to get a new piecewise affine linear map
![]() $f\in B_{\epsilon } (h)$
that is constant on
$f\in B_{\epsilon } (h)$
that is constant on
![]() $\sigma {}_{0}.$
The proof is similar to that of Step 4 of Theorem 3.8; however, we give the details here for clarity. To retain continuity, when we modify
$\sigma {}_{0}.$
The proof is similar to that of Step 4 of Theorem 3.8; however, we give the details here for clarity. To retain continuity, when we modify
![]() $f_{0}$
on
$f_{0}$
on
![]() $\sigma _{0}$
, we must also modify it on all m-simplices in
$\sigma _{0}$
, we must also modify it on all m-simplices in
![]() $\mathcal {K}^{\kern2pt(s)}$
adjacent to it. Let
$\mathcal {K}^{\kern2pt(s)}$
adjacent to it. Let
![]() $A:=\bigcup _{j=0}^{p}\sigma _{j}$
, where
$A:=\bigcup _{j=0}^{p}\sigma _{j}$
, where
![]() $\sigma _{j}$
is precisely an m-simplex in
$\sigma _{j}$
is precisely an m-simplex in
![]() $\mathcal {K}^{\kern2pt(s)}$
such that
$\mathcal {K}^{\kern2pt(s)}$
such that
![]() $\sigma _{j}\cap \sigma _{0}\ne \emptyset $
for all
$\sigma _{j}\cap \sigma _{0}\ne \emptyset $
for all
![]() $0\le j\le p$
. Then, clearly
$0\le j\le p$
. Then, clearly
![]() $A\subseteq W\subseteq \Delta^{0}$
, where W is as chosen in Step 3.
$A\subseteq W\subseteq \Delta^{0}$
, where W is as chosen in Step 3.
Let the vertices of
![]() $\sigma _{0}$
be
$\sigma _{0}$
be
![]() $u_{0},\ldots , u_{m-1}$
and
$u_{0},\ldots , u_{m-1}$
and
![]() $u_{m}$
, and let
$u_{m}$
, and let
![]() $v_{j}:=f_{0}(u_{j})$
for all
$v_{j}:=f_{0}(u_{j})$
for all
![]() $0\le j \le ~m$
. Then
$0\le j \le ~m$
. Then
![]() $v_{j}\ne u_{j}$
for all
$v_{j}\ne u_{j}$
for all
![]() $0\le j\le m$
, because
$0\le j\le m$
, because
![]() $u_{j}\in W$
for all
$u_{j}\in W$
for all
![]() $0\le j\le m$
and
$0\le j\le m$
and
![]() $f_{0}(W)\cap W=\emptyset $
. Also, as
$f_{0}(W)\cap W=\emptyset $
. Also, as
![]() $u_{0}, u_{1}, \ldots , u_{m}$
are geometrically independent vectors contained in
$u_{0}, u_{1}, \ldots , u_{m}$
are geometrically independent vectors contained in
![]() $\Delta $
, by result (ii) of Corollary 3.4, we see that
$\Delta $
, by result (ii) of Corollary 3.4, we see that
![]() $v_0, v_1,\ldots,v_m$
are geometrically independent. Further, by Step 2, they are all contained in the interior of a single simplex
$v_0, v_1,\ldots,v_m$
are geometrically independent. Further, by Step 2, they are all contained in the interior of a single simplex
![]() $\Delta {}_{1}$
of
$\Delta {}_{1}$
of
![]() ${\mathcal {K}}$
. Hence, by result (iii) of Corollary 3.4, we have
${\mathcal {K}}$
. Hence, by result (iii) of Corollary 3.4, we have
![]() $f_{0}(v_{j})\neq v_{j}$
for some
$f_{0}(v_{j})\neq v_{j}$
for some
![]() $0\le j\le m$
. Without loss of generality, we assume that
$0\le j\le m$
. Without loss of generality, we assume that
![]() $f_{0}(v_{0})\neq v_{0}.$
$f_{0}(v_{0})\neq v_{0}.$
Extend
![]() $\{u_{0}, \ldots , u_{m}\}$
to
$\{u_{0}, \ldots , u_{m}\}$
to
![]() $\{u_{0}, u_{1}, \ldots \}$
to include the vertices of all the simplices of
$\{u_{0}, u_{1}, \ldots \}$
to include the vertices of all the simplices of
![]() ${\mathcal K}^{(s)}$
and let
${\mathcal K}^{(s)}$
and let
![]() $v_{j}:= f_{0}(u_{j})$
for all
$v_{j}:= f_{0}(u_{j})$
for all
![]() $j \in \mathbb {Z}_{+}$
. Now, define f by
$j \in \mathbb {Z}_{+}$
. Now, define f by
 $$ \begin{align*} f(u_{j}) = \begin{cases} v_{0}&\text{if } 0\leq j\leq m,\\ v_{j}&\text{if } j>m,\end{cases} \end{align*} $$
$$ \begin{align*} f(u_{j}) = \begin{cases} v_{0}&\text{if } 0\leq j\leq m,\\ v_{j}&\text{if } j>m,\end{cases} \end{align*} $$
and extend it countably piecewise affine linearly to the whole of
![]() $|{\mathcal K}^{(s)}|= \mathbb {R}^{m}$
. Then
$|{\mathcal K}^{(s)}|= \mathbb {R}^{m}$
. Then
![]() $f_{0}$
is modified only on A and
$f_{0}$
is modified only on A and
![]() $f(x)=v_{0}$
for all
$f(x)=v_{0}$
for all
![]() $x\in \sigma _{0}$
.
$x\in \sigma _{0}$
.
Consider an arbitrary
![]() $x\in A$
. Then
$x\in A$
. Then
![]() $x\in \sigma _{j}$
for some
$x\in \sigma _{j}$
for some
![]() $0\le j\le p$
. Let
$0\le j\le p$
. Let
![]() $\sigma _{j}=\langle u_{j_{0}}, u_{j_{1}}, \ldots , u_{j_{m}}\rangle $
and
$\sigma _{j}=\langle u_{j_{0}}, u_{j_{1}}, \ldots , u_{j_{m}}\rangle $
and
![]() $x=\sum _{i=0}^{m}\alpha _{j_{i}}u_{j_{i}}$
with
$x=\sum _{i=0}^{m}\alpha _{j_{i}}u_{j_{i}}$
with
![]() $\sum _{i=0}^{m}\alpha _{j_{i}}=1$
. Then by equation (4.4), we have
$\sum _{i=0}^{m}\alpha _{j_{i}}=1$
. Then by equation (4.4), we have
 $$ \begin{align*} \|f(x)-f_{0}(x)\|_{\infty}\le \sum_{i=0}^{m}\alpha_{j_{i}}\|f(u_{j_{i}})-f_{0}(u_{j_{i}})\|_{\infty} \le \sum_{i=0}^{m}\alpha_{j_{i}}\mbox{diam}(f_0(\Delta)) < \frac{\epsilon}{2^{r+4}}, \end{align*} $$
$$ \begin{align*} \|f(x)-f_{0}(x)\|_{\infty}\le \sum_{i=0}^{m}\alpha_{j_{i}}\|f(u_{j_{i}})-f_{0}(u_{j_{i}})\|_{\infty} \le \sum_{i=0}^{m}\alpha_{j_{i}}\mbox{diam}(f_0(\Delta)) < \frac{\epsilon}{2^{r+4}}, \end{align*} $$
implying by equation (4.5) that
Therefore,
![]() $\rho _{r}(f, h)< {\epsilon }/{2^{r+2}}$
. Also, we have
$\rho _{r}(f, h)< {\epsilon }/{2^{r+2}}$
. Also, we have
![]() $\rho _{j}(f, h)=\rho _{j}(f_{0},h)<{\epsilon }/{2^{j+2}}$
for
$\rho _{j}(f, h)=\rho _{j}(f_{0},h)<{\epsilon }/{2^{j+2}}$
for
![]() $j\ne r$
. Hence,
$j\ne r$
. Hence,
![]() $D(f, h)< \sum _{j=1}^{\infty }({\epsilon }/{2^{j+2}})={\epsilon }/{4}$
, proving that
$D(f, h)< \sum _{j=1}^{\infty }({\epsilon }/{2^{j+2}})={\epsilon }/{4}$
, proving that
![]() $f\in B_{\epsilon }(h)$
.
$f\in B_{\epsilon }(h)$
.
Step 5. Prove that f has no square roots in
![]() $\mathcal {C}(\mathbb {R}^{m})$
. It is clear that
$\mathcal {C}(\mathbb {R}^{m})$
. It is clear that
![]() $f(v_{0})\neq v_{0}$
, because
$f(v_{0})\neq v_{0}$
, because
![]() $A\subseteq W$
,
$A\subseteq W$
,
![]() $f=f_{0}$
on
$f=f_{0}$
on
![]() $A^{c}$
and
$A^{c}$
and
![]() $f_{0}(W)\cap W=\emptyset $
. Also, by Step 3, we have
$f_{0}(W)\cap W=\emptyset $
. Also, by Step 3, we have
![]() $f_{0}^{-1}(\sigma _{0})\cap \sigma =\emptyset $
for all
$f_{0}^{-1}(\sigma _{0})\cap \sigma =\emptyset $
for all
![]() $\sigma \in {\mathcal K}^{(s)}$
with
$\sigma \in {\mathcal K}^{(s)}$
with
![]() $\sigma \cap \sigma _{0}\neq \emptyset $
, implying that
$\sigma \cap \sigma _{0}\neq \emptyset $
, implying that
![]() $f=f_{0}$
on
$f=f_{0}$
on
![]() $f_{0}^{-1}(\sigma _{0})$
. Further,
$f_{0}^{-1}(\sigma _{0})$
. Further,
![]() $f_{0}^{-1}(\sigma _{0})$
is uncountable, since
$f_{0}^{-1}(\sigma _{0})$
is uncountable, since
![]() $\sigma _{0}$
is uncountable and
$\sigma _{0}$
is uncountable and
![]() $\sigma _{0}\subseteq R(f_{0})^{0}$
. Therefore, as
$\sigma _{0}\subseteq R(f_{0})^{0}$
. Therefore, as
![]() $f^{-2}(v_{0})\supseteq f^{-1}(f^{-1}(v_{0}))\supseteq f^{-1}(\sigma _{0})\supseteq f_{0}^{-1}(\sigma _{0})$
, it follows that
$f^{-2}(v_{0})\supseteq f^{-1}(f^{-1}(v_{0}))\supseteq f^{-1}(\sigma _{0})\supseteq f_{0}^{-1}(\sigma _{0})$
, it follows that
![]() $f^{-2}(v_{0})$
is uncountable. Moreover,
$f^{-2}(v_{0})$
is uncountable. Moreover,
![]() $f|_{\sigma }$
is injective for every
$f|_{\sigma }$
is injective for every
![]() $\sigma \in \mathcal {K}^{\kern2pt(s)}$
with
$\sigma \in \mathcal {K}^{\kern2pt(s)}$
with
![]() $\sigma \neq \sigma _{0}$
by result (i) of Lemma 3.1, and hence
$\sigma \neq \sigma _{0}$
by result (i) of Lemma 3.1, and hence
![]() $f^{-1}(x)$
is countable for all
$f^{-1}(x)$
is countable for all
![]() $x\ne v_{0}$
in
$x\ne v_{0}$
in
![]() $\mathbb {R}^{m}$
. Thus, f satisfies the hypothesis of Case (iii) of Theorem 2.4, proving that f has no square roots in
$\mathbb {R}^{m}$
. Thus, f satisfies the hypothesis of Case (iii) of Theorem 2.4, proving that f has no square roots in
![]() $\mathcal {C}(\mathbb {R}^{m})$
.
$\mathcal {C}(\mathbb {R}^{m})$
.
We have seen in Theorem 3.8 (respectively Theorem 4.3) that each open neighborhood of each map in
![]() $\mathcal {C}(I^{m})$
(respectively in
$\mathcal {C}(I^{m})$
(respectively in
![]() $\mathcal {C}(\mathbb {R}^{m})$
) has a continuous map which does not have even discontinuous square roots. Additionally, if X and Y are locally compact Hausdorff spaces, and
$\mathcal {C}(\mathbb {R}^{m})$
) has a continuous map which does not have even discontinuous square roots. Additionally, if X and Y are locally compact Hausdorff spaces, and
![]() $\phi :X\to Y$
is a homeomorphism, then the map
$\phi :X\to Y$
is a homeomorphism, then the map
![]() $f\mapsto \phi \circ f\circ \phi ^{-1}$
is a homeomorphism of
$f\mapsto \phi \circ f\circ \phi ^{-1}$
is a homeomorphism of
![]() $\mathcal {C}(X)$
onto
$\mathcal {C}(X)$
onto
![]() $\mathcal {C}(Y)$
, where both
$\mathcal {C}(Y)$
, where both
![]() $\mathcal {C}(X)$
and
$\mathcal {C}(X)$
and
![]() $\mathcal {C}(Y)$
have the compact-open topology, and moreover
$\mathcal {C}(Y)$
have the compact-open topology, and moreover
![]() $f=g^{2}$
on X if and only if
$f=g^{2}$
on X if and only if
![]() $\phi \circ f\circ \phi ^{-1} = (\phi \circ g\circ \phi ^{-1})^{2}$
on Y. Hence, it follows that Theorem 3.8 (respectively Theorem 4.3) is true if
$\phi \circ f\circ \phi ^{-1} = (\phi \circ g\circ \phi ^{-1})^{2}$
on Y. Hence, it follows that Theorem 3.8 (respectively Theorem 4.3) is true if
![]() $I^{m}$
(respectively
$I^{m}$
(respectively
![]() $\mathbb {R}^{m}$
) is replaced by any topological space homeomorphic to it. For the same reason, Theorem 3.9 is also true if
$\mathbb {R}^{m}$
) is replaced by any topological space homeomorphic to it. For the same reason, Theorem 3.9 is also true if
![]() $I^{m}$
is replaced by any topological space homeomorphic to it.
$I^{m}$
is replaced by any topological space homeomorphic to it.
5
 $L^{p}$
denseness of iterative squares in
$L^{p}$
denseness of iterative squares in
 $\mathcal {C}(I^{m})$
$\mathcal {C}(I^{m})$
In this section, we prove that the iterative squares of continuous self-maps on
![]() $I^{m}$
are
$I^{m}$
are
![]() $L^{p}$
dense in
$L^{p}$
dense in
![]() $\mathcal {C}(I^{m})$
. Given any nontrivial compact subintervals
$\mathcal {C}(I^{m})$
. Given any nontrivial compact subintervals
![]() $I_{1}, I_{2}, \ldots , I_{m}$
of I, let
$I_{1}, I_{2}, \ldots , I_{m}$
of I, let
![]() $I_{1}\times I_{2}\times \cdots \times I_{m}$
denote the closed rectangular region in
$I_{1}\times I_{2}\times \cdots \times I_{m}$
denote the closed rectangular region in
![]() $I^{m}$
defined by
$I^{m}$
defined by
Consider
![]() $\mathcal {C}(I^{m})$
in the
$\mathcal {C}(I^{m})$
in the
![]() $L^{p}$
norm defined by
$L^{p}$
norm defined by
 $$ \begin{align*} \|f\|_{p}=\bigg(\int_{I^{m}}^{} \|f(x)\|_{\infty}^{p}\,d\mu(x) \bigg)^{{1}/{p}}, \end{align*} $$
$$ \begin{align*} \|f\|_{p}=\bigg(\int_{I^{m}}^{} \|f(x)\|_{\infty}^{p}\,d\mu(x) \bigg)^{{1}/{p}}, \end{align*} $$
where
![]() $\mu $
is the Lebesgue measure on
$\mu $
is the Lebesgue measure on
![]() ${\mathbb R}^{m}$
. First, we prove a result which gives a sufficient condition for extending a given function to a square.
${\mathbb R}^{m}$
. First, we prove a result which gives a sufficient condition for extending a given function to a square.
Theorem 5.1. Let K be a proper closed subset of
![]() $I^{m}$
and
$I^{m}$
and
![]() $f:K\to I^{m}$
be continuous. Then there exists a
$f:K\to I^{m}$
be continuous. Then there exists a
![]() $g\in \mathcal {C}(I^{m})$
such that
$g\in \mathcal {C}(I^{m})$
such that
![]() $f=g^{2}|_{K}$
.
$f=g^{2}|_{K}$
.
Proof. Let
![]() $I_{1}\times I_{2}\times \cdots \times I_{m}$
be a closed rectangular region in
$I_{1}\times I_{2}\times \cdots \times I_{m}$
be a closed rectangular region in
![]() $I^{m}\setminus K$
and
$I^{m}\setminus K$
and
![]() $\tilde {g}$
be a homeomorphism of K into
$\tilde {g}$
be a homeomorphism of K into
![]() $I_{1}\times I_{2}\times \cdots \times I_{m}$
. Extend
$I_{1}\times I_{2}\times \cdots \times I_{m}$
. Extend
![]() $\tilde {g}$
to
$\tilde {g}$
to
![]() $K\cup R(\tilde {g})$
by setting
$K\cup R(\tilde {g})$
by setting
![]() $g(x)=f(\tilde {g}^{-1}(x))$
for
$g(x)=f(\tilde {g}^{-1}(x))$
for
![]() $x\in R(\tilde {g})$
. Then g is continuous on the closed set
$x\in R(\tilde {g})$
. Then g is continuous on the closed set
![]() $K\cup R(\tilde {g})$
, and therefore, by an extension of Tietze’s extension theorem by Dugundji (see Theorem 4.1 and Corollary 4.2 of [Reference Dugundji11, pp. 357–358]), it has an extension to a continuous self-map of
$K\cup R(\tilde {g})$
, and therefore, by an extension of Tietze’s extension theorem by Dugundji (see Theorem 4.1 and Corollary 4.2 of [Reference Dugundji11, pp. 357–358]), it has an extension to a continuous self-map of
![]() $I^{m}$
, which also we denote by g. Further, for each
$I^{m}$
, which also we denote by g. Further, for each
![]() $x\in K$
, we have
$x\in K$
, we have
 $$ \begin{align*} g^{2}(x)&=g(g(x))\\[3pt] &=g(\tilde{g}(x))\\[3pt] &=f(\tilde{g}^{-1}(\tilde{g}(x)))~~(\text{since}~\tilde{g}(x)\in R(\tilde{g}))\\[3pt] &=f(x), \end{align*} $$
$$ \begin{align*} g^{2}(x)&=g(g(x))\\[3pt] &=g(\tilde{g}(x))\\[3pt] &=f(\tilde{g}^{-1}(\tilde{g}(x)))~~(\text{since}~\tilde{g}(x)\in R(\tilde{g}))\\[3pt] &=f(x), \end{align*} $$
implying that
![]() $f=g^{2}|_{K}$
.
$f=g^{2}|_{K}$
.
It is worth noting that the assumption in the above theorem that K is a proper subset of
![]() $I^{m}$
cannot be dropped. Indeed, if
$I^{m}$
cannot be dropped. Indeed, if
![]() $K=I$
, then the continuous map
$K=I$
, then the continuous map
![]() $f(x)=1-x$
on K has no square roots in
$f(x)=1-x$
on K has no square roots in
![]() $\mathcal {C}(I)$
(see [Reference Kuczma, Choczewski and Ger24, pp. 425–426] or Corollary 2.7). Such maps can be constructed on
$\mathcal {C}(I)$
(see [Reference Kuczma, Choczewski and Ger24, pp. 425–426] or Corollary 2.7). Such maps can be constructed on
![]() $K=I^{m}$
for general m using Theorem 2.6. We now prove our desired result.
$K=I^{m}$
for general m using Theorem 2.6. We now prove our desired result.
Theorem 5.2.
![]() $\mathcal {W}(2;I^{m})$
is
$\mathcal {W}(2;I^{m})$
is
![]() $L^{p}$
dense in
$L^{p}$
dense in
![]() $\mathcal {C}(I^{m})$
.
$\mathcal {C}(I^{m})$
.
Proof. Consider an arbitrary
![]() $f\in \mathcal {C}(I^{m})$
. Then, by Theorem 5.1, for each
$f\in \mathcal {C}(I^{m})$
. Then, by Theorem 5.1, for each
![]() $\epsilon>0$
, there exists a map
$\epsilon>0$
, there exists a map
![]() $g_{\epsilon } \in \mathcal {C}(I^{m})$
such that
$g_{\epsilon } \in \mathcal {C}(I^{m})$
such that
![]() $f|_{I_{\epsilon }\times I_{\epsilon }\times \cdots \times I_{\epsilon }}=g_{\epsilon }^{2}|_{I_{\epsilon }\times I_{\epsilon }\times \cdots \times I_{\epsilon }}$
, where
$f|_{I_{\epsilon }\times I_{\epsilon }\times \cdots \times I_{\epsilon }}=g_{\epsilon }^{2}|_{I_{\epsilon }\times I_{\epsilon }\times \cdots \times I_{\epsilon }}$
, where
![]() $I_{\epsilon }=[\epsilon , 1]$
. Now,
$I_{\epsilon }=[\epsilon , 1]$
. Now,
 $$ \begin{align*} \|g_{\epsilon}^{2}-f\|_{p}^{p}&=\int_{I^{m}}^{} \|g_{\epsilon}^{2}(x)-f(x)\|_{\infty }^{p}\,d\mu(x)\\[3pt] &=\int_{({I_{\epsilon}\times I_{\epsilon}\times \cdots \times I_{\epsilon}})^{c}}^{} \|g_{\epsilon}^{2}(x)-f(x)\|_{\infty}^{p}\,d\mu(x)\\[3pt] &\le \mu(({I_{\epsilon}\times I_{\epsilon}\times \cdots \times I_{\epsilon}})^{c})\\[3pt] &=1-(1-\epsilon)^{m}, \end{align*} $$
$$ \begin{align*} \|g_{\epsilon}^{2}-f\|_{p}^{p}&=\int_{I^{m}}^{} \|g_{\epsilon}^{2}(x)-f(x)\|_{\infty }^{p}\,d\mu(x)\\[3pt] &=\int_{({I_{\epsilon}\times I_{\epsilon}\times \cdots \times I_{\epsilon}})^{c}}^{} \|g_{\epsilon}^{2}(x)-f(x)\|_{\infty}^{p}\,d\mu(x)\\[3pt] &\le \mu(({I_{\epsilon}\times I_{\epsilon}\times \cdots \times I_{\epsilon}})^{c})\\[3pt] &=1-(1-\epsilon)^{m}, \end{align*} $$
implying that
![]() $\|g_{\epsilon }^{2}-f\|_{p} \to 0$
as
$\|g_{\epsilon }^{2}-f\|_{p} \to 0$
as
![]() $\epsilon \to 0$
. Hence,
$\epsilon \to 0$
. Hence,
![]() $\lim \nolimits _{\epsilon \to 0}g_{\epsilon }^{2}=f$
in
$\lim \nolimits _{\epsilon \to 0}g_{\epsilon }^{2}=f$
in
![]() $L^{p}$
, and the result follows.
$L^{p}$
, and the result follows.
Acknowledgements
The authors are grateful to the referee for his/her many helpful comments. B.V.R.B. is supported by J C Bose Fellowship of the Science and Engineering Board, India. C.G. is supported by the Indian Statistical Institute, Bangalore through J C Bose Fellowship of B.V.R.B., and by the National Board for Higher Mathematics, India through No: 0204/3/2021/R&D-II/7389.