1 Introduction
The representational theory of measurement (RTM) characterizes the conditions under which qualitative attributes can be represented numerically. Footnote 1 This is achieved with representation theorems that demonstrate the existence of a homomorphism between two types of structure. The domain of the homomorphism is an empirical relational structure—a structure satisfying an axiomatization of the nature of the attribute. The codomain is a numerical relational structure—typically a set of numbers with a set of mathematical relations defined over it.
The interpretation of the empirical relational structures preferred by the original architects of RTM is expressly operationalist. On their view, an empirical relational structure is taken to consist of a set of objects that all instantiate the qualitative attribute in question together with a collection of operationally interpreted relations defined over the set. The numerical relational structure is typically taken to be the real numbers with the standard order structure and the standard notion of addition. The existence of a homomorphism between these two structures establishes a clear sense in which the relations over the set in the empirical relational structure can be represented by the order and addition relations obtaining over the real numbers.
There have been a number of recent efforts to reinterpret the formalism of RTM for the purposes of articulating a realist metaphysics of quantity. Footnote 2 We are quite sympathetic to what we take to be one central aspect of this project: reinterpreting the empirical relational structures of RTM as property spaces provides an apt characterization of the nature of the quantities arising in physical theories. There is another aspect of recent realist reinterpretations of RTM, however, which requires more careful scrutiny. In particular, a number of authors have recently advocated that in addition to reinterpreting the empirical relational structure, we ought to strengthen the representation theorems so that they establish the existence of an isomorphism rather than a homomorphism.
The move from homomorphism to isomorphism amounts to demanding that all of the structure of the number system in which the representation is sought can be projected back onto the empirical relational structure. The difficulty with this requirement is that certain aspects of the representations furnished by RTM are conventional. The original proponents of RTM were well aware of this, and on their operationalist interpretation of the formalism the conventionality of the representations is entirely unproblematic. Our worry is that the conventionality, together with the demand that the representations take the form of isomorphisms, leads to an unjustified pattern of inference concerning the nature of the empirical relational structure.
In order to make this worry explicit, we establish a new form of conventionality in the representations afforded by RTM. What we show is that there is an important sense in which the very number system in which one represents quantities like mass and length turns out to be conventional. More precisely, what we show is that positive closed extensive structures (PCES) are homomorphically representable in both the real and the rational numbers. If one conventionally selects the representation in the reals, and then demands isomorphism, this prejudges substantive questions about the nature of the qualitative attribute being represented. We argue that such questions can only be resolved through empirical investigation of the nature of the qualitative attribute, and hence conventionality together with the requirement of isomorphism can lead to unjustified inferences concerning the nature of physical quantities.
Our argument proceeds as follows. In section 2, we recall the basic elements of RTM and its operationalist interpretation. We then discuss how to reinterpret the formalism in terms of property spaces. In the third section we prove a series of results concerning the numerical representability of positive closed extensive structures in both the real and rational numbers. In section 4 we argue that these results demonstrate an important sense of conventionality in the choice of numerical structure for a certain class of quantities, and we discuss the impact of this conclusion for efforts to leverage the results of the representational theory of measurement for the metaphysics of quantity.
2 Property space interpretations of RTM
According to the operational interpretation of RTM, the numerical representation of a physical quantity is achieved by first enumerating a set of objects
![]() $A$
that have the quantity in question as one of their attributes. In the case of length we might take
$A$
that have the quantity in question as one of their attributes. In the case of length we might take
![]() $A$
to be a set of rigid rods of varying lengths. Such a collection of rods can be compared to one another and we introduce a comparison relation, denoted by
$A$
to be a set of rigid rods of varying lengths. Such a collection of rods can be compared to one another and we introduce a comparison relation, denoted by
![]() $ \succsim $
, such that, for any
$ \succsim $
, such that, for any
![]() $a,b \in A$
,
$a,b \in A$
,
![]() $a \,\succsim\, \it b$
if and only if (iff) the length of
$a \,\succsim\, \it b$
if and only if (iff) the length of
![]() $a$
is greater than that of
$a$
is greater than that of
![]() $b$
. We also define a concatenation relation, denoted by
$b$
. We also define a concatenation relation, denoted by
![]() $ \circ $
, such that, for any
$ \circ $
, such that, for any
![]() $a,b \in A$
,
$a,b \in A$
,
![]() $a \circ b$
can enter into the comparison relation with any
$a \circ b$
can enter into the comparison relation with any
![]() $c \in A$
. Taken together,
$c \in A$
. Taken together,
![]() $\langle A, \succsim, \circ \rangle $
forms the empirical relational structure.
$\langle A, \succsim, \circ \rangle $
forms the empirical relational structure.
The operationalist nature of the interpretation stems from the interpretation of
![]() $\succsim $
and
$\succsim $
and
![]() $ \circ $
as concrete comparison and concatenation procedures. In the case of length, to compare rods
$ \circ $
as concrete comparison and concatenation procedures. In the case of length, to compare rods
![]() $a$
and
$a$
and
![]() $b$
we place them side by side with one end of each aligned with one another. If at the other end
$b$
we place them side by side with one end of each aligned with one another. If at the other end
![]() $a$
extends past
$a$
extends past
![]() $b$
then
$b$
then
![]() $a \succ b$
, if
$a \succ b$
, if
![]() $b$
extends past
$b$
extends past
![]() $a$
then
$a$
then
![]() $b \succ a$
, and if neither rod can be determined to extend past the other then we have
$b \succ a$
, and if neither rod can be determined to extend past the other then we have
![]() $a\sim b$
. Concatenation is interpreted as placing the rods end on end. If we compare
$a\sim b$
. Concatenation is interpreted as placing the rods end on end. If we compare
![]() $c$
with
$c$
with
![]() $a$
placed end on end with
$a$
placed end on end with
![]() $b$
and find that
$b$
and find that
![]() $c$
extends past
$c$
extends past
![]() $a \circ b$
, then we have
$a \circ b$
, then we have
![]() $c \succ a \circ b$
.
$c \succ a \circ b$
.
The sense of numerical representability employed in RTM is then given by the following definition.
Definition 2.1
An empirical relational structure
![]() $\langle A, \succsim, \circ \rangle $
is homomorphically representable in a numerical relational structure
$\langle A, \succsim, \circ \rangle $
is homomorphically representable in a numerical relational structure
![]() $\langle B, \ge, + \rangle $
iff there exists a function
$\langle B, \ge, + \rangle $
iff there exists a function
![]() $\phi :A \to B$
such that,
$\phi :A \to B$
such that,
![]() $\forall a,b \in A$
:
$\forall a,b \in A$
:
-
(i)
 $a\, \succsim\, \it b$
iff
$a\, \succsim\, \it b$
iff
 $\phi \left( a \right) \ge \phi \left( b \right)$
;
$\phi \left( a \right) \ge \phi \left( b \right)$
; -
(ii)
 $\phi \left( {a \circ b} \right) = \phi \left( a \right) + \phi \left( b \right)$
.
$\phi \left( {a \circ b} \right) = \phi \left( a \right) + \phi \left( b \right)$
.
To generate a representation theorem, we need to articulate a particular empirical relational structure and a particular numerical relational structure. The numerical relational structure is typically taken to be
![]() $\langle \mathbb{R}, \ge, + \rangle $
, or perhaps
$\langle \mathbb{R}, \ge, + \rangle $
, or perhaps
![]() $\langle {\mathbb{R}_ + }, \ge, + \rangle $
. The precise nature of the empirical relational structure is articulated with axioms that specify the properties of
$\langle {\mathbb{R}_ + }, \ge, + \rangle $
. The precise nature of the empirical relational structure is articulated with axioms that specify the properties of
![]() $ \succsim $
and
$ \succsim $
and
![]() $ \circ $
. For quantities such as mass and length, the following empirical relational structure is employed.
$ \circ $
. For quantities such as mass and length, the following empirical relational structure is employed.
Definition 2.2 (Krantz et al. Reference Krantz, Luce, Suppes and Tversky2007, Definition 3.1, 73). Let
![]() $A$
be a non-empty set, let
$A$
be a non-empty set, let
![]() $\succsim$
be a binary relation on
$\succsim$
be a binary relation on
![]() $A$
, and let
$A$
, and let
![]() $ \circ $
be a closed binary operation on
$ \circ $
be a closed binary operation on
![]() $A$
. An empirical relational structure
$A$
. An empirical relational structure
![]() $\langle A, \succsim, \circ \rangle $
is a positive closed extensive structure iff,
$\langle A, \succsim, \circ \rangle $
is a positive closed extensive structure iff,
![]() $\forall a,b,c \in A$
, each of the following are satisfied:
$\forall a,b,c \in A$
, each of the following are satisfied:
-
(Connectedness) Either
 $a\, \succsim\, \it b$
or
$a\, \succsim\, \it b$
or
 $b \,\succsim\, \it a$
.
$b \,\succsim\, \it a$
. -
(Transitivity) If
 $a\, \succsim\, \it b$
and
$a\, \succsim\, \it b$
and
 $b \,\succsim\, \it c$
, then
$b \,\succsim\, \it c$
, then
 $a \,\succsim\, \it c$
.
$a \,\succsim\, \it c$
. -
(Weak associativity)
 $a \circ \left( {b \circ c} \right)\sim \left( {a \circ b} \right) \circ c$
.
$a \circ \left( {b \circ c} \right)\sim \left( {a \circ b} \right) \circ c$
. -
(Monotonicity)
 $a\, \succsim\, \it b$
iff
$a\, \succsim\, \it b$
iff
 $a \circ c \,\succsim\, \it b \circ c$
iff
$a \circ c \,\succsim\, \it b \circ c$
iff
 $c \circ a \,\succsim\, \it c \circ b$
.
$c \circ a \,\succsim\, \it c \circ b$
. -
(Archimedean) There exists a positive integer
 $n$
such that
$n$
such that
 $na\, \succsim\, \it b$
, where
$na\, \succsim\, \it b$
, where
 $na$
is defined inductively as
$na$
is defined inductively as
 $1a = a$
,
$1a = a$
,
 $\left( {n + 1} \right)a = na \circ a$
.
$\left( {n + 1} \right)a = na \circ a$
. -
(Positivity)
 $a \circ b \succ a$
.
$a \circ b \succ a$
. -
(Solvability) If
 $a \succ b$
, then there exists
$a \succ b$
, then there exists
 $c \in A$
such that
$c \in A$
such that
 $a\sim b \circ c$
.
$a\sim b \circ c$
.
The representation theorem then takes the following form.
Theorem 2.1 (Krantz et al. Reference Krantz, Luce, Suppes and Tversky2007, Theorem 3.1, 74, 80–81). Let
![]() $A$
be a non-empty set, let
$A$
be a non-empty set, let
![]() $ \succsim $
be a binary relation on
$ \succsim $
be a binary relation on
![]() $A$
, and let
$A$
, and let
![]() $ \circ $
be a closed binary operation on
$ \circ $
be a closed binary operation on
![]() $A$
. Then the following are equivalent:
$A$
. Then the following are equivalent:
-
(i)
 $\langle A, \succsim, \circ \rangle $
is a positive closed extensive structure.
$\langle A, \succsim, \circ \rangle $
is a positive closed extensive structure.
-
(ii)
 $\langle A, \succsim, \circ \rangle $
is homomorphically representable in
$\langle A, \succsim, \circ \rangle $
is homomorphically representable in
 $\langle {\mathbb{R}_ + }, \ge, + \rangle $
.
$\langle {\mathbb{R}_ + }, \ge, + \rangle $
.
The operationalist interpretation of the empirical relational structure suited the purposes of the original architects of the theory, but it is deficient as the basis for a metaphysics of the quantities that appear in physical theories. To take just one example, a strict operationalist interpretation requires that there exists an actual rod of each length that we want to represent numerically. But of course, there are many possible lengths for which there is no corresponding rod. If one is interested in leveraging the results of the representational theory of measurement in support of more metaphysically committal views about the nature of the quantities, we need a new way to interpret the empirical relational structure.
In the metaphysics literature it has become common to treat quantities as determinable properties which admit of a collection of determinates as their possible values. One promising strategy for the reinterpretation of the empirical relational structure is to understand the underlying set as a property space. That is, we can take the set
![]() $A$
in the empirical relational structure to be the set of all of the possible determinate values of the quantity, and
$A$
in the empirical relational structure to be the set of all of the possible determinate values of the quantity, and
![]() $ \succsim $
and
$ \succsim $
and
![]() $ \circ $
to be relations between determinate values of the quantity.
$ \circ $
to be relations between determinate values of the quantity.
Reinterpreting the qualitative domain as a property space suggests additional constraints on the function
![]() $\phi $
. On an operationalist interpretation, the order on
$\phi $
. On an operationalist interpretation, the order on
![]() $A$
is not required to be antisymmetric, since there may be distinct objects
$A$
is not required to be antisymmetric, since there may be distinct objects
![]() $a,b$
such that both
$a,b$
such that both
![]() $a\, \succsim\, \it b$
and
$a\, \succsim\, \it b$
and
![]() $b\, \succsim \,\it a$
. But the determinates of a given quantity are such that no distinct determinates may be tied with each other with respect to their ordering. So on a property space interpretation, it is reasonable to require that the order on
$b\, \succsim \,\it a$
. But the determinates of a given quantity are such that no distinct determinates may be tied with each other with respect to their ordering. So on a property space interpretation, it is reasonable to require that the order on
![]() $A$
be antisymmetric. We thus characterize a property space by adding antisymmetry to the list of axioms given in Definition 2.2, resulting in the following definition.
$A$
be antisymmetric. We thus characterize a property space by adding antisymmetry to the list of axioms given in Definition 2.2, resulting in the following definition.
Definition 2.3
A positive closed extensive structure
![]() $\langle A, \succsim, \circ \rangle $
is simply ordered iff,
$\langle A, \succsim, \circ \rangle $
is simply ordered iff,
![]() $\forall a,b \in A$
, the following is satisfied:
$\forall a,b \in A$
, the following is satisfied:
(Antisymmetry) If both
![]() $a\, \succsim\, \it b$
and
$a\, \succsim\, \it b$
and
![]() $b \,\succsim \,\it a$
, then
$b \,\succsim \,\it a$
, then
![]() $a$
is (numerically) identical with
$a$
is (numerically) identical with
![]() $b$
.
$b$
.
In combination with the two conditions on homomorphic representability given in Definition 2.1, the antisymmetry of the order on
![]() $A$
implies that
$A$
implies that
![]() $\phi $
is injective. Realist adaptations of RTM often require that the homomorphism
$\phi $
is injective. Realist adaptations of RTM often require that the homomorphism
![]() $\phi $
also be surjective, thereby replacing the notion of homomorphic representation with that of isomorphic representation.
Footnote 3
This is captured in the following strengthened notion of numerical representation.
$\phi $
also be surjective, thereby replacing the notion of homomorphic representation with that of isomorphic representation.
Footnote 3
This is captured in the following strengthened notion of numerical representation.
Definition 2.4
An empirical relational structure
![]() $\langle A, \succsim, \circ \rangle $
is isomorphically representable in a numerical relational structure
$\langle A, \succsim, \circ \rangle $
is isomorphically representable in a numerical relational structure
![]() $\langle B, \ge, + \rangle $
iff there exists a function
$\langle B, \ge, + \rangle $
iff there exists a function
![]() $\phi :A \to B$
such that,
$\phi :A \to B$
such that,
![]() $\forall a,b \in A$
:
$\forall a,b \in A$
:
-
(i)
 $a\, \succsim\, \it b$
iff
$a\, \succsim\, \it b$
iff
 $\phi \left( a \right) \ge \phi \left( b \right)$
;
$\phi \left( a \right) \ge \phi \left( b \right)$
; -
(ii)
 $\phi \left( {a \circ b} \right) = \phi \left( a \right) + \phi \left( b \right)$
;
$\phi \left( {a \circ b} \right) = \phi \left( a \right) + \phi \left( b \right)$
; -
(iii)
 $\phi $
is a bijection.
$\phi $
is a bijection.
As Wolff has it, requiring
![]() $\phi $
to be an isomorphism captures the realist commitment that “the rich structure of the numerical representation is projected back to the physical world” (Wolff Reference Wolff2020, 96).
$\phi $
to be an isomorphism captures the realist commitment that “the rich structure of the numerical representation is projected back to the physical world” (Wolff Reference Wolff2020, 96).
We can now make our worry explicit. Once one moves to requiring isomorphic representation, some features of the representations which were unproblematic when the empirical relational structures were interpreted operationally start to look quite problematic when they are interpreted as property spaces. What we have in mind in particular are conventional elements of the representation. The original developers of RTM were explicit that the interpretation of the relations in the numerical relational structure were conventional. Alternative interpretations of those relations yield equally good numerical representations. We think there is a response available to advocates of isomorphic representation in the case of this sense of conventionality. However, in the next section we show that the number system itself is conventionally chosen. This raises serious problems for inferences that involve projecting structure from the numerical relational structure back to the empirical relational structure.
3 Numerical representability in
 $\mathbb{R}$
and
$\mathbb{R}$
and
 $\mathbb{Q}$
$\mathbb{Q}$
Theorem 2.1 establishes that a relational structure is a positive closed extensive structure iff it is homomorphically representable in
![]() $\langle {\mathbb{R}_ + }, \ge, + \rangle $
. In this section we show that the use of the reals as the underlying set in the numerical relational structure is a conventional choice. Our strategy is to determine a class of empirical relational structures that are homomorphically representable in
$\langle {\mathbb{R}_ + }, \ge, + \rangle $
. In this section we show that the use of the reals as the underlying set in the numerical relational structure is a conventional choice. Our strategy is to determine a class of empirical relational structures that are homomorphically representable in
![]() $\langle {\mathbb{Q}_ + }, \ge, + \rangle $
, and then to explore the constraints that homomorphic representability in
$\langle {\mathbb{Q}_ + }, \ge, + \rangle $
, and then to explore the constraints that homomorphic representability in
![]() $\langle {\mathbb{Q}_ + }, \ge, + \rangle $
imposes on an empirical relational structure. To start, we first establish that there exist PCES that are not homomorphically representable in
$\langle {\mathbb{Q}_ + }, \ge, + \rangle $
imposes on an empirical relational structure. To start, we first establish that there exist PCES that are not homomorphically representable in
![]() $\langle {\mathbb{Q}_ + }, \ge, + \rangle $
.
Footnote 4
$\langle {\mathbb{Q}_ + }, \ge, + \rangle $
.
Footnote 4
Theorem 3.1
Not all positive closed extensive structures are homomorphically representable in
![]() $\langle {\mathbb{Q}_ + }, \ge, + \rangle $
.
$\langle {\mathbb{Q}_ + }, \ge, + \rangle $
.
While all PCES are homomorphically representable in
![]() $\langle {\mathbb{R}_ + }, \ge, + \rangle $
, not all PCES are homomorphically representable in
$\langle {\mathbb{R}_ + }, \ge, + \rangle $
, not all PCES are homomorphically representable in
![]() $\langle {\mathbb{Q}_ + }, \ge, + \rangle $
: being a PCES is not sufficient for being homomorphically representable in
$\langle {\mathbb{Q}_ + }, \ge, + \rangle $
: being a PCES is not sufficient for being homomorphically representable in
![]() $\langle {\mathbb{Q}_ + }, \ge, + \rangle $
. The following theorem demonstrates that any empirical relational structure that is homomorphically representable in
$\langle {\mathbb{Q}_ + }, \ge, + \rangle $
. The following theorem demonstrates that any empirical relational structure that is homomorphically representable in
![]() $\langle {\mathbb{Q}_ + }, \ge, + \rangle $
is also homorphically representable in
$\langle {\mathbb{Q}_ + }, \ge, + \rangle $
is also homorphically representable in
![]() $\langle {\mathbb{R}_ + }, \ge, + \rangle $
.
$\langle {\mathbb{R}_ + }, \ge, + \rangle $
.
Theorem 3.2
Let
![]() $A$
be a non-empty set, let
$A$
be a non-empty set, let
![]() $ \succsim $
be a binary relation on
$ \succsim $
be a binary relation on
![]() $A$
, and let
$A$
, and let
![]() $ \circ $
be a closed binary operation on
$ \circ $
be a closed binary operation on
![]() $A$
. If
$A$
. If
![]() $\langle A, \succsim, \circ \rangle $
is homomorphically representable in
$\langle A, \succsim, \circ \rangle $
is homomorphically representable in
![]() $\langle {\mathbb{Q}_ + }, \ge, + \rangle $
then
$\langle {\mathbb{Q}_ + }, \ge, + \rangle $
then
![]() $\langle A, \succsim, \circ \rangle $
is homomorphically representable in
$\langle A, \succsim, \circ \rangle $
is homomorphically representable in
![]() $\langle {\mathbb{R}_ + }, \ge, + \rangle $
.
$\langle {\mathbb{R}_ + }, \ge, + \rangle $
.
From Theorems 2.1 and 3.2, it follows that homomorphic representability of an empirical relational structure
![]() $\langle A, \succsim, \circ \rangle $
in
$\langle A, \succsim, \circ \rangle $
in
![]() $\langle {\mathbb{Q}_ + }, \ge, + \rangle $
implies that
$\langle {\mathbb{Q}_ + }, \ge, + \rangle $
implies that
![]() $\langle A, \succsim, \circ \rangle $
is a PCES. Then, from Theorem 3.1, it follows that, in addition to the axioms for PCES, some further constraint delineates those structures that are homomorphically representable in
$\langle A, \succsim, \circ \rangle $
is a PCES. Then, from Theorem 3.1, it follows that, in addition to the axioms for PCES, some further constraint delineates those structures that are homomorphically representable in
![]() $\langle {\mathbb{Q}_ + }, \ge, + \rangle $
. This constraint is captured by the following axiom.
$\langle {\mathbb{Q}_ + }, \ge, + \rangle $
. This constraint is captured by the following axiom.
Definition 3.1 A positive closed extensive structure is commensurable if it satisfies the following axiom:
(Commensurability) For every
![]() $a,b \in A$
, there exists
$a,b \in A$
, there exists
![]() $c \in A$
and positive integers
$c \in A$
and positive integers
![]() $m,n$
such that
$m,n$
such that
![]() $a\sim mc$
and
$a\sim mc$
and
![]() $b\sim nc$
.
$b\sim nc$
.
A PCES is incommensurable if it does not satisfy commensurability.
Being a commensurable PCES is necessary and sufficient for being homomorphically representable in
![]() $\langle {\mathbb{Q}_ + }, \ge, + \rangle $
.
$\langle {\mathbb{Q}_ + }, \ge, + \rangle $
.
Theorem 3.3
Let
![]() $\langle A, \succsim, \circ \rangle $
be a positive closed extensive structure. Then the following are equivalent:
$\langle A, \succsim, \circ \rangle $
be a positive closed extensive structure. Then the following are equivalent:
-
(i)
 $\langle A, \succsim, \circ \rangle $
is commensurable.
$\langle A, \succsim, \circ \rangle $
is commensurable.
-
(ii)
 $\langle A, \succsim, \circ \rangle $
is homomorphically representable in
$\langle A, \succsim, \circ \rangle $
is homomorphically representable in
 $\langle {\mathbb{Q}_ + }, \ge, + \rangle $
.
$\langle {\mathbb{Q}_ + }, \ge, + \rangle $
.
Theorem 3.3 establishes that a representation theorem formulated in terms of necessary and sufficient conditions for homomorphic representation in
![]() $\langle {\mathbb{Q}_ + }, \ge, + \rangle $
is available, provided that the represented PCES is stipulated to be commensurable. Theorem 2.1 establishes that
$\langle {\mathbb{Q}_ + }, \ge, + \rangle $
is available, provided that the represented PCES is stipulated to be commensurable. Theorem 2.1 establishes that
![]() $\langle {\mathbb{R}_ + }, \ge, + \rangle $
can accommodate homomorphic representation of any PCES. This might be taken to suggest that
$\langle {\mathbb{R}_ + }, \ge, + \rangle $
can accommodate homomorphic representation of any PCES. This might be taken to suggest that
![]() $\langle {\mathbb{R}_ + }, \ge, + \rangle $
is to be favored for being generally applicable to any PCES, whereas the applicability of
$\langle {\mathbb{R}_ + }, \ge, + \rangle $
is to be favored for being generally applicable to any PCES, whereas the applicability of
![]() $\langle {\mathbb{Q}_ + }, \ge, + \rangle $
is limited to those PCES that are commensurable. It should be noted that this difference in scope of applicability is a result of the fact that
$\langle {\mathbb{Q}_ + }, \ge, + \rangle $
is limited to those PCES that are commensurable. It should be noted that this difference in scope of applicability is a result of the fact that
![]() $\langle {\mathbb{R}_ + }, \ge, + \rangle $
contains
$\langle {\mathbb{R}_ + }, \ge, + \rangle $
contains
![]() $\langle {\mathbb{Q}_ + }, \ge, + \rangle $
as a substructure, which implies that any homomorphism into
$\langle {\mathbb{Q}_ + }, \ge, + \rangle $
as a substructure, which implies that any homomorphism into
![]() $\langle {\mathbb{Q}_ + }, \ge, + \rangle $
can be regarded as a homomorphism into
$\langle {\mathbb{Q}_ + }, \ge, + \rangle $
can be regarded as a homomorphism into
![]() $\langle {\mathbb{R}_ + }, \ge, + \rangle $
. Thus, any empirical relational structure that is homomorphically representable in
$\langle {\mathbb{R}_ + }, \ge, + \rangle $
. Thus, any empirical relational structure that is homomorphically representable in
![]() $\langle {\mathbb{Q}_ + }, \ge, + \rangle $
is also homomorphically representable in
$\langle {\mathbb{Q}_ + }, \ge, + \rangle $
is also homomorphically representable in
![]() $\langle {\mathbb{R}_ + }, \ge, + \rangle $
.
$\langle {\mathbb{R}_ + }, \ge, + \rangle $
.
The situation is different if we require isomorphic representation. Being isomorphically representable in
![]() $\langle {\mathbb{R}_ + }, \ge, + \rangle $
and being isomorphically representable in
$\langle {\mathbb{R}_ + }, \ge, + \rangle $
and being isomorphically representable in
![]() $\langle {\mathbb{Q}_ + }, \ge, + \rangle $
are mutually exclusive. The general applicability of
$\langle {\mathbb{Q}_ + }, \ge, + \rangle $
are mutually exclusive. The general applicability of
![]() $\langle {\mathbb{R}_ + }, \ge, + \rangle $
for representation of PCES as established by Theorem 2.1 does not survive the move from homomorphic to isomorphic representation. To demand that a PCES be isomorphically representable in
$\langle {\mathbb{R}_ + }, \ge, + \rangle $
for representation of PCES as established by Theorem 2.1 does not survive the move from homomorphic to isomorphic representation. To demand that a PCES be isomorphically representable in
![]() $\langle {\mathbb{R}_ + }, \ge, + \rangle $
is effectively to stipulate that the PCES is incommensurable.
$\langle {\mathbb{R}_ + }, \ge, + \rangle $
is effectively to stipulate that the PCES is incommensurable.
In the context of homomorphic representation,
![]() $\langle {\mathbb{R}_ + }, \ge, + \rangle $
accommodates representation of both commensurable and incommensurable PCES. But isomorphic representation of a PCES in
$\langle {\mathbb{R}_ + }, \ge, + \rangle $
accommodates representation of both commensurable and incommensurable PCES. But isomorphic representation of a PCES in
![]() $\langle {\mathbb{R}_ + }, \ge, + \rangle $
requires that the represented PCES be incommensurable, as established by the next result.
$\langle {\mathbb{R}_ + }, \ge, + \rangle $
requires that the represented PCES be incommensurable, as established by the next result.
Theorem 3.4
Let
![]() $\langle A, \succsim, \circ \rangle $
be a positive, closed, extensive structure. If
$\langle A, \succsim, \circ \rangle $
be a positive, closed, extensive structure. If
![]() $\langle A, \succsim, \circ \rangle $
is isomorphically representable in
$\langle A, \succsim, \circ \rangle $
is isomorphically representable in
![]() $\langle {\mathbb{R}_ + }, \ge, + \rangle $
, then
$\langle {\mathbb{R}_ + }, \ge, + \rangle $
, then
![]() $\langle A, \succsim, \circ \rangle $
is incommensurable.
$\langle A, \succsim, \circ \rangle $
is incommensurable.
Theorem 2.1 establishes that any PCES is homomorphically representable in
![]() $\langle {\mathbb{R}_ + }, \ge, + \rangle $
, but this is not sufficient to determine whether the PCES is commensurable or incommensurable. If we demand a PCES to be isomorphically representable in
$\langle {\mathbb{R}_ + }, \ge, + \rangle $
, but this is not sufficient to determine whether the PCES is commensurable or incommensurable. If we demand a PCES to be isomorphically representable in
![]() $\langle {\mathbb{R}_ + }, \ge, + \rangle $
, then it follows from Theorem 3.4 that we thereby indirectly demand the PCES to be incommensurable. The following corollary emphasizes this point.
$\langle {\mathbb{R}_ + }, \ge, + \rangle $
, then it follows from Theorem 3.4 that we thereby indirectly demand the PCES to be incommensurable. The following corollary emphasizes this point.
Corollary 3.4.1. No commensurable PCES is isomorphically representable in
![]() $\langle {\mathbb{R}_ + }, \ge, + \rangle $
.
$\langle {\mathbb{R}_ + }, \ge, + \rangle $
.
Similarly, if we demand a PCES to be isomorphically representable in
![]() $\langle {\mathbb{Q}_ + }, \ge, + \rangle $
, then we indirectly demand that it is commensurable.
$\langle {\mathbb{Q}_ + }, \ge, + \rangle $
, then we indirectly demand that it is commensurable.
Theorem 3.5
Let
![]() $\langle A, \succsim, \circ \rangle $
be a positive, closed, extensive structure. If
$\langle A, \succsim, \circ \rangle $
be a positive, closed, extensive structure. If
![]() $\langle A, \succsim, \circ \rangle $
is isomorphically representable in
$\langle A, \succsim, \circ \rangle $
is isomorphically representable in
![]() $\langle {\mathbb{Q}_ + }, \ge, + \rangle $
, then
$\langle {\mathbb{Q}_ + }, \ge, + \rangle $
, then
![]() $\langle A, \succsim, \circ \rangle $
is commensurable.
$\langle A, \succsim, \circ \rangle $
is commensurable.
Corollary 3.5.1. No incommensurable PCES is isomorphically representable in
![]() $\langle {\mathbb{Q}_ + }, \ge, + \rangle $
.
$\langle {\mathbb{Q}_ + }, \ge, + \rangle $
.
Taken together, the results presented in this section establish a sense in which the the use of the reals in representations of PCES is conventional. There exist PCES which are homomorphically representable just as well in the rationals as they are in the reals. Absent additional argumentation, we don’t see any reason to prefer the representation in the reals to representation in the rationals. Defaulting to a representation based on one or the other of the number systems is to make a conventional choice. This conventionality combines with the move to isomorphic representation in a perhaps unexpected manner. If we naively demand that our conventional homomorphic representation in the reals can be extended to an isomorphic representation, we indirectly demand that the PCES exhibits incommensurability. If instead we conventionally start from the homomorphic representation in the rationals, and then demand isomorphism, we indirectly demand that the PCES exhibits commensurability. But conventional representational choices aren’t the sort of thing that can tell us anything at all about the nature of the structure being represented, and so we think that the motivations for making the switch to isomorphic representation require further elaboration.
4 Conclusion
The results of the last section are not intended to undermine metaphysical readings of the representational theory of measurement. Rather, they provide reason to revisit what the commitments of the realist about quantities are supposed to be. In recent discussions, realism has become bound up with the demand for isomorphic representation. We propose that realism about quantities need not be coupled with this demand. One can be a realist by taking a particular property space to capture the real structure of a physical quantity. That a quantity understood in this way can be represented in some number system isomorphically is an additional commitment that goes beyond realism.
A Proofs of theorems
Proof of Theorem 3.1. An example of a PCES that is not homomorphically representable in
![]() $\langle {\mathbb{Q}_ + }, \ge, + \rangle $
is as follows: Let
$\langle {\mathbb{Q}_ + }, \ge, + \rangle $
is as follows: Let
![]() $A = {\mathbb{R}_ + }$
, let
$A = {\mathbb{R}_ + }$
, let
![]() $ \succsim $
be
$ \succsim $
be
![]() $ \ge $
(the usual non-strict order on
$ \ge $
(the usual non-strict order on
![]() ${\mathbb{R}_ + }$
), and let
${\mathbb{R}_ + }$
), and let
![]() $ \circ $
be
$ \circ $
be
![]() $ + $
(the usual addition operation on
$ + $
(the usual addition operation on
![]() ${\mathbb{R}_ + }$
).
Footnote 5
Showing that
${\mathbb{R}_ + }$
).
Footnote 5
Showing that
![]() $\langle A, \succsim, \circ \rangle $
satisfies Definition 2.2 is straightforward. Suppose for contradiction that
$\langle A, \succsim, \circ \rangle $
satisfies Definition 2.2 is straightforward. Suppose for contradiction that
![]() $\langle A, \succsim, \circ \rangle $
is homomorphically representable in
$\langle A, \succsim, \circ \rangle $
is homomorphically representable in
![]() $\langle {\mathbb{Q}_ + }, \ge, + \rangle $
. Then there exists a function
$\langle {\mathbb{Q}_ + }, \ge, + \rangle $
. Then there exists a function
![]() $\phi :A \to {\mathbb{Q}_ + }$
satisfying the two conditions given in Definition 2.1. Since
$\phi :A \to {\mathbb{Q}_ + }$
satisfying the two conditions given in Definition 2.1. Since
![]() $A = {\mathbb{R}_ + }$
,
$A = {\mathbb{R}_ + }$
,
![]() $A$
is uncountable and, since
$A$
is uncountable and, since
![]() ${\mathbb{Q}_ + }$
is countable, we have that
${\mathbb{Q}_ + }$
is countable, we have that
![]() $\left| A \right| \gt \left| {{\mathbb{Q}_ + }} \right|$
. It follows that
$\left| A \right| \gt \left| {{\mathbb{Q}_ + }} \right|$
. It follows that
![]() $\phi :A \to {\mathbb{Q}_ + }$
is not injective, and thus there exist
$\phi :A \to {\mathbb{Q}_ + }$
is not injective, and thus there exist
![]() $a,b \in A$
such that
$a,b \in A$
such that
![]() $a \ne b$
and
$a \ne b$
and
![]() $\phi \left( a \right) = \phi \left( b \right)$
. Since
$\phi \left( a \right) = \phi \left( b \right)$
. Since
![]() $ \ge $
is a total order on
$ \ge $
is a total order on
![]() ${\mathbb{R}_ + }$
, we have that, for every
${\mathbb{R}_ + }$
, we have that, for every
![]() $x,y \in {\mathbb{R}_ + }$
,
$x,y \in {\mathbb{R}_ + }$
,
![]() $x \ne y$
iff either
$x \ne y$
iff either
![]() $x \gt y$
or
$x \gt y$
or
![]() $y \gt x$
(where
$y \gt x$
(where
![]() $ \gt $
is the strict total order associated with
$ \gt $
is the strict total order associated with
![]() $ \ge $
). There thus exist
$ \ge $
). There thus exist
![]() $a,b \in A$
such that either
$a,b \in A$
such that either
![]() $a \succ b$
or
$a \succ b$
or
![]() $b \succ a$
and
$b \succ a$
and
![]() $\phi \left( a \right) = \phi \left( b \right)$
. Suppose without loss of generality that
$\phi \left( a \right) = \phi \left( b \right)$
. Suppose without loss of generality that
![]() $a \succ b$
. From
$a \succ b$
. From
![]() $\phi \left( a \right) = \phi \left( b \right)$
we have
$\phi \left( a \right) = \phi \left( b \right)$
we have
![]() $\phi \left( b \right) \ge \phi \left( a \right)$
and thus, by Condition (i) from Definition 2.1,
$\phi \left( b \right) \ge \phi \left( a \right)$
and thus, by Condition (i) from Definition 2.1,
![]() $b \,\succsim \,\it a$
, a contradiction. □
$b \,\succsim \,\it a$
, a contradiction. □
Proof of Theorem 3.2. Suppose that
![]() $A$
is a non-empty set,
$A$
is a non-empty set,
![]() $ \succsim $
is a binary relation on
$ \succsim $
is a binary relation on
![]() $A$
,
$A$
,
![]() $ \circ $
is a closed binary operation on
$ \circ $
is a closed binary operation on
![]() $A$
, and that
$A$
, and that
![]() $\langle A, \succsim, \circ \rangle $
is homomorphically representable in
$\langle A, \succsim, \circ \rangle $
is homomorphically representable in
![]() $\langle {\mathbb{Q}_ + }, \ge, + \rangle $
. Then there exists a function
$\langle {\mathbb{Q}_ + }, \ge, + \rangle $
. Then there exists a function
![]() $\phi :A \to {\mathbb{Q}_ + }$
satisfying the two conditions given in Definition 2.1. Since
$\phi :A \to {\mathbb{Q}_ + }$
satisfying the two conditions given in Definition 2.1. Since
![]() $\langle {\mathbb{Q}_ + }, \ge, + \rangle $
is a substructure of
$\langle {\mathbb{Q}_ + }, \ge, + \rangle $
is a substructure of
![]() $\langle {\mathbb{R}_ + }, \ge, + \rangle $
we can define the function
$\langle {\mathbb{R}_ + }, \ge, + \rangle $
we can define the function
![]() $\psi :A \to {\mathbb{R}_ + }$
as
$\psi :A \to {\mathbb{R}_ + }$
as
![]() $\psi \left( a \right): = \phi \left( a \right)$
for every
$\psi \left( a \right): = \phi \left( a \right)$
for every
![]() $a \in A$
, and we have that
$a \in A$
, and we have that
![]() $\psi $
satisfies the two conditions given in Definition 2.1.□
$\psi $
satisfies the two conditions given in Definition 2.1.□
Proof of Theorem 3.3. Let
![]() $\langle A, \succsim, \circ \rangle $
be a PCES. Suppose that
$\langle A, \succsim, \circ \rangle $
be a PCES. Suppose that
![]() $\langle A, \succsim, \circ \rangle $
is commensurable. Let
$\langle A, \succsim, \circ \rangle $
is commensurable. Let
![]() $a,b \in A$
. By (Commensurability),
$a,b \in A$
. By (Commensurability),
![]() $\exists c \in A$
and
$\exists c \in A$
and
![]() $m,n \in {\mathbb{Z}_ + }$
such that
$m,n \in {\mathbb{Z}_ + }$
such that
![]() $a\sim mc$
and
$a\sim mc$
and
![]() $b\sim nc$
. Thus
$b\sim nc$
. Thus
Let
![]() ${F_{\left( {a,b} \right)}}$
be the set of all fractions
${F_{\left( {a,b} \right)}}$
be the set of all fractions
![]() $m/n$
such that
$m/n$
such that
![]() $na\sim mb$
.
$na\sim mb$
.
![]() ${F_{\left( {a,b} \right)}}$
is non-empty, and if
${F_{\left( {a,b} \right)}}$
is non-empty, and if
![]() ${m/n}, {m{\rm{'}}/n{\rm{'}}} \in {F_{\left( {a,b} \right)}}$
we have that
${m/n}, {m{\rm{'}}/n{\rm{'}}} \in {F_{\left( {a,b} \right)}}$
we have that
Thus,
![]() $\left( {n{\rm{'}}n} \right)a\sim \left( {mn{\rm{'}}} \right)b$
and
$\left( {n{\rm{'}}n} \right)a\sim \left( {mn{\rm{'}}} \right)b$
and
![]() $\left( {nm{\rm{'}}} \right)b\sim \left( {n{\rm{'}}n} \right)a$
, so that
$\left( {nm{\rm{'}}} \right)b\sim \left( {n{\rm{'}}n} \right)a$
, so that
![]() $\left( {mn{\rm{'}}} \right)b\sim \left( {nm{\rm{'}}} \right)b$
. By Lemma B.7, it follows that
$\left( {mn{\rm{'}}} \right)b\sim \left( {nm{\rm{'}}} \right)b$
. By Lemma B.7, it follows that
![]() $mn{\rm{'}} = nm{\rm{'}}$
. So, given any
$mn{\rm{'}} = nm{\rm{'}}$
. So, given any
![]() $\left( {a,b} \right) \in A \times A$
, the fractions in
$\left( {a,b} \right) \in A \times A$
, the fractions in
![]() ${F_{\left( {a,b} \right)}}$
are all equivalent, so that
${F_{\left( {a,b} \right)}}$
are all equivalent, so that
![]() ${F_{\left( {a,b} \right)}}$
determines a unique positive rational number. Now, choose an arbitrary
${F_{\left( {a,b} \right)}}$
determines a unique positive rational number. Now, choose an arbitrary
![]() $e \in A$
, and define the function
$e \in A$
, and define the function
![]() $\phi :A \to {\mathbb{Q}_ + }$
as follows:
$\phi :A \to {\mathbb{Q}_ + }$
as follows:
![]() $\phi \left( a \right) = m/n$
, where
$\phi \left( a \right) = m/n$
, where
![]() $na\sim me$
. We now show that
$na\sim me$
. We now show that
![]() $\phi $
satisfies both conditions stated in Definition 2.1.
$\phi $
satisfies both conditions stated in Definition 2.1.
Condition (ii):
![]() $\phi \left( {a \circ b} \right) = \phi \left( a \right) + \phi \left( b \right)$
. Let
$\phi \left( {a \circ b} \right) = \phi \left( a \right) + \phi \left( b \right)$
. Let
![]() $a,b \in A$
, and let
$a,b \in A$
, and let
![]() $\phi \left( a \right) = {m_a}/{n_a}$
and
$\phi \left( a \right) = {m_a}/{n_a}$
and
![]() $\phi \left( b \right) = {m_b}/{n_b}$
. Then
$\phi \left( b \right) = {m_b}/{n_b}$
. Then
![]() ${n_a}a\sim {m_a}e$
and
${n_a}a\sim {m_a}e$
and
![]() ${n_b}b\sim {m_b}e$
. Define
${n_b}b\sim {m_b}e$
. Define
![]() $n: = {n_a}{n_b}$
,
$n: = {n_a}{n_b}$
,
![]() $m: = {m_a}{n_b}$
,
$m: = {m_a}{n_b}$
,
![]() $m{\rm{'}}: = {m_b}{n_a}$
. Then
$m{\rm{'}}: = {m_b}{n_a}$
. Then
![]() $\phi \left( a \right) = {m_a}/{n_a} = m/n$
and
$\phi \left( a \right) = {m_a}/{n_a} = m/n$
and
![]() $\phi \left( b \right) = {m_b}/{n_b} = m{\rm{'}}/n$
, so that
$\phi \left( b \right) = {m_b}/{n_b} = m{\rm{'}}/n$
, so that
![]() $na\sim me$
and
$na\sim me$
and
![]() $nb\sim m{\rm{'}}e$
. Then, by Lemma B.3,
$nb\sim m{\rm{'}}e$
. Then, by Lemma B.3,
![]() $na \circ nb\sim me \circ m{\rm{'}}e$
, and, by Lemmas B.4 and B.1,
$na \circ nb\sim me \circ m{\rm{'}}e$
, and, by Lemmas B.4 and B.1,
![]() $n\left( {a \circ b} \right)\sim \left( {m + m{\rm{'}}} \right)e$
. Thus
$n\left( {a \circ b} \right)\sim \left( {m + m{\rm{'}}} \right)e$
. Thus
![]() $\phi \left( {a \circ b} \right) = \left( {m + m{\rm{'}}} \right)/n = \phi \left( a \right) + \phi \left( b \right)$
.
$\phi \left( {a \circ b} \right) = \left( {m + m{\rm{'}}} \right)/n = \phi \left( a \right) + \phi \left( b \right)$
.
Condition (i):
![]() $a\, \succsim\, b$
iff
$a\, \succsim\, b$
iff
![]() $\phi \left( a \right) \ge \phi \left( b \right)$
. Let
$\phi \left( a \right) \ge \phi \left( b \right)$
. Let
![]() $a,b \in A$
with
$a,b \in A$
with
![]() $a\, \succsim\, b$
. In the case where
$a\, \succsim\, b$
. In the case where
![]() $a\sim b$
, let
$a\sim b$
, let
![]() $\phi \left( a \right) = m/n$
.
$\phi \left( a \right) = m/n$
.
![]() $\phi \left( a \right) = m/n$
iff
$\phi \left( a \right) = m/n$
iff
![]() $na\sim me$
, and
$na\sim me$
, and
![]() $a\sim b$
iff
$a\sim b$
iff
![]() $na\sim nb$
(by Lemma B.7). Thus, (
$na\sim nb$
(by Lemma B.7). Thus, (
![]() $a\sim b$
and
$a\sim b$
and
![]() $\phi \left( a \right) = m/n$
) iff
$\phi \left( a \right) = m/n$
) iff
![]() $nb\sim me$
iff
$nb\sim me$
iff
![]() $\phi \left( b \right) = m/n$
. In the case where
$\phi \left( b \right) = m/n$
. In the case where
![]() $a \succ b$
, by (Solvability)
$a \succ b$
, by (Solvability)
![]() $\exists c \in A$
such that
$\exists c \in A$
such that
![]() $a\sim b \circ c$
. Conversely, if
$a\sim b \circ c$
. Conversely, if
![]() $a\sim b \circ c$
, then since
$a\sim b \circ c$
, then since
![]() $b \circ c \succ b$
—by (Positivity)—we have, by Lemma B.5, that
$b \circ c \succ b$
—by (Positivity)—we have, by Lemma B.5, that
![]() $a \succ b$
. Thus,
$a \succ b$
. Thus,
![]() $a \succ b$
iff
$a \succ b$
iff
![]() $\exists c \in A$
such that
$\exists c \in A$
such that
![]() $a\sim b \circ c$
. By the previous case,
$a\sim b \circ c$
. By the previous case,
![]() $a\sim b \circ c$
iff
$a\sim b \circ c$
iff
![]() $\phi \left( a \right) = \phi \left( {b \circ c} \right) = \phi \left( b \right) + \phi \left( c \right)$
, by Condition (ii). Since
$\phi \left( a \right) = \phi \left( {b \circ c} \right) = \phi \left( b \right) + \phi \left( c \right)$
, by Condition (ii). Since
![]() $\phi \left( c \right)$
is positive,
$\phi \left( c \right)$
is positive,
![]() $\phi \left( a \right) = \phi \left( b \right) + \phi \left( c \right)$
iff
$\phi \left( a \right) = \phi \left( b \right) + \phi \left( c \right)$
iff
![]() $\phi \left( a \right) \gt \phi \left( b \right)$
.
$\phi \left( a \right) \gt \phi \left( b \right)$
.
Next, suppose that
![]() $\langle A, \succsim, \circ \rangle $
is homomorphically representable in
$\langle A, \succsim, \circ \rangle $
is homomorphically representable in
![]() $\langle {\mathbb{Q}_ + }, \ge\!\!, + \rangle $
. Let
$\langle {\mathbb{Q}_ + }, \ge\!\!, + \rangle $
. Let
![]() $a,b \in A$
. We will show that
$a,b \in A$
. We will show that
![]() $\exists c \in A$
and
$\exists c \in A$
and
![]() $\exists m,n \in {\mathbb{Z}_ + }$
such that
$\exists m,n \in {\mathbb{Z}_ + }$
such that
![]() $a\sim nc$
and
$a\sim nc$
and
![]() $b\sim mc$
. The case where
$b\sim mc$
. The case where
![]() $a\sim b$
is trivial, so let
$a\sim b$
is trivial, so let
![]() $a \succ b$
. Let
$a \succ b$
. Let
![]() $N\left( {a,b} \right)$
be the greatest integer such that
$N\left( {a,b} \right)$
be the greatest integer such that
![]() $a \succ N\left( {a,b} \right)b$
—the (Archimedean) axiom ensures the existence of
$a \succ N\left( {a,b} \right)b$
—the (Archimedean) axiom ensures the existence of
![]() $N\left( {a,b} \right)$
. Then, by (Solvability),
$N\left( {a,b} \right)$
. Then, by (Solvability),
![]() $\exists {c_0} \in A$
such that
$\exists {c_0} \in A$
such that
![]() $a\sim N\left( {a,b} \right)b \circ {c_0}$
, and
$a\sim N\left( {a,b} \right)b \circ {c_0}$
, and
![]() $b\,\succsim\,\it {c_0}$
. If
$b\,\succsim\,\it {c_0}$
. If
![]() ${c_0}\sim b$
, then
${c_0}\sim b$
, then
![]() $a\sim \left[ {N\left( {a,b} \right) + 1} \right]b$
and then
$a\sim \left[ {N\left( {a,b} \right) + 1} \right]b$
and then
![]() $n = N\left( {a,b} \right) + 1$
,
$n = N\left( {a,b} \right) + 1$
,
![]() $m = 1$
,
$m = 1$
,
![]() $c = b$
gives the desired result. So let
$c = b$
gives the desired result. So let
![]() $b \succ {c_0}$
. Then
$b \succ {c_0}$
. Then
![]() $\exists {c_1} \in A$
such that
$\exists {c_1} \in A$
such that
![]() $b\sim N\left( {b,{c_0}} \right){c_0} \circ {c_1}$
, and
$b\sim N\left( {b,{c_0}} \right){c_0} \circ {c_1}$
, and
![]() ${c_0} \,\succsim\,\it {c_1}$
. If
${c_0} \,\succsim\,\it {c_1}$
. If
![]() ${c_1}\sim {c_0}$
, then
${c_1}\sim {c_0}$
, then
![]() $b\sim \left[ {N\left( {b,{c_0}} \right) + 1} \right]{c_0}$
and then
$b\sim \left[ {N\left( {b,{c_0}} \right) + 1} \right]{c_0}$
and then
![]() $n = N\left( {a,b} \right)\left[ {N\left( {b,{c_0}} \right) + 1} \right]$
,
$n = N\left( {a,b} \right)\left[ {N\left( {b,{c_0}} \right) + 1} \right]$
,
![]() $m = N\left( {b,{c_0}} \right) + 1$
,
$m = N\left( {b,{c_0}} \right) + 1$
,
![]() $c = {c_0}$
gives the desired result. Letting
$c = {c_0}$
gives the desired result. Letting
![]() ${c_0} \succ {c_1}$
, we may continue in this fashion:
${c_0} \succ {c_1}$
, we may continue in this fashion:
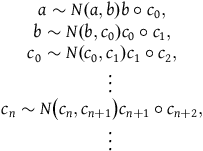 $$\matrix{ {a\sim N\left( {a,b} \right)b\circ {c_0},} \cr {b\sim N\left( {b,{c_0}} \right){c_0}\circ {c_1},} \cr {{c_0}\sim N\left( {{c_0},{c_1}} \right){c_1}\circ {c_2},} \cr {\;\;\; \vdots } \cr {{c_n}\sim N\left( {{c_n},{c_{n + 1}}} \right){c_{n + 1}}\circ {c_{n + 2}},} \cr {\;\;\; \vdots } \cr } $$
$$\matrix{ {a\sim N\left( {a,b} \right)b\circ {c_0},} \cr {b\sim N\left( {b,{c_0}} \right){c_0}\circ {c_1},} \cr {{c_0}\sim N\left( {{c_0},{c_1}} \right){c_1}\circ {c_2},} \cr {\;\;\; \vdots } \cr {{c_n}\sim N\left( {{c_n},{c_{n + 1}}} \right){c_{n + 1}}\circ {c_{n + 2}},} \cr {\;\;\; \vdots } \cr } $$
This process can be iterated for
![]() ${c_n}$
as long as
${c_n}$
as long as
![]() ${c_{n + 1}} \succ {c_{n + 2}}$
. If we arrive at a step for which
${c_{n + 1}} \succ {c_{n + 2}}$
. If we arrive at a step for which
![]() ${c_{n + 2}}\sim {c_{n + 1}}$
, we will have that
${c_{n + 2}}\sim {c_{n + 1}}$
, we will have that
![]() ${c_n}\sim \left[ {N\left( {{c_n},{c_{n + 1}}} \right) + 1} \right]{c_{n + 1}}$
and thus that
${c_n}\sim \left[ {N\left( {{c_n},{c_{n + 1}}} \right) + 1} \right]{c_{n + 1}}$
and thus that
![]() $a\sim N\left( {a,b} \right)b \circ N\left( {{c_0},{c_1}} \right){c_1} \circ N\left( {{c_2},{c_3}} \right){c_3} \circ \cdots \circ \left[ {N\left( {{c_n},{c_{n + 1}}} \right) + 1} \right]{c_{n + 1}}$
, from which it follows that
$a\sim N\left( {a,b} \right)b \circ N\left( {{c_0},{c_1}} \right){c_1} \circ N\left( {{c_2},{c_3}} \right){c_3} \circ \cdots \circ \left[ {N\left( {{c_n},{c_{n + 1}}} \right) + 1} \right]{c_{n + 1}}$
, from which it follows that
![]() $a\sim \left[ {N\left( {a,{c_{n + 1}}} \right) + 1} \right]{c_{n + 1}}$
and that
$a\sim \left[ {N\left( {a,{c_{n + 1}}} \right) + 1} \right]{c_{n + 1}}$
and that
![]() $b\sim \left[ {N\left( {b,{c_{n + 1}}} \right) + 1} \right]{c_{n + 1}}$
. So, if there exists
$b\sim \left[ {N\left( {b,{c_{n + 1}}} \right) + 1} \right]{c_{n + 1}}$
. So, if there exists
![]() $n{\rm{'}}$
such that
$n{\rm{'}}$
such that
![]() ${c_{n{\rm{'}} + 2}}\sim {c_{n{\rm{'}} + 1}}$
, then
${c_{n{\rm{'}} + 2}}\sim {c_{n{\rm{'}} + 1}}$
, then
![]() $n = N\left( {a,{c_{n{\rm{'}} + 1}}} \right) + 1$
,
$n = N\left( {a,{c_{n{\rm{'}} + 1}}} \right) + 1$
,
![]() $m = N\left( {b,{c_{n{\rm{'}} + 1}}} \right) + 1$
,
$m = N\left( {b,{c_{n{\rm{'}} + 1}}} \right) + 1$
,
![]() $c = {c_{n{\rm{'}} + 1}}$
gives the desired result. We show below that there exists
$c = {c_{n{\rm{'}} + 1}}$
gives the desired result. We show below that there exists
![]() $n{\rm{'}}$
such that
$n{\rm{'}}$
such that
![]() ${c_{n{\rm{'}} + 2}}\sim {c_{n{\rm{'}} + 1}}$
. By the supposition, there exists a function
${c_{n{\rm{'}} + 2}}\sim {c_{n{\rm{'}} + 1}}$
. By the supposition, there exists a function
![]() $\phi :A \to {\mathbb{Q}_ + }$
that satisfies Conditions (i) and (ii) from Definition 2.1. Thus, by the series of expressions in (1), we have that
$\phi :A \to {\mathbb{Q}_ + }$
that satisfies Conditions (i) and (ii) from Definition 2.1. Thus, by the series of expressions in (1), we have that
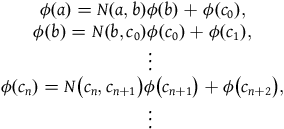 $$\matrix{ {\phi \left( a \right) = N\left( {a,b} \right)\phi \left( b \right) + \phi \left( {{c_0}} \right),} \cr {\phi \left( b \right) = N\left( {b,{c_0}} \right)\phi \left( {{c_0}} \right) + \phi \left( {{c_1}} \right),} \cr {\;\;\; \vdots } \cr {\phi \left( {{c_n}} \right) = N\left( {{c_n},{c_{n + 1}}} \right)\phi \left( {{c_{n + 1}}} \right) + \phi \left( {{c_{n + 2}}} \right),} \cr {\;\;\; \vdots } \cr } $$
$$\matrix{ {\phi \left( a \right) = N\left( {a,b} \right)\phi \left( b \right) + \phi \left( {{c_0}} \right),} \cr {\phi \left( b \right) = N\left( {b,{c_0}} \right)\phi \left( {{c_0}} \right) + \phi \left( {{c_1}} \right),} \cr {\;\;\; \vdots } \cr {\phi \left( {{c_n}} \right) = N\left( {{c_n},{c_{n + 1}}} \right)\phi \left( {{c_{n + 1}}} \right) + \phi \left( {{c_{n + 2}}} \right),} \cr {\;\;\; \vdots } \cr } $$
It follows that
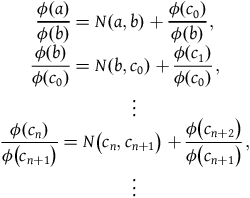 $${\matrix{ {\displaystyle{{\phi \left( a \right)} \over {\phi (b)}} = N\left( {a,b} \right) + {{\phi \left( {{c_0}} \right)} \over {\phi \left( b \right)}},} \cr {\displaystyle{{\phi \left( b \right)} \over {\phi \left( {{c_0}} \right)}} = N\left( {b,{c_0}} \right) + {{\phi \left( {{c_1}} \right)} \over {\phi \left( {{c_0}} \right)}},} \cr {\;\;\; \vdots } \cr {\displaystyle{{\phi \left( {{c_n}} \right)} \over {\phi \left( {{c_{n + 1}}} \right)}} = N\left( {{c_n},{c_{n + 1}}} \right) + {{\phi \left( {{c_{n + 2}}} \right)} \over {\phi \left( {{c_{n + 1}}} \right)}},} \cr {\;\;\; \vdots } \cr }} $$
$${\matrix{ {\displaystyle{{\phi \left( a \right)} \over {\phi (b)}} = N\left( {a,b} \right) + {{\phi \left( {{c_0}} \right)} \over {\phi \left( b \right)}},} \cr {\displaystyle{{\phi \left( b \right)} \over {\phi \left( {{c_0}} \right)}} = N\left( {b,{c_0}} \right) + {{\phi \left( {{c_1}} \right)} \over {\phi \left( {{c_0}} \right)}},} \cr {\;\;\; \vdots } \cr {\displaystyle{{\phi \left( {{c_n}} \right)} \over {\phi \left( {{c_{n + 1}}} \right)}} = N\left( {{c_n},{c_{n + 1}}} \right) + {{\phi \left( {{c_{n + 2}}} \right)} \over {\phi \left( {{c_{n + 1}}} \right)}},} \cr {\;\;\; \vdots } \cr }} $$
Notice that the second term of the right-hand side of each equation in series (3) is the reciprocal of the left-hand side of the subsequent equation. Thus,
![]() $\phi \left( a \right)/\phi \left( b \right)$
may be represented by the following continued fraction:
$\phi \left( a \right)/\phi \left( b \right)$
may be represented by the following continued fraction:
 $$N\left( {a,b} \right) + {1 \over {N\left( {b,{c_0}} \right) + \displaystyle{1 \over {N\left( {{c_0},{c_1}} \right) + \displaystyle{1 \over {N\left( {{c_1},{c_2}} \right) + \cdots }}}}}}$$
$$N\left( {a,b} \right) + {1 \over {N\left( {b,{c_0}} \right) + \displaystyle{1 \over {N\left( {{c_0},{c_1}} \right) + \displaystyle{1 \over {N\left( {{c_1},{c_2}} \right) + \cdots }}}}}}$$
A continued fraction is infinite iff its numerical value is irrational, and
![]() $\phi \left( a \right)/\phi \left( b \right) \in {\mathbb{Q}_ + }$
since
$\phi \left( a \right)/\phi \left( b \right) \in {\mathbb{Q}_ + }$
since
![]() $\phi \left( a \right),\phi \left( b \right) \in {\mathbb{Q}_ + }$
. The continued fraction (4) is therefore finite, and thus series (2) terminates at
$\phi \left( a \right),\phi \left( b \right) \in {\mathbb{Q}_ + }$
. The continued fraction (4) is therefore finite, and thus series (2) terminates at
![]() $\phi \left( {{c_{n{\rm{'}}}}} \right)$
, for some integer
$\phi \left( {{c_{n{\rm{'}}}}} \right)$
, for some integer
![]() $n{\rm{'}}$
. Thus, series (1) terminates with
$n{\rm{'}}$
. Thus, series (1) terminates with
![]() ${c_{n{\rm{'}}}}$
, which implies that
${c_{n{\rm{'}}}}$
, which implies that
![]() ${c_{n{\rm{'}} + 2}}\sim {c_{n{\rm{'}} + 1}}$
. □
${c_{n{\rm{'}} + 2}}\sim {c_{n{\rm{'}} + 1}}$
. □
Proof of Theorem 3.4. Let
![]() $\langle A, \succsim, \circ \rangle $
be a PCES and let
$\langle A, \succsim, \circ \rangle $
be a PCES and let
![]() $\phi :A \to {\mathbb{R}_ + }$
be a function satisfying Conditions (i), (ii), and (iii) from Definition 2.4. By Condition (iii),
$\phi :A \to {\mathbb{R}_ + }$
be a function satisfying Conditions (i), (ii), and (iii) from Definition 2.4. By Condition (iii),
![]() $\forall x \in {\mathbb{R}_ + }\exists !a \in A$
such that
$\forall x \in {\mathbb{R}_ + }\exists !a \in A$
such that
![]() $\phi \left( a \right) = x$
. Let
$\phi \left( a \right) = x$
. Let
![]() $a,e \in A$
be such that
$a,e \in A$
be such that
![]() $\phi \left( a \right) = \sqrt 2 $
and
$\phi \left( a \right) = \sqrt 2 $
and
![]() $\phi \left( e \right) = 1$
. Suppose for a contradiction that
$\phi \left( e \right) = 1$
. Suppose for a contradiction that
![]() $\exists c \in A$
and
$\exists c \in A$
and
![]() $\exists m,n \in {\mathbb{Z}_ + }$
such that
$\exists m,n \in {\mathbb{Z}_ + }$
such that
![]() $a\sim mc$
and
$a\sim mc$
and
![]() $e\sim nc$
. Then
$e\sim nc$
. Then
![]() $na\sim me$
, so that, by Condition (i),
$na\sim me$
, so that, by Condition (i),
![]() $\phi \left( {na} \right) = \phi \left( {me} \right)$
and thus, by Condition (ii),
$\phi \left( {na} \right) = \phi \left( {me} \right)$
and thus, by Condition (ii),
![]() $\phi \left( a \right) = \left( {m/n} \right)\phi \left( e \right) = \left( {m/n} \right)\left( 1 \right) = m/n$
. It follows that
$\phi \left( a \right) = \left( {m/n} \right)\phi \left( e \right) = \left( {m/n} \right)\left( 1 \right) = m/n$
. It follows that
![]() $\sqrt 2 = m/n$
where
$\sqrt 2 = m/n$
where
![]() $m,n \in {\mathbb{Z}_ + }$
, a contradiction. □
$m,n \in {\mathbb{Z}_ + }$
, a contradiction. □
Proof of Theorem 3.5. Let
![]() $\langle A, \succsim, \circ \rangle $
be a PCES and let
$\langle A, \succsim, \circ \rangle $
be a PCES and let
![]() $\phi :A \to {\mathbb{Q}_ + }$
be a function satisfying Conditions (i), (ii), and (iii) from Definition 2.4. Let
$\phi :A \to {\mathbb{Q}_ + }$
be a function satisfying Conditions (i), (ii), and (iii) from Definition 2.4. Let
![]() $a,b \in A$
, and let
$a,b \in A$
, and let
![]() ${m_a},{n_a},{m_b},{n_b} \in {\mathbb{Z}_ + }$
be such that
${m_a},{n_a},{m_b},{n_b} \in {\mathbb{Z}_ + }$
be such that
![]() $\phi \left( a \right) = {m_a}/{n_a}$
and
$\phi \left( a \right) = {m_a}/{n_a}$
and
![]() $\phi \left( b \right) = {m_b}/{n_b}$
. Then
$\phi \left( b \right) = {m_b}/{n_b}$
. Then
![]() $\phi \left( a \right) + \phi \left( b \right) = \left( {{m_a}{n_b} + {n_a}{m_b}} \right)/{n_a}{n_b} = \phi \left( {a \circ b} \right)$
. By Condition (iii),
$\phi \left( a \right) + \phi \left( b \right) = \left( {{m_a}{n_b} + {n_a}{m_b}} \right)/{n_a}{n_b} = \phi \left( {a \circ b} \right)$
. By Condition (iii),
![]() $\forall x \in {\mathbb{Q}_ + }\exists !a \in A$
such that
$\forall x \in {\mathbb{Q}_ + }\exists !a \in A$
such that
![]() $\phi \left( a \right) = x$
. Let
$\phi \left( a \right) = x$
. Let
![]() $c \in A$
be such that
$c \in A$
be such that
![]() $\phi \left( c \right) = 1/{n_a}{n_b}$
. Then
$\phi \left( c \right) = 1/{n_a}{n_b}$
. Then
![]() $\phi \left( a \right) = {m_a}{n_b}\phi \left( c \right)$
and
$\phi \left( a \right) = {m_a}{n_b}\phi \left( c \right)$
and
![]() $\phi \left( b \right) = {m_b}{n_a}\phi \left( c \right)$
. Thus, by Condition (ii),
$\phi \left( b \right) = {m_b}{n_a}\phi \left( c \right)$
. Thus, by Condition (ii),
![]() $\phi \left( a \right) = \phi \left( {{m_a}{n_b}c} \right)$
and
$\phi \left( a \right) = \phi \left( {{m_a}{n_b}c} \right)$
and
![]() $\phi \left( b \right) = \phi \left( {{m_b}{n_a}c} \right)$
. By Condition (i), it follows that
$\phi \left( b \right) = \phi \left( {{m_b}{n_a}c} \right)$
. By Condition (i), it follows that
![]() $a\sim {m_a}{n_b}c$
and
$a\sim {m_a}{n_b}c$
and
![]() $b\sim {m_b}{n_a}c$
.□
$b\sim {m_b}{n_a}c$
.□
B Lemmas
Let
![]() $a,b,c,d \in A$
, and let
$a,b,c,d \in A$
, and let
![]() $m,n$
be positive integers.
$m,n$
be positive integers.
Lemma B.1
![]() $ma \circ na\sim \left( {m + n} \right)a$
.
$ma \circ na\sim \left( {m + n} \right)a$
.
Lemma B.2
![]() $n\left( {ma} \right)\sim \left( {nm} \right)a$
.
$n\left( {ma} \right)\sim \left( {nm} \right)a$
.
Lemma B.3
If
![]() $a\sim b$
and
$a\sim b$
and
![]() $c\sim d$
, then
$c\sim d$
, then
![]() $a \circ c\sim b \circ d$
.
$a \circ c\sim b \circ d$
.
Lemma B.4
![]() $m\left( {a \circ b} \right)\sim ma \circ mb$
.
$m\left( {a \circ b} \right)\sim ma \circ mb$
.
Lemma B.5
Suppose that
![]() $b\sim c$
. Then
$b\sim c$
. Then
![]() $a \succ b$
iff
$a \succ b$
iff
![]() $a \succ c$
.
$a \succ c$
.
Lemma B.6
For any positive integer
![]() $n$
,
$n$
,
![]() $a\sim b$
iff
$a\sim b$
iff
![]() $na\sim nb$
.
$na\sim nb$
.
Lemma B.7
Suppose that
![]() $a\sim b$
. Then
$a\sim b$
. Then
![]() $na \succ mb$
iff
$na \succ mb$
iff
![]() $n \gt m$
.
$n \gt m$
.
Acknowledgments
We are grateful to Neil Dewar, Zee Perry, Eran Tal, and Jo Wolff for helpful discussion of the view developed in this paper. This work was supported by an Insight Grant from the Social Sciences and Humanities Research Council of Canada.



