2.1. MHD simulation set-up

We perform a simulation of incompressible visco-resistive MHD turbulence in a 3-D periodic box. The governing equations of the flow field $\boldsymbol{u}$ and the magnetic field $\boldsymbol{B}$ , which are given by (Biskamp Reference Biskamp2003)

(2.1a) \begin{align} \frac {\partial \boldsymbol{u}}{\partial t} +\boldsymbol{u} \boldsymbol{\cdot }\boldsymbol{\nabla }\boldsymbol{u} = \boldsymbol{B} \boldsymbol{\cdot }\boldsymbol{\nabla }\boldsymbol{B} -\boldsymbol{\nabla }p -\nu _h(-\varDelta )^h \boldsymbol{u} +\boldsymbol{f}, \quad \boldsymbol{\nabla }\boldsymbol{\cdot }\boldsymbol{u} = 0, \end{align}

(2.1b) \begin{align} \frac {\partial \boldsymbol{B}}{\partial t}+\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{\nabla }\boldsymbol{B} -\boldsymbol{B} \boldsymbol{\cdot }\boldsymbol{\nabla }\boldsymbol{u} = -\eta _h(-\varDelta )^h \boldsymbol{B}, \quad \boldsymbol{\nabla }\boldsymbol{\cdot }\boldsymbol{B} = 0, \end{align}

with hyper-viscosity $\nu _h$ and hyper-resistivity $\eta _h$ of order $h$ , are solved with our pseudo-spectral code SpecDyn (Wilbert, Giesecke & Grauer Reference Wilbert, Giesecke and Grauer2022; Wilbert Reference Wilbert2023). The equations are solved on a 3-D uniform grid with $1024^3$ points and periodic boundary conditions. The length of the domain is $L_{\mathrm{box}}=2\pi$ and the time scale of the flow is $T_{\mathrm{eddy}}=L_{\mathrm{box}}/u_{\mathrm{rms}}$ . We set $\nu _h=\eta _h$ , resulting in the magnetic Prandtl number $Pr_m=1$ . The magnetic field $\boldsymbol{B}$ , which is specified in Alfvénic units $[B]=[u]$ , is initialised with a small-amplitude seed field with zero magnetic helicity and zero net magnetic flux. The flow field $\boldsymbol{u}$ is driven by a large-scale force density $\boldsymbol{f}$ , operating on the wavenumber band $1\leqslant k\leqslant 2$ , with random amplitudes, which are $\delta$ -correlated in time to ensure constant power injection. The force density is constructed such that the injected net cross-helicity is zero (Alvelius Reference Alvelius1999). Due to the chosen wavenumber band of the forcing, the box contains only one flow correlation cell. We run the simulations until the magnetic energy has been amplified to a statistically saturated state, and then record eight snapshots of $\boldsymbol{u}(\boldsymbol{x})$ and $\boldsymbol{B}(\boldsymbol{x})$ separated in time by $T_{\mathrm{eddy}}$ .

We simulate (2.1) with $h=1$ as the baseline case and with $h=2$ as the production case. The parameters of the simulations are listed in table 1. Setting $h=2$ results in a sharper dissipative cut-off and, thus, an extended inertial range, which is reflected by the Reynolds numbers listed in table 1. Differences in the spectra and geometry are further reflected by the characteristic scales listed in table 2. For $h=2$ , the magnetic energy saturates at a higher level compared with $h=1$ (see also Brandenburg & Sarson Reference Brandenburg and Sarson2002); however, this does not matter for our test particle simulations, because we normalise the magnetic field to unit root-mean-square (r.m.s.) strength. Despite differences in the flux rope geometries, as indicated in table 2, we do not observe significant differences in our conditional particle statistics. Thus, subsequently, we only show the results for the case $h=2$ , which additionally allows for the meaningful inclusion of lower-energy particles due to the shorter dissipation scale.

See also § 2.3 for additional discussion of the geometric length scales.

Table 1. MHD simulation parameters, for grid size $1024^3$ , box length $L_{\mathrm{box}}=2\pi$ and fields $\boldsymbol{w}\in \{\boldsymbol{u},\boldsymbol{B}\}$ . The maximal resolved de-aliased wavenumber is $k_{\mathrm{max}}=341$ . The Reynolds numbers are based on the Taylor scale $k_{w,T}$ reported in table 2, and for $h=2$ , on the effective viscosity $\nu _{\mathrm{eff}}$ and effective resistivity $\eta _{\mathrm{eff}}$ (Haugen & Brandenburg Reference Haugen and Brandenburg2004).

Table 2. Characteristic length scales of the simulations. We report the correlation scale $k_{w,\mathrm{corr}}$ , Taylor scale $k_{w,T}$ and Kolmogorov dissipation scale $k_{w,\mathrm{diss}}$ for both fields $\boldsymbol{w}\in \{\boldsymbol{u},\boldsymbol{B}\}$ . Additionally, we show for the magnetic field, the characteristic parallel scale $k_\parallel$ , reversal scale $k_{\boldsymbol{B}\times \boldsymbol{j}}$ and perpendicular scale $k_{\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{j}}$ (see Schekochihin et al. Reference Schekochihin, Cowley, Taylor, Maron and McWilliams2004).

2.2. Test particle set-up

We then study the motion of cosmic rays in these static snapshots by integrating the Newton–Lorentz equations (see Appendix A)

(2.2) \begin{equation} \dot {\boldsymbol{X}}_t=\boldsymbol{V}_t, \quad \dot {\boldsymbol{V}}_t=\hat {\omega }_g\boldsymbol{V}_t {\times} \boldsymbol{B}(\boldsymbol{X}_t) \end{equation}

with the volume-preserving Boris scheme (Boris & Shanny Reference Boris and Shanny1971; Ripperda et al. Reference Ripperda, Bacchini, Teunissen, Xia, Porth, Sironi, Lapenta and Keppens2018). This test-particle approach is justified by assuming that relativistic cosmic rays with $V\approx c$ move in front of a non-relativistic plasma background with $u_{\mathrm{rms}}\ll c$ , such that the time scales of the MHD and test particle simulations are well separated, i.e. $T_{\mathrm{particle}}\ll T_{\mathrm{eddy}}$ with $T_{\mathrm{particle}}=L_{\mathrm{box}}/V_0$ . We can then neglect the influence of the electric field, implying conservation of energy for our test particles. The particles are parametrised by the normalised r.m.s. gyro frequency

(2.3) \begin{equation} \hat {\omega }_g=\frac {qB_{\mathrm{rms}}}{\gamma m}\frac {L_{\mathrm{box}}}{V_0}, \end{equation}

which includes the amplitudes $V_0$ of the particle velocity and $B_{\mathrm{rms}}$ of the magnetic field; (2.2) is accordingly normalised to $\|\boldsymbol{V}\|=1$ and $B_{\mathrm{rms}}=\langle \|\boldsymbol{B}\|^2\rangle ^{1/2}=1$ . The parameter $\hat {\omega }_g$ denotes how strongly particles are coupled to the magnetic field and inversely encodes their energy via $E=\gamma mc^2=qB_{\mathrm{rms}}L_{\mathrm{box}}c/\hat {\omega }_g$ , with $V_0=c$ . Table 3 provides a mapping to specific astrophysical systems, based on typical values of the magnetic field strengths and turbulence correlation scales. Due to limited numerical resolution and the requirement to constrain the particle gyro radii to the range of resolved turbulent fluctuations, the representable particle energies are very high for the respective physical systems. How our findings extend to lower energies, such as galactic GeV protons, can only be speculated about, as we attempt in § 4.1.

Table 3. Cosmic-ray protons affected by our considerations with $\hat {\omega }_g=64,\ldots ,256$ , characterised by the r.m.s. field strength $B_{\mathrm{rms}}$ and turbulence correlation scale $L_{\mathrm{corr}}\sim L_{\mathrm{box}}$ with values taken from: (1) Weygand et al. (Reference Weygand, Matthaeus, Dasso and Kivelson2011); (2) Weygand et al. (Reference Weygand, Matthaeus, Kivelson and Dasso2013); (3) Houde et al. (Reference Houde, Vaillancourt, Hildebrand, Chitsazzadeh and Kirby2009); (4) Crutcher (Reference Crutcher2012);, (5) Jansson & Farrar (Reference Jansson and Farrar2012); (6) Seta et al. (Reference Seta, Bushby, Shukurov and Wood2020); and (7) Domínguez Fernández (Reference Fernández2020). Note that values found in the literature tend to be widely spread due to the heterogeneous nature of astrophysical environments, as well as due to intrinsic observational uncertainties. The listed values serve merely as order-of-magnitude estimates. Also note that our fluctuating dynamo turbulence is not applicable to the anisotropic solar wind (Chen et al. Reference Chen2020; Wang et al. Reference Wang, Chhiber, Roy, Cuesta, Pecora, Yang, Fu, Li and Matthaeus2024) and that the reported particle energies are non-relativistic with $V_0=(0.037,\ldots ,0.009)\,c$ . For these reasons, the solar wind values are shown only for reference.

The typical gyro period is given by $T_g=2\pi \,\hat {\omega }_g^{-1}$ and we employ a fixed time step $\Delta t=10^{-2}\,T_g$ for the integration of (2.2). The r.m.s. and instantaneous normalised gyro radii are respectively estimated by $\langle \hat {r}_g\rangle =({\pi }/{2})\hat {\omega }_g^{-1}$ and $\hat {r}_{g,t}=\sqrt {1-\mu _t^2}\,\hat {\omega }_g^{-1}B^{-1}(\boldsymbol{X}_t)$ , where $\mu _t=\hat {\boldsymbol{V}}_t\boldsymbol{\cdot }\hat {\boldsymbol{B}\,}\!(\boldsymbol{X}_t)$ denotes the pitch angle cosine. We select five values between $\hat {\omega }_g=256$ and $\hat {\omega }_g=64$ , where particles with larger values follow field lines more closely, whereas particles with smaller values average magnetic structures more coarsely and exhibit behaviour akin to a random walk. The respective gyro scales $\langle \hat {r}_g\rangle ^{-1}$ are shown in figure 1 in relation to the radially averaged energy spectra of the flow and magnetic field.

Figure 1. Radially averaged power spectra of flow and magnetic field in the statistically saturated state of the simulation with $h=2$ . Indicated are the wavenumbers of the integral scales $k_u=2.139$ and $k_B=8.983$ , the effective Kolmogorov dissipation scales $k_\nu =409.148$ and $k_\eta =511.787$ , as well as the r.m.s. gyro wavenumbers ${(\pi /2)^{-1}}{\hat {\omega }_g}$ of the considered gyro frequencies $\hat {\omega }_g=64; 90.51; 128; 181.019; 256$ .

We solve (2.2) with our ParticlePusher code, which is able to record binned statistics of arbitrary quantities along particle trajectories. We use the local gyro average of a quantity $Q$ along a particle trajectory $\boldsymbol{X}_t$ , which is defined as

(2.4) \begin{equation} \bar {Q}(\boldsymbol{X}_t)=\frac {1}{\tilde {T}_g(\boldsymbol{X}_t)}\int \limits _0^{\tilde {T}_g(\boldsymbol{X}_t)}Q(\boldsymbol{X}_{t-t'})\mathop {}\!\mathrm{d}{t'}, \end{equation}

where the local gyro period is estimated as $\tilde {T}_g(\boldsymbol{X}_t)=2\pi ( {\hat {\omega }_g} \smallint _0^{T_g}B(\boldsymbol{X}_{t-t'})\mathop {}\!\mathrm{d}{t'} / T_g)^{-1}$ . In the magnetised limit $r_g\ll B/\boldsymbol{\nabla }B$ , particles coherently gyrate along an ordered field and $\bar {Q}$ describes the well-defined gyro-centre motion, while in the unmagnetised limit $r_g\gg B/\boldsymbol{\nabla }B$ , particles exhibit highly chaotic motion and $\bar {Q}$ quantifies the competition between the particle’s inertia and the quickly varying Lorentz force. Analogously, we define the local gyro variance as

(2.5) \begin{equation} \,\overline {\!{\delta Q}}^2(\boldsymbol{X}_t)=\,\overline {\!{\left (Q(\boldsymbol{X}_t)-\bar {Q}(\boldsymbol{X}_t)\right )^2}}. \end{equation}

To investigate scattering and transport behaviour of particles in the magnetised and unmagnetised regimes, we consult the geometric picture of Lemoine (Reference Lemoine2023) and Kempski et al. (Reference Kempski, Fielding, Quataert, Galishnikova, Kunz, Philippov and Ripperda2023) based on the field-line curvature

(2.6) \begin{equation} \kappa =\frac {\|\boldsymbol{B}/B\times (\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{\nabla }\boldsymbol{B})\|}{B^2}, \end{equation}

where $\kappa r_g\ll 1$ corresponds to the magnetised case, $\kappa r_g\gg 1$ corresponds to the unmagnetised case and for $\kappa r_g\sim 1$ order-unity variations of the magnetic moment,

(2.7) \begin{equation} M=\frac {\gamma m V_\perp ^2}{2B}=\frac {\gamma m \left (1-\mu ^2\right )}{2B} \end{equation}

are expected. Based on these definitions, we record the average of the relative variation of the magnetic moment conditional on the field-line curvature and particle gyro radius,

(2.8) \begin{equation} \left \langle \frac {\,\overline {\!{\delta M}}}{\,\overline {\!{M}}} \middle | \bar {\kappa }, \bar {r}_g \right \rangle . \end{equation}

Further, we record spatial mean squared displacements (MSDs) of particles

(2.9) \begin{equation} \langle \Delta X^2_\tau \,|\,\mathrm{cond.}\rangle =\langle \|\boldsymbol{X}_{t+\tau }-\boldsymbol{X}_t\|^2\,|\,\mathrm{cond.}\rangle , \end{equation}

conditional on the magnetisation criteria $\bar {\kappa }\bar {r}_g\lt 1$ and $\bar {\kappa }\bar {r}_g\gt 1$ , as well as an unconditional baseline. We assume stationarity $\langle \|\boldsymbol{X}_\tau -\boldsymbol{X}_0\|^2\rangle =\langle \|\boldsymbol{X}_{t+\tau }-\boldsymbol{X}_t\|^2\rangle$ , expressed by the local time scale $\tau$ . The MSD, obtained from the displacement of individual particles, measures the time-dependent spread of the underlying particle distribution function, and classifies the motion as super-, normal or sub-diffusive, depending on $\langle \Delta X^2_\tau \rangle \sim \tau ^\alpha$ scaling with $\alpha \gt 1$ , $=1$ or $\lt 1$ . For $\alpha =1$ , the classical diffusion coefficient is given by $D_\infty =\lim _{\tau \to \infty }\langle \Delta X^2_\tau \rangle /2\tau$ (Metzler & Klafter Reference Metzler and Klafter2000).

The unconditional MSD should be treated with care, because it averages over many different length scales, thus hiding relevant physical processes, which we address by conditioning on the magnetisation criterion. Further, since our simulation box only contains one flow correlation cell, and the parallel scale of the magnetic field $k_\parallel$ is comparable to the box size, $D_\infty$ converges only after particles traverse the periodic domain multiple times. In doing so, particles likely re-enter the box at a different position and thus sample different regions of the magnetic field, which results in a meaningful albeit biased value for $D_\infty$ .

To obtain the conditional statistics, we simulated for each $\hat {\omega }_g$ , in each of the eight statistically independent MHD snapshots, $400\,000$ independent test-particle trajectories for $1000$ gyro periods. The unconditional baseline MSD is, per snapshot, based on $40\,000$ independent test-particle trajectories with lengths of $10\,000$ gyro periods. This ensures that the tails of the joint density $p(\bar {\kappa },\bar {r}_g)$ are well resolved. However, the conditional MSD at large time scales is hard to resolve properly, even with increased sample sizes. This matter is discussed in more detail in § 3.2.

2.3. MHD simulation results

We start by inspecting the magnetic field snapshots extracted from the statistically saturated phase of the MHD simulation. Figure 2 shows isosurfaces of the magnetic field strength $B$ and the current density magnitude $j=\|\boldsymbol{\nabla }\boldsymbol{\cdot} \boldsymbol{B}\|$ at different zoom levels in the simulation box. The isosurfaces of $B$ reveal characteristic structures of the saturated fluctuating dynamo (Miller Reference Miller2019; Seta et al. Reference Seta, Bushby, Shukurov and Wood2020), which can be described as long flattened tubes with length $l$ , width $w$ and height $h$ , ordered as $l \gg w\gt h$ . As indicated in figure 4, they contain coherent bundles of field lines and approximately represent flux surfaces. Thus, henceforth, we refer to these coherent structures as flux tubes. The connection between field strength $B$ and coherent geometry with small curvatures $\kappa$ is formally expressed by the anti-correlation between the two quantities $B\sim \kappa ^{-1/2}$ (Schekochihin et al. Reference Schekochihin, Cowley, Taylor, Maron and McWilliams2004).

Figure 2. Isosurfaces of the magnetic field strength $B$ (blue) and the current density magnitude $j=\|\boldsymbol{\nabla }\boldsymbol{\cdot} \boldsymbol{B}\|$ (red). (a) Whole box with $B_{\mathrm{iso}}/B_{\mathrm{max}}=0.7$ and $j_{\mathrm{iso}}/j_{\mathrm{max}}=0.418$ . (b) Cutout with $B_{\mathrm{iso}}/B_{\mathrm{max}}=0.489$ and $j_{\mathrm{iso}}/j_{\mathrm{max}}=0.303$ . (c) Cutout with $B_{\mathrm{iso}}/B_{\mathrm{max}}=0.245$ and $j_{\mathrm{iso}}/j_{\mathrm{max}}=0.115$ . The subscript iso denotes the value at which the isosurfaces are drawn. The structures of the magnetic isosurfaces correspond to flux tubes, as indicated in figure 4, which are amplified by the fluctuating dynamo action. Most of the magnetic energy is concentrated on large scales in a few intense flux tubes, while small scales reveal less intense and tightly folded flux tubes. Current sheets appear in close proximity to intense flux tubes and are embedded between folds.

Figure 3. Slices through a magnetic flux tube, surrounded by tight folds, current sheets and plasmoids. (a) Field-line curvature divided by the field strength $\kappa /B$ for comparison with the magnetisation criterion $\kappa r_g\sim 1$ with $r_g\propto B^{-1}$ . (b) Magnitude of the current density $j$ indicating intense current sheets. (c) Alignment between the magnetic field and current density $\sigma _{j,B}=\hat {\boldsymbol{j}\,} \boldsymbol{\cdot }\hat {\boldsymbol{B}\,}\!$ indicating cellularisation into approximately force-free patches. Further indicated are the correlation scale of the magnetic field and the locations of the flux tube and example plasmoids.

Figure 4. Magnetic field lines coloured by field strength $B$ and test-particle trajectories coloured by pitch angle cosine $\mu$ in the (a) flux tube and (b) one of the plasmoids from figure 3. In the coherent flux tube, particles are closely bound to field lines with occasional large-scale mirroring. The plasmoid exhibits highly tangled field lines and effectively confines particles with a mixture of small-scale mirroring and unmagnetised scattering. The magnetic correlation scale is indicated for reference.

At the outermost zoom level in figure 2, we recognise that most of the magnetic energy is distributed intermittently throughout the domain, concentrated in a few intense flux tubes with almost circular cross-sections, which extend up to the flow correlation scale $l\lesssim L_u$ . These structures are sometimes observed wrapped up by intense current sheets. Further zooming into apparently quiet regions reveals a population of smaller, less intense, flattened flux tubes, organised in a tightly folded pattern (Schekochihin et al. Reference Schekochihin, Cowley, Taylor, Maron and McWilliams2004) with embedded current sheets. The networks of flux tubes and current sheets are dual to each other. Outside of coherent flux tubes, e.g. in the debris of disrupted structures, field lines tend to be chaotically tangled and highly disorganised. Additionally, reconnection (either due to resistive diffusion or due to tearing) of folded flux tubes is observed to seed small-scale plasmoids (Galishnikova, Kunz & Schekochihin Reference Galishnikova, Kunz and Schekochihin2022). This diverse picture is illustrated by a slice plot through an intense flux tube and its surroundings in figure 3.

The conventionally computed correlation wavenumber $k_{B,\mathrm{corr}}$ does not adequately reflect the geometric structure of the magnetic field, as indicated by its rather large value $O(10\,k_{\mathrm{forcing}})$ , because the intermittent and highly correlated flux tubes are averaged out. It is thus instructive to also report the characteristic geometric scales $k_\parallel$ , $k_{\boldsymbol{B}\boldsymbol{\cdot} \boldsymbol{j}}$ and $k_{\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{j}}$ , which are sensitive to the local direction of the magnetic field (see table 2; Schekochihin et al. Reference Schekochihin, Cowley, Taylor, Maron and McWilliams2004; Galishnikova et al. Reference Galishnikova, Kunz and Schekochihin2022). For $h=2$ , these values confirm elongated tube-like structures with length $l_\parallel \approx L_u$ and an approximate aspect ratio of $1:6:6$ . However, the flow $\boldsymbol{u}$ exhibits a lower degree of intermittency compared with $\boldsymbol{B}$ , so the correlation wavenumber is more suitable to characterise its correlation structure. The small discrepancy between $k_{u,\mathrm{corr}}$ and $k_{\mathrm{forcing}}$ results from the presence of a broadband turbulent energy spectrum (Seta et al. Reference Seta, Bushby, Shukurov and Wood2020).

2.4. Test particle results

Figure 4 shows examples of test-particle trajectories. Particles are clearly magnetised with $\bar {\kappa }\bar {r}_g\lt 1$ inside the intense flux tube, where they closely follow magnetic field lines. Due to large-scale variations of the illustrated flux tube, particles undergo occasional mirroring events, which appear as sudden reversals of direction. These rare reversals imply a long parallel MFP. Outside of the flux tube, particle motion is unmagnetised with $\bar {\kappa }\bar {r}_g\gt 1$ and appears much more erratic, as the particles bounce chaotically and with a short MFP through the tangled field. An additional interesting case is illustrated by the small-scale plasmoid, which appears to be an efficient device for trapping particles. However, since they appear to have a sub-dominant contribution in our statistics, and due to numerical concerns addressed in § 4.2, we focus here on the modelling of magnetised and unmagnetised motion, and leave a detailed study on the effect of plasmoids on particle transport for later work.

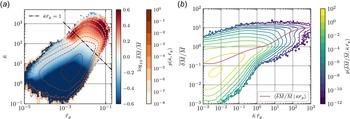
These observations are substantiated by the conditional statistics given by (2.8) and (2.9). First, figure 5 confirms that particles are magnetised in the sense that their magnetic moments are weakly conserved, $\,\overline {\!{\delta M}}/\,\overline {\!{M}}\lt 1$ , when their gyro radii are smaller than the experienced field-line curvature radius, i.e. $\bar {\kappa }\bar {r}_g\lt 1$ (Lemoine Reference Lemoine2023). If this condition is violated, i.e. $\bar {\kappa }\bar {r}_g\gt 1$ , large variations of the magnetic moment are expected. Although $\bar {\kappa }\bar {r}_g=1$ does not constitute an exact decision boundary, we consider it as a useful heuristic, because our ensuing results remain qualitatively robust under minor refinements of this condition. Appendix B shows results for an alternative magnetisation criterion based on the perpendicular reversal scale $\kappa _\perp$ introduced by Kempski et al. (Reference Kempski, Fielding, Quataert, Galishnikova, Kunz, Philippov and Ripperda2023), which can be approximated as $\bar {\kappa }_\perp \bar {r}_g^{1/2}\sim 30$ .

Figure 5. (a) Average of the relative magnetic moment variation $\,\overline {\!{\delta M}}/\,\overline {\!{M}}$ conditional on particle gyro radius $\bar {r}_g$ and field-line curvature $\bar {\kappa }$ . All recorded quantities are gyro-averaged. The colour scale is centred at $\,\overline {\!{\delta M}}/\,\overline {\!{M}}=1$ , where particles can be considered magnetised for smaller variations and unmagnetised for larger variations. Further, the colour scale is capped to $\log _{10}\,\overline {\!{\delta M}}/\,\overline {\!{M}}\in (-0.6, 0.6)$ to highlight the transition region. This transition region is compared with the magnetisation criterion $\bar {\kappa }\bar {r}_g\sim 1$ expected from the field-line curvature picture. The joint density $p(\bar {\kappa }, \bar {r}_g)$ is indicated for reference. (b) Conditional average $\langle \,\overline {\!{\delta M}}/\,\overline {\!{M}}|\bar {\kappa }\bar {r}_g\rangle$ also showing the transition from predominantly magnetised and to predominantly unmagnetised motion as $\bar {\kappa }\bar {r}_g$ increases, although the joint density $p(\,\overline {\!{\delta M}}/\,\overline {\!{M}},\bar {\kappa }\bar {r}_g)$ reveals some uncertainty of this criterion.

Figure 6. (a) MSD of the test particles, depending on the time lag $\tau$ , revealing initial ballistic propagation, transient subdiffusion and asymptotic diffusive behaviour. Notably, diffusion only occurs for mean square displacements beyond the simulation box size. (b) Conditional MSD for magnetised and unmagnetised transport for a selected test-particle energy, as well as the respective relative bin counts. Longer consecutively magnetised or unmagnetised segments have a lower probability than shorter ones, which leads to a systematically smaller sample size for the conditional averages at larger time scales $\tau$ . We describe magnetised transport by compound subdiffusion and unmagnetised transport by a Langevin equation. The discrepancy between magnetised data and model are likely due to this bias at large $\tau$ , which is addressed when tuning the combined model to the unconditional MSD, resulting in good agreement.

Second, figure 6 shows the unconditional MSD for our considered particles, as well as the conditional observations for $\hat {\omega }_g=181.019$ . The unconditional data reveal three time scales of transport: particles move ballistically on short time scales, followed by a transient subdiffusive phase, before becoming asymptotically diffusive. As noted in § 2.2, convergence to normal diffusion occurs only after the MSD reaches the box size, which means that particles may experience the same structures repeatedly due to the periodic boundary conditions. We address this issue partly by modelling the transport behaviour on short and intermediate time scales, where the bias of the periodic domain is negligible.

The conditional data support two distinct transport behaviours, where magnetised particles exhibit much longer MFPs compared with unmagnetised particles. Also indicated are the relative bin counts contributing to the conditional averages. This number strongly decreases for both cases for larger time scales, because the probability of finding an uninterrupted conditional trajectory segment decreases with its desired length. The conditional averages at large time scales are thus likely dominated by a few very intense flux tubes, implying a systematic bias caused by our heuristic magnetisation criterion $\bar {\kappa }\bar {r}_g\sim 1$ . Our methodology for modelling the conditional and unconditional data, as well as addressing this bias, is presented in § 3.

3.1. Stochastic differential equations

We start with describing the motion of field lines and unmagnetised particles by a 3-D Langevin equation (Chandrasekhar Reference Chandrasekhar1943; Bian & Li Reference Bian and Li2024)

(3.3) \begin{equation} \mathop {}\!\mathrm{d}{\boldsymbol{X}}_s=\boldsymbol{V}_s\mathop {}\!\mathrm{d}{s},\quad \mathop {}\!\mathrm{d}{\boldsymbol{V}}_s=-\theta \boldsymbol{V}_s\mathop {}\!\mathrm{d}{s}+\sqrt {\frac {2}{3}\theta v^2_{\mathrm{rms}}}\mathop {}\!\mathrm{d}{\boldsymbol{W}}_s, \end{equation}

where $\boldsymbol{V}_s$ and $\boldsymbol{X}_s$ denote velocity and position of the random walker at the generalised time or path parameter $s$ . The walker is parametrised by the scattering rate $\theta$ and thermal velocity $v_{\mathrm{rms}}$ , and driven by 3-D Gaussian white noise $\mathop {}\!\mathrm{d}{\boldsymbol{W}}_s$ with the correlation function $\langle \mathop {}\!\mathrm{d}{W}_{i,s}\mathop {}\!\mathrm{d}{W}_{j,s'}\rangle =\delta _{ij}\delta (s-s')$ . The MSD is given by (as shown in Appendix C.1)

(3.4) \begin{equation} \langle X^2_s \rangle = \langle \|\boldsymbol{X}_s\|^2 \rangle = \frac {2v^2_{\mathrm{rms}}}{\theta ^2}\left (e^{-\theta s}+\theta s-1\right ), \end{equation}

which scales asymptotically as $\langle X_s^2\rangle \underset {s\to 0}{\sim }v_{\mathrm{rms}}^2s^2$ and $\langle X_s^2\rangle \underset {s\to \infty }{\sim }{2v_{\mathrm{rms}}^2s}/{\theta }$ . The MFP is accordingly given by the scattering rate and thermal velocity as

(3.5) \begin{equation} \lambda =\frac {v_{\mathrm{rms}}}{\theta } =\frac {D_{xx}}{v_{\mathrm{rms}}}, \end{equation}

with $D_{xx}=\lim _{s\to \infty }{\langle X_s^2\rangle }/{2s}$ . In the following, we set $v_{\mathrm{rms}}=1$ for field lines and unmagnetised transport in accordance with the normalisation choices $\|\boldsymbol{V}\|=1$ and $\langle \|\boldsymbol{B}\|^2\rangle =1$ according to § 2.

Next, we describe pitch-angle motion of magnetised particles with an Itô stochastic differential equation of the form (Strauss & Effenberger Reference Strauss and Effenberger2017)

(3.6) \begin{equation} \mathop {}\!\mathrm{d}{s}_t=v_{\mathrm{eff}}\mu _t\mathop {}\!\mathrm{d}{t},\quad \mathop {}\!\mathrm{d}{\mu }_t= \frac {\mathop {}\!\mathrm{d}{D_{\mu \mu }(\mu _t)}}{\mathop {}\!\mathrm{d}{\mu }}\mathop {}\!\mathrm{d}{t} +\sqrt {2D_{\mu \mu }(\mu _t)}\mathop {}\!\mathrm{d}{W}_t, \end{equation}

where $s_t$ denotes the displacement along a field line at time $t$ and $\mu _t\in (-1,1)$ , with reflective boundary conditions, denotes the pitch angle cosine. The effective velocity $v_{\mathrm{eff}}$ reflects anisotropies of the pitch-angle-cosine distribution, where $v_{\mathrm{eff}}=1$ indicates an isotropic uniform distribution. The process is driven by uncorrelated Gaussian white noise with $\langle \mathop {}\!\mathrm{d}{W}_t\mathop {}\!\mathrm{d}{W}_{t'}\rangle =\delta (t-t')$ and is characterised by the pitch angle diffusion coefficient

(3.7) \begin{equation} D_{\mu \mu }(\mu )=D_0\left (1-\mu ^2\right ). \end{equation}

We choose this generic isotropic shape of $D_{\mu \mu }$ in accordance with the agnostic stance of this work towards the detailed pitch-angle physics (see also van den Berg, Els & Engelbrecht Reference van den Berg, Els and Engelbrecht2024). Analogously to (3.4), due to the Markovian nature of this process resulting in an exponential velocity correlation function, the MSD is given by

(3.8) \begin{equation} \langle s_t^2\rangle =\frac {2\lambda _\mu ^2}{3}\left (e^{-\theta _\mu t}+\theta _\mu t-1\right ), \end{equation}

where the additional factor $1/3$ comes from the variance of the uniform distribution $\mathcal{U}(-1, 1)$ . The MFP $\lambda _\mu =v_{\mathrm{eff}}/\theta _\mu$ of this process is known from the literature (Schlickeiser Reference Schlickeiser2002) as

(3.9) \begin{equation} \lambda _\mu =\frac {3D_{ss}}{v_{\mathrm{eff}}} =\frac {3v_{\mathrm{eff}}}{8}\int _{-1}^{+1}\frac {\left (1-\mu ^2\right )^2}{D_{\mu \mu }(\mu )}\mathop {}\!\mathrm{d}{\mu }, \end{equation}

with $D_{ss}=\lim _{t\to \infty }\langle s_t^2\rangle /2t$ , where the integral evaluates together with (3.7) to $\lambda _\mu =v_{\mathrm{eff}}/2D_0$ .

Further, a pitch-angle walker diffusing along a diffusing field line results in compound subdiffusion, with the MSD scaling as $t^{1/2}$ . The spatial position of such a random walker is found by evaluating the field-line trajectory $\boldsymbol{X}_{{\mathrm{fl}},s}$ , given by (3.3), at the pitch-angle displacement coordinate $s_t$ , given by (3.6), as

(3.10) \begin{equation} \boldsymbol{Y}_t=\boldsymbol{X}_{{\mathrm{fl}},s_t}. \end{equation}

This approach resembles Brownian yet non-Gaussian diffusion via subordination as presented by Chechkin et al. (Reference Chechkin, Seno, Metzler and Sokolov2017), and guided by their techniques, we can write the MSD as the integral

(3.11) \begin{equation} \left \langle Y_{t}^2\right \rangle =\int _{-\infty }^{+\infty }\left \langle X_{{\mathrm{fl}},|s|}^2\right \rangle \frac {1}{\sqrt {2\pi \langle s_t^2\rangle }} \exp \left ({-}\frac {s^2}{2\langle s_t^2\rangle }\right )\mathop {}\!\mathrm{d}{s}, \end{equation}

where the MSD of the field line $\langle X_{\mathrm{fl},s}^2\rangle$ is given by (3.4) and the MSD of the pitch-angle walker $\langle s_t^2\rangle$ is given by (3.8). For the purpose of fitting (3.11) to the data, we evaluate the integral numerically with an adaptive Gaussian quadrature rule; however, the asymptotic behaviour can be written explicitly as $\langle Y^2_{s_t}\rangle \underset {t\to 0}{\sim }v_{\mathrm{eff}}^2t^2/3$ and $\langle Y^2_{s_t}\rangle \underset {t\to \infty }{\sim }4\lambda _{\mathrm{fl}}\sqrt {v_{\mathrm{eff}}\lambda _\mu t}/3$ , as shown in Appendix C.2.

Based on these building blocks, we construct the combined stochastic model $\boldsymbol{Z}_{\mathrm{model},t}$ . A stochastic walker alternates between magnetised and unmagnetised transport behaviour, where the duration for each segment is sampled from the respective escape-time probability distributions $p(t|t^\ast _\mu )$ and $p(t|t^\ast _{\mathrm{scatter}})$ . For magnetised transport, we simulate a field line $\boldsymbol{X}_{\mathrm{fl},s}$ according to (3.3) and let the walker diffuse with $s_t$ along this field line according to (3.6). This behaviour is parametrised by the field-line and mirror MFPs $\lambda _{\mathrm{fl}}$ and $\lambda _\mu$ , the effective velocity $v_{\mathrm{eff}}$ , and the magnetised mean duration $t_\mu ^\ast$ . Note that we simulate a new independent field line for every time the walker enters magnetised behaviour. For unmagnetised transport, we simply simulate random scattering $\boldsymbol{X}_{\mathrm{scatter},t}$ according to (3.3), which is parametrised by the scattering MFP $\lambda _{\mathrm{scatter}}$ and the scattering mean duration $t_{\mathrm{scatter}}^\ast$ . The procedure is summarised in Algorithm 1.

Algorithm 1 Combined stochastic model

3.2. Fitting the model

As noted in § 2.4, finding connected segments of particle trajectories, which satisfy the desired conditions $\bar {\kappa }\bar {r}_g\lessgtr 1$ , becomes more difficult with increasing length of these segments. The reason for this is partly physical due to the distribution of field-line curvature, and partly methodical due to our magnetisation condition $\bar {\kappa }\bar {r}_g\sim 1$ being merely a heuristic. Thus, the conditional data $\langle \Delta X_\tau ^2|\bar {\kappa }\bar {r}_g\lessgtr 1\rangle$ come with the caveat that data points at larger time scales $\tau$ are backed by a much smaller sample size compared with data points at smaller $\tau$ . This is illustrated by the relative bin counts in figure 6(b). When fitting our models, we address this issue by truncating the data at a cut-off time scale $\tau _{\mathrm{cutoff}}$ , where the choice of $\tau _{\mathrm{cutoff}}$ should be small enough for sufficient statistical significance and large enough to provide a meaningful fit result. For the magnetised case, we choose $\tau _{\mathrm{cutoff}}=1.5\tau _{\mathrm{peak}}$ with $\tau _{\mathrm{peak}}=\mathop {\mathrm{argmax}}_\tau \langle \Delta X^2_\tau |\bar {\kappa }\bar {r}_g\lt 1\rangle /2t$ and ensure a minimum relative bin count of $1\%$ . Analogously for the unmagnetised case, we choose $\tau _{\mathrm{cutoff}}=1\tau _{\mathrm{peak}}$ with $\tau _{\mathrm{peak}}=\mathop {\mathrm{argmax}}_\tau \langle \Delta X^2_\tau |\bar {\kappa }\bar {r}_g\gt 1\rangle /2t$ and ensure a minimum relative bin count of $1\,\%$ as well. Despite these precautions, a systematic bias likely remains in the data, most notably in the conditional magnetised data, which is dominated at long time scales by a small number of very intense flux tubes. This remaining bias is addressed by the Bayesian optimisation of the magnetised mean duration $t^\ast _\mu$ and MFP $\lambda _\mu$ discussed later.

We proceed by fitting the compound subdiffusion model given by (3.11), which is parametrised by $\lambda _{\mathrm{fl}}$ , $\lambda _\mu$ and $v_{\mathrm{eff}}$ , to the magnetised data $\langle \Delta X^2_\tau |\bar {\kappa }\bar {r}_g\lt 1\rangle$ . Since a clear distinction of the two MFPs requires reliable data at large $\tau$ , we argue that large-scale magnetic mirrors mostly operate on the correlation scale of coherent flux tubes and fix $\lambda _{\mathrm{fl}}=\lambda _\mu$ , thereby reducing the number of free parameters by one. Further, we fit the Langevin model given by (3.4), which is parametrised by $\lambda _{\mathrm{scatter}}$ , to the unmagnetised data $\langle \Delta X_\tau ^2|\bar {\kappa }\bar {r}_g\gt 1\rangle$ . We employ a nonlinear least squares method for both cases (Branch, Coleman & Li Reference Branch, Coleman and Li1999). For comparison, the unconditional asymptotic MFP of the unconditional data is estimated as

(3.12) \begin{equation} \lambda _{\mathrm{asymp}}=\frac {D_\infty }{v_{\mathrm{rms}}} \end{equation}

with the asymptotic diffusion coefficient $D_\infty =\lim _{\tau \to \infty }\langle \Delta X_\tau ^2\rangle /2\tau$ and the particle r.m.s. velocity $v_{\mathrm{rms}}^2= ({3}/{2})\lim _{\tau \to 0}\langle \Delta X_\tau ^2\rangle /\tau ^2$ . This choice of $v_{\mathrm{rms}}$ ensures consistency with the Langevin model for the unmagnetised motion. The resulting MFPs are shown in figure 7(a) and discussed in § 3.3. The effective pitch angle velocities $v_{\mathrm{eff}}$ are shown in figure 7(b), where $v_{\mathrm{eff}}=1$ corresponds to an isotropic uniform pitch angle cosine distribution. We observe $v_{\mathrm{eff}}\gt 1$ for higher particle energies, which is likely due to shorter durations of magnetised segments, thus those particles experience less mirroring, which would isotropise the pitch angles.

Figure 7. (a) Fitted MFPs for conditional magnetised $\lambda _{\mathrm{fl}}$ and unmagnetised transport $\lambda _{\mathrm{scatter}}$ , as well as for the unconditional asymptotic case $\lambda _{\mathrm{asymp}}$ . As shown in the inset, $\lambda _{\mathrm{asymp}}$ converges to $\lambda _{\mathrm{scatter}}$ for high energies, where our magnetised model is no longer valid. Scalings $\hat {\omega }_g^{-1}$ and $\hat {\omega }_g^{-1/3}$ are indicated for reference. The field line MFP $\lambda _{\mathrm{fl}}$ is obtained twice: once by naively fitting (3.11) to the biased magnetised MSD (measured), and once by optimising the unbiased loss function given by (3.14) (optimised). Both values are scaled by a factor ${1}/{4}$ to simplify comparison with $\lambda _{\mathrm{scatter}}$ and $\lambda _{\mathrm{asymp}}$ . (b) Fitted effective velocity of magnetised pitch-angle diffusion. The error bars in both plots for the fitted models are given by $1.96\,\times$ the standard error produced by the respective fit routines. The error bars for $\lambda _{\mathrm{asymp}}$ are obtained by taking the mean and $1.96\,\times$ the standard deviation over the eight independent MHD snapshots.

Figure 8. Escape-time probability distributions estimated from the conditional test-particle averages. (a) Magnetised cases exhibit heavier tails than an exponential distribution, indicating that the magnetised motion has some memory. The power-law scaling $t^{-3/2}$ expected for the classical first-passage time distribution of a random walker on a finite line is indicated for reference. (b) Unmagnetised cases closely resemble exponential distributions, indicating a memory-less Markov nature of the unmagnetised motion.

Figure 9. (a) Measured and fitted mean durations $t^\ast _\mu$ and $t^\ast _{\mathrm{scatter}}$ . Box-crossing and decoupling time scales are given for reference. The measured magnetised mean duration is much smaller than the expected decoupling time scale due to neglecting the correlation of large-scale flux tubes. However, the optimised mean magnetised duration is comparable to the decoupling time scale. The error bars of the optimised results are given by $1.96\times$ the estimated confidence interval of the Bayesian optimisation procedure (see Appendix D). (b) Ratio of measured unmagnetised and magnetised mean durations, as a proxy for the volume filling fraction of scattering sites experienced by the test particles. The optimised mean scattering duration is determined by multiplying this measured ratio with the optimised mean magnetised duration.

Next, we estimate the escape-time probability distributions by recording the lengths of observed conditional magnetised and unmagnetised segments into histograms. The densities of the histogram are plotted in figure 8, revealing an exponential shape for the unmagnetised case, which corroborates the view of the unmagnetised motion as a memory-less random walk. However, the magnetised case roughly resembles a tempered power-law shape, indicating a process with long memory governed by extended flux tubes. When picturing a one-dimensional (1-D) pitch-angle walker on a field line with finite length, one would expect the classical first-passage time distribution (Krapivsky, Redner & Ben-Naim Reference Krapivsky, Redner and Ben-Naim2010), which scales as $t^{-3/2}$ . This scaling is indicated for reference.

To judge whether the results are reasonable, we compare the magnetised mean duration $t_\mu ^\ast$ with the typical box-crossing time scale $\tau _{\mathrm{box}}$ (see figure 6 a) and the decoupling time scale $\tau _{\mathrm{decouple}}$ , which is estimated as the inflection point of the unconditional running diffusion coefficient $\langle \Delta X_\tau ^2\rangle /2\tau$ as

(3.13) \begin{equation} \tau _{\mathrm{decouple}}=\mathop {\mathrm{argmin}}_{\tau \in (0,\infty )}\frac {\mathop {}\!\mathrm{d}{}\log {\langle \Delta X_\tau ^2\rangle }/{2\tau }}{\mathop {}\!\mathrm{d}{}\log \tau }. \end{equation}

First, since the dominant coherent structures which govern the particle transport are comparable to the fluid correlation scale $l\lesssim L_u\lt L_{\mathrm{box}}$ , we expect $t_\mu ^\ast \lt \tau _{\mathrm{box}}$ , i.e. that magnetised motion is clearly separated from the box-crossing time scale . Second, we assume that the initially ballistic and transiently subdiffusive behaviour of the unconditional MSD is given by magnetised transport, and asymptotic diffusion is linked to decoupling of particles from coherent field lines, so we expect $t^\ast _\mu \sim \tau _{\mathrm{decouple}}$ . The various time scales are shown in figure 9(a), which confirms the first expectations, but reveals that the measured magnetised mean durations are shorter than expected by an order of magnitude $\tau _{\mathrm{decouple}}/t_\mu ^\ast \sim O(10)$ . Additionally, the combined model given by Algorithm 1 does not reproduce the unconditional MSD with these naively measured parameters (not shown).

This severe underestimation is likely caused by the discrepancy between our combined stochastic model, which simulates a new independent stochastic field line for each magnetised segment, and test particles in MHD snapshots, where magnetised transport is governed by a finite number of spatially correlated intense flux tubes. To explore the capabilities of our combined model, we search for an optimal effective mean magnetised duration $t^\ast _\mu$ by means of Bayesian optimisation (see Appendix D for details). Specifically, we minimise the loss function

(3.14) \begin{equation} \mathcal{L}\big(t^\ast _\mu ,\lambda _{\mathrm{fl}}\big)= \max _{\tau \in (0,\tau _{\mathrm{max}})}\left |\log \frac {\langle \Delta X^2_\tau \rangle }{\big\langle Z_{\mathrm{model},\tau }^2|t^\ast _\mu ,\lambda _{\mathrm{fl}}\big\rangle }\right |, \end{equation}

which compares the unconditional MSD of test particles $\langle \Delta X_\tau ^2\rangle$ with the MSD of our combined model $\langle Z^2_{\mathrm{model},\tau }|t^\ast _\mu ,\lambda _{\mathrm{fl}}\rangle$ . We also take the field line MFP $\lambda _{\mathrm{fl}}$ as a tuneable parameter to account for the previously discussed bias of the magnetised data. Further, the effective pitch-angle walker velocity $v_{\mathrm{eff}}$ and scattering MFP $\lambda _{\mathrm{scatter}}$ are taken from the conditional fit results, the pitch angle MFP is fixed as $\lambda _\mu =\lambda _{\mathrm{fl}}$ , and the unmagnetised mean duration is determined from the fixed measured ratio $t^\ast _{\mathrm{scatter}}/t^\ast _\mu$ (see figure 9 b), which serves as a proxy for the volume filling fraction of scattering sites.

3.3. Model results

The MSDs of the combined model for the optimised values are plotted in figure 10 and agree well with the unconditional test-particle MSD for all considered particle energies. Note that the optimised magnetised mean durations are now comparable to the decoupling time scale, as shown in figure 9(a). Also plotted in figure 10 are the conditional MSDs and models, showing good agreement of the simple Langevin diffusion with the unmagnetised data, as well as some disagreement for the compound subdiffusion and the biased magnetised data. Specifically, as shown in figure 7(a), the optimisation procedure predicts for most particle energies smaller MFPs compared with the conditional data. These smaller values can account for transport by less intense flux tubes or constellations of strongly correlated flux tubes and, thus, correct the bias from the conditional magnetised data, dominated by isolated (intrinsic to the measurement methodology) and very intense flux tubes (fulfilling the heuristic magnetisation criterion for long time scales).

Figure 10. Time-dependent MSDs for conditional and unconditional test-particle measurements, as well as conditional and combined model results. The combined model with optimised parameters shows good agreement with the unconditional test-particle MSD. The compound subdiffusion model is also shown for the unbiased optimised parameters, thus some deviation from the biased conditional data is present.

5.1. Refinement of the combined stochastic model

We emphasise that our model is semi-empirical, where parameters are inferred from the test-particle data. It is essential for a proper transport theory to predict the involved MFPs and mean durations from the underlying turbulence. In particular, such a theory should account for the hierarchy of scales present in the problem, from scattering on gyro scales, over motion within individual coherent structures and up to large-scale network-like constellations of the population of coherent structures (Ntormousi et al. Reference Ntormousi, Vlahos, Konstantinou and Isliker2024). This task could be approached by projector-based coarse-graining of the dynamics, following the Mori–Zwanzig formalism (Hudson & Li Reference Hudson and Li2020; Lin et al. Reference Lin, Tian, Livescu and Anghel2021).

Another possible approach to accurately derive the required MFPs and mean durations would be to follow Drummond (Reference Drummond1982) and start with a path integral formulation of turbulent diffusion. However, in Drummond’s approach, the magnetic potential is assumed to be Gaussian. A possible, far from trivial approach would be a path integral formulation including the action $S_{\mathrm{MHD}}$ corresponding to the MHD dynamics plus the action $S_{\mathrm{particle}}$ of the particle dynamics and applying non-perturbative methods to approximate this complex path integral (see, e.g. Grafke, Grauer & Schäfer Reference Grafke, Grauer and Schäfer2015; Bureković et al. Reference Bureković, Schäfer and Grauer2024; Schorlepp & Grafke Reference Schorlepp and Grafke2025).

5.2. Alternative transport descriptions

A central assumption of our model is that all involved kinds of motion are Gaussian and sufficiently characterised by their MFPs or MSDs. While our combined model of Langevin and compound subdiffusion successfully reproduces the test-particle MSD, possibly relevant higher-order statistics are neglected. For instance, intermittent pitch-angle scattering (Zimbardo & Perri Reference Zimbardo and Perri2020) or streaming (Sampson et al. Reference Sampson, Beattie, Krumholz, Crocker, Federrath and Seta2023) can lead to superdiffusion of cosmic rays. In the context of our test-particle data, magnetised motion may be described by spatial superdiffusion (averaged over the pitch angle), and mirror-confinement in coherent structures may correspond to subdiffusion. A clever combination of Lévy walks and extended waiting times (Zaburdaev, Denisov & Klafter Reference Zaburdaev, Denisov and Klafter2015) with truncated distributions (Liang & Oh Reference Liang and Oh2025) may reproduce the intricate time evolution of the test-particle MSDs, while also accounting for possibly relevant higher-order statistics. In this case of competition between sub- and superdiffusion (Magdziarz & Weron Reference Magdziarz and Weron2007) of cosmic rays, a single (fractional) transport equation might be formulated that is equivalent to the stochastic model as presented for the superdiffusive case by Effenberger et al. (Reference Effenberger, Aerdker, Merten and Fichtner2024) and Aerdker et al. (Reference Aerdker, Merten, Effenberger, Fichtner and Becker Tjus2025).

Alternatively, especially when modelling large-scale ( $\gg L_u$ ) multiphase media, the structured nature of turbulence may be reflected by distinct diffusion coefficients. For the example of two spatially distinguishable phases, one can employ a regular Fokker–Planck equation $\partial _t f(\boldsymbol{x},t)=\Delta D(\boldsymbol{x})f(\boldsymbol{x},t)$ with a mixed diffusion coefficient $D(\boldsymbol{x})=D_1$ for $\boldsymbol{x}\in \text{phase 1}$ and $D(\boldsymbol{x})=D_2$ for $\boldsymbol{x}\in \text{phase 2}$ , which is readily applicable to astrophysical problems (see, e.g. Reichherzer et al. Reference Reichherzer, Bott, Ewart, Gregori, Kempski, Kunz and Schekochihin2025). Otherwise, a temporal switching Fokker–Planck equation $\partial _tf_i(\boldsymbol{x},t)=D_i\Delta f_i(\boldsymbol{x},t)+A_{ij}f_j(\boldsymbol{x},t)$ with Markovian switching rates $A_{ij}$ may be useful (see, e.g. Bressloff & Lawley Reference Bressloff and Lawley2017; Balcerek et al. Reference Balcerek, Wyłomańska, Burnecki, Metzler and Krapf2023), which could be applied as a sub-grid model for cosmic-ray transport.

All presented models involve a competition between two transport regimes to capture the transient phases of the observed MSD. Similar switching or competing models are also known in other complex systems (see, e.g. Doerries, Chechkin & Metzler Reference Doerries, Chechkin and Metzler2022; Datta, Beta & Großmann Reference Datta, Beta and Großmann2024).

5.3. Generalised transport equation

To study structure-mediated transport of cosmic rays in astrophysical applications, the physics described by our combined stochastic model needs to be encapsulated in a generalised transport equation for the $5+1$ -dimensional particle distribution function $f(\boldsymbol{x},\mu ,\hat {\omega }_g,t)$ . This transport equation takes the form $\partial _tf=\mathcal{D}[f]$ , where the generalised transport operator $\mathcal{D}[\boldsymbol{\cdot }]$ can describe a wide range and combination of processes, such as (anomalous) spatial diffusion $\mathcal{D}=D_{xx}\varDelta ^{(\alpha )}$ , pitch-angle diffusion $\mathcal{D}=\partial _\mu D_{\mu \mu }\partial _\mu$ or momentum diffusion $\mathcal{D}=p^{-2}\partial _pp^2D_{pp}\partial _p$ (with momentum $p\propto \hat {\omega }_g$ in our notation) (Metzler & Klafter Reference Metzler and Klafter2000; Schlickeiser Reference Schlickeiser2002). Since transport properties are strong functions of the local plasma conditions and cosmic rays can exert a dynamically relevant feedback on the plasma, the transport equation needs to be coupled with the astrophysical simulation for a self-consistent treatment (Bai et al. Reference Bai, Caprioli, Sironi and Spitkovsky2015; Pfrommer et al. Reference Pfrommer, Pakmor, Schaal, Simpson and Springel2017; Böss et al. Reference Böss, Steinwandel, Dolag and Lesch2023). With such a set-up, one could, for instance, study the effect of streaming on coherent structures (compare, e.g. Rieder & Teyssier Reference Rieder and Teyssier2017; Sampson et al. Reference Sampson, Beattie, Krumholz, Crocker, Federrath and Seta2023).

Possible approaches to construct an operator $\mathcal{D}$ , which describes the competition between two modes of transport, are contemplated in § 5.2. We also note that $\mathcal{D}$ must not necessarily be known explicitly, as it can be represented and solved by the corresponding stochastic differential equations (Effenberger et al. Reference Effenberger, Aerdker, Merten and Fichtner2024; Aerdker et al. Reference Aerdker, Merten, Effenberger, Fichtner and Becker Tjus2025). The remaining challenge is then to parametrise our transport model in terms of characteristic turbulence quantities, which may vary across the large-scale simulation domain, such as the turbulence correlation scale, turbulence strength or sonic Mach number.

Such an integrated study can provide data for validating this or other non-standard transport models against observational data. Ultimately, this study should not only be consistent with the data, but provide falsifiable predictions. Observational constraints for intermittent cosmic-ray scattering theories are, for instance, considered by Butsky et al. (Reference Butsky, Hopkins, Kempski, Ponnada, Quataert and Squire2024) and Kempski et al. (Reference Kempski, Li, Fielding, Quataert, Phinney, Kunz, Jow and Philippov2025).