Non-technical Summary
The current paper reviews the developmental gene hypothesis (DGH), which provides molecular support for the theory of punctuated equilibria. The author reviews and expands the DGH, using game theory and simulations to illustrate and predict the evolutionary patterns of stasis and punctuated change of developmental genes and their roles in the fossil record.
Punctuated Equilibria: A Historical Perspective
Although previous naturalists had noted the paucity of the nineteenth-century fossil record, it was Charles Darwin who most famously acknowledged its limitations in his book On the Origin of Species (Reference Darwin1859). Most importantly, he recognized that transitional forms were often lacking in the fossil record, which posed potential problems for his theory of gradualism. As a result, most Darwinists of the early to mid-twentieth century turned their attentions away from paleontology and instead toward the burgeoning young field of biology, which began exploration into areas such as cell biology, physiology, and embryology. By contrast, most paleontologists during the late nineteenth and early twentieth centuries were not outright Darwinists and either focused on descriptive studies outlining morphology and stratigraphy or adhered to a variety of other schools of evolutionary thought, including orthogenesis and Lamarckism, which placed less emphasis on gradualism (reviewed in Sepkoski Reference Sepkoski2012).
As early heredity studies and population genetics led to the school of thought we now know as the modern synthesis, paleontology was slowly brought into the fold (and sometimes under the heel) of the Neo-Darwinists. Interestingly, as Sepkoski (Reference Sepkoski2012) reviews in his history of paleobiology, many paleontologists before the modern synthesis had found saltational and macromutational explanations of evolution appealing and perhaps more in line with what they were seeing in the fossil record. Ernst Mayr, the evolutionary biologist, later recalled that “most paleontologists were either saltationists or orthogenesists, while those we believe to have been Neo-Darwinists failed to write general papers or books” (Mayr Reference Mayr, Mayr and Provine1980; Sepkoski Reference Sepkoski2012: p. 28).
Although American paleontologist, George Gaylord Simpson, eventually acquiesced to the hardline synthesis school of thought by the 1950s, his earlier work Tempo and Mode in Evolution (1944) argued strongly that the discontinuous nature of the fossil record across higher taxa indicated potential variability in the rates of evolution over time. Likewise, he was willing to accept that, unlike in the gradualist theory, these major shifts in evolutionary tempo should not necessarily be extrapolated from microevolutionary processes but may instead be unique. Simpson referred to this enhanced tempo as “quantum evolution” and dramatic evolutionary leaps as “mega-evolution.” Curiously, these terms were significantly downplayed in the subsequent revision of his book, retitled The Major Features of Evolution (Simpson Reference Simpson1953). By that time, his ideas had been impacted by the increasingly strict interpretation of the modern synthesis and the intense influence of other Neo-Darwinists like Theodosius Dobzhansky and Ernst Mayr. In fact, most paleontologists by the late 1960s adhered overwhelmingly to Neo-Darwinian views (reviewed in Sepkoski Reference Sepkoski2012).
It is well known that Darwin’s work was significantly influenced by Charles Lyell and his support for uniformitarianism, which emphasizes that geologic processes that shape the Earth are constant and usually quite slow (Rhodes Reference Rhodes1987). Darwin’s insistence on evolutionary gradualism was largely borne out of this intellectual admiration. Uniformitarianism, however, is in stark contrast to Georges Cuvier’s theory of catastrophism, which proposes that the large gaps present in the fossil record are the result of catastrophic events, leading to large-scale extinction. During the height of the modern synthesis, forms of catastrophism tended to be viewed as anathema and were often pushed to the fringes of science—that is, until the work of American invertebrate paleontologist Norman Newell.
Although Newell never referred to himself as a catastrophist, he provided strong evidence and open scientific support for the idea that discontinuity in the worldwide fossil record was the consequence of large-scale episodic events. Others, such as Raup and Sepkoski, also published on the periodicity of mass extinctions (Raup and Sepkoski Reference Raup and Sepkoski1984; Raup Reference Raup1991). Many of the mass extinction events we recognize today are the outcome of catastrophic geologic processes such as volcanism, major changes in climate, or even asteroid impacts. As a result of his standing within the paleontological community, his support gave significant weight to a theory that had been out of fashion since the time of Lyell. Not only did Newell’s research, as well as later work by Raup and Sepkoski (Raup and Sepkoski Reference Raup and Sepkoski1984; Raup Reference Raup1991), show that these fossil gaps were worldwide and not just localized inconsistencies, they were also closely followed by evolutionary radiations.
It is perhaps unsurprising, given Newell’s focus on mass extinctions and subsequent radiations, that he was mentor to both Niles Eldredge and Stephen Jay Gould, the authors of punctuated equilibria. Likewise, these young scientists were influenced by Simpson’s Tempo and Mode in Evolution, whose earliest iterations stressed the variability in evolutionary rate, as well as Mayr’s work on allopatric speciation, which emphasized the role of geographic isolation during speciation events (Mayr Reference Mayr, Huxley, Hardy and Ford1954). Each of these influences is clearly present in Eldredge’s Reference Eldredge1971 paper “The Allopatric Model and Phylogeny in Paleozoic Invertebrates,” which, short of naming the new theory, outlined much of what is considered the meat of punctuated equilibria. Throughout much of the first half of the twentieth century, genetics and paleontology were moderately separate disciplines with little collaborative overlap due in part to significant differences in methodology and fundamental schema. (See Mayr [Reference Mayr1982] for review on the methodological and conceptual differences that initially kept these fields apart.) By the middle of the century, paleontology appears to have been brought into the biological fold but in a manner subservient to the will of the Neo-Darwinists. However, with the 1970s paleontological renaissance—in which Gould and Eldredge were major figures—paleontology essentially broke free and began to reconnect with some of its roots.
Perhaps due to the rocky history of interaction between these two disciplines, as well as a dearth of viable ancient DNA material, paleontology and genetics have remained modestly siloed from one another, despite areas of convergence, such as phylogenetic analysis, molecular clock dating, and ancestral state reconstruction. However, with the completions of the Human Genome Project and subsequent sequencing of numerous other organismal genomes, computational and comparative studies have provided a wealth of information that is applicable to evolutionary theory and macroevolutionary processes (Venter et al. Reference Venter, Adams, Myers, Li, Mural, Sutton and Smith2001). And indeed, there have been some attempts to reconcile this fundamental divide, most notably by Eldredge et al. (Reference Eldredge, Thompson, Brakefield, Gavrilets, Jablonski, Jackson, Lenski, Lieberman, McPeek and Miller2005), a collaboration between paleontology and population genetics in which both groups ultimately agree on the importance of allopatry in speciation. However, prominent gaps still remain between the fields, particularly with regard to macroevolutionary theory.
Recently, Casanova and Konkel (Reference Casanova and Konkel2020) proposed the developmental gene hypothesis (DGH), which may address one of these important gaps. Notably, it supplies a genetic complement for the patterns visible within the fossil record, which were highlighted by Eldredge and Gould’s (Reference Eldredge, Gould and Schopf1972) theory of punctuated equilibria. The purpose of the current thesis is to review and expand this new theory, as well as integrate concepts of developmental constraint proposed by Gould (Reference Gould1980). In addition to expanding the DGH, game theory is used to model the behavior of developmental regulatory (DevReg) gene networks, which are fundamental to this new theory and may ultimately provide a better understanding of their roles in both stasis and speciation.
Developmental Constraints and Punctuated Equilibria
As Gould and Eldredge’s concepts surrounding punctuated equilibria continued to mature, their focus expanded beyond the pace of evolutionary change (gradual vs. punctuated), whose potential saltatory-like nature could, with some effort, be shoehorned into the traditional Neo-Darwinian paradigm. As Lewin implied with his Reference Lewin1986 article titled “Punctuated Equilibrium Is Now Old Hat,” the patterns of punctuated equilibria are “something everyone knew all along” (p. 672). See also Richard Dawkins’s allegory of the exodus of the Israelites in his book The Blind Watchmaker (1996) as further testament to these claims, in which he declares that simply because a process is gradual does not necessitate it occurs at a constant and steady pace. However, Darwin himself based his ideas of gradualism on a species’ “tendency to vary by generation,” which strongly implies a steady state of change insofar as generations are consistently spaced, suggesting that our definition of “gradual” has indeed been adapted over time and is no longer strictly Darwinian in nature (Darwin 1837–Reference Darwin and van Wyhe1838).
While still interested in the tempo of evolution, Gould and Eldredge instead focused on possible mechanisms underlying the stasis observed (Gould Reference Gould1977; Gould and Eldredge Reference Gould and Eldredge1977). Namely, they proposed a mechanism of “developmental constraint,” pulling from Karl Ernst von Baer’s laws of embryology, one of which states that “the more general characters of a large group appear earlier in the embryo than the more special characters” (translated in Huxley Reference Huxley1898). They also drew from Zuckerkandl (Reference Zuckerkandl, Rich and Davidson1968), who predicted that fetally expressed proteins would be more conserved than proteins expressed in adulthood. (I will talk more on this conservation in the next section, where I discuss the developmental hourglass model.) Importantly, these “developmental constraints” are an integral part of developmental selection (Frank Reference Frank1997).
Despite developmental selection being a series of natural phenomena well recognized within the broad field of evolutionary developmental biology (evo-devo), because it is not categorically subsumed under “natural selection” due to its reliance on intrinsic factors rather than the extrinsic environment, it is sometimes overlooked by adaptationists and population geneticists (Müller Reference Müller2007). The consequences of this are summarized elegantly by Müller:
Whereas in the Modern Synthesis framework the burden of explanation rests on the action of selection, with genetic variation representing the necessary boundary condition, the evo-devo framework assigns much of the explanatory weight to the generative properties of development, with natural selection providing the boundary condition. When natural selection is a general boundary condition, the specificity of the phenotypic outcome is determined by development. Thus, evo-devo moves the focus of evolutionary explanation from the external and contingent to the internal and inherent. (Müller Reference Müller2007: p. 947)
Developmental selection is not a minor player concerned with rare exceptions. As a case in point, approximately 30% of all human conceptions are miscarried, the majority due to major chromosomal rearrangements and other genetic variations not otherwise compatible with life (Wilcox et al. Reference Wilcox, Weinberg, O’Connor, Baird, Schlatterer, Canfield, Armstrong and Nisula1988; Choi et al. Reference Choi, Lee, Park, Jeong and Moon2014; Linnakaari et al. Reference Linnakaari, Helle, Mentula, Bloigu, Gissler, Heikinheimo and Niinimäki2019). In fact, according to a recent study by Soler et al. (Reference Soler, Morales, Mademont-Soler, Margarit, Borrell, Borobio, Muñoz and Sánchez2017) in which they studied more than 1000 chorionic villi samples, trisomy, triploidy, and tetraploidy occurred in approximately 20% of samples. These mutations are not weeded out via survival of the fittest adult forms, but rather survival of blastocystic, embryonic, and fetal forms. The rate at which these genetic variations occur and are weeded out cannot be discounted as rare exceptions. They shape the genome just as much as natural selection of the adult form. And yet we often think of these variations as “uncommon” or “rare,” because they are indeed uncommon in organisms that have survived beyond embryonic or larval stages—survival of the developmentally fittest.
Scientists such as Dawkins (Reference Dawkins1996) and Coyne (Reference Coyne2021) have criticized Gould and Eldredge for utilizing the idea of “developmental constraints” as explanation for the stasis within the fossil record.
As I said, the one respect in which punctuationists do differ from other schools of Darwinism is in their strong emphasis on stasis as something positive: as an active resistance to evolutionary change rather than as, simply, absence of evolutionary change. And this is the one respect in which they are quite probably wrong. (Dawkins Reference Dawkins1996: p. 248)
In contrast to Dawkins’s and Coyne’s claims, developmental systems and the genes that regulate them are in fact a perfect explanatory mechanism for the “active resistance” highlighted by Eldredge and Gould (Reference Eldredge, Gould and Schopf1972) and for which Casanova and Konkel (Reference Casanova and Konkel2020) provide support in their paper on the DGH. Other scientists beyond Gould have continued to explore ideas surrounding developmental constraints, such as Sean Carroll, who examined how gene regulatory networks constrain evolutionary paths; Wallace Arthur and Alessandro Minelli, each of whom have studied how developmental constraints influence morphology and diversity; and Günter Wagner, who proposed the concept of “homologues of process,” which refers to the conservation of certain developmental processes across different species (Minelli Reference Minelli2003; Arthur Reference Arthur2004; Carroll Reference Carroll2005; Wagner Reference Wagner2014). For a further in-depth treatment of these topics, please see these and related works.
Now I will turn my attention to a fundamental explanatory mechanism for the molecular basis of punctuated equilibria. In the following sections, I reintroduce the original DGH (Casanova and Konkel Reference Casanova and Konkel2020) and further expand the theory, integrating other areas of research such as the influence of gene flow on accumulation of weakly deleterious variations and the roles of DevReg genes in hybrid incompatibility and the maintenance of species integrity, and finally I will model stasis and compensatory adaptation using game theory in a fashion similar to John Maynard Smith (Maynard Smith and Price Reference Maynard Smith and Price1973; Maynard Smith Reference Maynard Smith1976).
The Developmental Gene Hypothesis
Critics claim that, in most cases, gene flow is simply too restricted to exert homogenizing influence and prevent differentiation. This produces a paradox: why, then, are species coherent (or even recognizable)? Why do groups of (relatively independent) local populations continue to display a fairly consistent phenotype that permits their recognition as a species?… The answer probably lies in a view of species and individuals as homeostatic systems—as amazingly well-buffered to resist change and maintain stability in the face of disturbing influences.… The coherence of species, therefore, is not maintained by interaction among its members (gene flow). It emerges, rather, as an historical consequence of the species’ origin as a peripherally isolated population that acquired its own powerful homeostatic system. (Eldredge and Gould Reference Eldredge, Gould and Schopf1972: pp. 112–114)
Although aspects of Eldredge and Gould’s theory of punctuated equilibria could be seen in earlier works such as Simpson’s (Reference Simpson1944) Tempo and Mode in Evolution and Mayr’s theory on allopatric speciation (1942), both authors felt that one of the most original features of their 1972 paper was that it highlighted “stasis,” a characteristic of the fossil record that had always been acknowledged but never truly recognized as scientifically relevant (reviewed in Sepkoski Reference Sepkoski2012). They predicted the existence of an endogenous homeostatic mechanism that regulated speciation by acting as a buffer against significant species change, although its precise biological basis was unknown at the time. This is in contrast to adaptationists, who assumed that alternating periods of speciation and stasis were the sole result of extrinsic environmental factors and the selection they wrought upon organisms (Eldredge and Gould Reference Eldredge, Gould and Schopf1972).
Sequencing and study of numerous species’ genomes have led to substantial advances in the field of evolutionary genomics, which has allowed scientists to reassess these earlier questions. Recently, Casanova and Konkel (Reference Casanova and Konkel2020) proposed a molecular mechanism (DGH) that may be responsible for the stasis present within the fossil record. In this paper, the authors describe a group of metazoan genes, known as DevReg genes, responsible for the regulation of morphological development, which are highly conserved across species and exhibit significant mutation intolerance. As Lidgard and Love (Reference Lidgard and Love2018) suggest, these genes may be considered “molecular living fossils” relative to other gene groups due to their conserved natures. While they are not mutation coldspots per se, they are often dosage sensitive, leading to relative intolerance of genetic variation (Makino and McLysaght Reference Makino and McLysaght2010). Although a variety of mechanisms may exist that lead to this dosage sensitivity, Rice and McLysaght (Reference Rice and McLysaght2017a,Reference Rice and McLysaghtb) contend that one key mechanism lies in the tendency for such gene products to form protein complexes and tightly regulated molecular pathways, each potentially sensitive to stoichiometric imbalance. In partial support of this, my own work has identified increased protein–protein interactions (PPI) and greater mutation intolerance in DevReg genes in humans (Casanova Reference Casanova2023). Variation in a single gene can lead to deviations in ratio within these complexes and can result in significant complex-wide impairment (further explored in the gene dosage balance hypothesis; Birchler and Veitia Reference Birchler and Veitia2012). Therefore, such genes must typically change in concert or not at all. In support of this, single copy number variations of these dosage-sensitive genes are rarely inherited but homologues of these same genes may be retained following whole-genome duplication (WGD) events (reviewed in Rice and McLysaght Reference Rice and McLysaght2017a,Reference Rice and McLysaghtb).
These genes also seem to be integral to the vertebrate phylotypic period of development and likely underlie the common archetype seen during these middle embryonic stages proposed by von Baer and captured in Ernst Haeckel’s famous drawings (Richardson et al. Reference Richardson, Hanken, Gooneratne, Pieau, Raynaud, Selwood and Wright1997; Irie and Kuratani Reference Irie and Kuratani2014). Interestingly, genes expressed during this developmental period exhibit conserved expression patterns compared with genes expressed in earlier and later stages, supporting the developmental hourglass model (Kalinka et al. Reference Kalinka, Varga, Gerrard, Preibisch, Corcoran, Jarrells, Ohler, Bergman and Tomancak2010; Raff, Reference Raff2012), as well as harkening back to work by Zuckerkandl (Reference Zuckerkandl, Rich and Davidson1968). (Interestingly, Zuckerkandl was not entirely correct: genes expressed in earliest development are not particularly well conserved across Vertebrata, nor are the later stages; instead, middle stages of development centered around organogenesis are most tightly conserved.) Most relevant to the current thesis, mutations targeting these developmental genes are under substantial purifying selection and are a singular candidate for the homeostatic mechanism proposed by Eldredge and Gould (Reference Eldredge, Gould and Schopf1972), considering they are key orchestrators in animalian morphology and therefore their influence should be keenly felt within the fossil record. While many of these genes radiated within the early vertebrates thanks to two rounds of WGD, a substantial subset of DevReg genes is also shared by the Bilateria and Eumetazoa, predating the vertebrate developmental archetype altogether, and their evolutionary rates are similarly low (Putnam et al. Reference Putnam, Butts, Ferrier, Furlong, Hellsten, Kawashima and Robinson-Rechavi2008; Casanova Reference Casanova2023).
In addition, the process [of heritable change] is stochastic rather than deterministic and so it only appears when averaged over many characters. (Penny Reference Penny1985: p. 202)
As we have shown, de novo variations in DevReg genes are infrequently inherited due to strong selective pressures promoting their stability. In contrast to Penny’s (Reference Penny1985) claim, this process is not random but considerably more deterministic than that of less-constrained functional gene groups. Penny goes on to state:
Where regulatory genes are known in any detail … these genes are subject to exactly the same type of point mutations, small deletions and insertions, and larger duplications that are found in structural genes.… The evidence we have is that regulatory genes do not differ genetically in any fundamental way from structural genes. (Penny Reference Penny1985: pp. 203–204)
While the genetic variations that have arisen in DevReg genes are usually not inherently different from the variations seen in other gene types, the heritability rate of those variations is divergent and comparatively conserved. Meanwhile, and in spite of this divergence, these developmental genes (especially neurodevelopmental genes) and their regulatory sequences are overrepresented in evolutionarily accelerated regions in humans, primates, and mammals, to name a few (Capra et al. Reference Capra, Erwin, McKinsey, Rubenstein and Pollard2013; Holloway et al. Reference Holloway, Bruneau, Sukonnik, Rubenstein and Pollard2016; Kostka et al. Reference Kostka, Holloway and Pollard2018; Girskis et al. Reference Girskis, Stergachis, DeGennaro, Doan, Qian, Johnson and Wang2021). This suggests that when speciation events do occur, the selective pressures on DevReg genes change and are overcome by extrinsic and/or intrinsic factors, such as major environmental shifts, reduced gene flow, hybridization events leading to chromosomal rearrangements or even WGD, or transposable element radiations. In further support of this, phenotypic divergence between humans and the other great apes is associated with rapid evolution in human-specific regulatory sequences, which are largely the result of recombination-associated exaptations of conserved regulatory sequences and human-specific insertions of tranposable elements (Glinsky Reference Glinsky2016). Therefore, these genes and the sequences that regulate them are not only major drivers of stasis, but are also prime targets for speciation. They are not wholly immutable but instead act as anchors; however, they are also targets for change under strong enough pressures, as in the case of new transposon radiations, a mechanism that we focused on in our original article (Zeh et al. Reference Zeh, Zeh and Ishida2009; Casanova and Konkel Reference Casanova and Konkel2020). Such pressures may force biology to effectively “weigh anchor.”
Expansion of the Developmental Gene Hypothesis
With the first publication of the DGH, our primary focus lay with the genetic mechanisms underlying stasis observable within the fossil record (Casanova and Konkel Reference Casanova and Konkel2020). However, in that earlier iteration, the proposed mechanisms responsible for punctuated speciation were vague, focusing on infrequent genomic events such as transposable element insertions. Within the present paper, I expand this thesis, integrating bodies of work on active and passive genomic evolvability; the neutral and nearly neutral theories of molecular evolution and the roles of reduced gene flow such as occurs with geographic isolation; the circumstances surrounding compensatory adaptation in conserved gene networks; and the roles DevReg genes play in hybrid incompatibility; and finally I explore the applicability of game theory to both the conservation and adaptation of DevReg networks as a predictive model for their behaviors and, ultimately, patterns within the fossil record (Kimura Reference Kimura1968; Eldredge and Gould Reference Eldredge, Gould and Schopf1972; Ohta Reference Ohta1992).
Active Evolvability
If species are in equilibrium for most of their durations, what causal agency of the punctuation can one invoke other than physical change?… Thus, the chief cause of population size reduction and allopatry in the history of life have probably derived from tectonic and climatic changes; and our finding that a species starts relatively small on its own prompts the hypothesis of speciation pulses. (Vrba Reference Vrba2005: pp. 158–159)
One of the great curiosities within the fossil record concerns coordinated multi-faunal patterns of stasis followed by abrupt change and speciation. This trend has been central to the theories of coordinated stasis (Brett et al. Reference Brett, Ivany and Schopf1996) and the turnover-pulse hypothesis (Vrba Reference Vrba1985, Reference Vrba1993). Much of the causal emphasis has been placed on the roles environmental upheaval plays in these processes; however, less consideration has been given to intrinsic factors at the organism level that may play a permissive and potentially adaptive role during environmental change. As such, it is better to view organisms not as molecularly passive pawns, but as active participants with the potential for rapid change in the face of destabilizing events. This tendency is known as “evolvability” and is an ongoing and active field of research (for review, see Müller Reference Müller2007).
The various ways in which environmental stressors can place strain on molecular networks and trigger increased phenotypic variability in ensuing generations is an active area of study. Notable stressors include hyperthermia, hypoxia, hyposmolarity, starvation, oxidation, and radiation—all of which trigger the cell stress response, which is a defensive (and evolved) strategy cells take in response to damage (Ray et al. Reference Ray, Huang and Tsuji2012; Masson and Ratcliffe Reference Masson and Ratcliffe2014; Efeyan et al. Reference Efeyan, Comb and Sabatini2015; Jeggo et al. Reference Jeggo, Pearl and Carr2016; Gomez-Pastor et al. Reference Gomez-Pastor, Burchfiel and Thiele2018). In particular, heat shock proteins, especially Hsp90, have received considerable attention (Fulda et al. Reference Fulda, Gorman, Hori and Samali2010). Hsp90 is a molecular chaperone that, under normal circumstances, coordinates folding, assembly, distribution, and turnover of proteins that are key to growth and survival (Whitesell et al. Reference Whitesell, Bagatell and Falsey2003). Under circumstances of cellular stress, during which protein production and repair are significantly increased, heat shock proteins can become overwhelmed.
Relevant to processes underlying adaptation, Hsp90 also functions as an “evolutionary capacitor” (i.e., switching mechanism), in that it indirectly regulates the phenotypic expression of otherwise cryptic genetic variation already present within the genome. As reviewed in Bergman and Siegal (Reference Bergman and Siegal2003), Hsp90 demonstrates three properties in its role as evolutionary capacitor: “(1) it suppresses phenotypic variation under normal conditions and releases this variation when functionally compromised; (2) its function is overwhelmed by environmental stress; and (3) it exerts pleiotropic effects on key developmental processes” (p. 549).
Earlier, Siegal and Bergman (Reference Siegal and Bergman2002) demonstrated that canalization, which is the phenotypic robustness of a system in the face of intrinsic (genetic) and extrinsic (environmental) change, is not unique to heat shock proteins but can be found throughout numerous developmental systems. Instead, the extent of canalization may instead be dependent on the complexity (connectedness) within a given molecular network.
According to Siegal and Bergman (Reference Siegal and Bergman2002), rather than requiring a dedicated mechanism, canalization instead arises as an emergent property of the complexity of these networks. When a particular component of that network is compromised, such as Hsp90, which would normally provide buffering in the face of stress, this promotes adaptation within the network toward a new optimal phenotype. During stasis, this network may be modeled as a Nash equilibrium, that is, “no single player, by changing his own part … can obtain higher utility if the others stick to their parts” (Kreps Reference Kreps, Eatwell, Milgate and Newman1989: p. 167). (See “Modeling Conservation” subsection for an expansion of this idea.) Interestingly, this emergent property was presaged by Dobzhansky himself:
But nature has not been kind enough to endow the organism with the ability to react purposefully to the needs of the changing environment by producing only beneficial mutations where and when needed. Mutations are random changes. Hence the necessity for the species to possess at all times a store of concealed, potential, variability. (Dobzhansky Reference Dobzhansky1937: p. 126)
While DevReg genes, such as transcription factors, tend to be highly conserved, the transcription factor binding sites to which they bind display a surprising potential for evolvability, suggesting a means for adaptation in the face of selective pressures (Payne and Wagner Reference Payne and Wagner2014).
The cell stress response also induces transposable element mobilization, providing new mutational capacity rather than forcing organisms to rely solely on cryptic variation (Kidwell et al. Reference Kidwell, Kidwell and Sved1977). One of the mechanisms by which this is achieved is the displacement of transposable element regulatory agents such as PIWI-interacting RNA (piRNA) to the lysosome for degradation (Cappucci et al. Reference Cappucci, Noro, Casale, Fanti, Berloco, Alagia, Grassi, Le Pera, Piacentini and Pimpinelli2019). Transposon insertions not only result in mutations that have the potential to disrupt nearby gene sequences, but due to the fact they often carry with them their own cis-regulatory elements (CREs) in order to exploit the host genome environment, these CRE sequences can subsequently influence host genes as well (Jordan et al. Reference Jordan, Rogozin, Glazko and Koonin2003; Sundaram and Wysocka Reference Sundaram and Wysocka2020). Further work is needed to truly address the functionality of these potential CREs (de Souza et al. Reference de Souza, Franchini and Rubinstein2013); however, examples of exaptation suggest they are a simple means to acquire potential regulatory material rapidly, lending toward speciation (for review, see Sundaram and Wysocka Reference Sundaram and Wysocka2020). Furthermore, evidence indicates that under linkage disequilibrium, cis–trans pairings can diverge rapidly between closely related species under selection (a genetic Red Queen race), providing a functional barrier to hybridization (Mack and Nachman Reference Mack and Nachman2017). Subsequently, such cis–trans divergence appears to lead to significant gene misexpression in sterile as compared with fertile hybrids (Mack et al. Reference Mack, Campbell and Nachman2016).
Together, these emergent properties, which themselves have been under selection, provide a rapid albeit risky means to increase phenotypic variability in the face of an unstable environment. Because some of these are mechanisms common even to bacteria (reviewed in Casacuberta and González Reference Casacuberta and González2013), they provide a universal and intrinsic means by which groups of unrelated organisms may actively adapt in the face of environmental upheaval.
Passive Evolvability: The Nearly Neutral Theory of Molecular Evolution, Compensatory Adaptation, and Species Integrity
Scientists such as Mayr (Reference Mayr1942), Eldredge and Gould (Reference Eldredge, Gould and Schopf1972), and Vrba (Reference Vrba2005) recognized the association of geographic isolation and environmental change as mechanisms integral to speciation. However, it is also important to review the roles of genetic drift in genome evolution and how gene flow is influenced by population size (Wright Reference Wright1931). It should be noted that even Darwin appears to have touched on the concept of allopatry in his earlier transmutation notebooks, but later downplayed it for the benefit of his preferred theory, “gradual change through time driven by natural selection” (reviewed in Eldredge Reference Eldredge2015). Darwin presciently stated:
One is tempted to exclaim that nature conscious of the principle of incessant change in her offspring has invented all kinds of plan to insure [sic] sterility, but isolate your species her plans are frustrated or rather a new principle is brought to bear. (Darwin Reference Darwin1838: pp. 52–53)
Of course, no discussion of genetic drift is complete without addressing the foundational work of Motoo Kimura. Kimura first published his radically new thesis, the neutral theory of molecular evolution, in 1968, outlining his ideas on the importance of genetic drift and the accumulation of neutral mutations as the dominant process in genome evolution rather than natural selection. He also stated that purifying selection, which acts to conserve the status quo and quickly purges deleterious variants from the gene pool, is far more common than positive selection of advantageous variants, which are comparatively rare (reviewed in Hughes Reference Hughes2008).
Later, Tomoko Ohta (Reference Ohta1992) extended this work, publishing the nearly neutral theory of molecular evolution, in which he further emphasized the role of population size in predicting the retention and accumulation of weakly deleterious variants. Specifically, Ohta showed that the smaller the size of a given breeding population, the higher its burden of nonsynonymous (i.e., weakly deleterious) variants. The theory predicts that as population size decreases and gene flow is reduced, weakly deleterious variants increase in frequency or even come to fixation, which may lead to higher genetic burden in small groups potentially undergoing speciation. Relevant examples of populations with evidence of higher genetic burden include the modern Greenlandic Inuit people, Neanderthals, Denisovans, some subspecies of gorilla, the African cheetah, and the black-faced spoonbill, to name just a few (Dobrynin et al. Reference Dobrynin, Liu, Tamazian, Xiong, Yurchenko, Krasheninnikova and Kliver2015; Harris and Nielsen Reference Harris and Nielsen2016; Simons and Sella Reference Simons and Sella2016; Pedersen et al. Reference Pedersen, Lohmueller, Grarup, Bjerregaard, Hansen, Siegismund, Moltke and Albrechtsen2017; Li et al. Reference Li, Liu, Yeh, Fu, Yeung, Lee and Chiu2022).
Ohto also recognized the importance of subsequent compensatory adaptation in the face of genetic drift in a small population and the accumulation of weakly deleterious variation; that is, the accumulation of new genetic variation ameliorates deleterious effects and, in essence, may create linkage disequilibrium between regions (epistasis). As reviewed by Hartl and Taubes (Reference Hartl and Taubes1996):
The result is that, as Ohta has pointed out, a significant fraction of mutations that are fixed in evolution are slightly detrimental. In the long run, the fixation of detrimental mutations in a gene increases the opportunity for the occurrence of a compensatory favorable mutation, either in the same gene or in an interacting gene. (p. 303)
Compensatory adaptation is a form of positive selection and, according to predictions by Kimura (Reference Kimura1968) and Ohta (Reference Ohta1992), is likely to be the predominant form of adaptation. In short, these variants are adaptive insomuch as they restore prior function. Compensatory adaptation has been identified within extended interacting gene networks and may be responsible for large islands of divergence in nascent species (i.e., accelerated regions) (Hartl and Taubes Reference Hartl and Taubes1996; Renaut et al. Reference Renaut, Maillet, Normandeau, Sauvage, Derome, Rogers and Bernatchez2012; Hubisz and Pollard Reference Hubisz and Pollard2014). However, it also occurs within the host gene itself, and variants are far more likely to arise closer to the original mutation site (Davis et al. Reference Davis, Poon and Whitlock2009).
As Maheshwari and Barbash (Reference Maheshwari and Barbash2011) note, most hybrid incompatibilities are due to genetic drift and compensatory adaptation rather than ecological adaptation. If hybrid incompatibility is the primary means for reinforcing species integrity and DevReg genes are, as previously proposed, integral to stasis and speciation, one might expect them to be implicated in such barriers (Casanova and Konkel Reference Casanova and Konkel2020). In fact, work by Renaut and Bernatchez (Reference Renaut and Bernatchez2011) implicates DevReg genes in postzygotic incompatibilities. While studying differences in gene expression patterns in backcross hybrids of normal and dwarf white lakefish, which exhibit strong but incomplete postzygotic isolation, the team found that developmentally abnormal hybrids exhibit dysregulated expression in more than 2000 genes compared with healthy hybrids. Developmental genes are significantly overrepresented in this dysregulated gene group, indicating that variation in DevReg genes is a key mechanism in preventing hybridization, helping to maintain species integrity, and potentially influencing speciation events (see also Renaut et al. Reference Renaut, Nolte and Bernatchez2009).
On the other hand, areas of the genome with lower rates of conservation may also be implicated in hybrid incompatibility, despite greater mutation tolerance. For instance, a number of studies have implicated mitochondrial DNA (mtDNA) mutations in such incompatibilities (Burton et al. Reference Burton, Ellison and Harrison2006; Pereira et al. Reference Pereira, Lima, Pierce-Ward, Chao and Burton2021; Burton Reference Burton2022). Aside from the fact that (1) mitochondria are continually exposed to the mutating effects of reactive oxygen species, (2) their DNA is not protected by histones, and (3) their DNA repair mechanisms are less effective than those of nuclear DNA, mtDNA also exhibits high rates of genetic drift due to the lack of recombination (Klungland et al. Reference Klungland, Höss, Gunz, Constantinou, Clarkson, Doetsch, Bolton, Wood and Lindahl1999; Birky Reference Birky2001; Alexeyev Reference Alexeyev2009; Kazak et al. Reference Kazak, Reyes, He, Wood, Brea-Calvo, Holen and Holt2013). While these genes may be less dosage sensitive than DevReg genes, differences in mitochondrial functionality may similarly prohibit hybridization, although incompatibilities may not arise as readily due to relative mutation tolerance.
Of particular interest, a recent study by Brownstein et al. (Reference Brownstein, MacGuigan, Kim, Orr, Yang, David, Kreiser and Near2024) has shown that gars and sturgeons (types of fish known as “living fossils”) exhibit unusually slow rates of genome evolution. The team also reported that two species of gar that share a last common ancestor over 100 Myr are able to successfully hybridize. The researchers suggest that highly effective DNA repair mechanisms may be responsible for the low rates of variation in both conserved and less conserved exonic sequences, indicating that divergence at the DNA level is a key factor in maintaining species integrity.
Regardless of the cause of variation, whether it results from active mechanisms of evolvability in reaction to environmental upheaval, from transposable element radiation or hybridization, or from passive genetic drift in combination with geographic isolation, DevReg genes networks are likely to respond similarly in the face of destabilizing events. Most disruptions (mutations) will be purified; meanwhile, a few variants will be modestly tolerated and may subsequently prompt compensatory adaptation over ensuing generations, further reinforcing the potential for species incompatibility. In the following section, I will model stasis, destabilization, and compensatory adaptation of DevReg genes using game theory.
Modeling Conservation and Compensatory Adaptation in Developmental Genes Using Game Theory
[The] stronger the constraint on a molecule, the lower is its rate of evolution. (Ohta Reference Ohta1992: p. 265)
The normal or stable state of DevReg gene networks can be likened to a Nash equilibrium, a type of game theory in which all “players” (genes) in a given “game” (network) are essentially best served by maintaining the status quo, because no individual can gain by changing its strategy while the strategies of the other players remain the same (Nash Reference Nash1950). John Maynard Smith (;aynard Smith and Price 1973, Maynard Smith Reference Maynard Smith1976) famously applied game theory to the organismal level (and later to the ecosystem and genetics levels) by using the metaphor of hawks versus doves vying for a limited resource (Lawlor and Maynard Smith Reference Lawlor and Smith1976; Maynard Smith Reference Maynard Smith1982). He also introduced the concept of an evolutionarily stable strategy (ESS), which is essentially any trait or behavior of an individual that depends on the behavior of other players, typically in a competitive scenario such as males vying for mates.
I will show why such a Nash equilibrium is also an appropriate means to model the ESS of stoichiometrically balanced dosage-sensitive DevReg genes and how loss of equilibrium predicts the subsequent compensatory adaptation seen in living systems (Hartl and Taubes Reference Hartl and Taubes1996; Davis et al. Reference Davis, Poon and Whitlock2009). Rather than a competitive format as modeled by Maynard Smith (Maynard Smith and Price Reference Maynard Smith and Price1973; Maynard Smith Reference Maynard Smith1982), this game will be cooperative in nature. First, however, it is important to understand how the probability of such an equilibrium scales with the size of the network, reflective of the larger sizes of the PPI networks of DevReg genes.
Let us mathematically represent a scenario with a variable number of genes (players)
$ \eta $
, assuming that the behavior (gene expression) of each dosage-sensitive gene can be expressed in three different ways: high (H), low (L), and optimal (O). The Nash equilibrium is the scenario in which all genes are expressed optimally (O, O, …, O). The total number of possible outcomes for
$ \eta $
genes is
$ {3}^{\eta } $
, as each gene can choose from three expression levels independently (H, L, O). This mimics the fact that DevReg genes are not mutation coldspots, as already reported, but new variants are instead under strong purifying selection (Makino and McLysaght Reference Makino and McLysaght2010). As such, the probability
$ P(NE) $
of achieving this equilibrium under the assumption that all outcomes are equally probable is:
$$ P\;(NE)=1/3\eta $$
With an increasing number of genes (players), reflective of the higher PPI seen in association with DevReg genes, the probability of maintaining a Nash equilibrium becomes progressively smaller. This may reflect the extreme conservation we see in these developmental networks. With two interacting gene partners and three possible outcomes (H, L, O), P(NE) = 1 in 9; with three interacting gene partners it is 1 in 27; with four it is 1 in 81. Figure 1 is a representative payoff matrix for three dosage-sensitive genes (players) with three possible outcomes per gene. Note that only a single outcome (O, O, O) (highlighted in yellow) maintains Nash equilibrium.
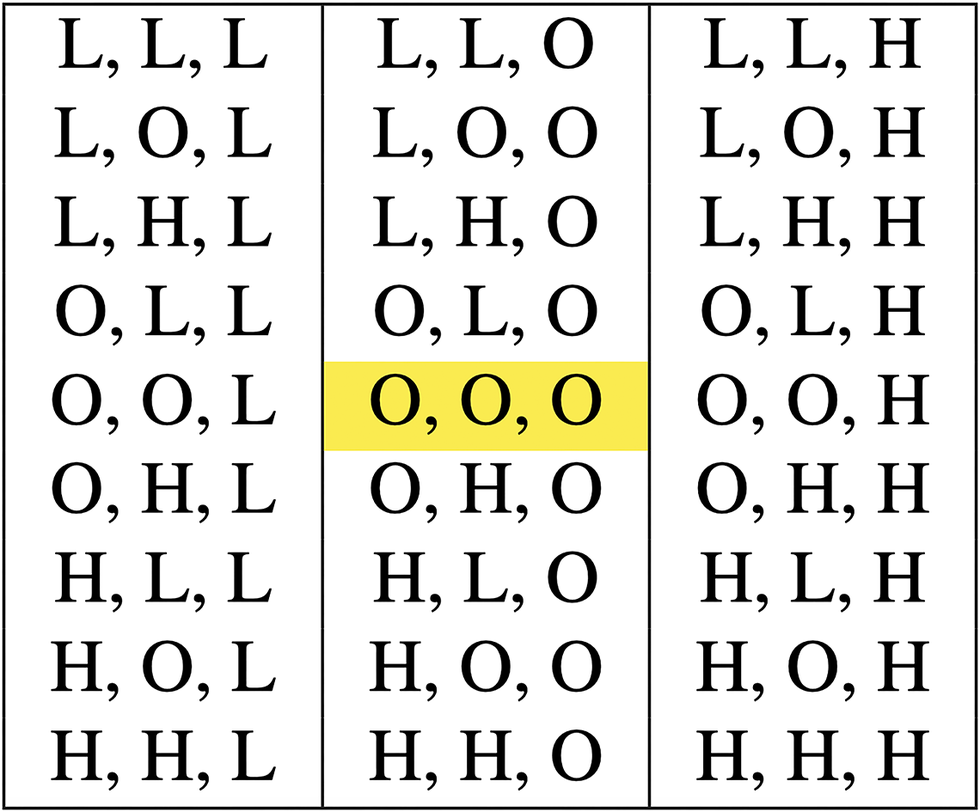
Figure 1. Payoff matrix for three genes (players) representing dosage-sensitive genes. Modeling three outcomes (high [H], optimal [O], low [L]) in which only a single outcome among all three genes (optimal [O, O, O], highlighted in yellow) maintains a Nash equilibrium. One out of 27 possible outcomes maintains equilibrium, mimicking the dosage sensitivity of the developmental regulatory (DevReg) gene group.
Subsequently, one may represent a three-gene network that is less dosage sensitive (e.g., recessively inherited gene variants), stipulating five possible outcomes to mimic this relative dosage insensitivity: high deleterious (HD), high tolerated (HT), optimal (O), low tolerated (LT), low deleterious (LD), in which three of the five (HT, O, LT) are each potentially acceptable outcomes and maintain equilibrium. Probability of equilibrium can be calculated as:
$$ P\;\left(\mathrm{Optimal}\right)=\mathrm{Number}\ \mathrm{of}\ \mathrm{optimal}\ \mathrm{outcomes}/\mathrm{total}\ \mathrm{possible}\ \mathrm{outcomes} $$
In this three-gene dosage-insensitive network, the probability of equilibrium is dramatically increased (27 of 125 outcomes) compared with previous examples. (A payoff matrix for this interaction network is not provided due to size restrictions, as it would extend 5 columns across and 25 rows deep.) If we compare this ratio to that of the earlier dosage-sensitive gene network with the same number of genes (players) using a two-proportions Z-test, we see that the difference between these scenarios is statistically significant (Z = −2.615, p = 0.009). In summary, less dosage-sensitive gene networks allow for more “wiggle room” when modeled in these types of payoff matrices, suggesting stabilizing selection affecting these mutation tolerant genes is weaker than that of DevReg genes, which is supported by data from living systems (Casanova Reference Casanova2023).
We can also model weakly deleterious variation and subsequent compensatory adaptation by understanding what occurs when a Nash equilibrium is lost. When a player changes its behavior (e.g., as a result of a new genetic variation that influences gene dosage), this can result in instability for a time as players search for a new equilibrium, during which time they frequently change strategies in an attempt to find a better outcome (i.e., compensatory adaptation) (Hartl and Taubes Reference Hartl and Taubes1996; Weibull Reference Weibull1997; Moore et al. Reference Moore, Rozen and Lenski2000). If we represent this using a simplified model of three genes and only a single optimal outcome, we can appreciate how the remaining genes adjust their strategies to seek a new equilibrium. Mathematically, this adaptation can be represented by adjusting the payoff functions to include the effects of compensatory strategies by applying a variant of a fitness landscape model (Wright Reference Wright1932). If we define a deviation function
$ D\left({c}_X,{c}_Y,{c}_z\right) $
that measures the distance from the optimum (0) as a whole, in which c = (new dosage/optimal dosage), indicating relative change of dosage in a given gene, and equilibrium is achieved when
$ D\left({c^{\ast}}_X,{c^{\ast}}_Y,{c^{\ast}}_Z\right)=0 $
, where all genes are in their optimal states. Subsequently, by using absolute differences between gene pairs, we can model the magnitude of deviation regardless of direction, as dosage-sensitive gene networks are vulnerable to bidirectional changes in dosage. A nonzero value would indicate a loss of Nash equilibrium:
$$ D\left( abs\left[{c^{\ast}}_X-{c^{\ast}}_Y\right], abs\left[{c^{\ast}}_X-{c^{\ast}}_Z\right], abs\left[{c^{\ast}}_Y-{c^{\ast}}_Z\right]\right)=0 $$
In applying this equation, let us model a single gene change in which Gene X experiences a 20% reduction in expression. Therefore,
$ {c}_X=\left(\frac{0.8}{1}\right) $
or 80% of the original dosage. As such:
$$ D\left( abs\left[0.8-1\right], abs\left[0.8-1\right], abs\left[1-1\right]\right)=\left(0.2,0.2,0\right)\ne 0 $$
Using game theory, this model demonstrates how equilibrium is lost and suggests how genes may adapt to disruptions in equilibrium by adjusting their strategies, seeking to optimize their outcomes within the new constraints of the system, such that once again
$ D\left({c}_X,{c}_Y,{c}_Z\right)=0 $
. In this instance, Gene X can readjust its dosage to come back into equilibrium with Genes Y and Z (probabilistically, the most likely scenario with the fewest number of steps, aka mutations) or Genes Y and Z can decrease their dosages accordingly (Davis et al. Reference Davis, Poon and Whitlock2009). By contrast, one can also appreciate how gene networks with laxer constraints are able to maintain relative equilibrium in the face of some variation by modeling a system with a range of acceptable outcomes, in which the value
$ \varepsilon $
represents that range:
$$ D\left( abs\left[{c^{\ast}}_X-{c^{\ast}}_Y\right], abs\left[{c^{\ast}}_X-{c^{\ast}}_Z\right], abs\left[{c^{\ast}}_Y-{c^{\ast}}_Z\right]\right)=\varepsilon $$
If one attempts to model equation (3) in R using a simulation, each “game” would produce three outcomes per iteration, for example, (0, 0, 0) or (0.8, 0, 0), which is difficult to plot in a simple graphic illustration. Therefore, one can convert equation (3) to the sum of these three deviations, such that:
$$ {D}_{sum}\left( abs\left[{c^{\ast}}_X-{c^{\ast}}_Y\right]+ abs\left[{c^{\ast}}_X-{c^{\ast}}_Z\right]+ abs\left[{c^{\ast}}_Y-{c^{\ast}}_Z\right]\right)=0 $$
This conversion will provide a single data point to plot per iteration. In actuality, equation (6) does not appropriately model a living system as, according to the simulation model, the likelihood of maintaining equilibrium
$ \left({D}_{sum}=0\right) $
is effectively zero even after 10,000 iterations (see Simulation #1 code in GitHub: https://github.com/flibbit1582/DGH/blob/main/Nasheek_simulation_code_4Github.R). As even the most dosage-sensitive genes are likely to tolerate a minor amount of variation, equation (7) is a more appropriate means to model the varied ranges of dosage sensitivity (
$ \varepsilon $
) in living systems. We can, therefore, use this equation to model both dosage-sensitive and dosage-insensitive gene networks, adapting the range of acceptable outcomes for the particular simulation:
$$ {D}_{sum}\left( abs\left[{c^{\ast}}_X-{c^{\ast}}_Y\right]+ abs\left[{c^{\ast}}_X-{c^{\ast}}_Z\right]+ abs\left[{c^{\ast}}_Y-{c^{\ast}}_Z\right]\right)=\varepsilon $$
In this way, we can simulate a dosage-sensitive range (Simulation #2, see code in GitHub), in this instance set at lower bound,
$ \varepsilon $
lower = 0, and an arbitrary upper bound,
$ \varepsilon $
upper = 0.3, and a dosage-insensitive example (Simulation #3, see code in GitHub) with a comparatively larger range of acceptable outcomes (
$ \varepsilon $
lower = 0,
$ \varepsilon $
upper = 0.9). Then we can run 1000 iterations to determine the likelihood of maintaining a Nash equilibrium in either set. (Ten thousand iterations would have been preferable according to modern convention, but would be difficult to represent graphically; therefore, 1000 iterations are used for illustrative purposes [Manly Reference Manly2018].) In the dosage-sensitive simulation (#2), any collective deviations (
$ \varepsilon $
) in any given “game” that falls beyond the upper boundary (0.3) are considered a loss of equilibrium (Fig. 2A, blue vs. red data points). Likewise, in the dosage-insensitive simulation (#3), any
$ \varepsilon $
falling above the upper boundary (0.9) results in a loss of equilibrium (Fig. 2B). The results of these two sets of simulations were compared using a chi-square analysis, indicating significant differences between groups in the likelihood that Nash equilibrium is maintained (dosage insensitive [51%] > dosage sensitive [6.1%]; X
2 = 491.430, OR = 2.757, p = 6.960 × 10−109). As can be noted in Figure 2A,B, the dosage-insensitive gene network is far more likely to maintain equilibrium than the dosage-sensitive network.
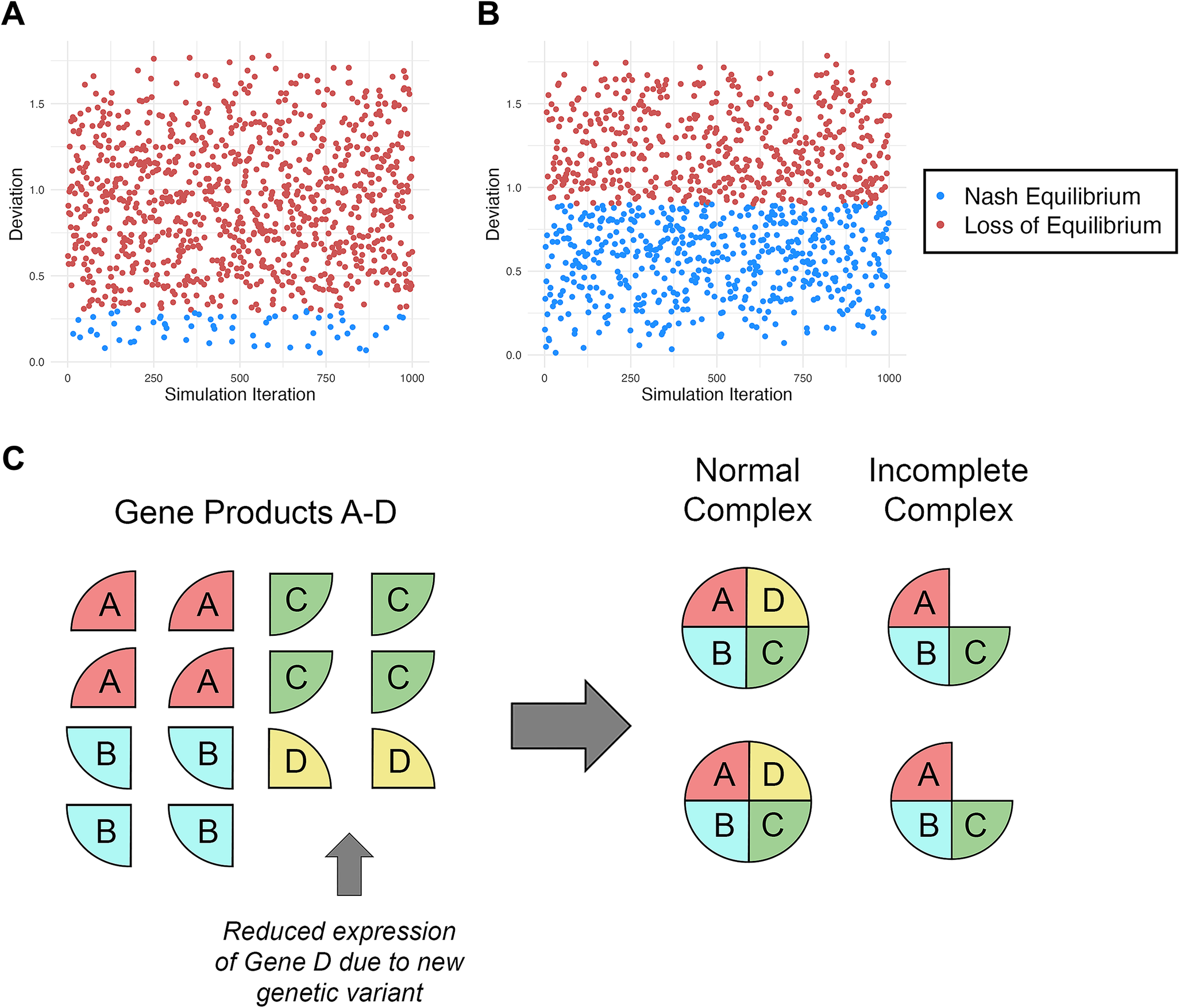
Figure 2
. A, Random simulation of 1000 iterations modeling equation (7) using a more dosage-sensitive range of acceptable outcomes (
$ \varepsilon $
= 0–0.3). B, Simulation of 1000 iterations modeling equation (7) using a dosage-insensitive range of acceptable outcomes (
$ \varepsilon $
= 0–0.9). C, Simple illustration of the gene dosage balance hypothesis (Birchler and Veitia Reference Birchler and Veitia2010) using four gene products (Proteins A–D), one of which (Protein D) is reduced in expression as a result of a new genetic variation. In this simplified scenario, this leads to a 50% reduction in the total amount of protein complex produced, illustrating the importance of ratios of closely interacting gene products.
In the case of living systems, once equilibrium is lost and if a new equilibrium cannot be reached quickly enough, this may result in suboptimal outcomes, potentially endangering the fitness of the organism or lineage (Nash Reference Nash1950; Fudenberg and Tirole Reference Fudenberg and Tirole1991; Osborne and Rubinstein Reference Osborne and Rubinstein1994; Jones Reference Jones2000). Although variation in DevReg genes is under strong purifying selection, in the case of small breeding population numbers, such as may occur with geographic isolation, weakly deleterious variants in these genes increase in likelihood (as they do with all genes), leading to more frequent loss of Nash equilibrium in gene networks and subsequent compensatory adaptation in the gene players within a given network until a new equilibrium is acquired.
Birchler and Veitia (Reference Birchler and Veitia2010) proposed the gene dosage balance hypothesis, which predicts that stoichiometric (proportional) balance of gene products forming key complexes or pathways is integral to their function. When this ratio is disturbed, cellular physiology can be negatively influenced (see Fig. 2C for illustration). Birchler and Veitia reported that gene products involved in regulatory pathways, signal transduction, and regulation of the structure and function of the genome are dosage sensitive and particularly prone to such disruptions. Each of these functions is enriched in DevReg genes (reviewed in Casanova Reference Casanova2023). As indicated earlier, the delicate balance among gene players in key developmental complexes and pathways makes Nash equilibrium an ideal model for predicting both their conservation and adaptation.
In conclusion, one would expect DevReg genes to remain in stasis longer than other functional gene groups, as even minor fluctuations in DevReg genes may lead to loss of Nash equilibrium with severe and sometimes lethal effects. The mutation intolerance and tight conservation of these gene sequences are testament to this prediction (Casanova Reference Casanova2023). However, in infrequent instances when variation does occur and is mildly tolerated in a DevReg gene in a conserved network, compensatory adaptation is likely to ensue until a new equilibrium is achieved. In addition, due to dosage sensitivity of developmental networks, they are liable to lead to hybrid incompatibility once reintroduction occurs as a result of dosage mismatch between genes in a given network. One can therefore predict that variation in dosage-sensitive genes will, on average, lead to hybrid incompatibility more often compared with less dosage-sensitive gene networks, as the latter can tolerate a wider range of variations, resulting in less frequent incompatibilities between mates. It should be noted that these generalizations are ones by degree: incompatibility may occur in more tolerant networks provided the effects of the variation are suitably severe, as in the case of recessive diseases, or enough variation has accumulated as a factor of separation time between two lineages (Amorim et al. Reference Amorim, Gao, Baker, Diesel, Simons, Haque, Pickrell and Przeworski2017).
Conclusion
As Darwin painstakingly developed his theory of evolution by natural selection, he envisioned adaptation of a species as a long series of “slight, successive, favourable variations” with subtle changes in phenotype driven by environmental demands (1859: p. 471). In his own words, these phenotypes would have the “tendency to vary by generation” (Darwin 1837–Reference Darwin and van Wyhe1838), suggesting he indeed used the term “gradual” to imply a slow, incremental, and relatively constant process—despite later scientists’ claims to the contrary (Dawkins Reference Dawkins1996).
It is from this vantage point that we must view the originality of the theory of punctuated equilibria, notwithstanding other authors who have attempted to walk back its novelty by slackening the definition of gradualism. Many synthesists during the middle of the twentieth century envisioned evolution of the genome as the accumulation of small genetic changes (Dobzhansky Reference Dobzhansky1937). Meanwhile, identification of the “molecular clock,” which suggested that point mutations occur at a steady pace, further supported the literal gradualist view (Kimura Reference Kimura1968). A mere 4 years after publication of Kimura’s molecular clock paper, punctuated equilibria happened on the scene and shook the prevailing paradigm, about which notable scientists continued to argue for the remainder of the twentieth century and into the next (Maynard Smith Reference Maynard Smith1982; Mayr Reference Mayr1982; Dennett Reference Dennett1995; Dawkins Reference Dawkins1996; Lynch and Walsh Reference Lynch and Walsh2007).
John Maynard Smith, though not an outright critic of punctuated equilibria, nevertheless questioned how the mechanics of the theory could be reconciled with genetic principles, advocating for a synthesis that included genetic explanations for macroevolutionary patterns (Maynard Smith Reference Maynard Smith1993, Reference Maynard Smith1998). Later, in his book Shaping Life: Genes, Embryos, and Evolution (Reference Maynard Smith1999), Maynard Smith proposed that the evolution of developmental genes and their regulatory elements could lead to rapid morphological change. However, he was also curious about the mechanisms underlying stasis, as he notably penned in his chapter “Paleontology at the High Table”:
What is new is the emphasis on stasis.… [The] existence today of pairs of species which are morphologically indistinguishable, or almost so, but whose proteins have diverged sufficiently to suggest that they have been separate for millions of years, supports the reality of stasis. Stasis, then, is a phenomenon that calls for an explanation. (Maynard Smith Reference Maynard Smith1988: p. 126)
The earlier iteration of the DGH did exactly that. It highlighted the roles of DevReg gene sequence conservation, with the prediction that morphology and the genes that regulate it should be more resistant to change than other gene groups, such as metabolic genes, resulting in slower evolutionary rates. Maynard Smith also doubted how the “splitting of lineages” (1988: p. 126) (e.g., allopatry) could be associated with rapid change—an idea emphasized by Eldredge and Gould (Reference Eldredge, Gould and Schopf1972). However, the current paper integrates work from population genetics, specifically highlighting the influence of small population sizes on fixation of deleterious mutations and subsequent compensatory adaptation, increasing the likelihood of hybrid incompatibility upon reintroduction. Finally, I model the DGH using game theory à la Maynard Smith, providing the reader with a predictive model for the workings of DevReg gene networks, both during periods of stasis (Nash equilibrium) and punctuated change (loss of equilibrium).
Steve Jones, the British geneticist, is said to have once quipped, “One man’s punctuation is another man’s gradualism” (Maynard Smith Reference Maynard Smith1988: p. 126). This observation is particularly poignant, as it zeroes in on a fundamental issue regarding the use of relativistic terms like “gradual” and “punctuated.” While swaths of time can be represented in the fossil record as the smallest of strata, relative to the span of a human life most evolutionary changes are bound to seem slow. Therefore, these types of relativistic terms are inevitably dependent on context and individual perception, making them subjective concepts, which are likely to lead to errors and confusion in communication (Kim Reference Kim and Ludwig2003).
Nevertheless, given the language Darwin frequently used to describe his conception of gradualism, it is apparent he intended the term to mean not only slow, but steady. Within that context, it is clear that the predictions of the DGH align more closely with punctuated equilibria than with gradualism. And thus, as per the request of Maynard Smith (Reference Maynard Smith1993, Reference Maynard Smith1998), the present thesis provides a genetic complement for both macroevolutionary patterns and stasis observable within the fossil record.
Acknowledgments
I am extremely grateful for the assistance of N. Eldredge and his feedback on this paper. The AI, Pria, was used for fine-tuning of the proposed equilibrium model in section on game theory (https://www.hiimpria.ai/pria). This research was not supported by any grants. The author declares no financial conflicts of interest.
Data Availability Statement
Original codes for the simulation series (1–3) are freely available at: https://github.com/flibbit1582/DGH/blob/main/Nasheek_simulation_code_4Github.R.
Open access
