1. Introduction
The self-focusing of a laser beam is a basic physical phenomenon in nonlinear optics, and it has been the focus of several investigations[Reference Rubenchik, Fedoruk and Turitsyn1–Reference Lee, Chae, YIM and Park4]. It has been shown that nonlinear self-focusing is the fundamental cause that affects the laser output power. The nonlinear effect makes the whole intensity distribution of the laser change. Jokipii et al. presented solutions for reduction or elimination of catastrophic self-focusing in a medium[Reference Jokipii and Marbmger5]. Beckwitt et al. [Reference Beckwitt, Wise, Qian, Wallker II and Canto-Said6] used cascade quadratic nonlinearity to compensate self-focusing. Another factor influencing the intensity is defects in the optical elements[Reference Neauport, Lamaignere, Bercegol, Pilon and Birolleau7, Reference Mainguy, Tovena-Pecault and Le Garrec8]. The presence of defects may lead to a more complex intensity distribution and worse beam quality, and may even cause small-scale self-focusing which may damage optical elements[Reference Bespalov and Talanov9, Reference Jia, Xu, Wang and Zhou10].
The rapid development of laser techniques has promoted the generation and improvement of broadband lasers[Reference Xu, Wang, Huang, Li, Lu and Leng11, Reference Johnston, Whittaker, Dowd, Davies, Linfield and Li12]. Increasing attention has been paid to broadband technology in high-power lasers: for example, the formation of a hot image from phase defects in high-power broadband laser beams[Reference Hu, Wang, Wen, Deng and Fan13], parametric characteristics of a broadband beam in free space[Reference Mao and Zhao14], the smoothing effect through a dispersive wedge[Reference Peng, Ye, Tang, Zhao, Wen and Fan15], and a broadband beam modulated by a hard-edged aperture[Reference Peng, Ye, Tang and Fan16] have been studied. However, little attention has been paid to high-power broadband lasers passing through a Kerr medium with defects, whose refractive index is dependent on the wavelength. In this paper, by treating a broadband laser as a superposition of several narrow-broadband lasers with different centre wavelengths, we study the propagation characteristics of a high-power broadband beam in a nonlinear medium, on the basis of the nonlinear Schrödinger equation. The influences of the bandwidth, the medium thickness, and the defects on the evolution of intensity are investigated. In particular, the role of the bandwidth in suppressing nonlinear self-focusing and improving uniformity is discussed. These results are important for high-power laser engineering.
2. Theory
In general, optical defects exist in optical materials, and when a high-power laser passes through optical materials, these optical defects may induce high-power laser self-focusing such that the optical materials could be severely damaged. The optical defects can be divided into two kinds: one is amplitude modulation defects, such as dirt, dust, and bubbles, and the other is phase modulation defects, such as protrusions, craters, and scratches. In a real situation, we assume that there is an amplitude defect with Gaussian-shaped amplitude transparency on the front surface of a Kerr medium. The mathematical description for this Gaussian-shaped amplitude modulation defect is
where ![]() $A$ is the modulation amplitude,
$A$ is the modulation amplitude, ![]() $a$ is the half-width of this defect, and (
$a$ is the half-width of this defect, and (![]() $x_{0}$,
$x_{0}$, ![]() $y_{0}$) are the amplitude modulation (AM) centre coordinates.
$y_{0}$) are the amplitude modulation (AM) centre coordinates.
It is known that the refractive index of a material depends on the wavelength of light. The widely used SF57 glass is taken as an example of a Kerr medium in this study; the dependence of the refractive index of SF57 glass on the wavelength can be expressed by dispersion formula (Sellmeier) as follows[17]:
where ![]() $B_{1}=1.81651371, B_{2}=0.428893641$,
$B_{1}=1.81651371, B_{2}=0.428893641$, ![]() $B_{3}=1.07186278$,
$B_{3}=1.07186278$, ![]() $C_{1}=0.0143704198$,
$C_{1}=0.0143704198$, ![]() $C_{2}=0.0592801172$, and
$C_{2}=0.0592801172$, and ![]() $C_{3}=121.419942$. The unit of wavelength (
$C_{3}=121.419942$. The unit of wavelength (![]() $\lambda $) is
$\lambda $) is ![]() $\mathrm {\mu} {\rm m}$.
$\mathrm {\mu} {\rm m}$.

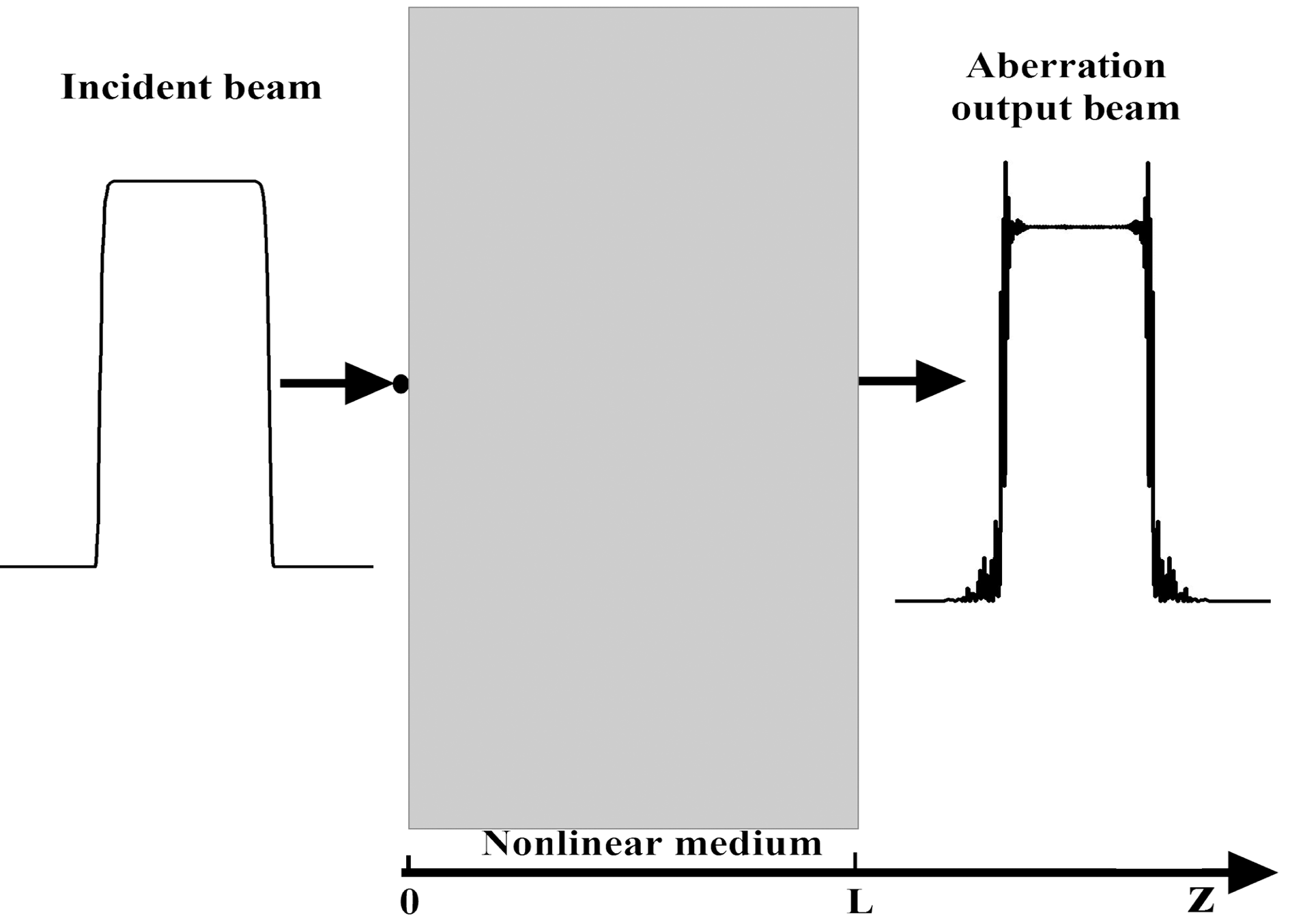
Figure 1. (Colour online) Schematic illustration of a super-Gaussian beam passing through a nonlinear medium.
The nonlinear refractive index ![]() $n_{2}$ of this glass in electro-static units (esu) has the form[17]
$n_{2}$ of this glass in electro-static units (esu) has the form[17]
The propagation of a laser beam through a nonlinear medium is illustrated in figure 1, in which a high-power broadband beam passes through a slab of a Kerr medium of thickness ![]() $L$, and then comes out of the medium and into free space. The propagation of the beam in the medium and in free space can be described by the nonlinear Schrödinger equation[Reference Agrawal18]
$L$, and then comes out of the medium and into free space. The propagation of the beam in the medium and in free space can be described by the nonlinear Schrödinger equation[Reference Agrawal18]
and by the paraxial wave equation
The nonlinear refractive index arises from both self-phase and cross-phase modulation[Reference Agrawal18]; it is expressed as
 $$\begin {equation} \label {eq5} \Delta n_j \left ({\lambda _j } \right ) = n_2 \left ({\lambda _j } \right )\left (\lvert {E_j }\rvert ^2 + 2\sum _{ jj = 1 \atop jj \ne j }^n \lvert {E_{jj}}\rvert ^2\right ). \end {equation}$$
$$\begin {equation} \label {eq5} \Delta n_j \left ({\lambda _j } \right ) = n_2 \left ({\lambda _j } \right )\left (\lvert {E_j }\rvert ^2 + 2\sum _{ jj = 1 \atop jj \ne j }^n \lvert {E_{jj}}\rvert ^2\right ). \end {equation}$$ Here, we divide the bandwidth ![]() $\Delta \lambda $ of the broadband laser beam into
$\Delta \lambda $ of the broadband laser beam into ![]() $n$ elements, in which each bandwidth is
$n$ elements, in which each bandwidth is ![]() $\Delta \lambda /n$, so that the transmission of the broadband laser can be considered as a superposition of monochromatic laser transmissions with different centre wavelengths
$\Delta \lambda /n$, so that the transmission of the broadband laser can be considered as a superposition of monochromatic laser transmissions with different centre wavelengths ![]() $\lambda _{j}$. In this case, Equations (4) and (5) can be written as:
$\lambda _{j}$. In this case, Equations (4) and (5) can be written as:
It is assumed that the electric field of the incident beam is super-Gaussian, so the field can be written as
where ![]() $w_{0}$ denotes the beam radius of the incident beam and
$w_{0}$ denotes the beam radius of the incident beam and ![]() $N$ is an integer representing the order of the super-Gaussian beam.
$N$ is an integer representing the order of the super-Gaussian beam.
We can numerically calculate Equations (7) and (8) by employing the split-step Fourier method. Based on Equations (1)–(9), the intensity distribution of the broadband laser beam can be obtained. In the following Section, we will discuss the influence of the bandwidth, the medium thickness and the surface defects on the intensity distribution of the laser beam.
3. Simulation results and discussion
3.1. The case of a nonlinear medium without defects
In this Section, unless other parameters are specified in the figure captions, we select the parameters as follows: the spatial sampling range is ![]() $1\ {\rm cm}\times 1\ {\rm cm}$, the transverse field is sampled over a grid of
$1\ {\rm cm}\times 1\ {\rm cm}$, the transverse field is sampled over a grid of ![]() $1024\times 1024$ points, for the incident super-Gaussian beam,
$1024\times 1024$ points, for the incident super-Gaussian beam, ![]() $N=4$,
$N=4$, ![]() $w_{0}=3\ {\rm mm}$, and the central wavelength of broadband beam
$w_{0}=3\ {\rm mm}$, and the central wavelength of broadband beam ![]() $\lambda _{0}=1053\ {\rm nm}$, the bandwidth
$\lambda _{0}=1053\ {\rm nm}$, the bandwidth ![]() $\Delta \lambda =40\ {\rm nm}$,
$\Delta \lambda =40\ {\rm nm}$, ![]() $n=20$,
$n=20$, ![]() $\Delta \lambda _{j}=2\ {\rm nm}$,
$\Delta \lambda _{j}=2\ {\rm nm}$, ![]() $I_{0j}=I_{0}=12\ {\rm GW}/{\rm cm}^{2}$. The intensity is normalized to the initial intensity
$I_{0j}=I_{0}=12\ {\rm GW}/{\rm cm}^{2}$. The intensity is normalized to the initial intensity ![]() $I_{0}$; the medium thickness
$I_{0}$; the medium thickness ![]() $L=6\ {\rm cm}$,
$L=6\ {\rm cm}$, ![]() $n_{2}(\lambda _{0})=2.28\times 10^{ - 6}\ {\rm cm}^{2}/{\rm GW}$,
$n_{2}(\lambda _{0})=2.28\times 10^{ - 6}\ {\rm cm}^{2}/{\rm GW}$, ![]() $n_{0}(\lambda _{0})=1.812$.
$n_{0}(\lambda _{0})=1.812$.
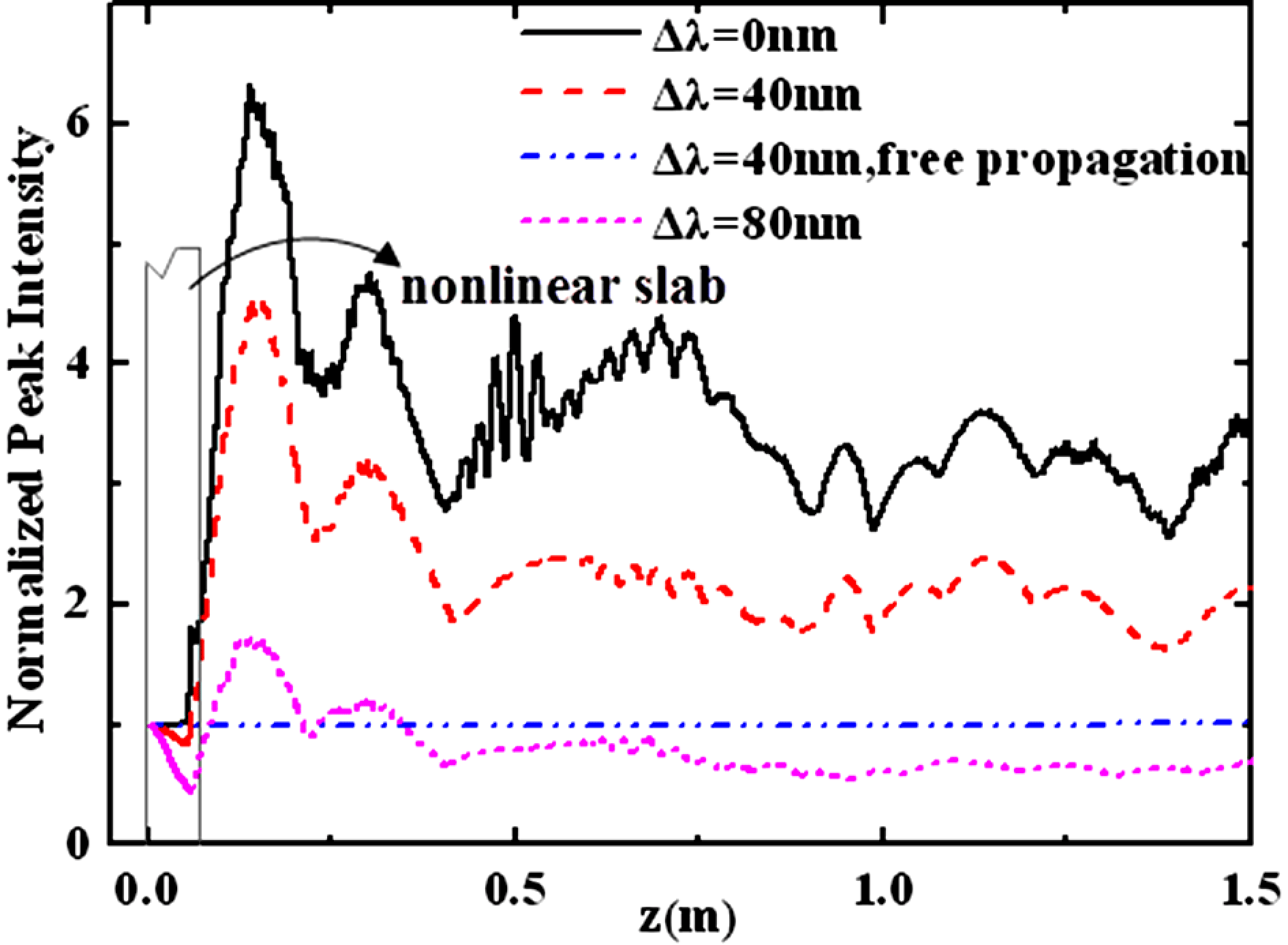
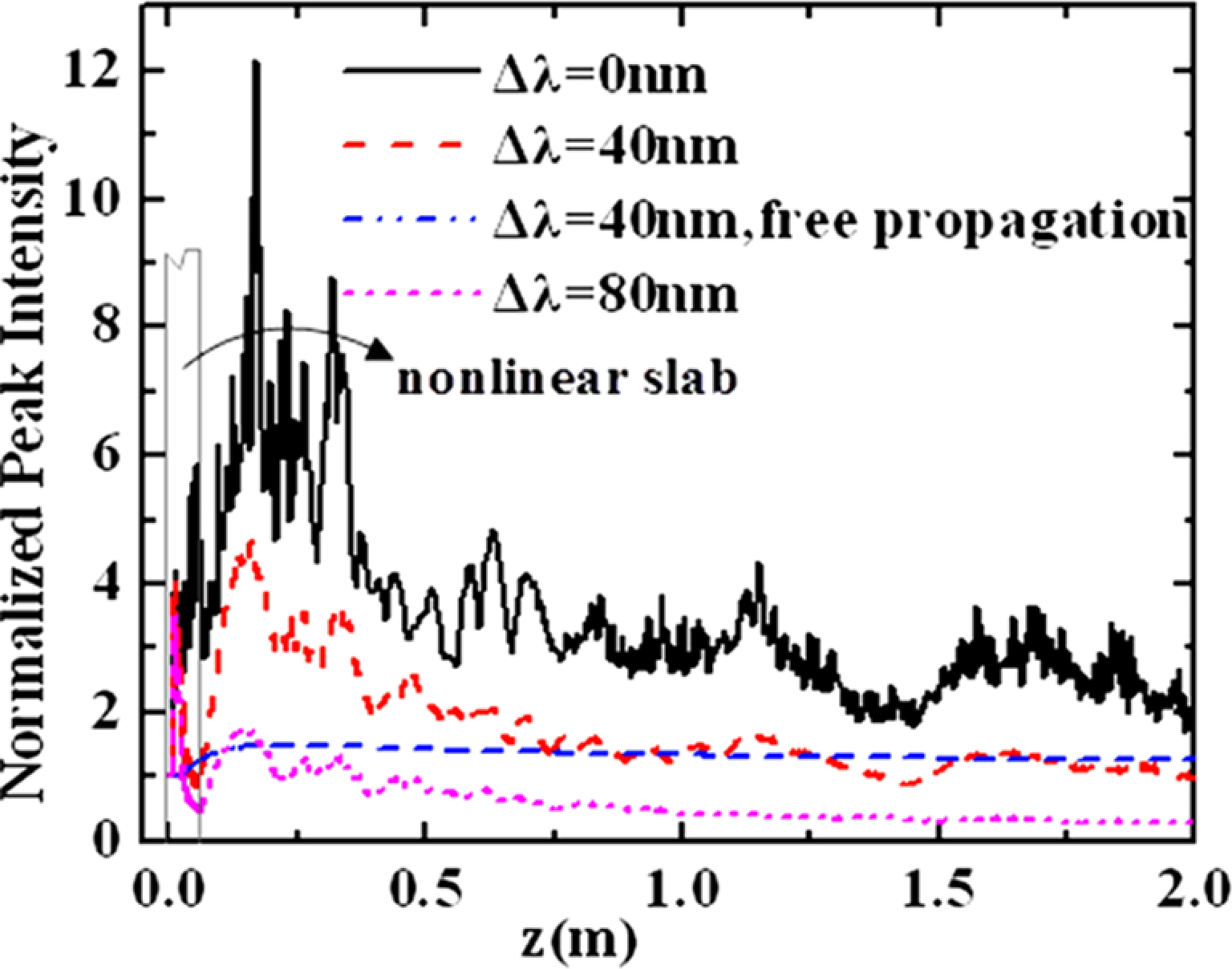
To clearly demonstrate the effect of bandwidth on the nonlinear transmission, we first compare the properties of the peak intensity produced by a broadband laser system to that by a narrowband laser system. For a narrowband laser, we consider the limiting case of a monochromatic laser (i.e. ![]() $\Delta \lambda =0\ {\rm nm}$). Figure 2 shows the variation of the normalized peak intensity of a laser beam with different bandwidths along the propagation distance. It is shown that when the incident laser is monochromatic, the maximum peak intensity reaches 6.3. We can find that the maximum peak intensity decreases with the increase of the bandwidth of broadband beam; i.e., when
$\Delta \lambda =0\ {\rm nm}$). Figure 2 shows the variation of the normalized peak intensity of a laser beam with different bandwidths along the propagation distance. It is shown that when the incident laser is monochromatic, the maximum peak intensity reaches 6.3. We can find that the maximum peak intensity decreases with the increase of the bandwidth of broadband beam; i.e., when ![]() $\Delta \lambda =40\ {\rm nm}$, the maximum peak intensity is 4.6, and when
$\Delta \lambda =40\ {\rm nm}$, the maximum peak intensity is 4.6, and when ![]() $\Delta \lambda =80\ {\rm nm}$, the maximum peak intensity decreases to 1.6. This result indicates that the increase of the bandwidth of the laser beam may effectively decrease the maximum peak intensity, so that decreases the risk of damage to the optical elements. The reason for decreasing the maximum peak intensity is due to the effect of dispersion for a broadband laser beam propagating in optical materials. The major effects of a monochromatic laser propagating in a nonlinear medium are diffraction and nonlinear effects: if the incident laser intensity is very high, the nonlinear effect is stronger than the diffraction effect, so the peak intensity of the laser beam increases with the propagation distance. Because a broadband beam propagating in a nonlinear medium is influenced by material dispersion, the self-focusing can be largely suppressed due to dispersion.
$\Delta \lambda =80\ {\rm nm}$, the maximum peak intensity decreases to 1.6. This result indicates that the increase of the bandwidth of the laser beam may effectively decrease the maximum peak intensity, so that decreases the risk of damage to the optical elements. The reason for decreasing the maximum peak intensity is due to the effect of dispersion for a broadband laser beam propagating in optical materials. The major effects of a monochromatic laser propagating in a nonlinear medium are diffraction and nonlinear effects: if the incident laser intensity is very high, the nonlinear effect is stronger than the diffraction effect, so the peak intensity of the laser beam increases with the propagation distance. Because a broadband beam propagating in a nonlinear medium is influenced by material dispersion, the self-focusing can be largely suppressed due to dispersion.

Figure 2. (Colour online) The normalized peak intensity of a super-Gaussian beam against the propagation distance for different bandwidths. ![]() $n_{0}(\lambda _{0})=1.812$,
$n_{0}(\lambda _{0})=1.812$, ![]() $n_{2}(\lambda _{0})=2.28\times 10^{ - 6}\ {\rm cm}^{2}/{\rm GW}$,
$n_{2}(\lambda _{0})=2.28\times 10^{ - 6}\ {\rm cm}^{2}/{\rm GW}$, ![]() $L=6\ {\rm cm}$, the super-Gaussian beam
$L=6\ {\rm cm}$, the super-Gaussian beam ![]() $I_{0}=12\ {\rm GW}/{\rm cm}^{2}$,
$I_{0}=12\ {\rm GW}/{\rm cm}^{2}$, ![]() $N=4$,
$N=4$, ![]() $w_{0}=3\ {\rm mm}$.
$w_{0}=3\ {\rm mm}$.
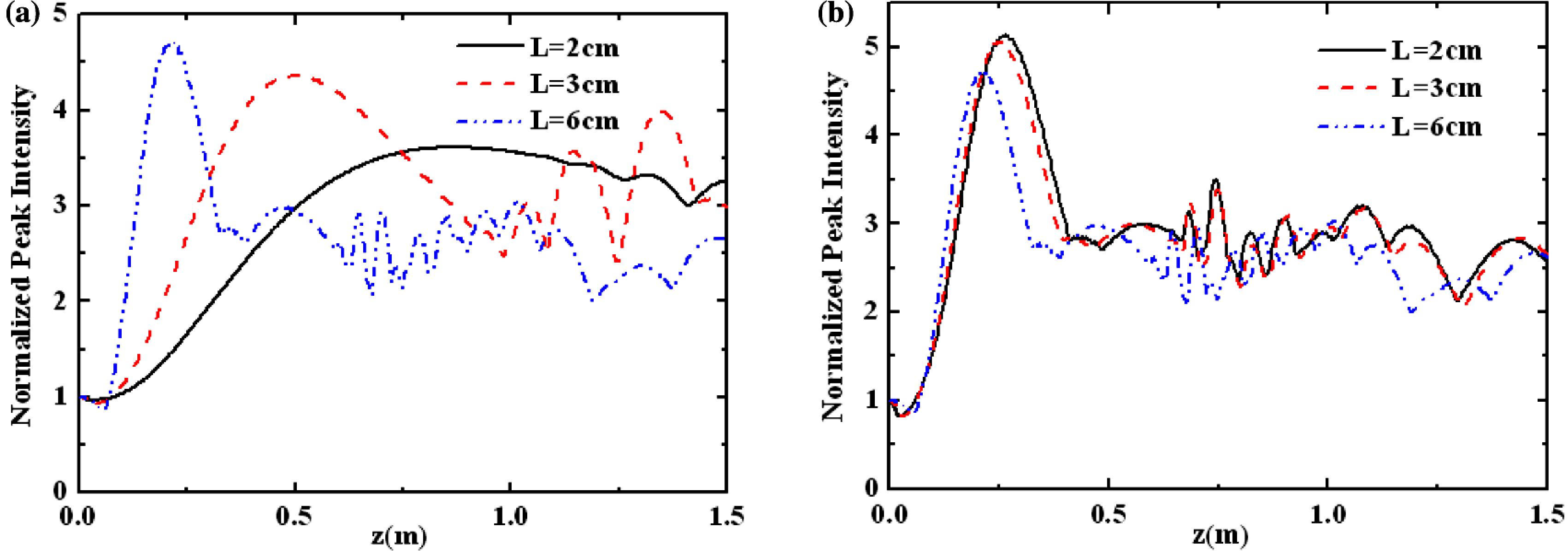
Figure 3 shows the evolution of the peak intensity of a broadband laser beam passing through a nonlinear medium with different thicknesses along the propagation direction. It is shown in figure 3(a) that, under a certain incident intensity (such as ![]() $I_{0}=12\ {\rm GW}/{\rm cm}^{2}$), a thicker medium will lead to a stronger self-focusing. This means that, for a thicker nonlinear medium, the focal position is closer to the left side. In figure 3(b), we plot the evolution of the peak intensity of a broadband laser beam passing through a nonlinear medium with different thicknesses along the propagation direction for the case that the
$I_{0}=12\ {\rm GW}/{\rm cm}^{2}$), a thicker medium will lead to a stronger self-focusing. This means that, for a thicker nonlinear medium, the focal position is closer to the left side. In figure 3(b), we plot the evolution of the peak intensity of a broadband laser beam passing through a nonlinear medium with different thicknesses along the propagation direction for the case that the ![]() $B$ integral is fixed. We can find that in this case the peak intensity is nearly constant.
$B$ integral is fixed. We can find that in this case the peak intensity is nearly constant.

Figure 3. (Colour online) Evolution of the normalized peak intensity of a broadband super-Gaussian beam passing through different thicknesses of nonlinear medium along the propagation direction. (a) The incident intensity is fixed, ![]() $I_{0} =12\ {\rm GW}/{\rm cm}^{2}$, (b) The
$I_{0} =12\ {\rm GW}/{\rm cm}^{2}$, (b) The ![]() $B$ integral is fixed.
$B$ integral is fixed. ![]() $I_{0} =36\ {\rm GW}/{\rm cm}^{2}$ when
$I_{0} =36\ {\rm GW}/{\rm cm}^{2}$ when ![]() $L=2\ {\rm cm}$;
$L=2\ {\rm cm}$; ![]() $I_{0} =24\ {\rm GW}/{\rm cm}^{2}$ when
$I_{0} =24\ {\rm GW}/{\rm cm}^{2}$ when ![]() $L=3\ {\rm cm}$;
$L=3\ {\rm cm}$; ![]() $ I_{0} =12\ {\rm GW}/{\rm cm}^{2}$ when
$ I_{0} =12\ {\rm GW}/{\rm cm}^{2}$ when ![]() $L=6\ {\rm cm}$.
$L=6\ {\rm cm}$. ![]() $N=4$,
$N=4$, ![]() $w_{0}=3\ {\rm mm}$, and
$w_{0}=3\ {\rm mm}$, and ![]() $\Delta \lambda =40\ {\rm nm}$.
$\Delta \lambda =40\ {\rm nm}$.
It has been assumed that the incident laser beam is a super-Gaussian one. A previous reported study has shown that a larger order ![]() $N$ of the super-Gaussian beam will result in stronger modulation on the laser beam; therefore, the uniformity of the light beam will be worse with a larger
$N$ of the super-Gaussian beam will result in stronger modulation on the laser beam; therefore, the uniformity of the light beam will be worse with a larger ![]() $N$. To clearly demonstrate the effect of the bandwidth of a laser beam on the beam uniformity, the order of the super-Gaussian laser beam is chosen as
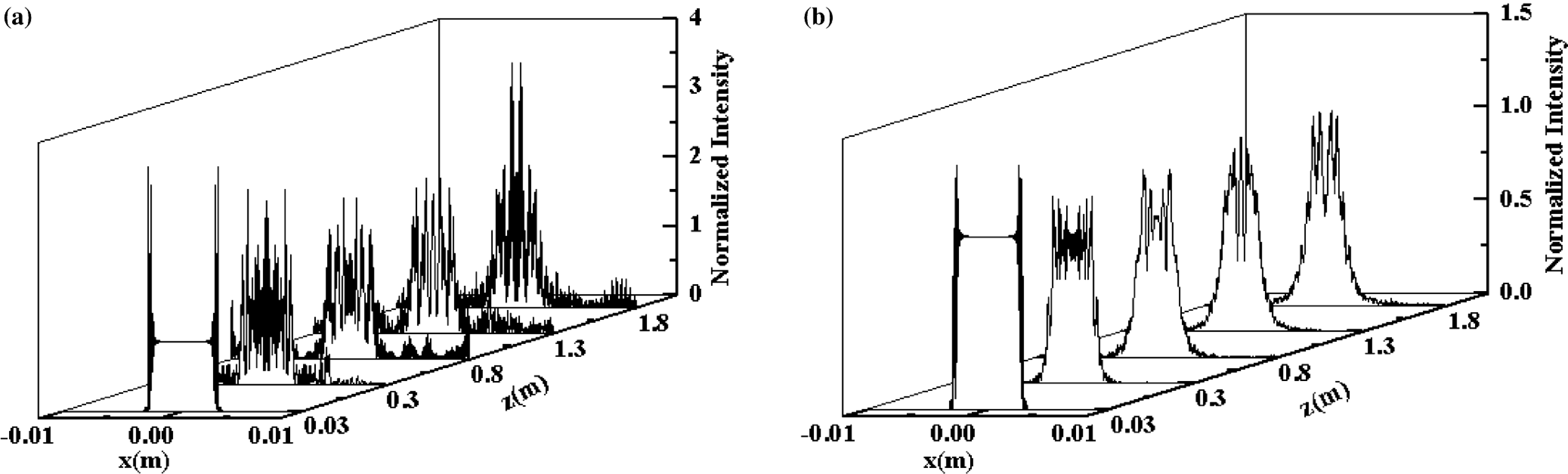
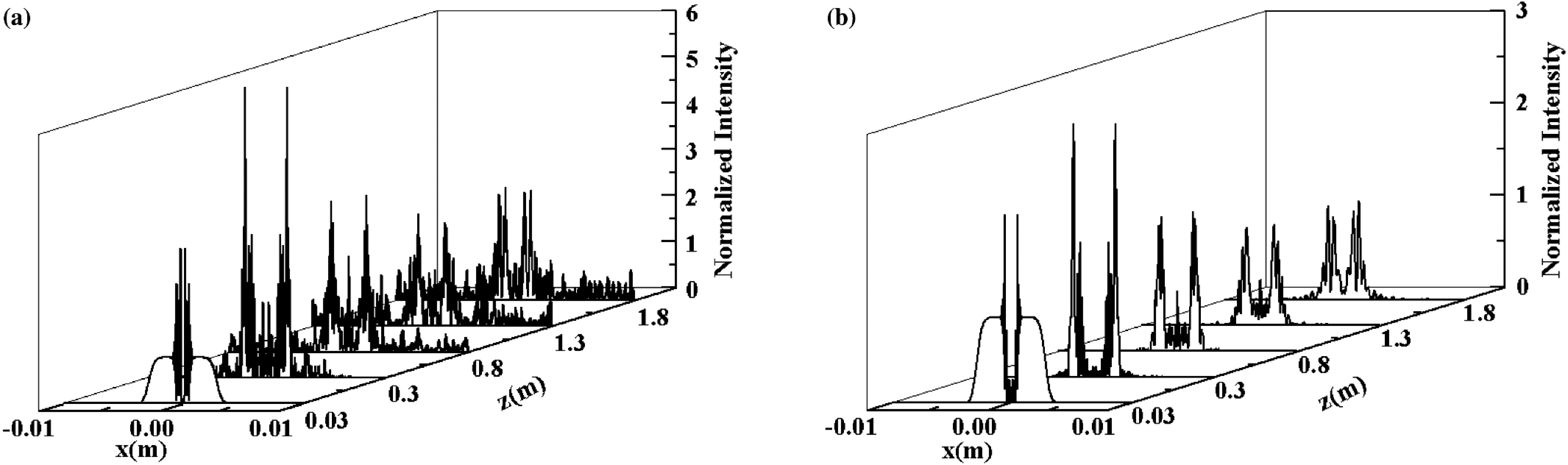
$N$. To clearly demonstrate the effect of the bandwidth of a laser beam on the beam uniformity, the order of the super-Gaussian laser beam is chosen as ![]() $N=20$. Figure 4 shows the evolution of the transverse intensity for laser beams of two different bandwidths (
$N=20$. Figure 4 shows the evolution of the transverse intensity for laser beams of two different bandwidths (![]() $\Delta \lambda =0\ {\rm nm}$ and
$\Delta \lambda =0\ {\rm nm}$ and ![]() $\Delta \lambda =40\ {\rm nm}$) propagating in a nonlinear medium and free space. It is found from figure 4(a) that the intensity distribution of the narrowband beam has many spikes; i.e., the uniformity of the light intensity is very poor. These spikes of intensity may induce damage in the optical medium. In figure 4(b), we plot the evolution of the transverse intensity distribution for the case of a broadband laser beam propagating in a nonlinear medium and free space. It is found that the spikes of the transverse intensity distribution are greatly decreased, and so the beam uniformity is improved. This phenomenon can be easily understood, because, for a different wavelength (or frequency), the transverse intensity distribution is slightly different, so the integrated intensity distribution for different wavelengths becomes uniform.
$\Delta \lambda =40\ {\rm nm}$) propagating in a nonlinear medium and free space. It is found from figure 4(a) that the intensity distribution of the narrowband beam has many spikes; i.e., the uniformity of the light intensity is very poor. These spikes of intensity may induce damage in the optical medium. In figure 4(b), we plot the evolution of the transverse intensity distribution for the case of a broadband laser beam propagating in a nonlinear medium and free space. It is found that the spikes of the transverse intensity distribution are greatly decreased, and so the beam uniformity is improved. This phenomenon can be easily understood, because, for a different wavelength (or frequency), the transverse intensity distribution is slightly different, so the integrated intensity distribution for different wavelengths becomes uniform.

Figure 4. Intensity distribution of a narrowband beam, ![]() $\Delta \lambda =0\ {\rm nm}$ (a) and a broadband beam,
$\Delta \lambda =0\ {\rm nm}$ (a) and a broadband beam, ![]() $\Delta \lambda =40\ {\rm nm}$ (b) at different distances.
$\Delta \lambda =40\ {\rm nm}$ (b) at different distances. ![]() $n_{0}(\lambda _{0})=1.812$,
$n_{0}(\lambda _{0})=1.812$, ![]() $n_{2}(\lambda _{0})=2.28\times 10^{ - 6}\ {\rm cm}^{2}/{\rm GW}$,
$n_{2}(\lambda _{0})=2.28\times 10^{ - 6}\ {\rm cm}^{2}/{\rm GW}$, ![]() $ L=6\ {\rm cm}$,
$ L=6\ {\rm cm}$, ![]() $I_{0} =12\ {\rm GW}/{\rm cm}^{2}$,
$I_{0} =12\ {\rm GW}/{\rm cm}^{2}$, ![]() $N=20$, and
$N=20$, and ![]() $w_{0}=3\ {\rm mm}$.
$w_{0}=3\ {\rm mm}$.

Figure 5. (Colour online) Evolution of the normalized peak intensity of a super-Gaussian beam for different bandwidths, considering the medium’s front surface to have a defect. The defect size ![]() $a=100\ \mathrm {\mu} {\rm m}$,
$a=100\ \mathrm {\mu} {\rm m}$, ![]() $A=1$,
$A=1$, ![]() $x_{0}=0$;
$x_{0}=0$; ![]() $n_{0}(\lambda _{0})=1.812$,
$n_{0}(\lambda _{0})=1.812$, ![]() $n_{2}(\lambda _{0})=2.28\times 10^{- 6}\ {\rm cm}^{2}/{\rm GW}$,
$n_{2}(\lambda _{0})=2.28\times 10^{- 6}\ {\rm cm}^{2}/{\rm GW}$, ![]() $ L=6\ {\rm cm}$,
$ L=6\ {\rm cm}$, ![]() $I_{0}=12\ {\rm GW}/{\rm cm}^{2}$,
$I_{0}=12\ {\rm GW}/{\rm cm}^{2}$, ![]() $N=4$, and
$N=4$, and ![]() $w_{0}=3\ {\rm mm}$.
$w_{0}=3\ {\rm mm}$.
3.2. The case of a nonlinear medium with defects
All of the above studies focus on the cases of an ideal medium (i.e., a medium without defects). Now we consider the case of a laser beam passing through a nonlinear optical medium with defects. Figure 5 presents the evolution of the maximum intensity of a laser beam propagating through a medium in the presence of an amplitude defect on the front surface. It is found that, for a narrowband laser beam (![]() $\Delta \lambda =0\ {\rm nm}$), the defect on the medium surface makes the maximum intensity larger, and that accelerates the self-focusing process. By comparing Figure 2 with Figure 5, we find that the propagation characteristic of a broadband beam passing through a nonlinear medium with defects is different from that for a broadband beam passing through a nonlinear medium without defects. It is shown that the maximum intensity reaches 12 for a narrowband laser beam, which is nearly twice that for the case with the non-defect medium. This indicates that, for a laser beam passing through a nonlinear medium with defects, the maximum intensity is shown to be larger; therefore it may increase the risk of damaging optical systems. We also find from Figure 5 that a broadband laser beam can make the maximum intensity decrease, and that decreases the risk of damaging optical systems.
$\Delta \lambda =0\ {\rm nm}$), the defect on the medium surface makes the maximum intensity larger, and that accelerates the self-focusing process. By comparing Figure 2 with Figure 5, we find that the propagation characteristic of a broadband beam passing through a nonlinear medium with defects is different from that for a broadband beam passing through a nonlinear medium without defects. It is shown that the maximum intensity reaches 12 for a narrowband laser beam, which is nearly twice that for the case with the non-defect medium. This indicates that, for a laser beam passing through a nonlinear medium with defects, the maximum intensity is shown to be larger; therefore it may increase the risk of damaging optical systems. We also find from Figure 5 that a broadband laser beam can make the maximum intensity decrease, and that decreases the risk of damaging optical systems.
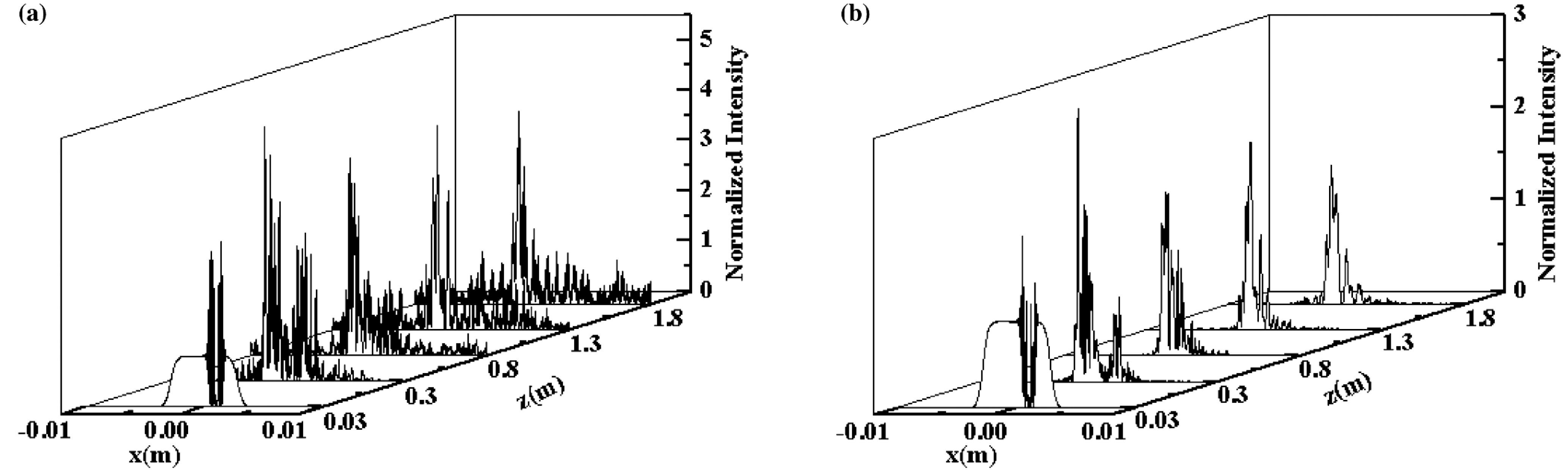
We plot the evolution of the transverse intensity distribution of a laser beam with two different bandwidths (![]() $\Delta \lambda =0\ {\rm nm}$ and
$\Delta \lambda =0\ {\rm nm}$ and ![]() $\Delta \lambda =40\ {\rm nm}$) passing through a nonlinear medium with a defect in figure 6, in which the parameters of the defect are the same as those in figure 5. It is shown from figure 6(a) that when the narrowband laser beam passes through a nonlinear medium with defects, the transverse intensity distribution has many spikes, being due to the high frequency modulation by the defect. This high frequency modulation seems to be an important reason for the acceleration of the nonlinear self-focusing effect. However, as shown in figure 6(b), the broadband beam can significantly suppress small-scale self-focusing, partially erasing the self-focusing filaments and burrs caused by the defect and the diffraction effect.
$\Delta \lambda =40\ {\rm nm}$) passing through a nonlinear medium with a defect in figure 6, in which the parameters of the defect are the same as those in figure 5. It is shown from figure 6(a) that when the narrowband laser beam passes through a nonlinear medium with defects, the transverse intensity distribution has many spikes, being due to the high frequency modulation by the defect. This high frequency modulation seems to be an important reason for the acceleration of the nonlinear self-focusing effect. However, as shown in figure 6(b), the broadband beam can significantly suppress small-scale self-focusing, partially erasing the self-focusing filaments and burrs caused by the defect and the diffraction effect.

Figure 6. The propagation of a narrowband beam, ![]() $\Delta \lambda =0\ {\rm nm}$ (a) and a broadband beam,
$\Delta \lambda =0\ {\rm nm}$ (a) and a broadband beam, ![]() $\Delta \lambda =40\ {\rm nm}$ (b) through a nonlinear medium whose front surface contains a defect. Here, the parameters are the same as in Figure 5.
$\Delta \lambda =40\ {\rm nm}$ (b) through a nonlinear medium whose front surface contains a defect. Here, the parameters are the same as in Figure 5.

Figure 7. The propagation of a narrowband beam (a) and a broadband beam (b) when the defect is not in the centre, ![]() $x_{0}=0.001\ {\rm m}$, the other parameters are the same as in Figure 6.
$x_{0}=0.001\ {\rm m}$, the other parameters are the same as in Figure 6.
In figure 7, we plot the evolution of the transverse intensity distribution at several propagation positions for the case that the position of the defect modulation point is not in the centre of the beam. It is seen that the transverse intensity distribution is asymmetric, and when the incident laser beam is of narrowband type, there also exist many spikes. We can find that when the incident laser beam is of broadband type, the transverse intensity distribution is also asymmetric; however, the spikes in the transverse intensity distribution have been largely suppressed.
4. Conclusions
In conclusion, we have studied the propagation characteristics of a high-power broadband laser beam in a nonlinear medium with defects or without defects. The effects of the bandwidth, the medium thickness, and defects on the evolution of the transverse intensity distribution have been studied. It has been found that, when the incident laser beam is of narrowband type, the transverse intensity distribution has many spikes, which may damage the optical medium. However when the incident laser beam is of broadband type, the spikes of the intensity distribution can be suppressed, decreasing the risk of the optical medium being damaged. The results of this paper are important for high-power laser engineering.
Acknowledgements
This research was supported by the National Natural Science Foundation of China (NSFC) under Grant Nos. 61178015 and 11304104, and the Open Research Fund of the National Laboratory on High Power Laser and Physics under Grant No. SG-001102.