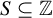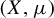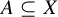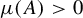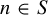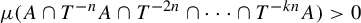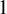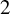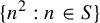1 Background and motivation
A probability measure-preserving system (or MPS) is a quadruple
![]() $(X,\mathcal B,\mu ,T)$
where
$(X,\mathcal B,\mu ,T)$
where
![]() $(X,\mathcal B,\mu )$
is a probability measure space and
$(X,\mathcal B,\mu )$
is a probability measure space and
![]() $T:X\to X$
is an invertible transformation preserving
$T:X\to X$
is an invertible transformation preserving
![]() $\mu $
, meaning
$\mu $
, meaning
![]() $\mu (T^{-1}A)=\mu (A)$
for every measurable set
$\mu (T^{-1}A)=\mu (A)$
for every measurable set
![]() $A\subseteq X$
.
$A\subseteq X$
.
We say that
![]() $S\subseteq \mathbb Z$
is a set of measurable recurrence if for every MPS
$S\subseteq \mathbb Z$
is a set of measurable recurrence if for every MPS
![]() $(X,\mathcal B,\mu ,T)$
and every
$(X,\mathcal B,\mu ,T)$
and every
![]() $A\subseteq X$
having
$A\subseteq X$
having
![]() $\mu (A)>0$
, there is an
$\mu (A)>0$
, there is an
![]() $n\in S$
such that
$n\in S$
such that
![]() $\mu (A\cap T^{-n}A)>0$
.
$\mu (A\cap T^{-n}A)>0$
.
For a fixed
![]() $k\in \mathbb N$
, we say S is a set of k-recurrence if under these hypotheses, there is an
$k\in \mathbb N$
, we say S is a set of k-recurrence if under these hypotheses, there is an
![]() $n\in S$
such that
$n\in S$
such that
![]() $\mu (\bigcap _{j=0}^{k} T^{-jn}A)>0$
; in this terminology, a set of measurable recurrence is a set of
$\mu (\bigcap _{j=0}^{k} T^{-jn}A)>0$
; in this terminology, a set of measurable recurrence is a set of
![]() $1$
-recurrence.
$1$
-recurrence.
Finally,
![]() $S\subseteq \mathbb Z$
is a set of Bohr recurrence if for all
$S\subseteq \mathbb Z$
is a set of Bohr recurrence if for all
![]() $d\in \mathbb N$
, every
$d\in \mathbb N$
, every
![]() $\boldsymbol {\alpha } \in \mathbb T^d$
, and all
$\boldsymbol {\alpha } \in \mathbb T^d$
, and all
![]() $\varepsilon>0$
, there is an
$\varepsilon>0$
, there is an
![]() $n\in S$
such that
$n\in S$
such that
![]() $\|n\boldsymbol {\alpha }\|<\varepsilon $
(see §3 for definitions and notation).
$\|n\boldsymbol {\alpha }\|<\varepsilon $
(see §3 for definitions and notation).
Frantzikinakis, Lesigne, and Wierdl [Reference Frantzikinakis, Lesigne and Wierdl10] proved that if
![]() $k\in \mathbb N$
and
$k\in \mathbb N$
and
![]() $S\subseteq \mathbb Z$
is a set of k-recurrence, then
$S\subseteq \mathbb Z$
is a set of k-recurrence, then
![]() $S^{\wedge k}:=\{n^k: n\in S\}$
is a set of Bohr recurrence. They ask (the remarks following [Reference Frantzikinakis, Lesigne and Wierdl10, Proposition 2.2]) whether this conclusion can be strengthened to ‘
$S^{\wedge k}:=\{n^k: n\in S\}$
is a set of Bohr recurrence. They ask (the remarks following [Reference Frantzikinakis, Lesigne and Wierdl10, Proposition 2.2]) whether this conclusion can be strengthened to ‘
![]() $S^{\wedge k}$
is a set of measurable recurrence,’ and the subsequent articles [Reference Frantzikinakis7, Reference Frantzikinakis8] reiterate ([Reference Frantzikinakis8, Problem 5] of the current version at arXiv:1103.3808) this question. Our main result, Theorem 1.1, provides a negative answer for the case
$S^{\wedge k}$
is a set of measurable recurrence,’ and the subsequent articles [Reference Frantzikinakis7, Reference Frantzikinakis8] reiterate ([Reference Frantzikinakis8, Problem 5] of the current version at arXiv:1103.3808) this question. Our main result, Theorem 1.1, provides a negative answer for the case
![]() $k=2$
. For
$k=2$
. For
![]() $k\geq 3$
, the question remains open. A related question in [Reference Frantzikinakis7] asks whether a set S which is a set of k-recurrence for every k must have the property that
$k\geq 3$
, the question remains open. A related question in [Reference Frantzikinakis7] asks whether a set S which is a set of k-recurrence for every k must have the property that
![]() $S^{\wedge 2}$
is a set of measurable recurrence. We discuss how our construction relates to these questions in §16.
$S^{\wedge 2}$
is a set of measurable recurrence. We discuss how our construction relates to these questions in §16.
Theorem 1.1. There is a set
![]() $S\subseteq \mathbb Z$
which is a set of
$S\subseteq \mathbb Z$
which is a set of
![]() $2$
-recurrence such that
$2$
-recurrence such that
![]() $S^{\wedge 2}$
is not a set of measurable recurrence.
$S^{\wedge 2}$
is not a set of measurable recurrence.
Reflecting on the known examples of sets of Bohr recurrence which are not sets of measurable recurrence, Frantzikinakis [Reference Frantzikinakis8] predicts that an example of a set of
![]() $2$
-recurrence S where
$2$
-recurrence S where
![]() $S^{\wedge 2}$
is not a set of measurable recurrence will be rather complicated. Our example is indeed complicated: while built from well-known constituents using standard methods, the proof that it is a set of
$S^{\wedge 2}$
is not a set of measurable recurrence will be rather complicated. Our example is indeed complicated: while built from well-known constituents using standard methods, the proof that it is a set of
![]() $2$
-recurrence uses several reductions—from general measure-preserving systems to totally ergodic systems to nilsystems to affine systems to Kronecker systems. The final reduction combines explicit computations of multiple ergodic averages in 2-step affine systems with classical estimates for three term arithmetic progressions in terms of Fourier coefficients.
$2$
-recurrence uses several reductions—from general measure-preserving systems to totally ergodic systems to nilsystems to affine systems to Kronecker systems. The final reduction combines explicit computations of multiple ergodic averages in 2-step affine systems with classical estimates for three term arithmetic progressions in terms of Fourier coefficients.
1.1 Outline of the article
Our approach is similar to Kriz’s construction [Reference Kříž18] proving that there is a set of topological recurrence which is not a set of measurable recurrence. Very roughly, our example S in Theorem 1.1 is
![]() $\{n:n^2 \in R\}$
, where R is Kriz’s example. While this description is not quite correct, it may help those familiar with [Reference Kříž18], [Reference Griesmer16] or [Reference Griesmer15] understand our construction.
$\{n:n^2 \in R\}$
, where R is Kriz’s example. While this description is not quite correct, it may help those familiar with [Reference Kříž18], [Reference Griesmer16] or [Reference Griesmer15] understand our construction.
The overall proof of Theorem 1.1 is presented at the end of §2. We outline its components here. Section 2 begins by collecting standard facts about the following finite approximations to recurrence properties.
Definition 1.2. Let
![]() $S\subseteq \mathbb Z$
and
$S\subseteq \mathbb Z$
and
![]() $k\in \mathbb N$
. We say that S is
$k\in \mathbb N$
. We say that S is
![]() $(\delta ,k)$
-recurrent if for every MPS
$(\delta ,k)$
-recurrent if for every MPS
![]() $(X,\mathcal B,\mu ,T)$
and every
$(X,\mathcal B,\mu ,T)$
and every
![]() $A\subseteq X$
with
$A\subseteq X$
with
![]() $\mu (A)>\delta $
, we have
$\mu (A)>\delta $
, we have
![]() $A\cap T^{-n}A\cap \cdots \cap T^{-kn}A\neq \varnothing $
for some
$A\cap T^{-n}A\cap \cdots \cap T^{-kn}A\neq \varnothing $
for some
![]() $n\in S$
.
$n\in S$
.
We say that S is
![]() $(\delta ,k)$
-non-recurrent if there is an MPS
$(\delta ,k)$
-non-recurrent if there is an MPS
![]() $(X,\mathcal B,\mu ,T)$
and
$(X,\mathcal B,\mu ,T)$
and
![]() $A\subseteq X$
with
$A\subseteq X$
with
![]() $\mu (A)>\delta $
such that
$\mu (A)>\delta $
such that
![]() $A\cap T^{-n}A\cap \cdots \cap T^{-kn}A=\varnothing $
.
$A\cap T^{-n}A\cap \cdots \cap T^{-kn}A=\varnothing $
.
We say S is
![]() $\delta $
-non-recurrent if it is
$\delta $
-non-recurrent if it is
![]() $(\delta ,1)$
-non-recurrent, meaning there is an MPS
$(\delta ,1)$
-non-recurrent, meaning there is an MPS
![]() $(X,\mathcal B,\mu ,T)$
and
$(X,\mathcal B,\mu ,T)$
and
![]() $A\subseteq X$
with
$A\subseteq X$
with
![]() $\mu (A)>\delta $
such that
$\mu (A)>\delta $
such that
![]() $A\cap T^{-n}A=\varnothing $
for all
$A\cap T^{-n}A=\varnothing $
for all
![]() $n\in S$
.
$n\in S$
.
Remark 1.3. The condition
![]() $A\cap T^{-n}A\cap \cdots \cap T^{-kn}A\neq \varnothing $
in the definition of
$A\cap T^{-n}A\cap \cdots \cap T^{-kn}A\neq \varnothing $
in the definition of
![]() $(\delta ,k)$
- recurrent may be replaced with
$(\delta ,k)$
- recurrent may be replaced with
![]() $\mu (A\cap T^{-n}A\cap \cdots \cap T^{-kn}A)>0$
; cf. Lemma 15.1.
$\mu (A\cap T^{-n}A\cap \cdots \cap T^{-kn}A)>0$
; cf. Lemma 15.1.
Lemma 2.1 says that if
![]() $S_1, S_2\subseteq \mathbb Z$
are finite,
$S_1, S_2\subseteq \mathbb Z$
are finite,
![]() $\delta _1$
-non-recurrent, and
$\delta _1$
-non-recurrent, and
![]() $\delta _2$
-non-recurrent, then for all sufficiently large m,
$\delta _2$
-non-recurrent, then for all sufficiently large m,
![]() $S_1\cup mS_2$
is
$S_1\cup mS_2$
is
![]() $2\delta _1\delta _2$
-non-recurrent. Thus, if
$2\delta _1\delta _2$
-non-recurrent. Thus, if
![]() $S_1^{\wedge 2}$
and
$S_1^{\wedge 2}$
and
![]() $S_2^{\wedge 2}$
are
$S_2^{\wedge 2}$
are
![]() $\delta _1$
-non-recurrent and
$\delta _1$
-non-recurrent and
![]() $\delta _2$
-non-recurrent, respectively, then
$\delta _2$
-non-recurrent, respectively, then
![]() $(S_1 \cup mS_2)^{\wedge 2}$
is
$(S_1 \cup mS_2)^{\wedge 2}$
is
![]() $2\delta _1\delta _2$
-non-recurrent for all sufficiently large m, as
$2\delta _1\delta _2$
-non-recurrent for all sufficiently large m, as
![]() $(S_1 \cup mS_2)^{\wedge 2} = S_1^{\wedge 2} \cup m^2S_2^{\wedge 2}$
.
$(S_1 \cup mS_2)^{\wedge 2} = S_1^{\wedge 2} \cup m^2S_2^{\wedge 2}$
.
Lemma 2.3 says that
![]() $S\subseteq \mathbb Z$
is
$S\subseteq \mathbb Z$
is
![]() $\delta $
-non-recurrent if and only if for all
$\delta $
-non-recurrent if and only if for all
![]() $\delta '< \delta $
and all finite subsets
$\delta '< \delta $
and all finite subsets
![]() $S'\subseteq S$
,
$S'\subseteq S$
,
![]() $S'$
is
$S'$
is
![]() $\delta '$
-non-recurrent. Likewise, if
$\delta '$
-non-recurrent. Likewise, if
![]() $S\subseteq \mathbb Z$
is
$S\subseteq \mathbb Z$
is
![]() $(\eta ,2)$
-recurrent, then for all
$(\eta ,2)$
-recurrent, then for all
![]() $\eta '<\eta $
, there is a finite subset
$\eta '<\eta $
, there is a finite subset
![]() $S'\subseteq S$
which is
$S'\subseteq S$
which is
![]() $(\eta ',2)$
-recurrent.
$(\eta ',2)$
-recurrent.
The proof of Theorem 1.1 is given at the end of §2; it explains in detail how finite approximations are assembled to form a
![]() $2$
-recurrent set whose perfect squares do not form a set of measurable recurrence. This reduces the problem to proving Lemma 2.4, which states that the required finite approximations exist. These approximations are based on Bohr–Hamming balls, which we introduce in §3. Bohr–Hamming balls were used in [Reference Griesmer15, Reference Kříž18] to construct sets with prescribed recurrence properties. Fixing
$2$
-recurrent set whose perfect squares do not form a set of measurable recurrence. This reduces the problem to proving Lemma 2.4, which states that the required finite approximations exist. These approximations are based on Bohr–Hamming balls, which we introduce in §3. Bohr–Hamming balls were used in [Reference Griesmer15, Reference Kříž18] to construct sets with prescribed recurrence properties. Fixing
![]() $\delta <\tfrac 12$
and
$\delta <\tfrac 12$
and
![]() $\eta>0$
, Lemmas 3.4 and 3.5 show that there is a Bohr–Hamming ball
$\eta>0$
, Lemmas 3.4 and 3.5 show that there is a Bohr–Hamming ball
![]() $BH$
which is
$BH$
which is
![]() $\delta $
-non-recurrent, while
$\delta $
-non-recurrent, while
![]() $\sqrt {BH}:=\{n\in \mathbb N: n^2\in BH\}$
is
$\sqrt {BH}:=\{n\in \mathbb N: n^2\in BH\}$
is
![]() $(\eta ,2)$
-recurrent.
$(\eta ,2)$
-recurrent.
The proof of Lemma 3.5 occupies §§4–15. It is proved by estimating multiple ergodic averages of the form
 $$ \begin{align} \lim_{N\to\infty} \frac{1}{N}\sum_{n=1}^N g(n^2\boldsymbol{\beta}) \int f\cdot f\circ T^n \cdot f\circ T^{2n}\, d\mu, \end{align} $$
$$ \begin{align} \lim_{N\to\infty} \frac{1}{N}\sum_{n=1}^N g(n^2\boldsymbol{\beta}) \int f\cdot f\circ T^n \cdot f\circ T^{2n}\, d\mu, \end{align} $$
where
![]() $(X,\mathcal B,\mu ,T)$
is a measure-preserving system,
$(X,\mathcal B,\mu ,T)$
is a measure-preserving system,
![]() $f:X\to [0,1]$
has
$f:X\to [0,1]$
has
![]() $\int f\, d\mu>\delta $
for some prescribed
$\int f\, d\mu>\delta $
for some prescribed
![]() $\delta>0$
,
$\delta>0$
,
![]() $\boldsymbol {\beta }\in \mathbb T^r$
for some
$\boldsymbol {\beta }\in \mathbb T^r$
for some
![]() $r\in \mathbb N$
, and
$r\in \mathbb N$
, and
![]() $g:\mathbb T^r\to [0,1]$
is Riemann integrable. Under certain hypotheses on g, we will prove the limit in equation (1.1) is positive; this is the inequality in equation (4.7) in the proof of Lemma 3.5. In §4, we show how the general case may be reduced to that where T is totally ergodic. The remainder of the article, outlined in §5.2, is dedicated to analyzing the limit in equation (1.1) when T is totally ergodic. Section 8 shows that the totally ergodic case can be further reduced to the study of standard
$g:\mathbb T^r\to [0,1]$
is Riemann integrable. Under certain hypotheses on g, we will prove the limit in equation (1.1) is positive; this is the inequality in equation (4.7) in the proof of Lemma 3.5. In §4, we show how the general case may be reduced to that where T is totally ergodic. The remainder of the article, outlined in §5.2, is dedicated to analyzing the limit in equation (1.1) when T is totally ergodic. Section 8 shows that the totally ergodic case can be further reduced to the study of standard
![]() $2$
-step Weyl systems, and §§9–13 are dedicated to simplifying and estimating equation (1.1) for these systems.
$2$
-step Weyl systems, and §§9–13 are dedicated to simplifying and estimating equation (1.1) for these systems.
Readers familiar with the theory of characteristic factors (especially [Reference Frantzikinakis6]) may find it most profitable to read §§2, 3, 5, and 8 in detail, and skim §4.
2 Constructing the example from finite approximations
We first require some standard facts about the properties mentioned in Definition 1.2. The following is [Reference Griesmer16, Lemma 3.6]; it is essentially [Reference Kříž18, Lemma 3.2]. Similar lemmas appear, often unnamed, in the variations on Kriz’s example [Reference Forrest5, Reference McCutcheon, Petersen and Salama20, Reference McCutcheon21, Reference Weiss25].
Lemma 2.1. Let
![]() $S_1, S_2\subseteq \mathbb N$
be finite. If
$S_1, S_2\subseteq \mathbb N$
be finite. If
![]() $S_1$
and
$S_1$
and
![]() $S_2$
are
$S_2$
are
![]() $\delta $
-non-recurrent and
$\delta $
-non-recurrent and
![]() $\eta $
-non-recurrent, respectively, then for all sufficiently large
$\eta $
-non-recurrent, respectively, then for all sufficiently large
![]() $m\in \mathbb N$
,
$m\in \mathbb N$
,
![]() $S_1\cup mS_2$
is
$S_1\cup mS_2$
is
![]() $2\delta \eta $
-non-recurrent.
$2\delta \eta $
-non-recurrent.
Lemma 2.2. Let
![]() $m\in \mathbb Z$
and
$m\in \mathbb Z$
and
![]() $\delta \geq 0$
. If
$\delta \geq 0$
. If
![]() $S\subseteq \mathbb Z$
is
$S\subseteq \mathbb Z$
is
![]() $(\delta ,2)$
-recurrent, then
$(\delta ,2)$
-recurrent, then
![]() $mS$
is also
$mS$
is also
![]() $(\delta ,2)$
-recurrent.
$(\delta ,2)$
-recurrent.
Proof. Fix
![]() $m\in \mathbb Z$
and let
$m\in \mathbb Z$
and let
![]() $S\subseteq \mathbb Z$
be a
$S\subseteq \mathbb Z$
be a
![]() $(\delta ,2)$
-recurrent set. Let
$(\delta ,2)$
-recurrent set. Let
![]() $(X,\mathcal B,\mu ,T)$
be an MPS, with
$(X,\mathcal B,\mu ,T)$
be an MPS, with
![]() $A\subseteq X$
having
$A\subseteq X$
having
![]() $\mu (A)>\delta $
. Consider the MPS
$\mu (A)>\delta $
. Consider the MPS
![]() $(X,\mathcal B,\mu ,T^m)$
. Since
$(X,\mathcal B,\mu ,T^m)$
. Since
![]() $\mu (A)>\delta $
, there exists
$\mu (A)>\delta $
, there exists
![]() $n\in S$
such that
$n\in S$
such that
![]() $\mu (A\cap (T^{m})^{-n}A \cap (T^{m})^{-2n}A)>0$
, meaning
$\mu (A\cap (T^{m})^{-n}A \cap (T^{m})^{-2n}A)>0$
, meaning
![]() $\mu (A\cap T^{-mn}A\cap T^{-2(mn)}A)>0$
. Since
$\mu (A\cap T^{-mn}A\cap T^{-2(mn)}A)>0$
. Since
![]() $mn\in mS$
, this proves
$mn\in mS$
, this proves
![]() $mS$
is
$mS$
is
![]() $(\delta ,2)$
-recurrent.
$(\delta ,2)$
-recurrent.
Our proof of Lemma 2.4 uses the following compactness properties for recurrence.
Lemma 2.3. Let
![]() $k\in \mathbb N$
and
$k\in \mathbb N$
and
![]() $\delta \geq 0$
. If
$\delta \geq 0$
. If
![]() $\delta '>\delta $
and every finite subset of S is
$\delta '>\delta $
and every finite subset of S is
![]() $(\delta ',k)$
-non-recurrent, then S is
$(\delta ',k)$
-non-recurrent, then S is
![]() $(\delta ,k)$
-non-recurrent.
$(\delta ,k)$
-non-recurrent.
Consequently, if S is
![]() $(\delta ,k)$
-recurrent, then for all
$(\delta ,k)$
-recurrent, then for all
![]() $\delta '>\delta $
, there is a finite
$\delta '>\delta $
, there is a finite
![]() $S'\subseteq S$
which is
$S'\subseteq S$
which is
![]() $(\delta ',k)$
-recurrent.
$(\delta ',k)$
-recurrent.
We prove Lemma 2.3 in §15. A special case, which is easily adapted to prove the general case, appears in [Reference Forrest5, Ch. 2].
Theorem 1.1 is proved by combining the following lemma with the others in this section.
Lemma 2.4. For all
![]() $\delta>0$
and
$\delta>0$
and
![]() $\eta <1/2$
, there exists
$\eta <1/2$
, there exists
![]() $S\subseteq \mathbb Z$
which is
$S\subseteq \mathbb Z$
which is
![]() $(\delta ,2)$
-recurrent such that
$(\delta ,2)$
-recurrent such that
![]() $S^{\wedge 2}$
is
$S^{\wedge 2}$
is
![]() $\eta $
-non-recurrent.
$\eta $
-non-recurrent.
By Lemma 2.3, we can take S to be finite in Lemma 2.4.
Lemmas 3.4 and 3.5 will prove Lemma 2.4; the proof of Lemma 3.5 forms the majority of this article.
Proof of Theorem 1.1
Let
![]() $\delta <\delta '<\tfrac 12$
. We will construct an increasing sequence of finite sets
$\delta <\delta '<\tfrac 12$
. We will construct an increasing sequence of finite sets
![]() $S_1\subseteq S_2\subseteq \cdots $
so that
$S_1\subseteq S_2\subseteq \cdots $
so that
![]() $S_n$
is
$S_n$
is
![]() $({1}/{n},2)$
-recurrent, and
$({1}/{n},2)$
-recurrent, and
![]() $S_n^{\wedge 2}$
is
$S_n^{\wedge 2}$
is
![]() $\delta '$
-non-recurrent. Setting
$\delta '$
-non-recurrent. Setting
![]() $S:=\bigcup _{n=1}^\infty S_n$
, we get that S is a set of
$S:=\bigcup _{n=1}^\infty S_n$
, we get that S is a set of
![]() $2$
-recurrence, while every finite subset of
$2$
-recurrence, while every finite subset of
![]() $S^{\wedge 2}$
is
$S^{\wedge 2}$
is
![]() $\delta '$
-non-recurrent. Lemma 2.3 then implies S is
$\delta '$
-non-recurrent. Lemma 2.3 then implies S is
![]() $\delta $
-non-recurrent.
$\delta $
-non-recurrent.
To define
![]() $S_1$
, we apply Lemma 2.4 to find an
$S_1$
, we apply Lemma 2.4 to find an
![]() $S_1\subseteq \mathbb Z$
which is
$S_1\subseteq \mathbb Z$
which is
![]() $(1,2)$
-recurrent, while
$(1,2)$
-recurrent, while
![]() $S_1^{\wedge 2}$
is
$S_1^{\wedge 2}$
is
![]() $\delta _1$
-non-recurrent for some
$\delta _1$
-non-recurrent for some
![]() $\delta _1>\delta '$
. We define the remaining
$\delta _1>\delta '$
. We define the remaining
![]() $S_n$
inductively: suppose
$S_n$
inductively: suppose
![]() $n\in \mathbb N$
and that
$n\in \mathbb N$
and that
![]() $S_n$
has been chosen to be
$S_n$
has been chosen to be
![]() $({1}/{n},2)$
-recurrent, while
$({1}/{n},2)$
-recurrent, while
![]() $S_n^{\wedge 2}$
is
$S_n^{\wedge 2}$
is
![]() $\delta _n$
-non-recurrent for some
$\delta _n$
-non-recurrent for some
![]() $\delta _n>\delta '$
. Let
$\delta _n>\delta '$
. Let
![]() $\eta <\tfrac 12$
so that
$\eta <\tfrac 12$
so that
![]() $2\eta \delta _n>\delta '$
. We will find
$2\eta \delta _n>\delta '$
. We will find
![]() $S_{n+1}\supset S_n$
so that
$S_{n+1}\supset S_n$
so that
![]() $S_{n+1}$
is
$S_{n+1}$
is
![]() $({1}/({n+1}),2)$
-recurrent and
$({1}/({n+1}),2)$
-recurrent and
![]() $S_{n+1}^{\wedge 2}$
is
$S_{n+1}^{\wedge 2}$
is
![]() $2\eta \delta _n$
-non-recurrent. To do so, apply Lemma 2.4 to find a finite
$2\eta \delta _n$
-non-recurrent. To do so, apply Lemma 2.4 to find a finite
![]() $R \subseteq \mathbb Z$
which is
$R \subseteq \mathbb Z$
which is
![]() $({1}/({n+1}),2)$
-recurrent such that
$({1}/({n+1}),2)$
-recurrent such that
![]() $R^{\wedge 2}$
is
$R^{\wedge 2}$
is
![]() $\eta $
-non-recurrent. By Lemma 2.1, choose
$\eta $
-non-recurrent. By Lemma 2.1, choose
![]() $m\in \mathbb N$
so that
$m\in \mathbb N$
so that
![]() $(S_n^{\wedge 2})\cup m^2(R^{\wedge 2})$
is
$(S_n^{\wedge 2})\cup m^2(R^{\wedge 2})$
is
![]() $2\eta \delta _n$
-non-recurrent. Now
$2\eta \delta _n$
-non-recurrent. Now
![]() $S_{n+1}:= S_n \cup mR$
is the desired set:
$S_{n+1}:= S_n \cup mR$
is the desired set:
![]() $mR$
is
$mR$
is
![]() $({1}/({n+1}),2)$
-recurrent, by Lemma 2.2, while
$({1}/({n+1}),2)$
-recurrent, by Lemma 2.2, while
![]() $S_{n+1}^{\wedge 2}= (S_n^{\wedge 2})\cup m^2(R^{\wedge 2})$
. Since
$S_{n+1}^{\wedge 2}= (S_n^{\wedge 2})\cup m^2(R^{\wedge 2})$
. Since
![]() $2\eta \delta _n> \delta '$
, this completes the inductive step of the construction.
$2\eta \delta _n> \delta '$
, this completes the inductive step of the construction.
3 Approximate Hamming balls in
 $\mathbb T^r$
and Bohr–Hamming balls in
$\mathbb T^r$
and Bohr–Hamming balls in
 $\mathbb Z$
$\mathbb Z$
Let
![]() $\mathbb T$
denote the group
$\mathbb T$
denote the group
![]() $\mathbb R/\mathbb Z$
with the usual topology. For
$\mathbb R/\mathbb Z$
with the usual topology. For
![]() $x\in \mathbb T$
, let
$x\in \mathbb T$
, let
![]() $\tilde {x}$
denote the unique element of
$\tilde {x}$
denote the unique element of
![]() $[0,1)$
such that
$[0,1)$
such that
![]() $x = \tilde {x}+\mathbb Z$
and define
$x = \tilde {x}+\mathbb Z$
and define
![]() $\|x\|:=\min \{|\tilde {x}-n|: n\in \mathbb Z\}$
. For
$\|x\|:=\min \{|\tilde {x}-n|: n\in \mathbb Z\}$
. For
![]() $r\in \mathbb N$
and
$r\in \mathbb N$
and
![]() $\mathbf x = (x_1,\ldots , x_r)\in \mathbb T^r$
, let
$\mathbf x = (x_1,\ldots , x_r)\in \mathbb T^r$
, let
![]() $\|\mathbf x\|:=\max _{j\leq r} \|x_j\|$
.
$\|\mathbf x\|:=\max _{j\leq r} \|x_j\|$
.
For
![]() $\varepsilon>0$
,
$\varepsilon>0$
,
![]() $r\in \mathbb N$
, and
$r\in \mathbb N$
, and
![]() $\mathbf x=(x_1,\ldots ,x_r)\in \mathbb T^r$
, let
$\mathbf x=(x_1,\ldots ,x_r)\in \mathbb T^r$
, let
So
![]() $w_\varepsilon (\mathbf x)$
is the number of coordinates of
$w_\varepsilon (\mathbf x)$
is the number of coordinates of
![]() $\mathbf x$
differing from
$\mathbf x$
differing from
![]() $0$
by at least
$0$
by at least
![]() $\varepsilon $
.
$\varepsilon $
.
Definition 3.1. For
![]() $k< r\in \mathbb N$
,
$k< r\in \mathbb N$
,
![]() $\mathbf y\in \mathbb T^r$
, and
$\mathbf y\in \mathbb T^r$
, and
![]() $\varepsilon>0$
, we define the approximate Hamming ball of radius
$\varepsilon>0$
, we define the approximate Hamming ball of radius
![]() $(k,\varepsilon )$
around
$(k,\varepsilon )$
around
![]() $\mathbf y$
as
$\mathbf y$
as
So
![]() $\operatorname {Hamm}(\mathbf y; k,\varepsilon )$
is the set of
$\operatorname {Hamm}(\mathbf y; k,\varepsilon )$
is the set of
![]() $\mathbf x=(x_1,\ldots ,x_r)\in \mathbb T^r$
, where at most k coordinates
$\mathbf x=(x_1,\ldots ,x_r)\in \mathbb T^r$
, where at most k coordinates
![]() $x_i$
differ from
$x_i$
differ from
![]() $y_i$
by at least
$y_i$
by at least
![]() $\varepsilon $
.
$\varepsilon $
.
If Z is a topological abelian group, we say
![]() $\alpha \in Z$
generates Z if the cyclic subgroup
$\alpha \in Z$
generates Z if the cyclic subgroup
![]() $\{n\alpha :n\in \mathbb Z\}$
is dense in Z. In other words,
$\{n\alpha :n\in \mathbb Z\}$
is dense in Z. In other words,
![]() $\alpha $
generates Z if Z is the smallest closed subgroup containing
$\alpha $
generates Z if Z is the smallest closed subgroup containing
![]() $\alpha $
.
$\alpha $
.
The group rotation system
![]() $(Z,\mathcal B, m_Z,R_{\alpha })$
, where
$(Z,\mathcal B, m_Z,R_{\alpha })$
, where
![]() $\mathcal B$
is the Borel
$\mathcal B$
is the Borel
![]() $\sigma $
-algebra on Z and
$\sigma $
-algebra on Z and
![]() $m_Z$
is Haar measure on Z, is given by
$m_Z$
is Haar measure on Z, is given by
![]() $R_{\alpha }z=z+\alpha $
.
$R_{\alpha }z=z+\alpha $
.
Definition 3.2. If
![]() $U=\operatorname {Hamm}(\mathbf y; k,\varepsilon ) \subseteq \mathbb T^r$
is an approximate Hamming ball and
$U=\operatorname {Hamm}(\mathbf y; k,\varepsilon ) \subseteq \mathbb T^r$
is an approximate Hamming ball and
![]() $\boldsymbol {\beta }\in \mathbb T^r$
, the corresponding Bohr–Hamming ball of radius
$\boldsymbol {\beta }\in \mathbb T^r$
, the corresponding Bohr–Hamming ball of radius
![]() $(k,\varepsilon )$
is
$(k,\varepsilon )$
is
If
![]() $\boldsymbol {\beta }$
generates
$\boldsymbol {\beta }$
generates
![]() $\mathbb T^r$
, we say that the corresponding Bohr–Hamming ball is proper.
$\mathbb T^r$
, we say that the corresponding Bohr–Hamming ball is proper.
We write m for Haar probability measure on
![]() $\mathbb T^r$
. Lemmas 3.3 and 3.4 here are implicit in [Reference Kříž18] and proved explicitly in [Reference Griesmer15].
$\mathbb T^r$
. Lemmas 3.3 and 3.4 here are implicit in [Reference Kříž18] and proved explicitly in [Reference Griesmer15].
Lemma 3.3. Let
![]() $k\in \mathbb N$
and
$k\in \mathbb N$
and
![]() $\eta <\tfrac 12$
. For all sufficiently large
$\eta <\tfrac 12$
. For all sufficiently large
![]() $r\in \mathbb N$
, there is an
$r\in \mathbb N$
, there is an
![]() $\varepsilon>0$
and
$\varepsilon>0$
and
![]() $E\subseteq \mathbb T^r$
with
$E\subseteq \mathbb T^r$
with
![]() $m(E)>\eta $
such that
$m(E)>\eta $
such that
![]() $E\cap (E+U)=\varnothing $
, where
$E\cap (E+U)=\varnothing $
, where
![]() $U=\operatorname {Hamm}(\mathbf y;k,\varepsilon )$
, with
$U=\operatorname {Hamm}(\mathbf y;k,\varepsilon )$
, with
![]() $\mathbf y = (\tfrac 12,\ldots , \tfrac 12)\in \mathbb T^r$
.
$\mathbf y = (\tfrac 12,\ldots , \tfrac 12)\in \mathbb T^r$
.
Lemma 3.3 is a consequence of [Reference Griesmer15, Lemma 7.1]. To derive the former from the latter, note that [Reference Griesmer15, Lemma 7.1] (in the case
![]() $p=2$
there) provides sets E,
$p=2$
there) provides sets E,
![]() $E'\subseteq \mathbb T^r$
with
$E'\subseteq \mathbb T^r$
with
![]() $\mu (E)>\eta $
, an approximate Hamming ball U around
$\mu (E)>\eta $
, an approximate Hamming ball U around
![]() $0_{\mathbb T^r}$
with radius
$0_{\mathbb T^r}$
with radius
![]() $(k,\varepsilon )$
for some
$(k,\varepsilon )$
for some
![]() $\varepsilon>0$
, such that
$\varepsilon>0$
, such that
![]() $E+U\subseteq E'$
and
$E+U\subseteq E'$
and
![]() $E'+ (\tfrac 12,\ldots ,\tfrac 12)$
is disjoint from
$E'+ (\tfrac 12,\ldots ,\tfrac 12)$
is disjoint from
![]() $E'$
.
$E'$
.
Lemma 3.4. Let
![]() $k\in \mathbb N$
and
$k\in \mathbb N$
and
![]() $\eta <\tfrac 12$
. For all sufficiently large
$\eta <\tfrac 12$
. For all sufficiently large
![]() $r\in \mathbb N$
, there is an
$r\in \mathbb N$
, there is an
![]() $\varepsilon>0$
such that for all
$\varepsilon>0$
such that for all
![]() $\boldsymbol {\beta }\in \mathbb T^r$
, the Bohr–Hamming ball
$\boldsymbol {\beta }\in \mathbb T^r$
, the Bohr–Hamming ball
![]() $BH(\boldsymbol {\beta },\mathbf y;k,\varepsilon )$
is
$BH(\boldsymbol {\beta },\mathbf y;k,\varepsilon )$
is
![]() $\eta $
-non-recurrent, where
$\eta $
-non-recurrent, where
![]() $\mathbf y = (\tfrac 12,\ldots ,\tfrac 12)\in \mathbb T^r$
.
$\mathbf y = (\tfrac 12,\ldots ,\tfrac 12)\in \mathbb T^r$
.
Proof. Let
![]() $\eta <\tfrac 12$
and choose r large enough to find the E and U provided by Lemma 3.3, with
$\eta <\tfrac 12$
and choose r large enough to find the E and U provided by Lemma 3.3, with
![]() $m(E)>\eta $
. Let
$m(E)>\eta $
. Let
![]() $(X,\mathcal B,\mu ,T) = (\mathbb T^r,\mathcal B,m,R_{\boldsymbol {\beta }})$
be the group rotation on
$(X,\mathcal B,\mu ,T) = (\mathbb T^r,\mathcal B,m,R_{\boldsymbol {\beta }})$
be the group rotation on
![]() $\mathbb T^r$
determined by
$\mathbb T^r$
determined by
![]() $\boldsymbol {\beta }$
. For
$\boldsymbol {\beta }$
. For
![]() $n\in BH(\boldsymbol {\beta },\mathbf y;k,\eta )$
, we have
$n\in BH(\boldsymbol {\beta },\mathbf y;k,\eta )$
, we have
![]() $R_{\boldsymbol {\beta }}^n E \subseteq E+U$
, so
$R_{\boldsymbol {\beta }}^n E \subseteq E+U$
, so
![]() $E\cap R_{\boldsymbol {\beta }}^n E=\varnothing .$
Since
$E\cap R_{\boldsymbol {\beta }}^n E=\varnothing .$
Since
![]() $R_{\boldsymbol {\beta }}$
is invertible, this means
$R_{\boldsymbol {\beta }}$
is invertible, this means
![]() $E\cap R_{\boldsymbol {\beta }}^{-n}E =\varnothing $
, as well.
$E\cap R_{\boldsymbol {\beta }}^{-n}E =\varnothing $
, as well.
For
![]() $S\subseteq \mathbb Z$
, let
$S\subseteq \mathbb Z$
, let
![]() $\sqrt {S}:=\{n\in \mathbb Z:n^2 \in S\}$
.
$\sqrt {S}:=\{n\in \mathbb Z:n^2 \in S\}$
.
Lemma 3.5. For all
![]() $\delta>0$
, there exists
$\delta>0$
, there exists
![]() $k_0\in \mathbb N$
such that for every
$k_0\in \mathbb N$
such that for every
![]() $r\in \mathbb N$
, every proper Bohr–Hamming ball
$r\in \mathbb N$
, every proper Bohr–Hamming ball
![]() $BH:=BH(\boldsymbol {\beta },\mathbf y; k, \varepsilon )$
with
$BH:=BH(\boldsymbol {\beta },\mathbf y; k, \varepsilon )$
with
![]() $k\geq k_0$
,
$k\geq k_0$
,
![]() $\varepsilon>0$
, and
$\varepsilon>0$
, and
![]() $\mathbf y\in \mathbb T^r$
,
$\mathbf y\in \mathbb T^r$
,
![]() $\sqrt {BH}$
is
$\sqrt {BH}$
is
![]() $(\delta ,2)$
-recurrent.
$(\delta ,2)$
-recurrent.
Lemma 3.5 is proved using multiple ergodic averages and characteristic factors. The main argument is given in §4, using several reductions developed in §§4–14.
Proof of Lemma 2.4
Let
![]() $\delta>0$
and
$\delta>0$
and
![]() $\eta <\tfrac 12$
. Choose k large enough to satisfy the conclusion of Lemma 3.5. With this k, choose
$\eta <\tfrac 12$
. Choose k large enough to satisfy the conclusion of Lemma 3.5. With this k, choose
![]() $r>k$
and
$r>k$
and
![]() $\varepsilon $
small enough to satisfy the conclusion of Lemma 3.4. Let
$\varepsilon $
small enough to satisfy the conclusion of Lemma 3.4. Let
![]() $\boldsymbol {\beta }\in \mathbb T^r$
be generating and let
$\boldsymbol {\beta }\in \mathbb T^r$
be generating and let
![]() $BH=BH(\boldsymbol {\beta },\mathbf y;k,\varepsilon )$
, where
$BH=BH(\boldsymbol {\beta },\mathbf y;k,\varepsilon )$
, where
![]() $\mathbf y=(\tfrac 12,\ldots ,\tfrac 12)\in \mathbb T^r$
, so that
$\mathbf y=(\tfrac 12,\ldots ,\tfrac 12)\in \mathbb T^r$
, so that
![]() $BH$
is
$BH$
is
![]() $\eta $
-non-recurrent. Finally, let
$\eta $
-non-recurrent. Finally, let
![]() $S=\sqrt {BH}$
, so that S is
$S=\sqrt {BH}$
, so that S is
![]() $(\delta ,2)$
-recurrent, by Lemma 3.5. Since
$(\delta ,2)$
-recurrent, by Lemma 3.5. Since
![]() $S^{\wedge 2}\subseteq BH$
, we get that
$S^{\wedge 2}\subseteq BH$
, we get that
![]() $S^{\wedge 2}$
is
$S^{\wedge 2}$
is
![]() $\eta $
-non-recurrent, as desired.
$\eta $
-non-recurrent, as desired.
3.1 Cylinders and Fourier coefficients
Here we define constituents of approximate Hamming balls.
Definition 3.6. Given
![]() $r\in \mathbb N$
,
$r\in \mathbb N$
,
![]() $I\subseteq \{1,\ldots ,r\}$
,
$I\subseteq \{1,\ldots ,r\}$
,
![]() $\eta>0$
, and
$\eta>0$
, and
![]() $\mathbf y\in \mathbb T^r$
, define the
$\mathbf y\in \mathbb T^r$
, define the
![]() $\eta $
-cylinder determined by I around
$\eta $
-cylinder determined by I around
![]() $\mathbf y$
to be
$\mathbf y$
to be
so that
 $$ \begin{align} U:=\operatorname{Hamm}(\mathbf y;k,\eta) = \bigcup_{\substack{I\subseteq \{1,\ldots, r\}\\ |I| = r-k}} V_{I,\mathbf y, \eta}. \end{align} $$
$$ \begin{align} U:=\operatorname{Hamm}(\mathbf y;k,\eta) = \bigcup_{\substack{I\subseteq \{1,\ldots, r\}\\ |I| = r-k}} V_{I,\mathbf y, \eta}. \end{align} $$
We say that
![]() $g:\mathbb T\to \mathbb R$
is a cylinder function subordinate to U if
$g:\mathbb T\to \mathbb R$
is a cylinder function subordinate to U if
![]() $g={m(V)}^{-1}1_V$
, where V is one of the cylinders
$g={m(V)}^{-1}1_V$
, where V is one of the cylinders
![]() $V_{I,\mathbf y,\eta }$
in equation (3.1). Note that each cylinder function subordinate to U is supported on U.
$V_{I,\mathbf y,\eta }$
in equation (3.1). Note that each cylinder function subordinate to U is supported on U.
Let
![]() $\mathcal S^1$
denote the circle group
$\mathcal S^1$
denote the circle group
![]() $\{z\in \mathbb C:|z|=1\}$
with the usual topology and the group operation of complex multiplication. If Z is a compact abelian group with Haar probability measure m,
$\{z\in \mathbb C:|z|=1\}$
with the usual topology and the group operation of complex multiplication. If Z is a compact abelian group with Haar probability measure m,
![]() $\widehat {Z}$
denotes its Pontryagin dual, meaning
$\widehat {Z}$
denotes its Pontryagin dual, meaning
![]() $\widehat {Z}$
is the group of continuous homomorphisms
$\widehat {Z}$
is the group of continuous homomorphisms
![]() $\chi :Z\to \mathcal S^1$
; such homomorphisms are called characters of Z. Given
$\chi :Z\to \mathcal S^1$
; such homomorphisms are called characters of Z. Given
![]() $f:Z\to \mathbb C$
, its Fourier transform is
$f:Z\to \mathbb C$
, its Fourier transform is
![]() $\hat {f}:\widehat {Z}\to \mathbb C$
given by
$\hat {f}:\widehat {Z}\to \mathbb C$
given by
![]() $\hat {f}(\chi )=\int f \overline {\chi }\, dm$
.
$\hat {f}(\chi )=\int f \overline {\chi }\, dm$
.
For
![]() $s\in Z$
, let
$s\in Z$
, let
![]() $f_s$
be the translate of f defined by
$f_s$
be the translate of f defined by
![]() $f_s(x):=f(x+s)$
. Then
$f_s(x):=f(x+s)$
. Then
![]() $\widehat {f_s}(\chi )=\chi (s)\hat {f}(\chi )$
for each
$\widehat {f_s}(\chi )=\chi (s)\hat {f}(\chi )$
for each
![]() $\chi \in \widehat {Z}$
.
$\chi \in \widehat {Z}$
.
As usual, for
![]() $f, g: Z\to \mathbb C$
,
$f, g: Z\to \mathbb C$
,
![]() $f*g$
denotes their convolution, defined as
$f*g$
denotes their convolution, defined as
![]() $f*g(x):=\int f(t)g(x-t)\, dm(t)$
. We will use the standard identity
$f*g(x):=\int f(t)g(x-t)\, dm(t)$
. We will use the standard identity
![]() $\widehat {f*g}=\hat {f}\hat {g}$
(the Fourier transform turns convolution into pointwise multiplication).
$\widehat {f*g}=\hat {f}\hat {g}$
(the Fourier transform turns convolution into pointwise multiplication).
Letting
![]() $\|f\|:=(\int |f|^2\, dm)^{1/2}$
denote the
$\|f\|:=(\int |f|^2\, dm)^{1/2}$
denote the
![]() $L^2(m)$
norm of f, we have the standard Plancherel identity in equation (3.2), which leads to the subsequent lemma,
$L^2(m)$
norm of f, we have the standard Plancherel identity in equation (3.2), which leads to the subsequent lemma,
 $$ \begin{align} \sum_{\chi\in \widehat{Z}} |\hat{f}(\chi)|^2 = \|f\|^2. \end{align} $$
$$ \begin{align} \sum_{\chi\in \widehat{Z}} |\hat{f}(\chi)|^2 = \|f\|^2. \end{align} $$
Lemma 3.7. Let Z be a compact abelian group with Haar probability measure m and
![]() $f\in L^2(m)$
. If
$f\in L^2(m)$
. If
![]() $\|f\|\leq 1$
and
$\|f\|\leq 1$
and
![]() $|\hat {f}(\chi _1)|,\ldots , |\hat {f}(\chi _k)|$
are the k largest values of
$|\hat {f}(\chi _1)|,\ldots , |\hat {f}(\chi _k)|$
are the k largest values of
![]() $|\hat {f}|$
, then
$|\hat {f}|$
, then
![]() $|\hat {f}(\chi )|< k^{-1/2}$
for all
$|\hat {f}(\chi )|< k^{-1/2}$
for all
![]() $\chi \in \widehat {Z}\setminus \{\chi _1,\ldots ,\chi _k\}$
.
$\chi \in \widehat {Z}\setminus \{\chi _1,\ldots ,\chi _k\}$
.
Proof. Let
![]() $S_1 = \{\chi _1,\ldots , \chi _k\}$
be the set of characters attaining the k largest values of
$S_1 = \{\chi _1,\ldots , \chi _k\}$
be the set of characters attaining the k largest values of
![]() $|\hat {f}|$
, let
$|\hat {f}|$
, let
![]() $S_2 = \widehat {Z}\setminus S_1$
, and let
$S_2 = \widehat {Z}\setminus S_1$
, and let
![]() $c=\max \{|\hat {f}(\chi )|:\chi \in S_2\}$
. By definition, we have
$c=\max \{|\hat {f}(\chi )|:\chi \in S_2\}$
. By definition, we have
![]() $|\hat {f}(\chi )|\geq c$
for all
$|\hat {f}(\chi )|\geq c$
for all
![]() $\chi \in S_1$
.
$\chi \in S_1$
.
We split the left-hand side of equation (3.2) into sums over
![]() $\chi \in S_1$
and
$\chi \in S_1$
and
![]() $\chi \in S_2$
, then subtract the sum over
$\chi \in S_2$
, then subtract the sum over
![]() $S_1$
to get
$S_1$
to get
Since
![]() $|\hat {f}(\chi )|\geq c$
for all
$|\hat {f}(\chi )|\geq c$
for all
![]() $\chi \in S_1$
, the right-hand side is bounded above by
$\chi \in S_1$
, the right-hand side is bounded above by
![]() $\|f\|^2 - kc^2$
. Since
$\|f\|^2 - kc^2$
. Since
![]() $c\leq |\hat {f}(\chi )|$
for at least one
$c\leq |\hat {f}(\chi )|$
for at least one
![]() $\chi \in S_2$
, the left-hand side above is bounded below by
$\chi \in S_2$
, the left-hand side above is bounded below by
![]() $c^2$
. So
$c^2$
. So
which implies
![]() $c^2\leq 1-kc^2$
. Solving, we get
$c^2\leq 1-kc^2$
. Solving, we get
![]() $c\leq (1+k)^{-1/2}$
. This means
$c\leq (1+k)^{-1/2}$
. This means
![]() $|\hat {f}(\chi )|< k^{-1/2}$
for all
$|\hat {f}(\chi )|< k^{-1/2}$
for all
![]() $\chi \in S_2$
.
$\chi \in S_2$
.
Remark 3.8. The exact form of the inequality in Lemma 3.7 is not important; we only need
![]() $\sup _{\chi \in \widehat {Z}\setminus \{\chi _1,\ldots ,\chi _k\}} |\hat {f}(\chi )|\leq c(k)$
, where
$\sup _{\chi \in \widehat {Z}\setminus \{\chi _1,\ldots ,\chi _k\}} |\hat {f}(\chi )|\leq c(k)$
, where
![]() $c(k)\to 0$
as
$c(k)\to 0$
as
![]() $k\to \infty $
, uniformly for
$k\to \infty $
, uniformly for
![]() $\|f\|\leq 1$
.
$\|f\|\leq 1$
.
Much of the proof of Lemma 3.5 is contained in Lemma 3.9. The actual application requires a technical generalization (Lemma 12.2).
Lemma 3.9. Fix
![]() $k<r\in \mathbb N$
, and let
$k<r\in \mathbb N$
, and let
![]() $U\subseteq \mathbb T^r$
be an approximate Hamming ball of radius
$U\subseteq \mathbb T^r$
be an approximate Hamming ball of radius
![]() $(k,\eta )$
with
$(k,\eta )$
with
![]() $\eta>0$
.
$\eta>0$
.
-
(i) Let
 $\chi _1,\ldots ,\chi _k\in \widehat {\mathbb T}^r$
be non-trivial. Then there is a cylinder function g subordinate to U such that for all
$\chi _1,\ldots ,\chi _k\in \widehat {\mathbb T}^r$
be non-trivial. Then there is a cylinder function g subordinate to U such that for all
 $s\in \mathbb T^r$
, we have
$s\in \mathbb T^r$
, we have  $$ \begin{align*} \widehat{{g}_{s}}(\chi_j)=0 \quad \text{for each } j\leq k. \end{align*} $$
$$ \begin{align*} \widehat{{g}_{s}}(\chi_j)=0 \quad \text{for each } j\leq k. \end{align*} $$
-
(ii) If
 $f\in L^2(m_{\mathbb T^r})$
with
$f\in L^2(m_{\mathbb T^r})$
with
 $\|f\|\leq 1$
, there is a cylinder function g subordinate to U so that
$\|f\|\leq 1$
, there is a cylinder function g subordinate to U so that  $$ \begin{align*} |\widehat{f*g}(\chi)|< k^{-1/2} \quad \text{for all } \chi\in\widehat{\mathbb T}^d. \end{align*} $$
$$ \begin{align*} |\widehat{f*g}(\chi)|< k^{-1/2} \quad \text{for all } \chi\in\widehat{\mathbb T}^d. \end{align*} $$
Proof. (i) Assuming k, r,
![]() $\chi _j$
, and U are as in the statement, we may write
$\chi _j$
, and U are as in the statement, we may write
![]() $\chi _j$
as
$\chi _j$
as
 $$ \begin{align} \chi_j(x_1,\ldots,x_r)=e\bigg( \sum_{l=1}^{r} n^{(j)}_lx_l\bigg), \end{align} $$
$$ \begin{align} \chi_j(x_1,\ldots,x_r)=e\bigg( \sum_{l=1}^{r} n^{(j)}_lx_l\bigg), \end{align} $$
where
![]() $e(t):=\exp (2\pi i t)$
and
$e(t):=\exp (2\pi i t)$
and
![]() $n^{(j)}_l\in \mathbb Z$
. Non-triviality of
$n^{(j)}_l\in \mathbb Z$
. Non-triviality of
![]() $\chi _j$
means that for each j, at least one of the
$\chi _j$
means that for each j, at least one of the
![]() $n^{(j)}_l$
is non-zero. So choose one such index
$n^{(j)}_l$
is non-zero. So choose one such index
![]() $l_j$
for each
$l_j$
for each
![]() $j\leq k$
and let
$j\leq k$
and let
![]() $I=\{1,\ldots ,r\}\setminus \{l_1,\ldots ,l_k\}$
. In case some of the
$I=\{1,\ldots ,r\}\setminus \{l_1,\ldots ,l_k\}$
. In case some of the
![]() $l_j$
repeat, remove additional elements from I so that
$l_j$
repeat, remove additional elements from I so that
![]() $|I|=r-k$
.
$|I|=r-k$
.
Writing U as
![]() $\operatorname {Hamm}(\mathbf y;k,\eta )$
, let
$\operatorname {Hamm}(\mathbf y;k,\eta )$
, let
![]() $V = V_{I,\mathbf y,\eta }=\{\mathbf x\in \mathbb T^d:\|y_l-x_l\|<\eta \text { for all } l \in I\}$
, so that
$V = V_{I,\mathbf y,\eta }=\{\mathbf x\in \mathbb T^d:\|y_l-x_l\|<\eta \text { for all } l \in I\}$
, so that
![]() $V\subseteq U$
. Let
$V\subseteq U$
. Let
![]() $g:={m(V)}^{-1}1_V$
, so that g is a cylinder function subordinate to U, and let
$g:={m(V)}^{-1}1_V$
, so that g is a cylinder function subordinate to U, and let
![]() $j\leq k$
. To prove that
$j\leq k$
. To prove that
![]() $\hat {g}(\chi _j)=0$
, note that g does not depend on any of the coordinates
$\hat {g}(\chi _j)=0$
, note that g does not depend on any of the coordinates
![]() $x_{l_j}$
, so we can simplify the right-hand side of equation (3.3) as
$x_{l_j}$
, so we can simplify the right-hand side of equation (3.3) as
![]() $e(\sum _{\substack {l=1 \\ l\neq l_j}}^{r} n_{l}^{(j)}x_l)e(n_{l_j}^{(j)} x_{l_j})$
and write
$e(\sum _{\substack {l=1 \\ l\neq l_j}}^{r} n_{l}^{(j)}x_l)e(n_{l_j}^{(j)} x_{l_j})$
and write
![]() $\hat {g}(\chi _j)=\int g \overline {\chi }_j \, dm$
as
$\hat {g}(\chi _j)=\int g \overline {\chi }_j \, dm$
as
 $$ \begin{align*} \int_{\mathbb T^{r-1}} g(x_1,\ldots,x_r) e\bigg(-\sum_{\substack{l=1 \\ l\neq l_j}}^{r} n_{l}^{(j)}x_l\bigg)\, dx_1\ldots \, dx_{l_{j-1}}\, dx_{l_{j+1}}\, \ldots \, dx_{r} \, \int_{\mathbb T} e(-n_{l_j}^{(j)} x_{l_j})\, dx_{l_j}. \end{align*} $$
$$ \begin{align*} \int_{\mathbb T^{r-1}} g(x_1,\ldots,x_r) e\bigg(-\sum_{\substack{l=1 \\ l\neq l_j}}^{r} n_{l}^{(j)}x_l\bigg)\, dx_1\ldots \, dx_{l_{j-1}}\, dx_{l_{j+1}}\, \ldots \, dx_{r} \, \int_{\mathbb T} e(-n_{l_j}^{(j)} x_{l_j})\, dx_{l_j}. \end{align*} $$
Since
![]() $\int e(-n_{l_j}^{(j)} x_{l_j})\, dx_{l_j}=0$
, we conclude that
$\int e(-n_{l_j}^{(j)} x_{l_j})\, dx_{l_j}=0$
, we conclude that
![]() $\hat {g}(\chi _j)=0$
for each j. To complete the proof of part (i), we observe that
$\hat {g}(\chi _j)=0$
for each j. To complete the proof of part (i), we observe that
![]() $\widehat {g_{s}}(\chi )=\chi (s)\hat {g}(\chi )$
for each
$\widehat {g_{s}}(\chi )=\chi (s)\hat {g}(\chi )$
for each
![]() $\chi $
.
$\chi $
.
To prove part (ii), assume
![]() $f:\mathbb T^r\to \mathbb C$
has
$f:\mathbb T^r\to \mathbb C$
has
![]() $\|f\|\leq 1$
, and let
$\|f\|\leq 1$
, and let
![]() $|\hat {f}(\chi _1)|, \ldots , |\hat {f}(\chi _k)|$
be the k largest values of
$|\hat {f}(\chi _1)|, \ldots , |\hat {f}(\chi _k)|$
be the k largest values of
![]() $|\hat {f}|$
. By part (i), choose a cylinder function g subordinate to U so that
$|\hat {f}|$
. By part (i), choose a cylinder function g subordinate to U so that
![]() $\hat {g}(\chi _j)=0$
for these
$\hat {g}(\chi _j)=0$
for these
![]() $\chi _j$
. Then
$\chi _j$
. Then
![]() $|\hat {f}(\chi )|< k^{-1/2}$
for all other
$|\hat {f}(\chi )|< k^{-1/2}$
for all other
![]() $\chi $
, by Lemma 3.7. Note that
$\chi $
, by Lemma 3.7. Note that
![]() $|\hat {g}(\chi )|\leq 1$
for all
$|\hat {g}(\chi )|\leq 1$
for all
![]() $\chi \in \widehat {\mathbb T}^d$
, since
$\chi \in \widehat {\mathbb T}^d$
, since
![]() $\int |g|\, dm =1$
. We therefore have
$\int |g|\, dm =1$
. We therefore have
![]() $\widehat {f*g}(\chi _j)=\hat {f}(\chi _j)\hat {g}(\chi _j)=0$
for
$\widehat {f*g}(\chi _j)=\hat {f}(\chi _j)\hat {g}(\chi _j)=0$
for
![]() $j=1,\ldots ,k$
, while
$j=1,\ldots ,k$
, while
![]() $|\widehat {f*g}(\chi )|\leq |\hat {f}(\chi )|<k^{-1/2}$
for all other
$|\widehat {f*g}(\chi )|\leq |\hat {f}(\chi )|<k^{-1/2}$
for all other
![]() $\chi $
.
$\chi $
.
4 Multiple ergodic averages
Some of our reductions use facts from the general theory of nilsystems, mainly contained in [Reference Frantzikinakis6, Reference Frantzikinakis and Kra9]. Readers who want a general introduction to the theory can consult [Reference Host and Kra17].
If
![]() $(X,\mathcal B,\mu ,T)$
is an MPS and f is a bounded function on X, let
$(X,\mathcal B,\mu ,T)$
is an MPS and f is a bounded function on X, let
 $$ \begin{align*} L_3(f,T):=\lim_{N\to\infty} \frac{1}{N}\sum_{n=1}^N \int f\cdot T^n f\cdot T^{2n}f\, d\mu. \end{align*} $$
$$ \begin{align*} L_3(f,T):=\lim_{N\to\infty} \frac{1}{N}\sum_{n=1}^N \int f\cdot T^n f\cdot T^{2n}f\, d\mu. \end{align*} $$
The existence of this limit was established in [Reference Furstenberg11, §Reference Bergelson, Host, McCutcheon and Parreau3].
In this section, we prove Lemma 3.5 using Lemma 4.4, which estimates variants of
![]() $L_3(f,T)$
. In §5.1, we state a more convenient form of Lemma 4.4 and outline its proof.
$L_3(f,T)$
. In §5.1, we state a more convenient form of Lemma 4.4 and outline its proof.
We will use the following known result, which follows by combining a special case of [Reference Bergelson, Host, McCutcheon and Parreau3, Theorem 2.1] with the multidimensional Szemerédi theorem [Reference Furstenberg and Katznelson13].
Theorem 4.1. For all
![]() $\delta>0$
, there exists
$\delta>0$
, there exists
![]() $c(\delta )>0$
such that for every MPS
$c(\delta )>0$
such that for every MPS
![]() $(X,\mathcal B,\mu ,T)$
and every
$(X,\mathcal B,\mu ,T)$
and every
![]() $f:X\to [0,1]$
with
$f:X\to [0,1]$
with
![]() $\int f\, d\mu> \delta $
, we have
$\int f\, d\mu> \delta $
, we have
Definition 4.2. We say that
![]() $\mathbf X=(X,\mathcal B,\mu ,T)$
is ergodic if
$\mathbf X=(X,\mathcal B,\mu ,T)$
is ergodic if
![]() $\mu (A\triangle T^{-1}A)=0$
implies
$\mu (A\triangle T^{-1}A)=0$
implies
![]() $\mu (A)=0$
or
$\mu (A)=0$
or
![]() $\mu (A)=1$
for every
$\mu (A)=1$
for every
![]() $A\in \mathcal B$
. We say that
$A\in \mathcal B$
. We say that
![]() $\mathbf X$
is totally ergodic if for every
$\mathbf X$
is totally ergodic if for every
![]() $m\in \mathbb N$
, the system
$m\in \mathbb N$
, the system
![]() $(X,\mathcal B,\mu ,T^m)$
is ergodic.
$(X,\mathcal B,\mu ,T^m)$
is ergodic.
Remark 4.3. When determining whether a set is a set of k-recurrence, we may restrict our attention to ergodic MPSs where
![]() $\mu $
is a regular Borel measure on a compact metric space X; cf. [Reference Einsiedler and Ward4, §§7.2.2 and 7.2.3].
$\mu $
is a regular Borel measure on a compact metric space X; cf. [Reference Einsiedler and Ward4, §§7.2.2 and 7.2.3].
When we say a sequence
![]() $(b_n)_{n\in \mathbb N}$
of natural numbers has linear growth, we mean that it is strictly increasing and
$(b_n)_{n\in \mathbb N}$
of natural numbers has linear growth, we mean that it is strictly increasing and
![]() $\limsup _{n\to \infty } b_n/n < \infty $
. Note that a strictly increasing sequence has linear growth if and only if the set of terms
$\limsup _{n\to \infty } b_n/n < \infty $
. Note that a strictly increasing sequence has linear growth if and only if the set of terms
![]() $B=\{b_n:n\in \mathbb N\}$
satisfies
$B=\{b_n:n\in \mathbb N\}$
satisfies
![]() . Enumerating the positive elements of
. Enumerating the positive elements of
![]() $\sqrt {BH}$
in increasing order, where
$\sqrt {BH}$
in increasing order, where
![]() $BH$
is a proper Bohr–Hamming ball always results in a sequence of linear growth. To see this, write
$BH$
is a proper Bohr–Hamming ball always results in a sequence of linear growth. To see this, write
![]() $\sqrt {BH}$
as
$\sqrt {BH}$
as
![]() $\{n\in \mathbb Z:n^2\boldsymbol {\beta }\in U\}$
for some approximate Hamming ball
$\{n\in \mathbb Z:n^2\boldsymbol {\beta }\in U\}$
for some approximate Hamming ball
![]() $U\subseteq \mathbb T^r$
and generator
$U\subseteq \mathbb T^r$
and generator
![]() $\boldsymbol {\beta }\in \mathbb T^r$
. Then,
$\boldsymbol {\beta }\in \mathbb T^r$
. Then,
 $$ \begin{align*}\lim_{N\to\infty}\frac{|\sqrt{BH} \cap [1,\ldots N]|}{N} = \lim_{N\to\infty} \frac{1}{N}\sum_{n=1}^N 1_U(n^2\boldsymbol{\beta}) = m(U),\end{align*} $$
$$ \begin{align*}\lim_{N\to\infty}\frac{|\sqrt{BH} \cap [1,\ldots N]|}{N} = \lim_{N\to\infty} \frac{1}{N}\sum_{n=1}^N 1_U(n^2\boldsymbol{\beta}) = m(U),\end{align*} $$
by Weyl’s theorem on uniform distribution of polynomials (see Lemma 10.3). Since
![]() $n = |\sqrt {BH}\cap [1,\ldots ,b_n]|$
, this implies
$n = |\sqrt {BH}\cap [1,\ldots ,b_n]|$
, this implies
![]() $b_n/n$
is bounded. Likewise, if g is a cylinder function subordinate to U (Definition 3.6), then enumerating
$b_n/n$
is bounded. Likewise, if g is a cylinder function subordinate to U (Definition 3.6), then enumerating
![]() $\{n\in \mathbb N: g(n^2\boldsymbol {\beta })>0\}$
in increasing order results in a sequence of linear growth.
$\{n\in \mathbb N: g(n^2\boldsymbol {\beta })>0\}$
in increasing order results in a sequence of linear growth.
The next lemma says that
![]() $L_3(f,T)$
can be approximated by averaging over elements of
$L_3(f,T)$
can be approximated by averaging over elements of
![]() $\sqrt {BH}$
, provided
$\sqrt {BH}$
, provided
![]() $\mathbf X$
is totally ergodic and
$\mathbf X$
is totally ergodic and
![]() $BH$
is a proper Bohr–Hamming ball of radius
$BH$
is a proper Bohr–Hamming ball of radius
![]() $(k,\eta )$
with k sufficiently large. In passing to the general case, we need to consider
$(k,\eta )$
with k sufficiently large. In passing to the general case, we need to consider
![]() $\sqrt {BH}/\ell :=\{n\in \mathbb Z: \ell n \in \sqrt {BH}\}$
.
$\sqrt {BH}/\ell :=\{n\in \mathbb Z: \ell n \in \sqrt {BH}\}$
.
Lemma 4.4. For all
![]() $\varepsilon>0$
, there is a
$\varepsilon>0$
, there is a
![]() $k\in \mathbb N$
such that for every totally ergodic MPS
$k\in \mathbb N$
such that for every totally ergodic MPS
![]() $(X,\mathcal B,\mu ,T)$
, every
$(X,\mathcal B,\mu ,T)$
, every
![]() $f:X\to [0,1]$
, every proper Bohr–Hamming ball
$f:X\to [0,1]$
, every proper Bohr–Hamming ball
![]() $BH$
of radius
$BH$
of radius
![]() $(k,\eta )$
(
$(k,\eta )$
(
![]() $\eta>0$
), and all
$\eta>0$
), and all
![]() $\ell \in \mathbb N$
, there is a sequence
$\ell \in \mathbb N$
, there is a sequence
![]() $b_n\in \sqrt {BH}/\ell $
having linear growth such that
$b_n\in \sqrt {BH}/\ell $
having linear growth such that
 $$ \begin{align} \lim_{N\to \infty} \bigg|\frac{1}{N}\sum_{n=1}^N \int f\cdot T^{b_n}f \cdot T^{2b_n}f\, d\mu - L_3(f,T)\bigg|<\varepsilon \|f\|^2. \end{align} $$
$$ \begin{align} \lim_{N\to \infty} \bigg|\frac{1}{N}\sum_{n=1}^N \int f\cdot T^{b_n}f \cdot T^{2b_n}f\, d\mu - L_3(f,T)\bigg|<\varepsilon \|f\|^2. \end{align} $$
Consequently, if
![]() $\int f\, d\mu>\delta $
and k is sufficiently large (depending only on
$\int f\, d\mu>\delta $
and k is sufficiently large (depending only on
![]() $\delta $
), we have
$\delta $
), we have
 $$ \begin{align} \lim_{N\to\infty} \frac{1}{N}\sum_{n=1}^N \int f\cdot T^{b_n}f \cdot T^{2b_n}f\, d\mu> c(\delta)/2, \end{align} $$
$$ \begin{align} \lim_{N\to\infty} \frac{1}{N}\sum_{n=1}^N \int f\cdot T^{b_n}f \cdot T^{2b_n}f\, d\mu> c(\delta)/2, \end{align} $$
where
![]() $c(\delta )$
is defined in Theorem 4.1.
$c(\delta )$
is defined in Theorem 4.1.
Lemma 5.1 is a convenient reformulation of Lemma 4.4. In §5.1, we outline its proof, which occupies the majority of this article.
Remark 4.5. We do not know whether the condition ‘totally ergodic’ can be replaced with ‘ergodic’ in Lemma 4.4. The main obstruction to this replacement is our lack of a convenient representation of ergodic, but not totally ergodic, 2-step affine nilsystems.
4.1 Factors and extensions
If
![]() $\mathbf X = (X,\mathcal B,\mu ,T)$
and
$\mathbf X = (X,\mathcal B,\mu ,T)$
and
![]() $\mathbf Y = (Y,\mathcal D,\nu ,S)$
are MPSs, we say that
$\mathbf Y = (Y,\mathcal D,\nu ,S)$
are MPSs, we say that
![]() $\mathbf Y$
is a factor of
$\mathbf Y$
is a factor of
![]() $\mathbf X$
if there is a measurable
$\mathbf X$
if there is a measurable
![]() $\pi : X\to Y$
intertwining S and T, meaning
$\pi : X\to Y$
intertwining S and T, meaning
and
![]() $\mu (\pi ^{-1}D) = \nu (D)$
for all
$\mu (\pi ^{-1}D) = \nu (D)$
for all
![]() $D\in \mathcal D$
. Strictly speaking, the factor is the pair
$D\in \mathcal D$
. Strictly speaking, the factor is the pair
![]() $(\pi , \mathbf Y)$
, and we refer to ‘the factor
$(\pi , \mathbf Y)$
, and we refer to ‘the factor
![]() $\pi :\mathbf X\to \mathbf Y$
’.
$\pi :\mathbf X\to \mathbf Y$
’.
If
![]() $\pi :\mathbf X\to \mathbf Y$
is a factor and
$\pi :\mathbf X\to \mathbf Y$
is a factor and
![]() $f\in L^2(\mu )$
is equal
$f\in L^2(\mu )$
is equal
![]() $\mu $
-almost everywhere to a function of the form
$\mu $
-almost everywhere to a function of the form
![]() $g\circ \pi $
, with
$g\circ \pi $
, with
![]() $g\in L^2(\nu )$
, we say that f is
$g\in L^2(\nu )$
, we say that f is
![]() $\mathbf Y$
-measurable. This is equivalent to saying that f is
$\mathbf Y$
-measurable. This is equivalent to saying that f is
![]() $\pi ^{-1}(\mathcal D)$
-measurable (modulo
$\pi ^{-1}(\mathcal D)$
-measurable (modulo
![]() $\mu $
). We denote by
$\mu $
). We denote by
![]() $P_{\mathbf Y}$
the orthogonal projection from
$P_{\mathbf Y}$
the orthogonal projection from
![]() $L^2(\mu )$
to the space of
$L^2(\mu )$
to the space of
![]() $\pi ^{-1}(\mathcal D)$
-measurable functions. Given
$\pi ^{-1}(\mathcal D)$
-measurable functions. Given
![]() $f\in L^2(\mu )$
, we identify
$f\in L^2(\mu )$
, we identify
![]() $P_{\mathbf Y}f$
with
$P_{\mathbf Y}f$
with
![]() $\tilde {f}\in L^2(\nu )$
satisfying
$\tilde {f}\in L^2(\nu )$
satisfying
![]() $P_{\mathbf Y} f = \tilde {f}\circ \pi $
.
$P_{\mathbf Y} f = \tilde {f}\circ \pi $
.
We repeatedly use, without comment, the fact that
![]() $P_{\mathbf Y}$
is a positive operator preserving integration with respect to
$P_{\mathbf Y}$
is a positive operator preserving integration with respect to
![]() $\mu $
. In other words, if
$\mu $
. In other words, if
![]() $f(x)\geq 0$
for
$f(x)\geq 0$
for
![]() $\mu $
-a.e. x, then
$\mu $
-a.e. x, then
![]() $P_{\mathbf Y}f(x)\geq 0$
for
$P_{\mathbf Y}f(x)\geq 0$
for
![]() $\mu $
-a.e. x, and
$\mu $
-a.e. x, and
![]() $\int f\, d\mu = \int P_{\mathbf Y} f\, d\mu $
. Consequently,
$\int f\, d\mu = \int P_{\mathbf Y} f\, d\mu $
. Consequently,
![]() $\sup f \geq \tilde {f}(y)\geq \inf f$
for
$\sup f \geq \tilde {f}(y)\geq \inf f$
for
![]() $\nu $
-a.e. y and
$\nu $
-a.e. y and
![]() $\int \tilde {f}\, d\nu = \int f\, d\mu $
.
$\int \tilde {f}\, d\nu = \int f\, d\mu $
.
Remark 4.6. When
![]() $\pi : \mathbf X\to \mathbf Y$
is a factor, we say that
$\pi : \mathbf X\to \mathbf Y$
is a factor, we say that
![]() $\mathbf X$
is an extension of
$\mathbf X$
is an extension of
![]() $\mathbf Y$
. If we wish to prove an inequality on ergodic averages for a system
$\mathbf Y$
. If we wish to prove an inequality on ergodic averages for a system
![]() $\mathbf Y$
, it suffices to prove that inequality for an extension
$\mathbf Y$
, it suffices to prove that inequality for an extension
![]() $\pi :\mathbf X\to \mathbf Y$
, since the integrals
$\pi :\mathbf X\to \mathbf Y$
, since the integrals
![]() $\int f_0\cdot S^af_1\cdot S^{b}f_2\, d\nu $
can be written as
$\int f_0\cdot S^af_1\cdot S^{b}f_2\, d\nu $
can be written as
![]() $\int h_0\cdot T^a h_1\cdot T^{b}h_2\, d\mu $
, where
$\int h_0\cdot T^a h_1\cdot T^{b}h_2\, d\mu $
, where
![]() $h_i = f_i\circ \pi $
. This observation will be used in §14.
$h_i = f_i\circ \pi $
. This observation will be used in §14.
4.2 Reducing to total ergodicity
The next lemma is used to deduce Lemma 3.5 from Lemma 4.4 and Theorem 4.1. Part (i) is a special case of [Reference Bergelson, Host and Kra2, Corollary 4.6], and part (ii) is an immediate consequence of part (i). Here ‘
![]() $\mathbf Y$
is an inverse limit of ergodic nilsystems’ means that for all
$\mathbf Y$
is an inverse limit of ergodic nilsystems’ means that for all
![]() $f\in L^\infty (\nu )$
and
$f\in L^\infty (\nu )$
and
![]() $\varepsilon>0$
, there is a factor
$\varepsilon>0$
, there is a factor
![]() $\pi :\mathbf Y\to \mathbf Z$
, where
$\pi :\mathbf Y\to \mathbf Z$
, where
![]() $\mathbf Z=(Z,\mathcal Z,\eta ,R)$
is an ergodic nilsystem and
$\mathbf Z=(Z,\mathcal Z,\eta ,R)$
is an ergodic nilsystem and
![]() $\|f-P_{\mathbf Z}f\|_{L^1(\nu )}<\varepsilon $
.
$\|f-P_{\mathbf Z}f\|_{L^1(\nu )}<\varepsilon $
.
Lemma 4.7. Let
![]() $\mathbf X=(X,\mathcal B,\mu ,T)$
be an ergodic measure-preserving system. There is a factor
$\mathbf X=(X,\mathcal B,\mu ,T)$
be an ergodic measure-preserving system. There is a factor
![]() $\pi :\mathbf X\to \mathbf Y=(Y,\mathcal D,\nu ,S)$
which is an inverse limit of ergodic nilsystems such that:
$\pi :\mathbf X\to \mathbf Y=(Y,\mathcal D,\nu ,S)$
which is an inverse limit of ergodic nilsystems such that:
-
(i) for all
 $f_i\in L^\infty (\mu )$
, letting
$f_i\in L^\infty (\mu )$
, letting
 $\tilde {f}_i\circ \pi =P_{\mathbf Y}f_i$
, we have
$\tilde {f}_i\circ \pi =P_{\mathbf Y}f_i$
, we have  $$ \begin{align*} \lim_{N\to \infty} \frac{1}{N}\sum_{n=1}^N \bigg| \int f_0\cdot T^n f_1\cdot T^{2n}f_2 \, d\mu - \int \tilde{f}_0\cdot S^n \tilde{f}_1\cdot S^{2n}\tilde f_2\, d\nu\bigg|=0; \end{align*} $$
$$ \begin{align*} \lim_{N\to \infty} \frac{1}{N}\sum_{n=1}^N \bigg| \int f_0\cdot T^n f_1\cdot T^{2n}f_2 \, d\mu - \int \tilde{f}_0\cdot S^n \tilde{f}_1\cdot S^{2n}\tilde f_2\, d\nu\bigg|=0; \end{align*} $$
-
(ii) if
 $(b_n)_{n\in \mathbb N}$
is a sequence of linear growth, then
$(b_n)_{n\in \mathbb N}$
is a sequence of linear growth, then  $$ \begin{align*} \lim_{N\to\infty} \frac{1}{N}\sum_{n=1}^N \bigg|\int f_0\cdot T^{b_n}f_1 \cdot T^{2b_n}f_2 \, d\mu - \int \tilde{f}_0\cdot S^{b_n}\tilde{f}_1 \cdot S^{2b_n}\tilde{f}_2\, d\nu\bigg|=0. \end{align*} $$
$$ \begin{align*} \lim_{N\to\infty} \frac{1}{N}\sum_{n=1}^N \bigg|\int f_0\cdot T^{b_n}f_1 \cdot T^{2b_n}f_2 \, d\mu - \int \tilde{f}_0\cdot S^{b_n}\tilde{f}_1 \cdot S^{2b_n}\tilde{f}_2\, d\nu\bigg|=0. \end{align*} $$
To derive part (ii) from part (i), note that
 $$ \begin{align*} &\frac{1}{N}\sum_{n=1}^N \bigg|\int f\cdot T^{b_n}f \cdot T^{2b_n}f \, d\mu - \int \tilde{f}\cdot S^{b_n}\tilde{f} \cdot S^{2b_n}\tilde{f}\, d\nu \bigg| \\ &\quad\leq \frac{b_N}{N} \cdot \frac{1}{b_N}\sum_{n=1}^{b_N}\bigg| \int f_0\cdot T^n f_1\cdot T^{2n}f_2 \, d\mu - \int \tilde{f}_0\cdot S^n \tilde{f}_1\cdot S^{2n}\tilde f_2\, d\nu\bigg|\\ &\quad\underset{N\to\infty}{\longrightarrow} 0, \end{align*} $$
$$ \begin{align*} &\frac{1}{N}\sum_{n=1}^N \bigg|\int f\cdot T^{b_n}f \cdot T^{2b_n}f \, d\mu - \int \tilde{f}\cdot S^{b_n}\tilde{f} \cdot S^{2b_n}\tilde{f}\, d\nu \bigg| \\ &\quad\leq \frac{b_N}{N} \cdot \frac{1}{b_N}\sum_{n=1}^{b_N}\bigg| \int f_0\cdot T^n f_1\cdot T^{2n}f_2 \, d\mu - \int \tilde{f}_0\cdot S^n \tilde{f}_1\cdot S^{2n}\tilde f_2\, d\nu\bigg|\\ &\quad\underset{N\to\infty}{\longrightarrow} 0, \end{align*} $$
since
![]() ${b_N}/{N}$
is bounded.
${b_N}/{N}$
is bounded.
We get the next result by combining the definition of ‘inverse limit’ with the fact that for every ergodic nilsystem
![]() $(Y,\mathcal D,\nu ,S)$
, there is an
$(Y,\mathcal D,\nu ,S)$
, there is an
![]() $\ell \in \mathbb N$
such that the ergodic components of
$\ell \in \mathbb N$
such that the ergodic components of
![]() $(Y,\mathcal D,\nu ,S^\ell )$
are totally ergodic; see [Reference Frantzikinakis6, Proposition 2.1] for justification.
$(Y,\mathcal D,\nu ,S^\ell )$
are totally ergodic; see [Reference Frantzikinakis6, Proposition 2.1] for justification.
Lemma 4.8. If
![]() $(X,\mathcal B,\mu ,T)$
is an inverse limit of ergodic nilsystems,
$(X,\mathcal B,\mu ,T)$
is an inverse limit of ergodic nilsystems,
![]() $f:X\to [0,1]$
, and
$f:X\to [0,1]$
, and
![]() $\varepsilon>0$
, there is a factor
$\varepsilon>0$
, there is a factor
![]() $\mathbf Y = (Y,\mathcal D,\nu ,S)$
and
$\mathbf Y = (Y,\mathcal D,\nu ,S)$
and
![]() $\ell \in \mathbb N$
such that:
$\ell \in \mathbb N$
such that:
-
(i)
 $\|f-P_{\mathbf Y}f\|_{L^1(\mu )}<\varepsilon $
;
$\|f-P_{\mathbf Y}f\|_{L^1(\mu )}<\varepsilon $
; -
(ii) the ergodic components of
 $(Y,\mathcal D,\nu ,S^\ell )$
are totally ergodic.
$(Y,\mathcal D,\nu ,S^\ell )$
are totally ergodic.
Notation 4.9. When Y is the phase space of an ergodic nilsystem where
![]() $(Y,\mathcal D,\nu ,S^\ell )$
is totally ergodic, we will enumerate its connected components as
$(Y,\mathcal D,\nu ,S^\ell )$
is totally ergodic, we will enumerate its connected components as
![]() $Y_1,\ldots ,Y_M$
, and write
$Y_1,\ldots ,Y_M$
, and write
![]() $\nu _i:=({1}/{M})\nu |_{Y_i}$
. Each
$\nu _i:=({1}/{M})\nu |_{Y_i}$
. Each
![]() $\mathbf Y_i:=(Y_i,\mathcal D_i,\nu _i,S^{\ell })$
is an ergodic component of
$\mathbf Y_i:=(Y_i,\mathcal D_i,\nu _i,S^{\ell })$
is an ergodic component of
![]() $(Y,\mathcal D,\nu _Y,S^\ell )$
. If
$(Y,\mathcal D,\nu _Y,S^\ell )$
. If
![]() $\mathbf X$
is an extension of
$\mathbf X$
is an extension of
![]() $\mathbf Y$
with factor map
$\mathbf Y$
with factor map
![]() $\pi :X\to Y$
, we let
$\pi :X\to Y$
, we let
![]() $X_i=\pi ^{-1}(Y_i)$
,
$X_i=\pi ^{-1}(Y_i)$
,
![]() $\mathbf \mu _i:= ({1}/{M})\mu |_{X_i}$
,
$\mathbf \mu _i:= ({1}/{M})\mu |_{X_i}$
,
![]() $\mathcal B_i:=\{B\cap X_i:B\in \mathcal B\}$
, and
$\mathcal B_i:=\{B\cap X_i:B\in \mathcal B\}$
, and
![]() $\mathbf X_i=(X_i,\mathcal B_i,\mu _i,T^{\ell })$
. It is easy to verify that
$\mathbf X_i=(X_i,\mathcal B_i,\mu _i,T^{\ell })$
. It is easy to verify that
![]() $\mathbf Y_i$
is a factor of
$\mathbf Y_i$
is a factor of
![]() $\mathbf X_i$
with factor map
$\mathbf X_i$
with factor map
![]() $\pi |_{X_i}$
.
$\pi |_{X_i}$
.
Remark 4.10. Here we identify a technical difficulty common in multiple recurrence arguments. Readers familiar with the use of Markov’s inequality to overcome this difficulty may skip to the proof of Lemma 3.5.
Our proof of Lemma 3.5 starts with an ergodic, but not totally ergodic, MPS
![]() $\mathbf X=(X,\mathcal B,\mu ,T)$
. By Lemma 4.7, it suffices to prove the lemma in the special case where
$\mathbf X=(X,\mathcal B,\mu ,T)$
. By Lemma 4.7, it suffices to prove the lemma in the special case where
![]() $\mathbf X$
is an inverse limit of ergodic nilsystems, so we assume
$\mathbf X$
is an inverse limit of ergodic nilsystems, so we assume
![]() $\mathbf X$
is such an inverse limit. We then consider
$\mathbf X$
is such an inverse limit. We then consider
![]() $f:X\to [0,1]$
with
$f:X\to [0,1]$
with
![]() $\int f\, d\mu>\delta $
. The goal is to find an
$\int f\, d\mu>\delta $
. The goal is to find an
![]() $\ell \in \mathbb N$
and a sequence
$\ell \in \mathbb N$
and a sequence
![]() $(b_n)$
of elements of
$(b_n)$
of elements of
![]() $\sqrt {BH}/\ell $
satisfying equation (4.7). The main difficulty arises when trying to exploit the structure of nilsystems: Lemma 4.4 requires total ergodicity, so we fix
$\sqrt {BH}/\ell $
satisfying equation (4.7). The main difficulty arises when trying to exploit the structure of nilsystems: Lemma 4.4 requires total ergodicity, so we fix
![]() $\varepsilon>0$
and choose a factor
$\varepsilon>0$
and choose a factor
![]() $\pi :\mathbf X\to \mathbf Y$
where
$\pi :\mathbf X\to \mathbf Y$
where
![]() $\mathbf Y$
is an ergodic nilsystem satisfying parts (i) and (ii) in Lemma 4.8. We choose
$\mathbf Y$
is an ergodic nilsystem satisfying parts (i) and (ii) in Lemma 4.8. We choose
![]() $\ell $
so that the ergodic components of
$\ell $
so that the ergodic components of
![]() $(Y,\mathcal D,\nu ,S^\ell )$
are totally ergodic, and we enumerate these components as
$(Y,\mathcal D,\nu ,S^\ell )$
are totally ergodic, and we enumerate these components as
![]() $\mathbf Y_i = (Y_i, \mathcal D_i, \nu _i,S^\ell )$
,
$\mathbf Y_i = (Y_i, \mathcal D_i, \nu _i,S^\ell )$
,
![]() ${i=1,\ldots ,M}$
. With Notation 4.9 defined above, let
${i=1,\ldots ,M}$
. With Notation 4.9 defined above, let
![]() $\tilde {f}\circ \pi =P_{\mathbf Y}f$
and
$\tilde {f}\circ \pi =P_{\mathbf Y}f$
and
![]() $\tilde {f}_i=\tilde {f}|_{Y_i}$
. Lemma 4.4 allows us to choose, for each ergodic component
$\tilde {f}_i=\tilde {f}|_{Y_i}$
. Lemma 4.4 allows us to choose, for each ergodic component
![]() $\mathbf Y_i$
where
$\mathbf Y_i$
where
![]() $\int \tilde {f}_i\, d\nu _i>\delta /2$
, a sequence
$\int \tilde {f}_i\, d\nu _i>\delta /2$
, a sequence
![]() $b_n^{(i)}\in \sqrt {BH}/\ell $
having linear growth, such that
$b_n^{(i)}\in \sqrt {BH}/\ell $
having linear growth, such that
 $$ \begin{align}\lim_{N\to\infty} \frac{1}{N}\sum_{n=1}^N \int \tilde{f}_i\cdot S^{\ell b_n^{(i)}} \tilde{f}_i \cdot S^{2\ell b_n^{(i)}}\tilde{f}_i\, d\nu_i>c(\delta/2)/2. \end{align} $$
$$ \begin{align}\lim_{N\to\infty} \frac{1}{N}\sum_{n=1}^N \int \tilde{f}_i\cdot S^{\ell b_n^{(i)}} \tilde{f}_i \cdot S^{2\ell b_n^{(i)}}\tilde{f}_i\, d\nu_i>c(\delta/2)/2. \end{align} $$
The choice of
![]() $b_{n}^{(i)}$
depends on
$b_{n}^{(i)}$
depends on
![]() $\mathbf Y_i$
, so equation (4.4) implies only that
$\mathbf Y_i$
, so equation (4.4) implies only that
 $$ \begin{align} \lim_{N\to\infty} \frac{1}{N}\sum_{n=1}^N \int \tilde{f}\cdot S^{\ell b_n^{(i)}} \tilde{f} \cdot S^{2\ell b_n^{(i)}}\tilde{f}\, d\nu> \frac{1}{M}\frac{c(\delta/2)}{2}. \end{align} $$
$$ \begin{align} \lim_{N\to\infty} \frac{1}{N}\sum_{n=1}^N \int \tilde{f}\cdot S^{\ell b_n^{(i)}} \tilde{f} \cdot S^{2\ell b_n^{(i)}}\tilde{f}\, d\nu> \frac{1}{M}\frac{c(\delta/2)}{2}. \end{align} $$
If M is large, then
![]() $\|f-P_{\mathbf Y}f\|_{L^1(\mu )}$
may be large compared with
$\|f-P_{\mathbf Y}f\|_{L^1(\mu )}$
may be large compared with
![]() $({1}/{M}){c(\delta /2)}/{2}$
, and equation (4.5) will not immediately imply equation (4.7). To overcome this obstacle, we want to find an i where equation (4.4) holds and
$({1}/{M}){c(\delta /2)}/{2}$
, and equation (4.5) will not immediately imply equation (4.7). To overcome this obstacle, we want to find an i where equation (4.4) holds and
![]() $({1}/{M})\|f_i-P_{\mathbf Y}f_i\|_{L^1(\mu )}$
is sufficiently small to make
$({1}/{M})\|f_i-P_{\mathbf Y}f_i\|_{L^1(\mu )}$
is sufficiently small to make
![]() $\int \tilde {f}_i\cdot S^{\ell a}\tilde {f}_i \cdot S^{\ell b}\tilde {f}_i\, d\nu _i$
close to
$\int \tilde {f}_i\cdot S^{\ell a}\tilde {f}_i \cdot S^{\ell b}\tilde {f}_i\, d\nu _i$
close to
![]() $\int f_i\cdot T^{\ell a}f_i\cdot T^{\ell b} f_i\, d\mu _i$
for all
$\int f_i\cdot T^{\ell a}f_i\cdot T^{\ell b} f_i\, d\mu _i$
for all
![]() $a, b$
. Such an i is provided by two straightforward applications of Markov’s inequality outlined in §15.3.
$a, b$
. Such an i is provided by two straightforward applications of Markov’s inequality outlined in §15.3.
Before proving Lemma 3.5, we recall its statement: for all
![]() $\delta>0$
, there is a
$\delta>0$
, there is a
![]() $k_0\in \mathbb N$
such that for every proper Bohr–Hamming ball
$k_0\in \mathbb N$
such that for every proper Bohr–Hamming ball
![]() $BH:=BH(\boldsymbol {\beta },\boldsymbol {y}; k, \eta )$
with
$BH:=BH(\boldsymbol {\beta },\boldsymbol {y}; k, \eta )$
with
![]() $k\geq k_0$
,
$k\geq k_0$
,
![]() $\eta>0$
, and
$\eta>0$
, and
![]() $\mathbf y\in \mathbb T^r$
,
$\mathbf y\in \mathbb T^r$
,
![]() $\sqrt {BH}$
is
$\sqrt {BH}$
is
![]() $(\delta ,2)$
-recurrent.
$(\delta ,2)$
-recurrent.
Proof of Lemma 3.5, assuming Lemma 4.4
Let
![]() $\delta>0$
and choose
$\delta>0$
and choose
![]() $k_0\in \mathbb N$
so that for all
$k_0\in \mathbb N$
so that for all
![]() $k\geq k_0$
, the inequality in equation (4.3) holds in Lemma 4.4 with
$k\geq k_0$
, the inequality in equation (4.3) holds in Lemma 4.4 with
![]() $c(\delta /2)$
in place of
$c(\delta /2)$
in place of
![]() $c(\delta )$
. Let
$c(\delta )$
. Let
![]() $BH$
be a proper Bohr–Hamming ball with radius
$BH$
be a proper Bohr–Hamming ball with radius
![]() $(k,\eta )$
for some
$(k,\eta )$
for some
![]() $\eta>0$
. It suffices to prove that for every MPS
$\eta>0$
. It suffices to prove that for every MPS
![]() $(X,\mathcal B,\mu ,T)$
with
$(X,\mathcal B,\mu ,T)$
with
![]() $A\subseteq X$
having
$A\subseteq X$
having
![]() $\mu (A)>\delta $
,
$\mu (A)>\delta $
,
By Remark 4.3, we need only consider ergodic MPSs. We will prove that if
![]() $\mathbf X$
is ergodic and
$\mathbf X$
is ergodic and
![]() $f:X\to [0,1]$
has
$f:X\to [0,1]$
has
![]() $\int f\, d\mu>\delta $
, then there is a sequence of elements
$\int f\, d\mu>\delta $
, then there is a sequence of elements
![]() $b_n\in \sqrt {BH}$
with linear growth such that
$b_n\in \sqrt {BH}$
with linear growth such that
 $$ \begin{align} \liminf_{N\to\infty} \frac{1}{N}\sum_{n=1}^N \int f\cdot T^{b_n}f\cdot T^{2b_n}f\, d\mu>0. \end{align} $$
$$ \begin{align} \liminf_{N\to\infty} \frac{1}{N}\sum_{n=1}^N \int f\cdot T^{b_n}f\cdot T^{2b_n}f\, d\mu>0. \end{align} $$
The special case of equation (4.7) where
![]() $f=1_A$
implies equation (4.6), as the integral then simplifies to
$f=1_A$
implies equation (4.6), as the integral then simplifies to
![]() $\mu (A\cap T^{-b_n}A\cap T^{-2b_n}A)$
.
$\mu (A\cap T^{-b_n}A\cap T^{-2b_n}A)$
.
By part (ii) of Lemma 4.7, it suffices to prove equation (4.7) when
![]() $\mathbf X=(X,\mathcal B,\mu ,T)$
is an inverse limit of ergodic nilsystems. We now fix such an
$\mathbf X=(X,\mathcal B,\mu ,T)$
is an inverse limit of ergodic nilsystems. We now fix such an
![]() $\mathbf X$
, and
$\mathbf X$
, and
![]() $f:X\to [0,1]$
with
$f:X\to [0,1]$
with
![]() $\int f\, d\mu>\delta $
.
$\int f\, d\mu>\delta $
.
Let
![]() $\varepsilon = ({\delta }/{24})c({\delta }/{2})$
, and let
$\varepsilon = ({\delta }/{24})c({\delta }/{2})$
, and let
![]() $\pi :\mathbf X\to \mathbf Y$
be the factor provided by Lemma 4.8 for this
$\pi :\mathbf X\to \mathbf Y$
be the factor provided by Lemma 4.8 for this
![]() $\varepsilon $
, with
$\varepsilon $
, with
![]() $\ell \in \mathbb N$
chosen so that the ergodic components
$\ell \in \mathbb N$
chosen so that the ergodic components
![]() $\mathbf Y_i$
of
$\mathbf Y_i$
of
![]() $(Y,\mathcal D,\nu ,S^{\ell })$
are totally ergodic. Let M be the number of ergodic components (we can take
$(Y,\mathcal D,\nu ,S^{\ell })$
are totally ergodic. Let M be the number of ergodic components (we can take
![]() $\ell = M$
, but we do not need this fact) so that
$\ell = M$
, but we do not need this fact) so that
![]() $\mu (Y_i)=1/M$
for each i.
$\mu (Y_i)=1/M$
for each i.
Let
![]() $X_i=\pi ^{-1}(Y_i)$
and let
$X_i=\pi ^{-1}(Y_i)$
and let
![]() $f_i=1_{X_i}f$
, so that the
$f_i=1_{X_i}f$
, so that the
![]() $X_i$
partition X into sets of measure
$X_i$
partition X into sets of measure
![]() $1/M$
, and
$1/M$
, and
![]() $\sum _i \int f_i \, d\mu = \int f \, d\mu>\delta $
. Observe that
$\sum _i \int f_i \, d\mu = \int f \, d\mu>\delta $
. Observe that
![]() $P_{\mathbf Y}f_i$
is supported on
$P_{\mathbf Y}f_i$
is supported on
![]() $X_i$
and
$X_i$
and
![]() $\int P_{\mathbf Y}f_i\, d\mu = \int f_i\, d\mu $
for each i.
$\int P_{\mathbf Y}f_i\, d\mu = \int f_i\, d\mu $
for each i.
Setting
![]() $\mathbf Y_{i}:=(Y_i,\mathcal D_i,\nu _i,S^{\ell })$
, where
$\mathbf Y_{i}:=(Y_i,\mathcal D_i,\nu _i,S^{\ell })$
, where
![]() $\nu _i:=M\nu |_{Y_i}$
, we get that
$\nu _i:=M\nu |_{Y_i}$
, we get that
![]() $\mathbf{Y}_{i}$
is a totally ergodic MPS. Likewise,
$\mathbf{Y}_{i}$
is a totally ergodic MPS. Likewise,
![]() $\mathbf X_{i}:= (X_i, \mathcal B_i, \mu _i,T^{\ell })$
, with
$\mathbf X_{i}:= (X_i, \mathcal B_i, \mu _i,T^{\ell })$
, with
![]() $\mu _i:=M\mu |_{X_i}$
is an MPS (possibly not ergodic), with
$\mu _i:=M\mu |_{X_i}$
is an MPS (possibly not ergodic), with
![]() $\pi |_{X_i}:X_i\to Y_i$
a factor map. To prove equation (4.7), we will find a sequence
$\pi |_{X_i}:X_i\to Y_i$
a factor map. To prove equation (4.7), we will find a sequence
![]() $b_n$
of elements of
$b_n$
of elements of
![]() $\sqrt {BH}/\ell $
having linear growth and
$\sqrt {BH}/\ell $
having linear growth and
![]() $i\leq M$
with
$i\leq M$
with
 $$ \begin{align} \liminf_{N\to\infty} \frac{1}{N}\sum_{n=1}^N \int f_i\cdot T^{\ell b_n}f_i\cdot T^{2\ell b_n} f_i\, d\mu> 0. \end{align} $$
$$ \begin{align} \liminf_{N\to\infty} \frac{1}{N}\sum_{n=1}^N \int f_i\cdot T^{\ell b_n}f_i\cdot T^{2\ell b_n} f_i\, d\mu> 0. \end{align} $$
We claim that there is an i such that
This i is provided by Lemmas 15.5 and 15.6: setting
 $$ \begin{align*}I:=\bigg\{i:\int f_i\, d\mu>\frac{\delta}{2M}\bigg\}, \quad J:=\bigg\{i: \int |f_i - P_{\mathbf Y}f_i|\, d\mu < \frac{c(\delta/2)}{12M}\bigg\},\end{align*} $$
$$ \begin{align*}I:=\bigg\{i:\int f_i\, d\mu>\frac{\delta}{2M}\bigg\}, \quad J:=\bigg\{i: \int |f_i - P_{\mathbf Y}f_i|\, d\mu < \frac{c(\delta/2)}{12M}\bigg\},\end{align*} $$
we get
![]() $|I|> M\delta /2$
and
$|I|> M\delta /2$
and
![]() $|J| > M(1-12\varepsilon/c(\delta/2)) = M(1-\delta/2)$
. Thus
$|J| > M(1-12\varepsilon/c(\delta/2)) = M(1-\delta/2)$
. Thus
![]() $|I|+|J|>M$
, implying
$|I|+|J|>M$
, implying
![]() $I\cap J$
is non-empty.
$I\cap J$
is non-empty.
Fix i satisfying inequalities (4.9) and (4.10). Note that inequality (4.9) and the definition of
![]() $\nu _i$
,
$\nu _i$
,
![]() $\mu _i$
, and
$\mu _i$
, and
![]() $\tilde {f}_i$
imply
$\tilde {f}_i$
imply
Since
![]() $(Y_i,\mathcal B_i,\nu _i,S^{\ell })$
is totally ergodic, we may apply Lemma 4.4 to choose a sequence of elements
$(Y_i,\mathcal B_i,\nu _i,S^{\ell })$
is totally ergodic, we may apply Lemma 4.4 to choose a sequence of elements
![]() $b_n\in \sqrt {BH}/\ell $
having linear growth and satisfying
$b_n\in \sqrt {BH}/\ell $
having linear growth and satisfying
 $$ \begin{align} \lim_{N\to\infty} \frac{1}{N}\sum_{n=1}^N \int \tilde{f}_i\cdot S^{\ell b_n}\tilde{f}_i \cdot S^{2\ell b_n} \tilde{f}_i\, d\nu_i> c(\delta/2)/2. \end{align} $$
$$ \begin{align} \lim_{N\to\infty} \frac{1}{N}\sum_{n=1}^N \int \tilde{f}_i\cdot S^{\ell b_n}\tilde{f}_i \cdot S^{2\ell b_n} \tilde{f}_i\, d\nu_i> c(\delta/2)/2. \end{align} $$
Inequality (4.10), the bounds
![]() $\|f_i\|_{\infty }\leq 1$
,
$\|f_i\|_{\infty }\leq 1$
,
![]() $\|P_{\mathbf Y}f_{i}\|_{\infty }\leq 1$
, and Lemma 15.7 imply
$\|P_{\mathbf Y}f_{i}\|_{\infty }\leq 1$
, and Lemma 15.7 imply
 $$ \begin{align} \bigg|\int f_i\cdot T^{\ell a} f_i \cdot T^{\ell b} f_i\, d\mu_i - \int P_{\mathbf Y_i}f_i\cdot T^{\ell a} P_{\mathbf Y_i}f_i \cdot T^{\ell b} P_{\mathbf Y_i}f_i\, d\mu_i\bigg|< \frac{1}{4}c(\delta/2) \end{align} $$
$$ \begin{align} \bigg|\int f_i\cdot T^{\ell a} f_i \cdot T^{\ell b} f_i\, d\mu_i - \int P_{\mathbf Y_i}f_i\cdot T^{\ell a} P_{\mathbf Y_i}f_i \cdot T^{\ell b} P_{\mathbf Y_i}f_i\, d\mu_i\bigg|< \frac{1}{4}c(\delta/2) \end{align} $$
for each
![]() $a,b\in \mathbb N$
. Recalling the definition of
$a,b\in \mathbb N$
. Recalling the definition of
![]() $\mu _i$
and
$\mu _i$
and
![]() $\nu _i$
, we see that for all sufficiently large N,
$\nu _i$
, we see that for all sufficiently large N,
 $$ \begin{align*} &\frac{1}{N} \sum_{n=1}^{N} \int f_i\cdot T^{\ell b_n} f_i \cdot T^{2\ell b_n} f_i\, d\mu\\ &\quad> \frac{1}{N}\sum_{n=1}^{N} \int \tilde{f}_i \cdot S^{\ell b_n} f_i \cdot S^{2\ell b_n} f_i\, d\nu - \frac{c(\delta/2)}{4M} \quad \text{by inequality}\ ({4.13})\\ &\quad> \frac{c(\delta/2)}{2M} - \frac{c(\delta/2)}{4M} \qquad\qquad\qquad\qquad\qquad\quad \ \text{ by inequality}\ ({4.12}) \\ &\quad= \frac{c(\delta/2)}{4M}. \end{align*} $$
$$ \begin{align*} &\frac{1}{N} \sum_{n=1}^{N} \int f_i\cdot T^{\ell b_n} f_i \cdot T^{2\ell b_n} f_i\, d\mu\\ &\quad> \frac{1}{N}\sum_{n=1}^{N} \int \tilde{f}_i \cdot S^{\ell b_n} f_i \cdot S^{2\ell b_n} f_i\, d\nu - \frac{c(\delta/2)}{4M} \quad \text{by inequality}\ ({4.13})\\ &\quad> \frac{c(\delta/2)}{2M} - \frac{c(\delta/2)}{4M} \qquad\qquad\qquad\qquad\qquad\quad \ \text{ by inequality}\ ({4.12}) \\ &\quad= \frac{c(\delta/2)}{4M}. \end{align*} $$
The above inequalities imply equation (4.8). Since
![]() $f\geq f_i$
pointwise and we chose
$f\geq f_i$
pointwise and we chose
![]() $b_n\in \sqrt {BH}/\ell $
, this implies equation (4.7) and completes the proof of Lemma 3.5.
$b_n\in \sqrt {BH}/\ell $
, this implies equation (4.7) and completes the proof of Lemma 3.5.
5 Reformulation of Lemma 4.4
5.1 Reformulation
Lemma 4.4 is an immediate consequence of the following reformulation. This version allows us to apply the theory of characteristic factors.
Lemma 5.1. Let
![]() $k<r\in \mathbb N$
,
$k<r\in \mathbb N$
,
![]() $\ell \in \mathbb N$
, let
$\ell \in \mathbb N$
, let
![]() $\boldsymbol {\beta }\in \mathbb T^r$
be generating, and let
$\boldsymbol {\beta }\in \mathbb T^r$
be generating, and let
![]() $U\subseteq \mathbb T^r$
be an approximate Hamming ball of radius
$U\subseteq \mathbb T^r$
be an approximate Hamming ball of radius
![]() $(k,\eta )$
for some
$(k,\eta )$
for some
![]() $\eta>0$
. For every totally ergodic MPS
$\eta>0$
. For every totally ergodic MPS
![]() $(X,\mathcal B,\mu ,T)$
, and every measurable
$(X,\mathcal B,\mu ,T)$
, and every measurable
![]() $f:X\to [0,1]$
, there is a cylinder function
$f:X\to [0,1]$
, there is a cylinder function
![]() $g={m(V)}^{-1}1_V$
subordinate to U such that
$g={m(V)}^{-1}1_V$
subordinate to U such that
 $$ \begin{align} \lim_{N\to \infty} \bigg|\frac{1}{N}\sum_{n=1}^N g(n^2\ell^2\boldsymbol{\beta})\int f\cdot T^{n} f \cdot T^{2n} f\, d\mu - L_3(f,T)\bigg|<2k^{-1/2}\|f\|^2. \end{align} $$
$$ \begin{align} \lim_{N\to \infty} \bigg|\frac{1}{N}\sum_{n=1}^N g(n^2\ell^2\boldsymbol{\beta})\int f\cdot T^{n} f \cdot T^{2n} f\, d\mu - L_3(f,T)\bigg|<2k^{-1/2}\|f\|^2. \end{align} $$
While U does not depend on f in Lemma 5.1, the choice of g to satisfy equation (5.1) does depend on f.
We prove Lemma 5.1 in §14. The derivation of Lemma 4.4 from Lemma 5.1 is an instance of the following general principle: if
![]() $a_n$
is a bounded sequence,
$a_n$
is a bounded sequence,
![]() $B\subseteq \mathbb N$
is enumerated as
$B\subseteq \mathbb N$
is enumerated as
![]() $\{b_1<b_2<\ldots \}$
, and
$\{b_1<b_2<\ldots \}$
, and
![]() $d(B):=\lim _{N\to \infty } ({|B\cap \{1,\ldots ,N\}|}/{N})>0$
, then
$d(B):=\lim _{N\to \infty } ({|B\cap \{1,\ldots ,N\}|}/{N})>0$
, then
 $$ \begin{align*} \lim_{N\to\infty} \frac{1}{N}\sum_{n=1}^N a_{b_n} = \lim_{N\to\infty} \frac{1}{Nd(B)}\sum_{n=1}^N1_{B}(n)a_n \end{align*} $$
$$ \begin{align*} \lim_{N\to\infty} \frac{1}{N}\sum_{n=1}^N a_{b_n} = \lim_{N\to\infty} \frac{1}{Nd(B)}\sum_{n=1}^N1_{B}(n)a_n \end{align*} $$
provided the limit on the right exists. Note that
![]() $(b_n)_{n\in \mathbb N}$
has linear growth if
$(b_n)_{n\in \mathbb N}$
has linear growth if
![]() $d(B)>0$
.
$d(B)>0$
.
We will apply this principle with
![]() $a_n = \int f\cdot T^{n} f \cdot T^{2n} f\, d\mu $
and
$a_n = \int f\cdot T^{n} f \cdot T^{2n} f\, d\mu $
and
![]() ${B=\{n:n^2\ell ^2\boldsymbol {\beta }\in V\}}$
, where V is a cylinder contained in U. Then,
${B=\{n:n^2\ell ^2\boldsymbol {\beta }\in V\}}$
, where V is a cylinder contained in U. Then,
![]() $g={m(V)}^{-1}1_V$
is a cylinder function subordinate to U, and
$g={m(V)}^{-1}1_V$
is a cylinder function subordinate to U, and
![]() $g(n^2\ell ^2\boldsymbol {\beta })={d(B)}^{-1}1_B(n)$
. The equation
$g(n^2\ell ^2\boldsymbol {\beta })={d(B)}^{-1}1_B(n)$
. The equation
![]() $d(B)=m(V)$
follows from Weyl’s theorem on uniform distribution (cf. §10). Note that this B is contained in
$d(B)=m(V)$
follows from Weyl’s theorem on uniform distribution (cf. §10). Note that this B is contained in
![]() $\sqrt {BH}/\ell $
, where
$\sqrt {BH}/\ell $
, where
![]() $BH$
is the Bohr–Hamming ball corresponding to U, with frequency
$BH$
is the Bohr–Hamming ball corresponding to U, with frequency
![]() $\boldsymbol {\beta }$
.
$\boldsymbol {\beta }$
.
Remark 5.2. The exact form of the bound in equation (5.1) is not important in the following. The only relevant property is that the coefficient of
![]() $\|f\|^2$
tends to
$\|f\|^2$
tends to
![]() $0$
as
$0$
as
![]() $k\to \infty $
.
$k\to \infty $
.
5.2 Outline of a special case of Lemma 15.1
This outline highlights the key steps in our proof while avoiding some complications.
We begin with an arbitrary totally ergodic measure-preserving system
![]() $\mathbf X=(X,\mathcal B,\mu ,T)$
,
$\mathbf X=(X,\mathcal B,\mu ,T)$
,
![]() $f: X\to [0,1]$
, and
$f: X\to [0,1]$
, and
![]() $k\in \mathbb N$
. We let
$k\in \mathbb N$
. We let
![]() $r>k$
,
$r>k$
,
![]() $\eta>0$
, and fix an approximate Hamming ball
$\eta>0$
, and fix an approximate Hamming ball
![]() $U=\operatorname {Hamm}(\mathbf y;k,\eta )\subseteq \mathbb T^r$
and a generator
$U=\operatorname {Hamm}(\mathbf y;k,\eta )\subseteq \mathbb T^r$
and a generator
![]() $\boldsymbol {\beta } \in \mathbb T^r$
. We want to find a cylinder function g subordinate to U so that
$\boldsymbol {\beta } \in \mathbb T^r$
. We want to find a cylinder function g subordinate to U so that
 $$ \begin{align} A_N(f,g):= \frac{1}{N}\sum_{n=1}^N g(n^2\boldsymbol{\beta})\int f\cdot T^nf\cdot T^{2n}f\, d\mu \end{align} $$
$$ \begin{align} A_N(f,g):= \frac{1}{N}\sum_{n=1}^N g(n^2\boldsymbol{\beta})\int f\cdot T^nf\cdot T^{2n}f\, d\mu \end{align} $$
satisfies
![]() $\lim _{N\to \infty } |A_N(f,g)-L_3(f,T)|<2k^{-1/2}\|f\|^2$
.
$\lim _{N\to \infty } |A_N(f,g)-L_3(f,T)|<2k^{-1/2}\|f\|^2$
.
In §§6–8, we will reduce to the case where
![]() $\mathbf X$
is a standard 2-step Weyl system. This means that
$\mathbf X$
is a standard 2-step Weyl system. This means that
![]() $(X,\mathcal B,\mu ,T)$
can be realized with
$(X,\mathcal B,\mu ,T)$
can be realized with
![]() $X=\mathbb T^d\times \mathbb T^d$
,
$X=\mathbb T^d\times \mathbb T^d$
,
![]() $d\in \mathbb N$
,
$d\in \mathbb N$
,
![]() $\mu =$
Haar probability measure on
$\mu =$
Haar probability measure on
![]() $\mathbb T^d\times \mathbb T^d$
, and T is given by
$\mathbb T^d\times \mathbb T^d$
, and T is given by
![]() $T(x, y)=( x+\boldsymbol {\alpha },y+ x)$
, for some generator
$T(x, y)=( x+\boldsymbol {\alpha },y+ x)$
, for some generator
![]() $\boldsymbol {\alpha }\in \mathbb T^d$
. The orbits of T can be computed explicitly:
$\boldsymbol {\alpha }\in \mathbb T^d$
. The orbits of T can be computed explicitly:
![]() $T^n(x,y)=(x+n\boldsymbol {\alpha }, y+nx+\tbinom {n}{2}\boldsymbol {\alpha })$
. This reduction relies on the theory of characteristic factors, especially [Reference Frantzikinakis6, Theorem B].
$T^n(x,y)=(x+n\boldsymbol {\alpha }, y+nx+\tbinom {n}{2}\boldsymbol {\alpha })$
. This reduction relies on the theory of characteristic factors, especially [Reference Frantzikinakis6, Theorem B].
To simplify this outline, we assume
![]() $r=d$
and
$r=d$
and
![]() $\boldsymbol {\beta } = \boldsymbol {\alpha }$
. We write functions on
$\boldsymbol {\beta } = \boldsymbol {\alpha }$
. We write functions on
![]() $\mathbb T^d\times \mathbb T^d$
with variables displayed as
$\mathbb T^d\times \mathbb T^d$
with variables displayed as
![]() $f(x,y)$
, where
$f(x,y)$
, where
![]() $x, y\in \mathbb T^d$
. Writing
$x, y\in \mathbb T^d$
. Writing
![]() $m\times m$
for Haar probability measure on
$m\times m$
for Haar probability measure on
![]() $\mathbb T^d\times \mathbb T^d$
, we write
$\mathbb T^d\times \mathbb T^d$
, we write
![]() $\int f\, dm\times m$
as
$\int f\, dm\times m$
as
![]() $\int f(x,y)\, dx\, dy$
, or
$\int f(x,y)\, dx\, dy$
, or
![]() $\int f\binom {x}{y}\, dx\, dy$
to save space. With these assumptions, the averages in equation (5.2) become
$\int f\binom {x}{y}\, dx\, dy$
to save space. With these assumptions, the averages in equation (5.2) become
 $$ \begin{align*} B_N := \frac{1}{N}\sum_{n=1}^N g(n^2\boldsymbol{\alpha}) \int_{\mathbb T^d\times \mathbb T^d} f\,\Big(\begin{matrix} x\\[-2pt]y \end{matrix}\Big) \, f \begin{pmatrix} x+n\boldsymbol{\alpha}\\[-1pt]y+nx+\tbinom{n}{2}\boldsymbol{\alpha} \end{pmatrix} f\begin{pmatrix} x+2n\boldsymbol{\alpha} \\[-1pt] y+2nx + \tbinom{2n}{2}\boldsymbol{\alpha} \end{pmatrix} \, dx\, dy. \end{align*} $$
$$ \begin{align*} B_N := \frac{1}{N}\sum_{n=1}^N g(n^2\boldsymbol{\alpha}) \int_{\mathbb T^d\times \mathbb T^d} f\,\Big(\begin{matrix} x\\[-2pt]y \end{matrix}\Big) \, f \begin{pmatrix} x+n\boldsymbol{\alpha}\\[-1pt]y+nx+\tbinom{n}{2}\boldsymbol{\alpha} \end{pmatrix} f\begin{pmatrix} x+2n\boldsymbol{\alpha} \\[-1pt] y+2nx + \tbinom{2n}{2}\boldsymbol{\alpha} \end{pmatrix} \, dx\, dy. \end{align*} $$
Proposition 13.1 provides an explicit formula for
![]() $\lim _{N\to \infty } B_N$
. Under the present assumptions, it says
$\lim _{N\to \infty } B_N$
. Under the present assumptions, it says
 $$ \begin{align} &\lim_{N\to\infty} B_N\nonumber\\ &\quad= \int_{(\mathbb T^d)^4} f(x,y)f(x+s,y+t) \bigg(\int_{\mathbb T^d} f(x+2s,y+2t+2w)g(w) \, dw\bigg) \, ds\, dt \, dx\, dy. \end{align} $$
$$ \begin{align} &\lim_{N\to\infty} B_N\nonumber\\ &\quad= \int_{(\mathbb T^d)^4} f(x,y)f(x+s,y+t) \bigg(\int_{\mathbb T^d} f(x+2s,y+2t+2w)g(w) \, dw\bigg) \, ds\, dt \, dx\, dy. \end{align} $$
Write I for the right-hand side above, and define
Using Lemma 12.2 (a generalization of Lemma 3.9), we choose a cylinder function g subordinate to U such that
![]() $|\widehat {f*_2 g}(\chi ,\psi )|<k^{-1/2}$
for all
$|\widehat {f*_2 g}(\chi ,\psi )|<k^{-1/2}$
for all
![]() $(\chi ,\psi )\in \widehat {\mathbb T}^d\times \widehat {\mathbb T}^d$
with
$(\chi ,\psi )\in \widehat {\mathbb T}^d\times \widehat {\mathbb T}^d$
with
![]() $\psi $
non-trivial. We set
$\psi $
non-trivial. We set
![]() $f'(x)\kern1.2pt{:=}\kern1.2pt\int f(x,y)\, dy$
and
$f'(x)\kern1.2pt{:=}\kern1.2pt\int f(x,y)\, dy$
and
![]() $J'\kern1.2pt{:=}\kern1.2pt \int \int f'(x)f'(x\kern1.2pt{+}\kern1.2pt s)f'(x\kern1.2pt{+}\kern1.2pt 2s)\, dx\, ds$
. By Lemma 11.1, the bound on
$J'\kern1.2pt{:=}\kern1.2pt \int \int f'(x)f'(x\kern1.2pt{+}\kern1.2pt s)f'(x\kern1.2pt{+}\kern1.2pt 2s)\, dx\, ds$
. By Lemma 11.1, the bound on
![]() $\widehat {f*_2 g}$
will imply
$\widehat {f*_2 g}$
will imply
We can also prove (directly, or using Theorem 7.1) that
![]() $L_3(f,T)=J'$
. Combining equation (5.4) with equation (5.3), we then have equation (5.1), completing the outline of this special case. The factor
$L_3(f,T)=J'$
. Combining equation (5.4) with equation (5.3), we then have equation (5.1), completing the outline of this special case. The factor
![]() $2$
on the right-hand side of equation (5.1) accounts for the reduction to Weyl systems.
$2$
on the right-hand side of equation (5.1) accounts for the reduction to Weyl systems.
In the general case, we must compute
![]() $\lim _{N\to \infty } A_N(f,g)$
for
$\lim _{N\to \infty } A_N(f,g)$
for
![]() $d\neq r$
and
$d\neq r$
and
![]() $\boldsymbol {\beta }\neq \boldsymbol {\alpha }$
. The integral
$\boldsymbol {\beta }\neq \boldsymbol {\alpha }$
. The integral
![]() $\int f(x+2s,y+2t +2w) g(w)\, dw$
in equation (5.3) will then be replaced by an integral over an affine joining of
$\int f(x+2s,y+2t +2w) g(w)\, dw$
in equation (5.3) will then be replaced by an integral over an affine joining of
![]() $\mathbb T^d$
with
$\mathbb T^d$
with
![]() $\mathbb T^r$
(Definition 9.4), but the computation in this case is not substantially different from the outline above.
$\mathbb T^r$
(Definition 9.4), but the computation in this case is not substantially different from the outline above.
5.3 Iterated integral notation
When all variables are displayed and there is no chance of confusion, we may omit all but one of the integral signs and the subscripts indicating the domain of integration. So the integral in equation (5.3) may be written as
6 Eigenvalues and ergodicity of products
An eigenfunction of an MPS
![]() $\mathbf X=(X,\mathcal B,\mu ,T)$
with eigenvalue
$\mathbf X=(X,\mathcal B,\mu ,T)$
with eigenvalue
![]() $\unicode{x3bb} \in \mathbb C$
is an
$\unicode{x3bb} \in \mathbb C$
is an
![]() $f\in L^2(\mu )$
satisfying
$f\in L^2(\mu )$
satisfying
![]() $\|f\|\neq 0$
and
$\|f\|\neq 0$
and
![]() $f\circ T=\unicode{x3bb} f$
. Since
$f\circ T=\unicode{x3bb} f$
. Since
![]() $\int |f\circ T|\, d\mu = \int |f|\, d\mu $
, we have
$\int |f\circ T|\, d\mu = \int |f|\, d\mu $
, we have
![]() $|\unicode{x3bb} |=1$
. We then have that
$|\unicode{x3bb} |=1$
. We then have that
![]() $|f\circ T|$
is T-invariant, so if
$|f\circ T|$
is T-invariant, so if
![]() $\mathbf X$
is ergodic, we get that
$\mathbf X$
is ergodic, we get that
![]() $|f|$
is equal
$|f|$
is equal
![]() $\mu $
-almost everywhere to a constant. We say an eigenvalue
$\mu $
-almost everywhere to a constant. We say an eigenvalue
![]() $\unicode{x3bb} $
of
$\unicode{x3bb} $
of
![]() $\mathbf X$
is non-trivial if
$\mathbf X$
is non-trivial if
![]() $\unicode{x3bb} \neq 1$
. Note that the eigenfunctions of
$\unicode{x3bb} \neq 1$
. Note that the eigenfunctions of
![]() $\mathbf X$
are the eigenvectors of the unitary operator
$\mathbf X$
are the eigenvectors of the unitary operator
![]() $U_T:L^2(\mu )\to L^2(\mu )$
defined by
$U_T:L^2(\mu )\to L^2(\mu )$
defined by
![]() $U_T f = f\circ T$
.
$U_T f = f\circ T$
.
Given two MPSs
![]() $\mathbf X = (X,\mathcal B,\mu ,T)$
and
$\mathbf X = (X,\mathcal B,\mu ,T)$
and
![]() $\mathbf Y = (Y,\mathcal D,\nu ,S)$
, we form the product system
$\mathbf Y = (Y,\mathcal D,\nu ,S)$
, we form the product system
![]() $\mathbf X\times \mathbf Y=(X\times Y, \mathcal B\otimes \mathcal D,\mu \times \nu , T\times S)$
. For
$\mathbf X\times \mathbf Y=(X\times Y, \mathcal B\otimes \mathcal D,\mu \times \nu , T\times S)$
. For
![]() $f\in L^2(\mu )$
and
$f\in L^2(\mu )$
and
![]() $g\in L^2(\nu )$
, we write
$g\in L^2(\nu )$
, we write
![]() $f\otimes g$
for the function defined by
$f\otimes g$
for the function defined by
![]() $f\otimes g(x,y)=f(x)g(y)$
.
$f\otimes g(x,y)=f(x)g(y)$
.
We need some standard consequences of the following, which is the specialization of [Reference Furstenberg12, Lemma 4.17, p. 91] to the case where
![]() $\mathcal H=L^2(\mu )$
,
$\mathcal H=L^2(\mu )$
,
![]() $\mathcal H'=L^2(\nu )$
for MPSs
$\mathcal H'=L^2(\nu )$
for MPSs
![]() $\mathbf X$
and
$\mathbf X$
and
![]() $\mathbf Y$
as above, with unitary operators
$\mathbf Y$
as above, with unitary operators
![]() $Uf:=f\circ T$
and
$Uf:=f\circ T$
and
![]() $U'g:=g\circ S$
.
$U'g:=g\circ S$
.
Lemma 6.1. Let
![]() $\mathbf X$
and
$\mathbf X$
and
![]() $\mathbf Y$
be measure-preserving systems as above, and let
$\mathbf Y$
be measure-preserving systems as above, and let
![]() $\mathbf X\times \mathbf Y$
be the product system. Let
$\mathbf X\times \mathbf Y$
be the product system. Let
![]() $h\in L^2(\mu \times \nu )$
be an eigenfunction of
$h\in L^2(\mu \times \nu )$
be an eigenfunction of
![]() $\mathbf X\times \mathbf Y$
with eigenvalue
$\mathbf X\times \mathbf Y$
with eigenvalue
![]() $\unicode{x3bb} $
, meaning
$\unicode{x3bb} $
, meaning
![]() $h\circ (T\times S)=\unicode{x3bb} h$
. Then
$h\circ (T\times S)=\unicode{x3bb} h$
. Then
![]() $h = \sum c_n f_n\otimes g_n$
, where
$h = \sum c_n f_n\otimes g_n$
, where
![]() $f_n\circ T=\unicode{x3bb} _nf_n$
,
$f_n\circ T=\unicode{x3bb} _nf_n$
,
![]() $g_n\circ S = \unicode{x3bb} _n'g_n$
,
$g_n\circ S = \unicode{x3bb} _n'g_n$
,
![]() $\unicode{x3bb} _n\unicode{x3bb} _n' = \unicode{x3bb} $
, and the sequences
$\unicode{x3bb} _n\unicode{x3bb} _n' = \unicode{x3bb} $
, and the sequences
![]() $\{f_n\}$
,
$\{f_n\}$
,
![]() $\{g_n\}$
are orthonormal in
$\{g_n\}$
are orthonormal in
![]() $L^2(\mu )$
and
$L^2(\mu )$
and
![]() $L^2(\nu )$
, respectively.
$L^2(\nu )$
, respectively.
To deduce Lemma 6.1 from of [Reference Furstenberg12, Lemma 4.17], note that if
![]() $\mu $
and
$\mu $
and
![]() $\nu $
are measure spaces,
$\nu $
are measure spaces,
![]() $L^2(\mu \times \nu )$
is isomorphic to the tensor product
$L^2(\mu \times \nu )$
is isomorphic to the tensor product
![]() $L^2(\mu )\otimes L^2(\nu )$
, and the obvious isomorphism identifies
$L^2(\mu )\otimes L^2(\nu )$
, and the obvious isomorphism identifies
![]() $U_{T\times S}$
with
$U_{T\times S}$
with
![]() $U_T\otimes U_S$
.
$U_T\otimes U_S$
.
The next lemma is a well-known consequence of Lemma 6.1; we omit its proof.
Lemma 6.2. If
![]() $\mathbf X$
and
$\mathbf X$
and
![]() $\mathbf Y$
are ergodic MPSs, the product system
$\mathbf Y$
are ergodic MPSs, the product system
![]() $\mathbf X\times \mathbf Y$
is ergodic if and only if
$\mathbf X\times \mathbf Y$
is ergodic if and only if
![]() $\mathbf X$
and
$\mathbf X$
and
![]() $\mathbf Y$
have no non-trivial eigenvalues in common.
$\mathbf Y$
have no non-trivial eigenvalues in common.
Another immediate consequence of Lemma 6.1 is the following lemma.
Lemma 6.3. If
![]() $\mathbf X=(X,\mathcal B,\mu ,T)$
and
$\mathbf X=(X,\mathcal B,\mu ,T)$
and
![]() $\mathbf Y=(Y,\mathcal D,\nu ,S)$
are MPSs such that
$\mathbf Y=(Y,\mathcal D,\nu ,S)$
are MPSs such that
![]() $\mathbf X\times \mathbf Y$
is ergodic and
$\mathbf X\times \mathbf Y$
is ergodic and
![]() $g\in L^2(\nu )$
is orthogonal to every eigenfunction of
$g\in L^2(\nu )$
is orthogonal to every eigenfunction of
![]() $\mathbf Y$
, then for every
$\mathbf Y$
, then for every
![]() $f\in L^2(\mu )$
,
$f\in L^2(\mu )$
,
![]() $f\otimes g$
is orthogonal to every eigenfunction of
$f\otimes g$
is orthogonal to every eigenfunction of
![]() $\mathbf X\times \mathbf Y$
.
$\mathbf X\times \mathbf Y$
.
7 Eigenfunctions and the Kronecker factor
Every ergodic MPS
![]() $\mathbf X$
has a factor
$\mathbf X$
has a factor
![]() $\pi :\mathbf X\to \mathbf Z$
where
$\pi :\mathbf X\to \mathbf Z$
where
![]() $\mathbf Z=(Z,\mathcal Z,m,R)$
is a compact abelian group rotation such that every eigenfunction of
$\mathbf Z=(Z,\mathcal Z,m,R)$
is a compact abelian group rotation such that every eigenfunction of
![]() $\mathbf X$
is
$\mathbf X$
is
![]() $\pi ^{-1}(\mathcal Z)$
-measurable. This factor is called the Kronecker factor of
$\pi ^{-1}(\mathcal Z)$
-measurable. This factor is called the Kronecker factor of
![]() $\mathbf X$
, and we write
$\mathbf X$
, and we write
![]() $\int _Z f(s)\, ds$
(or sometimes just
$\int _Z f(s)\, ds$
(or sometimes just
![]() $\int f(s)\,ds$
) to abbreviate
$\int f(s)\,ds$
) to abbreviate
![]() $\int f(s)\, dm(s)$
.
$\int f(s)\, dm(s)$
.
The following result is proved in [Reference Furstenberg11, §3]; we use the notation
![]() $L_3$
introduced in §4.
$L_3$
introduced in §4.
Theorem 7.1. If
![]() $\mathbf X=(X,\mathcal B,\mu ,T)$
is an ergodic MPS with Kronecker factor
$\mathbf X=(X,\mathcal B,\mu ,T)$
is an ergodic MPS with Kronecker factor
![]() $\pi :\mathbf X\to \mathbf Z$
,
$\pi :\mathbf X\to \mathbf Z$
,
![]() $\mathbf Z=(Z,\mathcal Z,m,R)$
, and
$\mathbf Z=(Z,\mathcal Z,m,R)$
, and
![]() $f_i:X\to [0,1]$
, then
$f_i:X\to [0,1]$
, then
 $$ \begin{align*}\lim_{N\to\infty} \frac{1}{N}\sum_{n=1}^N f_1(T^n x) f_2(T^{2n} x) = \int_Z \tilde{f}_1(\pi(x)+s)\tilde{f}_2(\pi(x)+2s)\, ds, \quad (\text{in} \ L^2(\mu)),\end{align*} $$
$$ \begin{align*}\lim_{N\to\infty} \frac{1}{N}\sum_{n=1}^N f_1(T^n x) f_2(T^{2n} x) = \int_Z \tilde{f}_1(\pi(x)+s)\tilde{f}_2(\pi(x)+2s)\, ds, \quad (\text{in} \ L^2(\mu)),\end{align*} $$
where
![]() $\tilde {f}_i\in L^\infty (m)$
satisfies
$\tilde {f}_i\in L^\infty (m)$
satisfies
![]() $\tilde {f}_i\circ \pi =P_{\mathbf Z}f_i$
. Furthermore,
$\tilde {f}_i\circ \pi =P_{\mathbf Z}f_i$
. Furthermore,
7.1 Kronecker factor of a standard 2-step Weyl system
A standard
![]() $2$
-step Weyl system is an MPS of the form
$2$
-step Weyl system is an MPS of the form
![]() $\mathbf Y = (Y, \mathcal B, m,S)$
, where
$\mathbf Y = (Y, \mathcal B, m,S)$
, where
![]() $Y=\mathbb T^d\times \mathbb T^d$
,
$Y=\mathbb T^d\times \mathbb T^d$
,
![]() $d\in \mathbb N$
, and
$d\in \mathbb N$
, and
![]() $S:Y\to Y$
is defined as
$S:Y\to Y$
is defined as
![]() $S(x,y)=(x+\alpha ,y+x)$
, for some fixed
$S(x,y)=(x+\alpha ,y+x)$
, for some fixed
![]() $\alpha =(\alpha _1,\ldots ,\alpha _d)$
generating
$\alpha =(\alpha _1,\ldots ,\alpha _d)$
generating
![]() $\mathbb T^d$
. There is an explicit formula for the orbits of S:
$\mathbb T^d$
. There is an explicit formula for the orbits of S:
which may be verified by induction. Ergodicity of
![]() $\mathbf Y$
is equivalent to
$\mathbf Y$
is equivalent to
![]() $\mathbf \alpha $
generating
$\mathbf \alpha $
generating
![]() $\mathbb T^d$
. For
$\mathbb T^d$
. For
![]() $d=1$
, this follows from [Reference Furstenberg12, Proposition 3.11, p. 67], and the general case follows from a nearly identical proof. Also explained in [Reference Furstenberg12] is the Kronecker factor of
$d=1$
, this follows from [Reference Furstenberg12, Proposition 3.11, p. 67], and the general case follows from a nearly identical proof. Also explained in [Reference Furstenberg12] is the Kronecker factor of
![]() $\mathbf Y$
: the eigenfunctions of
$\mathbf Y$
: the eigenfunctions of
![]() $\mathbf Y$
are exactly the functions
$\mathbf Y$
are exactly the functions
![]() $\chi $
on Y defined by
$\chi $
on Y defined by
for some
![]() $n_j\in \mathbb Z$
, so the group of eigenvalues of
$n_j\in \mathbb Z$
, so the group of eigenvalues of
![]() $\mathbf Y$
is
$\mathbf Y$
is
![]() $\{\exp (2\pi i (n_1\alpha _1+\cdots +n_d\alpha _d)) : n_j\in ~\mathbb Z\}$
. Thus, the Kronecker factor of
$\{\exp (2\pi i (n_1\alpha _1+\cdots +n_d\alpha _d)) : n_j\in ~\mathbb Z\}$
. Thus, the Kronecker factor of
![]() $\mathbf Y$
is obtained by setting
$\mathbf Y$
is obtained by setting
![]() $Z=\mathbb T^d$
and letting
$Z=\mathbb T^d$
and letting
![]() $\pi :\mathbb T^d\times \mathbb T^d \to \mathbb T^d$
be a projection onto the first coordinate. Since the span of the eigenfunctions of
$\pi :\mathbb T^d\times \mathbb T^d \to \mathbb T^d$
be a projection onto the first coordinate. Since the span of the eigenfunctions of
![]() $\mathbf Y$
consists solely of those functions depending on the first coordinate, the orthogonal projection
$\mathbf Y$
consists solely of those functions depending on the first coordinate, the orthogonal projection
![]() $P_{\mathbf Z}f(x,y)$
can be written as
$P_{\mathbf Z}f(x,y)$
can be written as
![]() $(P_{\mathbf Z}f)(x,y):=\int f(x,y)\, dy$
. Combining this with Theorem 7.1, we have the following observation.
$(P_{\mathbf Z}f)(x,y):=\int f(x,y)\, dy$
. Combining this with Theorem 7.1, we have the following observation.
Observation 7.2. The Kronecker factor
![]() $(Z,\mathcal Z,m,R)$
of a standard 2-step Weyl system
$(Z,\mathcal Z,m,R)$
of a standard 2-step Weyl system
![]() $(\mathbb T^d \times \mathbb T^d,\mathcal D,\mu ,S)$
is spanned by functions of the form
$(\mathbb T^d \times \mathbb T^d,\mathcal D,\mu ,S)$
is spanned by functions of the form
![]() $f(x,y)=g(x)$
(i.e. functions depending on only the first coordinate), and for all bounded
$f(x,y)=g(x)$
(i.e. functions depending on only the first coordinate), and for all bounded
![]() $f:\mathbb T^d\times \mathbb T^d\to \mathbb C$
, we have
$f:\mathbb T^d\times \mathbb T^d\to \mathbb C$
, we have
 $$ \begin{align*} \lim_{N\to\infty} \frac{1}{N}\sum_{n=1}^N \int f\cdot S^n f\cdot S^{2n}f \, d\mu = \int_{\mathbb T^d}\int_{\mathbb T^d} f'(x)f'(x+s)f'(x+2s)\, dx\, ds, \end{align*} $$
$$ \begin{align*} \lim_{N\to\infty} \frac{1}{N}\sum_{n=1}^N \int f\cdot S^n f\cdot S^{2n}f \, d\mu = \int_{\mathbb T^d}\int_{\mathbb T^d} f'(x)f'(x+s)f'(x+2s)\, dx\, ds, \end{align*} $$
where
![]() $f':\mathbb T^d\to \mathbb C$
is defined as
$f':\mathbb T^d\to \mathbb C$
is defined as
![]() $f'(x):=\int f(x,y)\, dy$
.
$f'(x):=\int f(x,y)\, dy$
.
8 Reduction to Weyl systems
The next lemma is one key step in the proof of Lemma 5.1. Its proof is similar to the proof of [Reference Ackelsberg, Bergelson and Best1, Lemma 8.1].
Lemma 8.1. Let
![]() $\mathbf X = (X,\mathcal B,\mu ,T)$
be a totally ergodic MPS and
$\mathbf X = (X,\mathcal B,\mu ,T)$
be a totally ergodic MPS and
![]() $f:X\to [0,1]$
. For all
$f:X\to [0,1]$
. For all
![]() $\varepsilon>0$
, there is a factor
$\varepsilon>0$
, there is a factor
![]() $\pi :\mathbf X\to \mathbf Y$
such that:
$\pi :\mathbf X\to \mathbf Y$
such that:
-
(i)
 $\mathbf Y$
is a factor of a standard 2-step Weyl system;
$\mathbf Y$
is a factor of a standard 2-step Weyl system; -
(ii) setting
 $\tilde {f}\circ \pi =P_{\mathbf Y}f$
, we have for every continuous
$\tilde {f}\circ \pi =P_{\mathbf Y}f$
, we have for every continuous $$ \begin{align*}\lim_{N\to\infty} \bigg|\frac{1}{N}\sum_{n=1}^N g(n^2 \boldsymbol{\beta})\int f \cdot T^{n}f\cdot T^{2n}f\, d\mu - g(n^2\boldsymbol{\beta}) \int \tilde{f}\cdot S^{n}\tilde{f}\cdot S^{2n}\tilde{f}\, d\nu\bigg|<\varepsilon\end{align*} $$
$$ \begin{align*}\lim_{N\to\infty} \bigg|\frac{1}{N}\sum_{n=1}^N g(n^2 \boldsymbol{\beta})\int f \cdot T^{n}f\cdot T^{2n}f\, d\mu - g(n^2\boldsymbol{\beta}) \int \tilde{f}\cdot S^{n}\tilde{f}\cdot S^{2n}\tilde{f}\, d\nu\bigg|<\varepsilon\end{align*} $$
 $g:\mathbb T^r\to [0,1]$
and every
$g:\mathbb T^r\to [0,1]$
and every
 $\boldsymbol {\beta }\in \mathbb T^r$
, for all
$\boldsymbol {\beta }\in \mathbb T^r$
, for all
 $r\in \mathbb N$
.
$r\in \mathbb N$
.
If we assume
![]() $\boldsymbol {\beta }$
generates
$\boldsymbol {\beta }$
generates
![]() $\mathbb T^r$
, then item (ii) holds for every Riemann integrable
$\mathbb T^r$
, then item (ii) holds for every Riemann integrable
![]() $g:\mathbb T^r\to [0,1]$
.
$g:\mathbb T^r\to [0,1]$
.
We prove Lemma 8.1 at the end of this section. Most of the proof is contained in the next lemma, an application of [Reference Frantzikinakis6, Theorem B]. It concerns the maximal
![]() $2$
-step affine factor
$2$
-step affine factor
![]() $\mathbf A_2$
of an ergodic MPS
$\mathbf A_2$
of an ergodic MPS
![]() $\mathbf X$
; see [Reference Frantzikinakis6] for discussion and exposition. Additionally, we use the standard fact that the Kronecker factor of
$\mathbf X$
; see [Reference Frantzikinakis6] for discussion and exposition. Additionally, we use the standard fact that the Kronecker factor of
![]() $\mathbf X$
is a factor of
$\mathbf X$
is a factor of
![]() $\mathbf A_2$
.
$\mathbf A_2$
.
If
![]() $\mathbf X$
is an MPS, we write
$\mathbf X$
is an MPS, we write
![]() $\mathcal E(\mathbf X)$
for the group of eigenvalues of
$\mathcal E(\mathbf X)$
for the group of eigenvalues of
![]() $\mathbf X$
(see §6). We continue to write
$\mathbf X$
(see §6). We continue to write
![]() $e(t)$
for
$e(t)$
for
![]() $\exp (2\pi i t)$
, and we use the notation
$\exp (2\pi i t)$
, and we use the notation
![]() $P_{\mathbf Y}$
introduced in §4.1.
$P_{\mathbf Y}$
introduced in §4.1.
Lemma 8.2. Let
![]() $\mathbf X=(X,\mathcal B,\mu ,T)$
be an ergodic measure-preserving system with maximal 2-step affine factor
$\mathbf X=(X,\mathcal B,\mu ,T)$
be an ergodic measure-preserving system with maximal 2-step affine factor
![]() $\mathbf A_2$
and let
$\mathbf A_2$
and let
![]() $\beta \in [0,1)$
. Then
$\beta \in [0,1)$
. Then
![]() $\mathbf A_2$
is characteristic for the averages
$\mathbf A_2$
is characteristic for the averages
 $$ \begin{align} B_N(f_1,f_2):=\frac{1}{N}\sum_{n=1}^N e(n^2\beta) \cdot T^n f_1 \cdot T^{2n}f_2, \end{align} $$
$$ \begin{align} B_N(f_1,f_2):=\frac{1}{N}\sum_{n=1}^N e(n^2\beta) \cdot T^n f_1 \cdot T^{2n}f_2, \end{align} $$
meaning
in
![]() $L^2(\mu )$
, for all bounded
$L^2(\mu )$
, for all bounded
![]() $f_1, f_2$
. Furthermore, if
$f_1, f_2$
. Furthermore, if
![]() $\beta $
is irrational and
$\beta $
is irrational and
then
![]() $\lim _{N\to \infty } B_N(f_1,f_2)=0$
in
$\lim _{N\to \infty } B_N(f_1,f_2)=0$
in
![]() $L^2(\mu )$
for all bounded measurable
$L^2(\mu )$
for all bounded measurable
![]() $f_i$
.
$f_i$
.
Remark 8.3. The existence of
![]() $\lim _{N\to \infty } B_N(f_1,f_2)$
is not immediately obvious, but the proof of Lemma 8.2 will show that it is a special case of the existence of limits of polynomial multiple ergodic averages found in [Reference Frantzikinakis6].
$\lim _{N\to \infty } B_N(f_1,f_2)$
is not immediately obvious, but the proof of Lemma 8.2 will show that it is a special case of the existence of limits of polynomial multiple ergodic averages found in [Reference Frantzikinakis6].
Proof. We first dispense with the case where
![]() $\beta $
is rational. In this case, the sequence
$\beta $
is rational. In this case, the sequence
![]() $e(n^2\beta )$
is periodic, so we fix a period
$e(n^2\beta )$
is periodic, so we fix a period
![]() $p\in \mathbb N$
such that
$p\in \mathbb N$
such that
![]() $e((pn+q)^2\beta )=e(q^2\beta )$
for every n and
$e((pn+q)^2\beta )=e(q^2\beta )$
for every n and
![]() $q\in \mathbb N$
. For
$q\in \mathbb N$
. For
![]() $0\leq r\leq p$
and
$0\leq r\leq p$
and
![]() $N\in \mathbb N$
, we can then write
$N\in \mathbb N$
, we can then write
![]() $B_{pN+r}(f_1,f_2)$
as
$B_{pN+r}(f_1,f_2)$
as
 $$ \begin{align*} \frac{1}{pN+r}\bigg(\sum_{n=pN+1}^{pN+r} e(n^2\beta)\cdot T^nf_1\cdot T^{2n}f_2+\sum_{q=1}^{p}e(q^2\beta)\sum_{n=0}^{N-1} T^{pn+q}f_1\cdot T^{2(pn+q)}f_2\bigg). \end{align*} $$
$$ \begin{align*} \frac{1}{pN+r}\bigg(\sum_{n=pN+1}^{pN+r} e(n^2\beta)\cdot T^nf_1\cdot T^{2n}f_2+\sum_{q=1}^{p}e(q^2\beta)\sum_{n=0}^{N-1} T^{pn+q}f_1\cdot T^{2(pn+q)}f_2\bigg). \end{align*} $$
For large N, the sum
![]() $\sum _{n=pN+1}^{pN+r} e(n^2\beta )\cdot T^nf_1\cdot T^{2n}f_2$
can be ignored, and we have
$\sum _{n=pN+1}^{pN+r} e(n^2\beta )\cdot T^nf_1\cdot T^{2n}f_2$
can be ignored, and we have
 $$ \begin{align*} \lim_{N\to\infty} B_{N}(f_1,f_2)= \lim_{N\to\infty} \frac{1}{p}\sum_{q=1}^{p}e(q^2\beta) \frac{1}{N}\sum_{n=0}^{N-1} T^{pn+q}f_1\cdot T^{2(pn+q)}f_2. \end{align*} $$
$$ \begin{align*} \lim_{N\to\infty} B_{N}(f_1,f_2)= \lim_{N\to\infty} \frac{1}{p}\sum_{q=1}^{p}e(q^2\beta) \frac{1}{N}\sum_{n=0}^{N-1} T^{pn+q}f_1\cdot T^{2(pn+q)}f_2. \end{align*} $$
Now, [Reference Frantzikinakis6, Theorem A] implies that the Kronecker factor of
![]() $\mathbf X$
(which is itself a factor of
$\mathbf X$
(which is itself a factor of
![]() $\mathbf A_2$
) is characteristic for the averages above. This proves the first assertion of the lemma when
$\mathbf A_2$
) is characteristic for the averages above. This proves the first assertion of the lemma when
![]() $\beta $
is rational.
$\beta $
is rational.
We now assume
![]() $\beta \in (0,1)$
is irrational and consider two cases, based on whether equation (8.3) holds. When equation (8.3) fails we write the coefficient
$\beta \in (0,1)$
is irrational and consider two cases, based on whether equation (8.3) holds. When equation (8.3) fails we write the coefficient
![]() $e(n^2\beta )$
in terms of
$e(n^2\beta )$
in terms of
![]() $\bar {g}T^{p(n)}g$
, where
$\bar {g}T^{p(n)}g$
, where
![]() $g\in L^\infty (\mu )$
and p is a polynomial. When equation (8.3) holds, we write
$g\in L^\infty (\mu )$
and p is a polynomial. When equation (8.3) holds, we write
![]() $e(n^2\beta )$
as
$e(n^2\beta )$
as
![]() $g_0S^ng_1S^{2n}g_2$
, where
$g_0S^ng_1S^{2n}g_2$
, where
![]() $\mathbf Y=(Y,\mathcal D,\nu ,S)$
is an ergodic
$\mathbf Y=(Y,\mathcal D,\nu ,S)$
is an ergodic
![]() $MPS$
such that
$MPS$
such that
![]() $\mathbf X\times \mathbf Y$
is ergodic and
$\mathbf X\times \mathbf Y$
is ergodic and
![]() $g_i\in L^\infty (\nu )$
. In each case, we write
$g_i\in L^\infty (\nu )$
. In each case, we write
![]() $B_N(f_1,f_2)$
as a familiar multiple ergodic average and apply known results.
$B_N(f_1,f_2)$
as a familiar multiple ergodic average and apply known results.
For the first case, we assume equation (8.3) fails. We fix
![]() $k\in \mathbb N$
such that
$k\in \mathbb N$
such that
![]() $1\neq e(k\beta )\in \mathcal E(\mathbf X)$
, meaning
$1\neq e(k\beta )\in \mathcal E(\mathbf X)$
, meaning
![]() $e(k\beta )$
is a non-trivial eigenvalue of
$e(k\beta )$
is a non-trivial eigenvalue of
![]() $\mathbf X$
. Let
$\mathbf X$
. Let
![]() $g\in L^2(\mu )$
be a corresponding eigenfunction, so that
$g\in L^2(\mu )$
be a corresponding eigenfunction, so that
![]() $g\circ T= e(k\beta ) g$
and
$g\circ T= e(k\beta ) g$
and
![]() $|g|= 1\, \mu $
-almost everywhere. Then
$|g|= 1\, \mu $
-almost everywhere. Then
![]() $e(k\beta )^m = \bar {g}\cdot T^{m}g \mu $
-almost everywhere. In particular,
$e(k\beta )^m = \bar {g}\cdot T^{m}g \mu $
-almost everywhere. In particular,
in
![]() $L^2(\mu )$
. Then,
$L^2(\mu )$
. Then,
 $$ \begin{align*} &\lim_{N\to\infty}B_N(f_1,f_2)\\&\quad= \lim_{N\to\infty}\frac{1}{k}\sum_{j=0}^{k-1} \frac{1}{N}\sum_{n=0}^{N-1} e((nk+j)^2\beta) T^{nk+j} f_1 \cdot T^{2nk+2j} f_2\\ &\quad= \lim_{N\to\infty} \frac{1}{k}\sum_{j=0}^{k-1} \frac{1}{N}\sum_{n=0}^{N-1} e(j^2\beta) e(k\beta)^{kn^2+2jn} T^{nk+j} f_1 \cdot T^{2nk+2j} f_2\\ &\quad= \lim_{N\to\infty} \frac{1}{k}\kern-2pt\sum_{j=0}^{k-1}\kern-2pt e(j^2\beta) \frac{1}{N }\!\sum_{n=0}^{N-1} \overline{g} \cdot T^{kn^2+2jn}g \cdot T^{nk+j}f_1 \cdot T^{2nk+2j}f_2 \quad \!\text{by equation}~({8.4})\kern-0.1pt. \end{align*} $$
$$ \begin{align*} &\lim_{N\to\infty}B_N(f_1,f_2)\\&\quad= \lim_{N\to\infty}\frac{1}{k}\sum_{j=0}^{k-1} \frac{1}{N}\sum_{n=0}^{N-1} e((nk+j)^2\beta) T^{nk+j} f_1 \cdot T^{2nk+2j} f_2\\ &\quad= \lim_{N\to\infty} \frac{1}{k}\sum_{j=0}^{k-1} \frac{1}{N}\sum_{n=0}^{N-1} e(j^2\beta) e(k\beta)^{kn^2+2jn} T^{nk+j} f_1 \cdot T^{2nk+2j} f_2\\ &\quad= \lim_{N\to\infty} \frac{1}{k}\kern-2pt\sum_{j=0}^{k-1}\kern-2pt e(j^2\beta) \frac{1}{N }\!\sum_{n=0}^{N-1} \overline{g} \cdot T^{kn^2+2jn}g \cdot T^{nk+j}f_1 \cdot T^{2nk+2j}f_2 \quad \!\text{by equation}~({8.4})\kern-0.1pt. \end{align*} $$
The polynomial exponents
![]() $p_1(n)=kn^2+2jn$
,
$p_1(n)=kn^2+2jn$
,
![]() $p_2(n)=nk+j$
,
$p_2(n)=nk+j$
,
![]() $p_3(n)=2nk+2j$
are, in the terminology of [Reference Frantzikinakis6], essentially distinct and not type (
$p_3(n)=2nk+2j$
are, in the terminology of [Reference Frantzikinakis6], essentially distinct and not type (
![]() $e_1$
). Therefore, [Reference Frantzikinakis6, Theorem B] asserts that
$e_1$
). Therefore, [Reference Frantzikinakis6, Theorem B] asserts that
![]() $f_1$
and
$f_1$
and
![]() $f_2$
in equation (8.1) can be replaced with
$f_2$
in equation (8.1) can be replaced with
![]() $P_{\mathbf A_2}f_1$
and
$P_{\mathbf A_2}f_1$
and
![]() $P_{\mathbf A_2}f_2$
, respectively, without changing the value of the limit. This proves the first assertion of the lemma in the case where
$P_{\mathbf A_2}f_2$
, respectively, without changing the value of the limit. This proves the first assertion of the lemma in the case where
![]() $\mathcal E(\mathbf X)\cap \{e(n\beta )\}_{n\in \mathbb Z}\neq \{1\}$
.
$\mathcal E(\mathbf X)\cap \{e(n\beta )\}_{n\in \mathbb Z}\neq \{1\}$
.
Now we assume that equation (8.3) holds. We will prove that
![]() $\lim _{N\to \infty } B_N(f_1,f_2)=0$
for all
$\lim _{N\to \infty } B_N(f_1,f_2)=0$
for all
![]() $f_1, f_2\in L^\infty (\mu )$
. This implies equation (8.2), since
$f_1, f_2\in L^\infty (\mu )$
. This implies equation (8.2), since
![]() $P_{\mathbf A_2} f_i \in L^\infty (\mu )$
.
$P_{\mathbf A_2} f_i \in L^\infty (\mu )$
.
Consider the system
![]() $\mathbf Y=(\mathbb T^2,\mathcal D,m,S)$
, where
$\mathbf Y=(\mathbb T^2,\mathcal D,m,S)$
, where
![]() $S(x,y)=(x+\beta ,y+x)$
; this
$S(x,y)=(x+\beta ,y+x)$
; this
![]() $\mathbf Y$
is ergodic since
$\mathbf Y$
is ergodic since
![]() $\beta $
is irrational. As discussed in §7.1, the eigenvalues of
$\beta $
is irrational. As discussed in §7.1, the eigenvalues of
![]() $\mathbf Y$
are
$\mathbf Y$
are
![]() $\{e(n\beta )\}_{n\in \mathbb Z}$
. Thus,
$\{e(n\beta )\}_{n\in \mathbb Z}$
. Thus,
![]() $\mathbf Y$
has no non-trivial eigenvalues in common with
$\mathbf Y$
has no non-trivial eigenvalues in common with
![]() $\mathbf X$
, by equation (8.3). The product system
$\mathbf X$
, by equation (8.3). The product system
![]() $(\mathbb T^2\times X, m \times \mu , S\times T)$
is therefore ergodic, by Lemma 6.2. We will write
$(\mathbb T^2\times X, m \times \mu , S\times T)$
is therefore ergodic, by Lemma 6.2. We will write
![]() $B_N(f_1,f_2)$
as an element of
$B_N(f_1,f_2)$
as an element of
![]() $L^2(m\times \mu )$
. First observe that for all
$L^2(m\times \mu )$
. First observe that for all
![]() $(x,y)\in \mathbb T^2$
, we have
$(x,y)\in \mathbb T^2$
, we have
 $$ \begin{align*} e(n^2\beta)&= e(y)e(-2y-2nx -n(n+1) \beta)e(y+2nx+n(2n+1)\beta) \\ &= g_0\cdot g_1(S^n(x,y)) \cdot g_2(S^{2n}(x,y)), \end{align*} $$
$$ \begin{align*} e(n^2\beta)&= e(y)e(-2y-2nx -n(n+1) \beta)e(y+2nx+n(2n+1)\beta) \\ &= g_0\cdot g_1(S^n(x,y)) \cdot g_2(S^{2n}(x,y)), \end{align*} $$
where
![]() $g_0(x,y):=e(y)$
,
$g_0(x,y):=e(y)$
,
![]() $g_1(x,y):=e(-2y)$
,
$g_1(x,y):=e(-2y)$
,
![]() $g_2(x,y):=e(y)$
. So
$g_2(x,y):=e(y)$
. So
When computing the limit of the averages of the right-hand side in equation (8.5), Theorem 7.1 allows us to replace each
![]() $g_i\otimes f_i$
with its projection
$g_i\otimes f_i$
with its projection
![]() $\phi _i:=P_{\mathbf Z}(g_i\otimes f_i)$
, where
$\phi _i:=P_{\mathbf Z}(g_i\otimes f_i)$
, where
![]() $\mathbf Z$
is the Kronecker factor of
$\mathbf Z$
is the Kronecker factor of
![]() $\mathbf Y\times \mathbf X$
. By Lemma 6.3 and Observation 7.2,
$\mathbf Y\times \mathbf X$
. By Lemma 6.3 and Observation 7.2,
![]() $g_i\otimes f_i$
is orthogonal to every eigenfunction of
$g_i\otimes f_i$
is orthogonal to every eigenfunction of
![]() $\mathbf Y\times \mathbf X$
, so
$\mathbf Y\times \mathbf X$
, so
![]() $\phi _i =0$
. Thus, the limit of the averages is
$\phi _i =0$
. Thus, the limit of the averages is
![]() $0$
in
$0$
in
![]() $L^2(m\times \mu )$
. Since
$L^2(m\times \mu )$
. Since
![]() $B_N(f_1,f_2)$
belongs to the natural embedding of
$B_N(f_1,f_2)$
belongs to the natural embedding of
![]() $L^2(\mu )$
in
$L^2(\mu )$
in
![]() $L^2(m\times \mu )$
, this proves
$L^2(m\times \mu )$
, this proves
![]() $\lim _{N\to \infty } B_N(f_1,f_2)=0$
in
$\lim _{N\to \infty } B_N(f_1,f_2)=0$
in
![]() $L^2(\mu )$
.
$L^2(\mu )$
.
Corollary 8.4. Let
![]() $(X,\mathcal B,\mu ,T)$
be an ergodic measure-preserving system and let
$(X,\mathcal B,\mu ,T)$
be an ergodic measure-preserving system and let
![]() ${\boldsymbol {\beta }=(\beta _1,\ldots ,\beta _r)\in \mathbb T^r}$
. If
${\boldsymbol {\beta }=(\beta _1,\ldots ,\beta _r)\in \mathbb T^r}$
. If
![]() $g:\mathbb T^r\to \mathbb C$
is continuous and
$g:\mathbb T^r\to \mathbb C$
is continuous and
![]() $f_i\in L^\infty (\mu )$
, then
$f_i\in L^\infty (\mu )$
, then
 $$ \begin{align*} \lim_{N\to\infty} \frac{1}{N}\sum_{n=1}^N g(n^2\boldsymbol{\beta}) \cdot T^{n} f_1 \cdot T^{2n} f_2= \lim_{N\to\infty} \frac{1}{N}\sum_{n=1}^N g(n^2\boldsymbol{\beta}) \cdot T^{n} \bar{f}_1 \cdot T^{2n}\bar{f}_2 \end{align*} $$
$$ \begin{align*} \lim_{N\to\infty} \frac{1}{N}\sum_{n=1}^N g(n^2\boldsymbol{\beta}) \cdot T^{n} f_1 \cdot T^{2n} f_2= \lim_{N\to\infty} \frac{1}{N}\sum_{n=1}^N g(n^2\boldsymbol{\beta}) \cdot T^{n} \bar{f}_1 \cdot T^{2n}\bar{f}_2 \end{align*} $$
in
![]() $L^2(\mu )$
, where
$L^2(\mu )$
, where
![]() $\mathbf A_2$
is the maximal 2-step affine factor of
$\mathbf A_2$
is the maximal 2-step affine factor of
![]() $\mathbf X$
, and
$\mathbf X$
, and
![]() $\bar {f}_i=P_{\mathbf A_2}f_i$
.
$\bar {f}_i=P_{\mathbf A_2}f_i$
.
Proof. Uniformly approximating g by trigonometric polynomials, it suffices to prove the lemma in the case where g is a character of
![]() $\mathbb T^r$
. In this case, we can write
$\mathbb T^r$
. In this case, we can write
![]() $g(n^2\boldsymbol {\beta })$
as
$g(n^2\boldsymbol {\beta })$
as
![]() $e(n^2\alpha )$
for some
$e(n^2\alpha )$
for some
![]() $\alpha \in [0,1)$
and apply Lemma 8.2.
$\alpha \in [0,1)$
and apply Lemma 8.2.
8.1 Nilsystems and their affine factors
The following is a restatement of part (i) of Lemma 4.7.
Lemma 8.5. Let
![]() $\mathbf X = (X,\mathcal B, \mu ,T)$
be an ergodic MPS,
$\mathbf X = (X,\mathcal B, \mu ,T)$
be an ergodic MPS,
![]() $f_i\in L^\infty (\mu )$
, and
$f_i\in L^\infty (\mu )$
, and
![]() $\varepsilon>0$
. There is a factor
$\varepsilon>0$
. There is a factor
![]() $\pi :\mathbf X\to \mathbf Y=(Y,\mathcal D,\nu ,S)$
which is a 2-step nilsystem such that for every bounded sequence
$\pi :\mathbf X\to \mathbf Y=(Y,\mathcal D,\nu ,S)$
which is a 2-step nilsystem such that for every bounded sequence
![]() $(c_n)_{n\in \mathbb N}$
, we have
$(c_n)_{n\in \mathbb N}$
, we have
 $$ \begin{align} \limsup_{N\to \infty} \bigg|\frac{1}{N}\sum_{n=1}^N c_n \int f_0\cdot T^{ n}f_1 \cdot T^{2 n}f_2\, d\mu - c_n\int \tilde{f}_0 \cdot S^{ n}\tilde{f}_1 \cdot S^{2 n}\tilde{f}_2 \, d\nu\bigg| <\varepsilon \sup_{n} |c_n|, \end{align} $$
$$ \begin{align} \limsup_{N\to \infty} \bigg|\frac{1}{N}\sum_{n=1}^N c_n \int f_0\cdot T^{ n}f_1 \cdot T^{2 n}f_2\, d\mu - c_n\int \tilde{f}_0 \cdot S^{ n}\tilde{f}_1 \cdot S^{2 n}\tilde{f}_2 \, d\nu\bigg| <\varepsilon \sup_{n} |c_n|, \end{align} $$
where
![]() $\tilde {f}_i\circ \pi :=P_{\mathbf Y}f_i$
.
$\tilde {f}_i\circ \pi :=P_{\mathbf Y}f_i$
.
When computing ergodic averages for ergodic 2-step affine nilsystems, the following lemma allows us to specialize to standard Weyl systems.
Lemma 8.6. [Reference Frantzikinakis and Kra9, Lemma 4.1]
Let
![]() $T:\mathbb T^d\to \mathbb T^d$
be defined by
$T:\mathbb T^d\to \mathbb T^d$
be defined by
![]() $T(x)=Ax+b$
, where A is a
$T(x)=Ax+b$
, where A is a
![]() $d\times d$
unipotent integer matrix and
$d\times d$
unipotent integer matrix and
![]() $b\in \mathbb T^d$
. Assume furthermore that T is ergodic. Then T is a factor of an ergodic affine transformation
$b\in \mathbb T^d$
. Assume furthermore that T is ergodic. Then T is a factor of an ergodic affine transformation
![]() $S:\mathbb T^d\to \mathbb T^d$
, where
$S:\mathbb T^d\to \mathbb T^d$
, where
![]() $S=S_1\times S_2\times \cdots \times S_s$
and for
$S=S_1\times S_2\times \cdots \times S_s$
and for
![]() $r=1,2,\ldots ,s$
,
$r=1,2,\ldots ,s$
,
![]() $S_r: \mathbb T^{d_r} \to \mathbb T^{d_r}$
has the form
$S_r: \mathbb T^{d_r} \to \mathbb T^{d_r}$
has the form
for some
![]() $b_r\in \mathbb T$
.
$b_r\in \mathbb T$
.
Although not explicitly stated in [Reference Frantzikinakis and Kra9], the proof there allows us to conclude that we have
![]() $d_r\leq D$
, where D is the degree of unipotency of A. Furthermore, if
$d_r\leq D$
, where D is the degree of unipotency of A. Furthermore, if
![]() $(A-I)^2=0$
, as is the case when T is 2-step affine, then we can take
$(A-I)^2=0$
, as is the case when T is 2-step affine, then we can take
![]() $d_r\leq 2$
for each r. For convenience, we may also assume that
$d_r\leq 2$
for each r. For convenience, we may also assume that
![]() $d_r=2$
for each r, and therefore
$d_r=2$
for each r, and therefore
![]() $s=1$
. With these specializations, the system given by S above is a standard 2-step Weyl system.
$s=1$
. With these specializations, the system given by S above is a standard 2-step Weyl system.
Proof of Lemma 8.1
Fix a totally ergodic MPS
![]() $\mathbf X = (X,\mathcal B,\mu ,T)$
, bounded measurable functions
$\mathbf X = (X,\mathcal B,\mu ,T)$
, bounded measurable functions
![]() $f_i$
on X,
$f_i$
on X,
![]() $r\in \mathbb N$
, and
$r\in \mathbb N$
, and
![]() $\boldsymbol {\beta }\in \mathbb T^r$
. Let
$\boldsymbol {\beta }\in \mathbb T^r$
. Let
![]() $g:\mathbb T^r\to [0,1]$
be continuous, and let
$g:\mathbb T^r\to [0,1]$
be continuous, and let
![]() $\varepsilon>0$
. Consider the averages
$\varepsilon>0$
. Consider the averages
 $$ \begin{align*} A_N: = \frac{1}{N}\sum_{n=1}^N g(n^2\boldsymbol{\beta})\int f_0 \cdot T^{n}f_1\cdot T^{2n}f_2\, d\mu. \end{align*} $$
$$ \begin{align*} A_N: = \frac{1}{N}\sum_{n=1}^N g(n^2\boldsymbol{\beta})\int f_0 \cdot T^{n}f_1\cdot T^{2n}f_2\, d\mu. \end{align*} $$
First apply Lemma 8.5 to find a 2-step nilsystem
![]() $\mathbf Y_0=(Y_0,\mathcal D_0,\nu _0,S)$
satisfying equation (8.6) with
$\mathbf Y_0=(Y_0,\mathcal D_0,\nu _0,S)$
satisfying equation (8.6) with
![]() $c_n=g(n^2\boldsymbol {\beta })$
, and write
$c_n=g(n^2\boldsymbol {\beta })$
, and write
![]() $B_N$
for the averages
$B_N$
for the averages
 $$ \begin{align*}\frac{1}{N}\sum_{n=1}^N g(n^2\boldsymbol{\beta}) \int \tilde{f}_0\cdot S^{n}\tilde{f}_1 \cdot S^{2n}\tilde{f}_2\, d\nu.\end{align*} $$
$$ \begin{align*}\frac{1}{N}\sum_{n=1}^N g(n^2\boldsymbol{\beta}) \int \tilde{f}_0\cdot S^{n}\tilde{f}_1 \cdot S^{2n}\tilde{f}_2\, d\nu.\end{align*} $$
Our application of Lemma 8.5 means that
![]() $\limsup _{N\to \infty } |A_N-B_N|<\varepsilon $
.
$\limsup _{N\to \infty } |A_N-B_N|<\varepsilon $
.
By Corollary 8.4, the factor
![]() $\mathbf Y:=\mathbf A_2(\mathbf Y_0)$
is characteristic for the averages
$\mathbf Y:=\mathbf A_2(\mathbf Y_0)$
is characteristic for the averages
![]() $B_N$
: we may replace each
$B_N$
: we may replace each
![]() $\tilde {f}_i$
with
$\tilde {f}_i$
with
![]() $P_{\mathbf Y}\tilde {f}_i$
without affecting
$P_{\mathbf Y}\tilde {f}_i$
without affecting
![]() $\lim _{N\to \infty } B_N$
. The total ergodicity of
$\lim _{N\to \infty } B_N$
. The total ergodicity of
![]() $\mathbf X$
implies every factor of
$\mathbf X$
implies every factor of
![]() $\mathbf X$
is also totally ergodic; in particular,
$\mathbf X$
is also totally ergodic; in particular,
![]() $\mathbf A_2(\mathbf Y_0)$
is totally ergodic. By Lemma 15.2, we conclude that
$\mathbf A_2(\mathbf Y_0)$
is totally ergodic. By Lemma 15.2, we conclude that
![]() $\mathbf A_2(\mathbf Y_0)$
is isomorphic to a unipotent
$\mathbf A_2(\mathbf Y_0)$
is isomorphic to a unipotent
![]() $2$
-step affine transformation on a finite-dimensional torus, and Lemma 8.6 allows us to conclude that
$2$
-step affine transformation on a finite-dimensional torus, and Lemma 8.6 allows us to conclude that
![]() $\mathbf A_2(\mathbf Y)$
is a factor of a standard 2-step Weyl system.
$\mathbf A_2(\mathbf Y)$
is a factor of a standard 2-step Weyl system.
To obtain the remark after part (ii) in the statement of the lemma, apply Lemma 15.8 with
![]() $y_n = n^2\boldsymbol {\beta }$
and
$y_n = n^2\boldsymbol {\beta }$
and
![]() $v_n = \int f \cdot T^{n}f\cdot T^{2n}f\, d\mu - \int \tilde {f}\cdot S^{n}\tilde {f}\cdot S^{2n}\tilde {f}\, d\nu $
. We may apply Lemma 15.8 since the Weyl criterion implies
$v_n = \int f \cdot T^{n}f\cdot T^{2n}f\, d\mu - \int \tilde {f}\cdot S^{n}\tilde {f}\cdot S^{2n}\tilde {f}\, d\nu $
. We may apply Lemma 15.8 since the Weyl criterion implies
![]() $n^2\boldsymbol {\beta }$
is uniformly distributed in
$n^2\boldsymbol {\beta }$
is uniformly distributed in
![]() $\mathbb T^r$
whenever
$\mathbb T^r$
whenever
![]() $\boldsymbol {\beta }$
is generating.
$\boldsymbol {\beta }$
is generating.
Remark 8.7. Our proof of Lemma 8.1 needs the hypothesis of total ergodicity to conclude that
![]() $\mathbf A_2(\mathbf Y)$
is isomorphic to a
$\mathbf A_2(\mathbf Y)$
is isomorphic to a
![]() $2$
-step affine transformation on a finite-dimensional torus. Without this hypothesis,
$2$
-step affine transformation on a finite-dimensional torus. Without this hypothesis,
![]() $\mathbf A_2(\mathbf X)$
may be more complicated: the underlying space may be disconnected, and may even have uncountably many connected components. In particular, the Kronecker factor of
$\mathbf A_2(\mathbf X)$
may be more complicated: the underlying space may be disconnected, and may even have uncountably many connected components. In particular, the Kronecker factor of
![]() $\mathbf X$
could be isomorphic to a rotation on a compact uncountable totally disconnected abelian group (such as the profinite compactification of
$\mathbf X$
could be isomorphic to a rotation on a compact uncountable totally disconnected abelian group (such as the profinite compactification of
![]() $\mathbb Z$
). This would cause two problems in the following: first, in §13, we exploit the fact that the connected component of a closed subgroup
$\mathbb Z$
). This would cause two problems in the following: first, in §13, we exploit the fact that the connected component of a closed subgroup
![]() $\Lambda $
of
$\Lambda $
of
![]() $\mathbb T^d$
has finite index in
$\mathbb T^d$
has finite index in
![]() $\Lambda $
(although this may not be crucial); second, we simply lack a convenient algebraic description of affine systems defined on disconnected groups, and such a description is required for our computation in Proposition 13.1.
$\Lambda $
(although this may not be crucial); second, we simply lack a convenient algebraic description of affine systems defined on disconnected groups, and such a description is required for our computation in Proposition 13.1.
For similar reasons, we cannot prove Lemma 8.1 starting with an arbitrary totally ergodic
![]() $\mathbf X$
and passing immediately to
$\mathbf X$
and passing immediately to
![]() $\mathbf A_2(\mathbf X)$
. While disconnectedness will not be a problem, it is possible that the Kronecker factor of
$\mathbf A_2(\mathbf X)$
. While disconnectedness will not be a problem, it is possible that the Kronecker factor of
![]() $\mathbf X$
is a group rotation on an infinite-dimensional torus, or a solenoid, and then
$\mathbf X$
is a group rotation on an infinite-dimensional torus, or a solenoid, and then
![]() $\mathbf A_2(\mathbf X)$
could be an affine transformation on such a group, which does not fit the hypothesis of Lemma 8.6.
$\mathbf A_2(\mathbf X)$
could be an affine transformation on such a group, which does not fit the hypothesis of Lemma 8.6.
9 Joinings of groups
Given two compact abelian groups Z and W with cartesian product
![]() $Z\times W$
, write
$Z\times W$
, write
![]() $\pi _1$
and
$\pi _1$
and
![]() $\pi _2$
for the projection maps onto Z and W, respectively. We say a subgroup
$\pi _2$
for the projection maps onto Z and W, respectively. We say a subgroup
![]() $\Gamma \subseteq Z\times W$
is a joining of Z with W if
$\Gamma \subseteq Z\times W$
is a joining of Z with W if
![]() $\Gamma $
is closed, and
$\Gamma $
is closed, and
![]() $\pi _1:\Gamma \to Z$
and
$\pi _1:\Gamma \to Z$
and
![]() $\pi _2:\Gamma \to W$
are both surjective.
$\pi _2:\Gamma \to W$
are both surjective.
Observation 9.1. If
![]() $\alpha \in Z$
and
$\alpha \in Z$
and
![]() $\beta \in W$
are generating elements, then the closed subgroup
$\beta \in W$
are generating elements, then the closed subgroup
![]() $\Gamma $
of
$\Gamma $
of
![]() $Z\times W$
generated by
$Z\times W$
generated by
![]() $(\alpha ,\beta )$
is a joining of Z with W:
$(\alpha ,\beta )$
is a joining of Z with W:
![]() $\pi _1(\Gamma )$
is generated by
$\pi _1(\Gamma )$
is generated by
![]() $\alpha $
and
$\alpha $
and
![]() $\pi _2(\Gamma )$
is generated by
$\pi _2(\Gamma )$
is generated by
![]() $\beta $
.
$\beta $
.
Joinings arise naturally in the computation of multiple ergodic averages. For example, let
![]() $\Gamma :=\{(t,t)\}: t\in Z\}$
(
$\Gamma :=\{(t,t)\}: t\in Z\}$
(
![]() $=$
the diagonal of
$=$
the diagonal of
![]() $Z\times Z$
), so that
$Z\times Z$
), so that
![]() $\Gamma $
is a joining of Z with itself. Then we can write the integral on the right-hand side of equation (7.1) as
$\Gamma $
is a joining of Z with itself. Then we can write the integral on the right-hand side of equation (7.1) as
The notation
![]() $\pi _i(t)$
will be cumbersome in our formulas, so we adopt the following abbreviation.
$\pi _i(t)$
will be cumbersome in our formulas, so we adopt the following abbreviation.
Notation 9.2. If
![]() $\Gamma $
is a joining of Z with W and
$\Gamma $
is a joining of Z with W and
![]() $t\in \Gamma $
, we write
$t\in \Gamma $
, we write
![]() $t_1$
for
$t_1$
for
![]() $\pi _1(t)$
and
$\pi _1(t)$
and
![]() $t_2$
for
$t_2$
for
![]() $\pi _2(t)$
.
$\pi _2(t)$
.
So the integral in equation (9.1) can be written as
![]() $\int _\Gamma \int _Z f(x)f(x+t_1)f(x+2t_2)\, dx \, dm_{\Gamma }(t)$
.
$\int _\Gamma \int _Z f(x)f(x+t_1)f(x+2t_2)\, dx \, dm_{\Gamma }(t)$
.
The joinings we consider will be closed subgroups of
![]() $\mathbb T^d\times \mathbb T^r$
; this allows us to exploit the well-known structure of such groups (detailed in [Reference Rudin24], for example).
$\mathbb T^d\times \mathbb T^r$
; this allows us to exploit the well-known structure of such groups (detailed in [Reference Rudin24], for example).
Observation 9.3. If
![]() $\Gamma $
is a joining of
$\Gamma $
is a joining of
![]() $\mathbb T^d$
with
$\mathbb T^d$
with
![]() $\mathbb T^r$
, then its identity component is also a joining of these groups. To see this, note that since
$\mathbb T^r$
, then its identity component is also a joining of these groups. To see this, note that since
![]() $\Gamma $
is a closed subgroup of a finite-dimensional torus, its identity component
$\Gamma $
is a closed subgroup of a finite-dimensional torus, its identity component
![]() $\Gamma _0$
has finite index in
$\Gamma _0$
has finite index in
![]() $\Gamma $
. The images of
$\Gamma $
. The images of
![]() $\pi _1$
and
$\pi _1$
and
![]() $\pi _2$
therefore have finite index in their respective codomains
$\pi _2$
therefore have finite index in their respective codomains
![]() $\mathbb T^d$
and
$\mathbb T^d$
and
![]() $\mathbb T^r$
. Since these codomains are connected, they have no proper closed finite index subgroups, so the images
$\mathbb T^r$
. Since these codomains are connected, they have no proper closed finite index subgroups, so the images
![]() $\pi _1(\Gamma _0)$
,
$\pi _1(\Gamma _0)$
,
![]() $\pi _2(\Gamma _0)$
must equal their respective codomains.
$\pi _2(\Gamma _0)$
must equal their respective codomains.
If G is a compact abelian group and H is a closed subgroup,
![]() $m_{H}$
denotes Haar probability measure on H. If
$m_{H}$
denotes Haar probability measure on H. If
![]() $H'$
is a coset
$H'$
is a coset
![]() $H+t$
of H,
$H+t$
of H,
![]() $m_{H'}$
denotes Haar measure on
$m_{H'}$
denotes Haar measure on
![]() $H'$
, i.e. the measure given by
$H'$
, i.e. the measure given by
![]() $\int f\, dm_{H'}:= \int f(x+t)\, dm_H(x)$
.
$\int f\, dm_{H'}:= \int f(x+t)\, dm_H(x)$
.
Definition 9.4. If
![]() $\Gamma _0$
is a joining of Z with W,
$\Gamma _0$
is a joining of Z with W,
![]() $\Gamma _j, j\leq k$
is a collection of cosets of
$\Gamma _j, j\leq k$
is a collection of cosets of
![]() $\Gamma _0$
, and
$\Gamma _0$
, and
![]() $c_j \in [0,1]$
satisfy
$c_j \in [0,1]$
satisfy
![]() $\sum _{j} c_j=1$
, we say that the
$\sum _{j} c_j=1$
, we say that the
![]() $\Gamma _j$
and
$\Gamma _j$
and
![]() $c_j$
form an affine joining
$c_j$
form an affine joining
![]() $\Gamma $
of Z with W, and define integration over
$\Gamma $
of Z with W, and define integration over
![]() $\Gamma $
by
$\Gamma $
by
 $$ \begin{align*} \int f \, dm_{\Gamma} := \sum_{j} c_j \int f\, dm_{\Gamma_j}. \end{align*} $$
$$ \begin{align*} \int f \, dm_{\Gamma} := \sum_{j} c_j \int f\, dm_{\Gamma_j}. \end{align*} $$
For example,
![]() $\Gamma _0 = \{(x,2x):x\in \mathbb T\}$
,
$\Gamma _0 = \{(x,2x):x\in \mathbb T\}$
,
![]() $\Gamma _1 = \{(x+\tfrac 14,2x):x\in \mathbb T\} \subseteq \mathbb T\times \mathbb T$
,
$\Gamma _1 = \{(x+\tfrac 14,2x):x\in \mathbb T\} \subseteq \mathbb T\times \mathbb T$
,
![]() $c_0 = \tfrac 13$
, and
$c_0 = \tfrac 13$
, and
![]() $c_1 = \tfrac 23$
determine an affine joining
$c_1 = \tfrac 23$
determine an affine joining
![]() $\Gamma $
of
$\Gamma $
of
![]() $\mathbb T$
with
$\mathbb T$
with
![]() $\mathbb T$
, and
$\mathbb T$
, and
 $$ \begin{align*} \int f\, dm_{\Gamma} = \frac{1}{3}\int f(x,2x) \, dx + \frac{2}{3} \int f\bigg(x+\frac{1}{4},2x\bigg)\, dx.\end{align*} $$
$$ \begin{align*} \int f\, dm_{\Gamma} = \frac{1}{3}\int f(x,2x) \, dx + \frac{2}{3} \int f\bigg(x+\frac{1}{4},2x\bigg)\, dx.\end{align*} $$
10 Application of Kronecker’s and Weyl’s theorems
The limits of ergodic averages we consider will be computed as integrals over affine joinings. To compute them explicitly, we need the following well-known results of Kronecker and Weyl.
Given a compact abelian group Z and
![]() $\alpha _1,\ldots ,\alpha _d\in Z$
, we write
$\alpha _1,\ldots ,\alpha _d\in Z$
, we write
![]() $\langle \alpha _1,\ldots , \alpha _d\rangle $
for the subgroup of Z generated by these elements. We write
$\langle \alpha _1,\ldots , \alpha _d\rangle $
for the subgroup of Z generated by these elements. We write
![]() $\overline {\langle \alpha _1,\ldots , \alpha _d\rangle }$
for its closure.
$\overline {\langle \alpha _1,\ldots , \alpha _d\rangle }$
for its closure.
Lemma 10.1. (Kronecker’s criterion)
Let
![]() $\alpha _1,\ldots ,\alpha _d$
be elements of a compact abelian group Z. Then
$\alpha _1,\ldots ,\alpha _d$
be elements of a compact abelian group Z. Then
![]() $\overline {\langle \alpha _1,\ldots , \alpha _d\rangle }=Z$
if and only if for every non-trivial character
$\overline {\langle \alpha _1,\ldots , \alpha _d\rangle }=Z$
if and only if for every non-trivial character
![]() $\chi \in \widehat {Z}$
,
$\chi \in \widehat {Z}$
,
![]() $\chi (\alpha _j)\neq 1$
for at least one of the
$\chi (\alpha _j)\neq 1$
for at least one of the
![]() $\alpha _j$
.
$\alpha _j$
.
Weyl’s theorem on uniform distribution of polynomials ([Reference Weyl26], or [Reference Kuipers and Niederreiter19, Theorem 3.2]) says that if
![]() $p(x)=c_mx^m + c_{m-1}x^{m-1} + \cdots + c_0$
is a polynomial with real coefficients and at least one of the
$p(x)=c_mx^m + c_{m-1}x^{m-1} + \cdots + c_0$
is a polynomial with real coefficients and at least one of the
![]() $c_j$
with
$c_j$
with
![]() $j>0$
is irrational, then
$j>0$
is irrational, then
 $$ \begin{align*} \lim_{N\to\infty} \frac{1}{N}\sum_{n=1}^N e(p(n)) = 0. \end{align*} $$
$$ \begin{align*} \lim_{N\to\infty} \frac{1}{N}\sum_{n=1}^N e(p(n)) = 0. \end{align*} $$
As usual,
![]() $e(t)$
denotes
$e(t)$
denotes
![]() $\exp (2\pi i t)$
.
$\exp (2\pi i t)$
.
Lemma 10.2. Let Z be a compact abelian group, let
![]() $\alpha $
,
$\alpha $
,
![]() $\beta \in Z$
, and let
$\beta \in Z$
, and let
![]() $\chi \in \widehat {Z}$
be such that
$\chi \in \widehat {Z}$
be such that
![]() $\chi (\alpha )$
,
$\chi (\alpha )$
,
![]() $\chi (\beta )$
are not both roots of unity. Then
$\chi (\beta )$
are not both roots of unity. Then
![]() $\lim _{N\to \infty } ({1}/{N})\sum _{n=1}^N \chi (n\alpha + n^2\beta )=0$
.
$\lim _{N\to \infty } ({1}/{N})\sum _{n=1}^N \chi (n\alpha + n^2\beta )=0$
.
Proof. Write
![]() $\chi (n\alpha + n^2\beta )$
as
$\chi (n\alpha + n^2\beta )$
as
![]() $\chi (\alpha )^n\chi (\beta )^{n^2} = e(n\gamma _1 + n^2\gamma _2)$
, where at least one of
$\chi (\alpha )^n\chi (\beta )^{n^2} = e(n\gamma _1 + n^2\gamma _2)$
, where at least one of
![]() $\gamma _1, \gamma _2\in [0,1)$
is irrational. Weyl’s theorem then implies the limit of the averages is
$\gamma _1, \gamma _2\in [0,1)$
is irrational. Weyl’s theorem then implies the limit of the averages is
![]() $0$
.
$0$
.
Lemma 10.3. Let Z be a compact abelian group with Haar probability measure m and let
![]() $\alpha , \beta $
generate Z.
$\alpha , \beta $
generate Z.
-
(i) If Z is connected, then for all continuous
 $f:Z\to \mathbb C$
, we have (10.1)
$f:Z\to \mathbb C$
, we have (10.1) $$ \begin{align} \lim_{N\to\infty} \frac{1}{N}\sum_{n=1}^N f(n\alpha + n^2\beta) = \int f\, dm. \end{align} $$
$$ \begin{align} \lim_{N\to\infty} \frac{1}{N}\sum_{n=1}^N f(n\alpha + n^2\beta) = \int f\, dm. \end{align} $$
-
(ii) If Z has finitely many connected components
 $Z_j$
, then the limit above can be written as
$Z_j$
, then the limit above can be written as
 $\sum c_j \int f\, dm_{Z_j}$
for some non-negative
$\sum c_j \int f\, dm_{Z_j}$
for some non-negative
 $c_j$
with
$c_j$
with
 $\sum c_j=1$
.
$\sum c_j=1$
. -
(iii) For fixed
 $\beta $
, if
$\beta $
, if
 $\alpha , \alpha '\in Z$
are such that
$\alpha , \alpha '\in Z$
are such that
 $\overline {\langle \alpha \rangle } = \overline {\langle \alpha '\rangle }$
and
$\overline {\langle \alpha \rangle } = \overline {\langle \alpha '\rangle }$
and
 $\overline {\langle \alpha \rangle }$
is connected, we have (10.2)
$\overline {\langle \alpha \rangle }$
is connected, we have (10.2) $$ \begin{align} \lim_{N\to\infty} \frac{1}{N}\sum_{n=1}^N f(n\alpha + n^2\beta) = \lim_{N\to\infty} \frac{1}{N}\sum_{n=1}^N f(n\alpha' + n^2\beta). \end{align} $$
$$ \begin{align} \lim_{N\to\infty} \frac{1}{N}\sum_{n=1}^N f(n\alpha + n^2\beta) = \lim_{N\to\infty} \frac{1}{N}\sum_{n=1}^N f(n\alpha' + n^2\beta). \end{align} $$
Proof. (i) Approximating f by trigonometric polynomials, it suffices to prove the special case where f is a non-trivial character
![]() $\chi \in \widehat {Z}$
. Under this assumption, we will show that the limit of the averages in equation (10.1) is
$\chi \in \widehat {Z}$
. Under this assumption, we will show that the limit of the averages in equation (10.1) is
![]() $0$
. In this case,
$0$
. In this case,
![]() $f(n\alpha +n^2\beta )=\chi (\alpha )^n\chi (\beta )^{n^2}$
. Connectedness of Z implies
$f(n\alpha +n^2\beta )=\chi (\alpha )^n\chi (\beta )^{n^2}$
. Connectedness of Z implies
![]() $\chi ^n\not \equiv 1$
for all
$\chi ^n\not \equiv 1$
for all
![]() $n\in \mathbb N$
. Since
$n\in \mathbb N$
. Since
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
generate Z, Lemma 10.1 implies
$\beta $
generate Z, Lemma 10.1 implies
![]() $\chi (\alpha )^n\neq 1$
or
$\chi (\alpha )^n\neq 1$
or
![]() $\chi (\beta )^n\neq 1$
for all
$\chi (\beta )^n\neq 1$
for all
![]() $n\in \mathbb N$
. Lemma 10.2 then implies
$n\in \mathbb N$
. Lemma 10.2 then implies
![]() $\lim _{N\to \infty } ({1}/{N})\sum _{n=1}^N \chi (n\alpha + n^2\beta )=0$
.
$\lim _{N\to \infty } ({1}/{N})\sum _{n=1}^N \chi (n\alpha + n^2\beta )=0$
.
(ii) Assuming Z has finitely many connected components
![]() $Z_j$
and identity component
$Z_j$
and identity component
![]() $Z_0$
, let
$Z_0$
, let
![]() $A_j:=\{n\in \mathbb Z:n\alpha +n^2\beta \in Z_j\}$
, and let p be the index of
$A_j:=\{n\in \mathbb Z:n\alpha +n^2\beta \in Z_j\}$
, and let p be the index of
![]() $Z_0$
in Z. We claim that each
$Z_0$
in Z. We claim that each
![]() $A_j$
is a union of infinite arithmetic progressions of the form
$A_j$
is a union of infinite arithmetic progressions of the form
![]() $p\mathbb Z+q$
. To prove this, it suffices to prove
$p\mathbb Z+q$
. To prove this, it suffices to prove
![]() $A_j+p = A_j$
. To do so, observe that
$A_j+p = A_j$
. To do so, observe that
![]() $p\alpha , p\beta \in Z_0$
. We will show that if
$p\alpha , p\beta \in Z_0$
. We will show that if
![]() $n\kern1.2pt{\in}\kern1.2pt A_j$
, then
$n\kern1.2pt{\in}\kern1.2pt A_j$
, then
![]() $n\kern1.2pt{-}\kern1.2pt p\kern1.2pt{\in}\kern1.2pt A_j$
; in other words, if
$n\kern1.2pt{-}\kern1.2pt p\kern1.2pt{\in}\kern1.2pt A_j$
; in other words, if
![]() $n\alpha \kern1.2pt{+}\kern1.2pt n^2\beta \kern1.2pt{\in}\kern1.2pt Z_j$
, then
$n\alpha \kern1.2pt{+}\kern1.2pt n^2\beta \kern1.2pt{\in}\kern1.2pt Z_j$
, then
![]() $(n\kern1.2pt{+}\kern1.2pt p)\alpha \kern1.2pt{+}\kern1.2pt (n\kern1.2pt{+}\kern1.2pt p)^2\beta \kern1.2pt{\in}\kern1.2pt Z_j$
. Now fix
$(n\kern1.2pt{+}\kern1.2pt p)\alpha \kern1.2pt{+}\kern1.2pt (n\kern1.2pt{+}\kern1.2pt p)^2\beta \kern1.2pt{\in}\kern1.2pt Z_j$
. Now fix
![]() $n,j$
with
$n,j$
with
![]() $n\alpha +n^2\beta \in Z_j$
. Then
$n\alpha +n^2\beta \in Z_j$
. Then
as desired. Similarly, we can show that if
![]() $n\in A_j$
, then
$n\in A_j$
, then
![]() $n+p\in A_j$
, so that
$n+p\in A_j$
, so that
![]() $A_j+p=A_j$
.
$A_j+p=A_j$
.
Fix
![]() $q\in \mathbb Z$
. We claim
$q\in \mathbb Z$
. We claim
![]() $\alpha _0:=(1+2q)p\alpha $
and
$\alpha _0:=(1+2q)p\alpha $
and
![]() $\beta _0:=p^2\beta $
generate
$\beta _0:=p^2\beta $
generate
![]() $Z_0$
. To see this, note that the closed subgroup they generate is contained in
$Z_0$
. To see this, note that the closed subgroup they generate is contained in
![]() $Z_0$
, and has finite index in the subgroup generated by
$Z_0$
, and has finite index in the subgroup generated by
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
, while
$\beta $
, while
![]() $Z_0$
has no proper finite index closed subgroup.
$Z_0$
has no proper finite index closed subgroup.
We decompose the limit in equation (10.1) as
 $$ \begin{align} \frac{1}{p}\sum_{q=0}^{p-1} \lim_{N\to\infty} \frac{1}{N}\sum_{n=1}^N f((pn+q)\alpha + (pn+q)^2\beta). \end{align} $$
$$ \begin{align} \frac{1}{p}\sum_{q=0}^{p-1} \lim_{N\to\infty} \frac{1}{N}\sum_{n=1}^N f((pn+q)\alpha + (pn+q)^2\beta). \end{align} $$
Thinking of q as fixed, so that
![]() $(pn+q)\alpha + (pn+q)^2\beta \in Z_i$
for some i, it suffices to prove that the limit is
$(pn+q)\alpha + (pn+q)^2\beta \in Z_i$
for some i, it suffices to prove that the limit is
![]() $0$
when f is a character
$0$
when f is a character
![]() $\chi $
of Z which is not constant on
$\chi $
of Z which is not constant on
![]() $Z_i$
(and therefore not constant on
$Z_i$
(and therefore not constant on
![]() $Z_0$
). We fix such a
$Z_0$
). We fix such a
![]() $\chi $
and write
$\chi $
and write
 $$ \begin{align*} \chi((pn+q)\alpha + (pn+q)^2\beta) &= \chi(q\alpha+q^2\beta)\chi(n(1+2q)p\alpha+n^2p^2\beta)\\ &=\chi(q\alpha+q^2\beta)\chi(n\alpha_0+n^2\beta_0). \end{align*} $$
$$ \begin{align*} \chi((pn+q)\alpha + (pn+q)^2\beta) &= \chi(q\alpha+q^2\beta)\chi(n(1+2q)p\alpha+n^2p^2\beta)\\ &=\chi(q\alpha+q^2\beta)\chi(n\alpha_0+n^2\beta_0). \end{align*} $$
Since
![]() $\alpha _0$
and
$\alpha _0$
and
![]() $\beta _0$
generate
$\beta _0$
generate
![]() $Z_0$
, we have
$Z_0$
, we have
 $$ \begin{align*} \lim_{N\to\infty} \frac{1}{N}\sum_{n=1}^N \chi((pn+q)\alpha + (pn+q)^2\beta) = \chi(q\alpha+q^2\beta) \lim_{N\to\infty} \frac{1}{N}\sum_{n=1}^N \chi(n\alpha_0+n^2\beta_0) = 0, \end{align*} $$
$$ \begin{align*} \lim_{N\to\infty} \frac{1}{N}\sum_{n=1}^N \chi((pn+q)\alpha + (pn+q)^2\beta) = \chi(q\alpha+q^2\beta) \lim_{N\to\infty} \frac{1}{N}\sum_{n=1}^N \chi(n\alpha_0+n^2\beta_0) = 0, \end{align*} $$
by part (i). This shows that the averages in equation (10.3) converge to
![]() $0$
when f is a character which is not constant on
$0$
when f is a character which is not constant on
![]() $Z_i$
, completing the proof of part (ii).
$Z_i$
, completing the proof of part (ii).
To prove part (iii), fix
![]() $\alpha ,\alpha ', \beta \in Z$
and assume
$\alpha ,\alpha ', \beta \in Z$
and assume
![]() $H:=\overline {\langle \alpha \rangle }=\overline {\langle \alpha '\rangle }$
is a connected subgroup of Z. It suffices to prove that equation (10.2) holds when f is a character
$H:=\overline {\langle \alpha \rangle }=\overline {\langle \alpha '\rangle }$
is a connected subgroup of Z. It suffices to prove that equation (10.2) holds when f is a character
![]() $\chi $
of Z. If
$\chi $
of Z. If
![]() $\chi (H)=\{1\}$
, then
$\chi (H)=\{1\}$
, then
![]() $\chi (n\alpha +n^2\beta )=\chi (n\alpha '+n^2\beta )=\chi (n^2\beta $
), so the averages in equation (10.2) are equal. Now assume
$\chi (n\alpha +n^2\beta )=\chi (n\alpha '+n^2\beta )=\chi (n^2\beta $
), so the averages in equation (10.2) are equal. Now assume
![]() $\chi (H)\neq \{1\}$
. We will prove that both sides of equation (10.2) are
$\chi (H)\neq \{1\}$
. We will prove that both sides of equation (10.2) are
![]() $0$
. First note that
$0$
. First note that
![]() $\chi (H)=\{z\in \mathbb C:|z|=1\}$
, since H is compact and connected, and its image under
$\chi (H)=\{z\in \mathbb C:|z|=1\}$
, since H is compact and connected, and its image under
![]() $\chi $
is a non-trivial compact connected subgroup of
$\chi $
is a non-trivial compact connected subgroup of
![]() $\mathcal S^1$
. Since
$\mathcal S^1$
. Since
![]() $\alpha $
and
$\alpha $
and
![]() $\alpha '$
generate dense subgroups of H,
$\alpha '$
generate dense subgroups of H,
![]() $\chi (\alpha )$
and
$\chi (\alpha )$
and
![]() $\chi (\alpha ')$
generate dense subgroups of
$\chi (\alpha ')$
generate dense subgroups of
![]() $\chi (H)$
, and hence they are both not roots of unity. Lemma 10.2 then implies both limits in part (iii) are
$\chi (H)$
, and hence they are both not roots of unity. Lemma 10.2 then implies both limits in part (iii) are
![]() $0$
.
$0$
.
Remark 10.4. Part (iii) of Lemma 10.3 says that when
![]() $\beta $
is fixed and
$\beta $
is fixed and
![]() $\overline {\langle \alpha \rangle } = \overline {\langle \alpha '\rangle }$
is connected, the
$\overline {\langle \alpha \rangle } = \overline {\langle \alpha '\rangle }$
is connected, the
![]() $c_j$
provided by part (ii) do not change when
$c_j$
provided by part (ii) do not change when
![]() $\alpha '$
replaces
$\alpha '$
replaces
![]() $\alpha $
.
$\alpha $
.
11 The Roth integral and Fourier coefficients
Let Z be a compact abelian group with Haar probability measure m and
![]() $f:Z\to [0,1]$
. We examine the multilinear form which ‘counts 3-term arithmetic progressions’ in the support of f:
$f:Z\to [0,1]$
. We examine the multilinear form which ‘counts 3-term arithmetic progressions’ in the support of f:
Roth [Reference Roth22, Reference Roth23] (cf. [Reference Gowers14]) and Furstenberg [Reference Furstenberg11] observed that if
![]() $|\hat {f}(\chi )|$
is small for all non-trivial
$|\hat {f}(\chi )|$
is small for all non-trivial
![]() $\chi \in \widehat {Z}$
, then
$\chi \in \widehat {Z}$
, then
![]() $I_3(f)\approx (\int f\, dm)^3$
. Lemma 11.1 is a minor generalization of this fact; to state it, we first introduce some notation.
$I_3(f)\approx (\int f\, dm)^3$
. Lemma 11.1 is a minor generalization of this fact; to state it, we first introduce some notation.
Let
![]() $W=Z/K$
be a quotient of Z by a closed subgroup K. For
$W=Z/K$
be a quotient of Z by a closed subgroup K. For
![]() $f\in L^2(m)$
, let
$f\in L^2(m)$
, let
Let
![]() $\pi : Z\to W$
be the quotient map, and identify
$\pi : Z\to W$
be the quotient map, and identify
![]() $\widehat {W}$
with
$\widehat {W}$
with
![]() $\{\chi \circ \pi : \chi \in \widehat {W}\}\subseteq \widehat {Z}$
. We have
$\{\chi \circ \pi : \chi \in \widehat {W}\}\subseteq \widehat {Z}$
. We have
 $$ \begin{align} \widehat{f'}(\chi)=\begin{cases} \hat{f}(\chi) & \mbox{if } \chi\in\widehat{W}, \\[-2pt] 0 & \mbox{if } \chi \notin\widehat{W}. \end{cases} \end{align} $$
$$ \begin{align} \widehat{f'}(\chi)=\begin{cases} \hat{f}(\chi) & \mbox{if } \chi\in\widehat{W}, \\[-2pt] 0 & \mbox{if } \chi \notin\widehat{W}. \end{cases} \end{align} $$
To see this, note that for
![]() $\chi \in \widehat {W}$
, we have
$\chi \in \widehat {W}$
, we have
![]() $\chi (z+y)=\chi (z)$
for all
$\chi (z+y)=\chi (z)$
for all
![]() $y\in K$
, so
$y\in K$
, so
 $$ \begin{align*} \hat{f}(\chi) = \int f(z)\overline{\chi(z)}\, dm(z) &= \int \int f(z+y)\overline{\chi(z+y)} \, dm(z) \, dm_K(y)\\ &= \int \int f(z+y) \, dm_K(y) \overline{\chi(z)}\, dm(z)\\ &= \int f' \overline{\chi}\, dm\\ &=\widehat{f'}(\chi). \end{align*} $$
$$ \begin{align*} \hat{f}(\chi) = \int f(z)\overline{\chi(z)}\, dm(z) &= \int \int f(z+y)\overline{\chi(z+y)} \, dm(z) \, dm_K(y)\\ &= \int \int f(z+y) \, dm_K(y) \overline{\chi(z)}\, dm(z)\\ &= \int f' \overline{\chi}\, dm\\ &=\widehat{f'}(\chi). \end{align*} $$
Now for
![]() $\chi \notin \widehat {W}$
, there exists
$\chi \notin \widehat {W}$
, there exists
![]() $t\in K$
such that
$t\in K$
such that
![]() $\chi (t)\neq 1$
. Since
$\chi (t)\neq 1$
. Since
![]() $f'(z+s)=f'(z)$
for all
$f'(z+s)=f'(z)$
for all
![]() $s\in K$
, we have
$s\in K$
, we have
 $$ \begin{align*} \widehat{f'}(\chi) = \int f'(z) \overline{\chi(z)} \, dm(z) &= \int f'(z+t)\overline{\chi(z+t)} \, dm(z)\\[-2pt] &= \int f'(z)\overline{\chi(z+t)}\, dm(z)\\[-2pt] &= \overline{\chi(t)}\int f'(z)\overline{\chi(z)}\, dm(z)\\[-2pt] &= \overline{\chi(t)}\widehat{f'}(\chi). \end{align*} $$
$$ \begin{align*} \widehat{f'}(\chi) = \int f'(z) \overline{\chi(z)} \, dm(z) &= \int f'(z+t)\overline{\chi(z+t)} \, dm(z)\\[-2pt] &= \int f'(z)\overline{\chi(z+t)}\, dm(z)\\[-2pt] &= \overline{\chi(t)}\int f'(z)\overline{\chi(z)}\, dm(z)\\[-2pt] &= \overline{\chi(t)}\widehat{f'}(\chi). \end{align*} $$
So
![]() $\widehat {f'}(\chi ) = \overline {\chi (t)}\widehat {f'}(\chi )$
, which is possible only if
$\widehat {f'}(\chi ) = \overline {\chi (t)}\widehat {f'}(\chi )$
, which is possible only if
![]() $\widehat {f'}(\chi )=0$
.
$\widehat {f'}(\chi )=0$
.
Below we will use
![]() $dz$
and
$dz$
and
![]() $dt$
to indicate integration over all of Z with respect to the displayed variable. Integration over K will be indicated by
$dt$
to indicate integration over all of Z with respect to the displayed variable. Integration over K will be indicated by
![]() $\,dm_K$
.
$\,dm_K$
.
Lemma 11.1. With Z, K, and W as defined above, let
![]() $f_0, f_1, f_2 \in L^\infty (m)$
, and write
$f_0, f_1, f_2 \in L^\infty (m)$
, and write
 $$ \begin{align*} I &:= \int \int f_0(z)f_1(z+t)f_2(z+2t)\, dz \, dt,\\ I_W&:= \int \int f_0'(z)f_1'(z+t)f_2'(z+2t) \, dz \, dt. \end{align*} $$
$$ \begin{align*} I &:= \int \int f_0(z)f_1(z+t)f_2(z+2t)\, dz \, dt,\\ I_W&:= \int \int f_0'(z)f_1'(z+t)f_2'(z+2t) \, dz \, dt. \end{align*} $$
Suppose
![]() $|\hat {f}_2(\chi )|\leq \kappa $
for all
$|\hat {f}_2(\chi )|\leq \kappa $
for all
![]() $\chi \in \widehat {Z} \setminus \widehat {W}$
. Assuming the map
$\chi \in \widehat {Z} \setminus \widehat {W}$
. Assuming the map
![]() $\chi \mapsto \chi ^2$
is injective on
$\chi \mapsto \chi ^2$
is injective on
![]() $\widehat {Z}$
, we have
$\widehat {Z}$
, we have
Proof. Let
![]() $I_2= \int \int f_0(z)f_1(z+t)f_2'(z+2t)\, dz\, dt$
. We will prove that
$I_2= \int \int f_0(z)f_1(z+t)f_2'(z+2t)\, dz\, dt$
. We will prove that
and that
![]() $I_2 = I_W$
. We first prove the special case where each
$I_2 = I_W$
. We first prove the special case where each
![]() $f_i$
is a trigonometric polynomial. Expanding each
$f_i$
is a trigonometric polynomial. Expanding each
![]() $f_i$
as
$f_i$
as
![]() $\sum _{\chi \in \widehat {Z}} \hat {f}_i(\chi )\chi $
and simplifying, we get
$\sum _{\chi \in \widehat {Z}} \hat {f}_i(\chi )\chi $
and simplifying, we get
 $$ \begin{align*} I &= \sum_{\chi, \psi,\tau \in \widehat{Z}} \int \hat{f}_0(\chi)\chi(z) \hat{f}_1(\psi)\psi(z+t) \hat{f}_2(\tau)\tau(z+2t)\, dz \, dt\\[-2pt] &= \sum_{\chi, \psi, \tau \in \widehat{Z}} \int \hat{f}_0(\chi) \hat{f}_1(\psi) \hat{f}_2(\tau) \chi\psi\tau(z) \psi\tau^2(t)\, dz\, dt\\[-2pt] &= \sum_{\chi,\psi,\tau\in\widehat{Z}} \hat{f}_0(\chi) \hat{f}_1(\psi) \hat{f}_2(\tau) \int \chi\psi\tau(z)\, dz \int \psi \tau^2(t)\, dt. \end{align*} $$
$$ \begin{align*} I &= \sum_{\chi, \psi,\tau \in \widehat{Z}} \int \hat{f}_0(\chi)\chi(z) \hat{f}_1(\psi)\psi(z+t) \hat{f}_2(\tau)\tau(z+2t)\, dz \, dt\\[-2pt] &= \sum_{\chi, \psi, \tau \in \widehat{Z}} \int \hat{f}_0(\chi) \hat{f}_1(\psi) \hat{f}_2(\tau) \chi\psi\tau(z) \psi\tau^2(t)\, dz\, dt\\[-2pt] &= \sum_{\chi,\psi,\tau\in\widehat{Z}} \hat{f}_0(\chi) \hat{f}_1(\psi) \hat{f}_2(\tau) \int \chi\psi\tau(z)\, dz \int \psi \tau^2(t)\, dt. \end{align*} $$
At least one of
![]() $\int \psi \tau ^2(t)\, dt$
or
$\int \psi \tau ^2(t)\, dt$
or
![]() $\int \chi \psi \tau (z)\, dz$
is zero unless
$\int \chi \psi \tau (z)\, dz$
is zero unless
![]() $\psi \tau ^2$
and
$\psi \tau ^2$
and
![]() $\chi \psi \tau $
are both trivial; this triviality occurs exactly when
$\chi \psi \tau $
are both trivial; this triviality occurs exactly when
![]() $\psi = \tau ^{-2}$
and
$\psi = \tau ^{-2}$
and
![]() $\chi =\tau $
. The sum in the last line above may therefore be restricted to values of
$\chi =\tau $
. The sum in the last line above may therefore be restricted to values of
![]() $\chi ,\psi ,$
and
$\chi ,\psi ,$
and
![]() $\tau $
satisfying these identities, and we get
$\tau $
satisfying these identities, and we get
 $$ \begin{align*} I=\sum_{\tau \in \widehat{Z}} \hat{f}_0(\tau)\hat{f}_1(\tau^{-2})\hat{f}_2(\tau). \end{align*} $$
$$ \begin{align*} I=\sum_{\tau \in \widehat{Z}} \hat{f}_0(\tau)\hat{f}_1(\tau^{-2})\hat{f}_2(\tau). \end{align*} $$
As noted in equation (11.2),
![]() $\hat {f}_2'(\tau ) = \hat {f}_2(\tau )$
for
$\hat {f}_2'(\tau ) = \hat {f}_2(\tau )$
for
![]() $\tau \in \widehat {W}$
and
$\tau \in \widehat {W}$
and
![]() $\widehat {f'}_2(\tau )=0$
for
$\widehat {f'}_2(\tau )=0$
for
![]() $\tau \notin \widehat {Z}\setminus \widehat {W},$
so
$\tau \notin \widehat {Z}\setminus \widehat {W},$
so
 $$ \begin{align*} I_2 = \sum_{\tau \in \widehat{W}} \hat{f}_0(\tau)\hat{f}_1(\tau^{-2})\hat{f}_2(\tau). \end{align*} $$
$$ \begin{align*} I_2 = \sum_{\tau \in \widehat{W}} \hat{f}_0(\tau)\hat{f}_1(\tau^{-2})\hat{f}_2(\tau). \end{align*} $$
Then,
 $$ \begin{align*} |I - I_2| & = \bigg|\sum_{\tau \notin \widehat{W}} \hat{f}_0(\tau)\hat{f}_1(\tau^{-2})\hat{f}_2(\tau)\bigg|\\ &\leq \sum_{\tau\in \widehat{Z}} \kappa |\hat{f}_0(\tau) \hat{f}_1(\tau^{-2 })| \ \ \quad \text{ since } |\hat{f}_2(\tau)|<\kappa \text{ for } \tau\notin \widehat{W}\\ &\leq \kappa \|\hat{f}_0\|_{l^2}\|\hat{f}_1\|_{l^2} \qquad\qquad \ \ \text{Cauchy--Schwarz, assuming } \tau\mapsto \tau^2 \text{ is injective}\\ &= \kappa \|f_0\|_{L^2(m)}\|f_1\|_{L^2(m)}, \quad \text{Plancherel}, \end{align*} $$
$$ \begin{align*} |I - I_2| & = \bigg|\sum_{\tau \notin \widehat{W}} \hat{f}_0(\tau)\hat{f}_1(\tau^{-2})\hat{f}_2(\tau)\bigg|\\ &\leq \sum_{\tau\in \widehat{Z}} \kappa |\hat{f}_0(\tau) \hat{f}_1(\tau^{-2 })| \ \ \quad \text{ since } |\hat{f}_2(\tau)|<\kappa \text{ for } \tau\notin \widehat{W}\\ &\leq \kappa \|\hat{f}_0\|_{l^2}\|\hat{f}_1\|_{l^2} \qquad\qquad \ \ \text{Cauchy--Schwarz, assuming } \tau\mapsto \tau^2 \text{ is injective}\\ &= \kappa \|f_0\|_{L^2(m)}\|f_1\|_{L^2(m)}, \quad \text{Plancherel}, \end{align*} $$
where
![]() $\|\cdot \|_{l^2}$
denotes the
$\|\cdot \|_{l^2}$
denotes the
![]() $l^2$
norm for functions on
$l^2$
norm for functions on
![]() $\widehat {Z}$
.
$\widehat {Z}$
.
To prove
![]() $I_2=I_W$
, replace t with
$I_2=I_W$
, replace t with
![]() $t+s$
in the
$t+s$
in the
![]() $dt$
integral in
$dt$
integral in
![]() $I_2$
, then integrate s over K, using the fact that
$I_2$
, then integrate s over K, using the fact that
![]() $f_2'(z+s)=f_2(z)$
for all
$f_2'(z+s)=f_2(z)$
for all
![]() $z\in Z$
,
$z\in Z$
,
![]() $s\in K$
:
$s\in K$
:
 $$ \begin{align*} I_2 &= \int \int f_0(z) f_1(z+t)f_2'(z+2t) \, dz \, dt\\[-2pt] &= \int_K \int \int f_0(z) f_1(z+t+s) f_2'(z+2t+2s) \, dz \, dt\, dm_K(s)\\[-2pt] &= \int \int f_0(z) \int_K f_1(z+t+s)\, dm_K(s)\, f_2'(z+2t) \, dz \, dt \\[-2pt] &= \int \int f_0(z) f_1'(z+t) f_2'(z+2t) \, dz\, dt. \end{align*} $$
$$ \begin{align*} I_2 &= \int \int f_0(z) f_1(z+t)f_2'(z+2t) \, dz \, dt\\[-2pt] &= \int_K \int \int f_0(z) f_1(z+t+s) f_2'(z+2t+2s) \, dz \, dt\, dm_K(s)\\[-2pt] &= \int \int f_0(z) \int_K f_1(z+t+s)\, dm_K(s)\, f_2'(z+2t) \, dz \, dt \\[-2pt] &= \int \int f_0(z) f_1'(z+t) f_2'(z+2t) \, dz\, dt. \end{align*} $$
A similar manipulation, replacing z with
![]() $z+s$
, lets us replace
$z+s$
, lets us replace
![]() $f_0$
with
$f_0$
with
![]() $f_0'$
, completing the proof that
$f_0'$
, completing the proof that
![]() $I_2=I_W$
, and hence
$I_2=I_W$
, and hence
![]() $|I - I_W|\leq \kappa \|f_0\|_{L^2(m)}\|f_1\|_{L^2(m)}$
. This proves eqaution (11.4).
$|I - I_W|\leq \kappa \|f_0\|_{L^2(m)}\|f_1\|_{L^2(m)}$
. This proves eqaution (11.4).
12 Annihilating characters
Let
![]() $d,r\in \mathbb N$
, let
$d,r\in \mathbb N$
, let
![]() $f:\mathbb T^d\times \mathbb T^d\to \mathbb C$
,
$f:\mathbb T^d\times \mathbb T^d\to \mathbb C$
,
![]() $g:\mathbb T^r\to \mathbb C$
, and let
$g:\mathbb T^r\to \mathbb C$
, and let
![]() $\Gamma $
be an affine joining of
$\Gamma $
be an affine joining of
![]() $\mathbb T^d$
with
$\mathbb T^d$
with
![]() $\mathbb T^r$
(Definition 9.4). The limits we compute in the proof of Lemma 5.1 will contain functions of the form
$\mathbb T^r$
(Definition 9.4). The limits we compute in the proof of Lemma 5.1 will contain functions of the form
![]() $f*_{\Gamma } g:\mathbb T^d\times \mathbb T^d\to \mathbb C$
, defined by
$f*_{\Gamma } g:\mathbb T^d\times \mathbb T^d\to \mathbb C$
, defined by
The next two lemmas let us bound the Fourier coefficients of
![]() $f*_{\Gamma } g$
. We use the abbreviation
$f*_{\Gamma } g$
. We use the abbreviation
![]() $w_i$
for
$w_i$
for
![]() $\pi _i(w)$
introduced in Notation 9.2.
$\pi _i(w)$
introduced in Notation 9.2.
Lemma 12.1. Let
![]() $k<r\in \mathbb N$
and
$k<r\in \mathbb N$
and
![]() $U\subseteq \mathbb T^r$
be an approximate Hamming ball of radius
$U\subseteq \mathbb T^r$
be an approximate Hamming ball of radius
![]() $(k,\eta )$
,
$(k,\eta )$
,
![]() $\eta>0$
. Then we have the following.
$\eta>0$
. Then we have the following.
-
(i) If Z is a compact abelian group,
 $\pi :Z\to \mathbb T^r $
is a continuous homomorphism, and
$\pi :Z\to \mathbb T^r $
is a continuous homomorphism, and
 $\chi _1,\ldots ,\chi _k\in \widehat {Z}$
are non-trivial, then there is a cylinder function g subordinate to U such that
$\chi _1,\ldots ,\chi _k\in \widehat {Z}$
are non-trivial, then there is a cylinder function g subordinate to U such that
 $\widehat {g_{s}\circ \pi }(\chi _j)=0$
for each j and each translate
$\widehat {g_{s}\circ \pi }(\chi _j)=0$
for each j and each translate
 $g_{s}$
of g.
$g_{s}$
of g. -
(ii) If
 $\Gamma $
is an affine joining of
$\Gamma $
is an affine joining of
 $\mathbb T^d$
with
$\mathbb T^d$
with
 $\mathbb T^r$
and
$\mathbb T^r$
and
 $\chi _1,\ldots ,\chi _k\in \widehat {\mathbb T}^d$
are non-trivial, then there is a cylinder function g subordinate to U such that
$\chi _1,\ldots ,\chi _k\in \widehat {\mathbb T}^d$
are non-trivial, then there is a cylinder function g subordinate to U such that
 $\int \chi _j(w_1) g(w_2)\, dm_{\Gamma }(w) = 0$
for each
$\int \chi _j(w_1) g(w_2)\, dm_{\Gamma }(w) = 0$
for each
 $j\leq k$
.
$j\leq k$
.
Proof. (i) Let
![]() $\chi _j \in \widehat {Z}$
for
$\chi _j \in \widehat {Z}$
for
![]() $j\leq k$
, and let K be the kernel of
$j\leq k$
, and let K be the kernel of
![]() $\pi $
. We first consider those
$\pi $
. We first consider those
![]() $\chi _j$
where
$\chi _j$
where
![]() $\chi _j|_K$
is constant. In this case,
$\chi _j|_K$
is constant. In this case,
![]() $\chi _j$
can be written as
$\chi _j$
can be written as
![]() $\chi _j'\circ \pi $
, where
$\chi _j'\circ \pi $
, where
![]() $\chi _j'\in \widehat {\mathbb T}^r$
, and
$\chi _j'\in \widehat {\mathbb T}^r$
, and
![]() $\int (g_{s}\circ \pi )\, \overline {\chi }_j\, dm$
can be written as
$\int (g_{s}\circ \pi )\, \overline {\chi }_j\, dm$
can be written as
So choose g by Lemma 3.9 to make these integrals vanish for such
![]() $\chi _j$
. For those j where
$\chi _j$
. For those j where
![]() $\chi _j|_K$
is not constant, write
$\chi _j|_K$
is not constant, write
![]() $\int _Z f(z)\, dz$
as
$\int _Z f(z)\, dz$
as
![]() $\int _{Z} \int _{K} f(z+t) dm_K(t)\, dm(z).$
Then
$\int _{Z} \int _{K} f(z+t) dm_K(t)\, dm(z).$
Then
 $$ \begin{align*} \widehat{g_s\circ \pi}(\chi_j)=\int g_{s}(\pi(z)) \overline{\chi_j(z)}\, dz &= \int \int g_{s}(\pi(z+t)) \overline{\chi_j(z+t) }\, dm_K(t)\, dz \\[-2pt] &= \int g_{s}(\pi(z))\overline{\chi_j(z)} \, dz\, \int_{K} \overline{\chi_j(t)}\, dm_K(t) \\[-2pt] &=0, \end{align*} $$
$$ \begin{align*} \widehat{g_s\circ \pi}(\chi_j)=\int g_{s}(\pi(z)) \overline{\chi_j(z)}\, dz &= \int \int g_{s}(\pi(z+t)) \overline{\chi_j(z+t) }\, dm_K(t)\, dz \\[-2pt] &= \int g_{s}(\pi(z))\overline{\chi_j(z)} \, dz\, \int_{K} \overline{\chi_j(t)}\, dm_K(t) \\[-2pt] &=0, \end{align*} $$
where the last line follows from the fact that
![]() $\chi _j|_K$
is a non-trivial character of K.
$\chi _j|_K$
is a non-trivial character of K.
(ii) Since
![]() $\Gamma $
is an affine joining of
$\Gamma $
is an affine joining of
![]() $\mathbb T^d$
with
$\mathbb T^d$
with
![]() $\mathbb T^r$
, by definition, there is a joining
$\mathbb T^r$
, by definition, there is a joining
![]() $\Gamma _0$
so that the integral over
$\Gamma _0$
so that the integral over
![]() $\Gamma $
is a convex combination of integrals over translates of
$\Gamma $
is a convex combination of integrals over translates of
![]() $\Gamma _0$
. To prove part (ii), it therefore suffices to find a g subordinate to U so that
$\Gamma _0$
. To prove part (ii), it therefore suffices to find a g subordinate to U so that
![]() $\int \chi (w_1)g(w_2)\, dm_{\Gamma +t}(w)=0$
for every
$\int \chi (w_1)g(w_2)\, dm_{\Gamma +t}(w)=0$
for every
![]() $t\in \mathbb T^{d}\times \mathbb T^{r}$
. We will use the identity
$t\in \mathbb T^{d}\times \mathbb T^{r}$
. We will use the identity
 $$ \begin{align} \int \chi(w_1)g(w_2)\, dm_{\Gamma+t}(w) = \chi(\pi_1(t)) \int_{\Gamma_0} \chi(w_1)g_{\pi_2(t)}(w_2)\, dm_{\Gamma_0}(w), \end{align} $$
$$ \begin{align} \int \chi(w_1)g(w_2)\, dm_{\Gamma+t}(w) = \chi(\pi_1(t)) \int_{\Gamma_0} \chi(w_1)g_{\pi_2(t)}(w_2)\, dm_{\Gamma_0}(w), \end{align} $$
which follows from the manipulations
 $$ \begin{align*} \int_{\Gamma_0+t} \chi(w_1)g(w_2)\, dm_{\Gamma_0+t}(w) &= \int_{\Gamma_0} \chi(\pi_1(w+t))g(\pi_2(w+t)) \, dm_{\Gamma_0}(w)\\[3pt] &= \int_{\Gamma_0} \chi(\pi_1(t)) \chi(\pi_1(w))g(\pi_2(w)+\pi_2(t))\, dm_{\Gamma_0}(w)\\[3pt] &= \chi(\pi_1(t)) \int_{\Gamma_0} \chi(w_1)g_{\pi_2(t)}(w_2)\, dm_{\Gamma_0}(w). \end{align*} $$
$$ \begin{align*} \int_{\Gamma_0+t} \chi(w_1)g(w_2)\, dm_{\Gamma_0+t}(w) &= \int_{\Gamma_0} \chi(\pi_1(w+t))g(\pi_2(w+t)) \, dm_{\Gamma_0}(w)\\[3pt] &= \int_{\Gamma_0} \chi(\pi_1(t)) \chi(\pi_1(w))g(\pi_2(w)+\pi_2(t))\, dm_{\Gamma_0}(w)\\[3pt] &= \chi(\pi_1(t)) \int_{\Gamma_0} \chi(w_1)g_{\pi_2(t)}(w_2)\, dm_{\Gamma_0}(w). \end{align*} $$
We can consider the functions
![]() $z\mapsto \chi _j(\pi _1(z))$
as characters
$z\mapsto \chi _j(\pi _1(z))$
as characters
![]() $\tilde {\chi }_j\ \mathrm{on}\ \Gamma _0$
. These characters are non-trivial since
$\tilde {\chi }_j\ \mathrm{on}\ \Gamma _0$
. These characters are non-trivial since
![]() $\pi _1:\Gamma _0\to \mathbb T^d$
is surjective, so we can apply part (i) of the present lemma (with
$\pi _1:\Gamma _0\to \mathbb T^d$
is surjective, so we can apply part (i) of the present lemma (with
![]() $\Gamma _0$
in place of Z and
$\Gamma _0$
in place of Z and
![]() $\pi _2$
in place of
$\pi _2$
in place of
![]() $\pi $
) to find g subordinate to U so that
$\pi $
) to find g subordinate to U so that
![]() $\int _{\Gamma _0} \chi _j(\pi _1(w)) g_{s}(\pi _2(w))\, dm_{\Gamma _0}(w)=: \widehat {g_s\circ \pi _2}(\tilde {\chi }_j)=0$
for every translate
$\int _{\Gamma _0} \chi _j(\pi _1(w)) g_{s}(\pi _2(w))\, dm_{\Gamma _0}(w)=: \widehat {g_s\circ \pi _2}(\tilde {\chi }_j)=0$
for every translate
![]() $g_{s}$
of g and every
$g_{s}$
of g and every
![]() $j\leq k$
. In light of equation (12.2), this proves part (ii).
$j\leq k$
. In light of equation (12.2), this proves part (ii).
The expression
![]() $f*_{\Gamma } g$
in the next lemma is defined in equation (12.1); for
$f*_{\Gamma } g$
in the next lemma is defined in equation (12.1); for
![]() $h:\mathbb T^d\times \mathbb T^d\to \mathbb C$
,
$h:\mathbb T^d\times \mathbb T^d\to \mathbb C$
,
![]() $h':\mathbb T^d\to \mathbb C$
is defined as
$h':\mathbb T^d\to \mathbb C$
is defined as
![]() $h'(x):=\int _{\mathbb T^d} h(x,y) \, dy$
.
$h'(x):=\int _{\mathbb T^d} h(x,y) \, dy$
.
Lemma 12.2. Let
![]() $k,d,r\in \mathbb N$
, and let
$k,d,r\in \mathbb N$
, and let
![]() $\Gamma $
be an affine joining of
$\Gamma $
be an affine joining of
![]() $\mathbb T^d$
with
$\mathbb T^d$
with
![]() $\mathbb T^r$
. Let
$\mathbb T^r$
. Let
![]() $U\subseteq \mathbb T^r$
be an approximate Hamming ball of radius
$U\subseteq \mathbb T^r$
be an approximate Hamming ball of radius
![]() $(k,\eta )$
for some
$(k,\eta )$
for some
![]() $\eta>0$
.
$\eta>0$
.
Let
![]() $f:\mathbb T^d\times \mathbb T^d\to [0,1]$
. Then there is a cylinder function g subordinate to U such that
$f:\mathbb T^d\times \mathbb T^d\to [0,1]$
. Then there is a cylinder function g subordinate to U such that
Proof. Let
![]() $(\chi ,\psi )_j$
,
$(\chi ,\psi )_j$
,
![]() $j\leq k$
, denote the characters of
$j\leq k$
, denote the characters of
![]() $\mathbb T^d\times \mathbb T^d$
having the k largest values of
$\mathbb T^d\times \mathbb T^d$
having the k largest values of
![]() $|\hat {f}(\chi ,\psi )|$
, among those where
$|\hat {f}(\chi ,\psi )|$
, among those where
![]() $\psi $
is non-trivial. Lemma 3.7 implies
$\psi $
is non-trivial. Lemma 3.7 implies
Applying part (ii) of Lemma 12.1 with
![]() $\psi ^2$
in place of the
$\psi ^2$
in place of the
![]() $\chi _j$
, we may choose a cylinder function g subordinate to U such that
$\chi _j$
, we may choose a cylinder function g subordinate to U such that
Expand f as a Fourier series
![]() $\sum _{(\chi ,\psi )\in \widehat {\mathbb T}^d\times \widehat {\mathbb T}^d} \hat {f}(\chi ,\psi )\chi \psi $
, so that
$\sum _{(\chi ,\psi )\in \widehat {\mathbb T}^d\times \widehat {\mathbb T}^d} \hat {f}(\chi ,\psi )\chi \psi $
, so that
 $$ \begin{align*} f*_{\Gamma}g&=\int f(x,y+2w_1)g(w_2)\, dm_{\Gamma}(w) \\ &= \sum_{(\chi,\psi)} \hat{f}(\chi,\psi)\chi(x)\int \psi(y+2w_1)g(w_2)\, dm_{\Gamma}(w)\\ &= \sum_{(\chi,\psi)} \hat{f}(\chi,\psi)\chi(x)\psi(y)\int \psi(2w_1)g(w_2)\, dm_{\Gamma}(w), \end{align*} $$
$$ \begin{align*} f*_{\Gamma}g&=\int f(x,y+2w_1)g(w_2)\, dm_{\Gamma}(w) \\ &= \sum_{(\chi,\psi)} \hat{f}(\chi,\psi)\chi(x)\int \psi(y+2w_1)g(w_2)\, dm_{\Gamma}(w)\\ &= \sum_{(\chi,\psi)} \hat{f}(\chi,\psi)\chi(x)\psi(y)\int \psi(2w_1)g(w_2)\, dm_{\Gamma}(w), \end{align*} $$
and
The integral in equation (12.7) is
![]() $0$
when
$0$
when
![]() $(\chi ,\psi )$
are among the
$(\chi ,\psi )$
are among the
![]() $(\chi ,\psi )_j$
, so the inequality in equation (12.3) is satisfied for these characters. For the remaining characters with
$(\chi ,\psi )_j$
, so the inequality in equation (12.3) is satisfied for these characters. For the remaining characters with
![]() $\psi $
non-trivial, note that
$\psi $
non-trivial, note that
![]() $\int |g|\, dm=1$
, so equation (12.7) implies
$\int |g|\, dm=1$
, so equation (12.7) implies
![]() $|\widehat {f*_{\Gamma }g}|\leq |\hat {f}|$
everywhere. Now equations (12.5) and (12.6) imply equation (12.3). To prove equation (12.4), write
$|\widehat {f*_{\Gamma }g}|\leq |\hat {f}|$
everywhere. Now equations (12.5) and (12.6) imply equation (12.3). To prove equation (12.4), write
 $$ \begin{align*} (f*_\Gamma g)'(x) &= \int \int f(x,y+w_1) g(w_2)\, dm_{\Gamma}(w)\, dy\\ &= \int \int f(x,y+w_1) \, dy \, g(w_2)\, dm_{\Gamma}(w)\\ &= f'(x) \int g(w_2)\, dm_{\Gamma}(w)\\ &= f'(x). \\[-3pc] \end{align*} $$
$$ \begin{align*} (f*_\Gamma g)'(x) &= \int \int f(x,y+w_1) g(w_2)\, dm_{\Gamma}(w)\, dy\\ &= \int \int f(x,y+w_1) \, dy \, g(w_2)\, dm_{\Gamma}(w)\\ &= f'(x) \int g(w_2)\, dm_{\Gamma}(w)\\ &= f'(x). \\[-3pc] \end{align*} $$
Lemma 12.3. With the hypotheses of Lemma 12.2, let
![]() $f: \mathbb T^d\times \mathbb T^d\to [0,1]$
, define
$f: \mathbb T^d\times \mathbb T^d\to [0,1]$
, define
![]() $f'\kern1.2pt{:}\kern1.2pt \mathbb T^d\kern1pt{\to}\kern1pt [0,1\kern-0.9pt]$
by
$f'\kern1.2pt{:}\kern1.2pt \mathbb T^d\kern1pt{\to}\kern1pt [0,1\kern-0.9pt]$
by
![]() $f'\kern-1pt(x\kern-0.2pt)\kern1pt{:=}\kern0.4pt\int _{\mathbb T^d} \kern-2pt f(x\kern-0.1pt,y\kern-0.2pt)\kern1pt dy$
, and let
$f'\kern-1pt(x\kern-0.2pt)\kern1pt{:=}\kern0.4pt\int _{\mathbb T^d} \kern-2pt f(x\kern-0.1pt,y\kern-0.2pt)\kern1pt dy$
, and let
![]() ${J'\kern1.2pt{:=}\kern-0.2pt \int\kern-3pt \int\kern-3pt f'\kern-1pt(x\kern-0.2pt)f'(x\kern1pt{+}\kern1pt s\kern-0.2pt) f'\kern-1pt(x\kern1pt{+}\kern1pt 2s\kern-0.2pt) \kern1pt ds \kern1pt dx}\kern-0.3pt$
. Then there is a cylinder function g subordinate to U such that
${J'\kern1.2pt{:=}\kern-0.2pt \int\kern-3pt \int\kern-3pt f'\kern-1pt(x\kern-0.2pt)f'(x\kern1pt{+}\kern1pt s\kern-0.2pt) f'\kern-1pt(x\kern1pt{+}\kern1pt 2s\kern-0.2pt) \kern1pt ds \kern1pt dx}\kern-0.3pt$
. Then there is a cylinder function g subordinate to U such that
satisfies
![]() $|J-J'|<k^{-1/2}$
.
$|J-J'|<k^{-1/2}$
.
Proof. Choose, by Lemma 12.2, a cylinder function g subordinate to U so that
Now we apply Lemma 11.1 with
![]() $Z = \mathbb T^d\times \mathbb T^d$
,
$Z = \mathbb T^d\times \mathbb T^d$
,
![]() $W = \mathbb T^d$
,
$W = \mathbb T^d$
,
![]() $K= \{0\}\times \mathbb T^d$
,
$K= \{0\}\times \mathbb T^d$
,
![]() $I= J$
, and
$I= J$
, and
![]() $I_W = \int f'(x)f'(x+s)(f*_{\Gamma } g)'(x+2s) \, dx\, ds$
, using
$I_W = \int f'(x)f'(x+s)(f*_{\Gamma } g)'(x+2s) \, dx\, ds$
, using
![]() $\kappa = k^{-1/2}$
as supplied by equation (12.8). We conclude that
$\kappa = k^{-1/2}$
as supplied by equation (12.8). We conclude that
![]() $|J-I_W|<k^{-1/2}$
. Since
$|J-I_W|<k^{-1/2}$
. Since
![]() $(f*_{\Gamma }g)'=f'$
, we have
$(f*_{\Gamma }g)'=f'$
, we have
![]() $I_W=J'$
, so this is the desired conclusion.
$I_W=J'$
, so this is the desired conclusion.
13 Averages for standard 2-step Weyl systems
In the next section, we will prove Lemma 5.1 by reducing the general statement to the special case where the totally ergodic system under consideration is a standard 2-step Weyl system. Proposition 13.1 will then allow us to compute the limit of the multiple ergodic averages appearing in equation (5.1).
For the remainder of this section, we fix
![]() $d, r\in \mathbb N$
,
$d, r\in \mathbb N$
,
![]() $\alpha \in \mathbb T^d$
,
$\alpha \in \mathbb T^d$
,
![]() $\beta \in \mathbb T^r$
and let
$\beta \in \mathbb T^r$
and let
![]() $S:(\mathbb T^d)^2\to (\mathbb T^d)^2$
be given by
$S:(\mathbb T^d)^2\to (\mathbb T^d)^2$
be given by
![]() $S( x, y) = ( x + 2\alpha , y + x)$
. We assume
$S( x, y) = ( x + 2\alpha , y + x)$
. We assume
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
generate
$\beta $
generate
![]() $\mathbb T^d$
and
$\mathbb T^d$
and
![]() $\mathbb T^r$
, respectively, and we write m for Haar probability measure on
$\mathbb T^r$
, respectively, and we write m for Haar probability measure on
![]() $\mathbb T^d$
. We maintain the notational conventions introduced in §5 and the intervening sections.
$\mathbb T^d$
. We maintain the notational conventions introduced in §5 and the intervening sections.
Proposition 13.1. With
![]() $d, r, \alpha , \beta $
, and S defined above, there is an affine joining
$d, r, \alpha , \beta $
, and S defined above, there is an affine joining
![]() $\Gamma $
of
$\Gamma $
of
![]() $\mathbb T^d$
with
$\mathbb T^d$
with
![]() $\mathbb T^r$
such that for all Riemann integrable
$\mathbb T^r$
such that for all Riemann integrable
![]() $g:\mathbb T^r\to \mathbb R$
and all bounded measurable
$g:\mathbb T^r\to \mathbb R$
and all bounded measurable
![]() $f: \mathbb T^d\times \mathbb T^d\to \mathbb R$
, we have
$f: \mathbb T^d\times \mathbb T^d\to \mathbb R$
, we have
 $$ \begin{align} &\lim_{N\to\infty} \frac{1}{N}\sum_{n=1}^N g(n^2\beta)\int f \cdot f\circ S^n\cdot f\circ S^{2n} \, d(m\times m) \nonumber\\ &\quad=\int f(x,y) f(x+s,y+t) f*_{\Gamma}g(x+2s, y+2t) \, ds\, dt \, dx\, dy, \end{align} $$
$$ \begin{align} &\lim_{N\to\infty} \frac{1}{N}\sum_{n=1}^N g(n^2\beta)\int f \cdot f\circ S^n\cdot f\circ S^{2n} \, d(m\times m) \nonumber\\ &\quad=\int f(x,y) f(x+s,y+t) f*_{\Gamma}g(x+2s, y+2t) \, ds\, dt \, dx\, dy, \end{align} $$
where
![]() $f*_\Gamma g$
defined in equation (12.1).
$f*_\Gamma g$
defined in equation (12.1).
Remark 13.2. We use ‘
![]() $2\alpha $
’ in place of ‘
$2\alpha $
’ in place of ‘
![]() $\alpha $
’ in our definition of S to simplify computations. Since every generating
$\alpha $
’ in our definition of S to simplify computations. Since every generating
![]() $\alpha \in \mathbb T^d$
can be written as
$\alpha \in \mathbb T^d$
can be written as
![]() $2\alpha '$
, where
$2\alpha '$
, where
![]() $\alpha '$
is generating, there is no loss of generality.
$\alpha '$
is generating, there is no loss of generality.
We first prove Lemma 13.4, which provides explicit limits of polynomial averages on
![]() $(\mathbb T^d)^4\times \mathbb T^r$
. Lemma 13.5 then provides an explicit pointwise-almost everywhere limit for the relevant averages in equation (13.1) when f and g are continuous. Corollary 13.6 uses these to establish
$(\mathbb T^d)^4\times \mathbb T^r$
. Lemma 13.5 then provides an explicit pointwise-almost everywhere limit for the relevant averages in equation (13.1) when f and g are continuous. Corollary 13.6 uses these to establish
![]() $L^2$
convergence with the same limit formula, for bounded measurable f and Riemann integrable g. Proposition 13.1 is then proved in the last paragraph of this section.
$L^2$
convergence with the same limit formula, for bounded measurable f and Riemann integrable g. Proposition 13.1 is then proved in the last paragraph of this section.
The following lemma is needed for the proof of Lemma 13.4; it is nothing but Fubini’s theorem together with the translation invariance of Haar measure.
Lemma 13.3. Let
![]() $\nu $
be a Borel probability measure on
$\nu $
be a Borel probability measure on
![]() $\mathbb T^d\times \mathbb T^r$
, let m be Haar measure on
$\mathbb T^d\times \mathbb T^r$
, let m be Haar measure on
![]() $\mathbb T^d$
, and let
$\mathbb T^d$
, and let
![]() $h:\mathbb T^d\times (\mathbb T^d\times \mathbb T^r)\to \mathbb C$
be continuous. Then,
$h:\mathbb T^d\times (\mathbb T^d\times \mathbb T^r)\to \mathbb C$
be continuous. Then,
where
![]() $\pi _1 :\mathbb T^d\times \mathbb T^r\to \mathbb T^d$
is the projection map.
$\pi _1 :\mathbb T^d\times \mathbb T^r\to \mathbb T^d$
is the projection map.
Let
![]() $G=(\mathbb T^d)^4\times \mathbb T^r$
, with elements of G written
$G=(\mathbb T^d)^4\times \mathbb T^r$
, with elements of G written
![]() $(z_1,z_2,z_3,z_4,z_5)$
,
$(z_1,z_2,z_3,z_4,z_5)$
,
![]() $z_i\in \mathbb T^d$
for
$z_i\in \mathbb T^d$
for
![]() $i\leq 4$
,
$i\leq 4$
,
![]() $z_5\in \mathbb T^r$
. Let
$z_5\in \mathbb T^r$
. Let
![]() $G_{3AP}$
be the closed connected subgroup
$G_{3AP}$
be the closed connected subgroup
![]() $\{(s,t,2s,2t,0):s,t\in \mathbb T^d\}\subseteq G$
.
$\{(s,t,2s,2t,0):s,t\in \mathbb T^d\}\subseteq G$
.
Lemma 13.4. With
![]() $\alpha $
,
$\alpha $
,
![]() $\beta $
, d, r, and G as above, let
$\beta $
, d, r, and G as above, let
![]() $\mathbf u = (0,\alpha ,0,4\alpha ,\beta )\in G$
. Then there is an affine joining
$\mathbf u = (0,\alpha ,0,4\alpha ,\beta )\in G$
. Then there is an affine joining
![]() $\Gamma $
of
$\Gamma $
of
![]() $\mathbb T^d$
with
$\mathbb T^d$
with
![]() $\mathbb T^r$
such that
$\mathbb T^r$
such that
 $$ \begin{align} \lim_{N\to\infty} \frac{1}{N}\sum_{n=1}^N F(n\mathbf c + n^2\mathbf u) = \int F(s,t,2s,2t+2w_1,w_2)\, dm_{\Gamma}(w) \, ds\, dt \end{align} $$
$$ \begin{align} \lim_{N\to\infty} \frac{1}{N}\sum_{n=1}^N F(n\mathbf c + n^2\mathbf u) = \int F(s,t,2s,2t+2w_1,w_2)\, dm_{\Gamma}(w) \, ds\, dt \end{align} $$
for every continuous
![]() $F:G\to \mathbb C$
and all
$F:G\to \mathbb C$
and all
![]() $\mathbf c\in G$
such that
$\mathbf c\in G$
such that
![]() $\overline {\langle \mathbf c \rangle } = G_{3AP}$
.
$\overline {\langle \mathbf c \rangle } = G_{3AP}$
.
Proof. Assume
![]() $\mathbf c\in G$
is such that
$\mathbf c\in G$
is such that
![]() $\overline {\langle \mathbf c \rangle } = G_{3AP}$
. Let
$\overline {\langle \mathbf c \rangle } = G_{3AP}$
. Let
![]() $\Lambda = \overline {\langle \mathbf u\rangle }$
and let
$\Lambda = \overline {\langle \mathbf u\rangle }$
and let
![]() $\Phi = \overline {\langle \mathbf c, \mathbf u\rangle }$
. Note that
$\Phi = \overline {\langle \mathbf c, \mathbf u\rangle }$
. Note that
![]() $\Phi = G_{3AP}+\Lambda $
. Also,
$\Phi = G_{3AP}+\Lambda $
. Also,
![]() $\Phi $
does not depend on
$\Phi $
does not depend on
![]() $\mathbf c$
(assuming
$\mathbf c$
(assuming
![]() $\mathbf c$
generates
$\mathbf c$
generates
![]() $G_{3AP}$
).
$G_{3AP}$
).
Since
![]() $\Phi $
is a closed subgroup of a finite-dimensional torus, its identity component
$\Phi $
is a closed subgroup of a finite-dimensional torus, its identity component
![]() $\Phi _0$
has finite index in
$\Phi _0$
has finite index in
![]() $\Phi $
. Part (ii) of Lemma 10.3 then provides cosets
$\Phi $
. Part (ii) of Lemma 10.3 then provides cosets
![]() $\Phi _j$
of
$\Phi _j$
of
![]() $\Phi _0$
in
$\Phi _0$
in
![]() $\Phi $
and non-negative
$\Phi $
and non-negative
![]() $c_j$
with
$c_j$
with
![]() $\sum c_j=1$
such that for every continuous
$\sum c_j=1$
such that for every continuous
![]() $F:G\to \mathbb C$
, we have
$F:G\to \mathbb C$
, we have
 $$ \begin{align} \lim_{N\to\infty} \frac{1}{N}\sum_{n=1}^N F(n\mathbf c + n^2\mathbf u) = \sum c_j \int F\, dm_{\Phi_j}. \end{align} $$
$$ \begin{align} \lim_{N\to\infty} \frac{1}{N}\sum_{n=1}^N F(n\mathbf c + n^2\mathbf u) = \sum c_j \int F\, dm_{\Phi_j}. \end{align} $$
Part (iii) of Lemma 10.3 implies that the
![]() $c_j$
do not depend on
$c_j$
do not depend on
![]() $\mathbf c$
, assuming
$\mathbf c$
, assuming
![]() $\overline {\langle \mathbf c\rangle }=G_{3AP}$
(which is connected). We will prove that for each coset
$\overline {\langle \mathbf c\rangle }=G_{3AP}$
(which is connected). We will prove that for each coset
![]() $\Phi _j$
of
$\Phi _j$
of
![]() $\Phi _0$
in
$\Phi _0$
in
![]() $\Phi $
, we can write
$\Phi $
, we can write
where
![]() $\Lambda _j$
is a coset of
$\Lambda _j$
is a coset of
![]() $\Lambda _0$
(
$\Lambda _0$
(
![]() $=$
the identity component of
$=$
the identity component of
![]() $\Lambda $
), and that
$\Lambda $
), and that
![]() $\Lambda _0$
can be viewed as a joining of
$\Lambda _0$
can be viewed as a joining of
![]() $\mathbb T^d$
with
$\mathbb T^d$
with
![]() $\mathbb T^r$
. Combining equation (13.4) with equation (13.3), we get equation (13.2), where
$\mathbb T^r$
. Combining equation (13.4) with equation (13.3), we get equation (13.2), where
![]() $\Gamma $
is the affine joining of
$\Gamma $
is the affine joining of
![]() $\mathbb T^d$
with
$\mathbb T^d$
with
![]() $\mathbb T^r$
determined by
$\mathbb T^r$
determined by
![]() $c_j$
and
$c_j$
and
![]() $\Lambda _j$
.
$\Lambda _j$
.
Claim
-
(i)
 $\Lambda $
is a joining of the closed subgroups
$\Lambda $
is a joining of the closed subgroups
 $H_1:=\{(0,z,0,4z,0):z\in \mathbb T^d\}$
and
$H_1:=\{(0,z,0,4z,0):z\in \mathbb T^d\}$
and
 $H_2:=\{(0,0,0,0,v):v\in \mathbb T^r\}$
. Its identity component
$H_2:=\{(0,0,0,0,v):v\in \mathbb T^r\}$
. Its identity component
 $\Lambda _0$
is also a joining of
$\Lambda _0$
is also a joining of
 $H_1$
and
$H_1$
and
 $H_2$
.
$H_2$
. -
(ii)
 $\Phi _0= G_{3AP}+\Lambda _0$
is the identity component of
$\Phi _0= G_{3AP}+\Lambda _0$
is the identity component of
 $G_{3AP}+\Lambda $
.
$G_{3AP}+\Lambda $
. -
(iii) Every coset of
 $\Phi _0$
in
$\Phi _0$
in
 $\Phi $
has the form
$\Phi $
has the form
 $G_{3AP}+\Lambda _j$
where
$G_{3AP}+\Lambda _j$
where
 $\Lambda _j$
is a coset of
$\Lambda _j$
is a coset of
 $\Lambda _0$
in
$\Lambda _0$
in
 $\Lambda $
.
$\Lambda $
.
Part (i) of the claim follows from Observation 9.1, the fact that
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are generating, and Observation 9.3.
$\beta $
are generating, and Observation 9.3.
To prove part (ii), note that
![]() $G_{3AP}$
is closed and connected, so
$G_{3AP}$
is closed and connected, so
![]() $G_{3AP}+\Lambda _0$
is a closed connected subgroup of
$G_{3AP}+\Lambda _0$
is a closed connected subgroup of
![]() $G_{3AP}+\Lambda $
. Since
$G_{3AP}+\Lambda $
. Since
![]() $\Lambda _0$
is the identity component of
$\Lambda _0$
is the identity component of
![]() $\Lambda $
, which is a closed subgroup of a finite-dimensional torus, we see that
$\Lambda $
, which is a closed subgroup of a finite-dimensional torus, we see that
![]() $\Lambda _0$
has finite index in
$\Lambda _0$
has finite index in
![]() $\Lambda $
. Thus,
$\Lambda $
. Thus,
![]() $G_{3AP}+\Lambda _0$
is a closed, connected, finite index subgroup of
$G_{3AP}+\Lambda _0$
is a closed, connected, finite index subgroup of
![]() $G_{3AP}+\Lambda $
, and therefore is its identity component. Part (iii) is an immediate consequence of part (ii) and the fact that
$G_{3AP}+\Lambda $
, and therefore is its identity component. Part (iii) is an immediate consequence of part (ii) and the fact that
![]() $G_{3AP}$
is connected.
$G_{3AP}$
is connected.
The claim allows us to write integrals with respect to Haar measure over
![]() $\Phi _j$
explicitly. We write integration over a coset
$\Phi _j$
explicitly. We write integration over a coset
![]() $\Lambda _j$
of
$\Lambda _j$
of
![]() $\Lambda _0$
in
$\Lambda _0$
in
![]() $\Lambda $
as
$\Lambda $
as
where the
![]() $m_{\Lambda _j}$
on the right is viewed as Haar probability measure on a coset of a joining of
$m_{\Lambda _j}$
on the right is viewed as Haar probability measure on a coset of a joining of
![]() $\mathbb T^d$
with
$\mathbb T^d$
with
![]() $\mathbb T^r$
; this identification is possible as
$\mathbb T^r$
; this identification is possible as
![]() $H_1$
and
$H_1$
and
![]() $H_2$
are isomorphic to
$H_2$
are isomorphic to
![]() $\mathbb T^d$
and
$\mathbb T^d$
and
![]() $\mathbb T^r$
, respectively. We then write integration over
$\mathbb T^r$
, respectively. We then write integration over
![]() $\Phi _j$
(=
$\Phi _j$
(=
![]() $G_{3AP}+\Lambda _j$
) as
$G_{3AP}+\Lambda _j$
) as
This is justified by the fact that the above integral is invariant under translation by elements of
![]() $G_{3AP}$
and by elements of
$G_{3AP}$
and by elements of
![]() $\Lambda _0$
, so the above integral is indeed integration with respect to Haar probability measure on
$\Lambda _0$
, so the above integral is indeed integration with respect to Haar probability measure on
![]() $G_{3AP}+\Lambda _j$
.
$G_{3AP}+\Lambda _j$
.
We may replace t with
![]() $t-w_1$
in equation (13.6). To see this, first observe that the order of the outer integrals can be changed to
$t-w_1$
in equation (13.6). To see this, first observe that the order of the outer integrals can be changed to
![]() $dt\, ds$
. For a fixed
$dt\, ds$
. For a fixed
![]() $s\in \mathbb T^d$
, define
$s\in \mathbb T^d$
, define
![]() $h_s$
on
$h_s$
on
![]() $\mathbb T^d \times (\mathbb T^d\times \mathbb T^r)$
by
$\mathbb T^d \times (\mathbb T^d\times \mathbb T^r)$
by
![]() $h_s(t,w):=F(s,t+w_1,2s,2t+4w_1,w_2)$
. The right-hand side of equation (13.6) can then be written as
$h_s(t,w):=F(s,t+w_1,2s,2t+4w_1,w_2)$
. The right-hand side of equation (13.6) can then be written as
![]() $\int \int h_s(t,w)\, dm_{\Lambda _j}(w)\, dt\, ds$
. We apply Lemma 13.3 with
$\int \int h_s(t,w)\, dm_{\Lambda _j}(w)\, dt\, ds$
. We apply Lemma 13.3 with
![]() $m_{\Lambda _0}$
in place of
$m_{\Lambda _0}$
in place of
![]() $\nu $
, and again change the order of integration. The integral in equation (13.6) therefore simplifies to yield equation (13.4), completing the proof.
$\nu $
, and again change the order of integration. The integral in equation (13.6) therefore simplifies to yield equation (13.4), completing the proof.
An immediate consequence of Lemma 13.4 is that for every continuous
![]() $F:G\to \mathbb C$
,
$F:G\to \mathbb C$
,
 $$ \begin{align} &\lim_{N\to\infty} \frac{1}{N}\sum_{n=1}^N F(\mathbf z + n\mathbf c +n^2\mathbf u)\nonumber\\ &\quad= \int F(z_1+s,z_2+t,z_3+ 2s, z_4 + 2t+2w_1, z_5+w_2)\, dm_{\Gamma}(w) \, ds\, dt \end{align} $$
$$ \begin{align} &\lim_{N\to\infty} \frac{1}{N}\sum_{n=1}^N F(\mathbf z + n\mathbf c +n^2\mathbf u)\nonumber\\ &\quad= \int F(z_1+s,z_2+t,z_3+ 2s, z_4 + 2t+2w_1, z_5+w_2)\, dm_{\Gamma}(w) \, ds\, dt \end{align} $$
for all
![]() $\mathbf z\in G$
, all
$\mathbf z\in G$
, all
![]() $\mathbf c\in G$
such that
$\mathbf c\in G$
such that
![]() $\overline {\langle \mathbf c\rangle }=G_{3AP}$
. This can be seen by applying Lemma 13.4 with the translate
$\overline {\langle \mathbf c\rangle }=G_{3AP}$
. This can be seen by applying Lemma 13.4 with the translate
![]() $F_{\mathbf z}$
in place of F.
$F_{\mathbf z}$
in place of F.
Lemma 13.5. With the above
![]() $d, r, \alpha , \beta $
, S, G, and the affine joining
$d, r, \alpha , \beta $
, S, G, and the affine joining
![]() $\Gamma $
provided by Lemma 13.4, there is a set
$\Gamma $
provided by Lemma 13.4, there is a set
![]() $W\subseteq \mathbb T^d$
with
$W\subseteq \mathbb T^d$
with
![]() $m(W)=1$
such that
$m(W)=1$
such that
 $$ \begin{align} &\lim_{N\to \infty} \frac{1}{N}\sum_{n=1}^N g(n^2\beta) \cdot f\circ S^{n}(x,y) \cdot f\circ S^{2n}(x,y) \nonumber\\ &\quad= \int f(x+s, y+ t)f(x+2s, y+2t+2w_1)g(w_2) \, dm_{\Gamma}(w) \, ds\, dt.\end{align} $$
$$ \begin{align} &\lim_{N\to \infty} \frac{1}{N}\sum_{n=1}^N g(n^2\beta) \cdot f\circ S^{n}(x,y) \cdot f\circ S^{2n}(x,y) \nonumber\\ &\quad= \int f(x+s, y+ t)f(x+2s, y+2t+2w_1)g(w_2) \, dm_{\Gamma}(w) \, ds\, dt.\end{align} $$
for all
![]() $x\in W$
, all
$x\in W$
, all
![]() $y\in \mathbb T^d$
, and all continuous
$y\in \mathbb T^d$
, and all continuous
![]() $f:(\mathbb T^d)^2\to \mathbb R$
,
$f:(\mathbb T^d)^2\to \mathbb R$
,
![]() $g: \mathbb T^r\to \mathbb R$
.
$g: \mathbb T^r\to \mathbb R$
.
Proof. Write the terms on the left-hand side of equation (13.8) as
 $$ \begin{align*} &g(n^2\beta)f(S^{n}(x,y))f(S^{2n}(x,y))\\&\quad= F(x+2n\alpha,y+nx+\tbinom{n}{2}2\alpha,x+4n\alpha,y+2nx+\tbinom{2n}{2}2\alpha,n^2\beta)\\ &\quad= F(\mathbf z_{x,y} + n\mathbf c_x + n^2\mathbf u), \end{align*} $$
$$ \begin{align*} &g(n^2\beta)f(S^{n}(x,y))f(S^{2n}(x,y))\\&\quad= F(x+2n\alpha,y+nx+\tbinom{n}{2}2\alpha,x+4n\alpha,y+2nx+\tbinom{2n}{2}2\alpha,n^2\beta)\\ &\quad= F(\mathbf z_{x,y} + n\mathbf c_x + n^2\mathbf u), \end{align*} $$
where
![]() $F:G\to \mathbb R$
is given by
$F:G\to \mathbb R$
is given by
![]() $F(x,y,x',y',z):=f(x,y)f(x',y')g(z)$
and
$F(x,y,x',y',z):=f(x,y)f(x',y')g(z)$
and
If f and g are continuous, then F is continuous, and we may apply Lemma 13.4 (and equation (13.7) in particular) to conclude that
 $$ \begin{align*} &\lim_{N\to\infty} \frac{1}{N}\sum_{n=1}^N F(\mathbf z_{x,y} + n\mathbf c_x + n^2\mathbf u)\\&\quad= \int F(x+s,y+t,x+2s,y+2t+2w_1,w_2) \, dm_{\Gamma}(w) \, ds\,dt \end{align*} $$
$$ \begin{align*} &\lim_{N\to\infty} \frac{1}{N}\sum_{n=1}^N F(\mathbf z_{x,y} + n\mathbf c_x + n^2\mathbf u)\\&\quad= \int F(x+s,y+t,x+2s,y+2t+2w_1,w_2) \, dm_{\Gamma}(w) \, ds\,dt \end{align*} $$
for all
![]() $x\in \mathbb T^d$
such that
$x\in \mathbb T^d$
such that
![]() $\overline {\langle \mathbf c_x \rangle }=G_{3AP}$
and all
$\overline {\langle \mathbf c_x \rangle }=G_{3AP}$
and all
![]() $y\in \mathbb T^d$
. This is equivalent to equation (13.8).
$y\in \mathbb T^d$
. This is equivalent to equation (13.8).
Let
![]() $W:=\{x\in \mathbb T^d: \overline {\langle \mathbf c_x \rangle }=G_{3AP}\}$
. To complete the proof, we will show that
$W:=\{x\in \mathbb T^d: \overline {\langle \mathbf c_x \rangle }=G_{3AP}\}$
. To complete the proof, we will show that
![]() $m(W)=1$
. Note that
$m(W)=1$
. Note that
![]() $x\in W$
if and only if
$x\in W$
if and only if
![]() $\chi (\mathbf c_x)\neq 1$
for every non-trivial character
$\chi (\mathbf c_x)\neq 1$
for every non-trivial character
![]() $\chi $
of
$\chi $
of
![]() $G_{3AP}$
, and there are only countably many characters, so it suffices to prove that for every such
$G_{3AP}$
, and there are only countably many characters, so it suffices to prove that for every such
![]() $\chi $
,
$\chi $
,
![]() $m(E_\chi )=0$
, where
$m(E_\chi )=0$
, where
![]() $E_\chi :=\{x\in \mathbb T^d: \chi (\mathbf c_x)=1\}$
. Every character of
$E_\chi :=\{x\in \mathbb T^d: \chi (\mathbf c_x)=1\}$
. Every character of
![]() $G_{3AP}$
can be written as
$G_{3AP}$
can be written as
![]() $\chi ((s,t,2s,2t,0))= \exp (2\pi i (\mathbf j\cdot s + \mathbf k \cdot t))$
for some
$\chi ((s,t,2s,2t,0))= \exp (2\pi i (\mathbf j\cdot s + \mathbf k \cdot t))$
for some
![]() $\mathbf j, \mathbf k\in \mathbb Z^d$
, and if
$\mathbf j, \mathbf k\in \mathbb Z^d$
, and if
![]() $\chi $
is non-trivial, then
$\chi $
is non-trivial, then
![]() $\mathbf j$
and
$\mathbf j$
and
![]() $\mathbf k$
are not both
$\mathbf k$
are not both
![]() $0$
. Thus,
$0$
. Thus,
![]() $\chi (\mathbf c_x)=1$
if and only if
$\chi (\mathbf c_x)=1$
if and only if
![]() $\mathbf k \cdot x = -(2\mathbf j + \mathbf k)\cdot \alpha $
. When
$\mathbf k \cdot x = -(2\mathbf j + \mathbf k)\cdot \alpha $
. When
![]() $\mathbf k=\mathbf 0$
and
$\mathbf k=\mathbf 0$
and
![]() $\mathbf j\neq \mathbf 0$
, we then have
$\mathbf j\neq \mathbf 0$
, we then have
![]() $E_{\chi }=\varnothing $
. When
$E_{\chi }=\varnothing $
. When
![]() $\mathbf k \neq \mathbf 0$
, we see that
$\mathbf k \neq \mathbf 0$
, we see that
![]() $E_{\chi }$
is contained in a coset of the closed proper subgroup
$E_{\chi }$
is contained in a coset of the closed proper subgroup
![]() $\{x\in \mathbb T^d: \mathbf k\cdot x = 0\}$
, so that
$\{x\in \mathbb T^d: \mathbf k\cdot x = 0\}$
, so that
![]() $m(E_\chi )=0$
.
$m(E_\chi )=0$
.
Corollary 13.6. With
![]() $d,r,\alpha ,\beta $
and S defined above, let
$d,r,\alpha ,\beta $
and S defined above, let
![]() $f\in L^\infty (m\times m)$
and let
$f\in L^\infty (m\times m)$
and let
![]() $g:\mathbb T^r\to \mathbb R$
be Riemann integrable. Define
$g:\mathbb T^r\to \mathbb R$
be Riemann integrable. Define
![]() $A_N\in L^\infty (m\times m)$
by
$A_N\in L^\infty (m\times m)$
by
 $$ \begin{align*}A_N:= \frac{1}{N}\sum_{n=1}^N g(n^2\beta) \cdot f\circ S^{n} \cdot f\circ S^{2n}\end{align*} $$
$$ \begin{align*}A_N:= \frac{1}{N}\sum_{n=1}^N g(n^2\beta) \cdot f\circ S^{n} \cdot f\circ S^{2n}\end{align*} $$
and let
![]() $A(x,y):=\int f(x+s, y+ t)f(x+2s, y+2t+2w_1)g(w_2) \, dm_{\Gamma }(w) \, ds\, dt$
, where
$A(x,y):=\int f(x+s, y+ t)f(x+2s, y+2t+2w_1)g(w_2) \, dm_{\Gamma }(w) \, ds\, dt$
, where
![]() $\Gamma $
is the affine joining given by Lemma 13.4. Then,
$\Gamma $
is the affine joining given by Lemma 13.4. Then,
![]() $\lim _{N\to \infty } A_N = A$
in
$\lim _{N\to \infty } A_N = A$
in
![]() $L^2(m\times m)$
.
$L^2(m\times m)$
.
Proof. Let W be the set provided by Lemma 13.5. To deduce Corollary 13.6, we first prove that equation (13.8) holds for all
![]() $x\in W$
,
$x\in W$
,
![]() $y\in \mathbb T^d$
, assuming f is continuous and g is Riemann integrable. To prove this, assume we have such x, y, f, and g. Let
$y\in \mathbb T^d$
, assuming f is continuous and g is Riemann integrable. To prove this, assume we have such x, y, f, and g. Let
![]() $h_0^{(k)}, h_1^{(k)}$
be continuous functions on
$h_0^{(k)}, h_1^{(k)}$
be continuous functions on
![]() $\mathbb T^r$
satisfying
$\mathbb T^r$
satisfying
![]() $\inf g \leq h_0^{(k)}\leq g \leq h_1^{(k)}\leq \sup g$
pointwise, such that
$\inf g \leq h_0^{(k)}\leq g \leq h_1^{(k)}\leq \sup g$
pointwise, such that
![]() $\lim _{k\to \infty } \int h_1^{(k)} - h_0^{(k)} \, dm_{\mathbb T^r}=0$
. For each k, Lemma 13.4 says that equation (13.8) holds with
$\lim _{k\to \infty } \int h_1^{(k)} - h_0^{(k)} \, dm_{\mathbb T^r}=0$
. For each k, Lemma 13.4 says that equation (13.8) holds with
![]() $h_i^{(k)}$
in place of g. Applying Lemma 15.8 with
$h_i^{(k)}$
in place of g. Applying Lemma 15.8 with
![]() $f\circ S^n(x,y)\cdot f\circ S^{2n}(x,y)$
in place of
$f\circ S^n(x,y)\cdot f\circ S^{2n}(x,y)$
in place of
![]() $v_n$
, we see that
$v_n$
, we see that
The pointwise inequalities
![]() $h_0^{(k)} \leq g \leq h_1^{(k)}$
and the assumption
$h_0^{(k)} \leq g \leq h_1^{(k)}$
and the assumption
![]() $\lim _{k\to \infty } \int h_1^{(k)} - h_0^{(k)}\, dm_{\mathbb T^d}=0$
now imply that
$\lim _{k\to \infty } \int h_1^{(k)} - h_0^{(k)}\, dm_{\mathbb T^d}=0$
now imply that
![]() $\lim _{k\to \infty } h_0^{(k)} = g$
in
$\lim _{k\to \infty } h_0^{(k)} = g$
in
![]() $L^2(m_{\mathbb T^r})$
. The limit on the right of equation (13.9) is therefore equal to
$L^2(m_{\mathbb T^r})$
. The limit on the right of equation (13.9) is therefore equal to
![]() $\int f(x+s,y+t)f(x+2s,y+2t+2w_1) g(w_2)\, dm_\Gamma (w)\, ds\, dt$
. This proves that
$\int f(x+s,y+t)f(x+2s,y+2t+2w_1) g(w_2)\, dm_\Gamma (w)\, ds\, dt$
. This proves that
![]() $A_N$
converges to A for
$A_N$
converges to A for
![]() $m\times m$
almost every
$m\times m$
almost every
![]() $(x,y)$
, and the dominated convergence theorem then implies
$(x,y)$
, and the dominated convergence theorem then implies
![]() $A_N$
converges to A in
$A_N$
converges to A in
![]() $L^2(m\times m)$
, in the special case where f is continuous and g is Riemann integrable.
$L^2(m\times m)$
, in the special case where f is continuous and g is Riemann integrable.
To prove the general case of Corollary 13.6, let
![]() $f\in L^\infty (m\times m)$
and let
$f\in L^\infty (m\times m)$
and let
![]() $\varepsilon>0$
. Assume, without loss of generality, that
$\varepsilon>0$
. Assume, without loss of generality, that
![]() $\sup (|g|)\leq 1$
. We write
$\sup (|g|)\leq 1$
. We write
![]() $\|\cdot \|$
for the
$\|\cdot \|$
for the
![]() $L^2$
norm given by
$L^2$
norm given by
![]() $m\times m$
. Let
$m\times m$
. Let
![]() $f_0:(\mathbb T^d)^2\to \mathbb R$
be continuous with
$f_0:(\mathbb T^d)^2\to \mathbb R$
be continuous with
![]() $\|f-f_0\|<\varepsilon $
.
$\|f-f_0\|<\varepsilon $
.
Let
![]() $A_N':=({1}/{N})\sum _{n=1}^N g(n^2\beta )\cdot f_0\circ S^n \cdot f_0\circ S^{2n}$
, and let
$A_N':=({1}/{N})\sum _{n=1}^N g(n^2\beta )\cdot f_0\circ S^n \cdot f_0\circ S^{2n}$
, and let
Note that
hence
![]() $\|A_N-A_N'\|\leq 2(\sup |g|)\|f-f_0\|$
for every N, and similarly
$\|A_N-A_N'\|\leq 2(\sup |g|)\|f-f_0\|$
for every N, and similarly
![]() $\|A-A'\|\leq 2(\sup |g|)\|f-f_0\|$
. Then
$\|A-A'\|\leq 2(\sup |g|)\|f-f_0\|$
. Then
 $$ \begin{align*} \|A_N-A\| &= \|A_N-A_N'+A_N' - A' + A'- A\|\\ &\leq \|A_N-A_N'\| + \|A_N' - A'\| + \|A'- A\|\\ &< 2\varepsilon + \|A_N' - A'\| + 2\varepsilon \quad \text{assuming } \sup(|g|)\leq 1. \end{align*} $$
$$ \begin{align*} \|A_N-A\| &= \|A_N-A_N'+A_N' - A' + A'- A\|\\ &\leq \|A_N-A_N'\| + \|A_N' - A'\| + \|A'- A\|\\ &< 2\varepsilon + \|A_N' - A'\| + 2\varepsilon \quad \text{assuming } \sup(|g|)\leq 1. \end{align*} $$
(Apply the identity
![]() $ab-cd = a(b-d)+(a-c)(d)$
with
$ab-cd = a(b-d)+(a-c)(d)$
with
![]() $a=f_0\circ S^n$
,
$a=f_0\circ S^n$
,
![]() $b=f_0\circ S^{2n}$
,
$b=f_0\circ S^{2n}$
,
![]() $c=f\circ S^n$
,
$c=f\circ S^n$
,
![]() $d=f\circ ~S^{2n}$
, note that
$d=f\circ ~S^{2n}$
, note that
![]() $\|f\circ S^n - f_0\circ S^n\|=\|f-f_0\|$
and likewise for
$\|f\circ S^n - f_0\circ S^n\|=\|f-f_0\|$
and likewise for
![]() $S^{2n}$
.)
$S^{2n}$
.)
From the first paragraph of this proof, we have
![]() $\|A_N'-A'\|\to 0$
as
$\|A_N'-A'\|\to 0$
as
![]() $N\to \infty $
. Combining this with the above inequalities, we get
$N\to \infty $
. Combining this with the above inequalities, we get
![]() $\limsup _{N\to \infty }\|A_N-A\| \leq 4\varepsilon $
. Since
$\limsup _{N\to \infty }\|A_N-A\| \leq 4\varepsilon $
. Since
![]() $\varepsilon $
was arbitrary and g is fixed, we have
$\varepsilon $
was arbitrary and g is fixed, we have
![]() $\|A_N-A\|\to 0$
as
$\|A_N-A\|\to 0$
as
![]() $N\to \infty $
.
$N\to \infty $
.
Proposition 13.1 now follows from Corollary 13.6, observing that the left-hand side of equation (13.1) is
![]() $\lim _{N\to \infty } \int f(x,y) A_N(x,y)\, dx\, dy$
, with
$\lim _{N\to \infty } \int f(x,y) A_N(x,y)\, dx\, dy$
, with
![]() $A_N$
as in Corollary 13.6, and the right-hand side of equation (13.1) can be written as
$A_N$
as in Corollary 13.6, and the right-hand side of equation (13.1) can be written as
![]() $\int f(x,y) A(x,y) \, dx\, dy$
(recalling the definition of
$\int f(x,y) A(x,y) \, dx\, dy$
(recalling the definition of
![]() $f*_{\Gamma } g$
from equation (12.1)).
$f*_{\Gamma } g$
from equation (12.1)).
14 Proof of Lemma 5.1
Recall the statement of Lemma 5.1: let
![]() $k<r\in \mathbb N$
,
$k<r\in \mathbb N$
,
![]() $\ell \in \mathbb N$
, let
$\ell \in \mathbb N$
, let
![]() $\boldsymbol {\beta }\in \mathbb T^r$
be generating, and let
$\boldsymbol {\beta }\in \mathbb T^r$
be generating, and let
![]() $U\subseteq \mathbb T^r$
be an approximate Hamming ball of radius
$U\subseteq \mathbb T^r$
be an approximate Hamming ball of radius
![]() $(k,\eta )$
for some
$(k,\eta )$
for some
![]() $\eta>0$
. For every totally ergodic MPS
$\eta>0$
. For every totally ergodic MPS
![]() $(X,\mathcal B,\mu ,T)$
and every measurable
$(X,\mathcal B,\mu ,T)$
and every measurable
![]() $f:X\to [0,1]$
, there is a cylinder function
$f:X\to [0,1]$
, there is a cylinder function
![]() $g={m(V)}^{-1}1_V$
subordinate to U such that
$g={m(V)}^{-1}1_V$
subordinate to U such that
 $$ \begin{align} \lim_{N\to \infty} \bigg|\frac{1}{N}\sum_{n=1}^N g(n^2\ell^2\boldsymbol{\beta})\int f\cdot T^{n} f \cdot T^{2n} f\, d\mu - L_3(f,T)\bigg|<2k^{-1/2}\|f\|^2. \end{align} $$
$$ \begin{align} \lim_{N\to \infty} \bigg|\frac{1}{N}\sum_{n=1}^N g(n^2\ell^2\boldsymbol{\beta})\int f\cdot T^{n} f \cdot T^{2n} f\, d\mu - L_3(f,T)\bigg|<2k^{-1/2}\|f\|^2. \end{align} $$
Proof. Let
![]() $(X,\mathcal B,\mu ,T)$
be a totally ergodic MPS,
$(X,\mathcal B,\mu ,T)$
be a totally ergodic MPS,
![]() $f:X\to [0,1]$
, and
$f:X\to [0,1]$
, and
![]() $k\in \mathbb N$
. Let
$k\in \mathbb N$
. Let
![]() $U\subset \mathbb T^r$
be an approximate Hamming ball of radius
$U\subset \mathbb T^r$
be an approximate Hamming ball of radius
![]() $(k,\eta)$
, let
$(k,\eta)$
, let
![]() ${\boldsymbol \beta} \in \mathbb T^r$
be generating, and let
${\boldsymbol \beta} \in \mathbb T^r$
be generating, and let
![]() $\ell\in \mathbb N$
. Note that
$\ell\in \mathbb N$
. Note that
![]() $\ell ^2\boldsymbol {\beta }$
is also generating. For a Riemann integrable
$\ell ^2\boldsymbol {\beta }$
is also generating. For a Riemann integrable
![]() $g:\mathbb T^r\to \mathbb R$
, write
$g:\mathbb T^r\to \mathbb R$
, write
 $$ \begin{align*} A(f,g):= \lim_{N\to\infty}\frac{1}{N}\sum_{n=1}^N g(n^2\ell^2\boldsymbol{\beta})\int f\cdot T^n f\cdot T^{2n} f\, d\mu. \end{align*} $$
$$ \begin{align*} A(f,g):= \lim_{N\to\infty}\frac{1}{N}\sum_{n=1}^N g(n^2\ell^2\boldsymbol{\beta})\int f\cdot T^n f\cdot T^{2n} f\, d\mu. \end{align*} $$
We will prove that there is a cylinder function g subordinate to U such that
Let
![]() $M={1}/{m(V)}$
, where V is one of the cylinders
$M={1}/{m(V)}$
, where V is one of the cylinders
![]() $V_{I,\mathbf y,\eta }$
in equation (3.1). In other words,
$V_{I,\mathbf y,\eta }$
in equation (3.1). In other words,
![]() $M = \|g\|_{\infty }$
for each cylinder function g subordinate to U. Choose, by Lemma 8.1, a factor
$M = \|g\|_{\infty }$
for each cylinder function g subordinate to U. Choose, by Lemma 8.1, a factor
![]() $\pi :\mathbf X\to \mathbf Y=(Y,\mathcal D,\nu ,S)$
so that
$\pi :\mathbf X\to \mathbf Y=(Y,\mathcal D,\nu ,S)$
so that
![]() $\mathbf Y$
is a factor of a standard 2-step Weyl system, and such that for all Riemann integrable
$\mathbf Y$
is a factor of a standard 2-step Weyl system, and such that for all Riemann integrable
![]() $g:\mathbb T^r\to [0,M]$
, we have
$g:\mathbb T^r\to [0,M]$
, we have
where
![]() $\tilde {f}\circ \pi \kern1.3pt{=}\kern1.3pt P_{\mathbf Y}f$
and
$\tilde {f}\circ \pi \kern1.3pt{=}\kern1.3pt P_{\mathbf Y}f$
and
![]() $B(\tilde {f},g)\kern1.3pt{:=}\kern1.3pt \lim _{N\to \infty }({1}/{N})\kern-1.3pt\sum _{n=1}^Ng(n^2\ell ^2\boldsymbol {\beta })\int \kern-1.3pt\tilde {f} \cdot S^{n}\tilde {f} \kern1.3pt{\cdot}\kern1.3pt S^{2 n}\tilde {f}\, d\nu $
. Let
$B(\tilde {f},g)\kern1.3pt{:=}\kern1.3pt \lim _{N\to \infty }({1}/{N})\kern-1.3pt\sum _{n=1}^Ng(n^2\ell ^2\boldsymbol {\beta })\int \kern-1.3pt\tilde {f} \cdot S^{n}\tilde {f} \kern1.3pt{\cdot}\kern1.3pt S^{2 n}\tilde {f}\, d\nu $
. Let
 $$ \begin{align*}C(\tilde{f}):= \lim_{N\to\infty}\frac{1}{N}\sum_{n=1}^N \int \tilde{f}\cdot S^n \tilde{f}\cdot S^{2n}\tilde{f}\, d\nu,\end{align*} $$
$$ \begin{align*}C(\tilde{f}):= \lim_{N\to\infty}\frac{1}{N}\sum_{n=1}^N \int \tilde{f}\cdot S^n \tilde{f}\cdot S^{2n}\tilde{f}\, d\nu,\end{align*} $$
so that
![]() $C(\tilde {f})=B(\tilde {f},\mathbf 1)$
. Note that
$C(\tilde {f})=B(\tilde {f},\mathbf 1)$
. Note that
![]() $A(f,\mathbf 1)= L_3(f,T)$
, so the special case of equation (14.3) with
$A(f,\mathbf 1)= L_3(f,T)$
, so the special case of equation (14.3) with
![]() $g= \mathbf 1$
yields
$g= \mathbf 1$
yields
Let
![]() $\tilde {\mathbf Y} = (\tilde {Y},\tilde {\mathcal D},\tilde {\nu },\tilde {S})$
be an extension of
$\tilde {\mathbf Y} = (\tilde {Y},\tilde {\mathcal D},\tilde {\nu },\tilde {S})$
be an extension of
![]() $\mathbf Y $
which is a standard 2-step Weyl system
$\mathbf Y $
which is a standard 2-step Weyl system
![]() $(\mathbb T^d\times \mathbb T^d, \mathcal B_{\mathbb T^d\times \mathbb T^d}, m, \tilde {S})$
, and view
$(\mathbb T^d\times \mathbb T^d, \mathcal B_{\mathbb T^d\times \mathbb T^d}, m, \tilde {S})$
, and view
![]() $\tilde {f}$
as a function on
$\tilde {f}$
as a function on
![]() $\tilde {Y}=\mathbb T^d\times \mathbb T^d$
(cf. Remark 4.6). By Proposition 13.1, there is an affine joining
$\tilde {Y}=\mathbb T^d\times \mathbb T^d$
(cf. Remark 4.6). By Proposition 13.1, there is an affine joining
![]() $\Gamma $
of
$\Gamma $
of
![]() $\mathbb T^d$
with
$\mathbb T^d$
with
![]() $\mathbb T^r$
such that for each Riemann integrable
$\mathbb T^r$
such that for each Riemann integrable
![]() $g:\mathbb T^r \to \mathbb R$
, we have
$g:\mathbb T^r \to \mathbb R$
, we have
Let J denote the integral above, define
![]() $\tilde {f}':\mathbb T^d\to [0,1]$
by
$\tilde {f}':\mathbb T^d\to [0,1]$
by
![]() $\tilde {f}'(x):=\int \tilde {f}(x,y)\, dy$
, and let
$\tilde {f}'(x):=\int \tilde {f}(x,y)\, dy$
, and let
Choose, by Lemma 12.3, a cylinder function g subordinate to U so that
Observation 7.2 means
![]() $J'= C(\tilde {f})$
, so equation (14.5) can be written as
$J'= C(\tilde {f})$
, so equation (14.5) can be written as
Combining equation (14.6) with equations (14.4), (14.3), and the triangle inequality, we get equation (14.2), completing the proof.
15 Auxiliary lemmas
In §15.1, we prove Lemma 2.3, essentially by repeating a routine proof of Furstenberg’s correspondence principle. Section 15.2 explains a fact needed in the proof of Lemma 8.2, and §15.3 states two immediate consequences of Markov’s inequality needed in the proof of Lemma 3.5.
15.1 Compactness
Here we write
![]() $[N]$
for the interval
$[N]$
for the interval
![]() $\{0,1,\ldots ,N-1\}$
in
$\{0,1,\ldots ,N-1\}$
in
![]() $\mathbb Z$
.
$\mathbb Z$
.
Lemma 15.1. Let
![]() $S\subseteq \mathbb Z$
,
$S\subseteq \mathbb Z$
,
![]() $k\in \mathbb N$
, and
$k\in \mathbb N$
, and
![]() $\delta \geq 0$
. The following conditions are equivalent.
$\delta \geq 0$
. The following conditions are equivalent.
-
(i) There is a measure preserving system
 $(X,\mathcal B,\mu ,T)$
and
$(X,\mathcal B,\mu ,T)$
and
 $A\subseteq X$
with
$A\subseteq X$
with
 $\mu (A)>\delta $
such that
$\mu (A)>\delta $
such that
 $\mu (\bigcap _{j=0}^k T^{-js}A)=0$
for all
$\mu (\bigcap _{j=0}^k T^{-js}A)=0$
for all
 $s\in S$
.
$s\in S$
. -
(ii) S is
 $(\delta ,k)$
-non-recurrent, meaning condition (i) holds with
$(\delta ,k)$
-non-recurrent, meaning condition (i) holds with
 $\bigcap _{j=0}^k T^{-js}A=\varnothing $
in place of
$\bigcap _{j=0}^k T^{-js}A=\varnothing $
in place of
 $\mu (\bigcap _{j=0}^k T^{-js}A)=0$
.
$\mu (\bigcap _{j=0}^k T^{-js}A)=0$
. -
(iii) There is a
 $\delta '>\delta $
such that for all
$\delta '>\delta $
such that for all
 $N\in \mathbb N$
, there is a set
$N\in \mathbb N$
, there is a set
 $B_N\subseteq [N]$
with
$B_N\subseteq [N]$
with
 $|B_N|\geq \delta ' N$
such that
$|B_N|\geq \delta ' N$
such that
 $\bigcap _{j=0}^{k} (B_N-js)=\varnothing $
for all
$\bigcap _{j=0}^{k} (B_N-js)=\varnothing $
for all
 $s\in S$
.
$s\in S$
.
Proof. To prove condition (i) implies condition (ii), let A satisfy condition (i), and let
![]() $A':=A\setminus \bigcup _{s\in S} \bigcap _{j=0}^k T^{-js}A$
. Then,
$A':=A\setminus \bigcup _{s\in S} \bigcap _{j=0}^k T^{-js}A$
. Then,
![]() $\mu (A')=\mu (A)>\delta $
, while
$\mu (A')=\mu (A)>\delta $
, while
![]() $A'\subseteq \bigcap _{j=0}^k T^{-js}A' \subseteq \bigcap _{j=0}^k T^{-js}A$
for every
$A'\subseteq \bigcap _{j=0}^k T^{-js}A' \subseteq \bigcap _{j=0}^k T^{-js}A$
for every
![]() $s\in S$
. Since
$s\in S$
. Since
![]() $A'$
is both a subset of and disjoint from
$A'$
is both a subset of and disjoint from
![]() $\bigcap _{j=0}^k T^{-js}A$
, we have
$\bigcap _{j=0}^k T^{-js}A$
, we have
![]() $\bigcap _{j=0}^k T^{-js}A'=\varnothing $
for every
$\bigcap _{j=0}^k T^{-js}A'=\varnothing $
for every
![]() $s\in S$
.
$s\in S$
.
To prove condition (ii) implies condition (iii), suppose A satisfies condition (ii). Let
![]() $\delta '$
be such that
$\delta '$
be such that
![]() $\mu (A)>\delta '>\delta $
. Fixing
$\mu (A)>\delta '>\delta $
. Fixing
![]() $x\in X$
and setting
$x\in X$
and setting
![]() $A_x:=A\cap \{T^nx:n\in \mathbb N\}$
, we have
$A_x:=A\cap \{T^nx:n\in \mathbb N\}$
, we have
![]() $\bigcap _{j=0}^{k} T^{-jn}A_x=\varnothing $
. Setting
$\bigcap _{j=0}^{k} T^{-jn}A_x=\varnothing $
. Setting
![]() $B_x:=\{n\in \mathbb Z:T^nx\in A\}$
, we have
$B_x:=\{n\in \mathbb Z:T^nx\in A\}$
, we have
![]() $\bigcap _{j=0}^{k} (B_x-jn) = \{n\in \mathbb Z: T^nx \in \bigcap _{j=0}^k T^{-jn}A\}$
. Thus,
$\bigcap _{j=0}^{k} (B_x-jn) = \{n\in \mathbb Z: T^nx \in \bigcap _{j=0}^k T^{-jn}A\}$
. Thus,
![]() $\bigcap _{j=0}^{k} (B_x-jn)=\varnothing $
whenever
$\bigcap _{j=0}^{k} (B_x-jn)=\varnothing $
whenever
![]() $\bigcap _{j=0}^k T^{-jn}A=\varnothing $
.
$\bigcap _{j=0}^k T^{-jn}A=\varnothing $
.
Set
![]() $F_N:=({1}/{N})\sum _{n=0}^{N-1} 1_A(T^nx)$
. Then,
$F_N:=({1}/{N})\sum _{n=0}^{N-1} 1_A(T^nx)$
. Then,
![]() $\int F_N(x)\, d\mu (x) = \mu (A).$
It follows that there is an
$\int F_N(x)\, d\mu (x) = \mu (A).$
It follows that there is an
![]() $x\in X$
such that
$x\in X$
such that
![]() $F_N(x) \geq \delta '$
. Our definition of
$F_N(x) \geq \delta '$
. Our definition of
![]() $F_N$
then implies
$F_N$
then implies
![]() $|B_x\cap [N]| \geq \mu (A)N$
.
$|B_x\cap [N]| \geq \mu (A)N$
.
To prove condition (iii) implies condition (i), suppose condition (iii) holds. Let
![]() $X=\{0,1\}^{\mathbb {Z}}$
with the product topology, and let
$X=\{0,1\}^{\mathbb {Z}}$
with the product topology, and let
![]() $\mathcal B$
be the corresponding Borel
$\mathcal B$
be the corresponding Borel
![]() $\sigma $
-algebra. Let
$\sigma $
-algebra. Let
![]() $T:X\to X$
be the left shift, meaning
$T:X\to X$
be the left shift, meaning
![]() $(Tx)(n)=x(n+1)$
. We will construct a Borel probability measure
$(Tx)(n)=x(n+1)$
. We will construct a Borel probability measure
![]() $\mu $
on
$\mu $
on
![]() $(X,\mathcal B)$
and find a clopen set
$(X,\mathcal B)$
and find a clopen set
![]() $A\subseteq X$
satisfying condition (i).
$A\subseteq X$
satisfying condition (i).
Let
![]() $A:=\{x\in X:x(0)=1\}$
(so A is the cylinder set where
$A:=\{x\in X:x(0)=1\}$
(so A is the cylinder set where
![]() $1$
appears at index
$1$
appears at index
![]() $0$
). For each
$0$
). For each
![]() $N\in \mathbb N$
, let
$N\in \mathbb N$
, let
![]() $y_N:=1_{B_N}\in X$
. Note that
$y_N:=1_{B_N}\in X$
. Note that
![]() $1_A(T^ny_N)=1$
if and only if
$1_A(T^ny_N)=1$
if and only if
![]() $n\in B_N$
, and similarly
$n\in B_N$
, and similarly
 $$ \begin{align} 1_{A \cap T^{-s}A \cap \cdots \cap T^{-ks}A} (T^n y_N) = 1 \quad \text{if and only if } n\in \bigcap_{j=0}^{k} (B_N-js). \end{align} $$
$$ \begin{align} 1_{A \cap T^{-s}A \cap \cdots \cap T^{-ks}A} (T^n y_N) = 1 \quad \text{if and only if } n\in \bigcap_{j=0}^{k} (B_N-js). \end{align} $$
Form a measure
![]() $\mu _N$
on X defined by
$\mu _N$
on X defined by
 $$ \begin{align*} \int f\, d\mu_N:= \frac{1}{N}\sum_{n=0}^{N-1}f(T^ny_N). \end{align*} $$
$$ \begin{align*} \int f\, d\mu_N:= \frac{1}{N}\sum_{n=0}^{N-1}f(T^ny_N). \end{align*} $$
Let
![]() $\mu $
be a weak
$\mu $
be a weak
![]() $^*$
limit of the
$^*$
limit of the
![]() $\mu _N$
(that is, choose a convergent subsequence of
$\mu _N$
(that is, choose a convergent subsequence of
![]() $\mu _N$
and let
$\mu _N$
and let
![]() $\mu $
be the limit). To see that
$\mu $
be the limit). To see that
![]() $\mu $
is T-invariant, note that
$\mu $
is T-invariant, note that
 $$ \begin{align*} \bigg|\int f\circ T\, d\mu_N - \int f\, d\mu_N\bigg| =\frac{1}{N}|f(T^Ny_N) - f(y_N)|\leq \frac{2}{N}\sup |f| \end{align*} $$
$$ \begin{align*} \bigg|\int f\circ T\, d\mu_N - \int f\, d\mu_N\bigg| =\frac{1}{N}|f(T^Ny_N) - f(y_N)|\leq \frac{2}{N}\sup |f| \end{align*} $$
for every N, so
![]() $\int f\circ T\, d\mu = \int f\, d\mu $
for every bounded continuous f. In particular,
$\int f\circ T\, d\mu = \int f\, d\mu $
for every bounded continuous f. In particular,
![]() $\mu (T^{-1}C)=\int 1_C\circ T\, d\mu = \int 1_C\, d\mu = \mu (C)$
for every clopen set
$\mu (T^{-1}C)=\int 1_C\circ T\, d\mu = \int 1_C\, d\mu = \mu (C)$
for every clopen set
![]() $C\subseteq X$
. Since the clopen subsets of X generate the Borel
$C\subseteq X$
. Since the clopen subsets of X generate the Borel
![]() $\sigma $
-algebra of X, this proves that T preserves
$\sigma $
-algebra of X, this proves that T preserves
![]() $\mu $
.
$\mu $
.
To see that
![]() $\mu (A)\geq \delta '$
, note that
$\mu (A)\geq \delta '$
, note that
 $$ \begin{align*}\mu(A) \geq \liminf_{N\to\infty} \frac{1}{N}\sum_{n=0}^{N-1}1_A(T^ny_N) \geq \liminf_{N\to\infty} \frac{1}{N}|B_N|\geq \delta'.\end{align*} $$
$$ \begin{align*}\mu(A) \geq \liminf_{N\to\infty} \frac{1}{N}\sum_{n=0}^{N-1}1_A(T^ny_N) \geq \liminf_{N\to\infty} \frac{1}{N}|B_N|\geq \delta'.\end{align*} $$
To prove that
![]() $\mu (\bigcap _{j=0}^{k}T^{-js}A)=0$
for all
$\mu (\bigcap _{j=0}^{k}T^{-js}A)=0$
for all
![]() $s\in S$
, fix
$s\in S$
, fix
![]() $s\in S$
and note that equation (15.1) implies
$s\in S$
and note that equation (15.1) implies
 $$ \begin{align*} \mu_N\bigg(\bigcap_{j=0}^{k}T^{-js}A\bigg) = \frac{1}{N}\sum_{n=0}^{N-1} 1_{A\cap T^{-s}A\cap \cdots \cap T^{-ks}A}(T^ny_N) \leq \frac{1}{N}\bigg|\bigcap_{j=0}^k(B_N-js)\bigg|=0 \end{align*} $$
$$ \begin{align*} \mu_N\bigg(\bigcap_{j=0}^{k}T^{-js}A\bigg) = \frac{1}{N}\sum_{n=0}^{N-1} 1_{A\cap T^{-s}A\cap \cdots \cap T^{-ks}A}(T^ny_N) \leq \frac{1}{N}\bigg|\bigcap_{j=0}^k(B_N-js)\bigg|=0 \end{align*} $$
for all
![]() $N\in \mathbb N$
. Since
$N\in \mathbb N$
. Since
![]() $C:=\bigcap _{j=0}^k T^{-js} A$
is clopen and
$C:=\bigcap _{j=0}^k T^{-js} A$
is clopen and
![]() $\mu $
is a weak
$\mu $
is a weak
![]() $^*$
limit of the
$^*$
limit of the
![]() $\mu _N$
, we have
$\mu _N$
, we have
![]() $\mu (C)=\lim _{N\to \infty } \mu _N(C)=0$
.
$\mu (C)=\lim _{N\to \infty } \mu _N(C)=0$
.
Recall the statement of Lemma 2.3: if
![]() $k\in \mathbb N$
,
$k\in \mathbb N$
,
![]() $0\leq \delta <\delta '$
, and
$0\leq \delta <\delta '$
, and
![]() $S\subseteq \mathbb Z$
is such that every finite subset of S is
$S\subseteq \mathbb Z$
is such that every finite subset of S is
![]() $(\delta ',k)$
-non-recurrent, then S is
$(\delta ',k)$
-non-recurrent, then S is
![]() $(\delta ,k)$
-non-recurrent.
$(\delta ,k)$
-non-recurrent.
Proof of Lemma 2.3
Suppose
![]() $S\subseteq \mathbb Z$
,
$S\subseteq \mathbb Z$
,
![]() $k\in \mathbb N$
,
$k\in \mathbb N$
,
![]() $0\leq \delta <\delta '$
, and that every finite subset of S is
$0\leq \delta <\delta '$
, and that every finite subset of S is
![]() $(\delta ',k)$
-non-recurrent. Applying Lemma 15.1 to the finite set
$(\delta ',k)$
-non-recurrent. Applying Lemma 15.1 to the finite set
![]() $S_N:=S\cap [-N,N]$
, we may choose, for each N, a set
$S_N:=S\cap [-N,N]$
, we may choose, for each N, a set
![]() $B_N\subseteq [N]$
such that
$B_N\subseteq [N]$
such that
![]() $|B_N|>\delta 'N$
and
$|B_N|>\delta 'N$
and
![]() $\bigcap _{j=0}^N (B_N-js)=\varnothing $
for all
$\bigcap _{j=0}^N (B_N-js)=\varnothing $
for all
![]() $s\in S\cap [-N,N]$
. Note that this implies
$s\in S\cap [-N,N]$
. Note that this implies
![]() $\bigcap _{j=0}^N (B_N-js)=\varnothing $
for all
$\bigcap _{j=0}^N (B_N-js)=\varnothing $
for all
![]() $s\in S$
, since
$s\in S$
, since
![]() $B_N-js$
is disjoint from
$B_N-js$
is disjoint from
![]() $[N]$
for every
$[N]$
for every
![]() $s\in S\setminus [-N,N]$
. This means S satisfies condition (iii) of Lemma 15.1, and we conclude that S is
$s\in S\setminus [-N,N]$
. This means S satisfies condition (iii) of Lemma 15.1, and we conclude that S is
![]() $\delta $
-non-recurrent.
$\delta $
-non-recurrent.
15.2 The 2-step affine factor of a totally ergodic nilsystem
A nilsystem is an MPS
![]() $(Y,\mathcal D,\nu ,S)$
where
$(Y,\mathcal D,\nu ,S)$
where
![]() $Y=G/\Gamma $
, with G a nilpotent Lie group and
$Y=G/\Gamma $
, with G a nilpotent Lie group and
![]() $\Gamma $
a cocompact discrete subgroup,
$\Gamma $
a cocompact discrete subgroup,
![]() $\mathcal D$
is the Borel
$\mathcal D$
is the Borel
![]() $\sigma $
-algebra of Y,
$\sigma $
-algebra of Y,
![]() $\nu $
is the unique probability measure on
$\nu $
is the unique probability measure on
![]() $(Y,\mathcal D)$
invariant under left multiplication, and
$(Y,\mathcal D)$
invariant under left multiplication, and
![]() $Sy = a y$
for some fixed
$Sy = a y$
for some fixed
![]() $a\in G$
.
$a\in G$
.
When G is a topological group, we write
![]() $G_0$
for the connected component of the identity. For Lie groups,
$G_0$
for the connected component of the identity. For Lie groups,
![]() $G_0$
is a closed subgroup of G. We will use the fact that an ergodic nilsystem
$G_0$
is a closed subgroup of G. We will use the fact that an ergodic nilsystem
![]() $(G/\Gamma ,\mathcal B,\mu ,T)$
is totally ergodic if and only if
$(G/\Gamma ,\mathcal B,\mu ,T)$
is totally ergodic if and only if
![]() $G/\Gamma $
is connected.
$G/\Gamma $
is connected.
Lemma 15.2 identifies the maximal
![]() $2$
-step affine factor of a totally ergodic nilsystem; the purpose of this subsection is to explain how it follows from the results of [Reference Frantzikinakis6], where it is essentially proved but not explicitly stated.
$2$
-step affine factor of a totally ergodic nilsystem; the purpose of this subsection is to explain how it follows from the results of [Reference Frantzikinakis6], where it is essentially proved but not explicitly stated.
Lemma 15.2. Let
![]() $\mathbf X=(X,\mathcal B,\mu ,T)$
be a totally ergodic nilsystem. The maximal
$\mathbf X=(X,\mathcal B,\mu ,T)$
be a totally ergodic nilsystem. The maximal
![]() $2$
-step affine factor
$2$
-step affine factor
![]() $\mathbf A_2(\mathbf X)$
of
$\mathbf A_2(\mathbf X)$
of
![]() $\mathbf X$
is isomorphic to
$\mathbf X$
is isomorphic to
![]() $(\mathbb T^d,\mathcal B,m,A)$
, where
$(\mathbb T^d,\mathcal B,m,A)$
, where
![]() $d\in \mathbb N$
and
$d\in \mathbb N$
and
![]() $A:\mathbb T^d\to \mathbb T^d$
is a
$A:\mathbb T^d\to \mathbb T^d$
is a
![]() $2$
-step unipotent affine transformation.
$2$
-step unipotent affine transformation.
We will use the following standard fact about factors: let
![]() $\pi _i:\mathbf X\to \mathbf X_i = (X_i,\mathcal B_i,\nu _i,T_i), i=1,2$
, be two factors of a system where
$\pi _i:\mathbf X\to \mathbf X_i = (X_i,\mathcal B_i,\nu _i,T_i), i=1,2$
, be two factors of a system where
![]() $(X_i,\mathcal B_i,\nu _i)$
are separable as measure spaces. Then,
$(X_i,\mathcal B_i,\nu _i)$
are separable as measure spaces. Then,
![]() $\mathbf X_1$
and
$\mathbf X_1$
and
![]() $\mathbf X_2$
are isomorphic (as measure-preserving systems) if the algebra of bounded
$\mathbf X_2$
are isomorphic (as measure-preserving systems) if the algebra of bounded
![]() $\mathbf X_1$
-measurable functions is equal, up to
$\mathbf X_1$
-measurable functions is equal, up to
![]() $\mu $
-measure
$\mu $
-measure
![]() $0$
, to the algebra of bounded
$0$
, to the algebra of bounded
![]() $\mathbf X_2$
-measurable functions. We also need the following lemma from [Reference Frantzikinakis and Kra9].
$\mathbf X_2$
-measurable functions. We also need the following lemma from [Reference Frantzikinakis and Kra9].
Lemma 15.3. [Reference Frantzikinakis and Kra9, Proposition 3.1]
Let
![]() $X=G/\Gamma $
be a connected nilmanifold such that
$X=G/\Gamma $
be a connected nilmanifold such that
![]() $G_0$
is abelian. Then any nilrotation
$G_0$
is abelian. Then any nilrotation
![]() $T_a(x)=ax$
defined on X with Haar measure
$T_a(x)=ax$
defined on X with Haar measure
![]() $\mu $
is isomorphic to a unipotent affine transformation U on some finite-dimensional torus.
$\mu $
is isomorphic to a unipotent affine transformation U on some finite-dimensional torus.
Remark 15.4. The computation in [Reference Frantzikinakis and Kra9] showing that the transformation U is unipotent also shows that when G is k-step nilpotent, U is k-step unipotent.
We now explain how Lemma 15.2 follows from [Reference Frantzikinakis6]. Let
![]() $\mathbf X$
be a totally ergodic nilsystem,
$\mathbf X$
be a totally ergodic nilsystem,
![]() $\mathbf X = (X,\mathcal B,\mu ,T)$
, where
$\mathbf X = (X,\mathcal B,\mu ,T)$
, where
![]() $X = G/\Gamma $
, G being a nilpotent Lie group,
$X = G/\Gamma $
, G being a nilpotent Lie group,
![]() $\Gamma $
a cocompact lattice in G, and
$\Gamma $
a cocompact lattice in G, and
![]() $\mu $
the unique left-translation invariant Borel probability measure on
$\mu $
the unique left-translation invariant Borel probability measure on
![]() $G/\Gamma $
,
$G/\Gamma $
,
![]() $Tx\Gamma :=ax\Gamma $
for some fixed
$Tx\Gamma :=ax\Gamma $
for some fixed
![]() $a\in G$
. It is shown by [Reference Frantzikinakis6, Proposition 2.4] that the algebra of functions measurable with respect to
$a\in G$
. It is shown by [Reference Frantzikinakis6, Proposition 2.4] that the algebra of functions measurable with respect to
![]() $\mathbf A_2(\mathbf X)$
coincides with the functions measurable with respect to the factor
$\mathbf A_2(\mathbf X)$
coincides with the functions measurable with respect to the factor
![]() $\pi _2:\mathbf X\to \mathbf Y$
, where
$\pi _2:\mathbf X\to \mathbf Y$
, where
![]() $\mathbf Y = (X',\mathcal B', \mu ',T')$
,
$\mathbf Y = (X',\mathcal B', \mu ',T')$
,
![]() $X':=G/(G_3[G_0,G_0]\Gamma )$
, the factor map is given by
$X':=G/(G_3[G_0,G_0]\Gamma )$
, the factor map is given by
![]() $\pi _2(x\Gamma ):= xG_3[G_0,G_0]\Gamma $
, and
$\pi _2(x\Gamma ):= xG_3[G_0,G_0]\Gamma $
, and
![]() $T'y = \pi _2(a)y$
. Furthermore, it is easy to verify (given the background suggested in [Reference Frantzikinakis6, §2.2]) that
$T'y = \pi _2(a)y$
. Furthermore, it is easy to verify (given the background suggested in [Reference Frantzikinakis6, §2.2]) that
![]() $X'$
can be written as
$X'$
can be written as
![]() $G'/\Gamma '$
, where
$G'/\Gamma '$
, where
![]() $\Gamma '$
is a cocompact lattice in
$\Gamma '$
is a cocompact lattice in
![]() $G':=G/(G_3[G_0,G_0])$
, and
$G':=G/(G_3[G_0,G_0])$
, and
![]() $G'$
is a 2-step nilpotent Lie group with abelian identity component. It is stated by [Reference Frantzikinakis and Kra9, Proposition 3.1] (cf. Remark 15.4 above) that
$G'$
is a 2-step nilpotent Lie group with abelian identity component. It is stated by [Reference Frantzikinakis and Kra9, Proposition 3.1] (cf. Remark 15.4 above) that
![]() $\mathbf Y$
is isomorphic to a
$\mathbf Y$
is isomorphic to a
![]() $2$
-step unipotent affine transformation A on a finite-dimensional torus. Since the
$2$
-step unipotent affine transformation A on a finite-dimensional torus. Since the
![]() $\mathbf A_2(\mathbf X)$
-measurable functions coincide with the
$\mathbf A_2(\mathbf X)$
-measurable functions coincide with the
![]() $\mathbf Y$
-measurable functions, we get that
$\mathbf Y$
-measurable functions, we get that
![]() $\mathbf A_2(\mathbf X)$
is itself isomorphic to
$\mathbf A_2(\mathbf X)$
is itself isomorphic to
![]() $\mathbf Y$
.
$\mathbf Y$
.
15.3 Consequences of Markov’s inequality
Let
![]() $(X,\mu )$
be a probability space partitioned into subsets
$(X,\mu )$
be a probability space partitioned into subsets
![]() $X_i$
,
$X_i$
,
![]() $0\leq i \leq M-1$
, with
$0\leq i \leq M-1$
, with
![]() $\mu (X_i)=1/M$
for each i, and let
$\mu (X_i)=1/M$
for each i, and let
![]() $f:X\to [0,1]$
have
$f:X\to [0,1]$
have
![]() $\int f\, d\mu>\delta $
. Let
$\int f\, d\mu>\delta $
. Let
![]() $f_i:=f1_{X_i}$
.
$f_i:=f1_{X_i}$
.
Lemma 15.5. With X, f, and
![]() $X_i$
specified above, let
$X_i$
specified above, let
![]() $I:=\{i: \int f_i\, d\mu> {\delta }/{2M}\}$
. Then,
$I:=\{i: \int f_i\, d\mu> {\delta }/{2M}\}$
. Then,
![]() $|I|> M\delta /2$
.
$|I|> M\delta /2$
.
Proof. Let
![]() $I':=\{0,\ldots ,M-1\}\setminus I$
. Note that
$I':=\{0,\ldots ,M-1\}\setminus I$
. Note that
 $$ \begin{align*}\delta<\!\int f\, d\mu = \sum_{i\in I'} \int f_i\, d\mu + \sum_{i\in I} \int f_i\, d\mu \leq \sum_{i\in I'} \frac{\delta}{2M} + \sum_{i\in I} \frac{1}{M} = \frac{\delta}{2M}(M-|I|)+\frac{1}{M}|I|, \end{align*} $$
$$ \begin{align*}\delta<\!\int f\, d\mu = \sum_{i\in I'} \int f_i\, d\mu + \sum_{i\in I} \int f_i\, d\mu \leq \sum_{i\in I'} \frac{\delta}{2M} + \sum_{i\in I} \frac{1}{M} = \frac{\delta}{2M}(M-|I|)+\frac{1}{M}|I|, \end{align*} $$
so
![]() $\delta < {\delta }/{2} + {|I|}/{M}(1-{\delta }/{2})$
. This can be rearranged to
$\delta < {\delta }/{2} + {|I|}/{M}(1-{\delta }/{2})$
. This can be rearranged to
![]() $M\delta /2 < |I|(1-\delta /2)$
, which implies
$M\delta /2 < |I|(1-\delta /2)$
, which implies
![]() $M\delta /2<|I|$
.
$M\delta /2<|I|$
.
Lemma 15.6. With X and
![]() $X_i$
as defined above, let
$X_i$
as defined above, let
![]() $c, \varepsilon>0$
and assume
$c, \varepsilon>0$
and assume
![]() $f, g:X\to \mathbb R$
satisfy
$f, g:X\to \mathbb R$
satisfy
![]() $\|f-g\|_{L^1(\mu )}<\varepsilon $
. Define
$\|f-g\|_{L^1(\mu )}<\varepsilon $
. Define
 $$ \begin{align*}J := \bigg\{i: \int_{X_i} |f-g|\, d\mu< \frac{c}{M} \bigg\}.\end{align*} $$
$$ \begin{align*}J := \bigg\{i: \int_{X_i} |f-g|\, d\mu< \frac{c}{M} \bigg\}.\end{align*} $$
Then,
![]() $|J|> M(1-{\varepsilon }/{c})$
.
$|J|> M(1-{\varepsilon }/{c})$
.
Proof. We estimate
![]() $J'$
, where
$J'$
, where
![]() $J':=\{0,\ldots ,M-1\}\setminus J$
. Let
$J':=\{0,\ldots ,M-1\}\setminus J$
. Let
![]() $\varepsilon _i := \int _{X_i} |f-g|\, d\mu $
.
$\varepsilon _i := \int _{X_i} |f-g|\, d\mu $
.
Note that
![]() $ \sum _{i=0}^{M-1} \varepsilon _i=\|f-g\|_{L^1(\mu )} < \varepsilon $
, so
$ \sum _{i=0}^{M-1} \varepsilon _i=\|f-g\|_{L^1(\mu )} < \varepsilon $
, so
![]() $J'=\{i : \varepsilon _i \geq c/M\}$
satisfies
$J'=\{i : \varepsilon _i \geq c/M\}$
satisfies
![]() $|J'|\cdot c/M<\varepsilon $
, meaning
$|J'|\cdot c/M<\varepsilon $
, meaning
![]() $|J'|<M\varepsilon /c$
. Thus,
$|J'|<M\varepsilon /c$
. Thus,
![]() $|J|=M-|J'|>M(1-{\varepsilon }/{c})$
.
$|J|=M-|J'|>M(1-{\varepsilon }/{c})$
.
The next lemma is an immediate consequence of the triangle inequality and the identity
 $$ \begin{align*} f_1 f_2\cdots f_k - h_1h_2\cdots h_k = \sum_{i=1}^k f_1\cdots f_{i-1}(f_i-h_i)h_{i+1}\cdots h_{k}. \end{align*} $$
$$ \begin{align*} f_1 f_2\cdots f_k - h_1h_2\cdots h_k = \sum_{i=1}^k f_1\cdots f_{i-1}(f_i-h_i)h_{i+1}\cdots h_{k}. \end{align*} $$
Lemma 15.7. If
![]() $(X,\mu )$
is a probability space,
$(X,\mu )$
is a probability space,
![]() $f_i, h_i: X\to [0,1]$
,
$f_i, h_i: X\to [0,1]$
,
![]() $i=1,\ldots ,k$
, and
$i=1,\ldots ,k$
, and
![]() $\|f_i-h_i\|_{L^1(\mu )}<\varepsilon $
for each i, then
$\|f_i-h_i\|_{L^1(\mu )}<\varepsilon $
for each i, then
![]() $|\int f_1 f_2\cdots f_k\, d\mu - \int h_1h_2\cdots h_k\, d\mu |<k\varepsilon $
.
$|\int f_1 f_2\cdots f_k\, d\mu - \int h_1h_2\cdots h_k\, d\mu |<k\varepsilon $
.
15.4 Convergence with Riemann integrable coefficients
Let
![]() $r\in \mathbb N$
. We say that a sequence
$r\in \mathbb N$
. We say that a sequence
![]() $(y_n)_{n\in \mathbb N}$
of elements of
$(y_n)_{n\in \mathbb N}$
of elements of
![]() $\mathbb T^r$
is uniformly distributed if
$\mathbb T^r$
is uniformly distributed if
 $$ \begin{align*}\lim_{N\to\infty} \frac{1}{N}\sum_{n=1}^N g(y_n)=\int g\, dm\end{align*} $$
$$ \begin{align*}\lim_{N\to\infty} \frac{1}{N}\sum_{n=1}^N g(y_n)=\int g\, dm\end{align*} $$
for every continuous
![]() $g:\mathbb T^r\to \mathbb C$
, where m is Haar probability measure on
$g:\mathbb T^r\to \mathbb C$
, where m is Haar probability measure on
![]() $\mathbb T^d$
.
$\mathbb T^d$
.
Lemma 15.8. Let
![]() $r\in \mathbb N$
, let
$r\in \mathbb N$
, let
![]() $(y_n)_{n\in \mathbb N}$
be a uniformly distributed sequence of elements of
$(y_n)_{n\in \mathbb N}$
be a uniformly distributed sequence of elements of
![]() $\mathbb T^r$
. If
$\mathbb T^r$
. If
![]() $(v_n)_{n\in \mathbb N}$
is a bounded sequence of real numbers such that
$(v_n)_{n\in \mathbb N}$
is a bounded sequence of real numbers such that
![]() $L(g):=\lim _{N\to \infty } ({1}/{N})\sum _{n=1}^N g(y_n)v_n$
exists for every continuous
$L(g):=\lim _{N\to \infty } ({1}/{N})\sum _{n=1}^N g(y_n)v_n$
exists for every continuous
![]() $g:\mathbb T^r\to \mathbb R$
, then
$g:\mathbb T^r\to \mathbb R$
, then
![]() $L(g)$
exists for all Riemann integrable g.
$L(g)$
exists for all Riemann integrable g.
Furthermore, if
![]() $h_0^{(k)}, h_1^{(k)}$
are continuous functions on
$h_0^{(k)}, h_1^{(k)}$
are continuous functions on
![]() $\mathbb T^r$
with
$\mathbb T^r$
with
![]() $h_0^{(k)}\leq g \leq h_1^{(k)}$
pointwise and
$h_0^{(k)}\leq g \leq h_1^{(k)}$
pointwise and
![]() $\lim _{k\to \infty } \int h_1^{(k)} -h_0^{(k)}\, dm=0$
, then
$\lim _{k\to \infty } \int h_1^{(k)} -h_0^{(k)}\, dm=0$
, then
![]() $L(g)=\lim _{k\to \infty } L(h_0^{(k)})=\lim _{k\to \infty } L(h_1^{(k)})$
.
$L(g)=\lim _{k\to \infty } L(h_0^{(k)})=\lim _{k\to \infty } L(h_1^{(k)})$
.
Finally, if
![]() $C>0$
and
$C>0$
and
![]() $|L(g)|\leq C$
for every continuous
$|L(g)|\leq C$
for every continuous
![]() $g:\mathbb T^r \to [0,1]$
, then
$g:\mathbb T^r \to [0,1]$
, then
![]() $|L(g)|\leq C$
for every Riemann integrable
$|L(g)|\leq C$
for every Riemann integrable
![]() $g:\mathbb T^r\to [0,1]$
.
$g:\mathbb T^r\to [0,1]$
.
Proof. Note that it suffices to prove the statement under the additional assumption that
![]() $v_n \in [0,1]$
for each n. The general case follows by linearity.
$v_n \in [0,1]$
for each n. The general case follows by linearity.
Let
![]() $g:\mathbb T^r\to \mathbb R$
be Riemann integrable. Let
$g:\mathbb T^r\to \mathbb R$
be Riemann integrable. Let
![]() $\varepsilon>0$
, and choose continuous
$\varepsilon>0$
, and choose continuous
![]() $g_0, g_1:\mathbb T^r\to \mathbb R$
so that
$g_0, g_1:\mathbb T^r\to \mathbb R$
so that
![]() $g_0\leq g \leq g_1$
,
$g_0\leq g \leq g_1$
,
![]() $\int g_1-g_0\, dm<\varepsilon $
. Let
$\int g_1-g_0\, dm<\varepsilon $
. Let
![]() $A_N(g):=({1}/{N})\sum _{n=1}^N g(y_n)v_n$
. We have
$A_N(g):=({1}/{N})\sum _{n=1}^N g(y_n)v_n$
. We have
and
 $L(g_1)-L(g_0) = L(g_1-g_0)\leq \lim _{N\to \infty } ({1}/{N})\sum _{n=1}^N g_1(y_n)-g_0(y_n) =\int g_1-g_0\, dm < \varepsilon $
. Since
$L(g_1)-L(g_0) = L(g_1-g_0)\leq \lim _{N\to \infty } ({1}/{N})\sum _{n=1}^N g_1(y_n)-g_0(y_n) =\int g_1-g_0\, dm < \varepsilon $
. Since
![]() $\varepsilon>0$
was arbitrary, this proves that
$\varepsilon>0$
was arbitrary, this proves that
![]() $A_N(g)$
converges, meaning
$A_N(g)$
converges, meaning
![]() $L(g)$
exists.
$L(g)$
exists.
A nearly identical argument will prove the second assertion of the lemma. The third assertion follows from the second, by assuming
![]() $h_i^{(k)}:\mathbb T^r\to [0,1]$
.
$h_i^{(k)}:\mathbb T^r\to [0,1]$
.
16 Remarks
16.1 More general
 $2$
-recurrence
$2$
-recurrence
We say that
![]() $S\subseteq \mathbb Z$
is good for k-recurrence of powers if for every MPS
$S\subseteq \mathbb Z$
is good for k-recurrence of powers if for every MPS
![]() $(X,\mathcal B,\mu ,T)$
, every
$(X,\mathcal B,\mu ,T)$
, every
![]() $A\subseteq X$
with
$A\subseteq X$
with
![]() $\mu (A)>0$
, and all
$\mu (A)>0$
, and all
![]() $c_1,\ldots ,c_k\in \mathbb N$
, there is an
$c_1,\ldots ,c_k\in \mathbb N$
, there is an
![]() $n\in S$
such that
$n\in S$
such that
![]() $A\cap T^{-c_1n}A\cap \cdots \cap T^{-c_k n}A\neq \varnothing $
.
$A\cap T^{-c_1n}A\cap \cdots \cap T^{-c_k n}A\neq \varnothing $
.
It is asked in [Reference Frantzikinakis8, Problem 5] whether
![]() $S\subseteq \mathbb Z$
being good for k-recurrence of powers implies
$S\subseteq \mathbb Z$
being good for k-recurrence of powers implies
![]() $S^{\wedge k}$
is a set of measurable recurrence. Our proof of Theorem 1.1 does not immediately resolve this question for
$S^{\wedge k}$
is a set of measurable recurrence. Our proof of Theorem 1.1 does not immediately resolve this question for
![]() $k=2$
, since we considered intersections of the form
$k=2$
, since we considered intersections of the form
![]() $A\cap T^{-n}A\cap T^{-2n}A$
(that is,
$A\cap T^{-n}A\cap T^{-2n}A$
(that is,
![]() $c_1=1, c_2=2$
only). We believe that our proof can be modified slightly to construct a set S which is good for
$c_1=1, c_2=2$
only). We believe that our proof can be modified slightly to construct a set S which is good for
![]() $2$
-recurrence of powers such that
$2$
-recurrence of powers such that
![]() $S^{\wedge 2}$
is not a set of measurable recurrence.
$S^{\wedge 2}$
is not a set of measurable recurrence.
16.2 Higher-order recurrence
For
![]() $k\geq 3$
, one possible approach to [Reference Frantzikinakis8, Problem 5] would be to prove that the set S we construct in the proof of Theorem 1.1 is actually a set of k-recurrence, or to prove that our construction necessarily results in a set which is not a set of k-recurrence. While our construction does not appear to restrict
$k\geq 3$
, one possible approach to [Reference Frantzikinakis8, Problem 5] would be to prove that the set S we construct in the proof of Theorem 1.1 is actually a set of k-recurrence, or to prove that our construction necessarily results in a set which is not a set of k-recurrence. While our construction does not appear to restrict
![]() $\mu (A\cap T^{-n}A\cap T^{-2n}A\cap T^{-3n}A)$
for
$\mu (A\cap T^{-n}A\cap T^{-2n}A\cap T^{-3n}A)$
for
![]() $n\in S$
, computations and estimates of
$n\in S$
, computations and estimates of
 $$ \begin{align} \lim_{N\to\infty} \frac{1}{N}\sum_{n=1}^N g(n^2\beta) \int f\cdot f\circ T^n \cdot f\circ T^{2n} \cdot f\circ T^{3n} \, d\mu \end{align} $$
$$ \begin{align} \lim_{N\to\infty} \frac{1}{N}\sum_{n=1}^N g(n^2\beta) \int f\cdot f\circ T^n \cdot f\circ T^{2n} \cdot f\circ T^{3n} \, d\mu \end{align} $$
analogous to those in §§13–14 seem to require more intricate reasoning. It may not be possible to specialize the limit in equation (16.1) to affine systems. Perhaps one must consider arbitrary
![]() $2$
-step totally ergodic nilsystems, or even more general systems.
$2$
-step totally ergodic nilsystems, or even more general systems.
For
![]() $k\geq 3$
, our approach to Theorem 1.1 leads to the following natural conjecture, an analogue of Lemma 3.5. Here,
$k\geq 3$
, our approach to Theorem 1.1 leads to the following natural conjecture, an analogue of Lemma 3.5. Here,
![]() $BH^{1/k}$
denotes
$BH^{1/k}$
denotes
![]() $\{n\in \mathbb N: n^k\in BH\}$
.
$\{n\in \mathbb N: n^k\in BH\}$
.
Conjecture 16.1. Let
![]() $k\in \mathbb{N}$
. For all
$k\in \mathbb{N}$
. For all
![]() $\delta>0$
, there exists
$\delta>0$
, there exists
![]() $m_0\in \mathbb N$
such that for every
$m_0\in \mathbb N$
such that for every
![]() $r\in \mathbb N$
, every proper Bohr–Hamming Ball
$r\in \mathbb N$
, every proper Bohr–Hamming Ball
![]() $BH:=BH(\boldsymbol {\beta }, \boldsymbol {y},m,\varepsilon )$
with
$BH:=BH(\boldsymbol {\beta }, \boldsymbol {y},m,\varepsilon )$
with
![]() $m\geq m_0$
,
$m\geq m_0$
,
![]() $\varepsilon>0$
and
$\varepsilon>0$
and
![]() $y\in \mathbb T^r$
,
$y\in \mathbb T^r$
,
![]() $BH^{1/k}$
is
$BH^{1/k}$
is
![]() $(\delta ,k)$
-recurrent.
$(\delta ,k)$
-recurrent.
Conjecture 16.1 could be proved with appropriate higher-order analogues of Lemma 8.1, Proposition 13.1, and Lemma 11.1. For
![]() $k\geq 3$
, it seems very unlikely that a reduction to
$k\geq 3$
, it seems very unlikely that a reduction to
![]() $2$
-step affine systems will be possible, and for
$2$
-step affine systems will be possible, and for
![]() $k\geq 4$
, it is nearly certain that explicit computations must be carried out for essentially arbitrary
$k\geq 4$
, it is nearly certain that explicit computations must be carried out for essentially arbitrary
![]() $(k-1)$
-step totally ergodic nilsystems. These computations seem forbidding, so we hope a more qualitative approach can be developed.
$(k-1)$
-step totally ergodic nilsystems. These computations seem forbidding, so we hope a more qualitative approach can be developed.
Acknowledgements
We thank Nikos Frantzikinakis for helpful comments. An anonymous referee contributed several corrections and improvements to exposition.