Introduction
Trapridge Glacier (lat. 61° 14’ N., long, 140° 20’ W.) is one of three small glaciers whose melt streams join to form a tributary of Hazard Creek on the eastern flanks of Mt Wood, Yukon Territory. Located within the Steele Creek drainage basin, wherein at least sixteen glaciers are known to surge, the Trapridge and neighbouring Rusty and Backe Glaciers: Fig. 1) have been identified as surge-type glaciers by Post (1969). Rusty Glacier experienced a surge sometime prior to 1950, from which its extended tongue, very apparent in 1951 aerial photographs, is now rapidly receding. Backe Glacier, inactive in 1951 (Fig. 1a) was surging in 1967 overriding the Rusty Glacier (Fig. 1b). At present a steep surge front and heavily crevassed surface remain; the Backe is unlikely to surge again for at least twenty years. Trapridge Glacier, although quiescent in 1939 (Reference Wood.Wood 1940), was advancing rapidly in 1941 (Reference Sharp.Sharp 1947, 1951). As Figures 1a and 1b show its surface disrupted in 1951 (shortly after the surge) and smooth again by 1967, we believe that this advance was its most recent. The glacier has now lain dormant for more than twenty years and, since the surge cycle of glaciers in this area is typically 20-30 years (Reference Meier. and PostMeier and Post, 1969), we anticipate a surge of Trapridge Glacier within the near future.
Deep ice temperatures measured on Rusty Glacier in the summer of 1969 and 1970 indicate a region of temperate basal ice in an otherwise cold glacier (Reference Classen, Clarke., Bushnell and RagleClassen and Clarke, 1971, 1972). This discovery suggested thermal control of glacier surging, possibly in the manner described by Reference Robin.deRobin 1955. Subsequent numerical modelling of a modified version of Robin’s theory has shown thermal instability to be an acceptable surge mechanism for many sub-polar glaciers (Reference HoffmannHoffmann, unpublished; Hoffmann and Clarke, 1973). As a further field lest of this mechanism a program of thermal drilling and deep-ice temperature measurement was conducted on Trapridge Glacier in the summer of 1972. In addition, radar depth sounding and surface-slake triangulation surveys were carried out by Reference Goodman., Goodman, Clarke, Jarvis, Collins and Metcalfe.Goodman and others (1975) and S. G. Collins of the Arctic Institute of North America, respectively.

Fig. 1.a Portion of Canadian Government air photograph A 13 136–44 showing Trapridge Glacier region in 1951.
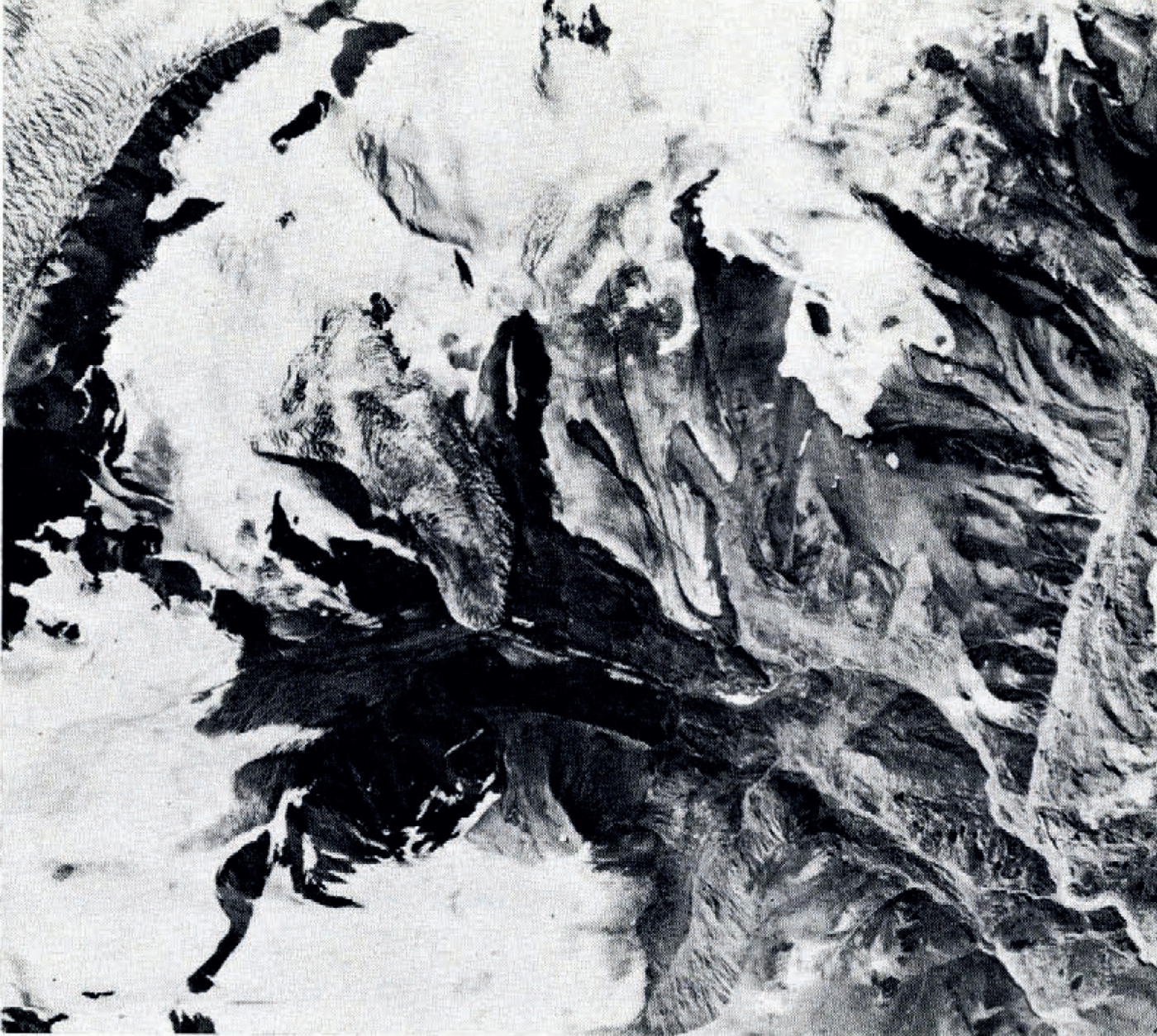
Fig. 1.b Portion of Canadian Government air photograph A20128–29 showing Trapridge Glacier region in 1967.
The radar depths were used to guide the selection of thermal drilling sites, temperate ice being most likely to occur at the deepest points. The triangulation survey, a continuation of work begun in 1969 (Reference Collins.Collins 1972), established the locations of radar stations and drilling sites to an accuracy of ± 0.40 m.
Thermistor preparation and field procedure
Fenwal GB34P2 glass-bead thermistors, with nominal resistance 11 k Ω at 0°C, were used throughout the project. These were calibrated in a Colora KT20S constant-temperature bath containing 80% water and 20% alcohol. The bath temperature was read digitally from a standard quartz thermometer to an accuracy of ±0.005. The corresponding thermistor resistances were measured with a Wheatstone bridge to an accuracy of ±5.0 Ω or ±0.05%. The resistance R of each thermistor was measured at four temperatures T in the range —10.00 ° C to 0.00° C and curves of the form R = exp (A+B/T+C/T2), where A, B, and C are constants, were fit to the resulting data. The calibrated thermistors were then installed in eight-conductor #22 A.W.G. cables following standard procedures (Reference Raspet., Raspet, Swartz, Lillard and Robertson.Raspet and others, 1966; Reference Robertson., Robertson., Raspet, Swartz. and Lillard.Robertson and others, 1966 ).
Electrically powered, cable-suspended, hot-point drills similar in design to those described by Classen (unpublished) were used throughout the field project and thermistor cables taped to the power lines were drawn into the ice by the descending probes. Further details of thermistor calibration and instrumentation are given in a thesis by jarvis (unpublished).
The thermal drilling program produced eight instrumented holes at seven locations on the glacier surface. A total of forty-nine thermistors was implanted in the depth range 10-87 m and the location of a single thermistor left in the lower tongue of the glacier by Classen (unpublished) was re-established. The positions of the drill sites as determined from surface survey data are indicated on the basal temperature map of Figure 5.
The average drilling speed was 4 m/h and the maximum depth attained was 87.5 m at hole no. 4. Drilling was terminated at each site for one of three reasons: sudden and prolonged reduction of drill speed (presumably due to englacial debris), probe burn-out, or hole closure by refreezing (Table I).
Table I. Drill-Hole Characteristics

Hot-point drilling alters the thermal regime of the glacier in the neighbourhood of each hole. After drilling has ceased, several weeks must pass before thermal contamination diffuses away. Temperatures indicated by newly installed thermistors will at first drop rapidly with time and then gradually approach the equilibrium temperatures which existed before drilling. To determine when each hole reached equilibrium, the resistances of all thermistors were measured every two or three days until the ice temperatures appeared stable. (Resistances were measured with a Fluke 8100A digital multimeter to an accuracy of ± 10 Ω, which corresponds to a temperature sensitivity of ±0.02 deg.) In most cases the temperatures became constant within twenty days. However, ice which was initially warmer than (approximately) —1°C took much longer to return to equilibrium, and by the end of the field season there was still some uncertainty in the final values of the warmer measurements. Also no temperatures were recorded at hole no. 8 since it was completed just three days before evacuation of the field camp. Consequently, in the summer of 1973 Trapridge Glacier was revisited and final temperatures were measured where possible. The temperatures recorded at the end of the 1972 field season and those observed in 1973 are listed in Table II.
Table II. Trapridge Glacier Temperature Data

Results
The data of Table II are presented as vertical temperature profiles in Figures 2, 3 and 4. All measured values were less than 0.00 °C and, other than at hole no. 8, ice temperatures generally increased with depth. Peculiarities of the profiles of holes no. 1 through no. 7 are discussed by Jarvis (unpublished). Hole no. 8, drilled directly above the outlet ice fall of a high cirque, was situated midway between large closely-spaced water-filled crevasses. Reference Jarvis. and ClarkeJarvis and Clarke 1974 have shown that thermal injection from water-filled crevasses in cold ice has a major warming influence on upper ice temperatures, resulting in temperature profiles similar to that at hole no. 8. The anomalous temperatures measured at this site are therefore attributed to the local crevassing; no extrapolation of this temperature profile was attempted. Results of radar depth sounding on Trapridge Glacier using a 620 MHz apparatus (Reference Goodman., Goodman, Clarke, Jarvis, Collins and Metcalfe.Goodman and others, 1975) enabled extrapolation of the remaining temperature profiles down to the glacier bed. Linear extrapolation from the deepest temperatures of each profile indicates the presence of temperate basal ice below five of the seven drill sites (Figures 2, 3and 4). This result supports thermal instability, as suggested by Robin (1955, 1969) or Hoffmann and Reference Clarke. and GoodmanClarke 1973, as the mechanism governing the surge behavior of Trapridge Glacier.
Although the extended temperature profiles of holes no. 1 through no. 6 all intersect the pressure melting point above the glacier bed, we do not interpret this as indicating the presence of a finite layer of temperate ice below the respective drilling sites. Such a situation would be thermally unstable as no geothermal heat, frictional heat of sliding, or latent heat of refreezing water could propagate upwards through the temperate ice. The total heat flux implied by the observed temperature gradients would then be due to viscous heat generation and latent energy exchange at the interface of cold and temperate ice. Reference LliboutryLliboutry 1966 has shown that in sufficiently deep ice sheets, strain heating may be able to account for measured heat fluxes. However the maximum measured depth on Trapridge Glacier was only 143± 10 m. Viscous heating in such shallow ice is insignificant (Jarvis, unpublished) and liquid inclusions in a basal layer of temperate ice would rapidly freeze (releasing latent heat) until the layer was removed. Hence it seems reasonable that the temperature gradients decrease close to the bed so that on average the pressure melting point is achieved only at the ice-rock interface, thereby allowing some of the geothermal heat to flow into the cold ice (Reference Lliboutry.Lliboutry 1966 , 1968; Paterson, 1969).
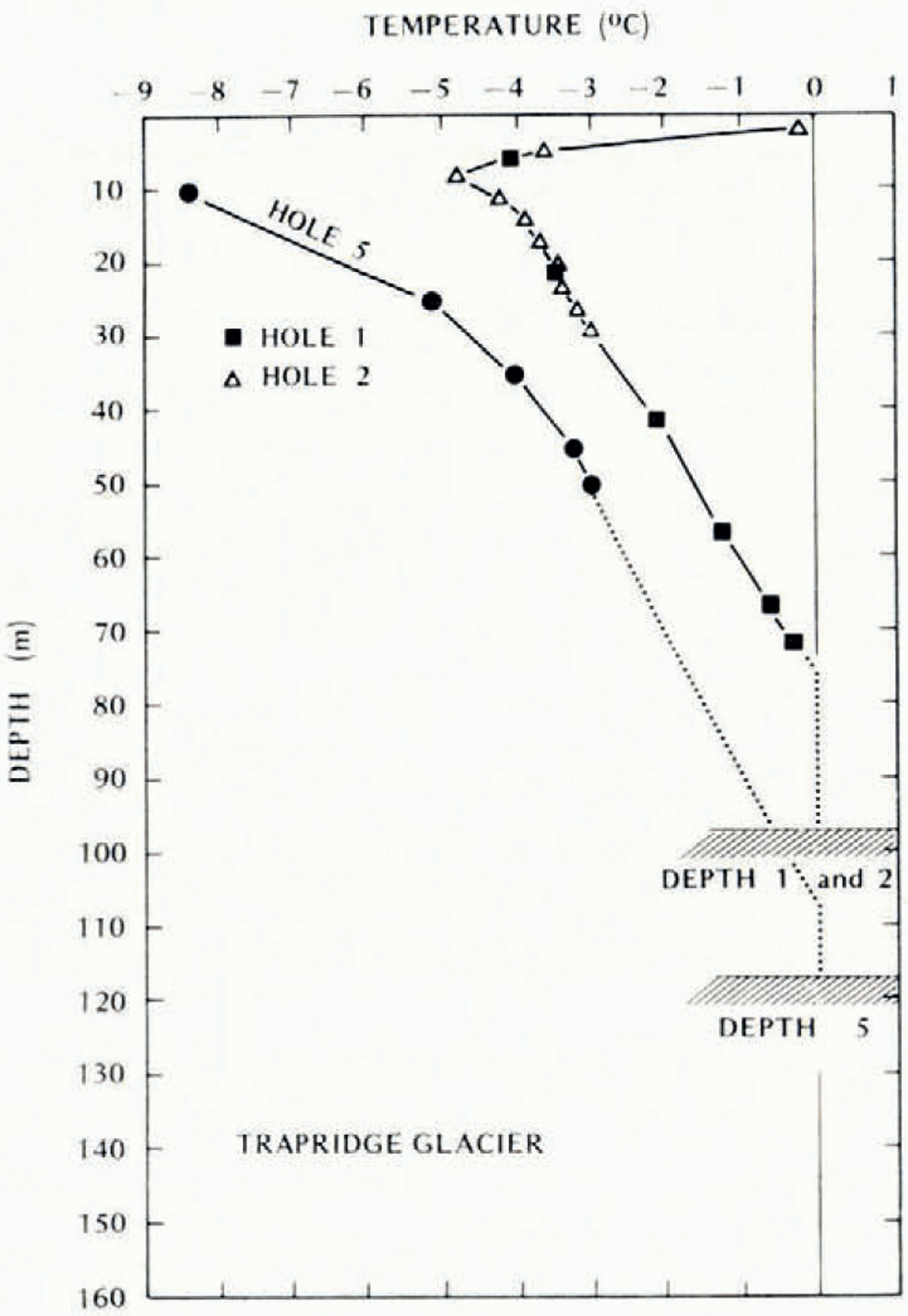
Fig. 2. Vertical temperature profiles: holes no. 1,2 and 5.

Fig. 3. Vertical temperature profiles: holes no. 3, 6 and 8.

Fig. 4. Vertical temperature profiles: holes no. 4 and 7.
A model of temperatures at the base of the glacier was constructed from the above observations. The glacier was divided into six zones centred on the drilling sites for which temperature extrapolations were made. Zone boundaries were determined by the right bisectors of lines joining adjacent centres, and depth control was obtained from a contour map of ice thickness, produced from the depth sounding results (Reference Goodman., Goodman, Clarke, Jarvis, Collins and Metcalfe.Goodman and others, 1975). For each region the observed 10 m temperature and the computed temperature gradient of the central drill site were applied over the whole zone. (Temperature gradients were computed from the 10 m temperatures and the points at which the extrapolated profiles intersected of 0° C (Figs 2,3 and4).) Below any point on the glacier the basal temperature could then be predicted by extrapolating along the appropriate gradient from the 10 m level down to the radar sounding depth. The extrapolation was performed for 101 points on the glacier bed and the predicted temperatures were contoured in one-degree intervals to produce the basal ice temperature map shown in Figure 5.
A cross-sectional view of the temperature regime of Trapridge Glacier was constructed from the vertical temperature profiles and the predicted basal temperatures. In Figure 6, this is superimposed on an ice depth profile given by Reference Goodman., Goodman, Clarke, Jarvis, Collins and Metcalfe.Goodman and others (1975). According to the model, the bedrock knoll between holes no. 1 and no. 4 prevents ice in this region from reaching its pressure melting point at the bed (Fig. 6a). However, no measurements have been made in this area due to the associated crevasse field and it is possible that the isotherms converge to follow the bed topography rather than cut through the local bedrock high.

Fig. 5. Trapridge Glacier map of basal temperature.
(Deep crevasses formed where ice flows over the rock dome allow summer melt water access to considerable ice depths. Refreezing of this water would contribute to the raising of basal temperatures (Reference Classen.Jarvis and Clarke 1974)-) In this case one continuous zone of temperate basal ice could exist from the neighbourhood of hole no. 3 down to hole no. 6 (Fig. 5).
Discussion of ice temperatures and surge behavior
The large regions of warm basal ice correlate well with the surface movement data of Reference Collins.Collins 1972. Up-glacier from survey marker G (indicated on Figure 6) as far as stake L our model of the bed temperatures predicts basal ice at the pressure melting point, and hence the rcgclation mechanism of glacier sliding could operate; in fact all measurable ice movement occurs above stake G. Down-glacier from G the basal ice is frozen to bedrock and Collins finds that this ice is stagnant. Between these regions of active and stagnant ice. exists a zone of positive ice emergence where flow lines bend sharply upwards above the horizontal. Collins suggests that this unusual deflection is caused by the lower tongue acting as an “ice dam” (as proposed by Reference Nielsen.Nielsen 1968, 1969), and our measurements indicate that the damming action is likely to be due to this ice being frozen to the bed. Since the basal slip component of the average ice velocity is eliminated in a cold tongue, the consequent slower ice motion in this region impedes the progress of sliding ice arriving from further up-glacier; in the case of Trapridge Glacier the thinness of the ice below G also causes the creep deformation component of ice flow to be reduced to an insignificant level. In larger glaciers with cold snouts, the “damming” action would be restricted to the elimination of basal sliding (and a reduction of creep deformation if the tongue is thinner or less steep than the upper regions). The observed strain-rate distribution (Reference Collins.Collins 1972) is consistent with this view of a cold glacier sliding on a partially temperate base. Above L (Fig. 6) tensile stresses exist, while below L compressive stress increases down-glacier culminating at G and rapidly decreases thereafter. The line marking the lower limit of the temperate ice follows very closely the zone of maximum compressive stress and coincides with a band of sharply increased surface slope.
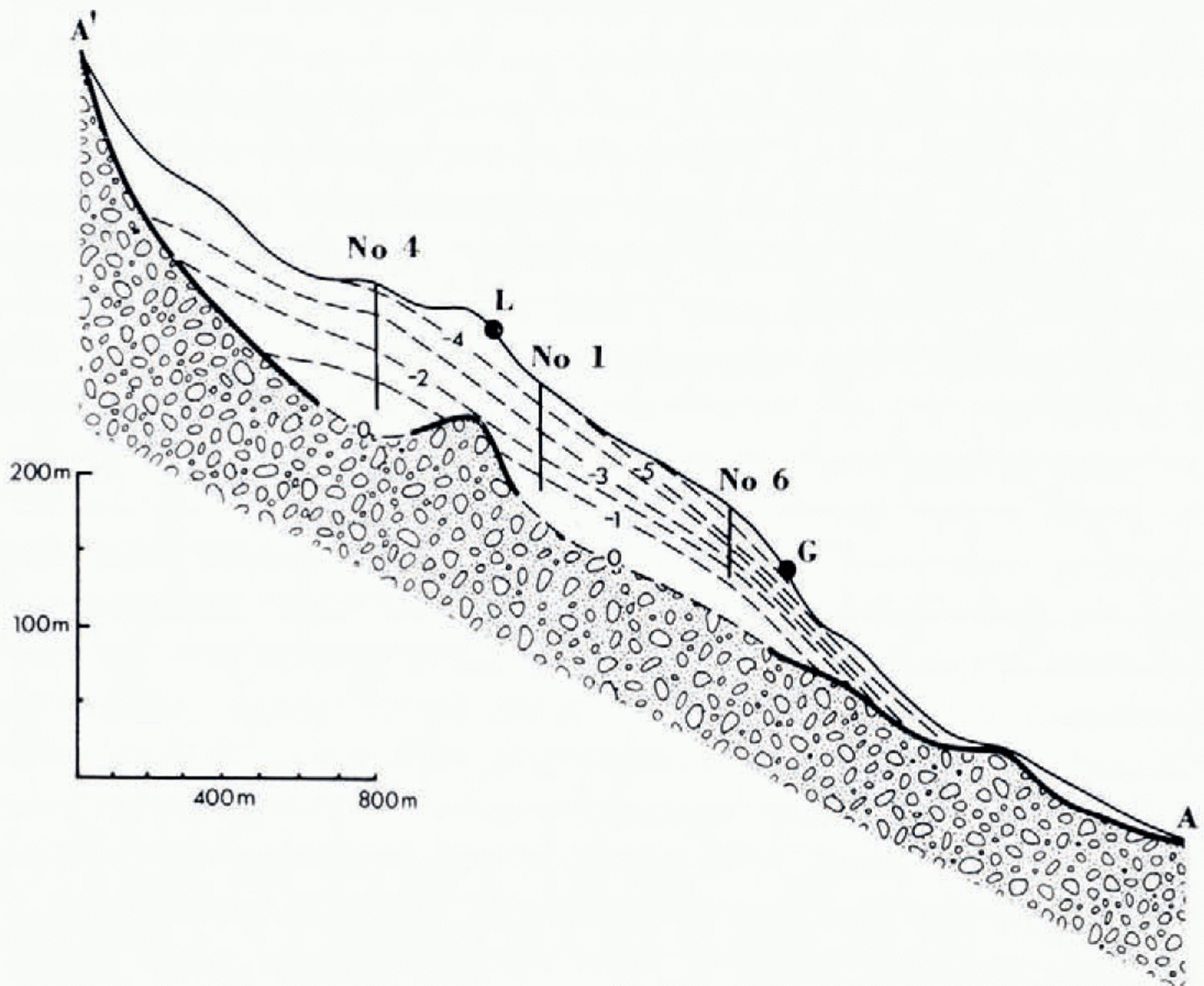
Fig. 6.a Cross-sectional view of Trapridge Glacier’ s temperature regime.

Fig. 6.b Cross-sectional view of Rusty Glacier’ s temperature regime.
The ice crest revealed by radar soundings (Fig. 6a), the intense zone of compressive stress, and the unusually large positive ice emergence, concurrent near survey stake G, suggest that a wave of ice thickening may be slowly moving down-glacier on the leading edge of the large zone of basal temperate ice. Consequent advection of the cold surface ice (in the vicinity of o) away from the bed may permit geothermal heat to extend the zone of temperate ice. Latent heat released by refreezing of basal water may also contribute to this effect (Reference Weertman.Weertman 1966). Thus an ice reservoir could be formed in the ablation area of the glacier causing it to thicken where it would otherwise thin. The ice crest on Trapridge Glacier is in fact one kilometer, or one-third of the total length of the glacier, below the firn line.
The cold tongue of Trapridge Glacier may also act as a thermal barrier to the flow of water which is produced at the bed by sliding friction and geothermal heat in the temperate zones. As each region of warm basal ice is encompassed by cold ice (Fig, 5) this water cannot escape along the bed and it is therefore trapped beneath the glacier. Some of this water will refreeze along the margins of the temperate ice zones. If an equal amount of melting and refreezing were to occur, there would be no net accumulation of water at the bed. However, since melt water can be produced throughout the temperate zones while refreezing is restricted primarily to the edges of these zones, it seems likely that melting will exceed refreezing. (It is not known whether a ring of cold ice can act as a dam for the movement of a sudden anomalous supply of water at the bed. Therefore the present description does not encompass the case of a sudden excess of water of sufficient quantity to crack open the ice-rock interface and allow water to How into the regions of cold ice.) As basal water accumulates, the bed roughness will be reduced locally by obstacle drowning (Reference Weertman.Weertman 1969) and the longitudinal stresses on either side of the lubricated zone will increase (Reference Robin.deRobin and Reference Weertman.Weertman 1973). At the same time, ablation of the stagnant lower glacier will continually weaken the ice dam. Eventually the increasing stress concentration below the ice crest should cause mechanical failure of the ice, and the reservoir will discharge overriding the inactive lower tongue, as illustrated in the 1941 photographs taken by Reference Sharp.Sharp (1947, 1951). In fact, Sharp referred to his “Glacier 13” (the Trapridge) as a small “superimposed glacier”. By 1951 the inactive snout was totally engulfed by the advancing surge front (Fig. 1a).
The speed and duration of the surge may be determined to a great extent by the amount of water accumulated at the bed. Although at the surge onset basal water production is greatly augmented by sliding friction, this is believed to be counteracted by the establishment of a basal drainage system allowing stored water to escape. As a result the glacier soon acquires a rougher bed, which retards sliding and thereby reduces water production. This may explain why the active phase of the surge cycle commences violently but, characteristically, is short-lived (Reference Meier. and PostMeier and Post, 1969).
Temperature, depth, and surface-movement studies of the nearby Rusty Glacier (Reference Classen. and ClarkeClassen and Clarke, 1971; Reference Clarke. and GoodmanClarke and Goodman 1975; Collins, 1972) show results strikingly similar to those presented here for Trapridge Glacier. The temperature distribution for Rusty Glacier is displayed in Figure 6b as isotherms along a longitudinal cross-section. As in the case of Trapridge Glacier, ice movement has been detected above the warm basal ice but not in the cold tongue (Collins, 1972).
In view of the observed temperature regimes of Rusty and Trapridge Glaciers, we feel that in cold glaciers the formation of an “ice reservoir” and “receiving area”, as discussed by Reference Meier. and PostMeier and Post (1969), may be due to the lower regions being frozen to the bedrock.
Relevance to large surging glaciers
Few temperature measurements have been made on large surge-type glaciers and it has been suggested that these are probably too deep to be cold at the bed (Reference Robin.deRobin and Weertman 1973). Flowever measurements have been made in the central region of Steele Glacier, Yukon Territory, (35 km long) two kilometers up-glacier from the stagnant “lower zone” of Reference Stanley.Stanley’s 1969 description (Jarvis and Clarke, 1974). The 114 m temperature was —6.7° C. For any reasonable ice temperature gradient, this observation implies cold ice for the upper few hundred metres; thus the lower zone of Steele Glacier may be frozen to its bed during the quiescent phase.
This conclusion is not incompatible with observations of internal and basal drainage in the lower tongue of Steele Glacier. Reference Weertman.Weertman 1972 has shown that water from the upper surface of a glacier which becomes englacial through moulins or deeply entrenched super-glacial streams (many of which have been noted on the Steele Glacier by Reference Wood.Wood 1936, Reference Classen. and ClarkeSharp (1947, 1951) and Reference Stanley.Stanley 1969) will probably drain through “Röthlisberger channels” at the bed (channels incised upwards into the overlying ice). Since Röthlisberger channels supplied by surface streams can be maintained without water melted from the bottom of the glacier (Reference Weertman.Weertman 1972; Reference Robin.deRobin and Weertman 1973), the observation of water emerging from ice tunnels at the bed is not necessarily evidence for basal melting. Further more, although internal water channels disturb cold ice temperatures locally, it is not believed that a regional influence sufficient to preclude a frozen snout would occur. In fact, actively draining moulins were observed in 1972, within 100 m of the site of temperature measurements of cold ice.
If the lower zone of Steele Glacier is frozen to its bed during quiescence, as only definitive ice temperature and depth measurements can prove, it may provide a thermal barrier to the flow of basal melt water produced in the upper regions. Up-glacier from a frozen snout, the drainage of upper-surface melt water through Röthlisberger channels at the bed is separated from the flow of basal melt water (Weertman, 1972) and hence is not expected to affect the damming of basal melt water by the frozen snout (Reference Robin.deRobin and Weertman, 1973).
The depth of Steele Glacier is not known, but 500 m would seem to be a reasonable upper value since 480 m was the largest depth estimate tabulated by Reference Meier. and PostMeier and Post (1969) for typical surging glaciers of western North America. The suggestion that this glacier may never be cold at its base implies, in the case of a temperate layer of basal ice of finite thickness, that no geothermal heat, latent heat of refreezing water, or frictional heat of sliding, can flow into the ice, and hence that the 114 m temperature stems from the mean annual surface temperature and internal viscous healing. Viscous heat generation would cause the ice tempera ture to increase with depth until the pressure melting point is attained. This occurs at what we refer to as the critical depth. Below the critical depth further viscous energy is dissipated in the formation of water within a layer of temperate ice which extends down to the glacier bed (Reference Lliboutry.Lliboutry 1966, 1968; Paterson, 1969). If the glacier depth is less than the critical depth, the basal ice must either be cold or at the melting point along the ice rock interface and in either case some (or all) of the incident geothermal, latent, or frictional heat must enter the glacier ice; thus cold ice must exist immediately above the bed.
An estimate of the critical depth of a glacier may indicate whether or not basal temperatures need be considered when studying its surge behaviour. If the ice depth over a major portion of a surge-type glacier is greater than the critical depth, basal temperatures are not likely to be significant. However, if large regions of a glacier are shallower than its critical depth the possibility of a frozen ice-bedrock interface exists. In the latter case the reduced ice thickness after a surge brings the cold upper ice closer to the bed, raises the pressure melting temperature at bedrock, and reduces the basal shear stress and hence the viscous heat generation near the bed. These factors may cause basal temperatures in certain regions to cool below freezing thereby enabling some form of thermal regulation (Reference Robin.deRobin 1955, 1969; Hoffmann and Clarke, 1973).
To obtain the desired estimate, a simple one-dimensional steady-state model of a glacier with ice thickness greater than the critical depth was considered. The temperature profile of the cold layer, from the critical depth up to the surface, can readily be calculated if a simple glacier geometry is assumed and flow-law constants are known. (Below the critical depth, temperatures follow the pressure melting curve down to the bed.) The steady-stale assumption facilitates analysis and roughly approximates conditions during the quiescent phase of a surge cycle. The boundary conditions for this problem are the mean surface temperature and the temperature at the critical depth (the pressure melting point of ice). At any inter mediate level, the temperature gradient must represent a heat flux which is equal to the integrated viscous heat generation from the critical depth up to that level. (The temperate layer below the critical depth insulates the cold upper ice from any geothermal, latent or frictional heating at the bed.)
If we consider an inclined-slab glacier model with coordinates x parallel to the glacier surface, y upward normal to the surface, and origin at the critical depth, the heat flux φ at any levels is given by
(where К is the thermal conductivity of ice and T the temperature), and the shear stress т is
where ρ is the ice density, g the gravitational acceleration, h the depth from the ice surface, and α the slope of the glacier surface. If the glacier surface is at y = H, then h = (H—y).
Viscous heat generation is simply
where εxy(y) is the shear strain-rate and εxy(y) is the shear stress. Using Glen’s flow law for ice, Equation (3) reduces to
where &3x0442;(y) has been substituted for тxy(y), is the temperature-dependent coefficient and n the power index of the flow law (Reference GlenGlen 1953, 1955).
For valley glaciers, т can be approximated by the introduction of a “form factor” f which accounts for the fact that some of the weight of the glacier is supported by the valley walls. Thus т =fρgh sin α. Values of f lie between zero and one, typically 0.7 ≤ f ≤ 0.9 (Reference Nye.Nye 1965; Paterson, 1969). Theoretical considerations suggest that the flow-law coefficient B varies with temperature in the following manner
where B0 is a constant, Q the activation energy of ice, R the universal gas constant, and T the absolute temperature (Reference GlenGlen 1953, 1955). Since values of B(T) are usually measured near To = 273 K, it is convenient to express B(T) in terms of B(To). Thus Equation (4) becomes
where the substitutions A = fpg sin α and h = (H—y) have been made.
Substitution of Equation (1) into Equation (6) yields the non-linear differential equation
where C = — B(To)An+1/K and D = Q/RTo . Equation (7) was solved by standard finite-difference methods to generate the complete solution T(y). In particular, the unique surface temperature Ts corresponding to critical depth H is determined as T s = T(H). In our calculations the spatial increment was chosen so that Ts would have an accuracy of ±0.01 deg.
The above model ignores changes of ice thickness. This may be partly justified by the following argument. Since an increase in ice thickness raises internal stresses, the subsequent additional viscous heating causes an equal increase in the thickness of the basal layer of temperate ice, and thus the critical depth as measured from the surface does not change. The temperature profile in the cold layer should again reflect the degree of visous heating and the surface temperature. Therefore the temperature profile in the cold layer can be considered approximately constant when measured in a coordinate system with origin at the critical depth.
In an early study of temperature profiles in cold ice Reference Robin.deRobin 1955 considered the effects of accumulation on stable ice sheets and fiat firn fields of small polar glaciers. Robin’s theory predicts that for an ice sheet 400 m thick, a net annual accumulation of 16 cm of ice causes basal temperatures to be approximately 4 deg colder than in the case of no accumulation. Although surging glaciers do not fit the model of stable ice sheets, this result suggests that accumulation in the upper regions may have a cooling effect on the deep ice temperatures. As this complication was not included in the one-dimensional model described above, our calculations probably underestimate the critical depth for regions above the firn line. Reference Robin.deRobin 1955 also points out that variation of temperatures with altitude produces a tendency to form inverse ice-temperature gradients close to the surface of the outer edges of polar ice sheets. This effect, if present in surge-type glaciers, may cause our estimates of the critical depth to be conservative in the ablation zone also.
The theoretical uniqueness of the relation between T s and H (for a given A) is lost in numerical calculations due to uncertainties in the values of the constants B(T0), n and Q. Hodge (unpublished), for example, has cited seventeen different measurements of B(T0) and n. Values of B(T 0) range from 0.040 bar−n to 0.849 bar−n a−1 and those of n from 2.1 to 5.2. Measured values of Q vary from 58520 J mol−1 to 132924 J mol −1 (Reference GlenGlen 1953, 1955; Raraty and Tabor, 1958). We have evaluated T s as a function of H for various glacier geometries (0.5 ≤ f ≤ 0.9; 1° ≤ α 15ΰ) over the above range of flow-law parameters and activation energies. A typical result is shown in Figure 7 in which the flow law parameters are according to Reference Nye.Nye 1953. Contours on this diagram connect points of equal critical depth H corresponding, in the steady state, to different combinations of Ts and A. The uncertainty in Q has been incorporated by the broadening of the contours. The lower edge of each broadened contour corresponds to Q= 132 924 J mol−1 while the upper edge is the curve for Q = 58520 J mol−1. The graph is relatively insensitive to this variation.

Fig. 7. Contours of critical depth H (see text) in a Cartesian space with coordinates Ts, the glacier’s mean surface temperature and A, a geometric term as defined in the text.
With the aid of Figure 7 the critical depth of a particular glacier can be determined once the geometrical term A and surface temperature Ts are known. In the case of Steele Glacier the surface slope a is approximately 2° (Reference Wood., Bushnell and RagleWood 1972) and ƒ is probably between 0.5 (semi circular cross section) and 1.0 (infinitely wide slab). Hence A may be anywhere between 15.4 × 10−5 N and 30.9 ×−5 N. The mean surface temperature T s is believed to be (— 8.0± 1)°C (Jarvis and Clarke, 1974). This scope for A and Ts is indicated as a rectangular section on Figure 7. Contours passing through this region indicate that the critical depth for Steele Glacier is between 350 m and 600 m. Specifically, for ƒ = 0.7 (a typical value for valley glaciers (Paterson, 1969; Reference Robin.deRobin and Weertman, 1973)) and Ts = —8.0° C, the critical depth is 450 m. This implies that wherever the glacier thickness does not exceed 450 m, geothermal heat must enter the glacier ice and a finite layer of temperate basal ice cannot exist. Further calculations show that for regions of glacier depth less than (approximately) 300 m, if we assume ф(о) = G the geothermal gradient, a value of Ts = —8.0° C can only be obtained from Equation (7) when T(o) < o° C. (C was taken as 20 deg km−1.) This predicted maximum ice thickness of the frozen snout (300 m) will be significantly reduced by the additional heat source of refreezing water at the bed. If sufficient energy is available from this source to double the temperature gradient in the basal ice, the predicted maximum depth for the frozen tongue becomes 200 m. (This figure would also be sensitive to anomalous geothermal gradients.) In either case, if the flow-law constants of Reference Nye.Nye(1953) are valid for Steele Glacier, large regions of this glacier may be frozen to bedrock.
Also indicated on Figure 7 are the areas appropriate to Finsterwalderbreen and Trapridge Glacier. The surface temperature and slope of Finsterwalderbreen, Spitsbergen, were taken from Reference Schytt.Schytt 1969 and Reference LiestφlLiestøl 1969. The slope of Trapridge Glacier was estimated from the surface survey data of Collins (1972). In both cases ƒ was assumed to lie between 0.5 and 1.0. The critical depths indicated for Finsterwalderbreen and Trapridge Glacier are approximately 400 m and 120 m respectively. No temperate layer of ice should exist at the base of these glaciers if their respective ice thicknesses are less than these values.
Our simple model of cold ice temperatures makes the unrealistic assumption that the mean surface temperature Ts and surface slope α are spatially constant. However, provided T s and a vary slowly with distance along the glacier, the model may be applied (approximately) at different locations by incorporating the local values. From Figure 7 it can be seen that for the larger Steele Glacier and Finsterwalderbre, a temperature variation of ±5 deg causes little change in the estimates of H. An increase or decrease in α by a factor of two would cause the predicted value of H for Steele Glacier to become 350 m or 700 m respectively.
The above discussion of critical depths has been based on Nye’s values of the flow-law constants, chosen because they lie in the middle of the range of values cited by Hodge . More (or less) viscous flow laws will naturally yield different critical depths. The critical depths of Steele Glacier, Finsterwalderbreen and Trapridge Glacier as predicted with the most viscous and least viscous (low laws tabulated by Hodge are presented in Table III. Although, as shown in this table, the critical depths vary significantly over the range of flow-law constants, we feel there is no reason to exclude the possibility of cold ice al the base of these sub-polar glaciers, particularly in the lower tongue regions.
Table III. Range Of values of critical depth corresponding to range of flow laws cited by hodge (unpublished)
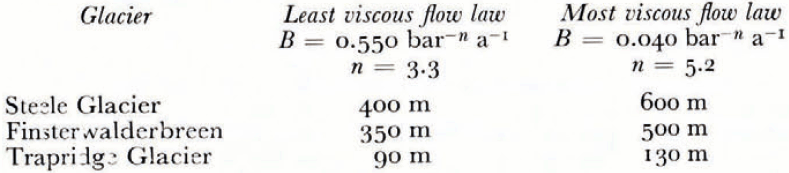
Concluding remarks
Reference Robin.deRobin and Weertman (1973) have proposed an attractive hypothesis for cyclic surging of presumably temperate glaciers which includes an active ice reservoir, with a steepening front, and stagnant receiving area. Finsterwalderbreen was cited as a surge-type glacier exhibiting the properties predicted by this hypothesis. However the gravity depth profile presented for this glacier (Reference Robin.deRobin and Weertman, 1973) never exceeds 350 m, in which case our calculations would indicate large regions of cold ice extending down to the base (Fig. 7). Melting temperatures should only prevail along the ice-rock interface under the deepest ice. Consequently the (low of Finsterwalderbreen may be thermally regulated in the same manner as that proposed for Rusty and Trapridge Glaciers.
It is interesting to note that the glaciers in Spitsbergen, where surging is a common mode of glacier advance, are all sub-polar (Reference LiestφlLiestøl 1969; Reference Schytt.Schytt 1969) and that the 23 m temperature measured on Bråsvellbreen (which has made the largest surge recorded in Spitsbergen) was -6.0° C. Schytt claims that the outer edges of ice caps in this region form a “ring of cold ice” frozen to the bed and J. T. Hollin (in discussion to Reference Schytt.Schytt 1969, p. 871) suggested that cold ice holding back warm ice may be favourable to surge development.
In conclusion it appears possible that a cold stagnant tongue acting both as a thermal and mechanical barrier may be responsible for the building up of ice reservoirs on many of the sub-polar glaciers in the Yukon Alaska region and in Spitsbergen.
Acknowledgements
We thank B. Chandra, B. B. Narod, and K. D. Schreiber for assistance in field preparations, and S. G. Collins, P. Dillon, R. H. Ragle, and P. Upton of the Arctic Institute of North America for encouragement and logistic support. We are especially grateful to Robert Metcalfe who was an extremely valuable field assistant. Financial support was provided by the University of British Columbia, Environment Canada and the National Research Council (Canada).














