1. Introduction
The polar regions of the Earth play a key role in determining the nature of global climate. While the tropics and subtropics are regions of net radiative input, there is net radiative loss over the high latitudes (i.e. outgoing longwave radiation exceeds absorbed shortwave radiation). It is the ‘task’ of the atmospheric (and to a lesser extent the oceanic) circulation to redress these imbalances (and to produce a quasi-steady climate) by transporting energy (primarily in the form of sensible heat, latent heat and potential energy) from the tropics to the polar regions. Seen from this perspective not only is the nature of the tropical processes and conditions important for the workings of the general circulation, but so too are the dispositions of the polar regions. For this and many other reasons, a comprehensive understanding of global dynamics and thermodynamics must involve consideration of the polar regions.
There is strong evidence to indicate that changes in the concentrations of ‘greenhouse’ gases in the atmosphere are leading to many changes in global climate. These changes are more marked in specific areas. For example, in recent decades the Arctic region surface temperature has increased by about twice the global average, the so-called ‘Arctic amplification’ (Reference Screen and SimmondsScreen and Simmonds, 2010). Many of the physical processes that dominate climate in the polar regions are strongly influenced by sea ice. For example, sea ice effectively forms a barrier between the ocean and the atmosphere and hence dramatically changes the nature of air-sea interaction. In addition, the shortwave albedo of ice is 0.8-0.9 while that of polar water is -0.1 and hence the radiative components of the surface energy budget greatly depend on whether ice is present or not. Recent research by, for example, Reference Screen and SimmondsScreen and Simmonds (2012) and Reference Pistone, Eisenman and RamanathanPistone and others (2014) has quantified the large role that this feedback plays in the radiative forcing. Hence, sea ice presents an additional complicating factor when considering the climate of polar regions.
It is the behaviour of sea ice in the two polar regions that is of interest in this paper. Only a few past studies have addressed this ‘bi-polar’ aspect, including Reference Turner and OverlandTurner and Overland (2009). In recent decades the Arctic sea-ice extent (SIE; defined as the area of ice that has a concentration in excess of 15%) has shown dramatic decreases, particularly in September. These reductions have been the subject of much research (e.g. Reference Walsh and ChapmanWalsh and Chapman, 2001; Reference Cavalieri and ParkinsonCavalieri and Parkinson, 2012; Reference ComisoComiso, 2012; Reference Stroeve, Serreze, Holland, Kay, Malanik and BarrettStroeve and others, 2012a; Reference WalshWalsh, 2013). On a longer timescale there are numerous studies that point to present Arctic SIE changes as being anomalous compared to events over the past few thousand years (e.g. Reference PolyakPolyak and others, 2010; Reference Kinnard, Zdanowicz, Fisher, Isaksson, Vernal and ThompsonKinnard and others, 2011; Reference SpielhagenSpielhagen and others, 2011). By contrast, it has been reported that the Antarctic SIE has exhibited ‘small’ increases over this period (Reference Cavalieri and ParkinsonCavalieri and Parkinson, 2008; Reference Cavalieri and ParkinsonParkinson and Cavalieri, 2012). This net increase in sea-ice extent comes about from the sum of positive and negative regional trends around the Antarctic periphery.
The morphology of the two polar regions is very different, so a priori it may not come as a surprise that their sea-ice trends differ. Most of the sea ice in the Northern Hemisphere (NH) is found in the Arctic Ocean. This ocean is centred approximately over the North Pole and is surrounded by continents. There is therefore limited oceanic access from the Arctic Ocean to the mid-latitudes, this being mainly through the relatively ‘narrow’ Bering and Fram Straits. Hence the sea-ice zone is far to the north of the mid-latitude storm tracks and not particularly subject to their influence. By contrast, the broad region about the South Pole is occupied by the Antarctic ice sheet whose elevation in places exceeds 4 km. The continent slopes down to meet the Southern Ocean at -70° S (depending on the longitude); the sea-ice zone then starts and has the whole Southern Ocean in front of it. The sea-ice zone extends, in some sectors and seasons, to -55° S, well into the westerlies (Reference Simmonds, Rafter, Cowan, Watkins and KeaySimmonds and others, 2005). Another aspect of difference between the two sea-ice regions is that the southern region is host to strong baroclinicity and frequent intense storms (Reference SimmondsSimmonds and others, 2003) which affect, and are affected by, the distribution of sea ice. In addition, the steep slopes and strong inversions over the Antarctic continent give rise to intense katabatic flows which have no counterpart in the Arctic. These flows play an important role in the generation and maintenance of coastal polynyas. The surface waters in the southern ice zone are ∼3-4psu (practical salinity units) more saline than those in the Arctic basin (Reference Zweng, Levitus and SilverZweng and others, 2013), while the Antarctic ice zone receives approximately three times as much precipitation (Reference AdlerAdler and others 2003). As a final point we comment that the modes of atmospheric variability that influence the Southern Ocean (e.g. Reference Simmonds and KingSimmonds and Jacka, 1995; Reference SimmondsSimmonds, 2003), and the scale and processes (including water mass formation) in the Southern Ocean are much more complex than those in the Arctic Ocean.
Sea ice is known to vary over a wide range of timescales, and hence the nature of diagnosed trends may be specific to the particular period chosen (Reference Watkins and SimmondsWatkins and Simmonds, 2000). In this paper, we analyse the satellite sea-ice record in the two hemispheres up to the present (1979-2013). This longer record grants us greater statistical confidence in the nature of variability and trends than has been possible heretofore, particularly in light of the extraordinary behaviour of Southern Hemisphere (SH) sea ice in 2013, namely record or near-record extents for all months of the year. We also perform analyses on the temporal behaviour of the global total (i.e. Arctic plus Antarctic) sea-ice coverage. We finally offer some comments on the comparison of Antarctic sea-ice trends in observations and the World Climate Research Program’s Coupled Model Intercomparison Project Phase 5 (CMIP5) models.
2. Data and Methods
The Arctic and Antarctic sea-ice data we use here are derived from a succession of satellite passive-microwave measurements which have provided an almost seamless global time series of coverage. Monthly mean data of SIE were downloaded from the National Snow and Ice Data Center (NSIDC, Boulder, CO, USA) for 35 years from November 1978 to December 2013.
These extents are derived from satellite passive-microwave data from the Scanning Multichannel Microwave Radiometer (SMMR) on the NASA Nimbus 7 satellite, the Special Sensor Microwave/Imager (SSMI) on the F8, F11 and F13 satellites of the US Defense Meteorological Satellite Program (DMSP), and the Special Sensor Microwave/Imager Sounder (SSMIS) on the DMSP F17 satellite. A large number of studies have established the accuracy of these datasets and, in particular, the techniques that have been used to account for the changes in the sensors used (and their resolution and sensitivity) over time (e.g. Reference Cavalieri, Parkinson, Gloersen, Comiso and ZwallyCavalieri and others, 1999, Reference Cavalieri and Parkinson2012; Parkinson and Reference Cavalieri and ParkinsonCavalieri, 2012; and references therein). A broad overview of these data is presented by Reference Fetterer, Knowles, Meier and SavoieFetterer and others (2002). The months December 1987 and January 1988 were flagged in the NSIDC archive as having insufficient satellite data available to process the extent values. Guided by the fact that sea-ice anomalies have significant multi-month persistence (e.g. Reference Blanchard-Wrigglesworth, Armour and BitzBlanchard-Wrigglesworth and others, 2011) we have here filled in these gaps by linear interpolation between the anomalies of November 1987 and February 1988. This approach to filling data gaps is clearly physically more realistic than others that have been used, such as filling gaps with linear interpolation between the same month in the previous year and following year (e.g. Reference Eisenman, Schneider, Battisti and BitzEisenman and others, 2011) or with the climatological mean (e.g. Reference Simpkins, Ciasto and EnglandSimpkins and others, 2013). The trends calculated below are determined from the straight line of best fit (using the standard least-squares approach), complemented by the calculation of the standard error. In some cases we fit a quadratic through the data, again following the standard least-squares method.
Our analysis includes the diagnosis of atmospheric structures which are associated with sea-ice behaviour. For this we have used the European Centre for Medium-Range Weather Forecasts’ ERA-Interim global reanalysis (Reference DeeDee and others, 2011). The choice of this reanalysis set was guided by its superior overall performance in the polar regions and, in particular, in high southern latitudes (e.g. Reference Bracegirdle and MarshallBracegirdle and Marshall, 2012), in comparison to other reanalyses. We use here the period 1979–2013.
The dominant mode of SH atmospheric variability is the Southern Annular Mode (SAM). The SAM is characterized by a meridional seiche of mass between about 40 and 658 S, and is intimately tied up with many circulation features of the SH and, in particular, the preferred paths of synoptic-scale weather systems (e.g. Reference Rashid and SimmondsRashid and Simmonds, 2005). As the index for this we have used the data provided by Marshall (2003) (and updates) http://www.nerc-bas.ac.uk/icd/gjma/sam.html, again using the period 1979–2013. In all the atmospheric analysis presented here, we follow the convention (e.g. Reference MarshallMarshall, 2003) that the year attributed to December–February (DJF) is the year of the December.
3. Results
3.1. Sea ice
We show in Figure 1 the mean annual cycle of NH and SH SIE compiled from the 35 year record. The Arctic curve reveals a maximum of 15.49x106km2 in March and a September minimum of 6.40x106km2. The analogous values for the Antarctic region are 18.83 x 106 km2 (September) and 3.06x106km2 (February). Also exhibited in the figure is the sum of the two time series, i.e. the annual cycle of the global total of sea ice. This shows a broad maximum during the austral winter and spring, with the absolute maximum occurring in November (27.30 x 106 km2). The graphs show that this maximum occurs after the austral maximum because at that time the rate of decrease of southern ice is more than compensated by the regrowth of northern ice. The annual means of the SIE are 11.77, 12.02 and 23.79 x 106 km2 for the NH, SH and globe, respectively. It is of interest to note that with the recent opposing SIE trends in the two hemispheres the annual mean in the south now exceeds that in the north.
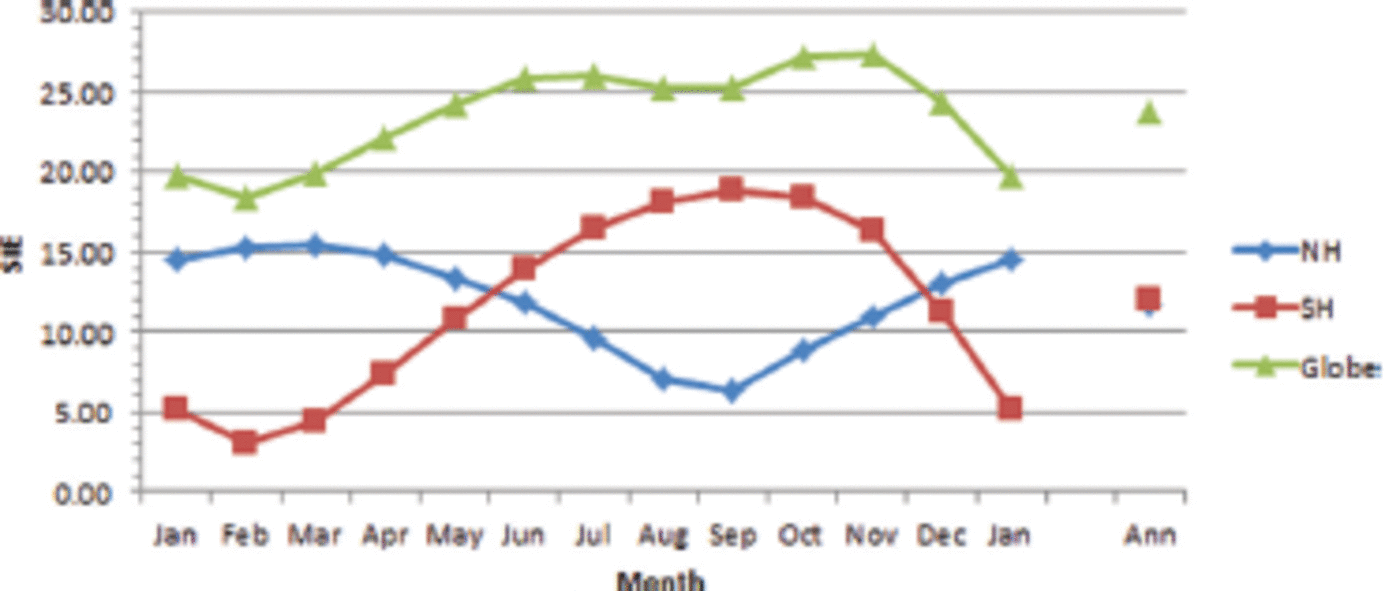
Fig. 1. Mean annual cycle of SIE (November 1978-December 2013) for the NH (blue diamonds), SH (red squares) and the globe (green triangles). Also shown are the annual means of the three series. Note that the symbol for the annual mean for the NH (11.77 x 106km2) lies beneath that for the SH (12.02 x 106km2).
The calendar-month trends of boreal SIE are determined from the least-squares line of best fit, and these are shown in Figure 2a. It is preferable to display these as absolute trends as we have done here rather than percentage (or ‘relative’) trends as are often shown, as the latter approach can distort the magnitude for months with low climatological sea-ice coverage. Another reason for considering absolute trends is that these have direct physical implications for changes in air-sea fluxes, air-ocean-sea-ice interactions, input of mechanical energy into the ocean, etc., associations that do not hold for relative changes. In addition, as pointed out by Reference WohllebenWohlleben and others (2013), the magnitude of the relative trend depends on the reference value or period used, which can cause confusion when the results from different studies are being compared. We are very much in accord with their view that ‘scientific studies involving the inter-comparison of trends should restrict themselves to the use of absolute trends to avoid ambiguity’.
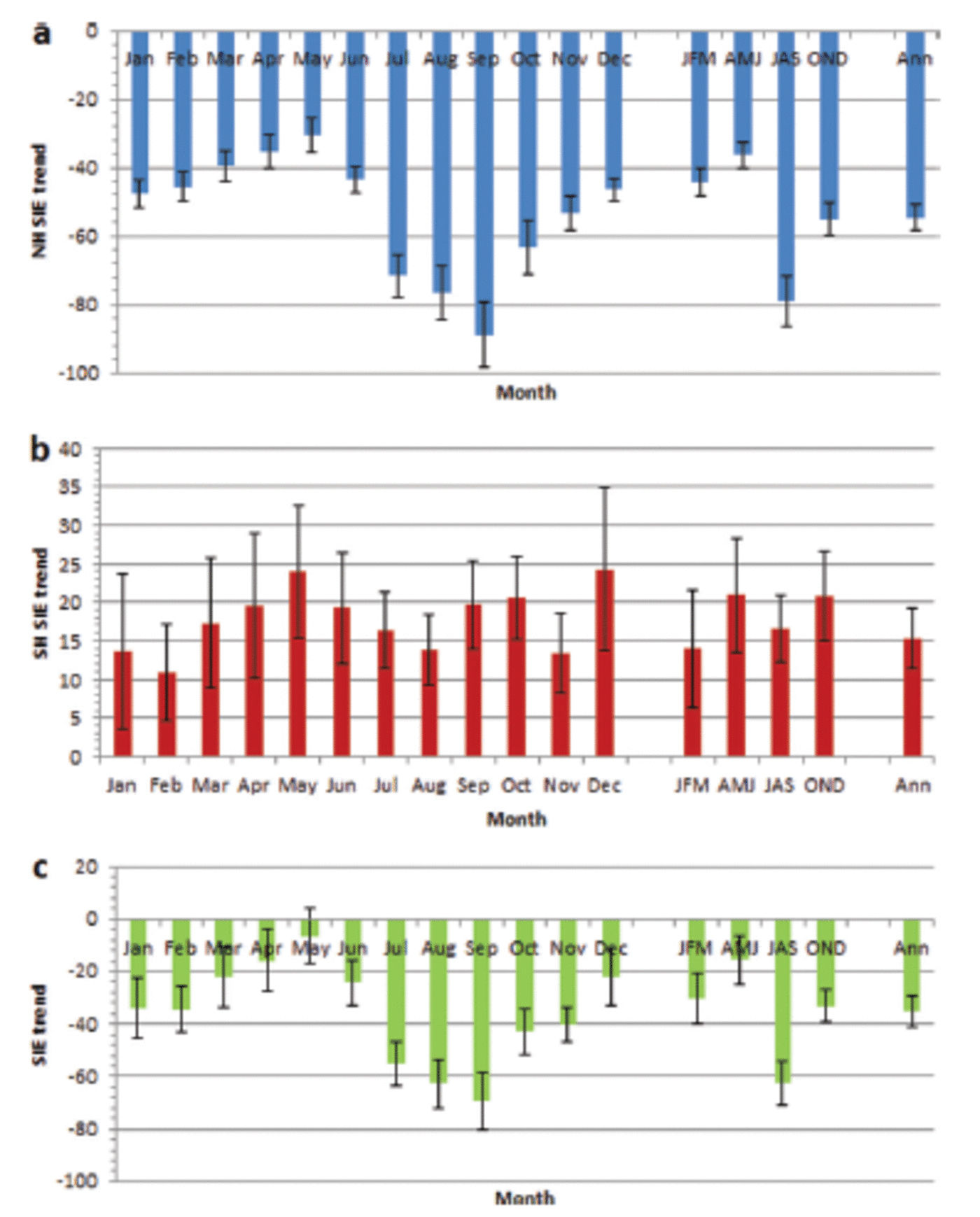
Fig. 2. Monthly trends in SIE (November 1978–December 2013) for (a) the NH, (b) the SH and (c) the globe. The whiskers indicate the standard errors. Also shown are the trends in the seasonal and annual time series.
The trends are negative in all months, with the smallest magnitude in May (-30.45 x 103 km2 a −1) and largest in September (-88.96 x 103 km2 a–1). The whiskers on the bars in Figure 2a indicate the standard error, and these are all much smaller than the trends. Table 1 presents the numerical values for these parameters, as well as indicating the statistical significance. The table indicates that the 12 monthly trends are significantly different from zero at the 99% confidence level (and indeed at p˂0.001). The second group of bars in Figure 2a indicates the trends in seasonal means (and we have here followed the ‘sea-ice’ season convention of Reference Cavalieri and ParkinsonCavalieri and Parkinson (2012) of defining boreal winter as January-March (JFM), etc.). All these seasonal trends are also highly significant (p˂0.01), with the greatest trend in summer (JAS). Finally, the last bar indicates a similarly robust downward trend in the annual means.
Table 1. Monthly, seasonal, and annual trends in SIE (November 1978–December 2013) for the NH, SH and the globe. The units are 103 km2 a–1. Also presented are the standard errors (SE). The statistical significance of the trends is indicated by the typeface: bold (p = 0.01), bold italic (p = 0.05) or italic (p = 0.10)

An analogous display for the SH is presented in Figure 2b (and Table 1). All monthly trends are seen to be positive, with the largest being found in May and December (the latter exhibiting 24.27 x 103 km2 a −1). The error bars suggest less confidence in the trends compared to the NH case. All trends, except for January, are significant at the 90% level, ten are significant at 95% and six at 99%, with these last tending to occur in the second half of the year. The seasonal and annual SH trends all reach the 99% level, with the exception of AMJ (p˃0.1).
The monthly trends of the global SIE are all positive (Fig. 2c; Table 1), and eight of these are significantly so (p˂0.01). The trend is not significant in April and May, and only marginally so (p˂0.1) in March and December. Overall, however, there is a significant (p˂0.01) trend in the global annual total of -35.29 x 103 km2 a–1. Three of the seasons also show this level of significance, while the trend identified in AMJ cannot be said to be above the noise level.
Complementing these, we show in Figure 3a the time series of Arctic SIE for the calendar month in which it exhibits its climatological maximum, i.e. March. As would be expected from the magnitude of the standard error presented in Table 1, there is considerable variability about the trend line, but we have seen the slope is significantly negative. The lowest value was recorded in 2006, with 2011 almost reaching that level. Figure 3b presents similar information for September, the month of least NH ice cover. The record low of 3.63 x 103 km2 was reached in 2012 and smashed the already dramatic record set in 2007 (Reference Simmonds and RudevaSimmonds and Rudeva, 2012). The highest September value was reached in 1996, and a number of authors have commented that the decay of the autumn sea ice appeared to accelerate in the 1990s (e.g. Reference Maslanik, Drobot, Fowler, Emery and BarryMaslanik and others, 2007; Reference Simmonds, Burke and KeaySimmonds and others, 2008; Reference Simmonds and KeaySimmonds and Keay, 2009). To highlight this, we show in the figure the quadratic curve of best fit to the data, and it serves to quantify the accelerating negative trend. Figure 3c plots the evolution of the annual mean Arctic SIE and its very strong downward trend. The year 2012 posted the lowest annual mean (10.65 x 106 km2), just beating the 10.68 x 106 km2 set in both 2007 and 2011.

Fig. 3. Time series of NH SIE in (a) March, (b) September and (c) for the annual mean. Each graph displays the straight line of best fit to the data. In (b) the quadratic line of best fit is also shown (dashed line). The r 2 of the linear fits are (a) 0.69, (b) 0.73 and (c) 0.74. The r 2 of the September quadratic fit is 0.79.
Figure 4 offers a comparable display for Antarctic SIE. The statistics indicate that the March trend of 17.23 x 103 km2 a–1 only just achieves significance at the 95% level. There is considerable sub-decadal variability in this and other time series, a point made by Reference Simpkins, Ciasto and EnglandSimpkins and others (2013). As an example of this timescale of variability, we point out that the minimum and maximum over the 35 year record are separated by only 2 years (2006 and 2008). The significance level of the increase in September is much greater, and we note that the record set in 2012 was broken in 2013 by quite a large margin. In fact the September 2013 SIE of 19.77 x 106 km2 was the greatest of any month of our 422 month sample. The time series of the annual mean SH SIE is shown in Figure 4c and, in particular, emphasizes how unusual 2013 was. The previous highest annual mean was 12.60 x 106 km2 (in 2008), but now that record stands at 12.85 x 106 km2. Consistent with this behaviour we remark that the last five months of 2013 recorded the greatest SIE (for their respective calendar months) over our analysis period. In the other seven months of the year the ice extent was at least the fifth most extensive, with the sole exception of January (eighth most extensive). We commented above that the September Arctic decrease appeared to have accelerated about the mid- to late 1990s. The structure of Figure 4c also suggests a change in trend about this time. The inclusion here also of the quadratic line of best fit reinforces this perspective of some quite rapid changes at the end of the data period, and we note that five of the heaviest SH sea-ice years have fallen in the last six years.

Fig. 4. Time series of SH SIE in (a) March, (b) September and (c) for the annual mean. Each graph displays the straight line of best fit to the data. In (c) the quadratic line of best fit is also shown (dashed line). The r 2 of the linear fits are (a) 0.11, (b) 0.26 and (c) 0.39. The r 2 of the annual quadratic fit is 0.43.
3.2. Atmospheric circulation
The distribution of sea ice is influenced by a number of factors, an important one of which is the atmospheric circulation (Reference Wassermann, Schmitt, Kottmeier and SimmondsWassermann and others, 2006; Reference Holland and KwokHolland and Kwok, 2012), and we wish here to explore the extent to which the trends documented above can be associated with circulation changes. In undertaking this, it is important to appreciate the background spatial structure of the mean sea-level pressure (SLP) distributions.
We present the mean SLP distributions in the four seasons (the seasons being defined here in the ‘meteorological’ sense of December–February (DJF), etc.). These are obtained from the ERA-Interim reanalysis for the period 1979–2013. Figure 5 shows that in DJF the high latitudes are strongly influenced by the Aleutian and Icelandic lows and the Siberian high, the last exerting a direct influence into the Arctic basin. In MAM these features become weaker and the centre of the Arctic high has moved from the Siberian coast to the central Arctic at ∼150°W. In JJA (boreal summer) the mean circulation is considerably weaker, with the polar high moving into the Beaufort Sea in this modern climatology and lower pressures dominating much of the Arctic basin. Finally, in SON the Arctic high has moved slightly to the west, and the mean sub-arctic pattern starts to resemble that in winter.
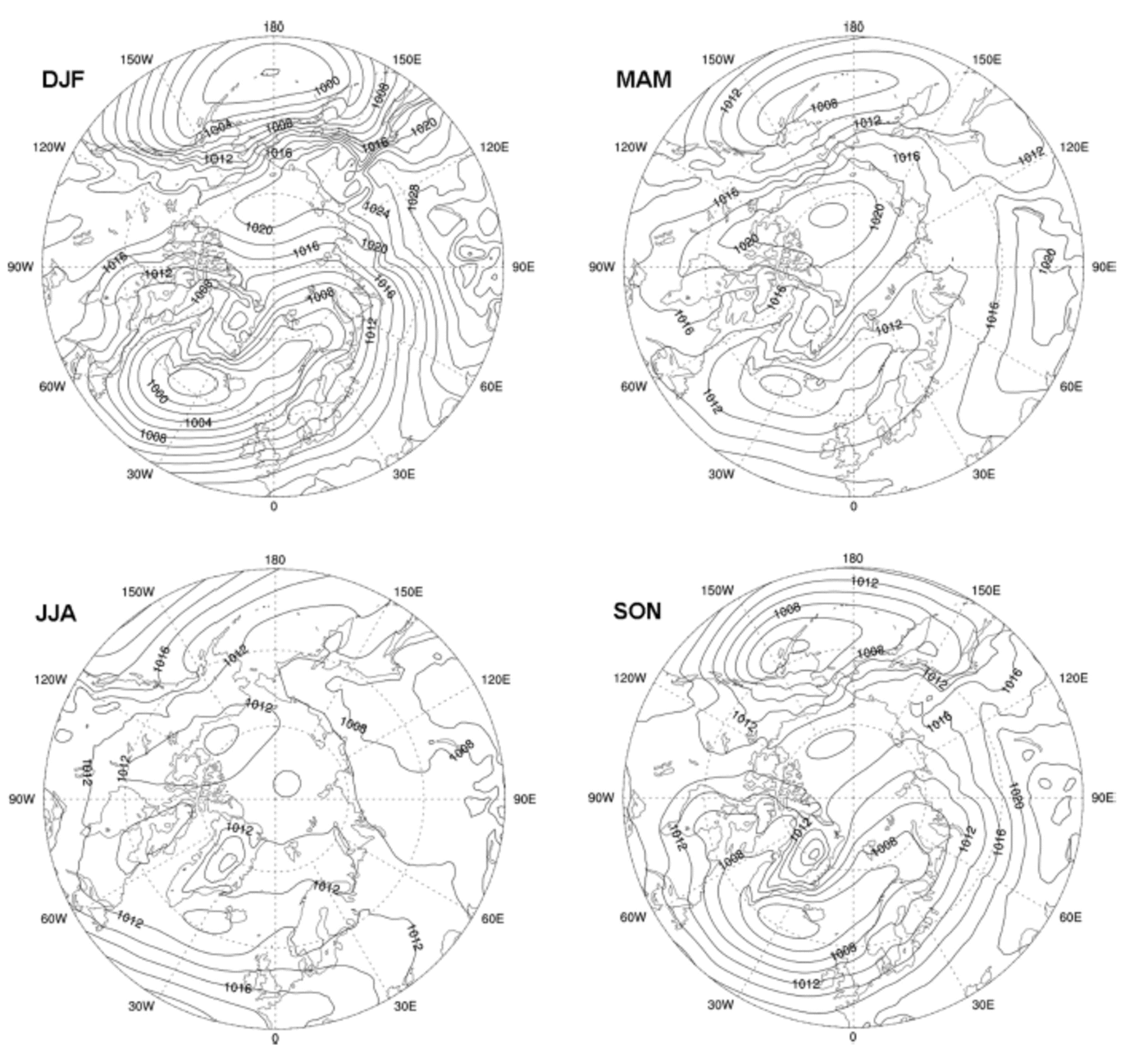
Fig. 5. High northern latitude climatological distributions of SLP for the four seasons for the period 1979–2013 in the ERA-Interim reanalysis. The contour interval is 2 hPa.
The 1979-2013 Antarctic SLP climatology (Fig. 6) shows the strong mid-latitude westerlies and the circumpolar trough (CPT) all year round. In DJF there are distinct lows within the CPT, located in the Amundsen/Bellingshausen Seas, off Dronning Maud Land, and a weaker system to the northwest of Wilkes Land. The SLP exhibits a strong semiannual oscillation (SAO) (Reference Simmonds and JonesSimmonds and Jones, 1998; Reference Simmonds and KingSimmonds and King, 2004) which drives the deepening of the trough seen in MAM and tends to make the SLP more zonally symmetric. The trough undergoes weakening into the austral winter (JJA), and there is a significant low centred just to the east of the Ross Sea. In SON as dictated by the dynamic and thermodynamic processes that drive the SAO, the CPT assumes its greatest annual depth (and associated increase in the westerlies) and the Ross Sea low starts its extension eastwards. SON is also the season in which the CPT assumes its more southerly position. In the SH the CPT and the sea-ice edge have different seasonal cycles, and their relative latitudinal positions have important implications for the meridional flux of ice. As discussed by Reference Enomoto and OhmuraEnomoto and Ohmura (1990) and Reference Simmonds, Rafter, Cowan, Watkins and KeaySimmonds and others (2005), in autumn the sea-ice edge lies mostly near, or south of, the trough, while in spring the edge is almost everywhere north of the CPT. The relative placement of the ice edge determines the meridional direction of the Ekman component of the sea-ice transport. In autumn the Ekman transport is to the south in most sectors and this discourages expansion of the ice edge, while in spring this transport is to the north, and the ice mass is, in turn, replenished by ice formed at higher latitudes.

Fig. 6. High southern latitude climatological distributions of SLP for the four seasons for the period 1979–2013 in the ERA-Interim reanalysis. The contour interval is 5 hPa.
The northern high-latitude SLP trends are shown in Figure 7 for the four seasons. The regions of interest here are of high interannual variability, and hence over many regions the trend is not significant (95%), even though it may be quite large. Among the significant changes of note are the SLP reduction over western Russia in MAM which, by strengthening the westward surface wind over the Barents Sea, has the potential to increase the southward ice flux through Fram Strait in the summer. Also of note is the dipole pattern in the Arctic region in JJA which has been implicated in the increase in flux out of the Arctic and SIE reductions in SON (Reference Maslanik, Drobot, Fowler, Emery and BarryMaslanik and others, 2007; Reference Ogi, Yamazaki and WallaceOgi and others, 2010; Reference Overland and WangOverland and Wang, 2010; Reference Screen, Simmonds and KeayScreen and others, 2011; Reference Ogi and WallaceOgi and Wallace, 2012; Reference Vihma, Tisler and UotilaVihma and others, 2012; Reference Ogi and RigorOgi and Rigor, 2013).

Fig. 7. High northern latitude SLP trends for the four seasons for the period 1979–2013 in the ERA-Interim reanalysis. Cross-hatching denotes regions over which the trends differ significantly from zero at the 9 5% confidence level.
In contrast to the north, the high southern latitudes SLPs have exhibited strong and significant changes over the 35 years considered here (Fig. 8). The summer season (DJF) shows a very strong annular structure to the trends, and the SAM is known to impact on sea-ice distribution (e.g. Reference Maksym, Stammerjohn, Ackley and MassomMaksym and others, 2012; Reference Pezza, Rashid and SimmondsPezza and others, 2012). The time series of the DJF SAM index in Figure 9a shows a significant positive trend (5.84±2.61 (100a)–1 p˂0.05). When considered against the structure of the background climatology (Fig. 6) these trends indicate that the CPT has deepened and moved south over the period. The MAM SLP tendencies (Fig. 8), while exhibiting considerable zonal asymmetry, do reflect aspects of the SAM spatial structure. There is a positive trend in the SAM index for this season (Fig. 9a), although its significance level is a little more modest (4.94 ±2.55 (100 a)–1 p˂ 0.10). There are no significant trends in winter or spring (1.07±3.05 and -0.32 ±3.31 (100a)–1respectively). In part the SIE trends can be related to the large-scale and regional anomalies displayed in Figure 8. In the austral summer the sea-ice edge is found to the south of -62°S at all longitudes (see, e.g., Fig. 1 of Reference Simmonds, Rafter, Cowan, Watkins and KeaySimmonds and others, 2005), and the SAM-like SLP trends indicate increasing westerly anomalies consistent with anomalous Ekman ice transport to the north. In autumn a similar process is evident, although the SAM is not as organized as in summer. By contrast, Figure 9b indicates no trend in the SAM in the other two seasons, suggesting more regional influences on the SIE. In JJA a negative SLP trend is centred to the north of the ice edge between 60 and 1208 W (Fig. 8), consistent with southward Ekman ice flux, and also an advection of ice towards the Ross Sea. Conversely, a trend to increasing westerly anomalies is evident in much of the Atlantic and Indian sectors, and an associated Ekman export of ice. Finally, in SON a cyclonic trend is evident in the Ross Sea sector just south of the ice edge, again consistent with northward Ekman export of ice (Reference Turner and OverlandTurner and others (2009) have commented on the association between the increase in the Ross Sea sector and enhanced cyclonic flow).

Fig. 8. Same as Figure 7, but for southern latitudes.
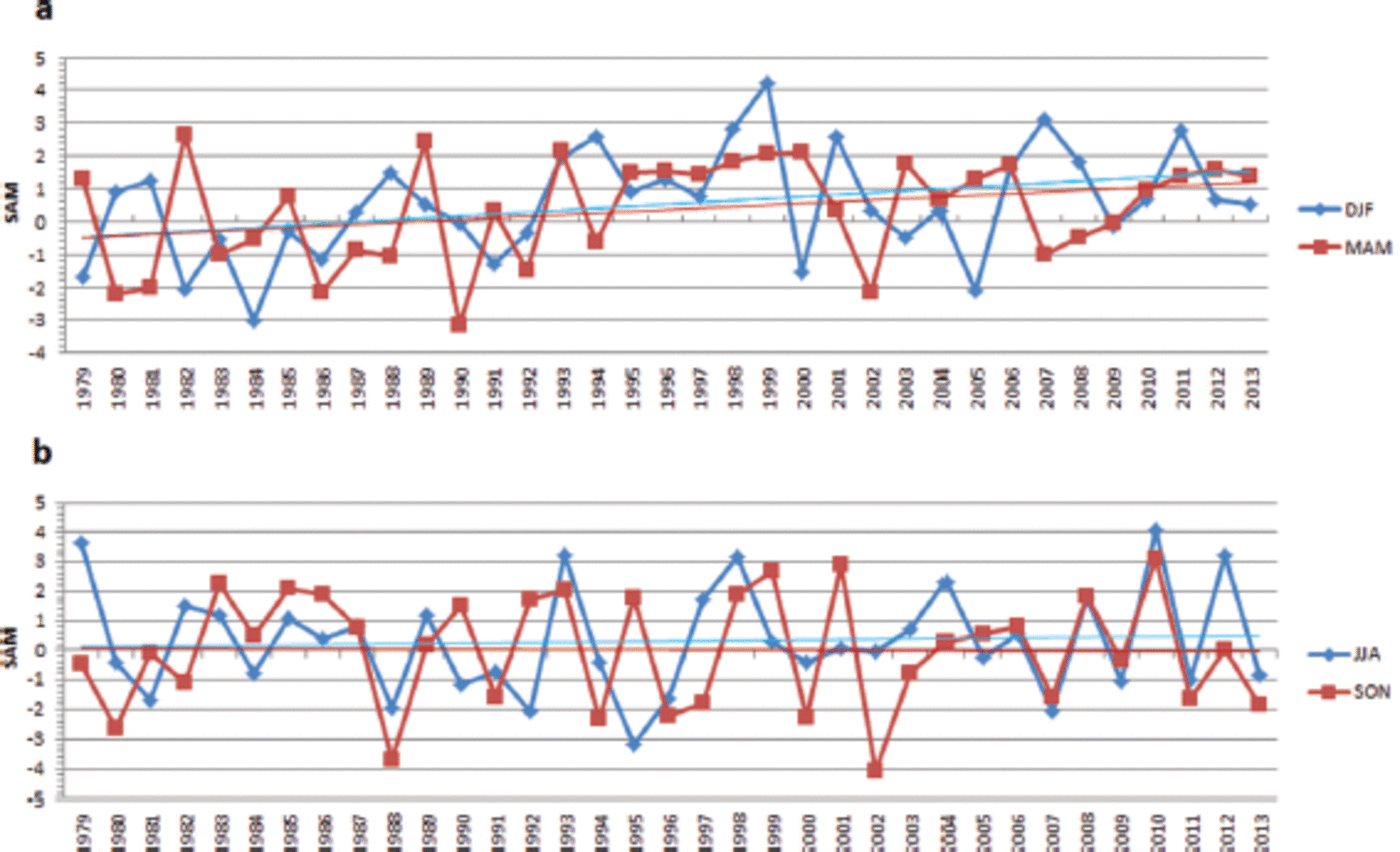
Fig. 9. Time series of the SAM index for (a) DJF and MAM and (b) JJA and SON for the period 1979–2013. The trend in DJF is significant (p ˂ 0.05, r 2 = 0.13), as is that for MAM (p ˂ 0.10, r 2 = 0.10). Significant trends are not detected in either JJA or SON.
4. Discussion
We have analysed the variability and change of sea-ice extent in the two polar regions using the satellite-era data up to the most recently available (namely 1979–2013). We have stressed that sea ice exhibits a broad spectrum of temporal variability, interannual, sub-decadal and multidecadal (e.g. Reference White and SimmondsWhite and Simmonds, 2006; Reference Bajish, Aoki, Taguchi, Komori and KimBajish and others, 2013). Given this, it is important to use as long a record as possible to avoid misinterpreting signals that may be present. Our analysis has revealed that over the 35 years of record the ice loss in the Arctic has continued and there has been a significant (p˂0.001) decrease in SIE in all 12 calendar months, with a maximum rate of loss in September ((88.96 ± 9.50) x 103 km2 a–1). This trend translates to a loss of 3 x 106km2 over the 35 years. The annual mean rate of attrition is a dramatic (54.58 ± 3.70) x 103 km2 a–1 (corresponding to a net loss of 1.86 x 106km2). The contrasting positive Antarctic SIE trends achieve their maximum of (24.27±10.59)x103km2a-1 in December, equivalent to growth of 0.83 x 106 km2 in 35 years. The increase in the SH annual mean, (15.29 ± 3.85) x 103 km2 a–1translates to just over 500 000 km2 over the period. This rate of growth of the annual means is ∼ 2 8% of the rate of loss from the NH, and hence can no longer be regarded as small.
The CMIP5 models perform quite well in the high northern latitudes, and capture the observed decrease in Arctic ice (while perhaps being too conservative as to the rate of loss) (Reference StroeveStroeve and others, 2012b). Similarly those models predict loss of Antarctic sea ice, a result in marked contrast to the observed increases we have documented above (Reference Bindoff and StockerBindoff and others, 2013). This conundrum is attracting a great deal of scientific interest as to what is behind this major discrepancy. One suggestion that has been made is that the opposing SH trends in the models and observations might not be incompatible when seen against the background of natural (or internal) variability. Following this line, Reference Polvani and SmithPolvani and Smith (2013) selected just four CMIP5 models, ran long integrations with ‘preindustrial’ forcings and concluded from the distribution of their 27year trends that the observed trend of annual mean Antarctic SIE over 1979-2005 (12.7 x 103 km2 a–1) ‘lies well within the natural variability of the modeled sea ice system’. There are a number of caveats associated with this conclusion, however. Firstly we have shown here that with recent acceleration the trend over the past 35 years has increased (15.29x 103km2a–1 p˂0.01) while at the same time the distributions of the models' natural variability over this longer period will be more narrow. Further, Reference Zunz, Goosse and MassonnetZunz and others (2013) examined a much larger sample of 24 CMIP model results and found that they greatly overestimated the variance of sea-ice extent (determined after the trends in sea-ice coverage were removed). They also showed very large differences in the abilities of the various models to capture the annual cycle of SIE, and concluded that while a critical role of the internal variability in the observed increase of sea-ice extent in the Southern Ocean could not be ruled out, ‘current models results appear inadequate to test more precisely this hypothesis’. Reference Mahlstein, Gent and SolomonMahlstein and others (2013) and Reference Turner, Bracegirdle, Phillips, Marshall and HoskingTurner and others (2013) have made similar comments and conclude that improvements are required for the modelling of climate and climate change in the Antarctic region (see also the recent comments of Reference Swart and FyfeSwart and Fyfe, 2012; Reference Bengtsson, Hodges, Koumoutsaris, Zahn and BerrisfordBengtsson and others 2013).
If natural variability is not the source of the paradox, there must be important physical processes that account for the Antarctic SIE increases over the past 35 years which are not considered or not treated correctly in climate models. There are a large number of such processes which could be relevant in the high southern latitudes. We will restrict ourselves here to mentioning one of these, namely the impact of calving or melting ice shelves. A number of investigators have documented that parts of the Antarctic ice sheet are losing ice at accelerating rates, much of which is a response to oceanic forcing, especially on the floating ice shelves (see, e.g., Reference HellmerHellmer, 2004, Reference Jacobs, Jenkins, Giulivi and DutrieuxJacobs and others, 2011; Reference Joughin, Alley and HollandJoughin and others, 2012; Reference Pritchard, Ligtenberg, Fricker, Vaughan, Broeke and PadmanPritchard and others, 2012; Reference Rignot, Jacobs, Mouginot and ScheuchlRignot and others, 2013). Basal melting of the shelves produces an influx of cool, fresh water near the surface of the ocean. A consequence of this is the stabilizing of the water column and cutting off the supply of heat from the warmer Circumpolar Deep Water. It is argued that this, in turn, would encourage more sea-ice formation at the surface. Whether in fact this is one of the key reasons for SIE increase is yet to be established, as a number of modelling studies have arrived at varying conclusions (Reference Stouffer, Seidov and HauptStouffer and others, 2007; Reference Bintanja, Van Oldenborgh, Drijfhout, Wouters and KatsmanBintanja and others 2013; Reference Swart and FyfeSwart and Fyfe, 2013) and it appears that the response to Southern Ocean freshening is very sensitive to how and where the freshwater flux was added. It is clear that many more challenges await us in modelling of the high southern latitude environment.
5. Concluding Remarks
In this paper we have explored the variation and trends in SIE in the two polar regions using the NSIDC sea-ice dataset for the 35 year period November 1978-December 2013. This is the longest period of record used up till now, and allows us to obtain more robust estimates of change than have been obtained heretofore. We have confined our analysis to considering only the total sea-ice coverage of the Arctic and of the Antarctic. We agree with the perspectives of Reference Lefebvre and GoosseLefebvre and Goosse (2008), Reference Cavalieri and ParkinsonCavalieri and Parkinson (2012), Parkinson and Reference Cavalieri and ParkinsonCavalieri (2012) and others that the investigation of sea-ice behaviour on a regional scale is of great importance in understanding this complex substance. However, the analysis of total coverage allows us a perspective on the net, integrated effect of regional processes and influences and is of great value in itself.
Our analysis has confirmed the ongoing loss of Arctic sea ice. We find significant (p˂0.001) negative trends in all months, seasons and in the annual mean. The greatest rate of decrease occurs in September, its trend of 88.96 ±9.50 x 103 km2 a–1 representing a reduction of 3 x 106 km2 over 35 years. The analysis also confirms that the Antarctic sea-ice expansion identified in earlier studies with shorter records has continued, and our longer record allows us to determine the magnitude of these trends with greater statistical confidence than heretofore. The trends in autumn, winter, spring and for the annual mean are highly significant (p˂0.01), and that in summer also achieves significance but at a low level of 90%. The positive trends in Antarctic ice can no longer be considered ‘small’, and the positive trend in the annual mean of (15.29 ±3.85) x 103 km2 a–1 is almost one-third of the magnitude of the NH annual mean decrease.
The contrasting trends in the two hemispheres raise interesting questions as to the evolution of the total amount (i.e. Arctic plus Antarctic) of sea ice over the globe. Our analysis applied to these combined data shows significant (p˂0.01) negative trends in three seasons (the trend in AMJ just fails to reach significance at the 90% level). The trend of the global annual mean time series, (-35.29 ± 5.75) x 103km2a–1is also highly significant.
We have commented that the Antarctic sea-ice trends simulated by the CMIP5 models have opposite signs to those revealed in our analysis of the satellite data. It has been suggested that these differences lie within the bounds of natural variability. One could argue that the longer record used here makes this suggested reason less likely. Instead, the reasons for the differences may have to be found within the physics of the models themselves. This is probably a hemisphere issue because the models perform well with respect to simulating Arctic ice and poorly for the Antarctic case.
Acknowledgements
Parts of this research were made possible by grants from the Australian Research Council and from the Australian Antarctic Science Advisory Committee.











