INTRODUCTION
The badger (Meles meles) is a wildlife species endemic in Ireland and the UK and many studies have been devoted to the subjects of badger ecology and behaviour. Mycobacterium bovis (M. bovis) infection is common in badgers. Cattle are also susceptible to this infection and the association of badgers with TB transmission in cattle is well recognized, both in Ireland and the UK [Reference Griffin1–Reference Donnelly3]. Aspects of the epidemiology of M. bovis in badger populations are well understood. It is known that badgers transmit the disease to each other and that there is spatial clustering of the disease in badgers [Reference Woodroffe2, Reference Delahay4–Reference Kelly6]. There is some understanding of badger home ranges from studies such as O'Corry-Crowe et al. [Reference O'Corry-Crowe7] and those in Smal [Reference Smal8] in Ireland and those by Tuyttens et al. [Reference Tuyttens9] and Woodroffe et al. [Reference Woodroffe10, Reference Woodroffe11] in the UK. However, while these studies have tracked badgers' social groupings and home ranges, less is known about the extent of badger ranges. This knowledge is particularly important in the understanding of disease transmission dynamics in the badger population and ultimately its control both in cattle and badgers. The main aim of this study is to estimate, using geostatistical methods, practical spatial ranges at which correlation of disease occurs in badger populations in Ireland.
METHODS
Study populations
The data for this study are drawn from the Four Area Project (FAP), a formal badger removal project undertaken in Ireland from September 1997 to August 2002, to assess the effect of badger culling on the incidence of bovine tuberculosis (TB). The study design and its results are published in detail elsewhere [Reference Griffin1]. Briefly, the FAP was conducted in matched removal and reference areas (average area of 245 km2) in four counties in Ireland: Cork, Donegal, Kilkenny and Monaghan. In addition, where natural barriers were absent, ‘buffer areas’ were created, up to 6 km in width, at the boundary of each selected removal area. These buffer areas will be referred to as outer removal areas. Badger removal was intensive and proactive throughout the study period in the removal areas (inner and outer), but reactive (culling only those badgers spatially associated with farms that had experienced severe TB outbreaks in cattle and where badgers were implicated) in the reference areas. Only cattle herds that had all their land located in the study areas are included in analyses here.
Prior to the study, all fields and hedgerows on participating farms were examined for badger setts. 5680 setts were found but only a fraction were active. During the course of the study, badgers were culled from 929 setts, 127 from the reference areas and 802 from the removal areas. TB status of badgers was based on culture results [Reference Costello12] and a sett was deemed positive if any badger captured therein was positive. All badgers in a sett were captured. Of these setts, 574 were negative, 338 were positive and 17 had unknown status. The percentage of positive setts in the removal areas ranged from 27% in Donegal to 42% in Cork. In the reference areas, the status of setts is unknown for the most part as little badger culling occurred there. Therefore, reference areas were not included in the current analyses.
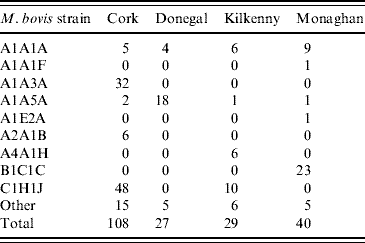
Records were complete for 2359 badgers culled in the removal areas regarding the date of capture, geographical area and specific sett from where the badgers were snared. The TB status was known for 2305 of these. The sett identifications used were based on surveys conducted as part of the FAP, and the geographical position of the sett at which badgers were caught was recorded in a GIS database. Our analyses were restricted to the first year of the FAP, September 1997 to August 1998, during which two culls were carried out in each county. The dates of the last culls in that year were in late May or June, varying with area. There were a total of 1113 badgers culled in the removal areas in the first year of the cull. Of these, 15 were cubs, i.e. badgers born in the previous 12 months, 1069 were adults (157 of which were yearlings) and 29 badgers with no age data recorded. Badgers without age data were excluded from the analysis, as were those without sex data or infection status and the 15 cubs (74 in total). We thus consider for study, the total of 1039 adult badgers culled, 304 in the outer removal areas and 735 in the inner removal areas for which the infection status, sex and age were known. The data are displayed in Table 1. Plots showing the locations of infected and non-infected badgers in the four counties are shown in Fig. 1. Of the 209 infected badgers under study, strain type information was available on 204. In all counties several strain types of M. bovis were found to infect badgers. Table 2 shows the distribution of each strain type for badgers by area.
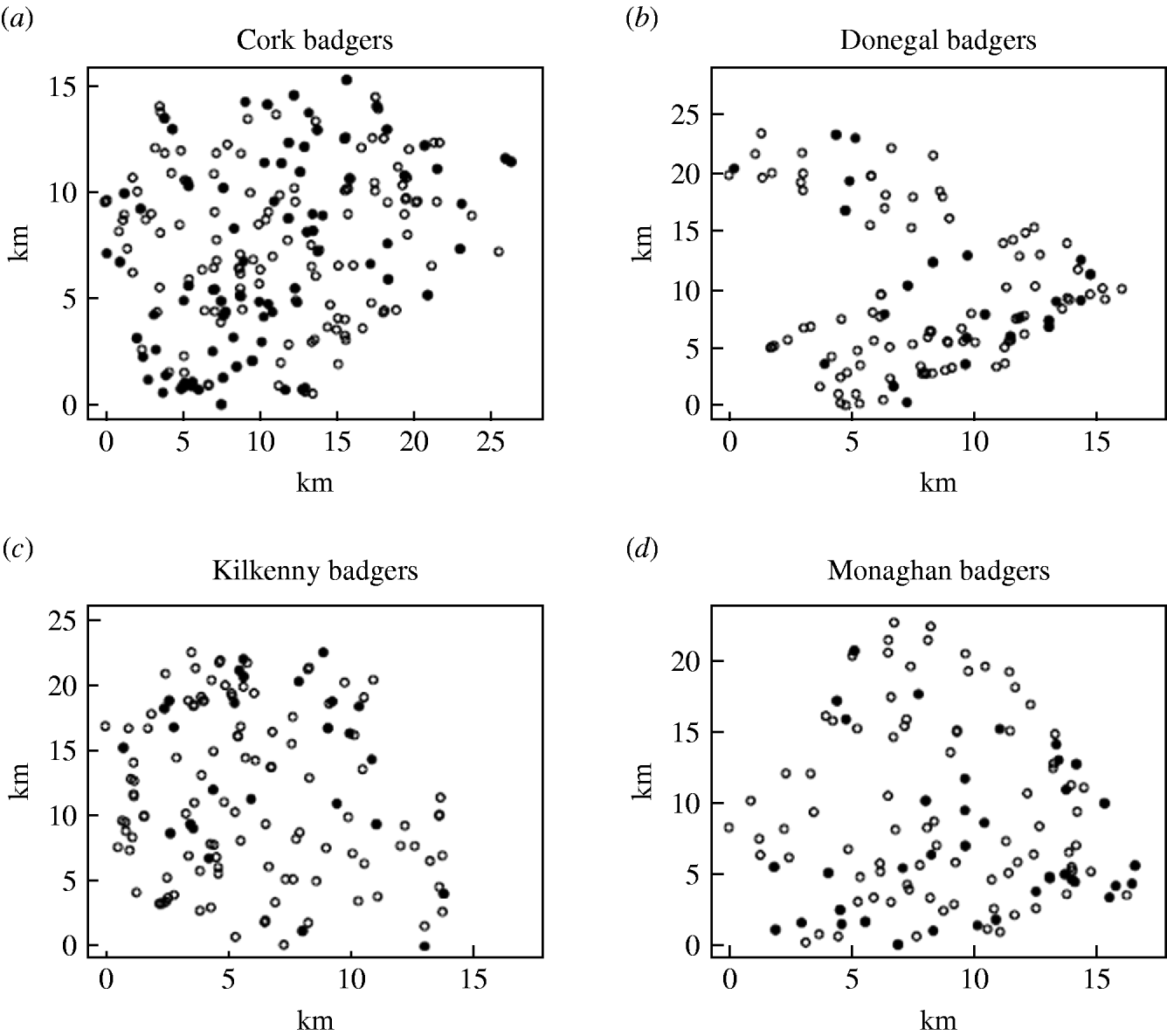
Fig. 1. Plots showing the locations of infected (•) and non-infected (○) badgers in the removal areas of the four counties.
Table 1. Summary statistics describing badgers captured in the initial 12-month period of proactive culling in the removal areas of the Four Area Project
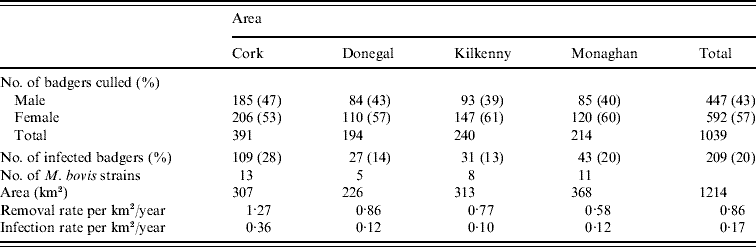
Table 2. Distribution of M. bovis strains in badgers captured in the initial 12-month period of proactive culling in the removal areas of the the Four Area Project
Statistical methods
Logistic regression was used to compare prevalence of TB across areas and between the sexes.
Second-order intensity functions
K-functions and second-order intensity functions were used to explore spatial associations of M. bovis infections in badgers. K-functions arise from the theory of spatial point processes [Reference Ripley13] and describe the distribution function of distances (d) between points (badger sett geographical locations) while second-order intensity functions describe the corresponding density function. We use distances based on nearest-neighbour distances badger–badger. K-functions for infected and non-infected badgers are estimated separately and the difference ![]() used to indicate clustering of disease [Reference Diggle and Chetwynd14]. Large values of D indicate clustering. Diggle & Chetwynd's [Reference Diggle and Chetwynd14] random labelling hypothesis is used that conditions on the set of all locations. The null hypothesis of no association is that each location is equally likely to be infected or uninfected. Data from badgers trapped at the same location (which shared the same distances to the nearest cattle herd) were condensed. A single location could contribute data both as TB infected (if one or more infected badgers were trapped there) and as uninfected (if one or more uninfected badgers were trapped there).
used to indicate clustering of disease [Reference Diggle and Chetwynd14]. Large values of D indicate clustering. Diggle & Chetwynd's [Reference Diggle and Chetwynd14] random labelling hypothesis is used that conditions on the set of all locations. The null hypothesis of no association is that each location is equally likely to be infected or uninfected. Data from badgers trapped at the same location (which shared the same distances to the nearest cattle herd) were condensed. A single location could contribute data both as TB infected (if one or more infected badgers were trapped there) and as uninfected (if one or more uninfected badgers were trapped there).
We evaluate the null sampling distribution of ![]() (d) by carrying out 99 Monte Carlo simulations in each of which disease labels are randomly assigned to locations. In each simulation the function
(d) by carrying out 99 Monte Carlo simulations in each of which disease labels are randomly assigned to locations. In each simulation the function ![]() (d) is re-calculated. The upper 97·5 and lower 2·5 percentiles of the simulated
(d) is re-calculated. The upper 97·5 and lower 2·5 percentiles of the simulated ![]() (d) values at each distance d are thus obtained. Differences between second-order intensities ID are also examined and upper and lower percentiles for these differences at each distance d are calculated using Monte Carlo simulation, as above. Here second-order intensity functions were calculated using K-function derivatives based on a bandwidth of 1 km, i.e. ID(d)=K(d+1) – K(d). Difference functions (D, ID) outside the upper confidence limit indicate clustering of infection. An alternative analysis of these data using the methods of Woodroffe et al. [Reference Woodroffe2] is presented in Kelly et al. [Reference Kelly6], for comparison purposes with that study.
(d) values at each distance d are thus obtained. Differences between second-order intensities ID are also examined and upper and lower percentiles for these differences at each distance d are calculated using Monte Carlo simulation, as above. Here second-order intensity functions were calculated using K-function derivatives based on a bandwidth of 1 km, i.e. ID(d)=K(d+1) – K(d). Difference functions (D, ID) outside the upper confidence limit indicate clustering of infection. An alternative analysis of these data using the methods of Woodroffe et al. [Reference Woodroffe2] is presented in Kelly et al. [Reference Kelly6], for comparison purposes with that study.
Spatial variation in risk-kernel probability maps
In the case of strain data we examined whether badgers with the same strain clustered and if so where they clustered. By spatial variation in risk we mean the strain (first-order) intensity functions are not proportional over the domain D of interest. As in Diggle & Ribeiro [Reference Diggle and Ribeiro15], the pattern of strains is assumed to be generated by a multivariate Poisson process with intensities λk(x) corresponding to strain type k at each location x. Then the probability a case at location x will be of type j, conditional on there being one of the s strain types at x, is
We say there is spatial segregation if the area can be partitioned approximately into subregions where one strain type predominates, i.e. complete segregation is if at each x in the subregion, pj (x)=1 for one of the j. We used the kernel regression estimator of p j given in Diggle & Ribeiro [Reference Diggle and Ribeiro15] where the smoothing parameter for p j is chosen by cross-validation. An ad-hoc statistic for a Monte Carlo test of clustering is then given by
To obtain the significance level of this test statistic, 999 Monte Carlo simulations were done where strain types were randomly assigned to locations but the frequency of strain occurrence was preserved. The estimated type-specific probability surfaces, ![]() vs. x, were plotted for each county using ArcView 9.2 (ESRI Inc., USA). Distance calculations related to strain types were done by two methods. In method 1, each badger contributed one observation for each strain type. In method 2, a capture location contributed one observation for each strain type as multiple strain types were occasionally found at the same location (see Table 1). As can be seen in Table 2, the number of cases of most strain types is too small for the application of non-parametric smoothing methods. Therefore, similar to the approach of Diggle et al. [Reference Diggle, Zheng and Durr16], analysis was restricted to the locations of the two main strain types in each county and in the case of Kilkenny the three main strain types.
vs. x, were plotted for each county using ArcView 9.2 (ESRI Inc., USA). Distance calculations related to strain types were done by two methods. In method 1, each badger contributed one observation for each strain type. In method 2, a capture location contributed one observation for each strain type as multiple strain types were occasionally found at the same location (see Table 1). As can be seen in Table 2, the number of cases of most strain types is too small for the application of non-parametric smoothing methods. Therefore, similar to the approach of Diggle et al. [Reference Diggle, Zheng and Durr16], analysis was restricted to the locations of the two main strain types in each county and in the case of Kilkenny the three main strain types.
Generalized linear geostatistical models (GLGMs)
Because second-order intensity function methods and kernel spatial maps do not take any covariates other than spatial location into account in any formal way, we also present GLGM analyses of these data. These models extend those of the logistic in that geographical information regarding badger sett locations are utilized in the models. We estimated practical spatial ranges at which clustering of disease occurs with these models. A separate model was constructed for the removal area of each county with infection status of the sett as the outcome variable. The covariates in the models are distance to the nearest cattle herd, log of herd size, restriction status of the herd in that year (1=restricted, 0=not restricted), previous history of TB in the herd (1=yes, 0=no) and interactions between these variables. In addition a random spatial effect u i is included in the logistic models, identified by the geographical coordinates s i of the ith badger sett.
The spatial correlation matrix S
The isotropic covariance models we considered for the spatial random effect have the form
where d ij denotes the distance between s i and s j. The following models were fitted:
(1) Spherical

(2) Exponential

(3) Gaussian

For these models, the parameter ρ refers to the geostatistical parameter ‘range’. In the exponential and Gaussian models covariances reach zero only asymptotically, thus the practical range is defined as the distance at which the correlations fall below 0·05. For the spherical model ρ equals the range; for the exponential model the practical range is 3ρ; in the Gaussian model it is ![]() . A likelihood ratio type test is used to compare models that are nested, i.e. a model with no spatial correlation ρ=0, to one with ρ≠0 (with critical value χ2α2 for a size-a test as in Lee et al. [17, p. 192]). Competing covariance models are compared using Akaike's Information Criterion [Reference Akaike, Petran and Csaki18].
. A likelihood ratio type test is used to compare models that are nested, i.e. a model with no spatial correlation ρ=0, to one with ρ≠0 (with critical value χ2α2 for a size-a test as in Lee et al. [17, p. 192]). Competing covariance models are compared using Akaike's Information Criterion [Reference Akaike, Petran and Csaki18].
Statistical calculations were performed using SAS software (SAS Institute, USA) and R [19].
RESULTS
Prevalence of M. bovis infection
The overall infection prevalence in adult badgers was 20%, ranging from 13% in Kilkenny to 28% in Cork. Of the 1039 adults studied, 448 (43·0%) were male. The adult sex ratio was female-biased in all counties (Table 1). Table 1 presents the prevalence of M. bovis infection in both male and female badgers. Using a logistic regression analysis we found prevalence varied substantially between areas (P<0·001). There was no significant effect of sex or interaction between sex and area on the risk of M. bovis infection. Thus prevalence was the same for the sexes within each area and for the sexes overall.
Clustering of infection using second-order intensity functions
The badger data consisted of 830 uninfected badgers at 491 locations and 209 infected badgers at 167 locations. Infected and uninfected badgers had comparable opportunities for contact with cattle. In the 12 months of the first year of badger culling, distances to the nearest herd were similar for infected and uninfected badgers (P=0·56, Wilcoxon rank sum test), the median distance was 0·55 km for uninfected badgers and 0·56 km for infected badgers. Figure 2 displays the difference in second-order intensity functions (ID(d)) for infected and uninfected badgers for each of the four areas. The figures show significant evidence of clustering of infection in badgers at all distances up to 8 km in counties Cork, Kilkenny and Monaghan. In Donegal, there was no significant difference in second-order intensity functions. When the number of Monte Carlo simulations for generating the confidence limits was increased from 99, results altered little, but computation time was greatly increased. Differences based on K-functions are not shown as these are less informative.
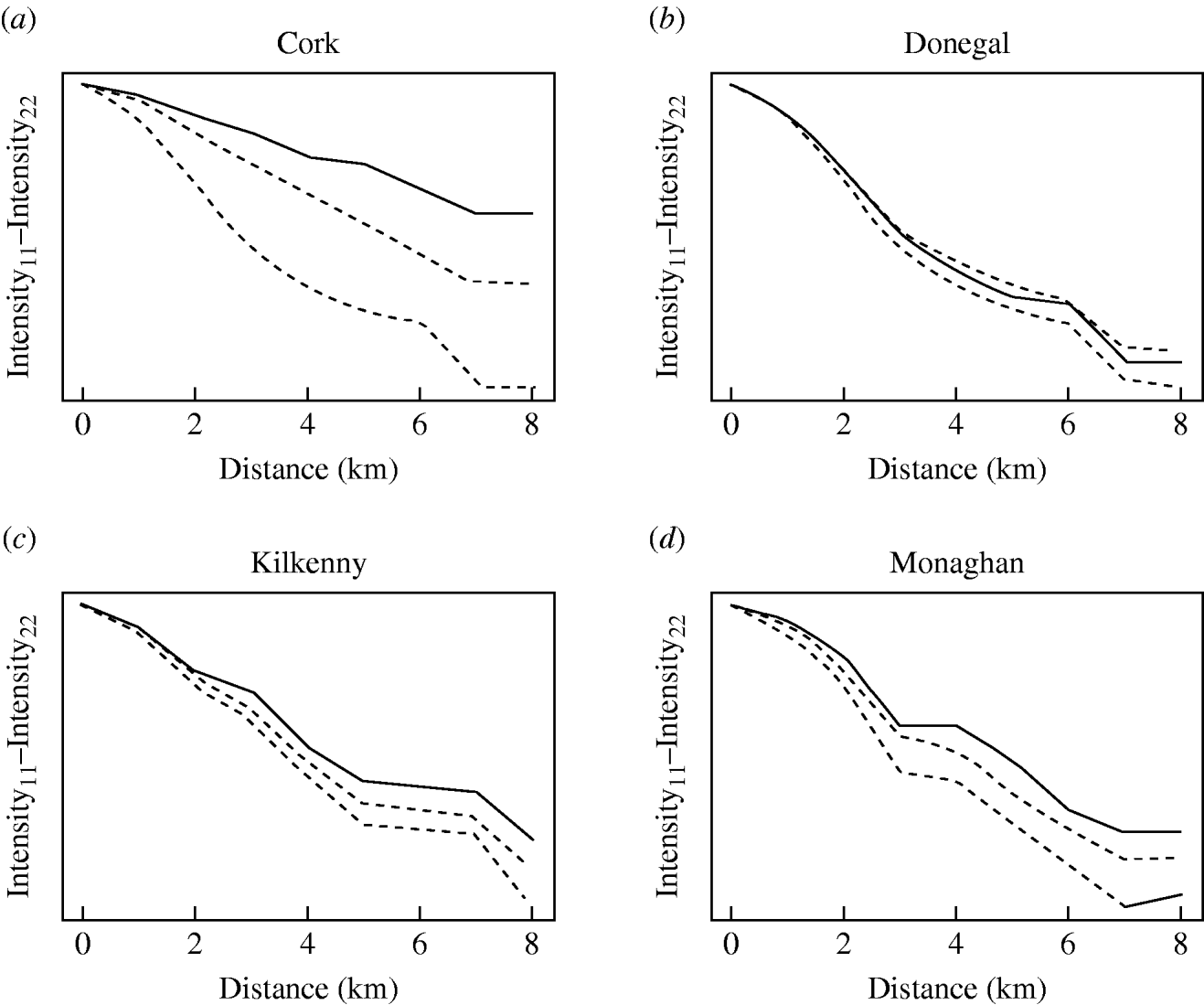
Fig. 2. Differences in second-order intensity functions of infected badgers to infected badgers and uninfected badgers to uninfected badgers in the removal areas of the Four Area Project. The dashed lines represent the upper 97·5 and lower 2·5 percentiles of simulated difference values at each distance d. Badger locations were condensed in the second-order intensity functions in that a single location could contribute data both as tuberculosis infected (if one or more infected badgers were captured there) and as uninfected (if one or more uninfected badgers were captured there).
Associations between strain types of M. bovis in badgers
Figure 3 shows the estimated type-specific probability surfaces for the main strain types in Cork, Donegal and Kilkenny using distance method 1 described above. The P values associated with Diggle's test of spatial segregation were, Cork (P<0·001), Donegal (P=0·128), and Kilkenny (P<0·001). In Monaghan, the estimated smoothing parameter was so large that the estimated probability surface is constant and there is no spatial segregation (P=1·0).
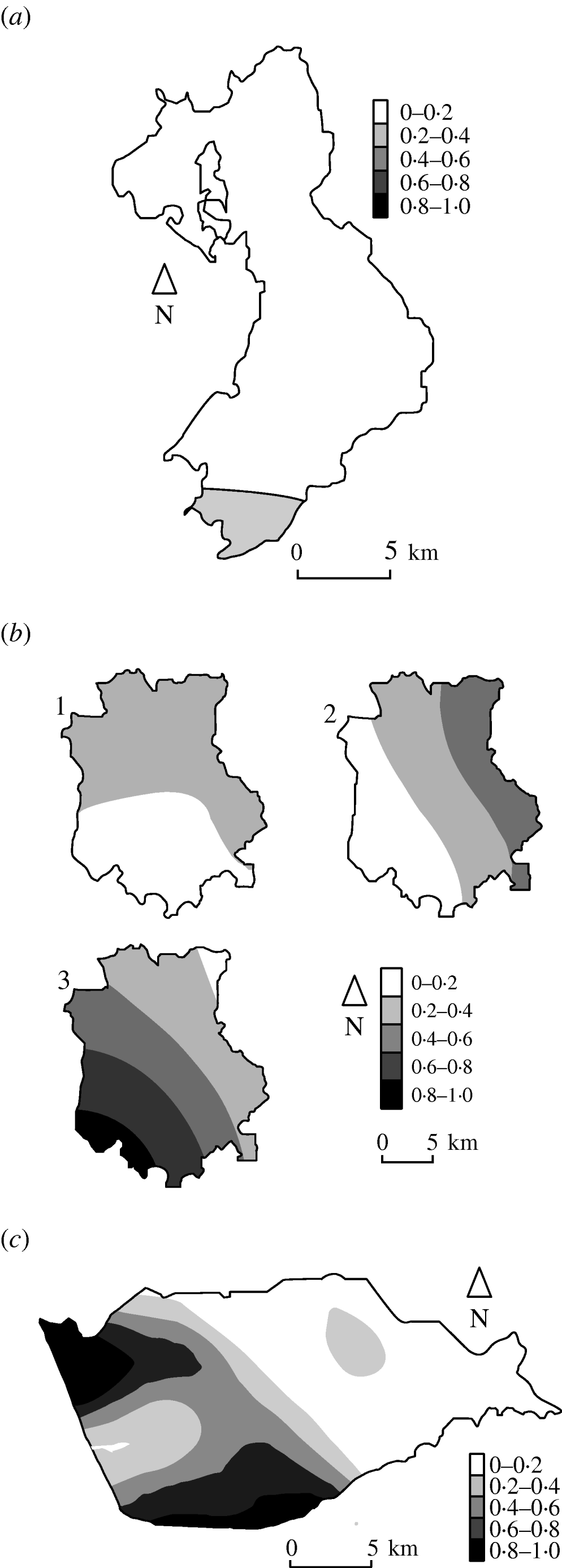
Fig. 3. Kernel estimates of badger strain-specific probability surfaces in three areas of the Four Area Project. (a) Donegal: kernel estimates of the A1A5A strain-specific probability surface. The estimate for A1A1A is 1 minus this (P=0·128 indicating some spatial segregation). (b) Kilkenny: kernel estimates of the A1A1A, A4A1H, C1H1J strain-specific probability surfaces (P<0·001 indicating spatial segregation). (c) Cork: kernel estimate of the A1A1A strain-specific probability surface. The estimate for C1H1J is 1 minus this (P<0·001 indicates spatial segregation).
GLGM results for removal areas
None of the covariates, distance to the nearest cattle herd, log of herd size, restriction status of the herd in that year, previous history of TB in the herd and interactions between these variables were significant in the models for any area. The exponential spatial covariance structure fitted best in all areas. The practical spatial correlation range was 4·47 km in Cork, 14·45 km in Donegal and 7·69 km in Monaghan. The spatial term was significant by the χ2α2 test: Cork (P=0·03), Donegal (P=0·02) and Monaghan (P=0·007). Examination of empirical variograms of the residuals from the models found no further spatial structure, indicating model adequacy. In Kilkenny, the exponential model did not give a positive definite covariance structure. A spherical correlation model did not give sensible answers in any county, but when the binary response is assumed Gaussian and a linear geostatistical model fitted, the estimated true range was 6·33 km in Cork, 10·44 km in Kilkenny, 18·7 km in Donegal and 14·66 km in Monaghan from this model.
DISCUSSION
Statistical issues
A second-order intensity function I(d) is essentially the density function associated with a K-function as outlined previously [Reference Schabenberger and Gotway20]. Using second-order intensities (rather than K functions) has the advantage of showing the exact distances at which clustering of disease occurs. We note the difference in K-functions D(d) (and thus also ID functions) tends to a positive constant as d →∞ [Reference Schabenberger and Gotway20], typical of clustered point processes. Diggle [Reference Diggle21] suggests the statistical information is greatest at small values of d, quite apart from the limitations imposed by the physical dimensions of the region under study. In the analysis of second-order intensities, we noted 95% of distances between animals fell within 15 km and thus as suggested in Diggle [Reference Diggle21], the difference in intensities, ID(d) is taken to 8 km in all counties. Thus, the extent of the investigation was limited by the dimensions of the study areas. In the case of strain data for infected badgers it is of interest to know not only if badgers with the same strain cluster but where they cluster. Numbers are now small and so computation of second-order intensity functions is not so appropriate. Kernel spatial mapping provides a method for locating clusters of infection. The GLGMs used here arise naturally from generalized linear models (GLM). A GLM can be easily extended to include a random effect using available statistical software. Such models are known as generalized linear mixed models (GLMMs) as they are extensions of GLMs that allow additional sources of variability due to unobservable random effects. A GLMM with spatially correlated random effects is a GLGM [Reference Diggle and Ribeiro15]. In the GLGM models, it was not possible to fit all types of correlation structure in each area due to convergence problems. However, in all areas except Kilkenny, models with exponential correlation structure did converge. In addition, the practical ranges assuming an exponential covariance structure with logistic regression or binary regression were remarkably similar (a further indication of model robustness). This is perhaps because sample sizes are large and the proportions of infected badgers in each area not too extreme (Table 1) [Reference Cox and Wermuth22]. Thus, we argue the estimates of ranges assuming a spherical covariance structure and Gaussian response are also reasonably valid. These ranges are necessarily larger than the practical ranges from an exponential covariance model. We also note the second-order intensity and GLGM approaches allow for spatially varying density of badgers throughout each region. However, they both require the assumption that the observed events constitute a partial realization of a stationary spatial point process. Thus the correlation is assumed to be the same for all pairs of equally distant locations and does not depend on direction. The extent to which this is not the case may account for differing results between Fig. 2 and the models. For example, most of the infection is located in one corner in Kilkenny and correlation may depend on direction.
Study findings
This work confirms that TB clusters in Irish badger populations. Using K-/second-order intensity functions, we found significant evidence of clustering of infection in badgers in Cork, Kilkenny and Monaghan and weaker evidence from Donegal, with clustering occurring at all distances up to 8 km, except for Donegal. We are uncertain as to the reason for reduced evidence of clustering in Donegal. We note Donegal is geographically distinct with sea inlets being a key feature [Reference Griffin1]. The results of the GLGMs also indicate spatial clustering of infection in each area. The results from the models with exponential correlation structure and spherical correlation structure show the same ordering of the areas in terms of magnitude of spatial ranges. The ranges in comparison to that of the second-order intensity results show no disagreement in Kilkenny and Monaghan. It is smaller in Cork. In Donegal the two approaches also show no disagreement, as a range of 18·7 km is at least half the largest diameter, and may just reflect spatial heterogeneity. Kilkenny had the lowest infection rate and thus has little variability in terms of infection and then necessarily the GLGM model will give a large spatial range. We note it is unlikely that the results from the GLGMs merely reflect spatial heterogeneity (apart from Donegal) given the results from the second-order intensity function analyses. Using two different types of measure, we found local associations between strains of M. bovis within the Irish badger population. We found that the main strains in three of the areas segregate, based on kernel probability estimates of strain-specific probability surfaces. Certain strain types dominate in defined areas (A1A3A in Cork, A1A5A in Donegal, C1H1J in Kilkenny and B1C1C in Monaghan) and this pattern is explained by local transmission of M. bovis within each area.
Comparisons with other studies
Our results are in agreement with other Irish work but with methodological differences. Olea-Popelka et al. [Reference Olea-Popelka23] found minimal spatial clustering of TB in badgers using nearest-neighbour methods, but their analysis did not adjust for the fact that negative badgers are more prevalent than positive ones and hence will be closer together. Using a measure based on nearest-neighbour distance ratios, Kelly et al. [Reference Kelly6] found clustering of infection when data from all counties were combined. Similar results using this type of measure were found by Olea-Popelka et al. [Reference Olea-Popelka5] with strain data. However, they used a different reference group, used a subset of the badger setts and no formal statistical test were carried out. Costello et al. [Reference Costello24] also report a diversity of strain types from the same sett, explained perhaps by badger movement and densities.
We restricted analyses to the first 12 months of the FAP, since the numbers of badgers captured in subsequent project years were too small to permit substantive second-order intensity function analysis. Moreover, years were not amalgamated, to avoid possible distorting effects of recent badger culling on the distribution of infection [Reference Tuyttens9, Reference Woodroffe10] and to permit comparison with UK studies. Our results are in general agreement with other reports from Britain of infection in badger populations [Reference Woodroffe2, Reference Delahay4, Reference Cheeseman25]. In the Randomized Badger Culling Trial (RBCT) analysis of Woodroffe et al. [Reference Woodroffe2], it was found that M. bovis infections were locally clustered within the badger populations; clustering was seen in nine of their ten trial areas (overall P<0·001). Spatial clustering of M. bovis infection was found at a scale of a few kilometers but the extent was not specified. Jenkins et al. [Reference Jenkins26] examined the changes in spatial associations in the RBCT data over successive culls. They obseved that 40% of distances from an uninfected badger to the nearest infected badger exceeded 1 km whereas the corresponding percentage for infected badger to the nearest infected badger was about 20%. Similar percentages were found in the current study for Cork, which had the highest infection rate in badgers (0·36 badgers/km2 per year, Table 1), and in this respect is the most similar to the RBCT. Thus, the spatial behaviour of infection in badgers in the FAP and RBCT appears to be similar, despite considerable differences in badger ecology [Reference Smal8, Reference O'Corry-Crowe, Eves, Hayden and Hayden27], population density [Reference Griffin1, Reference Donnelly28] and infection rates (Table 1). In terms of the latter, we calculated an infection rate in our study of 0·17 badgers/km2 per year (1039 adult badgers removed, area prevalence varying between 13% and 28%, overall prevalence 20%) compared to 0·29 badgers/km2 per year in the RBCT (2699 adult badgers removed in the initial cull, area prevalence varying between 2% and 38%, overall prevalence 12%).
Other issues
There is undoubtedly a complex relationship between density rates, previous badger removal, infection rates, the extent of badger ranges and the degree of contact between badgers, all of which may be factors in the scale at which clustering of infection was seen in these four areas. One badger cull had taken place during the period considered here and some badger removal from Kilkenny and Monaghan occurred shortly before the study began [Reference Griffin1]. Field studies, such as that of Tuyttens et al. [Reference Tuyttens9], reported that badger removal operations led to social disruption very soon after badger capture started and impacted setts at some distance from the main capturing areas. O'Corry-Crowe et al. [Reference O'Corry-Crowe7] noted that partial removal of a badger population may further increase the potential for cross-infection between badgers as the residual badgers range more widely. This has also been reported in Woodroffe et al. [Reference Woodroffe10]. O'Corry-Crowe et al. [Reference O'Corry-Crowe7] using bait-marking techniques put badger territories at between 0·87 and 1·17 km2 in an area of county Offaly with a badger density of 33·24 per km2. This corresponds roughly to a spatial range of between 0·53 km and 0·61 km. The spatial TB correlation range is necessarily larger than actual ranges as it involves only infected badgers. In our study we find it to be considerably larger, ranging from 6–15 km. However, the badger densities in the areas considered here are considerably lower, ranging from about 0·58 to 1·27 per km2. They are also lower than the 2·2 per km2 found in parts of Scotland, where territories could exceed 3 km2 as reported in Kruuk et al. [Reference Kruuk and Parish29]. Moreover, Sleeman et al. [Reference Sleeman, Mulcahy and Hayden30] detected considerable long-distance (up to 8 km) and sometimes extra-territorial, movements by some badgers in an Irish study. The long-distance movements were confined to badgers in the smaller social groups. O'Corry-Crowe et al. [Reference O'Corry-Crowe, Eves, Hayden and Hayden27] report a less stable social structure in low- density badger populations, i.e. less well-defined social groups. The interaction of the two factors – culling and density is complex. Two other recent studies [Reference Woodroffe11, Reference Macdonald, Riordan and Mathews31] concerning the effects of perturbation on TB in badgers suggest this. Mathematical models of infectious diseases [Reference Becker32] suggest that prevalence of infection in animals is likely to be density dependent. The degree of badger contact is also an obvious factor in disease transmission. The results on strain data here and other studies showing prevalence may be high in particular social groups concur with this [Reference Delahay4, Reference Cheeseman25].
In conclusion the data show strong evidence of spatial clustering of M. bovis infection within badger populations with the scale of the correlation exceeding 6 km in all areas. Moreover, badgers infected with the same strain of M. bovis are spatially segregated. Localized culling forms part of TB control policy in Ireland as outlined in Kelly et al. [Reference Kelly33]. Based on the results here, the scale for culling to be both feasible and effective requires further study. The implications of clustering on control policy have been discussed in the British context [Reference Woodroffe2, Reference Donnelly3, Reference Woodroffe10, Reference Donnelly28, Reference Macdonald, Riordan and Mathews31]. In Ireland, we face ongoing challenges with TB control in an environment where badgers are a protected and valued wildlife species contributing to biodiversity but are also an important reservoir of infection for cattle.
ACKNOWLEDGEMENTS
Thanks are due to the Centre for Veterinary Epidemiology and Risk Analysis, University College Dublin for providing the data for this study. Thanks also to Eamon Costello (Department of Agriculture, Fisheries and Food (DAFF), Central Veterinary Research Laboratory, Backweston Campus, Celbridge, Co. Kilkenny, Ireland) for providing the M. bovis culture data that were used in this study.
DECLARATION OF INTEREST
None.






