1 INTRODUCTION
Imaging spectroscopy over centimetre and decimetre wavelength range is important for addressing the problems of primary energy release, particle acceleration, and transportation processes (Bastian, Benz, & Dary Reference Bastian, Benz and Dary1998). Historically, the available solar observations image the Sun either at a few discrete frequencies, and spectroscopy without spatial resolution, such as the Nobeyama Radioheliograph (Nakajima et al. Reference Nakajima1994) and the Nancay Radioheliograph (Kerdraon & Delouis Reference Kerdraon, Delouis and Trottet1997) or with high spatial and spectral resolution but without time resolution, such as Owens Valley Solar Array (Gary & Hurford Reference Gary and Hurford1994). Three radio facilities with high spectral resolution are Culgoora (Prestage et al. Reference Prestage, Luckhurst, Paterson, Bevins and Yuile1994), Green Bank (Bastian et al. Reference Bastian, Bradley, White and Mastrantonio2005), and Zurich (Messmer, Benz, & Monstein Reference Messmer, Benz and Monstein1999). Broadband spectroscopy with high spectral and spatial resolution usually produces data covering a large instantaneous bandwidth and a large number of spectral channels, such as the Expanded Very Large Array (EVLA) (Perley et al. Reference Perley, Chandler, Butler and Wrobel2011). The Low Frequency Array (LOFAR), the planned Square Kilometre Array (SKA) and its precursor telescopes under construction, the Australia SKA Pathfinder(ASKAP) and the Karoo Array Telescopes (MeerKAT) in South Africa, are large next-generation radio telescopes with high sensitivity and high resolution (Beck et al. Reference Beck2013).
For diagnosing the radio emission from the Sun comprehensively, it was suggested to build a Chinese Spectral Radioheliograph (CSRH) in the decimetre to centimetre-wave range in recent years (Yan et al. Reference Yan, Zhang and Huang2004). The CSRH being developed will be a solar dedicated radio interferometric array that will observe spectroscopic imaging of the Sun, with high spatial resolution, high time resolution, and high frequency resolution images of the Sun simultaneously in the decimetre to centimetre wave range (Yan et al. Reference Yan, Zhang, Wang, Liu, Chen and Ji2009). CSRH is under construction and will be completed by the end of 2014.
Test bed plays a vital role in designing the instruments under construction. The design of the test bed is becoming increasingly complex and subtle. This paper describes the design and testing of the digital down conversion (DDC) subsystem test bed, which constructs a prototype and characterises the digital signal processing to be used for CSRH. As an important unit of CSRH, digital processing receiver affords to digitalising all analog intermediate frequency (IF) signal, filtering the signal with specified bandwidth and cross-correlating, etc. For the solar observations that are implemented at a few discrete frequencies, a small number of filters are used directly. But for the broadband observations, polyphase filter is usually used to obtain a great deal of narrow-band signals. Polyphase filtering technique uses a few low order filters instead of a high order filter. The data rate of each branch filter is only 1/D of the raw data rate (D is the number of branches). The technology is mature and easy to implement. However, with the increasing order of the filter, the complexity of hardware algorithm is increased, which causes heavy resources occupation.
An important feature of the subsystem test bed for CSRH is that any band needed can be selected. Meanwhile, the high-speed data can be processed by using less hardware resources. Through the design and simulation, we fully studied and mastered the digital signal processing of digital receiver of CSRH. The test bed provides the opportunity to simulate, verify, and calibrate for CSRH. Since Field Programmable Gate Array (FPGA) is highly modular, the test bed can optimise the algorithms.
The configuration and signals processing of CSRH are outlined in Chapter 2. The design and simulation of the test bed are presented in Chapter 3. The observation of geostationary satellite is analysed in Chapter 4. Finally, a conclusion is given in Chapter 5.
2 THE CONFIGURATION AND SIGNALS PROCESSING OF CSRH
In its present configuration, the CSRH consists of 100 equatorial mounted parabolic antennas including 40 4m diameter (CSRH I) and 60 2.5 m diameter (CSRH II) each, and is located at Inner-Mongolia (east longitude: 115°15′1.8′′; north latitude: 42°12′42.6′′) in China. The antennas are installed according to a three-arm spiral arrangement, and the maximal baseline is about 3 km. CSRH represents a major progress over other existing solar radio telescopes. It will perform broadband imaging spectroscopy over a frequency range of 0.4–15 GHZ, with high spatial, high temporal, and high spectral resolutions that are designed to exploit the dynamics of solar activity with good dynamic range.
The radio signals with left and right-handed circular polarisation are received by antennas in the 0.4–15 GHz range. Amplified by LNA and processed by optical transmitter, the signals are converted to optical signals, which is then transmitted to the optical receiver in the observation room by about 3400 m long optical fiber. The optical receiver is connected to the analog receiver in which the signal is mixed to IF signal by local oscillator(LO) signals and filtered to several 400 MHz bandwidth signals. Then the signal is input into digital receiver.
The digital receiver of CSRH consists of A/D converter, DDC, delay adjustment unit, fringe stopping unit, 2-bit quantiser and cross-correlator.
400 MHz bandwidth IF signal is digitised at 1 Gsps(Gigasample per second) by A/D converter. The A/D converter output, after filtered by polyphase filter bank with 16 channels, is truncated into 16 specified narrow-band signals with different centre frequencies. The narrow-band signals, after mixing with different LO signals, are converted to zero centre frequency signals. Then the narrow-band signals are to be quantised with 2-bit, adjusted by the delay adjustment unit and fringe stopping unit, finally input to the cross-correlator. The correlation results are stored in the hard disks. A brief system block diagram of CSRH is shown in Figure 1 (Wang et al. Reference Wang2013).

Figure 1. Brief system block diagram of CSRH.
3 THE DESIGN OF THE TEST BED
3.1 The basic design ideas
Considering the IF input to the digital receiver is broadband continuous spectrum, and the A/D converter of CSRH is 1 Gsps, on one hand, it is difficult to calculate and store data on hardware at such high rate; on the other hand, it will cause high-overhead resources occupation while flexibly obtaining any narrow-band signal from the broadband. Therefore, the input data stream must be mixed agilely, divided to several channels and extracted on FPGA.
Firstly, the IF digitised signal is down converted by the complex LO, the frequency of which is equal to the centre frequency of the needed bandwidth signal. The complex LO is alterable, therefore, the needed bandwidth signal with any centre frequency can be obtained easily. Secondly, the down converted signal is filtered by real filter, after that the narrow-band signal is obtained. The spectrum changes of the test bed are shown in Figure 2, in which spectrum A with even symmetry is shifted to spectrum B, and then is filtered to the spectrum C through the low-pass filter. The design makes the spectrum unfolded while the real mix may cause folded. In addition, the narrow-band signal at any centre frequency can be obtained by altering the LO equipped with only one real filter. The real filter with fix coefficients saves a lot of FPGA resources. The design of the test bed is introduced in detail as follows.

Figure 2. The spectrum changes of the test bed.
The complex mixing result is determined by the IF real input signal X(t) and LO frequency ω parameters, according to
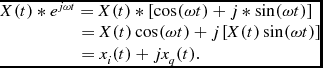 \begin{equation}
\begin{array}{l}X(t) * {e^{j\omega t}} = X(t) * \left[ {\cos (\omega t) + j * \sin (\omega t)} \right]\\
\,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = X(t)\cos (\omega t) + j\left[ {X(t)\sin (\omega t)} \right] \\
\,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = {x_i}(t) + j{x_q}(t). \\
\end{array}
\end{equation}
\begin{equation}
\begin{array}{l}X(t) * {e^{j\omega t}} = X(t) * \left[ {\cos (\omega t) + j * \sin (\omega t)} \right]\\
\,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = X(t)\cos (\omega t) + j\left[ {X(t)\sin (\omega t)} \right] \\
\,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = {x_i}(t) + j{x_q}(t). \\
\end{array}
\end{equation}
Where, x i (t) is the real of the mixed signal, and x q (t) is the image of the mixed signal. For reserving the alterable complex LO in the RAM of FPGA, two tables are designed to preset one period of orthogonal LO data respectively. The LO data are taken out periodically from the table and input to the mixer to multiply by IF signal. The LO is altered by updating the data in the RAM. There are many LO data stored in the host computer, which could be written to the RAM at all times. Thus the test bed has characteristics of flexible frequency conversion.
After mixing, in order to select the narrow-band signal, the complex output signal is filtered by the fixed real low-pass filter. The filtered equation is
Where, h(t) (n = 0, 1, 2, . . ., N-1) are the filter coefficients and N is the duration of the unit sample response of the filter. As mentioned above, the high-speed data flow needs to be divided to parallel channels and extracted. For this purpose, a high-speed parallel filter algorithm (Zhao et al. Reference Zhao, Yan, Chen, Liu, Wang and Chen2015) was used for designing a low-pass filter which is composed of parallel filter algorithm, bit-plane method, canonic-signed digit(CSD) coding (Hawley et al. Reference Hawley, Wong, Lin and Samueli1996) and extracting algorithm. The 1 GHz data flow is divided into 8 branches, which makes the data rate drop to 128 MHz each branch. The output of each branch(channel) is corresponding to the eight times extraction results from the output of serial filter algorithm. Therefore one branch output(128 MHz data rate) is selected from the parallel filter. Thus, the algorithm complexity and the hardware resources occupation are both reduced significantly. The main specifications of the test bed system, as driven by requirements of CSRH, are given in Table 1.
Table 1. The test bed specifications.

3.2 The simulation and testing of the test bed
In order to implement hardware and software algorithms properly, select the number of truncated data bits effectively, as well as investigate the effect of filter parameters on the internal signal processing, Matlab is initially used for simulating the test bed.
Two 10 MHz orthogonal LO modules are designed for complex mixer.
A low-pass equiripple filter with 127 order is designed by ‘Filter Design & Analysis Tool’ in Matlab. The pass band is [0, 0.01] Fnyq (Nyquist frequency). The maximum side lobe suppression level is − 60 dB.
The simulation of the digital signal processing of the test bed is shown in Figure 3, from the top to the bottom are the Gaussian white noise input signal in the time domain, the input signal spectrum, the signal spectrum after mixing, the signal spectrum after a low-pass filtering, the signal spectrum after extraction, and the self-correlation result.

Figure 3. The Matlab simulation of the test bed.
As shown in the simulation results, the self-correlation sequence value from the test bed could reach to the maximum when delay is 0, which is consistent with the theoretical expectations, and indicates that the design is feasible. Then the hardware algorithm could be designed and simulated.
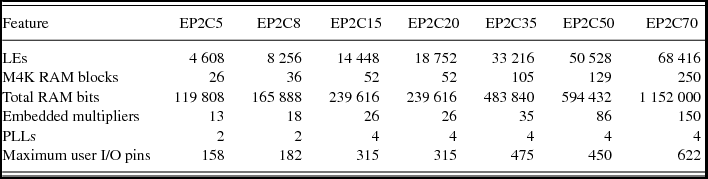
Altera Cyclone II series EP2C50F672 is selected as the main chip, matching with the ADC08D500. Based on the data handbook of Altera Corporation, Cyclone II FPGAs offer 60% higher performance and half the power consumption of competing 90 nm FPGAs. Table 2 lists the Cyclone II device family features. EP2C50F672 is suitable for the test bed by estimating the resources occupation. ModelSim-Altera 6.6c and Quartus II 9.0 are combined for FPGA simulation. The interface software, programmed by VC++6.0, allows the setting of parameters, such as the AD depth, the integration time, the length of displayed data sequence and the length of saved data.
Table 2. Cyclone II FPGA family features.
With respect to designing the hardware language algorithm, as shown in Figure 4, the 127-order filter coefficients are extracted and formed a 8*16 matrix (8 branches with 16 coefficients each). Every coefficient is quantised to 11 bits and coded with CSD, which constructs eight 11*16 matrices. Then bit-plane algorithm and parallel algorithm are applied to the matrices to achieve the high-speed filter algorithm. Two 10 MHz orthogonal LO modules are programmed into the mixer. The mixer and filter algorithm are integrated and tested on Cyclone II EP2C50F672. The comparison of FPGA resources occupation between the test bed as designed above and the DDC system based on the polyphase filter structure is shown in Table 3.

Figure 4. The algorithm logics of the test bed.
Table 3. The FPGA resource occupation.
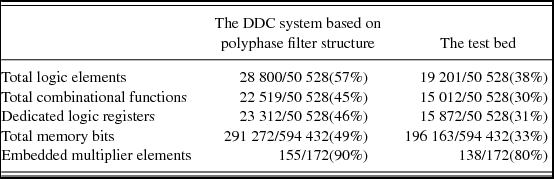
The test bed runs well at the sample clock of 1 GHz, and saves nearly 19% of the total logic elements and 16% of the total memory bits than the system based on polyphase filter. The saved hard resources can be applied to improving other parameters, which greatly enhances the system performance. The magnitude and phase response obtained from Matlab and Quartus II are shown in Figure 5, which shows consistent simulation results and further verifies the hardware algorithm on FPGA.

Figure 5. Magnitude and phase response.
4 OBSERVATION OF GEOSTATIONARY SATELLITE
To further test the design, the test bed is applied for processing the observation data of Fengyun-2E received by CSRH. Fengyun-2E is a geostationary satellite, which belongs to China’s meteorological satellite. It was launched in 2004 and is stationed along the equator at 105° east longitude. Fengyun-2E was chosen as observed source because its signals are stable and clear. Four antennas of CSRH are chosen for receiving the satellite signals. The selected antennas are close and at the same horizontal level so that they have better correlation and U-V coverage. The antenna arrangement of the CSRH central area which contains the selected antennas(A5, A6, C2, C4) is shown in Figure 6.

Figure 6. The antenna arrangement of the CSRH central area.
The Fengyun-2E satellite was observed on March 20, 2014 during 20:10–21:10. The observation bandwidth 1600 MHz–2000 MHz was selected because the frequency of the satellite is 1702.5 MHz. The integration time was set as 3 ms and the filter bandwidth was 10 MHz. The basic principle is to use the selected four antennas for receiving satellite signals. The signals are down-converted and filtered through the test bed as designed. Then the signals are quantised with 2-bit and cross-correlated with each other. Six results were obtained after the operation mentioned as above. It is assumed that the antenna signal S i (t) and S j (t) are obtained from the antenna i and j respectively. Thus the correlation output can be expressed as (Taylor, Carilli, & Perley Reference Taylor, Carilli and Perley1999):
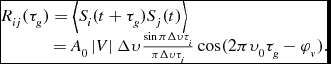 \begin{equation}
\begin{array}{l}R_{ij}({\tau _g}) = \left\langle {{S_i}(t + {\tau _g}){S_j}(t)} \right\rangle \\
\;\,\;\;\;\;\;\;\;\;\;= {A_0}\left| V \right|\Delta \upsilon \frac{{\sin \pi \Delta \upsilon {\tau _i}}}{{\pi \Delta \upsilon {\tau _i}}}\cos (2\pi {\upsilon _0}{\tau _g} - {\varphi _v}).
\end{array}
\end{equation}
\begin{equation}
\begin{array}{l}R_{ij}({\tau _g}) = \left\langle {{S_i}(t + {\tau _g}){S_j}(t)} \right\rangle \\
\;\,\;\;\;\;\;\;\;\;\;= {A_0}\left| V \right|\Delta \upsilon \frac{{\sin \pi \Delta \upsilon {\tau _i}}}{{\pi \Delta \upsilon {\tau _i}}}\cos (2\pi {\upsilon _0}{\tau _g} - {\varphi _v}).
\end{array}
\end{equation}
Where, τ g is the delay between the antenna i and antenna j, τ i is compensate deviation of the delay, R i j (τ g ) is the correlation result, A0 is the gain, |V| is the amplitude of the visibility function, Δυ is the correlation bandwidth, and φ v is the phase of the visibility function. R i j (τ g ) is modulated by function sinc. In actual measurement, the delay is adjusted gradually until the maximum of R i j (τ g ) is reached, meanwhile, the function sinc also reaches its maximum. At this point, the compensation delay is equal to the actual delay. The signals from the four antennas are processed through the test bed, adjusted delay for positive and negative 2 000 ns, and cross-correlated. Figure 7 shows the results. Six curves C12, C13, C14, C23, C24, and C34 correspond to six results of cross-correlation sequences. The number of 1, 2, 3, and 4 represents antenna A5, C2, C4, and A6 respectively.

Figure 7. The cross-correlation curves.
More accurate maximum peak can be obtained through Gaussian fitting on the cross-correlation sequences. Then the delay can be determined, which contains the device delay and the geometry delay. In order to better present Gaussian fitting, the curves are zoomed in and shifted as shown in Figure 8. The corresponding delays between each pair of antenna are shown in Table 4.

Figure 8. The Gaussian fitting curves.
Table 4. The delays between the antennas.

The closure relationships have proved to be very important in synthesis mapping (Thompson, Moran, & Swenson Reference Thompson, Moran and Swenson2001). We randomly selected any three antennas i, j, and k of the four. The delay of the three antennas should conform to the phase closure relationship (Taylor et al. Reference Taylor, Carilli and Perley1999), as:
As T= − dϕ/dω, for the same ω, T conforms to the delay closure relationship, as:
When applied to unsolved point sources, the noise term should be zero, and the phase closure should be zero (Wang et al. Reference Wang2013). Therefore, the delay closure should be zero too as explained above:
That equals to:
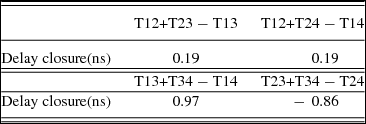
The results of delay closure are shown in Table 5, which are calculated according to equation (7).
Table 5. The results of delay closure.
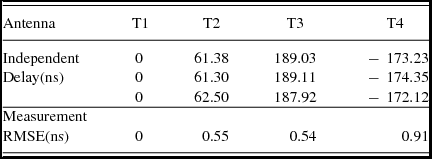
The delays between the antennas are relative delays. When T1 is assumed to be 0 ns, the independent delays can be calculated according to Table 4. Table 6 shows the independent delays and measurement errors.
Table 6. The independent delays and measurement errors.
The digital delay compensation has deviation with the actual delay. The deviation influences the amplitude and phase of the visibility function (Liu et al. Reference Liu, Yan, Zhao and Wang2013).
The phase error of the digital system is designed as 1° and the maximum bandwidth of IF is 25 MHz. Therefore the required delay compensation accuracy should be less than 1 ns, which meet the requirements of phase errors, the image dynamic range and digital delay compensation (Liu et al. Reference Liu, Yan, Zhao and Wang2013).
As shown in Tables 5 and 6, the values of the delay closure of satellite observation and the measurement RMSE are both less than 1 ns, which conforms to the requirement of delay compensation accuracy. Therefore the test bed is reasonable and feasible.
5 CONCLUSION
The simulations of Quartus II and Matlab demonstrate that the design of the test bed is reasonable and feasible. Furthermore, the satellite data from CSRH, after processed by the test bed, fulfill the delay closure relationship greatly, which further validates the design of the test bed. It provides a new method and support for testing and calibration for CSRH. Because of the modularity and good extension of FPGA, the design can also be applied to other radio astronomical observations.
ACKNOWLEDGEMENTS
We thank Jian Zhang from Peking University, who put forward many constructive comments. Linjie Chen, Lihong Geng, and Fei Liu are acknowledged for helpful discussions. We also thank Zhijun Chen, Donghao Liu and Cang Su for help with the observations. This research was supported by NSFC grants (No.11003028) and National Major Scientific Equipment Research and Design project (ZDYZ2009-3).

















