1. Introduction
High-end manufacturing fields such as ships and port machinery have developed rapidly in recent years, and the demand for on-site welding and polishing of large-scale complex structural components has increased sharply. Traditional industrial robots are difficult to adapt to the work requirements of complex constructive components on the spot, and the on-site work of large-scale complex structural components is mainly completed by the workers‘ handmade operations. There are problems such as a harsh working environment and great labor intensity of workers during the working process. Therefore, the development of a wall-climbing robot that meets the demands of large-scale, complex structural on-site work holds significant practical importance and broad application prospects. The wall-climbing robot is generally designed as a hybrid robot, which consists of two parts of the wall-climbing parallel mechanism (PM) and serial module. The accuracy of the operation requires high rigidity. Establishing the correct stiffness model is the basis for conducting dynamic analysis. Wu [Reference Wu, Li, Wang and Wang1–Reference Wu, Gao, Zhang and Wang3] established the stiffness model of PMs and explored new methods for evaluating their dynamic performance. The establishment of a static elastic stiffness model analyzed by the robot is of great significance for evaluating stiffness performance at the predesign stage of the robot.
Analytical methods can establish the required analytical expression between the external wrench and the corresponding deflection. Analytical methods fall into four categories: the virtual joint method (VJM), the screw theory method, the strain energy method, and the matrix structure analysis (MSA) method.
The VJM treats each link as a rigid link supported by springs with six degrees of freedom (DOFs) at both ends. Zhang [Reference Zhang, Zhao and Jin4] established an elastostatic stiffness model of the Exechon overconstrained PMs using the VJM. Shen [Reference Shen, Zhu and Meng5] established the stiffness model of the 2T1R PMs using the VJM. Kim [Reference Kim and Lipkin6] established stiffness models of the Tricept and 3-PRRR PMs by considering the flexibility of their links. However, the VJM may have redundant springs in certain directions, which requires combining sufficient number of deformation coordination equations to deal with these redundant spring constraints, makes the calculation process cumbersome; additionally, the VJM cannot obtain the compliance contribution matrix (CCM) and the elastic deflection contribution (EDC) for each elastic component in the robot [Reference Pashkevich, Klimchik and Chablat7, Reference Taghvaeipour, Angeles and Lessard8].
The screw theory method determines the constraint wrenches of the limb based on the screw theory, reducing the dimensions of the constraint wrenches imposed by each limb on the moving platform. This significantly reduces the required number of deformation coordination equations. Huang and Hu et al. [Reference Huang, Zhao and Liu9, Reference Hu10] established stiffness models of 4-R(CRR), 3-UPU, and 3-RPS PMs based on screw theory. They obtained the limb stiffness using the principle of superposition of deformations. Zhao [Reference Wang, Hikita, Kubo, Zhao, Huang and Ifukube11–Reference Xu, Liu, Yao and Zhao14] introduced the concept of limb constraint wrench stiffness matrices, and they analyzed overconstrained PMs such as 3-PRRR and 7-SS. However, the solution for limb stiffness matrices involves two projections, which makes the process somewhat cumbersome. Additionally, the CCM and EDC of each elastic member were not decoupled in the proposed modeling.
The strain energy method analyzes the strain energy of each elastic element and the entire mechanism based on material mechanics. It combines with the Castigliano’s theorem to establish the overall stiffness matrix of the mechanism. This method has a clear physical interpretation and is computationally straightforward. Rezaei and Yan [Reference Enferadi and Tootoonchi15–Reference Yan, Ong and Nee18] established stiffness models for 3-PSP, 3-RRP, 2PRR-PPR, and delta PMs using the strain energy method. However, they only analyzed constrained PMs. Yang [Reference Li, Chen and Xu19–Reference Yang, Li and Chen21] later developed their work and applied the strain energy method to overconstrained PMs to establish stiffness models for the 2UPR-RPU and 2PUR-PSR PMs. However, these models only analyze PMs and do not consider hybrid mechanisms. They also do not decouple the contribution of each elastic component to the small end deformation of hybrid robots.
The MSA method considers each link as a standard beam element and combines sufficient number of deformation coordination equations to assemble the overall stiffness matrix. The MSA method achieves a good balance between calculation accuracy and calculation time. Klimchik [Reference Klimchik, Pashkevich and Chablat22, Reference Klimchik, Chablat and Pashkevich23] presented a detailed process for the MSA method and established a stiffness model of the NaVaRo robot. Zhao [Reference Zhao, Guo, Zhang, Liu, Li and Deng24] established the stiffness model for n(3RR1S) robot based on the MSA method and the screw theory. Yu [Reference Yu, Wu and Wang25] obtained the overall stiffness matrix for a 3-DOF PM and Cammarata [Reference Cammarata26] established stiffness models of both a spherical parallel robot and a Ragnar robot by combining the MSA method with condensation techniques. However, the MSA method involves high-dimensional matrices for multibody systems [Reference Cammarata, Condorelli and Sinatra27–Reference Deblaise, Hernot and Maurine29], and the research based on the MSA method mentioned above did not obtain the CCM and EDC for each elastic component.
The previous studies primarily focused on establishing the overall matrix of the mechanism, with limited exploration of the contributions of each component to the overall stiffness performance of the mechanism. Therefore, this paper places emphasis on studying the contributions of each elastic component to the overall stiffness performance of the mechanism. This focus provides a theoretical foundation for the effective improvement of the mechanism’s stiffness performance.
The main contributions of this paper are as follows: (1) A decoupling method for the elastostatic stiffness model of hybrid robots is introduced. It is based on the rigidity principle, screw theory, strain energy, and Castigliano’s second theorem. This method derives analytical expressions for the decoupled static stiffness model of hybrid robots and is applicable to both constrained and overconstrained hybrid robots. (2) The CCM of each elastic component of the hybrid robot is obtained based on the strain energy and Castigliano’s theorem. (3) The linear and angular deflection contributions of each elastic component to the hybrid robots are decoupled to allow the contribution of each elastic component to the linear and angular stiffness performances of the hybrid robots to be evaluated quantitatively, thus providing a new approach for effective improvement of the linear/angular stiffness performances of the hybrid robots.
This paper is organized as follows. In Section 2, the decoupled elastostatic stiffness model based on the rigidity principle, screw theory, strain energy, and Castigliano’s second theorem is proposed. In Section 3, a 3SPR + 1R hybrid mechanism is used as an example to demonstrate the procedure of the proposed method. In Section 4, the elastostatic model of the 4SRRR-6R hybrid robot is presented. Finally, in Section 5, conclusions are drawn from the work presented.
2. Unified stiffness model of hybrid robots based on the screw theory
The following assumptions are made for the hybrid robots:
-
1. The weights of all components are negligible.
-
2. The motors, moving platform, and all joints are rigid.
-
3. All joints are considered to be frictionless.
-
4. The links are considered to be flexible and the spatial composite deformation of the links, including the tension (or compression), shear, torsional and bending deformation components, is considered.
-
5. The deformation of all components is linear and within the elastic range.
Figure 1 shows a general model of a hybrid robot consisting of parallel and serial modules without loss of generality. The parallel module consists of a moving platform connected to a fixed platform by n limbs. The serial module is fixed at point o on the moving platform. O-XYZ and o-xyz denote the fixed coordinate frame and the moving coordinate frame, respectively. W T = [f T ; m T ] is the external wrench exerted on the hybrid robot end, where f T = [f Tx , f Ty , f Tz ]T; m T = [m Tx , m Ty , m Tz ]T denote the external force and moment, respectively.
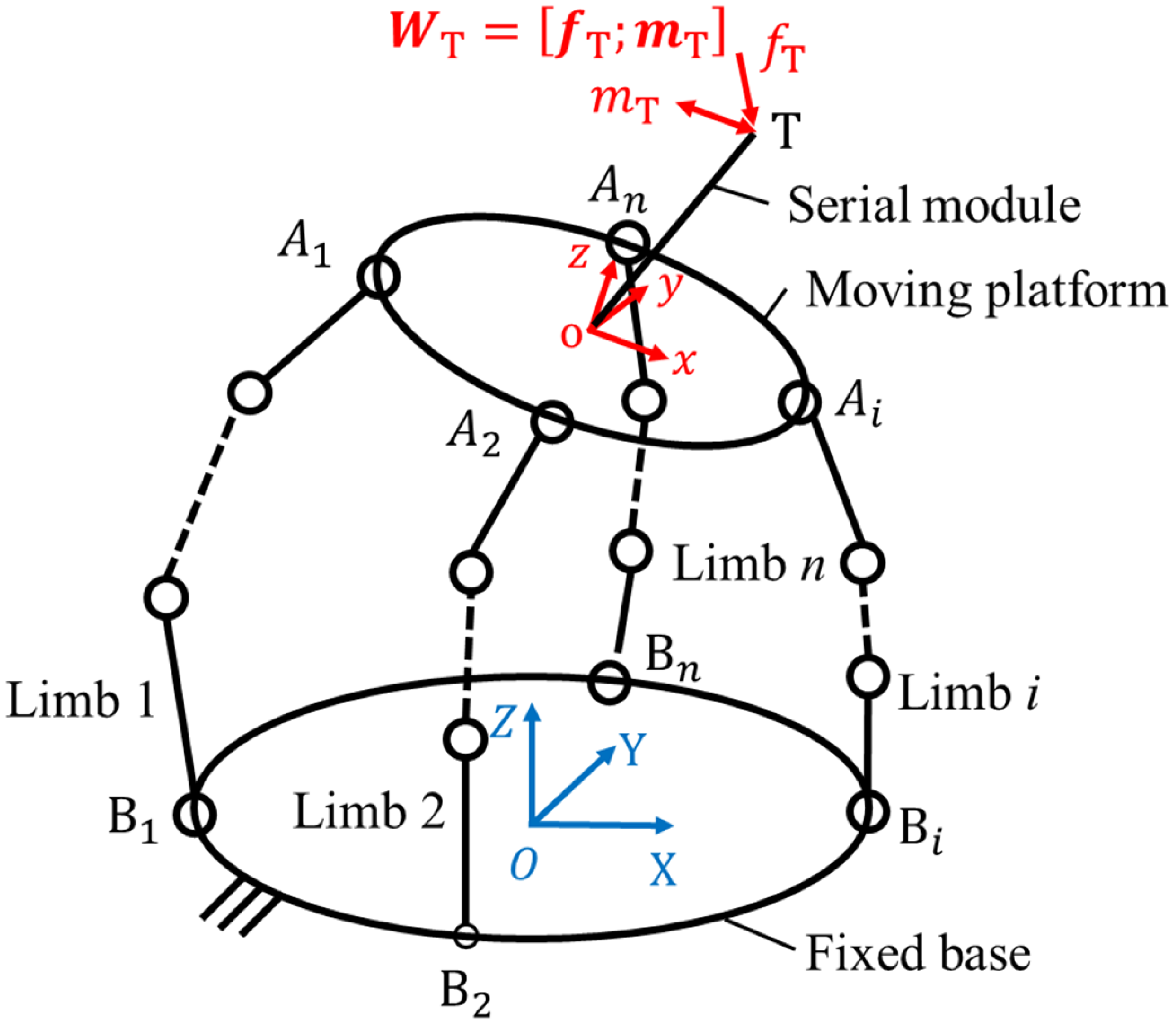
Figure 1. Schematic diagram of a general hybrid robot.
The theoretical model used in the work is based on the rigidity principle, screw theory, strain energy, Castigliano’s second theorem, and deformation compatibility equations (DCEs). Figure 2 shows the modeling process. The procedure of the proposed model in this paper is as follows: 1) According to the principle of superposition of deformation, the contribution of the hybrid robot to end deformation is equal to the superposition of the parallel and serial modules on end deformation. 2) Based on the rigidity principle, the contribution of the serial (parallel) module to end deformation can be obtained while the parallel (serial) module is considered to be rigid. 3) Decouple the total strain energy stored in the PM into the sum of the strain energy stored by each component (expressed based on external loads)
![]() $U=\sum _{i=1}\sum _{j=1}U_{ij}(\textbf{W}_{T})$
. 4) Based on the Castigliano’s second theorem, the contribution of each component to the end deformation of the hybrid robot can be obtained
$U=\sum _{i=1}\sum _{j=1}U_{ij}(\textbf{W}_{T})$
. 4) Based on the Castigliano’s second theorem, the contribution of each component to the end deformation of the hybrid robot can be obtained
![]() $\boldsymbol\Delta$
ij
= ∂U
ij
/∂W
T
. The detailed steps are as follows:
$\boldsymbol\Delta$
ij
= ∂U
ij
/∂W
T
. The detailed steps are as follows:

Figure 2. Decoupled elastostatic stiffness modeling of hybrid robots.
2.1. Elastic deformation of hybrid robot end caused by parallel module
2.1.1 The contribution to the robot end deformation of the parallel module
Based on the rigidity principle, the contribution of the parallel module to end deformation can be obtained while the serial module is considered to be rigid.
According to the wrench transfer formula, the wrench acting on the point o of the parallel module can be expressed as follows:
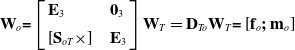 \begin{equation} \textbf{W}_{o}\textbf{=}\left[\begin{array}{l@{\quad}l} \textbf{E}_{3} & \textbf{0}_{3}\\[5pt] \left[\textbf{S}_{oT}\times \right] & \textbf{E}_{3} \end{array}\right]\textbf{W}_{T}=\textbf{D}_{To}\textbf{W}_{T}\textbf{=}\left[\textbf{f}_{o}\textbf{;}\;\textbf{m}_{o}\right] \end{equation}
\begin{equation} \textbf{W}_{o}\textbf{=}\left[\begin{array}{l@{\quad}l} \textbf{E}_{3} & \textbf{0}_{3}\\[5pt] \left[\textbf{S}_{oT}\times \right] & \textbf{E}_{3} \end{array}\right]\textbf{W}_{T}=\textbf{D}_{To}\textbf{W}_{T}\textbf{=}\left[\textbf{f}_{o}\textbf{;}\;\textbf{m}_{o}\right] \end{equation}
where D To denotes the mapping matrix from W T to W o . [S oT ×] denotes the skew-symmetric matrix of vector S oT .
The DCEs between limb end and the attachment point o of the moving platform of the parallel module can be obtained [Reference Li, Chen and Xu19] according to the principle of virtual work:
where
![]() $\boldsymbol\Delta$
i
denote the elastic deformation of the i
th limb; J
i
denote the unit constraint wrench system of the i
th limb; and
$\boldsymbol\Delta$
i
denote the elastic deformation of the i
th limb; J
i
denote the unit constraint wrench system of the i
th limb; and
![]() $\boldsymbol\Delta$
o
denotes the elastic deflection of the attachment point o of the moving platform.
$\boldsymbol\Delta$
o
denotes the elastic deflection of the attachment point o of the moving platform.
The following equation can be obtained according to DCEs and the equilibrium equation of the spatial force system [Reference Li, Chen and Xu19].
where K p denotes the overall stiffness matrix corresponding to the attachment point o of the moving platform of the parallel module.
Therefore, the elastic deflection of the attachment point of the moving platform under W o is
where C p denotes the overall flexibility matrix corresponding to attachment point o of the moving platform of the parallel module.
The hybrid-robot terminal elastic deflection caused by parallel module under the assumption that the serial module to be rigid can be obtained as follows.
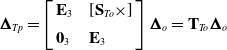 \begin{equation} \boldsymbol{\Delta }_{Tp}=\left[\begin{array}{l@{\quad}l} \textbf{E}_{3} & \left[\textbf{S}_{To}\times \right]\\[5pt] \textbf{0}_{3} & \textbf{E}_{3} \end{array}\right]\boldsymbol{\Delta }_{o}=\textbf{T}_{To}\boldsymbol{\Delta }_{o} \end{equation}
\begin{equation} \boldsymbol{\Delta }_{Tp}=\left[\begin{array}{l@{\quad}l} \textbf{E}_{3} & \left[\textbf{S}_{To}\times \right]\\[5pt] \textbf{0}_{3} & \textbf{E}_{3} \end{array}\right]\boldsymbol{\Delta }_{o}=\textbf{T}_{To}\boldsymbol{\Delta }_{o} \end{equation}
where E
3 and 0
3 denote the 3 × 3 identity matrix and zero matrix, respectively, [S
To
×] denotes the skew-symmetric matrix of vector S
To, and
T
To
denotes the mapping matrix from
![]() $\boldsymbol\Delta$
o
to
$\boldsymbol\Delta$
o
to
![]() $\boldsymbol\Delta$
Tp
.
$\boldsymbol\Delta$
Tp
.
From the analysis above, it is evident that to determine the contribution of the parallel module to the elastic deformation of the hybrid robot end, it is necessary to first calculate the overall stiffness matrix of the parallel module. The process for calculating the limb stiffness matrix and overall stiffness matrix of the parallel module can refer to [Reference Li, Chen and Xu19].
Figure 3 presents a general model of the limb. o ij -x ij y ij z ij denotes the coordinate frame of j th member of i th limb, and axis x ij is aligned with the direction of the limb member here.
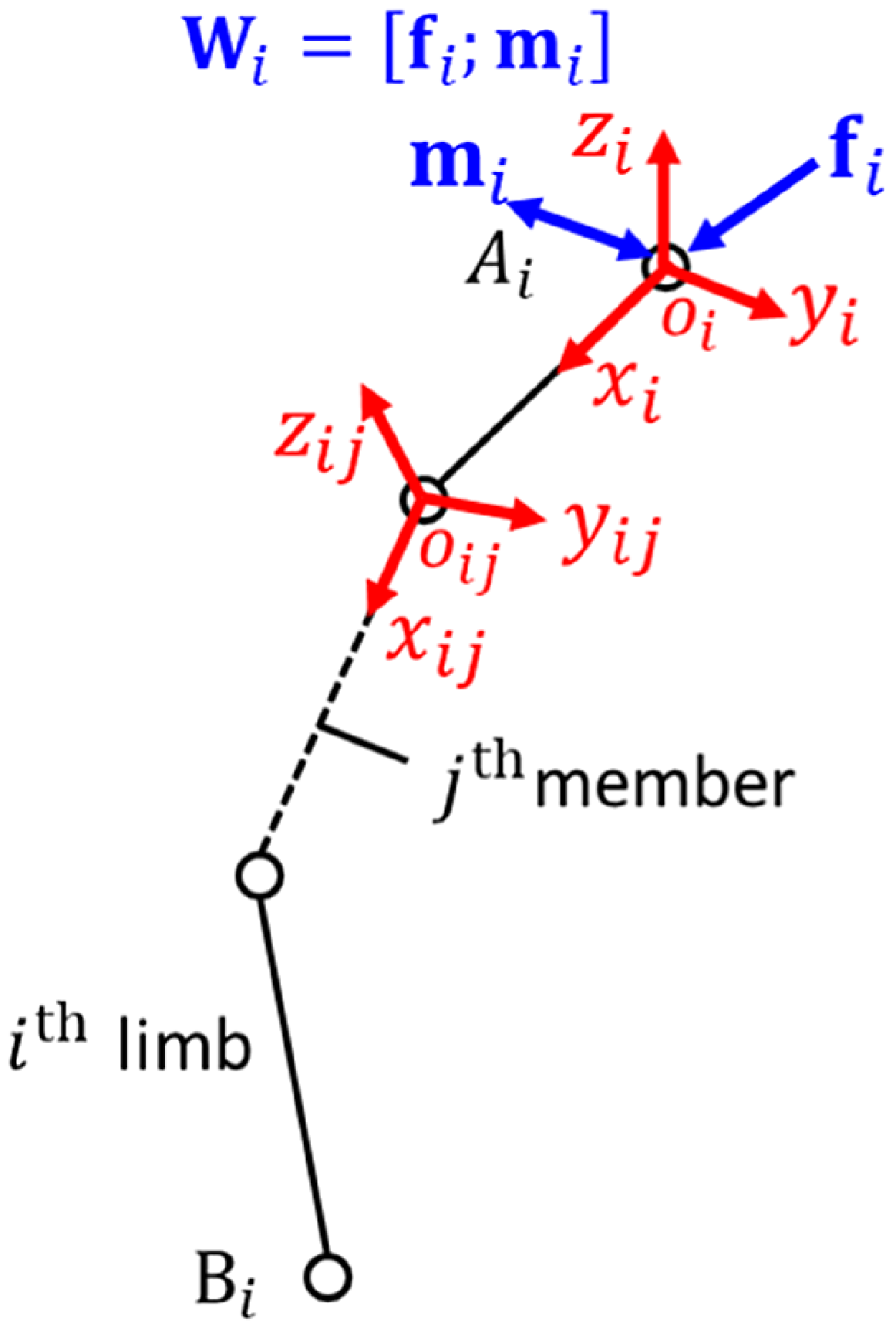
Figure 3. General model of limb.
Unit constraint wrench system
![]() $\textbf{J}_{i}=[\textbf{\$ }_{i1}^{r},\textbf{\$ }_{i2}^{r},\textbf{\$ }_{i3}^{r}]$
of the i
th limb can be established based on the reciprocal screw theory, where
$\textbf{J}_{i}=[\textbf{\$ }_{i1}^{r},\textbf{\$ }_{i2}^{r},\textbf{\$ }_{i3}^{r}]$
of the i
th limb can be established based on the reciprocal screw theory, where
![]() $\textbf{\$ }_{ij}^{r}=[\textbf{r}_{ij}^{r},\textbf{r}_{oij}^{r}\times \textbf{r}_{ij}^{r}]$
is the j
th unit constraint wrench of the i
th limb,
$\textbf{\$ }_{ij}^{r}=[\textbf{r}_{ij}^{r},\textbf{r}_{oij}^{r}\times \textbf{r}_{ij}^{r}]$
is the j
th unit constraint wrench of the i
th limb,
![]() $\textbf{r}_{ij}^{r}$
is a unit vector pointing along the direction of the screw axis, and
$\textbf{r}_{ij}^{r}$
is a unit vector pointing along the direction of the screw axis, and
![]() $\textbf{r}_{oij}^{r}$
is the position of any point on the screw axis, with a magnitude of W
i
= [f
i
; m
i
]. f
i
and m
i
denote constraint force and moment, respectively.
$\textbf{r}_{oij}^{r}$
is the position of any point on the screw axis, with a magnitude of W
i
= [f
i
; m
i
]. f
i
and m
i
denote constraint force and moment, respectively.
Based on screw theory and the principle of virtual work, the overall stiffness matrix of the parallel module can be established:
where K i denotes the stiffness matrix of the i th limb corresponding to W i .
2.1.2 The contribution to the robot end deformation of each component
Elastic deformation
![]() $\boldsymbol\Delta$
ij
of the i
th limb’s j
th member corresponding to W
i
can be obtained as follows according to Castigliano’s second theorem:
$\boldsymbol\Delta$
ij
of the i
th limb’s j
th member corresponding to W
i
can be obtained as follows according to Castigliano’s second theorem:
where U ij denotes the strain energy of the i th limb’s j th member; C ij denotes the flexibility matrix of the i th limb’s j th member corresponding to W i .
The strain energy of the i th limb’s j th member is given as
where f ij = [f ijx f ijy f ijz ]T, m ij = [m ijx m ijy m ijz ]T denotes the internal force of the i th limb’s j th member; E ij , G ij , and L ij denote the elastic modulus, shear modulus, and length of the i th limb’s j th member, respectively; A ij , A ijy , and A ijz denote the area and the effective shear area of the cross-section along the y ij and z ij axes, respectively; I ijy and I ijz denote the area moment of cross-section inertia about the y ij and z ij axes, respectively. Finally, I ijp denotes the polar moment of cross-section inertia.
The strain energy of the i th limb is as follows:
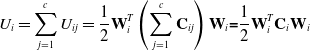 \begin{equation} U_{i}=\sum _{j=1}^{c}U_{ij}=\frac{1}{2}\textbf{W}_{i}^{T}\left(\sum _{j = 1}^{c}\textbf{C}_{ij}\right)\textbf{W}_{i}\textbf{=}\frac{1}{2}\textbf{W}_{i}^{T}\textbf{C}_{i}\textbf{W}_{i} \end{equation}
\begin{equation} U_{i}=\sum _{j=1}^{c}U_{ij}=\frac{1}{2}\textbf{W}_{i}^{T}\left(\sum _{j = 1}^{c}\textbf{C}_{ij}\right)\textbf{W}_{i}\textbf{=}\frac{1}{2}\textbf{W}_{i}^{T}\textbf{C}_{i}\textbf{W}_{i} \end{equation}
where C i denotes the flexibility matrix of the i th limb corresponding to W i ; c denotes the number of the member in the i th limb.
Elastic deformation
![]() $\boldsymbol\Delta$
i
of the i
th limb corresponding to W
i
is as follows according to Castigliano’s second theorem:
$\boldsymbol\Delta$
i
of the i
th limb corresponding to W
i
is as follows according to Castigliano’s second theorem:
The stiffness matrix of the i th limb constraint wrenches can be obtained as
Equations (1), (2), (3) and (10) lead to
Therefore, the strain energy of the i th limb’s j th member of parallel modules is as follows.
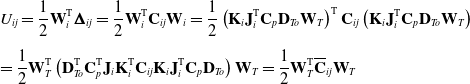 \begin{equation} \begin{array}{l} U_{ij}=\dfrac{1}{2}\textbf{W}_{i}^{\mathrm{T}}\boldsymbol{\Delta }_{ij}=\dfrac{1}{2}\textbf{W}_{i}^{\mathrm{T}}\textbf{C}_{ij}\textbf{W}_{i}=\dfrac{1}{2}\left(\textbf{K}_{i}\textbf{J}_{i}^{\mathrm{T}}\textbf{C}_{p}\textbf{D}_{To}\textbf{W}_{T}\right)^{\mathrm{T}}\textbf{C}_{ij}\left(\textbf{K}_{i}\textbf{J}_{i}^{\mathrm{T}}\textbf{C}_{p}\textbf{D}_{To}\textbf{W}_{T}\right)\\[12pt] =\dfrac{1}{2}\textbf{W}_{T}^{\mathrm{T}}\left(\textbf{D}_{To}^{\mathrm{T}}\textbf{C}_{p}^{\mathrm{T}}\textbf{J}_{i}\textbf{K}_{i}^{\mathrm{T}}\textbf{C}_{ij}\textbf{K}_{i}\textbf{J}_{i}^{\mathrm{T}}\textbf{C}_{p}\textbf{D}_{To}\right)\textbf{W}_{T}=\dfrac{1}{2}\textbf{W}_{T}^{\mathrm{T}}\overline{\textbf{C}}_{ij}\textbf{W}_{T} \end{array} \end{equation}
\begin{equation} \begin{array}{l} U_{ij}=\dfrac{1}{2}\textbf{W}_{i}^{\mathrm{T}}\boldsymbol{\Delta }_{ij}=\dfrac{1}{2}\textbf{W}_{i}^{\mathrm{T}}\textbf{C}_{ij}\textbf{W}_{i}=\dfrac{1}{2}\left(\textbf{K}_{i}\textbf{J}_{i}^{\mathrm{T}}\textbf{C}_{p}\textbf{D}_{To}\textbf{W}_{T}\right)^{\mathrm{T}}\textbf{C}_{ij}\left(\textbf{K}_{i}\textbf{J}_{i}^{\mathrm{T}}\textbf{C}_{p}\textbf{D}_{To}\textbf{W}_{T}\right)\\[12pt] =\dfrac{1}{2}\textbf{W}_{T}^{\mathrm{T}}\left(\textbf{D}_{To}^{\mathrm{T}}\textbf{C}_{p}^{\mathrm{T}}\textbf{J}_{i}\textbf{K}_{i}^{\mathrm{T}}\textbf{C}_{ij}\textbf{K}_{i}\textbf{J}_{i}^{\mathrm{T}}\textbf{C}_{p}\textbf{D}_{To}\right)\textbf{W}_{T}=\dfrac{1}{2}\textbf{W}_{T}^{\mathrm{T}}\overline{\textbf{C}}_{ij}\textbf{W}_{T} \end{array} \end{equation}
where
![]() $\overline{\textbf{C}}_{ij}$
denotes the overall flexibility contribution matrix caused by the i
th limb’s j
th member of parallel modules for the hybrid robot.
$\overline{\textbf{C}}_{ij}$
denotes the overall flexibility contribution matrix caused by the i
th limb’s j
th member of parallel modules for the hybrid robot.
The elastic deformation of the hybrid robot terminal caused by the i th limb’s j th member of parallel modules can be obtained based on the Castigliano’s second theorem.
Now, we have decoupled the elastic deformation of the hybrid robot end and the CCM caused by the i th limb’s j th member of parallel module of the hybrid robot through equation (14).
2.2. Elastic deformation of hybrid robot end caused by serial module
Elastic deformation
![]() $\boldsymbol\Delta$
si
of the j
th member of serial module corresponding to W
T
is as follows according to the strain energy and Castigliano’s second theorem.
$\boldsymbol\Delta$
si
of the j
th member of serial module corresponding to W
T
is as follows according to the strain energy and Castigliano’s second theorem.
where U sj denotes the strain energy of j th member of the serial module; C sj denotes the flexibility matrix corresponding to the W T of the j th member of serial module.
The strain energy of the serial module U s is as follows:
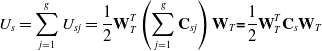 \begin{equation} U_{s}=\sum _{j=1}^{g}U_{sj}=\frac{1}{2}\textbf{W}_{T}^{T}\left(\sum _{j = 1}^{g}\textbf{C}_{sj}\right)\textbf{W}_{T}\textbf{=}\frac{1}{2}\textbf{W}_{T}^{T}\textbf{C}_{s}\textbf{W}_{T} \end{equation}
\begin{equation} U_{s}=\sum _{j=1}^{g}U_{sj}=\frac{1}{2}\textbf{W}_{T}^{T}\left(\sum _{j = 1}^{g}\textbf{C}_{sj}\right)\textbf{W}_{T}\textbf{=}\frac{1}{2}\textbf{W}_{T}^{T}\textbf{C}_{s}\textbf{W}_{T} \end{equation}
where C s denotes the flexibility matrix of the serial module corresponding to W T ; g denotes the number of members of the serial module.
The hybrid robot end elastic deformation caused by serial modules is as follows according to Castigliano’s second theorem:
2.3. Elastic deformation of hybrid robot end
Finally, the elastic deformation of the hybrid robot terminal is equal to the sum of elastic deformation caused by parallel and serial modules according to the rigidity principle.
where
![]() $\boldsymbol\Delta$
T
denotes the elastic deformation of the hybrid robot terminal; C
H
denotes the overall flexibility of the hybrid robot corresponding to external screw W
T
.
$\boldsymbol\Delta$
T
denotes the elastic deformation of the hybrid robot terminal; C
H
denotes the overall flexibility of the hybrid robot corresponding to external screw W
T
.
Reference [Reference Yang, Li and Chen21] decouples the contribution of each elastic element in the parallel module using the rigidity principle. In this approach, the contribution matrix of each elastic element to the stiffness of the mechanism becomes singular in some configurations, requiring the use of the generalized inverse operation to obtain the contribution of each elastic element to the end deformation of the mechanism. In contrast, in this paper, the parallel module operates entirely within the framework of strain energy and Castigliano’s second theorem, which has a clear physical interpretation and avoids the occurrence of singularity issues that can arise when using the rigidity principle in parallel module.
3. Example 1: 3SPR + 1R hybrid mechanism
First, we employ a 3SPR + 1R hybrid mechanism to systematically describe our model, as illustrated in Fig. 4a. The parallel module consists of a mobile platform, a fixed platform, and three identical SPR branches. Each limb comprises an active prismatic joint (P), a passive spherical joint (S), and a passive revolute joint (R). These three limbs are evenly distributed at 120° intervals with respect to the connection points on the mobile platform (or fixed platform). The serial module is formed by an active revolute joint (R) and is connected to the hybrid module at the geometric center o of the mobile platform. The entire hybrid mechanism includes a total of four active joints, serving as inputs for the mechanism. The mobile platform and joints are assumed to be rigid. The elastic rods are made of structural steel, sharing the same cross-sectional area with a diameter of d = 0.02m. The elastic modulus is E = 200 GPa, and the Poisson’s ratio is μ = 0.3. oA 1 = oA 2 = oA 3 = 0.13m, OB 1 = OB 2 = OB 3 = 0.18m.
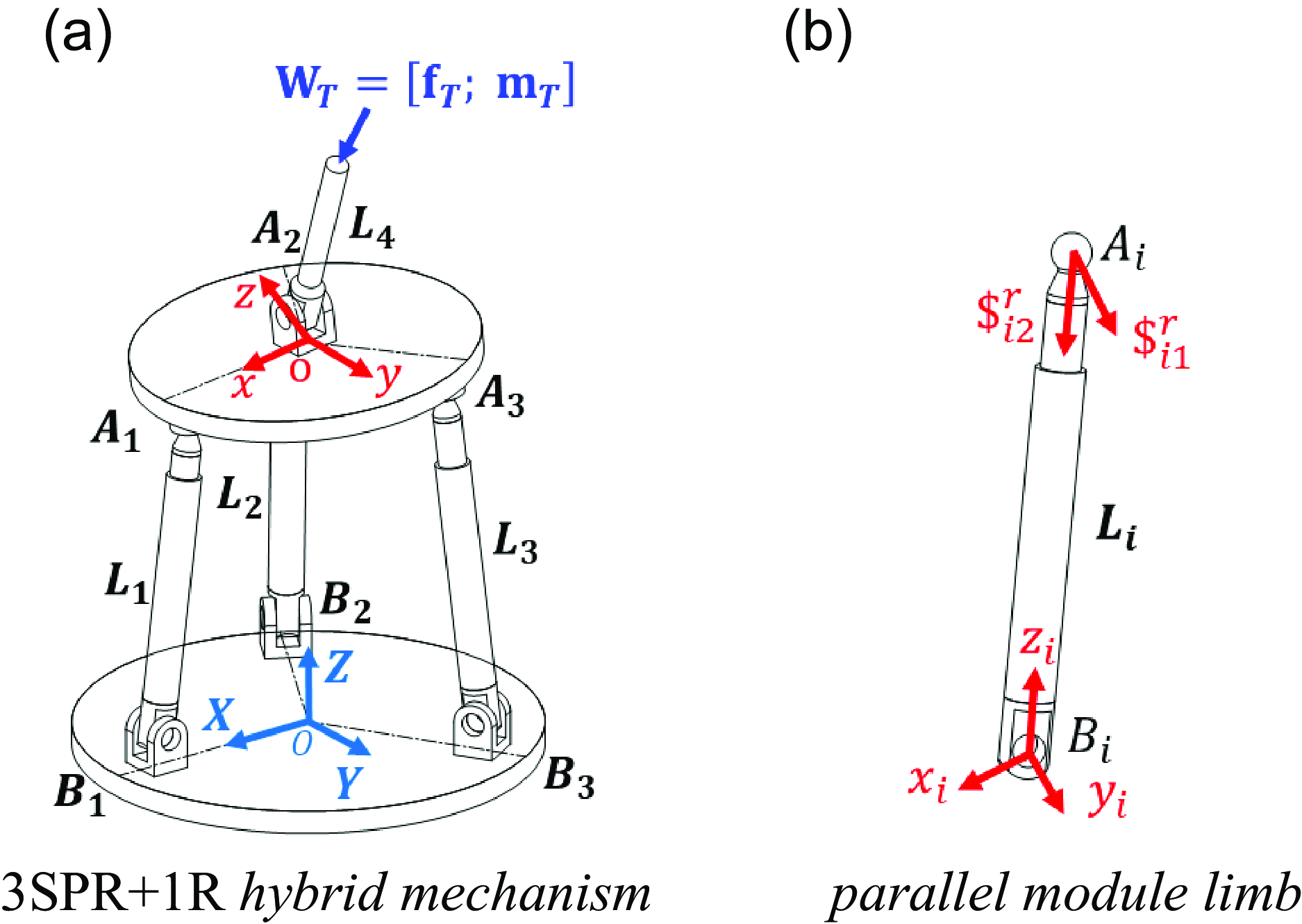
Figure 4. Coordinate system of 3SPR + 1R hybrid mechanism.
As shown in Fig. 4a, the parallel module’s moving coordinate system o-xyz has its origin o located at the geometric center of the mobile platform, the z-axis is perpendicular to the plane of the mobile platform, the x-axis is along the oA 1 direction, and the y-axis is determined by the right-hand rule. The fixed coordinate system O-XYZ has its origin at the geometric center of the fixed platform, the Z-axis is vertically oriented upward, the X-axis is along the OB 1 direction, and the Y-axis is determined by the right-hand rule. As shown in Fig. 4b, the local coordinate system B i -x i y i z i of the parallel module limb is depicted, the coordinate origin is located at point B i , where the y i -axis aligns with the direction of the revolute joint axis, and the z i -axis aligns with the direction of the limb rod, pointing toward point A i and the x i -axis is determined by the right-hand rule.
Based on screw and reciprocal screw theory, the reciprocal dot product of the motion screw and the constraint force screw is zero [Reference Ball30].
When the active prismatic joint of the limb is locked, the motion screw system of the limb can be represented based on the local coordinate system B i -x i y i z i :
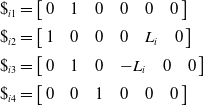 \begin{equation} \begin{array}{l} \$ _{i1}=\left[\begin{array}{l@{\quad}l@{\quad}l@{\quad}l@{\quad}l@{\quad}l} 0 & 1 & 0 & 0 & 0 & 0 \end{array}\right]\\[5pt] \$ _{i2}=\left[\begin{array}{l@{\quad}l@{\quad}l@{\quad}l@{\quad}l@{\quad}l} 1 & 0 & 0 & 0 & L_{i} & 0 \end{array}\right]\\[5pt] \$ _{i3}=\left[\begin{array}{l@{\quad}l@{\quad}l@{\quad}l@{\quad}l@{\quad}l} 0 & 1 & 0 & -L_{i} & 0 & 0 \end{array}\right]\\[5pt] \$ _{i4}=\left[\begin{array}{l@{\quad}l@{\quad}l@{\quad}l@{\quad}l@{\quad}l} 0 & 0 & 1 & 0 & 0 & 0 \end{array}\right] \end{array} \end{equation}
\begin{equation} \begin{array}{l} \$ _{i1}=\left[\begin{array}{l@{\quad}l@{\quad}l@{\quad}l@{\quad}l@{\quad}l} 0 & 1 & 0 & 0 & 0 & 0 \end{array}\right]\\[5pt] \$ _{i2}=\left[\begin{array}{l@{\quad}l@{\quad}l@{\quad}l@{\quad}l@{\quad}l} 1 & 0 & 0 & 0 & L_{i} & 0 \end{array}\right]\\[5pt] \$ _{i3}=\left[\begin{array}{l@{\quad}l@{\quad}l@{\quad}l@{\quad}l@{\quad}l} 0 & 1 & 0 & -L_{i} & 0 & 0 \end{array}\right]\\[5pt] \$ _{i4}=\left[\begin{array}{l@{\quad}l@{\quad}l@{\quad}l@{\quad}l@{\quad}l} 0 & 0 & 1 & 0 & 0 & 0 \end{array}\right] \end{array} \end{equation}
where L i represents the length of the limb rod.
According to equation (19), the constraint wrench system of the limb can be obtained as
According to the physical significance of reciprocal screw, we know that when the active prismatic joint of the limb is locked, the limb imposes two constraint forces on the mobile platform at point A i along the y i and z i axes, with magnitudes f i1 and f i2 (as shown in Fig. 4b). This can be expressed as W i = [0, f i1, f i2, 0, 0, 0]T = [f i , 0]T. In total, the three limbs collectively impose six constraint forces on the mobile platform. Therefore, the 3SPR + 1R hybrid mechanism is the underconstrained mechanism.
According to the knowledge of strain energy in material mechanics, the strain energy of limb can be expressed as
Table I. Elastic deflection of the hybrid robot terminal.

According to equation (10), the flexibility matrix C i of limb i is obtained as
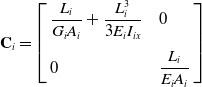 \begin{equation} \textbf{C}_{i}=\left[\begin{array}{l@{\quad}l} \dfrac{L_{i}}{G_{i}A_{i}}+\dfrac{L_{i}^{3}}{3E_{i}I_{ix}} & 0\\[12pt] 0 & \dfrac{L_{i}}{E_{i}A_{i}} \end{array}\right] \end{equation}
\begin{equation} \textbf{C}_{i}=\left[\begin{array}{l@{\quad}l} \dfrac{L_{i}}{G_{i}A_{i}}+\dfrac{L_{i}^{3}}{3E_{i}I_{ix}} & 0\\[12pt] 0 & \dfrac{L_{i}}{E_{i}A_{i}} \end{array}\right] \end{equation}
Stiffness matrix K
i
and overall stiffness matrix K
p
can be obtained by equations (6) and (11). The contribution of the parallel module to the elastic deformation of the hybrid robot end can be obtained by equation (5), where
![]() $\textbf{J}_{i}=[\boldsymbol{\$ }_{i1}^{r},\$ _{i2}^{r}]$
represents the constrained screw system of limb i. The overall flexibility matrix corresponding to the serial module and W
T
, as well as the contribution to the elastic deformation of the hybrid mechanism end, can be obtained according to the equations (16) and (17). The elastic deformation of the hybrid mechanism end is obtained according to the equation (18) after solving the contribution of the parallel and serial modules to the elastic deformation of the hybrid mechanism end, respectively.
$\textbf{J}_{i}=[\boldsymbol{\$ }_{i1}^{r},\$ _{i2}^{r}]$
represents the constrained screw system of limb i. The overall flexibility matrix corresponding to the serial module and W
T
, as well as the contribution to the elastic deformation of the hybrid mechanism end, can be obtained according to the equations (16) and (17). The elastic deformation of the hybrid mechanism end is obtained according to the equation (18) after solving the contribution of the parallel and serial modules to the elastic deformation of the hybrid mechanism end, respectively.
Validation is conducted using the finite element commercial software ANSYS software. In the ANSYS model, material and structural parameters are set based on those used in the theoretical model. The flexible limb rod is modeled using Beam 188 elements based on the Timoshenko beam theory, while the revolute joint and spherical joint are modeled using MPC184 elements in ANSYS. The configuration and structural parameters of the hybrid mechanism are as follows: When the active prismatic joint of the limb of the parallel module is locked, the length of limb rod is L 1 = 0.25m, L 2 = L 3 = 0.3m. The axis of the active revolute joint in the serial module is parallel to the x-axis of the moving coordinate o-xyz. When it is locked, the angle between the rod axis and the plane of the mobile platform is 60°, the length of the serial module rod is L 4 = 0.2m. Based on the fixed coordinate system O-XYZ, terminal external load is W T = [20N, 30N, −50N, 30N·m, −30N·m, 40N·m]T. The comparative results of end deformation for the hybrid mechanism are listed in Table 1, with the maximum error of 2.32%. This validates the accuracy of the proposed model in this paper. The FEA simulation results of the hybrid mechanism are illustrated in Fig. 5.
4. Example 2: 4SRRR + 6R hybrid robot
4.1. Introduction of 4SRRR + 6R
The hybrid robot composed of a four-legged wall-climbing robot and serial robotic arms is developed based on the on-site work requirements of large and complex structural parts (Fig. 6). The parallel module (four-legged wall-climbing robot) consists of a moving platform, a fixed platform (the fixed foot and the working wall form a fixed platform when the four-legged wall climbing robot reaches the working position), and four identical SRRR limbs. The limb legs are symmetrical and are composed of three active rotating joints (R) and one passive ball hinge joint (S). The serial module (serial robotic arm) is composed of six active rotating joints (R), and the axes of the last three rotating joints intersect at one point. There are a total of 18 active rotating joints in the parallel and serial module as the input of the mechanism. The mobile platform and joints of hybrid robot are assumed to be rigid, and the elastic rod components are made of aluminum alloy 7075-T6, with their physical and structural parameters shown in Table 2.
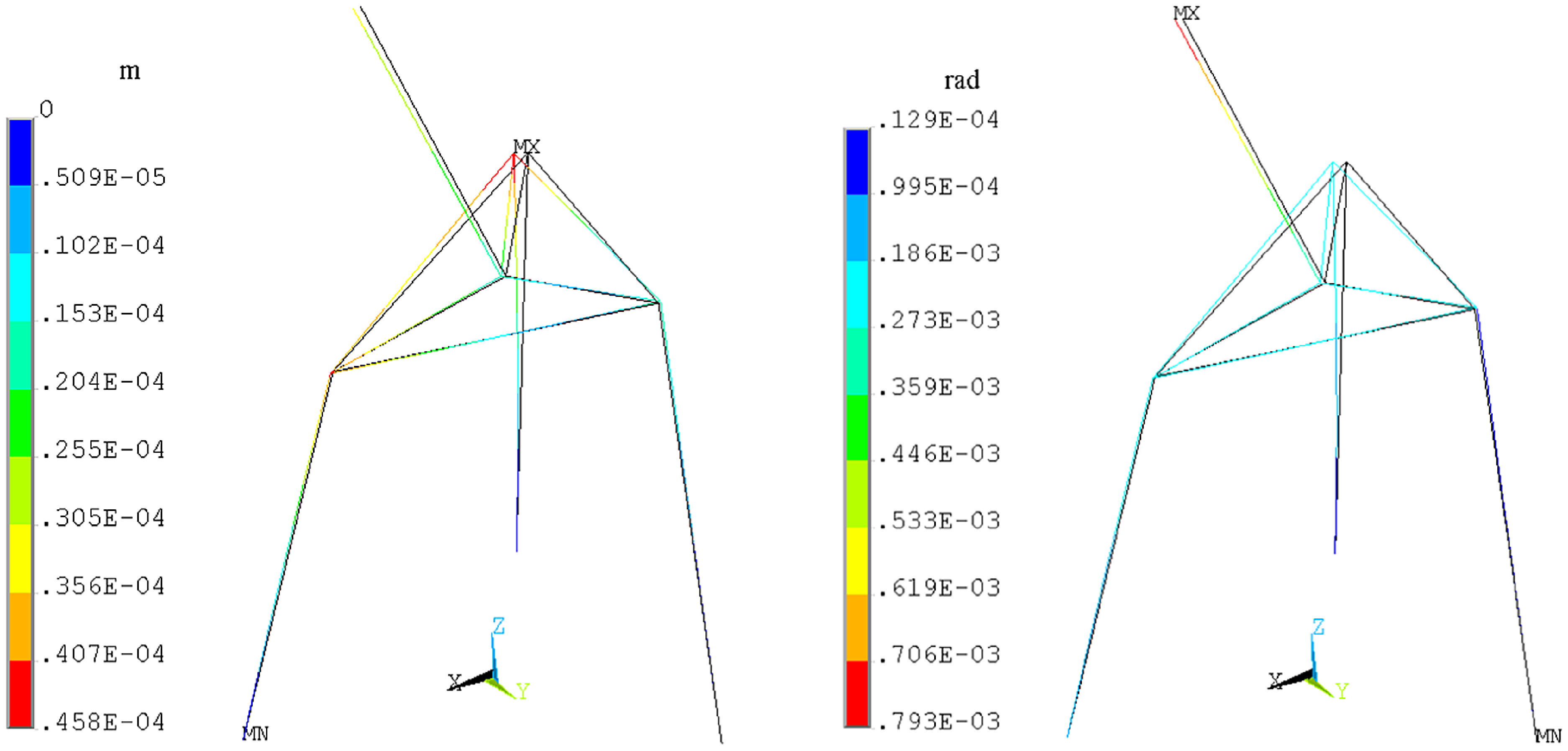
Figure 5. Contours of linear and angular displacement vectors.
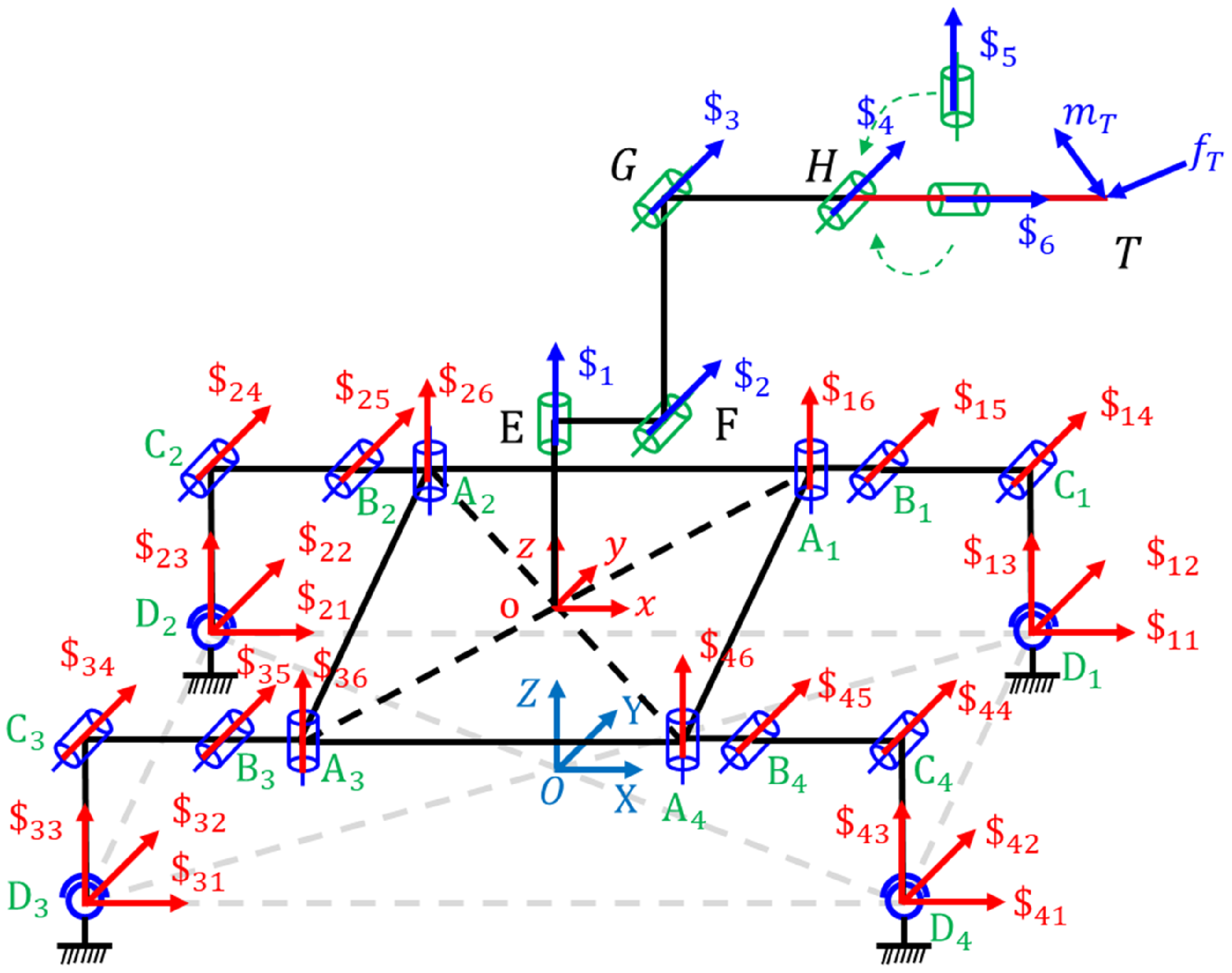
Figure 6. 4SRRR + 6R hybrid robot.
Table II. Physical and structure parameter values of the 4SRRR + 6R hybrid robot.
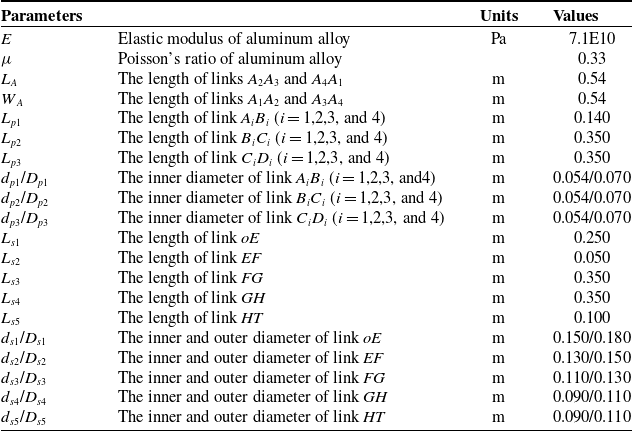
The origin of parallel module moving coordinate system o-xyz is located at the geometric center of the moving platform; the z-axis is perpendicular to the plane where the moving platform is located; the x-axis is parallel to line A 3 A 4; and the y-axis is determined by the right-hand rule. The origin of fixed coordinate system O-XYZ is located at the geometric center of the fixed platform. The Z-axis is vertically upward; the X-axis is parallel to the line of D 3 D 4; and the Y-axis is determined by the right-hand rule.
The parallel module limb is connected to the moving platform through R-joint at A i (the axis is perpendicular to the surface of the moving platform) and connected to the fixed platform through S-joint at D i (Fig. 7a). z i1, z i2, and z i3 of the local coordinate systems A i -x i1 y i1 z i1, B i -x i2 y i2 z i2, and C i -x i3 y i3 z i3 are along the axis of A i , B i , and C i , respectively. x i1, x i2, and x i3 point to the directions of A i B i , B i C i , and C i D i , respectively. The serial module establishes a coordinate system according to the DH method.
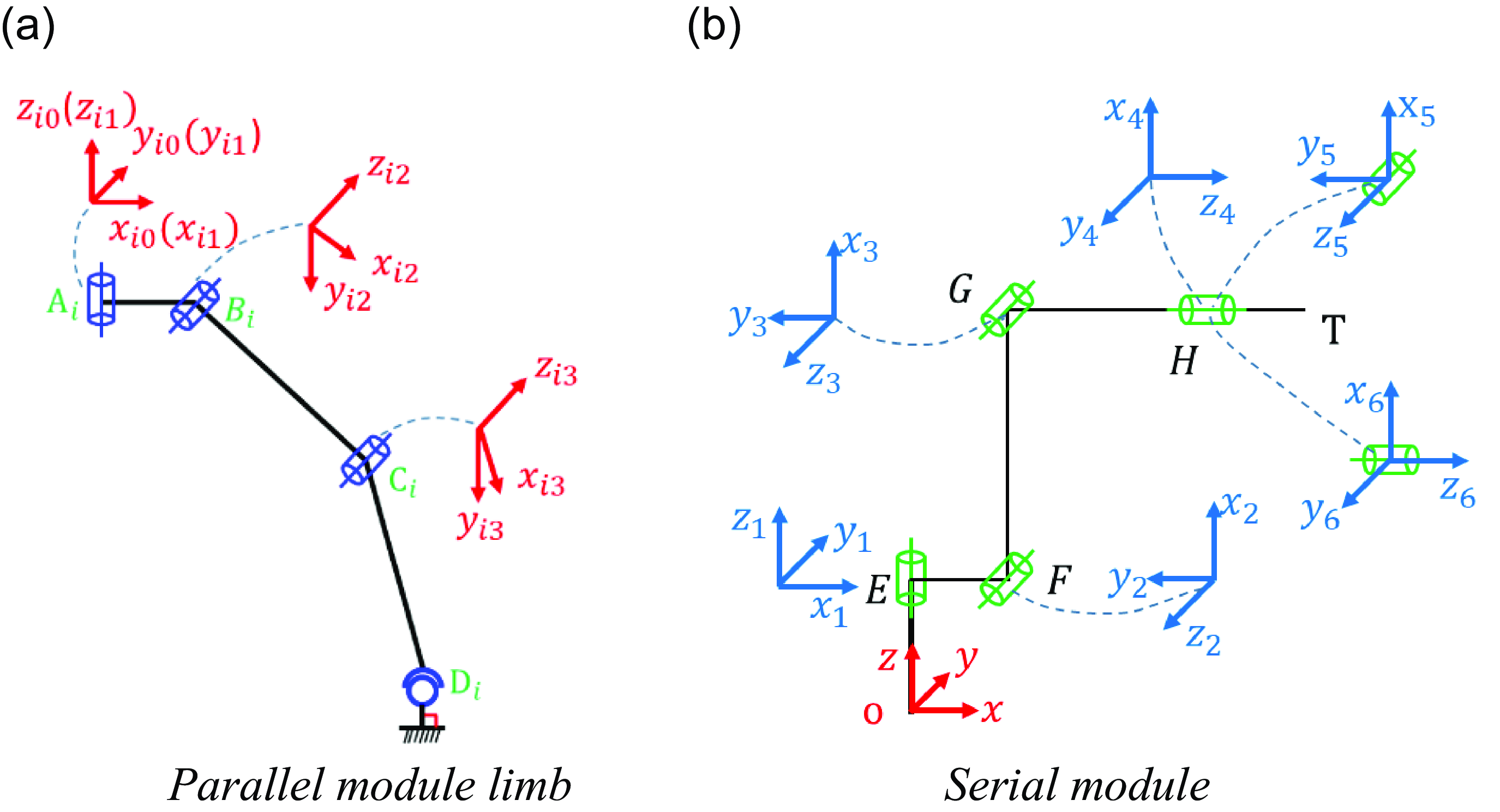
Figure 7. Coordinate system of parallel module limb and serial module.
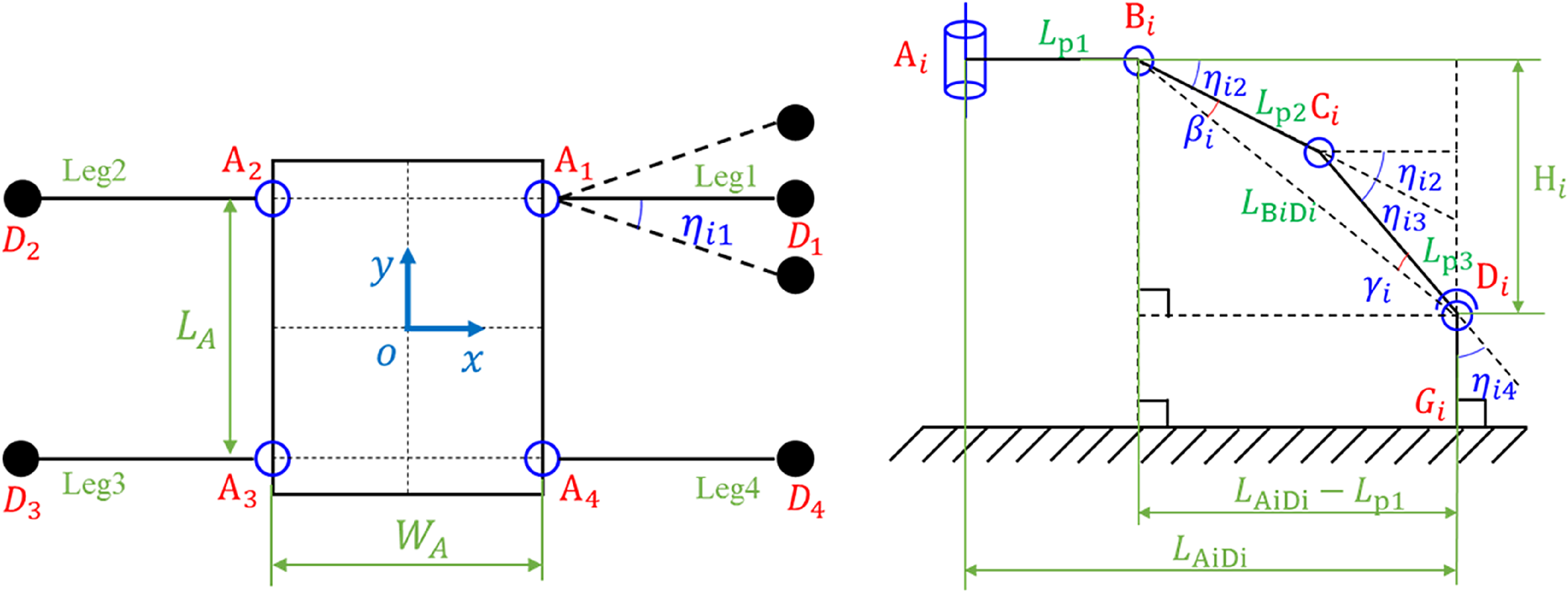
Figure 8. Inverse kinematics of 4SRRR wall climbing robot.
The foot must be perpendicular to the work surface due to the magnetic suction when the 4SRRR-6R hybrid robot is adsorbed on the work surface. Figure 8 illustrates the inverse kinematics calculation diagram of the limb of the 4SRRR-6R hybrid robot.
The coordinate of A i in the moving coordinate system is ( o x Ai , o y Ai , o z Ai ), and the coordinates of D i are ( o x Di , o y Di , o z Di ). The following equation according to the geometric relationships is
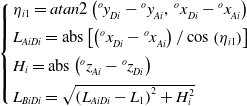 \begin{equation} \left\{\begin{array}{l} \eta _{i1}=atan2\left({}^{o}{y}{_{Di}^{}}-{}^{o}{y}{_{Ai}^{}},\,{}^{o}{x}{_{Di}^{}}-{}^{o}{x}{_{Ai}^{}}\right)\\[5pt] L_{AiDi}=\mathrm{abs}\left[\left({}^{o}{x}{_{Di}^{}}-{}^{o}{x}{_{Ai}^{}}\right)/\cos \left(\eta _{i1}\right)\right]\\[5pt] H_{i}=\mathrm{abs}\left({}^{o}{z}{_{Ai}^{}}-{}^{o}{z}{_{Di}^{}}\right)\\[5pt] L_{BiDi}=\sqrt{\left(L_{AiDi}-L_{1}\right)^{2}+H_{i}^{2}} \end{array}\right. \end{equation}
\begin{equation} \left\{\begin{array}{l} \eta _{i1}=atan2\left({}^{o}{y}{_{Di}^{}}-{}^{o}{y}{_{Ai}^{}},\,{}^{o}{x}{_{Di}^{}}-{}^{o}{x}{_{Ai}^{}}\right)\\[5pt] L_{AiDi}=\mathrm{abs}\left[\left({}^{o}{x}{_{Di}^{}}-{}^{o}{x}{_{Ai}^{}}\right)/\cos \left(\eta _{i1}\right)\right]\\[5pt] H_{i}=\mathrm{abs}\left({}^{o}{z}{_{Ai}^{}}-{}^{o}{z}{_{Di}^{}}\right)\\[5pt] L_{BiDi}=\sqrt{\left(L_{AiDi}-L_{1}\right)^{2}+H_{i}^{2}} \end{array}\right. \end{equation}
According to the cosine theorem,
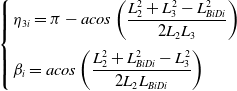 \begin{equation} \left\{\begin{array}{l} \eta _{3i}=\pi -acos\left(\dfrac{L_{2}^{2}+L_{3}^{2}-L_{BiDi}^{2}}{2L_{2}L_{3}}\right)\\[12pt] \beta _{i}=acos\left(\dfrac{L_{2}^{2}+L_{BiDi}^{2}-L_{3}^{2}}{2L_{2}L_{BiDi}}\right) \end{array}\right. \end{equation}
\begin{equation} \left\{\begin{array}{l} \eta _{3i}=\pi -acos\left(\dfrac{L_{2}^{2}+L_{3}^{2}-L_{BiDi}^{2}}{2L_{2}L_{3}}\right)\\[12pt] \beta _{i}=acos\left(\dfrac{L_{2}^{2}+L_{BiDi}^{2}-L_{3}^{2}}{2L_{2}L_{BiDi}}\right) \end{array}\right. \end{equation}
Then,
We can obtain
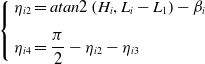 \begin{equation} \left\{\begin{array}{l} \eta _{i2}=atan2\left(H_{i},L_{i}-L_{1}\right)-\beta _{i}\\[9pt] \eta _{i4}=\dfrac{\pi }{2}-\eta _{i2}-\eta _{i3} \end{array}\right. \end{equation}
\begin{equation} \left\{\begin{array}{l} \eta _{i2}=atan2\left(H_{i},L_{i}-L_{1}\right)-\beta _{i}\\[9pt] \eta _{i4}=\dfrac{\pi }{2}-\eta _{i2}-\eta _{i3} \end{array}\right. \end{equation}
4.2. Static stiffness modeling of hybrid robots
Figure 9 shows the constraint wrench system imposed by the limb on the mobile platform. Utilizing the screw and reciprocal screw theory, the constraint wrench system of the limb can be obtained based on local coordinate systems A i -x i1 y i1 z i1:
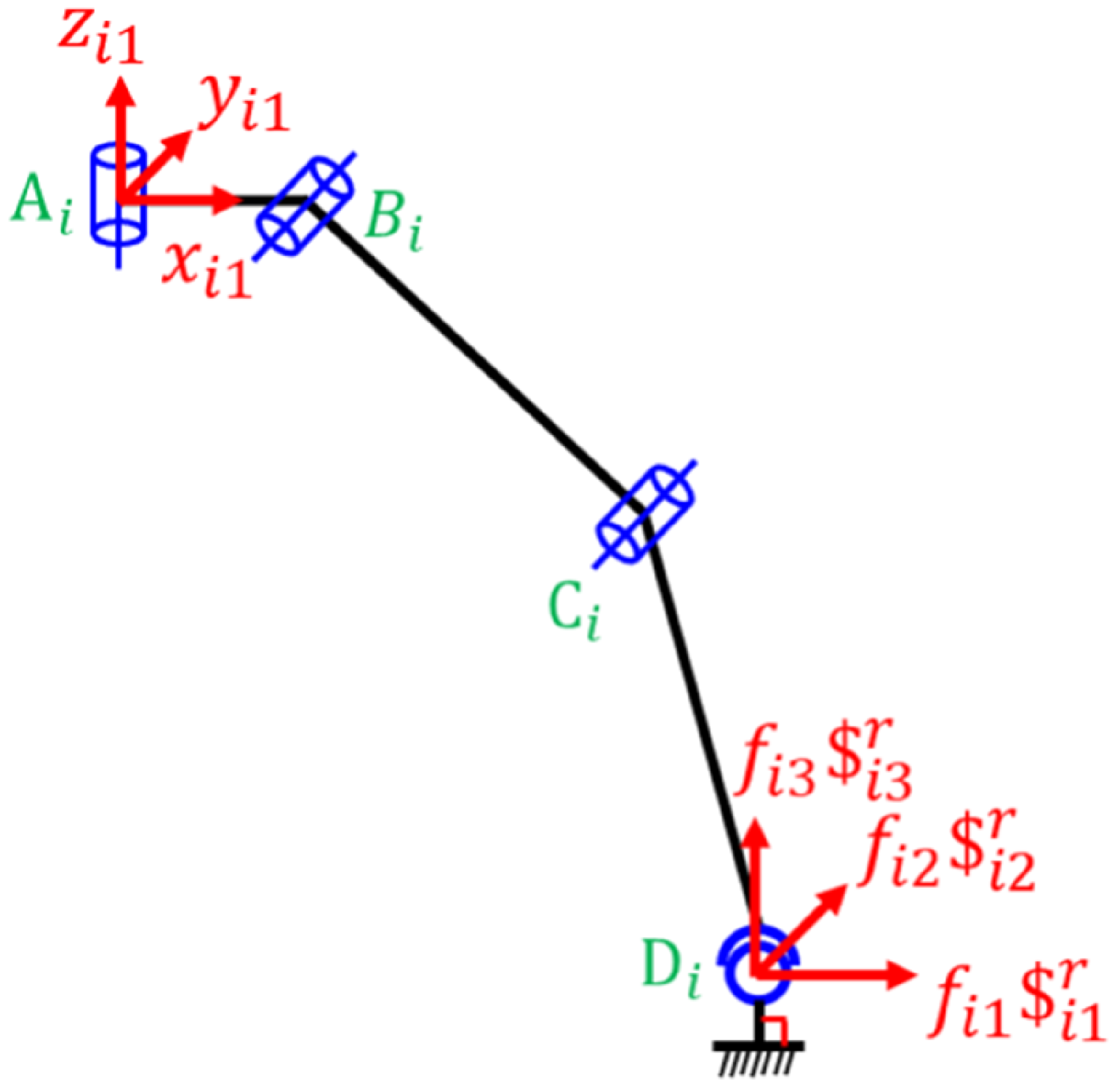
Figure 9. Constraint wrench system applied by the i th limb on the moving platform.
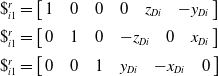 \begin{equation} \begin{array}{l} \$ _{i1}^{r}=\left[\begin{array}{l@{\quad}l@{\quad}l@{\quad}l@{\quad}l@{\quad}l} 1 & 0 & 0 & 0 & z_{Di} & -y_{Di} \end{array}\right]\\[5pt] \$ _{i1}^{r}=\left[\begin{array}{l@{\quad}l@{\quad}l@{\quad}l@{\quad}l@{\quad}l} 0 & 1 & 0 & -z_{Di} & 0 & x_{Di} \end{array}\right]\\[5pt] \$ _{i1}^{r}=\left[\begin{array}{l@{\quad}l@{\quad}l@{\quad}l@{\quad}l@{\quad}l} 0 & 0 & 1 & y_{Di} & -x_{Di} & 0 \end{array}\right] \end{array} \end{equation}
\begin{equation} \begin{array}{l} \$ _{i1}^{r}=\left[\begin{array}{l@{\quad}l@{\quad}l@{\quad}l@{\quad}l@{\quad}l} 1 & 0 & 0 & 0 & z_{Di} & -y_{Di} \end{array}\right]\\[5pt] \$ _{i1}^{r}=\left[\begin{array}{l@{\quad}l@{\quad}l@{\quad}l@{\quad}l@{\quad}l} 0 & 1 & 0 & -z_{Di} & 0 & x_{Di} \end{array}\right]\\[5pt] \$ _{i1}^{r}=\left[\begin{array}{l@{\quad}l@{\quad}l@{\quad}l@{\quad}l@{\quad}l} 0 & 0 & 1 & y_{Di} & -x_{Di} & 0 \end{array}\right] \end{array} \end{equation}
The limb leg exerts three constraint forces along the x i1, y i1, and z i1 axes on the robot mobile platform at point D i when the three active joints of the limb leg are all locked according to screw and reciprocal screw theory. The amplitudes are f i1, f i2, and f i3 (Fig. 9), that is, W i = [f i1 f i2 f i3 0 0 0]T = [f i 0]T. The four limb legs exert 12 constraint force on the robot’s moving platform. The solving requires simultaneous equations involving additional supplementary equations and static equilibrium equations. Therefore, the four-legged climbing robot is the overconstrained mechanism.
The force screw acting on the A i point can be expressed as follows under branch coordinate system A i -x i1 y i1 z i1 according to the translation principle of force in theoretical mechanics:
where f Ai represents the force at point A i , and f Ai = f i ; t Ai represents the torque at point A i , and t Ai = A i D i ×f i .
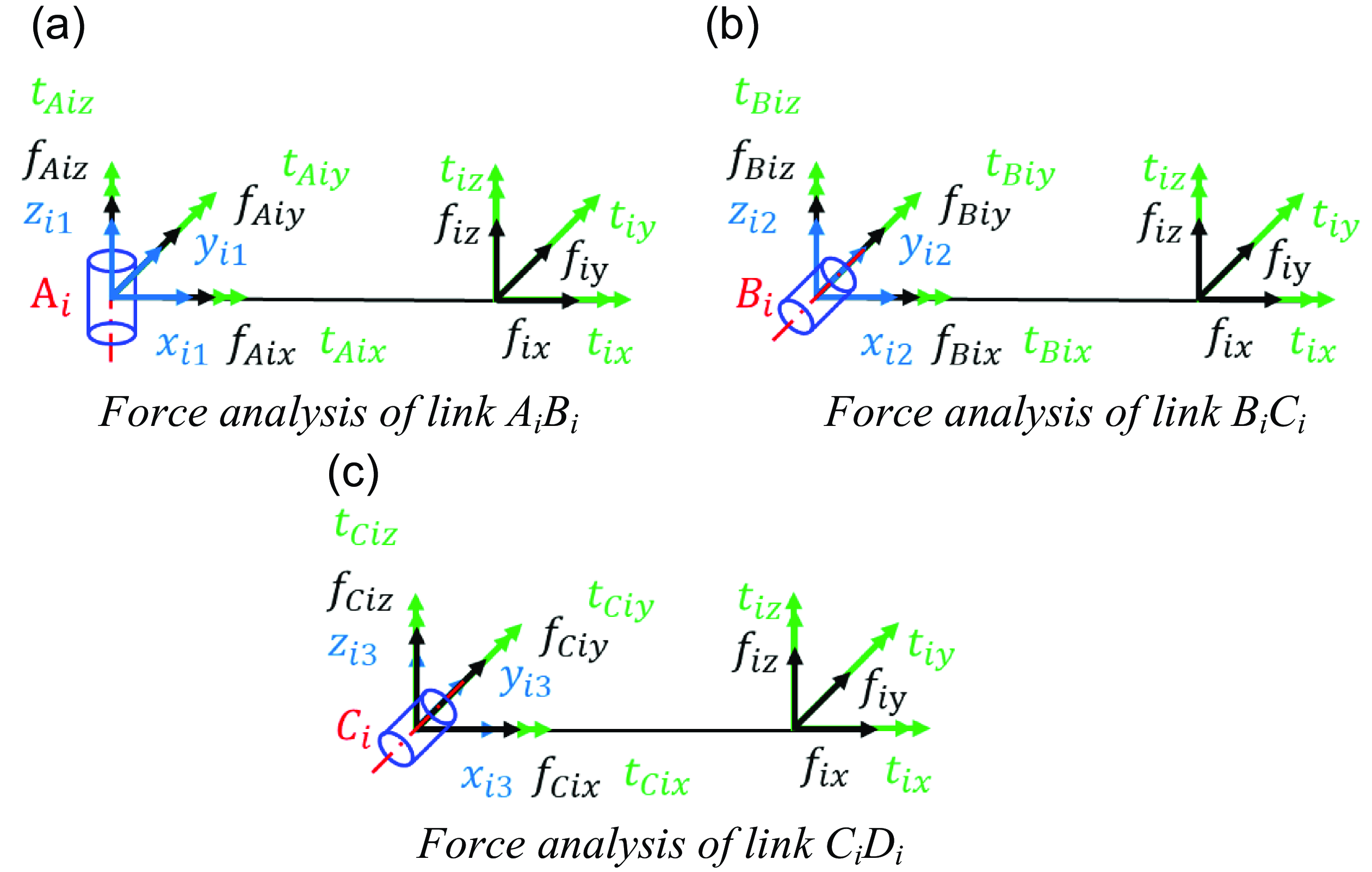
Figure 10. Force analysis of each component of the limb.
Figure 10a, 10b and 10c illustrate the force analysis of the A i B i , B i C i and C i D i rods within their respective branches based on the strain energy in material mechanics, and the strain energy of the A i B i , B i C i and C i D i rod in Branch i can be expressed as
where a ik1, a ik2 , …, and a ik6 (k = 1,2,3) are the coefficients obtained based on the equation with W i as the variable. C i1 can be solved according to the equation.
The strain energy of the i th limb is equal to the sum of the strain energy of each member.
where a ij = a i1j + a i2j + a i3j (j = 1, 2, …, 6).
The elastic deformation of the end of limb i along the axis of the constrained screw is as follows according to equation (7).
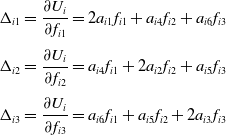 \begin{equation} \begin{array}{l} \Delta _{i1}=\dfrac{\partial U_{i}}{\partial f_{i1}}=2a_{i1}f_{i1}+a_{i4}f_{i2}+a_{i6}f_{i3}\\[12pt] \Delta _{i2}=\dfrac{\partial U_{i}}{\partial f_{i2}}=a_{i4}f_{i1}+2a_{i2}f_{i2}+a_{i5}f_{i3}\\[12pt] \Delta _{i3}=\dfrac{\partial U_{i}}{\partial f_{i3}}=a_{i6}f_{i1}+a_{i5}f_{i2}+2a_{i3}f_{i3} \end{array} \end{equation}
\begin{equation} \begin{array}{l} \Delta _{i1}=\dfrac{\partial U_{i}}{\partial f_{i1}}=2a_{i1}f_{i1}+a_{i4}f_{i2}+a_{i6}f_{i3}\\[12pt] \Delta _{i2}=\dfrac{\partial U_{i}}{\partial f_{i2}}=a_{i4}f_{i1}+2a_{i2}f_{i2}+a_{i5}f_{i3}\\[12pt] \Delta _{i3}=\dfrac{\partial U_{i}}{\partial f_{i3}}=a_{i6}f_{i1}+a_{i5}f_{i2}+2a_{i3}f_{i3} \end{array} \end{equation}
The flexibility matrix of limb i can be obtained as
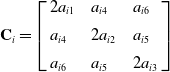 \begin{equation} \textbf{C}_{i}=\left[\begin{array}{l@{\quad}l@{\quad}l} 2a_{i1} & a_{i4} & a_{i6}\\[5pt] a_{i4} & 2a_{i2} & a_{i5}\\[5pt] a_{i6} & a_{i5} & 2a_{i3} \end{array}\right] \end{equation}
\begin{equation} \textbf{C}_{i}=\left[\begin{array}{l@{\quad}l@{\quad}l} 2a_{i1} & a_{i4} & a_{i6}\\[5pt] a_{i4} & 2a_{i2} & a_{i5}\\[5pt] a_{i6} & a_{i5} & 2a_{i3} \end{array}\right] \end{equation}
Stiffness matrix K
i
and overall stiffness matrix K
p
can be obtained by equations (6) and (11). The contribution of the parallel module to the elastic deformation of the hybrid robot end can be obtained by equation (5), and the contribution of each member of the parallel module to the elastic deformation of the hybrid robot end can be obtained by equation (14), where
![]() $\textbf{J}_{i}=[\boldsymbol{\$ }_{i1}^{r},\$ _{i2}^{r},\$ _{i3}^{r}]$
represents the constrained screw system of limb i.
$\textbf{J}_{i}=[\boldsymbol{\$ }_{i1}^{r},\$ _{i2}^{r},\$ _{i3}^{r}]$
represents the constrained screw system of limb i.
The decoupling flexibility matrix corresponding to serial module rod j and W T , as well as the contribution to the elastic deformation of the hybrid robot end, can be obtained according to the equation (15). The overall flexibility matrix corresponding to the serial module and W T , as well as the contribution to the elastic deformation of the hybrid robot end, can be obtained according to the equations (16) and (17).
The elastic deformation of the hybrid robot end is obtained according to the equation (18) after solving the contribution of the parallel and serial modules to the elastic deformation of the hybrid robot end, respectively.
4.3. Comparison between the analytical model and finite element model
The finite element commercial software ANSYS was used to verify the correctness and feasibility of the proposed method in the work. The material and structural parameters are given based on the parameters used in the theoretical model in the ANSYS model. The flexible limb is modeled using Beam 188 units based on the theory of Timoshenko.
Two typical working conditions of mobile welding are considered. Working pose 1: Four-legged wall-climbing robot (parallel module) limbs: θ i1 = 0°, θ i2 = 10°, and θ i3 = 70° (i = 1, 2, 3, 4). Serial module: joint angle θ s1 = 90°, θ s2 = −45°, θ s3 = 0°, θ s4 = 0°, θ s5 = −50°, and θ s6 = 0. Working pose 2: Four-legged wall-climbing robot (parallel module) limbs: θ i1 = 45°, θ i2 = 10°, and θ i3 = 70° (i = 1, 2, 3, 4). Serial module: joint angle θ s1 = 120°, θ s2 = −45°, θ s3 = 0°, θ s4 = 0°, θ s5 = −50°, and θ s6 = 0°. Terminal external load W T = [50N, 80N, −100N, 0, 0, 0]T.
Table 3 lists the comparison of tool terminal deformation results of the hybrid robot between the proposed analytical model and the finite element model (FEM), where the maximum error is 2.35%. The discrepancies between the theoretical model and the FEM mainly arise from differences in mesh partitioning and calculation errors. The correctness and accuracy of the proposed model are verified. Figure 11 shows the FEM results of the two poses of the hybrid robot.
4.4. Stiffness performance evaluation
The linear and angular displacements generated when the terminal of the hybrid robot works along the specified trajectory are used to evaluate the stiffness performance of the robot.
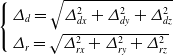 \begin{equation} \left\{\begin{array}{l} {\unicode{x1D6E5}}_{d}=\sqrt{{\unicode{x1D6E5}}_{\mathit{d}x}^{2}+{\unicode{x1D6E5}}_{dy}^{2}+{\unicode{x1D6E5}}_{dz}^{2}}\\[5pt] {\unicode{x1D6E5}}_{r}=\sqrt{{\unicode{x1D6E5}}_{rx}^{2}+{\unicode{x1D6E5}}_{ry}^{2}+{\unicode{x1D6E5}}_{rz}^{2}} \end{array}\right. \end{equation}
\begin{equation} \left\{\begin{array}{l} {\unicode{x1D6E5}}_{d}=\sqrt{{\unicode{x1D6E5}}_{\mathit{d}x}^{2}+{\unicode{x1D6E5}}_{dy}^{2}+{\unicode{x1D6E5}}_{dz}^{2}}\\[5pt] {\unicode{x1D6E5}}_{r}=\sqrt{{\unicode{x1D6E5}}_{rx}^{2}+{\unicode{x1D6E5}}_{ry}^{2}+{\unicode{x1D6E5}}_{rz}^{2}} \end{array}\right. \end{equation}
The robot performs welding or polishing work along a specified trajectory. The four-legged wall-climbing robot (parallel module) limbs: θ i1 = 45°, θ i2 = 10°, and θ i3 = 70° (i = 1, 2, 3, 4). The terminal tool of the robot works along the path of the sinusoidal curve (x = −0.3:0.02:0.3, y = 0.005sin(8πx) + 0.5, and z = 0.1) in a specific posture, and the external load is W T = [50N, 80N, −100N, 0, 0, 0]T. The linear and angular displacement reach their maximum values at the same time, which are 8.551e-5 m and 1.243e-4 rad, respectively, when the robot end is close to (−0.3 m, 0.495 m, 0.1 m) (Fig. 12).
Table III. Elastic deflection of the hybrid robot terminal.
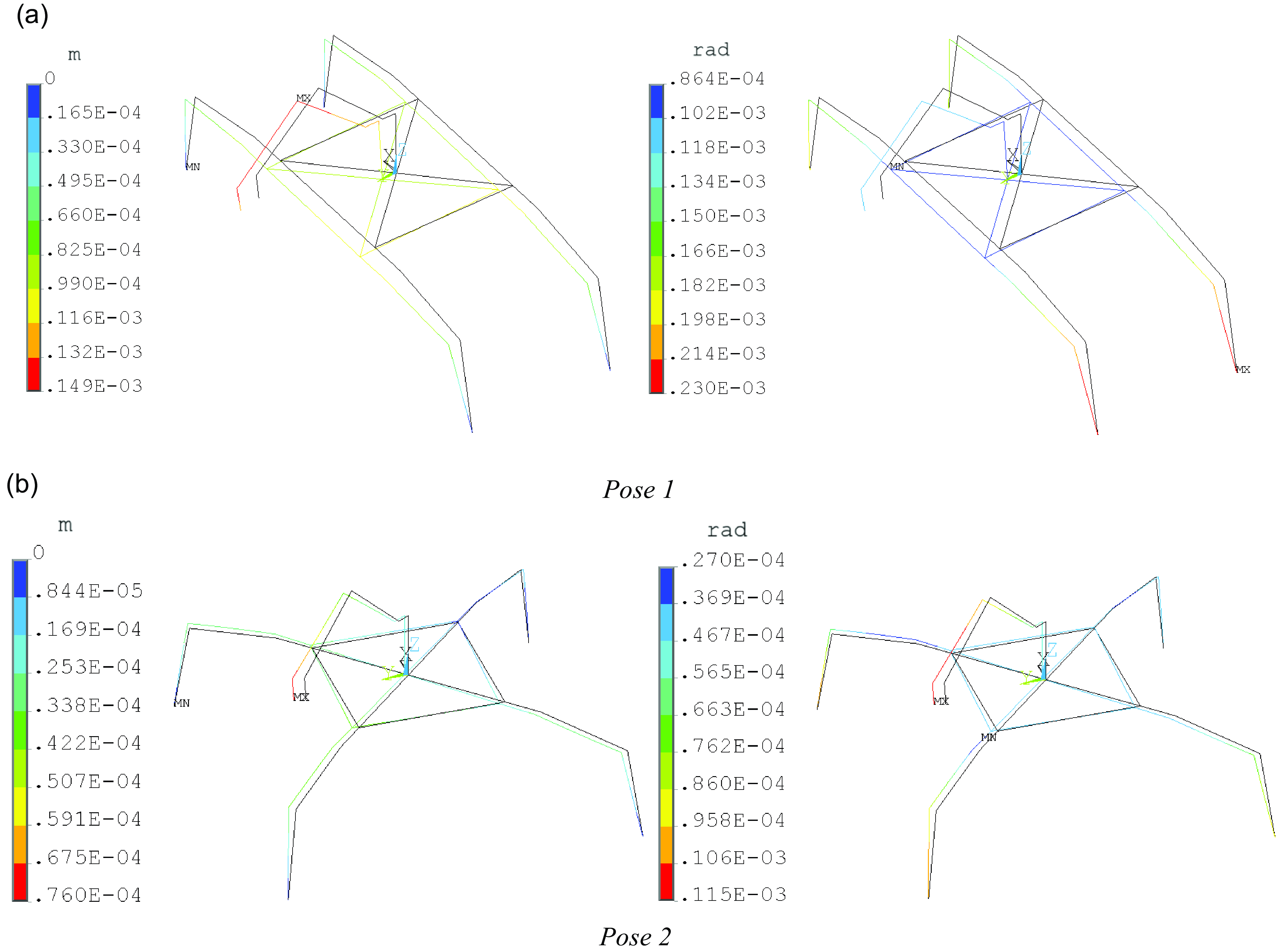
Figure 11. Contours of linear and angular displacement vectors.
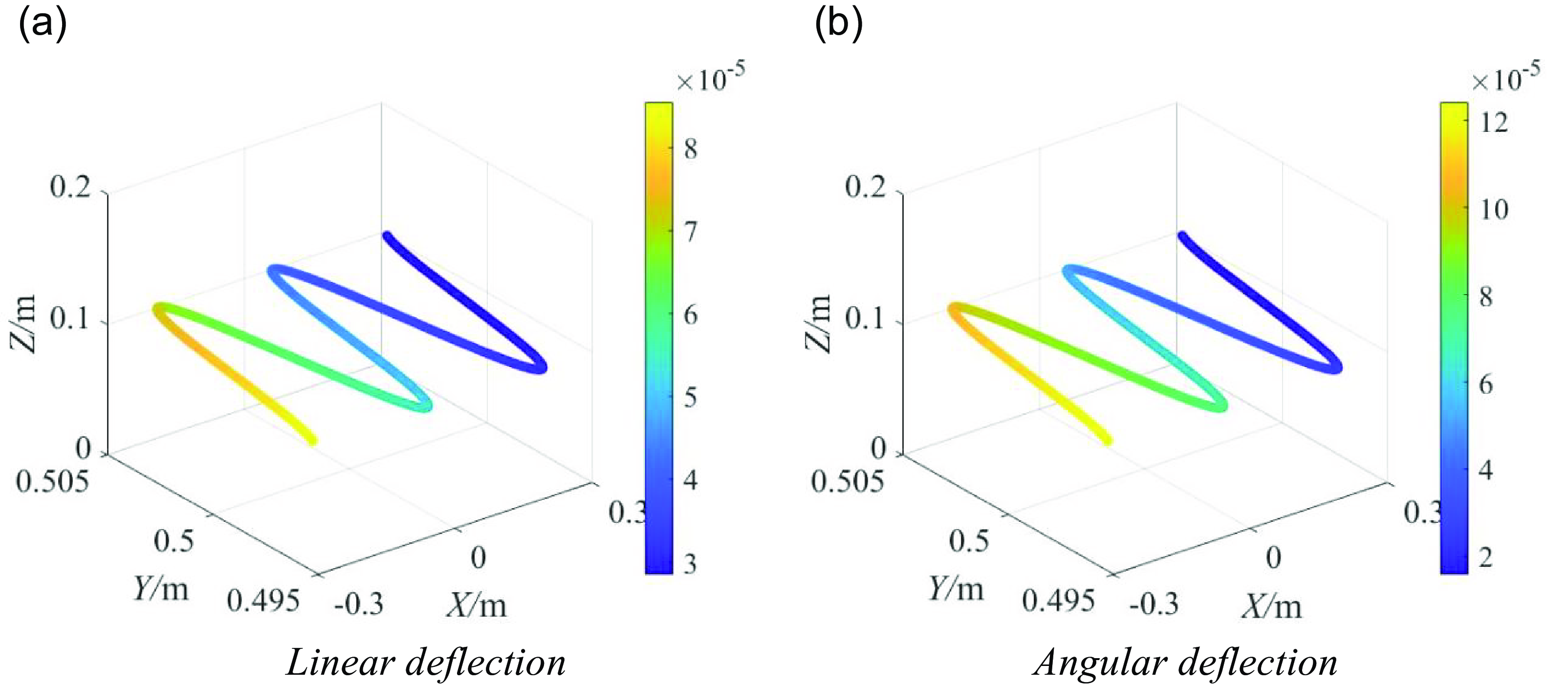
Figure 12. Linear and angular deflections of the hybrid robot terminal in the prescribed trajectory.
The contribution of each elastic element to the elastic deformation of the hybrid robot end is expressed by the equation as follows when the robot works along the specified trajectory.
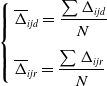 \begin{equation} \left\{\begin{array}{l} \overline{{\Delta} }_{ijd}=\dfrac{\sum {\Delta} _{ijd}}{N}\\[12pt] \overline{{\Delta} }_{ijr}=\dfrac{\sum {\Delta} _{ijr}}{N} \end{array}\right. \end{equation}
\begin{equation} \left\{\begin{array}{l} \overline{{\Delta} }_{ijd}=\dfrac{\sum {\Delta} _{ijd}}{N}\\[12pt] \overline{{\Delta} }_{ijr}=\dfrac{\sum {\Delta} _{ijr}}{N} \end{array}\right. \end{equation}
where
![]() ${\Delta} _{ijd}$
and
${\Delta} _{ijd}$
and
![]() ${\Delta} _{ijr}$
represent the linear and angular displacement of the elastic deformation of the robot end caused by the elastic deformation of limb i’s member j, respectively;
${\Delta} _{ijr}$
represent the linear and angular displacement of the elastic deformation of the robot end caused by the elastic deformation of limb i’s member j, respectively;
![]() $\overline{\unicode{x1D6E5}}_{ijd}$
and
$\overline{\unicode{x1D6E5}}_{ijd}$
and
![]() $\overline{\unicode{x1D6E5}}_{ijr}$
represent the average values of the linear and angular displacement caused by the elastic deformation of limb i’s member j when the hybrid robot end is working along a specified trajectory. N represents the number of discrete points in the work trajectory.
$\overline{\unicode{x1D6E5}}_{ijr}$
represent the average values of the linear and angular displacement caused by the elastic deformation of limb i’s member j when the hybrid robot end is working along a specified trajectory. N represents the number of discrete points in the work trajectory.
The average linear displacement of the hybrid robot end is 5.037 × 10−5m when it works along the sinusoidal curve path mentioned above (Fig. 12a). Table 4 shows the average linear displacement of each elastic element (the linear displacement along the x-, y-, and z-axes directions can be listed separately if necessary). The linear displacement at the tool end of the hybrid robot is mainly caused by the serial robot arm rod FG, followed by rods B 1 C 1, oE, and GH. Therefore, the serial robotic arm rod FG should be improved first to improve the linear stiffness of the hybrid robot.
The following five situations are considered to quantitatively evaluate the effect of improving the stiffness performance of each elastic element on the stiffness of the terminal line of the hybrid robot: (1) use the original physical parameters (Table 2), (2) the outer diameter of the FG of the serial robotic arm rod is increased by 20%, and the remaining parameters remain unchanged, (3) the outer diameter of parallel-module rod B 1 C 1 is increased by 20%, and the remaining parameters remain unchanged, (4) the outer diameter of the oE of the serial robotic arm rod is increased by 20%, and the remaining parameters remain unchanged, and (5) the outer diameter of the GH of the serial robotic arm rod is increased by 20%, and the remaining parameters remain unchanged.
Table 5 lists the influence of the above five conditions on the linear displacement of the terminal of the hybrid robot working along the specified trajectory. The linear displacement in working conditions (2)–(5) is reduced by 12.71%, 9.61%, 7.27%, and 6.06%, respectively, compared with that in working conditions (1). Improving the FG stiffness performance of the serial robotic arm rod can most improve the linear stiffness of the hybrid robot. In other words, the method proposed in this paper allows for effective control of the stiffness performance of the robot when the external wrench is known. This enables the maximization of robot stiffness performance or lightweight design. However, a limitation of this method is that it cannot pinpoint the components that have the greatest impact on the robot’s stiffness performance when the external wrench is unknown.
Similarly, the average angular displacement of the hybrid robot end when working along the sinusoidal curve path is 6.382 × 10−5 m (Fig. 12b). Table 6 shows the angular displacement of each elastic element (the angular displacement generated around the x-, y-, and z-axes can be listed separately if necessary). The angular displacement of the tool terminal of the hybrid robot is mainly caused by serial robot arm rod FG, followed by rod GH, oE, and A 2 B 2. Therefore, serial robotic arm rod FG should be improved first to improve the terminal line stiffness of the hybrid robot.
Table IV. Average linear elastic deflection contribution of each component of the 4SRRR + 6R.

Note:
![]() $\overline{\Delta }_{ijd}$
and
$\overline{\Delta }_{ijd}$
and
![]() $\overline{\Delta }_{sjd}$
denote the average linear elastic deflection contribution of the i
th limb’s j
th member of parallel modules and the j
th member of serial module, respectively, its unit is m.
$\overline{\Delta }_{sjd}$
denote the average linear elastic deflection contribution of the i
th limb’s j
th member of parallel modules and the j
th member of serial module, respectively, its unit is m.
Table V. Comparison of the effects of each elastic component on the resulting linear deflection of the 4SRRR + 6R.

Table VI. Average angular elastic deflection contribution of each component of the 4SRRR + 6R.

Note:
![]() $\overline{\Delta }_{ijr}$
and
$\overline{\Delta }_{ijr}$
and
![]() $\overline{\Delta }_{sjr}$
denote the average angular elastic deflection contribution of the i
th limb’s j
th member of parallel modules and the j
th member of serial module, respectively, its unit is rad.
$\overline{\Delta }_{sjr}$
denote the average angular elastic deflection contribution of the i
th limb’s j
th member of parallel modules and the j
th member of serial module, respectively, its unit is rad.
Table VII. Comparison of the effects of each elastic component on the resulting angular deflection of the 4SRRR + 6R.

The following five situations are considered to quantitatively evaluate the influence of each elastic element on the stiffness of the terminal angular of the hybrid robot: (1) use the original physical parameters (Table 2), (2) the outer diameter of the FG of the serial robotic arm rod is increased by 20%, and the remaining parameters remain unchanged, (3) the outer diameter of the parallel module rod GH increased by 20%, and the remaining parameters remained unchanged, (4) the outer diameter of the oE of the serial robotic arm rod is increased by 20%, and the remaining parameters remain unchanged, and (5) the outer diameter of the serial robotic arm rod A 2 B 2 increased by 20%, and the remaining parameters remained unchanged.
Table 7 shows the influence of the above five conditions on the angular displacement of the terminal of the hybrid robot working along the specified trajectory. The angular displacements of cases (2)–(5) are reduced by 23.69%, 7.87%, 5.26%, and 3.92%, respectively, compared with case (1). Improving the FG stiffness performance of the serial robotic arm rod can most improve the linear stiffness of the hybrid robot.Footnote 1
5. Conclusions
The decoupling method of the elastostatic stiffness model of hybrid robots is proposed in the work based on the rigidity principle, screw theory, strain energy, and Castigliano’s second theorem. The contribution of each elastic component to the stiffness performance of the robot is decoupled. This method decoupled the overall CCM of each elastic element to the robot based on the strain energy method, which avoided the singularity problem of that based on the rigidity principle.
This paper first introduces the model principles using a 3SPR hybrid mechanism and then applies them to a hybrid robot (4SRRR + 6R). The 4SRRR + 6R hybrid robot is composed of a four-legged wall-climbing robot and serial robotic arm. when the terminal of the robot tool is working along a specified trajectory, the rod FG has the greatest impact on the linear and angular displacement of the robot end. For the linear (angular) displacement, it is followed by the rod B 1 C 1, oE, GH (the rod GH, oE, A 2 B 2). Five situations are considered for linear (angular) displacement to verify the feasibility of the model proposed in the work: (1) In case 1, we use the original physical parameters; (2) In case 2, the outer diameter of the rod FG (FG) was increased by 20%. (3)In case 3, the outer diameter of the rod B 1 C 1 (GH) was increased by 20%. (4) In case 4, the outer diameter of the rod oE (oE) is increased by 20%. (5) In case 5, the outer diameter of the rod GH (A 2 B 2) is increased by 20%. As compared to case 1, the resulting linear (angular) deflections of case 2-5 are reduced by 12.71%, 9.61%, 7.27%, and 6.06% (23.69%, 7.87%, 5.26%, and 3.92%), respectively.
In conclusion, selectively improving the stiffness performance of a single elastic element can improve the overall linear and angular stiffness of the robot. It should be noted that if the improvement of linear stiffness and angular stiffness performance does not involve the same component, we need to make targeted choices based on engineering requirements. If the focus is more on linear stiffness performance, we can choose to enhance components that have a significant impact on linear stiffness. Alternatively, design personnel can skillfully balance between the two by assigning appropriate weight factors to components that significantly enhance both linear and angular stiffness based on experience. This enables a judicious distribution of quality. The model proposed in the work decoupled the contribution of each elastic element to the terminal linear and angular stiffness of the hybrid robot. The model has physical significance and provides a new way to improve the linear and angular stiffness of the hybrid robot.
Supplementary material
The supplementary material for this article can be found at https://doi.org/10.1017/S0263574724000675.
Author contributions
Yanzheng Zhao and Xudong Hu conceived and designed the study. Baoyu Wang and Peixing Li conducted investigation. Baoyu Wang and Peixing Li performed program coding. Baoyu Wang and Chao Yang wrote the article.
Financial support
This work was supported by National Key Planning (China) [No. 2017YFB1300603] and Department of Science and Technology in ZheJiang province [No. 2022C0065].
Competing interests
The authors declare no conflicts of interest exist.
Ethical approval
None.





















