Article contents
Rotating planar gravity currents at moderate Rossby numbers: fully resolved simulations and shallow-water modelling
Published online by Cambridge University Press: 20 March 2019
Abstract
The flow of a gravity current of finite volume and density 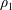 $\unicode[STIX]{x1D70C}_{1}$ released from rest from a rectangular lock (of height
$\unicode[STIX]{x1D70C}_{1}$ released from rest from a rectangular lock (of height 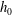 $h_{0}$) into an ambient fluid of density
$h_{0}$) into an ambient fluid of density 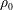 $\unicode[STIX]{x1D70C}_{0}$ (
$\unicode[STIX]{x1D70C}_{0}$ (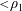 ${<}\unicode[STIX]{x1D70C}_{1}$) in a system rotating with
${<}\unicode[STIX]{x1D70C}_{1}$) in a system rotating with 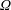 $\unicode[STIX]{x1D6FA}$ about the vertical
$\unicode[STIX]{x1D6FA}$ about the vertical  $z$ is investigated by means of fully resolved direct numerical simulations (DNS) and a theoretical model (based on shallow-water and Ekman layer spin-up theories, including mixing). The motion of the dense fluid includes several stages: propagation in the
$z$ is investigated by means of fully resolved direct numerical simulations (DNS) and a theoretical model (based on shallow-water and Ekman layer spin-up theories, including mixing). The motion of the dense fluid includes several stages: propagation in the  $x$-direction accompanied by Coriolis acceleration/deflection in the
$x$-direction accompanied by Coriolis acceleration/deflection in the 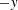 $-y$-direction, which produces a quasi-steady wedge-shaped structure with significant anticyclonic velocity
$-y$-direction, which produces a quasi-steady wedge-shaped structure with significant anticyclonic velocity 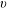 $v$, followed by a spin-up reduction of
$v$, followed by a spin-up reduction of 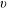 $v$ accompanied by a slow
$v$ accompanied by a slow  $x$ drift, and oscillation. The theoretical model aims to provide useful insights and approximations concerning the formation time and shape of wedge, and the subsequent spin-up effect. The main parameter is the Coriolis number,
$x$ drift, and oscillation. The theoretical model aims to provide useful insights and approximations concerning the formation time and shape of wedge, and the subsequent spin-up effect. The main parameter is the Coriolis number, 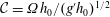 ${\mathcal{C}}=\unicode[STIX]{x1D6FA}h_{0}/(g^{\prime }h_{0})^{1/2}$, where
${\mathcal{C}}=\unicode[STIX]{x1D6FA}h_{0}/(g^{\prime }h_{0})^{1/2}$, where 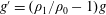 $g^{\prime }=(\unicode[STIX]{x1D70C}_{1}/\unicode[STIX]{x1D70C}_{0}-1)g$ is the reduced gravity. The DNS results are focused on a range of relatively small Coriolis numbers,
$g^{\prime }=(\unicode[STIX]{x1D70C}_{1}/\unicode[STIX]{x1D70C}_{0}-1)g$ is the reduced gravity. The DNS results are focused on a range of relatively small Coriolis numbers, 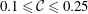 $0.1\leqslant {\mathcal{C}}\leqslant 0.25$ (i.e. Rossby number
$0.1\leqslant {\mathcal{C}}\leqslant 0.25$ (i.e. Rossby number 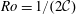 $Ro=1/(2{\mathcal{C}})$ in the range
$Ro=1/(2{\mathcal{C}})$ in the range  $2\leqslant Ro\leqslant 5$), and a large range of Schmidt numbers
$2\leqslant Ro\leqslant 5$), and a large range of Schmidt numbers 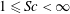 $1\leqslant Sc<\infty$; the Reynolds number is large in all cases. The current spreads out in the
$1\leqslant Sc<\infty$; the Reynolds number is large in all cases. The current spreads out in the  $x$ direction until it is arrested by the Coriolis effect (in
$x$ direction until it is arrested by the Coriolis effect (in 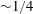 ${\sim}1/4$ revolution of the system). A complex motion develops about this state. First, we record oscillations on the inertial time scale
${\sim}1/4$ revolution of the system). A complex motion develops about this state. First, we record oscillations on the inertial time scale 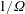 $1/\unicode[STIX]{x1D6FA}$ (which are a part of the geostrophic adjustment), accompanied by vortices at the interface. Second, we note the spread of the wedge on a significantly longer time scale; this is an indirect spin-up effect – mixing and entrainment reduce the lateral (angular) velocity, which in turn decreases the Coriolis support to the
$1/\unicode[STIX]{x1D6FA}$ (which are a part of the geostrophic adjustment), accompanied by vortices at the interface. Second, we note the spread of the wedge on a significantly longer time scale; this is an indirect spin-up effect – mixing and entrainment reduce the lateral (angular) velocity, which in turn decreases the Coriolis support to the 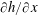 $\unicode[STIX]{x2202}h/\unicode[STIX]{x2202}x$ slope of the wedge shape. Contrary to non-rotating gravity currents, the front does not remain sharp as it is subject to (i) local stretching along the streamwise direction and (ii) convective mixing due to Kelvin–Helmholtz vortices generated by shear along the spanwise direction and stemming from Coriolis effects. The theoretical model predicts that the length of the wedge scales as
$\unicode[STIX]{x2202}h/\unicode[STIX]{x2202}x$ slope of the wedge shape. Contrary to non-rotating gravity currents, the front does not remain sharp as it is subject to (i) local stretching along the streamwise direction and (ii) convective mixing due to Kelvin–Helmholtz vortices generated by shear along the spanwise direction and stemming from Coriolis effects. The theoretical model predicts that the length of the wedge scales as 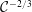 ${\mathcal{C}}^{-2/3}$ (in contrast to the Rossby radius
${\mathcal{C}}^{-2/3}$ (in contrast to the Rossby radius 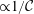 $\propto 1/{\mathcal{C}}$ which is relevant for large
$\propto 1/{\mathcal{C}}$ which is relevant for large 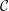 ${\mathcal{C}}$; and in contrast to
${\mathcal{C}}$; and in contrast to 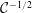 ${\mathcal{C}}^{-1/2}$ for the axisymmetric lens).
${\mathcal{C}}^{-1/2}$ for the axisymmetric lens).
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
Salinas et al. supplementary movie 1
Effect of the Coriolis number - cases (from top to bottom) S1-C25-F, S1-C15-F, S1-C10-F - side view of spanwise averaged density (Re=4000, Sc=1, free-slip)
Salinas et al. supplementary movie 2
Case S1-C15-F - top view of bottom density distribution (C=0.15, Ro=3.3, Re=4000, Sc=1, free-slip)
Salinas et al. supplementary movie 3
Case S5-C15-N - general view of the density surface rho=0.05 (C=0.15, Ro=3.3, Re=4000, Sc=5, no-slip)
Salinas et al. supplementary movie 4
Effect of the top-bottom boundary conditions - cases (from top to bottom) S1-C15-F, S1-C15-N - side view of spanwise averaged density (C=0.15, Ro=3.3, Re=4000, Sc=1)
Salinas et al. supplementary movie 5
Case SI-C15-N - general view of the density surfaces rho=0.1 and rho=0.9 (C=0.15, Ro=3.3, Re=4000, Sc=infinite, no-slip)
A correction has been issued for this article:
- 6
- Cited by
Linked content
Please note a has been issued for this article.

