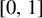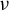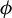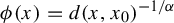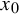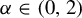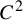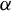1. Introduction
In this paper, we consider non-square-integrable observables
![]() $\phi : [0,1]\to {\mathbb R}$
on two simple classes of random dynamical system. One consists of randomly choosing in an independent and identically distributed (i.i.d.) manner from a finite set of maps which are strictly polynomially mixing with an indifferent fixed point at the origin, the other consisting of randomly choosing from a finite set of maps which are uniformly expanding and exponentially mixing. The main type of observable we consider is of the form
$\phi : [0,1]\to {\mathbb R}$
on two simple classes of random dynamical system. One consists of randomly choosing in an independent and identically distributed (i.i.d.) manner from a finite set of maps which are strictly polynomially mixing with an indifferent fixed point at the origin, the other consisting of randomly choosing from a finite set of maps which are uniformly expanding and exponentially mixing. The main type of observable we consider is of the form
![]() ${\phi (x) = |x-x_0|^{-{1}/{\alpha }}}$
,
${\phi (x) = |x-x_0|^{-{1}/{\alpha }}}$
,
![]() $\alpha \in (0,2)$
which, in the i.i.d. case, lies in the domain of attraction of a stable law of index
$\alpha \in (0,2)$
which, in the i.i.d. case, lies in the domain of attraction of a stable law of index
![]() $\alpha $
. For certain results, the point
$\alpha $
. For certain results, the point
![]() $x_0$
has to satisfy some non-genericity conditions and, in particular, not be a periodic point for almost every realization of the random system (see Definition 2.3). Some of our results, particularly those involving convergence to exponential and Poisson laws, hold for general observables that are regularly varying with index
$x_0$
has to satisfy some non-genericity conditions and, in particular, not be a periodic point for almost every realization of the random system (see Definition 2.3). Some of our results, particularly those involving convergence to exponential and Poisson laws, hold for general observables that are regularly varying with index
![]() $\alpha $
.
$\alpha $
.
The settings for investigations on stable limit laws for observables on dynamical systems tend to be of two broad types: (1) ‘good observables’ (typically Hölder) on slowly mixing non-uniformly hyperbolic systems; and (2) ‘bad’ observables (unbounded with fat tails) on fast mixing dynamical systems. As illustrative examples of both settings, we give two results.
Example of type (1): The LSV intermittent map
![]() $T_{\gamma }: [0,1]\to [0,1]$
,
$T_{\gamma }: [0,1]\to [0,1]$
,
![]() $\gamma \in (0,1)$
, is defined by
$\gamma \in (0,1)$
, is defined by
 $$ \begin{align*} T_{\gamma} (x) = \begin{cases} x(1+2^{\gamma}x^{\gamma}) & \mbox{if } 0 \leq x\le \tfrac12;\\ 2x-1 & \mbox{if } \tfrac12 <x < 1.\end{cases} \end{align*} $$
$$ \begin{align*} T_{\gamma} (x) = \begin{cases} x(1+2^{\gamma}x^{\gamma}) & \mbox{if } 0 \leq x\le \tfrac12;\\ 2x-1 & \mbox{if } \tfrac12 <x < 1.\end{cases} \end{align*} $$
The map
![]() $T_{\gamma }$
has a unique absolutely continuous invariant measure
$T_{\gamma }$
has a unique absolutely continuous invariant measure
![]() $\mu _{\gamma }$
.
$\mu _{\gamma }$
.
Gouëzel [Reference GouëzelGou04, Theorem 1.3] showed that if
![]() $\gamma>\tfrac 12$
and
$\gamma>\tfrac 12$
and
![]() $\phi : [0,1]\to {\mathbb R}$
is Hölder continuous with
$\phi : [0,1]\to {\mathbb R}$
is Hölder continuous with
![]() $\phi (0)\not =0$
,
$\phi (0)\not =0$
,
![]() $E_{\mu _{\gamma }}(\phi )=0$
, then for
$E_{\mu _{\gamma }}(\phi )=0$
, then for
![]() $\alpha ={1}/{\gamma }$
,
$\alpha ={1}/{\gamma }$
,
 $$ \begin{align*} \frac{1}{bn^{{1}/{\alpha}} }\sum_{j=0}^{n-1} \phi \circ T^j \to^{d} X_{\alpha,\beta} \end{align*} $$
$$ \begin{align*} \frac{1}{bn^{{1}/{\alpha}} }\sum_{j=0}^{n-1} \phi \circ T^j \to^{d} X_{\alpha,\beta} \end{align*} $$
(
![]() $\beta $
has a complicated expression).
$\beta $
has a complicated expression).
Example of type (2): Gouëzel [Reference GouëzelGou, Theorem 2.1] showed that if
![]() $T:[0,1] \to [0,1]$
is the doubling map
$T:[0,1] \to [0,1]$
is the doubling map
![]() $T(x)=2x$
(mod
$T(x)=2x$
(mod
![]() $1$
) with invariant measure m, Lebesgue, and
$1$
) with invariant measure m, Lebesgue, and
![]() ${\phi (x) =x^{-{{1}/{\alpha }}}}$
,
${\phi (x) =x^{-{{1}/{\alpha }}}}$
,
![]() $\alpha \in (0,2)$
, then there exists a sequence
$\alpha \in (0,2)$
, then there exists a sequence
![]() $c_n$
such that
$c_n$
such that
 $$ \begin{align*} \frac{2^{{1}/{\alpha}}-1}{n^{{1}/{\alpha}}} \sum_{j=0}^{n-1} \phi \circ T^j -c_n \to^{d} X_{\alpha,1}. \end{align*} $$
$$ \begin{align*} \frac{2^{{1}/{\alpha}}-1}{n^{{1}/{\alpha}}} \sum_{j=0}^{n-1} \phi \circ T^j -c_n \to^{d} X_{\alpha,1}. \end{align*} $$
For further results on the first type, we refer to the influential papers [Reference GouëzelGou04, Reference GouëzelGou07] and [Reference Melbourne and ZweimüllerMZ15]. In the setting of ‘good observables’ (typically Hölder) on slowly mixing non-uniformly hyperbolic systems, the technique of inducing on a subset of phase space and constructing a Young tower has been used with some success. ‘Good’ observables lift to well-behaved observables lying in a suitable Banach space on the Young tower. This is not the case with unbounded observables with fat tails, though in [Reference GouëzelGou04], the induction technique allows an observable to be unbounded at the fixed point in a family of intermittent maps.
For further results on the second type, we refer to the papers by Marta Tyran-Kaminska [Reference Tyran-KamińskaTK10a, Reference Tyran-KamińskaTK10b]. In the setting of Gibbs–Markov maps, she shows, among other results, that functions which are measurable with respect to the Gibbs–Markov partition and in the domain of attraction of a stable law with index
![]() $\alpha $
converge (under the appropriate scaling) in the
$\alpha $
converge (under the appropriate scaling) in the
![]() $J_1$
topology to a Lévy process of index
$J_1$
topology to a Lévy process of index
![]() $\alpha $
[Reference Tyran-KamińskaTK10b, Theorem 3.3, Corollaries 4.1 and 4.2].
$\alpha $
[Reference Tyran-KamińskaTK10b, Theorem 3.3, Corollaries 4.1 and 4.2].
For recent results on limit laws, though not stable laws, in the setting of skew-products with an ergodic base map and uniformly hyperbolic fiber maps, see also [Reference Dragičević, Froyland, González-Tokman and VaientiDFGTV20a]. For a still very useful survey of techniques and ideas in random dynamical systems, we refer to [Reference KiferKif98].
Our main results are given in §2. An introduction to stable laws and a discussion of modes of convergence are given in §§3 and 4. The Poisson point approach and its application to our random setting are detailed in §5. Results on convergence of return times to an exponential law and our point processes to a Poisson process are given in §6 (though the proofs of these results are delayed until §§8.1, 8.2, 9.1, and 9.2). The proofs of the main results are given in §10. We conclude in §11 with results on stable laws for the corresponding annealed systems.
2. Main results
For the sake of concreteness, we restrict ourselves to observables of the form
where
![]() $x_0$
is a non-recurrent point (see Definition 2.3) and
$x_0$
is a non-recurrent point (see Definition 2.3) and
![]() $\alpha \in (0,2)$
, but it is possible to consider more general regularly varying observables
$\alpha \in (0,2)$
, but it is possible to consider more general regularly varying observables
![]() $\phi $
which are piecewise monotonic with finitely many branches, see for instance [Reference Tyran-KamińskaTK10b, §4.2] in the deterministic case. Note that
$\phi $
which are piecewise monotonic with finitely many branches, see for instance [Reference Tyran-KamińskaTK10b, §4.2] in the deterministic case. Note that
![]() $\phi _{x_0}$
is regularity varying with index
$\phi _{x_0}$
is regularity varying with index
![]() $\alpha $
.
$\alpha $
.
We will be considering the following set-up with
![]() $(\Omega , \sigma )$
the full two-sided shift on finitely many symbols. In most of our settings, we take
$(\Omega , \sigma )$
the full two-sided shift on finitely many symbols. In most of our settings, we take
![]() $Y=[0,1]$
.
$Y=[0,1]$
.
Let
![]() $\sigma : \Omega \to \Omega $
be an invertible ergodic measure-preserving transformation on a probability space
$\sigma : \Omega \to \Omega $
be an invertible ergodic measure-preserving transformation on a probability space
![]() $(\Omega , {\mathcal F}, {\mathbb P})$
. For a measurable space
$(\Omega , {\mathcal F}, {\mathbb P})$
. For a measurable space
![]() $(Y, {\mathcal B})$
, let
$(Y, {\mathcal B})$
, let
![]() $\sigma :\Omega \to \Omega $
be the usual full shift and define
$\sigma :\Omega \to \Omega $
be the usual full shift and define
by
We assume F preserves a probability measure
![]() $\nu $
on
$\nu $
on
![]() $\Omega \times Y$
. We assume that
$\Omega \times Y$
. We assume that
![]() $\nu $
admits a disintegration given by
$\nu $
admits a disintegration given by
![]() $\nu (d \omega , dx) = {\mathbb P}(d \omega ) \nu ^\omega (dx)$
. For all
$\nu (d \omega , dx) = {\mathbb P}(d \omega ) \nu ^\omega (dx)$
. For all
![]() $n \ge 1$
, we have
$n \ge 1$
, we have
where
which satisfies the equivariance relations
![]() $(T_\omega ^n)_{*} \nu ^\omega = \nu ^{\sigma ^n \omega }$
for
$(T_\omega ^n)_{*} \nu ^\omega = \nu ^{\sigma ^n \omega }$
for
![]() ${\mathbb P}$
-almost every (a.e.)
${\mathbb P}$
-almost every (a.e.)
![]() ${\omega \in \Omega} $
.
${\omega \in \Omega} $
.
For each
![]() $\omega \in \Omega $
, we denote by
$\omega \in \Omega $
, we denote by
![]() $P_\omega $
the transfer operator of
$P_\omega $
the transfer operator of
![]() $T_\omega $
with respect to the Lebesgue measure m: for all
$T_\omega $
with respect to the Lebesgue measure m: for all
![]() $\phi \in L^\infty (m)$
and
$\phi \in L^\infty (m)$
and
![]() $\psi \in L^1(m)$
,
$\psi \in L^1(m)$
,
 $$ \begin{align*} \int_{[0,1]} (\phi \circ T_\omega) \cdot \psi \, dm = \int_{[0,1]} \phi \cdot P_\omega \psi \, dm. \end{align*} $$
$$ \begin{align*} \int_{[0,1]} (\phi \circ T_\omega) \cdot \psi \, dm = \int_{[0,1]} \phi \cdot P_\omega \psi \, dm. \end{align*} $$
We can then form, for
![]() $\omega \in \Omega $
and
$\omega \in \Omega $
and
![]() $n \ge 1$
, the cocycle
$n \ge 1$
, the cocycle
Definition 2.1. (Scaling constants)
We consider a sequence
![]() $(b_n)_{n \ge 1}$
of positive real numbers such that
$(b_n)_{n \ge 1}$
of positive real numbers such that
Definition 2.2. (Centering constants)
We define the centering sequence
![]() $(c_n)_{n \ge 1}$
by
$(c_n)_{n \ge 1}$
by

We now introduce two classes of random dynamical system (RDS) for which we are able to establish stable limit laws.
2.1. Random uniformly expanding maps
We consider random i.i.d. compositions with additional assumptions of uniform expansion. Let
![]() ${\mathcal S}$
be a finite collection of m piecewise
${\mathcal S}$
be a finite collection of m piecewise
![]() $C^2$
uniformly expanding maps of the unit interval
$C^2$
uniformly expanding maps of the unit interval
![]() $[0,1]$
. More precisely, we assume that for each
$[0,1]$
. More precisely, we assume that for each
![]() $T \in {\mathcal S}$
, there exist a finite partition
$T \in {\mathcal S}$
, there exist a finite partition
![]() ${\mathcal A}_T$
of
${\mathcal A}_T$
of
![]() $[0,1]$
into intervals, such that for each
$[0,1]$
into intervals, such that for each
![]() $I \in {\mathcal A}_T$
, T can be continuously extended as a strictly monotonic
$I \in {\mathcal A}_T$
, T can be continuously extended as a strictly monotonic
![]() $C^2$
function on
$C^2$
function on
![]() $\bar {I}$
and
$\bar {I}$
and
The maps
![]() $T_\omega $
(determined by the zeroth coordinate of
$T_\omega $
(determined by the zeroth coordinate of
![]() $\omega $
) are chosen from
$\omega $
) are chosen from
![]() ${\mathcal S}$
in an i.i.d. fashion according to a Bernoulli probability measure
${\mathcal S}$
in an i.i.d. fashion according to a Bernoulli probability measure
![]() ${\mathbb P}$
on
${\mathbb P}$
on
![]() $\Omega := \{1, \ldots , m\}^{{\mathbb Z}}$
. We will denote by
$\Omega := \{1, \ldots , m\}^{{\mathbb Z}}$
. We will denote by
![]() ${\mathcal A}_\omega $
the partition of monotonicity of
${\mathcal A}_\omega $
the partition of monotonicity of
![]() $T_\omega $
, and by
$T_\omega $
, and by
![]() ${\mathcal A}_\omega ^n = \vee _{k=0}^{n-1} (T_\omega ^k)^{-1}({\mathcal A}_{\sigma ^k \omega })$
the partition associated to
${\mathcal A}_\omega ^n = \vee _{k=0}^{n-1} (T_\omega ^k)^{-1}({\mathcal A}_{\sigma ^k \omega })$
the partition associated to
![]() $T_\omega ^n$
. We introduce
$T_\omega ^n$
. We introduce
the set of discontinuities of all the maps
![]() $T_\omega ^n$
. Note that
$T_\omega ^n$
. Note that
![]() ${\mathcal D}$
is at most a countable set.
${\mathcal D}$
is at most a countable set.
In the uniformly expanding case, we also assume the conditions (LY), (Dec), and (Min). Condition (LY) is the usual Lasota–Yorke inequality while conditions (Dec) and (Min) were introduced by Conze and Raugi [Reference Conze, Raugi and AssaniCR07].
-
(LY) There exist
 $r \ge 1$
,
$r \ge 1$
,
 $M>0$
and
$M>0$
and
 $D> 0$
and
$D> 0$
and
 $\rho \in (0,1)$
such that for all
$\rho \in (0,1)$
such that for all
 $\omega \in \Omega $
and all
$\omega \in \Omega $
and all
 $f \in \mathrm {BV}$
, and
$f \in \mathrm {BV}$
, and $$ \begin{align*} \|P_\omega f\|_{\mathrm{BV}} \le M \|f\|_{\mathrm{BV}} \end{align*} $$
$$ \begin{align*} \|P_\omega f\|_{\mathrm{BV}} \le M \|f\|_{\mathrm{BV}} \end{align*} $$
 $$ \begin{align*} \mathrm{Var}(P_\omega^r f) \le \rho \mathrm{Var}(f) + D \|f\|_{L^1(m)}. \end{align*} $$
$$ \begin{align*} \mathrm{Var}(P_\omega^r f) \le \rho \mathrm{Var}(f) + D \|f\|_{L^1(m)}. \end{align*} $$
-
(Dec) There exist
 $C>0$
and
$C>0$
and
 $\theta \in (0,1)$
such that for all
$\theta \in (0,1)$
such that for all
 $n \ge 1$
, all
$n \ge 1$
, all
 $\omega \in \Omega $
, and all
$\omega \in \Omega $
, and all
 ${f \in \mathrm {BV}}$
with
${f \in \mathrm {BV}}$
with
 ${\mathbb E}_m(f) = 0$
:
${\mathbb E}_m(f) = 0$
:  $$ \begin{align*} \| P_\omega^n f \|_{\mathrm{BV}} \le C \theta^n \|f\|_{\mathrm{BV}}. \end{align*} $$
$$ \begin{align*} \| P_\omega^n f \|_{\mathrm{BV}} \le C \theta^n \|f\|_{\mathrm{BV}}. \end{align*} $$
-
(Min) There exist
 $c>0$
such that for all
$c>0$
such that for all
 $n\ge 1$
and all
$n\ge 1$
and all
 $\omega \in \Omega $
,
$\omega \in \Omega $
, 
Definition 2.3. We say that
![]() $x_0$
is non-recurrent if
$x_0$
is non-recurrent if
![]() $x_0$
satisfies the condition
$x_0$
satisfies the condition
![]() $T^n_{\omega } (x_0)\not =x_0$
for all
$T^n_{\omega } (x_0)\not =x_0$
for all
![]() $n\ge 1$
for
$n\ge 1$
for
![]() ${\mathbb P}$
-a.e.
${\mathbb P}$
-a.e.
![]() $\omega \in \Omega $
.
$\omega \in \Omega $
.
Theorem 2.4. In the setting of expanding maps, assume conditions (LY), (Min), and (Dec). Suppose that
![]() $x_0 \notin {\mathcal D}$
is non-recurrent and consider the observable
$x_0 \notin {\mathcal D}$
is non-recurrent and consider the observable
![]() $\phi _{x_0}$
.
$\phi _{x_0}$
.
If
![]() $\alpha \in (0,1)$
, then for
$\alpha \in (0,1)$
, then for
![]() ${\mathbb P}$
-a.e.
${\mathbb P}$
-a.e.
![]() $\omega \in \Omega $
, the functional stable limit holds:
$\omega \in \Omega $
, the functional stable limit holds:
 $$ \begin{align*} X_n^\omega(t) := \frac{1}{b_n} \bigg[\sum_{j=0}^{\lfloor nt \rfloor - 1 } \phi_{x_0} \circ T_\omega^j - t c_n\bigg] \: \, {\stackrel{d}{\to} \,} X_{(\alpha)}(t) \quad \text{in } {\mathbb D}[0, \infty) \end{align*} $$
$$ \begin{align*} X_n^\omega(t) := \frac{1}{b_n} \bigg[\sum_{j=0}^{\lfloor nt \rfloor - 1 } \phi_{x_0} \circ T_\omega^j - t c_n\bigg] \: \, {\stackrel{d}{\to} \,} X_{(\alpha)}(t) \quad \text{in } {\mathbb D}[0, \infty) \end{align*} $$
in the
![]() $J_1$
topology under the probability measure
$J_1$
topology under the probability measure
![]() $\nu ^\omega $
, where
$\nu ^\omega $
, where
![]() $X_{(\alpha )}(t)$
is the
$X_{(\alpha )}(t)$
is the
![]() $\alpha $
-stable process with Lévy measure
$\alpha $
-stable process with Lévy measure
![]() $d\Pi _\alpha (dx) = \alpha |x|^{-(\alpha + 1)}$
on
$d\Pi _\alpha (dx) = \alpha |x|^{-(\alpha + 1)}$
on
![]() $[0,\infty )$
.
$[0,\infty )$
.
If
![]() $\alpha \in [1,2)$
, then the same result holds for m-a.e.
$\alpha \in [1,2)$
, then the same result holds for m-a.e.
![]() $x_0$
.
$x_0$
.
Example 2.5. (
 $\beta $
-transformations)
$\beta $
-transformations)
A simple example of a class of maps satisfying conditions (LY), (Dec), and (Min) [Reference Conze, Raugi and AssaniCR07] is to take m
![]() $\beta $
-maps of the unit interval,
$\beta $
-maps of the unit interval,
![]() $T_{\beta _i } (x)=\beta _i x$
(mod
$T_{\beta _i } (x)=\beta _i x$
(mod
![]() $1$
). We suppose
$1$
). We suppose
![]() $\beta _i>1+a$
,
$\beta _i>1+a$
,
![]() $a>0$
, for all
$a>0$
, for all
![]() $\beta _i$
,
$\beta _i$
,
![]() $i=1,\ldots ,m$
.
$i=1,\ldots ,m$
.
2.2. Random intermittent maps
Now we consider a simple class of intermittent type maps.
Liverani, Saussol, and Vaienti [Reference Liverani, Saussol and VaientiLSV99] introduced the map
![]() $T_{\gamma }$
as a simple model for intermittent dynamics:
$T_{\gamma }$
as a simple model for intermittent dynamics:
 $$ \begin{align*} T_{\gamma}:[0,1] \to [0,1], \quad T_{\gamma} (x) := \begin{cases} (2^{\gamma}x^{\gamma} +1)x& \mbox{if } 0 \leq x<\tfrac12;\\ 2x-1 & \mbox{if } \tfrac12 \le x \le 1. \end{cases} \end{align*} $$
$$ \begin{align*} T_{\gamma}:[0,1] \to [0,1], \quad T_{\gamma} (x) := \begin{cases} (2^{\gamma}x^{\gamma} +1)x& \mbox{if } 0 \leq x<\tfrac12;\\ 2x-1 & \mbox{if } \tfrac12 \le x \le 1. \end{cases} \end{align*} $$
If
![]() $0\le \gamma <1$
, then
$0\le \gamma <1$
, then
![]() $T_{\gamma }$
has an absolutely continuous invariant measure
$T_{\gamma }$
has an absolutely continuous invariant measure
![]() $\mu _{\gamma }$
with density
$\mu _{\gamma }$
with density
![]() $h_{\gamma }$
bounded away from zero and satisfying
$h_{\gamma }$
bounded away from zero and satisfying
![]() $h_{\gamma } (x)\sim C x^{-\gamma }$
for x near zero.
$h_{\gamma } (x)\sim C x^{-\gamma }$
for x near zero.
We form a random dynamical system by selecting
![]() $\gamma _i\in (0,1)$
,
$\gamma _i\in (0,1)$
,
![]() $i=1,\ldots ,m$
in an i.i.d. fashion and setting
$i=1,\ldots ,m$
in an i.i.d. fashion and setting
![]() $T_i:=T_{\gamma _i}$
. The associated Markov process on
$T_i:=T_{\gamma _i}$
. The associated Markov process on
![]() $[0,1]$
has a stationary invariant measure
$[0,1]$
has a stationary invariant measure
![]() $\nu $
which is absolutely continuous, with density h bounded away from zero.
$\nu $
which is absolutely continuous, with density h bounded away from zero.
We denote
![]() $\gamma _{\mathrm {max}}:=\max _{1\le i \le m} \{\gamma _i\}$
and
$\gamma _{\mathrm {max}}:=\max _{1\le i \le m} \{\gamma _i\}$
and
![]() $\gamma _{\mathrm {min}}:=\min _{1\le i \le m} \{\gamma _i\}$
.
$\gamma _{\mathrm {min}}:=\min _{1\le i \le m} \{\gamma _i\}$
.
Theorem 2.6. In the setting of an i.i.d. random composition of intermittent maps, suppose
![]() $\alpha \in (0,1)$
and
$\alpha \in (0,1)$
and
![]() $\gamma _{\mathrm {max}}<\tfrac 13$
. Then, for m-a.e.
$\gamma _{\mathrm {max}}<\tfrac 13$
. Then, for m-a.e.
![]() $x_0$
,
$x_0$
,
![]() $({1}/{b_n})\sum _{j=0}^{n-1}\phi _{x_0}\circ T_{\omega }^j \, {\stackrel {d}{\to } \,} X_{(\alpha )}(1)$
under the probability measure
$({1}/{b_n})\sum _{j=0}^{n-1}\phi _{x_0}\circ T_{\omega }^j \, {\stackrel {d}{\to } \,} X_{(\alpha )}(1)$
under the probability measure
![]() $\nu ^{\omega }$
for
$\nu ^{\omega }$
for
![]() ${\mathbb P}$
-a.e.
${\mathbb P}$
-a.e.
![]() $\omega $
(recall that
$\omega $
(recall that
![]() $c_n=0$
for
$c_n=0$
for
![]() $\alpha \in (0,1)$
).
$\alpha \in (0,1)$
).
Remark 2.7. (Convergence with respect to Lebesgue measure)
We state our limiting theorems with respect to the fiberwise measures
![]() $\nu ^{\omega }$
, but by general results of Eagleson [Reference EaglesonEag76] (see also [Reference ZweimüllerZwe07]), the convergence holds with respect to any measure
$\nu ^{\omega }$
, but by general results of Eagleson [Reference EaglesonEag76] (see also [Reference ZweimüllerZwe07]), the convergence holds with respect to any measure
![]() $\mu $
for which
$\mu $
for which
![]() $\mu \ll \nu ^{\omega }$
, in particular, our convergence results hold with respect to Lebesgue measure m. Further details are given in the Appendix.
$\mu \ll \nu ^{\omega }$
, in particular, our convergence results hold with respect to Lebesgue measure m. Further details are given in the Appendix.
Our proofs are based on a Poisson process approach developed for dynamical systems by Tyran-Kaminska [Reference Tyran-KamińskaTK10a, Reference Tyran-KamińskaTK10b].
3. Probabilistic tools
In this section, we review some topics from probability theory.
3.1. Regularly varying functions and domains of attraction
We refer to Feller [Reference FellerFel71] or Bingham, Goldie, and Teugels [Reference Bingham, Goldie and TeugelsBGT87] for the relations between domains of attraction of stable laws and regularly varying functions. For
![]() $\phi $
regularly varying, we define the constants
$\phi $
regularly varying, we define the constants
![]() $b_n$
and
$b_n$
and
![]() $c_n$
as in the case of
$c_n$
as in the case of
![]() $\phi _{x_0}$
.
$\phi _{x_0}$
.
Remark 3.1. When
![]() $\alpha \in (0,1)$
, then
$\alpha \in (0,1)$
, then
![]() $\phi $
is not integrable and one can choose the centering sequence
$\phi $
is not integrable and one can choose the centering sequence
![]() $(c_n)$
to be identically
$(c_n)$
to be identically
![]() $0$
. When
$0$
. When
![]() $\alpha = 1$
, it might happen that
$\alpha = 1$
, it might happen that
![]() $\phi $
is not integrable, and it is then necessary to define
$\phi $
is not integrable, and it is then necessary to define
![]() $c_n$
with suitably truncated moments as above. If
$c_n$
with suitably truncated moments as above. If
![]() $\phi $
is integrable, then center by
$\phi $
is integrable, then center by
![]() $c_n = n{\mathbb E}_\nu (\phi )$
.
$c_n = n{\mathbb E}_\nu (\phi )$
.
We will use the following asymptotics for truncated moments, which can be deduced from Karamata’s results concerning the tail behavior of regularly varying functions. Define p by
![]() $ \lim _{x \to \infty } ({\nu (\phi>x)}/{\nu (|\phi |>x)}) = p$
.
$ \lim _{x \to \infty } ({\nu (\phi>x)}/{\nu (|\phi |>x)}) = p$
.
Proposition 3.2. (Karamata)
Let
![]() $\phi $
be regularly varying with index
$\phi $
be regularly varying with index
![]() $\alpha \in (0,2)$
. Then, setting
$\alpha \in (0,2)$
. Then, setting
![]() $\beta := 2p -1$
and, for
$\beta := 2p -1$
and, for
![]() $\epsilon> 0$
,
$\epsilon> 0$
,
 $$ \begin{align} c_\alpha(\epsilon) := \begin{cases} 0 &\text{if } \alpha \in (0,1);\cr - \beta \log \epsilon & \text{if } \alpha = 1; \cr \epsilon^{1 - \alpha} \beta \alpha / (\alpha - 1) & \text{if } \alpha \in(1,2), \end{cases} \end{align} $$
$$ \begin{align} c_\alpha(\epsilon) := \begin{cases} 0 &\text{if } \alpha \in (0,1);\cr - \beta \log \epsilon & \text{if } \alpha = 1; \cr \epsilon^{1 - \alpha} \beta \alpha / (\alpha - 1) & \text{if } \alpha \in(1,2), \end{cases} \end{align} $$
and the following hold for all
![]() $\epsilon>0$
:
$\epsilon>0$
:
-
(a)

-
(b) if
 $\alpha \in (0,1)$
,
$\alpha \in (0,1)$
, 
-
(c) if
 $\alpha \in (1,2)$
,
$\alpha \in (1,2)$
, 
-
(d) if
 $\alpha = 1$
,
$\alpha = 1$
, 
-
(e) if
 $\alpha = 1$
,
$\alpha = 1$
, 
for a slowly varying function
 $\widetilde {L}$
.
$\widetilde {L}$
.
3.2. Lévy
 $\alpha $
-stable processes
$\alpha $
-stable processes
A helpful and more detailed discussion can be found, e.g., in [Reference Tyran-KamińskaTK10a, Reference Tyran-KamińskaTK10b].
The
![]() $X(t)$
is a Lévy stable process if
$X(t)$
is a Lévy stable process if
![]() $X(0)=0$
, X has stationary independent increments, and
$X(0)=0$
, X has stationary independent increments, and
![]() $X(1)$
has an
$X(1)$
has an
![]() $\alpha $
-stable distribution.
$\alpha $
-stable distribution.
The Lévy–Khintchine representation for the characteristic function of an
![]() $\alpha $
-stable random variable
$\alpha $
-stable random variable
![]() $X_{\alpha ,\beta }$
with index
$X_{\alpha ,\beta }$
with index
![]() $\alpha \in (0,2)$
and parameter
$\alpha \in (0,2)$
and parameter
![]() $\beta \in [-1,1]$
has the form:
$\beta \in [-1,1]$
has the form:
 $$ \begin{align*} {\mathbb E}[e^{itX}]=\mbox{exp}\bigg[ita_{\alpha}+\int (e^{itx}-1-itx1_{[-1,1]} (x))\Pi_{\alpha}(dx)\bigg], \end{align*} $$
$$ \begin{align*} {\mathbb E}[e^{itX}]=\mbox{exp}\bigg[ita_{\alpha}+\int (e^{itx}-1-itx1_{[-1,1]} (x))\Pi_{\alpha}(dx)\bigg], \end{align*} $$
where:
-
•
 $ a_{\alpha }= \begin {cases} \beta ({\alpha }/({1-\alpha })) & \alpha \not = 1;\\ 0 &\alpha =1;\end {cases}$
$ a_{\alpha }= \begin {cases} \beta ({\alpha }/({1-\alpha })) & \alpha \not = 1;\\ 0 &\alpha =1;\end {cases}$
-
•
 $\Pi _{\alpha }$
is a Lévy measure given by
$\Pi _{\alpha }$
is a Lévy measure given by  $$ \begin{align*} d \Pi_{\alpha} =\alpha (p1_{(0,\infty)} (x)+(1-p)1_{(-\infty,0)} (x) ) |x|^{-\alpha -1}\,dx; \end{align*} $$
$$ \begin{align*} d \Pi_{\alpha} =\alpha (p1_{(0,\infty)} (x)+(1-p)1_{(-\infty,0)} (x) ) |x|^{-\alpha -1}\,dx; \end{align*} $$
-
•
 $ p=({\beta +1})/{2}.$
$ p=({\beta +1})/{2}.$
Note that p and
![]() $\beta $
may equally serve as parameters for
$\beta $
may equally serve as parameters for
![]() $X_{\alpha ,\beta }$
. We will drop the
$X_{\alpha ,\beta }$
. We will drop the
![]() $\beta $
from
$\beta $
from
![]() $X_{\alpha ,\beta }$
, as is common in the literature, for simplicity of notation and when it plays no essential role.
$X_{\alpha ,\beta }$
, as is common in the literature, for simplicity of notation and when it plays no essential role.
3.3. Poisson point processes
Let
![]() $(T_n)_{n \ge 1}$
be a sequence of measurable transformations on a probability space
$(T_n)_{n \ge 1}$
be a sequence of measurable transformations on a probability space
![]() $(Y, {\mathcal B}, \mu )$
. For
$(Y, {\mathcal B}, \mu )$
. For
![]() $n \ge 1$
, we denote
$n \ge 1$
, we denote
Given
![]() $\phi : Y \to {\mathbb R}$
measurable, recall that we define the scaled Birkhoff sum by
$\phi : Y \to {\mathbb R}$
measurable, recall that we define the scaled Birkhoff sum by
 $$ \begin{align} S_n:= \frac{1}{b_n} \bigg[\sum_{j=0}^{ n - 1} \phi \circ T_1^j - c_n\bigg] \end{align} $$
$$ \begin{align} S_n:= \frac{1}{b_n} \bigg[\sum_{j=0}^{ n - 1} \phi \circ T_1^j - c_n\bigg] \end{align} $$
for some real constants
![]() $b_n> 0$
,
$b_n> 0$
,
![]() $c_n$
and the scaled random process
$c_n$
and the scaled random process
![]() $X_n(t)$
,
$X_n(t)$
,
![]() $n\ge 1$
, by
$n\ge 1$
, by
 $$ \begin{align} X_n(t) := \frac{1}{b_n} \bigg[\sum_{j=0}^{\lfloor nt \rfloor - 1} \phi \circ T_1^j - t c_n\bigg], \quad t \ge 0, \end{align} $$
$$ \begin{align} X_n(t) := \frac{1}{b_n} \bigg[\sum_{j=0}^{\lfloor nt \rfloor - 1} \phi \circ T_1^j - t c_n\bigg], \quad t \ge 0, \end{align} $$
For
![]() $X_{\alpha }(t)$
, a Lévy
$X_{\alpha }(t)$
, a Lévy
![]() $\alpha $
-stable process, and
$\alpha $
-stable process, and
![]() $B\in \mathcal {B} ((0,\infty ) \times ({\mathbb R} \setminus \{0\}))$
, define
$B\in \mathcal {B} ((0,\infty ) \times ({\mathbb R} \setminus \{0\}))$
, define
where
![]() $\Delta X_{\alpha }(t):=X_{\alpha }(t)-X_{\alpha }(t^-)$
.
$\Delta X_{\alpha }(t):=X_{\alpha }(t)-X_{\alpha }(t^-)$
.
The random variable
![]() $N_{(\alpha )}(B)$
, which counts the jumps (and their time) of the Lévy process that lie in B, is finite almost surely (a.s.) if and only if
$N_{(\alpha )}(B)$
, which counts the jumps (and their time) of the Lévy process that lie in B, is finite almost surely (a.s.) if and only if
![]() $(m \times \Pi _\alpha ) (B)< \infty $
. In that case,
$(m \times \Pi _\alpha ) (B)< \infty $
. In that case,
![]() $N_{(\alpha )}(B)$
has a Poisson distribution with mean
$N_{(\alpha )}(B)$
has a Poisson distribution with mean
![]() $(m \times \Pi _\alpha ) (B)$
.
$(m \times \Pi _\alpha ) (B)$
.
Similarly define
 $$ \begin{align*} N_n(B) := \# \bigg\{ j \ge 1 : \bigg(\frac{j}{n} , \frac{\phi \circ T_1^{j-1}}{b_n} \bigg) \in B \bigg\}, \quad n \ge 1, \end{align*} $$
$$ \begin{align*} N_n(B) := \# \bigg\{ j \ge 1 : \bigg(\frac{j}{n} , \frac{\phi \circ T_1^{j-1}}{b_n} \bigg) \in B \bigg\}, \quad n \ge 1, \end{align*} $$
![]() $N_n(B)$
counts the jumps of the process in equation (3.4) that lie in B. When a realization
$N_n(B)$
counts the jumps of the process in equation (3.4) that lie in B. When a realization
![]() $\omega \in \Omega $
is fixed, we define
$\omega \in \Omega $
is fixed, we define
 $$ \begin{align*} N_n^\omega(B) := \# \bigg\{ j \ge 1 : \bigg(\frac{j}{n} , \frac{\phi \circ T_\omega^{j-1}}{b_n} \bigg) \in B \bigg\}, \quad n \ge 1. \end{align*} $$
$$ \begin{align*} N_n^\omega(B) := \# \bigg\{ j \ge 1 : \bigg(\frac{j}{n} , \frac{\phi \circ T_\omega^{j-1}}{b_n} \bigg) \in B \bigg\}, \quad n \ge 1. \end{align*} $$
Definition 3.3. We say
![]() $N_n$
converges in distribution to
$N_n$
converges in distribution to
![]() $N_{(\alpha )}$
and write
$N_{(\alpha )}$
and write
if and only if
![]() $N_n(B) \, {\stackrel {d}{\to } \,} N_{(\alpha )}(B)$
for all
$N_n(B) \, {\stackrel {d}{\to } \,} N_{(\alpha )}(B)$
for all
![]() $B \in B((0, \infty ) \kern1.3pt{\times}\kern1.3pt ({\mathbb R} \setminus \{ 0 \}))$
with
$B \in B((0, \infty ) \kern1.3pt{\times}\kern1.3pt ({\mathbb R} \setminus \{ 0 \}))$
with
![]() ${(m \kern1.3pt{\times} \Pi _\alpha ) (B) \kern1.3pt{<}\kern1.3pt \infty }$
and
${(m \kern1.3pt{\times} \Pi _\alpha ) (B) \kern1.3pt{<}\kern1.3pt \infty }$
and
![]() $(m \times \Pi _\alpha ) (\partial B) = 0$
.
$(m \times \Pi _\alpha ) (\partial B) = 0$
.
4. Modes of convergence
Consider the process
![]() $X_{\alpha }$
determined by the observable
$X_{\alpha }$
determined by the observable
![]() $\phi $
(that is, an i.i.d. version of
$\phi $
(that is, an i.i.d. version of
![]() $\phi $
which regularly varies with the same index
$\phi $
which regularly varies with the same index
![]() $\alpha $
and parameter p). We are interested in the following limits.
$\alpha $
and parameter p). We are interested in the following limits.
-
(A) Poisson point process convergence.
with respect to $$ \begin{align*} ~N^{\omega}_n \, {\stackrel{d}{\to} \,} N_{(\alpha)} \end{align*} $$
$$ \begin{align*} ~N^{\omega}_n \, {\stackrel{d}{\to} \,} N_{(\alpha)} \end{align*} $$
 $\nu ^{\omega }$
for
$\nu ^{\omega }$
for
 ${\mathbb P}$
a.e.
${\mathbb P}$
a.e.
 $\omega $
, where
$\omega $
, where
 $N_{(\alpha )}$
is the Poisson point process of an
$N_{(\alpha )}$
is the Poisson point process of an
 $\alpha $
-stable process with parameter determined by
$\alpha $
-stable process with parameter determined by
 $\nu $
, the annealed measure.
$\nu $
, the annealed measure.
-
(B) Stable law convergence.
for $$ \begin{align*} ~S_n^{\omega}:=\frac{1}{b_n} \bigg[\sum_{j=0}^{n-1} \phi\circ T_{\omega}^j -c_n\bigg] \, {\stackrel{d}{\to} \,} X_{\alpha}(1) \end{align*} $$
$$ \begin{align*} ~S_n^{\omega}:=\frac{1}{b_n} \bigg[\sum_{j=0}^{n-1} \phi\circ T_{\omega}^j -c_n\bigg] \, {\stackrel{d}{\to} \,} X_{\alpha}(1) \end{align*} $$
 ${\mathbb P}$
-a.e.
${\mathbb P}$
-a.e.
 $\omega $
, with respect to
$\omega $
, with respect to
 $\nu ^{\omega }$
, for
$\nu ^{\omega }$
, for
 $\phi $
regularly varying with index
$\phi $
regularly varying with index
 $\alpha $
and
$\alpha $
and
 $X_{\alpha }(t)$
the corresponding
$X_{\alpha }(t)$
the corresponding
 $\alpha $
-stable process, for suitable scaling and centering constants
$\alpha $
-stable process, for suitable scaling and centering constants
 $b_n$
and
$b_n$
and
 $c_n$
.
$c_n$
.
-
(C) Functional stable law convergence.
in $$ \begin{align*} ~X_n^{\omega} (t) := \frac{1}{b_n}\bigg[ \sum_{j=0}^{\lfloor nt \rfloor-1} \phi \circ T_{\omega}^j - tc_n\bigg] \, {\stackrel{d}{\to} \,} X_{\alpha} (t) \end{align*} $$
$$ \begin{align*} ~X_n^{\omega} (t) := \frac{1}{b_n}\bigg[ \sum_{j=0}^{\lfloor nt \rfloor-1} \phi \circ T_{\omega}^j - tc_n\bigg] \, {\stackrel{d}{\to} \,} X_{\alpha} (t) \end{align*} $$
 ${\mathbb D}[0,\infty )$
in the
${\mathbb D}[0,\infty )$
in the
 $J_1$
topology
$J_1$
topology
 ${\mathbb P}$
-a.e.
${\mathbb P}$
-a.e.
 $\omega $
, with respect to
$\omega $
, with respect to
 $\nu ^{\omega }$
for
$\nu ^{\omega }$
for
 $\phi $
regularly varying with index
$\phi $
regularly varying with index
 $\alpha $
and
$\alpha $
and
 $X_{\alpha }(t)$
the corresponding
$X_{\alpha }(t)$
the corresponding
 $\alpha $
-stable process.
$\alpha $
-stable process.
For the cases we are considering, the scaling constants
![]() $b_n$
are given by equation (2.2) in Definition 2.1, and the centering constants
$b_n$
are given by equation (2.2) in Definition 2.1, and the centering constants
![]() $c_n$
are given in Definition 2.2 (see also Remark 3.1).
$c_n$
are given in Definition 2.2 (see also Remark 3.1).
Remark 4.1. In the limit laws for quenched systems that we obtain of type (B) and (C), the centering sequence
![]() $c_n$
does not depend on the realization
$c_n$
does not depend on the realization
![]() $\omega $
. This is in contrast to the case of the central limit theorem (CLT), where a random centering is necessary; see [Reference Abdelkader and AiminoAA16, Theorem 9] and [Reference Nicol, Pereira and TörökNPT21, Theorem 5.3].
$\omega $
. This is in contrast to the case of the central limit theorem (CLT), where a random centering is necessary; see [Reference Abdelkader and AiminoAA16, Theorem 9] and [Reference Nicol, Pereira and TörökNPT21, Theorem 5.3].
5. A Poisson point process approach to random and sequential dynamical systems
Our results are based on the Poisson point process approach developed by Tyran-Kamińska [Reference Tyran-KamińskaTK10a, Reference Tyran-KamińskaTK10b] adapted to our random setting (see Theorems 5.1 and 5.3). Namely, convergence to a stable law or a Lévy process follows from the convergence of the corresponding (Poisson) jump processes, and control of the small jumps.
A key role is played by Kallenberg’s theorem [Reference KallenbergKal76, Theorem 4.7] to check convergence of the Poisson point processes,
![]() $N_n\, {\stackrel {d}{\to } \,} N_{(\alpha )} $
. Kallenberg’s theorem does not assume stationarity and hence we may use it in our setting.
$N_n\, {\stackrel {d}{\to } \,} N_{(\alpha )} $
. Kallenberg’s theorem does not assume stationarity and hence we may use it in our setting.
In this section, we provide general conditions ensuring weak convergence to Lévy stable processes for non-stationary dynamical systems, following closely the approach of Tyran-Kamińska [Reference Tyran-KamińskaTK10b]. We start from the very general setting of non-autonomous sequential dynamics and then specialize to the case of quenched random dynamical systems, which will be useful to treat i.i.d. random compositions in the later sections.
5.1. Sequential transformations
Recall the notation introduced in §3.3. Here,
![]() $(T_n)_{n \ge 1}$
is a sequence of measurable transformations on a probability space
$(T_n)_{n \ge 1}$
is a sequence of measurable transformations on a probability space
![]() $(Y, {\mathcal B}, \mu )$
. For
$(Y, {\mathcal B}, \mu )$
. For
![]() $n \ge 1$
, recall we define
$n \ge 1$
, recall we define
The proof of the following statement is essentially the same as the proof of [Reference Tyran-KamińskaTK10b, Theorem 1.1].
Note that the measure
![]() $\mu $
does not have to be invariant. Moreover (see [Reference Tyran-KamińskaTK10b, Remark 2.1]), the convergence
$\mu $
does not have to be invariant. Moreover (see [Reference Tyran-KamińskaTK10b, Remark 2.1]), the convergence
![]() $X_n \, {\stackrel {d}{\to } \,} X_{(\alpha )}$
holds even without the condition
$X_n \, {\stackrel {d}{\to } \,} X_{(\alpha )}$
holds even without the condition
![]() $\mu (\phi \circ T_1^j \neq 0) = 1$
, which is used only for the converse implication of the ‘if and only if’.
$\mu (\phi \circ T_1^j \neq 0) = 1$
, which is used only for the converse implication of the ‘if and only if’.
Theorem 5.1. (Functional stable limit law, [Reference Tyran-KamińskaTK10b, Theorem 1.1])
Let
![]() $\alpha \in (0,2)$
and suppose that
$\alpha \in (0,2)$
and suppose that
![]() $\mu (\phi \circ T_1^j \neq 0) = 1$
for all
$\mu (\phi \circ T_1^j \neq 0) = 1$
for all
![]() $j\ge 0$
. Then
$j\ge 0$
. Then
![]() $X_n \, {\stackrel {d}{\to } \,} X_{(\alpha )}$
in
$X_n \, {\stackrel {d}{\to } \,} X_{(\alpha )}$
in
![]() ${\mathbb D}[0, \infty )$
under the probability measure
${\mathbb D}[0, \infty )$
under the probability measure
![]() $\mu $
for some constants
$\mu $
for some constants
![]() $b_n>0$
and
$b_n>0$
and
![]() $c_n$
if and only if:
$c_n$
if and only if:
-
•
 $N_n \, {\stackrel {d}{\to } \,} N_{(\alpha )}$
and
$N_n \, {\stackrel {d}{\to } \,} N_{(\alpha )}$
and -
• for all
 $\delta> 0$
,
$\delta> 0$
,
 $\ell \ge 1$
, with
$\ell \ge 1$
, with
 $c_\alpha (\epsilon )$
given by equation (3.1), (5.1)
$c_\alpha (\epsilon )$
given by equation (3.1), (5.1)
Remark 5.2. In some cases, the convergence
![]() $N_n \, {\stackrel {d}{\to } \,} N_{(\alpha )}$
does not hold, but one has convergence of the marginals,
$N_n \, {\stackrel {d}{\to } \,} N_{(\alpha )}$
does not hold, but one has convergence of the marginals,
![]() $N_n((0,1] \times \cdot ) \, {\stackrel {d}{\to } \,} N_{(\alpha )}((0,1] \times \cdot )$
. In this case, although unable to obtain a functional stable law convergence of type (C), we can in some settings prove the convergence to a stable law for the Birkhoff sums (convergence of type (B)).
$N_n((0,1] \times \cdot ) \, {\stackrel {d}{\to } \,} N_{(\alpha )}((0,1] \times \cdot )$
. In this case, although unable to obtain a functional stable law convergence of type (C), we can in some settings prove the convergence to a stable law for the Birkhoff sums (convergence of type (B)).
In particular, we are unable to prove
![]() $N_n^\omega \, {\stackrel {d}{\to } \,} N_{(\alpha )}$
for the case of random intermittent maps. However, in the setting of random uniformly expanding maps, we use the spectral gap to show that
$N_n^\omega \, {\stackrel {d}{\to } \,} N_{(\alpha )}$
for the case of random intermittent maps. However, in the setting of random uniformly expanding maps, we use the spectral gap to show that
![]() $N_n^\omega \, {\stackrel {d}{\to } \,} N_{(\alpha )}$
, and then obtain the functional stable limit law.
$N_n^\omega \, {\stackrel {d}{\to } \,} N_{(\alpha )}$
, and then obtain the functional stable limit law.
The next statement is [Reference Tyran-KamińskaTK10b, Lemma 2.2, part (2)], which follows from [Reference Tyran-KamińskaTK10a, Theorem 3.2]. Again, the measure does not have to be invariant.
Theorem 5.3. (Stable limit law, [Reference Tyran-KamińskaTK10b, Lemma 2.2])
For
![]() $\alpha \in (0,2)$
, consider an observable
$\alpha \in (0,2)$
, consider an observable
![]() $\phi $
on the probability measure
$\phi $
on the probability measure
![]() $\mu $
, and
$\mu $
, and
![]() $c_\alpha (\epsilon )$
given by equation (3.1).
$c_\alpha (\epsilon )$
given by equation (3.1).
If
and, for all
![]() $\delta> 0$
,
$\delta> 0$
,

then
 $$ \begin{align*} \frac{1}{b_n}\bigg[\sum_{j=0}^{n-1}\phi\circ T_{1}^j - c_n\bigg] \, {\stackrel{d}{\to} \,} X_{(\alpha)}(1) \end{align*} $$
$$ \begin{align*} \frac{1}{b_n}\bigg[\sum_{j=0}^{n-1}\phi\circ T_{1}^j - c_n\bigg] \, {\stackrel{d}{\to} \,} X_{(\alpha)}(1) \end{align*} $$
under the probability measure
![]() $\mu $
.
$\mu $
.
5.2. Random dynamical systems
Let
![]() $\phi : Y \to {\mathbb R}$
be a measurable function such that
$\phi : Y \to {\mathbb R}$
be a measurable function such that
![]() $\nu ^\omega ( \phi \neq 0) = 1$
.
$\nu ^\omega ( \phi \neq 0) = 1$
.
Proposition 5.4. [Reference Tyran-KamińskaTK10b, proof of Theorem 1.2]
Let
![]() $\alpha \in (0,1)$
. With
$\alpha \in (0,1)$
. With
![]() $b_n$
as in Definition 2.1 and
$b_n$
as in Definition 2.1 and
![]() $c_n=0$
, suppose that for
$c_n=0$
, suppose that for
![]() ${\mathbb P}$
-a.e.
${\mathbb P}$
-a.e.
![]() $\omega \in \Omega $
,
$\omega \in \Omega $
,

and
Then
![]() $X_n^\omega \, {\stackrel {d}{\to } \,} X_{(\alpha )}$
in
$X_n^\omega \, {\stackrel {d}{\to } \,} X_{(\alpha )}$
in
![]() ${\mathbb D}[0, \infty )$
under the probability measure
${\mathbb D}[0, \infty )$
under the probability measure
![]() $\nu ^\omega $
for
$\nu ^\omega $
for
![]() ${\mathbb P}$
-a.e.
${\mathbb P}$
-a.e.
![]() $\omega \in \Omega $
.
$\omega \in \Omega $
.
Proof. We will check that the hypothesis of Theorem 5.1 is met for
![]() ${\mathbb P}$
-a.e.
${\mathbb P}$
-a.e.
![]() $\omega $
with
$\omega $
with
![]() ${T_n = T_{\sigma ^{n-1} \omega }}$
,
${T_n = T_{\sigma ^{n-1} \omega }}$
,
![]() $\mu = \nu ^\omega $
. Recall that
$\mu = \nu ^\omega $
. Recall that
![]() $c_n=c_\alpha (\epsilon ) = 0$
when
$c_n=c_\alpha (\epsilon ) = 0$
when
![]() $\alpha \in (0,1)$
. Using [Reference Kounias and WengKW69, Theorem 1] (see Theorem 5.6) and the equivariance of the family of measures
$\alpha \in (0,1)$
. Using [Reference Kounias and WengKW69, Theorem 1] (see Theorem 5.6) and the equivariance of the family of measures
![]() $\{ \nu ^\omega \}_{\omega \in \Omega }$
, we have
$\{ \nu ^\omega \}_{\omega \in \Omega }$
, we have

which shows that the condition in equation (5.3) implies the condition in equation (5.1) for all
![]() $\delta> 0$
and
$\delta> 0$
and
![]() $\ell \ge 1$
.
$\ell \ge 1$
.
Remark 5.5. One could replace the condition in equation (5.3) by one similar to that in equation (5.5), and use the argument in the proof of Proposition 5.7.
Theorem 5.6. (Kounias and Weng [Reference Kounias and WengKW69, special case of Theorem 1 therein])
Assume the random variables
![]() $X_k$
are in
$X_k$
are in
![]() $L^1(\mu )$
. Then
$L^1(\mu )$
. Then
 $$ \begin{align*} \mu\bigg(\max_{1\le k \le n} \bigg|\sum_{\ell=1}^k X_\ell\bigg| \ge \delta\bigg) \le \frac{1}{\delta} \sum_{k=1}^n {\mathbb E}_\mu(|X_k|). \end{align*} $$
$$ \begin{align*} \mu\bigg(\max_{1\le k \le n} \bigg|\sum_{\ell=1}^k X_\ell\bigg| \ge \delta\bigg) \le \frac{1}{\delta} \sum_{k=1}^n {\mathbb E}_\mu(|X_k|). \end{align*} $$
Proposition 5.7. Let
![]() $\alpha \in [1, 2)$
.
$\alpha \in [1, 2)$
.
With
![]() $b_n$
and
$b_n$
and
![]() $c_n$
as in Definitions 2.1 and 2.2, and
$c_n$
as in Definitions 2.1 and 2.2, and
![]() $c_\alpha (\epsilon )$
as in equation (3.1), suppose that for all
$c_\alpha (\epsilon )$
as in equation (3.1), suppose that for all
![]() $\epsilon> 0$
and all
$\epsilon> 0$
and all
![]() $\ell \ge 1$
,
$\ell \ge 1$
,

and that for all
![]() $\delta> 0$
,
$\delta> 0$
,

If
![]() $N_n^\omega \, {\stackrel {d}{\to } \,} N_{(\alpha )}$
for
$N_n^\omega \, {\stackrel {d}{\to } \,} N_{(\alpha )}$
for
![]() ${\mathbb P}$
-a.e.
${\mathbb P}$
-a.e.
![]() $\omega \in \Omega $
, then
$\omega \in \Omega $
, then
![]() $X_n^\omega \, {\stackrel {d}{\to } \,} X_{(\alpha )}$
in
$X_n^\omega \, {\stackrel {d}{\to } \,} X_{(\alpha )}$
in
![]() ${\mathbb D}[0, \infty )$
under the probability measure
${\mathbb D}[0, \infty )$
under the probability measure
![]() $\nu ^\omega $
for
$\nu ^\omega $
for
![]() ${\mathbb P}$
-a.e.
${\mathbb P}$
-a.e.
![]() $\omega \in \Omega $
.
$\omega \in \Omega $
.
Proof. As in the proof of Proposition 5.4, we check the hypothesis of Theorem 5.1 with
![]() $T_n = T_{\sigma ^{n-1} \omega }$
,
$T_n = T_{\sigma ^{n-1} \omega }$
,
![]() $\mu = \nu ^\omega $
for
$\mu = \nu ^\omega $
for
![]() ${\mathbb P}$
-a.e.
${\mathbb P}$
-a.e.
![]() $\omega \in \Omega $
. We will see that equation (5.1) follows from equations (5.4) and (5.5).
$\omega \in \Omega $
. We will see that equation (5.1) follows from equations (5.4) and (5.5).
Using the equivariance of
![]() $\{ \nu ^\omega \}_{\omega \in \Omega }$
, we see that the condition in equation (5.1) is implied by the equation (5.4) and
$\{ \nu ^\omega \}_{\omega \in \Omega }$
, we see that the condition in equation (5.1) is implied by the equation (5.4) and

We next show that the condition in equation (5.5) implies equation (5.6).
Since

we obtain that, using again the equivariance, for
![]() ${\mathbb P}$
-a.e.
${\mathbb P}$
-a.e.
![]() $\omega \in \Omega $
,
$\omega \in \Omega $
,

Thus, the condition in equation (5.5) implies equation (5.6), which concludes the proof.
The analog for the convergence to a stable law is the following proposition.
Proposition 5.8. Suppose that for
![]() ${\mathbb P}$
-a.e.
${\mathbb P}$
-a.e.
![]() $\omega \in \Omega $
, we have
$\omega \in \Omega $
, we have
If
![]() $\alpha \in (0,1)$
(so
$\alpha \in (0,1)$
(so
![]() $c_n = 0$
), we require in addition that
$c_n = 0$
), we require in addition that

If
![]() $\alpha \in [1,2)$
, we require instead of equation (5.7) that for all
$\alpha \in [1,2)$
, we require instead of equation (5.7) that for all
![]() $\epsilon>0$
,
$\epsilon>0$
,

and

Then
 $$ \begin{align*} \frac{1}{b_n}\bigg[\sum_{j=0}^{n-1}\phi\circ T_{\omega}^j - c_n \bigg]\, {\stackrel{d}{\to} \,} X_{(\alpha)}(1) \end{align*} $$
$$ \begin{align*} \frac{1}{b_n}\bigg[\sum_{j=0}^{n-1}\phi\circ T_{\omega}^j - c_n \bigg]\, {\stackrel{d}{\to} \,} X_{(\alpha)}(1) \end{align*} $$
under the probability measure
![]() $\nu ^\omega $
for
$\nu ^\omega $
for
![]() ${\mathbb P}$
-a.e.
${\mathbb P}$
-a.e.
![]() $\omega \in \Omega $
.
$\omega \in \Omega $
.
5.3. The annealed transfer operator
We assume that the random dynamical system
![]() $F:\Omega \times [0,1]\to \Omega \times [0,1]$
,
$F:\Omega \times [0,1]\to \Omega \times [0,1]$
,
which can also be viewed as a Markov process on
![]() $[0,1]$
, has a stationary measure
$[0,1]$
, has a stationary measure
![]() $\nu $
with density h. The map
$\nu $
with density h. The map
![]() $F: \Omega \times [0,1] \to \Omega \times [0,1]$
will preserve
$F: \Omega \times [0,1] \to \Omega \times [0,1]$
will preserve
![]() ${\mathbb P}\times \nu $
. Recall that
${\mathbb P}\times \nu $
. Recall that
![]() ${{\mathbb P}:=\{(p_1, \ldots , p_m)\}^{\mathbb {Z}}}$
.
${{\mathbb P}:=\{(p_1, \ldots , p_m)\}^{\mathbb {Z}}}$
.
We use the notation
![]() $P_{\mu ,i}$
for the transfer operator of
$P_{\mu ,i}$
for the transfer operator of
![]() $T_i:[0,1]\to [0,1]$
with respect to a measure
$T_i:[0,1]\to [0,1]$
with respect to a measure
![]() $\mu $
on
$\mu $
on
![]() $[0,1]$
, that is,
$[0,1]$
, that is,
The annealed transfer operator is defined by
 $$ \begin{align*} P_{\mu} (f):=\sum_{i=1}^{m}p_i P_{\mu,i} (f) \end{align*} $$
$$ \begin{align*} P_{\mu} (f):=\sum_{i=1}^{m}p_i P_{\mu,i} (f) \end{align*} $$
with adjoint
 $$ \begin{align*} U(f):=\sum_{i=1}^m p_i f\circ T_{i} \end{align*} $$
$$ \begin{align*} U(f):=\sum_{i=1}^m p_i f\circ T_{i} \end{align*} $$
which satisfies the duality relation
As above, we assume there are sample measures
![]() $d \nu ^\omega = h_{\omega }\,d x $
on each fiber
$d \nu ^\omega = h_{\omega }\,d x $
on each fiber
![]() $[0,1]$
of the skew product such that
$[0,1]$
of the skew product such that
where
![]() $P_{\omega }$
is the transfer operator of
$P_{\omega }$
is the transfer operator of
![]() $T_{\omega _0}$
with respect to the Lebesgue measure.
$T_{\omega _0}$
with respect to the Lebesgue measure.
Therefore,
 $$ \begin{align*} \nu (A)=\int_{\Omega} \bigg[\int_A h_{\omega}\,dx\bigg] d{\mathbb P}(\omega) \end{align*} $$
$$ \begin{align*} \nu (A)=\int_{\Omega} \bigg[\int_A h_{\omega}\,dx\bigg] d{\mathbb P}(\omega) \end{align*} $$
for all Borel sets
![]() $A\subset [0,1]$
.
$A\subset [0,1]$
.
5.4. Decay of correlations
We now consider the decay of correlation properties of the annealed systems associated to maps satisfying conditions (LY), (Dec), and (Min) and intermittent maps.
By [Reference Aimino, Nicol and VaientiANV15, Proposition 3.1] in the setting of maps satisfying conditions (LY), (Dec), and (Min), we have exponential decay in BV against
![]() $L^1$
: there are
$L^1$
: there are
![]() $C>0$
,
$C>0$
,
![]() $0<\unicode{x3bb} <1$
such that
$0<\unicode{x3bb} <1$
such that
 $$ \begin{align*} \bigg| \int f g\circ U^n\,d\nu -\int f\,d\nu \int g\,d\nu \bigg|\le C \unicode{x3bb}^n \|f\|_{\mathrm{BV}} \|g\|_{L^1 (\nu)}. \end{align*} $$
$$ \begin{align*} \bigg| \int f g\circ U^n\,d\nu -\int f\,d\nu \int g\,d\nu \bigg|\le C \unicode{x3bb}^n \|f\|_{\mathrm{BV}} \|g\|_{L^1 (\nu)}. \end{align*} $$
In the setting of intermittent maps, by [Reference Bahsoun and BoseBB16, Theorem 1.2], we have polynomial decay in Hölder against
![]() $L^{\infty }$
: there exists
$L^{\infty }$
: there exists
![]() $C>0$
such that
$C>0$
such that
 $$ \begin{align*} \bigg| \int f g\circ U^n\,d\nu -\int f\,d\nu \int g\,d\nu \bigg|\le C n^{1-{1}/{\gamma_{\mathrm{min}}}} \|f\|_{\text{H}\ddot{\mathrm{o}}\text{lder}} \|g\|_{L^{\infty} (\nu)}. \end{align*} $$
$$ \begin{align*} \bigg| \int f g\circ U^n\,d\nu -\int f\,d\nu \int g\,d\nu \bigg|\le C n^{1-{1}/{\gamma_{\mathrm{min}}}} \|f\|_{\text{H}\ddot{\mathrm{o}}\text{lder}} \|g\|_{L^{\infty} (\nu)}. \end{align*} $$
We now consider a useful property satisfied by our class of random uniformly expanding maps.
Definition 5.9. (Condition U)
We assume that almost each
![]() $\nu ^\omega $
is absolutely continuous with respect to the Lebesgue measure m, and
$\nu ^\omega $
is absolutely continuous with respect to the Lebesgue measure m, and
Consequently, the stationary measure
![]() $\nu $
is also absolutely continuous with respect to m, with density
$\nu $
is also absolutely continuous with respect to m, with density
![]() $h \in L^\infty (m)$
given by
$h \in L^\infty (m)$
given by
![]() $h(x) = \int _\Omega h_\omega (x) {\mathbb P}(d\omega )$
and satisfying equation (5.8).
$h(x) = \int _\Omega h_\omega (x) {\mathbb P}(d\omega )$
and satisfying equation (5.8).
Lemma 5.10. Properties (LY), (Min), and (Dec) imply Condition U. Namely, there exists a unique Hölder map
![]() $\omega \in \Omega \mapsto h_\omega \in \mathrm {BV}$
such that
$\omega \in \Omega \mapsto h_\omega \in \mathrm {BV}$
such that
![]() $P_\omega h_\omega = h_{\sigma \omega }$
and equations (5.8) and (5.9) are satisfied by [Reference Aimino, Nicol and VaientiANV15].
$P_\omega h_\omega = h_{\sigma \omega }$
and equations (5.8) and (5.9) are satisfied by [Reference Aimino, Nicol and VaientiANV15].
Proof. By condition (Dec), and as all the operators
![]() $P_\omega $
are Markov with respect to m, we have
$P_\omega $
are Markov with respect to m, we have
which proves that ![]() is a Cauchy sequence in BV converging to a unique limit
is a Cauchy sequence in BV converging to a unique limit
![]() $h_\omega \in BV$
satisfying
$h_\omega \in BV$
satisfying
![]() $P_\omega h_\omega = h_{\sigma \omega }$
for all
$P_\omega h_\omega = h_{\sigma \omega }$
for all
![]() $\omega $
. The lower bound in equation (5.8) follows from the condition (Min), while the upper bound is a consequence of the uniform Lasota–Yorke inequality of condition (LY), as actually the family
$\omega $
. The lower bound in equation (5.8) follows from the condition (Min), while the upper bound is a consequence of the uniform Lasota–Yorke inequality of condition (LY), as actually the family
![]() $\{h_\omega \}_{\omega \in \Omega }$
is bounded in BV. To prove the Hölder continuity of
$\{h_\omega \}_{\omega \in \Omega }$
is bounded in BV. To prove the Hölder continuity of
![]() $\omega \mapsto h_\omega $
with respect to the distance
$\omega \mapsto h_\omega $
with respect to the distance
![]() $d_\theta $
, we remark that if
$d_\theta $
, we remark that if
![]() $\omega $
and
$\omega $
and
![]() $\omega '$
agree in coordinates
$\omega '$
agree in coordinates
![]() $|k| \le n$
, then
$|k| \le n$
, then
Remark 5.11. Note that the density h of the stationary measure
![]() $\nu $
also belongs to BV and is uniformly bounded from above and below, as the average of
$\nu $
also belongs to BV and is uniformly bounded from above and below, as the average of
![]() $h_\omega $
over
$h_\omega $
over
![]() $\Omega $
.
$\Omega $
.
5.4.1. The sample measures
 $h_\omega $
$h_\omega $
The regularity properties of the sample measures
![]() $h_{\omega }$
, both as functions of
$h_{\omega }$
, both as functions of
![]() $\omega $
and as functions of x on
$\omega $
and as functions of x on
![]() $[0,1]$
, play a key role in our estimates. We will first recall how the sample measures are constructed. Suppose
$[0,1]$
, play a key role in our estimates. We will first recall how the sample measures are constructed. Suppose
![]() ${\omega :=(\ldots , \omega _{-1}, \omega _0,\omega _1,\ldots , \omega _n,\ldots ,)}$
and define
${\omega :=(\ldots , \omega _{-1}, \omega _0,\omega _1,\ldots , \omega _n,\ldots ,)}$
and define
![]() $h_n (\omega )=P_{\omega _{-1}}\ldots P_{\omega _{-n} }1$
as a sequence of functions on the fiber I above
$h_n (\omega )=P_{\omega _{-1}}\ldots P_{\omega _{-n} }1$
as a sequence of functions on the fiber I above
![]() $\omega $
. In the setting both of random uniformly expanding maps and of intermittent maps
$\omega $
. In the setting both of random uniformly expanding maps and of intermittent maps
![]() $\{h_n (\omega ) \}$
is a Cauchy sequence and has a limit
$\{h_n (\omega ) \}$
is a Cauchy sequence and has a limit
![]() $h_{\omega }$
.
$h_{\omega }$
.
In the setting of random expanding maps,
![]() $h_\omega $
is uniformly BV in
$h_\omega $
is uniformly BV in
![]() $\omega $
as
$\omega $
as
In the setting of intermittent maps with
![]() $\gamma _{\mathrm {max}}=\max _{1\le i \le m} \{\gamma _i\}$
, the densities
$\gamma _{\mathrm {max}}=\max _{1\le i \le m} \{\gamma _i\}$
, the densities
![]() $h_\omega $
lie in the cone
$h_\omega $
lie in the cone
 $$ \begin{align*} \begin{array}{ll} L:=\big\{ f\in \mathcal{C}^0((0,1])\cap L^1(m), & f\geq 0,\ f \text{ non-increasing}, \\ & X^{\gamma_{\mathrm{max}}+1}f \text{ increasing}, f(x)\leq ax^{-\gamma_{\mathrm{max}}}m(f)\big\}\end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{ll} L:=\big\{ f\in \mathcal{C}^0((0,1])\cap L^1(m), & f\geq 0,\ f \text{ non-increasing}, \\ & X^{\gamma_{\mathrm{max}}+1}f \text{ increasing}, f(x)\leq ax^{-\gamma_{\mathrm{max}}}m(f)\big\}\end{array} \end{align*} $$
where
![]() $X(x) = x$
is the identity function and
$X(x) = x$
is the identity function and
![]() $m(f)$
is the integral of f with respect to m. In [Reference Aimino, Hu, Nicol, Török and VaientiAHN+
15
], it is proven that for a fixed value of
$m(f)$
is the integral of f with respect to m. In [Reference Aimino, Hu, Nicol, Török and VaientiAHN+
15
], it is proven that for a fixed value of
![]() $\gamma _{\mathrm {max}} \in (0,1)$
, provided that the constant a is big enough, the cone L is invariant under the action of all transfer operators
$\gamma _{\mathrm {max}} \in (0,1)$
, provided that the constant a is big enough, the cone L is invariant under the action of all transfer operators
![]() $P_{\gamma _i}$
with
$P_{\gamma _i}$
with
![]() $0<\gamma _i \leq \gamma _{\mathrm {max}}$
and so (see e.g. [Reference Nicol, Pereira and TörökNPT21, Proposition 3.3], which summarizes results of [Reference Nicol, Török and VaientiNTV18])
$0<\gamma _i \leq \gamma _{\mathrm {max}}$
and so (see e.g. [Reference Nicol, Pereira and TörökNPT21, Proposition 3.3], which summarizes results of [Reference Nicol, Török and VaientiNTV18])
 $$ \begin{align*} \|h_n (\omega)-h_{n+k} (\omega)\|_{L^1(m)} &\le \|P_{\omega_{-1}} P_{\omega_{-2}} \ldots P_{\omega_{-n}} (1-P_{\omega_{-n-1} } \ldots P_{\omega_{-n-k} }1 )\|_{L^1(m)}\\ &\le C_{\gamma_{\mathrm{max}} } n^{1-{1}/{\gamma_{\mathrm{max}}}} (\log n)^{{1}/{\gamma_{\mathrm{max}}}}, \end{align*} $$
$$ \begin{align*} \|h_n (\omega)-h_{n+k} (\omega)\|_{L^1(m)} &\le \|P_{\omega_{-1}} P_{\omega_{-2}} \ldots P_{\omega_{-n}} (1-P_{\omega_{-n-1} } \ldots P_{\omega_{-n-k} }1 )\|_{L^1(m)}\\ &\le C_{\gamma_{\mathrm{max}} } n^{1-{1}/{\gamma_{\mathrm{max}}}} (\log n)^{{1}/{\gamma_{\mathrm{max}}}}, \end{align*} $$
whence
![]() $h_\omega \in L^1(m)$
. In later arguments, we will use the approximation
$h_\omega \in L^1(m)$
. In later arguments, we will use the approximation
We mention also the recent paper [Reference Korepanov and LeppänenKL21], where the logarithm term in equation (5.11) is shown to be unnecessary and moment estimates are given.
We now show that
![]() $h_{\omega }$
is a Hölder function of
$h_{\omega }$
is a Hölder function of
![]() $\omega $
on
$\omega $
on
![]() $(\Omega , d_{\theta })$
in the setting of random expanding maps.
$(\Omega , d_{\theta })$
in the setting of random expanding maps.
For
![]() $\theta \in (0,1)$
, we introduce on
$\theta \in (0,1)$
, we introduce on
![]() $\Omega $
the symbolic metric
$\Omega $
the symbolic metric
where
![]() $s(\omega , \omega ') = \inf \{k \ge 0 : \omega _\ell \neq \omega _\ell ' \text { for some } |\ell |\le k\}$
.
$s(\omega , \omega ') = \inf \{k \ge 0 : \omega _\ell \neq \omega _\ell ' \text { for some } |\ell |\le k\}$
.
Suppose
![]() $\omega $
,
$\omega $
,
![]() $\omega '$
agree in coordinates
$\omega '$
agree in coordinates
![]() $|k| \le n$
(that is, backwards and forwards in time) so that
$|k| \le n$
(that is, backwards and forwards in time) so that
![]() $d_{\theta } (\omega , \omega ^{\prime }) \le \theta ^n$
in the symbolic metric on
$d_{\theta } (\omega , \omega ^{\prime }) \le \theta ^n$
in the symbolic metric on
![]() $\Omega $
. Then
$\Omega $
. Then
 $$ \begin{align*} \|h_{\omega}-h_{\omega'}\|_{\mathrm{BV}} &\le \|P_{\omega_{-1}} P_{\omega_1} \ldots P_{\omega_{-n+1}}(h_{(\sigma^{-n+1} \omega)}-h_{(\sigma^{-n+1} \omega')})\|_{\mathrm{BV}}\\ &\le C \unicode{x3bb}^{n-1} = C' d_{\theta} (\omega,\omega')^{\log_\theta \unicode{x3bb}}. \end{align*} $$
$$ \begin{align*} \|h_{\omega}-h_{\omega'}\|_{\mathrm{BV}} &\le \|P_{\omega_{-1}} P_{\omega_1} \ldots P_{\omega_{-n+1}}(h_{(\sigma^{-n+1} \omega)}-h_{(\sigma^{-n+1} \omega')})\|_{\mathrm{BV}}\\ &\le C \unicode{x3bb}^{n-1} = C' d_{\theta} (\omega,\omega')^{\log_\theta \unicode{x3bb}}. \end{align*} $$
Recall that
![]() $\|f\|_{\infty } \le C \|f\|_{\mathrm {BV}}$
, see e.g. [Reference Boyarsky and GóraBG97, Lemma 2.3.1].
$\|f\|_{\infty } \le C \|f\|_{\mathrm {BV}}$
, see e.g. [Reference Boyarsky and GóraBG97, Lemma 2.3.1].
That is, Condition U (see Definition 5.9) holds for random expanding maps.
The map
![]() $\omega \mapsto h_{\omega }$
is not Hölder in the setting of intermittent maps; in several arguments, we will use the regularity properties of the approximation
$\omega \mapsto h_{\omega }$
is not Hölder in the setting of intermittent maps; in several arguments, we will use the regularity properties of the approximation
![]() $h_n(\omega )$
for
$h_n(\omega )$
for
![]() $h_\omega $
.
$h_\omega $
.
However, on intervals that stay away from zero, all functions in the cone L are comparable to their mean. Therefore, on sets that are uniformly away from zero, all the above densities/measures (
![]() $d \nu = h\,dx$
,
$d \nu = h\,dx$
,
![]() $h_\omega $
,
$h_\omega $
,
![]() $h_n(\omega )$
) are still comparable.
$h_n(\omega )$
) are still comparable.
Namely,
 $$ \begin{align} &\text{ for any } \delta \in (0,1), \text{ there is } C_\delta> 0 \text{ such that }\nonumber\\ &\quad h \in L \implies 1/C_\delta < h(x)/m(h) < C_\delta \text{ for } x\in [\delta, 1]. \end{align} $$
$$ \begin{align} &\text{ for any } \delta \in (0,1), \text{ there is } C_\delta> 0 \text{ such that }\nonumber\\ &\quad h \in L \implies 1/C_\delta < h(x)/m(h) < C_\delta \text{ for } x\in [\delta, 1]. \end{align} $$
Indeed,
![]() $h/m(h)$
is bounded below by [Reference Liverani, Saussol and VaientiLSV99, Lemma 2.4], and the upper bound follows from the definition of the cone.
$h/m(h)$
is bounded below by [Reference Liverani, Saussol and VaientiLSV99, Lemma 2.4], and the upper bound follows from the definition of the cone.
6. Ancilliary results
Let
![]() $x_0 \in [0,1]$
, and, for
$x_0 \in [0,1]$
, and, for
![]() $\alpha \in (0,2)$
, recall we define the function
$\alpha \in (0,2)$
, recall we define the function
![]() $\phi _{x_0}(x) = |x - x_0|^{ - {1}/{\alpha }}$
. It is easy to see that
$\phi _{x_0}(x) = |x - x_0|^{ - {1}/{\alpha }}$
. It is easy to see that
![]() $\phi _{x_0}$
is regularity varying with index
$\phi _{x_0}$
is regularity varying with index
![]() $\alpha $
and that
$\alpha $
and that
![]() $p=1$
.
$p=1$
.
6.1. Exponential law and point process results
We denote by
![]() ${\mathcal J}$
the family of all finite unions of intervals of the form
${\mathcal J}$
the family of all finite unions of intervals of the form
![]() $(x, y]$
, where
$(x, y]$
, where
![]() $-\infty \le x < y \le \infty $
and
$-\infty \le x < y \le \infty $
and
![]() $0 \notin [x,y]$
.
$0 \notin [x,y]$
.
For a measurable subset
![]() $U \subset [0,1]$
, we define the hitting time of
$U \subset [0,1]$
, we define the hitting time of
![]() $(\omega , x) \in \Omega \times [0,1]$
to U by
$(\omega , x) \in \Omega \times [0,1]$
to U by
Recall that
![]() $\phi _{x_0}(x):=d(x,x_0)^{-{1}/{\alpha }}$
depends on the choice of
$\phi _{x_0}(x):=d(x,x_0)^{-{1}/{\alpha }}$
depends on the choice of
![]() $x_0 \in [0,1]$
. Recall also that
$x_0 \in [0,1]$
. Recall also that
the set of discontinuities of all the maps
![]() $T_\omega ^n$
.
$T_\omega ^n$
.
Theorem 6.1. In the setting of §2.1, assume conditions (LY), (Min), and (Dec). If
![]() $x_0 \notin {\mathcal D}$
is non-recurrent, then, for
$x_0 \notin {\mathcal D}$
is non-recurrent, then, for
![]() ${\mathbb P}$
-a.e.
${\mathbb P}$
-a.e.
![]() $\omega \in \Omega $
and all
$\omega \in \Omega $
and all
![]() $0 \le s < t$
,
$0 \le s < t$
,
where
![]() $A_n := \phi _{x_0}^{-1}(b_n J)$
,
$A_n := \phi _{x_0}^{-1}(b_n J)$
,
![]() $J \in {\mathcal J}$
.
$J \in {\mathcal J}$
.
Theorem 6.2. In the setting of intermittent maps, assume that
![]() $\gamma _{\mathrm {max}} <\tfrac 13$
. Then for m-a.e.
$\gamma _{\mathrm {max}} <\tfrac 13$
. Then for m-a.e.
![]() $x_0$
for
$x_0$
for
![]() ${\mathbb P}$
-a.e.
${\mathbb P}$
-a.e.
![]() $\omega \in \Omega $
and all
$\omega \in \Omega $
and all
![]() $0 \le s < t$
,
$0 \le s < t$
,
where
![]() $A_n := \phi _{x_0}^{-1}(b_n J)$
,
$A_n := \phi _{x_0}^{-1}(b_n J)$
,
![]() $J \in {\mathcal J}$
.
$J \in {\mathcal J}$
.
Theorem 6.3. In the setting of §2.1, assume conditions (LY), (Min), and (Dec). If
![]() $x_0 \notin {\mathcal D}$
is non-recurrent, then for
$x_0 \notin {\mathcal D}$
is non-recurrent, then for
![]() ${\mathbb P}$
-a.e.
${\mathbb P}$
-a.e.
![]() $\omega \in \Omega $
,
$\omega \in \Omega $
,
under the probability
![]() $\nu ^\omega $
.
$\nu ^\omega $
.
Theorem 6.4. In the setting of intermittent maps for m-a.e.
![]() $x_0$
for
$x_0$
for
![]() ${\mathbb P}$
-a.e.
${\mathbb P}$
-a.e.
![]() $\omega $
,
$\omega $
,
After some preliminary lemmas and results, Theorem 6.1 is proved in §8.1, Theorem 6.2 in §8.2, Theorem 6.3 in §9.1, and Theorem 6.4 in §9.2.
7. Scheme of proofs
7.1. Two useful lemmas
We now proceed to the proofs of the main results. We will use the following technical propositions which are a form of spatial ergodic theorem which allows us to prove exponential and Poisson limit laws.
Lemma 7.1. Assume Condition U and let
![]() $\chi _n : Y \to {\mathbb R}$
be a sequence of functions in
$\chi _n : Y \to {\mathbb R}$
be a sequence of functions in
![]() $L^1(m)$
such that
$L^1(m)$
such that
![]() ${\mathbb E}_m(| \chi _n |) = {\mathcal O}(n^{-1} \widetilde {L}(n))$
for some slowly varying function
${\mathbb E}_m(| \chi _n |) = {\mathcal O}(n^{-1} \widetilde {L}(n))$
for some slowly varying function
![]() $\widetilde {L}$
. Then, for
$\widetilde {L}$
. Then, for
![]() ${\mathbb P}$
-a.e.
${\mathbb P}$
-a.e.
![]() $\omega \in \Omega $
and for all
$\omega \in \Omega $
and for all
![]() $\ell \ge 1$
,
$\ell \ge 1$
,
 $$ \begin{align*} \lim_{n \to \infty} \sup_{0 \le k \le \ell} \bigg| \sum_{j=0}^{kn - 1} ({\mathbb E}_{\nu^{\sigma^j \omega}}( \chi_n) - {\mathbb E}_\nu(\chi_n) )\bigg| = 0. \end{align*} $$
$$ \begin{align*} \lim_{n \to \infty} \sup_{0 \le k \le \ell} \bigg| \sum_{j=0}^{kn - 1} ({\mathbb E}_{\nu^{\sigma^j \omega}}( \chi_n) - {\mathbb E}_\nu(\chi_n) )\bigg| = 0. \end{align*} $$
Therefore, given
![]() $( s, t] \subset [0, \infty )$
and
$( s, t] \subset [0, \infty )$
and
![]() $\epsilon> 0$
, for
$\epsilon> 0$
, for
![]() ${\mathbb P}$
-a.e.
${\mathbb P}$
-a.e.
![]() $\omega $
, there exists
$\omega $
, there exists
![]() $N(\omega )$
such that
$N(\omega )$
such that
 $$ \begin{align*} \bigg|\sum_{r=\lfloor n s \rfloor +1}^{\lfloor n t \rfloor} ({\mathbb E}_{\nu^{\sigma^j \omega}}( \chi_n) - {\mathbb E}_\nu(\chi_n))\bigg|\le \epsilon \end{align*} $$
$$ \begin{align*} \bigg|\sum_{r=\lfloor n s \rfloor +1}^{\lfloor n t \rfloor} ({\mathbb E}_{\nu^{\sigma^j \omega}}( \chi_n) - {\mathbb E}_\nu(\chi_n))\bigg|\le \epsilon \end{align*} $$
for all
![]() $n \ge N(\omega )$
.
$n \ge N(\omega )$
.
Proof. We obtain the second claim by taking the difference between two values of
![]() $\ell $
in the first claim.
$\ell $
in the first claim.
Fix
![]() $\ell \ge 1$
. For
$\ell \ge 1$
. For
![]() $\delta>0$
, let
$\delta>0$
, let
 $$ \begin{align*} U_k^n(\delta) = \bigg\{ \omega \in \Omega : \bigg| \sum_{j=0}^{kn -1} ({\mathbb E}_{\nu^{\sigma^j \omega}}(\chi_n) - {\mathbb E}_\nu(\chi_n) ) \bigg| \ge \delta \bigg\} \end{align*} $$
$$ \begin{align*} U_k^n(\delta) = \bigg\{ \omega \in \Omega : \bigg| \sum_{j=0}^{kn -1} ({\mathbb E}_{\nu^{\sigma^j \omega}}(\chi_n) - {\mathbb E}_\nu(\chi_n) ) \bigg| \ge \delta \bigg\} \end{align*} $$
and
 $$ \begin{align*} B^n(\delta) = \bigg\{ \omega \in \Omega : \sup_{0 \le k \le \ell} \bigg| \sum_{j=0}^{kn -1} ({\mathbb E}_{\nu^{\sigma^j \omega}}(\chi_n) - {\mathbb E}_\nu(\chi_n) ) \bigg| \ge \delta \bigg\}. \end{align*} $$
$$ \begin{align*} B^n(\delta) = \bigg\{ \omega \in \Omega : \sup_{0 \le k \le \ell} \bigg| \sum_{j=0}^{kn -1} ({\mathbb E}_{\nu^{\sigma^j \omega}}(\chi_n) - {\mathbb E}_\nu(\chi_n) ) \bigg| \ge \delta \bigg\}. \end{align*} $$
Note that
 $$ \begin{align*} B^n(\delta) = \bigcup_{k=0}^\ell U_k^n(\delta). \end{align*} $$
$$ \begin{align*} B^n(\delta) = \bigcup_{k=0}^\ell U_k^n(\delta). \end{align*} $$
We define
![]() $f_n(\omega ) = {\mathbb E}_{\nu ^\omega }(\chi _n)$
and
$f_n(\omega ) = {\mathbb E}_{\nu ^\omega }(\chi _n)$
and
![]() $\overline {f}_n = {\mathbb E}_{{\mathbb P}}(f_n)$
. We claim that
$\overline {f}_n = {\mathbb E}_{{\mathbb P}}(f_n)$
. We claim that
![]() $f_n:\Omega \to \mathbb {R}$
is Hölder with norm
$f_n:\Omega \to \mathbb {R}$
is Hölder with norm
![]() $\|f_n \|_\theta = {\mathcal O}(n^{-1}\widetilde {L}(n))$
. Indeed, for
$\|f_n \|_\theta = {\mathcal O}(n^{-1}\widetilde {L}(n))$
. Indeed, for
![]() $\omega \in \Omega $
, we have
$\omega \in \Omega $
, we have
 $$ \begin{align*} |f_n(\omega)| = \bigg| \int_Y \chi_n(x) \,d \nu^\omega(x) \bigg| \le \|h_\omega\|_{L^\infty_m} \|\chi_n\|_{L^1_m} \le \frac{C}{n}\widetilde{L}(n), \end{align*} $$
$$ \begin{align*} |f_n(\omega)| = \bigg| \int_Y \chi_n(x) \,d \nu^\omega(x) \bigg| \le \|h_\omega\|_{L^\infty_m} \|\chi_n\|_{L^1_m} \le \frac{C}{n}\widetilde{L}(n), \end{align*} $$
and for
![]() $\omega , \omega ' \in \Omega $
, we have
$\omega , \omega ' \in \Omega $
, we have
 $$ \begin{align*} |f_n(\omega) - f_n(\omega')| &= \bigg|\int_Y \chi_n(x) \,d \nu^\omega(x) - \int_Y \chi_n(x) \,d\nu^{\omega'}(x) \bigg| \\ & \le \int_Y | \chi_n(x) | \cdot |h_\omega(x) - h_{\omega'}(x)| \,dm(x) \\ & \le \| h_\omega - h_{\omega'}\|_{L^\infty_m} \| \chi_n \|_{L^1_m} \\ & \le \frac C n \widetilde{L}(n) d_\theta(\omega, \omega'), \end{align*} $$
$$ \begin{align*} |f_n(\omega) - f_n(\omega')| &= \bigg|\int_Y \chi_n(x) \,d \nu^\omega(x) - \int_Y \chi_n(x) \,d\nu^{\omega'}(x) \bigg| \\ & \le \int_Y | \chi_n(x) | \cdot |h_\omega(x) - h_{\omega'}(x)| \,dm(x) \\ & \le \| h_\omega - h_{\omega'}\|_{L^\infty_m} \| \chi_n \|_{L^1_m} \\ & \le \frac C n \widetilde{L}(n) d_\theta(\omega, \omega'), \end{align*} $$
since
![]() $\omega \in \Omega \mapsto h_\omega \in L^\infty (m)$
is Hölder continuous. In particular, we also have that
$\omega \in \Omega \mapsto h_\omega \in L^\infty (m)$
is Hölder continuous. In particular, we also have that
![]() ${\overline {f}_n = {\mathcal O}(n^{-1}\widetilde {L}(n))}$
.
${\overline {f}_n = {\mathcal O}(n^{-1}\widetilde {L}(n))}$
.
We have, using Chebyshev’s inequality,
 $$ \begin{align*} {\mathbb P}(U_k^n(\delta)) &= {\mathbb P}\bigg( \bigg\{ \omega \in \Omega : \bigg|\sum_{j=0}^{kn -1} ( f_n \circ \sigma^j - \overline{f}_n ) \bigg| \ge \delta \bigg\}\bigg) \\ & \le \frac{1}{\delta^2} {\mathbb E}_{{\mathbb P}}\bigg(\bigg(\sum_{j=0}^{kn -1} ( f_n \circ \sigma^j - \overline{f}_n )\bigg)^2 \bigg) \\ & \le \frac{1}{\delta^2} \bigg[ \sum_{j=0}^{kn - 1} ({\mathbb E}_{{\mathbb P}} |f_n \circ \sigma^j - \overline{f}_n|^2\\ &\quad+ 2 \sum_{0 \le i < j \le kn - 1} {\mathbb E}_{{\mathbb P}}((f_n \circ \sigma^i - \overline{f}_n)(f_n \circ \sigma^j - \overline{f}_n)) \bigg]. \end{align*} $$
$$ \begin{align*} {\mathbb P}(U_k^n(\delta)) &= {\mathbb P}\bigg( \bigg\{ \omega \in \Omega : \bigg|\sum_{j=0}^{kn -1} ( f_n \circ \sigma^j - \overline{f}_n ) \bigg| \ge \delta \bigg\}\bigg) \\ & \le \frac{1}{\delta^2} {\mathbb E}_{{\mathbb P}}\bigg(\bigg(\sum_{j=0}^{kn -1} ( f_n \circ \sigma^j - \overline{f}_n )\bigg)^2 \bigg) \\ & \le \frac{1}{\delta^2} \bigg[ \sum_{j=0}^{kn - 1} ({\mathbb E}_{{\mathbb P}} |f_n \circ \sigma^j - \overline{f}_n|^2\\ &\quad+ 2 \sum_{0 \le i < j \le kn - 1} {\mathbb E}_{{\mathbb P}}((f_n \circ \sigma^i - \overline{f}_n)(f_n \circ \sigma^j - \overline{f}_n)) \bigg]. \end{align*} $$
By the
![]() $\sigma $
-invariance of
$\sigma $
-invariance of
![]() ${\mathbb P}$
, we have
${\mathbb P}$
, we have
and, since
![]() $(\Omega , {\mathbb P}, \sigma )$
admits exponential decay of correlations for Hölder observables, there exist
$(\Omega , {\mathbb P}, \sigma )$
admits exponential decay of correlations for Hölder observables, there exist
![]() $\unicode{x3bb} \in (0,1)$
and
$\unicode{x3bb} \in (0,1)$
and
![]() $C>0$
such that
$C>0$
such that
 $$ \begin{align*} {\mathbb E}_{{\mathbb P}}((f_n \circ \sigma^i - \overline{f}_n)(f_n \circ \sigma^j - \overline{f}_n)) &= {\mathbb E}_{{\mathbb P}}((f_n - \overline{f}_n)(f_n \circ \sigma^{j-i}- \overline{f}_n)) \\ & \le C \unicode{x3bb}^{j-i} \| f_n - \overline{f}_n\|_\theta^2. \end{align*} $$
$$ \begin{align*} {\mathbb E}_{{\mathbb P}}((f_n \circ \sigma^i - \overline{f}_n)(f_n \circ \sigma^j - \overline{f}_n)) &= {\mathbb E}_{{\mathbb P}}((f_n - \overline{f}_n)(f_n \circ \sigma^{j-i}- \overline{f}_n)) \\ & \le C \unicode{x3bb}^{j-i} \| f_n - \overline{f}_n\|_\theta^2. \end{align*} $$
We then obtain that
 $$ \begin{align*} {\mathbb P}(U_k^n(\delta)) &\le \frac{C}{\delta^2} \bigg[kn \|f_n - \overline{f}_n\|_{L^2_m}^2 + 2 \sum_{0 \le i < j \le kn - 1} \unicode{x3bb}^{j-i} \| f_n - \overline{f}_n\|_\theta^2 \bigg]\\ & \le C \frac{nk}{\delta^2} \|f_n\|_\theta^2 \\ &\le C \frac{k}{n \delta^2}(\widetilde{L}(n))^2, \end{align*} $$
$$ \begin{align*} {\mathbb P}(U_k^n(\delta)) &\le \frac{C}{\delta^2} \bigg[kn \|f_n - \overline{f}_n\|_{L^2_m}^2 + 2 \sum_{0 \le i < j \le kn - 1} \unicode{x3bb}^{j-i} \| f_n - \overline{f}_n\|_\theta^2 \bigg]\\ & \le C \frac{nk}{\delta^2} \|f_n\|_\theta^2 \\ &\le C \frac{k}{n \delta^2}(\widetilde{L}(n))^2, \end{align*} $$
which implies that
Let
![]() $\eta>0$
. By the Borel–Cantelli lemma, it follows that for
$\eta>0$
. By the Borel–Cantelli lemma, it follows that for
![]() ${\mathbb P}$
-a.e.
${\mathbb P}$
-a.e.
![]() $\omega \in \Omega $
, there exists
$\omega \in \Omega $
, there exists
![]() $N(\omega , \delta ) \ge 1$
such that
$N(\omega , \delta ) \ge 1$
such that
![]() $\omega \notin B^{\lfloor p^{1+\eta }\rfloor } (\delta )$
for all
$\omega \notin B^{\lfloor p^{1+\eta }\rfloor } (\delta )$
for all
![]() $p \ge N(\omega , \delta )$
.
$p \ge N(\omega , \delta )$
.
Let now
![]() $P:= \lfloor p^{1+\eta } \rfloor < n \le P' = \lfloor (p+1)^{1+\eta } \rfloor $
for p large enough. Let
$P:= \lfloor p^{1+\eta } \rfloor < n \le P' = \lfloor (p+1)^{1+\eta } \rfloor $
for p large enough. Let
![]() $0 \le k \le \ell $
. Then, since
$0 \le k \le \ell $
. Then, since
![]() $\|f_n\|_\infty = {\mathcal O}(n^{-1}\widetilde {L}(n))$
,
$\|f_n\|_\infty = {\mathcal O}(n^{-1}\widetilde {L}(n))$
,
 $$ \begin{align*} \bigg| \sum_{j=0}^{kP -1 } (f_n(\sigma^j \omega) - \overline{f}_n ) - \sum_{j=0}^{kn - 1}(f_n(\sigma^j \omega) - \overline{f}_n )\bigg| &\le \sum_{j=kP}^{kn - 1} |f_n(\sigma^j \omega) - \overline{f}_n | \\ & \le C \frac{P' - P}{P} \widetilde{L}(n) \le C \frac{\widetilde{L}(p^{1 + \eta})}{p}, \end{align*} $$
$$ \begin{align*} \bigg| \sum_{j=0}^{kP -1 } (f_n(\sigma^j \omega) - \overline{f}_n ) - \sum_{j=0}^{kn - 1}(f_n(\sigma^j \omega) - \overline{f}_n )\bigg| &\le \sum_{j=kP}^{kn - 1} |f_n(\sigma^j \omega) - \overline{f}_n | \\ & \le C \frac{P' - P}{P} \widetilde{L}(n) \le C \frac{\widetilde{L}(p^{1 + \eta})}{p}, \end{align*} $$
because on the one hand,
 $$ \begin{align*} \frac{P' - P}{P} = \frac{\lfloor (p+1)^{1+\eta} \rfloor- \lfloor p^{1+\eta}\rfloor }{\lfloor p^{1+\eta} \rfloor} = {\mathcal O} \bigg( \frac 1 p \bigg), \end{align*} $$
$$ \begin{align*} \frac{P' - P}{P} = \frac{\lfloor (p+1)^{1+\eta} \rfloor- \lfloor p^{1+\eta}\rfloor }{\lfloor p^{1+\eta} \rfloor} = {\mathcal O} \bigg( \frac 1 p \bigg), \end{align*} $$
and on the other hand, by Potter’s bounds, for
![]() $\tau> 0$
,
$\tau> 0$
,
 $$ \begin{align*} \widetilde{L}(n) \le C \widetilde{L}(P) \bigg( \frac{n}{P} \bigg)^\tau \le C \widetilde{L}(P) \bigg( \frac{P'}{P} \bigg)^\tau \le C\widetilde{L}(P). \end{align*} $$
$$ \begin{align*} \widetilde{L}(n) \le C \widetilde{L}(P) \bigg( \frac{n}{P} \bigg)^\tau \le C \widetilde{L}(P) \bigg( \frac{P'}{P} \bigg)^\tau \le C\widetilde{L}(P). \end{align*} $$
Since
 $$ \begin{align*} \bigg| \sum_{j=0}^{kP -1} (f_n(\sigma^j \omega) - \overline{f}_n ) \bigg| < \delta \end{align*} $$
$$ \begin{align*} \bigg| \sum_{j=0}^{kP -1} (f_n(\sigma^j \omega) - \overline{f}_n ) \bigg| < \delta \end{align*} $$
for all
![]() $0 \le k \le \ell $
, it follows that for
$0 \le k \le \ell $
, it follows that for
![]() ${\mathbb P}$
-a.e.
${\mathbb P}$
-a.e.
![]() $\omega $
, there exists
$\omega $
, there exists
![]() $N(\omega , \delta )$
such that
$N(\omega , \delta )$
such that
![]() $\omega \notin B^n(2 \delta )$
for all
$\omega \notin B^n(2 \delta )$
for all
![]() $n \ge N(\omega , \delta )$
, which concludes the proof.
$n \ge N(\omega , \delta )$
, which concludes the proof.
We now consider a corresponding result to Lemma 7.1 in the setting of intermittent maps.
Lemma 7.2. Assume that
![]() $\gamma _{\mathrm {max}} < 1/2$
, and that
$\gamma _{\mathrm {max}} < 1/2$
, and that
![]() $\chi _n \in L^1(m)$
is such that
$\chi _n \in L^1(m)$
is such that
![]() ${\mathbb E}_m( |\chi _n|) = {\mathcal O}(n^{-1})$
,
${\mathbb E}_m( |\chi _n|) = {\mathcal O}(n^{-1})$
,
![]() $\|\chi _n\|_\infty = {\mathcal O}(1)$
and there is
$\|\chi _n\|_\infty = {\mathcal O}(1)$
and there is
![]() $\delta>0$
such that
$\delta>0$
such that
![]() $\mathrm {supp}(\chi _n) \subset [\delta ,1]$
for all n.
$\mathrm {supp}(\chi _n) \subset [\delta ,1]$
for all n.
Then, for
![]() ${\mathbb P}$
-a.e.
${\mathbb P}$
-a.e.
![]() $\omega \in \Omega $
and for all
$\omega \in \Omega $
and for all
![]() $\ell \ge 1$
,
$\ell \ge 1$
,
 $$ \begin{align*} \lim_{n \to \infty} \sup_{0 \le k \le \ell} \bigg| \sum_{j=0}^{kn - 1} ({\mathbb E}_{\nu^{\sigma^j \omega}}( \chi_n) - {\mathbb E}_\nu(\chi_n) )\bigg| = 0. \end{align*} $$
$$ \begin{align*} \lim_{n \to \infty} \sup_{0 \le k \le \ell} \bigg| \sum_{j=0}^{kn - 1} ({\mathbb E}_{\nu^{\sigma^j \omega}}( \chi_n) - {\mathbb E}_\nu(\chi_n) )\bigg| = 0. \end{align*} $$
Proof. In the setting of intermittent maps, we must modify the argument of Lemma 7.1 slightly as
![]() $h_\omega $
is not a Hölder function of
$h_\omega $
is not a Hölder function of
![]() $\omega $
. Instead, we consider
$\omega $
. Instead, we consider ![]() and use that, by equation (5.11),
and use that, by equation (5.11),
Note that
![]() $h^i_{\omega }$
is the ith approximate to
$h^i_{\omega }$
is the ith approximate to
![]() $h_{\omega }$
in the pullback construction of
$h_{\omega }$
in the pullback construction of
![]() $h_{\omega }$
. Let
$h_{\omega }$
. Let
![]() $\nu _\omega ^i$
be the measure such that
$\nu _\omega ^i$
be the measure such that
![]() ${d \nu _\omega ^i}/{dm} = h_\omega ^i$
.
${d \nu _\omega ^i}/{dm} = h_\omega ^i$
.
Consider
By equation (5.12), on the set
![]() $[\delta , 1]$
, the densities involved (
$[\delta , 1]$
, the densities involved (
![]() $h_\omega ^k, h_\omega , h=d \nu /d m$
) are uniformly bounded above and away from zero. Thus,
$h_\omega ^k, h_\omega , h=d \nu /d m$
) are uniformly bounded above and away from zero. Thus,
![]() $\|f_n^i \|_\infty = {\mathcal O}(n^{-1})$
.
$\|f_n^i \|_\infty = {\mathcal O}(n^{-1})$
.
Pick
![]() $0<a<1$
such that
$0<a<1$
such that
![]() $\beta :=(({1}/{\gamma _{\mathrm {max}}})-1)a -1>0$
.
$\beta :=(({1}/{\gamma _{\mathrm {max}}})-1)a -1>0$
.
For a given n, take
![]() $i=i_n=n^a$
. By equation (7.1), for all
$i=i_n=n^a$
. By equation (7.1), for all
![]() $\omega $
, n, and
$\omega $
, n, and
![]() $i=n^a$
,
$i=n^a$
,
Then
and
 $$ \begin{align*} \bigg|\sum_{r=0}^{kn - 1} [f_{n}^i (\sigma^r \omega)-f_n (\sigma^r \omega)] \bigg|\le C \ell n^{-\beta}. \end{align*} $$
$$ \begin{align*} \bigg|\sum_{r=0}^{kn - 1} [f_{n}^i (\sigma^r \omega)-f_n (\sigma^r \omega)] \bigg|\le C \ell n^{-\beta}. \end{align*} $$
Given
![]() $\epsilon $
, choose n large enough that for all
$\epsilon $
, choose n large enough that for all
![]() $0 \le k \le \ell $
,
$0 \le k \le \ell $
,
 $$ \begin{align*} \bigg\{ \omega \in \Omega : \bigg| \sum_{r=0}^{kn -1} (f_n (\sigma^r \omega)- \overline{f}_n) \bigg|>\epsilon\bigg\} \subset \bigg\{ \omega \in \Omega : \bigg| \sum_{r=0}^{kn-1} (f^i_n (\sigma^r \omega)-\overline{f}^i_n) \bigg| >\frac{\epsilon}{2}\bigg\}. \end{align*} $$
$$ \begin{align*} \bigg\{ \omega \in \Omega : \bigg| \sum_{r=0}^{kn -1} (f_n (\sigma^r \omega)- \overline{f}_n) \bigg|>\epsilon\bigg\} \subset \bigg\{ \omega \in \Omega : \bigg| \sum_{r=0}^{kn-1} (f^i_n (\sigma^r \omega)-\overline{f}^i_n) \bigg| >\frac{\epsilon}{2}\bigg\}. \end{align*} $$
By Chebyshev,
 $$ \begin{align*} &{\mathbb P} \bigg(\ \bigg| \sum_{r=0}^{kn-1} (f^i_n \circ \sigma^r-\overline{f}^i_n)\bigg|>\frac{\epsilon}{2}\bigg) \le \frac{4}{\epsilon^2} \sum_{r=0}^{kn-1} {\mathbb E}_{{\mathbb P}} \bigg( [f_n^i \circ \sigma^r -\overline{f}^i_n]^2 \bigg)\\ &\quad +\frac{4}{\epsilon^2} \bigg[2 \sum_{r=0}^{kn-1} \sum_{u=r+1}^{kn-1} | {\mathbb E}_{{\mathbb P}}[(f^i_n \circ \sigma^r -\overline{f}^i_n)(f_n^i \circ\sigma^u-\overline{f}^i_n)]|\bigg]. \end{align*} $$
$$ \begin{align*} &{\mathbb P} \bigg(\ \bigg| \sum_{r=0}^{kn-1} (f^i_n \circ \sigma^r-\overline{f}^i_n)\bigg|>\frac{\epsilon}{2}\bigg) \le \frac{4}{\epsilon^2} \sum_{r=0}^{kn-1} {\mathbb E}_{{\mathbb P}} \bigg( [f_n^i \circ \sigma^r -\overline{f}^i_n]^2 \bigg)\\ &\quad +\frac{4}{\epsilon^2} \bigg[2 \sum_{r=0}^{kn-1} \sum_{u=r+1}^{kn-1} | {\mathbb E}_{{\mathbb P}}[(f^i_n \circ \sigma^r -\overline{f}^i_n)(f_n^i \circ\sigma^u-\overline{f}^i_n)]|\bigg]. \end{align*} $$
We bound
 $$ \begin{align*} \sum_{r=0}^{kn-1} {\mathbb E}_{{\mathbb P}} ( [f_n^i -\overline{f}^i_n]^2 ) \le C \sum_{r=0}^{kn-1} \|f_n^i\|_\infty^2 \le \frac{C \ell}{ n} \end{align*} $$
$$ \begin{align*} \sum_{r=0}^{kn-1} {\mathbb E}_{{\mathbb P}} ( [f_n^i -\overline{f}^i_n]^2 ) \le C \sum_{r=0}^{kn-1} \|f_n^i\|_\infty^2 \le \frac{C \ell}{ n} \end{align*} $$
and note that if
![]() $|r-u|>n^{a}$
, then by independence,
$|r-u|>n^{a}$
, then by independence,
and hence, we may bound
 $$ \begin{align*} \sum_{r=0}^{kn-1} \sum_{u=r+1}^{kn-1} | {\mathbb E}_{{\mathbb P}}[(f^i_n \circ \sigma^r -\overline{f}^i_n)(f_n^i \circ\sigma^u-\overline{f}^i_n)]| \le \frac{C \ell}{n^{1-a}}. \end{align*} $$
$$ \begin{align*} \sum_{r=0}^{kn-1} \sum_{u=r+1}^{kn-1} | {\mathbb E}_{{\mathbb P}}[(f^i_n \circ \sigma^r -\overline{f}^i_n)(f_n^i \circ\sigma^u-\overline{f}^i_n)]| \le \frac{C \ell}{n^{1-a}}. \end{align*} $$
Thus, for n large enough,
 $$ \begin{align*} {\mathbb P} \bigg( \bigg\{ \omega \in \Omega : \bigg| \sum_{r=0}^{kn-1} [f_n (\sigma^r \omega)-\overline{f}_n]\bigg|>\epsilon \bigg\}\bigg) \le \frac{C\ell}{n^{1-a}\epsilon^2}. \end{align*} $$
$$ \begin{align*} {\mathbb P} \bigg( \bigg\{ \omega \in \Omega : \bigg| \sum_{r=0}^{kn-1} [f_n (\sigma^r \omega)-\overline{f}_n]\bigg|>\epsilon \bigg\}\bigg) \le \frac{C\ell}{n^{1-a}\epsilon^2}. \end{align*} $$
The rest of the argument proceeds as in the case of Lemma 7.1 using a speedup along a sequence
![]() $n=p^{1+\eta }$
, where
$n=p^{1+\eta }$
, where
![]() $\eta>{a}/({1-a})$
, since
$\eta>{a}/({1-a})$
, since
![]() $\|f_n\|_\infty = {\mathcal O}(n^{-1})$
still holds.
$\|f_n\|_\infty = {\mathcal O}(n^{-1})$
still holds.
7.2. Criteria for stable laws and functional limit laws
The next theorem shows that for regularly varying observables, Poisson convergence and Condition U imply convergence in the
![]() $J_1$
topology if
$J_1$
topology if
![]() $\alpha \in (0,1)$
and gives an additional condition to be verified in the case
$\alpha \in (0,1)$
and gives an additional condition to be verified in the case
![]() $\alpha \in [1,2)$
.
$\alpha \in [1,2)$
.
Note that equation (7.2) is essentially the condition in equation (5.5) of Proposition 5.7.
Theorem 7.3. Assume
![]() $\phi $
is regularly varying, Condition U holds, and that
$\phi $
is regularly varying, Condition U holds, and that
for
![]() ${\mathbb P}$
-a.e.
${\mathbb P}$
-a.e.
![]() $\omega \in \Omega $
.
$\omega \in \Omega $
.
If
![]() $\alpha \in [1, 2)$
, assume furthermore that for all
$\alpha \in [1, 2)$
, assume furthermore that for all
![]() $\delta> 0$
and
$\delta> 0$
and
![]() ${\mathbb P}$
-a.e.
${\mathbb P}$
-a.e.
![]() $\omega \in \Omega $
,
$\omega \in \Omega $
,

Then
![]() $X_n^\omega \, {\stackrel {d}{\to } \,} X_{(\alpha )}$
in
$X_n^\omega \, {\stackrel {d}{\to } \,} X_{(\alpha )}$
in
![]() ${\mathbb D}[0, \infty )$
under the probability measure
${\mathbb D}[0, \infty )$
under the probability measure
![]() $\nu ^\omega $
for
$\nu ^\omega $
for
![]() ${\mathbb P}$
-a.e.
${\mathbb P}$
-a.e.
![]() $\omega \in \Omega $
.
$\omega \in \Omega $
.
Remark 7.4. From equation (5.8) and Theorem 5.1, it follows that the convergence of
![]() $X_n^\omega $
also holds under the probability measure
$X_n^\omega $
also holds under the probability measure
![]() $\nu $
.
$\nu $
.
Proof of Theorem 7.3
When
![]() $\alpha \in (0,1)$
, we check the hypothesis of Proposition 5.4. Using equation (5.8), we have
$\alpha \in (0,1)$
, we check the hypothesis of Proposition 5.4. Using equation (5.8), we have

Using Proposition 3.2, we see that the condition in equation (5.3) is satisfied since
![]() $\alpha <1$
, thus proving the theorem in this case.
$\alpha <1$
, thus proving the theorem in this case.
When
![]() $\alpha \in [1,2)$
, we consider instead Proposition 5.7. First, we remark that the condition in equation (5.5) is implied by equations (7.2) and (5.8). It remains to check the condition in equation (5.4), which constitutes the rest of the proof.
$\alpha \in [1,2)$
, we consider instead Proposition 5.7. First, we remark that the condition in equation (5.5) is implied by equations (7.2) and (5.8). It remains to check the condition in equation (5.4), which constitutes the rest of the proof.
If
![]() $\alpha \in (1,2)$
, we have
$\alpha \in (1,2)$
, we have

with
 $$ \begin{align*} A_n^\omega(t) = \bigg| \frac{1}{b_n} \bigg[ \sum_{j=0}^{\lfloor nt \rfloor - 1} {\mathbb E}_{\nu^{\sigma^j \omega}}(\phi) - t c_n \bigg] \bigg|, \end{align*} $$
$$ \begin{align*} A_n^\omega(t) = \bigg| \frac{1}{b_n} \bigg[ \sum_{j=0}^{\lfloor nt \rfloor - 1} {\mathbb E}_{\nu^{\sigma^j \omega}}(\phi) - t c_n \bigg] \bigg|, \end{align*} $$

and

Since
![]() $\phi $
is regularity varying with index
$\phi $
is regularity varying with index
![]() $\alpha>1$
, it is integrable and the function
$\alpha>1$
, it is integrable and the function
![]() ${\omega \mapsto {\mathbb E}_{\nu ^\omega }(\phi )}$
is Hölder. Hence, it satisfies the law of the iterated logarithm, and we have for
${\omega \mapsto {\mathbb E}_{\nu ^\omega }(\phi )}$
is Hölder. Hence, it satisfies the law of the iterated logarithm, and we have for
![]() ${\mathbb P}$
-a.e.
${\mathbb P}$
-a.e.
![]() $\omega \in \Omega $
,
$\omega \in \Omega $
,
 $$ \begin{align*} \bigg|\frac{1}{k} \sum_{j=0}^{k-1} {\mathbb E}_{\nu^{\sigma^j \omega}}(\phi) - {\mathbb E}_\nu(\phi) \bigg| = {\mathcal O}\bigg( \frac{\sqrt{\log \log k}}{\sqrt k}\bigg). \end{align*} $$
$$ \begin{align*} \bigg|\frac{1}{k} \sum_{j=0}^{k-1} {\mathbb E}_{\nu^{\sigma^j \omega}}(\phi) - {\mathbb E}_\nu(\phi) \bigg| = {\mathcal O}\bigg( \frac{\sqrt{\log \log k}}{\sqrt k}\bigg). \end{align*} $$
Thus, we have
 $$ \begin{align*} \sup_{0 \le t \le \ell} A_n^\omega(t) = \mathcal{O} \bigg( \frac{\sqrt{n \ell} \sqrt{\log \log (n \ell)}}{b_n} \bigg). \end{align*} $$
$$ \begin{align*} \sup_{0 \le t \le \ell} A_n^\omega(t) = \mathcal{O} \bigg( \frac{\sqrt{n \ell} \sqrt{\log \log (n \ell)}}{b_n} \bigg). \end{align*} $$
As a consequence, we can deduce that
![]() $\lim _{n \to \infty } \sup _{0 \le t \le \ell } A_n^\omega (t) = 0 $
since
$\lim _{n \to \infty } \sup _{0 \le t \le \ell } A_n^\omega (t) = 0 $
since
![]() $b_n = n^{\frac {1}{\alpha }} \widetilde {L}(n)$
for a slowly varying function
$b_n = n^{\frac {1}{\alpha }} \widetilde {L}(n)$
for a slowly varying function
![]() $\widetilde {L}$
, with
$\widetilde {L}$
, with
![]() $\alpha <2$
.
$\alpha <2$
.
By Proposition 3.2, we also have
In particular, we have
This also implies that
![]() ${\mathbb E}_m(| \chi _n| ) = {\mathcal O}(n^{-1})$
if we define
${\mathbb E}_m(| \chi _n| ) = {\mathcal O}(n^{-1})$
if we define ![]() . From Lemma 7.1, it follows that
. From Lemma 7.1, it follows that
![]() $\lim _{n \to \infty } \sup _{0 \le t \le \ell } B_{n, \epsilon }^\omega (t) = 0$
.
$\lim _{n \to \infty } \sup _{0 \le t \le \ell } B_{n, \epsilon }^\omega (t) = 0$
.
Putting all these estimates together concludes the proof when
![]() $\alpha \in (1,2)$
.
$\alpha \in (1,2)$
.
When
![]() $\alpha = 1$
, we estimate the right-hand side of equation (7.3) by
$\alpha = 1$
, we estimate the right-hand side of equation (7.3) by
![]() $A_{n, \epsilon }^\omega (t) + B_{n, \epsilon }^\omega (t)$
with
$A_{n, \epsilon }^\omega (t) + B_{n, \epsilon }^\omega (t)$
with

and

We define ![]() . By Proposition 3.2, we have
. By Proposition 3.2, we have
![]() ${\mathbb E}_m(| \chi _n |) = {\mathcal O}(n^{-1} \widetilde {L}(n))$
for some slowly varying function
${\mathbb E}_m(| \chi _n |) = {\mathcal O}(n^{-1} \widetilde {L}(n))$
for some slowly varying function
![]() $\widetilde {L}$
, and so by Lemma 7.1,
$\widetilde {L}$
, and so by Lemma 7.1,
However, by Proposition 3.2, we have
and so
![]() $\lim _{n \to \infty } \sup _{0 \le t \le \ell } B_{n, \epsilon }^\omega (t) = 0$
which completes the proof.
$\lim _{n \to \infty } \sup _{0 \le t \le \ell } B_{n, \epsilon }^\omega (t) = 0$
which completes the proof.
8. An exponential law
We denote by
![]() ${\mathcal J}$
the family of all finite unions of intervals of the form
${\mathcal J}$
the family of all finite unions of intervals of the form
![]() $(x, y]$
, where
$(x, y]$
, where
![]() ${- \infty \le x < y \le \infty }$
and
${- \infty \le x < y \le \infty }$
and
![]() $0 \notin [x,y]$
. For
$0 \notin [x,y]$
. For
![]() $J \in {\mathcal J}$
, we will establish a quenched exponential law for the sequence of sets
$J \in {\mathcal J}$
, we will establish a quenched exponential law for the sequence of sets
![]() $A_n = (\phi _{x_0})^{-1}(b_n J)$
. Similar results were obtained in [Reference Crimmins and FroylandCF20, Reference Freitas, Freitas and VaientiFFV17, Reference Haydn, Rousseau and YangHRY20, Reference Rousseau, Saussol and VarandasRSV14, Reference Rousseau and ToddRT15].
$A_n = (\phi _{x_0})^{-1}(b_n J)$
. Similar results were obtained in [Reference Crimmins and FroylandCF20, Reference Freitas, Freitas and VaientiFFV17, Reference Haydn, Rousseau and YangHRY20, Reference Rousseau, Saussol and VarandasRSV14, Reference Rousseau and ToddRT15].
Since
![]() $\phi $
is regularly varying, it is easy to verify that
$\phi $
is regularly varying, it is easy to verify that
In particular,
![]() $ m(A_n) = {\mathcal O}(n^{-1})$
.
$ m(A_n) = {\mathcal O}(n^{-1})$
.
Lemma 8.1. Assume Condition U and that
![]() $\phi $
is regularly varying with index
$\phi $
is regularly varying with index
![]() $\alpha $
.
$\alpha $
.
If
![]() $A_n \subset [0,1]$
is a sequence of measurable subsets such that
$A_n \subset [0,1]$
is a sequence of measurable subsets such that
![]() $m(A_n) = {\mathcal O}(n^{-1})$
, then for all
$m(A_n) = {\mathcal O}(n^{-1})$
, then for all
![]() $0 \le s < t$
,
$0 \le s < t$
,
 $$ \begin{align*} \lim_{n \to \infty} \bigg(\bigg[ \sum_{j=\lfloor ns \rfloor +1}^{\lfloor nt \rfloor} \nu^{\sigma^j \omega}(A_n) \bigg] - n(t-s) \nu(A_n) \bigg) = 0. \end{align*} $$
$$ \begin{align*} \lim_{n \to \infty} \bigg(\bigg[ \sum_{j=\lfloor ns \rfloor +1}^{\lfloor nt \rfloor} \nu^{\sigma^j \omega}(A_n) \bigg] - n(t-s) \nu(A_n) \bigg) = 0. \end{align*} $$
The same result holds in the setting of intermittent maps if
![]() $A_n \subset [\delta , 1]$
for some
$A_n \subset [\delta , 1]$
for some
![]() $\delta>0$
with
$\delta>0$
with
![]() $m(A_n) = {\mathcal O}(n^{-1})$
. In particular, if
$m(A_n) = {\mathcal O}(n^{-1})$
. In particular, if
![]() $A_n = \phi _{x_0}^{-1}(b_n J)$
for
$A_n = \phi _{x_0}^{-1}(b_n J)$
for
![]() $J \in {\mathcal J}$
and
$J \in {\mathcal J}$
and
![]() $x_0 \neq 0$
, then for all
$x_0 \neq 0$
, then for all
![]() $0 \le s < t$
,
$0 \le s < t$
,
 $$ \begin{align*} \lim_{n \to \infty} \sum_{j=\lfloor ns \rfloor+1}^{\lfloor nt \rfloor} \nu^{\sigma^j \omega}(A_n) = (t-s) \Pi_\alpha(J). \end{align*} $$
$$ \begin{align*} \lim_{n \to \infty} \sum_{j=\lfloor ns \rfloor+1}^{\lfloor nt \rfloor} \nu^{\sigma^j \omega}(A_n) = (t-s) \Pi_\alpha(J). \end{align*} $$
Proof. For the first statement, it suffices to apply Lemma 7.1 or Lemma 7.2 with ![]() . The second statement immediately follows since
. The second statement immediately follows since
![]() $\lim _n n \nu (A_n) = \Pi _\alpha (J)$
.
$\lim _n n \nu (A_n) = \Pi _\alpha (J)$
.
Corollary 8.2. Assume the hypothesis of Lemma 8.1.
Let
![]() $J \in {\mathcal J}$
and set
$J \in {\mathcal J}$
and set
![]() $A_n = \phi ^{-1}(b_n J)$
. Then for
$A_n = \phi ^{-1}(b_n J)$
. Then for
![]() ${\mathbb P}$
-a.e.
${\mathbb P}$
-a.e.
![]() $ \omega \in \Omega $
and all
$ \omega \in \Omega $
and all
![]() $0 \le s < t$
,
$0 \le s < t$
,
 $$ \begin{align*} \lim_{n \to \infty} \prod_{j=\lfloor ns \rfloor +1}^{\lfloor nt \rfloor} ( 1 - \nu^{\sigma^j \omega}(A_n)) = e^{-(t-s) \Pi_\alpha(J)}. \end{align*} $$
$$ \begin{align*} \lim_{n \to \infty} \prod_{j=\lfloor ns \rfloor +1}^{\lfloor nt \rfloor} ( 1 - \nu^{\sigma^j \omega}(A_n)) = e^{-(t-s) \Pi_\alpha(J)}. \end{align*} $$
Proof. Since
![]() $\nu ^{\omega }(A_n)$
is of order at most
$\nu ^{\omega }(A_n)$
is of order at most
![]() $n^{-1}$
uniformly in
$n^{-1}$
uniformly in
![]() $\omega \in \Omega $
, it follows that
$\omega \in \Omega $
, it follows that
 $$ \begin{align*} \log \bigg[\prod_{j=\lfloor ns \rfloor +1}^{\lfloor nt \rfloor} ( 1 - \nu^{\sigma^j \omega}(A_n)) \bigg] = - \bigg( \sum_{j=\lfloor ns \rfloor +1}^{\lfloor nt \rfloor} \nu^{\sigma^j \omega}(A_n) \bigg) + {\mathcal O}(n^{-1}). \end{align*} $$
$$ \begin{align*} \log \bigg[\prod_{j=\lfloor ns \rfloor +1}^{\lfloor nt \rfloor} ( 1 - \nu^{\sigma^j \omega}(A_n)) \bigg] = - \bigg( \sum_{j=\lfloor ns \rfloor +1}^{\lfloor nt \rfloor} \nu^{\sigma^j \omega}(A_n) \bigg) + {\mathcal O}(n^{-1}). \end{align*} $$
By Lemma 8.1,
 $$ \begin{align*} \lim_{n \to \infty} \sum_{j=\lfloor ns \rfloor}^{\lfloor nt \rfloor - 1} \nu^{\sigma^j \omega}(A_n) = (t-s) \Pi_\alpha(J), \end{align*} $$
$$ \begin{align*} \lim_{n \to \infty} \sum_{j=\lfloor ns \rfloor}^{\lfloor nt \rfloor - 1} \nu^{\sigma^j \omega}(A_n) = (t-s) \Pi_\alpha(J), \end{align*} $$
which yields the conclusion.
Definition 8.3. For a measurable subset
![]() $U \subset Y = [0,1]$
, we define the hitting time of
$U \subset Y = [0,1]$
, we define the hitting time of
![]() $(\omega , x) \in \Omega \times Y$
to U by
$(\omega , x) \in \Omega \times Y$
to U by
and the induced measure by
![]() $\nu $
on U by
$\nu $
on U by
To establish our exponential law, we will first obtain a few estimates, based on the proof of [Reference Hirata, Saussol and VaientiHSV99, Theorem 2.1], to relate
![]() $\nu ^\omega (R_{A_n}(\omega )> \lfloor nt \rfloor )$
to
$\nu ^\omega (R_{A_n}(\omega )> \lfloor nt \rfloor )$
to
![]() $\sum _{j=0}^{\lfloor nt \rfloor - 1} \nu ^{\sigma ^j \omega }(A_n)$
so that we are able to invoke Corollary 8.2.
$\sum _{j=0}^{\lfloor nt \rfloor - 1} \nu ^{\sigma ^j \omega }(A_n)$
so that we are able to invoke Corollary 8.2.
The next lemma is basically [Reference Rousseau, Saussol and VarandasRSV14, Lemma 6].
Lemma 8.4. For every measurable set
![]() $U \subset [0,1]$
, we have the bound
$U \subset [0,1]$
, we have the bound
 $$ \begin{align*} &\bigg| \nu^{\omega} (R_U(\omega)> k) - \prod_{j=1}^{k} (1-\nu^{\sigma^j \omega}(U)) \bigg|\\ &\quad\le \sum_{j=1}^k \nu^{\sigma^j\omega} (U) \; c_{\sigma^j \omega}(k-j, U) \prod_{i=1}^{j-1} (1-\nu^{\sigma^i \omega}(U)) \\ &\quad \le \sum_{j=1}^k \nu^{\sigma^j\omega} (U) \; c_{\sigma^j \omega}(U), \end{align*} $$
$$ \begin{align*} &\bigg| \nu^{\omega} (R_U(\omega)> k) - \prod_{j=1}^{k} (1-\nu^{\sigma^j \omega}(U)) \bigg|\\ &\quad\le \sum_{j=1}^k \nu^{\sigma^j\omega} (U) \; c_{\sigma^j \omega}(k-j, U) \prod_{i=1}^{j-1} (1-\nu^{\sigma^i \omega}(U)) \\ &\quad \le \sum_{j=1}^k \nu^{\sigma^j\omega} (U) \; c_{\sigma^j \omega}(U), \end{align*} $$
where
and
Proof. Note that
![]() $\{R_U(\omega )> k\}=[T_{\omega }^{1}]^{-1} (U^c \cap \{R_U(\sigma \omega ) > k-1\})$
and so, using the equivariance of
$\{R_U(\omega )> k\}=[T_{\omega }^{1}]^{-1} (U^c \cap \{R_U(\sigma \omega ) > k-1\})$
and so, using the equivariance of
![]() $\{\nu ^\omega \}_{\omega \in \Omega }$
,
$\{\nu ^\omega \}_{\omega \in \Omega }$
,
Hence,
We note that
 $$ \begin{align*} \nu^{\omega} (R_U(\omega)> k) &=\nu^{\sigma \omega} (R_U(\sigma \omega) > k-1)\\&\quad -\nu^{\sigma \omega} (U) [\nu^{\sigma \omega} (R_U(\sigma \omega) > k-1 )+ c_{\sigma\omega}(k-1,U)] \\ & = (1 - \nu^{\sigma \omega}(U)) \nu^{\sigma \omega}(R_U(\sigma \omega) > k-1) - \nu^{\sigma \omega}(U) c_{\sigma \omega}(k-1, U). \end{align*} $$
$$ \begin{align*} \nu^{\omega} (R_U(\omega)> k) &=\nu^{\sigma \omega} (R_U(\sigma \omega) > k-1)\\&\quad -\nu^{\sigma \omega} (U) [\nu^{\sigma \omega} (R_U(\sigma \omega) > k-1 )+ c_{\sigma\omega}(k-1,U)] \\ & = (1 - \nu^{\sigma \omega}(U)) \nu^{\sigma \omega}(R_U(\sigma \omega) > k-1) - \nu^{\sigma \omega}(U) c_{\sigma \omega}(k-1, U). \end{align*} $$
Iterating we obtain, using the fact that for
![]() ${\mathbb P}$
-a.e.
${\mathbb P}$
-a.e.
![]() $\omega $
,
$\omega $
,
![]() $\nu ^{\omega } (R_U(\omega )\ge 1)=1$
,
$\nu ^{\omega } (R_U(\omega )\ge 1)=1$
,
 $$ \begin{align*} \nu^{\omega} (R_U(\omega)> k)= \prod_{j=1}^{k} (1-\nu^{\sigma^j \omega}(U)) - \sum_{j=1}^k \nu^{\sigma^j\omega} (U) c_{\sigma^j \omega}(k-j, U) \prod_{i=1}^{j-1} (1-\nu^{\sigma^i \omega}(U)), \end{align*} $$
$$ \begin{align*} \nu^{\omega} (R_U(\omega)> k)= \prod_{j=1}^{k} (1-\nu^{\sigma^j \omega}(U)) - \sum_{j=1}^k \nu^{\sigma^j\omega} (U) c_{\sigma^j \omega}(k-j, U) \prod_{i=1}^{j-1} (1-\nu^{\sigma^i \omega}(U)), \end{align*} $$
which yields the conclusion.
We will estimate now the coefficients
![]() $c_\omega (U)$
.
$c_\omega (U)$
.
Lemma 8.5. For any measurable subset
![]() $U \subset Y$
such that
$U \subset Y$
such that ![]() , we have, for all N,
, we have, for all N,
and
 $$ \begin{align} \nu_U^{\omega} (R_U(\omega) \le N) \le \frac{1}{\nu^\omega(U)} \nu^{\omega} (R_U(\omega) \le N), \quad \nu^{\omega} (R_U(\omega) \le N) \le \sum_{i=1}^N \nu^{\sigma^i \omega}(U). \end{align} $$
$$ \begin{align} \nu_U^{\omega} (R_U(\omega) \le N) \le \frac{1}{\nu^\omega(U)} \nu^{\omega} (R_U(\omega) \le N), \quad \nu^{\omega} (R_U(\omega) \le N) \le \sum_{i=1}^N \nu^{\sigma^i \omega}(U). \end{align} $$
Proof. The estimates in equation (8.2) follow from
 $$ \begin{align*} \{R_U(\omega) \le N\} = \bigcup_{i=1}^N (T^i_\omega)^{-1}(U), \end{align*} $$
$$ \begin{align*} \{R_U(\omega) \le N\} = \bigcup_{i=1}^N (T^i_\omega)^{-1}(U), \end{align*} $$
and therefore
 $$ \begin{align*} \nu^{\omega} (R_U(\omega) \le N) \le \sum_{i=1}^N \nu^{\sigma^i \omega}(U). \end{align*} $$
$$ \begin{align*} \nu^{\omega} (R_U(\omega) \le N) \le \sum_{i=1}^N \nu^{\sigma^i \omega}(U). \end{align*} $$
For equation (8.1), note that
If
![]() $j \le N$
, then
$j \le N$
, then
If
![]() $j> N$
, we write
$j> N$
, we write
 $$ \begin{align*} &\nu_U^{\omega} (R_U(\omega) \le j)-\nu^{\omega} (R_U(\omega) \le j)\\ &\quad=~\nu_U^{\omega} (R_U(\omega) \le j) - \nu_{U}^{\omega}(T_{\omega}^{-N} (R_U(\sigma^N \omega) \le j-N)) \\ &\qquad+~ \nu_{U}^{\omega}(T_{\omega}^{-N} (R_U(\sigma^N \omega) \le j-N)) - \nu^{\omega}(T_{\omega}^{-N} (R_U(\sigma^N \omega) \le j-N)) \\ &\qquad+~\nu^{\omega}(T_{\omega}^{-N} (R_U(\sigma^N \omega) \le j-N))-\nu^{\omega} (R_U(\omega) \le j) \\ &\quad= (a) + (b) + (c). \end{align*} $$
$$ \begin{align*} &\nu_U^{\omega} (R_U(\omega) \le j)-\nu^{\omega} (R_U(\omega) \le j)\\ &\quad=~\nu_U^{\omega} (R_U(\omega) \le j) - \nu_{U}^{\omega}(T_{\omega}^{-N} (R_U(\sigma^N \omega) \le j-N)) \\ &\qquad+~ \nu_{U}^{\omega}(T_{\omega}^{-N} (R_U(\sigma^N \omega) \le j-N)) - \nu^{\omega}(T_{\omega}^{-N} (R_U(\sigma^N \omega) \le j-N)) \\ &\qquad+~\nu^{\omega}(T_{\omega}^{-N} (R_U(\sigma^N \omega) \le j-N))-\nu^{\omega} (R_U(\omega) \le j) \\ &\quad= (a) + (b) + (c). \end{align*} $$
To bound terms (a) and (c), note that
so
and similarly for
![]() $\nu _U^{\omega }$
.
$\nu _U^{\omega }$
.
To bound term (b), we use the decay of
![]() $P_\omega ^k$
. Setting
$P_\omega ^k$
. Setting
![]() $V = \{ R_U(\sigma ^N \omega ) \le j - N \}$
, we have
$V = \{ R_U(\sigma ^N \omega ) \le j - N \}$
, we have

8.1. Exponential law: proof of Theorem 6.1
We can now prove the exponential law for
![]() $A_n = \phi ^{-1}(b_n J)$
,
$A_n = \phi ^{-1}(b_n J)$
,
![]() $J \in {\mathcal J}$
.
$J \in {\mathcal J}$
.
Proof of Theorem 6.1
Due to rounding errors when taking the integer parts, we have
 $$ \begin{align*} &| \nu^{\sigma^{\lfloor ns \rfloor}\omega} (R_{A_n}(\sigma^{\lfloor ns \rfloor}\omega)> \lfloor n(t-s) \rfloor) - \nu^{\sigma^{\lfloor ns \rfloor}\omega} (R_{A_n}(\sigma^{\lfloor ns \rfloor}\omega) > \lfloor nt \rfloor - \lfloor ns \rfloor )| \\ &\quad\le \nu^{\sigma^{\lfloor nt \rfloor}\omega}(A_n) \le C m(A_n) \to 0, \end{align*} $$
$$ \begin{align*} &| \nu^{\sigma^{\lfloor ns \rfloor}\omega} (R_{A_n}(\sigma^{\lfloor ns \rfloor}\omega)> \lfloor n(t-s) \rfloor) - \nu^{\sigma^{\lfloor ns \rfloor}\omega} (R_{A_n}(\sigma^{\lfloor ns \rfloor}\omega) > \lfloor nt \rfloor - \lfloor ns \rfloor )| \\ &\quad\le \nu^{\sigma^{\lfloor nt \rfloor}\omega}(A_n) \le C m(A_n) \to 0, \end{align*} $$
and it is thus enough to prove the convergence of
![]() $\nu ^{\sigma ^{\lfloor ns \rfloor }\omega } (R_{A_n}(\sigma ^{\lfloor ns \rfloor }\omega )> \lfloor nt \rfloor - \lfloor ns \rfloor )$
.
$\nu ^{\sigma ^{\lfloor ns \rfloor }\omega } (R_{A_n}(\sigma ^{\lfloor ns \rfloor }\omega )> \lfloor nt \rfloor - \lfloor ns \rfloor )$
.
By Lemmas 8.4 and 8.5, for all
![]() $N \ge 1$
, we have
$N \ge 1$
, we have
 $$ \begin{align} \bigg| \nu^{\sigma^{\lfloor ns \rfloor}\omega} (R_{A_n}(\sigma^{\lfloor ns \rfloor}\omega)> \lfloor nt \rfloor - \lfloor ns \rfloor ) - \prod_{j = \lfloor ns \rfloor +1}^{\lfloor nt \rfloor} (1 - \nu^{\sigma^j \omega}(A_n) )\bigg| \le \mathrm{(I)} + \mathrm{(II)} + \mathrm{(III)}, \end{align} $$
$$ \begin{align} \bigg| \nu^{\sigma^{\lfloor ns \rfloor}\omega} (R_{A_n}(\sigma^{\lfloor ns \rfloor}\omega)> \lfloor nt \rfloor - \lfloor ns \rfloor ) - \prod_{j = \lfloor ns \rfloor +1}^{\lfloor nt \rfloor} (1 - \nu^{\sigma^j \omega}(A_n) )\bigg| \le \mathrm{(I)} + \mathrm{(II)} + \mathrm{(III)}, \end{align} $$
with
 $$ \begin{align*} \mathrm{(I)} = \sum_{j = \lfloor ns \rfloor +1}^{\lfloor nt \rfloor}\nu^{\sigma^j \omega}(A_n \cap \{R_{A_n}(\sigma^j \omega) \le N \}), \end{align*} $$
$$ \begin{align*} \mathrm{(I)} = \sum_{j = \lfloor ns \rfloor +1}^{\lfloor nt \rfloor}\nu^{\sigma^j \omega}(A_n \cap \{R_{A_n}(\sigma^j \omega) \le N \}), \end{align*} $$
 $$ \begin{align*} \mathrm{(II)} = \sum_{j = \lfloor ns \rfloor +1}^{\lfloor nt \rfloor} \nu^{\sigma^j \omega}(A_n) \nu^{\sigma^j \omega}(R_{A_n}(\sigma^j \omega) \le N), \end{align*} $$
$$ \begin{align*} \mathrm{(II)} = \sum_{j = \lfloor ns \rfloor +1}^{\lfloor nt \rfloor} \nu^{\sigma^j \omega}(A_n) \nu^{\sigma^j \omega}(R_{A_n}(\sigma^j \omega) \le N), \end{align*} $$
and

To estimate (I), we choose
![]() $\epsilon> 0$
such that
$\epsilon> 0$
such that
![]() $J \subset \{ |x|> \epsilon \}$
and we introduce
$J \subset \{ |x|> \epsilon \}$
and we introduce
![]() ${V_n = \{ | \phi |> \epsilon b_n \}}$
. For a measurable subset
${V_n = \{ | \phi |> \epsilon b_n \}}$
. For a measurable subset
![]() $V \subset Y$
, we also define the shortest return to V by
$V \subset Y$
, we also define the shortest return to V by
and we set
We have

It follows from condition (Dec) that

as BV is a Banach algebra, and both ![]() and
and
![]() $\|h_{\sigma ^j \omega } \|_{\mathrm { BV}}$
are uniformly bounded. (Recall that, from the definition of
$\|h_{\sigma ^j \omega } \|_{\mathrm { BV}}$
are uniformly bounded. (Recall that, from the definition of
![]() $\phi $
, it follows that
$\phi $
, it follows that
![]() $V_n$
is an open interval, and thus
$V_n$
is an open interval, and thus ![]() has a uniformly bounded BV norm.)
has a uniformly bounded BV norm.)
Consequently,
 $$ \begin{align*} \mathrm{(I)} & \le \sum_{j = \lfloor ns \rfloor +1}^{\lfloor nt \rfloor} \sum_{i=r_{\sigma^j \omega}(V_n)}^N [ \nu^{\sigma^j \omega}(V_n) \nu^{\sigma^{i+j} \omega}(V_n) + {\mathcal O}( \theta^i m(V_n))] \\ & \le C (m(V_n)^2 n N + m(V_n) n \theta^{r(V_n)} ). \end{align*} $$
$$ \begin{align*} \mathrm{(I)} & \le \sum_{j = \lfloor ns \rfloor +1}^{\lfloor nt \rfloor} \sum_{i=r_{\sigma^j \omega}(V_n)}^N [ \nu^{\sigma^j \omega}(V_n) \nu^{\sigma^{i+j} \omega}(V_n) + {\mathcal O}( \theta^i m(V_n))] \\ & \le C (m(V_n)^2 n N + m(V_n) n \theta^{r(V_n)} ). \end{align*} $$
However, we have by equation (8.2),
 $$ \begin{align*} \mathrm{(II)} & \le \sum_{j = \lfloor ns \rfloor +1}^{\lfloor nt \rfloor} \nu^{\sigma^j \omega}(A_n) \sum_{i=1}^N \nu^{\sigma^{i+j} \omega}(A_n) \\ & \le C n N m(A_n)^2, \end{align*} $$
$$ \begin{align*} \mathrm{(II)} & \le \sum_{j = \lfloor ns \rfloor +1}^{\lfloor nt \rfloor} \nu^{\sigma^j \omega}(A_n) \sum_{i=1}^N \nu^{\sigma^{i+j} \omega}(A_n) \\ & \le C n N m(A_n)^2, \end{align*} $$
and it follows from condition (Dec) that

since
![]() $\{h_\omega \}_{\omega \in \Omega }$
is a bounded family in BV,
$\{h_\omega \}_{\omega \in \Omega }$
is a bounded family in BV,
![]() $A_n$
is the union of at most two intervals, and thus
$A_n$
is the union of at most two intervals, and thus ![]() is uniformly bounded. We can thus bound equation (8.4) by
is uniformly bounded. We can thus bound equation (8.4) by
and, assuming for the moment that
![]() $r(V_n) \to + \infty $
, we obtain the conclusion by choosing
$r(V_n) \to + \infty $
, we obtain the conclusion by choosing
![]() $N = N(n) = 2 \log n$
and letting
$N = N(n) = 2 \log n$
and letting
![]() $n \to \infty $
.
$n \to \infty $
.
It thus remains to show that
![]() $r(V_n) \to + \infty $
. Recall that
$r(V_n) \to + \infty $
. Recall that
![]() $V_n$
is the ball of center
$V_n$
is the ball of center
![]() $x_0$
and radius
$x_0$
and radius
![]() $b^{-1} \epsilon ^{-\alpha } n^{-1}$
. Let
$b^{-1} \epsilon ^{-\alpha } n^{-1}$
. Let
![]() $R \ge 1$
be a positive integer. Since
$R \ge 1$
be a positive integer. Since
![]() $x_0$
is assumed to be non-recurrent, and that the collection of maps
$x_0$
is assumed to be non-recurrent, and that the collection of maps
![]() $T_\omega ^j$
for
$T_\omega ^j$
for
![]() $\omega \in \Omega $
and
$\omega \in \Omega $
and
![]() $0 \le j < R$
is finite, we have that
$0 \le j < R$
is finite, we have that
is positive. Since all the maps
![]() $T_\omega ^j$
are continuous at
$T_\omega ^j$
are continuous at
![]() $x_0$
by assumption, there exists
$x_0$
by assumption, there exists
![]() $n_R \ge 1$
such that for all
$n_R \ge 1$
such that for all
![]() $n \ge n_R$
,
$n \ge n_R$
,
![]() $j < R$
, and
$j < R$
, and
![]() $\omega \in \Omega $
,
$\omega \in \Omega $
,
Increasing
![]() $n_R$
if necessary, we can assume that
$n_R$
if necessary, we can assume that
![]() $b^{-1} \epsilon ^{-\alpha } n^{-1} < ({\delta _R}/{2})$
for all
$b^{-1} \epsilon ^{-\alpha } n^{-1} < ({\delta _R}/{2})$
for all
![]() $n \ge n_R$
.
$n \ge n_R$
.
Then, for all
![]() $n \ge n_R$
,
$n \ge n_R$
,
![]() $\omega \in \Omega $
,
$\omega \in \Omega $
,
![]() $j < R$
, and
$j < R$
, and
![]() $x \in V_n$
, we have
$x \in V_n$
, we have
and thus
![]() $T_\omega ^j(x) \notin V_n$
.
$T_\omega ^j(x) \notin V_n$
.
This implies that
![]() $r(V_n)> R$
for all
$r(V_n)> R$
for all
![]() $n \ge n_R$
, which concludes the proof as R is arbitrary.
$n \ge n_R$
, which concludes the proof as R is arbitrary.
Remark 8.6. A quenched exponential law for random piecewise expanding maps of the interval is proved in [Reference Haydn, Rousseau and YangHRY20, Theorem 7.1]. Our proof follows the same standard approach. We are able to specify that Theorem 6.1 holds for non-recurrent
![]() $x_0$
, since our assumptions imply decay of correlations against
$x_0$
, since our assumptions imply decay of correlations against
![]() $L^1$
observables, which is known to be necessary for this purpose, see [Reference Aytaç, Freitas and VaientiAFV15, §3.1]. Our proof is shorter, as we consider the simpler setting of finitely many maps, which are all uniformly expanding. In addition, we use the exponential law in the intermittent case of [Reference Haydn, Rousseau and YangHRY20, Theorem 7.2] to establish the short returns condition of Lemma 8.7 below.
$L^1$
observables, which is known to be necessary for this purpose, see [Reference Aytaç, Freitas and VaientiAFV15, §3.1]. Our proof is shorter, as we consider the simpler setting of finitely many maps, which are all uniformly expanding. In addition, we use the exponential law in the intermittent case of [Reference Haydn, Rousseau and YangHRY20, Theorem 7.2] to establish the short returns condition of Lemma 8.7 below.
8.2. Exponential law: proof of Theorem 6.2
To prove the exponential law in the intermittent setting, Theorem 6.2, we need a genericity condition on the point
![]() $x_0$
in the definition (2.1) of
$x_0$
in the definition (2.1) of
![]() $\phi _{x_0}$
.
$\phi _{x_0}$
.
Lemma 8.7. If
![]() $\gamma _{\mathrm {max}}<\tfrac 13$
, for m-a.e.
$\gamma _{\mathrm {max}}<\tfrac 13$
, for m-a.e.
![]() $x_0$
and for
$x_0$
and for
![]() ${\mathbb P}$
-a.e.
${\mathbb P}$
-a.e.
![]() $\omega \in \Omega $
,
$\omega \in \Omega $
,
 $$ \begin{align*} \lim_{n \to \infty} \sum_{j=\lfloor sn\rfloor +1}^{\lfloor tn \rfloor} m (B_{c n^{-1}}(x_0) \cap \{ R_{B_{c n^{-1}}(x_0)}^{\sigma^j \omega} \le \lfloor n (\log n)^{-1} \rfloor \} ) = 0 \end{align*} $$
$$ \begin{align*} \lim_{n \to \infty} \sum_{j=\lfloor sn\rfloor +1}^{\lfloor tn \rfloor} m (B_{c n^{-1}}(x_0) \cap \{ R_{B_{c n^{-1}}(x_0)}^{\sigma^j \omega} \le \lfloor n (\log n)^{-1} \rfloor \} ) = 0 \end{align*} $$
for all
![]() $c>0$
and all
$c>0$
and all
![]() $0 \le s < t$
.
$0 \le s < t$
.
Proof. Let
![]() $N = \lfloor n (\log n)^{-1} \rfloor $
an
$N = \lfloor n (\log n)^{-1} \rfloor $
an
![]() $V_n = B_{c n^{-1}}(x_0)$
. First, we remark that for m-a.e.
$V_n = B_{c n^{-1}}(x_0)$
. First, we remark that for m-a.e.
![]() $x_0$
and
$x_0$
and
![]() ${\mathbb P}$
-a.e.
${\mathbb P}$
-a.e.
![]() $\omega $
,
$\omega $
,
This is a consequence of [Reference Haydn, Rousseau and YangHRY20, Theorem 7.2]. Their result is stated for two intermittent LSV maps both with
![]() $\gamma <\tfrac 13$
but generalizes immediately to a finite collection of maps with a uniform bound of
$\gamma <\tfrac 13$
but generalizes immediately to a finite collection of maps with a uniform bound of
![]() $\gamma _{\mathrm {max}}<\tfrac 13$
. The exponential law for return times to nested balls implies that for a fixed t, for m-a.e
$\gamma _{\mathrm {max}}<\tfrac 13$
. The exponential law for return times to nested balls implies that for a fixed t, for m-a.e
![]() $x_0$
, and
$x_0$
, and
![]() ${\mathbb P}$
-a.e.
${\mathbb P}$
-a.e.
![]() $\omega $
,
$\omega $
,
which shows in particular, since
![]() $\{R_{V_n}(\omega ) \le N \} \subset \{R_{V_n}(\omega ) \le nt \}$
for all n large enough, that for all
$\{R_{V_n}(\omega ) \le N \} \subset \{R_{V_n}(\omega ) \le nt \}$
for all n large enough, that for all
![]() $t>0$
, m-a.e
$t>0$
, m-a.e
![]() $x_0$
, and
$x_0$
, and
![]() ${\mathbb P}$
-a.e.
${\mathbb P}$
-a.e.
![]() $\omega $
,
$\omega $
,
Using equation (5.12), taking the limit
![]() $t \to 0$
proves equation (8.5). Note that, even though the set of full measure of
$t \to 0$
proves equation (8.5). Note that, even though the set of full measure of
![]() $x_0$
and
$x_0$
and
![]() $\omega $
such that equation (8.6) holds may depend on t, it is enough to consider only a sequence
$\omega $
such that equation (8.6) holds may depend on t, it is enough to consider only a sequence
![]() $t_k \to 0$
.
$t_k \to 0$
.
Now, for
![]() $k \ge 0$
and
$k \ge 0$
and
![]() $n_0 \ge 1$
, we introduce the set
$n_0 \ge 1$
, we introduce the set
 $$ \begin{align*} \Omega_k^{n_0} = \bigg\{ \omega \in \Omega : m(V_n \cap \{R_{V_n}(\omega) \le N \} ) \le \frac{2^{-k}}{n} \text{ for all } n \ge n_0 \bigg\}. \end{align*} $$
$$ \begin{align*} \Omega_k^{n_0} = \bigg\{ \omega \in \Omega : m(V_n \cap \{R_{V_n}(\omega) \le N \} ) \le \frac{2^{-k}}{n} \text{ for all } n \ge n_0 \bigg\}. \end{align*} $$
According to equation (8.5), we have for all
![]() $k \ge 0$
,
$k \ge 0$
,
 $$ \begin{align*} \lim_{n_0 \to \infty} {\mathbb P}(\Omega_k^{n_0}) = {\mathbb P}\bigg( \bigcup_{n_0 \ge 1} \Omega_k^{n_0} \bigg) = 1. \end{align*} $$
$$ \begin{align*} \lim_{n_0 \to \infty} {\mathbb P}(\Omega_k^{n_0}) = {\mathbb P}\bigg( \bigcup_{n_0 \ge 1} \Omega_k^{n_0} \bigg) = 1. \end{align*} $$
By the Birkhoff ergodic theorem, for all
![]() $k \ge 0$
,
$k \ge 0$
,
![]() $n_0 \ge 1$
, and
$n_0 \ge 1$
, and
![]() ${\mathbb P}$
-a.e.
${\mathbb P}$
-a.e.
![]() $\omega $
,
$\omega $
,

which implies that for all
![]() $0 \le s < t$
,
$0 \le s < t$
,

Let
![]() $n_0 = n_0(\omega , k)$
such that
$n_0 = n_0(\omega , k)$
such that
![]() ${\mathbb P}(\Omega _k^{n_0}) \ge 1 - 2^{-k}$
, and for all
${\mathbb P}(\Omega _k^{n_0}) \ge 1 - 2^{-k}$
, and for all
![]() $n \ge n_0$
,
$n \ge n_0$
,

Then, for all
![]() $n \ge n_0(\omega , k)$
, we have
$n \ge n_0(\omega , k)$
, we have

Consequently,
 $$ \begin{align*} \sum_{\lfloor ns \rfloor +1}^{\lfloor nt \rfloor} m(V_n \cap \{R_{V_n}(\omega) \le N \} ) \le (\lfloor nt \rfloor - \lfloor ns \rfloor ) \frac{2^{-k}}{n} + (\lfloor nt \rfloor - \lfloor ns \rfloor ) 2^{-(k-1)} m(V_n). \end{align*} $$
$$ \begin{align*} \sum_{\lfloor ns \rfloor +1}^{\lfloor nt \rfloor} m(V_n \cap \{R_{V_n}(\omega) \le N \} ) \le (\lfloor nt \rfloor - \lfloor ns \rfloor ) \frac{2^{-k}}{n} + (\lfloor nt \rfloor - \lfloor ns \rfloor ) 2^{-(k-1)} m(V_n). \end{align*} $$
This proves that
 $$ \begin{align*} \limsup_{n \to \infty} \sum_{\lfloor ns \rfloor +1}^{\lfloor nt \rfloor} m(V_n \cap \{R_{V_n}(\omega) \le N \} ) \le C \, 2^{-k} \end{align*} $$
$$ \begin{align*} \limsup_{n \to \infty} \sum_{\lfloor ns \rfloor +1}^{\lfloor nt \rfloor} m(V_n \cap \{R_{V_n}(\omega) \le N \} ) \le C \, 2^{-k} \end{align*} $$
and the result follows by taking the limit
![]() $k \to \infty $
.
$k \to \infty $
.
Note that the set of
![]() $x_0$
and
$x_0$
and
![]() $\omega $
for which the lemma holds depends a priori on
$\omega $
for which the lemma holds depends a priori on
![]() $c>0$
, but it is enough to consider a countable and dense set of c, since for
$c>0$
, but it is enough to consider a countable and dense set of c, since for
![]() $c < c'$
,
$c < c'$
,
The exponential law for random intermittent maps follows from Lemma 8.7.
Proof of Theorem 6.2
We consider the three terms in equation (8.4) with
![]() ${N = \lfloor n (\log n)^{-1} \rfloor }$
.
${N = \lfloor n (\log n)^{-1} \rfloor }$
.
Let
![]() $V_n = \{ | \phi |> \epsilon b_n\}$
, where
$V_n = \{ | \phi |> \epsilon b_n\}$
, where
![]() $\epsilon>0$
is such that
$\epsilon>0$
is such that
![]() $A_n \subset V_n$
for all
$A_n \subset V_n$
for all
![]() $n\ge 1$
. Since
$n\ge 1$
. Since
![]() $V_n$
is a ball of center
$V_n$
is a ball of center
![]() $x_0$
and radius
$x_0$
and radius
![]() $b^{-1} \epsilon ^{-\alpha } n^{-1}$
, and since
$b^{-1} \epsilon ^{-\alpha } n^{-1}$
, and since
![]() $V_n \subset [\delta , 1]$
, the term
$V_n \subset [\delta , 1]$
, the term
 $$ \begin{align*} \mathrm{(I)} = \sum_{j = \lfloor ns \rfloor +1}^{\lfloor nt \rfloor}\nu^{\sigma^j \omega}(A_n \cap \{R_{A_n}(\sigma^j \omega) \le N \}) \le C \sum_{j = \lfloor ns \rfloor +1}^{\lfloor nt \rfloor} m(V_n \cap \{R_{V_n}(\sigma^j \omega) \le N \}) \end{align*} $$
$$ \begin{align*} \mathrm{(I)} = \sum_{j = \lfloor ns \rfloor +1}^{\lfloor nt \rfloor}\nu^{\sigma^j \omega}(A_n \cap \{R_{A_n}(\sigma^j \omega) \le N \}) \le C \sum_{j = \lfloor ns \rfloor +1}^{\lfloor nt \rfloor} m(V_n \cap \{R_{V_n}(\sigma^j \omega) \le N \}) \end{align*} $$
tends to zero by Lemma 8.7 for m-a.e
![]() $x_0$
.
$x_0$
.
The term
 $$ \begin{align*} \mathrm{(II)} = \sum_{j = \lfloor ns \rfloor +1}^{\lfloor nt \rfloor} \nu^{\sigma^j \omega}(A_n) \nu^{\sigma^j \omega}(R_{A_n}(\sigma^j \omega) \le N) \le CnNm(A_n)^2 \end{align*} $$
$$ \begin{align*} \mathrm{(II)} = \sum_{j = \lfloor ns \rfloor +1}^{\lfloor nt \rfloor} \nu^{\sigma^j \omega}(A_n) \nu^{\sigma^j \omega}(R_{A_n}(\sigma^j \omega) \le N) \le CnNm(A_n)^2 \end{align*} $$
also tends to zero since
![]() $N=o(n)$
. Lastly, we consider
$N=o(n)$
. Lastly, we consider

We approximate ![]() by a
by a
![]() $C^1$
function g such that
$C^1$
function g such that
![]() $\|g\|_{C^1}\le n^{\tau }$
,
$\|g\|_{C^1}\le n^{\tau }$
, ![]() on
on
![]() $A_n$
, and
$A_n$
, and ![]() (recall
(recall
![]() $A_n$
is two intervals of length roughly
$A_n$
is two intervals of length roughly
![]() ${1}/{n}$
so a simple smoothing at the endpoints of the intervals allows us to find such a function g). Later we will specify
${1}/{n}$
so a simple smoothing at the endpoints of the intervals allows us to find such a function g). Later we will specify
![]() $\tau>1$
as needed. By [Reference Nicol, Pereira and TörökNPT21, Lemma 3.4] with
$\tau>1$
as needed. By [Reference Nicol, Pereira and TörökNPT21, Lemma 3.4] with
![]() $h = h_\omega $
and
$h = h_\omega $
and
![]() ${\varphi = g - m(g h_\omega )}$
, for all
${\varphi = g - m(g h_\omega )}$
, for all
![]() $\omega $
,
$\omega $
,
 $$ \begin{align*} \| P_{\omega}^N ([g-m(g h_\omega)] h_{\omega})\|_{L^1}&\le C n^\tau N^{1-{1}/{\gamma_{\mathrm{max}}}} (\log N)^{{1}/{\gamma_{\mathrm{max}}}} \\ & \le C n^{\tau +1 - {1}/{\gamma_{\mathrm{max}}}} (\log n)^{({2}/{\gamma_{\mathrm{max}}}) - 1}. \end{align*} $$
$$ \begin{align*} \| P_{\omega}^N ([g-m(g h_\omega)] h_{\omega})\|_{L^1}&\le C n^\tau N^{1-{1}/{\gamma_{\mathrm{max}}}} (\log N)^{{1}/{\gamma_{\mathrm{max}}}} \\ & \le C n^{\tau +1 - {1}/{\gamma_{\mathrm{max}}}} (\log n)^{({2}/{\gamma_{\mathrm{max}}}) - 1}. \end{align*} $$
Using the decomposition ![]() , we estimate, leaving out the log term,
, we estimate, leaving out the log term,
where the value of C may change line to line. Taking
![]() $\gamma _{\mathrm {max}}<\tfrac 13$
and
$\gamma _{\mathrm {max}}<\tfrac 13$
and
![]() $1<\tau <({1}/{\gamma _{\mathrm {max}}})-2$
suffices.
$1<\tau <({1}/{\gamma _{\mathrm {max}}})-2$
suffices.
9. Point process results
We now proceed to the proof of the Poisson convergence. In §11, we will consider an annealed version of our results.
9.1. Uniformly expanding maps: proof of Theorem 6.3
Recall Theorem 6.3: under the conditions of §2.1, in particular conditions (LY), (Min), and (Dec), if
![]() $x_0 \notin {\mathcal D}$
is non-recurrent, then for
$x_0 \notin {\mathcal D}$
is non-recurrent, then for
![]() ${\mathbb P}$
-a.e.
${\mathbb P}$
-a.e.
![]() $\omega \in \Omega $
,
$\omega \in \Omega $
,
under the probability measure
![]() $\nu ^\omega $
.
$\nu ^\omega $
.
Our proof of Theorem 6.3 uses the existence of a spectral gap for the associated transfer operators
![]() $P^n_{\omega }$
, and breaks down in the setting of intermittent maps. The use of the spectral gap is encapsulated in the following lemma.
$P^n_{\omega }$
, and breaks down in the setting of intermittent maps. The use of the spectral gap is encapsulated in the following lemma.
Lemma 9.1. Assume condition (LY). Then there exists
![]() $C>0$
such that for all
$C>0$
such that for all
![]() $\omega \in \Omega $
, all
$\omega \in \Omega $
, all
![]() $f, f_n \in \mathrm {BV}$
with
$f, f_n \in \mathrm {BV}$
with
we have
 $$ \begin{align*} \sup_{n \ge 0} \bigg\| P_\omega^n \bigg( f \cdot \prod_{j=1}^n f_j \circ T_\omega^j \bigg)\bigg\|_{\mathrm{BV}} \le C \|f\|_{\mathrm{BV}} \Big( \sup_{j \ge 1} \| f_j \|_{\mathrm{BV}} \Big). \end{align*} $$
$$ \begin{align*} \sup_{n \ge 0} \bigg\| P_\omega^n \bigg( f \cdot \prod_{j=1}^n f_j \circ T_\omega^j \bigg)\bigg\|_{\mathrm{BV}} \le C \|f\|_{\mathrm{BV}} \Big( \sup_{j \ge 1} \| f_j \|_{\mathrm{BV}} \Big). \end{align*} $$
Proof. We proceed in four steps.
Step 1. We define
 $$ \begin{align*} g_\omega^n = \prod_{j=0}^n f_j \circ T_\omega^j, \end{align*} $$
$$ \begin{align*} g_\omega^n = \prod_{j=0}^n f_j \circ T_\omega^j, \end{align*} $$
where we have set ![]() . We observe that for all
. We observe that for all
![]() $n \ge 0$
, there exists
$n \ge 0$
, there exists
![]() $C_n> 0$
such that for all
$C_n> 0$
such that for all
![]() $\omega \in \Omega $
,
$\omega \in \Omega $
,
 $$ \begin{align} \|g_\omega^n \|_{L^\infty(m)} \le \Big( \sup_{j \ge 1} \| f_j \|_{L^\infty(m)} \Big)^{n+1} \le 1 \: \text{ and } \: \|g_\omega^n\|_{\mathrm{BV}} \le C_n \Big( \sup_{j \ge 1} \|f_j\|_{\mathrm{BV}} \Big). \end{align} $$
$$ \begin{align} \|g_\omega^n \|_{L^\infty(m)} \le \Big( \sup_{j \ge 1} \| f_j \|_{L^\infty(m)} \Big)^{n+1} \le 1 \: \text{ and } \: \|g_\omega^n\|_{\mathrm{BV}} \le C_n \Big( \sup_{j \ge 1} \|f_j\|_{\mathrm{BV}} \Big). \end{align} $$
The first estimate is immediate, and the second follows, because
 $$ \begin{align*} \mathrm{Var}(g_\omega^{n+1}) &\le \mathrm{Var}(g_\omega^n) \|f_{n+1} \circ T_\omega^{n+1}\|_{L^\infty(m)} + \|g_\omega^n\|_{L^\infty(m)} \mathrm{Var}(f_{n+1}\circ T_\omega^{n+1}) \\ & \le \mathrm{Var}(g_\omega^n) + \mathrm{Var}(f_{n+1}\circ T_\omega^{n+1}) \\ & = \mathrm{Var}(g_\omega^n) + \sum_{I \in {\mathcal A}_\omega^{n+1}} \mathrm{Var}_I(f_{n+1}\circ T_\omega^{n+1}) \\ & = \mathrm{Var}(g_\omega^n) + \sum_{I \in {\mathcal A}_\omega^{n+1}} \mathrm{Var}_{T_\omega^{n+1}(I)}(f_{n+1}) \\ & \le \mathrm{Var}(g_\omega^n) + (\# {\mathcal A}_\omega^{n+1}) \mathrm{Var}(f_{n+1}), \end{align*} $$
$$ \begin{align*} \mathrm{Var}(g_\omega^{n+1}) &\le \mathrm{Var}(g_\omega^n) \|f_{n+1} \circ T_\omega^{n+1}\|_{L^\infty(m)} + \|g_\omega^n\|_{L^\infty(m)} \mathrm{Var}(f_{n+1}\circ T_\omega^{n+1}) \\ & \le \mathrm{Var}(g_\omega^n) + \mathrm{Var}(f_{n+1}\circ T_\omega^{n+1}) \\ & = \mathrm{Var}(g_\omega^n) + \sum_{I \in {\mathcal A}_\omega^{n+1}} \mathrm{Var}_I(f_{n+1}\circ T_\omega^{n+1}) \\ & = \mathrm{Var}(g_\omega^n) + \sum_{I \in {\mathcal A}_\omega^{n+1}} \mathrm{Var}_{T_\omega^{n+1}(I)}(f_{n+1}) \\ & \le \mathrm{Var}(g_\omega^n) + (\# {\mathcal A}_\omega^{n+1}) \mathrm{Var}(f_{n+1}), \end{align*} $$
and so we can define by induction
![]() $C_{n+1} = C_n + \sup _{\omega \in \Omega } \# {\mathcal A}_\omega ^{n+1}$
which is finite, as there are only finitely many maps in
$C_{n+1} = C_n + \sup _{\omega \in \Omega } \# {\mathcal A}_\omega ^{n+1}$
which is finite, as there are only finitely many maps in
![]() ${\mathcal S}$
.
${\mathcal S}$
.
Step 2. We first prove the lemma in the case where
![]() $r=1$
in the condition (LY). Before, we claim that for
$r=1$
in the condition (LY). Before, we claim that for
![]() $f \in \mathrm {BV}$
and sequences
$f \in \mathrm {BV}$
and sequences
![]() $(f_j) \subset \mathrm {BV}$
as in the statement, we have
$(f_j) \subset \mathrm {BV}$
as in the statement, we have
 $$ \begin{align} \mathrm{Var}(P_\omega^n(f g_\omega^n)) &\le \sum_{j=0}^n \rho^j \| P_\omega^{n-j}(f g_\omega^{n-j-1}) \|_{L^\infty(m)} \|f_{n-j}\|_{\mathrm{BV}} \nonumber\\ &\quad + D \sum_{j=0}^{n-1} \rho^j \|P_\omega^{n-1-j}(f g_{\omega}^{n-1-j})\|_{L^1(m)} \|f_{n-j}\|_{L^\infty(m)}. \end{align} $$
$$ \begin{align} \mathrm{Var}(P_\omega^n(f g_\omega^n)) &\le \sum_{j=0}^n \rho^j \| P_\omega^{n-j}(f g_\omega^{n-j-1}) \|_{L^\infty(m)} \|f_{n-j}\|_{\mathrm{BV}} \nonumber\\ &\quad + D \sum_{j=0}^{n-1} \rho^j \|P_\omega^{n-1-j}(f g_{\omega}^{n-1-j})\|_{L^1(m)} \|f_{n-j}\|_{L^\infty(m)}. \end{align} $$
This implies the lemma when
![]() $r=1$
, since
$r=1$
, since
and
We prove the claim by induction on
![]() $n \ge 0$
. It is immediate for
$n \ge 0$
. It is immediate for
![]() $n=0$
, and for the induction step, we have, using condition (LY),
$n=0$
, and for the induction step, we have, using condition (LY),
 $$ \begin{align*} &\mathrm{Var} (P_\omega^{n+1} (f g_\omega^{n+1})) \\ &\!\!\quad = \mathrm{Var}(P_\omega^{n+1}(f g_\omega^n f_{n+1} \circ T_\omega^{n+1})) = \mathrm{Var}(P_\omega^{n+1}(f g_\omega^n) f_{n+1}) \\ &\!\!\quad \le \mathrm{Var}(P_\omega^{n+1}(f g_\omega^n)) \|f_{n+1}\|_{L^\infty(m)} + \|P_\omega^{n+1} (f g_\omega^n) \|_{L^\infty(m)} \mathrm{Var}(f_{n+1}) \\ &\!\!\quad \le ( \rho \mathrm{Var}(P_\omega^{n}(f g_\omega^n)) + D \|P_\omega^n (f g_\omega^n) \|_{L^1(m)} ) \|f_{n+1}\|_{L^\infty(m)}\\ &\!\!\qquad + \|P_\omega^{n+1} (f g_\omega^n) \|_{L^\infty(m)} \mathrm{Var}(f_{n+1}) \\ &\!\!\quad \le \rho \mathrm{Var}(P_\omega^{n}(f g_\omega^n)) \kern1.3pt{+}\kern1.3pt D \|P_\omega^n (f g_\omega^n) \|_{L^1(m)} \|f_{n+1}\|_{L^\infty(m)} \kern1.3pt{+}\kern1.3pt \|P_\omega^{n+1} (f g_\omega^n) \|_{L^\infty(m)} \|f_{n+1}\|_{\mathrm{BV}}, \end{align*} $$
$$ \begin{align*} &\mathrm{Var} (P_\omega^{n+1} (f g_\omega^{n+1})) \\ &\!\!\quad = \mathrm{Var}(P_\omega^{n+1}(f g_\omega^n f_{n+1} \circ T_\omega^{n+1})) = \mathrm{Var}(P_\omega^{n+1}(f g_\omega^n) f_{n+1}) \\ &\!\!\quad \le \mathrm{Var}(P_\omega^{n+1}(f g_\omega^n)) \|f_{n+1}\|_{L^\infty(m)} + \|P_\omega^{n+1} (f g_\omega^n) \|_{L^\infty(m)} \mathrm{Var}(f_{n+1}) \\ &\!\!\quad \le ( \rho \mathrm{Var}(P_\omega^{n}(f g_\omega^n)) + D \|P_\omega^n (f g_\omega^n) \|_{L^1(m)} ) \|f_{n+1}\|_{L^\infty(m)}\\ &\!\!\qquad + \|P_\omega^{n+1} (f g_\omega^n) \|_{L^\infty(m)} \mathrm{Var}(f_{n+1}) \\ &\!\!\quad \le \rho \mathrm{Var}(P_\omega^{n}(f g_\omega^n)) \kern1.3pt{+}\kern1.3pt D \|P_\omega^n (f g_\omega^n) \|_{L^1(m)} \|f_{n+1}\|_{L^\infty(m)} \kern1.3pt{+}\kern1.3pt \|P_\omega^{n+1} (f g_\omega^n) \|_{L^\infty(m)} \|f_{n+1}\|_{\mathrm{BV}}, \end{align*} $$
which proves equation (9.2) for
![]() $n+1$
, assuming it holds for n.
$n+1$
, assuming it holds for n.
Step 3. Now, we consider the general case
![]() $r \ge 1$
and we assume that n is of the particular form
$r \ge 1$
and we assume that n is of the particular form
![]() $n = pr$
, with
$n = pr$
, with
![]() $p \ge 0$
. We note that the random system defined with
$p \ge 0$
. We note that the random system defined with
![]() ${\mathcal T} = \{ T_\omega ^r \}_{\omega \in \Omega }$
satisfies the condition (LY) with
${\mathcal T} = \{ T_\omega ^r \}_{\omega \in \Omega }$
satisfies the condition (LY) with
![]() $r = 1$
. Consequently, by the second step and equation (9.1), we have
$r = 1$
. Consequently, by the second step and equation (9.1), we have
 $$ \begin{align*} \| P_\omega^n (f g_\omega^n)\|_{\mathrm{BV}} & = \| P_{\sigma^{r-1} \omega}^r \circ \cdots \circ P_\omega^r \bigg(f \prod_{j=1}^p g_{\sigma^{jr}\omega}^r \circ T_\omega^{jr}\bigg ) \|_{\mathrm{BV}} \\ & \le C \|f\|_{\mathrm{BV}} \Big( \sup_{j \ge 1} \| g_{\sigma^{jr} \omega}^r \|_{\mathrm{BV}}\Big) \le C C_r \|f\|_{\mathrm{BV}} \Big(\sup_{j \ge 1} \|f_j\|_{\mathrm{BV}} \Big). \end{align*} $$
$$ \begin{align*} \| P_\omega^n (f g_\omega^n)\|_{\mathrm{BV}} & = \| P_{\sigma^{r-1} \omega}^r \circ \cdots \circ P_\omega^r \bigg(f \prod_{j=1}^p g_{\sigma^{jr}\omega}^r \circ T_\omega^{jr}\bigg ) \|_{\mathrm{BV}} \\ & \le C \|f\|_{\mathrm{BV}} \Big( \sup_{j \ge 1} \| g_{\sigma^{jr} \omega}^r \|_{\mathrm{BV}}\Big) \le C C_r \|f\|_{\mathrm{BV}} \Big(\sup_{j \ge 1} \|f_j\|_{\mathrm{BV}} \Big). \end{align*} $$
Step 4. Finally, if
![]() $n = pr + q$
, with
$n = pr + q$
, with
![]() $p \ge 0$
and
$p \ge 0$
and
![]() $q \in \{0, \ldots , r-1\}$
, as an immediate consequence of condition (LY), we obtain
$q \in \{0, \ldots , r-1\}$
, as an immediate consequence of condition (LY), we obtain
 $$ \begin{align*} \|P_\omega^n(f g_\omega^n) \|_{\mathrm{BV}} & = \|P_{\sigma^{pr}\omega}^q P_\omega^{pr}(f g_\omega^{pr} g_{\sigma^{pr}\omega}^q \circ T_\omega^{pr})\|_{\mathrm{BV}} \\ & = \|P_{\sigma^{pr}\omega}^q (P_\omega^{pr}(f g_\omega^{pr})g_{\sigma^{pr} \omega}^q) \|_{\mathrm{BV}} \le C \| P_\omega^{pr}(f g_\omega^{pr})g_{\sigma^{pr} \omega}^q\|_{\mathrm{BV}}. \end{align*} $$
$$ \begin{align*} \|P_\omega^n(f g_\omega^n) \|_{\mathrm{BV}} & = \|P_{\sigma^{pr}\omega}^q P_\omega^{pr}(f g_\omega^{pr} g_{\sigma^{pr}\omega}^q \circ T_\omega^{pr})\|_{\mathrm{BV}} \\ & = \|P_{\sigma^{pr}\omega}^q (P_\omega^{pr}(f g_\omega^{pr})g_{\sigma^{pr} \omega}^q) \|_{\mathrm{BV}} \le C \| P_\omega^{pr}(f g_\omega^{pr})g_{\sigma^{pr} \omega}^q\|_{\mathrm{BV}}. \end{align*} $$
However, from Step 3, we have
 $$ \begin{align*} \| P_\omega^{pr}(f g_\omega^{pr})g_{\sigma^{pr} \omega}^q \|_{L^1(m)} & \le \| g_{\sigma^{pr} \omega}^q \|_{L^\infty(m)} \| P_\omega^{pr} (f g_\omega^{pr})\|_{L^1(m)} \\ & \le \| P_\omega^{pr} (f g_\omega^{pr})\|_{L^1(m)} \le C \|f\|_{\mathrm{BV}} \Big(\sup_{j \ge 1} \|f_j \|_{\mathrm{BV}}\Big), \end{align*} $$
$$ \begin{align*} \| P_\omega^{pr}(f g_\omega^{pr})g_{\sigma^{pr} \omega}^q \|_{L^1(m)} & \le \| g_{\sigma^{pr} \omega}^q \|_{L^\infty(m)} \| P_\omega^{pr} (f g_\omega^{pr})\|_{L^1(m)} \\ & \le \| P_\omega^{pr} (f g_\omega^{pr})\|_{L^1(m)} \le C \|f\|_{\mathrm{BV}} \Big(\sup_{j \ge 1} \|f_j \|_{\mathrm{BV}}\Big), \end{align*} $$
and, using equation (9.1),
 $$ \begin{align*} \mathrm{Var}( P_\omega^{pr}(f g_\omega^{pr})g_{\sigma^{pr} \omega}^q) & \le \|P_\omega^{pr}(f g_\omega^{pr})\|_{L^\infty(m)} \mathrm{Var}(g_{\sigma^{pr}\omega}^q)\\ &\quad+ \mathrm{Var}(P_\omega^{pr}(f g_\omega^{pr})) \| g_{\sigma^{pr}\omega}^q \|_{L^\infty(m)} \\ & \le [ C_q \|g_\omega^{pr}\|_{L^\infty(m)} \|P_\omega^{pr} |f|\|_{L^\infty(m)} + C \|f\|_{\mathrm{BV}}] \Big( \sup_{j \ge 1 } \| f_j\|_{\mathrm{BV}}\Big) \\ & \le C \Big( 1 + \max_{q = 0, \ldots, r-1} C_q \Big) \|f\|_{\mathrm{BV}} \Big( \sup_{j \ge 1 } \| f_j\|_{\mathrm{ BV}}\Big), \end{align*} $$
$$ \begin{align*} \mathrm{Var}( P_\omega^{pr}(f g_\omega^{pr})g_{\sigma^{pr} \omega}^q) & \le \|P_\omega^{pr}(f g_\omega^{pr})\|_{L^\infty(m)} \mathrm{Var}(g_{\sigma^{pr}\omega}^q)\\ &\quad+ \mathrm{Var}(P_\omega^{pr}(f g_\omega^{pr})) \| g_{\sigma^{pr}\omega}^q \|_{L^\infty(m)} \\ & \le [ C_q \|g_\omega^{pr}\|_{L^\infty(m)} \|P_\omega^{pr} |f|\|_{L^\infty(m)} + C \|f\|_{\mathrm{BV}}] \Big( \sup_{j \ge 1 } \| f_j\|_{\mathrm{BV}}\Big) \\ & \le C \Big( 1 + \max_{q = 0, \ldots, r-1} C_q \Big) \|f\|_{\mathrm{BV}} \Big( \sup_{j \ge 1 } \| f_j\|_{\mathrm{ BV}}\Big), \end{align*} $$
which concludes the proof of the lemma.
Proof of Theorem 6.3
We denote by
![]() ${\mathcal R}$
the family of finite unions of rectangles R of the form
${\mathcal R}$
the family of finite unions of rectangles R of the form
![]() $R = (s,t] \times J$
with
$R = (s,t] \times J$
with
![]() $J \in {\mathcal J}$
. By Kallenberg’s theorem, see [Reference KallenbergKal76, Theorem 4.7] or [Reference ResnickRes87, Proposition 3.22],
$J \in {\mathcal J}$
. By Kallenberg’s theorem, see [Reference KallenbergKal76, Theorem 4.7] or [Reference ResnickRes87, Proposition 3.22],
![]() $N_n^\omega \, {\stackrel {d}{\to } \,} N_{(\alpha )}$
if for any
$N_n^\omega \, {\stackrel {d}{\to } \,} N_{(\alpha )}$
if for any
![]() $R \in {\mathcal R}$
,
$R \in {\mathcal R}$
,
and
We first prove equation (b). We write
 $$ \begin{align*} R = \bigcup_{i=1}^k R_i, \end{align*} $$
$$ \begin{align*} R = \bigcup_{i=1}^k R_i, \end{align*} $$
with
![]() $R_i = (s_i, t_i] \times J_i$
disjoint.
$R_i = (s_i, t_i] \times J_i$
disjoint.
Then
 $$ \begin{align*} {\mathbb E} N_{(\alpha)}(R) = \sum_{i=1}^k (t_i - s_i) \Pi_\alpha(J_i) \end{align*} $$
$$ \begin{align*} {\mathbb E} N_{(\alpha)}(R) = \sum_{i=1}^k (t_i - s_i) \Pi_\alpha(J_i) \end{align*} $$
and

By Lemma 8.1, for
![]() ${\mathbb P}$
-a.e.
${\mathbb P}$
-a.e.
![]() $\omega \in \Omega $
, we have
$\omega \in \Omega $
, we have
 $$ \begin{align*} \lim_{n \to \infty} \sum_{i=1}^k \sum_{j=\lfloor ns_i \rfloor}^{\lfloor nt_i \rfloor - 1} \nu^{\sigma^j \omega}(\phi_{x_0}^{-1}(b_n J_i)) = (t_i - s_i) \Pi_\alpha(J_i), \end{align*} $$
$$ \begin{align*} \lim_{n \to \infty} \sum_{i=1}^k \sum_{j=\lfloor ns_i \rfloor}^{\lfloor nt_i \rfloor - 1} \nu^{\sigma^j \omega}(\phi_{x_0}^{-1}(b_n J_i)) = (t_i - s_i) \Pi_\alpha(J_i), \end{align*} $$
which proves equation (b).
We next establish equation (a). We will use induction on the number of ‘time’ intervals
![]() $(s_i,t_i] \subset (0,\infty ]$
. Let
$(s_i,t_i] \subset (0,\infty ]$
. Let
![]() $R=(s_1,t_1]\times J_1$
, where
$R=(s_1,t_1]\times J_1$
, where
![]() $J_1\in \mathcal {J}$
. Define
$J_1\in \mathcal {J}$
. Define
Since
 $$ \begin{align*} \{N_n^{\omega} (R)=0\} & = \{ x: T_{\omega}^j (x)\not \in A_n, ns_1<j+1 \le nt_1 \} \\ &= \{ 1_{A_n^c}\circ T_{\omega}^{\lfloor ns_1 \rfloor} \cdot 1_{A_n^c}\circ T_{\omega}^{\lfloor ns_1 \rfloor+1} \cdot \cdots \cdot 1_{A_n^c}\circ T_{\omega}^{\lfloor nt_1 \rfloor-1} \not= 0\} \\ & = \bigg\{ x: \bigg(\prod_{j=0}^{\lfloor n t_1 \rfloor -1 - \lfloor n s_1 \rfloor}1_{A_n^c}\circ T_{\sigma^{\lfloor n s_1 \rfloor}\omega}^{j}\bigg) \circ T_{\omega}^{\lfloor n s_1 \rfloor}(x) \not= 0\bigg\}, \end{align*} $$
$$ \begin{align*} \{N_n^{\omega} (R)=0\} & = \{ x: T_{\omega}^j (x)\not \in A_n, ns_1<j+1 \le nt_1 \} \\ &= \{ 1_{A_n^c}\circ T_{\omega}^{\lfloor ns_1 \rfloor} \cdot 1_{A_n^c}\circ T_{\omega}^{\lfloor ns_1 \rfloor+1} \cdot \cdots \cdot 1_{A_n^c}\circ T_{\omega}^{\lfloor nt_1 \rfloor-1} \not= 0\} \\ & = \bigg\{ x: \bigg(\prod_{j=0}^{\lfloor n t_1 \rfloor -1 - \lfloor n s_1 \rfloor}1_{A_n^c}\circ T_{\sigma^{\lfloor n s_1 \rfloor}\omega}^{j}\bigg) \circ T_{\omega}^{\lfloor n s_1 \rfloor}(x) \not= 0\bigg\}, \end{align*} $$
we have that
 $$ \begin{align} |\nu^{\omega} (N_n^{\omega} (R)&=0) - \nu^{\sigma^{\lfloor ns_1 \rfloor} \omega} (R_{A_n}(\sigma^{\lfloor ns_1 \rfloor} \omega)> \lfloor n(t_1-s_1) \rfloor )|\notag \\ &\ \ \le \nu^{\sigma^{\lfloor n s_1 \rfloor} \omega}(R_{A_n}(\sigma^{\lfloor n s_1 \rfloor}\omega) = 0) = \nu^{\sigma^{\lfloor n s_1 \rfloor}\omega}(A_n) \le C m(A_n)\to 0, \end{align} $$
$$ \begin{align} |\nu^{\omega} (N_n^{\omega} (R)&=0) - \nu^{\sigma^{\lfloor ns_1 \rfloor} \omega} (R_{A_n}(\sigma^{\lfloor ns_1 \rfloor} \omega)> \lfloor n(t_1-s_1) \rfloor )|\notag \\ &\ \ \le \nu^{\sigma^{\lfloor n s_1 \rfloor} \omega}(R_{A_n}(\sigma^{\lfloor n s_1 \rfloor}\omega) = 0) = \nu^{\sigma^{\lfloor n s_1 \rfloor}\omega}(A_n) \le C m(A_n)\to 0, \end{align} $$
because, due to rounding when taking integer parts,
![]() $\lfloor n t_1 \rfloor - \lfloor n s_1 \rfloor -1$
is either equal to
$\lfloor n t_1 \rfloor - \lfloor n s_1 \rfloor -1$
is either equal to
![]() $\lfloor n( t_1 - s_1) \rfloor -1$
or to
$\lfloor n( t_1 - s_1) \rfloor -1$
or to
![]() $\lfloor n(t_1 - s_1) \rfloor $
. By Theorem 6.1,
$\lfloor n(t_1 - s_1) \rfloor $
. By Theorem 6.1,
as desired.
Now let
![]() $R=\bigcup _{j=1}^k (s_i, t_i]\times J_i$
with
$R=\bigcup _{j=1}^k (s_i, t_i]\times J_i$
with
![]() $0\le s_1 < t_1<\cdots < s_k < t_k$
and
$0\le s_1 < t_1<\cdots < s_k < t_k$
and
![]() $J_i \in \mathcal {J}$
. Furthermore, define
$J_i \in \mathcal {J}$
. Furthermore, define
![]() $s_i'=s_i-s_1$
and
$s_i'=s_i-s_1$
and
![]() $t_i'=t_i-s_1$
.
$t_i'=t_i-s_1$
.
Observe that, accounting for the rounding errors when taking integer parts as for equation (9.3), we get
 $$ \begin{align} &\bigg|\nu^{\omega} \bigg(N_n^{\omega} \bigg(\bigcup_{i=1}^k (s_i,t_i]\times J_i\bigg)=0\bigg) -\nu^{\sigma^{\lfloor n s_1 \rfloor}\omega} \bigg(N_n^{\sigma^{\lfloor n s_1 \rfloor}\omega} \bigg(\bigcup_{i=1}^k (s'_i,t'_i]\times J_i\bigg)=0\bigg)\bigg| \nonumber\\ &\quad\le 2C \sum_{i=1}^k m (\phi_{x_0}^{-1}(b_n J_i)) \to 0 \end{align} $$
$$ \begin{align} &\bigg|\nu^{\omega} \bigg(N_n^{\omega} \bigg(\bigcup_{i=1}^k (s_i,t_i]\times J_i\bigg)=0\bigg) -\nu^{\sigma^{\lfloor n s_1 \rfloor}\omega} \bigg(N_n^{\sigma^{\lfloor n s_1 \rfloor}\omega} \bigg(\bigcup_{i=1}^k (s'_i,t'_i]\times J_i\bigg)=0\bigg)\bigg| \nonumber\\ &\quad\le 2C \sum_{i=1}^k m (\phi_{x_0}^{-1}(b_n J_i)) \to 0 \end{align} $$
so, after replacing
![]() $\omega $
by
$\omega $
by
![]() $\sigma ^{\lfloor n s_1 \rfloor }\omega $
, we can assume that
$\sigma ^{\lfloor n s_1 \rfloor }\omega $
, we can assume that
![]() $s_1=0$
. Let
$s_1=0$
. Let
 $$ \begin{align*} &R_1=(0,t_1] \times J_1, \\ &R_2=\bigcup_{i=2}^k (s_i,t_i]\times J_i,\\ &R'_2=\bigcup_{i=2}^k (s_i-s_2,t_i-s_2]\times J_i. \end{align*} $$
$$ \begin{align*} &R_1=(0,t_1] \times J_1, \\ &R_2=\bigcup_{i=2}^k (s_i,t_i]\times J_i,\\ &R'_2=\bigcup_{i=2}^k (s_i-s_2,t_i-s_2]\times J_i. \end{align*} $$
Then, with
![]() $A_n =\phi _{x_0}^{-1} (b_n J_1)$
,
$A_n =\phi _{x_0}^{-1} (b_n J_1)$
,
as
![]() $n\to \infty $
, uniformly in
$n\to \infty $
, uniformly in
![]() $\eta \in \Omega $
, as in equation (9.4). Moreover, as we check below,
$\eta \in \Omega $
, as in equation (9.4). Moreover, as we check below,
 $$ \begin{align} &\vert\nu^{\eta} [\{R_{A_n}(\eta)> \lfloor nt_1 \rfloor\} \cap T_{\eta}^{-\lfloor ns_2 \rfloor} (N_n^{\sigma^{\lfloor ns_2\rfloor}\eta}(R'_2)=0)] \nonumber\\ &\quad- \nu^{\eta} (R_{A_n}(\eta)> \lfloor nt_1 \rfloor)\cdot \nu^{\eta} (N_n^{\eta}(R_2)=0) \vert\to 0 \end{align} $$
$$ \begin{align} &\vert\nu^{\eta} [\{R_{A_n}(\eta)> \lfloor nt_1 \rfloor\} \cap T_{\eta}^{-\lfloor ns_2 \rfloor} (N_n^{\sigma^{\lfloor ns_2\rfloor}\eta}(R'_2)=0)] \nonumber\\ &\quad- \nu^{\eta} (R_{A_n}(\eta)> \lfloor nt_1 \rfloor)\cdot \nu^{\eta} (N_n^{\eta}(R_2)=0) \vert\to 0 \end{align} $$
as
![]() $n\to \infty $
, uniformly in
$n\to \infty $
, uniformly in
![]() $\eta \in \Omega $
. Therefore, setting
$\eta \in \Omega $
. Therefore, setting
![]() $\eta = \sigma ^{\lfloor n s_2 \rfloor } \omega $
in equations (9.5) and (9.6), we have, by Theorem 6.1,
$\eta = \sigma ^{\lfloor n s_2 \rfloor } \omega $
in equations (9.5) and (9.6), we have, by Theorem 6.1,
which gives the induction step in the proof of equation (a).
We prove now equation (9.6). Our proof uses the spectral gap for
![]() $P^{n}_{\omega }$
and breaks down for random intermittent maps.
$P^{n}_{\omega }$
and breaks down for random intermittent maps.
Similarly to equation (9.4),
We have, using the notation
that

where the last inequality follows from the decay, uniform in
![]() $\eta $
, of
$\eta $
, of
![]() $\{P_{\eta }^k\}_{k}$
in BV (condition (Dec)).
$\{P_{\eta }^k\}_{k}$
in BV (condition (Dec)).
However,
which proves equation (9.6). This follows from Lemma 9.1 applied to
![]() $f = h_\eta $
and
$f = h_\eta $
and ![]() , because
, because

and both
![]() $\|h_\eta \|_{\mathrm {BV}}$
and
$\|h_\eta \|_{\mathrm {BV}}$
and ![]() are uniformly bounded. Note that for the stationary case, the estimate in equation (9.7) is used in the proof of [Reference Tyran-KamińskaTK10b, Theorem 4.4], which refers to [Reference Aaronson, Denker, Sarig and ZweimüllerADSZ04, Proposition 4].
are uniformly bounded. Note that for the stationary case, the estimate in equation (9.7) is used in the proof of [Reference Tyran-KamińskaTK10b, Theorem 4.4], which refers to [Reference Aaronson, Denker, Sarig and ZweimüllerADSZ04, Proposition 4].
9.2. Intermittent maps: proof of Theorem 6.4
We prove a weaker form of convergence in the setting of intermittent maps, which suffices to establish stable limit laws but not functional limit laws.
In the setting of intermittent maps, we will show that for
![]() ${\mathbb P}$
-a.e.
${\mathbb P}$
-a.e.
![]() $\omega $
,
$\omega $
,
Proof of Theorem 6.4
We will show that for
![]() ${\mathbb P}$
-a.e.
${\mathbb P}$
-a.e.
![]() $\omega \in \Omega $
, the assumptions of Kallenberg’s theorem [Reference KallenbergKal76, Theorem 4.7] hold.
$\omega \in \Omega $
, the assumptions of Kallenberg’s theorem [Reference KallenbergKal76, Theorem 4.7] hold.
Recall that
![]() $\mathcal {J}$
denotes the set of all finite unions of intervals of the form
$\mathcal {J}$
denotes the set of all finite unions of intervals of the form
![]() $(x,y]$
, where
$(x,y]$
, where
![]() $x <y$
and
$x <y$
and
![]() $0\not \in [x,y]$
.
$0\not \in [x,y]$
.
By Kallenberg’s theorem [Reference KallenbergKal76, Theorem 4.7],
![]() $N^{\omega }_n[(0,1]\times \cdot ) \to ^{d} N_{(\alpha )} ((0,1] \times \cdot )$
if for all
$N^{\omega }_n[(0,1]\times \cdot ) \to ^{d} N_{(\alpha )} ((0,1] \times \cdot )$
if for all
![]() $J \in \mathcal {J}$
,
$J \in \mathcal {J}$
,
and
We prove first equation (b) following [Reference Tyran-KamińskaTK10b, p. 12]. Write
 $$ \begin{align*} J=\bigcup_{i=1}^k J_i \end{align*} $$
$$ \begin{align*} J=\bigcup_{i=1}^k J_i \end{align*} $$
with
![]() $J_i=(x_i,y_i]$
disjoint.
$J_i=(x_i,y_i]$
disjoint.
Then
 $$ \begin{align*} {\mathbb E} N_{(\alpha)} ((0,1]\times J)=\sum_{i=1}^k \Pi_{\alpha} (J_i)=\Pi_{\alpha} (J) \end{align*} $$
$$ \begin{align*} {\mathbb E} N_{(\alpha)} ((0,1]\times J)=\sum_{i=1}^k \Pi_{\alpha} (J_i)=\Pi_{\alpha} (J) \end{align*} $$
and

We check that

for
![]() $J=\bigcup _{i=1}^k J_i$
.
$J=\bigcup _{i=1}^k J_i$
.
Write
![]() $A_n:=\phi _{x_0}^{-1} (b_n J)$
. Then
$A_n:=\phi _{x_0}^{-1} (b_n J)$
. Then
hence

by Lemma 7.2.
Now we prove equation (a), that is,
for all
![]() $J \in \mathcal {J}$
.
$J \in \mathcal {J}$
.
Let
![]() $J \in \mathcal {J}$
and denote as above
$J \in \mathcal {J}$
and denote as above
![]() $A_n := \phi _{x_0}^{-1} (b_n J)\subset X =[0,1]$
. Then
$A_n := \phi _{x_0}^{-1} (b_n J)\subset X =[0,1]$
. Then
Hence,
and by Theorem 6.2, for m-a.e.
![]() $x_0$
$x_0$
This proves equation (a).
10. Stable laws and functional limit laws
10.1. Uniformly expanding maps: proof of Theorem 2.4
In this section, we prove Theorem 2.4, under the conditions given in §2.1, in particular, conditions (LY), (Dec), and (Min).
For this purpose, we consider first some technical lemmas regarding short returns. For
![]() $\omega \in \Omega $
,
$\omega \in \Omega $
,
![]() $n \ge 1$
, and
$n \ge 1$
, and
![]() $\epsilon>0$
, let
$\epsilon>0$
, let
Lemma 10.1. There exists
![]() $C>0$
such that for all
$C>0$
such that for all
![]() $\omega \in \Omega $
,
$\omega \in \Omega $
,
![]() $n \ge 1$
, and
$n \ge 1$
, and
![]() $\epsilon>0$
,
$\epsilon>0$
,
Proof. We follow the proof of [Reference Holland, Nicol and TörökHNT12, Lemma 3.4], conveniently adapted to our setting of random non-Markov maps. Recall that
![]() ${\mathcal A}_\omega ^n$
is the partition of monotonicity associated to the map
${\mathcal A}_\omega ^n$
is the partition of monotonicity associated to the map
![]() $T_\omega ^n$
. Consider
$T_\omega ^n$
. Consider
![]() $I \in {\mathcal A}_\omega ^n$
. Since
$I \in {\mathcal A}_\omega ^n$
. Since
![]() $\inf _I |(T_\omega ^n)'| \ge \unicode{x3bb} ^n> 1$
, there exists at most one solution
$\inf _I |(T_\omega ^n)'| \ge \unicode{x3bb} ^n> 1$
, there exists at most one solution
![]() $x_I^\pm \in I$
to the equation
$x_I^\pm \in I$
to the equation
and since there is no sign change of
![]() $(T_\omega ^n)'$
on I, we have
$(T_\omega ^n)'$
on I, we have
We have
and by the mean value theorem,
Consequently,
 $$ \begin{align} | x_I^+ - x_I^- | \le \bigg( \sup_I \frac{1}{|(T_\omega^n)'|} \bigg) [ | x_I^+ - x_I^-| + 2 \epsilon ] \le \unicode{x3bb}^{-n} | x_I^+ - x_I^-| + 2 \epsilon \sup_I \frac{1}{|(T_\omega^n)'|}. \end{align} $$
$$ \begin{align} | x_I^+ - x_I^- | \le \bigg( \sup_I \frac{1}{|(T_\omega^n)'|} \bigg) [ | x_I^+ - x_I^-| + 2 \epsilon ] \le \unicode{x3bb}^{-n} | x_I^+ - x_I^-| + 2 \epsilon \sup_I \frac{1}{|(T_\omega^n)'|}. \end{align} $$
Note that if there is no solutions to equation (10.1), then the estimate in equation (10.3) is actually improved. Rearranging equation (10.3) and summing over
![]() $I\in {\mathcal A}_\omega ^n$
, we obtain, thanks to equation (10.2),
$I\in {\mathcal A}_\omega ^n$
, we obtain, thanks to equation (10.2),
 $$ \begin{align*} m({\mathcal E}_n^\omega(\epsilon)) \le \sum_{I \in {\mathcal A}_\omega^n} | x_I^+ - x_I^-| \le \frac{2 \epsilon}{1 - \unicode{x3bb}^{-n}} \sum_{I \in {\mathcal A}_\omega^n} \sup_I \frac{1}{|(T_\omega^n)'|} \le C \epsilon. \end{align*} $$
$$ \begin{align*} m({\mathcal E}_n^\omega(\epsilon)) \le \sum_{I \in {\mathcal A}_\omega^n} | x_I^+ - x_I^-| \le \frac{2 \epsilon}{1 - \unicode{x3bb}^{-n}} \sum_{I \in {\mathcal A}_\omega^n} \sup_I \frac{1}{|(T_\omega^n)'|} \le C \epsilon. \end{align*} $$
The fact that
 $$ \begin{align} \sum_{I \in {\mathcal A}_\omega^n} \sup_I \frac{1}{|(T_\omega^n)'|} \le C \end{align} $$
$$ \begin{align} \sum_{I \in {\mathcal A}_\omega^n} \sup_I \frac{1}{|(T_\omega^n)'|} \le C \end{align} $$
for a constant
![]() $C>0$
independent from
$C>0$
independent from
![]() $\omega $
and n follows from a standard distortion argument for one-dimensional maps that can be found in the proof of [Reference Aimino, Nicol and VaientiANV15, Lemma 8.5(3)] (see also [Reference Aimino and RousseauAR16, Lemma 7]), where finitely many piecewise
$\omega $
and n follows from a standard distortion argument for one-dimensional maps that can be found in the proof of [Reference Aimino, Nicol and VaientiANV15, Lemma 8.5(3)] (see also [Reference Aimino and RousseauAR16, Lemma 7]), where finitely many piecewise
![]() $C^2$
uniformly expanding maps with finitely many discontinuities are also considered. Since it follows from condition (LY) that
$C^2$
uniformly expanding maps with finitely many discontinuities are also considered. Since it follows from condition (LY) that
![]() $\| P_\omega ^n f \|_{\mathrm {BV}} \le C \|f\|_{\mathrm {BV}}$
for some uniform
$\| P_\omega ^n f \|_{\mathrm {BV}} \le C \|f\|_{\mathrm {BV}}$
for some uniform
![]() $C>0$
, we do not have to average equation (10.4) over
$C>0$
, we do not have to average equation (10.4) over
![]() $\omega $
as in [Reference Aimino, Nicol and VaientiANV15], but instead, we can simply have an estimate that holds uniformly in
$\omega $
as in [Reference Aimino, Nicol and VaientiANV15], but instead, we can simply have an estimate that holds uniformly in
![]() $\omega $
.
$\omega $
.
Recall that, for a measurable subset U,
![]() $R_U^\omega (x) \ge 1$
is the hitting time of
$R_U^\omega (x) \ge 1$
is the hitting time of
![]() $(\omega , x)$
to U defined by equation (6.1).
$(\omega , x)$
to U defined by equation (6.1).
Lemma 10.2. Let
![]() $a>0$
,
$a>0$
,
![]() $\frac 2 3 < \psi < 1$
, and
$\frac 2 3 < \psi < 1$
, and
![]() $0 < \kappa < 3 \psi - 2$
. Then there exist sequences
$0 < \kappa < 3 \psi - 2$
. Then there exist sequences
![]() $(\gamma _1(n))_{n \ge 1}$
and
$(\gamma _1(n))_{n \ge 1}$
and
![]() $(\gamma _2(n))_{n \ge 1}$
with
$(\gamma _2(n))_{n \ge 1}$
with
![]() $\gamma _1(n) = {\mathcal O}(n^{- \kappa })$
and
$\gamma _1(n) = {\mathcal O}(n^{- \kappa })$
and
![]() $\gamma _2(n) = o(1)$
, and for all
$\gamma _2(n) = o(1)$
, and for all
![]() $\omega \in \Omega $
, a sequence of measurable subsets
$\omega \in \Omega $
, a sequence of measurable subsets
![]() $(A_n^\omega )_{n \ge 1}$
of
$(A_n^\omega )_{n \ge 1}$
of
![]() $[0,1]$
with
$[0,1]$
with
![]() $m(A_n^\omega ) \le \gamma _1(n)$
and such that for all
$m(A_n^\omega ) \le \gamma _1(n)$
and such that for all
![]() $x_0 \notin A_n^\omega $
,
$x_0 \notin A_n^\omega $
,
 $$ \begin{align*} (\log n) \sum_{i=0}^{n-1} m( B_{n^{-\psi}}(x_0) \cap \{R_{ B_{n^{-\psi}}(x_0)}^{\sigma^i \omega} \le \lfloor a \log n \rfloor \}) \le \gamma_2(n). \end{align*} $$
$$ \begin{align*} (\log n) \sum_{i=0}^{n-1} m( B_{n^{-\psi}}(x_0) \cap \{R_{ B_{n^{-\psi}}(x_0)}^{\sigma^i \omega} \le \lfloor a \log n \rfloor \}) \le \gamma_2(n). \end{align*} $$
Proof. Let
Since
![]() $ B_{n^{-\psi }}(x_0) \cap \{R_{ B_{n^{-\psi }}(x_0)}^{\sigma ^i \omega } \le \lfloor a \log n \rfloor \} \subset B_{n^{-\psi }}(x_0) \cap E_n^{\sigma ^i \omega }$
, it is enough to consider
$ B_{n^{-\psi }}(x_0) \cap \{R_{ B_{n^{-\psi }}(x_0)}^{\sigma ^i \omega } \le \lfloor a \log n \rfloor \} \subset B_{n^{-\psi }}(x_0) \cap E_n^{\sigma ^i \omega }$
, it is enough to consider
 $$ \begin{align*} (\log n) \sum_{i=0}^{n-1} m( B_{n^{-\psi}}(x_0) \cap E_n^{\sigma^i \omega}). \end{align*} $$
$$ \begin{align*} (\log n) \sum_{i=0}^{n-1} m( B_{n^{-\psi}}(x_0) \cap E_n^{\sigma^i \omega}). \end{align*} $$
According to Lemma 10.1, we have
 $$ \begin{align*} m(E_n^\omega) \le \sum_{j=1}^{\lfloor a \log n \rfloor } m( {\mathcal E}_j^\omega(2n^{-\psi})) \le C \frac{\log n}{n^\psi}. \end{align*} $$
$$ \begin{align*} m(E_n^\omega) \le \sum_{j=1}^{\lfloor a \log n \rfloor } m( {\mathcal E}_j^\omega(2n^{-\psi})) \le C \frac{\log n}{n^\psi}. \end{align*} $$
We introduce the maximal function

By [Reference RudinRud87, Equation (5), p. 138], for all
![]() $\unicode{x3bb}> 0$
, we have
$\unicode{x3bb}> 0$
, we have

Let
![]() $\rho>0$
and
$\rho>0$
and
![]() $\xi>0$
to be determined later. We define
$\xi>0$
to be determined later. We define
so that we have

By definition of the maximal function
![]() $M_n^\omega $
, this implies that
$M_n^\omega $
, this implies that

from which it follows, by equation (10.5) with
![]() $\unicode{x3bb} = ( \log n) n^{\xi - \psi \rho }$
,
$\unicode{x3bb} = ( \log n) n^{\xi - \psi \rho }$
,
where

If
![]() $x_0 \notin A_n^\omega $
, then
$x_0 \notin A_n^\omega $
, then

Since
![]() $\tfrac 23 < \psi < 1$
and
$\tfrac 23 < \psi < 1$
and
![]() $0 < \kappa < 3 \psi - 2$
, it is possible to choose
$0 < \kappa < 3 \psi - 2$
, it is possible to choose
![]() $\rho>0$
and
$\rho>0$
and
![]() $\xi>0$
such that
$\xi>0$
such that
![]() $\kappa = \xi + (1-\rho )\psi - 1$
,
$\kappa = \xi + (1-\rho )\psi - 1$
,
![]() $\psi> \xi $
, and
$\psi> \xi $
, and
![]() $\psi (1+\rho )>1$
(for instance, take
$\psi (1+\rho )>1$
(for instance, take
![]() $\xi = \psi - \delta $
and
$\xi = \psi - \delta $
and
![]() $\rho = \psi ^{-1} - 1 + \delta \psi ^{-1}$
with
$\rho = \psi ^{-1} - 1 + \delta \psi ^{-1}$
with
![]() $\delta = ({3 \psi - 2 - \kappa })/{2}$
), which concludes the proof.
$\delta = ({3 \psi - 2 - \kappa })/{2}$
), which concludes the proof.
Lemma 10.3. Suppose that
![]() $a>0$
and
$a>0$
and
![]() $\frac 3 4 < \psi < 1$
. Then for m-a.e.
$\frac 3 4 < \psi < 1$
. Then for m-a.e.
![]() $x_0 \in [0,1]$
and
$x_0 \in [0,1]$
and
![]() ${\mathbb P}$
-a.e.
${\mathbb P}$
-a.e.
![]() $\omega \in \Omega $
and, we have
$\omega \in \Omega $
and, we have
 $$ \begin{align*} \lim_{n \to \infty} (\log n) \sum_{i=0}^{n-1} m( B_{n^{-\psi}}(x_0) \cap \{R_{ B_{n^{-\psi}}(x_0)}^{\sigma^i \omega} \le \lfloor a \log n \rfloor \}) = 0. \end{align*} $$
$$ \begin{align*} \lim_{n \to \infty} (\log n) \sum_{i=0}^{n-1} m( B_{n^{-\psi}}(x_0) \cap \{R_{ B_{n^{-\psi}}(x_0)}^{\sigma^i \omega} \le \lfloor a \log n \rfloor \}) = 0. \end{align*} $$
Proof. Let
![]() $0 < \kappa < 3 \psi - 2$
to be determined later. Consider the sets
$0 < \kappa < 3 \psi - 2$
to be determined later. Consider the sets
![]() $(A_n^\omega )_{n \ge 1}$
given by Lemma 10.2, with
$(A_n^\omega )_{n \ge 1}$
given by Lemma 10.2, with
![]() $m(A_n^\omega ) \le \gamma _1(n) = {\mathcal O}(n^{- \kappa })$
. Since
$m(A_n^\omega ) \le \gamma _1(n) = {\mathcal O}(n^{- \kappa })$
. Since
![]() $\kappa < 1$
, we need to consider a subsequence
$\kappa < 1$
, we need to consider a subsequence
![]() $(n_k)_{k \ge 1}$
such that
$(n_k)_{k \ge 1}$
such that
![]() $\sum _{k \ge 1} \gamma _1(n_k) < \infty $
. For such a subsequence, by the Borel–Cantelli lemma, for m-a.e.
$\sum _{k \ge 1} \gamma _1(n_k) < \infty $
. For such a subsequence, by the Borel–Cantelli lemma, for m-a.e.
![]() $x_0$
, there exists
$x_0$
, there exists
![]() $K = K(x_0, \omega )$
such that for all
$K = K(x_0, \omega )$
such that for all
![]() $k \ge K$
,
$k \ge K$
,
![]() $x_0 \notin A_{n_k}^\omega $
. Since
$x_0 \notin A_{n_k}^\omega $
. Since
![]() $\lim _{k \to \infty } \gamma _2(n_k) = 0$
, this implies
$\lim _{k \to \infty } \gamma _2(n_k) = 0$
, this implies
 $$ \begin{align*} \lim_{k \to \infty} (\log n_k) \sum_{i=0}^{n_k - 1} m( B_{n_k^{-\psi}}(x_0) \cap \{R_{ B_{n_k^{-\psi}}(x_0)}^{\sigma^i \omega} \le \lfloor a \log n_k \rfloor \}) = 0. \end{align*} $$
$$ \begin{align*} \lim_{k \to \infty} (\log n_k) \sum_{i=0}^{n_k - 1} m( B_{n_k^{-\psi}}(x_0) \cap \{R_{ B_{n_k^{-\psi}}(x_0)}^{\sigma^i \omega} \le \lfloor a \log n_k \rfloor \}) = 0. \end{align*} $$
We take
![]() $n_k = \lfloor k^\zeta \rfloor $
for some
$n_k = \lfloor k^\zeta \rfloor $
for some
![]() $\zeta>0$
to be determined later. To have
$\zeta>0$
to be determined later. To have
![]() $\sum _{k \ge 1} \gamma _1(n_k) < \infty $
, we need to require that
$\sum _{k \ge 1} \gamma _1(n_k) < \infty $
, we need to require that
![]() $\kappa \zeta> 1$
. Set
$\kappa \zeta> 1$
. Set
![]() $U_n^\omega (x_0) = B_{n^{-\psi }}(x_0) \cap \{R_{ B_{n^{-\psi }}(x_0)}^\omega \le \lfloor a \log n \rfloor \}$
. To obtain the convergence to
$U_n^\omega (x_0) = B_{n^{-\psi }}(x_0) \cap \{R_{ B_{n^{-\psi }}(x_0)}^\omega \le \lfloor a \log n \rfloor \}$
. To obtain the convergence to
![]() $0$
of the whole sequence, we need to prove that
$0$
of the whole sequence, we need to prove that
 $$ \begin{align} \lim_{k \to \infty} \sup_{n_k \le n < n_{k+1}} \bigg| (\log n) \sum_{i=0}^{n-1} m(U_n^{\sigma^i \omega}(x_0)) - (\log n_k ) \sum_{i=0}^{n_k - 1} m(U_{n_k}^{\sigma^i \omega}(x_0)) \bigg| = 0. \end{align} $$
$$ \begin{align} \lim_{k \to \infty} \sup_{n_k \le n < n_{k+1}} \bigg| (\log n) \sum_{i=0}^{n-1} m(U_n^{\sigma^i \omega}(x_0)) - (\log n_k ) \sum_{i=0}^{n_k - 1} m(U_{n_k}^{\sigma^i \omega}(x_0)) \bigg| = 0. \end{align} $$
For this purpose, we estimate
 $$ \begin{align*} &\bigg| (\log n) \sum_{i=0}^{n-1} m(U_n^{\sigma^i \omega}(x_0)) - (\log n_k ) \sum_{i=0}^{n_k - 1} m(U_{n_k}^{\sigma^i \omega}(x_0)) \bigg|\\ &\quad\le \mathrm{(I)} + \mathrm{(II)} + \mathrm{(III)} + \mathrm{ (IV)} + \mathrm{(V)}, \end{align*} $$
$$ \begin{align*} &\bigg| (\log n) \sum_{i=0}^{n-1} m(U_n^{\sigma^i \omega}(x_0)) - (\log n_k ) \sum_{i=0}^{n_k - 1} m(U_{n_k}^{\sigma^i \omega}(x_0)) \bigg|\\ &\quad\le \mathrm{(I)} + \mathrm{(II)} + \mathrm{(III)} + \mathrm{ (IV)} + \mathrm{(V)}, \end{align*} $$
where
 $$ \begin{align*} \mathrm{(I)} = | \log n - \log n_k| \sum_{i=0}^{n-1} m(U_n^{\sigma^i \omega}(x_0)), \: \: \mathrm{(II)} = (\log n_k) \sum_{i=n_k}^{n-1} m(U_n^{\sigma^i \omega}(x_0)), \end{align*} $$
$$ \begin{align*} \mathrm{(I)} = | \log n - \log n_k| \sum_{i=0}^{n-1} m(U_n^{\sigma^i \omega}(x_0)), \: \: \mathrm{(II)} = (\log n_k) \sum_{i=n_k}^{n-1} m(U_n^{\sigma^i \omega}(x_0)), \end{align*} $$
 $$ \begin{align*} \mathrm{(III)} &= (\log n_k) \sum_{i=0}^{n_k - 1} | m(B_{n^{-\psi}}(x_0) \cap \{R_{ B_{n^{-\psi}}(x_0)}^{\sigma^i \omega} \le\lfloor a \log n \rfloor \})\\ &\quad- m(B_{n_k^{-\psi}}(x_0) \cap \{R_{ B_{n^{-\psi}}(x_0)}^{\sigma^i \omega} \le \lfloor a \log n \rfloor \})|, \end{align*} $$
$$ \begin{align*} \mathrm{(III)} &= (\log n_k) \sum_{i=0}^{n_k - 1} | m(B_{n^{-\psi}}(x_0) \cap \{R_{ B_{n^{-\psi}}(x_0)}^{\sigma^i \omega} \le\lfloor a \log n \rfloor \})\\ &\quad- m(B_{n_k^{-\psi}}(x_0) \cap \{R_{ B_{n^{-\psi}}(x_0)}^{\sigma^i \omega} \le \lfloor a \log n \rfloor \})|, \end{align*} $$
 $$ \begin{align*} \mathrm{(IV)} &= (\log n_k) \sum_{i=0}^{n_k - 1} |m(B_{n_k^{-\psi}}(x_0) \cap \{R_{ B_{n^{-\psi}}(x_0)}^{\sigma^i \omega} \le \lfloor a \log n \rfloor \})\\ &\quad- m(B_{n_k^{-\psi}}(x_0) \cap \{R_{ B_{n_k^{-\psi}}(x_0)}^{\sigma^i \omega} \le \lfloor a \log n \rfloor \}) |, \end{align*} $$
$$ \begin{align*} \mathrm{(IV)} &= (\log n_k) \sum_{i=0}^{n_k - 1} |m(B_{n_k^{-\psi}}(x_0) \cap \{R_{ B_{n^{-\psi}}(x_0)}^{\sigma^i \omega} \le \lfloor a \log n \rfloor \})\\ &\quad- m(B_{n_k^{-\psi}}(x_0) \cap \{R_{ B_{n_k^{-\psi}}(x_0)}^{\sigma^i \omega} \le \lfloor a \log n \rfloor \}) |, \end{align*} $$
 $$ \begin{align*} \mathrm{(V)} &= (\log n_k) \sum_{i=0}^{n_k - 1} | m( B_{n_k^{-\psi}}(x_0) \cap \{R_{ B_{n_k^{-\psi}}(x_0)}^{\sigma^i \omega} \le \lfloor a \log n \rfloor \} )\\ &\quad - m( B_{n_k^{-\psi}}(x_0) \cap \{R_{ B_{n_k^{-\psi}}(x_0)}^{\sigma^i \omega} \le \lfloor a \log n_k \rfloor \} ) |. \end{align*} $$
$$ \begin{align*} \mathrm{(V)} &= (\log n_k) \sum_{i=0}^{n_k - 1} | m( B_{n_k^{-\psi}}(x_0) \cap \{R_{ B_{n_k^{-\psi}}(x_0)}^{\sigma^i \omega} \le \lfloor a \log n \rfloor \} )\\ &\quad - m( B_{n_k^{-\psi}}(x_0) \cap \{R_{ B_{n_k^{-\psi}}(x_0)}^{\sigma^i \omega} \le \lfloor a \log n_k \rfloor \} ) |. \end{align*} $$
Before proceeding to estimate each term, we note that
![]() $|n_{k+1} - n_k| = {\mathcal O}(k^{-(1- \zeta )})$
,
$|n_{k+1} - n_k| = {\mathcal O}(k^{-(1- \zeta )})$
,
![]() $|n_{k+1}^{- \psi } - n_k^{-\psi }| = {\mathcal O}(k^{-(1 + \zeta \psi )})$
,
$|n_{k+1}^{- \psi } - n_k^{-\psi }| = {\mathcal O}(k^{-(1 + \zeta \psi )})$
,
![]() $| \log n_{k+1} - \log n_k | = {\mathcal O}(k^{-1})$
and
$| \log n_{k+1} - \log n_k | = {\mathcal O}(k^{-1})$
and
![]() $m(U_n^\omega (x_0)) \le m(B_{n^{-\psi }}(x_0)) = {\mathcal O}(k^{-\zeta \psi })$
.
$m(U_n^\omega (x_0)) \le m(B_{n^{-\psi }}(x_0)) = {\mathcal O}(k^{-\zeta \psi })$
.
From these observations, it follows
 $$ \begin{align*} \mathrm{(III)} &\le C (\log n_k) n_k m(B_{n_k^{-\psi}}(x_0) \setminus B_{n^{-\psi}}(x_0))\\ &\le C (\log n_k) n_k | n_{k+1}^{-\psi} - n_k^{-\psi}| \le C (\log k) k^{-(1 - (1 - \psi) \zeta)}, \end{align*} $$
$$ \begin{align*} \mathrm{(III)} &\le C (\log n_k) n_k m(B_{n_k^{-\psi}}(x_0) \setminus B_{n^{-\psi}}(x_0))\\ &\le C (\log n_k) n_k | n_{k+1}^{-\psi} - n_k^{-\psi}| \le C (\log k) k^{-(1 - (1 - \psi) \zeta)}, \end{align*} $$
 $$ \begin{align*} \mathrm{(IV)} & \le C (\log n_k) \sum_{i=0}^{n_k - 1} m (B_{n_k^{-\psi}}(x_0) \cap \{ R_{B_{n_k^{-\psi}}(x_0) \setminus B_{n^{-\psi}}(x_0)}^{\sigma^i \omega} \le \lfloor a \log n \rfloor \} ) \\ & \le C (\log n_k) \sum_{i=0}^{n_k - 1} a (\log n) m(B_{n_k^{-\psi}}(x_0) \setminus B_{n^{-\psi}}(x_0)) \\ & \le C (\log k)^2 k^{-(1 - (1 - \psi) \zeta)}, \end{align*} $$
$$ \begin{align*} \mathrm{(IV)} & \le C (\log n_k) \sum_{i=0}^{n_k - 1} m (B_{n_k^{-\psi}}(x_0) \cap \{ R_{B_{n_k^{-\psi}}(x_0) \setminus B_{n^{-\psi}}(x_0)}^{\sigma^i \omega} \le \lfloor a \log n \rfloor \} ) \\ & \le C (\log n_k) \sum_{i=0}^{n_k - 1} a (\log n) m(B_{n_k^{-\psi}}(x_0) \setminus B_{n^{-\psi}}(x_0)) \\ & \le C (\log k)^2 k^{-(1 - (1 - \psi) \zeta)}, \end{align*} $$
and
 $$ \begin{align*} \mathrm{(V)} & \le C (\log n_k) \sum_{i=0}^{n_k -1} m( B_{n_k^{-\psi}}(x_0) \cap \{ \lfloor a \log n_k \rfloor < R_{ B_{n_k^{-\psi}}(x_0)}^{\sigma^i \omega} \le \lfloor a \log n \rfloor \}) \\ & \le C (\log n_k) \sum_{i=0}^{n_k-1 } a | \log n_{k+1} - \log n_k | m(B_{n_k^{-\psi}}(x_0)) \\ & \le C (\log k) k^{-(1 - (1 - \psi) \zeta)}. \end{align*} $$
$$ \begin{align*} \mathrm{(V)} & \le C (\log n_k) \sum_{i=0}^{n_k -1} m( B_{n_k^{-\psi}}(x_0) \cap \{ \lfloor a \log n_k \rfloor < R_{ B_{n_k^{-\psi}}(x_0)}^{\sigma^i \omega} \le \lfloor a \log n \rfloor \}) \\ & \le C (\log n_k) \sum_{i=0}^{n_k-1 } a | \log n_{k+1} - \log n_k | m(B_{n_k^{-\psi}}(x_0)) \\ & \le C (\log k) k^{-(1 - (1 - \psi) \zeta)}. \end{align*} $$
To obtain equation (10.6), it is thus sufficient to choose
![]() $\kappa>0$
and
$\kappa>0$
and
![]() $\zeta>0$
such that
$\zeta>0$
such that
![]() $\kappa < 3 \psi - 2$
,
$\kappa < 3 \psi - 2$
,
![]() $\kappa \zeta> 1$
, and
$\kappa \zeta> 1$
, and
![]() $(1 - \psi ) \zeta < 1$
, which is possible if
$(1 - \psi ) \zeta < 1$
, which is possible if
![]() $\psi> \frac 3 4$
.
$\psi> \frac 3 4$
.
We can now prove the functional convergence to a Lévy stable process for i.i.d. uniformly expanding maps.
Proof of Theorem 2.4
We apply Theorem 7.3. By Theorem 6.3, we have
![]() $N_n^\omega \, {\stackrel {d}{\to } \,} N_{(\alpha )}$
under the probability
$N_n^\omega \, {\stackrel {d}{\to } \,} N_{(\alpha )}$
under the probability
![]() $\nu ^\omega $
for
$\nu ^\omega $
for
![]() ${\mathbb P}$
-a.e.
${\mathbb P}$
-a.e.
![]() $\omega \in \Omega $
. It thus remains to check that equation (7.2) holds for m-a.e.
$\omega \in \Omega $
. It thus remains to check that equation (7.2) holds for m-a.e.
![]() $x_0$
when
$x_0$
when
![]() $\alpha \in [1,2)$
to complete the proof. For this purpose, we will use a reverse martingale argument from [Reference Nicol, Török and VaientiNTV18] (see also [Reference Aimino and RousseauAR16, Proposition 13]). Because of equation (5.8), it is enough to work on the probability space
$\alpha \in [1,2)$
to complete the proof. For this purpose, we will use a reverse martingale argument from [Reference Nicol, Török and VaientiNTV18] (see also [Reference Aimino and RousseauAR16, Proposition 13]). Because of equation (5.8), it is enough to work on the probability space
![]() $([0,1], \nu ^\omega )$
for
$([0,1], \nu ^\omega )$
for
![]() ${\mathbb P}$
-a.e.
${\mathbb P}$
-a.e.
![]() $\omega \in \Omega $
. Let
$\omega \in \Omega $
. Let
![]() $\mathcal {B}$
denote the
$\mathcal {B}$
denote the
![]() $\sigma $
-algebra of Borel sets on
$\sigma $
-algebra of Borel sets on
![]() $[0,1]$
and
$[0,1]$
and
To simplify notation a bit, let
From equation (5.8), it follows that
![]() ${\mathbb E}_m(|f_{\omega , j, n}|) \le C \epsilon b_n$
, and from the explicit definition of
${\mathbb E}_m(|f_{\omega , j, n}|) \le C \epsilon b_n$
, and from the explicit definition of
![]() $\phi $
, we can estimate the total variation of
$\phi $
, we can estimate the total variation of
![]() $f_{\omega ,j,n}$
and obtain the existence of
$f_{\omega ,j,n}$
and obtain the existence of
![]() $C> 0$
, independent of
$C> 0$
, independent of
![]() $\omega $
,
$\omega $
,
![]() $\epsilon $
, n, and j, such that
$\epsilon $
, n, and j, such that
We define
 $$ \begin{align*} S_{\omega, k, n}:=\sum_{j=0}^{k-1} f_{\omega, j, n}\circ T_{\omega}^j \end{align*} $$
$$ \begin{align*} S_{\omega, k, n}:=\sum_{j=0}^{k-1} f_{\omega, j, n}\circ T_{\omega}^j \end{align*} $$
and
Hence,
![]() $H_{\omega , 1, n}=0$
and an explicit formula for
$H_{\omega , 1, n}=0$
and an explicit formula for
![]() $H_{\omega , k, n}$
is
$H_{\omega , k, n}$
is
 $$ \begin{align*} H_{\omega, k, n}=\frac{1}{ h_{\sigma^k \omega}} \sum_{j=0}^{k-1} P_{\sigma^j \omega}^{k-j}(f_{\omega, j, n} h_{\sigma^j \omega}). \end{align*} $$
$$ \begin{align*} H_{\omega, k, n}=\frac{1}{ h_{\sigma^k \omega}} \sum_{j=0}^{k-1} P_{\sigma^j \omega}^{k-j}(f_{\omega, j, n} h_{\sigma^j \omega}). \end{align*} $$
From the explicit formula, the exponential decay in the BV norm of
![]() $P_{\sigma ^j \omega }^{n-j}$
from condition (Dec), equations (5.8) and (10.7), we see that
$P_{\sigma ^j \omega }^{n-j}$
from condition (Dec), equations (5.8) and (10.7), we see that
![]() $\|H_{\omega , k, n}\|_{\mathrm {BV}}\le C \epsilon b_n$
, where the constant C may be taken as constant over
$\|H_{\omega , k, n}\|_{\mathrm {BV}}\le C \epsilon b_n$
, where the constant C may be taken as constant over
![]() $\omega \in \Omega $
. If we define
$\omega \in \Omega $
. If we define
then the sequence
![]() $\{ M_{\omega , k, n}\}_{k \ge 1}$
is a reverse martingale difference for the decreasing filtration
$\{ M_{\omega , k, n}\}_{k \ge 1}$
is a reverse martingale difference for the decreasing filtration
![]() $\mathcal {B}_{\omega , k}=(T_{\omega }^n)^{-1}( \mathcal {B})$
as
$\mathcal {B}_{\omega , k}=(T_{\omega }^n)^{-1}( \mathcal {B})$
as
The martingale reverse differences are
where
We see from the
![]() $L^{\infty }$
bounds on
$L^{\infty }$
bounds on
![]() $\| H_{\omega , k, n}\|_{\infty } \le C b_n \epsilon $
and the telescoping sum that
$\| H_{\omega , k, n}\|_{\infty } \le C b_n \epsilon $
and the telescoping sum that
 $$ \begin{align} \bigg|\sum_{j=0}^{k-1} \psi_{\omega, j, n}\circ T_{\omega}^j -\sum_{j=0}^{k-1} f_{\omega, j, n}\circ T_{\omega}^j \bigg|\le C\epsilon b_n. \end{align} $$
$$ \begin{align} \bigg|\sum_{j=0}^{k-1} \psi_{\omega, j, n}\circ T_{\omega}^j -\sum_{j=0}^{k-1} f_{\omega, j, n}\circ T_{\omega}^j \bigg|\le C\epsilon b_n. \end{align} $$
By Doob’s martingale maximal inequality,
 $$ \begin{align*} \nu^\omega \bigg\{ \max_{1\le k \le n} \bigg| \sum_{j=0}^{k-1} \psi_{\omega, j, n}\circ T_{\omega}^j \bigg|\ge b_n \delta \bigg\} \le \frac{1}{b_n^2 \delta^2} {\mathbb E}_{\nu^\omega} \bigg|\sum_{j=0}^{n-1} \psi_{\omega, j, n} \circ T_{\omega}^j \bigg|^2. \end{align*} $$
$$ \begin{align*} \nu^\omega \bigg\{ \max_{1\le k \le n} \bigg| \sum_{j=0}^{k-1} \psi_{\omega, j, n}\circ T_{\omega}^j \bigg|\ge b_n \delta \bigg\} \le \frac{1}{b_n^2 \delta^2} {\mathbb E}_{\nu^\omega} \bigg|\sum_{j=0}^{n-1} \psi_{\omega, j, n} \circ T_{\omega}^j \bigg|^2. \end{align*} $$
Note that
 $$ \begin{align*} \sum_{j=0}^{n-1} {\mathbb E}_{\nu^\omega} [\psi^2_{\omega, j, n} \circ T_{\omega}^j]={\mathbb E}_{\nu^\omega} \bigg[\sum_{j=0}^{n-1} \psi_{\omega, j, n} \circ T_{\omega}^j\bigg]^{2} \end{align*} $$
$$ \begin{align*} \sum_{j=0}^{n-1} {\mathbb E}_{\nu^\omega} [\psi^2_{\omega, j, n} \circ T_{\omega}^j]={\mathbb E}_{\nu^\omega} \bigg[\sum_{j=0}^{n-1} \psi_{\omega, j, n} \circ T_{\omega}^j\bigg]^{2} \end{align*} $$
by pairwise orthogonality of martingale reverse differences.
As in [Reference Haydn, Nicol, Török and VaientiHNTV17, Lemma 6],
 $$ \begin{align*} {\mathbb E}_{\nu^\omega} [(S_{\omega, n, n})^2]=\sum_{j=0}^{n-1} {\mathbb E}_{\nu^\omega} [\psi^2_{\omega, j, n} \circ T_{\omega}^j]+ {\mathbb E}_{\nu^\omega}[H_{\omega, 1, n}^2]- {\mathbb E}_{\nu^\omega}[H_{\omega, n, n}^2\circ T_{\omega}^{n}]. \end{align*} $$
$$ \begin{align*} {\mathbb E}_{\nu^\omega} [(S_{\omega, n, n})^2]=\sum_{j=0}^{n-1} {\mathbb E}_{\nu^\omega} [\psi^2_{\omega, j, n} \circ T_{\omega}^j]+ {\mathbb E}_{\nu^\omega}[H_{\omega, 1, n}^2]- {\mathbb E}_{\nu^\omega}[H_{\omega, n, n}^2\circ T_{\omega}^{n}]. \end{align*} $$
So we see that
 $$ \begin{align} \nu^\omega \bigg\{ \max_{1\le k \le n} \bigg| \sum_{j=0}^{k-1} \psi_{\omega, j, n}\circ T_{\omega}^j \bigg|\ge b_n \delta \bigg\} \le \frac{1}{b_n^2 \delta^2} {\mathbb E}_{\nu^\omega} [(S_{\omega, n, n})^2] +2 \frac{C^2 \epsilon^2 }{\delta^2}, \end{align} $$
$$ \begin{align} \nu^\omega \bigg\{ \max_{1\le k \le n} \bigg| \sum_{j=0}^{k-1} \psi_{\omega, j, n}\circ T_{\omega}^j \bigg|\ge b_n \delta \bigg\} \le \frac{1}{b_n^2 \delta^2} {\mathbb E}_{\nu^\omega} [(S_{\omega, n, n})^2] +2 \frac{C^2 \epsilon^2 }{\delta^2}, \end{align} $$
where we have used
![]() $\| H^2_{\omega , j, n}\|_{\infty } \le C^2 b_n^2 \epsilon ^2$
.
$\| H^2_{\omega , j, n}\|_{\infty } \le C^2 b_n^2 \epsilon ^2$
.
Now we estimate
 $$ \begin{align} {\mathbb E}_{\nu^\omega} [(S_{\omega, n, n})^2]\le \sum_{j=0}^{n-1} {\mathbb E}_{\nu^\omega}[f^2_{\omega, j, n} \circ T_{\omega}^j]+2\sum_{i=0}^{n-1} \sum_{i < j} {\mathbb E}_{ \nu^\omega} [f_{\omega, j, n} \circ T_{\omega}^j \cdot f_{\omega, i, n} \circ T_{\omega}^i]. \end{align} $$
$$ \begin{align} {\mathbb E}_{\nu^\omega} [(S_{\omega, n, n})^2]\le \sum_{j=0}^{n-1} {\mathbb E}_{\nu^\omega}[f^2_{\omega, j, n} \circ T_{\omega}^j]+2\sum_{i=0}^{n-1} \sum_{i < j} {\mathbb E}_{ \nu^\omega} [f_{\omega, j, n} \circ T_{\omega}^j \cdot f_{\omega, i, n} \circ T_{\omega}^i]. \end{align} $$
Using the equivariance of the measures
![]() $\{ \nu ^\omega \}_{\omega \in \Omega }$
and equation (5.8), we have
$\{ \nu ^\omega \}_{\omega \in \Omega }$
and equation (5.8), we have

by Proposition 3.2 and that
since
![]() $\phi _{x_0}$
is regularly varying.
$\phi _{x_0}$
is regularly varying.
However, we are going to show that for m-a.e.
![]() $x_0$
,
$x_0$
,
 $$ \begin{align} \lim_{\epsilon \to 0} \limsup_{n \to \infty} \frac{1}{b_n^2}\sum_{i=0}^{n-1} \sum_{i< j} {\mathbb E}_{\nu^\omega} [f_{\omega, j, n} \circ T_{\omega}^j \cdot f_{\omega, i, n} \circ T^i_{\omega}] = 0. \end{align} $$
$$ \begin{align} \lim_{\epsilon \to 0} \limsup_{n \to \infty} \frac{1}{b_n^2}\sum_{i=0}^{n-1} \sum_{i< j} {\mathbb E}_{\nu^\omega} [f_{\omega, j, n} \circ T_{\omega}^j \cdot f_{\omega, i, n} \circ T^i_{\omega}] = 0. \end{align} $$
The first observation is that, due to condition (Dec),
where
![]() $\theta <1$
. Hence, there exists
$\theta <1$
. Hence, there exists
![]() $a> 0$
independently of n and
$a> 0$
independently of n and
![]() $\epsilon $
such that
$\epsilon $
such that
 $$ \begin{align*}\sum_{j-i> \lfloor a \log n \rfloor}{\mathbb E}_{\nu^\omega} [f_{\omega, j, n} \circ T_{\omega}^j \cdot f_{\omega, i, n} \circ T^i_{\omega}]\le C \epsilon^2 n^{-2} b_n^2\end{align*} $$
$$ \begin{align*}\sum_{j-i> \lfloor a \log n \rfloor}{\mathbb E}_{\nu^\omega} [f_{\omega, j, n} \circ T_{\omega}^j \cdot f_{\omega, i, n} \circ T^i_{\omega}]\le C \epsilon^2 n^{-2} b_n^2\end{align*} $$
and it is enough to prove that for
![]() $\epsilon> 0$
,
$\epsilon> 0$
,
 $$ \begin{align*} \sum_{i=0}^{n-1} \sum_{j = i+1}^{i + \lfloor a \log n \rfloor} {\mathbb E}_{\nu^\omega} [f_{\omega, j, n} \circ T_{\omega}^j \cdot f_{\omega, i, n} \circ T^i_{\omega}] = o(b_n^2) = o(n^{ 2/ \alpha}). \end{align*} $$
$$ \begin{align*} \sum_{i=0}^{n-1} \sum_{j = i+1}^{i + \lfloor a \log n \rfloor} {\mathbb E}_{\nu^\omega} [f_{\omega, j, n} \circ T_{\omega}^j \cdot f_{\omega, i, n} \circ T^i_{\omega}] = o(b_n^2) = o(n^{ 2/ \alpha}). \end{align*} $$
By construction, the term
![]() ${\mathbb E}_{\nu ^\omega }[f_{\omega , i, n} \circ T_\omega ^i \cdot f_{\omega , j, n} \circ T_\omega ^j]$
is a covariance, and since
${\mathbb E}_{\nu ^\omega }[f_{\omega , i, n} \circ T_\omega ^i \cdot f_{\omega , j, n} \circ T_\omega ^j]$
is a covariance, and since
![]() $\phi $
is positive, we can bound this quantity by
$\phi $
is positive, we can bound this quantity by
![]() ${\mathbb E}_{\nu ^\omega }[f \circ T_\omega ^i \cdot f \circ T_\omega ^j] = {\mathbb E}_{\nu ^{\sigma ^i \omega }}[f_n \cdot f_n \circ T_{\sigma ^i \omega }^{j-i}]$
, where
${\mathbb E}_{\nu ^\omega }[f \circ T_\omega ^i \cdot f \circ T_\omega ^j] = {\mathbb E}_{\nu ^{\sigma ^i \omega }}[f_n \cdot f_n \circ T_{\sigma ^i \omega }^{j-i}]$
, where ![]() . Then, since the densities are uniformly bounded by equation (5.8), we are left to estimate
. Then, since the densities are uniformly bounded by equation (5.8), we are left to estimate
 $$ \begin{align} \sum_{i=0}^{n-1} \sum_{j= i+1}^{i + \lfloor a \log n \rfloor} {\mathbb E}_m[f_n \cdot f_n \circ T_{\sigma^i \omega}^{j-i}]. \end{align} $$
$$ \begin{align} \sum_{i=0}^{n-1} \sum_{j= i+1}^{i + \lfloor a \log n \rfloor} {\mathbb E}_m[f_n \cdot f_n \circ T_{\sigma^i \omega}^{j-i}]. \end{align} $$
Let
![]() $\tfrac 3 4 < \psi < 1$
and
$\tfrac 3 4 < \psi < 1$
and
![]() $U_n = B_{n^{-\psi }}(x_0)$
. We bound equation (10.14) by
$U_n = B_{n^{-\psi }}(x_0)$
. We bound equation (10.14) by
![]() $\mathrm {(I)} + \mathrm {(II)} + \mathrm {(III)}$
, where
$\mathrm {(I)} + \mathrm {(II)} + \mathrm {(III)}$
, where
 $$ \begin{align*} \mathrm{(I)} = \sum_{i=0}^{n-1} \sum_{j= i+1}^{i + \lfloor a \log n \rfloor} \int_{U_n \cap (T_{\sigma^i \omega}^{j-i})^{-1}(U_n)} f_n \cdot f_n \circ T_{\sigma^i \omega}^{j-i} \,dm, \end{align*} $$
$$ \begin{align*} \mathrm{(I)} = \sum_{i=0}^{n-1} \sum_{j= i+1}^{i + \lfloor a \log n \rfloor} \int_{U_n \cap (T_{\sigma^i \omega}^{j-i})^{-1}(U_n)} f_n \cdot f_n \circ T_{\sigma^i \omega}^{j-i} \,dm, \end{align*} $$
 $$ \begin{align*} \mathrm{(II)} = \sum_{i=0}^{n-1} \sum_{j= i+1}^{i + \lfloor a \log n \rfloor} \int_{U_n \cap (T_{\sigma^i \omega}^{j-i})^{-1}(U_n^c)} f_n \cdot f_n \circ T_{\sigma^i \omega}^{j-i} \,dm, \end{align*} $$
$$ \begin{align*} \mathrm{(II)} = \sum_{i=0}^{n-1} \sum_{j= i+1}^{i + \lfloor a \log n \rfloor} \int_{U_n \cap (T_{\sigma^i \omega}^{j-i})^{-1}(U_n^c)} f_n \cdot f_n \circ T_{\sigma^i \omega}^{j-i} \,dm, \end{align*} $$
and
 $$ \begin{align*} \mathrm{(III)} = \sum_{i=0}^{n-1} \sum_{j= i+1}^{i + \lfloor a \log n \rfloor} \int_{U_n^c} f_n \cdot f_n \circ T_{\sigma^i \omega}^{j-i} \,dm. \end{align*} $$
$$ \begin{align*} \mathrm{(III)} = \sum_{i=0}^{n-1} \sum_{j= i+1}^{i + \lfloor a \log n \rfloor} \int_{U_n^c} f_n \cdot f_n \circ T_{\sigma^i \omega}^{j-i} \,dm. \end{align*} $$
Since
![]() $\|f_n\|_\infty \le \epsilon b_n$
, it follows that
$\|f_n\|_\infty \le \epsilon b_n$
, it follows that
 $$ \begin{align*} \mathrm{(I)} &\le \epsilon^2 b_n^2 \sum_{i=0}^{n-1} \sum_{j=i +1}^{i + \lfloor a \log n \rfloor }m(U_n \cap (T_{\sigma^i \omega}^{j-i})^{-1}(U_n)) \\ & \le a \epsilon^2 b_n^2 (\log n) \sum_{i=0}^{n-1} m(U_n \cap \{ R_{U_n}^{\sigma^i \omega} \le a \log n \} ), \end{align*} $$
$$ \begin{align*} \mathrm{(I)} &\le \epsilon^2 b_n^2 \sum_{i=0}^{n-1} \sum_{j=i +1}^{i + \lfloor a \log n \rfloor }m(U_n \cap (T_{\sigma^i \omega}^{j-i})^{-1}(U_n)) \\ & \le a \epsilon^2 b_n^2 (\log n) \sum_{i=0}^{n-1} m(U_n \cap \{ R_{U_n}^{\sigma^i \omega} \le a \log n \} ), \end{align*} $$
which by Lemma 10.3 is a
![]() $o(b_n^2)$
as
$o(b_n^2)$
as
![]() $n \to \infty $
for m-a.e.
$n \to \infty $
for m-a.e.
![]() $x_0$
.
$x_0$
.
To estimate terms (II) and (III), we will use Hölder’s inequality. We first observe by a direct computation that
 $$ \begin{align} \int_{U_n^c} \phi_{x_0}^2 \,dm = {\mathcal O}(n^{\psi ({2}/{\alpha} - 1 )}). \end{align} $$
$$ \begin{align} \int_{U_n^c} \phi_{x_0}^2 \,dm = {\mathcal O}(n^{\psi ({2}/{\alpha} - 1 )}). \end{align} $$
We consider term (III) first. Let
![]() $ A = U_n^c$
. We have
$ A = U_n^c$
. We have
 $$ \begin{align} \int_{U_n^c} f_n \cdot f_n \circ T_{\sigma^i \omega}^{j-i} \,dm &\le \int_A \phi_{x_0} \cdot f_n \circ T_{\sigma^i \omega}^{j-i} \,dm\nonumber\\ &\le \bigg( \int_A \phi_{x_0}^2 \,dm \bigg)^{ 1/ 2} \bigg( \int f_n^2 \circ T_{\sigma^i \omega}^{j-i} \,dm \bigg)^{ 1/ 2} \end{align} $$
$$ \begin{align} \int_{U_n^c} f_n \cdot f_n \circ T_{\sigma^i \omega}^{j-i} \,dm &\le \int_A \phi_{x_0} \cdot f_n \circ T_{\sigma^i \omega}^{j-i} \,dm\nonumber\\ &\le \bigg( \int_A \phi_{x_0}^2 \,dm \bigg)^{ 1/ 2} \bigg( \int f_n^2 \circ T_{\sigma^i \omega}^{j-i} \,dm \bigg)^{ 1/ 2} \end{align} $$
 $$ \begin{align} &\qquad\qquad\ \le C \bigg( \int_A \phi_{x_0}^2 \,dm \bigg)^{1/ 2} \bigg( \int f_n^2 \,dm \bigg)^{ 1/ 2}. \end{align} $$
$$ \begin{align} &\qquad\qquad\ \le C \bigg( \int_A \phi_{x_0}^2 \,dm \bigg)^{1/ 2} \bigg( \int f_n^2 \,dm \bigg)^{ 1/ 2}. \end{align} $$
By equation (10.15),
![]() $( \int _A \phi _{x_0}^2\,dm )^{ 1/ 2} \le C n^{{\psi }/{2} ({2}/{\alpha } - 1 )}$
and by Proposition 3.2,
$( \int _A \phi _{x_0}^2\,dm )^{ 1/ 2} \le C n^{{\psi }/{2} ({2}/{\alpha } - 1 )}$
and by Proposition 3.2,
![]() $( \int f_n^2\,dm )^{ 1/ 2} \le C n^{{1}/{\alpha } - 1 /2}$
. Hence, we may bound equation (10.16) by
$( \int f_n^2\,dm )^{ 1/ 2} \le C n^{{1}/{\alpha } - 1 /2}$
. Hence, we may bound equation (10.16) by
![]() $C n^{(1+\psi )({1}/{\alpha } - 1 /2)}$
.
$C n^{(1+\psi )({1}/{\alpha } - 1 /2)}$
.
To bound term (II), let
![]() $B= U_n \cap (T_{\sigma ^i \omega }^{j-i})^{-1}(U_n^c)$
. Then,
$B= U_n \cap (T_{\sigma ^i \omega }^{j-i})^{-1}(U_n^c)$
. Then,
 $$ \begin{align} \int_{U_n \cap (T_{\sigma^i \omega}^{j-i})^{-1}(U_n^c)} f_n \cdot f_n \circ T_{\sigma^i \omega}^{j-i} \,dm &\le \int_B f_n \cdot \phi_{x_0} \circ T_{\sigma^i \omega}^{j-i} \,dm\nonumber\\ & \le \bigg( \int f_n^2 \,dm \bigg)^{ 1/ 2} \bigg( \int_B \phi_{x_0}^2 \circ T_{\sigma^i \omega}^{j-i} \,dm \bigg)^{ 1/ 2}. \end{align} $$
$$ \begin{align} \int_{U_n \cap (T_{\sigma^i \omega}^{j-i})^{-1}(U_n^c)} f_n \cdot f_n \circ T_{\sigma^i \omega}^{j-i} \,dm &\le \int_B f_n \cdot \phi_{x_0} \circ T_{\sigma^i \omega}^{j-i} \,dm\nonumber\\ & \le \bigg( \int f_n^2 \,dm \bigg)^{ 1/ 2} \bigg( \int_B \phi_{x_0}^2 \circ T_{\sigma^i \omega}^{j-i} \,dm \bigg)^{ 1/ 2}. \end{align} $$
As before,
![]() $( \int f_n^2 dm )^{ 1 /2} \le C n^{{1}/{\alpha } - 1 /2}$
and
$( \int f_n^2 dm )^{ 1 /2} \le C n^{{1}/{\alpha } - 1 /2}$
and

by equation (10.15), and so equation (10.18) is bounded by
![]() $C n^{(1+\psi )({1}/{\alpha } - 1 /2)}$
.
$C n^{(1+\psi )({1}/{\alpha } - 1 /2)}$
.
It follows that
![]() $\mathrm {(II)} + \mathrm {(III)} \le C (\log n) n^{1 + (1+\psi )({1}/{\alpha } - 1/ 2)} = o(n^{ 2/ \alpha })$
, since
$\mathrm {(II)} + \mathrm {(III)} \le C (\log n) n^{1 + (1+\psi )({1}/{\alpha } - 1/ 2)} = o(n^{ 2/ \alpha })$
, since
![]() $ \psi < 1$
. This proves that equation (10.14) is
$ \psi < 1$
. This proves that equation (10.14) is
![]() $o(b_n^2)$
and concludes the proof of equation (10.13).
$o(b_n^2)$
and concludes the proof of equation (10.13).
Finally, from equations (10.11), (10.12), and (10.13), we obtain
 $$ \begin{align} \lim_{\epsilon \to 0} \limsup_{n \to \infty} \frac{1}{b_n^2} {\mathbb E}_{\nu^\omega}[(S_{\omega, n, n})^2] = 0, \end{align} $$
$$ \begin{align} \lim_{\epsilon \to 0} \limsup_{n \to \infty} \frac{1}{b_n^2} {\mathbb E}_{\nu^\omega}[(S_{\omega, n, n})^2] = 0, \end{align} $$
which gives the result by taking the limit first in n and then in
![]() $\epsilon $
in equation (10.10).
$\epsilon $
in equation (10.10).
10.2. Intermittent maps: proof of Theorem 2.6
We prove convergence to a stable law in the setting of intermittent maps when
![]() $\alpha \in (0,1)$
.
$\alpha \in (0,1)$
.
Proof of Theorem 2.6
We apply Proposition 5.8. By Theorem 6.4, it remains to prove equation (5.7), since
![]() $\alpha \in (0,1)$
. We will need an estimate for
$\alpha \in (0,1)$
. We will need an estimate for ![]() which is independent of
which is independent of
![]() $\omega $
. For this purpose, we introduce the absolutely continuous probability measure
$\omega $
. For this purpose, we introduce the absolutely continuous probability measure
![]() $\nu _{\mathrm {\max }}$
whose density is given by
$\nu _{\mathrm {\max }}$
whose density is given by
![]() $h_{\mathrm {\max }}(x) = \kappa x^{- \gamma _{\mathrm {\max }}}$
. Since all densities
$h_{\mathrm {\max }}(x) = \kappa x^{- \gamma _{\mathrm {\max }}}$
. Since all densities
![]() $h_\omega $
belong to the cone L, we have that
$h_\omega $
belong to the cone L, we have that
![]() $h_\omega \le ({a}/{\kappa }) h_{\mathrm {\max }}$
for all
$h_\omega \le ({a}/{\kappa }) h_{\mathrm {\max }}$
for all
![]() $\omega $
. Thus,
$\omega $
. Thus,

We can easily verify that
![]() $\phi _{x_0}$
is regularly varying of index
$\phi _{x_0}$
is regularly varying of index
![]() $\alpha $
with respect to
$\alpha $
with respect to
![]() $\nu _{\mathrm {\max }}$
, with scaling sequence equal to
$\nu _{\mathrm {\max }}$
, with scaling sequence equal to
![]() $(b_n)_{n \ge 1}$
up to a multiplicative constant factor. Consequently, by Proposition 3.2, we have that, for some constant
$(b_n)_{n \ge 1}$
up to a multiplicative constant factor. Consequently, by Proposition 3.2, we have that, for some constant
![]() $c>0$
,
$c>0$
,
which implies equation (5.7).
11. The annealed case
In this section, we consider the annealed counterparts of our results. Even though the annealed versions do not seem to follow immediately from the quenched version, it is easy to obtain them from our proofs in the quenched case. We take
![]() $\phi _{x_0} (x)=d(x,x_0)^{-{1}/{\alpha }}$
as before we consider the convergence on the measure space
$\phi _{x_0} (x)=d(x,x_0)^{-{1}/{\alpha }}$
as before we consider the convergence on the measure space
![]() $\Omega \times [0,1]$
with respect to
$\Omega \times [0,1]$
with respect to
![]() $\nu (d\omega , dx)={\mathbb P} (d \omega ) \nu ^{\omega } (dx)$
. We give precise annealed results in the case of Theorems 2.4 and 2.6, where we consider
$\nu (d\omega , dx)={\mathbb P} (d \omega ) \nu ^{\omega } (dx)$
. We give precise annealed results in the case of Theorems 2.4 and 2.6, where we consider
 $$ \begin{align*} X^a_n(\omega, x)(t) := \frac{1}{b_n} \bigg[ \sum_{j=0}^{\lfloor nt \rfloor - 1} \phi_{x_0}(T_\omega^j x) - t c_n\bigg], \: t \ge 0, \end{align*} $$
$$ \begin{align*} X^a_n(\omega, x)(t) := \frac{1}{b_n} \bigg[ \sum_{j=0}^{\lfloor nt \rfloor - 1} \phi_{x_0}(T_\omega^j x) - t c_n\bigg], \: t \ge 0, \end{align*} $$
viewed as a random process defined on the probability space
![]() $(\Omega \times [0,1], \nu )$
.
$(\Omega \times [0,1], \nu )$
.
Theorem 11.1. Under the same assumptions as Theorem 2.4, the random process
![]() $X^a_n (t)$
converges in the
$X^a_n (t)$
converges in the
![]() $J_1$
topology to the Lévy
$J_1$
topology to the Lévy
![]() $\alpha $
-stable process
$\alpha $
-stable process
![]() $X_{(\alpha )}(t)$
under the probability measure
$X_{(\alpha )}(t)$
under the probability measure
![]() $\nu $
.
$\nu $
.
Proof. We apply [Reference Tyran-KamińskaTK10b, Theorem 1.2] to the skew-product system
![]() $(\Omega \times [0,1], F, \nu )$
and the observable
$(\Omega \times [0,1], F, \nu )$
and the observable
![]() $\phi _{x_0}$
naturally extended to
$\phi _{x_0}$
naturally extended to
![]() $\Omega \times [0,1]$
. Recall that
$\Omega \times [0,1]$
. Recall that
![]() $\nu $
is given by the disintegration
$\nu $
is given by the disintegration
![]() $\nu (d \omega , dx) = {\mathbb P}(d \omega ) \nu ^\omega (dx)$
.
$\nu (d \omega , dx) = {\mathbb P}(d \omega ) \nu ^\omega (dx)$
.
We have to prove that:
-
(a)
 $N_n \, {\stackrel {d}{\to } \,} N_{(\alpha )}$
;
$N_n \, {\stackrel {d}{\to } \,} N_{(\alpha )}$
; -
(b) if
 $\alpha \in [1, 2)$
, for all
$\alpha \in [1, 2)$
, for all
 $\delta> 0$
,
$\delta> 0$
, 
where
 $$ \begin{align*} N_n(\omega, x)(B):= N_n^\omega(x)(B) = \# \bigg\{ j \ge 1 : \bigg( \frac{j}{n}, \frac{\phi_{x_0}(T_\omega^{j-1}(x))}{b_n}\bigg) \in B \bigg\}, \; n \ge 1. \end{align*} $$
$$ \begin{align*} N_n(\omega, x)(B):= N_n^\omega(x)(B) = \# \bigg\{ j \ge 1 : \bigg( \frac{j}{n}, \frac{\phi_{x_0}(T_\omega^{j-1}(x))}{b_n}\bigg) \in B \bigg\}, \; n \ge 1. \end{align*} $$
To prove item (a), we take
![]() $f \in C_K^+((0, \infty ) \times ({\mathbb R} \setminus \{ 0 \}))$
arbitrary. Then, by Theorem 6.3, we have for
$f \in C_K^+((0, \infty ) \times ({\mathbb R} \setminus \{ 0 \}))$
arbitrary. Then, by Theorem 6.3, we have for
![]() ${\mathbb P}$
-a.e.
${\mathbb P}$
-a.e.
![]() $\omega $
,
$\omega $
,
Integrating with respect to
![]() ${\mathbb P}$
and using the dominated convergence theorem yields
${\mathbb P}$
and using the dominated convergence theorem yields
which proves item (a).
To prove item (b), we simply have to integrate with respect to
![]() ${\mathbb P}$
in the estimates in the proof of Theorem 2.4, which hold uniformly in
${\mathbb P}$
in the estimates in the proof of Theorem 2.4, which hold uniformly in
![]() $\omega \in \Omega $
, and then to take the limits as
$\omega \in \Omega $
, and then to take the limits as
![]() $n \to \infty $
and
$n \to \infty $
and
![]() $\epsilon \to 0$
.
$\epsilon \to 0$
.
Similarly, we have the following theorem.
Theorem 11.2. Under the same assumptions as Theorem 2.6,
![]() $X_n^a(1) \, {\stackrel {d}{\to } \,} X_{(\alpha )}(1)$
under the probability measure
$X_n^a(1) \, {\stackrel {d}{\to } \,} X_{(\alpha )}(1)$
under the probability measure
![]() $\nu $
.
$\nu $
.
Proof. We can proceed as for Theorem 11.1 to check the assumptions of [Reference Tyran-KamińskaTK10b, Theorem 1.3] for the skew-product system
![]() $(\Omega \times [0,1], F, \nu )$
and the observable
$(\Omega \times [0,1], F, \nu )$
and the observable
![]() $\phi _{x_0}$
.
$\phi _{x_0}$
.
Acknowledgements
R.A. was partially supported by FCT project PTDC/MAT-PUR/ 4048/2021, with national funds, and by CMUP, which is financed by national funds through FCT – Fundação para a Ciência e a Tecnologia, I.P., under the project with reference UIDB/00144/2020. M.N. was supported in part by NSF Grants DMS 1600780 and DMS 2009923. A.T. was supported in part by NSF Grant DMS 1816315. R.A. would like to thank Jorge Freitas for several very insightful discussions about return time statistics and point processes. We wish to thank an anonymous referee for helpful comments. Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.
A. Appendix
The observation that our distributional limit theorems hold for any measures
![]() $\mu \ll \nu ^{\omega }$
follows from Zweimüller’s work [Reference ZweimüllerZwe07, Theorem 1, Corollary 1, and Corollary 3].
$\mu \ll \nu ^{\omega }$
follows from Zweimüller’s work [Reference ZweimüllerZwe07, Theorem 1, Corollary 1, and Corollary 3].
Let
 $$ \begin{align*} S_n (x)=\frac{1}{b_n} \bigg[\sum_{j=0}^{n-1} \phi\circ T_{\omega}^j (x)-a_n \bigg] \end{align*} $$
$$ \begin{align*} S_n (x)=\frac{1}{b_n} \bigg[\sum_{j=0}^{n-1} \phi\circ T_{\omega}^j (x)-a_n \bigg] \end{align*} $$
and suppose
where Y is a Lévy random variable.
We consider first the set-up of intermittent maps. We will show that for any measure
![]() $\nu $
with density h that is
$\nu $
with density h that is
![]() $d\nu =h\,dm$
in the cone L, in particular Lebesgue measure m with
$d\nu =h\,dm$
in the cone L, in particular Lebesgue measure m with
![]() $h=1$
,
$h=1$
,
We focus on m. According to [Reference ZweimüllerZwe07, Theorem 1], it is enough to show that
for any
![]() $\psi : {\mathbb R} \rightarrow {\mathbb R}$
which is bounded and uniformly Lipschitz.
$\psi : {\mathbb R} \rightarrow {\mathbb R}$
which is bounded and uniformly Lipschitz.
Fix such a
![]() $\psi $
and consider
$\psi $
and consider
 $$ \begin{align*} &\int \psi \bigg(\frac{1}{b_n} \bigg[\sum_{j=0}^{n-1} \phi\circ T_{\omega}^j (x)-a_n \bigg]\bigg) (h_{\omega} -1)\,dm\\ &\quad\le \int \psi \bigg(\frac{1}{b_n} \bigg[\sum_{j=0}^{n-1} \phi\circ T_{\sigma^k \omega}^j (x)-a_n \bigg]\bigg) P_{\omega}^k (h_{\omega} -1)\,dm\\ &\quad\le \|\psi\|_{\infty} \|P_{\omega}^k (h_{\omega} -1)\|_{L^{1}(m)}. \end{align*} $$
$$ \begin{align*} &\int \psi \bigg(\frac{1}{b_n} \bigg[\sum_{j=0}^{n-1} \phi\circ T_{\omega}^j (x)-a_n \bigg]\bigg) (h_{\omega} -1)\,dm\\ &\quad\le \int \psi \bigg(\frac{1}{b_n} \bigg[\sum_{j=0}^{n-1} \phi\circ T_{\sigma^k \omega}^j (x)-a_n \bigg]\bigg) P_{\omega}^k (h_{\omega} -1)\,dm\\ &\quad\le \|\psi\|_{\infty} \|P_{\omega}^k (h_{\omega} -1)\|_{L^{1}(m)}. \end{align*} $$
Since
![]() $\|P_{\omega }^k (h_{\omega } -1)\|_{L^{1}_m}\to 0$
in case of Example 2.2 and maps satisfying conditions (LY), (Dec), and (Min), the assertion is proved. By [Reference ZweimüllerZwe07, Corollary 3], the proof for continuous time distributional limits follows immediately.
$\|P_{\omega }^k (h_{\omega } -1)\|_{L^{1}_m}\to 0$
in case of Example 2.2 and maps satisfying conditions (LY), (Dec), and (Min), the assertion is proved. By [Reference ZweimüllerZwe07, Corollary 3], the proof for continuous time distributional limits follows immediately.