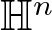1. Introduction
In this paper, we are interested in local behaviour of the weak solutions to nonlocal double phase problem in the Heisenberg group ![]() ${{\mathbb{H}}^n}$, whose prototype is
${{\mathbb{H}}^n}$, whose prototype is
 \begin{align}
\mathrm{P.V.}\int_{\mathbb{H}^n}\bigg[&\frac{|u(\xi)-u(\eta)|^{p-2}(u(\xi)-u(\eta))}{\|\eta^{-1}\circ\xi\|^{Q+sp}_{\mathbb{H}^n}} \nonumber \\
&+a(\xi,\eta)
\frac{|u(\xi)-u(\eta)|^{q-2}(u(\xi)-u(\eta))}{\|\eta^{-1}\circ\xi\|^{Q+tq}_{\mathbb{H}^n}}\bigg]\,d\eta=0 \quad \text{in } \Omega,
\end{align}
\begin{align}
\mathrm{P.V.}\int_{\mathbb{H}^n}\bigg[&\frac{|u(\xi)-u(\eta)|^{p-2}(u(\xi)-u(\eta))}{\|\eta^{-1}\circ\xi\|^{Q+sp}_{\mathbb{H}^n}} \nonumber \\
&+a(\xi,\eta)
\frac{|u(\xi)-u(\eta)|^{q-2}(u(\xi)-u(\eta))}{\|\eta^{-1}\circ\xi\|^{Q+tq}_{\mathbb{H}^n}}\bigg]\,d\eta=0 \quad \text{in } \Omega,
\end{align} where ![]() $1 \lt p\le q \lt \infty$,
$1 \lt p\le q \lt \infty$, ![]() $s,t\in(0,1)$,
$s,t\in(0,1)$, ![]() $ a(\cdot,\cdot)\ge 0$,
$ a(\cdot,\cdot)\ge 0$, ![]() $Q=2n+2$ is the homogeneous dimension and Ω is an open bounded subset of
$Q=2n+2$ is the homogeneous dimension and Ω is an open bounded subset of ![]() $\mathbb{H}^n$ (
$\mathbb{H}^n$ (![]() $n\ge1$). In the display above,
$n\ge1$). In the display above, ![]() $\|\cdot\|_{\mathbb{H}^n}$ and
$\|\cdot\|_{\mathbb{H}^n}$ and ![]() $\mathrm{P.V.}$ mean the standard Heisenberg norm and “in the principal value sense”, respectively. The main feature of the integro-differential equation (1.1) is that the leading operator could change between two different fractional elliptic phases according to whether the modulating coefficient a is zero or not.
$\mathrm{P.V.}$ mean the standard Heisenberg norm and “in the principal value sense”, respectively. The main feature of the integro-differential equation (1.1) is that the leading operator could change between two different fractional elliptic phases according to whether the modulating coefficient a is zero or not.
We observe that, if the coefficient ![]() $a\equiv0$, equation (1.1) is reduced to the p-fractional subLaplace equation arising in many diverse contexts, such as quantum mechanics, image segmentation models, ferromagnetic analysis and so on. Let us pay attention to the linear scenario first, i.e., p = 2. This kind of problems can be regarded as an extension of the conformally invariant fractional subLaplacian
$a\equiv0$, equation (1.1) is reduced to the p-fractional subLaplace equation arising in many diverse contexts, such as quantum mechanics, image segmentation models, ferromagnetic analysis and so on. Let us pay attention to the linear scenario first, i.e., p = 2. This kind of problems can be regarded as an extension of the conformally invariant fractional subLaplacian ![]() $\left(-\Delta_{\mathbb{H}^n}\right)^s$ in
$\left(-\Delta_{\mathbb{H}^n}\right)^s$ in ![]() $\mathbb{H}^n$ proposed initially in [Reference Branson, Fontana and Morpurgo2] by the spectral formula
$\mathbb{H}^n$ proposed initially in [Reference Branson, Fontana and Morpurgo2] by the spectral formula
 \begin{equation*}
\left(-\Delta_{\mathbb{H}^n}\right)^s:= {2^s}{\left| T \right|^s}\frac{{\Gamma \left( {- \frac{1}{2}{\Delta _H}{{\left| T \right|}^{- 1}} + \frac{{1 + s}}{2}} \right)}}{{\Gamma\left( {- \frac{1}{2}{\Delta _H}{{\left| T \right|}^{- 1}} + \frac{{1 - s}}{2}} \right)}},\;\;s \in \left( {0,1} \right),
\end{equation*}
\begin{equation*}
\left(-\Delta_{\mathbb{H}^n}\right)^s:= {2^s}{\left| T \right|^s}\frac{{\Gamma \left( {- \frac{1}{2}{\Delta _H}{{\left| T \right|}^{- 1}} + \frac{{1 + s}}{2}} \right)}}{{\Gamma\left( {- \frac{1}{2}{\Delta _H}{{\left| T \right|}^{- 1}} + \frac{{1 - s}}{2}} \right)}},\;\;s \in \left( {0,1} \right),
\end{equation*} where ![]() $s\in(0,1)$,
$s\in(0,1)$, ![]() $\Gamma(\cdot)$ is the Euler Gamma function, T is the vertical vector field, and
$\Gamma(\cdot)$ is the Euler Gamma function, T is the vertical vector field, and ![]() $\Delta_{\mathbb{H}^n}$ is the typical Kohn–Spencer subLaplacian on
$\Delta_{\mathbb{H}^n}$ is the typical Kohn–Spencer subLaplacian on ![]() $\mathbb{H}^n$. Subsequently, Roncal and Thangavelu [Reference Roncal and Thangavelu36] demonstrated the representation as below
$\mathbb{H}^n$. Subsequently, Roncal and Thangavelu [Reference Roncal and Thangavelu36] demonstrated the representation as below
 \begin{equation}
\left(-\Delta_{\mathbb{H}^n}\right)^su(\xi):=
C(n,s)\mathrm{P.V.}\int_{{\mathbb{H}^n}} {\frac{{u\left( \xi \right) - u\left( \eta \right)}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + 2s}}}d\eta }, \quad \xi\in\mathbb{H}^n,
\end{equation}
\begin{equation}
\left(-\Delta_{\mathbb{H}^n}\right)^su(\xi):=
C(n,s)\mathrm{P.V.}\int_{{\mathbb{H}^n}} {\frac{{u\left( \xi \right) - u\left( \eta \right)}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + 2s}}}d\eta }, \quad \xi\in\mathbb{H}^n,
\end{equation} holds true for ![]() $C(n,s) \gt 0$ depending only on
$C(n,s) \gt 0$ depending only on ![]() $n,s$. During the last decade, several aspects of the fractional operator of the type (1.2) have been investigated, such as Hardy and uncertainty inequalities on stratified Lie groups [Reference Ciatti, Cowling and Ricci6], Sobolev and Morrey-type embedding theory for fractional Sobolev space
$n,s$. During the last decade, several aspects of the fractional operator of the type (1.2) have been investigated, such as Hardy and uncertainty inequalities on stratified Lie groups [Reference Ciatti, Cowling and Ricci6], Sobolev and Morrey-type embedding theory for fractional Sobolev space ![]() $H^s(\mathbb{H}^n)$ [Reference Adimurthi and Mallick1], Harnack and Hölder estimates in Carnot groups [Reference Ferrari and Franchi18], Liouville-type theorem [Reference Cinti and Tan7]. One can refer to [Reference Ferrari, Miranda, Pallara, Pinamonti and Sire19–Reference Garofalo and Tralli22] and references therein for more results on the linear case. Regarding the nonlinear analogue to (1.2), the p-growth scenario is considered (
$H^s(\mathbb{H}^n)$ [Reference Adimurthi and Mallick1], Harnack and Hölder estimates in Carnot groups [Reference Ferrari and Franchi18], Liouville-type theorem [Reference Cinti and Tan7]. One can refer to [Reference Ferrari, Miranda, Pallara, Pinamonti and Sire19–Reference Garofalo and Tralli22] and references therein for more results on the linear case. Regarding the nonlinear analogue to (1.2), the p-growth scenario is considered (![]() $p\not=2$). For what concerns the regularity properties of weak solutions to the fractional p-subLaplace equations on the Heisenberg group, Manfredini et al. [Reference Manfredini, Palatucci, Piccinini and Polidoro31] established the interior boundedness and Hölder continuity via employing the De Giorge–Nash–Moser iteration; see also [Reference Palatucci and Piccinini32] for the nonlocal Harnack inequality, where the asymptotic behaviour of fractional linear operator was proved as well. In addition, as for the obstacle problems connected with the nonlocal p-subLaplacian, we refer to [Reference Piccinini34] in which Piccinini studied systematically solvability, semicontinuity, boundedness and Hölder regularity up to the boundary for weak solutions. More interesting estimates or fundamental functional inequalities can be found in [Reference Kassymov and Suragan27, Reference Kassymov and Surgan28, Reference Palatucci and Piccinini33]. To some extent, we can see that the results mentioned above extended the counterparts of the fractional Euclidean setting in [Reference Di Castro, Kuusi and Palatucci13, Reference Di Castro, Kuusi and Palatucci14, Reference Iannizzotto, Mosconi and Squassina26, Reference Korvenpää, Kuusi and Palatucci29, Reference Korvenpää, Kuusi and Palatucci30] to the Heisenberg framework.
$p\not=2$). For what concerns the regularity properties of weak solutions to the fractional p-subLaplace equations on the Heisenberg group, Manfredini et al. [Reference Manfredini, Palatucci, Piccinini and Polidoro31] established the interior boundedness and Hölder continuity via employing the De Giorge–Nash–Moser iteration; see also [Reference Palatucci and Piccinini32] for the nonlocal Harnack inequality, where the asymptotic behaviour of fractional linear operator was proved as well. In addition, as for the obstacle problems connected with the nonlocal p-subLaplacian, we refer to [Reference Piccinini34] in which Piccinini studied systematically solvability, semicontinuity, boundedness and Hölder regularity up to the boundary for weak solutions. More interesting estimates or fundamental functional inequalities can be found in [Reference Kassymov and Suragan27, Reference Kassymov and Surgan28, Reference Palatucci and Piccinini33]. To some extent, we can see that the results mentioned above extended the counterparts of the fractional Euclidean setting in [Reference Di Castro, Kuusi and Palatucci13, Reference Di Castro, Kuusi and Palatucci14, Reference Iannizzotto, Mosconi and Squassina26, Reference Korvenpää, Kuusi and Palatucci29, Reference Korvenpää, Kuusi and Palatucci30] to the Heisenberg framework.
Equation (1.1) could be viewed naturally as the nonlocal version of the classical double phase problem of the following type
Within the Euclidean context, the regularity theory of weak solutions to (1.3) or minimizers of the corresponding functionals has been developed extensively, beginning with the pioneering papers of Colombo and Mingione [Reference Colombo and Mingione8, Reference Colombo and Mingione9]. Under ![]() $a\in L^\infty_{\rm loc}(\Omega)$ and,
$a\in L^\infty_{\rm loc}(\Omega)$ and,  $p\le q\le \frac{np}{n-p}$ if p < n, or
$p\le q\le \frac{np}{n-p}$ if p < n, or ![]() $p\le q \lt \infty$ if
$p\le q \lt \infty$ if ![]() $p\ge n$, local boundedness for u was shown; and further under
$p\ge n$, local boundedness for u was shown; and further under ![]() $u\in L^\infty_{\rm loc}(\Omega)$,
$u\in L^\infty_{\rm loc}(\Omega)$,  $a\in C^{0,\alpha}_{\rm loc}(\Omega)$ and
$a\in C^{0,\alpha}_{\rm loc}(\Omega)$ and ![]() $p\le q\le p+\alpha$, Hölder continuity of u was obtained as well, see, e.g. [Reference Colombo and Mingione9, Reference Cupini, Marcellini and Mascolo10].
$p\le q\le p+\alpha$, Hölder continuity of u was obtained as well, see, e.g. [Reference Colombo and Mingione9, Reference Cupini, Marcellini and Mascolo10].
Very recently, the investigation of nonlocal problems with nonstandard growth, especially of those with (p, q)-growth condition, has been attracting increasing attention, however only in the fractional Euclidean spaces. In this respect, De Filippis and Palatucci [Reference De Filippis and Palatucci12] introduced nonlocal double phase equations of the form (1.1) in the Euclidean spaces, and established Hölder continuity for bounded viscosity solutions. Weak theory on this class of nonlocal equations was rapidly explored in hot pursuit, for example, [Reference Scott and Mengesha37] for self-improving inequalities on bounded weak solutions, [Reference Fang and Zhang17] for Hölder regularity and relationship between weak and viscosity solutions in the differentiability exponents ![]() $s\ge t$, [Reference Byun, Ok and Song4] for Hölder property with weaker assumption on solutions in the case s < t, [Reference Giacomoni, Kumar and Sreenadh24] for the sharp Hölder index and the parabolic version. Concerning more regularity and related results for nonlocal problems possessing nonuniform growth, one can see [Reference Byun, Kim and Ok3, Reference Chaker, Kim and Weidner5, Reference Fang and Zhang16, Reference Giacomoni, Kumar and Sreenadh23, Reference Prasad and Tewary35] and references therein.
$s\ge t$, [Reference Byun, Ok and Song4] for Hölder property with weaker assumption on solutions in the case s < t, [Reference Giacomoni, Kumar and Sreenadh24] for the sharp Hölder index and the parabolic version. Concerning more regularity and related results for nonlocal problems possessing nonuniform growth, one can see [Reference Byun, Kim and Ok3, Reference Chaker, Kim and Weidner5, Reference Fang and Zhang16, Reference Giacomoni, Kumar and Sreenadh23, Reference Prasad and Tewary35] and references therein.
In particular, we would like to mention that Palatucci, Piccinini, et al. in a series of papers [Reference Manfredini, Palatucci, Piccinini and Polidoro31–Reference Palatucci and Piccinini33] proposed the open problems about the regualrity of solutions to the so-called nonlocal double phase equation in the Heisenberg group ![]() $\mathbb{H}^n$. In this paper, influenced by the works [Reference Byun, Ok and Song4, Reference Di Castro, Kuusi and Palatucci14] we answer this question and develop the local regularity theory for the weak solutions of such equations in the Heisenberg group
$\mathbb{H}^n$. In this paper, influenced by the works [Reference Byun, Ok and Song4, Reference Di Castro, Kuusi and Palatucci14] we answer this question and develop the local regularity theory for the weak solutions of such equations in the Heisenberg group ![]() $\mathbb{H}^n$, including the boundedness and Hölder continuity of solutions. The main difficulties which are different from the previous ones are mainly two parts. One is that equation (1.1) not only possesses the nonlocal feature of the embraced integro-differential operators and the noneuclidean geometrical structure of the Heisenberg group, but also inherits the typical characteristics exhibited by the (local) double phase problems due to the (p, q)-growth condition and the presence of the nonnegative variable coefficient a. We need to find some appropriate assumptions on the summability exponents
$\mathbb{H}^n$, including the boundedness and Hölder continuity of solutions. The main difficulties which are different from the previous ones are mainly two parts. One is that equation (1.1) not only possesses the nonlocal feature of the embraced integro-differential operators and the noneuclidean geometrical structure of the Heisenberg group, but also inherits the typical characteristics exhibited by the (local) double phase problems due to the (p, q)-growth condition and the presence of the nonnegative variable coefficient a. We need to find some appropriate assumptions on the summability exponents ![]() $p,q\in (1, \infty)$ and differentiability exponents
$p,q\in (1, \infty)$ and differentiability exponents ![]() $s,t\in (0,1)$ together with the variable coefficient a in order to locally rebalance the non-uniform ellipticity of the operator. The other one is that the existing Sobolev embedding theorem, lemma 2.2, cannot be applied to our setting directly. To overcome this point, we have to establish a suitable Sobolev–Poincaré type inequality on balls in the Heisenberg group
$s,t\in (0,1)$ together with the variable coefficient a in order to locally rebalance the non-uniform ellipticity of the operator. The other one is that the existing Sobolev embedding theorem, lemma 2.2, cannot be applied to our setting directly. To overcome this point, we have to establish a suitable Sobolev–Poincaré type inequality on balls in the Heisenberg group ![]() $\mathbb{H}^n$. It may be of independent interest and potential applications when investigating regularity properties for some other nonlocal equations in the Heisenberg group. These difficulties make the current study more challenging than the fractional p-subLaplacian case.
$\mathbb{H}^n$. It may be of independent interest and potential applications when investigating regularity properties for some other nonlocal equations in the Heisenberg group. These difficulties make the current study more challenging than the fractional p-subLaplacian case.
Now we are in a position to state our main contributions. We first collect some notations, definitions as well as assumptions. Let ![]() $s,\;t$ and
$s,\;t$ and ![]() $p,\;q$ satisfy
$p,\;q$ satisfy
and the coefficient ![]() $a:{\mathbb{H}^n}\times {\mathbb{H}^n} \to {\mathbb{R}^+}$ fulfil
$a:{\mathbb{H}^n}\times {\mathbb{H}^n} \to {\mathbb{R}^+}$ fulfil
and
 \begin{equation}
\left| {a\left( {\xi ,\eta } \right) - a\left( {\xi ',\eta '} \right)} \right| \le {\left[ a \right]_\alpha }{\left( {{\| {{{\xi '}^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}} + {\| {{{\eta '}^{- 1}} \circ \eta } \|_{{\mathbb{H}^n}}}} \right)^\alpha},
\end{equation}
\begin{equation}
\left| {a\left( {\xi ,\eta } \right) - a\left( {\xi ',\eta '} \right)} \right| \le {\left[ a \right]_\alpha }{\left( {{\| {{{\xi '}^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}} + {\| {{{\eta '}^{- 1}} \circ \eta } \|_{{\mathbb{H}^n}}}} \right)^\alpha},
\end{equation} for ![]() $\left( {\xi ,\eta } \right),\left( {\xi ',\eta '} \right) \in {\mathbb{H}^n} \times {\mathbb{H}^n}$ and
$\left( {\xi ,\eta } \right),\left( {\xi ',\eta '} \right) \in {\mathbb{H}^n} \times {\mathbb{H}^n}$ and ![]() $\alpha \in \left( {0,1} \right]$.
$\alpha \in \left( {0,1} \right]$.
For convenience, we introduce the following notations:
 \begin{equation*}
H\left( {\xi ,\eta ,\tau } \right): = \frac{{{\tau ^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{sp}}} + a\left( {\xi ,\eta } \right)\frac{{{\tau ^q}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{tq}}}, \quad \xi ,\eta \in {\mathbb{H}^n}\;\hbox{and}\;\;\tau \gt 0,
\end{equation*}
\begin{equation*}
H\left( {\xi ,\eta ,\tau } \right): = \frac{{{\tau ^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{sp}}} + a\left( {\xi ,\eta } \right)\frac{{{\tau ^q}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{tq}}}, \quad \xi ,\eta \in {\mathbb{H}^n}\;\hbox{and}\;\;\tau \gt 0,
\end{equation*}and
with ![]() ${\tau _1},{\tau _2} \in \mathbb{R}$ and
${\tau _1},{\tau _2} \in \mathbb{R}$ and ![]() $l \in \{p,q\}$, and
$l \in \{p,q\}$, and
 \begin{equation*}
\rho \left( {u ;\Omega } \right) = \int_\Omega {\int_\Omega {H\left( {\xi ,\eta ,|u(\xi) -u(\eta)|} \right)\frac{{d\xi d\eta }}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^Q}}} },
\end{equation*}
\begin{equation*}
\rho \left( {u ;\Omega } \right) = \int_\Omega {\int_\Omega {H\left( {\xi ,\eta ,|u(\xi) -u(\eta)|} \right)\frac{{d\xi d\eta }}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^Q}}} },
\end{equation*} for every measurable set ![]() $\Omega \subset {\mathbb{H}^n}$ and
$\Omega \subset {\mathbb{H}^n}$ and ![]() $u: \Omega \to \mathbb{R}$. A function space related to weak solutions to (1.1) is defined as
$u: \Omega \to \mathbb{R}$. A function space related to weak solutions to (1.1) is defined as
 \begin{align*}{\mathcal{A}}\left( \Omega \right): & = \left\{u :{\mathbb{H}^n} \to \mathbb{R}: u {|_\Omega } \in {L^p}\left( \Omega \right)\;\;\hbox{and}\;\;\right. \nonumber\\
& \left.\iint_{\mathcal{C}_\Omega} H(\xi ,\eta ,|u(\xi)-u(\eta)|)\frac{d\xi d\eta }{\|\eta^{-1}\circ\xi\|_{\mathbb{H}^n}^Q} \lt \infty \right\},\end{align*}
\begin{align*}{\mathcal{A}}\left( \Omega \right): & = \left\{u :{\mathbb{H}^n} \to \mathbb{R}: u {|_\Omega } \in {L^p}\left( \Omega \right)\;\;\hbox{and}\;\;\right. \nonumber\\
& \left.\iint_{\mathcal{C}_\Omega} H(\xi ,\eta ,|u(\xi)-u(\eta)|)\frac{d\xi d\eta }{\|\eta^{-1}\circ\xi\|_{\mathbb{H}^n}^Q} \lt \infty \right\},\end{align*}where
Additionally, in view of the nonlocal nature of this problem, we need define a tail space
 \begin{equation*}
L^{q-1}_{sp}(\mathbb{H}^n):=\left\{u\in L_{\rm loc}^{q-1}(\mathbb H^n) : \int_{\mathbb{H}^n}\frac{|u(\xi)|^{q-1}}{(1+\|\xi\|_{\mathbb{H}^n})^{Q+sp}}
\,d\xi \lt \infty\right\},
\end{equation*}
\begin{equation*}
L^{q-1}_{sp}(\mathbb{H}^n):=\left\{u\in L_{\rm loc}^{q-1}(\mathbb H^n) : \int_{\mathbb{H}^n}\frac{|u(\xi)|^{q-1}}{(1+\|\xi\|_{\mathbb{H}^n})^{Q+sp}}
\,d\xi \lt \infty\right\},
\end{equation*}and the nonlocal tail
 \begin{equation*}
T\left( {u;\xi_0, r} \right): = \int_{{\mathbb{H}^n}\backslash {B_r(\xi_0)}} {\left( {\frac{{{{\left| {u \left( \xi \right)} \right|}^{p - 1}}}}{{\| {\xi _0^{- 1} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}} + {{\| a \|}_{{L^\infty }}}\frac{{{{\left| {u \left( \xi \right)} \right|}^{q - 1}}}}{{\| {\xi _0^{- 1} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + tq}}}} \right)\;d\xi .}
\end{equation*}
\begin{equation*}
T\left( {u;\xi_0, r} \right): = \int_{{\mathbb{H}^n}\backslash {B_r(\xi_0)}} {\left( {\frac{{{{\left| {u \left( \xi \right)} \right|}^{p - 1}}}}{{\| {\xi _0^{- 1} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}} + {{\| a \|}_{{L^\infty }}}\frac{{{{\left| {u \left( \xi \right)} \right|}^{q - 1}}}}{{\| {\xi _0^{- 1} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + tq}}}} \right)\;d\xi .}
\end{equation*} We can notice that the quantity T is finite if  $u\in L^{q-1}_{sp}(\mathbb{H}^n)$.
$u\in L^{q-1}_{sp}(\mathbb{H}^n)$.
We now give the definition of weak solutions to (1.1).
Definition 1.1. weak solution
If ![]() $u \in {\mathcal{A}}\left( \Omega \right)$ satisfies
$u \in {\mathcal{A}}\left( \Omega \right)$ satisfies
 \begin{align}
\iint_{\mathcal{C}_\Omega}\Bigg[\frac{J_p(u(\xi)-u(\eta))(\varphi(\xi)-\varphi(\eta))}{\|\eta^{-1}\circ\xi\|_{\mathbb{H}^n}^{Q+sp}} + a(\xi,\eta)\frac{J_q(u(\xi)-u(\eta))(\varphi(\xi)-\varphi(\eta))}{\|\eta^{-1}\circ\xi\|_{\mathbb{H}^n}^{Q+tq}}\Bigg]\,d\xi d\eta = 0,
\end{align}
\begin{align}
\iint_{\mathcal{C}_\Omega}\Bigg[\frac{J_p(u(\xi)-u(\eta))(\varphi(\xi)-\varphi(\eta))}{\|\eta^{-1}\circ\xi\|_{\mathbb{H}^n}^{Q+sp}} + a(\xi,\eta)\frac{J_q(u(\xi)-u(\eta))(\varphi(\xi)-\varphi(\eta))}{\|\eta^{-1}\circ\xi\|_{\mathbb{H}^n}^{Q+tq}}\Bigg]\,d\xi d\eta = 0,
\end{align} for every ![]() $\varphi \in {\mathcal{A}}\left( \Omega \right)$ with φ = 0 a.e. in
$\varphi \in {\mathcal{A}}\left( \Omega \right)$ with φ = 0 a.e. in ![]() ${\mathbb{H}^n}\backslash \Omega $, then we call u a weak solution to (1.1).
${\mathbb{H}^n}\backslash \Omega $, then we call u a weak solution to (1.1).
Note that ![]() $u\in {\mathcal{A}}( \Omega)$ implies
$u\in {\mathcal{A}}( \Omega)$ implies ![]() $u\in{HW}^{s,p}\left( \Omega \right)$, i.e.,
$u\in{HW}^{s,p}\left( \Omega \right)$, i.e., ![]() ${\mathcal{A}}\left( \Omega \right) \subset {HW}^{s,p}\left( \Omega \right)$. Hence in this work, we only consider the case
${\mathcal{A}}\left( \Omega \right) \subset {HW}^{s,p}\left( \Omega \right)$. Hence in this work, we only consider the case ![]() $sp \le Q$. Otherwise, the complementary scenario sp > Q ensures the local boundedness and Hölder continuity directly because of the fractional Morrey embedding in the Heisenberg group [Reference Adimurthi and Mallick1].
$sp \le Q$. Otherwise, the complementary scenario sp > Q ensures the local boundedness and Hölder continuity directly because of the fractional Morrey embedding in the Heisenberg group [Reference Adimurthi and Mallick1].
Our main results are stated as follows. The first one is the local boundedness of weak solutions.
Theorem 1.2 Let the conditions (1.4) and (1.5) be in force. If
 \begin{align}
\left\{\begin{array}{l}
p \le q \le \frac{{Qp}}{{Q - sp}} \quad \textrm{when } sp \lt Q,\\[2mm]
p \le q \lt \infty \qquad\,\, \textrm{when } sp \ge Q,
\end{array} \right.\;
\end{align}
\begin{align}
\left\{\begin{array}{l}
p \le q \le \frac{{Qp}}{{Q - sp}} \quad \textrm{when } sp \lt Q,\\[2mm]
p \le q \lt \infty \qquad\,\, \textrm{when } sp \ge Q,
\end{array} \right.\;
\end{align} then every weak solution  $u\in {\mathcal{A}}(\Omega ) \cap L_{sp}^{q - 1}\left({{\mathbb{H}^n}}\right)$ to (1.1) is locally bounded in Ω.
$u\in {\mathcal{A}}(\Omega ) \cap L_{sp}^{q - 1}\left({{\mathbb{H}^n}}\right)$ to (1.1) is locally bounded in Ω.
The second one is about the Hölder regularity of weak solutions to (1.1) via supposing ![]() $a(\cdot,\cdot)$ is Hölder continuous and the distance between q and p is small. For simplicity, we denote
$a(\cdot,\cdot)$ is Hölder continuous and the distance between q and p is small. For simplicity, we denote
as the set of basic parameters intervening in the problem.
Theorem 1.3 Let the conditions (1.4)–(1.6) with
be in force. If weak solution  $u\in {\mathcal{A}}(\Omega ) \cap L_{sp}^{q - 1}\left({{\mathbb{H}^n}}\right)$ to (1.1) has local boundedness in Ω, then it is locally Hölder continuous as well, that is, for any subset
$u\in {\mathcal{A}}(\Omega ) \cap L_{sp}^{q - 1}\left({{\mathbb{H}^n}}\right)$ to (1.1) has local boundedness in Ω, then it is locally Hölder continuous as well, that is, for any subset ![]() $\Omega'\subset\subset\Omega$, u belongs to
$\Omega'\subset\subset\Omega$, u belongs to  $C^{0,\beta}_{\rm loc}(\Omega')$ with some
$C^{0,\beta}_{\rm loc}(\Omega')$ with some  $\beta\in\left(0,\frac{sp}{q-1}\right)$ depending on
$\beta\in\left(0,\frac{sp}{q-1}\right)$ depending on ![]() $\mathrm{\mathbf{data}}$ and
$\mathrm{\mathbf{data}}$ and ![]() $\|u\|_{L^\infty(\Omega')}$.
$\|u\|_{L^\infty(\Omega')}$.
Putting these two theorems above, Hölder continuity is immediately obtained without local boundedness assumption under the intersecting conditions.
Remark 1.4. For the case s > t, local boundedness can be obtained under (1.5), (1.8) by checking the proof of theorem 1.2. Meanwhile, following the proof of theorem 1.3 and making a few slight modifications, we can deduce, under the same preconditions of theorem 1.3, that weak solutions are also of the class  $C^{0,\beta}_{\rm loc}(\Omega')$ with some
$C^{0,\beta}_{\rm loc}(\Omega')$ with some  $\beta\in\left(0,\frac{\min\{sp,tq\}}{q-1}\right)$.
$\beta\in\left(0,\frac{\min\{sp,tq\}}{q-1}\right)$.
This paper is organized as follows. In ![]() $\S$ 2, we introduce the Heisenberg group and function spaces, and then deduce some needful Sobolev embedding theorems. Section 3 is dedicated to proving local boundedness of weak solutions by the Caccioppoli-type estimate. At last, we shall show that the locally bounded weak solutions to (1.1) are Hölder continuous via establishing Logarithmic-type inequality in
$\S$ 2, we introduce the Heisenberg group and function spaces, and then deduce some needful Sobolev embedding theorems. Section 3 is dedicated to proving local boundedness of weak solutions by the Caccioppoli-type estimate. At last, we shall show that the locally bounded weak solutions to (1.1) are Hölder continuous via establishing Logarithmic-type inequality in ![]() $\S$ 4.
$\S$ 4.
2. Functional setting
In this section, we introduce the Heisenberg group ![]() ${{\mathbb{H}}^n}$ and some function spaces, and establish several important Sobolev embedding results. The Euclidean space
${{\mathbb{H}}^n}$ and some function spaces, and establish several important Sobolev embedding results. The Euclidean space ![]() ${{\mathbb{R}}^{2n + 1}}\;(n \ge 1)$ with the group multiplication
${{\mathbb{R}}^{2n + 1}}\;(n \ge 1)$ with the group multiplication
 \begin{equation*}\;\xi \circ \eta = \left( {{x_1} + {y_1},{x_2} + {y_2}, \cdots ,{x_{2n}} + {y_{2n}},\tau + \tau' + \frac{1}{2}\sum\limits_{i = 1}^n {\left( {{x_i}{y_{n + i}} - {x_{n + i}}{y_i}} \right)} } \right),\end{equation*}
\begin{equation*}\;\xi \circ \eta = \left( {{x_1} + {y_1},{x_2} + {y_2}, \cdots ,{x_{2n}} + {y_{2n}},\tau + \tau' + \frac{1}{2}\sum\limits_{i = 1}^n {\left( {{x_i}{y_{n + i}} - {x_{n + i}}{y_i}} \right)} } \right),\end{equation*} where ![]() $\xi = \left( {{x_1},{x_2}, \cdots ,{x_{2n}},\tau} \right),$
$\xi = \left( {{x_1},{x_2}, \cdots ,{x_{2n}},\tau} \right),$ ![]() $\eta = \left( {{y_1},{y_2}, \cdots ,{y_{2n}},\tau'} \right) \in {{\mathbb{R}}^{2n+1}},$ leads to the Heisenberg group
$\eta = \left( {{y_1},{y_2}, \cdots ,{y_{2n}},\tau'} \right) \in {{\mathbb{R}}^{2n+1}},$ leads to the Heisenberg group ![]() ${{\mathbb{H}}^n}$. The left invariant vector field on
${{\mathbb{H}}^n}$. The left invariant vector field on ![]() ${{\mathbb{H}}^n}$ is of the form
${{\mathbb{H}}^n}$ is of the form
 \begin{equation*}
{X_i} = {\partial _{{x_i}}} - \frac{{{x_{n + i}}}}{2}{\partial _\tau},\;{X_{n + i}} = {\partial _{{x_{n + i}}}} + \frac{{{x_i}}}{2}{\partial _\tau},\quad 1 \le i \le n,
\end{equation*}
\begin{equation*}
{X_i} = {\partial _{{x_i}}} - \frac{{{x_{n + i}}}}{2}{\partial _\tau},\;{X_{n + i}} = {\partial _{{x_{n + i}}}} + \frac{{{x_i}}}{2}{\partial _\tau},\quad 1 \le i \le n,
\end{equation*}and a non-trivial commutator is
We call that ![]() ${X_1},{X_2}, \cdots ,{X_{2n}}$ are the horizontal vector fields on
${X_1},{X_2}, \cdots ,{X_{2n}}$ are the horizontal vector fields on ![]() ${{\mathbb{H}}^n}$ and T the vertical vector field. Denote the horizontal gradient of a smooth function u on
${{\mathbb{H}}^n}$ and T the vertical vector field. Denote the horizontal gradient of a smooth function u on ![]() ${{\mathbb{H}}^n}$ by
${{\mathbb{H}}^n}$ by
The Haar measure in ![]() ${{\mathbb{H}}^n}$ is equivalent to the Lebesgue measure in
${{\mathbb{H}}^n}$ is equivalent to the Lebesgue measure in ![]() ${{\mathbb{R}}^{2n+1}}$. We denote the Lebesgue measure of a measurable set
${{\mathbb{R}}^{2n+1}}$. We denote the Lebesgue measure of a measurable set ![]() $E \subset {{\mathbb{H}}^n}$ by
$E \subset {{\mathbb{H}}^n}$ by ![]() $\left| E \right|$. For
$\left| E \right|$. For ![]() $\xi = \left( {{x_1},{x_2}, \cdots ,{x_{2n}},\tau} \right),$ we define its module as
$\xi = \left( {{x_1},{x_2}, \cdots ,{x_{2n}},\tau} \right),$ we define its module as
 \begin{equation*}{\| \xi \|_{{{\mathbb{H}}^n}}} = {\left( {{{\left( {\sum\limits_{i = 1}^{2n} {{x_i}^2} } \right)}^2} + {\tau^2}} \right)^{\frac{1}{4}}}.\end{equation*}
\begin{equation*}{\| \xi \|_{{{\mathbb{H}}^n}}} = {\left( {{{\left( {\sum\limits_{i = 1}^{2n} {{x_i}^2} } \right)}^2} + {\tau^2}} \right)^{\frac{1}{4}}}.\end{equation*} The Carnot-Carathéodary metric between two points ξ and η in ![]() ${{\mathbb{H}}^n}$ is the shortest length of the horizontal curve joining them, denoted by
${{\mathbb{H}}^n}$ is the shortest length of the horizontal curve joining them, denoted by ![]() $d(\xi,\eta)$. The C-C metric is equivalent to the Korànyi metric, i.e.,
$d(\xi,\eta)$. The C-C metric is equivalent to the Korànyi metric, i.e., ![]() $d\left( {\xi,\eta} \right) \sim {\| {{\xi^{- 1}}\circ \eta} \|_{{{\mathbb{H}}^n}}}$. The ball
$d\left( {\xi,\eta} \right) \sim {\| {{\xi^{- 1}}\circ \eta} \|_{{{\mathbb{H}}^n}}}$. The ball
is defined by the C-C metric d. When not important or clear from the context, we will omit the center as follows: ![]() $B_r:=B_r( \xi_0)$.
$B_r:=B_r( \xi_0)$.
Let ![]() $1 \le p \lt \infty ,\;s \in \left( {0,1} \right)$, and
$1 \le p \lt \infty ,\;s \in \left( {0,1} \right)$, and ![]() $v:{{\mathbb{H}}^n} \to {\mathbb{R}}$ be a measurable function. The Gagliardo semi-norm of v is defined as
$v:{{\mathbb{H}}^n} \to {\mathbb{R}}$ be a measurable function. The Gagliardo semi-norm of v is defined as
 \begin{equation*}{\left[ v \right]_{H{W^{s,p}}\left( {{{\mathbb{H}}^n}} \right)}} = {\left( {\int_{{{\mathbb{H}}^n}} {\int_{{{\mathbb{H}}^n}} {\frac{{{{\left| {v\left( \xi \right) - v\left( \eta \right)} \right|}^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{{\mathbb{H}}^n}}^{Q + sp}}}\,d\xi } d\eta } } \right)^{\frac{1}{p}}},\end{equation*}
\begin{equation*}{\left[ v \right]_{H{W^{s,p}}\left( {{{\mathbb{H}}^n}} \right)}} = {\left( {\int_{{{\mathbb{H}}^n}} {\int_{{{\mathbb{H}}^n}} {\frac{{{{\left| {v\left( \xi \right) - v\left( \eta \right)} \right|}^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{{\mathbb{H}}^n}}^{Q + sp}}}\,d\xi } d\eta } } \right)^{\frac{1}{p}}},\end{equation*} and the fractional Sobolev spaces ![]() $H{W^{s,p}}\left( {{{\mathbb{H}}^n}} \right)$ on the Heisenberg group are defined as
$H{W^{s,p}}\left( {{{\mathbb{H}}^n}} \right)$ on the Heisenberg group are defined as
 \begin{equation*}H{W^{s,p}}\left( {{{\mathbb{H}}^n}} \right) = \left\{{v \in {L^p}\left( {{{\mathbb{H}}^n}} \right):{{\left[ v \right]}_{H{W^{s,p}}\left( {{{\mathbb{H}}^n}} \right)}} \lt \infty } \right\},\end{equation*}
\begin{equation*}H{W^{s,p}}\left( {{{\mathbb{H}}^n}} \right) = \left\{{v \in {L^p}\left( {{{\mathbb{H}}^n}} \right):{{\left[ v \right]}_{H{W^{s,p}}\left( {{{\mathbb{H}}^n}} \right)}} \lt \infty } \right\},\end{equation*}endowed with the natural fractional norm
 \begin{equation*}{\| v \|_{H{W^{s,p}}\left( {{{\mathbb{H}}^n}} \right)}} = {\left( {\| v \|_{{L^p}\left( {{{\mathbb{H}}^n}} \right)}^p + \left[ v \right]_{H{W^{s,p}}\left( {{{\mathbb{H}}^n}} \right)}^p} \right)^{\frac{1}{p}}}.\end{equation*}
\begin{equation*}{\| v \|_{H{W^{s,p}}\left( {{{\mathbb{H}}^n}} \right)}} = {\left( {\| v \|_{{L^p}\left( {{{\mathbb{H}}^n}} \right)}^p + \left[ v \right]_{H{W^{s,p}}\left( {{{\mathbb{H}}^n}} \right)}^p} \right)^{\frac{1}{p}}}.\end{equation*} For any open set ![]() $\Omega \subset {{\mathbb{H}}^n}$, we can define similarly fractional Sobolev spaces
$\Omega \subset {{\mathbb{H}}^n}$, we can define similarly fractional Sobolev spaces ![]() $H{W^{s,p}}\left( \Omega \right)$ and fractional norm
$H{W^{s,p}}\left( \Omega \right)$ and fractional norm ![]() ${\| v \|_{H{W^{s,p}}\left( \Omega \right)}}$. The space
${\| v \|_{H{W^{s,p}}\left( \Omega \right)}}$. The space ![]() $HW_0^{s,p}\left( \Omega \right)$ is the closure of
$HW_0^{s,p}\left( \Omega \right)$ is the closure of ![]() $C_0^\infty \left( \Omega \right)$ in
$C_0^\infty \left( \Omega \right)$ in ![]() $H{W^{s,p}}\left( \Omega \right)$. Throughout this paper, we denote a generic positive constant as c or C. If necessary, relevant dependencies on parameters will be illustrated by parentheses, i.e.,
$H{W^{s,p}}\left( \Omega \right)$. Throughout this paper, we denote a generic positive constant as c or C. If necessary, relevant dependencies on parameters will be illustrated by parentheses, i.e., ![]() $c=c(n,p)$ means that c depends on
$c=c(n,p)$ means that c depends on ![]() $n,p$. Now we recall the fractional Poincaré type inequality and Sobolev embedding in the Heisenberg group
$n,p$. Now we recall the fractional Poincaré type inequality and Sobolev embedding in the Heisenberg group ![]() $\mathbb{H}^n$; see [Reference Piccinini34, proposition 2.7] and [Reference Kassymov and Surgan28, theorem 2.5], respectively.
$\mathbb{H}^n$; see [Reference Piccinini34, proposition 2.7] and [Reference Kassymov and Surgan28, theorem 2.5], respectively.
Lemma 2.1. Poincaré type inequality
Let ![]() $ p\ge1,\;s \in \left( {0,1} \right)$ and
$ p\ge1,\;s \in \left( {0,1} \right)$ and ![]() $v \in HW^{s,p}( B_r)$. Then we have
$v \in HW^{s,p}( B_r)$. Then we have
 \begin{equation*}\int_{{B_r}} {{{\left| {v - {{\left( v \right)}_r}} \right|}^p}\,d\xi } \le c{r^{sp}}\int_{{B_r}} {\int_{{B_r}} {\frac{{{{\left| {v\left( \xi \right) - v\left( \eta \right)} \right|}^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}}\,d\xi d\eta } } ,\end{equation*}
\begin{equation*}\int_{{B_r}} {{{\left| {v - {{\left( v \right)}_r}} \right|}^p}\,d\xi } \le c{r^{sp}}\int_{{B_r}} {\int_{{B_r}} {\frac{{{{\left| {v\left( \xi \right) - v\left( \eta \right)} \right|}^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}}\,d\xi d\eta } } ,\end{equation*} where ![]() $c=c(n,p) \gt 0$,
$c=c(n,p) \gt 0$,  ${\left( v \right)_r} = -\!\!\!\!\!\!\int_{{B_r}} {vd\xi } $.
${\left( v \right)_r} = -\!\!\!\!\!\!\int_{{B_r}} {vd\xi } $.
Lemma 2.2. Let ![]() $1 \lt p \lt \infty ,\;s \in \left( {0,1} \right)$ such that sp < Q. Let also
$1 \lt p \lt \infty ,\;s \in \left( {0,1} \right)$ such that sp < Q. Let also ![]() $v:{{\mathbb{H}}^n} \to {\mathbb{R}}$ be a measurable compactly supported function. Then there is a positive constant
$v:{{\mathbb{H}}^n} \to {\mathbb{R}}$ be a measurable compactly supported function. Then there is a positive constant ![]() $c = c\left( {n,p,s} \right)$ such that
$c = c\left( {n,p,s} \right)$ such that
 \begin{equation*}\| v \|_{{L^{{p_s^*}}}\left( {{{\mathbb{H}}^n}} \right)}^p \le c\left[ v \right]_{H{W^{s,p}}\left( {{{\mathbb{H}}^n}} \right)}^p,\end{equation*}
\begin{equation*}\| v \|_{{L^{{p_s^*}}}\left( {{{\mathbb{H}}^n}} \right)}^p \le c\left[ v \right]_{H{W^{s,p}}\left( {{{\mathbb{H}}^n}} \right)}^p,\end{equation*} with  ${p_s^*} = \frac{{Qp}}{{Q - sp}}$ being a critical Sobolev exponent.
${p_s^*} = \frac{{Qp}}{{Q - sp}}$ being a critical Sobolev exponent.
Now we also give the following result, a truncation lemma near ![]() $\partial\Omega$.
$\partial\Omega$.
Lemma 2.3. Let ![]() $ p \ge 1 ,\;s \in \left( {0,1} \right)$ and
$ p \ge 1 ,\;s \in \left( {0,1} \right)$ and ![]() $v \in HW^{s,p}\left( {{B_r}} \right)$. If
$v \in HW^{s,p}\left( {{B_r}} \right)$. If ![]() $\varphi \in {C^{0,1}}\left( {{B_r}} \right) \cap {L^\infty }\left( {{B_r}} \right)$, then it holds that
$\varphi \in {C^{0,1}}\left( {{B_r}} \right) \cap {L^\infty }\left( {{B_r}} \right)$, then it holds that ![]() $\varphi v \in HW^{s,p}\left( {{B_r}} \right)$ and
$\varphi v \in HW^{s,p}\left( {{B_r}} \right)$ and ![]() ${\| {\varphi v} \|_{H{W^{s,p}}\left( {{B_r}} \right)}} \le c{\| v \|_{H{W^{s,p}}\left( {{B_r}} \right)}}$ with c > 0 depending on
${\| {\varphi v} \|_{H{W^{s,p}}\left( {{B_r}} \right)}} \le c{\| v \|_{H{W^{s,p}}\left( {{B_r}} \right)}}$ with c > 0 depending on ![]() $n,p,s,r\;\hbox{and}\;\varphi.$
$n,p,s,r\;\hbox{and}\;\varphi.$
The proof of this lemma is very similar to that of [Reference Di Nezza, Palatucci and Valdinoci15, lemma 5.3], so we omit it here. Based on lemmas 2.1–2.3, we could conclude a Sobolev–Poincaré inequality on balls in the Heisenberg group, which plays a crucial role in proving regularity of solutions.
Proposition 2.4. Sobolev–Poincaré type inequality
Let ![]() $1 \lt p \lt \infty ,\;s \in \left( {0,1} \right)$ fulfil sp < Q. Suppose that
$1 \lt p \lt \infty ,\;s \in \left( {0,1} \right)$ fulfil sp < Q. Suppose that ![]() $v \in H{W^{s,p}}\left( {{B_R(\xi_0)}} \right)$ and
$v \in H{W^{s,p}}\left( {{B_R(\xi_0)}} \right)$ and ![]() ${B_r(\xi_0)} \subset {B_R(\xi_0)}\;(0 \lt r \lt R)$ are concentric balls. Then there exists a positive constant
${B_r(\xi_0)} \subset {B_R(\xi_0)}\;(0 \lt r \lt R)$ are concentric balls. Then there exists a positive constant ![]() $c=c(n,p,s)$ such that
$c=c(n,p,s)$ such that
 \begin{equation*}{\left( {{-\!\!\!\!\!\!\int_{{B_r}}}{{\left| {v - {{\left( v \right)}_{{r}}}} \right|}^{p_s^*}}\,d\xi } \right)^{\frac{p}{{p_s^*}}}} \le c{D_1}(R,r){-\!\!\!\!\!\!\int_{{B_R}}}\int_{{B_R}} {\frac{{{{\left| {v\left( \xi \right) - v\left( \eta \right)} \right|}^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}}\,d\xi } d\eta , \end{equation*}
\begin{equation*}{\left( {{-\!\!\!\!\!\!\int_{{B_r}}}{{\left| {v - {{\left( v \right)}_{{r}}}} \right|}^{p_s^*}}\,d\xi } \right)^{\frac{p}{{p_s^*}}}} \le c{D_1}(R,r){-\!\!\!\!\!\!\int_{{B_R}}}\int_{{B_R}} {\frac{{{{\left| {v\left( \xi \right) - v\left( \eta \right)} \right|}^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}}\,d\xi } d\eta , \end{equation*}where
 \begin{equation*}
{D_1}(R,r): = {r^{sp}}{\left( {\frac{R}{r}} \right)^{2Q}}\left[ {{{\left( {\frac{R}{{R - r}}} \right)}^p} + {{\left( {\frac{R}{{R - r}}} \right)}^{Q + sp}}} \right].
\end{equation*}
\begin{equation*}
{D_1}(R,r): = {r^{sp}}{\left( {\frac{R}{r}} \right)^{2Q}}\left[ {{{\left( {\frac{R}{{R - r}}} \right)}^p} + {{\left( {\frac{R}{{R - r}}} \right)}^{Q + sp}}} \right].
\end{equation*}Proof. Take ![]() $\varphi \left( \xi \right) \in C_0^\infty \left( {{B_R}\left( {{\xi _0}} \right)} \right)$ as a cut-off function such that
$\varphi \left( \xi \right) \in C_0^\infty \left( {{B_R}\left( {{\xi _0}} \right)} \right)$ as a cut-off function such that ![]() $0 \le \varphi \le 1,\;\varphi \equiv 1$ in
$0 \le \varphi \le 1,\;\varphi \equiv 1$ in ![]() ${{B_r}\left( {{\xi _0}} \right)}$,
${{B_r}\left( {{\xi _0}} \right)}$,  ${\rm supp}\, \varphi \subset B_\frac{R+r}{2}( \xi _0)$ and
${\rm supp}\, \varphi \subset B_\frac{R+r}{2}( \xi _0)$ and ![]() $\left| {{\nabla _H}\varphi } \right| \le \frac{c}{{R - r}}$ in
$\left| {{\nabla _H}\varphi } \right| \le \frac{c}{{R - r}}$ in ![]() ${{B_R}\left( {{\xi _0}} \right)}$. Then
${{B_R}\left( {{\xi _0}} \right)}$. Then ![]() $(v-(v)_r)\varphi \in HW_0^{s,p}(B_R)$ and further
$(v-(v)_r)\varphi \in HW_0^{s,p}(B_R)$ and further ![]() $(v-(v)_r)\varphi\in HW_0^{s,p}( {\mathbb{H}^n})$ by zero extension. We split
$(v-(v)_r)\varphi\in HW_0^{s,p}( {\mathbb{H}^n})$ by zero extension. We split ![]() ${\mathbb{H}^n} \times {\mathbb{H}^n}$ into
${\mathbb{H}^n} \times {\mathbb{H}^n}$ into
By virtue of lemma 2.2 and the definition of φ, we get
 \begin{align*}
{\left( {\int_{{B_r}} {{{\left| {v - {{\left( v \right)}_r}} \right|}^{p_s^*}}\,d\xi } } \right)^{\frac{p}{{p_s^*}}}} &\le {\left( {\int_{{\mathbb{H}^n}} {{{\left| {\left( {v - {{\left( v \right)}_r}} \right)\varphi } \right|}^{p_s^*}}\,d\xi } } \right)^{\frac{p}{{p_s^*}}}} \\
&\le c\int_{{\mathbb{H}^n}} {\int_{{\mathbb{H}^n}} {\frac{{{{\left| {\left( {v\left( \xi \right) - {{\left( v \right)}_r}} \right)\varphi \left( \xi \right) - \left( {v\left( \eta \right) - {{\left( v \right)}_r}} \right)\varphi \left( \eta \right)} \right|}^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}}\,d\xi } d\eta } \\
&\le c\int_{{B_R}} {\int_{{B_R}} {\frac{{{{\left| {\left( {v\left( \xi \right) - {{\left( v \right)}_r}} \right)\varphi \left( \xi \right) - \left( {v\left( \eta \right) - {{\left( v \right)}_r}} \right)\varphi \left( \eta \right)} \right|}^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}}{\mkern 1mu} d\xi d\eta } } \\
& \quad+ c \int_{{B_R}} {\int_{{H^n}\backslash {B_R}} {\frac{{{{\left| {\left( {v\left( \eta \right) - {{\left( v \right)}_r}} \right)\varphi \left( \eta \right)} \right|}^p}}}{{\left\| {{\eta ^{- 1}} \circ \xi } \right\|_{{\mathbb{H}^n}}^{Q + sp}}}{\mkern 1mu} d\xi d\eta } } \\
&=: {J_1} + {J_2}.
\end{align*}
\begin{align*}
{\left( {\int_{{B_r}} {{{\left| {v - {{\left( v \right)}_r}} \right|}^{p_s^*}}\,d\xi } } \right)^{\frac{p}{{p_s^*}}}} &\le {\left( {\int_{{\mathbb{H}^n}} {{{\left| {\left( {v - {{\left( v \right)}_r}} \right)\varphi } \right|}^{p_s^*}}\,d\xi } } \right)^{\frac{p}{{p_s^*}}}} \\
&\le c\int_{{\mathbb{H}^n}} {\int_{{\mathbb{H}^n}} {\frac{{{{\left| {\left( {v\left( \xi \right) - {{\left( v \right)}_r}} \right)\varphi \left( \xi \right) - \left( {v\left( \eta \right) - {{\left( v \right)}_r}} \right)\varphi \left( \eta \right)} \right|}^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}}\,d\xi } d\eta } \\
&\le c\int_{{B_R}} {\int_{{B_R}} {\frac{{{{\left| {\left( {v\left( \xi \right) - {{\left( v \right)}_r}} \right)\varphi \left( \xi \right) - \left( {v\left( \eta \right) - {{\left( v \right)}_r}} \right)\varphi \left( \eta \right)} \right|}^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}}{\mkern 1mu} d\xi d\eta } } \\
& \quad+ c \int_{{B_R}} {\int_{{H^n}\backslash {B_R}} {\frac{{{{\left| {\left( {v\left( \eta \right) - {{\left( v \right)}_r}} \right)\varphi \left( \eta \right)} \right|}^p}}}{{\left\| {{\eta ^{- 1}} \circ \xi } \right\|_{{\mathbb{H}^n}}^{Q + sp}}}{\mkern 1mu} d\xi d\eta } } \\
&=: {J_1} + {J_2}.
\end{align*}Note that
 \begin{align*}
{J_1}& \le c\int_{{B_R}} {\int_{{B_R}} {\frac{{{{\left| {v\left( \xi \right) - v\left( \eta \right)} \right|}^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}}\,d\xi } d\eta } + c\int_{{B_R}} {\int_{{B_R}} {\frac{{{{\left| {\varphi \left( \xi \right) - \varphi \left( \eta \right)} \right|}^p}{{\left| {\left( {v\left( \eta \right) - {{\left( v \right)}_r}} \right)} \right|}^p}}}{{\left\| {{\eta ^{- 1}} \circ \xi } \right\|_{{\mathbb{H}^n}}^{Q + sp}}}{\mkern 1mu} d\xi d\eta } } \\
& =:c\int_{{B_R}} {\int_{{B_R}} {\frac{{{{\left| {v\left( \xi \right) - v\left( \eta \right)} \right|}^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}}\,d\xi } d\eta } +J_{11}.
\end{align*}
\begin{align*}
{J_1}& \le c\int_{{B_R}} {\int_{{B_R}} {\frac{{{{\left| {v\left( \xi \right) - v\left( \eta \right)} \right|}^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}}\,d\xi } d\eta } + c\int_{{B_R}} {\int_{{B_R}} {\frac{{{{\left| {\varphi \left( \xi \right) - \varphi \left( \eta \right)} \right|}^p}{{\left| {\left( {v\left( \eta \right) - {{\left( v \right)}_r}} \right)} \right|}^p}}}{{\left\| {{\eta ^{- 1}} \circ \xi } \right\|_{{\mathbb{H}^n}}^{Q + sp}}}{\mkern 1mu} d\xi d\eta } } \\
& =:c\int_{{B_R}} {\int_{{B_R}} {\frac{{{{\left| {v\left( \xi \right) - v\left( \eta \right)} \right|}^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}}\,d\xi } d\eta } +J_{11}.
\end{align*}We first evaluate J 11 as
 \begin{align*}
{J_{11}} & \le \frac{c}{{{{\left( {R - r} \right)}^p}}}\int_{{B_R}} {\int_{{B_R}} {\frac{{{{\left| {{v\left( \eta \right) - {{\left( v \right)}_r}} } \right|}^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + p\left( {s - 1} \right)}}}\,d\xi d\eta } } \\
& \le \frac{c}{{{{\left( {R - r} \right)}^p}}}\int_{{B_R}} {{{\left| {{v\left( \eta \right) - {{\left( v \right)}_r}} } \right|}^p}\int_{{B_{2R}}\left( \eta \right)} {\frac{1}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + p\left( {s - 1} \right)}}}\,d\xi d\eta } } \\
& \le c{\left( {\frac{R}{{R - r}}} \right)^p}{R^{- sp}}\int_{{B_R}} {{{\left| {{v\left( \eta \right) - {{\left( v \right)}_r}} } \right|}^p}\,d\eta } \\
& \le c{\left( {\frac{R}{{R - r}}} \right)^p}{R^{- sp}}\left( {\int_{{B_R}} {{{\left| {{v\left( \eta \right) - {{\left( v \right)}_R}} } \right|}^p}\,d\eta } + \int_{{B_R}} {{{\left| {{{{\left( v \right)}_R} - {{\left( v \right)}_r}} } \right|}^p}\,d\eta } } \right)\\
&\le c{\left( {\frac{R}{{R - r}}} \right)^p}\!\!{R^{- sp}}\left( {{R^{sp}}\int_{{B_R}} {\int_{{B_R}} {\frac{{{{\left| {{v\left( \xi \right) - v\left( \eta \right)} } \right|}^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}}\,d\xi d\eta } } + {{\left| {{{\left( v \right)}_R} - {{\left( v \right)}_r}} \right|}^p}\left| {{B_R}} \right|} \right),
\end{align*}
\begin{align*}
{J_{11}} & \le \frac{c}{{{{\left( {R - r} \right)}^p}}}\int_{{B_R}} {\int_{{B_R}} {\frac{{{{\left| {{v\left( \eta \right) - {{\left( v \right)}_r}} } \right|}^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + p\left( {s - 1} \right)}}}\,d\xi d\eta } } \\
& \le \frac{c}{{{{\left( {R - r} \right)}^p}}}\int_{{B_R}} {{{\left| {{v\left( \eta \right) - {{\left( v \right)}_r}} } \right|}^p}\int_{{B_{2R}}\left( \eta \right)} {\frac{1}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + p\left( {s - 1} \right)}}}\,d\xi d\eta } } \\
& \le c{\left( {\frac{R}{{R - r}}} \right)^p}{R^{- sp}}\int_{{B_R}} {{{\left| {{v\left( \eta \right) - {{\left( v \right)}_r}} } \right|}^p}\,d\eta } \\
& \le c{\left( {\frac{R}{{R - r}}} \right)^p}{R^{- sp}}\left( {\int_{{B_R}} {{{\left| {{v\left( \eta \right) - {{\left( v \right)}_R}} } \right|}^p}\,d\eta } + \int_{{B_R}} {{{\left| {{{{\left( v \right)}_R} - {{\left( v \right)}_r}} } \right|}^p}\,d\eta } } \right)\\
&\le c{\left( {\frac{R}{{R - r}}} \right)^p}\!\!{R^{- sp}}\left( {{R^{sp}}\int_{{B_R}} {\int_{{B_R}} {\frac{{{{\left| {{v\left( \xi \right) - v\left( \eta \right)} } \right|}^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}}\,d\xi d\eta } } + {{\left| {{{\left( v \right)}_R} - {{\left( v \right)}_r}} \right|}^p}\left| {{B_R}} \right|} \right),
\end{align*}where in the last line we have utilized lemma 2.1. On the other hand,
 \begin{align*}
{\left| {{{\left( v \right)}_R} - {{\left( v \right)}_r}} \right|^p}\left| {{B_R}} \right|& = \left| {{B_R}} \right|{\left| {-\!\!\!\!\!\!\int_{{B_r}} {\left( {v - {{\left( v \right)}_R}} \right)d\xi } } \right|^p} \\
&\le \left| {{B_R}} \right|-\!\!\!\!\!\!\int_{{B_r}} {{{\left| {v - {{\left( v \right)}_R}} \right|}^p}d\xi } \\
& \le \frac{{\left| {{B_R}} \right|}}{{\left| {{B_r}} \right|}}\int_{{B_R}} {{{\left| {v - {{\left( v \right)}_R}} \right|}^p}d\xi }\\
& \le c{\left( {\frac{R}{r}} \right)^Q}{R^{sp}}\int_{{B_R}} {\int_{{B_R}} {\frac{{{{\left| {{v\left( \xi \right) - v\left( \eta \right)} } \right|}^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}}d\xi d\eta } }.
\end{align*}
\begin{align*}
{\left| {{{\left( v \right)}_R} - {{\left( v \right)}_r}} \right|^p}\left| {{B_R}} \right|& = \left| {{B_R}} \right|{\left| {-\!\!\!\!\!\!\int_{{B_r}} {\left( {v - {{\left( v \right)}_R}} \right)d\xi } } \right|^p} \\
&\le \left| {{B_R}} \right|-\!\!\!\!\!\!\int_{{B_r}} {{{\left| {v - {{\left( v \right)}_R}} \right|}^p}d\xi } \\
& \le \frac{{\left| {{B_R}} \right|}}{{\left| {{B_r}} \right|}}\int_{{B_R}} {{{\left| {v - {{\left( v \right)}_R}} \right|}^p}d\xi }\\
& \le c{\left( {\frac{R}{r}} \right)^Q}{R^{sp}}\int_{{B_R}} {\int_{{B_R}} {\frac{{{{\left| {{v\left( \xi \right) - v\left( \eta \right)} } \right|}^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}}d\xi d\eta } }.
\end{align*}Thus
 \begin{align*}
{J_1}& \le c\left( {1 + {{\left( {\frac{R}{{R - r}}} \right)}^p} + {{\left( {\frac{R}{r}} \right)}^Q}{{\left( {\frac{R}{{R - r}}} \right)}^p}} \right)\int_{{B_R}} {\int_{{B_R}} {\frac{{{{\left| {v\left( \xi \right) - v\left( \eta \right)} \right|}^p}}}{{\left\| {{\eta ^{- 1}} \circ \xi } \right\|_{{\mathbb{H}^n}}^{Q + sp}}}{\mkern 1mu} d\xi d\eta } } \\
& \le c{\left( {\frac{R}{r}} \right)^Q}{\left( {\frac{R}{{R - r}}} \right)^p}\int_{{B_R}} {\int_{{B_R}} {\frac{{{{\left| {v\left( \xi \right) - v\left( \eta \right)} \right|}^p}}}{{\left\| {{\eta ^{- 1}} \circ \xi } \right\|_{{{\mathbb{H}^n}^n}}^{Q + sp}}}{\mkern 1mu} d\xi d\eta } }.
\end{align*}
\begin{align*}
{J_1}& \le c\left( {1 + {{\left( {\frac{R}{{R - r}}} \right)}^p} + {{\left( {\frac{R}{r}} \right)}^Q}{{\left( {\frac{R}{{R - r}}} \right)}^p}} \right)\int_{{B_R}} {\int_{{B_R}} {\frac{{{{\left| {v\left( \xi \right) - v\left( \eta \right)} \right|}^p}}}{{\left\| {{\eta ^{- 1}} \circ \xi } \right\|_{{\mathbb{H}^n}}^{Q + sp}}}{\mkern 1mu} d\xi d\eta } } \\
& \le c{\left( {\frac{R}{r}} \right)^Q}{\left( {\frac{R}{{R - r}}} \right)^p}\int_{{B_R}} {\int_{{B_R}} {\frac{{{{\left| {v\left( \xi \right) - v\left( \eta \right)} \right|}^p}}}{{\left\| {{\eta ^{- 1}} \circ \xi } \right\|_{{{\mathbb{H}^n}^n}}^{Q + sp}}}{\mkern 1mu} d\xi d\eta } }.
\end{align*} Moreover, for ![]() $\xi \in {{\mathbb{H}^n}\backslash {B_R}}$,
$\xi \in {{\mathbb{H}^n}\backslash {B_R}}$,  $\eta \in {B_{\frac{{R + r}}{2}}}$, owing to the triangle inequality [Reference Cygan11] there holds that
$\eta \in {B_{\frac{{R + r}}{2}}}$, owing to the triangle inequality [Reference Cygan11] there holds that
 \begin{align*}
{\| {{\xi ^{- 1}} \circ \xi_0 } \|_{{\mathbb{H}^n}}} & \le \left( {1 + \frac{{{{\| {{\eta ^{- 1}} \circ {\xi_0}} \|}_{{\mathbb{H}^n}}}}}{{{{\| {{\xi ^{- 1}} \circ \eta } \|}_{{\mathbb{H}^n}}}}}} \right){\| {{\xi ^{- 1}} \circ \eta } \|_{{\mathbb{H}^n}}} \\
& \le \left(1 + \frac{(R+r)/2}{(R-r)/2} \right){\| {{\xi^{- 1}} \circ \eta } \|_{{\mathbb{H}^n}}} = \frac{{2R}}{{R - r}}{\| {{\xi ^{- 1}} \circ \eta } \|_{{\mathbb{H}^n}}}.
\end{align*}
\begin{align*}
{\| {{\xi ^{- 1}} \circ \xi_0 } \|_{{\mathbb{H}^n}}} & \le \left( {1 + \frac{{{{\| {{\eta ^{- 1}} \circ {\xi_0}} \|}_{{\mathbb{H}^n}}}}}{{{{\| {{\xi ^{- 1}} \circ \eta } \|}_{{\mathbb{H}^n}}}}}} \right){\| {{\xi ^{- 1}} \circ \eta } \|_{{\mathbb{H}^n}}} \\
& \le \left(1 + \frac{(R+r)/2}{(R-r)/2} \right){\| {{\xi^{- 1}} \circ \eta } \|_{{\mathbb{H}^n}}} = \frac{{2R}}{{R - r}}{\| {{\xi ^{- 1}} \circ \eta } \|_{{\mathbb{H}^n}}}.
\end{align*}From this, it follows that
 \begin{align*}
{J_{2}}& \le c \int_{{B_{\frac{{R + r}}{2}}}} {\int_{{\mathbb{H}^n}\backslash {B_R}} {\frac{{{{\left| {{v \left( \eta \right)- {{\left( v \right)}_r}} } \right|}^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}}\,d\xi d\eta } }\\
& \le c{\left( {\frac{R}{{R - r}}} \right)^{Q + sp}}\int_{{\mathbb{H}^n}\backslash {B_R}} {\frac{1}{{\| {{\xi ^{- 1}} \circ {\xi _0}} \|_{{\mathbb{H}^n}}^{Q + sp}}}d\xi \int_{{B_{\frac{{R + r}}{2}}}} {{{\left| {v\left( \eta \right) - {{\left( v \right)}_r}} \right|}^p}\,d\eta } } \\
& \le c\frac{{{R^Q}}}{{{{\left( {R - r} \right)}^{Q + sp}}}}\int_{{B_R}} {{{\left| {v\left( \eta \right) - {{\left( v \right)}_r}} \right|}^p}\,d\eta } \\
& \le c\frac{{{R^Q}}}{{{{\left( {R - r} \right)}^{Q + sp}}}}\left(R^{sp} + \frac{R^{Q + sp}}{r^Q}\right) \int_{B_R}\int_{B_R} \frac{|v( \xi) - v( \eta)|^p}{\|\eta ^{- 1} \circ \xi \|_{\mathbb{H}^n}^{Q + sp}}\,d\xi d\eta\\
& \le c{\left( {\frac{R}{r}} \right)^Q}{\left( {\frac{R}{{R - r}}} \right)^{Q+sp}}\int_{{B_R}} {\int_{{B_R}} {\frac{{{{\left| {v\left( \xi \right) - v\left( \eta \right)} \right|}^p}}}{{\left\| {{\eta ^{- 1}} \circ \xi } \right\|_{{{\mathbb{H}^n}^n}}^{Q + sp}}}{\mkern 1mu} d\xi d\eta } },
\end{align*}
\begin{align*}
{J_{2}}& \le c \int_{{B_{\frac{{R + r}}{2}}}} {\int_{{\mathbb{H}^n}\backslash {B_R}} {\frac{{{{\left| {{v \left( \eta \right)- {{\left( v \right)}_r}} } \right|}^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}}\,d\xi d\eta } }\\
& \le c{\left( {\frac{R}{{R - r}}} \right)^{Q + sp}}\int_{{\mathbb{H}^n}\backslash {B_R}} {\frac{1}{{\| {{\xi ^{- 1}} \circ {\xi _0}} \|_{{\mathbb{H}^n}}^{Q + sp}}}d\xi \int_{{B_{\frac{{R + r}}{2}}}} {{{\left| {v\left( \eta \right) - {{\left( v \right)}_r}} \right|}^p}\,d\eta } } \\
& \le c\frac{{{R^Q}}}{{{{\left( {R - r} \right)}^{Q + sp}}}}\int_{{B_R}} {{{\left| {v\left( \eta \right) - {{\left( v \right)}_r}} \right|}^p}\,d\eta } \\
& \le c\frac{{{R^Q}}}{{{{\left( {R - r} \right)}^{Q + sp}}}}\left(R^{sp} + \frac{R^{Q + sp}}{r^Q}\right) \int_{B_R}\int_{B_R} \frac{|v( \xi) - v( \eta)|^p}{\|\eta ^{- 1} \circ \xi \|_{\mathbb{H}^n}^{Q + sp}}\,d\xi d\eta\\
& \le c{\left( {\frac{R}{r}} \right)^Q}{\left( {\frac{R}{{R - r}}} \right)^{Q+sp}}\int_{{B_R}} {\int_{{B_R}} {\frac{{{{\left| {v\left( \xi \right) - v\left( \eta \right)} \right|}^p}}}{{\left\| {{\eta ^{- 1}} \circ \xi } \right\|_{{{\mathbb{H}^n}^n}}^{Q + sp}}}{\mkern 1mu} d\xi d\eta } },
\end{align*}the procedure of which is analogous to J 1. Eventually, we obtain
 \begin{align*}
&\quad {\left( {\int_{{B_r}} {{{\left| {v - {{\left( v \right)}_r}} \right|}^{p_s^*}}\,d\xi } } \right)^{\frac{p}{{p_s^*}}}}\\
& \le c{\left( {\frac{R}{r}} \right)^Q}\left[ {\left( {\frac{R}{{R - r}}} \right)^{p}}+{\left( {\frac{R}{{R - r}}} \right)^{Q+sp}} \right]\int_{{B_R}} {\int_{{B_R}} {\frac{{{{\left| {v\left( \xi \right) - v\left( \eta \right)} \right|}^p}}}{{\left\| {{\eta ^{- 1}} \circ \xi } \right\|_{{{\mathbb{H}^n}^n}}^{Q + sp}}}{\mkern 1mu} d\xi d\eta }},
\end{align*}
\begin{align*}
&\quad {\left( {\int_{{B_r}} {{{\left| {v - {{\left( v \right)}_r}} \right|}^{p_s^*}}\,d\xi } } \right)^{\frac{p}{{p_s^*}}}}\\
& \le c{\left( {\frac{R}{r}} \right)^Q}\left[ {\left( {\frac{R}{{R - r}}} \right)^{p}}+{\left( {\frac{R}{{R - r}}} \right)^{Q+sp}} \right]\int_{{B_R}} {\int_{{B_R}} {\frac{{{{\left| {v\left( \xi \right) - v\left( \eta \right)} \right|}^p}}}{{\left\| {{\eta ^{- 1}} \circ \xi } \right\|_{{{\mathbb{H}^n}^n}}^{Q + sp}}}{\mkern 1mu} d\xi d\eta }},
\end{align*}which implies the statement.
If we let ![]() $R=2r$ in the preceding Sobolev–Poincaré inequality, then we can get the very simple version below.
$R=2r$ in the preceding Sobolev–Poincaré inequality, then we can get the very simple version below.
Corollary 2.5. Let ![]() $1 \lt p \lt \infty,s \in (0,1)$ fulfil sp < Q. Suppose that
$1 \lt p \lt \infty,s \in (0,1)$ fulfil sp < Q. Suppose that ![]() $v\in H{W^{s,p}}(B_{2r})$ and
$v\in H{W^{s,p}}(B_{2r})$ and ![]() $B_r \subset B_{2r}$ are concentric balls. Then there exists a positive constant
$B_r \subset B_{2r}$ are concentric balls. Then there exists a positive constant ![]() $c(n,p,s)$ such that
$c(n,p,s)$ such that
 \begin{equation*}{\left( {{-\!\!\!\!\!\!\int_{{B_r}}}{{\left| {v - {{\left( v \right)}_{{r}}}} \right|}^{p_s^*}}\,d\xi } \right)^{\frac{p}{{p_s^*}}}} \le cr^{sp}{-\!\!\!\!\!\!\int_{B_{2r}}}\int_{B_{2r}} {\frac{{{{\left| {v\left( \xi \right) - v\left( \eta \right)} \right|}^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}}\,d\xi } d\eta . \end{equation*}
\begin{equation*}{\left( {{-\!\!\!\!\!\!\int_{{B_r}}}{{\left| {v - {{\left( v \right)}_{{r}}}} \right|}^{p_s^*}}\,d\xi } \right)^{\frac{p}{{p_s^*}}}} \le cr^{sp}{-\!\!\!\!\!\!\int_{B_{2r}}}\int_{B_{2r}} {\frac{{{{\left| {v\left( \xi \right) - v\left( \eta \right)} \right|}^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}}\,d\xi } d\eta . \end{equation*} The following result shows an embedding relation between the fractional Sobolev spaces ![]() $HW^{t,q}(\Omega)$ and
$HW^{t,q}(\Omega)$ and ![]() $HW^{s,p}(\Omega)$.
$HW^{s,p}(\Omega)$.
Lemma 2.6. Let ![]() $1 \lt p \le q$ and
$1 \lt p \le q$ and ![]() $0 \lt s \lt t \lt 1$. Let also Ω be a bounded measurable subset of
$0 \lt s \lt t \lt 1$. Let also Ω be a bounded measurable subset of ![]() $\mathbb{H}^n$. Then there holds that, for each
$\mathbb{H}^n$. Then there holds that, for each ![]() $v \in HW^{t,q}(\Omega)$,
$v \in HW^{t,q}(\Omega)$,
 \begin{equation*}{\left( {\int_\Omega {\int_\Omega {\frac{{{{\left| {{v\left( \xi \right) - v\left( \eta \right)} } \right|}^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}}d\xi d\eta } } } \right)^{\frac{1}{p}}} \le c{\left| \Omega \right|^{\frac{{q - p}}{{pq}}}}{\left( {\mathrm{diam}\left( \Omega \right)} \right)^{t - s}}{\left( {\int_\Omega {\int_\Omega {\frac{{{{\left| {{v\left( \xi \right) - v\left( \eta \right)} } \right|}^q}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + tq}}}d\xi d\eta } } } \right)^{\frac{1}{q}}},\end{equation*}
\begin{equation*}{\left( {\int_\Omega {\int_\Omega {\frac{{{{\left| {{v\left( \xi \right) - v\left( \eta \right)} } \right|}^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}}d\xi d\eta } } } \right)^{\frac{1}{p}}} \le c{\left| \Omega \right|^{\frac{{q - p}}{{pq}}}}{\left( {\mathrm{diam}\left( \Omega \right)} \right)^{t - s}}{\left( {\int_\Omega {\int_\Omega {\frac{{{{\left| {{v\left( \xi \right) - v\left( \eta \right)} } \right|}^q}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + tq}}}d\xi d\eta } } } \right)^{\frac{1}{q}}},\end{equation*} where c > 0 depends upon ![]() $n,p,q,s,t$.
$n,p,q,s,t$.
Proof. For p < q, we first utilize the Hölder inequality to get
 \begin{align*}
&\quad \int_\Omega {\int_\Omega {\frac{{{{\left| {{v\left( \xi \right) - v\left( \eta \right)}} \right|}^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}}\,d\xi d\eta } }\\
& = \int_\Omega {\int_\Omega {\frac{{{{\left| {{v\left( \xi \right) - v\left( \eta \right)} } \right|}^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{\left( {Q + tq} \right)\frac{p}{q}}}}\frac{1}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q\frac{{q - p}}{q} + (s - t)p}}}\,d\xi d\eta } } \\
& \le {\left( {\int_\Omega {\int_\Omega {\frac{{{{\left| {{v\left( \xi \right) - v\left( \eta \right)} } \right|}^q}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + tq}}}\,d\xi d\eta } } } \right)^{\frac{p}{q}}}{\left( {\int_\Omega {\int_\Omega {\frac{1}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + \frac{{(s - t)pq}}{{q - p}}}}}\,d\xi d\eta } } } \right)^{\frac{{q - p}}{q}}}.
\end{align*}
\begin{align*}
&\quad \int_\Omega {\int_\Omega {\frac{{{{\left| {{v\left( \xi \right) - v\left( \eta \right)}} \right|}^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}}\,d\xi d\eta } }\\
& = \int_\Omega {\int_\Omega {\frac{{{{\left| {{v\left( \xi \right) - v\left( \eta \right)} } \right|}^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{\left( {Q + tq} \right)\frac{p}{q}}}}\frac{1}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q\frac{{q - p}}{q} + (s - t)p}}}\,d\xi d\eta } } \\
& \le {\left( {\int_\Omega {\int_\Omega {\frac{{{{\left| {{v\left( \xi \right) - v\left( \eta \right)} } \right|}^q}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + tq}}}\,d\xi d\eta } } } \right)^{\frac{p}{q}}}{\left( {\int_\Omega {\int_\Omega {\frac{1}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + \frac{{(s - t)pq}}{{q - p}}}}}\,d\xi d\eta } } } \right)^{\frac{{q - p}}{q}}}.
\end{align*}On the other hand,
 \begin{align*}
\int_\Omega {\int_\Omega {\frac{1}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + \frac{{(s - t)pq}}{{q - p}}}}}\,d\xi d\eta } } & \le \int_\Omega {\int_{{B_d}\left( \eta \right)} {\frac{1}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{{\mathbb{H}}^n}}^{Q + \frac{{(s - t)pq}}{{q - p}}}}}\,d\xi d\eta } }\\
&\le Q\left| {{B_1}} \right|\int_\Omega {\int_0^d {{\rho ^{\frac{{(t - s)pq}}{{q - p}} - 1}}\,d\rho d\eta } } \nonumber\\
&= \frac{{Q\left| {{B_1}} \right|\left( {q - p} \right)}}{{(t - s)pq}}{d^{\frac{{(t - s)pq}}{{q - p}}}}\left| \Omega \right|,
\end{align*}
\begin{align*}
\int_\Omega {\int_\Omega {\frac{1}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + \frac{{(s - t)pq}}{{q - p}}}}}\,d\xi d\eta } } & \le \int_\Omega {\int_{{B_d}\left( \eta \right)} {\frac{1}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{{\mathbb{H}}^n}}^{Q + \frac{{(s - t)pq}}{{q - p}}}}}\,d\xi d\eta } }\\
&\le Q\left| {{B_1}} \right|\int_\Omega {\int_0^d {{\rho ^{\frac{{(t - s)pq}}{{q - p}} - 1}}\,d\rho d\eta } } \nonumber\\
&= \frac{{Q\left| {{B_1}} \right|\left( {q - p} \right)}}{{(t - s)pq}}{d^{\frac{{(t - s)pq}}{{q - p}}}}\left| \Omega \right|,
\end{align*} with ![]() $d: =\mathrm{diam}\left( \Omega \right)$. The combination of preceding inequalities implies the desired display.
$d: =\mathrm{diam}\left( \Omega \right)$. The combination of preceding inequalities implies the desired display.
If q = p, noting ![]() ${\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}} \le \mathrm{diam}\left( \Omega \right)$ for
${\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}} \le \mathrm{diam}\left( \Omega \right)$ for ![]() $\xi,\eta \in \Omega$ and s < t, we can readily obtain
$\xi,\eta \in \Omega$ and s < t, we can readily obtain
 \begin{align*}
{\left( {\int_\Omega {\int_\Omega {\frac{{{{\left| {{v\left( \xi \right) - v\left( \eta \right)} } \right|}^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}}\,d\xi d\eta } } } \right)^{\frac{1}{p}}}
&= {\left( {\int_\Omega {\int_\Omega {\frac{{{{\left| {{v\left( \xi \right) - v\left( \eta \right)} } \right|}^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + tp}}}\frac{1}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{(s - t)p}}}\,d\xi d\eta } } } \right)^{\frac{1}{p}}}\\
& \le {\left( {\mathrm{diam}\left( \Omega \right)} \right)^{t - s}}{\left( {\int_\Omega {\int_\Omega {\frac{{{{\left| {{v\left( \xi \right) - v\left( \eta \right)} } \right|}^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + tp}}}\,d\xi d\eta } } } \right)^{\frac{1}{p}}}.
\end{align*}
\begin{align*}
{\left( {\int_\Omega {\int_\Omega {\frac{{{{\left| {{v\left( \xi \right) - v\left( \eta \right)} } \right|}^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}}\,d\xi d\eta } } } \right)^{\frac{1}{p}}}
&= {\left( {\int_\Omega {\int_\Omega {\frac{{{{\left| {{v\left( \xi \right) - v\left( \eta \right)} } \right|}^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + tp}}}\frac{1}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{(s - t)p}}}\,d\xi d\eta } } } \right)^{\frac{1}{p}}}\\
& \le {\left( {\mathrm{diam}\left( \Omega \right)} \right)^{t - s}}{\left( {\int_\Omega {\int_\Omega {\frac{{{{\left| {{v\left( \xi \right) - v\left( \eta \right)} } \right|}^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + tp}}}\,d\xi d\eta } } } \right)^{\frac{1}{p}}}.
\end{align*}Now, we complete the proof.
The forthcoming two lemmas are the consequences of these results above, which will be exploited in the proof of boundedness and Hölder continuity for solutions.
Lemma 2.7. Assume that ![]() $s,t\in (0,1)$,
$s,t\in (0,1)$, ![]() $1 \lt p\le q$ and (1.8) hold. Then for every
$1 \lt p\le q$ and (1.8) hold. Then for every ![]() $f \in H{W^{s,p}}\left( {{B_r}} \right)$ we infer that
$f \in H{W^{s,p}}\left( {{B_r}} \right)$ we infer that
 \begin{align*}
-\!\!\!\!\!\!\int_{{B_r}} {\left( {{{\left| {\frac{f}{{{r^s}}}} \right|}^p} + {a_0}{{\left| {\frac{f}{{{r^t}}}} \right|}^q}} \right)\,d\xi }
& \le c{a_0}\frac{{D_1^{\frac{q}{p}}(R,r)}}{{{r^{tq}}}}{\left( {-\!\!\!\!\!\!\int_{{B_R}} {\int_{{B_R}} {\frac{{{{\left| {f\left( \xi \right) - f\left( \eta \right)} \right|}^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}}\,d\xi } d\eta } } \right)^{\frac{q}{p}}}\\
&\quad + c\frac{{{D_1}(R,r)}}{{{r^{sp}}}}{\left( {\frac{{\left| {{\rm{supp}}\,f} \right|}}{{\left| {{B_r}} \right|}}} \right)^{\frac{{sp}}{Q}}}-\!\!\!\!\!\!\int_{{B_R}} {\int_{{B_R}} {\frac{{{{\left| {f\left( \xi \right) - f\left( \eta \right)} \right|}^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}}\,d\xi } d\eta } \\
& \quad + c {{{\left(\frac{R}{r}\right)^Q\left( {\frac{{\left| {{\rm{supp}}\,f} \right|}}{{\left| {{B_r}} \right|}}} \right)}^{p - 1}} }-\!\!\!\!\!\!\int_{{B_R}} {\left( {{{\left| {\frac{f}{{{r^s}}}} \right|}^p} + {a_0}{{\left| {\frac{f}{{{r^t}}}} \right|}^q}} \right)\,d\xi },
\end{align*}
\begin{align*}
-\!\!\!\!\!\!\int_{{B_r}} {\left( {{{\left| {\frac{f}{{{r^s}}}} \right|}^p} + {a_0}{{\left| {\frac{f}{{{r^t}}}} \right|}^q}} \right)\,d\xi }
& \le c{a_0}\frac{{D_1^{\frac{q}{p}}(R,r)}}{{{r^{tq}}}}{\left( {-\!\!\!\!\!\!\int_{{B_R}} {\int_{{B_R}} {\frac{{{{\left| {f\left( \xi \right) - f\left( \eta \right)} \right|}^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}}\,d\xi } d\eta } } \right)^{\frac{q}{p}}}\\
&\quad + c\frac{{{D_1}(R,r)}}{{{r^{sp}}}}{\left( {\frac{{\left| {{\rm{supp}}\,f} \right|}}{{\left| {{B_r}} \right|}}} \right)^{\frac{{sp}}{Q}}}-\!\!\!\!\!\!\int_{{B_R}} {\int_{{B_R}} {\frac{{{{\left| {f\left( \xi \right) - f\left( \eta \right)} \right|}^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}}\,d\xi } d\eta } \\
& \quad + c {{{\left(\frac{R}{r}\right)^Q\left( {\frac{{\left| {{\rm{supp}}\,f} \right|}}{{\left| {{B_r}} \right|}}} \right)}^{p - 1}} }-\!\!\!\!\!\!\int_{{B_R}} {\left( {{{\left| {\frac{f}{{{r^s}}}} \right|}^p} + {a_0}{{\left| {\frac{f}{{{r^t}}}} \right|}^q}} \right)\,d\xi },
\end{align*} where ![]() ${\rm{supp}}\,f: = \{{B_r}:f \ne 0\} $, and c > 0 depends only upon
${\rm{supp}}\,f: = \{{B_r}:f \ne 0\} $, and c > 0 depends only upon ![]() $n,p,q,s,t$, and
$n,p,q,s,t$, and ![]() ${a_0}$ is any positive constant.
${a_0}$ is any positive constant.
Proof. By the Hölder inequality and proposition 2.4, we obtain
 \begin{align*}
-\!\!\!\!\!\!\int_{{B_r}} {{{\left| {\frac{f}{{{r^s}}}} \right|}^p}\,d\xi } &\le c-\!\!\!\!\!\!\int_{{B_r}} {{{\left| {\frac{{f - {{\left( f \right)}_r}}}{{{r^s}}}} \right|}^p}\chi_{\{f\neq0\}}\,d\xi } + c{\left| {\frac{{{{\left( f \right)}_r}}}{{{r^s}}}} \right|^p} \\
&\le c{\left( {\frac{{\left| {{\rm{supp}}\,f} \right|}}{{\left| {{B_r}} \right|}}} \right)^{\frac{{sp}}{Q}}}{\left( {-\!\!\!\!\!\!\int_{{B_r}} {{{\left| {\frac{{f - {{\left( f \right)}_r}}}{{{r^s}}}} \right|}^{p_s^*}}\,d\xi } } \right)^{\frac{p}{{p_s^*}}}} + c{\left| {\frac{{{{\left( f \right)}_r}}}{{{r^s}}}} \right|^p}\\
&\le c\frac{{{D_1}(R,r)}}{{{r^{sp}}}}{\left( {\frac{{\left| {{\rm{supp}}\,f} \right|}}{{\left| {{B_r}} \right|}}} \right)^{\frac{{sp}}{Q}}}-\!\!\!\!\!\!\int_{{B_R}} {\int_{{B_R}} {\frac{{{{\left| {f\left( \xi \right) - f\left( \eta \right)} \right|}^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}}\,d\xi } d\eta } \\
&\quad+ c{\left( {\frac{{\left| {{\rm{supp}}\,f} \right|}}{{\left| {{B_r}} \right|}}} \right)^{p - 1}}-\!\!\!\!\!\!\int_{{B_r}} {{{\left| {\frac{f}{{{r^s}}}} \right|}^p}\,d\xi },
\end{align*}
\begin{align*}
-\!\!\!\!\!\!\int_{{B_r}} {{{\left| {\frac{f}{{{r^s}}}} \right|}^p}\,d\xi } &\le c-\!\!\!\!\!\!\int_{{B_r}} {{{\left| {\frac{{f - {{\left( f \right)}_r}}}{{{r^s}}}} \right|}^p}\chi_{\{f\neq0\}}\,d\xi } + c{\left| {\frac{{{{\left( f \right)}_r}}}{{{r^s}}}} \right|^p} \\
&\le c{\left( {\frac{{\left| {{\rm{supp}}\,f} \right|}}{{\left| {{B_r}} \right|}}} \right)^{\frac{{sp}}{Q}}}{\left( {-\!\!\!\!\!\!\int_{{B_r}} {{{\left| {\frac{{f - {{\left( f \right)}_r}}}{{{r^s}}}} \right|}^{p_s^*}}\,d\xi } } \right)^{\frac{p}{{p_s^*}}}} + c{\left| {\frac{{{{\left( f \right)}_r}}}{{{r^s}}}} \right|^p}\\
&\le c\frac{{{D_1}(R,r)}}{{{r^{sp}}}}{\left( {\frac{{\left| {{\rm{supp}}\,f} \right|}}{{\left| {{B_r}} \right|}}} \right)^{\frac{{sp}}{Q}}}-\!\!\!\!\!\!\int_{{B_R}} {\int_{{B_R}} {\frac{{{{\left| {f\left( \xi \right) - f\left( \eta \right)} \right|}^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}}\,d\xi } d\eta } \\
&\quad+ c{\left( {\frac{{\left| {{\rm{supp}}\,f} \right|}}{{\left| {{B_r}} \right|}}} \right)^{p - 1}}-\!\!\!\!\!\!\int_{{B_r}} {{{\left| {\frac{f}{{{r^s}}}} \right|}^p}\,d\xi },
\end{align*}where we used the inequality below,
 \begin{equation*}{\left| {\frac{{{{\left( f \right)}_r}}}{{{r^s}}}} \right|^p} = {r^{- sp}}{\left| {-\!\!\!\!\!\!\int_{{B_r}} {f{\chi _{\left\{{f \ne 0} \right\}}}\,d\xi } } \right|^p} \le {\left( {\frac{{\left| {{\rm{supp}}\;f} \right|}}{{\left| {{B_r}} \right|}}} \right)^{p - 1}}-\!\!\!\!\!\!\int_{{B_r}} {{{\left| {\frac{f}{{{r^s}}}} \right|}^p}\,d\xi } .\end{equation*}
\begin{equation*}{\left| {\frac{{{{\left( f \right)}_r}}}{{{r^s}}}} \right|^p} = {r^{- sp}}{\left| {-\!\!\!\!\!\!\int_{{B_r}} {f{\chi _{\left\{{f \ne 0} \right\}}}\,d\xi } } \right|^p} \le {\left( {\frac{{\left| {{\rm{supp}}\;f} \right|}}{{\left| {{B_r}} \right|}}} \right)^{p - 1}}-\!\!\!\!\!\!\int_{{B_r}} {{{\left| {\frac{f}{{{r^s}}}} \right|}^p}\,d\xi } .\end{equation*}On the other hand, via the Hölder inequality and proposition 2.4 again,
 \begin{align*}
-\!\!\!\!\!\!\int_{{B_r}} {{{\left| {\frac{f}{{{r^t}}}} \right|}^q}d\xi }
&\le c{\left( {-\!\!\!\!\!\!\int_{{B_r}} {{{\left| {\frac{{f - {{\left( f \right)}_r}}}{{{r^t}}}} \right|}^{p_s^*}}d\xi } } \right)^{\frac{q}{{p_s^*}}}} + c{\left| {\frac{{{{\left( f \right)}_r}}}{{{r^t}}}} \right|^q} \\
&\le c\frac{{D_1^{\frac{q}{p}}(R,r)}}{{{r^{tq}}}}{\left( {-\!\!\!\!\!\!\int_{{B_R}} {\int_{{B_R}} {\frac{{{{\left| {f\left( \xi \right) - f\left( \eta \right)} \right|}^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}}\,d\xi } d\eta } } \right)^{\frac{q}{p}}}+ c{\left| {\frac{{{{\left( f \right)}_r}}}{{{r^t}}}} \right|^q}\\
&\le c\frac{{D_1^{\frac{q}{p}}(R,r)}}{{{r^{tq}}}}{\left( {-\!\!\!\!\!\!\int_{{B_R}} {\int_{{B_R}} {\frac{{{{\left| {f\left( \xi \right) - f\left( \eta \right)} \right|}^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}}\,d\xi } d\eta } } \right)^{\frac{q}{p}}}\\
&\quad+ c{\left( {\frac{{\left| {{\rm{supp}}\,f} \right|}}{{\left| {{B_r}} \right|}}} \right)^{p - 1}}-\!\!\!\!\!\!\int_{{B_r}} {{{\left| {\frac{f}{{{r^t}}}} \right|}^q}\,d\xi},
\end{align*}
\begin{align*}
-\!\!\!\!\!\!\int_{{B_r}} {{{\left| {\frac{f}{{{r^t}}}} \right|}^q}d\xi }
&\le c{\left( {-\!\!\!\!\!\!\int_{{B_r}} {{{\left| {\frac{{f - {{\left( f \right)}_r}}}{{{r^t}}}} \right|}^{p_s^*}}d\xi } } \right)^{\frac{q}{{p_s^*}}}} + c{\left| {\frac{{{{\left( f \right)}_r}}}{{{r^t}}}} \right|^q} \\
&\le c\frac{{D_1^{\frac{q}{p}}(R,r)}}{{{r^{tq}}}}{\left( {-\!\!\!\!\!\!\int_{{B_R}} {\int_{{B_R}} {\frac{{{{\left| {f\left( \xi \right) - f\left( \eta \right)} \right|}^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}}\,d\xi } d\eta } } \right)^{\frac{q}{p}}}+ c{\left| {\frac{{{{\left( f \right)}_r}}}{{{r^t}}}} \right|^q}\\
&\le c\frac{{D_1^{\frac{q}{p}}(R,r)}}{{{r^{tq}}}}{\left( {-\!\!\!\!\!\!\int_{{B_R}} {\int_{{B_R}} {\frac{{{{\left| {f\left( \xi \right) - f\left( \eta \right)} \right|}^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}}\,d\xi } d\eta } } \right)^{\frac{q}{p}}}\\
&\quad+ c{\left( {\frac{{\left| {{\rm{supp}}\,f} \right|}}{{\left| {{B_r}} \right|}}} \right)^{p - 1}}-\!\!\!\!\!\!\int_{{B_r}} {{{\left| {\frac{f}{{{r^t}}}} \right|}^q}\,d\xi},
\end{align*}where we can see that
 \begin{equation*}{\left| {\frac{{{{\left( f \right)}_r}}}{{{r^t}}}} \right|^q} \le {\left( {\frac{{\left| {{\rm{supp}}\,f} \right|}}{{\left| {{B_r}} \right|}}} \right)^{q - 1}}-\!\!\!\!\!\!\int_{{B_r}} {{{\left| {\frac{f}{{{r^t}}}} \right|}^q}\,d\xi } \le {\left( {\frac{{\left| {{\rm{supp}}\,f} \right|}}{{\left| {{B_r}} \right|}}} \right)^{p - 1}}-\!\!\!\!\!\!\int_{{B_r}} {{{\left| {\frac{f}{{{r^t}}}} \right|}^q}\,d\xi }. \end{equation*}
\begin{equation*}{\left| {\frac{{{{\left( f \right)}_r}}}{{{r^t}}}} \right|^q} \le {\left( {\frac{{\left| {{\rm{supp}}\,f} \right|}}{{\left| {{B_r}} \right|}}} \right)^{q - 1}}-\!\!\!\!\!\!\int_{{B_r}} {{{\left| {\frac{f}{{{r^t}}}} \right|}^q}\,d\xi } \le {\left( {\frac{{\left| {{\rm{supp}}\,f} \right|}}{{\left| {{B_r}} \right|}}} \right)^{p - 1}}-\!\!\!\!\!\!\int_{{B_r}} {{{\left| {\frac{f}{{{r^t}}}} \right|}^q}\,d\xi }. \end{equation*}We finally observe the plain relation that
 \begin{equation*}
-\!\!\!\!\!\!\int_{{B_r}}\left|\frac{f}{r^s}\right|^p+a_0\left|\frac{f}{r^t}\right|^q\,d\xi\le c\left(\frac{R}{r}\right)^Q-\!\!\!\!\!\!\int_{{B_R}}\left|\frac{f}{r^s}\right|^p+a_0\left|\frac{f}{r^t}\right|^q\,d\xi.
\end{equation*}
\begin{equation*}
-\!\!\!\!\!\!\int_{{B_r}}\left|\frac{f}{r^s}\right|^p+a_0\left|\frac{f}{r^t}\right|^q\,d\xi\le c\left(\frac{R}{r}\right)^Q-\!\!\!\!\!\!\int_{{B_R}}\left|\frac{f}{r^s}\right|^p+a_0\left|\frac{f}{r^t}\right|^q\,d\xi.
\end{equation*}In summary, we combine all the previous inequalities to arrive at the desired display.
Now denote
 \begin{equation*}a_R^ + : = \mathop {\sup }\limits_{{B_R} \times {B_R}} a\left( {\cdot,\cdot} \right) \quad \text{and} \quad a_R^ - : = \mathop {\inf }\limits_{{B_R} \times {B_R}} a\left( {\cdot,\cdot} \right).\end{equation*}
\begin{equation*}a_R^ + : = \mathop {\sup }\limits_{{B_R} \times {B_R}} a\left( {\cdot,\cdot} \right) \quad \text{and} \quad a_R^ - : = \mathop {\inf }\limits_{{B_R} \times {B_R}} a\left( {\cdot,\cdot} \right).\end{equation*}Lemma 2.8. Let ![]() $s,t \in (0,1)$,
$s,t \in (0,1)$, ![]() $1 \lt p\le q$ and
$1 \lt p\le q$ and ![]() $a(\cdot,\cdot)$ satisfy (1.6) and (1.9). Assume
$a(\cdot,\cdot)$ satisfy (1.6) and (1.9). Assume ![]() $f \in H{W^{t,q}}\left( {{B_{\bar R}}} \right) \cap {L^\infty }\left( {{B_{\bar R}}} \right)$ with
$f \in H{W^{t,q}}\left( {{B_{\bar R}}} \right) \cap {L^\infty }\left( {{B_{\bar R}}} \right)$ with ![]() ${\bar R} \le 1$. Then for
${\bar R} \le 1$. Then for  $\gamma : = \min \left\{{\frac{{p_s^*}}{p},\frac{{q_t^*}}{q}} \right\} \gt 1$, we have
$\gamma : = \min \left\{{\frac{{p_s^*}}{p},\frac{{q_t^*}}{q}} \right\} \gt 1$, we have
 \begin{align*}
& \quad{\left[ {-\!\!\!\!\!\!\int_{{B_r}} {{{\left( {{{\left| {\frac{f}{{{r^s}}}} \right|}^p} + a_{\bar R}^ + {{\left| {\frac{f}{{{r^t}}}} \right|}^q}} \right)}^\gamma }\,d\xi } } \right]^{\frac{1}{\gamma }}} \\
& \le c\left( {1 + \| f \|_{{L^\infty }\left( {{B_r}} \right)}^{q - p}} \right)\left( {\frac{{{D_1}\left( {R,r} \right)}}{{{r^{sp}}}} + \frac{{{\widetilde D}_1\left( {R,r} \right)}}{{{r^{tq}}}}} \right)-\!\!\!\!\!\!\int_{{B_R}} {\int_{{B_R}} {\frac{{H\left( {\xi ,\eta ,\left| {f\left( \xi \right) - f\left( \eta \right)} \right|} \right)}}{{\| {{\eta ^{- 1}}\circ \xi } \|_{{\mathbb{H}^n}}^Q}}\,d\xi d\eta } } \\
&\quad + c\left( {1 + \| f \|_{{L^\infty }\left( {{B_r}} \right)}^{q - p}} \right)-\!\!\!\!\!\!\int_{{B_R}} {\left( {{{\left| {\frac{f}{{{r^s}}}} \right|}^p} + a_{\bar R}^ - {{\left| {\frac{f}{{{r^t}}}} \right|}^q}} \right)\,d\xi},
\end{align*}
\begin{align*}
& \quad{\left[ {-\!\!\!\!\!\!\int_{{B_r}} {{{\left( {{{\left| {\frac{f}{{{r^s}}}} \right|}^p} + a_{\bar R}^ + {{\left| {\frac{f}{{{r^t}}}} \right|}^q}} \right)}^\gamma }\,d\xi } } \right]^{\frac{1}{\gamma }}} \\
& \le c\left( {1 + \| f \|_{{L^\infty }\left( {{B_r}} \right)}^{q - p}} \right)\left( {\frac{{{D_1}\left( {R,r} \right)}}{{{r^{sp}}}} + \frac{{{\widetilde D}_1\left( {R,r} \right)}}{{{r^{tq}}}}} \right)-\!\!\!\!\!\!\int_{{B_R}} {\int_{{B_R}} {\frac{{H\left( {\xi ,\eta ,\left| {f\left( \xi \right) - f\left( \eta \right)} \right|} \right)}}{{\| {{\eta ^{- 1}}\circ \xi } \|_{{\mathbb{H}^n}}^Q}}\,d\xi d\eta } } \\
&\quad + c\left( {1 + \| f \|_{{L^\infty }\left( {{B_r}} \right)}^{q - p}} \right)-\!\!\!\!\!\!\int_{{B_R}} {\left( {{{\left| {\frac{f}{{{r^s}}}} \right|}^p} + a_{\bar R}^ - {{\left| {\frac{f}{{{r^t}}}} \right|}^q}} \right)\,d\xi},
\end{align*} where ![]() ${B_r} \subset {B_R} \subseteq {B_{\bar R}}$ are concentric balls with
${B_r} \subset {B_R} \subseteq {B_{\bar R}}$ are concentric balls with  $\frac{1}{2}\bar R \le r \lt R \le \bar R$, and c > 0 depends only on
$\frac{1}{2}\bar R \le r \lt R \le \bar R$, and c > 0 depends only on ![]() $n,p,q,s,t$ and
$n,p,q,s,t$ and ![]() ${\left[ a \right]_\alpha }$. Here
${\left[ a \right]_\alpha }$. Here  ${\widetilde D}_1(R,r)$ is the corresponding
${\widetilde D}_1(R,r)$ is the corresponding ![]() ${D_1}\left( {R,r} \right)$ defined in proposition 2.4 with sp replaced by tq.
${D_1}\left( {R,r} \right)$ defined in proposition 2.4 with sp replaced by tq.
Proof. In view of Hölder continuity of a, we have
 \begin{equation*}a_{\bar R}^ + \le a_{\bar R}^ - + 4{\left[ a \right]_\alpha }{{\bar R}^\alpha } \le a_{\bar R}^ - + 8{\left[ a \right]_\alpha }{r^\alpha }.\end{equation*}
\begin{equation*}a_{\bar R}^ + \le a_{\bar R}^ - + 4{\left[ a \right]_\alpha }{{\bar R}^\alpha } \le a_{\bar R}^ - + 8{\left[ a \right]_\alpha }{r^\alpha }.\end{equation*} Then we by employing ![]() $tq \le sp+\alpha$,
$tq \le sp+\alpha$, ![]() $r \le 1$ have
$r \le 1$ have
 \begin{equation*}a_{\bar R}^ + {\left| {\frac{f}{{{r^t}}}} \right|^q} \le a_{\bar R}^ - {\left| {\frac{f}{{{r^t}}}} \right|^q} + c{r^{\alpha - tq + sp}}{\left| f \right|^{q - p}}{\left| {\frac{f}{{{r^s}}}} \right|^p}.\end{equation*}
\begin{equation*}a_{\bar R}^ + {\left| {\frac{f}{{{r^t}}}} \right|^q} \le a_{\bar R}^ - {\left| {\frac{f}{{{r^t}}}} \right|^q} + c{r^{\alpha - tq + sp}}{\left| f \right|^{q - p}}{\left| {\frac{f}{{{r^s}}}} \right|^p}.\end{equation*}Thus
 \begin{align*}
&\quad{\left[ {-\!\!\!\!\!\!\int_{{B_r}} {{{\left( {{{\left| {\frac{f}{{{r^s}}}} \right|}^p} + a_{\bar R}^ + {{\left| {\frac{f}{{{r^t}}}} \right|}^q}} \right)}^\gamma }\,d\xi } } \right]^{\frac{1}{\gamma }}}\\
&\le c\left( {1 + \| f \|_{{L^\infty }\left( {{B_r}} \right)}^{q - p}} \right){\left[ {-\!\!\!\!\!\!\int_{{B_r}} {{{\left( {{{\left| {\frac{f}{{{r^s}}}} \right|}^p} + a_{\bar R}^ - {{\left| {\frac{f}{{{r^t}}}} \right|}^q}} \right)}^\gamma }\,d\xi } } \right]^{\frac{1}{\gamma }}}\\
&\le c\left( {1 + \| f \|_{{L^\infty }\left( {{B_r}} \right)}^{q - p}} \right){\left[ {-\!\!\!\!\!\!\int_{{B_r}} {{{\left( {{{\left| {\frac{{f - {{\left( f \right)}_r}}}{{{r^s}}}} \right|}^p} + a_{\bar R}^ - {{\left| {\frac{{f - {{\left( f \right)}_r}}}{{{r^t}}}} \right|}^q}} \right)}^\gamma }\,d\xi } } \right]^{\frac{1}{\gamma }}}\\
&\quad + c\left( {1 + \| f \|_{{L^\infty }\left( {{B_r}} \right)}^{q - p}} \right)\left( {{{\left| {\frac{{{{\left( f \right)}_r}}}{{{r^s}}}} \right|}^p} + a_{\bar R}^ - {{\left| {\frac{{{{\left( f \right)}_r}}}{{{r^t}}}} \right|}^q}} \right).
\end{align*}
\begin{align*}
&\quad{\left[ {-\!\!\!\!\!\!\int_{{B_r}} {{{\left( {{{\left| {\frac{f}{{{r^s}}}} \right|}^p} + a_{\bar R}^ + {{\left| {\frac{f}{{{r^t}}}} \right|}^q}} \right)}^\gamma }\,d\xi } } \right]^{\frac{1}{\gamma }}}\\
&\le c\left( {1 + \| f \|_{{L^\infty }\left( {{B_r}} \right)}^{q - p}} \right){\left[ {-\!\!\!\!\!\!\int_{{B_r}} {{{\left( {{{\left| {\frac{f}{{{r^s}}}} \right|}^p} + a_{\bar R}^ - {{\left| {\frac{f}{{{r^t}}}} \right|}^q}} \right)}^\gamma }\,d\xi } } \right]^{\frac{1}{\gamma }}}\\
&\le c\left( {1 + \| f \|_{{L^\infty }\left( {{B_r}} \right)}^{q - p}} \right){\left[ {-\!\!\!\!\!\!\int_{{B_r}} {{{\left( {{{\left| {\frac{{f - {{\left( f \right)}_r}}}{{{r^s}}}} \right|}^p} + a_{\bar R}^ - {{\left| {\frac{{f - {{\left( f \right)}_r}}}{{{r^t}}}} \right|}^q}} \right)}^\gamma }\,d\xi } } \right]^{\frac{1}{\gamma }}}\\
&\quad + c\left( {1 + \| f \|_{{L^\infty }\left( {{B_r}} \right)}^{q - p}} \right)\left( {{{\left| {\frac{{{{\left( f \right)}_r}}}{{{r^s}}}} \right|}^p} + a_{\bar R}^ - {{\left| {\frac{{{{\left( f \right)}_r}}}{{{r^t}}}} \right|}^q}} \right).
\end{align*}Observe that
 \begin{equation*}{\left| {\frac{{{{\left( f \right)}_r}}}{{{r^s}}}} \right|^p} + a_{\bar R}^ - {\left| {\frac{{{{\left( f \right)}_r}}}{{{r^t}}}} \right|^q} \le -\!\!\!\!\!\!\int_{{B_r}} {{{\left( {{{\left| {\frac{f}{{{r^s}}}} \right|}^p} + a_{\bar R}^ - {{\left| {\frac{f}{{{r^t}}}} \right|}^q}} \right)} }\,d\xi } .\end{equation*}
\begin{equation*}{\left| {\frac{{{{\left( f \right)}_r}}}{{{r^s}}}} \right|^p} + a_{\bar R}^ - {\left| {\frac{{{{\left( f \right)}_r}}}{{{r^t}}}} \right|^q} \le -\!\!\!\!\!\!\int_{{B_r}} {{{\left( {{{\left| {\frac{f}{{{r^s}}}} \right|}^p} + a_{\bar R}^ - {{\left| {\frac{f}{{{r^t}}}} \right|}^q}} \right)} }\,d\xi } .\end{equation*}Moreover, it follows from proposition 2.4 that
 \begin{align*}
{\left[ {-\!\!\!\!\!\!\int_{{B_r}} {{{\left| {\frac{{f - {{\left( f \right)}_r}}}{{{r^s}}}} \right|}^{p\gamma }}\,d\xi } } \right]^{\frac{1}{\gamma }}}
&\le {\left( {-\!\!\!\!\!\!\int_{{B_r}} {{{\left| {\frac{{f - {{\left( f \right)}_r}}}{{{r^s}}}} \right|}^{p_s^*}}\,d\xi } } \right)^{\frac{p}{{p_s^*}}}} \\
&\le \frac{{{cD_1}\left( {R,r} \right)}}{{{r^{sp}}}}-\!\!\!\!\!\!\int_{{B_R}} {\int_{{B_R}} {\frac{{{{\left| {f\left( \xi \right) - f\left( \eta \right)} \right|}^p}}}{{\| {{\eta ^{- 1}}\circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}}\,d\xi d\eta } },
\end{align*}
\begin{align*}
{\left[ {-\!\!\!\!\!\!\int_{{B_r}} {{{\left| {\frac{{f - {{\left( f \right)}_r}}}{{{r^s}}}} \right|}^{p\gamma }}\,d\xi } } \right]^{\frac{1}{\gamma }}}
&\le {\left( {-\!\!\!\!\!\!\int_{{B_r}} {{{\left| {\frac{{f - {{\left( f \right)}_r}}}{{{r^s}}}} \right|}^{p_s^*}}\,d\xi } } \right)^{\frac{p}{{p_s^*}}}} \\
&\le \frac{{{cD_1}\left( {R,r} \right)}}{{{r^{sp}}}}-\!\!\!\!\!\!\int_{{B_R}} {\int_{{B_R}} {\frac{{{{\left| {f\left( \xi \right) - f\left( \eta \right)} \right|}^p}}}{{\| {{\eta ^{- 1}}\circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}}\,d\xi d\eta } },
\end{align*}and
 \begin{align*}
{\left[ {-\!\!\!\!\!\!\int_{{B_r}} {{{\left| {\frac{{f - {{\left( f \right)}_r}}}{{{r^t}}}} \right|}^{q\gamma }}d\xi } } \right]^{\frac{1}{\gamma }}}
&\le {\left( {-\!\!\!\!\!\!\int_{{B_r}} {{{\left| {\frac{{f - {{\left( f \right)}_r}}}{{{r^t}}}} \right|}^{q_t^*}}\,d\xi } } \right)^{\frac{q}{{q_t^*}}}} \\
&\le \frac{{{c{\widetilde D}_1}\left( {R,r} \right)}}{{{r^{tq}}}}-\!\!\!\!\!\!\int_{{B_R}} {\int_{{B_R}} {\frac{{{{\left| {f\left( \xi \right) - f\left( \eta \right)} \right|}^q}}}{{\| {{\eta ^{- 1}}\circ \xi } \|_{{\mathbb{H}^n}}^{Q + tq}}}\,d\xi d\eta } }.
\end{align*}
\begin{align*}
{\left[ {-\!\!\!\!\!\!\int_{{B_r}} {{{\left| {\frac{{f - {{\left( f \right)}_r}}}{{{r^t}}}} \right|}^{q\gamma }}d\xi } } \right]^{\frac{1}{\gamma }}}
&\le {\left( {-\!\!\!\!\!\!\int_{{B_r}} {{{\left| {\frac{{f - {{\left( f \right)}_r}}}{{{r^t}}}} \right|}^{q_t^*}}\,d\xi } } \right)^{\frac{q}{{q_t^*}}}} \\
&\le \frac{{{c{\widetilde D}_1}\left( {R,r} \right)}}{{{r^{tq}}}}-\!\!\!\!\!\!\int_{{B_R}} {\int_{{B_R}} {\frac{{{{\left| {f\left( \xi \right) - f\left( \eta \right)} \right|}^q}}}{{\| {{\eta ^{- 1}}\circ \xi } \|_{{\mathbb{H}^n}}^{Q + tq}}}\,d\xi d\eta } }.
\end{align*}Merging the last four inequalities leads to
 \begin{align*}
&\quad {\left[ {-\!\!\!\!\!\!\int_{{B_r}} {{{\left( {{{\left| {\frac{f}{{{r^s}}}} \right|}^p} + a_{\bar R}^ + {{\left| {\frac{f}{{{r^t}}}} \right|}^q}} \right)}^\gamma }\,d\xi } } \right]^{\frac{1}{\gamma }}} \\
&\le c\left( {1 + \| f \|_{{L^\infty }\left( {{B_r}} \right)}^{q - p}} \right)\left( {\frac{{{D_1}\left( {R,r} \right)}}{{{r^{sp}}}} + \frac{{{{\widetilde D}_1}\left( {R,r} \right)}}{{{r^{tq}}}}} \right)\\
&\qquad\cdot-\!\!\!\!\!\!\int_{{B_R}} {\int_{{B_R}} {\left( {\frac{{{{\left| {f\left( \xi \right) - f\left( \eta \right)} \right|}^p}}}{{\| {{\eta ^{- 1}}\circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}} + a_{\bar R}^ - \frac{{{{\left| {f\left( \xi \right) - f\left( \eta \right)} \right|}^q}}}{{\| {{\eta ^{- 1}}\circ \xi } \|_{{\mathbb{H}^n}}^{Q + tq}}}} \right)\,d\xi d\eta } } \\
&\quad + c\left( {1 + \| f \|_{{L^\infty }\left( {{B_r}} \right)}^{q - p}} \right)-\!\!\!\!\!\!\int_{{B_R}} {\left( {{{\left| {\frac{f}{{{r^s}}}} \right|}^p} + a_{\bar R}^ - {{\left| {\frac{f}{{{r^t}}}} \right|}^q}} \right)\,d\xi } \\
& \le c\left( {1 + \| f \|_{{L^\infty }\left( {{B_r}} \right)}^{q - p}} \right)\left( {\frac{{{D_1}\left( {R,r} \right)}}{{{r^{sp}}}} + \frac{{{{\widetilde D}_1}\left( {R,r} \right)}}{{{r^{tq}}}}} \right)-\!\!\!\!\!\!\int_{{B_R}} {\int_{{B_R}} {\frac{{H\left( {\xi ,\eta ,\left| {f\left( \xi \right) - f\left( \eta \right)} \right|} \right)}}{{\| {{\eta ^{- 1}}\circ \xi } \|_{{\mathbb{H}^n}}^Q}}\,d\xi d\eta } } \\
&\quad + c\left( {1 + \| f \|_{{L^\infty }\left( {{B_r}} \right)}^{q - p}} \right)-\!\!\!\!\!\!\int_{{B_R}} {\left( {{{\left| {\frac{f}{{{r^s}}}} \right|}^p} + a_{\bar R}^ - {{\left| {\frac{f}{{{r^t}}}} \right|}^q}} \right)\,d\xi } .
\end{align*}
\begin{align*}
&\quad {\left[ {-\!\!\!\!\!\!\int_{{B_r}} {{{\left( {{{\left| {\frac{f}{{{r^s}}}} \right|}^p} + a_{\bar R}^ + {{\left| {\frac{f}{{{r^t}}}} \right|}^q}} \right)}^\gamma }\,d\xi } } \right]^{\frac{1}{\gamma }}} \\
&\le c\left( {1 + \| f \|_{{L^\infty }\left( {{B_r}} \right)}^{q - p}} \right)\left( {\frac{{{D_1}\left( {R,r} \right)}}{{{r^{sp}}}} + \frac{{{{\widetilde D}_1}\left( {R,r} \right)}}{{{r^{tq}}}}} \right)\\
&\qquad\cdot-\!\!\!\!\!\!\int_{{B_R}} {\int_{{B_R}} {\left( {\frac{{{{\left| {f\left( \xi \right) - f\left( \eta \right)} \right|}^p}}}{{\| {{\eta ^{- 1}}\circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}} + a_{\bar R}^ - \frac{{{{\left| {f\left( \xi \right) - f\left( \eta \right)} \right|}^q}}}{{\| {{\eta ^{- 1}}\circ \xi } \|_{{\mathbb{H}^n}}^{Q + tq}}}} \right)\,d\xi d\eta } } \\
&\quad + c\left( {1 + \| f \|_{{L^\infty }\left( {{B_r}} \right)}^{q - p}} \right)-\!\!\!\!\!\!\int_{{B_R}} {\left( {{{\left| {\frac{f}{{{r^s}}}} \right|}^p} + a_{\bar R}^ - {{\left| {\frac{f}{{{r^t}}}} \right|}^q}} \right)\,d\xi } \\
& \le c\left( {1 + \| f \|_{{L^\infty }\left( {{B_r}} \right)}^{q - p}} \right)\left( {\frac{{{D_1}\left( {R,r} \right)}}{{{r^{sp}}}} + \frac{{{{\widetilde D}_1}\left( {R,r} \right)}}{{{r^{tq}}}}} \right)-\!\!\!\!\!\!\int_{{B_R}} {\int_{{B_R}} {\frac{{H\left( {\xi ,\eta ,\left| {f\left( \xi \right) - f\left( \eta \right)} \right|} \right)}}{{\| {{\eta ^{- 1}}\circ \xi } \|_{{\mathbb{H}^n}}^Q}}\,d\xi d\eta } } \\
&\quad + c\left( {1 + \| f \|_{{L^\infty }\left( {{B_r}} \right)}^{q - p}} \right)-\!\!\!\!\!\!\int_{{B_R}} {\left( {{{\left| {\frac{f}{{{r^s}}}} \right|}^p} + a_{\bar R}^ - {{\left| {\frac{f}{{{r^t}}}} \right|}^q}} \right)\,d\xi } .
\end{align*}We now finish the proof.
3. Local boundedness
This section is devoted to showing the interior boundedness of weak solutions to equation (1.1) by means of the key ingredient, a Caccioppoli-type inequality in the nonlocal framework. The forthcoming lemma indicates the multiplication of each function in ![]() $\mathcal{A}(\Omega)$ and a cut-off function also belongs to
$\mathcal{A}(\Omega)$ and a cut-off function also belongs to ![]() $\mathcal{A}(\Omega)$.
$\mathcal{A}(\Omega)$.
Lemma 3.1. Let ![]() $s,t,p$ and q satisfy (1.4) and
$s,t,p$ and q satisfy (1.4) and  $\varphi \in HW_0^{1,\infty }\left( {{B_r}} \right), v \in {\mathcal A}(\Omega)$. If one of the following two conditions holds:
$\varphi \in HW_0^{1,\infty }\left( {{B_r}} \right), v \in {\mathcal A}(\Omega)$. If one of the following two conditions holds:
(i) The inequality (1.8) holds and
 $v \in {L^p}\left( {{B_{2r}}} \right)$ satisfies
$v \in {L^p}\left( {{B_{2r}}} \right)$ satisfies  $\rho \left( {v ;{B_{2r}}} \right) \lt \infty$;
$\rho \left( {v ;{B_{2r}}} \right) \lt \infty$;(ii)
 $v \in {L^q}\left( {{B_{2r}}} \right)$ satisfies
$v \in {L^q}\left( {{B_{2r}}} \right)$ satisfies  $\rho \left( {v ;{B_{2r}}} \right) \lt \infty $,
$\rho \left( {v ;{B_{2r}}} \right) \lt \infty $,
then ![]() $\rho \left( {v \varphi ;\mathbb{H}^n} \right) \lt \infty $. In particular,
$\rho \left( {v \varphi ;\mathbb{H}^n} \right) \lt \infty $. In particular, ![]() $v \varphi \in {\mathcal A}(\Omega)$ whenever
$v \varphi \in {\mathcal A}(\Omega)$ whenever ![]() $ {B_{2r}}\subset\Omega$.
$ {B_{2r}}\subset\Omega$.
Proof. By ![]() $v \in {\mathcal A}(\Omega)$, proposition 2.4 and (1.8), we get
$v \in {\mathcal A}(\Omega)$, proposition 2.4 and (1.8), we get  $v \in {L^q}\left( {{B_{3r/2}}} \right)$ in (i). Thus, we just consider condition (ii). By the definition of
$v \in {L^q}\left( {{B_{3r/2}}} \right)$ in (i). Thus, we just consider condition (ii). By the definition of ![]() $\rho \left( {v \varphi ;\mathbb{H}^n} \right)$, we have
$\rho \left( {v \varphi ;\mathbb{H}^n} \right)$, we have
 \begin{align}
\rho \left( {v \varphi ;{\mathbb{H}^n}} \right)
&= 2\int_{{\mathbb{H}^n}\backslash {B_{3r/2}}} {\int_{{B_{3r/2}}} {H\left( {\xi ,\eta ,\left| {v \left( \xi \right)\varphi \left( \xi \right) - v \left( \eta \right)\varphi \left( \eta \right)} \right|} \right)\frac{{d\xi d\eta }}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^Q}}} }\nonumber \\
&\quad + \int_{{B_{3r/2}}} {\int_{{B_{3r/2}}} {H\left( {\xi ,\eta ,\left| {v \left( \xi \right)\varphi \left( \xi \right) - v \left( \eta \right)\varphi \left( \eta \right)} \right|} \right)\frac{{d\xi d\eta }}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^Q}}} } \nonumber \\
&=: 2{I_1} + {I_2}.
\end{align}
\begin{align}
\rho \left( {v \varphi ;{\mathbb{H}^n}} \right)
&= 2\int_{{\mathbb{H}^n}\backslash {B_{3r/2}}} {\int_{{B_{3r/2}}} {H\left( {\xi ,\eta ,\left| {v \left( \xi \right)\varphi \left( \xi \right) - v \left( \eta \right)\varphi \left( \eta \right)} \right|} \right)\frac{{d\xi d\eta }}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^Q}}} }\nonumber \\
&\quad + \int_{{B_{3r/2}}} {\int_{{B_{3r/2}}} {H\left( {\xi ,\eta ,\left| {v \left( \xi \right)\varphi \left( \xi \right) - v \left( \eta \right)\varphi \left( \eta \right)} \right|} \right)\frac{{d\xi d\eta }}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^Q}}} } \nonumber \\
&=: 2{I_1} + {I_2}.
\end{align} Owing to  $\varphi \in HW_0^{1,\infty }\left( {{B_r}} \right)$, we find
$\varphi \in HW_0^{1,\infty }\left( {{B_r}} \right)$, we find
 \begin{align}
{I_1}
&\le {\left( {{{\| \varphi \|}_{{L^\infty }\left( {{B_r}} \right)}} + 1} \right)^q}\int_{{\mathbb{H}^n}\backslash {B_{3r/2}}} {\int_{{B_r}} {\left( {\frac{{{{\left| {v \left( \xi \right)} \right|}^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}} + {{\| a \|}_{{L^\infty }}}\frac{{{{\left| {v \left( \xi \right)} \right|}^q}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + tq}}}} \right)\;d\xi d\eta } } \nonumber\\
&\le c{\left( {{{\| \varphi \|}_{{L^\infty }\left( {{B_r}} \right)}} + 1} \right)^q}\left( {{r^{- sp}}\int_{{B_r}} {{{\left| {v \left( \xi \right)} \right|}^p}\;d\xi } + {{\| a \|}_{{L^\infty }}}{r^{- tq}}\int_{{B_r}} {{{\left| {v \left( \xi \right)} \right|}^q}\;d\xi } } \right) \lt \infty .
\end{align}
\begin{align}
{I_1}
&\le {\left( {{{\| \varphi \|}_{{L^\infty }\left( {{B_r}} \right)}} + 1} \right)^q}\int_{{\mathbb{H}^n}\backslash {B_{3r/2}}} {\int_{{B_r}} {\left( {\frac{{{{\left| {v \left( \xi \right)} \right|}^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}} + {{\| a \|}_{{L^\infty }}}\frac{{{{\left| {v \left( \xi \right)} \right|}^q}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + tq}}}} \right)\;d\xi d\eta } } \nonumber\\
&\le c{\left( {{{\| \varphi \|}_{{L^\infty }\left( {{B_r}} \right)}} + 1} \right)^q}\left( {{r^{- sp}}\int_{{B_r}} {{{\left| {v \left( \xi \right)} \right|}^p}\;d\xi } + {{\| a \|}_{{L^\infty }}}{r^{- tq}}\int_{{B_r}} {{{\left| {v \left( \xi \right)} \right|}^q}\;d\xi } } \right) \lt \infty .
\end{align}The term I 2 is estimated as
 \begin{align}
{I_2}
&\le c\int_{B_{3r/2}} {\int_{B_{3r/2}} {H\left( {\xi ,\eta ,\left| {\left( {v \left( \xi \right) - v \left( \eta \right)} \right)\varphi \left( \eta \right)} \right|} \right)\frac{{d\xi d\eta }}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^Q}}} }\nonumber \\
&\quad + c\int_{B_{3r/2}} {\int_{B_{3r/2}} {H\left( {\xi ,\eta ,\left| {v \left( \xi \right)\left( {\varphi \left( \xi \right) - \varphi \left( \eta \right)} \right)} \right|} \right)\frac{{d\xi d\eta }}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^Q}}} } \nonumber\\
&\le c{\left( {{{\| \varphi \|}_{{L^\infty }\left( {{B_r}} \right)}} + 1} \right)^q}\int_{B_{3r/2}} {\int_{B_{3r/2}} {H\left( {\xi ,\eta ,\left| {v \left( \xi \right)} \right|} \right)\frac{{d\xi d\eta }}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^Q}}} } \nonumber\\
&\quad + c\| {{\nabla _H}\varphi } \|_{{L^\infty }\left( {{B_r}} \right)}^p\int_{B_{3r/2}} {{{\left| {v \left( \xi \right)} \right|}^p}\int_{B_{3r}} {\frac{{d\eta }}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + (s - 1)p}}}} } \;d\xi \nonumber\\
&\quad + c\| {{\nabla _H}\varphi } \|_{{L^\infty }\left( {{B_r}} \right)}^q{\| a \|_{{L^\infty }}}\int_{B_{3r/2}} {{{\left| {v \left( \xi \right)} \right|}^q}\int_{B_{3r}} {\frac{{d\eta }}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + (t - 1)p}}}} } \;d\xi \nonumber\\
&\le c{\left( {{{\| \varphi \|}_{{L^\infty }\left( {{B_r}} \right)}} + 1} \right)^q}\rho \left( {v ;{B_{2r}}} \right) + c\| {{\nabla _H}\varphi } \|_{{L^\infty }\left( {{B_r}} \right)}^p{r^{\left( {1 - s} \right)p}}\int_{{B_{2r}}} {{{\left| {v \left( \xi \right)} \right|}^p}} \;d\xi \nonumber\\
&\quad + c\| {{\nabla _H}\varphi } \|_{{L^\infty }\left( {{B_r}} \right)}^q{\| a \|_{{L^\infty }}}{r^{\left( {1 - t} \right)q}}\int_{{B_{2r}}} {{{\left| {v \left( \xi \right)} \right|}^q}} \;d\xi \nonumber\\
& \lt \infty .
\end{align}
\begin{align}
{I_2}
&\le c\int_{B_{3r/2}} {\int_{B_{3r/2}} {H\left( {\xi ,\eta ,\left| {\left( {v \left( \xi \right) - v \left( \eta \right)} \right)\varphi \left( \eta \right)} \right|} \right)\frac{{d\xi d\eta }}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^Q}}} }\nonumber \\
&\quad + c\int_{B_{3r/2}} {\int_{B_{3r/2}} {H\left( {\xi ,\eta ,\left| {v \left( \xi \right)\left( {\varphi \left( \xi \right) - \varphi \left( \eta \right)} \right)} \right|} \right)\frac{{d\xi d\eta }}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^Q}}} } \nonumber\\
&\le c{\left( {{{\| \varphi \|}_{{L^\infty }\left( {{B_r}} \right)}} + 1} \right)^q}\int_{B_{3r/2}} {\int_{B_{3r/2}} {H\left( {\xi ,\eta ,\left| {v \left( \xi \right)} \right|} \right)\frac{{d\xi d\eta }}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^Q}}} } \nonumber\\
&\quad + c\| {{\nabla _H}\varphi } \|_{{L^\infty }\left( {{B_r}} \right)}^p\int_{B_{3r/2}} {{{\left| {v \left( \xi \right)} \right|}^p}\int_{B_{3r}} {\frac{{d\eta }}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + (s - 1)p}}}} } \;d\xi \nonumber\\
&\quad + c\| {{\nabla _H}\varphi } \|_{{L^\infty }\left( {{B_r}} \right)}^q{\| a \|_{{L^\infty }}}\int_{B_{3r/2}} {{{\left| {v \left( \xi \right)} \right|}^q}\int_{B_{3r}} {\frac{{d\eta }}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + (t - 1)p}}}} } \;d\xi \nonumber\\
&\le c{\left( {{{\| \varphi \|}_{{L^\infty }\left( {{B_r}} \right)}} + 1} \right)^q}\rho \left( {v ;{B_{2r}}} \right) + c\| {{\nabla _H}\varphi } \|_{{L^\infty }\left( {{B_r}} \right)}^p{r^{\left( {1 - s} \right)p}}\int_{{B_{2r}}} {{{\left| {v \left( \xi \right)} \right|}^p}} \;d\xi \nonumber\\
&\quad + c\| {{\nabla _H}\varphi } \|_{{L^\infty }\left( {{B_r}} \right)}^q{\| a \|_{{L^\infty }}}{r^{\left( {1 - t} \right)q}}\int_{{B_{2r}}} {{{\left| {v \left( \xi \right)} \right|}^q}} \;d\xi \nonumber\\
& \lt \infty .
\end{align} Thus, it follows ![]() $\rho \left( {v \varphi ;{\mathbb{H}^n}} \right) \lt \infty$ by combining (3.2), (3.3) with (3.1).
$\rho \left( {v \varphi ;{\mathbb{H}^n}} \right) \lt \infty$ by combining (3.2), (3.3) with (3.1).
Next, we prove a nonlocal Caccioppoli-type inequality. Define
 \begin{equation}
h\left( {\xi ,\eta ,\tau } \right): = \frac{{{\tau ^{p - 1}}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{sp}}} + a\left( {\xi ,\eta } \right)\frac{{{\tau ^{q - 1}}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{tq}}},\;\;\;\;\xi ,\eta \in {\mathbb{H}^n}\;\hbox{and}\;\;\tau \gt 0.
\end{equation}
\begin{equation}
h\left( {\xi ,\eta ,\tau } \right): = \frac{{{\tau ^{p - 1}}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{sp}}} + a\left( {\xi ,\eta } \right)\frac{{{\tau ^{q - 1}}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{tq}}},\;\;\;\;\xi ,\eta \in {\mathbb{H}^n}\;\hbox{and}\;\;\tau \gt 0.
\end{equation}The numerical inequality below, to be exploited frequently, is from [Reference Di Castro, Kuusi and Palatucci14, lemma 3.1].
Lemma 3.2. Let ![]() $p \ge 1$ and
$p \ge 1$ and ![]() $a,b \ge 0$. Then we have
$a,b \ge 0$. Then we have
and
for any ![]() $\varepsilon \in \left( {0,1} \right)$ and some
$\varepsilon \in \left( {0,1} \right)$ and some ![]() $c=c(p) \gt 0$.
$c=c(p) \gt 0$.
Lemma 3.3. Caccioppoli-type inequality
Let ![]() ${B_{2r}}\left( {{\xi _0}} \right) \subset \subset \Omega $,
${B_{2r}}\left( {{\xi _0}} \right) \subset \subset \Omega $, ![]() $1 \lt p\le q$, (1.5) and (1.8) hold. Assume
$1 \lt p\le q$, (1.5) and (1.8) hold. Assume ![]() $u\in {\mathcal{A}}(\Omega )$ is a weak solution to (1.1). Then for any
$u\in {\mathcal{A}}(\Omega )$ is a weak solution to (1.1). Then for any ![]() $\phi \in C_0^\infty \left( {{B_r}} \right)$ with
$\phi \in C_0^\infty \left( {{B_r}} \right)$ with ![]() $0\le \phi \le 1$, we have
$0\le \phi \le 1$, we have
 \begin{align}
& \int_{{B_r}} {\int_{{B_r}} {H\left( {\xi ,\eta ,\left| {{w_\pm }\left( \xi \right) - {w_\pm }\left( \eta \right)} \right|} \right)\left( {{\phi ^q}\left( \xi \right) + {\phi ^q}\left( \eta \right)} \right)\frac{{d\xi d\eta }}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^Q}}} }\nonumber \\
\le& c\int_{{B_r}} {\int_{{B_r}} {H\left( {\xi ,\eta ,\left| {\left( {\phi \left( \xi \right) - \phi \left( \eta \right)} \right)\left( {{w_\pm }\left( \xi \right) + {w_\pm }\left( \eta \right)} \right)} \right|} \right)\frac{{d\xi d\eta }}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^Q}}} } \nonumber\\
& + c\left( {\mathop {\sup }\limits_{\xi \in \rm{supp}\,\phi } \int_{{\mathbb{H}^n}\backslash {B_r}} {h\left( {\xi ,\eta ,\left| {{w_\pm }\left( \eta \right)} \right|} \right)\frac{{d\eta }}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^Q}}} } \right)\int_{{B_r}} {{w_\pm }\left( \xi \right){\phi ^q}\left( \xi \right)d\xi },
\end{align}
\begin{align}
& \int_{{B_r}} {\int_{{B_r}} {H\left( {\xi ,\eta ,\left| {{w_\pm }\left( \xi \right) - {w_\pm }\left( \eta \right)} \right|} \right)\left( {{\phi ^q}\left( \xi \right) + {\phi ^q}\left( \eta \right)} \right)\frac{{d\xi d\eta }}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^Q}}} }\nonumber \\
\le& c\int_{{B_r}} {\int_{{B_r}} {H\left( {\xi ,\eta ,\left| {\left( {\phi \left( \xi \right) - \phi \left( \eta \right)} \right)\left( {{w_\pm }\left( \xi \right) + {w_\pm }\left( \eta \right)} \right)} \right|} \right)\frac{{d\xi d\eta }}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^Q}}} } \nonumber\\
& + c\left( {\mathop {\sup }\limits_{\xi \in \rm{supp}\,\phi } \int_{{\mathbb{H}^n}\backslash {B_r}} {h\left( {\xi ,\eta ,\left| {{w_\pm }\left( \eta \right)} \right|} \right)\frac{{d\eta }}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^Q}}} } \right)\int_{{B_r}} {{w_\pm }\left( \xi \right){\phi ^q}\left( \xi \right)d\xi },
\end{align} for some ![]() $c:=c(n,s,t,p,q) \gt 0$, where
$c:=c(n,s,t,p,q) \gt 0$, where ![]() ${w_\pm }:=(u-k)_ \pm$ with
${w_\pm }:=(u-k)_ \pm$ with ![]() $k \ge 0$.
$k \ge 0$.
Proof. We just consider the estimate for ![]() $w_+$, since the estimate for
$w_+$, since the estimate for ![]() $w_-$ can be proved similarly. By lemma 3.1, it follows that
$w_-$ can be proved similarly. By lemma 3.1, it follows that ![]() ${w_+}{\phi ^q} \in {\mathcal{A}}(\Omega )$ from
${w_+}{\phi ^q} \in {\mathcal{A}}(\Omega )$ from ![]() $u \in {\mathcal{A}}(\Omega )$ and
$u \in {\mathcal{A}}(\Omega )$ and  $\phi \in C_0^\infty \left( {{B_r}} \right) \subset HW_0^{1,\infty} \left( {{B_r}} \right)$, so we can take the testing function
$\phi \in C_0^\infty \left( {{B_r}} \right) \subset HW_0^{1,\infty} \left( {{B_r}} \right)$, so we can take the testing function ![]() $\varphi={w_+}{\phi ^q}$ in (1.7). Then we have
$\varphi={w_+}{\phi ^q}$ in (1.7). Then we have
 \begin{align}
0
&= \int_{{B_r}} {\int_{{B_r}} {\Bigg[\frac{{{J _p}( {u( \xi) - u( \eta)})( {{w_ + }( \xi ){\phi^q}( \xi) - {w_ + }( \eta ){\phi^q}( \eta)})}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}}} } \nonumber\\
&\quad + a(\xi ,\eta )\frac{{{J _q}( {u( \xi) - u( \eta )} )( {{w_ + }( \xi ){\phi^q}( \xi ) - {w_ + }( \eta){\phi^q}( \eta)})}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + tq}}}\Bigg]\,d\xi d\eta \nonumber\\
&\quad +2{\int _{{\mathbb{H}^n}\backslash {B_r}}}\int_{{B_r}} \Bigg[\frac{{{J _p}( {u( \xi ) - u( \eta)}){w_ + }( \xi){\phi^q}( \xi)}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}}\nonumber\\
&\quad + a( \xi ,\eta)\frac{{{J _q}( {u( \xi) - u( \eta)}){w_ + }( \xi){\phi^q}( \xi)}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + tq}}}\Bigg]\,d\xi d\eta \nonumber\\
&=: J_1+J_2.
\end{align}
\begin{align}
0
&= \int_{{B_r}} {\int_{{B_r}} {\Bigg[\frac{{{J _p}( {u( \xi) - u( \eta)})( {{w_ + }( \xi ){\phi^q}( \xi) - {w_ + }( \eta ){\phi^q}( \eta)})}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}}} } \nonumber\\
&\quad + a(\xi ,\eta )\frac{{{J _q}( {u( \xi) - u( \eta )} )( {{w_ + }( \xi ){\phi^q}( \xi ) - {w_ + }( \eta){\phi^q}( \eta)})}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + tq}}}\Bigg]\,d\xi d\eta \nonumber\\
&\quad +2{\int _{{\mathbb{H}^n}\backslash {B_r}}}\int_{{B_r}} \Bigg[\frac{{{J _p}( {u( \xi ) - u( \eta)}){w_ + }( \xi){\phi^q}( \xi)}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}}\nonumber\\
&\quad + a( \xi ,\eta)\frac{{{J _q}( {u( \xi) - u( \eta)}){w_ + }( \xi){\phi^q}( \xi)}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + tq}}}\Bigg]\,d\xi d\eta \nonumber\\
&=: J_1+J_2.
\end{align} We first estimate J 1. Since J 1 is symmetry for ξ and η, we may suppose without loss of generality that ![]() ${u\left( \xi \right) \ge u\left( \eta \right)}$. Then for
${u\left( \xi \right) \ge u\left( \eta \right)}$. Then for ![]() $l \in \{p,q\}$, it yields
$l \in \{p,q\}$, it yields
 \begin{align*}
&\quad {J _l}\left( {u\left( \xi \right) - u\left( \eta \right)} \right)\left( {{w_+ }\left( \xi \right){\phi^q}\left( \xi \right) - {w_+ }\left( \eta \right){\phi^q}\left( \eta \right)} \right) \\
& = \left\{\begin{array}{l}
{\left( {{w_+ }\left( \xi \right) - {w_+ }\left( \eta \right)} \right)^{l - 1}}\left( {{w_+ }\left( \xi \right){\phi^q}\left( \xi \right) - {w_+ }\left( \eta \right){\phi^q}\left( \eta \right)} \right),\quad \text{if } u\left( \xi \right) \ge u\left( \eta \right) \ge k\\
{\left( {u\left( \xi \right) - u\left( \eta \right)} \right)^{l - 1}}{w_+ }\left( \xi \right){\phi^q}\left( \xi \right),\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad \;\text{if } u\left( \xi \right) \ge k \ge u\left( \eta \right)\\
0,\quad\quad\quad\quad\quad\quad\quad\quad \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\;\;\;\quad\text{if } k \ge u\left( \xi \right) \ge u\left( \eta \right)
\end{array} \right.\\
&\ge {J _l}\left( {{w_+ }\left( \xi \right) - {w_+ }\left( \eta \right)} \right)\left( {{w_+ }\left( \xi \right){\phi^q}\left( \xi \right) - {w_+ }\left( \eta \right){\phi^q}\left( \eta \right)} \right).
\end{align*}
\begin{align*}
&\quad {J _l}\left( {u\left( \xi \right) - u\left( \eta \right)} \right)\left( {{w_+ }\left( \xi \right){\phi^q}\left( \xi \right) - {w_+ }\left( \eta \right){\phi^q}\left( \eta \right)} \right) \\
& = \left\{\begin{array}{l}
{\left( {{w_+ }\left( \xi \right) - {w_+ }\left( \eta \right)} \right)^{l - 1}}\left( {{w_+ }\left( \xi \right){\phi^q}\left( \xi \right) - {w_+ }\left( \eta \right){\phi^q}\left( \eta \right)} \right),\quad \text{if } u\left( \xi \right) \ge u\left( \eta \right) \ge k\\
{\left( {u\left( \xi \right) - u\left( \eta \right)} \right)^{l - 1}}{w_+ }\left( \xi \right){\phi^q}\left( \xi \right),\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad \;\text{if } u\left( \xi \right) \ge k \ge u\left( \eta \right)\\
0,\quad\quad\quad\quad\quad\quad\quad\quad \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\;\;\;\quad\text{if } k \ge u\left( \xi \right) \ge u\left( \eta \right)
\end{array} \right.\\
&\ge {J _l}\left( {{w_+ }\left( \xi \right) - {w_+ }\left( \eta \right)} \right)\left( {{w_+ }\left( \xi \right){\phi^q}\left( \xi \right) - {w_+ }\left( \eta \right){\phi^q}\left( \eta \right)} \right).
\end{align*}Moreover,
 \begin{align*}
&\quad {w_+ }\left( \xi \right){\phi^q}\left( \xi \right) - {w_+ }\left( \eta \right){\phi^q}\left( \eta \right) \\
& = \frac{{{w_+ }\left( \xi \right) - {w_+ }\left( \eta \right)}}{2}\left( {{\phi^q}\left( \xi \right) + {\phi^q}\left( \eta \right)} \right) + \frac{{{w_+ }\left( \xi \right) + {w_+ }\left( \eta \right)}}{2}\left( {{\phi^q}\left( \xi \right) - {\phi^q}\left( \eta \right)} \right),
\end{align*}
\begin{align*}
&\quad {w_+ }\left( \xi \right){\phi^q}\left( \xi \right) - {w_+ }\left( \eta \right){\phi^q}\left( \eta \right) \\
& = \frac{{{w_+ }\left( \xi \right) - {w_+ }\left( \eta \right)}}{2}\left( {{\phi^q}\left( \xi \right) + {\phi^q}\left( \eta \right)} \right) + \frac{{{w_+ }\left( \xi \right) + {w_+ }\left( \eta \right)}}{2}\left( {{\phi^q}\left( \xi \right) - {\phi^q}\left( \eta \right)} \right),
\end{align*}which implies
 \begin{align*}
&\quad {J _l}\left( {{w_+ }\left( \xi \right) - {w_+ }\left( \eta \right)} \right)\left( {{w_+ }\left( \xi \right){\phi^q}\left( \xi \right) - {w_+ }\left( \eta \right){\phi^q}\left( \eta \right)} \right) \\
&\ge {| {{w_+ }( \xi) - {w_+ }( \eta)}|^l}\frac{{{\phi^q}( \xi) + {\phi^q}( \eta)}}{2} - {| {{w_+ }( \xi) - {w_+ }( \eta)}|^{l - 1}}\frac{{{w_+ }( \xi) + {w_+ }( \eta)}}{2}| {{\phi^q}( \xi) - {\phi^q}( \eta)}|.
\end{align*}
\begin{align*}
&\quad {J _l}\left( {{w_+ }\left( \xi \right) - {w_+ }\left( \eta \right)} \right)\left( {{w_+ }\left( \xi \right){\phi^q}\left( \xi \right) - {w_+ }\left( \eta \right){\phi^q}\left( \eta \right)} \right) \\
&\ge {| {{w_+ }( \xi) - {w_+ }( \eta)}|^l}\frac{{{\phi^q}( \xi) + {\phi^q}( \eta)}}{2} - {| {{w_+ }( \xi) - {w_+ }( \eta)}|^{l - 1}}\frac{{{w_+ }( \xi) + {w_+ }( \eta)}}{2}| {{\phi^q}( \xi) - {\phi^q}( \eta)}|.
\end{align*}Since
 \begin{align*}
\left| {{\phi^q}\left( \xi \right) - {\phi^q}\left( \eta \right)} \right| &\le q\left( {{\phi^{q - 1}}\left( \xi \right) + {\phi^{q - 1}}\left( \eta \right)} \right)\left| {\phi\left( \xi \right) - \phi\left( \eta \right)} \right| \\
& \le c\left( q \right){\left( {{\phi^q}\left( \xi \right) +{\phi^q}\left( \eta \right)} \right)^{\frac{{q - 1}}{q}}}\left| {\phi \left( \xi \right) - \phi\left( \eta \right)} \right|,
\end{align*}
\begin{align*}
\left| {{\phi^q}\left( \xi \right) - {\phi^q}\left( \eta \right)} \right| &\le q\left( {{\phi^{q - 1}}\left( \xi \right) + {\phi^{q - 1}}\left( \eta \right)} \right)\left| {\phi\left( \xi \right) - \phi\left( \eta \right)} \right| \\
& \le c\left( q \right){\left( {{\phi^q}\left( \xi \right) +{\phi^q}\left( \eta \right)} \right)^{\frac{{q - 1}}{q}}}\left| {\phi \left( \xi \right) - \phi\left( \eta \right)} \right|,
\end{align*} from lemma 3.2, we use Young’s inequality, ![]() $0\le \phi\le 1$ and
$0\le \phi\le 1$ and  ${\frac{{q - 1}}{q}} \gt 0$ to deduce that
${\frac{{q - 1}}{q}} \gt 0$ to deduce that
 \begin{align*}
&\quad {\left| {{w_+ }\left( \xi \right) - {w_+ }\left( \eta \right)} \right|^{l - 1}}\frac{{{w_+ }\left( \xi \right) + {w_+ }\left( \eta \right)}}{2}\left| {{\phi^q}\left( \xi \right) - {\phi^q}\left( \eta \right)} \right| \\
&\le c\left( q \right){\left| {{w_+ }\left( \xi \right) - {w_+ }\left( \eta \right)} \right|^{l - 1}}\left( {{w_+ }\left( \xi \right) + {w_+ }\left( \eta \right)} \right){\left( {{\phi^q}\left( \xi \right) + {\phi^q}\left( \eta \right)} \right)^{\frac{{l - 1}}{l} + \frac{{q - l}}{{ql}}}}\left| {\phi\left( \xi \right) - \phi\left( \eta \right)} \right|\\
&\le \varepsilon {\left| {{w_+ }\left( \xi \right) - {w_+ }\left( \eta \right)} \right|^l}\left( {{\phi^q}\left( \xi \right) + {\phi^q}\left( \eta \right)} \right) \\
&\quad+ c\left( {\varepsilon ,q} \right){\left( {{\phi^q}\left( \xi \right) + {\phi^q}\left( \eta \right)} \right)^{\frac{{q - l}}{q}}}{\left| {\phi\left( \xi \right) -\phi\left( \eta \right)} \right|^l}{\left( {{w_+ }\left( \xi \right) + {w_+ }\left( \eta \right)} \right)^l}\\
& \le \varepsilon {\left| {{w_+ }\left( \xi \right) - {w_+ }\left( \eta \right)} \right|^l}\left( {{\phi^q}\left( \xi \right) + {\phi^q}\left( \eta \right)} \right) + c\left( {\varepsilon ,q} \right){\left| {\phi\left( \xi \right) -\phi\left( \eta \right)} \right|^l}{\left( {{w_+ }\left( \xi \right) + {w_+ }\left( \eta \right)} \right)^l}.
\end{align*}
\begin{align*}
&\quad {\left| {{w_+ }\left( \xi \right) - {w_+ }\left( \eta \right)} \right|^{l - 1}}\frac{{{w_+ }\left( \xi \right) + {w_+ }\left( \eta \right)}}{2}\left| {{\phi^q}\left( \xi \right) - {\phi^q}\left( \eta \right)} \right| \\
&\le c\left( q \right){\left| {{w_+ }\left( \xi \right) - {w_+ }\left( \eta \right)} \right|^{l - 1}}\left( {{w_+ }\left( \xi \right) + {w_+ }\left( \eta \right)} \right){\left( {{\phi^q}\left( \xi \right) + {\phi^q}\left( \eta \right)} \right)^{\frac{{l - 1}}{l} + \frac{{q - l}}{{ql}}}}\left| {\phi\left( \xi \right) - \phi\left( \eta \right)} \right|\\
&\le \varepsilon {\left| {{w_+ }\left( \xi \right) - {w_+ }\left( \eta \right)} \right|^l}\left( {{\phi^q}\left( \xi \right) + {\phi^q}\left( \eta \right)} \right) \\
&\quad+ c\left( {\varepsilon ,q} \right){\left( {{\phi^q}\left( \xi \right) + {\phi^q}\left( \eta \right)} \right)^{\frac{{q - l}}{q}}}{\left| {\phi\left( \xi \right) -\phi\left( \eta \right)} \right|^l}{\left( {{w_+ }\left( \xi \right) + {w_+ }\left( \eta \right)} \right)^l}\\
& \le \varepsilon {\left| {{w_+ }\left( \xi \right) - {w_+ }\left( \eta \right)} \right|^l}\left( {{\phi^q}\left( \xi \right) + {\phi^q}\left( \eta \right)} \right) + c\left( {\varepsilon ,q} \right){\left| {\phi\left( \xi \right) -\phi\left( \eta \right)} \right|^l}{\left( {{w_+ }\left( \xi \right) + {w_+ }\left( \eta \right)} \right)^l}.
\end{align*}Then, by choosing ɛ small enough, we have
 \begin{align*}
& {J _l}\left( {{w_+ }\left( \xi \right) - {w_+ }\left( \eta \right)} \right)\left( {{w_+ }\left( \xi \right){\phi^q}\left( \xi \right) - {w_+ }\left( \eta \right){\phi^q}\left( \eta \right)} \right) \\
\ge & {\left| {{w_+ }\left( \xi \right) - {w_+ }\left( \eta \right)} \right|^l}\frac{{{\phi^q}\left( \xi \right) + {\phi^q}\left( \eta \right)}}{4} - c{\left| {\phi( \xi) -\phi\left( \eta \right)} \right|^l}{\left( {{w_+ }\left( \xi \right) + {w_+ }\left( \eta \right)} \right)^l}.
\end{align*}
\begin{align*}
& {J _l}\left( {{w_+ }\left( \xi \right) - {w_+ }\left( \eta \right)} \right)\left( {{w_+ }\left( \xi \right){\phi^q}\left( \xi \right) - {w_+ }\left( \eta \right){\phi^q}\left( \eta \right)} \right) \\
\ge & {\left| {{w_+ }\left( \xi \right) - {w_+ }\left( \eta \right)} \right|^l}\frac{{{\phi^q}\left( \xi \right) + {\phi^q}\left( \eta \right)}}{4} - c{\left| {\phi( \xi) -\phi\left( \eta \right)} \right|^l}{\left( {{w_+ }\left( \xi \right) + {w_+ }\left( \eta \right)} \right)^l}.
\end{align*}Thus, we get
 \begin{align}
{J_1} \ge&\int_{{B_r}} {\int_{{B_r}} {\Bigg[ {\frac{{{{| {{w_ + }( \xi) - {w_ + }( \eta)}|}^p}(\phi^q(\xi) + \phi^q( \eta))/4 - c{{| {\phi( \xi) - \phi( \eta)}|}^p}{{( {{w_ + }( \xi ) + {w_ + }( \eta)})}^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}}} } } \nonumber \\
&+ a( {\xi ,\eta })\frac{{{\left| {{w_ + }\left( \xi \right) - {w_ + }\left( \eta \right)} \right|}^q}(\phi^q(\xi) +\phi^q(\eta))/4 }{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + tq}}}\nonumber\\
& - \frac{c{{\left| {\phi( \xi) -\phi( \eta)} \right|}^q}{\left( {{w_ + }\left( \xi \right) + {w_ + }\left( \eta \right)} \right)}^q}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + tq}}}
\Bigg]d\xi d\eta \nonumber \\
\ge& {\int_{{B_r}} {H\left( {\xi ,\eta ,\left| {{w_+ }\left( \xi \right) - {w_+ }\left( \eta \right)} \right|} \right)\left( {\phi^q\left( \xi \right) + {\phi^q}\left( \eta \right)} \right)\frac{{d\xi d\eta }}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^Q}}} } \nonumber\\
&-c\int_{{B_r}} {\int_{{B_r}} {H\left( {\xi ,\eta ,\left| {\phi( \xi) -\phi( \eta)} \right|\left( {{w_+ }\left( \xi \right) + {w_+ }\left( \eta \right)} \right)} \right)\frac{{d\xi d\eta }}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^Q}}} } .
\end{align}
\begin{align}
{J_1} \ge&\int_{{B_r}} {\int_{{B_r}} {\Bigg[ {\frac{{{{| {{w_ + }( \xi) - {w_ + }( \eta)}|}^p}(\phi^q(\xi) + \phi^q( \eta))/4 - c{{| {\phi( \xi) - \phi( \eta)}|}^p}{{( {{w_ + }( \xi ) + {w_ + }( \eta)})}^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}}} } } \nonumber \\
&+ a( {\xi ,\eta })\frac{{{\left| {{w_ + }\left( \xi \right) - {w_ + }\left( \eta \right)} \right|}^q}(\phi^q(\xi) +\phi^q(\eta))/4 }{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + tq}}}\nonumber\\
& - \frac{c{{\left| {\phi( \xi) -\phi( \eta)} \right|}^q}{\left( {{w_ + }\left( \xi \right) + {w_ + }\left( \eta \right)} \right)}^q}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + tq}}}
\Bigg]d\xi d\eta \nonumber \\
\ge& {\int_{{B_r}} {H\left( {\xi ,\eta ,\left| {{w_+ }\left( \xi \right) - {w_+ }\left( \eta \right)} \right|} \right)\left( {\phi^q\left( \xi \right) + {\phi^q}\left( \eta \right)} \right)\frac{{d\xi d\eta }}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^Q}}} } \nonumber\\
&-c\int_{{B_r}} {\int_{{B_r}} {H\left( {\xi ,\eta ,\left| {\phi( \xi) -\phi( \eta)} \right|\left( {{w_+ }\left( \xi \right) + {w_+ }\left( \eta \right)} \right)} \right)\frac{{d\xi d\eta }}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^Q}}} } .
\end{align}Now we estimate J 2. Note that
 \begin{equation}
{J _l}\left( {u\left( \xi \right) - u\left( \eta \right)} \right){w_+ }\left( \xi \right) \ge - w_+ ^{l - 1}\left( \eta \right){w_+ }\left( \xi \right).
\end{equation}
\begin{equation}
{J _l}\left( {u\left( \xi \right) - u\left( \eta \right)} \right){w_+ }\left( \xi \right) \ge - w_+ ^{l - 1}\left( \eta \right){w_+ }\left( \xi \right).
\end{equation} In fact, when ![]() $u\left( \xi \right) \ge u\left( \eta \right)$, it easy to see that the inequality (3.8) holds. When
$u\left( \xi \right) \ge u\left( \eta \right)$, it easy to see that the inequality (3.8) holds. When ![]() $u\left( \xi \right) \lt u\left( \eta \right)$ and
$u\left( \xi \right) \lt u\left( \eta \right)$ and ![]() $u\left( \xi \right)\le k$,
$u\left( \xi \right)\le k$, ![]() ${w_+ }\left( \xi \right)=0$, the inequality (3.8) also holds. When
${w_+ }\left( \xi \right)=0$, the inequality (3.8) also holds. When ![]() $k \lt u\left( \xi \right) \lt u\left( \eta \right)$,
$k \lt u\left( \xi \right) \lt u\left( \eta \right)$,
 \begin{align*}
{J _l}( {u( \xi) - u( \eta)}){w_+ }( \xi)
= - {| {{w_+ }( \xi) - {w_+ }( \eta)}|^{l - 1}}{w_+ }( \xi) \ge - w_+ ^{l - 1}( \eta){w_+ }( \xi).
\end{align*}
\begin{align*}
{J _l}( {u( \xi) - u( \eta)}){w_+ }( \xi)
= - {| {{w_+ }( \xi) - {w_+ }( \eta)}|^{l - 1}}{w_+ }( \xi) \ge - w_+ ^{l - 1}( \eta){w_+ }( \xi).
\end{align*}Thus, we apply (3.8) and (3.4) to get
 \begin{align}
J_2 &= 2{\int _{{\mathbb{H}^n}\backslash {B_r}}}\int_{{B_r}} \Bigg[\frac{{{J _p}( {u( \xi ) - u( \eta )}){w_ + }( \xi){\phi^q}( \xi )}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}}+ a( {\xi ,\eta })\frac{{{J _q}( {u( \xi) - u( \eta )} ){w_ + }( \xi){\phi^q}( \xi)}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + tq}}}\Bigg]\nonumber\\
& \quad \times\,d\xi d\eta \nonumber\\
&\ge - c{\int _{{\mathbb{H}^n}\backslash {B_r}}}\int_{{B_r}} {\left[ {\frac{{w_+ ^{p - 1}( \eta ){w_+ }( \xi){\phi^q}( \xi)}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{sp}}} + a(\xi ,\eta)\frac{{w_+ ^{q - 1}( \eta){w_+ }( \xi){\phi^q}( \xi)}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{tq}}}} \right]\frac{{d\xi d\eta }}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^Q}}} \nonumber \\
&\ge - c\left( {\mathop {\sup }\limits_{\xi \in {\rm{supp}}\;\phi} \int_{{\mathbb{H}^n}\backslash {B_r}} {h( {\xi ,\eta ,{w_+ }( \eta )})\frac{d\eta }{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^Q}}} } \right)\int_{{B_r}} {{w_\pm }( \xi){\phi^q}( \xi)\,d\xi }.
\end{align}
\begin{align}
J_2 &= 2{\int _{{\mathbb{H}^n}\backslash {B_r}}}\int_{{B_r}} \Bigg[\frac{{{J _p}( {u( \xi ) - u( \eta )}){w_ + }( \xi){\phi^q}( \xi )}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}}+ a( {\xi ,\eta })\frac{{{J _q}( {u( \xi) - u( \eta )} ){w_ + }( \xi){\phi^q}( \xi)}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + tq}}}\Bigg]\nonumber\\
& \quad \times\,d\xi d\eta \nonumber\\
&\ge - c{\int _{{\mathbb{H}^n}\backslash {B_r}}}\int_{{B_r}} {\left[ {\frac{{w_+ ^{p - 1}( \eta ){w_+ }( \xi){\phi^q}( \xi)}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{sp}}} + a(\xi ,\eta)\frac{{w_+ ^{q - 1}( \eta){w_+ }( \xi){\phi^q}( \xi)}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{tq}}}} \right]\frac{{d\xi d\eta }}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^Q}}} \nonumber \\
&\ge - c\left( {\mathop {\sup }\limits_{\xi \in {\rm{supp}}\;\phi} \int_{{\mathbb{H}^n}\backslash {B_r}} {h( {\xi ,\eta ,{w_+ }( \eta )})\frac{d\eta }{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^Q}}} } \right)\int_{{B_r}} {{w_\pm }( \xi){\phi^q}( \xi)\,d\xi }.
\end{align}The following standard iteration lemma can be found in [Reference Giusti25, lemma 7.1].
Lemma 3.4. Let ![]() $\left\{{{y_i}} \right\}_{i = 0}^\infty $ be a sequence of nonnegative numbers satisfying
$\left\{{{y_i}} \right\}_{i = 0}^\infty $ be a sequence of nonnegative numbers satisfying
 \begin{equation*}{y_{i + 1}} \le {b_1}b_2^iy_i^{1 + \beta },\;i = 0,1,2, \cdots \end{equation*}
\begin{equation*}{y_{i + 1}} \le {b_1}b_2^iy_i^{1 + \beta },\;i = 0,1,2, \cdots \end{equation*} for some constants ![]() $b_1,\;\beta \gt 0$ and
$b_1,\;\beta \gt 0$ and ![]() $b_2 \gt 1$. If
$b_2 \gt 1$. If
 \begin{equation*}{y_0} \le b_1^{- \frac{1}{\beta }}b_2^{- \frac{1}{{{\beta ^2}}}},\end{equation*}
\begin{equation*}{y_0} \le b_1^{- \frac{1}{\beta }}b_2^{- \frac{1}{{{\beta ^2}}}},\end{equation*} then ![]() ${y_i} \to 0$ as
${y_i} \to 0$ as ![]() $i \to \infty$.
$i \to \infty$.
We end this section by providing the proof of boundedness. Lemmas 2.7 and 3.3 play the vital roles in the process.
Proof of theorem 1.2. For convenience, denote
Let ![]() ${B_{r}} \equiv {B_{r}}\left( {{\xi _0}} \right) \subset \subset \Omega $ be a fixed ball with
${B_{r}} \equiv {B_{r}}\left( {{\xi _0}} \right) \subset \subset \Omega $ be a fixed ball with ![]() $r \le 1$. For
$r \le 1$. For ![]() $i=0,1,2,\cdots$ and
$i=0,1,2,\cdots$ and ![]() $k_0 \gt 0$, we write
$k_0 \gt 0$, we write
 \begin{equation*}{r_i}: = \frac{r}{2}\left( {1 + {2^{- i}}} \right),\quad {\sigma _i}: = \;\frac{{{r_{i - 1}} + {r_i}}}{2}, \quad {k_i}: = 2{k_0}\left( {1 - {2^{- i - 1}}} \right)\end{equation*}
\begin{equation*}{r_i}: = \frac{r}{2}\left( {1 + {2^{- i}}} \right),\quad {\sigma _i}: = \;\frac{{{r_{i - 1}} + {r_i}}}{2}, \quad {k_i}: = 2{k_0}\left( {1 - {2^{- i - 1}}} \right)\end{equation*}and
 \begin{equation*}{y_i}: = \int_{{A^ + }\left( {{k_i},{r_i}} \right)} {{H_0}\left( {\left( {u\left( \xi \right) - {k_i}} \right){_ + }} \right)\;d\xi } .\end{equation*}
\begin{equation*}{y_i}: = \int_{{A^ + }\left( {{k_i},{r_i}} \right)} {{H_0}\left( {\left( {u\left( \xi \right) - {k_i}} \right){_ + }} \right)\;d\xi } .\end{equation*}In addition, we denote
 \begin{equation*}{A^ + }\left( {{k_i},{r_i}} \right): = \left\{{\xi \in {B_{{r_i}}}:u\left( \xi \right) \ge {k_i}} \right\}.\end{equation*}
\begin{equation*}{A^ + }\left( {{k_i},{r_i}} \right): = \left\{{\xi \in {B_{{r_i}}}:u\left( \xi \right) \ge {k_i}} \right\}.\end{equation*} Then via ![]() ${\left( {u\left( \xi \right) - k_i} \right)_ + }\le {\left( {u\left( \xi \right) - k_{i-1}} \right)_ + }$,
${\left( {u\left( \xi \right) - k_i} \right)_ + }\le {\left( {u\left( \xi \right) - k_{i-1}} \right)_ + }$,
Moreover, for ![]() $\xi \in {A^ + }\left( {{k_i},{r_i}} \right)$, we have
$\xi \in {A^ + }\left( {{k_i},{r_i}} \right)$, we have
 \begin{equation*}{\left( {u\left( \xi \right) - k_{i-1}} \right)_ + } = u\left( \xi \right) - k_{i-1} \ge k_i - k_{i-1}=2^{-i}k_0.\end{equation*}
\begin{equation*}{\left( {u\left( \xi \right) - k_{i-1}} \right)_ + } = u\left( \xi \right) - k_{i-1} \ge k_i - k_{i-1}=2^{-i}k_0.\end{equation*}Thus, it deduces
 \begin{align}
\left| {{A^ + }\left( {k_i,r_i } \right)} \right| & \le \int_{{A^ + }\left( {k_i,r_i } \right)} {\frac{{\left( {u\left( \xi \right) - k_{i-1}} \right)_ + ^p}}{{{{\left( {k_i - k_{i-1}} \right)}^p}}}d\xi }\le{k_0^{-p}}2^{ip}y_{i-1}
\end{align}
\begin{align}
\left| {{A^ + }\left( {k_i,r_i } \right)} \right| & \le \int_{{A^ + }\left( {k_i,r_i } \right)} {\frac{{\left( {u\left( \xi \right) - k_{i-1}} \right)_ + ^p}}{{{{\left( {k_i - k_{i-1}} \right)}^p}}}d\xi }\le{k_0^{-p}}2^{ip}y_{i-1}
\end{align}and
 \begin{align}
\int_{{B_{r_{i-1}} }} {{{\left( {u\left( \xi \right) - k_i} \right)}_ + }\;d\xi }
& \le \int_{{B_{r_{i-1}} }} {{{\left( {u\left( \xi \right) - k_{i-1}} \right)}_ + }{{\left( {\frac{{{{\left( {u\left( \xi \right) - k_{i-1}} \right)}_ + }}}{{k_i - k_{i-1}}}} \right)}^{p - 1}}\;d\xi } \nonumber\\
& \le {{{k_0^{1-p}}{2^{i(p - 1)}}}}\int_{{B_{r_{i-1}} }} {{H_0}\left( {{{\left( {u\left( \xi \right) - k_{i-1}} \right)}_ + }} \right)\;d\xi } \nonumber\\
&={{{k_0^{1-p}}{2^{i(p - 1)}}}}y_{i-1}.
\end{align}
\begin{align}
\int_{{B_{r_{i-1}} }} {{{\left( {u\left( \xi \right) - k_i} \right)}_ + }\;d\xi }
& \le \int_{{B_{r_{i-1}} }} {{{\left( {u\left( \xi \right) - k_{i-1}} \right)}_ + }{{\left( {\frac{{{{\left( {u\left( \xi \right) - k_{i-1}} \right)}_ + }}}{{k_i - k_{i-1}}}} \right)}^{p - 1}}\;d\xi } \nonumber\\
& \le {{{k_0^{1-p}}{2^{i(p - 1)}}}}\int_{{B_{r_{i-1}} }} {{H_0}\left( {{{\left( {u\left( \xi \right) - k_{i-1}} \right)}_ + }} \right)\;d\xi } \nonumber\\
&={{{k_0^{1-p}}{2^{i(p - 1)}}}}y_{i-1}.
\end{align} We use lemma 2.7 with ![]() $f:= {\left( {u - k} \right)_ + }, a_0:=\|a\|_{L^\infty}$ and (3.11) to get
$f:= {\left( {u - k} \right)_ + }, a_0:=\|a\|_{L^\infty}$ and (3.11) to get
 \begin{align}
{y_i}
&\le c{r_i^Q}-\!\!\!\!\!\!\int_{{B_{{r_i}}}} {{H_0}\left( {{{\left( {u\left( \xi \right) - {k_i}} \right)}_ + }} \right)\;d\xi }\nonumber\\
& \le cr_i^{Q + sp } -\!\!\!\!\!\!\int_{{B_{{{r _i}}}}} {\left( {{{\left| {\frac{{{{\left( {u\left( \xi \right) - {k_i}} \right)}_ + }}}{{{r_i^s}}}} \right|}^p} + {\left\| a \right\|_{{L^\infty }}}{{\left| {\frac{{{{\left( {u\left( \xi \right) - {k_i}} \right)}_ + }}}{{{r_i^t}}}} \right|}^q}} \right)\;d\xi } \nonumber\\
& \le c{\left\| a \right\|_{{L^\infty }}}r_i^{Q + sp - tq}D_1^{\frac{q}{p}}({\sigma _i},{r_i}){\left( {-\!\!\!\!\!\!\int_{{B_{{\sigma _i}}}} {\int_{{B_{{{\sigma _i}}}}} {\frac{{{{\left| {{{\left( {u\left( \xi \right) - {k_i}} \right)}_ + } - {{\left( {u\left( \eta \right) - {k_i}} \right)}_ + }} \right|}^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}}\;d\xi } d\eta } } \right)^{\frac{q}{p}}}\nonumber\\
& \quad+ cr_i^{Q - sp}{D_1}({\sigma _i},r_i){\left( {{A^ + }\left( {{k_i},{r_i}} \right)} \right)^{\frac{{sp}}{Q}}}-\!\!\!\!\!\!\int_{{B_{{\sigma _i}}}} {\int_{{B_{{\sigma _i}}}} {\frac{{{{\left| {{{\left( {u\left( \xi \right) - {k_i}} \right)}_ + } - {{\left( {u\left( \eta \right) - {k_i}} \right)}_ + }} \right|}^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}}\;d\xi } d\eta } \nonumber\\
&\quad + cr_i^{Q + sp} {{\left( {\frac{{{A^ + }\left( {{k_i},{r_i}} \right)}}{{\left| {{B_{{r_i}}}} \right|}}} \right)}^{p - 1}} -\!\!\!\!\!\!\int_{{B_{{{\sigma _i}}}}} {\left( {{{\left| {\frac{{{{\left( {u\left( \xi \right) - {k_i}} \right)}_ + }}}{{{r_i^s}}}} \right|}^p} + {\left\| a \right\|_{{L^\infty }}}{{\left| {\frac{{{{\left( {u\left( \xi \right) - {k_i}} \right)}_ + }}}{{{r_i^t}}}} \right|}^q}} \right)\;d\xi } \nonumber\\
& \le c{\left\| a \right\|_{{L^\infty }}}r_i^{Q + sp - tq}D_1^{\frac{q}{p}}({\sigma _i},{r_i}){\left( {-\!\!\!\!\!\!\int_{{B_{{{\sigma _i}}}}} {\int_{{B_{{{\sigma _i}}}}} {\frac{{{{\left| {{{\left( {u\left( \xi \right) - {k_i}} \right)}_ + } - {{\left( {u\left( \eta \right) - {k_i}} \right)}_ + }} \right|}^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}}\;d\xi } d\eta } } \right)^{\frac{q}{p}}}\nonumber\\
&\quad + ck_0^{- \frac{{s{p^2}}}{Q}}r_i^{Q - sp}{2^{i\frac{{s{p^2}}}{Q}}}{D_1}({\sigma _i},r_i)y_{i - 1}^{\frac{{sp}}{Q}}-\!\!\!\!\!\!\int_{{B_{{\sigma _i}}}} {\int_{{B_{{\sigma _i}}}} {\frac{{{{\left| {{{\left( {u\left( \xi \right) - {k_i}} \right)}_ + } - {{\left( {u\left( \eta \right) - {k_i}} \right)}_ + }} \right|}^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}}\;d\xi } d\eta } \nonumber\\
& \quad + cr_i^{Q + sp-tq}
{{\left( {\frac{{k_0^{- p}{2^{ip}}{y_{i - 1}}}}{{\left| {{B_{{r_i}}}} \right|}}} \right)}^{p - 1}} -\!\!\!\!\!\!\int_{{B_{{\sigma _i}}}} {{H_0}\left( {{{\left( {u\left( \xi \right) - {k_i}} \right)}_ + }} \right)\;d\xi } .
\end{align}
\begin{align}
{y_i}
&\le c{r_i^Q}-\!\!\!\!\!\!\int_{{B_{{r_i}}}} {{H_0}\left( {{{\left( {u\left( \xi \right) - {k_i}} \right)}_ + }} \right)\;d\xi }\nonumber\\
& \le cr_i^{Q + sp } -\!\!\!\!\!\!\int_{{B_{{{r _i}}}}} {\left( {{{\left| {\frac{{{{\left( {u\left( \xi \right) - {k_i}} \right)}_ + }}}{{{r_i^s}}}} \right|}^p} + {\left\| a \right\|_{{L^\infty }}}{{\left| {\frac{{{{\left( {u\left( \xi \right) - {k_i}} \right)}_ + }}}{{{r_i^t}}}} \right|}^q}} \right)\;d\xi } \nonumber\\
& \le c{\left\| a \right\|_{{L^\infty }}}r_i^{Q + sp - tq}D_1^{\frac{q}{p}}({\sigma _i},{r_i}){\left( {-\!\!\!\!\!\!\int_{{B_{{\sigma _i}}}} {\int_{{B_{{{\sigma _i}}}}} {\frac{{{{\left| {{{\left( {u\left( \xi \right) - {k_i}} \right)}_ + } - {{\left( {u\left( \eta \right) - {k_i}} \right)}_ + }} \right|}^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}}\;d\xi } d\eta } } \right)^{\frac{q}{p}}}\nonumber\\
& \quad+ cr_i^{Q - sp}{D_1}({\sigma _i},r_i){\left( {{A^ + }\left( {{k_i},{r_i}} \right)} \right)^{\frac{{sp}}{Q}}}-\!\!\!\!\!\!\int_{{B_{{\sigma _i}}}} {\int_{{B_{{\sigma _i}}}} {\frac{{{{\left| {{{\left( {u\left( \xi \right) - {k_i}} \right)}_ + } - {{\left( {u\left( \eta \right) - {k_i}} \right)}_ + }} \right|}^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}}\;d\xi } d\eta } \nonumber\\
&\quad + cr_i^{Q + sp} {{\left( {\frac{{{A^ + }\left( {{k_i},{r_i}} \right)}}{{\left| {{B_{{r_i}}}} \right|}}} \right)}^{p - 1}} -\!\!\!\!\!\!\int_{{B_{{{\sigma _i}}}}} {\left( {{{\left| {\frac{{{{\left( {u\left( \xi \right) - {k_i}} \right)}_ + }}}{{{r_i^s}}}} \right|}^p} + {\left\| a \right\|_{{L^\infty }}}{{\left| {\frac{{{{\left( {u\left( \xi \right) - {k_i}} \right)}_ + }}}{{{r_i^t}}}} \right|}^q}} \right)\;d\xi } \nonumber\\
& \le c{\left\| a \right\|_{{L^\infty }}}r_i^{Q + sp - tq}D_1^{\frac{q}{p}}({\sigma _i},{r_i}){\left( {-\!\!\!\!\!\!\int_{{B_{{{\sigma _i}}}}} {\int_{{B_{{{\sigma _i}}}}} {\frac{{{{\left| {{{\left( {u\left( \xi \right) - {k_i}} \right)}_ + } - {{\left( {u\left( \eta \right) - {k_i}} \right)}_ + }} \right|}^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}}\;d\xi } d\eta } } \right)^{\frac{q}{p}}}\nonumber\\
&\quad + ck_0^{- \frac{{s{p^2}}}{Q}}r_i^{Q - sp}{2^{i\frac{{s{p^2}}}{Q}}}{D_1}({\sigma _i},r_i)y_{i - 1}^{\frac{{sp}}{Q}}-\!\!\!\!\!\!\int_{{B_{{\sigma _i}}}} {\int_{{B_{{\sigma _i}}}} {\frac{{{{\left| {{{\left( {u\left( \xi \right) - {k_i}} \right)}_ + } - {{\left( {u\left( \eta \right) - {k_i}} \right)}_ + }} \right|}^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}}\;d\xi } d\eta } \nonumber\\
& \quad + cr_i^{Q + sp-tq}
{{\left( {\frac{{k_0^{- p}{2^{ip}}{y_{i - 1}}}}{{\left| {{B_{{r_i}}}} \right|}}} \right)}^{p - 1}} -\!\!\!\!\!\!\int_{{B_{{\sigma _i}}}} {{H_0}\left( {{{\left( {u\left( \xi \right) - {k_i}} \right)}_ + }} \right)\;d\xi } .
\end{align} When we apply lemma 3.3, we choose a cut-off function  $\phi \in C_0^\infty \left( {{B_{\frac{{\sigma _i + {r_{i - 1}}}}{2}}}} \right)$ satisfying
$\phi \in C_0^\infty \left( {{B_{\frac{{\sigma _i + {r_{i - 1}}}}{2}}}} \right)$ satisfying ![]() $0 \le \phi\le 1,\;\phi\equiv 1 $ in
$0 \le \phi\le 1,\;\phi\equiv 1 $ in ![]() $B_{\sigma _i}$ and
$B_{\sigma _i}$ and  $\left| {{\nabla _H}\phi } \right| \le \frac{c}{{r_{i-1}-\sigma _i }}=\frac{c}{r}2^i$. Then we have that, from (3.12),
$\left| {{\nabla _H}\phi } \right| \le \frac{c}{{r_{i-1}-\sigma _i }}=\frac{c}{r}2^i$. Then we have that, from (3.12),
 \begin{align*}
&\quad -\!\!\!\!\!\!\int_{{B_{{\sigma _i}}}} {\int_{{B_{{\sigma _i}}}} {\frac{{{{\left| {{{\left( {u\left( \xi \right) - {k_i}} \right)}_ + } - {{\left( {u\left( \eta \right) - {k_i}} \right)}_ + }} \right|}^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}}\;d\xi } d\eta } \\
&\le -\!\!\!\!\!\!\int_{{B_{{\sigma _i}}}} {\int_{{B_{{\sigma _i}}}} {H\left( {\xi ,\eta ,\left| {{{\left( {u\left( \xi \right) - {k_i}} \right)}_ + } - {{\left( {u\left( \eta \right) - {k_i}} \right)}_ + }} \right|} \right)\frac{{d\xi d\eta }}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^Q}}} } \\
&\le c{r^{- p}}{2^{ip}}-\!\!\!\!\!\!\int_{{B_{{r_{i - 1}}}}} {\left( {u\left( \xi \right) - {k_{i }}} \right)_ + ^p\int_{{B_{{r_{i - 1}}}}} {\frac{{d\xi d\eta }}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + (s - 1)p}}}} } \\
&\quad + c{\| a \|_{{L^\infty }}}{r^{- q}}{2^{iq}}-\!\!\!\!\!\!\int_{{B_{{r_{i - 1}}}}} {\left( {u\left( \xi \right) - {k_{i }}} \right)_ + ^q\int_{{B_{{r_{i - 1}}}}} {\frac{{d\xi d\eta }}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + (t - 1)q}}}} } \\
&\quad + c {\mathop {\sup }\limits_{\xi \in {\rm{supp}}\;\phi } \int_{{\mathbb{H}^n}\backslash {B_{{r_{i - 1}}}}} {\left( {\frac{{\left( {u\left( \eta \right) - k_{i }} \right)_ + ^{p - 1}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}} + {{\| a \|}_{{L^\infty }}}\frac{{\left( {u\left( \eta \right) - k_{i }} \right)_ + ^{q - 1}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + tq}}}} \right)\;d\eta } } \\
&\qquad\cdot-\!\!\!\!\!\!\int_{{B_{{r_{i - 1}}}}} {{{\left( {u\left( \xi \right) - k_{i }} \right)}_ + }\;d\xi } \\
& \le c{r^{- p}}{2^{ip}}r_{i - 1}^{\left( {1 - s} \right)p}-\!\!\!\!\!\!\int_{{B_{{r_{i - 1}}}}} {\left( {u\left( \xi \right) - {k_{i }}} \right)_ + ^p\;d\xi} \\
&\quad+ c{\| a \|_{{L^\infty }}}{r^{- q}}{2^{iq}}r_{i - 1}^{\left( {1 - t} \right)q}-\!\!\!\!\!\!\int_{{B_{{r_{i - 1}}}}} {\left( {u\left( \xi \right) - {k_{i }}} \right)_ + ^q\;d\xi}+ c{\left( {\frac{{{r_{i - 1}} + {\sigma _i}}}{{{r_{i - 1}} - {\sigma _i}}}} \right)^{Q + tq}} \\
&\qquad\cdot {\int_{{\mathbb{H}^n}\backslash {B_{{r_{i - 1}}}}} {\left( {\frac{{\left( {u\left( \eta \right) - k_{i }} \right)_ + ^{p - 1}}}{{\| {{\eta ^{- 1}} \circ {\xi _0}} \|_{{\mathbb{H}^n}}^{Q + sp}}} + {{\| a \|}_{{L^\infty }}}\frac{{\left( {u\left( \eta \right) - k_{i }} \right)_ + ^{q - 1}}}{{\| {{\eta ^{- 1}} \circ {\xi _0}} \|_{{\mathbb{H}^n}}^{Q + tq}}}} \right)\;d\eta } } -\!\!\!\!\!\!\int_{{B_{{r_{i - 1}}}}} \!\!\!\!{{{\left( {u\left( \xi \right) - k_{i }} \right)}_ + }\;d\xi } \\
& \le c{r^{- q}}{2^{iq}}r_{i - 1}^{\left( {1 - t} \right)p}-\!\!\!\!\!\!\int_{{B_{{r_{i - 1}}}}} {{H_0}\left( {{{\left( {u\left( \xi \right) - {k_i}} \right)}_ + }} \right)\;d\xi } \\
&\quad+ c{2^{i\left( {Q + tq} \right)}}T\left( {{{\left( {u - {k_i}} \right)}_ + };\xi_0,{r_{i - 1}}} \right)-\!\!\!\!\!\!\int_{{B_{{r_{i - 1}}}}} {{{\left( {u\left( \xi \right) - k_i} \right)}_ + }\;d\xi }\\
&\le c{2^{i\left( {Q + q + p-1 } \right)}}{y_{i - 1}},
\end{align*}
\begin{align*}
&\quad -\!\!\!\!\!\!\int_{{B_{{\sigma _i}}}} {\int_{{B_{{\sigma _i}}}} {\frac{{{{\left| {{{\left( {u\left( \xi \right) - {k_i}} \right)}_ + } - {{\left( {u\left( \eta \right) - {k_i}} \right)}_ + }} \right|}^p}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}}\;d\xi } d\eta } \\
&\le -\!\!\!\!\!\!\int_{{B_{{\sigma _i}}}} {\int_{{B_{{\sigma _i}}}} {H\left( {\xi ,\eta ,\left| {{{\left( {u\left( \xi \right) - {k_i}} \right)}_ + } - {{\left( {u\left( \eta \right) - {k_i}} \right)}_ + }} \right|} \right)\frac{{d\xi d\eta }}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^Q}}} } \\
&\le c{r^{- p}}{2^{ip}}-\!\!\!\!\!\!\int_{{B_{{r_{i - 1}}}}} {\left( {u\left( \xi \right) - {k_{i }}} \right)_ + ^p\int_{{B_{{r_{i - 1}}}}} {\frac{{d\xi d\eta }}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + (s - 1)p}}}} } \\
&\quad + c{\| a \|_{{L^\infty }}}{r^{- q}}{2^{iq}}-\!\!\!\!\!\!\int_{{B_{{r_{i - 1}}}}} {\left( {u\left( \xi \right) - {k_{i }}} \right)_ + ^q\int_{{B_{{r_{i - 1}}}}} {\frac{{d\xi d\eta }}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + (t - 1)q}}}} } \\
&\quad + c {\mathop {\sup }\limits_{\xi \in {\rm{supp}}\;\phi } \int_{{\mathbb{H}^n}\backslash {B_{{r_{i - 1}}}}} {\left( {\frac{{\left( {u\left( \eta \right) - k_{i }} \right)_ + ^{p - 1}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}} + {{\| a \|}_{{L^\infty }}}\frac{{\left( {u\left( \eta \right) - k_{i }} \right)_ + ^{q - 1}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + tq}}}} \right)\;d\eta } } \\
&\qquad\cdot-\!\!\!\!\!\!\int_{{B_{{r_{i - 1}}}}} {{{\left( {u\left( \xi \right) - k_{i }} \right)}_ + }\;d\xi } \\
& \le c{r^{- p}}{2^{ip}}r_{i - 1}^{\left( {1 - s} \right)p}-\!\!\!\!\!\!\int_{{B_{{r_{i - 1}}}}} {\left( {u\left( \xi \right) - {k_{i }}} \right)_ + ^p\;d\xi} \\
&\quad+ c{\| a \|_{{L^\infty }}}{r^{- q}}{2^{iq}}r_{i - 1}^{\left( {1 - t} \right)q}-\!\!\!\!\!\!\int_{{B_{{r_{i - 1}}}}} {\left( {u\left( \xi \right) - {k_{i }}} \right)_ + ^q\;d\xi}+ c{\left( {\frac{{{r_{i - 1}} + {\sigma _i}}}{{{r_{i - 1}} - {\sigma _i}}}} \right)^{Q + tq}} \\
&\qquad\cdot {\int_{{\mathbb{H}^n}\backslash {B_{{r_{i - 1}}}}} {\left( {\frac{{\left( {u\left( \eta \right) - k_{i }} \right)_ + ^{p - 1}}}{{\| {{\eta ^{- 1}} \circ {\xi _0}} \|_{{\mathbb{H}^n}}^{Q + sp}}} + {{\| a \|}_{{L^\infty }}}\frac{{\left( {u\left( \eta \right) - k_{i }} \right)_ + ^{q - 1}}}{{\| {{\eta ^{- 1}} \circ {\xi _0}} \|_{{\mathbb{H}^n}}^{Q + tq}}}} \right)\;d\eta } } -\!\!\!\!\!\!\int_{{B_{{r_{i - 1}}}}} \!\!\!\!{{{\left( {u\left( \xi \right) - k_{i }} \right)}_ + }\;d\xi } \\
& \le c{r^{- q}}{2^{iq}}r_{i - 1}^{\left( {1 - t} \right)p}-\!\!\!\!\!\!\int_{{B_{{r_{i - 1}}}}} {{H_0}\left( {{{\left( {u\left( \xi \right) - {k_i}} \right)}_ + }} \right)\;d\xi } \\
&\quad+ c{2^{i\left( {Q + tq} \right)}}T\left( {{{\left( {u - {k_i}} \right)}_ + };\xi_0,{r_{i - 1}}} \right)-\!\!\!\!\!\!\int_{{B_{{r_{i - 1}}}}} {{{\left( {u\left( \xi \right) - k_i} \right)}_ + }\;d\xi }\\
&\le c{2^{i\left( {Q + q + p-1 } \right)}}{y_{i - 1}},
\end{align*}where we used the fact that
 \begin{equation*}T\left( {{{\left( {u - {k_i}} \right)}_ + };\xi_0,{r_{i - 1}}} \right) \le T\left( {u;\xi_0,\frac{r}{2}} \right) \lt \infty ,\end{equation*}
\begin{equation*}T\left( {{{\left( {u - {k_i}} \right)}_ + };\xi_0,{r_{i - 1}}} \right) \le T\left( {u;\xi_0,\frac{r}{2}} \right) \lt \infty ,\end{equation*}and
 \begin{equation*}\frac{{\| {{\eta ^{- 1}} \circ {\xi _0}} \|_{{\mathbb{H}^n}}^{}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{}}} \le 1 + \frac{{\| {\xi _0^{- 1} \circ \xi } \|_{{\mathbb{H}^n}}^{}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{}}} \le 1 + \frac{{{r_{i - 1}} + {\sigma _i}}}{{{r_{i - 1}} - {\sigma _i}}} \le 2\frac{{{r_{i - 1}} + {\sigma _i}}}{{{r_{i - 1}} - {\sigma _i}}} \le c{2^i}\end{equation*}
\begin{equation*}\frac{{\| {{\eta ^{- 1}} \circ {\xi _0}} \|_{{\mathbb{H}^n}}^{}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{}}} \le 1 + \frac{{\| {\xi _0^{- 1} \circ \xi } \|_{{\mathbb{H}^n}}^{}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{}}} \le 1 + \frac{{{r_{i - 1}} + {\sigma _i}}}{{{r_{i - 1}} - {\sigma _i}}} \le 2\frac{{{r_{i - 1}} + {\sigma _i}}}{{{r_{i - 1}} - {\sigma _i}}} \le c{2^i}\end{equation*} for ![]() ${\xi \in {\rm{supp}}\;\phi }$ and
${\xi \in {\rm{supp}}\;\phi }$ and ![]() $\eta \in {{\mathbb{H}^n}\backslash {B_{r_{i - 1}} }}$. Noting that
$\eta \in {{\mathbb{H}^n}\backslash {B_{r_{i - 1}} }}$. Noting that ![]() ${D_1}({\sigma _i},{r_i}) \le c{2^{i\left( {Q + p} \right)}}$, it follows from (3.13) that
${D_1}({\sigma _i},{r_i}) \le c{2^{i\left( {Q + p} \right)}}$, it follows from (3.13) that
 \begin{align}
{y_i} \le
c{2^{i\left[ {\frac{{q\left( {Q + p} \right)}}{p} + \frac{{q\left( {Q + q + p} \right)}}{p}} \right]}}y_{i - 1}^{\frac{q}{p}} + c{2^{i\left( {\frac{{{p^2}}}{Q} + Q + p + \frac{{q\left( {Q + q + p} \right)}}{p}} \right)}}y_{i - 1}^{\frac{{sp}}{Q} + 1} + c{2^{ip(p - 1)}}y_{i - 1}^p.
\end{align}
\begin{align}
{y_i} \le
c{2^{i\left[ {\frac{{q\left( {Q + p} \right)}}{p} + \frac{{q\left( {Q + q + p} \right)}}{p}} \right]}}y_{i - 1}^{\frac{q}{p}} + c{2^{i\left( {\frac{{{p^2}}}{Q} + Q + p + \frac{{q\left( {Q + q + p} \right)}}{p}} \right)}}y_{i - 1}^{\frac{{sp}}{Q} + 1} + c{2^{ip(p - 1)}}y_{i - 1}^p.
\end{align} Since ![]() ${H_0}\left( u \right) \in {L^1}\left( \Omega \right)$ from the assumption (1.8), we get that
${H_0}\left( u \right) \in {L^1}\left( \Omega \right)$ from the assumption (1.8), we get that
 \begin{equation*}{y_0} = \int_{{A^ + }\left( {{k_0},r} \right)} {{H_0}\left( {\left( {u\left( \xi \right) - {k_0}} \right){_ + }} \right)\;d\xi } \to 0\quad \text{as } k_0 \to \infty .\end{equation*}
\begin{equation*}{y_0} = \int_{{A^ + }\left( {{k_0},r} \right)} {{H_0}\left( {\left( {u\left( \xi \right) - {k_0}} \right){_ + }} \right)\;d\xi } \to 0\quad \text{as } k_0 \to \infty .\end{equation*} First, we consider ![]() $k_0 \gt 1$ so large that
$k_0 \gt 1$ so large that
Then, we have from (3.14) that
 \begin{equation*}{y_i} \le c{2^{\theta i}}y_{i - 1}^\beta ,\end{equation*}
\begin{equation*}{y_i} \le c{2^{\theta i}}y_{i - 1}^\beta ,\end{equation*}where
 \begin{equation*}\theta = 2\left(\frac{{\left( {Q + p + q} \right)q}}{p} + {p^2}\right),\;\;\;\;\;\beta = \min \left\{{\frac{{q }}{p}-1,\frac{{sp}}{Q},p - 1} \right\}.\end{equation*}
\begin{equation*}\theta = 2\left(\frac{{\left( {Q + p + q} \right)q}}{p} + {p^2}\right),\;\;\;\;\;\beta = \min \left\{{\frac{{q }}{p}-1,\frac{{sp}}{Q},p - 1} \right\}.\end{equation*}Finally, we can choose k 0 so large that
 \begin{equation*}{y_0} \le {{\tilde c}^{- \frac{1}{\beta }}}{2^{- \frac{\theta }{{{\beta ^2}}}}}\end{equation*}
\begin{equation*}{y_0} \le {{\tilde c}^{- \frac{1}{\beta }}}{2^{- \frac{\theta }{{{\beta ^2}}}}}\end{equation*}holds. Then lemma 3.4 implies
 \begin{equation*}{y_\infty } = \int_{{A^ + }\left( {2{k_0},\frac{r}{2}} \right)} {{H_0}\left( {\left( {u\left( \xi \right) - 2{k_0}} \right){_ + }} \right)\;d\xi } = 0,\end{equation*}
\begin{equation*}{y_\infty } = \int_{{A^ + }\left( {2{k_0},\frac{r}{2}} \right)} {{H_0}\left( {\left( {u\left( \xi \right) - 2{k_0}} \right){_ + }} \right)\;d\xi } = 0,\end{equation*} which means that ![]() $u \le 2{k_0}$ a.e. in
$u \le 2{k_0}$ a.e. in  ${B_{\frac{r}{2}}}$.
${B_{\frac{r}{2}}}$.
Applying the same argument to −u, we consequently obtain  $u \in {L^\infty }( {{B_{\frac{r}{2}}}} )$.
$u \in {L^\infty }( {{B_{\frac{r}{2}}}} )$.
4. Hölder continuity
We are going to demonstrate the Hölder regularity of weak solutions to equation (1.1) in the last section. First, the second important tool, logarithmic estimate, is established as follows. Throughout this part, we fix any subdomain ![]() $\Omega ' \subset \subset \Omega $.
$\Omega ' \subset \subset \Omega $.
Lemma 4.1. Logarithmic inequality
Let ![]() $s,t,p,q$ satisfy (1.4) and
$s,t,p,q$ satisfy (1.4) and ![]() $a(\cdot, \cdot)$ fulfil (1.5), (1.6) with (1.9). Let also
$a(\cdot, \cdot)$ fulfil (1.5), (1.6) with (1.9). Let also ![]() $u\in \mathcal{A}(\Omega)$ be a weak solution of (1.1) such that
$u\in \mathcal{A}(\Omega)$ be a weak solution of (1.1) such that ![]() $u\in L^{\infty}(\Omega')$ and
$u\in L^{\infty}(\Omega')$ and ![]() $u \ge 0$ in
$u \ge 0$ in ![]() $B_R: = {B_R}\left( {{\xi _0}} \right) \subset \Omega '$ with
$B_R: = {B_R}\left( {{\xi _0}} \right) \subset \Omega '$ with ![]() $R\le 1$. Then for any
$R\le 1$. Then for any  $0 \lt r\le \frac{R}{2}$ and d > 0,
$0 \lt r\le \frac{R}{2}$ and d > 0,
 \begin{align*}
& \int_{{B_r}} {\int_{{B_r}} {\left| {\log \frac{{u\left( \xi \right) + d}}{{u\left( \eta \right) + d}}} \right|} } \frac{{d\xi d\eta }}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^Q}} \\
\le & c{K^2}\left( {{r^Q} + \frac{{{r^{Q + sp}}}}{{{d^{p - 1}}}}\int_{{\mathbb{H}^n}\backslash {B_R}} \!\!{\frac{{u_ - ^{p - 1}\left( \eta \right) + u_ - ^{q - 1}\left( \eta \right)}}{{\| {{\eta ^{- 1}} \circ \xi_0 } \|_{{\mathbb{H}^n}}^{Q + sp}}}\,d\eta } + \frac{{{r^{Q + tq}}}}{{{d^{q - 1}}}}\int_{{\mathbb{H}^n}\backslash {B_R}} \!\!{\frac{{u_ - ^{q - 1}\left( \eta \right)}}{{\| {{\eta ^{- 1}} \circ \xi_0 } \|_{{\mathbb{H}^n}}^{Q + tq}}}\,d\eta}}\right),
\end{align*}
\begin{align*}
& \int_{{B_r}} {\int_{{B_r}} {\left| {\log \frac{{u\left( \xi \right) + d}}{{u\left( \eta \right) + d}}} \right|} } \frac{{d\xi d\eta }}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^Q}} \\
\le & c{K^2}\left( {{r^Q} + \frac{{{r^{Q + sp}}}}{{{d^{p - 1}}}}\int_{{\mathbb{H}^n}\backslash {B_R}} \!\!{\frac{{u_ - ^{p - 1}\left( \eta \right) + u_ - ^{q - 1}\left( \eta \right)}}{{\| {{\eta ^{- 1}} \circ \xi_0 } \|_{{\mathbb{H}^n}}^{Q + sp}}}\,d\eta } + \frac{{{r^{Q + tq}}}}{{{d^{q - 1}}}}\int_{{\mathbb{H}^n}\backslash {B_R}} \!\!{\frac{{u_ - ^{q - 1}\left( \eta \right)}}{{\| {{\eta ^{- 1}} \circ \xi_0 } \|_{{\mathbb{H}^n}}^{Q + tq}}}\,d\eta}}\right),
\end{align*} holds true. Here  $K:=1+d^{q-p}+\| u \|_{{L^\infty }\left( {\Omega '} \right)}^{q - p}$ and the constant
$K:=1+d^{q-p}+\| u \|_{{L^\infty }\left( {\Omega '} \right)}^{q - p}$ and the constant ![]() $c\ge1$ depends on
$c\ge1$ depends on ![]() $\mathrm{\textbf{data}}$.
$\mathrm{\textbf{data}}$.
Proof. Let us give some notations as below,
 \begin{equation*}{H_\rho }\left( {\xi ,\eta ,\tau } \right) = \frac{{{\tau ^p}}}{{{\rho ^{sp}}}} + a\left( {\xi ,\eta } \right)\frac{{{\tau ^q}}}{{{\rho ^{tq}}}},\;\;\;{h_\rho}\left( {\xi ,\eta ,\tau } \right) = \frac{{{\tau ^{p - 1}}}}{{{\rho^{sp}}}} + a\left( {\xi ,\eta } \right)\frac{{{\tau ^{q - 1}}}}{{{\rho^{tq}}}}\end{equation*}
\begin{equation*}{H_\rho }\left( {\xi ,\eta ,\tau } \right) = \frac{{{\tau ^p}}}{{{\rho ^{sp}}}} + a\left( {\xi ,\eta } \right)\frac{{{\tau ^q}}}{{{\rho ^{tq}}}},\;\;\;{h_\rho}\left( {\xi ,\eta ,\tau } \right) = \frac{{{\tau ^{p - 1}}}}{{{\rho^{sp}}}} + a\left( {\xi ,\eta } \right)\frac{{{\tau ^{q - 1}}}}{{{\rho^{tq}}}}\end{equation*}and
 \begin{equation*}{G_\rho }\left( \tau \right) = \frac{{{\tau ^p}}}{{{\rho ^{sp}}}} + a_\rho ^ + \frac{{{\tau ^q}}}{{{\rho ^{tq}}}},\;\;\;{g_\rho }\left( \tau \right) = \frac{{{\tau ^{p - 1}}}}{{{\rho ^{sp}}}} + a_\rho ^ + \frac{{{\tau ^{q - 1}}}}{{{\rho ^{tq}}}},\end{equation*}
\begin{equation*}{G_\rho }\left( \tau \right) = \frac{{{\tau ^p}}}{{{\rho ^{sp}}}} + a_\rho ^ + \frac{{{\tau ^q}}}{{{\rho ^{tq}}}},\;\;\;{g_\rho }\left( \tau \right) = \frac{{{\tau ^{p - 1}}}}{{{\rho ^{sp}}}} + a_\rho ^ + \frac{{{\tau ^{q - 1}}}}{{{\rho ^{tq}}}},\end{equation*} with  $a_\rho ^ + : = \mathop {\sup }\limits_{{B_\rho } \times {B_\rho }} a\left( {\cdot , \cdot } \right)$ and
$a_\rho ^ + : = \mathop {\sup }\limits_{{B_\rho } \times {B_\rho }} a\left( {\cdot , \cdot } \right)$ and ![]() $\tau \ge 0$.
$\tau \ge 0$.
Consider a cut-off function  $\phi\in C_0^\infty \left( {{B_{\frac{{3r}}{2}}}\left( {{\xi _0}} \right)} \right)$ satisfying
$\phi\in C_0^\infty \left( {{B_{\frac{{3r}}{2}}}\left( {{\xi _0}} \right)} \right)$ satisfying
 \begin{equation*}
0 \le \phi\le 1, \quad \phi\equiv 1 \text{in} B_r \quad \text{and} \quad \left| {{\nabla _H}\phi} \right| \le \frac{c}{r} \text{in} {{B_{\frac{{3r}}{2}}}}.
\end{equation*}
\begin{equation*}
0 \le \phi\le 1, \quad \phi\equiv 1 \text{in} B_r \quad \text{and} \quad \left| {{\nabla _H}\phi} \right| \le \frac{c}{r} \text{in} {{B_{\frac{{3r}}{2}}}}.
\end{equation*} Taking the test function  $\varphi \left( \xi \right): = \frac{{\phi^q\left( \xi \right)}}{{{g_{2r}}\left( {u\left( \xi \right) + d} \right)}}$, we have from the weak formulation that
$\varphi \left( \xi \right): = \frac{{\phi^q\left( \xi \right)}}{{{g_{2r}}\left( {u\left( \xi \right) + d} \right)}}$, we have from the weak formulation that
 \begin{align}
0 &= \int_{{B_{2r}}} {\int_{{B_{2r}}} {\Bigg[\frac{{{J_p}(u( \xi) - u( \eta))}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}}} } \left( {\frac{{{\phi^q}( \xi)}}{{{g_{2r}}(\overline{u}(\xi))}} - \frac{{\phi^q( \eta)}}{{{g_{2r}}( {\overline{u}( \eta)} )}}} \right)\nonumber \\
& \quad+ a( \xi ,\eta )\frac{{{J_q}( u( \xi) - u( \eta))}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + tq}}}\left( {\frac{{\phi^q( \xi)}}{{{g_{2r}}( \bar u( \xi))}} - \frac{{\phi^q( \eta)}}{{{g_{2r}}(\bar u( \eta))}}}\right)\Bigg]\,d\xi d\eta \nonumber \\
&\quad +2{\int _{{\mathbb{H}^n}\backslash {B_{2r}}}}\int_{{B_{2r}}} {\left[\frac{{{J_p}( u( \xi) - u( \eta ))}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}} + a(\xi ,\eta )\frac{{{J_q}( u( \xi) - u( \eta))}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + tq}}}\right]\frac{\phi^q(\xi)}{g_{2r}(\overline{u}(\xi))}\,d\xi d\eta } \nonumber \\
&=:I_1+I_2,
\end{align}
\begin{align}
0 &= \int_{{B_{2r}}} {\int_{{B_{2r}}} {\Bigg[\frac{{{J_p}(u( \xi) - u( \eta))}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}}} } \left( {\frac{{{\phi^q}( \xi)}}{{{g_{2r}}(\overline{u}(\xi))}} - \frac{{\phi^q( \eta)}}{{{g_{2r}}( {\overline{u}( \eta)} )}}} \right)\nonumber \\
& \quad+ a( \xi ,\eta )\frac{{{J_q}( u( \xi) - u( \eta))}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + tq}}}\left( {\frac{{\phi^q( \xi)}}{{{g_{2r}}( \bar u( \xi))}} - \frac{{\phi^q( \eta)}}{{{g_{2r}}(\bar u( \eta))}}}\right)\Bigg]\,d\xi d\eta \nonumber \\
&\quad +2{\int _{{\mathbb{H}^n}\backslash {B_{2r}}}}\int_{{B_{2r}}} {\left[\frac{{{J_p}( u( \xi) - u( \eta ))}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}} + a(\xi ,\eta )\frac{{{J_q}( u( \xi) - u( \eta))}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + tq}}}\right]\frac{\phi^q(\xi)}{g_{2r}(\overline{u}(\xi))}\,d\xi d\eta } \nonumber \\
&=:I_1+I_2,
\end{align} with ![]() $\bar u: = u + d$.
$\bar u: = u + d$.
In what follows, we deal with I 1 in the case ![]() $\bar u\left( \xi \right) \ge \bar u\left( \eta \right)$ that is divided into two subcases:
$\bar u\left( \xi \right) \ge \bar u\left( \eta \right)$ that is divided into two subcases:
 \begin{equation}
\bar u\left( \xi \right) \ge \bar u\left( \eta \right)\ge \frac{1}{2}\bar u\left( \xi \right),
\end{equation}
\begin{equation}
\bar u\left( \xi \right) \ge \bar u\left( \eta \right)\ge \frac{1}{2}\bar u\left( \xi \right),
\end{equation}and
If (4.2) occurs, we first observe that
 \begin{align}
&\quad \frac{{{\phi ^q}\left( \xi \right)}}{{{g_{2r}}\left( {\bar u\left( \xi \right)} \right)}} - \frac{{{\phi^q}\left( \eta \right)}}{{{g_{2r}}\left( {\bar u\left( \eta \right)} \right)}}\nonumber \\
&\le \frac{c{{\phi^{q - 1}}\left( \xi \right)\sup_{B_{3R/2}} \left| {{\nabla _H}\phi} \right|{{\| {{\eta ^{- 1}} \circ \xi } \|}_{{\mathbb{H}^n}}}}}{{{g_{2r}}\left( {\bar u\left( \eta \right)} \right)}} \nonumber \\
&+{\phi^q}\left( \xi \right)\int_0^1 {\frac{d}{{d\sigma }}\left( {g_{2r}^{- 1}\left( {\sigma \bar u\left( \xi \right) + (1 - \sigma )\bar u\left( \eta \right)} \right)} \right)\,d\sigma } \nonumber \\
& \le \frac{c{{\phi^{q - 1}}\left( \xi \right){r^{- 1}}{{\| {{\eta ^{- 1}} \circ \xi } \|}_{{\mathbb{H}^n}}}}}{{{g_{2r}}\left( {\bar u\left( \eta \right)} \right)}} - \frac{{\left( {p - 1} \right){\phi^q}\left( \xi \right)\left( {\bar u\left( \xi \right) - \bar u\left( \eta \right)} \right)}}{{{2^q}{G_{2r}}\left( {\bar u\left( \eta \right)} \right)}},
\end{align}
\begin{align}
&\quad \frac{{{\phi ^q}\left( \xi \right)}}{{{g_{2r}}\left( {\bar u\left( \xi \right)} \right)}} - \frac{{{\phi^q}\left( \eta \right)}}{{{g_{2r}}\left( {\bar u\left( \eta \right)} \right)}}\nonumber \\
&\le \frac{c{{\phi^{q - 1}}\left( \xi \right)\sup_{B_{3R/2}} \left| {{\nabla _H}\phi} \right|{{\| {{\eta ^{- 1}} \circ \xi } \|}_{{\mathbb{H}^n}}}}}{{{g_{2r}}\left( {\bar u\left( \eta \right)} \right)}} \nonumber \\
&+{\phi^q}\left( \xi \right)\int_0^1 {\frac{d}{{d\sigma }}\left( {g_{2r}^{- 1}\left( {\sigma \bar u\left( \xi \right) + (1 - \sigma )\bar u\left( \eta \right)} \right)} \right)\,d\sigma } \nonumber \\
& \le \frac{c{{\phi^{q - 1}}\left( \xi \right){r^{- 1}}{{\| {{\eta ^{- 1}} \circ \xi } \|}_{{\mathbb{H}^n}}}}}{{{g_{2r}}\left( {\bar u\left( \eta \right)} \right)}} - \frac{{\left( {p - 1} \right){\phi^q}\left( \xi \right)\left( {\bar u\left( \xi \right) - \bar u\left( \eta \right)} \right)}}{{{2^q}{G_{2r}}\left( {\bar u\left( \eta \right)} \right)}},
\end{align} where the first inequality holds naturally when ![]() $\phi(\xi) \le \phi(\eta)$. Here, we have used (4.2) and
$\phi(\xi) \le \phi(\eta)$. Here, we have used (4.2) and
 \begin{align*}
\int_0^1 {\frac{d}{{d\sigma }}\left( {g_{2r}^{- 1}\left( {\sigma \bar u\left( \xi \right) + (1 - \sigma )\bar u\left( \eta \right)} \right)} \right)\,d\sigma } &\ge \frac{{\left( {p - 1} \right)\left( {\bar u\left( \xi \right) - \bar u\left( \eta \right)} \right)}}{{{G_{2r}}\left( {\bar u\left( \xi \right)} \right)}} \nonumber\\
&\ge \frac{{\left( {p - 1} \right)\left( {\bar u\left( \xi \right) - \bar u\left( \eta \right)} \right)}}{{{2^q}{G_{2r}}\left( {\bar u\left( \eta \right)} \right)}},
\end{align*}
\begin{align*}
\int_0^1 {\frac{d}{{d\sigma }}\left( {g_{2r}^{- 1}\left( {\sigma \bar u\left( \xi \right) + (1 - \sigma )\bar u\left( \eta \right)} \right)} \right)\,d\sigma } &\ge \frac{{\left( {p - 1} \right)\left( {\bar u\left( \xi \right) - \bar u\left( \eta \right)} \right)}}{{{G_{2r}}\left( {\bar u\left( \xi \right)} \right)}} \nonumber\\
&\ge \frac{{\left( {p - 1} \right)\left( {\bar u\left( \xi \right) - \bar u\left( \eta \right)} \right)}}{{{2^q}{G_{2r}}\left( {\bar u\left( \eta \right)} \right)}},
\end{align*}the details of which can be found in [Reference Byun, Ok and Song4]. Then, combining (4.4) and Young’s inequality yields
 \begin{align}
F\left( {\xi ,\eta } \right)&:= \left( {\frac{{{J_p}\left( {u\left( \xi \right) - u\left( \eta \right)} \right)}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{sp}}} + a\left( {\xi ,\eta } \right)\frac{{{J_q}\left( {u\left( \xi \right) - u\left( \eta \right)} \right)}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{tq}}}} \right)\left( {\frac{{{\phi^q}\left( \xi \right)}}{{{g_{2r}}\left( {\bar u\left( \xi \right)} \right)}} - \frac{{{\phi^q}( \eta)}}{{{g_{2r}}\left( {\bar u\left( \eta \right)} \right)}}} \right)\nonumber \\
&\le \frac{{c{\phi^{q - 1}}\left( \xi \right){r^{- 1}}{{\| {{\eta ^{- 1}} \circ \xi } \|}_{{\mathbb{H}^n}}}\bar u\left( \eta \right)}}{{{G_{2r}}\left( {\bar u\left( \eta \right)} \right)}}\nonumber\\
&\left( {\frac{{{{\left| {\bar u\left( \xi \right) - \bar u\left( \eta \right)} \right|}^{p - 1}}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{sp}}} + a\left( {\xi ,\eta } \right)\frac{{{{\left| {\bar u\left( \xi \right) - \bar u\left( \eta \right)} \right|}^{q - 1}}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{tq}}}} \right)\nonumber \\
&\quad - \frac{{\left( {p - 1} \right){\phi^q}\left( \xi \right)H\left( {\xi ,\eta ,\bar u\left( \xi \right) - \bar u\left( \eta \right)} \right)}}{{{2^q}{G_{2r}}\left( {\bar u\left( \eta \right)} \right)}} \nonumber \\
&\le \frac{{\varepsilon {\phi^{\frac{{\left( {q - 1} \right)p}}{{p - 1}}}}\left( \xi \right){{\left| {\bar u\left( \xi \right) - \bar u\left( \eta \right)} \right|}^p}}}{{{G_{2r}}\left( {\bar u\left( \eta \right)} \right)\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{sp}}} + a\left( {\xi ,\eta } \right)\frac{{\varepsilon {\phi^q}\left( \xi \right){{\left| {\bar u\left( \xi \right) - \bar u\left( \eta \right)} \right|}^q}}}{{{G_{2r}}\left( {\bar u\left( \eta \right)} \right)\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{tq}}} \nonumber \\
&\quad - \frac{{\left( {p - 1} \right){\phi^q}\left( \xi \right)H\left( {\xi ,\eta ,\bar u\left( \xi \right) - \bar u\left( \eta \right)} \right)}}{{{2^q}{G_{2r}}\left( {\bar u\left( \eta \right)} \right)}}\nonumber \\
&\quad + c\left( \varepsilon \right)\frac{{{r^{- p}}\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^p{{\left| {\bar u\left( \eta \right)} \right|}^p}}}{{{G_{2r}}\left( {\bar u\left( \eta \right)} \right)\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{sp}}} + c\left( \varepsilon \right)a_{2r}^ + \frac{{{r^{- q}}\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^q{{\left| {\bar u\left( \eta \right)} \right|}^q}}}{{{G_{2r}}\left( {\bar u\left( \eta \right)} \right)\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{tq}}}\nonumber \\
&\le - \frac{{\left( {p - 1} \right){\phi^q}\left( \xi \right)H\left( {\xi ,\eta ,\bar u\left( \xi \right) - \bar u\left( \eta \right)} \right)}}{{{2^{q + 1}}{G_{2r}}\left( {\bar u\left( \eta \right)} \right)}} + c\frac{{{r^{p\left( {s - 1} \right)}}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{p\left( {s - 1} \right)}}} + c\frac{{{r^{q\left( {t - 1} \right)}}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{q\left( {t - 1} \right)}}},
\end{align}
\begin{align}
F\left( {\xi ,\eta } \right)&:= \left( {\frac{{{J_p}\left( {u\left( \xi \right) - u\left( \eta \right)} \right)}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{sp}}} + a\left( {\xi ,\eta } \right)\frac{{{J_q}\left( {u\left( \xi \right) - u\left( \eta \right)} \right)}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{tq}}}} \right)\left( {\frac{{{\phi^q}\left( \xi \right)}}{{{g_{2r}}\left( {\bar u\left( \xi \right)} \right)}} - \frac{{{\phi^q}( \eta)}}{{{g_{2r}}\left( {\bar u\left( \eta \right)} \right)}}} \right)\nonumber \\
&\le \frac{{c{\phi^{q - 1}}\left( \xi \right){r^{- 1}}{{\| {{\eta ^{- 1}} \circ \xi } \|}_{{\mathbb{H}^n}}}\bar u\left( \eta \right)}}{{{G_{2r}}\left( {\bar u\left( \eta \right)} \right)}}\nonumber\\
&\left( {\frac{{{{\left| {\bar u\left( \xi \right) - \bar u\left( \eta \right)} \right|}^{p - 1}}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{sp}}} + a\left( {\xi ,\eta } \right)\frac{{{{\left| {\bar u\left( \xi \right) - \bar u\left( \eta \right)} \right|}^{q - 1}}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{tq}}}} \right)\nonumber \\
&\quad - \frac{{\left( {p - 1} \right){\phi^q}\left( \xi \right)H\left( {\xi ,\eta ,\bar u\left( \xi \right) - \bar u\left( \eta \right)} \right)}}{{{2^q}{G_{2r}}\left( {\bar u\left( \eta \right)} \right)}} \nonumber \\
&\le \frac{{\varepsilon {\phi^{\frac{{\left( {q - 1} \right)p}}{{p - 1}}}}\left( \xi \right){{\left| {\bar u\left( \xi \right) - \bar u\left( \eta \right)} \right|}^p}}}{{{G_{2r}}\left( {\bar u\left( \eta \right)} \right)\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{sp}}} + a\left( {\xi ,\eta } \right)\frac{{\varepsilon {\phi^q}\left( \xi \right){{\left| {\bar u\left( \xi \right) - \bar u\left( \eta \right)} \right|}^q}}}{{{G_{2r}}\left( {\bar u\left( \eta \right)} \right)\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{tq}}} \nonumber \\
&\quad - \frac{{\left( {p - 1} \right){\phi^q}\left( \xi \right)H\left( {\xi ,\eta ,\bar u\left( \xi \right) - \bar u\left( \eta \right)} \right)}}{{{2^q}{G_{2r}}\left( {\bar u\left( \eta \right)} \right)}}\nonumber \\
&\quad + c\left( \varepsilon \right)\frac{{{r^{- p}}\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^p{{\left| {\bar u\left( \eta \right)} \right|}^p}}}{{{G_{2r}}\left( {\bar u\left( \eta \right)} \right)\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{sp}}} + c\left( \varepsilon \right)a_{2r}^ + \frac{{{r^{- q}}\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^q{{\left| {\bar u\left( \eta \right)} \right|}^q}}}{{{G_{2r}}\left( {\bar u\left( \eta \right)} \right)\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{tq}}}\nonumber \\
&\le - \frac{{\left( {p - 1} \right){\phi^q}\left( \xi \right)H\left( {\xi ,\eta ,\bar u\left( \xi \right) - \bar u\left( \eta \right)} \right)}}{{{2^{q + 1}}{G_{2r}}\left( {\bar u\left( \eta \right)} \right)}} + c\frac{{{r^{p\left( {s - 1} \right)}}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{p\left( {s - 1} \right)}}} + c\frac{{{r^{q\left( {t - 1} \right)}}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{q\left( {t - 1} \right)}}},
\end{align} where ɛ was chosen as  $\frac{{p - 1}}{{{2^{q + 1}}}}$,
$\frac{{p - 1}}{{{2^{q + 1}}}}$,  $\frac{{\left( {q - 1} \right)p}}{{p - 1}} \gt q$ and c > 0 is independent of a. We proceed to evaluate
$\frac{{\left( {q - 1} \right)p}}{{p - 1}} \gt q$ and c > 0 is independent of a. We proceed to evaluate ![]() ${{G_{2r}}\left( {\bar u\left( \eta \right)} \right)}$. For
${{G_{2r}}\left( {\bar u\left( \eta \right)} \right)}$. For ![]() $\xi,\eta \in B_{2r}$, recalling the Hölder continuity of a, we get
$\xi,\eta \in B_{2r}$, recalling the Hölder continuity of a, we get
Thus this implies by the facts that ![]() $r\le 1$ and
$r\le 1$ and ![]() $tq \le sp+\alpha$ that
$tq \le sp+\alpha$ that
 \begin{align}
{G_{2r}}\left( {\bar u\left( \eta \right)} \right) & \le \frac{{{{\bar u}^p}\left( \eta \right)}}{{{{\left( {2r} \right)}^{sp}}}} + 2{\left[ a \right]_\alpha }{\left( {4r} \right)^\alpha }\frac{{{{\bar u}^q}\left( \eta \right)}}{{{{\left( {2r} \right)}^{tq}}}} + a\left( {\xi ,\eta } \right)\frac{{{{\bar u}^q}\left( \eta \right)}}{{{{\left( {2r} \right)}^{tq}}}}\nonumber \\
& \le \left( {1 + 8{{\left[ a \right]}_\alpha }{r^{\alpha + sp - tq}}\| u \|_{{L^\infty }\left( {\Omega '} \right)}^{q - p}} \right)\frac{{{{\bar u}^p}\left( \eta \right)}}{{{{\left( {2r} \right)}^{sp}}}} + a\left( {\xi ,\eta } \right)\frac{{{{\bar u}^q}\left( \eta \right)}}{{{{\left( {2r} \right)}^{tq}}}}\nonumber\\
& \le c\left( {1 + \| u \|_{{L^\infty }\left( {\Omega '} \right)}^{q - p}} \right){H_{2r}}\left( {\xi ,\eta ,\bar u\left( \eta \right)} \right).
\end{align}
\begin{align}
{G_{2r}}\left( {\bar u\left( \eta \right)} \right) & \le \frac{{{{\bar u}^p}\left( \eta \right)}}{{{{\left( {2r} \right)}^{sp}}}} + 2{\left[ a \right]_\alpha }{\left( {4r} \right)^\alpha }\frac{{{{\bar u}^q}\left( \eta \right)}}{{{{\left( {2r} \right)}^{tq}}}} + a\left( {\xi ,\eta } \right)\frac{{{{\bar u}^q}\left( \eta \right)}}{{{{\left( {2r} \right)}^{tq}}}}\nonumber \\
& \le \left( {1 + 8{{\left[ a \right]}_\alpha }{r^{\alpha + sp - tq}}\| u \|_{{L^\infty }\left( {\Omega '} \right)}^{q - p}} \right)\frac{{{{\bar u}^p}\left( \eta \right)}}{{{{\left( {2r} \right)}^{sp}}}} + a\left( {\xi ,\eta } \right)\frac{{{{\bar u}^q}\left( \eta \right)}}{{{{\left( {2r} \right)}^{tq}}}}\nonumber\\
& \le c\left( {1 + \| u \|_{{L^\infty }\left( {\Omega '} \right)}^{q - p}} \right){H_{2r}}\left( {\xi ,\eta ,\bar u\left( \eta \right)} \right).
\end{align} Next, we will obtain an estimate on ![]() $\log \bar u$. It is easy to find
$\log \bar u$. It is easy to find
 \begin{align*}
\log \frac{{\bar u\left( \xi \right)}}{{\bar u\left( \eta \right)}}= \int_0^1 {\frac{{\bar u\left( \xi \right) - \bar u\left( \eta \right)}}{{\bar u\left( \eta \right) + \sigma \left( {\bar u\left( \xi \right) - \bar u\left( \eta \right)} \right)}}}\, d\sigma
\le \frac{(\bar u( \xi)-\bar u(\eta))/\|\eta ^{-1}\circ \xi \|_{{\mathbb{H}^n}}^s}
{\bar u(\eta)/(2r)^s} \frac{\|\eta ^{- 1}\circ \xi\|_{{\mathbb{H}^n}}^s}{(2r)^s},
\end{align*}
\begin{align*}
\log \frac{{\bar u\left( \xi \right)}}{{\bar u\left( \eta \right)}}= \int_0^1 {\frac{{\bar u\left( \xi \right) - \bar u\left( \eta \right)}}{{\bar u\left( \eta \right) + \sigma \left( {\bar u\left( \xi \right) - \bar u\left( \eta \right)} \right)}}}\, d\sigma
\le \frac{(\bar u( \xi)-\bar u(\eta))/\|\eta ^{-1}\circ \xi \|_{{\mathbb{H}^n}}^s}
{\bar u(\eta)/(2r)^s} \frac{\|\eta ^{- 1}\circ \xi\|_{{\mathbb{H}^n}}^s}{(2r)^s},
\end{align*} so, by the monotonicity of the function  $f(\tau)=(\tau^p+a(\xi,\eta)\tau^q\|\eta ^{-1}\circ \xi \|_{\mathbb{H}^n}^{-(t-s)q})/\tau$ with
$f(\tau)=(\tau^p+a(\xi,\eta)\tau^q\|\eta ^{-1}\circ \xi \|_{\mathbb{H}^n}^{-(t-s)q})/\tau$ with ![]() $\tau\ge0$,
$\tau\ge0$,
 \begin{align}
\log \frac{\bar u(\xi)}{u(\eta)}&\le\frac{\|\eta ^{- 1} \circ \xi \|_{\mathbb{H}^n}^s}{(2r)^s}\left[\frac{\left(\frac{\bar u(\xi)-\bar u(\eta)}{\|\eta^{-1}\circ\xi\|_{\mathbb{H}^n}^s}\right)^p+a(\xi,\eta)\left(\frac{\bar u(\xi)-\bar u(\eta)}{\|\eta^{-1}\circ\xi\|_{\mathbb{H}^n}^s}\right)^q\|\eta^{-1}\circ\xi\|_{\mathbb{H}^n}^{-(t-s)q}}{\left(\frac{\bar u(\eta)}{(2r)^s}\right)^p+a(\xi,\eta)\left(\frac{\bar u(\eta)}{(2r)^s}\right)^q\|\eta^{-1}\circ\xi\|_{\mathbb{H}^n}^{-(t-s)q}}+ 1\right] \nonumber\\
&\le \frac{{cH\left( {\xi ,\eta ,\bar u\left( \xi \right) - \bar u\left( \eta \right)} \right)}}{{{H_{2r}}\left( {\xi ,\eta ,\bar u\left( \eta \right)} \right)}} + \frac{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^s}}{{{{\left( {2r} \right)}^s}}},
\end{align}
\begin{align}
\log \frac{\bar u(\xi)}{u(\eta)}&\le\frac{\|\eta ^{- 1} \circ \xi \|_{\mathbb{H}^n}^s}{(2r)^s}\left[\frac{\left(\frac{\bar u(\xi)-\bar u(\eta)}{\|\eta^{-1}\circ\xi\|_{\mathbb{H}^n}^s}\right)^p+a(\xi,\eta)\left(\frac{\bar u(\xi)-\bar u(\eta)}{\|\eta^{-1}\circ\xi\|_{\mathbb{H}^n}^s}\right)^q\|\eta^{-1}\circ\xi\|_{\mathbb{H}^n}^{-(t-s)q}}{\left(\frac{\bar u(\eta)}{(2r)^s}\right)^p+a(\xi,\eta)\left(\frac{\bar u(\eta)}{(2r)^s}\right)^q\|\eta^{-1}\circ\xi\|_{\mathbb{H}^n}^{-(t-s)q}}+ 1\right] \nonumber\\
&\le \frac{{cH\left( {\xi ,\eta ,\bar u\left( \xi \right) - \bar u\left( \eta \right)} \right)}}{{{H_{2r}}\left( {\xi ,\eta ,\bar u\left( \eta \right)} \right)}} + \frac{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^s}}{{{{\left( {2r} \right)}^s}}},
\end{align} where we need to note ![]() ${\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}} \le 4r$. It follows from (4.5)–(4.7) that
${\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}} \le 4r$. It follows from (4.5)–(4.7) that
 \begin{equation*}F\left( {\xi ,\eta } \right) \le - \frac{{{\phi^q}\left( \xi \right)}}{{cK}}\log \frac{{\bar u\left( \xi \right)}}{{\bar u\left( \eta \right)}} + \frac{{c\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^s}}{{{{\left( {2r} \right)}^s}}} + \frac{{c\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{p(1 - s)}}}{{{{\left( {2r} \right)}^{p(1 - s)}}}} + \frac{{c\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{q(1 - t)}}}{{{{\left( {2r} \right)}^{q(1 - t)}}}}.\end{equation*}
\begin{equation*}F\left( {\xi ,\eta } \right) \le - \frac{{{\phi^q}\left( \xi \right)}}{{cK}}\log \frac{{\bar u\left( \xi \right)}}{{\bar u\left( \eta \right)}} + \frac{{c\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^s}}{{{{\left( {2r} \right)}^s}}} + \frac{{c\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{p(1 - s)}}}{{{{\left( {2r} \right)}^{p(1 - s)}}}} + \frac{{c\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{q(1 - t)}}}{{{{\left( {2r} \right)}^{q(1 - t)}}}}.\end{equation*} Second, we in the case (4.3) tackle the integral I 1. Applying lemma 3.2 and the relation ![]() $\bar u\left( \xi \right) \ge 2\bar u\left( \eta \right)$, we could derive
$\bar u\left( \xi \right) \ge 2\bar u\left( \eta \right)$, we could derive
 \begin{align*}
\frac{{{\phi^q}\left( \xi \right)}}{{{g_{2r}}\left( {\bar u\left( \xi \right)} \right)}} - \frac{{{\phi^q}( \eta)}}{{{g_{2r}}\left( {\bar u\left( \eta \right)} \right)}}&\le \frac{{{\phi^q}\left( \xi \right) - {\phi^q}\left( \eta \right)}}{{{g_{2r}}\left( {\bar u\left( \xi \right)} \right)}} + {\phi ^q}\left( \eta \right)\left( {\frac{1}{{{g_{2r}}\left( {2\bar u\left( \eta \right)} \right)}} - \frac{1}{{{g_{2r}}\left( {\bar u\left( \eta \right)} \right)}}} \right)\\
&\le\frac{{\varepsilon {\phi^q}\left( \eta \right) + c\left( \varepsilon \right){{\left| {\phi\left( \xi \right) - \phi\left( \eta \right)} \right|}^q}}}{{{g_{2r}}\left( {\bar u\left( \xi \right)} \right)}} - \frac{{{2^{p - 1}} - 1}}{{{2^{p - 1}}}}\frac{{\phi ^q( \eta)}}{{{g_{2r}}\left( {\bar u\left( \eta \right)} \right)}}\\
&\le\frac{{c{{\left| {\phi( \xi) - \phi( \eta)} \right|}^q}}}{{{g_{2r}}\left( {\bar u\left( \xi \right)} \right)}} - \frac{{\left( {{2^{p - 1}} - 1} \right){\phi^q}\left( \eta \right)}}{{{2^p}{g_{2r}}\left( {\bar u\left( \eta \right)} \right)},}
\end{align*}
\begin{align*}
\frac{{{\phi^q}\left( \xi \right)}}{{{g_{2r}}\left( {\bar u\left( \xi \right)} \right)}} - \frac{{{\phi^q}( \eta)}}{{{g_{2r}}\left( {\bar u\left( \eta \right)} \right)}}&\le \frac{{{\phi^q}\left( \xi \right) - {\phi^q}\left( \eta \right)}}{{{g_{2r}}\left( {\bar u\left( \xi \right)} \right)}} + {\phi ^q}\left( \eta \right)\left( {\frac{1}{{{g_{2r}}\left( {2\bar u\left( \eta \right)} \right)}} - \frac{1}{{{g_{2r}}\left( {\bar u\left( \eta \right)} \right)}}} \right)\\
&\le\frac{{\varepsilon {\phi^q}\left( \eta \right) + c\left( \varepsilon \right){{\left| {\phi\left( \xi \right) - \phi\left( \eta \right)} \right|}^q}}}{{{g_{2r}}\left( {\bar u\left( \xi \right)} \right)}} - \frac{{{2^{p - 1}} - 1}}{{{2^{p - 1}}}}\frac{{\phi ^q( \eta)}}{{{g_{2r}}\left( {\bar u\left( \eta \right)} \right)}}\\
&\le\frac{{c{{\left| {\phi( \xi) - \phi( \eta)} \right|}^q}}}{{{g_{2r}}\left( {\bar u\left( \xi \right)} \right)}} - \frac{{\left( {{2^{p - 1}} - 1} \right){\phi^q}\left( \eta \right)}}{{{2^p}{g_{2r}}\left( {\bar u\left( \eta \right)} \right)},}
\end{align*} with  $\varepsilon = \frac{{{2^{p - 1}} - 1}}{{{2^p}}}$. Thereby, it holds that
$\varepsilon = \frac{{{2^{p - 1}} - 1}}{{{2^p}}}$. Thereby, it holds that
 \begin{align*}
F\left( {\xi ,\eta } \right)& \le \frac{{ch\left( {\xi ,\eta ,\bar u\left( \xi \right) - \bar u\left( \eta \right)} \right){{| {\phi( \xi) -\phi( \eta)}|}^q}}}{{{g_{2r}}\left( {\bar u\left( \xi \right)} \right)}} - \frac{{h\left( {\xi ,\eta ,\bar u\left( \xi \right) - \bar u\left( \eta \right)} \right){\phi ^q}\left( \eta \right)}}{{c{g_{2r}}\left( {\bar u\left( \eta \right)} \right)}} \\
& \le \frac{{c{{\left( {2r} \right)}^{- q}}\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^qh\left( {\xi ,\eta ,\bar u\left( \xi \right) - \bar u\left( \eta \right)} \right)}}{{{g_{2r}}\left( {\bar u\left( \xi \right)} \right)}} - \frac{{h\left( {\xi ,\eta ,\bar u\left( \xi \right) - \bar u\left( \eta \right)} \right){\phi^q}\left( \eta \right)}}{{cK{h_{2r}}\left( {\xi ,\eta ,\bar u\left( \eta \right)} \right)}}.
\end{align*}
\begin{align*}
F\left( {\xi ,\eta } \right)& \le \frac{{ch\left( {\xi ,\eta ,\bar u\left( \xi \right) - \bar u\left( \eta \right)} \right){{| {\phi( \xi) -\phi( \eta)}|}^q}}}{{{g_{2r}}\left( {\bar u\left( \xi \right)} \right)}} - \frac{{h\left( {\xi ,\eta ,\bar u\left( \xi \right) - \bar u\left( \eta \right)} \right){\phi ^q}\left( \eta \right)}}{{c{g_{2r}}\left( {\bar u\left( \eta \right)} \right)}} \\
& \le \frac{{c{{\left( {2r} \right)}^{- q}}\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^qh\left( {\xi ,\eta ,\bar u\left( \xi \right) - \bar u\left( \eta \right)} \right)}}{{{g_{2r}}\left( {\bar u\left( \xi \right)} \right)}} - \frac{{h\left( {\xi ,\eta ,\bar u\left( \xi \right) - \bar u\left( \eta \right)} \right){\phi^q}\left( \eta \right)}}{{cK{h_{2r}}\left( {\xi ,\eta ,\bar u\left( \eta \right)} \right)}}.
\end{align*} Here ![]() $F\left( {\xi ,\eta } \right)$ is the same as that in (4.5) and the estimate for
$F\left( {\xi ,\eta } \right)$ is the same as that in (4.5) and the estimate for ![]() ${{g_{2r}}\left( {\bar u\left( \eta \right)} \right)}$ is similar to (4.6). Moreover, via
${{g_{2r}}\left( {\bar u\left( \eta \right)} \right)}$ is similar to (4.6). Moreover, via ![]() $\bar u\left( \xi \right) \ge 2\bar u\left( \eta \right)\ge 0$ in
$\bar u\left( \xi \right) \ge 2\bar u\left( \eta \right)\ge 0$ in ![]() $B_{2r}$,
$B_{2r}$,
 \begin{align*}
\frac{{h\left( {\xi ,\eta ,\bar u( \xi) - \bar u( \eta)} \right)}}{{{g_{2r}}( {\bar u( \xi)})}}
&\le \frac{\frac{|\bar u(\xi)-\bar u(\eta)|^{p-1}}{\|\eta^{-1} \circ \xi\|_{\mathbb{H}^n}^{sp}}+a(\xi,\eta)\frac{|\bar u(\xi)-\bar u(\eta)|^{q-1}}{\|\eta^{-1} \circ \xi\|_{\mathbb{H}^n}^{tq}}}{\frac{|\bar u(\xi)-\bar u(\eta)|^{p-1}}{(2r)^{sp}}+a_{2r}^ +\frac{|\bar u(\xi)-\bar u(\eta)|^{q-1}}{(2r)^{tq}}}
\\
&\le \frac{{{{\left( {2r} \right)}^{sp}}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{sp}}} + \frac{{{{\left( {2r} \right)}^{tq}}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{tq}}},
\end{align*}
\begin{align*}
\frac{{h\left( {\xi ,\eta ,\bar u( \xi) - \bar u( \eta)} \right)}}{{{g_{2r}}( {\bar u( \xi)})}}
&\le \frac{\frac{|\bar u(\xi)-\bar u(\eta)|^{p-1}}{\|\eta^{-1} \circ \xi\|_{\mathbb{H}^n}^{sp}}+a(\xi,\eta)\frac{|\bar u(\xi)-\bar u(\eta)|^{q-1}}{\|\eta^{-1} \circ \xi\|_{\mathbb{H}^n}^{tq}}}{\frac{|\bar u(\xi)-\bar u(\eta)|^{p-1}}{(2r)^{sp}}+a_{2r}^ +\frac{|\bar u(\xi)-\bar u(\eta)|^{q-1}}{(2r)^{tq}}}
\\
&\le \frac{{{{\left( {2r} \right)}^{sp}}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{sp}}} + \frac{{{{\left( {2r} \right)}^{tq}}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{tq}}},
\end{align*}and further
 \begin{equation*}F\left( {\xi ,\eta } \right) \le \frac{{c\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{q - sp}}}{{{{\left( {2r} \right)}^{q - sp}}}} + \frac{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{q\left( {1 - t} \right)}}}{{{{\left( {2r} \right)}^{q\left( {1 - t} \right)}}}} - \frac{{h\left( {\xi ,\eta ,\bar u\left( \xi \right) - \bar u\left( \eta \right)} \right){\phi ^q}\left( \eta \right)}}{{cK{h_{2r}}\left( {\xi ,\eta ,\bar u\left( \eta \right)} \right)}}.\end{equation*}
\begin{equation*}F\left( {\xi ,\eta } \right) \le \frac{{c\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{q - sp}}}{{{{\left( {2r} \right)}^{q - sp}}}} + \frac{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{q\left( {1 - t} \right)}}}{{{{\left( {2r} \right)}^{q\left( {1 - t} \right)}}}} - \frac{{h\left( {\xi ,\eta ,\bar u\left( \xi \right) - \bar u\left( \eta \right)} \right){\phi ^q}\left( \eta \right)}}{{cK{h_{2r}}\left( {\xi ,\eta ,\bar u\left( \eta \right)} \right)}}.\end{equation*} Now we obtain an estimate on  $\log \frac{{\bar u\left( \xi \right)}}{{\bar u\left( \eta \right)}}$ under (4.3). Notice
$\log \frac{{\bar u\left( \xi \right)}}{{\bar u\left( \eta \right)}}$ under (4.3). Notice ![]() $\bar u(\xi)\le 2(\bar u( \xi) - \bar u( \eta))$. we get
$\bar u(\xi)\le 2(\bar u( \xi) - \bar u( \eta))$. we get
 \begin{align*}
&\quad\log \frac{\bar u(\xi)}{\bar u( \eta)}\\
&\le \frac{c\left( (\bar u(\xi) - \bar u( \eta))/\|\eta ^{- 1} \circ \xi\|_{\mathbb{H}^n}^s\right)^{p - 1}}{(\bar u(\eta)/(2r)^s)^{p - 1}} \frac{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{s\left( {p - 1} \right)}}}{{{{\left( {2r} \right)}^{s\left( {p - 1} \right)}}}}\\
&\le c\frac{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{s\left( {p - 1} \right)}}}{{{{\left( {2r} \right)}^{s\left( {p - 1} \right)}}}}\left[\frac{\left(\frac{\bar u(\xi)-\bar u(\eta)}{\|\eta^{-1}\circ\xi\|_{\mathbb{H}^n}^s}\right)^{p-1}+a(\xi,\eta)\left(\frac{\bar u(\xi)-\bar u(\eta)}{\|\eta^{-1}\circ\xi\|_{\mathbb{H}^n}^s}\right)^{q-1}\|\eta^{-1}\circ\xi\|_{\mathbb{H}^n}^{-(t-s)q}}{\left(\frac{\bar u(\eta)}{(2r)^s}\right)^{p-1}+a(\xi,\eta)\left(\frac{\bar u(\eta)}{(2r)^s}\right)^{q-1}\|\eta^{-1}\circ\xi\|_{\mathbb{H}^n}^{-(t-s)q}}+ 1\right]\\
&\le \frac{{ch\left( {\xi ,\eta ,\bar u\left( \xi \right) - \bar u\left( \eta \right)} \right)}}{{{h_{2r}}\left( {\xi ,\eta ,\bar u\left( \eta \right)} \right)}} + \frac{{c\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{s\left( {p - 1} \right)}}}{{{{\left( {2r} \right)}^{s\left( {p - 1} \right)}}}},
\end{align*}
\begin{align*}
&\quad\log \frac{\bar u(\xi)}{\bar u( \eta)}\\
&\le \frac{c\left( (\bar u(\xi) - \bar u( \eta))/\|\eta ^{- 1} \circ \xi\|_{\mathbb{H}^n}^s\right)^{p - 1}}{(\bar u(\eta)/(2r)^s)^{p - 1}} \frac{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{s\left( {p - 1} \right)}}}{{{{\left( {2r} \right)}^{s\left( {p - 1} \right)}}}}\\
&\le c\frac{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{s\left( {p - 1} \right)}}}{{{{\left( {2r} \right)}^{s\left( {p - 1} \right)}}}}\left[\frac{\left(\frac{\bar u(\xi)-\bar u(\eta)}{\|\eta^{-1}\circ\xi\|_{\mathbb{H}^n}^s}\right)^{p-1}+a(\xi,\eta)\left(\frac{\bar u(\xi)-\bar u(\eta)}{\|\eta^{-1}\circ\xi\|_{\mathbb{H}^n}^s}\right)^{q-1}\|\eta^{-1}\circ\xi\|_{\mathbb{H}^n}^{-(t-s)q}}{\left(\frac{\bar u(\eta)}{(2r)^s}\right)^{p-1}+a(\xi,\eta)\left(\frac{\bar u(\eta)}{(2r)^s}\right)^{q-1}\|\eta^{-1}\circ\xi\|_{\mathbb{H}^n}^{-(t-s)q}}+ 1\right]\\
&\le \frac{{ch\left( {\xi ,\eta ,\bar u\left( \xi \right) - \bar u\left( \eta \right)} \right)}}{{{h_{2r}}\left( {\xi ,\eta ,\bar u\left( \eta \right)} \right)}} + \frac{{c\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{s\left( {p - 1} \right)}}}{{{{\left( {2r} \right)}^{s\left( {p - 1} \right)}}}},
\end{align*} where the fact ![]() ${\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}} \le 4r$ was utilized. Noting
${\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}} \le 4r$ was utilized. Noting ![]() $q\ge p$ and
$q\ge p$ and ![]() ${\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}} \le 4r$ again,
${\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}} \le 4r$ again,
 \begin{align*}
F\left( {\xi ,\eta } \right) \le - \frac{{{\phi^q}\left( \xi \right)}}{{cK}}\log \frac{{\bar u\left( \xi \right)}}{{\bar u\left( \eta \right)}} + \frac{{c\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{p\left( {1 - s} \right)}}}{{{{\left( {2r} \right)}^{p\left( {1 - s} \right)}}}} + \frac{{c\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{q(1 - t)}}}{{{{\left( {2r} \right)}^{q(1 - t)}}}} + \frac{{c\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{s(p - 1)}}}{{{{\left( {2r} \right)}^{s(p - 1)}}}}.
\end{align*}
\begin{align*}
F\left( {\xi ,\eta } \right) \le - \frac{{{\phi^q}\left( \xi \right)}}{{cK}}\log \frac{{\bar u\left( \xi \right)}}{{\bar u\left( \eta \right)}} + \frac{{c\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{p\left( {1 - s} \right)}}}{{{{\left( {2r} \right)}^{p\left( {1 - s} \right)}}}} + \frac{{c\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{q(1 - t)}}}{{{{\left( {2r} \right)}^{q(1 - t)}}}} + \frac{{c\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{s(p - 1)}}}{{{{\left( {2r} \right)}^{s(p - 1)}}}}.
\end{align*} At this moment, for ![]() $\bar u\left( \xi \right) \ge \bar u\left( \eta \right)$, the integral I 1 is evaluated as
$\bar u\left( \xi \right) \ge \bar u\left( \eta \right)$, the integral I 1 is evaluated as
 \begin{align}
I_1 &\le -\frac{1}{cK}\int_{B_{2r}}\int_{B_{2r}}\min\left\{\phi^q(\xi),\phi^q(\eta)\right\}\left|\log\frac{\bar u(\xi)}{\bar u(\eta)}\right| \frac{d\xi d\eta }{\|\eta^{-1}\circ\xi\|_{\mathbb{H}^n}^Q}\nonumber \\
& + c\int_{B_{2r}}\int_{B_{2r}}\Bigg[\frac{\|\eta^{-1} \circ \xi \|_{\mathbb{H}^n}^{p - sp}}{r^{p(1 - s)}}\nonumber \\
&+ \frac{\|\eta^{-1}\circ\xi\|_{\mathbb{H}^n}^{q(1 - t)}}{r^{q(1 - t)}} + \frac{\|\eta^{-1} \circ \xi\|_{\mathbb{H}^n}^{s(p - 1)}}{r^{s(p - 1)}} + \frac{\|\eta^{-1}\circ\xi\|_{\mathbb{H}^n}^s}{r^s}\Bigg]\frac{d\xi d\eta}{\|\eta^{-1}\circ\xi\|_{\mathbb{H}^n}^Q} \nonumber \\
& \le -\frac{1}{cK}\int_{B_{2r}}\int_{B_{2r}} \left|\log\frac{\bar u(\xi)}{\bar u(\eta)}\right|\frac{d\xi d\eta }{\|\eta^{-1}\circ \xi\|_{\mathbb{H}^n}^Q}+ cr^Q,
\end{align}
\begin{align}
I_1 &\le -\frac{1}{cK}\int_{B_{2r}}\int_{B_{2r}}\min\left\{\phi^q(\xi),\phi^q(\eta)\right\}\left|\log\frac{\bar u(\xi)}{\bar u(\eta)}\right| \frac{d\xi d\eta }{\|\eta^{-1}\circ\xi\|_{\mathbb{H}^n}^Q}\nonumber \\
& + c\int_{B_{2r}}\int_{B_{2r}}\Bigg[\frac{\|\eta^{-1} \circ \xi \|_{\mathbb{H}^n}^{p - sp}}{r^{p(1 - s)}}\nonumber \\
&+ \frac{\|\eta^{-1}\circ\xi\|_{\mathbb{H}^n}^{q(1 - t)}}{r^{q(1 - t)}} + \frac{\|\eta^{-1} \circ \xi\|_{\mathbb{H}^n}^{s(p - 1)}}{r^{s(p - 1)}} + \frac{\|\eta^{-1}\circ\xi\|_{\mathbb{H}^n}^s}{r^s}\Bigg]\frac{d\xi d\eta}{\|\eta^{-1}\circ\xi\|_{\mathbb{H}^n}^Q} \nonumber \\
& \le -\frac{1}{cK}\int_{B_{2r}}\int_{B_{2r}} \left|\log\frac{\bar u(\xi)}{\bar u(\eta)}\right|\frac{d\xi d\eta }{\|\eta^{-1}\circ \xi\|_{\mathbb{H}^n}^Q}+ cr^Q,
\end{align}where
 \begin{align*}
\int_{{B_{2r}}} {\int_{{B_{2r}}} {\frac{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^l}}{{{r^l}}}\frac{{d\xi d\eta }}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^Q}}} } & \le \int_{{B_{2r}}} {\int_{{B_{4r}(\eta)}} {\frac{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^l}}{{{r^l}}}\frac{{d\xi d\eta }}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^Q}}} } \\
&\le \frac{c}{r^l}\int_{{B_{2r}}}\int^{4r}_0\rho^{l-1}\,d\rho d\eta \le c{r^Q}.
\end{align*}
\begin{align*}
\int_{{B_{2r}}} {\int_{{B_{2r}}} {\frac{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^l}}{{{r^l}}}\frac{{d\xi d\eta }}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^Q}}} } & \le \int_{{B_{2r}}} {\int_{{B_{4r}(\eta)}} {\frac{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^l}}{{{r^l}}}\frac{{d\xi d\eta }}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^Q}}} } \\
&\le \frac{c}{r^l}\int_{{B_{2r}}}\int^{4r}_0\rho^{l-1}\,d\rho d\eta \le c{r^Q}.
\end{align*} Furthermore, if ![]() $\bar u\left( \xi \right) \lt \bar u\left( \eta \right)$, the same estimate still holds true through exchanging the roles of ξ and η.
$\bar u\left( \xi \right) \lt \bar u\left( \eta \right)$, the same estimate still holds true through exchanging the roles of ξ and η.
For the second contribution I 2 in (4.1), we first observe that if ![]() $\eta \in {B_R}$, then
$\eta \in {B_R}$, then ![]() ${( {u\left( \xi \right) - u\left( \eta \right)} )_ + }$
${( {u\left( \xi \right) - u\left( \eta \right)} )_ + }$ ![]() $\le u\left( \xi \right) + d$ by
$\le u\left( \xi \right) + d$ by ![]() $u\left( \eta \right) \ge 0$, and that if
$u\left( \eta \right) \ge 0$, and that if ![]() $\eta \in {\mathbb{H}^n}\backslash {B_R}$, then
$\eta \in {\mathbb{H}^n}\backslash {B_R}$, then ![]() ${\left( {u\left( \xi \right) - u\left( \eta \right)} \right)_ + } \le u\left( \xi \right) + u_-\left( \eta \right) \le \bar u\left( \xi \right) + u_-\left( \eta \right)$. From this and
${\left( {u\left( \xi \right) - u\left( \eta \right)} \right)_ + } \le u\left( \xi \right) + u_-\left( \eta \right) \le \bar u\left( \xi \right) + u_-\left( \eta \right)$. From this and  ${\rm supp}\, \phi\subset {B_{\frac{{3r}}{2}}}$, we can evaluate I 2 as
${\rm supp}\, \phi\subset {B_{\frac{{3r}}{2}}}$, we can evaluate I 2 as
 \begin{align}
I_2 &\le 2{\int _{{B_R}\backslash {B_{2r}}}}\int_{{B_{\frac{{3r}}{2}}}} {\left[\frac{{\left( {u\left( \xi \right) - u\left( \eta \right)} \right)_ + ^{p - 1}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}} + a\left( {\xi ,\eta } \right)\frac{{\left( {u\left( \xi \right) - u\left( \eta \right)} \right)_ + ^{q - 1}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + tq}}}\right]\frac{{d\xi d\eta }}{{{g_{2r}}\left( {\bar u\left( \xi \right)} \right)}}} \nonumber \\
&\quad + 2{\int _{{\mathbb{H}^n}\backslash {B_R}}}\int_{{B_{\frac{{3r}}{2}}}} {\left[\frac{{\left( {u\left( \xi \right) - u\left( \eta \right)} \right)_ + ^{p - 1}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}} + a\left( {\xi ,\eta } \right)\frac{{\left( {u\left( \xi \right) - u\left( \eta \right)} \right)_ + ^{q - 1}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + tq}}}\right]\frac{{d\xi d\eta }}{{{g_{2r}}\left( {\bar u\left( \xi \right)} \right)}}}\nonumber \\
& \le {\int _{{\mathbb{H}^n}\backslash {B_{2r}}}}\int_{{B_{\frac{{3r}}{2}}}} {\frac{c{h\left( {\xi ,\eta ,\bar u\left( \xi \right)} \right)}}{{{g_{2r}}\left( {\bar u\left( \xi \right)} \right)\| {{\eta ^{- 1}} \circ \xi }\|_{{\mathbb{H}^n}}^Q}}\,d\xi d\eta }
+ {\int _{{\mathbb{H}^n}\backslash {B_R}}}\int_{{B_{\frac{{3r}}{2}}}}\nonumber\\
&{\frac{c{h\left( {\xi ,\eta ,u\left( \eta \right)} \right)}}{{{g_{2r}}\left( {\bar u\left( \xi \right)} \right)\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^Q}}\,d\xi d\eta } \nonumber \\
&= :{I_{21}} + {I_{22}}.
\end{align}
\begin{align}
I_2 &\le 2{\int _{{B_R}\backslash {B_{2r}}}}\int_{{B_{\frac{{3r}}{2}}}} {\left[\frac{{\left( {u\left( \xi \right) - u\left( \eta \right)} \right)_ + ^{p - 1}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}} + a\left( {\xi ,\eta } \right)\frac{{\left( {u\left( \xi \right) - u\left( \eta \right)} \right)_ + ^{q - 1}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + tq}}}\right]\frac{{d\xi d\eta }}{{{g_{2r}}\left( {\bar u\left( \xi \right)} \right)}}} \nonumber \\
&\quad + 2{\int _{{\mathbb{H}^n}\backslash {B_R}}}\int_{{B_{\frac{{3r}}{2}}}} {\left[\frac{{\left( {u\left( \xi \right) - u\left( \eta \right)} \right)_ + ^{p - 1}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}} + a\left( {\xi ,\eta } \right)\frac{{\left( {u\left( \xi \right) - u\left( \eta \right)} \right)_ + ^{q - 1}}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + tq}}}\right]\frac{{d\xi d\eta }}{{{g_{2r}}\left( {\bar u\left( \xi \right)} \right)}}}\nonumber \\
& \le {\int _{{\mathbb{H}^n}\backslash {B_{2r}}}}\int_{{B_{\frac{{3r}}{2}}}} {\frac{c{h\left( {\xi ,\eta ,\bar u\left( \xi \right)} \right)}}{{{g_{2r}}\left( {\bar u\left( \xi \right)} \right)\| {{\eta ^{- 1}} \circ \xi }\|_{{\mathbb{H}^n}}^Q}}\,d\xi d\eta }
+ {\int _{{\mathbb{H}^n}\backslash {B_R}}}\int_{{B_{\frac{{3r}}{2}}}}\nonumber\\
&{\frac{c{h\left( {\xi ,\eta ,u\left( \eta \right)} \right)}}{{{g_{2r}}\left( {\bar u\left( \xi \right)} \right)\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^Q}}\,d\xi d\eta } \nonumber \\
&= :{I_{21}} + {I_{22}}.
\end{align} We now intend to control precisely the term  $\frac{{h\left( {\xi ,\eta ,\bar u\left( \xi \right)} \right)}}{{{g_{2r}}\left( {\bar u\left( \xi \right)} \right)}}$ by some constants. In view of the condition (1.6), there holds that, for
$\frac{{h\left( {\xi ,\eta ,\bar u\left( \xi \right)} \right)}}{{{g_{2r}}\left( {\bar u\left( \xi \right)} \right)}}$ by some constants. In view of the condition (1.6), there holds that, for ![]() $\xi \in B_{2r}$ and
$\xi \in B_{2r}$ and ![]() $\eta \in \mathbb{H}^n$,
$\eta \in \mathbb{H}^n$,
 \begin{align}
a\left( {\xi ,\eta } \right)& \le a\left( {\xi ,\eta } \right) - a\left( {\xi ,\xi } \right) + a_{2r}^ + \nonumber \\
& \le {\left( {2{{\| a \|}_{{L^\infty }}}} \right)^{1 - \frac{{tq - sp}}{\alpha }}}{\left| {a\left( {\xi ,\eta } \right) - a\left( {\xi ,\xi } \right)} \right|^{\frac{{tq - sp}}{\alpha }}} + a_{2r}^ + \nonumber \\
& \le c\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{tq - sp} + a_{2r}^ + .
\end{align}
\begin{align}
a\left( {\xi ,\eta } \right)& \le a\left( {\xi ,\eta } \right) - a\left( {\xi ,\xi } \right) + a_{2r}^ + \nonumber \\
& \le {\left( {2{{\| a \|}_{{L^\infty }}}} \right)^{1 - \frac{{tq - sp}}{\alpha }}}{\left| {a\left( {\xi ,\eta } \right) - a\left( {\xi ,\xi } \right)} \right|^{\frac{{tq - sp}}{\alpha }}} + a_{2r}^ + \nonumber \\
& \le c\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{tq - sp} + a_{2r}^ + .
\end{align}This indicates
 \begin{align*}
{I_{21}} & \le c{\int _{{\mathbb{H}^n}\backslash {B_{2r}}}}\int_{{B_{\frac{{3r}}{2}}}} {\frac{{\frac{{{{\bar u}^{p - 1}}\left( \xi \right) + {{\bar u}^{q - 1}}\left( \xi \right)}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{sp}}} + a_{2r}^ + \frac{{{{\bar u}^{q - 1}}\left( \xi \right)}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{tq}}}}}{{\frac{{{{\bar u}^{p - 1}}\left( \xi \right)}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{sp}}}\frac{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{sp}}}{{{{\left( {2r} \right)}^{sp}}}} + a_{2r}^ + \frac{{{{\bar u}^{q - 1}}\left( \xi \right)}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{tq}}}\frac{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{tq}}}{{{{\left( {2r} \right)}^{tq}}}}}}\frac{{d\xi d\eta }}{{\| {{\eta ^{- 1}} \circ \xi } \|_{\mathbb{H}{^n}}^Q}}} \\
& \le cK{\int _{{\mathbb{H}^n}\backslash {B_{2r}}}}\int_{{B_{\frac{{3r}}{2}}}} {\frac{(r/2)^{sp}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}}\,d\xi d\eta,}
\end{align*}
\begin{align*}
{I_{21}} & \le c{\int _{{\mathbb{H}^n}\backslash {B_{2r}}}}\int_{{B_{\frac{{3r}}{2}}}} {\frac{{\frac{{{{\bar u}^{p - 1}}\left( \xi \right) + {{\bar u}^{q - 1}}\left( \xi \right)}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{sp}}} + a_{2r}^ + \frac{{{{\bar u}^{q - 1}}\left( \xi \right)}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{tq}}}}}{{\frac{{{{\bar u}^{p - 1}}\left( \xi \right)}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{sp}}}\frac{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{sp}}}{{{{\left( {2r} \right)}^{sp}}}} + a_{2r}^ + \frac{{{{\bar u}^{q - 1}}\left( \xi \right)}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{tq}}}\frac{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{tq}}}{{{{\left( {2r} \right)}^{tq}}}}}}\frac{{d\xi d\eta }}{{\| {{\eta ^{- 1}} \circ \xi } \|_{\mathbb{H}{^n}}^Q}}} \\
& \le cK{\int _{{\mathbb{H}^n}\backslash {B_{2r}}}}\int_{{B_{\frac{{3r}}{2}}}} {\frac{(r/2)^{sp}}{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^{Q + sp}}}\,d\xi d\eta,}
\end{align*} by virtue of  ${\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}} \gt \frac{r}{2}$. For
${\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}} \gt \frac{r}{2}$. For  $\xi \in {B_{\frac{{3r}}{2}}}$ and
$\xi \in {B_{\frac{{3r}}{2}}}$ and ![]() $\eta \in \mathbb{H}^n\backslash {B_{2r}}$, via the triangle inequality,
$\eta \in \mathbb{H}^n\backslash {B_{2r}}$, via the triangle inequality,
 \begin{align}
{\| {{\eta ^{- 1}} \circ {\xi _0}} \|_{{\mathbb{H}^n}}} &
\le\left( {1 + \frac{{{{\| {{\xi ^{- 1}} \circ {\xi _0}} \|}_{{\mathbb{H}^n}}}}}{{{{\| {{\eta ^{- 1}} \circ \xi } \|}_{{\mathbb{H}^n}}}}}} \right){\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}} \nonumber\\
& \le \left( 1 + \frac{3r/2}{r/2} \right){\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}} = 4{\| {{\eta ^{- 1}} \circ \xi }\|_{{\mathbb{H}^n}}},
\end{align}
\begin{align}
{\| {{\eta ^{- 1}} \circ {\xi _0}} \|_{{\mathbb{H}^n}}} &
\le\left( {1 + \frac{{{{\| {{\xi ^{- 1}} \circ {\xi _0}} \|}_{{\mathbb{H}^n}}}}}{{{{\| {{\eta ^{- 1}} \circ \xi } \|}_{{\mathbb{H}^n}}}}}} \right){\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}} \nonumber\\
& \le \left( 1 + \frac{3r/2}{r/2} \right){\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}} = 4{\| {{\eta ^{- 1}} \circ \xi }\|_{{\mathbb{H}^n}}},
\end{align}Thus by [Reference Manfredini, Palatucci, Piccinini and Polidoro31, Lemma 2.6],
 \begin{equation}
{I_{21}} \le cK\left| {{B_{\frac{{3r}}{2}}}} \right|{\int _{{\mathbb{H}^n}\backslash {B_{2r}}}}\frac{{{r^{sp}}}}{{\| {{\eta ^{- 1}} \circ {\xi _0}} \|_{{\mathbb{H}^n}}^{Q + sp}}}\,d\eta \le cK{r^Q}.
\end{equation}
\begin{equation}
{I_{21}} \le cK\left| {{B_{\frac{{3r}}{2}}}} \right|{\int _{{\mathbb{H}^n}\backslash {B_{2r}}}}\frac{{{r^{sp}}}}{{\| {{\eta ^{- 1}} \circ {\xi _0}} \|_{{\mathbb{H}^n}}^{Q + sp}}}\,d\eta \le cK{r^Q}.
\end{equation} Let us proceed to examine I 22. With the aid of (4.10), (4.11) and ![]() $u(\xi)\ge 0$ in
$u(\xi)\ge 0$ in  ${{B_{\frac{{3r}}{2}}}}$,
${{B_{\frac{{3r}}{2}}}}$,
 \begin{align}
I_{22} & \le c{\int _{{\mathbb{H}^n}\backslash {B_R}}}\int_{{B_{\frac{{3r}}{2}}}} {\left( {\frac{{u_ - ^{p - 1}( \eta) + u_ - ^{q - 1}( \eta)}}{{\| {{\eta ^{- 1}} \circ \xi }\|_{{\mathbb{H}^n}}^{Q + sp}}} + a_{2r}^ + \frac{{u_ - ^{q - 1}( \eta )}}{{\| {{\eta ^{- 1}} \circ \xi }\|_{{\mathbb{H}^n}}^{Q + tq}}}} \right){g^{- 1}}( d)\,d\xi d\eta } \nonumber \\
& \le c{r^Q}{g^{- 1}}( d){\int _{{\mathbb{H}^n}\backslash {B_R}}}\left( {\frac{{u_ - ^{p - 1}( \eta) + u_ - ^{q - 1}( \eta)}}{{\| {{\eta ^{- 1}} \circ {\xi _0}}\|_{{\mathbb{H}^n}}^{Q + sp}}} + a_{2r}^ + \frac{{u_ - ^{q - 1}(\eta)}}{{\| {{\eta ^{- 1}} \circ {\xi _0}}\|_{{\mathbb{H}^n}}^{Q + tq}}}} \right)\,d\eta\nonumber \\
& \le c{r^{Q+sp}}{d^{1 - p}}{\int _{{\mathbb{H}^n}\backslash {B_R}}}\frac{{u_ - ^{p - 1}( \eta) + u_ - ^{q - 1}( \eta)}}{{\| {{\eta ^{- 1}} \circ {\xi _0}}\|_{{\mathbb{H}^n}}^{Q + sp}}}d\eta \nonumber \\
&\quad + c{r^{Q + tq}}{d^{1 - q}}{\int _{{\mathbb{H}^n}\backslash {B_R}}}\frac{{u_ - ^{q - 1}( \eta)}}{{\| {{\eta ^{- 1}} \circ {\xi _0}}\|_{{\mathbb{H}^n}}^{Q + tq}}}\,d\eta,
\end{align}
\begin{align}
I_{22} & \le c{\int _{{\mathbb{H}^n}\backslash {B_R}}}\int_{{B_{\frac{{3r}}{2}}}} {\left( {\frac{{u_ - ^{p - 1}( \eta) + u_ - ^{q - 1}( \eta)}}{{\| {{\eta ^{- 1}} \circ \xi }\|_{{\mathbb{H}^n}}^{Q + sp}}} + a_{2r}^ + \frac{{u_ - ^{q - 1}( \eta )}}{{\| {{\eta ^{- 1}} \circ \xi }\|_{{\mathbb{H}^n}}^{Q + tq}}}} \right){g^{- 1}}( d)\,d\xi d\eta } \nonumber \\
& \le c{r^Q}{g^{- 1}}( d){\int _{{\mathbb{H}^n}\backslash {B_R}}}\left( {\frac{{u_ - ^{p - 1}( \eta) + u_ - ^{q - 1}( \eta)}}{{\| {{\eta ^{- 1}} \circ {\xi _0}}\|_{{\mathbb{H}^n}}^{Q + sp}}} + a_{2r}^ + \frac{{u_ - ^{q - 1}(\eta)}}{{\| {{\eta ^{- 1}} \circ {\xi _0}}\|_{{\mathbb{H}^n}}^{Q + tq}}}} \right)\,d\eta\nonumber \\
& \le c{r^{Q+sp}}{d^{1 - p}}{\int _{{\mathbb{H}^n}\backslash {B_R}}}\frac{{u_ - ^{p - 1}( \eta) + u_ - ^{q - 1}( \eta)}}{{\| {{\eta ^{- 1}} \circ {\xi _0}}\|_{{\mathbb{H}^n}}^{Q + sp}}}d\eta \nonumber \\
&\quad + c{r^{Q + tq}}{d^{1 - q}}{\int _{{\mathbb{H}^n}\backslash {B_R}}}\frac{{u_ - ^{q - 1}( \eta)}}{{\| {{\eta ^{- 1}} \circ {\xi _0}}\|_{{\mathbb{H}^n}}^{Q + tq}}}\,d\eta,
\end{align} where we notice ![]() $\eta \in {\mathbb{H}^n}\backslash {B_R} \subset {\mathbb{H}^n}\backslash {B_{2r}}$.
$\eta \in {\mathbb{H}^n}\backslash {B_R} \subset {\mathbb{H}^n}\backslash {B_{2r}}$.
Merging (4.8), (4.9), (4.12), (4.13) with (4.1) arrives eventually at the desired estimate with the positive constant c depending upon ![]() $n,p,q,s,t,\alpha,[a]_{\alpha} $ and
$n,p,q,s,t,\alpha,[a]_{\alpha} $ and ![]() $\| a \|_{L^\infty }$.
$\| a \|_{L^\infty }$.
Corollary 4.2. Let the assumptions of lemma 4.1 be in force. Define
 \begin{equation*}w: = \min \left\{{{{\left( {\log \left( {\tau + d} \right) - \log \left( {u + d} \right)} \right)}_ + },\log b} \right\}\end{equation*}
\begin{equation*}w: = \min \left\{{{{\left( {\log \left( {\tau + d} \right) - \log \left( {u + d} \right)} \right)}_ + },\log b} \right\}\end{equation*} with ![]() $\tau,d \gt 0$ and b > 1. Then for the weak solution u of (1.1) it holds that
$\tau,d \gt 0$ and b > 1. Then for the weak solution u of (1.1) it holds that
 \begin{align*}
&\quad -\!\!\!\!\!\!\int_{{B_r}} {| {w - {{( w)}_r}}|\,d\eta } \\
&\le c{K^2}\left(1 + \frac{r^{sp}}{d^{p -1}}{\int _{{\mathbb{H}^n}\backslash {B_R}}}\frac{{u_ - ^{p - 1}( \eta) + u_ - ^{q - 1}( \eta)}}{{\| {{\eta ^{- 1}} \circ {\xi _0}} \|_{{\mathbb{H}^n}}^{Q + sp}}}\,d\eta
+ \frac{r^{tq}}{d^{q - 1}}{\int _{{\mathbb{H}^n}\backslash {B_R}}}\frac{{u_ - ^{q - 1}( \eta)}}{{\| {{\eta ^{- 1}} \circ {\xi _0}}\|_{{\mathbb{H}^n}}^{Q + tq}}}\,d\eta \right),
\end{align*}
\begin{align*}
&\quad -\!\!\!\!\!\!\int_{{B_r}} {| {w - {{( w)}_r}}|\,d\eta } \\
&\le c{K^2}\left(1 + \frac{r^{sp}}{d^{p -1}}{\int _{{\mathbb{H}^n}\backslash {B_R}}}\frac{{u_ - ^{p - 1}( \eta) + u_ - ^{q - 1}( \eta)}}{{\| {{\eta ^{- 1}} \circ {\xi _0}} \|_{{\mathbb{H}^n}}^{Q + sp}}}\,d\eta
+ \frac{r^{tq}}{d^{q - 1}}{\int _{{\mathbb{H}^n}\backslash {B_R}}}\frac{{u_ - ^{q - 1}( \eta)}}{{\| {{\eta ^{- 1}} \circ {\xi _0}}\|_{{\mathbb{H}^n}}^{Q + tq}}}\,d\eta \right),
\end{align*} where c > 1 depends on ![]() $\mathrm{\textbf{data}}$, and K is defined as in lemma 4.1.
$\mathrm{\textbf{data}}$, and K is defined as in lemma 4.1.
Proof. Notice that, since w is a truncation of ![]() $\log (u+d)$,
$\log (u+d)$,
 \begin{align*}
-\!\!\!\!\!\!\int_{{B_r}} {| {w - {( w)}_r}|\,d\eta } & \le -\!\!\!\!\!\!\int_{{B_r}} {\left| {-\!\!\!\!\!\!\int_{{B_r}} {( {w( \eta) - w( \xi)})\,d\xi } } \right|\,d\eta } \\
& \le -\!\!\!\!\!\!\int_{{B_r}} {-\!\!\!\!\!\!\int_{{B_r}} {| {w( \xi ) - w( \eta)}|\,d\xi } d\eta } \\
& \le -\!\!\!\!\!\!\int_{{B_r}} {-\!\!\!\!\!\!\int_{{B_r}} {\frac{{\left| {\log \left( {u\left( \xi \right) + d} \right) - \log \left( {u\left( \eta \right) + d} \right)} \right|}}{{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^Q}/{{{\left( {2r} \right)}^Q}}}}\,d\xi } d\eta } \\
& \le -\!\!\!\!\!\!\int_{{B_r}} {\int_{{B_r}} {\left| {\log \frac{{u\left( \xi \right) + d}}{{u\left( \eta \right) + d}}} \right|\frac{{d\xi d\eta }}{{\| {{\eta ^{- 1}} \circ \xi }\|_{{\mathbb{H}^n}}^Q}}} }.
\end{align*}
\begin{align*}
-\!\!\!\!\!\!\int_{{B_r}} {| {w - {( w)}_r}|\,d\eta } & \le -\!\!\!\!\!\!\int_{{B_r}} {\left| {-\!\!\!\!\!\!\int_{{B_r}} {( {w( \eta) - w( \xi)})\,d\xi } } \right|\,d\eta } \\
& \le -\!\!\!\!\!\!\int_{{B_r}} {-\!\!\!\!\!\!\int_{{B_r}} {| {w( \xi ) - w( \eta)}|\,d\xi } d\eta } \\
& \le -\!\!\!\!\!\!\int_{{B_r}} {-\!\!\!\!\!\!\int_{{B_r}} {\frac{{\left| {\log \left( {u\left( \xi \right) + d} \right) - \log \left( {u\left( \eta \right) + d} \right)} \right|}}{{{\| {{\eta ^{- 1}} \circ \xi } \|_{{\mathbb{H}^n}}^Q}/{{{\left( {2r} \right)}^Q}}}}\,d\xi } d\eta } \\
& \le -\!\!\!\!\!\!\int_{{B_r}} {\int_{{B_r}} {\left| {\log \frac{{u\left( \xi \right) + d}}{{u\left( \eta \right) + d}}} \right|\frac{{d\xi d\eta }}{{\| {{\eta ^{- 1}} \circ \xi }\|_{{\mathbb{H}^n}}^Q}}} }.
\end{align*}Then the desired result is a plain consequence of lemma 4.1.
In the end, we will focus on establishing Hölder regularity of weak solutions. For this aim, it is sufficient to show an oscillation improvement result, theorem 4.3. Before proceeding, let us introduce some notations. For ![]() $j\in\mathbb{N}\cup\{0\}$, set
$j\in\mathbb{N}\cup\{0\}$, set
 \begin{equation*}
r_j:=\sigma^jr, \quad \sigma\in(0,1/4] ,\quad B_j:=B_{r_j}(\xi_0) \quad\text{and} \quad 2B_j:=B_{2r_j},
\end{equation*}
\begin{equation*}
r_j:=\sigma^jr, \quad \sigma\in(0,1/4] ,\quad B_j:=B_{r_j}(\xi_0) \quad\text{and} \quad 2B_j:=B_{2r_j},
\end{equation*} where we fix any ball ![]() $B_{2r}(\xi_0)\subset\Omega'\subset\subset\Omega$. Furthermore, define
$B_{2r}(\xi_0)\subset\Omega'\subset\subset\Omega$. Furthermore, define
 \begin{align*}
\omega(r_0):=2\sup_{B_r}|u|&+\left(r^{sp}\int_{\mathbb{H}^n\setminus B_r}\frac{|u|^{p-1}+|u|^{q-1}}{\|\xi_0^{-1}\circ\xi\|_{\mathbb{H}^n}^{Q+sp}}\,d\xi\right)^\frac{1}{p-1}\nonumber\\
&+\left(r^{tq}\int_{\mathbb{H}^n\setminus B_r}\frac{|u|^{q-1}}{\|\xi_0^{-1}\circ\xi\|_{\mathbb{H}^n}^{Q+tq}}\,d\xi\right)^\frac{1}{q-1},
\end{align*}
\begin{align*}
\omega(r_0):=2\sup_{B_r}|u|&+\left(r^{sp}\int_{\mathbb{H}^n\setminus B_r}\frac{|u|^{p-1}+|u|^{q-1}}{\|\xi_0^{-1}\circ\xi\|_{\mathbb{H}^n}^{Q+sp}}\,d\xi\right)^\frac{1}{p-1}\nonumber\\
&+\left(r^{tq}\int_{\mathbb{H}^n\setminus B_r}\frac{|u|^{q-1}}{\|\xi_0^{-1}\circ\xi\|_{\mathbb{H}^n}^{Q+tq}}\,d\xi\right)^\frac{1}{q-1},
\end{align*}and
 \begin{equation*}
\omega(r_j):=\left(\frac{r_j}{r_0}\right)^\beta\omega(r_0)=\sigma^{j\beta}\omega(r) \quad\text{for some } 0 \lt \beta \lt \frac{sp}{q-1}.
\end{equation*}
\begin{equation*}
\omega(r_j):=\left(\frac{r_j}{r_0}\right)^\beta\omega(r_0)=\sigma^{j\beta}\omega(r) \quad\text{for some } 0 \lt \beta \lt \frac{sp}{q-1}.
\end{equation*}Let us point out that σ and β are to be determined later.
Now we are in a position to prove the following iteration lemma, which suggests ![]() $u\in C^{0,\beta}(B_r)$.
$u\in C^{0,\beta}(B_r)$.
Theorem 4.3 Let  $u\in \mathcal{A}(\Omega)\cap L^{q-1}_{sp}(\mathbb{H}^n)$ be a weak solution to (1.1). Under the conditions (1.4), (1.5) and (1.6) with
$u\in \mathcal{A}(\Omega)\cap L^{q-1}_{sp}(\mathbb{H}^n)$ be a weak solution to (1.1). Under the conditions (1.4), (1.5) and (1.6) with ![]() $tq\le sp+\alpha$, there holds that
$tq\le sp+\alpha$, there holds that
 \begin{equation*}
\mathop{\rm osc}\limits_{B_j}u\le \omega(r_j) \quad\text{for any } j\in\mathbb{N}\cup\{0\},
\end{equation*}
\begin{equation*}
\mathop{\rm osc}\limits_{B_j}u\le \omega(r_j) \quad\text{for any } j\in\mathbb{N}\cup\{0\},
\end{equation*}where these notations are fixed as above.
Proof. Argue by induction. The conclusion is obvious for j = 0 and then assume it holds true for ![]() $i\le j$. Now we show this claim for j + 1. Let us notice the simple fact that either
$i\le j$. Now we show this claim for j + 1. Let us notice the simple fact that either
 \begin{equation}
\left|2B_{j+1}\cap\left\{u\ge \inf_{B_j}u+\omega(r_j)/2\right\}\right|\ge\frac{1}{2}|2B_{j+1}|,
\end{equation}
\begin{equation}
\left|2B_{j+1}\cap\left\{u\ge \inf_{B_j}u+\omega(r_j)/2\right\}\right|\ge\frac{1}{2}|2B_{j+1}|,
\end{equation}or
 \begin{equation}
\left|2B_{j+1}\cap\left\{u \lt \inf_{B_j}u+\omega(r_j)/2\right\}\right|\ge\frac{1}{2}|2B_{j+1}|.
\end{equation}
\begin{equation}
\left|2B_{j+1}\cap\left\{u \lt \inf_{B_j}u+\omega(r_j)/2\right\}\right|\ge\frac{1}{2}|2B_{j+1}|.
\end{equation}Define
 \begin{equation*}
u_j=\begin{cases}u-\inf_{B_j}u, &\text{if (4.14) occurs},\\[2mm]
\sup_{B_j}u-u, &\text{if (4.15) occurs}.
\end{cases}
\end{equation*}
\begin{equation*}
u_j=\begin{cases}u-\inf_{B_j}u, &\text{if (4.14) occurs},\\[2mm]
\sup_{B_j}u-u, &\text{if (4.15) occurs}.
\end{cases}
\end{equation*} Obviously, ![]() $u_j\ge0$ in Bj and
$u_j\ge0$ in Bj and
 \begin{equation}
|2B_{j+1}\cap\{u_j\geq\omega(r_j)/2\}|\ge\frac{1}{2}|2B_{j+1}|.
\end{equation}
\begin{equation}
|2B_{j+1}\cap\{u_j\geq\omega(r_j)/2\}|\ge\frac{1}{2}|2B_{j+1}|.
\end{equation}Moreover, uj is a weak solution to (1.1) such that
 \begin{equation}
\sup_{B_i}|u_j|\le \omega(r_i) \quad\text{for any } i\in\{0,1,2,\cdots,j\}.
\end{equation}
\begin{equation}
\sup_{B_i}|u_j|\le \omega(r_i) \quad\text{for any } i\in\{0,1,2,\cdots,j\}.
\end{equation}Now we set an auxiliary function
 \begin{equation*}
w:=\min\left\{\left[\log\left(\frac{\omega(r_j)/2+d}{u_j+d}\right)\right]_+,k\right\} \quad\text{with } k \gt 0.
\end{equation*}
\begin{equation*}
w:=\min\left\{\left[\log\left(\frac{\omega(r_j)/2+d}{u_j+d}\right)\right]_+,k\right\} \quad\text{with } k \gt 0.
\end{equation*}Applying corollary 4.2 derives
 \begin{align}
&\quad-\!\!\!\!\!\!\int_{2B_{j+1}}|w-(w)_{2B_{j+1}}|\,d\xi \nonumber\\
&\leq CK^2\left(1+d^{1-p}r^{sp}_{j+1}\int_{\mathbb{H}^n\setminus B_j}\frac{|u_j|^{p-1}+|u_j|^{q-1}}{\|\xi_0^{-1}\circ\xi\|_{\mathbb{H}^n}^{Q+sp}}\,d\xi+d^{1-q}r^{tq}_{j+1}\int_{\mathbb{H}^n\setminus B_j}\frac{|u_j|^{q-1}}{\|\xi_0^{-1}\circ\xi\|_{\mathbb{H}^n}^{Q+tq}}\,d\xi\right),
\end{align}
\begin{align}
&\quad-\!\!\!\!\!\!\int_{2B_{j+1}}|w-(w)_{2B_{j+1}}|\,d\xi \nonumber\\
&\leq CK^2\left(1+d^{1-p}r^{sp}_{j+1}\int_{\mathbb{H}^n\setminus B_j}\frac{|u_j|^{p-1}+|u_j|^{q-1}}{\|\xi_0^{-1}\circ\xi\|_{\mathbb{H}^n}^{Q+sp}}\,d\xi+d^{1-q}r^{tq}_{j+1}\int_{\mathbb{H}^n\setminus B_j}\frac{|u_j|^{q-1}}{\|\xi_0^{-1}\circ\xi\|_{\mathbb{H}^n}^{Q+tq}}\,d\xi\right),
\end{align} with K defined as in lemma 4.1. We evaluate the second integral at the right-hand side. By means of (4.17) and the definition of ![]() $\omega(r_0)$,
$\omega(r_0)$,
 \begin{align}
&\quad r^{tq}_{j+1}\int_{\mathbb{H}^n\setminus B_j}\frac{|u_j|^{q-1}}{\|\xi_0^{-1}\circ\xi\|_{\mathbb{H}^n}^{Q+tq}}\,d\xi \nonumber\\ &=r^{tq}_j\sum^j_{i=1}\int_{B_{i-1}\setminus B_i}\frac{|u_j|^{q-1}}{\|\xi_0^{-1}\circ\xi\|_{\mathbb{H}^n}^{Q+tq}}\,d\xi
+r^{tq}_j\int_{\mathbb{H}^n\setminus B_0}\frac{|u_j|^{q-1}}{\|\xi_0^{-1}\circ\xi\|_{\mathbb{H}^n}^{Q+tq}}\,d\xi \nonumber\\
&\leq\sum^j_{i=1}\omega(r_{i-1})^{q-1}\left(\frac{r_j}{r_i}\right)^{tq}+Cr^{tq}_j\int_{\mathbb{H}^n\setminus B_0}\frac{|u|^{q-1}+(\sup_{B_0}|u|)^{q-1}}{\|\xi_0^{-1}\circ\xi\|_{\mathbb{H}^n}^{Q+tq}}\,d\xi \nonumber\\
&\leq C\sum^j_{i=1}\left(\frac{r_j}{r_i}\right)^{tq}\omega(r_{i-1})^{q-1} \nonumber\\
&\le C\frac{4^{tq-\beta(q-1)}}{(tq-\beta(q-1))\log4}\sigma^{-\beta(q-1)}\omega(r_j)^{q-1},
\end{align}
\begin{align}
&\quad r^{tq}_{j+1}\int_{\mathbb{H}^n\setminus B_j}\frac{|u_j|^{q-1}}{\|\xi_0^{-1}\circ\xi\|_{\mathbb{H}^n}^{Q+tq}}\,d\xi \nonumber\\ &=r^{tq}_j\sum^j_{i=1}\int_{B_{i-1}\setminus B_i}\frac{|u_j|^{q-1}}{\|\xi_0^{-1}\circ\xi\|_{\mathbb{H}^n}^{Q+tq}}\,d\xi
+r^{tq}_j\int_{\mathbb{H}^n\setminus B_0}\frac{|u_j|^{q-1}}{\|\xi_0^{-1}\circ\xi\|_{\mathbb{H}^n}^{Q+tq}}\,d\xi \nonumber\\
&\leq\sum^j_{i=1}\omega(r_{i-1})^{q-1}\left(\frac{r_j}{r_i}\right)^{tq}+Cr^{tq}_j\int_{\mathbb{H}^n\setminus B_0}\frac{|u|^{q-1}+(\sup_{B_0}|u|)^{q-1}}{\|\xi_0^{-1}\circ\xi\|_{\mathbb{H}^n}^{Q+tq}}\,d\xi \nonumber\\
&\leq C\sum^j_{i=1}\left(\frac{r_j}{r_i}\right)^{tq}\omega(r_{i-1})^{q-1} \nonumber\\
&\le C\frac{4^{tq-\beta(q-1)}}{(tq-\beta(q-1))\log4}\sigma^{-\beta(q-1)}\omega(r_j)^{q-1},
\end{align} where we used the fact that  $\beta \lt \frac{sp}{q-1}\left(\le \frac{tq}{q-1}\right)$. Analogously,
$\beta \lt \frac{sp}{q-1}\left(\le \frac{tq}{q-1}\right)$. Analogously,
 \begin{align}
r^{sp}_j\int_{\mathbb{H}^n\setminus B_j}\frac{|u_j|^{p-1}+|u_j|^{q-1}}{\|\xi_0^{-1}\circ\xi\|_{\mathbb{H}^n}^{Q+sp}}\,d\xi &\le C(1+\|u\|^{q-p}_{L^\infty(\Omega')})\sum^j_{i=1}\left(\frac{r_j}{r_i}\right)^{sp}\omega(r_{i-1})^{p-1} \nonumber\\
&\le CN\sigma^{-\beta(p-1)}\omega(r_j)^{p-1},
\end{align}
\begin{align}
r^{sp}_j\int_{\mathbb{H}^n\setminus B_j}\frac{|u_j|^{p-1}+|u_j|^{q-1}}{\|\xi_0^{-1}\circ\xi\|_{\mathbb{H}^n}^{Q+sp}}\,d\xi &\le C(1+\|u\|^{q-p}_{L^\infty(\Omega')})\sum^j_{i=1}\left(\frac{r_j}{r_i}\right)^{sp}\omega(r_{i-1})^{p-1} \nonumber\\
&\le CN\sigma^{-\beta(p-1)}\omega(r_j)^{p-1},
\end{align} with  $\beta \lt \frac{sp}{q-1}\left(\le \frac{sp}{p-1}\right)$, where
$\beta \lt \frac{sp}{q-1}\left(\le \frac{sp}{p-1}\right)$, where  $N:=1+\|u\|^{q-p}_{L^\infty(\Omega')}$ and the derivation of
$N:=1+\|u\|^{q-p}_{L^\infty(\Omega')}$ and the derivation of  $\|u\|^{q-p}_{L^\infty(\Omega')}$ is from the term
$\|u\|^{q-p}_{L^\infty(\Omega')}$ is from the term ![]() $|u_j|^{q-1}$, and C > 0 depends on
$|u_j|^{q-1}$, and C > 0 depends on ![]() $n,p,s$ and the difference of
$n,p,s$ and the difference of  $\frac{sp}{p-1}$ and β. Combining (4.19), (4.20) with (4.18) and remembering
$\frac{sp}{p-1}$ and β. Combining (4.19), (4.20) with (4.18) and remembering  $\frac{r_{j+1}}{r_j}=\sigma$, we get
$\frac{r_{j+1}}{r_j}=\sigma$, we get
 \begin{align*}
&\quad -\!\!\!\!\!\!\int_{2B_{j+1}}|w-(w)_{2B_{j+1}}|\,d\xi
\\
&\leq CK^2\left(1+Nd^{1-p}\sigma^{sp-\beta(p-1)}\omega(r_j)^{p-1}+d^{1-q}\sigma^{tq-\beta(q-1)}\omega(r_j)^{q-1}\right),
\end{align*}
\begin{align*}
&\quad -\!\!\!\!\!\!\int_{2B_{j+1}}|w-(w)_{2B_{j+1}}|\,d\xi
\\
&\leq CK^2\left(1+Nd^{1-p}\sigma^{sp-\beta(p-1)}\omega(r_j)^{p-1}+d^{1-q}\sigma^{tq-\beta(q-1)}\omega(r_j)^{q-1}\right),
\end{align*} where C depends on ![]() $n,p,q,s,t$ and the difference of β and
$n,p,q,s,t$ and the difference of β and  $\frac{tq}{q-1}$, and
$\frac{tq}{q-1}$, and  $\frac{sp}{p-1}$.
$\frac{sp}{p-1}$.
In what follows, picking
 \begin{equation*}
d:=\sigma^{\frac{sp}{q-1}-\beta}\omega(r_j),
\end{equation*}
\begin{equation*}
d:=\sigma^{\frac{sp}{q-1}-\beta}\omega(r_j),
\end{equation*} and recalling ![]() $\omega(r_j)=\sigma^{j\beta}\omega(r_0)$, we find
$\omega(r_j)=\sigma^{j\beta}\omega(r_0)$, we find
 \begin{align*}
&\quad-\!\!\!\!\!\!\int_{2B_{j+1}}|w-(w)_{2B_{j+1}}|\,d\xi \\
&\leq CK^2\left[1+N\sigma^{\left({\frac{sp}{q-1}-\beta}\right)(1-p)+\left({\frac{sp}{p-1}-\beta}\right)(p-1)}
+\sigma^{\left({\frac{sp}{q-1}-\beta}\right)(1-q)+\left({\frac{tq}{q-1}-\beta}\right)(q-1)}\right] \leq CN^3,
\end{align*}
\begin{align*}
&\quad-\!\!\!\!\!\!\int_{2B_{j+1}}|w-(w)_{2B_{j+1}}|\,d\xi \\
&\leq CK^2\left[1+N\sigma^{\left({\frac{sp}{q-1}-\beta}\right)(1-p)+\left({\frac{sp}{p-1}-\beta}\right)(p-1)}
+\sigma^{\left({\frac{sp}{q-1}-\beta}\right)(1-q)+\left({\frac{tq}{q-1}-\beta}\right)(q-1)}\right] \leq CN^3,
\end{align*} where C depends on ![]() $n,p,q,s,t,\alpha,[a]_\alpha,\|a\|_{L^\infty}$ and the difference of β and
$n,p,q,s,t,\alpha,[a]_\alpha,\|a\|_{L^\infty}$ and the difference of β and  $\frac{tq}{q-1}$, and
$\frac{tq}{q-1}$, and  $\frac{sp}{p-1}$. Here we need to utilize the definition of K as in lemma 4.1, and
$\frac{sp}{p-1}$. Here we need to utilize the definition of K as in lemma 4.1, and ![]() $\omega(r_j)\le 2\|u\|_{L^\infty(\Omega')}$. From the last inequality,
$\omega(r_j)\le 2\|u\|_{L^\infty(\Omega')}$. From the last inequality,
 \begin{equation*}
\frac{|2B_{j+1}\cap\{w=k\}|}{|2B_{j+1}|}\le \frac{CN^3}{k}.
\end{equation*}
\begin{equation*}
\frac{|2B_{j+1}\cap\{w=k\}|}{|2B_{j+1}|}\le \frac{CN^3}{k}.
\end{equation*}We refer to [Reference Di Castro, Kuusi and Palatucci14, page 1296] for the details. By taking
 \begin{equation*}
k=\log\left(\frac{\omega(r_j)/2+\varepsilon\omega(r_j)}{3\varepsilon\omega(r_j)}\right)=\log\left(\frac{1/2+\varepsilon}{3\varepsilon}\right)\approx\log\frac{1}{\varepsilon},
\end{equation*}
\begin{equation*}
k=\log\left(\frac{\omega(r_j)/2+\varepsilon\omega(r_j)}{3\varepsilon\omega(r_j)}\right)=\log\left(\frac{1/2+\varepsilon}{3\varepsilon}\right)\approx\log\frac{1}{\varepsilon},
\end{equation*} with  $\varepsilon:=\sigma^{\frac{sp}{q-1}-\beta}$, it holds that
$\varepsilon:=\sigma^{\frac{sp}{q-1}-\beta}$, it holds that
 \begin{equation}
\frac{|2B_{j+1}\cap\{u_j\leq2\varepsilon\omega(r_j)\}|}{|2B_{j+1}|}\le \frac{CN^3}{k}\le \frac{C_{\rm log}N^3}{\log\frac{1}{\sigma}}
\end{equation}
\begin{equation}
\frac{|2B_{j+1}\cap\{u_j\leq2\varepsilon\omega(r_j)\}|}{|2B_{j+1}|}\le \frac{CN^3}{k}\le \frac{C_{\rm log}N^3}{\log\frac{1}{\sigma}}
\end{equation} for the constant ![]() $C_{\rm log} \gt 0$ depending on
$C_{\rm log} \gt 0$ depending on ![]() $n,p,q,s,t,\alpha,[a]_\alpha,\|a\|_{L^\infty}$ and β.
$n,p,q,s,t,\alpha,[a]_\alpha,\|a\|_{L^\infty}$ and β.
At this moment, we are going to perform a suitable iteration. For each ![]() $i=0,1,\cdots$, let
$i=0,1,\cdots$, let
 \begin{equation*}
\rho_i=r_{j+1}+2^{-i}r_{j+1}, \quad \hat{\rho_i}=\frac{\rho_i+3\rho_{i+1}}{4}, \quad \tilde{\rho_i}=\frac{3\rho_i+\rho_{i+1}}{4},
\end{equation*}
\begin{equation*}
\rho_i=r_{j+1}+2^{-i}r_{j+1}, \quad \hat{\rho_i}=\frac{\rho_i+3\rho_{i+1}}{4}, \quad \tilde{\rho_i}=\frac{3\rho_i+\rho_{i+1}}{4},
\end{equation*}and the corresponding balls
 \begin{equation*}
B^i=B_{\rho_i}, \quad \hat{B}^i=B_{\hat{\rho_i}}, \quad \tilde{B}^i=B_{\tilde{\rho_i}}.
\end{equation*}
\begin{equation*}
B^i=B_{\rho_i}, \quad \hat{B}^i=B_{\hat{\rho_i}}, \quad \tilde{B}^i=B_{\tilde{\rho_i}}.
\end{equation*} Then take the cut-off functions ![]() $\psi_i\in C^\infty_0(\tilde{B}^i)$ such that
$\psi_i\in C^\infty_0(\tilde{B}^i)$ such that
 \begin{equation*}
0\le \psi_i\le 1, \quad \psi_i\equiv 1 \text{in } \hat{B}^{i} \quad\text{and} \quad |\nabla_H\psi_i|\le 2^{i+2}r^{-1}_{j+1}.
\end{equation*}
\begin{equation*}
0\le \psi_i\le 1, \quad \psi_i\equiv 1 \text{in } \hat{B}^{i} \quad\text{and} \quad |\nabla_H\psi_i|\le 2^{i+2}r^{-1}_{j+1}.
\end{equation*}Besides, set
and
 \begin{equation*}
A_i=\frac{|B^i\cap \{u_j\leq k_i\}|}{|B^i|}=\frac{|B^i\cap \{w_j\ge0\}|}{|B^i|}.
\end{equation*}
\begin{equation*}
A_i=\frac{|B^i\cap \{u_j\leq k_i\}|}{|B^i|}=\frac{|B^i\cap \{w_j\ge0\}|}{|B^i|}.
\end{equation*}Observe the apparent facts that
and denote
 \begin{equation*}
a^+_{j+1}:=\sup_{B_{2r_{j+1}}\times B_{2r_{j+1}}}a(\cdot,\cdot),\ \ \ a^-_{j+1}:=\inf_{B_{2r_{j+1}}\times B_{2r_{j+1}}}a(\cdot,\cdot),\ \ \
\overline{G}(\tau):=\frac{\tau^p}{r^{sp}_{j+1}}+a^+_{j+1}\frac{\tau^q}{r^{tq}_{j+1}}.
\end{equation*}
\begin{equation*}
a^+_{j+1}:=\sup_{B_{2r_{j+1}}\times B_{2r_{j+1}}}a(\cdot,\cdot),\ \ \ a^-_{j+1}:=\inf_{B_{2r_{j+1}}\times B_{2r_{j+1}}}a(\cdot,\cdot),\ \ \
\overline{G}(\tau):=\frac{\tau^p}{r^{sp}_{j+1}}+a^+_{j+1}\frac{\tau^q}{r^{tq}_{j+1}}.
\end{equation*}With the help of Caccioppoli inequality (lemma 3.3), we derive
 \begin{align}
&\quad-\!\!\!\!\!\!\int_{\hat{B}^i}\int_{\hat{B}^i}\frac{H(\xi,\eta,|w_i(\xi)-w_i(\eta)|)}{\|\eta^{-1}\circ\xi\|^Q_{\mathbb{H}^n}}\,d\xi d\eta \nonumber\\
&\le C-\!\!\!\!\!\!\int_{B^i}\int_{B^i}\frac{H(\xi,\eta,(w_i(\xi)+w_i(\eta))|\psi_i(\xi)-\psi_i(\eta)|)}{\|\eta^{-1}\circ\xi\|^Q_{\mathbb{H}^n}}\,d\xi d\eta \nonumber\\
&\quad +C-\!\!\!\!\!\!\int_{B^i}w_i\psi_i^q\,d\xi\left(\sup_{\eta\in \tilde{B}^i}\int_{\mathbb{H}^n\setminus B^i}\frac{h(\xi,\eta,w_i(\xi))}{\|\eta^{-1}\circ\xi\|^Q_{\mathbb{H}^n}}\,d\xi\right) \nonumber\\
&=:J_1+J_2.
\end{align}
\begin{align}
&\quad-\!\!\!\!\!\!\int_{\hat{B}^i}\int_{\hat{B}^i}\frac{H(\xi,\eta,|w_i(\xi)-w_i(\eta)|)}{\|\eta^{-1}\circ\xi\|^Q_{\mathbb{H}^n}}\,d\xi d\eta \nonumber\\
&\le C-\!\!\!\!\!\!\int_{B^i}\int_{B^i}\frac{H(\xi,\eta,(w_i(\xi)+w_i(\eta))|\psi_i(\xi)-\psi_i(\eta)|)}{\|\eta^{-1}\circ\xi\|^Q_{\mathbb{H}^n}}\,d\xi d\eta \nonumber\\
&\quad +C-\!\!\!\!\!\!\int_{B^i}w_i\psi_i^q\,d\xi\left(\sup_{\eta\in \tilde{B}^i}\int_{\mathbb{H}^n\setminus B^i}\frac{h(\xi,\eta,w_i(\xi))}{\|\eta^{-1}\circ\xi\|^Q_{\mathbb{H}^n}}\,d\xi\right) \nonumber\\
&=:J_1+J_2.
\end{align}Via the definition of wi and ψi, J 1 is evaluated as
 \begin{align}
J_1&\leq C\frac{2^{ip}k_i^p}{r_{j+1}^p}\int_{B^i\cap \{u_j\le k_i\}}-\!\!\!\!\!\!\int_{B^i}\|\eta^{-1}\circ\xi\|_{\mathbb{H}^n}^{-Q+(1-s)p}\,d\xi d\eta \nonumber\\
&\quad+Ca^+_{j+1}\frac{2^{iq}k_i^q}{r_{j+1}^q}\int_{B^i\cap \{u_j\le k_i\}}-\!\!\!\!\!\!\int_{B^i}\|\eta^{-1}\circ\xi\|_{\mathbb{H}^n}^{-Q+(1-t)q}\,d\xi d\eta \nonumber\\
&\leq C2^{iq}\overline{G}(k_i)A_i,
\end{align}
\begin{align}
J_1&\leq C\frac{2^{ip}k_i^p}{r_{j+1}^p}\int_{B^i\cap \{u_j\le k_i\}}-\!\!\!\!\!\!\int_{B^i}\|\eta^{-1}\circ\xi\|_{\mathbb{H}^n}^{-Q+(1-s)p}\,d\xi d\eta \nonumber\\
&\quad+Ca^+_{j+1}\frac{2^{iq}k_i^q}{r_{j+1}^q}\int_{B^i\cap \{u_j\le k_i\}}-\!\!\!\!\!\!\int_{B^i}\|\eta^{-1}\circ\xi\|_{\mathbb{H}^n}^{-Q+(1-t)q}\,d\xi d\eta \nonumber\\
&\leq C2^{iq}\overline{G}(k_i)A_i,
\end{align}and moreover, we have
 \begin{equation*}
-\!\!\!\!\!\!\int_{B^i}w_i\psi_i^q\,d\xi\le Ck_iA_i.
\end{equation*}
\begin{equation*}
-\!\!\!\!\!\!\int_{B^i}w_i\psi_i^q\,d\xi\le Ck_iA_i.
\end{equation*} As for the nonlocal integral in J 2, we first note that if ![]() $\eta\in\tilde{B}^i$ and
$\eta\in\tilde{B}^i$ and ![]() $\xi\in\mathbb{H}^n\setminus B^i$, then
$\xi\in\mathbb{H}^n\setminus B^i$, then
 \begin{equation*}
\|\xi_0^{-1}\circ\xi\|_{\mathbb{H}^n}\le\left(1+\frac{\|\xi_0^{-1}\circ\eta\|_{\mathbb{H}^n}}{\|\eta^{-1}\circ\xi\|_{\mathbb{H}^n}}\right)\|\eta^{-1}\circ\xi\|_{\mathbb{H}^n}
\le2^{i+4}\|\eta^{-1}\circ\xi\|_{\mathbb{H}^n}.
\end{equation*}
\begin{equation*}
\|\xi_0^{-1}\circ\xi\|_{\mathbb{H}^n}\le\left(1+\frac{\|\xi_0^{-1}\circ\eta\|_{\mathbb{H}^n}}{\|\eta^{-1}\circ\xi\|_{\mathbb{H}^n}}\right)\|\eta^{-1}\circ\xi\|_{\mathbb{H}^n}
\le2^{i+4}\|\eta^{-1}\circ\xi\|_{\mathbb{H}^n}.
\end{equation*} Furthermore, ![]() $w_i\le k_i\le2\varepsilon\omega(r_j)$ in Bj (by
$w_i\le k_i\le2\varepsilon\omega(r_j)$ in Bj (by ![]() $u_j\ge0$ in Bj), and
$u_j\ge0$ in Bj), and ![]() $w_i\le k_i+|u|$ in
$w_i\le k_i+|u|$ in ![]() $\mathbb{H}^n\setminus B_j$. In a similar way to treat I 2 in the proof of lemma 4.1, by applying (4.19), (4.20), the definition of ɛ and
$\mathbb{H}^n\setminus B_j$. In a similar way to treat I 2 in the proof of lemma 4.1, by applying (4.19), (4.20), the definition of ɛ and ![]() $B_{j+1}\subset B^i$ we derive
$B_{j+1}\subset B^i$ we derive
 \begin{align*}
&\quad \sup_{\eta\in \tilde{B}^i}\int_{\mathbb{H}^n\setminus B^i}\frac{h(\xi,\eta,w_i(\xi))}{\|\eta^{-1}\circ\xi\|^Q_{\mathbb{H}^n}}\,d\xi \\
&\leq \sup_{\eta\in \tilde{B}^i}\int_{\mathbb{H}^n\setminus B^i}\frac{w_i^{p-1}+w_i^{q-1}}{\|\eta^{-1}\circ\xi\|^{Q+sp}_{\mathbb{H}^n}}
+a^+_{j+1}\frac{w_i^{q-1}}{\|\eta^{-1}\circ\xi\|^{Q+tq}_{\mathbb{H}^n}}\,d\xi\\
&\leq C2^{i(Q+sp+tq)}\int_{\mathbb{H}^n\setminus B_{j+1}}\frac{w_i^{p-1}+w_i^{q-1}}{\|\xi_0^{-1}\circ\xi\|^{Q+sp}_{\mathbb{H}^n}}
+a^+_{j+1}\frac{w_i^{q-1}}{\|\xi_0^{-1}\circ\xi\|^{Q+tq}_{\mathbb{H}^n}}\,d\xi\\
&\leq C2^{i(Q+sp+tq)}\int_{\mathbb{H}^n\setminus B_{j}}\frac{|u_j|^{p-1}+|u_j|^{q-1}}{\|\xi_0^{-1}\circ\xi\|^{Q+sp}_{\mathbb{H}^n}}+
a^+_{j+1}\frac{|u_j|^{q-1}}{\|\xi_0^{-1}\circ\xi\|^{Q+tq}_{\mathbb{H}^n}}\,d\xi\\
&\quad+ C2^{i(Q+sp+tq)}\int_{\mathbb{H}^n\setminus B_{j+1}}\frac{k_i^{p-1}+k_i^{q-1}}{\|\xi_0^{-1}\circ\xi\|^{Q+sp}_{\mathbb{H}^n}}+
a^+_{j+1}\frac{k_i^{q-1}}{\|\xi_0^{-1}\circ\xi\|^{Q+tq}_{\mathbb{H}^n}}\,d\xi\\
&\leq C2^{i(Q+sp+tq)}\left(\frac{N\omega(r_j)^{p-1}}{r_j^{sp}\sigma^{\beta(p-1)}}+a^+_{j+1}\frac{\omega(r_j)^{q-1}}{r_j^{tq}\sigma^{\beta(q-1)}}
+\frac{k_i^{p-1}+k_i^{q-1}}{r_{j+1}^{sp}}+a^+_{j+1}\frac{k_i^{q-1}}{r_{j+1}^{tq}}\right) \\
&\leq C2^{i(Q+sp+tq)}\left(\frac{Nk_i^{p-1}}{\varepsilon^{p-1}r_j^{sp}\sigma^{\beta(p-1)}}+a^+_{j+1}\frac{k_i^{q-1}}{\varepsilon^{q-1}r_j^{tq}\sigma^{\beta(q-1)}}
+\frac{Nk_i^{p-1}}{r_{j+1}^{sp}}+a^+_{j+1}\frac{k_i^{q-1}}{r_{j+1}^{tq}}\right) \\
&\leq CN2^{i(Q+sp+tq)}\left(\frac{\sigma^{sp-\frac{sp(p-1)}{q-1}}k_i^{p-1}}{r_{j+1}^{sp}}+a^+_{j+1}\frac{\sigma^{tq-sp}k_i^{q-1}}{r_{j+1}^{tq}}
+\frac{\overline{G}(k_i)}{k_i}\right) \\
&\le CN2^{i(Q+sp+tq)}\frac{\overline{G}(k_i)}{k_i}.
\end{align*}
\begin{align*}
&\quad \sup_{\eta\in \tilde{B}^i}\int_{\mathbb{H}^n\setminus B^i}\frac{h(\xi,\eta,w_i(\xi))}{\|\eta^{-1}\circ\xi\|^Q_{\mathbb{H}^n}}\,d\xi \\
&\leq \sup_{\eta\in \tilde{B}^i}\int_{\mathbb{H}^n\setminus B^i}\frac{w_i^{p-1}+w_i^{q-1}}{\|\eta^{-1}\circ\xi\|^{Q+sp}_{\mathbb{H}^n}}
+a^+_{j+1}\frac{w_i^{q-1}}{\|\eta^{-1}\circ\xi\|^{Q+tq}_{\mathbb{H}^n}}\,d\xi\\
&\leq C2^{i(Q+sp+tq)}\int_{\mathbb{H}^n\setminus B_{j+1}}\frac{w_i^{p-1}+w_i^{q-1}}{\|\xi_0^{-1}\circ\xi\|^{Q+sp}_{\mathbb{H}^n}}
+a^+_{j+1}\frac{w_i^{q-1}}{\|\xi_0^{-1}\circ\xi\|^{Q+tq}_{\mathbb{H}^n}}\,d\xi\\
&\leq C2^{i(Q+sp+tq)}\int_{\mathbb{H}^n\setminus B_{j}}\frac{|u_j|^{p-1}+|u_j|^{q-1}}{\|\xi_0^{-1}\circ\xi\|^{Q+sp}_{\mathbb{H}^n}}+
a^+_{j+1}\frac{|u_j|^{q-1}}{\|\xi_0^{-1}\circ\xi\|^{Q+tq}_{\mathbb{H}^n}}\,d\xi\\
&\quad+ C2^{i(Q+sp+tq)}\int_{\mathbb{H}^n\setminus B_{j+1}}\frac{k_i^{p-1}+k_i^{q-1}}{\|\xi_0^{-1}\circ\xi\|^{Q+sp}_{\mathbb{H}^n}}+
a^+_{j+1}\frac{k_i^{q-1}}{\|\xi_0^{-1}\circ\xi\|^{Q+tq}_{\mathbb{H}^n}}\,d\xi\\
&\leq C2^{i(Q+sp+tq)}\left(\frac{N\omega(r_j)^{p-1}}{r_j^{sp}\sigma^{\beta(p-1)}}+a^+_{j+1}\frac{\omega(r_j)^{q-1}}{r_j^{tq}\sigma^{\beta(q-1)}}
+\frac{k_i^{p-1}+k_i^{q-1}}{r_{j+1}^{sp}}+a^+_{j+1}\frac{k_i^{q-1}}{r_{j+1}^{tq}}\right) \\
&\leq C2^{i(Q+sp+tq)}\left(\frac{Nk_i^{p-1}}{\varepsilon^{p-1}r_j^{sp}\sigma^{\beta(p-1)}}+a^+_{j+1}\frac{k_i^{q-1}}{\varepsilon^{q-1}r_j^{tq}\sigma^{\beta(q-1)}}
+\frac{Nk_i^{p-1}}{r_{j+1}^{sp}}+a^+_{j+1}\frac{k_i^{q-1}}{r_{j+1}^{tq}}\right) \\
&\leq CN2^{i(Q+sp+tq)}\left(\frac{\sigma^{sp-\frac{sp(p-1)}{q-1}}k_i^{p-1}}{r_{j+1}^{sp}}+a^+_{j+1}\frac{\sigma^{tq-sp}k_i^{q-1}}{r_{j+1}^{tq}}
+\frac{\overline{G}(k_i)}{k_i}\right) \\
&\le CN2^{i(Q+sp+tq)}\frac{\overline{G}(k_i)}{k_i}.
\end{align*}Therefore,
 \begin{equation}
J_2\le CN2^{i(Q+sp+tq)}\overline{G}(k_i)A_i.
\end{equation}
\begin{equation}
J_2\le CN2^{i(Q+sp+tq)}\overline{G}(k_i)A_i.
\end{equation} On the other hand, making use of lemma 2.8 with ![]() $u:=w_i$ yields that
$u:=w_i$ yields that
 \begin{align}
&\quad A^\frac{1}{\gamma}_{i+1}\overline{G}(k_i-k_{i+1})\nonumber\\
&\le\left(-\!\!\!\!\!\!\int_{B^{i+1}}\left(\left|\frac{w_i}{r^s_{j+1}}\right|^p+a^+_{j+1}\left|\frac{w_i}{r^t_{j+1}}\right|^q\right)^\gamma\,d\xi\right)
^\frac{1}{\gamma} \nonumber\\
&\leq CN\left(\frac{D_1(\hat{\rho}_i,\rho_{i+1})}{r_{j+1}^{sp}}+\frac{\widetilde{D}_1(\hat{\rho}_i,\rho_{i+1})}{r_{j+1}^{tq}}\right)
-\!\!\!\!\!\!\int_{\hat{B}^i}\int_{\hat{B}^i}\frac{H(\xi,\eta,|w_i(\xi)-w_i(\eta)|)}{\|\eta^{-1}\circ\xi\|^Q_{\mathbb{H}^n}}\,d\xi d\eta \nonumber\\
&\quad+CN-\!\!\!\!\!\!\int_{\hat{B}^i}\left|\frac{w_i}{r^s_{j+1}}\right|^p
+a^-_{j+1}\left|\frac{w_i}{r^t_{j+1}}\right|^q\,d\xi.
\end{align}
\begin{align}
&\quad A^\frac{1}{\gamma}_{i+1}\overline{G}(k_i-k_{i+1})\nonumber\\
&\le\left(-\!\!\!\!\!\!\int_{B^{i+1}}\left(\left|\frac{w_i}{r^s_{j+1}}\right|^p+a^+_{j+1}\left|\frac{w_i}{r^t_{j+1}}\right|^q\right)^\gamma\,d\xi\right)
^\frac{1}{\gamma} \nonumber\\
&\leq CN\left(\frac{D_1(\hat{\rho}_i,\rho_{i+1})}{r_{j+1}^{sp}}+\frac{\widetilde{D}_1(\hat{\rho}_i,\rho_{i+1})}{r_{j+1}^{tq}}\right)
-\!\!\!\!\!\!\int_{\hat{B}^i}\int_{\hat{B}^i}\frac{H(\xi,\eta,|w_i(\xi)-w_i(\eta)|)}{\|\eta^{-1}\circ\xi\|^Q_{\mathbb{H}^n}}\,d\xi d\eta \nonumber\\
&\quad+CN-\!\!\!\!\!\!\int_{\hat{B}^i}\left|\frac{w_i}{r^s_{j+1}}\right|^p
+a^-_{j+1}\left|\frac{w_i}{r^t_{j+1}}\right|^q\,d\xi.
\end{align} Thanks to the definitions of ![]() $D_1,\widetilde{D}_1$ and
$D_1,\widetilde{D}_1$ and ![]() $\hat{\rho}_i,\rho_{i+1}$, we from
$\hat{\rho}_i,\rho_{i+1}$, we from ![]() $\hat{\rho}_i\approx\rho_{i+1}\approx r_{j+1}$ and
$\hat{\rho}_i\approx\rho_{i+1}\approx r_{j+1}$ and ![]() $\hat{\rho}_i-\rho_{i+1}=2^{-i-3}r_{j+1}$ calculate
$\hat{\rho}_i-\rho_{i+1}=2^{-i-3}r_{j+1}$ calculate
 \begin{equation*}
\frac{D_1(\hat{\rho}_i,\rho_{i+1})}{r_{j+1}^{sp}}\le C2^{i(Q+sp+p)}, \quad \frac{\widetilde{D}_1(\hat{\rho}_i,\rho_{i+1})}{r_{j+1}^{tq}}\le C2^{i(Q+tq+q)}.
\end{equation*}
\begin{equation*}
\frac{D_1(\hat{\rho}_i,\rho_{i+1})}{r_{j+1}^{sp}}\le C2^{i(Q+sp+p)}, \quad \frac{\widetilde{D}_1(\hat{\rho}_i,\rho_{i+1})}{r_{j+1}^{tq}}\le C2^{i(Q+tq+q)}.
\end{equation*}It is easy to obtain
 \begin{equation}
-\!\!\!\!\!\!\int_{\hat{B}^i}\left|\frac{w_i}{r^s_{j+1}}\right|^p
+a^-_{j+1}\left|\frac{w_i}{r^t_{j+1}}\right|^q\,d\xi\le C-\!\!\!\!\!\!\int_{{B}^i}\overline{G}(w_i)\,d\xi\le C\overline{G}(k_i)A_i.
\end{equation}
\begin{equation}
-\!\!\!\!\!\!\int_{\hat{B}^i}\left|\frac{w_i}{r^s_{j+1}}\right|^p
+a^-_{j+1}\left|\frac{w_i}{r^t_{j+1}}\right|^q\,d\xi\le C-\!\!\!\!\!\!\int_{{B}^i}\overline{G}(w_i)\,d\xi\le C\overline{G}(k_i)A_i.
\end{equation}It follows from (4.22)–(4.26) that
 \begin{equation*}
\begin{split}
A^\frac{1}{\gamma}_{i+1}\overline{G}(2^{-i-1}\varepsilon\omega(r_j))&=A^\frac{1}{\gamma}_{i+1}\overline{G}(k_i-k_{i+1})\\
&\le
CN^22^{i2(Q+2q)}\overline{G}(k_i)A_i\\
&\le CN^2 2^{i2(Q+2q)}\overline{G}(\varepsilon\omega(r_j))A_i,
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
A^\frac{1}{\gamma}_{i+1}\overline{G}(2^{-i-1}\varepsilon\omega(r_j))&=A^\frac{1}{\gamma}_{i+1}\overline{G}(k_i-k_{i+1})\\
&\le
CN^22^{i2(Q+2q)}\overline{G}(k_i)A_i\\
&\le CN^2 2^{i2(Q+2q)}\overline{G}(\varepsilon\omega(r_j))A_i,
\end{split}
\end{equation*}and further
 \begin{equation*}
A_{i+1}\le CN^{2\gamma}2^{i2(Q+3q)\gamma}A^\gamma_i,
\end{equation*}
\begin{equation*}
A_{i+1}\le CN^{2\gamma}2^{i2(Q+3q)\gamma}A^\gamma_i,
\end{equation*} where  $\gamma=\min\left\{\frac{p^*_s}{p},\frac{q^*_t}{q}\right\} \gt 1$ and C depends on
$\gamma=\min\left\{\frac{p^*_s}{p},\frac{q^*_t}{q}\right\} \gt 1$ and C depends on ![]() $\mathrm{\textbf{data}}$ and β.
$\mathrm{\textbf{data}}$ and β.
Now if A 0 fulfils
 \begin{align}
A_0=\frac{|2B_{j+1}\cap\{u_j\leq 2\varepsilon\omega(r_j)\}|}{|2B_{j+1}|}\leq (CN^{2\gamma})^{-\frac{1}{\gamma-1}}2^{-\frac{2\gamma(Q+3q)}{(\gamma-1)^2}}=:\mu,
\end{align}
\begin{align}
A_0=\frac{|2B_{j+1}\cap\{u_j\leq 2\varepsilon\omega(r_j)\}|}{|2B_{j+1}|}\leq (CN^{2\gamma})^{-\frac{1}{\gamma-1}}2^{-\frac{2\gamma(Q+3q)}{(\gamma-1)^2}}=:\mu,
\end{align} then by lemma 3.4 we deduce ![]() $A_i\rightarrow0$ as
$A_i\rightarrow0$ as ![]() $i\rightarrow\infty$. This means
$i\rightarrow\infty$. This means
which together with (4.17) leads to
 \begin{equation*}
\mathop{\rm osc}\limits_{B_{j+1}}u\le (1-\varepsilon)\omega(r_j)=(1-\varepsilon)\sigma^{-\beta}\omega(r_{j+1}).
\end{equation*}
\begin{equation*}
\mathop{\rm osc}\limits_{B_{j+1}}u\le (1-\varepsilon)\omega(r_j)=(1-\varepsilon)\sigma^{-\beta}\omega(r_{j+1}).
\end{equation*} Finally, choosing  $\beta\in\left(0,\frac{sp}{q-1}\right)$ small enough such that
$\beta\in\left(0,\frac{sp}{q-1}\right)$ small enough such that
 \begin{equation*}
\sigma^\beta\geq 1-\varepsilon=1-\sigma^{\frac{sp}{q-1}-\beta},
\end{equation*}
\begin{equation*}
\sigma^\beta\geq 1-\varepsilon=1-\sigma^{\frac{sp}{q-1}-\beta},
\end{equation*} then  $\mathrm{osc}_{B_{j+1}}u\leq\omega(r_{j+1})$, and β depends on
$\mathrm{osc}_{B_{j+1}}u\leq\omega(r_{j+1})$, and β depends on ![]() $\mathrm{\textbf{data}}$ and
$\mathrm{\textbf{data}}$ and ![]() $\|u\|_{L^\infty(\Omega')}$. Indeed, due to (4.21), it yields that
$\|u\|_{L^\infty(\Omega')}$. Indeed, due to (4.21), it yields that
 \begin{equation*}
A_0\le \frac{C_{\rm log}N^3}{\log\frac{1}{\sigma}}\leq \mu,
\end{equation*}
\begin{equation*}
A_0\le \frac{C_{\rm log}N^3}{\log\frac{1}{\sigma}}\leq \mu,
\end{equation*} by picking  $\sigma\le \mathrm{exp}\left(-\frac{C_{\rm log}N^3}{\mu}\right)$. Then, we select
$\sigma\le \mathrm{exp}\left(-\frac{C_{\rm log}N^3}{\mu}\right)$. Then, we select  $\sigma=\min\left\{\frac{1}{4},\mathrm{exp}\left(-\frac{C_{\rm log}N^3}{\mu}\right)\right\}$ to ensure the condition (4.27) does hold true. Now we finish the proof.
$\sigma=\min\left\{\frac{1}{4},\mathrm{exp}\left(-\frac{C_{\rm log}N^3}{\mu}\right)\right\}$ to ensure the condition (4.27) does hold true. Now we finish the proof.
Acknowledgements
The authors wish to thank the anonymous reviewer for valuable comments and suggestions to improve the manuscript. This work was supported by the National Natural Science Foundation of China (No. 12071098), the Postdoctoral Science Foundation of Heilongjiang Province (No. LBH-Z22177), the National Postdoctoral Program for Innovative Talents of China (No. BX20220381), the Fundamental Research Funds for the Central Universities (No. 2022FRFK060022) and the Natural Science Basic Research Program of Shaanxi (No. 2024JC-YBQN-0054).
Declarations
Conflict of interest
The authors declare that there is no conflict of interest. We also declare that this manuscript has no associated data.
Data availability
Data sharing is not applicable to this article as no datasets were generated or analysed during the current study.