INTRODUCTION
Epidemiological models can be developed to represent and simulate the spread of a pathogen in a population according to the main factors influencing its transmission [Reference Anderson and May1–Reference Andersson and Britton3]. They allow the investigation of the expected dynamics of the pathogen's spread for various initial situations (herds, herd managements, proportions of susceptible animals) under various control actions. The model results are the prediction of extent and duration of infection under various control strategies. Relevance of results obtained from predictive models depends on the assumptions made on the population structure and dynamics (host only if microparasite, host and parasite otherwise), on the biology of the host–parasite interaction (transmission, recovery or removal) and on the mathematical modelling assumptions to specify them [Reference Daley and Gani4]. The complexity of the models depends on the assumptions and on the retained modelling options.
Bovine viral diarrhoea virus (BVDV) is a microparasite infection transmitted from infected animals both vertically and horizontally by direct contact or indirectly via contaminated equipment. When a susceptible animal is infected (horizontal transmission), it becomes transiently infected and excretes the virus in a low amount during a short time period before becoming protected against a new BVDV infection [Reference Radostits and Littlejohns5–Reference Houe7]. The main feature of an infection by BVDV is that transplacental transmission of the virus (vertical transmission) can lead to the birth of a persistently infected (PI) animal (immunotolerance induced by a fetal infection in early pregnancy). PI animals excrete the virus lifelong in a greater amount than transiently infected animals [Reference Houe7]. They are the main source of new BVDV infections [Reference Radostits and Littlejohns5, Reference Houe8]. Thus, to model BVDV spread dynamics, classical SIR models are too simple. In a SIR model, animals are separated into three exclusive statuses: S for susceptible, I for infectious and R for immune. For BVDV, transiently infected and PI animals cannot be regrouped in one infectious status, and both vertical and horizontal transmissions should be considered. Moreover, a cattle herd is a structured population, managed, with a small controlled size and animals enter by birth or possible purchase, particularities which are not considered in a simple SIR model. The herd structure and dynamics influence BVDV spread. In a dairy herd, animals are separated into subgroups (same age or physiological status) inducing a contact structure (heterogeneous mixing) and then a heterogeneity of virus transmission between subgroups. A form of transmission rate should be chosen according to assumptions on the horizontal transmission, considering the contact structure and the two different levels of excretion by infected animals [Reference De Jong, Diekmann, Heesterbeek and Mollison9, Reference McCallum, Barlow and Hone10]. The population has a small controlled size, and is managed by the farmer, contrary to human population dynamics (not controlled, large size). The particularities of the population structure and dynamics should be taken into account in models dealing with slow spreading animal diseases, i.e. where transmission occurs mainly by close contact (nose to nose).
The objectives of this paper were to review published models for BVDV spread in a cattle herd, to describe and discuss the main modelling options and assumptions used and to propose possible ways to improve existing models. Comparison of model results was not an objective of this review. In the following, the characteristics of BVDV infection and transmission are detailed throughout the description of the modelling options and assumptions.
SELECTED MODELS
Published models were systematically searched. To identify papers, a literature search was conducted of the CAB (Commonwealth Abstract Bureau, Oxon, UK) and Medline (National Library of Medicine, Rockville Pike, USA) databases for papers indexed between 1972 and 2005. The search terms used were (Bovine and Virus and Diarrh* and Model*) wherever in title, abstract, descriptors and subject headings. Only articles published in peer-reviewed journals and written in English were retained. Only papers describing models that aimed at describing the virus spread in cattle herds were considered. Economic models aiming at assessing the cost of the disease, but either not relying on virus transmission modelling or not providing any information on the dynamics of the virus spread were not selected (e.g. [Reference Hartley and Richards11–Reference Stott14]). Two papers initially selected were excluded from this review because their models did not predict the virus spread in a herd. In one non-selected paper, a model was proposed assuming only transiently infected animals as excreting animals in a simple group of susceptible lactating cows [Reference Moerman15]. This simple model aimed at estimating a horizontal transmission coefficient by fitting the model to data observed in a specific population, but did not represent a full herd. In ref. [Reference Innocent16], a deterministic model was proposed to compare its results to the average output of another published stochastic model [Reference Innocent17]. This model aiming at verification only was excluded. One other paper [Reference Humphry, Stott and Gunn18] initially selected was not considered further. In ref. [Reference Humphry, Stott and Gunn18], an individual-based model was proposed as a modification of a previously published model [Reference Gunn, Stott and Humphry19] assuming that all individuals are identified. As assumptions on BVDV spread and on dynamics of the herd were the same in the two models, only the model [Reference Gunn, Stott and Humphry19] was considered.
Finally, six models were selected [Reference Innocent17, Reference Gunn, Stott and Humphry19–Reference Viet23]. All models represented BVDV spread within a dairy herd except the model [Reference Gunn, Stott and Humphry19] that was within a beef herd. The objectives, as mentioned by the authors, were either to predict the virus spread within a herd under different assumptions [Reference Innocent17, Reference Cherry, Reeves and Smith22, Reference Viet23], or to also include the economic assessment of the disease consequences at the herd level [Reference Gunn, Stott and Humphry19–Reference Sørensen, Enevoldsen and Houe21]. BVDV spread was simulated over either 2 years [Reference Pasman, Dijkhuizen and Wentink20, Reference Cherry, Reeves and Smith22] or 10 years [Reference Innocent17, Reference Gunn, Stott and Humphry19, Reference Sørensen, Enevoldsen and Houe21, Reference Viet23]. The initial herds were either derived from a sample of herds [Reference Pasman, Dijkhuizen and Wentink20], or directly observed [Reference Sørensen, Enevoldsen and Houe21] or defined a priori [Reference Innocent17, Reference Gunn, Stott and Humphry19, Reference Sørensen, Enevoldsen and Houe21–Reference Viet23]. Results were expressed in terms of the extent of infection (proportions or number of animals in the different infection statuses at different time after virus introduction), of the virus persistence and of the virus disappearance from the herd.
TYPES OF MODELS
To characterize the selected models, three modelling characteristics used in the classification of epidemiological models proposed in ref. [Reference Hurd and Kaneene24] were retained in the present review: effect of chance (i.e. variability), mathematical treatment of time (continuous or discrete) and treatment of individuals (continuous-entity: if the individuals in any state are treated as a real number; discrete-entity: if all individuals are tracked over time or if the individuals in any state are treated as an entire number). We added another characteristic, the time dependency of the transitions. The transitions can be independent of time (Markov assumption), or depend only on the time spent in the states (semi-Markov assumption) or be time-dependent (non-Markov assumption). The modelling options of the selected models are presented in Table 1. The model complexity, due to the considered factors influencing the virus spread and the level of representation in the model of the disease mechanisms, are described in the next sections and not included here. The six selected models were classified into three general types.
Table 1. Modelling options and simulation procedure of six bovine viral diarrhoea virus models

n.a., Not applicable; n.g., not given.
* Treatment of animals.
† Time-dependence of transition: The transitions can be triggered independently of time, depend only on time spent or be time dependent.
‡ Variables represent the total number of animals in each infection status or the density of animals in each infection status (number of animals per unit area).
Three models were discrete-entity stochastic models [Reference Innocent17, Reference Sørensen, Enevoldsen and Houe21, Reference Viet23]. In stochastic models, the variability of the dynamics of the virus spread within a herd can be assessed by carrying out several replications with the same input. Clearance of the virus is a possible behaviour (i.e. disappearance of all excreting animals and animals carrying a PI foetus) and the probability of clearance can be estimated. These models are frequently studied by simulation. The virus transmission can be modelled in herds of different sizes. In discrete-entity models, either the number of animals in any state is an entire number (no fraction of animals) or every animal is tracked over time. In models tracking each animal over time, the evolution of the population is the sum of the evolution of all animals. The individual-animal characteristics are known over time (e.g. age, parity, time spent in different subgroups). The discrete-entity approach allows the modelling of herd dynamics and herd management considering either a high number of subpopulations or the individual characteristics of each animal.
Two models were continuous-entity deterministic models [Reference Pasman, Dijkhuizen and Wentink20, Reference Cherry, Reeves and Smith22]. In deterministic models, only an average behaviour of the modelled system is obtained. The results are easier to obtain than with stochastic models and sometimes with analytical methods. It is not possible to represent variability and to estimate any probability because all the replications with the same input lead to the same output. When the population is small, the deterministic models would not provide a realistic approximation of the average behaviour. When the population size is sufficiently large, deterministic models are often considered as approximations of corresponding stochastic Markov models. The model [Reference Cherry, Reeves and Smith22] was defined for a population of 67 animals by km2 and the model [Reference Pasman, Dijkhuizen and Wentink20] defined for a population of 100 animals separated into three groups with no mixing, which is not a very large population. In ref. [Reference Innocent16], the proportions of animals in each health status simulated with the stochastic and deterministic models were similar for a herd size >40 (assuming a homogeneous mixed population). In continuous-entity models, the individual animals are not identified and fractions of animals exist. Introducing some individual animal characteristics is possible (through definition of subpopulations) but increases the model complexity. Otherwise, identical transition rates are applied to all animals. For example, a single exit rate was applied to all animals whatever their age in ref. [Reference Cherry, Reeves and Smith22]. The reviewed deterministic continuous-entity models had no [Reference Cherry, Reeves and Smith22] or three [Reference Pasman, Dijkhuizen and Wentink20] subpopulations and can hardly account for either the complexity of BVDV spread or the dynamics of a cattle herd. In ref. [Reference Cherry, Reeves and Smith22], the authors stated that their model was a possible approximation of more complete stochastic models, but provided a more transparent behaviour (i.e. effects of parameter values on the model behaviour were easy to identify). The deterministic continuous-entity models are easy to study. Some theoretical results are available for simple models to estimate the minimum level of vaccination required to induce pathogen clearance (one aim of ref. [Reference Cherry, Reeves and Smith22]). Such models may be used for a very large population when only average results are needed.
One model [Reference Gunn, Stott and Humphry19] was a continuous-entity stochastic model. The stochastic part of this model was limited. Only a random element was considered: in the case of a number of PI animals between 0 and 1, the simulated number of PI animals was triggered randomly to 0 or 1. This model is less complex than discrete-entity models and allowed the simulation of a range of behaviours (an advantage of stochastic models). The complexity of BVDV spread within a herd is simplified in ref. [Reference Gunn, Stott and Humphry19].
ASSUMPTIONS IN MODELS
Virus spread
The biology of an infectious disease occurring at the individual level, such as illness, duration of excretion after an infection, immune responses, and transmission, is represented in a model by mathematical expressions with different underlying assumptions which are often implicit in published model descriptions.
BVDV infection status and excretion
Animals with no previous exposure to BVDV are susceptible. When infected, they first become latently infected (i.e. in an incubation period with no virus excretion) and then transiently infected (i.e. infectious) during a few days to a few weeks. After the transiently infected status, animals become immune and this immunity is assumed to be lifelong [Reference Houe7]. Calves from immune dams receive maternal antibodies via the colostrum (passive immunity). The maternal antibodies disappear between the ages of 6 and 8 months [Reference Coria and McClurkin25, Reference Menanteau-Horta26] and more rapidly (4–8 weeks) for PI animals [Reference Palfi, Houe and Philipsen27]. After vertical transmission, some animals are born persistently infected (see next section) and excrete the virus lifelong.
Different BVDV infection statuses were modelled (Table 2). PI animals were always modelled as excreting animals contrary to transiently infected animals. Ignoring excretion by transiently infected animals ([Reference Gunn, Stott and Humphry19, Reference Sørensen, Enevoldsen and Houe21]) may result in underestimating the virus spread in a herd. In ref. [Reference Innocent17], the authors compared the behaviour of their model considering virus transmission, on the one hand, by both transiently infected and PI animals, and, on the other hand, by PI animals only. They concluded that the dynamics of the virus spread differed. New infections occurred more frequently at the beginning of the simulation period if both transiently infected and PI animals were assumed to excrete the virus. No data was available yet to study the accuracy of this dynamic of BVDV spread. However, virus spread was shown to be possible in a herd without any PI animals [Reference Moerman15]. Transiently infected status should then be included in models. The duration of excretion varied, but available information also reported different durations resulting in a wide confidence interval. Improved knowledge on the distribution of duration of excretion is needed. The duration modelled in ref. [Reference Cherry, Reeves and Smith22] was consistent with the duration reported in ref. [Reference Duffell and Harkness28] (15 days) but longer than the average duration modelled in ref. [Reference Viet23], which was consistent with the one estimated in ref. [Reference McGowan6] (5–6 days). The transiently infected status was not introduced as a specific status of animals in two models [Reference Innocent17, Reference Pasman, Dijkhuizen and Wentink20]. Nevertheless, an estimation of the excretion by transiently infected animals was considered for the transmission modelling in ref. [Reference Innocent17], assuming that all newly seroconverted animals have excreted the virus during a period of 10 days. These models were discrete-time models with lengthy time-stepping (3 months and 1 month). As the time spent in a status cannot be shorter than the time-step, duration of excretion by transiently infected animals and then virus transmission by transiently infected animals would be overestimated with such long time-steps if a specific status is defined.
Table 2. Bovine viral diarrhoea virus infection statuses and virus excretion considered in the six selected models

E, Excreting the virus; NE, not excreting the virus; —, not in the model; PI, persistently infected; n.g., not given.
* Values within parentheses are mean duration in the status.
† Status not modelled but approximated from number of seroconverting animals.
‡ Direct and indirect transmission.
In ref. [Reference Cherry, Reeves and Smith22], the period between infection and immunity was split into two infection statuses: latently infected (i.e. infected with no virus excretion) and transiently infected (infected with virus excretion). When the latently infected status is not modelled, the corresponding period can either be ignored or added to the period of excretion. The former option anticipates the arrival of newly infected animals in the transiently infected status. The latter option induces an overestimation of the virus transmission by transiently infected animals. In ref. [Reference Cherry, Reeves and Smith22], the simulated virus spread, with and without a latent period with a constant duration of transient excretion were compared. The authors concluded a negligible effect on the model behaviour. Thus for BVDV, the latent period can be ignored when predicting virus spread.
Via the colostrum, maternal antibodies protect against BVDV infection during a few months [Reference Kendrick and Franti29]. All models considered this protective passive immunity with two exceptions [Reference Gunn, Stott and Humphry19, Reference Pasman, Dijkhuizen and Wentink20]. If the corresponding status was modelled, the duration was consistent with available observations [Reference Coria and McClurkin25, Reference Menanteau-Horta26]. Ignoring the protection during this period results in simulating infection of calves earlier than if there was passive protection. Then, a higher proportion of heifers would have reached the immune status before pregnancy. With passive protection, some of these heifers could be still susceptible in pregnancy. Therefore, not considering passive protection could lead to an underestimation of the number of infections during pregnancy and to an underestimation of the number of births of PI calves.
Horizontal transmission
The horizontal transmission corresponds to the transmission of an agent from one infected host to a susceptible host by direct contact or indirectly. In models, horizontal transmission for an animal was defined as a transition from susceptible status to either the latently infected status [Reference Cherry, Reeves and Smith22] or the transiently infected status [Reference Innocent17, Reference Gunn, Stott and Humphry19, Reference Sørensen, Enevoldsen and Houe21, Reference Viet23], or the immune status [Reference Pasman, Dijkhuizen and Wentink20]. The transmission rate per susceptible animal is called the force of infection. The force of infection is defined either as a probability of infection for a susceptible animal during a time-step in the case of discrete-time models [Reference Innocent17, Reference Gunn, Stott and Humphry19–Reference Sørensen, Enevoldsen and Houe21] or as a rate of infection per susceptible animal per unit of time in the case of continuous-time models [Reference Cherry, Reeves and Smith22, Reference Viet23]. Forms of the force of infection rely on assumptions on transmission routes and mechanisms.
For BVDV, the virus transmission occurs mainly by direct contact, but also indirectly via contaminated equipments (such as tools, needles, boots, clothes) or is airborne at short distances [Reference Lang-Ree30, Reference Niskanen and Lindberg31]. In ref. [Reference Viet23], a transition rate was defined as the sum of a direct transmission rate within a subgroup and an indirect transmission rate between subgroups (see section ‘Separation into subgroups’). In other models, either a homogeneous mixing of all animals was considered [Reference Innocent17, Reference Gunn, Stott and Humphry19, Reference Sørensen, Enevoldsen and Houe21, Reference Cherry, Reeves and Smith22] or indirect virus transmission between subgroups was ignored [Reference Pasman, Dijkhuizen and Wentink20].
Form of the force of infection
Four types of the force of infection were used in the reviewed models (Reed–Frost, density-dependent, frequency-dependent, constant). The assumptions generally underlying these types are presented Table 3. In each type, susceptibility of animals and amount of virus excreted by animals in one excreting status are assumed to be, on average, identical whatever the population studied.
(a) Reed–Frost type [Reference Innocent17, Reference Gunn, Stott and Humphry19]. This type of transmission rate is used in discrete-time models. The probability of a susceptible animal still alive at the end of the time-step to be infected during this time-step is expressed as 1 minus the probability of not being infected:
(1)where r is the force of infection, c the probability that a contact between a susceptible and an excreting animal occurs and is effective, and I the number of excreting animals.
(b) Density-dependent type [Reference Cherry, Reeves and Smith22]. This type of the transmission rate is used mainly in continuous-time models and sometimes in discrete-time models. The density of new infections (number of newly infected animals per unit area) per unit of time was proportional to the density of susceptible animals and to the density of excreting animals. The transmission rate was defined as:
(2)where β is the transmission coefficient (rate of effective contacts between susceptible and excreting animals; this coefficient includes rate of contacts and effectiveness of transmission), and i the density of excreting animals.
(c) Frequency-dependent type [Reference Viet23]. This type of transmission rate is used mainly in continuous-time models and sometimes in discrete-time models. The rate of a new infection for a susceptible animal by direct transmission depends on the proportion of excreting animals in its subgroup. The direct transmission rate was defined as :
(3)where βd is the transmission coefficient, I the number of excreting animals and N the total number of animals in the subgroup.
(d) Constant rate [Reference Pasman, Dijkhuizen and Wentink20, Reference Sørensen, Enevoldsen and Houe21]. Transmission occurs, as soon as one excreting animal is present, independently of the number of excreting animals (constant r).
To model indirect transmission, an adapted frequency-dependent form was used in ref. [Reference Viet23]. The probability that equipment was contaminated by contact with PI animals from subgroup a depends on their proportion within subgroup a. The probability that a susceptible animal in subgroup b was in contact with this contaminated equipment depends on the subgroup size. The force of infection from PI animals in subgroup a was given by:
where r indirect(a|b) is the indirect transmission rate per susceptible animal in subgroup b from excreting animals in subgroup a; βab is the indirect transmission coefficient from subgroup a to subgroup b; I a is the number of excreting animals in subgroup a; N b is the total number of animals in subgroup b (where the susceptible animal is), and N a is the total number of animals in subgroup a.
Table 3. Forms, underlying assumptions and coefficient values of transmission rates used in the selected models to represent the horizontal transmission of the bovine viral diarrhoea virus

d, Day; wk, week; mo., month; yr, year.
* Values of the transmission rate given within the period in parentheses when at least one persistently infected animal was present.
† Three values of the transmission coefficient for persistently infected animals were considered.
Assumptions underlying the choice of transmission rates were implicit in the reviewed papers and differed. As BVDV transmission occurs mainly by contacts between susceptible and excreting animals, the probability that a contact involves an excreting animal is likely to be overestimated when considering the number of excreting animals but not the group size to calculate the transmission rate. Frequency-dependent rates can be assumed to be more appropriate, as well as density-dependent rates in the case of a constant total density (as in ref. [Reference Cherry, Reeves and Smith22]) that also induced a herd-size dependence. By contrast, the Reed–Frost type transmission rate used [Reference Innocent17, Reference Gunn, Stott and Humphry19] did not account for the herd size.
Aggregating excretion from two sources
PI and transiently infected animals excrete the virus in different amounts and can both induce horizontal transmission [Reference Houe7]. Models with these two types of excreting animals used either the same value of transmission coefficient whatever the type of excreting animals [Reference Innocent17] or two different transmission coefficients assuming different levels of excretion [Reference Cherry, Reeves and Smith22, Reference Viet23]. In the former case, transiently infected animals were then assumed to excrete the virus in the same amount as PI animals, which seems incorrect [Reference Houe7]. In the latter case, the transmission rate was the sum of two transmission rates:
where β1 and β2 are the coefficient of transmission by transiently infected animals and PI animals respectively, I T the number of transiently infected animals, I P the number of PI animals, and f(.) a function of a number of animals corresponding to the density (in ref. [Reference Cherry, Reeves and Smith22]) or to the proportion (in ref. [Reference Viet23]).
Values of the force of infection
The values of the transmission coefficients were determined according to experts' belief [Reference Innocent17, Reference Pasman, Dijkhuizen and Wentink20, Reference Sørensen, Enevoldsen and Houe21], or to literature review [Reference Gunn, Stott and Humphry19, Reference Viet23] or estimated from observed data [Reference Cherry, Reeves and Smith22]. Direct comparison of the value of the transmission coefficients was not possible as different forms of force of infection are used. The comparison of the horizontal transmission rates on the overall epidemic curves was not possible. The overall epidemic curve depends not only on the modelling of horizontal transmission but also on vertical transmission and herd dynamics, which differed in reviewed models. To compare the transmission rates used in the different models of the force of infection associated with the horizontal transmission by PI animals, we calculated the epidemic curves obtained in a similar stable population (theoretical situation). We approximated the proportion over time of animals infected by one PI animal in a closed group of constant size (no births and no deaths) assuming no excretion by transiently infected animals. We used the transmission rates proposed by each author in a deterministic model with either the time-step defined by the authors or a time-step of 1 day in case of initial continuous-time models (Table 3, Fig. 1). Using the coefficients of transmission by PI animals, the simulated epidemic curves differed between models (Fig. 1): the virus spread was fast for three models ([Reference Gunn, Stott and Humphry19] assuming a high transmission rate, and [Reference Sørensen, Enevoldsen and Houe21, Reference Cherry, Reeves and Smith22]), very low for one model [Reference Innocent17], and intermediate for other models [Reference Gunn, Stott and Humphry19, Reference Pasman, Dijkhuizen and Wentink20, Reference Viet23].
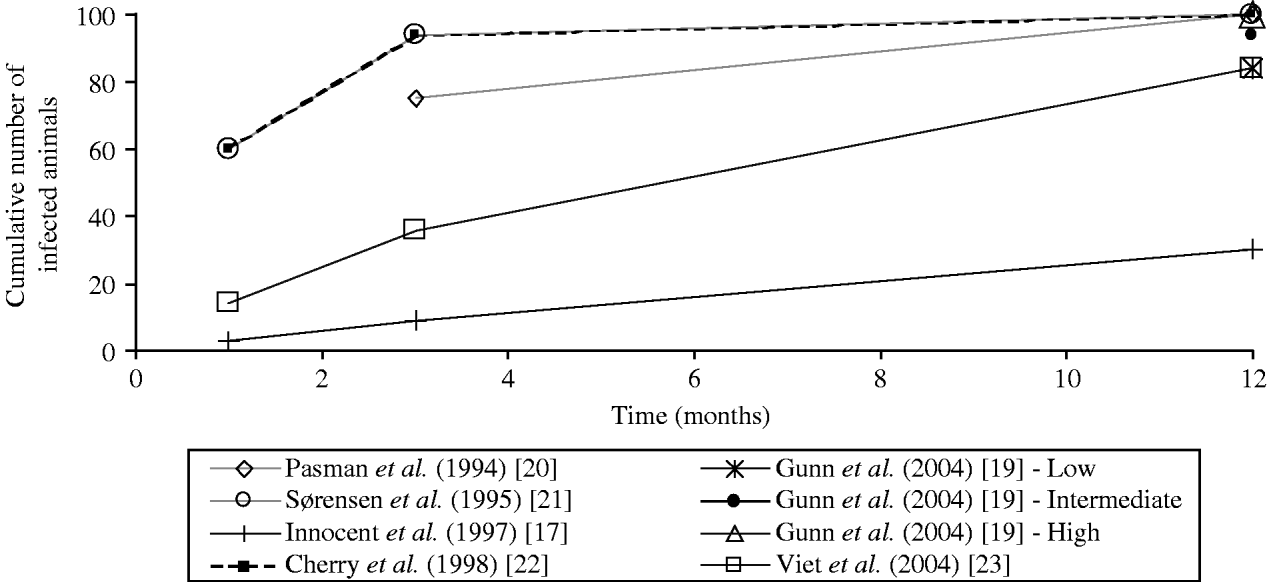
Fig. 1. Comparison of the values of horizontal transmission coefficients considered in six bovine viral diarrhoea virus models: estimation of the epidemic curves obtained in a similar stable population. The cumulative numbers of infected animals were estimated at 1, 3 and 12 months assuming an introduction of one persistently infected animal in a closed group of 100 animals with no excretion by transiently infected animals, no births and no deaths. A precautious approach should be followed when interpreting the figure: the straight lines between data marks are drawn to connect estimates for one transmission coefficient but do not correspond to a linear relationship.
The coefficient of virus transmission by PI animals was shown to influence the virus spread in two models [Reference Gunn, Stott and Humphry19, Reference Viet23]. No difference in the number of PI animals at equilibrium was reported when increasing the coefficient [Reference Cherry, Reeves and Smith22], which was not surprising as the authors’ initial coefficient induced a high virus spread (Fig. 1). For high values of the transmission coefficient by PI animals, no effect on the virus persistence was observed [Reference Viet23]. In ref. [Reference Innocent17], although the transmission rate was low, the authors reported that the use of a higher value for their transmission coefficient had no impact on the final epidemic size in their model. This result may be explained by the interaction of horizontal transmission with vertical transmission and herd dynamics. Further data are needed to increase knowledge on virus transmission level and then reduce the uncertainty on the transmission coefficient by PI animals.
In the two models where transiently infected animals were assumed to be excreting [Reference Cherry, Reeves and Smith22, Reference Viet23], the force of infection associated with transmission by transiently infected animals were equivalent (if assuming a subgroup size of 15 in ref. [Reference Viet23]). The values were in accord with the estimation from observed data in ref. [Reference Moerman15], assuming a virus excretion during 6 days. The model [Reference Viet23] was not sensitive to a small variation of the coefficient of virus transmission by transiently infected animals.
Vertical transmission
The vertical transmission corresponds to the virus transmission from a pregnant infected dam (PI or transiently infected) to her foetus. Calves born from PI dams are always PI. In the case of an infection of a susceptible dam, various outcomes can occur according to the age of the foetus (or embryo) at the time of the dam's infection: early or late embryonic death, abortion, congenital defect, birth of immune calf, birth of PI calf [Reference Radostits and Littlejohns5]. It is widely acknowledged that the occurrence of the different outcomes depends on the stage of pregnancy at time of infection [Reference Kendrick32, Reference Done33]. But, the use of published data to define a probability of outcomes according to the stage of pregnancy is difficult due to the large range of values in published data.
Calves born from PI dams were PI in all selected models. In the case of infection of a susceptible dam, the pregnancy period was split into 2–5 different stages determining the probabilities of the different possible consequences (Fig. 2). In discrete-entity models [Reference Innocent17, Reference Sørensen, Enevoldsen and Houe21, Reference Viet23], outcome of a transplacental transmission depended on the exact stage of pregnancy of each animal at the time of infection. Such an approach allows a more precise modelling of the vertical transmission, but requires precise data to define the probability of each outcome for each stage of pregnancy. In the continuous-entity model [Reference Cherry, Reeves and Smith22], because individual stages of pregnancy were not modelled, the population of susceptible animals becoming infected was split at random into three categories according to the average time spent in each category (not pregnant, ⩽150 days of pregnancy, >150 days of pregnancy). This modelling approach is simpler than the previous one with discrete-entity, but it assumes that the proportion of animals in each category is the same at each time-step. In ref. [Reference Gunn, Stott and Humphry19], the time-step was 1 year. The pregnancy could not then be divided into stages. For susceptible animals infected during the year, the infection status of the newborn calves was determined randomly. In ref. [Reference Pasman, Dijkhuizen and Wentink20], no information on the modelling of vertical transmission was provided.
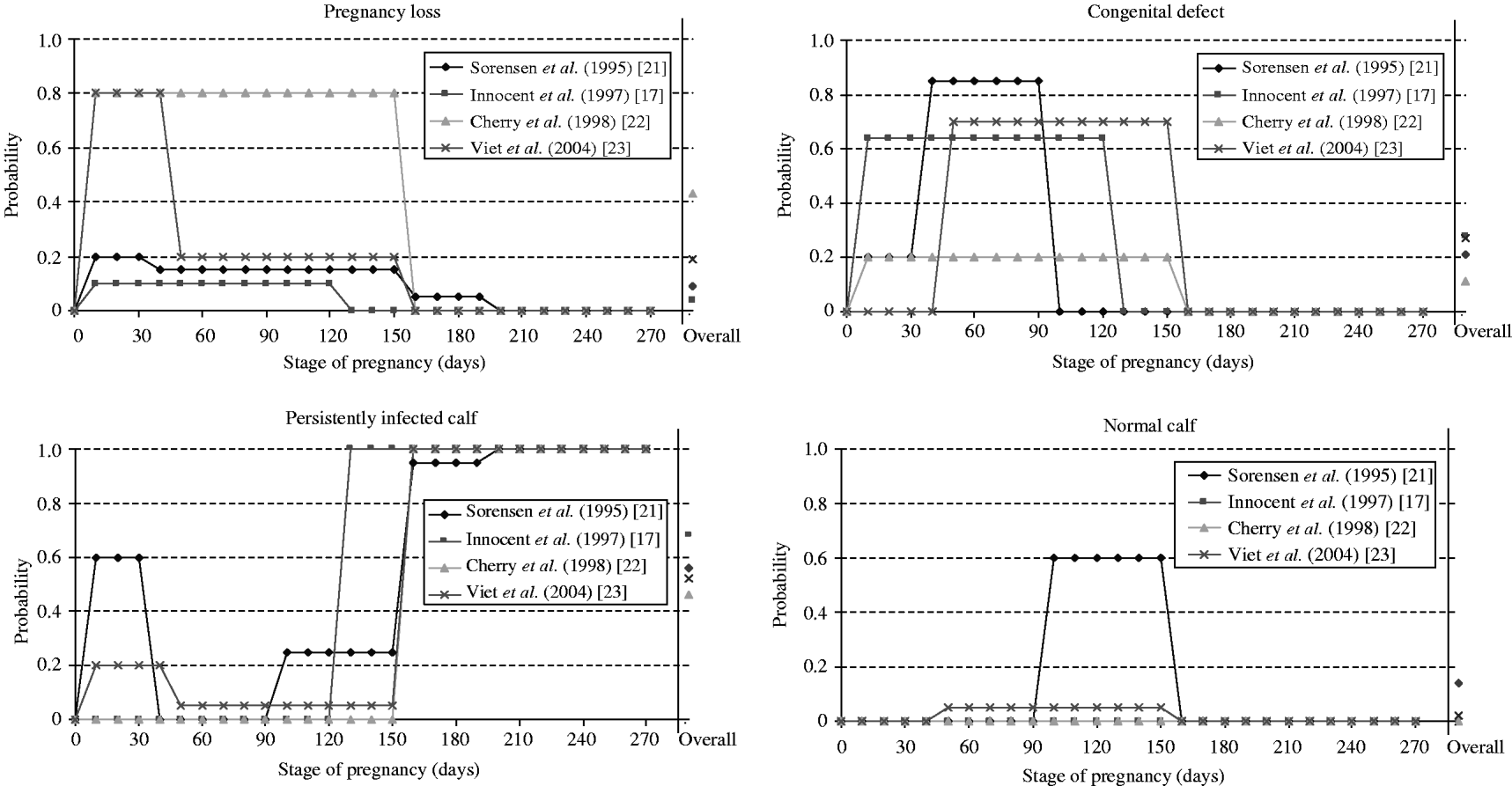
Fig. 2. Probabilities of consequences of an infection by the bovine viral diarrhoea virus during pregnancy used in four selected models for dams and embryo or foetus according to pregnancy stage at infection. An overall probability was estimated by us assuming a uniform distribution of the time of infection during pregnancy for comparison between the different models.
Among the consequences of an infection during pregnancy, the birth of a PI animal is the only one with a direct effect on the virus spread. The overall probability of vertical transmission differed widely between models (Fig. 2). Overall, birth of a PI calf was 2·5 times more likely to occur after an infection of a pregnant cow in refs [Reference Innocent17, Reference Viet23] than in ref. [Reference Cherry, Reeves and Smith22]. In ref. [Reference Cherry, Reeves and Smith22], considering a shorter period (duration of 105 days rather than 150 days) reduced the proportion of PI animals in the herd at equilibrium (from 1·2% to 0·9%). As PI animals are the main source of BVDV transmission, there is a need for further data to quantify the probability of vertical transmission.
Consequences of infection on herd demography
Different consequences of BVDV infections can influence the herd demography such as reproductive failures, abortions, growth retardation [Reference Houe8], and reduced lifespan of PI animals [Reference Duffell and Harkness28]. These production effects therefore influence the virus spread, through modification of the population dynamics. Other population effects (e.g. reduced milk yield) are important when considering economic consequences of the infection but they are not reported here, as they do not influence directly the virus spread within a herd.
Consequences on reproduction
Failure to conceive at artificial insemination (AI) can be induced by a BVDV infection [Reference McGowan6, Reference Grahn, Fahning and Zemjanis34]. As pregnancy losses induce either culling or increased calving intervals, BVDV spread can strongly influence herd dynamics.
Different effects of BVDV infection on reproduction were included in the models:
● delayed first heat after calving [Reference Sørensen, Enevoldsen and Houe21];
● reduced probability of conception after AI [Reference Pasman, Dijkhuizen and Wentink20, Reference Sørensen, Enevoldsen and Houe21, Reference Viet23];
● pregnancy loss including embryonic death, fetal death and abortion [Reference Innocent17, Reference Pasman, Dijkhuizen and Wentink20–Reference Viet23]. Probabilities of pregnancy losses differed according to stage of pregnancy (Fig. 2).
In ref. [Reference Gunn, Stott and Humphry19], the authors reported that the effect of abortion, conception failure and re-absorption due to BVDV infections were considered in their model but provided no information on their modelling assumptions.
The overall probability of pregnancy losses varied by 10-fold between models. Underestimating the pregnancy losses results in a higher birth rate of PI calves in the simulated herd and thus is likely to strongly influence the simulated virus spread. Further observed data are needed to more precisely estimate these effects because large variations are reported in the literature [Reference Kendrick32, Reference McClurkin35, Reference Rüfenacht36].
Reduced lifespan of PI animals
On average, the lifespan of PI animals is observed to be reduced (either because of direct effects of primary infection or because of mucosal disease after re-infection) [Reference Radostits and Littlejohns5]. About half of the PI animals die before the age of 1 year [Reference Duffell and Harkness28]. As PI animals can infect many susceptible animals due to their high level of virus excretion, the PI animals' lifespan is assumed to influence the virus spread.
A reduction of the PI animals' lifespan was introduced in all models except ref. [Reference Pasman, Dijkhuizen and Wentink20]. The mortality rate of PI animals was increased for all animals whatever their age in the continuous-entity model [Reference Cherry, Reeves and Smith22], only for PI calves [Reference Innocent17], and equally for PI heifers and PI cows [Reference Sørensen, Enevoldsen and Houe21]. In ref. [Reference Innocent17], PI cows were culled earlier (after the second lactation, whereas others were culled after the fifth lactation). A specific probability of PI animals leaving the herd was defined during all their life [Reference Viet23], and only within the first year of life due to culling [Reference Gunn, Stott and Humphry19].
Early death of PI animals influences the virus spread within a herd because it results in a decrease in the number of excreting animals. This effect was obvious and strong in refs [Reference Innocent17, Reference Cherry, Reeves and Smith22]. In ref. [Reference Cherry, Reeves and Smith22], a reduction of the mortality rate of PI animals (from 0·02 to 0·0002) resulted in an increase of the proportion of PI animals at steady state (from 0·02% to 3·6%). In ref. [Reference Innocent17], the probability for clearance of the virus in a herd within 10 years increased 10-fold when a 50% loss of PI calves before age 1 year was modelled compared to no reduction of lifespan (0·033 vs. 0·301).
Herd management influencing the virus spread
Herd is a structured population controlled by farmers. Some herd-management decisions are likely to influence the virus spread in a herd, although they do not specifically aim at controlling the infection. In models, a too-simplified representation of the population dynamics could lead to an incorrect representation of BVDV spread within the herd.
Separation into subgroups
In herds, animals are often separated into subgroups according to their age and reproductive status. Such separation induces a homogeneous mixing within each subgroup and a heterogeneous mixing between subgroups with a contact structure. According to the contact structure (subgroups in different pens or buildings), the virus spread can be limited between subgroups [Reference Taylor, Danzen and van Donkersgoed37].
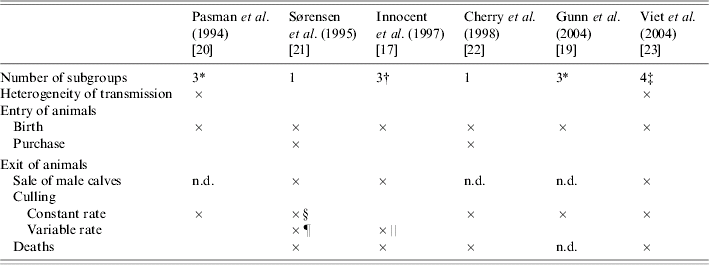
Separation of animals into subgroups was introduced into four models (Table 4). Movements between subgroups were related to age [Reference Innocent17, Reference Gunn, Stott and Humphry19, Reference Pasman, Dijkhuizen and Wentink20]. In ref. [Reference Viet23], transitions between subgroups depended on the time spent in the current subgroup (semi-Markov process). In only two of the four models that considered a separation into subgroups, the herd structure was assumed to influence the virus transmission between animals (Table 4). In ref. [Reference Pasman, Dijkhuizen and Wentink20], transmission was modelled only within each subgroup contrary to ref. [Reference Viet23] where both direct transmission within each subgroup and indirect transmission between subgroups were considered. In two other models [Reference Innocent17, Reference Gunn, Stott and Humphry19], the transmission rate was defined assuming a homogeneous mixing of all animals. Ignoring heterogeneous mixing, as in these two models, is likely to result in overestimating the number of new infections. The effect of the contact level between subgroups on BVDV spread was shown in ref. [Reference Viet38].
Table 4. Dynamics and structure of the herd in six bovine viral diarrhoea virus models
n.d., Not determined.
* <1 year, between 1 and 2 years, >2 years.
† Cows, heifers, calves.
‡ Cows, heifers ready for breeding, heifers before breeding, calves.
§ Involuntary culling.
¶ Different animals characteristics are taken into account: days open, current milk production.
‖ Different animals characteristics are taken into account: lactation number, failure to conceive after three services.
Sale, culling and control of the herd size
As the number of new BVDV infections due to a PI animal depends on the length of its stay in the herd, the sale and culling (such as an exit other than sale) should be considered in the models. Moreover, for quotas and housing, herd size is often kept nearly constant. Either culling is limited or animals are purchased to control the herd size within a small range. Such control of herd size may also influence the pathogen spread.
In dairy herds (depending on the farming systems), male calves are either sold systematically before weaning or kept in the herd. If they are sold, the number of new PI animals will decrease on average by half. This is likely to influence BVDV spread strongly. In the selected models, all male calves were sold at birth in two models [Reference Innocent17, Reference Sørensen, Enevoldsen and Houe21] and at 10 days old in one model [Reference Viet23]. In two continuous-entity models, male calves were not identified [Reference Pasman, Dijkhuizen and Wentink20, Reference Cherry, Reeves and Smith22].
In beef cattle herds, the male calves can be kept in the herd or sold. In ref. [Reference Gunn, Stott and Humphry19], no specific information was given on male calves.
Farmers' sale and culling decisions on heifers and cows are based on both animal characteristics (including reproductive status) and the herd situation (quotas, number of cows and heifers). BVDV infection can increase the rate of so-called involuntary reproductive culling, and then the replacement rate. Immune animals are likely to be culled and susceptible animals to be introduced. The number of new BVDV infections might then increase (as simulated in ref. [Reference Sørensen, Enevoldsen and Houe21]). Culling was introduced in all models (Table 4). A constant overall culling rate was used to model both the culling and the sale of animals [Reference Cherry, Reeves and Smith22]. Culling of young stock was modelled in three models [Reference Pasman, Dijkhuizen and Wentink20, Reference Sørensen, Enevoldsen and Houe21, Reference Viet23]. Constant culling rates for heifers just before insemination or in pregnancy, and for cows were considered in ref. [Reference Viet23]. The culling rate for cows depended on the characteristics of the individual animals in refs [Reference Innocent17, Reference Sørensen, Enevoldsen and Houe21] (Table 4). A constant number of cows were assumed to be culled per year [Reference Gunn, Stott and Humphry19]. Additional decision rules were defined in ref. [Reference Viet23] to keep within small ranges the size of the subgroup of heifers (just before insemination or in pregnancy) and the subgroup of cows. In ref. [Reference Sørensen, Enevoldsen and Houe21], sales of heifers were determined according to the number of cows in the herd. In ref. [Reference Cherry, Reeves and Smith22], the number of purchased animals was calculated to compensate for the mortality and reduced birth rates. In ref. [Reference Gunn, Stott and Humphry19], the herd size was constant without any description on how this was achieved.
The overall culling rate influenced the total number of cows infected in a 10-year period in a fully susceptible herd but not in a herd with mainly immune animals [Reference Sørensen, Enevoldsen and Houe21]. In a susceptible herd, the total number of cows infected in a 10-year period was higher with a high (36%) rather than with a low culling rate (23%).
Purchase
The purchase of animals is a major route for virus introduction in a herd [Reference Houe8]. In open herds where animals are purchased, the risk of virus introduction should be modelled. The study of the dynamics of the virus spread with virus re-introductions in a herd would then be possible. The purchase of animals over time was considered in two models [Reference Sørensen, Enevoldsen and Houe21, Reference Cherry, Reeves and Smith22] but not modelled as a possible route for virus introduction.
Disease control
To control the spread of BVDV, different measures are available to farmers: vaccination, test-and-cull consisting in monitoring and screening for detection and elimination of PI animals [Reference Harkness39].
The effectiveness of specific control measures on virus spread within a herd was investigated in refs [Reference Pasman, Dijkhuizen and Wentink20, Reference Cherry, Reeves and Smith22]. In ref. [Reference Pasman, Dijkhuizen and Wentink20], two scenarios were simulated: BVDV spread (1) with, and (2) without a strategy consisting of a systematic removal of all PI animals. The authors concluded that this strategy is economically unattractive assuming a virus re-introduction. In ref. [Reference Cherry, Reeves and Smith22], the authors estimated (i) the rate of removal of PI animals which induced clearance and (ii) the minimum required vaccination coverage (defined as the minimum percentage of animals in the herd which had to be vaccinated) to limit virus spread. They did not compare the effectiveness of these two strategies. To ensure clearance, they estimated (i) that PI animals should be removed before 11 days old and (ii) the proportion of animals to be vaccinated. However, the proposed removal of PI animals at this age is not possible using available tests in field conditions. No reviewed model represented stages of control actions such as tests of target populations for the detection and the removal of PI animals with imperfect laboratory tests, and booster injections for vaccination. The comparison of different strategies (such as do nothing, vaccination, test and removal of PI animals) was not presented in the reviewed models.
VALIDATION
A model is a simplified representation of a real system and has to properly represent its behaviour in order to use the model results. Validation consists of assessing the agreement between the behaviours of the model and of the real system that is represented [Reference Kleijnen40].
A step of qualitative validation consists of verifying that different observed behaviours can be mimicked by the model. Such a validation was described in ref. [Reference Sørensen, Enevoldsen and Houe21] using a case report and in ref. [Reference Viet23] using data from a survey. In ref. [Reference Sørensen, Enevoldsen and Houe21], among the behaviours obtained with the stochastic model, one simulation was presented where numbers and dates of occurrence of abortions, birth of a PI calf, and death of PI animals were consistent with the observations in one real herd. In ref. [Reference Viet23], observed data were compared to simulated data for behaviour corresponding to new infections of a susceptible herd. Simulated and observed data were consistent. In refs [Reference Pasman, Dijkhuizen and Wentink20, Reference Cherry, Reeves and Smith22], the authors did not describe any validation of their model. Other authors reported in the discussion some comparisons with observed or published data and concluded on the consistency with their results but did not describe their validation in detail [Reference Innocent17, Reference Gunn, Stott and Humphry19].
Quantitative validation consists of comparing results obtained in a sample of simulations with observed data in a sample of herds. It relies on the goodness-of-fit approach. To be able to do a quantitative validation, observed data representing either the main dynamic of virus spread after virus introduction in the case of deterministic models or all possible dynamics in the case of stochastic models are required. As outlined in ref. [Reference Sørensen, Enevoldsen and Houe21], datasets covering all situations do not exist. For instance, if the virus disappears very quickly after its introduction in a herd, it is probable that infection would be silent and not detected. The proportion of such behaviours cannot be known from observed data. It probably explains why no author reported any quantitative validation.
DISCUSSION
We reviewed different models published to study BVDV spread within a cattle herd (beef or dairy). Difficulties occurred in reviewing the models because main assumptions were not systematically detailed in the papers. The precise description of a model may be long and, consequently, may not be accepted by most journals. Thus, a balance needs to be chosen between a very long description and sufficient information on assumptions and modelling options allowing the further use and generalization of results. In particular, the assumptions on the modelling of virus transmission, on herd dynamics, on interaction between virus spread and herd dynamics, the type of model, the model states and the transitions between states should be given in the paper.
According to the analysis of modelling options, and implicit and explicit assumptions presented in the reviewed papers, the main identified modelling assumptions taken into account in the reviewed BVDV models are summarized in Table 5. Based on this review, the following critical points were identified and suggested further research.
Table 5. Main identified assumptions to model the bovine viral diarrhoea virus in a herd (structured population)
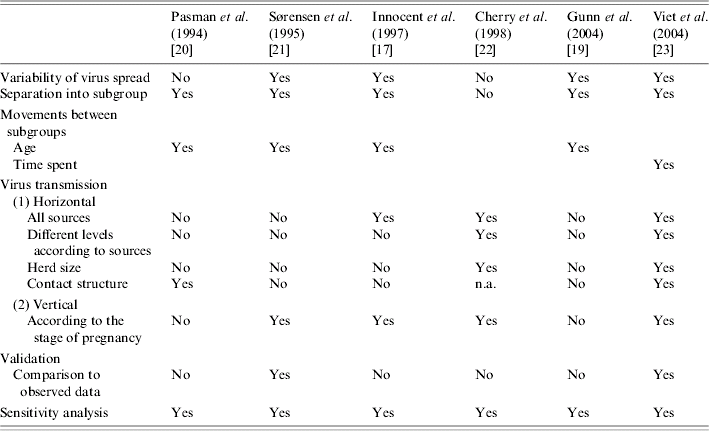
n.a., Not applicable.
When a separation into subgroups was modelled in the reviewed models, transitions between subgroups were related to age or to time spent in the subgroup (semi-Markov assumption) [Reference Innocent17, Reference Gunn, Stott and Humphry19, Reference Pasman, Dijkhuizen and Wentink20, Reference Viet23]. The use of semi-Markov transitions induces a higher complexity of the models than Markov transitions. The mathematical analysis of the model behaviour is then more complex. No comparison of the effect on BVDV spread of the definition of transitions between subgroups with a Markov rather a semi-Markov assumption has yet been published.
For horizontal BVDV transmission, the form of the force of infection has to be chosen according to the transmission mechanisms and the contact structure in the population (heterogeneous mixing due to subgroups). Within a homogeneous subgroup, modelling the force of infection, dependent on the number of excreting animals and on herd size (or subgroup size) as in refs [Reference Cherry, Reeves and Smith22, Reference Viet23] seems to be relevant. For a discrete-time model, a modified form of the Reed–Frost type accounting for herd size was proposed in refs [Reference De Jong41, Reference Allen and Burgin42] and could be used. Due to the separation of the population into subgroups, the indirect transmission between subgroups should be modelled as dependent on the contact structure. To our knowledge, no method or criterion to define the form of the force of infection representing the indirect transmission along with the estimation of the corresponding transmission rates (dependent on the contact structure) has been proposed yet.
Modelling the vertical transmission depending on the stage of pregnancy at time of infection is critical for the BVDV. Two modelling approaches were identified in this review: (1) the stage of pregnancy is known at time of infection [Reference Sørensen, Enevoldsen and Houe21, Reference Viet23]; (2) a probability distribution is used as in a continuous-entity model [Reference Cherry, Reeves and Smith22]. A comparison should be carried out to determine if approach (2) with a probability distribution leads to consistent results or not with approach (1) where the exact stage of pregnancy is considered.
In all the reviewed models, the parameter values were estimated from published data. For some parameters, such as the transmission coefficients, very few (published) data were available. Observed or experimental data are necessary to improve the parameter estimation. Nevertheless, detailed observations of the spread of the pathogen, such as that presented in ref. [Reference Sørensen, Enevoldsen and Houe21], are not often available. Even without detailed data, model parameters may be estimated using different methods, depending on the available observed data [Reference Becker and Britton43]. For example, a Bayesian approach with augmented data can be used with partial observed data as in ref. [Reference O'Neill and Roberts44] where only recovery times after infection were observed. In surveys for BVDV, the antibody level is often measured either in the bulk-tank milk or in individual serum. Further research is needed to study the potential use of such repeated measures taking into account the uncertainty of the tests results according to the sensitivity and the specificity of the test. If no observed data are available, sensitivity analyses to parameters with uncertainty have to be thoroughly investigated in order to identify key parameters to be estimated in priority.
For validation, detailed follow-up of infected herds when available are often biased or partial (e.g. no detection of early extinction; no information on virus introduction and on possible re-infection; often obtained during the screening of a herd to detect PI animals). Nevertheless, they could be used only for qualitative or partial validation until a specific data collection is completed (as in ref. [Reference Viet45]). Moreover, specific sampling schemes may be represented in the model in order to produce model outcomes similar to those available from sampling observed data. Thus, validation should be considered when defining the model.
A model is a simplified representation of the observed system. Models with parsimony are often considered as too simplified to represent the reality. Globally, the reviewed models were not parsimonious. It can be explained by the fact that the models aim to be as close as possible to the reality. Due to increased computer capability, models are more and more complex. More assumptions are included and more parameters are needed. The drawback of such models is the uncertainty for some parameter values. Among the complex models, the individual-based approach was often used but without justifying the need of the resulting complexity [Reference Grimm46]. To be used, the model should be as simple as possible without losing the main characteristics of the disease and the factors influencing the considered pathogen spread. For some assumptions, simplifications can be chosen a priori. Nevertheless, before simplifying assumptions assumed to influence the pathogen spread, consequences of these simplifications on the pathogen spread should be evaluated.
Different BVDV models were proposed representing different situations (country, herd size, herd management, etc.) and with different objectives (simulation, studying control measure, economic calculation). To conclude, we proposed the following guidelines for further BVDV models:
● The model should be as simple as possible regarding the objective of the model. If the objective is to provide outputs for economic calculation, the model should include production losses (such as milk yield reduction). However, the modelling of production losses is not needed when studying only the effect on the epidemic size of control measures.
● To be used for a population of finite size, a model should be able to mimic the variability of virus spread in a given situation (from early clearance to persistence of the virus). Here, the model should be stochastic.
● Horizontal transmission of BVDV depends on contacts between excreting animals and susceptible animals. First, the two types of animals (transiently infective and PI animals) excreting the virus with different amounts should be modelled. Second, the structure of contacts should be represented either between subgroups of animals or between animals. To model the horizontal transmission, as the herd size is kept nearly constant and assuming a constant area per animal whatever the herd size, the force of infection should depend on the number of excreting animals and on the herd size.
● Vertical transmission should be represented as it influences the number of PI animals in the herd.
● Factors in herd management reported as influencing virus spread should be taken into account in the model. Some factors are common in cattle herds (separation into subgroups, culling and sales) whereas other depends on farmers (calving season, purchase). At least, the models should include the common herd management factors (either by defining subpopulations or by considering characteristics of each individual).
● Values of the parameters of virus spread (virus transmission, duration of health status, probability of vertical transmission) have to be calibrated as precisely as possible from available observed or experimental data.
● Validation of the model by comparison of observed data with model outcomes should be realized. If no observed data are available, sensitivity analyses to parameters with uncertainty have to be thoroughly investigated.
ACKNOWLEDGEMENTS
The authors thank Christine Jacob (Unité de Mathématiques et Informatique Appliquées, INRA), Pauline Ezanno and Thierry Hoch (Unit of Animal Health Management, Veterinary School & INRA) for their comments on this paper.
DECLARATION OF INTEREST
None.








