Introduction
The problem of the flow of ice in glaciers and ice caps has been treated by Nye in a series of very illuminating papersReference Nye 1 , Reference Nye 2 , Reference Nye 3 , Reference Nye 4 , Reference Nye 5 . One problem that has not been analyzed by his methods is the creep of floating ice shelves. ‘The analyses which have been given by Nye are inapplicable to this special problem because his solutions require a finite shear stress to exist at the bottom of the mass of ice being considered. At the bottom of a floating ice shelf the shear stress, of course, must be zero. This paper presents an analysis for this problem using Glen’s creep lawReference Glen 6 for ice and Nye’s relationReference Nye 1 of steady-state creep (the analogue of the Lévy-Mises relation in plasticity theory). It turns out that the solution is almost trivial. It is equivalent to the solution of the problem of a weightless material being compressed by frictionless plates.
Theory
We consider a floating ice shelf such as is shown in Fig. 1. The shelf is assumed to be in a steady-state condition, its thickness h remaining constant in time. The thickness of the shelf is assumed to be many orders of magnitude smaller than its length. The direction y is perpendicular to the surface of the shelf, x is parallel to the surface and perpendicular to the ice front, and z is parallel both to the surface and the ice front. Consider the case where creep movement can occur in the x and y direction but not in the z direction. In the Appendix is given a case where creep in the z direction is permitted.

Fig. 1 Cross section of floating ice shelf
The equations for equilibrium are

where σ ij are the usual stress components (σ ii is positive when in tension), g is the gravitational acceleration, and ρ I is the density of the ice. An average density is used in the following analysis. It is a simple matter, however, to give an exact solution to the problem using a density which is a function of y.
We now make the assumption, which we believe to be quite reasonable, that at a position far from the edge of the shelf all the stress components must be independent of x and z. This assumption along with the condition that the shear stress at the top and bottom surface of the shelf must be equal to zero reduces Eqs. (1) to
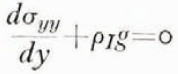
and
Integrating Eq. (2) gives
The stresses σ xx and σ zz must still be determined.
Nye’s relationReference Nye 1 of steady-state creep (based on Glen’s creep lawReference Glen 6 ) is
where
and
and
Here n is a constant, A is a constant which depends on the temperature and may depend on the density, δ ij is equal to zero when i does not equal j and equals one when they are equal, and

where u i is a velocity component.
Since the creep rate is zero in the z direction the term
These equations are consistent with Eq. (9) only if
Setting
The plus sign is used when K is positive, an expanding shelf; the minus sign when K is negative, a shrinking shelf. Both the stresses σ xx and σ yy are functions of y. For an expanding shelf the values of σ xx are such that it is in tension at the top of the shelf and in compression at the bottom. The stress σ yy is always in compression.
We now take advantage of the fact that the shelf is floating in the sea. Let ρ W be the density of the sea water. Then σ xx must obey the equation

Setting σ xx given by Eq. (12) into Eq. (13) one obtains for K

This equation gives the result that we are seeking, namely, the creep rate of the shelf. It is a particularly simple result; the creep rate in the shelf from top to bottom is constant. It turns out that K can only be positive. Therefore a shrinking shelf cannot exist.
The solution just found for the stresses and creep rate in an ice shelf applies only far from the edges of the shelf. Near an edge the stress distribution must change. Since

(the torque exerted across a unit cross-section of the shelf, perpendicular to the surface and parallel to the ice front) is not equal to zero, a torque of this magnitude must exist at either end of a shelf in order to maintain mechanical equilibrium. Such a torque may be maintained in several ways such as, for example, by means of an overhanging cliff at the ice front of the shelf.
Comparison with Experiment
We wish to compare now an observed creep rate of the ice shelf at Maudheim with that predicted by Eq. (4). SchyttReference Schytt 7 states that a two kilometer base line stretched at a rate of 30 cm./month. This speed gives a creep rate of 1.8 × 10−3 years−1. The shelf at Maudheim was approximately 185 m. thick. The temperature of the shelf varied from −17.5° C. near the top surface to −16.5° C. at a depth of 100 m. Temperatures below 100 m. were not known. Presumably the temperature. at the bottom surface is about −1.5° C. The density of the ice varied from 0.50 gm. cm.−3 near the top surface to 0.80 gm. cm.−3 at a depth of 55 m. and then approached the value of solid ice (0.91 gm. cm.−3).
The constant A appearing in Eq. (14) can be obtained from the results of Glen on the creep of ice. Glen found that if σ is the uniaxial stress applied to a laboratory specimen then the creep rate is given by
where T is the temperature, T m is the melting point of ice, B is a constant equal to 0.017 bars−4.2 years−1 (one bar is equal to 106 dynes cm.−2), Q is an activation energy and is equal to 32,000 cal/ mol., n is a constant equal to 4.2, and R is the gas constant. In terms of the quantities entering into Eq. (15) the constant A is given by
(See NyeReference Nye 1 for the reason for the inclusion of the factor in front of B.)
The term
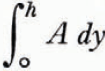
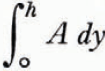
The author wishes to thank Professor R. P. Sharp for drawing his attention to the work of Schytt.
Appendix
Consider a detached floating ice sheet which is free to creep in both the x and z direction. Consider the situation far from the edge of the sheet. Assume again that the various stresses are independent of x and z. Eqs. (2), (3), and (4) will still be valid. It is reasonable in this situation to take σ xx equal to σ zz since an arbitrary rotation of the axes about the y axis ought not to change the form of the solution. Eq. (10) now takes the form

Proceeding as before we find for K

The creep rate predicted by Eq. (17) is a factor (2/√3) n /√3~1.1 larger than that predicted by Eq. (14). The creep rate predicted by Eq. (17) is isotropic. That is, any base line on the shelf, regardless of its orientation, will stretch at this rate. For Eq. (14) only a base line perpendicular to the sea front will stretch. In any actual situation in the Antarctic the truth probably lies somewhere between Eqs. (14) and (17).
When the density of ice, ρ I , is a function of the depth, the term



