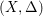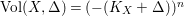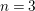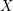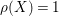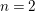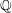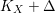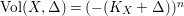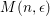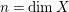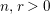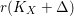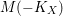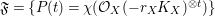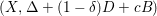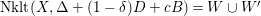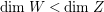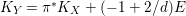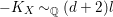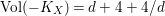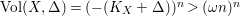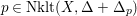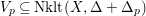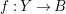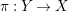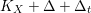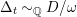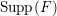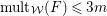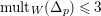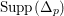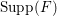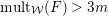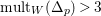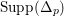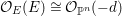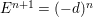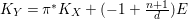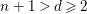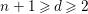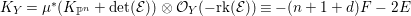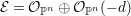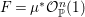According to the minimal model program, Fano varieties are the building blocks for varieties of negative Kodaira dimension. The set of Fano varieties of a given dimension is expected to satisfy certain boundedness properties. For example, the set of all the
![]() $n$
-dimensional smooth Fano manifolds forms a bounded family by [Reference Kollár, Miyaoka and MoriKMM92]. Since the need of singularities arises naturally in the minimal model program, the set of mildly singular Fano varieties is also expected to be bounded. This is known for terminal
$n$
-dimensional smooth Fano manifolds forms a bounded family by [Reference Kollár, Miyaoka and MoriKMM92]. Since the need of singularities arises naturally in the minimal model program, the set of mildly singular Fano varieties is also expected to be bounded. This is known for terminal
![]() $\mathbb{Q}$
-Fano
$\mathbb{Q}$
-Fano
![]() $\mathbb{Q}$
-factorial threefolds of Picard number one by [Reference KawamataKaw92] and for canonical
$\mathbb{Q}$
-factorial threefolds of Picard number one by [Reference KawamataKaw92] and for canonical
![]() $\mathbb{Q}$
-Fano threefolds by [Reference Kollár, Miyaoka, Mori and TakagiKMMT00]. However, if one considers the set of all klt
$\mathbb{Q}$
-Fano threefolds by [Reference Kollár, Miyaoka, Mori and TakagiKMMT00]. However, if one considers the set of all klt
![]() $\mathbb{Q}$
-Fano varieties with Picard number one of a given dimension, [Reference LinLin03] and [Reference OkadaOka09] have shown that (birational) boundedness fails. The problem is that the category of klt singularities is too big to be bounded as it contains finite quotients of arbitrarily large order. Instead, one restricts to a smaller class of singularities, known as
$\mathbb{Q}$
-Fano varieties with Picard number one of a given dimension, [Reference LinLin03] and [Reference OkadaOka09] have shown that (birational) boundedness fails. The problem is that the category of klt singularities is too big to be bounded as it contains finite quotients of arbitrarily large order. Instead, one restricts to a smaller class of singularities, known as
![]() $\unicode[STIX]{x1D716}$
-klt singularities where
$\unicode[STIX]{x1D716}$
-klt singularities where
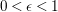 $0<\unicode[STIX]{x1D716}<1$
. Since the notion of log pairs naturally arises in the context of minimal model program, we also consider log Fano varieties.
$0<\unicode[STIX]{x1D716}<1$
. Since the notion of log pairs naturally arises in the context of minimal model program, we also consider log Fano varieties.
Definition.
A pair
![]() $(X,\unicode[STIX]{x1D6E5})$
consists of a normal projective variety
$(X,\unicode[STIX]{x1D6E5})$
consists of a normal projective variety
![]() $X$
and an effective Weil
$X$
and an effective Weil
![]() $\mathbb{Q}$
-divisor
$\mathbb{Q}$
-divisor
![]() $\unicode[STIX]{x1D6E5}$
such that
$\unicode[STIX]{x1D6E5}$
such that
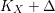 $K_{X}+\unicode[STIX]{x1D6E5}$
is
$K_{X}+\unicode[STIX]{x1D6E5}$
is
![]() $\mathbb{Q}$
-Cartier. Let
$\mathbb{Q}$
-Cartier. Let
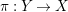 $\unicode[STIX]{x1D70B}:Y\rightarrow X$
be a log resolution of a pair
$\unicode[STIX]{x1D70B}:Y\rightarrow X$
be a log resolution of a pair
![]() $(X,\unicode[STIX]{x1D6E5})$
and write
$(X,\unicode[STIX]{x1D6E5})$
and write
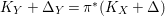 $K_{Y}+\unicode[STIX]{x1D6E5}_{Y}=\unicode[STIX]{x1D70B}^{\ast }(K_{X}+\unicode[STIX]{x1D6E5})$
. For
$K_{Y}+\unicode[STIX]{x1D6E5}_{Y}=\unicode[STIX]{x1D70B}^{\ast }(K_{X}+\unicode[STIX]{x1D6E5})$
. For
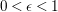 $0<\unicode[STIX]{x1D716}<1$
, we say that the pair
$0<\unicode[STIX]{x1D716}<1$
, we say that the pair
![]() $(X,\unicode[STIX]{x1D6E5})$
is
$(X,\unicode[STIX]{x1D6E5})$
is
![]() $\unicode[STIX]{x1D716}$
-klt if all the coefficients of
$\unicode[STIX]{x1D716}$
-klt if all the coefficients of
![]() $\unicode[STIX]{x1D6E5}_{Y}$
are less than
$\unicode[STIX]{x1D6E5}_{Y}$
are less than
![]() $1-\unicode[STIX]{x1D716}$
. In particular, all the coefficients of
$1-\unicode[STIX]{x1D716}$
. In particular, all the coefficients of
![]() $\unicode[STIX]{x1D6E5}$
lie in
$\unicode[STIX]{x1D6E5}$
lie in
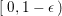 $[0,1-\unicode[STIX]{x1D716})$
. Note that smaller
$[0,1-\unicode[STIX]{x1D716})$
. Note that smaller
![]() $\unicode[STIX]{x1D716}$
corresponds to worse singularities.
$\unicode[STIX]{x1D716}$
corresponds to worse singularities.
An
![]() $\unicode[STIX]{x1D716}$
-klt (weak) log
$\unicode[STIX]{x1D716}$
-klt (weak) log
![]() $\mathbb{Q}$
-Fano variety is an
$\mathbb{Q}$
-Fano variety is an
![]() $\unicode[STIX]{x1D716}$
-klt pair
$\unicode[STIX]{x1D716}$
-klt pair
![]() $(X,\unicode[STIX]{x1D6E5})$
such that the
$(X,\unicode[STIX]{x1D6E5})$
such that the
![]() $\mathbb{Q}$
-Cartier divisor
$\mathbb{Q}$
-Cartier divisor
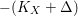 $-(K_{X}+\unicode[STIX]{x1D6E5})$
is ample (resp. nef and big).
$-(K_{X}+\unicode[STIX]{x1D6E5})$
is ample (resp. nef and big).
Definition.
We say that a collection of varieties
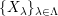 $\{X_{\unicode[STIX]{x1D706}}\}_{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}}$
is bounded if there exists a morphism of finite type of Noetherian schemes
$\{X_{\unicode[STIX]{x1D706}}\}_{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}}$
is bounded if there exists a morphism of finite type of Noetherian schemes
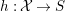 $h:{\mathcal{X}}\rightarrow S$
such that for each
$h:{\mathcal{X}}\rightarrow S$
such that for each
![]() $X_{\unicode[STIX]{x1D706}}$
,
$X_{\unicode[STIX]{x1D706}}$
,
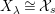 $X_{\unicode[STIX]{x1D706}}\cong {\mathcal{X}}_{s}$
for some closed point
$X_{\unicode[STIX]{x1D706}}\cong {\mathcal{X}}_{s}$
for some closed point
![]() $s\in S$
.
$s\in S$
.
In this paper, we are interested in the following conjecture which is still open in dimension three and higher.
Borisov–Alexeev–Borisov Conjecture.
Fix
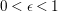 $0<\unicode[STIX]{x1D716}<1$
, an integer
$0<\unicode[STIX]{x1D716}<1$
, an integer
![]() $n>0$
, and consider the set of all the
$n>0$
, and consider the set of all the
![]() $n$
-dimensional
$n$
-dimensional
![]() $\unicode[STIX]{x1D716}$
-klt log
$\unicode[STIX]{x1D716}$
-klt log
![]() $\mathbb{Q}$
-Fano pairs
$\mathbb{Q}$
-Fano pairs
![]() $(X,\unicode[STIX]{x1D6E5})$
. Then the set of underlying varieties
$(X,\unicode[STIX]{x1D6E5})$
. Then the set of underlying varieties
![]() $\{X\}$
is bounded.
$\{X\}$
is bounded.
A. Borisov and L. Borisov establish the B–A–B Conjecture for toric varieties in [Reference Borisov and BorisovBB92]. Alexeev establishes the two-dimensional B–A–B Conjecture in [Reference AlexeevAle94] with a simplified argument given in [Reference Alexeev and MoriAM04]. The author’s original motivation of studying the B–A–B Conjecture is that it is related to the conjectural termination of flips in the minimal model program: According to [Reference Birkar and ShokurovBS10], log minimal model program, ACCFootnote
1
for minimal log discrepancies, and B–A–B Conjecture in dimension
![]() ${\leqslant}d$
implies termination of log flips in dimension
${\leqslant}d$
implies termination of log flips in dimension
![]() ${\leqslant}d+1$
for effective pairs.
${\leqslant}d+1$
for effective pairs.
The following statements concerning log
![]() $\mathbb{Q}$
-Fano pairs
$\mathbb{Q}$
-Fano pairs
![]() $(X,\unicode[STIX]{x1D6E5})$
are relevant to the B–A–B Conjecture:
$(X,\unicode[STIX]{x1D6E5})$
are relevant to the B–A–B Conjecture:
-
(i) The Cartier index of
 $K_{X}+\unicode[STIX]{x1D6E5}$
of an
$K_{X}+\unicode[STIX]{x1D6E5}$
of an
 $n$
-dimensional
$n$
-dimensional
 $\unicode[STIX]{x1D716}$
-klt log
$\unicode[STIX]{x1D716}$
-klt log
 $\mathbb{Q}$
-Fano pair
$\mathbb{Q}$
-Fano pair
 $(X,\unicode[STIX]{x1D6E5})$
is bounded from above by a fixed integer
$(X,\unicode[STIX]{x1D6E5})$
is bounded from above by a fixed integer
 $r(n,\unicode[STIX]{x1D716})$
depending only on
$r(n,\unicode[STIX]{x1D716})$
depending only on
 $n=\dim X$
and
$n=\dim X$
and
 $\unicode[STIX]{x1D716}$
.
$\unicode[STIX]{x1D716}$
. -
(ii) The anticanonical volume
 $\text{Vol}(X,\unicode[STIX]{x1D6E5})=(-(K_{X}+\unicode[STIX]{x1D6E5}))^{n}$
of an
$\text{Vol}(X,\unicode[STIX]{x1D6E5})=(-(K_{X}+\unicode[STIX]{x1D6E5}))^{n}$
of an
 $n$
-dimensional
$n$
-dimensional
 $\unicode[STIX]{x1D716}$
-klt log
$\unicode[STIX]{x1D716}$
-klt log
 $\mathbb{Q}$
-Fano pair
$\mathbb{Q}$
-Fano pair
 $(X,\unicode[STIX]{x1D6E5})$
is bounded from above by a fixed integer
$(X,\unicode[STIX]{x1D6E5})$
is bounded from above by a fixed integer
 $M(n,\unicode[STIX]{x1D716})$
depending only on
$M(n,\unicode[STIX]{x1D716})$
depending only on
 $n=\dim X$
and
$n=\dim X$
and
 $\unicode[STIX]{x1D716}$
.
$\unicode[STIX]{x1D716}$
. -
(iii) (Batyrev Conjecture) For given integers
 $n,r>0$
, consider the set of all the
$n,r>0$
, consider the set of all the
 $n$
-dimensional klt log
$n$
-dimensional klt log
 $\mathbb{Q}$
-Fano pairs
$\mathbb{Q}$
-Fano pairs
 $(X,\unicode[STIX]{x1D6E5})$
such that
$(X,\unicode[STIX]{x1D6E5})$
such that
 $r(K_{X}+\unicode[STIX]{x1D6E5})$
is Cartier. Then the set of underlying varieties
$r(K_{X}+\unicode[STIX]{x1D6E5})$
is Cartier. Then the set of underlying varieties
 $\{X\}$
is bounded.
$\{X\}$
is bounded.
It is clear that the B–A–B Conjecture follows from (i) and (iii) (cf., Proposition below). The Batyrev Conjecture (iii) in dimension three is established by Borisov, [Reference BorisovBor96, Reference BorisovBor01]. Recently Hacon, McKernan, and Xu have announced a proof of the Batyrev Conjecture (iii) in any dimension. In general, it is very hard to establish (i). Ambro in [Reference AmbroAmb09] has proved (i) for toric singularities assuming that only the standard coefficients
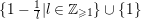 $\{1-\frac{1}{l}|l\in \mathbb{Z}_{{\geqslant}1}\}\cup \{1\}$
are allowed to be the coefficients of
$\{1-\frac{1}{l}|l\in \mathbb{Z}_{{\geqslant}1}\}\cup \{1\}$
are allowed to be the coefficients of
![]() $\unicode[STIX]{x1D6E5}$
. A necessary condition for (i) is that the coefficients of
$\unicode[STIX]{x1D6E5}$
. A necessary condition for (i) is that the coefficients of
![]() $\unicode[STIX]{x1D6E5}$
must lie in a fixed DCC set: A counterexample is given by the set of pairs
$\unicode[STIX]{x1D6E5}$
must lie in a fixed DCC set: A counterexample is given by the set of pairs
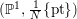 $(\mathbb{P}^{1},\frac{1}{N}\{\text{pt}\})$
for
$(\mathbb{P}^{1},\frac{1}{N}\{\text{pt}\})$
for
![]() $N\geqslant 1$
.
$N\geqslant 1$
.
For convenience of the reader, we include a well-known (to the experts) argument establishing the B–A–B Conjecture under conditions (i) and (ii) in the case when
![]() $\unicode[STIX]{x1D6E5}=0$
, or
$\unicode[STIX]{x1D6E5}=0$
, or
![]() $X$
is
$X$
is
![]() $\mathbb{Q}$
-factional of
$\mathbb{Q}$
-factional of
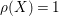 $\unicode[STIX]{x1D70C}(X)=1$
.
$\unicode[STIX]{x1D70C}(X)=1$
.
Proposition.
Suppose that
![]() $\unicode[STIX]{x1D6E5}=0$
or
$\unicode[STIX]{x1D6E5}=0$
or
![]() $X$
is
$X$
is
![]() $\mathbb{Q}$
-factional of
$\mathbb{Q}$
-factional of
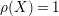 $\unicode[STIX]{x1D70C}(X)=1$
, then the B–A–B Conjecture follows from the statements (i) and (ii) above.
$\unicode[STIX]{x1D70C}(X)=1$
, then the B–A–B Conjecture follows from the statements (i) and (ii) above.
Proof. Let
![]() $X$
be an
$X$
be an
![]() $\unicode[STIX]{x1D716}$
-klt
$\unicode[STIX]{x1D716}$
-klt
![]() $\mathbb{Q}$
-Fano variety of dimension
$\mathbb{Q}$
-Fano variety of dimension
![]() $n$
and let
$n$
and let
![]() $r_{X}$
be the Cartier index of
$r_{X}$
be the Cartier index of
![]() $K_{X}$
. The following statements together imply boundedness:
$K_{X}$
. The following statements together imply boundedness:
-
(1) There is an upper bound
 $r(n,\unicode[STIX]{x1D716})$
of the Cartier index
$r(n,\unicode[STIX]{x1D716})$
of the Cartier index
 $r_{X}$
of
$r_{X}$
of
 $K_{X}$
depending only on
$K_{X}$
depending only on
 $n$
and
$n$
and
 $\unicode[STIX]{x1D716}$
;
$\unicode[STIX]{x1D716}$
; -
(2) The divisor
 $M(-K_{X})$
is a very ample line bundle for a fixed
$M(-K_{X})$
is a very ample line bundle for a fixed
 $M$
depending only on
$M$
depending only on
 $n$
and
$n$
and
 $\unicode[STIX]{x1D716}$
;
$\unicode[STIX]{x1D716}$
; -
(3) The set of Hilbert polynomials
 $\mathfrak{F}=\{P(t)=\unicode[STIX]{x1D712}({\mathcal{O}}_{X}(-r_{X}K_{X})^{\otimes t})\}$
associated to all the
$\mathfrak{F}=\{P(t)=\unicode[STIX]{x1D712}({\mathcal{O}}_{X}(-r_{X}K_{X})^{\otimes t})\}$
associated to all the
 $n$
-dimensional
$n$
-dimensional
 $\unicode[STIX]{x1D716}$
-klt
$\unicode[STIX]{x1D716}$
-klt
 $\mathbb{Q}$
-Fano variety is finite.
$\mathbb{Q}$
-Fano variety is finite.
In fact,
![]() $(2)$
and
$(2)$
and
![]() $(3)$
imply that the set of
$(3)$
imply that the set of
![]() $n$
-dimensional
$n$
-dimensional
![]() $\unicode[STIX]{x1D716}$
-klt
$\unicode[STIX]{x1D716}$
-klt
![]() $\mathbb{Q}$
-Fano varieties is contained in the finite union of Hilbert schemes
$\mathbb{Q}$
-Fano varieties is contained in the finite union of Hilbert schemes
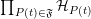 $\prod _{P(t)\in \mathfrak{F}}{\mathcal{H}}_{P(t)}$
, where each
$\prod _{P(t)\in \mathfrak{F}}{\mathcal{H}}_{P(t)}$
, where each
![]() ${\mathcal{H}}_{P(t)}$
is Noetherian. Note that
${\mathcal{H}}_{P(t)}$
is Noetherian. Note that
![]() $(1)$
is essential for getting
$(1)$
is essential for getting
![]() $(2)$
.
$(2)$
.
The statement (1) is simply (i).
Let
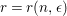 $r=r(n,\unicode[STIX]{x1D716})$
as in (i). Since
$r=r(n,\unicode[STIX]{x1D716})$
as in (i). Since
![]() $rK_{X}$
is a line bundle, by [Reference KollárKol93]
$rK_{X}$
is a line bundle, by [Reference KollárKol93]
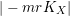 $|-mrK_{X}|$
is base point free for any
$|-mrK_{X}|$
is base point free for any
![]() $m>0$
divisible by a constant
$m>0$
divisible by a constant
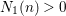 $N_{1}(n)>0$
depending only on
$N_{1}(n)>0$
depending only on
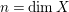 $n=\dim X$
. Since
$n=\dim X$
. Since
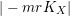 $|-mrK_{X}|$
is ample and base point free for
$|-mrK_{X}|$
is ample and base point free for
![]() $m>0$
sufficiently divisible, it defines a finite morphism. By [Reference KollárKol97, Theorem 5.9], the map induced by
$m>0$
sufficiently divisible, it defines a finite morphism. By [Reference KollárKol97, Theorem 5.9], the map induced by
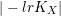 $|-lrK_{X}|$
for
$|-lrK_{X}|$
for
![]() $l>0$
divisible by
$l>0$
divisible by
![]() $N_{2}(n)$
is birational where
$N_{2}(n)$
is birational where
![]() $N_{2}(n)$
also depends only on
$N_{2}(n)$
also depends only on
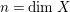 $n=\dim X$
. Since a finite birational morphism of normal varieties is an isomorphism, it follows that there exists an effective embedding by
$n=\dim X$
. Since a finite birational morphism of normal varieties is an isomorphism, it follows that there exists an effective embedding by
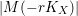 $|M(-rK_{X})|$
for some fixed
$|M(-rK_{X})|$
for some fixed
![]() $M>0$
depending only on
$M>0$
depending only on
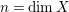 $n=\dim X$
and
$n=\dim X$
and
![]() $\unicode[STIX]{x1D716}$
. This is
$\unicode[STIX]{x1D716}$
. This is
![]() $(2)$
.
$(2)$
.
By [Reference Kollár and MatsusakaKM83], the coefficients of the Hilbert polynomial
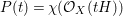 $P(t)=\unicode[STIX]{x1D712}({\mathcal{O}}_{X}(tH))$
of a polarized variety
$P(t)=\unicode[STIX]{x1D712}({\mathcal{O}}_{X}(tH))$
of a polarized variety
![]() $(X,H)$
with
$(X,H)$
with
![]() $H$
an ample line bundle can be bounded by
$H$
an ample line bundle can be bounded by
![]() $H^{n}$
and
$H^{n}$
and
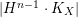 $|H^{n-1}\cdot K_{X}|$
. Since by (1) there exists an integer
$|H^{n-1}\cdot K_{X}|$
. Since by (1) there exists an integer
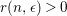 $r(n,\unicode[STIX]{x1D716})>0$
depending only on
$r(n,\unicode[STIX]{x1D716})>0$
depending only on
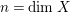 $n=\dim X$
and
$n=\dim X$
and
![]() $\unicode[STIX]{x1D716}$
such that
$\unicode[STIX]{x1D716}$
such that
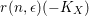 $r(n,\unicode[STIX]{x1D716})(-K_{X})$
is an ample line bundle, set
$r(n,\unicode[STIX]{x1D716})(-K_{X})$
is an ample line bundle, set
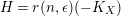 $H=r(n,\unicode[STIX]{x1D716})(-K_{X})$
and apply (ii), it follows that there are only finitely many Hilbert polynomials for the set of anticanonically polarized
$H=r(n,\unicode[STIX]{x1D716})(-K_{X})$
and apply (ii), it follows that there are only finitely many Hilbert polynomials for the set of anticanonically polarized
![]() $\unicode[STIX]{x1D716}$
-klt Fano varieties
$\unicode[STIX]{x1D716}$
-klt Fano varieties
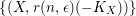 $\{(X,r(n,\unicode[STIX]{x1D716})(-K_{X}))\}$
. This proves
$\{(X,r(n,\unicode[STIX]{x1D716})(-K_{X}))\}$
. This proves
![]() $(3)$
.
$(3)$
.
If
![]() $X$
is
$X$
is
![]() $\mathbb{Q}$
-factorial of
$\mathbb{Q}$
-factorial of
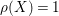 $\unicode[STIX]{x1D70C}(X)=1$
, then
$\unicode[STIX]{x1D70C}(X)=1$
, then
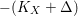 $-(K_{X}+\unicode[STIX]{x1D6E5})$
being ample implies that
$-(K_{X}+\unicode[STIX]{x1D6E5})$
being ample implies that
![]() $-K_{X}$
is also ample. It is clear that
$-K_{X}$
is also ample. It is clear that
![]() $X$
is also
$X$
is also
![]() $\unicode[STIX]{x1D716}$
-klt and hence boundedness follows from the same proof as above.◻
$\unicode[STIX]{x1D716}$
-klt and hence boundedness follows from the same proof as above.◻
An effective upper bound in (ii) is obtained for smooth Fano
![]() $n$
-folds in [Reference Kollár, Miyaoka and MoriKMM92] and for canonical
$n$
-folds in [Reference Kollár, Miyaoka and MoriKMM92] and for canonical
![]() $\mathbb{Q}$
-Fano threefolds in [Reference Kollár, Miyaoka, Mori and TakagiKMMT00]. In this work, we obtain an effective answer to question (ii) in dimension two, that is, for log del Pezzo surfaces (cf., Theorem 4.3).
$\mathbb{Q}$
-Fano threefolds in [Reference Kollár, Miyaoka, Mori and TakagiKMMT00]. In this work, we obtain an effective answer to question (ii) in dimension two, that is, for log del Pezzo surfaces (cf., Theorem 4.3).
Theorem A.
Let
![]() $(X,\unicode[STIX]{x1D6E5})$
be an
$(X,\unicode[STIX]{x1D6E5})$
be an
![]() $\unicode[STIX]{x1D716}$
-klt weak log del Pezzo surface, then the anticanonical volume
$\unicode[STIX]{x1D716}$
-klt weak log del Pezzo surface, then the anticanonical volume
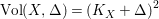 $\text{Vol}(X,\unicode[STIX]{x1D6E5})=(K_{X}+\unicode[STIX]{x1D6E5})^{2}$
satisfies
$\text{Vol}(X,\unicode[STIX]{x1D6E5})=(K_{X}+\unicode[STIX]{x1D6E5})^{2}$
satisfies
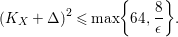 $$\begin{eqnarray}(K_{X}+\unicode[STIX]{x1D6E5})^{2}\leqslant \max \biggl\{64,\frac{8}{\unicode[STIX]{x1D716}}\biggr\}.\end{eqnarray}$$
$$\begin{eqnarray}(K_{X}+\unicode[STIX]{x1D6E5})^{2}\leqslant \max \biggl\{64,\frac{8}{\unicode[STIX]{x1D716}}\biggr\}.\end{eqnarray}$$
Moreover, this upper bound is in a sharp form: There exists a sequence of
![]() $\unicode[STIX]{x1D716}$
-klt del Pezzo surfaces whose volume grows linearly with respect to
$\unicode[STIX]{x1D716}$
-klt del Pezzo surfaces whose volume grows linearly with respect to
![]() $1/\unicode[STIX]{x1D716}$
.
$1/\unicode[STIX]{x1D716}$
.
Let
![]() $(X,\unicode[STIX]{x1D6E5})$
be an
$(X,\unicode[STIX]{x1D6E5})$
be an
![]() $\unicode[STIX]{x1D716}$
-klt weak log del Pezzo surface and
$\unicode[STIX]{x1D716}$
-klt weak log del Pezzo surface and
![]() $X_{\text{min}}$
be the minimal resolution of
$X_{\text{min}}$
be the minimal resolution of
![]() $(X,\unicode[STIX]{x1D6E5})$
. Alexeev and Mori have shown in [Reference Alexeev and MoriAM04, Theorem 1.8] that
$(X,\unicode[STIX]{x1D6E5})$
. Alexeev and Mori have shown in [Reference Alexeev and MoriAM04, Theorem 1.8] that
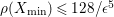 $\unicode[STIX]{x1D70C}(X_{\text{min}})\leqslant 128/\unicode[STIX]{x1D716}^{5}$
. Also from [Reference Alexeev and MoriAM04, Lemma 1.2] (or see the proof of Theorem 4.3), an exceptional curve
$\unicode[STIX]{x1D70C}(X_{\text{min}})\leqslant 128/\unicode[STIX]{x1D716}^{5}$
. Also from [Reference Alexeev and MoriAM04, Lemma 1.2] (or see the proof of Theorem 4.3), an exceptional curve
![]() $E$
on
$E$
on
![]() $X_{\text{min}}$
over
$X_{\text{min}}$
over
![]() $X$
satisfies
$X$
satisfies
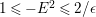 $1\leqslant -E^{2}\leqslant 2/\unicode[STIX]{x1D716}$
. In case
$1\leqslant -E^{2}\leqslant 2/\unicode[STIX]{x1D716}$
. In case
![]() $\unicode[STIX]{x1D6E5}=0$
, since the Cartier index of
$\unicode[STIX]{x1D6E5}=0$
, since the Cartier index of
![]() $K_{X}$
is bounded from above by the determinant of the intersection matrix
$K_{X}$
is bounded from above by the determinant of the intersection matrix
![]() $(E_{i}.E_{j})$
of the exceptional curves
$(E_{i}.E_{j})$
of the exceptional curves
![]() $E_{i}$
’s on
$E_{i}$
’s on
![]() $X_{\text{min}}$
over
$X_{\text{min}}$
over
![]() $X$
, it follows that the Cartier index bound
$X$
, it follows that the Cartier index bound
![]() $r(2,\unicode[STIX]{x1D716})$
in statement (i) satisfies
$r(2,\unicode[STIX]{x1D716})$
in statement (i) satisfies
 $$\begin{eqnarray}r(2,\unicode[STIX]{x1D716})\leqslant 2(2/\unicode[STIX]{x1D716})^{128/\unicode[STIX]{x1D716}^{5}}.\end{eqnarray}$$
$$\begin{eqnarray}r(2,\unicode[STIX]{x1D716})\leqslant 2(2/\unicode[STIX]{x1D716})^{128/\unicode[STIX]{x1D716}^{5}}.\end{eqnarray}$$
Remark 0.1. An upper bound of
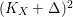 $(K_{X}+\unicode[STIX]{x1D6E5})^{2}$
is implicitly mentioned in [Reference AlexeevAle94] but not clearly written down. It is also not clear if the upper bound (◇) is optimal. In view of Theorem A, this seems unlikely.
$(K_{X}+\unicode[STIX]{x1D6E5})^{2}$
is implicitly mentioned in [Reference AlexeevAle94] but not clearly written down. It is also not clear if the upper bound (◇) is optimal. In view of Theorem A, this seems unlikely.
We also obtain an upper bound of the anticanonical volumes for
![]() $\unicode[STIX]{x1D716}$
-klt
$\unicode[STIX]{x1D716}$
-klt
![]() $\mathbb{Q}$
-factorial log
$\mathbb{Q}$
-factorial log
![]() $\mathbb{Q}$
-Fano threefolds of Picard number one (cf., Theorem 5.17).
$\mathbb{Q}$
-Fano threefolds of Picard number one (cf., Theorem 5.17).
Theorem B.
Let
![]() $(X,\unicode[STIX]{x1D6E5})$
be an
$(X,\unicode[STIX]{x1D6E5})$
be an
![]() $\unicode[STIX]{x1D716}$
-klt
$\unicode[STIX]{x1D716}$
-klt
![]() $\mathbb{Q}$
-factorial log
$\mathbb{Q}$
-factorial log
![]() $\mathbb{Q}$
-Fano threefold of
$\mathbb{Q}$
-Fano threefold of
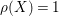 $\unicode[STIX]{x1D70C}(X)=1$
. Then the degree
$\unicode[STIX]{x1D70C}(X)=1$
. Then the degree
![]() $-K_{X}^{3}$
satisfies
$-K_{X}^{3}$
satisfies
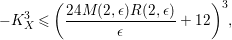 $$\begin{eqnarray}-K_{X}^{3}\leqslant \biggl(\frac{24M(2,\unicode[STIX]{x1D716})R(2,\unicode[STIX]{x1D716})}{\unicode[STIX]{x1D716}}+12\biggr)^{3},\end{eqnarray}$$
$$\begin{eqnarray}-K_{X}^{3}\leqslant \biggl(\frac{24M(2,\unicode[STIX]{x1D716})R(2,\unicode[STIX]{x1D716})}{\unicode[STIX]{x1D716}}+12\biggr)^{3},\end{eqnarray}$$
where
![]() $R(2,\unicode[STIX]{x1D716})$
is an upper bound of the Cartier index of
$R(2,\unicode[STIX]{x1D716})$
is an upper bound of the Cartier index of
![]() $K_{S}$
for
$K_{S}$
for
![]() $S$
any
$S$
any
![]() $\unicode[STIX]{x1D716}/2$
-klt log del Pezzo surface of
$\unicode[STIX]{x1D716}/2$
-klt log del Pezzo surface of
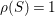 $\unicode[STIX]{x1D70C}(S)=1$
and
$\unicode[STIX]{x1D70C}(S)=1$
and
![]() $M(2,\unicode[STIX]{x1D716})$
is an upper bound of the anticanonical volume
$M(2,\unicode[STIX]{x1D716})$
is an upper bound of the anticanonical volume
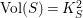 $\text{Vol}(S)=K_{S}^{2}$
for
$\text{Vol}(S)=K_{S}^{2}$
for
![]() $S$
any
$S$
any
![]() $\unicode[STIX]{x1D716}/2$
-klt log del Pezzo surface of
$\unicode[STIX]{x1D716}/2$
-klt log del Pezzo surface of
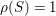 $\unicode[STIX]{x1D70C}(S)=1$
. Note that
$\unicode[STIX]{x1D70C}(S)=1$
. Note that
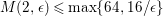 $M(2,\unicode[STIX]{x1D716})\leqslant \max \{64,16/\unicode[STIX]{x1D716}\}$
from Theorem A and
$M(2,\unicode[STIX]{x1D716})\leqslant \max \{64,16/\unicode[STIX]{x1D716}\}$
from Theorem A and
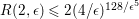 $R(2,\unicode[STIX]{x1D716})\leqslant 2(4/\unicode[STIX]{x1D716})^{128/\unicode[STIX]{x1D716}^{5}}$
from ( ◇).
$R(2,\unicode[STIX]{x1D716})\leqslant 2(4/\unicode[STIX]{x1D716})^{128/\unicode[STIX]{x1D716}^{5}}$
from ( ◇).
For a
![]() $\mathbb{Q}$
-factorial
$\mathbb{Q}$
-factorial
![]() $\unicode[STIX]{x1D716}$
-klt log
$\unicode[STIX]{x1D716}$
-klt log
![]() $\mathbb{Q}$
-Fano pair
$\mathbb{Q}$
-Fano pair
![]() $(X,\unicode[STIX]{x1D6E5})$
of
$(X,\unicode[STIX]{x1D6E5})$
of
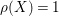 $\unicode[STIX]{x1D70C}(X)=1$
, since
$\unicode[STIX]{x1D70C}(X)=1$
, since
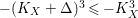 $-(K_{X}+\unicode[STIX]{x1D6E5})^{3}\leqslant -K_{X}^{3}$
and
$-(K_{X}+\unicode[STIX]{x1D6E5})^{3}\leqslant -K_{X}^{3}$
and
![]() $X$
is also
$X$
is also
![]() $\unicode[STIX]{x1D716}$
-klt, by Theorem B we get an upper bound of the anticanonical volume
$\unicode[STIX]{x1D716}$
-klt, by Theorem B we get an upper bound of the anticanonical volume
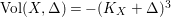 $\text{Vol}(X,\unicode[STIX]{x1D6E5})=-(K_{X}+\unicode[STIX]{x1D6E5})^{3}$
. However, it is not expected that the bound in Theorem B is sharp or in a sharp form. As a corollary of Theorem B, this gives a proof of the Batyrev conjecture in the case of log
$\text{Vol}(X,\unicode[STIX]{x1D6E5})=-(K_{X}+\unicode[STIX]{x1D6E5})^{3}$
. However, it is not expected that the bound in Theorem B is sharp or in a sharp form. As a corollary of Theorem B, this gives a proof of the Batyrev conjecture in the case of log
![]() $\mathbb{Q}$
-Fano threefolds of Picard number one.
$\mathbb{Q}$
-Fano threefolds of Picard number one.
Note that
![]() $\mathbb{Q}$
-factoriality is a technical assumption. However, this condition is natural in the sense that starting from a smooth variety, each variety constructed by a step of the minimal model program remains
$\mathbb{Q}$
-factoriality is a technical assumption. However, this condition is natural in the sense that starting from a smooth variety, each variety constructed by a step of the minimal model program remains
![]() $\mathbb{Q}$
-factorial. In dimension two, surfaces with rational singularities, for example, klt singularities, are always
$\mathbb{Q}$
-factorial. In dimension two, surfaces with rational singularities, for example, klt singularities, are always
![]() $\mathbb{Q}$
-factorial.
$\mathbb{Q}$
-factorial.
Instead of using deformation theory of rational curves as in [Reference Kollár, Miyaoka, Mori and TakagiKMMT00], the Riemann–Roch formula as in [Reference KawamataKaw92], or the sandwich argument of [Reference AlexeevAle94], we aim to create isolated non-klt centers by the method developed in [McK02]. The point is that deformation theory for rational curves on klt varieties is much harder and so far no effective Riemann–Roch formula is known for klt threefolds.
This paper is organized as follows: In Section 1, we study non-klt centers. In Section 2, we illustrate the general method in [McK02] for obtaining an upper bound of anticanonical volumes in Theorems A and B. In Section 3, we review the theory of families of non-klt centers in [McK02]. In Section 4, we study weak log del Pezzo surfaces and prove Theorem A. In Section 5, we prove Theorem B.
Through this article we work over field of complex numbers
![]() $\mathbb{C}$
.
$\mathbb{C}$
.
1 Non-klt centers
For the definition and properties of the singularities in the minimal model program, we refer to [Reference Kollár and MoriKM98].
Definition 1.1. Let
![]() $(X,\unicode[STIX]{x1D6E5})$
be a log pair. A subvariety
$(X,\unicode[STIX]{x1D6E5})$
be a log pair. A subvariety
![]() $V\subseteq X$
is called a non-klt center if it is the image of a divisor of discrepancy at most -1. A non-klt place is a valuation corresponding to a divisor of discrepancy at most -1. The non-klt locus
$V\subseteq X$
is called a non-klt center if it is the image of a divisor of discrepancy at most -1. A non-klt place is a valuation corresponding to a divisor of discrepancy at most -1. The non-klt locus
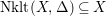 $\text{Nklt}(X,\unicode[STIX]{x1D6E5})\subseteq X$
is the union of the non-klt centers. If there is a unique non-klt place lying over the generic point of a non-klt center
$\text{Nklt}(X,\unicode[STIX]{x1D6E5})\subseteq X$
is the union of the non-klt centers. If there is a unique non-klt place lying over the generic point of a non-klt center
![]() $V$
, then we say that
$V$
, then we say that
![]() $V$
is exceptional. If
$V$
is exceptional. If
![]() $(X,\unicode[STIX]{x1D6E5})$
is log canonical along the generic point of a non-klt center
$(X,\unicode[STIX]{x1D6E5})$
is log canonical along the generic point of a non-klt center
![]() $V$
, then we say that
$V$
, then we say that
![]() $V$
is pure.
$V$
is pure.
The non-klt places/centers here are the log canonical (lc) places/centers in [McK02].
A standard way of creating a non-klt center on an
![]() $n$
-dimensional variety
$n$
-dimensional variety
![]() $X$
is to find a very singular divisor: Fix
$X$
is to find a very singular divisor: Fix
![]() $p\in X$
a smooth point. If
$p\in X$
a smooth point. If
![]() $\unicode[STIX]{x1D6E5}$
is a
$\unicode[STIX]{x1D6E5}$
is a
![]() $\mathbb{Q}$
-Cartier divisor on
$\mathbb{Q}$
-Cartier divisor on
![]() $X$
with
$X$
with
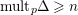 $\text{mult}_{p}\unicode[STIX]{x1D6E5}\geqslant n$
, then
$\text{mult}_{p}\unicode[STIX]{x1D6E5}\geqslant n$
, then
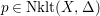 $p\in \text{Nklt}(X,\unicode[STIX]{x1D6E5})$
. Indeed, consider the blow up
$p\in \text{Nklt}(X,\unicode[STIX]{x1D6E5})$
. Indeed, consider the blow up
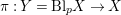 $\unicode[STIX]{x1D70B}:Y=\text{Bl}_{p}X\rightarrow X$
and let
$\unicode[STIX]{x1D70B}:Y=\text{Bl}_{p}X\rightarrow X$
and let
![]() $E$
be the unique exceptional divisor with
$E$
be the unique exceptional divisor with
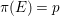 $\unicode[STIX]{x1D70B}(E)=p$
, then the discrepancy
$\unicode[STIX]{x1D70B}(E)=p$
, then the discrepancy
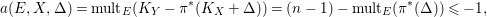 $$\begin{eqnarray}a(E,X,\unicode[STIX]{x1D6E5})=\text{mult}_{E}(K_{Y}-\unicode[STIX]{x1D70B}^{\ast }(K_{X}+\unicode[STIX]{x1D6E5}))=(n-1)-\text{mult}_{E}(\unicode[STIX]{x1D70B}^{\ast }(\unicode[STIX]{x1D6E5}))\leqslant -1,\end{eqnarray}$$
$$\begin{eqnarray}a(E,X,\unicode[STIX]{x1D6E5})=\text{mult}_{E}(K_{Y}-\unicode[STIX]{x1D70B}^{\ast }(K_{X}+\unicode[STIX]{x1D6E5}))=(n-1)-\text{mult}_{E}(\unicode[STIX]{x1D70B}^{\ast }(\unicode[STIX]{x1D6E5}))\leqslant -1,\end{eqnarray}$$
as
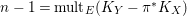 $n-1=\text{mult}_{E}(K_{Y}-\unicode[STIX]{x1D70B}^{\ast }K_{X})$
and
$n-1=\text{mult}_{E}(K_{Y}-\unicode[STIX]{x1D70B}^{\ast }K_{X})$
and
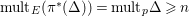 $\text{mult}_{E}(\unicode[STIX]{x1D70B}^{\ast }(\unicode[STIX]{x1D6E5}))=\text{mult}_{p}\unicode[STIX]{x1D6E5}\geqslant n$
.
$\text{mult}_{E}(\unicode[STIX]{x1D70B}^{\ast }(\unicode[STIX]{x1D6E5}))=\text{mult}_{p}\unicode[STIX]{x1D6E5}\geqslant n$
.
Existence of singular divisors can be shown by the following standard estimation.
Lemma 1.2. Let
![]() $X$
be an
$X$
be an
![]() $n$
-dimensional complete complex variety and
$n$
-dimensional complete complex variety and
![]() $D$
be a divisor with
$D$
be a divisor with
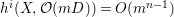 $h^{i}(X,{\mathcal{O}}(mD))=O(m^{n-1})$
for all
$h^{i}(X,{\mathcal{O}}(mD))=O(m^{n-1})$
for all
![]() $i>0$
, for example, when
$i>0$
, for example, when
![]() $D$
is big and nef. Fix a positive rational number
$D$
is big and nef. Fix a positive rational number
![]() $\unicode[STIX]{x1D6FC}$
with
$\unicode[STIX]{x1D6FC}$
with
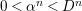 $0<\unicode[STIX]{x1D6FC}^{n}<D^{n}$
. Then for
$0<\unicode[STIX]{x1D6FC}^{n}<D^{n}$
. Then for
![]() $m\gg 0$
and any
$m\gg 0$
and any
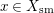 $x\in X_{\text{sm}}$
, there exists a divisor
$x\in X_{\text{sm}}$
, there exists a divisor
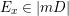 $E_{x}\in |mD|$
with
$E_{x}\in |mD|$
with
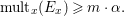 $\text{mult}_{x}(E_{x})\geqslant m\cdot \unicode[STIX]{x1D6FC}.$
$\text{mult}_{x}(E_{x})\geqslant m\cdot \unicode[STIX]{x1D6FC}.$
Proof. This is [Reference LazarsfeldLaz04, Proposition 1.1.31]. ◻
We will apply Lemma 1.2 to the case where
![]() $(X,\unicode[STIX]{x1D6E5})$
is an
$(X,\unicode[STIX]{x1D6E5})$
is an
![]() $n$
-dimensional log
$n$
-dimensional log
![]() $\mathbb{Q}$
-Fano variety: Write
$\mathbb{Q}$
-Fano variety: Write
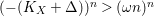 $(-(K_{X}+\unicode[STIX]{x1D6E5}))^{n}>(\unicode[STIX]{x1D714}n)^{n}$
for some rational number
$(-(K_{X}+\unicode[STIX]{x1D6E5}))^{n}>(\unicode[STIX]{x1D714}n)^{n}$
for some rational number
![]() $\unicode[STIX]{x1D714}>0$
, then as the cohomology groups
$\unicode[STIX]{x1D714}>0$
, then as the cohomology groups
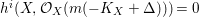 $h^{i}(X,{\mathcal{O}}_{X}(m(-K_{X}+\unicode[STIX]{x1D6E5})))=0$
for
$h^{i}(X,{\mathcal{O}}_{X}(m(-K_{X}+\unicode[STIX]{x1D6E5})))=0$
for
![]() $i>0$
and
$i>0$
and
![]() $m>0$
sufficiently divisible by Kawamata–Viehweg vanishing theorem, we can find for each
$m>0$
sufficiently divisible by Kawamata–Viehweg vanishing theorem, we can find for each
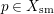 $p\in X_{\text{sm}}$
an effective
$p\in X_{\text{sm}}$
an effective
![]() $\mathbb{Q}$
-divisor
$\mathbb{Q}$
-divisor
![]() $\unicode[STIX]{x1D6E5}_{p}$
such that
$\unicode[STIX]{x1D6E5}_{p}$
such that
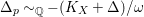 $\unicode[STIX]{x1D6E5}_{p}{\sim}_{\mathbb{Q}}-(K_{X}+\unicode[STIX]{x1D6E5})/\unicode[STIX]{x1D714}$
with
$\unicode[STIX]{x1D6E5}_{p}{\sim}_{\mathbb{Q}}-(K_{X}+\unicode[STIX]{x1D6E5})/\unicode[STIX]{x1D714}$
with
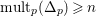 $\text{mult}_{p}(\unicode[STIX]{x1D6E5}_{p})\geqslant n$
. In particular,
$\text{mult}_{p}(\unicode[STIX]{x1D6E5}_{p})\geqslant n$
. In particular,
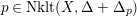 $p\in \text{Nklt}(X,\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6E5}_{p})$
.
$p\in \text{Nklt}(X,\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6E5}_{p})$
.
The non-klt centers satisfy the following Connectedness Lemma of Kollár and Shokurov, whose proof is simply a formal consequence of the Kawamata–Viehweg vanishing theorem. This is the most important ingredient in this work.
Lemma 1.3. Let
![]() $(X,\unicode[STIX]{x1D6E5})$
be a log pair. Let
$(X,\unicode[STIX]{x1D6E5})$
be a log pair. Let
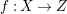 $f:X\rightarrow Z$
be a projective morphism with connected fibers such that the image of every component of
$f:X\rightarrow Z$
be a projective morphism with connected fibers such that the image of every component of
![]() $\unicode[STIX]{x1D6E5}$
with negative coefficient is of codimension at least two in
$\unicode[STIX]{x1D6E5}$
with negative coefficient is of codimension at least two in
![]() $Z$
. Assume that
$Z$
. Assume that
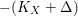 $-(K_{X}+\unicode[STIX]{x1D6E5})$
is big and nef over
$-(K_{X}+\unicode[STIX]{x1D6E5})$
is big and nef over
![]() $Z$
, then the intersection of
$Z$
, then the intersection of
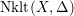 $\text{Nklt}(X,\unicode[STIX]{x1D6E5})$
with each fiber
$\text{Nklt}(X,\unicode[STIX]{x1D6E5})$
with each fiber
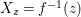 $X_{z}=f^{-1}(z)$
is connected.
$X_{z}=f^{-1}(z)$
is connected.
Proof. For simplicity, we assume that
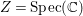 $Z=\text{Spec}(\mathbb{C})$
is a point and
$Z=\text{Spec}(\mathbb{C})$
is a point and
![]() $(X,\unicode[STIX]{x1D6E5})$
is log smooth, that is,
$(X,\unicode[STIX]{x1D6E5})$
is log smooth, that is,
![]() $X$
is smooth and
$X$
is smooth and
![]() $\unicode[STIX]{x1D6E5}$
has simple normal crossing support. Then the identity map
$\unicode[STIX]{x1D6E5}$
has simple normal crossing support. Then the identity map
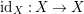 $\text{id}_{X}:X\rightarrow X$
is a log resolution of
$\text{id}_{X}:X\rightarrow X$
is a log resolution of
![]() $(X,\unicode[STIX]{x1D6E5})$
and
$(X,\unicode[STIX]{x1D6E5})$
and
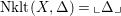 $\text{Nklt}(X,\unicode[STIX]{x1D6E5})=\llcorner \unicode[STIX]{x1D6E5}\lrcorner$
. Consider the exact sequence
$\text{Nklt}(X,\unicode[STIX]{x1D6E5})=\llcorner \unicode[STIX]{x1D6E5}\lrcorner$
. Consider the exact sequence
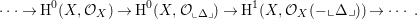 $$\begin{eqnarray}\cdots \rightarrow \text{H}^{0}(X,{\mathcal{O}}_{X})\rightarrow \text{H}^{0}(X,{\mathcal{O}}_{\llcorner \unicode[STIX]{x1D6E5}\lrcorner })\rightarrow \text{H}^{1}(X,{\mathcal{O}}_{X}(-\llcorner \unicode[STIX]{x1D6E5}\lrcorner ))\rightarrow \cdots \,.\end{eqnarray}$$
$$\begin{eqnarray}\cdots \rightarrow \text{H}^{0}(X,{\mathcal{O}}_{X})\rightarrow \text{H}^{0}(X,{\mathcal{O}}_{\llcorner \unicode[STIX]{x1D6E5}\lrcorner })\rightarrow \text{H}^{1}(X,{\mathcal{O}}_{X}(-\llcorner \unicode[STIX]{x1D6E5}\lrcorner ))\rightarrow \cdots \,.\end{eqnarray}$$
Since
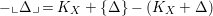 $-\llcorner \unicode[STIX]{x1D6E5}\lrcorner =K_{X}+\{\unicode[STIX]{x1D6E5}\}-(K_{X}+\unicode[STIX]{x1D6E5})$
and
$-\llcorner \unicode[STIX]{x1D6E5}\lrcorner =K_{X}+\{\unicode[STIX]{x1D6E5}\}-(K_{X}+\unicode[STIX]{x1D6E5})$
and
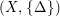 $(X,\{\unicode[STIX]{x1D6E5}\})$
is klt, we have
$(X,\{\unicode[STIX]{x1D6E5}\})$
is klt, we have
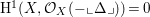 $\text{H}^{1}(X,{\mathcal{O}}_{X}(-\llcorner \unicode[STIX]{x1D6E5}\lrcorner ))=0$
by Kawamata–Viehweg vanishing theorem as
$\text{H}^{1}(X,{\mathcal{O}}_{X}(-\llcorner \unicode[STIX]{x1D6E5}\lrcorner ))=0$
by Kawamata–Viehweg vanishing theorem as
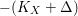 $-(K_{X}+\unicode[STIX]{x1D6E5})$
is nef and big. Since
$-(K_{X}+\unicode[STIX]{x1D6E5})$
is nef and big. Since
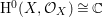 $\text{H}^{0}(X,{\mathcal{O}}_{X})\cong \mathbb{C}$
, we see that
$\text{H}^{0}(X,{\mathcal{O}}_{X})\cong \mathbb{C}$
, we see that
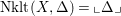 $\text{Nklt}(X,\unicode[STIX]{x1D6E5})=\llcorner \unicode[STIX]{x1D6E5}\lrcorner$
is connected.
$\text{Nklt}(X,\unicode[STIX]{x1D6E5})=\llcorner \unicode[STIX]{x1D6E5}\lrcorner$
is connected.
For general case, see [Reference CortiCor07, Theorem 17.4]. ◻
Here is a nonexample showing that
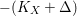 $-(K_{X}+\unicode[STIX]{x1D6E5})$
being nef and big is necessary in the Connectedness Lemma 1.3.
$-(K_{X}+\unicode[STIX]{x1D6E5})$
being nef and big is necessary in the Connectedness Lemma 1.3.
Example 1.4. Let
![]() $X$
be
$X$
be
![]() $\mathbb{P}^{1}\times \mathbb{P}^{1}$
and denote
$\mathbb{P}^{1}\times \mathbb{P}^{1}$
and denote
![]() $F$
(resp.
$F$
(resp.
![]() $G$
) to be the fiber of the first (resp. second) projection to
$G$
) to be the fiber of the first (resp. second) projection to
![]() $\mathbb{P}^{1}$
. Consider
$\mathbb{P}^{1}$
. Consider
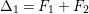 $\unicode[STIX]{x1D6E5}_{1}=F_{1}+F_{2}$
the sum of two distinct fibers of the first projection to
$\unicode[STIX]{x1D6E5}_{1}=F_{1}+F_{2}$
the sum of two distinct fibers of the first projection to
![]() $\mathbb{P}^{1}$
and
$\mathbb{P}^{1}$
and
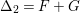 $\unicode[STIX]{x1D6E5}_{2}=F+G$
the sum of two fibers with respect to two different projections to
$\unicode[STIX]{x1D6E5}_{2}=F+G$
the sum of two fibers with respect to two different projections to
![]() $\mathbb{P}^{1}$
’s. Then
$\mathbb{P}^{1}$
’s. Then
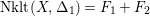 $\text{Nklt}(X,\unicode[STIX]{x1D6E5}_{1})=F_{1}+F_{2}$
is not connected while
$\text{Nklt}(X,\unicode[STIX]{x1D6E5}_{1})=F_{1}+F_{2}$
is not connected while
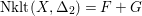 $\text{Nklt}(X,\unicode[STIX]{x1D6E5}_{2})=F+G$
is connected. Note that
$\text{Nklt}(X,\unicode[STIX]{x1D6E5}_{2})=F+G$
is connected. Note that
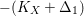 $-(K_{X}+\unicode[STIX]{x1D6E5}_{1})$
is nef but not big while
$-(K_{X}+\unicode[STIX]{x1D6E5}_{1})$
is nef but not big while
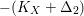 $-(K_{X}+\unicode[STIX]{x1D6E5}_{2})$
is nef and big.
$-(K_{X}+\unicode[STIX]{x1D6E5}_{2})$
is nef and big.
Later on, we will try to produce not only non-klt centers but isolated non-klt centers. The following theorem is the main technique which allows us to cut down the dimension of non-klt centers.
Theorem 1.5. [Reference KollárKol97, Theorem 6.8.1]
Let
![]() $(X,\unicode[STIX]{x1D6E5})$
be klt, projective and
$(X,\unicode[STIX]{x1D6E5})$
be klt, projective and
![]() $x\in X$
a closed point. Let
$x\in X$
a closed point. Let
![]() $D$
be an effective
$D$
be an effective
![]() $\mathbb{Q}$
-Cartier
$\mathbb{Q}$
-Cartier
![]() $\mathbb{Q}$
-divisor on
$\mathbb{Q}$
-divisor on
![]() $X$
such that
$X$
such that
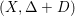 $(X,\unicode[STIX]{x1D6E5}+D)$
is log canonical in a neighborhood of
$(X,\unicode[STIX]{x1D6E5}+D)$
is log canonical in a neighborhood of
![]() $x$
. Assume that
$x$
. Assume that
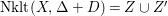 $\text{Nklt}(X,\unicode[STIX]{x1D6E5}+D)=Z\cup Z^{\prime }$
where
$\text{Nklt}(X,\unicode[STIX]{x1D6E5}+D)=Z\cup Z^{\prime }$
where
![]() $Z$
is irreducible,
$Z$
is irreducible,
![]() $x\in Z$
, and
$x\in Z$
, and
![]() $x\notin Z^{\prime }$
. Set
$x\notin Z^{\prime }$
. Set
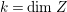 $k=\dim Z$
. Let
$k=\dim Z$
. Let
![]() $H$
be an ample
$H$
be an ample
![]() $\mathbb{Q}$
-divisor on
$\mathbb{Q}$
-divisor on
![]() $X$
such that
$X$
such that
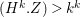 $(H^{k}.Z)>k^{k}$
. Then there is an effective
$(H^{k}.Z)>k^{k}$
. Then there is an effective
![]() $\mathbb{Q}$
-divisor
$\mathbb{Q}$
-divisor
![]() $B\equiv H$
and rational numbers
$B\equiv H$
and rational numbers
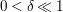 $0<\unicode[STIX]{x1D6FF}\ll 1$
and
$0<\unicode[STIX]{x1D6FF}\ll 1$
and
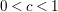 $0<c<1$
such that
$0<c<1$
such that
-
(1)
 $(X,\unicode[STIX]{x1D6E5}+(1-\unicode[STIX]{x1D6FF})D+cB)$
is non-klt in a neighborhood of
$(X,\unicode[STIX]{x1D6E5}+(1-\unicode[STIX]{x1D6FF})D+cB)$
is non-klt in a neighborhood of
 $x$
, and
$x$
, and -
(2)
 $\text{Nklt}(X,\unicode[STIX]{x1D6E5}+(1-\unicode[STIX]{x1D6FF})D+cB)=W\cup W^{\prime }$
where
$\text{Nklt}(X,\unicode[STIX]{x1D6E5}+(1-\unicode[STIX]{x1D6FF})D+cB)=W\cup W^{\prime }$
where
 $W$
is irreducible,
$W$
is irreducible,
 $x\in W$
,
$x\in W$
,
 $x\notin W^{\prime }$
and
$x\notin W^{\prime }$
and
 $\dim W<\dim Z$
.
$\dim W<\dim Z$
.
2 Guiding example
The idea in [McK02] for obtaining an upper bound of the anticanonical volumes is to create isolated non-klt centers and then use the Connectedness Lemma 1.3: For simplicity, we assume that
![]() $\unicode[STIX]{x1D6E5}=0$
. Write
$\unicode[STIX]{x1D6E5}=0$
. Write
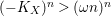 $(-K_{X})^{n}>(\unicode[STIX]{x1D714}n)^{n}$
for a positive rational number
$(-K_{X})^{n}>(\unicode[STIX]{x1D714}n)^{n}$
for a positive rational number
![]() $\unicode[STIX]{x1D714}$
. For each
$\unicode[STIX]{x1D714}$
. For each
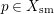 $p\in X_{\text{sm}}$
, we can find an effective
$p\in X_{\text{sm}}$
, we can find an effective
![]() $\mathbb{Q}$
-divisor
$\mathbb{Q}$
-divisor
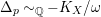 $\unicode[STIX]{x1D6E5}_{p}{\sim}_{\mathbb{Q}}-K_{X}/\unicode[STIX]{x1D714}$
such that
$\unicode[STIX]{x1D6E5}_{p}{\sim}_{\mathbb{Q}}-K_{X}/\unicode[STIX]{x1D714}$
such that
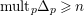 $\text{mult}_{p}\unicode[STIX]{x1D6E5}_{p}\geqslant n$
and hence
$\text{mult}_{p}\unicode[STIX]{x1D6E5}_{p}\geqslant n$
and hence
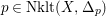 $p\in \text{Nklt}(X,\unicode[STIX]{x1D6E5}_{p})$
. The observation is that if
$p\in \text{Nklt}(X,\unicode[STIX]{x1D6E5}_{p})$
. The observation is that if
![]() $\unicode[STIX]{x1D714}\gg 0$
, then for general
$\unicode[STIX]{x1D714}\gg 0$
, then for general
![]() $p\in X$
,
$p\in X$
,
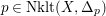 $p\in \text{Nklt}(X,\unicode[STIX]{x1D6E5}_{p})$
cannot be an isolated point. Indeed, if this is not true, then for two general points
$p\in \text{Nklt}(X,\unicode[STIX]{x1D6E5}_{p})$
cannot be an isolated point. Indeed, if this is not true, then for two general points
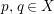 $p,q\in X$
, the set
$p,q\in X$
, the set
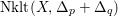 $\text{Nklt}(X,\unicode[STIX]{x1D6E5}_{p}+\unicode[STIX]{x1D6E5}_{q})$
would contain
$\text{Nklt}(X,\unicode[STIX]{x1D6E5}_{p}+\unicode[STIX]{x1D6E5}_{q})$
would contain
![]() $\{p,q\}$
as isolated non-klt centers. But the pair
$\{p,q\}$
as isolated non-klt centers. But the pair
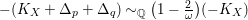 $-(K_{X}+\unicode[STIX]{x1D6E5}_{p}+\unicode[STIX]{x1D6E5}_{q}){\sim}_{\mathbb{Q}}\big(1-\frac{2}{\unicode[STIX]{x1D714}}\big)(-K_{X})$
is nef and big for
$-(K_{X}+\unicode[STIX]{x1D6E5}_{p}+\unicode[STIX]{x1D6E5}_{q}){\sim}_{\mathbb{Q}}\big(1-\frac{2}{\unicode[STIX]{x1D714}}\big)(-K_{X})$
is nef and big for
![]() $\unicode[STIX]{x1D714}>2$
. By the Connectedness Lemma 1.3,
$\unicode[STIX]{x1D714}>2$
. By the Connectedness Lemma 1.3,
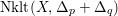 $\text{Nklt}(X,\unicode[STIX]{x1D6E5}_{p}+\unicode[STIX]{x1D6E5}_{q})$
must be connected, a contradiction.
$\text{Nklt}(X,\unicode[STIX]{x1D6E5}_{p}+\unicode[STIX]{x1D6E5}_{q})$
must be connected, a contradiction.
Therefore, for general
![]() $p\in X$
the minimal non-klt center
$p\in X$
the minimal non-klt center
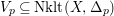 $V_{p}\subseteq \text{Nklt}(X,\unicode[STIX]{x1D6E5}_{p})$
passing through
$V_{p}\subseteq \text{Nklt}(X,\unicode[STIX]{x1D6E5}_{p})$
passing through
![]() $p$
is typically positive dimensional. We would like to show that the restricted volume
$p$
is typically positive dimensional. We would like to show that the restricted volume
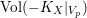 $\text{Vol}(-K_{X}|_{V_{p}})$
on the minimal non-klt center
$\text{Vol}(-K_{X}|_{V_{p}})$
on the minimal non-klt center
![]() $V_{p}$
is large if
$V_{p}$
is large if
![]() $\unicode[STIX]{x1D714}\gg 0$
. Hence, we can cut down the dimension of non-klt centers by Theorem 1.5. After doing this finitely many times, we get isolated non-klt centers and we are done.
$\unicode[STIX]{x1D714}\gg 0$
. Hence, we can cut down the dimension of non-klt centers by Theorem 1.5. After doing this finitely many times, we get isolated non-klt centers and we are done.
In general, it is hard to find a lower bound of the restricted volume
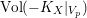 $\text{Vol}(-K_{X}|_{V_{p}})$
on the minimal non-klt center
$\text{Vol}(-K_{X}|_{V_{p}})$
on the minimal non-klt center
![]() $V_{p}$
. We illustrate McKernan’s method of obtaining a lower bound of the restricted volumes on the non-klt center of an
$V_{p}$
. We illustrate McKernan’s method of obtaining a lower bound of the restricted volumes on the non-klt center of an
![]() $\unicode[STIX]{x1D716}$
-klt log
$\unicode[STIX]{x1D716}$
-klt log
![]() $\mathbb{Q}$
-Fano variety by the following guiding example (cf., [McK02]).
$\mathbb{Q}$
-Fano variety by the following guiding example (cf., [McK02]).
Example 2.1. Let
![]() $X$
be the projective cone over a rational normal curve of degree
$X$
be the projective cone over a rational normal curve of degree
![]() $d\geqslant 2$
with the unique singular point
$d\geqslant 2$
with the unique singular point
![]() $O\in X$
. The blow up
$O\in X$
. The blow up
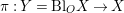 $\unicode[STIX]{x1D70B}:Y=\text{Bl}_{O}X\rightarrow X$
is a resolution of
$\unicode[STIX]{x1D70B}:Y=\text{Bl}_{O}X\rightarrow X$
is a resolution of
![]() $X$
where
$X$
where
![]() $Y$
is a
$Y$
is a
![]() $\mathbb{P}^{1}$
-bundle
$\mathbb{P}^{1}$
-bundle
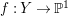 $f:Y\rightarrow \mathbb{P}^{1}$
over
$f:Y\rightarrow \mathbb{P}^{1}$
over
![]() $\mathbb{P}^{1}$
:
$\mathbb{P}^{1}$
:
It is easy to show that
-
(a)
 $K_{Y}=\unicode[STIX]{x1D70B}^{\ast }K_{X}+(-1+2/d)E$
, where
$K_{Y}=\unicode[STIX]{x1D70B}^{\ast }K_{X}+(-1+2/d)E$
, where
 $E$
is the unique
$E$
is the unique
 $\unicode[STIX]{x1D70B}$
-exceptional divisor and hence
$\unicode[STIX]{x1D70B}$
-exceptional divisor and hence
 $X$
is
$X$
is
 $\unicode[STIX]{x1D716}$
-klt for
$\unicode[STIX]{x1D716}$
-klt for
 $\unicode[STIX]{x1D716}=1/d$
;
$\unicode[STIX]{x1D716}=1/d$
; -
(b)
 $X$
is
$X$
is
 $\mathbb{Q}$
-factorial of Picard number one and
$\mathbb{Q}$
-factorial of Picard number one and
 $-K_{X}{\sim}_{\mathbb{Q}}(d+2)l$
is an ample
$-K_{X}{\sim}_{\mathbb{Q}}(d+2)l$
is an ample
 $\mathbb{Q}$
-Cartier divisor, where
$\mathbb{Q}$
-Cartier divisor, where
 $l$
is the class of a ruling of
$l$
is the class of a ruling of
 $X$
. Hence
$X$
. Hence
 $X$
is an
$X$
is an
 $\unicode[STIX]{x1D716}$
-klt del Pezzo surface;
$\unicode[STIX]{x1D716}$
-klt del Pezzo surface; -
(c)
 $\text{Vol}(-K_{X})=d+4+4/d$
is a linear function of
$\text{Vol}(-K_{X})=d+4+4/d$
is a linear function of
 $d=1/\unicode[STIX]{x1D716}$
and provides the required example in Theorem A.
$d=1/\unicode[STIX]{x1D716}$
and provides the required example in Theorem A.
Let
![]() $p\in X$
be a general point. Then
$p\in X$
be a general point. Then
![]() $p$
is not the vertex
$p$
is not the vertex
![]() $O$
and the unique ruling
$O$
and the unique ruling
![]() $l_{p}$
passing through
$l_{p}$
passing through
![]() $p$
is the non-klt center of the log pair
$p$
is the non-klt center of the log pair
![]() $(X,l_{p})$
, that is,
$(X,l_{p})$
, that is,
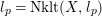 $l_{p}=\text{Nklt}(X,l_{p})$
. Moreover, the proper transform
$l_{p}=\text{Nklt}(X,l_{p})$
. Moreover, the proper transform
![]() $F_{p}$
of
$F_{p}$
of
![]() $l_{p}$
on
$l_{p}$
on
![]() $Y$
is a fiber of the
$Y$
is a fiber of the
![]() $\mathbb{P}^{1}$
-bundle
$\mathbb{P}^{1}$
-bundle
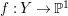 $f:Y\rightarrow \mathbb{P}^{1}$
. In this case, one interprets the
$f:Y\rightarrow \mathbb{P}^{1}$
. In this case, one interprets the
![]() $\mathbb{P}^{1}$
-bundle structure of
$\mathbb{P}^{1}$
-bundle structure of
![]() $Y$
as a covering family of non-klt centers of
$Y$
as a covering family of non-klt centers of
![]() $X$
since the map
$X$
since the map
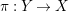 $\unicode[STIX]{x1D70B}:Y\rightarrow X$
is dominant.
$\unicode[STIX]{x1D70B}:Y\rightarrow X$
is dominant.
For
 $p,q\in X$
two general points, let
$p,q\in X$
two general points, let
![]() $l_{p}$
and
$l_{p}$
and
![]() $l_{q}$
be the rulings passing through
$l_{q}$
be the rulings passing through
![]() $p$
and
$p$
and
![]() $q$
respectively. Consider the pair
$q$
respectively. Consider the pair
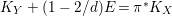 $K_{Y}+(1-2/d)E=\unicode[STIX]{x1D70B}^{\ast }K_{X}$
. By the Connectedness Lemma 1.3, the non-klt locus
$K_{Y}+(1-2/d)E=\unicode[STIX]{x1D70B}^{\ast }K_{X}$
. By the Connectedness Lemma 1.3, the non-klt locus
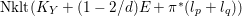 $\text{Nklt}(K_{Y}+(1-2/d)E+\unicode[STIX]{x1D70B}^{\ast }(l_{p}+l_{q}))$
containing
$\text{Nklt}(K_{Y}+(1-2/d)E+\unicode[STIX]{x1D70B}^{\ast }(l_{p}+l_{q}))$
containing
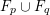 $F_{p}\cup F_{q}$
is connected as
$F_{p}\cup F_{q}$
is connected as
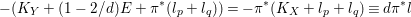 $$\begin{eqnarray}-(K_{Y}+(1-2/d)E+\unicode[STIX]{x1D70B}^{\ast }(l_{p}+l_{q}))=-\unicode[STIX]{x1D70B}^{\ast }(K_{X}+l_{p}+l_{q})\equiv d\unicode[STIX]{x1D70B}^{\ast }l\end{eqnarray}$$
$$\begin{eqnarray}-(K_{Y}+(1-2/d)E+\unicode[STIX]{x1D70B}^{\ast }(l_{p}+l_{q}))=-\unicode[STIX]{x1D70B}^{\ast }(K_{X}+l_{p}+l_{q})\equiv d\unicode[STIX]{x1D70B}^{\ast }l\end{eqnarray}$$
is nef and big. In fact, the fibers
![]() $F_{p}$
and
$F_{p}$
and
![]() $F_{q}$
are connected by
$F_{q}$
are connected by
![]() $E$
in
$E$
in
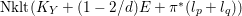 $\text{Nklt}(K_{Y}+(1-2/d)E+\unicode[STIX]{x1D70B}^{\ast }(l_{p}+l_{q}))$
as
$\text{Nklt}(K_{Y}+(1-2/d)E+\unicode[STIX]{x1D70B}^{\ast }(l_{p}+l_{q}))$
as
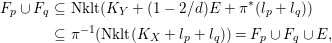 $$\begin{eqnarray}\displaystyle F_{p}\cup F_{q} & \subseteq & \displaystyle \text{Nklt}(K_{Y}+(1-2/d)E+\unicode[STIX]{x1D70B}^{\ast }(l_{p}+l_{q}))\nonumber\\ \displaystyle & \subseteq & \displaystyle \unicode[STIX]{x1D70B}^{-1}(\text{Nklt}(K_{X}+l_{p}+l_{q}))=F_{p}\cup F_{q}\cup E,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{p}\cup F_{q} & \subseteq & \displaystyle \text{Nklt}(K_{Y}+(1-2/d)E+\unicode[STIX]{x1D70B}^{\ast }(l_{p}+l_{q}))\nonumber\\ \displaystyle & \subseteq & \displaystyle \unicode[STIX]{x1D70B}^{-1}(\text{Nklt}(K_{X}+l_{p}+l_{q}))=F_{p}\cup F_{q}\cup E,\nonumber\end{eqnarray}$$
where the second inclusion follows from the definition of non-klt centers. In particular,
 $$\begin{eqnarray}\text{mult}_{E}(\unicode[STIX]{x1D70B}^{\ast }(l_{p}+l_{q}))\geqslant \frac{2}{d}=2\unicode[STIX]{x1D716}.\end{eqnarray}$$
$$\begin{eqnarray}\text{mult}_{E}(\unicode[STIX]{x1D70B}^{\ast }(l_{p}+l_{q}))\geqslant \frac{2}{d}=2\unicode[STIX]{x1D716}.\end{eqnarray}$$
By symmetry,
![]() $\unicode[STIX]{x1D70B}^{\ast }l_{p}$
must contribute multiplicity at least
$\unicode[STIX]{x1D70B}^{\ast }l_{p}$
must contribute multiplicity at least
![]() $1/d=\unicode[STIX]{x1D716}$
to the component
$1/d=\unicode[STIX]{x1D716}$
to the component
![]() $E$
(and in fact is exactly
$E$
(and in fact is exactly
![]() $1/d$
in this case), that is,
$1/d$
in this case), that is,
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}^{\ast }l_{p}\geqslant \unicode[STIX]{x1D716}E.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}^{\ast }l_{p}\geqslant \unicode[STIX]{x1D716}E.\end{eqnarray}$$
Note that
 $$\begin{eqnarray}l_{p}{\sim}_{\mathbb{Q}}\frac{-K_{X}}{\sqrt{d}\cdot \sqrt{\text{V ol }(X)}}.\end{eqnarray}$$
$$\begin{eqnarray}l_{p}{\sim}_{\mathbb{Q}}\frac{-K_{X}}{\sqrt{d}\cdot \sqrt{\text{V ol }(X)}}.\end{eqnarray}$$
By intersecting both sides of (2.1) with a general fiber
![]() $F$
of
$F$
of
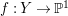 $f:Y\rightarrow \mathbb{P}^{1}$
, we get for the ruling
$f:Y\rightarrow \mathbb{P}^{1}$
, we get for the ruling
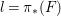 $l=\unicode[STIX]{x1D70B}_{\ast }(F)$
,
$l=\unicode[STIX]{x1D70B}_{\ast }(F)$
,
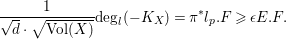 $$\begin{eqnarray}\frac{1}{\sqrt{d}\cdot \sqrt{\text{V ol }(X)}}\text{deg}_{l}(-K_{X})=\unicode[STIX]{x1D70B}^{\ast }l_{p}.F\geqslant \unicode[STIX]{x1D716}E.F.\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{\sqrt{d}\cdot \sqrt{\text{V ol }(X)}}\text{deg}_{l}(-K_{X})=\unicode[STIX]{x1D70B}^{\ast }l_{p}.F\geqslant \unicode[STIX]{x1D716}E.F.\end{eqnarray}$$
Since
![]() $F$
is a general fiber meeting the horizontal divisor
$F$
is a general fiber meeting the horizontal divisor
![]() $E$
at a smooth point,
$E$
at a smooth point,
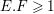 $E.F\geqslant 1$
. (In this case
$E.F\geqslant 1$
. (In this case
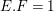 $E.F=1$
.) Combining all of these, we obtain a lower bound of the restricted volume
$E.F=1$
.) Combining all of these, we obtain a lower bound of the restricted volume
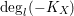 $\text{deg}_{l}(-K_{X})$
,
$\text{deg}_{l}(-K_{X})$
,
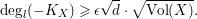 $$\begin{eqnarray}\text{deg}_{l}(-K_{X})\geqslant \unicode[STIX]{x1D716}\sqrt{d}\cdot \sqrt{\text{V ol }(X)}.\end{eqnarray}$$
$$\begin{eqnarray}\text{deg}_{l}(-K_{X})\geqslant \unicode[STIX]{x1D716}\sqrt{d}\cdot \sqrt{\text{V ol }(X)}.\end{eqnarray}$$
Note that since in this case
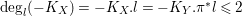 $\text{deg}_{l}(-K_{X})=-K_{X}.l=-K_{Y}.\unicode[STIX]{x1D70B}^{\ast }l\leqslant 2$
, it follows that the anticanonical volume
$\text{deg}_{l}(-K_{X})=-K_{X}.l=-K_{Y}.\unicode[STIX]{x1D70B}^{\ast }l\leqslant 2$
, it follows that the anticanonical volume
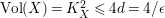 $\text{Vol}(X)=K_{X}^{2}\leqslant 4d=4/\unicode[STIX]{x1D716}$
.
$\text{Vol}(X)=K_{X}^{2}\leqslant 4d=4/\unicode[STIX]{x1D716}$
.
In summary, the method of getting an upper bound of the anticanonical volumes is to obtain a lower bound of the restricted volume
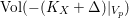 $\text{Vol}(-(K_{X}+\unicode[STIX]{x1D6E5})|_{V_{p}})$
on the non-klt center
$\text{Vol}(-(K_{X}+\unicode[STIX]{x1D6E5})|_{V_{p}})$
on the non-klt center
![]() $V_{p}$
. This is outlined in the following steps:
$V_{p}$
. This is outlined in the following steps:
-
∙ Suppose that
 $\text{Vol}(X,\unicode[STIX]{x1D6E5})=(-(K_{X}+\unicode[STIX]{x1D6E5}))^{n}>(\unicode[STIX]{x1D714}n)^{n}$
for a positive rational number
$\text{Vol}(X,\unicode[STIX]{x1D6E5})=(-(K_{X}+\unicode[STIX]{x1D6E5}))^{n}>(\unicode[STIX]{x1D714}n)^{n}$
for a positive rational number
 $\unicode[STIX]{x1D714}$
. We will show that
$\unicode[STIX]{x1D714}$
. We will show that
 $\unicode[STIX]{x1D714}>0$
cannot be arbitrarily large.
$\unicode[STIX]{x1D714}>0$
cannot be arbitrarily large. -
∙ For general
 $p\in X$
, choose so that
$p\in X$
, choose so that $$\begin{eqnarray}\unicode[STIX]{x1D6E5}_{p}{\sim}_{\mathbb{Q}}\frac{-(K_{X}+\unicode[STIX]{x1D6E5})}{\unicode[STIX]{x1D714}}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E5}_{p}{\sim}_{\mathbb{Q}}\frac{-(K_{X}+\unicode[STIX]{x1D6E5})}{\unicode[STIX]{x1D714}}\end{eqnarray}$$
 $p\in \text{Nklt}(X,\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6E5}_{p})$
. Let
$p\in \text{Nklt}(X,\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6E5}_{p})$
. Let
 $V_{p}\subseteq \text{Nklt}(X,\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6E5}_{p})$
be the minimal non-klt center containing
$V_{p}\subseteq \text{Nklt}(X,\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6E5}_{p})$
be the minimal non-klt center containing
 $p$
.
$p$
.
-
∙ Construct covering families of non-klt centers by “lining up” (part of the) non-klt centers
 $\{V_{p}\}$
; see Section 3. This is the generalization of the
$\{V_{p}\}$
; see Section 3. This is the generalization of the
 $\mathbb{P}^{1}$
-bundle structure in the Example 2.1 and is called the covering families of tigers in [McK02].
$\mathbb{P}^{1}$
-bundle structure in the Example 2.1 and is called the covering families of tigers in [McK02]. -
∙ Use the Connectedness Lemma 1.3 to obtain a lower bound of the restricted volume
on the non-klt center $$\begin{eqnarray}\text{Vol}(-(K_{X}+\unicode[STIX]{x1D6E5})|_{V_{p}})=(-(K_{X}+\unicode[STIX]{x1D6E5})|_{V_{p}})^{\dim V_{p}}\end{eqnarray}$$
$$\begin{eqnarray}\text{Vol}(-(K_{X}+\unicode[STIX]{x1D6E5})|_{V_{p}})=(-(K_{X}+\unicode[STIX]{x1D6E5})|_{V_{p}})^{\dim V_{p}}\end{eqnarray}$$
 $V_{p}$
in terms of
$V_{p}$
in terms of
 $\unicode[STIX]{x1D714}$
and
$\unicode[STIX]{x1D714}$
and
 $\unicode[STIX]{x1D716}$
. This is the most technical part.
$\unicode[STIX]{x1D716}$
. This is the most technical part.
-
∙ If
 $\unicode[STIX]{x1D714}\gg 0$
, then we cut down the dimension of non-klt centers by Theorem 1.5. After finitely many steps, we get isolated non-klt centers and hence a contradiction to the Connectedness Lemma 1.3.
$\unicode[STIX]{x1D714}\gg 0$
, then we cut down the dimension of non-klt centers by Theorem 1.5. After finitely many steps, we get isolated non-klt centers and hence a contradiction to the Connectedness Lemma 1.3.
The difficulty of this argument arises in dimensions three in many places. First of all, the non-klt centers can be of dimension one or two and we have to deal them separately. When we have one-dimensional covering families of tigers, it is subtle to detect the contribution of the
![]() $\unicode[STIX]{x1D716}$
-klt condition from some horizontal subvariety, which is the analogue to the exceptional curve
$\unicode[STIX]{x1D716}$
-klt condition from some horizontal subvariety, which is the analogue to the exceptional curve
![]() $E$
in the Example 2.1. This is done by applying a differentiation argument to construct a better behaved covering family of tigers; see 5.3. In case we have two-dimensional non-klt centers, complications arise for computing intersection numbers as the total space
$E$
in the Example 2.1. This is done by applying a differentiation argument to construct a better behaved covering family of tigers; see 5.3. In case we have two-dimensional non-klt centers, complications arise for computing intersection numbers as the total space
![]() $Y$
of a covering family of tigers is in general not
$Y$
of a covering family of tigers is in general not
![]() $\mathbb{Q}$
-factorial. This can be fixed by replacing
$\mathbb{Q}$
-factorial. This can be fixed by replacing
![]() $Y$
with a suitable birational model. To finish the proof, we also need to run a relative minimal model on the covering families of tigers and study the geometry of all possible outcomes.
$Y$
with a suitable birational model. To finish the proof, we also need to run a relative minimal model on the covering families of tigers and study the geometry of all possible outcomes.
3 Covering families of tigers
The main reference for this section is [McK02].
Definition 3.1. [McK02, Definition 3.1]
Let
![]() $(X,\unicode[STIX]{x1D6E5})$
be a log pair with
$(X,\unicode[STIX]{x1D6E5})$
be a log pair with
![]() $X$
projective and
$X$
projective and
![]() $D$
a
$D$
a
![]() $\mathbb{Q}$
-Cartier divisor. We say that pairs of the form
$\mathbb{Q}$
-Cartier divisor. We say that pairs of the form
![]() $(\unicode[STIX]{x1D6E5}_{t},V_{t})$
form a covering family of tigers of dimension
$(\unicode[STIX]{x1D6E5}_{t},V_{t})$
form a covering family of tigers of dimension
![]() $k$
and weight
$k$
and weight
![]() $\unicode[STIX]{x1D714}$
if
$\unicode[STIX]{x1D714}$
if
-
(1) there is a projective morphism
 $f:Y\rightarrow B$
of normal projective varieties such that the general fiber of
$f:Y\rightarrow B$
of normal projective varieties such that the general fiber of
 $f$
over
$f$
over
 $t\in B$
is
$t\in B$
is
 $V_{t}$
;
$V_{t}$
; -
(2) there is a morphism of
 $B$
to the Hilbert scheme of
$B$
to the Hilbert scheme of
 $X$
such that
$X$
such that
 $B$
is the normalization of its image and
$B$
is the normalization of its image and
 $f$
is obtained by taking the normalization of the universal family;
$f$
is obtained by taking the normalization of the universal family; -
(3) If
 $\unicode[STIX]{x1D70B}:Y\rightarrow X$
is the natural morphism, then
$\unicode[STIX]{x1D70B}:Y\rightarrow X$
is the natural morphism, then
 $\unicode[STIX]{x1D70B}(V_{t})$
is a pure non-klt center of
$\unicode[STIX]{x1D70B}(V_{t})$
is a pure non-klt center of
 $K_{X}+\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6E5}_{t}$
;
$K_{X}+\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6E5}_{t}$
; -
(4)
 $\unicode[STIX]{x1D70B}$
is generically finite and dominant;
$\unicode[STIX]{x1D70B}$
is generically finite and dominant; -
(5)
 $\unicode[STIX]{x1D6E5}_{t}{\sim}_{\mathbb{Q}}D/\unicode[STIX]{x1D714}$
, where
$\unicode[STIX]{x1D6E5}_{t}{\sim}_{\mathbb{Q}}D/\unicode[STIX]{x1D714}$
, where
 $\unicode[STIX]{x1D6E5}_{t}$
is effective;
$\unicode[STIX]{x1D6E5}_{t}$
is effective; -
(6) the dimension of
 $V_{t}$
is
$V_{t}$
is
 $k$
.
$k$
.
Note that by definition
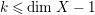 $k\leqslant \dim X-1$
and
$k\leqslant \dim X-1$
and
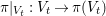 $\unicode[STIX]{x1D70B}|_{V_{t}}:V_{t}\rightarrow \unicode[STIX]{x1D70B}(V_{t})$
is finite and birational. A covering family of tigers is illustrated in the following diagram:
$\unicode[STIX]{x1D70B}|_{V_{t}}:V_{t}\rightarrow \unicode[STIX]{x1D70B}(V_{t})$
is finite and birational. A covering family of tigers is illustrated in the following diagram:
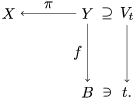
We will sometimes also refer
![]() $V_{p}$
as a pure non-klt center of
$V_{p}$
as a pure non-klt center of
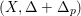 $(X,\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6E5}_{p})$
containing
$(X,\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6E5}_{p})$
containing
![]() $p$
.
$p$
.
For
![]() $(X,\unicode[STIX]{x1D6E5})$
a log
$(X,\unicode[STIX]{x1D6E5})$
a log
![]() $\mathbb{Q}$
-Fano variety, we will always assume that
$\mathbb{Q}$
-Fano variety, we will always assume that
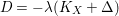 $D=-\unicode[STIX]{x1D706}(K_{X}+\unicode[STIX]{x1D6E5})$
for some
$D=-\unicode[STIX]{x1D706}(K_{X}+\unicode[STIX]{x1D6E5})$
for some
![]() $\unicode[STIX]{x1D706}>0$
. In particular,
$\unicode[STIX]{x1D706}>0$
. In particular,
![]() $D$
is big and semiample.
$D$
is big and semiample.
The existence of a covering family of tigers is achieved by constructing non-klt centers at general points of
![]() $X$
and then fitting a subcollection of them into a family. In order to fit the non-klt centers into a family, we use exceptional non-klt centers where we patch up the unique non-klt place associated to each of them; see Lemma 3.3. The following lemma allows us to create exceptional non-klt centers.
$X$
and then fitting a subcollection of them into a family. In order to fit the non-klt centers into a family, we use exceptional non-klt centers where we patch up the unique non-klt place associated to each of them; see Lemma 3.3. The following lemma allows us to create exceptional non-klt centers.
Lemma 3.2. Let
![]() $(X,\unicode[STIX]{x1D6E5})$
be a log pair and let
$(X,\unicode[STIX]{x1D6E5})$
be a log pair and let
![]() $D$
be a big and semiample
$D$
be a big and semiample
![]() $\mathbb{Q}$
-Cartier divisor. Write
$\mathbb{Q}$
-Cartier divisor. Write
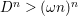 $D^{n}>(\unicode[STIX]{x1D714}n)^{n}$
for some positive rational number
$D^{n}>(\unicode[STIX]{x1D714}n)^{n}$
for some positive rational number
![]() $\unicode[STIX]{x1D714}$
. For every
$\unicode[STIX]{x1D714}$
. For every
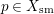 $p\in X_{\text{sm}}$
, we can find an effective
$p\in X_{\text{sm}}$
, we can find an effective
![]() $\mathbb{Q}$
-divisor
$\mathbb{Q}$
-divisor
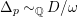 $\unicode[STIX]{x1D6E5}_{p}{\sim}_{\mathbb{Q}}D/\unicode[STIX]{x1D714}$
such that the unique minimal non-klt center
$\unicode[STIX]{x1D6E5}_{p}{\sim}_{\mathbb{Q}}D/\unicode[STIX]{x1D714}$
such that the unique minimal non-klt center
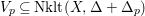 $V_{p}\subseteq \text{Nklt}(X,\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6E5}_{p})$
containing
$V_{p}\subseteq \text{Nklt}(X,\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6E5}_{p})$
containing
![]() $p$
is exceptional.
$p$
is exceptional.
Proof. Fix a rational number
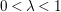 $0<\unicode[STIX]{x1D706}<1$
. By Lemma 1.2, for any
$0<\unicode[STIX]{x1D706}<1$
. By Lemma 1.2, for any
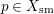 $p\in X_{\text{sm}}$
we can find an effective divisor
$p\in X_{\text{sm}}$
we can find an effective divisor
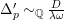 $\unicode[STIX]{x1D6E5}_{p}^{\prime }{\sim}_{\mathbb{Q}}\frac{D}{\unicode[STIX]{x1D706}\unicode[STIX]{x1D714}}$
such that
$\unicode[STIX]{x1D6E5}_{p}^{\prime }{\sim}_{\mathbb{Q}}\frac{D}{\unicode[STIX]{x1D706}\unicode[STIX]{x1D714}}$
such that
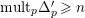 $\text{mult}_{p}\unicode[STIX]{x1D6E5}_{p}^{\prime }\geqslant n$
and hence
$\text{mult}_{p}\unicode[STIX]{x1D6E5}_{p}^{\prime }\geqslant n$
and hence
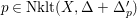 $p\in \text{Nklt}(X,\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6E5}_{p}^{\prime })$
.
$p\in \text{Nklt}(X,\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6E5}_{p}^{\prime })$
.
Fix
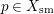 $p\in X_{\text{sm}}$
, pick
$p\in X_{\text{sm}}$
, pick
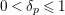 $0<\unicode[STIX]{x1D6FF}_{p}\leqslant 1$
the unique rational number such that
$0<\unicode[STIX]{x1D6FF}_{p}\leqslant 1$
the unique rational number such that
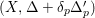 $(X,\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6FF}_{p}\unicode[STIX]{x1D6E5}_{p}^{\prime })$
is log canonical but not klt at
$(X,\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6FF}_{p}\unicode[STIX]{x1D6E5}_{p}^{\prime })$
is log canonical but not klt at
![]() $p$
. By [Reference AmbroAmb98, Proposition 3.2], we can find an effective divisor
$p$
. By [Reference AmbroAmb98, Proposition 3.2], we can find an effective divisor
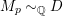 $M_{p}{\sim}_{\mathbb{Q}}D$
and some rational number
$M_{p}{\sim}_{\mathbb{Q}}D$
and some rational number
![]() $a>0$
such that for any rational number
$a>0$
such that for any rational number
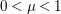 $0<\unicode[STIX]{x1D707}<1$
, the pair
$0<\unicode[STIX]{x1D707}<1$
, the pair
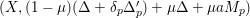 $(X,(1-\unicode[STIX]{x1D707})(\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6FF}_{p}\unicode[STIX]{x1D6E5}_{p}^{\prime })+\unicode[STIX]{x1D707}\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D707}aM_{p})$
has a unique minimal non-klt center
$(X,(1-\unicode[STIX]{x1D707})(\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6FF}_{p}\unicode[STIX]{x1D6E5}_{p}^{\prime })+\unicode[STIX]{x1D707}\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D707}aM_{p})$
has a unique minimal non-klt center
![]() $V_{p}$
passing through
$V_{p}$
passing through
![]() $p$
which is exceptional. If we write
$p$
which is exceptional. If we write
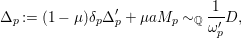 $$\begin{eqnarray}\unicode[STIX]{x1D6E5}_{p}:=(1-\unicode[STIX]{x1D707})\unicode[STIX]{x1D6FF}_{p}\unicode[STIX]{x1D6E5}_{p}^{\prime }+\unicode[STIX]{x1D707}aM_{p}{\sim}_{\mathbb{Q}}\frac{1}{\unicode[STIX]{x1D714}_{p}^{\prime }}D,\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E5}_{p}:=(1-\unicode[STIX]{x1D707})\unicode[STIX]{x1D6FF}_{p}\unicode[STIX]{x1D6E5}_{p}^{\prime }+\unicode[STIX]{x1D707}aM_{p}{\sim}_{\mathbb{Q}}\frac{1}{\unicode[STIX]{x1D714}_{p}^{\prime }}D,\end{eqnarray}$$
then
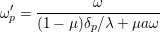 $$\begin{eqnarray}\unicode[STIX]{x1D714}_{p}^{\prime }=\frac{\unicode[STIX]{x1D714}}{(1-\unicode[STIX]{x1D707})\unicode[STIX]{x1D6FF}_{p}/\unicode[STIX]{x1D706}+\unicode[STIX]{x1D707}a\unicode[STIX]{x1D714}}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D714}_{p}^{\prime }=\frac{\unicode[STIX]{x1D714}}{(1-\unicode[STIX]{x1D707})\unicode[STIX]{x1D6FF}_{p}/\unicode[STIX]{x1D706}+\unicode[STIX]{x1D707}a\unicode[STIX]{x1D714}}\end{eqnarray}$$
satisfies
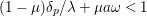 $$\begin{eqnarray}(1-\unicode[STIX]{x1D707})\unicode[STIX]{x1D6FF}_{p}/\unicode[STIX]{x1D706}+\unicode[STIX]{x1D707}a\unicode[STIX]{x1D714}<1\end{eqnarray}$$
$$\begin{eqnarray}(1-\unicode[STIX]{x1D707})\unicode[STIX]{x1D6FF}_{p}/\unicode[STIX]{x1D706}+\unicode[STIX]{x1D707}a\unicode[STIX]{x1D714}<1\end{eqnarray}$$
for
![]() $\unicode[STIX]{x1D6FF}_{p}\approx \unicode[STIX]{x1D706}$
and
$\unicode[STIX]{x1D6FF}_{p}\approx \unicode[STIX]{x1D706}$
and
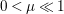 $0<\unicode[STIX]{x1D707}\ll 1$
. Hence
$0<\unicode[STIX]{x1D707}\ll 1$
. Hence
![]() $\unicode[STIX]{x1D714}_{p}^{\prime }>\unicode[STIX]{x1D714}$
. Since
$\unicode[STIX]{x1D714}_{p}^{\prime }>\unicode[STIX]{x1D714}$
. Since
![]() $D$
is semiample, we can add a small multiple of
$D$
is semiample, we can add a small multiple of
![]() $D$
to
$D$
to
![]() $\unicode[STIX]{x1D6E5}_{p}$
so that
$\unicode[STIX]{x1D6E5}_{p}$
so that
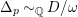 $\unicode[STIX]{x1D6E5}_{p}{\sim}_{\mathbb{Q}}D/\unicode[STIX]{x1D714}$
is the required divisor.◻
$\unicode[STIX]{x1D6E5}_{p}{\sim}_{\mathbb{Q}}D/\unicode[STIX]{x1D714}$
is the required divisor.◻
For a topological space
![]() $X$
, we say that a subset
$X$
, we say that a subset
![]() $P$
is countably dense if
$P$
is countably dense if
![]() $P$
is not contained in the union of countably many proper closed subsets of
$P$
is not contained in the union of countably many proper closed subsets of
![]() $X$
. The following proposition is the construction of the covering family of tigers; see also [McK02, Lemma 3.2] or [Reference TodorovTod07, Lemma 3.2].
$X$
. The following proposition is the construction of the covering family of tigers; see also [McK02, Lemma 3.2] or [Reference TodorovTod07, Lemma 3.2].
Proposition 3.3. Let
![]() $(X,\unicode[STIX]{x1D6E5})$
and
$(X,\unicode[STIX]{x1D6E5})$
and
![]() $\unicode[STIX]{x1D6E5}_{p}$
be the same as in Lemma 3.2. Then there exists a covering family of tigers
$\unicode[STIX]{x1D6E5}_{p}$
be the same as in Lemma 3.2. Then there exists a covering family of tigers
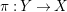 $\unicode[STIX]{x1D70B}:Y\rightarrow X$
of weight
$\unicode[STIX]{x1D70B}:Y\rightarrow X$
of weight
![]() $\unicode[STIX]{x1D714}$
with
$\unicode[STIX]{x1D714}$
with
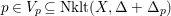 $p\in V_{p}\subseteq \text{Nklt}(X,\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6E5}_{p})$
.
$p\in V_{p}\subseteq \text{Nklt}(X,\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6E5}_{p})$
.
Proof. For each
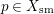 $p\in X_{\text{sm}}$
, there is an integer
$p\in X_{\text{sm}}$
, there is an integer
![]() $m_{p}$
such that
$m_{p}$
such that
![]() $m_{p}\unicode[STIX]{x1D6E5}_{p}$
and
$m_{p}\unicode[STIX]{x1D6E5}_{p}$
and
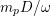 $m_{p}D/\unicode[STIX]{x1D714}$
are linearly equivalent Cartier divisors. For
$m_{p}D/\unicode[STIX]{x1D714}$
are linearly equivalent Cartier divisors. For
![]() $m>0$
such that
$m>0$
such that
![]() $mD/\unicode[STIX]{x1D714}$
is Cartier, set
$mD/\unicode[STIX]{x1D714}$
is Cartier, set
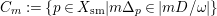 $C_{m}:=\{p\in X_{\text{sm}}|m\unicode[STIX]{x1D6E5}_{p}\in |mD/\unicode[STIX]{x1D714}|\}$
. Then by construction
$C_{m}:=\{p\in X_{\text{sm}}|m\unicode[STIX]{x1D6E5}_{p}\in |mD/\unicode[STIX]{x1D714}|\}$
. Then by construction
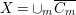 $X=\cup _{m}\overline{C_{m}}$
, where the union is taken over all
$X=\cup _{m}\overline{C_{m}}$
, where the union is taken over all
![]() $m>0$
such that
$m>0$
such that
![]() $mD/\unicode[STIX]{x1D714}$
is Cartier. Since
$mD/\unicode[STIX]{x1D714}$
is Cartier. Since
![]() $X$
is countably dense, there is an integer
$X$
is countably dense, there is an integer
![]() $m>0$
such that
$m>0$
such that
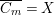 $\overline{C_{m}}=X$
.
$\overline{C_{m}}=X$
.
Choose
![]() $m>0$
an integer as above so that
$m>0$
an integer as above so that
![]() $mD/\unicode[STIX]{x1D714}$
is integral Cartier and
$mD/\unicode[STIX]{x1D714}$
is integral Cartier and
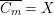 $\overline{C_{m}}=X$
. Let
$\overline{C_{m}}=X$
. Let
![]() $B$
be the Zariski closure of the set of points
$B$
be the Zariski closure of the set of points
 $\{m\unicode[STIX]{x1D6E5}_{p}|p\in X_{\text{sm}}\}\subseteq |mD/\unicode[STIX]{x1D714}|$
in the projective space
$\{m\unicode[STIX]{x1D6E5}_{p}|p\in X_{\text{sm}}\}\subseteq |mD/\unicode[STIX]{x1D714}|$
in the projective space
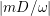 $|mD/\unicode[STIX]{x1D714}|$
. Replace
$|mD/\unicode[STIX]{x1D714}|$
. Replace
![]() $B$
by an irreducible component which contains an uncountable subset
$B$
by an irreducible component which contains an uncountable subset
![]() $Q$
of
$Q$
of
![]() $B$
such that the set
$B$
such that the set
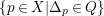 $\{p\in X|\unicode[STIX]{x1D6E5}_{p}\in Q\}$
is dense in
$\{p\in X|\unicode[STIX]{x1D6E5}_{p}\in Q\}$
is dense in
![]() $X$
. This is possible since
$X$
. This is possible since
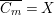 $\overline{C_{m}}=X$
and
$\overline{C_{m}}=X$
and
![]() $X$
is countably dense. Let
$X$
is countably dense. Let
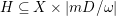 $H\subseteq X\times |mD/\unicode[STIX]{x1D714}|$
be the universal family of divisors defined by the incidence relation and
$H\subseteq X\times |mD/\unicode[STIX]{x1D714}|$
be the universal family of divisors defined by the incidence relation and
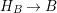 $H_{B}\rightarrow B$
the restriction to
$H_{B}\rightarrow B$
the restriction to
![]() $B$
. Take a log resolution of
$B$
. Take a log resolution of
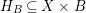 $H_{B}\subseteq X\times B$
over the generic point of
$H_{B}\subseteq X\times B$
over the generic point of
![]() $B$
and extend it over an open subset
$B$
and extend it over an open subset
![]() $U$
of
$U$
of
![]() $B$
. By assumption the log resolution over the generic point of
$B$
. By assumption the log resolution over the generic point of
![]() $B$
has a unique exceptional divisor of log discrepancy zero since it is true over
$B$
has a unique exceptional divisor of log discrepancy zero since it is true over
![]() $Q\subseteq B$
. Let
$Q\subseteq B$
. Let
![]() $Y$
be the image of this unique exceptional divisor in
$Y$
be the image of this unique exceptional divisor in
![]() $X\times B$
with the natural projection map
$X\times B$
with the natural projection map
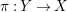 $\unicode[STIX]{x1D70B}:Y\rightarrow X$
. By construction
$\unicode[STIX]{x1D70B}:Y\rightarrow X$
. By construction
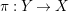 $\unicode[STIX]{x1D70B}:Y\rightarrow X$
dominates
$\unicode[STIX]{x1D70B}:Y\rightarrow X$
dominates
![]() $X$
.
$X$
.
Possibly taking a finite cover of
![]() $B$
and passing to an open subset of
$B$
and passing to an open subset of
![]() $B$
, we may assume that any fiber
$B$
, we may assume that any fiber
![]() $V_{t}$
of
$V_{t}$
of
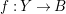 $f:Y\rightarrow B$
over
$f:Y\rightarrow B$
over
![]() $t\in B$
is a non-klt center of
$t\in B$
is a non-klt center of
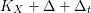 $K_{X}+\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6E5}_{t}$
. Possibly passing to an open subset of
$K_{X}+\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6E5}_{t}$
. Possibly passing to an open subset of
![]() $B$
, we may assume that
$B$
, we may assume that
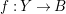 $f:Y\rightarrow B$
is flat and
$f:Y\rightarrow B$
is flat and
![]() $B$
maps into the Hilbert scheme. Replace
$B$
maps into the Hilbert scheme. Replace
![]() $B$
by the normalization of the closure of its image in the Hilbert scheme and
$B$
by the normalization of the closure of its image in the Hilbert scheme and
![]() $Y$
by the normalization of the pullback of the universal family. After possibly cutting by hyperplanes in
$Y$
by the normalization of the pullback of the universal family. After possibly cutting by hyperplanes in
![]() $B$
, we may assume that
$B$
, we may assume that
![]() $\unicode[STIX]{x1D70B}$
is generically finite and dominant. The resulted family is a required covering family of tigers.◻
$\unicode[STIX]{x1D70B}$
is generically finite and dominant. The resulted family is a required covering family of tigers.◻
In fact, the original construction of covering families of tigers is carried out in a more general setting.
Corollary 3.4. Let
![]() $(X,\unicode[STIX]{x1D6E5})$
be an
$(X,\unicode[STIX]{x1D6E5})$
be an
![]() $n$
-dimensional log pair and let
$n$
-dimensional log pair and let
![]() $D$
be a big
$D$
be a big
![]() $\mathbb{Q}$
-Cartier divisor. Let
$\mathbb{Q}$
-Cartier divisor. Let
![]() $\unicode[STIX]{x1D714}$
be a positive rational number such that
$\unicode[STIX]{x1D714}$
be a positive rational number such that
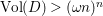 $\text{Vol}(D)>(\unicode[STIX]{x1D714}n)^{n}$
. Let
$\text{Vol}(D)>(\unicode[STIX]{x1D714}n)^{n}$
. Let
![]() $P$
be a countably dense subset of
$P$
be a countably dense subset of
![]() $X$
. Suppose that for every point
$X$
. Suppose that for every point
![]() $p\in P$
we may find a pair
$p\in P$
we may find a pair
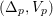 $(\unicode[STIX]{x1D6E5}_{p},V_{p})$
such that
$(\unicode[STIX]{x1D6E5}_{p},V_{p})$
such that
![]() $V_{p}$
is a pure non-klt center of
$V_{p}$
is a pure non-klt center of
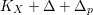 $K_{X}+\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6E5}_{p}$
where
$K_{X}+\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6E5}_{p}$
where
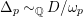 $\unicode[STIX]{x1D6E5}_{p}{\sim}_{\mathbb{Q}}D/\unicode[STIX]{x1D714}_{p}$
for some
$\unicode[STIX]{x1D6E5}_{p}{\sim}_{\mathbb{Q}}D/\unicode[STIX]{x1D714}_{p}$
for some
![]() $\unicode[STIX]{x1D714}_{p}>\unicode[STIX]{x1D714}$
. Then we may find a covering family of tigers of weight
$\unicode[STIX]{x1D714}_{p}>\unicode[STIX]{x1D714}$
. Then we may find a covering family of tigers of weight
![]() $\unicode[STIX]{x1D714}$
together with a countably dense subset
$\unicode[STIX]{x1D714}$
together with a countably dense subset
![]() $Q$
of
$Q$
of
![]() $P$
such that for all
$P$
such that for all
![]() $q\in Q$
,
$q\in Q$
,
![]() $V_{q}$
is a fiber of
$V_{q}$
is a fiber of
![]() $\unicode[STIX]{x1D70B}$
.
$\unicode[STIX]{x1D70B}$
.
Proof. See [McK02, Lemma 3.2] or [Reference TodorovTod07, Lemma 3.2]. ◻
The following lemma shows that we can assume the covering families of tigers under our consideration are always positive dimensional as suggested in the guiding example 2.1.
Lemma 3.5. Let
![]() $(X,\unicode[STIX]{x1D6E5})$
be a projective klt pair and
$(X,\unicode[STIX]{x1D6E5})$
be a projective klt pair and
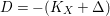 $D=-(K_{X}+\unicode[STIX]{x1D6E5})$
be a big and nef
$D=-(K_{X}+\unicode[STIX]{x1D6E5})$
be a big and nef
![]() $\mathbb{Q}$
-Cartier divisor. Then a covering family of tigers
$\mathbb{Q}$
-Cartier divisor. Then a covering family of tigers
![]() $(\unicode[STIX]{x1D6E5}_{t},V_{t})$
of weight
$(\unicode[STIX]{x1D6E5}_{t},V_{t})$
of weight
![]() $\unicode[STIX]{x1D714}>2$
is positive dimensional, that is,
$\unicode[STIX]{x1D714}>2$
is positive dimensional, that is,
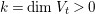 $k=\dim V_{t}>0$
.
$k=\dim V_{t}>0$
.
Proof. This is [McK02, Lemma 3.4] and we include the proof for convenience of the reader. Suppose that there exists a zero-dimensional covering family of tigers of weight
![]() $\unicode[STIX]{x1D714}>2$
. For
$\unicode[STIX]{x1D714}>2$
. For
![]() $p_{1}$
and
$p_{1}$
and
![]() $p_{2}$
general, there are divisors
$p_{2}$
general, there are divisors
![]() $\unicode[STIX]{x1D6E5}_{1}$
and
$\unicode[STIX]{x1D6E5}_{1}$
and
![]() $\unicode[STIX]{x1D6E5}_{2}$
with
$\unicode[STIX]{x1D6E5}_{2}$
with
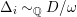 $\unicode[STIX]{x1D6E5}_{i}{\sim}_{\mathbb{Q}}D/\unicode[STIX]{x1D714}$
such that
$\unicode[STIX]{x1D6E5}_{i}{\sim}_{\mathbb{Q}}D/\unicode[STIX]{x1D714}$
such that
![]() $p_{i}$
is an isolated non-klt center of
$p_{i}$
is an isolated non-klt center of
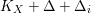 $K_{X}+\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6E5}_{i}$
. As
$K_{X}+\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6E5}_{i}$
. As
![]() $p_{1}$
and
$p_{1}$
and
![]() $p_{2}$
are general, it follows that
$p_{2}$
are general, it follows that
![]() $\unicode[STIX]{x1D6E5}_{2}$
does not contain
$\unicode[STIX]{x1D6E5}_{2}$
does not contain
![]() $p_{1}$
and
$p_{1}$
and
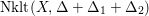 $\text{Nklt}(X,\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6E5}_{1}+\unicode[STIX]{x1D6E5}_{2})$
contains
$\text{Nklt}(X,\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6E5}_{1}+\unicode[STIX]{x1D6E5}_{2})$
contains
![]() $p_{1}$
and
$p_{1}$
and
![]() $p_{2}$
as disconnected non-klt centers. But
$p_{2}$
as disconnected non-klt centers. But
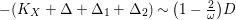 $-(K_{X}+\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6E5}_{1}+\unicode[STIX]{x1D6E5}_{2})\sim \big(1-\frac{2}{\unicode[STIX]{x1D714}}\big)D$
is nef and big if
$-(K_{X}+\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6E5}_{1}+\unicode[STIX]{x1D6E5}_{2})\sim \big(1-\frac{2}{\unicode[STIX]{x1D714}}\big)D$
is nef and big if
![]() $\unicode[STIX]{x1D714}>2$
. This contradicts to Lemma 1.3.◻
$\unicode[STIX]{x1D714}>2$
. This contradicts to Lemma 1.3.◻
Recall that we want to obtain a lower bound of restricted volumes on the non-klt centers by studying the associated covering families of tigers so that we can cut down the dimension via Theorem 1.5 to get isolated non-klt centers. If the new non-klt centers after cutting down the dimension are still positive dimensional, then we have to create new covering families of tigers and repeat the process. The following proposition due to McKernan, [McK02, Lemma 5.3], enables us to create covering families of tigers of new non-klt centers after cutting down the dimension. We include the proof here for the convenience of the readers. It starts with two lemmas.
Lemma 3.6. Let
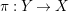 $\unicode[STIX]{x1D70B}:Y\rightarrow X$
be a smooth morphism of smooth varieties. Let
$\unicode[STIX]{x1D70B}:Y\rightarrow X$
be a smooth morphism of smooth varieties. Let
![]() $\unicode[STIX]{x1D6E5}_{1}$
be a
$\unicode[STIX]{x1D6E5}_{1}$
be a
![]() $\mathbb{Q}$
-divisor on
$\mathbb{Q}$
-divisor on
![]() $X$
and let
$X$
and let
![]() $\unicode[STIX]{x1D6E4}_{1}$
be the pullback of
$\unicode[STIX]{x1D6E4}_{1}$
be the pullback of
![]() $\unicode[STIX]{x1D6E5}_{1}$
to
$\unicode[STIX]{x1D6E5}_{1}$
to
![]() $Y$
. Let
$Y$
. Let
![]() $\unicode[STIX]{x1D6E4}_{2}$
be a boundary on
$\unicode[STIX]{x1D6E4}_{2}$
be a boundary on
![]() $Y$
, such that the support
$Y$
, such that the support
![]() $B$
of
$B$
of
![]() $\unicode[STIX]{x1D6E4}_{2}$
dominates
$\unicode[STIX]{x1D6E4}_{2}$
dominates
![]() $X$
and
$X$
and
![]() $\unicode[STIX]{x1D70B}|_{B}$
is smooth. Then
$\unicode[STIX]{x1D70B}|_{B}$
is smooth. Then
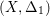 $(X,\unicode[STIX]{x1D6E5}_{1})$
is log canonical (respectively Kawamata log terminal, etc.) if and only if
$(X,\unicode[STIX]{x1D6E5}_{1})$
is log canonical (respectively Kawamata log terminal, etc.) if and only if
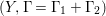 $(Y,\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E4}_{1}+\unicode[STIX]{x1D6E4}_{2})$
is log canonical (respectively Kawamata log terminal, etc.).
$(Y,\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E4}_{1}+\unicode[STIX]{x1D6E4}_{2})$
is log canonical (respectively Kawamata log terminal, etc.).
Proof. The property of being log canonical is local in the analytic topology. On the other hand, locally in the analytic topology,
![]() $Y$
is a product
$Y$
is a product
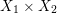 $X_{1}\times X_{2}$
, where
$X_{1}\times X_{2}$
, where
![]() $X_{1}$
is isomorphic to
$X_{1}$
is isomorphic to
![]() $X$
and
$X$
and
![]() $\unicode[STIX]{x1D6E4}_{2}$
is the pullback of a divisor
$\unicode[STIX]{x1D6E4}_{2}$
is the pullback of a divisor
![]() $\unicode[STIX]{x1D6E5}_{2}$
on
$\unicode[STIX]{x1D6E5}_{2}$
on
![]() $X_{2}$
whose support is smooth, so that
$X_{2}$
whose support is smooth, so that
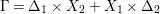 $\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E5}_{1}\times X_{2}+X_{1}\times \unicode[STIX]{x1D6E5}_{2}$
. The result follows from the same computation as in [Reference KollárKol97, Proposition 8.21].◻
$\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E5}_{1}\times X_{2}+X_{1}\times \unicode[STIX]{x1D6E5}_{2}$
. The result follows from the same computation as in [Reference KollárKol97, Proposition 8.21].◻
Lemma 3.7. Let
![]() $(X,\unicode[STIX]{x1D6E5})$
be a log pair where
$(X,\unicode[STIX]{x1D6E5})$
be a log pair where
![]() $X$
is projective and
$X$
is projective and
![]() $\unicode[STIX]{x1D6E5}$
is effective. Suppose that
$\unicode[STIX]{x1D6E5}$
is effective. Suppose that
![]() $V$
is an exceptional log canonical center of
$V$
is an exceptional log canonical center of
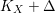 $K_{X}+\unicode[STIX]{x1D6E5}$
. Then there is an open subset
$K_{X}+\unicode[STIX]{x1D6E5}$
. Then there is an open subset
![]() $U$
of the smooth locus of
$U$
of the smooth locus of
![]() $V$
with the following property:
$V$
with the following property:
For all divisors
![]() $\unicode[STIX]{x1D6E9}$
on
$\unicode[STIX]{x1D6E9}$
on
![]() $X$
, which do not contain the generic point of
$X$
, which do not contain the generic point of
![]() $V$
and subvarieties
$V$
and subvarieties
![]() $W$
of
$W$
of
![]() $V$
such that
$V$
such that
![]() $W|_{U}$
is a pure log canonical center of
$W|_{U}$
is a pure log canonical center of
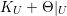 $K_{U}+\unicode[STIX]{x1D6E9}|_{U}$
, then
$K_{U}+\unicode[STIX]{x1D6E9}|_{U}$
, then
![]() $W$
is a pure log canonical center of
$W$
is a pure log canonical center of
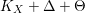 $K_{X}+\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6E9}$
.
$K_{X}+\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6E9}$
.
Proof. This result is local about the generic point of
![]() $V$
so we are free to replace
$V$
so we are free to replace
![]() $X$
by any open set that contains the generic point of
$X$
by any open set that contains the generic point of
![]() $V$
. The idea is to reduce to the case of a divisor, when the result becomes an easy consequence of inversion of adjunction. Pick a log resolution
$V$
. The idea is to reduce to the case of a divisor, when the result becomes an easy consequence of inversion of adjunction. Pick a log resolution
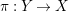 $\unicode[STIX]{x1D70B}:Y\rightarrow X$
of the pair
$\unicode[STIX]{x1D70B}:Y\rightarrow X$
of the pair
![]() $(X,\unicode[STIX]{x1D6E5})$
and let
$(X,\unicode[STIX]{x1D6E5})$
and let
![]() $\unicode[STIX]{x1D6E4}$
be the divisor defined by
$\unicode[STIX]{x1D6E4}$
be the divisor defined by
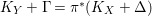 $K_{Y}+\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D70B}^{\ast }(K_{X}+\unicode[STIX]{x1D6E5})$
. By assumption there is a unique divisor
$K_{Y}+\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D70B}^{\ast }(K_{X}+\unicode[STIX]{x1D6E5})$
. By assumption there is a unique divisor
![]() $E$
lying over
$E$
lying over
![]() $V$
of log discrepancy zero. Let
$V$
of log discrepancy zero. Let
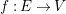 $f:E\rightarrow V$
be the restriction of
$f:E\rightarrow V$
be the restriction of
![]() $\unicode[STIX]{x1D70B}$
to
$\unicode[STIX]{x1D70B}$
to
![]() $E$
. Replacing
$E$
. Replacing
![]() $X$
by an open subset, we may assume that
$X$
by an open subset, we may assume that
![]() $f$
and
$f$
and
![]() $V$
are both smooth, and that
$V$
are both smooth, and that
![]() $K_{V}$
and
$K_{V}$
and
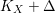 $K_{X}+\unicode[STIX]{x1D6E5}$
are
$K_{X}+\unicode[STIX]{x1D6E5}$
are
![]() $\mathbb{Q}$
-linearly equivalent to zero. Passing to a smaller open set of
$\mathbb{Q}$
-linearly equivalent to zero. Passing to a smaller open set of
![]() $X$
, we can assume that
$X$
, we can assume that
![]() $\unicode[STIX]{x1D6E4}\geqslant 0$
. By adjunction we may write
$\unicode[STIX]{x1D6E4}\geqslant 0$
. By adjunction we may write
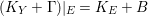 $(K_{Y}+\unicode[STIX]{x1D6E4})|_{E}=K_{E}+B$
for some effective divisor
$(K_{Y}+\unicode[STIX]{x1D6E4})|_{E}=K_{E}+B$
for some effective divisor
![]() $B$
, where both sides are
$B$
, where both sides are
![]() $\mathbb{Q}$
-linearly equivalent to zero. Passing to a smaller open set again, we may assume that every component of
$\mathbb{Q}$
-linearly equivalent to zero. Passing to a smaller open set again, we may assume that every component of
![]() $B$
dominates
$B$
dominates
![]() $V$
and that
$V$
and that
![]() $f|_{B}$
is smooth. Then
$f|_{B}$
is smooth. Then
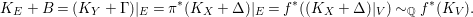 $$\begin{eqnarray}K_{E}+B=(K_{Y}+\unicode[STIX]{x1D6E4})|_{E}=\unicode[STIX]{x1D70B}^{\ast }(K_{X}+\unicode[STIX]{x1D6E5})|_{E}=f^{\ast }((K_{X}+\unicode[STIX]{x1D6E5})|_{V}){\sim}_{\mathbb{Q}}f^{\ast }(K_{V}).\end{eqnarray}$$
$$\begin{eqnarray}K_{E}+B=(K_{Y}+\unicode[STIX]{x1D6E4})|_{E}=\unicode[STIX]{x1D70B}^{\ast }(K_{X}+\unicode[STIX]{x1D6E5})|_{E}=f^{\ast }((K_{X}+\unicode[STIX]{x1D6E5})|_{V}){\sim}_{\mathbb{Q}}f^{\ast }(K_{V}).\end{eqnarray}$$
Suppose that
![]() $W$
is a pure log canonical center of
$W$
is a pure log canonical center of
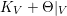 $K_{V}+\unicode[STIX]{x1D6E9}|_{V}$
. Set
$K_{V}+\unicode[STIX]{x1D6E9}|_{V}$
. Set
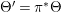 $\unicode[STIX]{x1D6E9}^{\prime }=\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D6E9}$
. As
$\unicode[STIX]{x1D6E9}^{\prime }=\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D6E9}$
. As
![]() $\unicode[STIX]{x1D6E9}$
does not contain the generic point of
$\unicode[STIX]{x1D6E9}$
does not contain the generic point of
![]() $V$
,
$V$
,
![]() $E$
is not a component of
$E$
is not a component of
![]() $\unicode[STIX]{x1D6E9}^{\prime }$
, so that
$\unicode[STIX]{x1D6E9}^{\prime }$
, so that
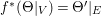 $f^{\ast }(\unicode[STIX]{x1D6E9}|_{V})=\unicode[STIX]{x1D6E9}^{\prime }|_{E}$
. It follows by Lemma 3.6 that
$f^{\ast }(\unicode[STIX]{x1D6E9}|_{V})=\unicode[STIX]{x1D6E9}^{\prime }|_{E}$
. It follows by Lemma 3.6 that
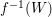 $f^{-1}(W)$
is a pure log canonical center of
$f^{-1}(W)$
is a pure log canonical center of
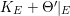 $K_{E}+\unicode[STIX]{x1D6E9}^{\prime }|_{E}$
.
$K_{E}+\unicode[STIX]{x1D6E9}^{\prime }|_{E}$
.
The result now follows from the inversion of subadjunction (cf., (17.1.1), (17.6) and (17.7) of [Reference KollárKol92]). ◻
Proposition 3.8. Let
![]() $(X,\unicode[STIX]{x1D6E5})$
be a log pair and let
$(X,\unicode[STIX]{x1D6E5})$
be a log pair and let
![]() $D$
be a
$D$
be a
![]() $\mathbb{Q}$
-Cartier divisor of the form
$\mathbb{Q}$
-Cartier divisor of the form
![]() $A+E$
where
$A+E$
where
![]() $A$
is ample and
$A$
is ample and
![]() $E$
is effective. Let
$E$
is effective. Let
![]() $(\unicode[STIX]{x1D6E5}_{t},V_{t})$
be a covering family of tigers of weight
$(\unicode[STIX]{x1D6E5}_{t},V_{t})$
be a covering family of tigers of weight
![]() $\unicode[STIX]{x1D714}$
and dimension
$\unicode[STIX]{x1D714}$
and dimension
![]() $k$
. Let
$k$
. Let
![]() $A_{t}$
be
$A_{t}$
be
![]() $A|_{V_{t}}$
. Suppose that there is an open subset
$A|_{V_{t}}$
. Suppose that there is an open subset
![]() $U\subseteq B$
such that for all
$U\subseteq B$
such that for all
![]() $t\in U$
we may find a covering family of tigers
$t\in U$
we may find a covering family of tigers
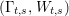 $(\unicode[STIX]{x1D6E4}_{t,s},W_{t,s})$
on
$(\unicode[STIX]{x1D6E4}_{t,s},W_{t,s})$
on
![]() $V_{t}$
of weight
$V_{t}$
of weight
![]() $\unicode[STIX]{x1D714}^{\prime }$
with respect to
$\unicode[STIX]{x1D714}^{\prime }$
with respect to
![]() $A_{t}$
. Then for
$A_{t}$
. Then for
![]() $(X,\unicode[STIX]{x1D6E5})$
we can find a covering family of tigers
$(X,\unicode[STIX]{x1D6E5})$
we can find a covering family of tigers
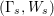 $(\unicode[STIX]{x1D6E4}_{s},W_{s})$
of dimension less than
$(\unicode[STIX]{x1D6E4}_{s},W_{s})$
of dimension less than
![]() $k$
and weight
$k$
and weight
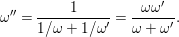 $$\begin{eqnarray}\unicode[STIX]{x1D714}^{\prime \prime }=\frac{1}{1/\unicode[STIX]{x1D714}+1/\unicode[STIX]{x1D714}^{\prime }}=\frac{\unicode[STIX]{x1D714}\unicode[STIX]{x1D714}^{\prime }}{\unicode[STIX]{x1D714}+\unicode[STIX]{x1D714}^{\prime }}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D714}^{\prime \prime }=\frac{1}{1/\unicode[STIX]{x1D714}+1/\unicode[STIX]{x1D714}^{\prime }}=\frac{\unicode[STIX]{x1D714}\unicode[STIX]{x1D714}^{\prime }}{\unicode[STIX]{x1D714}+\unicode[STIX]{x1D714}^{\prime }}.\end{eqnarray}$$
Proof. Pick
![]() $r$
so that
$r$
so that
![]() $rA$
is Cartier and let
$rA$
is Cartier and let
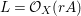 $L={\mathcal{O}}_{X}(rA)$
be the corresponding line bundle. Note that by Serre vanishing
$L={\mathcal{O}}_{X}(rA)$
be the corresponding line bundle. Note that by Serre vanishing
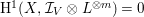 $\text{H}^{1}(X,{\mathcal{I}}_{V}\otimes L^{\otimes m})=0$
for
$\text{H}^{1}(X,{\mathcal{I}}_{V}\otimes L^{\otimes m})=0$
for
![]() $m$
large enough. Hence we may lift
$m$
large enough. Hence we may lift
![]() $\unicode[STIX]{x1D6E4}_{t,s}$
to a
$\unicode[STIX]{x1D6E4}_{t,s}$
to a
![]() $\mathbb{Q}$
-divisor
$\mathbb{Q}$
-divisor
![]() $\unicode[STIX]{x1D6E9}_{t,s}$
on
$\unicode[STIX]{x1D6E9}_{t,s}$
on
![]() $X$
$X$
![]() $\mathbb{Q}$
-linearly equivalent to the same multiple of
$\mathbb{Q}$
-linearly equivalent to the same multiple of
![]() $A$
. Adding on a multiple of
$A$
. Adding on a multiple of
![]() $E$
we may assume that
$E$
we may assume that
![]() $\unicode[STIX]{x1D6E9}_{t,s}$
is in fact a multiple of
$\unicode[STIX]{x1D6E9}_{t,s}$
is in fact a multiple of
![]() $D$
. Since adding
$D$
. Since adding
![]() $E$
only effect a proper closed subset of
$E$
only effect a proper closed subset of
![]() $X$
, there is a countably dense collection
$X$
, there is a countably dense collection
![]() $(\unicode[STIX]{x1D6E5}_{t},V_{t})$
satisfying the hypothesis of Lemma 3.7. Thus by Corollary 3.4 applied to
$(\unicode[STIX]{x1D6E5}_{t},V_{t})$
satisfying the hypothesis of Lemma 3.7. Thus by Corollary 3.4 applied to
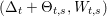 $(\unicode[STIX]{x1D6E5}_{t}+\unicode[STIX]{x1D6E9}_{t,s},W_{t,s})$
, we may find a covering family of tigers
$(\unicode[STIX]{x1D6E5}_{t}+\unicode[STIX]{x1D6E9}_{t,s},W_{t,s})$
, we may find a covering family of tigers
 $(\unicode[STIX]{x1D6E4}_{s},W_{s})$
of weight
$(\unicode[STIX]{x1D6E4}_{s},W_{s})$
of weight
![]() $\unicode[STIX]{x1D714}^{\prime \prime }$
.◻
$\unicode[STIX]{x1D714}^{\prime \prime }$
.◻
We will apply Proposition 3.8 with the ample divisor
 $D=-(K_{X}+\unicode[STIX]{x1D6E5})$
and only in the case when we have a two-dimensional covering family of tigers
$D=-(K_{X}+\unicode[STIX]{x1D6E5})$
and only in the case when we have a two-dimensional covering family of tigers
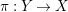 $\unicode[STIX]{x1D70B}:Y\rightarrow X$
with
$\unicode[STIX]{x1D70B}:Y\rightarrow X$
with
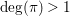 $\deg (\unicode[STIX]{x1D70B})>1$
.
$\deg (\unicode[STIX]{x1D70B})>1$
.
In the process of obtaining lower bound of the restricted volume on the non-klt centers, if we have one-dimensional non-klt centers, then we can control the restricted volume of
![]() $D$
(cf., [McK02, Lemma 5.3]).
$D$
(cf., [McK02, Lemma 5.3]).
Corollary 3.9. Let
![]() $(X,\unicode[STIX]{x1D6E5})$
be a log pair and let
$(X,\unicode[STIX]{x1D6E5})$
be a log pair and let
![]() $D$
be an ample divisor. Let
$D$
be an ample divisor. Let
![]() $(\unicode[STIX]{x1D6E5}_{t},V_{t})$
be a covering family of tigers of weight
$(\unicode[STIX]{x1D6E5}_{t},V_{t})$
be a covering family of tigers of weight
![]() $\unicode[STIX]{x1D714}>2$
and dimension one. Then
$\unicode[STIX]{x1D714}>2$
and dimension one. Then
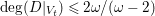 $\text{deg}(D|_{V_{t}})\leqslant 2\unicode[STIX]{x1D714}/(\unicode[STIX]{x1D714}-2)$
.
$\text{deg}(D|_{V_{t}})\leqslant 2\unicode[STIX]{x1D714}/(\unicode[STIX]{x1D714}-2)$
.
Proof. Suppose that
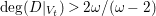 $\text{deg}(D|_{V_{t}})>2\unicode[STIX]{x1D714}/(\unicode[STIX]{x1D714}-2)$
, then by Lemma 3.2, Theorem 1.5, and Corollary 3.4 we may find a covering family
$\text{deg}(D|_{V_{t}})>2\unicode[STIX]{x1D714}/(\unicode[STIX]{x1D714}-2)$
, then by Lemma 3.2, Theorem 1.5, and Corollary 3.4 we may find a covering family
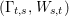 $(\unicode[STIX]{x1D6E4}_{t,s},W_{s,t})$
of tigers of weight
$(\unicode[STIX]{x1D6E4}_{t,s},W_{s,t})$
of tigers of weight
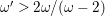 $\unicode[STIX]{x1D714}^{\prime }>2\unicode[STIX]{x1D714}/(\unicode[STIX]{x1D714}-2)$
and dimension zero on
$\unicode[STIX]{x1D714}^{\prime }>2\unicode[STIX]{x1D714}/(\unicode[STIX]{x1D714}-2)$
and dimension zero on
![]() $V_{t}$
. By Proposition 3.8, there exists a covering family of tigers of dimension zero and weight
$V_{t}$
. By Proposition 3.8, there exists a covering family of tigers of dimension zero and weight
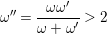 $$\begin{eqnarray}\unicode[STIX]{x1D714}^{\prime \prime }=\frac{\unicode[STIX]{x1D714}\unicode[STIX]{x1D714}^{\prime }}{\unicode[STIX]{x1D714}+\unicode[STIX]{x1D714}^{\prime }}>2\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D714}^{\prime \prime }=\frac{\unicode[STIX]{x1D714}\unicode[STIX]{x1D714}^{\prime }}{\unicode[STIX]{x1D714}+\unicode[STIX]{x1D714}^{\prime }}>2\end{eqnarray}$$
for
![]() $X$
. This contradicts Lemma 3.5.◻
$X$
. This contradicts Lemma 3.5.◻
4 Log Del Pezzo surfaces
Let
![]() $(X,\unicode[STIX]{x1D6E5})$
be an
$(X,\unicode[STIX]{x1D6E5})$
be an
![]() $\unicode[STIX]{x1D716}$
-klt weak log del Pezzo surface. The minimal resolution
$\unicode[STIX]{x1D716}$
-klt weak log del Pezzo surface. The minimal resolution
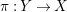 $\unicode[STIX]{x1D70B}:Y\rightarrow X$
of
$\unicode[STIX]{x1D70B}:Y\rightarrow X$
of
![]() $(X,\unicode[STIX]{x1D6E5})$
is the unique proper birational morphism such that
$(X,\unicode[STIX]{x1D6E5})$
is the unique proper birational morphism such that
![]() $Y$
is a smooth projective surface and
$Y$
is a smooth projective surface and
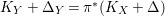 $K_{Y}+\unicode[STIX]{x1D6E5}_{Y}=\unicode[STIX]{x1D70B}^{\ast }(K_{X}+\unicode[STIX]{x1D6E5})$
for some effective
$K_{Y}+\unicode[STIX]{x1D6E5}_{Y}=\unicode[STIX]{x1D70B}^{\ast }(K_{X}+\unicode[STIX]{x1D6E5})$
for some effective
![]() $\mathbb{Q}$
-divisor
$\mathbb{Q}$
-divisor
![]() $\unicode[STIX]{x1D6E5}_{Y}$
on
$\unicode[STIX]{x1D6E5}_{Y}$
on
![]() $Y$
. Note that minimal resolutions always exist for two-dimensional log pairs. It is easy to see that
$Y$
. Note that minimal resolutions always exist for two-dimensional log pairs. It is easy to see that
 $(Y,\unicode[STIX]{x1D6E5}_{Y})$
is also an
$(Y,\unicode[STIX]{x1D6E5}_{Y})$
is also an
![]() $\unicode[STIX]{x1D716}$
-klt weak log del Pezzo surface with volume
$\unicode[STIX]{x1D716}$
-klt weak log del Pezzo surface with volume
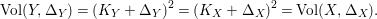 $$\begin{eqnarray}\text{Vol}(Y,\unicode[STIX]{x1D6E5}_{Y})=(K_{Y}+\unicode[STIX]{x1D6E5}_{Y})^{2}=(K_{X}+\unicode[STIX]{x1D6E5}_{X})^{2}=\text{Vol}(X,\unicode[STIX]{x1D6E5}_{X}).\end{eqnarray}$$
$$\begin{eqnarray}\text{Vol}(Y,\unicode[STIX]{x1D6E5}_{Y})=(K_{Y}+\unicode[STIX]{x1D6E5}_{Y})^{2}=(K_{X}+\unicode[STIX]{x1D6E5}_{X})^{2}=\text{Vol}(X,\unicode[STIX]{x1D6E5}_{X}).\end{eqnarray}$$
Hence replacing
![]() $(X,\unicode[STIX]{x1D6E5})$
by its minimal resolution, we can assume that
$(X,\unicode[STIX]{x1D6E5})$
by its minimal resolution, we can assume that
![]() $X$
is smooth.
$X$
is smooth.
Write
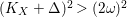 $(K_{X}+\unicode[STIX]{x1D6E5})^{2}>(2\unicode[STIX]{x1D714})^{2}$
. For a general point
$(K_{X}+\unicode[STIX]{x1D6E5})^{2}>(2\unicode[STIX]{x1D714})^{2}$
. For a general point
![]() $p\in X$
, let
$p\in X$
, let
 $\unicode[STIX]{x1D6E5}_{p}{\sim}_{\mathbb{Q}}-(K_{X}+\unicode[STIX]{x1D6E5})/\unicode[STIX]{x1D714}$
be an effective
$\unicode[STIX]{x1D6E5}_{p}{\sim}_{\mathbb{Q}}-(K_{X}+\unicode[STIX]{x1D6E5})/\unicode[STIX]{x1D714}$
be an effective
![]() $\mathbb{Q}$
-divisor constructed from Lemma 1.2 such that
$\mathbb{Q}$
-divisor constructed from Lemma 1.2 such that
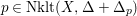 $p\in \text{Nklt}(X,\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6E5}_{p})$
. Assume that
$p\in \text{Nklt}(X,\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6E5}_{p})$
. Assume that
![]() $\unicode[STIX]{x1D714}>2$
, then by Lemma 3.5 the unique minimal non-klt center
$\unicode[STIX]{x1D714}>2$
, then by Lemma 3.5 the unique minimal non-klt center
![]() $F_{p}$
of
$F_{p}$
of
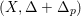 $(X,\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6E5}_{p})$
containing
$(X,\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6E5}_{p})$
containing
![]() $p$
is one-dimensional. Note that for general
$p$
is one-dimensional. Note that for general
![]() $p\in X$
,
$p\in X$
,
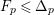 $F_{p}\leqslant \unicode[STIX]{x1D6E5}_{p}$
.
$F_{p}\leqslant \unicode[STIX]{x1D6E5}_{p}$
.
Lemma 4.1. For a very general point
![]() $p\in X$
, the numerical class
$p\in X$
, the numerical class
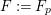 $F:=F_{p}$
on
$F:=F_{p}$
on
![]() $X$
is well defined and
$X$
is well defined and
![]() $F$
is nef.
$F$
is nef.
Proof. An effective integral one-cycles
![]() $F_{p}$
satisfies
$F_{p}$
satisfies
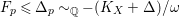 $F_{p}\leqslant \unicode[STIX]{x1D6E5}_{p}{\sim}_{\mathbb{Q}}-(K_{X}+\unicode[STIX]{x1D6E5})/\unicode[STIX]{x1D714}$
and hence forms a bounded set in the Mori cone of curves. As
$F_{p}\leqslant \unicode[STIX]{x1D6E5}_{p}{\sim}_{\mathbb{Q}}-(K_{X}+\unicode[STIX]{x1D6E5})/\unicode[STIX]{x1D714}$
and hence forms a bounded set in the Mori cone of curves. As
![]() $\mathbb{C}$
is uncountable, for
$\mathbb{C}$
is uncountable, for
![]() $p\in X$
a very general point the numerical class
$p\in X$
a very general point the numerical class
 $F:=F_{p}$
is well defined. Since
$F:=F_{p}$
is well defined. Since
![]() $\{F_{p}\}$
moves, the class
$\{F_{p}\}$
moves, the class
![]() $F$
is nef.◻
$F$
is nef.◻
The following lemma shows that if we assume the weight
![]() $\unicode[STIX]{x1D714}$
is large, then the non-klt centers
$\unicode[STIX]{x1D714}$
is large, then the non-klt centers
![]() $\{F_{p}\}$
on
$\{F_{p}\}$
on
![]() $X$
already possess a nearly fiber bundle structure analogous to a covering family of tigers.
$X$
already possess a nearly fiber bundle structure analogous to a covering family of tigers.
Lemma 4.2. Assume that
![]() $\unicode[STIX]{x1D714}>4$
, then
$\unicode[STIX]{x1D714}>4$
, then
![]() $F^{2}=0$
, that is,
$F^{2}=0$
, that is,
 $F_{p}\cap F_{q}=\emptyset$
for
$F_{p}\cap F_{q}=\emptyset$
for
 $p,q\in X$
two very general points.
$p,q\in X$
two very general points.
Proof. Suppose that
![]() $\unicode[STIX]{x1D714}>4$
and assume that
$\unicode[STIX]{x1D714}>4$
and assume that
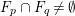 $F_{p}\cap F_{q}\neq \emptyset$
for
$F_{p}\cap F_{q}\neq \emptyset$
for
 $p,q\in X$
two very general points. Since by Lemma 4.1 the curve class
$p,q\in X$
two very general points. Since by Lemma 4.1 the curve class
![]() $F=F_{p}$
is nef, then for
$F=F_{p}$
is nef, then for
 $H=-(K_{X}+\unicode[STIX]{x1D6E5})/\unicode[STIX]{x1D714}$
we have
$H=-(K_{X}+\unicode[STIX]{x1D6E5})/\unicode[STIX]{x1D714}$
we have
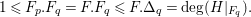 $$\begin{eqnarray}1\leqslant F_{p}.F_{q}=F.F_{q}\leqslant F.\unicode[STIX]{x1D6E5}_{q}=\text{deg}(H|_{F_{q}}).\end{eqnarray}$$
$$\begin{eqnarray}1\leqslant F_{p}.F_{q}=F.F_{q}\leqslant F.\unicode[STIX]{x1D6E5}_{q}=\text{deg}(H|_{F_{q}}).\end{eqnarray}$$
Since
![]() $H$
is big and nef, one can cut down the dimension of the non-klt centers by Theorem 1.5.Footnote
2
$H$
is big and nef, one can cut down the dimension of the non-klt centers by Theorem 1.5.Footnote
2
To be precise, choose
![]() $x$
an intersection point of
$x$
an intersection point of
![]() $F_{p}$
and
$F_{p}$
and
![]() $F_{q}$
. Pick
$F_{q}$
. Pick
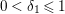 $0<\unicode[STIX]{x1D6FF}_{1}\leqslant 1$
such that
$0<\unicode[STIX]{x1D6FF}_{1}\leqslant 1$
such that
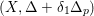 $(X,\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6FF}_{1}\unicode[STIX]{x1D6E5}_{p})$
is log canonical at
$(X,\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6FF}_{1}\unicode[STIX]{x1D6E5}_{p})$
is log canonical at
![]() $x$
. If
$x$
. If
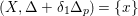 $(X,\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6FF}_{1}\unicode[STIX]{x1D6E5}_{p})=\{x\}$
, then this contradicts the Connected Lemma 1.3 as
$(X,\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6FF}_{1}\unicode[STIX]{x1D6E5}_{p})=\{x\}$
, then this contradicts the Connected Lemma 1.3 as
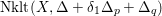 $\text{Nklt}(X,\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6FF}_{1}\unicode[STIX]{x1D6E5}_{p}+\unicode[STIX]{x1D6E5}_{q})$
containing
$\text{Nklt}(X,\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6FF}_{1}\unicode[STIX]{x1D6E5}_{p}+\unicode[STIX]{x1D6E5}_{q})$
containing
![]() $x$
and
$x$
and
![]() $F_{q}$
is disconnected but
$F_{q}$
is disconnected but
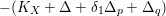 $-(K_{X}+\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6FF}_{1}\unicode[STIX]{x1D6E5}_{p}+\unicode[STIX]{x1D6E5}_{q})$
is nef and big. Hence we may assume that
$-(K_{X}+\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6FF}_{1}\unicode[STIX]{x1D6E5}_{p}+\unicode[STIX]{x1D6E5}_{q})$
is nef and big. Hence we may assume that
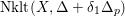 $\text{Nklt}(X,\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6FF}_{1}\unicode[STIX]{x1D6E5}_{p})$
is one-dimensional. By Theorem 1.5, there exists rational numbers
$\text{Nklt}(X,\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6FF}_{1}\unicode[STIX]{x1D6E5}_{p})$
is one-dimensional. By Theorem 1.5, there exists rational numbers
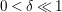 $0<\unicode[STIX]{x1D6FF}\ll 1$
,
$0<\unicode[STIX]{x1D6FF}\ll 1$
,
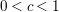 $0<c<1$
, and an effective
$0<c<1$
, and an effective
![]() $\mathbb{Q}$
-divisor
$\mathbb{Q}$
-divisor
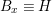 $B_{x}\equiv H$
such that
$B_{x}\equiv H$
such that
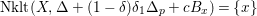 $\text{Nklt}(X,\unicode[STIX]{x1D6E5}+(1-\unicode[STIX]{x1D6FF})\unicode[STIX]{x1D6FF}_{1}\unicode[STIX]{x1D6E5}_{p}+cB_{x})=\{x\}$
in a neighborhood of
$\text{Nklt}(X,\unicode[STIX]{x1D6E5}+(1-\unicode[STIX]{x1D6FF})\unicode[STIX]{x1D6FF}_{1}\unicode[STIX]{x1D6E5}_{p}+cB_{x})=\{x\}$
in a neighborhood of
![]() $x$
. By switching
$x$
. By switching
![]() $p$
and
$p$
and
![]() $q$
, we can assume that
$q$
, we can assume that
![]() $q\neq x$
. Similarly we have
$q\neq x$
. Similarly we have
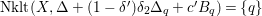 $\text{Nklt}(X,\unicode[STIX]{x1D6E5}+(1-\unicode[STIX]{x1D6FF}^{\prime })\unicode[STIX]{x1D6FF}_{2}\unicode[STIX]{x1D6E5}_{q}+c^{\prime }B_{q})=\{q\}$
in a neighborhood of
$\text{Nklt}(X,\unicode[STIX]{x1D6E5}+(1-\unicode[STIX]{x1D6FF}^{\prime })\unicode[STIX]{x1D6FF}_{2}\unicode[STIX]{x1D6E5}_{q}+c^{\prime }B_{q})=\{q\}$
in a neighborhood of
![]() $q$
for some divisor
$q$
for some divisor
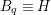 $B_{q}\equiv H$
and rational numbers
$B_{q}\equiv H$
and rational numbers
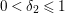 $0<\unicode[STIX]{x1D6FF}_{2}\leqslant 1$
,
$0<\unicode[STIX]{x1D6FF}_{2}\leqslant 1$
,
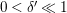 $0<\unicode[STIX]{x1D6FF}^{\prime }\ll 1$
, and
$0<\unicode[STIX]{x1D6FF}^{\prime }\ll 1$
, and
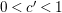 $0<c^{\prime }<1$
. The set
$0<c^{\prime }<1$
. The set
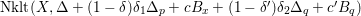 $\text{Nklt}(X,\unicode[STIX]{x1D6E5}+(1-\unicode[STIX]{x1D6FF})\unicode[STIX]{x1D6FF}_{1}\unicode[STIX]{x1D6E5}_{p}+cB_{x}+(1-\unicode[STIX]{x1D6FF}^{\prime })\unicode[STIX]{x1D6FF}_{2}\unicode[STIX]{x1D6E5}_{q}+c^{\prime }B_{q})$
contains isolated non-klt centers
$\text{Nklt}(X,\unicode[STIX]{x1D6E5}+(1-\unicode[STIX]{x1D6FF})\unicode[STIX]{x1D6FF}_{1}\unicode[STIX]{x1D6E5}_{p}+cB_{x}+(1-\unicode[STIX]{x1D6FF}^{\prime })\unicode[STIX]{x1D6FF}_{2}\unicode[STIX]{x1D6E5}_{q}+c^{\prime }B_{q})$
contains isolated non-klt centers
![]() $x$
and
$x$
and
![]() $q$
and hence is disconnected. Since the pair is numerically equivalent to
$q$
and hence is disconnected. Since the pair is numerically equivalent to
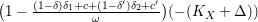 $\big(1-\frac{(1-\unicode[STIX]{x1D6FF})\unicode[STIX]{x1D6FF}_{1}+c+(1-\unicode[STIX]{x1D6FF}^{\prime })\unicode[STIX]{x1D6FF}_{2}+c^{\prime }}{\unicode[STIX]{x1D714}}\big)(-(K_{X}+\unicode[STIX]{x1D6E5}))$
which is nef and big if
$\big(1-\frac{(1-\unicode[STIX]{x1D6FF})\unicode[STIX]{x1D6FF}_{1}+c+(1-\unicode[STIX]{x1D6FF}^{\prime })\unicode[STIX]{x1D6FF}_{2}+c^{\prime }}{\unicode[STIX]{x1D714}}\big)(-(K_{X}+\unicode[STIX]{x1D6E5}))$
which is nef and big if
![]() $\unicode[STIX]{x1D714}>4$
, we have a contradiction to the Connectedness Lemma 1.3.◻
$\unicode[STIX]{x1D714}>4$
, we have a contradiction to the Connectedness Lemma 1.3.◻
Recall that for any two Weil divisors
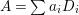 $A=\sum a_{i}D_{i}$
and
$A=\sum a_{i}D_{i}$
and
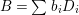 $B=\sum b_{i}D_{i}$
, we define
$B=\sum b_{i}D_{i}$
, we define
![]() $A\wedge B$
to be
$A\wedge B$
to be
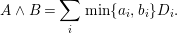 $$\begin{eqnarray}A\wedge B=\mathop{\sum }_{i}\min \{a_{i},b_{i}\}D_{i}.\end{eqnarray}$$
$$\begin{eqnarray}A\wedge B=\mathop{\sum }_{i}\min \{a_{i},b_{i}\}D_{i}.\end{eqnarray}$$
Theorem 4.3. Let
![]() $(X,\unicode[STIX]{x1D6E5})$
be an
$(X,\unicode[STIX]{x1D6E5})$
be an
![]() $\unicode[STIX]{x1D716}$
-klt weak log del Pezzo surface. Then the anticanonical volume
$\unicode[STIX]{x1D716}$
-klt weak log del Pezzo surface. Then the anticanonical volume
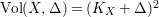 $\text{Vol}(X,\unicode[STIX]{x1D6E5})=(K_{X}+\unicode[STIX]{x1D6E5})^{2}$
satisfies
$\text{Vol}(X,\unicode[STIX]{x1D6E5})=(K_{X}+\unicode[STIX]{x1D6E5})^{2}$
satisfies
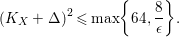 $$\begin{eqnarray}(K_{X}+\unicode[STIX]{x1D6E5})^{2}\leqslant \max \biggl\{64,\frac{8}{\unicode[STIX]{x1D716}}\biggr\}.\end{eqnarray}$$
$$\begin{eqnarray}(K_{X}+\unicode[STIX]{x1D6E5})^{2}\leqslant \max \biggl\{64,\frac{8}{\unicode[STIX]{x1D716}}\biggr\}.\end{eqnarray}$$
Proof. Replacing
![]() $(X,\unicode[STIX]{x1D6E5})$
by its minimal resolution, we may assume that
$(X,\unicode[STIX]{x1D6E5})$
by its minimal resolution, we may assume that
![]() $X$
is smooth. Write
$X$
is smooth. Write
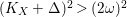 $(K_{X}+\unicode[STIX]{x1D6E5})^{2}>(2\unicode[STIX]{x1D714})^{2}$
, then for each general point
$(K_{X}+\unicode[STIX]{x1D6E5})^{2}>(2\unicode[STIX]{x1D714})^{2}$
, then for each general point
![]() $p\in X$
there exists an effective
$p\in X$
there exists an effective
![]() $\mathbb{Q}$
-divisor
$\mathbb{Q}$
-divisor
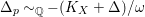 $\unicode[STIX]{x1D6E5}_{p}{\sim}_{\mathbb{Q}}-(K_{X}+\unicode[STIX]{x1D6E5})/\unicode[STIX]{x1D714}$
such that
$\unicode[STIX]{x1D6E5}_{p}{\sim}_{\mathbb{Q}}-(K_{X}+\unicode[STIX]{x1D6E5})/\unicode[STIX]{x1D714}$
such that
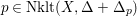 $p\in \text{Nklt}(X,\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6E5}_{p})$
. From Lemma 3.5, we may assume that
$p\in \text{Nklt}(X,\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6E5}_{p})$
. From Lemma 3.5, we may assume that
![]() $\unicode[STIX]{x1D714}>2$
and the unique minimal non-klt center
$\unicode[STIX]{x1D714}>2$
and the unique minimal non-klt center
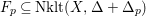 $F_{p}\subseteq \text{Nklt}(X,\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6E5}_{p})$
containing
$F_{p}\subseteq \text{Nklt}(X,\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6E5}_{p})$
containing
![]() $p$
is one-dimensional. Note that
$p$
is one-dimensional. Note that
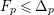 $F_{p}\leqslant \unicode[STIX]{x1D6E5}_{p}$
for general
$F_{p}\leqslant \unicode[STIX]{x1D6E5}_{p}$
for general
![]() $p\in X$
. By Lemmas 4.1 and 4.2, we may assume that
$p\in X$
. By Lemmas 4.1 and 4.2, we may assume that
![]() $\unicode[STIX]{x1D714}>4$
and for very general
$\unicode[STIX]{x1D714}>4$
and for very general
![]() $p\in X$
the numerical class
$p\in X$
the numerical class
![]() $F$
of
$F$
of
![]() $F_{p}$
is well defined and nef with
$F_{p}$
is well defined and nef with
![]() $F^{2}=0$
.
$F^{2}=0$
.
For two very general points
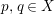 $p,q\in X$
,
$p,q\in X$
,
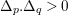 $\unicode[STIX]{x1D6E5}_{p}.\unicode[STIX]{x1D6E5}_{q}>0$
and hence
$\unicode[STIX]{x1D6E5}_{p}.\unicode[STIX]{x1D6E5}_{q}>0$
and hence
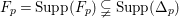 $F_{p}=\text{Supp}(F_{p})\subsetneq \text{Supp}(\unicode[STIX]{x1D6E5}_{p})$
: Otherwise
$F_{p}=\text{Supp}(F_{p})\subsetneq \text{Supp}(\unicode[STIX]{x1D6E5}_{p})$
: Otherwise
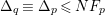 $\unicode[STIX]{x1D6E5}_{q}\equiv \unicode[STIX]{x1D6E5}_{p}\leqslant NF_{p}$
for some
$\unicode[STIX]{x1D6E5}_{q}\equiv \unicode[STIX]{x1D6E5}_{p}\leqslant NF_{p}$
for some
![]() $N>0$
and
$N>0$
and
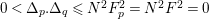 $0<\unicode[STIX]{x1D6E5}_{p}.\unicode[STIX]{x1D6E5}_{q}\leqslant N^{2}F_{p}^{2}=N^{2}F^{2}=0$
, a contradiction. Denote
$0<\unicode[STIX]{x1D6E5}_{p}.\unicode[STIX]{x1D6E5}_{q}\leqslant N^{2}F_{p}^{2}=N^{2}F^{2}=0$
, a contradiction. Denote
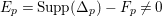 $E_{p}=\text{Supp}(\unicode[STIX]{x1D6E5}_{p})-F_{p}\neq 0$
. By the Connectedness Lemma 1.3,
$E_{p}=\text{Supp}(\unicode[STIX]{x1D6E5}_{p})-F_{p}\neq 0$
. By the Connectedness Lemma 1.3,
 $\text{Nklt}(X,\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6E5}_{p}+\unicode[STIX]{x1D6E5}_{q})\supseteq F_{p}\cup F_{q}$
is connected. By Lemma 4.2,
$\text{Nklt}(X,\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6E5}_{p}+\unicode[STIX]{x1D6E5}_{q})\supseteq F_{p}\cup F_{q}$
is connected. By Lemma 4.2,
 $F_{p}\cap F_{q}=\emptyset$
and hence
$F_{p}\cap F_{q}=\emptyset$
and hence
![]() $E_{p}$
must contain a connected curve
$E_{p}$
must contain a connected curve
![]() $E\leqslant E_{p}$
such that
$E\leqslant E_{p}$
such that
 $F_{p}.E\neq 0$
,
$F_{p}.E\neq 0$
,
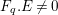 $F_{q}.E\neq 0$
, and
$F_{q}.E\neq 0$
, and
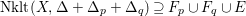 $\text{Nklt}(X,\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6E5}_{p}+\unicode[STIX]{x1D6E5}_{q})\supseteq F_{p}\cup F_{q}\cup E$
. Furthermore, we can assume that
$\text{Nklt}(X,\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6E5}_{p}+\unicode[STIX]{x1D6E5}_{q})\supseteq F_{p}\cup F_{q}\cup E$
. Furthermore, we can assume that
![]() $E$
is irreducible since
$E$
is irreducible since
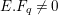 $E.F_{q}\neq 0$
as
$E.F_{q}\neq 0$
as
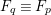 $F_{q}\equiv F_{p}$
for
$F_{q}\equiv F_{p}$
for
![]() $q\in X$
a very general point. By symmetry and the
$q\in X$
a very general point. By symmetry and the
![]() $\unicode[STIX]{x1D716}$
-klt condition,
$\unicode[STIX]{x1D716}$
-klt condition,
![]() $E$
satisfies
$E$
satisfies
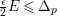 $\frac{\unicode[STIX]{x1D716}}{2}E\leqslant \unicode[STIX]{x1D6E5}_{p}$
(cf., Example 2.1).
$\frac{\unicode[STIX]{x1D716}}{2}E\leqslant \unicode[STIX]{x1D6E5}_{p}$
(cf., Example 2.1).
Suppose that
![]() $E^{2}\geqslant 0$
, then as
$E^{2}\geqslant 0$
, then as
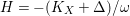 $H=-(K_{X}+\unicode[STIX]{x1D6E5})/\unicode[STIX]{x1D714}$
is nef
$H=-(K_{X}+\unicode[STIX]{x1D6E5})/\unicode[STIX]{x1D714}$
is nef
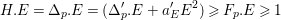 $$\begin{eqnarray}H.E=\unicode[STIX]{x1D6E5}_{p}.E=(\unicode[STIX]{x1D6E5}_{p}^{\prime }.E+a_{E}^{\prime }E^{2})\geqslant F_{p}.E\geqslant 1\end{eqnarray}$$
$$\begin{eqnarray}H.E=\unicode[STIX]{x1D6E5}_{p}.E=(\unicode[STIX]{x1D6E5}_{p}^{\prime }.E+a_{E}^{\prime }E^{2})\geqslant F_{p}.E\geqslant 1\end{eqnarray}$$
where we write
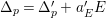 $\unicode[STIX]{x1D6E5}_{p}=\unicode[STIX]{x1D6E5}_{p}^{\prime }+a_{E}^{\prime }E$
with
$\unicode[STIX]{x1D6E5}_{p}=\unicode[STIX]{x1D6E5}_{p}^{\prime }+a_{E}^{\prime }E$
with
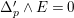 $\unicode[STIX]{x1D6E5}_{p}^{\prime }\wedge E=0$
,
$\unicode[STIX]{x1D6E5}_{p}^{\prime }\wedge E=0$
,
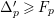 $\unicode[STIX]{x1D6E5}_{p}^{\prime }\geqslant F_{p}$
, and
$\unicode[STIX]{x1D6E5}_{p}^{\prime }\geqslant F_{p}$
, and
![]() $a_{E}^{\prime }>0$
. In particular, we can use Theorem 1.5 again to cut down the dimension of non-klt centers as in Lemma 4.2. This contradicts the Connectedness Lemma 1.3.
$a_{E}^{\prime }>0$
. In particular, we can use Theorem 1.5 again to cut down the dimension of non-klt centers as in Lemma 4.2. This contradicts the Connectedness Lemma 1.3.
We may assume that
![]() $E^{2}<0$
, and thus
$E^{2}<0$
, and thus
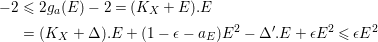 $$\begin{eqnarray}\displaystyle -2 & {\leqslant} & \displaystyle 2g_{a}(E)-2=(K_{X}+E).E\nonumber\\ \displaystyle & = & \displaystyle (K_{X}+\unicode[STIX]{x1D6E5}).E+(1-\unicode[STIX]{x1D716}-a_{E})E^{2}-\unicode[STIX]{x1D6E5}^{\prime }.E+\unicode[STIX]{x1D716}E^{2}\leqslant \unicode[STIX]{x1D716}E^{2}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle -2 & {\leqslant} & \displaystyle 2g_{a}(E)-2=(K_{X}+E).E\nonumber\\ \displaystyle & = & \displaystyle (K_{X}+\unicode[STIX]{x1D6E5}).E+(1-\unicode[STIX]{x1D716}-a_{E})E^{2}-\unicode[STIX]{x1D6E5}^{\prime }.E+\unicode[STIX]{x1D716}E^{2}\leqslant \unicode[STIX]{x1D716}E^{2}\nonumber\end{eqnarray}$$
where
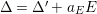 $\unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D6E5}^{\prime }+a_{E}E$
with
$\unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D6E5}^{\prime }+a_{E}E$
with
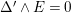 $\unicode[STIX]{x1D6E5}^{\prime }\wedge E=0$
and
$\unicode[STIX]{x1D6E5}^{\prime }\wedge E=0$
and
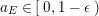 $a_{E}\in [0,1-\unicode[STIX]{x1D716})$
by the
$a_{E}\in [0,1-\unicode[STIX]{x1D716})$
by the
![]() $\unicode[STIX]{x1D716}$
-klt condition. This implies that
$\unicode[STIX]{x1D716}$
-klt condition. This implies that
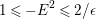 $$\begin{eqnarray}1\leqslant -E^{2}\leqslant 2/\unicode[STIX]{x1D716}\end{eqnarray}$$
$$\begin{eqnarray}1\leqslant -E^{2}\leqslant 2/\unicode[STIX]{x1D716}\end{eqnarray}$$
where the first inequality follows from the fact that
![]() $E^{2}\in \mathbb{Z}$
as
$E^{2}\in \mathbb{Z}$
as
![]() $X$
is smooth. Since
$X$
is smooth. Since
![]() $F^{2}=0$
for
$F^{2}=0$
for
![]() $F$
the numerical class of
$F$
the numerical class of
![]() $F_{p}$
, where
$F_{p}$
, where
![]() $p\in X$
is very general, by Nakai’s criterion the divisor
$p\in X$
is very general, by Nakai’s criterion the divisor
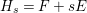 $H_{s}=F+sE$
with
$H_{s}=F+sE$
with
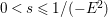 $0<s\leqslant 1/(-E^{2})$
is nef and big. By the Hodge index theorem (see [Reference HartshorneHar77, V 1.1.9(a)]), we get the inequality
$0<s\leqslant 1/(-E^{2})$
is nef and big. By the Hodge index theorem (see [Reference HartshorneHar77, V 1.1.9(a)]), we get the inequality
 $$\begin{eqnarray}(K_{X}+\unicode[STIX]{x1D6E5})^{2}\leqslant \frac{(-(K_{X}+\unicode[STIX]{x1D6E5}).H_{s})^{2}}{H_{s}^{2}}.\end{eqnarray}$$
$$\begin{eqnarray}(K_{X}+\unicode[STIX]{x1D6E5})^{2}\leqslant \frac{(-(K_{X}+\unicode[STIX]{x1D6E5}).H_{s})^{2}}{H_{s}^{2}}.\end{eqnarray}$$
From
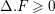 $\unicode[STIX]{x1D6E5}.F\geqslant 0$
and
$\unicode[STIX]{x1D6E5}.F\geqslant 0$
and
![]() $F^{2}=0$
, we have that
$F^{2}=0$
, we have that
 $$\begin{eqnarray}-(K_{X}+\unicode[STIX]{x1D6E5}).F\leqslant -(K_{X}+F).F\leqslant 2.\end{eqnarray}$$
$$\begin{eqnarray}-(K_{X}+\unicode[STIX]{x1D6E5}).F\leqslant -(K_{X}+F).F\leqslant 2.\end{eqnarray}$$
Also for
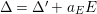 $\unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D6E5}^{\prime }+a_{E}E$
with
$\unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D6E5}^{\prime }+a_{E}E$
with
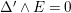 $\unicode[STIX]{x1D6E5}^{\prime }\wedge E=0$
and
$\unicode[STIX]{x1D6E5}^{\prime }\wedge E=0$
and
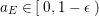 $a_{E}\in [0,1-\unicode[STIX]{x1D716})$
, we have that
$a_{E}\in [0,1-\unicode[STIX]{x1D716})$
, we have that
 $$\begin{eqnarray}\displaystyle -(K_{X}+\unicode[STIX]{x1D6E5}).E & = & \displaystyle -K_{X}.E-\unicode[STIX]{x1D6E5}^{\prime }.E-a_{E}E^{2}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle E^{2}+2-a_{E}E^{2}=(a_{E}-1)(-E^{2})+2\leqslant 2-\unicode[STIX]{x1D716}(-E^{2}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle -(K_{X}+\unicode[STIX]{x1D6E5}).E & = & \displaystyle -K_{X}.E-\unicode[STIX]{x1D6E5}^{\prime }.E-a_{E}E^{2}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle E^{2}+2-a_{E}E^{2}=(a_{E}-1)(-E^{2})+2\leqslant 2-\unicode[STIX]{x1D716}(-E^{2}).\end{eqnarray}$$
Put
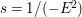 $s=1/(-E^{2})$
, all together we get
$s=1/(-E^{2})$
, all together we get
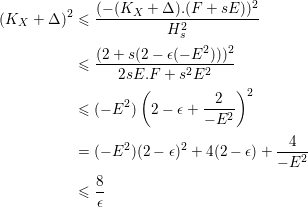 $$\begin{eqnarray}\displaystyle (K_{X}+\unicode[STIX]{x1D6E5})^{2} & {\leqslant} & \displaystyle \frac{(-(K_{X}+\unicode[STIX]{x1D6E5}).(F+sE))^{2}}{H_{s}^{2}}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \frac{(2+s(2-\unicode[STIX]{x1D716}(-E^{2})))^{2}}{2sE.F+s^{2}E^{2}}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle (-E^{2})\left(2-\unicode[STIX]{x1D716}+\frac{2}{-E^{2}}\right)^{2}\nonumber\\ \displaystyle & = & \displaystyle (-E^{2})(2-\unicode[STIX]{x1D716})^{2}+4(2-\unicode[STIX]{x1D716})+\frac{4}{-E^{2}}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \frac{8}{\unicode[STIX]{x1D716}}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (K_{X}+\unicode[STIX]{x1D6E5})^{2} & {\leqslant} & \displaystyle \frac{(-(K_{X}+\unicode[STIX]{x1D6E5}).(F+sE))^{2}}{H_{s}^{2}}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \frac{(2+s(2-\unicode[STIX]{x1D716}(-E^{2})))^{2}}{2sE.F+s^{2}E^{2}}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle (-E^{2})\left(2-\unicode[STIX]{x1D716}+\frac{2}{-E^{2}}\right)^{2}\nonumber\\ \displaystyle & = & \displaystyle (-E^{2})(2-\unicode[STIX]{x1D716})^{2}+4(2-\unicode[STIX]{x1D716})+\frac{4}{-E^{2}}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \frac{8}{\unicode[STIX]{x1D716}}\nonumber\end{eqnarray}$$
where the first inequality is (1), the second inequality follows from (2), (3), and
![]() $F^{2}=0$
, and the third inequality is given by
$F^{2}=0$
, and the third inequality is given by
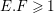 $E.F\geqslant 1$
, and thus
$E.F\geqslant 1$
, and thus
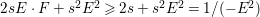 $2sE\cdot F+s^{2}E^{2}\geqslant 2s+s^{2}E^{2}=1/(-E^{2})$
. The last inequality follows from the fact that the function
$2sE\cdot F+s^{2}E^{2}\geqslant 2s+s^{2}E^{2}=1/(-E^{2})$
. The last inequality follows from the fact that the function
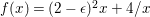 $f(x)=(2-\unicode[STIX]{x1D716})^{2}x+4/x$
, defined on
$f(x)=(2-\unicode[STIX]{x1D716})^{2}x+4/x$
, defined on
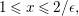 $1\leqslant x\leqslant 2/\unicode[STIX]{x1D716},$
achieves its maximum at
$1\leqslant x\leqslant 2/\unicode[STIX]{x1D716},$
achieves its maximum at
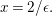 $x=2/\unicode[STIX]{x1D716}.$
◻
$x=2/\unicode[STIX]{x1D716}.$
◻
5 Log Fano threefolds of Picard number one
Let
![]() $(X,\unicode[STIX]{x1D6E5})$
be an
$(X,\unicode[STIX]{x1D6E5})$
be an
![]() $\unicode[STIX]{x1D716}$
-klt
$\unicode[STIX]{x1D716}$
-klt
![]() $\mathbb{Q}$
-factorial log
$\mathbb{Q}$
-factorial log
![]() $\mathbb{Q}$
-Fano threefold of Picard number
$\mathbb{Q}$
-Fano threefold of Picard number
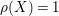 $\unicode[STIX]{x1D70C}(X)=1$
. Note that by hypothesis
$\unicode[STIX]{x1D70C}(X)=1$
. Note that by hypothesis
![]() $X$
is
$X$
is
![]() $\unicode[STIX]{x1D716}$
-klt and
$\unicode[STIX]{x1D716}$
-klt and
![]() $-K_{X}$
is ample with
$-K_{X}$
is ample with
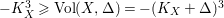 $-K_{X}^{3}\geqslant \text{Vol}(X,\unicode[STIX]{x1D6E5})=-(K_{X}+\unicode[STIX]{x1D6E5})^{3}$
. Hence it is sufficient to assume that
$-K_{X}^{3}\geqslant \text{Vol}(X,\unicode[STIX]{x1D6E5})=-(K_{X}+\unicode[STIX]{x1D6E5})^{3}$
. Hence it is sufficient to assume that
![]() $X$
is an
$X$
is an
![]() $\unicode[STIX]{x1D716}$
-klt
$\unicode[STIX]{x1D716}$
-klt
![]() $\mathbb{Q}$
-factorial
$\mathbb{Q}$
-factorial
![]() $\mathbb{Q}$
-Fano threefold of Picard number
$\mathbb{Q}$
-Fano threefold of Picard number
 $\unicode[STIX]{x1D70C}(X)=1$
and to find an upper bound of
$\unicode[STIX]{x1D70C}(X)=1$
and to find an upper bound of
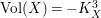 $\text{Vol}(X)=-K_{X}^{3}$
.
$\text{Vol}(X)=-K_{X}^{3}$
.
We will obtain an upper bound of the volumes by studying covering families of tigers. The weight of any covering families of tigers in our study will always be the weight with respect to
![]() $-K_{X}$
.
$-K_{X}$
.
Let
![]() $X$
be an
$X$
be an
![]() $\unicode[STIX]{x1D716}$
-klt
$\unicode[STIX]{x1D716}$
-klt
![]() $\mathbb{Q}$
-factorial
$\mathbb{Q}$
-factorial
![]() $\mathbb{Q}$
-Fano threefold of Picard number
$\mathbb{Q}$
-Fano threefold of Picard number
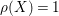 $\unicode[STIX]{x1D70C}(X)=1$
and write
$\unicode[STIX]{x1D70C}(X)=1$
and write
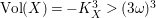 $\text{Vol}(X)=-K_{X}^{3}>(3\unicode[STIX]{x1D714})^{3}$
for some positive rational number
$\text{Vol}(X)=-K_{X}^{3}>(3\unicode[STIX]{x1D714})^{3}$
for some positive rational number
![]() $\unicode[STIX]{x1D714}$
. Denote
$\unicode[STIX]{x1D714}$
. Denote
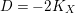 $D=-2K_{X}$
, we have
$D=-2K_{X}$
, we have
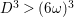 $D^{3}>(6\unicode[STIX]{x1D714})^{3}$
. By Lemma 1.2, we can fix an affine open subset
$D^{3}>(6\unicode[STIX]{x1D714})^{3}$
. By Lemma 1.2, we can fix an affine open subset
![]() $U\subseteq X$
such that for each
$U\subseteq X$
such that for each
![]() $p\in U$
there exists an effective divisor
$p\in U$
there exists an effective divisor
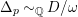 $\unicode[STIX]{x1D6E5}_{p}{\sim}_{\mathbb{Q}}D/\unicode[STIX]{x1D714}$
with
$\unicode[STIX]{x1D6E5}_{p}{\sim}_{\mathbb{Q}}D/\unicode[STIX]{x1D714}$
with
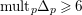 $\text{mult}_{p}\unicode[STIX]{x1D6E5}_{p}\geqslant 6$
. We do not assume that
$\text{mult}_{p}\unicode[STIX]{x1D6E5}_{p}\geqslant 6$
. We do not assume that
![]() $\unicode[STIX]{x1D6E5}_{p}$
creates exceptional non-klt centers as in Lemma 3.2, otherwise we lose control on multiplicity. We pick divisors
$\unicode[STIX]{x1D6E5}_{p}$
creates exceptional non-klt centers as in Lemma 3.2, otherwise we lose control on multiplicity. We pick divisors
![]() $\unicode[STIX]{x1D6E5}_{p}$
’s in the following systematic way so that we can control their multiplicities uniformly.
$\unicode[STIX]{x1D6E5}_{p}$
’s in the following systematic way so that we can control their multiplicities uniformly.
5.1 Construction
Let
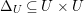 $\unicode[STIX]{x1D6E5}_{U}\subseteq U\times U$
be the diagonal and
$\unicode[STIX]{x1D6E5}_{U}\subseteq U\times U$
be the diagonal and
![]() ${\mathcal{I}}_{{\mathcal{Z}}}$
be the ideal sheaf of
${\mathcal{I}}_{{\mathcal{Z}}}$
be the ideal sheaf of
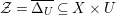 ${\mathcal{Z}}=\overline{\unicode[STIX]{x1D6E5}_{U}}\subseteq X\times U$
. For each
${\mathcal{Z}}=\overline{\unicode[STIX]{x1D6E5}_{U}}\subseteq X\times U$
. For each
![]() $p\in U$
, by the existence of
$p\in U$
, by the existence of
![]() $\mathbb{Q}$
-divisor
$\mathbb{Q}$
-divisor
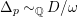 $\unicode[STIX]{x1D6E5}_{p}{\sim}_{\mathbb{Q}}D/\unicode[STIX]{x1D714}$
with
$\unicode[STIX]{x1D6E5}_{p}{\sim}_{\mathbb{Q}}D/\unicode[STIX]{x1D714}$
with
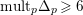 $\text{mult}_{p}\unicode[STIX]{x1D6E5}_{p}\geqslant 6$
, there exists
$\text{mult}_{p}\unicode[STIX]{x1D6E5}_{p}\geqslant 6$
, there exists
![]() $m_{p}>0$
such that
$m_{p}>0$
such that
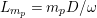 $L_{m_{p}}=m_{p}D/\unicode[STIX]{x1D714}$
is Cartier and
$L_{m_{p}}=m_{p}D/\unicode[STIX]{x1D714}$
is Cartier and
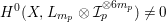 $H^{0}(X,L_{m_{p}}\otimes {\mathcal{I}}_{p}^{\otimes 6m_{p}})\neq 0$
, where
$H^{0}(X,L_{m_{p}}\otimes {\mathcal{I}}_{p}^{\otimes 6m_{p}})\neq 0$
, where
![]() ${\mathcal{I}}_{p}$
is the ideal sheaf of
${\mathcal{I}}_{p}$
is the ideal sheaf of
![]() $p\in U$
. In particular, we can write
$p\in U$
. In particular, we can write
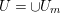 $U=\cup U_{m}$
where
$U=\cup U_{m}$
where
![]() $m>0$
runs through all sufficiently divisible integers such that
$m>0$
runs through all sufficiently divisible integers such that
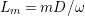 $L_{m}=mD/\unicode[STIX]{x1D714}$
is Cartier and
$L_{m}=mD/\unicode[STIX]{x1D714}$
is Cartier and
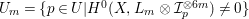 $U_{m}=\{p\in U|H^{0}(X,L_{m}\otimes {\mathcal{I}}_{p}^{\otimes 6m})\neq 0\}$
. In particular, each
$U_{m}=\{p\in U|H^{0}(X,L_{m}\otimes {\mathcal{I}}_{p}^{\otimes 6m})\neq 0\}$
. In particular, each
![]() $\overline{U_{m}}$
is closed in
$\overline{U_{m}}$
is closed in
![]() $X$
and
$X$
and
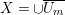 $X=\cup \overline{U_{m}}$
. Since the base field
$X=\cup \overline{U_{m}}$
. Since the base field
![]() $\mathbb{C}$
is uncountable,
$\mathbb{C}$
is uncountable,
![]() $X$
cannot be a countable union of proper closed subsets and there exists some
$X$
cannot be a countable union of proper closed subsets and there exists some
![]() $m>0$
such that
$m>0$
such that
![]() $U_{m}$
is dense in
$U_{m}$
is dense in
![]() $X$
.
$X$
.
Fix an
![]() $m>0$
so that
$m>0$
so that
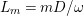 $L_{m}=mD/\unicode[STIX]{x1D714}$
is Cartier and
$L_{m}=mD/\unicode[STIX]{x1D714}$
is Cartier and
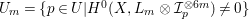 $U_{m}=\{p\in U|H^{0}(X,L_{m}\otimes {\mathcal{I}}_{p}^{\otimes 6m})\neq 0\}$
is dense in
$U_{m}=\{p\in U|H^{0}(X,L_{m}\otimes {\mathcal{I}}_{p}^{\otimes 6m})\neq 0\}$
is dense in
![]() $X$
. Denote
$X$
. Denote
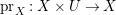 $\text{pr}_{X}:X\times U\rightarrow X$
and
$\text{pr}_{X}:X\times U\rightarrow X$
and
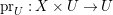 $\text{pr}_{U}:X\times U\rightarrow U$
the projection maps. Since
$\text{pr}_{U}:X\times U\rightarrow U$
the projection maps. Since
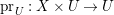 $\text{pr}_{U}:X\times U\rightarrow U$
is flat, by [Reference HartshorneHar77, III 12.11] after restricting to a smaller open affine subset of
$\text{pr}_{U}:X\times U\rightarrow U$
is flat, by [Reference HartshorneHar77, III 12.11] after restricting to a smaller open affine subset of
![]() $U$
, we can assume that the map
$U$
, we can assume that the map
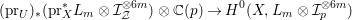 $$\begin{eqnarray}(\text{pr}_{U})_{\ast }(\text{pr}_{X}^{\ast }L_{m}\otimes {\mathcal{I}}_{{\mathcal{Z}}}^{\otimes 6m})\otimes \mathbb{C}(p)\rightarrow H^{0}(X,L_{m}\otimes {\mathcal{I}}_{p}^{\otimes 6m})\end{eqnarray}$$
$$\begin{eqnarray}(\text{pr}_{U})_{\ast }(\text{pr}_{X}^{\ast }L_{m}\otimes {\mathcal{I}}_{{\mathcal{Z}}}^{\otimes 6m})\otimes \mathbb{C}(p)\rightarrow H^{0}(X,L_{m}\otimes {\mathcal{I}}_{p}^{\otimes 6m})\end{eqnarray}$$
is isomorphic for each
![]() $p\in U$
. Since
$p\in U$
. Since
![]() $U_{m}$
is dense in
$U_{m}$
is dense in
![]() $U$
, the sheaf
$U$
, the sheaf
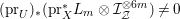 $(\text{pr}_{U})_{\ast }(\text{pr}_{X}^{\ast }L_{m}\otimes {\mathcal{I}}_{{\mathcal{Z}}}^{\otimes 6m})\neq 0$
on
$(\text{pr}_{U})_{\ast }(\text{pr}_{X}^{\ast }L_{m}\otimes {\mathcal{I}}_{{\mathcal{Z}}}^{\otimes 6m})\neq 0$
on
![]() $U$
and hence
$U$
and hence
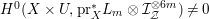 $H^{0}(X\times U,\text{pr}_{X}^{\ast }L_{m}\otimes {\mathcal{I}}_{{\mathcal{Z}}}^{\otimes 6m})\neq 0$
as
$H^{0}(X\times U,\text{pr}_{X}^{\ast }L_{m}\otimes {\mathcal{I}}_{{\mathcal{Z}}}^{\otimes 6m})\neq 0$
as
![]() $U$
is affine. Let
$U$
is affine. Let
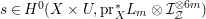 $s\in H^{0}(X\times U,\text{pr}_{X}^{\ast }L_{m}\otimes {\mathcal{I}}_{{\mathcal{Z}}}^{\otimes 6m})$
be a nonzero section with
$s\in H^{0}(X\times U,\text{pr}_{X}^{\ast }L_{m}\otimes {\mathcal{I}}_{{\mathcal{Z}}}^{\otimes 6m})$
be a nonzero section with
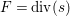 $F=\text{div}(s)$
the corresponding divisor on
$F=\text{div}(s)$
the corresponding divisor on
![]() $X\times U$
. For each
$X\times U$
. For each
![]() $p\in U$
, denote
$p\in U$
, denote
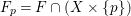 $F_{p}=F\cap (X\times \{p\})$
the associated divisor on
$F_{p}=F\cap (X\times \{p\})$
the associated divisor on
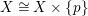 $X\cong X\times \{p\}$
. Since
$X\cong X\times \{p\}$
. Since
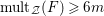 $\text{mult}_{{\mathcal{Z}}}(F)\geqslant 6m$
, by Lemma 5.1 below the
$\text{mult}_{{\mathcal{Z}}}(F)\geqslant 6m$
, by Lemma 5.1 below the
![]() $\mathbb{Q}$
-divisor
$\mathbb{Q}$
-divisor
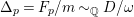 $\unicode[STIX]{x1D6E5}_{p}=F_{p}/m{\sim}_{\mathbb{Q}}D/\unicode[STIX]{x1D714}$
on
$\unicode[STIX]{x1D6E5}_{p}=F_{p}/m{\sim}_{\mathbb{Q}}D/\unicode[STIX]{x1D714}$
on
![]() $X$
satisfies
$X$
satisfies
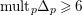 $\text{mult}_{p}\unicode[STIX]{x1D6E5}_{p}\geqslant 6$
for general
$\text{mult}_{p}\unicode[STIX]{x1D6E5}_{p}\geqslant 6$
for general
![]() $p\in U$
.
$p\in U$
.
Lemma 5.1. [Reference LazarsfeldLaz04, Lemma 5.2.11]
Let
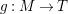 $g:M\rightarrow T$
be a morphism of smooth varieties, and suppose that
$g:M\rightarrow T$
be a morphism of smooth varieties, and suppose that
![]() ${\mathcal{Z}}\subseteq M$
is an irreducible subvariety dominating
${\mathcal{Z}}\subseteq M$
is an irreducible subvariety dominating
![]() $T$
:
$T$
:
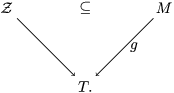
Let
![]() $F\subseteq M$
be an effective divisor. Then for a general point
$F\subseteq M$
be an effective divisor. Then for a general point
![]() $t\in T$
and any irreducible component
$t\in T$
and any irreducible component
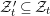 ${\mathcal{Z}}_{t}^{\prime }\subseteq {\mathcal{Z}}_{t}$
,
${\mathcal{Z}}_{t}^{\prime }\subseteq {\mathcal{Z}}_{t}$
,
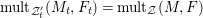 $$\begin{eqnarray}\text{mult}_{{\mathcal{Z}}_{t}^{\prime }}(M_{t},F_{t})=\text{mult}_{{\mathcal{Z}}}(M,F)\end{eqnarray}$$
$$\begin{eqnarray}\text{mult}_{{\mathcal{Z}}_{t}^{\prime }}(M_{t},F_{t})=\text{mult}_{{\mathcal{Z}}}(M,F)\end{eqnarray}$$
where
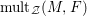 $\text{mult}_{{\mathcal{Z}}}(M,F)$
is the multiplicity of the divisor
$\text{mult}_{{\mathcal{Z}}}(M,F)$
is the multiplicity of the divisor
![]() $F$
on
$F$
on
![]() $M$
along a general point of the irreducible subvariety
$M$
along a general point of the irreducible subvariety
![]() ${\mathcal{Z}}\subseteq M$
and similarly for
${\mathcal{Z}}\subseteq M$
and similarly for
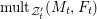 $\text{mult}_{{\mathcal{Z}}_{t}^{\prime }}(M_{t},F_{t})$
.
$\text{mult}_{{\mathcal{Z}}_{t}^{\prime }}(M_{t},F_{t})$
.
For a given collection of
![]() $\mathbb{Q}$
-divisors
$\mathbb{Q}$
-divisors
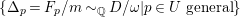 $\{\unicode[STIX]{x1D6E5}_{p}=F_{p}/m{\sim}_{\mathbb{Q}}D/\unicode[STIX]{x1D714}|p\in U~\text{general}\}$
associated to a nonzero section in
$\{\unicode[STIX]{x1D6E5}_{p}=F_{p}/m{\sim}_{\mathbb{Q}}D/\unicode[STIX]{x1D714}|p\in U~\text{general}\}$
associated to a nonzero section in
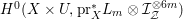 $H^{0}(X\times U,\text{pr}_{X}^{\ast }L_{m}\otimes {\mathcal{I}}_{{\mathcal{Z}}}^{\otimes 6m})$
as above, by Lemma 3.2 we can modify
$H^{0}(X\times U,\text{pr}_{X}^{\ast }L_{m}\otimes {\mathcal{I}}_{{\mathcal{Z}}}^{\otimes 6m})$
as above, by Lemma 3.2 we can modify
![]() $\unicode[STIX]{x1D6E5}_{p}$
’s such that the unique non-klt centers
$\unicode[STIX]{x1D6E5}_{p}$
’s such that the unique non-klt centers
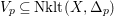 $V_{p}\subseteq \text{Nklt}(X,\unicode[STIX]{x1D6E5}_{p})$
passing through
$V_{p}\subseteq \text{Nklt}(X,\unicode[STIX]{x1D6E5}_{p})$
passing through
![]() $p$
are exceptional. By Lemma 3.3 (or in general Corollary 3.4), we can construct covering families of tigers from these divisors.
$p$
are exceptional. By Lemma 3.3 (or in general Corollary 3.4), we can construct covering families of tigers from these divisors.
In order to obtain an upper bound of
![]() $\unicode[STIX]{x1D714}$
, which is enough for bounding the volumes, we will pick up a “well-behaved” nonzero section
$\unicode[STIX]{x1D714}$
, which is enough for bounding the volumes, we will pick up a “well-behaved” nonzero section
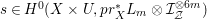 $s\in H^{0}(X\times U,pr_{X}^{\ast }L_{m}\otimes {\mathcal{I}}_{{\mathcal{Z}}}^{\otimes 6m})$
and study the corresponding covering families of tigers.
$s\in H^{0}(X\times U,pr_{X}^{\ast }L_{m}\otimes {\mathcal{I}}_{{\mathcal{Z}}}^{\otimes 6m})$
and study the corresponding covering families of tigers.
5.2 Cases
By 5.1, there exists an open affine subset
![]() $U\subseteq X$
and an integer
$U\subseteq X$
and an integer
![]() $m>0$
such that
$m>0$
such that
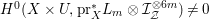 $H^{0}(X\times U,\text{pr}_{X}^{\ast }L_{m}\otimes {\mathcal{I}}_{{\mathcal{Z}}}^{\otimes 6m})\neq 0$
. Let
$H^{0}(X\times U,\text{pr}_{X}^{\ast }L_{m}\otimes {\mathcal{I}}_{{\mathcal{Z}}}^{\otimes 6m})\neq 0$
. Let
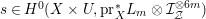 $s\in H^{0}(X\times U,\text{pr}_{X}^{\ast }L_{m}\otimes {\mathcal{I}}_{{\mathcal{Z}}}^{\otimes 6m})$
be a nonzero section with divisor
$s\in H^{0}(X\times U,\text{pr}_{X}^{\ast }L_{m}\otimes {\mathcal{I}}_{{\mathcal{Z}}}^{\otimes 6m})$
be a nonzero section with divisor
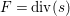 $F=\text{div}(s)$
on
$F=\text{div}(s)$
on
![]() $X\times U$
and
$X\times U$
and
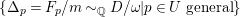 $\{\unicode[STIX]{x1D6E5}_{p}=F_{p}/m{\sim}_{\mathbb{Q}}D/\unicode[STIX]{x1D714}|p\in U~\text{general}\}$
be the associated collection of
$\{\unicode[STIX]{x1D6E5}_{p}=F_{p}/m{\sim}_{\mathbb{Q}}D/\unicode[STIX]{x1D714}|p\in U~\text{general}\}$
be the associated collection of
![]() $\mathbb{Q}$
-divisors. We consider two cases:
$\mathbb{Q}$
-divisors. We consider two cases:
-
(1) (Small multiplicity) For each irreducible component
 ${\mathcal{W}}$
of
${\mathcal{W}}$
of
 $\text{Supp}(F)$
passing through
$\text{Supp}(F)$
passing through
 ${\mathcal{Z}}$
,
${\mathcal{Z}}$
,
 $\text{mult}_{{\mathcal{W}}}(F)\leqslant 3m$
, that is, for general
$\text{mult}_{{\mathcal{W}}}(F)\leqslant 3m$
, that is, for general
 $p\in U$
we have
$p\in U$
we have
 $\text{mult}_{W}(\unicode[STIX]{x1D6E5}_{p})\leqslant 3$
for any irreducible component
$\text{mult}_{W}(\unicode[STIX]{x1D6E5}_{p})\leqslant 3$
for any irreducible component
 $W$
of
$W$
of
 $\text{Supp}(\unicode[STIX]{x1D6E5}_{p})$
passing through
$\text{Supp}(\unicode[STIX]{x1D6E5}_{p})$
passing through
 $p$
. After differentiating
$p$
. After differentiating
 $F$
, we will construct a “well-behaved” covering family of tigers of dimension one. We will derive an upper bound of
$F$
, we will construct a “well-behaved” covering family of tigers of dimension one. We will derive an upper bound of
 $\unicode[STIX]{x1D714}$
by studying this well-behaved covering family of tigers. See Section 5.3.
$\unicode[STIX]{x1D714}$
by studying this well-behaved covering family of tigers. See Section 5.3. -
(2) (Big multiplicity) There exists an irreducible component
 ${\mathcal{W}}$
of
${\mathcal{W}}$
of
 $\text{Supp}(F)$
passing through
$\text{Supp}(F)$
passing through
 ${\mathcal{Z}}$
with multiplicity
${\mathcal{Z}}$
with multiplicity
 $\text{mult}_{{\mathcal{W}}}(F)>3m$
, that is, for general
$\text{mult}_{{\mathcal{W}}}(F)>3m$
, that is, for general
 $p\in U$
we have
$p\in U$
we have
 $\text{mult}_{W}(\unicode[STIX]{x1D6E5}_{p})>3$
for an irreducible component
$\text{mult}_{W}(\unicode[STIX]{x1D6E5}_{p})>3$
for an irreducible component
 $W$
of
$W$
of
 $\text{Supp}(\unicode[STIX]{x1D6E5}_{p})$
passing through
$\text{Supp}(\unicode[STIX]{x1D6E5}_{p})$
passing through
 $p$
. We will construct a covering family of tigers of dimension two and derive an upper bound of
$p$
. We will construct a covering family of tigers of dimension two and derive an upper bound of
 $\unicode[STIX]{x1D714}$
by studying the geometry of this covering family of tigers. See Section 5.4.
$\unicode[STIX]{x1D714}$
by studying the geometry of this covering family of tigers. See Section 5.4.
To pick up a “well-behaved” nonzero section in
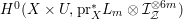 $H^{0}(X\times U,\text{pr}_{X}^{\ast }L_{m}\otimes {\mathcal{I}}_{{\mathcal{Z}}}^{\otimes 6m})$
, we will apply the following proposition.
$H^{0}(X\times U,\text{pr}_{X}^{\ast }L_{m}\otimes {\mathcal{I}}_{{\mathcal{Z}}}^{\otimes 6m})$
, we will apply the following proposition.
Proposition 5.2. [Reference LazarsfeldLaz04, Proposition 5.2.13]
Let
![]() $X$
and
$X$
and
![]() $U$
be smooth irreducible varieties, with
$U$
be smooth irreducible varieties, with
![]() $U$
affine, and suppose that
$U$
affine, and suppose that
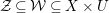 $$\begin{eqnarray}{\mathcal{Z}}\subseteq {\mathcal{W}}\subseteq X\times U\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{Z}}\subseteq {\mathcal{W}}\subseteq X\times U\end{eqnarray}$$
are irreducible subvarieties such that
![]() ${\mathcal{W}}$
dominates
${\mathcal{W}}$
dominates
![]() $X$
. Fix a line bundle
$X$
. Fix a line bundle
![]() $L$
on
$L$
on
![]() $X$
, and suppose given on
$X$
, and suppose given on
![]() $X\times U$
a divisor
$X\times U$
a divisor
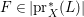 $F\in |\text{pr}_{X}^{\ast }(L)|$
. Write
$F\in |\text{pr}_{X}^{\ast }(L)|$
. Write
 $$\begin{eqnarray}l=\text{mult}_{{\mathcal{Z}}}(F),\qquad k=\text{mult}_{{\mathcal{W}}}(F).\end{eqnarray}$$
$$\begin{eqnarray}l=\text{mult}_{{\mathcal{Z}}}(F),\qquad k=\text{mult}_{{\mathcal{W}}}(F).\end{eqnarray}$$
Then after differentiating in the parameter directions, there exists a divisor
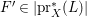 $F^{\prime }\in |\text{pr}_{X}^{\ast }(L)|$
on
$F^{\prime }\in |\text{pr}_{X}^{\ast }(L)|$
on
![]() $X\times U$
with the property that
$X\times U$
with the property that
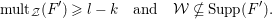 $$\begin{eqnarray}\text{mult}_{{\mathcal{Z}}}(F^{\prime })\geqslant l-k\quad \text{and}\quad {\mathcal{W}}\nsubseteq \text{Supp}(F^{\prime }).\end{eqnarray}$$
$$\begin{eqnarray}\text{mult}_{{\mathcal{Z}}}(F^{\prime })\geqslant l-k\quad \text{and}\quad {\mathcal{W}}\nsubseteq \text{Supp}(F^{\prime }).\end{eqnarray}$$
5.3 Small multiplicity
Let
![]() $X$
be an
$X$
be an
![]() $\unicode[STIX]{x1D716}$
-klt
$\unicode[STIX]{x1D716}$
-klt
![]() $\mathbb{Q}$
-Fano threefold of Picard number one and write
$\mathbb{Q}$
-Fano threefold of Picard number one and write
 $\text{Vol}(X)=-K_{X}^{3}>(3\unicode[STIX]{x1D714})^{3}$
for some positive rational number
$\text{Vol}(X)=-K_{X}^{3}>(3\unicode[STIX]{x1D714})^{3}$
for some positive rational number
![]() $\unicode[STIX]{x1D714}$
. Denote
$\unicode[STIX]{x1D714}$
. Denote
 $D=-2K_{X}$
, we have
$D=-2K_{X}$
, we have
 $D^{3}>(6\unicode[STIX]{x1D714})^{3}$
. From 5.1, there is an integer
$D^{3}>(6\unicode[STIX]{x1D714})^{3}$
. From 5.1, there is an integer
![]() $m>0$
such that
$m>0$
such that
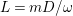 $L=mD/\unicode[STIX]{x1D714}$
is Cartier and an open affine subset
$L=mD/\unicode[STIX]{x1D714}$
is Cartier and an open affine subset
![]() $U\subseteq X$
such that
$U\subseteq X$
such that
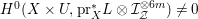 $H^{0}(X\times U,\text{pr}_{X}^{\ast }L\otimes {\mathcal{I}}_{{\mathcal{Z}}}^{\otimes 6m})\neq 0$
. We fix a nonzero section
$H^{0}(X\times U,\text{pr}_{X}^{\ast }L\otimes {\mathcal{I}}_{{\mathcal{Z}}}^{\otimes 6m})\neq 0$
. We fix a nonzero section
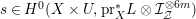 $s\in H^{0}(X\times U,\text{pr}_{X}^{\ast }L\otimes {\mathcal{I}}_{{\mathcal{Z}}}^{\otimes 6m})$
with
$s\in H^{0}(X\times U,\text{pr}_{X}^{\ast }L\otimes {\mathcal{I}}_{{\mathcal{Z}}}^{\otimes 6m})$
with
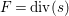 $F=\text{div}(s)$
on
$F=\text{div}(s)$
on
![]() $X\times U$
.
$X\times U$
.
Proposition 5.3. With the above set up, assume that
![]() $\unicode[STIX]{x1D714}>4$
. Suppose that we are in the case where all the irreducible components
$\unicode[STIX]{x1D714}>4$
. Suppose that we are in the case where all the irreducible components
![]() ${\mathcal{W}}$
of
${\mathcal{W}}$
of
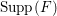 $\text{Supp}(F)$
passing through
$\text{Supp}(F)$
passing through
![]() ${\mathcal{Z}}$
satisfy
${\mathcal{Z}}$
satisfy
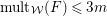 $\text{mult}_{{\mathcal{W}}}(F)\leqslant 3m$
, then we have
$\text{mult}_{{\mathcal{W}}}(F)\leqslant 3m$
, then we have
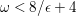 $\unicode[STIX]{x1D714}<8/\unicode[STIX]{x1D716}+4$
. In particular, there is an upper bound of the volume
$\unicode[STIX]{x1D714}<8/\unicode[STIX]{x1D716}+4$
. In particular, there is an upper bound of the volume
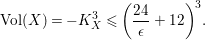 $$\begin{eqnarray}\text{Vol}(X)=-K_{X}^{3}\leqslant \biggl(\frac{24}{\unicode[STIX]{x1D716}}+12\biggr)^{3}.\end{eqnarray}$$
$$\begin{eqnarray}\text{Vol}(X)=-K_{X}^{3}\leqslant \biggl(\frac{24}{\unicode[STIX]{x1D716}}+12\biggr)^{3}.\end{eqnarray}$$
Proof. Let
![]() $M$
be the maximum of
$M$
be the maximum of
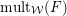 $\text{mult}_{{\mathcal{W}}}(F)$
amongst all the irreducible components
$\text{mult}_{{\mathcal{W}}}(F)$
amongst all the irreducible components
![]() ${\mathcal{W}}$
of
${\mathcal{W}}$
of
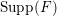 $\text{Supp}(F)$
passing through
$\text{Supp}(F)$
passing through
![]() ${\mathcal{Z}}$
, then
${\mathcal{Z}}$
, then
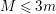 $M\leqslant 3m$
from the hypothesis. For
$M\leqslant 3m$
from the hypothesis. For
![]() ${\mathcal{W}}$
of
${\mathcal{W}}$
of
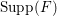 $\text{Supp}(F)$
a fixed irreducible component passing through
$\text{Supp}(F)$
a fixed irreducible component passing through
![]() ${\mathcal{Z}}$
, take
${\mathcal{Z}}$
, take
![]() $M$
times differentiation of
$M$
times differentiation of
![]() $F$
by Proposition 5.2. Then we obtain a divisor
$F$
by Proposition 5.2. Then we obtain a divisor
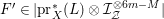 $F^{\prime }\in |\text{pr}_{X}^{\ast }(L)\otimes {\mathcal{I}}_{{\mathcal{Z}}}^{\otimes 6m-M}|$
with the property that
$F^{\prime }\in |\text{pr}_{X}^{\ast }(L)\otimes {\mathcal{I}}_{{\mathcal{Z}}}^{\otimes 6m-M}|$
with the property that
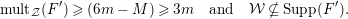 $$\begin{eqnarray}\text{mult}_{{\mathcal{Z}}}(F^{\prime })\geqslant (6m-M)\geqslant 3m\quad \text{and}\quad {\mathcal{W}}\nsubseteq \text{Supp}(F^{\prime }).\end{eqnarray}$$
$$\begin{eqnarray}\text{mult}_{{\mathcal{Z}}}(F^{\prime })\geqslant (6m-M)\geqslant 3m\quad \text{and}\quad {\mathcal{W}}\nsubseteq \text{Supp}(F^{\prime }).\end{eqnarray}$$
Since there are only finitely many irreducible components of
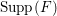 $\text{Supp}(F)$
passing through
$\text{Supp}(F)$
passing through
![]() ${\mathcal{Z}}$
and we are taking a generic differentiation, indeed for a general divisor
${\mathcal{Z}}$
and we are taking a generic differentiation, indeed for a general divisor
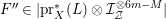 $F^{\prime \prime }\in |\text{pr}_{X}^{\ast }(L)\otimes {\mathcal{I}}_{{\mathcal{Z}}}^{\otimes 6m-M}|$
we have
$F^{\prime \prime }\in |\text{pr}_{X}^{\ast }(L)\otimes {\mathcal{I}}_{{\mathcal{Z}}}^{\otimes 6m-M}|$
we have
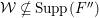 ${\mathcal{W}}\nsubseteq \text{Supp}(F^{\prime \prime })$
for any
${\mathcal{W}}\nsubseteq \text{Supp}(F^{\prime \prime })$
for any
![]() ${\mathcal{W}}$
an irreducible component of
${\mathcal{W}}$
an irreducible component of
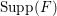 $\text{Supp}(F)$
passing through
$\text{Supp}(F)$
passing through
![]() ${\mathcal{Z}}$
. In particular, the base locus
${\mathcal{Z}}$
. In particular, the base locus
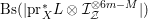 $\text{Bs}(|\text{pr}_{X}^{\ast }L\otimes {\mathcal{I}}_{{\mathcal{Z}}}^{\otimes 6m-M}|)$
contains no codimension one components in a neighborhood of
$\text{Bs}(|\text{pr}_{X}^{\ast }L\otimes {\mathcal{I}}_{{\mathcal{Z}}}^{\otimes 6m-M}|)$
contains no codimension one components in a neighborhood of
![]() ${\mathcal{Z}}$
.
${\mathcal{Z}}$
.
Let
![]() $G$
be a general divisor in
$G$
be a general divisor in
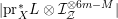 $|\text{pr}_{X}^{\ast }L\otimes {\mathcal{I}}_{{\mathcal{Z}}}^{\otimes 6m-M}|$
and
$|\text{pr}_{X}^{\ast }L\otimes {\mathcal{I}}_{{\mathcal{Z}}}^{\otimes 6m-M}|$
and
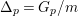 $\unicode[STIX]{x1D6E5}_{p}=G_{p}/m$
for
$\unicode[STIX]{x1D6E5}_{p}=G_{p}/m$
for
![]() $p\in U$
general be the corresponding
$p\in U$
general be the corresponding
![]() $\mathbb{Q}$
-divisors on
$\mathbb{Q}$
-divisors on
![]() $X$
. It follows that
$X$
. It follows that
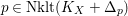 $p\in \text{Nklt}(K_{X}+\unicode[STIX]{x1D6E5}_{p})$
as
$p\in \text{Nklt}(K_{X}+\unicode[STIX]{x1D6E5}_{p})$
as
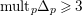 $\text{mult}_{p}\unicode[STIX]{x1D6E5}_{p}\geqslant 3$
. The minimal non-klt center
$\text{mult}_{p}\unicode[STIX]{x1D6E5}_{p}\geqslant 3$
. The minimal non-klt center
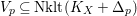 $V_{p}\subseteq \text{Nklt}(K_{X}+\unicode[STIX]{x1D6E5}_{p})$
passing through
$V_{p}\subseteq \text{Nklt}(K_{X}+\unicode[STIX]{x1D6E5}_{p})$
passing through
![]() $p$
must be positive dimensional by Lemma 3.5 as the weight of
$p$
must be positive dimensional by Lemma 3.5 as the weight of
![]() $\unicode[STIX]{x1D6E5}_{p}$
is
$\unicode[STIX]{x1D6E5}_{p}$
is
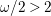 $\unicode[STIX]{x1D714}/2>2$
. Also
$\unicode[STIX]{x1D714}/2>2$
. Also
![]() $V_{p}$
can only be one-dimensional, as by construction
$V_{p}$
can only be one-dimensional, as by construction
![]() $m\geqslant 2$
, and hence
$m\geqslant 2$
, and hence
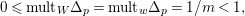 $$\begin{eqnarray}0\leqslant \text{mult}_{W}\unicode[STIX]{x1D6E5}_{p}=\text{mult}_{w}\unicode[STIX]{x1D6E5}_{p}=1/m<1,\end{eqnarray}$$
$$\begin{eqnarray}0\leqslant \text{mult}_{W}\unicode[STIX]{x1D6E5}_{p}=\text{mult}_{w}\unicode[STIX]{x1D6E5}_{p}=1/m<1,\end{eqnarray}$$
where
![]() $W$
is any irreducible component of
$W$
is any irreducible component of
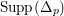 $\text{Supp}(\unicode[STIX]{x1D6E5}_{p})$
and
$\text{Supp}(\unicode[STIX]{x1D6E5}_{p})$
and
![]() $w\in W$
is a general point.
$w\in W$
is a general point.
Let
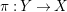 $\unicode[STIX]{x1D70B}:Y\rightarrow X$
with
$\unicode[STIX]{x1D70B}:Y\rightarrow X$
with
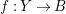 $f:Y\rightarrow B$
be a one-dimensional covering family of tigers of weight
$f:Y\rightarrow B$
be a one-dimensional covering family of tigers of weight
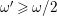 $\unicode[STIX]{x1D714}^{\prime }\geqslant \unicode[STIX]{x1D714}/2$
constructed from
$\unicode[STIX]{x1D714}^{\prime }\geqslant \unicode[STIX]{x1D714}/2$
constructed from
![]() $\unicode[STIX]{x1D6E5}_{p}$
’s by Lemma 3.2 and Proposition 3.3. By abusing of the notation, we still denote
$\unicode[STIX]{x1D6E5}_{p}$
’s by Lemma 3.2 and Proposition 3.3. By abusing of the notation, we still denote
![]() $\unicode[STIX]{x1D6E5}_{p}$
’s the divisors associated to this covering family of tigers.
$\unicode[STIX]{x1D6E5}_{p}$
’s the divisors associated to this covering family of tigers.
Choose
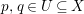 $p,q\in U\subseteq X$
general. By Lemma 1.3, the non-klt locus
$p,q\in U\subseteq X$
general. By Lemma 1.3, the non-klt locus
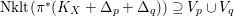 $\text{Nklt}(\unicode[STIX]{x1D70B}^{\ast }(K_{X}+\unicode[STIX]{x1D6E5}_{p}+\unicode[STIX]{x1D6E5}_{q}))\supseteq V_{p}\cup V_{q}$
on
$\text{Nklt}(\unicode[STIX]{x1D70B}^{\ast }(K_{X}+\unicode[STIX]{x1D6E5}_{p}+\unicode[STIX]{x1D6E5}_{q}))\supseteq V_{p}\cup V_{q}$
on
![]() $Y$
is connected and there is a one-cycle
$Y$
is connected and there is a one-cycle
![]() $C_{p,q}$
connecting
$C_{p,q}$
connecting
![]() $V_{p}$
and
$V_{p}$
and
![]() $V_{q}$
. Since
$V_{q}$
. Since
![]() $Y$
is normal, an irreducible component
$Y$
is normal, an irreducible component
![]() $C$
of
$C$
of
![]() $C_{p,q}$
intersecting
$C_{p,q}$
intersecting
![]() $V_{q}$
satisfies
$V_{q}$
satisfies
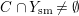 $C\cap Y_{\text{sm}}\neq \emptyset$
for
$C\cap Y_{\text{sm}}\neq \emptyset$
for
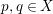 $p,q\in X$
general. Since
$p,q\in X$
general. Since
![]() $C$
is in
$C$
is in
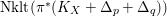 $\text{Nklt}(\unicode[STIX]{x1D70B}^{\ast }(K_{X}+\unicode[STIX]{x1D6E5}_{p}+\unicode[STIX]{x1D6E5}_{q}))$
, by symmetry we have
$\text{Nklt}(\unicode[STIX]{x1D70B}^{\ast }(K_{X}+\unicode[STIX]{x1D6E5}_{p}+\unicode[STIX]{x1D6E5}_{q}))$
, by symmetry we have
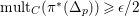 $\text{mult}_{C}(\unicode[STIX]{x1D70B}^{\ast }(\unicode[STIX]{x1D6E5}_{p}))\geqslant \unicode[STIX]{x1D716}/2$
. Choose a general point
$\text{mult}_{C}(\unicode[STIX]{x1D70B}^{\ast }(\unicode[STIX]{x1D6E5}_{p}))\geqslant \unicode[STIX]{x1D716}/2$
. Choose a general point
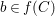 $b\in f(C)$
, then
$b\in f(C)$
, then
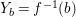 $Y_{b}=f^{-1}(b)$
is a general fiber of
$Y_{b}=f^{-1}(b)$
is a general fiber of
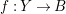 $f:Y\rightarrow B$
and one has
$f:Y\rightarrow B$
and one has
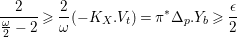 $$\begin{eqnarray}\frac{2}{\frac{\unicode[STIX]{x1D714}}{2}-2}\geqslant \frac{2}{\unicode[STIX]{x1D714}}(-K_{X}.V_{t})=\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D6E5}_{p}.Y_{b}\geqslant \frac{\unicode[STIX]{x1D716}}{2}\end{eqnarray}$$
$$\begin{eqnarray}\frac{2}{\frac{\unicode[STIX]{x1D714}}{2}-2}\geqslant \frac{2}{\unicode[STIX]{x1D714}}(-K_{X}.V_{t})=\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D6E5}_{p}.Y_{b}\geqslant \frac{\unicode[STIX]{x1D716}}{2}\end{eqnarray}$$
where the first inequality follows from Corollary 3.9. For the second inequality, note that we can make
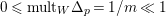 $0\leqslant \text{mult}_{W}\unicode[STIX]{x1D6E5}_{p}=1/m\ll 1$
for
$0\leqslant \text{mult}_{W}\unicode[STIX]{x1D6E5}_{p}=1/m\ll 1$
for
![]() $W$
any irreducible component of
$W$
any irreducible component of
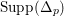 $\text{Supp}(\unicode[STIX]{x1D6E5}_{p})$
. In fact, in 5.2 we can start with the section
$\text{Supp}(\unicode[STIX]{x1D6E5}_{p})$
. In fact, in 5.2 we can start with the section
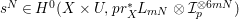 $s^{N}\in H^{0}(X\times U,pr_{X}^{\ast }L_{mN}\otimes {\mathcal{I}}_{p}^{\otimes 6mN})$
for
$s^{N}\in H^{0}(X\times U,pr_{X}^{\ast }L_{mN}\otimes {\mathcal{I}}_{p}^{\otimes 6mN})$
for
![]() $N\gg 0$
. The dichotomy into small and big multiplicities are the same and the above argument still goes through.
$N\gg 0$
. The dichotomy into small and big multiplicities are the same and the above argument still goes through.
Hence
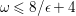 $\unicode[STIX]{x1D714}\leqslant 8/\unicode[STIX]{x1D716}+4$
.◻
$\unicode[STIX]{x1D714}\leqslant 8/\unicode[STIX]{x1D716}+4$
.◻
Remark 5.4. The difficulty here when we have covering families of tigers of dimension one is that in general the one-cycle
![]() $C$
as in the above proof might be contained in
$C$
as in the above proof might be contained in
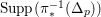 $\text{Supp}(\unicode[STIX]{x1D70B}_{\ast }^{-1}(\unicode[STIX]{x1D6E5}_{p}))$
. In this case, one cannot see the contribution of the
$\text{Supp}(\unicode[STIX]{x1D70B}_{\ast }^{-1}(\unicode[STIX]{x1D6E5}_{p}))$
. In this case, one cannot see the contribution of the
![]() $\unicode[STIX]{x1D716}$
-klt condition from the intersection number
$\unicode[STIX]{x1D716}$
-klt condition from the intersection number
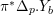 $\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D6E5}_{p}.Y_{b}$
for
$\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D6E5}_{p}.Y_{b}$
for
![]() $Y_{b}$
a general fiber over
$Y_{b}$
a general fiber over
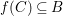 $f(C)\subseteq B$
, since
$f(C)\subseteq B$
, since
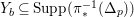 $Y_{b}\subseteq \text{Supp}(\unicode[STIX]{x1D70B}_{\ast }^{-1}(\unicode[STIX]{x1D6E5}_{p}))$
(cf., Example 2.1). The differentiation argument eliminates the contribution of irreducible codimension one components of
$Y_{b}\subseteq \text{Supp}(\unicode[STIX]{x1D70B}_{\ast }^{-1}(\unicode[STIX]{x1D6E5}_{p}))$
(cf., Example 2.1). The differentiation argument eliminates the contribution of irreducible codimension one components of
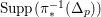 $\text{Supp}(\unicode[STIX]{x1D70B}_{\ast }^{-1}(\unicode[STIX]{x1D6E5}_{p}))$
along
$\text{Supp}(\unicode[STIX]{x1D70B}_{\ast }^{-1}(\unicode[STIX]{x1D6E5}_{p}))$
along
![]() $Y_{b}$
and hence we can proceed as in Proposition 5.3.
$Y_{b}$
and hence we can proceed as in Proposition 5.3.
5.4 Big multiplicity
Again, let
![]() $X$
be an
$X$
be an
![]() $\unicode[STIX]{x1D716}$
-klt
$\unicode[STIX]{x1D716}$
-klt
![]() $\mathbb{Q}$
-factorial
$\mathbb{Q}$
-factorial
![]() $\mathbb{Q}$
-Fano threefold of Picard number one. Write
$\mathbb{Q}$
-Fano threefold of Picard number one. Write
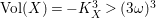 $\text{Vol}(X)=-K_{X}^{3}>(3\unicode[STIX]{x1D714})^{3}$
for some positive rational number
$\text{Vol}(X)=-K_{X}^{3}>(3\unicode[STIX]{x1D714})^{3}$
for some positive rational number
![]() $\unicode[STIX]{x1D714}$
and denote
$\unicode[STIX]{x1D714}$
and denote
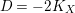 $D=-2K_{X}$
. As before, from 5.1 there is an integer
$D=-2K_{X}$
. As before, from 5.1 there is an integer
![]() $m>0$
such that
$m>0$
such that
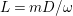 $L=mD/\unicode[STIX]{x1D714}$
is Cartier and an open affine subset
$L=mD/\unicode[STIX]{x1D714}$
is Cartier and an open affine subset
![]() $U\subseteq X$
such that
$U\subseteq X$
such that
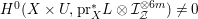 $H^{0}(X\times U,\text{pr}_{X}^{\ast }L\otimes {\mathcal{I}}_{{\mathcal{Z}}}^{\otimes 6m})\neq 0$
. We fix a nonzero section
$H^{0}(X\times U,\text{pr}_{X}^{\ast }L\otimes {\mathcal{I}}_{{\mathcal{Z}}}^{\otimes 6m})\neq 0$
. We fix a nonzero section
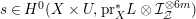 $s\in H^{0}(X\times U,\text{pr}_{X}^{\ast }L\otimes {\mathcal{I}}_{{\mathcal{Z}}}^{\otimes 6m})$
with
$s\in H^{0}(X\times U,\text{pr}_{X}^{\ast }L\otimes {\mathcal{I}}_{{\mathcal{Z}}}^{\otimes 6m})$
with
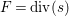 $F=\text{div}(s)$
on
$F=\text{div}(s)$
on
![]() $X\times U$
. We now consider the case where there exists an irreducible component
$X\times U$
. We now consider the case where there exists an irreducible component
![]() ${\mathcal{W}}$
of
${\mathcal{W}}$
of
 $\text{Supp}(F)$
passing through
$\text{Supp}(F)$
passing through
![]() ${\mathcal{Z}}$
with multiplicity
${\mathcal{Z}}$
with multiplicity
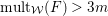 $\text{mult}_{{\mathcal{W}}}(F)>3m$
.
$\text{mult}_{{\mathcal{W}}}(F)>3m$
.
Lemma 5.5. Suppose that there exists an irreducible component
![]() ${\mathcal{W}}$
of
${\mathcal{W}}$
of
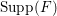 $\text{Supp}(F)$
passing through
$\text{Supp}(F)$
passing through
![]() ${\mathcal{Z}}$
with multiplicity
${\mathcal{Z}}$
with multiplicity
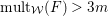 $\text{mult}_{{\mathcal{W}}}(F)>3m$
, then there exists a covering family of tigers of dimension two and weight
$\text{mult}_{{\mathcal{W}}}(F)>3m$
, then there exists a covering family of tigers of dimension two and weight
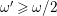 $\unicode[STIX]{x1D714}^{\prime }\geqslant \unicode[STIX]{x1D714}/2$
.
$\unicode[STIX]{x1D714}^{\prime }\geqslant \unicode[STIX]{x1D714}/2$
.
Proof. Fix
![]() ${\mathcal{W}}$
to be one of these irreducible components. Cutting down by hyperplanes on
${\mathcal{W}}$
to be one of these irreducible components. Cutting down by hyperplanes on
![]() $U$
and restrict to a smaller open subset of
$U$
and restrict to a smaller open subset of
![]() $U$
, we may assume that
$U$
, we may assume that
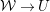 ${\mathcal{W}}\rightarrow U$
factors through a Hilbert scheme of
${\mathcal{W}}\rightarrow U$
factors through a Hilbert scheme of
![]() $X$
and
$X$
and
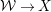 ${\mathcal{W}}\rightarrow X$
is generically finite. Replace
${\mathcal{W}}\rightarrow X$
is generically finite. Replace
![]() $U$
by the normalization of the closure of its image in the Hilbert scheme and
$U$
by the normalization of the closure of its image in the Hilbert scheme and
![]() ${\mathcal{W}}$
by the normalization of universal family, we obtain maps
${\mathcal{W}}$
by the normalization of universal family, we obtain maps
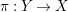 $\unicode[STIX]{x1D70B}:Y\rightarrow X$
and
$\unicode[STIX]{x1D70B}:Y\rightarrow X$
and
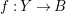 $f:Y\rightarrow B$
. Note that a general fiber
$f:Y\rightarrow B$
. Note that a general fiber
![]() $Y_{b}$
is two-dimensional. We claim that the pairs
$Y_{b}$
is two-dimensional. We claim that the pairs
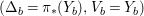 $(\unicode[STIX]{x1D6E5}_{b}=\unicode[STIX]{x1D70B}_{\ast }(Y_{b}),V_{b}=Y_{b})$
is a two-dimensional covering of tigers of weight
$(\unicode[STIX]{x1D6E5}_{b}=\unicode[STIX]{x1D70B}_{\ast }(Y_{b}),V_{b}=Y_{b})$
is a two-dimensional covering of tigers of weight
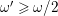 $\unicode[STIX]{x1D714}^{\prime }\geqslant \unicode[STIX]{x1D714}/2$
.
$\unicode[STIX]{x1D714}^{\prime }\geqslant \unicode[STIX]{x1D714}/2$
.
Since
![]() $X$
is
$X$
is
![]() $\mathbb{Q}$
-factorial and
$\mathbb{Q}$
-factorial and
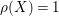 $\unicode[STIX]{x1D70C}(X)=1$
, the integral divisor
$\unicode[STIX]{x1D70C}(X)=1$
, the integral divisor
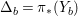 $\unicode[STIX]{x1D6E5}_{b}=\unicode[STIX]{x1D70B}_{\ast }(Y_{b})$
for any
$\unicode[STIX]{x1D6E5}_{b}=\unicode[STIX]{x1D70B}_{\ast }(Y_{b})$
for any
![]() $b\in B$
on
$b\in B$
on
![]() $X$
is
$X$
is
![]() $\mathbb{Q}$
-linearly equivalent to a multiple of
$\mathbb{Q}$
-linearly equivalent to a multiple of
![]() $-K_{X}$
. Also
$-K_{X}$
. Also
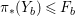 $\unicode[STIX]{x1D70B}_{\ast }(Y_{b})\leqslant F_{b}$
since by construction this is true for the divisor
$\unicode[STIX]{x1D70B}_{\ast }(Y_{b})\leqslant F_{b}$
since by construction this is true for the divisor
![]() ${\mathcal{W}}_{b}$
. In particular,
${\mathcal{W}}_{b}$
. In particular,
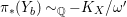 $\unicode[STIX]{x1D70B}_{\ast }(Y_{b}){\sim}_{\mathbb{Q}}-K_{X}/\unicode[STIX]{x1D714}^{\prime }$
for some
$\unicode[STIX]{x1D70B}_{\ast }(Y_{b}){\sim}_{\mathbb{Q}}-K_{X}/\unicode[STIX]{x1D714}^{\prime }$
for some
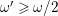 $\unicode[STIX]{x1D714}^{\prime }\geqslant \unicode[STIX]{x1D714}/2$
. Since any two general divisors
$\unicode[STIX]{x1D714}^{\prime }\geqslant \unicode[STIX]{x1D714}/2$
. Since any two general divisors
![]() $\unicode[STIX]{x1D70B}_{\ast }(Y_{b_{i}})$
,
$\unicode[STIX]{x1D70B}_{\ast }(Y_{b_{i}})$
,
![]() $i=1,2$
, on
$i=1,2$
, on
![]() $X$
are
$X$
are
![]() $\mathbb{Q}$
-linearly equivalent as the base field is uncountable, and it is clear that
$\mathbb{Q}$
-linearly equivalent as the base field is uncountable, and it is clear that
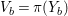 $V_{b}=\unicode[STIX]{x1D70B}(Y_{b})$
is a pure non-klt center of
$V_{b}=\unicode[STIX]{x1D70B}(Y_{b})$
is a pure non-klt center of
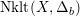 $\text{Nklt}(X,\unicode[STIX]{x1D6E5}_{b})$
, the claim follows.◻
$\text{Nklt}(X,\unicode[STIX]{x1D6E5}_{b})$
, the claim follows.◻
Let
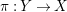 $\unicode[STIX]{x1D70B}:Y\rightarrow X$
with
$\unicode[STIX]{x1D70B}:Y\rightarrow X$
with
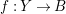 $f:Y\rightarrow B$
be a covering family of tigers of dimension two and weight
$f:Y\rightarrow B$
be a covering family of tigers of dimension two and weight
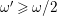 $\unicode[STIX]{x1D714}^{\prime }\geqslant \unicode[STIX]{x1D714}/2$
from Lemma 5.5. We first deal with case where
$\unicode[STIX]{x1D714}^{\prime }\geqslant \unicode[STIX]{x1D714}/2$
from Lemma 5.5. We first deal with case where
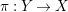 $\unicode[STIX]{x1D70B}:Y\rightarrow X$
is not birational.
$\unicode[STIX]{x1D70B}:Y\rightarrow X$
is not birational.
Proposition 5.6. Suppose that the two-dimensional covering family of tigers
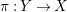 $\unicode[STIX]{x1D70B}:Y\rightarrow X$
with
$\unicode[STIX]{x1D70B}:Y\rightarrow X$
with
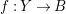 $f:Y\rightarrow B$
of weight
$f:Y\rightarrow B$
of weight
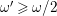 $\unicode[STIX]{x1D714}^{\prime }\geqslant \unicode[STIX]{x1D714}/2$
is not birational and assume that
$\unicode[STIX]{x1D714}^{\prime }\geqslant \unicode[STIX]{x1D714}/2$
is not birational and assume that
![]() $\unicode[STIX]{x1D714}>12$
, then
$\unicode[STIX]{x1D714}>12$
, then
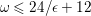 $\unicode[STIX]{x1D714}\leqslant 24/\unicode[STIX]{x1D716}+12$
. In particular, there is an upper bound of volume
$\unicode[STIX]{x1D714}\leqslant 24/\unicode[STIX]{x1D716}+12$
. In particular, there is an upper bound of volume
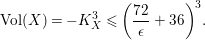 $$\begin{eqnarray}\text{Vol}(X)=-K_{X}^{3}\leqslant \biggl(\frac{72}{\unicode[STIX]{x1D716}}+36\biggr)^{3}.\end{eqnarray}$$
$$\begin{eqnarray}\text{Vol}(X)=-K_{X}^{3}\leqslant \biggl(\frac{72}{\unicode[STIX]{x1D716}}+36\biggr)^{3}.\end{eqnarray}$$
Proof. Let
![]() $d\geqslant 2$
be the degree of
$d\geqslant 2$
be the degree of
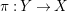 $\unicode[STIX]{x1D70B}:Y\rightarrow X$
. Fix an open subset
$\unicode[STIX]{x1D70B}:Y\rightarrow X$
. Fix an open subset
![]() $U\subseteq X$
such that for a general point
$U\subseteq X$
such that for a general point
![]() $p\in U$
, there are
$p\in U$
, there are
![]() $d$
divisors
$d$
divisors
![]() $\unicode[STIX]{x1D6E5}_{p}^{t_{i}}$
for some
$\unicode[STIX]{x1D6E5}_{p}^{t_{i}}$
for some
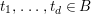 $t_{1},\ldots ,t_{d}\in B$
such that
$t_{1},\ldots ,t_{d}\in B$
such that
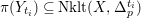 $\unicode[STIX]{x1D70B}(Y_{t_{i}})\subseteq \text{Nklt}(X,\unicode[STIX]{x1D6E5}_{p}^{t_{i}})$
is the unique minimal non-klt center passing through
$\unicode[STIX]{x1D70B}(Y_{t_{i}})\subseteq \text{Nklt}(X,\unicode[STIX]{x1D6E5}_{p}^{t_{i}})$
is the unique minimal non-klt center passing through
![]() $p$
. Consider the collection of
$p$
. Consider the collection of
![]() $\mathbb{Q}$
-divisors
$\mathbb{Q}$
-divisors
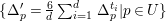 $\{\unicode[STIX]{x1D6E5}_{p}^{\prime }=\frac{6}{d}\sum _{i=1}^{d}\unicode[STIX]{x1D6E5}_{p}^{t_{i}}|p\in U\}$
, then
$\{\unicode[STIX]{x1D6E5}_{p}^{\prime }=\frac{6}{d}\sum _{i=1}^{d}\unicode[STIX]{x1D6E5}_{p}^{t_{i}}|p\in U\}$
, then
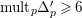 $\text{mult}_{p}\unicode[STIX]{x1D6E5}_{p}^{\prime }\geqslant 6$
,
$\text{mult}_{p}\unicode[STIX]{x1D6E5}_{p}^{\prime }\geqslant 6$
,
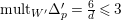 $\text{mult}_{W^{\prime }}\unicode[STIX]{x1D6E5}_{p}^{\prime }=\frac{6}{d}\leqslant 3$
for
$\text{mult}_{W^{\prime }}\unicode[STIX]{x1D6E5}_{p}^{\prime }=\frac{6}{d}\leqslant 3$
for
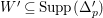 $W^{\prime }\subseteq \text{Supp}(\unicode[STIX]{x1D6E5}_{p}^{\prime })$
any irreducible component, and
$W^{\prime }\subseteq \text{Supp}(\unicode[STIX]{x1D6E5}_{p}^{\prime })$
any irreducible component, and
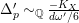 $\unicode[STIX]{x1D6E5}_{p}^{\prime }{\sim}_{\mathbb{Q}}\frac{-K_{X}}{d\unicode[STIX]{x1D714}^{\prime }/6}$
.
$\unicode[STIX]{x1D6E5}_{p}^{\prime }{\sim}_{\mathbb{Q}}\frac{-K_{X}}{d\unicode[STIX]{x1D714}^{\prime }/6}$
.
By the same construction as in 5.1, possibly after shrinking
![]() $U$
to a smaller open affine subset, there exists an integer
$U$
to a smaller open affine subset, there exists an integer
![]() $m>0$
such that
$m>0$
such that
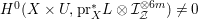 $H^{0}(X\times U,\text{pr}_{X}^{\ast }L\otimes {\mathcal{I}}_{{\mathcal{Z}}}^{\otimes 6m})\neq 0$
where
$H^{0}(X\times U,\text{pr}_{X}^{\ast }L\otimes {\mathcal{I}}_{{\mathcal{Z}}}^{\otimes 6m})\neq 0$
where
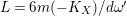 $L=6m(-K_{X})/d\unicode[STIX]{x1D714}^{\prime }$
is Cartier. Let
$L=6m(-K_{X})/d\unicode[STIX]{x1D714}^{\prime }$
is Cartier. Let
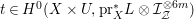 $t\in H^{0}(X\times U,\text{pr}_{X}^{\ast }L\otimes {\mathcal{I}}_{{\mathcal{Z}}}^{\otimes 6m})$
be a general nonzero section and
$t\in H^{0}(X\times U,\text{pr}_{X}^{\ast }L\otimes {\mathcal{I}}_{{\mathcal{Z}}}^{\otimes 6m})$
be a general nonzero section and
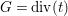 $G=\text{div}(t)$
be the associated divisor on
$G=\text{div}(t)$
be the associated divisor on
![]() $X\times U$
. Note that
$X\times U$
. Note that
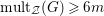 $\text{mult}_{{\mathcal{Z}}}(G)\geqslant 6m$
and
$\text{mult}_{{\mathcal{Z}}}(G)\geqslant 6m$
and
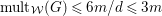 $\text{mult}_{{\mathcal{W}}}(G)\leqslant 6m/d\leqslant 3m$
for
$\text{mult}_{{\mathcal{W}}}(G)\leqslant 6m/d\leqslant 3m$
for
![]() ${\mathcal{W}}$
any irreducible component of
${\mathcal{W}}$
any irreducible component of
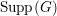 $\text{Supp}(G)$
passing through
$\text{Supp}(G)$
passing through
![]() ${\mathcal{Z}}$
. This is true since for general
${\mathcal{Z}}$
. This is true since for general
![]() $p\in U$
there is a special divisor
$p\in U$
there is a special divisor
![]() $\unicode[STIX]{x1D6E5}_{p}^{\prime }$
with
$\unicode[STIX]{x1D6E5}_{p}^{\prime }$
with
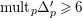 $\text{mult}_{p}\unicode[STIX]{x1D6E5}_{p}^{\prime }\geqslant 6$
and
$\text{mult}_{p}\unicode[STIX]{x1D6E5}_{p}^{\prime }\geqslant 6$
and
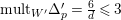 $\text{mult}_{W^{\prime }}\unicode[STIX]{x1D6E5}_{p}^{\prime }=\frac{6}{d}\leqslant 3$
for
$\text{mult}_{W^{\prime }}\unicode[STIX]{x1D6E5}_{p}^{\prime }=\frac{6}{d}\leqslant 3$
for
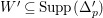 $W^{\prime }\subseteq \text{Supp}(\unicode[STIX]{x1D6E5}_{p}^{\prime })$
any irreducible component, but
$W^{\prime }\subseteq \text{Supp}(\unicode[STIX]{x1D6E5}_{p}^{\prime })$
any irreducible component, but
![]() $t$
is a general section and we can use Lemma 5.1 to compute the multiplicity of the general section
$t$
is a general section and we can use Lemma 5.1 to compute the multiplicity of the general section
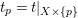 $t_{p}=t|_{X\times \{p\}}$
.
$t_{p}=t|_{X\times \{p\}}$
.
By a differentiation argument and the same construction as in Proposition 5.3, there is a covering family of tigers
![]() $(\unicode[STIX]{x1D6E5}_{t},V_{t})$
of dimension one and weight
$(\unicode[STIX]{x1D6E5}_{t},V_{t})$
of dimension one and weight
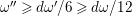 $\unicode[STIX]{x1D714}^{\prime \prime }\geqslant d\unicode[STIX]{x1D714}^{\prime }/6\geqslant d\unicode[STIX]{x1D714}/12$
which satisfies the property that the base locus
$\unicode[STIX]{x1D714}^{\prime \prime }\geqslant d\unicode[STIX]{x1D714}^{\prime }/6\geqslant d\unicode[STIX]{x1D714}/12$
which satisfies the property that the base locus
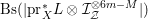 $\text{Bs}(|\text{pr}_{X}^{\ast }L\otimes {\mathcal{I}}_{{\mathcal{Z}}}^{\otimes 6m-M}|)$
contains no codimension one components in a neighborhood of
$\text{Bs}(|\text{pr}_{X}^{\ast }L\otimes {\mathcal{I}}_{{\mathcal{Z}}}^{\otimes 6m-M}|)$
contains no codimension one components in a neighborhood of
![]() ${\mathcal{Z}}$
, where
${\mathcal{Z}}$
, where
![]() $M$
is the maximum of
$M$
is the maximum of
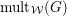 $\text{mult}_{{\mathcal{W}}}(G)$
amongst all the irreducible components
$\text{mult}_{{\mathcal{W}}}(G)$
amongst all the irreducible components
![]() ${\mathcal{W}}$
of
${\mathcal{W}}$
of
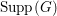 $\text{Supp}(G)$
passing through
$\text{Supp}(G)$
passing through
![]() ${\mathcal{Z}}$
. Hence by Corollary 3.9 again, we get
${\mathcal{Z}}$
. Hence by Corollary 3.9 again, we get
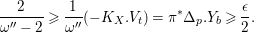 $$\begin{eqnarray}\frac{2}{\unicode[STIX]{x1D714}^{\prime \prime }-2}\geqslant \frac{1}{\unicode[STIX]{x1D714}^{\prime \prime }}(-K_{X}.V_{t})=\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D6E5}_{p}.Y_{b}\geqslant \frac{\unicode[STIX]{x1D716}}{2}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{2}{\unicode[STIX]{x1D714}^{\prime \prime }-2}\geqslant \frac{1}{\unicode[STIX]{x1D714}^{\prime \prime }}(-K_{X}.V_{t})=\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D6E5}_{p}.Y_{b}\geqslant \frac{\unicode[STIX]{x1D716}}{2}.\end{eqnarray}$$
In particular,
 $$\begin{eqnarray}\frac{4}{\unicode[STIX]{x1D716}}+2\geqslant \unicode[STIX]{x1D714}^{\prime \prime }\geqslant \frac{d\unicode[STIX]{x1D714}}{12}\geqslant \frac{\unicode[STIX]{x1D714}}{6}\end{eqnarray}$$
$$\begin{eqnarray}\frac{4}{\unicode[STIX]{x1D716}}+2\geqslant \unicode[STIX]{x1D714}^{\prime \prime }\geqslant \frac{d\unicode[STIX]{x1D714}}{12}\geqslant \frac{\unicode[STIX]{x1D714}}{6}\end{eqnarray}$$
and
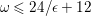 $\unicode[STIX]{x1D714}\leqslant 24/\unicode[STIX]{x1D716}+12$
.◻
$\unicode[STIX]{x1D714}\leqslant 24/\unicode[STIX]{x1D716}+12$
.◻
Assumption 5.7. From now on, we assume that
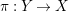 $\unicode[STIX]{x1D70B}:Y\rightarrow X$
with
$\unicode[STIX]{x1D70B}:Y\rightarrow X$
with
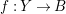 $f:Y\rightarrow B$
is a birational covering family of tigers of dimension two and weight
$f:Y\rightarrow B$
is a birational covering family of tigers of dimension two and weight
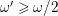 $\unicode[STIX]{x1D714}^{\prime }\geqslant \unicode[STIX]{x1D714}/2$
. Write
$\unicode[STIX]{x1D714}^{\prime }\geqslant \unicode[STIX]{x1D714}/2$
. Write
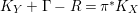 $K_{Y}+\unicode[STIX]{x1D6E4}-R=\unicode[STIX]{x1D70B}^{\ast }K_{X}$
where
$K_{Y}+\unicode[STIX]{x1D6E4}-R=\unicode[STIX]{x1D70B}^{\ast }K_{X}$
where
![]() $\unicode[STIX]{x1D6E4}$
and
$\unicode[STIX]{x1D6E4}$
and
![]() $R$
are effective divisors on
$R$
are effective divisors on
![]() $Y$
with no common components.
$Y$
with no common components.
Lemma 5.8. There is a
![]() $\unicode[STIX]{x1D70B}$
-exceptional divisor
$\unicode[STIX]{x1D70B}$
-exceptional divisor
![]() $E$
on
$E$
on
![]() $Y$
dominating
$Y$
dominating
![]() $B$
. In particular,
$B$
. In particular,
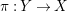 $\unicode[STIX]{x1D70B}:Y\rightarrow X$
is not small.
$\unicode[STIX]{x1D70B}:Y\rightarrow X$
is not small.
Proof. Suppose that there is no
![]() $\unicode[STIX]{x1D70B}$
-exceptional divisors dominating
$\unicode[STIX]{x1D70B}$
-exceptional divisors dominating
![]() $B$
. Let
$B$
. Let
![]() $A_{B}$
be a sufficiently ample divisor on
$A_{B}$
be a sufficiently ample divisor on
![]() $B$
and
$B$
and
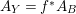 $A_{Y}=f^{\ast }A_{B}$
the pullback. Since
$A_{Y}=f^{\ast }A_{B}$
the pullback. Since
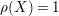 $\unicode[STIX]{x1D70C}(X)=1$
, the divisor
$\unicode[STIX]{x1D70C}(X)=1$
, the divisor
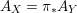 $A_{X}=\unicode[STIX]{x1D70B}_{\ast }A_{Y}$
on
$A_{X}=\unicode[STIX]{x1D70B}_{\ast }A_{Y}$
on
![]() $X$
is ample and
$X$
is ample and
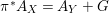 $\unicode[STIX]{x1D70B}^{\ast }A_{X}=A_{Y}+G$
for some effective
$\unicode[STIX]{x1D70B}^{\ast }A_{X}=A_{Y}+G$
for some effective
![]() $\unicode[STIX]{x1D70B}$
-exceptional divisor
$\unicode[STIX]{x1D70B}$
-exceptional divisor
![]() $G$
. By assumption
$G$
. By assumption
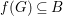 $f(G)\subseteq B$
has codimension one and hence
$f(G)\subseteq B$
has codimension one and hence
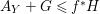 $A_{Y}+G\leqslant f^{\ast }H$
for some divisor
$A_{Y}+G\leqslant f^{\ast }H$
for some divisor
![]() $H$
on
$H$
on
![]() $B$
. This is a contradiction since then
$B$
. This is a contradiction since then
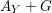 $A_{Y}+G$
is not big but
$A_{Y}+G$
is not big but
![]() $\unicode[STIX]{x1D70B}^{\ast }A_{X}$
is.◻
$\unicode[STIX]{x1D70B}^{\ast }A_{X}$
is.◻
The following lemma is crucial for computing the restricted volume. The key point is that it allows us to control the negative part of the subadjunction
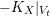 $-K_{X}|_{V_{t}}$
. Note that the proof fails in higher dimensions (cf., [McK02, Lemma 6.2]).
$-K_{X}|_{V_{t}}$
. Note that the proof fails in higher dimensions (cf., [McK02, Lemma 6.2]).
Lemma 5.9. Let
![]() $E$
be a
$E$
be a
![]() $\unicode[STIX]{x1D70B}$
-exceptional divisor dominating
$\unicode[STIX]{x1D70B}$
-exceptional divisor dominating
![]() $B$
, then for general points
$B$
, then for general points
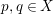 $p,q\in X$
we have that
$p,q\in X$
we have that
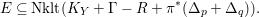 $$\begin{eqnarray}E\subseteq \text{Nklt}(K_{Y}+\unicode[STIX]{x1D6E4}-R+\unicode[STIX]{x1D70B}^{\ast }(\unicode[STIX]{x1D6E5}_{p}+\unicode[STIX]{x1D6E5}_{q})).\end{eqnarray}$$
$$\begin{eqnarray}E\subseteq \text{Nklt}(K_{Y}+\unicode[STIX]{x1D6E4}-R+\unicode[STIX]{x1D70B}^{\ast }(\unicode[STIX]{x1D6E5}_{p}+\unicode[STIX]{x1D6E5}_{q})).\end{eqnarray}$$
In particular, if we denote
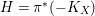 $H=\unicode[STIX]{x1D70B}^{\ast }(-K_{X})$
, then for any
$H=\unicode[STIX]{x1D70B}^{\ast }(-K_{X})$
, then for any
![]() $\unicode[STIX]{x1D70B}$
-exceptional divisor
$\unicode[STIX]{x1D70B}$
-exceptional divisor
![]() $E$
dominating
$E$
dominating
![]() $B$
we have
$B$
we have
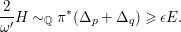 $$\begin{eqnarray}\frac{2}{\unicode[STIX]{x1D714}^{\prime }}H{\sim}_{\mathbb{Q}}\unicode[STIX]{x1D70B}^{\ast }(\unicode[STIX]{x1D6E5}_{p}+\unicode[STIX]{x1D6E5}_{q})\geqslant \unicode[STIX]{x1D716}E.\end{eqnarray}$$
$$\begin{eqnarray}\frac{2}{\unicode[STIX]{x1D714}^{\prime }}H{\sim}_{\mathbb{Q}}\unicode[STIX]{x1D70B}^{\ast }(\unicode[STIX]{x1D6E5}_{p}+\unicode[STIX]{x1D6E5}_{q})\geqslant \unicode[STIX]{x1D716}E.\end{eqnarray}$$
Proof. Since the construction of covering families of tigers is done by the Hilbert scheme,
![]() $\unicode[STIX]{x1D70B}$
is finite on the general fibers
$\unicode[STIX]{x1D70B}$
is finite on the general fibers
![]() $V_{t}$
of
$V_{t}$
of
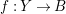 $f:Y\rightarrow B$
. Recall that
$f:Y\rightarrow B$
. Recall that
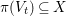 $\unicode[STIX]{x1D70B}(V_{t})\subseteq X$
is a pure non-klt center of
$\unicode[STIX]{x1D70B}(V_{t})\subseteq X$
is a pure non-klt center of
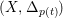 $(X,\unicode[STIX]{x1D6E5}_{p(t)})$
for some
$(X,\unicode[STIX]{x1D6E5}_{p(t)})$
for some
![]() $\unicode[STIX]{x1D6E5}_{p(t)}$
passing through a general point
$\unicode[STIX]{x1D6E5}_{p(t)}$
passing through a general point
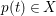 $p(t)\in X$
. We denote
$p(t)\in X$
. We denote
![]() $\unicode[STIX]{x1D6E5}_{p(t)}$
by
$\unicode[STIX]{x1D6E5}_{p(t)}$
by
![]() $\unicode[STIX]{x1D6E5}_{t}$
for simplicity.
$\unicode[STIX]{x1D6E5}_{t}$
for simplicity.
Let
![]() $E$
be a
$E$
be a
![]() $\unicode[STIX]{x1D70B}$
-exceptional divisor dominating
$\unicode[STIX]{x1D70B}$
-exceptional divisor dominating
![]() $B$
. Take
$B$
. Take
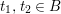 $t_{1},t_{2}\in B$
general, and consider
$t_{1},t_{2}\in B$
general, and consider
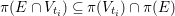 $\unicode[STIX]{x1D70B}(E\cap V_{t_{i}})\subseteq \unicode[STIX]{x1D70B}(V_{t_{i}})\cap \unicode[STIX]{x1D70B}(E)$
. Since
$\unicode[STIX]{x1D70B}(E\cap V_{t_{i}})\subseteq \unicode[STIX]{x1D70B}(V_{t_{i}})\cap \unicode[STIX]{x1D70B}(E)$
. Since
![]() $\unicode[STIX]{x1D70B}$
is finite on the general fibers of
$\unicode[STIX]{x1D70B}$
is finite on the general fibers of
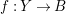 $f:Y\rightarrow B$
,
$f:Y\rightarrow B$
,
![]() $\unicode[STIX]{x1D70B}(E)$
is an irreducible curve contained in
$\unicode[STIX]{x1D70B}(E)$
is an irreducible curve contained in
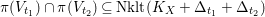 $\unicode[STIX]{x1D70B}(V_{t_{1}})\cap \unicode[STIX]{x1D70B}(V_{t_{2}})\subseteq \text{Nklt}(K_{X}+\unicode[STIX]{x1D6E5}_{t_{1}}+\unicode[STIX]{x1D6E5}_{t_{2}})$
. Pick a general point
$\unicode[STIX]{x1D70B}(V_{t_{1}})\cap \unicode[STIX]{x1D70B}(V_{t_{2}})\subseteq \text{Nklt}(K_{X}+\unicode[STIX]{x1D6E5}_{t_{1}}+\unicode[STIX]{x1D6E5}_{t_{2}})$
. Pick a general point
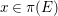 $x\in \unicode[STIX]{x1D70B}(E)$
and consider its preimage on
$x\in \unicode[STIX]{x1D70B}(E)$
and consider its preimage on
![]() $V_{t_{i}}$
. Since
$V_{t_{i}}$
. Since
![]() $\unicode[STIX]{x1D70B}$
is finite on the general fiber
$\unicode[STIX]{x1D70B}$
is finite on the general fiber
![]() $V_{t}$
,
$V_{t}$
,
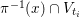 $\unicode[STIX]{x1D70B}^{-1}(x)\cap V_{t_{i}}$
can only be finitely many points. Choose
$\unicode[STIX]{x1D70B}^{-1}(x)\cap V_{t_{i}}$
can only be finitely many points. Choose
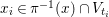 $x_{i}\in \unicode[STIX]{x1D70B}^{-1}(x)\cap V_{t_{i}}$
over
$x_{i}\in \unicode[STIX]{x1D70B}^{-1}(x)\cap V_{t_{i}}$
over
![]() $x$
for
$x$
for
![]() $i=1,2$
. By the Connectedness Lemma 1.3 applied to the pair
$i=1,2$
. By the Connectedness Lemma 1.3 applied to the pair
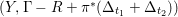 $(Y,\unicode[STIX]{x1D6E4}-R+\unicode[STIX]{x1D70B}^{\ast }(\unicode[STIX]{x1D6E5}_{t_{1}}+\unicode[STIX]{x1D6E5}_{t_{2}}))$
over
$(Y,\unicode[STIX]{x1D6E4}-R+\unicode[STIX]{x1D70B}^{\ast }(\unicode[STIX]{x1D6E5}_{t_{1}}+\unicode[STIX]{x1D6E5}_{t_{2}}))$
over
![]() $X$
, there is a (possibly reducible) curve contained in
$X$
, there is a (possibly reducible) curve contained in
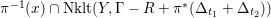 $\unicode[STIX]{x1D70B}^{-1}(x)\cap \text{Nklt}(Y,\unicode[STIX]{x1D6E4}-R+\unicode[STIX]{x1D70B}^{\ast }(\unicode[STIX]{x1D6E5}_{t_{1}}+\unicode[STIX]{x1D6E5}_{t_{2}}))$
connecting
$\unicode[STIX]{x1D70B}^{-1}(x)\cap \text{Nklt}(Y,\unicode[STIX]{x1D6E4}-R+\unicode[STIX]{x1D70B}^{\ast }(\unicode[STIX]{x1D6E5}_{t_{1}}+\unicode[STIX]{x1D6E5}_{t_{2}}))$
connecting
![]() $x_{1}$
and
$x_{1}$
and
![]() $x_{2}$
. The component of this curve containing
$x_{2}$
. The component of this curve containing
![]() $x_{1}$
cannot lie on
$x_{1}$
cannot lie on
![]() $V_{t_{1}}$
as the map
$V_{t_{1}}$
as the map
![]() $\unicode[STIX]{x1D70B}$
is finite on
$\unicode[STIX]{x1D70B}$
is finite on
![]() $V_{t_{1}}$
. As
$V_{t_{1}}$
. As
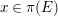 $x\in \unicode[STIX]{x1D70B}(E)$
is general, this curve deforms into a dimension two set by moving
$x\in \unicode[STIX]{x1D70B}(E)$
is general, this curve deforms into a dimension two set by moving
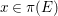 $x\in \unicode[STIX]{x1D70B}(E)$
. Denote
$x\in \unicode[STIX]{x1D70B}(E)$
. Denote
![]() $\tilde{E}$
the closure of this two-dimensional set, which is another
$\tilde{E}$
the closure of this two-dimensional set, which is another
![]() $\unicode[STIX]{x1D70B}$
-exceptional divisor mapping onto
$\unicode[STIX]{x1D70B}$
-exceptional divisor mapping onto
![]() $\unicode[STIX]{x1D70B}(E)$
and intersects along
$\unicode[STIX]{x1D70B}(E)$
and intersects along
![]() $E\cap V_{t_{1}}$
. Since there are only finitely many exceptional divisors over
$E\cap V_{t_{1}}$
. Since there are only finitely many exceptional divisors over
![]() $\unicode[STIX]{x1D70B}(E)$
and
$\unicode[STIX]{x1D70B}(E)$
and
![]() $t_{1}$
is general, we can assume
$t_{1}$
is general, we can assume
![]() $\tilde{E}=E$
as
$\tilde{E}=E$
as
![]() $E$
is irreducible, and hence
$E$
is irreducible, and hence
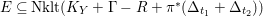 $E\subseteq \text{Nklt}(K_{Y}+\unicode[STIX]{x1D6E4}-R+\unicode[STIX]{x1D70B}^{\ast }(\unicode[STIX]{x1D6E5}_{t_{1}}+\unicode[STIX]{x1D6E5}_{t_{2}}))$
. In particular,
$E\subseteq \text{Nklt}(K_{Y}+\unicode[STIX]{x1D6E4}-R+\unicode[STIX]{x1D70B}^{\ast }(\unicode[STIX]{x1D6E5}_{t_{1}}+\unicode[STIX]{x1D6E5}_{t_{2}}))$
. In particular,
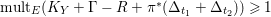 $\text{mult}_{E}(K_{Y}+\unicode[STIX]{x1D6E4}-R+\unicode[STIX]{x1D70B}^{\ast }(\unicode[STIX]{x1D6E5}_{t_{1}}+\unicode[STIX]{x1D6E5}_{t_{2}}))\geqslant 1$
and we get
$\text{mult}_{E}(K_{Y}+\unicode[STIX]{x1D6E4}-R+\unicode[STIX]{x1D70B}^{\ast }(\unicode[STIX]{x1D6E5}_{t_{1}}+\unicode[STIX]{x1D6E5}_{t_{2}}))\geqslant 1$
and we get
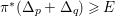 $\unicode[STIX]{x1D70B}^{\ast }(\unicode[STIX]{x1D6E5}_{p}+\unicode[STIX]{x1D6E5}_{q})\geqslant E$
if
$\unicode[STIX]{x1D70B}^{\ast }(\unicode[STIX]{x1D6E5}_{p}+\unicode[STIX]{x1D6E5}_{q})\geqslant E$
if
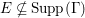 $E\nsubseteq \text{Supp}(\unicode[STIX]{x1D6E4})$
and
$E\nsubseteq \text{Supp}(\unicode[STIX]{x1D6E4})$
and
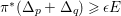 $\unicode[STIX]{x1D70B}^{\ast }(\unicode[STIX]{x1D6E5}_{p}+\unicode[STIX]{x1D6E5}_{q})\geqslant \unicode[STIX]{x1D716}E$
if
$\unicode[STIX]{x1D70B}^{\ast }(\unicode[STIX]{x1D6E5}_{p}+\unicode[STIX]{x1D6E5}_{q})\geqslant \unicode[STIX]{x1D716}E$
if
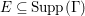 $E\subseteq \text{Supp}(\unicode[STIX]{x1D6E4})$
from the fact that
$E\subseteq \text{Supp}(\unicode[STIX]{x1D6E4})$
from the fact that
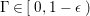 $\unicode[STIX]{x1D6E4}\in [0,1-\unicode[STIX]{x1D716})$
as
$\unicode[STIX]{x1D6E4}\in [0,1-\unicode[STIX]{x1D716})$
as
![]() $X$
is
$X$
is
![]() $\unicode[STIX]{x1D716}$
-klt.◻
$\unicode[STIX]{x1D716}$
-klt.◻
To study the geometry of the covering family
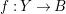 $f:Y\rightarrow B$
, we would like to run a relative minimal model program of
$f:Y\rightarrow B$
, we would like to run a relative minimal model program of
![]() $(Y,\unicode[STIX]{x1D6E4})$
over
$(Y,\unicode[STIX]{x1D6E4})$
over
![]() $B$
. However,
$B$
. However,
![]() $Y$
is normal but possibly not
$Y$
is normal but possibly not
![]() $\mathbb{Q}$
-factorial. To get a
$\mathbb{Q}$
-factorial. To get a
![]() $\mathbb{Q}$
-factorial model of
$\mathbb{Q}$
-factorial model of
![]() $(Y,\unicode[STIX]{x1D6E4})$
, we adopt Hacon’s dlt models (cf., [Reference Kollár and KovácsKK10, Theorem 3.1]). In fact, since the volume bound will be obtained by doing a computation on a general fiber
$(Y,\unicode[STIX]{x1D6E4})$
, we adopt Hacon’s dlt models (cf., [Reference Kollár and KovácsKK10, Theorem 3.1]). In fact, since the volume bound will be obtained by doing a computation on a general fiber
![]() $Y_{b}$
, it suffices to modify
$Y_{b}$
, it suffices to modify
![]() $Y$
over an open subset
$Y$
over an open subset
![]() $U\subseteq B$
.
$U\subseteq B$
.
Lemma 5.10. After restricting to an open subset
![]() $U\subseteq B$
and replacing
$U\subseteq B$
and replacing
![]() $Y$
by a suitable birational model, we can assume that
$Y$
by a suitable birational model, we can assume that
![]() $Y$
is
$Y$
is
![]() $\mathbb{Q}$
-factorial and
$\mathbb{Q}$
-factorial and
![]() $(Y,\unicode[STIX]{x1D6E4})$
is
$(Y,\unicode[STIX]{x1D6E4})$
is
![]() $\unicode[STIX]{x1D716}/2$
-klt. Moreover, we can assume that for
$\unicode[STIX]{x1D716}/2$
-klt. Moreover, we can assume that for
![]() $E$
any
$E$
any
![]() $\unicode[STIX]{x1D70B}$
-exceptional divisor dominating
$\unicode[STIX]{x1D70B}$
-exceptional divisor dominating
![]() $U$
and
$U$
and
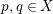 $p,q\in X$
general, we have that
$p,q\in X$
general, we have that
 $$\begin{eqnarray}\frac{2}{\unicode[STIX]{x1D714}^{\prime }}H{\sim}_{\mathbb{Q}}\unicode[STIX]{x1D70B}^{\ast }(\unicode[STIX]{x1D6E5}_{p}+\unicode[STIX]{x1D6E5}_{q})\geqslant \frac{\unicode[STIX]{x1D716}}{2}E.\end{eqnarray}$$
$$\begin{eqnarray}\frac{2}{\unicode[STIX]{x1D714}^{\prime }}H{\sim}_{\mathbb{Q}}\unicode[STIX]{x1D70B}^{\ast }(\unicode[STIX]{x1D6E5}_{p}+\unicode[STIX]{x1D6E5}_{q})\geqslant \frac{\unicode[STIX]{x1D716}}{2}E.\end{eqnarray}$$
Proof. Fix
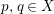 $p,q\in X$
general and consider the pair
$p,q\in X$
general and consider the pair
 $$\begin{eqnarray}K_{Y}+\unicode[STIX]{x1D6E4}-R_{\text{d}}+\unicode[STIX]{x1D70B}^{\ast }(\unicode[STIX]{x1D6E5}_{p}+\unicode[STIX]{x1D6E5}_{q})-R_{\text{e}}{\sim}_{\mathbb{Q}}\unicode[STIX]{x1D70B}^{\ast }(K_{X}+\unicode[STIX]{x1D6E5}_{p}+\unicode[STIX]{x1D6E5}_{q})\end{eqnarray}$$
$$\begin{eqnarray}K_{Y}+\unicode[STIX]{x1D6E4}-R_{\text{d}}+\unicode[STIX]{x1D70B}^{\ast }(\unicode[STIX]{x1D6E5}_{p}+\unicode[STIX]{x1D6E5}_{q})-R_{\text{e}}{\sim}_{\mathbb{Q}}\unicode[STIX]{x1D70B}^{\ast }(K_{X}+\unicode[STIX]{x1D6E5}_{p}+\unicode[STIX]{x1D6E5}_{q})\end{eqnarray}$$
where
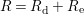 $R=R_{\text{d}}+R_{\text{e}}$
with
$R=R_{\text{d}}+R_{\text{e}}$
with
![]() $(-)_{\text{d}}$
the sum of components dominating
$(-)_{\text{d}}$
the sum of components dominating
![]() $B$
and
$B$
and
![]() $(-)_{\text{e}}$
the sum of components mapping to points in
$(-)_{\text{e}}$
the sum of components mapping to points in
![]() $B$
. Restricting
$B$
. Restricting
![]() $Y$
to
$Y$
to
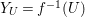 $Y_{U}=f^{-1}(U)$
for a suitable nonempty open set
$Y_{U}=f^{-1}(U)$
for a suitable nonempty open set
![]() $U\subseteq B$
, we may assume that
$U\subseteq B$
, we may assume that
![]() $R_{\text{e}}=0$
and the pair (
♯
) becomes the effective pair
$R_{\text{e}}=0$
and the pair (
♯
) becomes the effective pair
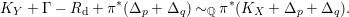 $$\begin{eqnarray}K_{Y}+\unicode[STIX]{x1D6E4}-R_{\text{d}}+\unicode[STIX]{x1D70B}^{\ast }(\unicode[STIX]{x1D6E5}_{p}+\unicode[STIX]{x1D6E5}_{q}){\sim}_{\mathbb{Q}}\unicode[STIX]{x1D70B}^{\ast }(K_{X}+\unicode[STIX]{x1D6E5}_{p}+\unicode[STIX]{x1D6E5}_{q}).\end{eqnarray}$$
$$\begin{eqnarray}K_{Y}+\unicode[STIX]{x1D6E4}-R_{\text{d}}+\unicode[STIX]{x1D70B}^{\ast }(\unicode[STIX]{x1D6E5}_{p}+\unicode[STIX]{x1D6E5}_{q}){\sim}_{\mathbb{Q}}\unicode[STIX]{x1D70B}^{\ast }(K_{X}+\unicode[STIX]{x1D6E5}_{p}+\unicode[STIX]{x1D6E5}_{q}).\end{eqnarray}$$
We abuse the notation:
![]() $Y$
is understood to be
$Y$
is understood to be
![]() $Y_{U}$
if not specified.
$Y_{U}$
if not specified.
Denote
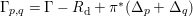 $\unicode[STIX]{x1D6E4}_{p,q}=\unicode[STIX]{x1D6E4}-R_{\text{d}}+\unicode[STIX]{x1D70B}^{\ast }(\unicode[STIX]{x1D6E5}_{p}+\unicode[STIX]{x1D6E5}_{q})$
and let
$\unicode[STIX]{x1D6E4}_{p,q}=\unicode[STIX]{x1D6E4}-R_{\text{d}}+\unicode[STIX]{x1D70B}^{\ast }(\unicode[STIX]{x1D6E5}_{p}+\unicode[STIX]{x1D6E5}_{q})$
and let
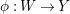 $\unicode[STIX]{x1D719}:W\rightarrow Y$
be a log resolution of
$\unicode[STIX]{x1D719}:W\rightarrow Y$
be a log resolution of
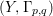 $(Y,\unicode[STIX]{x1D6E4}_{p,q})$
. Write
$(Y,\unicode[STIX]{x1D6E4}_{p,q})$
. Write
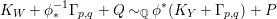 $$\begin{eqnarray}K_{W}+\unicode[STIX]{x1D719}_{\ast }^{-1}\unicode[STIX]{x1D6E4}_{p,q}+Q{\sim}_{\mathbb{Q}}\unicode[STIX]{x1D719}^{\ast }(K_{Y}+\unicode[STIX]{x1D6E4}_{p,q})+P\end{eqnarray}$$
$$\begin{eqnarray}K_{W}+\unicode[STIX]{x1D719}_{\ast }^{-1}\unicode[STIX]{x1D6E4}_{p,q}+Q{\sim}_{\mathbb{Q}}\unicode[STIX]{x1D719}^{\ast }(K_{Y}+\unicode[STIX]{x1D6E4}_{p,q})+P\end{eqnarray}$$
where
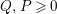 $Q,P\geqslant 0$
are
$Q,P\geqslant 0$
are
![]() $\unicode[STIX]{x1D719}$
-exceptional divisors with
$\unicode[STIX]{x1D719}$
-exceptional divisors with
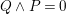 $Q\wedge P=0$
. We aim to modify
$Q\wedge P=0$
. We aim to modify
![]() $W$
by running a relative minimal model program over
$W$
by running a relative minimal model program over
![]() $Y$
with scaling of an ample divisor so that it contracts
$Y$
with scaling of an ample divisor so that it contracts
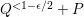 $Q^{{<}1-\unicode[STIX]{x1D716}/2}+P$
.
$Q^{{<}1-\unicode[STIX]{x1D716}/2}+P$
.
Consider
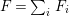 $F=\sum _{i}F_{i}$
where the sum runs over all the
$F=\sum _{i}F_{i}$
where the sum runs over all the
![]() $\unicode[STIX]{x1D719}$
-exceptional divisors with log discrepancy in
$\unicode[STIX]{x1D719}$
-exceptional divisors with log discrepancy in
![]() $(\unicode[STIX]{x1D716}/2,1]$
with respect to
$(\unicode[STIX]{x1D716}/2,1]$
with respect to
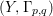 $(Y,\unicode[STIX]{x1D6E4}_{p,q})$
, then
$(Y,\unicode[STIX]{x1D6E4}_{p,q})$
, then
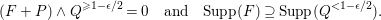 $$\begin{eqnarray}(F+P)\wedge Q^{{\geqslant}1-\unicode[STIX]{x1D716}/2}=0\quad \text{and}\quad \text{Supp}(F)\supseteq \text{Supp}(Q^{{<}1-\unicode[STIX]{x1D716}/2}).\end{eqnarray}$$
$$\begin{eqnarray}(F+P)\wedge Q^{{\geqslant}1-\unicode[STIX]{x1D716}/2}=0\quad \text{and}\quad \text{Supp}(F)\supseteq \text{Supp}(Q^{{<}1-\unicode[STIX]{x1D716}/2}).\end{eqnarray}$$
Since
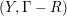 $(Y,\unicode[STIX]{x1D6E4}-R)$
is
$(Y,\unicode[STIX]{x1D6E4}-R)$
is
![]() $\unicode[STIX]{x1D716}$
-klt, the divisor
$\unicode[STIX]{x1D716}$
-klt, the divisor
![]() $\unicode[STIX]{x1D6E4}$
on
$\unicode[STIX]{x1D6E4}$
on
![]() $Y$
as well as
$Y$
as well as
![]() $\unicode[STIX]{x1D719}_{\ast }^{-1}\unicode[STIX]{x1D6E4}$
on
$\unicode[STIX]{x1D719}_{\ast }^{-1}\unicode[STIX]{x1D6E4}$
on
![]() $W$
has coefficients in
$W$
has coefficients in
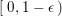 $[0,1-\unicode[STIX]{x1D716})$
. For rational numbers
$[0,1-\unicode[STIX]{x1D716})$
. For rational numbers
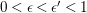 $0<\unicode[STIX]{x1D716}<\unicode[STIX]{x1D716}^{\prime }<1$
and
$0<\unicode[STIX]{x1D716}<\unicode[STIX]{x1D716}^{\prime }<1$
and
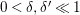 $0<\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FF}^{\prime }\ll 1$
, we have the following
$0<\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FF}^{\prime }\ll 1$
, we have the following
![]() $\unicode[STIX]{x1D716}/2$
-klt pair
$\unicode[STIX]{x1D716}/2$
-klt pair
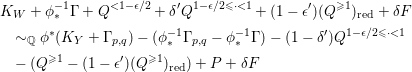 $$\begin{eqnarray}\displaystyle & & \displaystyle K_{W}+\unicode[STIX]{x1D719}_{\ast }^{-1}\unicode[STIX]{x1D6E4}+Q^{{<}1-\unicode[STIX]{x1D716}/2}+\unicode[STIX]{x1D6FF}^{\prime }Q^{1-\unicode[STIX]{x1D716}/2\leqslant \cdot <1}+(1-\unicode[STIX]{x1D716}^{\prime })(Q^{{\geqslant}1})_{\text{red}}+\unicode[STIX]{x1D6FF}F\nonumber\\ \displaystyle & & \displaystyle \quad {\sim}_{\mathbb{Q}}\unicode[STIX]{x1D719}^{\ast }(K_{Y}+\unicode[STIX]{x1D6E4}_{p,q})-(\unicode[STIX]{x1D719}_{\ast }^{-1}\unicode[STIX]{x1D6E4}_{p,q}-\unicode[STIX]{x1D719}_{\ast }^{-1}\unicode[STIX]{x1D6E4})-(1-\unicode[STIX]{x1D6FF}^{\prime })Q^{1-\unicode[STIX]{x1D716}/2\leqslant \cdot <1}\nonumber\\ \displaystyle & & \displaystyle \quad -\,(Q^{{\geqslant}1}-(1-\unicode[STIX]{x1D716}^{\prime })(Q^{{\geqslant}1})_{\text{red}})+P+\unicode[STIX]{x1D6FF}F\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle K_{W}+\unicode[STIX]{x1D719}_{\ast }^{-1}\unicode[STIX]{x1D6E4}+Q^{{<}1-\unicode[STIX]{x1D716}/2}+\unicode[STIX]{x1D6FF}^{\prime }Q^{1-\unicode[STIX]{x1D716}/2\leqslant \cdot <1}+(1-\unicode[STIX]{x1D716}^{\prime })(Q^{{\geqslant}1})_{\text{red}}+\unicode[STIX]{x1D6FF}F\nonumber\\ \displaystyle & & \displaystyle \quad {\sim}_{\mathbb{Q}}\unicode[STIX]{x1D719}^{\ast }(K_{Y}+\unicode[STIX]{x1D6E4}_{p,q})-(\unicode[STIX]{x1D719}_{\ast }^{-1}\unicode[STIX]{x1D6E4}_{p,q}-\unicode[STIX]{x1D719}_{\ast }^{-1}\unicode[STIX]{x1D6E4})-(1-\unicode[STIX]{x1D6FF}^{\prime })Q^{1-\unicode[STIX]{x1D716}/2\leqslant \cdot <1}\nonumber\\ \displaystyle & & \displaystyle \quad -\,(Q^{{\geqslant}1}-(1-\unicode[STIX]{x1D716}^{\prime })(Q^{{\geqslant}1})_{\text{red}})+P+\unicode[STIX]{x1D6FF}F\nonumber\end{eqnarray}$$
where
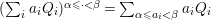 $(\sum _{i}a_{i}Q_{i})^{\unicode[STIX]{x1D6FC}\leqslant \cdot <\unicode[STIX]{x1D6FD}}=\sum _{\unicode[STIX]{x1D6FC}\leqslant a_{i}<\unicode[STIX]{x1D6FD}}a_{i}Q_{i}$
and
$(\sum _{i}a_{i}Q_{i})^{\unicode[STIX]{x1D6FC}\leqslant \cdot <\unicode[STIX]{x1D6FD}}=\sum _{\unicode[STIX]{x1D6FC}\leqslant a_{i}<\unicode[STIX]{x1D6FD}}a_{i}Q_{i}$
and
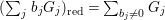 $(\sum _{j}b_{j}G_{j})_{\text{red}}=\sum _{b_{j}\neq 0}G_{j}$
. We denote this pair by
$(\sum _{j}b_{j}G_{j})_{\text{red}}=\sum _{b_{j}\neq 0}G_{j}$
. We denote this pair by
![]() $(W,\unicode[STIX]{x1D6EF})$
where
$(W,\unicode[STIX]{x1D6EF})$
where
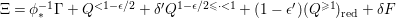 $\unicode[STIX]{x1D6EF}=\unicode[STIX]{x1D719}_{\ast }^{-1}\unicode[STIX]{x1D6E4}+Q^{{<}1-\unicode[STIX]{x1D716}/2}+\unicode[STIX]{x1D6FF}^{\prime }Q^{1-\unicode[STIX]{x1D716}/2\leqslant \cdot <1}+(1-\unicode[STIX]{x1D716}^{\prime })(Q^{{\geqslant}1})_{\text{red}}+\unicode[STIX]{x1D6FF}F$
.
$\unicode[STIX]{x1D6EF}=\unicode[STIX]{x1D719}_{\ast }^{-1}\unicode[STIX]{x1D6E4}+Q^{{<}1-\unicode[STIX]{x1D716}/2}+\unicode[STIX]{x1D6FF}^{\prime }Q^{1-\unicode[STIX]{x1D716}/2\leqslant \cdot <1}+(1-\unicode[STIX]{x1D716}^{\prime })(Q^{{\geqslant}1})_{\text{red}}+\unicode[STIX]{x1D6FF}F$
.
By [BCHM10], a relative minimal model program with scaling of an ample divisor of the pair
![]() $(W,\unicode[STIX]{x1D6EF})$
over
$(W,\unicode[STIX]{x1D6EF})$
over
![]() $Y$
terminates with a birational model
$Y$
terminates with a birational model
 $\unicode[STIX]{x1D713}:W{\dashrightarrow}W^{\prime }$
over
$\unicode[STIX]{x1D713}:W{\dashrightarrow}W^{\prime }$
over
![]() $Y$
with
$Y$
with
 $\unicode[STIX]{x1D719}^{\prime }:W^{\prime }\rightarrow Y$
the induced map. We obtain the following diagram:
$\unicode[STIX]{x1D719}^{\prime }:W^{\prime }\rightarrow Y$
the induced map. We obtain the following diagram:
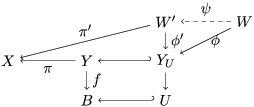
where
 $\unicode[STIX]{x1D70B}^{\prime }:W^{\prime }\rightarrow X$
is the induced map.
$\unicode[STIX]{x1D70B}^{\prime }:W^{\prime }\rightarrow X$
is the induced map.
Write
 $K_{W^{\prime }}+\unicode[STIX]{x1D6E4}_{W^{\prime }}-R_{W^{\prime }}{\sim}_{\mathbb{Q}}{\unicode[STIX]{x1D70B}^{\prime }}^{\ast }K_{X}$
where
$K_{W^{\prime }}+\unicode[STIX]{x1D6E4}_{W^{\prime }}-R_{W^{\prime }}{\sim}_{\mathbb{Q}}{\unicode[STIX]{x1D70B}^{\prime }}^{\ast }K_{X}$
where
 $\unicode[STIX]{x1D70B}^{\prime }=\unicode[STIX]{x1D719}^{\prime }\circ \unicode[STIX]{x1D70B}$
. Note that
$\unicode[STIX]{x1D70B}^{\prime }=\unicode[STIX]{x1D719}^{\prime }\circ \unicode[STIX]{x1D70B}$
. Note that
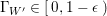 $\unicode[STIX]{x1D6E4}_{W^{\prime }}\in [0,1-\unicode[STIX]{x1D716})$
by the
$\unicode[STIX]{x1D6E4}_{W^{\prime }}\in [0,1-\unicode[STIX]{x1D716})$
by the
![]() $\unicode[STIX]{x1D716}$
-klt condition and
$\unicode[STIX]{x1D716}$
-klt condition and
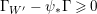 $\unicode[STIX]{x1D6E4}_{W^{\prime }}-\unicode[STIX]{x1D713}_{\ast }\unicode[STIX]{x1D6E4}\geqslant 0$
is
$\unicode[STIX]{x1D6E4}_{W^{\prime }}-\unicode[STIX]{x1D713}_{\ast }\unicode[STIX]{x1D6E4}\geqslant 0$
is
![]() $\unicode[STIX]{x1D719}^{\prime }$
-exceptional. It follows by the construction that
$\unicode[STIX]{x1D719}^{\prime }$
-exceptional. It follows by the construction that
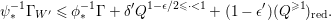 $$\begin{eqnarray}\unicode[STIX]{x1D713}_{\ast }^{-1}\unicode[STIX]{x1D6E4}_{W^{\prime }}\leqslant \unicode[STIX]{x1D719}_{\ast }^{-1}\unicode[STIX]{x1D6E4}+\unicode[STIX]{x1D6FF}^{\prime }Q^{1-\unicode[STIX]{x1D716}/2\leqslant \cdot <1}+(1-\unicode[STIX]{x1D716}^{\prime })(Q^{{\geqslant}1})_{\text{r ed}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D713}_{\ast }^{-1}\unicode[STIX]{x1D6E4}_{W^{\prime }}\leqslant \unicode[STIX]{x1D719}_{\ast }^{-1}\unicode[STIX]{x1D6E4}+\unicode[STIX]{x1D6FF}^{\prime }Q^{1-\unicode[STIX]{x1D716}/2\leqslant \cdot <1}+(1-\unicode[STIX]{x1D716}^{\prime })(Q^{{\geqslant}1})_{\text{r ed}}.\end{eqnarray}$$
In particular,
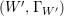 $(W^{\prime },\unicode[STIX]{x1D6E4}_{W^{\prime }})$
is
$(W^{\prime },\unicode[STIX]{x1D6E4}_{W^{\prime }})$
is
![]() $\unicode[STIX]{x1D716}/2$
-klt as the pair
$\unicode[STIX]{x1D716}/2$
-klt as the pair
![]() $(W,\unicode[STIX]{x1D6EF})$
is
$(W,\unicode[STIX]{x1D6EF})$
is
![]() $\unicode[STIX]{x1D716}/2$
-klt and the minimal model program does not make singularities worse.
$\unicode[STIX]{x1D716}/2$
-klt and the minimal model program does not make singularities worse.
On
![]() $W^{\prime }$
, the divisor
$W^{\prime }$
, the divisor
 $$\begin{eqnarray}\displaystyle G & = & \displaystyle \unicode[STIX]{x1D713}_{\ast }(-(\unicode[STIX]{x1D719}_{\ast }^{-1}\unicode[STIX]{x1D6E4}_{p,q}-\unicode[STIX]{x1D719}_{\ast }^{-1}\unicode[STIX]{x1D6E4})-(1-\unicode[STIX]{x1D6FF}^{\prime })Q^{1-\unicode[STIX]{x1D716}/2\leqslant \cdot <1}\nonumber\\ \displaystyle & & \displaystyle \qquad -(Q^{{\geqslant}1}-(1-\unicode[STIX]{x1D716}^{\prime })(Q^{{\geqslant}1})_{\text{red}})+P+\unicode[STIX]{x1D6FF}F)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle G & = & \displaystyle \unicode[STIX]{x1D713}_{\ast }(-(\unicode[STIX]{x1D719}_{\ast }^{-1}\unicode[STIX]{x1D6E4}_{p,q}-\unicode[STIX]{x1D719}_{\ast }^{-1}\unicode[STIX]{x1D6E4})-(1-\unicode[STIX]{x1D6FF}^{\prime })Q^{1-\unicode[STIX]{x1D716}/2\leqslant \cdot <1}\nonumber\\ \displaystyle & & \displaystyle \qquad -(Q^{{\geqslant}1}-(1-\unicode[STIX]{x1D716}^{\prime })(Q^{{\geqslant}1})_{\text{red}})+P+\unicode[STIX]{x1D6FF}F)\nonumber\end{eqnarray}$$
is
![]() $\unicode[STIX]{x1D719}^{\prime }$
-nef with
$\unicode[STIX]{x1D719}^{\prime }$
-nef with
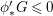 $\unicode[STIX]{x1D719}_{\ast }^{\prime }G\leqslant 0$
. By [Reference Kollár and MoriKM98, Negativity Lemma 3.39], we have that
$\unicode[STIX]{x1D719}_{\ast }^{\prime }G\leqslant 0$
. By [Reference Kollár and MoriKM98, Negativity Lemma 3.39], we have that
![]() $G\leqslant 0$
. Since
$G\leqslant 0$
. Since
![]() $F$
is
$F$
is
![]() $\unicode[STIX]{x1D719}$
-exceptional and
$\unicode[STIX]{x1D719}$
-exceptional and
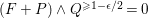 $(F+P)\wedge Q^{{\geqslant}1-\unicode[STIX]{x1D716}/2}=0$
, it follows that
$(F+P)\wedge Q^{{\geqslant}1-\unicode[STIX]{x1D716}/2}=0$
, it follows that
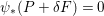 $\unicode[STIX]{x1D713}_{\ast }(P+\unicode[STIX]{x1D6FF}F)=0$
. In particular, all the
$\unicode[STIX]{x1D713}_{\ast }(P+\unicode[STIX]{x1D6FF}F)=0$
. In particular, all the
![]() $\unicode[STIX]{x1D719}^{\prime }$
-exceptional divisors on
$\unicode[STIX]{x1D719}^{\prime }$
-exceptional divisors on
![]() $W^{\prime }$
have log discrepancies less than or equal to
$W^{\prime }$
have log discrepancies less than or equal to
![]() $\unicode[STIX]{x1D716}/2$
with respect to
$\unicode[STIX]{x1D716}/2$
with respect to
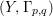 $(Y,\unicode[STIX]{x1D6E4}_{p,q})$
.
$(Y,\unicode[STIX]{x1D6E4}_{p,q})$
.
We now show that for any
![]() $\unicode[STIX]{x1D70B}^{\prime }$
-exceptional divisor
$\unicode[STIX]{x1D70B}^{\prime }$
-exceptional divisor
![]() $E^{\prime }$
on
$E^{\prime }$
on
![]() $W^{\prime }$
dominating
$W^{\prime }$
dominating
![]() $U$
,
$U$
,
![]() $E^{\prime }$
satisfies the inequality
$E^{\prime }$
satisfies the inequality
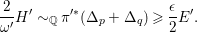 $$\begin{eqnarray}\frac{2}{\unicode[STIX]{x1D714}^{\prime }}H^{\prime }{\sim}_{\mathbb{ Q}}{\unicode[STIX]{x1D70B}^{\prime }}^{\ast }(\unicode[STIX]{x1D6E5}_{p}+\unicode[STIX]{x1D6E5}_{q})\geqslant \frac{\unicode[STIX]{x1D716}}{2}E^{\prime }.\end{eqnarray}$$
$$\begin{eqnarray}\frac{2}{\unicode[STIX]{x1D714}^{\prime }}H^{\prime }{\sim}_{\mathbb{ Q}}{\unicode[STIX]{x1D70B}^{\prime }}^{\ast }(\unicode[STIX]{x1D6E5}_{p}+\unicode[STIX]{x1D6E5}_{q})\geqslant \frac{\unicode[STIX]{x1D716}}{2}E^{\prime }.\end{eqnarray}$$
where
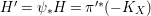 $H^{\prime }=\unicode[STIX]{x1D713}_{\ast }H={\unicode[STIX]{x1D70B}^{\prime }}^{\ast }(-K_{X})$
. This is easy to see: If
$H^{\prime }=\unicode[STIX]{x1D713}_{\ast }H={\unicode[STIX]{x1D70B}^{\prime }}^{\ast }(-K_{X})$
. This is easy to see: If
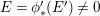 $E=\unicode[STIX]{x1D719}_{\ast }^{\prime }(E^{\prime })\neq 0$
on
$E=\unicode[STIX]{x1D719}_{\ast }^{\prime }(E^{\prime })\neq 0$
on
![]() $Y_{U}$
, then by Lemma 5.9
$Y_{U}$
, then by Lemma 5.9
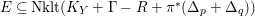 $E\subseteq \text{Nklt}(K_{Y}+\unicode[STIX]{x1D6E4}-R+\unicode[STIX]{x1D70B}^{\ast }(\unicode[STIX]{x1D6E5}_{p}+\unicode[STIX]{x1D6E5}_{q}))$
and hence
$E\subseteq \text{Nklt}(K_{Y}+\unicode[STIX]{x1D6E4}-R+\unicode[STIX]{x1D70B}^{\ast }(\unicode[STIX]{x1D6E5}_{p}+\unicode[STIX]{x1D6E5}_{q}))$
and hence
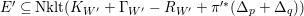 $E^{\prime }\subseteq \text{Nklt}(K_{W^{\prime }}+\unicode[STIX]{x1D6E4}_{W^{\prime }}-R_{W^{\prime }}+{\unicode[STIX]{x1D70B}^{\prime }}^{\ast }(\unicode[STIX]{x1D6E5}_{p}+\unicode[STIX]{x1D6E5}_{q}))$
. The inequality then follows from the same argument as in Lemma 5.9. If
$E^{\prime }\subseteq \text{Nklt}(K_{W^{\prime }}+\unicode[STIX]{x1D6E4}_{W^{\prime }}-R_{W^{\prime }}+{\unicode[STIX]{x1D70B}^{\prime }}^{\ast }(\unicode[STIX]{x1D6E5}_{p}+\unicode[STIX]{x1D6E5}_{q}))$
. The inequality then follows from the same argument as in Lemma 5.9. If
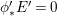 $\unicode[STIX]{x1D719}_{\ast }^{\prime }E^{\prime }=0$
, then by construction
$\unicode[STIX]{x1D719}_{\ast }^{\prime }E^{\prime }=0$
, then by construction
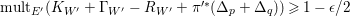 $\text{mult}_{E^{\prime }}(K_{W^{\prime }}+\unicode[STIX]{x1D6E4}_{W^{\prime }}-R_{W^{\prime }}+{\unicode[STIX]{x1D70B}^{\prime }}^{\ast }(\unicode[STIX]{x1D6E5}_{p}+\unicode[STIX]{x1D6E5}_{q}))\geqslant 1-\unicode[STIX]{x1D716}/2$
. Suppose that
$\text{mult}_{E^{\prime }}(K_{W^{\prime }}+\unicode[STIX]{x1D6E4}_{W^{\prime }}-R_{W^{\prime }}+{\unicode[STIX]{x1D70B}^{\prime }}^{\ast }(\unicode[STIX]{x1D6E5}_{p}+\unicode[STIX]{x1D6E5}_{q}))\geqslant 1-\unicode[STIX]{x1D716}/2$
. Suppose that
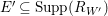 $E^{\prime }\subseteq \text{Supp}(R_{W^{\prime }})$
, then
$E^{\prime }\subseteq \text{Supp}(R_{W^{\prime }})$
, then
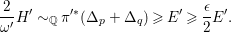 $$\begin{eqnarray}\frac{2}{\unicode[STIX]{x1D714}^{\prime }}H^{\prime }{\sim}_{\mathbb{ Q}}{\unicode[STIX]{x1D70B}^{\prime }}^{\ast }(\unicode[STIX]{x1D6E5}_{p}+\unicode[STIX]{x1D6E5}_{q})\geqslant E^{\prime }\geqslant \frac{\unicode[STIX]{x1D716}}{2}E^{\prime }.\end{eqnarray}$$
$$\begin{eqnarray}\frac{2}{\unicode[STIX]{x1D714}^{\prime }}H^{\prime }{\sim}_{\mathbb{ Q}}{\unicode[STIX]{x1D70B}^{\prime }}^{\ast }(\unicode[STIX]{x1D6E5}_{p}+\unicode[STIX]{x1D6E5}_{q})\geqslant E^{\prime }\geqslant \frac{\unicode[STIX]{x1D716}}{2}E^{\prime }.\end{eqnarray}$$
If
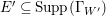 $E^{\prime }\subseteq \text{Supp}(\unicode[STIX]{x1D6E4}_{W^{\prime }})$
, then as
$E^{\prime }\subseteq \text{Supp}(\unicode[STIX]{x1D6E4}_{W^{\prime }})$
, then as
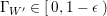 $\unicode[STIX]{x1D6E4}_{W^{\prime }}\in [0,1-\unicode[STIX]{x1D716})$
we get
$\unicode[STIX]{x1D6E4}_{W^{\prime }}\in [0,1-\unicode[STIX]{x1D716})$
we get
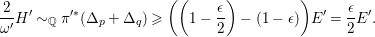 $$\begin{eqnarray}\frac{2}{\unicode[STIX]{x1D714}^{\prime }}H^{\prime }{\sim}_{\mathbb{ Q}}{\unicode[STIX]{x1D70B}^{\prime }}^{\ast }(\unicode[STIX]{x1D6E5}_{p}+\unicode[STIX]{x1D6E5}_{q})\geqslant \biggl(\biggl(1-\frac{\unicode[STIX]{x1D716}}{2}\biggr)-(1-\unicode[STIX]{x1D716})\biggr)E^{\prime }=\frac{\unicode[STIX]{x1D716}}{2}E^{\prime }.\end{eqnarray}$$
$$\begin{eqnarray}\frac{2}{\unicode[STIX]{x1D714}^{\prime }}H^{\prime }{\sim}_{\mathbb{ Q}}{\unicode[STIX]{x1D70B}^{\prime }}^{\ast }(\unicode[STIX]{x1D6E5}_{p}+\unicode[STIX]{x1D6E5}_{q})\geqslant \biggl(\biggl(1-\frac{\unicode[STIX]{x1D716}}{2}\biggr)-(1-\unicode[STIX]{x1D716})\biggr)E^{\prime }=\frac{\unicode[STIX]{x1D716}}{2}E^{\prime }.\end{eqnarray}$$
It follows that
![]() $W^{\prime }$
is a required model.◻
$W^{\prime }$
is a required model.◻
Remark 5.11. Write
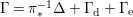 $\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D70B}_{\ast }^{-1}\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6E4}_{\text{d}}+\unicode[STIX]{x1D6E4}_{\text{e}}$
and
$\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D70B}_{\ast }^{-1}\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6E4}_{\text{d}}+\unicode[STIX]{x1D6E4}_{\text{e}}$
and
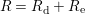 $R=R_{\text{d}}+R_{\text{e}}$
, where
$R=R_{\text{d}}+R_{\text{e}}$
, where
![]() $(-)_{\text{d}}$
is the sum of components dominating
$(-)_{\text{d}}$
is the sum of components dominating
![]() $B$
and
$B$
and
![]() $(-)_{\text{e}}$
is the sum of components mapping to points in
$(-)_{\text{e}}$
is the sum of components mapping to points in
![]() $B$
. From the proof of Lemma 5.10, we deduce the following two inequalities:
$B$
. From the proof of Lemma 5.10, we deduce the following two inequalities:
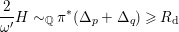 $$\begin{eqnarray}\frac{2}{\unicode[STIX]{x1D714}^{\prime }}H{\sim}_{\mathbb{Q}}\unicode[STIX]{x1D70B}^{\ast }(\unicode[STIX]{x1D6E5}_{p}+\unicode[STIX]{x1D6E5}_{q})\geqslant R_{\text{d}}\end{eqnarray}$$
$$\begin{eqnarray}\frac{2}{\unicode[STIX]{x1D714}^{\prime }}H{\sim}_{\mathbb{Q}}\unicode[STIX]{x1D70B}^{\ast }(\unicode[STIX]{x1D6E5}_{p}+\unicode[STIX]{x1D6E5}_{q})\geqslant R_{\text{d}}\end{eqnarray}$$
and
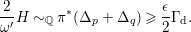 $$\begin{eqnarray}\frac{2}{\unicode[STIX]{x1D714}^{\prime }}H{\sim}_{\mathbb{Q}}\unicode[STIX]{x1D70B}^{\ast }(\unicode[STIX]{x1D6E5}_{p}+\unicode[STIX]{x1D6E5}_{q})\geqslant \frac{\unicode[STIX]{x1D716}}{2}\unicode[STIX]{x1D6E4}_{\text{d}}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{2}{\unicode[STIX]{x1D714}^{\prime }}H{\sim}_{\mathbb{Q}}\unicode[STIX]{x1D70B}^{\ast }(\unicode[STIX]{x1D6E5}_{p}+\unicode[STIX]{x1D6E5}_{q})\geqslant \frac{\unicode[STIX]{x1D716}}{2}\unicode[STIX]{x1D6E4}_{\text{d}}.\end{eqnarray}$$
Now let
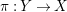 $\unicode[STIX]{x1D70B}:Y\rightarrow X$
with
$\unicode[STIX]{x1D70B}:Y\rightarrow X$
with
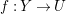 $f:Y\rightarrow U$
be the modified birational covering family of tigers of dimension two and weight
$f:Y\rightarrow U$
be the modified birational covering family of tigers of dimension two and weight
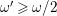 $\unicode[STIX]{x1D714}^{\prime }\geqslant \unicode[STIX]{x1D714}/2$
given by Lemma 5.10 where
$\unicode[STIX]{x1D714}^{\prime }\geqslant \unicode[STIX]{x1D714}/2$
given by Lemma 5.10 where
![]() $Y$
is now
$Y$
is now
![]() $\mathbb{Q}$
-factorial. Write
$\mathbb{Q}$
-factorial. Write
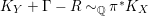 $K_{Y}+\unicode[STIX]{x1D6E4}-R{\sim}_{\mathbb{Q}}\unicode[STIX]{x1D70B}^{\ast }K_{X}$
, where
$K_{Y}+\unicode[STIX]{x1D6E4}-R{\sim}_{\mathbb{Q}}\unicode[STIX]{x1D70B}^{\ast }K_{X}$
, where
![]() $\unicode[STIX]{x1D6E4}\geqslant 0$
,
$\unicode[STIX]{x1D6E4}\geqslant 0$
,
![]() $R\geqslant 0$
are
$R\geqslant 0$
are
![]() $\unicode[STIX]{x1D70B}$
-exceptional, and
$\unicode[STIX]{x1D70B}$
-exceptional, and
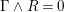 $\unicode[STIX]{x1D6E4}\wedge R=0$
. The pair
$\unicode[STIX]{x1D6E4}\wedge R=0$
. The pair
![]() $(Y,\unicode[STIX]{x1D6E4})$
is
$(Y,\unicode[STIX]{x1D6E4})$
is
![]() $\unicode[STIX]{x1D716}/2$
-klt with
$\unicode[STIX]{x1D716}/2$
-klt with
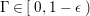 $\unicode[STIX]{x1D6E4}\in [0,1-\unicode[STIX]{x1D716})$
and note that
$\unicode[STIX]{x1D6E4}\in [0,1-\unicode[STIX]{x1D716})$
and note that
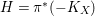 $H=\unicode[STIX]{x1D70B}^{\ast }(-K_{X})$
is semiample and big on
$H=\unicode[STIX]{x1D70B}^{\ast }(-K_{X})$
is semiample and big on
![]() $Y$
.
$Y$
.
Recall that for a projective morphism
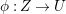 $\unicode[STIX]{x1D719}:Z\rightarrow U$
, a divisor
$\unicode[STIX]{x1D719}:Z\rightarrow U$
, a divisor
![]() $D$
on
$D$
on
![]() $Z$
is pseudo-effective (PSEF) over
$Z$
is pseudo-effective (PSEF) over
![]() $U$
if the restriction of
$U$
if the restriction of
![]() $D$
to the generic fiber is pseudo-effective.
$D$
to the generic fiber is pseudo-effective.
Lemma 5.12. Assume that
![]() $\unicode[STIX]{x1D714}^{\prime }>2$
and consider the pseudo-effective threshold of
$\unicode[STIX]{x1D714}^{\prime }>2$
and consider the pseudo-effective threshold of
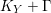 $K_{Y}+\unicode[STIX]{x1D6E4}$
over
$K_{Y}+\unicode[STIX]{x1D6E4}$
over
![]() $U$
with respect to
$U$
with respect to
![]() $H$
$H$
 $$\begin{eqnarray}\unicode[STIX]{x1D70F}:=\inf \{t>0|K_{Y}+\unicode[STIX]{x1D6E4}+tH~\text{is PSEF over}~B\},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70F}:=\inf \{t>0|K_{Y}+\unicode[STIX]{x1D6E4}+tH~\text{is PSEF over}~B\},\end{eqnarray}$$
then
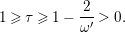 $$\begin{eqnarray}1\geqslant \unicode[STIX]{x1D70F}\geqslant 1-\frac{2}{\unicode[STIX]{x1D714}^{\prime }}>0.\end{eqnarray}$$
$$\begin{eqnarray}1\geqslant \unicode[STIX]{x1D70F}\geqslant 1-\frac{2}{\unicode[STIX]{x1D714}^{\prime }}>0.\end{eqnarray}$$
Proof. Since
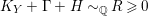 $K_{Y}+\unicode[STIX]{x1D6E4}+H{\sim}_{\mathbb{Q}}R\geqslant 0$
, the first inequality is clear. When restrict to a general fiber
$K_{Y}+\unicode[STIX]{x1D6E4}+H{\sim}_{\mathbb{Q}}R\geqslant 0$
, the first inequality is clear. When restrict to a general fiber
![]() $Y_{u}$
of
$Y_{u}$
of
![]() $Y$
over
$Y$
over
![]() $U$
, we have
$U$
, we have
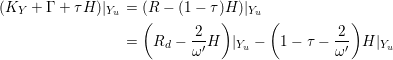 $$\begin{eqnarray}\displaystyle (K_{Y}+\unicode[STIX]{x1D6E4}+\unicode[STIX]{x1D70F}H)|_{Y_{u}} & = & \displaystyle (R-(1-\unicode[STIX]{x1D70F})H)|_{Y_{u}}\nonumber\\ \displaystyle & = & \displaystyle \biggl(R_{d}-\frac{2}{\unicode[STIX]{x1D714}^{\prime }}H\biggr)|_{Y_{u}}-\biggl(1-\unicode[STIX]{x1D70F}-\frac{2}{\unicode[STIX]{x1D714}^{\prime }}\biggr)H|_{Y_{u}}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (K_{Y}+\unicode[STIX]{x1D6E4}+\unicode[STIX]{x1D70F}H)|_{Y_{u}} & = & \displaystyle (R-(1-\unicode[STIX]{x1D70F})H)|_{Y_{u}}\nonumber\\ \displaystyle & = & \displaystyle \biggl(R_{d}-\frac{2}{\unicode[STIX]{x1D714}^{\prime }}H\biggr)|_{Y_{u}}-\biggl(1-\unicode[STIX]{x1D70F}-\frac{2}{\unicode[STIX]{x1D714}^{\prime }}\biggr)H|_{Y_{u}}\nonumber\end{eqnarray}$$
which cannot be PSEF if
![]() $\unicode[STIX]{x1D714}^{\prime }>2$
and
$\unicode[STIX]{x1D714}^{\prime }>2$
and
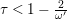 $\unicode[STIX]{x1D70F}<1-\frac{2}{\unicode[STIX]{x1D714}^{\prime }}$
since the first term is nonpositive by (5.2) and the second term is negative.◻
$\unicode[STIX]{x1D70F}<1-\frac{2}{\unicode[STIX]{x1D714}^{\prime }}$
since the first term is nonpositive by (5.2) and the second term is negative.◻
Now we run a relative minimal model program with scaling of the covering family of tigers
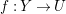 $f:Y\rightarrow U$
. Since
$f:Y\rightarrow U$
. Since
![]() $(Y,\unicode[STIX]{x1D6E4})$
is
$(Y,\unicode[STIX]{x1D6E4})$
is
![]() $\unicode[STIX]{x1D716}/2$
-klt and
$\unicode[STIX]{x1D716}/2$
-klt and
![]() $H$
is semiample and big, we may assume that
$H$
is semiample and big, we may assume that
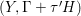 $(Y,\unicode[STIX]{x1D6E4}+\unicode[STIX]{x1D70F}^{\prime }H)$
remains
$(Y,\unicode[STIX]{x1D6E4}+\unicode[STIX]{x1D70F}^{\prime }H)$
remains
![]() $\unicode[STIX]{x1D716}/2$
-klt for a rational number
$\unicode[STIX]{x1D716}/2$
-klt for a rational number
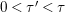 $0<\unicode[STIX]{x1D70F}^{\prime }<\unicode[STIX]{x1D70F}$
. Run a relative minimal model program of
$0<\unicode[STIX]{x1D70F}^{\prime }<\unicode[STIX]{x1D70F}$
. Run a relative minimal model program of
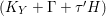 $(K_{Y}+\unicode[STIX]{x1D6E4}+\unicode[STIX]{x1D70F}^{\prime }H)$
with scaling of
$(K_{Y}+\unicode[STIX]{x1D6E4}+\unicode[STIX]{x1D70F}^{\prime }H)$
with scaling of
![]() $H$
over
$H$
over
![]() $U$
. By [BCHM10], it terminates with a relative Mori fiber space
$U$
. By [BCHM10], it terminates with a relative Mori fiber space
![]() $Y^{\prime }\rightarrow T$
over
$Y^{\prime }\rightarrow T$
over
![]() $U$
with
$U$
with
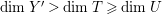 $\dim Y^{\prime }>\dim T\geqslant \dim U$
. Denote the induced maps by
$\dim Y^{\prime }>\dim T\geqslant \dim U$
. Denote the induced maps by
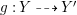 $g:Y{\dashrightarrow}Y^{\prime }$
,
$g:Y{\dashrightarrow}Y^{\prime }$
,
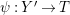 $\unicode[STIX]{x1D713}:Y^{\prime }\rightarrow T$
, and
$\unicode[STIX]{x1D713}:Y^{\prime }\rightarrow T$
, and
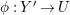 $\unicode[STIX]{x1D719}:Y^{\prime }\rightarrow U$
, we get the following diagram:
$\unicode[STIX]{x1D719}:Y^{\prime }\rightarrow U$
, we get the following diagram:
For a general fiber
![]() $Y_{t}^{\prime }$
of
$Y_{t}^{\prime }$
of
 $\unicode[STIX]{x1D713}:Y^{\prime }\rightarrow T$
, the Picard number
$\unicode[STIX]{x1D713}:Y^{\prime }\rightarrow T$
, the Picard number
 $\unicode[STIX]{x1D70C}(Y_{t}^{\prime })=1$
and
$\unicode[STIX]{x1D70C}(Y_{t}^{\prime })=1$
and
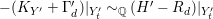 $-(K_{Y^{\prime }}+\unicode[STIX]{x1D6E4}_{d}^{\prime })|_{Y_{t}^{\prime }}{\sim}_{\mathbb{Q}}(H^{\prime }-R_{d})|_{Y_{t}^{\prime }}$
is ample.
$-(K_{Y^{\prime }}+\unicode[STIX]{x1D6E4}_{d}^{\prime })|_{Y_{t}^{\prime }}{\sim}_{\mathbb{Q}}(H^{\prime }-R_{d})|_{Y_{t}^{\prime }}$
is ample.
Lemma 5.13. There exists a divisor
![]() $E^{\prime }$
on
$E^{\prime }$
on
![]() $Y^{\prime }$
which is exceptional over
$Y^{\prime }$
which is exceptional over
![]() $X$
and dominates
$X$
and dominates
![]() $T$
.
$T$
.
Proof. Recall that there is a natural map
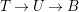 $T\rightarrow U\rightarrow B$
. Hence we can extend
$T\rightarrow U\rightarrow B$
. Hence we can extend
 $\unicode[STIX]{x1D713}:Y^{\prime }\rightarrow T$
to
$\unicode[STIX]{x1D713}:Y^{\prime }\rightarrow T$
to
 $\overline{\unicode[STIX]{x1D713}}:\overline{Y^{\prime }}\rightarrow \overline{T}$
over
$\overline{\unicode[STIX]{x1D713}}:\overline{Y^{\prime }}\rightarrow \overline{T}$
over
![]() $B$
where
$B$
where
![]() $\overline{(-)}$
stands for a projective compactification of
$\overline{(-)}$
stands for a projective compactification of
![]() $(-)$
. Take a common resolution
$(-)$
. Take a common resolution
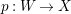 $p:W\rightarrow X$
and
$p:W\rightarrow X$
and
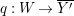 $q:W\rightarrow \overline{Y^{\prime }}$
and let
$q:W\rightarrow \overline{Y^{\prime }}$
and let
![]() $A_{\overline{T}}$
be a sufficiently ample divisor on
$A_{\overline{T}}$
be a sufficiently ample divisor on
![]() $\overline{T}$
. Let
$\overline{T}$
. Let
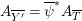 $A_{\overline{Y^{\prime }}}=\overline{\unicode[STIX]{x1D713}}^{\ast }A_{\overline{T}}$
,
$A_{\overline{Y^{\prime }}}=\overline{\unicode[STIX]{x1D713}}^{\ast }A_{\overline{T}}$
,
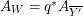 $A_{W}=q^{\ast }A_{\overline{Y^{\prime }}}$
, and
$A_{W}=q^{\ast }A_{\overline{Y^{\prime }}}$
, and
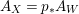 $A_{X}=p_{\ast }A_{W}$
. Then
$A_{X}=p_{\ast }A_{W}$
. Then
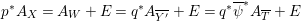 $p^{\ast }A_{X}=A_{W}+E=q^{\ast }A_{\overline{Y^{\prime }}}+E=q^{\ast }\overline{\unicode[STIX]{x1D713}}^{\ast }A_{\overline{T}}+E$
for an effective divisor
$p^{\ast }A_{X}=A_{W}+E=q^{\ast }A_{\overline{Y^{\prime }}}+E=q^{\ast }\overline{\unicode[STIX]{x1D713}}^{\ast }A_{\overline{T}}+E$
for an effective divisor
![]() $E$
on
$E$
on
![]() $W$
which is exceptional over
$W$
which is exceptional over
![]() $X$
. Since
$X$
. Since
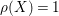 $\unicode[STIX]{x1D70C}(X)=1$
, it follows by the same argument as in Lemma 5.8 that one of the irreducible components of
$\unicode[STIX]{x1D70C}(X)=1$
, it follows by the same argument as in Lemma 5.8 that one of the irreducible components of
![]() $E$
maps to a divisor
$E$
maps to a divisor
![]() $E^{\prime }$
on
$E^{\prime }$
on
![]() $\overline{Y^{\prime }}$
. By the same argument as in Lemma 5.8 again, one of the irreducible components of the nonzero divisor
$\overline{Y^{\prime }}$
. By the same argument as in Lemma 5.8 again, one of the irreducible components of the nonzero divisor
![]() $q_{\ast }(E)$
dominates
$q_{\ast }(E)$
dominates
![]() $\overline{T}$
.◻
$\overline{T}$
.◻
Proposition 5.14. If
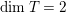 $\dim T=2$
, then
$\dim T=2$
, then
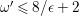 $\unicode[STIX]{x1D714}^{\prime }\leqslant 8/\unicode[STIX]{x1D716}+2$
.
$\unicode[STIX]{x1D714}^{\prime }\leqslant 8/\unicode[STIX]{x1D716}+2$
.
Proof. By Lemma 5.13, there exists a divisor
![]() $E^{\prime }$
on
$E^{\prime }$
on
![]() $Y^{\prime }$
which is exceptional over
$Y^{\prime }$
which is exceptional over
![]() $X$
and dominates
$X$
and dominates
![]() $T$
. Note that
$T$
. Note that
![]() $Y^{\prime }$
is normal and hence
$Y^{\prime }$
is normal and hence
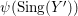 $\unicode[STIX]{x1D713}(\text{Sing}(Y^{\prime }))$
is a proper subset of
$\unicode[STIX]{x1D713}(\text{Sing}(Y^{\prime }))$
is a proper subset of
![]() $T$
. In particular, a general fiber
$T$
. In particular, a general fiber
![]() $Y_{t}^{\prime }$
of
$Y_{t}^{\prime }$
of
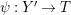 $\unicode[STIX]{x1D713}:Y^{\prime }\rightarrow T$
is a smooth projective curve and hence
$\unicode[STIX]{x1D713}:Y^{\prime }\rightarrow T$
is a smooth projective curve and hence
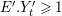 $E^{\prime }.Y_{t}^{\prime }\geqslant 1$
. Since
$E^{\prime }.Y_{t}^{\prime }\geqslant 1$
. Since
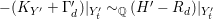 $-(K_{Y^{\prime }}+\unicode[STIX]{x1D6E4}_{d}^{\prime })|_{Y_{t}^{\prime }}{\sim}_{\mathbb{Q}}(H^{\prime }-R_{d})|_{Y_{t}^{\prime }}$
is ample, a general fiber
$-(K_{Y^{\prime }}+\unicode[STIX]{x1D6E4}_{d}^{\prime })|_{Y_{t}^{\prime }}{\sim}_{\mathbb{Q}}(H^{\prime }-R_{d})|_{Y_{t}^{\prime }}$
is ample, a general fiber
![]() $Y_{t}^{\prime }$
is a smooth rational curve
$Y_{t}^{\prime }$
is a smooth rational curve
![]() $\mathbb{P}^{1}$
. From (5.1), we know that
$\mathbb{P}^{1}$
. From (5.1), we know that
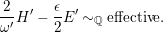 $$\begin{eqnarray}\frac{2}{\unicode[STIX]{x1D714}^{\prime }}H^{\prime }-\frac{\unicode[STIX]{x1D716}}{2}E^{\prime }{\sim}_{\mathbb{ Q}}\text{effective}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{2}{\unicode[STIX]{x1D714}^{\prime }}H^{\prime }-\frac{\unicode[STIX]{x1D716}}{2}E^{\prime }{\sim}_{\mathbb{ Q}}\text{effective}.\end{eqnarray}$$
Also from (5.2),
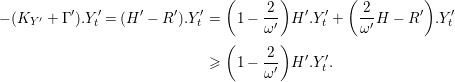 $$\begin{eqnarray}\displaystyle -(K_{Y^{\prime }}+\unicode[STIX]{x1D6E4}^{\prime }).Y_{t}^{\prime }=(H^{\prime }-R^{\prime }).Y_{t}^{\prime } & = & \displaystyle \biggl(1-\frac{2}{\unicode[STIX]{x1D714}^{\prime }}\biggr)H^{\prime }.Y_{t}^{\prime }+\biggl(\frac{2}{\unicode[STIX]{x1D714}^{\prime }}H-R^{\prime }\biggr).Y_{t}^{\prime }\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \biggl(1-\frac{2}{\unicode[STIX]{x1D714}^{\prime }}\biggr)H^{\prime }.Y_{t}^{\prime }.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle -(K_{Y^{\prime }}+\unicode[STIX]{x1D6E4}^{\prime }).Y_{t}^{\prime }=(H^{\prime }-R^{\prime }).Y_{t}^{\prime } & = & \displaystyle \biggl(1-\frac{2}{\unicode[STIX]{x1D714}^{\prime }}\biggr)H^{\prime }.Y_{t}^{\prime }+\biggl(\frac{2}{\unicode[STIX]{x1D714}^{\prime }}H-R^{\prime }\biggr).Y_{t}^{\prime }\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \biggl(1-\frac{2}{\unicode[STIX]{x1D714}^{\prime }}\biggr)H^{\prime }.Y_{t}^{\prime }.\nonumber\end{eqnarray}$$
It follows that
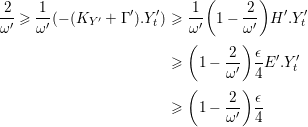 $$\begin{eqnarray}\displaystyle \frac{2}{\unicode[STIX]{x1D714}^{\prime }}\geqslant \frac{1}{\unicode[STIX]{x1D714}^{\prime }}(-(K_{Y^{\prime }}+\unicode[STIX]{x1D6E4}^{\prime }).Y_{t}^{\prime }) & {\geqslant} & \displaystyle \frac{1}{\unicode[STIX]{x1D714}^{\prime }}\biggl(1-\frac{2}{\unicode[STIX]{x1D714}^{\prime }}\biggr)H^{\prime }.Y_{t}^{\prime }\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \biggl(1-\frac{2}{\unicode[STIX]{x1D714}^{\prime }}\biggr)\frac{\unicode[STIX]{x1D716}}{4}E^{\prime }.Y_{t}^{\prime }\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \biggl(1-\frac{2}{\unicode[STIX]{x1D714}^{\prime }}\biggr)\frac{\unicode[STIX]{x1D716}}{4}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{2}{\unicode[STIX]{x1D714}^{\prime }}\geqslant \frac{1}{\unicode[STIX]{x1D714}^{\prime }}(-(K_{Y^{\prime }}+\unicode[STIX]{x1D6E4}^{\prime }).Y_{t}^{\prime }) & {\geqslant} & \displaystyle \frac{1}{\unicode[STIX]{x1D714}^{\prime }}\biggl(1-\frac{2}{\unicode[STIX]{x1D714}^{\prime }}\biggr)H^{\prime }.Y_{t}^{\prime }\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \biggl(1-\frac{2}{\unicode[STIX]{x1D714}^{\prime }}\biggr)\frac{\unicode[STIX]{x1D716}}{4}E^{\prime }.Y_{t}^{\prime }\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \biggl(1-\frac{2}{\unicode[STIX]{x1D714}^{\prime }}\biggr)\frac{\unicode[STIX]{x1D716}}{4}\nonumber\end{eqnarray}$$
where the first inequality is by the adjunction formula on
![]() $\mathbb{P}^{1}$
. Hence
$\mathbb{P}^{1}$
. Hence
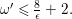 $\unicode[STIX]{x1D714}^{\prime }\leqslant \frac{8}{\unicode[STIX]{x1D716}}+2.$
◻
$\unicode[STIX]{x1D714}^{\prime }\leqslant \frac{8}{\unicode[STIX]{x1D716}}+2.$
◻
Proposition 5.15. If
 $\dim T=1$
, then
$\dim T=1$
, then
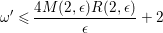 $$\begin{eqnarray}\unicode[STIX]{x1D714}^{\prime }\leqslant \frac{4M(2,\unicode[STIX]{x1D716})R(2,\unicode[STIX]{x1D716})}{\unicode[STIX]{x1D716}}+2\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D714}^{\prime }\leqslant \frac{4M(2,\unicode[STIX]{x1D716})R(2,\unicode[STIX]{x1D716})}{\unicode[STIX]{x1D716}}+2\end{eqnarray}$$
where
![]() $R(2,\unicode[STIX]{x1D716})$
is an upper bound of the Cartier index of
$R(2,\unicode[STIX]{x1D716})$
is an upper bound of the Cartier index of
![]() $K_{S}$
for
$K_{S}$
for
![]() $S$
any
$S$
any
![]() $\unicode[STIX]{x1D716}/2$
-klt log del Pezzo surface of
$\unicode[STIX]{x1D716}/2$
-klt log del Pezzo surface of
 $\unicode[STIX]{x1D70C}(S)=1$
and
$\unicode[STIX]{x1D70C}(S)=1$
and
![]() $M(2,\unicode[STIX]{x1D716})$
is an upper bound of the volume
$M(2,\unicode[STIX]{x1D716})$
is an upper bound of the volume
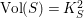 $\text{Vol}(S)=K_{S}^{2}$
for
$\text{Vol}(S)=K_{S}^{2}$
for
![]() $S$
any
$S$
any
![]() $\unicode[STIX]{x1D716}/2$
-klt log del Pezzo surface of
$\unicode[STIX]{x1D716}/2$
-klt log del Pezzo surface of
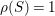 $\unicode[STIX]{x1D70C}(S)=1$
.
$\unicode[STIX]{x1D70C}(S)=1$
.
Proof. Since
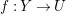 $f:Y\rightarrow U$
has connected fibers,
$f:Y\rightarrow U$
has connected fibers,
![]() $T\cong U$
. Since
$T\cong U$
. Since
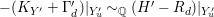 $-(K_{Y^{\prime }}+\unicode[STIX]{x1D6E4}_{d}^{\prime })|_{Y_{u}^{\prime }}{\sim}_{\mathbb{Q}}(H^{\prime }-R_{d})|_{Y_{u}^{\prime }}$
is ample and
$-(K_{Y^{\prime }}+\unicode[STIX]{x1D6E4}_{d}^{\prime })|_{Y_{u}^{\prime }}{\sim}_{\mathbb{Q}}(H^{\prime }-R_{d})|_{Y_{u}^{\prime }}$
is ample and
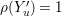 $\unicode[STIX]{x1D70C}(Y_{u}^{\prime })=1$
for a general point
$\unicode[STIX]{x1D70C}(Y_{u}^{\prime })=1$
for a general point
![]() $u\in U$
, we see that
$u\in U$
, we see that
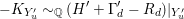 $$\begin{eqnarray}-K_{Y_{u}^{\prime }}{\sim}_{\mathbb{Q}}(H^{\prime }+\unicode[STIX]{x1D6E4}_{d}^{\prime }-R_{d})|_{Y_{u}^{\prime }}\end{eqnarray}$$
$$\begin{eqnarray}-K_{Y_{u}^{\prime }}{\sim}_{\mathbb{Q}}(H^{\prime }+\unicode[STIX]{x1D6E4}_{d}^{\prime }-R_{d})|_{Y_{u}^{\prime }}\end{eqnarray}$$
is ample. By Lemma 5.13, let
![]() $E^{\prime }$
be a divisor on
$E^{\prime }$
be a divisor on
![]() $Y^{\prime }$
exceptional over
$Y^{\prime }$
exceptional over
![]() $X$
which dominates
$X$
which dominates
![]() $U$
, then
$U$
, then
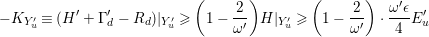 $$\begin{eqnarray}-K_{Y_{u}^{\prime }}\equiv (H^{\prime }+\unicode[STIX]{x1D6E4}_{d}^{\prime }-R_{d})|_{Y_{u}^{\prime }}\geqslant \biggl(1-\frac{2}{\unicode[STIX]{x1D714}^{\prime }}\biggr)H|_{Y_{u}^{\prime }}\geqslant \biggl(1-\frac{2}{\unicode[STIX]{x1D714}^{\prime }}\biggr)\cdot \frac{\unicode[STIX]{x1D714}^{\prime }\unicode[STIX]{x1D716}}{4}E_{u}^{\prime }\end{eqnarray}$$
$$\begin{eqnarray}-K_{Y_{u}^{\prime }}\equiv (H^{\prime }+\unicode[STIX]{x1D6E4}_{d}^{\prime }-R_{d})|_{Y_{u}^{\prime }}\geqslant \biggl(1-\frac{2}{\unicode[STIX]{x1D714}^{\prime }}\biggr)H|_{Y_{u}^{\prime }}\geqslant \biggl(1-\frac{2}{\unicode[STIX]{x1D714}^{\prime }}\biggr)\cdot \frac{\unicode[STIX]{x1D714}^{\prime }\unicode[STIX]{x1D716}}{4}E_{u}^{\prime }\end{eqnarray}$$
where the second inequality follows by dropping
![]() $\unicode[STIX]{x1D6E4}_{d}^{\prime }$
and applying (5.2) while the last one from (5.1). By intersecting with the ample divisor
$\unicode[STIX]{x1D6E4}_{d}^{\prime }$
and applying (5.2) while the last one from (5.1). By intersecting with the ample divisor
![]() $-K_{Y_{u}^{\prime }}$
, this implies that
$-K_{Y_{u}^{\prime }}$
, this implies that
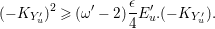 $$\begin{eqnarray}(-K_{Y_{u}^{\prime }})^{2}\geqslant (\unicode[STIX]{x1D714}^{\prime }-2)\frac{\unicode[STIX]{x1D716}}{4}E_{u}^{\prime }.(-K_{Y_{u}^{\prime }}).\end{eqnarray}$$
$$\begin{eqnarray}(-K_{Y_{u}^{\prime }})^{2}\geqslant (\unicode[STIX]{x1D714}^{\prime }-2)\frac{\unicode[STIX]{x1D716}}{4}E_{u}^{\prime }.(-K_{Y_{u}^{\prime }}).\end{eqnarray}$$
Now
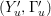 $(Y_{u}^{\prime },\unicode[STIX]{x1D6E4}_{u}^{\prime })$
is an
$(Y_{u}^{\prime },\unicode[STIX]{x1D6E4}_{u}^{\prime })$
is an
![]() $\unicode[STIX]{x1D716}/2$
-klt log del Pezzo surfaces of Picard number one. Hence
$\unicode[STIX]{x1D716}/2$
-klt log del Pezzo surfaces of Picard number one. Hence
![]() $Y_{u}^{\prime }$
is an
$Y_{u}^{\prime }$
is an
![]() $\unicode[STIX]{x1D716}/2$
-klt del Pezzo surfaces of Picard number
$\unicode[STIX]{x1D716}/2$
-klt del Pezzo surfaces of Picard number
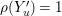 $\unicode[STIX]{x1D70C}(Y_{u}^{\prime })=1$
. By Theorem 4.3,
$\unicode[STIX]{x1D70C}(Y_{u}^{\prime })=1$
. By Theorem 4.3,
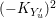 $(-K_{Y_{u}^{\prime }})^{2}$
is bounded above by a positive number
$(-K_{Y_{u}^{\prime }})^{2}$
is bounded above by a positive number
![]() $M(2,\unicode[STIX]{x1D716})$
satisfying
$M(2,\unicode[STIX]{x1D716})$
satisfying
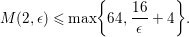 $$\begin{eqnarray}M(2,\unicode[STIX]{x1D716})\leqslant \max \biggl\{64,\frac{16}{\unicode[STIX]{x1D716}}+4\biggr\}.\end{eqnarray}$$
$$\begin{eqnarray}M(2,\unicode[STIX]{x1D716})\leqslant \max \biggl\{64,\frac{16}{\unicode[STIX]{x1D716}}+4\biggr\}.\end{eqnarray}$$
Also, by (◇) the Cartier index of
![]() $K_{Y_{u}^{\prime }}$
has an upper bound,
$K_{Y_{u}^{\prime }}$
has an upper bound,
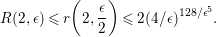 $$\begin{eqnarray}R(2,\unicode[STIX]{x1D716})\leqslant r\biggl(2,\frac{\unicode[STIX]{x1D716}}{2}\biggr)\leqslant 2(4/\unicode[STIX]{x1D716})^{128/\unicode[STIX]{x1D716}^{5}}.\end{eqnarray}$$
$$\begin{eqnarray}R(2,\unicode[STIX]{x1D716})\leqslant r\biggl(2,\frac{\unicode[STIX]{x1D716}}{2}\biggr)\leqslant 2(4/\unicode[STIX]{x1D716})^{128/\unicode[STIX]{x1D716}^{5}}.\end{eqnarray}$$
It follows that
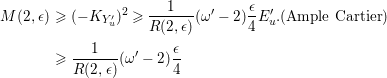 $$\begin{eqnarray}\displaystyle M(2,\unicode[STIX]{x1D716}) & {\geqslant} & \displaystyle (-K_{Y_{u}^{\prime }})^{2}\geqslant \frac{1}{R(2,\unicode[STIX]{x1D716})}(\unicode[STIX]{x1D714}^{\prime }-2)\frac{\unicode[STIX]{x1D716}}{4}E_{u}^{\prime }.(\text{Ample Cartier})\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \frac{1}{R(2,\unicode[STIX]{x1D716})}(\unicode[STIX]{x1D714}^{\prime }-2)\frac{\unicode[STIX]{x1D716}}{4}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle M(2,\unicode[STIX]{x1D716}) & {\geqslant} & \displaystyle (-K_{Y_{u}^{\prime }})^{2}\geqslant \frac{1}{R(2,\unicode[STIX]{x1D716})}(\unicode[STIX]{x1D714}^{\prime }-2)\frac{\unicode[STIX]{x1D716}}{4}E_{u}^{\prime }.(\text{Ample Cartier})\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \frac{1}{R(2,\unicode[STIX]{x1D716})}(\unicode[STIX]{x1D714}^{\prime }-2)\frac{\unicode[STIX]{x1D716}}{4}\nonumber\end{eqnarray}$$
and hence we get an upper bound,
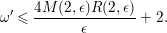 $$\begin{eqnarray}\unicode[STIX]{x1D714}^{\prime }\leqslant \frac{4M(2,\unicode[STIX]{x1D716})R(2,\unicode[STIX]{x1D716})}{\unicode[STIX]{x1D716}}+2.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D714}^{\prime }\leqslant \frac{4M(2,\unicode[STIX]{x1D716})R(2,\unicode[STIX]{x1D716})}{\unicode[STIX]{x1D716}}+2.\end{eqnarray}$$
Remark 5.16. It has been shown in [Reference BelousovBel08] that a klt log del Pezzo surface has at most four isolated singularities. Also surface klt singularities are classified by Alexeev in [Reference CortiCor07]. Hence we expect that it is possible to obtain a better upper bound for
![]() $R(2,\unicode[STIX]{x1D716})$
and
$R(2,\unicode[STIX]{x1D716})$
and
![]() $M(2,\unicode[STIX]{x1D716})$
in Proposition 5.15.
$M(2,\unicode[STIX]{x1D716})$
in Proposition 5.15.
Theorem 5.17. Let
![]() $(X,\unicode[STIX]{x1D6E5})$
be an
$(X,\unicode[STIX]{x1D6E5})$
be an
![]() $\unicode[STIX]{x1D716}$
-klt log
$\unicode[STIX]{x1D716}$
-klt log
![]() $\mathbb{Q}$
-Fano threefold of
$\mathbb{Q}$
-Fano threefold of
 $\unicode[STIX]{x1D70C}(X)=1$
. Then the degree
$\unicode[STIX]{x1D70C}(X)=1$
. Then the degree
![]() $-K_{X}^{3}$
satisfies
$-K_{X}^{3}$
satisfies
 $$\begin{eqnarray}-K_{X}^{3}\leqslant \biggl(\frac{24M(2,\unicode[STIX]{x1D716})R(2,\unicode[STIX]{x1D716})}{\unicode[STIX]{x1D716}}+12\biggr)^{3}\end{eqnarray}$$
$$\begin{eqnarray}-K_{X}^{3}\leqslant \biggl(\frac{24M(2,\unicode[STIX]{x1D716})R(2,\unicode[STIX]{x1D716})}{\unicode[STIX]{x1D716}}+12\biggr)^{3}\end{eqnarray}$$
where where
![]() $R(2,\unicode[STIX]{x1D716})$
is an upper bound of the Cartier index of
$R(2,\unicode[STIX]{x1D716})$
is an upper bound of the Cartier index of
![]() $K_{S}$
for
$K_{S}$
for
![]() $S$
any
$S$
any
![]() $\unicode[STIX]{x1D716}/2$
-klt log del Pezzo surface of
$\unicode[STIX]{x1D716}/2$
-klt log del Pezzo surface of
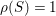 $\unicode[STIX]{x1D70C}(S)=1$
and
$\unicode[STIX]{x1D70C}(S)=1$
and
![]() $M(2,\unicode[STIX]{x1D716})$
is an upper bound of the volume
$M(2,\unicode[STIX]{x1D716})$
is an upper bound of the volume
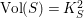 $\text{Vol}(S)=K_{S}^{2}$
for
$\text{Vol}(S)=K_{S}^{2}$
for
![]() $S$
any
$S$
any
![]() $\unicode[STIX]{x1D716}/2$
-klt log del Pezzo surface of
$\unicode[STIX]{x1D716}/2$
-klt log del Pezzo surface of
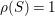 $\unicode[STIX]{x1D70C}(S)=1$
. Note that we have
$\unicode[STIX]{x1D70C}(S)=1$
. Note that we have
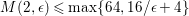 $M(2,\unicode[STIX]{x1D716})\leqslant \max \{64,16/\unicode[STIX]{x1D716}+4\}$
from Theorem 4.3 and
$M(2,\unicode[STIX]{x1D716})\leqslant \max \{64,16/\unicode[STIX]{x1D716}+4\}$
from Theorem 4.3 and
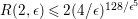 $R(2,\unicode[STIX]{x1D716})\leqslant 2(4/\unicode[STIX]{x1D716})^{128/\unicode[STIX]{x1D716}^{5}}$
from ( ◇).
$R(2,\unicode[STIX]{x1D716})\leqslant 2(4/\unicode[STIX]{x1D716})^{128/\unicode[STIX]{x1D716}^{5}}$
from ( ◇).
Proof. Recall that
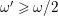 $\unicode[STIX]{x1D714}^{\prime }\geqslant \unicode[STIX]{x1D714}/2$
. The theorem then follows from Propositions 5.3, 5.14 and 5.15.◻
$\unicode[STIX]{x1D714}^{\prime }\geqslant \unicode[STIX]{x1D714}/2$
. The theorem then follows from Propositions 5.3, 5.14 and 5.15.◻
The following example shows that the cone construction analogous to Example 2.1 only provides
![]() $\unicode[STIX]{x1D716}$
-klt Fano threefolds with volumes of order
$\unicode[STIX]{x1D716}$
-klt Fano threefolds with volumes of order
![]() $1/\unicode[STIX]{x1D716}^{2}$
.
$1/\unicode[STIX]{x1D716}^{2}$
.
Example 5.18. (Projective cone of projective spaces)
For
![]() $n\geqslant 1$
and
$n\geqslant 1$
and
![]() $d\geqslant 2$
, let
$d\geqslant 2$
, let
 $\mathbb{P}^{n}{\hookrightarrow}\mathbb{P}^{N}$
be the embedding by
$\mathbb{P}^{n}{\hookrightarrow}\mathbb{P}^{N}$
be the embedding by
![]() $|{\mathcal{O}}(d)|$
and
$|{\mathcal{O}}(d)|$
and
![]() $X$
be the associated projective cone. The projective variety
$X$
be the associated projective cone. The projective variety
![]() $X$
is normal
$X$
is normal
![]() $\mathbb{Q}$
-factorial of Picard number one with the unique singularity at the vertex
$\mathbb{Q}$
-factorial of Picard number one with the unique singularity at the vertex
![]() $O$
.
$O$
.
![]() $X$
admits a resolution
$X$
admits a resolution
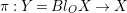 $\unicode[STIX]{x1D70B}:Y=Bl_{O}X\rightarrow X$
with exceptional divisor
$\unicode[STIX]{x1D70B}:Y=Bl_{O}X\rightarrow X$
with exceptional divisor
![]() $E\cong \mathbb{P}^{n}$
of normal bundle
$E\cong \mathbb{P}^{n}$
of normal bundle
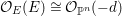 ${\mathcal{O}}_{E}(E)\cong {\mathcal{O}}_{\mathbb{P}^{n}}(-d)$
. The variety
${\mathcal{O}}_{E}(E)\cong {\mathcal{O}}_{\mathbb{P}^{n}}(-d)$
. The variety
![]() $Y$
is the projective bundle
$Y$
is the projective bundle
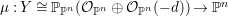 $\unicode[STIX]{x1D707}:Y\cong \mathbb{P}_{\mathbb{P}^{n}}({\mathcal{O}}_{\mathbb{P}^{n}}\oplus {\mathcal{O}}_{\mathbb{P}^{n}}(-d))\rightarrow \mathbb{P}^{n}$
with tautological bundle
$\unicode[STIX]{x1D707}:Y\cong \mathbb{P}_{\mathbb{P}^{n}}({\mathcal{O}}_{\mathbb{P}^{n}}\oplus {\mathcal{O}}_{\mathbb{P}^{n}}(-d))\rightarrow \mathbb{P}^{n}$
with tautological bundle
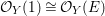 ${\mathcal{O}}_{Y}(1)\cong {\mathcal{O}}_{Y}(E)$
. We have:
${\mathcal{O}}_{Y}(1)\cong {\mathcal{O}}_{Y}(E)$
. We have:
-
∙
 ${\mathcal{O}}_{E}(E)\cong {\mathcal{O}}_{\mathbb{P}^{n}}(-d)$
and hence
${\mathcal{O}}_{E}(E)\cong {\mathcal{O}}_{\mathbb{P}^{n}}(-d)$
and hence
 $E^{n+1}=(-d)^{n}$
;
$E^{n+1}=(-d)^{n}$
; -
∙
 $K_{Y}=\unicode[STIX]{x1D70B}^{\ast }K_{X}+(-1+\frac{n+1}{d})E$
and hence
$K_{Y}=\unicode[STIX]{x1D70B}^{\ast }K_{X}+(-1+\frac{n+1}{d})E$
and hence
 $X$
is always klt.
$X$
is always klt.
 $X$
is terminal (resp. canonical) if and only if
$X$
is terminal (resp. canonical) if and only if
 $n+1>d\geqslant 2$
(resp.
$n+1>d\geqslant 2$
(resp.
 $n+1\geqslant d\geqslant 2$
);
$n+1\geqslant d\geqslant 2$
); -
∙
 $K_{Y}=\unicode[STIX]{x1D707}^{\ast }(K_{\mathbb{P}^{n}}+\det ({\mathcal{E}}))\otimes {\mathcal{O}}_{Y}(-\text{rk}({\mathcal{E}}))\equiv -(n+1+d)F-2E$
where
$K_{Y}=\unicode[STIX]{x1D707}^{\ast }(K_{\mathbb{P}^{n}}+\det ({\mathcal{E}}))\otimes {\mathcal{O}}_{Y}(-\text{rk}({\mathcal{E}}))\equiv -(n+1+d)F-2E$
where
 ${\mathcal{E}}={\mathcal{O}}_{\mathbb{P}^{n}}\oplus {\mathcal{O}}_{\mathbb{P}^{n}}(-d)$
and
${\mathcal{E}}={\mathcal{O}}_{\mathbb{P}^{n}}\oplus {\mathcal{O}}_{\mathbb{P}^{n}}(-d)$
and
 $F=\unicode[STIX]{x1D707}^{\ast }{\mathcal{O}}_{\mathbb{P}}^{n}(1)$
;
$F=\unicode[STIX]{x1D707}^{\ast }{\mathcal{O}}_{\mathbb{P}}^{n}(1)$
; -
∙
 $F^{n+1}=0$
and
$F^{n+1}=0$
and
 $F^{n+1-k}.E^{k}=(-d)^{k-1}$
for
$F^{n+1-k}.E^{k}=(-d)^{k-1}$
for
 $1\leqslant k\leqslant n+1$
;
$1\leqslant k\leqslant n+1$
; -
∙
 $K_{Y}^{n+1}=K_{X}^{n+1}+(-1+\frac{n+1}{d})^{n+1}E^{n+1}$
and
$K_{Y}^{n+1}=K_{X}^{n+1}+(-1+\frac{n+1}{d})^{n+1}E^{n+1}$
and  $$\begin{eqnarray}\displaystyle K_{Y}^{n+1} & = & \displaystyle \frac{-1}{d}\mathop{\sum }_{k=1}^{n+1}\left(\begin{array}{@{}c@{}}n+1-k\\ k\end{array}\right)\biggl(-1+\frac{n+1}{d}\biggr)^{n+1-k}(2d)^{k}\nonumber\\ \displaystyle & = & \displaystyle \frac{-1}{d}((d-n-1)^{n+1}-(-(d+n+1)^{n+1}));\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle K_{Y}^{n+1} & = & \displaystyle \frac{-1}{d}\mathop{\sum }_{k=1}^{n+1}\left(\begin{array}{@{}c@{}}n+1-k\\ k\end{array}\right)\biggl(-1+\frac{n+1}{d}\biggr)^{n+1-k}(2d)^{k}\nonumber\\ \displaystyle & = & \displaystyle \frac{-1}{d}((d-n-1)^{n+1}-(-(d+n+1)^{n+1}));\nonumber\end{eqnarray}$$
-
∙ In summary,
 $-K_{X}$
is ample with
$-K_{X}$
is ample with  $$\begin{eqnarray}(-K_{X})^{n+1}=\frac{(d+n+1)^{n+1}}{d}.\end{eqnarray}$$
$$\begin{eqnarray}(-K_{X})^{n+1}=\frac{(d+n+1)^{n+1}}{d}.\end{eqnarray}$$
If
![]() $n=2$
, then we have an
$n=2$
, then we have an
![]() $\unicode[STIX]{x1D716}$
-klt Fano threefold of Picard number one with
$\unicode[STIX]{x1D716}$
-klt Fano threefold of Picard number one with
![]() $\unicode[STIX]{x1D716}=1/d$
. The volume
$\unicode[STIX]{x1D716}=1/d$
. The volume
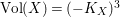 $\text{Vol}(X)=(-K_{X})^{3}$
is of order
$\text{Vol}(X)=(-K_{X})^{3}$
is of order
![]() $1/\unicode[STIX]{x1D716}^{2}$
.
$1/\unicode[STIX]{x1D716}^{2}$
.
In view of Theorem 5.17, it is then interesting to see whether
![]() $\unicode[STIX]{x1D716}$
-klt Fano threefolds with big volumes exist.
$\unicode[STIX]{x1D716}$
-klt Fano threefolds with big volumes exist.
Question 5.19. Can one find an
![]() $\unicode[STIX]{x1D716}$
-klt
$\unicode[STIX]{x1D716}$
-klt
![]() $\mathbb{Q}$
-factorial
$\mathbb{Q}$
-factorial
![]() $\mathbb{Q}$
-Fano threefold
$\mathbb{Q}$
-Fano threefold
![]() $X$
of
$X$
of
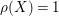 $\unicode[STIX]{x1D70C}(X)=1$
with volume
$\unicode[STIX]{x1D70C}(X)=1$
with volume
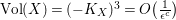 $\text{Vol}(X)=(-K_{X})^{3}=O\big(\frac{1}{\unicode[STIX]{x1D716}^{c}}\big)$
for
$\text{Vol}(X)=(-K_{X})^{3}=O\big(\frac{1}{\unicode[STIX]{x1D716}^{c}}\big)$
for
![]() $c\geqslant 3$
?
$c\geqslant 3$
?
Acknowledgments
The author is grateful to Professor Christopher Hacon, Professor James McKernan, and Professor Chenyang Xu for many useful discussions and suggestions. The author thanks Professor James McKernan for allowing him to include in this article his theory of the covering families of tigers in [McK02]. The author also thanks the referees for their careful reading and very helpful suggestions for improving the presentation of this paper.