Introduction
Over the last three decades, the concept of a ‘neutrino telescope’ has gained increasing traction within the world's astrophysics community (Chiarusi and Spurio, Reference Chiarusi and Spurio2010). Owing to their inertness to electromagnetic interactions (on which the light-based telescopes which have dominated astronomy for the last four centuries are based), neutrinos offer direct information on the internal processes, otherwise obscured to light-based telescopes, that drive the most explosive cosmic accelerators. From a particle physics perspective, whereas photon ‘messengers’ probe electromagnetic force interactions, neutrino messengers probe weak force interactions. Experimental measurements of cosmic ray protons or heavier atomic nuclei probe strong force, weak force and also electromagnetic interactions. This has given rise to the emerging field of ‘multi-messenger astronomy’ (Bartos and Kowalski, Reference Bartos and Kowalski2017), which has, as its primary goal, formulating a complete picture of the high-energy Universe (Mészáros and others, Reference Mészáros, Fox, Hanna and Murase2019). Synthesis of measurements from contemporary gamma-ray, charged cosmic-ray, neutrino and even gravitational wave observatories allows considerably enhanced refinement of astrophysical models than afforded by one cosmic messenger alone.
Owing to their inertness, however, a neutrino telescope requires a massive instrumented volume in order to register statistically significant event rates; this challenge grows at the highest neutrino energies due to the precipitously falling flux with increasing neutrino energy. The Earth's polar ice sheets comprise a large and nearly homogeneous target volume for cosmic neutrinos, which can then be detected via the Cherenkov radiation following an interaction of a neutrino with an ice molecule. At the highest neutrino energies, detection of coherent radio-frequency emissions is perhaps the most cost-effective approach given the high transparency of cold polar ice to radio waves (Barwick and others, Reference Barwick, Besson, Gorham and Saltzberg2005; Besson, Reference Besson2008; Barrella and others, Reference Barrella, Barwick and Saltzberg2011; Allison, Reference Allison2012; Avva and others, Reference Avva, Kovac, Miki, Saltzberg and Vieregg2014; Hanson, Reference Hanson2015; Aguilar and others, Reference Aguilar2022). Detailed site-specific ice dielectric measurements are required to confidently quantify the expected neutrino detection rate at a given location. The imaginary component of the permittivity, for example, determines the amount of absorption per unit length as signal propagates from interaction point to measurement point, and therefore the total effective neutrino target volume.
The recently initiated Radio Neutrino Observatory in Greenland (RNO-G), located at Summit Station on the Greenland ice sheet, seeks first-ever detection of so-called ‘cosmogenic’ neutrinos (Aguilar, Reference Aguilar2021). In tandem with the deployment of the first radio receivers in the summer of 2021, an extensive data sample was accumulated to quantify the ice radio-glaciological characteristics at Summit Station. Below, we detail measurements, not only of the bulk ice attenuation length, but also of the reflective characteristics of radio-scattering layers embedded within the ice sheet itself. Via reflection back to a surface receiver, such layers also afford a measurement of the polarization dependence of the in-ice wavespeed (‘birefringence’), as well as variation of wavespeed with frequency (‘dispersion’).
Summit Station radioglaciology
The Summit Station site is among the best-studied glaciological sites in the world. The original drilling and extraction of the 3027-m GRIP and 3053-m GISP-2 cores in the 1990s was followed by comprehensive conductivity and chemistry analysis (Taylor and others, Reference Taylor1993). This has been complemented by aerial and ground-based radar sounding (Corr and others, Reference Corr, Moore and Nicholls1993; Paden and others, Reference Paden, Akins, Dunson, Allen and Gogineni2010), providing both extensive layering and ice thickness information in the vicinity of the Summit. Relevant to the measurements outlined below:
• As revealed by aerial surveys, the bedrock topography in the vicinity of Summit is observed to be highly faceted (Paden and others, Reference Paden, Akins, Dunson, Allen and Gogineni2010).
• Consistent with expectations for a dome, ice flow is minimal at Summit, with measured velocities of order 1 m a−1 in the direction of Grid West (Hawley and others, Reference Hawley, Neumann, Stevens, Brunt and Sutterley2020).
• Ice fabric measurements indicate that the ĉ-axis (defined as a normal to the englacial ice crystal face) distribution, projected onto the horizontal plane is approximately isotropic in azimuth (i.e. ‘uniaxial’, such that the horizontal directional eigenvalues of the fabric orientation ellipsoids E1 and E2 are approximately equal, but differ from the vertical eigenvalue E3), consistent with the slow ice flow at the top of a dome. The ĉ-axis alignment with vertical grows approximately linearly with depth (Thorsteinsson and others, Reference Thorsteinsson, Kipfstuhl and Miller1997); by a depth of 3 km, the ĉ-axis distribution is almost entirely vertically aligned.
The last two considerations suggest that the refractive indices for signals propagating vertically, but with polarization pointing in any arbitrary direction in the horizontal plane are approximately uniform (n 1 ≈ n 2, where n 1 and n 2 are the refractive indices for signals with polarizations pointing parallel and perpendicular, respectively, to the local ice-flow direction in the horizontal plane). This uniaxial behavior contrasts with the ice fabric at South Pole, for which n 1 ≈ 0.996n 2; n 2 ≈ n 3 (Jordan and others, Reference Jordan2019); here n 3 is the refractive index for vertical signal polarizations.
Methods
Measurements
Our 2021 ice calibration campaign had several aspects, including:
(1) The attenuation length ($L_\alpha$
 ) determines the neutrino detector effective volume for in-ice radio receiver arrays at high neutrino energies ($E_\nu \gtrsim 1$
) determines the neutrino detector effective volume for in-ice radio receiver arrays at high neutrino energies ($E_\nu \gtrsim 1$ EeV).
EeV).(2) Reflection of radio-frequency signals by internal layers can both complicate signal recognition and also present a potential background channel when above-surface radio-frequency noise propagating into the ice may be reflected upward toward a shallower receiver (Rx) antenna. This necessitates an accurate measurement of the absolute reflectivity of those layers.
(3) Since a depth-dependent refractive index profile (n(z)) results in curved, rather than rectilinear ray trajectories, some neutrino interaction vertices are inaccessible to shallow radio receivers. The functional form of n(z) therefore determines the degree of ‘shadowing’ for signals arriving from primarily horizontal directions; this effect is most important at the lowest detectable energy neutrinos using the radio technique ($E_\nu \lesssim 100$
 PeV). Numerically, n(z) can be extracted by comparing the time difference between two optical paths, one directly connecting a radio transmitter to a receiver, and the other determined from reflection off either an internal layer or the ice–air interface.
PeV). Numerically, n(z) can be extracted by comparing the time difference between two optical paths, one directly connecting a radio transmitter to a receiver, and the other determined from reflection off either an internal layer or the ice–air interface.(4) Anisotropy in signal velocity with electric-field $\vec {E}$
 polarization direction (‘birefringence’) leads to signal splitting and rotation of polarization vectors (Matsuoka and others, Reference Matsuoka, Wilen, Hurley and Raymond2008; Besson and others, Reference Besson, Kravchenko, Ramos and Remmers2010; Jordan and others, Reference Jordan2019; Connolly, Reference Connolly2022; Heyer and Glaser, Reference Heyer and Glaser2023), depending on propagation and polarization directions, with signal arrival time staggers of order 1–10 ns km−1 of distance propagated, and quantified by comparing arrival times for a variety of geometries.
polarization direction (‘birefringence’) leads to signal splitting and rotation of polarization vectors (Matsuoka and others, Reference Matsuoka, Wilen, Hurley and Raymond2008; Besson and others, Reference Besson, Kravchenko, Ramos and Remmers2010; Jordan and others, Reference Jordan2019; Connolly, Reference Connolly2022; Heyer and Glaser, Reference Heyer and Glaser2023), depending on propagation and polarization directions, with signal arrival time staggers of order 1–10 ns km−1 of distance propagated, and quantified by comparing arrival times for a variety of geometries.(5) To the extent that the polar ice medium is dispersive in the relevant frequency regime (hundreds of MHz), a sharp, nanosecond-scale signal produced by neutrino collisions with molecular ice can spread in the time domain and arrive at the receiver with a considerably diminished peak amplitude. We measure this by comparing signal propagation velocities as a function of frequency. Since antenna group delays lead to similar effects, those must be unfolded to quantify dispersion resulting from the ice medium itself.
Experimental configuration
Data were taken using the same experimental configuration as recently reported for the in-ice radio-frequency attenuation length measurement, calculated by normalizing to through-air propagation (Fig. 1, reproduced from Aguilar and others, Reference Aguilar2022). Schematically, the set-up is typical of bi-static radar experiments. A high-gain transmitter antenna beams signal downward into the ice and the reflected signals are recorded in a similar, downward-facing high-gain receiver antenna, connected to a low-noise amplifier (LNA), and horizontally displaced by ~244 m. To improve the signal coupling to the surface snow, both transmitter and receiver antennas were buried ~2 m. The signal trigger is provided by a direct above-ice transmitter$\to$![]() above-ice receiver antenna. We use a sharp (~1 ns rise time) pulsed signal to elucidate sharp internal features, rather than the ~microsecond-duration fixed-frequency tones often employed for mapping ice thickness and bedrock topography (Rodriguez-Morales and others, Reference Rodriguez-Morales2013).
above-ice receiver antenna. We use a sharp (~1 ns rise time) pulsed signal to elucidate sharp internal features, rather than the ~microsecond-duration fixed-frequency tones often employed for mapping ice thickness and bedrock topography (Rodriguez-Morales and others, Reference Rodriguez-Morales2013).

Figure 1. Set up for data-taking at Summit Station, Greenland during August 2021. Signal chain is as follows: FID, Inc. FPG6-1PNK Signal Generator at the highest amplitude setting $\to$![]() Mini-Circuits, Inc. NHP-100 100 MHz high-pass filter →10 m LMA-400 coaxial cable $\to$
Mini-Circuits, Inc. NHP-100 100 MHz high-pass filter →10 m LMA-400 coaxial cable $\to$![]() RNO-G LPDA $\to$
RNO-G LPDA $\to$![]() ice reflector $\to$
ice reflector $\to$![]() RNO-G LPDA →10 m LMA-400 coaxial cable $\to$
RNO-G LPDA →10 m LMA-400 coaxial cable $\to$![]() VHF 145+ high-pass filter $\to$
VHF 145+ high-pass filter $\to$![]() RNO-G surface amplifier (~59 dB gain) $\to$
RNO-G surface amplifier (~59 dB gain) $\to$![]() NLF 575+ low-pass filter$\to$
NLF 575+ low-pass filter$\to$![]() Tektronix digital oscilloscope for data recording at 5 GSa s−1.
Tektronix digital oscilloscope for data recording at 5 GSa s−1.
The detailed signal chain is as follows: an FID model FPG6-1PNK signal generator (the same unit described in Besson and others, Reference Besson, Kravchenko, Ramos and Remmers2010) set to maximum signal amplitude is connected to a high-pass filter (Mini-Circuits NHP-100) to inhibit potentially damaging reflections due to poor impedance mismatch outside of the system bandpass. An additional 10 m of LMR-400 coaxial cable is then connected to a commercially available log-periodic dipole antenna (LPDA, CREATE Corp., model CLP5130-2n [http://www.cd-corp.com/eng/cma/clp5130.pdf], and used as surface antennas for both the ARIANNA (Barwick, Reference Barwick2015) and also RNO-G (Aguilar, Reference Aguilar2021) experiments) directed downward into the snow. The LPDA has excellent response (VSWR<2) over the passband, and approximately uniform +10 dB forward gain. At the receiver end, an identical, downward-pointing LPDA, with the receiver antenna plane oriented parallel to the transmitter (Tx) antenna plane (i.e. co-polarized transmitter and receiver orientation) feeds signal into a +59 dB custom amplifier, and, finally, to a Tektronix digital oscilloscope, for digitization and storage. Owing to the frequency-dependent group delay typical of LPDA antennas, the nanosecond-scale pulsed signal broadens to an observed temporal extent of 20 ns, when captured on the digital oscilloscope at the receiver.
Since the return signal strength may depend on the electric field polarization direction, four additional datasets (analyzed for the birefringence measurement) were also taken for which the transmitter and receiver antennas were placed on the surface (again, facing down) and moved to a separation ~10% of the original separation, with the trigger provided by the through-air ‘leakage’ from the transmitter side lobe to the receiver. Those four datasets correspond to azimuthal antenna polarizations co-rotated in 30$^\circ$![]() increments (designated ϕ 0, ϕ 30, ϕ 60 and ϕ 90) from parallel to the local ice-flow direction, to perpendicular to the local ice-flow direction. This angular range should bracket the full range of possible polarization orientations.
increments (designated ϕ 0, ϕ 30, ϕ 60 and ϕ 90) from parallel to the local ice-flow direction, to perpendicular to the local ice-flow direction. This angular range should bracket the full range of possible polarization orientations.
Results and analysis
Coherence of in-ice scattering
In addition to coherent scattering expected from discrete conducting layers, radar signals may be reflected incoherently by either faceted scatterers comparable in size to one wavelength, or sparse individual scatterers with spacing larger than the characteristic radar signal wavelength. Rayleigh scattering (Rayleigh, Reference Rayleigh1881), for example, formally describes the case for which the optical wavelength is much larger than the size of atmospherically distributed scatterers, leading to incoherent 1/r 4 amplitude dependence with distance, and scattering angles increasing with frequency (and therefore often out of our signal beam).
Detailed first-principles calculations of the volumetric scattering expected for airborne ice-penetrating radar (Davis and Moore, Reference Davis and Moore1993) concluded that, although surface and layered scattering dominates in the low-elevation regions of Greenland, volume scattering should dominate airborne radar surveys over the interior plateau (e.g. East Antarctica, Dome C, Vostok and South Pole). Calculations of radio-frequency attenuation lengths using the ‘slopes’ of radar data echograms typically exclude consideration of volume contributions (Matsuoka and others, Reference Matsuoka, MacGregor and Pattyn2012; Stockham and others, Reference Stockham, Macy and Besson2016), although the validity of this assumption that volume scattering can be neglected has not yet been rigorously demonstrated. We note, parenthetically, that attenuation length determinations based on bedrock echoes implicitly include any processes (either due to the bulk volume or discrete layers) which scatter signal out of the main beam. The volume contribution is not only of interest glaciologically, but also important for experiments seeking to measure neutrinos above some radio-frequency background using radar echoes (Prohira, Reference Prohira2021); some of that background may be due to intrinsic thermal, black-body radiation, and some may be due to volume scattering.
Measuring coherent vs incoherent scattering
During data-taking, the digital oscilloscope recorded ~50 μs of data, including 4.5 μs prior to the event trigger, and ~10 μs beyond the deepest observed echo, corresponding to the bedrock at a depth of ≈3 km. To numerically quantify the relative contributions of coherent (e.g. layer scattering) vs incoherent (including volume scattering) signals, 20 separate runs, each comprising an average of 10 000 individual echo waveform triggers, were taken at Summit Station. For each run, a single data file, consisting of the 10K-averaged waveform, was written to the digital oscilloscope memory. Experimentally, for purely coherent/incoherent signal summation, the phase of the return signal observed at a given time t (measured simply as a voltage at a given time) relative to the data-acquisition trigger time (t 0) is identical/random trigger-to-trigger. For N summed waveform files, coherent scattering amplitudes scale linearly with the number of files co-added (N files) whereas incoherently summed waveform amplitudes vary as $\sqrt {N_{{\rm files}}}$![]() ; the latter corresponds to the expectations for summing thermal noise. Similarly, averaging waveforms for N files will not change the amplitude of a coherent signal, while the RMS for incoherent signals will decrease by a factor ${1}/{\sqrt {N_{{\rm files}}}}$
; the latter corresponds to the expectations for summing thermal noise. Similarly, averaging waveforms for N files will not change the amplitude of a coherent signal, while the RMS for incoherent signals will decrease by a factor ${1}/{\sqrt {N_{{\rm files}}}}$![]() .
.
To apply the approach outlined above to the full waveform capture, we separate our observed echograms into four time regimes. For t < 0 μs, i.e. before the first signals from the transmitting antenna arrive, and prior to the t ≈ 0 trigger signal, data are dominated by noise from the environment, which can serve as a control region for entirely incoherent signals. Some of the radio signal broadcast from the downward-facing transmitter antenna leaks sideways and, via a through-air route, is strong enough to saturate the nearby receiver antenna over the time interval $0\, {\rm \mu }{\rm s} < t\lesssim 5\, {\rm \mu }{\rm s}$![]() . Over this time interval, recorded Rx voltages are dominated by the ringdown of the saturated amplifier, which are identical trigger-to-trigger, and can therefore be used as a control coherent region. This is followed by return signals from any reflectors inside the ice (either coherent or incoherent), until the noise floor is reached at t echo ~ 20 μs.
. Over this time interval, recorded Rx voltages are dominated by the ringdown of the saturated amplifier, which are identical trigger-to-trigger, and can therefore be used as a control coherent region. This is followed by return signals from any reflectors inside the ice (either coherent or incoherent), until the noise floor is reached at t echo ~ 20 μs.
This is demonstrated by the fits in Figure 2, comparing the averaged waveforms for the two specified (pre-trigger ‘control’ incoherent and immediately post-trigger ‘control’ coherent) time intervals.
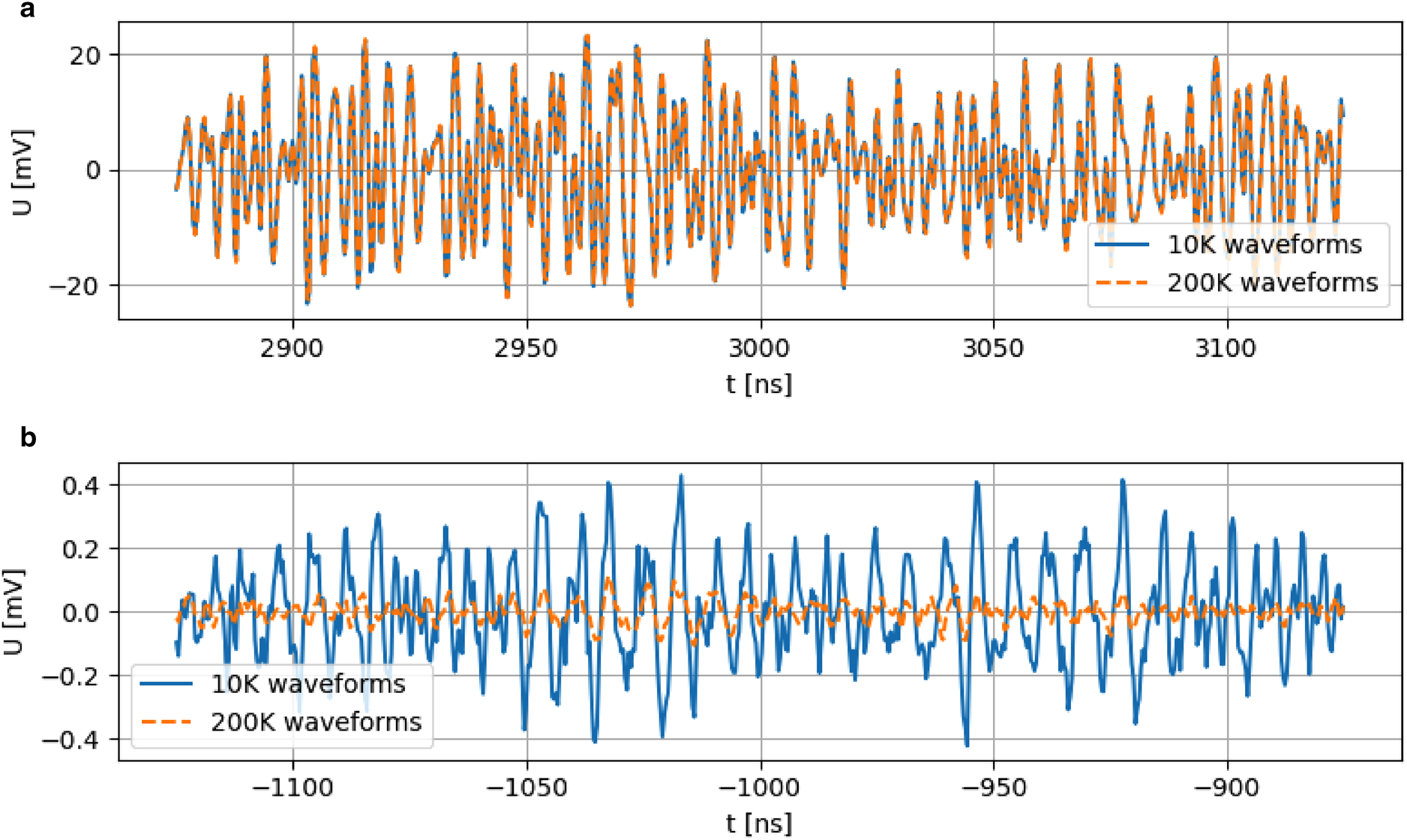
Figure 2. Comparison of the averages from 10 000 waveforms (N files = 1; blue) vs 200 000 waveforms (N files = 20; orange) inside a time window dominated by coherent waveform summation (a) and one dominated by incoherent noise (b).
This statistical contrast between a coherent vs incoherent average allows us to quantify the fractional contribution f c of coherent scattering in our echo data sample.
We measure f c by calculating the root mean square voltage σ V (N files) of the sum of the waveforms for N files, as shown for the two control regions in Figure 3. We then solve for the coherence fraction at a given echo time f c(t echo) by fitting a function of the form
to the σ V (N files) distribution, normalized to σ V (20) = 1, in slices of echo time t echo. The initial result of this exercise, for one of our transmitter/receiver polarization orientations, is shown in Figure 3b. Our experimental data indicate completely coherent scattering for the first 15 μs, after which observed signal amplitudes degrade and become comparable to the t < 0 incoherent control region, albeit with a slight positive offset.
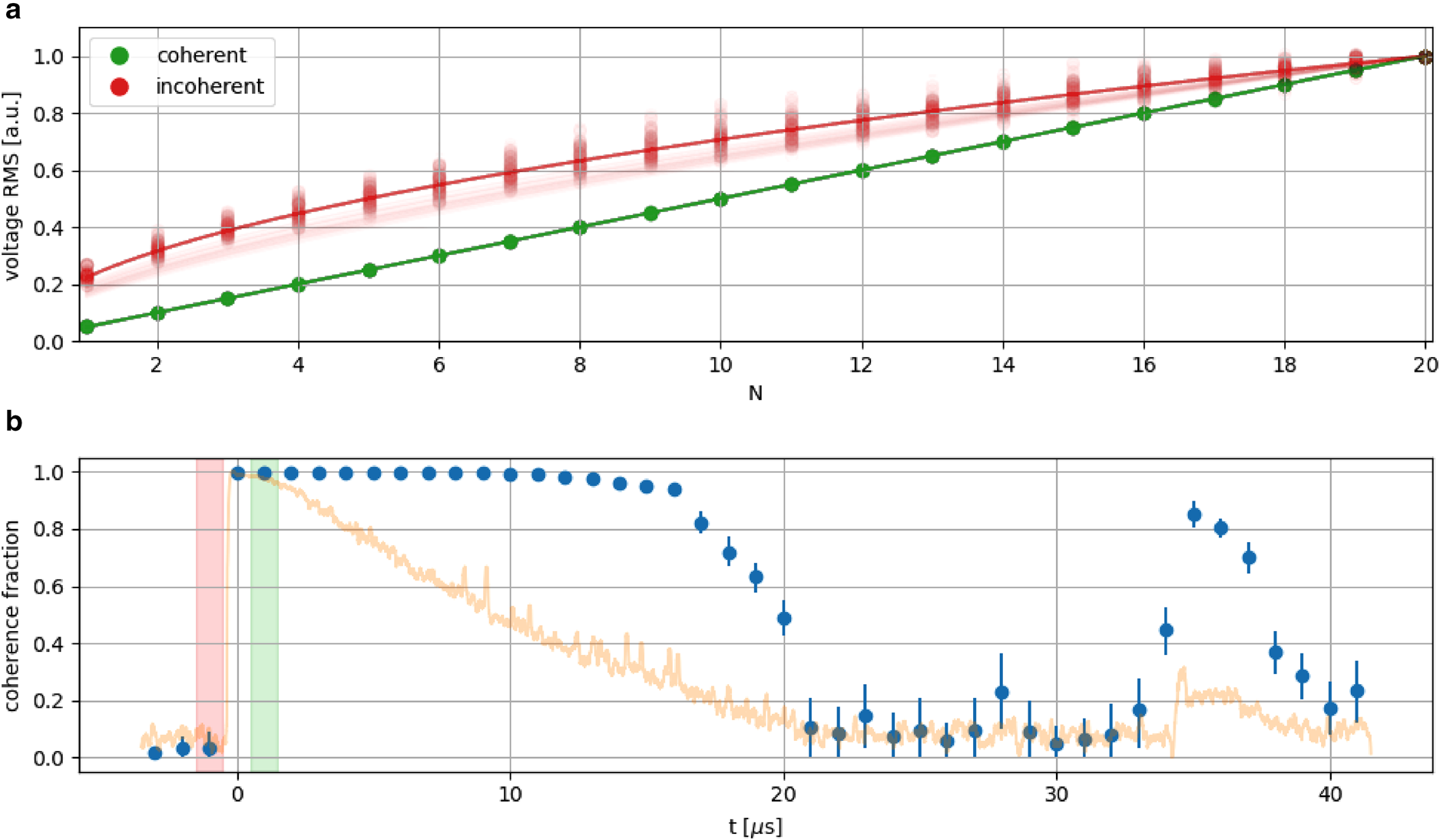
Figure 3. (a) Variation in the root mean square voltage (σ V(N files)) of the sum of the waveforms from N files of 10 000 triggers each, with fits to a linear (green) or square root (red) dependence overlaid. Green shows the result for pure, incoherent noise, red for a time window where the amplifier was saturated and recorded identical voltages event-to-event. Scatter in the green points shows the variation obtained by shuffling the order by which runs are added to the average, to ensure no time-dependent bias in the result. (b) Estimated (pre-corrections; see below) relative contribution of coherent scattering to the return signal as a function of signal travel time. The green and red shaded areas mark the time window used for panel (a). For reference, the logarithm of the return power of the return signal (arbitrarily normalized) is overlaid in orange, showing the simultaneity of the bedrock echo at ≈35 μs with an interval of high coherence.
Cross-checks
We have performed several cross-checks of the result presented above, as follows:
(1) Data-driven vs parameterized fitting procedure: In addition to fitting our data as described above, we can also perform a bin-by-bin χ 2 fit to the σ V(N files) distributions, for a given bin of echo return time. In this case, we use our ‘control’ incoherent vs coherent histograms (Fig. 3a) as inputs, and, for an arbitrary time slice, directly fit to the linear sum of the two histograms that gives the best match to the observed σ V(N files) distribution for a non-control echo time bin. This procedure is observed to give essentially identical results to the parametric fitting approach outlined above.
(2) Dependence on number of sub-samples used for fitting. Rather than fitting our data using 20 data points (one per file), we can combine data samples pairwise and refit to 10 points of 20 K events per point. As expected, this gives consistent results – the smaller number of data points is compensated by the smaller scatter point-to-point.
(3) Dependence on return echo binning. We have verified that binning our results in 1 μs echo return bins vs 250 ns echo return bins yields consistent results.
(4) To allow for the possibility that the LNA gain may slightly change over time, or that a data file may have been contaminated by background triggers, we repeated the fitting procedure by shuffling (i.e. randomizing) the order by which each of the 20 files were added to the average. This resulted in no change in our final coherence plot.
(5) Check of amplitude independence of f C ≡ 1. We have verified that our procedure returns complete coherence, independent of amplitude, by inputting the same 10 K data file 20 times to our fitting algorithms and recovering 100% coherence over the entire duration of the echogram, as expected.
(6) We have extracted the fractional coherence using a phase-variation technique for which we measure the RMS spread δ V between the measured voltages, for a given time bin, run-to-run. We use the voltage recorded at a given time in a given trace as a proxy for the phase of the signal; this parameter has previously been shown to have utility in decoding englacial and sub-glacial characteristics from radar measurements (Hills and others, Reference Hills2022). As outlined previously, in the case of complete coherence, the measured phase/voltage at a given waveform time should be identical run-to-run; in the case of incomplete coherence, the measured phase/voltage at a given time should vary randomly. To map the true δ Phase,true to our observed δ Phase,measured distribution, we use a ‘toy’ Monte Carlo, which eschews all experimental hardware details, and simulates only the calculational aspects of our coherence determination. This Monte Carlo allows us to vary the relative input fractions of incoherent Gaussian noise and a coherent sinusoid, and determine a correction function $R_{\rm C}^{{\rm true}}( \delta _{{\rm Phase, measured}})$
 . After correction, this phase-based approach yields coherence results consistent with those obtained by tracking the RMS dependence on N files. (We have verified that any arbitrary coherent function having the same simulated voltage for each time bin in the simulated data file, other than a sinusoid, gives identical results.)
. After correction, this phase-based approach yields coherence results consistent with those obtained by tracking the RMS dependence on N files. (We have verified that any arbitrary coherent function having the same simulated voltage for each time bin in the simulated data file, other than a sinusoid, gives identical results.)(7) We find reasonable consistency between our results for four different datasets, corresponding to data collected at the four different azimuthal polarization orientations.
In principle, the 15 μs time interval preceding the bedrock echo can have contributions from both incoherent volume scattering and also thermal noise. We conclude that thermal noise dominates this interval, based on: (a) the expected inverse quartic dependence of volume scattering with distance would imply a depth-variable contribution varying by approximately an order of magnitude (10 dB) over this echo interval, inconsistent with our data, which shows a relatively flat dependence on echo time (Fig. 4). (b) A direct comparison of data taken while the transmitter was off compared to data taken while the transmitter was on shows approximately identical RMS voltages over this interval, as well (Fig. 4). (c) Performing an absolute calculation of the expected level of thermal noise, using P thermal = k BTB (here, k B is Boltzmann's constant, T is the ambient temperature in Kelvin, taken to be 250 K and B is the bandwidth of our system, taken to be 400 MHz) also yields an expectation for a thermal noise contribution within ~25% of observation.

Figure 4. Comparison of traces (10 K trigger averages) recorded for transmitter off (black) vs transmitter on (red); we qualitatively note approximate consistency of the RMS voltages in the 20 → 35 μs time interval, as well as prior to the event trigger, at negative times.
Corrections
Our calculation of the fractional coherence assumes a linear interpolation between the zero-coherence and the full-coherence control samples. That is although we have verified that we measure f c ≡ 1 for a completely coherent data sample, and f c ≡ 0 for a completely incoherent data sample, it is not necessarily the case that 50% coherence will yield f c = 0.5. Using the same toy Monte Carlo as described above, we can similarly determine a correction function, that we apply to the extracted f c(σ V(Nfiles)) distribution shown in Figure 3. Figure 5a shows the mapping from an input f c value in our simulation to a measured value. After applying a correction based on that mapping, we obtain the results presented in Figure 5. Qualitatively, we obtain f c values similar to Figure 3; the primary difference is that the corrected peak bedrock coherence is reduced by ~50%. For echo times up to 15 μs, we verify nearly complete coherence in the echo returns.
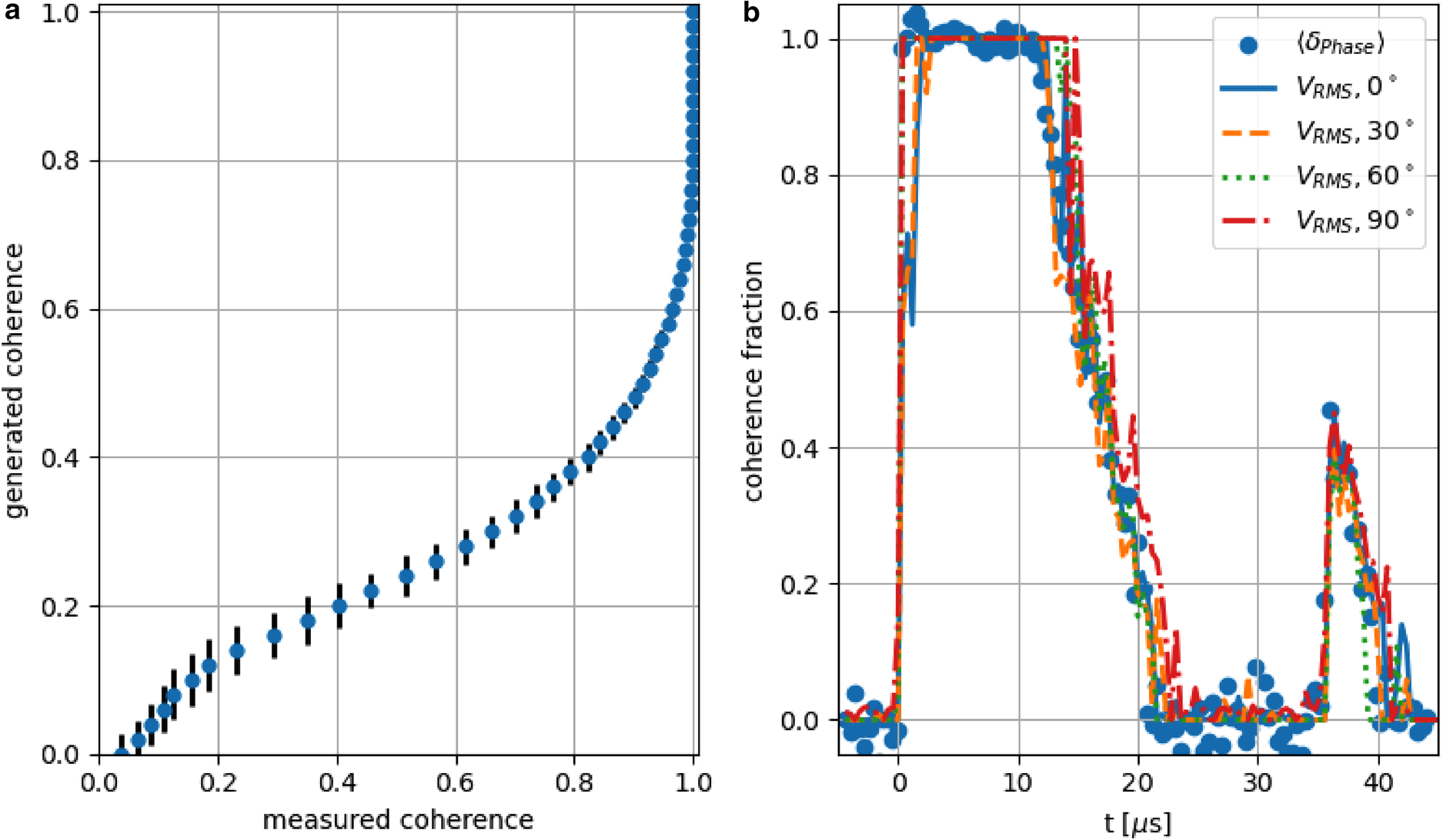
Figure 5. (a) Generated coherence (f c) vs measured coherence, as obtained from Monte Carlo simulations. (b) Coherence fraction f c, after applying toy Monte Carlo-based corrections to coherence extracted using data-driven fit, without constraining relative incoherent/coherent fractions to be bounded by (0,1). Overlaid are results extracted using bin-by-bin phase coherence, from four data samples (taken with varying horizontal polarization angles referenced relative to the local ice-flow direction, as indicated in the legend), as well as after applying a correction to the f c value extracted using the procedure described above, to obtain Figure 3. We note some bins where the extracted coherence fraction either exceeds 1 or is <0. We interpret the scatter about those physical limits as indicative of the systematic errors inherent in our procedure.
Alternatively, rather than extracting the coherence using the RMS of the linear sum of the coherent and incoherent voltage components in our Monte Carlo simulation, we can also consider a quadrature voltage sum as $\sigma _V( {N}_{\rm files}) = \sqrt {\sigma ^2_{V, {\rm coherent}} + \sigma ^2_{V, {\rm incoherent}}}$![]() . This leads to a linear dependence of measured f c value to input f c value in our simulation, and, ultimately, the same measured coherence fraction, as a function of time.
. This leads to a linear dependence of measured f c value to input f c value in our simulation, and, ultimately, the same measured coherence fraction, as a function of time.
Our procedure indicates complete coherence (f c ≡ 1, after averaging 10 K triggers per file) over the echo return interval for which our measured signals significantly exceed the irreducible noise contribution, corresponding to return times <15 μs.
Three caveats are appropriate here:
• A higher-power transmitter would likely have greater depth reach in probing coherence and be capable of extending the coherence regime beyond 15 μs, and/or yield a larger measured bedrock coherence. The results presented herein therefore can be interpreted as a lower limit on the coherence fraction.
• Our results are specific for our data averaging. We cannot exclude the possibility that, event-by-event, incoherent volume scattering significantly contributes to the time interval over which we measure complete coherence (t < 15 μs), since that component has already been reduced by a factor of 100 owing to the 10 K averaging, prior to waveform recording.
• For the bedrock, we stress that our measured coherence is distinct from the intrinsic reflectivity of the subglacial bed, which itself has been the subject of extensive study (Schroeder and others, Reference Schroeder, Blankenship, Raney and Grima2014; Jordan and others, Reference Jordan2017) – in our data, for example, we observe complete coherence for shallower layers with very small intrinsic reflectivities (discussed later).
Attenuation length
Absolutely calculated frequency-dependent attenuation length
We now describe an ‘absolute’ attenuation length measurement, based solely on the strength of the observed through-ice, bedrock-reflected signal, combined with our laboratory-derived values for the system transfer function. This provides a partially independent check on the recently published measurement (Aguilar and others, Reference Aguilar2022) derived by normalizing the observed in-ice bedrock reflection to a through-air Tx → Rx broadcast. Note that one of the primary uncertainties in that prior measurement (the bedrock signal reflectivity R) remains in this measurement, as well. As previously outlined (Aguilar and others, Reference Aguilar2022), the ‘absolute’ extraction of the attenuation length can be derived from standard radar expressions. The Friis equation (Shaw, Reference Shaw2013) prescribes the free space wavelength-dependent received power P Rx given the power output from a transmitter P Tx, over the frequency band overlapping with the receiver frequency response, for propagation over a distance d through a medium with frequency-dependent average field attenuation length $\langle L_\alpha \rangle$![]() :
:
here, F is a flux-focusing factor, R the bedrock reflectivity, λ the wavelength being broadcast (since the signal is impulsive, we transform into the frequency domain and calculate transmission amplitudes in frequency bins), ${{\cal G_{\rm LNA}}}$![]() the gain of the LNA, and ${{\cal G}_{\rm Tx}}$
the gain of the LNA, and ${{\cal G}_{\rm Tx}}$![]() and ${{\cal G}_{\rm Rx}}$
and ${{\cal G}_{\rm Rx}}$![]() refer to the gain of the transmitter and receiver antennas, respectively.
refer to the gain of the transmitter and receiver antennas, respectively.
To quantify the bedrock echo signal power, we use the same power integration window (0.5 μs) used in the companion analysis (Aguilar and others, Reference Aguilar2022). The numerical values for the quantities needed to extract the attenuation length are similarly taken from the companion paper; the primary difference is that the gain characteristics of the amplifiers and losses in cables and connectors must be explicitly inserted as multiplicative corrections to the value of P Tx input to the equations above, whereas in the previous measurement these systematics largely cancel. Applying the Friis equation to the frequency-binned signal power, we obtain the attenuation length, as a function of frequency, as shown in Figure 6. As in the companion paper, we use a Monte Carlo method, where each parameter is varied randomly within its uncertainties and the total error estimated from the resulting distribution of attenuation lengths. We draw uncertainties on the bedrock reflectivity R, the signal propagation distance d and the focusing factor F from the previous publication. The relative uncertainty in the gain of the LNA is estimated as σ LNA = 0.1, based on Aguilar, Reference Aguilar2021, and the gain of the antennas, which are identical to those used by the ARIANNA experiment, has an estimated relative gain uncertainty $\sigma _{\cal G} = 0.15$![]() (Barwick, Reference Barwick2017).
(Barwick, Reference Barwick2017).

Figure 6. Calculated attenuation length, as a function of frequency, obtained by Friis calculation of bedrock echo power measured in a receiver LPDA relative to the calculated signal power transmitted into the ice sheet by an identical LPDA, at Summit Station, Greenland. The prior results obtained using the in-air normalization are overlaid (Aguilar and others, Reference Aguilar2022). Downward-pointing arrows indicate that negative error bars extend beyond the lower limit of the plot.
We obtain final values typically within 10% of results previously reported using the through-air normalization technique (Aguilar and others, Reference Aguilar2022), albeit consistently lower. We consider this level of agreement adequate to justify applying this calculational machinery to a measurement of internal layer reflectivity (described below), which was one of the original science goals.
Cross-check of attenuation measurement using envelope of return power profile
The measurement shown in the previous section yields the average attenuation through the entire thickness of the ice sheet. The bulk attenuation is expected to be dominated by the deepest (and warmest) ~1 km of the ice sheet, while the most relevant region for radio neutrino detectors is the upper ~1.5 km, where the majority of detectable neutrino interactions are expected to occur.
The power envelope from in-ice scattering, which (as demonstrated previously) should coherently scale with distance as 1/r 2 provides an additional measure of attenuation in the upper portion of the ice sheet. Having measured the total two-way loss to the bedrock and back, we invoke a model of relative attenuation, as a function of depth to infer the total signal diminution to an arbitrary depth within the ice, as detailed in the companion measurement (Aguilar and others, Reference Aguilar2022). We attribute any additional loss, beyond inverse quadratic, to attenuation (Corr and others, Reference Corr, Moore and Nicholls1993; Matsuoka and others, Reference Matsuoka, MacGregor and Pattyn2012; MacGregor and others, Reference MacGregor2007, Reference MacGregor2015). This approach is complementary to the ground echo measurement, as it is not affected by the deeper parts of the ice sheets and very little affected by systematic uncertainties in the instrumental response.
We follow MacGregor and others, Reference MacGregor2015 for the depth dependence of the attenuation length, which takes into account the conductivity variation with temperature of impurities in the ice. Figure 7 shows the measured return power as a function of echo time, calculated by integrating the square of the voltages over a 100 ns sliding time window. Superimposed is the expectation using the model of MacGregor and others for attenuation, as a function of depth. The measured return power has been re-scaled to match the expectation at early times, when the amplifier has just recovered from saturation. For comparison, the expected return power if only the effect of ice temperature is considered, but impurities are ignored (referred to as the pure ice model) is also shown. The pure ice model predicts a longer attenuation length ~1100 m at 150 MHz) at shallower depths compared to the MacGregor model ~850 m at 150 MHz), for which impurities in the ice decrease the attenuation length over the upper ~1500 m of the ice sheet. We observe that the MacGregor model qualitatively matches the shape of the measured return power with depth somewhat better than the pure ice model (other models, such as Paden and others, Reference Paden, Akins, Dunson, Allen and Gogineni2010 give predictions similar to MacGregor and others). These results therefore indicate internal consistency between our measured attenuation length dependence on depth, and the shape of the return echo power envelope measured in our data.

Figure 7. Measured return power of the reflected radio signal overlaid with expectations for attenuation models based on MacGregor and others (Reference MacGregor2015), if impurities are included (purple) or ignored (green).
Englacial layer reflectivity
Internal layers are a well-studied radioglaciological feature (Eisen and others, Reference Eisen, Wilhelms, Nixdorf and Miller2003). If the reflectivity of internal layers is sufficiently high, radio signals generated by down-going ultra-high energy cosmic ray air showers impacting the snow surface, and subsequently reflected upward to a shallower radio receiver may present an irreducible background to neutrino searches (De Kockere and others, Reference De Kockere, de Vries and van Eijndhoven2021; Rice-Smith, Reference Rice-Smith2022). We directly apply the formalism described previously, used to ‘absolutely’ extract the attenuation length to a calculation of the absolute reflectivity of the observed internal layers. In this case, rather than inputting a value for the bedrock reflectivity, as we do for the attenuation length measurement, we use the measured return strength at a given echo time to extract the reflectivity itself. We use our own measurement of attenuation length, as a function of depth, to quantify the in-ice signal absorption, down to a given layer depth (Aguilar and others, Reference Aguilar2022). Figure 8a highlights the layers considered; the right panel shows, for each of the considered layers, the Friis-derived reflectivity as a function of frequency. Reflectivities are ~−65 dB, with no clear dependence on frequency or depth.

Figure 8. (a) Return power as a function of signal propagation time. The colored bands mark the position of the considered radio reflectors. (b, c) Calculated (color-coded) reflectivities, as a function of frequency. For better readability, the measurements have been split between two figures, with (b) showing the first five reflectors and (c) the last six reflectors.
Systematic errors for this absolute reflectivity measurement are assessed using a simulation, similar to that used for the absolute attenuation length measurement (Aguilar and others, Reference Aguilar2022). The uncertainties in the antenna and amplifier gains, firn focusing and the refractive index are identical to Aguilar and others (Reference Aguilar2022); the integrated attenuation to a given layer is calculated using our own attenuation length measurement, and also varied within the corresponding errors. We ignore any possible correlated errors between the varied quantities, which yields a conservative estimate of our total uncertainties after adding all errors in quadrature. During the measurements to check for birefringence (see the following section), we noticed that the magnitude of the return power from bulk ice reflections varied between different antenna orientations relative to the direction of ice flow by as much as 40%. Admitting the possibility that this may have been an instrumental effect, we correspondingly assume an additional 40% uncertainty on the return power in our calculation of the total error.
Polarization dependence and birefringence
Unlike South Pole, for which the measured crystal orientation fabric (COF) exhibits a strong variation in the horizontal plane (Voigt, Reference Voigt2017), the measured COF at Summit Station is significantly more azimuthally isotropic, corresponding to a uniaxial, rather than biaxial, COF. Figure 9 (Thorsteinsson and others, Reference Thorsteinsson, Kipfstuhl and Miller1997) shows the published eigenvalues of the crystal-orientation fabric ellipsoid, illustrating the near equivalence of the E1- (parallel to ice flow) and E2- (perpendicular to ice flow, in the horizontal plane) eigenvalues and the increasing dominance of the E3-eigenvalue (ẑ-direction) with depth, as compression effects increasingly rotate the ĉ-axis toward the vertical.

Figure 9. Published Summit Station magnitudes of horizontal (E1 and E2) vs vertical (E3) components of COF tensor for data (Thorsteinsson and others, Reference Thorsteinsson, Kipfstuhl and Miller1997), referenced relative to local ice-flow direction, and also direction of vertical.
Consequently, we expect birefringent effects to be less evident for a vertically propagating signal at Summit Station compared to South Pole. To test this, we considered the radar echo datasets taken at varying azimuths relative to the local ice flow (approximately due west [$\phi _0 = 0^\circ$![]() ], at a velocity an order of magnitude smaller than for South Pole (Hawley and others, Reference Hawley, Neumann, Stevens, Brunt and Sutterley2020)). Biaxial birefringence can result in a ϕ-dependent wave velocity in ice – at South Pole, this corresponds to maximum time lag δ(t) ~ 10 ns km−1 of traversed ice for vertical echoes reflected from the bedrock (Allison, Reference Allison2020).
], at a velocity an order of magnitude smaller than for South Pole (Hawley and others, Reference Hawley, Neumann, Stevens, Brunt and Sutterley2020)). Biaxial birefringence can result in a ϕ-dependent wave velocity in ice – at South Pole, this corresponds to maximum time lag δ(t) ~ 10 ns km−1 of traversed ice for vertical echoes reflected from the bedrock (Allison, Reference Allison2020).
Assuming the Summit dome is a geologically stable location, the maximal effect should be observable for configurations parallel vs perpendicular to the local ice-flow direction. To quantify birefringence, we therefore window the summed and averaged waveforms ±2 μs around the observed onset of the bedrock echo for (a) azimuthal polarization parallel to the flow axis (ϕ 0) and (b) azimuthal polarization perpendicular to the flow axis (ϕ 90). We find that the value of the cross-correlation between these two-windowed waveforms is maximized when we apply a time offset of +1.6 ns to the perpendicular-flow waveform. (As a cross-check, we verified that the 30 and 60$^\circ$![]() data samples, relative to ϕ 0 were statistically consistent with zero-time offset.) To quantify uncertainties, we perform a similarly windowed cross-correlation between all unique pairs of the twenty event files (each comprising 10 K averaged events) corresponding to a single ϕ orientation; the distribution of time offsets peaks at 0.10 ns (consistent with zero, as expected), with a std dev. of 3.3 ns. We therefore quote a birefringent time asymmetry of 1.6 ± 3.3 ns, compared with a central value of 53 ns measured at the South Pole (Besson and others, Reference Besson, Kravchenko, Ramos and Remmers2010), over a 6% shorter pathlength. Our measured value is considerably smaller than the group delay of typical radio neutrino experiments, indicating that birefringence will not be as important a consideration in reconstructing neutrino signals following primarily vertical trajectories, compared to South Pole. Additional work is needed to quantify this effect for horizontal trajectories, which admit both vertical and also horizontal polarizations.
data samples, relative to ϕ 0 were statistically consistent with zero-time offset.) To quantify uncertainties, we perform a similarly windowed cross-correlation between all unique pairs of the twenty event files (each comprising 10 K averaged events) corresponding to a single ϕ orientation; the distribution of time offsets peaks at 0.10 ns (consistent with zero, as expected), with a std dev. of 3.3 ns. We therefore quote a birefringent time asymmetry of 1.6 ± 3.3 ns, compared with a central value of 53 ns measured at the South Pole (Besson and others, Reference Besson, Kravchenko, Ramos and Remmers2010), over a 6% shorter pathlength. Our measured value is considerably smaller than the group delay of typical radio neutrino experiments, indicating that birefringence will not be as important a consideration in reconstructing neutrino signals following primarily vertical trajectories, compared to South Pole. Additional work is needed to quantify this effect for horizontal trajectories, which admit both vertical and also horizontal polarizations.
Dispersion
Among the ice parameters critical to the design of an in-ice radio-frequency neutrino detection experiment is the variation of refractive index over the relevant system frequency band, i.e. dispersion. Laboratory studies of pure ice indicate that the dependence of wavespeed on frequency at radio-frequencies (n(ω)) should be insignificant over the signal propagation distances typical of experiments such as RNO-G (Fujita and others, Reference Fujita, Matsuoka, Morishima and Mae1993). Nevertheless, there are relatively few direct in situ determinations of dispersion (Besson and others, Reference Besson, Kravchenko, Ramos and Remmers2010). One approach for measuring this critical parameter is to measure the simultaneity of the bedrock echo as one sweeps in frequency, using bi-static surface radar.
Given the λ 2 dependence of the antenna effective area, we have banded our data into two frequency bins, spanning 150–190 and 190–340 MHz, respectively. Owing to the intrinsically dispersive nature of the transmitter and receiver LPDA antennas, we expect that the observed signals should exhibit ~10–20 ns offset between the signal onset for the lower- vs higher-frequency signal bands. The high-frequency signal arrival for the through-air path is, indeed, observed to precede the low-frequency signal arrival by 22.5 ± 4.2 ns (Fig. 10).

Figure 10. Frequency-banded signals for in-air broadcasts between LPDA surface transmitter and LPDA surface receiver. The observed time shift in signal arrival times is consistent with the known, intrinsically dispersive properties of the LPDA antennas.
Cross-correlating the observed high-frequency bedrock echo with the observed low-frequency bedrock echo yields a time offset of 21.4 ± 4.0 ns, statistically consistent with the offset observed for the through-air path. Subtracting that offset, we obtain a time difference between the two bands of 1.1 ± 5.6 ns (adding the statistical uncertainties on the bed and through-air offsets in quadrature). Normalized to the total bedrock echo time of 35.5 μs implies a dispersive slope (3.1 ± 15.8) × 10−5 per 100 MHz. This value is statistically consistent with the value obtained at the South Pole (Besson and others, Reference Besson, Kravchenko, Ramos and Remmers2010), albeit with a larger attendant error, due in part to the more dispersive LPDA antennas used as transmitter/receiver, and in part owing to the more restricted frequency band over which these measurements were made.
Conclusions
We summarize our results as follows:
(1) Based on the statistics of our observed signals, and the dependence of the measured RMS-voltage with sample size, we find no clear evidence for incoherent scattering within the ice-sheet volume, after averaging N trigger=10 K triggers per recorded waveform. However, we cannot exclude the possibility that incoherent scattering may contribute more significantly as N trigger approaches 1.
(2) Using the Friis equation, we determine the radio-frequency ice attenuation length at Summit Station and reproduce (to ≈10%) the values previously calculated by normalizing the in-ice reflection to a through-air broadcast (Aguilar and others, Reference Aguilar2022). These results are supported by an analysis of the slope of the radar return power envelope.
(3) Using the same approach as for the bedrock reflector, we similarly measure the reflectivity of internal layers at Summit Station. We obtain values in the range −60 to −70 dB, roughly consistent with values obtained in a similar analysis at South Pole (Besson and others, Reference Besson, Kravchenko and Nivedita2023).
(4) Consistent with expectations based on the known crystal fabric at Summit Station, Greenland, no significant birefringent effects are observed in our radar sounding data for vertically propagating signals.
(5) We observe no statistically significant evidence for dispersion of radio-frequency signals propagating in ice, over the frequency interval 150–340 MHz.
Overall, from a radio-glaciological perspective, Summit Station is an extremely propitious site for in-ice neutrino detection. Given the importance of ice properties to neutrino detection, future campaigns anticipate an expansion of the calibration measurements cited herein, including measurements of birefringence along horizontal trajectories, more precise parameterizations of the refractive index dependence on depth, and measurement of both cross-polarized reflection strengths, as well as those of internal layer reflections in the upper 200 m of the ice sheet.
Acknowledgements
We thank the staff at Summit Station and Polar Field Services for their unflagging and superb logistical support. We thank our home institutions and funding agencies for supporting the RNO-G work; in particular the Belgian Funds for Scientific Research (FRS-FNRS and FWO) and the FWO program for International Research Infrastructure (IRI), the National Science Foundation through the NSF Awards 2118315 and 2112352 and the IceCube EPSCoR Initiative (Award ID 2019597), the German research foundation (DFG, Grant NE 2031/2-1), the Helmholtz Association (Initiative and Networking Fund, W2/W3 Program), the University of Chicago Research Computing Center, and the European Research Council under the European Union's Horizon 2020 research and innovation program (grant agreement No. 805486).





















