1. Introduction
Conditionals of the form ‘if A then usually B’ state a conneQction between the antecedent A and the consequent B that is plausible, but that also carries uncertainty and is defeasible. A semantics for conditional belief bases
![]() $\Delta$
consisting of a set of conditionals typically provides a means for ordering the underlying possible worlds
$\Delta$
consisting of a set of conditionals typically provides a means for ordering the underlying possible worlds
![]() $\Omega$
according to their plausibility. Ranking functions
$\Omega$
according to their plausibility. Ranking functions
![]() $\kappa$
(Spohn, Reference Spohn, Harper and Skyrms1988) do this by assigning a degree of implausibility to the worlds via a mapping
$\kappa$
(Spohn, Reference Spohn, Harper and Skyrms1988) do this by assigning a degree of implausibility to the worlds via a mapping
![]() $\kappa\;:\; \Omega \rightarrow \mathbb{N} \cup \{\infty\}$
; the higher the rank
$\kappa\;:\; \Omega \rightarrow \mathbb{N} \cup \{\infty\}$
; the higher the rank
![]() $\kappa(\omega)$
of a possible world
$\kappa(\omega)$
of a possible world
![]() $\omega$
, the less plausible or the more surprising it is, with a rank of infinity indicating that a world is completely implausible. A ranking function
$\omega$
, the less plausible or the more surprising it is, with a rank of infinity indicating that a world is completely implausible. A ranking function
![]() $\kappa$
models a conditional ‘if A then usually B’, formally denoted by
$\kappa$
models a conditional ‘if A then usually B’, formally denoted by
![]() ${{(B|A)}}$
, if the verification of
${{(B|A)}}$
, if the verification of
![]() ${{(B|A)}}$
is strictly more plausible than its falsification, that is, if
${{(B|A)}}$
is strictly more plausible than its falsification, that is, if
![]() $\kappa(AB) \lt \kappa(A\overline{B})$
.
$\kappa(AB) \lt \kappa(A\overline{B})$
.
The well-known consistency test for conditional belief bases given by Goldszmidt and Pearl (Reference Goldszmidt and Pearl1996) yields a rather strong notion of consistency. It requires that for
![]() $\Delta$
to be consistent there must exist a ranking function
$\Delta$
to be consistent there must exist a ranking function
![]() $\kappa$
modelling all conditionals in
$\kappa$
modelling all conditionals in
![]() $\Delta$
such that
$\Delta$
such that
![]() $\kappa$
assigns to each world
$\kappa$
assigns to each world
![]() $\omega$
a natural number
$\omega$
a natural number
![]() $\kappa(\omega) \lt \infty$
. Thus, this notion of consistency, which we will refer to as strong consistency in the following, enforces that every world has at least some plausibility, that is, prohiting any completely implausible world
$\kappa(\omega) \lt \infty$
. Thus, this notion of consistency, which we will refer to as strong consistency in the following, enforces that every world has at least some plausibility, that is, prohiting any completely implausible world
![]() $\omega$
with
$\omega$
with
![]() $\kappa(\omega) = \infty$
. Here, we will take a broader view on consistency of belief bases that allows that only a subset of worlds is considered feasible, while other worlds may be infeasible and thus fully implausible, expressed by
$\kappa(\omega) = \infty$
. Here, we will take a broader view on consistency of belief bases that allows that only a subset of worlds is considered feasible, while other worlds may be infeasible and thus fully implausible, expressed by
![]() $\kappa(\omega) = \infty$
. Belief bases satisfying this generalized notion of consistency are called weakly consistent (Haldimann et al., Reference Haldimann, Beierle, Kern-Isberner, Meyer, Chun and Franklin2023). Contrary to strongly consistent belief bases that only contain defeasible beliefs, weakly consistent belief bases can also contain strict beliefs (Casini & Straccia, Reference Casini and Straccia2013). Such strict beliefs correspond to the requirement that some worlds are infeasible, forcing all worlds
$\kappa(\omega) = \infty$
. Belief bases satisfying this generalized notion of consistency are called weakly consistent (Haldimann et al., Reference Haldimann, Beierle, Kern-Isberner, Meyer, Chun and Franklin2023). Contrary to strongly consistent belief bases that only contain defeasible beliefs, weakly consistent belief bases can also contain strict beliefs (Casini & Straccia, Reference Casini and Straccia2013). Such strict beliefs correspond to the requirement that some worlds are infeasible, forcing all worlds
![]() $\omega$
not satisfying a strict belief to have rank
$\omega$
not satisfying a strict belief to have rank
![]() $\kappa(\omega) = \infty$
.
$\kappa(\omega) = \infty$
.
The significance of weakly consistent belief bases is given by their increased expressive power. In a strongly consistent belief base, one can state that a formula A holds plausibly, but one can not express that A definitely holds and that therefore
![]() $\neg A$
is completely ruled out, while this can be expressed straightforwardly in a weakly consistent belief base. Thus, using the concept of weak consistency, one can also realize reasoning from belief bases that contain both conditionals stating defeasible beliefs and formulas in classical logic stating undefeasible strict beliefs.
$\neg A$
is completely ruled out, while this can be expressed straightforwardly in a weakly consistent belief base. Thus, using the concept of weak consistency, one can also realize reasoning from belief bases that contain both conditionals stating defeasible beliefs and formulas in classical logic stating undefeasible strict beliefs.
Inductive inference from a conditional belief base
![]() $\Delta$
means to complete the set of explicit beliefs given in
$\Delta$
means to complete the set of explicit beliefs given in
![]() $\Delta$
to an inference relation representing the beliefs entailed by
$\Delta$
to an inference relation representing the beliefs entailed by
![]() $\Delta$
. The resulting inference relation will contain both the beliefs stated explicitly in
$\Delta$
. The resulting inference relation will contain both the beliefs stated explicitly in
![]() $\Delta$
as well as the beliefs entailed by
$\Delta$
as well as the beliefs entailed by
![]() $\Delta$
. Because
$\Delta$
. Because
![]() $\Delta$
contains defeasible beliefs, the resulting relation is a nonmonotonic inference relation. There is no generally accepted ‘best’ answer to the question what a belief base should entail (Lehmann & Magidor, Reference Lehmann and Magidor1992). For formally capturing the process of inductive inference from
$\Delta$
contains defeasible beliefs, the resulting relation is a nonmonotonic inference relation. There is no generally accepted ‘best’ answer to the question what a belief base should entail (Lehmann & Magidor, Reference Lehmann and Magidor1992). For formally capturing the process of inductive inference from
![]() $\Delta$
, the notion of an inductive inference operator mapping each
$\Delta$
, the notion of an inductive inference operator mapping each
![]() $\Delta$
to an inference relation
$\Delta$
to an inference relation
![]() $\mathord{{|\hspace{-2pt}}{\sim}^{}_{\Delta}}$
has been introduced (Kern-Isberner et al., Reference Kern-Isberner, Beierle, Brewka, Calvanese, Erdem and Thielscher2020). Employing the viewpoint of inductive inference operators, we will consider various inference methods in this article, starting with the seminal p-entailment, that can be characterized by system P (Adams, Reference Adams1975; Kraus et al., Reference Kraus, Lehmann and Magidor1990), and Pearl’s system Z that has been shown to coincide with rational closure (Lehmann, Reference Lehmann, Brachman, Levesque and Reiter1989; Goldszmidt & Pearl, Reference Goldszmidt and Pearl1996). We recall how these inductive inference operators deal with weakly consistent belief bases and how characterizations of them can be used for implementing them.
$\mathord{{|\hspace{-2pt}}{\sim}^{}_{\Delta}}$
has been introduced (Kern-Isberner et al., Reference Kern-Isberner, Beierle, Brewka, Calvanese, Erdem and Thielscher2020). Employing the viewpoint of inductive inference operators, we will consider various inference methods in this article, starting with the seminal p-entailment, that can be characterized by system P (Adams, Reference Adams1975; Kraus et al., Reference Kraus, Lehmann and Magidor1990), and Pearl’s system Z that has been shown to coincide with rational closure (Lehmann, Reference Lehmann, Brachman, Levesque and Reiter1989; Goldszmidt & Pearl, Reference Goldszmidt and Pearl1996). We recall how these inductive inference operators deal with weakly consistent belief bases and how characterizations of them can be used for implementing them.
We then focus on the c-representations (Kern-Isberner, Reference Kern-Isberner2001, Reference Kern-Isberner2004) of a belief base
![]() $\Delta$
, a special kind of ranking functions modelling
$\Delta$
, a special kind of ranking functions modelling
![]() $\Delta$
. c-Representations define inductive inference operators that satisfy most advanced properties of nonmonotonic inference, particularly syntax splitting and conditional syntax splitting (Kern-Isberner et al., Reference Kern-Isberner, Beierle, Brewka, Calvanese, Erdem and Thielscher2020; Heyninck et al., Reference Heyninck, Kern-Isberner, Meyer, Haldimann, Beierle, Williams, Chen and Neville2023; Beierle et al., Reference Beierle, Spiegel, Haldimann, Wilhelm, Heyninck, Kern-Isberner, Marquis, Ortiz and Pagnucco2024). While initially introduced only for belief bases satisfying the strong notion of consistency described above, in this paper, we define extended c-representations that also cover belief bases satisfying the weaker notion of consistency where some possible worlds may be assigned a rank of
$\Delta$
. c-Representations define inductive inference operators that satisfy most advanced properties of nonmonotonic inference, particularly syntax splitting and conditional syntax splitting (Kern-Isberner et al., Reference Kern-Isberner, Beierle, Brewka, Calvanese, Erdem and Thielscher2020; Heyninck et al., Reference Heyninck, Kern-Isberner, Meyer, Haldimann, Beierle, Williams, Chen and Neville2023; Beierle et al., Reference Beierle, Spiegel, Haldimann, Wilhelm, Heyninck, Kern-Isberner, Marquis, Ortiz and Pagnucco2024). While initially introduced only for belief bases satisfying the strong notion of consistency described above, in this paper, we define extended c-representations that also cover belief bases satisfying the weaker notion of consistency where some possible worlds may be assigned a rank of
![]() $\infty$
indicating them to be completely infeasible according to
$\infty$
indicating them to be completely infeasible according to
![]() $\Delta$
. This allows for realizing a kind of paraconsistent conditional reasoning based on the strong structural concept of c-representations. The notion of c-inference was introduced in Beierle et al. (Reference Beierle, Eichhorn, Kern-Isberner, Gyssens and Simari2016a Reference Beierle, Eichhorn, Kern-Isberner and Kutsch2018) as nonmonotonic inference taking all c-representations into account, inheriting the restriction that it is only defined for strongly consistent belief bases. Using extended c-representations, we will introduce an extended version of c-inference that also covers weakly consistent belief bases.
$\Delta$
. This allows for realizing a kind of paraconsistent conditional reasoning based on the strong structural concept of c-representations. The notion of c-inference was introduced in Beierle et al. (Reference Beierle, Eichhorn, Kern-Isberner, Gyssens and Simari2016a Reference Beierle, Eichhorn, Kern-Isberner and Kutsch2018) as nonmonotonic inference taking all c-representations into account, inheriting the restriction that it is only defined for strongly consistent belief bases. Using extended c-representations, we will introduce an extended version of c-inference that also covers weakly consistent belief bases.
The c-representations of a belief base
![]() $\Delta$
can be characterized by a CSP, and in Beierle et al. (Reference Beierle, Eichhorn, Kern-Isberner, Gyssens and Simari2016a); Reference Beierle, Eichhorn, Kern-Isberner and Kutsch2018), it is shown that c-inference can also be realized by a CSP. Here, we develop both a CSP that characterizes all extended c-representations and a simplified version of this CSP the solutions of which still cover all c-representations relevant for c-inference. Furthermore, we show how extended c-inference can be realized by a CSP.
$\Delta$
can be characterized by a CSP, and in Beierle et al. (Reference Beierle, Eichhorn, Kern-Isberner, Gyssens and Simari2016a); Reference Beierle, Eichhorn, Kern-Isberner and Kutsch2018), it is shown that c-inference can also be realized by a CSP. Here, we develop both a CSP that characterizes all extended c-representations and a simplified version of this CSP the solutions of which still cover all c-representations relevant for c-inference. Furthermore, we show how extended c-inference can be realized by a CSP.
An inductive inference operator satisfies syntax splitting if it satisfies the axioms of independence (Ind) and relevance (Rel) (Kern-Isberner et al., Reference Kern-Isberner, Beierle, Brewka, Calvanese, Erdem and Thielscher2020). While these axioms have been developed taking only strongly consistent belief bases into account, here we employ versions of (Ind) and (Rel) adapted to our setting of weakly consistent belief bases and prove that extended c-inference complies with syntax splitting.
While c-inference is skeptical in the sense that it takes every c-representation of
![]() $\Delta$
into account, also credulous and weakly skeptical c-inference have been introduced, the latter lying between the cautious skeptical and the bold credulous reasoning method (Beierle et al., Reference Beierle, Eichhorn, Kern-Isberner and Kutsch2018; Beierle et al., Reference Beierle, Eichhorn, Kern-Isberner and Kutsch2021). We introduce extended versions of these inductive inference methods that cover also weakly consistent belief bases, characterize them by CSPs that can be used for implementations, and show how they relate to the unextended versions requiring strong consistency.
$\Delta$
into account, also credulous and weakly skeptical c-inference have been introduced, the latter lying between the cautious skeptical and the bold credulous reasoning method (Beierle et al., Reference Beierle, Eichhorn, Kern-Isberner and Kutsch2018; Beierle et al., Reference Beierle, Eichhorn, Kern-Isberner and Kutsch2021). We introduce extended versions of these inductive inference methods that cover also weakly consistent belief bases, characterize them by CSPs that can be used for implementations, and show how they relate to the unextended versions requiring strong consistency.
In summary, the main contributions of this article are
-
• Compactly presenting the notion of weak consistency and how its treatment by p-entailment (or system P) and system Z can be characterized and implemented;
-
• Generalizing the concept of c-representations to cover also weakly consistent belief bases and characterizing them as solutions of a CSP;
-
• Extending c-inference by taking all extended c-representations of a belief base into account to cover also weakly consistent belief bases;
-
• Modelling extended c-inference by a CSP, thus providing a basis for implementations;
-
• Proving that extended c-inference fully complies with the syntax splitting postulates for inductive inference operators;
-
• Extending credulous and weakly skeptical c-inference to cover also weakly consistent belief bases, modelling them by CSPs, and evaluating the resulting inductive inference operators.
This article is a revised and largely extended version of our FoIKS-2024 conference paper Haldimann et al. (Reference Haldimann, Beierle, Kern-Isberner, Meier and Ortiz2024). The additions include in particlar the following aspects. We added full proofs for all propositions and lemmas that have been left out in the conference paper. We elaborate methods for checking weak consistency of a belief base and compactly recall how p-entailment and system Z handle weakly consistent belief bases. We investigate conditional indifference of extended c-representations and evaluate extended c-inference with respect to semi-monotony and rational monotony and weakened versions thereof. Furthermore, we develop extended versions of credulous and weakly skeptical c-inference and their modelling as CSPs, and we provide a map of all arising inference operators and their interrelationships.
The remainder of this article is organized as follows: We recall the background on conditional logic in Section 2 and inductive inference in Section 3. In Section 4, we elaborate and illustrate the different kinds of consistency and address the treatment of weakly consistent belief bases by p-entailment and system Z. We develop extended c-representations in Section 5, extended c-inference in Section 6, and present a corresponding CSP-characterizations in Section 7. In Section 8, we address syntax splitting, and Section 9 deals with credulous and weakly skeptical inference. In Section 10, we conclude and point out future work.
2. Conditional logic
A (propositional) signature is a finite set
![]() $\Sigma$
of propositional variables. Assuming an underlying signature
$\Sigma$
of propositional variables. Assuming an underlying signature
![]() $\Sigma$
, we denote the resulting propositional language by
$\Sigma$
, we denote the resulting propositional language by
![]() ${{\mathcal{L}_{\Sigma}}}$
. Usually, we denote elements of signatures with lowercase letters
${{\mathcal{L}_{\Sigma}}}$
. Usually, we denote elements of signatures with lowercase letters
![]() $a, b, c, \dots$
and formulas with uppercase letters
$a, b, c, \dots$
and formulas with uppercase letters
![]() $A, B, C, \dots$
. We may denote a conjunction
$A, B, C, \dots$
. We may denote a conjunction
![]() $A \wedge B$
by AB and a negation
$A \wedge B$
by AB and a negation
![]() $\neg A$
by
$\neg A$
by
![]() $\overline{A}$
for brevity of notation. The set of interpretations over the underlying signature is denoted as
$\overline{A}$
for brevity of notation. The set of interpretations over the underlying signature is denoted as
![]() ${{\Omega_{\Sigma}}}$
. Interpretations are also called worlds and
${{\Omega_{\Sigma}}}$
. Interpretations are also called worlds and
![]() ${{\Omega_{\Sigma}}}$
the universe. An interpretation
${{\Omega_{\Sigma}}}$
the universe. An interpretation
![]() $\omega \in {{\Omega_{\Sigma}}}$
is a model of a formula
$\omega \in {{\Omega_{\Sigma}}}$
is a model of a formula
![]() $A \in {{\mathcal{L}}}$
if A holds in
$A \in {{\mathcal{L}}}$
if A holds in
![]() $\omega$
, denoted as
$\omega$
, denoted as
![]() $\omega \models A$
. The set of models of a formula (over a signature
$\omega \models A$
. The set of models of a formula (over a signature
![]() $\Sigma$
) is denoted as
$\Sigma$
) is denoted as
![]() ${Mod}\,_\Sigma(A) = \{\omega \in {{\Omega_{\Sigma}}} \mid \omega \models A\}$
or short as
${Mod}\,_\Sigma(A) = \{\omega \in {{\Omega_{\Sigma}}} \mid \omega \models A\}$
or short as
![]() $\Omega_A$
. The
$\Omega_A$
. The
![]() $\Sigma$
in
$\Sigma$
in
![]() $\Omega_\Sigma$
,
$\Omega_\Sigma$
,
![]() ${{\mathcal{L}_{\Sigma}}}$
and
${{\mathcal{L}_{\Sigma}}}$
and
![]() ${Mod}\,_\Sigma(A)$
can be omitted if the signature is clear from the context or if the underlying signature is not relevant. A formula A entails a formula B, denoted by
${Mod}\,_\Sigma(A)$
can be omitted if the signature is clear from the context or if the underlying signature is not relevant. A formula A entails a formula B, denoted by
![]() $A \models B$
, if
$A \models B$
, if
![]() $\Omega_{A} \subseteq \Omega_{B}$
. A formula A is satisfiable if
$\Omega_{A} \subseteq \Omega_{B}$
. A formula A is satisfiable if
![]() $\Omega_{A} \neq \emptyset$
. By slight abuse of notation we sometimes interpret worlds as the corresponding complete conjunction of all elements in the signature in either positive or negated form.
$\Omega_{A} \neq \emptyset$
. By slight abuse of notation we sometimes interpret worlds as the corresponding complete conjunction of all elements in the signature in either positive or negated form.
A conditional
![]() ${{(B|A)}}$
connects two formulas A, B and represents the rule ‘If A then usually B’, where A is called the antecedent and B the consequent of the conditional. The conditional language is denoted as
${{(B|A)}}$
connects two formulas A, B and represents the rule ‘If A then usually B’, where A is called the antecedent and B the consequent of the conditional. The conditional language is denoted as
![]() ${{{{(\mathcal{L}|\mathcal{L})}}_{\Sigma}}} = \{{{(B|A)}} \mid A, B \in {{\mathcal{L}_{\Sigma}}}\}$
. A finite set of conditionals is called a belief base. We use a three-valued semantics of conditionals in this paper (de Finetti, Reference de Finetti1937). For a world
${{{{(\mathcal{L}|\mathcal{L})}}_{\Sigma}}} = \{{{(B|A)}} \mid A, B \in {{\mathcal{L}_{\Sigma}}}\}$
. A finite set of conditionals is called a belief base. We use a three-valued semantics of conditionals in this paper (de Finetti, Reference de Finetti1937). For a world
![]() $\omega$
a conditional
$\omega$
a conditional
![]() ${{(B|A)}}$
is either verified by
${{(B|A)}}$
is either verified by
![]() $\omega$
if
$\omega$
if
![]() $\omega \models AB$
, falsified by
$\omega \models AB$
, falsified by
![]() $\omega$
if
$\omega$
if
![]() $\omega \models A\overline{B}$
, or not applicable to
$\omega \models A\overline{B}$
, or not applicable to
![]() $\omega$
if
$\omega$
if
![]() $\omega \models \overline{A}$
. Popular models for belief bases are ranking functions (also called ordinal conditional functions, OCF) (Spohn, Reference Spohn, Harper and Skyrms1988, Reference Spohn2012) and total preorders (TPO) on
$\omega \models \overline{A}$
. Popular models for belief bases are ranking functions (also called ordinal conditional functions, OCF) (Spohn, Reference Spohn, Harper and Skyrms1988, Reference Spohn2012) and total preorders (TPO) on
![]() $\Omega_\Sigma$
(Darwiche & Pearl, Reference Darwiche and Pearl1997). An OCF
$\Omega_\Sigma$
(Darwiche & Pearl, Reference Darwiche and Pearl1997). An OCF
![]() $\kappa\;:\; \Omega_\Sigma \rightarrow \mathbb{N} \cup \{\infty\}$
maps worlds to a rank such that at least one world has rank 0, that is,
$\kappa\;:\; \Omega_\Sigma \rightarrow \mathbb{N} \cup \{\infty\}$
maps worlds to a rank such that at least one world has rank 0, that is,
![]() $\kappa^{-1}(0) \neq \emptyset$
. OCFs have been first introduced by Spohn (Reference Spohn, Harper and Skyrms1988) in a more general form. The intuition is that worlds with lower ranks are more plausible than worlds with higher ranks; worlds with rank
$\kappa^{-1}(0) \neq \emptyset$
. OCFs have been first introduced by Spohn (Reference Spohn, Harper and Skyrms1988) in a more general form. The intuition is that worlds with lower ranks are more plausible than worlds with higher ranks; worlds with rank
![]() $\infty$
are considered infeasible. OCFs are lifted to formulas by mapping a formula A to the smallest rank of a model of A, or to
$\infty$
are considered infeasible. OCFs are lifted to formulas by mapping a formula A to the smallest rank of a model of A, or to
![]() $\infty$
if A has no models. An OCF
$\infty$
if A has no models. An OCF
![]() $\kappa$
is a model of a conditional
$\kappa$
is a model of a conditional
![]() ${{(B|A)}}$
, denoted as
${{(B|A)}}$
, denoted as
![]() $\kappa \models {{(B|A)}}$
, if
$\kappa \models {{(B|A)}}$
, if
![]() $\kappa(A) = \infty$
or if
$\kappa(A) = \infty$
or if
![]() $\kappa(AB) \lt \kappa(A\overline{B})$
;
$\kappa(AB) \lt \kappa(A\overline{B})$
;
![]() $\kappa$
is a model of a belief base
$\kappa$
is a model of a belief base
![]() $\Delta$
, denoted as
$\Delta$
, denoted as
![]() $\kappa \models \Delta$
, if it is a model of every conditional in
$\kappa \models \Delta$
, if it is a model of every conditional in
![]() $\Delta$
. For
$\Delta$
. For
![]() $\Sigma' \subseteq \Sigma$
the marginalization of a ranking function
$\Sigma' \subseteq \Sigma$
the marginalization of a ranking function
![]() $\kappa\;:\; {{\Omega_{\Sigma}}} \rightarrow \mathbb{N} \cup \{\infty\}$
to
$\kappa\;:\; {{\Omega_{\Sigma}}} \rightarrow \mathbb{N} \cup \{\infty\}$
to
![]() $\Sigma'$
is the ranking function
$\Sigma'$
is the ranking function
![]() ${\kappa}_{|\Sigma'}\;:\; {{\Omega_{\Sigma'}}} \rightarrow \mathbb{N} \cup \{\infty\}$
defined by
${\kappa}_{|\Sigma'}\;:\; {{\Omega_{\Sigma'}}} \rightarrow \mathbb{N} \cup \{\infty\}$
defined by
![]() ${\kappa}_{|\Sigma'}(\omega') = \min \{\kappa(\omega) \mid {\omega}_{\mid {\Sigma'}} = \omega'\}$
.
${\kappa}_{|\Sigma'}(\omega') = \min \{\kappa(\omega) \mid {\omega}_{\mid {\Sigma'}} = \omega'\}$
.
Lemma 1. Let
![]() $\kappa\;:\; {{\Omega_{\Sigma}}} \rightarrow \mathbb{N} \cup \{\infty\}$
be a ranking function. Let
$\kappa\;:\; {{\Omega_{\Sigma}}} \rightarrow \mathbb{N} \cup \{\infty\}$
be a ranking function. Let
![]() $\Sigma' \subseteq \Sigma$
and let
$\Sigma' \subseteq \Sigma$
and let
![]() $\kappa' = {\kappa}_{|\Sigma'}$
. Then, for any formula
$\kappa' = {\kappa}_{|\Sigma'}$
. Then, for any formula
![]() $A \in {{\mathcal{L}_{\Sigma'}}}$
we have that
$A \in {{\mathcal{L}_{\Sigma'}}}$
we have that
![]() $\kappa(A) = \kappa'(A)$
.
$\kappa(A) = \kappa'(A)$
.
Proof. We can obtain the models of A with respect to
![]() $\Sigma$
by extending the models of A with respect to
$\Sigma$
by extending the models of A with respect to
![]() $\Sigma'$
by any possible valuation of
$\Sigma'$
by any possible valuation of
![]() $\Sigma \setminus \Sigma'$
, that is,
$\Sigma \setminus \Sigma'$
, that is,
![]() ${Mod}\,_{\Sigma}(A) = \{(\omega^a \cdot \omega^b) \mid \omega^a \in {Mod}\,_{\Sigma'}(A), \omega^b \in {{\Omega_{\Sigma \setminus \Sigma'}}}\}$
. By definition, we have that
${Mod}\,_{\Sigma}(A) = \{(\omega^a \cdot \omega^b) \mid \omega^a \in {Mod}\,_{\Sigma'}(A), \omega^b \in {{\Omega_{\Sigma \setminus \Sigma'}}}\}$
. By definition, we have that
![]() $\kappa'(\omega') = \min \{\kappa(\omega) \mid \omega \in {{\Omega_{\Sigma}}}, {\omega}_{\mid {\Sigma'}} = \omega'\} = \min \{\kappa(\omega' \cdot \omega^b) \mid \omega^b \in {{\Omega_{\Sigma \setminus \Sigma'}}}\}$
. Therefore,
$\kappa'(\omega') = \min \{\kappa(\omega) \mid \omega \in {{\Omega_{\Sigma}}}, {\omega}_{\mid {\Sigma'}} = \omega'\} = \min \{\kappa(\omega' \cdot \omega^b) \mid \omega^b \in {{\Omega_{\Sigma \setminus \Sigma'}}}\}$
. Therefore,
Lemma 2. Let
![]() $\kappa\;:\; {{\Omega_{\Sigma}}} \rightarrow \mathbb{N} \cup \{\infty\}$
be a ranking function. Let
$\kappa\;:\; {{\Omega_{\Sigma}}} \rightarrow \mathbb{N} \cup \{\infty\}$
be a ranking function. Let
![]() $\Sigma' \subseteq \Sigma$
and let
$\Sigma' \subseteq \Sigma$
and let
![]() $\kappa' = {\kappa}_{|\Sigma'}$
. Then, for formulas
$\kappa' = {\kappa}_{|\Sigma'}$
. Then, for formulas
![]() $A, B \in {{\mathcal{L}_{\Sigma'}}}$
we have that
$A, B \in {{\mathcal{L}_{\Sigma'}}}$
we have that
![]() $\kappa \models {{(B|A)}}$
iff
$\kappa \models {{(B|A)}}$
iff
![]() $\kappa' \models {{(B|A)}}$
.
$\kappa' \models {{(B|A)}}$
.
Proof. Using Lemma 1, we have
![]() $\kappa(A) = \kappa'(A)$
and
$\kappa(A) = \kappa'(A)$
and
![]() $\kappa(AB) = \kappa'(AB)$
and
$\kappa(AB) = \kappa'(AB)$
and
![]() $\kappa(A\overline{B}) = \kappa'(A\overline{B})$
. Therefore,
$\kappa(A\overline{B}) = \kappa'(A\overline{B})$
. Therefore,
![]() $\kappa \models {{(B|A)}}$
iff
$\kappa \models {{(B|A)}}$
iff
![]() $\kappa' \models {{(B|A)}}$
.
$\kappa' \models {{(B|A)}}$
.
It is also possible to combine ranking functions
![]() $\kappa_1, \kappa_2$
over disjoint subsignatures
$\kappa_1, \kappa_2$
over disjoint subsignatures
![]() $\Sigma_1, \Sigma_2$
. For
$\Sigma_1, \Sigma_2$
. For
![]() $\kappa_1\;:\; {{\Omega_{\Sigma_1}}} \rightarrow \mathbb{N} \cup \{\infty\}$
and
$\kappa_1\;:\; {{\Omega_{\Sigma_1}}} \rightarrow \mathbb{N} \cup \{\infty\}$
and
![]() $\kappa_2\;:\; {{\Omega_{\Sigma_2}}} \rightarrow \mathbb{N} \cup \{\infty\}$
, the combination of
$\kappa_2\;:\; {{\Omega_{\Sigma_2}}} \rightarrow \mathbb{N} \cup \{\infty\}$
, the combination of
![]() $\kappa_1$
and
$\kappa_1$
and
![]() $\kappa_2$
, denoted by
$\kappa_2$
, denoted by
![]() $\kappa_{\oplus} = \kappa_1 \oplus \kappa_2$
, is defined by
$\kappa_{\oplus} = \kappa_1 \oplus \kappa_2$
, is defined by
![]() $\kappa_{\oplus}(\omega) = \kappa_1({\omega}_{\mid {\Sigma_1}}) + \kappa_2({\omega}_{\mid {\Sigma_2}})$
.
$\kappa_{\oplus}(\omega) = \kappa_1({\omega}_{\mid {\Sigma_1}}) + \kappa_2({\omega}_{\mid {\Sigma_2}})$
.
Lemma 3. Let
![]() $\Sigma_1, \Sigma_2$
be disjoint, let
$\Sigma_1, \Sigma_2$
be disjoint, let
![]() $\kappa_1\;:\; {{\Omega_{\Sigma_1}}} \rightarrow \mathbb{N} \cup \{\infty\}$
and
$\kappa_1\;:\; {{\Omega_{\Sigma_1}}} \rightarrow \mathbb{N} \cup \{\infty\}$
and
![]() $\kappa_2\;:\; {{\Omega_{\Sigma_2}}} \rightarrow \mathbb{N} \cup \{\infty\}$
, and let
$\kappa_2\;:\; {{\Omega_{\Sigma_2}}} \rightarrow \mathbb{N} \cup \{\infty\}$
, and let
![]() $\kappa_{\oplus} = \kappa_1 \oplus \kappa_2$
. For formulas
$\kappa_{\oplus} = \kappa_1 \oplus \kappa_2$
. For formulas
![]() $A \in {{\mathcal{L}_{\Sigma_1}}}, B \in {{\mathcal{L}_{\Sigma_2}}}$
it holds that
$A \in {{\mathcal{L}_{\Sigma_1}}}, B \in {{\mathcal{L}_{\Sigma_2}}}$
it holds that
![]() $\kappa_{\oplus}(AB) = \kappa_1(A) + \kappa_2(B)$
.
$\kappa_{\oplus}(AB) = \kappa_1(A) + \kappa_2(B)$
.
Proof. Let
![]() $\Sigma = \Sigma_1 \cup \Sigma_2$
. Because
$\Sigma = \Sigma_1 \cup \Sigma_2$
. Because
![]() $A \in {{\mathcal{L}_{\Sigma_1}}}$
and
$A \in {{\mathcal{L}_{\Sigma_1}}}$
and
![]() $B \in {{\mathcal{L}_{\Sigma_2}}}$
, we have that
$B \in {{\mathcal{L}_{\Sigma_2}}}$
, we have that
![]() ${Mod}\,_{\Sigma}(AB) = \{(\omega^1 \cdot \omega^2) \mid \omega^1 \in {Mod}\,_{\Sigma_1}(A), \omega^2 \in {Mod}\,_{\Sigma_2}(B)\}$
. Therefore, it holds that
${Mod}\,_{\Sigma}(AB) = \{(\omega^1 \cdot \omega^2) \mid \omega^1 \in {Mod}\,_{\Sigma_1}(A), \omega^2 \in {Mod}\,_{\Sigma_2}(B)\}$
. Therefore, it holds that
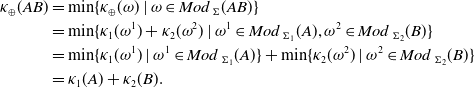 \begin{align*} \kappa_{\oplus}(AB) &= \min \{\kappa_{\oplus}(\omega) \mid \omega \in {Mod}\,_{\Sigma}(AB)\} \\ &= \min \{\kappa_1(\omega^1) + \kappa_2(\omega^2) \mid \omega^1 \in {Mod}\,_{\Sigma_1}(A), \omega^2 \in {Mod}\,_{\Sigma_2}(B)\} \\ &= \min \{\kappa_1(\omega^1) \mid \omega^1 \in {Mod}\,_{\Sigma_1}(A)\} + \min \{\kappa_2(\omega^2) \mid \omega^2 \in {Mod}\,_{\Sigma_2}(B)\} \\ &= \kappa_1(A) + \kappa_2(B).\end{align*}
\begin{align*} \kappa_{\oplus}(AB) &= \min \{\kappa_{\oplus}(\omega) \mid \omega \in {Mod}\,_{\Sigma}(AB)\} \\ &= \min \{\kappa_1(\omega^1) + \kappa_2(\omega^2) \mid \omega^1 \in {Mod}\,_{\Sigma_1}(A), \omega^2 \in {Mod}\,_{\Sigma_2}(B)\} \\ &= \min \{\kappa_1(\omega^1) \mid \omega^1 \in {Mod}\,_{\Sigma_1}(A)\} + \min \{\kappa_2(\omega^2) \mid \omega^2 \in {Mod}\,_{\Sigma_2}(B)\} \\ &= \kappa_1(A) + \kappa_2(B).\end{align*}
Lemma 4 (Kern-Isberner & Brewka, Reference Kern-Isberner and Brewka2017). Let
![]() $\Sigma_1, \Sigma_2$
be disjoint signatures and let
$\Sigma_1, \Sigma_2$
be disjoint signatures and let
![]() $\kappa_1\;:\; {{\Omega_{\Sigma_1}}} \rightarrow \mathbb{N} \cup \{\infty\}$
and
$\kappa_1\;:\; {{\Omega_{\Sigma_1}}} \rightarrow \mathbb{N} \cup \{\infty\}$
and
![]() $\kappa_2\;:\; {{\Omega_{\Sigma_2}}} \rightarrow \mathbb{N} \cup \{\infty\}$
be ranking functions. Let
$\kappa_2\;:\; {{\Omega_{\Sigma_2}}} \rightarrow \mathbb{N} \cup \{\infty\}$
be ranking functions. Let
![]() $\kappa_{\oplus} = \kappa_1 \oplus \kappa_2$
. Then
$\kappa_{\oplus} = \kappa_1 \oplus \kappa_2$
. Then
![]() ${\kappa_{\oplus}}_{|\Sigma_1} = \kappa_1$
.
${\kappa_{\oplus}}_{|\Sigma_1} = \kappa_1$
.
Proof. Let
![]() $\omega^1$
be any world in
$\omega^1$
be any world in
![]() ${{\Omega_{\Sigma_1}}}$
. Let
${{\Omega_{\Sigma_1}}}$
. Let
![]() $\omega^2 \in {{\Omega_{\Sigma_1}}}$
such that
$\omega^2 \in {{\Omega_{\Sigma_1}}}$
such that
![]() $\kappa_2(\omega^2) = 0$
. We have that
$\kappa_2(\omega^2) = 0$
. We have that
 \begin{align*} {\kappa_{\oplus}}_{|\Sigma_1}(\omega^1) &= \min \{\kappa(\omega) \mid \omega \in {{\Omega_{\Sigma}}}, {\omega}_{\mid {\Sigma_1}} = \omega^1\}\\ &= \min \{\kappa_1(\omega^1) + \kappa_2(\omega_{\mid {\Sigma_2}}) \mid \omega \in {{\Omega_{\Sigma}}}\}\\ &\overset{*}{=} \kappa_1(\omega^1). \end{align*}
\begin{align*} {\kappa_{\oplus}}_{|\Sigma_1}(\omega^1) &= \min \{\kappa(\omega) \mid \omega \in {{\Omega_{\Sigma}}}, {\omega}_{\mid {\Sigma_1}} = \omega^1\}\\ &= \min \{\kappa_1(\omega^1) + \kappa_2(\omega_{\mid {\Sigma_2}}) \mid \omega \in {{\Omega_{\Sigma}}}\}\\ &\overset{*}{=} \kappa_1(\omega^1). \end{align*}
Equation
![]() $(\!*\!)$
holds because we can choose, for example,
$(\!*\!)$
holds because we can choose, for example,
![]() $\omega = (\omega^1 \cdot \omega^2)$
, resulting in
$\omega = (\omega^1 \cdot \omega^2)$
, resulting in
![]() $\kappa_2(\omega_{\mid {\Sigma_2}}) = 0$
.
$\kappa_2(\omega_{\mid {\Sigma_2}}) = 0$
.
Lemmas 1–4 will be helpful when proving properties regarding syntax splitting in the sequel.
3. Inductive inference
The conditional beliefs of an agent are formally captured by a binary relation
![]() $\mathord{{|\hspace{-2pt}}{\sim}}$
on propositional formulas with
$\mathord{{|\hspace{-2pt}}{\sim}}$
on propositional formulas with
![]() $A \mathord{{|\hspace{-2pt}}{\sim}} B$
representing that A (defeasibly) entails B; this relation is called inference or entailment relation. Different sets of properties for inference relations have been suggested, and often the set of postulates called system P (Adams, Reference Adams1975; Kraus et al., Reference Kraus, Lehmann and Magidor1990) is considered as minimal requirement for inference relations. Inference relations satisfying system P are called preferential inference relations, for details we refer to Adams (Reference Adams1975), Kraus et al. (Reference Kraus, Lehmann and Magidor1990), see Figure 1.
$A \mathord{{|\hspace{-2pt}}{\sim}} B$
representing that A (defeasibly) entails B; this relation is called inference or entailment relation. Different sets of properties for inference relations have been suggested, and often the set of postulates called system P (Adams, Reference Adams1975; Kraus et al., Reference Kraus, Lehmann and Magidor1990) is considered as minimal requirement for inference relations. Inference relations satisfying system P are called preferential inference relations, for details we refer to Adams (Reference Adams1975), Kraus et al. (Reference Kraus, Lehmann and Magidor1990), see Figure 1.
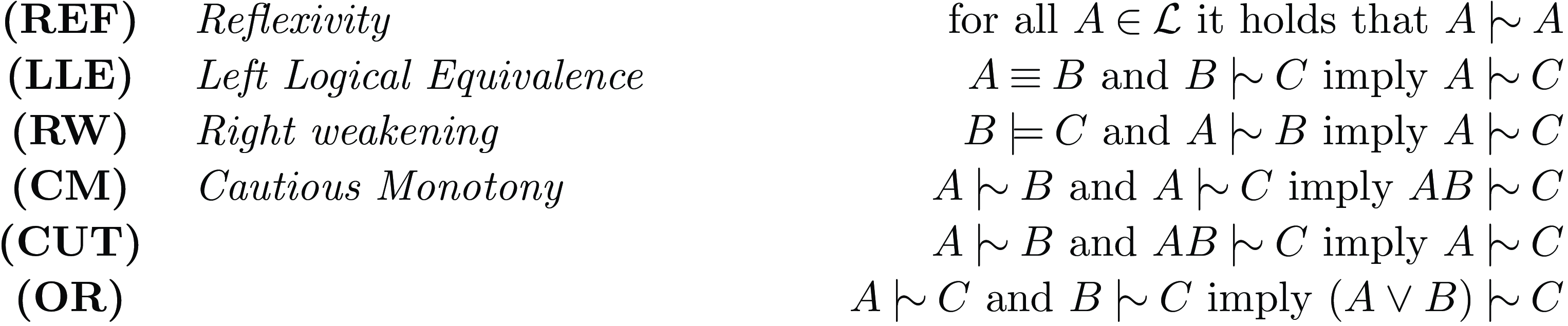
Figure 1. The system P postulates for nonmonotonic inference relations.
Every ranking function
![]() $\kappa$
induces a preferential inference relation
$\kappa$
induces a preferential inference relation
![]() $|\hspace{-2pt} {\sim}_{\kappa}$
by
$|\hspace{-2pt} {\sim}_{\kappa}$
by
Note that the condition
![]() $\kappa(A) = \infty$
in (1) ensures that system P’s axiom (Reflexivity):
$\kappa(A) = \infty$
in (1) ensures that system P’s axiom (Reflexivity):
![]() $A |\hspace{-2pt} {\sim}_{\kappa} A$
is satisfied for
$A |\hspace{-2pt} {\sim}_{\kappa} A$
is satisfied for
![]() $A \equiv \bot$
.
$A \equiv \bot$
.
Regarding the inference induced by a marginalized ranking function, the following lemma holds.
Lemma 5. Let
![]() $\kappa\;:\; {{\Omega_{\Sigma}}} \rightarrow \mathbb{N} \cup \{\infty\}$
be a ranking function. Let
$\kappa\;:\; {{\Omega_{\Sigma}}} \rightarrow \mathbb{N} \cup \{\infty\}$
be a ranking function. Let
![]() $\Sigma' \subseteq \Sigma$
and let
$\Sigma' \subseteq \Sigma$
and let
![]() $\kappa' = {\kappa}_{|\Sigma'}$
. Then, for formulas
$\kappa' = {\kappa}_{|\Sigma'}$
. Then, for formulas
![]() $A, B \in {{\mathcal{L}_{\Sigma'}}}$
we have that
$A, B \in {{\mathcal{L}_{\Sigma'}}}$
we have that
![]() $A |\hspace{-2pt} {\sim}_{\kappa} B$
iff
$A |\hspace{-2pt} {\sim}_{\kappa} B$
iff
![]() $A |\hspace{-2pt} {\sim}_{\kappa'} B$
.
$A |\hspace{-2pt} {\sim}_{\kappa'} B$
.
Proof. Using Lemma 1 we have
![]() $\kappa(A) = \kappa'(A)$
and
$\kappa(A) = \kappa'(A)$
and
![]() $\kappa(AB) = \kappa'(AB)$
and
$\kappa(AB) = \kappa'(AB)$
and
![]() $\kappa(A\overline{B}) = \kappa'(A\overline{B})$
. Therefore,
$\kappa(A\overline{B}) = \kappa'(A\overline{B})$
. Therefore,
![]() $A |\hspace{-2pt} {\sim}_{\kappa} B$
iff
$A |\hspace{-2pt} {\sim}_{\kappa} B$
iff
![]() $A |\hspace{-2pt} {\sim}_{\kappa'} B$
.
$A |\hspace{-2pt} {\sim}_{\kappa'} B$
.
Inductive inference is the process of completing a given belief base to an inference relation. To formally capture this, we use inductive inference operators.
Definition 6 (inductive inference operator, Kern-Isberner et al., Reference Kern-Isberner, Beierle, Brewka, Calvanese, Erdem and Thielscher2020). An inductive inference operator is a mapping
![]() $C\;:\; \Delta \mapsto \mathord{{|\hspace{-2pt}}{\sim}^{}_{\Delta}}$
that maps each belief base to an inference relation s.t. direct inference (DI) and trivial vacuity (TV) are fulfilled, that is,
$C\;:\; \Delta \mapsto \mathord{{|\hspace{-2pt}}{\sim}^{}_{\Delta}}$
that maps each belief base to an inference relation s.t. direct inference (DI) and trivial vacuity (TV) are fulfilled, that is,
-
(DI) if
 ${{(B|A)}} \in \Delta$
then
${{(B|A)}} \in \Delta$
then
 $A |\hspace{-2pt} {\sim}_{\Delta} B$
, and
$A |\hspace{-2pt} {\sim}_{\Delta} B$
, and -
(TV) if
 $\Delta = \emptyset$
and
$\Delta = \emptyset$
and
 $A |\hspace{-2pt} {\sim}_{\Delta} B$
, then
$A |\hspace{-2pt} {\sim}_{\Delta} B$
, then
 $A \models B$
.
$A \models B$
.
An inductive inference operator C is a preferential inductive inference operator if every inference relation
![]() $|\hspace{-2pt} {\sim}_{\Delta}$
in the image of C satisfies system P.
$|\hspace{-2pt} {\sim}_{\Delta}$
in the image of C satisfies system P.
p-Entailment (Adams, Reference Adams1975; Kraus et al., Reference Kraus, Lehmann and Magidor1990)
![]() $C^p\;:\; \Delta \mapsto\mathord{{|\hspace{-2pt}}{\sim}^{\,p}_{\Delta}}$
is the most cautious preferential inductive inference operator. It is characterized by system P in the way that it only licenses inferences that can be obtained by iteratively applying the rules of system P to the belief base. Every other preferential inductive inference operator extends p-entailment. While extending p-entailment and adding some more inferences to the induced inference relations is usually desired, p-entailment can act as a basic guidance for inferences of the form
$C^p\;:\; \Delta \mapsto\mathord{{|\hspace{-2pt}}{\sim}^{\,p}_{\Delta}}$
is the most cautious preferential inductive inference operator. It is characterized by system P in the way that it only licenses inferences that can be obtained by iteratively applying the rules of system P to the belief base. Every other preferential inductive inference operator extends p-entailment. While extending p-entailment and adding some more inferences to the induced inference relations is usually desired, p-entailment can act as a basic guidance for inferences of the form
![]() $A \mathord{{|\hspace{-2pt}}{\sim}} \bot$
which can be seen as representations of ‘strict’ beliefs (i.e., A is completely unfeasible).
$A \mathord{{|\hspace{-2pt}}{\sim}} \bot$
which can be seen as representations of ‘strict’ beliefs (i.e., A is completely unfeasible).
Postulate (Classic Preservation) 1. (adapted from Casini et al., Reference Casini, Meyer, Varzinczak, Calimeri, Leone and Manna2019). An inductive inference operator
![]() $C\;:\; \Delta \mapsto \mathord{{|\hspace{-2pt}}{\sim}^{}_{\Delta}}$
satisfies (Classic Preservation) if for all belief bases
$C\;:\; \Delta \mapsto \mathord{{|\hspace{-2pt}}{\sim}^{}_{\Delta}}$
satisfies (Classic Preservation) if for all belief bases
![]() $\Delta$
and
$\Delta$
and
![]() $A \in {{\mathcal{L}}}$
it holds that
$A \in {{\mathcal{L}}}$
it holds that
![]() $A|\hspace{-2pt} {\sim}_{\Delta} \bot$
iff
$A|\hspace{-2pt} {\sim}_{\Delta} \bot$
iff
![]() $A |\hspace{-2pt} {\sim}^{p}_{\Delta} \bot$
.
$A |\hspace{-2pt} {\sim}^{p}_{\Delta} \bot$
.
4. Consistency of belief bases
There are different definitions of consistency of a belief base in the literature, for example, Goldszmidt and Pearl (Reference Goldszmidt and Pearl1996), Giordano et al. (Reference Giordano, Gliozzi, Olivetti and Pozzato2015), Casini et al. (Reference Casini, Meyer, Varzinczak, Calimeri, Leone and Manna2019). To distinguish two different notions of consistency that commonly occur and are both used in this paper, we call one notion of consistency strong consistency and the other notion weak consistency, as suggested in Haldimann et al. (Reference Haldimann, Beierle, Kern-Isberner, Meyer, Chun and Franklin2023).
Definition 7 (Haldimann et al., Reference Haldimann, Beierle, Kern-Isberner, Meyer, Chun and Franklin2023). A belief base
![]() $\Delta$
is called strongly consistent if there exists at least one ranking function
$\Delta$
is called strongly consistent if there exists at least one ranking function
![]() $\kappa$
with
$\kappa$
with
![]() $\kappa \models \Delta$
and
$\kappa \models \Delta$
and
![]() $\kappa^{-1}(\infty) = \emptyset$
. A belief base
$\kappa^{-1}(\infty) = \emptyset$
. A belief base
![]() $\Delta$
is weakly consistent if there is a ranking function
$\Delta$
is weakly consistent if there is a ranking function
![]() $\kappa$
with
$\kappa$
with
![]() $\kappa \models \Delta$
.
$\kappa \models \Delta$
.
Thus,
![]() $\Delta$
is strongly consistent if there is at least one ranking function modelling
$\Delta$
is strongly consistent if there is at least one ranking function modelling
![]() $\Delta$
that considers all worlds feasible. This notion of consistency is used in many approaches, for example, Goldszmidt and Pearl (Reference Goldszmidt and Pearl1996). The notion of weak consistency is equivalent to the more relaxed notion of consistency that is used in, for example, Giordano et al. (Reference Giordano, Gliozzi, Olivetti and Pozzato2015), Casini et al. (Reference Casini, Meyer, Varzinczak, Calimeri, Leone and Manna2019). Trivially, strong consistency implies weak consistency.
$\Delta$
that considers all worlds feasible. This notion of consistency is used in many approaches, for example, Goldszmidt and Pearl (Reference Goldszmidt and Pearl1996). The notion of weak consistency is equivalent to the more relaxed notion of consistency that is used in, for example, Giordano et al. (Reference Giordano, Gliozzi, Olivetti and Pozzato2015), Casini et al. (Reference Casini, Meyer, Varzinczak, Calimeri, Leone and Manna2019). Trivially, strong consistency implies weak consistency.
Example 8. Let
![]() $\Sigma = \{a,b,c,d\}$
. The belief base
$\Sigma = \{a,b,c,d\}$
. The belief base
![]() $\Delta_1 = \{{{(\bot|\top)}}\}$
is not weakly consistent. If there were any ranking function
$\Delta_1 = \{{{(\bot|\top)}}\}$
is not weakly consistent. If there were any ranking function
![]() $\kappa$
with
$\kappa$
with
![]() $\kappa \models \Delta_1$
then there would be a world
$\kappa \models \Delta_1$
then there would be a world
![]() $\omega$
such that
$\omega$
such that
![]() $\kappa(\omega) = 0$
and therefore
$\kappa(\omega) = 0$
and therefore
![]() $\kappa(\top) = 0$
. For
$\kappa(\top) = 0$
. For
![]() $\kappa$
to model
$\kappa$
to model
![]() ${{(\bot|\top)}}$
, we need
${{(\bot|\top)}}$
, we need
![]() $\kappa(\top \wedge \bot) \lt \kappa(\top \wedge \top) = 0$
, which is clearly impossible.
$\kappa(\top \wedge \bot) \lt \kappa(\top \wedge \top) = 0$
, which is clearly impossible.
![]() $\Delta_2 = \{{{(\bot|a)}},{{(\overline{b}|\overline{a})}}, {{(b|\overline{a})}}\}$
is also not weakly consistent. The conditional
$\Delta_2 = \{{{(\bot|a)}},{{(\overline{b}|\overline{a})}}, {{(b|\overline{a})}}\}$
is also not weakly consistent. The conditional
![]() ${{(\bot|a)}}$
enforces that for every ranking function
${{(\bot|a)}}$
enforces that for every ranking function
![]() $\kappa$
with
$\kappa$
with
![]() $\kappa \models \Delta_2$
and any model
$\kappa \models \Delta_2$
and any model
![]() $\omega$
of a we have
$\omega$
of a we have
![]() $\kappa(a) = \infty$
. The conditionals
$\kappa(a) = \infty$
. The conditionals
![]() ${{(\overline{b}|\overline{a})}}, {{(b|\overline{a})}}$
in combination enforce that the rank of any model of
${{(\overline{b}|\overline{a})}}, {{(b|\overline{a})}}$
in combination enforce that the rank of any model of
![]() $\overline{a}$
must have rank infinity. Because every ranking function must assign rank 0 to at least one world, there is no ranking function modelling
$\overline{a}$
must have rank infinity. Because every ranking function must assign rank 0 to at least one world, there is no ranking function modelling
![]() $\Delta_2$
. Because
$\Delta_2$
. Because
![]() $\Delta_1$
and
$\Delta_1$
and
![]() $\Delta_2$
are not weakly consistent, they are not strongly consistent.
$\Delta_2$
are not weakly consistent, they are not strongly consistent.
The belief bases
![]() $\Delta_3 = \{{{(\overline{b}|\overline{a})}}, {{(b|\overline{a})}}\}$
and
$\Delta_3 = \{{{(\overline{b}|\overline{a})}}, {{(b|\overline{a})}}\}$
and
![]() $\Delta_4 = \{{{(\bot|a)}}\}$
, both subsets of
$\Delta_4 = \{{{(\bot|a)}}\}$
, both subsets of
![]() $\Delta_2$
, are weakly consistent but not strongly consistent.
$\Delta_2$
, are weakly consistent but not strongly consistent.
![]() $\Delta_3$
requires all ranking functions modelling it to assign rank
$\Delta_3$
requires all ranking functions modelling it to assign rank
![]() $\infty$
to models of
$\infty$
to models of
![]() $\overline{a}$
, and
$\overline{a}$
, and
![]() $\Delta_4$
requires all ranking functions modelling it to assign rank
$\Delta_4$
requires all ranking functions modelling it to assign rank
![]() $\infty$
to models of a.
$\infty$
to models of a.
The belief base
![]() $\Delta_5 = \{{{(b|a)}}, {{(d|c)}}\}$
is strongly consistent and thus also weakly consistent.
$\Delta_5 = \{{{(b|a)}}, {{(d|c)}}\}$
is strongly consistent and thus also weakly consistent.
Lemma 9. For every weakly consistent belief base
![]() $\Delta$
there is an
$\Delta$
there is an
![]() $\omega \in \Omega$
such that
$\omega \in \Omega$
such that
![]() $\omega$
does not falsify any conditional in
$\omega$
does not falsify any conditional in
![]() $\Delta$
.
$\Delta$
.
Proof. Because
![]() $\Delta$
is weakly consistent, there is a ranking function
$\Delta$
is weakly consistent, there is a ranking function
![]() $\kappa$
with
$\kappa$
with
![]() $\kappa \models \Delta$
. Let
$\kappa \models \Delta$
. Let
![]() $\omega \in \kappa^{-1}(0)$
. Towards a contradiction, assume that there is a
$\omega \in \kappa^{-1}(0)$
. Towards a contradiction, assume that there is a
![]() ${{(B|A)}} \in \Delta$
that is falsified by
${{(B|A)}} \in \Delta$
that is falsified by
![]() $\omega$
, that is,
$\omega$
, that is,
![]() $\omega \models A\overline{B}$
. For
$\omega \models A\overline{B}$
. For
![]() $\kappa$
to accept
$\kappa$
to accept
![]() ${{(B|A)}}$
it must be either
${{(B|A)}}$
it must be either
![]() $\kappa(A) = \infty$
or
$\kappa(A) = \infty$
or
![]() $\kappa(AB) \lt \kappa(A\overline{B})$
. Because
$\kappa(AB) \lt \kappa(A\overline{B})$
. Because
![]() $\omega \models A$
and
$\omega \models A$
and
![]() $\kappa(\omega) =0$
we have
$\kappa(\omega) =0$
we have
![]() $\kappa(A) \neq \infty$
. Because
$\kappa(A) \neq \infty$
. Because
![]() $\kappa(A\overline{B}) \leqslant 0$
and there are no ranks below 0 the condition
$\kappa(A\overline{B}) \leqslant 0$
and there are no ranks below 0 the condition
![]() $\kappa(AB) \lt \kappa(A\overline{B})$
does not hold. This is a contradiction; hence,
$\kappa(AB) \lt \kappa(A\overline{B})$
does not hold. This is a contradiction; hence,
![]() $\omega$
does not falsify any conditional in
$\omega$
does not falsify any conditional in
![]() $\Delta$
.
$\Delta$
.
Lemma 10. Let
![]() $\Delta$
be a belief base. If there is an
$\Delta$
be a belief base. If there is an
![]() $\omega \in \Omega$
such that
$\omega \in \Omega$
such that
![]() $\omega$
does not falsify any conditional in
$\omega$
does not falsify any conditional in
![]() $\Delta$
, then
$\Delta$
, then
![]() $\Delta$
is weakly consistent.
$\Delta$
is weakly consistent.
Proof. Assume there is a world
![]() $\omega^*$
that does not falsify any conditional in
$\omega^*$
that does not falsify any conditional in
![]() $\Delta$
. Then
$\Delta$
. Then
 \[\kappa(\omega) = \begin{cases} 0 & \text{if } \omega = \omega^*\\ \infty & \text{otherwise} \end{cases}\]
\[\kappa(\omega) = \begin{cases} 0 & \text{if } \omega = \omega^*\\ \infty & \text{otherwise} \end{cases}\]
is a model of
![]() $\Delta$
. Therefore,
$\Delta$
. Therefore,
![]() $\Delta$
is weakly consistent.
$\Delta$
is weakly consistent.
An interpretation
![]() $\omega$
falsifies a conditional
$\omega$
falsifies a conditional
![]() ${{(B|A)}}$
iff it is not a model of its material implication counterpart
${{(B|A)}}$
iff it is not a model of its material implication counterpart
![]() $A \rightarrow B$
, which is equivalent to
$A \rightarrow B$
, which is equivalent to
![]() $\neg A \vee B$
. Therefore, Lemmas 9 and 10 imply that checking a belief base for weak consistency can be reduced to a single SAT check.
$\neg A \vee B$
. Therefore, Lemmas 9 and 10 imply that checking a belief base for weak consistency can be reduced to a single SAT check.
Proposition 11. A belief base
![]() $\Delta$
is weakly consistent if
$\Delta$
is weakly consistent if
is satisfiable.
The original definition of an inductive inference operator in Kern-Isberner et al. (Reference Kern-Isberner, Beierle, Brewka, Calvanese, Erdem and Thielscher2020) implicitly assumes all belief bases to be strongly consistent. However, the definition can be extended to cover all belief bases. Some inductive inference operators known from literature are defined only for strongly consistent belief bases, while other operators are defined for all belief bases. In particular, inference operators of the second type are able to draw inferences from all weakly consistent belief bases. For example, system Z is an inductive inference operator that is defined based on the Z-partition of a belief base. It was first defined for strongly consistent belief bases (Pearl, Reference Pearl1990). Then an extended version of system Z was introduced (Goldszmidt & Pearl, Reference Goldszmidt and Pearl1990) that also covers weakly consistent belief bases and that was shown to be equivalent to rational closure (Lehmann, Reference Lehmann, Brachman, Levesque and Reiter1989) in Goldszmidt and Pearl (Reference Goldszmidt and Pearl1990).
Definition 12 ((extended) Z-partition). A conditional
![]() ${{(B|A)}}$
is tolerated by
${{(B|A)}}$
is tolerated by
![]() $\Delta = \{{{(B_i|A_i)}} \mid i=1, \dots, n\}$
if there is a world
$\Delta = \{{{(B_i|A_i)}} \mid i=1, \dots, n\}$
if there is a world
![]() $\omega \in \Omega$
such that
$\omega \in \Omega$
such that
![]() $\omega$
verifies
$\omega$
verifies
![]() ${{(B|A)}}$
and
${{(B|A)}}$
and
![]() $\omega$
does not falsify any conditional in
$\omega$
does not falsify any conditional in
![]() $\Delta$
, that is,
$\Delta$
, that is,
![]() $\omega \models AB$
and
$\omega \models AB$
and
![]() $\omega \models \bigwedge_{i=1}^n (\overline{A_i} \vee B_i)$
.
$\omega \models \bigwedge_{i=1}^n (\overline{A_i} \vee B_i)$
.
The (extended) Z-partition
![]() ${{{{{\mathit{EZP}}}}(\Delta)}} = (\Delta^0, \dots, \Delta^k, \Delta^\infty)$
of a belief base
${{{{{\mathit{EZP}}}}(\Delta)}} = (\Delta^0, \dots, \Delta^k, \Delta^\infty)$
of a belief base
![]() $\Delta$
is the ordered partition of
$\Delta$
is the ordered partition of
![]() $\Delta$
constructed by letting
$\Delta$
constructed by letting
![]() $\Delta^i$
be the inclusion maximal subset of
$\Delta^i$
be the inclusion maximal subset of
![]() $\bigcup_{j=i}^n \Delta^j$
that is tolerated by
$\bigcup_{j=i}^n \Delta^j$
that is tolerated by
![]() $\bigcup_{j=i}^n \Delta^j$
until
$\bigcup_{j=i}^n \Delta^j$
until
![]() $\Delta^{k+1} = \emptyset$
. The set
$\Delta^{k+1} = \emptyset$
. The set
![]() $\Delta^\infty$
is the remaining set of conditionals containing no conditional tolerated by
$\Delta^\infty$
is the remaining set of conditionals containing no conditional tolerated by
![]() $\Delta^\infty$
.
$\Delta^\infty$
.
Because the
![]() $\Delta^i$
are chosen inclusion-maximal, the Z-partition is unique (Pearl, Reference Pearl1990).
$\Delta^i$
are chosen inclusion-maximal, the Z-partition is unique (Pearl, Reference Pearl1990).
Definition 13 ((extended) system Z). Let
![]() $\Delta$
be a belief base with
$\Delta$
be a belief base with
![]() ${{{{{\mathit{EZP}}}}(\Delta)}} = (\Delta^0, \dots, \Delta^k, \Delta^\infty)$
. If
${{{{{\mathit{EZP}}}}(\Delta)}} = (\Delta^0, \dots, \Delta^k, \Delta^\infty)$
. If
![]() $\Delta$
is not weakly consistent, let
$\Delta$
is not weakly consistent, let
![]() $A |\hspace{-2pt} {\sim}^{z}_{\Delta} B$
for any
$A |\hspace{-2pt} {\sim}^{z}_{\Delta} B$
for any
![]() $A, B \in {{\mathcal{L}}}$
. Otherwise, the (extended) Z-ranking function
$A, B \in {{\mathcal{L}}}$
. Otherwise, the (extended) Z-ranking function
![]() $\kappa_\Delta^z$
is defined as follows: For
$\kappa_\Delta^z$
is defined as follows: For
![]() $\omega \in \Omega$
, if a conditional in
$\omega \in \Omega$
, if a conditional in
![]() $\Delta^\infty$
is applicable to
$\Delta^\infty$
is applicable to
![]() $\omega$
define
$\omega$
define
![]() $\kappa_\Delta^z(\omega) = \infty$
. If not, let
$\kappa_\Delta^z(\omega) = \infty$
. If not, let
![]() $\Delta^j$
be the last element in
$\Delta^j$
be the last element in
![]() ${{{{{\mathit{EZP}}}}(\Delta)}}$
that contains a conditional falsified by
${{{{{\mathit{EZP}}}}(\Delta)}}$
that contains a conditional falsified by
![]() $\omega$
. Then let
$\omega$
. Then let
![]() $\kappa_\Delta^z(\omega) = j+1$
. If
$\kappa_\Delta^z(\omega) = j+1$
. If
![]() $\omega$
does not falsify any conditional in
$\omega$
does not falsify any conditional in
![]() $\Delta$
, then let
$\Delta$
, then let
![]() $\kappa_\Delta^z(\omega) = 0$
. (Extended) system Z maps
$\kappa_\Delta^z(\omega) = 0$
. (Extended) system Z maps
![]() $\Delta$
to the inference relation
$\Delta$
to the inference relation
![]() $|\hspace{-2pt} {\sim}^{z}_{\Delta}$
induced by
$|\hspace{-2pt} {\sim}^{z}_{\Delta}$
induced by
![]() $\kappa_\Delta^z$
.
$\kappa_\Delta^z$
.
For weakly consistent belief bases
![]() $\Delta$
the OCF
$\Delta$
the OCF
![]() $\kappa^z_{\Delta}$
is a model of
$\kappa^z_{\Delta}$
is a model of
![]() $\Delta$
. For strongly consistent belief bases extended system Z coincides with system Z in Pearl (Reference Pearl1990), Goldszmidt and Pearl (Reference Goldszmidt and Pearl1996).
$\Delta$
. For strongly consistent belief bases extended system Z coincides with system Z in Pearl (Reference Pearl1990), Goldszmidt and Pearl (Reference Goldszmidt and Pearl1996).
Lemma 14 (Haldimann et al., Reference Haldimann, Beierle, Kern-Isberner, Meyer, Chun and Franklin2023). For a weakly consistent belief base
![]() $\Delta$
and a formula A we have
$\Delta$
and a formula A we have
![]() $\kappa^z_{\Delta}(A) = \infty$
iff
$\kappa^z_{\Delta}(A) = \infty$
iff
![]() $A |\hspace{-2pt} {\sim}^{p}_{\Delta} \bot$
.
$A |\hspace{-2pt} {\sim}^{p}_{\Delta} \bot$
.
Lemma 15 (Haldimann et al., Reference Haldimann, Beierle, Kern-Isberner, Meyer, Chun and Franklin2023). Let
![]() $\Delta$
be with
$\Delta$
be with
![]() ${{{{{\mathit{EZP}}}}(\Delta)}} = (\Delta^0, \dots, \Delta^k, \Delta^\infty)$
. A world
${{{{{\mathit{EZP}}}}(\Delta)}} = (\Delta^0, \dots, \Delta^k, \Delta^\infty)$
. A world
![]() $\omega \in \Omega$
falsifies a conditional in
$\omega \in \Omega$
falsifies a conditional in
![]() $\Delta^\infty$
iff a conditional in
$\Delta^\infty$
iff a conditional in
![]() $\Delta^\infty$
is applicable in
$\Delta^\infty$
is applicable in
![]() $\omega$
.
$\omega$
.
Proof. Direction
![]() $\Rightarrow$
: Assume that
$\Rightarrow$
: Assume that
![]() $\omega$
falsifies a conditional in
$\omega$
falsifies a conditional in
![]() $\Delta^\infty$
. Then this conditional is applicable for
$\Delta^\infty$
. Then this conditional is applicable for
![]() $\omega$
.
$\omega$
.
Direction
![]() $\Leftarrow$
: Assume that at least one conditional
$\Leftarrow$
: Assume that at least one conditional
![]() ${{(B|A)}} \in \Delta^\infty$
is applicable in
${{(B|A)}} \in \Delta^\infty$
is applicable in
![]() $\omega$
. There are two possible cases: Either
$\omega$
. There are two possible cases: Either
![]() $\omega$
falsifies one of the other conditionals in
$\omega$
falsifies one of the other conditionals in
![]() $\Delta^\infty$
or not. In the first case the lemma holds. In the second case, towards a contradiction, we assume that
$\Delta^\infty$
or not. In the first case the lemma holds. In the second case, towards a contradiction, we assume that
![]() $\omega$
does not falsify
$\omega$
does not falsify
![]() ${{(B|A)}}$
. If
${{(B|A)}}$
. If
![]() ${{(B|A)}}$
is applicable in
${{(B|A)}}$
is applicable in
![]() $\omega$
and
$\omega$
and
![]() $\omega$
does not falsify
$\omega$
does not falsify
![]() ${{(B|A)}}$
then
${{(B|A)}}$
then
![]() $\omega$
must verify
$\omega$
must verify
![]() ${{(B|A)}}$
. That implies that
${{(B|A)}}$
. That implies that
![]() ${{(B|A)}}$
is tolerated by
${{(B|A)}}$
is tolerated by
![]() $\Delta^\infty$
which contradicts the construction of
$\Delta^\infty$
which contradicts the construction of
![]() ${{{{{\mathit{EZP}}}}(\Delta)}}$
.
${{{{{\mathit{EZP}}}}(\Delta)}}$
.
It is well-known that the construction of the extended Z-partition
![]() ${{{{{\mathit{EZP}}}}(\Delta)}}$
is successful with
${{{{{\mathit{EZP}}}}(\Delta)}}$
is successful with
![]() $\Delta^\infty = \emptyset$
iff
$\Delta^\infty = \emptyset$
iff
![]() $\Delta$
is strongly consistent (Goldszmidt & Pearl, Reference Goldszmidt and Pearl1996). We can also use the extended Z-partition to check for weak consistency. The following proposition summarizes the relations between
$\Delta$
is strongly consistent (Goldszmidt & Pearl, Reference Goldszmidt and Pearl1996). We can also use the extended Z-partition to check for weak consistency. The following proposition summarizes the relations between
![]() ${{{{{\mathit{EZP}}}}(\Delta)}}$
and the consistency of
${{{{{\mathit{EZP}}}}(\Delta)}}$
and the consistency of
![]() $\Delta$
.
$\Delta$
.
Proposition 16. Let
![]() $\Delta = \{{{(B_1|A_1)}}, \dots, {{(B_n|A_n)}}\}$
be a belief base with
$\Delta = \{{{(B_1|A_1)}}, \dots, {{(B_n|A_n)}}\}$
be a belief base with
![]() ${{{{{\mathit{EZP}}}}(\Delta)}} = (\Delta^0, \dots, \Delta^k, \Delta^\infty)$
.
${{{{{\mathit{EZP}}}}(\Delta)}} = (\Delta^0, \dots, \Delta^k, \Delta^\infty)$
.
-
1.
 $\Delta$
is strongly consistent iff
$\Delta$
is strongly consistent iff
 $\Delta^\infty = \emptyset$
.
$\Delta^\infty = \emptyset$
. -
2.
 $\Delta$
is weakly consistent iff
$\Delta$
is weakly consistent iff
 $\Delta^\infty \neq \Delta$
or
$\Delta^\infty \neq \Delta$
or
 $A_1 \vee \dots \vee A_n \not\equiv \top$
.
$A_1 \vee \dots \vee A_n \not\equiv \top$
. -
3.
 $\Delta$
is not weakly consistent iff
$\Delta$
is not weakly consistent iff
 $\Delta^\infty = \Delta$
and
$\Delta^\infty = \Delta$
and
 $A_1 \vee \dots \vee A_n \equiv \top$
.
$A_1 \vee \dots \vee A_n \equiv \top$
.
Continuing Example 8, for the not weakly consistent
![]() $\Delta_2$
we have
$\Delta_2$
we have
![]() ${{{{{\mathit{EZP}}}}(\Delta_2)}} = (\Delta_2^\infty)$
with
${{{{{\mathit{EZP}}}}(\Delta_2)}} = (\Delta_2^\infty)$
with
![]() $\Delta_2^\infty = \Delta$
and
$\Delta_2^\infty = \Delta$
and
![]() $a \vee \overline{a} \vee \overline{a} \equiv \top$
. For the weakly consistent
$a \vee \overline{a} \vee \overline{a} \equiv \top$
. For the weakly consistent
![]() $\Delta_3$
we have
$\Delta_3$
we have
![]() ${{{{{\mathit{EZP}}}}(\Delta_3)}} = (\Delta_3^\infty)$
with
${{{{{\mathit{EZP}}}}(\Delta_3)}} = (\Delta_3^\infty)$
with
![]() $\Delta_3^\infty = \Delta$
but
$\Delta_3^\infty = \Delta$
but
![]() $a \not\equiv \top$
. For the strongly consistent
$a \not\equiv \top$
. For the strongly consistent
![]() $\Delta_3$
we have
$\Delta_3$
we have
![]() ${{{{{\mathit{EZP}}}}(\Delta_4)}} = (\Delta_4^0)$
with
${{{{{\mathit{EZP}}}}(\Delta_4)}} = (\Delta_4^0)$
with
![]() $\Delta_4^0 = \Delta$
and
$\Delta_4^0 = \Delta$
and
![]() $\Delta_4^\infty = \emptyset$
.
$\Delta_4^\infty = \emptyset$
.
The extended Z-partition
![]() ${{{{{\mathit{EZP}}}}(\Delta)}}$
can be computed with the algorithm provided by Pearl (Reference Pearl1990). Having
${{{{{\mathit{EZP}}}}(\Delta)}}$
can be computed with the algorithm provided by Pearl (Reference Pearl1990). Having
![]() ${{{{{\mathit{EZP}}}}(\Delta)}}$
at hand,
${{{{{\mathit{EZP}}}}(\Delta)}}$
at hand,
![]() $\kappa^z_{\Delta}$
can be computed directly along the lines of Definition 13, leading to an implementation of system Z inference induced by
$\kappa^z_{\Delta}$
can be computed directly along the lines of Definition 13, leading to an implementation of system Z inference induced by
![]() $\kappa^z_{\Delta}$
for every weakly consistent belief base
$\kappa^z_{\Delta}$
for every weakly consistent belief base
![]() $\Delta$
.
$\Delta$
.
For p-entailment with respect to strongly consistent belief bases, it is well known that the relation
![]() $A|\hspace{-2pt} {\sim}^{p}_{\Delta} B$
holds iff
$A|\hspace{-2pt} {\sim}^{p}_{\Delta} B$
holds iff
![]() $\Delta \cup \{{{(\overline{B}|A)}}\}$
is not strongly consistent (Goldszmidt & Pearl, Reference Goldszmidt and Pearl1996). Obviously, this characterization of p-entailment is not applicable for belief bases that are only weakly consistent. For p-entailment with respect to a weakly consistent belief base
$\Delta \cup \{{{(\overline{B}|A)}}\}$
is not strongly consistent (Goldszmidt & Pearl, Reference Goldszmidt and Pearl1996). Obviously, this characterization of p-entailment is not applicable for belief bases that are only weakly consistent. For p-entailment with respect to a weakly consistent belief base
![]() $\Delta$
, Lehmann and Magidor (Reference Lehmann and Magidor1992), p. 41, say that Dix pointed out to them how rational closure, and thus extended system Z, yields a method for deciding whether
$\Delta$
, Lehmann and Magidor (Reference Lehmann and Magidor1992), p. 41, say that Dix pointed out to them how rational closure, and thus extended system Z, yields a method for deciding whether
![]() $A|\hspace{-2pt} {\sim}^{p}_{\Delta} B$
holds. We state this observation in the following proposition.
$A|\hspace{-2pt} {\sim}^{p}_{\Delta} B$
holds. We state this observation in the following proposition.
Proposition 17 (Lehmann & Magidor, Reference Lehmann and Magidor1992, p. 41, adapted). Let
![]() $\Delta = \{{{(B_1|A_1)}}, \dots, {{(B_n|A_n)}}\}$
be a weakly consistent belief base, and let A, B be formulas. Then the following holds:
$\Delta = \{{{(B_1|A_1)}}, \dots, {{(B_n|A_n)}}\}$
be a weakly consistent belief base, and let A, B be formulas. Then the following holds:
An immediate consequence of Proposition 17 is the following.
Proposition 18. Let
![]() $\Delta = \{{{(B_1|A_1)}}, \dots, {{(B_n|A_n)}}\}$
be a weakly consistent belief base, and let A, B be formulas. Then the following holds:
$\Delta = \{{{(B_1|A_1)}}, \dots, {{(B_n|A_n)}}\}$
be a weakly consistent belief base, and let A, B be formulas. Then the following holds:
Proof. The claim follows from Proposition 17 because for every ranking function
![]() $\kappa$
, the relation
$\kappa$
, the relation
![]() $A |\hspace{-2pt} {\sim}_{\kappa} \bot$
iff
$A |\hspace{-2pt} {\sim}_{\kappa} \bot$
iff
![]() $\kappa(A) = \infty$
holds according to Equation (1).
$\kappa(A) = \infty$
holds according to Equation (1).
Hence, an implementation of (extended) system Z and its underlying ranking function can be used to obtain an implementation of p-entailment, and thus of system P, for every weakly consistent belief base.
5. Generalizing c-representations
c-Representations are a special type of ranking model of a belief base. They are obtained from natural number impacts associated with the conditionals in the belief base that can be seen as penalty points for worlds falsifying the corresponding conditional.
Definition 19 (c-representation, Kern-Isberner, Reference Kern-Isberner2001, Reference Kern-Isberner2004). A c-representation of a belief base
![]() $\Delta = \{{{(B_1|A_1)}}, \dots, {{(B_n|A_n)}}\}$
over
$\Delta = \{{{(B_1|A_1)}}, \dots, {{(B_n|A_n)}}\}$
over
![]() $\Sigma$
is a ranking function
$\Sigma$
is a ranking function
![]() $\kappa_{\vec{\eta}}$
constructed from integers
$\kappa_{\vec{\eta}}$
constructed from integers
![]() $\vec{\eta} = (\eta_{1}\, , \ldots \, , \eta_{n})$
, also called impacts, with
$\vec{\eta} = (\eta_{1}\, , \ldots \, , \eta_{n})$
, also called impacts, with
![]() $\eta_{i} \in \mathbb{N}_0, i \in \{1, \ldots, n \}$
assigned to each conditional
$\eta_{i} \in \mathbb{N}_0, i \in \{1, \ldots, n \}$
assigned to each conditional
![]() ${{(B_i|A_i)}}$
such that
${{(B_i|A_i)}}$
such that
![]() $\kappa_{\vec{\eta}}$
accepts
$\kappa_{\vec{\eta}}$
accepts
![]() $\Delta$
and is given by:
$\Delta$
and is given by:
We will denote the set of all c-representations of
![]() $\Delta$
by
$\Delta$
by
![]() ${Mod}\,^{c}_{\Sigma}(\Delta)$
.
${Mod}\,^{c}_{\Sigma}(\Delta)$
.
Note that the impact
![]() $\eta_{i}$
assigned to the conditional
$\eta_{i}$
assigned to the conditional
![]() ${{(B_i|A_i)}}$
decreases the plausibility of a world
${{(B_i|A_i)}}$
decreases the plausibility of a world
![]() $\omega$
if
$\omega$
if
![]() $\omega$
falsifies
$\omega$
falsifies
![]() ${{(B_i|A_i)}}$
, and that the rank of
${{(B_i|A_i)}}$
, and that the rank of
![]() $\omega$
under the c-representation
$\omega$
under the c-representation
![]() $\kappa_{\vec{\eta}}$
induced by the impact vector
$\kappa_{\vec{\eta}}$
induced by the impact vector
![]() $\vec{\eta}$
is the sum of the impacts assigned to the conditionals which are falsified by
$\vec{\eta}$
is the sum of the impacts assigned to the conditionals which are falsified by
![]() $\omega$
.
$\omega$
.
A belief base
![]() $\Delta$
that is not strongly consistent has no c-representation: by Definition 19, a c-representation of
$\Delta$
that is not strongly consistent has no c-representation: by Definition 19, a c-representation of
![]() $\Delta$
is a finite ranking function modelling
$\Delta$
is a finite ranking function modelling
![]() $\Delta$
; if
$\Delta$
; if
![]() $\Delta$
is not strongly consistent, such a ranking function cannot exist. For belief bases that are only weakly consistent, we need a more general definition of c-representations. A ranking function that is a model of a weakly but not strongly consistent belief base must assign rank
$\Delta$
is not strongly consistent, such a ranking function cannot exist. For belief bases that are only weakly consistent, we need a more general definition of c-representations. A ranking function that is a model of a weakly but not strongly consistent belief base must assign rank
![]() $\infty$
to some worlds. To achieve this while keeping a construction of c-representations similar to the one given in (4), we extend the definition of c-representations to allow infinite impacts.
$\infty$
to some worlds. To achieve this while keeping a construction of c-representations similar to the one given in (4), we extend the definition of c-representations to allow infinite impacts.
Definition 20 (extended c-representation). An extended c-representation of a belief base
![]() $\Delta = \{{{(B_1|A_1)}}, \dots, {{(B_n|A_n)}}\}$
over
$\Delta = \{{{(B_1|A_1)}}, \dots, {{(B_n|A_n)}}\}$
over
![]() $\Sigma$
is a ranking function
$\Sigma$
is a ranking function
![]() $\kappa_{\vec{\eta}}$
constructed from impacts
$\kappa_{\vec{\eta}}$
constructed from impacts
![]() $\vec{\eta} = (\eta_{1}\, , \ldots \, , \eta_{n}) $
with
$\vec{\eta} = (\eta_{1}\, , \ldots \, , \eta_{n}) $
with
![]() $\eta_{i} \in \mathbb{N}_0 \cup \{\infty\}, i \in \{1, \ldots, n \}$
assigned to each conditional
$\eta_{i} \in \mathbb{N}_0 \cup \{\infty\}, i \in \{1, \ldots, n \}$
assigned to each conditional
![]() ${{(B_i|A_i)}}$
such that
${{(B_i|A_i)}}$
such that
![]() $\kappa_{\vec{\eta}}$
accepts
$\kappa_{\vec{\eta}}$
accepts
![]() $\Delta$
and is given by
$\Delta$
and is given by
We will denote the set of all extended c-representations of
![]() $\Delta$
by
$\Delta$
by
![]() $\mbox{Mod}\,^{ec}_{\Sigma}(\Delta)$
.
$\mbox{Mod}\,^{ec}_{\Sigma}(\Delta)$
.
Example 21. Let
![]() $\Sigma = \{b, p, f\}$
and
$\Sigma = \{b, p, f\}$
and
![]() $\Delta = \{{{(b|p)}}, {{(f|b)}}, {{(\overline{b}|p)}}\}$
. Note that
$\Delta = \{{{(b|p)}}, {{(f|b)}}, {{(\overline{b}|p)}}\}$
. Note that
![]() $\Delta$
is weakly consistent but not strongly consistent. The OCF
$\Delta$
is weakly consistent but not strongly consistent. The OCF
![]() $\kappa_{\vec{\eta}}$
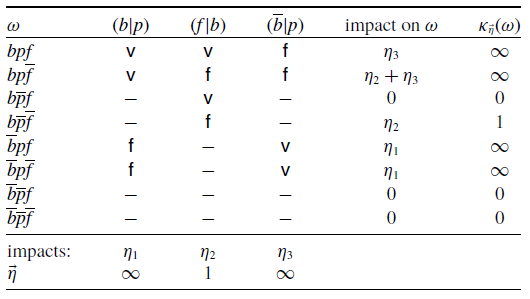
displayed in Table 1 is an extended c-representation of
$\kappa_{\vec{\eta}}$
displayed in Table 1 is an extended c-representation of
![]() $\Delta$
induced by the impacts
$\Delta$
induced by the impacts
![]() $\vec{\eta} = (\infty, 1,\infty)$
.
$\vec{\eta} = (\infty, 1,\infty)$
.
Every c-representation of a strongly consistent belief base
![]() $\Delta$
is obviously an extended c-representation of
$\Delta$
is obviously an extended c-representation of
![]() $\Delta$
, and every weakly consistent belief base has at least one extended c-representation.
$\Delta$
, and every weakly consistent belief base has at least one extended c-representation.
Table 1. Verification (
![]() ${\textsf{v}}$
) and falsification (
${\textsf{v}}$
) and falsification (
![]() ${\textsf{f}}$
) of the conditionals in
${\textsf{f}}$
) of the conditionals in
![]() $\Delta$
from Example 21 and their corresponding impacts. The ranking function
$\Delta$
from Example 21 and their corresponding impacts. The ranking function
![]() $\kappa_{\vec{\eta}}$
induced by the impacts
$\kappa_{\vec{\eta}}$
induced by the impacts
![]() $\vec{\eta} = (\eta_{1}, \eta_{2}, \eta_{3}) = (\infty, 1, \infty)$
is an extended c-representation for
$\vec{\eta} = (\eta_{1}, \eta_{2}, \eta_{3}) = (\infty, 1, \infty)$
is an extended c-representation for
![]() $\Delta$
$\Delta$
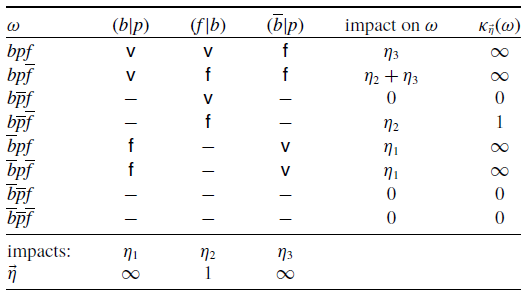
Proposition 22. Let
![]() $\Delta$
be a strongly consistent belief base. Every c-representation
$\Delta$
be a strongly consistent belief base. Every c-representation
![]() $\kappa_{\vec{\eta}}$
of
$\kappa_{\vec{\eta}}$
of
![]() $\Delta$
is an extended c-representation of
$\Delta$
is an extended c-representation of
![]() $\Delta$
.
$\Delta$
.
Proposition 23. Let
![]() $\Delta$
be a weakly consistent belief base. Then
$\Delta$
be a weakly consistent belief base. Then
![]() $\kappa_{\vec{\eta}}$
with
$\kappa_{\vec{\eta}}$
with
![]() $\vec{\eta} = (\infty, \dots, \infty)$
is an extended c-representation of
$\vec{\eta} = (\infty, \dots, \infty)$
is an extended c-representation of
![]() $\Delta$
.
$\Delta$
.
Proof. Because
![]() $\Delta$
is weakly consistent, there is at least one world
$\Delta$
is weakly consistent, there is at least one world
![]() $\omega \in \Omega_\Sigma$
that does not falsify any of the conditionals (see Lemma 9). This implies
$\omega \in \Omega_\Sigma$
that does not falsify any of the conditionals (see Lemma 9). This implies
![]() $\kappa_{\vec{\eta}}(\omega) = 0$
. Thus,
$\kappa_{\vec{\eta}}(\omega) = 0$
. Thus,
![]() $\kappa_{\vec{\eta}}$
is a ranking function.
$\kappa_{\vec{\eta}}$
is a ranking function.
For every
![]() ${{(B|A)}} \in \Delta$
it holds that
${{(B|A)}} \in \Delta$
it holds that
![]() $\kappa_{\vec{\eta}}(A\overline{B}) = \infty$
because every model of
$\kappa_{\vec{\eta}}(A\overline{B}) = \infty$
because every model of
![]() $A\overline{B}$
falsifies the conditional
$A\overline{B}$
falsifies the conditional
![]() ${{(B|A)}}$
with impact
${{(B|A)}}$
with impact
![]() $\infty$
. For
$\infty$
. For
![]() $\kappa_{\vec{\eta}}(AB)$
we have either (1)
$\kappa_{\vec{\eta}}(AB)$
we have either (1)
![]() $\kappa_{\vec{\eta}}(AB) = 0$
or (2)
$\kappa_{\vec{\eta}}(AB) = 0$
or (2)
![]() $\kappa_{\vec{\eta}}(AB) = \infty$
. In case (1) we have
$\kappa_{\vec{\eta}}(AB) = \infty$
. In case (1) we have
![]() $\kappa_{\vec{\eta}}(AB) = 0 \lt \infty = \kappa_{\vec{\eta}}(A\overline{B})$
. In case (2) we have
$\kappa_{\vec{\eta}}(AB) = 0 \lt \infty = \kappa_{\vec{\eta}}(A\overline{B})$
. In case (2) we have
![]() $\kappa_{\vec{\eta}}(AB) = \infty$
and
$\kappa_{\vec{\eta}}(AB) = \infty$
and
![]() $\kappa_{\vec{\eta}}(A\overline{B}) = \infty$
and therefore
$\kappa_{\vec{\eta}}(A\overline{B}) = \infty$
and therefore
![]() $\kappa_{\vec{\eta}}(A) = \infty$
because
$\kappa_{\vec{\eta}}(A) = \infty$
because
![]() $\kappa_{\vec{\eta}}(A) = \min \{\kappa_{\vec{\eta}}(AB), \kappa_{\vec{\eta}}(A\overline{B})\}$
. In both cases,
$\kappa_{\vec{\eta}}(A) = \min \{\kappa_{\vec{\eta}}(AB), \kappa_{\vec{\eta}}(A\overline{B})\}$
. In both cases,
![]() $\kappa_{\vec{\eta}}$
accepts
$\kappa_{\vec{\eta}}$
accepts
![]() ${{(B|A)}}$
. Thus,
${{(B|A)}}$
. Thus,
![]() $\kappa_{\vec{\eta}} \models \Delta$
.
$\kappa_{\vec{\eta}} \models \Delta$
.
Proposition 23 also illustrates that in extended c-representations worlds may have rank infinity without the belief base requiring this. In an extended c-representation of
![]() $\Delta$
only those worlds need to have rank infinity that have rank infinity in the z-ranking
$\Delta$
only those worlds need to have rank infinity that have rank infinity in the z-ranking
![]() $\kappa^z_{\Delta}$
of
$\kappa^z_{\Delta}$
of
![]() $\Delta$
. This is shown in the following two lemmas.
$\Delta$
. This is shown in the following two lemmas.
Lemma 24. Let
![]() $\Delta$
be a weakly consistent belief base. If
$\Delta$
be a weakly consistent belief base. If
![]() $\kappa^z_{\Delta}(\omega) = \infty$
for a world
$\kappa^z_{\Delta}(\omega) = \infty$
for a world
![]() $\omega$
, then
$\omega$
, then
![]() $\kappa_{\vec{\eta}}(\omega) = \infty$
for all extended c-representations
$\kappa_{\vec{\eta}}(\omega) = \infty$
for all extended c-representations
![]() $\kappa_{\vec{\eta}}$
of
$\kappa_{\vec{\eta}}$
of
![]() $\Delta$
.
$\Delta$
.
Proof. Assume that
![]() $\kappa^z_{\Delta}(\omega) = \infty$
. Let
$\kappa^z_{\Delta}(\omega) = \infty$
. Let
![]() ${{{{{\mathit{EZP}}}}(\Delta)}} = \{\Delta^0, \dots, \Delta^m, \Delta^\infty\}$
be the extended Z-partition of
${{{{{\mathit{EZP}}}}(\Delta)}} = \{\Delta^0, \dots, \Delta^m, \Delta^\infty\}$
be the extended Z-partition of
![]() $\Delta$
. By definition of
$\Delta$
. By definition of
![]() $\kappa^z_{\Delta}$
there exists a conditional
$\kappa^z_{\Delta}$
there exists a conditional
![]() ${{(B|A)}} \in \Delta^\infty$
s.t.
${{(B|A)}} \in \Delta^\infty$
s.t.
![]() $\omega \models A$
. Because
$\omega \models A$
. Because
![]() ${{(B|A)}} \in \Delta^\infty$
the conditional
${{(B|A)}} \in \Delta^\infty$
the conditional
![]() ${{(B|A)}}$
is not tolerated by
${{(B|A)}}$
is not tolerated by
![]() $\Delta^\infty$
, so there is a conditional
$\Delta^\infty$
, so there is a conditional
![]() ${{(B'|A')}} \in \Delta^\infty$
that is falsified by
${{(B'|A')}} \in \Delta^\infty$
that is falsified by
![]() $\omega$
(this can be
$\omega$
(this can be
![]() ${{(B|A)}}$
again).
${{(B|A)}}$
again).
Towards a contradiction assume that there is a c-representation
![]() $\kappa_{\vec{\eta}}$
of
$\kappa_{\vec{\eta}}$
of
![]() $\Delta$
with
$\Delta$
with
![]() $\kappa_{\vec{\eta}}(\omega) \lt \infty$
. As
$\kappa_{\vec{\eta}}(\omega) \lt \infty$
. As
![]() $\kappa_{\vec{\eta}}$
models
$\kappa_{\vec{\eta}}$
models
![]() $\Delta$
and thus also
$\Delta$
and thus also
![]() ${{(B'|A')}}$
there must be a world
${{(B'|A')}}$
there must be a world
![]() $\omega^1$
that verifies
$\omega^1$
that verifies
![]() ${{(B'|A')}}$
and satisfies
${{(B'|A')}}$
and satisfies
![]() $\kappa_{\vec{\eta}}(\omega^1) \lt \kappa_{\vec{\eta}}(\omega)$
. With the same argumentation there must be another conditional
$\kappa_{\vec{\eta}}(\omega^1) \lt \kappa_{\vec{\eta}}(\omega)$
. With the same argumentation there must be another conditional
![]() ${{(B^1|A^1)}} \in \Delta^\infty$
that is falsified by
${{(B^1|A^1)}} \in \Delta^\infty$
that is falsified by
![]() $\omega^1$
, and another world
$\omega^1$
, and another world
![]() $\omega_2$
that verifies
$\omega_2$
that verifies
![]() ${{(B^1|A^1)}}$
and satisfies
${{(B^1|A^1)}}$
and satisfies
![]() $\kappa_{\vec{\eta}}(\omega^2) \lt \kappa_{\vec{\eta}}(\omega^1)$
. Repeating this argumentation, we obtain an infinite chain of worlds
$\kappa_{\vec{\eta}}(\omega^2) \lt \kappa_{\vec{\eta}}(\omega^1)$
. Repeating this argumentation, we obtain an infinite chain of worlds
![]() $\omega_1, \omega_2, \dots$
s.t.
$\omega_1, \omega_2, \dots$
s.t.
![]() $\kappa_{\vec{\eta}}(\omega_1) \gt \kappa_{\vec{\eta}}(\omega_2) \gt \dots$
. But as there are only finitely many worlds (and also because there are only finitely many ranks below
$\kappa_{\vec{\eta}}(\omega_1) \gt \kappa_{\vec{\eta}}(\omega_2) \gt \dots$
. But as there are only finitely many worlds (and also because there are only finitely many ranks below
![]() $\kappa_{\vec{\eta}}(\omega_1)$
) such a chain cannot exist. Contradiction.
$\kappa_{\vec{\eta}}(\omega_1)$
) such a chain cannot exist. Contradiction.
Lemma 25. Let
![]() $\Delta$
be a weakly consistent belief base. There is a c-representation
$\Delta$
be a weakly consistent belief base. There is a c-representation
![]() $\kappa_{\vec{\eta}}$
of
$\kappa_{\vec{\eta}}$
of
![]() $\Delta$
with
$\Delta$
with
![]() $\kappa_{\vec{\eta}}(\omega) \lt \infty$
for all worlds
$\kappa_{\vec{\eta}}(\omega) \lt \infty$
for all worlds
![]() $\omega$
with
$\omega$
with
![]() $\kappa^z_{\Delta}(\omega) \lt \infty$
.
$\kappa^z_{\Delta}(\omega) \lt \infty$
.
Proof. Let
![]() $\Delta = \{{{(B_1|A_1)}}, \dots, {{(B_n|A_n)}}\}$
be a weakly consistent belief base. Let
$\Delta = \{{{(B_1|A_1)}}, \dots, {{(B_n|A_n)}}\}$
be a weakly consistent belief base. Let
![]() ${{{{{\mathit{EZP}}}}(\Delta)}} = \{\Delta^0, \dots, \Delta^m, \Delta^\infty\}$
be the extended Z-partition of
${{{{{\mathit{EZP}}}}(\Delta)}} = \{\Delta^0, \dots, \Delta^m, \Delta^\infty\}$
be the extended Z-partition of
![]() $\Delta$
. Construct an impact vector
$\Delta$
. Construct an impact vector
![]() $\vec{\eta}$
for
$\vec{\eta}$
for
![]() $\Delta$
as follows. Let
$\Delta$
as follows. Let
![]() $\mu^0 = 1$
and
$\mu^0 = 1$
and
![]() $\mu^j = |\Delta^0 \cup \dots \cup \Delta^{j-1}| \cdot \mu^{j-1} +1$
for
$\mu^j = |\Delta^0 \cup \dots \cup \Delta^{j-1}| \cdot \mu^{j-1} +1$
for
![]() $j=1, \dots, m$
. For
$j=1, \dots, m$
. For
![]() ${{(B_i|A_i)}}$
with
${{(B_i|A_i)}}$
with
![]() ${{(B_i|A_i)}} \in \Delta^j$
let
${{(B_i|A_i)}} \in \Delta^j$
let
![]() $\eta_{i} = \mu^j$
for
$\eta_{i} = \mu^j$
for
![]() $j \lt \infty$
and
$j \lt \infty$
and
![]() $\eta_{j} = \infty$
for
$\eta_{j} = \infty$
for
![]() $j = \infty$
. By construction, for worlds
$j = \infty$
. By construction, for worlds
![]() $\omega$
that do not falsify a conditional from
$\omega$
that do not falsify a conditional from
![]() $\Delta^j \cup \dots \cup \Delta^m \cup \Delta^\infty$
we have
$\Delta^j \cup \dots \cup \Delta^m \cup \Delta^\infty$
we have
![]() $\kappa_{\vec{\eta}}(\omega) \lt \mu^j$
.
$\kappa_{\vec{\eta}}(\omega) \lt \mu^j$
.
![]() $\kappa_{\vec{\eta}}$
is a c-representation of
$\kappa_{\vec{\eta}}$
is a c-representation of
![]() $\Delta$
: Let
$\Delta$
: Let
![]() ${{(B_i|A_i)}}$
be any conditional in
${{(B_i|A_i)}}$
be any conditional in
![]() $\Delta$
. If
$\Delta$
. If
![]() ${{(B_i|A_i)}} \in \Delta^\infty$
then
${{(B_i|A_i)}} \in \Delta^\infty$
then
![]() $\kappa^z_{\Delta}(A_i) = \infty$
by the definition of
$\kappa^z_{\Delta}(A_i) = \infty$
by the definition of
![]() $\kappa^z_{\Delta}$
which implies with Proposition 26 that
$\kappa^z_{\Delta}$
which implies with Proposition 26 that
![]() $\kappa_{\vec{\eta}}(A_i) = \infty$
and therefore
$\kappa_{\vec{\eta}}(A_i) = \infty$
and therefore
![]() $\kappa_{\vec{\eta}} \models {{(B_i|A_i)}}$
. Otherwise, we have
$\kappa_{\vec{\eta}} \models {{(B_i|A_i)}}$
. Otherwise, we have
![]() ${{(B_i|A_i)}} \in \Delta^j$
with
${{(B_i|A_i)}} \in \Delta^j$
with
![]() $j \lt \infty$
. Then for any world
$j \lt \infty$
. Then for any world
![]() $\omega'$
falsifying
$\omega'$
falsifying
![]() ${{(B_i|A_i)}}$
we have
${{(B_i|A_i)}}$
we have
![]() $\kappa_{\vec{\eta}}(\omega) \gt \mu^j$
; hence
$\kappa_{\vec{\eta}}(\omega) \gt \mu^j$
; hence
![]() $\kappa_{\vec{\eta}}(A_i \overline{B_i}) \geqslant \mu_j$
. Because
$\kappa_{\vec{\eta}}(A_i \overline{B_i}) \geqslant \mu_j$
. Because
![]() ${{(B_i|A_i)}} \in \Delta^j$
, there is a world
${{(B_i|A_i)}} \in \Delta^j$
, there is a world
![]() $\omega'$
that verifies
$\omega'$
that verifies
![]() ${{(B_i|A_i)}}$
and does not falsify a conditional in
${{(B_i|A_i)}}$
and does not falsify a conditional in
![]() $\Delta^j \cup \dots \cup \Delta^m \cup \Delta^\infty$
. Therefore,
$\Delta^j \cup \dots \cup \Delta^m \cup \Delta^\infty$
. Therefore,
![]() $\kappa_{\vec{\eta}}(A_i B_i)\lt \mu_j$
. Thus,
$\kappa_{\vec{\eta}}(A_i B_i)\lt \mu_j$
. Thus,
![]() $\kappa_{\vec{\eta}}(A_i B_i)\lt \mu_j \leqslant \kappa_{\vec{\eta}}(A_i \overline{B_i})$
and
$\kappa_{\vec{\eta}}(A_i B_i)\lt \mu_j \leqslant \kappa_{\vec{\eta}}(A_i \overline{B_i})$
and
![]() $\kappa_{\vec{\eta}} \models {{(B_i|A_i)}}$
.
$\kappa_{\vec{\eta}} \models {{(B_i|A_i)}}$
.
Furthermore, it holds that
![]() $\kappa_{\vec{\eta}}(\omega) = \infty$
iff
$\kappa_{\vec{\eta}}(\omega) = \infty$
iff
![]() $\omega$
falsifies a conditional in
$\omega$
falsifies a conditional in
![]() $\Delta^\infty$
. Therefore,
$\Delta^\infty$
. Therefore,
![]() $\kappa_{\vec{\eta}}(\omega) \lt \infty$
for all worlds
$\kappa_{\vec{\eta}}(\omega) \lt \infty$
for all worlds
![]() $\omega$
with
$\omega$
with
![]() $\kappa^z_{\Delta}(\omega) \lt \infty$
.
$\kappa^z_{\Delta}(\omega) \lt \infty$
.
Lemmas 24 and 25 can be summarized by the following proposition.
Proposition 26. Let
![]() $\Delta$
be a weakly consistent belief base. If
$\Delta$
be a weakly consistent belief base. If
![]() $\kappa^z_{\Delta}(\omega) = \infty$
for a world
$\kappa^z_{\Delta}(\omega) = \infty$
for a world
![]() $\omega$
, then
$\omega$
, then
![]() $\kappa_{\vec{\eta}}(\omega) = \infty$
for all extended c-representations
$\kappa_{\vec{\eta}}(\omega) = \infty$
for all extended c-representations
![]() $\kappa_{\vec{\eta}}$
of
$\kappa_{\vec{\eta}}$
of
![]() $\Delta$
.
$\Delta$
.
Moreover, there is an extended c-representation
![]() $\kappa_{\vec{\eta}}$
of
$\kappa_{\vec{\eta}}$
of
![]() $\Delta$
with
$\Delta$
with
![]() $\kappa_{\vec{\eta}}(\omega) \lt \infty$
for all worlds
$\kappa_{\vec{\eta}}(\omega) \lt \infty$
for all worlds
![]() $\omega$
with
$\omega$
with
![]() $\kappa^z_{\Delta}(\omega) \lt \infty$
.
$\kappa^z_{\Delta}(\omega) \lt \infty$
.
As a consequence of this proposition, for a weakly consistent
![]() $\Delta$
, there is an extended c-representation
$\Delta$
, there is an extended c-representation
![]() ${{\kappa_{\vec{\eta}}}}$
such that
${{\kappa_{\vec{\eta}}}}$
such that
![]() ${{\kappa_{\vec{\eta}}}}(\omega) \lt \infty$
iff
${{\kappa_{\vec{\eta}}}}(\omega) \lt \infty$
iff
![]() $\kappa^z_{\Delta}(\omega) \lt \infty$
. Using Lemma 14, we have
$\kappa^z_{\Delta}(\omega) \lt \infty$
. Using Lemma 14, we have
![]() $\kappa_{\vec{\eta}}(\omega) \lt \infty$
iff
$\kappa_{\vec{\eta}}(\omega) \lt \infty$
iff
![]() $\omega$
does not entail
$\omega$
does not entail
![]() $\bot$
with p-entailment.
$\bot$
with p-entailment.
Lemma 27. Let
![]() $\Delta$
be a weakly consistent belief base. There is an extended c-representation
$\Delta$
be a weakly consistent belief base. There is an extended c-representation
![]() $\kappa_{\vec{\eta}}$
of
$\kappa_{\vec{\eta}}$
of
![]() $\Delta$
such that for all
$\Delta$
such that for all
![]() $\omega \in \Omega$
we have
$\omega \in \Omega$
we have
![]() $\kappa_{\vec{\eta}}(\omega) \lt \infty$
iff
$\kappa_{\vec{\eta}}(\omega) \lt \infty$
iff
![]() $ \omega |\hspace{-2pt} {\sim}\!\!\!\!/^{\,p}_{\Delta} \bot $
, where the world
$ \omega |\hspace{-2pt} {\sim}\!\!\!\!/^{\,p}_{\Delta} \bot $
, where the world
![]() $\omega$
is considered as a formula on the right side of the ‘iff’.
$\omega$
is considered as a formula on the right side of the ‘iff’.
Another consequence of Proposition 26 is the following.
Proposition 28. Let
![]() $\Delta$
be a belief base with
$\Delta$
be a belief base with
![]() ${{{{{\mathit{EZP}}}}(\Delta)}} = \{\Delta^0, \dots, \Delta^m, \Delta^\infty\}$
, and let
${{{{{\mathit{EZP}}}}(\Delta)}} = \{\Delta^0, \dots, \Delta^m, \Delta^\infty\}$
, and let
![]() $\omega \in \Omega$
. We have that
$\omega \in \Omega$
. We have that
![]() $\kappa(\omega) = \infty$
for all
$\kappa(\omega) = \infty$
for all
![]() $\kappa \in {Mod}\,^{ec}_{\Delta}$
iff
$\kappa \in {Mod}\,^{ec}_{\Delta}$
iff
![]() $\omega \models A$
for some
$\omega \models A$
for some
![]() ${{(B|A)}} \in \Delta^\infty$
.
${{(B|A)}} \in \Delta^\infty$
.
Proof.
Direction
![]() $\Rightarrow$
If
$\Rightarrow$
If
![]() $\kappa(\omega) = \infty$
for all
$\kappa(\omega) = \infty$
for all
![]() $\kappa \in {Mod}\,^{ec}_{\Delta}$
, then there is no
$\kappa \in {Mod}\,^{ec}_{\Delta}$
, then there is no
![]() $\kappa_{\vec{\eta}} \in {Mod}\,^{ec}_{\Delta}$
with
$\kappa_{\vec{\eta}} \in {Mod}\,^{ec}_{\Delta}$
with
![]() $\kappa_{\vec{\eta}}(\omega) \lt \infty$
. With Proposition 26 this implies
$\kappa_{\vec{\eta}}(\omega) \lt \infty$
. With Proposition 26 this implies
![]() $\kappa^z_{\Delta}(\omega) = \infty$
. By Definition 13, this is the case if a conditional in
$\kappa^z_{\Delta}(\omega) = \infty$
. By Definition 13, this is the case if a conditional in
![]() $\Delta^\infty$
is applicable for
$\Delta^\infty$
is applicable for
![]() $\omega$
.
$\omega$
.
Direction
![]() $\Leftarrow$
Assume
$\Leftarrow$
Assume
![]() $\omega \models A$
for some
$\omega \models A$
for some
![]() ${{(B|A)}} \in \Delta^\infty$
. Then
${{(B|A)}} \in \Delta^\infty$
. Then
![]() $\kappa^z_{\Delta}(\omega) = \infty$
and with Proposition 26 we have
$\kappa^z_{\Delta}(\omega) = \infty$
and with Proposition 26 we have
![]() $\kappa(\omega) = \infty$
for all
$\kappa(\omega) = \infty$
for all
![]() $\kappa \in {Mod}\,^{ec}_{\Delta}$
.
$\kappa \in {Mod}\,^{ec}_{\Delta}$
.
When general c-representations were introduced in Kern-Isberner (Reference Kern-Isberner2001), they were shown to be conditionally indifferent with respect to the inducing knowledge base. Very briefly, conditional indifference is an invariance property for models of a knowledge base which claims that possible worlds should be assigned the same semantic value if they behave the same with respect to the conditionals in the knowledge base, that is, if they verify and falsify exactly the same conditionals. Equivalently, this means that any difference in the semantic evaluation of two worlds can be explained by differences in the conditional-logical evaluation of the worlds with respect to the knowledge base. This links the numerical values assigned to worlds clearly to the logical structure provided by the conditionals in the base.
We adapt a simplified version of conditional indifference to the setting of inducing ranking models from weakly consistent knowledge bases on which we focus in this paper.
Definition 29 (conditional indifference, adapted from Kern-Isberner, Reference Kern-Isberner2001). Let
![]() $\Delta$
be a conditional belief base and let
$\Delta$
be a conditional belief base and let
![]() $\kappa\;:\; \Omega \rightarrow \mathbb{N} \cup \{\infty\}$
be a ranking function. Then
$\kappa\;:\; \Omega \rightarrow \mathbb{N} \cup \{\infty\}$
be a ranking function. Then
![]() $\kappa$
is conditionally indifferent with respect to
$\kappa$
is conditionally indifferent with respect to
![]() $\Delta$
, if the following two conditions hold:
$\Delta$
, if the following two conditions hold:
-
1. If
 $\kappa(\omega) = \infty$
, then there is a conditional
$\kappa(\omega) = \infty$
, then there is a conditional
 ${{(B|A)}} \in \Delta$
that is either falsified in or not applicable to
${{(B|A)}} \in \Delta$
that is either falsified in or not applicable to
 $\omega$
, and
$\omega$
, and
 $\kappa(\omega') = \infty$
for every
$\kappa(\omega') = \infty$
for every
 $\omega' \in \Omega$
that behaves the same with respect to
$\omega' \in \Omega$
that behaves the same with respect to
 ${{(B|A)}}$
as
${{(B|A)}}$
as
 $\omega$
, that is,
$\omega$
, that is,
 ${{(B|A)}}$
also falsifies resp. is not applicable to
${{(B|A)}}$
also falsifies resp. is not applicable to
 $\omega'$
.
$\omega'$
. -
2.
 $\kappa(\omega) = \kappa(\omega')$
for every
$\kappa(\omega) = \kappa(\omega')$
for every
 $\omega, \omega' \in \Omega$
that verify and falsify exactly the same conditionals in
$\omega, \omega' \in \Omega$
that verify and falsify exactly the same conditionals in
 $\Delta$
.
$\Delta$
.
The following proposition shows that also extended c-representations of weakly consistent knowledge bases satisfy conditional indifference.
Proposition 30. Let
![]() $\Delta$
be a conditional belief base and let
$\Delta$
be a conditional belief base and let
![]() $\kappa\;:\; \Omega \rightarrow \mathbb{N} \cup \{\infty\}$
be an extended c-representation of
$\kappa\;:\; \Omega \rightarrow \mathbb{N} \cup \{\infty\}$
be an extended c-representation of
![]() $\Delta$
. Then the following two conditions hold:
$\Delta$
. Then the following two conditions hold:
-
1. If
 $\kappa(\omega) = \infty$
, then there is a conditional
$\kappa(\omega) = \infty$
, then there is a conditional
 ${{(B|A)}} \in \Delta$
that is either falsified in or not applicable to
${{(B|A)}} \in \Delta$
that is either falsified in or not applicable to
 $\omega$
, and
$\omega$
, and
 $\kappa(\omega') = \infty$
for every
$\kappa(\omega') = \infty$
for every
 $\omega' \in \Omega$
that behaves the same with respect to
$\omega' \in \Omega$
that behaves the same with respect to
 ${{(B|A)}}$
as
${{(B|A)}}$
as
 $\omega$
, that is,
$\omega$
, that is,
 ${{(B|A)}}$
also falsifies resp. is not applicable to
${{(B|A)}}$
also falsifies resp. is not applicable to
 $\omega'$
.
$\omega'$
. -
2.
 $\kappa(\omega) = \kappa(\omega')$
for every
$\kappa(\omega) = \kappa(\omega')$
for every
 $\omega, \omega' \in \Omega$
that verify and falsify exactly the same conditionals in
$\omega, \omega' \in \Omega$
that verify and falsify exactly the same conditionals in
 $\Delta$
.
$\Delta$
.
Proof.
Ad 1: Let
![]() $\omega$
be a world with
$\omega$
be a world with
![]() $\kappa(\omega)=\infty$
. Because
$\kappa(\omega)=\infty$
. Because
![]() $\kappa(\omega)$
is the sum of the impacts of the conditionals falsified by
$\kappa(\omega)$
is the sum of the impacts of the conditionals falsified by
![]() $\omega$
and
$\omega$
and
![]() $\Delta$
is finite,
$\Delta$
is finite,
![]() $\omega$
must falsify at least one conditional
$\omega$
must falsify at least one conditional
![]() ${{(B_i|A_i)}}$
with impact
${{(B_i|A_i)}}$
with impact
![]() $\eta_{i} = \infty$
. This
$\eta_{i} = \infty$
. This
![]() ${{(B_i|A_i)}}$
satisfies the first part of condition (1). Moreover, all worlds
${{(B_i|A_i)}}$
satisfies the first part of condition (1). Moreover, all worlds
![]() $\omega'$
that also falsify
$\omega'$
that also falsify
![]() ${{(B_i|A_i)}}$
will have rank
${{(B_i|A_i)}}$
will have rank
![]() $\kappa(\omega') = \infty$
, too. Therefore, also the second part of condition (1) is satisfied by
$\kappa(\omega') = \infty$
, too. Therefore, also the second part of condition (1) is satisfied by
![]() ${{(B_i|A_i)}}$
, and the condition holds.
${{(B_i|A_i)}}$
, and the condition holds.
Ad 2: The rank
![]() $\kappa(\omega)$
of a world
$\kappa(\omega)$
of a world
![]() $\omega$
only depends on which conditionals in
$\omega$
only depends on which conditionals in
![]() $\Delta$
the world falsifies. Therefore, if two worlds
$\Delta$
the world falsifies. Therefore, if two worlds
![]() $\omega, \omega'$
verify and falsify the same conditionals in
$\omega, \omega'$
verify and falsify the same conditionals in
![]() $\Delta$
they will have the same rank.
$\Delta$
they will have the same rank.
With extended c-representations we can now define extended c-inference.
6. Extending c-inference
c-Inference (Beierle et al., Reference Beierle, Eichhorn, Kern-Isberner, Gyssens and Simari2016a; Reference Beierle, Eichhorn, Kern-Isberner and Kutsch2018) is an inference operator taking all c-representations of a belief base
![]() $\Delta$
into account. It was originally defined for strongly consistent belief bases.
$\Delta$
into account. It was originally defined for strongly consistent belief bases.
Definition 31 (c-inference,
![]() $|\hspace{-2pt} {\sim}^{c}_{\Delta}$
Beierle et al., Reference Beierle, Eichhorn, Kern-Isberner, Gyssens and Simari2016a). Let
$|\hspace{-2pt} {\sim}^{c}_{\Delta}$
Beierle et al., Reference Beierle, Eichhorn, Kern-Isberner, Gyssens and Simari2016a). Let
![]() $\Delta$
be a strongly consistent belief base and let A, B be formulas. B is a c-inference from A in the context of
$\Delta$
be a strongly consistent belief base and let A, B be formulas. B is a c-inference from A in the context of
![]() $\Delta$
, denoted by
$\Delta$
, denoted by
![]() $A|\hspace{-2pt} {\sim}^{c}_{\Delta} B$
, iff
$A|\hspace{-2pt} {\sim}^{c}_{\Delta} B$
, iff
![]() $A|\hspace{-2pt} {\sim}_{\kappa} B$
holds for all c-representations
$A|\hspace{-2pt} {\sim}_{\kappa} B$
holds for all c-representations
![]() $\kappa$
of
$\kappa$
of
![]() $\Delta$
.
$\Delta$
.
Now we use extended c-representations to extend c-inference for belief bases that may be only weakly consistent.
Definition 32 (extended c-inference,
![]() $|\hspace{-2pt} {\sim}^{ec}_{\Delta}$
). Let
$|\hspace{-2pt} {\sim}^{ec}_{\Delta}$
). Let
![]() $\Delta$
be a belief base and let
$\Delta$
be a belief base and let
![]() $A, B \in {{\mathcal{L}}}$
. Then B is an extended c-inference from A in the context of
$A, B \in {{\mathcal{L}}}$
. Then B is an extended c-inference from A in the context of
![]() $\Delta$
, denoted by
$\Delta$
, denoted by
![]() $A|\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
, iff
$A|\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
, iff
![]() $A|\hspace{-2pt} {\sim}_{\kappa} B$
holds for all extended c-representations
$A|\hspace{-2pt} {\sim}_{\kappa} B$
holds for all extended c-representations
![]() $\kappa$
of
$\kappa$
of
![]() $\Delta$
.
$\Delta$
.
First, let us verify that extended c-inference is indeed an inductive inference operator that coincides with c-inference for strongly consistent belief bases.
Proposition 33. Extended c-inference is an inductive inference operator, that is, it satisfies (DI) and (TV).
Proof. We need to show that extended c-inference satisfies (DI) and (TV). (DI) is trivial: Every c-representation of
![]() $\Delta$
accepts the conditionals in
$\Delta$
accepts the conditionals in
![]() $\Delta$
by definition. Therefore,
$\Delta$
by definition. Therefore,
![]() $A |\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
for every
$A |\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
for every
![]() ${{(B|A)}} \in \Delta$
. (TV) is also clear: For
${{(B|A)}} \in \Delta$
. (TV) is also clear: For
![]() $\Delta = \emptyset$
, the only c-representation is
$\Delta = \emptyset$
, the only c-representation is
![]() $\kappa_u$
with
$\kappa_u$
with
![]() $\kappa_u(\omega) = 0$
for all
$\kappa_u(\omega) = 0$
for all
![]() $\omega \in \Omega$
. In this case,
$\omega \in \Omega$
. In this case,
![]() $\kappa_u$
accepts only conditionals
$\kappa_u$
accepts only conditionals
![]() ${{(B|A)}}$
with
${{(B|A)}}$
with
![]() $A\overline{B} = \bot$
, which are conditionals with
$A\overline{B} = \bot$
, which are conditionals with
![]() $A \models B$
.
$A \models B$
.
Proposition 34. For strongly consistent belief bases, extended c-inference coincides with normal c-inference.
Proof. Let
![]() $\Delta = \{{{(B_1|A_1)}}, \dots, {{(B_n|A_n)}}\}$
be a strongly consistent belief base and
$\Delta = \{{{(B_1|A_1)}}, \dots, {{(B_n|A_n)}}\}$
be a strongly consistent belief base and
![]() $C, D \in {{\mathcal{L}}}$
. We need to show that
$C, D \in {{\mathcal{L}}}$
. We need to show that
![]() $C |\hspace{-2pt} {\sim}^{ec}_{\Delta} D$
iff
$C |\hspace{-2pt} {\sim}^{ec}_{\Delta} D$
iff
![]() $C |\hspace{-2pt} {\sim}^{c}_{\Delta} D$
.
$C |\hspace{-2pt} {\sim}^{c}_{\Delta} D$
.
Direction
![]() $\Rightarrow$
: Let
$\Rightarrow$
: Let
![]() $C |\hspace{-2pt} {\sim}^{ec}_{\Delta} D$
, that is, every extended c-representation models
$C |\hspace{-2pt} {\sim}^{ec}_{\Delta} D$
, that is, every extended c-representation models
![]() ${{(D|C)}}$
. As every c-representation is an extended c-representation (Proposition 22), every c-representation models
${{(D|C)}}$
. As every c-representation is an extended c-representation (Proposition 22), every c-representation models
![]() ${{(D|C)}}$
. Thus,
${{(D|C)}}$
. Thus,
![]() $D |\hspace{-2pt} {\sim}^{c}_{kb} C$
.
$D |\hspace{-2pt} {\sim}^{c}_{kb} C$
.
Direction
![]() $\Leftarrow$
: Let
$\Leftarrow$
: Let
![]() $C |\hspace{-2pt} {\sim}^{c}_{\Delta} D$
, that is, every c-representation models
$C |\hspace{-2pt} {\sim}^{c}_{\Delta} D$
, that is, every c-representation models
![]() ${{(D|C)}}$
. We need to show that any extended c-representation
${{(D|C)}}$
. We need to show that any extended c-representation
![]() $\kappa_{\vec{\eta}}$
models
$\kappa_{\vec{\eta}}$
models
![]() ${{(D|C)}}$
. If
${{(D|C)}}$
. If
![]() $\vec{\eta}$
contains only finite values, it is a c-representation and thus models
$\vec{\eta}$
contains only finite values, it is a c-representation and thus models
![]() ${{(D|C)}}$
by assumption.
${{(D|C)}}$
by assumption.
Assume that
![]() $\vec{\eta}$
contains infinite entries. Let
$\vec{\eta}$
contains infinite entries. Let
![]() ${{{{{\mathit{OP}}}}(\Delta)}} = \{\Delta^0, \dots, \Delta^m, \Delta^\infty\}$
be the extended tolerance partition of
${{{{{\mathit{OP}}}}(\Delta)}} = \{\Delta^0, \dots, \Delta^m, \Delta^\infty\}$
be the extended tolerance partition of
![]() $\Delta$
. Because
$\Delta$
. Because
![]() $\Delta$
is strongly consistent, we have
$\Delta$
is strongly consistent, we have
![]() $\Delta^\infty = \emptyset$
. Let
$\Delta^\infty = \emptyset$
. Let
![]() $\mathit{fin}(\vec{\eta}) = \{\eta_{i} \mid i \in \{0,\dots, n\}, \eta_{i} \lt \infty\}$
be the set of finite values in impact vector
$\mathit{fin}(\vec{\eta}) = \{\eta_{i} \mid i \in \{0,\dots, n\}, \eta_{i} \lt \infty\}$
be the set of finite values in impact vector
![]() $\vec{\eta}$
and
$\vec{\eta}$
and
![]() $f_0 = 1+ |\mathit{fin}(\vec{\eta})| \cdot \max (\mathit{fin}(\vec{\eta}))$
. Now construct
$f_0 = 1+ |\mathit{fin}(\vec{\eta})| \cdot \max (\mathit{fin}(\vec{\eta}))$
. Now construct
![]() $\vec{\eta}^f$
from
$\vec{\eta}^f$
from
![]() $\vec{\eta}$
as follows. For
$\vec{\eta}$
as follows. For
![]() ${{(B_i|A_i)}} \in \Delta^0$
with
${{(B_i|A_i)}} \in \Delta^0$
with
![]() $\eta_{i} = \infty$
let
$\eta_{i} = \infty$
let
![]() $\eta_{i}^f = f_0$
. Let
$\eta_{i}^f = f_0$
. Let
![]() $f_1 = (f_0+1) \cdot | \{{{(B_i|A_i)}} \in \Delta^0 \mid \eta_{i} = \infty\} |$
. For
$f_1 = (f_0+1) \cdot | \{{{(B_i|A_i)}} \in \Delta^0 \mid \eta_{i} = \infty\} |$
. For
![]() ${{(B_i|A_i)}} \in \Delta^1$
with
${{(B_i|A_i)}} \in \Delta^1$
with
![]() $\eta_{i} = \infty$
let
$\eta_{i} = \infty$
let
![]() $\eta_{i}^f = f_1$
. Let
$\eta_{i}^f = f_1$
. Let
![]() $f_2 = (f_1+1) \cdot \big| \{{{(B_i|A_i)}} \in \Delta^1 \mid \eta_{i} = \infty\} \big|$
. For
$f_2 = (f_1+1) \cdot \big| \{{{(B_i|A_i)}} \in \Delta^1 \mid \eta_{i} = \infty\} \big|$
. For
![]() ${{(B_i|A_i)}} \in \Delta^1$
with
${{(B_i|A_i)}} \in \Delta^1$
with
![]() $\eta_{i} = \infty$
let
$\eta_{i} = \infty$
let
![]() $\eta_{i}^f = f_2$
; and so on. By construction the sum of the impacts in
$\eta_{i}^f = f_2$
; and so on. By construction the sum of the impacts in
![]() $\mathit{fin}(\vec{\eta})$
is less than
$\mathit{fin}(\vec{\eta})$
is less than
![]() $f_0$
and the sum of the impacts of the conditionals in
$f_0$
and the sum of the impacts of the conditionals in
![]() $\Delta^0 \cup \dots \cup \Delta^j$
is less than
$\Delta^0 \cup \dots \cup \Delta^j$
is less than
![]() $f_j$
for
$f_j$
for
![]() $j=0, \dots, m$
.
$j=0, \dots, m$
.
Let
![]() $\kappa^f = \kappa_{\vec{\eta}^f}$
. Now verify that:
$\kappa^f = \kappa_{\vec{\eta}^f}$
. Now verify that:
-
1.
 $\kappa^f$
is a c-representation of
$\kappa^f$
is a c-representation of
 $\Delta$
. For this we need to check that
$\Delta$
. For this we need to check that
 $\kappa^f$
models all conditionals in
$\kappa^f$
models all conditionals in
 $\Delta$
.
$\Delta$
. -
2.
 $\mathord{{|\hspace{-2pt}}{\sim}^{}_{\kappa^f}} \subseteq \mathord{{|\hspace{-2pt}}{\sim}^{}_{\kappa_{\vec{\eta}}}}$
, that is, every inference in
$\mathord{{|\hspace{-2pt}}{\sim}^{}_{\kappa^f}} \subseteq \mathord{{|\hspace{-2pt}}{\sim}^{}_{\kappa_{\vec{\eta}}}}$
, that is, every inference in
 $|\hspace{-2pt} {\sim}_{\kappa^f}$
is also an inference in
$|\hspace{-2pt} {\sim}_{\kappa^f}$
is also an inference in
 $|\hspace{-2pt} {\sim}_{\kappa_{\vec{\eta}}}$
.
$|\hspace{-2pt} {\sim}_{\kappa_{\vec{\eta}}}$
.
From (1) it follows that
![]() $\kappa^f$
is a model of
$\kappa^f$
is a model of
![]() ${{(D|C)}}$
because
${{(D|C)}}$
because
![]() $C |\hspace{-2pt} {\sim}^{c}_{\Delta}D$
. With (2.) it follows that
$C |\hspace{-2pt} {\sim}^{c}_{\Delta}D$
. With (2.) it follows that
![]() ${{(D|C)}}$
is modelled by
${{(D|C)}}$
is modelled by
![]() $\kappa_{\vec{\eta}}$
.
$\kappa_{\vec{\eta}}$
.
Ad (1): Let
![]() ${{(B_i|A_i)}} \in \Delta$
. We distinguish three cases.
${{(B_i|A_i)}} \in \Delta$
. We distinguish three cases.
Case 1:
![]() $\kappa_{\vec{\eta}}(A_i B_i) \lt \kappa_{\vec{\eta}}(A_i \overline{B_i}) \lt \infty$
$\kappa_{\vec{\eta}}(A_i B_i) \lt \kappa_{\vec{\eta}}(A_i \overline{B_i}) \lt \infty$
In this case
![]() $\kappa^f(A_i B_i) \lt \kappa^f(A_i \overline{B_i}) \lt f_0$
and therefore
$\kappa^f(A_i B_i) \lt \kappa^f(A_i \overline{B_i}) \lt f_0$
and therefore
![]() $\kappa^f \models {{(B_i|A_i)}}$
.
$\kappa^f \models {{(B_i|A_i)}}$
.
Case 2:
![]() $\kappa_{\vec{\eta}}(A_i B_i) \lt \infty$
and
$\kappa_{\vec{\eta}}(A_i B_i) \lt \infty$
and
![]() $\kappa_{\vec{\eta}}(A_i \overline{B_i}) = \infty$
$\kappa_{\vec{\eta}}(A_i \overline{B_i}) = \infty$
In this case
![]() $\kappa^f(A_i B_i) \lt f_0 \lt \kappa^f(A_i \overline{B_i})$
and therefore
$\kappa^f(A_i B_i) \lt f_0 \lt \kappa^f(A_i \overline{B_i})$
and therefore
![]() $\kappa^f \models {{(B_i|A_i)}}$
.
$\kappa^f \models {{(B_i|A_i)}}$
.
Case 3:
![]() $\kappa_{\vec{\eta}}(A_i B_i) = \infty$
and
$\kappa_{\vec{\eta}}(A_i B_i) = \infty$
and
![]() $\kappa_{\vec{\eta}}(A_i \overline{B_i}) = \infty$
$\kappa_{\vec{\eta}}(A_i \overline{B_i}) = \infty$
Assume that
![]() ${{(B_i|A_i)}}$
is in
${{(B_i|A_i)}}$
is in
![]() $\Delta^j$
. Then there is a world
$\Delta^j$
. Then there is a world
![]() $\omega$
s.t.
$\omega$
s.t.
![]() $\omega \models A_i B_i$
and
$\omega \models A_i B_i$
and
![]() $\omega$
falsifies no conditional in
$\omega$
falsifies no conditional in
![]() $\Delta^0 \cup \dots \cup \Delta^j$
. Therefore,
$\Delta^0 \cup \dots \cup \Delta^j$
. Therefore,
![]() $\kappa^f(\omega) \lt f_j$
and thus
$\kappa^f(\omega) \lt f_j$
and thus
![]() $\kappa^f(A_i B_i) \lt f_j$
. Any model of
$\kappa^f(A_i B_i) \lt f_j$
. Any model of
![]() $A_i \overline{B_i}$
falsifies
$A_i \overline{B_i}$
falsifies
![]() ${{(B_i|A_i)}}$
, therefore,
${{(B_i|A_i)}}$
, therefore,
![]() $\kappa^f(A_i \overline{B_i}) \gt f_j$
. Thus, we have
$\kappa^f(A_i \overline{B_i}) \gt f_j$
. Thus, we have
![]() $\kappa^f(A_i B_i) \lt f_j \lt \kappa^f(A_i \overline{B_i})$
and therefore
$\kappa^f(A_i B_i) \lt f_j \lt \kappa^f(A_i \overline{B_i})$
and therefore
![]() $\kappa^f \models {{(B_i|A_i)}}$
.
$\kappa^f \models {{(B_i|A_i)}}$
.
Ad (2): Assume that
![]() $X |\hspace{-2pt} {\sim}_{\kappa^f}Y$
. There are two cases.
$X |\hspace{-2pt} {\sim}_{\kappa^f}Y$
. There are two cases.
Case 1:
![]() $\kappa^f(X \overline{Y}) \lt f_0$
$\kappa^f(X \overline{Y}) \lt f_0$
In this case
![]() $\kappa^f(XY) \lt \kappa^f(X \overline{Y}) \lt f_0$
and therefore
$\kappa^f(XY) \lt \kappa^f(X \overline{Y}) \lt f_0$
and therefore
![]() $\kappa_{\vec{\eta}}(XY) \lt \kappa_{\vec{\eta}}(X \overline{Y}) \lt \infty$
. Hence,
$\kappa_{\vec{\eta}}(XY) \lt \kappa_{\vec{\eta}}(X \overline{Y}) \lt \infty$
. Hence,
![]() $X |\hspace{-2pt} {\sim}_{\kappa_{\vec{\eta}}} Y$
.
$X |\hspace{-2pt} {\sim}_{\kappa_{\vec{\eta}}} Y$
.
Case 2:
![]() $ \kappa^f(X \overline{Y}) \geqslant f_0$
$ \kappa^f(X \overline{Y}) \geqslant f_0$
In this case
![]() $\kappa_{\vec{\eta}}(X \overline{Y}) = \infty$
and therefore
$\kappa_{\vec{\eta}}(X \overline{Y}) = \infty$
and therefore
![]() $X |\hspace{-2pt} {\sim}_{\kappa_{\vec{\eta}}} Y$
.
$X |\hspace{-2pt} {\sim}_{\kappa_{\vec{\eta}}} Y$
.
Because extended c-inference is defined as skeptical inference over a set of ranking functions it is also a preferential inference operator.
Proposition 35. Extended c-inference is preferential, that is, it satisfies system P.
Proof. Every ranking function, and thus every extended c-representation, induces a preferential inference relation. The intersection of two preferential inference relations is again preferential. As extended c-inference is the intersection of the inference relations induced by each extended c-representation, extended c-inference is preferential.
Proposition 35 implies that extended c-inference captures p-entailment, that is, if
![]() $A |\hspace{-2pt} {\sim}^{p}_{\Delta} B$
, then
$A |\hspace{-2pt} {\sim}^{p}_{\Delta} B$
, then
![]() $A |\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
. Furthermore, extended c-inference coincides with p-entailment on entailments of the form
$A |\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
. Furthermore, extended c-inference coincides with p-entailment on entailments of the form
![]() $A \mathord{{|\hspace{-2pt}}{\sim}} \bot$
, which can be seen as representations of ‘strict’ beliefs (i.e., A is completely unfeasible).
$A \mathord{{|\hspace{-2pt}}{\sim}} \bot$
, which can be seen as representations of ‘strict’ beliefs (i.e., A is completely unfeasible).
Proposition 36. Extended c-inference satisfies (Classic Preservation).
Proof. We need to show that
![]() $A |\hspace{-2pt} {\sim}^{ec}_{\Delta} \bot$
iff
$A |\hspace{-2pt} {\sim}^{ec}_{\Delta} \bot$
iff
![]() $A |\hspace{-2pt} {\sim}^{p}_{\Delta} \bot$
. Using Lemma 14, it is sufficient to show that
$A |\hspace{-2pt} {\sim}^{p}_{\Delta} \bot$
. Using Lemma 14, it is sufficient to show that
![]() $A |\hspace{-2pt} {\sim}^{ec}_{\Delta} \bot$
iff
$A |\hspace{-2pt} {\sim}^{ec}_{\Delta} \bot$
iff
![]() $\kappa^z(A) = \infty$
.
$\kappa^z(A) = \infty$
.
Direction
![]() $\Leftarrow$
: Let
$\Leftarrow$
: Let
![]() $\kappa^z_{\Delta}(A) = \infty$
. Then Proposition 26 states that
$\kappa^z_{\Delta}(A) = \infty$
. Then Proposition 26 states that
![]() $\kappa_{\vec{\eta}}(A) = \infty$
for every extended c-representation
$\kappa_{\vec{\eta}}(A) = \infty$
for every extended c-representation
![]() $\kappa_{\vec{\eta}}(A)$
of
$\kappa_{\vec{\eta}}(A)$
of
![]() $\Delta$
. Thus,
$\Delta$
. Thus,
![]() $A |\hspace{-2pt} {\sim}^{ec}_{\Delta} \bot$
.
$A |\hspace{-2pt} {\sim}^{ec}_{\Delta} \bot$
.
Direction
![]() $\Rightarrow$
: Let
$\Rightarrow$
: Let
![]() $A |\hspace{-2pt} {\sim}^{ec}_{\Delta} \bot$
, that is, there is no extended c-representation
$A |\hspace{-2pt} {\sim}^{ec}_{\Delta} \bot$
, that is, there is no extended c-representation
![]() $\kappa_{\vec{\eta}}$
of
$\kappa_{\vec{\eta}}$
of
![]() $\Delta$
s.t.
$\Delta$
s.t.
![]() $\kappa_{\vec{\eta}}(A) \lt \infty$
. By Proposition 26, we have
$\kappa_{\vec{\eta}}(A) \lt \infty$
. By Proposition 26, we have
![]() $\kappa^z_{\Delta}(A) = \infty$
.
$\kappa^z_{\Delta}(A) = \infty$
.
Besides Cautious Monotony (CM) ensured by system P, other postulates capturing versions of monotony have been introduced. One of these is Rational Monotony (Kraus et al., Reference Kraus, Lehmann and Magidor1990) which in combination with system P characterizes the class of inference relations that can be induced by ranking functions (Lehmann & Magidor, Reference Lehmann and Magidor1992).
Another monotony postulate is Semi Monotony (Reiter, Reference Reiter1980; Goldszmidt & Pearl, Reference Goldszmidt and Pearl1996), which states that the set of possible inferences only increases if conditionals are added to the belief base.
Extended c-inference does not satisfy (RM) as c-inference already violates (RM) (Beierle et al., Reference Beierle, Kutsch, Breuers, Barták and Brawner2019a). Analogously, extended c-inference does not satisfy (SM) (Kutsch, Reference Kutsch2021). However, we can show that extended c-inference satisfies weaker versions of these two postulates: weak Rational Monotony (Rott, Reference Rott2001) and weak Semi Monotony (Wilhelm et al., Reference Wilhelm, Kern-Isberner, Beierle, Meier and Ortiz2024).
c-Inference satisfies weak rational monotony (Beierle et al., Reference Beierle, Kutsch, Breuers, Barták and Brawner2019a), and this also holds for the extended version.
Proposition 37. Extended c-inference satisfies (wRM).
Proof. Let
![]() $\Delta$
be a belief base with
$\Delta$
be a belief base with
![]() $\top |\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
and
$\top |\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
and
![]() $\top \mathord{{|\hspace{-2pt}}{\sim}\!\!\!\!/\;\;}^{ec}_{\Delta} \overline{A}$
. If
$\top \mathord{{|\hspace{-2pt}}{\sim}\!\!\!\!/\;\;}^{ec}_{\Delta} \overline{A}$
. If
![]() $\Delta$
is not weakly consistent,
$\Delta$
is not weakly consistent,
![]() $A |\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
holds trivially. For the remainder of the proof assume that
$A |\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
holds trivially. For the remainder of the proof assume that
![]() $\Delta$
is weakly consistent. Let
$\Delta$
is weakly consistent. Let
![]() $\kappa$
be any extended c-representation of
$\kappa$
be any extended c-representation of
![]() $\Delta$
, and let
$\Delta$
, and let
![]() $\Omega_{\mathit{zero}} = \kappa^{-1}(0)$
be the set of worlds with rank 0 with respect to
$\Omega_{\mathit{zero}} = \kappa^{-1}(0)$
be the set of worlds with rank 0 with respect to
![]() $\kappa$
. Then,
$\kappa$
. Then,
![]() $\top |\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
implies that
$\top |\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
implies that
![]() $\kappa(B) \lt \kappa(\overline{B})$
and therefore that for every
$\kappa(B) \lt \kappa(\overline{B})$
and therefore that for every
![]() $\omega \in \Omega_{\mathit{zero}}$
we have
$\omega \in \Omega_{\mathit{zero}}$
we have
![]() $\omega \models B$
. Because
$\omega \models B$
. Because
![]() $\top \mathord{{|\hspace{-2pt}}{\sim}\!\!\!\!/\;\;}^{ec}_{\Delta} \overline{A}$
there is at least one
$\top \mathord{{|\hspace{-2pt}}{\sim}\!\!\!\!/\;\;}^{ec}_{\Delta} \overline{A}$
there is at least one
![]() $\omega \in \Omega_{\mathit{zero}}$
with
$\omega \in \Omega_{\mathit{zero}}$
with
![]() $\omega \models A$
. This
$\omega \models A$
. This
![]() $\omega$
is a model of AB implying that
$\omega$
is a model of AB implying that
![]() $\kappa(AB) = 0$
. We also have that
$\kappa(AB) = 0$
. We also have that
![]() $\kappa(A\overline{B}) \gt 0$
because there are no models of B with rank 0. In summary, we have
$\kappa(A\overline{B}) \gt 0$
because there are no models of B with rank 0. In summary, we have
![]() $\kappa(AB) = 0 \lt \kappa(A\overline{B})$
implying that
$\kappa(AB) = 0 \lt \kappa(A\overline{B})$
implying that
![]() $A |\hspace{-2pt} {\sim}_{\kappa} B$
. Because the c-representation
$A |\hspace{-2pt} {\sim}_{\kappa} B$
. Because the c-representation
![]() $\kappa$
was chosen arbitrarily, we have
$\kappa$
was chosen arbitrarily, we have
![]() $A |\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
.
$A |\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
.
While c-Inference and its extended version fail to satisfy semi monotony (Kutsch, Reference Kutsch2021), both satisfy the only recently introduced (Wilhelm et al., Reference Wilhelm, Kern-Isberner, Beierle, Meier and Ortiz2024) weaker notion of it.
Proposition 38. c-Inference and extended c-inference satisfy (wSM).
Proof. We first show that extended c-inference satisfies (wSM). Let
![]() $\Delta, \Delta'$
be belief bases with
$\Delta, \Delta'$
be belief bases with
![]() $\Delta \subseteq \Delta'$
and
$\Delta \subseteq \Delta'$
and
![]() $\top |\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
. If
$\top |\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
. If
![]() $\Delta'$
is not weakly consistent,
$\Delta'$
is not weakly consistent,
![]() $\top |\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
holds trivially. For the remainder of the proof assume that
$\top |\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
holds trivially. For the remainder of the proof assume that
![]() $\Delta'$
and therefore also
$\Delta'$
and therefore also
![]() $\Delta$
is weakly consistent. Let
$\Delta$
is weakly consistent. Let
![]() $\kappa'$
be an extended c-representation of
$\kappa'$
be an extended c-representation of
![]() $\Delta'$
, and let
$\Delta'$
, and let
![]() $\Omega_{\mathit{zero}} = \kappa^{\prime-1}(0)$
be the set of worlds with rank 0 with respect to
$\Omega_{\mathit{zero}} = \kappa^{\prime-1}(0)$
be the set of worlds with rank 0 with respect to
![]() $\kappa'$
. Let
$\kappa'$
. Let
![]() $\omega$
be any world in
$\omega$
be any world in
![]() $\Omega_{\mathit{zero}}$
. Because
$\Omega_{\mathit{zero}}$
. Because
![]() $\kappa' \models \Delta'$
, the world
$\kappa' \models \Delta'$
, the world
![]() $\omega$
cannot falsify any conditional in
$\omega$
cannot falsify any conditional in
![]() $\Delta'$
. Thus,
$\Delta'$
. Thus,
![]() $\omega$
also does not falsify any conditional in
$\omega$
also does not falsify any conditional in
![]() $\Delta$
. Let
$\Delta$
. Let
![]() $\kappa$
be an extended c-representation of
$\kappa$
be an extended c-representation of
![]() $\Delta$
. Because
$\Delta$
. Because
![]() $\omega$
does not falsify any conditional in
$\omega$
does not falsify any conditional in
![]() $\Delta$
, we have
$\Delta$
, we have
![]() $\kappa(\omega) = 0$
. Since
$\kappa(\omega) = 0$
. Since
![]() $\top |\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
implies that
$\top |\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
implies that
![]() $\kappa(B) \lt \kappa(\overline{B})$
, we have
$\kappa(B) \lt \kappa(\overline{B})$
, we have
![]() $\omega \models B$
. As
$\omega \models B$
. As
![]() $\omega$
was chosen arbitrarily, every world in
$\omega$
was chosen arbitrarily, every world in
![]() $\Omega_{\mathit{zero}}$
is a model of B. Thus
$\Omega_{\mathit{zero}}$
is a model of B. Thus
![]() $\kappa'(B) = 0 \lt \kappa'(\overline{B})$
, implying
$\kappa'(B) = 0 \lt \kappa'(\overline{B})$
, implying
![]() $\top |\hspace{-2pt} {\sim}_{\kappa'} B$
. Because
$\top |\hspace{-2pt} {\sim}_{\kappa'} B$
. Because
![]() $\kappa'$
was chosen arbitrarily among the extended c-representations of
$\kappa'$
was chosen arbitrarily among the extended c-representations of
![]() $\Delta'$
, we have
$\Delta'$
, we have
![]() $\top |\hspace{-2pt} {\sim}^{ec}_{\Delta'} B$
.
$\top |\hspace{-2pt} {\sim}^{ec}_{\Delta'} B$
.
Since c-inference and extended c-inference coincide for strongly consistent belief bases, c-inference satisfies (wSM) as well.
In summary, we showed that extended c-inference is the natural extension of c-inference to weakly consistent belief bases.
7. CSPs for extended c-representations
In this section, we investigate CSPs dealing with extended c-representations. In Section 7.1, we present a constraint system describing all extended c-representations of a belief base. Then we develop a simplification of this constraint system that takes the effects of conditionals in
![]() $\Delta^\infty$
into account right from the beginning. In Section 7.2, we show how extended c-inference can be realized by a CSP.
$\Delta^\infty$
into account right from the beginning. In Section 7.2, we show how extended c-inference can be realized by a CSP.
7.1. Describing extended c-representations by CSPs
The c-representations of a belief base
![]() $\Delta$
can conveniently be characterized by the solutions of a CSP (Kern-Isberner, Reference Kern-Isberner2001). In Beierle et al. (Reference Beierle, Eichhorn, Kern-Isberner and Kutsch2018), the following modelling of c-representations as solutions of a CSP is introduced. For a belief base
$\Delta$
can conveniently be characterized by the solutions of a CSP (Kern-Isberner, Reference Kern-Isberner2001). In Beierle et al. (Reference Beierle, Eichhorn, Kern-Isberner and Kutsch2018), the following modelling of c-representations as solutions of a CSP is introduced. For a belief base
![]() $\Delta = \{{{(B_1|A_1)}},\ldots,{{(B_n|A_n)}}\}$
over
$\Delta = \{{{(B_1|A_1)}},\ldots,{{(B_n|A_n)}}\}$
over
![]() $\Sigma$
the CSP for c-representations of
$\Sigma$
the CSP for c-representations of
![]() $\Delta$
, denoted by
$\Delta$
, denoted by
![]() ${{\mathit{CR}_{\Sigma}(\Delta)}}$
, on the constraint variables
${{\mathit{CR}_{\Sigma}(\Delta)}}$
, on the constraint variables
![]() $\{\eta_{1}, \ldots, \eta_{n}\}$
ranging over
$\{\eta_{1}, \ldots, \eta_{n}\}$
ranging over
![]() $\mathbb{N}_0$
is given by the constraints
$\mathbb{N}_0$
is given by the constraints
![]() ${{{{\mathit{cr}^{\Delta}_{i}}}}}$
, for all
${{{{\mathit{cr}^{\Delta}_{i}}}}}$
, for all
![]() $i \in \{1,\ldots,n\}$
:
$i \in \{1,\ldots,n\}$
:
 \begin{align*} {{{{{\mathit{\ }}}}}} \hspace{4.5cm} \def\lumina\hspace{1cm} \eta_{i} \,\, \gt \,\, \min_{\substack{\omega \in \Omega_\Sigma\\\omega \models A_i B_i}} \sum_{\substack{j \neq i \\ \omega \models A_j \overline{B_j}}} \eta_{j} \,\, - \,\, \min_{\substack{\omega \in \Omega_\Sigma\\\omega \models A_i \overline{B}_i}} \sum_{\substack{j \neq i \\ \omega \models A_j \overline{B_j}}} \eta_{j} \hspace{3.5cm} ({{{{{\mathit{cr}^{\Delta}_{i}}}}}}) \end{align*}
\begin{align*} {{{{{\mathit{\ }}}}}} \hspace{4.5cm} \def\lumina\hspace{1cm} \eta_{i} \,\, \gt \,\, \min_{\substack{\omega \in \Omega_\Sigma\\\omega \models A_i B_i}} \sum_{\substack{j \neq i \\ \omega \models A_j \overline{B_j}}} \eta_{j} \,\, - \,\, \min_{\substack{\omega \in \Omega_\Sigma\\\omega \models A_i \overline{B}_i}} \sum_{\substack{j \neq i \\ \omega \models A_j \overline{B_j}}} \eta_{j} \hspace{3.5cm} ({{{{{\mathit{cr}^{\Delta}_{i}}}}}}) \end{align*}
The constraint
![]() $({{{{\mathit{cr}^{\Delta}_{i}}}}})$
is the constraint corresponding to the conditional
$({{{{\mathit{cr}^{\Delta}_{i}}}}})$
is the constraint corresponding to the conditional
![]() ${{(B_i|A_i)}}$
. The sum terms are induced by the worlds verifying and falsifying
${{(B_i|A_i)}}$
. The sum terms are induced by the worlds verifying and falsifying
![]() ${{(B_i|A_i)}}$
, respectively. A solution of
${{(B_i|A_i)}}$
, respectively. A solution of
![]() ${{\mathit{CR}_{\Sigma}(\Delta)}}$
is an n-tuple
${{\mathit{CR}_{\Sigma}(\Delta)}}$
is an n-tuple
![]() $(\eta_{1}, \ldots, \eta_{n}) \in \mathbb{N}_0^n .$
For a constraint satisfaction problem
$(\eta_{1}, \ldots, \eta_{n}) \in \mathbb{N}_0^n .$
For a constraint satisfaction problem
![]() $\mathit{CSP}$
, the set of solutions is denoted by
$\mathit{CSP}$
, the set of solutions is denoted by
![]() ${{\mathit{Sol}(\mathit{CSP})}}$
. Thus, with
${{\mathit{Sol}(\mathit{CSP})}}$
. Thus, with
![]() ${{\mathit{Sol}({{\mathit{CR}_{\Sigma}(\Delta))}}}}$
, we denote the set of all solutions of
${{\mathit{Sol}({{\mathit{CR}_{\Sigma}(\Delta))}}}}$
, we denote the set of all solutions of
![]() ${{\mathit{CR}_{\Sigma}(\Delta)}}$
. The solutions of
${{\mathit{CR}_{\Sigma}(\Delta)}}$
. The solutions of
![]() ${{\mathit{CR}_{\Sigma}(\Delta)}}$
correspond to the c-representations of
${{\mathit{CR}_{\Sigma}(\Delta)}}$
correspond to the c-representations of
![]() $\Delta$
.
$\Delta$
.
Proposition 39 (soundness and completeness of
![]() ${{\mathit{CR}_{\Sigma}(\Delta)}}$
, Beierle et al., Reference Beierle, Eichhorn, Kern-Isberner and Kutsch2018). Let
${{\mathit{CR}_{\Sigma}(\Delta)}}$
, Beierle et al., Reference Beierle, Eichhorn, Kern-Isberner and Kutsch2018). Let
![]() $\Delta = \{{{(B_1|A_1)}}, \ldots, {{(B_n|A_n)}} \}$
be a belief base over
$\Delta = \{{{(B_1|A_1)}}, \ldots, {{(B_n|A_n)}} \}$
be a belief base over
![]() $\Sigma$
. Then we have:
$\Sigma$
. Then we have:
If we want to construct a similar CSP for extended c-representations, we have to take worlds and formulas with infinite rank into account.
Definition 40 (
![]() ${{\mathit{CR}^{ex}_{\Sigma}(\Delta)}}$
). Let
${{\mathit{CR}^{ex}_{\Sigma}(\Delta)}}$
). Let
![]() $ \Delta = \{{{(B_1|A_1)}}, \ldots, {{(B_n|A_n)}}\} $
be a belief base over
$ \Delta = \{{{(B_1|A_1)}}, \ldots, {{(B_n|A_n)}}\} $
be a belief base over
![]() $\Sigma$
. The CSP for extended c-representations of
$\Sigma$
. The CSP for extended c-representations of
![]() $\Delta$
, denoted by
$\Delta$
, denoted by
![]() ${{\mathit{CR}^{ex}_{\Sigma}(\Delta)}}$
, on the constraint variables
${{\mathit{CR}^{ex}_{\Sigma}(\Delta)}}$
, on the constraint variables
![]() $\{\eta_{1}, \ldots, \eta_{n}\}$
ranging over
$\{\eta_{1}, \ldots, \eta_{n}\}$
ranging over
![]() $\mathbb{N}_0 \cup \{\infty\}$
is given by the constraints
$\mathbb{N}_0 \cup \{\infty\}$
is given by the constraints
![]() ${{{{\mathit{cr}^{ex\,\Delta}_{i}}}}}$
, for all
${{{{\mathit{cr}^{ex\,\Delta}_{i}}}}}$
, for all
![]() $i \in \{1,\ldots,n\}$
:
$i \in \{1,\ldots,n\}$
:

Again, each constraint (
![]() ${{{{\mathit{cr}^{ex\,\Delta}_{i}}}}}$
) corresponds to the conditional
${{{{\mathit{cr}^{ex\,\Delta}_{i}}}}}$
) corresponds to the conditional
![]() ${{(B_i|A_i)}} \in \Delta$
.
${{(B_i|A_i)}} \in \Delta$
.
Proposition 41 (soundness and completeness of
![]() ${{\mathit{CR}^{ex}_{\Sigma}(\Delta)}}$
). Let
${{\mathit{CR}^{ex}_{\Sigma}(\Delta)}}$
). Let
![]() $\Delta = \{{{(B_1|A_1)}}, \ldots, {{(B_n|A_n)}} \}$
be a weakly consistent belief base over
$\Delta = \{{{(B_1|A_1)}}, \ldots, {{(B_n|A_n)}} \}$
be a weakly consistent belief base over
![]() $\Sigma$
. Then we have
$\Sigma$
. Then we have
Proof.
Soundness: Let
![]() $\vec{\eta}$
be an impact vector in
$\vec{\eta}$
be an impact vector in
![]() ${{\mathit{Sol}({{\mathit{CR}^{ex}_{\Sigma}(\Delta)}})}}$
. Because
${{\mathit{Sol}({{\mathit{CR}^{ex}_{\Sigma}(\Delta)}})}}$
. Because
![]() $\Delta$
is weakly consistent, there is a world
$\Delta$
is weakly consistent, there is a world
![]() $\omega$
that does not falsify any conditional in
$\omega$
that does not falsify any conditional in
![]() $\Delta$
; therefore,
$\Delta$
; therefore,
![]() $\kappa_{\vec{\eta}}(\omega)=0$
and
$\kappa_{\vec{\eta}}(\omega)=0$
and
![]() $\kappa_{\vec{\eta}}$
is a ranking function. It is left to show that
$\kappa_{\vec{\eta}}$
is a ranking function. It is left to show that
![]() $\kappa_{\vec{\eta}}$
satisfies all conditionals in
$\kappa_{\vec{\eta}}$
satisfies all conditionals in
![]() $\Delta$
.
$\Delta$
.
Let
![]() ${{(B_i|A_i)}} \in \Delta$
. There are three cases.
${{(B_i|A_i)}} \in \Delta$
. There are three cases.
Case 1:
![]() $\kappa_{\vec{\eta}}(A_i \overline{B_i}) = \infty$
and
$\kappa_{\vec{\eta}}(A_i \overline{B_i}) = \infty$
and
![]() $\kappa_{\vec{\eta}}(A_i B_i) = \infty$
$\kappa_{\vec{\eta}}(A_i B_i) = \infty$
In this case
![]() $\kappa_{\vec{\eta}}(A_i) = \infty$
and therefore
$\kappa_{\vec{\eta}}(A_i) = \infty$
and therefore
![]() $\kappa_{\vec{\eta}} \models {{(B_i|A_i)}}$
.
$\kappa_{\vec{\eta}} \models {{(B_i|A_i)}}$
.
Case 2:
![]() $\kappa_{\vec{\eta}}(A_i \overline{B_i}) = \infty$
and
$\kappa_{\vec{\eta}}(A_i \overline{B_i}) = \infty$
and
![]() $\kappa_{\vec{\eta}}(A_i B_i) \lt \infty$
$\kappa_{\vec{\eta}}(A_i B_i) \lt \infty$
In this case,
![]() $\kappa_{\vec{\eta}}(A_i \overline{B_i} \gt \kappa_{\vec{\eta}}(A_i B_i) \lt \infty$
and therefore
$\kappa_{\vec{\eta}}(A_i \overline{B_i} \gt \kappa_{\vec{\eta}}(A_i B_i) \lt \infty$
and therefore
![]() $\kappa_{\vec{\eta}} \models {{(B_i|A_i)}}$
.
$\kappa_{\vec{\eta}} \models {{(B_i|A_i)}}$
.
Case 3:
![]() $\kappa_{\vec{\eta}}(A_i \overline{B_i}) \lt \infty$
$\kappa_{\vec{\eta}}(A_i \overline{B_i}) \lt \infty$
In this case,
![]() $\min_{\substack{\omega \in \Omega_\Sigma\\\omega \models A_i}} \,\, \sum_{\substack{1 \leqslant j \leqslant n \\ \omega \models A_j \overline{B_j}} } \eta_{j} = \kappa_{\vec{\eta}}(A_i \overline{B_i}) \lt \infty$
; hence, the condition in (
$\min_{\substack{\omega \in \Omega_\Sigma\\\omega \models A_i}} \,\, \sum_{\substack{1 \leqslant j \leqslant n \\ \omega \models A_j \overline{B_j}} } \eta_{j} = \kappa_{\vec{\eta}}(A_i \overline{B_i}) \lt \infty$
; hence, the condition in (
![]() ${{{{\mathit{cr}^{ex\,\Delta}_{i}}}}}$
) before the or is not satisfied.
${{{{\mathit{cr}^{ex\,\Delta}_{i}}}}}$
) before the or is not satisfied.
Because
![]() $\vec{\eta} \in {{\mathit{Sol}({{\mathit{CR}^{ex}_{\Sigma}(\Delta)}})}}$
it must satisfy all constraints in
$\vec{\eta} \in {{\mathit{Sol}({{\mathit{CR}^{ex}_{\Sigma}(\Delta)}})}}$
it must satisfy all constraints in
![]() ${{\mathit{CR}^{ex}_{\Sigma}(\Delta)}}$
including
${{\mathit{CR}^{ex}_{\Sigma}(\Delta)}}$
including
![]() $({{{{{\mathit{cr}^{ex\,\Delta}_{i}}}}}})$
. Because the condition before the or is violated, it must hold that
$({{{{{\mathit{cr}^{ex\,\Delta}_{i}}}}}})$
. Because the condition before the or is violated, it must hold that
 \begin{align*} &&\eta_{i} \,\, \gt \,\, \min_{\substack{\omega \in \Omega_\Sigma\\\omega \models A_i B_i}} \sum_{\substack{j \neq i \\ \omega \models A_j \overline{B_j}}} \eta_{j} \,\, &- \,\, \min_{\substack{\omega \in \Omega_\Sigma\\\omega \models A_i \overline{B}_i}} \sum_{\substack{j \neq i \\ \omega \models A_j \overline{B_j}}} \eta_{j} \\ \Leftrightarrow&&\eta_{i} \,\, + \,\, \min_{\substack{\omega \in \Omega_\Sigma\\\omega \models A_i \overline{B}_i}} \sum_{\substack{j \neq i \\ \omega \models A_j \overline{B_j}}} \eta_{j} \,\, &\gt \,\, \min_{\substack{\omega \in \Omega_\Sigma\\\omega \models A_i B_i}} \sum_{\substack{j \neq i \\ \omega \models A_j \overline{B_j}}} \eta_{j} \\ \Leftrightarrow&&\min_{\substack{\omega \in \Omega_\Sigma\\\omega \models A_i \overline{B}_i}} \sum_{\substack{1 \leqslant j \leqslant n \\ \omega \models A_j \overline{B_j}}} \eta_{j} \,\, &\gt \,\, \min_{\substack{\omega \in \Omega_\Sigma\\\omega \models A_i B_i}} \sum_{\substack{1 \leqslant j \leqslant n \\ \omega \models A_j \overline{B_j}}} \eta_{j} \\ \Leftrightarrow&&\kappa_{\vec{\eta}}(A_i\overline{B_i}) \,\, &\gt \,\, \kappa_{\vec{\eta}}(A_i B_i) \end{align*}
\begin{align*} &&\eta_{i} \,\, \gt \,\, \min_{\substack{\omega \in \Omega_\Sigma\\\omega \models A_i B_i}} \sum_{\substack{j \neq i \\ \omega \models A_j \overline{B_j}}} \eta_{j} \,\, &- \,\, \min_{\substack{\omega \in \Omega_\Sigma\\\omega \models A_i \overline{B}_i}} \sum_{\substack{j \neq i \\ \omega \models A_j \overline{B_j}}} \eta_{j} \\ \Leftrightarrow&&\eta_{i} \,\, + \,\, \min_{\substack{\omega \in \Omega_\Sigma\\\omega \models A_i \overline{B}_i}} \sum_{\substack{j \neq i \\ \omega \models A_j \overline{B_j}}} \eta_{j} \,\, &\gt \,\, \min_{\substack{\omega \in \Omega_\Sigma\\\omega \models A_i B_i}} \sum_{\substack{j \neq i \\ \omega \models A_j \overline{B_j}}} \eta_{j} \\ \Leftrightarrow&&\min_{\substack{\omega \in \Omega_\Sigma\\\omega \models A_i \overline{B}_i}} \sum_{\substack{1 \leqslant j \leqslant n \\ \omega \models A_j \overline{B_j}}} \eta_{j} \,\, &\gt \,\, \min_{\substack{\omega \in \Omega_\Sigma\\\omega \models A_i B_i}} \sum_{\substack{1 \leqslant j \leqslant n \\ \omega \models A_j \overline{B_j}}} \eta_{j} \\ \Leftrightarrow&&\kappa_{\vec{\eta}}(A_i\overline{B_i}) \,\, &\gt \,\, \kappa_{\vec{\eta}}(A_i B_i) \end{align*}
and therefore
![]() $\kappa_{\vec{\eta}} \models {{(B_i|A_i)}}$
.
$\kappa_{\vec{\eta}} \models {{(B_i|A_i)}}$
.
Completeness: Let
![]() $\kappa_{\vec{\eta}}$
be an extended c-representation of
$\kappa_{\vec{\eta}}$
be an extended c-representation of
![]() $\Delta$
with impact vector
$\Delta$
with impact vector
![]() $\vec{\eta}$
. We need to show that
$\vec{\eta}$
. We need to show that
![]() $\vec{\eta} \in {{\mathit{Sol}({{\mathit{CR}^{ex}_{\Sigma}(\Delta)}})}}$
, that is, that
$\vec{\eta} \in {{\mathit{Sol}({{\mathit{CR}^{ex}_{\Sigma}(\Delta)}})}}$
, that is, that
![]() $\vec{\eta}$
satisfies every constraint (
$\vec{\eta}$
satisfies every constraint (
![]() ${{{{\mathit{cr}^{ex\,\Delta}_{i}}}}}$
) in
${{{{\mathit{cr}^{ex\,\Delta}_{i}}}}}$
) in
![]() ${{\mathit{CR}^{ex}_{\Sigma}(\Delta)}}$
. Because
${{\mathit{CR}^{ex}_{\Sigma}(\Delta)}}$
. Because
![]() $\kappa_{\vec{\eta}}$
is an extended c-representation of
$\kappa_{\vec{\eta}}$
is an extended c-representation of
![]() $\Delta$
, we have
$\Delta$
, we have
![]() $\kappa_{\vec{\eta}} \models {{(B_i|A_i)}}$
. This requires either (1)
$\kappa_{\vec{\eta}} \models {{(B_i|A_i)}}$
. This requires either (1)
![]() $\kappa_{\vec{\eta}}(A_i) = \infty$
or (2)
$\kappa_{\vec{\eta}}(A_i) = \infty$
or (2)
![]() $\kappa_{\vec{\eta}}(A_i\overline{B_i}) \gt \kappa_{\vec{\eta}}(A_i B_i)$
. In case (1), it is
$\kappa_{\vec{\eta}}(A_i\overline{B_i}) \gt \kappa_{\vec{\eta}}(A_i B_i)$
. In case (1), it is
![]() $\min_{\substack{\omega \in \Omega_\Sigma\\\omega \models A_i}} \,\, \sum_{\substack{1 \leqslant j \leqslant n \\ \omega \models A_j \overline{B_j}} } \eta_{j} = \kappa_{\vec{\eta}}(A_i \overline{B_i}) = \infty$
and the condition before the or in (
$\min_{\substack{\omega \in \Omega_\Sigma\\\omega \models A_i}} \,\, \sum_{\substack{1 \leqslant j \leqslant n \\ \omega \models A_j \overline{B_j}} } \eta_{j} = \kappa_{\vec{\eta}}(A_i \overline{B_i}) = \infty$
and the condition before the or in (
![]() ${{{{\mathit{cr}^{ex\,\Delta}_{i}}}}}$
) is satisfied. In case (2), we can see with the equivelence transformations in the Soundness part of this proof that the condition behind the or is satisfied. In both cases
${{{{\mathit{cr}^{ex\,\Delta}_{i}}}}}$
) is satisfied. In case (2), we can see with the equivelence transformations in the Soundness part of this proof that the condition behind the or is satisfied. In both cases
![]() $\vec{\eta}$
satisfies (
$\vec{\eta}$
satisfies (
![]() ${{{{\mathit{cr}^{ex\,\Delta}_{i}}}}}$
).
${{{{\mathit{cr}^{ex\,\Delta}_{i}}}}}$
).
The requirement for weak consistency in Proposition 41 is necessary because for a belief base
![]() $\Delta$
that is not weakly consistent it holds that
$\Delta$
that is not weakly consistent it holds that
![]() $\mathit{CMod}^{ec}_{\Delta} = \emptyset$
but
$\mathit{CMod}^{ec}_{\Delta} = \emptyset$
but
![]() ${{\mathit{Sol}({{\mathit{CR}^{ex}_{\Sigma}(\Delta)}})}} = \{(\infty, \dots, \infty)\}$
.
${{\mathit{Sol}({{\mathit{CR}^{ex}_{\Sigma}(\Delta)}})}} = \{(\infty, \dots, \infty)\}$
.
The resulting CSP
![]() ${{\mathit{CR}^{ex}_{\Sigma}(\Delta)}}$
is not a conjunction of inequalities any more, but it now contains disjunctions and is thus more complex. However, for the computation of extended c-inference, we can construct a simplified CSP
${{\mathit{CR}^{ex}_{\Sigma}(\Delta)}}$
is not a conjunction of inequalities any more, but it now contains disjunctions and is thus more complex. However, for the computation of extended c-inference, we can construct a simplified CSP
![]() ${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}}$
that still yields all extended c-representations relevant for c-inference. This is possible, because from Proposition 26 we already know which worlds must have rank infinity and which worlds may have finite rank in the extended c-representations of
${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}}$
that still yields all extended c-representations relevant for c-inference. This is possible, because from Proposition 26 we already know which worlds must have rank infinity and which worlds may have finite rank in the extended c-representations of
![]() $\Delta$
. The simplified CSP not only uses fewer constraint variables but also fewer constraints than
$\Delta$
. The simplified CSP not only uses fewer constraint variables but also fewer constraints than
![]() ${{\mathit{CR}^{ex}_{\Sigma}(\Delta)}}$
for weakly but not strongly consistent belief bases. Before stating
${{\mathit{CR}^{ex}_{\Sigma}(\Delta)}}$
for weakly but not strongly consistent belief bases. Before stating
![]() ${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}}$
, we show some proposition we will use for proving the correctness of
${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}}$
, we show some proposition we will use for proving the correctness of
![]() ${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}}$
.
${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}}$
.
We can assume the impacts of conditionals in
![]() $\Delta^\infty$
to be infinity.
$\Delta^\infty$
to be infinity.
Proposition 42. Let
![]() $\Delta$
be a weakly consistent belief base with extended Z-partition
$\Delta$
be a weakly consistent belief base with extended Z-partition
![]() ${{{{{\mathit{EZP}}}}(\Delta)}} = \{\Delta^0, \dots, \Delta^m, \Delta^\infty\}$
. Let
${{{{{\mathit{EZP}}}}(\Delta)}} = \{\Delta^0, \dots, \Delta^m, \Delta^\infty\}$
. Let
![]() $\vec{\eta}$
be impacts such that
$\vec{\eta}$
be impacts such that
![]() $\kappa_{\vec{\eta}}$
is an extended c-representation of
$\kappa_{\vec{\eta}}$
is an extended c-representation of
![]() $\Delta$
. Let
$\Delta$
. Let
![]() $\vec{\eta}^{\prime}$
be the impact vector defined by
$\vec{\eta}^{\prime}$
be the impact vector defined by
![]() $\eta_{i}' = \infty$
if
$\eta_{i}' = \infty$
if
![]() ${{(B_i|A_i)}} \in \Delta^\infty$
and
${{(B_i|A_i)}} \in \Delta^\infty$
and
![]() $\eta_{i}' = \eta_{i}$
otherwise. Then
$\eta_{i}' = \eta_{i}$
otherwise. Then
![]() $\kappa_{\vec{\eta}} = \kappa_{\vec{\eta}'}$
.
$\kappa_{\vec{\eta}} = \kappa_{\vec{\eta}'}$
.
Proof. Let
![]() $\omega$
be a world. There are two cases.
$\omega$
be a world. There are two cases.
Case 1: There is a conditional
![]() ${{(B_i|A_i)}} \in \Delta^\infty$
that is falsified by
${{(B_i|A_i)}} \in \Delta^\infty$
that is falsified by
![]() $\omega$
. Then
$\omega$
. Then
![]() $\kappa^z_{\Delta}(\omega) = \infty$
and therefore
$\kappa^z_{\Delta}(\omega) = \infty$
and therefore
![]() $\kappa_{\vec{\eta}}(\omega) = \infty$
by Proposition 26. Because
$\kappa_{\vec{\eta}}(\omega) = \infty$
by Proposition 26. Because
![]() $\eta_{i}' = \infty$
we have
$\eta_{i}' = \infty$
we have
![]() $\kappa_{\vec{\eta}'}(\omega) = \sum\limits_{\substack{1 \leqslant j \leqslant n\\\omega\models A_j\overline{B}_j}}\eta_{j}' = \infty = \kappa_{\vec{\eta}}(\omega)$
.
$\kappa_{\vec{\eta}'}(\omega) = \sum\limits_{\substack{1 \leqslant j \leqslant n\\\omega\models A_j\overline{B}_j}}\eta_{j}' = \infty = \kappa_{\vec{\eta}}(\omega)$
.
Case 2: There is no conditional in
![]() $\Delta^\infty$
that is falsified by
$\Delta^\infty$
that is falsified by
![]() $\omega$
. Because
$\omega$
. Because
![]() $\eta_{i} = \eta_{i}'$
for all i with
$\eta_{i} = \eta_{i}'$
for all i with
![]() $\omega\models A_j\overline{B}_j$
we have
$\omega\models A_j\overline{B}_j$
we have
![]() $\kappa_{\vec{\eta}'}(\omega) = \sum\limits_{\substack{1 \leqslant j \leqslant n\\\omega\models A_j\overline{B}_j}}\eta_{j}' = \sum\limits_{\substack{1 \leqslant j \leqslant n\\\omega\models A_j\overline{B}_j}}\eta_{j} = \kappa_{\vec{\eta}}(\omega)$
.
$\kappa_{\vec{\eta}'}(\omega) = \sum\limits_{\substack{1 \leqslant j \leqslant n\\\omega\models A_j\overline{B}_j}}\eta_{j}' = \sum\limits_{\substack{1 \leqslant j \leqslant n\\\omega\models A_j\overline{B}_j}}\eta_{j} = \kappa_{\vec{\eta}}(\omega)$
.
Extended c-representations can assign rank infinity to conditionals without this being enforced by the belief base (cf. Proposition 23). In the following, we introduce conservative extended c-representations, which assign rank infinity only to worlds that also have rank infinity in the Z-ranking function
![]() $\kappa^z_{\Delta}$
.
$\kappa^z_{\Delta}$
.
Definition 43. Let
![]() $\Delta$
be a belief base. Then
$\Delta$
be a belief base. Then
![]() $\mathit{CMod}^{ec}_{\Delta}$
is the set of conservative extended c-representations
$\mathit{CMod}^{ec}_{\Delta}$
is the set of conservative extended c-representations
![]() $\kappa_{\vec{\eta}}$
of
$\kappa_{\vec{\eta}}$
of
![]() $\Delta$
with
$\Delta$
with
![]() $\kappa_{\vec{\eta}}(\omega) \lt \infty$
for all worlds
$\kappa_{\vec{\eta}}(\omega) \lt \infty$
for all worlds
![]() $\omega$
with
$\omega$
with
![]() $\kappa^z_{\Delta}(\omega) \lt \infty$
.
$\kappa^z_{\Delta}(\omega) \lt \infty$
.
For c-inference, it is sufficient to take only conservative extended c-representations of a belief base into account.
Proposition 44. Let
![]() $\Delta$
be a belief base. Then
$\Delta$
be a belief base. Then
![]() $A|\hspace{-2pt} {\sim}_{\kappa} B$
for all c-representations
$A|\hspace{-2pt} {\sim}_{\kappa} B$
for all c-representations
![]() $\kappa$
in
$\kappa$
in
![]() $\mathit{CMod}^{ec}_{\Delta}$
iff
$\mathit{CMod}^{ec}_{\Delta}$
iff
![]() $A|\hspace{-2pt} {\sim}_{\kappa} B$
holds for all c-representations
$A|\hspace{-2pt} {\sim}_{\kappa} B$
holds for all c-representations
![]() $\kappa$
in
$\kappa$
in
![]() ${{\mathit{Mod}^{ec}_{\Sigma}({\Delta})}}$
.
${{\mathit{Mod}^{ec}_{\Sigma}({\Delta})}}$
.
Proof. Direction
![]() $\Leftarrow$
: Observe that
$\Leftarrow$
: Observe that
![]() $\mathit{CMod}^{ec}_{\Delta} \subseteq {Mod}\,^{ec}_{\Delta}$
. Therefore, if
$\mathit{CMod}^{ec}_{\Delta} \subseteq {Mod}\,^{ec}_{\Delta}$
. Therefore, if
![]() $A|\hspace{-2pt} {\sim}_{\kappa} B$
holds for all c-representations
$A|\hspace{-2pt} {\sim}_{\kappa} B$
holds for all c-representations
![]() $\kappa$
in
$\kappa$
in
![]() ${Mod}\,^{ec}_{\Delta}$
, then
${Mod}\,^{ec}_{\Delta}$
, then
![]() $A|\hspace{-2pt} {\sim}_{\kappa} B$
holds for all c-representations
$A|\hspace{-2pt} {\sim}_{\kappa} B$
holds for all c-representations
![]() $\kappa$
in
$\kappa$
in
![]() $\mathit{CMod}^{ec}_{\Delta}$
.
$\mathit{CMod}^{ec}_{\Delta}$
.
Direction
![]() $\Rightarrow$
: Show this by contraposition. Assume that
$\Rightarrow$
: Show this by contraposition. Assume that
![]() $\kappa \in \mathit{CMod}^{ec}_{\Delta}$
with
$\kappa \in \mathit{CMod}^{ec}_{\Delta}$
with
![]() $A \mathrel{{|\hspace{-2pt} {\sim}}^{}_{\kappa}} B$
. Using the construction of
$A \mathrel{{|\hspace{-2pt} {\sim}}^{}_{\kappa}} B$
. Using the construction of
![]() $\kappa^f$
in the proof of Proposition 11 we can find a
$\kappa^f$
in the proof of Proposition 11 we can find a
![]() $\kappa' = \kappa^f$
that is a c-inference of
$\kappa' = \kappa^f$
that is a c-inference of
![]() $\Delta$
and satisfies
$\Delta$
and satisfies
![]() $\mathord{{|\hspace{-2pt}}{\sim}^{}_{\kappa'}} \subseteq \mathord{{|\hspace{-2pt}}{\sim}^{}_{\kappa}}$
. Therefore, if
$\mathord{{|\hspace{-2pt}}{\sim}^{}_{\kappa'}} \subseteq \mathord{{|\hspace{-2pt}}{\sim}^{}_{\kappa}}$
. Therefore, if
![]() $A \mathrel{{|\hspace{-2pt} {\sim}}^{}_{\kappa}} B$
then
$A \mathrel{{|\hspace{-2pt} {\sim}}^{}_{\kappa}} B$
then
![]() $A \mathrel{{|\hspace{-2pt} {\sim}}^{}_{\kappa'}} B$
. Hence, there is a c-representation
$A \mathrel{{|\hspace{-2pt} {\sim}}^{}_{\kappa'}} B$
. Hence, there is a c-representation
![]() $\kappa'$
with
$\kappa'$
with
![]() $A \mathrel{{|\hspace{-2pt} {\sim}}^{}_{\kappa'}} B$
.
$A \mathrel{{|\hspace{-2pt} {\sim}}^{}_{\kappa'}} B$
.
As indicated above, the c-representations in
![]() $\mathit{CMod}^{ec}_{\Delta}$
can then be characterized by a simplified CSP.
$\mathit{CMod}^{ec}_{\Delta}$
can then be characterized by a simplified CSP.
Definition 45 (
![]() ${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}}$
). Let
${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}}$
). Let
![]() $ \Delta = \{{{(B_1|A_1)}}, \ldots, {{(B_n|A_n)}}\} $
be a belief base over
$ \Delta = \{{{(B_1|A_1)}}, \ldots, {{(B_n|A_n)}}\} $
be a belief base over
![]() $\Sigma$
with the extended Z-partition
$\Sigma$
with the extended Z-partition
![]() ${{{{{\mathit{EZP}}}}(\Delta)}} = \{\Delta^0, \dots, \Delta^m, \Delta^\infty\}$
. Let
${{{{{\mathit{EZP}}}}(\Delta)}} = \{\Delta^0, \dots, \Delta^m, \Delta^\infty\}$
. Let
The simplified CSP for extended c-inference of
![]() $\Delta$
, denoted by
$\Delta$
, denoted by
![]() ${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}}$
, on the constraint variables
${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}}$
, on the constraint variables
![]() $\{\eta_{j_1}, \ldots, \eta_{j_l}\},\, j_k \in J_\Delta$
ranging over
$\{\eta_{j_1}, \ldots, \eta_{j_l}\},\, j_k \in J_\Delta$
ranging over
![]() $\mathbb{N}_0$
is given by the constraints
$\mathbb{N}_0$
is given by the constraints
![]() ${{{{\mathit{crs}^{ex\,\Delta}_{j}}}}}$
, for all
${{{{\mathit{crs}^{ex\,\Delta}_{j}}}}}$
, for all
![]() $j \in J_\Delta$
:
$j \in J_\Delta$
:
 \begin{align*} {{{{{\mathit{\ }}}}}} \hspace{4.1cm} \def\lumina\hspace{1cm} \eta_{i} \,\, \gt \,\, \min_{\substack{\omega \in \Omega_\Sigma\\\omega \models A_i B_i}} \sum_{\substack{j \in J_\Delta\\j \neq i \\ \omega \models A_j \overline{B_j}}} \eta_{j} \,\, - \,\, \min_{\substack{\omega \in \Omega_\Sigma\\\omega \models A_i \overline{B}_i}} \sum_{\substack{j \in J_\Delta\\j \neq i \\ \omega \models A_j \overline{B_j}}} \eta_{j} \hspace{3.6cm} ({{{{{\mathit{crs}^{ex\,\Delta}_{j}}}}}}) \end{align*}
\begin{align*} {{{{{\mathit{\ }}}}}} \hspace{4.1cm} \def\lumina\hspace{1cm} \eta_{i} \,\, \gt \,\, \min_{\substack{\omega \in \Omega_\Sigma\\\omega \models A_i B_i}} \sum_{\substack{j \in J_\Delta\\j \neq i \\ \omega \models A_j \overline{B_j}}} \eta_{j} \,\, - \,\, \min_{\substack{\omega \in \Omega_\Sigma\\\omega \models A_i \overline{B}_i}} \sum_{\substack{j \in J_\Delta\\j \neq i \\ \omega \models A_j \overline{B_j}}} \eta_{j} \hspace{3.6cm} ({{{{{\mathit{crs}^{ex\,\Delta}_{j}}}}}}) \end{align*}
The condition
![]() $A_j \overline{B_j} \wedge \big(\bigwedge_{{{(D|C)}} \in \Delta^\infty} (\overline{C} \vee D) \big) \not\equiv \bot$
in the definition of
$A_j \overline{B_j} \wedge \big(\bigwedge_{{{(D|C)}} \in \Delta^\infty} (\overline{C} \vee D) \big) \not\equiv \bot$
in the definition of
![]() $J_\Delta$
is equivalent to there being an
$J_\Delta$
is equivalent to there being an
![]() $\omega \in \Omega_{A_j \overline{B_j}}$
that does not falsify conditionals in
$\omega \in \Omega_{A_j \overline{B_j}}$
that does not falsify conditionals in
![]() $\Delta^\infty$
.
$\Delta^\infty$
.
Definition 46. Let
![]() $\Delta$
be a belief base,
$\Delta$
be a belief base,
![]() $n = |\Delta|$
, and let
$n = |\Delta|$
, and let
![]() $J_\Delta$
be defined as above. For
$J_\Delta$
be defined as above. For
![]() $\vec{\eta}^J \in {{\mathit{Sol}({{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}})}}$
let
$\vec{\eta}^J \in {{\mathit{Sol}({{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}})}}$
let
![]() $\vec{\eta}^{J+\infty} \in (\mathbb{N}_0 \cup \{\infty\})^n$
be the impact vector with
$\vec{\eta}^{J+\infty} \in (\mathbb{N}_0 \cup \{\infty\})^n$
be the impact vector with
 \[\eta_{i}^{J+\infty} = \begin{cases} \eta_{i} & \text{for } i \in J_\Delta \\ \infty & \text{otherwise.}\end{cases}\]
\[\eta_{i}^{J+\infty} = \begin{cases} \eta_{i} & \text{for } i \in J_\Delta \\ \infty & \text{otherwise.}\end{cases}\]
Then
![]() $Sol^{J+\infty}_\Delta \;:\!=\; \{ \vec{\eta}^{J+\infty} \mid \vec{\eta}^J \in Sol({{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}}) \}$
.
$Sol^{J+\infty}_\Delta \;:\!=\; \{ \vec{\eta}^{J+\infty} \mid \vec{\eta}^J \in Sol({{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}}) \}$
.
Proposition 47. (soundness and completeness of
![]() ${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}}$
). Let
${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}}$
). Let
![]() $\Delta$
be a weakly consistent belief base over
$\Delta$
be a weakly consistent belief base over
![]() $\Sigma$
. Then
$\Sigma$
. Then
Proof. Let
![]() ${{{{{\mathit{EZP}}}}(\Delta)}} = (\Delta^0, \dots, \Delta^k, \Delta^\infty)$
, and let
${{{{{\mathit{EZP}}}}(\Delta)}} = (\Delta^0, \dots, \Delta^k, \Delta^\infty)$
, and let
![]() $J_\Delta$
be defined as in Definition 45.
$J_\Delta$
be defined as in Definition 45.
Soundness: Let
![]() $\vec{\eta} \in Sol^{J+\infty}_\Delta$
. By definition, there is a vector
$\vec{\eta} \in Sol^{J+\infty}_\Delta$
. By definition, there is a vector
![]() $\vec{\eta}^J \in {{\mathit{Sol}({{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}})}}$
such that
$\vec{\eta}^J \in {{\mathit{Sol}({{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}})}}$
such that
![]() $\vec{\eta} = \vec{\eta}^{J+\infty}$
.
$\vec{\eta} = \vec{\eta}^{J+\infty}$
.
Because
![]() $\eta_{i} = \infty$
for every
$\eta_{i} = \infty$
for every
![]() ${{(B_i|A_i)}} \in \Delta^\infty$
and due to Lemma 9, all worlds
${{(B_i|A_i)}} \in \Delta^\infty$
and due to Lemma 9, all worlds
![]() $\omega$
for which one of the conditionals in
$\omega$
for which one of the conditionals in
![]() $\Delta^\infty$
is applicable have rank
$\Delta^\infty$
is applicable have rank
![]() $\kappa_{\vec{\eta}}(\omega) = \infty$
. Therefore, all conditionals in
$\kappa_{\vec{\eta}}(\omega) = \infty$
. Therefore, all conditionals in
![]() $\Delta^\infty$
are accepted by
$\Delta^\infty$
are accepted by
![]() $\kappa_{\vec{\eta}}$
.
$\kappa_{\vec{\eta}}$
.
For any conditional
![]() ${{(B_i|A_i)}} \in \Delta \setminus \Delta^\infty$
, there is at least one world
${{(B_i|A_i)}} \in \Delta \setminus \Delta^\infty$
, there is at least one world
![]() $\omega$
that verifies
$\omega$
that verifies
![]() ${{(B_i|A_i)}}$
without falsifying a conditional in
${{(B_i|A_i)}}$
without falsifying a conditional in
![]() $\Delta^\infty$
(otherwise
$\Delta^\infty$
(otherwise
![]() ${{(B_i|A_i)}}$
would not be tolerated by
${{(B_i|A_i)}}$
would not be tolerated by
![]() $\Delta^\infty$
). Because every world that falsifies a conditional
$\Delta^\infty$
). Because every world that falsifies a conditional
![]() ${{(B_j|A_j)}}$
with
${{(B_j|A_j)}}$
with
![]() $j \notin J_\Delta$
also falsifies a conditional in
$j \notin J_\Delta$
also falsifies a conditional in
![]() $\Delta^\infty$
, the world
$\Delta^\infty$
, the world
![]() $\omega$
does not falsify any such conditional
$\omega$
does not falsify any such conditional
![]() ${{(B_j|A_j)}}$
with impact
${{(B_j|A_j)}}$
with impact
![]() $\infty$
. Therefore,
$\infty$
. Therefore,
![]() $\kappa_{\vec{\eta}}(A_i B_i) \lt \infty$
. If
$\kappa_{\vec{\eta}}(A_i B_i) \lt \infty$
. If
![]() $\kappa_{\vec{\eta}}(A_i \overline{B_i}) = \infty$
then
$\kappa_{\vec{\eta}}(A_i \overline{B_i}) = \infty$
then
![]() $\kappa_{\vec{\eta}} \models {{(B_i|A_i)}}$
. Otherwise, for
$\kappa_{\vec{\eta}} \models {{(B_i|A_i)}}$
. Otherwise, for
![]() $\kappa_{\vec{\eta}}(A_i \overline{B_i}) \lt \infty$
, there is a world that falsifies
$\kappa_{\vec{\eta}}(A_i \overline{B_i}) \lt \infty$
, there is a world that falsifies
![]() ${{(B|A)}}$
without falsifying a conditional in
${{(B|A)}}$
without falsifying a conditional in
![]() $\Delta^\infty$
. In this case it is
$\Delta^\infty$
. In this case it is
![]() $i \in J_\Delta$
and the CSP
$i \in J_\Delta$
and the CSP
![]() ${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}}$
contains the constraint
${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}}$
contains the constraint
![]() $({{{{\mathit{crs}^{ex\,\Delta}_{j}}}}})$
which must hold for
$({{{{\mathit{crs}^{ex\,\Delta}_{j}}}}})$
which must hold for
![]() $\vec{\eta}^J$
:
$\vec{\eta}^J$
:
 \begin{align*} &&\eta_{i} \,\, \gt \,\, \min_{\substack{\omega \in \Omega_\Sigma\\\omega \models A_i B_i}} \sum_{\substack{j \in J_\Delta j \neq i \\ \omega \models A_j \overline{B_j}}} \eta_{j} \,\, &- \,\, \min_{\substack{\omega \in \Omega_\Sigma\\\omega \models A_i \overline{B}_i}} \sum_{\substack{j \in J_\Delta j \neq i \\ \omega \models A_j \overline{B_j}}} \eta_{j} \\ \Leftrightarrow&&\eta_{i} \,\, + \,\, \min_{\substack{\omega \in \Omega_\Sigma\\\omega \models A_i \overline{B}_i}} \sum_{\substack{j \in J_\Delta j \neq i \\ \omega \models A_j \overline{B_j}}} \eta_{j} \,\, &\gt \,\, \min_{\substack{\omega \in \Omega_\Sigma\\\omega \models A_i B_i}} \sum_{\substack{j \in J_\Delta j \neq i \\ \omega \models A_j \overline{B_j}}} \eta_{j} \\ \Leftrightarrow&&\min_{\substack{\omega \in \Omega_\Sigma\\\omega \models A_i \overline{B}_i}} \sum_{\substack{j \in J_\Delta \\ \omega \models A_j \overline{B_j}}} \eta_{j} \,\, &\gt \,\, \min_{\substack{\omega \in \Omega_\Sigma\\\omega \models A_i B_i}} \sum_{\substack{j \in J_\Delta \\ \omega \models A_j \overline{B_j}}} \eta_{j} \\ \overset{(*)}{\Leftrightarrow}&&\min_{\substack{\omega \in \Omega_\Sigma\\\omega \models A_i \overline{B}_i}} \sum_{\substack{1 \leqslant j \leqslant n \\ \omega \models A_j \overline{B_j}}} \eta_{j} \,\, &\gt \,\, \min_{\substack{\omega \in \Omega_\Sigma\\\omega \models A_i B_i}} \sum_{\substack{1 \leqslant j \leqslant n \\ \omega \models A_j \overline{B_j}}} \eta_{j} \\ \Leftrightarrow&&\kappa_{\vec{\eta}}(A_i\overline{B_i}) \,\, &\gt \,\, \kappa_{\vec{\eta}}(A_i B_i). \end{align*}
\begin{align*} &&\eta_{i} \,\, \gt \,\, \min_{\substack{\omega \in \Omega_\Sigma\\\omega \models A_i B_i}} \sum_{\substack{j \in J_\Delta j \neq i \\ \omega \models A_j \overline{B_j}}} \eta_{j} \,\, &- \,\, \min_{\substack{\omega \in \Omega_\Sigma\\\omega \models A_i \overline{B}_i}} \sum_{\substack{j \in J_\Delta j \neq i \\ \omega \models A_j \overline{B_j}}} \eta_{j} \\ \Leftrightarrow&&\eta_{i} \,\, + \,\, \min_{\substack{\omega \in \Omega_\Sigma\\\omega \models A_i \overline{B}_i}} \sum_{\substack{j \in J_\Delta j \neq i \\ \omega \models A_j \overline{B_j}}} \eta_{j} \,\, &\gt \,\, \min_{\substack{\omega \in \Omega_\Sigma\\\omega \models A_i B_i}} \sum_{\substack{j \in J_\Delta j \neq i \\ \omega \models A_j \overline{B_j}}} \eta_{j} \\ \Leftrightarrow&&\min_{\substack{\omega \in \Omega_\Sigma\\\omega \models A_i \overline{B}_i}} \sum_{\substack{j \in J_\Delta \\ \omega \models A_j \overline{B_j}}} \eta_{j} \,\, &\gt \,\, \min_{\substack{\omega \in \Omega_\Sigma\\\omega \models A_i B_i}} \sum_{\substack{j \in J_\Delta \\ \omega \models A_j \overline{B_j}}} \eta_{j} \\ \overset{(*)}{\Leftrightarrow}&&\min_{\substack{\omega \in \Omega_\Sigma\\\omega \models A_i \overline{B}_i}} \sum_{\substack{1 \leqslant j \leqslant n \\ \omega \models A_j \overline{B_j}}} \eta_{j} \,\, &\gt \,\, \min_{\substack{\omega \in \Omega_\Sigma\\\omega \models A_i B_i}} \sum_{\substack{1 \leqslant j \leqslant n \\ \omega \models A_j \overline{B_j}}} \eta_{j} \\ \Leftrightarrow&&\kappa_{\vec{\eta}}(A_i\overline{B_i}) \,\, &\gt \,\, \kappa_{\vec{\eta}}(A_i B_i). \end{align*}
Therefore,
![]() $\kappa_{\vec{\eta}} \models {{(B_i|A_i)}}$
.
$\kappa_{\vec{\eta}} \models {{(B_i|A_i)}}$
.
The equivalence
![]() $(*)$
holds, because there is a model for
$(*)$
holds, because there is a model for
![]() $A_i\dot{B_i}$
that does not falsify a conditional in
$A_i\dot{B_i}$
that does not falsify a conditional in
![]() $\Delta^\infty$
, we have
$\Delta^\infty$
, we have
![]() $\eta_{j} = \infty$
for all
$\eta_{j} = \infty$
for all
![]() ${{(B_j|A_j)}}$
with
${{(B_j|A_j)}}$
with
![]() $j \notin J_\Delta$
, and therefore
$j \notin J_\Delta$
, and therefore
 \[ \min_{\substack{\omega \in \Omega_\Sigma\\\omega \models A_i \dot{B_i}}} \sum_{\substack{j \in J_\Delta \\ \omega \models A_j \overline{B_j}}} \eta_{j} = \min_{\substack{\omega \in \Omega_\Sigma\\\omega \models A_i \dot{B_i}}} \sum_{\substack{1 \leqslant j \leqslant n \\ \omega \models A_j \overline{B_j}}} \eta_{j}. \]
\[ \min_{\substack{\omega \in \Omega_\Sigma\\\omega \models A_i \dot{B_i}}} \sum_{\substack{j \in J_\Delta \\ \omega \models A_j \overline{B_j}}} \eta_{j} = \min_{\substack{\omega \in \Omega_\Sigma\\\omega \models A_i \dot{B_i}}} \sum_{\substack{1 \leqslant j \leqslant n \\ \omega \models A_j \overline{B_j}}} \eta_{j}. \]
For any world
![]() $\omega$
with
$\omega$
with
![]() $\kappa^z_{\Delta}(\omega) \lt \infty$
it holds that all conditionals in
$\kappa^z_{\Delta}(\omega) \lt \infty$
it holds that all conditionals in
![]() $\Delta^\infty$
are not applicable in
$\Delta^\infty$
are not applicable in
![]() $\omega$
. Therefore,
$\omega$
. Therefore,
![]() $\kappa_{\vec{\eta}}(\omega)$
is the sum of some of the impacts in
$\kappa_{\vec{\eta}}(\omega)$
is the sum of some of the impacts in
![]() $\vec{\eta}^J$
; and because
$\vec{\eta}^J$
; and because
![]() $\vec{\eta}^J \in \mathbb{N}_0^l$
we have
$\vec{\eta}^J \in \mathbb{N}_0^l$
we have
![]() $\kappa_{\vec{\eta}}(\omega) \lt \infty$
.
$\kappa_{\vec{\eta}}(\omega) \lt \infty$
.
In summary,
![]() $\kappa_{\vec{\eta}} \in \mathit{CMod}^{ec}_{\Delta}$
.
$\kappa_{\vec{\eta}} \in \mathit{CMod}^{ec}_{\Delta}$
.
Completeness: Let
![]() $\kappa \in \mathit{CMod}^{ec}_{\Delta}$
be an extended c-representation. Let
$\kappa \in \mathit{CMod}^{ec}_{\Delta}$
be an extended c-representation. Let
![]() $\vec{\eta} \in (\mathbb{N}_0 \cup {\infty})^n$
be an impact vector such that
$\vec{\eta} \in (\mathbb{N}_0 \cup {\infty})^n$
be an impact vector such that
![]() $\kappa = \kappa_{\vec{\eta}}$
. Because of Proposition 42, w.l.o.g. we can assume
$\kappa = \kappa_{\vec{\eta}}$
. Because of Proposition 42, w.l.o.g. we can assume
![]() $\eta_{i} = \infty$
for all
$\eta_{i} = \infty$
for all
![]() ${{(B_i|A_i)}} \in \Delta^\infty$
. Furthermore, w.l.o.g, we can assume
${{(B_i|A_i)}} \in \Delta^\infty$
. Furthermore, w.l.o.g, we can assume
![]() $\eta_{i} = \infty$
for all conditionals
$\eta_{i} = \infty$
for all conditionals
![]() ${{(B_i|A_i)}} \in \Delta\setminus\Delta^\infty$
which are falsified only by worlds
${{(B_i|A_i)}} \in \Delta\setminus\Delta^\infty$
which are falsified only by worlds
![]() $\omega$
that also falsify a conditional in
$\omega$
that also falsify a conditional in
![]() $\Delta^\infty$
– all worlds for which these impacts apply already have rank
$\Delta^\infty$
– all worlds for which these impacts apply already have rank
![]() $\infty$
because of the impacts for
$\infty$
because of the impacts for
![]() $\Delta^\infty$
.
$\Delta^\infty$
.
The vector
![]() $\vec{\eta}$
is a combination of a vector
$\vec{\eta}$
is a combination of a vector
![]() $\vec{\eta}^J$
of impacts
$\vec{\eta}^J$
of impacts
![]() $\eta_{j}$
for
$\eta_{j}$
for
![]() $j \in J_\Delta$
, and a vector
$j \in J_\Delta$
, and a vector
![]() $(\infty, \dots, \infty)$
of size
$(\infty, \dots, \infty)$
of size
![]() $n - |J_\Delta|$
of impacts for conditionals
$n - |J_\Delta|$
of impacts for conditionals
![]() ${{(B_j|A_j)}}$
with
${{(B_j|A_j)}}$
with
![]() $j \notin J_\Delta$
.
$j \notin J_\Delta$
.
For every
![]() $i \in J_\Delta$
, by construction of
$i \in J_\Delta$
, by construction of
![]() $J_\Delta$
there is at least one world
$J_\Delta$
there is at least one world
![]() $\omega$
falsifying
$\omega$
falsifying
![]() ${{(B_i|A_i)}}$
without falsifying a conditional in
${{(B_i|A_i)}}$
without falsifying a conditional in
![]() $\Delta^\infty$
. Then,
$\Delta^\infty$
. Then,
![]() $\kappa^z_{\Delta}(\omega) \lt \infty$
because
$\kappa^z_{\Delta}(\omega) \lt \infty$
because
![]() $\omega$
falsifies no conditionals in
$\omega$
falsifies no conditionals in
![]() $\Delta^\infty$
and due to Lemma 15; therefore
$\Delta^\infty$
and due to Lemma 15; therefore
![]() $\eta_{i} \lt \kappa_{\vec{\eta}}(\omega) \lt \infty$
because
$\eta_{i} \lt \kappa_{\vec{\eta}}(\omega) \lt \infty$
because
![]() $\kappa_{\vec{\eta}} \in \mathit{CMod}^{ec}_{\Delta}$
. Hence,
$\kappa_{\vec{\eta}} \in \mathit{CMod}^{ec}_{\Delta}$
. Hence,
![]() $\vec{\eta}^J \in \mathbb{N}_0$
.
$\vec{\eta}^J \in \mathbb{N}_0$
.
It is left to show that
![]() $\vec{\eta}^J$
is a solution of
$\vec{\eta}^J$
is a solution of
![]() ${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}}$
, that is, that for every
${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}}$
, that is, that for every
![]() $j \in J_\Delta$
it satisfies the constraint
$j \in J_\Delta$
it satisfies the constraint
![]() $({{{{\mathit{crs}^{ex\,\Delta}_{j}}}}})$
. As
$({{{{\mathit{crs}^{ex\,\Delta}_{j}}}}})$
. As
![]() $\kappa_{\vec{\eta}}$
is a model of
$\kappa_{\vec{\eta}}$
is a model of
![]() $\Delta$
, it satisfies the conditional
$\Delta$
, it satisfies the conditional
![]() ${{(B_j|A_j)}} \in \Delta$
. By construction of
${{(B_j|A_j)}} \in \Delta$
. By construction of
![]() $J_\Delta$
, there is at least one world
$J_\Delta$
, there is at least one world
![]() $\omega$
falsifying
$\omega$
falsifying
![]() ${{(B_j|A_j)}}$
without falsifying a conditional in
${{(B_j|A_j)}}$
without falsifying a conditional in
![]() $\Delta^\infty$
. As established above, the rank of such a world in
$\Delta^\infty$
. As established above, the rank of such a world in
![]() $\kappa_{\vec{\eta}}$
is finite, and thus
$\kappa_{\vec{\eta}}$
is finite, and thus
![]() $\kappa_{\vec{\eta}}(A)$
is finite. To satisfy
$\kappa_{\vec{\eta}}(A)$
is finite. To satisfy
![]() ${{(B_j|A_j)}}$
it is necessary that
${{(B_j|A_j)}}$
it is necessary that
![]() $\kappa_{\vec{\eta}}(A_i \overline{B_i}) \gt \kappa_{\vec{\eta}}(A_i B_i)$
. Using the equivalence transformation in the Soundness part of this proof, we obtain that
$\kappa_{\vec{\eta}}(A_i \overline{B_i}) \gt \kappa_{\vec{\eta}}(A_i B_i)$
. Using the equivalence transformation in the Soundness part of this proof, we obtain that
![]() $({{{{\mathit{crs}^{ex\,\Delta}_{j}}}}})$
holds for
$({{{{\mathit{crs}^{ex\,\Delta}_{j}}}}})$
holds for
![]() $\eta_{j}$
.
$\eta_{j}$
.
Propositions 44 and 47 imply the following result.
Proposition 48. Let
![]() $\Delta$
be a weakly consistent belief base. Then
$\Delta$
be a weakly consistent belief base. Then
![]() $A |\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
iff
$A |\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
iff
![]() $A |\hspace{-2pt} {\sim}_{\kappa_{\vec{\eta}}} {B}$
for every
$A |\hspace{-2pt} {\sim}_{\kappa_{\vec{\eta}}} {B}$
for every
![]() $\vec{\eta} \in Sol^{J+\infty}_\Delta$
.
$\vec{\eta} \in Sol^{J+\infty}_\Delta$
.
The following example illustrates how
![]() ${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}}$
is simpler than
${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}}$
is simpler than
![]() ${{\mathit{CR}^{ex}_{\Sigma}(\Delta)}}$
.
${{\mathit{CR}^{ex}_{\Sigma}(\Delta)}}$
.
Example 49. Let
![]() $\Sigma = \{a, b, c\}$
and
$\Sigma = \{a, b, c\}$
and
![]() $\Delta = \{{{(\bot|a)}}, {{(\overline{a}|b)}}, {{(b|c)}}\}$
. The CSP
$\Delta = \{{{(\bot|a)}}, {{(\overline{a}|b)}}, {{(b|c)}}\}$
. The CSP
![]() ${{\mathit{CR}^{ex}_{\Sigma}(\Delta)}}$
over
${{\mathit{CR}^{ex}_{\Sigma}(\Delta)}}$
over
![]() $\eta_{1}, \eta_{1}, \eta_{3} \in \mathbb{N}_0 \cup \{\infty\}$
contains the constraints
$\eta_{1}, \eta_{1}, \eta_{3} \in \mathbb{N}_0 \cup \{\infty\}$
contains the constraints
 \begin{align*} ({{{{{\mathit{cr}^{ex\,\Delta}_{1}}}}}}) \hspace{.30cm} &\min_{\substack{\omega \in \Omega_\Sigma\\\omega \models a}} \,\, \sum_{\substack{1 \leqslant j \leqslant n \\ \omega \models A_j \overline{B_j}} } \def\lumina\hspace{-1.7mm} \eta_{j} = \infty \quad \text{or} \quad \eta_{1} \,\, \gt \min_{\substack{\omega \in \Omega_\Sigma\\\omega \models a \wedge \bot}} \sum_{\substack{j \neq 1 \\ \omega \models A_j \overline{B_j}}} \def\lumina\hspace{-1.7mm} \eta_{j} \,\, - \min_{\substack{\omega \in \Omega_\Sigma\\\omega \models a \wedge \top}} \sum_{\substack{j \neq 1 \\ \omega \models A_j \overline{B_j}}} \def\lumina\hspace{-1.7mm} \eta_{j}, \\ ({{{{{\mathit{cr}^{ex\,\Delta}_{2}}}}}}) \hspace{.30cm} &\min_{\substack{\omega \in \Omega_\Sigma\\\omega \models b}} \,\, \sum_{\substack{1 \leqslant j \leqslant n \\ \omega \models A_j \overline{B_j}} } \def\lumina\hspace{-1.7mm} \eta_{j} = \infty \quad \text{or} \quad \eta_{i} \,\, \gt \,\, \min_{\substack{\omega \in \Omega_\Sigma\\\omega \models b \overline{a}}} \sum_{\substack{j \neq 2 \\ \omega \models A_j \overline{B_j}}} \def\lumina\hspace{-1.7mm} \eta_{j} \,\, - \,\, \min_{\substack{\omega \in \Omega_\Sigma\\\omega \models b a}} \sum_{\substack{j \neq 2 \\ \omega \models A_j \overline{B_j}}} \def\lumina\hspace{-1.7mm} \eta_{j}, \\ ({{{{{\mathit{cr}^{ex\,\Delta}_{3}}}}}}) \hspace{.30cm} &\min_{\substack{\omega \in \Omega_\Sigma\\\omega \models c}} \,\, \sum_{\substack{1 \leqslant j \leqslant n \\ \omega \models A_j \overline{B_j}} } \def\lumina\hspace{-1.7mm} \eta_{j} = \infty \quad \text{or} \quad \eta_{i} \,\, \gt \,\, \min_{\substack{\omega \in \Omega_\Sigma\\\omega \models c b}} \sum_{\substack{j \neq 3 \\ \omega \models A_j \overline{B_j}}} \def\lumina\hspace{-1.7mm} \eta_{j} \,\, - \,\, \min_{\substack{\omega \in \Omega_\Sigma\\\omega \models c \overline{b}}} \sum_{\substack{j \neq 3 \\ \omega \models A_j \overline{B_j}}} \def\lumina\hspace{-1.7mm} \eta_{j}. \end{align*}
\begin{align*} ({{{{{\mathit{cr}^{ex\,\Delta}_{1}}}}}}) \hspace{.30cm} &\min_{\substack{\omega \in \Omega_\Sigma\\\omega \models a}} \,\, \sum_{\substack{1 \leqslant j \leqslant n \\ \omega \models A_j \overline{B_j}} } \def\lumina\hspace{-1.7mm} \eta_{j} = \infty \quad \text{or} \quad \eta_{1} \,\, \gt \min_{\substack{\omega \in \Omega_\Sigma\\\omega \models a \wedge \bot}} \sum_{\substack{j \neq 1 \\ \omega \models A_j \overline{B_j}}} \def\lumina\hspace{-1.7mm} \eta_{j} \,\, - \min_{\substack{\omega \in \Omega_\Sigma\\\omega \models a \wedge \top}} \sum_{\substack{j \neq 1 \\ \omega \models A_j \overline{B_j}}} \def\lumina\hspace{-1.7mm} \eta_{j}, \\ ({{{{{\mathit{cr}^{ex\,\Delta}_{2}}}}}}) \hspace{.30cm} &\min_{\substack{\omega \in \Omega_\Sigma\\\omega \models b}} \,\, \sum_{\substack{1 \leqslant j \leqslant n \\ \omega \models A_j \overline{B_j}} } \def\lumina\hspace{-1.7mm} \eta_{j} = \infty \quad \text{or} \quad \eta_{i} \,\, \gt \,\, \min_{\substack{\omega \in \Omega_\Sigma\\\omega \models b \overline{a}}} \sum_{\substack{j \neq 2 \\ \omega \models A_j \overline{B_j}}} \def\lumina\hspace{-1.7mm} \eta_{j} \,\, - \,\, \min_{\substack{\omega \in \Omega_\Sigma\\\omega \models b a}} \sum_{\substack{j \neq 2 \\ \omega \models A_j \overline{B_j}}} \def\lumina\hspace{-1.7mm} \eta_{j}, \\ ({{{{{\mathit{cr}^{ex\,\Delta}_{3}}}}}}) \hspace{.30cm} &\min_{\substack{\omega \in \Omega_\Sigma\\\omega \models c}} \,\, \sum_{\substack{1 \leqslant j \leqslant n \\ \omega \models A_j \overline{B_j}} } \def\lumina\hspace{-1.7mm} \eta_{j} = \infty \quad \text{or} \quad \eta_{i} \,\, \gt \,\, \min_{\substack{\omega \in \Omega_\Sigma\\\omega \models c b}} \sum_{\substack{j \neq 3 \\ \omega \models A_j \overline{B_j}}} \def\lumina\hspace{-1.7mm} \eta_{j} \,\, - \,\, \min_{\substack{\omega \in \Omega_\Sigma\\\omega \models c \overline{b}}} \sum_{\substack{j \neq 3 \\ \omega \models A_j \overline{B_j}}} \def\lumina\hspace{-1.7mm} \eta_{j}. \end{align*}
The extended Z-partition of
![]() $\Delta$
is
$\Delta$
is
![]() ${{{{{\mathit{EZP}}}}(\Delta)}} = (\Delta^0, \Delta^\infty)$
with
${{{{{\mathit{EZP}}}}(\Delta)}} = (\Delta^0, \Delta^\infty)$
with
![]() $\Delta^0 = \{{{(\overline{a}|b)}}, {{(b|c)}}\}$
and
$\Delta^0 = \{{{(\overline{a}|b)}}, {{(b|c)}}\}$
and
![]() $\Delta^\infty = \{{{(\bot|a)}}\}$
. The conditional
$\Delta^\infty = \{{{(\bot|a)}}\}$
. The conditional
![]() ${{(\overline{a}|b)}}$
cannot be falsified without also falsifying
${{(\overline{a}|b)}}$
cannot be falsified without also falsifying
![]() ${{(\bot|a)}} \in \Delta^\infty$
. Therefore,
${{(\bot|a)}} \in \Delta^\infty$
. Therefore,
![]() $J_\Delta = \{3\}$
and the CSP
$J_\Delta = \{3\}$
and the CSP
![]() ${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}}$
over
${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}}$
over
![]() $\eta_{3} \in \mathbb{N}_0$
contains only the constraint
$\eta_{3} \in \mathbb{N}_0$
contains only the constraint
 \begin{align*} ({{{{{\mathit{crs}^{ex\,\Delta}_{3}}}}}}) \hspace{1.0cm} \def\lumina\hspace{1cm} \eta_{3} \,\, \gt \,\, \min_{\substack{\omega \in \Omega_\Sigma\\\omega \models b c}} \sum_{\substack{j \in J_\Delta\\j \neq 3 \\ \omega \models A_j \overline{B_j}}} \eta_{j} \,\, - \,\, \min_{\substack{\omega \in \Omega_\Sigma\\\omega \models b \overline{c}}} \sum_{\substack{j \in J_\Delta\\j \neq 3 \\ \omega \models A_j \overline{B_j}}} \eta_{j} \end{align*}
\begin{align*} ({{{{{\mathit{crs}^{ex\,\Delta}_{3}}}}}}) \hspace{1.0cm} \def\lumina\hspace{1cm} \eta_{3} \,\, \gt \,\, \min_{\substack{\omega \in \Omega_\Sigma\\\omega \models b c}} \sum_{\substack{j \in J_\Delta\\j \neq 3 \\ \omega \models A_j \overline{B_j}}} \eta_{j} \,\, - \,\, \min_{\substack{\omega \in \Omega_\Sigma\\\omega \models b \overline{c}}} \sum_{\substack{j \in J_\Delta\\j \neq 3 \\ \omega \models A_j \overline{B_j}}} \eta_{j} \end{align*}
which simplifies to
![]() $\eta_{3} \gt 0$
. For
$\eta_{3} \gt 0$
. For
![]() $\vec{\eta} \in Sol^{J+\infty}_\Delta$
it holds that
$\vec{\eta} \in Sol^{J+\infty}_\Delta$
it holds that
![]() $\eta_{1} = \eta_{2} = \infty$
and
$\eta_{1} = \eta_{2} = \infty$
and
![]() $\eta_{3} \in {{\mathit{Sol}({{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}})}}$
.
$\eta_{3} \in {{\mathit{Sol}({{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}})}}$
.
7.2. Characterizing extended c-inference by a CSP
In Beierle et al. (Reference Beierle, Eichhorn, Kern-Isberner and Kutsch2018) a method is developed that realizes c-inference as a CSP. The idea of this approach is that in order to check whether
![]() $A |\hspace{-2pt} {\sim}^{c}_{\Delta}B$
holds, a constraint encoding that
$A |\hspace{-2pt} {\sim}^{c}_{\Delta}B$
holds, a constraint encoding that
![]() $A |\hspace{-2pt} {\sim}_{\kappa_{\vec{\eta}}} B$
does not hold is added to
$A |\hspace{-2pt} {\sim}_{\kappa_{\vec{\eta}}} B$
does not hold is added to
![]() ${{\mathit{CR}_{\Sigma}(\Delta)}}$
. If the resulting CSP is unsovable,
${{\mathit{CR}_{\Sigma}(\Delta)}}$
. If the resulting CSP is unsovable,
![]() $A |\hspace{-2pt} {\sim}_{\kappa_{\vec{\eta}}} B$
holds for all solutions
$A |\hspace{-2pt} {\sim}_{\kappa_{\vec{\eta}}} B$
holds for all solutions
![]() $\vec{\eta}$
of
$\vec{\eta}$
of
![]() ${{\mathit{CR}_{\Sigma}(\Delta)}}$
. Based on this idea, we develop a CSP that allows doing something similar for extended c-inference.
${{\mathit{CR}_{\Sigma}(\Delta)}}$
. Based on this idea, we develop a CSP that allows doing something similar for extended c-inference.
First we need a constraint encoding that
![]() $A |\hspace{-2pt} {\sim}_{\kappa_{\vec{\eta}}} B$
does not hold for an extended c-representation
$A |\hspace{-2pt} {\sim}_{\kappa_{\vec{\eta}}} B$
does not hold for an extended c-representation
![]() ${{\kappa_{\vec{\eta}}}}$
.
${{\kappa_{\vec{\eta}}}}$
.
Definition 50. Let
![]() $\Delta = \{{{(B_1|A_1)}}, \dots, {{(B_n|A_n)}}\}$
be a belief base and let
$\Delta = \{{{(B_1|A_1)}}, \dots, {{(B_n|A_n)}}\}$
be a belief base and let
![]() $J_\Delta$
be as defined in Definition 45. The constraint
$J_\Delta$
be as defined in Definition 45. The constraint
![]() ${{\neg{{\mathit{CR}_{\Delta}{{(B|A)}}}}}}$
is given by
${{\neg{{\mathit{CR}_{\Delta}{{(B|A)}}}}}}$
is given by
Using this constraint and the CSP
![]() ${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}}$
developed in Section 7.1 we can check if
${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}}$
developed in Section 7.1 we can check if
![]() $A |\hspace{-2pt} {\sim}^{ec}_{\Delta}B$
with the following proposition.
$A |\hspace{-2pt} {\sim}^{ec}_{\Delta}B$
with the following proposition.
Proposition 51. Let
![]() $\Delta$
be weakly consistent. Then
$\Delta$
be weakly consistent. Then
![]() $A |\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
iff (i)
$A |\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
iff (i)
![]() $\kappa^z_{\Delta}(A\overline{B}) = \infty$
or (ii)
$\kappa^z_{\Delta}(A\overline{B}) = \infty$
or (ii)
![]() $\kappa^z_{\Delta}(A\overline{B})\lt\infty$
,
$\kappa^z_{\Delta}(A\overline{B})\lt\infty$
,
![]() $\kappa^z_{\Delta}(AB) \lt \infty$
and
$\kappa^z_{\Delta}(AB) \lt \infty$
and
![]() ${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}} \cup {{\neg{{\mathit{CR}_{\Delta}{{(B|A)}}}}}}$
is unsolvable.
${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}} \cup {{\neg{{\mathit{CR}_{\Delta}{{(B|A)}}}}}}$
is unsolvable.
Proof.
Direction
![]() $\Rightarrow$
: Assume that
$\Rightarrow$
: Assume that
![]() $A |\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
and that
$A |\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
and that
![]() $\kappa^z_{\Delta}(A\overline{B}) \lt \infty$
. Then
$\kappa^z_{\Delta}(A\overline{B}) \lt \infty$
. Then
![]() $\kappa(A \overline{B}) \lt \infty$
for all
$\kappa(A \overline{B}) \lt \infty$
for all
![]() $\kappa \in \mathit{CMod}^{ec}_{\Delta}$
by the definition of
$\kappa \in \mathit{CMod}^{ec}_{\Delta}$
by the definition of
![]() $\mathit{CMod}^{ec}_{\Delta}$
. Therefore,
$\mathit{CMod}^{ec}_{\Delta}$
. Therefore,
![]() $\kappa(A) \lt \infty$
for all
$\kappa(A) \lt \infty$
for all
![]() $\kappa \in \mathit{CMod}^{ec}_{\Delta}$
. Furthermore,
$\kappa \in \mathit{CMod}^{ec}_{\Delta}$
. Furthermore,
![]() $A |\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
implies that for every
$A |\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
implies that for every
![]() $\kappa \in \mathit{CMod}^{ec}_{\Delta}$
, we have
$\kappa \in \mathit{CMod}^{ec}_{\Delta}$
, we have
![]() $A |\hspace{-2pt} {\sim}_{\kappa} B$
. Therefore,
$A |\hspace{-2pt} {\sim}_{\kappa} B$
. Therefore,
![]() $\kappa(A B) \lt \kappa(A \overline{B})$
for every
$\kappa(A B) \lt \kappa(A \overline{B})$
for every
![]() $\kappa \in \mathit{CMod}^{ec}_{\Delta}$
, and because of Proposition 47
$\kappa \in \mathit{CMod}^{ec}_{\Delta}$
, and because of Proposition 47
![]() $\kappa_{\vec{\eta}}(A B) \lt \kappa_{\vec{\eta}}(A \overline{B})$
for every
$\kappa_{\vec{\eta}}(A B) \lt \kappa_{\vec{\eta}}(A \overline{B})$
for every
![]() $\vec{\eta} \in Sol^{J+\infty}_\Delta$
. We have
$\vec{\eta} \in Sol^{J+\infty}_\Delta$
. We have
 \begin{align*} &&\kappa_{\vec{\eta}}(A B) &\lt \kappa_{\vec{\eta}}(A \overline{B}) \\ \Leftrightarrow&&\min_{\omega \models AB} \sum_{\substack{1 \leqslant i \leqslant n \\ \omega \models A_i \overline{B_i}}} \eta_{i} &\lt \min_{\omega \models A\overline{B}} \sum_{\substack{1 \leqslant i \leqslant n \\ \omega \models A_i \overline{B_i}}} \eta_{i} \\ \overset{(*)}{\Leftrightarrow}&&\min_{\omega \models AB} \sum_{\substack{i \in J_\Delta \\ \omega \models A_i \overline{B_i}}} \eta_{i} \ \ &\lt \ \ \min_{\omega \models A \overline{B}} \sum_{\substack{i \in J_\Delta \\ \omega \models A_i \overline{B_i}}} \eta_{i}. \end{align*}
\begin{align*} &&\kappa_{\vec{\eta}}(A B) &\lt \kappa_{\vec{\eta}}(A \overline{B}) \\ \Leftrightarrow&&\min_{\omega \models AB} \sum_{\substack{1 \leqslant i \leqslant n \\ \omega \models A_i \overline{B_i}}} \eta_{i} &\lt \min_{\omega \models A\overline{B}} \sum_{\substack{1 \leqslant i \leqslant n \\ \omega \models A_i \overline{B_i}}} \eta_{i} \\ \overset{(*)}{\Leftrightarrow}&&\min_{\omega \models AB} \sum_{\substack{i \in J_\Delta \\ \omega \models A_i \overline{B_i}}} \eta_{i} \ \ &\lt \ \ \min_{\omega \models A \overline{B}} \sum_{\substack{i \in J_\Delta \\ \omega \models A_i \overline{B_i}}} \eta_{i}. \end{align*}
Equivalence
![]() $(*)$
holds because the ranks of the minimal models of A B and
$(*)$
holds because the ranks of the minimal models of A B and
![]() $A \overline{B}$
are finite and therefore do not violate a conditional
$A \overline{B}$
are finite and therefore do not violate a conditional
![]() ${{(B_i|A_i)}}$
with
${{(B_i|A_i)}}$
with
![]() $i \notin J_\Delta$
.
$i \notin J_\Delta$
.
Therefore,
![]() ${{\neg{{\mathit{CR}_{\Delta}{{(B|A)}}}}}}$
does not hold for any solution of
${{\neg{{\mathit{CR}_{\Delta}{{(B|A)}}}}}}$
does not hold for any solution of
![]() ${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}}$
, implying that
${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}}$
, implying that
![]() ${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}} \cup {{\neg{{\mathit{CR}_{\Delta}{{(B|A)}}}}}}$
is unsolvable.
${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}} \cup {{\neg{{\mathit{CR}_{\Delta}{{(B|A)}}}}}}$
is unsolvable.
Direction
![]() $\Leftarrow$
: Assume that either
$\Leftarrow$
: Assume that either
![]() $\kappa^z_{\Delta}(A\overline{B}) = \infty$
or
$\kappa^z_{\Delta}(A\overline{B}) = \infty$
or
![]() $\big($
$\big($
![]() $\kappa^z_{\Delta}(AB) \lt \infty$
and
$\kappa^z_{\Delta}(AB) \lt \infty$
and
![]() ${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}} \cup {{\neg{{\mathit{CR}_{\Delta}{{(B|A)}}}}}}$
is unsolvable
${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}} \cup {{\neg{{\mathit{CR}_{\Delta}{{(B|A)}}}}}}$
is unsolvable
![]() $\big)$
. There are three cases.
$\big)$
. There are three cases.
Case 1:
![]() $\kappa^z_{\Delta}(A B) = \infty$
and
$\kappa^z_{\Delta}(A B) = \infty$
and
![]() $\kappa^z_{\Delta}(A \overline{B}) = \infty$
$\kappa^z_{\Delta}(A \overline{B}) = \infty$
Then
![]() $\kappa^z_{\Delta}(A) = \infty$
and, by Proposition 26,
$\kappa^z_{\Delta}(A) = \infty$
and, by Proposition 26,
![]() $\kappa(A) = \infty$
for every
$\kappa(A) = \infty$
for every
![]() $\kappa \in {Mod}\,^{ec}_{\Delta}$
. Therefore
$\kappa \in {Mod}\,^{ec}_{\Delta}$
. Therefore
![]() $A |\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
.
$A |\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
.
Case 2:
![]() $\kappa^z_{\Delta}(A B) \lt \infty$
and
$\kappa^z_{\Delta}(A B) \lt \infty$
and
![]() $\kappa^z_{\Delta}(A \overline{B}) = \infty$
$\kappa^z_{\Delta}(A \overline{B}) = \infty$
Then, by the definition of
![]() $\mathit{CMod}^{ec}_{\Delta}$
, we have
$\mathit{CMod}^{ec}_{\Delta}$
, we have
![]() $\kappa(A B) \lt \infty$
and, by Proposition 26,
$\kappa(A B) \lt \infty$
and, by Proposition 26,
![]() $\kappa(A\overline{B}) = \infty$
for every
$\kappa(A\overline{B}) = \infty$
for every
![]() $\kappa \in \mathit{CMod}^{ec}_{\Delta}$
. Therefore,
$\kappa \in \mathit{CMod}^{ec}_{\Delta}$
. Therefore,
![]() $\kappa(A B) \lt \kappa(A \overline{B})$
for every
$\kappa(A B) \lt \kappa(A \overline{B})$
for every
![]() $\kappa \in \mathit{CMod}^{ec}_{\Delta}$
and hence
$\kappa \in \mathit{CMod}^{ec}_{\Delta}$
and hence
![]() $A |\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
by Proposition 44.
$A |\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
by Proposition 44.
Case 3:
![]() $\kappa^z_{\Delta}(A \overline{B}) \lt \infty$
$\kappa^z_{\Delta}(A \overline{B}) \lt \infty$
Then, by assumption,
![]() ${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}} \cup {{\neg{{\mathit{CR}_{\Delta}{{(B|A)}}}}}}$
is unsolvable and
${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}} \cup {{\neg{{\mathit{CR}_{\Delta}{{(B|A)}}}}}}$
is unsolvable and
![]() $\kappa^z_{\Delta}(A B) \lt \infty$
. This implies that
$\kappa^z_{\Delta}(A B) \lt \infty$
. This implies that
![]() ${{\neg{{\mathit{CR}_{\Delta}{{(B|A)}}}}}}$
is false for every
${{\neg{{\mathit{CR}_{\Delta}{{(B|A)}}}}}}$
is false for every
![]() $\vec{\eta}^J \in {{\mathit{Sol}({{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}})}}$
. In this case, using the equivalence transformations in the part of the proof for Direction
$\vec{\eta}^J \in {{\mathit{Sol}({{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}})}}$
. In this case, using the equivalence transformations in the part of the proof for Direction
![]() $\Rightarrow$
, we have
$\Rightarrow$
, we have
![]() $\kappa_{\vec{\eta}}(AB) \lt \kappa_{\vec{\eta}}(A\overline{B})$
for every
$\kappa_{\vec{\eta}}(AB) \lt \kappa_{\vec{\eta}}(A\overline{B})$
for every
![]() $\vec{\eta} \in Sol^{J+\infty}_\Delta$
. With Proposition 48 it follows that
$\vec{\eta} \in Sol^{J+\infty}_\Delta$
. With Proposition 48 it follows that
![]() $A |\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
.
$A |\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
.
This realization of extended c-inference by a CSP yields a starting point for an implementation of extended c-inference as a SAT or SMT problem (Beierle et al., Reference Beierle, von Berg, Sanin, Keshtkar and Franklin2022; von Berg et al., Reference von Berg, Sanin, Beierle, Bouraoui, Jabbour and Vesic2023).
8. Syntax splitting
The concept of syntax splittings was originally developed by Parikh (Reference Parikh1999) describing that a belief set contains independent information over different parts of the signature. The notion of syntax splitting was later extended to other representations of beliefs (Kern-Isberner & Brewka, Reference Kern-Isberner and Brewka2017; Kern-Isberner et al., Reference Kern-Isberner, Beierle, Brewka, Calvanese, Erdem and Thielscher2020). In Kern-Isberner et al. (Reference Kern-Isberner, Beierle, Brewka, Calvanese, Erdem and Thielscher2020) not only inductive inference operators were introduced, but also the postulates (Rel), (Ind), (SynSplit) for inductive inference operators that govern inference from strongly consistent belief bases with syntax splitting. Notably, c-inference satisfies these postulates. In this section we show that also extended c-inference respects syntax splittings on belief bases.
Definition 52 (syntax splitting for belief bases, Kern-Isberner et al., Reference Kern-Isberner, Beierle, Brewka, Calvanese, Erdem and Thielscher2020). Let
![]() $\Delta$
be a belief base over
$\Delta$
be a belief base over
![]() $\Sigma$
. A partition
$\Sigma$
. A partition
![]() $\{\Sigma_1, \dots, \Sigma_n\}$
of
$\{\Sigma_1, \dots, \Sigma_n\}$
of
![]() $\Sigma$
is a syntax splitting for
$\Sigma$
is a syntax splitting for
![]() $\Delta$
if there is a partition
$\Delta$
if there is a partition
![]() $\{\Delta_1, \dots, \Delta_n\}$
of
$\{\Delta_1, \dots, \Delta_n\}$
of
![]() $\Delta$
s.t.
$\Delta$
s.t.
![]() $\Delta_i \subseteq {{{{(\mathcal{L}|\mathcal{L})}}_{\Sigma_i}}}$
for every
$\Delta_i \subseteq {{{{(\mathcal{L}|\mathcal{L})}}_{\Sigma_i}}}$
for every
![]() $i = 1, \dots, n$
.
$i = 1, \dots, n$
.
In this paper, we only consider syntax splittings with two parts. Such a splitting
![]() $\{\Sigma_1, \Sigma_2\}$
of
$\{\Sigma_1, \Sigma_2\}$
of
![]() $\Delta$
with corresponding partition
$\Delta$
with corresponding partition
![]() $\{\Delta_1, \Delta_2\}$
is denoted as (Kern-Isberner et al., Reference Kern-Isberner, Beierle, Brewka, Calvanese, Erdem and Thielscher2020)
$\{\Delta_1, \Delta_2\}$
is denoted as (Kern-Isberner et al., Reference Kern-Isberner, Beierle, Brewka, Calvanese, Erdem and Thielscher2020)
![]() $\Delta = \Delta_1 \bigcup\limits_{\Sigma_1, \Sigma_2} \Delta_2$
. Results for syntax splittings with more than two parts can be obtained by iteratively applying the postulates presented here.
$\Delta = \Delta_1 \bigcup\limits_{\Sigma_1, \Sigma_2} \Delta_2$
. Results for syntax splittings with more than two parts can be obtained by iteratively applying the postulates presented here.
Here, we present slightly adapted versions of the splitting postulates, (Rel
![]() $^{+}$
), (Ind
$^{+}$
), (Ind
![]() $^{+}$
), and (SynSplit
$^{+}$
), and (SynSplit
![]() $^{+}$
) (Kern-Isberner et al., Reference Kern-Isberner, Beierle, Brewka, Calvanese, Erdem and Thielscher2020; Haldimann et al., Reference Haldimann, Beierle, Kern-Isberner, Meyer, Chun and Franklin2023), that are intended for inference operators that are defined for all belief bases, including only weakly consistent belief bases.
$^{+}$
) (Kern-Isberner et al., Reference Kern-Isberner, Beierle, Brewka, Calvanese, Erdem and Thielscher2020; Haldimann et al., Reference Haldimann, Beierle, Kern-Isberner, Meyer, Chun and Franklin2023), that are intended for inference operators that are defined for all belief bases, including only weakly consistent belief bases.
For belief bases with syntax splitting, the postulate relevance (Rel
![]() $^{+}$
) requires that for an inference using only atoms from one part of the syntax splitting only conditionals from the corresponding part of the belief base are relevant.
$^{+}$
) requires that for an inference using only atoms from one part of the syntax splitting only conditionals from the corresponding part of the belief base are relevant.
(Rel
+
) An inductive inference operator
![]() $C\;:\; \Delta \mapsto \mathord{{|\hspace{-2pt}}{\sim}^{}_{\Delta}}$
satisfies (Rel
$C\;:\; \Delta \mapsto \mathord{{|\hspace{-2pt}}{\sim}^{}_{\Delta}}$
satisfies (Rel
![]() $^{+}$
) if for a weakly consistent
$^{+}$
) if for a weakly consistent
![]() $\Delta = \Delta_1 \bigcup\limits_{\Sigma_1, \Sigma_2} \Delta_2$
, for
$\Delta = \Delta_1 \bigcup\limits_{\Sigma_1, \Sigma_2} \Delta_2$
, for
![]() $i = 1, 2$
, and for
$i = 1, 2$
, and for
![]() $A, B \in {{\mathcal{L}_{\Sigma_i}}}$
we have
$A, B \in {{\mathcal{L}_{\Sigma_i}}}$
we have
The postulate independence (Ind
![]() $^{+}$
) requires that an inference using only atoms from one part of the syntax splitting should be drawn independently of additional beliefs about other parts of the splitting.
$^{+}$
) requires that an inference using only atoms from one part of the syntax splitting should be drawn independently of additional beliefs about other parts of the splitting.
(Ind
+
) An inductive inference operator
![]() $C\;:\; \Delta \mapsto \mathord{{|\hspace{-2pt}}{\sim}^{}_{\Delta}}$
satisfies (Ind
$C\;:\; \Delta \mapsto \mathord{{|\hspace{-2pt}}{\sim}^{}_{\Delta}}$
satisfies (Ind
![]() $^{+}$
) if for any weakly consistent
$^{+}$
) if for any weakly consistent
![]() $\Delta = \Delta_1 \bigcup\limits_{\Sigma_1, \Sigma_2} \Delta_2$
, and for
$\Delta = \Delta_1 \bigcup\limits_{\Sigma_1, \Sigma_2} \Delta_2$
, and for
![]() $i, j \in \{1, 2\}, i \neq j$
and for any
$i, j \in \{1, 2\}, i \neq j$
and for any
![]() $A, B \in {{\mathcal{L}_{\Sigma_i}}}$
,
$A, B \in {{\mathcal{L}_{\Sigma_i}}}$
,
![]() $D \in {{\mathcal{L}_{\Sigma_j}}}$
such that
$D \in {{\mathcal{L}_{\Sigma_j}}}$
such that
![]() $D \mathord{{|\hspace{-2pt}}{\sim}\!\!\!\!/\;\;}_{\Delta} \bot$
, we have
$D \mathord{{|\hspace{-2pt}}{\sim}\!\!\!\!/\;\;}_{\Delta} \bot$
, we have
The difference of these postulates to (Rel) and (Ind) is that also weakly consistent belief bases are considered. Additionally, in (Ind
![]() $^{+}$
) the requirement
$^{+}$
) the requirement
![]() $D \mathord{{|\hspace{-2pt}}{\sim}\!\!\!\!/\;\;}_{\Delta} \bot$
was added. Otherwise, the postulate would have some clearly unintended implications. For any formula
$D \mathord{{|\hspace{-2pt}}{\sim}\!\!\!\!/\;\;}_{\Delta} \bot$
was added. Otherwise, the postulate would have some clearly unintended implications. For any formula
![]() $A \in {{\mathcal{L}_{\Sigma_1}}}$
with (Ind) we would have
$A \in {{\mathcal{L}_{\Sigma_1}}}$
with (Ind) we would have
![]() $AD |\hspace{-2pt} {\sim}_{\Delta} \bot$
for any
$AD |\hspace{-2pt} {\sim}_{\Delta} \bot$
for any
![]() $D \in {{\mathcal{L}_{\Sigma_2}}}$
with
$D \in {{\mathcal{L}_{\Sigma_2}}}$
with
![]() $D |\hspace{-2pt} {\sim}_{\Delta} \bot$
. Then, (Ind) would imply that
$D |\hspace{-2pt} {\sim}_{\Delta} \bot$
. Then, (Ind) would imply that
![]() $A \mathord{{|\hspace{-2pt}}{\sim}\!\!\!\!/\;\;}_{\Delta} \bot$
. The condition
$A \mathord{{|\hspace{-2pt}}{\sim}\!\!\!\!/\;\;}_{\Delta} \bot$
. The condition
![]() $D \mathord{{|\hspace{-2pt}}{\sim}\!\!\!\!/\;\;}_{\Delta} \bot$
avoids this unintended consequence.
$D \mathord{{|\hspace{-2pt}}{\sim}\!\!\!\!/\;\;}_{\Delta} \bot$
avoids this unintended consequence.
(SynSplit
+
) An inductive inference operator
![]() $C\;:\; \Delta \mapsto \mathord{{|\hspace{-2pt}}{\sim}^{}_{\Delta}}$
satisfies (SynSplit
$C\;:\; \Delta \mapsto \mathord{{|\hspace{-2pt}}{\sim}^{}_{\Delta}}$
satisfies (SynSplit
![]() $^{+}$
) if it satisfies both (Rel
$^{+}$
) if it satisfies both (Rel
![]() $^{+}$
) and (Ind
$^{+}$
) and (Ind
![]() $^{+}$
).
$^{+}$
).
For our proof that extended c-inference complies with syntax splitting, we need some lemmas on the behaviour of c-representations in the context of a syntax splitting
![]() $\Delta = \Delta_1 \bigcup\limits_{\Sigma_1, \Sigma_2} \Delta_2$
. Differing from the proof that c-inference satisfies (SynSplit) in Kern-Isberner et al. (Reference Kern-Isberner, Beierle, Brewka, Calvanese, Erdem and Thielscher2020), in the following we argue about the sets of extended c-inferences
$\Delta = \Delta_1 \bigcup\limits_{\Sigma_1, \Sigma_2} \Delta_2$
. Differing from the proof that c-inference satisfies (SynSplit) in Kern-Isberner et al. (Reference Kern-Isberner, Beierle, Brewka, Calvanese, Erdem and Thielscher2020), in the following we argue about the sets of extended c-inferences
![]() ${{\mathit{Mod}^{ec}_{\Sigma}({\Delta})}}$
directly instead of the sets of solutions of the corresponding CSPs. This is mainly because the CSPs characterizing all extended c-representations are more involved than the CSPs for c-representations. First observe that the combination of any extended c-inference of
${{\mathit{Mod}^{ec}_{\Sigma}({\Delta})}}$
directly instead of the sets of solutions of the corresponding CSPs. This is mainly because the CSPs characterizing all extended c-representations are more involved than the CSPs for c-representations. First observe that the combination of any extended c-inference of
![]() $\Delta_1$
with an extended c-inference of
$\Delta_1$
with an extended c-inference of
![]() $\Delta_2$
is an extended c-inference of
$\Delta_2$
is an extended c-inference of
![]() $\Delta$
.
$\Delta$
.
Lemma 53. Let
![]() $\Delta = \Delta_1 \bigcup\limits_{\Sigma_1, \Sigma_2} \Delta_2$
be a weakly consistent belief base with syntax splitting. Let
$\Delta = \Delta_1 \bigcup\limits_{\Sigma_1, \Sigma_2} \Delta_2$
be a weakly consistent belief base with syntax splitting. Let
![]() $\kappa_1 \in {{\mathit{Mod}^{ec}_{\Sigma_1}({\Delta_1})}}$
and
$\kappa_1 \in {{\mathit{Mod}^{ec}_{\Sigma_1}({\Delta_1})}}$
and
![]() $\kappa_2 \in {{\mathit{Mod}^{ec}_{\Sigma_2}({\Delta_2})}}$
. Then
$\kappa_2 \in {{\mathit{Mod}^{ec}_{\Sigma_2}({\Delta_2})}}$
. Then
![]() $\kappa_{\oplus} = \kappa_1 \oplus \kappa_2$
is an extended c-representation of
$\kappa_{\oplus} = \kappa_1 \oplus \kappa_2$
is an extended c-representation of
![]() $\Delta$
, that is,
$\Delta$
, that is,
![]() $\kappa_{\oplus} \in {{\mathit{Mod}^{ec}_{\Sigma}({\Delta})}}$
.
$\kappa_{\oplus} \in {{\mathit{Mod}^{ec}_{\Sigma}({\Delta})}}$
.
Proof. Let
![]() ${{(B_1|A_1)}}, \dots, {{(B_k|A_k)}}$
be the conditionals in
${{(B_1|A_1)}}, \dots, {{(B_k|A_k)}}$
be the conditionals in
![]() $\Delta_1$
and let
$\Delta_1$
and let
![]() ${{(B_{k+1}|A_{k+1})}}, \dots, {{(B_n|A_n)}}$
be the conditionals in
${{(B_{k+1}|A_{k+1})}}, \dots, {{(B_n|A_n)}}$
be the conditionals in
![]() $\Delta_2$
. Let
$\Delta_2$
. Let
![]() $\vec{\eta}^1$
be an impact vector inducing
$\vec{\eta}^1$
be an impact vector inducing
![]() $\kappa_1$
and let
$\kappa_1$
and let
![]() $\vec{\eta}^2$
be an impact vector inducing
$\vec{\eta}^2$
be an impact vector inducing
![]() $\kappa_2$
. Let
$\kappa_2$
. Let
![]() $\omega$
be any world in
$\omega$
be any world in
![]() ${{\Omega_{\Sigma}}}$
. Because of the syntax splitting,
${{\Omega_{\Sigma}}}$
. Because of the syntax splitting,
![]() ${\omega}_{\mid {\Sigma_1}}$
falsifies the same worlds in
${\omega}_{\mid {\Sigma_1}}$
falsifies the same worlds in
![]() $\Delta_1$
as
$\Delta_1$
as
![]() $\omega$
and
$\omega$
and
![]() ${\omega}_{\mid {\Sigma_2}}$
falsifies the same worlds in
${\omega}_{\mid {\Sigma_2}}$
falsifies the same worlds in
![]() $\Delta_2$
as
$\Delta_2$
as
![]() $\omega$
. Let
$\omega$
. Let
![]() $\vec{\eta}$
be the impact vector for
$\vec{\eta}$
be the impact vector for
![]() $\Delta$
that combines the impacts from
$\Delta$
that combines the impacts from
![]() $\vec{\eta}^1$
and
$\vec{\eta}^1$
and
![]() $\vec{\eta}^2$
. We have that
$\vec{\eta}^2$
. We have that
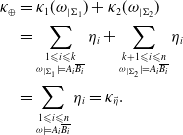 \begin{align} \begin{split} \kappa_{\oplus} &= \kappa_1({\omega}_{\mid {\Sigma_1}}) + \kappa_2({\omega}_{\mid {\Sigma_2}}) \\ &= \sum_{\substack{1 \leqslant i \leqslant k\\ {\omega}_{\mid {\Sigma_1}} \models A_i\overline{B_i}}} \eta_{i} + \sum_{\substack{k+1 \leqslant i \leqslant n\\{\omega}_{\mid {\Sigma_2}} \models A_i\overline{B_i}}} \eta_{i} \\ &= \sum_{\substack{1 \leqslant i \leqslant n\\ \omega \models A_i\overline{B_i}}} \eta_{i} = {{{\kappa_{\vec{\eta}}}}.} \end{split} \end{align}
\begin{align} \begin{split} \kappa_{\oplus} &= \kappa_1({\omega}_{\mid {\Sigma_1}}) + \kappa_2({\omega}_{\mid {\Sigma_2}}) \\ &= \sum_{\substack{1 \leqslant i \leqslant k\\ {\omega}_{\mid {\Sigma_1}} \models A_i\overline{B_i}}} \eta_{i} + \sum_{\substack{k+1 \leqslant i \leqslant n\\{\omega}_{\mid {\Sigma_2}} \models A_i\overline{B_i}}} \eta_{i} \\ &= \sum_{\substack{1 \leqslant i \leqslant n\\ \omega \models A_i\overline{B_i}}} \eta_{i} = {{{\kappa_{\vec{\eta}}}}.} \end{split} \end{align}
Additionally, because
![]() $\kappa_1 = {\kappa_{\oplus}}_{\mid {\Sigma_1}}$
and
$\kappa_1 = {\kappa_{\oplus}}_{\mid {\Sigma_1}}$
and
![]() $\kappa_2 = {\kappa_{\oplus}}_{\mid {\Sigma_2}}$
(see Lemma 4), Lemma 2 yields that
$\kappa_2 = {\kappa_{\oplus}}_{\mid {\Sigma_2}}$
(see Lemma 4), Lemma 2 yields that
![]() $\kappa_{\oplus}$
models the conditionals in
$\kappa_{\oplus}$
models the conditionals in
![]() $\Delta_1$
and in
$\Delta_1$
and in
![]() $\Delta_2$
. Therefore,
$\Delta_2$
. Therefore,
![]() $\kappa_{\oplus}$
is an extended c-representation of
$\kappa_{\oplus}$
is an extended c-representation of
![]() $\Delta$
.
$\Delta$
.
In the other direction, Lemma 54 shows how an extended c-representation of
![]() $\Delta$
splits for certain formulas.
$\Delta$
splits for certain formulas.
Lemma 54. Let
![]() $\Delta = \Delta_1 \bigcup\limits_{\Sigma_1, \Sigma_2} \Delta_2$
be a weakly consistent belief base with syntax splitting. Let
$\Delta = \Delta_1 \bigcup\limits_{\Sigma_1, \Sigma_2} \Delta_2$
be a weakly consistent belief base with syntax splitting. Let
![]() ${{\kappa_{\vec{\eta}}}} \in {{\mathit{Mod}^{ec}_{\Sigma}({\Delta})}}$
be an extended c-representation induced by impact vector
${{\kappa_{\vec{\eta}}}} \in {{\mathit{Mod}^{ec}_{\Sigma}({\Delta})}}$
be an extended c-representation induced by impact vector
![]() $\vec{\eta}$
. Let
$\vec{\eta}$
. Let
![]() $\vec{\eta}^1$
be the impact vector containing the impacts from
$\vec{\eta}^1$
be the impact vector containing the impacts from
![]() $\vec{\eta}$
for
$\vec{\eta}$
for
![]() $\Delta_1$
and let
$\Delta_1$
and let
![]() $\vec{\eta}^2$
be the impact vector containing the impacts from
$\vec{\eta}^2$
be the impact vector containing the impacts from
![]() $\vec{\eta}$
for
$\vec{\eta}$
for
![]() $\Delta_2$
. Then, for
$\Delta_2$
. Then, for
![]() $X \in {{\mathcal{L}_{\Sigma_1}}}, Y \in {{\mathcal{L}_{\Sigma_2}}}$
we have
$X \in {{\mathcal{L}_{\Sigma_1}}}, Y \in {{\mathcal{L}_{\Sigma_2}}}$
we have
![]() $\kappa(XY) = {{\kappa_{\vec{\eta}^1}}}(X) + {{\kappa_{\vec{\eta}^2}}}(Y)$
.
$\kappa(XY) = {{\kappa_{\vec{\eta}^1}}}(X) + {{\kappa_{\vec{\eta}^2}}}(Y)$
.
Proof. Let
![]() ${{(B_1|A_1)}}, \dots, {{(B_k|A_k)}}$
be the conditionals in
${{(B_1|A_1)}}, \dots, {{(B_k|A_k)}}$
be the conditionals in
![]() $\Delta_1$
and let
$\Delta_1$
and let
![]() ${{(B_{k+1}|A_{k+1})}}, \dots, {{(B_n|A_n)}}$
be the conditionals in
${{(B_{k+1}|A_{k+1})}}, \dots, {{(B_n|A_n)}}$
be the conditionals in
![]() $\Delta_2$
. For any
$\Delta_2$
. For any
![]() $\omega \in {{\Omega_{\Sigma}}}$
we have that
$\omega \in {{\Omega_{\Sigma}}}$
we have that
Because
![]() $X \in {{\mathcal{L}_{\Sigma_1}}}$
and
$X \in {{\mathcal{L}_{\Sigma_1}}}$
and
![]() $Y \in {{\mathcal{L}_{\Sigma_2}}}$
we have that
$Y \in {{\mathcal{L}_{\Sigma_2}}}$
we have that
![]() ${Mod}\,_{\Sigma}(XY) = \{(\omega^x \cdot \omega^y) \mid \omega^x \in {Mod}\,_{\Sigma_1}(X), \omega^y \in {Mod}\,_{\Sigma_2}(Y)\}$
. In summary, we have that
${Mod}\,_{\Sigma}(XY) = \{(\omega^x \cdot \omega^y) \mid \omega^x \in {Mod}\,_{\Sigma_1}(X), \omega^y \in {Mod}\,_{\Sigma_2}(Y)\}$
. In summary, we have that
 \begin{align*} \begin{split} \kappa(XY) &= \min \{\kappa(\omega) \mid \omega \in {Mod}\,_{\Sigma}(XY)\} \\ &= \min \{\kappa(\omega^x \cdot \omega^y) \mid \omega^x \in {Mod}\,_{\Sigma_1}(X), \omega^y \in {Mod}\,_{\Sigma_2}(Y)\} \\ &= \min \{{{\kappa_{\vec{\eta}^1}}}(\omega^x) + {{\kappa_{\vec{\eta}^2}}}(\omega^y) \mid \omega^x \in {Mod}\,_{\Sigma_1}(X), \omega^y \in {Mod}\,_{\Sigma_2}(Y)\} \\ &= \min \{{{\kappa_{\vec{\eta}^1}}}(\omega^x) \mid \omega^x \in {Mod}\,_{\Sigma_1}(X)\} + \min \{{{\kappa_{\vec{\eta}^2}}}(\omega^y) \mid \omega^y \in {Mod}\,_{\Sigma_2}(Y)\} \\ &= {{\kappa_{\vec{\eta}^1}}}(X) + {{\kappa_{\vec{\eta}^2}}}(Y). \end{split} \end{align*}
\begin{align*} \begin{split} \kappa(XY) &= \min \{\kappa(\omega) \mid \omega \in {Mod}\,_{\Sigma}(XY)\} \\ &= \min \{\kappa(\omega^x \cdot \omega^y) \mid \omega^x \in {Mod}\,_{\Sigma_1}(X), \omega^y \in {Mod}\,_{\Sigma_2}(Y)\} \\ &= \min \{{{\kappa_{\vec{\eta}^1}}}(\omega^x) + {{\kappa_{\vec{\eta}^2}}}(\omega^y) \mid \omega^x \in {Mod}\,_{\Sigma_1}(X), \omega^y \in {Mod}\,_{\Sigma_2}(Y)\} \\ &= \min \{{{\kappa_{\vec{\eta}^1}}}(\omega^x) \mid \omega^x \in {Mod}\,_{\Sigma_1}(X)\} + \min \{{{\kappa_{\vec{\eta}^2}}}(\omega^y) \mid \omega^y \in {Mod}\,_{\Sigma_2}(Y)\} \\ &= {{\kappa_{\vec{\eta}^1}}}(X) + {{\kappa_{\vec{\eta}^2}}}(Y). \end{split} \end{align*}
Lemma 55 states that marginalizing an extended c-representation of
![]() $\Delta$
to the subsignature
$\Delta$
to the subsignature
![]() $\Sigma_i$
,
$\Sigma_i$
,
![]() $i \in \{1, 2\}$
leads to an extended c-representation of
$i \in \{1, 2\}$
leads to an extended c-representation of
![]() $\Delta_i$
.
$\Delta_i$
.
Lemma 55. Let
![]() $\Delta = \Delta_1 \bigcup\limits_{\Sigma_1, \Sigma_2} \Delta_2$
be a weakly consistent belief base with syntax splitting. If
$\Delta = \Delta_1 \bigcup\limits_{\Sigma_1, \Sigma_2} \Delta_2$
be a weakly consistent belief base with syntax splitting. If
![]() $\kappa \in {{\mathit{Mod}^{ec}_{\Sigma}({\Delta})}}$
then
$\kappa \in {{\mathit{Mod}^{ec}_{\Sigma}({\Delta})}}$
then
![]() ${\kappa}_{|\Sigma_1} \in {{\mathit{Mod}^{ec}_{\Sigma_1}({\Delta_1})}}$
.
${\kappa}_{|\Sigma_1} \in {{\mathit{Mod}^{ec}_{\Sigma_1}({\Delta_1})}}$
.
Proof. Let
![]() $\kappa \in {{\mathit{Mod}^{ec}_{\Sigma}({\Delta})}}$
. By Lemma 2,
$\kappa \in {{\mathit{Mod}^{ec}_{\Sigma}({\Delta})}}$
. By Lemma 2,
![]() ${\kappa}_{|\Sigma_1}$
models the same conditionals in
${\kappa}_{|\Sigma_1}$
models the same conditionals in
![]() ${{{{(\mathcal{L}|\mathcal{L})}}_{\Sigma_1}}}$
as
${{{{(\mathcal{L}|\mathcal{L})}}_{\Sigma_1}}}$
as
![]() $\kappa$
. Especially,
$\kappa$
. Especially,
![]() ${\kappa}_{|\Sigma_1}$
models all conditionals in
${\kappa}_{|\Sigma_1}$
models all conditionals in
![]() $\Delta_1$
. It remains to be shown that
$\Delta_1$
. It remains to be shown that
![]() ${\kappa}_{|\Sigma_1}$
can be constructed from integer impacts.
${\kappa}_{|\Sigma_1}$
can be constructed from integer impacts.
For this let
![]() ${{(B_1|A_1)}}, \dots, {{(B_k|A_k)}}$
be the conditionals in
${{(B_1|A_1)}}, \dots, {{(B_k|A_k)}}$
be the conditionals in
![]() $\Delta_1$
and let
$\Delta_1$
and let
![]() ${{(B_{k+1}|A_{k+1})}}, \dots, {{(B_n|A_n)}}$
be the conditionals in
${{(B_{k+1}|A_{k+1})}}, \dots, {{(B_n|A_n)}}$
be the conditionals in
![]() $\Delta_2$
. Let
$\Delta_2$
. Let
![]() $\vec{\eta}$
be an impact vector inducing
$\vec{\eta}$
be an impact vector inducing
![]() $\kappa$
, and let
$\kappa$
, and let
![]() $\vec{\eta}^1$
be the impact vector containing the impacts from
$\vec{\eta}^1$
be the impact vector containing the impacts from
![]() $\vec{\eta}$
for
$\vec{\eta}$
for
![]() $\Delta_1$
. Let
$\Delta_1$
. Let
![]() $\omega^0 \in {{\Omega_{\Sigma}}}$
be a world that does not falsify any conditional in
$\omega^0 \in {{\Omega_{\Sigma}}}$
be a world that does not falsify any conditional in
![]() $\Delta$
(see Lemma 9). Let
$\Delta$
(see Lemma 9). Let
![]() $\omega'$
be any world in
$\omega'$
be any world in
![]() ${{\Omega_{\Sigma_1}}}$
. All worlds
${{\Omega_{\Sigma_1}}}$
. All worlds
![]() $\omega$
with
$\omega$
with
![]() ${\omega}_{\mid {\Sigma_1}} = \omega'$
falsify the same conditionals in
${\omega}_{\mid {\Sigma_1}} = \omega'$
falsify the same conditionals in
![]() $\Delta_1$
. The world
$\Delta_1$
. The world
![]() $\omega^* = (\omega' \cdot {\omega^0}_{\mid {\Sigma_2}})$
falsifies no conditional in
$\omega^* = (\omega' \cdot {\omega^0}_{\mid {\Sigma_2}})$
falsifies no conditional in
![]() $\Delta_2$
and is thus one of the worlds with the lowest rank in
$\Delta_2$
and is thus one of the worlds with the lowest rank in
![]() $\kappa$
that coincides with
$\kappa$
that coincides with
![]() $\omega'$
on
$\omega'$
on
![]() $\Sigma_1$
. We have that
$\Sigma_1$
. We have that
 \begin{align*} {\kappa}_{|\Sigma_1}(\omega') &= \min \{\kappa(\omega) \mid {\omega}_{\mid {\Sigma_1}} = \omega'\}\\ &= \min \{\sum_{\substack{1 \leqslant i \leqslant n\\\omega \models A_i\overline{B_i}}} \eta_{i} \mid {\omega}_{\mid {\Sigma_1}} = \omega'\} \\ &= \sum_{\substack{1 \leqslant i \leqslant n\\\omega^* \models A_i\overline{B_i}}} \eta_{i} = \sum_{\substack{1 \leqslant i \leqslant k\\\omega' \models A_i\overline{B_i}}} \eta_{i} = {{\kappa_{\vec{\eta}^1}}}(\omega'). \end{align*}
\begin{align*} {\kappa}_{|\Sigma_1}(\omega') &= \min \{\kappa(\omega) \mid {\omega}_{\mid {\Sigma_1}} = \omega'\}\\ &= \min \{\sum_{\substack{1 \leqslant i \leqslant n\\\omega \models A_i\overline{B_i}}} \eta_{i} \mid {\omega}_{\mid {\Sigma_1}} = \omega'\} \\ &= \sum_{\substack{1 \leqslant i \leqslant n\\\omega^* \models A_i\overline{B_i}}} \eta_{i} = \sum_{\substack{1 \leqslant i \leqslant k\\\omega' \models A_i\overline{B_i}}} \eta_{i} = {{\kappa_{\vec{\eta}^1}}}(\omega'). \end{align*}
Therefore,
![]() ${\kappa}_{|\Sigma_1}$
is an extended c-representation of
${\kappa}_{|\Sigma_1}$
is an extended c-representation of
![]() $\Delta_1$
.
$\Delta_1$
.
One of the key observations for proving that c-inference satisfies (SynSplit) in Kern-Isberner et al. (Reference Kern-Isberner, Beierle, Brewka, Calvanese, Erdem and Thielscher2020) is Kern-Isberner et al. (Reference Kern-Isberner, Beierle, Brewka, Calvanese, Erdem and Thielscher2020), Proposition 8. Given a belief base with syntax splitting
![]() $\Delta = \Delta_1 \bigcup\limits_{\Sigma_1, \Sigma_2} \Delta_2$
, this proposition states that the c-representations of
$\Delta = \Delta_1 \bigcup\limits_{\Sigma_1, \Sigma_2} \Delta_2$
, this proposition states that the c-representations of
![]() $\Delta$
are exactly the combinations of the c-representations of
$\Delta$
are exactly the combinations of the c-representations of
![]() $\Delta_1$
with the c-representations of
$\Delta_1$
with the c-representations of
![]() $\Delta_2$
. In combination, the Lemmas 53, 54, and 55 yield a corresponding observation for extended c-representations as expressed in the following lemma.
$\Delta_2$
. In combination, the Lemmas 53, 54, and 55 yield a corresponding observation for extended c-representations as expressed in the following lemma.
Lemma 56. Let
![]() $\Delta = \Delta_1 \bigcup\limits_{\Sigma_1, \Sigma_2} \Delta_2$
be a weakly consistent belief base with syntax splitting. Then
$\Delta = \Delta_1 \bigcup\limits_{\Sigma_1, \Sigma_2} \Delta_2$
be a weakly consistent belief base with syntax splitting. Then
![]() $\kappa \in {{\mathit{Mod}^{ec}_{\Sigma}({\Delta})}}$
iff there are
$\kappa \in {{\mathit{Mod}^{ec}_{\Sigma}({\Delta})}}$
iff there are
![]() $\kappa_1 \in {{\mathit{Mod}^{ec}_{\Sigma_1}({\Delta_1})}}$
and
$\kappa_1 \in {{\mathit{Mod}^{ec}_{\Sigma_1}({\Delta_1})}}$
and
![]() $\kappa_2 \in {{\mathit{Mod}^{ec}_{\Sigma_2}({\Delta_2})}}$
such that
$\kappa_2 \in {{\mathit{Mod}^{ec}_{\Sigma_2}({\Delta_2})}}$
such that
![]() $\kappa = \kappa_1 \oplus \kappa_2$
.
$\kappa = \kappa_1 \oplus \kappa_2$
.
Proof. Direction
![]() $\Leftarrow$
follows from Lemma 54. In the other direction
$\Leftarrow$
follows from Lemma 54. In the other direction
![]() $\Rightarrow$
, with Lemma 54 we can see that there are
$\Rightarrow$
, with Lemma 54 we can see that there are
![]() $\kappa_1\;:\; {{\Omega_{\Sigma_1}}} \rightarrow \mathbb{N} \cup \{\infty\}$
and
$\kappa_1\;:\; {{\Omega_{\Sigma_1}}} \rightarrow \mathbb{N} \cup \{\infty\}$
and
![]() $\kappa_1\;:\; {{\Omega_{\Sigma_1}}} \rightarrow \mathbb{N} \cup \{\infty\}$
such that
$\kappa_1\;:\; {{\Omega_{\Sigma_1}}} \rightarrow \mathbb{N} \cup \{\infty\}$
such that
![]() $\kappa = \kappa_1 \oplus \kappa_2$
. By Lemma 4 we have that
$\kappa = \kappa_1 \oplus \kappa_2$
. By Lemma 4 we have that
![]() $\kappa_i = {(\kappa_1 \oplus \kappa_2)}_{|\Sigma_i} = {\kappa}_{|\Sigma_i}$
for
$\kappa_i = {(\kappa_1 \oplus \kappa_2)}_{|\Sigma_i} = {\kappa}_{|\Sigma_i}$
for
![]() $i \in \{1, 2\}$
and therefore, with Lemma 55, that
$i \in \{1, 2\}$
and therefore, with Lemma 55, that
![]() $\kappa_1 \in {{\mathit{Mod}^{ec}_{\Sigma_1}({\Delta_1})}}$
and
$\kappa_1 \in {{\mathit{Mod}^{ec}_{\Sigma_1}({\Delta_1})}}$
and
![]() $\kappa_2 \in {{\mathit{Mod}^{ec}_{\Sigma_1}({\Delta_1})}}$
.
$\kappa_2 \in {{\mathit{Mod}^{ec}_{\Sigma_1}({\Delta_1})}}$
.
Extended c-inference does not change if unused atoms are added to or removed from the signature. This is captured by the following Lemma 57.
Lemma 57. Let
![]() $\Sigma$
be a signature,
$\Sigma$
be a signature,
![]() $\Sigma' \subseteq \Sigma$
, and
$\Sigma' \subseteq \Sigma$
, and
![]() $\Delta$
be a belief base over
$\Delta$
be a belief base over
![]() $\Sigma'$
. For
$\Sigma'$
. For
![]() $A, B \in {{\mathcal{L}_{\Sigma'}}}$
we have
$A, B \in {{\mathcal{L}_{\Sigma'}}}$
we have
![]() $A |\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
with respect to
$A |\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
with respect to
![]() $\Sigma$
iff
$\Sigma$
iff
![]() $A |\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
with respect to
$A |\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
with respect to
![]() $\Sigma'$
.
$\Sigma'$
.
Proof. Show both directions of the iff.
Direction
![]() $\Rightarrow$
: Let
$\Rightarrow$
: Let
![]() $A |\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
with respect to
$A |\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
with respect to
![]() $\Sigma$
. Let
$\Sigma$
. Let
![]() $\kappa' \in {{\mathit{Mod}^{ec}_{\Sigma'}({\Delta})}}$
. We can see
$\kappa' \in {{\mathit{Mod}^{ec}_{\Sigma'}({\Delta})}}$
. We can see
![]() $\Delta$
as a belief base with syntax splitting
$\Delta$
as a belief base with syntax splitting
![]() $\Delta = \Delta \bigcup\limits_{\Sigma', \Sigma\setminus\Sigma'} \emptyset$
. The only extended c-representation in
$\Delta = \Delta \bigcup\limits_{\Sigma', \Sigma\setminus\Sigma'} \emptyset$
. The only extended c-representation in
![]() ${{\mathit{Mod}^{ec}_{\Sigma\setminus\Sigma'}({\emptyset})}}$
is
${{\mathit{Mod}^{ec}_{\Sigma\setminus\Sigma'}({\emptyset})}}$
is
![]() $\kappa^0$
with
$\kappa^0$
with
![]() $\kappa^0(\omega) = 0$
for all
$\kappa^0(\omega) = 0$
for all
![]() $\omega \in {{\Omega_{\Sigma \setminus \Sigma'}}}$
. By Lemma 53,
$\omega \in {{\Omega_{\Sigma \setminus \Sigma'}}}$
. By Lemma 53,
![]() $\kappa_{\oplus} = \kappa' \oplus \kappa^0$
is in
$\kappa_{\oplus} = \kappa' \oplus \kappa^0$
is in
![]() ${{\mathit{Mod}^{ec}_{\Sigma}({\Delta})}}$
, and therefore
${{\mathit{Mod}^{ec}_{\Sigma}({\Delta})}}$
, and therefore
![]() $A |\hspace{-2pt} {\sim}_{\kappa_{\oplus}} B$
. By Lemma 5, this implies that
$A |\hspace{-2pt} {\sim}_{\kappa_{\oplus}} B$
. By Lemma 5, this implies that
![]() $A |\hspace{-2pt} {\sim}_{\kappa'} B$
because
$A |\hspace{-2pt} {\sim}_{\kappa'} B$
because
![]() $\kappa' = {\kappa_{\oplus}}_{|\Sigma'}$
(see Lemma 4). Hence, in summary we have that
$\kappa' = {\kappa_{\oplus}}_{|\Sigma'}$
(see Lemma 4). Hence, in summary we have that
![]() $A |\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
with respect to
$A |\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
with respect to
![]() $\Sigma'$
.
$\Sigma'$
.
Direction
![]() $\Leftarrow$
: Let
$\Leftarrow$
: Let
![]() $A |\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
with respect to
$A |\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
with respect to
![]() $\Sigma'$
. Let
$\Sigma'$
. Let
![]() $\kappa \in {{\mathit{Mod}^{ec}_{\Sigma}({\Delta})}}$
be an extended c-representation. Again, we can see
$\kappa \in {{\mathit{Mod}^{ec}_{\Sigma}({\Delta})}}$
be an extended c-representation. Again, we can see
![]() $\Delta$
as a belief base with syntax splitting
$\Delta$
as a belief base with syntax splitting
![]() $\Delta = \Delta \bigcup\limits_{\Sigma', \Sigma\setminus\Sigma'} \emptyset$
. By Lemma 55,
$\Delta = \Delta \bigcup\limits_{\Sigma', \Sigma\setminus\Sigma'} \emptyset$
. By Lemma 55,
![]() $\kappa' = {\kappa}_{|\Sigma'}$
is an extended c-representation in
$\kappa' = {\kappa}_{|\Sigma'}$
is an extended c-representation in
![]() ${{\mathit{Mod}^{ec}_{\Sigma'}({\Delta})}}$
, and therefore
${{\mathit{Mod}^{ec}_{\Sigma'}({\Delta})}}$
, and therefore
![]() $A |\hspace{-2pt} {\sim}_{\kappa'} B$
. Then Lemma 5 implies that
$A |\hspace{-2pt} {\sim}_{\kappa'} B$
. Then Lemma 5 implies that
![]() $A |\hspace{-2pt} {\sim}_{\kappa} B$
. Hence, in summary we have that
$A |\hspace{-2pt} {\sim}_{\kappa} B$
. Hence, in summary we have that
![]() $A |\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
with respect to
$A |\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
with respect to
![]() $\Sigma$
.
$\Sigma$
.
Using the lemmas above, we can now show that extended c-inference satisfies (Rel
![]() $^{+}$
). Observe that the proof for the next Proposition 58 does not need to deal explicitly with the case that a formula/world is infeasible (i.e., has rank
$^{+}$
). Observe that the proof for the next Proposition 58 does not need to deal explicitly with the case that a formula/world is infeasible (i.e., has rank
![]() $\infty$
). In this proof, all situations where a world or formula has rank
$\infty$
). In this proof, all situations where a world or formula has rank
![]() $\infty$
are already covered by the underlying definitions and results.
$\infty$
are already covered by the underlying definitions and results.
Proposition 58. Extended c-inference satisfies (Rel
![]() $^{+}$
).
$^{+}$
).
Proof. Let
![]() $\Delta = \Delta_1 \bigcup\limits_{\Sigma_1, \Sigma_2} \Delta_2$
be weakly consistent. W.l.o.g. let
$\Delta = \Delta_1 \bigcup\limits_{\Sigma_1, \Sigma_2} \Delta_2$
be weakly consistent. W.l.o.g. let
![]() $i=1$
and
$i=1$
and
![]() $A, B \in {{\mathcal{L}_{\Sigma_1}}}$
. We need to show that
$A, B \in {{\mathcal{L}_{\Sigma_1}}}$
. We need to show that
![]() $A |\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
iff
$A |\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
iff
![]() $A |\hspace{-2pt} {\sim}^{ec}_{\Delta_1} B$
.
$A |\hspace{-2pt} {\sim}^{ec}_{\Delta_1} B$
.
Direction
![]() $\Rightarrow$
: Assume that
$\Rightarrow$
: Assume that
![]() $A |\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
. Because of Lemma 57 it is sufficient to show that
$A |\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
. Because of Lemma 57 it is sufficient to show that
![]() $A |\hspace{-2pt} {\sim}^{ec}_{\Delta_1} B$
w.r.t.
$A |\hspace{-2pt} {\sim}^{ec}_{\Delta_1} B$
w.r.t.
![]() $\Sigma_1$
. Let
$\Sigma_1$
. Let
![]() $\kappa_1 \in {{\mathit{Mod}^{ec}_{\Sigma_1}({\Delta_1})}}$
be any extended c-representation of
$\kappa_1 \in {{\mathit{Mod}^{ec}_{\Sigma_1}({\Delta_1})}}$
be any extended c-representation of
![]() $\Delta_1$
. We need to show that
$\Delta_1$
. We need to show that
![]() $A |\hspace{-2pt} {\sim}_{\kappa_1} B$
.
$A |\hspace{-2pt} {\sim}_{\kappa_1} B$
.
Let
![]() $\kappa_2 \in {{\mathit{Mod}^{ec}_{\Sigma_2}({\Delta_2})}}$
and
$\kappa_2 \in {{\mathit{Mod}^{ec}_{\Sigma_2}({\Delta_2})}}$
and
![]() $\kappa_{\oplus} = \kappa_1 \oplus \kappa_2$
. By Lemma 53 we have
$\kappa_{\oplus} = \kappa_1 \oplus \kappa_2$
. By Lemma 53 we have
![]() $\kappa_{\oplus} \in {{\mathit{Mod}^{ec}_{\Sigma}({\Delta})}}$
. Therefore, by assumption we have
$\kappa_{\oplus} \in {{\mathit{Mod}^{ec}_{\Sigma}({\Delta})}}$
. Therefore, by assumption we have
![]() $A |\hspace{-2pt} {\sim}_{\kappa_{\oplus}} B$
. Because
$A |\hspace{-2pt} {\sim}_{\kappa_{\oplus}} B$
. Because
![]() $\kappa_1 = {\kappa_{\oplus}}_{|\Sigma_1}$
, with Lemma 5 we have that
$\kappa_1 = {\kappa_{\oplus}}_{|\Sigma_1}$
, with Lemma 5 we have that
![]() $A |\hspace{-2pt} {\sim}_{\kappa_1} B$
.
$A |\hspace{-2pt} {\sim}_{\kappa_1} B$
.
Direction
![]() $\Leftarrow$
: Assume that
$\Leftarrow$
: Assume that
![]() $A |\hspace{-2pt} {\sim}^{ec}_{\Delta_1} B$
(w.r.t.
$A |\hspace{-2pt} {\sim}^{ec}_{\Delta_1} B$
(w.r.t.
![]() $\Sigma$
). Let
$\Sigma$
). Let
![]() $\kappa \in {{\mathit{Mod}^{ec}_{\Sigma}({\Delta})}}$
be any extended c-representation of
$\kappa \in {{\mathit{Mod}^{ec}_{\Sigma}({\Delta})}}$
be any extended c-representation of
![]() $\Delta$
. We need to show that
$\Delta$
. We need to show that
![]() $A |\hspace{-2pt} {\sim}_{\kappa} B$
.
$A |\hspace{-2pt} {\sim}_{\kappa} B$
.
With Lemma 55 we have that
![]() $\kappa_1 = {\kappa}_{|\Sigma_1}$
is an extended c-representation of
$\kappa_1 = {\kappa}_{|\Sigma_1}$
is an extended c-representation of
![]() $\Delta_1$
. With Lemma 57 we have that
$\Delta_1$
. With Lemma 57 we have that
![]() $A |\hspace{-2pt} {\sim}^{ec}_{\Delta_1} B$
w.r.t.
$A |\hspace{-2pt} {\sim}^{ec}_{\Delta_1} B$
w.r.t.
![]() $\Sigma_1$
, and therefore
$\Sigma_1$
, and therefore
![]() $A |\hspace{-2pt} {\sim}_{\kappa_1} B$
. Using Lemma 5 we have that
$A |\hspace{-2pt} {\sim}_{\kappa_1} B$
. Using Lemma 5 we have that
![]() $A |\hspace{-2pt} {\sim}_{\kappa} B$
.
$A |\hspace{-2pt} {\sim}_{\kappa} B$
.
For proving (Ind
![]() $^{+}$
), in contrast to proving (Rel
$^{+}$
), in contrast to proving (Rel
![]() $^{+}$
) in Proposition 58, we have to distinguish explicitly between the case that an entailment holds because its antecedent is infeasible and the case that an entailment holds because its verification has a lower rank than its falsification.
$^{+}$
) in Proposition 58, we have to distinguish explicitly between the case that an entailment holds because its antecedent is infeasible and the case that an entailment holds because its verification has a lower rank than its falsification.
Proposition 59. Extended c-inference satisfies (Ind
![]() $^{+}$
).
$^{+}$
).
Proof. Let
![]() $\Delta = \Delta_1 \bigcup\limits_{\Sigma_1, \Sigma_2} \Delta_2$
be weakly consistent. W.l.o.g. let
$\Delta = \Delta_1 \bigcup\limits_{\Sigma_1, \Sigma_2} \Delta_2$
be weakly consistent. W.l.o.g. let
![]() $i=1, j=2$
and
$i=1, j=2$
and
![]() $A, B \in {{\mathcal{L}_{\Sigma_1}}}, D \in {{\mathcal{L}_{\Sigma_2}}}$
such that
$A, B \in {{\mathcal{L}_{\Sigma_1}}}, D \in {{\mathcal{L}_{\Sigma_2}}}$
such that
![]() $D \mathord{{|\hspace{-2pt}}{\sim}\!\!\!\!/\;\;}^{ec}_{\Delta} \bot$
. We need to show that
$D \mathord{{|\hspace{-2pt}}{\sim}\!\!\!\!/\;\;}^{ec}_{\Delta} \bot$
. We need to show that
![]() $A |\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
iff
$A |\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
iff
![]() $AD |\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
.
$AD |\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
.
Direction
![]() $\Rightarrow$
: Assume
$\Rightarrow$
: Assume
![]() $A |\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
. We show
$A |\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
. We show
![]() $AD |\hspace{-2pt} {\sim}_{\kappa} B$
for every
$AD |\hspace{-2pt} {\sim}_{\kappa} B$
for every
![]() $\kappa \in {{\mathit{Mod}^{ec}_{\Sigma}({\Delta})}}$
.
$\kappa \in {{\mathit{Mod}^{ec}_{\Sigma}({\Delta})}}$
.
Let
![]() $\kappa \in {{\mathit{Mod}^{ec}_{\Sigma}({\Delta})}}$
be any extended c-representation of
$\kappa \in {{\mathit{Mod}^{ec}_{\Sigma}({\Delta})}}$
be any extended c-representation of
![]() $\Delta$
. Because
$\Delta$
. Because
![]() $A |\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
we have that
$A |\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
we have that
![]() $A |\hspace{-2pt} {\sim}_{\kappa} B$
. Let
$A |\hspace{-2pt} {\sim}_{\kappa} B$
. Let
![]() $\vec{\eta}$
be the impact vector inducing
$\vec{\eta}$
be the impact vector inducing
![]() $\kappa$
, that is,
$\kappa$
, that is,
![]() $\kappa = {{\kappa_{\vec{\eta}}}}$
. Because
$\kappa = {{\kappa_{\vec{\eta}}}}$
. Because
![]() $\Delta = \Delta_1 \cup \Delta_2$
, we can sort the impacts in
$\Delta = \Delta_1 \cup \Delta_2$
, we can sort the impacts in
![]() $\vec{\eta}$
into an impact vector
$\vec{\eta}$
into an impact vector
![]() $\vec{\eta}^1$
for
$\vec{\eta}^1$
for
![]() $\Delta_1$
and an impact vector
$\Delta_1$
and an impact vector
![]() $\vec{\eta}^2$
for
$\vec{\eta}^2$
for
![]() $\Delta_2$
. We can distinguish three cases.
$\Delta_2$
. We can distinguish three cases.
Case 1:
![]() ${{\kappa_{\vec{\eta}}}}(A) = \infty$
Applying Lemma 54, we have
${{\kappa_{\vec{\eta}}}}(A) = \infty$
Applying Lemma 54, we have
![]() ${{\kappa_{\vec{\eta}}}}(A) = {{\kappa_{\vec{\eta}}}}(A \wedge \top) = {{\kappa_{\vec{\eta}^1}}}(A) + {{\kappa_{\vec{\eta}^2}}}(\top)$
. Because
${{\kappa_{\vec{\eta}}}}(A) = {{\kappa_{\vec{\eta}}}}(A \wedge \top) = {{\kappa_{\vec{\eta}^1}}}(A) + {{\kappa_{\vec{\eta}^2}}}(\top)$
. Because
![]() $\Delta$
is weakly consistent, there is at least one world
$\Delta$
is weakly consistent, there is at least one world
![]() $\omega$
that does not falsify a conditional in
$\omega$
that does not falsify a conditional in
![]() $\Delta$
. Therefore, we have
$\Delta$
. Therefore, we have
![]() ${{\kappa_{\vec{\eta}^2}}}(\top) = 0$
. Hence,
${{\kappa_{\vec{\eta}^2}}}(\top) = 0$
. Hence,
![]() ${{\kappa_{\vec{\eta}^1}}}(A) = \infty$
. This implies
${{\kappa_{\vec{\eta}^1}}}(A) = \infty$
. This implies
![]() ${{\kappa_{\vec{\eta}}}}(AD) = {{\kappa_{\vec{\eta}^1}}}(A) + {{\kappa_{\vec{\eta}^2}}}(D) = \infty + {{\kappa_{\vec{\eta}^2}}}(D) = \infty$
. Thus,
${{\kappa_{\vec{\eta}}}}(AD) = {{\kappa_{\vec{\eta}^1}}}(A) + {{\kappa_{\vec{\eta}^2}}}(D) = \infty + {{\kappa_{\vec{\eta}^2}}}(D) = \infty$
. Thus,
![]() $AD |\hspace{-2pt} {\sim}_{\kappa} B$
.
$AD |\hspace{-2pt} {\sim}_{\kappa} B$
.
Case 2:
![]() ${{\kappa_{\vec{\eta}}}}(A) \lt \infty$
and
${{\kappa_{\vec{\eta}}}}(A) \lt \infty$
and
![]() ${{\kappa_{\vec{\eta}}}}(D) = \infty$
With a similar argumentation as in Case 1, we have
${{\kappa_{\vec{\eta}}}}(D) = \infty$
With a similar argumentation as in Case 1, we have
![]() ${{\kappa_{\vec{\eta}^2}}}(D) = \infty$
. This implies
${{\kappa_{\vec{\eta}^2}}}(D) = \infty$
. This implies
![]() ${{\kappa_{\vec{\eta}}}}(AD) = {{\kappa_{\vec{\eta}^1}}}(A) + {{\kappa_{\vec{\eta}^2}}}(D) = {{\kappa_{\vec{\eta}^1}}}(A) + \infty = \infty$
. Thus,
${{\kappa_{\vec{\eta}}}}(AD) = {{\kappa_{\vec{\eta}^1}}}(A) + {{\kappa_{\vec{\eta}^2}}}(D) = {{\kappa_{\vec{\eta}^1}}}(A) + \infty = \infty$
. Thus,
![]() $AD |\hspace{-2pt} {\sim}_{{{\kappa_{\vec{\eta}}}}} B$
.
$AD |\hspace{-2pt} {\sim}_{{{\kappa_{\vec{\eta}}}}} B$
.
Case 3:
![]() ${{\kappa_{\vec{\eta}}}}(A) \lt \infty$
and
${{\kappa_{\vec{\eta}}}}(A) \lt \infty$
and
![]() ${{\kappa_{\vec{\eta}}}}(D) \lt \infty$
Because
${{\kappa_{\vec{\eta}}}}(D) \lt \infty$
Because
![]() $A |\hspace{-2pt} {\sim}_{{{\kappa_{\vec{\eta}}}}} B$
in this case it is necessary that
$A |\hspace{-2pt} {\sim}_{{{\kappa_{\vec{\eta}}}}} B$
in this case it is necessary that
![]() ${{\kappa_{\vec{\eta}}}}(AB) \lt {{\kappa_{\vec{\eta}}}}(A\overline{B})$
.
${{\kappa_{\vec{\eta}}}}(AB) \lt {{\kappa_{\vec{\eta}}}}(A\overline{B})$
.
Applying Lemma 54, we have
![]() ${{\kappa_{\vec{\eta}}}}(AB) = {{\kappa_{\vec{\eta}}}}(AB \wedge \top) = {{\kappa_{\vec{\eta}^1}}}(AB) + {{\kappa_{\vec{\eta}^2}}}(\top)$
. Because
${{\kappa_{\vec{\eta}}}}(AB) = {{\kappa_{\vec{\eta}}}}(AB \wedge \top) = {{\kappa_{\vec{\eta}^1}}}(AB) + {{\kappa_{\vec{\eta}^2}}}(\top)$
. Because
![]() $\Delta$
is weakly consistent, with Lemma 9 there is at least one world
$\Delta$
is weakly consistent, with Lemma 9 there is at least one world
![]() $\omega$
that does not falsify a conditional in
$\omega$
that does not falsify a conditional in
![]() $\Delta$
. Therefore, we have
$\Delta$
. Therefore, we have
![]() ${{\kappa_{\vec{\eta}^2}}}(\top) = 0$
. Hence,
${{\kappa_{\vec{\eta}^2}}}(\top) = 0$
. Hence,
![]() ${{\kappa_{\vec{\eta}^1}}}(AB) = {{\kappa_{\vec{\eta}}}}(AB)$
. Analogously,
${{\kappa_{\vec{\eta}^1}}}(AB) = {{\kappa_{\vec{\eta}}}}(AB)$
. Analogously,
![]() ${{\kappa_{\vec{\eta}^1}}}(A\overline{B}) = {{\kappa_{\vec{\eta}}}}(A\overline{B})$
and
${{\kappa_{\vec{\eta}^1}}}(A\overline{B}) = {{\kappa_{\vec{\eta}}}}(A\overline{B})$
and
![]() ${{\kappa_{\vec{\eta}^2}}}(D) = {{\kappa_{\vec{\eta}}}}(D) \lt \infty$
. Therefore,
${{\kappa_{\vec{\eta}^2}}}(D) = {{\kappa_{\vec{\eta}}}}(D) \lt \infty$
. Therefore,
![]() ${{\kappa_{\vec{\eta}^1}}}(AB) \lt {{\kappa_{\vec{\eta}^1}}}(A\overline{B})$
. Lemma 54 also yields
${{\kappa_{\vec{\eta}^1}}}(AB) \lt {{\kappa_{\vec{\eta}^1}}}(A\overline{B})$
. Lemma 54 also yields
![]() ${{\kappa_{\vec{\eta}}}}(ABD) = {{\kappa_{\vec{\eta}^1}}}(AB) + {{\kappa_{\vec{\eta}^2}}}(D)$
and
${{\kappa_{\vec{\eta}}}}(ABD) = {{\kappa_{\vec{\eta}^1}}}(AB) + {{\kappa_{\vec{\eta}^2}}}(D)$
and
![]() ${{\kappa_{\vec{\eta}}}}(A\overline{B}D) = {{\kappa_{\vec{\eta}^1}}}(A\overline{B}) + {{\kappa_{\vec{\eta}^2}}}(D)$
. Together, we have that
${{\kappa_{\vec{\eta}}}}(A\overline{B}D) = {{\kappa_{\vec{\eta}^1}}}(A\overline{B}) + {{\kappa_{\vec{\eta}^2}}}(D)$
. Together, we have that
![]() ${{\kappa_{\vec{\eta}}}}(ABD) = {{\kappa_{\vec{\eta}^1}}}(AB) + {{\kappa_{\vec{\eta}^2}}}(D) \lt {{\kappa_{\vec{\eta}^1}}}(A\overline{B}) + {{\kappa_{\vec{\eta}^2}}}(D) = {{\kappa_{\vec{\eta}}}}(A\overline{B}D)$
and thus
${{\kappa_{\vec{\eta}}}}(ABD) = {{\kappa_{\vec{\eta}^1}}}(AB) + {{\kappa_{\vec{\eta}^2}}}(D) \lt {{\kappa_{\vec{\eta}^1}}}(A\overline{B}) + {{\kappa_{\vec{\eta}^2}}}(D) = {{\kappa_{\vec{\eta}}}}(A\overline{B}D)$
and thus
![]() $AD |\hspace{-2pt} {\sim}_{{{\kappa_{\vec{\eta}}}}} B$
.
$AD |\hspace{-2pt} {\sim}_{{{\kappa_{\vec{\eta}}}}} B$
.
Direction
![]() $\Leftarrow$
: Assume
$\Leftarrow$
: Assume
![]() $AD |\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
. We show
$AD |\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
. We show
![]() $A |\hspace{-2pt} {\sim}_{\kappa} B$
for every
$A |\hspace{-2pt} {\sim}_{\kappa} B$
for every
![]() $\kappa \in {{\mathit{Mod}^{ec}_{\Sigma}({\Delta})}}$
.
$\kappa \in {{\mathit{Mod}^{ec}_{\Sigma}({\Delta})}}$
.
Let
![]() $\kappa \in {{\mathit{Mod}^{ec}_{\Sigma}({\Delta})}}$
be any extended c-representation of
$\kappa \in {{\mathit{Mod}^{ec}_{\Sigma}({\Delta})}}$
be any extended c-representation of
![]() $\Delta$
. Because
$\Delta$
. Because
![]() $AD \mathord{{|\hspace{-2pt}}{\sim}\!\!\!\!/\;\;}^{ec}_{\Delta} B$
we have
$AD \mathord{{|\hspace{-2pt}}{\sim}\!\!\!\!/\;\;}^{ec}_{\Delta} B$
we have
![]() $AD |\hspace{-2pt} {\sim}_{\kappa} B$
. Because
$AD |\hspace{-2pt} {\sim}_{\kappa} B$
. Because
![]() $D \mathord{{|\hspace{-2pt}}{\sim}\!\!\!\!/\;\;}^{ec}_{\Delta} \bot$
, there is a
$D \mathord{{|\hspace{-2pt}}{\sim}\!\!\!\!/\;\;}^{ec}_{\Delta} \bot$
, there is a
![]() $\kappa' \in {{\mathit{Mod}^{ec}_{\Sigma}({\Delta})}}$
such that
$\kappa' \in {{\mathit{Mod}^{ec}_{\Sigma}({\Delta})}}$
such that
![]() $D \mathord{{|\hspace{-2pt}}{\sim}\!\!\!\!/\;\;}_{\kappa'} \bot$
which implies
$D \mathord{{|\hspace{-2pt}}{\sim}\!\!\!\!/\;\;}_{\kappa'} \bot$
which implies
![]() $\kappa'(D) \lt \infty$
. Using Lemma 55 we have
$\kappa'(D) \lt \infty$
. Using Lemma 55 we have
![]() ${\kappa'}_{|\Sigma_2} \in {{\mathit{Mod}^{ec}_{\Sigma_2}({\Delta_2})}}$
. With Lemma 1 we have
${\kappa'}_{|\Sigma_2} \in {{\mathit{Mod}^{ec}_{\Sigma_2}({\Delta_2})}}$
. With Lemma 1 we have
![]() ${\kappa'}_{|\Sigma_2}(D) = \kappa'(D)$
. Analogously, we have
${\kappa'}_{|\Sigma_2}(D) = \kappa'(D)$
. Analogously, we have
![]() ${\kappa}_{|\Sigma_1} \in {{\mathit{Mod}^{ec}_{\Sigma_1}({\Delta_1})}}$
and
${\kappa}_{|\Sigma_1} \in {{\mathit{Mod}^{ec}_{\Sigma_1}({\Delta_1})}}$
and
![]() ${\kappa}_{|\Sigma_1}(A) = \kappa(A)$
and
${\kappa}_{|\Sigma_1}(A) = \kappa(A)$
and
![]() ${\kappa}_{|\Sigma_1}(AB) = \kappa(AB)$
and
${\kappa}_{|\Sigma_1}(AB) = \kappa(AB)$
and
![]() ${\kappa}_{|\Sigma_1}(A\overline{B}) = \kappa(A\overline{B})$
. Let
${\kappa}_{|\Sigma_1}(A\overline{B}) = \kappa(A\overline{B})$
. Let
![]() $\kappa_{\oplus} = {\kappa}_{|\Sigma_1} \oplus {\kappa'}_{|\Sigma_2}$
. With Lemma 53 we have
$\kappa_{\oplus} = {\kappa}_{|\Sigma_1} \oplus {\kappa'}_{|\Sigma_2}$
. With Lemma 53 we have
![]() $\kappa_{\oplus} \in {{\mathit{Mod}^{ec}_{\Sigma}({\Delta})}}$
. Because
$\kappa_{\oplus} \in {{\mathit{Mod}^{ec}_{\Sigma}({\Delta})}}$
. Because
![]() $AD |\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
this entails that
$AD |\hspace{-2pt} {\sim}^{ec}_{\Delta} B$
this entails that
![]() $AD |\hspace{-2pt} {\sim}_{\kappa_{\oplus}} B$
. We can distinguish two cases.
$AD |\hspace{-2pt} {\sim}_{\kappa_{\oplus}} B$
. We can distinguish two cases.
Case 1:
![]() $\kappa_{\oplus}(AD) = \infty$
Because of Lemma 3 we have
$\kappa_{\oplus}(AD) = \infty$
Because of Lemma 3 we have
![]() $\kappa_\oplus(AD) = {\kappa}_{|\Sigma_1}(A) + {\kappa'}_{|\Sigma_2}(D)$
, and with
$\kappa_\oplus(AD) = {\kappa}_{|\Sigma_1}(A) + {\kappa'}_{|\Sigma_2}(D)$
, and with
![]() ${\kappa'}_{|\Sigma_2}(D) = \kappa'(D) \lt \infty$
we have
${\kappa'}_{|\Sigma_2}(D) = \kappa'(D) \lt \infty$
we have
![]() ${\kappa}_{|\Sigma_1}(A) = \infty$
. Therefore,
${\kappa}_{|\Sigma_1}(A) = \infty$
. Therefore,
![]() $\kappa(A) = {\kappa}_{|\Sigma_1}(A) = \infty$
and thus
$\kappa(A) = {\kappa}_{|\Sigma_1}(A) = \infty$
and thus
![]() $A |\hspace{-2pt} {\sim}_{\kappa} B$
.
$A |\hspace{-2pt} {\sim}_{\kappa} B$
.
Case 2:
![]() $\kappa_{\oplus}(AD) \lt \infty$
Because
$\kappa_{\oplus}(AD) \lt \infty$
Because
![]() $AD |\hspace{-2pt} {\sim}_{\kappa_{\oplus}} B$
we have
$AD |\hspace{-2pt} {\sim}_{\kappa_{\oplus}} B$
we have
![]() $\kappa_{\oplus}(ABD) \lt \kappa_{\oplus}(A\overline{B}D)$
. With Lemma 3 we have
$\kappa_{\oplus}(ABD) \lt \kappa_{\oplus}(A\overline{B}D)$
. With Lemma 3 we have
![]() $\kappa_\oplus(ABD) = {\kappa}_{|\Sigma_1}(AB) + {\kappa'}_{|\Sigma_2}(D)$
and
$\kappa_\oplus(ABD) = {\kappa}_{|\Sigma_1}(AB) + {\kappa'}_{|\Sigma_2}(D)$
and
![]() $\kappa_\oplus(A\overline{B}D) = {\kappa}_{|\Sigma_1}(A\overline{B}) + {\kappa'}_{|\Sigma_2}(D)$
. This implies that
$\kappa_\oplus(A\overline{B}D) = {\kappa}_{|\Sigma_1}(A\overline{B}) + {\kappa'}_{|\Sigma_2}(D)$
. This implies that
![]() ${\kappa}_{|\Sigma_1}(AB) + {\kappa'}_{|\Sigma_2}(D) \lt {\kappa}_{|\Sigma_1}(A\overline{B}) + {\kappa'}_{|\Sigma_2}(D)$
and therefore that
${\kappa}_{|\Sigma_1}(AB) + {\kappa'}_{|\Sigma_2}(D) \lt {\kappa}_{|\Sigma_1}(A\overline{B}) + {\kappa'}_{|\Sigma_2}(D)$
and therefore that
![]() $\kappa(AB) \lt \kappa(A\overline{B})$
. Thus,
$\kappa(AB) \lt \kappa(A\overline{B})$
. Thus,
![]() $A |\hspace{-2pt} {\sim}_{\kappa} B$
.
$A |\hspace{-2pt} {\sim}_{\kappa} B$
.
Note that for Direction
![]() $\Leftarrow$
of the proof of Proposition 59 for showing that
$\Leftarrow$
of the proof of Proposition 59 for showing that
![]() $A |\hspace{-2pt} {\sim}_{\kappa} B$
we had to pay special attention to the case where
$A |\hspace{-2pt} {\sim}_{\kappa} B$
we had to pay special attention to the case where
![]() $\kappa(D) = \infty$
even though
$\kappa(D) = \infty$
even though
![]() $D \mathord{{|\hspace{-2pt}}{\sim}\!\!\!\!/\;\;}^{ec}_{\Delta} \bot$
. Therefore, in the proof we employ the extended c-representation
$D \mathord{{|\hspace{-2pt}}{\sim}\!\!\!\!/\;\;}^{ec}_{\Delta} \bot$
. Therefore, in the proof we employ the extended c-representation
![]() $\kappa_{\oplus}$
derived from
$\kappa_{\oplus}$
derived from
![]() $\kappa$
that satisfies
$\kappa$
that satisfies
![]() $\kappa_{\oplus}(D) \lt \infty$
and is used to show that
$\kappa_{\oplus}(D) \lt \infty$
and is used to show that
![]() $A |\hspace{-2pt} {\sim}_{\kappa} B$
.
$A |\hspace{-2pt} {\sim}_{\kappa} B$
.
Combining Propositions 58 and 59 yields that extended c-inference satisfies (SynSplit
![]() $^{+}$
):
$^{+}$
):
Proposition 60. Extended c-inference satisfies (SynSplit
![]() $^{+}$
).
$^{+}$
).
While p-entailment and system Z already do not satisfy syntax splitting for strongly consistent belief bases (Kern-Isberner et al., Reference Kern-Isberner, Beierle, Brewka, Calvanese, Erdem and Thielscher2020), the results above make c-inference the only other inductive inference operator besides system W (Komo & Beierle, Reference Komo, Beierle, Schmid, Klügl and Wolter2020, Reference Komo and Beierle2022; Haldimann et al., Reference Haldimann, Beierle, Kern-Isberner, Meyer, Chun and Franklin2023) that has been shown to fully comply with syntax splitting for weakly consistent belief bases.
9. Extended credulous and weakly skeptical c-inference
In the previous sections, we considered skeptical reasoning about the (extended) c-representations of a belief base, that is, the inference operator licenses entailments that hold in all considered ranking functions. In Beierle et al. (Reference Beierle, Eichhorn, Kern-Isberner, Kutsch, Kaminka, Fox, Bouquet, Hüllermeier, Dignum, Dignum and van Harmelen2016b) two other modes of reasoning are investigated: credulous and weakly skeptical reasoning. Instantiated for c-representations, these reasoning modes yield the inference operators credulous c-inference and weakly skeptical c-inference.
Definition 61 (credulous/weakly skeptical c-inference, Beierle et al., Reference Beierle, Eichhorn, Kern-Isberner and Kutsch2021). Let
![]() $\Delta$
be a strongly consistent belief base and let A, B be formulas.
$\Delta$
be a strongly consistent belief base and let A, B be formulas.
-
• B is a credulous c-inference from A in the context of
 $\Delta$
, denoted by
$\Delta$
, denoted by
 $A|\hspace{-2pt} {\sim}^{cr}_{\Delta} B$
, iff there is a c-representation
$A|\hspace{-2pt} {\sim}^{cr}_{\Delta} B$
, iff there is a c-representation
 $\kappa$
of
$\kappa$
of
 $\Delta$
with
$\Delta$
with
 $A|\hspace{-2pt} {\sim}_{\kappa} B$
.
$A|\hspace{-2pt} {\sim}_{\kappa} B$
. -
• B is a weakly skeptical c-inference from A in the context of
 $\Delta$
, denoted by
$\Delta$
, denoted by
 $A|\hspace{-2pt} {\sim}^{ws}_{\Delta} B$
, iff
$A|\hspace{-2pt} {\sim}^{ws}_{\Delta} B$
, iff
 $A \equiv \bot$
or there is a c-representation
$A \equiv \bot$
or there is a c-representation
 $\kappa$
of
$\kappa$
of
 $\Delta$
with
$\Delta$
with
 $A|\hspace{-2pt} {\sim}_{\kappa} B$
and there is no c-representation
$A|\hspace{-2pt} {\sim}_{\kappa} B$
and there is no c-representation
 $\kappa'$
of
$\kappa'$
of
 $\Delta$
with
$\Delta$
with
 $A|\hspace{-2pt} {\sim}_{\kappa'} \overline{B}$
.
$A|\hspace{-2pt} {\sim}_{\kappa'} \overline{B}$
.
In the following we will explore how these two inference operators can be extended to belief bases that are not strongly consistent by using extended c-representations.
9.1. Extended credulous c-inference
A straightforward way of adapting credulous c-inference to using extended c-representations is to define it as credulous inference over all extended c-representations.
Definition 62 (extended credulous c-inference). Let
![]() $\Delta$
be a belief base and let A, B be formulas. B is an extended credulous c-inference from A in the context of
$\Delta$
be a belief base and let A, B be formulas. B is an extended credulous c-inference from A in the context of
![]() $\Delta$
, denoted by
$\Delta$
, denoted by
![]() $A|\hspace{-2pt} {\sim}^{ecr}_{\Delta} B$
, iff (i)
$A|\hspace{-2pt} {\sim}^{ecr}_{\Delta} B$
, iff (i)
![]() $\Delta$
is not weakly consistent or (ii) there is an extended c-representation
$\Delta$
is not weakly consistent or (ii) there is an extended c-representation
![]() $\kappa$
of
$\kappa$
of
![]() $\Delta$
with
$\Delta$
with
![]() $A|\hspace{-2pt} {\sim}_{\kappa} B$
.
$A|\hspace{-2pt} {\sim}_{\kappa} B$
.
Lemma 63. Extended credulous c-inference is an inductive inference operator, that is, it satisfies (DI) and (TV).
Proof. For belief bases that are not weakly consistent (DI) holds trivially. For weakly consistent belief bases the proof is analogous to the proof of Proposition 33.
In comparison to credulous c-inference, extended credulous c-inference is even bolder in the sense that it is based additionally on extended c-representations. This leads to the somewhat unexpected observation that extended credulous c-inference coincides with classical deduction with respect to the material counterparts
![]() $A \rightarrow B$
of the conditionals
$A \rightarrow B$
of the conditionals
![]() ${{(B|A)}} \in \Delta$
.
${{(B|A)}} \in \Delta$
.
Proposition 64. Let
![]() $\Delta$
be a belief base and A, B be formulas. Let
$\Delta$
be a belief base and A, B be formulas. Let
![]() $\widetilde{\Delta} = \{ A_i \rightarrow B_i \mid {{(B_i|A_i)}} \in \Delta$
be the material counterpart of
$\widetilde{\Delta} = \{ A_i \rightarrow B_i \mid {{(B_i|A_i)}} \in \Delta$
be the material counterpart of
![]() $\Delta$
. Then
$\Delta$
. Then
Proof. For belief bases
![]() $\Delta$
that are not weakly consistent,
$\Delta$
that are not weakly consistent,
![]() $\widetilde{\Delta}$
is unsatisfiable; then the proposition holds because both
$\widetilde{\Delta}$
is unsatisfiable; then the proposition holds because both
![]() $A |\hspace{-2pt} {\sim}^{ecr}_{\Delta} B$
and
$A |\hspace{-2pt} {\sim}^{ecr}_{\Delta} B$
and
![]() $\widetilde{\Delta} \models A \rightarrow B$
. For weakly consistent belief bases we show both directions of the ‘iff”.
$\widetilde{\Delta} \models A \rightarrow B$
. For weakly consistent belief bases we show both directions of the ‘iff”.
Direction
![]() $\Rightarrow$
Assume that
$\Rightarrow$
Assume that
![]() $A |\hspace{-2pt} {\sim}^{ecr}_{\Delta} B$
. Therefore there is an extended c-representation
$A |\hspace{-2pt} {\sim}^{ecr}_{\Delta} B$
. Therefore there is an extended c-representation
![]() $\kappa$
with
$\kappa$
with
![]() $A |\hspace{-2pt} {\sim}_{\kappa} B$
, that is, either
$A |\hspace{-2pt} {\sim}_{\kappa} B$
, that is, either
![]() $\kappa(A) = \infty$
or
$\kappa(A) = \infty$
or
![]() $\kappa(AB) \lt \kappa(A\overline{B})$
. Let us distinguish these two cases.
$\kappa(AB) \lt \kappa(A\overline{B})$
. Let us distinguish these two cases.
Case 1:
![]() $\kappa(A) = \infty$
$\kappa(A) = \infty$
This implies that every model of A has rank
![]() $\infty$
. As
$\infty$
. As
![]() $\kappa$
is an extended c-representation,
$\kappa$
is an extended c-representation,
![]() $\kappa(\omega) \gt 0$
for some
$\kappa(\omega) \gt 0$
for some
![]() $\omega$
implies that
$\omega$
implies that
![]() $\omega$
falsifies at least one conditional in
$\omega$
falsifies at least one conditional in
![]() $\Delta$
. Therefore, all models of A falsify at least one conditional in
$\Delta$
. Therefore, all models of A falsify at least one conditional in
![]() $\Delta$
. Because the models of
$\Delta$
. Because the models of
![]() $\widetilde{\Delta}$
are exactly the worlds that do not falsify any conditional in
$\widetilde{\Delta}$
are exactly the worlds that do not falsify any conditional in
![]() $\Delta$
, we have that
$\Delta$
, we have that
![]() $\widetilde{\Delta} \models \neg A$
and therefore
$\widetilde{\Delta} \models \neg A$
and therefore
![]() $\widetilde{\Delta} \models A \rightarrow B$
.
$\widetilde{\Delta} \models A \rightarrow B$
.
Case 2:
![]() $\kappa(AB) \lt \kappa(A\overline{B})$
$\kappa(AB) \lt \kappa(A\overline{B})$
In this case especially
![]() $\kappa(A \overline{B}) \gt 0$
, implying that every model of
$\kappa(A \overline{B}) \gt 0$
, implying that every model of
![]() $A\overline{B}$
falsifies at least one conditional. Therefore,
$A\overline{B}$
falsifies at least one conditional. Therefore,
![]() $\widetilde{\Delta} \models \neg (A\overline{B})$
which is equivalent to
$\widetilde{\Delta} \models \neg (A\overline{B})$
which is equivalent to
![]() $\widetilde{\Delta} \models A \rightarrow B$
.
$\widetilde{\Delta} \models A \rightarrow B$
.
Direction
![]() $\Leftarrow$
Assume that
$\Leftarrow$
Assume that
![]() $\widetilde{\Delta} \models A \rightarrow B$
. Let
$\widetilde{\Delta} \models A \rightarrow B$
. Let
![]() $\kappa$
be the extended c-representation obtained from the impact vector
$\kappa$
be the extended c-representation obtained from the impact vector
![]() $\vec{\eta} = (\infty, \dots, \infty)$
. Then
$\vec{\eta} = (\infty, \dots, \infty)$
. Then
 \[ \kappa(\omega) = \begin{cases} 0 & \text{if } \omega \models \widetilde{\Delta} \\ \infty & \text{otherwise.} \end{cases} \]
\[ \kappa(\omega) = \begin{cases} 0 & \text{if } \omega \models \widetilde{\Delta} \\ \infty & \text{otherwise.} \end{cases} \]
We will show that
![]() $A |\hspace{-2pt} {\sim}_{\kappa} B$
by distinguishing two cases.
$A |\hspace{-2pt} {\sim}_{\kappa} B$
by distinguishing two cases.
Case 1:
![]() $\widetilde{\Delta} \not\models \neg A$
$\widetilde{\Delta} \not\models \neg A$
Let
![]() $\omega \in {Mod}\,_{\Sigma}(\widetilde{\Delta} \cup \{A\})$
. We have that
$\omega \in {Mod}\,_{\Sigma}(\widetilde{\Delta} \cup \{A\})$
. We have that
![]() $\kappa(\omega) = 0$
. Because
$\kappa(\omega) = 0$
. Because
![]() $\widetilde{\Delta} \models A \rightarrow B$
, we know that
$\widetilde{\Delta} \models A \rightarrow B$
, we know that
![]() $\omega \models B$
. Hence,
$\omega \models B$
. Hence,
![]() $\kappa(AB) = 0$
. Furthermore,
$\kappa(AB) = 0$
. Furthermore,
![]() $\widetilde{\Delta} \models A \rightarrow B$
yields that
$\widetilde{\Delta} \models A \rightarrow B$
yields that
![]() $\kappa(A\overline{B}) \gt 0$
. Thus,
$\kappa(A\overline{B}) \gt 0$
. Thus,
![]() $\kappa(AB) \lt \kappa(A\overline{B})$
and
$\kappa(AB) \lt \kappa(A\overline{B})$
and
![]() $A |\hspace{-2pt} {\sim}_{\kappa} B$
.
$A |\hspace{-2pt} {\sim}_{\kappa} B$
.
Case 2:
![]() $\widetilde{\Delta} \models \neg A$
$\widetilde{\Delta} \models \neg A$
In this case,
![]() $\kappa(A) = \infty$
and thus
$\kappa(A) = \infty$
and thus
![]() $A |\hspace{-2pt} {\sim}_{\kappa} B$
.
$A |\hspace{-2pt} {\sim}_{\kappa} B$
.
It should also be noted that for strongly consistent belief bases, every credulous c-inference is also an extended credulous c-inference, but not the other way round.
Proposition 65. (1) For every strongly consistent
![]() $\Delta$
and formulas A, B, if
$\Delta$
and formulas A, B, if
![]() $A |\hspace{-2pt} {\sim}^{cr}_{\Delta} B$
then
$A |\hspace{-2pt} {\sim}^{cr}_{\Delta} B$
then
![]() $A |\hspace{-2pt} {\sim}^{ecr}_{\Delta} B$
. (2) There are
$A |\hspace{-2pt} {\sim}^{ecr}_{\Delta} B$
. (2) There are
![]() $\Delta, A, B$
such that
$\Delta, A, B$
such that
![]() $A \mathord{{|\hspace{-2pt}}{\sim}\!\!\!\!/\;\;}^{cr}_{\Delta} B$
but
$A \mathord{{|\hspace{-2pt}}{\sim}\!\!\!\!/\;\;}^{cr}_{\Delta} B$
but
![]() $A |\hspace{-2pt} {\sim}^{ecr}_{\Delta} B$
.
$A |\hspace{-2pt} {\sim}^{ecr}_{\Delta} B$
.
Proof. Ad (1): This follows directly from Proposition 22 and the definitions of credulous c-inference and extended credulous c-inference.
Ad (2): Consider
![]() $\Delta = \{{{(b|p)}}, {{(f|b)}}, {{(\overline{f}|p)}}\}$
over
$\Delta = \{{{(b|p)}}, {{(f|b)}}, {{(\overline{f}|p)}}\}$
over
![]() $\Sigma = \{p, b, f\}$
. Then
$\Sigma = \{p, b, f\}$
. Then
![]() $p \mathord{{|\hspace{-2pt}}{\sim}\!\!\!\!/\;\;}^{cr}_{\Delta} f$
but
$p \mathord{{|\hspace{-2pt}}{\sim}\!\!\!\!/\;\;}^{cr}_{\Delta} f$
but
![]() $p |\hspace{-2pt} {\sim}^{ecr}_{\Delta} f$
because for
$p |\hspace{-2pt} {\sim}^{ecr}_{\Delta} f$
because for
![]() $\vec{\eta} = (\infty, \infty, \infty)$
we have
$\vec{\eta} = (\infty, \infty, \infty)$
we have
![]() ${{\kappa_{\vec{\eta}}}}(p) = \infty$
and thus
${{\kappa_{\vec{\eta}}}}(p) = \infty$
and thus
![]() $p |\hspace{-2pt} {\sim}_{{{\kappa_{\vec{\eta}}}}} f$
.
$p |\hspace{-2pt} {\sim}_{{{\kappa_{\vec{\eta}}}}} f$
.
Furthermore, extended credulous c-inference fails to satisfy (Classic Preservation). For instance, continuing the example in the proof of Proposition 65 (2), we have
![]() $p \mathord{{|\hspace{-2pt}}{\sim}\!\!\!\!/\;\;}^{p}_{\Delta} \bot$
but
$p \mathord{{|\hspace{-2pt}}{\sim}\!\!\!\!/\;\;}^{p}_{\Delta} \bot$
but
![]() $p |\hspace{-2pt} {\sim}^{ecr}_{\Delta} \bot$
because
$p |\hspace{-2pt} {\sim}^{ecr}_{\Delta} \bot$
because
![]() ${{\kappa_{\vec{\eta}}}}(p) = \infty$
for
${{\kappa_{\vec{\eta}}}}(p) = \infty$
for
![]() $\vec{\eta} = (\infty, \infty, \infty)$
. This motivates the introduction of a version of extended credulous c-inference which coincides with credulous c-inference on strongly consistent belief bases and which complies with (Classic Preservation). This can be achieved by taking only the conservative extended c-representations in
$\vec{\eta} = (\infty, \infty, \infty)$
. This motivates the introduction of a version of extended credulous c-inference which coincides with credulous c-inference on strongly consistent belief bases and which complies with (Classic Preservation). This can be achieved by taking only the conservative extended c-representations in
![]() $\mathit{CMod}^{ec}_{\Delta}$
into account.
$\mathit{CMod}^{ec}_{\Delta}$
into account.
Definition 66 (conservative extended credulous c-inference). Let
![]() $\Delta$
be a belief base and let A, B be formulas. B is a conservative extended credulous c-inference from A in the context of
$\Delta$
be a belief base and let A, B be formulas. B is a conservative extended credulous c-inference from A in the context of
![]() $\Delta$
, denoted by
$\Delta$
, denoted by
![]() $A|\hspace{-2pt} {\sim}^{cecr}_{\Delta} B$
, iff (i)
$A|\hspace{-2pt} {\sim}^{cecr}_{\Delta} B$
, iff (i)
![]() $\Delta$
is not weakly consistent or (ii) there is a conservative extended c-representation
$\Delta$
is not weakly consistent or (ii) there is a conservative extended c-representation
![]() $\kappa \in \mathit{CMod}^{ec}_{\Delta}$
of
$\kappa \in \mathit{CMod}^{ec}_{\Delta}$
of
![]() $\Delta$
with
$\Delta$
with
![]() $A|\hspace{-2pt} {\sim}_{\kappa} B$
.
$A|\hspace{-2pt} {\sim}_{\kappa} B$
.
Lemma 67. Conservative extended credulous c-inference is an inductive inference operator, that is, it satisfies (DI) and (TV).
Proof. Analogous to the proof of Proposition 33.
Lemma 68. For strongly consistent belief bases, conservative extended credulous c-inference coincides with credulous c-inference.
Proof. Let
![]() $\Delta$
be a strongly consistent belief base. In this case we have
$\Delta$
be a strongly consistent belief base. In this case we have
![]() $\kappa^z_{\Delta}(\omega) \lt \infty$
for all
$\kappa^z_{\Delta}(\omega) \lt \infty$
for all
![]() $\omega \in \Omega$
. By definition of
$\omega \in \Omega$
. By definition of
![]() $\mathit{CMod}^{ec}_{\Delta}$
(cf. Definition 43), we have
$\mathit{CMod}^{ec}_{\Delta}$
(cf. Definition 43), we have
![]() $\kappa(\omega) \lt \infty$
for all
$\kappa(\omega) \lt \infty$
for all
![]() $\kappa \in \mathit{CMod}^{ec}_{\Delta}$
and for all
$\kappa \in \mathit{CMod}^{ec}_{\Delta}$
and for all
![]() $\omega \in \Omega$
. Thus
$\omega \in \Omega$
. Thus
![]() $\mathit{CMod}^{ec}_{\Delta}$
coincides with the set of c-representations of
$\mathit{CMod}^{ec}_{\Delta}$
coincides with the set of c-representations of
![]() $\Delta$
, and the inferences that can be made with extended credulous c-inference from
$\Delta$
, and the inferences that can be made with extended credulous c-inference from
![]() $\Delta$
coincide with the inferences that can be made with credulous c-inference from
$\Delta$
coincide with the inferences that can be made with credulous c-inference from
![]() $\Delta$
.
$\Delta$
.
Proposition 69. Conservative extended credulous c-inference satisfies (Classic Preservation).
Proof. We have to show that
![]() $A |\hspace{-2pt} {\sim}^{cecr}_{\Delta} \bot$
iff
$A |\hspace{-2pt} {\sim}^{cecr}_{\Delta} \bot$
iff
![]() $A |\hspace{-2pt} {\sim}^{p}_{\Delta} \bot$
. Using Lemma 14, it suffices to show that
$A |\hspace{-2pt} {\sim}^{p}_{\Delta} \bot$
. Using Lemma 14, it suffices to show that
![]() $A |\hspace{-2pt} {\sim}^{cecr}_{\Delta} \bot$
iff
$A |\hspace{-2pt} {\sim}^{cecr}_{\Delta} \bot$
iff
![]() $\kappa^z_{\Delta}(A) = \infty$
. Combining Definition 43 and Lemma 24 yields that
$\kappa^z_{\Delta}(A) = \infty$
. Combining Definition 43 and Lemma 24 yields that
![]() $\kappa(\omega) = \infty$
iff
$\kappa(\omega) = \infty$
iff
![]() $\kappa^z_{\Delta}(\omega) = \infty$
for every
$\kappa^z_{\Delta}(\omega) = \infty$
for every
![]() $\kappa \in \mathit{CMod}^{ec}_{\Delta}$
and every
$\kappa \in \mathit{CMod}^{ec}_{\Delta}$
and every
![]() $\omega \in \Omega$
. Thus, the proposition holds.
$\omega \in \Omega$
. Thus, the proposition holds.
In the following we will show how conservative extended credulous c-inference can be realized by a CSP. This approach is inspired by the CSP characterization of credulous c-inference in Beierle et al. (Reference Beierle, Kutsch and Sauerwald2019b) and the CSP realization of extended (skeptical) c-inference in Subsection 7.2. We will again use the CSP
![]() ${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}}$
characterizing all extended c-inferences in
${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}}$
characterizing all extended c-inferences in
![]() $\mathit{CMod}^{ec}_{\Delta}$
(cf. Proposition 47).
$\mathit{CMod}^{ec}_{\Delta}$
(cf. Proposition 47).
The following constraint encodes that
![]() $A |\hspace{-2pt} {\sim}_{\kappa_{\vec{\eta}}} B$
holds for an extended c-representation
$A |\hspace{-2pt} {\sim}_{\kappa_{\vec{\eta}}} B$
holds for an extended c-representation
![]() ${{\kappa_{\vec{\eta}}}}$
.
${{\kappa_{\vec{\eta}}}}$
.
Definition 70. Let
![]() $\Delta = \{{{(B_1|A_1)}}, \dots, {{(B_n|A_n)}}\}$
be a belief base and let
$\Delta = \{{{(B_1|A_1)}}, \dots, {{(B_n|A_n)}}\}$
be a belief base and let
![]() $J_\Delta$
be as defined in Definition 45. The constraint
$J_\Delta$
be as defined in Definition 45. The constraint
![]() ${{\mathit{CR}_{\Delta}{{(B|A)}}}}$
is given by
${{\mathit{CR}_{\Delta}{{(B|A)}}}}$
is given by
By combining this constraint with the CSP
![]() ${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}}$
, we can check whether
${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}}$
, we can check whether
![]() $A |\hspace{-2pt} {\sim}^{cecr}_{\Delta} B$
with the following proposition.
$A |\hspace{-2pt} {\sim}^{cecr}_{\Delta} B$
with the following proposition.
Proposition 71. Let
![]() $\Delta$
be a weakly consistent belief base. Then
$\Delta$
be a weakly consistent belief base. Then
![]() $A |\hspace{-2pt} {\sim}^{cecr}_{\Delta} B$
iff either (i)
$A |\hspace{-2pt} {\sim}^{cecr}_{\Delta} B$
iff either (i)
![]() $\kappa^z_{\Delta}(A\overline{B}) = \infty$
, or (ii)
$\kappa^z_{\Delta}(A\overline{B}) = \infty$
, or (ii)
![]() $\kappa^z_{\Delta}(A\overline{B}) \lt \infty$
,
$\kappa^z_{\Delta}(A\overline{B}) \lt \infty$
,
![]() $ \kappa^z_{\Delta}(AB) \lt \infty$
and
$ \kappa^z_{\Delta}(AB) \lt \infty$
and
![]() ${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}} \cup {{\mathit{CR}_{\Delta}{{(B|A)}}}}$
is solvable.
${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}} \cup {{\mathit{CR}_{\Delta}{{(B|A)}}}}$
is solvable.
Proof.
Direction
![]() $\Rightarrow$
Assume that
$\Rightarrow$
Assume that
![]() $A |\hspace{-2pt} {\sim}^{cecr}_{\Delta} B$
and that
$A |\hspace{-2pt} {\sim}^{cecr}_{\Delta} B$
and that
![]() $\kappa^z_{\Delta}(A\overline{B}) \lt \infty$
. Then
$\kappa^z_{\Delta}(A\overline{B}) \lt \infty$
. Then
![]() $\kappa(A \overline{B}) \lt \infty$
for all
$\kappa(A \overline{B}) \lt \infty$
for all
![]() $\kappa \in \mathit{CMod}^{ec}_{\Delta}$
by the definition of
$\kappa \in \mathit{CMod}^{ec}_{\Delta}$
by the definition of
![]() $\mathit{CMod}^{ec}_{\Delta}$
. Therefore,
$\mathit{CMod}^{ec}_{\Delta}$
. Therefore,
![]() $\kappa(A) \lt \infty$
for all
$\kappa(A) \lt \infty$
for all
![]() $\kappa \in \mathit{CMod}^{ec}_{\Delta}$
. Because
$\kappa \in \mathit{CMod}^{ec}_{\Delta}$
. Because
![]() $A |\hspace{-2pt} {\sim}^{cecr}_{\Delta} B$
, there is at least one ranking function
$A |\hspace{-2pt} {\sim}^{cecr}_{\Delta} B$
, there is at least one ranking function
![]() $\kappa^* \in \mathit{CMod}^{ec}_{\Delta}$
with
$\kappa^* \in \mathit{CMod}^{ec}_{\Delta}$
with
![]() $A |\hspace{-2pt} {\sim}_{\kappa^*} B$
and thus
$A |\hspace{-2pt} {\sim}_{\kappa^*} B$
and thus
![]() $\kappa^*(AB) \lt \kappa^*(A\overline{B})$
. This implies that
$\kappa^*(AB) \lt \kappa^*(A\overline{B})$
. This implies that
![]() $\kappa^*(AB) \lt \infty$
and, by the definition of
$\kappa^*(AB) \lt \infty$
and, by the definition of
![]() $\mathit{CMod}^{ec}_{\Delta}$
,
$\mathit{CMod}^{ec}_{\Delta}$
,
![]() $\kappa^z_{\Delta}(AB) \lt \infty$
. Because of Proposition 47 there must be an
$\kappa^z_{\Delta}(AB) \lt \infty$
. Because of Proposition 47 there must be an
![]() $\vec{\eta}^* \in Sol^{J+\infty}_\Delta$
with
$\vec{\eta}^* \in Sol^{J+\infty}_\Delta$
with
![]() $\kappa^* = \kappa_{\vec{\eta}^*}$
and thus
$\kappa^* = \kappa_{\vec{\eta}^*}$
and thus
![]() $\kappa_{\vec{\eta}^*}(A B) \lt \kappa_{\vec{\eta}^*}(A \overline{B})$
. We have
$\kappa_{\vec{\eta}^*}(A B) \lt \kappa_{\vec{\eta}^*}(A \overline{B})$
. We have
 \begin{align*} &&\kappa_{\vec{\eta}^*}(A B) &\lt \kappa_{\vec{\eta}^*}(A \overline{B}) \\ \Leftrightarrow&&\min_{\omega \models AB} \sum_{\substack{1 \leqslant i \leqslant n \\ \omega \models A_i \overline{B_i}}} \eta_{i}^* &\lt \min_{\omega \models A\overline{B}} \sum_{\substack{1 \leqslant i \leqslant n \\ \omega \models A_i \overline{B_i}}} \eta_{i}^* \\ \overset{(*)}{\Leftrightarrow}&&\min_{\omega \models AB} \sum_{\substack{i \in J_\Delta \\ \omega \models A_i \overline{B_i}}} \eta_{i}^* \ \ &\lt \ \ \min_{\omega \models A \overline{B}} \sum_{\substack{i \in J_\Delta \\ \omega \models A_i \overline{B_i}}} \eta_{i}^*. \end{align*}
\begin{align*} &&\kappa_{\vec{\eta}^*}(A B) &\lt \kappa_{\vec{\eta}^*}(A \overline{B}) \\ \Leftrightarrow&&\min_{\omega \models AB} \sum_{\substack{1 \leqslant i \leqslant n \\ \omega \models A_i \overline{B_i}}} \eta_{i}^* &\lt \min_{\omega \models A\overline{B}} \sum_{\substack{1 \leqslant i \leqslant n \\ \omega \models A_i \overline{B_i}}} \eta_{i}^* \\ \overset{(*)}{\Leftrightarrow}&&\min_{\omega \models AB} \sum_{\substack{i \in J_\Delta \\ \omega \models A_i \overline{B_i}}} \eta_{i}^* \ \ &\lt \ \ \min_{\omega \models A \overline{B}} \sum_{\substack{i \in J_\Delta \\ \omega \models A_i \overline{B_i}}} \eta_{i}^*. \end{align*}
Equivalence
![]() $(*)$
holds because the ranks of the minimal models of A B and
$(*)$
holds because the ranks of the minimal models of A B and
![]() $A \overline{B}$
are finite and therefore do not violate a conditional
$A \overline{B}$
are finite and therefore do not violate a conditional
![]() ${{(B_i|A_i)}}$
with
${{(B_i|A_i)}}$
with
![]() $i \notin J_\Delta$
.
$i \notin J_\Delta$
.
Therefore,
![]() ${{\mathit{CR}_{\Delta}{{(B|A)}}}}$
holds for the solution of
${{\mathit{CR}_{\Delta}{{(B|A)}}}}$
holds for the solution of
![]() ${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}}$
corresponding to
${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}}$
corresponding to
![]() $\vec{\eta}^*$
, implying that
$\vec{\eta}^*$
, implying that
![]() ${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}} \cup {{\mathit{CR}_{\Delta}{{(B|A)}}}}$
is solvable.
${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}} \cup {{\mathit{CR}_{\Delta}{{(B|A)}}}}$
is solvable.
Direction
![]() $\Leftarrow$
Assume that either
$\Leftarrow$
Assume that either
![]() $\kappa^z_{\Delta}(A\overline{B}) = \infty$
or
$\kappa^z_{\Delta}(A\overline{B}) = \infty$
or
![]() $\big($
$\big($
![]() $\kappa^z_{\Delta}(A\overline{B}) \lt \infty$
,
$\kappa^z_{\Delta}(A\overline{B}) \lt \infty$
,
![]() $ \kappa^z_{\Delta}(AB) \lt \infty$
and
$ \kappa^z_{\Delta}(AB) \lt \infty$
and
![]() ${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}} \cup {{\mathit{CR}_{\Delta}{{(B|A)}}}}$
is solvable
${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}} \cup {{\mathit{CR}_{\Delta}{{(B|A)}}}}$
is solvable
![]() $\big)$
. There are three cases.
$\big)$
. There are three cases.
Case 1:
![]() $\kappa^z_{\Delta}(A B) = \infty$
and
$\kappa^z_{\Delta}(A B) = \infty$
and
![]() $\kappa^z_{\Delta}(A \overline{B}) = \infty$
$\kappa^z_{\Delta}(A \overline{B}) = \infty$
Then
![]() $\kappa^z_{\Delta}(A) = \infty$
and, by Proposition 26,
$\kappa^z_{\Delta}(A) = \infty$
and, by Proposition 26,
![]() $\kappa(A) = \infty$
for every
$\kappa(A) = \infty$
for every
![]() $\kappa \in \mathit{CMod}^{ec}_{\Delta}$
. Because
$\kappa \in \mathit{CMod}^{ec}_{\Delta}$
. Because
![]() $\mathit{CMod}^{ec}_{\Delta}$
contains at least one c-representation,
$\mathit{CMod}^{ec}_{\Delta}$
contains at least one c-representation,
![]() $A |\hspace{-2pt} {\sim}^{ecr}_{\Delta} B$
.
$A |\hspace{-2pt} {\sim}^{ecr}_{\Delta} B$
.
Case 2:
![]() $\kappa^z_{\Delta}(A B) \lt \infty$
and
$\kappa^z_{\Delta}(A B) \lt \infty$
and
![]() $\kappa^z_{\Delta}(A \overline{B}) = \infty$
$\kappa^z_{\Delta}(A \overline{B}) = \infty$
Then, by the definition of
![]() $\mathit{CMod}^{ec}_{\Delta}$
, we have
$\mathit{CMod}^{ec}_{\Delta}$
, we have
![]() $\kappa(A B) \lt \infty$
and, by Proposition 26,
$\kappa(A B) \lt \infty$
and, by Proposition 26,
![]() $\kappa(A\overline{B}) = \infty$
for every
$\kappa(A\overline{B}) = \infty$
for every
![]() $\kappa \in \mathit{CMod}^{ec}_{\Delta}$
. Therefore,
$\kappa \in \mathit{CMod}^{ec}_{\Delta}$
. Therefore,
![]() $\kappa(A B) \lt \kappa(A \overline{B})$
for every
$\kappa(A B) \lt \kappa(A \overline{B})$
for every
![]() $\kappa \in \mathit{CMod}^{ec}_{\Delta}$
, and because
$\kappa \in \mathit{CMod}^{ec}_{\Delta}$
, and because
![]() $\mathit{CMod}^{ec}_{\Delta}$
contains at least one c-representation,
$\mathit{CMod}^{ec}_{\Delta}$
contains at least one c-representation,
![]() $A |\hspace{-2pt} {\sim}^{cecr}_{\Delta} B$
.
$A |\hspace{-2pt} {\sim}^{cecr}_{\Delta} B$
.
Case 3:
![]() $\kappa^z_{\Delta}(A \overline{B}) \lt \infty$
$\kappa^z_{\Delta}(A \overline{B}) \lt \infty$
Then, by assumption,
![]() ${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}} \cup {{\mathit{CR}_{\Delta}{{(B|A)}}}}$
is solvable and
${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}} \cup {{\mathit{CR}_{\Delta}{{(B|A)}}}}$
is solvable and
![]() $\kappa^z_{\Delta}(A B) \lt \infty$
. This implies that there is an
$\kappa^z_{\Delta}(A B) \lt \infty$
. This implies that there is an
![]() $\vec{\eta}^J \in {{\mathit{Sol}({{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}})}}$
satisfying
$\vec{\eta}^J \in {{\mathit{Sol}({{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}})}}$
satisfying
![]() ${{\mathit{CR}_{\Delta}{{(B|A)}}}}$
. Using the equivalence transformations in the part of the proof for Direction
${{\mathit{CR}_{\Delta}{{(B|A)}}}}$
. Using the equivalence transformations in the part of the proof for Direction
![]() $\Rightarrow$
, there is an
$\Rightarrow$
, there is an
![]() $\vec{\eta}^* \in Sol^{J+\infty}_\Delta$
constructed from
$\vec{\eta}^* \in Sol^{J+\infty}_\Delta$
constructed from
![]() $\vec{\eta}^J$
with
$\vec{\eta}^J$
with
![]() $\kappa_{\vec{\eta}^*}(AB) \lt \kappa_{\vec{\eta}^*}(A\overline{B})$
. With Proposition 47, it follows that
$\kappa_{\vec{\eta}^*}(AB) \lt \kappa_{\vec{\eta}^*}(A\overline{B})$
. With Proposition 47, it follows that
![]() $A |\hspace{-2pt} {\sim}^{cecr}_{\Delta} B$
.
$A |\hspace{-2pt} {\sim}^{cecr}_{\Delta} B$
.
9.2. Extended weakly skeptical c-inference
Analogous to extended credulous c-inference, we can define extended weakly skeptical c-inference as weakly skeptical inference over all extended c-representations.
Definition 72 (extended weakly skeptical c-inference). Let
![]() $\Delta$
be a belief base and let A, B be formulas. B is an extended weakly skeptical c-inference from A in the context of
$\Delta$
be a belief base and let A, B be formulas. B is an extended weakly skeptical c-inference from A in the context of
![]() $\Delta$
, denoted by
$\Delta$
, denoted by
![]() $A|\hspace{-2pt} {\sim}^{ews}_{\Delta} B$
, iff (i)
$A|\hspace{-2pt} {\sim}^{ews}_{\Delta} B$
, iff (i)
![]() $\Delta$
is not weakly consistent, (ii) there is an extended c-representation
$\Delta$
is not weakly consistent, (ii) there is an extended c-representation
![]() $\kappa^{\circ}$
of
$\kappa^{\circ}$
of
![]() $\Delta$
with
$\Delta$
with
![]() $\kappa^\circ(A) = \infty$
, or (iii) there is an extended c-representation
$\kappa^\circ(A) = \infty$
, or (iii) there is an extended c-representation
![]() $\kappa$
of
$\kappa$
of
![]() $\Delta$
with
$\Delta$
with
![]() $A|\hspace{-2pt} {\sim}_{\kappa} B$
and there is no extended c-representation
$A|\hspace{-2pt} {\sim}_{\kappa} B$
and there is no extended c-representation
![]() $\kappa'$
of
$\kappa'$
of
![]() $\Delta$
with
$\Delta$
with
![]() $A|\hspace{-2pt} {\sim}_{\kappa'} \overline{B}$
.
$A|\hspace{-2pt} {\sim}_{\kappa'} \overline{B}$
.
Lemma 73. Extended weakly skeptical c-inference is an inductive inference operator, that is, it satisfies (DI) and (TV).
Proof.
(DI): Let
![]() ${{(B_i|A_i)}} \in \Delta$
. We need to show that
${{(B_i|A_i)}} \in \Delta$
. We need to show that
![]() $A_i |\hspace{-2pt} {\sim}^{ews}_{\Delta} B_i$
. If
$A_i |\hspace{-2pt} {\sim}^{ews}_{\Delta} B_i$
. If
![]() $\Delta$
is not weakly consistent or if there is an extended c-representation
$\Delta$
is not weakly consistent or if there is an extended c-representation
![]() $\kappa^{\circ}$
with
$\kappa^{\circ}$
with
![]() $\kappa^{\circ}(A_i) = \infty$
, then
$\kappa^{\circ}(A_i) = \infty$
, then
![]() $A_i |\hspace{-2pt} {\sim}^{ews}_{\Delta} B_i$
by definition. For the remainder of the proof assume that
$A_i |\hspace{-2pt} {\sim}^{ews}_{\Delta} B_i$
by definition. For the remainder of the proof assume that
![]() $\Delta$
is weakly consistent and
$\Delta$
is weakly consistent and
![]() $\kappa(A_i) \lt \infty$
for every extended c-representation
$\kappa(A_i) \lt \infty$
for every extended c-representation
![]() $\kappa$
of
$\kappa$
of
![]() $\Delta$
. Every extended c-representation
$\Delta$
. Every extended c-representation
![]() $\kappa$
is a model of
$\kappa$
is a model of
![]() ${{(B_i|A_i)}}$
and therefore must satisfy
${{(B_i|A_i)}}$
and therefore must satisfy
![]() $\kappa(A_i B_i) \lt \kappa(A_i \overline{B_i})$
. Thus,
$\kappa(A_i B_i) \lt \kappa(A_i \overline{B_i})$
. Thus,
![]() $A_i |\hspace{-2pt} {\sim}^{ews}_{\Delta} B_i$
.
$A_i |\hspace{-2pt} {\sim}^{ews}_{\Delta} B_i$
.
(TV): Analogous to the proof of Proposition 33.
Interestingly, this inference operator also coincides with classical deduction with respect to the material counterparts of the conditionals.
Proposition 74. Let
![]() $\Delta$
be a belief base and A, B be formulas. Let
$\Delta$
be a belief base and A, B be formulas. Let
![]() $\widetilde{\Delta} = \{ A_i \rightarrow B_i \mid {{(B_i|A_i)}} \in \Delta$
.
$\widetilde{\Delta} = \{ A_i \rightarrow B_i \mid {{(B_i|A_i)}} \in \Delta$
.
Proof. For belief bases
![]() $\Delta$
that are not weakly consistent,
$\Delta$
that are not weakly consistent,
![]() $\widetilde{\Delta}$
is unsatisfiable; then the proposition holds because both
$\widetilde{\Delta}$
is unsatisfiable; then the proposition holds because both
![]() $A |\hspace{-2pt} {\sim}^{ews}_{\Delta} B$
and
$A |\hspace{-2pt} {\sim}^{ews}_{\Delta} B$
and
![]() $\widetilde{\Delta} \models A \rightarrow B$
. For weakly consistent belief bases we show both directions of the ‘iff’.
$\widetilde{\Delta} \models A \rightarrow B$
. For weakly consistent belief bases we show both directions of the ‘iff’.
Direction
![]() $\Rightarrow$
Assume that
$\Rightarrow$
Assume that
![]() $A |\hspace{-2pt} {\sim}^{ews}_{\Delta} B$
. We can distinguish two cases.
$A |\hspace{-2pt} {\sim}^{ews}_{\Delta} B$
. We can distinguish two cases.
Case 1: There is an extended c-representation
![]() $\kappa^\circ$
with
$\kappa^\circ$
with
![]() $\kappa^\circ(A) = \infty$
$\kappa^\circ(A) = \infty$
Then every model of A falsifies at least one conditional in
![]() $\Delta$
. But by the construction of
$\Delta$
. But by the construction of
![]() $\widetilde{\Delta}$
, the models of
$\widetilde{\Delta}$
, the models of
![]() $\widetilde{\Delta}$
do not falsify any conditional in
$\widetilde{\Delta}$
do not falsify any conditional in
![]() $\Delta$
. Thus,
$\Delta$
. Thus,
![]() $\widetilde{\Delta} \models \neg A$
and therefore
$\widetilde{\Delta} \models \neg A$
and therefore
![]() $\widetilde{\Delta} \models A \rightarrow B$
.
$\widetilde{\Delta} \models A \rightarrow B$
.
Case 2: There is no such
![]() $\kappa^\circ$
with
$\kappa^\circ$
with
![]() $\kappa^\circ(A) = \infty$
$\kappa^\circ(A) = \infty$
Then there must be an extended c-representation
![]() $\kappa$
with
$\kappa$
with
![]() $A |\hspace{-2pt} {\sim}_{\kappa} B$
. In this case it cannot be that
$A |\hspace{-2pt} {\sim}_{\kappa} B$
. In this case it cannot be that
![]() $\kappa(A) = \infty$
, therefore we have
$\kappa(A) = \infty$
, therefore we have
![]() $\kappa(AB) \lt \kappa(A\overline{B})$
. Especially, we have
$\kappa(AB) \lt \kappa(A\overline{B})$
. Especially, we have
![]() $\kappa(A \overline{B}) \gt 0$
, implying that every model of
$\kappa(A \overline{B}) \gt 0$
, implying that every model of
![]() $A\overline{B}$
falsifies at least one conditional and thus is not a model of
$A\overline{B}$
falsifies at least one conditional and thus is not a model of
![]() $\widetilde{\Delta}$
. Therefore,
$\widetilde{\Delta}$
. Therefore,
![]() $\widetilde{\Delta} \models \neg (A \overline{B})$
which is equivalent to
$\widetilde{\Delta} \models \neg (A \overline{B})$
which is equivalent to
![]() $\widetilde{\Delta} \models A \rightarrow B$
.
$\widetilde{\Delta} \models A \rightarrow B$
.
Direction
![]() $\Leftarrow$
Assume that
$\Leftarrow$
Assume that
![]() $\widetilde{\Delta} \models A \rightarrow B$
. Let
$\widetilde{\Delta} \models A \rightarrow B$
. Let
![]() $\kappa$
be the extended c-inference obtained from the impact vector
$\kappa$
be the extended c-inference obtained from the impact vector
![]() $\vec{\eta} = (\infty, \dots, \infty)$
. Then
$\vec{\eta} = (\infty, \dots, \infty)$
. Then
 \[ \kappa(\omega) = \begin{cases} 0 & \text{if } \omega \models \widetilde{\Delta} \\ \infty & \text{otherwise.} \end{cases} \]
\[ \kappa(\omega) = \begin{cases} 0 & \text{if } \omega \models \widetilde{\Delta} \\ \infty & \text{otherwise.} \end{cases} \]
We can distinguish two cases.
Case 1:
![]() $\widetilde{\Delta} \cup \{A\}$
is satisfiable
$\widetilde{\Delta} \cup \{A\}$
is satisfiable
Then there is at least one model
![]() $\omega$
of A that does not falsify any conditional. Because
$\omega$
of A that does not falsify any conditional. Because
![]() $\widetilde{\Delta} \models A \rightarrow B$
we have
$\widetilde{\Delta} \models A \rightarrow B$
we have
![]() $\omega \models AB$
. Therefore,
$\omega \models AB$
. Therefore,
![]() $\kappa(AB) = 0$
. Furthermore, every model of
$\kappa(AB) = 0$
. Furthermore, every model of
![]() $A\overline{B}$
must falsify at least one conditional, implying that
$A\overline{B}$
must falsify at least one conditional, implying that
![]() $\kappa(A\overline{B}) = \infty$
. Therefore,
$\kappa(A\overline{B}) = \infty$
. Therefore,
![]() $\kappa(AB) \lt \kappa(A\overline{B})$
and
$\kappa(AB) \lt \kappa(A\overline{B})$
and
![]() $A |\hspace{-2pt} {\sim}_{\kappa} B$
.
$A |\hspace{-2pt} {\sim}_{\kappa} B$
.
Additionally, because
![]() $\widetilde{\Delta} \models A \rightarrow B$
we have
$\widetilde{\Delta} \models A \rightarrow B$
we have
![]() $\kappa'(AB) = 0$
for every extended c-representation
$\kappa'(AB) = 0$
for every extended c-representation
![]() $\kappa'$
of
$\kappa'$
of
![]() $\Delta$
. This implies that there is no extended c-representation
$\Delta$
. This implies that there is no extended c-representation
![]() $\kappa'$
with
$\kappa'$
with
![]() $A |\hspace{-2pt} {\sim}_{\kappa} \overline{B}$
. In summary,
$A |\hspace{-2pt} {\sim}_{\kappa} \overline{B}$
. In summary,
![]() $A |\hspace{-2pt} {\sim}^{ews}_{\Delta} B$
.
$A |\hspace{-2pt} {\sim}^{ews}_{\Delta} B$
.
Case 2:
![]() $\widetilde{\Delta} \cup \{A\}$
is not satisfiable
$\widetilde{\Delta} \cup \{A\}$
is not satisfiable
Then every model of A falsifies at least one conditional in
![]() $\Delta$
, implying that
$\Delta$
, implying that
![]() $\kappa(A) = \infty$
. This implies
$\kappa(A) = \infty$
. This implies
![]() $A |\hspace{-2pt} {\sim}^{ews}_{\Delta} B$
.
$A |\hspace{-2pt} {\sim}^{ews}_{\Delta} B$
.
Thus, credulous and weakly skeptical c-inference over all extended c-representations coincide because
according to Propositions 64 and 74. Moreover, analogously to extended credulous c-inference (Proposition 65), we observe that for strongly consistent belief bases, extended weakly skeptical c-inference extends weakly skeptical c-inference but does not coincide with it.
Proposition 75. (1) For every strongly consistent
![]() $\Delta$
and formulas A, B, if
$\Delta$
and formulas A, B, if
![]() $A |\hspace{-2pt} {\sim}^{ws}_{\Delta} B$
then
$A |\hspace{-2pt} {\sim}^{ws}_{\Delta} B$
then
![]() $A |\hspace{-2pt} {\sim}^{ews}_{\Delta} B$
. (2) There are
$A |\hspace{-2pt} {\sim}^{ews}_{\Delta} B$
. (2) There are
![]() $\Delta, A, B$
such that
$\Delta, A, B$
such that
![]() $A \mathord{{|\hspace{-2pt}}{\sim}\!\!\!\!/\;\;}^{ws}_{\Delta} B$
but
$A \mathord{{|\hspace{-2pt}}{\sim}\!\!\!\!/\;\;}^{ws}_{\Delta} B$
but
![]() $A |\hspace{-2pt} {\sim}^{ews}_{\Delta}B$
.
$A |\hspace{-2pt} {\sim}^{ews}_{\Delta}B$
.
Proof.
Ad (1): Let
![]() $A |\hspace{-2pt} {\sim}^{ws}_{\Delta} B$
. This implies that
$A |\hspace{-2pt} {\sim}^{ws}_{\Delta} B$
. This implies that
![]() $A |\hspace{-2pt} {\sim}^{cr}_{\Delta} B$
(Beierle et al., Reference Beierle, Eichhorn, Kern-Isberner and Kutsch2021) and with Proposition 65 that
$A |\hspace{-2pt} {\sim}^{cr}_{\Delta} B$
(Beierle et al., Reference Beierle, Eichhorn, Kern-Isberner and Kutsch2021) and with Proposition 65 that
![]() $A |\hspace{-2pt} {\sim}^{ecr}_{\Delta} B$
. By Propositions 64 and 74 we have
$A |\hspace{-2pt} {\sim}^{ecr}_{\Delta} B$
. By Propositions 64 and 74 we have
![]() $A |\hspace{-2pt} {\sim}^{ews}_{\Delta} B$
.
$A |\hspace{-2pt} {\sim}^{ews}_{\Delta} B$
.
Ad (2): Consider
![]() $\Delta = \{{{(b|p)}}, {{(f|b)}}, {{(\overline{f}|p)}}\}$
over
$\Delta = \{{{(b|p)}}, {{(f|b)}}, {{(\overline{f}|p)}}\}$
over
![]() $\Sigma = \{p, b, f\}$
. Then
$\Sigma = \{p, b, f\}$
. Then
![]() $p \mathord{{|\hspace{-2pt}}{\sim}\!\!\!\!/\;\;}^{ws}_{\Delta} f$
but
$p \mathord{{|\hspace{-2pt}}{\sim}\!\!\!\!/\;\;}^{ws}_{\Delta} f$
but
![]() $p |\hspace{-2pt} {\sim}^{ews}_{\Delta} f$
because for
$p |\hspace{-2pt} {\sim}^{ews}_{\Delta} f$
because for
![]() $\vec{\eta} = (\infty, \infty, \infty)$
we have
$\vec{\eta} = (\infty, \infty, \infty)$
we have
![]() ${{\kappa_{\vec{\eta}}}}(p) = \infty$
.
${{\kappa_{\vec{\eta}}}}(p) = \infty$
.
Furthermore, similar to the credulous case, also extended weakly skeptical inference fails to satisfy (Classic Preservation). For instance, continuing the example in the proof of Proposition 75 (2), we have
![]() $p \mathord{{|\hspace{-2pt}}{\sim}\!\!\!\!/\;\;}^{p}_{\Delta} \bot$
but
$p \mathord{{|\hspace{-2pt}}{\sim}\!\!\!\!/\;\;}^{p}_{\Delta} \bot$
but
![]() $p |\hspace{-2pt} {\sim}^{ecr}_{\Delta} \bot$
because
$p |\hspace{-2pt} {\sim}^{ecr}_{\Delta} \bot$
because
![]() ${{\kappa_{\vec{\eta}}}}(p) = \infty$
for
${{\kappa_{\vec{\eta}}}}(p) = \infty$
for
![]() $\vec{\eta} = (\infty, \infty, \infty)$
. Therefore, we consider weakly skeptical inference only over the conservative extended c-representations of a belief base.
$\vec{\eta} = (\infty, \infty, \infty)$
. Therefore, we consider weakly skeptical inference only over the conservative extended c-representations of a belief base.
Definition 76 (conservative extended weakly skeptical c-inference). Let
![]() $\Delta$
be a belief base and let A, B be formulas. B is a conservative extended weakly skeptical c-inference from A in the context of
$\Delta$
be a belief base and let A, B be formulas. B is a conservative extended weakly skeptical c-inference from A in the context of
![]() $\Delta$
, denoted by
$\Delta$
, denoted by
![]() $A|\hspace{-2pt} {\sim}^{cews}_{\Delta} B$
, iff (i)
$A|\hspace{-2pt} {\sim}^{cews}_{\Delta} B$
, iff (i)
![]() $\Delta$
is not weakly consistent, (ii) there is a conservative extended c-representation
$\Delta$
is not weakly consistent, (ii) there is a conservative extended c-representation
![]() $\kappa^{\circ}$
of
$\kappa^{\circ}$
of
![]() $\Delta$
with
$\Delta$
with
![]() $\kappa^{\circ}(A) = \infty$
, or (iii) there is a conservative extended c-representation
$\kappa^{\circ}(A) = \infty$
, or (iii) there is a conservative extended c-representation
![]() $\kappa$
of
$\kappa$
of
![]() $\Delta$
with
$\Delta$
with
![]() $A|\hspace{-2pt} {\sim}_{\kappa} B$
and there is no conservative extended c-representation
$A|\hspace{-2pt} {\sim}_{\kappa} B$
and there is no conservative extended c-representation
![]() $\kappa'$
of
$\kappa'$
of
![]() $\Delta$
with
$\Delta$
with
![]() $A|\hspace{-2pt} {\sim}_{\kappa'} \overline{B}$
.
$A|\hspace{-2pt} {\sim}_{\kappa'} \overline{B}$
.
Lemma 77. Conservative extended weakly skeptical c-inference is an inductive inference operator, that is, it satisfies (DI) and (TV).
Proof.
(DI): Let
![]() $A |\hspace{-2pt} {\sim}^{p}_{\Delta} B$
. If
$A |\hspace{-2pt} {\sim}^{p}_{\Delta} B$
. If
![]() $\Delta$
is not weakly consistent or if there is a conservative extended c-representation
$\Delta$
is not weakly consistent or if there is a conservative extended c-representation
![]() $\kappa^\circ$
with
$\kappa^\circ$
with
![]() $\kappa^\circ(A) = \infty$
then
$\kappa^\circ(A) = \infty$
then
![]() $A |\hspace{-2pt} {\sim}^{cews}_{\Delta} B$
follows immediately. Assume for the remainder of this proof that
$A |\hspace{-2pt} {\sim}^{cews}_{\Delta} B$
follows immediately. Assume for the remainder of this proof that
![]() $\Delta$
is weakly consistent and
$\Delta$
is weakly consistent and
![]() $\kappa(A) \lt \infty$
for all conservative extended c-representations
$\kappa(A) \lt \infty$
for all conservative extended c-representations
![]() $\kappa$
of
$\kappa$
of
![]() $\Delta$
. For every conservative extended c-representations
$\Delta$
. For every conservative extended c-representations
![]() $\kappa$
of
$\kappa$
of
![]() $\Delta$
it holds that
$\Delta$
it holds that
![]() $A |\hspace{-2pt} {\sim}_{\kappa} B$
. Because
$A |\hspace{-2pt} {\sim}_{\kappa} B$
. Because
![]() $\kappa(A) \lt \infty$
this implies that
$\kappa(A) \lt \infty$
this implies that
![]() $\kappa(AB) \lt \kappa(A\overline{B})$
. Thus,
$\kappa(AB) \lt \kappa(A\overline{B})$
. Thus,
![]() $A \mathord{{|\hspace{-2pt}}{\sim}\!\!\!\!/\;\;}_{\kappa} \overline{B}$
. In summary we have
$A \mathord{{|\hspace{-2pt}}{\sim}\!\!\!\!/\;\;}_{\kappa} \overline{B}$
. In summary we have
![]() $A |\hspace{-2pt} {\sim}^{cews}_{\Delta} B$
.
$A |\hspace{-2pt} {\sim}^{cews}_{\Delta} B$
.
(TV): Analogous to the proof of Proposition 33.
Lemma 78. For strongly consistent belief bases, conservative extended weakly skeptical c-inference coincides with weakly skeptical c-inference.
Proof. Let
![]() $\Delta$
be a strongly consistent belief base. In this case we have
$\Delta$
be a strongly consistent belief base. In this case we have
![]() $\kappa^z_{\Delta}(\omega) \lt \infty$
for all
$\kappa^z_{\Delta}(\omega) \lt \infty$
for all
![]() $\omega \in \Omega$
. By definition of
$\omega \in \Omega$
. By definition of
![]() $\mathit{CMod}^{ec}_{\Delta}$
(cf. Definition 43), it is
$\mathit{CMod}^{ec}_{\Delta}$
(cf. Definition 43), it is
![]() $\kappa(\omega) \lt \infty$
for all
$\kappa(\omega) \lt \infty$
for all
![]() $\kappa \in \mathit{CMod}^{ec}_{\Delta}$
and
$\kappa \in \mathit{CMod}^{ec}_{\Delta}$
and
![]() $\omega \in \Omega$
. We have
$\omega \in \Omega$
. We have
![]() $\kappa(A) = \infty$
iff
$\kappa(A) = \infty$
iff
![]() $A \equiv \bot$
for all
$A \equiv \bot$
for all
![]() $\kappa \in \mathit{CMod}^{ec}_{\Delta}$
. Thus,
$\kappa \in \mathit{CMod}^{ec}_{\Delta}$
. Thus,
![]() $\mathit{CMod}^{ec}_{\Delta}$
coincides with the set of c-representations of
$\mathit{CMod}^{ec}_{\Delta}$
coincides with the set of c-representations of
![]() $\Delta$
, and the inferences that can be made with conservative extended weakly skeptical c-inference from
$\Delta$
, and the inferences that can be made with conservative extended weakly skeptical c-inference from
![]() $\Delta$
coincide with the inferences that can be made with weakly skeptical c-inferences from
$\Delta$
coincide with the inferences that can be made with weakly skeptical c-inferences from
![]() $\Delta$
.
$\Delta$
.
Proposition 79. Conservative extended weakly skeptical c-inference satisfies (Classic Preservation).
Proof. We have to show that
![]() $A |\hspace{-2pt} {\sim}^{cews}_{\Delta} \bot$
iff
$A |\hspace{-2pt} {\sim}^{cews}_{\Delta} \bot$
iff
![]() $A |\hspace{-2pt} {\sim}^{p}_{\Delta} \bot$
. For
$A |\hspace{-2pt} {\sim}^{p}_{\Delta} \bot$
. For
![]() $\Delta$
not weakly consistent, we have both
$\Delta$
not weakly consistent, we have both
![]() $A |\hspace{-2pt} {\sim}^{cews}_{\Delta} \bot$
and
$A |\hspace{-2pt} {\sim}^{cews}_{\Delta} \bot$
and
![]() $A |\hspace{-2pt} {\sim}^{p}_{\Delta} \bot$
and thus the proposition holds. For weakly consistent
$A |\hspace{-2pt} {\sim}^{p}_{\Delta} \bot$
and thus the proposition holds. For weakly consistent
![]() $\Delta$
, using Lemma 14, it suffices to show that
$\Delta$
, using Lemma 14, it suffices to show that
![]() $A |\hspace{-2pt} {\sim}^{cews}_{\Delta} \bot$
iff
$A |\hspace{-2pt} {\sim}^{cews}_{\Delta} \bot$
iff
![]() $\kappa^z_{\Delta}(A) = \infty$
. Combining Definition 43 and Lemma 24 yields that
$\kappa^z_{\Delta}(A) = \infty$
. Combining Definition 43 and Lemma 24 yields that
![]() $\kappa(\omega) = \infty$
iff
$\kappa(\omega) = \infty$
iff
![]() $\kappa^z_{\Delta}(\omega) = \infty$
for every
$\kappa^z_{\Delta}(\omega) = \infty$
for every
![]() $\kappa \in \mathit{CMod}^{ec}_{\Delta}$
and every
$\kappa \in \mathit{CMod}^{ec}_{\Delta}$
and every
![]() $\omega \in \Omega$
. Thus, the proposition holds.
$\omega \in \Omega$
. Thus, the proposition holds.
We will now realize conservative extended weakly skeptical c-inference by a CSP. Inspired by the CSP characterization of weakly skeptical c-inference in Beierle et al. (Reference Beierle, Kutsch and Sauerwald2019b) we will again use the CSPs
![]() ${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}}$
and
${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}}$
and
![]() ${{\mathit{CR}_{\Delta}{{(B|A)}}}}$
and
${{\mathit{CR}_{\Delta}{{(B|A)}}}}$
and
![]() ${{\neg{{\mathit{CR}_{\Delta}{{(B|A)}}}}}}$
as in Propositions 71 and 51.
${{\neg{{\mathit{CR}_{\Delta}{{(B|A)}}}}}}$
as in Propositions 71 and 51.
Proposition 80. Let
![]() $\Delta$
be a weakly consistent belief base. Then
$\Delta$
be a weakly consistent belief base. Then
![]() $A |\hspace{-2pt} {\sim}^{cews}_{\Delta} B$
iff either (i)
$A |\hspace{-2pt} {\sim}^{cews}_{\Delta} B$
iff either (i)
![]() $\kappa^z_{\Delta}(A\overline{B}) = \infty$
or (ii)
$\kappa^z_{\Delta}(A\overline{B}) = \infty$
or (ii)
![]() $\kappa^z_{\Delta}(A\overline{B}) \lt \infty$
,
$\kappa^z_{\Delta}(A\overline{B}) \lt \infty$
,
![]() $\kappa^z_{\Delta}(AB) \lt \infty$
and
$\kappa^z_{\Delta}(AB) \lt \infty$
and
![]() ${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}} \cup {{\mathit{CR}_{\Delta}{{(B|A)}}}}$
is solvable and
${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}} \cup {{\mathit{CR}_{\Delta}{{(B|A)}}}}$
is solvable and
![]() ${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}} \cup {{\mathit{CR}_{\Delta}{{(\overline{B}|A)}}}}$
is unsolvable.
${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}} \cup {{\mathit{CR}_{\Delta}{{(\overline{B}|A)}}}}$
is unsolvable.
Proof.
Direction
![]() $\Rightarrow$
Assume that
$\Rightarrow$
Assume that
![]() $A |\hspace{-2pt} {\sim}^{cews}_{\Delta} B$
and that
$A |\hspace{-2pt} {\sim}^{cews}_{\Delta} B$
and that
![]() $\kappa^z_{\Delta}(A\overline{B}) \lt \infty$
. Then
$\kappa^z_{\Delta}(A\overline{B}) \lt \infty$
. Then
![]() $\kappa(A \overline{B}) \lt \infty$
for all
$\kappa(A \overline{B}) \lt \infty$
for all
![]() $\kappa \in \mathit{CMod}^{ec}_{\Delta}$
by the definition of
$\kappa \in \mathit{CMod}^{ec}_{\Delta}$
by the definition of
![]() $\mathit{CMod}^{ec}_{\Delta}$
. Therefore,
$\mathit{CMod}^{ec}_{\Delta}$
. Therefore,
![]() $\kappa(A) \lt \infty$
for all
$\kappa(A) \lt \infty$
for all
![]() $\kappa \in \mathit{CMod}^{ec}_{\Delta}$
.
$\kappa \in \mathit{CMod}^{ec}_{\Delta}$
.
Because
![]() $A |\hspace{-2pt} {\sim}^{cews}_{\Delta} B$
, there is at least one ranking function
$A |\hspace{-2pt} {\sim}^{cews}_{\Delta} B$
, there is at least one ranking function
![]() $\kappa^* \in \mathit{CMod}^{ec}_{\Delta}$
with
$\kappa^* \in \mathit{CMod}^{ec}_{\Delta}$
with
![]() $A |\hspace{-2pt} {\sim}_{\kappa^*} B$
and thus
$A |\hspace{-2pt} {\sim}_{\kappa^*} B$
and thus
![]() $\kappa^*(AB) \lt \kappa^*(A\overline{B})$
. This implies that
$\kappa^*(AB) \lt \kappa^*(A\overline{B})$
. This implies that
![]() $\kappa^*(AB) \lt \infty$
and, by Proposition 26,
$\kappa^*(AB) \lt \infty$
and, by Proposition 26,
![]() $\kappa^z_{\Delta}(AB) \lt \infty$
. Because of Proposition 74 there must be an
$\kappa^z_{\Delta}(AB) \lt \infty$
. Because of Proposition 74 there must be an
![]() $\vec{\eta}^* \in Sol^{J+\infty}_\Delta$
with
$\vec{\eta}^* \in Sol^{J+\infty}_\Delta$
with
![]() $\kappa^* = \kappa_{\vec{\eta}^*}$
and thus
$\kappa^* = \kappa_{\vec{\eta}^*}$
and thus
![]() $\kappa_{\vec{\eta}^*}(A B) \lt \kappa_{\vec{\eta}^*}(A \overline{B})$
. Analogously to the proof of Proposition 71, we can show that this is equivalent to the satisfication of
$\kappa_{\vec{\eta}^*}(A B) \lt \kappa_{\vec{\eta}^*}(A \overline{B})$
. Analogously to the proof of Proposition 71, we can show that this is equivalent to the satisfication of
![]() ${{\mathit{CR}_{\Delta}{{(B|A)}}}}$
. Therefore,
${{\mathit{CR}_{\Delta}{{(B|A)}}}}$
. Therefore,
![]() ${{\mathit{CR}_{\Delta}{{(B|A)}}}}$
holds for the solution of
${{\mathit{CR}_{\Delta}{{(B|A)}}}}$
holds for the solution of
![]() ${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}}$
corresponding to
${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}}$
corresponding to
![]() $\vec{\eta}^*$
, implying that
$\vec{\eta}^*$
, implying that
![]() ${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}} \cup {{\mathit{CR}_{\Delta}{{(B|A)}}}}$
is solvable.
${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}} \cup {{\mathit{CR}_{\Delta}{{(B|A)}}}}$
is solvable.
![]() $A |\hspace{-2pt} {\sim}^{cews}_{\Delta} B$
also implies that there is no conservative extended c-representation
$A |\hspace{-2pt} {\sim}^{cews}_{\Delta} B$
also implies that there is no conservative extended c-representation
![]() $\kappa' \in \mathit{CMod}^{ec}_{\Delta}$
with
$\kappa' \in \mathit{CMod}^{ec}_{\Delta}$
with
![]() $A |\hspace{-2pt} {\sim}_{\kappa'} \overline{B}$
. This implies that there is no
$A |\hspace{-2pt} {\sim}_{\kappa'} \overline{B}$
. This implies that there is no
![]() $\kappa'$
with
$\kappa'$
with
![]() $\kappa'(A\overline{B}) \lt \kappa'(AB)$
. Because of Proposition 47 there cannot be an
$\kappa'(A\overline{B}) \lt \kappa'(AB)$
. Because of Proposition 47 there cannot be an
![]() $\vec{\eta}' \in Sol^{J+\infty}_\Delta$
with
$\vec{\eta}' \in Sol^{J+\infty}_\Delta$
with
![]() $\kappa_{\vec{\eta}'}(A \overline{B}) \lt \kappa_{\vec{\eta}'}(A B)$
. Analogously to the proof of Proposition 71, we can show that
$\kappa_{\vec{\eta}'}(A \overline{B}) \lt \kappa_{\vec{\eta}'}(A B)$
. Analogously to the proof of Proposition 71, we can show that
![]() $\kappa_{\vec{\eta}}(A \overline{B}) \lt \kappa_{\vec{\eta}}(A B)$
is equivalent to
$\kappa_{\vec{\eta}}(A \overline{B}) \lt \kappa_{\vec{\eta}}(A B)$
is equivalent to
![]() ${{\mathit{CR}_{\Delta}{{(\overline{B}|A)}}}}$
. Therefore, there cannot be a solution of
${{\mathit{CR}_{\Delta}{{(\overline{B}|A)}}}}$
. Therefore, there cannot be a solution of
![]() ${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}}$
that satisfies
${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}}$
that satisfies
![]() ${{\mathit{CR}_{\Delta}{{(\overline{B}|A)}}}}$
, implying that
${{\mathit{CR}_{\Delta}{{(\overline{B}|A)}}}}$
, implying that
![]() ${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}} \cup {{\mathit{CR}_{\Delta}{{(\overline{B}|A)}}}}$
is unsolvable.
${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}} \cup {{\mathit{CR}_{\Delta}{{(\overline{B}|A)}}}}$
is unsolvable.
Direction
![]() $\Leftarrow$
Assume that either
$\Leftarrow$
Assume that either
![]() $\kappa^z_{\Delta}(A\overline{B}) = \infty$
, or
$\kappa^z_{\Delta}(A\overline{B}) = \infty$
, or
![]() $\big(\!\!$
$\big(\!\!$
![]() $\kappa^z_{\Delta}(A\overline{B}) \lt \infty$
,
$\kappa^z_{\Delta}(A\overline{B}) \lt \infty$
,
![]() $\kappa^z_{\Delta}(AB) \lt \infty$
and
$\kappa^z_{\Delta}(AB) \lt \infty$
and
![]() ${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}} \cup {{\mathit{CR}_{\Delta}{{(B|A)}}}}$
is solvable and
${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}} \cup {{\mathit{CR}_{\Delta}{{(B|A)}}}}$
is solvable and
![]() ${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}} \cup {{\mathit{CR}_{\Delta}{{(\overline{B}|A)}}}}$
is unsolvable
${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}} \cup {{\mathit{CR}_{\Delta}{{(\overline{B}|A)}}}}$
is unsolvable
![]() $\!\big)$
. There are three cases.
$\!\big)$
. There are three cases.
Case 1:
![]() $\kappa^z_{\Delta}(A B) = \infty$
and
$\kappa^z_{\Delta}(A B) = \infty$
and
![]() $\kappa^z_{\Delta}(A \overline{B}) = \infty$
$\kappa^z_{\Delta}(A \overline{B}) = \infty$
Then
![]() $\kappa^z_{\Delta}(A) = \infty$
. Because
$\kappa^z_{\Delta}(A) = \infty$
. Because
![]() $\Delta$
is weakly consistent there is at least one conservative extended c-representation
$\Delta$
is weakly consistent there is at least one conservative extended c-representation
![]() $\kappa \in \mathit{CMod}^{ec}_{\Delta}$
and, by Proposition 26,
$\kappa \in \mathit{CMod}^{ec}_{\Delta}$
and, by Proposition 26,
![]() $\kappa(A) = \infty$
. Therefore,
$\kappa(A) = \infty$
. Therefore,
![]() $A |\hspace{-2pt} {\sim}^{cews}_{\Delta} B$
.
$A |\hspace{-2pt} {\sim}^{cews}_{\Delta} B$
.
Case 2:
![]() $\kappa^z_{\Delta}(A B) \lt \infty$
and
$\kappa^z_{\Delta}(A B) \lt \infty$
and
![]() $\kappa^z_{\Delta}(A \overline{B}) = \infty$
$\kappa^z_{\Delta}(A \overline{B}) = \infty$
Then, by the definition of
![]() $\mathit{CMod}^{ec}_{\Delta}$
, we have
$\mathit{CMod}^{ec}_{\Delta}$
, we have
![]() $\kappa(A B) \lt \infty$
and, by Proposition 26,
$\kappa(A B) \lt \infty$
and, by Proposition 26,
![]() $\kappa(A\overline{B}) = \infty$
for every
$\kappa(A\overline{B}) = \infty$
for every
![]() $\kappa \in \mathit{CMod}^{ec}_{\Delta}$
. Therefore,
$\kappa \in \mathit{CMod}^{ec}_{\Delta}$
. Therefore,
![]() $\kappa(A B) \lt \kappa(A \overline{B})$
for every
$\kappa(A B) \lt \kappa(A \overline{B})$
for every
![]() $\kappa \in \mathit{CMod}^{ec}_{\Delta}$
. Because
$\kappa \in \mathit{CMod}^{ec}_{\Delta}$
. Because
![]() $\Delta$
is weakly consistent there is at least one
$\Delta$
is weakly consistent there is at least one
![]() $\kappa^* \in \mathit{CMod}^{ec}_{\Delta}$
with
$\kappa^* \in \mathit{CMod}^{ec}_{\Delta}$
with
![]() $\kappa^*(AB) \lt \kappa^*(A\overline{B})$
and thus
$\kappa^*(AB) \lt \kappa^*(A\overline{B})$
and thus
![]() $A |\hspace{-2pt} {\sim}_{\kappa^*} B$
. Furthermore, there cannot be a conservative extended c-representation
$A |\hspace{-2pt} {\sim}_{\kappa^*} B$
. Furthermore, there cannot be a conservative extended c-representation
![]() $\kappa'$
with
$\kappa'$
with
![]() $A |\hspace{-2pt} {\sim}_{\kappa'} \overline{B}$
, because this would imply
$A |\hspace{-2pt} {\sim}_{\kappa'} \overline{B}$
, because this would imply
![]() $\kappa'(A) = \infty$
or
$\kappa'(A) = \infty$
or
![]() $\kappa'(A\overline{B}) \lt \kappa'(AB)$
, contradicting the results above. Thus,
$\kappa'(A\overline{B}) \lt \kappa'(AB)$
, contradicting the results above. Thus,
![]() $A |\hspace{-2pt} {\sim}^{cews}_{\Delta} B$
.
$A |\hspace{-2pt} {\sim}^{cews}_{\Delta} B$
.
Case 3:
![]() $\kappa^z_{\Delta}(A \overline{B}) \lt \infty$
$\kappa^z_{\Delta}(A \overline{B}) \lt \infty$
Then, by assumption,
![]() $\kappa^z_{\Delta}(AB) \lt \infty$
, the CSP
$\kappa^z_{\Delta}(AB) \lt \infty$
, the CSP
![]() ${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}} \cup {{\mathit{CR}_{\Delta}{{(B|A)}}}}$
is solvable, and
${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}} \cup {{\mathit{CR}_{\Delta}{{(B|A)}}}}$
is solvable, and
![]() ${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}} \cup {{\mathit{CR}_{\Delta}{{(\overline{B}|A)}}}}$
is unsolvable.
${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}} \cup {{\mathit{CR}_{\Delta}{{(\overline{B}|A)}}}}$
is unsolvable.
![]() ${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}} \cup {{\mathit{CR}_{\Delta}{{(B|A)}}}}$
being solvable implies that there is an
${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}} \cup {{\mathit{CR}_{\Delta}{{(B|A)}}}}$
being solvable implies that there is an
![]() $\vec{\eta}^J \in {{\mathit{Sol}({{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}})}}$
satisfying
$\vec{\eta}^J \in {{\mathit{Sol}({{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}})}}$
satisfying
![]() ${{\mathit{CR}_{\Delta}{{(B|A)}}}}$
. Using the equivalence transformations as in the proof for Proposition 71, Direction
${{\mathit{CR}_{\Delta}{{(B|A)}}}}$
. Using the equivalence transformations as in the proof for Proposition 71, Direction
![]() $\Rightarrow$
, there is an
$\Rightarrow$
, there is an
![]() $\vec{\eta}^* \in Sol^{J+\infty}_\Delta$
constructed from
$\vec{\eta}^* \in Sol^{J+\infty}_\Delta$
constructed from
![]() $\vec{\eta}^J$
with
$\vec{\eta}^J$
with
![]() $\kappa_{\vec{\eta}^*}(AB) \lt \kappa_{\vec{\eta}^*}(A\overline{B})$
. With Proposition 47, it follows that
$\kappa_{\vec{\eta}^*}(AB) \lt \kappa_{\vec{\eta}^*}(A\overline{B})$
. With Proposition 47, it follows that
![]() $\kappa_{\vec{\eta}^*} \in \mathit{CMod}^{ec}_{\Delta}$
. Thus, we found a conservative extended c-representation
$\kappa_{\vec{\eta}^*} \in \mathit{CMod}^{ec}_{\Delta}$
. Thus, we found a conservative extended c-representation
![]() $\kappa^* = \kappa_{\vec{\eta}^*}$
with
$\kappa^* = \kappa_{\vec{\eta}^*}$
with
![]() $A |\hspace{-2pt} {\sim}_{\kappa^*} B$
.
$A |\hspace{-2pt} {\sim}_{\kappa^*} B$
.
Analogously,
![]() ${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}} \cup {{\mathit{CR}_{\Delta}{{(\overline{B}|A)}}}}$
being unsolvable implies that
${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}} \cup {{\mathit{CR}_{\Delta}{{(\overline{B}|A)}}}}$
being unsolvable implies that
![]() ${{\mathit{CR}_{\Delta}{{(\overline{B}|A)}}}}$
is violated for every solution of
${{\mathit{CR}_{\Delta}{{(\overline{B}|A)}}}}$
is violated for every solution of
![]() ${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}}$
. Using the equivalence transformation from the proof for Proposition 71, Direction
${{\mathit{CRS}^{ex}_{\Sigma}(\Delta)}}$
. Using the equivalence transformation from the proof for Proposition 71, Direction
![]() $\Rightarrow$
, this implies that for every
$\Rightarrow$
, this implies that for every
![]() $\vec{\eta} \in Sol^{J+\infty}_\Delta$
we have
$\vec{\eta} \in Sol^{J+\infty}_\Delta$
we have
![]() ${{\kappa_{\vec{\eta}}}}(AB) \not\lt {{\kappa_{\vec{\eta}}}}(A\overline{B})$
and thus, with Proposition 47,
${{\kappa_{\vec{\eta}}}}(AB) \not\lt {{\kappa_{\vec{\eta}}}}(A\overline{B})$
and thus, with Proposition 47,
![]() $\kappa(AB) \not\lt \kappa(A\overline{B})$
for every
$\kappa(AB) \not\lt \kappa(A\overline{B})$
for every
![]() $\kappa \in \mathit{CMod}^{ec}_{\Delta}$
. Therefore, there cannot be a conservative extended c-representation
$\kappa \in \mathit{CMod}^{ec}_{\Delta}$
. Therefore, there cannot be a conservative extended c-representation
![]() $\kappa'$
with
$\kappa'$
with
![]() $A |\hspace{-2pt} {\sim}_{\kappa'} \overline{B}$
, because this would imply
$A |\hspace{-2pt} {\sim}_{\kappa'} \overline{B}$
, because this would imply
![]() $\kappa'(A) = \infty$
or
$\kappa'(A) = \infty$
or
![]() $\kappa'(A\overline{B}) \lt \kappa'(AB)$
, contradicting the results above.
$\kappa'(A\overline{B}) \lt \kappa'(AB)$
, contradicting the results above.
In summary, it follows that
![]() $A |\hspace{-2pt} {\sim}^{cews}_{\Delta} B$
.
$A |\hspace{-2pt} {\sim}^{cews}_{\Delta} B$
.
The inductive inference operators developed and addressed in this article together with their interrelationships are summarized and illustrated in Figure 2.
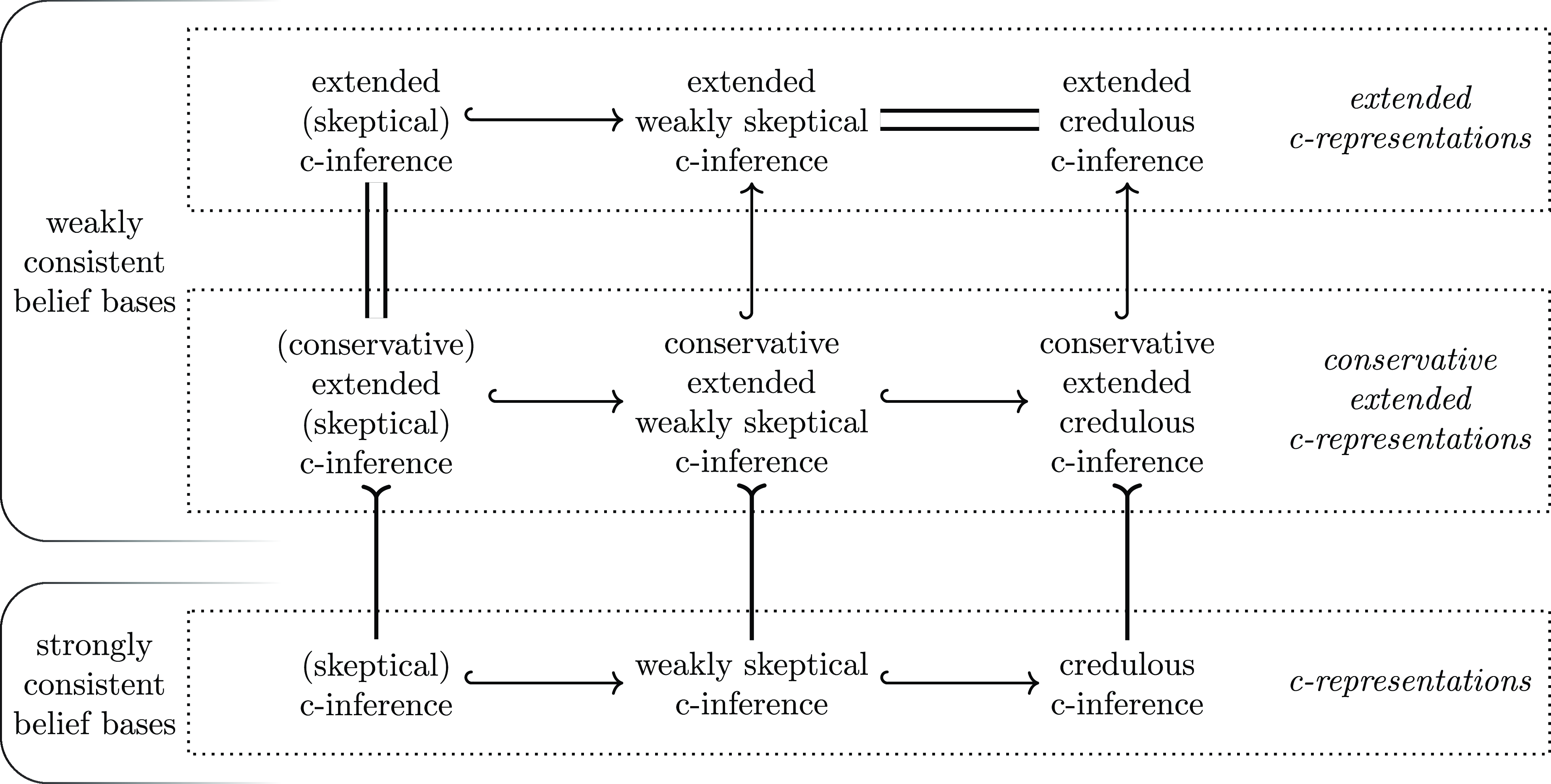
Figure 2. A Summary of inductive inference operators and theirinterrelationships. The left-most column indicates whether theinference operator is defined on weakly consistent belief bases or onstrongly consistent belief bases only. The right-most columnindicates the class of c-representations that the inference operator takes into account. An arrow
![]() $I_1\, {-\!\!-\!\!\!\lt}\ I_2$
indicates that the inductive inference operator
$I_1\, {-\!\!-\!\!\!\lt}\ I_2$
indicates that the inductive inference operator
![]() $I_1$
and the restriction of
$I_1$
and the restriction of
![]() $I_2$
to strongly consistent belief bases coincide. A double line
$I_2$
to strongly consistent belief bases coincide. A double line
![]() $I_1 = I_2$
indicates that
$I_1 = I_2$
indicates that
![]() $I_1$
and
$I_1$
and
![]() $I_2$
coincide. An arrow
$I_2$
coincide. An arrow
![]() $I_1 \, {\hookrightarrow} \, I_2$
indicates that
$I_1 \, {\hookrightarrow} \, I_2$
indicates that
![]() $I_1$
is captured by
$I_1$
is captured by
![]() $I_2$
and that
$I_2$
and that
![]() $I_1$
is strictly extended by
$I_1$
is strictly extended by
![]() $I_2$
for some belief bases.
$I_2$
for some belief bases.
10. Conclusions and future work
Weakly consistent belief bases are belief bases that may enforce some worlds to be completely implausible. In this article, we investigated how the knowledge given in a conditional belief base that is not strongly consistent, but only weakly consistent, can be completed by applying an inductive inference operator. After presenting the treatment of weakly consistent belief bases by p-entailment and system Z, we focussed on c-representations. For c-inference extended to weakly consistent belief bases, we developed a CSP characterizing it. We showed that extended c-inference can be realized equivalently by a specialized CSP taking just conservative extended c-representations into account. Moreover, we showed that extended c-inference inherits highly desirable inference properties, in particular, that extended c-inference fully complies with syntax splitting. For this, we proved that extended c-inference satisfies adapted versions of (Rel) and (Ind) that also take inference from weakly consistent belief bases into account. We also extended credulous and weakly skeptical c-inference and provided realizations for them as CSPs. We observed that for credulous and weakly skeptical c-inference, the distinction whether extended or only conservative extended c-representations are taken into account is significant, leading to a map of interesting, specific interrelationsships among the various inference operators. In Haldimann and Beierle (Reference Haldimann and Beierle2024), a comprehensive map of the relationships of extended c-inference to other inductive inference operators taking weakly consistent belief bases into account can be found.
Future work includes investigating how the reasoning with infeasible worlds relates to approaches to paraconsistent reasoning like Priest’s logic LP (Priest, Reference Priest1979). Furthermore, similarly as it has been done for c-inference, we will employ compilation techniques (Beierle et al., Reference Beierle, Kutsch and Sauerwald2019b) for extended c-inference and we will realize it as a SAT and as an SMT problem (Beierle et al., Reference Beierle, von Berg, Sanin, Keshtkar and Franklin2022; von Berg et al., Reference von Berg, Sanin, Beierle, Bouraoui, Jabbour and Vesic2023, Reference von Berg, Sanin, Beierle, Meier and Ortiz2024) and implement it in the InfOCF reasoning platform (Beierle et al., Reference Beierle, Eichhorn and Kutsch2017; Kutsch & Beierle, Reference Kutsch and Beierle2021; Beierle et al., Reference Beierle, Spiegel, Haldimann, Wilhelm, Heyninck, Kern-Isberner, Marquis, Ortiz and Pagnucco2024, Reference Beierle, Haldimann, Sanin, Spang, Spiegel, von Berg, Casini, Dundua and Kutsia2025). We will also generalize the implementations of p-entailment and system Z existing in InfOCF to the treatment of weakly consistent belief bases as described in this article.
Acknowledgements
This work was supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)—512363537, grant BE 1700/12-1 awarded to Christoph Beierle.
This work was partially supported by the Austrian Science Fund (FWF) projects P30873, PIN8884924, and the FWF and netidee SCIENCE project T1349-N.