Introduction
The melting of sea ice is a much more complex process than the melting of freshwater ice. In the latter case, the ice has a well-defined melting temperature (0°C), at which it transforms from its solid state into its liquid state. If both the bottom and the top of a piece of freshwater ice are at melting temperature, phase changes only take place at these surfaces, while the interior of the ice remains solid at a temperature that will quickly adjust to 0°C, too.
The melting of sea ice, in contrast, is complicated by the fact that sea ice is a mixture, primarily of pure freshwater ice and interstitial brine. At the boundary between these two phases, phase equilibrium is always maintained. As such, sea ice does not have a specific, single melting temperature, but changes some of its freshwater ice into liquid whenever it is heated (Reference NotzNotz, 2005). This phase change during any temperature change of sea ice causes its heat capacity to be significantly higher than that of freshwater ice, since the effective heat capacity of sea ice must also take into account the heat required for the internal phase change. For the same external forcing, the interior of sea ice therefore changes its temperature much more slowly than freshwater ice.
While these differences have long been known (e.g. Reference MalmgrenMalmgren, 1927) and have been shown through model studies to affect the amplitude and the phase of the seasonal cycle of sea ice (e.g. Reference SemtnerSemtner, 1984; Reference FichefetFichefet and Morales Maqueda, 1997), systematic studies of how they affect the melt rate are largely lacking. Reference Vancoppenolle and FichefetVancoppenolle and others (2005) found that less saline ice sometimes melts faster than more saline ice because of its lower heat capacity, and sometimes melts more slowly because of its higher solid fraction. Here we quantitatively investigate the melt rates of sea ice and freshwater ice in a laboratory set-up and in temperature-salinity simulations. Combining the laboratory experiments with one-dimensional (1-D) modelling provides additional insight into the physical processes that govern the melting of sea ice and of pure ice: once the model is shown to reproduce the laboratory experiments, we can use it to examine the relationship of the various processes that occur in ice under similar conditions.
A laboratory set-up is obviously a simplification of the real world. For example, we neglect the impact of solar radiation, of horizontal inhomogeneities, of snowfall, of changing meteorological and oceanographic conditions, etc. On the other hand, this simplification allows us to investigate specific processes which occur during the melting of sea ice under controlled conditions and with a high level of detail.
We introduce our laboratory set-up and the model in the following section. We then try to answer the three main questions that motivated this study: First, we investigate the temporal evolution of the melt rate of sea ice and freshwater ice. Second, we examine how the evolving internal temperature field interacts with the evolving salinity profile to explain the observed melt rates. And third, we examine how the surface temperature of the two ice types evolves during melting, which is of particular relevance for the outgoing longwave radiation and the remote sensing of sea ice from satellites. These questions are all answered in a purely 1-D framework. We close with a short discussion and a summary of our findings.
Experimental Set-Up and Model Configuration
In our laboratory experiments, we carried out melting experiments with sea ice and pure ice under controlled, largely reproducible conditions. This allowed us to directly compare the evolution of pure ice in one experiment with that of sea ice in another experiment. Because of the limited dimensions of our tank and the limited time we had available for this study, we focused on relatively thin ice with a thickness of ∼0.1 m.
Experimental set-up
The ice was grown and melted in a 1.94 m long, 0.66 m wide tank which was filled with water up to a height of ∼0.9m. Styrofoam plates 0.05 m thick insulated the tank walls and bottom thermally to ensure that the heat exchange with the ambient air occurred only through the air-water interface. Heating plates installed at the water level around the whole tank kept the ice from freezing to the walls.
The tank was placed in a cold room, whose air temperature was varied according to the experimental protocol described below. The surface of the ice and water in the tank was continuously monitored with both a standard webcam and an infrared camera ('VarioCAM high resolution' from InfraTec). A standard meteorological thermometer (Young platinum temperature probe, model 41342) was used to measure air temperature inside the cold room just above the tank and hence ∼0.2 m above the water level. Inside the tank, a ruler was mounted that was subsequently frozen into the ice, which allowed us to visually measure the ice thickness. The ruler was mounted within our main measuring area close to the centre of the tank. About 0.3 m from this ruler, a thermistor chain with 29 thermistors was mounted that measured the ice temperature every 10s with a spatial resolution of up to 0.005 m. The thermistor chain had a counterweight to prevent the ice from being pulled underneath the water surface by the weight of the thermistor chain. In order to simulate an oceanic heat flux and to prevent supercooling in the water, we installed a heating wire at the bottom of the tank, which continuously provided a heat flux of 15 Wm 2 . This heat flux was determined by dividing the input of electric power to the wire by the tank surface area. At the height of the tank rim a ventilator mixed the air inside the cold room to avoid an accumulation of cold air inside the tank directly above the ice surface, which otherwise occurs during melting conditions. The water itself was stirred by two pumps during the cooling phase preceding the actual experiments described here. During the freezing and melting cycles described here, those pumps were turned off. Hence, the ice in our experiments was grown under calm conditions and we expect it to be columnar straight from the beginning. Unfortunately, we did not observe the stratigraphy in our experiments to firmly support this assumption. Further details of our experimental set-up are given by Reference WieseWiese (2012).
The tank was placed in a cold room, whose air temperature was varied according to the experimental protocol described below. The surface of the ice and water in the tank was continuously monitored with both a standard webcam and an infrared camera ('VarioCAM high resolution' from InfraTec). A standard meteorological thermometer (Young platinum temperature probe, model 41342) was used to measure air temperature inside the cold room just above the tank and hence ∼0.2 m above the water level. Inside the tank, a ruler was mounted that was subsequently frozen into the ice, which allowed us to visually measure the ice thickness. The ruler was mounted within our main measuring area close to the centre of the tank. About 0.3 m from this ruler, a thermistor chain with 29 thermistors was mounted that measured the ice temperature every 10s with a spatial resolution of up to 0.005 m. The thermistor chain had a counterweight to prevent the ice from being pulled underneath the water surface by the weight of the thermistor chain. In order to simulate an oceanic heat flux and to prevent supercooling in the water, we installed a heating wire at the bottom of the tank, which continuously provided a heat flux of 15 Wm 2 . This heat flux was determined by dividing the input of electric power to the wire by the tank surface area. At the height of the tank rim a ventilator mixed the air inside the cold room to avoid an accumulation of cold air inside the tank directly above the ice surface, which otherwise occurs during melting conditions. The water itself was stirred by two pumps during the cooling phase preceding the actual experiments described here. During the freezing and melting cycles described here, those pumps were turned off. Hence, the ice in our experiments was grown under calm conditions and we expect it to be columnar straight from the beginning. Unfortunately, we did not observe the stratigraphy in our experiments to firmly support this assumption. Further details of our experimental set-up are given by Reference WieseWiese (2012).
For the experiments the tank was filled with water of a particular salinity, being 0g kg-1 for the pure-ice experiments and 12, 28 and 3 3 g kg-1, respectively, for different sea-ice experiments. These different salinities were chosen to examine the impact of initial salinity on the resulting sea-ice melting. For all experiments, ice was grown to a thickness of 0.1 m at a temperature of -20°C. Once that thickness was reached, the air temperature was either increased directly to +10°C or increased stepwise to simulate a slower transition from freezing to melting conditions. All in all, we conducted two freshwater-ice experiments and 14 sea-ice experiments. Because of space constraints, here we only discuss results from two freshwater ice and three sea-ice experiments. Our findings are, however, generally valid for all our experiments and hence not affected by this subsampling. Details for the other experiments are given by Reference WieseWiese (2012).
During all experiments, the ice thickness was measured manually once every hour during daytime by reading off the position of the ice bottom at the location of the ruler that was frozen into the ice. No measurements were carried out during night-time. Towards the end of the melting period, the ice thickness became horizontally very inhomogeneous. Once the ice was subjectively too inhomogeneous to allow a meaningful ice-thickness measurement, we stopped the manual ice-thickness measurement and instead relied on webcam images to determine the time of the total loss of ice from the tank. This time then defined the end of our experiments. We estimate the absolute accuracy of the thickness reading to be better than 0.004 m. During ice growth, this error is dominated by a possible parallax error, since we only had a single ruler frozen into the ice. During melting, the bottom of the ice becomes uneven, and the error becomes dominated by the subjective averaging across this unevenness that amounted to a few millimetres. The relative error of the thickness reading is better than 0.004 m, since an individual observer usually makes a similar parallax error between measurements. Based on this and on our hourly sampling rate, we trust that the error in melt rate is ˂ 0 . 0 0 4 m h-1 . The accuracy of the temperature measurements with the thermistors was better than ±0.2°C.
Model configuration
To understand the evolution of the melting ice in the laboratory experiments, we carried out corroborating simulations with the 1-D multiphase sea-ice model SAMSIM (Reference Griewank and NotzGriewank and Notz, 2013). This model simulates vertical desalination processes such as gravity drainage, which is the convective overturning of brine with underlying sea water, and flushing, which describes the removal of brine by percolating surface meltwater. The changes in phase composition that result from these desalination processes are simulated based on the mushy-layer description of sea ice (see also Reference Hunke, Notz and VancoppenolleHunke and others, 2011). The flushing parameterization was slightly simplified for this study compared to the original description by disregarding horizontal fluxes during flushing as the melting laboratory ice is much more horizontally homogeneous than ice of the same thickness under field conditions.
The model grid finely resolves the profiles of temperature, salinity, enthalpy and mass towards the top and the bottom of the ice, with a possible coarser resolution in the ice's interior. The number of gridcells increases up to a fixed value as the ice thickens in the simulations. For the simulations presented here, the number of gridcells was limited to 70, the minimum layer thickness is 0.002 m and the time step was set to 1 s.
The boundary condition for the model that dominates ice growth and melt is the atmospheric heat flux. No measurements were taken of the radiative, latent and sensible heat fluxes in the cooling chamber. In the absence of data we assume that the atmospheric heat flux is proportional to the temperature difference between the air temperature and the ice-surface temperature. This rather crude approximation requires a proportionality constant which depends on the thermal radiation and the airflow in the cooling chamber. In an attempt to take into account the stratification above the ice, each experiment has one proportionality constant for freezing and another constant for melting as the stable stratification above the melting ice substantially reduces heat transfer. The proportionality constants were chosen to replicate the thickness measurements and ranged from 12.5 to 1 6 W m -2 K -1 for growing ice and were up to 30% smaller for melting ice.
All other experimental parameters such as the oceanic heat flux, the water salinity, the air temperature and the duration of ice growth were directly taken from the laboratory measurements. For technical reasons, however, the air temperature in the model does not change continuously, but is only updated once every hour.
Results
Melt rate and internal temperature
We now turn to a presentation of experimental results, starting with the melt rate and its relationship to the internal temperature of the ice. We use the term 'melt rate' somewhat loosely to refer to the change in ice thickness per unit time both for sea ice and for freshwater ice. More precisely, one would refer to this thickness change for sea ice by a more general term that accounts for the fact that sea ice usually does not melt, but that its freshwater ice content is instead dissolved into the surrounding brine. This explains why the thinning of sea ice and its internal phase changes usually occur at temperatures below 0°C, where melting of its freshwater ice crystals is impossible (see also Reference WoodsWoods, 1992). In line with common terminology, we nevertheless decided to refer to the thickness change of sea ice as melting.
Freshwater ice
The thinning of freshwater ice, in contrast, indeed occurs through melting, and the melting process can easily be captured mathematically. For melting to occur in freshwater ice, its temperature must be increased to its melting temperature T m=0°C. For freshwater ice as thin as in our
experiment, we can assume that the entire body of ice is warmed to that temperature from an initially linear temperature gradient with a surface temperature Ts and a bottom temperature Tb = 0°C. The energy ΔH needed to warm the entire layer of ice with a thickness h to the melting temperature Tm = Tb is then given by
where p920 kg m 3 is cp ≈ 2000 kJ kg 1 K 1 is its heat capacity. For a given heat flux Q, the time t needed until the ice starts melting is then simply given by AH/Q. Once that time is passed, the ice will start thinning at a rate h given by the latent heat of fusion L of ice according to
In our experiments, we had a heat flux of ∼60 W m 2 towards the ice surface after the increase of the cold room's air temperature to +10 °C, plus an additional heat flux of 15 W m 2 from the heating wire in the tank. For our freshwater experiments with an ice thickness h = 0.1 m and an initial surface temperature of around -7°C, such heat flux can warm the ice to its melting temperature within t ≈ 3 hours. The relatively short adjustment time until the freshwater ice has reached its melting temperature throughout is seen both in the experiment and in the model simulation (black lines in Fig. 1). The adjustment time is in our case a few hours longer than predicted by the simple calculation because of a ∼5hour long time span that the cold room's temperature needed to reach its new steady state. This timescale of a few hours for the temperature adjustment of freshwater ice is comparable to the diffusive timescale h2/(k/(pcp)), which is for a heat conductivity k ≈ 2 W m 2 K - 1 and a thickness of h = 0.1 m around 3 hours. This suggests that indeed the temperature profile will remain close to linear throughout the experiment.
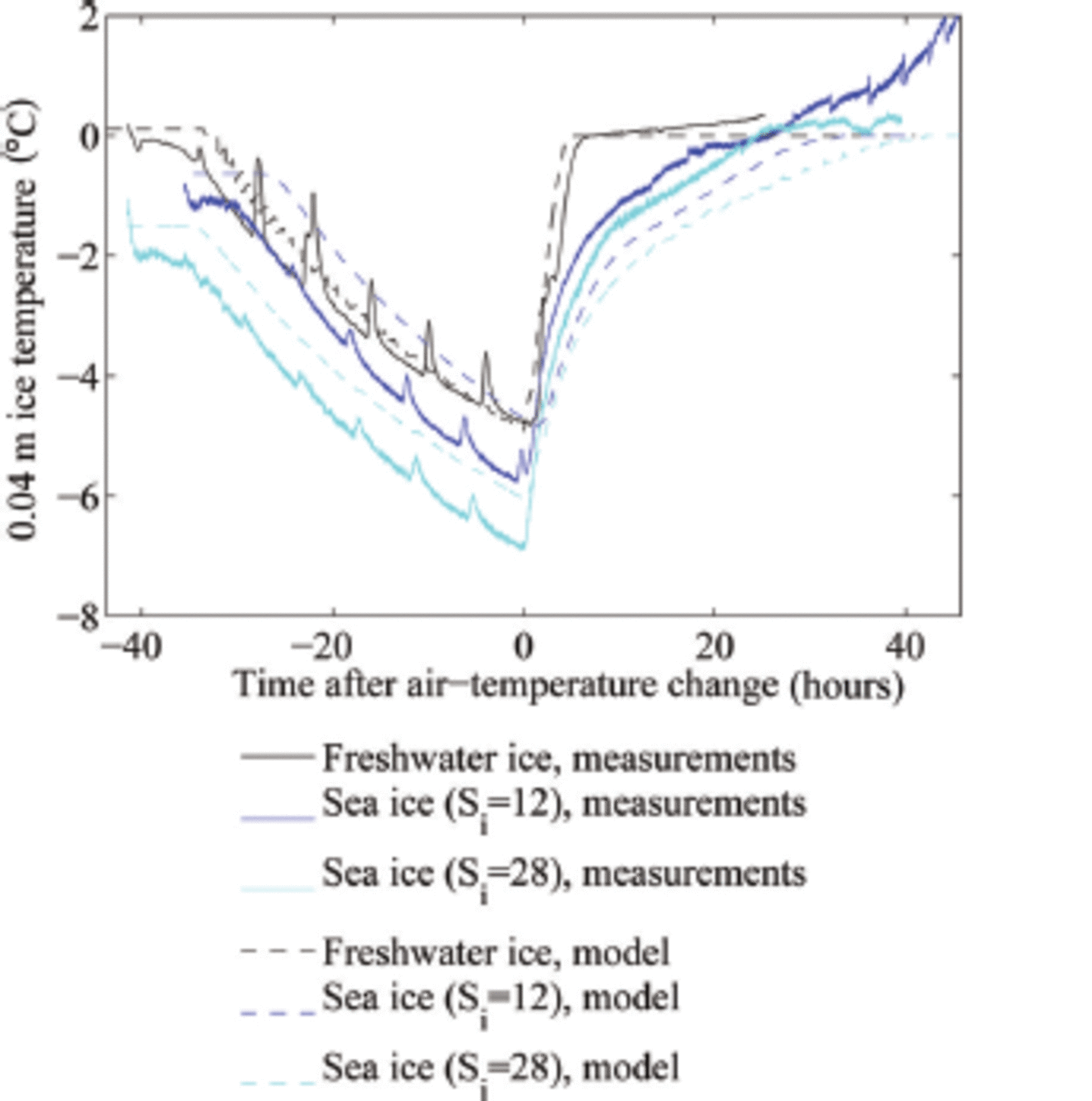
Fig. 1. Evolution of the ice temperature at 0.04 m depth in the laboratory and model experiments. The regular increase in temperature every 6 hours is caused by the defrost cycle of our cold room.
For the evolution of ice thickness the initial fast adjustment in the temperature field causes a quick transition from a growth rate of ∼0.001 m h- 1 to a melt rate of ∼0.001 m h- 1, which is then roughly constant for at least 50 hours in the experiments (red lines in Fig. 2c). After that time, the ice thickness in the tank became too inhomogeneous the density to allow of meaningful the ice and measurements of ice thickness until the ice was completely melted. Hence, for the final 24 hours of the freshwater experiments, the calculated melt rates are only very crude approximations. The initial, constant melt rate is close to the theoretical value given by Eqn (1), which is h = 0.0011 m h- 1 for the combined atmospheric and oceanic heat flux of Q = 75 W m 2 . The thinning is split according to the fractionation of the heat fluxes, with about four-fifths of the melting occurring at the surface, where the atmospheric heat flux is about Q = 60 W m- 2, and one-fifth occurring at the bottom, where the oceanic heat flux is about Q = 15 W m 2.
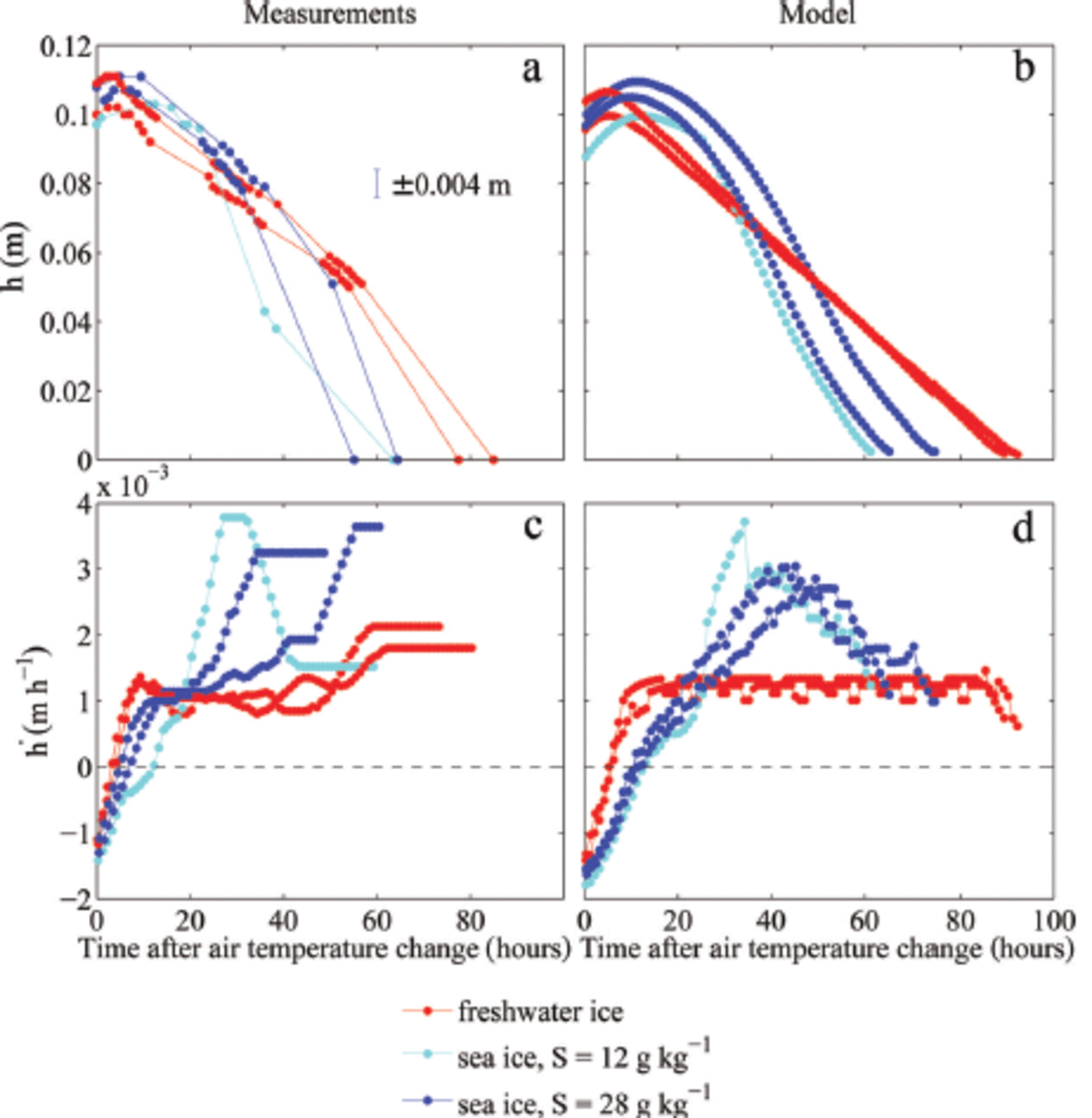
Fig. 2. Measured and modelled temporal evolution of the ice thickness h (a, b) and melt rates (c, d). Only the melting period is shown, and accordingly the time is given in hours after the air temperature change to 10°C. The ice grew in water with different initial salinities S. Each dot in (a) marks one ice-thickness measurement. The melt rate in (c) is calculated from 1 hourly ice-thickness values obtained by linear interpolation. A running mean with a window of 8 hours is applied both to the measured and modelled melt rate.
The model simulations show a very similar behaviour of the melt-rate evolution to that seen in the experiments (red lines in Fig. 2d). However, since no unaccounted lateral heat fluxes exist in the model, the model simulations are in better agreement with theoretical expectations. The simulated melt rate is roughly constant until the ice is fully melted in the model. The slight short-term temporal fluctuations in melt rate are caused by the discrete disappearance of gridcells from the model domain as the ice thinned. Although the amplitude and frequency of these fluctuations depend on the chosen vertical resolution, the mean melt rate evolution is resolution-independent.
Sea ice
The thinning of sea ice, in contrast, shows a much more complex evolution of melt rates, both in the experiment and in the model simulations (blue lines in Fig. 2c and d): The melt rate increases more slowly than that of freshwater ice, eventually reaches a much higher value than that of freshwater ice and finally decreases again to values close to the melt rate of freshwater ice. The initial salinity of the water is also crucial, with the ice grown from less salty water showing an initially slower increase in melt rate and a higher maximum melt rate (light blue lines in Fig. 2c and d).
To understand this behaviour, it is useful to carry out a simple calculation similar to that outlined above for freshwater ice. However, to calculate the time that it would take the ice to warm to a temperature close to its liquidus temperature, we now have to take the temperature dependence of the heat capacity into account: during the warming of sea ice not only the brine and the ice warm, some of the solid ice is also dissolved into the surrounding brine. To calculate the energy needed to warm the ice from a temperature T 1 to a temperature T2 it is easiest to consider the change in enthalpy between these two temperatures. Generally, the enthalpy content of sea ice is given by
(e.g. Reference NotzNotz, 2005). Here subscripts s and br denote solid and brine, respectively, and ϕ is solid fraction. The equality of the two lines follows from the fact that Hbr Hs is the latent heat L The liquid fraction 1 is given as the ratio of bulk salinity to brine salinity, Sbu/S br, where the former is the salinity of a melted sea-ice sample and the latter can be approximated as T/α, where a is the proportionality constant that approximately links the brine salinity to its respective liquidus temperature. The enthalpy change between two temperatures T 1 and T2 is then directly given as
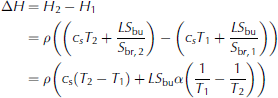
see also Reference Vancoppenolle and FichefetUntersteiner, 1961), where c s = œ•H/œ•T is the heat capacity of the solid ice. Since in our set-up the temperature profile of sea ice is roughly linear at the end of the freezing period, we can use the bottom line of Eqn (3) to approximate the total amount of energy needed to warm the entire ice layer to its liquidus temperature depending on its respective bulk salinity. We find that for a mean bulk salinity of 1-15g kg 1, a surface temperature of about 7°C, a bottom temperature of about -2°C and a heat flux of Q = 75Wm-2we would need between 75 hours for S bu =15gkg-1 and 93 hours for S bu = 1 g kg -1 to heat the entire ice layer to its liquidus temperature. The time span needed to warm freshwater ice is much shorter than for sea ice, because we actually completely transform the sea ice into water by heating the ice to its liquidus temperature. This is also the reason why the calculation gives a longer time for the warming of the ice with a lower bulk salinity: the ice has a higher solid fraction, which needs more energy to be completely changed into liquid.
Because the typical timescale for the heating of the sea ice is much longer than the diffusive timescale of ∼3 hours, the temperature profile during the heating will no longer be linear (see Fig. 3). Instead, we expect a temperature minimum in the interior of the ice, which indeed we find both in the experiments and in the simulations. This implies that we can no longer roughly separate an initial period of warming of the ice from a consecutive period of thinning of the ice, as was the case for freshwater ice. For sea ice, the ice still keeps warming significantly in its interior as the surface is already at its liquidus temperature (cf. blue lines in Fig. 1).

Fig. 3. Measured (a) and modelled (b) temperature profiles of freshwater ice and sea ice (initial water salinity S =28 g kg 1) during ice growth (35 hours after start of experiment) and melting (60 hours after start of experiment). The depth is given as distance from the first thermistor above the ice surface. The dotted line indicates 0°C.
This slow heating of the ice's interior explains the initial shape of the observed and modelled evolution of the melt rates that is shown in Figure 2c and d: as the ice's interior gets warmer during the heating, the heat flux into the ice's interior becomes smaller. Therefore, more energy remains available to thin the ice at the bottom and at the surface, which explains the initial increase in melt rate. Compared to freshwater ice, the initial melting is slower because more energy is used to warm the interior of the sea ice and to decrease its solid fraction. At later stages, however, this initial investment of energy pays off, and the by then much less solid sea ice thins faster than freshwater ice. To understand why the thinning of the sea ice eventually slows down again, we need to consider the vertical inhomogeneity of the bulk salinity within the ice. Since we do not have direct measurements of bulk salinity available, we use for our analysis the simulated bulk salinity evolution shown in Figure 4.
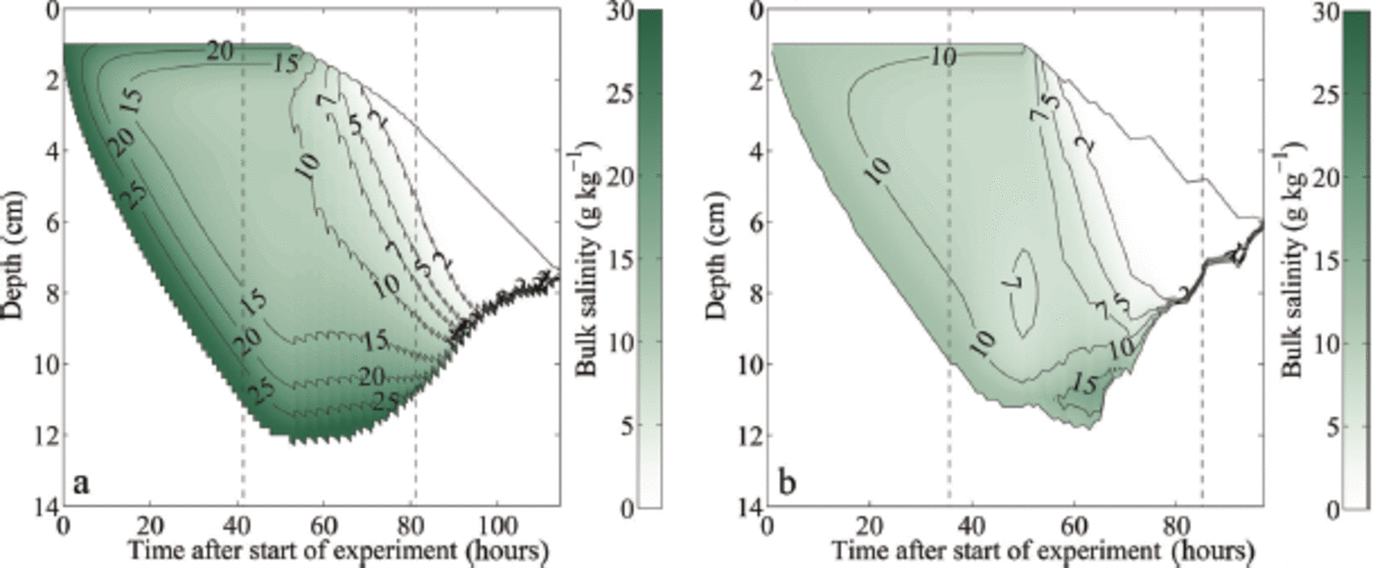
Fig. 4. Modelled temporal evolution of the bulk salinity during growth and melting of sea ice: (a) initial water salinity S = 28 gkg-1; (b) initial water salinity S = 12 gkg-1 . The depth is given as distance from the first thermistor above the ice surface. The black solid lines indicate the modelled ice surface and bottom. The left black dashed line in each panel indicates the time when the air temperature was switched to melting conditions, while the right black dashed line indicates the time when the ice had completely melted around the thermistor chain in the laboratory experiment, which occurred several hours before the complete melting of the ice in the tank.
The simulations show clearly that after the onset of surface warming, flushing sets in, which transports cold and salty brine from higher up in the ice to the region close to the ice-ocean interface. Heat diffusion from the ice-ocean interface into the ice and the negative heat advection of the cold flushing brine cools the lower layers for a short time after the onset of melting. This cooling keeps the highly saline lowest layers with a low solid fraction from being melted away by the oceanic heat flux. In the 12g kg-1 simulation the sum of the diffusive heat flux from the ice-ocean interface and the negative heat advection of the cold brine is stronger than the oceanic heat flux, which causes some ice to grow at the ice-ocean interface (Fig. 4). However, once the heat flux from the interior ice is depleted, a relatively rapid bottom ablation occurs, since only ice with a comparably low solid fraction needs to be completely dissolved to thin the bottom ice. This initially slow melt followed by a rapid thinning is visible in all sea-ice experiments and simulations (Fig. 2).
Once the salty layer at the bottom is fully eroded, bottom ablation slows down significantly, since then ice with a much higher solid fraction is present at the ice-ocean interface. For example, ice grown in water with an initial water salinity of 28 gkg-1 has a very low bulk salinity close to 0gkg-1 about 95 hours after the start of the experiment and the bottom ablation decreases from this moment on (Fig. 4). It is primarily this decrease in bottom ablation that causes the observed and modelled slowdown of the thinning after the initial acceleration. This process is amplified by the fact that flushing continues to very effectively desalinate the ice, which is seen in the almost complete loss of bulk salinity in the simulations as time progresses. Hence, the solid fraction of the remaining ice becomes higher and higher, making it more and more difficult to thin that remaining ice. The melt rates of the sea ice therefore approach those of freshwater ice towards the end of the experiment, both in the laboratory and in the numerical model. In line with expectations, we always find that sea ice is fully melted faster than freshwater ice, because sea ice has a lower overall solid content and hence requires less time to melt for any given heat flux than the fully solid freshwater ice.
The observed differences between the thickness evolution of the sea ice grown from water of 12 gkg-1 initial salinity and that grown from 28g kg-1 are simulated well by the numerical model. Both in the experiment and in the simulations the less salty ice that formed from the less salty water has initially a slightly slower increase in melt rate than the saltier ice. This reflects the larger amount of energy that is transformed through internal phase changes in the more solid, less saline ice.
The maximum melt rate eventually reached is higher in the less salty ice than in the saltier ice. This seems to be primarily related to the evolution of bottom ablation, which shows larger variations in the less salty ice grown from water of 12 g kg-1 initial salinity compared to the ice grown from 28gkg-1 . In the 12gkg-1 case, about half of the thinning occurs at the bottom, while in the 28 gkg-1 case the bottom melt accounts for only about one-third of the total thinning. These fractions are different to those seen in freshwater ice which were given by the ratio of the atmospheric to oceanic heat fluxes. This exemplifies the impact of the internal thermodynamics of sea ice on thinning rates. However, the stronger thinning from below for the less salty compared to the saltier ice is not fully understood yet. In the simulations, a more extensive region of very low solid fraction forms towards the bottom of the less saline ice, which is then quickly eroded away, explaining the high rates of thinning roughly 30-40 hours after the increase in cold-room temperature. The formation of ice with such low solid fractions is highly dependent on the salt and heat fluxes at the ice-water interface which are only crudely included in the model. Despite the model limitations the amplitude and timing of the maximum melt rate agree very well between simulations and experiment, and the evolution of the temperature field is also captured well in the model for all ice types (Fig. 5).
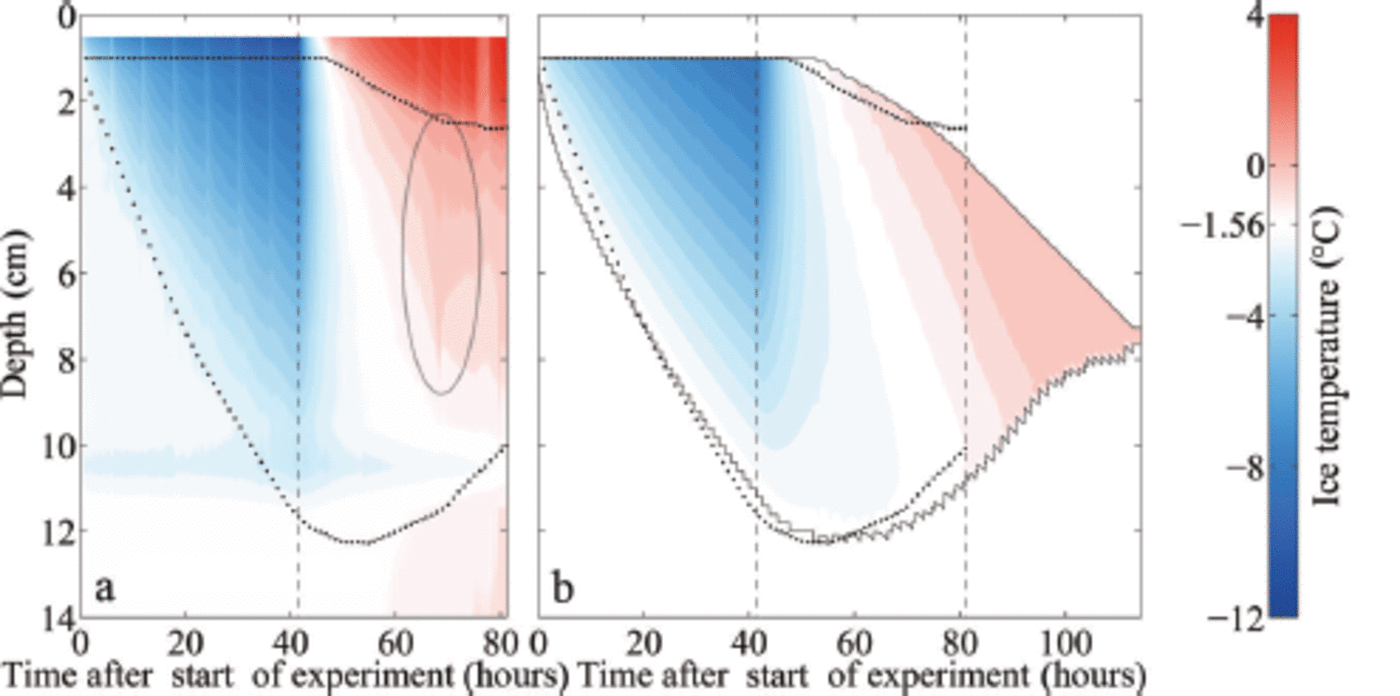
Fig. 5. Measured (a) and modelled (b) temporal evolution of the ice temperature during growth and melting of sea ice (initial water salinity S =28 g kg 1 ) . The depth is given as distance from the first thermistor above the ice surface. The upper dotted line indicates the ice surface, during melting given by the maximum temperature gradient. The lower dotted line indicates the bottom as obtained from the addition of the measured ice thickness to the position of the ice surface. The black solid lines indicate the modelled ice surface and bottom. The left black dashed line in each panel indicates the time when the air temperature was switched to melting conditions, while the right black dashed line indicates the time when the ice had completely melted around the thermistor chain in the laboratory experiment, which occurred several hours before the complete melting of the ice in the tank. White areas indicate the respective freezing point of the water. The ellipse in (a) marks a flushing event.
One final notable feature related to the evolution of internal temperature in our experiments is the signature of a localized flushing event (ellipse in Fig. 5a): Around 25 hours after we raised the air temperature, the ice temperature increased strongly and subsequently decreased again in the upper two-thirds of the ice within a few hours. The measured temperature reaches 0°C and even higher. The sudden onset and short duration of this event point towards a localized flushing event, where penetrating comparably fresh meltwater from the surface desalinates a small region of ice quickly. The rapid desalination leads to a short release of latent heat, as a fraction of the percolated water freezes in order to reach thermal equilibrium. Once the desalination ends, much of the percolated freshwater refreezes in the interior of the ice due to heat diffusion from the colder surrounding ice which was not desalinated by the localized flushing event.
In our set-up, it is likely that the thermistor chain sticking in the ice supported or even induced this localized flushing event due to additional heat conduction that let the ice melt around the chain. After the flushing event the measured temperatures stay above 0°C in the upper 0.02-0.03 m of the ice, which indicates that the thermistors are no longer in
contact with the ice, but instead with comparably warm meltwater. Note, however, that a similar flushing event was observed by Reference Pringle and EickenPringle and others (2007) in a set-up with only horizontal thermistor strings. In any case, such a localized flushing event cannot be reproduced in the 1-D model as a 1-D model cannot account for horizontal variations.
Surface temperature
We now turn to the surface temperatures measured duringour experiments. We measured the surface temperature with an infrared (IR) camera, which we calibrated against temperatures taken by a Seabird CTD SBE 37 to an accuracy of 0.1 K. The camera took pictures of the ice surface every 15-30min.
We found that the structure of the ice surface of growing ice and that of melting ice look quite different. During ice growth the surface of both freshwater ice and sea ice was smooth, except for small areas where frost flowers formed on the surface. During melting the surface of freshwater ice stayed smooth while that of sea ice became uneven. Meltwater from ice and frost flowers accumulated in small surface irregularities and formed small meltwater patches with a diameter of ∼0.01 m (Fig. 6). We are not aware of similar observations from thicker natural sea ice, which suggests that these patches might only form on thin ice where their surface can be in equilibrium with the surrounding water level. If this were the case, these small features would quickly drain away in thicker ice. Because of the potential impact of these small-scale features on both outgoing longwave radiation and microwave emission, we nevertheless find it important to report on this finding.

Fig. 6. A photograph of the sea-ice surface during melting. The picture shows the surface irregularities that cause the mean surface temperature of the ice to be ˃0°C in our melting experiments. The scale on the ruler is labelled in centimetres.
To analyse these surface irregularities more quantitatively, we examine the temperature evolution inside a square of 30x30 pixels taken by the IR camera (Fig. 7). This square is located in the middle of the ice surface to reduce influences from the tank sides. Since the spatial resolution of the IR image is ∼0.003 m in the measuring area, the cm-scale meltwater patches on the ice surface are partly captured.

Fig. 7. The measured surface temperature T s in each pixel inside the measuring area. The pixel length is between 0.003 and 0.004 m due to the tilted viewing angle of the IR camera. The data shown here stem from the melting phase of an experiment where sea ice was grown from water with a salinity of 33 gkg 1 . We performed more experiments with this salinity, in which we melted the ice at different air temperatures, and analyse them in greater detail.
The measured surface temperature is a combination of the ice-surface temperature and the surface temperature of the liquid patches. This causes the surface temperature of individual pixels within our sampling area to often be above 0°C, which shows that the meltwater patches are not in thermal equilibrium with the surrounding ice but significantly warmer. That other individual pixels are below zero indicates bulk salinities above zero, suggesting that flushing leads to salinity variations on sub-centimetre scales at the surface. We find that the variations in surface temperature are larger for salty ice than for freshwater ice (Fig. 8). This is probably due to the lack of horizontal salinity variations in freshwater ice and to the occurrence of much fewer meltwater patches on its surface.
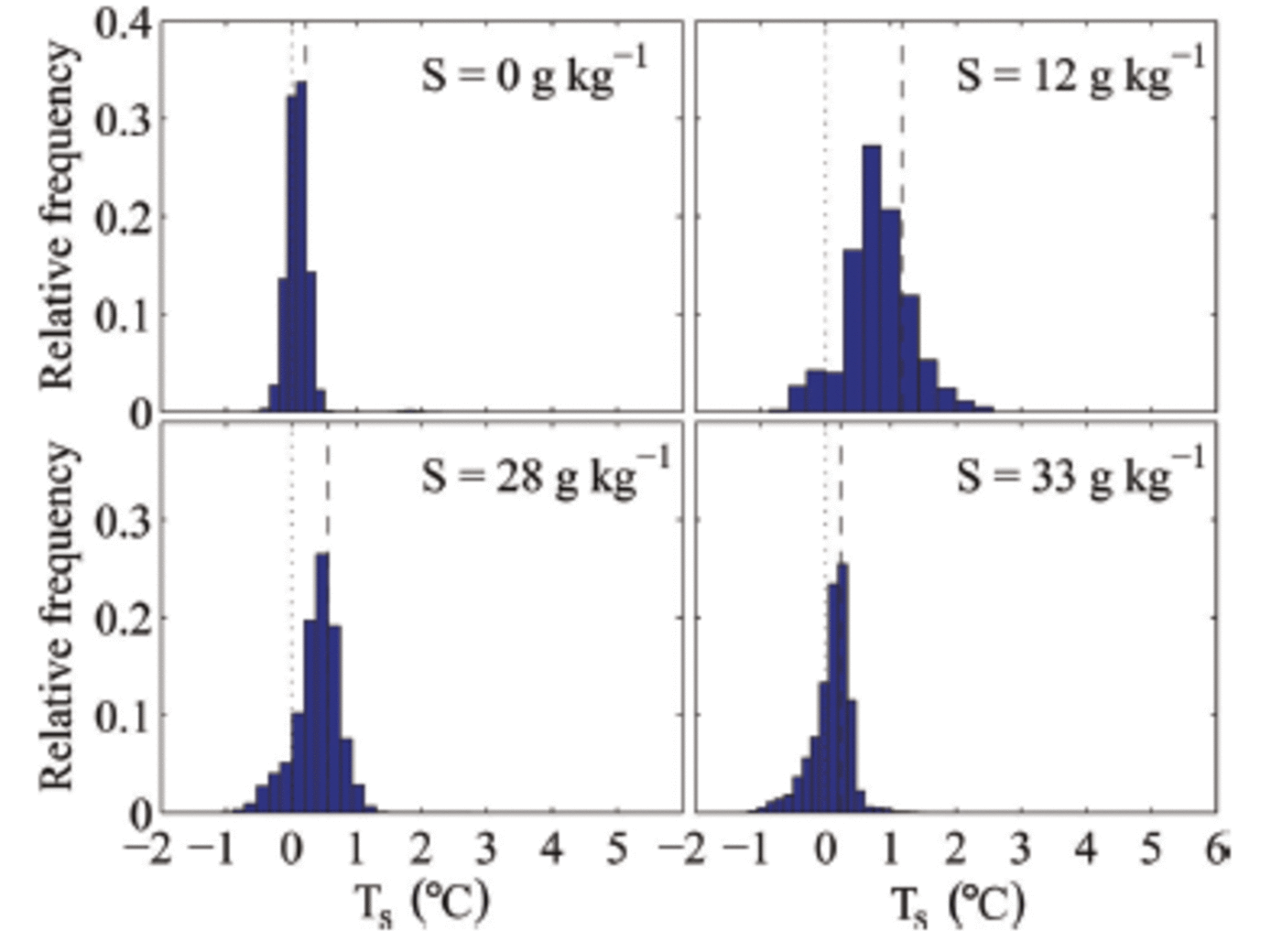
Fig. 8. Histograms of the surface temperature T s in the measuring area during melting of ice grown out of water with different initial salinities S. The black dashed line indicates the mean surface temperature in the measuring area, and the black dotted line indicates 0°C.
For some of the sea-ice experiments with an initial water salinity of 33g kg-1we slowly increased the air temperature, which allows us to study the surface temperature as a function of ambient air temperature (Fig. 9). We find that the surface temperature increases for higher air temperatures, which we interpret as a stronger warming of the meltwater patches for warmer ambient air.

Fig. 9. The measured surface temperature T s as a function of the air temperature T a during melting. The data shown here stem from the melting phase of an experiment where sea ice was grown from water with a salinity of 33 g kg 1.
We also find that the surface temperature depends on the salinity of the sea ice (cf. mean temperature as shown in Fig. 8). For higher bulk salinity of the ice, i.e. for ice grown from higher-salinity water, we find a lower mean surface temperature for the same environmental conditions than for sea ice with a lower bulk salinity. We can currently only speculate on the reason for this relationship, which we believe to be caused by higher bulk salinities near the surface. The higher salinities cause lower liquidus temperatures and increase the permeability of the ice, which could lead to a reduction of melt patches as the higher permeability makes it easier for the surface meltwater to percolate into the ice.
Discussion
So far we have primarily described the laboratory and model results. We will now discuss the general implications of this work, in particular its relevance for the understanding of sea-ice melting under natural conditions.
The first implication we draw from our results is the following. Since all measured parameters agree well with the model simulations, the SAMSIM model and the assumptions it is based on are sufficient to capture the underlying processes occurring in our laboratory experiments. This agreement is the more striking given that we only crudely approximated the surface heat flux in the simulations to be proportional to the temperature difference between the air and the ice surface. Also, the assumption of horizontal homogeneity on which the 1-D model is based is only partially fulfilled in the tank. These two model limitations combined with heat conduction in the thermistor are likely why the ice is up to 1°C warmer in the simulations during ice growth and up to 1°C colder during melting conditions. Building on the skill of SAMSIM to simulate melting conditions in a simplified setting, we extended the model to include, among others, the interaction of snow and of shortwave radiation with melting sea ice. This allowed us to simulate and to understand the salinity profiles measured in Arctic sea ice, as described in a separate paper (Reference Griewank and NotzGriewank and Notz, 2014).
We can also gain some insights into the real-world evolution of sea ice based on the experiments and simulations presented here. Our first finding is that, as expected, sea ice and freshwater ice melt very differently. The heat exchange that occurs during warming because of internal phase changes has a large effect. Very simple formulations of sea-ice melting which cannot capture this heat exchange, such as the zero-layer model of Reference SemtnerSemtner (1976), therefore cause significant changes in the amplitude and seasonal cycle of sea-ice evolution, as pointed out already by Reference SemtnerSemtner (1984) and Reference FichefetFichefet and Morales Maqueda (1997). We also find that the salinity evolution during the melting process affects the temporal evolution of the ice thinning (see also Reference Vancoppenolle and FichefetVancoppenolle and others, 2005). At the surface, this is only of minor importance since salinity fluctuations there are generally quite small. At the ice bottom, however, much larger differences in bulk salinity occur during bottom ablation, ranging from the initially very high saline layer that forms at the bottom of the ice to ice almost completely desalinated by flushing. Therefore, the melt rates of sea ice can become similar to those of freshwater ice towards the end of the melting period.
We have found mean surface temperatures that were several tenths of a degree above zero in our detailed observations of surface temperatures. These higher values are related to meltwater patches that partially cover the ice surface. A temperature offset of 1K could change the outgoing longwave radiation by 5 Wm 2and could hence significantly impact the surface thermal balance. Therefore it is important to find out if such small-scale changes in surface temperature also occur on sea ice under natural conditions, and if so, which environmental and sea-ice conditions foster their formation.
Obviously, it is impossible to reproduce actual field conditions in a laboratory experiment. This therefore was not the aim of our study, in which we instead primarily wanted to investigate some fundamental differences between the melting of sea ice and freshwater ice. Nevertheless, because our findings are based in fundamental physics, they will largely carry over to conditions encountered in the real world. The main differences in a real-world setting compared to our laboratory experiments are the presence of solar radiation during melting and the usually larger sea-ice thickness in polar regions. For a comparison of the melting of freshwater ice and sea ice, the presence of solar radiation will amplify most of our findings: Because freshwater ice is much more translucent than sea ice, the latter will absorb more of the incoming shortwave radiation in its interior, which will further increase the melt rate compared to freshwater ice. The larger ice thickness in reality might quantitatively affect our results, which, however, are qualitatively valid independent of ice thickness. For a more quantitative analysis of these aspects, we plan to carry out dedicated modelling studies with SAMSIM after it has been evaluated successfully against measurements in the present study.
Conclusions
We have systematically examined differences between the melting of sea ice and that of freshwater ice. We did so by carrying out dedicated laboratory experiments and numerical model simulations with the 1-D thermohaline sea-ice model SAMSIM.
In line with theoretical expectations, the temperature of freshwater ice quickly adjusts to 0°C when the air temperature exceeds freezing temperatures (Fig. 1). For the thin ice that we consider here, the adjustment occurs on a timescale comparable to the diffusive timescale. In sea ice, the internal temperature adjusts much more slowly to warm air temperatures due to the internal phase changes in the ice (Fig. 1).
Once the temperature of freshwater ice has reached 0°C, constant forcing causes a constant melt rate (Fig. 2c and d). The ratio of the thinning at the surface and at the bottom is the same as the ratio of the atmospheric and the oceanic heat flux. For sea ice, the melt rate is not constant over time (Fig. 2c and d) and is linked to the temporal evolution of the solid fraction of the ice. The melt rate initially slowly increases because of a decrease in the heat transfer into the interior of the ice. After reaching a maximum, the melt rate decreases again, reflecting the comparably high solid fraction of the remaining ice (Fig. 4). Because of its lower solid content, for equal forcing sea ice always melts away faster than freshwater ice of the same thickness. The thinning of freshwater ice, however, sets in slightly earlier because of the faster adjustment of its internal temperature (Fig. 1 and 2).
The average surface temperature of sea ice can exceed 0°C during melting, because cm-scale meltwater patches accumulate at the ice surface (Fig. 6 and 7). The mean surface temperature is higher for less saline sea ice (Fig. 8) and for higher air temperature (Fig. 9).
Because model simulations with SAMSIM agree favourably with laboratory experiments, the underlying mushy-layer equations and the parameterizations used in the model apparently capture the governing physics. This enhances our trust that SAMSIM is a useful tool to study sea ice.
Acknowledgement
This work was funded through a Max Planck Research Group scholarship.











