INTRODUCTION
Due to the half-life of radiocarbon (14C, 5730 yr) and industrial fossil fuel and other effects in the atmosphere, traditional 14C dating is mainly applicable to samples older than ca. 300 yr. For younger samples it has been demonstrated that bomb-pulse 14C dating can give reliable and accurate results, especially for samples with rapid turnover (Wild et al. Reference Wild, Arlamosky, Golser, Kurchera, Priller, Puchegger, Rom, Steiner and Wycudilik2000). Such dating has proven helpful to estimate time of death and birth of unidentified humans in missing persons’ forensic cases (Johnstone-Bedford and Blau Reference Johnstone-Bedford and Blau2020).
Prior to the nuclear bomb testing in the 1950s and early 1960s the global atmospheric 14C level was relatively stable. However, during the bomb testing the 14C level in the atmosphere increased dramatically. Since the test ban treaty in 1963, the atmospheric 14C concentration has been dropping exponentially due to mixing with terrestrial and marine carbon reservoirs and has now almost reached the relatively stable 14C level prior to the testing. This artificial 14C bomb pulse is captured in organic material through the food chain and can thus be utilized as a calibration curve for 14C dating in modern forensic cases.
14C dating has however to rely on modeled corrections due to slow collagen carbon turnover and possible marine reservoir effects. Thus, the interpretation of the 14C results can only reflect the true age if the aforementioned substantial corrections are reliable. Here, the age of the individual at death and the type of tissues sampled are important factors.
The turnover rate refers to the fact that only a fraction of the bone collagen is renewed, and bone collagen therefore reflects an individual’s diet over a long period, which can be substantially more than 10 yr (Hedges et al. Reference Hedges, Clement, Thomas and O’Connell2007). The turnover rate varies between sexes and with age and different bone types. Studies have found that turnover is faster in females than males and varies substantially between adolescence and maturity (see e.g., Hedges et al. Reference Hedges, Clement, Thomas and O’Connell2007). Thus, turnover rate corrections must reflect both lifetime integrated turnover rate and the bomb pulse shape, and thus depend on time of birth and age at death. According to Hedges et al. (Reference Hedges, Clement, Thomas and O’Connell2007), a 35-yr-old individual with a 4% annual turnover rate will contain >50% contribution of collagen from the time of greatest growth i.e., from the teenage years. Type of bone is also important as total turnover varies considerably between bone types and texture (Ubelaker et al. Reference Ubelaker, Plens, Soriano, Diniz, de Almeida Junior, Daruge, Francesquini and Machado2022). For cortical bone material, such as the main component of femoral, the turnover is considered to be as long as 30 yr, whereas for mainly trabecular bone, such as rib and the inner part of femoral, the collagen turnover is much faster, of the order of 4 yr (Yaemsiri et al. Reference Yaemsiri, Hou, Slining and He2010).
As pointed out by Wild et al. (Reference Wild, Arlamosky, Golser, Kurchera, Priller, Puchegger, Rom, Steiner and Wycudilik2000), the best results when determining time of death in forensic cases are obtained by selecting material with a high turnover rate. In many cases, however, collagen from a single bone or bone fragment is the only material available and thus it is of utmost importance to develop models that describe the time dependence of collagen turnover in human bones. Often, a simple approach of correcting for a death-age dependent time lag is used (e.g., Ubelaker et al. Reference Ubelaker, Thomas and Olson2015, Reference Ubelaker, Plens, Soriano, Diniz, de Almeida Junior, Daruge, Francesquini and Machado2022). However, we find the approach of Hedges et al. (Reference Hedges, Clement, Thomas and O’Connell2007) more useful and reliable, as it incorporates the important factor of the time of birth in a detailed modeling of the 14C content remaining in the bone collagen of a person who has lived through parts of the atmospheric bomb pulse (see discussion for details). In the present paper, we thus use this approach to analyze and interpret our results. Thus, for details of the model and the actual parameters we use, see Hedges et al. (Reference Hedges, Clement, Thomas and O’Connell2007).
In 2017 and 2019 the Icelandic police approached us with the request of 14C dating an unidentified human bone in order to determine whether it was recent and of forensic relevance. However, after our analyses and reports to the police, DNA analyses were conducted from which the police were able to identify both individuals. Accordingly, we now know their time of birth as well as their death dates (or at least disappearance dates). The purpose of this paper is to critically assess our initial findings on the time of death, and to investigate if collagen turnover modeling of the 14C concentration in bones could explain the discrepancy between the actual time of death and our reported time of death in our initial report.
THE FORENSIC CASES
Case 1 (AAR-26566) involves a bone that was discovered in 2017 in a fisherman’s net in the seas, just off the southwest coast of Iceland. The bone was long and grayish-white with no soft tissue. A forensic pathologist identified it as a humeral bone, probably the left humerus from a relatively large body structure, most likely a male. It was very well preserved and cortical material was sampled at the distal end close to the knee joint as shown in Figure 1A. After submission of our results, the person was later identified by DNA analysis as a male born April 13, 1974, and disappeared December 26, 2015, the most likely time of death.

Figure 1 Photos of the human bones discussed in the paper. Panel A shows the humeral bone discovered in fishermen’s net off the Southwest coast of Iceland (AAR-26566). Panel B shows the scull found in the southwest lowlands, Iceland (AAR-30392).
Case 2 (AAR-30392) involves a human cranium found in 1995 in South Iceland, about 50 km from Reykjavík, the capital of Iceland. It was very well preserved with no soft tissue, and cortical material was sampled at the lower back (Figure 1B). After submission of our results, the cranium was later identified by DNA analysis to belong to a male born in 1940 who disappeared December 24, 1987, the most likely time of death.
METHODS
Samples obtained from the cranium and left humerus were pretreated following a modified Longin procedure with ultrafiltration (Longin Reference Longin1971; Brown et al. Reference Brown, Nelson, Vogel and Southon1988; Brock et al. Reference Brock, Geoghegan, Thomas, Jurkschat and Higham2013). The bone samples were demineralized in hydrochloric acid (HCl) at 4°C for several days. The acid was renewed regularly until the mineral fraction was removed completely. Humic substances were removed using 0.2M sodium hydroxide (NaOH) at 20°C. The sodium hydroxide was replaced every 20 minutes until the solution stayed clear. The samples were subsequently rinsed with 0.01M HCl and gelatinized in 0.01M HCl at 58°C overnight. The extracted “collagen” was ultra-filtered in pre-cleaned Amicon Ultra Centrifugal Filters (Ultracel − 30K). The >30kDa fractions were weighed after ultrafiltration and freeze-drying and used for 14C analysis.
The collagen was converted to CO2 by combustion in sealed evacuated quartz tubes with 200 mg CuO. The CO2 was reduced to graphite by the H2 reduction method using an iron catalyst and MgClO4 to remove the water (Vogel et al. Reference Vogel, Southon, Nelson and Brown1984; Santos et al. Reference Santos, Southon, Griffin, Beaupre and Druffel2007). The samples were 14C dated using the HVE 1MV tandetron accelerator AMS system at the Aarhus AMS Centre (AARAMS) (Olsen et al. Reference Olsen, Tikhomirov, Grosen, Heinemeier and Klein2017). 14C dates are reported as uncalibrated F14C values (Reimer et al. Reference Reimer, Brown and Reimer2004) and are normalized to δ13C −25‰ according to international convention using the online 13C/12C ratios (Stuiver and Polach Reference Stuiver and Polach1977).
Stable isotopes δ13C and δ15N were measured using a continuous-flow IsoPrime IRMS coupled to an Elementar PyroCube elemental analyzer at AARAMS, Aarhus University, Denmark. An in-house standard Gel-A was used as primary standard yielding ±0.2‰ and ±0.3‰ precision for carbon and nitrogen analysis respectively. Further, secondary in-house and international standard were used to check the normalization to the VPDB and AIR scale.
The F14C values are calibrated with the Northern Hemisphere bomb calibration curve (Bomb21NH1_2021; Hua et al. Reference Hua, Turnbull, Santos, Rakowski, Ancapichún, De Pol-Holz, Hammer, Lehman, Levin, Miller, J. Palmer and Turney2022) using OxCal 4.4 (Bronk Ramsey et al. Reference Bronk Ramsey, Dee, Lee, Nakagawa and Staff2010). Calculations and modeling are performed using MatLab 2020 version 9.8.0.145134.
MODELING THE 14C CONTENT OF BONE COLLAGEN AS A FUNCTION OF AGE
The 14C concentration of collagen in human bones is controlled by the 14C concentration in the consumed diet and the carbon exchange rate between bone collagen and the consumed diet, i.e., the collagen carbon turnover rate.
Firstly, to model the 14C concentration of bone collagen over the time span of an individual it is necessary to estimate the bone-collagen carbon turnover rate (f) as a function of age. We use the approach as well as the modeled collagen turnover rates of Hedges et al. (Reference Hedges, Clement, Thomas and O’Connell2007) (Figure 2B). This model is derived from a modeled turnover template defined by four (decreasing) turnover rate values at four time points, two of which are fixed, and two of which can vary: At age 0 (fixed, age of birth), at age between 10 and 20 (adolescence), at age between 19–30 (cessation of growth), and at age of 100 (fixed, age by which all subjects are dead). There are therefore six adjustable parameters (4 turnover rate values and 2 varying time points, i.e., adolescence and cessation of growth), for linear interpolation to evaluate the turnover rate at any given age (for details, see Hedges et al. [Reference Hedges, Clement, Thomas and O’Connell2007] and discussion section below).

Figure 2 Panel A: The Northern Hemisphere bomb calibration curve (Bomb21NH1_2021; Hua et al. Reference Hua, Turnbull, Santos, Rakowski, Ancapichún, De Pol-Holz, Hammer, Lehman, Levin, Miller, J. Palmer and Turney2022). In addition, the calculated terrestrial diet curve is shown together with examples of mixed marine diet curves in shades of blue. The marine curve is constructed using data from the north Icelandic shelf (Wanamaker et al. Reference Wanamaker, Butler, Scourse, Heinemeier, Eiríksson, Knudsen and Richardson2012). Panel B: Bone collagen turnover rates f taken from Table 2 in Hedges et al. (Reference Hedges, Clement, Thomas and O’Connell2007). (Please see online version for color figures.)
Secondly, the 14C concentration of the diet must be known. In case of a purely terrestrial diet a 14C diet curve can be constructed from the atmospheric 14C concentration by assuming a time lag of 1–2 yr between the atmosphere and the consumed diet. We use the Northern Hemisphere 14C calibration curve (Bomb21NH1; Hua et al. Reference Hua, Turnbull, Santos, Rakowski, Ancapichún, De Pol-Holz, Hammer, Lehman, Levin, Miller, J. Palmer and Turney2022) as the atmospheric input and calculate a 14C diet curve (F14Cdiet) by a 2-yr backwards moving average and standard deviation:
where Yi range between 1940 and 2020.
In case of mixed terrestrial and marine diet the situation is much more complex because the 14C concentration of the surface ocean is not distributed uniformly geographically (e.g., Wanamaker et al. Reference Wanamaker, Butler, Scourse, Heinemeier, Eiríksson, Knudsen and Richardson2012). We use the surface ocean 14C datasets from Grimsey and Siglufjordur from the Icelandic shelf as our marine diet curve input (Wanamaker et al. Reference Wanamaker, Butler, Scourse, Heinemeier, Eiríksson, Knudsen and Richardson2012). The 14C marine surface ocean curve is constructed using a 3-yr moving average and standard deviation of the two datasets. The 14C marine surface ocean curve is subsequently extrapolated to 2020. A mixed terrestrial and marine 14C diet curve is then constructed by taking the relative fraction of the terrestrial 14C diet curve and the 14C surface ocean curve (see Figure 2A).
Having constructed a 14C diet curve, F14Cdiet curve, the F14Cbone at birth can be estimated as F14Cdiet curve(Ybirth), thus
After birth, the bone F14Cbone is modeled using two components: the exchangeable and non-exchangeable carbon. The fraction of exchangeable carbon is estimated as the bone collagen carbon turnover rate in percent (f) using the Hedges et al. (Reference Hedges, Clement, Thomas and O’Connell2007) model as f i , where i range from 1 to 100 yr (Figure 2B). Further, the exchangeable carbon 14C content is estimated using the F14Cdiet. The non-exchangeable carbon (1–f i ) is estimated using the F14Cbone content from the previous year taking into account the 14C decay. Thus, the F14Cbone collagen over lifetime of an individual is modeled as:
 $$\hskip -4pt{F^{14}}{C_{bone}}\left( {{Y_{birth}} + i} \right) = {f_i}\cdot{F^{14}}{C_{diet}}\left( {{Y_{birth}} + i} \right) + \!\left( {1 - {f_i}} \right)\cdot{F^{14}}{C_{bone}}\left( {{Y_{birth}} + i - 1} \right)\cdot exp\left( { - {1 \over {8267}}} \right)$$
$$\hskip -4pt{F^{14}}{C_{bone}}\left( {{Y_{birth}} + i} \right) = {f_i}\cdot{F^{14}}{C_{diet}}\left( {{Y_{birth}} + i} \right) + \!\left( {1 - {f_i}} \right)\cdot{F^{14}}{C_{bone}}\left( {{Y_{birth}} + i - 1} \right)\cdot exp\left( { - {1 \over {8267}}} \right)$$
Where i ranges from 1 to 100 yr and the last latter term is taking into account the 14C decay. Error estimates on the calculated F14Cbone are calculated by resampling the 14C diet curve (F14Cdiet curve) and bone collagen turnover rate (f) 1000 times, assuming all uncertainties to be normally distributed. As an approximate further constraint, the bone collagen turnover rate (f) is required to be decreasing with age (∂f / ∂age <0) and f to be strictly greater than 0%.
RESULTS—RADIOCARBON ANALYSIS
Results are reported in Table 1 and the calibrated 14C ages are shown in Figure 3.
Table 1 Radiocarbon and stable isotope data as well as known birth and death years for the two individuals Case 1 and 2.


Figure 3 Shown is the Northern Hemisphere bomb calibration curve (Bomb21NH1_2021; Hua et al. Reference Hua, Turnbull, Santos, Rakowski, Ancapichún, De Pol-Holz, Hammer, Lehman, Levin, Miller, J. Palmer and Turney2022) together with the calibrated probability distributions (white; Bronk Ramsey et al. Reference Bronk Ramsey, Dee, Lee, Nakagawa and Staff2010) for each individual (AAR-26566 and AAR-30392). The provided age ranges are uncorrected for collagen turnover rates. The arrows indicate a 10-yr shift of the probability distribution representing a simple lag-time correction for collagen turnover in human bones (gray). Shown are also the period of death for both individuals.
Case 1
The 14C analysis was performed in 2017 (AAR-26566). The extracted collagen was of good quality, with a yield of 11%. Isotope data showed no or limited indication of marine diet, with a δ13C of –20.3‰, a δ15N value of 11.4‰ and C/N ratio of 3. 3. The 14C date demonstrates that the individual is modern with a F14C value of 1.1217 ± 0.0041, falling within the bomb-pulse period. As shown in Figure 3, the calibrated age using 95% probability gives a very slim probability (only 2.7%) that the bone is from the years 1958.2 AD to 1958.5. More likely (92.7% probability) the time of death would be during the years from 1993.7–1996.7 AD. In reality, the ambiguity as to the relevant side of the bomb peak is unresolved. To provide a quick forensic result to the police, we took the naïve approach of a standard 10-yr time-lag correction for bone collagen turnover and no marine correction. This yields the possible time of death at 1968 or, more likely, in the time interval 2004–2007.
Case 2
The 14C analysis was performed in 2019 (AAR-30392). The extracted collagen was of good quality, with a yield of 9.9%. Isotope data showed limited indication of marine diet, with a δ13C of –19.2‰, a δ15N of 12.7‰ and a C/N ratio of 3.4. The F14C value demonstrated that the individual was modern (1.1622 ± 0.0034), falling within the bomb-pulse period. As shown in Figure 3, the calibrated age using 95% probability gives 17.7% probability of a time of death during the years 1958.5 AD to 1959.0, and 77.8% probability during 1989.2 AD to 1990.6. Again, to provide a quick forensic result to the police, we added a 10-yr time-lag correction for bone collagen turnover (i.e., year 2000) and assumed no marine correction. As the cranium was found in 1995 the latter time was ruled out, and we suggested that the most likely time of death was around 1970.
In hindsight, the application of unqualified lag-time turnover corrections is simply not generally valid in connection with bomb-pulse dating as demonstrated by our modeling results below and Figure 4.

Figure 4 Panel A and B: the Northern Hemisphere bomb calibration curve (Bomb21NH1_2021; Hua et al. Reference Hua, Turnbull, Santos, Rakowski, Ancapichún, De Pol-Holz, Hammer, Lehman, Levin, Miller, J. Palmer and Turney2022). Panel A shows the modeling results for AAR-25566 (Case 1) whereas Panel B shows the modeling results for AAR-30392 (Case 2). Both panel A and B show the modeled F14Cbone curves from the time of birth using either a terrestrial diet curve or a 30% marine diet curve. The time of death is indicated with the vertical grey bar for each individual (for further details please consult the main text).
RESULTS—14C BONE COLLAGEN MODELING
The bone collagen models for the individuals of the two cases are presented in Figure 4 and Table 2. Using the known year of birth, a total of 7 models are calculated for each individual: one model representing a purely terrestrial diet and 6 models ranging from 10–60% marine diet. Table 2 provides the calculated F14Cbone for the year of death which is then compared to the measured F14C value presented by the difference between the measured F14C (Table 1) and the F14Cbone values (ΔF14C; Table 2). Further, the Z-score, as defined in Table 2, is calculated for the ΔF14C values.
Table 2 Bone F14C modeling for the two individuals. F14Cbone indicates the modeled F14C value using either a purely terrestrial diet curve or mixed curves with 10–60% marine influence. The ΔF14C is calculated as difference between the measured F14C value and the modeled F14Cbone. The Z-score indicates the ΔF14C in units of the standard deviation by dividing the ΔF14C value by the error on the ΔF14C value.
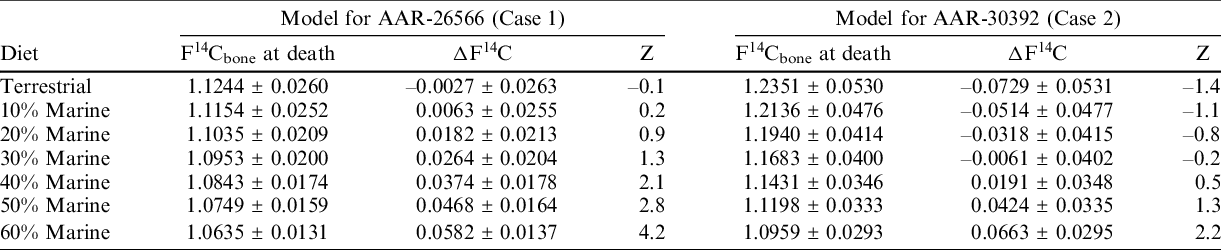
For Case 1 (AAR-26566), the purely terrestrial model appears to represent the best statistical agreement with the measured F14C value with a possibility of up to 20% marine diet (Table 2). For Case 2 (AAR-30392), a 30% marine diet appears to represent the best statistical agreement with the measured F14C value with a possible marine diet range between 20–40% (Table 2). Note, however, that the modeling for this individual, with a birth date in 1940, yields an extremely wide range (1960–2000) of possible death dates, too wide to be of practical value in a forensic case.
DISCUSSION
As mentioned above, direct calibration of post 1950 using the bomb calibration curve is only useful if the turnover rate of the sample can be assumed to be less than 1–2 yr. Often a time-lag correction is applied to the calibrated age probability distributions in order to correct for longer turnover rates (e.g., Ubelaker and Buchholz Reference Ubelaker and Buchholz2005). Our initial time lag correction of 10 yr is clearly incorrect when compared to the actual time of death (Table 1; Figure 3). Both men were in their forties when they disappeared (41 and 47 yr old respectively) and in both cases, we estimated their time of death too early by ca. 10 and 17 yr, respectively. The most likely explanation for this discrepancy is our initial naive approach to correcting for the bone-collagen turnover rate. A more sophisticated approach would have been to apply an age dependent time lag as suggested by Ubelaker and Buchholz (Reference Ubelaker and Buchholz2005). Ubelaker et al. (Reference Ubelaker, Thomas and Olson2015) studied published literature on modern 14C values of human bones to analyze correlation between age of death and the 14C time lag. In their study, they used 39 individuals with known birth and death dates. They reported the lag time for decadal intervals of age at death of the individuals. A clear lag time increase was observed with advancing age, but the study failed to detect significant sex differences. The average time lag for individuals dying in their forties is 16.78 ± 9.86 yr according to their study. However, the range around this mean is very large, from 3 yr to 30.34 yr, probably because of the importance of the birth year not being accounted for. The mean lag time is thus not very helpful to correct accurately for the collagen turnover rate, at least not for the 40–50-yr age interval. It is important to note, that even this age dependent time-lag method would not have made our initial estimate of death more accurate.
Hedges et al. (Reference Hedges, Clement, Thomas and O’Connell2007) took a different approach in their study of collagen extracted from mid-shaft femur of 67 Australian individuals who died during the years 1991–1993 at the age range from 40 to 97 yr. They defined turnover as a function of biological age, i.e., percentage of collagen lost and replaced each year in a lifespan and compared the model calculations with actual time of death. Considerable scatter was found when 14C content of collagen was plotted versus date at death, attributed to uncertainty in individual turnover rate (Fig. 2 in Hedges et al. Reference Hedges, Clement, Thomas and O’Connell2007). Their model describes turnover as an age-dependent function and integrates diet and turnover throughout life. This means that calculations of the 14C level of bone collagen of each individual is carried out iteratively for each year from birth (Y0) to death (YD).
In our study, using their approach with the turnover rates they obtained by parameter fitting to their data set, we constructed a suite of models where a range from a purely terrestrial to a 60% marine diet was used on each individual. It was found that a 0–20% marine diet could explain the measured F14C value at time of death for individual 1, whereas the model results suggest a 20–40% marine diet for individual 2 (Table 2; Figure 4). This is perhaps not surprising, but turnover correction methods often seem to overlook the possible influence from a marine diet, which can be very important since the atmosphere-sea difference in 14C concentration can be close to a factor of 2 during the peak of the bomb pulse, which strongly dampened in the surface ocean.
Interpreting diet using δ13C values for modern humans is complicated because of the Suess effect (the 13C depletion of the atmosphere since the industrial revolution) and because of the food production where C4 plants like maize may make up a significant proportion. However, if it is assumed that C4 plants play an insignificant role and further that we have a simple two-component system consisting of the terrestrial and marine environments, then the stable isotopes may estimate the marine diet fraction. The average C3 plant δ13C values is ca. 2‰ lower than the preindustrial value (Kohn Reference Kohn2010). Therefore, the terrestrial δ13C endpoint for collagen can be estimated to –23‰, and the marine δ13C endpoint can be assumed to be –12‰. On this basis, the marine diet of the individual of Case 1 is roughly estimated to 24% and for the individual of Case 2 marine diet is roughly 34%. With consideration to the uncertainties with respect to the marine diet calculation, this appears to agree with percent marine diet as suggested from our bone collagen model.
CONCLUSIONS
Provided that the birth year is known, we have demonstrated that we are able to explain the measured F14C value and time of death. Our finding warns against simple time-lag corrections in forensic cases of 14C dating of human bones. However, without knowing the birth year our method is of little help in providing the time of death. We suggest that in forensic cases the possible age of the person should be estimated by the anthropologist and shared with the 14C laboratory, which then may produce families of curves for different birth years and year of death. From the suite of curves, a range of possible death years may be produced.
So, how can we contribute to identify a missing unidentified person if only few skeletal remains are available and no information on birth date nor date or age at death?
As a first step, 14C dating should be performed to determine whether the individual is recent and of forensic relevance (Bomb pulse age).
If so, the police could inform of unsolved missing persons, and their birth dates as well as date of their disappearance.
After running the model, we can inform the police, which of the missing persons have dates of birth and disappearance/death in accordance with the model results of the submitted remains.








