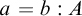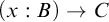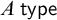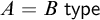1 Introduction
One thing most philosophers agree on about the analytic–synthetic distinction is that a proposition is analytic when true solely by virtue of its meaning and synthetic otherwise. I believe this is a semantic distinction that deserves to be accounted for not only classically but also within the opposing school of constructive semantics. Roughly, its basic tenets are that meaning and truth are rooted in provability. They can be traced back to the so-called proof explanation of the intuitionistic logical constants established by Brouwer, Heyting, Kolmogorov and many others [Reference Troelstra and van Dalen32]. I am particularly interested in the kind of constructive semantics that originated in the work of Martin-Löf [Reference Martin-Löf21] as a generalization of the proof explanation to type-theoretic contexts. The question I want to address in this paper is: how should the analytic–synthetic distinction be drawn?
To be precise, this constructive semantics takes the form of a body of informal meaning explanations used to justify the axioms and rules of inference of constructive type theory, a class of formal systems in which every object is assigned a type and every operation is restricted to objects of a certain type [Reference Martin-Löf, Rose and Shepherdson20]. The type theory is constructive since the objects of a type can be interpreted as proofs of a proposition in such a way that the disjunction property holds and all existential claims have witnesses. In fact, the meaning explanations generalize the proof explanation given that the objects of a type can also be regarded as elements of a set and propositions as sets that consist of their proofs.
The reason I wish to draw special attention to this remarkable form of constructive semantics is that Martin-Löf [Reference Martin-Löf and Parrini25] also supplemented it with the proposal of a distinction between analytic and synthetic judgments for his constructive type theory. His thoughts on the matter have been particularly influential, and his distinction has been widely accepted by those sympathetic to his constructivism without ever being challenged until now.Footnote 1 Proposing a revision of his views on analyticity and syntheticity is precisely my aim in this paper. My criticism of Martin-Löf’s distinction will be directed to the following six points:
-
1. It should concern judgments and not forms of judgments, for the expressions that occur in a form of judgment are metavariables and have no meaning per se.
-
2. It presupposes a vague characterization of analyticity (and thus also syntheticity), lacking an explanation of what the meaning of an expression actually is.
-
3. It is based on an unfounded claim that all judgments of the form
 $a : A$
and
$a : A$
and
 $a = b : A$
are analytic due to the vagueness mentioned above.
$a = b : A$
are analytic due to the vagueness mentioned above. -
4. It completely leaves out the issue of the analyticity or syntheticity of judgments of the forms
 $A \> \mathsf {type}$
and
$A \> \mathsf {type}$
and
 $A = B \> \mathsf {type}$
and, more importantly, hypothetical judgments.
$A = B \> \mathsf {type}$
and, more importantly, hypothetical judgments. -
5. It must ultimately be rooted in the meaning explanations, thus decidability in a formal system has nothing to do with the analyticity or syntheticity of a judgment.
-
6. It is wrong that all synthetic judgments are “grounded on” analytic judgments, so both analyticity and syntheticity are equally basic and important notions.
These points will be thoroughly explained and elaborated upon in due course. The view I will arrive at is that a judgment must be analytic when its correctness is exclusively due to the evaluation of the expressions that occur in the judgment. Given that it is common to understand the meaning of an expression referentially by means of the evaluation of the program it expresses in constructive semantics [Reference Bentzen3], my account of analyticity can be regarded as a refinement of Martin-Löf’s working principle that an analytic judgment is correct only by virtue of the meanings of the expressions that occur in it.
I argue that Martin-Löf should not have claimed that all judgments of the form
![]() $a : A$
and
$a : A$
and
![]() $a = b : A$
are analytic. Because analyticity is not a property of forms of judgments but judgments themselves, we must examine each judgment and the meaning of its expressions individually to support this claim. Yet, as we shall see, when A evaluates to a dependent function type
$a = b : A$
are analytic. Because analyticity is not a property of forms of judgments but judgments themselves, we must examine each judgment and the meaning of its expressions individually to support this claim. Yet, as we shall see, when A evaluates to a dependent function type
![]() $(x : B) \to C$
, all judgments of these forms fail to be analytic and therefore end up as synthetic. Evaluation cannot be decisive for their correctness because of the meaning explanation given for dependent function types, which is dependent on the purely extensional meaning explanation of hypothetical judgments. Going beyond the scope of Martin-Löf’s distinction, I also argue that all hypothetical judgments are synthetic and show how my analytic–synthetic distinction accommodates judgments of the forms
$(x : B) \to C$
, all judgments of these forms fail to be analytic and therefore end up as synthetic. Evaluation cannot be decisive for their correctness because of the meaning explanation given for dependent function types, which is dependent on the purely extensional meaning explanation of hypothetical judgments. Going beyond the scope of Martin-Löf’s distinction, I also argue that all hypothetical judgments are synthetic and show how my analytic–synthetic distinction accommodates judgments of the forms
![]() $A \> \mathsf {type}$
and
$A \> \mathsf {type}$
and
![]() $A = B \> \mathsf {type}$
. Although there are several instances of analytic judgments of these forms, just as with
$A = B \> \mathsf {type}$
. Although there are several instances of analytic judgments of these forms, just as with
![]() $a : A$
and
$a : A$
and
![]() $a = b : A$
syntheticity is the norm whenever A evaluates to a dependent function type. To conclude, I consider and reject an alternative account of analyticity as decidability and assess Martin-Löf’s position on the analytic grounding of synthetic judgments.
$a = b : A$
syntheticity is the norm whenever A evaluates to a dependent function type. To conclude, I consider and reject an alternative account of analyticity as decidability and assess Martin-Löf’s position on the analytic grounding of synthetic judgments.
The remainder of this paper is structured as follows. Section 2 gives a general overview of all the forms of judgment of constructive type theory and discusses the analytic–synthetic distinction proposed by Martin-Löf [Reference Martin-Löf and Parrini25]. Section 3 presents the meaning explanations of the basic forms of judgment in detail. In Section 4 I advance my own views through a systematic criticism of Martin-Löf’s analytic–synthetic distinction following the points mentioned above. Section 5 replies to some possible objections and general concerns. Finally, Section 6 contains some concluding remarks and outlines directions for future work.
2 Analyticity and syntheticity in Martin-Löf
The aim of this section is to present Martin-Löf’s original views on the distinction between analytic and synthetic judgments in constructive type theory. My own critical assessment of his ideas will have to wait until the next sections. Before I begin, however, I want to stress that his analytic–synthetic distinction is drawn in the domain of judgments and not that of propositions as it is common in the literature on classical semantics. Allow me to start by elaborating on the role of judgments in the development of the logic tradition.
Judgments are what can be conferred assertive force and be subject to rules of inference. They convey the idea that one or more objects have a property or stand in a relation. By making a judgment one expresses the knowledge that what is being judged is the case, so judgments may be regarded as objects of knowledge [Reference Martin-Löf22, p. 19]. When different sorts of properties or relations describe the content of two judgments, we typically say that these judgments have different forms. To know a judgment of a certain form is to know that the objects involved have the properties in question or stand in the relevant relation. I shall also call a judgment that can be made or known a correct judgment.
Throughout the history of logic, various forms of judgment have been observed. For instance, the Aristotelian tradition rests on judgments of the subject-copula-predicate form,
![]() $S \textsf { is } P$
, which constitute the premises and conclusions of a syllogism. Judgments of this form express that a particular subject S has a certain property P. Indeed, the Kantian analytic–synthetic distinction is famously proposed for judgments of the
$S \textsf { is } P$
, which constitute the premises and conclusions of a syllogism. Judgments of this form express that a particular subject S has a certain property P. Indeed, the Kantian analytic–synthetic distinction is famously proposed for judgments of the
![]() $S \text { is } P$
form [Reference Kant17, B10]. Since especially the works of Bolzano and Frege, modern logic has adopted a new primitive form of judgment,
$S \text { is } P$
form [Reference Kant17, B10]. Since especially the works of Bolzano and Frege, modern logic has adopted a new primitive form of judgment,
![]() $A \> \mathsf {true}$
, thereby departing from the Aristotelian tradition.Footnote
2
Judgments of this modern form express that a proposition is true and even today continue to figure in both the premises and the conclusion of an inference. Although Frege stressed the importance of making the truth particle explicit in judgments of this form, as famously demonstrated by his use of the turnstile symbol in his notation, this particle is typically omitted when referring to judgments of this form in the contemporary literature. This has resulted in a confusion between the judgment
$A \> \mathsf {true}$
, thereby departing from the Aristotelian tradition.Footnote
2
Judgments of this modern form express that a proposition is true and even today continue to figure in both the premises and the conclusion of an inference. Although Frege stressed the importance of making the truth particle explicit in judgments of this form, as famously demonstrated by his use of the turnstile symbol in his notation, this particle is typically omitted when referring to judgments of this form in the contemporary literature. This has resulted in a confusion between the judgment
![]() $A \> \mathsf {true}$
and the proposition A. The former states that a proposition A is true while the latter simply stands for a proposition A that may either be true or not. When one characterizes a true proposition A as analytic or synthetic one is thus saying that the judgment
$A \> \mathsf {true}$
and the proposition A. The former states that a proposition A is true while the latter simply stands for a proposition A that may either be true or not. When one characterizes a true proposition A as analytic or synthetic one is thus saying that the judgment
![]() $A \> \mathsf {true}$
is analytic or synthetic. This is especially evident in Frege [Reference Frege13, sec. 3]. Yet, because there is only one form of judgment in the background,
$A \> \mathsf {true}$
is analytic or synthetic. This is especially evident in Frege [Reference Frege13, sec. 3]. Yet, because there is only one form of judgment in the background,
![]() $A \> \mathsf {true}$
, it still makes sense to say that the analytic–synthetic distinction is drawn for true propositions. In fact, the distinction still operates at the level of judgments like it does in Kant, the difference is that we are restricting all judgments to the one form that states that a proposition is true.
$A \> \mathsf {true}$
, it still makes sense to say that the analytic–synthetic distinction is drawn for true propositions. In fact, the distinction still operates at the level of judgments like it does in Kant, the difference is that we are restricting all judgments to the one form that states that a proposition is true.
Propositions are what can serve as truth bearers and are connected by the logical connectives. They lack assertive power and may only figure as the content of
![]() $A \> \mathsf {true}$
. Constructively, a proposition is defined by prescribing how its canonical proofs may be formed and how they can be recognized as the same [Reference Martin-Löf23, pp. 412–413], that is, by specifying what are the direct ways to prove a proposition and when two such proofs are identical. To illustrate, implication is defined as follows: the canonical way to prove
$A \> \mathsf {true}$
. Constructively, a proposition is defined by prescribing how its canonical proofs may be formed and how they can be recognized as the same [Reference Martin-Löf23, pp. 412–413], that is, by specifying what are the direct ways to prove a proposition and when two such proofs are identical. To illustrate, implication is defined as follows: the canonical way to prove
![]() $A \to B$
is by providing a method that yields a proof of B when applied to a proof of A. Additionally, two such methods are the same when they produce identical proofs of B given a proof of A. The knowledge that something is a proposition therefore amounts to the knowledge of what its canonical proofs are and when two such canonical proofs are the same. Martin-Löf [Reference Martin-Löf, Rose and Shepherdson20] noticed that the modern one-dimensional judgment structure
$A \to B$
is by providing a method that yields a proof of B when applied to a proof of A. Additionally, two such methods are the same when they produce identical proofs of B given a proof of A. The knowledge that something is a proposition therefore amounts to the knowledge of what its canonical proofs are and when two such canonical proofs are the same. Martin-Löf [Reference Martin-Löf, Rose and Shepherdson20] noticed that the modern one-dimensional judgment structure
![]() $A \> \mathsf {true}$
was not enough to effectively capture the subtleties of knowledge in constructive semantics. He then introduced a more complex judgment structure with his constructive type theory in order to accurately express knowledge from a constructive perspective within a formal system.
$A \> \mathsf {true}$
was not enough to effectively capture the subtleties of knowledge in constructive semantics. He then introduced a more complex judgment structure with his constructive type theory in order to accurately express knowledge from a constructive perspective within a formal system.
Constructive type theory expresses knowledge through not one but four fundamental forms of judgment that say that something is a type, two things are the same type, something is an object of a type, and two things are the same objects of a type, respectively:
Perhaps a few words are in order to motivate these four forms of judgment. First, notice that Martin-Löf diverges from the modern tradition of Frege and Bolzano and regards
![]() $a : A$
and
$a : A$
and
![]() $a = b : A$
as primitive forms of judgment, as opposed to
$a = b : A$
as primitive forms of judgment, as opposed to
![]() $A \> \mathsf {true}$
. Well, this adjustment is only natural from the constructive standpoint, given that these two forms of judgment can be respectively read as “a is a proof of A” and “a and b are equal proofs of A” and what makes a proposition true is a proof of it. Thus,
$A \> \mathsf {true}$
. Well, this adjustment is only natural from the constructive standpoint, given that these two forms of judgment can be respectively read as “a is a proof of A” and “a and b are equal proofs of A” and what makes a proposition true is a proof of it. Thus,
![]() $a : A$
and
$a : A$
and
![]() $a = b : A$
are more basic than
$a = b : A$
are more basic than
![]() $A \> \mathsf {true}$
. Under this logical reading the other two forms of judgment
$A \> \mathsf {true}$
. Under this logical reading the other two forms of judgment
![]() $A \> \mathsf {type}$
and
$A \> \mathsf {type}$
and
![]() $A = B \> \mathsf {type}$
simply express that “A is a proposition” and that “A and B are equal propositions.” In Section 3, we will see that these forms of judgment extend beyond propositions and proofs to include sets and their elements as well, which can also be interpreted as types and their objects.
$A = B \> \mathsf {type}$
simply express that “A is a proposition” and that “A and B are equal propositions.” In Section 3, we will see that these forms of judgment extend beyond propositions and proofs to include sets and their elements as well, which can also be interpreted as types and their objects.
I think I have said all I need to put Martin-Löf’s distinction into proper perspective. Classically, it is not harmful to locate the analytic–synthetic distinction on the level of true propositions because there is only one form of judgment,
![]() $A \> \mathsf {true}$
. But with the complex judgment structure required by constructive semantics, as Martin-Löf understands it, we are forced to look for a more elaborate analytic–synthetic distinction that attributes analyticity and syntheticity to judgments having the forms
$A \> \mathsf {true}$
. But with the complex judgment structure required by constructive semantics, as Martin-Löf understands it, we are forced to look for a more elaborate analytic–synthetic distinction that attributes analyticity and syntheticity to judgments having the forms
![]() $A \> \mathsf {type}, A = B \> \mathsf {type}, a : A$
, and
$A \> \mathsf {type}, A = B \> \mathsf {type}, a : A$
, and
![]() $a = b : A$
. This understanding is sufficient for us to comprehend his central claims. I leave a fully detailed account of the meaning explanations of these forms of judgment to the next section.
$a = b : A$
. This understanding is sufficient for us to comprehend his central claims. I leave a fully detailed account of the meaning explanations of these forms of judgment to the next section.
2.1 Analytic judgments
Martin-Löf embraces the now widespread view that an analytic judgment is one which is correct only in virtue of the meanings of the terms that occur in it [Reference Martin-Löf and Parrini25, p. 88]. According to him, this “current formulation” of analyticity, as he calls it, is in essential agreement with the Kantian insight that analytic judgments are explicative. After a brief exposition of some basic rules of inference valid in his constructive type theory, which I shall omit here since they are not directly relevant to our discussion, Martin-Löf claims that the forms of judgment
![]() $a : A$
and
$a : A$
and
![]() $a = b : A$
are both analytic:
$a = b : A$
are both analytic:
Now, whatever type
![]() $\alpha $
that we choose, the two forms of judgement
$\alpha $
that we choose, the two forms of judgement
![]() $a : \alpha $
and
$a : \alpha $
and
![]() $a = b : \alpha $
are both analytic. You see, if a judgement of one of these two forms is evident at all, then it is evident solely by virtue of the meanings of the terms that occur in it. [Reference Martin-Löf and Parrini25, p. 93]
$a = b : \alpha $
are both analytic. You see, if a judgement of one of these two forms is evident at all, then it is evident solely by virtue of the meanings of the terms that occur in it. [Reference Martin-Löf and Parrini25, p. 93]
The reason given is simply that the correctness for such forms of judgment follows from the meanings of the expressions that occur in them and nothing else. This is unfortunately all Martin-Löf tells us about analyticity on this occasion. But later in his paper, he adds that the analytic–synthetic distinction is crucial for a proper understanding of the incompleteness and undecidability phenomena in logic, observing that judgments of the two analytic forms
![]() $a : A$
and
$a : A$
and
![]() $a = b : A$
are decidable and, consequently, complete too:
$a = b : A$
are decidable and, consequently, complete too:
![]() $[$
…
$[$
…
![]() $]$
if you have a judgement of one of the two analytical forms, that is, one of the two forms
$]$
if you have a judgement of one of the two analytical forms, that is, one of the two forms
![]() $a : \alpha $
and
$a : \alpha $
and
![]() $a = b : \alpha $
, then it can be checked, or decided, whether or not that judgement is derivable by means of the formal rules, and the algorithm for doing that is what the computer scientists call the type checking algorithm, which is so to speak the formal, or logical, heart of the computer proof systems that I just mentioned. [Reference Martin-Löf and Parrini25, p. 97]
$a = b : \alpha $
, then it can be checked, or decided, whether or not that judgement is derivable by means of the formal rules, and the algorithm for doing that is what the computer scientists call the type checking algorithm, which is so to speak the formal, or logical, heart of the computer proof systems that I just mentioned. [Reference Martin-Löf and Parrini25, p. 97]
For Martin-Löf the “logic of analytic judgments,” as he calls it, is complete and decidable because there is an algorithm to check whether
![]() $a : A$
and
$a : A$
and
![]() $a = b : A$
are derivable. The kind of decidability referred to here therefore amounts to derivability in a formal system. This is an important point that I shall soon return to in Section 4.5. The requirement that typechecking be decidable in the theory is closely related to Kreisel’s [Reference Kreisel19] dictum that we must recognize a proof when we see one, given the propositions-as-types correspondence. Note that the completeness of the “logic of analytic judgments” follows because decidability guarantees that every judgment
$a = b : A$
are derivable. The kind of decidability referred to here therefore amounts to derivability in a formal system. This is an important point that I shall soon return to in Section 4.5. The requirement that typechecking be decidable in the theory is closely related to Kreisel’s [Reference Kreisel19] dictum that we must recognize a proof when we see one, given the propositions-as-types correspondence. Note that the completeness of the “logic of analytic judgments” follows because decidability guarantees that every judgment
![]() $a : A$
and
$a : A$
and
![]() $a = b : A$
is either correct or not.
$a = b : A$
is either correct or not.
2.2 Synthetic judgments
Having concluded that the forms of judgment
![]() $a : A$
and
$a : A$
and
![]() $a = b : A$
are analytic, Martin-Löf asks where do synthetic judgments come from. To understand his account of syntheticity it is necessary we first discuss how his constructive semantics incorporates the tenet that provability has conceptual priority over truth. The truth of a proposition is expressed with the introduction of a fifth form of judgment
$a = b : A$
are analytic, Martin-Löf asks where do synthetic judgments come from. To understand his account of syntheticity it is necessary we first discuss how his constructive semantics incorporates the tenet that provability has conceptual priority over truth. The truth of a proposition is expressed with the introduction of a fifth form of judgment
![]() $A \> \mathsf {true}$
that is explained to be correct provided some judgment
$A \> \mathsf {true}$
that is explained to be correct provided some judgment
![]() $a : A$
is correct in the presence of some a. In other words, the new form of judgment
$a : A$
is correct in the presence of some a. In other words, the new form of judgment
![]() $A \> \mathsf {true}$
is derived from the primitive
$A \> \mathsf {true}$
is derived from the primitive
![]() $a : A$
and the notion of existence. Some comments on the role of existence in Martin-Löf’s thought will be helpful.
$a : A$
and the notion of existence. Some comments on the role of existence in Martin-Löf’s thought will be helpful.
Existence must enter the analysis of judgments of the form
![]() $A \> \mathsf {true}$
because for Martin-Löf a proposition A is true only if there exists a proof of A. It is imperative to acknowledge that existence cannot be examined through the use of the existential quantifiers here. This attempt would only lead to an infinite regress of questioning what it means for the resulting existentially quantified proposition to be true [Reference Martin-Löf24, pp. 138–139]. We should instead make use of the traditional philosophical notion of concept instantiation, viewing, as Martin-Löf [Reference Martin-Löf and Parrini25, p. 93] says, the existence of A in terms of objects falling under A. This passage holds special philosophical significance as it illustrates how Martin-Löf treats concepts and types as synonymous philosophical notions. He even explicitly alludes to a Kantian interpretation of types as categories [Reference Martin-Löf and Parrini25, p. 91]. Unfortunately, to delve any further into this difficult topic would take us too far astray, so I will simply take his claim for granted and think of objects falling under concepts as objects belonging to a type.Footnote
3
The suggestion is then that we can say that A is true whenever the type A is inhabited. To put it differently, whenever it is the case that some a is an object of A, it follows that A is true. This meaning stipulation can be more clearly stated in the form of a semantic rule:
$A \> \mathsf {true}$
because for Martin-Löf a proposition A is true only if there exists a proof of A. It is imperative to acknowledge that existence cannot be examined through the use of the existential quantifiers here. This attempt would only lead to an infinite regress of questioning what it means for the resulting existentially quantified proposition to be true [Reference Martin-Löf24, pp. 138–139]. We should instead make use of the traditional philosophical notion of concept instantiation, viewing, as Martin-Löf [Reference Martin-Löf and Parrini25, p. 93] says, the existence of A in terms of objects falling under A. This passage holds special philosophical significance as it illustrates how Martin-Löf treats concepts and types as synonymous philosophical notions. He even explicitly alludes to a Kantian interpretation of types as categories [Reference Martin-Löf and Parrini25, p. 91]. Unfortunately, to delve any further into this difficult topic would take us too far astray, so I will simply take his claim for granted and think of objects falling under concepts as objects belonging to a type.Footnote
3
The suggestion is then that we can say that A is true whenever the type A is inhabited. To put it differently, whenever it is the case that some a is an object of A, it follows that A is true. This meaning stipulation can be more clearly stated in the form of a semantic rule:
Martin-Löf argues that the form of judgment
![]() $A \> \mathsf {true}$
is the synthetic form of judgment. Conceptual analysis alone does not suffice to establish correctness, because
$A \> \mathsf {true}$
is the synthetic form of judgment. Conceptual analysis alone does not suffice to establish correctness, because
![]() $A \> \mathsf {true}$
is correct only when there exists an a such that
$A \> \mathsf {true}$
is correct only when there exists an a such that
![]() $a : A$
is correct, so to know that
$a : A$
is correct, so to know that
![]() $A \> \mathsf {true}$
one has to go beyond what is contained in the judgment and find an object of the relevant type:
$A \> \mathsf {true}$
one has to go beyond what is contained in the judgment and find an object of the relevant type:
The synthetic form of judgement is precisely the existential form of judgement that I have just introduced. […] To see why, we have to ask ourselves, what does its evidence rest on? Is it merely on conceptual analysis, or do we have to go beyond what is contained entirely within the judgement in order to make it evident? Well, its evidence rests on a construction: you see, we arrive at an existential judgment
![]() $\alpha $
exists, say through the construction of an object which falls under the concept
$\alpha $
exists, say through the construction of an object which falls under the concept
![]() $\alpha $
, that is, through the construction of the concept […] in Kantian terminology. [Reference Martin-Löf and Parrini25, p. 94]
$\alpha $
, that is, through the construction of the concept […] in Kantian terminology. [Reference Martin-Löf and Parrini25, p. 94]
Since according to Martin-Löf the synthetic judgment is obtained by suppressing part of the underlying analytic judgment, he concludes that every synthetic judgment is “grounded on” an analytic judgment in this sense [Reference Martin-Löf and Parrini25, p. 95]. He sees this as the reason for why the notion of analyticity is more basic and important than that of syntheticity. What does it mean to say that
![]() $A \> \mathsf {true}$
suppresses part of the underlying analytic judgment? Another point made by Martin-Löf is that the judgment
$A \> \mathsf {true}$
suppresses part of the underlying analytic judgment? Another point made by Martin-Löf is that the judgment
![]() $A \> \mathsf {true}$
is some kind of incomplete or abbreviated judgment, where leave out the object a of the judgment
$A \> \mathsf {true}$
is some kind of incomplete or abbreviated judgment, where leave out the object a of the judgment
![]() $a : A$
and choose to retain only the relevant information that A is inhabited [Reference Martin-Löf24, p. 139].
$a : A$
and choose to retain only the relevant information that A is inhabited [Reference Martin-Löf24, p. 139].
Later in the paper when discussing incompleteness and undecidability, Martin-Löf states that the source of the phenomena is the fact that in the synthetic form of judgment
![]() $A \> \mathsf {true}$
the object a such that
$A \> \mathsf {true}$
the object a such that
![]() $a : A$
claimed to exist has been suppressed:
$a : A$
claimed to exist has been suppressed:
![]() $[$
…
$[$
…
![]() $]$
we have to search for an object a of type
$]$
we have to search for an object a of type
![]() $\alpha $
, and, even if we limit ourselves to a particular formal system, that search procedure will not necessarily terminate, let alone then if we put no limitation on the axioms that we are allowed to invoke in the course of that procedure. [Reference Martin-Löf and Parrini25, pp. 97–98]
$\alpha $
, and, even if we limit ourselves to a particular formal system, that search procedure will not necessarily terminate, let alone then if we put no limitation on the axioms that we are allowed to invoke in the course of that procedure. [Reference Martin-Löf and Parrini25, pp. 97–98]
Incompleteness and undecidability have the same source, Martin-Löf suggests. If we fix a formal system and consider a type A that can be formulated in it, he says, then it may be the case that the judgment
![]() $A \> \mathsf {true}$
is not derivable just because there is no
$A \> \mathsf {true}$
is not derivable just because there is no
![]() $a : A$
that can be expressed in the system. However, by considering an extension of the original system with other axioms or rules of inference, it is possible that now there is a derivation of
$a : A$
that can be expressed in the system. However, by considering an extension of the original system with other axioms or rules of inference, it is possible that now there is a derivation of
![]() $a : A$
. Martin-Löf connects this observation with Gödel’s discovery:
$a : A$
. Martin-Löf connects this observation with Gödel’s discovery:
It was this phenomenon that Gödel discovered by taking the original system to be first order arithmetic, say, and constructing a particular first order arithmetical proposition A which is such that there is no proof of A in first order arithmetic […] [Reference Martin-Löf and Parrini25, p. 98]
3 Overview of the meaning explanations
The analytic–synthetic distinction is drawn in terms of meaning, so a closer look on how the meanings of these judgments are explained in constructive type theory will be helpful in my assessment of Martin-Löf’s distinction. My exposition follows the earliest formulation of the meaning explanations by Martin-Löf [Reference Martin-Löf21] based on a lower-order type structure. The only difference is that I adopt an intensional approach to type equality to simplify the presentation following Constable et al. [Reference Constable, Allen, Bromley, Cleaveland, Cremer, Harper, Howe, Knoblock, Mendler, Panangaden, Sasaki and Smith9] and Allen [Reference Allen1]. This early formulation differs from the later version of the meaning explanations considered by Martin-Löf [Reference Martin-Löf and Parrini25] on top of a higher-order structure that places sets and propositions at the bottom level as ground types and builds higher types as function types. However, these are minor differences that are completely orthogonal to my criticism of Martin-Löf’s analytic–synthetic distinction and my own characterization of analyticity and syntheticity. I address objections against the neutrality of my particular formulation of the meaning explanations in Section 5.
The meaning explanations fix the intended interpretation of constructive type theory with a systematic account of what a judgment of each one of its forms means. This is done with an explanation of what one knows when one knows a judgment of one of the forms. So if
![]() $\mathcal {J}$
is a judgment its meaning explanation goes as “to know
$\mathcal {J}$
is a judgment its meaning explanation goes as “to know
![]() $\mathcal {J}$
is to know ….” Roughly, we explain the four primitive forms of judgment according to the following pattern:
$\mathcal {J}$
is to know ….” Roughly, we explain the four primitive forms of judgment according to the following pattern:
-
(i) To know
 $A \> \mathsf {type}$
is to know that A evaluates to a canonical type; To know a canonical type is to know:
$A \> \mathsf {type}$
is to know that A evaluates to a canonical type; To know a canonical type is to know:-
(a) how to construct a canonical object of it;
-
(b) how to show that two of its canonical objects are equal.
-
-
(ii) To know
 $A = B \> \mathsf {type}$
is to know that A and B evaluate to the same canonical type.
$A = B \> \mathsf {type}$
is to know that A and B evaluate to the same canonical type. -
(iii) To know
 $a : A$
is to know that a evaluates to a canonical object in A.
$a : A$
is to know that a evaluates to a canonical object in A. -
(iv) To know
 $a = b : A$
is to know that a and b evaluate to the same canonical object in A.
$a = b : A$
is to know that a and b evaluate to the same canonical object in A.
We do not need to add
![]() $A \> \mathsf {true}$
to the list above because the semantic rule from Section 2.2 allows for us to explain its meaning directly from the meaning explanation of
$A \> \mathsf {true}$
to the list above because the semantic rule from Section 2.2 allows for us to explain its meaning directly from the meaning explanation of
![]() $a : A$
. Now, since each judgment in constructive type theory can depend, or not, on some hypotheses, the meaning explanations will actually fall into two groups. When there is dependence on a finite list of hypotheses, judgments are said to be hypothetical and when no assumptions are made they are said to be categorical. If the judgment is hypothetical, the list of hypotheses it depends on will be displayed within braces to the right as
$a : A$
. Now, since each judgment in constructive type theory can depend, or not, on some hypotheses, the meaning explanations will actually fall into two groups. When there is dependence on a finite list of hypotheses, judgments are said to be hypothetical and when no assumptions are made they are said to be categorical. If the judgment is hypothetical, the list of hypotheses it depends on will be displayed within braces to the right as
![]() $\mathcal {J} (\mathcal {J}_1, ..., \mathcal {J}_n)$
.
$\mathcal {J} (\mathcal {J}_1, ..., \mathcal {J}_n)$
.
3.1 Categorical judgments
The meaning explanations of categorical judgments begin with the specification of a native model of computation as the point of departure. This is the most fundamental assumption underlying the meaning explanations because objects will be assigned to types depending on their computational behavior. For example, the meaning of the categorical judgment
![]() $a : A$
will be explained based on what values a and A evaluate to. It follows from this order of priority that the model of computation taken as primitive in the explanation of type membership must itself be an untyped one to avoid circularity. It can be specified with the prescription of the syntax of a primitive programming language and its operational semantics.
$a : A$
will be explained based on what values a and A evaluate to. It follows from this order of priority that the model of computation taken as primitive in the explanation of type membership must itself be an untyped one to avoid circularity. It can be specified with the prescription of the syntax of a primitive programming language and its operational semantics.
The model of computation adopted here is a form of untyped lambda-calculus extended with constants for some types and their respective constructors and eliminators. They are the dependent function type, equality type, empty type, and natural number type, which will suffice for the point I want to make in this paper. Our syntax is as follows:
 $$ \begin{align*} \mathsf{var} &:=\: \mathsf{x_0} \mid \mathsf{x_1} \mid \mathsf{x_2} \mid \ldots \\ \mathsf{expr} & :=\: \mathsf{var} \mid \lambda \mathsf{var.}\mathsf{expr} \mid \mathsf{app}(\mathsf{expr},\mathsf{expr}) \mid (\mathsf{var} : \mathsf{expr}) \to \mathsf{expr} \\ & \mid \mathsf{refl} \mid \mathsf{Id}(\mathsf{expr},\mathsf{expr},\mathsf{expr}) \mid \mathsf{void} \mid \mathsf{0} \mid \mathsf{s}(\mathsf{expr}) \\ & \mid \mathsf{natrec}(\mathsf{expr},\mathsf{expr},\mathsf{expr}) \mid \mathsf{nat} \end{align*} $$
$$ \begin{align*} \mathsf{var} &:=\: \mathsf{x_0} \mid \mathsf{x_1} \mid \mathsf{x_2} \mid \ldots \\ \mathsf{expr} & :=\: \mathsf{var} \mid \lambda \mathsf{var.}\mathsf{expr} \mid \mathsf{app}(\mathsf{expr},\mathsf{expr}) \mid (\mathsf{var} : \mathsf{expr}) \to \mathsf{expr} \\ & \mid \mathsf{refl} \mid \mathsf{Id}(\mathsf{expr},\mathsf{expr},\mathsf{expr}) \mid \mathsf{void} \mid \mathsf{0} \mid \mathsf{s}(\mathsf{expr}) \\ & \mid \mathsf{natrec}(\mathsf{expr},\mathsf{expr},\mathsf{expr}) \mid \mathsf{nat} \end{align*} $$
Now that we have fixed the syntax of our programming language; let me briefly introduce the four types we will be talking about before we proceed. It is easier to explain them by reference to the sets and propositions that each of them corresponds to:
-
• We can think of the dependent function type
 $(x : A) \to B$
as the Cartesian product of a family of sets B indexed by A, set-theoretically. When the type family B is constant and does not depend on objects of A this is simply the set of functions from A to B. Under the propositions-as-types paradigm [Reference Howard, Seldin and Hindley15], the type
$(x : A) \to B$
as the Cartesian product of a family of sets B indexed by A, set-theoretically. When the type family B is constant and does not depend on objects of A this is simply the set of functions from A to B. Under the propositions-as-types paradigm [Reference Howard, Seldin and Hindley15], the type
 $(x : A) \to B$
plays the role of universal quantification and can be translated as “all As are Bs.” It also boils down to the implication
$(x : A) \to B$
plays the role of universal quantification and can be translated as “all As are Bs.” It also boils down to the implication
 $A \to B$
when there is no dependence, hence the arrow notation. Objects of this type can be constructed as lambda functions
$A \to B$
when there is no dependence, hence the arrow notation. Objects of this type can be constructed as lambda functions
 $\lambda x. a$
and they can be used by means of function application with the eliminator
$\lambda x. a$
and they can be used by means of function application with the eliminator
 $\mathsf {app}(f,a)$
.
$\mathsf {app}(f,a)$
. -
• The equality type
 $\mathsf {Id}(A,a,b)$
is the type of identifications of objects a and b of the type A. One straightforward interpretation in set theory views it as a set that is nonempty when a and b are equal elements of A and empty otherwise. At the same time, it can be regarded as a proposition that expresses the identity of a and b and is governed by Leibniz’s Law. Objects of this type are then just reflexivity proofs
$\mathsf {Id}(A,a,b)$
is the type of identifications of objects a and b of the type A. One straightforward interpretation in set theory views it as a set that is nonempty when a and b are equal elements of A and empty otherwise. At the same time, it can be regarded as a proposition that expresses the identity of a and b and is governed by Leibniz’s Law. Objects of this type are then just reflexivity proofs
 $\mathsf {refl}$
. Notice that there is no constant associated with an elimination rule for equality. There is no need for one because the meaning explanations validate the reflection rule (see Section 3.2), which allows us to assert
$\mathsf {refl}$
. Notice that there is no constant associated with an elimination rule for equality. There is no need for one because the meaning explanations validate the reflection rule (see Section 3.2), which allows us to assert
 $a = b :A$
when given a
$a = b :A$
when given a
 $p : \mathsf {Id}(A,a,b)$
under any assumptions, and this already serves as the elimination rule for this type.
$p : \mathsf {Id}(A,a,b)$
under any assumptions, and this already serves as the elimination rule for this type. -
• The empty type
 $\mathsf {void}$
is the type that has no constructors. Its counterpart in set theory is the empty set and, in logic, the proposition it corresponds to is absurdity. The elimination rule for this type validated by the meaning explanations is a stronger version of ex falso quodlibet which states that given an object of
$\mathsf {void}$
is the type that has no constructors. Its counterpart in set theory is the empty set and, in logic, the proposition it corresponds to is absurdity. The elimination rule for this type validated by the meaning explanations is a stronger version of ex falso quodlibet which states that given an object of
 $\mathsf {void}$
any judgment
$\mathsf {void}$
any judgment
 $\mathcal {J}$
can be derived (see Section 3.2). Thus, again, there is no need to include a constant to act as an elimination rule for it in our programming language.
$\mathcal {J}$
can be derived (see Section 3.2). Thus, again, there is no need to include a constant to act as an elimination rule for it in our programming language. -
• The natural number type
 $\mathsf {nat}$
is the type that has a zero
$\mathsf {nat}$
is the type that has a zero
 $\mathsf {0}$
and successor
$\mathsf {0}$
and successor
 $\mathsf {s}(n)$
constructor. Its eliminator
$\mathsf {s}(n)$
constructor. Its eliminator
 $\mathsf {natrec}(n,a,f)$
generalizes the principle of mathematical induction by roughly allowing us to define dependent functions over natural numbers by recursion. The type
$\mathsf {natrec}(n,a,f)$
generalizes the principle of mathematical induction by roughly allowing us to define dependent functions over natural numbers by recursion. The type
 $\mathsf {nat}$
has an obvious interpretation in set theory as the set of natural numbers. Drawing inspiration from the propositions-as-types paradigm, one may also want to think of
$\mathsf {nat}$
has an obvious interpretation in set theory as the set of natural numbers. Drawing inspiration from the propositions-as-types paradigm, one may also want to think of
 $\mathsf {nat}$
as a proposition that has countably many proofs
$\mathsf {nat}$
as a proposition that has countably many proofs
 $\mathsf {0}$
and
$\mathsf {0}$
and
 $\mathsf {s}(n)$
[Reference Martin-Löf24, p. 163], but this reading is so unnatural in that it has absolutely no noticeable counterpart in logic. It is for this reason I am inclined to think of the propositions-as-types not as an isomorphism, as it is often referred to, but as an embedding of propositions into types. The term “isomorphism” suggests an interpretation that goes in both ways, but there is no question that many types normally considered as part of constructive type theory (especially inductive types and universes) fail to have a natural counterpart in logic as propositions. It is of course expected that a foundational system of mathematics like constructive type theory go beyond logic. It is in this sense that we say that the meaning explanations generalize the proof explanation.
$\mathsf {s}(n)$
[Reference Martin-Löf24, p. 163], but this reading is so unnatural in that it has absolutely no noticeable counterpart in logic. It is for this reason I am inclined to think of the propositions-as-types not as an isomorphism, as it is often referred to, but as an embedding of propositions into types. The term “isomorphism” suggests an interpretation that goes in both ways, but there is no question that many types normally considered as part of constructive type theory (especially inductive types and universes) fail to have a natural counterpart in logic as propositions. It is of course expected that a foundational system of mathematics like constructive type theory go beyond logic. It is in this sense that we say that the meaning explanations generalize the proof explanation.
We may now endow our language with an operational semantics. The collection of valid programs in this language is determined by a binary transition relation over expressions with no occurrence of free variables (closed expressions). The relation is reflexive on the closed expressions that cannot be computed any further and are taken as values. This relation, written as
![]() $M \longmapsto M'$
to indicate that M transitions to
$M \longmapsto M'$
to indicate that M transitions to
![]() $M'$
, can be defined as the smallest relation closed under the three groups of reduction rules given below:
$M'$
, can be defined as the smallest relation closed under the three groups of reduction rules given below:
 $$ \begin{align*} \frac{M \longmapsto M'}{\mathsf{app}(M,N) \longmapsto \mathsf{app}(M',N)} \end{align*} $$
$$ \begin{align*} \frac{M \longmapsto M'}{\mathsf{app}(M,N) \longmapsto \mathsf{app}(M',N)} \end{align*} $$
 $$ \begin{align*} \frac{M \longmapsto M'}{\mathsf{natrec}(M,N,O) \longmapsto \mathsf{natrec}(M',N,O)} \end{align*} $$
$$ \begin{align*} \frac{M \longmapsto M'}{\mathsf{natrec}(M,N,O) \longmapsto \mathsf{natrec}(M',N,O)} \end{align*} $$
Instead of using distinct kinds of letters a, b, f, n, A, B for the metavariables to suggest the expressions they stand for, as I did in the discussion above, I insisted to write them all uniformly as M, N, etc. to emphasize the fact that computation is untyped.
How should the reduction rules above be read? The first group of rules determines what expressions are values using a lazy evaluation strategy, which postpones the reduction of an expression until it becomes necessary to determine its value. This means that an expression may be a value even when some of its parts may not. One example of a value is
![]() $\mathsf {s}(\mathsf {2}+\mathsf {2})$
since it is already a successor, even though we could still evaluate
$\mathsf {s}(\mathsf {2}+\mathsf {2})$
since it is already a successor, even though we could still evaluate
![]() $\mathsf {2}+\mathsf {2}$
further. The second and third groups describe the reduction rules for dependent functions and natural numbers respectively, telling us what happens when a function is applied to an argument and when a recursor operates on a natural number. For example,
$\mathsf {2}+\mathsf {2}$
further. The second and third groups describe the reduction rules for dependent functions and natural numbers respectively, telling us what happens when a function is applied to an argument and when a recursor operates on a natural number. For example,
![]() $\mathsf {app}(\lambda x. x+\mathsf {2},\mathsf {2})$
reduces to
$\mathsf {app}(\lambda x. x+\mathsf {2},\mathsf {2})$
reduces to
![]() $\mathsf {2}+\mathsf {2}$
given that the function that adds two yields two plus two when applied to two as argument. To reduce
$\mathsf {2}+\mathsf {2}$
given that the function that adds two yields two plus two when applied to two as argument. To reduce
![]() $\lambda x. \mathsf {app}(M,x)$
to M we require that M has no free occurrences of x as usual. The reduction rules for
$\lambda x. \mathsf {app}(M,x)$
to M we require that M has no free occurrences of x as usual. The reduction rules for
![]() $\mathsf {natrec}$
simply reflect the principles of definition by recursion. They state, in particular, that
$\mathsf {natrec}$
simply reflect the principles of definition by recursion. They state, in particular, that
![]() $m+\mathsf {0}$
reduces to m and
$m+\mathsf {0}$
reduces to m and
![]() $m+\mathsf {s}(n)$
reduces to
$m+\mathsf {s}(n)$
reduces to
![]() $\mathsf {s}(m+n)$
. For better readability, I am treating the addition sign as an abbreviation for the addition operation
$\mathsf {s}(m+n)$
. For better readability, I am treating the addition sign as an abbreviation for the addition operation
![]() $m+n$
that can be defined by recursion on the second argument as
$m+n$
that can be defined by recursion on the second argument as
![]() $\mathsf {natrec}(n, m, \lambda k. \lambda f. \mathsf {s}(f))$
. I am also using numerals to abbreviate
$\mathsf {natrec}(n, m, \lambda k. \lambda f. \mathsf {s}(f))$
. I am also using numerals to abbreviate
![]() $\mathsf {s}(\mathsf {0})$
as
$\mathsf {s}(\mathsf {0})$
as
![]() $\mathsf {1}$
,
$\mathsf {1}$
,
![]() $\mathsf {s}(\mathsf {1})$
as
$\mathsf {s}(\mathsf {1})$
as
![]() $\mathsf {2}$
, and so on. Together, all these rules make closed expressions into programs that when executed may output a value after a finite number of reduction steps. If there is a sequence of reductions that starts with M and ends with value
$\mathsf {2}$
, and so on. Together, all these rules make closed expressions into programs that when executed may output a value after a finite number of reduction steps. If there is a sequence of reductions that starts with M and ends with value
![]() $M'$
, we say that M evaluates to
$M'$
, we say that M evaluates to
![]() $M'$
and write
$M'$
and write
![]() $M \downarrow M'$
. Reductions need not always simplify an expression and evaluations may even go forever and never terminate.
$M \downarrow M'$
. Reductions need not always simplify an expression and evaluations may even go forever and never terminate.
3.1.1 Typehood and type equality
Knowing that A is a type means knowing that A evaluates to a canonical type. To begin with, therefore, I shall explain what being a canonical type means. Recall that the meaning explanations are always given in terms of what it is to know something. Knowing that A is a canonical type is to know how to construct a canonical object of A and the conditions under which two canonical objects of A are equal. To illustrate the idea, we have:
-
• We know that
 $(x : A) \to B$
is canonical because we prescribe that the function
$(x : A) \to B$
is canonical because we prescribe that the function
 $\lambda x.b$
is a canonical object of it provided that b is an object of B given some object x of A; moreover, two functions
$\lambda x.b$
is a canonical object of it provided that b is an object of B given some object x of A; moreover, two functions
 $\lambda x.b$
and
$\lambda x.b$
and
 $\lambda x.c$
are equal canonical objects of this canonical type when b and c are equal objects of B assuming that x is some object of A.
$\lambda x.c$
are equal canonical objects of this canonical type when b and c are equal objects of B assuming that x is some object of A. -
• We know that
 $\mathsf {Id}(A,a,b)$
is canonical because we prescribe that
$\mathsf {Id}(A,a,b)$
is canonical because we prescribe that
 $\mathsf {refl}$
is a canonical object of it provided a and b are equal objects of A; moreover,
$\mathsf {refl}$
is a canonical object of it provided a and b are equal objects of A; moreover,
 $\mathsf {refl}$
is equal to itself.
$\mathsf {refl}$
is equal to itself. -
• We know that
 $\mathsf {void}$
is canonical because we prescribe it has no canonical objects. I should stress that this stipulation does tell us how to construct objects of this type and when they are equal, namely, under absolutely no circumstances.
$\mathsf {void}$
is canonical because we prescribe it has no canonical objects. I should stress that this stipulation does tell us how to construct objects of this type and when they are equal, namely, under absolutely no circumstances. -
• We know that
 $\mathsf {nat}$
is a canonical type because we prescribe that
$\mathsf {nat}$
is a canonical type because we prescribe that
 $\mathsf {0}$
is a canonical object of it and that so is
$\mathsf {0}$
is a canonical object of it and that so is
 $\mathsf {s}(n)$
when is n an object of
$\mathsf {s}(n)$
when is n an object of
 $\mathsf {nat}$
(which may be non-canonical); moreover,
$\mathsf {nat}$
(which may be non-canonical); moreover,
 $\mathsf {0}$
is equal to itself and
$\mathsf {0}$
is equal to itself and
 $\mathsf {s}(n)$
equals
$\mathsf {s}(n)$
equals
 $\mathsf {s}(m)$
when n and m are equal objects of
$\mathsf {s}(m)$
when n and m are equal objects of
 $\mathsf {nat}$
.
$\mathsf {nat}$
.
In general, the meaning of a judgment of the form
![]() $A \> \mathsf {type}$
is explained as: to know that A is a type is to know that A evaluates to an
$A \> \mathsf {type}$
is explained as: to know that A is a type is to know that A evaluates to an
![]() $A'$
that we know is a canonical type. Nevertheless, the precise format of the explanation depends on the canonical type under consideration. Our task at hand is to provide a concrete explanation of the meaning of
$A'$
that we know is a canonical type. Nevertheless, the precise format of the explanation depends on the canonical type under consideration. Our task at hand is to provide a concrete explanation of the meaning of
![]() $A \> \mathsf {type}$
for each of the canonical types introduced above, namely, dependent function types
$A \> \mathsf {type}$
for each of the canonical types introduced above, namely, dependent function types
![]() $(x : A) \to B$
, equality types
$(x : A) \to B$
, equality types
![]() $\mathsf {Id}(A,a,b)$
, the empty type
$\mathsf {Id}(A,a,b)$
, the empty type
![]() $\mathsf {void}$
, and natural number type
$\mathsf {void}$
, and natural number type
![]() $\mathsf {nat}$
.
$\mathsf {nat}$
.
After that, we will need to explain the meaning of judgments of the form
![]() $A = B \> \mathsf {type}$
. These judgments are known whenever A and B evaluate to the same canonical type, so, again, the particular form of the explanation is contingent on the canonical types in question. Instead of giving two separate meaning explanations, first explaining
$A = B \> \mathsf {type}$
. These judgments are known whenever A and B evaluate to the same canonical type, so, again, the particular form of the explanation is contingent on the canonical types in question. Instead of giving two separate meaning explanations, first explaining
![]() $A \> \mathsf {type}$
and then
$A \> \mathsf {type}$
and then
![]() $A = B \> \mathsf {type}$
, I observe that the explanation of the meaning of
$A = B \> \mathsf {type}$
, I observe that the explanation of the meaning of
![]() $A \> \mathsf {type}$
is just an instance of the more comprehensive meaning explanation of the judgment
$A \> \mathsf {type}$
is just an instance of the more comprehensive meaning explanation of the judgment
![]() $A = B \> \mathsf {type}$
in the specific case where A and B happen to be syntactically identical as expressions.Footnote
4
Thus, to avoid unnecessary repetition, I shall focus exclusively on the meaning explanation of
$A = B \> \mathsf {type}$
in the specific case where A and B happen to be syntactically identical as expressions.Footnote
4
Thus, to avoid unnecessary repetition, I shall focus exclusively on the meaning explanation of
![]() $A = B \> \mathsf {type}$
from this point on, implicitly treating the meaning explanation of
$A = B \> \mathsf {type}$
from this point on, implicitly treating the meaning explanation of
![]() $A \> \mathsf {type}$
as that of
$A \> \mathsf {type}$
as that of
![]() $A = A \> \mathsf {type}$
.
$A = A \> \mathsf {type}$
.
We explain the meaning of the type equality judgment
![]() $A = B \> \mathsf {type}$
by saying that to know that A and B are equal types is to know that they evaluate to the same canonical type. For atomic types such as the empty type
$A = B \> \mathsf {type}$
by saying that to know that A and B are equal types is to know that they evaluate to the same canonical type. For atomic types such as the empty type
![]() $\mathsf {void}$
and natural number type
$\mathsf {void}$
and natural number type
![]() $\mathsf {nat}$
which cannot be broken down into smaller parts this simply amounts to syntactic equality of canonical types. The idea can be more clearly illustrated in the rule format displayed below. To avoid confusion, one should not forget that these are semantic stipulations and not rules of inference:
$\mathsf {nat}$
which cannot be broken down into smaller parts this simply amounts to syntactic equality of canonical types. The idea can be more clearly illustrated in the rule format displayed below. To avoid confusion, one should not forget that these are semantic stipulations and not rules of inference:
For compound types such as the dependent function and equality types, which are composed of other types as their parts, the meaning explanation above tells us that type equality is dependent on that of the canonical types that their parts evaluate to. In particular, we have
 $$ \begin{align*}\frac{A \downarrow (x : A') \to C' \quad B \downarrow (x : B') \to D' \quad A' = B' \> \mathsf{type} \quad C' = D' \> \mathsf{type}\ (x : A')} { A = B \> \mathsf{type}} \end{align*} $$
$$ \begin{align*}\frac{A \downarrow (x : A') \to C' \quad B \downarrow (x : B') \to D' \quad A' = B' \> \mathsf{type} \quad C' = D' \> \mathsf{type}\ (x : A')} { A = B \> \mathsf{type}} \end{align*} $$
 $$ \begin{align*} \frac{A \downarrow \mathsf{Id}(A',a,c) \quad B \downarrow \mathsf{Id}(B',b,d) \quad A' = B' \> \mathsf{type} \quad a = b : A' \quad c = d : B'}{ A = B \> \mathsf{type}}. \end{align*} $$
$$ \begin{align*} \frac{A \downarrow \mathsf{Id}(A',a,c) \quad B \downarrow \mathsf{Id}(B',b,d) \quad A' = B' \> \mathsf{type} \quad a = b : A' \quad c = d : B'}{ A = B \> \mathsf{type}}. \end{align*} $$
Since the evaluation of a closed expression may not always terminate, the problem of whether or not A is a type according to the meaning explanations is not decidable, even though in the formalism the judgment
![]() $A \> \mathsf {type}$
is often decidable. Indeed, as we shall soon see, the meaning of judgments of the form
$A \> \mathsf {type}$
is often decidable. Indeed, as we shall soon see, the meaning of judgments of the form
![]() $a : A$
and
$a : A$
and
![]() $a = b : A$
will be explained by means of evaluation as well, so they too are undecidable in general. This discrepancy with the intended interpretation is due to the fact that the axioms and rules of inference chosen for the formal system may not be rich enough to fully capture this aspect of the meaning explanations. The failure of decidability in the meaning explanations is a highly significant point, in view of the role it plays in Martin-Löf’s analytic–synthetic distinction. I am not contradicting his claims that
$a = b : A$
will be explained by means of evaluation as well, so they too are undecidable in general. This discrepancy with the intended interpretation is due to the fact that the axioms and rules of inference chosen for the formal system may not be rich enough to fully capture this aspect of the meaning explanations. The failure of decidability in the meaning explanations is a highly significant point, in view of the role it plays in Martin-Löf’s analytic–synthetic distinction. I am not contradicting his claims that
![]() $a : A$
and
$a : A$
and
![]() $a = b : A$
are decidable in a particular formal system. I am stating that they fail to be decidable in its intended interpretation, the meaning explanations. Another important semantic element responsible for this lack of decidability is the explanation of the meaning of hypothetical judgments. I shall go back to this point in Section 3.2.
$a = b : A$
are decidable in a particular formal system. I am stating that they fail to be decidable in its intended interpretation, the meaning explanations. Another important semantic element responsible for this lack of decidability is the explanation of the meaning of hypothetical judgments. I shall go back to this point in Section 3.2.
3.1.2 Type membership and member equality
We explain the meaning of
![]() $a : A$
under the assumption that A is a type. Knowing that a is an object of the type A, assuming the knowledge that A evaluates to a canonical type
$a : A$
under the assumption that A is a type. Knowing that a is an object of the type A, assuming the knowledge that A evaluates to a canonical type
![]() $A'$
, is knowing that a evaluates to a canonical object of the canonical type
$A'$
, is knowing that a evaluates to a canonical object of the canonical type
![]() $A'$
. We shall also derive this meaning explanation from a more general meaning explanation for
$A'$
. We shall also derive this meaning explanation from a more general meaning explanation for
![]() $a = b : A$
in the particular case where a and b are syntactically identical. Therefore, we shall only be concerned with the meaning explanation for
$a = b : A$
in the particular case where a and b are syntactically identical. Therefore, we shall only be concerned with the meaning explanation for
![]() $a = b : A$
in what follows.
$a = b : A$
in what follows.
Knowing from the assumption that A is a type that it evaluates to the canonical type
![]() $A'$
, we say that to know that
$A'$
, we say that to know that
![]() $a = b : A$
is to know that a and b both evaluate to equal canonical objects of
$a = b : A$
is to know that a and b both evaluate to equal canonical objects of
![]() $A'$
, where we have stipulated above which canonical objects belong to which types and when they are equal. The meaning explanation of
$A'$
, where we have stipulated above which canonical objects belong to which types and when they are equal. The meaning explanation of
![]() $a = b : A$
is immediately clear in cases when objects evaluate to strictly the same canonical object:
$a = b : A$
is immediately clear in cases when objects evaluate to strictly the same canonical object:
For other pairs of objects of the same type that evaluate to more complex canonical objects that need not be strictly identical to one another, we just demand the knowledge that the parts of their values be equal objects of the same type. With this, we are given meaning explanations for all objects of the natural number, dependent function, equality, and empty type. The latter only gets covered through a vacuous explanation that consists of no rules since the empty type has no canonical objects that can be evaluated to. Thus the explanations are
Note that the meaning explanations for dependent function types given above for
![]() $a = b : A$
and earlier for
$a = b : A$
and earlier for
![]() $A = B \> \mathsf {type}$
presuppose a meaning explanation for hypothetical judgments. I shall now explain what the meaning of a hypothetical judgment is.
$A = B \> \mathsf {type}$
presuppose a meaning explanation for hypothetical judgments. I shall now explain what the meaning of a hypothetical judgment is.
3.2 Hypothetical judgments
We will be exclusively concerned with hypothetical judgments that depend on a finite list of type membership judgments
![]() $x_1 : A_1, ..., x_n : A_n$
where each
$x_1 : A_1, ..., x_n : A_n$
where each
![]() $x_i$
is a variable. We may think of the closed expressions that occur in a categorical judgment as complete programs in the sense that they can be executed in isolation anytime. Then the open expressions which occur in a hypothetical judgment depending on a finite list of typed variables are best seen as incomplete programs that need parameters for their execution. We can then think of the hypotheses
$x_i$
is a variable. We may think of the closed expressions that occur in a categorical judgment as complete programs in the sense that they can be executed in isolation anytime. Then the open expressions which occur in a hypothetical judgment depending on a finite list of typed variables are best seen as incomplete programs that need parameters for their execution. We can then think of the hypotheses
![]() $x_1 : A_1, ..., x_n : A_n$
as variable declarations. These incomplete programs behave functionally given that they only serve to yield complete programs whenever other complete programs are passed as parameters of appropriate types to replace their variables.
$x_1 : A_1, ..., x_n : A_n$
as variable declarations. These incomplete programs behave functionally given that they only serve to yield complete programs whenever other complete programs are passed as parameters of appropriate types to replace their variables.
Hypothetical judgments are explained by induction on the length of their list of declared variables that for the sake briefness we shall denote as
![]() $\Gamma $
. Since the base case is that of a categorical judgment, it suffices that we focus our attention on the inductive step. Assuming that we already know what a hypothetical judgment
$\Gamma $
. Since the base case is that of a categorical judgment, it suffices that we focus our attention on the inductive step. Assuming that we already know what a hypothetical judgment
![]() $\mathcal {J} \ (\Gamma )$
means for any judgment
$\mathcal {J} \ (\Gamma )$
means for any judgment
![]() $\mathcal {J}$
, we can deal with the inductive case through the stipulation that to know
$\mathcal {J}$
, we can deal with the inductive case through the stipulation that to know
![]() $\mathcal {J} \ (\Gamma , x : A)$
is to know that
$\mathcal {J} \ (\Gamma , x : A)$
is to know that
![]() $\mathcal {J}[M/x]\ (\Gamma )$
for any
$\mathcal {J}[M/x]\ (\Gamma )$
for any
![]() $M : A \ (\Gamma )$
. Put differently, this means that
$M : A \ (\Gamma )$
. Put differently, this means that
is correct when every single categorical judgment
![]() $\mathcal {J}[a_1/x_1, ..., a_n/x_n]$
is correct for all
$\mathcal {J}[a_1/x_1, ..., a_n/x_n]$
is correct for all
We also require additional conditions demanding that hypothetical judgments have functional extensionality with respect to type and object equality [Reference Martin-Löf21, pp. 164–166], but the simplified picture we have drawn here will be enough for our purposes.
To illustrate how the meaning explanation of hypothetical judgments works, I want to call attention to two of its notable implications that result in undecidability. They involve the validation in the meaning explanations of the reflection rule and judgmental ex falso rule mentioned earlier in Section 3.1. First, the reflection rule states that if the hypothetical judgment that a certain equality type is inhabited is known
then the hypothetical judgment that the relevant objects are equal is also known
This rule is valid, for according to the explanation of the meaning of hypothetical judgments, the assumption that the former judgment is known means that the categorical judgment
![]() $p [a_1/x_1, ..., a_n/x_n] : \mathsf {Id}(A [a_1/x_1, ..., a_n/x_n],x[a_1/x_1, ..., a_n/x_n], y[a_1/x_1, ..., a_n/x_n])$
is known no matter what closed objects
$p [a_1/x_1, ..., a_n/x_n] : \mathsf {Id}(A [a_1/x_1, ..., a_n/x_n],x[a_1/x_1, ..., a_n/x_n], y[a_1/x_1, ..., a_n/x_n])$
is known no matter what closed objects
![]() $a_1 : A_1, ..., a_n : A_n [a_1/x_1, ..., a_{n-1}/x_{n-1}]$
we choose. This, in turn, as seen in Section 3.1.2, means we know that
$a_1 : A_1, ..., a_n : A_n [a_1/x_1, ..., a_{n-1}/x_{n-1}]$
we choose. This, in turn, as seen in Section 3.1.2, means we know that
![]() $p [a_1/x_1, ..., a_n/x_n] \downarrow \mathsf {refl}$
and
$p [a_1/x_1, ..., a_n/x_n] \downarrow \mathsf {refl}$
and
![]() $x[a_1/x_1, ..., a_n/x_n] = y[a_1/x_1, ..., a_n/x_n] : A[a_1/x_1, ..., a_n/x_n]$
[Reference Dybjer, Dybjer, Lindström, Palmgren and Sundholm12, sec. 11.2.7].
$x[a_1/x_1, ..., a_n/x_n] = y[a_1/x_1, ..., a_n/x_n] : A[a_1/x_1, ..., a_n/x_n]$
[Reference Dybjer, Dybjer, Lindström, Palmgren and Sundholm12, sec. 11.2.7].
Second, we note that a stronger version of the ex falso quodlibet rule in which the explosion takes place at the level of judgments is valid. Specifically, as there are no closed objects
![]() $a : \mathsf {void}$
to account for, since
$a : \mathsf {void}$
to account for, since
![]() $\mathsf {void}$
has no canonical objects, any hypothetical judgment
$\mathsf {void}$
has no canonical objects, any hypothetical judgment
![]() $\mathcal {J} \ (x : \mathsf {void})$
is vacuously correct for any judgment
$\mathcal {J} \ (x : \mathsf {void})$
is vacuously correct for any judgment
![]() $\mathcal {J}$
expressible in our language. Or, more generally, the judgment
$\mathcal {J}$
expressible in our language. Or, more generally, the judgment
![]() $\mathcal {J} \ (x : A)$
is known for any type A that is known not to be inhabited.Footnote
5
$\mathcal {J} \ (x : A)$
is known for any type A that is known not to be inhabited.Footnote
5
Both the reflection and generalized ex falso rules are causes of undecidability of judgments of the form
![]() $a : A$
or
$a : A$
or
![]() $a = b : A$
in the meaning explanations, given that we cannot generally decide when their correctness is a consequence of one of these rules. That would imply a decision method for when a type is inhabited, since the reflection rule asks when equality types are inhabited and the judgmental ex falso rule when types are not inhabited.
$a = b : A$
in the meaning explanations, given that we cannot generally decide when their correctness is a consequence of one of these rules. That would imply a decision method for when a type is inhabited, since the reflection rule asks when equality types are inhabited and the judgmental ex falso rule when types are not inhabited.
4 Our account of analyticity and syntheticity
Now that we have discussed the meaning explanations in the previous section, it is time to take a critical look at the analytic–synthetic distinction proposed by Martin-Löf [Reference Martin-Löf and Parrini25] and already examined at length in Section 2. In what follows, I will level six charges against his distinction and overcome them by proposing and defending my own. My criticism is motivated by six fundamental questions that I will ask about his distinction:
-
1. Does it do justice to the “current formulation” of analytic judgment as one which is correct solely by virtue of the meanings of the expressions involved?
-
2. Does it explain what the meaning of an expression in the “current formulation” is?
-
3. Can the meaning explanations justify the central claims that the judgments of the two analytic forms are
 $a : A$
and
$a : A$
and
 $a = b : A$
and that the synthetic form is
$a = b : A$
and that the synthetic form is
 $A \> \mathsf {true}$
?
$A \> \mathsf {true}$
? -
4. Does it conclusively attribute analyticity or syntheticity to all correct judgments?
-
5. Can the connections drawn between decidability and analyticity be defended by appealing to the meaning explanations?
-
6. Can the claim that synthetic judgments are “grounded on” analytic ones be supported?
All questions will be answered negatively due to the problems indicated in Section 1. I shall address each problem in turn in the subsections to follow while advancing, at the same time, an alternative account of analyticity and syntheticity that can remedy them.
Given that I will establish my proposal through a systematic critique and reconstruction of Martin-Löf’s ideas, a major part of my argumentation will be negative. Yet, a crucial positive argument underlies my discussion of the first two questions, which runs as follows: firstly, if a judgment is analytic when correct only in virtue of the meaning of the expressions occurring in it and synthetic otherwise then we should examine what the expressions in the judgment in question mean before attributing analyticity or syntheticity; secondly, the meaning of an expression here should be understood as reference, which, from a constructive standpoint, is traditionally understood as evaluation of programs. Recall that evaluation is conceived by means of the computational model described in Section 3.1. Therefore, the analytic–synthetic distinction should center around the evaluation of expressions occurring in the judgment. This is how I will arrive at my own definition of analytic and synthetic judgments:
Definition 1 (Analyticity and syntheticity)
A judgment is analytic when its correctness is entirely a consequence of the evaluation of the expressions that occur in it and nothing else. A judgment is synthetic when its correctness cannot be established just by evaluation.
As I hope to show, my definition of analyticity and syntheticity is simply a more careful rendering of the “current formulation” of analyticity invoked by Martin-Löf [Reference Martin-Löf and Parrini25, p. 88] when the relevant notion of meaning is investigated more thoroughly. After we analyze what the meaning of an expression is, we realize that some judgments of the form
![]() $a : A$
and
$a : A$
and
![]() $a = b : A$
cannot be correct only in virtue of meaning, that we should also investigate the analytic or synthetic character of judgments of the form
$a = b : A$
cannot be correct only in virtue of meaning, that we should also investigate the analytic or synthetic character of judgments of the form
![]() $A \> \mathsf {type}$
and
$A \> \mathsf {type}$
and
![]() $A = B \> \mathsf {type}$
, that questions of decidability are peripheral to those of analyticity and syntheticity, and that synthetic judgments are not grounded on analytic ones, revealing that both are basic notions.
$A = B \> \mathsf {type}$
, that questions of decidability are peripheral to those of analyticity and syntheticity, and that synthetic judgments are not grounded on analytic ones, revealing that both are basic notions.
4.1 Analyticity according to the “current formulation”
Recall that the so-called “current formulation” of analyticity states that an analytic judgment is correct solely by virtue of the meaning of the expressions that occur in it. Is it upheld in his distinction as Martin-Löf [Reference Martin-Löf and Parrini25, p. 93] claims it is? I do not think so. Some passages quoted in Section 2 suggest that he attributes analyticity to the two forms of judgment
![]() $a : A$
and
$a : A$
and
![]() $a = b : A$
themselves, not to the actual judgments expressible in the language that have these forms. For instance,
$a = b : A$
themselves, not to the actual judgments expressible in the language that have these forms. For instance,
![]() $\mathsf {0} : \mathsf {nat}$
or
$\mathsf {0} : \mathsf {nat}$
or
![]() $\mathsf {s}(\mathsf {0}) = \mathsf {s}(\mathsf {0}) : \mathsf {nat}$
. The crucial observation is that forms of judgments are not judgments themselves. Being a form of judgment means that whenever the metavariables are replaced with expressions of the language the result is a judgment. So
$\mathsf {s}(\mathsf {0}) = \mathsf {s}(\mathsf {0}) : \mathsf {nat}$
. The crucial observation is that forms of judgments are not judgments themselves. Being a form of judgment means that whenever the metavariables are replaced with expressions of the language the result is a judgment. So
![]() $a : A$
and
$a : A$
and
![]() $a = b : A$
are forms of judgment but not in fact judgments themselves, given that the metavariables a, b, and A that occur in them are not part of the syntax of the language. Martin-Löf also seems to attribute syntheticity to the form of judgment
$a = b : A$
are forms of judgment but not in fact judgments themselves, given that the metavariables a, b, and A that occur in them are not part of the syntax of the language. Martin-Löf also seems to attribute syntheticity to the form of judgment
![]() $A \> \mathsf {true}$
, rather than to judgments of this form such as
$A \> \mathsf {true}$
, rather than to judgments of this form such as
![]() $\mathsf {Id}(\mathsf {nat},\mathsf {2}+\mathsf {2},\mathsf {4}) \> \mathsf {true}$
. This practice of relocating the distinction to the realm of forms of judgments is illustrated in Martin-Löf [Reference Martin-Löf and Parrini25] in many places through statements and expressions such as:
$\mathsf {Id}(\mathsf {nat},\mathsf {2}+\mathsf {2},\mathsf {4}) \> \mathsf {true}$
. This practice of relocating the distinction to the realm of forms of judgments is illustrated in Martin-Löf [Reference Martin-Löf and Parrini25] in many places through statements and expressions such as:
“[…] the two forms of judgement
![]() $a : \alpha $
and
$a : \alpha $
and
![]() $a = b : \alpha $
are both analytic.” (p. 93)
$a = b : \alpha $
are both analytic.” (p. 93)
“The synthetic form of judgement is precisely the existential form of judgement that I have just introduced.” (p. 94)
“[…] it is only [A is true] which is a form of synthetic judgment.” (p. 96)
“[…] a judgement of one of the two analytical forms […]” (p. 97)
To my mind, this is an inaccurate way of phrasing the analytic–synthetic distinction. If analyticity is indeed correctness by virtue of the meaning of expressions in a judgment, as Martin-Löf insists with his allusion to the “current formulation,” then it can never be predicated of forms of judgments. The expressions that occur in a form of judgment are metavariables that have no meaning. Forms of judgments are not even bearers of correctness, so phrases like the “synthetic form of judgment” or “form of analytic judgment” reveal a misleading façon de parler. To offer a charitable reading of Martin-Löf’s claim, one could say that all judgments that have the forms
![]() $a : A$
and
$a : A$
and
![]() $a = b : A$
are analytic and all judgments having the form
$a = b : A$
are analytic and all judgments having the form
![]() $A \> \mathsf {true}$
are synthetic. I believe this is the most profitable way of understanding his claim, so this is how I will interpret his distinction in the rest of this paper. Yet, his terminology of analytic and synthetic forms indicates that the form takes priority over the content of a judgment in questions of analyticity and syntheticity.
$A \> \mathsf {true}$
are synthetic. I believe this is the most profitable way of understanding his claim, so this is how I will interpret his distinction in the rest of this paper. Yet, his terminology of analytic and synthetic forms indicates that the form takes priority over the content of a judgment in questions of analyticity and syntheticity.
In this regard, Martin-Löf breaks with the tradition of Kant, Frege, Carnap and others, where two judgments may share the same form but still have different analytic or synthetic status depending on their content. For instance, in Kant’s [Reference Kant17, B11] view, you can have the judgment “all bodies are extended” as analytic and “all bodies are heavy” as synthetic, even though both ultimately share the same form
![]() $S \textsf { is } P$
. Kant says that the former is analytic because one needs only to analyze the concept of a body to find extension therein. In the latter we cannot find heaviness as a predicate no matter how hard we analyze the subject. These examples indicate that, generally, to determine analyticity or syntheticity for a judgment having the form
$S \textsf { is } P$
. Kant says that the former is analytic because one needs only to analyze the concept of a body to find extension therein. In the latter we cannot find heaviness as a predicate no matter how hard we analyze the subject. These examples indicate that, generally, to determine analyticity or syntheticity for a judgment having the form
![]() $S \textsf { is } P$
in Kant we must first analyze the content of the judgment, which in this case is the particular subject S and predicate P involved in the judgment. And in Frege’s writings, to give another example, we can see that some judgments having the same form
$S \textsf { is } P$
in Kant we must first analyze the content of the judgment, which in this case is the particular subject S and predicate P involved in the judgment. And in Frege’s writings, to give another example, we can see that some judgments having the same form
![]() $A~\> \mathsf {true}$
can be analytic while others are synthetic, as he believed that the truths of arithmetic were analytic but those of geometry were synthetic [Reference Frege13, secs. 89 and 90]. The distinction does not rest on the form of the judgment. This suggests that the analytic–synthetic distinction has been traditionally conceived as a contentual one: a judgment is analytic or synthetic just in virtue of the meanings of the expressions contained in it and not its form.
$A~\> \mathsf {true}$
can be analytic while others are synthetic, as he believed that the truths of arithmetic were analytic but those of geometry were synthetic [Reference Frege13, secs. 89 and 90]. The distinction does not rest on the form of the judgment. This suggests that the analytic–synthetic distinction has been traditionally conceived as a contentual one: a judgment is analytic or synthetic just in virtue of the meanings of the expressions contained in it and not its form.
Unlike the philosophical tradition, Martin-Löf’s distinction is purely formal. What decides whether a judgment is analytic or synthetic is not the meanings of the expressions involved but the form the judgment has,
![]() $A \> \mathsf {type}$
,
$A \> \mathsf {type}$
,
![]() $A = B \> \mathsf {type}$
,
$A = B \> \mathsf {type}$
,
![]() $a : A$
,
$a : A$
,
![]() $a = b : A$
, or
$a = b : A$
, or
![]() $A \> \mathsf {true}$
. If two judgments share the same form they are either both analytic or synthetic. This is a questionable approach, for one cannot adhere to the “current formulation” and focus on the meaning of expressions while endorsing this formal attitude. When a judgment is analytic, in Martin-Löf’s view, it is due to having one of his two “analytical forms,”
$A \> \mathsf {true}$
. If two judgments share the same form they are either both analytic or synthetic. This is a questionable approach, for one cannot adhere to the “current formulation” and focus on the meaning of expressions while endorsing this formal attitude. When a judgment is analytic, in Martin-Löf’s view, it is due to having one of his two “analytical forms,”
![]() $a : A$
or
$a : A$
or
![]() $a = b : A$
. So how can its analyticity be derived from the meaning of the expressions? To properly adhere to the “current formulation” we must first examine what the expressions occurring in a judgment mean and then attribute analyticity or syntheticity to it depending of their meaning. Note that this is precisely the approach of Definition 1, where meaning is explained as evaluation. My definition of analyticity and syntheticity is thus well aligned with the tradition. However, it remains to be seen why meaning should be understood as evaluation.
$a = b : A$
. So how can its analyticity be derived from the meaning of the expressions? To properly adhere to the “current formulation” we must first examine what the expressions occurring in a judgment mean and then attribute analyticity or syntheticity to it depending of their meaning. Note that this is precisely the approach of Definition 1, where meaning is explained as evaluation. My definition of analyticity and syntheticity is thus well aligned with the tradition. However, it remains to be seen why meaning should be understood as evaluation.
4.2 Meaning as evaluation
In Section 2 we discussed Martin-Löf’s claim that all judgments of forms
![]() $a : A$
and
$a : A$
and
![]() $a = b : A$
are analytic because the correctness of a judgment of these forms is “solely by virtue of the meanings of the terms that occur in it” [Reference Martin-Löf and Parrini25, p. 93]. Unfortunately, this claim is presented without any accompanying argument in support of it. Even worse, it has an alarming air of vagueness, as it is unclear what it is for a judgment to be correct solely by virtue of the meaning of the expressions occurring in it. What is the meaning of an expression? To support Martin-Löf’s claim this notion of meaning of expression must be clarified.
$a = b : A$
are analytic because the correctness of a judgment of these forms is “solely by virtue of the meanings of the terms that occur in it” [Reference Martin-Löf and Parrini25, p. 93]. Unfortunately, this claim is presented without any accompanying argument in support of it. Even worse, it has an alarming air of vagueness, as it is unclear what it is for a judgment to be correct solely by virtue of the meaning of the expressions occurring in it. What is the meaning of an expression? To support Martin-Löf’s claim this notion of meaning of expression must be clarified.
This matter is not settled in the meaning explanations. They say what a judgment means, but tell nothing directly about the meaning of an expression occurring in a judgment. This is a gap that we must fill ourselves to understand the imprecise account of analyticity Martin-Löf appeals to in his claim that all
![]() $a : A$
and
$a : A$
and
![]() $a = b : A$
are analytic. We shall do this as follows. There are two primary dimensions of meaning for expressions, sense and reference. Which one is most fitting to clarify the notion of meaning Martin-Löf needs in his claim?
$a = b : A$
are analytic. We shall do this as follows. There are two primary dimensions of meaning for expressions, sense and reference. Which one is most fitting to clarify the notion of meaning Martin-Löf needs in his claim?
It is a commonly accepted view in constructive semantics that the sense of an expression is the program it expresses when endowed by an operational semantics and that its reference is determined by evaluation as the value of the program it expresses. This program-value interpretation of sense and reference was suggested by Dummett [Reference Dummett11, p. 133]. His ideas were further developed in a constructive setting in 1992 at a talk delivered in Leiden whose transcript was published recently [Reference Dummett10]. In 2001, his interpretation was refined and adapted to constructive type theory by Martin-Löf [Reference Martin-Löf27].Footnote
6
For our purposes, it will suffice to mention that the reading of meaning as sense emphasizes the way the program expressed by an expression computes its value. The reading of meaning as reference stresses the value output by the program, regardless of how it was computed. For example, the senses of
![]() $\mathsf {2}+\mathsf {2}$
and
$\mathsf {2}+\mathsf {2}$
and
![]() $\mathsf {4}$
are different, but they have the same reference, as both evaluate to
$\mathsf {4}$
are different, but they have the same reference, as both evaluate to
![]() $\mathsf {4}$
. As we shall see, the referential reading of meaning squares better with the conceptualization of analyticity presupposed by Martin-Löf and it is thus the notion of meaning we shall adopt.
$\mathsf {4}$
. As we shall see, the referential reading of meaning squares better with the conceptualization of analyticity presupposed by Martin-Löf and it is thus the notion of meaning we shall adopt.
Referentially, the meaning of any expression M definable in our programming language is understood by means of the evaluation
![]() $M \downarrow M'$
in accordance to the operational semantics we have already prescribed in Section 3.1. Therefore, to say that a judgment of the forms
$M \downarrow M'$
in accordance to the operational semantics we have already prescribed in Section 3.1. Therefore, to say that a judgment of the forms
![]() $a : A$
or
$a : A$
or
![]() $a = b : B$
is analytic would be the same as saying that when it is correct, its correctness is entirely due to the evaluation of the expressions a and A, or a, b, A, and B, respectively. This referential reading seems to be implicit, for example, in Sundholm [Reference Sundholm, Niiniluoto, Sintonen and Woleński29]:
$a = b : B$
is analytic would be the same as saying that when it is correct, its correctness is entirely due to the evaluation of the expressions a and A, or a, b, A, and B, respectively. This referential reading seems to be implicit, for example, in Sundholm [Reference Sundholm, Niiniluoto, Sintonen and Woleński29]:
![]() $[a : \alpha $
and
$[a : \alpha $
and
![]() $a = b : \alpha]$
have the required analytic character. It is enough to have a and
$a = b : \alpha]$
have the required analytic character. It is enough to have a and
![]() $\alpha $
in order to decide whether
$\alpha $
in order to decide whether
![]() $a : \alpha $
(and similarly for judgements of equality. For both kinds of judgement, the means of decision utilizes evaluation to, and inspection of, relevant canonical forms). [Reference Sundholm, Niiniluoto, Sintonen and Woleński29, p. 456]
$a : \alpha $
(and similarly for judgements of equality. For both kinds of judgement, the means of decision utilizes evaluation to, and inspection of, relevant canonical forms). [Reference Sundholm, Niiniluoto, Sintonen and Woleński29, p. 456]
Under the referential reading, Martin-Löf’s claim that all judgments of the forms
![]() $a : A$
or
$a : A$
or
![]() $a = b : B$
are analytic has in common with the meaning explanations given for these forms of judgment the fact that their correctness is a consequence of evaluation. This may seem to count as evidence in favor of his claim. However, upon closer inspection, although a few correct judgments of the forms
$a = b : B$
are analytic has in common with the meaning explanations given for these forms of judgment the fact that their correctness is a consequence of evaluation. This may seem to count as evidence in favor of his claim. However, upon closer inspection, although a few correct judgments of the forms
![]() $a : A$
or
$a : A$
or
![]() $a = b : B$
indeed come out as analytic, some do not. This can be observed after a more detailed examination of the meaning explanations.
$a = b : B$
indeed come out as analytic, some do not. This can be observed after a more detailed examination of the meaning explanations.
4.3 Revisiting Martin-Löf’s claims
There is a number of simple cases in which analyticity is easy to see. The correctness of several judgments of the form
![]() $a : A$
or
$a : A$
or
![]() $a = b : A$
can be determined after some reflection on the meaning of the expressions involved, that is, by evaluating them. I will focus mainly on the type of natural numbers here because the computation of arithmetical expressions is a simple task we are all sufficiently familiar with. Take, for example, the correct judgment
$a = b : A$
can be determined after some reflection on the meaning of the expressions involved, that is, by evaluating them. I will focus mainly on the type of natural numbers here because the computation of arithmetical expressions is a simple task we are all sufficiently familiar with. Take, for example, the correct judgment
![]() $\mathsf {0} : \mathsf {nat}$
. From the meanings of
$\mathsf {0} : \mathsf {nat}$
. From the meanings of
![]() $\mathsf {0}$
and
$\mathsf {0}$
and
![]() $\mathsf {nat}$
alone it can be concluded that
$\mathsf {nat}$
alone it can be concluded that
![]() $\mathsf {0} \downarrow \mathsf {0}$
and
$\mathsf {0} \downarrow \mathsf {0}$
and
![]() $\mathsf {nat} \downarrow \mathsf {nat}$
. This is all that is needed to know to immediately check that the judgment
$\mathsf {nat} \downarrow \mathsf {nat}$
. This is all that is needed to know to immediately check that the judgment
![]() $\mathsf {0} : \mathsf {nat}$
is correct according to the zero clause from Section 3.1.2, given that this is a valid instance:
$\mathsf {0} : \mathsf {nat}$
is correct according to the zero clause from Section 3.1.2, given that this is a valid instance:
Similarly, we can show that any judgment
![]() $\mathsf {n} : \mathsf {nat}$
is analytic, where, for the sake of briefness, a numeral
$\mathsf {n} : \mathsf {nat}$
is analytic, where, for the sake of briefness, a numeral
![]() $\mathsf {n}$
is used as a short for a string of n-many successors
$\mathsf {n}$
is used as a short for a string of n-many successors
![]() $\mathsf {s}(...)$
followed by
$\mathsf {s}(...)$
followed by
![]() $\mathsf {0}$
. The meaning of the expressions occurring in, say,
$\mathsf {0}$
. The meaning of the expressions occurring in, say,
![]() $\mathsf {1} : \mathsf {nat}$
, is, given that
$\mathsf {1} : \mathsf {nat}$
, is, given that
![]() $\mathsf {1}$
abbreviates
$\mathsf {1}$
abbreviates
![]() $\mathsf {s}(\mathsf {0})$
, fixed by the evaluations
$\mathsf {s}(\mathsf {0})$
, fixed by the evaluations
![]() $\mathsf {0} \downarrow \mathsf {0}$
,
$\mathsf {0} \downarrow \mathsf {0}$
,
![]() $\mathsf {s}(\mathsf {0}) \downarrow \mathsf {s}(\mathsf {0})$
and
$\mathsf {s}(\mathsf {0}) \downarrow \mathsf {s}(\mathsf {0})$
and
![]() $\mathsf {nat} \downarrow \mathsf {nat}$
, which include all expressions that have occurrences in the judgment. Then, since we have just seen that the correctness of
$\mathsf {nat} \downarrow \mathsf {nat}$
, which include all expressions that have occurrences in the judgment. Then, since we have just seen that the correctness of
![]() $\mathsf {0} : \mathsf {nat}$
follows entirely from the meanings of
$\mathsf {0} : \mathsf {nat}$
follows entirely from the meanings of
![]() $\mathsf {0}$
and
$\mathsf {0}$
and
![]() $\mathsf {nat}$
, we have all we need to show its correctness using the successor clause from Section 3.1.2 via the instance:
$\mathsf {nat}$
, we have all we need to show its correctness using the successor clause from Section 3.1.2 via the instance:
 $$ \begin{align*} \frac{\mathsf{nat} \downarrow \mathsf{nat} \quad \mathsf{s}(\mathsf{0}) \downarrow \mathsf{s}(\mathsf{0}) \quad \mathsf{0} : \mathsf{nat}}{ \mathsf{s}(\mathsf{0}) : \mathsf{nat}}. \end{align*} $$
$$ \begin{align*} \frac{\mathsf{nat} \downarrow \mathsf{nat} \quad \mathsf{s}(\mathsf{0}) \downarrow \mathsf{s}(\mathsf{0}) \quad \mathsf{0} : \mathsf{nat}}{ \mathsf{s}(\mathsf{0}) : \mathsf{nat}}. \end{align*} $$
It is not hard to check the analyticity of
![]() $\mathsf {2}+ \mathsf {2} = \mathsf {4} : \mathsf {nat}$
and similar arithmetical judgments. Again,
$\mathsf {2}+ \mathsf {2} = \mathsf {4} : \mathsf {nat}$
and similar arithmetical judgments. Again,
![]() $m+n$
abbreviates
$m+n$
abbreviates
![]() $\mathsf {natrec}(n, m, \lambda k. \lambda f. \mathsf {s}(f))$
. Correctness follows directly from the meanings of the expressions occurring in it because
$\mathsf {natrec}(n, m, \lambda k. \lambda f. \mathsf {s}(f))$
. Correctness follows directly from the meanings of the expressions occurring in it because
![]() $\mathsf {2}+ \mathsf {2} \downarrow \mathsf {4}$
and
$\mathsf {2}+ \mathsf {2} \downarrow \mathsf {4}$
and
![]() $\mathsf {4} : \mathsf {nat}$
is analytic. I take this as sufficient evidence that all judgments of the form
$\mathsf {4} : \mathsf {nat}$
is analytic. I take this as sufficient evidence that all judgments of the form
![]() $a : A$
and
$a : A$
and
![]() $a = b : A$
are analytic when A is
$a = b : A$
are analytic when A is
![]() $\mathsf {nat}$
. To be exact, this claim extends to any particular type A such that
$\mathsf {nat}$
. To be exact, this claim extends to any particular type A such that
![]() $A \downarrow \mathsf {nat}$
.
$A \downarrow \mathsf {nat}$
.
Simple cases like this in which all we need to do to determine correctness is a calculation from the meanings of the expressions were perhaps what Martin-Löf had in mind. But what happens when A evaluates to a more complex type like dependent function types?
Martin-Löf’s claim that all
![]() $a : A$
and
$a : A$
and
![]() $a = b : A$
are analytic breaks down because it leaves out any type A that evaluates to a dependent function type,
$a = b : A$
are analytic breaks down because it leaves out any type A that evaluates to a dependent function type,
![]() $A \downarrow (x : B) \to C$
. This failure is due to the meaning explanation given for hypothetical judgments. I remarked in Section 3.1.2 that all meaning explanations involving dependent function types depend on the meaning explanation for hypothetical judgments. That is, in cases where
$A \downarrow (x : B) \to C$
. This failure is due to the meaning explanation given for hypothetical judgments. I remarked in Section 3.1.2 that all meaning explanations involving dependent function types depend on the meaning explanation for hypothetical judgments. That is, in cases where
![]() $A \downarrow (x : B) \to C$
,
$A \downarrow (x : B) \to C$
,
![]() $a : A$
is correct only if
$a : A$
is correct only if
![]() $a \downarrow \lambda x. c$
and the hypothetical judgment
$a \downarrow \lambda x. c$
and the hypothetical judgment
![]() $ c : C \ (x : B)$
is correct. More generally, the correctness of
$ c : C \ (x : B)$
is correct. More generally, the correctness of
![]() $a = b : A$
follows only when
$a = b : A$
follows only when
![]() $ c = d : C \ (x : B)$
is correct, assuming that
$ c = d : C \ (x : B)$
is correct, assuming that
![]() $a \downarrow \lambda x. c$
and
$a \downarrow \lambda x. c$
and
![]() $b \downarrow \lambda x. d$
. To sum up, when A evaluates to a dependent function type
$b \downarrow \lambda x. d$
. To sum up, when A evaluates to a dependent function type
![]() $(x : B) \to C$
, the judgments
$(x : B) \to C$
, the judgments
![]() $a : A$
and
$a : A$
and
![]() $a = b : A$
are analytic only if so are the hypothetical judgments
$a = b : A$
are analytic only if so are the hypothetical judgments
![]() $ c : C \ (x : B)$
and
$ c : C \ (x : B)$
and
![]() $ c = d : C \ (x : B)$
they respectively presuppose. But the problem is that no hypothetical judgments can be analytic. Their correctness is never in virtue of evaluation alone but due to their intrinsic “extensional” nature: the fact that all resulting categorical judgments remain correct for all objects passed as parameters.
$ c = d : C \ (x : B)$
they respectively presuppose. But the problem is that no hypothetical judgments can be analytic. Their correctness is never in virtue of evaluation alone but due to their intrinsic “extensional” nature: the fact that all resulting categorical judgments remain correct for all objects passed as parameters.
Recall from Section 3.2 that the meaning explanation for hypothetical judgments is given functionally, reducing, for instance, the correctness of
to the correctness of every categorical judgment
that holds for all
So, given how the correctness of multiple categorical judgments needs to be checked before we can establish the correctness of judgments involving dependent function types, we can see why a conceptual analysis by means of evaluation cannot be conclusive. In fact, we could never expect evaluation to determine the correctness of a hypothetical judgment in general, for, as we stipulated in Section 3.1, only closed expressions can be evaluated.
Let me now turn to a few concrete cases where any hope for analyticity is extinguished by the semantic stipulation for hypothetical judgments. Recall that we can, for example, draw the absurd conclusion that
![]() $\mathsf {1} : \mathsf {nat} \to \mathsf {nat}$
under the assumption that
$\mathsf {1} : \mathsf {nat} \to \mathsf {nat}$
under the assumption that
![]() $x : \mathsf {void}$
. This is an instance of the judgmental ex falso rule validated in Section 3.2. Thus, we have
$x : \mathsf {void}$
. This is an instance of the judgmental ex falso rule validated in Section 3.2. Thus, we have
But it does not matter how we try to analyze the meanings of the expressions involved. We will never be able to assert this judgment based on evaluation alone. Actually no further evaluation is possible since
![]() $\lambda x. \mathsf {1} \downarrow \lambda x. \mathsf {1}$
and
$\lambda x. \mathsf {1} \downarrow \lambda x. \mathsf {1}$
and
![]() $\mathsf {void} \to (\mathsf {nat} \to \mathsf {nat}) \downarrow \mathsf {void} \to (\mathsf {nat} \to \mathsf {nat})$
. Yet this information does not suffice to determine that
$\mathsf {void} \to (\mathsf {nat} \to \mathsf {nat}) \downarrow \mathsf {void} \to (\mathsf {nat} \to \mathsf {nat})$
. Yet this information does not suffice to determine that
![]() $\lambda x. \mathsf {1} : \mathsf {void} \to (\mathsf {nat} \to \mathsf {nat})$
is correct. The key issue is that its correctness depends on the correctness of
$\lambda x. \mathsf {1} : \mathsf {void} \to (\mathsf {nat} \to \mathsf {nat})$
is correct. The key issue is that its correctness depends on the correctness of
![]() $ \mathsf {1} : \mathsf {nat} \to \mathsf {nat} \ (x : \mathsf {void})$
. So, as indicated above, we need to justify its correctness with an extensional argument that checks the correctness of every resulting categorical judgment for all objects as parameters. The point is that we need to go beyond the meanings of the expressions involved.
$ \mathsf {1} : \mathsf {nat} \to \mathsf {nat} \ (x : \mathsf {void})$
. So, as indicated above, we need to justify its correctness with an extensional argument that checks the correctness of every resulting categorical judgment for all objects as parameters. The point is that we need to go beyond the meanings of the expressions involved.
One may wonder if the above example is not too specific since functions from empty domains correspond to vacuously true implications under the propositions-as-types interpretation. I believe a more common example of a function will provide a more general and illuminating picture of the failure of analyticity. The simplest example of such a synthetic judgment may be the judgment that the identity function is a function
![]() $\lambda x. x : A \to A$
. It is correct, but its correctness does not follow from the evaluation of the expressions alone. Again,
$\lambda x. x : A \to A$
. It is correct, but its correctness does not follow from the evaluation of the expressions alone. Again,
![]() $\lambda x. x$
and
$\lambda x. x$
and
![]() $A \to A$
are already values, that is,
$A \to A$
are already values, that is,
![]() $\lambda x. x \downarrow \lambda x. x$
and
$\lambda x. x \downarrow \lambda x. x$
and
![]() $A \to A \downarrow A \to A$
. The judgment is only correct due to the trivial extensional argument that for any
$A \to A \downarrow A \to A$
. The judgment is only correct due to the trivial extensional argument that for any
![]() $a : A$
we have
$a : A$
we have
![]() $a : A$
.
$a : A$
.
The example above suggests that all judgments of the form
![]() $a : A$
are synthetic when A evaluates to a dependent function type. Judgments of the form
$a : A$
are synthetic when A evaluates to a dependent function type. Judgments of the form
![]() $a = b : A$
can be synthetic too. What I am trying to convey can already be seen for unary arithmetic functions
$a = b : A$
can be synthetic too. What I am trying to convey can already be seen for unary arithmetic functions
![]() $\mathsf {nat} \to \mathsf {nat}$
. Using the definition of addition by recursion on the second argument mentioned earlier, consider two extensionally equal functions, one that adds two to something
$\mathsf {nat} \to \mathsf {nat}$
. Using the definition of addition by recursion on the second argument mentioned earlier, consider two extensionally equal functions, one that adds two to something
![]() $\lambda x. x + \mathsf {2}$
and one that adds something to two
$\lambda x. x + \mathsf {2}$
and one that adds something to two
![]() $\lambda x. \mathsf {2} + x$
. The judgment that expresses their equality
$\lambda x. \mathsf {2} + x$
. The judgment that expresses their equality
is correct because so is the hypothetical judgment
That is, for any closed number
![]() $n : \mathsf {nat}$
,
$n : \mathsf {nat}$
,
![]() $n + \mathsf {2} = \mathsf {2} + n : \mathsf {nat}$
is correct. But, again, the equality of these two functions is not a consequence of the evaluation of the expressions involved. From the facts that
$n + \mathsf {2} = \mathsf {2} + n : \mathsf {nat}$
is correct. But, again, the equality of these two functions is not a consequence of the evaluation of the expressions involved. From the facts that
![]() $\mathsf {nat} \to \mathsf {nat} \downarrow \mathsf {nat} \to \mathsf {nat}$
,
$\mathsf {nat} \to \mathsf {nat} \downarrow \mathsf {nat} \to \mathsf {nat}$
,
![]() $ \lambda x. x + \mathsf {2} \downarrow \lambda x. x + \mathsf {2} $
, and
$ \lambda x. x + \mathsf {2} \downarrow \lambda x. x + \mathsf {2} $
, and
![]() $ \lambda x. \mathsf {2}+x \downarrow \lambda x. \mathsf {2}+x$
alone there is no way to know that
$ \lambda x. \mathsf {2}+x \downarrow \lambda x. \mathsf {2}+x$
alone there is no way to know that
![]() $\lambda x. x + \mathsf {2} = \lambda x. \mathsf {2} + x : \mathsf {nat} \to \mathsf {nat}$
. We must appeal to extensionality and check that the equality holds for every natural number
$\lambda x. x + \mathsf {2} = \lambda x. \mathsf {2} + x : \mathsf {nat} \to \mathsf {nat}$
. We must appeal to extensionality and check that the equality holds for every natural number
![]() $n : \mathsf {nat}$
. But, of course, this can never be checked analytically, that is, by means of evaluation alone.
$n : \mathsf {nat}$
. But, of course, this can never be checked analytically, that is, by means of evaluation alone.
In summary, upon closer interpretation and examination, Martin-Löf’s assertion that all judgments of the forms
![]() $a : A$
and
$a : A$
and
![]() $a = b : A$
are analytic lacks a solid foundation. Some judgments of these forms are indeed analytic as he observes. But others are synthetic. All judgments of these forms are synthetic when A evaluates to a dependent function type.
$a = b : A$
are analytic lacks a solid foundation. Some judgments of these forms are indeed analytic as he observes. But others are synthetic. All judgments of these forms are synthetic when A evaluates to a dependent function type.
4.4 Martin-Löf’s missing judgments
Another problem with Martin-Löf’s distinction is that it does not exhaustively apply to all judgments expressible in the language of constructive type theory. It neglects the status of hypothetical judgments and the forms
![]() $A \> \mathsf {type}$
and
$A \> \mathsf {type}$
and
![]() $A = B \> \mathsf {type}$
, in particular. But, first of all, why should we expect that Martin-Löf’s analytic–synthetic distinction be exhaustive?
$A = B \> \mathsf {type}$
, in particular. But, first of all, why should we expect that Martin-Löf’s analytic–synthetic distinction be exhaustive?
One might attempt to counter my objection by noting that Kant [Reference Kant17] originally only considered categorical judgments, so Martin-Löf is simply following the Kantian tradition. I hesitate to think this is a convincing analogy for two reasons:
-
• Martin-Löf already omits categorical judgments of the forms
 $A \> \mathsf {type}$
and
$A \> \mathsf {type}$
and
 $A = B \> \mathsf {type}$
, which are needed to establish the correctness of all
$A = B \> \mathsf {type}$
, which are needed to establish the correctness of all
 $a : A$
and
$a : A$
and
 $a = b : A$
. As long as we adhere to the “current formulation,” viewing analyticity as correctness from the meaning of expressions, I do not see how one can claim that
$a = b : A$
. As long as we adhere to the “current formulation,” viewing analyticity as correctness from the meaning of expressions, I do not see how one can claim that
 $a : A$
and
$a : A$
and
 $a = b : A$
are analytic without understanding the status of the more basic
$a = b : A$
are analytic without understanding the status of the more basic
 $A \> \mathsf {type}$
and
$A \> \mathsf {type}$
and
 $A = B \> \mathsf {type}$
.
$A = B \> \mathsf {type}$
. -
• Unlike in the Kantian background, the correctness of hypothetical judgments is a precondition for the correctness of some of Martin-Löf’s categorical judgments. These are not only the instances of
 $a : A$
and
$a : A$
and
 $a = b : A$
we have considered before, where A evaluates to a dependent function type, but also those of
$a = b : A$
we have considered before, where A evaluates to a dependent function type, but also those of
 $A \> \mathsf {type}$
and
$A \> \mathsf {type}$
and
 $A = B \> \mathsf {type}$
. Again, there is no way to examine how these categorical judgments are correct solely by virtue of the meaning of their expressions without extending one’s examination to the hypothetical judgments that their correctness presuppose.
$A = B \> \mathsf {type}$
. Again, there is no way to examine how these categorical judgments are correct solely by virtue of the meaning of their expressions without extending one’s examination to the hypothetical judgments that their correctness presuppose.
The account proposed here is general enough to be applicable to any correct judgment. I just showed in Section 4.3 that all judgments
![]() $a : A$
and
$a : A$
and
![]() $a = b : A$
will fail to be analytic whenever
$a = b : A$
will fail to be analytic whenever
![]() $A \downarrow (x : B) \to C$
, for their correctness is not verifiable purely by evaluation. It is implied in my previous considerations that every hypothetical judgment is synthetic. This is the real reason of the failure of analyticity for
$A \downarrow (x : B) \to C$
, for their correctness is not verifiable purely by evaluation. It is implied in my previous considerations that every hypothetical judgment is synthetic. This is the real reason of the failure of analyticity for
![]() $a : A$
and
$a : A$
and
![]() $a = b : A$
when
$a = b : A$
when
![]() $A \downarrow (x : B) \to C$
.
$A \downarrow (x : B) \to C$
.
What about the typehood and type equality judgments? I trust that the reader can see that
![]() $\mathsf {void} = \mathsf {void} \> \mathsf {type}$
and
$\mathsf {void} = \mathsf {void} \> \mathsf {type}$
and
![]() $\mathsf {Id}(\mathsf {nat},0,0) \> \mathsf {type}$
are analytic, for example. Is it possible for a judgment of these forms to be synthetic? Yes, due to the syntheticity of hypothetical judgments,
$\mathsf {Id}(\mathsf {nat},0,0) \> \mathsf {type}$
are analytic, for example. Is it possible for a judgment of these forms to be synthetic? Yes, due to the syntheticity of hypothetical judgments,
![]() $A \> \mathsf {type}$
and
$A \> \mathsf {type}$
and
![]() $A = B \> \mathsf {type}$
will be synthetic whenever
$A = B \> \mathsf {type}$
will be synthetic whenever
![]() $A \downarrow (x : B) \to C$
. One simple example of a synthetic judgment of one of these forms is
$A \downarrow (x : B) \to C$
. One simple example of a synthetic judgment of one of these forms is
![]() $(x : \mathsf {nat}) \to \mathsf {Id}(\mathsf {nat},x,x) \> \mathsf {type}$
. Its correctness owes to the correctness of the hypothetical judgment
$(x : \mathsf {nat}) \to \mathsf {Id}(\mathsf {nat},x,x) \> \mathsf {type}$
. Its correctness owes to the correctness of the hypothetical judgment
![]() $\mathsf {Id}(\mathsf {nat},x,x) \> \mathsf {type} \ (x : \mathsf {nat})$
.
$\mathsf {Id}(\mathsf {nat},x,x) \> \mathsf {type} \ (x : \mathsf {nat})$
.
4.5 Decidability and incompleteness
Perhaps my demonstration of the failure of analyticity for some judgments of the forms
![]() $a : A$
and
$a : A$
and
![]() $a = b : A$
may be taken as evidence that a completely distinct characterization of meaning of expression underlies Martin-Löf’s [Reference Martin-Löf and Parrini25] claim. So, in his defense, it may be objected that, since his conclusions are erroneous under our referential reading of meaning as evaluation, he must have endorsed a different account of analyticity.
$a = b : A$
may be taken as evidence that a completely distinct characterization of meaning of expression underlies Martin-Löf’s [Reference Martin-Löf and Parrini25] claim. So, in his defense, it may be objected that, since his conclusions are erroneous under our referential reading of meaning as evaluation, he must have endorsed a different account of analyticity.
The closest thing to an argument that could provide a justification for his claim of analyticity is found in his discussion of decidability [Reference Martin-Löf and Parrini25, pp. 97–99]. This is not the first time analyticity has been connected with decidability in the philosophical tradition. Indeed, Wittgenstein thought that we should be able to decide by a mechanical calculation of symbols alone whether a proposition is analytic, as Sundholm [Reference Sundholm, Rudolf and Brandl31, pp. 59–60] notes. What is special about Martin-Löf’s view is that the analytic status he attributes to
![]() $a : A$
and
$a : A$
and
![]() $a = b : A$
is intimately related to our possession of a type-checking algorithm which can decide whether or not they are derivable in a fixed formal system for constructive type theory.
$a = b : A$
is intimately related to our possession of a type-checking algorithm which can decide whether or not they are derivable in a fixed formal system for constructive type theory.
Clearly, the meaning of an expression has to be understood along the same lines if this connection between analyticity and decidability is to be taken seriously. Martin-Löf does not explain in what sense of “meaning” the decidability of
![]() $a : A$
and
$a : A$
and
![]() $a = b : A$
leads to correctness in virtue of the meaning of the expressions that occur in them. But one thing we can say for sure is that meaning has to be understood in terms of the information needed to decide whether these judgments are derivable or not. For example, we can say that the meaning of an expression consists of all the axioms and rules of inference of the formal system in consideration that say something about this expression. Needless to say, making this approach to meaning fully precise requires a bit more work than this. But, no matter how much we refine the idea, the formal line of reasoning it hinges on is too problematic. The correlation with decidability inevitably put matters of analyticity at the level of the particular formal system our type-checking algorithm is based on. Nevertheless, the analytic–synthetic distinction is supposed to have a semantic, as opposed to a formal nature.Footnote
7
$a = b : A$
leads to correctness in virtue of the meaning of the expressions that occur in them. But one thing we can say for sure is that meaning has to be understood in terms of the information needed to decide whether these judgments are derivable or not. For example, we can say that the meaning of an expression consists of all the axioms and rules of inference of the formal system in consideration that say something about this expression. Needless to say, making this approach to meaning fully precise requires a bit more work than this. But, no matter how much we refine the idea, the formal line of reasoning it hinges on is too problematic. The correlation with decidability inevitably put matters of analyticity at the level of the particular formal system our type-checking algorithm is based on. Nevertheless, the analytic–synthetic distinction is supposed to have a semantic, as opposed to a formal nature.Footnote
7
Since the intended semantics of constructive type theory is the meaning explanations, the analytic–synthetic distinction must be rooted in reflections on the meaning explanations and not on the particulars of one formal system they justify. My proposed account of analyticity in terms of evaluation conforms to this principle, but the one discussed here violates it. Its formal approach is incapable of offering a sustainable answer because the same meaning explanations can be used to justify vastly different formal systems (e.g., [Reference Martin-Löf, Rose and Shepherdson20, Reference Martin-Löf21]). All of them are imperfect approximations of the meaning explanations. They can never portray the full picture due to Gödel’s incompleteness theorems. Once the set of all correct judgments encompasses all arithmetical truths, as it should under the standard interpretation of the natural numbers in the meaning explanations, it ceases to be recursively enumerable. The totality of correct judgments outstrips a single body of axioms and rules of inference.Footnote 8
Each one of these different formal systems for constructive type theory simply isolates a limited range of semantic properties of the meaning explanations it emphasizes. That is, from a certain formal viewpoint, if we are careful enough to see that only the “right” axioms and rules of inference are included in the proof system, the result will indeed be a formalism in which
![]() $a : A$
and
$a : A$
and
![]() $a = b : A$
are decidable [Reference Martin-Löf, Rose and Shepherdson20]. However, decidability only holds because the axioms and rules of inference that we chose to accept are incapable of fully capturing this rich aspect of the meaning explanations.
$a = b : A$
are decidable [Reference Martin-Löf, Rose and Shepherdson20]. However, decidability only holds because the axioms and rules of inference that we chose to accept are incapable of fully capturing this rich aspect of the meaning explanations.
As it was seen in Section 3, the judgments
![]() $a : A$
and
$a : A$
and
![]() $a = b : A$
are undecidable from the semantic perspective of the meaning explanations. It is thus to be expected that these judgments will be undecidable in a different but still justifiable formal system. One such a formalism with undecidable type-checking is outlined in Martin-Löf [Reference Martin-Löf21] with the adoption of the reflection rule as the elimination rule for the equality type.
$a = b : A$
are undecidable from the semantic perspective of the meaning explanations. It is thus to be expected that these judgments will be undecidable in a different but still justifiable formal system. One such a formalism with undecidable type-checking is outlined in Martin-Löf [Reference Martin-Löf21] with the adoption of the reflection rule as the elimination rule for the equality type.
The greatest challenge for this tentative formal account of analyticity as decidability in some formal system is how to decide which axioms and rules of inference count as the “right” ones when other rules that lead to undecidability are validated by the meaning explanations. As far as I can see, a proper defense would involve abandoning the meaning explanations completely in favor of another intended constructive semantics or at least restricting its decisive role in the justification of type-theoretic formal systems to some extent.Footnote 9
One could, for instance, maintain that formal systems where
![]() $a : A$
and
$a : A$
and
![]() $a = b : A$
are decidable have a privileged status for some other reason extraneous to the meaning explanations. To be fair, I am willing to concede that decidability of type-checking is a useful feature to have for practical purposes like formal proof verification in the mechanization of mathematics.
$a = b : A$
are decidable have a privileged status for some other reason extraneous to the meaning explanations. To be fair, I am willing to concede that decidability of type-checking is a useful feature to have for practical purposes like formal proof verification in the mechanization of mathematics.
Perhaps Kreisel’s [Reference Kreisel19] dictum that we should recognize a proof when we see one best expresses why decidability is held in high regard by many as an ideal proof-theoretic feature. Implicit in this welcoming attitude toward decidability is a rough treatment of
![]() $a : A$
as “a is a formal proof of the theorem A.” Is there a chance that with some refinements to the idea this could give rise to a different intended semantics for constructive type theory that could rival the meaning explanations? Well, worries similar to those expressed on page would arise, considering that it is hard to think of judgments not restricted to logic such as
$a : A$
as “a is a formal proof of the theorem A.” Is there a chance that with some refinements to the idea this could give rise to a different intended semantics for constructive type theory that could rival the meaning explanations? Well, worries similar to those expressed on page would arise, considering that it is hard to think of judgments not restricted to logic such as
![]() $\mathsf {2}+\mathsf {2} : \mathsf {nat}$
as formal proofs of the theorem
$\mathsf {2}+\mathsf {2} : \mathsf {nat}$
as formal proofs of the theorem
![]() $\mathsf {nat}$
. Such judgments are unproblematic in the meaning explanations where all objects are programs and
$\mathsf {nat}$
. Such judgments are unproblematic in the meaning explanations where all objects are programs and
![]() $a : A$
means “a is a program with values in A.” Though every formal proof can be regarded as a program by the very finitistic nature of a formal system, not every program should be identified with a formal proof. Until a solution to this problem is found, it is unclear how this treatment of objects as formal proofs could lead to an interpretation for all types considered in constructive type theory.
$a : A$
means “a is a program with values in A.” Though every formal proof can be regarded as a program by the very finitistic nature of a formal system, not every program should be identified with a formal proof. Until a solution to this problem is found, it is unclear how this treatment of objects as formal proofs could lead to an interpretation for all types considered in constructive type theory.
4.6 Analytic and synthetic grounding
Finally, I want to emphasize that Martin-Löf’s [Reference Martin-Löf and Parrini25] view that every synthetic judgment of the form
![]() $A \> \mathsf {true}$
is “grounded on” an analytic one is false under our proposed account. I do not dispute his conclusion that all
$A \> \mathsf {true}$
is “grounded on” an analytic one is false under our proposed account. I do not dispute his conclusion that all
![]() $A \> \mathsf {true}$
are synthetic, since it is not possible to establish their correctness with some
$A \> \mathsf {true}$
are synthetic, since it is not possible to establish their correctness with some
![]() $a : A$
only by evaluating A. But, as we have seen, it is possible that the judgment
$a : A$
only by evaluating A. But, as we have seen, it is possible that the judgment
![]() $a : A$
that makes
$a : A$
that makes
![]() $A \> \mathsf {true}$
correct is synthetic. This will happen in any truth judgment involving the dependent function type. To give an example, notice that we have both synthetic judgments in the premise and the conclusion of the following valid rule:
$A \> \mathsf {true}$
correct is synthetic. This will happen in any truth judgment involving the dependent function type. To give an example, notice that we have both synthetic judgments in the premise and the conclusion of the following valid rule:
 $$ \begin{align*}\frac{ \lambda x. \lambda y. x : A \to (B \to A)}{ A \to (B \to A) \> \mathsf{true}}.\end{align*} $$
$$ \begin{align*}\frac{ \lambda x. \lambda y. x : A \to (B \to A)}{ A \to (B \to A) \> \mathsf{true}}.\end{align*} $$
So we end up with two classes of synthetic judgments of the form
![]() $A \> \mathsf {true}$
, namely, those that can be grounded on an analytic judgment
$A \> \mathsf {true}$
, namely, those that can be grounded on an analytic judgment
![]() $a : A$
and those that cannot. In this sense, judgments of the first class are more fundamentally synthetic than those of the second class. Is this subtle difference between so-to-speak “synthetic-synthetic” and “synthetic-analytic” judgments of the form
$a : A$
and those that cannot. In this sense, judgments of the first class are more fundamentally synthetic than those of the second class. Is this subtle difference between so-to-speak “synthetic-synthetic” and “synthetic-analytic” judgments of the form
![]() $A \> \mathsf {true}$
able to capture any useful philosophical distinction? I believe so, though for reasons of space I can only offer a short example to convince the reader. Via the propositions-as-types paradigm, my proposal allows us to distinguish the syntheticity of any logical laws saying something about implication or universal quantification from that of simpler judgments like
$A \> \mathsf {true}$
able to capture any useful philosophical distinction? I believe so, though for reasons of space I can only offer a short example to convince the reader. Via the propositions-as-types paradigm, my proposal allows us to distinguish the syntheticity of any logical laws saying something about implication or universal quantification from that of simpler judgments like
![]() $\mathsf {nat} \> \mathsf {true}$
or
$\mathsf {nat} \> \mathsf {true}$
or
![]() $\mathsf {Id}(\mathsf {nat},\mathsf {0},\mathsf {0}) \> \mathsf {true}$
which have an analytic grounding. Martin-Löf’s account of syntheticity is unable to explain this difference.
$\mathsf {Id}(\mathsf {nat},\mathsf {0},\mathsf {0}) \> \mathsf {true}$
which have an analytic grounding. Martin-Löf’s account of syntheticity is unable to explain this difference.
5 Some possible objections
Before I conclude, I would like to address some possible objections and general concerns that may arise regarding the legitimacy of my criticism of Martin-Löf’s views and some implications of the analytic–synthetic distinction I proposed above.
5.1 Particulars of the meaning explanations
It may be objected that my critical remarks rely heavily on the particular formulation of the meaning explanations favored in Section 3. The version I presented is a variant of the original formulation of Martin-Löf [Reference Martin-Löf21] that adopts an intensional explanation of type equality judgments. In his own meaning explanations, however, he explains type equality extensionally by saying instead that the judgment
![]() $A = B \> \mathsf {type}$
is known whenever the knowledge of
$A = B \> \mathsf {type}$
is known whenever the knowledge of
![]() $a : A$
follows from the knowledge of
$a : A$
follows from the knowledge of
![]() $a : B$
and vice-versa. This extensional explanation is rejected in this paper for going against what I see as the most fundamental principle of the meaning explanations: the core idea that computational behavior determines meaning is entirely absent in the extensional account of type equality. That is, unlike its intensional counterpart I adopt, the meaning of
$a : B$
and vice-versa. This extensional explanation is rejected in this paper for going against what I see as the most fundamental principle of the meaning explanations: the core idea that computational behavior determines meaning is entirely absent in the extensional account of type equality. That is, unlike its intensional counterpart I adopt, the meaning of
![]() $A = B \> \mathsf {type}$
is not determined by taking into account how closed expressions are evaluated to their canonical forms. For this reason, under the extensional approach we cannot explain
$A = B \> \mathsf {type}$
is not determined by taking into account how closed expressions are evaluated to their canonical forms. For this reason, under the extensional approach we cannot explain
![]() $A \> \mathsf {type}$
as
$A \> \mathsf {type}$
as
![]() $A = A \> \mathsf {type}$
. Still, none of my arguments in Section 4 are contingent upon the adoption of intensional type equality.
$A = A \> \mathsf {type}$
. Still, none of my arguments in Section 4 are contingent upon the adoption of intensional type equality.
I have also opted to follow the early meaning explanations of Martin-Löf [Reference Martin-Löf21], wherein the elements of a set and proofs of a proposition are treated as objects of a type. This approach, commonly referred to as a lower-order formulation, is distinct from the later higher-order formulation proposed by Martin-Löf [Reference Martin-Löf24], which employs a complex type structure where the elements of a set and proofs of a proposition are distinct from objects of a type. It also features a typed evaluation relation instead. This higher-order structure is assumed in the background of Martin-Löf’s [Reference Martin-Löf and Parrini25, pp. 91–94] distinction. I avoided it here due to its significant conceptual complexity, which I believe would complicate the presentation. Moreover, I am not entirely convinced the presupposition of a typed evaluation relation in an explanation of what it means to be a type is a coherent philosophical move to make. This is an issue worth exploring, but due to space constraints, I cannot do so here. Most importantly, my adoption of a lower-order formulation does not result in any loss of generality in my arguments. The only features of the meaning explanations I rely on in my refutation of Martin-Löf’s claim that all
![]() $a : A$
and
$a : A$
and
![]() $a = b : A$
are analytic in Sections 4.3 and 4.5 are found in both the lower- and higher-order formulations. In particular, the explanation of the meaning of hypothetical judgments and thus the semantical undecidability of
$a = b : A$
are analytic in Sections 4.3 and 4.5 are found in both the lower- and higher-order formulations. In particular, the explanation of the meaning of hypothetical judgments and thus the semantical undecidability of
![]() $a : A$
and
$a : A$
and
![]() $a = b : A$
. The interested reader can compare [Reference Martin-Löf21, pp. 164–166] with [Reference Martin-Löf24, pp. 35–39].
$a = b : A$
. The interested reader can compare [Reference Martin-Löf21, pp. 164–166] with [Reference Martin-Löf24, pp. 35–39].
5.2 Why the formal approach is left behind?
Recall I accept Martin-Löf’s claim that all judgments of the form
![]() $A \> \mathsf {true}$
are synthetic. If some
$A \> \mathsf {true}$
are synthetic. If some
![]() $A \> \mathsf {true}$
were analytic, their correctness would follow from the evaluation of A alone. But to make this judgment one needs an object a such that the judgment
$A \> \mathsf {true}$
were analytic, their correctness would follow from the evaluation of A alone. But to make this judgment one needs an object a such that the judgment
![]() $a : A$
is correct. As I reject Martin-Löf’s formal approach in Section 4.1, I must add that the syntheticity of every judgment of the form
$a : A$
is correct. As I reject Martin-Löf’s formal approach in Section 4.1, I must add that the syntheticity of every judgment of the form
![]() $A \> \mathsf {true}$
is not a consequence of the form of judgment that they all share, but our failure to establish their correctness based only on an analysis of the meaning of A. I follow the contentual tradition of Kant, Frege and others, since two judgments having the same form can have different analytic or synthetic status according to my proposal. I see the type membership
$A \> \mathsf {true}$
is not a consequence of the form of judgment that they all share, but our failure to establish their correctness based only on an analysis of the meaning of A. I follow the contentual tradition of Kant, Frege and others, since two judgments having the same form can have different analytic or synthetic status according to my proposal. I see the type membership
![]() $\mathsf {0} : \mathsf {nat}$
as analytic but
$\mathsf {0} : \mathsf {nat}$
as analytic but
![]() $\lambda x. x : A \to A$
as synthetic, for instance. This is a result of the difference in meaning of the expressions occurring in them.
$\lambda x. x : A \to A$
as synthetic, for instance. This is a result of the difference in meaning of the expressions occurring in them.
5.3 Typehood judgments cannot be synthetic
It may be objected that my claim that some judgments of the forms
![]() $A \> \mathsf {type}$
or
$A \> \mathsf {type}$
or
![]() $A = B \> \mathsf {type}$
are synthetic is counterintuitive or even contradictory. To say that something is a type is, in some sense, to say that it is meaningful, but this, as I claim, may not always follow from an analysis of the meaning of the expressions. There is a confusion between the meaningfulness an expression is supposed to have when it is known to be a type and the notion of meaning of expression I pin down to understand analyticity with. When
$A = B \> \mathsf {type}$
are synthetic is counterintuitive or even contradictory. To say that something is a type is, in some sense, to say that it is meaningful, but this, as I claim, may not always follow from an analysis of the meaning of the expressions. There is a confusion between the meaningfulness an expression is supposed to have when it is known to be a type and the notion of meaning of expression I pin down to understand analyticity with. When
![]() $A \> \mathsf {type}$
is correct, A is meaningful in that we know from the meaning explanations what it means for it to be a type. This cannot be the notion of meaning we invoke in our discussion of analyticity. If it were, we would be forced to say, for instance, that
$A \> \mathsf {type}$
is correct, A is meaningful in that we know from the meaning explanations what it means for it to be a type. This cannot be the notion of meaning we invoke in our discussion of analyticity. If it were, we would be forced to say, for instance, that
![]() $\mathsf {nat} \> \mathsf {true}$
is analytic. When one knows that
$\mathsf {nat} \> \mathsf {true}$
is analytic. When one knows that
![]() $\mathsf {nat}$
is a type one knows how to construct a canonical object of it. Thus, from the meaningfulness
$\mathsf {nat}$
is a type one knows how to construct a canonical object of it. Thus, from the meaningfulness
![]() $\mathsf {nat}$
has as a type one could conclude that
$\mathsf {nat}$
has as a type one could conclude that
![]() $0 : \mathsf {nat}$
and therefore that
$0 : \mathsf {nat}$
and therefore that
![]() $\mathsf {nat} \> \mathsf {true}$
. Under my view, the meaning of an expression is the value it expresses as a program.
$\mathsf {nat} \> \mathsf {true}$
. Under my view, the meaning of an expression is the value it expresses as a program.
5.4 Empirical judgments
Given that the status of identity judgments is a recurring concern in classical approaches to the analytic–synthetic distinction, one may wonder how the distinction proposed in this paper can be applied to identity judgments beyond the ideal realm of mathematics. For example, what is the status of a judgment such as
![]() $\text {Hesperus}=\text {Phosphorus} : \text {Planet}$
? One problem is how to understand types of empirical objects and the correctness of judgments about them. Elsewhere Martin-Löf [Reference Martin-Löf26, p. 5] states that to explain what an empirical proposition is one has to first explain the notion of an empirical quantity. Instead of giving a definition he provides examples such as the eye color of some individual, the length of a table, or the number of geese that cackled on the Capitol a particular night in 390 BC. Martin-Löf adds that these empirical quantities all have their own types. For eye colors we have a type that contains brown, blue, green and so on. For lengths and geese we have natural numbers. We can then perhaps say that Mercury, Venus, Earth, Mars, Jupiter, Saturn, Uranus, and Neptune are all empirical quantities of the type
$\text {Hesperus}=\text {Phosphorus} : \text {Planet}$
? One problem is how to understand types of empirical objects and the correctness of judgments about them. Elsewhere Martin-Löf [Reference Martin-Löf26, p. 5] states that to explain what an empirical proposition is one has to first explain the notion of an empirical quantity. Instead of giving a definition he provides examples such as the eye color of some individual, the length of a table, or the number of geese that cackled on the Capitol a particular night in 390 BC. Martin-Löf adds that these empirical quantities all have their own types. For eye colors we have a type that contains brown, blue, green and so on. For lengths and geese we have natural numbers. We can then perhaps say that Mercury, Venus, Earth, Mars, Jupiter, Saturn, Uranus, and Neptune are all empirical quantities of the type
![]() $\text {Planet}$
. However, a more serious problem is that it is less clear how we should evaluate empirical quantities. Martin-Löf [Reference Martin-Löf26, p. 5] contrasts calculation for mathematical objects with “experiments” for empirical objects in a broad sense. For example, taking a look at my eyes to tell what color they are, or using a ruler to measure the height of a table both count as experiments in his view. If we follow this line of reasoning then, because an experiment revels that both Hesperus and Phosphorus turn out to be the planet Venus, we should take
$\text {Planet}$
. However, a more serious problem is that it is less clear how we should evaluate empirical quantities. Martin-Löf [Reference Martin-Löf26, p. 5] contrasts calculation for mathematical objects with “experiments” for empirical objects in a broad sense. For example, taking a look at my eyes to tell what color they are, or using a ruler to measure the height of a table both count as experiments in his view. If we follow this line of reasoning then, because an experiment revels that both Hesperus and Phosphorus turn out to be the planet Venus, we should take
![]() $\text {Hesperus}=\text {Phosphorus} : \text {Planet}$
as analytic. They are non-canonical empirical quantities of that type, so to speak. But to provide a comprehensive analysis of this proposal, a rigorous examination of empirical types is necessary. One might think a viable approach for refining the conception of experimentation could be the formulation of a general theory of intuition and fulfillment-chains in the sense of Husserl [Reference Husserl16, VI, sec. 18]. However, some strong objections to the idea that Husserl’s views on intuition are compatible with a constructivist interpretation have been raised recently [Reference Bentzen5]. In any case, further investigation of judgments outside of mathematics is beyond the scope of this paper.
$\text {Hesperus}=\text {Phosphorus} : \text {Planet}$
as analytic. They are non-canonical empirical quantities of that type, so to speak. But to provide a comprehensive analysis of this proposal, a rigorous examination of empirical types is necessary. One might think a viable approach for refining the conception of experimentation could be the formulation of a general theory of intuition and fulfillment-chains in the sense of Husserl [Reference Husserl16, VI, sec. 18]. However, some strong objections to the idea that Husserl’s views on intuition are compatible with a constructivist interpretation have been raised recently [Reference Bentzen5]. In any case, further investigation of judgments outside of mathematics is beyond the scope of this paper.
6 Concluding remarks
I have proposed an analytic–synthetic distinction that remedies all the six problems with Martin-Löf’s proposal mentioned in Section 1. My account of analyticity and syntheticity is supported by the meaning explanations and a constructive reading of meaning as evaluation. It would be important to investigate in future work to what extent the correctness of synthetic judgments requires appeal to intuition, a theme that was so central in Kant. For that we would first have to develop a notion of intuition for constructive type theory. With some modifications that can overcome a problem of ontological explosion raised in [Reference Bentzen6], perhaps Brouwer’s theory of the intuition of twoity may be a promising start.
Acknowledgments
I thank Ansten Klev, Antonio Piccolomini d’Aragona, Will Stafford, Göran Sundholm, Colin Zwanziger, and two anonymous reviewers for helpful comments on an early version of this paper. I am especially indebted to Bob Harper. My understanding of the meaning explanations and the computational approach to type theory has been shaped by many long conversations with him over the years.
Funding
This work was funded by the grant 23YJRC04ZD-2YB from the Zhejiang Federation of Humanities and Social Sciences.