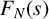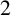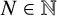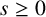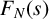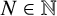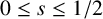1 Introduction
For a sequence
![]() $(x_n)_{n \in \mathbb {N}}$
of elements in
$(x_n)_{n \in \mathbb {N}}$
of elements in
![]() $[0,1]$
, a natural number
$[0,1]$
, a natural number
![]() $N \in \mathbb {N}$
and
$N \in \mathbb {N}$
and
![]() $s \in \mathbb {R}^+_0$
, we define
$s \in \mathbb {R}^+_0$
, we define
where
![]() $\lVert \cdot \rVert $
is the distance of a number from its nearest integer. It measures the behaviour of gaps between the first N elements of
$\lVert \cdot \rVert $
is the distance of a number from its nearest integer. It measures the behaviour of gaps between the first N elements of
![]() $(x_n)_{n \in \mathbb {N}}$
on a local scale. A sequence
$(x_n)_{n \in \mathbb {N}}$
on a local scale. A sequence
![]() $(x_n)_{n \in \mathbb {N}}$
is said to have Poissonian pair correlations (see, for example, [Reference El-Baz, Marklof and Vinogradov2, Reference Weiß and Skill14]) if
$(x_n)_{n \in \mathbb {N}}$
is said to have Poissonian pair correlations (see, for example, [Reference El-Baz, Marklof and Vinogradov2, Reference Weiß and Skill14]) if
![]() ${F(s):= \lim _{N \to \infty } F_{N}(s) = 2s}$
for all
${F(s):= \lim _{N \to \infty } F_{N}(s) = 2s}$
for all
![]() $s \geq 0$
. As (1.1) corresponds to the N-point correlation in [Reference Lutsko and Technau6, Reference Lutsko and Technau7] (with the f in the definition therein being chosen as the indicator function), we also call
$s \geq 0$
. As (1.1) corresponds to the N-point correlation in [Reference Lutsko and Technau6, Reference Lutsko and Technau7] (with the f in the definition therein being chosen as the indicator function), we also call
![]() $F_N(s)$
the N-point correlation of
$F_N(s)$
the N-point correlation of
![]() $(x_n)_{n \in \mathbb {N}}$
. To distinguish it from
$(x_n)_{n \in \mathbb {N}}$
. To distinguish it from
![]() $F_N(s)$
, we call
$F_N(s)$
, we call
![]() $F(s)$
the limiting pair correlation function.
$F(s)$
the limiting pair correlation function.
A generic uniformly distributed random sequence in
![]() $[0,1]$
drawn from the uniform distribution has Poissonian pair correlations (see [Reference Marklof, Granville and Rudnick8] for a proof). Nonetheless, there are few explicitly known such examples (see [Reference El-Baz, Marklof and Vinogradov2] and more recent examples in [Reference Lutsko, Sourmelidis and Technau5, Reference Lutsko and Technau7]). One of the reasons why such examples are difficult to find is that it is, in general, hard to completely describe the gap structure of a finite sequence, that is, the lengths and combinatorics of gaps between neighbouring points (see [Reference Weiß12]). Although research has mainly focused on the generic (Poissonian) case, the nongeneric case has also attracted more attention in recent times. In [Reference Marklof and Strömbergsson9], it is shown that the limiting gap distribution of
$[0,1]$
drawn from the uniform distribution has Poissonian pair correlations (see [Reference Marklof, Granville and Rudnick8] for a proof). Nonetheless, there are few explicitly known such examples (see [Reference El-Baz, Marklof and Vinogradov2] and more recent examples in [Reference Lutsko, Sourmelidis and Technau5, Reference Lutsko and Technau7]). One of the reasons why such examples are difficult to find is that it is, in general, hard to completely describe the gap structure of a finite sequence, that is, the lengths and combinatorics of gaps between neighbouring points (see [Reference Weiß12]). Although research has mainly focused on the generic (Poissonian) case, the nongeneric case has also attracted more attention in recent times. In [Reference Marklof and Strömbergsson9], it is shown that the limiting gap distribution of
![]() $(\{\log (n)\})_{n \in \mathbb {N}}$
, where
$(\{\log (n)\})_{n \in \mathbb {N}}$
, where
![]() $\{ \cdot \}$
denotes the fractional part of a number, has an explicit distribution which is not a Poissonian distribution but close to an exponential distribution. In [Reference Weiß13], the limiting pair correlation function of
$\{ \cdot \}$
denotes the fractional part of a number, has an explicit distribution which is not a Poissonian distribution but close to an exponential distribution. In [Reference Weiß13], the limiting pair correlation function of
![]() $( \{ {\log (2n-1)}/{\log (2)} \} )_{n \in \mathbb {N}}$
is explicitly calculated by exploiting the simple gap structure of this sequence. Another result in [Reference Lutsko4] describes the limiting pair correlation function of orbits of a point in hyperbolic space under the action of a discrete subgroup. Finally, in [Reference Sayous11], the nongeneric pair correlation statistic of the sequence
$( \{ {\log (2n-1)}/{\log (2)} \} )_{n \in \mathbb {N}}$
is explicitly calculated by exploiting the simple gap structure of this sequence. Another result in [Reference Lutsko4] describes the limiting pair correlation function of orbits of a point in hyperbolic space under the action of a discrete subgroup. Finally, in [Reference Sayous11], the nongeneric pair correlation statistic of the sequence
![]() $({n^\alpha })_{n \in \mathbb {N}}$
is studied for
$({n^\alpha })_{n \in \mathbb {N}}$
is studied for
![]() $0 < \alpha < 1$
.
$0 < \alpha < 1$
.
In this note, we add to the growing body of literature by calculating for all
![]() $N \in \mathbb {N}$
and
$N \in \mathbb {N}$
and
![]() $s \geq 0$
the N-point correlation
$s \geq 0$
the N-point correlation
![]() $F_N(s)$
of the van der Corput sequence in base
$F_N(s)$
of the van der Corput sequence in base
![]() $2$
. The van der Corput sequence is a classical example of a low-discrepancy sequence and thus, in particular, a uniformly distributed sequence. Because of their importance in uniform distribution theory, their intuitive geometry and their generalisations to higher dimensions, van der Corput sequences are widely discussed in the literature (see [Reference Drmota and Tichy1, Reference Kuipers and Niederreiter3, Reference Niederreiter10, Reference Weiß and Skill14]).
$2$
. The van der Corput sequence is a classical example of a low-discrepancy sequence and thus, in particular, a uniformly distributed sequence. Because of their importance in uniform distribution theory, their intuitive geometry and their generalisations to higher dimensions, van der Corput sequences are widely discussed in the literature (see [Reference Drmota and Tichy1, Reference Kuipers and Niederreiter3, Reference Niederreiter10, Reference Weiß and Skill14]).
Recall that for an integer
![]() $b \geq 2$
, the b-ary representation of
$b \geq 2$
, the b-ary representation of
![]() $n \in {\mathbb {N}}$
is
$n \in {\mathbb {N}}$
is
![]() $n = \sum _{j=0}^\infty e_j b^j$
with
$n = \sum _{j=0}^\infty e_j b^j$
with
![]() $0 \leq e_j = e_j(n) < b$
. The radical-inverse function is defined by
$0 \leq e_j = e_j(n) < b$
. The radical-inverse function is defined by
![]() $g_b(n)=\sum _{j=0}^\infty e_j b^{-j-1}$
for all
$g_b(n)=\sum _{j=0}^\infty e_j b^{-j-1}$
for all
![]() $n \in {\mathbb {N}}$
and the van der Corput sequence in base b is given by
$n \in {\mathbb {N}}$
and the van der Corput sequence in base b is given by
![]() $x_i := g_b(i-1)$
for
$x_i := g_b(i-1)$
for
![]() $i \geq 2$
. For convenience, we add
$i \geq 2$
. For convenience, we add
![]() $x_1 = 0$
as the first element of a van der Corput sequence because it simplifies the presentation of results in our context.
$x_1 = 0$
as the first element of a van der Corput sequence because it simplifies the presentation of results in our context.
Theorem 1.1. Let
![]() $N \in \mathbb {N}$
and
$N \in \mathbb {N}$
and
![]() $s \geq 0$
. Let the
$s \geq 0$
. Let the
![]() $2$
-ary representation of N be
$2$
-ary representation of N be
![]() $N = \sum _{j=0}^M e_j2^j$
with the coefficients
$N = \sum _{j=0}^M e_j2^j$
with the coefficients
![]() $e_0, e_1, \ldots , e_M \in \{ 0,1\}$
. Then for the van der Corput sequence
$e_0, e_1, \ldots , e_M \in \{ 0,1\}$
. Then for the van der Corput sequence
![]() $(x_n)_{n \in \mathbb {N}}$
in base
$(x_n)_{n \in \mathbb {N}}$
in base
![]() $b=2$
we have
$b=2$
we have
 $$ \begin{align} F_N(s) = \frac{1}{N} \sum_{k=0}^M e_k \bigg( \bigg\lfloor \frac{s}{N} 2^k \bigg\rfloor + \sum_{l=k+1}^{N} e_l \cdot 2 \cdot \bigg\lceil \frac{1}{2}\bigg\lfloor\frac{s}{N} 2^{l+1}\bigg\rfloor \bigg\rceil \bigg) 2^{k+1}. \end{align} $$
$$ \begin{align} F_N(s) = \frac{1}{N} \sum_{k=0}^M e_k \bigg( \bigg\lfloor \frac{s}{N} 2^k \bigg\rfloor + \sum_{l=k+1}^{N} e_l \cdot 2 \cdot \bigg\lceil \frac{1}{2}\bigg\lfloor\frac{s}{N} 2^{l+1}\bigg\rfloor \bigg\rceil \bigg) 2^{k+1}. \end{align} $$
To the best of our knowledge, this constitutes the first example of an exact closed-form expression of
![]() $F_N(s)$
for all
$F_N(s)$
for all
![]() $N \in \mathbb {N}$
and all
$N \in \mathbb {N}$
and all
![]() $s \geq 0$
, where the right-hand side does not rely on explicit knowledge of the involved sequence. Moreover, the expression on the right-hand side is surprisingly simple. The formula is superior in terms of running time because the time needed to evaluate the N-point correlation from the definition grows quadratically in N, while the running time to compute the right-hand side of (1.2) only grows logarithmically. For example, it would be almost infeasible to calculate the N-point correlation for a given
$s \geq 0$
, where the right-hand side does not rely on explicit knowledge of the involved sequence. Moreover, the expression on the right-hand side is surprisingly simple. The formula is superior in terms of running time because the time needed to evaluate the N-point correlation from the definition grows quadratically in N, while the running time to compute the right-hand side of (1.2) only grows logarithmically. For example, it would be almost infeasible to calculate the N-point correlation for a given
![]() $s> 0$
and
$s> 0$
and
![]() $N = 10^9$
on a standard computer via (1.1), while the evaluation of (1.2) takes less than a second.
$N = 10^9$
on a standard computer via (1.1), while the evaluation of (1.2) takes less than a second.
The main step in proving Theorem 1.1 is to decompose the set
into several subsets, where the indices of the elements of
![]() $(x_n)_{n \in \mathbb {N}}$
depend on powers of
$(x_n)_{n \in \mathbb {N}}$
depend on powers of
![]() $2$
instead of N. This idea goes back to [Reference Weiß and Skill14], where the weak limiting pair correlation function of van der Corput sequences was calculated. In principle, our proof technique could be applied to van der Corput sequences in arbitrary base but the expression on the right-hand side of (1.2) would be much longer and more complex. Therefore, we decided here to restrict to the case where a short formula can be given. The reason why this can only be done in base
$2$
instead of N. This idea goes back to [Reference Weiß and Skill14], where the weak limiting pair correlation function of van der Corput sequences was calculated. In principle, our proof technique could be applied to van der Corput sequences in arbitrary base but the expression on the right-hand side of (1.2) would be much longer and more complex. Therefore, we decided here to restrict to the case where a short formula can be given. The reason why this can only be done in base
![]() $b=2$
is that there are only at most two different gap lengths for all
$b=2$
is that there are only at most two different gap lengths for all
![]() $N \in \mathbb {N}$
, while there are up to three different gap lengths for all bases
$N \in \mathbb {N}$
, while there are up to three different gap lengths for all bases
![]() $b \geq 3$
.
$b \geq 3$
.
Our formula has the following application.
Corollary 1.2. The limit
![]() $\lim _{N \to \infty } F_N(s)$
exists if and only if
$\lim _{N \to \infty } F_N(s)$
exists if and only if
![]() $0 \leq s \leq \tfrac {1}{2}$
. In this case,
$0 \leq s \leq \tfrac {1}{2}$
. In this case,
![]() $F(s) = 0$
.
$F(s) = 0$
.
2 Proof of results
We prove our main result for the van der Corput sequence in base
![]() $b = 2$
by applying the same decomposition of (1.1) into subsets as in [Reference Weiß and Skill14].
$b = 2$
by applying the same decomposition of (1.1) into subsets as in [Reference Weiß and Skill14].
Proof of Theorem 1.1.
Let us write the N-point correlation as
 $$ \begin{align*} N \cdot F_N(s) & = \# \underbrace{\bigg\{ \lVert{x_i-x_j}\rVert \leq \frac{s}{N} : 1 \leq i \neq j \leq 2^M \bigg\}}_{=:A(s,M,N)} \\ &\quad + 2 \# \underbrace{\bigg\{ \lVert{x_i-x_j}\rVert \leq \frac{s}{N} : 1 \leq i \leq 2^M, 2^{M} + 1 \leq j \leq N \bigg\}}_{=:B(s,M,N)} \\ &\quad + \# \underbrace{\bigg\{ \lVert{x_i-x_j}\rVert \leq \frac{s}{N} : 2^M+1 \leq i \neq j \leq N \bigg\}.}_{=:C(s,M,N)} \end{align*} $$
$$ \begin{align*} N \cdot F_N(s) & = \# \underbrace{\bigg\{ \lVert{x_i-x_j}\rVert \leq \frac{s}{N} : 1 \leq i \neq j \leq 2^M \bigg\}}_{=:A(s,M,N)} \\ &\quad + 2 \# \underbrace{\bigg\{ \lVert{x_i-x_j}\rVert \leq \frac{s}{N} : 1 \leq i \leq 2^M, 2^{M} + 1 \leq j \leq N \bigg\}}_{=:B(s,M,N)} \\ &\quad + \# \underbrace{\bigg\{ \lVert{x_i-x_j}\rVert \leq \frac{s}{N} : 2^M+1 \leq i \neq j \leq N \bigg\}.}_{=:C(s,M,N)} \end{align*} $$
Since the set
![]() $A(s,M,N)$
consists of all points
$A(s,M,N)$
consists of all points
![]() $x_i$
which are numbers of the form
$x_i$
which are numbers of the form
![]() ${k}/{2^M}$
with
${k}/{2^M}$
with
![]() $0 \leq k < 2^{M}$
, its magnitude can be calculated immediately as
$0 \leq k < 2^{M}$
, its magnitude can be calculated immediately as
In the definition of the set
![]() $B(s,M,N)$
, the
$B(s,M,N)$
, the
![]() $x_i$
are again of the form
$x_i$
are again of the form
![]() ${k}/{2^M}$
with
${k}/{2^M}$
with
![]() ${0 \leq k \leq 2^{M}}$
, while the
${0 \leq k \leq 2^{M}}$
, while the
![]() $x_j$
all have the form
$x_j$
all have the form
![]() ${l}/{2^{M+1}}$
with odd l such that
${l}/{2^{M+1}}$
with odd l such that
![]() $1 \leq l < 2^{M+1}$
by the definition of van der Corput sequences. Hence, it follows that
$1 \leq l < 2^{M+1}$
by the definition of van der Corput sequences. Hence, it follows that
Thus, it only remains to calculate
![]() $C(s,M,N)$
. To do that, we first see that
$C(s,M,N)$
. To do that, we first see that
![]() $(x_j)_{j=2^M+1}^N$
is the van der Corput sequence
$(x_j)_{j=2^M+1}^N$
is the van der Corput sequence
![]() $(x_j)_{j=1}^{N-2^{M}+1}$
translated to the right by
$(x_j)_{j=1}^{N-2^{M}+1}$
translated to the right by
![]() $2^{-(M+1)}$
. Note that
$2^{-(M+1)}$
. Note that
![]() $\lVert {x_i-x_j}\rVert $
is invariant under simultaneous translation of
$\lVert {x_i-x_j}\rVert $
is invariant under simultaneous translation of
![]() $x_i$
and
$x_i$
and
![]() $x_j$
. If we treat the simpler situation
$x_j$
. If we treat the simpler situation
![]() $N = 2^M + 2^k$
with
$N = 2^M + 2^k$
with
![]() $k < M$
, then we can proceed inductively and apply the formula for
$k < M$
, then we can proceed inductively and apply the formula for
![]() $A(s,M,N)$
which yields
$A(s,M,N)$
which yields
because the set of type B is empty here. In the general case,
 $$ \begin{align*}C(s,M,N) = \sum e_k \cdot \bigg( a(s,k,N) + 2 \cdot b\bigg(s,k,N-\sum_{l=k+1}^M e_l 2^l\bigg) \bigg), \end{align*} $$
$$ \begin{align*}C(s,M,N) = \sum e_k \cdot \bigg( a(s,k,N) + 2 \cdot b\bigg(s,k,N-\sum_{l=k+1}^M e_l 2^l\bigg) \bigg), \end{align*} $$
where the factor
![]() $2$
appears because sets of type B are counted twice. Substituting the corresponding expressions for
$2$
appears because sets of type B are counted twice. Substituting the corresponding expressions for
![]() $A(\cdot )$
and
$A(\cdot )$
and
![]() $B(\cdot )$
yields a sum of the form
$B(\cdot )$
yields a sum of the form
 $$ \begin{align*}\sum_{k=1}^N e_k \bigg( \bigg\lfloor \frac{s}{M} 2^k \bigg\rfloor 2^{k+1} + 4 \bigg\lceil \frac{1}{2}\bigg\lfloor\frac{s}{M} 2^{k+1}\bigg\rfloor \bigg\rceil \sum_{l=1}^{k-1} e_l 2^l \bigg).\end{align*} $$
$$ \begin{align*}\sum_{k=1}^N e_k \bigg( \bigg\lfloor \frac{s}{M} 2^k \bigg\rfloor 2^{k+1} + 4 \bigg\lceil \frac{1}{2}\bigg\lfloor\frac{s}{M} 2^{k+1}\bigg\rfloor \bigg\rceil \sum_{l=1}^{k-1} e_l 2^l \bigg).\end{align*} $$
Collecting powers of
![]() $2$
yields the formula on the right-hand side of (1.2).
$2$
yields the formula on the right-hand side of (1.2).
Having (1.2) at hand, it is not hard to calculate the limiting behaviour of
![]() $F_N(s)$
.
$F_N(s)$
.
Proof of Corollary 1.2.
For
![]() $2^{M} \leq N < 2^{M+1}$
, the
$2^{M} \leq N < 2^{M+1}$
, the
![]() $2$
-ary representation of
$2$
-ary representation of
![]() $N \in \mathbb {N}$
is of the form
$N \in \mathbb {N}$
is of the form
![]() $N = 2^M + \sum _{k=1}^M e_k 2^k$
. Thus,
$N = 2^M + \sum _{k=1}^M e_k 2^k$
. Thus,
for
![]() $0 \leq s \leq \tfrac 12$
and the limit is
$0 \leq s \leq \tfrac 12$
and the limit is
![]() $F_N(s) = 0$
by Theorem 1.1. Now let
$F_N(s) = 0$
by Theorem 1.1. Now let
![]() $s \in [l, l + 1)$
for some
$s \in [l, l + 1)$
for some
![]() $l \in \mathbb {N}_0$
. Then, we have
$l \in \mathbb {N}_0$
. Then, we have
![]() $F_N(s) = 2l$
for
$F_N(s) = 2l$
for
![]() $N = 2^M$
, again by Theorem 1.1. If
$N = 2^M$
, again by Theorem 1.1. If
![]() ${s \in (1/2 + l, 1/2 + l + 1]}$
for some
${s \in (1/2 + l, 1/2 + l + 1]}$
for some
![]() $l \in \mathbb {N}_0$
, we choose N big enough such that
$l \in \mathbb {N}_0$
, we choose N big enough such that
Then
![]() $F_N(s) \geq {2^{M+1}}/{(2^M+1)}$
for all
$F_N(s) \geq {2^{M+1}}/{(2^M+1)}$
for all
![]() $N = 2^{M+k} + 2^k$
with
$N = 2^{M+k} + 2^k$
with
![]() $k \in \mathbb {N}$
. Thus,
$k \in \mathbb {N}$
. Thus,
![]() $F_N(s)$
cannot converge for
$F_N(s)$
cannot converge for
![]() $s> \tfrac {1}{2}$
.
$s> \tfrac {1}{2}$
.
Acknowledgement
Research on this article was conducted during a stay at the Université de Montréal, whom the author would like to thank for their hospitality.