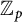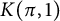1 Introduction
1.1 To understand the p-adic étale cohomology of a p-adic variety, Faltings [Reference Gabber and RameroFal88] introduced a new ringed topos as a bridge linking the p-adic étale cohomology with various p-adic cohomologies originating from differential forms. He proved that the cohomology of his ringed topos is (almost) isomorphic to the p-adic étale cohomology of the variety. This result is known as Faltings’ main p-adic comparison theorem. The local nature of this ringed topos allows to compute its cohomology by Galois cohomology and hence to relate it to differential forms.
1.2 More precisely, let
![]() $\mathcal {O}_K$
be a complete discrete valuation ring extension of
$\mathcal {O}_K$
be a complete discrete valuation ring extension of
![]() $\mathbb {Z}_p$
, let K be its fraction field, let
$\mathbb {Z}_p$
, let K be its fraction field, let
![]() $\overline {K}$
be an algebraic closure of K, let X be a proper smooth
$\overline {K}$
be an algebraic closure of K, let X be a proper smooth
![]() $\mathcal {O}_K$
-scheme, and let
$\mathcal {O}_K$
-scheme, and let
![]() $Y=X_{\overline {K}}$
be the geometric generic fiber of X. Faltings introduced a ringed site
$Y=X_{\overline {K}}$
be the geometric generic fiber of X. Faltings introduced a ringed site
![]() $(\mathbf {E}_{Y \to X}^{\mathrm {\acute {e}t}},\overline {\mathscr {B}})$
which admits natural morphisms of sites
$(\mathbf {E}_{Y \to X}^{\mathrm {\acute {e}t}},\overline {\mathscr {B}})$
which admits natural morphisms of sites
where
![]() $X_{\mathrm {\acute {e}t}}$
denotes the étale site of X. The underlying category of
$X_{\mathrm {\acute {e}t}}$
denotes the étale site of X. The underlying category of
![]() $\mathbf {E}_{Y \to X}^{\mathrm {\acute {e}t}}$
is a fibered category over
$\mathbf {E}_{Y \to X}^{\mathrm {\acute {e}t}}$
is a fibered category over
![]() $X_{\mathrm {\acute {e}t}}$
, whose fiber over an étale X-scheme U is the finite étale site of
$X_{\mathrm {\acute {e}t}}$
, whose fiber over an étale X-scheme U is the finite étale site of
![]() $U_{\overline {K}}$
(see 3.1 for a precise definition). The sheaves
$U_{\overline {K}}$
(see 3.1 for a precise definition). The sheaves
![]() $\mathrm {R}^q\sigma _*(\overline {\mathscr {B}}/p^n\overline {\mathscr {B}})$
(
$\mathrm {R}^q\sigma _*(\overline {\mathscr {B}}/p^n\overline {\mathscr {B}})$
(
![]() $q,n\in \mathbb {N}$
) are computed by Galois cohomology and hence can be related to differential forms of X over
$q,n\in \mathbb {N}$
) are computed by Galois cohomology and hence can be related to differential forms of X over
![]() $\mathcal {O}_K$
. On the other hand, Faltings proved that for any finite locally constant abelian sheaf
$\mathcal {O}_K$
. On the other hand, Faltings proved that for any finite locally constant abelian sheaf
![]() $\mathbb {F}$
on
$\mathbb {F}$
on
![]() $Y_{\mathrm {\acute {e}t}}$
and any integer
$Y_{\mathrm {\acute {e}t}}$
and any integer
![]() $q\geq 0$
, there is a canonical morphism,
$q\geq 0$
, there is a canonical morphism,
which is an almost isomorphism, that is, its kernel and cokernel are killed by
![]() $p^r$
for any rational number
$p^r$
for any rational number
![]() $r>0$
. The right-hand side of (1.2.2) can be related to various p-adic cohomologies of X, leading to various p-adic comparison theorems. For instance, the Hodge–Tate decomposition theorem (i.e., the comparison with the Hodge cohomologies) is obtained from the Cartan–Leray spectral sequence for the composed functor
$r>0$
. The right-hand side of (1.2.2) can be related to various p-adic cohomologies of X, leading to various p-adic comparison theorems. For instance, the Hodge–Tate decomposition theorem (i.e., the comparison with the Hodge cohomologies) is obtained from the Cartan–Leray spectral sequence for the composed functor
![]() $\mathrm {R}\Gamma (X_{\mathrm {\acute {e}t}},-)\circ \mathrm {R}\sigma _*$
taking for
$\mathrm {R}\Gamma (X_{\mathrm {\acute {e}t}},-)\circ \mathrm {R}\sigma _*$
taking for
![]() $\mathbb {F}$
some constant torsion sheaves, see [Reference Abbes and GrosAG20]. Faltings pushed further this strategy by developing a p-adic Simpson correspondence that compares the p-adic étale cohomology of a p-adic local system with the Dolbeault cohomology of the associated Higgs bundle [Reference GrothendieckFal05] (cf. [Reference AchingerAGT16]).
$\mathbb {F}$
some constant torsion sheaves, see [Reference Abbes and GrosAG20]. Faltings pushed further this strategy by developing a p-adic Simpson correspondence that compares the p-adic étale cohomology of a p-adic local system with the Dolbeault cohomology of the associated Higgs bundle [Reference GrothendieckFal05] (cf. [Reference AchingerAGT16]).
1.3 Faltings formulated also a relative version of his main comparison theorem relating the relative étale cohomology and the relative cohomology of his ringed topos for a proper log-smooth morphism of log-smooth
![]() $\mathcal {O}_K$
-schemes. He only roughly sketched the proof in [Reference GrothendieckFal02], but a complete proof was provided recently by Abbes and Gros [Reference Abbes and GrosAG20]. They used this relative version in their construction of the relative Hodge–Tate spectral sequence and more generally in their study of the functoriality of the p-adic Simpson correspondence by higher direct images [Reference Abbes, Gros and TsujiAG22]. As we have seen above, Faltings topos builds on an integral model of the p-adic variety, whose (logarithmic) smoothness seems necessary for good properties of Faltings topos and thus for the proofs of the comparison theorems. The goal of this article is to get rid of the smoothness assumptions in Faltings’ main comparison theorems, not only on the integral models but also on the generic fibers.
$\mathcal {O}_K$
-schemes. He only roughly sketched the proof in [Reference GrothendieckFal02], but a complete proof was provided recently by Abbes and Gros [Reference Abbes and GrosAG20]. They used this relative version in their construction of the relative Hodge–Tate spectral sequence and more generally in their study of the functoriality of the p-adic Simpson correspondence by higher direct images [Reference Abbes, Gros and TsujiAG22]. As we have seen above, Faltings topos builds on an integral model of the p-adic variety, whose (logarithmic) smoothness seems necessary for good properties of Faltings topos and thus for the proofs of the comparison theorems. The goal of this article is to get rid of the smoothness assumptions in Faltings’ main comparison theorems, not only on the integral models but also on the generic fibers.
1.4 In fact, we generalize Faltings’ main comparison theorem to any proper and finitely presented morphism of coherent schemes (i.e., quasi-compact and quasi-separated schemes) over an absolute integral closure of
![]() $\mathbb {Z}_p$
(without any further assumption on smoothness or finiteness) for torsion abelian étale sheaves (not necessarily finite locally constant). This generalization takes place in a variant of Faltings site with v-topology, that we introduced and called the v-site of integrally closed schemes. We have shown in [Reference HeHe23] that both the étale cohomology and the cohomology of Faltings ringed topos can be computed by this v-site. The latter implies a cohomological descent for Faltings ringed topos along proper hypercoverings, which allows us to reduce the proof of our generalization to Faltings’ main comparison theorem for proper log-smooth morphisms of log-smooth
$\mathbb {Z}_p$
(without any further assumption on smoothness or finiteness) for torsion abelian étale sheaves (not necessarily finite locally constant). This generalization takes place in a variant of Faltings site with v-topology, that we introduced and called the v-site of integrally closed schemes. We have shown in [Reference HeHe23] that both the étale cohomology and the cohomology of Faltings ringed topos can be computed by this v-site. The latter implies a cohomological descent for Faltings ringed topos along proper hypercoverings, which allows us to reduce the proof of our generalization to Faltings’ main comparison theorem for proper log-smooth morphisms of log-smooth
![]() $\mathcal {O}_K$
-schemes using a variant of de Jong’s alteration theorem for morphisms of schemes due to Gabber–Illusie–Temkin. Moreover, it allows us to deduce generalizations of Faltings’ main comparison theorems for the original Faltings site both in the absolute and the relative cases. We remark that Scholze has generalized Faltings’ main comparison theorem to proper smooth morphisms of rigid analytic varieties for finite locally constant abelian sheaves [Reference ScholzeSch13a, 5.11], and to proper morphisms of algebraic varieties for torsion abelian sheaves [Reference ScholzeSch13b, 3.13]. Compared to his results, our arguments are purely scheme theoretic and our generalization for torsion abelian sheaves holds for proper morphisms of more general schemes (i.e., less restrictive on finiteness). On the other hand, it is not clear whether our generalization and Scholze’s can be directly deduced from each other.
$\mathcal {O}_K$
-schemes using a variant of de Jong’s alteration theorem for morphisms of schemes due to Gabber–Illusie–Temkin. Moreover, it allows us to deduce generalizations of Faltings’ main comparison theorems for the original Faltings site both in the absolute and the relative cases. We remark that Scholze has generalized Faltings’ main comparison theorem to proper smooth morphisms of rigid analytic varieties for finite locally constant abelian sheaves [Reference ScholzeSch13a, 5.11], and to proper morphisms of algebraic varieties for torsion abelian sheaves [Reference ScholzeSch13b, 3.13]. Compared to his results, our arguments are purely scheme theoretic and our generalization for torsion abelian sheaves holds for proper morphisms of more general schemes (i.e., less restrictive on finiteness). On the other hand, it is not clear whether our generalization and Scholze’s can be directly deduced from each other.
Firstly, we state our generalization of Faltings’ main comparison theorem in the absolute case.
Theorem 1.5 (see 5.17)
Let A be a valuation ring extension of
![]() $\mathbb {Z}_p$
with algebraically closed fraction field. Consider a Cartesian square of coherent schemes:
$\mathbb {Z}_p$
with algebraically closed fraction field. Consider a Cartesian square of coherent schemes:

Assume that X is proper of finite presentation over A. Then, for any finite locally constant abelian sheaf
![]() $\mathbb {F}$
on
$\mathbb {F}$
on
![]() $Y_{\mathrm {\acute {e}t}}$
, there exists a canonical morphism
$Y_{\mathrm {\acute {e}t}}$
, there exists a canonical morphism
which is an almost isomorphism, where
![]() $\psi :Y_{\mathrm {\acute {e}t}} \to \mathbf {E}_{Y \to X}^{\mathrm {\acute {e}t}}$
is the natural morphism of sites (see 3.2).
$\psi :Y_{\mathrm {\acute {e}t}} \to \mathbf {E}_{Y \to X}^{\mathrm {\acute {e}t}}$
is the natural morphism of sites (see 3.2).
We remark that the natural morphism of sites
![]() $\psi :Y_{\mathrm {\acute {e}t}} \to \mathbf {E}_{Y \to X}^{\mathrm {\acute {e}t}}$
induces an equivalence of the categories of finite locally constant abelian sheaves on
$\psi :Y_{\mathrm {\acute {e}t}} \to \mathbf {E}_{Y \to X}^{\mathrm {\acute {e}t}}$
induces an equivalence of the categories of finite locally constant abelian sheaves on
![]() $Y_{\mathrm {\acute {e}t}}$
and
$Y_{\mathrm {\acute {e}t}}$
and
![]() $\mathbf {E}_{Y \to X}^{\mathrm {\acute {e}t}}$
(5.3)
$\mathbf {E}_{Y \to X}^{\mathrm {\acute {e}t}}$
(5.3)

1.6 One of the key ingredients of the proof of 1.5 is our cohomological descent for Faltings ringed topos [Reference HeHe23]. Roughly speaking, it allows us to descend important results on Faltings topos associated with nice integral models to Faltings topos associated with general integral model. More concretely, we adopt the following strategy:
-
(1) Firstly, we use de Jong–Gabber–Illusie–Temkin’s alteration theorem for morphisms of schemes [Reference Illusie, Laszlo and OrgogozoILO14, X.3] to obtain a proper surjective morphism of finite presentation
 $X'\to X$
such that the morphism
$X'\to X$
such that the morphism
 $X'\to \mathop {\mathrm {Spec}}(A)$
is the cofiltered limit of a system of “nice” morphisms
$X'\to \mathop {\mathrm {Spec}}(A)$
is the cofiltered limit of a system of “nice” morphisms
 $X^{\prime }_\lambda \to T_\lambda $
of “nice” models over
$X^{\prime }_\lambda \to T_\lambda $
of “nice” models over
 $\mathcal {O}_{K_\lambda }$
, where
$\mathcal {O}_{K_\lambda }$
, where
 $K_\lambda $
is a finite extension of
$K_\lambda $
is a finite extension of
 $\mathbb {Q}_p$
(see 4.11).
$\mathbb {Q}_p$
(see 4.11). -
(2) Then, we can apply Faltings’ main comparison theorem in the relative case to the “nice” morphisms
 $X^{\prime }_\lambda \to T_\lambda $
(formulated by Faltings [Reference GrothendieckFal02, Theorem 6, page 266] and proved by Abbes and Gros [Reference Abbes and GrosAG20, 5.7.4], see 5.13). By a limit argument, we get the comparison theorem for
$X^{\prime }_\lambda \to T_\lambda $
(formulated by Faltings [Reference GrothendieckFal02, Theorem 6, page 266] and proved by Abbes and Gros [Reference Abbes and GrosAG20, 5.7.4], see 5.13). By a limit argument, we get the comparison theorem for
 $X'$
.
$X'$
. -
(3) Finally, using our cohomological descent for Faltings ringed topos along a proper hypercovering (see 3.10), we deduce the comparison theorem for X.
1.7 In fact, even the construction of Faltings’ comparison morphism (1.5.2) is not trivial, even in the smooth case (1.2.2). It relies on the acyclicity of the morphism
![]() $\psi $
for any finite locally constant abelian sheaf
$\psi $
for any finite locally constant abelian sheaf
![]() $\mathbb {F}$
, i.e.,
$\mathbb {F}$
, i.e.,
![]() $\psi _*\mathbb {F}=\mathrm {R}\psi _*\mathbb {F}$
. Faltings’ comparison morphism is obtained from the canonical morphisms
$\psi _*\mathbb {F}=\mathrm {R}\psi _*\mathbb {F}$
. Faltings’ comparison morphism is obtained from the canonical morphisms
The acyclicity of
![]() $\psi $
is a consequence of Achinger’s result on
$\psi $
is a consequence of Achinger’s result on
![]() $K(\pi ,1)$
-schemes (see 5.6 and 5.8).
$K(\pi ,1)$
-schemes (see 5.6 and 5.8).
We don’t know if
![]() $\psi $
is acyclic for more general coefficients. This is also one of the reasons why Faltings consider only local systems in his main comparison theorems. We propose a new way to construct Faltings’ comparison morphism in the derived category of almost modules using our cohomological descent result [Reference HeHe23] (see also 3.9), that avoids the acyclicity of
$\psi $
is acyclic for more general coefficients. This is also one of the reasons why Faltings consider only local systems in his main comparison theorems. We propose a new way to construct Faltings’ comparison morphism in the derived category of almost modules using our cohomological descent result [Reference HeHe23] (see also 3.9), that avoids the acyclicity of
![]() $\psi $
and that holds for more general coefficients. Indeed, there is a natural commutative diagram of sites (see 3.6):
$\psi $
and that holds for more general coefficients. Indeed, there is a natural commutative diagram of sites (see 3.6):

where
![]() $(\mathbf {Sch}^{\mathrm {coh}}_{/Y})_{\mathrm {v}}$
is the v-site of coherent Y-schemes,
$(\mathbf {Sch}^{\mathrm {coh}}_{/Y})_{\mathrm {v}}$
is the v-site of coherent Y-schemes,
![]() $\mathbf {I}_{Y \to X^Y}$
is the v-site of Y-integrally closed coherent
$\mathbf {I}_{Y \to X^Y}$
is the v-site of Y-integrally closed coherent
![]() $X^Y$
-schemes (1.4). Moreover,
$X^Y$
-schemes (1.4). Moreover,
![]() $\varepsilon $
is actually a morphism of ringed sites
$\varepsilon $
is actually a morphism of ringed sites
Recall the following facts:
-
(1) (Acyclicity of
 $\Psi $
, see 3.8) The morphism
$\Psi $
, see 3.8) The morphism
 $\Psi $
is acyclic for any torsion abelian sheaf
$\Psi $
is acyclic for any torsion abelian sheaf
 $\mathcal {F}$
on
$\mathcal {F}$
on
 $Y_{\mathrm {\acute {e}t}}$
, i.e.,
$Y_{\mathrm {\acute {e}t}}$
, i.e.,
 $\Psi _*(a^{-1}\mathcal {F})=\mathrm {R}\Psi _*(a^{-1}\mathcal {F})$
, which allows more general coefficients and whose proof [Reference HeHe23, 3.27] is much easier than that for
$\Psi _*(a^{-1}\mathcal {F})=\mathrm {R}\Psi _*(a^{-1}\mathcal {F})$
, which allows more general coefficients and whose proof [Reference HeHe23, 3.27] is much easier than that for
 $\psi $
, as we could reduce to the case of valuation rings.
$\psi $
, as we could reduce to the case of valuation rings. -
(2) (Cohomological descent for étale cohomology, see 3.4) For any torsion abelian sheaf
 $\mathcal {F}$
on
$\mathcal {F}$
on
 $Y_{\mathrm {\acute {e}t}}$
, the canonical morphism
$Y_{\mathrm {\acute {e}t}}$
, the canonical morphism
 $\mathcal {F}\to \mathrm {R} a_*a^{-1}\mathcal {F}$
is an isomorphism.
$\mathcal {F}\to \mathrm {R} a_*a^{-1}\mathcal {F}$
is an isomorphism. -
(3) (Cohomological descent for Faltings ringed topos, see 3.9) For any finite locally constant abelian sheaf
 $\mathbb {L}$
over
$\mathbb {L}$
over
 $\mathbf {E}_{Y \to X}^{\mathrm {\acute {e}t}}$
, the canonical morphism
$\mathbf {E}_{Y \to X}^{\mathrm {\acute {e}t}}$
, the canonical morphism
 $\mathbb {L}\otimes _{\mathbb {Z}} \overline {\mathscr {B}}\to \mathrm {R}\varepsilon _*(\varepsilon ^{-1}\mathbb {L}\otimes _{\mathbb {Z}}\mathscr {O})$
is an almost isomorphism.
$\mathbb {L}\otimes _{\mathbb {Z}} \overline {\mathscr {B}}\to \mathrm {R}\varepsilon _*(\varepsilon ^{-1}\mathbb {L}\otimes _{\mathbb {Z}}\mathscr {O})$
is an almost isomorphism.
From these facts, we obtain a new construction of Faltings’ comparison morphism, which does not give a “real morphism” (1.5.2) but a canonical morphism in the derived category of almost modules (see 6.6).
1.8 As we have seen above, the v-variant of Faltings site
![]() $\mathbf {I}_{Y \to X^Y}$
computes the étale cohomology of Y for torsion abelian sheaves (by the facts (1) and (2) in Section 1.7), and it describes well the cohomological descent for Faltings ringed topos ((3) in Section 1.7). These facts enable us to reformulate Faltings’ main comparison theorem using
$\mathbf {I}_{Y \to X^Y}$
computes the étale cohomology of Y for torsion abelian sheaves (by the facts (1) and (2) in Section 1.7), and it describes well the cohomological descent for Faltings ringed topos ((3) in Section 1.7). These facts enable us to reformulate Faltings’ main comparison theorem using
![]() $\mathbf {I}_{Y \to X^Y}$
instead of
$\mathbf {I}_{Y \to X^Y}$
instead of
![]() $\mathbf {E}_{Y \to X}^{\mathrm {\acute {e}t}}$
, which then provides a relative statement for more general coefficients.
$\mathbf {E}_{Y \to X}^{\mathrm {\acute {e}t}}$
, which then provides a relative statement for more general coefficients.
Theorem 1.9 (see 6.12)
With the same notation in 1.5, let
![]() $\mathcal {F}$
be a torsion abelian sheaf on
$\mathcal {F}$
be a torsion abelian sheaf on
![]() $Y_{\mathrm {\acute {e}t}}$
and we set
$Y_{\mathrm {\acute {e}t}}$
and we set
![]() $\mathscr {F}=\Psi _*a^{-1}\mathcal {F}$
. Then, there is a canonical almost isomorphism
$\mathscr {F}=\Psi _*a^{-1}\mathcal {F}$
. Then, there is a canonical almost isomorphism
Indeed, the canonical morphism (1.9.1) is obtained from the canonical morphisms
Thus, 1.9 is a direct corollary of the following relative statement.
Theorem 1.10 (see 6.11)
Let
![]() $\overline {\mathbb {Z}_p}$
be the integral closure of
$\overline {\mathbb {Z}_p}$
be the integral closure of
![]() $\mathbb {Z}_p$
in an algebraic closure
$\mathbb {Z}_p$
in an algebraic closure
![]() $\overline {\mathbb {Q}_p}$
of
$\overline {\mathbb {Q}_p}$
of
![]() $\mathbb {Q}_p$
. Consider a Cartesian square of coherent schemes:
$\mathbb {Q}_p$
. Consider a Cartesian square of coherent schemes:

where
![]() $Y\to X$
is Cartesian over
$Y\to X$
is Cartesian over
![]() $\mathop {\mathrm {Spec}}(\overline {\mathbb {Q}_p})\to \mathop {\mathrm {Spec}}(\overline {\mathbb {Z}_p})$
. Assume that
$\mathop {\mathrm {Spec}}(\overline {\mathbb {Q}_p})\to \mathop {\mathrm {Spec}}(\overline {\mathbb {Z}_p})$
. Assume that
![]() $X'\to X$
is proper of finite presentation. Let
$X'\to X$
is proper of finite presentation. Let
![]() $\mathcal {F}'$
be a torsion abelian sheaf on
$\mathcal {F}'$
be a torsion abelian sheaf on
![]() $Y^{\prime }_{\mathrm {\acute {e}t}}$
and
$Y^{\prime }_{\mathrm {\acute {e}t}}$
and
![]() $\mathscr {F}'=\Psi ^{\prime }_*a^{{\prime }-1}\mathcal {F}'$
(see (1.7.2)). Then, the canonical morphism
$\mathscr {F}'=\Psi ^{\prime }_*a^{{\prime }-1}\mathcal {F}'$
(see (1.7.2)). Then, the canonical morphism
is an almost isomorphism, where
![]() $f_{\mathbf {I}}:(\mathbf {I}_{Y' \to X^{{\prime }Y'}},\mathscr {O}')\longrightarrow (\mathbf {I}_{Y \to X^Y},\mathscr {O})$
is the natural morphism of ringed sites defined by the functoriality of (1.7.2).
$f_{\mathbf {I}}:(\mathbf {I}_{Y' \to X^{{\prime }Y'}},\mathscr {O}')\longrightarrow (\mathbf {I}_{Y \to X^Y},\mathscr {O})$
is the natural morphism of ringed sites defined by the functoriality of (1.7.2).
1.11 We remark that if
![]() $\mathcal {F}'=\mathbb {Z}/p^n\mathbb {Z}$
, then
$\mathcal {F}'=\mathbb {Z}/p^n\mathbb {Z}$
, then
![]() $\mathscr {F}'=\mathbb {Z}/p^n\mathbb {Z}$
(see 6.2), and that
$\mathscr {F}'=\mathbb {Z}/p^n\mathbb {Z}$
(see 6.2), and that
![]() $\mathrm {R}^q f_{\mathbf {I} *}\mathscr {F}'$
is the sheafification in v-topology of the qth étale cohomologies of
$\mathrm {R}^q f_{\mathbf {I} *}\mathscr {F}'$
is the sheafification in v-topology of the qth étale cohomologies of
![]() $Y'$
over Y with coefficients in
$Y'$
over Y with coefficients in
![]() $\mathcal {F}'$
(see 6.13). Roughly speaking, objects of
$\mathcal {F}'$
(see 6.13). Roughly speaking, objects of
![]() $\mathbf {I}_{Y \to X^Y}$
are “locally” the spectrums of valuation rings, and the “stalks” of (1.10.2) are Faltings’ comparison morphisms (1.5.2) when
$\mathbf {I}_{Y \to X^Y}$
are “locally” the spectrums of valuation rings, and the “stalks” of (1.10.2) are Faltings’ comparison morphisms (1.5.2) when
![]() $\mathcal {F}'$
is finite locally constant (see 6.5). This enables us to prove 1.10 for such
$\mathcal {F}'$
is finite locally constant (see 6.5). This enables us to prove 1.10 for such
![]() $\mathcal {F}'$
by reducing to the absolute case 1.5. Then, standard techniques in [SGA 4III
, IX.2] allow us to extend the conclusion to general
$\mathcal {F}'$
by reducing to the absolute case 1.5. Then, standard techniques in [SGA 4III
, IX.2] allow us to extend the conclusion to general
![]() $\mathcal {F}'$
. Theorem 1.10 can be regarded as a generalization of Scholze’s comparison theorem for proper morphisms of algebraic varieties [Reference ScholzeSch13b, 3.13]. Finally, we generalize Faltings’ main comparison theorem in the relative case for the original Faltings site using 1.10 and the cohomological descent for Faltings ringed topos (3.9).
$\mathcal {F}'$
. Theorem 1.10 can be regarded as a generalization of Scholze’s comparison theorem for proper morphisms of algebraic varieties [Reference ScholzeSch13b, 3.13]. Finally, we generalize Faltings’ main comparison theorem in the relative case for the original Faltings site using 1.10 and the cohomological descent for Faltings ringed topos (3.9).
Theorem 1.12 (see 6.14 and 6.15)
With the same notation in 1.10, assume that
![]() $Y'\to Y$
is smooth and that
$Y'\to Y$
is smooth and that
![]() $X'\to X$
is proper of finite presentation. Then, for any finite locally constant abelian sheaf
$X'\to X$
is proper of finite presentation. Then, for any finite locally constant abelian sheaf
![]() $\mathbb {F}'$
on
$\mathbb {F}'$
on
![]() $Y^{\prime }_{\mathrm {\acute {e}t}}$
, there exists a canonical morphism
$Y^{\prime }_{\mathrm {\acute {e}t}}$
, there exists a canonical morphism
which is an almost isomorphism, and where
![]() $f_{\mathrm {\acute {e}t}}:Y^{\prime }_{\mathrm {\acute {e}t}}\to Y_{\mathrm {\acute {e}t}}$
and
$f_{\mathrm {\acute {e}t}}:Y^{\prime }_{\mathrm {\acute {e}t}}\to Y_{\mathrm {\acute {e}t}}$
and
![]() $f_{\mathbf {E}}:\mathbf {E}_{Y' \to X'}^{\mathrm {\acute {e}t}}\to \mathbf {E}_{Y \to X}^{\mathrm {\acute {e}t}}$
are the natural morphisms of sites. In particular, there exists a canonical morphism
$f_{\mathbf {E}}:\mathbf {E}_{Y' \to X'}^{\mathrm {\acute {e}t}}\to \mathbf {E}_{Y \to X}^{\mathrm {\acute {e}t}}$
are the natural morphisms of sites. In particular, there exists a canonical morphism
which is an almost isomorphism, for any integer q.
1.13 The article is structured as follows. In Section 3, we summarize the main results of [Reference HeHe23] including the cohomological descent for Faltings ringed topos. In Section 4, we review de Jong–Gabber–Illusie–Temkin’s alteration theorem and apply it to schemes over a valuation ring of height
![]() $1$
. Section 5 is devoted to proving our generalization of Faltings’ main comparison theorem in the absolute case. Finally, we give a new construction of Faltings’ comparison morphism and our generalization of Faltings’ main comparison theorem in the relative case in Section 6.
$1$
. Section 5 is devoted to proving our generalization of Faltings’ main comparison theorem in the absolute case. Finally, we give a new construction of Faltings’ comparison morphism and our generalization of Faltings’ main comparison theorem in the relative case in Section 6.
2 Notation and conventions
2.1 We fix a prime number p throughout this paper. For a ring R, we denote by
![]() $R^\times $
the group of units of R. A ring R is called absolutely integrally closed if any monic polynomial
$R^\times $
the group of units of R. A ring R is called absolutely integrally closed if any monic polynomial
![]() $f\in R[T]$
has a root in R [Sta23, 0DCK]. We remark that quotients, localizations, and products of absolutely integrally closed rings are still absolutely integrally closed.
$f\in R[T]$
has a root in R [Sta23, 0DCK]. We remark that quotients, localizations, and products of absolutely integrally closed rings are still absolutely integrally closed.
Recall that a valuation ring is a domain V such that for any element x in its fraction field, if
![]() $x\notin V,$
then
$x\notin V,$
then
![]() $x^{-1}\in V$
. The family of ideals of V is totally ordered by the inclusion relation [Reference BourbakiBou06, VI.§1.2, Theorem 1]. In particular, a radical ideal of V is a prime ideal. Moreover, any quotient of V by a prime ideal and any localization of V are still valuations rings [Sta23, 088Y]. We remark that V is normal, and that V is absolutely integrally closed if and only if its fraction field is algebraically closed. An extension of valuation rings is an injective and local homomorphism of valuation rings.
$x^{-1}\in V$
. The family of ideals of V is totally ordered by the inclusion relation [Reference BourbakiBou06, VI.§1.2, Theorem 1]. In particular, a radical ideal of V is a prime ideal. Moreover, any quotient of V by a prime ideal and any localization of V are still valuations rings [Sta23, 088Y]. We remark that V is normal, and that V is absolutely integrally closed if and only if its fraction field is algebraically closed. An extension of valuation rings is an injective and local homomorphism of valuation rings.
2.2 Following [SGA 4II
, VI.1.22], a coherent scheme (resp. morphism of schemes) stands for a quasi-compact and quasi-separated scheme (resp. morphism of schemes). For a coherent morphism
![]() $Y \to X$
of schemes, we denote by
$Y \to X$
of schemes, we denote by
![]() $X^Y$
the integral closure of X in Y [Sta23, 0BAK]. For an X-scheme Z, we say that Z is Y-integrally closed if
$X^Y$
the integral closure of X in Y [Sta23, 0BAK]. For an X-scheme Z, we say that Z is Y-integrally closed if
![]() $Z=Z^{Y \times _X Z}$
.
$Z=Z^{Y \times _X Z}$
.
2.3 Throughout this paper, we fix two universes
![]() $\mathbb {U}$
and
$\mathbb {U}$
and
![]() $\mathbb {V}$
such that the set of natural numbers
$\mathbb {V}$
such that the set of natural numbers
![]() $\mathbb {N}$
is an element of
$\mathbb {N}$
is an element of
![]() $\mathbb {U}$
and that
$\mathbb {U}$
and that
![]() $\mathbb {U}$
is an element of
$\mathbb {U}$
is an element of
![]() $\mathbb {V}$
[SGA 4I
, I.0]. In most cases, we won’t emphasize this set theoretical issue. Unless stated otherwise, we only consider
$\mathbb {V}$
[SGA 4I
, I.0]. In most cases, we won’t emphasize this set theoretical issue. Unless stated otherwise, we only consider
![]() $\mathbb {U}$
-small schemes and we denote by
$\mathbb {U}$
-small schemes and we denote by
![]() $\mathbf {Sch}$
the category of
$\mathbf {Sch}$
the category of
![]() $\mathbb {U}$
-small schemes, which is a
$\mathbb {U}$
-small schemes, which is a
![]() $\mathbb {V}$
-small category.
$\mathbb {V}$
-small category.
2.4 Let C be a category. We denote by
![]() $\widehat {C}$
the category of presheaves of
$\widehat {C}$
the category of presheaves of
![]() $\mathbb {V}$
-small sets on C. If C is a
$\mathbb {V}$
-small sets on C. If C is a
![]() $\mathbb {V}$
-site [SGA 4I
, II.3.0.2], we denote by
$\mathbb {V}$
-site [SGA 4I
, II.3.0.2], we denote by
![]() $\widetilde {C}$
the topos of sheaves of
$\widetilde {C}$
the topos of sheaves of
![]() $\mathbb {V}$
-small sets on C. We denote by
$\mathbb {V}$
-small sets on C. We denote by
![]() $h^C : C \to \widehat {C}$
,
$h^C : C \to \widehat {C}$
,
![]() $x\mapsto h_x^C$
the Yoneda embedding [SGA 4I
, I.1.3], and by
$x\mapsto h_x^C$
the Yoneda embedding [SGA 4I
, I.1.3], and by
![]() $\widehat {C} \to \widetilde {C}$
,
$\widehat {C} \to \widetilde {C}$
,
![]() $\mathcal {F} \mapsto \mathcal {F}^{\mathrm {a}}$
the sheafification functor [SGA 4I
, II.3.4].
$\mathcal {F} \mapsto \mathcal {F}^{\mathrm {a}}$
the sheafification functor [SGA 4I
, II.3.4].
2.5 Let
![]() $u^+ : C \to D$
be a functor of categories. We denote by
$u^+ : C \to D$
be a functor of categories. We denote by
![]() $u^{\mathrm {p}} : \widehat {D} \to \widehat {C}$
the functor that associates to a presheaf
$u^{\mathrm {p}} : \widehat {D} \to \widehat {C}$
the functor that associates to a presheaf
![]() $\mathcal {G}$
of
$\mathcal {G}$
of
![]() $\mathbb {V}$
-small sets on D the presheaf
$\mathbb {V}$
-small sets on D the presheaf
![]() $u^{\mathrm {p}} \mathcal {G} = \mathcal {G} \circ u^+$
. If C is
$u^{\mathrm {p}} \mathcal {G} = \mathcal {G} \circ u^+$
. If C is
![]() $\mathbb {V}$
-small and D is a
$\mathbb {V}$
-small and D is a
![]() $\mathbb {V}$
-category, then
$\mathbb {V}$
-category, then
![]() $u^{\mathrm {p}}$
admits a left adjoint
$u^{\mathrm {p}}$
admits a left adjoint
![]() $u_{\mathrm {p}}$
[Sta23, 00VC] and a right adjoint
$u_{\mathrm {p}}$
[Sta23, 00VC] and a right adjoint
![]() ${}_{\mathrm {p}}u$
[Sta23, 00XF] (cf. [SGA 4I
, I.5]). So we have a sequence of adjoint functors
${}_{\mathrm {p}}u$
[Sta23, 00XF] (cf. [SGA 4I
, I.5]). So we have a sequence of adjoint functors
If, moreover, C and D are
![]() $\mathbb {V}$
-sites, then we denote by
$\mathbb {V}$
-sites, then we denote by
![]() $u_{\mathrm {s}} , u^{\mathrm {s}} , {}_{\mathrm {s}}u$
the functors of the topoi
$u_{\mathrm {s}} , u^{\mathrm {s}} , {}_{\mathrm {s}}u$
the functors of the topoi
![]() $\widetilde {C}$
and
$\widetilde {C}$
and
![]() $\widetilde {D}$
of sheaves of
$\widetilde {D}$
of sheaves of
![]() $\mathbb {V}$
-small sets induced by composing the sheafification functor with the functors
$\mathbb {V}$
-small sets induced by composing the sheafification functor with the functors
![]() $u_{\mathrm {p}} , u^{\mathrm {p}} , {}_{\mathrm {p}}u$
, respectively. If finite limits are representable in C and D and if
$u_{\mathrm {p}} , u^{\mathrm {p}} , {}_{\mathrm {p}}u$
, respectively. If finite limits are representable in C and D and if
![]() $u^+$
is left exact and continuous, then
$u^+$
is left exact and continuous, then
![]() $u^+$
gives a morphism of sites
$u^+$
gives a morphism of sites
![]() $u:D\to C$
[SGA 4I
, IV.4.9.2] and we also denote by
$u:D\to C$
[SGA 4I
, IV.4.9.2] and we also denote by
the associated morphism of topoi, where
![]() $u^{-1}=u_{\mathrm {s}}$
and
$u^{-1}=u_{\mathrm {s}}$
and
![]() $u_*=u^{\mathrm {s}}=u^{\mathrm {p}}|_{\widetilde {D}}$
. If, moreover, u is a morphism of ringed sites
$u_*=u^{\mathrm {s}}=u^{\mathrm {p}}|_{\widetilde {D}}$
. If, moreover, u is a morphism of ringed sites
![]() $u:(D,\mathcal {O}_D)\to (C,\mathcal {O}_C)$
, then we denote by
$u:(D,\mathcal {O}_D)\to (C,\mathcal {O}_C)$
, then we denote by
![]() $u^*=\mathcal {O}_D\otimes _{u^{-1}\mathcal {O}_C}u^{-1}$
the pullback functor of modules. We remark that the notation here, adopted by [Sta23], is slightly different from that in [SGA 4I
] (see [Sta23, 0CMZ]).
$u^*=\mathcal {O}_D\otimes _{u^{-1}\mathcal {O}_C}u^{-1}$
the pullback functor of modules. We remark that the notation here, adopted by [Sta23], is slightly different from that in [SGA 4I
] (see [Sta23, 0CMZ]).
3 Brief review on cohomological descent for faltings ringed topos
For the convenience of readers and preparation of new notation used later, we briefly summarize some main notions and results in [Reference HeHe23].
3.1 Firstly, we recall the definition of the Faltings site associated with a morphism of coherent schemes
![]() $Y\to X$
(see [Reference HeHe23, 7.7]). Let
$Y\to X$
(see [Reference HeHe23, 7.7]). Let
![]() $\mathbf {E}_{Y\to X}^{\mathrm {\acute {e}t}}$
be the category of morphisms of coherent schemes
$\mathbf {E}_{Y\to X}^{\mathrm {\acute {e}t}}$
be the category of morphisms of coherent schemes
![]() $V\to U$
over
$V\to U$
over
![]() $Y\to X$
, i.e., commutative diagrams
$Y\to X$
, i.e., commutative diagrams

such that U is étale over X and that V is finite étale over
![]() $Y\times _X U$
. We endow
$Y\times _X U$
. We endow
![]() $\mathbf {E}_{Y\to X}^{\mathrm {\acute {e}t}}$
with the topology generated by the following types of families of morphisms:
$\mathbf {E}_{Y\to X}^{\mathrm {\acute {e}t}}$
with the topology generated by the following types of families of morphisms:
-
(v)
 $\{(V_m \to U) \to (V \to U)\}_{m \in M}$
, where M is a finite set and
$\{(V_m \to U) \to (V \to U)\}_{m \in M}$
, where M is a finite set and
 $\coprod _{m\in M} V_m\to V$
is surjective;
$\coprod _{m\in M} V_m\to V$
is surjective; -
(c)
 $\{(V\times _U{U_n} \to U_n) \to (V \to U)\}_{n \in N}$
, where N is a finite set and
$\{(V\times _U{U_n} \to U_n) \to (V \to U)\}_{n \in N}$
, where N is a finite set and
 $\coprod _{n\in N} U_n\to U$
is surjective.
$\coprod _{n\in N} U_n\to U$
is surjective.
Consider the presheaf
![]() $\overline {\mathscr {B}}$
on
$\overline {\mathscr {B}}$
on
![]() $\mathbf {E}_{Y\to X}^{\mathrm {\acute {e}t}}$
defined by
$\mathbf {E}_{Y\to X}^{\mathrm {\acute {e}t}}$
defined by
where
![]() $U^V$
is the integral closure of U in V. It is indeed a sheaf of rings, called the structural sheaf of
$U^V$
is the integral closure of U in V. It is indeed a sheaf of rings, called the structural sheaf of
![]() $\mathbf {E}_{Y\to X}^{\mathrm {\acute {e}t}}$
(see [Reference HeHe23, 7.6]).
$\mathbf {E}_{Y\to X}^{\mathrm {\acute {e}t}}$
(see [Reference HeHe23, 7.6]).
3.2 Let
![]() $Y \to X$
be a morphism of coherent schemes. The natural left exact and continuous functors
$Y \to X$
be a morphism of coherent schemes. The natural left exact and continuous functors
induce a natural commutative diagram of sites (2.5),

where
![]() $\rho : Y_{\mathrm {\acute {e}t}} \to Y_{\mathrm {f\acute {e}t}}$
is defined by the inclusion functor (see [Reference HeHe23, 7.8]).
$\rho : Y_{\mathrm {\acute {e}t}} \to Y_{\mathrm {f\acute {e}t}}$
is defined by the inclusion functor (see [Reference HeHe23, 7.8]).
3.3 Recall that a morphism of coherent schemes
![]() $T\to S$
is called a v-covering if for any morphism
$T\to S$
is called a v-covering if for any morphism
![]() $\mathop {\mathrm {Spec}}(A)\to S$
with A a valuation ring, there exists an extension of valuation rings
$\mathop {\mathrm {Spec}}(A)\to S$
with A a valuation ring, there exists an extension of valuation rings
![]() $A\to B$
and a lifting
$A\to B$
and a lifting
![]() $\mathop {\mathrm {Spec}}(B)\to T$
[Reference HeHe23, 3.1(1)]. Let
$\mathop {\mathrm {Spec}}(B)\to T$
[Reference HeHe23, 3.1(1)]. Let
![]() $\mathbf {Sch}^{\mathrm {coh}}$
be the category of coherent schemes. We endow it with the topology generated by the pretopology formed by families of morphisms
$\mathbf {Sch}^{\mathrm {coh}}$
be the category of coherent schemes. We endow it with the topology generated by the pretopology formed by families of morphisms
![]() $\{S_i \to S\}_{i \in I}$
with I finite such that
$\{S_i \to S\}_{i \in I}$
with I finite such that
![]() $\coprod _{i \in I} S_i \to S$
is a v-covering, and we denote the corresponding site by
$\coprod _{i \in I} S_i \to S$
is a v-covering, and we denote the corresponding site by
![]() $\mathbf {Sch}^{\mathrm {coh}}_{\mathrm {v}}$
[Reference HeHe23, 3.3]. For any object S of
$\mathbf {Sch}^{\mathrm {coh}}_{\mathrm {v}}$
[Reference HeHe23, 3.3]. For any object S of
![]() $\mathbf {Sch}^{\mathrm {coh}}_{\mathrm {v}}$
, we denote by
$\mathbf {Sch}^{\mathrm {coh}}_{\mathrm {v}}$
, we denote by
![]() $(\mathbf {Sch}^{\mathrm {coh}}_{/S})_{\mathrm {v}}$
the localization of the v-site
$(\mathbf {Sch}^{\mathrm {coh}}_{/S})_{\mathrm {v}}$
the localization of the v-site
![]() $\mathbf {Sch}^{\mathrm {coh}}_{\mathrm {v}}$
at S. The cohomological descent for étale cohomology can be stated as follows:
$\mathbf {Sch}^{\mathrm {coh}}_{\mathrm {v}}$
at S. The cohomological descent for étale cohomology can be stated as follows:
Theorem 3.4 ([Reference HeHe23, 3.9])
Let S be a coherent scheme, let
![]() $\mathcal {F}$
be a torsion abelian sheaf on the site
$\mathcal {F}$
be a torsion abelian sheaf on the site
![]() $S_{\mathrm {\acute {e}t}}$
formed by coherent étale S-schemes endowed with the étale topology, and let
$S_{\mathrm {\acute {e}t}}$
formed by coherent étale S-schemes endowed with the étale topology, and let
![]() $a: (\mathbf {Sch}^{\mathrm {coh}}_{/S})_{\mathrm {v}} \to S_{\mathrm {\acute {e}t}}$
be the morphism of sites defined by the inclusion functor. Then, the canonical morphism
$a: (\mathbf {Sch}^{\mathrm {coh}}_{/S})_{\mathrm {v}} \to S_{\mathrm {\acute {e}t}}$
be the morphism of sites defined by the inclusion functor. Then, the canonical morphism
![]() $\mathcal {F} \to \mathrm {R} a_*a^{-1}\mathcal {F}$
is an isomorphism.
$\mathcal {F} \to \mathrm {R} a_*a^{-1}\mathcal {F}$
is an isomorphism.
Definition 3.5 ([Reference HeHe23, 3.23])
Let
![]() $S^\circ \to S$
be an open immersion of coherent schemes such that S is integrally closed in
$S^\circ \to S$
be an open immersion of coherent schemes such that S is integrally closed in
![]() $S^\circ $
. We define a site
$S^\circ $
. We define a site
![]() $\mathbf {I}_{S^\circ \to S}$
as follows:
$\mathbf {I}_{S^\circ \to S}$
as follows:
-
(1) The underlying category is formed by coherent S-schemes T which are integrally closed in
 $S^\circ \times _S T$
.
$S^\circ \times _S T$
. -
(2) The topology is generated by covering families
 $\{T_i\to T\}_{i\in I}$
in the v-topology.
$\{T_i\to T\}_{i\in I}$
in the v-topology.
We call
![]() $\mathbf {I}_{S^\circ \to S}$
the v-site of
$\mathbf {I}_{S^\circ \to S}$
the v-site of
![]() $S^\circ $
-integrally closed coherent S-schemes, and we call the sheaf
$S^\circ $
-integrally closed coherent S-schemes, and we call the sheaf
![]() $\mathscr {O}$
on
$\mathscr {O}$
on
![]() $\mathbf {I}_{S^\circ \to S}$
associated with the presheaf
$\mathbf {I}_{S^\circ \to S}$
associated with the presheaf
![]() $T\mapsto \Gamma (T,\mathcal {O}_T)$
the structural sheaf of
$T\mapsto \Gamma (T,\mathcal {O}_T)$
the structural sheaf of
![]() $\mathbf {I}_{S^\circ \to S}$
.
$\mathbf {I}_{S^\circ \to S}$
.
3.6 Let
![]() $Y \to X$
be a morphism of coherent schemes such that
$Y \to X$
be a morphism of coherent schemes such that
![]() $Y \to X^Y$
is an open immersion, where
$Y \to X^Y$
is an open immersion, where
![]() $X^Y$
denotes the integral closure of X in Y (2.2). The natural left exact and continuous functors
$X^Y$
denotes the integral closure of X in Y (2.2). The natural left exact and continuous functors
induce natural morphisms of sites (see [Reference HeHe23, 3.26, 8.6])
Combining with the morphisms of sites defined in 3.2 and 3.4, we obtain the following natural commutative diagram of sites:

Moreover,
![]() $\varepsilon ^+$
actually defines a morphism of ringed sites (see [Reference HeHe23, 8.6])
$\varepsilon ^+$
actually defines a morphism of ringed sites (see [Reference HeHe23, 8.6])
Lemma 3.7 (cf. [Reference HeHe23, 7.9])
Let X be the spectrum of an absolutely integrally closed valuation ring, and let Y be a quasi-compact open subscheme of X. Then, for any presheaf
![]() $\mathcal {F}$
on
$\mathcal {F}$
on
![]() $\mathbf {E}_{Y \to X}^{\mathrm {\acute {e}t}}$
(resp.
$\mathbf {E}_{Y \to X}^{\mathrm {\acute {e}t}}$
(resp.
![]() $\mathbf {I}_{Y \to X^Y}$
), we have
$\mathbf {I}_{Y \to X^Y}$
), we have
![]() $\mathcal {F}^{\mathrm {a}}(Y\to X)=\mathcal {F}(Y \to X)$
(resp.
$\mathcal {F}^{\mathrm {a}}(Y\to X)=\mathcal {F}(Y \to X)$
(resp.
![]() $\mathcal {F}^{\mathrm {a}}(X^Y)=\mathcal {F}(X^Y)$
). In particular, the associated topos of
$\mathcal {F}^{\mathrm {a}}(X^Y)=\mathcal {F}(X^Y)$
). In particular, the associated topos of
![]() $\mathbf {E}_{Y \to X}^{\mathrm {\acute {e}t}}$
(resp.
$\mathbf {E}_{Y \to X}^{\mathrm {\acute {e}t}}$
(resp.
![]() $\mathbf {I}_{Y \to X^Y}$
) is local [SGA 4II
, VI.8.4.6].
$\mathbf {I}_{Y \to X^Y}$
) is local [SGA 4II
, VI.8.4.6].
Proof The statement for
![]() $\mathbf {E}_{Y \to X^Y}^{\mathrm {\acute {e}t}}$
is proved in [Reference HeHe23, 7.9]. The same arguments work for
$\mathbf {E}_{Y \to X^Y}^{\mathrm {\acute {e}t}}$
is proved in [Reference HeHe23, 7.9]. The same arguments work for
![]() $\mathbf {I}_{Y \to X^Y}$
.
$\mathbf {I}_{Y \to X^Y}$
.
Proposition 3.8 ([Reference HeHe23, 3.27])
We keep the notation in 3.6.
-
(1) For any torsion abelian sheaf
 $\mathcal {F}$
on
$\mathcal {F}$
on
 $Y_{\mathrm {\acute {e}t}}$
, the canonical morphism
$Y_{\mathrm {\acute {e}t}}$
, the canonical morphism
 $\Psi _*(a^{-1}\mathcal {F}) \to \mathrm {R}\Psi _*(a^{-1}\mathcal {F})$
is an isomorphism.
$\Psi _*(a^{-1}\mathcal {F}) \to \mathrm {R}\Psi _*(a^{-1}\mathcal {F})$
is an isomorphism. -
(2) For any locally constant torsion abelian sheaf
 $\mathbb {L}$
on
$\mathbb {L}$
on
 $\mathbf {I}_{Y \to X^Y}$
, the canonical morphism
$\mathbf {I}_{Y \to X^Y}$
, the canonical morphism
 $\mathbb {L} \to \mathrm {R}\Psi _*\Psi ^{-1}\mathbb {L}$
is an isomorphism.
$\mathbb {L} \to \mathrm {R}\Psi _*\Psi ^{-1}\mathbb {L}$
is an isomorphism.
Combining 3.8(1) with 3.4, we see that the cohomology of
![]() $\mathbf {I}_{Y \to X^Y}$
computes the étale cohomology of Y. Moreover, it also computes the cohomology of Faltings ringed topos in the following sense.
$\mathbf {I}_{Y \to X^Y}$
computes the étale cohomology of Y. Moreover, it also computes the cohomology of Faltings ringed topos in the following sense.
Theorem 3.9 ([Reference HeHe23, 8.14])
Let K be a pre-perfectoid field of mixed characteristic
![]() $(0, p)$
(i.e., a valuation field whose valuation ring
$(0, p)$
(i.e., a valuation field whose valuation ring
![]() $\mathcal {O}_K$
is non-discrete, extension of
$\mathcal {O}_K$
is non-discrete, extension of
![]() $\mathbb {Z}_p$
and of height
$\mathbb {Z}_p$
and of height
![]() $1$
such that the Frobenius map on
$1$
such that the Frobenius map on
![]() $\mathcal {O}_K/p\mathcal {O}_K$
is surjective, see [Reference HeHe23, 5.1]),
$\mathcal {O}_K/p\mathcal {O}_K$
is surjective, see [Reference HeHe23, 5.1]),
![]() $\eta = \mathop {\mathrm {Spec}}(K)$
,
$\eta = \mathop {\mathrm {Spec}}(K)$
,
![]() $S = \mathop {\mathrm {Spec}} (\mathcal {O}_K)$
,
$S = \mathop {\mathrm {Spec}} (\mathcal {O}_K)$
,
![]() $Y \to X$
a morphism of coherent schemes such that
$Y \to X$
a morphism of coherent schemes such that
![]() $X^Y$
is an S-scheme with generic fiber
$X^Y$
is an S-scheme with generic fiber
![]() $(X^Y)_\eta =Y$
(in particular,
$(X^Y)_\eta =Y$
(in particular,
![]() $X^Y$
is an object of
$X^Y$
is an object of
![]() $\mathbf {I}_{\eta \to S}$
). Then, for any finite locally constant abelian sheaf
$\mathbf {I}_{\eta \to S}$
). Then, for any finite locally constant abelian sheaf
![]() $\mathbb {L}$
on
$\mathbb {L}$
on
![]() $\mathbf {E}_{Y\to X}^{\mathrm {\acute {e}t}}$
, the canonical morphism (3.6)
$\mathbf {E}_{Y\to X}^{\mathrm {\acute {e}t}}$
, the canonical morphism (3.6)
is an almost isomorphism [Reference HeHe23, 5.7].
The cohomological descent for Faltings ringed topos along a proper hypercovering is stated as follows:
Corollary 3.10 ([Reference HeHe23, 8.18])
Under the assumptions in 3.9 and with the same notation, let
![]() $X_\bullet \to X$
be an augmentation of simplicial coherent scheme, and let
$X_\bullet \to X$
be an augmentation of simplicial coherent scheme, and let
![]() $Y_\bullet =Y \times _X X_\bullet $
,
$Y_\bullet =Y \times _X X_\bullet $
,
![]() $b: \mathbf {E}_{Y_\bullet \to X_\bullet }^{\mathrm {\acute {e}t}} \to \mathbf {E}_{Y \to X}^{\mathrm {\acute {e}t}}$
be the augmentation of simplicial site [Reference HeHe23, 8.17]. If
$b: \mathbf {E}_{Y_\bullet \to X_\bullet }^{\mathrm {\acute {e}t}} \to \mathbf {E}_{Y \to X}^{\mathrm {\acute {e}t}}$
be the augmentation of simplicial site [Reference HeHe23, 8.17]. If
![]() $X_\bullet ^{Y_\bullet } \to X^Y$
is a hypercovering in
$X_\bullet ^{Y_\bullet } \to X^Y$
is a hypercovering in
![]() $\mathbf {I}_{\eta \to S}$
, then the canonical morphism
$\mathbf {I}_{\eta \to S}$
, then the canonical morphism
is an almost isomorphism [Reference HeHe23, 5.7].
4 Complements on logarithmic geometry
We briefly recall some notions and facts of logarithmic geometry which will be used in the rest of the paper. We refer to [Reference GrothendieckGR04, Reference KatoKat89, Reference KatoKat94, Reference OgusOgu18] for a systematic development of logarithmic geometry, and to [Reference AchingerAGT16, II.5] for a brief summary of the theory.
4.1 We only consider logarithmic structures in étale topology. More precisely, let X be a scheme, let
![]() $X_{\mathrm {\acute {e}t}}$
be the étale site of X, let
$X_{\mathrm {\acute {e}t}}$
be the étale site of X, let
![]() $\mathcal {O}_{X_{\mathrm {\acute {e}t}}}$
be the structure sheaf on
$\mathcal {O}_{X_{\mathrm {\acute {e}t}}}$
be the structure sheaf on
![]() $X_{\mathrm {\acute {e}t}}$
, and let
$X_{\mathrm {\acute {e}t}}$
, and let
![]() $\mathcal {O}_{X_{\mathrm {\acute {e}t}}}^\times $
be the subsheaf of units of
$\mathcal {O}_{X_{\mathrm {\acute {e}t}}}^\times $
be the subsheaf of units of
![]() $\mathcal {O}_{X_{\mathrm {\acute {e}t}}}$
. A logarithmic structure on X is a homomorphism of sheaves of monoids
$\mathcal {O}_{X_{\mathrm {\acute {e}t}}}$
. A logarithmic structure on X is a homomorphism of sheaves of monoids
![]() $\alpha :\mathscr {M} \to \mathcal {O}_{X_{\mathrm {\acute {e}t}}}$
on
$\alpha :\mathscr {M} \to \mathcal {O}_{X_{\mathrm {\acute {e}t}}}$
on
![]() $X_{\mathrm {\acute {e}t}}$
which induces an isomorphism
$X_{\mathrm {\acute {e}t}}$
which induces an isomorphism
![]() $\alpha ^{-1}(\mathcal {O}_{X_{\mathrm {\acute {e}t}}}^\times ) \stackrel {\sim }{\longrightarrow } \mathcal {O}_{X_{\mathrm {\acute {e}t}}}^\times $
. We denote by
$\alpha ^{-1}(\mathcal {O}_{X_{\mathrm {\acute {e}t}}}^\times ) \stackrel {\sim }{\longrightarrow } \mathcal {O}_{X_{\mathrm {\acute {e}t}}}^\times $
. We denote by
![]() $(X,\mathscr {M})$
the associated logarithmic scheme (cf. [Reference AchingerAGT16, II.5.11]).
$(X,\mathscr {M})$
the associated logarithmic scheme (cf. [Reference AchingerAGT16, II.5.11]).
4.2 Let
![]() $(X,\mathscr {M})$
be a coherent log scheme (cf. [Reference AchingerAGT16, II.5.15]). Then, there is a maximal open subscheme
$(X,\mathscr {M})$
be a coherent log scheme (cf. [Reference AchingerAGT16, II.5.15]). Then, there is a maximal open subscheme
![]() $X^{\mathrm {tr}}$
of X on which
$X^{\mathrm {tr}}$
of X on which
![]() $\mathscr {M}$
is trivial, and moreover it is functorial in
$\mathscr {M}$
is trivial, and moreover it is functorial in
![]() $(X,\mathscr {M})$
[Reference OgusOgu18, III.1.2.8]. Let
$(X,\mathscr {M})$
[Reference OgusOgu18, III.1.2.8]. Let
![]() $(X,\mathscr {M}) \to (S,\mathscr {L}) \leftarrow (Y,\mathscr {N})$
be a diagram of fine and saturated log schemes (cf. [Reference AchingerAGT16, II.5.15]). Then, the fibered product is representable in the category of fine and saturated log schemes by
$(X,\mathscr {M}) \to (S,\mathscr {L}) \leftarrow (Y,\mathscr {N})$
be a diagram of fine and saturated log schemes (cf. [Reference AchingerAGT16, II.5.15]). Then, the fibered product is representable in the category of fine and saturated log schemes by
![]() $(Z,\mathscr {P})=(X,\mathscr {M}) \times _{(S,\mathscr {L})}^{\mathrm {fs}} (Y,\mathscr {N})$
. We remark that
$(Z,\mathscr {P})=(X,\mathscr {M}) \times _{(S,\mathscr {L})}^{\mathrm {fs}} (Y,\mathscr {N})$
. We remark that
![]() $Z^{\mathrm {tr}}= X^{\mathrm {tr}} \times _{S^{\mathrm {tr}}} Y^{\mathrm {tr}}$
, that
$Z^{\mathrm {tr}}= X^{\mathrm {tr}} \times _{S^{\mathrm {tr}}} Y^{\mathrm {tr}}$
, that
![]() $Z \to X \times _S Y$
is finite, and that
$Z \to X \times _S Y$
is finite, and that
![]() $Z^{\mathrm {tr}} \to Z$
is Cartesian over
$Z^{\mathrm {tr}} \to Z$
is Cartesian over
![]() $X^{\mathrm {tr}} \times _{S^{\mathrm {tr}}} Y^{\mathrm {tr}} \to X \times _S Y$
[Reference OgusOgu18, III 2.1.2, 2.1.6]. Moreover, if
$X^{\mathrm {tr}} \times _{S^{\mathrm {tr}}} Y^{\mathrm {tr}} \to X \times _S Y$
[Reference OgusOgu18, III 2.1.2, 2.1.6]. Moreover, if
![]() $X^{\mathrm {tr}}=X$
, then
$X^{\mathrm {tr}}=X$
, then
![]() $Z=X \times _S Y$
[Reference OgusOgu18, III.2.1.3].
$Z=X \times _S Y$
[Reference OgusOgu18, III.2.1.3].
4.3 For an open immersion
![]() $j:Y \to X$
, we denote by
$j:Y \to X$
, we denote by
![]() $j_{\mathrm {\acute {e}t}}: Y_{\mathrm {\acute {e}t}} \to X_{\mathrm {\acute {e}t}}$
the morphism of their étale sites defined by the base change by j. Let
$j_{\mathrm {\acute {e}t}}: Y_{\mathrm {\acute {e}t}} \to X_{\mathrm {\acute {e}t}}$
the morphism of their étale sites defined by the base change by j. Let
![]() $\mathscr {M}_{Y \to X}$
be the preimage of
$\mathscr {M}_{Y \to X}$
be the preimage of
![]() $j_{\mathrm {\acute {e}t}*} \mathcal {O}_{Y_{\mathrm {\acute {e}t}}}^\times $
under the natural map
$j_{\mathrm {\acute {e}t}*} \mathcal {O}_{Y_{\mathrm {\acute {e}t}}}^\times $
under the natural map
![]() $\mathcal {O}_{X_{\mathrm {\acute {e}t}}}\to j_{\mathrm {\acute {e}t}*}\mathcal {O}_{Y_{\mathrm {\acute {e}t}}}$
, and we endow X with the logarithmic structure
$\mathcal {O}_{X_{\mathrm {\acute {e}t}}}\to j_{\mathrm {\acute {e}t}*}\mathcal {O}_{Y_{\mathrm {\acute {e}t}}}$
, and we endow X with the logarithmic structure
![]() $\mathscr {M}_{Y \to X} \to \mathcal {O}_{X_{\mathrm {\acute {e}t}}}$
, which is called the compactifying log structure associated with the open immersion j [Reference OgusOgu18, III.1.6.1]. Sometimes we write
$\mathscr {M}_{Y \to X} \to \mathcal {O}_{X_{\mathrm {\acute {e}t}}}$
, which is called the compactifying log structure associated with the open immersion j [Reference OgusOgu18, III.1.6.1]. Sometimes we write
![]() $\mathscr {M}_{Y \to X}$
as
$\mathscr {M}_{Y \to X}$
as
![]() $\mathscr {M}_{X}$
if Y is clear in the context.
$\mathscr {M}_{X}$
if Y is clear in the context.
4.4 Let
![]() $(X,\mathscr {M})$
be a fine and saturated log scheme which is regular ([Reference KatoKat94, 2.1], [Reference NiziołNiz06, 2.3]). Then, X is locally Noetherian and normal, and
$(X,\mathscr {M})$
be a fine and saturated log scheme which is regular ([Reference KatoKat94, 2.1], [Reference NiziołNiz06, 2.3]). Then, X is locally Noetherian and normal, and
![]() $X^{\mathrm {tr}}$
is regular and dense in X [Reference KatoKat94, 4.1]. Moreover, there is a natural isomorphism
$X^{\mathrm {tr}}$
is regular and dense in X [Reference KatoKat94, 4.1]. Moreover, there is a natural isomorphism
![]() $\mathscr {M} \stackrel {\sim }{\longrightarrow } \mathscr {M}_{X^{\mathrm {tr}} \to X}$
([Reference KatoKat94, 11.6], [Reference NiziołNiz06, 2.6]). We remark that if X is a regular scheme with a strict normal crossings divisor D, then
$\mathscr {M} \stackrel {\sim }{\longrightarrow } \mathscr {M}_{X^{\mathrm {tr}} \to X}$
([Reference KatoKat94, 11.6], [Reference NiziołNiz06, 2.6]). We remark that if X is a regular scheme with a strict normal crossings divisor D, then
![]() $(X,\mathscr {M}_{X\setminus D \to X})$
is fine, saturated, and regular [Reference OgusOgu18, III.1.11.9].
$(X,\mathscr {M}_{X\setminus D \to X})$
is fine, saturated, and regular [Reference OgusOgu18, III.1.11.9].
Let
![]() $f:(X,\mathscr {M}) \to (S,\mathscr {L})$
be a smooth (resp. saturated) morphism of fine and saturated log schemes (cf. [Reference AchingerAGT16, II 5.25, 5.18]). Then, f remains smooth (resp. saturated) under the base change in the category of fine and saturated log schemes ([Reference OgusOgu18, IV.3.1.2, IV.3.1.11], resp. [Reference OgusOgu18, III.2.5.3]). We remark that if f is smooth, then
$f:(X,\mathscr {M}) \to (S,\mathscr {L})$
be a smooth (resp. saturated) morphism of fine and saturated log schemes (cf. [Reference AchingerAGT16, II 5.25, 5.18]). Then, f remains smooth (resp. saturated) under the base change in the category of fine and saturated log schemes ([Reference OgusOgu18, IV.3.1.2, IV.3.1.11], resp. [Reference OgusOgu18, III.2.5.3]). We remark that if f is smooth, then
![]() $f^{\mathrm {tr}}:X^{\mathrm {tr}}\to S^{\mathrm {tr}}$
is a smooth morphism of schemes. If, moreover,
$f^{\mathrm {tr}}:X^{\mathrm {tr}}\to S^{\mathrm {tr}}$
is a smooth morphism of schemes. If, moreover,
![]() $(S,\mathscr {L})$
is regular, then
$(S,\mathscr {L})$
is regular, then
![]() $(X,\mathscr {M})$
is also regular [Reference OgusOgu18, IV.3.5.3]. We also remark that if f is saturated, then for any fibered product in the category of fine and saturated log schemes
$(X,\mathscr {M})$
is also regular [Reference OgusOgu18, IV.3.5.3]. We also remark that if f is saturated, then for any fibered product in the category of fine and saturated log schemes
![]() $(Z,\mathscr {P})=(X,\mathscr {M}) \times _{(S,\mathscr {L})}^{\mathrm {fs}} (Y,\mathscr {N})$
, we have
$(Z,\mathscr {P})=(X,\mathscr {M}) \times _{(S,\mathscr {L})}^{\mathrm {fs}} (Y,\mathscr {N})$
, we have
![]() $Z=X\times _S Y$
[Reference TsujiTsu19, II.2.13].
$Z=X\times _S Y$
[Reference TsujiTsu19, II.2.13].
4.5 Let K be a complete discrete valuation field with valuation ring
![]() $\mathcal {O}_K$
, let k be the residue field of
$\mathcal {O}_K$
, let k be the residue field of
![]() $\mathcal {O}_K$
, and let
$\mathcal {O}_K$
, and let
![]() $\pi $
be a uniformizer of
$\pi $
be a uniformizer of
![]() $\mathcal {O}_K$
. We set
$\mathcal {O}_K$
. We set
![]() $\eta =\mathop {\mathrm {Spec}}(K)$
,
$\eta =\mathop {\mathrm {Spec}}(K)$
,
![]() $S= \mathop {\mathrm {Spec}}(\mathcal {O}_K)$
and
$S= \mathop {\mathrm {Spec}}(\mathcal {O}_K)$
and
![]() $s=\mathop {\mathrm {Spec}}(k)$
. Then,
$s=\mathop {\mathrm {Spec}}(k)$
. Then,
![]() $(S,\mathscr {M}_{\eta \to S})$
is fine, saturated, and regular, since
$(S,\mathscr {M}_{\eta \to S})$
is fine, saturated, and regular, since
![]() $\mathbb {N} \to \Gamma (S,\mathscr {M}_{\eta \to S})$
sending
$\mathbb {N} \to \Gamma (S,\mathscr {M}_{\eta \to S})$
sending
![]() $1$
to
$1$
to
![]() $\pi $
forms a chart of
$\pi $
forms a chart of
![]() $(S,\mathscr {M}_{\eta \to S})$
(cf. [Reference AchingerAGT16, II.5.13, II.6.1]). Recall that an open immersion
$(S,\mathscr {M}_{\eta \to S})$
(cf. [Reference AchingerAGT16, II.5.13, II.6.1]). Recall that an open immersion
![]() $Y \to X$
of quasi-compact and separated schemes over
$Y \to X$
of quasi-compact and separated schemes over
![]() $\eta \to S$
is strictly semi-stable [Reference de JongdJ96, 6.3] if and only if the following conditions are satisfied ([Reference de JongdJ96, 6.4], [Reference GrothendieckEGA IV4
, 17.5.3]):
$\eta \to S$
is strictly semi-stable [Reference de JongdJ96, 6.3] if and only if the following conditions are satisfied ([Reference de JongdJ96, 6.4], [Reference GrothendieckEGA IV4
, 17.5.3]):
-
(i) For each point x of the generic fiber
 $X_\eta $
, there is an open neighborhood
$X_\eta $
, there is an open neighborhood
 $U\subseteq X_\eta $
of x and a smooth K-morphism (4.5.1)such that f maps x to the point associated with the maximal ideal
$U\subseteq X_\eta $
of x and a smooth K-morphism (4.5.1)such that f maps x to the point associated with the maximal ideal $$ \begin{align} f:U\longrightarrow \mathop{\mathrm{Spec}}(K[s_1,\dots,s_m]) \end{align} $$
$$ \begin{align} f:U\longrightarrow \mathop{\mathrm{Spec}}(K[s_1,\dots,s_m]) \end{align} $$
 $(s_1,\dots ,s_m)$
and that
$(s_1,\dots ,s_m)$
and that
 $U\setminus Y$
is the inverse image of the closed subset defined by
$U\setminus Y$
is the inverse image of the closed subset defined by
 $s_1\dots s_m=0$
.
$s_1\dots s_m=0$
.
-
(ii) For each point x of the special fiber
 $X_s$
, there is an open neighborhood
$X_s$
, there is an open neighborhood
 $U\subseteq X$
of x and a smooth
$U\subseteq X$
of x and a smooth
 $\mathcal {O}_K$
-morphism (4.5.2)such that f maps x to the point associated with the maximal ideal
$\mathcal {O}_K$
-morphism (4.5.2)such that f maps x to the point associated with the maximal ideal $$ \begin{align} f:U\longrightarrow \mathop{\mathrm{Spec}}(\mathcal{O}_K[t_1,\dots,t_n, s_1,\dots,s_m]/(\pi-t_1\dots t_n)) \end{align} $$
$$ \begin{align} f:U\longrightarrow \mathop{\mathrm{Spec}}(\mathcal{O}_K[t_1,\dots,t_n, s_1,\dots,s_m]/(\pi-t_1\dots t_n)) \end{align} $$
 $(t_1,\dots ,t_n, s_1,\dots ,s_m)$
and that
$(t_1,\dots ,t_n, s_1,\dots ,s_m)$
and that
 $U\setminus Y$
is the inverse image of the closed subset defined by
$U\setminus Y$
is the inverse image of the closed subset defined by
 $t_1\dots t_n\cdot s_1\dots s_m=0$
.
$t_1\dots t_n\cdot s_1\dots s_m=0$
.
We say that an open immersion
![]() $Y \to X$
of quasi-compact and separated schemes over
$Y \to X$
of quasi-compact and separated schemes over
![]() $\eta \to S$
is semi-stable if for any point x of X there is an étale neighborhood U of x such that
$\eta \to S$
is semi-stable if for any point x of X there is an étale neighborhood U of x such that
![]() $Y\times _X U\to U$
is strictly semi-stable. In this case,
$Y\times _X U\to U$
is strictly semi-stable. In this case,
![]() $(X,\mathscr {M}_{Y \to X})$
is a fine, saturated, and regular log scheme smooth and saturated over
$(X,\mathscr {M}_{Y \to X})$
is a fine, saturated, and regular log scheme smooth and saturated over
![]() $(S,\mathscr {M}_{\eta \to S})$
, since for any point x of X there is an étale neighborhood U of x such that there exists a chart for the morphism
$(S,\mathscr {M}_{\eta \to S})$
, since for any point x of X there is an étale neighborhood U of x such that there exists a chart for the morphism
![]() $(U,\mathscr {M}_{Y\times _X U \to U})\to (S,\mathscr {M}_{\eta \to S})$
subordinate to the morphism
$(U,\mathscr {M}_{Y\times _X U \to U})\to (S,\mathscr {M}_{\eta \to S})$
subordinate to the morphism
![]() $\mathbb {N} \to \mathbb {N}^n\oplus \mathbb {N}^m$
sending
$\mathbb {N} \to \mathbb {N}^n\oplus \mathbb {N}^m$
sending
![]() $1$
to
$1$
to
![]() $(1,\dots ,1,0,\dots ,0)$
such that the induced morphism
$(1,\dots ,1,0,\dots ,0)$
such that the induced morphism
![]() $U\to S\times _{\mathbb {A}_{\mathbb {N}}}\mathbb {A}_{\mathbb {N}^n\oplus \mathbb {N}^m}$
is smooth (cf. [Reference OgusOgu18, II.2.4.1, IV.3.1.18]).
$U\to S\times _{\mathbb {A}_{\mathbb {N}}}\mathbb {A}_{\mathbb {N}^n\oplus \mathbb {N}^m}$
is smooth (cf. [Reference OgusOgu18, II.2.4.1, IV.3.1.18]).
4.6 Recall that a morphism of schemes
![]() $f:X\to S$
is called generically finite if there exists a dense open subscheme U of S such that
$f:X\to S$
is called generically finite if there exists a dense open subscheme U of S such that
![]() $f^{-1}(U)\to U$
is finite. We remark that for a morphism
$f^{-1}(U)\to U$
is finite. We remark that for a morphism
![]() $f:X\to S$
of finite type between Noetherian schemes which maps generic points to generic points, f is generically finite if and only if the residue field of any generic point
$f:X\to S$
of finite type between Noetherian schemes which maps generic points to generic points, f is generically finite if and only if the residue field of any generic point
![]() $\eta $
of X is a finite field extension of the residue field of
$\eta $
of X is a finite field extension of the residue field of
![]() $f(\eta )$
[Reference Illusie, Laszlo and OrgogozoILO14, II.1.1.7].
$f(\eta )$
[Reference Illusie, Laszlo and OrgogozoILO14, II.1.1.7].
4.7 Let K be a complete discrete valuation field with valuation ring
![]() $\mathcal {O}_K$
, let L be an algebraically closed valuation field of height
$\mathcal {O}_K$
, let L be an algebraically closed valuation field of height
![]() $1$
extension of K with valuation ring
$1$
extension of K with valuation ring
![]() $\mathcal {O}_L$
, and let
$\mathcal {O}_L$
, and let
![]() $\overline {K}$
be the algebraic closure of K in L.
$\overline {K}$
be the algebraic closure of K in L.
Consider the category
![]() $\mathscr {C}$
of open immersions between integral affine schemes
$\mathscr {C}$
of open immersions between integral affine schemes
![]() $U\to T$
over
$U\to T$
over
![]() $\mathop {\mathrm {Spec}}(K)\to \mathop {\mathrm {Spec}}(\mathcal {O}_K)$
under
$\mathop {\mathrm {Spec}}(K)\to \mathop {\mathrm {Spec}}(\mathcal {O}_K)$
under
![]() $\mathop {\mathrm {Spec}}(L)\to \mathop {\mathrm {Spec}}(\mathcal {O}_L)$
such that T is of finite type over
$\mathop {\mathrm {Spec}}(L)\to \mathop {\mathrm {Spec}}(\mathcal {O}_L)$
such that T is of finite type over
![]() $\mathcal {O}_K$
and that
$\mathcal {O}_K$
and that
![]() $\mathop {\mathrm {Spec}}(L)\to U$
is dominant. Let
$\mathop {\mathrm {Spec}}(L)\to U$
is dominant. Let
![]() $\mathscr {C}_{\mathrm {car}}$
be the full subcategory of
$\mathscr {C}_{\mathrm {car}}$
be the full subcategory of
![]() $\mathscr {C}$
formed by those objects
$\mathscr {C}$
formed by those objects
![]() $U \to T$
Cartesian over
$U \to T$
Cartesian over
![]() $\mathop {\mathrm {Spec}}(K) \to \mathop {\mathrm {Spec}}(\mathcal {O}_K)$
.
$\mathop {\mathrm {Spec}}(K) \to \mathop {\mathrm {Spec}}(\mathcal {O}_K)$
.

We note that the objects of
![]() $\mathscr {C}$
are of the form
$\mathscr {C}$
are of the form
![]() $(U=\mathop {\mathrm {Spec}}(B) \to T=\mathop {\mathrm {Spec}}(A)),$
where A (resp. B) is a finitely generated
$(U=\mathop {\mathrm {Spec}}(B) \to T=\mathop {\mathrm {Spec}}(A)),$
where A (resp. B) is a finitely generated
![]() $\mathcal {O}_K$
-subalgebra of
$\mathcal {O}_K$
-subalgebra of
![]() $\mathcal {O}_L$
(resp. K-subalgebra of L) with
$\mathcal {O}_L$
(resp. K-subalgebra of L) with
![]() $A\subseteq B$
such that
$A\subseteq B$
such that
![]() $\mathop {\mathrm {Spec}}(B) \to \mathop {\mathrm {Spec}}(A)$
is an open immersion.
$\mathop {\mathrm {Spec}}(B) \to \mathop {\mathrm {Spec}}(A)$
is an open immersion.
Lemma 4.8 With the notation in 4.7, we have:
-
(1) The category
 $\mathscr {C}$
is cofiltered, and the subcategory
$\mathscr {C}$
is cofiltered, and the subcategory
 $\mathscr {C}_{\mathrm {car}}$
is initial in
$\mathscr {C}_{\mathrm {car}}$
is initial in
 $\mathscr {C}$
.
$\mathscr {C}$
. -
(2) The morphism
 $\mathop {\mathrm {Spec}}(L) \to \mathop {\mathrm {Spec}}(\mathcal {O}_L)$
represents the cofiltered limit of morphisms
$\mathop {\mathrm {Spec}}(L) \to \mathop {\mathrm {Spec}}(\mathcal {O}_L)$
represents the cofiltered limit of morphisms
 $U \to T$
indexed by
$U \to T$
indexed by
 $\mathscr {C}$
in the category of morphisms of schemes (see [Reference HeHe23, 7.1]).
$\mathscr {C}$
in the category of morphisms of schemes (see [Reference HeHe23, 7.1]). -
(3) There exists a directed inverse system
 $(U_\lambda \to T_\lambda )_{\lambda \in \Lambda }$
of objects of
$(U_\lambda \to T_\lambda )_{\lambda \in \Lambda }$
of objects of
 $\mathscr {C}_{\mathrm {car}}$
over a directed inverse system
$\mathscr {C}_{\mathrm {car}}$
over a directed inverse system
 $(\mathop {\mathrm {Spec}}(K_\lambda ) \to \mathop {\mathrm {Spec}}(\mathcal {O}_{K_\lambda }))_{\lambda \in \Lambda }$
of objects of
$(\mathop {\mathrm {Spec}}(K_\lambda ) \to \mathop {\mathrm {Spec}}(\mathcal {O}_{K_\lambda }))_{\lambda \in \Lambda }$
of objects of
 $\mathscr {C}_{\mathrm {car}}$
such that
$\mathscr {C}_{\mathrm {car}}$
such that
 $K_\lambda $
is a finite field extension of K in L, that
$K_\lambda $
is a finite field extension of K in L, that
 $\overline {K}=\bigcup _{\lambda \in \Lambda } K_\lambda $
, that
$\overline {K}=\bigcup _{\lambda \in \Lambda } K_\lambda $
, that
 $U_\lambda \to T_\lambda $
is strictly semi-stable over
$U_\lambda \to T_\lambda $
is strictly semi-stable over
 $\mathop {\mathrm {Spec}}(K_\lambda ) \to \mathop {\mathrm {Spec}}(\mathcal {O}_{K_\lambda })$
(4.5), and that
$\mathop {\mathrm {Spec}}(K_\lambda ) \to \mathop {\mathrm {Spec}}(\mathcal {O}_{K_\lambda })$
(4.5), and that
 $(U_\lambda \to T_\lambda )_{\lambda \in \Lambda }$
forms an initial full subcategory of
$(U_\lambda \to T_\lambda )_{\lambda \in \Lambda }$
forms an initial full subcategory of
 $\mathscr {C}_{\mathrm {car}}$
.
$\mathscr {C}_{\mathrm {car}}$
.
Proof (1) For a diagram
![]() $(U_1\to T_1)\to (U_0 \to T_0) \leftarrow (U_2 \to T_2)$
in
$(U_1\to T_1)\to (U_0 \to T_0) \leftarrow (U_2 \to T_2)$
in
![]() $\mathscr {C}$
, let T be the scheme theoretic image of
$\mathscr {C}$
, let T be the scheme theoretic image of
![]() $\mathop {\mathrm {Spec}}(L) \to T_1\times _{T_0} T_2$
, and let U be the intersection of
$\mathop {\mathrm {Spec}}(L) \to T_1\times _{T_0} T_2$
, and let U be the intersection of
![]() $U_1\times _{U_0} U_2$
with T. It is clear that T is of finite type over
$U_1\times _{U_0} U_2$
with T. It is clear that T is of finite type over
![]() $\mathcal {O}_K$
as
$\mathcal {O}_K$
as
![]() $\mathcal {O}_K$
is Noetherian, that U and T are integral and affine, that
$\mathcal {O}_K$
is Noetherian, that U and T are integral and affine, that
![]() $\mathop {\mathrm {Spec}}(L) \to U$
is dominant, and that
$\mathop {\mathrm {Spec}}(L) \to U$
is dominant, and that
![]() $\mathop {\mathrm {Spec}}(L)\to T$
factors through
$\mathop {\mathrm {Spec}}(L)\to T$
factors through
![]() $\mathop {\mathrm {Spec}}(\mathcal {O}_L)$
. Thus,
$\mathop {\mathrm {Spec}}(\mathcal {O}_L)$
. Thus,
![]() $U \to T$
is an object of
$U \to T$
is an object of
![]() $\mathscr {C}$
, which shows that
$\mathscr {C}$
, which shows that
![]() $\mathscr {C}$
is cofiltered. For an object
$\mathscr {C}$
is cofiltered. For an object
![]() $(U=\mathop {\mathrm {Spec}}(B)\to T=\mathop {\mathrm {Spec}}(A))$
of
$(U=\mathop {\mathrm {Spec}}(B)\to T=\mathop {\mathrm {Spec}}(A))$
of
![]() $\mathscr {C}$
, we write
$\mathscr {C}$
, we write
![]() $\mathcal {O}_L$
as a filtered union of finitely generated A-subalgebras
$\mathcal {O}_L$
as a filtered union of finitely generated A-subalgebras
![]() $A_i$
. Let
$A_i$
. Let
![]() $\pi $
be a uniformizer of K. Notice that
$\pi $
be a uniformizer of K. Notice that
![]() $L=\mathcal {O}_L[1/\pi ]=\mathop {\mathrm {colim}} A_i[1/\pi ]$
and that
$L=\mathcal {O}_L[1/\pi ]=\mathop {\mathrm {colim}} A_i[1/\pi ]$
and that
![]() $\mathrm {Hom}_{K\textrm {-}\mathbf {Alg}}(B,L)=\mathop {\mathrm {colim}} \mathrm {Hom}_{K\textrm {-}\mathbf {Alg}}(B,A_i[1/\pi ])$
by [Reference GrothendieckEGA IV3
, 8.14.2.2]. Thus, there exists an index i such that
$\mathrm {Hom}_{K\textrm {-}\mathbf {Alg}}(B,L)=\mathop {\mathrm {colim}} \mathrm {Hom}_{K\textrm {-}\mathbf {Alg}}(B,A_i[1/\pi ])$
by [Reference GrothendieckEGA IV3
, 8.14.2.2]. Thus, there exists an index i such that
![]() $\mathop {\mathrm {Spec}}(A_i[1/\pi ]) \to \mathop {\mathrm {Spec}}(A_i)$
is an object of
$\mathop {\mathrm {Spec}}(A_i[1/\pi ]) \to \mathop {\mathrm {Spec}}(A_i)$
is an object of
![]() $\mathscr {C}_{\mathrm {car}}$
over
$\mathscr {C}_{\mathrm {car}}$
over
![]() $U \to T$
.
$U \to T$
.
(2) It follows immediately from the arguments above.
(3) Consider the category
![]() $\mathscr {D}$
of morphisms of
$\mathscr {D}$
of morphisms of
![]() $\mathscr {C}_{\mathrm {car}}$
,
$\mathscr {C}_{\mathrm {car}}$
,

such that
![]() $K'$
is a finite field extension of K. Similarly, this category is also cofiltered with limit of diagrams of schemes
$K'$
is a finite field extension of K. Similarly, this category is also cofiltered with limit of diagrams of schemes
![]() $(\mathop {\mathrm {Spec}}(L) \to \mathop {\mathrm {Spec}}(\mathcal {O}_L)) \to (\mathop {\mathrm {Spec}}(\overline {K}) \to \mathop {\mathrm {Spec}}(\mathcal {O}_{\overline {K}}))$
. It suffices to show that the full subcategory of
$(\mathop {\mathrm {Spec}}(L) \to \mathop {\mathrm {Spec}}(\mathcal {O}_L)) \to (\mathop {\mathrm {Spec}}(\overline {K}) \to \mathop {\mathrm {Spec}}(\mathcal {O}_{\overline {K}}))$
. It suffices to show that the full subcategory of
![]() $\mathscr {D}$
formed by strictly semi-stable objects is initial. For any object
$\mathscr {D}$
formed by strictly semi-stable objects is initial. For any object
![]() $U \to T$
of
$U \to T$
of
![]() $\mathscr {C}_{\mathrm {car}}$
, by de Jong’s alteration theorem [Reference de JongdJ96, 6.5], there exists a proper surjective and generically finite morphism
$\mathscr {C}_{\mathrm {car}}$
, by de Jong’s alteration theorem [Reference de JongdJ96, 6.5], there exists a proper surjective and generically finite morphism
![]() $T' \to T$
of integral schemes such that
$T' \to T$
of integral schemes such that
![]() $U'=U\times _T T' \to T'$
is strictly semi-stable over
$U'=U\times _T T' \to T'$
is strictly semi-stable over
![]() $\mathop {\mathrm {Spec}}(K') \to \mathop {\mathrm {Spec}}(\mathcal {O}_{K'})$
for a finite field extension
$\mathop {\mathrm {Spec}}(K') \to \mathop {\mathrm {Spec}}(\mathcal {O}_{K'})$
for a finite field extension
![]() $K\to K'$
. Since L is algebraically closed, the dominant morphism
$K\to K'$
. Since L is algebraically closed, the dominant morphism
![]() $\mathop {\mathrm {Spec}}(L)\to U$
lifts to a dominant morphism
$\mathop {\mathrm {Spec}}(L)\to U$
lifts to a dominant morphism
![]() $\mathop {\mathrm {Spec}}(L)\to U'$
(4.6), which further extends to a lifting
$\mathop {\mathrm {Spec}}(L)\to U'$
(4.6), which further extends to a lifting
![]() $\mathop {\mathrm {Spec}}(\mathcal {O}_L) \to T'$
of
$\mathop {\mathrm {Spec}}(\mathcal {O}_L) \to T'$
of
![]() $\mathop {\mathrm {Spec}}(\mathcal {O}_L) \to T$
by the valuative criterion. After replacing
$\mathop {\mathrm {Spec}}(\mathcal {O}_L) \to T$
by the valuative criterion. After replacing
![]() $T'$
by an affine open neighborhood of the image of the closed point of
$T'$
by an affine open neighborhood of the image of the closed point of
![]() $\mathop {\mathrm {Spec}}(\mathcal {O}_L)$
, we obtain a strictly semi-stable object of
$\mathop {\mathrm {Spec}}(\mathcal {O}_L)$
, we obtain a strictly semi-stable object of
![]() $\mathscr {D}$
over
$\mathscr {D}$
over
![]() $(U \to T)\to (\mathop {\mathrm {Spec}}(K) \to \mathop {\mathrm {Spec}}(\mathcal {O}_K))$
, which completes the proof.
$(U \to T)\to (\mathop {\mathrm {Spec}}(K) \to \mathop {\mathrm {Spec}}(\mathcal {O}_K))$
, which completes the proof.
Theorem 4.9 ([Reference Illusie, Laszlo and OrgogozoILO14, X 3.5, 3.7])
Let K be a complete discrete valuation field with valuation ring
![]() $\mathcal {O}_K$
, and let
$\mathcal {O}_K$
, and let
![]() $(Y\to X) \to (U \to T)$
be a morphism of dominant open immersions over
$(Y\to X) \to (U \to T)$
be a morphism of dominant open immersions over
![]() $\mathop {\mathrm {Spec}}(K) \to \mathop {\mathrm {Spec}}(\mathcal {O}_K)$
between irreducible
$\mathop {\mathrm {Spec}}(K) \to \mathop {\mathrm {Spec}}(\mathcal {O}_K)$
between irreducible
![]() $\mathcal {O}_K$
-schemes of finite type such that
$\mathcal {O}_K$
-schemes of finite type such that
![]() $X\to T$
is proper surjective. Then, there exists a commutative diagram of dominant open immersions between irreducible
$X\to T$
is proper surjective. Then, there exists a commutative diagram of dominant open immersions between irreducible
![]() $\mathcal {O}_K$
-schemes of finite type
$\mathcal {O}_K$
-schemes of finite type

satisfying the following conditions:
-
(i) We have
 $Y'=\beta ^{-1}(Y)\cap f^{{\prime }-1}(U')$
, i.e.,
$Y'=\beta ^{-1}(Y)\cap f^{{\prime }-1}(U')$
, i.e.,
 $Y'\to X'$
is Cartesian over
$Y'\to X'$
is Cartesian over
 $U'\times _{U}Y \to T'\times _{T} X$
(see [Reference HeHe23, 7.1]).
$U'\times _{U}Y \to T'\times _{T} X$
(see [Reference HeHe23, 7.1]). -
(ii) The morphism
 $(X',\mathscr {M}_{Y'\to X'})\to (T',\mathscr {M}_{U'\to T'})$
induced by
$(X',\mathscr {M}_{Y'\to X'})\to (T',\mathscr {M}_{U'\to T'})$
induced by
 $(f^{{\prime }\circ },f')$
is a smooth and saturated morphism of fine, saturated, and regular log schemes.
$(f^{{\prime }\circ },f')$
is a smooth and saturated morphism of fine, saturated, and regular log schemes. -
(iii) The morphisms
 $\alpha $
and
$\alpha $
and
 $\beta $
are proper surjective and generically finite, and
$\beta $
are proper surjective and generically finite, and
 $f'$
is projective surjective.
$f'$
is projective surjective.
Proof We may assume that T is nonempty. Recall that
![]() $\mathop {\mathrm {Spec}}(\mathcal {O}_K)$
is universally
$\mathop {\mathrm {Spec}}(\mathcal {O}_K)$
is universally
![]() $\mathbb {Q}$
-resolvable [Reference Illusie, Laszlo and OrgogozoILO14, X.3.3] by de Jong’s alteration theorem [Reference de JongdJ96, 6.5]. Thus, T is also universally
$\mathbb {Q}$
-resolvable [Reference Illusie, Laszlo and OrgogozoILO14, X.3.3] by de Jong’s alteration theorem [Reference de JongdJ96, 6.5]. Thus, T is also universally
![]() $\mathbb {Q}$
-resolvable by [Reference Illusie, Laszlo and OrgogozoILO14, X 3.5, 3.5.2] so that we can apply [Reference Illusie, Laszlo and OrgogozoILO14, X.3.5] to the proper surjective morphism f and the nowhere dense closed subset
$\mathbb {Q}$
-resolvable by [Reference Illusie, Laszlo and OrgogozoILO14, X 3.5, 3.5.2] so that we can apply [Reference Illusie, Laszlo and OrgogozoILO14, X.3.5] to the proper surjective morphism f and the nowhere dense closed subset
![]() $X\setminus Y$
. Then, we obtain a commutative diagram of schemes
$X\setminus Y$
. Then, we obtain a commutative diagram of schemes

and dense open subsets
![]() $U'{\kern-1pt}\subseteq{\kern-1pt} T'$
,
$U'{\kern-1pt}\subseteq{\kern-1pt} T'$
,
![]() $Y'{\kern-1pt}={\kern-1pt}\beta ^{-1}(Y){\kern-1pt}\cap{\kern-1pt} f^{{\prime }-1}(U'){\kern-1pt}\subseteq{\kern-1pt} X'$
such that
$Y'{\kern-1pt}={\kern-1pt}\beta ^{-1}(Y){\kern-1pt}\cap{\kern-1pt} f^{{\prime }-1}(U'){\kern-1pt}\subseteq{\kern-1pt} X'$
such that
![]() $(X',\mathscr {M}_{Y'\to X'})$
and
$(X',\mathscr {M}_{Y'\to X'})$
and
![]() $(T',\mathscr {M}_{U'\to T'})$
are fine, saturated, and regular, that
$(T',\mathscr {M}_{U'\to T'})$
are fine, saturated, and regular, that
![]() $(X',\mathscr {M}_{Y'\to X'})\to (T',\mathscr {M}_{U'\to T'})$
is smooth, that
$(X',\mathscr {M}_{Y'\to X'})\to (T',\mathscr {M}_{U'\to T'})$
is smooth, that
![]() $\alpha , \beta $
are proper surjective and generically finite morphisms which map generic points to generic points, and that
$\alpha , \beta $
are proper surjective and generically finite morphisms which map generic points to generic points, and that
![]() $f'$
is projective (since f is proper, cf. [Reference Illusie, Laszlo and OrgogozoILO14, X 3.1.6, 3.1.7]). Since X (resp. T) is irreducible and
$f'$
is projective (since f is proper, cf. [Reference Illusie, Laszlo and OrgogozoILO14, X 3.1.6, 3.1.7]). Since X (resp. T) is irreducible and
![]() $X'$
(resp.
$X'$
(resp.
![]() $T'$
) is a disjoint union of normal integral schemes (4.4), after firstly replacing
$T'$
) is a disjoint union of normal integral schemes (4.4), after firstly replacing
![]() $X'$
by an irreducible component and then replacing
$X'$
by an irreducible component and then replacing
![]() $T'$
by the irreducible component under
$T'$
by the irreducible component under
![]() $X'$
, we may assume that
$X'$
, we may assume that
![]() $X'$
and
$X'$
and
![]() $T'$
are irreducible. Then,
$T'$
are irreducible. Then,
![]() $Y'\to U'$
is dominant (so that
$Y'\to U'$
is dominant (so that
![]() $f'$
is projective surjective), since it is smooth and
$f'$
is projective surjective), since it is smooth and
![]() $Y'$
is nonempty [Reference GrothendieckEGA IV2
, 2.3.4]. We claim that
$Y'$
is nonempty [Reference GrothendieckEGA IV2
, 2.3.4]. We claim that
![]() $\alpha $
maps
$\alpha $
maps
![]() $U'$
into U. Indeed, if there exists a point
$U'$
into U. Indeed, if there exists a point
![]() $u\in U'$
with
$u\in U'$
with
![]() $\alpha (u)\notin U$
, then
$\alpha (u)\notin U$
, then
![]() $f^{{\prime }-1}(u)\cap Y'=\emptyset $
. However, endowing u with the trivial log structure, the log scheme
$f^{{\prime }-1}(u)\cap Y'=\emptyset $
. However, endowing u with the trivial log structure, the log scheme
![]() $(u,\mathcal {O}_{u_{\mathrm {\acute {e}t}}}^\times )$
is fine, saturated, and regular, and the fibered product in the category of fine and saturated log schemes
$(u,\mathcal {O}_{u_{\mathrm {\acute {e}t}}}^\times )$
is fine, saturated, and regular, and the fibered product in the category of fine and saturated log schemes
is regular with underlying scheme
![]() $f^{{\prime }-1}(u)$
(4.4, 4.2). Thus,
$f^{{\prime }-1}(u)$
(4.4, 4.2). Thus,
![]() $f^{{\prime }-1}(u)\cap Y'$
is dense in
$f^{{\prime }-1}(u)\cap Y'$
is dense in
![]() $f^{{\prime }-1}(u)$
, which contradicts the assumption that
$f^{{\prime }-1}(u)$
, which contradicts the assumption that
![]() $f^{{\prime }-1}(u)\cap Y'=\emptyset $
since
$f^{{\prime }-1}(u)\cap Y'=\emptyset $
since
![]() $f'$
is surjective. Thus, we obtain a diagram (4.9.1) satisfying all the conditions except the saturatedness of
$f'$
is surjective. Thus, we obtain a diagram (4.9.1) satisfying all the conditions except the saturatedness of
![]() $(X',\mathscr {M}_{Y'\to X'})\to (T',\mathscr {M}_{U'\to T'})$
.
$(X',\mathscr {M}_{Y'\to X'})\to (T',\mathscr {M}_{U'\to T'})$
.
To make
![]() $(X',\mathscr {M}_{Y'\to X'})\to (T',\mathscr {M}_{U'\to T'})$
saturated, we apply [Reference Illusie, Laszlo and OrgogozoILO14, X.3.7] to the morphism
$(X',\mathscr {M}_{Y'\to X'})\to (T',\mathscr {M}_{U'\to T'})$
saturated, we apply [Reference Illusie, Laszlo and OrgogozoILO14, X.3.7] to the morphism
![]() $(f^{{\prime }\circ }, f')$
. We obtain a Cartesian morphism
$(f^{{\prime }\circ }, f')$
. We obtain a Cartesian morphism
![]() $(\gamma ^{\circ }, \gamma ):(U" \to T")\to (U' \to T') $
of dominant open immersions such that
$(\gamma ^{\circ }, \gamma ):(U" \to T")\to (U' \to T') $
of dominant open immersions such that
![]() $(T",\mathscr {M}_{U" \to T"})$
is a fine, saturated, and regular log scheme, that
$(T",\mathscr {M}_{U" \to T"})$
is a fine, saturated, and regular log scheme, that
![]() $\gamma $
is a proper surjective and generically finite morphism which maps generic points of
$\gamma $
is a proper surjective and generically finite morphism which maps generic points of
![]() $T"$
to the generic point of
$T"$
to the generic point of
![]() $T'$
, and that the fibered product in the category of fine and saturated log schemes
$T'$
, and that the fibered product in the category of fine and saturated log schemes
is saturated over
![]() $(T",\mathscr {M}_{U" \to T"})$
. The fibered product (4.9.4) is still smooth over
$(T",\mathscr {M}_{U" \to T"})$
. The fibered product (4.9.4) is still smooth over
![]() $(T",\mathscr {M}_{U" \to T"})$
, and thus it is regular (4.4). Let
$(T",\mathscr {M}_{U" \to T"})$
, and thus it is regular (4.4). Let
![]() $X"$
be the underlying scheme of it, and let
$X"$
be the underlying scheme of it, and let
![]() $Y"=(X")^{\mathrm {tr}}$
. Then, the fibered product (4.9.4) is isomorphic to
$Y"=(X")^{\mathrm {tr}}$
. Then, the fibered product (4.9.4) is isomorphic to
![]() $(X",\mathscr {M}_{Y"\to X"})$
(4.4). Thus, we obtain a commutative diagram of dominant open immersions of schemes:
$(X",\mathscr {M}_{Y"\to X"})$
(4.4). Thus, we obtain a commutative diagram of dominant open immersions of schemes:

Notice that
![]() $Y"= U" \times _{U'} Y'$
and
$Y"= U" \times _{U'} Y'$
and
![]() $X" \to T" \times _{T'} X'$
is finite, and that
$X" \to T" \times _{T'} X'$
is finite, and that
![]() $Y"\to X"$
is Cartesian over
$Y"\to X"$
is Cartesian over
![]() $U" \times _{U'} Y' \to T" \times _{T'} X'$
(4.2). Thus, we see that
$U" \times _{U'} Y' \to T" \times _{T'} X'$
(4.2). Thus, we see that
![]() $Y"\to X"$
is Cartesian over
$Y"\to X"$
is Cartesian over
![]() $U" \times _{U} Y \to T" \times _{T} X$
and that
$U" \times _{U} Y \to T" \times _{T} X$
and that
![]() $f"$
is projective. Since
$f"$
is projective. Since
![]() $T'$
(resp.
$T'$
(resp.
![]() $X'$
) is irreducible and
$X'$
) is irreducible and
![]() $T"$
(resp.
$T"$
(resp.
![]() $X"$
) is a disjoint union of normal integral schemes (4.4), after firstly replacing
$X"$
) is a disjoint union of normal integral schemes (4.4), after firstly replacing
![]() $T"$
by an irreducible component and then replacing
$T"$
by an irreducible component and then replacing
![]() $X"$
by an irreducible component on which the restriction of
$X"$
by an irreducible component on which the restriction of
![]() $\delta ^{\circ }$
is dominant, we may assume that
$\delta ^{\circ }$
is dominant, we may assume that
![]() $T"$
and
$T"$
and
![]() $X"$
are irreducible. In particular,
$X"$
are irreducible. In particular,
![]() $\delta $
is generically finite and so is
$\delta $
is generically finite and so is
![]() $\beta \circ \delta $
(4.6), and again
$\beta \circ \delta $
(4.6), and again
![]() $Y"\to U"$
is dominant so that
$Y"\to U"$
is dominant so that
![]() $f"$
is projective surjective.
$f"$
is projective surjective.
Lemma 4.10 Let X be a scheme of finite type over a valuation ring A of height
![]() $1$
. Then, the underlying topological space of X is Noetherian.
$1$
. Then, the underlying topological space of X is Noetherian.
Proof Let
![]() $\eta $
and s be the generic point and closed point of
$\eta $
and s be the generic point and closed point of
![]() $\mathop {\mathrm {Spec}}(A),$
respectively. Then, the generic fiber
$\mathop {\mathrm {Spec}}(A),$
respectively. Then, the generic fiber
![]() $X_\eta $
and the special fiber
$X_\eta $
and the special fiber
![]() $X_s$
are both Noetherian. As a union of
$X_s$
are both Noetherian. As a union of
![]() $X_\eta $
and
$X_\eta $
and
![]() $X_s$
, the underlying topological space of X is also Noetherian [Sta23, 0053].
$X_s$
, the underlying topological space of X is also Noetherian [Sta23, 0053].
Proposition 4.11 With the notation in 4.7 and 4.8, let
![]() $Y\to X$
be a quasi-compact dominant open immersion over
$Y\to X$
be a quasi-compact dominant open immersion over
![]() $\mathop {\mathrm {Spec}}(L) \to \mathop {\mathrm {Spec}}(\mathcal {O}_L)$
such that
$\mathop {\mathrm {Spec}}(L) \to \mathop {\mathrm {Spec}}(\mathcal {O}_L)$
such that
![]() $X \to \mathop {\mathrm {Spec}}(\mathcal {O}_L)$
is proper of finite presentation. Then, there exists a proper surjective
$X \to \mathop {\mathrm {Spec}}(\mathcal {O}_L)$
is proper of finite presentation. Then, there exists a proper surjective
![]() $\mathcal {O}_L$
-morphism of finite presentation
$\mathcal {O}_L$
-morphism of finite presentation
![]() $X' \to X$
, an index
$X' \to X$
, an index
![]() $\lambda _1\in \Lambda $
, and a directed inverse system of open immersions
$\lambda _1\in \Lambda $
, and a directed inverse system of open immersions
![]() $(Y^{\prime }_\lambda \to X^{\prime }_\lambda )_{\lambda \geq \lambda _1}$
over
$(Y^{\prime }_\lambda \to X^{\prime }_\lambda )_{\lambda \geq \lambda _1}$
over
![]() $(U_\lambda \to T_\lambda )_{\lambda \geq \lambda _1}$
satisfying the following conditions for each
$(U_\lambda \to T_\lambda )_{\lambda \geq \lambda _1}$
satisfying the following conditions for each
![]() $\lambda \geq \lambda _1$
:
$\lambda \geq \lambda _1$
:
-
(i) We have
 $Y'=Y\times _X X'=\lim _{\lambda \geq \lambda _1} Y^{\prime }_\lambda $
and
$Y'=Y\times _X X'=\lim _{\lambda \geq \lambda _1} Y^{\prime }_\lambda $
and
 $X'=\lim _{\lambda \geq \lambda _1} X^{\prime }_\lambda $
.
$X'=\lim _{\lambda \geq \lambda _1} X^{\prime }_\lambda $
. -
(ii) The log scheme
 $(X^{\prime }_\lambda ,\mathscr {M}_{Y^{\prime }_\lambda \to X^{\prime }_\lambda })$
is fine, saturated, and regular.
$(X^{\prime }_\lambda ,\mathscr {M}_{Y^{\prime }_\lambda \to X^{\prime }_\lambda })$
is fine, saturated, and regular. -
(iii) The morphism
 $(X^{\prime }_\lambda ,\mathscr {M}_{Y^{\prime }_\lambda \to X^{\prime }_\lambda })\to (T_\lambda ,\mathscr {M}_{U_\lambda \to T_\lambda })$
is smooth and saturated, and
$(X^{\prime }_\lambda ,\mathscr {M}_{Y^{\prime }_\lambda \to X^{\prime }_\lambda })\to (T_\lambda ,\mathscr {M}_{U_\lambda \to T_\lambda })$
is smooth and saturated, and
 $X^{\prime }_\lambda \to T_\lambda $
is projective.
$X^{\prime }_\lambda \to T_\lambda $
is projective. -
(iv) If, moreover,
 $Y= \mathop {\mathrm {Spec}}(L) \times _{\mathop {\mathrm {Spec}}(\mathcal {O}_L)} X$
, then we can require that
$Y= \mathop {\mathrm {Spec}}(L) \times _{\mathop {\mathrm {Spec}}(\mathcal {O}_L)} X$
, then we can require that
 $Y^{\prime }_\lambda = U_\lambda \times _{T_\lambda }X^{\prime }_\lambda $
.
$Y^{\prime }_\lambda = U_\lambda \times _{T_\lambda }X^{\prime }_\lambda $
.
Proof We follow closely the proof of [Reference Adiprasito, Liu, Pak and TemkinALPT19, 5.2.19]. Since the underlying topological space of X is Noetherian by 4.10, each irreducible component Z of X admits a closed subscheme structure such that
![]() $Z\to X$
is of finite presentation [Sta23, 01PH]. After replacing X by the disjoint union of its irreducible components, we may assume that X is irreducible. Then, the generic fiber of
$Z\to X$
is of finite presentation [Sta23, 01PH]. After replacing X by the disjoint union of its irreducible components, we may assume that X is irreducible. Then, the generic fiber of
![]() $X\to \mathop {\mathrm {Spec}}(\mathcal {O}_L)$
is also irreducible as an open subset of X. Using [Reference GrothendieckEGA IV3
, 8.8.2, 8.10.5], there exists an index
$X\to \mathop {\mathrm {Spec}}(\mathcal {O}_L)$
is also irreducible as an open subset of X. Using [Reference GrothendieckEGA IV3
, 8.8.2, 8.10.5], there exists an index
![]() $\lambda _0 \in \Lambda $
, a proper
$\lambda _0 \in \Lambda $
, a proper
![]() $T_{\lambda _0}$
-scheme
$T_{\lambda _0}$
-scheme
![]() $X_{\lambda _0}$
, and an open subscheme
$X_{\lambda _0}$
, and an open subscheme
![]() $Y_{\lambda _0}$
of
$Y_{\lambda _0}$
of
![]() $U_{\lambda _0}\times _{T_{\lambda _0}} X_{\lambda _0}$
, such that
$U_{\lambda _0}\times _{T_{\lambda _0}} X_{\lambda _0}$
, such that
![]() $X=\mathop {\mathrm {Spec}}(\mathcal {O}_L) \times _{T_{\lambda _0}} X_{\lambda _0}$
and that
$X=\mathop {\mathrm {Spec}}(\mathcal {O}_L) \times _{T_{\lambda _0}} X_{\lambda _0}$
and that
![]() $Y=\mathop {\mathrm {Spec}}(L) \times _{U_{\lambda _0}} Y_{\lambda _0}$
. Let
$Y=\mathop {\mathrm {Spec}}(L) \times _{U_{\lambda _0}} Y_{\lambda _0}$
. Let
![]() $\eta $
denote the generic point of X,
$\eta $
denote the generic point of X,
![]() $\eta _{\lambda _0}$
the image of
$\eta _{\lambda _0}$
the image of
![]() $\eta $
under the morphism
$\eta $
under the morphism
![]() $X\to X_{\lambda _0}$
,
$X\to X_{\lambda _0}$
,
![]() $Z_{\lambda _0}$
the scheme theoretic closure of
$Z_{\lambda _0}$
the scheme theoretic closure of
![]() $\eta _{\lambda _0}$
in
$\eta _{\lambda _0}$
in
![]() $X_{\lambda _0}$
. Notice that
$X_{\lambda _0}$
. Notice that
![]() $\mathop {\mathrm {Spec}}(\mathcal {O}_L)\times _{T_{\lambda _0}} Z_{\lambda _0}\to X$
is a surjective finitely presented closed immersion. After replacing X by
$\mathop {\mathrm {Spec}}(\mathcal {O}_L)\times _{T_{\lambda _0}} Z_{\lambda _0}\to X$
is a surjective finitely presented closed immersion. After replacing X by
![]() $\mathop {\mathrm {Spec}}(\mathcal {O}_L)\times _{T_{\lambda _0}} Z_{\lambda _0}$
and replacing
$\mathop {\mathrm {Spec}}(\mathcal {O}_L)\times _{T_{\lambda _0}} Z_{\lambda _0}$
and replacing
![]() $X_{\lambda _0}$
by
$X_{\lambda _0}$
by
![]() $Z_{\lambda _0}$
, we may assume that
$Z_{\lambda _0}$
, we may assume that
![]() $X\to X_{\lambda _0}$
is a dominant morphism of irreducible schemes. Since
$X\to X_{\lambda _0}$
is a dominant morphism of irreducible schemes. Since
![]() $T_{\lambda _0}$
is irreducible and L is algebraically closed, the generic fiber of
$T_{\lambda _0}$
is irreducible and L is algebraically closed, the generic fiber of
![]() $f:X_{\lambda _0}\to T_{\lambda _0}$
is geometrically irreducible. In particular, if
$f:X_{\lambda _0}\to T_{\lambda _0}$
is geometrically irreducible. In particular, if
![]() $\xi _{\lambda _0}$
(resp.
$\xi _{\lambda _0}$
(resp.
![]() $\eta _{\lambda _0}$
) denotes the generic point of
$\eta _{\lambda _0}$
) denotes the generic point of
![]() $T_{\lambda _0}$
(resp.
$T_{\lambda _0}$
(resp.
![]() $X_{\lambda _0}$
), then
$X_{\lambda _0}$
), then
![]() $\eta =\mathop {\mathrm {Spec}}(L)\times _{\xi _{\lambda _0}}\eta _{\lambda _0}$
[Reference GrothendieckEGA IV2
, 4.5.9]. In the situation of (iv), we can moreover assume that
$\eta =\mathop {\mathrm {Spec}}(L)\times _{\xi _{\lambda _0}}\eta _{\lambda _0}$
[Reference GrothendieckEGA IV2
, 4.5.9]. In the situation of (iv), we can moreover assume that
![]() $Y_{\lambda _0}= U_{\lambda _0} \times _{T_{\lambda _0}} X_{\lambda _0}$
.
$Y_{\lambda _0}= U_{\lambda _0} \times _{T_{\lambda _0}} X_{\lambda _0}$
.
By 4.9, there exists a commutative diagram of dominant open immersions of irreducible schemes,

where
![]() $Y^{\prime }_{\lambda _0}\to X^{\prime }_{\lambda _0}$
is Cartesian over
$Y^{\prime }_{\lambda _0}\to X^{\prime }_{\lambda _0}$
is Cartesian over
![]() $U^{\prime }_{\lambda _0}\times _{U_{\lambda _0}}Y_{\lambda _0} \to T^{\prime }_{\lambda _0}\times _{T_{\lambda _0}} X_{\lambda _0}$
, and where
$U^{\prime }_{\lambda _0}\times _{U_{\lambda _0}}Y_{\lambda _0} \to T^{\prime }_{\lambda _0}\times _{T_{\lambda _0}} X_{\lambda _0}$
, and where
![]() $(X^{\prime }_{\lambda _0},\mathscr {M}_{Y^{\prime }_{\lambda _0}\to X^{\prime }_{\lambda _0}})\to (T^{\prime }_{\lambda _0},\mathscr {M}_{U^{\prime }_{\lambda _0}\to T^{\prime }_{\lambda _0}})$
is a smooth and saturated morphism of fine, saturated, and regular log schemes, and where
$(X^{\prime }_{\lambda _0},\mathscr {M}_{Y^{\prime }_{\lambda _0}\to X^{\prime }_{\lambda _0}})\to (T^{\prime }_{\lambda _0},\mathscr {M}_{U^{\prime }_{\lambda _0}\to T^{\prime }_{\lambda _0}})$
is a smooth and saturated morphism of fine, saturated, and regular log schemes, and where
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are proper surjective and generically finite, and where
$\beta $
are proper surjective and generically finite, and where
![]() $f'$
is projective surjective. We take a dominant morphism
$f'$
is projective surjective. We take a dominant morphism
![]() $\gamma ^{\circ }:\mathop {\mathrm {Spec}}(L)\to U_{\lambda _0}'$
which lifts
$\gamma ^{\circ }:\mathop {\mathrm {Spec}}(L)\to U_{\lambda _0}'$
which lifts
![]() $\mathop {\mathrm {Spec}}(L)\to U_{\lambda _0}$
since L is algebraically closed and
$\mathop {\mathrm {Spec}}(L)\to U_{\lambda _0}$
since L is algebraically closed and
![]() $\alpha $
is generically finite, the morphism
$\alpha $
is generically finite, the morphism
![]() $\mathop {\mathrm {Spec}}(\mathcal {O}_L) \to T_{\lambda _0}$
lifts to
$\mathop {\mathrm {Spec}}(\mathcal {O}_L) \to T_{\lambda _0}$
lifts to
![]() $\gamma :\mathop {\mathrm {Spec}}(\mathcal {O}_L) \to T^{\prime }_{\lambda _0}$
by the valuative criterion. We set
$\gamma :\mathop {\mathrm {Spec}}(\mathcal {O}_L) \to T^{\prime }_{\lambda _0}$
by the valuative criterion. We set
![]() $Y'=\mathop {\mathrm {Spec}}(L)\times _{U^{\prime }_{\lambda _0}}Y^{\prime }_{\lambda _0}$
and
$Y'=\mathop {\mathrm {Spec}}(L)\times _{U^{\prime }_{\lambda _0}}Y^{\prime }_{\lambda _0}$
and
![]() $X'=\mathop {\mathrm {Spec}}(\mathcal {O}_L)\times _{T^{\prime }_{\lambda _0}} X^{\prime }_{\lambda _0}$
. It is clear that
$X'=\mathop {\mathrm {Spec}}(\mathcal {O}_L)\times _{T^{\prime }_{\lambda _0}} X^{\prime }_{\lambda _0}$
. It is clear that
![]() $Y'\to X'$
is Cartesian over
$Y'\to X'$
is Cartesian over
![]() $Y \to X$
by base change. Let
$Y \to X$
by base change. Let
![]() $\xi ^{\prime }_{\lambda _0}$
(resp.
$\xi ^{\prime }_{\lambda _0}$
(resp.
![]() $\eta ^{\prime }_{\lambda _0}$
) be the generic point of
$\eta ^{\prime }_{\lambda _0}$
) be the generic point of
![]() $T^{\prime }_{\lambda _0}$
(resp.
$T^{\prime }_{\lambda _0}$
(resp.
![]() $X^{\prime }_{\lambda _0}$
). Since the generic fiber of f is geometrically irreducible,
$X^{\prime }_{\lambda _0}$
). Since the generic fiber of f is geometrically irreducible,
![]() $\xi ^{\prime }_{\lambda _0}\times _{\xi _{\lambda _0}}\eta _{\lambda _0}$
is a single point and
$\xi ^{\prime }_{\lambda _0}\times _{\xi _{\lambda _0}}\eta _{\lambda _0}$
is a single point and
![]() $\eta ^{\prime }_{\lambda _0}$
maps to it [Reference GrothendieckEGA IV2
, 4.5.9]. Since
$\eta ^{\prime }_{\lambda _0}$
maps to it [Reference GrothendieckEGA IV2
, 4.5.9]. Since
![]() $\mathop {\mathrm {Spec}}(L)\times _{\xi _{\lambda _0}}\eta _{\lambda _0}$
is the generic point of X, we see that
$\mathop {\mathrm {Spec}}(L)\times _{\xi _{\lambda _0}}\eta _{\lambda _0}$
is the generic point of X, we see that
![]() $X' \to X$
is proper surjective and of finite presentation. It remains to construct
$X' \to X$
is proper surjective and of finite presentation. It remains to construct
![]() $(Y^{\prime }_\lambda \to X^{\prime }_\lambda )_{\lambda \geq \lambda _1}$
.
$(Y^{\prime }_\lambda \to X^{\prime }_\lambda )_{\lambda \geq \lambda _1}$
.
After replacing
![]() $T^{\prime }_{\lambda _0}$
by an affine open neighborhood of the image of the closed point of
$T^{\prime }_{\lambda _0}$
by an affine open neighborhood of the image of the closed point of
![]() $\mathop {\mathrm {Spec}}(\mathcal {O}_L)$
, Lemma 4.8 implies that there exists an index
$\mathop {\mathrm {Spec}}(\mathcal {O}_L)$
, Lemma 4.8 implies that there exists an index
![]() $\lambda _1 \geq \lambda _0$
such that the transition morphism
$\lambda _1 \geq \lambda _0$
such that the transition morphism
![]() $(U_{\lambda _1}\to T_{\lambda _1}) \to (U_{\lambda _0}\to T_{\lambda _0})$
factors through
$(U_{\lambda _1}\to T_{\lambda _1}) \to (U_{\lambda _0}\to T_{\lambda _0})$
factors through
![]() $(U^{\prime }_{\lambda _0}\to T^{\prime }_{\lambda _0})$
. For each index
$(U^{\prime }_{\lambda _0}\to T^{\prime }_{\lambda _0})$
. For each index
![]() $\lambda \geq \lambda _1$
, consider the fibered product in the category of fine and saturated log schemes
$\lambda \geq \lambda _1$
, consider the fibered product in the category of fine and saturated log schemes
which is a fine, saturated, and regular log scheme smooth and saturated over
![]() $(T_{\lambda },\mathscr {M}_{U_{\lambda }\to T_{\lambda }})$
(4.2, 4.4). Moreover, we have
$(T_{\lambda },\mathscr {M}_{U_{\lambda }\to T_{\lambda }})$
(4.2, 4.4). Moreover, we have
![]() $Y^{\prime }_\lambda = U_\lambda \times _{U^{\prime }_{\lambda _0}} Y^{\prime }_{\lambda _0}$
,
$Y^{\prime }_\lambda = U_\lambda \times _{U^{\prime }_{\lambda _0}} Y^{\prime }_{\lambda _0}$
,
![]() $X^{\prime }_\lambda = T_\lambda \times _{T^{\prime }_{\lambda _0}} X^{\prime }_{\lambda _0}$
, and in the situation of (iv),
$X^{\prime }_\lambda = T_\lambda \times _{T^{\prime }_{\lambda _0}} X^{\prime }_{\lambda _0}$
, and in the situation of (iv),
![]() $Y^{\prime }_\lambda =U_\lambda \times _{T_\lambda }X^{\prime }_\lambda $
by base change. Therefore,
$Y^{\prime }_\lambda =U_\lambda \times _{T_\lambda }X^{\prime }_\lambda $
by base change. Therefore,
![]() $(Y^{\prime }_\lambda \to X^{\prime }_\lambda )_{\lambda \geq \lambda _1}$
meets our requirements.
$(Y^{\prime }_\lambda \to X^{\prime }_\lambda )_{\lambda \geq \lambda _1}$
meets our requirements.
5 Faltings’ main p-adic comparison theorem: the absolute case
Lemma 5.1 Let Y be a coherent scheme, and let V be a finite étale Y-scheme. Then, there exists a finite étale surjective morphism
![]() $Y'\to Y$
such that
$Y'\to Y$
such that
![]() $Y'\times _Y V$
is isomorphic to a finite disjoint union of
$Y'\times _Y V$
is isomorphic to a finite disjoint union of
![]() $Y'$
.
$Y'$
.
Proof If Y is connected, let
![]() $\overline {y}$
be a geometric point of Y,
$\overline {y}$
be a geometric point of Y,
![]() $\pi _1(Y,\overline {y})$
the fundamental group of Y with base point
$\pi _1(Y,\overline {y})$
the fundamental group of Y with base point
![]() $\overline {y}$
. Then,
$\overline {y}$
. Then,
![]() $Y_{\mathrm {f\acute {e}t}}$
is equivalent to the category of finite
$Y_{\mathrm {f\acute {e}t}}$
is equivalent to the category of finite
![]() $\pi _1(Y,\overline {y})$
-sets so that the lemma holds [Sta23, 0BND].
$\pi _1(Y,\overline {y})$
-sets so that the lemma holds [Sta23, 0BND].
In general, for any connected component Z of Y, let
![]() $(Y_\lambda )_{\lambda \in \Lambda _Z}$
be the directed inverse system of all open and closed subschemes of Y which contain Z and whose transition morphisms are inclusions. Notice that
$(Y_\lambda )_{\lambda \in \Lambda _Z}$
be the directed inverse system of all open and closed subschemes of Y which contain Z and whose transition morphisms are inclusions. Notice that
![]() $\lim _{\lambda \in \Lambda _Z} Y_\lambda $
is a closed subscheme of Y with underlying topological space Z by [Sta23, 04PL] and [Reference GrothendieckEGA IV3
, 8.2.9]. We endow Z with the closed subscheme structure of
$\lim _{\lambda \in \Lambda _Z} Y_\lambda $
is a closed subscheme of Y with underlying topological space Z by [Sta23, 04PL] and [Reference GrothendieckEGA IV3
, 8.2.9]. We endow Z with the closed subscheme structure of
![]() $\lim _{\lambda \in \Lambda _Z} Y_\lambda $
. The first paragraph shows that there exists a finite étale surjective morphism
$\lim _{\lambda \in \Lambda _Z} Y_\lambda $
. The first paragraph shows that there exists a finite étale surjective morphism
![]() $Z'\to Z$
such that
$Z'\to Z$
such that
![]() $Z'\times _Y V=\coprod _{i=1}^r Z'$
. Using [Reference GrothendieckEGA IV3
, 8.8.2, 8.10.5] and [Reference GrothendieckEGA IV4
, 17.7.8], there exists an index
$Z'\times _Y V=\coprod _{i=1}^r Z'$
. Using [Reference GrothendieckEGA IV3
, 8.8.2, 8.10.5] and [Reference GrothendieckEGA IV4
, 17.7.8], there exists an index
![]() $\lambda _0\in \Lambda _Z$
, a finite étale surjective morphism
$\lambda _0\in \Lambda _Z$
, a finite étale surjective morphism
![]() $Y^{\prime }_{\lambda _0}\to Y_{\lambda _0}$
and an isomorphism
$Y^{\prime }_{\lambda _0}\to Y_{\lambda _0}$
and an isomorphism
![]() $Y^{\prime }_{\lambda _0}\times _Y V = \coprod _{i=1}^r Y^{\prime }_{\lambda _0}$
. Notice that
$Y^{\prime }_{\lambda _0}\times _Y V = \coprod _{i=1}^r Y^{\prime }_{\lambda _0}$
. Notice that
![]() $Y^{\prime }_{\lambda _0}$
is also finite étale over Y. Since Z is an arbitrary connected component of Y, the conclusion follows from the quasi-compactness of Y.
$Y^{\prime }_{\lambda _0}$
is also finite étale over Y. Since Z is an arbitrary connected component of Y, the conclusion follows from the quasi-compactness of Y.
Lemma 5.2 Let Y be a coherent scheme, and let
![]() $\rho :Y_{\mathrm {\acute {e}t}} \to Y_{\mathrm {f\acute {e}t}}$
be the morphism of sites defined by the inclusion functor. Then, the functor
$\rho :Y_{\mathrm {\acute {e}t}} \to Y_{\mathrm {f\acute {e}t}}$
be the morphism of sites defined by the inclusion functor. Then, the functor
![]() of the associated topoi induces an equivalence
of the associated topoi induces an equivalence
![]() $\rho ^{-1}:\mathbf {LocSys}(Y_{\mathrm {f\acute {e}t}}) \to \mathbf {LocSys}(Y_{\mathrm {\acute {e}t}})$
between the categories of finite locally constant abelian sheaves with quasi-inverse
$\rho ^{-1}:\mathbf {LocSys}(Y_{\mathrm {f\acute {e}t}}) \to \mathbf {LocSys}(Y_{\mathrm {\acute {e}t}})$
between the categories of finite locally constant abelian sheaves with quasi-inverse
![]() $\rho _*$
.
$\rho _*$
.
Proof Since any finite locally constant sheaf on
![]() $Y_{\mathrm {\acute {e}t}}$
(resp.
$Y_{\mathrm {\acute {e}t}}$
(resp.
![]() $Y_{\mathrm {f\acute {e}t}}$
) is representable by a finite étale Y-scheme by faithfully flat descent (cf. [Sta23, 03RV]), the Yoneda embeddings induce a commutative diagram:
$Y_{\mathrm {f\acute {e}t}}$
) is representable by a finite étale Y-scheme by faithfully flat descent (cf. [Sta23, 03RV]), the Yoneda embeddings induce a commutative diagram:

where the horizontal arrows are fully faithful. In particular,
![]() $\rho ^{-1}$
is fully faithful. For a finite locally constant abelian sheaf
$\rho ^{-1}$
is fully faithful. For a finite locally constant abelian sheaf
![]() $\mathbb {F}$
on
$\mathbb {F}$
on
![]() $Y_{\mathrm {\acute {e}t}}$
, let V be a finite étale Y-scheme representing
$Y_{\mathrm {\acute {e}t}}$
, let V be a finite étale Y-scheme representing
![]() $\mathbb {F}$
, and let
$\mathbb {F}$
, and let
![]() $h_V^{\mathrm {\acute {e}t}}$
(resp.
$h_V^{\mathrm {\acute {e}t}}$
(resp.
![]() $h_V^{\mathrm {f\acute {e}t}}$
) be the representable sheaf associated with V on
$h_V^{\mathrm {f\acute {e}t}}$
) be the representable sheaf associated with V on
![]() $Y_{\mathrm {\acute {e}t}}$
(resp.
$Y_{\mathrm {\acute {e}t}}$
(resp.
![]() $Y_{\mathrm {f\acute {e}t}}$
) (see 2.4). We have
$Y_{\mathrm {f\acute {e}t}}$
) (see 2.4). We have
![]() $\mathbb {F}=h_V^{\mathrm {\acute {e}t}}=\rho ^{-1}h_V^{\mathrm {f\acute {e}t}}$
[Sta23, 04D3]. By 5.1,
$\mathbb {F}=h_V^{\mathrm {\acute {e}t}}=\rho ^{-1}h_V^{\mathrm {f\acute {e}t}}$
[Sta23, 04D3]. By 5.1,
![]() $h_V^{\mathrm {f\acute {e}t}}$
is finite locally constant. It is clear that the adjunction morphism
$h_V^{\mathrm {f\acute {e}t}}$
is finite locally constant. It is clear that the adjunction morphism
![]() $h_V^{\mathrm {f\acute {e}t}}\to \rho _*h_V^{\mathrm {\acute {e}t}}$
is an isomorphism, which shows that
$h_V^{\mathrm {f\acute {e}t}}\to \rho _*h_V^{\mathrm {\acute {e}t}}$
is an isomorphism, which shows that
![]() $h_V^{\mathrm {f\acute {e}t}}$
is an abelian sheaf. Thus,
$h_V^{\mathrm {f\acute {e}t}}$
is an abelian sheaf. Thus,
![]() $\rho ^{-1}$
is essentially surjective. Moreover, the argument also shows that
$\rho ^{-1}$
is essentially surjective. Moreover, the argument also shows that
![]() $\rho _*$
induces a functor
$\rho _*$
induces a functor
![]() $\rho _*:\mathbf {LocSys}(Y_{\mathrm {\acute {e}t}}) \to \mathbf {LocSys}(Y_{\mathrm {f\acute {e}t}})$
which is a quasi-inverse of
$\rho _*:\mathbf {LocSys}(Y_{\mathrm {\acute {e}t}}) \to \mathbf {LocSys}(Y_{\mathrm {f\acute {e}t}})$
which is a quasi-inverse of
![]() $\rho ^{-1}$
.
$\rho ^{-1}$
.
Proposition 5.3 Let
![]() $Y \to X$
be a morphism of coherent schemes. With the notation in 3.2, the functors between the categories of finite locally constant abelian sheaves
$Y \to X$
be a morphism of coherent schemes. With the notation in 3.2, the functors between the categories of finite locally constant abelian sheaves
are equivalences with quasi-inverses
![]() $\beta _*$
and
$\beta _*$
and
![]() $\psi _*$
, respectively.
$\psi _*$
, respectively.
Proof Notice that for any finite locally constant abelian sheaf
![]() $\mathbb {G}$
on
$\mathbb {G}$
on
![]() $Y_{\mathrm {f\acute {e}t}}$
, the canonical morphism
$Y_{\mathrm {f\acute {e}t}}$
, the canonical morphism
![]() $\beta ^{-1}\mathbb {G}\to \psi _*\rho ^{-1}\mathbb {G}$
, which is induced by the adjunction
$\beta ^{-1}\mathbb {G}\to \psi _*\rho ^{-1}\mathbb {G}$
, which is induced by the adjunction
![]() $\mathrm {id} \to \psi _*\psi ^{-1}$
and by the identity
$\mathrm {id} \to \psi _*\psi ^{-1}$
and by the identity
![]() $\psi ^{-1}\beta ^{-1}=\rho ^{-1}$
, is an isomorphism by 5.2 and the proof of [Reference AchingerAGT16, VI.6.3(iii)]. For a finite locally constant abelian sheaf
$\psi ^{-1}\beta ^{-1}=\rho ^{-1}$
, is an isomorphism by 5.2 and the proof of [Reference AchingerAGT16, VI.6.3(iii)]. For a finite locally constant abelian sheaf
![]() $\mathbb {F}$
over
$\mathbb {F}$
over
![]() $Y_{\mathrm {\acute {e}t}}$
, we write
$Y_{\mathrm {\acute {e}t}}$
, we write
![]() $\mathbb {F}=\rho ^{-1}\mathbb {G}$
by 5.2. Then,
$\mathbb {F}=\rho ^{-1}\mathbb {G}$
by 5.2. Then,
![]() $\mathbb {F}=\psi ^{-1}\beta ^{-1}\mathbb {G}\stackrel {\sim }{\longrightarrow }\psi ^{-1}\psi _*\rho ^{-1}\mathbb {G}=\psi ^{-1}\psi _*\mathbb {F}$
, whose inverse is the adjunction map
$\mathbb {F}=\psi ^{-1}\beta ^{-1}\mathbb {G}\stackrel {\sim }{\longrightarrow }\psi ^{-1}\psi _*\rho ^{-1}\mathbb {G}=\psi ^{-1}\psi _*\mathbb {F}$
, whose inverse is the adjunction map
![]() $\psi ^{-1}\psi _*\mathbb {F} \to \mathbb {F}$
since the composition of
$\psi ^{-1}\psi _*\mathbb {F} \to \mathbb {F}$
since the composition of
![]() $\psi ^{-1}(\beta ^{-1}\mathbb {G}) \to \psi ^{-1}(\psi _*\psi ^{-1})(\beta ^{-1}\mathbb {G})=(\psi ^{-1}\psi _*)\psi ^{-1}(\beta ^{-1}\mathbb {G})\to \psi ^{-1}(\beta ^{-1}\mathbb {G})$
is the identity. On the other hand, for a finite locally constant abelian sheaf
$\psi ^{-1}(\beta ^{-1}\mathbb {G}) \to \psi ^{-1}(\psi _*\psi ^{-1})(\beta ^{-1}\mathbb {G})=(\psi ^{-1}\psi _*)\psi ^{-1}(\beta ^{-1}\mathbb {G})\to \psi ^{-1}(\beta ^{-1}\mathbb {G})$
is the identity. On the other hand, for a finite locally constant abelian sheaf
![]() $\mathbb {L}$
over
$\mathbb {L}$
over
![]() $\mathbf {E}_{Y \to X}^{\mathrm {\acute {e}t}}$
, we claim that
$\mathbf {E}_{Y \to X}^{\mathrm {\acute {e}t}}$
, we claim that
![]() $\mathbb {L} \to \psi _*\psi ^{-1}\mathbb {L}$
is an isomorphism. The problem is local on
$\mathbb {L} \to \psi _*\psi ^{-1}\mathbb {L}$
is an isomorphism. The problem is local on
![]() $\mathbf {E}_{Y \to X}^{\mathrm {\acute {e}t}}$
. Thus, we may assume that
$\mathbf {E}_{Y \to X}^{\mathrm {\acute {e}t}}$
. Thus, we may assume that
![]() $\mathbb {L}$
is the constant sheaf with value L, where L is a finite abelian group. Let
$\mathbb {L}$
is the constant sheaf with value L, where L is a finite abelian group. Let
![]() $\underline {L}$
be the constant sheaf with value L on
$\underline {L}$
be the constant sheaf with value L on
![]() $Y_{\mathrm {f\acute {e}t}}$
. Then,
$Y_{\mathrm {f\acute {e}t}}$
. Then,
![]() $\mathbb {L}=\beta ^{-1}\underline {L}$
, and the isomorphism
$\mathbb {L}=\beta ^{-1}\underline {L}$
, and the isomorphism
![]() $\mathbb {L}=\beta ^{-1}\underline {L}\stackrel {\sim }{\longrightarrow } \psi _*\rho ^{-1}\underline {L}=\psi _*\psi ^{-1}\mathbb {L}$
coincides with the adjunction map
$\mathbb {L}=\beta ^{-1}\underline {L}\stackrel {\sim }{\longrightarrow } \psi _*\rho ^{-1}\underline {L}=\psi _*\psi ^{-1}\mathbb {L}$
coincides with the adjunction map
![]() $\mathbb {L} \to \psi _*\psi ^{-1}\mathbb {L}$
. Therefore,
$\mathbb {L} \to \psi _*\psi ^{-1}\mathbb {L}$
. Therefore,
![]() $\psi ^{-1}:\mathbf {LocSys}(\mathbf {E}_{Y \to X}^{\mathrm {\acute {e}t}}) \to \mathbf {LocSys}(Y_{\mathrm {\acute {e}t}}) $
is an equivalence with quasi-inverse
$\psi ^{-1}:\mathbf {LocSys}(\mathbf {E}_{Y \to X}^{\mathrm {\acute {e}t}}) \to \mathbf {LocSys}(Y_{\mathrm {\acute {e}t}}) $
is an equivalence with quasi-inverse
![]() $\psi _*$
. The conclusion follows from 5.2.
$\psi _*$
. The conclusion follows from 5.2.
5.4 Let
![]() $f:(Y' \to X')\to (Y \to X)$
be a morphism of morphisms between coherent schemes over
$f:(Y' \to X')\to (Y \to X)$
be a morphism of morphisms between coherent schemes over
![]() $\mathop {\mathrm {Spec}}(\mathbb {Q}_p)\to \mathop {\mathrm {Spec}}(\mathbb {Z}_p)$
. The base change by f induces a commutative diagram of sites (see 3.2):
$\mathop {\mathrm {Spec}}(\mathbb {Q}_p)\to \mathop {\mathrm {Spec}}(\mathbb {Z}_p)$
. The base change by f induces a commutative diagram of sites (see 3.2):

Let
![]() $\mathbb {F}'$
be a finite locally constant abelian sheaf on
$\mathbb {F}'$
be a finite locally constant abelian sheaf on
![]() $Y^{\prime }_{\mathrm {\acute {e}t}}$
. Remark that the sheaf
$Y^{\prime }_{\mathrm {\acute {e}t}}$
. Remark that the sheaf
![]() $\overline {\mathscr {B}}$
on
$\overline {\mathscr {B}}$
on
![]() $\mathbf {E}_{Y \to X}^{\mathrm {\acute {e}t}}$
is flat over
$\mathbf {E}_{Y \to X}^{\mathrm {\acute {e}t}}$
is flat over
![]() $\mathbb {Z}$
. Consider the natural morphisms in the derived category
$\mathbb {Z}$
. Consider the natural morphisms in the derived category
![]() $\mathbf {D}(\overline {\mathscr {B}}\textrm {-}\mathbf {Mod}_{\mathbf {E}_{Y \to X}^{\mathrm {\acute {e}t}}})$
,
$\mathbf {D}(\overline {\mathscr {B}}\textrm {-}\mathbf {Mod}_{\mathbf {E}_{Y \to X}^{\mathrm {\acute {e}t}}})$
,
where
![]() $\alpha _1$
is induced by the canonical morphism
$\alpha _1$
is induced by the canonical morphism
![]() $\psi ^{\prime }_*\mathbb {F}' \to \mathrm {R}\psi ^{\prime }_*\mathbb {F}'$
, and
$\psi ^{\prime }_*\mathbb {F}' \to \mathrm {R}\psi ^{\prime }_*\mathbb {F}'$
, and
![]() $\alpha _2$
is the canonical morphism.
$\alpha _2$
is the canonical morphism.
5.5 We keep the notation in 5.4 and assume that X is the spectrum of an absolutely integrally closed valuation ring A and that Y is a quasi-compact open subscheme of X. Then, the associated topos of
![]() $\mathbf {E}_{Y \to X}^{\mathrm {\acute {e}t}}$
is local (3.7). By applying the functor
$\mathbf {E}_{Y \to X}^{\mathrm {\acute {e}t}}$
is local (3.7). By applying the functor
![]() $\mathrm {R}\Gamma (Y \to X,-)$
on (5.4.2), we obtain the natural morphisms in the derived category
$\mathrm {R}\Gamma (Y \to X,-)$
on (5.4.2), we obtain the natural morphisms in the derived category
![]() $\mathbf {D}(A\textrm {-}\mathbf {Mod})$
,
$\mathbf {D}(A\textrm {-}\mathbf {Mod})$
,
Definition 5.6 ([Reference Abbes and GrosAG20, 4.8.13, 5.7.4])
Under the assumptions in 5.4 (resp. 5.5) and with the same notation, if
![]() $\alpha _1$
is an isomorphism (for instance, if the canonical morphism
$\alpha _1$
is an isomorphism (for instance, if the canonical morphism
![]() $\psi ^{\prime }_*\mathbb {F}' \to \mathrm {R}\psi ^{\prime }_*\mathbb {F}'$
is an isomorphism), then we call the canonical morphism
$\psi ^{\prime }_*\mathbb {F}' \to \mathrm {R}\psi ^{\prime }_*\mathbb {F}'$
is an isomorphism), then we call the canonical morphism
the relative (resp. absolute) Faltings’ comparison morphism associated with
![]() $f:(Y' \to X')\to (Y \to X)$
and
$f:(Y' \to X')\to (Y \to X)$
and
![]() $\mathbb {F}'$
. In this case, we say that the relative (resp. absolute) Faltings’ comparison morphism exists.
$\mathbb {F}'$
. In this case, we say that the relative (resp. absolute) Faltings’ comparison morphism exists.
Theorem 5.7 [Reference Abbes and GrosAch17, Corollary 6.9], cf. [Reference Abbes and GrosAG20, 4.4.2]
Let
![]() $\mathcal {O}_K$
be a strictly Henselian discrete valuation ring with fraction field K of characteristic
$\mathcal {O}_K$
be a strictly Henselian discrete valuation ring with fraction field K of characteristic
![]() $0$
and residue field of characteristic p. We fix an algebraic closure
$0$
and residue field of characteristic p. We fix an algebraic closure
![]() $\overline {K}$
of K. Let X be an
$\overline {K}$
of K. Let X be an
![]() $\mathcal {O}_K$
-scheme of finite type, let
$\mathcal {O}_K$
-scheme of finite type, let
![]() $\mathbb {F}$
be a finite locally constant abelian sheaf on
$\mathbb {F}$
be a finite locally constant abelian sheaf on
![]() $X_{\overline {K},\mathrm {\acute {e}t}}$
, and let
$X_{\overline {K},\mathrm {\acute {e}t}}$
, and let
![]() $\psi :X_{\overline {K},\mathrm {\acute {e}t}} \to \mathbf {E}_{X_{\overline {K}} \to X}^{\mathrm {\acute {e}t}}$
be the morphism of sites defined in 3.2. Then, the canonical morphism
$\psi :X_{\overline {K},\mathrm {\acute {e}t}} \to \mathbf {E}_{X_{\overline {K}} \to X}^{\mathrm {\acute {e}t}}$
be the morphism of sites defined in 3.2. Then, the canonical morphism
![]() $\psi _*\mathbb {F} \to \mathrm {R}\psi _*\mathbb {F}$
is an isomorphism.
$\psi _*\mathbb {F} \to \mathrm {R}\psi _*\mathbb {F}$
is an isomorphism.
Corollary 5.8 Let
![]() $\mathcal {O}_K$
be a strictly Henselian discrete valuation ring with fraction field K of characteristic
$\mathcal {O}_K$
be a strictly Henselian discrete valuation ring with fraction field K of characteristic
![]() $0$
and residue field of characteristic p. We fix an algebraic closure
$0$
and residue field of characteristic p. We fix an algebraic closure
![]() $\overline {K}$
of K. Let X be a coherent
$\overline {K}$
of K. Let X be a coherent
![]() $\mathcal {O}_{\overline {K}}$
-scheme,
$\mathcal {O}_{\overline {K}}$
-scheme,
![]() $Y=\mathop {\mathrm {Spec}}(\overline {K})\times _{\mathop {\mathrm {Spec}}(\mathcal {O}_{\overline {K}})} X$
, let
$Y=\mathop {\mathrm {Spec}}(\overline {K})\times _{\mathop {\mathrm {Spec}}(\mathcal {O}_{\overline {K}})} X$
, let
![]() $\mathbb {F}$
be a finite locally constant abelian sheaf on
$\mathbb {F}$
be a finite locally constant abelian sheaf on
![]() $Y_{\mathrm {\acute {e}t}}$
, and let
$Y_{\mathrm {\acute {e}t}}$
, and let
![]() $\psi :Y_{\mathrm {\acute {e}t}} \to \mathbf {E}_{Y \to X}^{\mathrm {\acute {e}t}}$
be the morphism of sites defined in 3.2. Then, the canonical morphism
$\psi :Y_{\mathrm {\acute {e}t}} \to \mathbf {E}_{Y \to X}^{\mathrm {\acute {e}t}}$
be the morphism of sites defined in 3.2. Then, the canonical morphism
![]() $\psi _*\mathbb {F} \to \mathrm {R}\psi _*\mathbb {F}$
is an isomorphism.
$\psi _*\mathbb {F} \to \mathrm {R}\psi _*\mathbb {F}$
is an isomorphism.
We emphasize that we don’t need any finiteness condition of X over
![]() $\mathcal {O}_{\overline {K}}$
in 5.8. In fact, one can replace
$\mathcal {O}_{\overline {K}}$
in 5.8. In fact, one can replace
![]() $\mathcal {O}_{\overline {K}}$
by
$\mathcal {O}_{\overline {K}}$
by
![]() $\overline {\mathbb {Z}_p}$
without loss of generality, where
$\overline {\mathbb {Z}_p}$
without loss of generality, where
![]() $\overline {\mathbb {Z}_p}$
is the integral closure of
$\overline {\mathbb {Z}_p}$
is the integral closure of
![]() $\mathbb {Z}_p$
in an algebraic closure of
$\mathbb {Z}_p$
in an algebraic closure of
![]() $\mathbb {Q}_p$
. We keep working over
$\mathbb {Q}_p$
. We keep working over
![]() $\mathcal {O}_{\overline {K}}$
only for the continuation of our usage of notation.
$\mathcal {O}_{\overline {K}}$
only for the continuation of our usage of notation.
Proof of 5.8
We take a directed inverse system
![]() $(X_\lambda \to \mathop {\mathrm {Spec}}(\mathcal {O}_{K_\lambda }))_{\lambda \in \Lambda }$
of morphisms of finite type of schemes by Noetherian approximation, such that
$(X_\lambda \to \mathop {\mathrm {Spec}}(\mathcal {O}_{K_\lambda }))_{\lambda \in \Lambda }$
of morphisms of finite type of schemes by Noetherian approximation, such that
![]() $K_\lambda $
is a finite field extension of K and
$K_\lambda $
is a finite field extension of K and
![]() $\overline {K}=\bigcup _{\lambda \in \Lambda }K_\lambda $
, and that the transition morphisms
$\overline {K}=\bigcup _{\lambda \in \Lambda }K_\lambda $
, and that the transition morphisms
![]() $X_{\lambda '} \to X_\lambda $
are affine and
$X_{\lambda '} \to X_\lambda $
are affine and
![]() $X=\lim _{\lambda \in \Lambda } X_\lambda $
(cf. [Sta23, 09MV]). For each
$X=\lim _{\lambda \in \Lambda } X_\lambda $
(cf. [Sta23, 09MV]). For each
![]() $\lambda \in \Lambda $
, we set
$\lambda \in \Lambda $
, we set
![]() $Y_\lambda =\mathop {\mathrm {Spec}}(\overline {K}) \times _{\mathop {\mathrm {Spec}}(\mathcal {O}_{K_\lambda })}X_\lambda $
. Notice that
$Y_\lambda =\mathop {\mathrm {Spec}}(\overline {K}) \times _{\mathop {\mathrm {Spec}}(\mathcal {O}_{K_\lambda })}X_\lambda $
. Notice that
![]() $Y=\lim Y_\lambda $
. Then, there exists an index
$Y=\lim Y_\lambda $
. Then, there exists an index
![]() $\lambda _0\in \Lambda $
and a finite locally constant abelian sheaf
$\lambda _0\in \Lambda $
and a finite locally constant abelian sheaf
![]() $\mathbb {F}_{\lambda _0}$
on
$\mathbb {F}_{\lambda _0}$
on
![]() $Y_{\lambda _0,\mathrm {\acute {e}t}}$
such that
$Y_{\lambda _0,\mathrm {\acute {e}t}}$
such that
![]() $\mathbb {F}$
is the pullback of
$\mathbb {F}$
is the pullback of
![]() $\mathbb {F}_{\lambda _0}$
by
$\mathbb {F}_{\lambda _0}$
by
![]() $Y_{\mathrm {\acute {e}t}} \to Y_{\lambda _0,\mathrm {\acute {e}t}}$
(cf. [Sta23, 09YU]). Let
$Y_{\mathrm {\acute {e}t}} \to Y_{\lambda _0,\mathrm {\acute {e}t}}$
(cf. [Sta23, 09YU]). Let
![]() $\mathbb {F}_\lambda $
be the pullback of
$\mathbb {F}_\lambda $
be the pullback of
![]() $\mathbb {F}_{\lambda _0}$
by
$\mathbb {F}_{\lambda _0}$
by
![]() $Y_{\lambda ,\mathrm {\acute {e}t}} \to Y_{\lambda _0,\mathrm {\acute {e}t}}$
for each
$Y_{\lambda ,\mathrm {\acute {e}t}} \to Y_{\lambda _0,\mathrm {\acute {e}t}}$
for each
![]() $\lambda \geq \lambda _0$
. Notice that
$\lambda \geq \lambda _0$
. Notice that
![]() $\mathcal {O}_{K_\lambda }$
also satisfies the conditions in 5.7. Let
$\mathcal {O}_{K_\lambda }$
also satisfies the conditions in 5.7. Let
![]() $\psi _\lambda :Y_{\lambda ,\mathrm {\acute {e}t}} \to \mathbf {E}_{Y_\lambda \to X_\lambda }^{\mathrm {\acute {e}t}}$
be the morphism of sites defined in 3.2, and let
$\psi _\lambda :Y_{\lambda ,\mathrm {\acute {e}t}} \to \mathbf {E}_{Y_\lambda \to X_\lambda }^{\mathrm {\acute {e}t}}$
be the morphism of sites defined in 3.2, and let
![]() $\varphi _\lambda : \mathbf {E}_{Y \to X}^{\mathrm {\acute {e}t}}\to \mathbf {E}_{Y_\lambda \to X_\lambda }^{\mathrm {\acute {e}t}}$
be the morphism of sites defined by the transition morphism. Then, we have
$\varphi _\lambda : \mathbf {E}_{Y \to X}^{\mathrm {\acute {e}t}}\to \mathbf {E}_{Y_\lambda \to X_\lambda }^{\mathrm {\acute {e}t}}$
be the morphism of sites defined by the transition morphism. Then, we have
![]() $\mathrm {R}^q\psi _{\lambda *}\mathbb {F}_\lambda =0$
for each integer
$\mathrm {R}^q\psi _{\lambda *}\mathbb {F}_\lambda =0$
for each integer
![]() $q>0$
by 5.7, and moreover,
$q>0$
by 5.7, and moreover,
by [Reference HeHe23, 7.12], [SGA 4II , VII.5.6], and [SGA 4II , VI.8.7.3] whose conditions are satisfied because each object in each concerned site is quasi-compact.
Lemma 5.9 With the notation in 5.4, let
![]() $\mathbb {F}$
be a finite locally constant abelian sheaf on
$\mathbb {F}$
be a finite locally constant abelian sheaf on
![]() $Y_{\mathrm {\acute {e}t}}$
. Then, the canonical morphism
$Y_{\mathrm {\acute {e}t}}$
. Then, the canonical morphism
![]() $f_{\mathbf {E}}^{-1}\psi _*\mathbb {F}\to \psi ^{\prime }_*f_{\mathrm {\acute {e}t}}^{-1}\mathbb {F}$
is an isomorphism.
$f_{\mathbf {E}}^{-1}\psi _*\mathbb {F}\to \psi ^{\prime }_*f_{\mathrm {\acute {e}t}}^{-1}\mathbb {F}$
is an isomorphism.
Proof The base change morphism
![]() $f_{\mathbf {E}}^{-1}\psi _*\mathbb {F}\to \psi ^{\prime }_*f_{\mathrm {\acute {e}t}}^{-1}\mathbb {F}$
is the composition of the adjunction morphisms [SGA 4III
, XVII.2.1.3]
$f_{\mathbf {E}}^{-1}\psi _*\mathbb {F}\to \psi ^{\prime }_*f_{\mathrm {\acute {e}t}}^{-1}\mathbb {F}$
is the composition of the adjunction morphisms [SGA 4III
, XVII.2.1.3]
which are both isomorphisms by 5.3.
5.10 Let K be a complete discrete valuation field of characteristic
![]() $0$
with valuation ring
$0$
with valuation ring
![]() $\mathcal {O}_K$
whose residue field k is algebraically closed (a condition required by [Reference Abbes and GrosAG20, 4.1.3, 5.1.3]) of characteristic
$\mathcal {O}_K$
whose residue field k is algebraically closed (a condition required by [Reference Abbes and GrosAG20, 4.1.3, 5.1.3]) of characteristic
![]() $p>0$
, and let
$p>0$
, and let
![]() $\overline {K}$
be an algebraic closure of K,
$\overline {K}$
be an algebraic closure of K,
![]() $\mathcal {O}_{\overline {K}}$
the integral closure of
$\mathcal {O}_{\overline {K}}$
the integral closure of
![]() $\mathcal {O}_K$
in
$\mathcal {O}_K$
in
![]() $\overline {K}$
,
$\overline {K}$
,
![]() $\eta = \mathop {\mathrm {Spec}} (K)$
,
$\eta = \mathop {\mathrm {Spec}} (K)$
,
![]() $\overline {\eta }=\mathop {\mathrm {Spec}}(\overline {K})$
,
$\overline {\eta }=\mathop {\mathrm {Spec}}(\overline {K})$
,
![]() $S=\mathop {\mathrm {Spec}} (\mathcal {O}_K)$
,
$S=\mathop {\mathrm {Spec}} (\mathcal {O}_K)$
,
![]() $\overline {S}=\mathop {\mathrm {Spec}}(\mathcal {O}_{\overline {K}})$
,
$\overline {S}=\mathop {\mathrm {Spec}}(\mathcal {O}_{\overline {K}})$
,
![]() $s=\mathop {\mathrm {Spec}} (k)$
. Remark that
$s=\mathop {\mathrm {Spec}} (k)$
. Remark that
![]() $\overline {K}$
is a pre-perfectoid field with valuation ring
$\overline {K}$
is a pre-perfectoid field with valuation ring
![]() $\mathcal {O}_{\overline {K}}$
so we are also in the situation of 3.9.
$\mathcal {O}_{\overline {K}}$
so we are also in the situation of 3.9.
5.11 With the notation in 5.10, let X be an S-scheme, and let Y be an open subscheme of the generic fiber
![]() $X_\eta $
. We simply denote by
$X_\eta $
. We simply denote by
![]() $\mathscr {M}_X$
the compactifying log structure
$\mathscr {M}_X$
the compactifying log structure
![]() $\mathscr {M}_{X_\eta \to X}$
(4.3). Following [Reference AchingerAGT16, III.4.7], we say that
$\mathscr {M}_{X_\eta \to X}$
(4.3). Following [Reference AchingerAGT16, III.4.7], we say that
![]() $Y\to X$
is adequate over
$Y\to X$
is adequate over
![]() $\eta \to S$
if the following conditions are satisfied:
$\eta \to S$
if the following conditions are satisfied:
-
(i) X is of finite type over S.
-
(ii) Any point of the special fiber
 $X_s$
admits an étale neighborhood U such that
$X_s$
admits an étale neighborhood U such that
 $U_\eta \to \eta $
is smooth and that
$U_\eta \to \eta $
is smooth and that
 $U_\eta \setminus Y$
is the support of a strict normal crossings divisor on
$U_\eta \setminus Y$
is the support of a strict normal crossings divisor on
 $U_\eta $
.
$U_\eta $
. -
(iii)
 $(X,\mathscr {M}_{Y \to X})$
is a fine log scheme and the structure morphism
$(X,\mathscr {M}_{Y \to X})$
is a fine log scheme and the structure morphism
 $(X,\mathscr {M}_{Y \to X}) \to (S,\mathscr {M}_{S})$
is smooth and saturated.
$(X,\mathscr {M}_{Y \to X}) \to (S,\mathscr {M}_{S})$
is smooth and saturated.
In this case,
![]() $(X,\mathscr {M}_{Y \to X}) \to (S,\mathscr {M}_{S})$
is adequate in the sense of [Reference AchingerAGT16, III.4.7]. We remark that for any adequate
$(X,\mathscr {M}_{Y \to X}) \to (S,\mathscr {M}_{S})$
is adequate in the sense of [Reference AchingerAGT16, III.4.7]. We remark that for any adequate
![]() $(S,\mathscr {M}_{S})$
-log scheme
$(S,\mathscr {M}_{S})$
-log scheme
![]() $(X,\mathscr {M})$
,
$(X,\mathscr {M})$
,
![]() $X^{\mathrm {tr}}\to X$
is adequate over
$X^{\mathrm {tr}}\to X$
is adequate over
![]() $\eta \to S$
and
$\eta \to S$
and
![]() $(X,\mathscr {M})=(X,\mathscr {M}_{X^{\mathrm {tr}}\to X})$
(see 4.4 and 4.5). Note that if
$(X,\mathscr {M})=(X,\mathscr {M}_{X^{\mathrm {tr}}\to X})$
(see 4.4 and 4.5). Note that if
![]() $Y \to X$
is semi-stable over
$Y \to X$
is semi-stable over
![]() $\eta \to S$
then it is adequate (see 4.5).
$\eta \to S$
then it is adequate (see 4.5).
5.12 We recall the statement of Faltings’ main p-adic comparison theorem following Abbes and Gros [Reference Abbes and GrosAG20]. We take the notation and assumptions in 5.10. Firstly, recall that for any adequate open immersion of schemes
![]() $X^\circ \to X$
over
$X^\circ \to X$
over
![]() $\eta \to S$
and any finite locally constant abelian sheaf
$\eta \to S$
and any finite locally constant abelian sheaf
![]() $\mathbb {F}$
on
$\mathbb {F}$
on
![]() $X^\circ _{\overline {\eta },\mathrm {\acute {e}t}}$
, the canonical morphism
$X^\circ _{\overline {\eta },\mathrm {\acute {e}t}}$
, the canonical morphism
![]() $\psi _*\mathbb {F} \to \mathrm {R}\psi _*\mathbb {F}$
is an isomorphism, where
$\psi _*\mathbb {F} \to \mathrm {R}\psi _*\mathbb {F}$
is an isomorphism, where
![]() $\psi :X^\circ _{\overline {\eta },\mathrm {\acute {e}t}} \to \mathbf {E}_{X_{\overline {\eta }}^\circ \to X}^{\mathrm {\acute {e}t}}$
is the morphism of sites defined in 3.2 [Reference Abbes and GrosAG20, 4.4.2].
$\psi :X^\circ _{\overline {\eta },\mathrm {\acute {e}t}} \to \mathbf {E}_{X_{\overline {\eta }}^\circ \to X}^{\mathrm {\acute {e}t}}$
is the morphism of sites defined in 3.2 [Reference Abbes and GrosAG20, 4.4.2].
Let
![]() $(X^{{\prime }\triangleright }\to X') \to (X^\circ \to X)$
be a morphism of adequate open immersions of schemes over
$(X^{{\prime }\triangleright }\to X') \to (X^\circ \to X)$
be a morphism of adequate open immersions of schemes over
![]() $\eta \to S$
such that
$\eta \to S$
such that
![]() $X' \to X$
is projective and that the induced morphism
$X' \to X$
is projective and that the induced morphism
![]() $(X',\mathscr {M}_{X^{{\prime }\triangleright } \to X'})\to (X,\mathscr {M}_{X^\circ \to X})$
is smooth and saturated. Let
$(X',\mathscr {M}_{X^{{\prime }\triangleright } \to X'})\to (X,\mathscr {M}_{X^\circ \to X})$
is smooth and saturated. Let
![]() $Y'=\overline {\eta }\times _{\eta } X^{{\prime }\triangleright }$
,
$Y'=\overline {\eta }\times _{\eta } X^{{\prime }\triangleright }$
,
![]() $Y=\overline {\eta }\times _{\eta } X^\circ $
,
$Y=\overline {\eta }\times _{\eta } X^\circ $
,
![]() $f:(Y' \to X') \to (Y\to X)$
be the natural morphism, and let
$f:(Y' \to X') \to (Y\to X)$
be the natural morphism, and let
![]() $\mathbb {F}'$
be a finite locally constant abelian sheaf on
$\mathbb {F}'$
be a finite locally constant abelian sheaf on
![]() $Y^{\prime }_{\mathrm {\acute {e}t}}$
. By the first paragraph, we have the relative Faltings’ comparison morphism associated with f and
$Y^{\prime }_{\mathrm {\acute {e}t}}$
. By the first paragraph, we have the relative Faltings’ comparison morphism associated with f and
![]() $\mathbb {F}'$
(5.6.1),
$\mathbb {F}'$
(5.6.1),
Remark that under our assumption, the sheaf
![]() $\mathrm {R}^q f_{\mathrm {\acute {e}t} *} \mathbb {F}'$
on
$\mathrm {R}^q f_{\mathrm {\acute {e}t} *} \mathbb {F}'$
on
![]() $Y_{\mathrm {\acute {e}t}}$
is finite locally constant for each integer q [Reference Abbes and GrosAG20, 2.2.25].
$Y_{\mathrm {\acute {e}t}}$
is finite locally constant for each integer q [Reference Abbes and GrosAG20, 2.2.25].
Theorem 5.13 [Reference GrothendieckFal02, Theorem 6, page 266], [Reference Abbes and GrosAG20, 5.7.4]
Under the assumptions in 5.12 and with the same notation, the relative Faltings’ comparison morphism associated with f and
![]() $\mathbb {F}'$
is an almost isomorphism in the derived category
$\mathbb {F}'$
is an almost isomorphism in the derived category
![]() $\mathbf {D}(\mathcal {O}_{\overline {K}}\textrm {-}\mathbf {Mod}_{\mathbf {E}_{Y \to X}^{\mathrm {\acute {e}t}}})$
[Reference HeHe23, 5.7], and it induces an almost isomorphism
$\mathbf {D}(\mathcal {O}_{\overline {K}}\textrm {-}\mathbf {Mod}_{\mathbf {E}_{Y \to X}^{\mathrm {\acute {e}t}}})$
[Reference HeHe23, 5.7], and it induces an almost isomorphism
of
![]() $\mathcal {O}_{\overline {K}}$
-modules for each integer q.
$\mathcal {O}_{\overline {K}}$
-modules for each integer q.
Proposition 5.14 With the notation in 5.10, let A be an absolutely integrally closed valuation ring of height
![]() $1$
extension of
$1$
extension of
![]() $\mathcal {O}_{\overline {K}}$
, let X be a proper A-scheme of finite presentation,
$\mathcal {O}_{\overline {K}}$
, let X be a proper A-scheme of finite presentation,
![]() $Y= \mathop {\mathrm {Spec}}(A[1/p]) \times _{\mathop {\mathrm {Spec}}(A)} X$
, and let
$Y= \mathop {\mathrm {Spec}}(A[1/p]) \times _{\mathop {\mathrm {Spec}}(A)} X$
, and let
![]() $\mathbb {F}$
be a finite locally constant abelian sheaf on
$\mathbb {F}$
be a finite locally constant abelian sheaf on
![]() $Y_{\mathrm {\acute {e}t}}$
. Then, there exists a proper surjective morphism
$Y_{\mathrm {\acute {e}t}}$
. Then, there exists a proper surjective morphism
![]() $X' \to X$
of finite presentation such that the relative and absolute Faltings’ comparison morphisms associated with
$X' \to X$
of finite presentation such that the relative and absolute Faltings’ comparison morphisms associated with
![]() $f':(Y' \to X') \to (\mathop {\mathrm {Spec}}(A[1/p])\to \mathop {\mathrm {Spec}}(A))$
and
$f':(Y' \to X') \to (\mathop {\mathrm {Spec}}(A[1/p])\to \mathop {\mathrm {Spec}}(A))$
and
![]() $\mathbb {F}'$
(which exist by 5.8) are almost isomorphisms, where
$\mathbb {F}'$
(which exist by 5.8) are almost isomorphisms, where
![]() $Y'=Y\times _X X'$
and
$Y'=Y\times _X X'$
and
![]() $\mathbb {F}'$
is the pullback of
$\mathbb {F}'$
is the pullback of
![]() $\mathbb {F}$
on
$\mathbb {F}$
on
![]() $Y^{\prime }_{\mathrm {\acute {e}t}}$
.
$Y^{\prime }_{\mathrm {\acute {e}t}}$
.
Proof Since the underlying topological space of X is Noetherian by 4.10, each irreducible component Z of X admits a closed subscheme structure such that
![]() ${Z\to X}$
is of finite presentation [Sta23, 01PH]. After replacing X by the disjoint union of its irreducible components, we may assume that X is irreducible. If Y is empty, then we take
${Z\to X}$
is of finite presentation [Sta23, 01PH]. After replacing X by the disjoint union of its irreducible components, we may assume that X is irreducible. If Y is empty, then we take
![]() $X'=X$
and thus the relative (resp. absolute) Faltings’ comparison morphism associated with
$X'=X$
and thus the relative (resp. absolute) Faltings’ comparison morphism associated with
![]() $f'$
and
$f'$
and
![]() $\mathbb {F}'$
is an isomorphism between zero objects. If Y is not empty, then we are in the situation of 4.11(iv) by taking
$\mathbb {F}'$
is an isomorphism between zero objects. If Y is not empty, then we are in the situation of 4.11(iv) by taking
![]() $\mathcal {O}_L=A$
. With the notation in 4.11, we check that the morphism
$\mathcal {O}_L=A$
. With the notation in 4.11, we check that the morphism
![]() $X' \to X$
meets our requirements. We set
$X' \to X$
meets our requirements. We set
![]() $\eta _\lambda =\mathop {\mathrm {Spec}}(K_\lambda )$
,
$\eta _\lambda =\mathop {\mathrm {Spec}}(K_\lambda )$
,
![]() $S_\lambda =\mathop {\mathrm {Spec}}(\mathcal {O}_{K_\lambda })$
,
$S_\lambda =\mathop {\mathrm {Spec}}(\mathcal {O}_{K_\lambda })$
,
![]() $T_{\lambda ,\overline {\eta _\lambda }} =\overline {\eta }\times _{\eta _\lambda } U_\lambda $
,
$T_{\lambda ,\overline {\eta _\lambda }} =\overline {\eta }\times _{\eta _\lambda } U_\lambda $
,
![]() $X^{\prime }_{\lambda ,\overline {\eta _\lambda }}=\overline {\eta }\times _{\eta _\lambda } Y^{\prime }_\lambda $
, and denote by
$X^{\prime }_{\lambda ,\overline {\eta _\lambda }}=\overline {\eta }\times _{\eta _\lambda } Y^{\prime }_\lambda $
, and denote by
![]() $f^{\prime }_\lambda :(X^{\prime }_{\lambda ,\overline {\eta _\lambda }} \to X^{\prime }_\lambda ) \to (T_{\lambda ,\overline {\eta _\lambda }} \to T_\lambda )$
the natural morphism. We obtain a commutative diagram:
$f^{\prime }_\lambda :(X^{\prime }_{\lambda ,\overline {\eta _\lambda }} \to X^{\prime }_\lambda ) \to (T_{\lambda ,\overline {\eta _\lambda }} \to T_\lambda )$
the natural morphism. We obtain a commutative diagram:

Firstly, notice that the site
![]() $Y^{\prime }_{\mathrm {\acute {e}t}}$
(resp.
$Y^{\prime }_{\mathrm {\acute {e}t}}$
(resp.
![]() $\mathop {\mathrm {Spec}}(A[1/p])_{\mathrm {\acute {e}t}}$
) is the limit of the sites
$\mathop {\mathrm {Spec}}(A[1/p])_{\mathrm {\acute {e}t}}$
) is the limit of the sites
![]() $X^{\prime }_{\lambda ,\overline {\eta _\lambda },\mathrm {\acute {e}t}}$
(resp.
$X^{\prime }_{\lambda ,\overline {\eta _\lambda },\mathrm {\acute {e}t}}$
(resp.
![]() $T_{\lambda ,\overline {\eta _\lambda },\mathrm {\acute {e}t}}$
) and the site
$T_{\lambda ,\overline {\eta _\lambda },\mathrm {\acute {e}t}}$
) and the site
![]() $\mathbf {E}_{Y' \to X'}^{\mathrm {\acute {e}t}}$
(resp.
$\mathbf {E}_{Y' \to X'}^{\mathrm {\acute {e}t}}$
(resp.
![]() $\mathbf {E}_{\mathop {\mathrm {Spec}}(A[1/p]) \to \mathop {\mathrm {Spec}}(A)}^{\mathrm {\acute {e}t}}$
) is the limit of the sites
$\mathbf {E}_{\mathop {\mathrm {Spec}}(A[1/p]) \to \mathop {\mathrm {Spec}}(A)}^{\mathrm {\acute {e}t}}$
) is the limit of the sites
![]() $\mathbf {E}_{X^{\prime }_{\lambda ,\overline {\eta _\lambda }} \to X^{\prime }_\lambda }^{\mathrm {\acute {e}t}}$
(resp.
$\mathbf {E}_{X^{\prime }_{\lambda ,\overline {\eta _\lambda }} \to X^{\prime }_\lambda }^{\mathrm {\acute {e}t}}$
(resp.
![]() $\mathbf {E}_{T_{\lambda ,\overline {\eta _\lambda }} \to T_\lambda }^{\mathrm {\acute {e}t}}$
) ([SGA 4II
, VII.5.6] and [Reference HeHe23, 7.12]). There exists an index
$\mathbf {E}_{T_{\lambda ,\overline {\eta _\lambda }} \to T_\lambda }^{\mathrm {\acute {e}t}}$
) ([SGA 4II
, VII.5.6] and [Reference HeHe23, 7.12]). There exists an index
![]() $\lambda _0\in \Lambda $
and a finite locally constant abelian sheaf
$\lambda _0\in \Lambda $
and a finite locally constant abelian sheaf
![]() $\mathbb {F}^{\prime }_{\lambda _0}$
on
$\mathbb {F}^{\prime }_{\lambda _0}$
on
![]() $X^{\prime }_{\lambda _0,\overline {\eta _{\lambda _0}},\mathrm {\acute {e}t}}$
such that
$X^{\prime }_{\lambda _0,\overline {\eta _{\lambda _0}},\mathrm {\acute {e}t}}$
such that
![]() $\mathbb {F}'$
is the pullback of
$\mathbb {F}'$
is the pullback of
![]() $\mathbb {F}^{\prime }_{\lambda _0}$
by
$\mathbb {F}^{\prime }_{\lambda _0}$
by
![]() $Y^{\prime }_{\mathrm {\acute {e}t}} \to X^{\prime }_{\lambda _0,\overline {\eta _{\lambda _0}},\mathrm {\acute {e}t}}$
(cf. [Sta23, 09YU]). Let
$Y^{\prime }_{\mathrm {\acute {e}t}} \to X^{\prime }_{\lambda _0,\overline {\eta _{\lambda _0}},\mathrm {\acute {e}t}}$
(cf. [Sta23, 09YU]). Let
![]() $\mathbb {F}^{\prime }_\lambda $
be the pullback of
$\mathbb {F}^{\prime }_\lambda $
be the pullback of
![]() $\mathbb {F}^{\prime }_{\lambda _0}$
by
$\mathbb {F}^{\prime }_{\lambda _0}$
by
![]() $X^{\prime }_{\lambda ,\overline {\eta _{\lambda }},\mathrm {\acute {e}t}} \to X^{\prime }_{\lambda _0,\overline {\eta _{\lambda _0}},\mathrm {\acute {e}t}}$
for each
$X^{\prime }_{\lambda ,\overline {\eta _{\lambda }},\mathrm {\acute {e}t}} \to X^{\prime }_{\lambda _0,\overline {\eta _{\lambda _0}},\mathrm {\acute {e}t}}$
for each
![]() $\lambda \geq \lambda _0$
. We also have
$\lambda \geq \lambda _0$
. We also have
![]() $\overline {\mathscr {B}}'=\mathop {\mathrm {colim}} g_{\lambda ,\mathbf {E}}^{-1}\overline {\mathscr {B}}'$
(resp.
$\overline {\mathscr {B}}'=\mathop {\mathrm {colim}} g_{\lambda ,\mathbf {E}}^{-1}\overline {\mathscr {B}}'$
(resp.
![]() $\overline {\mathscr {B}}=\mathop {\mathrm {colim}} h_{\lambda ,\mathbf {E}}^{-1}\overline {\mathscr {B}}$
) by [Reference HeHe23, 7.12]. According to [SGA 4II
, VI.8.7.3], whose conditions are satisfied because each object in each concerned site is quasi-compact, there are canonical isomorphisms for each integer q,
$\overline {\mathscr {B}}=\mathop {\mathrm {colim}} h_{\lambda ,\mathbf {E}}^{-1}\overline {\mathscr {B}}$
) by [Reference HeHe23, 7.12]. According to [SGA 4II
, VI.8.7.3], whose conditions are satisfied because each object in each concerned site is quasi-compact, there are canonical isomorphisms for each integer q,
On the other hand,
![]() $(X^{\prime }_\lambda ,\mathscr {M}_{X^{\prime }_\lambda }) \to (T_\lambda ,\mathscr {M}_{T_\lambda })$
is a smooth and saturated morphism of adequate
$(X^{\prime }_\lambda ,\mathscr {M}_{X^{\prime }_\lambda }) \to (T_\lambda ,\mathscr {M}_{T_\lambda })$
is a smooth and saturated morphism of adequate
![]() $(S_\lambda ,\mathscr {M}_{S_\lambda })$
-log schemes with
$(S_\lambda ,\mathscr {M}_{S_\lambda })$
-log schemes with
![]() $X^{\prime }_\lambda \to T_\lambda $
projective for each
$X^{\prime }_\lambda \to T_\lambda $
projective for each
![]() $\lambda \in \Lambda $
by construction. Thus, we are in the situation of 5.13, which implies that the relative Faltings’ comparison morphism associated with
$\lambda \in \Lambda $
by construction. Thus, we are in the situation of 5.13, which implies that the relative Faltings’ comparison morphism associated with
![]() $f^{\prime }_\lambda $
and
$f^{\prime }_\lambda $
and
![]() $\mathbb {F}^{\prime }_\lambda $
,
$\mathbb {F}^{\prime }_\lambda $
,
is an almost isomorphism for each
![]() $\lambda \geq \lambda _0$
. Combining with (5.14.2) and (5.14.3), we see that the relative Faltings’ comparison morphism associated with
$\lambda \geq \lambda _0$
. Combining with (5.14.2) and (5.14.3), we see that the relative Faltings’ comparison morphism associated with
![]() $f'$
and
$f'$
and
![]() $\mathbb {F}'$
,
$\mathbb {F}'$
,
is an almost isomorphism (and thus so is the absolute one).
Corollary 5.15 Under the assumptions in 5.14 and with the same notation, there exists a proper hypercovering
![]() $X_\bullet \to X$
of coherent schemes [Sta23, 0DHI] such that for each degree n, the relative and absolute Faltings’ comparison morphisms associated with
$X_\bullet \to X$
of coherent schemes [Sta23, 0DHI] such that for each degree n, the relative and absolute Faltings’ comparison morphisms associated with
![]() $f_n:(Y_n \to X_n) \to (\mathop {\mathrm {Spec}}(A[1/p])\to \mathop {\mathrm {Spec}}(A))$
and
$f_n:(Y_n \to X_n) \to (\mathop {\mathrm {Spec}}(A[1/p])\to \mathop {\mathrm {Spec}}(A))$
and
![]() $\mathbb {F}_n$
(which exist by 5.8) are almost isomorphisms, where
$\mathbb {F}_n$
(which exist by 5.8) are almost isomorphisms, where
![]() $Y_n=Y\times _X X_n$
and
$Y_n=Y\times _X X_n$
and
![]() $\mathbb {F}_n$
is the pullback of
$\mathbb {F}_n$
is the pullback of
![]() $\mathbb {F}$
by the natural morphism
$\mathbb {F}$
by the natural morphism
![]() $Y_{n,\mathrm {\acute {e}t}} \to Y_{\mathrm {\acute {e}t}}$
. In particular,
$Y_{n,\mathrm {\acute {e}t}} \to Y_{\mathrm {\acute {e}t}}$
. In particular,
![]() $Y_\bullet \to Y$
is a proper hypercovering and
$Y_\bullet \to Y$
is a proper hypercovering and
![]() $X_\bullet ^{Y_\bullet }\to X^Y$
is a hypercovering in
$X_\bullet ^{Y_\bullet }\to X^Y$
is a hypercovering in
![]() $\mathbf {I}_{\overline {\eta }\to \overline {S}}$
.
$\mathbf {I}_{\overline {\eta }\to \overline {S}}$
.
Proof Let
![]() $\mathscr {C}$
be the category of proper A-schemes of finite presentation endowed with the pretopology formed by families of morphisms
$\mathscr {C}$
be the category of proper A-schemes of finite presentation endowed with the pretopology formed by families of morphisms
![]() $\{f_i:X_i \to X\}_{i \in I}$
with I finite and
$\{f_i:X_i \to X\}_{i \in I}$
with I finite and
![]() $X=\bigcup _{i \in I} f_i(X_i)$
. Consider the functor
$X=\bigcup _{i \in I} f_i(X_i)$
. Consider the functor
![]() $u^+:\mathscr {C} \to \mathbf {I}_{\mathop {\mathrm {Spec}}(A[1/p]) \to \mathop {\mathrm {Spec}}(A)}$
sending X to
$u^+:\mathscr {C} \to \mathbf {I}_{\mathop {\mathrm {Spec}}(A[1/p]) \to \mathop {\mathrm {Spec}}(A)}$
sending X to
![]() $X^{Y}$
, where
$X^{Y}$
, where
![]() $Y=\mathop {\mathrm {Spec}}(A[1/p])\times _{\mathop {\mathrm {Spec}}(A)} X$
. It is well-defined by [Reference HeHe23, 3.19(4)] and commutes with fibered products by [Reference HeHe23, 3.21] and is continuous by [Reference HeHe23, 3.15]. Proposition 5.14 allows us to take a hypercovering
$Y=\mathop {\mathrm {Spec}}(A[1/p])\times _{\mathop {\mathrm {Spec}}(A)} X$
. It is well-defined by [Reference HeHe23, 3.19(4)] and commutes with fibered products by [Reference HeHe23, 3.21] and is continuous by [Reference HeHe23, 3.15]. Proposition 5.14 allows us to take a hypercovering
![]() $X_\bullet \to X$
in
$X_\bullet \to X$
in
![]() $\mathscr {C}$
meeting our requirement by [Sta23, 094K and 0DB1]. We see that
$\mathscr {C}$
meeting our requirement by [Sta23, 094K and 0DB1]. We see that
![]() $Y_\bullet \to Y$
is a proper hypercovering and that
$Y_\bullet \to Y$
is a proper hypercovering and that
![]() $X_\bullet ^{Y_\bullet }\to X^Y$
is a hypercovering in
$X_\bullet ^{Y_\bullet }\to X^Y$
is a hypercovering in
![]() $\mathbf {I}_{\overline {\eta }\to \overline {S}}$
by the properties of
$\mathbf {I}_{\overline {\eta }\to \overline {S}}$
by the properties of
![]() $u^+$
[Sta23, 0DAY].
$u^+$
[Sta23, 0DAY].
Lemma 5.16 Let
![]() $\overline {\mathbb {Z}_p}$
be the integral closure of
$\overline {\mathbb {Z}_p}$
be the integral closure of
![]() $\mathbb {Z}_p$
in an algebraic closure of
$\mathbb {Z}_p$
in an algebraic closure of
![]() $\mathbb {Q}_p$
, let A be a
$\mathbb {Q}_p$
, let A be a
![]() $\overline {\mathbb {Z}_p}$
-algebra which is an absolutely integrally closed valuation ring, let X be a proper A-scheme of finite presentation,
$\overline {\mathbb {Z}_p}$
-algebra which is an absolutely integrally closed valuation ring, let X be a proper A-scheme of finite presentation,
![]() $Y= \mathop {\mathrm {Spec}}(A[1/p]) \times _{\mathop {\mathrm {Spec}}(A)} X$
, and let
$Y= \mathop {\mathrm {Spec}}(A[1/p]) \times _{\mathop {\mathrm {Spec}}(A)} X$
, and let
![]() $\mathbb {F}$
be a finite locally constant abelian sheaf on
$\mathbb {F}$
be a finite locally constant abelian sheaf on
![]() $Y_{\mathrm {\acute {e}t}}$
. Let
$Y_{\mathrm {\acute {e}t}}$
. Let
![]() $A'=((A/\cap _{n>0}p^nA)_{\sqrt {pA}})^\wedge $
(p-adic completion),
$A'=((A/\cap _{n>0}p^nA)_{\sqrt {pA}})^\wedge $
(p-adic completion),
![]() $X'=X_{A'}$
,
$X'=X_{A'}$
,
![]() $Y'=Y_{A'}$
,
$Y'=Y_{A'}$
,
![]() $\mathbb {F}'$
the pullback of
$\mathbb {F}'$
the pullback of
![]() $\mathbb {F}$
on
$\mathbb {F}$
on
![]() $Y^{\prime }_{\mathrm {\acute {e}t}}$
. Then, the following statements are equivalent:
$Y^{\prime }_{\mathrm {\acute {e}t}}$
. Then, the following statements are equivalent:
-
(1) The absolute Faltings’ comparison morphism associated with
 $f:(Y\to X) \to (\mathop {\mathrm {Spec}}(A[1/p]) \to \mathop {\mathrm {Spec}}(A))$
and
$f:(Y\to X) \to (\mathop {\mathrm {Spec}}(A[1/p]) \to \mathop {\mathrm {Spec}}(A))$
and
 $\mathbb {F}$
(which exists by 5.8) is an almost isomorphism.
$\mathbb {F}$
(which exists by 5.8) is an almost isomorphism. -
(2) The absolute Faltings’ comparison morphism associated with
 $f':(Y'\to X') \to (\mathop {\mathrm {Spec}}(A'[1/p]) \to \mathop {\mathrm {Spec}}(A'))$
and
$f':(Y'\to X') \to (\mathop {\mathrm {Spec}}(A'[1/p]) \to \mathop {\mathrm {Spec}}(A'))$
and
 $\mathbb {F}'$
(which exists by 5.8) is an almost isomorphism.
$\mathbb {F}'$
(which exists by 5.8) is an almost isomorphism.
Proof If p is zero (resp. invertible) in A, then the absolute Faltings’ comparison morphisms are both isomorphisms between zero objects, since Y and
![]() $Y'$
are empty (resp. the abelian sheaves
$Y'$
are empty (resp. the abelian sheaves
![]() $\mathbb {F}$
and
$\mathbb {F}$
and
![]() $\mathbb {F}'$
are zero after inverting p). Thus, we may assume that p is a nonzero element of the maximal ideal of A. Notice that
$\mathbb {F}'$
are zero after inverting p). Thus, we may assume that p is a nonzero element of the maximal ideal of A. Notice that
![]() $\cap _{n>0}p^nA$
is the maximal prime ideal of A not containing p and that
$\cap _{n>0}p^nA$
is the maximal prime ideal of A not containing p and that
![]() $\sqrt {pA}$
is the minimal prime ideal of A containing p (2.1). Thus,
$\sqrt {pA}$
is the minimal prime ideal of A containing p (2.1). Thus,
![]() $(A/\cap _{n>0}p^nA)_{\sqrt {pA}}$
is an absolutely integrally closed valuation ring of height
$(A/\cap _{n>0}p^nA)_{\sqrt {pA}}$
is an absolutely integrally closed valuation ring of height
![]() $1$
extension of
$1$
extension of
![]() $\overline {\mathbb {Z}_p}$
(2.1) and thus so is its p-adic completion
$\overline {\mathbb {Z}_p}$
(2.1) and thus so is its p-adic completion
![]() $A'$
.
$A'$
.
We denote by
![]() $u:(Y' \to X') \to (Y \to X)$
the natural morphism. We have
$u:(Y' \to X') \to (Y \to X)$
the natural morphism. We have
![]() $\mathbb {F}'=u_{\mathrm {\acute {e}t}}^{-1}\mathbb {F}$
. The natural morphisms in (5.5.1) induce a commutative diagram:
$\mathbb {F}'=u_{\mathrm {\acute {e}t}}^{-1}\mathbb {F}$
. The natural morphisms in (5.5.1) induce a commutative diagram:

where
![]() $\gamma _1$
is induced by the canonical morphism
$\gamma _1$
is induced by the canonical morphism
![]() $\mathbb {F} \to \mathrm {R} u_{\mathrm {\acute {e}t} *}u_{\mathrm {\acute {e}t}}^{-1}\mathbb {F}$
, and
$\mathbb {F} \to \mathrm {R} u_{\mathrm {\acute {e}t} *}u_{\mathrm {\acute {e}t}}^{-1}\mathbb {F}$
, and
![]() $\gamma _2$
(resp.
$\gamma _2$
(resp.
![]() $\gamma _3$
) is induced by the composition of
$\gamma _3$
) is induced by the composition of
![]() $\psi _*\mathbb {F} \to \mathrm {R} u_{\mathbf {E} *} u_{\mathbf {E}}^{-1}\psi _*\mathbb {F} \to \mathrm {R} u_{\mathbf {E} *}\psi ^{\prime }_*u_{\mathrm {\acute {e}t}}^{-1}\mathbb {F}$
(resp. and by the canonical morphism
$\psi _*\mathbb {F} \to \mathrm {R} u_{\mathbf {E} *} u_{\mathbf {E}}^{-1}\psi _*\mathbb {F} \to \mathrm {R} u_{\mathbf {E} *}\psi ^{\prime }_*u_{\mathrm {\acute {e}t}}^{-1}\mathbb {F}$
(resp. and by the canonical morphism
![]() $\overline {\mathscr {B}} \to \mathrm {R} u_{\mathbf {E} *}\overline {\mathscr {B}}'$
). Since
$\overline {\mathscr {B}} \to \mathrm {R} u_{\mathbf {E} *}\overline {\mathscr {B}}'$
). Since
![]() $\alpha _1$
and
$\alpha _1$
and
![]() $\alpha _1'$
are isomorphisms by 5.8, it suffices to show that
$\alpha _1'$
are isomorphisms by 5.8, it suffices to show that
![]() $\gamma _1$
and
$\gamma _1$
and
![]() $\gamma _3$
are almost isomorphisms.
$\gamma _3$
are almost isomorphisms.
Since
![]() $A/\cap _{n>0}p^nA\to (A/\cap _{n>0}p^nA)_{\sqrt {pA}}$
is injective whose cokernel is killed by
$A/\cap _{n>0}p^nA\to (A/\cap _{n>0}p^nA)_{\sqrt {pA}}$
is injective whose cokernel is killed by
![]() $\sqrt {pA}$
[Reference HeHe23, 4.7], the morphism
$\sqrt {pA}$
[Reference HeHe23, 4.7], the morphism
![]() $A \to A'$
induces an almost isomorphism
$A \to A'$
induces an almost isomorphism
![]() $A/p^nA \to A'/p^nA'$
for each n. Then, for any torsion abelian group M, the natural morphism
$A/p^nA \to A'/p^nA'$
for each n. Then, for any torsion abelian group M, the natural morphism
![]() $M\otimes _{\mathbb {Z}} A \to M \otimes _{\mathbb {Z}} A'$
is an almost isomorphism. Therefore,
$M\otimes _{\mathbb {Z}} A \to M \otimes _{\mathbb {Z}} A'$
is an almost isomorphism. Therefore,
![]() $\gamma _1$
is an almost isomorphism by the proper base change theorem over the strictly Henselian local ring
$\gamma _1$
is an almost isomorphism by the proper base change theorem over the strictly Henselian local ring
![]() $A[1/p]$
[SGA 4III
, XII 5.5, 5.4]. For
$A[1/p]$
[SGA 4III
, XII 5.5, 5.4]. For
![]() $\gamma _3$
, it suffices to show that the canonical morphism
$\gamma _3$
, it suffices to show that the canonical morphism
![]() $\psi _*\mathbb {F}\otimes \overline {\mathscr {B}} \to \mathrm {R} u_{\mathbf {E}*} (\psi ^{\prime }_*\mathbb {F}'\otimes \overline {\mathscr {B}}')$
is an almost isomorphism. The problem is local on
$\psi _*\mathbb {F}\otimes \overline {\mathscr {B}} \to \mathrm {R} u_{\mathbf {E}*} (\psi ^{\prime }_*\mathbb {F}'\otimes \overline {\mathscr {B}}')$
is an almost isomorphism. The problem is local on
![]() $\mathbf {E}_{Y \to X}^{\mathrm {\acute {e}t}}$
, thus we may assume that
$\mathbf {E}_{Y \to X}^{\mathrm {\acute {e}t}}$
, thus we may assume that
![]() $\psi _*\mathbb {F}$
is the constant sheaf with value
$\psi _*\mathbb {F}$
is the constant sheaf with value
![]() $\mathbb {Z}/p^n\mathbb {Z}$
by 5.3. Then,
$\mathbb {Z}/p^n\mathbb {Z}$
by 5.3. Then,
![]() $\psi ^{\prime }_*\mathbb {F}'$
is also the constant sheaf with value
$\psi ^{\prime }_*\mathbb {F}'$
is also the constant sheaf with value
![]() $\mathbb {Z}/p^n\mathbb {Z}$
by 5.9. Thus, it remains to show that
$\mathbb {Z}/p^n\mathbb {Z}$
by 5.9. Thus, it remains to show that
![]() $\overline {\mathscr {B}}/p^n\overline {\mathscr {B}} \to \mathrm {R} u_{\mathbf {E}*} (\overline {\mathscr {B}}'/p^n\overline {\mathscr {B}}')$
is an almost isomorphism. Consider the following commutative diagram of ringed sites (see 3.6):
$\overline {\mathscr {B}}/p^n\overline {\mathscr {B}} \to \mathrm {R} u_{\mathbf {E}*} (\overline {\mathscr {B}}'/p^n\overline {\mathscr {B}}')$
is an almost isomorphism. Consider the following commutative diagram of ringed sites (see 3.6):

By the cohomological descent for Faltings ringed topos (3.9), it remains to show that
![]() $\mathscr {O}/p^n\mathscr {O} \to \mathrm {R} u_{\mathbf {E}*} (\mathscr {O}'/p^n\mathscr {O}')$
is an almost isomorphism. Let W be an object of
$\mathscr {O}/p^n\mathscr {O} \to \mathrm {R} u_{\mathbf {E}*} (\mathscr {O}'/p^n\mathscr {O}')$
is an almost isomorphism. Let W be an object of
![]() $\mathbf {I}_{Y \to X^Y}$
such that W is the spectrum of a
$\mathbf {I}_{Y \to X^Y}$
such that W is the spectrum of a
![]() $\overline {\mathbb {Z}_p}$
-algebra R which is almost pre-perfectoid [Reference HeHe23, 5.19]. Since the almost isomorphisms
$\overline {\mathbb {Z}_p}$
-algebra R which is almost pre-perfectoid [Reference HeHe23, 5.19]. Since the almost isomorphisms
![]() $R/p^n \to (R\otimes _A A')/p^n$
(
$R/p^n \to (R\otimes _A A')/p^n$
(
![]() $n\geq 1$
) induces an almost isomorphism of the p-adic completions
$n\geq 1$
) induces an almost isomorphism of the p-adic completions
![]() $\widehat {R}\to R\widehat {\otimes }_A A'$
, the
$\widehat {R}\to R\widehat {\otimes }_A A'$
, the
![]() $\overline {\mathbb {Z}_p}$
-algebra
$\overline {\mathbb {Z}_p}$
-algebra
![]() $R\otimes _A A'$
is still almost pre-perfectoid [Reference HeHe23, 5.19]. The pullback of W in
$R\otimes _A A'$
is still almost pre-perfectoid [Reference HeHe23, 5.19]. The pullback of W in
![]() $\mathbf {I}_{Y' \to X^{{\prime }Y'}}$
is the spectrum of the integral closure
$\mathbf {I}_{Y' \to X^{{\prime }Y'}}$
is the spectrum of the integral closure
![]() $R'$
of
$R'$
of
![]() $R\otimes _A A'$
in
$R\otimes _A A'$
in
![]() $R\otimes _A A'[1/p]$
[Reference HeHe23, (3.21.1)]. Since
$R\otimes _A A'[1/p]$
[Reference HeHe23, (3.21.1)]. Since
![]() $R\otimes _A A'$
is almost pre-perfectoid,
$R\otimes _A A'$
is almost pre-perfectoid,
![]() $R'$
is also almost pre-perfectoid and the morphism
$R'$
is also almost pre-perfectoid and the morphism
![]() $(R\otimes _A A')/p^n \to R'/p^n$
is an almost isomorphism by [Reference HeHe23, 5.30]. Recall that such W forms a topological generating family of
$(R\otimes _A A')/p^n \to R'/p^n$
is an almost isomorphism by [Reference HeHe23, 5.30]. Recall that such W forms a topological generating family of
![]() $\mathbf {I}_{Y \to X^Y}$
[Reference HeHe23, 8.10]. Therefore, the morphism
$\mathbf {I}_{Y \to X^Y}$
[Reference HeHe23, 8.10]. Therefore, the morphism
![]() $\mathscr {O}/p^n\mathscr {O} \to \mathrm {R} u_{\mathbf {E}*} (\mathscr {O}'/p^n\mathscr {O}')$
is an almost isomorphism by [Reference HeHe23, 8.11].
$\mathscr {O}/p^n\mathscr {O} \to \mathrm {R} u_{\mathbf {E}*} (\mathscr {O}'/p^n\mathscr {O}')$
is an almost isomorphism by [Reference HeHe23, 8.11].
Theorem 5.17 Let
![]() $\overline {\mathbb {Z}_p}$
be the integral closure of
$\overline {\mathbb {Z}_p}$
be the integral closure of
![]() $\mathbb {Z}_p$
in an algebraic closure of
$\mathbb {Z}_p$
in an algebraic closure of
![]() $\mathbb {Q}_p$
, let A be a
$\mathbb {Q}_p$
, let A be a
![]() $\overline {\mathbb {Z}_p}$
-algebra which is an absolutely integrally closed valuation ring, let X be a proper A-scheme of finite presentation,
$\overline {\mathbb {Z}_p}$
-algebra which is an absolutely integrally closed valuation ring, let X be a proper A-scheme of finite presentation,
![]() $Y= \mathop {\mathrm {Spec}}(A[1/p]) \times _{\mathop {\mathrm {Spec}}(A)} X$
, and let
$Y= \mathop {\mathrm {Spec}}(A[1/p]) \times _{\mathop {\mathrm {Spec}}(A)} X$
, and let
![]() $\mathbb {F}$
be a finite locally constant abelian sheaf on
$\mathbb {F}$
be a finite locally constant abelian sheaf on
![]() $Y_{\mathrm {\acute {e}t}}$
. Then, the absolute Faltings’ comparison morphism associated with
$Y_{\mathrm {\acute {e}t}}$
. Then, the absolute Faltings’ comparison morphism associated with
![]() $f:(Y \to X) \to (\mathop {\mathrm {Spec}}(A[1/p])\to \mathop {\mathrm {Spec}}(A))$
and
$f:(Y \to X) \to (\mathop {\mathrm {Spec}}(A[1/p])\to \mathop {\mathrm {Spec}}(A))$
and
![]() $\mathbb {F}$
(5.6.2) (which exists by 5.8),
$\mathbb {F}$
(5.6.2) (which exists by 5.8),
is an almost isomorphism in
![]() $\mathbf {D}(\overline {\mathbb {Z}_p}\textrm {-}\mathbf {Mod})$
[Reference HeHe23, 5.7].
$\mathbf {D}(\overline {\mathbb {Z}_p}\textrm {-}\mathbf {Mod})$
[Reference HeHe23, 5.7].
Proof Let K be the p-adic completion of the maximal unramified extension of
![]() $\mathbb {Q}_p$
. By 5.16, we may assume that A is a valuation ring of height
$\mathbb {Q}_p$
. By 5.16, we may assume that A is a valuation ring of height
![]() $1$
extension of
$1$
extension of
![]() $\mathcal {O}_{\overline {K}}$
. Let
$\mathcal {O}_{\overline {K}}$
. Let
![]() $X_\bullet \to X$
be the proper hypercovering of coherent schemes constructed in 5.15. For each degree n, the canonical morphisms (5.6.2),
$X_\bullet \to X$
be the proper hypercovering of coherent schemes constructed in 5.15. For each degree n, the canonical morphisms (5.6.2),
are, respectively, an isomorphism and an almost isomorphism, where
![]() $\mathbb {F}_n$
is the pullback of
$\mathbb {F}_n$
is the pullback of
![]() $\mathbb {F}$
by the natural morphism
$\mathbb {F}$
by the natural morphism
![]() $Y_{n,\mathrm {\acute {e}t}} \to Y_{\mathrm {\acute {e}t}}$
. Consider the commutative diagram:
$Y_{n,\mathrm {\acute {e}t}} \to Y_{\mathrm {\acute {e}t}}$
. Consider the commutative diagram:

where
![]() $\mathbb {F}_\bullet =(\mathbb {F}_n)_{[n]\in \mathrm {Ob}(\Delta )}$
(see [Reference HeHe23, 6.5] for the notation). By the functorial spectral sequence of simplicial sites [Sta23, 09WJ], we deduce from (5.17.2) that
$\mathbb {F}_\bullet =(\mathbb {F}_n)_{[n]\in \mathrm {Ob}(\Delta )}$
(see [Reference HeHe23, 6.5] for the notation). By the functorial spectral sequence of simplicial sites [Sta23, 09WJ], we deduce from (5.17.2) that
![]() $\alpha _{1\bullet }$
is an isomorphism and
$\alpha _{1\bullet }$
is an isomorphism and
![]() $\alpha _{2\bullet }$
is an almost isomorphism. Since
$\alpha _{2\bullet }$
is an almost isomorphism. Since
![]() $\alpha _1$
is an isomorphism by 5.8, it remains to show that the left vertical arrow is an isomorphism and the right vertical arrow is an almost isomorphism.
$\alpha _1$
is an isomorphism by 5.8, it remains to show that the left vertical arrow is an isomorphism and the right vertical arrow is an almost isomorphism.
We denote by
![]() $b:\mathbf {E}_{Y_{\bullet } \to X_\bullet }^{\mathrm {\acute {e}t}}\to \mathbf {E}_{Y \to X}^{\mathrm {\acute {e}t}}$
the augmentation of simplicial site and by
$b:\mathbf {E}_{Y_{\bullet } \to X_\bullet }^{\mathrm {\acute {e}t}}\to \mathbf {E}_{Y \to X}^{\mathrm {\acute {e}t}}$
the augmentation of simplicial site and by
![]() $b_n:\mathbf {E}_{Y_{n} \to X_n}^{\mathrm {\acute {e}t}}\to \mathbf {E}_{Y \to X}^{\mathrm {\acute {e}t}}$
the natural morphism of sites. Notice that
$b_n:\mathbf {E}_{Y_{n} \to X_n}^{\mathrm {\acute {e}t}}\to \mathbf {E}_{Y \to X}^{\mathrm {\acute {e}t}}$
the natural morphism of sites. Notice that
![]() $b^{-1}\psi _*\mathbb {F}=(b_n^{-1}\psi _*\mathbb {F})_{[n]\in \mathrm {Ob}(\Delta )}=(\psi _{n *}\mathbb {F}_n)_{[n]\in \mathrm {Ob}(\Delta )}=\psi _{\bullet *}\mathbb {F}_\bullet $
by 5.9 [Sta23, 0D70]. Since
$b^{-1}\psi _*\mathbb {F}=(b_n^{-1}\psi _*\mathbb {F})_{[n]\in \mathrm {Ob}(\Delta )}=(\psi _{n *}\mathbb {F}_n)_{[n]\in \mathrm {Ob}(\Delta )}=\psi _{\bullet *}\mathbb {F}_\bullet $
by 5.9 [Sta23, 0D70]. Since
![]() $X_\bullet ^{Y_\bullet } \to X^Y$
forms a hypercovering in
$X_\bullet ^{Y_\bullet } \to X^Y$
forms a hypercovering in
![]() $\mathbf {I}_{\overline {\eta }\to \overline {S}}$
, the right vertical arrow is an almost isomorphism by 5.3 and 3.10. Finally, the left vertical arrow is an isomorphism by the cohomological descent for étale cohomology [Sta23, 0DHL].
$\mathbf {I}_{\overline {\eta }\to \overline {S}}$
, the right vertical arrow is an almost isomorphism by 5.3 and 3.10. Finally, the left vertical arrow is an isomorphism by the cohomological descent for étale cohomology [Sta23, 0DHL].
6 Faltings’ main p-adic comparison theorem: the relative case
6.1 Let
![]() $Y \to X$
be a morphism of coherent schemes such that
$Y \to X$
be a morphism of coherent schemes such that
![]() $Y \to X^Y$
is an open immersion. Recall that there is a natural commutative diagram of sites (see 3.6):
$Y \to X^Y$
is an open immersion. Recall that there is a natural commutative diagram of sites (see 3.6):

Lemma 6.2 With the notation in 6.1, for any finite locally constant abelian sheaf
![]() $\mathbb {F}$
on
$\mathbb {F}$
on
![]() $Y_{\mathrm {\acute {e}t}}$
, the canonical morphism
$Y_{\mathrm {\acute {e}t}}$
, the canonical morphism
![]() $\varepsilon ^{-1}\psi _*\mathbb {F}\to \Psi _*a^{-1}\mathbb {F}$
is an isomorphism.
$\varepsilon ^{-1}\psi _*\mathbb {F}\to \Psi _*a^{-1}\mathbb {F}$
is an isomorphism.
Proof The base change morphism
![]() $\varepsilon ^{-1}\psi _*\mathbb {F}\to \Psi _*a^{-1}\mathbb {F}$
is the composition of the adjunction morphisms [SGA 4III
, XVII.2.1.3]
$\varepsilon ^{-1}\psi _*\mathbb {F}\to \Psi _*a^{-1}\mathbb {F}$
is the composition of the adjunction morphisms [SGA 4III
, XVII.2.1.3]
6.3 We fix an algebraic closure
![]() $\overline {\mathbb {Q}_p}$
of
$\overline {\mathbb {Q}_p}$
of
![]() $\mathbb {Q}_p$
and we denote by
$\mathbb {Q}_p$
and we denote by
![]() $\overline {\mathbb {Z}_p}$
the integral closure of
$\overline {\mathbb {Z}_p}$
the integral closure of
![]() $\mathbb {Z}_p$
in
$\mathbb {Z}_p$
in
![]() $\overline {\mathbb {Q}_p}$
. We set
$\overline {\mathbb {Q}_p}$
. We set
![]() $\eta = \mathop {\mathrm {Spec}} (\mathbb {Q}_p)$
,
$\eta = \mathop {\mathrm {Spec}} (\mathbb {Q}_p)$
,
![]() $\overline {\eta }=\mathop {\mathrm {Spec}}(\overline {\mathbb {Q}_p})$
,
$\overline {\eta }=\mathop {\mathrm {Spec}}(\overline {\mathbb {Q}_p})$
,
![]() $S=\mathop {\mathrm {Spec}} (\mathbb {Z}_p)$
,
$S=\mathop {\mathrm {Spec}} (\mathbb {Z}_p)$
,
![]() $\overline {S}=\mathop {\mathrm {Spec}}(\overline {\mathbb {Z}_p})$
. Remark that
$\overline {S}=\mathop {\mathrm {Spec}}(\overline {\mathbb {Z}_p})$
. Remark that
![]() $\overline {\mathbb {Q}_p}$
is a pre-perfectoid field with valuation ring
$\overline {\mathbb {Q}_p}$
is a pre-perfectoid field with valuation ring
![]() $\overline {\mathbb {Z}_p}$
so we are also in the situation of 3.9. Let
$\overline {\mathbb {Z}_p}$
so we are also in the situation of 3.9. Let
![]() $f:(Y'\to X')\to (Y\to X)$
be a Cartesian morphism of morphisms of coherent schemes with a Cartesian morphism
$f:(Y'\to X')\to (Y\to X)$
be a Cartesian morphism of morphisms of coherent schemes with a Cartesian morphism
![]() $(Y\to X^Y)\to (\overline {\eta } \to \overline {S})$
(then,
$(Y\to X^Y)\to (\overline {\eta } \to \overline {S})$
(then,
![]() $Y'\to X^{{\prime }Y'}$
is Cartesian over
$Y'\to X^{{\prime }Y'}$
is Cartesian over
![]() $\overline {\eta } \to \overline {S}$
by [Reference HeHe23, 3.19(4)]). Thus,
$\overline {\eta } \to \overline {S}$
by [Reference HeHe23, 3.19(4)]). Thus,
![]() $X^Y$
and
$X^Y$
and
![]() $X^{{\prime }Y'}$
are objects of
$X^{{\prime }Y'}$
are objects of
![]() $\mathbf {I}_{\overline {\eta } \to \overline {S}}$
. Consider the following commutative diagram of sites associated with f (see 3.6):
$\mathbf {I}_{\overline {\eta } \to \overline {S}}$
. Consider the following commutative diagram of sites associated with f (see 3.6):

6.4 Following 6.3, let
![]() $g: (\widetilde {Y}\to \widetilde {X})\to (Y\to X)$
be a morphism of coherent schemes such that
$g: (\widetilde {Y}\to \widetilde {X})\to (Y\to X)$
be a morphism of coherent schemes such that
![]() $\widetilde {Y}{\kern-1pt}\to{\kern-1pt} \widetilde {X}^{\widetilde {Y}}$
is also Cartesian over
$\widetilde {Y}{\kern-1pt}\to{\kern-1pt} \widetilde {X}^{\widetilde {Y}}$
is also Cartesian over
![]() $\overline {\eta } {\kern-1pt}\to{\kern-1pt} \overline {S}$
. We denote by
$\overline {\eta } {\kern-1pt}\to{\kern-1pt} \overline {S}$
. We denote by
![]() $g':(\widetilde {Y'}{\kern-1pt}\to{\kern-1pt} \widetilde {X'}){\kern-1pt}\to (Y'\to X')$
the base change of g by f, and denote by
$g':(\widetilde {Y'}{\kern-1pt}\to{\kern-1pt} \widetilde {X'}){\kern-1pt}\to (Y'\to X')$
the base change of g by f, and denote by
![]() $\widetilde {f}: (\widetilde {Y'}\to \widetilde {X'})\to (\widetilde {Y}\to \widetilde {X})$
the natural morphism which is Cartesian by base change. Thus,
$\widetilde {f}: (\widetilde {Y'}\to \widetilde {X'})\to (\widetilde {Y}\to \widetilde {X})$
the natural morphism which is Cartesian by base change. Thus,
![]() $\widetilde {X}^{\widetilde {Y}}$
and
$\widetilde {X}^{\widetilde {Y}}$
and
![]() $\widetilde {X'}^{\widetilde {Y'}}$
are also objects of
$\widetilde {X'}^{\widetilde {Y'}}$
are also objects of
![]() $\mathbf {I}_{\overline {\eta } \to \overline {S}}$
. We write the diagram (6.3.1) associated with
$\mathbf {I}_{\overline {\eta } \to \overline {S}}$
. We write the diagram (6.3.1) associated with
![]() $\widetilde {f}$
by equipping all labels with tildes.
$\widetilde {f}$
by equipping all labels with tildes.
Lemma 6.5 With the notation in 6.3 and 6.4, let
![]() $\mathbb {F}'$
be a finite locally constant abelian sheaf on
$\mathbb {F}'$
be a finite locally constant abelian sheaf on
![]() $Y^{\prime }_{\mathrm {\acute {e}t}}$
and we set
$Y^{\prime }_{\mathrm {\acute {e}t}}$
and we set
![]() $\mathscr {F}'=\Psi ^{\prime }_*a^{{\prime }-1}\mathbb {F}'$
. Let
$\mathscr {F}'=\Psi ^{\prime }_*a^{{\prime }-1}\mathbb {F}'$
. Let
![]() $\widetilde {X}$
be an object of
$\widetilde {X}$
be an object of
![]() $\mathbf {I}_{Y\to X^Y}$
,
$\mathbf {I}_{Y\to X^Y}$
,
![]() $\widetilde {Y}=\overline {\eta }\times _{\overline {S}} \widetilde {X}$
,
$\widetilde {Y}=\overline {\eta }\times _{\overline {S}} \widetilde {X}$
,
![]() $\widetilde {\mathbb {F}'}=g^{{\prime }-1}_{\mathrm {\acute {e}t}}\mathbb {F}'$
, q an integer.
$\widetilde {\mathbb {F}'}=g^{{\prime }-1}_{\mathrm {\acute {e}t}}\mathbb {F}'$
, q an integer.
-
(1) The sheaf
 $\mathrm {R}^q f_{\mathbf {I} *}\mathscr {F}'$
on
$\mathrm {R}^q f_{\mathbf {I} *}\mathscr {F}'$
on
 $\mathbf {I}_{Y \to X^{Y}}$
is canonically isomorphic to the sheaf associated with the presheaf
$\mathbf {I}_{Y \to X^{Y}}$
is canonically isomorphic to the sheaf associated with the presheaf
 $\widetilde {X}\mapsto H^q_{\mathrm {\acute {e}t}}(\widetilde {Y'},\widetilde {\mathbb {F}'})$
.
$\widetilde {X}\mapsto H^q_{\mathrm {\acute {e}t}}(\widetilde {Y'},\widetilde {\mathbb {F}'})$
. -
(2) The sheaf
 $\mathrm {R}^q f_{\mathbf {I} *}(\mathscr {F}'\otimes _{\mathbb {Z}}\mathscr {O}')$
on
$\mathrm {R}^q f_{\mathbf {I} *}(\mathscr {F}'\otimes _{\mathbb {Z}}\mathscr {O}')$
on
 $\mathbf {I}_{Y \to X^{Y}}$
is canonically almost isomorphic to the sheaf associated with the presheaf
$\mathbf {I}_{Y \to X^{Y}}$
is canonically almost isomorphic to the sheaf associated with the presheaf
 $\widetilde {X}\mapsto H^q(\mathbf {E}_{\widetilde {Y'}\to \widetilde {X'}}^{\mathrm {\acute {e}t}},\widetilde {\psi '}_*\widetilde {\mathbb {F}'}\otimes _{\mathbb {Z}}\overline {\mathscr {B}}')$
.
$\widetilde {X}\mapsto H^q(\mathbf {E}_{\widetilde {Y'}\to \widetilde {X'}}^{\mathrm {\acute {e}t}},\widetilde {\psi '}_*\widetilde {\mathbb {F}'}\otimes _{\mathbb {Z}}\overline {\mathscr {B}}')$
. -
(3) The canonical morphism
 $(\mathrm {R}^q f_{\mathbf {I} *}\mathscr {F}')\otimes _{\mathbb {Z}}\mathscr {O}\to (\mathrm {R}^q f_{\mathbf {I} *}\mathscr {F}'\otimes _{\mathbb {Z}}\mathscr {O}')$
is compatible with the canonical morphisms
$(\mathrm {R}^q f_{\mathbf {I} *}\mathscr {F}')\otimes _{\mathbb {Z}}\mathscr {O}\to (\mathrm {R}^q f_{\mathbf {I} *}\mathscr {F}'\otimes _{\mathbb {Z}}\mathscr {O}')$
is compatible with the canonical morphisms
 $H^q_{\mathrm {\acute {e}t}}(\widetilde {Y'},\widetilde {\mathbb {F}'})\otimes _{\mathbb {Z}} R \stackrel {\alpha _1}{\longleftarrow } H^q(\mathbf {E}_{\widetilde {Y'}\to \widetilde {X'}}^{\mathrm {\acute {e}t}},\widetilde {\psi '}_*\widetilde {\mathbb {F}'})\otimes _{\mathbb {Z}} R\stackrel {\alpha _2}{\longrightarrow } H^q(\mathbf {E}_{\widetilde {Y'}\to \widetilde {X'}}^{\mathrm {\acute {e}t}},\widetilde {\psi '}_*\widetilde {\mathbb {F}'}\otimes _{\mathbb {Z}}\overline {\mathscr {B}}')$
, where
$H^q_{\mathrm {\acute {e}t}}(\widetilde {Y'},\widetilde {\mathbb {F}'})\otimes _{\mathbb {Z}} R \stackrel {\alpha _1}{\longleftarrow } H^q(\mathbf {E}_{\widetilde {Y'}\to \widetilde {X'}}^{\mathrm {\acute {e}t}},\widetilde {\psi '}_*\widetilde {\mathbb {F}'})\otimes _{\mathbb {Z}} R\stackrel {\alpha _2}{\longrightarrow } H^q(\mathbf {E}_{\widetilde {Y'}\to \widetilde {X'}}^{\mathrm {\acute {e}t}},\widetilde {\psi '}_*\widetilde {\mathbb {F}'}\otimes _{\mathbb {Z}}\overline {\mathscr {B}}')$
, where
 $R=\overline {\mathscr {B}}(\widetilde {Y}\to \widetilde {X})$
(cf. (5.5.1)).
$R=\overline {\mathscr {B}}(\widetilde {Y}\to \widetilde {X})$
(cf. (5.5.1)).
Proof Let
![]() $\widetilde {\mathscr {F}'}$
be the restriction of
$\widetilde {\mathscr {F}'}$
be the restriction of
![]() $\mathscr {F}'$
on
$\mathscr {F}'$
on
![]() $\mathbf {I}_{\widetilde {Y'}\to \widetilde {X'}^{\widetilde {Y'}}}$
. We have
$\mathbf {I}_{\widetilde {Y'}\to \widetilde {X'}^{\widetilde {Y'}}}$
. We have
![]() $\widetilde {\mathscr {F}'}=\widetilde {\Psi '}_*\widetilde {a'}^{-1}\widetilde {\mathbb {F}'}$
. We set
$\widetilde {\mathscr {F}'}=\widetilde {\Psi '}_*\widetilde {a'}^{-1}\widetilde {\mathbb {F}'}$
. We set
![]() $\widetilde {\mathbb {L}'}=\widetilde {\psi '}_*\widetilde {\mathbb {F}'}$
which is a finite locally constant abelian sheaf on
$\widetilde {\mathbb {L}'}=\widetilde {\psi '}_*\widetilde {\mathbb {F}'}$
which is a finite locally constant abelian sheaf on
![]() $\mathbf {E}_{\widetilde {Y'} \to \widetilde {X'}}^{\mathrm {\acute {e}t}}$
by 5.3. Notice that the canonical morphisms
$\mathbf {E}_{\widetilde {Y'} \to \widetilde {X'}}^{\mathrm {\acute {e}t}}$
by 5.3. Notice that the canonical morphisms
![]() $\widetilde {\psi '}^{-1}\widetilde {\mathbb {L}'}\to \widetilde {\mathbb {F}'}$
and
$\widetilde {\psi '}^{-1}\widetilde {\mathbb {L}'}\to \widetilde {\mathbb {F}'}$
and
![]() $\widetilde {\varepsilon '}^{-1}\widetilde {\mathbb {L}'} \to \widetilde {\mathscr {F}'}$
are isomorphisms by 5.3 and 6.2, respectively.
$\widetilde {\varepsilon '}^{-1}\widetilde {\mathbb {L}'} \to \widetilde {\mathscr {F}'}$
are isomorphisms by 5.3 and 6.2, respectively.
(1) It follows from the canonical isomorphisms
where
![]() $\gamma _1$
is induced by the canonical isomorphism
$\gamma _1$
is induced by the canonical isomorphism
![]() $\widetilde {\varepsilon '}^{-1}\widetilde {\mathbb {L}'}\stackrel {\sim }{\longrightarrow } \mathrm {R}\widetilde {\Psi '}_*\widetilde {\Psi '}^{-1}\widetilde {\varepsilon '}^{-1}\widetilde {\mathbb {L}'}$
(3.8(2)), and
$\widetilde {\varepsilon '}^{-1}\widetilde {\mathbb {L}'}\stackrel {\sim }{\longrightarrow } \mathrm {R}\widetilde {\Psi '}_*\widetilde {\Psi '}^{-1}\widetilde {\varepsilon '}^{-1}\widetilde {\mathbb {L}'}$
(3.8(2)), and
![]() $\gamma _2$
is induced by the canonical isomorphism
$\gamma _2$
is induced by the canonical isomorphism
![]() $\widetilde {\psi '}^{-1}\widetilde {\mathbb {L}'}\to \mathrm {R}\widetilde {a'}_*\widetilde {a'}^{-1}\widetilde {\psi '}^{-1}\widetilde {\mathbb {L}'}$
(3.4).
$\widetilde {\psi '}^{-1}\widetilde {\mathbb {L}'}\to \mathrm {R}\widetilde {a'}_*\widetilde {a'}^{-1}\widetilde {\psi '}^{-1}\widetilde {\mathbb {L}'}$
(3.4).
(2) It follows from the canonical almost isomorphism
which is induced by the canonical almost isomorphism
![]() $\widetilde {\mathbb {L}'}{\kern-1pt}\otimes _{\mathbb {Z}}\overline {\mathscr {B}}'{\kern-1pt}\to{\kern-1pt} \mathrm {R}\widetilde {\varepsilon '}_*(\widetilde {\varepsilon '}^{-1}\widetilde {\mathbb {L}'}{\kern-1pt}\otimes{\kern-1pt} \mathscr {O}')$
(3.9).
$\widetilde {\mathbb {L}'}{\kern-1pt}\otimes _{\mathbb {Z}}\overline {\mathscr {B}}'{\kern-1pt}\to{\kern-1pt} \mathrm {R}\widetilde {\varepsilon '}_*(\widetilde {\varepsilon '}^{-1}\widetilde {\mathbb {L}'}{\kern-1pt}\otimes{\kern-1pt} \mathscr {O}')$
(3.9).
(3) Consider the following diagram:

where the unlabeled vertical arrow is induced by the canonical morphism
![]() $\widetilde {\mathbb {L}'}\to \mathrm {R}\widetilde {\varepsilon '}_*\widetilde {\varepsilon '}^{-1}\widetilde {\mathbb {L}'}$
, and the unlabeled horizontal arrow is the canonical morphism which induces
$\widetilde {\mathbb {L}'}\to \mathrm {R}\widetilde {\varepsilon '}_*\widetilde {\varepsilon '}^{-1}\widetilde {\mathbb {L}'}$
, and the unlabeled horizontal arrow is the canonical morphism which induces
![]() $(\mathrm {R}^q f_{\mathbf {I} *}\mathscr {F}')\otimes _{\mathbb {Z}}\mathscr {O}\to \mathrm {R}^q f_{\mathbf {I} *}(\mathscr {F}'\otimes _{\mathbb {Z}}\mathscr {O}')$
on
$(\mathrm {R}^q f_{\mathbf {I} *}\mathscr {F}')\otimes _{\mathbb {Z}}\mathscr {O}\to \mathrm {R}^q f_{\mathbf {I} *}(\mathscr {F}'\otimes _{\mathbb {Z}}\mathscr {O}')$
on
![]() $\mathbf {I}_{Y \to X^{Y}}$
by sheafification. It is clear that the diagram (6.5.3) is commutative, which completes the proof.
$\mathbf {I}_{Y \to X^{Y}}$
by sheafification. It is clear that the diagram (6.5.3) is commutative, which completes the proof.
6.6 We remark that 6.5 gives a new definition of the relative (resp. absolute) Faltings’ comparison morphism without using 5.8. Following 6.3, let
![]() $\mathbb {F}'$
be a finite locally constant abelian sheaf on
$\mathbb {F}'$
be a finite locally constant abelian sheaf on
![]() $Y^{\prime }_{\mathrm {\acute {e}t}}$
and we set
$Y^{\prime }_{\mathrm {\acute {e}t}}$
and we set
![]() $\mathscr {F}'=\Psi ^{\prime }_*a^{{\prime }-1}\mathbb {F}'$
. We set
$\mathscr {F}'=\Psi ^{\prime }_*a^{{\prime }-1}\mathbb {F}'$
. We set
![]() $\mathbb {L}'=\psi ^{\prime }_*\mathbb {F}'$
, which is a finite locally constant abelian sheaf on
$\mathbb {L}'=\psi ^{\prime }_*\mathbb {F}'$
, which is a finite locally constant abelian sheaf on
![]() $\mathbf {E}_{Y'\to X'}^{\mathrm {\acute {e}t}}$
by 5.3. Remark that the canonical morphisms
$\mathbf {E}_{Y'\to X'}^{\mathrm {\acute {e}t}}$
by 5.3. Remark that the canonical morphisms
![]() $\psi ^{{\prime }-1}\mathbb {L}'\to \mathbb {F}'$
and
$\psi ^{{\prime }-1}\mathbb {L}'\to \mathbb {F}'$
and
![]() $\varepsilon ^{{\prime }-1}\mathbb {L}'\to \mathscr {F}'$
are isomorphisms by 5.3 and 6.2, respectively. We also remark that
$\varepsilon ^{{\prime }-1}\mathbb {L}'\to \mathscr {F}'$
are isomorphisms by 5.3 and 6.2, respectively. We also remark that
![]() $\overline {\mathscr {B}}$
,
$\overline {\mathscr {B}}$
,
![]() $\mathscr {O}$
are flat over
$\mathscr {O}$
are flat over
![]() $\mathbb {Z}$
. The canonical morphisms in the derived category
$\mathbb {Z}$
. The canonical morphisms in the derived category
![]() $\mathbf {D}(\overline {\mathscr {B}}\textrm {-}\mathbf {Mod}_{\mathbf {E}_{Y \to X}^{\mathrm {\acute {e}t}}})$
(cf. (5.4.2)),
$\mathbf {D}(\overline {\mathscr {B}}\textrm {-}\mathbf {Mod}_{\mathbf {E}_{Y \to X}^{\mathrm {\acute {e}t}}})$
(cf. (5.4.2)),
fit into the following commutative diagram:

-
(1) The morphism
 $\alpha _3$
is induced by the canonical isomorphism
$\alpha _3$
is induced by the canonical isomorphism
 $\psi ^{{\prime }-1}\mathbb {L}'\to \mathrm {R} a^{\prime }_*a^{{\prime }-1} (\psi ^{{\prime }-1}\mathbb {L}')$
by 3.4, and thus
$\psi ^{{\prime }-1}\mathbb {L}'\to \mathrm {R} a^{\prime }_*a^{{\prime }-1} (\psi ^{{\prime }-1}\mathbb {L}')$
by 3.4, and thus
 $\alpha _3$
is an isomorphism.
$\alpha _3$
is an isomorphism. -
(2) The morphism
 $\alpha _5$
is induced by the canonical isomorphism
$\alpha _5$
is induced by the canonical isomorphism
 $\varepsilon ^{{\prime }-1}\mathbb {L}' \to \mathrm {R} \Psi ^{\prime }_*\Psi ^{{\prime }-1}\varepsilon ^{{\prime }-1}\mathbb {L}'$
by 3.8(2), and thus
$\varepsilon ^{{\prime }-1}\mathbb {L}' \to \mathrm {R} \Psi ^{\prime }_*\Psi ^{{\prime }-1}\varepsilon ^{{\prime }-1}\mathbb {L}'$
by 3.8(2), and thus
 $\alpha _5$
is an isomorphism.
$\alpha _5$
is an isomorphism. -
(3) The unlabeled arrow is induced by the canonical morphism
 $\mathbb {L}\to \mathrm {R}\varepsilon ^{\prime }_*\varepsilon ^{{\prime }-1}\mathbb {L}$
.
$\mathbb {L}\to \mathrm {R}\varepsilon ^{\prime }_*\varepsilon ^{{\prime }-1}\mathbb {L}$
. -
(4) The morphism
 $\alpha _4$
is induced by the canonical almost isomorphism
$\alpha _4$
is induced by the canonical almost isomorphism
 $\mathbb {L}'\otimes _{\mathbb {Z}} \overline {\mathscr {B}}' \to \mathrm {R} \varepsilon ^{\prime }_* (\varepsilon ^{{\prime }-1}\mathbb {L}'\otimes _{\mathbb {Z}} \mathscr {O}')$
by 3.9, and thus
$\mathbb {L}'\otimes _{\mathbb {Z}} \overline {\mathscr {B}}' \to \mathrm {R} \varepsilon ^{\prime }_* (\varepsilon ^{{\prime }-1}\mathbb {L}'\otimes _{\mathbb {Z}} \mathscr {O}')$
by 3.9, and thus
 $\alpha _4$
is an almost isomorphism.
$\alpha _4$
is an almost isomorphism. -
(5) The morphism
 $\alpha _6$
is the composition of (6.6.3)
$\alpha _6$
is the composition of (6.6.3) $$ \begin{align} \mathrm{R} \varepsilon_*(\mathrm{R} f_{\mathbf{I} *}\varepsilon^{{\prime}-1}\mathbb{L}') \otimes_{\mathbb{Z}}^{\mathrm{L}} \overline{\mathscr{B}} &\longrightarrow \mathrm{R} \varepsilon_*((\mathrm{R} f_{\mathbf{I} *}\varepsilon^{{\prime}-1}\mathbb{L}') \otimes_{\mathbb{Z}}^{\mathrm{L}} \mathscr{O}) \end{align} $$
(6.6.4)
$$ \begin{align} \mathrm{R} \varepsilon_*(\mathrm{R} f_{\mathbf{I} *}\varepsilon^{{\prime}-1}\mathbb{L}') \otimes_{\mathbb{Z}}^{\mathrm{L}} \overline{\mathscr{B}} &\longrightarrow \mathrm{R} \varepsilon_*((\mathrm{R} f_{\mathbf{I} *}\varepsilon^{{\prime}-1}\mathbb{L}') \otimes_{\mathbb{Z}}^{\mathrm{L}} \mathscr{O}) \end{align} $$
(6.6.4) $$ \begin{align} \textrm{ with } \mathrm{R} \varepsilon_*((\mathrm{R} f_{\mathbf{I} *}\varepsilon^{{\prime}-1}\mathbb{L}') \otimes_{\mathbb{Z}}^{\mathrm{L}} \mathscr{O}) &\longrightarrow \mathrm{R} \varepsilon_* \mathrm{R} f_{\mathbf{I} *}(\varepsilon^{{\prime}-1}\mathbb{L}'\otimes_{\mathbb{Z}} \mathscr{O}'). \end{align} $$
$$ \begin{align} \textrm{ with } \mathrm{R} \varepsilon_*((\mathrm{R} f_{\mathbf{I} *}\varepsilon^{{\prime}-1}\mathbb{L}') \otimes_{\mathbb{Z}}^{\mathrm{L}} \mathscr{O}) &\longrightarrow \mathrm{R} \varepsilon_* \mathrm{R} f_{\mathbf{I} *}(\varepsilon^{{\prime}-1}\mathbb{L}'\otimes_{\mathbb{Z}} \mathscr{O}'). \end{align} $$
In conclusion, the arrows
![]() $\alpha _3$
,
$\alpha _3$
,
![]() $\alpha _5$
,
$\alpha _5$
,
![]() $\alpha _6$
and
$\alpha _6$
and
![]() $\alpha _4$
induce an arrow
$\alpha _4$
induce an arrow
in the derived category of almost
![]() $\overline {\mathbb {Z}_p}$
-modules on
$\overline {\mathbb {Z}_p}$
-modules on
![]() $\mathbf {E}_{Y \to X}^{\mathrm {\acute {e}t}}$
[Reference HeHe23, 5.7]. Remark that we don’t assume that
$\mathbf {E}_{Y \to X}^{\mathrm {\acute {e}t}}$
[Reference HeHe23, 5.7]. Remark that we don’t assume that
![]() $\alpha _1$
is an isomorphism here. We also call (6.6.5) the relative Faltings’ comparison morphism. Indeed, if
$\alpha _1$
is an isomorphism here. We also call (6.6.5) the relative Faltings’ comparison morphism. Indeed, if
![]() $\alpha _1$
is an isomorphism, then the relative Faltings’ comparison morphism (5.6.1) induces (6.6.5) in
$\alpha _1$
is an isomorphism, then the relative Faltings’ comparison morphism (5.6.1) induces (6.6.5) in
![]() $\mathbf {D}(\overline {\mathbb {Z}_p}^{\mathrm {al}}\textrm {-}\mathbf {Mod})$
(the derived category of almost
$\mathbf {D}(\overline {\mathbb {Z}_p}^{\mathrm {al}}\textrm {-}\mathbf {Mod})$
(the derived category of almost
![]() $\overline {\mathbb {Z}_p}$
-modules, see [Reference HeHe23, 5.7]) due to the commutativity of the diagram (6.6.2).
$\overline {\mathbb {Z}_p}$
-modules, see [Reference HeHe23, 5.7]) due to the commutativity of the diagram (6.6.2).
If X is the spectrum of an absolutely integrally closed valuation ring A and if
![]() $Y=\overline {\eta }\times _{\overline {S}} X$
, then applying the functor
$Y=\overline {\eta }\times _{\overline {S}} X$
, then applying the functor
![]() $\mathrm {R}\Gamma (Y \to X,-)$
on (6.6.2) we obtain the natural morphisms in the derived category
$\mathrm {R}\Gamma (Y \to X,-)$
on (6.6.2) we obtain the natural morphisms in the derived category
![]() $\mathbf {D}(A\textrm {-}\mathbf {Mod})$
by 3.7 making the following diagram commutative.
$\mathbf {D}(A\textrm {-}\mathbf {Mod})$
by 3.7 making the following diagram commutative.

The arrows
![]() $\alpha _3$
,
$\alpha _3$
,
![]() $\alpha _5$
,
$\alpha _5$
,
![]() $\alpha _6,$
and
$\alpha _6,$
and
![]() $\alpha _4$
induce an arrow
$\alpha _4$
induce an arrow
in the derived category
![]() $\mathbf {D}(\overline {\mathbb {Z}_p}^{\mathrm {al}}\textrm {-}\mathbf {Mod})$
of almost
$\mathbf {D}(\overline {\mathbb {Z}_p}^{\mathrm {al}}\textrm {-}\mathbf {Mod})$
of almost
![]() $\overline {\mathbb {Z}_p}$
-modules [Reference HeHe23, 5.7]. We also call (6.6.7) the absolute Faltings’ comparison morphism.
$\overline {\mathbb {Z}_p}$
-modules [Reference HeHe23, 5.7]. We also call (6.6.7) the absolute Faltings’ comparison morphism.
Lemma 6.7 With the notation in 6.3, let
![]() $\mathbb {F}'$
be a finite locally constant abelian sheaf on
$\mathbb {F}'$
be a finite locally constant abelian sheaf on
![]() $Y^{\prime }_{\mathrm {\acute {e}t}}$
and we set
$Y^{\prime }_{\mathrm {\acute {e}t}}$
and we set
![]() $\mathscr {F}'=\Psi ^{\prime }_*a^{{\prime }-1}\mathbb {F}'$
. Assume that
$\mathscr {F}'=\Psi ^{\prime }_*a^{{\prime }-1}\mathbb {F}'$
. Assume that
![]() $X' \to X$
is proper of finite presentation. Then, the canonical morphism
$X' \to X$
is proper of finite presentation. Then, the canonical morphism
is an almost isomorphism.
Proof Following 6.5, consider the following presheaves on
![]() $\mathbf {I}_{Y \to X^{Y}}$
for each integer q:
$\mathbf {I}_{Y \to X^{Y}}$
for each integer q:
They satisfy the limit-preserving condition [Reference HeHe23, 3.25(ii)] by [Reference HeHe23, 7.12], [SGA 4II
, VII.5.6], and [SGA 4II
, VI 8.5.9, 8.7.3]. Moreover, if
![]() $\widetilde {X}=\mathop {\mathrm {Spec}}(A),$
where A is an absolutely integrally closed valuation ring with p nonzero in A, then the canonical morphisms
$\widetilde {X}=\mathop {\mathrm {Spec}}(A),$
where A is an absolutely integrally closed valuation ring with p nonzero in A, then the canonical morphisms
are, respectively, an isomorphism and an almost isomorphism by 5.17. Thus, the canonical morphisms
![]() $\mathcal {H}_1^q\leftarrow \mathcal {H}_2^q \to \mathcal {H}_3^q$
induce an isomorphism and an almost isomorphism of their sheafifications by [Reference HeHe23, 3.25]. The conclusion follows from 6.5.
$\mathcal {H}_1^q\leftarrow \mathcal {H}_2^q \to \mathcal {H}_3^q$
induce an isomorphism and an almost isomorphism of their sheafifications by [Reference HeHe23, 3.25]. The conclusion follows from 6.5.
Lemma 6.8 Let
![]() $Y\to X$
be an open immersion of coherent schemes,
$Y\to X$
be an open immersion of coherent schemes,
![]() $Y' \to Y$
a finite morphism of finite presentation. Then, there exists a finite morphism
$Y' \to Y$
a finite morphism of finite presentation. Then, there exists a finite morphism
![]() $X'\to X$
of finite presentation whose base change by
$X'\to X$
of finite presentation whose base change by
![]() $Y\to X$
is
$Y\to X$
is
![]() $Y'\to Y$
.
$Y'\to Y$
.
Proof Firstly, assume that X is Noetherian. We have
![]() $Y'=Y\times _X X^Y$
by [Reference HeHe23, 3.19(4)]. We write
$Y'=Y\times _X X^Y$
by [Reference HeHe23, 3.19(4)]. We write
![]() $X^Y=\mathop {\mathrm {Spec}}_X(\mathcal {A})$
where
$X^Y=\mathop {\mathrm {Spec}}_X(\mathcal {A})$
where
![]() $\mathcal {A}$
is an integral quasi-coherent
$\mathcal {A}$
is an integral quasi-coherent
![]() $\mathcal {O}_X$
-algebra on X, and we write
$\mathcal {O}_X$
-algebra on X, and we write
![]() $\mathcal {A}$
as a filtered colimit of its finite quasi-coherent
$\mathcal {A}$
as a filtered colimit of its finite quasi-coherent
![]() $\mathcal {O}_X$
-subalgebras
$\mathcal {O}_X$
-subalgebras
![]() $\mathcal {A}=\mathop {\mathrm {colim}} \mathcal {A}_\alpha $
[Sta23, 0817]. Let
$\mathcal {A}=\mathop {\mathrm {colim}} \mathcal {A}_\alpha $
[Sta23, 0817]. Let
![]() $\mathcal {B}_\alpha $
be the restriction of
$\mathcal {B}_\alpha $
be the restriction of
![]() $\mathcal {A}_\alpha $
to Y. Then,
$\mathcal {A}_\alpha $
to Y. Then,
![]() $\mathcal {B}=\mathop {\mathrm {colim}} \mathcal {B}_\alpha $
is a filtered colimit of finite quasi-coherent
$\mathcal {B}=\mathop {\mathrm {colim}} \mathcal {B}_\alpha $
is a filtered colimit of finite quasi-coherent
![]() $\mathcal {O}_Y$
-algebras with injective transition morphisms. Since
$\mathcal {O}_Y$
-algebras with injective transition morphisms. Since
![]() $Y'=\mathop {\mathrm {Spec}}_Y(\mathcal {B})$
is finite over Y, there exists an index
$Y'=\mathop {\mathrm {Spec}}_Y(\mathcal {B})$
is finite over Y, there exists an index
![]() $\alpha _0$
such that
$\alpha _0$
such that
![]() $Y'=\mathop {\mathrm {Spec}}_Y(\mathcal {B}_{\alpha _0})$
. Therefore,
$Y'=\mathop {\mathrm {Spec}}_Y(\mathcal {B}_{\alpha _0})$
. Therefore,
![]() $X'=\mathop {\mathrm {Spec}}_X(\mathcal {A}_{\alpha _0})$
meets our requirements.
$X'=\mathop {\mathrm {Spec}}_X(\mathcal {A}_{\alpha _0})$
meets our requirements.
In general, we write X as a cofiltered limit of coherent schemes of finite type over
![]() $\mathbb {Z}$
with affine transition morphisms
$\mathbb {Z}$
with affine transition morphisms
![]() $X=\lim _{\lambda \in \Lambda } X_\lambda $
[Sta23, 01ZA]. Since
$X=\lim _{\lambda \in \Lambda } X_\lambda $
[Sta23, 01ZA]. Since
![]() $Y\to X$
is an open immersion of finite presentation, using [Reference GrothendieckEGA IV3
, 8.8.2, 8.10.5] there exists an index
$Y\to X$
is an open immersion of finite presentation, using [Reference GrothendieckEGA IV3
, 8.8.2, 8.10.5] there exists an index
![]() $\lambda _0\in \Lambda $
, an open immersion
$\lambda _0\in \Lambda $
, an open immersion
![]() $Y_{\lambda _0}\to X_{\lambda _0}$
and a finite morphism
$Y_{\lambda _0}\to X_{\lambda _0}$
and a finite morphism
![]() $Y^{\prime }_{\lambda _0}\to Y_{\lambda _0}$
such that the base change of the morphisms
$Y^{\prime }_{\lambda _0}\to Y_{\lambda _0}$
such that the base change of the morphisms
![]() $Y^{\prime }_{\lambda _0}\to Y_{\lambda _0} \to X_{\lambda _0}$
by
$Y^{\prime }_{\lambda _0}\to Y_{\lambda _0} \to X_{\lambda _0}$
by
![]() $X\to X_{\lambda _0}$
are the morphisms
$X\to X_{\lambda _0}$
are the morphisms
![]() $Y'\to Y \to X$
. By the first paragraph, there exists a finite morphism
$Y'\to Y \to X$
. By the first paragraph, there exists a finite morphism
![]() $X^{\prime }_{\lambda _0}\to X_{\lambda _0}$
of finite presentation such that
$X^{\prime }_{\lambda _0}\to X_{\lambda _0}$
of finite presentation such that
![]() $Y^{\prime }_{\lambda _0}=Y_{\lambda _0}\times _{X_{\lambda _0}} X^{\prime }_{\lambda _0}$
. We see that the base change
$Y^{\prime }_{\lambda _0}=Y_{\lambda _0}\times _{X_{\lambda _0}} X^{\prime }_{\lambda _0}$
. We see that the base change
![]() $X'\to X$
of
$X'\to X$
of
![]() $X^{\prime }_{\lambda _0}\to X_{\lambda _0}$
by
$X^{\prime }_{\lambda _0}\to X_{\lambda _0}$
by
![]() $X\to X_{\lambda _0}$
meets our requirements.
$X\to X_{\lambda _0}$
meets our requirements.
Lemma 6.9 With the notation in 6.3, let
![]() $g:Y"\to Y'$
be a finite morphism of finite presentation, let
$g:Y"\to Y'$
be a finite morphism of finite presentation, let
![]() $\mathbb {F}"$
be a finite locally constant abelian sheaf on
$\mathbb {F}"$
be a finite locally constant abelian sheaf on
![]() $Y^{{\prime }\prime }_{\mathrm {\acute {e}t}}$
and we set
$Y^{{\prime }\prime }_{\mathrm {\acute {e}t}}$
and we set
![]() ${\mathscr {F}'=\Psi ^{\prime }_*a^{{\prime }-1}(g_{\mathrm {\acute {e}t}*}\mathbb {F}")}$
. Assume that
${\mathscr {F}'=\Psi ^{\prime }_*a^{{\prime }-1}(g_{\mathrm {\acute {e}t}*}\mathbb {F}")}$
. Assume that
![]() $X' \to X$
is proper of finite presentation. Then, the canonical morphism
$X' \to X$
is proper of finite presentation. Then, the canonical morphism
is an almost isomorphism.
Proof There exists a Cartesian morphism
![]() $g:(Y"\to X")\to (Y'\to X^{Y}\times _X X')$
of open immersions of coherent schemes such that
$g:(Y"\to X")\to (Y'\to X^{Y}\times _X X')$
of open immersions of coherent schemes such that
![]() $X" \to X^{Y}\times _X X'$
is finite and of finite presentation by 6.8. Consider the diagram (6.3.1) associated with g:
$X" \to X^{Y}\times _X X'$
is finite and of finite presentation by 6.8. Consider the diagram (6.3.1) associated with g:

We set
![]() $\mathscr {G}"=\Psi ^{{\prime }\prime }_*a^{{\prime }{\prime }-1}\mathbb {F}"$
. As
$\mathscr {G}"=\Psi ^{{\prime }\prime }_*a^{{\prime }{\prime }-1}\mathbb {F}"$
. As
![]() $g:Y"\to Y'$
is finite, the base change morphism
$g:Y"\to Y'$
is finite, the base change morphism
![]() $a^{{\prime }-1}g_{\mathrm {\acute {e}t} *}\to g_{\mathrm {v}*}a^{{\prime }{\prime }-1}$
induces a canonical isomorphism
$a^{{\prime }-1}g_{\mathrm {\acute {e}t} *}\to g_{\mathrm {v}*}a^{{\prime }{\prime }-1}$
induces a canonical isomorphism
![]() $\mathscr {F}'\stackrel {\sim }{\longrightarrow } g_{\mathbf {I}*}\mathscr {G}"$
by [Reference HeHe23, 3.10]. Moreover, the canonical morphism
$\mathscr {F}'\stackrel {\sim }{\longrightarrow } g_{\mathbf {I}*}\mathscr {G}"$
by [Reference HeHe23, 3.10]. Moreover, the canonical morphism
![]() $g_{\mathbf {I} *}\mathscr {G}" \to \mathrm {R} g_{\mathbf {I} *} \mathscr {G}"$
is an isomorphism by 6.5(1) and [Reference HeHe23, 3.25], since
$g_{\mathbf {I} *}\mathscr {G}" \to \mathrm {R} g_{\mathbf {I} *} \mathscr {G}"$
is an isomorphism by 6.5(1) and [Reference HeHe23, 3.25], since
![]() $g:Y"\to Y'$
is finite [SGA 4II
, VIII.5.6]. By applying 6.7 to g and
$g:Y"\to Y'$
is finite [SGA 4II
, VIII.5.6]. By applying 6.7 to g and
![]() $\mathbb {F}"$
, the canonical morphism
$\mathbb {F}"$
, the canonical morphism
is an almost isomorphism. Let h be the composition of
![]() $(Y"\to X")\to (Y'\to X^{Y} \times _X X')\to (Y\to X^Y)$
. Note that
$(Y"\to X")\to (Y'\to X^{Y} \times _X X')\to (Y\to X^Y)$
. Note that
![]() $X"\to X^Y$
is also proper of finite presentation. By applying 6.7 to h and
$X"\to X^Y$
is also proper of finite presentation. By applying 6.7 to h and
![]() $\mathbb {F}"$
, the canonical morphism
$\mathbb {F}"$
, the canonical morphism
is an almost isomorphism. It is clear that
![]() $h_{\mathbf {I}}=f_{\mathbf {I}}\circ g_{\mathbf {I}}$
. The conclusion follows from the canonical isomorphism
$h_{\mathbf {I}}=f_{\mathbf {I}}\circ g_{\mathbf {I}}$
. The conclusion follows from the canonical isomorphism
![]() $\mathscr {F}'\to \mathrm {R} g_{\mathbf {I} *}\mathscr {G}"$
and the canonical almost isomorphisms (6.9.3) and (6.9.4).
$\mathscr {F}'\to \mathrm {R} g_{\mathbf {I} *}\mathscr {G}"$
and the canonical almost isomorphisms (6.9.3) and (6.9.4).
Lemma 6.10 With the notation in 6.3, let
![]() $\mathcal {F}'$
be a constructible abelian sheaf on
$\mathcal {F}'$
be a constructible abelian sheaf on
![]() $Y^{\prime }_{\mathrm {\acute {e}t}}$
and we set
$Y^{\prime }_{\mathrm {\acute {e}t}}$
and we set
![]() $\mathscr {F}'=\Psi ^{\prime }_*a^{{\prime }-1}\mathcal {F}'$
. Assume that
$\mathscr {F}'=\Psi ^{\prime }_*a^{{\prime }-1}\mathcal {F}'$
. Assume that
![]() $X' \to X$
is proper of finite presentation. Then, the canonical morphism
$X' \to X$
is proper of finite presentation. Then, the canonical morphism
is an almost isomorphism.
Proof We prove by induction on an integer q that the canonical morphism
![]() $(\mathrm {R}^q f_{\mathbf {I} *}\mathscr {F}')\otimes _{\mathbb {Z}} \mathscr {O} \to \mathrm {R}^q f_{\mathbf {I} *}(\mathscr {F}'\otimes _{\mathbb {Z}} \mathscr {O}')$
is an almost isomorphism. It holds trivially for each
$(\mathrm {R}^q f_{\mathbf {I} *}\mathscr {F}')\otimes _{\mathbb {Z}} \mathscr {O} \to \mathrm {R}^q f_{\mathbf {I} *}(\mathscr {F}'\otimes _{\mathbb {Z}} \mathscr {O}')$
is an almost isomorphism. It holds trivially for each
![]() $q\leq -1$
. Notice that there exists a finite morphism
$q\leq -1$
. Notice that there exists a finite morphism
![]() $g:Y"\to Y'$
of finite presentation, a finite locally constant abelian sheaf
$g:Y"\to Y'$
of finite presentation, a finite locally constant abelian sheaf
![]() $\mathbb {F}"$
on
$\mathbb {F}"$
on
![]() $Y^{{\prime }\prime }_{\mathrm {\acute {e}t}}$
and an injective morphism
$Y^{{\prime }\prime }_{\mathrm {\acute {e}t}}$
and an injective morphism
![]() $\mathcal {F}'\to g_{\mathrm {\acute {e}t}*}\mathbb {F}"$
by [Sta23, 09Z7] (cf. [SGA 4III
, IX.2.14]). Let
$\mathcal {F}'\to g_{\mathrm {\acute {e}t}*}\mathbb {F}"$
by [Sta23, 09Z7] (cf. [SGA 4III
, IX.2.14]). Let
![]() $\mathcal {G}'$
be the quotient of
$\mathcal {G}'$
be the quotient of
![]() $\mathcal {F}'\to g_{\mathrm {\acute {e}t}*}\mathbb {F}"$
, which is also a constructible abelian sheaf on
$\mathcal {F}'\to g_{\mathrm {\acute {e}t}*}\mathbb {F}"$
, which is also a constructible abelian sheaf on
![]() $Y^{\prime }_{\mathrm {\acute {e}t}}$
since
$Y^{\prime }_{\mathrm {\acute {e}t}}$
since
![]() $g_{\mathrm {\acute {e}t}*}\mathbb {F}"$
is so [Sta23, 095R, 03RZ]. The exact sequence
$g_{\mathrm {\acute {e}t}*}\mathbb {F}"$
is so [Sta23, 095R, 03RZ]. The exact sequence
![]() $0\to \mathcal {F}' \to g_{\mathrm {\acute {e}t}*}\mathbb {F}" \to \mathcal {G}'\to 0$
induces an exact sequence by 3.8(1),
$0\to \mathcal {F}' \to g_{\mathrm {\acute {e}t}*}\mathbb {F}" \to \mathcal {G}'\to 0$
induces an exact sequence by 3.8(1),
We set
![]() $\mathscr {H}'=\Psi ^{\prime }_*a^{{\prime }-1}(g_{\mathrm {\acute {e}t}*}\mathbb {F}")$
and
$\mathscr {H}'=\Psi ^{\prime }_*a^{{\prime }-1}(g_{\mathrm {\acute {e}t}*}\mathbb {F}")$
and
![]() $\mathscr {G}'=\Psi ^{\prime }_*a^{{\prime }-1}\mathcal {G}'$
. Then, we obtain a morphism of long exact sequences:
$\mathscr {G}'=\Psi ^{\prime }_*a^{{\prime }-1}\mathcal {G}'$
. Then, we obtain a morphism of long exact sequences:

Notice that
![]() $\gamma _1$
and
$\gamma _1$
and
![]() $\gamma _2$
are almost isomorphisms by induction, and that
$\gamma _2$
are almost isomorphisms by induction, and that
![]() $\gamma _4$
is an almost isomorphism by 6.9. Thus, applying the 5-lemma [Sta23, 05QA] in the abelian category of almost
$\gamma _4$
is an almost isomorphism by 6.9. Thus, applying the 5-lemma [Sta23, 05QA] in the abelian category of almost
![]() $\overline {\mathbb {Z}_p}$
-modules over
$\overline {\mathbb {Z}_p}$
-modules over
![]() $\mathbf {I}_{Y \to X^{Y}}$
, we see that
$\mathbf {I}_{Y \to X^{Y}}$
, we see that
![]() $\gamma _3$
is almost injective. Since
$\gamma _3$
is almost injective. Since
![]() $\mathcal {F}'$
is an arbitrary constructible abelian sheaf, the morphism
$\mathcal {F}'$
is an arbitrary constructible abelian sheaf, the morphism
![]() $\gamma _5$
is also almost injective. Thus,
$\gamma _5$
is also almost injective. Thus,
![]() $\gamma _3$
is an almost isomorphism.
$\gamma _3$
is an almost isomorphism.
Theorem 6.11 With the notation in 6.3, let
![]() $\mathcal {F}'$
be a torsion abelian sheaf on
$\mathcal {F}'$
be a torsion abelian sheaf on
![]() $Y^{\prime }_{\mathrm {\acute {e}t}}$
and we set
$Y^{\prime }_{\mathrm {\acute {e}t}}$
and we set
![]() $\mathscr {F}'=\Psi ^{\prime }_*a^{{\prime }-1}\mathcal {F}'$
. Assume that
$\mathscr {F}'=\Psi ^{\prime }_*a^{{\prime }-1}\mathcal {F}'$
. Assume that
![]() $X' \to X$
is proper of finite presentation. Then, the canonical morphism
$X' \to X$
is proper of finite presentation. Then, the canonical morphism
is an almost isomorphism in the derived category
![]() $\mathbf {D}(\overline {\mathbb {Z}_p}\textrm {-}\mathbf {Mod}_{\mathbf {I}_{Y \to X^Y}})$
[Reference HeHe23, 5.7].
$\mathbf {D}(\overline {\mathbb {Z}_p}\textrm {-}\mathbf {Mod}_{\mathbf {I}_{Y \to X^Y}})$
[Reference HeHe23, 5.7].
Proof We write
![]() $\mathcal {F}'$
as a filtered colimit of constructible abelian sheaves
$\mathcal {F}'$
as a filtered colimit of constructible abelian sheaves
![]() $\mathcal {F}'=\mathop {\mathrm {colim}}_{\lambda \in \Lambda }\mathcal {F}^{\prime }_\lambda $
([Sta23, 03SA], cf. [SGA 4III
, IX.2.7.2]). We set
$\mathcal {F}'=\mathop {\mathrm {colim}}_{\lambda \in \Lambda }\mathcal {F}^{\prime }_\lambda $
([Sta23, 03SA], cf. [SGA 4III
, IX.2.7.2]). We set
![]() $\mathscr {F}^{\prime }_\lambda =\Psi ^{\prime }_*a^{{\prime }-1}\mathcal {F}_\lambda $
. We have
$\mathscr {F}^{\prime }_\lambda =\Psi ^{\prime }_*a^{{\prime }-1}\mathcal {F}_\lambda $
. We have
![]() $\mathscr {F}'=\mathop {\mathrm {colim}}_{\lambda \in \Lambda }\mathscr {F}^{\prime }_\lambda $
by [SGA 4II
, VI.5.1] whose conditions are satisfied since each object in each concerned site is quasi-compact. Moreover, for each integer q, we have
$\mathscr {F}'=\mathop {\mathrm {colim}}_{\lambda \in \Lambda }\mathscr {F}^{\prime }_\lambda $
by [SGA 4II
, VI.5.1] whose conditions are satisfied since each object in each concerned site is quasi-compact. Moreover, for each integer q, we have
The conclusion follows from 6.10.
Corollary 6.12 Let
![]() $\overline {\mathbb {Z}_p}$
be the integral closure of
$\overline {\mathbb {Z}_p}$
be the integral closure of
![]() $\mathbb {Z}_p$
in an algebraic closure of
$\mathbb {Z}_p$
in an algebraic closure of
![]() $\mathbb {Q}_p$
, let A be a
$\mathbb {Q}_p$
, let A be a
![]() $\overline {\mathbb {Z}_p}$
-algebra which is an absolutely integrally closed valuation ring, let X be a proper A-scheme of finite presentation,
$\overline {\mathbb {Z}_p}$
-algebra which is an absolutely integrally closed valuation ring, let X be a proper A-scheme of finite presentation,
![]() $Y= \mathop {\mathrm {Spec}}(A[1/p]) \times _{\mathop {\mathrm {Spec}}(A)} X$
, and let
$Y= \mathop {\mathrm {Spec}}(A[1/p]) \times _{\mathop {\mathrm {Spec}}(A)} X$
, and let
![]() $\mathcal {F}$
be a torsion abelian sheaf on
$\mathcal {F}$
be a torsion abelian sheaf on
![]() $Y_{\mathrm {\acute {e}t}}$
and we set
$Y_{\mathrm {\acute {e}t}}$
and we set
![]() $\mathscr {F}=\Psi _*a^{-1}\mathcal {F}$
with the notation in 3.6. Then, there is a canonical isomorphism
$\mathscr {F}=\Psi _*a^{-1}\mathcal {F}$
with the notation in 3.6. Then, there is a canonical isomorphism
and the canonical morphism
is an almost isomorphism in the derived category
![]() $\mathbf {D}(\overline {\mathbb {Z}_p}\textrm {-}\mathbf {Mod}_{\mathbf {I}_{Y \to X^Y}})$
[Reference HeHe23, 5.7].
$\mathbf {D}(\overline {\mathbb {Z}_p}\textrm {-}\mathbf {Mod}_{\mathbf {I}_{Y \to X^Y}})$
[Reference HeHe23, 5.7].
Proof The first assertion follows from the canonical isomorphisms
 $\mathrm {R}\Gamma (Y_{\mathrm {\acute {e}t}},\mathcal {F})\stackrel {\sim }{\longrightarrow } \mathrm {R}\Gamma ((\mathbf {Sch}^{\mathrm {coh}}_{/Y})_{\mathrm {v}},a^{-1}\mathcal {F})=\mathrm {R}\Gamma (\mathbf {I}_{Y \to X^Y},\mathrm {R}\Psi _*a^{-1}\mathcal {F}) \stackrel {\sim }{\longleftarrow }\mathrm {R}\Gamma (\mathbf {I}_{Y \to X^Y},\Psi _*a^{-1}\mathcal {F})$
by 3.4 and 3.8(1) (cf. 6.13(1)). The second assertion follows from applying 6.11 to the morphism
$\mathrm {R}\Gamma (Y_{\mathrm {\acute {e}t}},\mathcal {F})\stackrel {\sim }{\longrightarrow } \mathrm {R}\Gamma ((\mathbf {Sch}^{\mathrm {coh}}_{/Y})_{\mathrm {v}},a^{-1}\mathcal {F})=\mathrm {R}\Gamma (\mathbf {I}_{Y \to X^Y},\mathrm {R}\Psi _*a^{-1}\mathcal {F}) \stackrel {\sim }{\longleftarrow }\mathrm {R}\Gamma (\mathbf {I}_{Y \to X^Y},\Psi _*a^{-1}\mathcal {F})$
by 3.4 and 3.8(1) (cf. 6.13(1)). The second assertion follows from applying 6.11 to the morphism
![]() $X\to \mathop {\mathrm {Spec}}(A)$
and from the fact that the associated topos of
$X\to \mathop {\mathrm {Spec}}(A)$
and from the fact that the associated topos of
![]() $\mathbf {I}_{\mathop {\mathrm {Spec}}(A[1/p])\to \mathop {\mathrm {Spec}}(A)}$
is local (3.7).
$\mathbf {I}_{\mathop {\mathrm {Spec}}(A[1/p])\to \mathop {\mathrm {Spec}}(A)}$
is local (3.7).
Lemma 6.13 (cf. 6.5(1))
With the notation in 6.3 and 6.4, let
![]() $\mathcal {F}'$
be a torsion abelian sheaf on
$\mathcal {F}'$
be a torsion abelian sheaf on
![]() $Y^{\prime }_{\mathrm {\acute {e}t}}$
,
$Y^{\prime }_{\mathrm {\acute {e}t}}$
,
![]() $\mathcal {H}=\mathrm {R} f_{\mathrm {\acute {e}t} *}\mathcal {F}'$
, and we set
$\mathcal {H}=\mathrm {R} f_{\mathrm {\acute {e}t} *}\mathcal {F}'$
, and we set
![]() $\mathscr {F}'=\Psi ^{\prime }_*a^{{\prime }-1}\mathcal {F}'$
,
$\mathscr {F}'=\Psi ^{\prime }_*a^{{\prime }-1}\mathcal {F}'$
,
![]() $\mathscr {H}=\mathrm {R}\Psi _*a^{-1}\mathcal {H}$
. Let
$\mathscr {H}=\mathrm {R}\Psi _*a^{-1}\mathcal {H}$
. Let
![]() $\widetilde {X}$
be an object of
$\widetilde {X}$
be an object of
![]() $\mathbf {I}_{Y\to X^Y}$
,
$\mathbf {I}_{Y\to X^Y}$
,
![]() $\widetilde {Y}=\overline {\eta }\times _{\overline {S}} \widetilde {X}$
,
$\widetilde {Y}=\overline {\eta }\times _{\overline {S}} \widetilde {X}$
,
![]() $\widetilde {\mathcal {F}'}=g^{{\prime }-1}_{\mathrm {\acute {e}t}}\mathcal {F}'$
.
$\widetilde {\mathcal {F}'}=g^{{\prime }-1}_{\mathrm {\acute {e}t}}\mathcal {F}'$
.
-
(1) The sheaf
 $\mathrm {R}^q f_{\mathbf {I} *}\mathscr {F}'$
is canonically isomorphic to the presheaf
$\mathrm {R}^q f_{\mathbf {I} *}\mathscr {F}'$
is canonically isomorphic to the presheaf
 $\widetilde {X}\mapsto H^q_{\mathrm {\acute {e}t}}(\widetilde {Y'}, \widetilde {\mathcal {F}'})$
for each integer q.
$\widetilde {X}\mapsto H^q_{\mathrm {\acute {e}t}}(\widetilde {Y'}, \widetilde {\mathcal {F}'})$
for each integer q. -
(2) If
 $Y'\to Y$
is proper, then there exists a canonical isomorphism
$Y'\to Y$
is proper, then there exists a canonical isomorphism
 $\mathscr {H}\stackrel {\sim }{\longrightarrow } \mathrm {R} f_{\mathbf {I} *}\mathscr {F}' $
.
$\mathscr {H}\stackrel {\sim }{\longrightarrow } \mathrm {R} f_{\mathbf {I} *}\mathscr {F}' $
.
Proof Note that the canonical morphism
![]() $\mathscr {F}'\to \mathrm {R}\Psi ^{\prime }_*a^{{\prime }-1}\mathcal {F}'$
is an isomorphism by 3.8(1). Thus,
$\mathscr {F}'\to \mathrm {R}\Psi ^{\prime }_*a^{{\prime }-1}\mathcal {F}'$
is an isomorphism by 3.8(1). Thus,
![]() $\mathrm {R} f_{\mathbf {I} *}\mathscr {F}'=\mathrm {R}(\Psi \circ f_{\mathrm {v}})_*a^{{\prime }-1}\mathcal {F}'$
, whose qth cohomology is the sheaf associated with the presheaf
$\mathrm {R} f_{\mathbf {I} *}\mathscr {F}'=\mathrm {R}(\Psi \circ f_{\mathrm {v}})_*a^{{\prime }-1}\mathcal {F}'$
, whose qth cohomology is the sheaf associated with the presheaf
![]() $\widetilde {X}\mapsto H^q_{\mathrm {v}}(\widetilde {Y'}, \widetilde {a'}^{-1}\widetilde {\mathcal {F}'})=H^q_{\mathrm {\acute {e}t}}(\widetilde {Y'}, \widetilde {\mathcal {F}'})$
by 3.4, and thus (1) follows. If
$\widetilde {X}\mapsto H^q_{\mathrm {v}}(\widetilde {Y'}, \widetilde {a'}^{-1}\widetilde {\mathcal {F}'})=H^q_{\mathrm {\acute {e}t}}(\widetilde {Y'}, \widetilde {\mathcal {F}'})$
by 3.4, and thus (1) follows. If
![]() $Y'\to Y$
is proper, then the base change morphism
$Y'\to Y$
is proper, then the base change morphism
![]() $a^{-1}\mathrm {R} f_{\mathrm {\acute {e}t} *}\to \mathrm {R} f_{\mathrm {v}*}a^{{\prime }-1}$
induces an isomorphism
$a^{-1}\mathrm {R} f_{\mathrm {\acute {e}t} *}\to \mathrm {R} f_{\mathrm {v}*}a^{{\prime }-1}$
induces an isomorphism
![]() $a^{-1} \mathcal {H}\stackrel {\sim }{\longrightarrow } \mathrm {R} f_{\mathrm {v}*}a^{{\prime }-1}\mathcal {F}'$
by [Reference HeHe23, 3.10], and thus (2) follows.
$a^{-1} \mathcal {H}\stackrel {\sim }{\longrightarrow } \mathrm {R} f_{\mathrm {v}*}a^{{\prime }-1}\mathcal {F}'$
by [Reference HeHe23, 3.10], and thus (2) follows.
Theorem 6.14 With the notation in 6.3, let
![]() $\mathbb {F}'$
be a finite locally constant abelian sheaf on
$\mathbb {F}'$
be a finite locally constant abelian sheaf on
![]() $Y^{\prime }_{\mathrm {\acute {e}t}}$
. Assume that:
$Y^{\prime }_{\mathrm {\acute {e}t}}$
. Assume that:
-
(i) the morphism
 $X' \to X$
is proper of finite presentation, and that
$X' \to X$
is proper of finite presentation, and that -
(ii) the sheaf
 $\mathrm {R}^q f_{\mathrm {\acute {e}t}*} \mathbb {F}'$
is finite locally constant for each integer q and nonzero for finitely many q, and that
$\mathrm {R}^q f_{\mathrm {\acute {e}t}*} \mathbb {F}'$
is finite locally constant for each integer q and nonzero for finitely many q, and that -
(iii) we have
 $\mathrm {R}^q\psi _*\mathbb {H}=0$
(resp.
$\mathrm {R}^q\psi _*\mathbb {H}=0$
(resp.
 $\mathrm {R}^q\psi ^{\prime }_*\mathbb {H}=0$
) for any finite locally constant abelian sheaf
$\mathrm {R}^q\psi ^{\prime }_*\mathbb {H}=0$
) for any finite locally constant abelian sheaf
 $\mathbb {H}$
on
$\mathbb {H}$
on
 $Y_{\mathrm {\acute {e}t}}$
(resp.
$Y_{\mathrm {\acute {e}t}}$
(resp.
 $Y^{\prime }_{\mathrm {\acute {e}t}}$
) and any integer
$Y^{\prime }_{\mathrm {\acute {e}t}}$
) and any integer
 $q>0$
.
$q>0$
.
Then, the relative Faltings’ comparison morphism associated with f and
![]() $\mathbb {F}'$
(5.6.1) (which exists by (iii)) is an almost isomorphism in the derived category
$\mathbb {F}'$
(5.6.1) (which exists by (iii)) is an almost isomorphism in the derived category
![]() $\mathbf {D}(\overline {\mathbb {Z}_p}\textrm {-}\mathbf {Mod}_{\mathbf {E}_{Y \to X}^{\mathrm {\acute {e}t}}})$
[Reference HeHe23, 5.7], and it induces an almost isomorphism
$\mathbf {D}(\overline {\mathbb {Z}_p}\textrm {-}\mathbf {Mod}_{\mathbf {E}_{Y \to X}^{\mathrm {\acute {e}t}}})$
[Reference HeHe23, 5.7], and it induces an almost isomorphism
of
![]() $\overline {\mathbb {Z}_p}$
-modules for each integer q.
$\overline {\mathbb {Z}_p}$
-modules for each integer q.
Proof We follow the discussion of 6.6 and set
![]() $\mathscr {F}'=\Psi ^{\prime }_*a^{{\prime }-1}\mathbb {F}'$
. The canonical morphism (6.6.4)
$\mathscr {F}'=\Psi ^{\prime }_*a^{{\prime }-1}\mathbb {F}'$
. The canonical morphism (6.6.4)
is an almost isomorphism by 6.7. It remains to show that the canonical morphism (6.6.3)
is also an almost isomorphism. With the notation in 6.13 by taking
![]() $\mathcal {F}'=\mathbb {F}'$
, the complex
$\mathcal {F}'=\mathbb {F}'$
, the complex
![]() $\mathcal {H}$
is a bounded complex whose cohomologies
$\mathcal {H}$
is a bounded complex whose cohomologies
![]() $H^q(\mathcal {H})$
are finite locally constant abelian sheaves by condition (ii). Consider the commutative diagram (3.6.4):
$H^q(\mathcal {H})$
are finite locally constant abelian sheaves by condition (ii). Consider the commutative diagram (3.6.4):

We set
![]() $\mathcal {L}=\mathrm {R}\psi _*\mathcal {H}$
. Then,
$\mathcal {L}=\mathrm {R}\psi _*\mathcal {H}$
. Then,
![]() $H^q(\mathcal {L})=\psi _*H^q(\mathcal {H})$
by Cartan–Leray spectral sequence and condition (iii). Hence,
$H^q(\mathcal {L})=\psi _*H^q(\mathcal {H})$
by Cartan–Leray spectral sequence and condition (iii). Hence,
![]() $\mathcal {L}$
is a bounded complex of abelian sheaves whose cohomologies are finite locally constant by 5.3 so that the canonical morphism
$\mathcal {L}$
is a bounded complex of abelian sheaves whose cohomologies are finite locally constant by 5.3 so that the canonical morphism
is an almost isomorphism by 3.9 (cf. [Reference HeHe23, 8.15]).
On the other hand,
![]() $H^q(\mathscr {H})=\Psi _*a^{-1}H^q(\mathcal {H})$
by Cartan–Leray spectral sequence and 3.8(1). Thus, the base change morphism
$H^q(\mathscr {H})=\Psi _*a^{-1}H^q(\mathcal {H})$
by Cartan–Leray spectral sequence and 3.8(1). Thus, the base change morphism
![]() $\varepsilon ^{-1}\mathrm {R}\psi _*\to \mathrm {R}\Psi _*a^{-1}$
induces an isomorphism
$\varepsilon ^{-1}\mathrm {R}\psi _*\to \mathrm {R}\Psi _*a^{-1}$
induces an isomorphism
![]() $\varepsilon ^{-1}\mathcal {L}\stackrel {\sim }{\longrightarrow } \mathscr {H}$
by 6.2. Moreover, the canonical morphism
$\varepsilon ^{-1}\mathcal {L}\stackrel {\sim }{\longrightarrow } \mathscr {H}$
by 6.2. Moreover, the canonical morphism
![]() $\mathcal {L}\to \mathrm {R}\varepsilon _*\varepsilon ^{-1}\mathcal {L}=\mathrm {R}\varepsilon _*\mathscr {H}=\mathrm {R}\psi _*\mathrm {R} a_*a^{-1}\mathcal {H}$
is an isomorphism by 3.4. Thus, the canonical morphism
$\mathcal {L}\to \mathrm {R}\varepsilon _*\varepsilon ^{-1}\mathcal {L}=\mathrm {R}\varepsilon _*\mathscr {H}=\mathrm {R}\psi _*\mathrm {R} a_*a^{-1}\mathcal {H}$
is an isomorphism by 3.4. Thus, the canonical morphism
is an almost isomorphism by (6.14.5). In conclusion, (6.14.3) is an almost isomorphism by (6.14.6) and by the canonical isomorphisms
![]() $\varepsilon ^{-1}\mathcal {L}\stackrel {\sim }{\longrightarrow } \mathscr {H}\stackrel {\sim }{\longrightarrow } \mathrm {R} f_{\mathbf {I} *}\mathscr {F}'$
.
$\varepsilon ^{-1}\mathcal {L}\stackrel {\sim }{\longrightarrow } \mathscr {H}\stackrel {\sim }{\longrightarrow } \mathrm {R} f_{\mathbf {I} *}\mathscr {F}'$
.
Remark 6.15 We give two concrete situations where the conditions in 6.14 are satisfied:
-
(1) Let
 $\overline {\mathbb {Z}_p}$
be the integral closure of
$\overline {\mathbb {Z}_p}$
be the integral closure of
 $\mathbb {Z}_p$
in an algebraic closure
$\mathbb {Z}_p$
in an algebraic closure
 $\overline {\mathbb {Q}_p}$
of
$\overline {\mathbb {Q}_p}$
of
 $\mathbb {Q}_p$
, let
$\mathbb {Q}_p$
, let
 $X'\to X$
be a proper and finitely presented morphism of coherent
$X'\to X$
be a proper and finitely presented morphism of coherent
 $\overline {\mathbb {Z}_p}$
-schemes, and let
$\overline {\mathbb {Z}_p}$
-schemes, and let
 $Y'\to Y$
be the base change of
$Y'\to Y$
be the base change of
 $X'\to X$
by
$X'\to X$
by
 $\mathop {\mathrm {Spec}}(\overline {\mathbb {Q}_p})\to \mathop {\mathrm {Spec}}(\overline {\mathbb {Z}_p})$
. Assume that
$\mathop {\mathrm {Spec}}(\overline {\mathbb {Q}_p})\to \mathop {\mathrm {Spec}}(\overline {\mathbb {Z}_p})$
. Assume that
 $Y'\to Y$
is smooth. Then, the condition (ii) is guaranteed by [SGA 4III
, XVI.2.2 and XVII.5.2.8.1], and the condition (iii) is guaranteed by 5.8.
$Y'\to Y$
is smooth. Then, the condition (ii) is guaranteed by [SGA 4III
, XVI.2.2 and XVII.5.2.8.1], and the condition (iii) is guaranteed by 5.8. -
(2) Let
 $\mathcal {O}_K$
be a strictly Henselian discrete valuation ring with fraction field K of characteristic
$\mathcal {O}_K$
be a strictly Henselian discrete valuation ring with fraction field K of characteristic
 $0$
and residue field of characteristic p, let
$0$
and residue field of characteristic p, let
 $\overline {K}$
be an algebraic closure of K, let
$\overline {K}$
be an algebraic closure of K, let
 $X'\to X$
be a proper morphism of
$X'\to X$
be a proper morphism of
 $\mathcal {O}_K$
-schemes of finite type, and let
$\mathcal {O}_K$
-schemes of finite type, and let
 $Y'\to Y$
be the base change of
$Y'\to Y$
be the base change of
 $X'\to X$
by
$X'\to X$
by
 $\mathop {\mathrm {Spec}}(\overline {K})\to \mathop {\mathrm {Spec}}(\mathcal {O}_K)$
. Assume that
$\mathop {\mathrm {Spec}}(\overline {K})\to \mathop {\mathrm {Spec}}(\mathcal {O}_K)$
. Assume that
 $Y'\to Y$
is smooth. Then, the condition (ii) is guaranteed by [SGA 4III
, XVI.2.2 and XVII.5.2.8.1], and the condition (iii) is guaranteed by 5.7.
$Y'\to Y$
is smooth. Then, the condition (ii) is guaranteed by [SGA 4III
, XVI.2.2 and XVII.5.2.8.1], and the condition (iii) is guaranteed by 5.7.
Acknowledgments
This work is part of my thesis prepared at Université Paris-Saclay and Institut des Hautes Études Scientifiques. I would like to express my sincere gratitude to my doctoral supervisor, Ahmed Abbes, for his guidance to this project, his thorough review of this work, and his plenty of helpful suggestions on both research and writing.