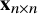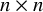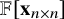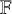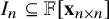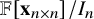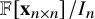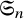1 Introduction
Let
![]() ${\mathbf {x}}$
be a finite set of variables, and let
${\mathbf {x}}$
be a finite set of variables, and let
![]() ${\mathbb {F}}[{\mathbf {x}}]$
be the polynomial ring in these variables over a field
${\mathbb {F}}[{\mathbf {x}}]$
be the polynomial ring in these variables over a field
![]() ${\mathbb {F}}$
. If
${\mathbb {F}}$
. If
![]() $I \subseteq {\mathbb {F}}[{\mathbf {x}}]$
is a homogeneous ideal, the quotient ring
$I \subseteq {\mathbb {F}}[{\mathbf {x}}]$
is a homogeneous ideal, the quotient ring
![]() ${\mathbb {F}}[{\mathbf {x}}]/I$
has the structure of a graded vector space. The Hilbert series of
${\mathbb {F}}[{\mathbf {x}}]/I$
has the structure of a graded vector space. The Hilbert series of
![]() ${\mathbb {F}}[{\mathbf {x}}]/I$
is the graded dimension of the vector space, viz.
${\mathbb {F}}[{\mathbf {x}}]/I$
is the graded dimension of the vector space, viz.
Macaulay [Reference Macaulay13] characterized the polynomials
![]() $a_0 + a_1 \cdot q + \cdots + a_d \cdot q^d$
with positive integer coefficients which arise as the Hilbert series of a graded quotient of the form
$a_0 + a_1 \cdot q + \cdots + a_d \cdot q^d$
with positive integer coefficients which arise as the Hilbert series of a graded quotient of the form
![]() ${\mathbb {F}}[{\mathbf {x}}]/I$
. Following the exposition of Stanley [Reference Stanley19, Thm. 1.3], for positive integers a and i, there is a unique representation
${\mathbb {F}}[{\mathbf {x}}]/I$
. Following the exposition of Stanley [Reference Stanley19, Thm. 1.3], for positive integers a and i, there is a unique representation
![]() $a = {b_i \choose i} + {b_{i-1} \choose i-1} + \cdots + {b_j \choose j}$
, where
$a = {b_i \choose i} + {b_{i-1} \choose i-1} + \cdots + {b_j \choose j}$
, where
![]() $b_i> b_{i-1} > \cdots > b_j \geq j \geq 1$
. Let
$b_i> b_{i-1} > \cdots > b_j \geq j \geq 1$
. Let
![]() $a^{\langle i \rangle } := {b_i + 1 \choose i+1} + \cdots + {b_j + 1 \choose j +1}$
. Then
$a^{\langle i \rangle } := {b_i + 1 \choose i+1} + \cdots + {b_j + 1 \choose j +1}$
. Then
![]() $a_0 + a_1 \cdot q + \cdots + a_d \cdot q^d$
is the Hilbert series of some graded quotient
$a_0 + a_1 \cdot q + \cdots + a_d \cdot q^d$
is the Hilbert series of some graded quotient
![]() ${\mathbb {F}}[{\mathbf {x}}]/I$
if and only if
${\mathbb {F}}[{\mathbf {x}}]/I$
if and only if
![]() $a_{i+1} \leq a_i^{\langle i+1 \rangle }$
for
$a_{i+1} \leq a_i^{\langle i+1 \rangle }$
for
![]() $0 \leq i \leq d-1$
.
$0 \leq i \leq d-1$
.
In this paper, we show that a generating function arising from increasing subsequences of permutations is the Hilbert series of a natural graded ring. Write
![]() ${\mathfrak {S}}_n$
for the symmetric group on
${\mathfrak {S}}_n$
for the symmetric group on
![]() $[n] := \{1, \dots , n \}$
. If
$[n] := \{1, \dots , n \}$
. If
![]() $w \in {\mathfrak {S}}_n$
is a permutation, an increasing subsequence in w is a set of positions
$w \in {\mathfrak {S}}_n$
is a permutation, an increasing subsequence in w is a set of positions
![]() $1 \leq i_1 < \cdots < i_k \leq n$
whose images under w satisfy
$1 \leq i_1 < \cdots < i_k \leq n$
whose images under w satisfy
![]() $w(i_1) < \cdots < w(i_k)$
. The integer k is the length of this increasing subsequence. We write
$w(i_1) < \cdots < w(i_k)$
. The integer k is the length of this increasing subsequence. We write
for the length of the longest increasing subsequence of w and
for the number of permutations in
![]() ${\mathfrak {S}}_n$
whose longest increasing subsequence has length k. For any positive integer n, the sequence
${\mathfrak {S}}_n$
whose longest increasing subsequence has length k. For any positive integer n, the sequence
![]() $(a_{n,1}, a_{n,2}, \dots , a_{n,n})$
was conjectured by Chen [Reference Chen4, Conj. 1.1] to be log-concave, that is,
$(a_{n,1}, a_{n,2}, \dots , a_{n,n})$
was conjectured by Chen [Reference Chen4, Conj. 1.1] to be log-concave, that is,
![]() $a_{n,i}^2 \geq a_{n,i-1} \cdot a_{n,i+1}$
for all
$a_{n,i}^2 \geq a_{n,i-1} \cdot a_{n,i+1}$
for all
![]() $1 < i < n$
. When
$1 < i < n$
. When
![]() $n = 4$
, this sequence reads
$n = 4$
, this sequence reads
![]() $(a_{4,1},a_{4,2},a_{4,3},a_{4,4}) = (1,13,9,1)$
.
$(a_{4,1},a_{4,2},a_{4,3},a_{4,4}) = (1,13,9,1)$
.
The following ideal
![]() $I_n$
is our object of study. Despite the simplicity of its generating set, it will turn out to have deep connections to the combinatorics of increasing subsequences.
$I_n$
is our object of study. Despite the simplicity of its generating set, it will turn out to have deep connections to the combinatorics of increasing subsequences.
Definition 1.1. Let
![]() ${\mathbf {x}}_{n \times n}$
be an
${\mathbf {x}}_{n \times n}$
be an
![]() $n \times n$
matrix of variables
$n \times n$
matrix of variables
![]() $(x_{i,j})_{1 \leq i , j \leq n}$
, and consider the polynomial ring
$(x_{i,j})_{1 \leq i , j \leq n}$
, and consider the polynomial ring
![]() ${\mathbb {F}}[{\mathbf {x}}_{n \times n}]$
over these variables. Let
${\mathbb {F}}[{\mathbf {x}}_{n \times n}]$
over these variables. Let
![]() $I_n \subseteq {\mathbb {F}}[{\mathbf {x}}_{n \times n}]$
be the ideal generated by
$I_n \subseteq {\mathbb {F}}[{\mathbf {x}}_{n \times n}]$
be the ideal generated by
-
• any product
 $x_{i,j} \cdot x_{i,j'}$
for
$x_{i,j} \cdot x_{i,j'}$
for
 $1 \leq i \leq n$
and
$1 \leq i \leq n$
and
 $1 \leq j, j' \leq n$
of variables in the same row,
$1 \leq j, j' \leq n$
of variables in the same row, -
• any product
 $x_{i,j} \cdot x_{i',j}$
for
$x_{i,j} \cdot x_{i',j}$
for
 $1 \leq i, i' \leq n$
and
$1 \leq i, i' \leq n$
and
 $1 \leq j \leq n$
of variables in the same column,
$1 \leq j \leq n$
of variables in the same column, -
• any row sum
 $x_{i,1} + \cdots + x_{i,n}$
for
$x_{i,1} + \cdots + x_{i,n}$
for
 $1 \leq i \leq n$
, and
$1 \leq i \leq n$
, and -
• and column sum
 $x_{1,j} + \cdots + x_{n,j}$
for
$x_{1,j} + \cdots + x_{n,j}$
for
 $1 \leq j \leq n$
.
$1 \leq j \leq n$
.
The ideal
![]() $I_n \subseteq {\mathbb {F}}[{\mathbf {x}}_{n \times n}]$
is homogeneous, so
$I_n \subseteq {\mathbb {F}}[{\mathbf {x}}_{n \times n}]$
is homogeneous, so
![]() ${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
is a graded
${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
is a graded
![]() ${\mathbb {F}}$
-algebra. The natural action of the group
${\mathbb {F}}$
-algebra. The natural action of the group
![]() ${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
on the variable matrix
${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
on the variable matrix
![]() ${\mathbf {x}}_{n \times n}$
given by independent row and column permutation induces an action on
${\mathbf {x}}_{n \times n}$
given by independent row and column permutation induces an action on
![]() ${\mathbb {F}}[{\mathbf {x}}_{n \times n}]$
which stabilizes
${\mathbb {F}}[{\mathbf {x}}_{n \times n}]$
which stabilizes
![]() $I_n$
so that
$I_n$
so that
![]() ${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
is a graded
${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
is a graded
![]() ${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
-module.
${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
-module.
When
![]() $n = 1$
, we have
$n = 1$
, we have
![]() $I_1 = (x_{1,1}) \subseteq {\mathbb {F}}[{\mathbf {x}}_{1 \times 1}]$
so that
$I_1 = (x_{1,1}) \subseteq {\mathbb {F}}[{\mathbf {x}}_{1 \times 1}]$
so that
![]() ${\mathbb {F}}[{\mathbf {x}}_{1 \times 1}]/I_1 = {\mathbb {F}}$
. When
${\mathbb {F}}[{\mathbf {x}}_{1 \times 1}]/I_1 = {\mathbb {F}}$
. When
![]() $n = 2$
, the ideal
$n = 2$
, the ideal
![]() $I_2 \subseteq {\mathbb {F}}[{\mathbf {x}}_{2 \times 2}]$
has generators
$I_2 \subseteq {\mathbb {F}}[{\mathbf {x}}_{2 \times 2}]$
has generators
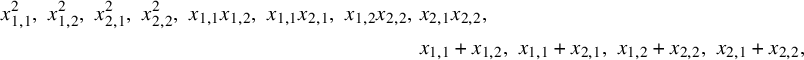 $$ \begin{align*} x_{1,1}^2, \, \,x_{1,2}^2, \, \, x_{2,1}^2, \, \, x_{2,2}^2, \, \, x_{1,1} x_{1,2}, \, \, x_{1,1} x_{2,1}, \, \, x_{1,2} x_{2,2}, \, \, & x_{2,1} x_{2,2}, \\ & x_{1,1} + x_{1,2}, \, \, x_{1,1} + x_{2,1}, \, \, x_{1,2} + x_{2,2}, \, \, x_{2,1} + x_{2,2}, \end{align*} $$
$$ \begin{align*} x_{1,1}^2, \, \,x_{1,2}^2, \, \, x_{2,1}^2, \, \, x_{2,2}^2, \, \, x_{1,1} x_{1,2}, \, \, x_{1,1} x_{2,1}, \, \, x_{1,2} x_{2,2}, \, \, & x_{2,1} x_{2,2}, \\ & x_{1,1} + x_{1,2}, \, \, x_{1,1} + x_{2,1}, \, \, x_{1,2} + x_{2,2}, \, \, x_{2,1} + x_{2,2}, \end{align*} $$
and it is not hard to check that
![]() ${\mathbb {F}}[{\mathbf {x}}_{2 \times 2}]/I_2$
has Hilbert series
${\mathbb {F}}[{\mathbf {x}}_{2 \times 2}]/I_2$
has Hilbert series
![]() $1 + q$
and that the set of monomials
$1 + q$
and that the set of monomials
![]() $\{1, x_{1,2} \}$
descends to a basis.
$\{1, x_{1,2} \}$
descends to a basis.
We prove (Corollary 3.13) that the Hilbert series of
![]() ${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
is given by
${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
is given by
so that the (reversal of the) generating function for permutations in
![]() ${\mathfrak {S}}_n$
by longest increasing subsequence is the Hilbert series of
${\mathfrak {S}}_n$
by longest increasing subsequence is the Hilbert series of
![]() ${\mathbb {F}}[{\mathbf {x}}_{n \times n}] / I_n$
. In particular, the polynomial
${\mathbb {F}}[{\mathbf {x}}_{n \times n}] / I_n$
. In particular, the polynomial
![]() $a_{n,n} + a_{n,n-1} \cdot q + \cdots + a_{n,1} \cdot q^{n-1}$
satisfies Macaulay’s criterion, a fact which seems difficult to prove directly from the combinatorics of increasing subsequences. Taking
$a_{n,n} + a_{n,n-1} \cdot q + \cdots + a_{n,1} \cdot q^{n-1}$
satisfies Macaulay’s criterion, a fact which seems difficult to prove directly from the combinatorics of increasing subsequences. Taking
![]() $q \to 1$
, the ungraded vector space
$q \to 1$
, the ungraded vector space
![]() ${\mathbb {F}}[{\mathbf {x}}_{n \times n}] / I_n$
has dimension
${\mathbb {F}}[{\mathbf {x}}_{n \times n}] / I_n$
has dimension
We will attach (Definition 3.9) a monomial
![]() ${\mathfrak {s}}(w)$
in the variables
${\mathfrak {s}}(w)$
in the variables
![]() $x_{i,j}$
to any permutation
$x_{i,j}$
to any permutation
![]() $w \in {\mathfrak {S}}_n$
such that
$w \in {\mathfrak {S}}_n$
such that
and prove (Theorem 3.12) that
descends to a vector space basis of
![]() ${\mathbb {F}}[{\mathbf {x}}_{n \times n}] / I_n$
. In fact, this will be the standard monomial basis of
${\mathbb {F}}[{\mathbf {x}}_{n \times n}] / I_n$
. In fact, this will be the standard monomial basis of
![]() ${\mathbb {F}}[{\mathbf {x}}_{n \times n}] / I_n$
with respect to a ‘Toeplitz term order’
${\mathbb {F}}[{\mathbf {x}}_{n \times n}] / I_n$
with respect to a ‘Toeplitz term order’
![]() $<_{\mathrm {Top}}$
(Definition 3.8). The notation
$<_{\mathrm {Top}}$
(Definition 3.8). The notation
![]() ${\mathfrak {s}}$
refers to the use of Viennot’s shadow line formulation [Reference Viennot, Foata and Notes20] of the Schensted correspondence in the definition of
${\mathfrak {s}}$
refers to the use of Viennot’s shadow line formulation [Reference Viennot, Foata and Notes20] of the Schensted correspondence in the definition of
![]() ${\mathfrak {s}}(w)$
. Our results may be interpreted as the ideal
${\mathfrak {s}}(w)$
. Our results may be interpreted as the ideal
![]() $I_n \subseteq {\mathbb {F}}[{\mathbf {x}}_{n \times n}]$
together with the term order
$I_n \subseteq {\mathbb {F}}[{\mathbf {x}}_{n \times n}]$
together with the term order
![]() $<_{\mathrm {Top}}$
‘seeing’ the Viennot shadow line construction.
$<_{\mathrm {Top}}$
‘seeing’ the Viennot shadow line construction.
When the field
![]() ${\mathbb {F}}$
has characteristic zero or characteristic
${\mathbb {F}}$
has characteristic zero or characteristic
![]() $p> n$
, we characterize the structure of
$p> n$
, we characterize the structure of
![]() ${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
as an ungraded (Corollary 4.1) and graded (Theorem 4.2) module over the product group
${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
as an ungraded (Corollary 4.1) and graded (Theorem 4.2) module over the product group
![]() ${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
. The module structure of
${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
. The module structure of
![]() ${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
relates to a family of
${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
relates to a family of
![]() ${\mathfrak {S}}_n$
-characters considered by Novak and the author [Reference Novak and Rhoades14] in a strengthening of Chen’s log-concavity conjecture.
${\mathfrak {S}}_n$
-characters considered by Novak and the author [Reference Novak and Rhoades14] in a strengthening of Chen’s log-concavity conjecture.
For
![]() $1 \leq k \leq n$
, define a character
$1 \leq k \leq n$
, define a character
![]() $\alpha _{n,k}: {\mathfrak {S}}_n \rightarrow {\mathbb {F}}$
by the rule
$\alpha _{n,k}: {\mathfrak {S}}_n \rightarrow {\mathbb {F}}$
by the rule
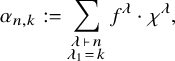 $$ \begin{align} \alpha_{n,k} := \sum_{\substack{\lambda \, \vdash \, n \\ \lambda_1 \, = \, k}} f^{\lambda} \cdot \chi^{\lambda}, \end{align} $$
$$ \begin{align} \alpha_{n,k} := \sum_{\substack{\lambda \, \vdash \, n \\ \lambda_1 \, = \, k}} f^{\lambda} \cdot \chi^{\lambda}, \end{align} $$
where the sum is over partitions of n whose first row has length k. Here,
![]() $\chi ^{\lambda }: {\mathfrak {S}}_n \rightarrow {\mathbb {F}}$
is the irreducible character of
$\chi ^{\lambda }: {\mathfrak {S}}_n \rightarrow {\mathbb {F}}$
is the irreducible character of
![]() ${\mathfrak {S}}_n$
attached to the partition
${\mathfrak {S}}_n$
attached to the partition
![]() $\lambda $
and
$\lambda $
and
![]() $f^\lambda = \chi ^\lambda (e)$
is the dimension of the irreducible
$f^\lambda = \chi ^\lambda (e)$
is the dimension of the irreducible
![]() ${\mathfrak {S}}_n$
-module attached to
${\mathfrak {S}}_n$
-module attached to
![]() $\lambda $
. We have
$\lambda $
. We have
![]() $\alpha _{n,k}(e) = a_{n,k}$
, so the sequence
$\alpha _{n,k}(e) = a_{n,k}$
, so the sequence
![]() $(\alpha _{n,1}, \dots , \alpha _{n,n})$
of class functions is a representation-theoretic refinement of the sequence
$(\alpha _{n,1}, \dots , \alpha _{n,n})$
of class functions is a representation-theoretic refinement of the sequence
![]() $(a_{n,1}, \dots , a_{n,n})$
appearing in Chen’s conjecture.
$(a_{n,1}, \dots , a_{n,n})$
appearing in Chen’s conjecture.
Novak and the author conjectured [Reference Novak and Rhoades14, Conj. 2] the the difference
![]() $\alpha _{n,k} * \alpha _{n,k} - \alpha _{n,k-1} * \alpha _{n,k+1}$
is a genuine (rather than merely virtual) character of
$\alpha _{n,k} * \alpha _{n,k} - \alpha _{n,k-1} * \alpha _{n,k+1}$
is a genuine (rather than merely virtual) character of
![]() ${\mathfrak {S}}_n$
for all
${\mathfrak {S}}_n$
for all
![]() $1 < k < n$
, where
$1 < k < n$
, where
![]() $*$
denotes the Kronecker product of class functions on
$*$
denotes the Kronecker product of class functions on
![]() ${\mathfrak {S}}_n$
. Since
${\mathfrak {S}}_n$
. Since
![]() $\alpha _{n,k}(e) = a_{n,k}$
, this would imply Chen’s conjecture. One way to prove this stronger conjecture would be to describe an
$\alpha _{n,k}(e) = a_{n,k}$
, this would imply Chen’s conjecture. One way to prove this stronger conjecture would be to describe an
![]() ${\mathfrak {S}}_n$
-module which has
${\mathfrak {S}}_n$
-module which has
![]() $\alpha _{n,k} * \alpha _{n,k} - \alpha _{n,k-1} * \alpha _{n,k+1}$
as its character. We prove (Corollary 4.3) that
$\alpha _{n,k} * \alpha _{n,k} - \alpha _{n,k-1} * \alpha _{n,k+1}$
as its character. We prove (Corollary 4.3) that
![]() $\alpha _{n,k}$
is the character of the degree
$\alpha _{n,k}$
is the character of the degree
![]() $n-k$
piece of the quotient
$n-k$
piece of the quotient
![]() ${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
, restricted from the product
${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
, restricted from the product
![]() ${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
to either factor of
${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
to either factor of
![]() ${\mathfrak {S}}_n$
. To the author’s knowledge, this is the simplest explicit module with character
${\mathfrak {S}}_n$
. To the author’s knowledge, this is the simplest explicit module with character
![]() $\alpha _{n,k}$
. We hope that this representation-theoretic model for
$\alpha _{n,k}$
. We hope that this representation-theoretic model for
![]() $\alpha _{n,k}$
can give new insight on the Novak–Rhoades conjecture. In fact, it appears that a stronger equivariant log-concavity result holds without restriction from
$\alpha _{n,k}$
can give new insight on the Novak–Rhoades conjecture. In fact, it appears that a stronger equivariant log-concavity result holds without restriction from
![]() ${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
to one of its factors; see Conjecture 4.4.
${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
to one of its factors; see Conjecture 4.4.
Our results have application to permutation statistics. For
![]() $k \geq 0$
, a statistic
$k \geq 0$
, a statistic
![]() $f: {\mathfrak {S}}_n \rightarrow {\mathbb {F}}$
is k-local [Reference Dafni, Filmus, Lifshitz, Lindzey and Vinyals5, Reference Hamaker and Rhoades10] if f is an
$f: {\mathfrak {S}}_n \rightarrow {\mathbb {F}}$
is k-local [Reference Dafni, Filmus, Lifshitz, Lindzey and Vinyals5, Reference Hamaker and Rhoades10] if f is an
![]() ${\mathbb {F}}$
-linear combination of indicator statistics which detect whether a permutation w carries a given list of k positions onto another given list of k values. The locality of a permutation statistic is a measure of its complexity; for example, the 0-local statistics are precisely the constant functions
${\mathbb {F}}$
-linear combination of indicator statistics which detect whether a permutation w carries a given list of k positions onto another given list of k values. The locality of a permutation statistic is a measure of its complexity; for example, the 0-local statistics are precisely the constant functions
![]() ${\mathfrak {S}}_n \rightarrow {\mathbb {F}}$
. While the vector space of k-local statistics is defined via a spanning set, finding an explicit basis for this vector space was an open problem in [Reference Hamaker and Rhoades10]. Our Gröbner-theoretic methods yield (Theorem 3.16) a solution to this problem.
${\mathfrak {S}}_n \rightarrow {\mathbb {F}}$
. While the vector space of k-local statistics is defined via a spanning set, finding an explicit basis for this vector space was an open problem in [Reference Hamaker and Rhoades10]. Our Gröbner-theoretic methods yield (Theorem 3.16) a solution to this problem.
To prove our results, we apply the method of orbit harmonics to the locus
![]() $P_n \subseteq {\mathbb {F}}^{n \times n}$
of permutation matrices inside the affine space
$P_n \subseteq {\mathbb {F}}^{n \times n}$
of permutation matrices inside the affine space
![]() ${\mathbb {F}}^{n \times n}$
of
${\mathbb {F}}^{n \times n}$
of
![]() $n \times n$
matrices over
$n \times n$
matrices over
![]() ${\mathbb {F}}$
. Orbit harmonics is a general method of transforming finite point loci
${\mathbb {F}}$
. Orbit harmonics is a general method of transforming finite point loci
![]() $Z \subseteq {\mathbb {F}}^N$
into graded quotients
$Z \subseteq {\mathbb {F}}^N$
into graded quotients
![]() ${\mathbb {F}}[{\mathbf {x}}_N]/{\mathrm {gr}} \, {\mathbf {I}}(Z)$
of the polynomial ring
${\mathbb {F}}[{\mathbf {x}}_N]/{\mathrm {gr}} \, {\mathbf {I}}(Z)$
of the polynomial ring
![]() ${\mathbb {F}}[{\mathbf {x}}_N]$
. This method dates back to at least the work of Kostant [Reference Kostant11] and has been used to study modules arising in Macdonald theory [Reference Garsia and Procesi7, Reference Griffin8, Reference Haglund, Rhoades and Shimozono9], understand cyclic sieving results [Reference Oh and Rhoades15], and interpret Donaldson–Thomas invariants of symmetric quivers as orbit enumerations in the lattice points of break divisor polytopes [Reference Reineke, Rhoades and Tewari16].
${\mathbb {F}}[{\mathbf {x}}_N]$
. This method dates back to at least the work of Kostant [Reference Kostant11] and has been used to study modules arising in Macdonald theory [Reference Garsia and Procesi7, Reference Griffin8, Reference Haglund, Rhoades and Shimozono9], understand cyclic sieving results [Reference Oh and Rhoades15], and interpret Donaldson–Thomas invariants of symmetric quivers as orbit enumerations in the lattice points of break divisor polytopes [Reference Reineke, Rhoades and Tewari16].
The rest of the paper is organized as follows. In Section 2
, we give background material on Gröbner bases, orbit harmonics and the Schensted correspondence. In Section 3
, we use Viennot’s shadow line interpretation of the Schensted correspondence to find a monomial basis of
![]() ${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
indexed by permutations in
${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
indexed by permutations in
![]() ${\mathfrak {S}}_n$
. We also give a basis for the space of k-local permutation statistics. In Section 4
, we describe the structure of
${\mathfrak {S}}_n$
. We also give a basis for the space of k-local permutation statistics. In Section 4
, we describe the structure of
![]() ${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
as a module over the product group
${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
as a module over the product group
![]() ${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
. We close in Section 5
with directions for future research.
${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
. We close in Section 5
with directions for future research.
2 Background
2.1 Gröbner theory
Let
![]() ${\mathbf {x}} = (x_1, \dots , x_N)$
be a finite list of variables, and let
${\mathbf {x}} = (x_1, \dots , x_N)$
be a finite list of variables, and let
![]() ${\mathbb {F}}[{\mathbf {x}}_N]$
be the polynomial ring in these variables over a field
${\mathbb {F}}[{\mathbf {x}}_N]$
be the polynomial ring in these variables over a field
![]() ${\mathbb {F}}$
. A total order
${\mathbb {F}}$
. A total order
![]() $<$
on the monomials in
$<$
on the monomials in
![]() ${\mathbb {F}}[{\mathbf {x}}_N]$
is a term order if
${\mathbb {F}}[{\mathbf {x}}_N]$
is a term order if
-
• we have
 $1 \leq m$
for all monomials m, and
$1 \leq m$
for all monomials m, and -
• if
 $m_1, m_2, m_3$
are monomials with
$m_1, m_2, m_3$
are monomials with
 $m_1 \leq m_2$
, then
$m_1 \leq m_2$
, then
 $m_1 m_3 \leq m_2 m_3$
.
$m_1 m_3 \leq m_2 m_3$
.
If
![]() $f \in {\mathbb {F}}[{\mathbf {x}}_N]$
is a nonzero polynomial and
$f \in {\mathbb {F}}[{\mathbf {x}}_N]$
is a nonzero polynomial and
![]() $<$
is a term order, write
$<$
is a term order, write
![]() ${\mathrm {in}}_< (f)$
for the largest monomial with respect to
${\mathrm {in}}_< (f)$
for the largest monomial with respect to
![]() $<$
which appears with nonzero coefficient in f.
$<$
which appears with nonzero coefficient in f.
Let
![]() $I \subseteq {\mathbb {F}}[{\mathbf {x}}_N]$
be an ideal, and let
$I \subseteq {\mathbb {F}}[{\mathbf {x}}_N]$
be an ideal, and let
![]() $<$
be a term order. The initial ideal
$<$
be a term order. The initial ideal
![]() ${\mathrm {in}}_< (I) \subseteq {\mathbb {F}}[{\mathbf {x}}_N]$
associated to I is given by
${\mathrm {in}}_< (I) \subseteq {\mathbb {F}}[{\mathbf {x}}_N]$
associated to I is given by
In other words, the ideal
![]() ${\mathrm {in}}_< (I)$
is generated by the
${\mathrm {in}}_< (I)$
is generated by the
![]() $<$
-leading monomials of all nonzero polynomials in I. A subset
$<$
-leading monomials of all nonzero polynomials in I. A subset
![]() $G = \{ g_1, \dots , g_r \} \subseteq I$
is a Gröbner basis of I if
$G = \{ g_1, \dots , g_r \} \subseteq I$
is a Gröbner basis of I if
If
![]() $G = \{ g_1, \dots , g_r \}$
is a Gröbner basis of I, it follows that
$G = \{ g_1, \dots , g_r \}$
is a Gröbner basis of I, it follows that
![]() $I = \langle g_1, \dots , g_r \rangle $
.
$I = \langle g_1, \dots , g_r \rangle $
.
Given an ideal
![]() $I \subseteq {\mathbb {F}}[{\mathbf {x}}_N]$
and a term order
$I \subseteq {\mathbb {F}}[{\mathbf {x}}_N]$
and a term order
![]() $<$
, a monomial m in the variables
$<$
, a monomial m in the variables
![]() ${\mathbf {x}}_N$
is a standard monomial if
${\mathbf {x}}_N$
is a standard monomial if
![]() $m \neq {\mathrm {in}}_< (f)$
for any nonzero
$m \neq {\mathrm {in}}_< (f)$
for any nonzero
![]() $f \in I$
. It is known that the family of cosets
$f \in I$
. It is known that the family of cosets
descends to a vector space basis of
![]() ${\mathbb {F}}[{\mathbf {x}}_N]/I$
. This is referred to as the standard monomial basis.
${\mathbb {F}}[{\mathbf {x}}_N]/I$
. This is referred to as the standard monomial basis.
2.2 Orbit harmonics
Let
![]() $Z \subseteq {\mathbb {F}}^N$
be a finite locus of points, and consider the ideal
$Z \subseteq {\mathbb {F}}^N$
be a finite locus of points, and consider the ideal
of polynomials in
![]() ${\mathbb {F}}[{\mathbf {x}}_N]$
which vanish on Z. The ideal
${\mathbb {F}}[{\mathbf {x}}_N]$
which vanish on Z. The ideal
![]() ${\mathbf {I}}(Z)$
is usually not homogeneous. Since Z is finite, we have an identification
${\mathbf {I}}(Z)$
is usually not homogeneous. Since Z is finite, we have an identification
of the vector space
![]() ${\mathbb {F}}[Z]$
of functions
${\mathbb {F}}[Z]$
of functions
![]() $Z \rightarrow {\mathbb {F}}$
and the typically ungraded quotient space
$Z \rightarrow {\mathbb {F}}$
and the typically ungraded quotient space
![]() ${\mathbb {F}}[{\mathbf {x}}_N]/{\mathbf {I}}(Z)$
.
${\mathbb {F}}[{\mathbf {x}}_N]/{\mathbf {I}}(Z)$
.
Given a nonzero polynomial
![]() $f \in {\mathbb {F}}[{\mathbf {x}}_N]$
, let
$f \in {\mathbb {F}}[{\mathbf {x}}_N]$
, let
![]() $\tau (f)$
be the highest degree homogeneous component of f. That is, if
$\tau (f)$
be the highest degree homogeneous component of f. That is, if
![]() $f = f_d + \cdots + f_1 + f_0$
where
$f = f_d + \cdots + f_1 + f_0$
where
![]() $f_i$
is homogeneous of degree i and
$f_i$
is homogeneous of degree i and
![]() $f_d \neq 0$
, we have
$f_d \neq 0$
, we have
![]() $\tau (f) = f_d$
. If
$\tau (f) = f_d$
. If
![]() $I \subseteq {\mathbb {F}}[{\mathbf {x}}_N]$
is an ideal, the associated graded ideal is
$I \subseteq {\mathbb {F}}[{\mathbf {x}}_N]$
is an ideal, the associated graded ideal is
In other words, the ideal
![]() ${\mathrm {gr}} \, I$
is generated by the top homogeneous components of all nonzero polynomials in I. The associated graded ideal
${\mathrm {gr}} \, I$
is generated by the top homogeneous components of all nonzero polynomials in I. The associated graded ideal
![]() ${\mathrm {gr}} \, I \subseteq {\mathbb {F}}[{\mathbf {x}}_N]$
is homogeneous by construction.
${\mathrm {gr}} \, I \subseteq {\mathbb {F}}[{\mathbf {x}}_N]$
is homogeneous by construction.
Returning to the setting of our finite locus
![]() $Z \subseteq {\mathbb {F}}^N$
, we may extend the chain (2.5) of ungraded
$Z \subseteq {\mathbb {F}}^N$
, we may extend the chain (2.5) of ungraded
![]() ${\mathbb {F}}$
-vector space isomorphisms
${\mathbb {F}}$
-vector space isomorphisms
where the last quotient
![]() ${\mathbb {F}}[{\mathbf {x}}_N] / {\mathrm {gr}} \, {\mathbf {I}}(Z)$
has the additional structure of a graded
${\mathbb {F}}[{\mathbf {x}}_N] / {\mathrm {gr}} \, {\mathbf {I}}(Z)$
has the additional structure of a graded
![]() ${\mathbb {F}}$
-vector space.
${\mathbb {F}}$
-vector space.
When the locus Z possesses symmetry, more can be said. Let
![]() $G \subseteq GL_N({\mathbb {F}})$
be a finite matrix group, and assume that the group algebra
$G \subseteq GL_N({\mathbb {F}})$
be a finite matrix group, and assume that the group algebra
![]() ${\mathbb {F}}[G]$
is semisimple. Equivalently, this means that
${\mathbb {F}}[G]$
is semisimple. Equivalently, this means that
![]() $|G| \neq 0$
in
$|G| \neq 0$
in
![]() ${\mathbb {F}}$
. The natural action of G on
${\mathbb {F}}$
. The natural action of G on
![]() ${\mathbb {F}}^N$
induces an action on
${\mathbb {F}}^N$
induces an action on
![]() ${\mathbb {F}}[{\mathbf {x}}_N]$
by linear substitutions. If Z is stable under the action of G, the isomorphisms (2.7) hold in the category of
${\mathbb {F}}[{\mathbf {x}}_N]$
by linear substitutions. If Z is stable under the action of G, the isomorphisms (2.7) hold in the category of
![]() ${\mathbb {F}}[G]$
-modules, and the last quotient
${\mathbb {F}}[G]$
-modules, and the last quotient
![]() ${\mathbb {F}}[{\mathbf {x}}_N] / {\mathrm {gr}} \, {\mathbf {I}}(Z)$
has the additional structure of a graded
${\mathbb {F}}[{\mathbf {x}}_N] / {\mathrm {gr}} \, {\mathbf {I}}(Z)$
has the additional structure of a graded
![]() ${\mathbb {F}}[G]$
-module.
${\mathbb {F}}[G]$
-module.
2.3 The Schensted correspondence
Given
![]() $n \geq 0$
, a partition of n is a weakly decreasing sequence
$n \geq 0$
, a partition of n is a weakly decreasing sequence
![]() $\lambda = (\lambda _1 \geq \cdots \geq \lambda _k)$
of positive integers which satisfy
$\lambda = (\lambda _1 \geq \cdots \geq \lambda _k)$
of positive integers which satisfy
![]() $\lambda _1 + \cdots + \lambda _k = n$
. We write
$\lambda _1 + \cdots + \lambda _k = n$
. We write
![]() $\lambda \vdash n$
to indicate that
$\lambda \vdash n$
to indicate that
![]() $\lambda $
is a partition of n. We identify a partition
$\lambda $
is a partition of n. We identify a partition
![]() $\lambda = (\lambda _1, \dots , \lambda _k)$
with its (English) Young diagram consisting of
$\lambda = (\lambda _1, \dots , \lambda _k)$
with its (English) Young diagram consisting of
![]() $\lambda _i$
left-justified boxes in row i.
$\lambda _i$
left-justified boxes in row i.
Let
![]() $\lambda \vdash n$
be a partition. A tableau of shape
$\lambda \vdash n$
be a partition. A tableau of shape
![]() $\lambda $
is an assignment
$\lambda $
is an assignment
![]() $T: \lambda \rightarrow \{1,2,\dots \}$
of positive integers to the boxes of
$T: \lambda \rightarrow \{1,2,\dots \}$
of positive integers to the boxes of
![]() $\lambda $
. A standard tableau of shape
$\lambda $
. A standard tableau of shape
![]() $\lambda $
is a bijective filling
$\lambda $
is a bijective filling
![]() $T: \lambda \rightarrow [n]$
of the boxes of
$T: \lambda \rightarrow [n]$
of the boxes of
![]() $\lambda $
with
$\lambda $
with
![]() $1, 2, \dots , n$
which is increasing across rows and down columns. We display, from left to right, the Young diagram of
$1, 2, \dots , n$
which is increasing across rows and down columns. We display, from left to right, the Young diagram of
![]() $\lambda = (4,2,2) \vdash 8$
, a standard tableau of shape
$\lambda = (4,2,2) \vdash 8$
, a standard tableau of shape
![]() $\lambda $
and two tableaux of shape
$\lambda $
and two tableaux of shape
![]() $\lambda $
which are not standard.
$\lambda $
which are not standard.

Although the above tableau
![]() $T: \lambda \rightarrow \{1,2, \dots \}$
on the far right is not standard, it is an injective filling which is (strictly) increasing across rows and down columns. We call a tableau satisfying these conditions a partial standard tableau.
$T: \lambda \rightarrow \{1,2, \dots \}$
on the far right is not standard, it is an injective filling which is (strictly) increasing across rows and down columns. We call a tableau satisfying these conditions a partial standard tableau.
The famous Schensted correspondence [Reference Schensted18] is a bijection
which sends a permutation
![]() $w \in {\mathfrak {S}}_n$
to a pair
$w \in {\mathfrak {S}}_n$
to a pair
![]() $(P(w), Q(w))$
of standard tableaux with the same n-box shape. The Schensted correspondence is most commonly defined using an insertion algorithm (see, e.g., [Reference Sagan17] for details). We will not need the insertion formulation of the Schensted bijection, but an equivalent ‘geometric’ formulation due to Viennot [Reference Viennot, Foata and Notes20] recalled in the next section will be crucial in our work. Schensted proved that his bijection relates to increasing subsequences as follows.
$(P(w), Q(w))$
of standard tableaux with the same n-box shape. The Schensted correspondence is most commonly defined using an insertion algorithm (see, e.g., [Reference Sagan17] for details). We will not need the insertion formulation of the Schensted bijection, but an equivalent ‘geometric’ formulation due to Viennot [Reference Viennot, Foata and Notes20] recalled in the next section will be crucial in our work. Schensted proved that his bijection relates to increasing subsequences as follows.
Theorem 2.1. (Schensted [Reference Schensted18, Thm. 1]).
Let
![]() $w \in {\mathfrak {S}}_n$
, and suppose that
$w \in {\mathfrak {S}}_n$
, and suppose that
![]() $w \mapsto (P(w), Q(w))$
under the Schensted bijection where
$w \mapsto (P(w), Q(w))$
under the Schensted bijection where
![]() $P(w)$
and
$P(w)$
and
![]() $Q(w)$
have shape
$Q(w)$
have shape
![]() $\lambda \vdash n$
. The first part
$\lambda \vdash n$
. The first part
![]() $\lambda _1$
of the partition
$\lambda _1$
of the partition
![]() $\lambda $
is the length of the longest increasing subsequence of w.
$\lambda $
is the length of the longest increasing subsequence of w.
2.4
 ${\mathfrak {S}}_n$
-representation theory
${\mathfrak {S}}_n$
-representation theory
Let
![]() ${\mathbb {F}}$
be a field in which
${\mathbb {F}}$
be a field in which
![]() $n \neq 0$
so that the group algebra
$n \neq 0$
so that the group algebra
![]() ${\mathbb {F}}[{\mathfrak {S}}_n]$
is semisimple. There is a one-to-one correspondence between partitions of n and irreducible representations of
${\mathbb {F}}[{\mathfrak {S}}_n]$
is semisimple. There is a one-to-one correspondence between partitions of n and irreducible representations of
![]() ${\mathfrak {S}}_n$
over
${\mathfrak {S}}_n$
over
![]() ${\mathbb {F}}$
. If
${\mathbb {F}}$
. If
![]() $\lambda \vdash n$
is a partition, we write
$\lambda \vdash n$
is a partition, we write
![]() $V^\lambda $
for the corresponding irreducible module,
$V^\lambda $
for the corresponding irreducible module,
![]() $\chi ^\lambda : {\mathfrak {S}}_n \rightarrow {\mathbb {F}}$
for its character, and
$\chi ^\lambda : {\mathfrak {S}}_n \rightarrow {\mathbb {F}}$
for its character, and
![]() $f^\lambda := \dim V^\lambda $
for its dimension. The number
$f^\lambda := \dim V^\lambda $
for its dimension. The number
![]() $f^\lambda $
counts standard tableaux of shape
$f^\lambda $
counts standard tableaux of shape
![]() $\lambda $
.
$\lambda $
.
The vector space
![]() ${\mathrm {Class}}({\mathfrak {S}}_n,{\mathbb {F}})$
of
${\mathrm {Class}}({\mathfrak {S}}_n,{\mathbb {F}})$
of
![]() ${\mathbb {F}}$
-valued class functions on
${\mathbb {F}}$
-valued class functions on
![]() ${\mathfrak {S}}_n$
has basis
${\mathfrak {S}}_n$
has basis
![]() $\{ \chi ^\lambda \,:\, \lambda \vdash n \}$
given by irreducible characters. The Kronecker product
$\{ \chi ^\lambda \,:\, \lambda \vdash n \}$
given by irreducible characters. The Kronecker product
![]() $*$
on
$*$
on
![]() ${\mathrm {Class}}({\mathfrak {S}}_n,{\mathbb {F}})$
is defined by
${\mathrm {Class}}({\mathfrak {S}}_n,{\mathbb {F}})$
is defined by
for any
![]() $\varphi , \psi \in {\mathrm {Class}}({\mathfrak {S}}_n,{\mathbb {F}})$
and
$\varphi , \psi \in {\mathrm {Class}}({\mathfrak {S}}_n,{\mathbb {F}})$
and
![]() $w \in {\mathfrak {S}}_n$
. If
$w \in {\mathfrak {S}}_n$
. If
![]() $V_1$
and
$V_1$
and
![]() $V_2$
are
$V_2$
are
![]() ${\mathfrak {S}}_n$
-modules, their vector space tensor product
${\mathfrak {S}}_n$
-modules, their vector space tensor product
![]() $V_1 \otimes V_2$
carries a diagonal action of
$V_1 \otimes V_2$
carries a diagonal action of
![]() ${\mathfrak {S}}_n$
by the rule
${\mathfrak {S}}_n$
by the rule
![]() $w \cdot (v_1 \otimes v_2) := (w \cdot v_1) \otimes (w \cdot v_2)$
. The characters
$w \cdot (v_1 \otimes v_2) := (w \cdot v_1) \otimes (w \cdot v_2)$
. The characters
![]() $\chi _{V_1}, \chi _{V_2}, \chi _{V_1 \otimes V_2}: {\mathfrak {S}}_n \rightarrow {\mathbb {F}}$
of these modules are related by
$\chi _{V_1}, \chi _{V_2}, \chi _{V_1 \otimes V_2}: {\mathfrak {S}}_n \rightarrow {\mathbb {F}}$
of these modules are related by
![]() $\chi _{V_1 \otimes V_2} = \chi _{V_1} * \chi _{V_2}$
.
$\chi _{V_1 \otimes V_2} = \chi _{V_1} * \chi _{V_2}$
.
3 Hilbert series and standard monomial basis
3.1 The injection relations
In order to analyze the quotients
![]() ${\mathbb {F}}[{\mathbf {x}}_{n \times n}] / I_n$
, we start by exhibiting strategic elements of the ideal
${\mathbb {F}}[{\mathbf {x}}_{n \times n}] / I_n$
, we start by exhibiting strategic elements of the ideal
![]() $I_n$
. Given two subsets
$I_n$
. Given two subsets
![]() $S, T \subseteq [n]$
, define elements
$S, T \subseteq [n]$
, define elements
![]() $a_{S,T}, b_{S,T} \in {\mathbb {F}}[{\mathbf {x}}_{n \times n}]$
by
$a_{S,T}, b_{S,T} \in {\mathbb {F}}[{\mathbf {x}}_{n \times n}]$
by
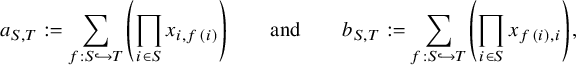 $$ \begin{align} a_{S,T} := \sum_{f: S \hookrightarrow T} \left( \prod_{ i \in S } x_{i,f(i)} \right) \quad \quad \text{and} \quad \quad b_{S,T} := \sum_{f: S \hookrightarrow T} \left( \prod_{ i \in S } x_{f(i),i} \right), \end{align} $$
$$ \begin{align} a_{S,T} := \sum_{f: S \hookrightarrow T} \left( \prod_{ i \in S } x_{i,f(i)} \right) \quad \quad \text{and} \quad \quad b_{S,T} := \sum_{f: S \hookrightarrow T} \left( \prod_{ i \in S } x_{f(i),i} \right), \end{align} $$
where both sums are over injective functions
![]() $f: S \hookrightarrow T$
. For example, if
$f: S \hookrightarrow T$
. For example, if
![]() $S = \{2,4\}$
and
$S = \{2,4\}$
and
![]() $T = \{1,3,4\}$
, we have
$T = \{1,3,4\}$
, we have
In general, the polynomials
![]() $a_{S,T}$
and
$a_{S,T}$
and
![]() $b_{S,T}$
are obtained from one another by transposing the matrix
$b_{S,T}$
are obtained from one another by transposing the matrix
![]() ${\mathbf {x}}_{n \times n}$
of variables. We have
${\mathbf {x}}_{n \times n}$
of variables. We have
![]() $a_{S,T} = b_{S,T} = 0$
whenever
$a_{S,T} = b_{S,T} = 0$
whenever
![]() $|S|> |T|$
.
$|S|> |T|$
.
Since the product of any two variables in the same row or column of
![]() ${\mathbf {x}}_{n \times n}$
is a generator of
${\mathbf {x}}_{n \times n}$
is a generator of
![]() $I_n$
, we have the congruences
$I_n$
, we have the congruences
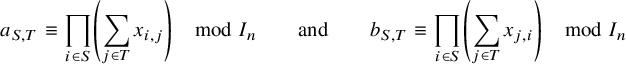 $$ \begin{align} a_{S,T} \equiv \prod_{i \in S} \left( \sum_{j \in T} x_{i,j} \right) \quad\mod I_n \quad \quad \text{and} \quad \quad b_{S,T} \equiv \prod_{i \in S} \left( \sum_{j \in T} x_{j,i} \right) \quad\mod I_n \end{align} $$
$$ \begin{align} a_{S,T} \equiv \prod_{i \in S} \left( \sum_{j \in T} x_{i,j} \right) \quad\mod I_n \quad \quad \text{and} \quad \quad b_{S,T} \equiv \prod_{i \in S} \left( \sum_{j \in T} x_{j,i} \right) \quad\mod I_n \end{align} $$
modulo
![]() $I_n$
. In other words, as far as the quotient
$I_n$
. In other words, as far as the quotient
![]() ${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
is concerned, we could have defined
${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
is concerned, we could have defined
![]() $a_{S,T}$
and
$a_{S,T}$
and
![]() $b_{S,T}$
using all functions
$b_{S,T}$
using all functions
![]() $S \rightarrow T$
, not just injections. Our first lemma states that
$S \rightarrow T$
, not just injections. Our first lemma states that
![]() $a_{S,T}$
and
$a_{S,T}$
and
![]() $b_{S,T}$
are members of
$b_{S,T}$
are members of
![]() $I_n$
provided that
$I_n$
provided that
![]() $|S| + |T|> n$
.
$|S| + |T|> n$
.
Lemma 3.1. Let
![]() $S, T \subseteq [n]$
be subsets. If
$S, T \subseteq [n]$
be subsets. If
![]() $|S| + |T|> n$
, we have
$|S| + |T|> n$
, we have
![]() $a_{S,T}, b_{S,T} \in I_n$
.
$a_{S,T}, b_{S,T} \in I_n$
.
Proof. The polynomial
![]() $b_{S,T}$
is obtained from
$b_{S,T}$
is obtained from
![]() $a_{S,T}$
by transposing the matrix
$a_{S,T}$
by transposing the matrix
![]() ${\mathbf {x}}_{n \times n}$
of variables, an operation under which
${\mathbf {x}}_{n \times n}$
of variables, an operation under which
![]() $I_n$
is stable. As such, it suffices to prove the lemma for
$I_n$
is stable. As such, it suffices to prove the lemma for
![]() $a_{S,T}$
. Furthermore, by the congruences (3.2) it suffices to prove the lemma when
$a_{S,T}$
. Furthermore, by the congruences (3.2) it suffices to prove the lemma when
![]() $|S| + |T| = n+1$
. Finally, since
$|S| + |T| = n+1$
. Finally, since
![]() $I_n$
is stable under the action of the product group
$I_n$
is stable under the action of the product group
![]() ${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
on the rows and columns of
${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
on the rows and columns of
![]() ${\mathbf {x}}_{n \times n}$
, it is enough to consider the case where
${\mathbf {x}}_{n \times n}$
, it is enough to consider the case where
![]() $S = [s]$
and
$S = [s]$
and
![]() $T = [t]$
for
$T = [t]$
for
![]() $s + t = n+1$
.
$s + t = n+1$
.
We argue by increasing induction on s (and decreasing induction on t). If
![]() $s = 1$
, then
$s = 1$
, then
![]() $t = n$
and
$t = n$
and
![]() $a_{S,T} = x_{1,1} + x_{1,2} + \cdots + x_{1,n}$
is a generator of the ideal
$a_{S,T} = x_{1,1} + x_{1,2} + \cdots + x_{1,n}$
is a generator of the ideal
![]() $I_n$
. If
$I_n$
. If
![]() $s> 1$
, we have
$s> 1$
, we have
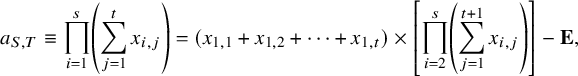 $$ \begin{align} a_{S,T} \equiv \prod_{i = 1}^s \left( \sum_{j = 1}^t x_{i,j} \right) = (x_{1,1} + x_{1,2} + \cdots + x_{1,t}) \times \left[ \prod_{i = 2}^s \left( \sum_{j = 1}^{t+1} x_{i,j} \right) \right] - {\mathbf {E}}, \end{align} $$
$$ \begin{align} a_{S,T} \equiv \prod_{i = 1}^s \left( \sum_{j = 1}^t x_{i,j} \right) = (x_{1,1} + x_{1,2} + \cdots + x_{1,t}) \times \left[ \prod_{i = 2}^s \left( \sum_{j = 1}^{t+1} x_{i,j} \right) \right] - {\mathbf {E}}, \end{align} $$
where the congruence modulo
![]() $I_n$
follows from Equation (3.2), the expression
$I_n$
follows from Equation (3.2), the expression
![]() $[ \, \cdots ]$
in square brackets lies in
$[ \, \cdots ]$
in square brackets lies in
![]() $I_n$
by induction and the ‘error term’
$I_n$
by induction and the ‘error term’
![]() ${\mathbf {E}}$
is given by
${\mathbf {E}}$
is given by
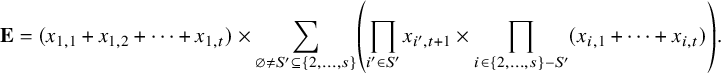 $$ \begin{align} {\mathbf {E}} = (x_{1,1} + x_{1,2} + \cdots + x_{1,t}) \times \sum_{\varnothing \neq S' \subseteq \{2, \dots, s\}} \left( \prod_{i' \in S'} x_{i',t+1} \times \prod_{i \in \{2,\dots,s\} - S'} (x_{i,1} + \cdots + x_{i,t}) \right). \end{align} $$
$$ \begin{align} {\mathbf {E}} = (x_{1,1} + x_{1,2} + \cdots + x_{1,t}) \times \sum_{\varnothing \neq S' \subseteq \{2, \dots, s\}} \left( \prod_{i' \in S'} x_{i',t+1} \times \prod_{i \in \{2,\dots,s\} - S'} (x_{i,1} + \cdots + x_{i,t}) \right). \end{align} $$
It suffices to show that
![]() ${\mathbf {E}} \in I_n$
. When the
${\mathbf {E}} \in I_n$
. When the
![]() $|S'|> 1$
and
$|S'|> 1$
and
![]() $i^{\prime }_1, i^{\prime }_2 \in S'$
are distinct, the corresponding summand in
$i^{\prime }_1, i^{\prime }_2 \in S'$
are distinct, the corresponding summand in
![]() ${\mathbf {E}}$
contains the product
${\mathbf {E}}$
contains the product
![]() $x_{i^{\prime }_1,t+1} \cdot x_{i^{\prime }_2,t+1}$
and so lies in
$x_{i^{\prime }_1,t+1} \cdot x_{i^{\prime }_2,t+1}$
and so lies in
![]() $I_n$
. We conclude that
$I_n$
. We conclude that
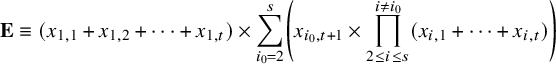 $$ \begin{align} {\mathbf {E}} \equiv (x_{1,1} + x_{1,2} + \cdots + x_{1,t}) \times \sum_{i_0 = 2}^s \left( x_{i_0,t+1} \times \prod_{2 \leq i \leq s}^{i \neq i_0} (x_{i,1} + \cdots + x_{i,t}) \right) \end{align} $$
$$ \begin{align} {\mathbf {E}} \equiv (x_{1,1} + x_{1,2} + \cdots + x_{1,t}) \times \sum_{i_0 = 2}^s \left( x_{i_0,t+1} \times \prod_{2 \leq i \leq s}^{i \neq i_0} (x_{i,1} + \cdots + x_{i,t}) \right) \end{align} $$
modulo
![]() $I_n$
. Applying the congruences (3.2) and the defining relations of
$I_n$
. Applying the congruences (3.2) and the defining relations of
![]() $I_n$
, we arrive at
$I_n$
, we arrive at
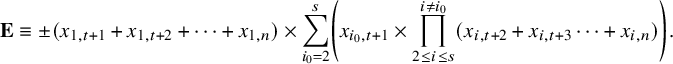 $$ \begin{align} {\mathbf {E}} \equiv \pm (x_{1,t+1} + x_{1,t+2} + \cdots + x_{1,n}) \times \sum_{i_0 = 2}^s \left( x_{i_0,t+1} \times \prod_{2 \leq i \leq s}^{i \neq i_0} (x_{i,t+2} + x_{i,t+3} \cdots + x_{i,n}) \right). \end{align} $$
$$ \begin{align} {\mathbf {E}} \equiv \pm (x_{1,t+1} + x_{1,t+2} + \cdots + x_{1,n}) \times \sum_{i_0 = 2}^s \left( x_{i_0,t+1} \times \prod_{2 \leq i \leq s}^{i \neq i_0} (x_{i,t+2} + x_{i,t+3} \cdots + x_{i,n}) \right). \end{align} $$
The sum
![]() $(x_{i,t+2} + x_{i,t+3} \cdots + x_{i,n}) $
contains
$(x_{i,t+2} + x_{i,t+3} \cdots + x_{i,n}) $
contains
![]() $n-t-1 = n - (n+1-s) - 1 = s - 2$
terms. The pigeonhole principle implies that every term in the expansion of the right-hand side of the congruence (3.6) will contain a product of variables
$n-t-1 = n - (n+1-s) - 1 = s - 2$
terms. The pigeonhole principle implies that every term in the expansion of the right-hand side of the congruence (3.6) will contain a product of variables
![]() $x_{i,j} \cdot x_{i',j}$
for some
$x_{i,j} \cdot x_{i',j}$
for some
![]() $i \neq i'$
so that
$i \neq i'$
so that
![]() ${\mathbf {E}} \in I_n$
. We conclude that
${\mathbf {E}} \in I_n$
. We conclude that
![]() $a_{S,T} \in I_n$
, and the lemma is proven.
$a_{S,T} \in I_n$
, and the lemma is proven.
3.2 Shadow sets
We represent a permutation
![]() $w = [w(1), \dots , w(n)] \in {\mathfrak {S}}_n$
with its graph, that is, the collection of points
$w = [w(1), \dots , w(n)] \in {\mathfrak {S}}_n$
with its graph, that is, the collection of points
![]() $\{ (i,w(i)) \,:\, 1 \leq i \leq n \}$
on the grid
$\{ (i,w(i)) \,:\, 1 \leq i \leq n \}$
on the grid
![]() $[n] \times [n]$
. For example, the permutation
$[n] \times [n]$
. For example, the permutation
![]() $w = [4,1,8,5,3,6,2,7] \in {\mathfrak {S}}_8$
is given below in bullets.
$w = [4,1,8,5,3,6,2,7] \in {\mathfrak {S}}_8$
is given below in bullets.
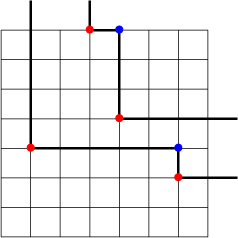
Viennot used [Reference Viennot, Foata and Notes20] the graph of a permutation w to obtain its image
![]() $(P(w),Q(w))$
under the Schensted correspondence as follows. Shine a flashlight northeast from the origin (0,0). Each bullet in the permutation casts a shadow to its northeast. The boundary of the shaded region is the first shadow line; in our example, it is as follows.
$(P(w),Q(w))$
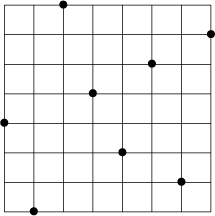
under the Schensted correspondence as follows. Shine a flashlight northeast from the origin (0,0). Each bullet in the permutation casts a shadow to its northeast. The boundary of the shaded region is the first shadow line; in our example, it is as follows.
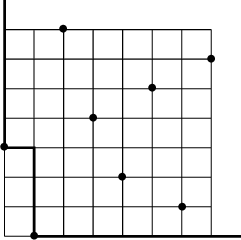
Removing the points on the first shadow line and repeating this procedure, we obtain the second shadow line. Iterating, we obtain the third shadow line, the fourth shadow line and so on. In our example, the shadow lines are shown below.
Let
![]() $w \in {\mathfrak {S}}_n$
and suppose that the shadow lines of w are given by
$w \in {\mathfrak {S}}_n$
and suppose that the shadow lines of w are given by
![]() $L_1, \dots , L_r$
from southwest to northeast. Viennot proved [Reference Viennot, Foata and Notes20] that if
$L_1, \dots , L_r$
from southwest to northeast. Viennot proved [Reference Viennot, Foata and Notes20] that if
![]() $w \mapsto (P(w), Q(w))$
under the Schensted correspondence, then the y-coordinates of the infinite horizontal rays in
$w \mapsto (P(w), Q(w))$
under the Schensted correspondence, then the y-coordinates of the infinite horizontal rays in
![]() $L_1, \dots , L_r$
form the first row of
$L_1, \dots , L_r$
form the first row of
![]() $P(w)$
and the x-coordinates of the infinite vertical rays of
$P(w)$
and the x-coordinates of the infinite vertical rays of
![]() $L_1, \dots , L_r$
form the first row of
$L_1, \dots , L_r$
form the first row of
![]() $Q(w)$
. In our example, the first row of
$Q(w)$
. In our example, the first row of
![]() $P(w)$
is
$P(w)$
is ![]() while the first row of
while the first row of
![]() $Q(w)$
is
$Q(w)$
is ![]() . In particular, the common length of the first row of
. In particular, the common length of the first row of
![]() $P(w)$
and
$P(w)$
and
![]() $Q(w)$
is the number of shadow lines. The northeast corners of the shadow lines played an important role in Viennot’s work and will for us as well.
$Q(w)$
is the number of shadow lines. The northeast corners of the shadow lines played an important role in Viennot’s work and will for us as well.
Definition 3.2. The shadow set
![]() ${\mathcal {S}}(w)$
of a permutation
${\mathcal {S}}(w)$
of a permutation
![]() $w \in {\mathfrak {S}}_n$
is the collection of points
$w \in {\mathfrak {S}}_n$
is the collection of points
![]() $(i,j)$
in the grid
$(i,j)$
in the grid
![]() $[n] \times [n]$
which lie at the northeast corner of a shadow line of w.
$[n] \times [n]$
which lie at the northeast corner of a shadow line of w.
In our example, the points in the shadow set
![]() ${\mathcal {S}}(w) = \{ (2,4), (4,8), (5,5), (7,3) \}$
are drawn in red. For any permutation
${\mathcal {S}}(w) = \{ (2,4), (4,8), (5,5), (7,3) \}$
are drawn in red. For any permutation
![]() $w \in {\mathfrak {S}}_n$
, the shadow set
$w \in {\mathfrak {S}}_n$
, the shadow set
![]() ${\mathcal {S}}(w)$
contains at most one point in any row or column. Such subsets of the square grid have a name.
${\mathcal {S}}(w)$
contains at most one point in any row or column. Such subsets of the square grid have a name.
Definition 3.3. A subset
![]() ${\mathcal {R}} \subseteq [n] \times [n]$
is a (nonattacking) rook placement if
${\mathcal {R}} \subseteq [n] \times [n]$
is a (nonattacking) rook placement if
![]() ${\mathcal {R}}$
contains at most one point in any row or column.
${\mathcal {R}}$
contains at most one point in any row or column.
Rook placements are also known as ‘partial permutations’. Importantly, the Viennot shadow line construction may be performed on an arbitrary rook placement, not just on the graph of a permutation.
Although every permutation shadow set is a rook placement, not every rook placement is the shadow set of a permutation. For example, shadow sets contain no points in row 1 or column 1. In Lemma 3.6 below, we give a combinatorial criterion for deciding whether a rook placement is a shadow set.
Returning to our permutation
![]() $w \in {\mathfrak {S}}_n$
, we may iterate the shadow line construction on the shadow set
$w \in {\mathfrak {S}}_n$
, we may iterate the shadow line construction on the shadow set
![]() ${\mathcal {S}}(w)$
. In our
${\mathcal {S}}(w)$
. In our
![]() $n = 8$
example, this yields the shadow lines.
$n = 8$
example, this yields the shadow lines.
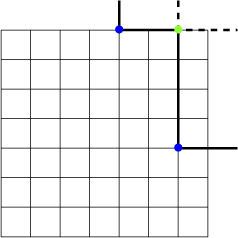
Viennot proved that the horizontal and vertical rays of these ‘iterated’ shadow lines give the second rows of
![]() $P(w)$
and
$P(w)$
and
![]() $Q(w)$
, respectively. In our example, the second row of
$Q(w)$
, respectively. In our example, the second row of
![]() $P(w)$
is
$P(w)$
is ![]() and the second row of
and the second row of
![]() $Q(w)$
is
$Q(w)$
is ![]() . These iterated shadow lines produce an iterated shadow set
. These iterated shadow lines produce an iterated shadow set
![]() ${\mathcal {S}}({\mathcal {S}}(w))$
whose points are drawn in blue. Repeating this procedure in our example yields the iterated shadow sets and shadow lines
${\mathcal {S}}({\mathcal {S}}(w))$
whose points are drawn in blue. Repeating this procedure in our example yields the iterated shadow sets and shadow lines
and we conclude that the tableaux
![]() $P(w)$
and
$P(w)$
and
![]() $Q(w)$
are given by
$Q(w)$
are given by
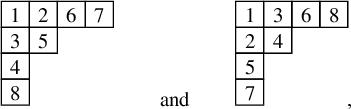
respectively.
Theorem 3.4. (Viennot [Reference Viennot, Foata and Notes20]).
The shadow line procedure described above computes the image
![]() $(P(w), Q(w))$
of a permutation
$(P(w), Q(w))$
of a permutation
![]() $w \in {\mathfrak {S}}_n$
under the Schensted correspondence.
$w \in {\mathfrak {S}}_n$
under the Schensted correspondence.
For our purposes, we may take Theorem 3.4 as the definition of the Schensted correspondence. Combining Theorem 3.4 with Schensted’s Theorem 2.1 yields the following result immediately.
Lemma 3.5. Let
![]() $w \in {\mathfrak {S}}_n$
. The size
$w \in {\mathfrak {S}}_n$
. The size
![]() $|{\mathcal {S}}(w)|$
of the shadow set of w is given by
$|{\mathcal {S}}(w)|$
of the shadow set of w is given by
We close this subsection with a combinatorial criterion for deciding when a rook placement
![]() ${\mathcal {R}}$
is the shadow set of some permutation
${\mathcal {R}}$
is the shadow set of some permutation
![]() $w \in {\mathfrak {S}}_n$
. We use the fact that the shadow line construction may be applied to
$w \in {\mathfrak {S}}_n$
. We use the fact that the shadow line construction may be applied to
![]() ${\mathcal {R}}$
. This will yield a pair
${\mathcal {R}}$
. This will yield a pair
![]() $(P,Q)$
of partial standard tableaux with the same shape such that the y-coordinates of
$(P,Q)$
of partial standard tableaux with the same shape such that the y-coordinates of
![]() ${\mathcal {R}}$
are the entries in P and the x-coordinates in
${\mathcal {R}}$
are the entries in P and the x-coordinates in
![]() ${\mathcal {R}}$
are the entries in Q.
${\mathcal {R}}$
are the entries in Q.
Lemma 3.6. Let
![]() ${\mathcal {R}} \subseteq [n] \times [n]$
be a rook placement, and apply the shadow line construction to
${\mathcal {R}} \subseteq [n] \times [n]$
be a rook placement, and apply the shadow line construction to
![]() ${\mathcal {R}}$
. Let
${\mathcal {R}}$
. Let
![]() $L_1, \dots , L_r$
be the shadow lines so obtained. Define two length n sequences
$L_1, \dots , L_r$
be the shadow lines so obtained. Define two length n sequences
![]() $x_1 x_2 \dots x_n$
and
$x_1 x_2 \dots x_n$
and
![]() $y_1 y_2 \dots y_n$
over the alphabet
$y_1 y_2 \dots y_n$
over the alphabet
![]() $\{1,0,-1\}$
by
$\{1,0,-1\}$
by
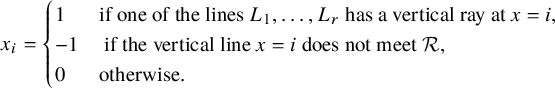 $$ \begin{align} x_i = \begin{cases} 1 & \text{if one of the lines } L_1, \dots, L_r \text{ has a vertical ray at } x = i, \\ -1 & \text{ if the vertical line } x = i \text{ does not meet } {\mathcal {R}}, \\ 0 & \text{otherwise.} \end{cases} \end{align} $$
$$ \begin{align} x_i = \begin{cases} 1 & \text{if one of the lines } L_1, \dots, L_r \text{ has a vertical ray at } x = i, \\ -1 & \text{ if the vertical line } x = i \text{ does not meet } {\mathcal {R}}, \\ 0 & \text{otherwise.} \end{cases} \end{align} $$
and
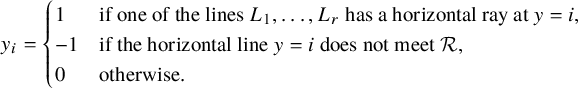 $$ \begin{align} y_i = \begin{cases} 1 & \text{if one of the lines } L_1, \dots, L_r \text{ has a horizontal ray at } y = i, \\ -1 & \text{if the horizontal line } y = i \text{ does not meet } {\mathcal {R}}, \\ 0 & \text{otherwise.} \end{cases} \end{align} $$
$$ \begin{align} y_i = \begin{cases} 1 & \text{if one of the lines } L_1, \dots, L_r \text{ has a horizontal ray at } y = i, \\ -1 & \text{if the horizontal line } y = i \text{ does not meet } {\mathcal {R}}, \\ 0 & \text{otherwise.} \end{cases} \end{align} $$
Then
![]() ${\mathcal {R}} = {\mathcal {S}}(w)$
is the shadow set of some permutation
${\mathcal {R}} = {\mathcal {S}}(w)$
is the shadow set of some permutation
![]() $w \in {\mathfrak {S}}_n$
if and only if for all
$w \in {\mathfrak {S}}_n$
if and only if for all
![]() $1 \leq i \leq n$
we have
$1 \leq i \leq n$
we have
![]() $x_1 + x_2 + \cdots + x_i \leq 0$
and
$x_1 + x_2 + \cdots + x_i \leq 0$
and
![]() $y_1 + y_2 + \cdots + y_i \leq 0$
.
$y_1 + y_2 + \cdots + y_i \leq 0$
.
Proof. Suppose
![]() ${\mathcal {R}} = {\mathcal {S}}(w)$
is the shadow set of a permutation
${\mathcal {R}} = {\mathcal {S}}(w)$
is the shadow set of a permutation
![]() $w \in {\mathfrak {S}}_n$
. If
$w \in {\mathfrak {S}}_n$
. If
![]() $w \mapsto (P(w), Q(w))$
under the Schensted correspondence, the horizontal rays of
$w \mapsto (P(w), Q(w))$
under the Schensted correspondence, the horizontal rays of
![]() $L_1, \dots , L_r$
give the second row of
$L_1, \dots , L_r$
give the second row of
![]() $P(w)$
and the vertical rays of
$P(w)$
and the vertical rays of
![]() $L_1, \dots , L_r$
give the second row of
$L_1, \dots , L_r$
give the second row of
![]() $Q(w)$
. The y-coordinates which do not appear in
$Q(w)$
. The y-coordinates which do not appear in
![]() ${\mathcal {R}}$
give the first row of
${\mathcal {R}}$
give the first row of
![]() $P(w)$
and the x-coordinates which do not appear in
$P(w)$
and the x-coordinates which do not appear in
![]() ${\mathcal {R}}$
give the first row of
${\mathcal {R}}$
give the first row of
![]() $Q(w)$
. Since
$Q(w)$
. Since
![]() $P(w)$
and
$P(w)$
and
![]() $Q(w)$
are standard, all prefix sums of the sequences
$Q(w)$
are standard, all prefix sums of the sequences
![]() $x_1 x_2 \dots x_n$
and
$x_1 x_2 \dots x_n$
and
![]() $y_1 y_2 \dots y_n$
are nonpositive.
$y_1 y_2 \dots y_n$
are nonpositive.
Now, assume that all prefix sums of
![]() $x_1 x_2 \dots x_n$
and
$x_1 x_2 \dots x_n$
and
![]() $y_1 y_2 \dots y_n$
are nonpositive. We may apply Viennot’s construction to the set
$y_1 y_2 \dots y_n$
are nonpositive. We may apply Viennot’s construction to the set
![]() ${\mathcal {R}}$
to get a pair
${\mathcal {R}}$
to get a pair
![]() $(P',Q')$
of partial standard tableaux where the entries of
$(P',Q')$
of partial standard tableaux where the entries of
![]() $P'$
are the y-coordinates in
$P'$
are the y-coordinates in
![]() ${\mathcal {R}}$
and the entries of
${\mathcal {R}}$
and the entries of
![]() $Q'$
are the x-coordinates in
$Q'$
are the x-coordinates in
![]() ${\mathcal {R}}$
. By the assumption on prefixes, the tableaux P and Q obtained by adding a first row to P and Q consisting of those y-coordinates and x-coordinates which do not appear in
${\mathcal {R}}$
. By the assumption on prefixes, the tableaux P and Q obtained by adding a first row to P and Q consisting of those y-coordinates and x-coordinates which do not appear in
![]() ${\mathcal {R}}$
(respectively) are both standard. If we let
${\mathcal {R}}$
(respectively) are both standard. If we let
![]() $w \in {\mathfrak {S}}_n$
be the unique permutation such that
$w \in {\mathfrak {S}}_n$
be the unique permutation such that
![]() $w \mapsto (P,Q)$
, Viennot’s Theorem 3.4 implies that
$w \mapsto (P,Q)$
, Viennot’s Theorem 3.4 implies that
![]() ${\mathcal {S}}(w) = {\mathcal {R}}$
.
${\mathcal {S}}(w) = {\mathcal {R}}$
.
An example may help in understanding Lemma 3.6 and its proof. Let
![]() $n = 8$
, and let
$n = 8$
, and let
![]() ${\mathcal {R}}$
be the rook placement
${\mathcal {R}}$
be the rook placement
of size 5. Applying the Viennot shadow line construction to
![]() ${\mathcal {R}}$
yields
${\mathcal {R}}$
yields
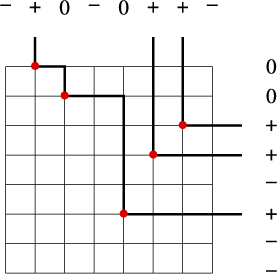
where the sequences
![]() $x_1 x_2 \dots x_8$
and
$x_1 x_2 \dots x_8$
and
![]() $y_1 y_2 \cdots y_8$
in
$y_1 y_2 \cdots y_8$
in
![]() $\{1,0,-1\}$
are shown horizontally and vertically, respectively. A
$\{1,0,-1\}$
are shown horizontally and vertically, respectively. A
![]() $+1$
in a given row (or column) corresponds to an infinite ray of a shadow line, a 0 corresponds to a shadow line segment which is not an infinite ray, and a
$+1$
in a given row (or column) corresponds to an infinite ray of a shadow line, a 0 corresponds to a shadow line segment which is not an infinite ray, and a
![]() $-1$
corresponds to that row (or column) not containing an element of
$-1$
corresponds to that row (or column) not containing an element of
![]() ${\mathcal {R}}$
. We have
${\mathcal {R}}$
. We have
![]() $x_1 + x_2 + \cdots + x_7 = 1> 0$
, so by Lemma 3.6 the set
$x_1 + x_2 + \cdots + x_7 = 1> 0$
, so by Lemma 3.6 the set
![]() ${\mathcal {R}}$
is not the shadow set of a permutation in
${\mathcal {R}}$
is not the shadow set of a permutation in
![]() ${\mathfrak {S}}_8$
. Indeed, applying Schensted insertion to the rook placement
${\mathfrak {S}}_8$
. Indeed, applying Schensted insertion to the rook placement
![]() ${\mathcal {R}}$
yields the pair of tableaux
${\mathcal {R}}$
yields the pair of tableaux
![]() $P'$
and
$P'$
and
![]() $Q'$
given by
$Q'$
given by
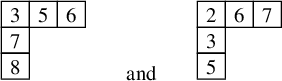
(respectively), and adding the row ![]() corresponding to the positions of the
corresponding to the positions of the
![]() $-1$
’s in the sequence
$-1$
’s in the sequence
![]() $x_1 x_2 \dots x_8$
to the top row of
$x_1 x_2 \dots x_8$
to the top row of
![]() $Q'$
would not yield a standard tableau.
$Q'$
would not yield a standard tableau.
3.3 Shadow monomials and spanning
Our next task is to convert the combinatorics of the previous subsection into a spanning set for the quotient ring
![]() ${\mathbb {F}}[{\mathbf {x}}_{n \times n}] / I_n$
. Given any set
${\mathbb {F}}[{\mathbf {x}}_{n \times n}] / I_n$
. Given any set
![]() ${\mathcal {S}} \subseteq [n] \times [n]$
of grid points, let
${\mathcal {S}} \subseteq [n] \times [n]$
of grid points, let
![]() $m({\mathcal {S}}) = \prod _{(i,j) \in {\mathcal {S}}} x_{i,j}$
be the corresponding squarefree monomial in
$m({\mathcal {S}}) = \prod _{(i,j) \in {\mathcal {S}}} x_{i,j}$
be the corresponding squarefree monomial in
![]() ${\mathbb {F}}[{\mathbf {x}}_{n \times n}]$
.
${\mathbb {F}}[{\mathbf {x}}_{n \times n}]$
.
Lemma 3.7. The family of monomials
![]() $m({\mathcal {R}})$
corresponding to rook placements
$m({\mathcal {R}})$
corresponding to rook placements
![]() ${\mathcal {R}} \subseteq [n] \times [n]$
descends to a spanning set of
${\mathcal {R}} \subseteq [n] \times [n]$
descends to a spanning set of
![]() ${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
.
${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
.
Proof. This is immediate from the fact that generating set of
![]() $I_n$
contains all squares
$I_n$
contains all squares
![]() $x_{i,j}^2$
of variables and all products of two variables in a given row or column.
$x_{i,j}^2$
of variables and all products of two variables in a given row or column.
The spanning set of Lemma 3.7 is far from a basis. In order to extract a basis from this spanning set, we introduce a strategic term order. Recall that the lexicographical order on monomials in an ordered set of variables
![]() $y_1> y_2 > \cdots > y_N$
is given by
$y_1> y_2 > \cdots > y_N$
is given by
![]() $y_1^{a_1} \cdots y_N^{a_N} < y_1^{b_1} \cdots y_N^{b_N}$
if there exists
$y_1^{a_1} \cdots y_N^{a_N} < y_1^{b_1} \cdots y_N^{b_N}$
if there exists
![]() $1 \leq j \leq N$
with
$1 \leq j \leq N$
with
![]() $a_i = b_i$
for
$a_i = b_i$
for
![]() $i < j$
and
$i < j$
and
![]() $a_j < b_j$
.
$a_j < b_j$
.
Definition 3.8. The Toeplitz term order
![]() $<_{\mathrm {Top}}$
on monomials in
$<_{\mathrm {Top}}$
on monomials in
![]() ${\mathbb {F}}[{\mathbf {x}}_{n \times n}]$
is the lexicographical term order with respect to the order on variables given by
${\mathbb {F}}[{\mathbf {x}}_{n \times n}]$
is the lexicographical term order with respect to the order on variables given by
Roughly speaking, the Toeplitz term order weights a variable
![]() $x_{a,b}$
heavier than
$x_{a,b}$
heavier than
![]() $x_{c,d}$
whenever
$x_{c,d}$
whenever
![]() $a + b < c + d$
and then breaks ties lexicographically. In fact, this tie breaking process among variables
$a + b < c + d$
and then breaks ties lexicographically. In fact, this tie breaking process among variables
![]() $x_{i,j}$
with
$x_{i,j}$
with
![]() $i + j$
constant will be irrelevant for the arguments that follow; all that is important is the relative weight of the variables
$i + j$
constant will be irrelevant for the arguments that follow; all that is important is the relative weight of the variables
![]() $x_{i,j}$
for which
$x_{i,j}$
for which
![]() $i + j$
differs. The word ‘Toeplitz’ comes from Toeplitz matrices (which are constant along diagonals). Since all of the relations we apply will be homogeneous, we could have also defined
$i + j$
differs. The word ‘Toeplitz’ comes from Toeplitz matrices (which are constant along diagonals). Since all of the relations we apply will be homogeneous, we could have also defined
![]() $<_{\mathrm {Top}}$
by ordering by total degree first and then using the lexicographical order with respect to the indicated variable order to break ties.
$<_{\mathrm {Top}}$
by ordering by total degree first and then using the lexicographical order with respect to the indicated variable order to break ties.
Definition 3.9. Let
![]() $w \in {\mathfrak {S}}_n$
. The shadow monomial
$w \in {\mathfrak {S}}_n$
. The shadow monomial
![]() ${\mathfrak {s}}(w) \in {\mathbb {F}}[{\mathbf {x}}_{n \times n}] / I_n$
is the squarefree monomial corresponding to the shadow set of w. In symbols, we have
${\mathfrak {s}}(w) \in {\mathbb {F}}[{\mathbf {x}}_{n \times n}] / I_n$
is the squarefree monomial corresponding to the shadow set of w. In symbols, we have
![]() ${\mathfrak {s}}(w) = m({\mathcal {S}}(w))$
.
${\mathfrak {s}}(w) = m({\mathcal {S}}(w))$
.
For example, if
![]() $w = [4,1,8,5,3,6,2,7] \in {\mathfrak {S}}_8$
we have
$w = [4,1,8,5,3,6,2,7] \in {\mathfrak {S}}_8$
we have
![]() ${\mathcal {S}}(w) = \{ (2,4), (4,8), (5,5), (7,3) \}$
so that
${\mathcal {S}}(w) = \{ (2,4), (4,8), (5,5), (7,3) \}$
so that
![]() ${\mathfrak {s}}(w) = x_{2,4} \cdot x_{4,8} \cdot x_{5,5} \cdot x_{7,3}$
. Our next lemma shows that the shadow monomials of permutations span the quotient ring
${\mathfrak {s}}(w) = x_{2,4} \cdot x_{4,8} \cdot x_{5,5} \cdot x_{7,3}$
. Our next lemma shows that the shadow monomials of permutations span the quotient ring
![]() ${\mathbb {F}}[{\mathbf {x}}_{n \times n}] / I_n$
. The key tools in its proof are the relations in
${\mathbb {F}}[{\mathbf {x}}_{n \times n}] / I_n$
. The key tools in its proof are the relations in
![]() ${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
coming from Lemma 3.1 and the characterization (Lemma 3.6) of when a rook placement monomial
${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
coming from Lemma 3.1 and the characterization (Lemma 3.6) of when a rook placement monomial
![]() $m({\mathcal {R}})$
is the shadow monomial
$m({\mathcal {R}})$
is the shadow monomial
![]() ${\mathfrak {s}}(w)$
of a permutation
${\mathfrak {s}}(w)$
of a permutation
![]() $w \in {\mathfrak {S}}_n$
. To begin, we record the
$w \in {\mathfrak {S}}_n$
. To begin, we record the
![]() $<_{\mathrm {Top}}$
-leading terms of the elements of
$<_{\mathrm {Top}}$
-leading terms of the elements of
![]() $I_n$
appearing in Lemma 3.1.
$I_n$
appearing in Lemma 3.1.
Observation 3.10. Let
![]() $S = \{s_1 < \cdots < s_p \}$
and
$S = \{s_1 < \cdots < s_p \}$
and
![]() $T = \{t_1 < \cdots < t_q \}$
be subsets of
$T = \{t_1 < \cdots < t_q \}$
be subsets of
![]() $[n]$
with
$[n]$
with
![]() $p \leq q$
. Then
$p \leq q$
. Then
In other words, the leading monomials of
![]() $a_{S,T}$
and
$a_{S,T}$
and
![]() $b_{S,T}$
correspond to the injection
$b_{S,T}$
correspond to the injection
![]() $S \hookrightarrow T$
which assigns the elements of S to the smallest
$S \hookrightarrow T$
which assigns the elements of S to the smallest
![]() $|S|$
elements of T in an order-preserving fashion. If
$|S|$
elements of T in an order-preserving fashion. If
![]() $S = \{2,4\}$
and
$S = \{2,4\}$
and
![]() $T = \{1,4,5\}$
, then
$T = \{1,4,5\}$
, then
![]() $a_{S,T}$
given by
$a_{S,T}$
given by
with its
![]() $<_{\mathrm {Top}}$
-leading term underlined. We have all the pieces we need to prove our spanning result.
$<_{\mathrm {Top}}$
-leading term underlined. We have all the pieces we need to prove our spanning result.
Lemma 3.11. The shadow monomials
![]() $\{ {\mathfrak {s}}(w) \,:\, w \in {\mathfrak {S}}_n \}$
descend to a spanning set of the quotient ring
$\{ {\mathfrak {s}}(w) \,:\, w \in {\mathfrak {S}}_n \}$
descend to a spanning set of the quotient ring
![]() ${\mathbb {F}}[{\mathbf {x}}_{n \times n}] / I_n$
.
${\mathbb {F}}[{\mathbf {x}}_{n \times n}] / I_n$
.
Proof. Let
![]() ${\mathcal {R}} \subseteq [n] \times [n]$
be a rook placement. By Lemma 3.7, it suffices to show that
${\mathcal {R}} \subseteq [n] \times [n]$
be a rook placement. By Lemma 3.7, it suffices to show that
![]() $m({\mathcal {R}})$
lies in the span of
$m({\mathcal {R}})$
lies in the span of
![]() $\{ {\mathfrak {s}}(w) \,:\, w \in {\mathfrak {S}}_n \}$
modulo
$\{ {\mathfrak {s}}(w) \,:\, w \in {\mathfrak {S}}_n \}$
modulo
![]() $I_n$
. If
$I_n$
. If
![]() ${\mathcal {R}} = {\mathcal {S}}(w)$
for some permutation
${\mathcal {R}} = {\mathcal {S}}(w)$
for some permutation
![]() $w \in {\mathfrak {S}}_n$
, then
$w \in {\mathfrak {S}}_n$
, then
![]() $m({\mathcal {R}}) = {\mathfrak {s}}(w)$
and this is clear, so assume that
$m({\mathcal {R}}) = {\mathfrak {s}}(w)$
and this is clear, so assume that
![]() ${\mathcal {R}} \neq {\mathcal {S}}(w)$
for all
${\mathcal {R}} \neq {\mathcal {S}}(w)$
for all
![]() $w \in {\mathfrak {S}}_n$
.
$w \in {\mathfrak {S}}_n$
.
Apply Viennot’s shadow line construction to the rook placement
![]() ${\mathcal {R}}$
. Let
${\mathcal {R}}$
. Let
![]() $L_1, \dots , L_r$
be the shadow lines so obtained, ordered from southwest to northeast, and let
$L_1, \dots , L_r$
be the shadow lines so obtained, ordered from southwest to northeast, and let
![]() $x_1 x_2 \dots x_n$
and
$x_1 x_2 \dots x_n$
and
![]() $y_1 y_2 \dots y_n$
be the sequences appearing in the statement of Lemma 3.6. Since
$y_1 y_2 \dots y_n$
be the sequences appearing in the statement of Lemma 3.6. Since
![]() ${\mathcal {R}}$
is not the shadow set of a permutation, Lemma 3.6 implies that at least one of the sequences
${\mathcal {R}}$
is not the shadow set of a permutation, Lemma 3.6 implies that at least one of the sequences
![]() $x_1 x_2 \dots x_n$
and
$x_1 x_2 \dots x_n$
and
![]() $y_1 y_2 \dots y_n$
has a prefix with a strictly positive sum. We assume that
$y_1 y_2 \dots y_n$
has a prefix with a strictly positive sum. We assume that
![]() $x_1 x_2 \dots x_n$
has a prefix with strictly positive sum; the case of
$x_1 x_2 \dots x_n$
has a prefix with strictly positive sum; the case of
![]() $y_1 y_2 \dots y_n$
is similar.
$y_1 y_2 \dots y_n$
is similar.
Choose
![]() $1 \leq a \leq n$
minimal such that
$1 \leq a \leq n$
minimal such that
![]() $x_1 + x_2 + \cdots + x_a> 0$
. By the minimality of a, we have
$x_1 + x_2 + \cdots + x_a> 0$
. By the minimality of a, we have
![]() $x_a = 1$
so that
$x_a = 1$
so that
![]() $x = a$
is the vertical ray of one of the shadow lines
$x = a$
is the vertical ray of one of the shadow lines
![]() $L_p$
for some
$L_p$
for some
![]() $1 \leq p \leq r$
. We define a size p subset
$1 \leq p \leq r$
. We define a size p subset
![]() $\{ (i_1, j_1), \dots , (i_p, j_p) \} \subseteq {\mathcal {R}}$
as follows. Starting at the vertical ray of
$\{ (i_1, j_1), \dots , (i_p, j_p) \} \subseteq {\mathcal {R}}$
as follows. Starting at the vertical ray of
![]() $L_p$
, let
$L_p$
, let
![]() $(i_p,j_p)$
be the first element of
$(i_p,j_p)$
be the first element of
![]() ${\mathcal {R}}$
encountered by marching south (in particular, we have
${\mathcal {R}}$
encountered by marching south (in particular, we have
![]() $i_p = a$
). Now, march west from
$i_p = a$
). Now, march west from
![]() $(i_p,j_p)$
until one encounters a vertical segment of the shadow line
$(i_p,j_p)$
until one encounters a vertical segment of the shadow line
![]() $L_{p-1}$
. March south along this segment until one reaches a point
$L_{p-1}$
. March south along this segment until one reaches a point
![]() $(i_{p-1},j_{p-1}) \in {\mathcal {R}}$
. Now, march west from
$(i_{p-1},j_{p-1}) \in {\mathcal {R}}$
. Now, march west from
![]() $(i_{p-1},j_{p-1})$
until one encounters a vertical segment of the shadow line
$(i_{p-1},j_{p-1})$
until one encounters a vertical segment of the shadow line
![]() $L_{p-2}$
. March south along this segment until one reaches a point
$L_{p-2}$
. March south along this segment until one reaches a point
![]() $(i_{p-2}, j_{p-2}) \in {\mathcal {R}}$
. Continuing this process, we arrive at a subset
$(i_{p-2}, j_{p-2}) \in {\mathcal {R}}$
. Continuing this process, we arrive at a subset
![]() $\{ (i_1, j_1), \dots , (i_p, j_p) \} \subseteq {\mathcal {R}}$
such that
$\{ (i_1, j_1), \dots , (i_p, j_p) \} \subseteq {\mathcal {R}}$
such that
-
• the point
 $(i_q, j_q)$
lies on the shadow line
$(i_q, j_q)$
lies on the shadow line
 $L_q$
for each
$L_q$
for each
 $1 \leq q \leq p$
,
$1 \leq q \leq p$
, -
• we have
 $i_1 < \cdots < i_p$
, and
$i_1 < \cdots < i_p$
, and -
• we have
 $j_1 < \cdots < j_p$
.
$j_1 < \cdots < j_p$
.
Let
![]() ${\mathcal {R}}' := {\mathcal {R}} - \{ (i_1, j_1), \dots , (i_p, j_p) \}$
be the complement of
${\mathcal {R}}' := {\mathcal {R}} - \{ (i_1, j_1), \dots , (i_p, j_p) \}$
be the complement of
![]() $\{ (i_1, j_1), \dots , (i_p, j_p) \}$
in
$\{ (i_1, j_1), \dots , (i_p, j_p) \}$
in
![]() ${\mathcal {R}}$
.
${\mathcal {R}}$
.
An example may help in understanding these constructions. Let
![]() $n = 11$
and consider the rook placement
$n = 11$
and consider the rook placement
![]() ${\mathcal {R}} \subseteq [11] \times [11]$
given by
${\mathcal {R}} \subseteq [11] \times [11]$
given by
The sequence
![]() $(x_1, x_2, \dots , x_{11})$
is given by
$(x_1, x_2, \dots , x_{11})$
is given by
the figure below shows the shadow lines of
![]() ${\mathcal {R}}$
. By Lemma 3.6, the rook placement
${\mathcal {R}}$
. By Lemma 3.6, the rook placement
![]() ${\mathcal {R}}$
is not the shadow set of a permutation in
${\mathcal {R}}$
is not the shadow set of a permutation in
![]() ${\mathfrak {S}}_8$
because
${\mathfrak {S}}_8$
because
Furthermore, the prefix
![]() $x_1 x_2 \dots x_8$
is the shortest positive sum prefix of the word
$x_1 x_2 \dots x_8$
is the shortest positive sum prefix of the word
![]() $x_1 x_2 \dots x_{11}$
. We conclude that
$x_1 x_2 \dots x_{11}$
. We conclude that
![]() $a = 8$
. Our marching procedure on the shadow line diagram of
$a = 8$
. Our marching procedure on the shadow line diagram of
![]() ${\mathcal {R}}$
is shown in dashed and blue as follows.
${\mathcal {R}}$
is shown in dashed and blue as follows.
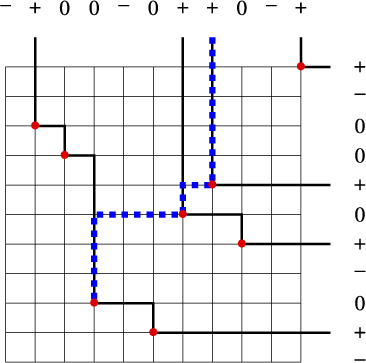
We conclude that
![]() $(i_1, j_1) = (4,3), (i_2, j_2) = (7,6)$
and
$(i_1, j_1) = (4,3), (i_2, j_2) = (7,6)$
and
![]() $(i_3, j_3) = (8,7)$
. Furthermore, we have the set
$(i_3, j_3) = (8,7)$
. Furthermore, we have the set
of rooks in
![]() ${\mathcal {R}}$
which are not visited by the dashed blue line.
${\mathcal {R}}$
which are not visited by the dashed blue line.
Consider the squarefree monomial
![]() $m({\mathcal {R}}')$
corresponding to the rooks in
$m({\mathcal {R}}')$
corresponding to the rooks in
![]() ${\mathcal {R}}' \subseteq {\mathcal {R}}$
which are not reached by our marching procedure. The ideal
${\mathcal {R}}' \subseteq {\mathcal {R}}$
which are not reached by our marching procedure. The ideal
![]() $m({\mathcal {R}}') \cdot {\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
generated by
$m({\mathcal {R}}') \cdot {\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
generated by
![]() $m({\mathcal {R}}')$
in the ring
$m({\mathcal {R}}')$
in the ring
![]() ${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
admits a morphism from a smaller quotient of the same form. More precisely, let
${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
admits a morphism from a smaller quotient of the same form. More precisely, let
![]() $\bar {n} := n - |{\mathcal {R}}'|$
, and let
$\bar {n} := n - |{\mathcal {R}}'|$
, and let
![]() $\bar {{\mathbf {x}}}$
be the
$\bar {{\mathbf {x}}}$
be the
![]() $\bar {n} \times \bar {n}$
matrix of variables
$\bar {n} \times \bar {n}$
matrix of variables
In our example above, the matrix
![]() $\bar {{\mathbf {x}}}$
consists of the variables
$\bar {{\mathbf {x}}}$
consists of the variables
![]() $x_{i,j}$
indexed by
$x_{i,j}$
indexed by
![]() $i \in \{1,4,5,7,8,10\}$
and
$i \in \{1,4,5,7,8,10\}$
and
![]() $j \in \{1,3,4,6,7,10\}$
. Let
$j \in \{1,3,4,6,7,10\}$
. Let
![]() ${\mathbb {F}}[\bar {{\mathbf {x}}}]$
be the polynomial ring over the variables in
${\mathbb {F}}[\bar {{\mathbf {x}}}]$
be the polynomial ring over the variables in
![]() $\bar {{\mathbf {x}}}$
, and let
$\bar {{\mathbf {x}}}$
, and let
![]() $\bar {I} \subseteq {\mathbb {F}}[\bar {{\mathbf {x}}}]$
be the natural copy of the ideal
$\bar {I} \subseteq {\mathbb {F}}[\bar {{\mathbf {x}}}]$
be the natural copy of the ideal
![]() $I_{\bar {n}}$
in the square variable matrix
$I_{\bar {n}}$
in the square variable matrix
![]() $\bar {{\mathbf {x}}}$
. The map
$\bar {{\mathbf {x}}}$
. The map
induced by
![]() $f \mapsto m({\mathcal {R}}') \cdot f$
is easily seen to be a (well-defined) homomorphism of
$f \mapsto m({\mathcal {R}}') \cdot f$
is easily seen to be a (well-defined) homomorphism of
![]() ${\mathbb {F}}[\bar {{\mathbf {x}}}]$
-modules; one simply checks that for any generator
${\mathbb {F}}[\bar {{\mathbf {x}}}]$
-modules; one simply checks that for any generator
![]() $g \in {\mathbb {F}}[\bar {{\mathbf {x}}}]$
of
$g \in {\mathbb {F}}[\bar {{\mathbf {x}}}]$
of
![]() $\bar {I}$
, we have
$\bar {I}$
, we have
![]() $m({\mathcal {R}}') \cdot g \in I_n$
. We consider the sets
$m({\mathcal {R}}') \cdot g \in I_n$
. We consider the sets
and
In our example, we have
![]() $T = \{4,7,8,10\}$
and
$T = \{4,7,8,10\}$
and
![]() $S = \{3,6,7\}$
.
$S = \{3,6,7\}$
.
By the definitions of S and T, the polynomial
![]() $b_{S,T} \in {\mathbb {F}}[\bar {{\mathbf {x}}}]$
does not involve any of the variables which share a row or column with a rook
$b_{S,T} \in {\mathbb {F}}[\bar {{\mathbf {x}}}]$
does not involve any of the variables which share a row or column with a rook
![]() $(i,j) \in {\mathcal {R}}'$
which is not visited by our marching procedure. Since
$(i,j) \in {\mathcal {R}}'$
which is not visited by our marching procedure. Since
![]() $i_p = a$
and we have the prefix inequality
$i_p = a$
and we have the prefix inequality
![]() $x_1 + x_2 + \cdots + x_a> 0$
, we have
$x_1 + x_2 + \cdots + x_a> 0$
, we have
![]() $|S| + |T|> \bar {n}$
. Lemma 3.1 applies to give
$|S| + |T|> \bar {n}$
. Lemma 3.1 applies to give
Since the map
![]() $\varphi $
of Equation (3.13) is a homomorphism of
$\varphi $
of Equation (3.13) is a homomorphism of
![]() ${\mathbb {F}}[\bar {{\mathbf {x}}}]$
-modules we obtain
${\mathbb {F}}[\bar {{\mathbf {x}}}]$
-modules we obtain
Observation 3.10 implies that the Toeplitz-leading term of
![]() $m({\mathcal {R}}') \cdot b_{S,T}$
is
$m({\mathcal {R}}') \cdot b_{S,T}$
is
![]() $m({\mathcal {R}})$
, so the membership (3.17) yields
$m({\mathcal {R}})$
, so the membership (3.17) yields
where
![]() $\Sigma $
is a
$\Sigma $
is a
![]() ${\mathbb {F}}$
-linear combination of monomials which are
${\mathbb {F}}$
-linear combination of monomials which are
![]() $<_{\mathrm {Top}} m({\mathcal {R}})$
. By induction on the Toeplitz order, the lemma is proven.
$<_{\mathrm {Top}} m({\mathcal {R}})$
. By induction on the Toeplitz order, the lemma is proven.
Lemma 3.11 (and its proof) give a Gröbner basis for the ideal
![]() $I_n \subseteq {\mathbb {F}}[{\mathbf {x}}_{n \times n}]$
with respect to the Toeplitz order which consists of
$I_n \subseteq {\mathbb {F}}[{\mathbf {x}}_{n \times n}]$
with respect to the Toeplitz order which consists of
-
• any product of two variables in
 ${\mathbf {x}}_{n \times n}$
which lie in the same row or column, and
${\mathbf {x}}_{n \times n}$
which lie in the same row or column, and -
• in the notation of the proof of Lemma 3.11 and polynomial of the form
 $m({\mathcal {R}}') \cdot b_{S,T}$
for a rook placement
$m({\mathcal {R}}') \cdot b_{S,T}$
for a rook placement
 ${\mathcal {R}} \subseteq [n] \times [n]$
which is not the shadow set of a permutation
${\mathcal {R}} \subseteq [n] \times [n]$
which is not the shadow set of a permutation
 $w \in {\mathfrak {S}}_n$
for which some prefix of the word
$w \in {\mathfrak {S}}_n$
for which some prefix of the word
 $x_1 x_2 \dots x_n$
is positive, and the image of
$x_1 x_2 \dots x_n$
is positive, and the image of
 $m({\mathcal {R}}') \cdot b_{S,T}$
under the involution
$m({\mathcal {R}}') \cdot b_{S,T}$
under the involution
 ${\mathbb {F}}[{\mathbf {x}}_{n \times n}]$
which interchanges
${\mathbb {F}}[{\mathbf {x}}_{n \times n}]$
which interchanges
 $x_{i,j}$
and
$x_{i,j}$
and
 $x_{j,i}$
.
$x_{j,i}$
.
This Gröbner basis is far from minimal. We leave the computation of a minimal (or reduced) Gröbner basis of
![]() $I_n$
as an open problem.
$I_n$
as an open problem.
3.4 Standard monomial basis and Hilbert series
Lemma 3.11 bounds the quotient ring
![]() ${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
from above by giving an
${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
from above by giving an
![]() ${\mathbb {F}}$
-linear spanning set. In this subsection, we use orbit harmonics to bound this quotient from below.
${\mathbb {F}}$
-linear spanning set. In this subsection, we use orbit harmonics to bound this quotient from below.
Let
![]() ${\mathbb {F}}^{n \times n}$
be the affine space of
${\mathbb {F}}^{n \times n}$
be the affine space of
![]() $n \times n$
matrices over
$n \times n$
matrices over
![]() ${\mathbb {F}}$
with coordinate ring
${\mathbb {F}}$
with coordinate ring
![]() ${\mathbb {F}}[{\mathbf {x}}_{n \times n}]$
. Write
${\mathbb {F}}[{\mathbf {x}}_{n \times n}]$
. Write
![]() $P_n \subseteq {\mathbb {F}}^{n \times n}$
for the locus of permutation matrices. That is, the set
$P_n \subseteq {\mathbb {F}}^{n \times n}$
for the locus of permutation matrices. That is, the set
![]() $P_n$
consists of 0,1-matrices with a unique 1 in each row and column. The vanishing ideal
$P_n$
consists of 0,1-matrices with a unique 1 in each row and column. The vanishing ideal
![]() ${\mathbf {I}}(P_n) \subseteq {\mathbb {F}}[{\mathbf {x}}_{n \times n}]$
of the permutation matrix locus is generated by
${\mathbf {I}}(P_n) \subseteq {\mathbb {F}}[{\mathbf {x}}_{n \times n}]$
of the permutation matrix locus is generated by
-
•
 $x_{i,j}^2 - x_{i,j}$
for all
$x_{i,j}^2 - x_{i,j}$
for all
 $1 \leq i, j \leq n$
,
$1 \leq i, j \leq n$
, -
•
 $x_{i,j} \cdot x_{i',j}$
for all
$x_{i,j} \cdot x_{i',j}$
for all
 $1 \leq i < i' \leq n$
and
$1 \leq i < i' \leq n$
and
 $i \leq j \leq n$
,
$i \leq j \leq n$
, -
•
 $x_{i,j} \cdot x_{i,j'}$
for all
$x_{i,j} \cdot x_{i,j'}$
for all
 $1 \leq i \leq n$
and
$1 \leq i \leq n$
and
 $1 \leq j < j' \leq n$
,
$1 \leq j < j' \leq n$
, -
•
 $x_{i,1} + \cdots + x_{i,n} - 1$
for all
$x_{i,1} + \cdots + x_{i,n} - 1$
for all
 $1 \leq i \leq n$
, and
$1 \leq i \leq n$
, and -
•
 $x_{1,j} + \cdots + x_{n,j} - 1$
for all
$x_{1,j} + \cdots + x_{n,j} - 1$
for all
 $1 \leq j \leq n$
.
$1 \leq j \leq n$
.
Indeed, the generators in the first bullet point come from the
![]() $(i,j)$
-entry of a permutation matrix being 0 or 1, the generators in the second and third bullet points come from products of distinct entries in a row or column of a permutation matrix vanishing, and the generators in the fourth and fifth bullet points come from the row and columns summing to 1. Comparing these generators with Definition 1.1, we get the containment
$(i,j)$
-entry of a permutation matrix being 0 or 1, the generators in the second and third bullet points come from products of distinct entries in a row or column of a permutation matrix vanishing, and the generators in the fourth and fifth bullet points come from the row and columns summing to 1. Comparing these generators with Definition 1.1, we get the containment
Although the highest degree components
![]() $\tau (g_1), \dots , \tau (g_r)$
of a generating set
$\tau (g_1), \dots , \tau (g_r)$
of a generating set
![]() $\{ g_1, \dots , g_r \}$
of an ideal I are in general insufficient to generate
$\{ g_1, \dots , g_r \}$
of an ideal I are in general insufficient to generate
![]() ${\mathrm {gr}} \, I$
, in our case the containment (3.19) is an equality.
${\mathrm {gr}} \, I$
, in our case the containment (3.19) is an equality.
Theorem 3.12. We have the equality of ideals
![]() $I_n = {\mathrm {gr}} \, {\mathbf {I}}(P_n)$
of
$I_n = {\mathrm {gr}} \, {\mathbf {I}}(P_n)$
of
![]() ${\mathbb {F}}[{\mathbf {x}}_{n \times n}]$
. Furthermore, the set
${\mathbb {F}}[{\mathbf {x}}_{n \times n}]$
. Furthermore, the set
![]() $\{ {\mathfrak {s}}(w) \,:\, w \in {\mathfrak {S}}_n \}$
of shadow monomials of permutations in
$\{ {\mathfrak {s}}(w) \,:\, w \in {\mathfrak {S}}_n \}$
of shadow monomials of permutations in
![]() ${\mathfrak {S}}_n$
descends to a basis of
${\mathfrak {S}}_n$
descends to a basis of
![]() ${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
. This is the standard monomial basis of
${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
. This is the standard monomial basis of
![]() ${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
with respect to the Toeplitz term order
${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
with respect to the Toeplitz term order
![]() $<_{\mathrm {Top}}$
.
$<_{\mathrm {Top}}$
.
Standard monomial bases of quotient rings
![]() ${\mathbb {F}}[{\mathbf {x}}]/I$
can be unpredictable, even for nicely presented ideals I. However, Theorem 3.12 informally suggests that the Toeplitz term order
${\mathbb {F}}[{\mathbf {x}}]/I$
can be unpredictable, even for nicely presented ideals I. However, Theorem 3.12 informally suggests that the Toeplitz term order
![]() $<_{\mathrm {Top}}$
and the homogeneous ideal
$<_{\mathrm {Top}}$
and the homogeneous ideal
![]() $I_n$
‘know’ the Viennot shadow line incarnation of the Schensted correspondence
$I_n$
‘know’ the Viennot shadow line incarnation of the Schensted correspondence
![]() $w \mapsto (P(w), Q(w))$
.
$w \mapsto (P(w), Q(w))$
.
Proof. The chain (2.7) of
![]() ${\mathbb {F}}$
-vector space isomorphisms coming from orbit harmonics reads
${\mathbb {F}}$
-vector space isomorphisms coming from orbit harmonics reads
Lemma 3.11 and the containment (3.19) of ideals yield the chain of (in)equalities
which forces
![]() $I_n = {\mathrm {gr}} \, {\mathbf {I}}(P_n)$
and
$I_n = {\mathrm {gr}} \, {\mathbf {I}}(P_n)$
and
![]() $\dim {\mathbb {F}}[{\mathbf {x}}_{n \times n}] / I_n = n!$
. Another application of Lemma 3.11 shows that the spanning set
$\dim {\mathbb {F}}[{\mathbf {x}}_{n \times n}] / I_n = n!$
. Another application of Lemma 3.11 shows that the spanning set
![]() $\{ {\mathfrak {s}}(w) \,:\, w \in {\mathfrak {S}}_n \}$
of
$\{ {\mathfrak {s}}(w) \,:\, w \in {\mathfrak {S}}_n \}$
of
![]() ${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
is in fact a basis. The proof of Lemma 3.11 shows that
${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
is in fact a basis. The proof of Lemma 3.11 shows that
![]() $\{ {\mathfrak {s}}(w) \,:\, w \in {\mathfrak {S}}_n \}$
is the standard monomial basis of
$\{ {\mathfrak {s}}(w) \,:\, w \in {\mathfrak {S}}_n \}$
is the standard monomial basis of
![]() ${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
with respect to
${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
with respect to
![]() $<_{\mathrm {Top}}$
.
$<_{\mathrm {Top}}$
.
As a corollary, we get our promised relationship between the Hilbert series of
![]() ${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
and longest increasing subsequences in permutations.
${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
and longest increasing subsequences in permutations.
Corollary 3.13. Let
![]() $a_{n,k}$
be the number of permutations in
$a_{n,k}$
be the number of permutations in
![]() ${\mathfrak {S}}_n$
whose longest increasing sequence has length k. The quotient ring
${\mathfrak {S}}_n$
whose longest increasing sequence has length k. The quotient ring
![]() ${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
has Hilbert series
${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
has Hilbert series
3.5 Local permutation statistics
Corollary 3.13 gives the structure of
![]() ${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
as a graded vector space. Our next goal is the structure of this quotient as a graded
${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
as a graded vector space. Our next goal is the structure of this quotient as a graded
![]() ${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
module (at least when
${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
module (at least when
![]() $n! \neq 0$
in
$n! \neq 0$
in
![]() ${\mathbb {F}}$
). Our calculation of the module structure of
${\mathbb {F}}$
). Our calculation of the module structure of
![]() ${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
will make crucial use of a notion of complexity on permutation statistics due to Hamaker and the author [Reference Hamaker and Rhoades10] called ‘locality’.
${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
will make crucial use of a notion of complexity on permutation statistics due to Hamaker and the author [Reference Hamaker and Rhoades10] called ‘locality’.
A permutation statistic (with values in the field
![]() ${\mathbb {F}}$
) is a function
${\mathbb {F}}$
) is a function
![]() $f: {\mathfrak {S}}_n \rightarrow {\mathbb {F}}$
. The study of permutation statistics is an important subfield of combinatorics. Examples include the exceedance, inversion, and peak numbers given by
$f: {\mathfrak {S}}_n \rightarrow {\mathbb {F}}$
. The study of permutation statistics is an important subfield of combinatorics. Examples include the exceedance, inversion, and peak numbers given by
Following [Reference Hamaker and Rhoades10], we define a notion of locality for permutation statistics as follows. If
![]() ${\mathcal {R}} \subseteq [n] \times [n]$
is a rook placement and
${\mathcal {R}} \subseteq [n] \times [n]$
is a rook placement and
![]() $w \in {\mathfrak {S}}_n$
is a permutation, we say that w extends
$w \in {\mathfrak {S}}_n$
is a permutation, we say that w extends
![]() ${\mathcal {R}}$
if we have the containment of sets
${\mathcal {R}}$
if we have the containment of sets
![]() ${\mathcal {R}} \subseteq \{ (i,w(i)) \,:\, 1 \leq i \leq n \}$
. Given a rook placement
${\mathcal {R}} \subseteq \{ (i,w(i)) \,:\, 1 \leq i \leq n \}$
. Given a rook placement
![]() ${\mathcal {R}} \subseteq [n] \times [n]$
, let
${\mathcal {R}} \subseteq [n] \times [n]$
, let
![]() ${\mathbf {1}}_{{\mathcal {R}}}: {\mathfrak {S}}_n \rightarrow {\mathbb {F}}$
be the indicator permutation statistic
${\mathbf {1}}_{{\mathcal {R}}}: {\mathfrak {S}}_n \rightarrow {\mathbb {F}}$
be the indicator permutation statistic
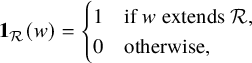 $$ \begin{align} {\mathbf {1}}_{{\mathcal {R}}}(w) = \begin{cases} 1 & \text{if } w \text{ extends } {\mathcal {R}}, \\ 0 & \text{otherwise,} \end{cases} \end{align} $$
$$ \begin{align} {\mathbf {1}}_{{\mathcal {R}}}(w) = \begin{cases} 1 & \text{if } w \text{ extends } {\mathcal {R}}, \\ 0 & \text{otherwise,} \end{cases} \end{align} $$
which detects whether w extends
![]() ${\mathcal {R}}$
. A permutation statistic
${\mathcal {R}}$
. A permutation statistic
![]() $f: {\mathfrak {S}}_n \rightarrow {\mathbb {F}}$
is k-local if there exist field elements
$f: {\mathfrak {S}}_n \rightarrow {\mathbb {F}}$
is k-local if there exist field elements
![]() $c_{{\mathcal {R}}} \in {\mathbb {F}}$
such that
$c_{{\mathcal {R}}} \in {\mathbb {F}}$
such that
as functions
![]() ${\mathfrak {S}}_n \rightarrow {\mathbb {F}}$
where the sum is over all rook placements
${\mathfrak {S}}_n \rightarrow {\mathbb {F}}$
where the sum is over all rook placements
![]() ${\mathcal {R}} \subseteq [n] \times [n]$
with k rooks.
${\mathcal {R}} \subseteq [n] \times [n]$
with k rooks.
Remark 3.14. A k-local statistic
![]() $f: {\mathfrak {S}}_n \rightarrow {\mathbb {F}}$
is also known to have ‘degree at most k’ elsewhere in the literature, for example, [Reference Dafni, Filmus, Lifshitz, Lindzey and Vinyals5]. We avoid this terminology to guard against confusion with the degree of a character.
$f: {\mathfrak {S}}_n \rightarrow {\mathbb {F}}$
is also known to have ‘degree at most k’ elsewhere in the literature, for example, [Reference Dafni, Filmus, Lifshitz, Lindzey and Vinyals5]. We avoid this terminology to guard against confusion with the degree of a character.
Roughly speaking, the locality of a permutation statistic bounds its complexity. The only 0-local statistics are constant functions
![]() ${\mathfrak {S}}_n \rightarrow {\mathbb {F}}$
. The statistic
${\mathfrak {S}}_n \rightarrow {\mathbb {F}}$
. The statistic
![]() ${\mathrm {exc}}$
is 1-local, the statistic
${\mathrm {exc}}$
is 1-local, the statistic
![]() ${\mathrm {inv}}$
is 2-local, and the statistic
${\mathrm {inv}}$
is 2-local, and the statistic
![]() ${\mathrm {peak}}$
is 3-local. Following Hamaker and the author [Reference Hamaker and Rhoades10], we consider the
${\mathrm {peak}}$
is 3-local. Following Hamaker and the author [Reference Hamaker and Rhoades10], we consider the
![]() ${\mathbb {F}}$
-vector space
${\mathbb {F}}$
-vector space
of k-local statistics on
![]() ${\mathfrak {S}}_n$
. It is not hard to see that any k-local statistic is also
${\mathfrak {S}}_n$
. It is not hard to see that any k-local statistic is also
![]() $(k+1)$
-local so that
$(k+1)$
-local so that
![]() ${\mathrm {Loc}}_k({\mathfrak {S}}_n,{\mathbb {F}}) \subseteq {\mathrm {Loc}}_{k+1}({\mathfrak {S}}_n,{\mathbb {F}})$
. Furthermore, any permutation statistic
${\mathrm {Loc}}_k({\mathfrak {S}}_n,{\mathbb {F}}) \subseteq {\mathrm {Loc}}_{k+1}({\mathfrak {S}}_n,{\mathbb {F}})$
. Furthermore, any permutation statistic
![]() ${\mathfrak {S}}_n \rightarrow {\mathbb {F}}$
is
${\mathfrak {S}}_n \rightarrow {\mathbb {F}}$
is
![]() $(n-1)$
-local. The vector spaces
$(n-1)$
-local. The vector spaces
![]() ${\mathrm {Loc}}_k({\mathfrak {S}}_n,{\mathbb {F}})$
will play an important role in the module structure of
${\mathrm {Loc}}_k({\mathfrak {S}}_n,{\mathbb {F}})$
will play an important role in the module structure of
![]() ${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
(Theorem 4.2); for now we use shadow monomials to solve an open problem from [Reference Hamaker and Rhoades10] about the spaces
${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
(Theorem 4.2); for now we use shadow monomials to solve an open problem from [Reference Hamaker and Rhoades10] about the spaces
![]() ${\mathrm {Loc}}_k({\mathfrak {S}}_n,{\mathbb {F}})$
themselves.
${\mathrm {Loc}}_k({\mathfrak {S}}_n,{\mathbb {F}})$
themselves.
By definition, the set
![]() $\{ {\mathbf {1}}_{{\mathcal {R}}} \,:\, | {\mathcal {R}} | = k \}$
of indicator statistics corresponding to rook placements
$\{ {\mathbf {1}}_{{\mathcal {R}}} \,:\, | {\mathcal {R}} | = k \}$
of indicator statistics corresponding to rook placements
![]() ${\mathcal {R}} \subseteq [n] \times [n]$
of size k is a spanning set of
${\mathcal {R}} \subseteq [n] \times [n]$
of size k is a spanning set of
![]() ${\mathrm {Loc}}_k({\mathfrak {S}}_n,{\mathbb {F}})$
, but this spanning set is almost always linearly dependent. In [Reference Hamaker and Rhoades10, Cor. 4.7] it is proven that when
${\mathrm {Loc}}_k({\mathfrak {S}}_n,{\mathbb {F}})$
, but this spanning set is almost always linearly dependent. In [Reference Hamaker and Rhoades10, Cor. 4.7] it is proven that when
![]() ${\mathbb {F}} = \mathbb {R}$
is the field of real numbers, the dimension of
${\mathbb {F}} = \mathbb {R}$
is the field of real numbers, the dimension of
![]() ${\mathrm {Loc}}_k({\mathfrak {S}}_n,{\mathbb {F}})$
equals to the number
${\mathrm {Loc}}_k({\mathfrak {S}}_n,{\mathbb {F}})$
equals to the number
![]() $a_{n,n-k} + \cdots + a_{n,n-1} + a_{n,n}$
of permutations in
$a_{n,n-k} + \cdots + a_{n,n-1} + a_{n,n}$
of permutations in
![]() ${\mathfrak {S}}_n$
which have an increasing subsequence of length at least
${\mathfrak {S}}_n$
which have an increasing subsequence of length at least
![]() $n-k$
. The methods of [Reference Hamaker and Rhoades10] apply whenever
$n-k$
. The methods of [Reference Hamaker and Rhoades10] apply whenever
![]() ${\mathbb {F}}$
has characteristic 0 or characteristic
${\mathbb {F}}$
has characteristic 0 or characteristic
![]() $p> n$
; we will see (Theorem 3.16) that this is true over any field.
$p> n$
; we will see (Theorem 3.16) that this is true over any field.
The paper [Reference Hamaker and Rhoades10] did not give an explicit basis of the space of k-local statistics consisting of statistics of the form
![]() ${\mathbf {1}}_{\mathcal {R}}$
; we solve this problem in Theorem 3.16 below. Although the members
${\mathbf {1}}_{\mathcal {R}}$
; we solve this problem in Theorem 3.16 below. Although the members
![]() ${\mathbf {1}}_{\mathcal {R}}$
of our basis for
${\mathbf {1}}_{\mathcal {R}}$
of our basis for
![]() ${\mathrm {Loc}}_k({\mathfrak {S}}_n,{\mathbb {F}})$
can correspond to rook placements with
${\mathrm {Loc}}_k({\mathfrak {S}}_n,{\mathbb {F}})$
can correspond to rook placements with
![]() $|{\mathcal {R}}| < k$
in general, we will obtain a nested family of bases for the chain of vector spaces
$|{\mathcal {R}}| < k$
in general, we will obtain a nested family of bases for the chain of vector spaces
![]() ${\mathrm {Loc}}_0({\mathfrak {S}}_n,{\mathbb {F}}) \subseteq {\mathrm {Loc}}_1({\mathfrak {S}}_n,{\mathbb {F}}) \subseteq \cdots \subseteq {\mathrm {Loc}}_{n-1}({\mathfrak {S}}_n,{\mathbb {F}})$
. To achieve these goals, we recall a standard fact about associated graded ideals.
${\mathrm {Loc}}_0({\mathfrak {S}}_n,{\mathbb {F}}) \subseteq {\mathrm {Loc}}_1({\mathfrak {S}}_n,{\mathbb {F}}) \subseteq \cdots \subseteq {\mathrm {Loc}}_{n-1}({\mathfrak {S}}_n,{\mathbb {F}})$
. To achieve these goals, we recall a standard fact about associated graded ideals.
Let
![]() ${\mathbf {x}}$
be a finite set of variables, and consider the polynomial ring
${\mathbf {x}}$
be a finite set of variables, and consider the polynomial ring
![]() ${\mathbb {F}}[{\mathbf {x}}]$
over these variables. Given
${\mathbb {F}}[{\mathbf {x}}]$
over these variables. Given
![]() $d \geq 0$
and a graded
$d \geq 0$
and a graded
![]() ${\mathbb {F}}$
-algebra A, let
${\mathbb {F}}$
-algebra A, let
![]() $A_{\leq d} \subseteq A$
be the subspace of elements of degree at most d. We have a filtration
$A_{\leq d} \subseteq A$
be the subspace of elements of degree at most d. We have a filtration
![]() ${\mathbb {F}}[{\mathbf {x}}]_{\leq 0} \subseteq {\mathbb {F}}[{\mathbf {x}}]_{\leq 1} \subseteq {\mathbb {F}}[{\mathbf {x}}]_{\leq 2} \subseteq \cdots $
of
${\mathbb {F}}[{\mathbf {x}}]_{\leq 0} \subseteq {\mathbb {F}}[{\mathbf {x}}]_{\leq 1} \subseteq {\mathbb {F}}[{\mathbf {x}}]_{\leq 2} \subseteq \cdots $
of
![]() ${\mathbb {F}}[{\mathbf {x}}]$
by finite-dimensional subspaces.
${\mathbb {F}}[{\mathbf {x}}]$
by finite-dimensional subspaces.
Lemma 3.15. Let
![]() $I \subseteq {\mathbb {F}}[{\mathbf {x}}]$
be an ideal, and let
$I \subseteq {\mathbb {F}}[{\mathbf {x}}]$
be an ideal, and let
![]() ${\mathrm {gr}} \, I \subseteq {\mathbb {F}}[{\mathbf {x}}]$
be the associated graded ideal of I. Fix an integer
${\mathrm {gr}} \, I \subseteq {\mathbb {F}}[{\mathbf {x}}]$
be the associated graded ideal of I. Fix an integer
![]() $d \geq 0$
, and let
$d \geq 0$
, and let
![]() ${\mathcal {B}} \subseteq {\mathbb {F}}[{\mathbf {x}}]_{\leq d}$
be a family of homogeneous polynomials of degree at most d. Suppose that
${\mathcal {B}} \subseteq {\mathbb {F}}[{\mathbf {x}}]_{\leq d}$
be a family of homogeneous polynomials of degree at most d. Suppose that
![]() ${\mathcal {B}}$
descends to a basis of the vector space
${\mathcal {B}}$
descends to a basis of the vector space
![]() $( {\mathbb {F}}[{\mathbf {x}}] / {\mathrm {gr}} \, I )_{\leq d}$
. Then
$( {\mathbb {F}}[{\mathbf {x}}] / {\mathrm {gr}} \, I )_{\leq d}$
. Then
![]() ${\mathcal {B}}$
descends to a basis of the vector space
${\mathcal {B}}$
descends to a basis of the vector space
![]() ${\mathbb {F}}[{\mathbf {x}}]_{\leq d} / (I \cap {\mathbb {F}}[{\mathbf {x}}]_{\leq d} )$
.
${\mathbb {F}}[{\mathbf {x}}]_{\leq d} / (I \cap {\mathbb {F}}[{\mathbf {x}}]_{\leq d} )$
.
Lemma 3.15 is the heart of the orbit harmonics isomorphisms (2.7). We include its straightforward proof for completeness.
Proof. If
![]() ${\mathcal {B}}$
were not linearly independent modulo
${\mathcal {B}}$
were not linearly independent modulo
![]() $I \cap {\mathbb {F}}[{\mathbf {x}}]_{\leq d}$
, there would exist scalars
$I \cap {\mathbb {F}}[{\mathbf {x}}]_{\leq d}$
, there would exist scalars
![]() $c_b \in {\mathbb {F}}$
not all zero and an element
$c_b \in {\mathbb {F}}$
not all zero and an element
![]() $g \in I$
with
$g \in I$
with
![]() $\deg (g) \leq d$
such that
$\deg (g) \leq d$
such that
![]() $\sum _{b \in {\mathcal {B}}} c_b \cdot b = g$
. Since the elements of
$\sum _{b \in {\mathcal {B}}} c_b \cdot b = g$
. Since the elements of
![]() ${\mathcal {B}}$
are homogeneous, taking the highest degree component of both sides of this equation would result in a linear dependence of
${\mathcal {B}}$
are homogeneous, taking the highest degree component of both sides of this equation would result in a linear dependence of
![]() ${\mathcal {B}}$
modulo
${\mathcal {B}}$
modulo
![]() ${\mathrm {gr}} \, I$
, a contradiction.
${\mathrm {gr}} \, I$
, a contradiction.
If
![]() ${\mathcal {B}}$
did not span
${\mathcal {B}}$
did not span
![]() ${\mathbb {F}}[{\mathbf {x}}]_{\leq d} / (I \cap {\mathbb {F}}[{\mathbf {x}}]_{\leq d} )$
, there would be some homogeneous polynomial
${\mathbb {F}}[{\mathbf {x}}]_{\leq d} / (I \cap {\mathbb {F}}[{\mathbf {x}}]_{\leq d} )$
, there would be some homogeneous polynomial
![]() $h \in {\mathbb {F}}[{\mathbf {x}}]_{\leq d}$
such that g does not lie in the span of
$h \in {\mathbb {F}}[{\mathbf {x}}]_{\leq d}$
such that g does not lie in the span of
![]() ${\mathcal {B}}$
modulo
${\mathcal {B}}$
modulo
![]() $I \cap {\mathbb {F}}[{\mathbf {x}}]_{\leq d}$
. Choose such an h with
$I \cap {\mathbb {F}}[{\mathbf {x}}]_{\leq d}$
. Choose such an h with
![]() $\deg (h)$
minimal. There exist scalars
$\deg (h)$
minimal. There exist scalars
![]() $c_b \in {\mathbb {F}}$
such that
$c_b \in {\mathbb {F}}$
such that
![]() $\sum _{b \in {\mathcal {B}}} c_b \cdot b = h + \tau (g)$
for some
$\sum _{b \in {\mathcal {B}}} c_b \cdot b = h + \tau (g)$
for some
![]() $g \in I$
with
$g \in I$
with
![]() $\deg (g) = \deg (h)$
(so that in particular
$\deg (g) = \deg (h)$
(so that in particular
![]() $g \in I \cap {\mathbb {F}}[{\mathbf {x}}]_{\leq d}$
), where
$g \in I \cap {\mathbb {F}}[{\mathbf {x}}]_{\leq d}$
), where
![]() $\tau (g)$
is the highest degree component of g. Discarding redundant terms if necessary, we may assume that
$\tau (g)$
is the highest degree component of g. Discarding redundant terms if necessary, we may assume that
![]() $c_b = 0$
whenever
$c_b = 0$
whenever
![]() $\deg (b) \neq \deg (h)$
. We conclude that
$\deg (b) \neq \deg (h)$
. We conclude that
![]() $h + g - \sum _{b \in {\mathcal {B}}} c_b \cdot b$
has degree
$h + g - \sum _{b \in {\mathcal {B}}} c_b \cdot b$
has degree
![]() $< \deg (h)$
, so by our choice of h there exist
$< \deg (h)$
, so by our choice of h there exist
![]() $c^{\prime }_b \in {\mathbb {F}}$
and
$c^{\prime }_b \in {\mathbb {F}}$
and
![]() $g' \in I \cap {\mathbb {F}}[{\mathbf {x}}]_{\leq d}$
with
$g' \in I \cap {\mathbb {F}}[{\mathbf {x}}]_{\leq d}$
with
so that
![]() $h = \sum _{b \in {\mathcal {B}}} (c^{\prime }_b - c_b) \cdot b - (g' + g)$
lies in the span of
$h = \sum _{b \in {\mathcal {B}}} (c^{\prime }_b - c_b) \cdot b - (g' + g)$
lies in the span of
![]() ${\mathcal {B}}$
modulo
${\mathcal {B}}$
modulo
![]() $I \cap {\mathbb {F}}[{\mathbf {x}}]_{\leq d}$
, a contradiction.
$I \cap {\mathbb {F}}[{\mathbf {x}}]_{\leq d}$
, a contradiction.
An application of Lemma 3.15 gives a basis of the vector space
![]() ${\mathrm {Loc}}_k({\mathfrak {S}}_n,{\mathbb {F}})$
.
${\mathrm {Loc}}_k({\mathfrak {S}}_n,{\mathbb {F}})$
.
Theorem 3.16. The vector space
![]() ${\mathrm {Loc}}_k({\mathfrak {S}}_n,{\mathbb {F}})$
of k-local statistics
${\mathrm {Loc}}_k({\mathfrak {S}}_n,{\mathbb {F}})$
of k-local statistics
![]() ${\mathfrak {S}}_n \rightarrow {\mathbb {F}}$
has basis
${\mathfrak {S}}_n \rightarrow {\mathbb {F}}$
has basis
given by indicator functions of shadow sets of permutations in
![]() ${\mathfrak {S}}_n$
which contain an increasing subsequence of length
${\mathfrak {S}}_n$
which contain an increasing subsequence of length
![]() $n-k$
.
$n-k$
.
Other authors (see, e.g., [Reference Dafni, Filmus, Lifshitz, Lindzey and Vinyals5]) refer to the functions
![]() ${\mathbf {1}}_{\mathcal {R}}$
as juntas. So Theorem 3.16 describes a basis of shadow juntas.
${\mathbf {1}}_{\mathcal {R}}$
as juntas. So Theorem 3.16 describes a basis of shadow juntas.
Proof. For
![]() $\ell \leq k$
, any
$\ell \leq k$
, any
![]() $\ell $
-local permutation statistic is also k-local, so the indicator functions in question are members of
$\ell $
-local permutation statistic is also k-local, so the indicator functions in question are members of
![]() ${\mathrm {Loc}}_k({\mathfrak {S}}_n,{\mathbb {F}})$
by Lemma 3.5. Identifying
${\mathrm {Loc}}_k({\mathfrak {S}}_n,{\mathbb {F}})$
by Lemma 3.5. Identifying
![]() ${\mathfrak {S}}_n = P_n$
with the locus of permutation matrices in
${\mathfrak {S}}_n = P_n$
with the locus of permutation matrices in
![]() ${\mathbb {F}}^{n \times n}$
, the indicator function
${\mathbb {F}}^{n \times n}$
, the indicator function
![]() ${\mathbf {1}}_{{\mathcal {R}}}$
corresponding to a rook placement
${\mathbf {1}}_{{\mathcal {R}}}$
corresponding to a rook placement
![]() ${\mathcal {R}} \subseteq [n] \times [n]$
is represented by the degree
${\mathcal {R}} \subseteq [n] \times [n]$
is represented by the degree
![]() $|{\mathcal {R}}|$
monomial
$|{\mathcal {R}}|$
monomial
![]() $m({\mathcal {R}}) \in {\mathbb {F}}[{\mathbf {x}}_{n \times n}]$
. It follows that we have an isomorphism
$m({\mathcal {R}}) \in {\mathbb {F}}[{\mathbf {x}}_{n \times n}]$
. It follows that we have an isomorphism
of
![]() ${\mathbb {F}}$
-vector spaces given by
${\mathbb {F}}$
-vector spaces given by
![]() ${\mathbf {1}}_{\mathcal {R}} \mapsto m({\mathcal {R}}) + ( {\mathbf {I}}(P_n) \cap {\mathbb {F}}[{\mathbf {x}}_{n \times n}]_{\leq k} )$
. Write
${\mathbf {1}}_{\mathcal {R}} \mapsto m({\mathcal {R}}) + ( {\mathbf {I}}(P_n) \cap {\mathbb {F}}[{\mathbf {x}}_{n \times n}]_{\leq k} )$
. Write
for the set of monomials representing the indicator functions in the statement. Theorem 3.12 implies that
![]() ${\mathcal {B}}$
descends to a basis for the
${\mathcal {B}}$
descends to a basis for the
![]() ${\mathbb {F}}$
-vector space
${\mathbb {F}}$
-vector space
![]() $( {\mathbb {F}}[{\mathbf {x}}_{n \times n}] / {\mathrm {gr}} \, {\mathbf {I}}(P_n) )_{\leq k}$
. An application of Lemma 3.15 shows that
$( {\mathbb {F}}[{\mathbf {x}}_{n \times n}] / {\mathrm {gr}} \, {\mathbf {I}}(P_n) )_{\leq k}$
. An application of Lemma 3.15 shows that
![]() ${\mathcal {B}}$
also descends to a basis for
${\mathcal {B}}$
also descends to a basis for
![]() ${\mathbb {F}}[{\mathbf {x}}_{n \times n}]_{\leq k} / ( {\mathbf {I}}(P_n) \cap {\mathbb {F}}[{\mathbf {x}}_{n \times n}]_{\leq k} )$
, and the isomorphism (3.30) completes the proof.
${\mathbb {F}}[{\mathbf {x}}_{n \times n}]_{\leq k} / ( {\mathbf {I}}(P_n) \cap {\mathbb {F}}[{\mathbf {x}}_{n \times n}]_{\leq k} )$
, and the isomorphism (3.30) completes the proof.
The nested shadow junta bases of
![]() ${\mathrm {Loc}}_0({\mathfrak {S}}_3,{\mathbb {F}}) \subset {\mathrm {Loc}}_1({\mathfrak {S}}_3,{\mathbb {F}}) \subset {\mathrm {Loc}}_2({\mathfrak {S}}_3,{\mathbb {F}})$
are as follows.
${\mathrm {Loc}}_0({\mathfrak {S}}_3,{\mathbb {F}}) \subset {\mathrm {Loc}}_1({\mathfrak {S}}_3,{\mathbb {F}}) \subset {\mathrm {Loc}}_2({\mathfrak {S}}_3,{\mathbb {F}})$
are as follows.

It may be interesting to find a basis of
![]() ${\mathrm {Loc}}_k({\mathfrak {S}}_n,{\mathbb {F}})$
drawn from the spanning set
${\mathrm {Loc}}_k({\mathfrak {S}}_n,{\mathbb {F}})$
drawn from the spanning set
![]() $\{ {\mathbf {1}}_{\mathcal {R}} \,:\, |{\mathcal {R}}| = k \}$
. By Theorem 3.12, the above monomials also form a vector space basis of
$\{ {\mathbf {1}}_{\mathcal {R}} \,:\, |{\mathcal {R}}| = k \}$
. By Theorem 3.12, the above monomials also form a vector space basis of
![]() ${\mathbb {F}}[{\mathbf {x}}_{3 \times 3}]/I_3$
.
${\mathbb {F}}[{\mathbf {x}}_{3 \times 3}]/I_3$
.
The results we have proven so far hold when the field
![]() ${\mathbb {F}}$
is replaced by a commutative ring R. More precisely, we have an ideal
${\mathbb {F}}$
is replaced by a commutative ring R. More precisely, we have an ideal
![]() $I_n^R \subseteq R[{\mathbf {x}}_{n \times n}]$
with the same generating set as in Definition 1.1.
$I_n^R \subseteq R[{\mathbf {x}}_{n \times n}]$
with the same generating set as in Definition 1.1.
-
• The proofs of Lemmas 3.1 and 3.11 goes through to show that the shadow monomials
 $\{ {\mathfrak {s}}(w) \,:\, w \in {\mathfrak {S}}_n \}$
span
$\{ {\mathfrak {s}}(w) \,:\, w \in {\mathfrak {S}}_n \}$
span
 $R[{\mathbf {x}}_{n \times n}]/I_n^R$
over R. Here, we use the fact that the coefficients in the polynomials
$R[{\mathbf {x}}_{n \times n}]/I_n^R$
over R. Here, we use the fact that the coefficients in the polynomials
 $a_{S,T}, b_{S,T}$
appearing in Lemma 3.1 are all
$a_{S,T}, b_{S,T}$
appearing in Lemma 3.1 are all
 $\pm 1$
.
$\pm 1$
. -
• When
 $R = {\mathbb {Z}}$
, a linear dependence of
$R = {\mathbb {Z}}$
, a linear dependence of
 $\{ {\mathfrak {s}}(w) \,:\, w \in {\mathfrak {S}}_n \}$
modulo
$\{ {\mathfrak {s}}(w) \,:\, w \in {\mathfrak {S}}_n \}$
modulo
 $I_n^{\mathbb {Z}}$
would induce a linear dependence modulo
$I_n^{\mathbb {Z}}$
would induce a linear dependence modulo
 $I_n^{\mathbb {Q}}$
. By Theorem 3.12,
$I_n^{\mathbb {Q}}$
. By Theorem 3.12,
 $\{ {\mathfrak {s}}(w) \,:\, w \in {\mathfrak {S}}_n \}$
descends to a
$\{ {\mathfrak {s}}(w) \,:\, w \in {\mathfrak {S}}_n \}$
descends to a
 ${\mathbb {Z}}$
-basis of
${\mathbb {Z}}$
-basis of
 ${\mathbb {Z}}[{\mathbf {x}}_{n \times n}]/I_n^{\mathbb {Z}}$
.
${\mathbb {Z}}[{\mathbf {x}}_{n \times n}]/I_n^{\mathbb {Z}}$
. -
• Since
 $R[{\mathbf {x}}_{n \times n}]/I_n^R = R \otimes _{\mathbb {Z}} {\mathbb {Z}}[{\mathbf {x}}_{n \times n}]/I_n^{\mathbb {Z}}$
, the set
$R[{\mathbf {x}}_{n \times n}]/I_n^R = R \otimes _{\mathbb {Z}} {\mathbb {Z}}[{\mathbf {x}}_{n \times n}]/I_n^{\mathbb {Z}}$
, the set
 $\{ {\mathfrak {s}}(w) \,:\, w \in {\mathfrak {S}}_n \}$
descends to a R-basis of
$\{ {\mathfrak {s}}(w) \,:\, w \in {\mathfrak {S}}_n \}$
descends to a R-basis of
 $R[{\mathbf {x}}_{n \times n}]/I_n^R$
for any R. The proof of Lemma 3.15 holds over R, so the shadow juntas
$R[{\mathbf {x}}_{n \times n}]/I_n^R$
for any R. The proof of Lemma 3.15 holds over R, so the shadow juntas
 $\{ {\mathbf {1}}_{{\mathcal {S}}(w)} \,:\, w \in {\mathfrak {S}}_n, \, \, {\mathrm {lis}}(w) \geq n-k \}$
form an R-basis of
$\{ {\mathbf {1}}_{{\mathcal {S}}(w)} \,:\, w \in {\mathfrak {S}}_n, \, \, {\mathrm {lis}}(w) \geq n-k \}$
form an R-basis of
 ${\mathrm {Loc}}_k({\mathfrak {S}}_n,R)$
.
${\mathrm {Loc}}_k({\mathfrak {S}}_n,R)$
.
4 Module structure
As explained in the introduction, the self-product
![]() ${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
of the rank n symmetric group acts on the matrix
${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
of the rank n symmetric group acts on the matrix
![]() ${\mathbf {x}}_{n \times n}$
of variables by independent row and column permutation. This induces an action of
${\mathbf {x}}_{n \times n}$
of variables by independent row and column permutation. This induces an action of
![]() ${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
on
${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
on
![]() $I_n$
and endows
$I_n$
and endows
![]() ${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
with the structure of a graded
${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
with the structure of a graded
![]() ${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
-module. The purpose of this section is to study this action. To do so, for the remainder of the section we made the following assumption on the characteristic of
${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
-module. The purpose of this section is to study this action. To do so, for the remainder of the section we made the following assumption on the characteristic of
![]() ${\mathbb {F}}$
.
${\mathbb {F}}$
.
Assumption. The field
![]() ${\mathbb {F}}$
either has characteristic zero or has characteristic
${\mathbb {F}}$
either has characteristic zero or has characteristic
![]() $p> n$
.
$p> n$
.
This assumption guarantees that the group algebras
![]() ${\mathbb {F}}[{\mathfrak {S}}_n]$
and
${\mathbb {F}}[{\mathfrak {S}}_n]$
and
![]() ${\mathbb {F}}[{\mathfrak {S}}_n \times {\mathfrak {S}}_n]$
are semisimple. We may immediately describe the ungraded
${\mathbb {F}}[{\mathfrak {S}}_n \times {\mathfrak {S}}_n]$
are semisimple. We may immediately describe the ungraded
![]() ${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
-structure of
${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
-structure of
![]() ${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
.
${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
.
Corollary 4.1. Let
![]() ${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
act on the locus
${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
act on the locus
![]() $P_n \subseteq {\mathbb {F}}^{n \times n}$
by independent row and column permutation. We have an isomorphism
$P_n \subseteq {\mathbb {F}}^{n \times n}$
by independent row and column permutation. We have an isomorphism
![]() ${\mathbb {F}}[P_n] \cong {\mathbb {F}}[{\mathbf {x}}_{n \times n}] / I_n$
of ungraded
${\mathbb {F}}[P_n] \cong {\mathbb {F}}[{\mathbf {x}}_{n \times n}] / I_n$
of ungraded
![]() ${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
-modules.
${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
-modules.
Corollary 4.1 may be given as a decomposition into
![]() ${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
irreducibles as follows. If
${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
irreducibles as follows. If
![]() $\lambda \vdash n$
is a partition of n, recall that
$\lambda \vdash n$
is a partition of n, recall that
![]() $V^{\lambda }$
denotes the corresponding irreducible
$V^{\lambda }$
denotes the corresponding irreducible
![]() ${\mathfrak {S}}_n$
-module. Irreducible representations of the product group
${\mathfrak {S}}_n$
-module. Irreducible representations of the product group
![]() ${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
are given by tensor products
${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
are given by tensor products
![]() $V^{\lambda } \otimes V^{\mu }$
for ordered pairs of partitions
$V^{\lambda } \otimes V^{\mu }$
for ordered pairs of partitions
![]() $(\lambda , \mu )$
of n. Corollary 4.1 asserts that
$(\lambda , \mu )$
of n. Corollary 4.1 asserts that
![]() ${\mathbb {F}}[{\mathbf {x}}_{n \times n}] / I_n \cong \bigoplus _{\lambda \vdash n} V^\lambda \otimes V^\lambda $
as ungraded
${\mathbb {F}}[{\mathbf {x}}_{n \times n}] / I_n \cong \bigoplus _{\lambda \vdash n} V^\lambda \otimes V^\lambda $
as ungraded
![]() ${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
-modules.
${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
-modules.
Proof. By Theorem 3.12, we have an isomorphism and an equality
of ungraded
![]() ${\mathbb {F}}$
-vector spaces. By our assumption on the characteristic of
${\mathbb {F}}$
-vector spaces. By our assumption on the characteristic of
![]() ${\mathbb {F}}$
, these upgrade to an isomorphism and an equality of ungraded
${\mathbb {F}}$
, these upgrade to an isomorphism and an equality of ungraded
![]() ${\mathbb {F}}[{\mathfrak {S}}_n \times {\mathfrak {S}}_n]$
-modules.
${\mathbb {F}}[{\mathfrak {S}}_n \times {\mathfrak {S}}_n]$
-modules.
We enhance Corollary 4.1 by describing the graded module structure of
![]() ${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
. As suggested by Corollary 3.13, the graded refinement of the isomorphism
${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
. As suggested by Corollary 3.13, the graded refinement of the isomorphism
![]() ${\mathbb {F}}[{\mathbf {x}}_{n \times n}] / I_n \cong _{{\mathfrak {S}}_n \times {\mathfrak {S}}_n} \bigoplus _{\lambda \vdash n} V^\lambda \otimes V^\lambda $
is obtained by focusing on the length of the first row of
${\mathbb {F}}[{\mathbf {x}}_{n \times n}] / I_n \cong _{{\mathfrak {S}}_n \times {\mathfrak {S}}_n} \bigoplus _{\lambda \vdash n} V^\lambda \otimes V^\lambda $
is obtained by focusing on the length of the first row of
![]() $\lambda $
.
$\lambda $
.
Theorem 4.2. For any
![]() $k \geq 0$
, the degree k piece of
$k \geq 0$
, the degree k piece of
![]() ${\mathbb {F}}[{\mathbf {x}}_{n \times n}] / I_n$
has
${\mathbb {F}}[{\mathbf {x}}_{n \times n}] / I_n$
has
![]() ${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
-module structure
${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
-module structure
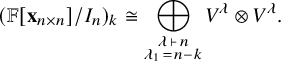 $$ \begin{align} ( {\mathbb {F}}[{\mathbf {x}}_{n \times n}] / I_n )_k \cong \bigoplus_{\substack{\lambda \, \vdash \, n \\ \lambda_1 \, = \, n-k}} V^{\lambda} \otimes V^{\lambda}. \end{align} $$
$$ \begin{align} ( {\mathbb {F}}[{\mathbf {x}}_{n \times n}] / I_n )_k \cong \bigoplus_{\substack{\lambda \, \vdash \, n \\ \lambda_1 \, = \, n-k}} V^{\lambda} \otimes V^{\lambda}. \end{align} $$
Proof. If W is any
![]() ${\mathfrak {S}}_n$
-module over
${\mathfrak {S}}_n$
-module over
![]() ${\mathbb {F}}$
, the vector space
${\mathbb {F}}$
, the vector space
![]() ${\mathrm {End}}_{\mathbb {F}}(W)$
of
${\mathrm {End}}_{\mathbb {F}}(W)$
of
![]() ${\mathbb {F}}$
-linear maps
${\mathbb {F}}$
-linear maps
![]() $\varphi : W \rightarrow W$
is a
$\varphi : W \rightarrow W$
is a
![]() ${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
-module via
${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
-module via
We have
![]() ${\mathrm {End}}_{\mathbb {F}}(W) \cong W \otimes W^*$
, and since
${\mathrm {End}}_{\mathbb {F}}(W) \cong W \otimes W^*$
, and since
![]() ${\mathfrak {S}}_n$
-modules are self-dual, we have
${\mathfrak {S}}_n$
-modules are self-dual, we have
as
![]() ${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
-modules.
${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
-modules.
The group algebra
![]() ${\mathbb {F}}[{\mathfrak {S}}_n]$
is naturally a
${\mathbb {F}}[{\mathfrak {S}}_n]$
is naturally a
![]() ${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
-module under left and right multiplication. Since
${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
-module under left and right multiplication. Since
![]() ${\mathbb {F}}[{\mathfrak {S}}_n]$
is semisimple, the Artin–Wedderburn theorem gives an isomorphism of
${\mathbb {F}}[{\mathfrak {S}}_n]$
is semisimple, the Artin–Wedderburn theorem gives an isomorphism of
![]() ${\mathbb {F}}$
-algebras
${\mathbb {F}}$
-algebras
Given
![]() $a \in {\mathbb {F}}[{\mathfrak {S}}_n]$
, the
$a \in {\mathbb {F}}[{\mathfrak {S}}_n]$
, the
![]() $\lambda ^{th}$
component of
$\lambda ^{th}$
component of
![]() $\Psi (a)$
acts on
$\Psi (a)$
acts on
![]() $V^{\lambda }$
by the
$V^{\lambda }$
by the
![]() ${\mathbb {F}}$
-linear map
${\mathbb {F}}$
-linear map
![]() $\Psi (a): v \mapsto a \cdot v$
.
$\Psi (a): v \mapsto a \cdot v$
.
Returning to the statement of the theorem, since
![]() ${\mathbb {F}}[{\mathfrak {S}}_n]$
is semisimple, by induction on k it suffices to establish the isomorphism
${\mathbb {F}}[{\mathfrak {S}}_n]$
is semisimple, by induction on k it suffices to establish the isomorphism
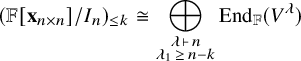 $$ \begin{align} ( {\mathbb {F}}[{\mathbf {x}}_{n \times n}] / I_n )_{\leq k} \cong \bigoplus_{\substack{\lambda \, \vdash \, n \\ \lambda_1 \, \geq \, n-k}} {\mathrm {End}}_{\mathbb {F}}(V^{\lambda}) \end{align} $$
$$ \begin{align} ( {\mathbb {F}}[{\mathbf {x}}_{n \times n}] / I_n )_{\leq k} \cong \bigoplus_{\substack{\lambda \, \vdash \, n \\ \lambda_1 \, \geq \, n-k}} {\mathrm {End}}_{\mathbb {F}}(V^{\lambda}) \end{align} $$
in the category of ungraded
![]() ${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
-modules. To this end, Theorem 3.12 gives rise to the identifications
${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
-modules. To this end, Theorem 3.12 gives rise to the identifications
of ungraded
![]() ${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
-modules. Let
${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
-modules. Let
![]() $L_k$
be the image of
$L_k$
be the image of
![]() ${\mathbb {F}}[{\mathbf {x}}_{n \times n}]_{\leq k}$
in
${\mathbb {F}}[{\mathbf {x}}_{n \times n}]_{\leq k}$
in
![]() ${\mathbb {F}}[{\mathbf {x}}_{n \times n}] / {\mathbf {I}}(P_n)$
, i.e.
${\mathbb {F}}[{\mathbf {x}}_{n \times n}] / {\mathbf {I}}(P_n)$
, i.e.
Lemma 3.15 implies that
As explained in the proof of Theorem 3.16, under the correspondence
![]() ${\mathbb {F}}[{\mathfrak {S}}_n] = {\mathbb {F}}[P_n] \cong {\mathbb {F}}[{\mathbf {x}}_{n \times n}]/{\mathbf {I}}(P_n)$
we have the identification
${\mathbb {F}}[{\mathfrak {S}}_n] = {\mathbb {F}}[P_n] \cong {\mathbb {F}}[{\mathbf {x}}_{n \times n}]/{\mathbf {I}}(P_n)$
we have the identification
with the
![]() ${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
-module of k-local statistics
${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
-module of k-local statistics
![]() ${\mathfrak {S}}_n \rightarrow {\mathbb {F}}$
. Lemma 3.15 and the chain (4.7) of isomorphisms give rise to the further identification
${\mathfrak {S}}_n \rightarrow {\mathbb {F}}$
. Lemma 3.15 and the chain (4.7) of isomorphisms give rise to the further identification
of
![]() ${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
-modules.
${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
-modules.
By the last paragraph, we are reduced to establishing the isomorphism
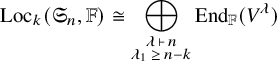 $$ \begin{align} {\mathrm {Loc}}_k({\mathfrak {S}}_n,{\mathbb {F}}) \cong \bigoplus_{\substack{\lambda \, \vdash \, n \\ \lambda_1 \, \geq \, n-k}} {\mathrm {End}}_{\mathbb {F}}(V^{\lambda}) \end{align} $$
$$ \begin{align} {\mathrm {Loc}}_k({\mathfrak {S}}_n,{\mathbb {F}}) \cong \bigoplus_{\substack{\lambda \, \vdash \, n \\ \lambda_1 \, \geq \, n-k}} {\mathrm {End}}_{\mathbb {F}}(V^{\lambda}) \end{align} $$
of ungraded
![]() ${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
-modules. Embed
${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
-modules. Embed
![]() ${\mathfrak {S}}_{n-k} \subseteq {\mathfrak {S}}_n$
by acting on the first
${\mathfrak {S}}_{n-k} \subseteq {\mathfrak {S}}_n$
by acting on the first
![]() $n-k$
letters, let
$n-k$
letters, let
be the group algebra element which symmetrizes over these letters, and let
![]() $J_k \subseteq {\mathbb {F}}[{\mathfrak {S}}_n]$
be the two-sided ideal generated by
$J_k \subseteq {\mathbb {F}}[{\mathfrak {S}}_n]$
be the two-sided ideal generated by
![]() $\eta _{n-k}$
. The correspondence between functions
$\eta _{n-k}$
. The correspondence between functions
![]() $f: {\mathfrak {S}}_n \rightarrow {\mathbb {F}}$
and group algebra elements
$f: {\mathfrak {S}}_n \rightarrow {\mathbb {F}}$
and group algebra elements
![]() $\sum _{w \in {\mathfrak {S}}_n} f(w) \cdot w$
gives rise to an identification
$\sum _{w \in {\mathfrak {S}}_n} f(w) \cdot w$
gives rise to an identification
of ungraded
![]() ${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
-modules. Indeed, the group algebra element
${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
-modules. Indeed, the group algebra element
![]() $\eta _{n-k} \in {\mathbb {F}}[{\mathfrak {S}}_n]$
corresponds to the indicator permutation statistic
$\eta _{n-k} \in {\mathbb {F}}[{\mathfrak {S}}_n]$
corresponds to the indicator permutation statistic
![]() ${\mathbf {1}}_{{\mathcal {R}}}: {\mathfrak {S}}_n \to {\mathbb {F}}$
indexed by the rook placement
${\mathbf {1}}_{{\mathcal {R}}}: {\mathfrak {S}}_n \to {\mathbb {F}}$
indexed by the rook placement
Multiplying
![]() $\eta _{n-k}$
on the left and right by permutations of
$\eta _{n-k}$
on the left and right by permutations of
![]() ${\mathfrak {S}}_n$
corresponds to interchanging rows and columns in the rook placement
${\mathfrak {S}}_n$
corresponds to interchanging rows and columns in the rook placement
![]() ${\mathcal {R}}_0$
; any rook placement with k rooks may be obtained in this way.
${\mathcal {R}}_0$
; any rook placement with k rooks may be obtained in this way.
Thanks to the identification (4.14), we are reduced to showing
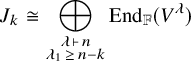 $$ \begin{align} J_k \cong \bigoplus_{\substack{\lambda \, \vdash \, n \\ \lambda_1 \, \geq \, n-k}} {\mathrm {End}}_{\mathbb {F}}(V^{\lambda}) \end{align} $$
$$ \begin{align} J_k \cong \bigoplus_{\substack{\lambda \, \vdash \, n \\ \lambda_1 \, \geq \, n-k}} {\mathrm {End}}_{\mathbb {F}}(V^{\lambda}) \end{align} $$
as
![]() ${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
-modules. The image
${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
-modules. The image
![]() $\Psi (J_k)$
of the ideal
$\Psi (J_k)$
of the ideal
![]() $J_k \subseteq {\mathbb {F}}[{\mathfrak {S}}_n]$
under the Artin–Wedderburn isomorphism (4.5) is an ideal in the direct sum
$J_k \subseteq {\mathbb {F}}[{\mathfrak {S}}_n]$
under the Artin–Wedderburn isomorphism (4.5) is an ideal in the direct sum
![]() $\bigoplus _{\lambda \vdash n} {\mathrm {End}}_{\mathbb {F}}(V^{\lambda })$
of matrix rings. Since each summand
$\bigoplus _{\lambda \vdash n} {\mathrm {End}}_{\mathbb {F}}(V^{\lambda })$
of matrix rings. Since each summand
![]() ${\mathrm {End}}_{\mathbb {F}}(V^{\lambda })$
is simple, there is a set
${\mathrm {End}}_{\mathbb {F}}(V^{\lambda })$
is simple, there is a set
![]() $P(k)$
of partitions of n such that
$P(k)$
of partitions of n such that
The definitions of
![]() $\Psi $
and
$\Psi $
and
![]() $J_k$
imply that
$J_k$
imply that
It remains to show that
![]() $P(k) = \{ \lambda \vdash n \,:\, \lambda _1 \geq n-k \}$
. To this end, observe that for any
$P(k) = \{ \lambda \vdash n \,:\, \lambda _1 \geq n-k \}$
. To this end, observe that for any
![]() ${\mathfrak {S}}_n$
-module W, the image
${\mathfrak {S}}_n$
-module W, the image
![]() $\eta _{n-k} \cdot W$
may be characterized as the trivial component
$\eta _{n-k} \cdot W$
may be characterized as the trivial component
of the restriction of W from
![]() ${\mathfrak {S}}_n$
to
${\mathfrak {S}}_n$
to
![]() ${\mathfrak {S}}_{n-k}$
. In particular, for
${\mathfrak {S}}_{n-k}$
. In particular, for
![]() $\lambda \vdash n$
we have
$\lambda \vdash n$
we have
By the branching rule for symmetric group representations (see, e.g., [Reference Sagan17, Thm. 2.8.3]), the restriction
![]() $ {\mathrm {Res}}^{{\mathfrak {S}}_n}_{{\mathfrak {S}}_{n-k}} V^\lambda $
has a nonzero trivial component if and only if
$ {\mathrm {Res}}^{{\mathfrak {S}}_n}_{{\mathfrak {S}}_{n-k}} V^\lambda $
has a nonzero trivial component if and only if
![]() $\lambda _1 \geq n-k$
. This proves the isomorphism (4.12) and the theorem.
$\lambda _1 \geq n-k$
. This proves the isomorphism (4.12) and the theorem.
The ring
![]() ${\mathbb {F}}[{\mathbf {x}}_{n \times n}]$
carries a natural involution
${\mathbb {F}}[{\mathbf {x}}_{n \times n}]$
carries a natural involution
![]() $\sigma : x_{i,j} \mapsto x_{j,i}$
which transposes the matrix
$\sigma : x_{i,j} \mapsto x_{j,i}$
which transposes the matrix
![]() ${\mathbf {x}}_{n \times n}$
of variables. This induces a homogeneous involution on the quotient ring
${\mathbf {x}}_{n \times n}$
of variables. This induces a homogeneous involution on the quotient ring
![]() ${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
, also denoted
${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
, also denoted
![]() $\sigma $
. The proof technique of Theorem 4.2 applies to show that in the isomorphism
$\sigma $
. The proof technique of Theorem 4.2 applies to show that in the isomorphism
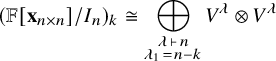 $$ \begin{align} ( {\mathbb {F}}[{\mathbf {x}}_{n \times n}] / I_n )_k \cong \bigoplus_{\substack{\lambda \, \vdash \, n \\ \lambda_1 \, = \, n-k}} V^{\lambda} \otimes V^{\lambda} \end{align} $$
$$ \begin{align} ( {\mathbb {F}}[{\mathbf {x}}_{n \times n}] / I_n )_k \cong \bigoplus_{\substack{\lambda \, \vdash \, n \\ \lambda_1 \, = \, n-k}} V^{\lambda} \otimes V^{\lambda} \end{align} $$
of
![]() ${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
-modules, the action of
${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
-modules, the action of
![]() $\sigma $
on the left-hand side intertwines with the automorphism
$\sigma $
on the left-hand side intertwines with the automorphism
![]() $(w,u) \mapsto (u,w)$
of the group
$(w,u) \mapsto (u,w)$
of the group
![]() ${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
.
${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
.
Recall from the introduction that
![]() $\alpha _{n,k}$
is the character of
$\alpha _{n,k}$
is the character of
![]() ${\mathfrak {S}}_n$
given by
${\mathfrak {S}}_n$
given by
![]() $\alpha _{n,k} = \sum _{\lambda _1 = k} f^{\lambda } \cdot \chi ^\lambda $
, where the sum is over partitions
$\alpha _{n,k} = \sum _{\lambda _1 = k} f^{\lambda } \cdot \chi ^\lambda $
, where the sum is over partitions
![]() $\lambda \vdash n$
whose first row has length k. As an immediate application of Theorem 4.2, we get an explicit
$\lambda \vdash n$
whose first row has length k. As an immediate application of Theorem 4.2, we get an explicit
![]() ${\mathfrak {S}}_n$
-module with character
${\mathfrak {S}}_n$
-module with character
![]() $\alpha _{n,k}$
.
$\alpha _{n,k}$
.
Corollary 4.3. The class function
![]() $\alpha _{n,k}: {\mathfrak {S}}_n \rightarrow {\mathbb {F}}$
is the character of the restriction of the degree
$\alpha _{n,k}: {\mathfrak {S}}_n \rightarrow {\mathbb {F}}$
is the character of the restriction of the degree
![]() $n-k$
part of
$n-k$
part of
![]() ${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
to either factor of
${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
to either factor of
![]() ${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
. In symbols, we have
${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
. In symbols, we have
where
![]() $\chi _V: {\mathfrak {S}}_n \times {\mathfrak {S}}_n \rightarrow {\mathbb {F}}$
denotes the character of an
$\chi _V: {\mathfrak {S}}_n \times {\mathfrak {S}}_n \rightarrow {\mathbb {F}}$
denotes the character of an
![]() ${\mathbb {F}}[{\mathfrak {S}}_n \times {\mathfrak {S}}_n]$
-module V.
${\mathbb {F}}[{\mathfrak {S}}_n \times {\mathfrak {S}}_n]$
-module V.
The space
![]() $({\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n)_{n-k}$
is the cleanest representation-theoretic model for
$({\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n)_{n-k}$
is the cleanest representation-theoretic model for
![]() $\alpha _{n,k}$
known to the author. There is another model for
$\alpha _{n,k}$
known to the author. There is another model for
![]() $\alpha _{n,k}$
involving quotient spaces. For any d, we have an action of
$\alpha _{n,k}$
involving quotient spaces. For any d, we have an action of
![]() ${\mathfrak {S}}_n$
on
${\mathfrak {S}}_n$
on
![]() ${\mathrm {Loc}}_d({\mathfrak {S}}_n,{\mathbb {F}})$
given by
${\mathrm {Loc}}_d({\mathfrak {S}}_n,{\mathbb {F}})$
given by
![]() $(w \cdot f)(v) := f(w^{-1} v)$
for
$(w \cdot f)(v) := f(w^{-1} v)$
for
![]() $w, v \in {\mathfrak {S}}_n$
and
$w, v \in {\mathfrak {S}}_n$
and
![]() $f \in {\mathrm {Loc}}_d({\mathfrak {S}}_n,{\mathbb {F}})$
. The isomorphism (4.12) implies that the sum
$f \in {\mathrm {Loc}}_d({\mathfrak {S}}_n,{\mathbb {F}})$
. The isomorphism (4.12) implies that the sum
![]() $\alpha _{n,k} + \alpha _{n,k+1} + \cdots + \alpha _{n,n}$
is the character of
$\alpha _{n,k} + \alpha _{n,k+1} + \cdots + \alpha _{n,n}$
is the character of
![]() ${\mathrm {Loc}}_{n-k}({\mathfrak {S}}_n,{\mathbb {F}})$
. Therefore, the quotient module
${\mathrm {Loc}}_{n-k}({\mathfrak {S}}_n,{\mathbb {F}})$
. Therefore, the quotient module
![]() ${\mathrm {Loc}}_{n-k}({\mathfrak {S}}_n,{\mathbb {F}})/{\mathrm {Loc}}_{n-k-1}({\mathfrak {S}}_n,{\mathbb {F}})$
has character
${\mathrm {Loc}}_{n-k}({\mathfrak {S}}_n,{\mathbb {F}})/{\mathrm {Loc}}_{n-k-1}({\mathfrak {S}}_n,{\mathbb {F}})$
has character
![]() $\alpha _{n,k}$
.
$\alpha _{n,k}$
.
Sums of the characters
![]() $\alpha _{n,k}$
also arise in the context of Schur–Weyl duality. Let
$\alpha _{n,k}$
also arise in the context of Schur–Weyl duality. Let
![]() ${\mathbb {F}} = {\mathbb {C}}$
, let
${\mathbb {F}} = {\mathbb {C}}$
, let
![]() $V = {\mathbb {C}}^d$
, and let
$V = {\mathbb {C}}^d$
, and let
![]() $V^{\otimes n} = V \otimes \cdots \otimes V$
be the n-fold tensor power of V. The vector space
$V^{\otimes n} = V \otimes \cdots \otimes V$
be the n-fold tensor power of V. The vector space
![]() $V^{\otimes n}$
carries a diagonal action of
$V^{\otimes n}$
carries a diagonal action of
![]() $GL(V)$
, viz.
$GL(V)$
, viz.
Let
![]() ${\mathrm {End}}_{GL(V)}(V^{\otimes n})$
be the algebra of linear maps
${\mathrm {End}}_{GL(V)}(V^{\otimes n})$
be the algebra of linear maps
![]() $\varphi : V^{\otimes n} \rightarrow V^{\otimes n}$
which commute with the action of
$\varphi : V^{\otimes n} \rightarrow V^{\otimes n}$
which commute with the action of
![]() $GL(V)$
. We have an algebra homomorphism
$GL(V)$
. We have an algebra homomorphism
![]() $\Phi : {\mathbb {C}}[{\mathfrak {S}}_n] \rightarrow {\mathrm {End}}_{GL(V)}(V^{\otimes n})$
induced by
$\Phi : {\mathbb {C}}[{\mathfrak {S}}_n] \rightarrow {\mathrm {End}}_{GL(V)}(V^{\otimes n})$
induced by
Schur–Weyl duality asserts that the homomorphism
![]() $\Phi $
is surjective, but when
$\Phi $
is surjective, but when
![]() $d < n$
, the kernel of
$d < n$
, the kernel of
![]() $\Phi $
is nonzero. In fact, the character of the
$\Phi $
is nonzero. In fact, the character of the
![]() ${\mathfrak {S}}_n$
-module
${\mathfrak {S}}_n$
-module
![]() ${\mathrm {End}}_{GL(V)}(V^{\otimes n})$
is given by
${\mathrm {End}}_{GL(V)}(V^{\otimes n})$
is given by
where
![]() ${\mathrm {sign}}$
is the degree 1 sign character. In other words, we have
${\mathrm {sign}}$
is the degree 1 sign character. In other words, we have
![]() $\chi _{{\mathrm {End}}_{GL(V)}(V^{\otimes n})} = \sum _{\lambda ^{\prime }_1 \leq d} f^{\lambda } \cdot \chi ^{\lambda }$
where the sum is over partitions
$\chi _{{\mathrm {End}}_{GL(V)}(V^{\otimes n})} = \sum _{\lambda ^{\prime }_1 \leq d} f^{\lambda } \cdot \chi ^{\lambda }$
where the sum is over partitions
![]() $\lambda \vdash n$
whose first column has length at most d. By Corollary 4.3, we have an isomorphism of
$\lambda \vdash n$
whose first column has length at most d. By Corollary 4.3, we have an isomorphism of
![]() ${\mathfrak {S}}_n$
-modules
${\mathfrak {S}}_n$
-modules
It may be interesting to give a formula for this isomorphism.
By Corollary 4.3, finding an explicit family of linear injections
which commute with either the row or column action of
![]() ${\mathfrak {S}}_n$
on
${\mathfrak {S}}_n$
on
![]() ${\mathbf {x}}_{n \times n}$
would prove the Novak–Rhoades conjecture [Reference Novak and Rhoades14] and imply Chen’s conjecture [Reference Chen4]. In fact, computations suggest that such an injection can be found which commutes with both row and column permutation.
${\mathbf {x}}_{n \times n}$
would prove the Novak–Rhoades conjecture [Reference Novak and Rhoades14] and imply Chen’s conjecture [Reference Chen4]. In fact, computations suggest that such an injection can be found which commutes with both row and column permutation.
Conjecture 4.4. Given any degree
![]() $d \geq 0$
, let
$d \geq 0$
, let
![]() ${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
act on
${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
act on
![]() $ ({\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n)_d$
by independent row and column permutation. For all
$ ({\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n)_d$
by independent row and column permutation. For all
![]() $0 < d < n-1$
, there exists a linear injection
$0 < d < n-1$
, there exists a linear injection
which commutes with the diagonal action of
![]() ${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
defined by
${\mathfrak {S}}_n \times {\mathfrak {S}}_n$
defined by
for
![]() $(w,v) \in {\mathfrak {S}}_n \times {\mathfrak {S}}_n$
and
$(w,v) \in {\mathfrak {S}}_n \times {\mathfrak {S}}_n$
and
![]() $f, g \in {\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
.
$f, g \in {\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
.
Conjecture 4.4 would imply both the Novak–Rhoades conjecture [Reference Novak and Rhoades14] and Chen’s conjecture [Reference Chen4]. The existence of a map
![]() $\varphi $
as in Conjecture 4.4 has been checked for
$\varphi $
as in Conjecture 4.4 has been checked for
![]() $n \leq 15$
.
$n \leq 15$
.
5 Conclusion
This paper established a connection between the algebra of
![]() ${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
and the combinatorics of
${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
and the combinatorics of
![]() ${\mathfrak {S}}_n$
. It may be interesting to find analogous results for other combinatorial structures. As motivation, Bóna, Lackner, and Sagan [Reference Bóna, Lackner and Sagan3] conjectured that the sequence
${\mathfrak {S}}_n$
. It may be interesting to find analogous results for other combinatorial structures. As motivation, Bóna, Lackner, and Sagan [Reference Bóna, Lackner and Sagan3] conjectured that the sequence
![]() $(i_{n,1}, \dots , i_{n,k})$
given by
$(i_{n,1}, \dots , i_{n,k})$
given by
which counts involutions in
![]() ${\mathfrak {S}}_n$
with longest increasing subsequence of length k is log-concave. Novak and the author made (unpublished) the stronger conjecture [Reference Novak and Rhoades14] that the sequence
${\mathfrak {S}}_n$
with longest increasing subsequence of length k is log-concave. Novak and the author made (unpublished) the stronger conjecture [Reference Novak and Rhoades14] that the sequence
![]() $(\iota _{n,1}, \dots , \iota _{n,n})$
of characters
$(\iota _{n,1}, \dots , \iota _{n,n})$
of characters
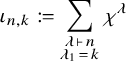 $$ \begin{align} \iota_{n,k} := \sum_{\substack{\lambda \, \vdash \, n \\ \lambda_1 \, = \, k }} \chi^{\lambda} \end{align} $$
$$ \begin{align} \iota_{n,k} := \sum_{\substack{\lambda \, \vdash \, n \\ \lambda_1 \, = \, k }} \chi^{\lambda} \end{align} $$
is log-concave with respect to the Kronecker product (where a class function is ‘nonnegative’ if it is a genuine character). On the commutative algebra side, adding the differences
![]() $x_{i,j} - x_{j,i}$
to the ideal
$x_{i,j} - x_{j,i}$
to the ideal
![]() $I_n \subseteq {\mathbb {F}}[{\mathbf {x}}_{n \times n}]$
gives a candidate quotient ring which could be used to study these conjectures.
$I_n \subseteq {\mathbb {F}}[{\mathbf {x}}_{n \times n}]$
gives a candidate quotient ring which could be used to study these conjectures.
A key tool for understanding the structure of
![]() ${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
was the orbit harmonics method applied to the locus
${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/I_n$
was the orbit harmonics method applied to the locus
![]() $P_n \subseteq {\mathbb {F}}^{n \times n}$
of permutation matrices; it was proven that
$P_n \subseteq {\mathbb {F}}^{n \times n}$
of permutation matrices; it was proven that
![]() $I_n = {\mathrm {gr}} \, {\mathbf {I}}(P_n)$
. It may be interesting to compute
$I_n = {\mathrm {gr}} \, {\mathbf {I}}(P_n)$
. It may be interesting to compute
![]() ${\mathrm {gr}} \, {\mathbf {I}}(M_n)$
for other matrix loci
${\mathrm {gr}} \, {\mathbf {I}}(M_n)$
for other matrix loci
![]() $M_n \subseteq {\mathbb {F}}^{n \times n}$
. Four suggestions in this direction are as follows.
$M_n \subseteq {\mathbb {F}}^{n \times n}$
. Four suggestions in this direction are as follows.
-
1. The set
 $M_n = {\mathcal {I}}_n$
of symmetric permutation matrices corresponding to involutions in
$M_n = {\mathcal {I}}_n$
of symmetric permutation matrices corresponding to involutions in
 ${\mathfrak {S}}_n$
. The ideal
${\mathfrak {S}}_n$
. The ideal
 ${\mathrm {gr}} \, {\mathbf {I}}({\mathcal {I}}_n)$
could have application to the Bóna-Lackner–Sagan conjecture [Reference Bóna, Lackner and Sagan3] and the Kronecker log-concavity of the character sequence
${\mathrm {gr}} \, {\mathbf {I}}({\mathcal {I}}_n)$
could have application to the Bóna-Lackner–Sagan conjecture [Reference Bóna, Lackner and Sagan3] and the Kronecker log-concavity of the character sequence
 $(\iota _{n,1}, \dots , \iota _{n,n})$
.
$(\iota _{n,1}, \dots , \iota _{n,n})$
. -
2. The set
 $M_n = G$
of elements of a complex reflection group. The Hilbert series of
$M_n = G$
of elements of a complex reflection group. The Hilbert series of
 ${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/{\mathrm {gr}} \, {\mathbf {I}}(G)$
should be generating functions for a ‘longest increasing subsequence’ statistic on G.Footnote
1
${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/{\mathrm {gr}} \, {\mathbf {I}}(G)$
should be generating functions for a ‘longest increasing subsequence’ statistic on G.Footnote
1
-
3. The set
 $M_n = A_n$
of
$M_n = A_n$
of
 $n \times n$
alternating sign matrices. A standard monomial basis of
$n \times n$
alternating sign matrices. A standard monomial basis of
 ${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/{\mathrm {gr}} \, {\mathbf {I}}(A_n)$
could give a clues about a Schensted correspondence for ASMs.
${\mathbb {F}}[{\mathbf {x}}_{n \times n}]/{\mathrm {gr}} \, {\mathbf {I}}(A_n)$
could give a clues about a Schensted correspondence for ASMs.
It may also be interesting to consider loci of rectangular
![]() $m \times n$
matrices for which
$m \times n$
matrices for which
![]() $m \neq n$
. For example, fixing sequences
$m \neq n$
. For example, fixing sequences
![]() $\lambda = (\lambda _1, \dots , \lambda _n)$
and
$\lambda = (\lambda _1, \dots , \lambda _n)$
and
![]() $\mu = (\mu _1, \dots , \mu _n)$
, one could consider the contingency table locus of
$\mu = (\mu _1, \dots , \mu _n)$
, one could consider the contingency table locus of
![]() ${\mathbb {Z}}_{\geq 0}$
-matrices with column sums
${\mathbb {Z}}_{\geq 0}$
-matrices with column sums
![]() $\lambda $
and row sums
$\lambda $
and row sums
![]() $\mu $
. Fulton’s matrix-ball construction [Reference Fulton6] generalizes Viennot shadow lines from permutation matrices to contingency tables; perhaps the matrix-ball construction is also related to standard monomial theory.
$\mu $
. Fulton’s matrix-ball construction [Reference Fulton6] generalizes Viennot shadow lines from permutation matrices to contingency tables; perhaps the matrix-ball construction is also related to standard monomial theory.
The genesis of this paper was an email from Pierre Briaud and Morten Øygarden to the author regarding a problem in cryptography. We close by describing this problem and its relationship to our work.
Let q be a prime power, and let
![]() ${\mathbb {F}}_q$
be the finite field with q elements. Given a known matrix
${\mathbb {F}}_q$
be the finite field with q elements. Given a known matrix
![]() ${\mathbf {A}} \in {\mathbb {F}}_q^{m \times n}$
and a known vector
${\mathbf {A}} \in {\mathbb {F}}_q^{m \times n}$
and a known vector
![]() ${\mathbf {v}} \in {\mathbb {F}}_q^n$
, the permuted kernel problem (PKP) [Reference Beullens, Faugère, Koussa, Macario-Rat, Patarin and Perret1, Def. 1] seeks to recover an unknown permutation
${\mathbf {v}} \in {\mathbb {F}}_q^n$
, the permuted kernel problem (PKP) [Reference Beullens, Faugère, Koussa, Macario-Rat, Patarin and Perret1, Def. 1] seeks to recover an unknown permutation
![]() $w \in {\mathfrak {S}}_n$
of the coordinates of
$w \in {\mathfrak {S}}_n$
of the coordinates of
![]() ${\mathbf {v}}$
which lies in the right kernel of
${\mathbf {v}}$
which lies in the right kernel of
![]() ${\mathbf {A}}$
. The parameters
${\mathbf {A}}$
. The parameters
![]() $q, m,$
and n are chosen so that
$q, m,$
and n are chosen so that
![]() $n! \approx q^m$
, and there exists a unique such
$n! \approx q^m$
, and there exists a unique such
![]() $w \in {\mathfrak {S}}_n$
with high probability. The PKP amounts to solving a polynomial system in the
$w \in {\mathfrak {S}}_n$
with high probability. The PKP amounts to solving a polynomial system in the
![]() $n^2$
variables
$n^2$
variables
![]() ${\mathbf {x}}_{n \times n}$
over the field
${\mathbf {x}}_{n \times n}$
over the field
![]() ${\mathbb {F}}_q$
consisting of
${\mathbb {F}}_q$
consisting of
-
1. the polynomials which express
 ${\mathbf {x}}_{n \times n}$
as a permutation matrix, and
${\mathbf {x}}_{n \times n}$
as a permutation matrix, and -
2. the m polynomials coming from the vector equation
 ${\mathbf {A}} \cdot {\mathbf {x}}_{n \times n} \cdot {\mathbf {v}} = {\mathbf {0}}$
.
${\mathbf {A}} \cdot {\mathbf {x}}_{n \times n} \cdot {\mathbf {v}} = {\mathbf {0}}$
.
In cryptography, one wants to know the difficulty in solving this system using Gröbner methods.Footnote
2
This paper analyzed the system of polynomials coming from
![]() $(1)$
alone; we hope that this will lead to a better understanding of the more cryptographically relevant system
$(1)$
alone; we hope that this will lead to a better understanding of the more cryptographically relevant system
![]() $(1) \cup (2)$
. The Hilbert series of a quotient similar to that by
$(1) \cup (2)$
. The Hilbert series of a quotient similar to that by
![]() $(1) \cup (2)$
was studied by Briaud and Øygarden in [Reference Briaud and Øygarden2] when the linear system analogous to (2) is sufficiently generic.
$(1) \cup (2)$
was studied by Briaud and Øygarden in [Reference Briaud and Øygarden2] when the linear system analogous to (2) is sufficiently generic.
Acknowledgements
The author is very thankful to Pierre Briaud and Morten Øygarden for sharing their conjecture on the Hilbert series of
![]() ${\mathbb {F}}[{\mathbf {x}}_{n \times n}] / {\mathrm {gr}} \, {\mathbf {I}}(P_n)$
and for many very helpful email interactions throughout this project (and their comments on and corrections to earlier versions of this manuscript). The author is also grateful to Dennis Stanton and Jessica Striker for helpful conversations. The author thanks four anonymous referees for their careful reading of and helpful comments on this paper.
${\mathbb {F}}[{\mathbf {x}}_{n \times n}] / {\mathrm {gr}} \, {\mathbf {I}}(P_n)$
and for many very helpful email interactions throughout this project (and their comments on and corrections to earlier versions of this manuscript). The author is also grateful to Dennis Stanton and Jessica Striker for helpful conversations. The author thanks four anonymous referees for their careful reading of and helpful comments on this paper.
Competing interest
The authors have no competing interest to declare.
Funding statement
The author was partially supported by NSF Grants DMS-1953781 and DMS-2246846.
Ethical standards
The research meets all ethical guidelines, including adherence to the legal requirements of the study country.