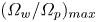1. Introduction
Recently, many researchers have been attracted to and have shown great interest in investigating the interaction of laser pulses with plasma due to the significant advances in the production of short and high-intensity laser pulses (Hooker et al. Reference Hooker, Brunetti, Esarey, Gallacher, Geddes, Gonsalves, Jaroszynski, Kamperidis, Kneip and Krushelnick2007; Joshi Reference Joshi2007; Lundh et al. Reference Lundh, Lim, Rechatin, Ammoura, Ben-Ismaïl, Davoine, Gallot, Goddet, Lefebvre and Malka2011; Hooker Reference Hooker2013; Abedi-Varaki & Jafari Reference Abedi-Varaki and Jafari2017a; Abedi-Varaki Reference Abedi-Varaki2018a). One of the areas of interest for researchers is the study into the effects of external fields such as the wiggler field and the uniform magnetic fields on the interactions of intense laser pulses with plasma. These fields have a centralizing role on the electron beam that is employed to accelerate within the plasma (Abedi-Varaki Reference Abedi-Varaki2017; Abedi-Varaki & Jafari Reference Abedi-Varaki and Jafari2017a,Reference Abedi-Varaki and Jafarib, Reference Abedi-Varaki and Jafari2018a,Reference Abedi-Varaki and Jafarib,Reference Abedi-Varaki and Jafaric; Abedi-Varaki & Panahi Reference Abedi-Varaki and Panahi2019; Gopal et al. Reference Gopal, Gupta, Jain, Hur and Suk2021a). The electron acceleration in the laser–plasma interaction leads to nonlinear effects such as self-focusing, self-modulation, filamentation, second-harmonic generation, terahertz radiation generation and so on. In fact, nonlinear effects cause changes in the distribution of the input pulse intensity of the laser, which is applied in advanced technologies such as laser fusion, laser-plasma accelerators, laser ablation, X-ray lasers and inertial confinement fusion (ICF) (Abedi-Varaki & Jafari Reference Abedi-Varaki and Jafari2017b; Abedi-Varaki Reference Abedi-Varaki2018c; Reference Abedi-Varaki2020; Haines et al. Reference Haines, Shah, Smidt, Albright, Cardenas, Douglas, Forrest, Glebov, Gunderson and Hamilton2020; Kautz, Phillips & Harilal Reference Kautz, Phillips and Harilal2020; Sherlock & Bissell Reference Sherlock and Bissell2020; Tajima & Malka Reference Tajima and Malka2020; Yadav, Gupta & Sharma Reference Yadav, Gupta and Sharma2020). To investigate electron acceleration in vacuum and plasmas in terms of theoretical and experimental aspects, several models have been proposed and developed (Abedi-Varaki Reference Abedi-Varaki2018b; Reference Abedi-Varaki2019; Gupta, Kant & Singh Reference Gupta, Kant and Singh2018; Caizergues et al. Reference Caizergues, Smartsev, Malka and Thaury2020; Yadav et al. Reference Yadav, Gupta and Sharma2020; Gopal, Gupta & Suk Reference Gopal, Gupta and Suk2021b). The main focus has been on the production of high-energy particles, using ultra-short and ultra-intense lasers in the plasmas via compact ultrahigh gradient accelerators (Malik, Kumar, & Nishida Reference Malik, Kumar and Nishida2007; Leemans et al. Reference Leemans, Gonsalves, Mao, Nakamura, Benedetti, Schroeder, Tóth, Daniels, Mittelberger and Bulanov2014; Litos et al. Reference Litos, Adli, An, Clarke, Clayton, Corde, Delahaye, England, Fisher and Frederico2014). Generation of large amplitude plasma waves has been studied under several schemes and in numerous accelerators such as the plasma wakefield accelerator, laser wakefield accelerator (LWFA), resonant laser-plasma accelerator and the self-modulated laser wakefield accelerator (SMLWFA) (Lindberg et al. Reference Lindberg, Charman, Wurtele and Friedland2004; Hooker et al. Reference Hooker, Brunetti, Esarey, Gallacher, Geddes, Gonsalves, Jaroszynski, Kamperidis, Kneip and Krushelnick2007; Chen et al. Reference Chen, Chang, Lin, Noble and Sydora2009; Esarey, Schroeder & Leemans Reference Esarey, Schroeder and Leemans2009; Jha, Saroch & Mishra Reference Jha, Saroch and Mishra2013; Gupta et al. Reference Gupta, Gopal, Nam, Kulagin and Suk2014; Albert et al. Reference Albert, Lemos, Shaw, Pollock, Goyon, Schumaker, Saunders, Marsh, Pak and Ralph2017). Recently, laser-plasma accelerators have been investigated from both an experimental and theoretical perspective. Tajima and Dawson (Reference Tajima and Dawson1979) studied laser-plasma accelerators. They found that the structures of wakes and sheaths in plasma are in conflict. When the large amplitude of wakefields involves collective resonance oscillations of the eigenmode of the entire plasma electrons, the wake phase velocity ~c and ultrafastness of the laser pulse introduce the wake stability and rigidity. When the phase velocity declines, wakefields turn into sheaths more suitable for ion acceleration. The outcomes of a nonlinear plasma wakefield accelerator (PWFA), high transformer ratio experiment has been reported by Roussel et al. (Reference Roussel, Andonian, Lynn, Sanwalka, Robles, Hansel, Deng, Lawler, Rosenzweig and Ha2020) applying high-charge, longitudinally asymmetric drive beams in a plasma cell. Moreover, single-shot wakefield measurements of a PWFA in the nonlinear regime by controlling over-drive beam shaping have also been illustrated in their experiment. A recorded transformer ratio of 7.8 ± 2.3 from a linearly ramped beam and the observation of a near uniform decelerating field for a drive beam with a parabolic head are two main outcomes of their experimental investigations. Some initial applications that probably came into view from plasma-based accelerator research have been examined by Joshi, Corde & Mori (Reference Joshi, Corde and Mori2020). These applications include incoherent directional X-ray beams for science and technology, electron beam radiotherapy, near single cycle continuously tunable infrared pulses for spectroscopy as well as non-perturbative quantum electrodynamics enabled by plasma-based accelerator electron beams. The progression of these near-term applications has been promised and anticipated in the next decades, performing coordinated attempts. Emittance preservation through density ramp matching sections in a plasma wakefield accelerator has been studied by Zhao et al. (Reference Zhao, An, Xu, Li, Hildebrand, Hogan, Yakimenko, Joshi and Mori2020). It has been realized that the beam emittance can be preserved under the matching condition even while the beam has an initial energy spread.
In this article, we intend to investigate the influence of a wiggler magnetic field on electron acceleration and the wakefield produced resulting from GL, SG and BG laser pulses in plasma. The main body of the paper is divided into three sections. Section 2 refers to the derivation of fundamental equations and methods for the analysis of the laser wakefield in GL, SG and BG of laser pulses. The numerical results for wakefield properties on the electron acceleration are achieved and analysed in § 3. Finally, § 4 is devoted to the conclusions of the research.
2. Fundamental equations for analysis of laser wakefield
Propagation of electromagnetic waves through plasma has been considered in the presence of a planar magnetostatic wiggler in a weakly nonlinear regime. Our considered physical configuration comprises an intense laser pulse propagating through a cold collisionless plasma containing a periodic planar wiggler field $({\boldsymbol{B}_w} = {B_w}{\hat{e}_y})$![]() . The wiggler field can be expressed as (Abedi-Varaki & Jafari Reference Abedi-Varaki and Jafari2017c, Reference Abedi-Varaki and Jafari2017d, Reference Abedi-Varaki and Jafari2018a)
. The wiggler field can be expressed as (Abedi-Varaki & Jafari Reference Abedi-Varaki and Jafari2017c, Reference Abedi-Varaki and Jafari2017d, Reference Abedi-Varaki and Jafari2018a)
where ${B_w}$![]() and ${k_w} = 2{\rm \pi}/{\lambda _w}$
and ${k_w} = 2{\rm \pi}/{\lambda _w}$![]() are the amplitude and wavenumber of the wiggler field, respectively. A schematic illustration of this configuration is shown in figure 1.
are the amplitude and wavenumber of the wiggler field, respectively. A schematic illustration of this configuration is shown in figure 1.
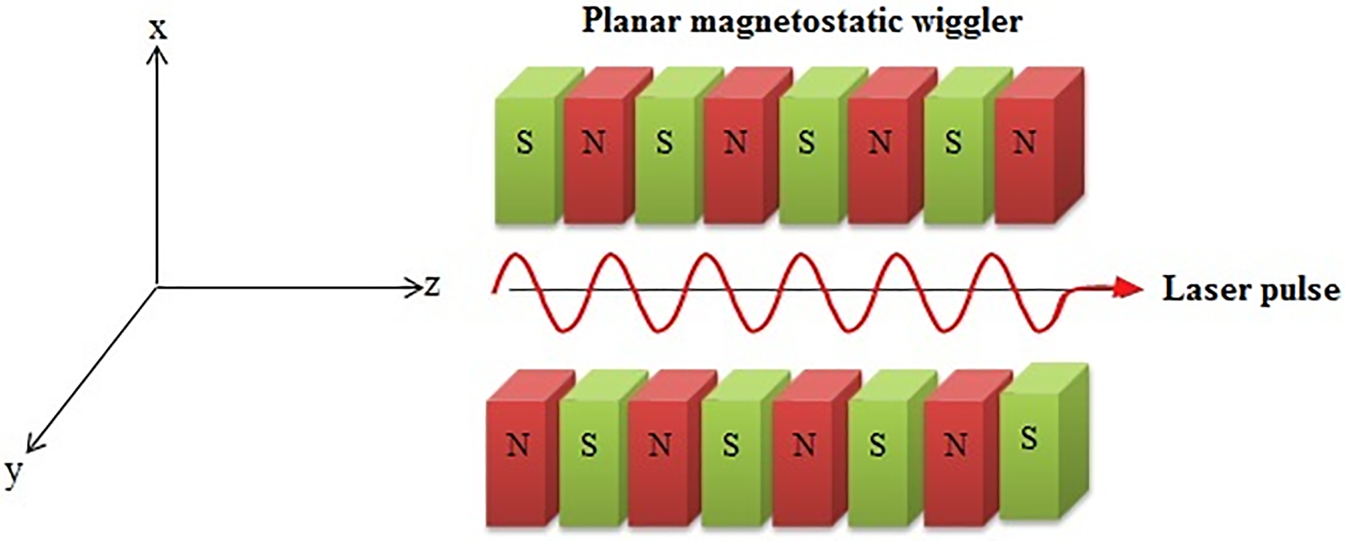
Figure 1. Schematic illustration of laser pulse trajectory in the presence of a planar magnetostatic wiggler.
Applying the following equations in plasma, a laser–plasma interaction in a nonlinear regime and in the presence of a wiggler field is yielded as follows:
in which $\boldsymbol{E} = E(\zeta ){\hat{e}_x}$![]() and $\boldsymbol{B} = B(\zeta ){\hat{e}_y}$
and $\boldsymbol{B} = B(\zeta ){\hat{e}_y}$![]() are the electric and magnetic fields of an electromagnetic wave, ${n_e}$
are the electric and magnetic fields of an electromagnetic wave, ${n_e}$![]() stands for the density of an electron, $\boldsymbol{J}$
stands for the density of an electron, $\boldsymbol{J}$![]() is the current density of electrons of plasma, e refers to the magnitude of electron charge,$\boldsymbol{u}$
is the current density of electrons of plasma, e refers to the magnitude of electron charge,$\boldsymbol{u}$![]() is the electron velocity and $\boldsymbol{p} = \gamma m\boldsymbol{u}$
is the electron velocity and $\boldsymbol{p} = \gamma m\boldsymbol{u}$![]() denotes the relativistic momentum where the relativistic Lorentz factor $(\gamma )$
denotes the relativistic momentum where the relativistic Lorentz factor $(\gamma )$![]() can be shown as (Abedi-Varaki & Kant Reference Abedi-Varaki and Kant2022)
can be shown as (Abedi-Varaki & Kant Reference Abedi-Varaki and Kant2022)

Considering the fact that the mass of the electron is lighter than the ion mass, the motion of the ion can be supposed to be negligible and the corresponding plasma can be considered in an equilibrium state. In this condition, plasma density ${n_0}$![]() and drift velocity ${\boldsymbol{u}_0}$
and drift velocity ${\boldsymbol{u}_0}$![]() are constant and zero, respectively. Additionally, the laser pulse propagation is considered in the z-axis direction and the plasma electron density is mentioned as ${n_e} = {n_0} + {n^{\prime}_e}$
are constant and zero, respectively. Additionally, the laser pulse propagation is considered in the z-axis direction and the plasma electron density is mentioned as ${n_e} = {n_0} + {n^{\prime}_e}$![]() , where ${n^{\prime}_e}$
, where ${n^{\prime}_e}$![]() is the electron density perturbation due to the laser pulse. As all the characteristics depend only on $\zeta = z - {u_g}t$
is the electron density perturbation due to the laser pulse. As all the characteristics depend only on $\zeta = z - {u_g}t$![]() and by using the weakly nonlinear regime where${u_z} \gg {u_x}$
and by using the weakly nonlinear regime where${u_z} \gg {u_x}$![]() , the result is
, the result is
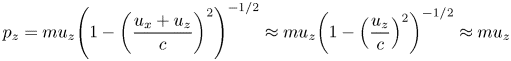
and
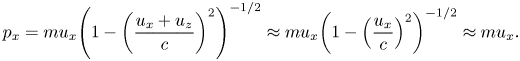
Applying the perturbation technique along with (2.1)–(2.7), while the wiggler field is present, will result in
in which ${u_g} = c{(1 - \varOmega _p^2/{\varOmega ^2})^{1/2}}$![]() , ${\varOmega _w} = e{B_w}/mc$
, ${\varOmega _w} = e{B_w}/mc$![]() and ${\varOmega _p} = {({n_0}{e^2}/m{\varepsilon _0})^{1/2}}$
and ${\varOmega _p} = {({n_0}{e^2}/m{\varepsilon _0})^{1/2}}$![]() are the group velocity, the wiggler frequency and the plasma frequency, respectively. The following equation can be derived by using (2.11)–(2.16):
are the group velocity, the wiggler frequency and the plasma frequency, respectively. The following equation can be derived by using (2.11)–(2.16):
Using the weakly nonlinear regime and considering small perturbations $({n^{\prime}_e} \ll {n_0})$![]() , derivations will be as follows:
, derivations will be as follows:
Integration of (2.18) by using (2.14)–(2.16) under the condition that ${n^{\prime}_e},{u_x}$![]() and ${u_z}$
and ${u_z}$![]() vanish as $|\zeta |\to \infty$
vanish as $|\zeta |\to \infty$![]() leads to wake potential as
leads to wake potential as
where $\beta = c/{u_g}$![]() and ${k_p} = {\varOmega _p}/{u_g} = 2{\rm \pi}/{\lambda _p}$
and ${k_p} = {\varOmega _p}/{u_g} = 2{\rm \pi}/{\lambda _p}$![]() is the plasma wavenumber. Equation (2.19) generally represents the wake potential. As a matter of fact, the wake potential equation has a dependence on the external magnetic field, the electric field and the group velocity of the laser pulse. Furthermore, the force term that relates to the pondermotive force and drives the wakefield is indicated via the last term of (2.19). For formulating the electron acceleration and the interaction between electrons and the wakefield, (2.2) is considered as
is the plasma wavenumber. Equation (2.19) generally represents the wake potential. As a matter of fact, the wake potential equation has a dependence on the external magnetic field, the electric field and the group velocity of the laser pulse. Furthermore, the force term that relates to the pondermotive force and drives the wakefield is indicated via the last term of (2.19). For formulating the electron acceleration and the interaction between electrons and the wakefield, (2.2) is considered as
For simplifying the mathematical processes, the variable $\eta = {k_p}(\zeta - L/2)$![]() which is associated with the wakefield phase has been introduced. Considering the one-dimensional motion of electron and taking $\zeta = z - {u_g}t$
which is associated with the wakefield phase has been introduced. Considering the one-dimensional motion of electron and taking $\zeta = z - {u_g}t$![]() , we can achieve following relations:
, we can achieve following relations:
As a consequence, dividing ${\rm d}\gamma /{\rm d}t$![]() by ${\rm d}\eta /{\rm d}t$
by ${\rm d}\eta /{\rm d}t$![]() and taking into account ${\rm d}z/{\rm d}t = {u_z} = c{(1 - 1/{\gamma ^2})^{1/2}}$
and taking into account ${\rm d}z/{\rm d}t = {u_z} = c{(1 - 1/{\gamma ^2})^{1/2}}$![]() and their integration will consequently result in
and their integration will consequently result in
Equation (2.22) represents the general equation that governs the electron acceleration in the wakefield. By assuming the initial value $\gamma$![]() as ${\gamma _0}$
as ${\gamma _0}$![]() at $\zeta = 0$
at $\zeta = 0$![]() and by integrating the above equation, $\Delta \gamma$
and by integrating the above equation, $\Delta \gamma$![]() can be expressed as
can be expressed as
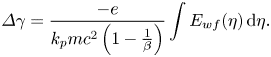
Thus, the electron energy gain is achieved by the electron acceleration in the wakefield excited by the laser pulses by employing $\varDelta W = m{c^2}\varDelta \gamma$![]() .
.
The main goal of this paper is to focus on the electron acceleration in the wakefield excited by GL, SG and BG laser pulses in the presence of a planar magnetostatic wiggler.
2.1. GL laser pulse
The profiles of the field distributions of the GL laser pulse are given as
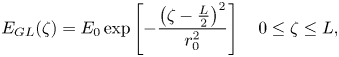
in which ${E_0}$![]() is the maximum amplitude of the Gaussian electric field, L is the pulse length and ${r_0}$
is the maximum amplitude of the Gaussian electric field, L is the pulse length and ${r_0}$![]() is the laser pulse waist. By putting (2.24) in (2.19), the wakefield potential ${\varphi _{WGL}}$
is the laser pulse waist. By putting (2.24) in (2.19), the wakefield potential ${\varphi _{WGL}}$![]() behind the GL can be extracted as
behind the GL can be extracted as
Here, ${\alpha _{GL}}$![]() can be presented as
can be presented as
In addition, the wakefield of the GL laser pulse is given by
The density perturbations behind the GL pulse can be achieved by using (2.19) in combination with the weakly nonlinear regime as
Additionally, the electron energy gain of GL laser pulse in the presence of a planar magnetostatic wiggler can be derived by replacing (2.27) in (2.23) as
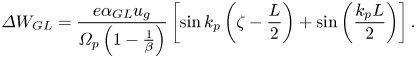
2.2. SG laser pulse
For this type of pulse, the profiles of the field distributions are taken as
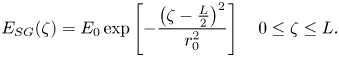
Replacing (2.30) in (2.19) under the same conditions as § 2 will lead to the wakefield potential ${\varphi _{WSG}}$![]() and ${E_{WSG}}$
and ${E_{WSG}}$![]() behind the SG as
behind the SG as
Furthermore, the generalized hyper-geometric function is introduced in the following equation (Górska & Penson Reference Górska and Penson2013):
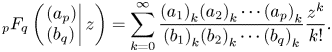
Here, ${b_j} \ne 0, - 1, - 2, \ldots ,\;j = 1,2, \ldots q$![]() . It is worth mentioning that ${(a)_k} = \varGamma (a + k)/\varGamma (a)$
. It is worth mentioning that ${(a)_k} = \varGamma (a + k)/\varGamma (a)$![]() stands for the Pochhammer symbol in which $\varGamma$
stands for the Pochhammer symbol in which $\varGamma$![]() is the gamma function. Employing (2.33) and mathematical processes, the coefficient of ${\alpha _{SG}}$
is the gamma function. Employing (2.33) and mathematical processes, the coefficient of ${\alpha _{SG}}$![]() is obtained as (Hörmander Reference Hörmander1967)
is obtained as (Hörmander Reference Hörmander1967)
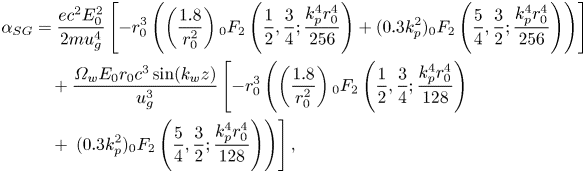
where $_0{F_2}(a,b;c)$![]() is a hyper-geometric function. We can obtain the density perturbations behind the SG pulse by using (2.18) and employing (2.31) and (2.32) to get
is a hyper-geometric function. We can obtain the density perturbations behind the SG pulse by using (2.18) and employing (2.31) and (2.32) to get
As a result, we can compute the electron energy gain in the wakefield excited by SG laser pulse as
2.3. BG laser pulse
Finally, the case of wakefield excitation has been analysed with a BG laser pulse. The profiles of the field distributions of the BG laser pulse are given as follows (Li, Lee & Wolf Reference Li, Lee and Wolf2004):
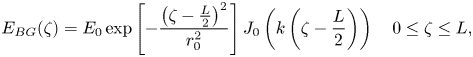
in which k and ${J_0}$![]() are the transverse wavenumber and the zero-order Bessel function, respectively. Using (2.37), (2.19) will be obtained under the conditions that the wake potential is zero at the middle of pulse $(\zeta = L/2)$
are the transverse wavenumber and the zero-order Bessel function, respectively. Using (2.37), (2.19) will be obtained under the conditions that the wake potential is zero at the middle of pulse $(\zeta = L/2)$![]() as
as
Employing the expansion of Bessel function, the coefficient of ${\alpha _{BG}}$![]() in (2.38) is achieved as follows (Fallah & Khorashadizadeh Reference Fallah and Khorashadizadeh2019):
in (2.38) is achieved as follows (Fallah & Khorashadizadeh Reference Fallah and Khorashadizadeh2019):
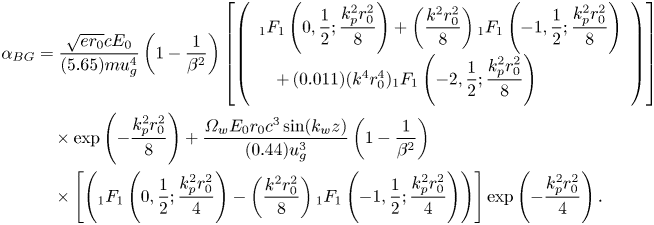
Here, $_1{F_1}(a,b;c)$![]() is the confluent hyper-geometric function. Furthermore, the wakefield of the BG laser pulse is calculated as
is the confluent hyper-geometric function. Furthermore, the wakefield of the BG laser pulse is calculated as
By inserting (2.40) in (2.23), the electron energy gain of the GL laser pulse in the presence of a wiggler field is obtained as follows:
Equation (2.41) denotes the electron energy gain in the wakefield produced by a BG laser pulse in the presence of a planar magnetostatic wiggler in cold collisionless plasma.
3. Numerical results and discussion
Analytical solutions of equations including Maxwell's equations, hydrodynamics fluid equations as well as perturbation technique for laser wakefields induced by GL, SG and BG laser pulses in the weakly nonlinear regime reveal that the amplitude of the wakefield depends on some parameters such as frequency, energy, intensity, length of laser pulses as well as wiggler field and plasma electron density. Thus, the influence of such parameters on the electron acceleration and wakefield is considered and investigated for three shapes of GL, SG and BG laser pulses in the presence of a planar magnetostatic wiggler. To study the mentioned parameters effects, laser frequency, laser intensity and plasma electron density are assumed as 2.4 × 1015 Hz, 3 × 1022 W m−2 and ${n_0} = 2.5 \times {10^{24}}\;{\textrm{m}^{ - 3}}$![]() , respectively, on the basis of a wavelength of λ = 800 nm.
, respectively, on the basis of a wavelength of λ = 800 nm.
As an outcome of the numerical results of this research, we will finally be able to understand and analyse how a wiggler magnetic field can result in considerable variations in the amplitude of the wakefield and also boost the energy of accelerated electrons in a cold collisionless plasma.
3.1. Evaluation of GL, SG and BG wakefields
3.1.1. Influence of laser intensity
As can be seen from figure 2(a–c), by considering different values of the laser intensity as 0.75 × 1022 W m−2, 1.5 × 1022 W m−2, 2.25 × 1022 W m−2 and 3 × 1022 W m−2, the variation of the wakefield versus the distance for BG, SG and GL laser pulses in Bw = 50 T has been illustrated. It is clearly understood through these figures that an increase in laser intensity from 0.75 × 1022 W m−2 to 3 × 1022 W m−2 for three different shapes of BG, SG and GL laser pulses leads to an increase in the wakefield. Additionally, (2.28) and (2.35) disclose the direct association of the wakefield amplitude with $E_0^2$![]() . As a result, it is promising that the higher intensity laser pulses will excite a larger amplitude owing to the larger density perturbations in collisionless plasma and correspondingly a larger wakefield will be generated.
. As a result, it is promising that the higher intensity laser pulses will excite a larger amplitude owing to the larger density perturbations in collisionless plasma and correspondingly a larger wakefield will be generated.
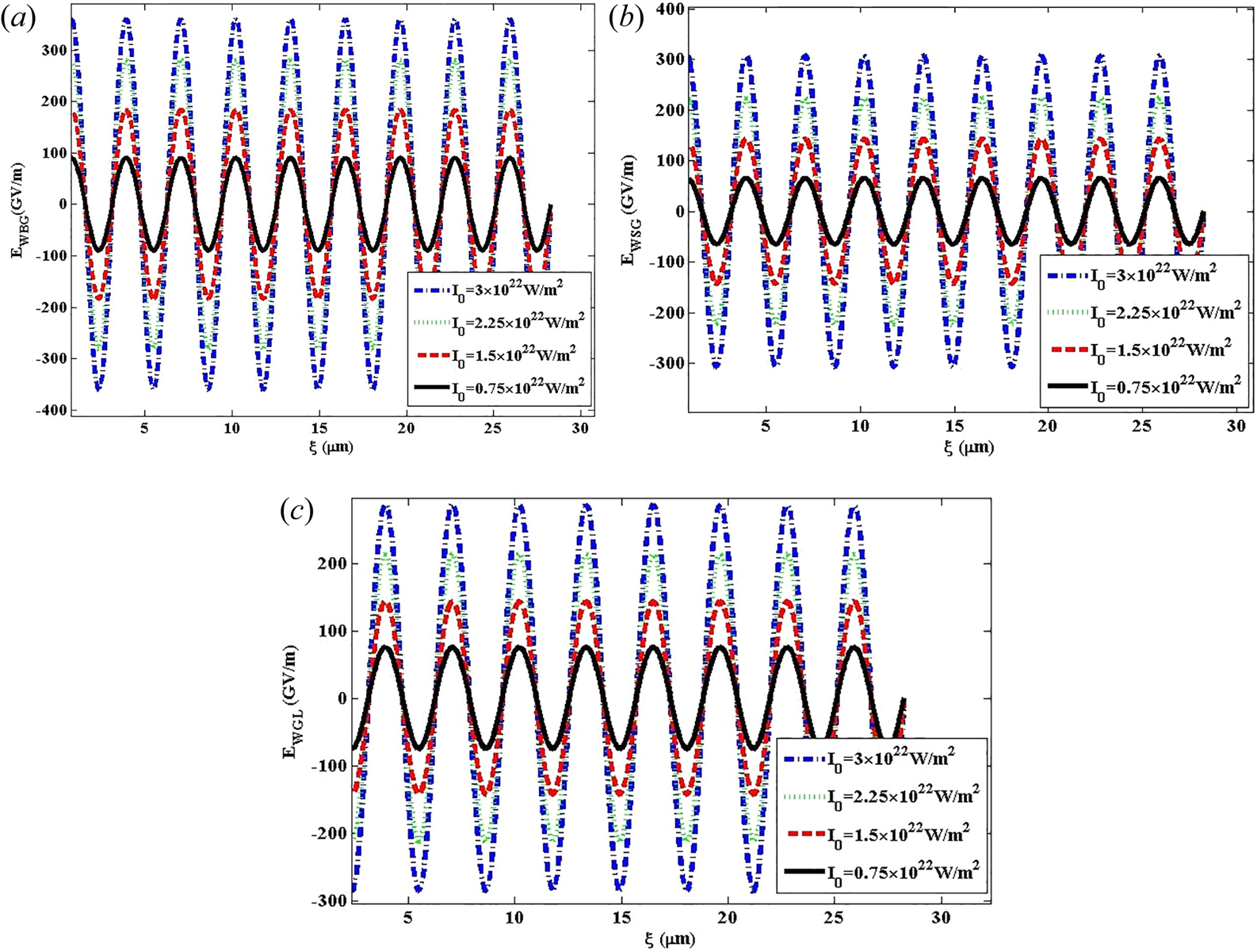
Figure 2. Variation of the wakefield versus the distance for (a) BG, (b) SG and (c) GL laser pulses at laser intensities of 0.75 × 1022 W m−2, 1.5 × 1022 W m−2, 2.25 × 1022 W m−2 and 3 × 1022 W m−2 when Bw = 50 T.
3.1.2. Influence of laser frequency
Variation of the wakefield amplitude with respect to the laser frequency has been illustrated in figure 3(a–c) for BG, SG and GL laser pulses. It is worth mentioning that for this case, the intensity of the laser has been considered 3 × 1022 W m−2 and the wiggler field has different values of Bw = 18 T, 34 T, 50 T and 66 T. These curves clearly show that an increase in the wiggler magnetic field and laser frequency yields an increased wakefield amplitude. It sounds that the main reason for the growth in wakefield amplitude is the laser group velocity. In other words, the frequency of the laser pulse is completely dependent on the laser group velocity. It is deduced that a slight variation in group velocity of the laser pulse due to the laser frequency results in a more significant variation in factor $({\beta ^2} - 1)$![]() that appears in (2.19). Additionally, it is inferred that with increasing laser group velocity for larger frequencies, the electron energy gain gets larger with enhancing laser frequency. It is important to emphasize that the electron energy gain is proportional to the factor $1/(\beta - 1)$
that appears in (2.19). Additionally, it is inferred that with increasing laser group velocity for larger frequencies, the electron energy gain gets larger with enhancing laser frequency. It is important to emphasize that the electron energy gain is proportional to the factor $1/(\beta - 1)$![]() . Moreover, a greater effectiveness of the wiggler field on the BG laser pulse in comparison with SG and GL laser pulses is the predominant outcome of this section.
. Moreover, a greater effectiveness of the wiggler field on the BG laser pulse in comparison with SG and GL laser pulses is the predominant outcome of this section.
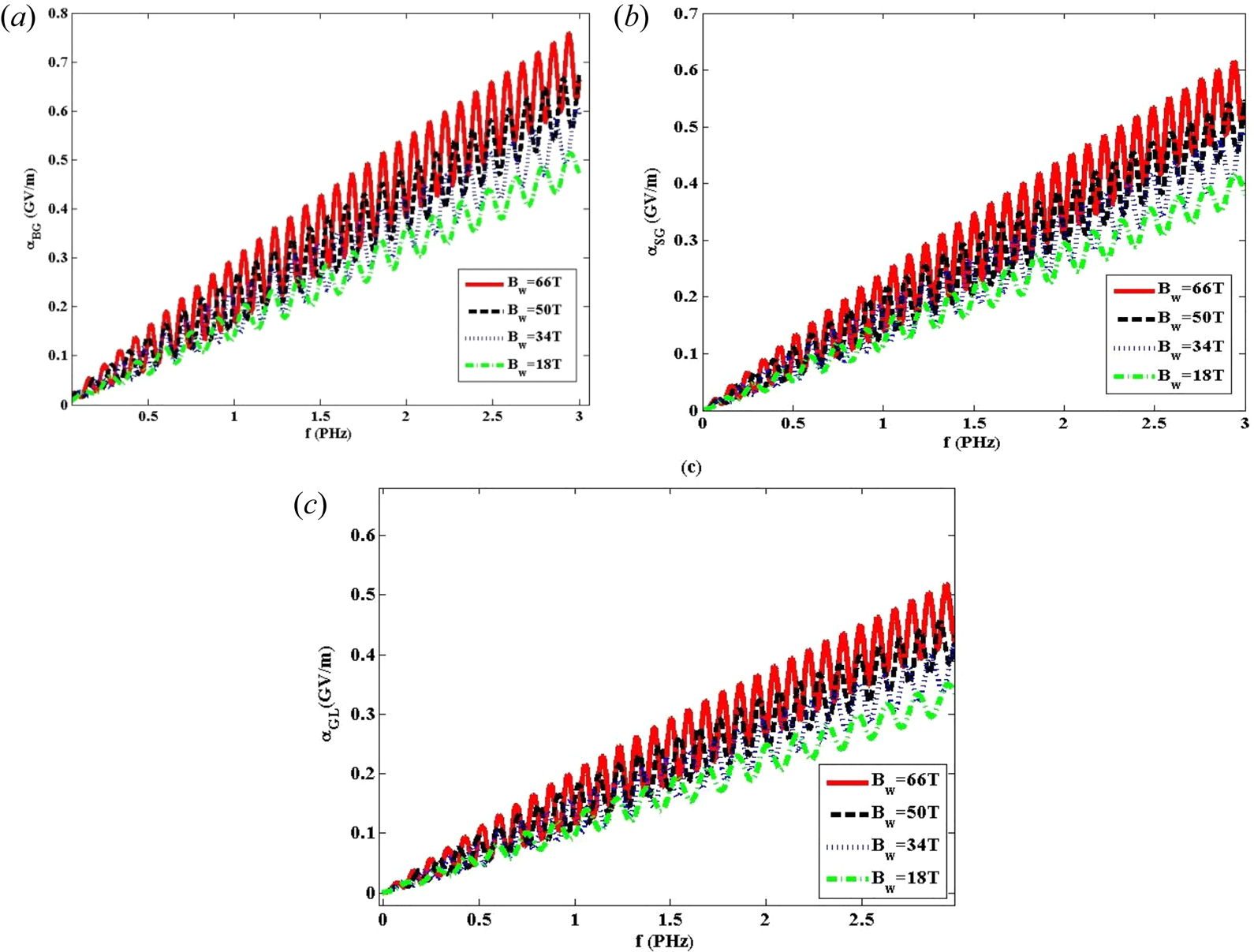
Figure 3. Variation of the wakefield amplitude versus the laser frequency for (a) BG, (b) SG and (c) GL laser pulses at laser intensity 3 × 1022 W m−2 for Bw = 18 T, 34 T, 50 T and 66 T.
3.1.3. Influence of the electron energy gain
Variation of the electron energy gain versus the plasma electron density and laser intensity for BG, SG and GL laser pulses in the presence of a wiggler magnetic field has been demonstrated in figures 4 and 5. It is obvious from figure 4(a–c) that the electron energy gain has first a sharp upward trend and then follows a moderate drop while the laser intensity is raised from 0.75 × 1022 W m−2 to 3 × 1022 W m−2 for BG, SG and GL laser pulses. Indeed, with increasing laser intensity, the difference in the electron energy gain has an increasing trend and eventually reaches a maximum of 18.88 MeV, 15.84 MeV and 13.64 MeV for a specific plasma electron density in BG, SG and GL laser pulses, respectively. In addition, it is specified that the electron energy gain has the largest amount for the BG laser pulse in comparison with SG and GL laser pulses. With consideration of figure 5, we will encounter an upward trend in electron energy gain for all three shapes of laser pulses while the laser intensity increases. To provide more details, the periodic behaviour is dominant and then the electron energy gain shows a considerable ascending trend to 511 MeV, 414 MeV and 322 MeV for BG, SG and GL laser pulses, respectively. Correspondingly, it can be comprehended that the electron accelerating force and subsequently the electron velocity increase as the wakefield amplitude increases, which consequently results in a higher electron energy gain. Also, a comparison among the energy gain obtained in the wakefield excited by BG, SG and GL laser pulses in the presence of a planar magnetostatic wiggler reveals the trend WBG > WSG > WGL for the electron energy gain.
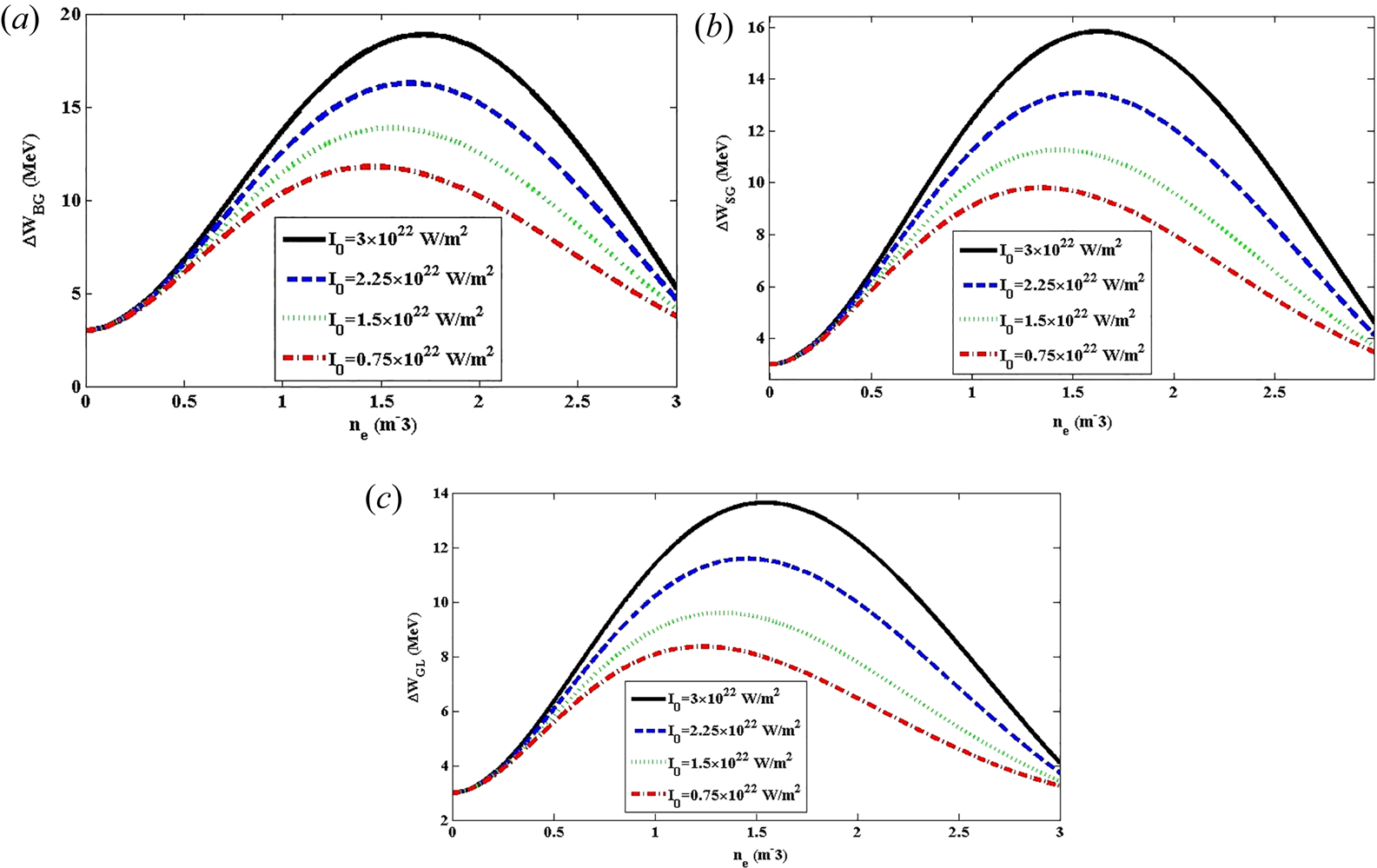
Figure 4. Variation of the electron energy gain versus the plasma electron density for (a) BG, (b) SG and (c) GL laser pulses. The chosen parameters are λ = 0.8 μm, Bw = 50 T and L = 25 μm.
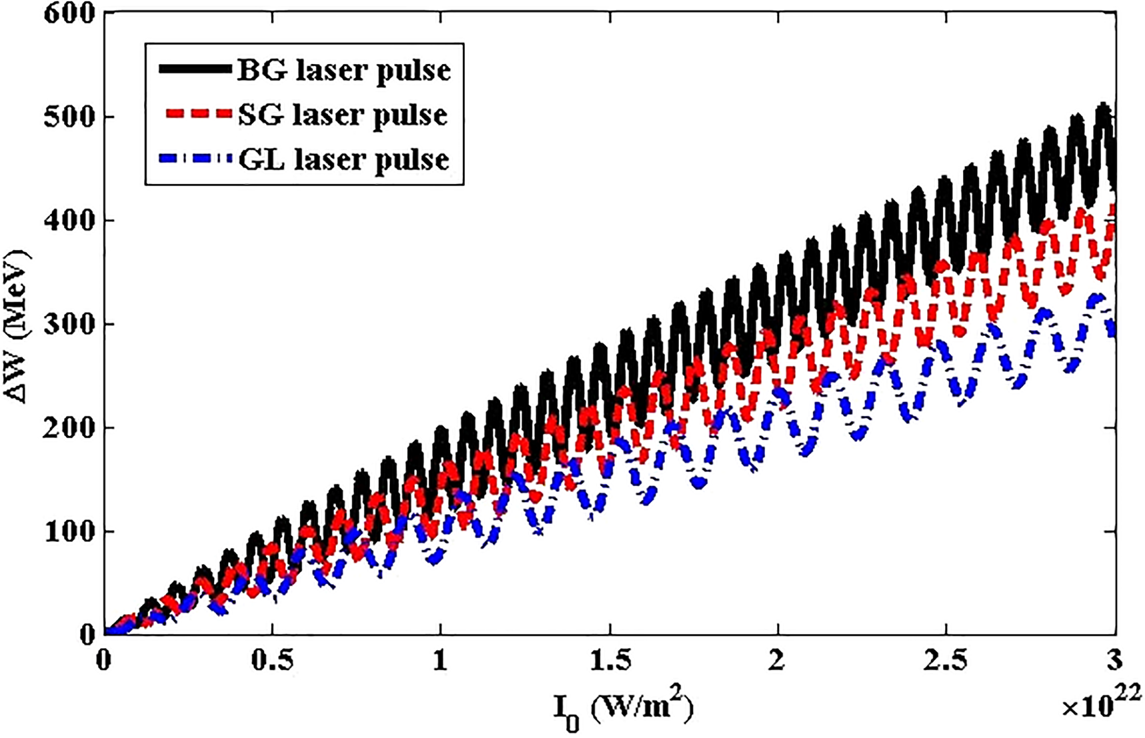
Figure 5. Variation of the electron energy gain versus the laser intensity for (a) BG (b) SG and (c) GL laser pulses. The chosen parameters are λ = 0.8 μm, Bw = 50 T, L = 25 μm and n 0 = 2.5 × 1024 m−3.
3.1.4. Influence of pulse length
Variation of the wakefield amplitude versus Ωw/Ωp for BG, SG and GL laser pulses at laser intensity 3 × 1022 W m−2 and different values of the pulse length as L = 24 μm, 25 μm, 26 μm and 27 μm is demonstrated in figures 6(a) and 6(b). It is understood from these figures that increasing the pulse length yields a decline in the wakefield amplitude so that L = 27 μm reaches minimum values of ${\alpha _{BG}} = 2.66\;\textrm{GV}\;{\textrm{m}^{ - 1}}$![]() , ${\alpha _{SG}} = 1.77\;\textrm{GV}\;{\textrm{m}^{ - 1}}$
, ${\alpha _{SG}} = 1.77\;\textrm{GV}\;{\textrm{m}^{ - 1}}$![]() and ${\alpha _{GL}} = 1.32\;\textrm{GV}\;{\textrm{m}^{ - 1}}$
and ${\alpha _{GL}} = 1.32\;\textrm{GV}\;{\textrm{m}^{ - 1}}$![]() at the resonance positions shift of ${({\varOmega _w}/{\varOmega _p})_{min}} = 0.46,\;{({\varOmega _w}/{\varOmega _p})_{min}} = 0.44$
at the resonance positions shift of ${({\varOmega _w}/{\varOmega _p})_{min}} = 0.46,\;{({\varOmega _w}/{\varOmega _p})_{min}} = 0.44$![]() and ${({\varOmega _w}/{\varOmega _p})_{min}} = 0.42$
and ${({\varOmega _w}/{\varOmega _p})_{min}} = 0.42$![]() for BG, SG and GL laser pulses, respectively. Additionally, the remarkable role of the pulse length in wakefield excitation has been revealed and has been shown that the amplitude of the wakefield is enhanced while the pulse length decreases, resulting in a shift to the higher number of resonant positions ${({\varOmega _w}/{\varOmega _p})_{max}}$
for BG, SG and GL laser pulses, respectively. Additionally, the remarkable role of the pulse length in wakefield excitation has been revealed and has been shown that the amplitude of the wakefield is enhanced while the pulse length decreases, resulting in a shift to the higher number of resonant positions ${({\varOmega _w}/{\varOmega _p})_{max}}$![]() .
.
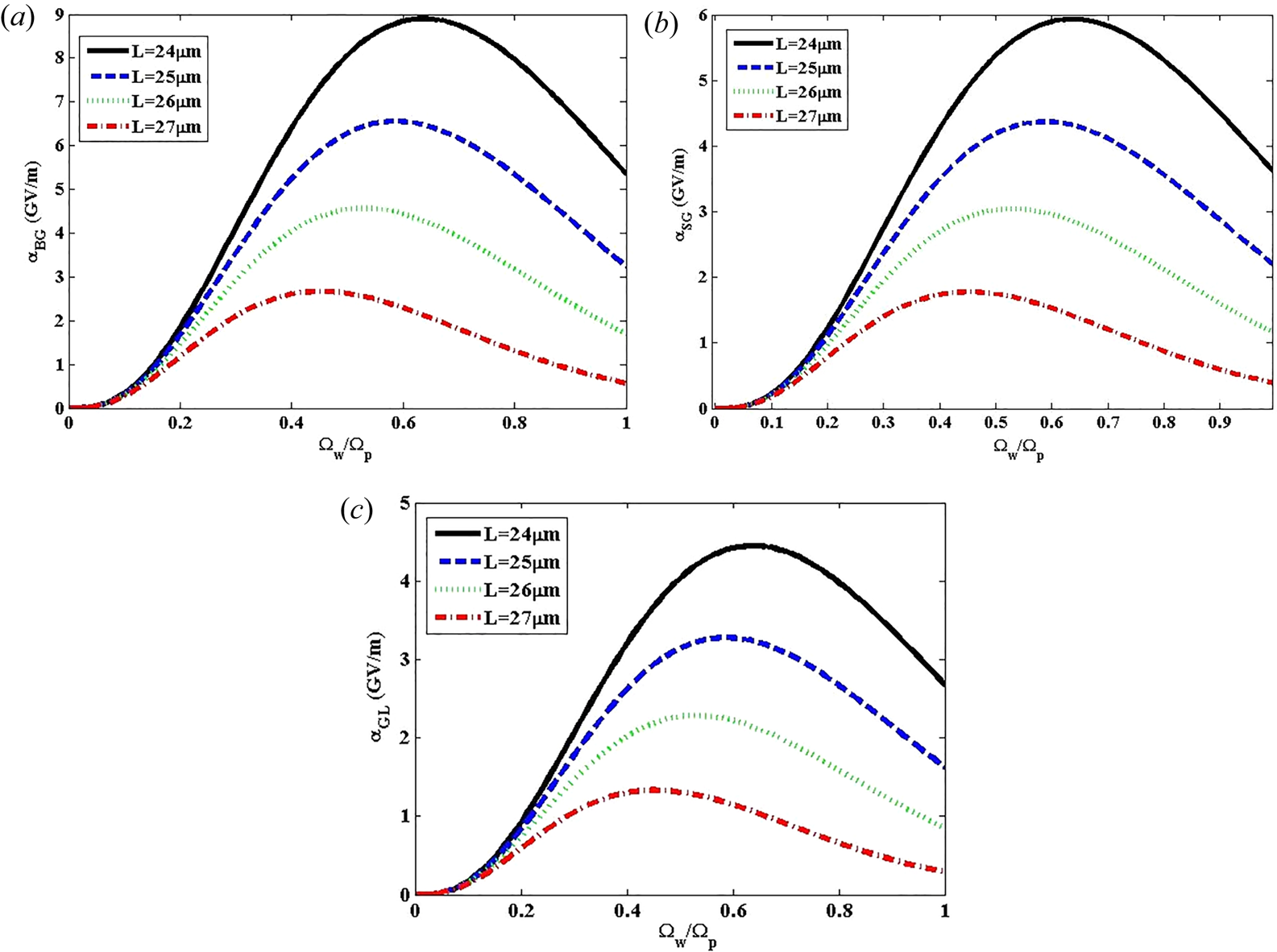
Figure 6. Variation of the wakefield amplitude versus the Ωw/Ωp at laser intensity 3 × 1022 W m−2 for (a) BG, (b) SG and (c) GL laser pulses for different values of L = 24 μm, 25 μm, 26 μm and 27 μm.
3.1.5. Influence of wiggler magnetic field
Variation of the wakefield with respect to the distance at laser intensity ${I_0} = 3 \times {10^{22}}\;\textrm{W}\;{\textrm{m}^{ - 2}}$![]() for BG, SG and GL laser pulses has been demonstrated in figure 7(a–c). For this case, the wiggler magnetic field has different values of Bw = 0 T, 18 T, 34 T and 50 T. As shown, changes in the wiggler magnetic field have substantial effects on the amplitude of the wakefield. As analysed, although the overall behaviour of the wakefield does not change, the wakefield amplitude shows an increasing trend when the wiggler magnetic field increases. As can be seen, compared to the cases of SG and GL laser pulses, when the wiggler field is increased, the wakefield amplitude excited by the BG laser pulse will be larger. Moreover, (2.19) implies that the wake potential is related to the wiggler field. Hence, a rise in the wiggler field gives rise to a larger wakefield.
for BG, SG and GL laser pulses has been demonstrated in figure 7(a–c). For this case, the wiggler magnetic field has different values of Bw = 0 T, 18 T, 34 T and 50 T. As shown, changes in the wiggler magnetic field have substantial effects on the amplitude of the wakefield. As analysed, although the overall behaviour of the wakefield does not change, the wakefield amplitude shows an increasing trend when the wiggler magnetic field increases. As can be seen, compared to the cases of SG and GL laser pulses, when the wiggler field is increased, the wakefield amplitude excited by the BG laser pulse will be larger. Moreover, (2.19) implies that the wake potential is related to the wiggler field. Hence, a rise in the wiggler field gives rise to a larger wakefield.
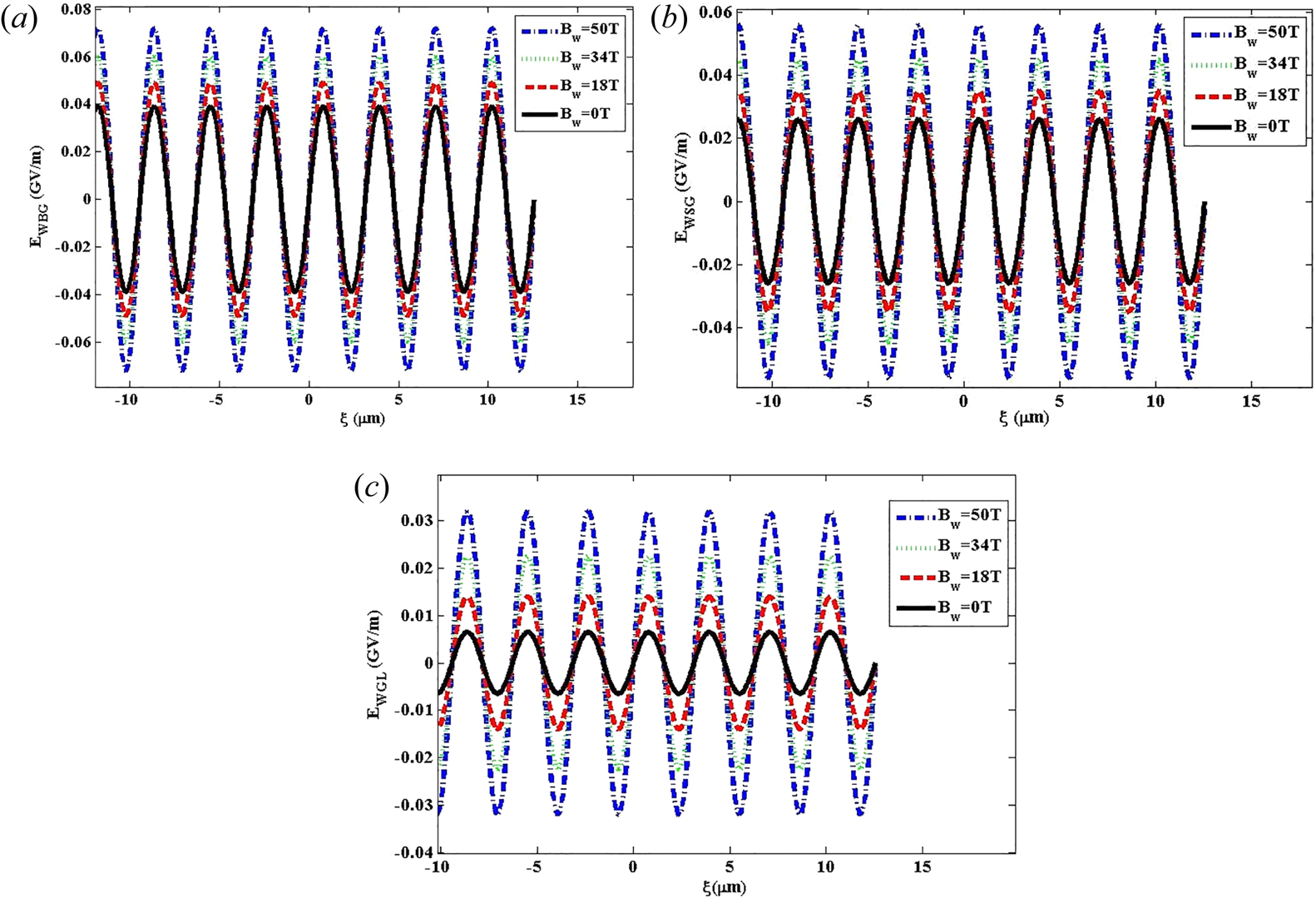
Figure 7. Variation of the wakefield versus the distance for (a) BG, (b) SG and (c) GL laser pulses at laser intensity 3 × 1022 W m−2 for different values of Bw = 0 T, 18 T, 34 T and 50 T.
3.1.6. Influence of the plasma electron density
Variations of the wakefield versus the distance for BG, SG and GL laser pulses in Bw = 50 T and laser intensity ${I_0} = 3 \times {10^{22}}\;\textrm{W}\;{\textrm{m}^{ - 2}}$![]() have been illustrated in figure 8(a–c). In this case, the plasma electron density has different values of 0.62 × 1024 m−3, 1.25 × 1024 m−3, 1.87 × 1024 m−3 and 2.5 × 1024 m−3. As evident for the BG laser pulse, the wakefield increases to 527 GV/m as the plasma electron density increases. Moreover, it is comprehensible that compared to SG and GL laser pulses, the wakefield excited by the BG laser pulse is stronger. In fact, as can be realized, lower densities represent a larger electron bunch, and alteration in the background electron density leads to variations in the amplitude of the wakefield. Moreover, it is found that the plasma electron density can be affected by the wakefield position behind the laser pulse.
have been illustrated in figure 8(a–c). In this case, the plasma electron density has different values of 0.62 × 1024 m−3, 1.25 × 1024 m−3, 1.87 × 1024 m−3 and 2.5 × 1024 m−3. As evident for the BG laser pulse, the wakefield increases to 527 GV/m as the plasma electron density increases. Moreover, it is comprehensible that compared to SG and GL laser pulses, the wakefield excited by the BG laser pulse is stronger. In fact, as can be realized, lower densities represent a larger electron bunch, and alteration in the background electron density leads to variations in the amplitude of the wakefield. Moreover, it is found that the plasma electron density can be affected by the wakefield position behind the laser pulse.
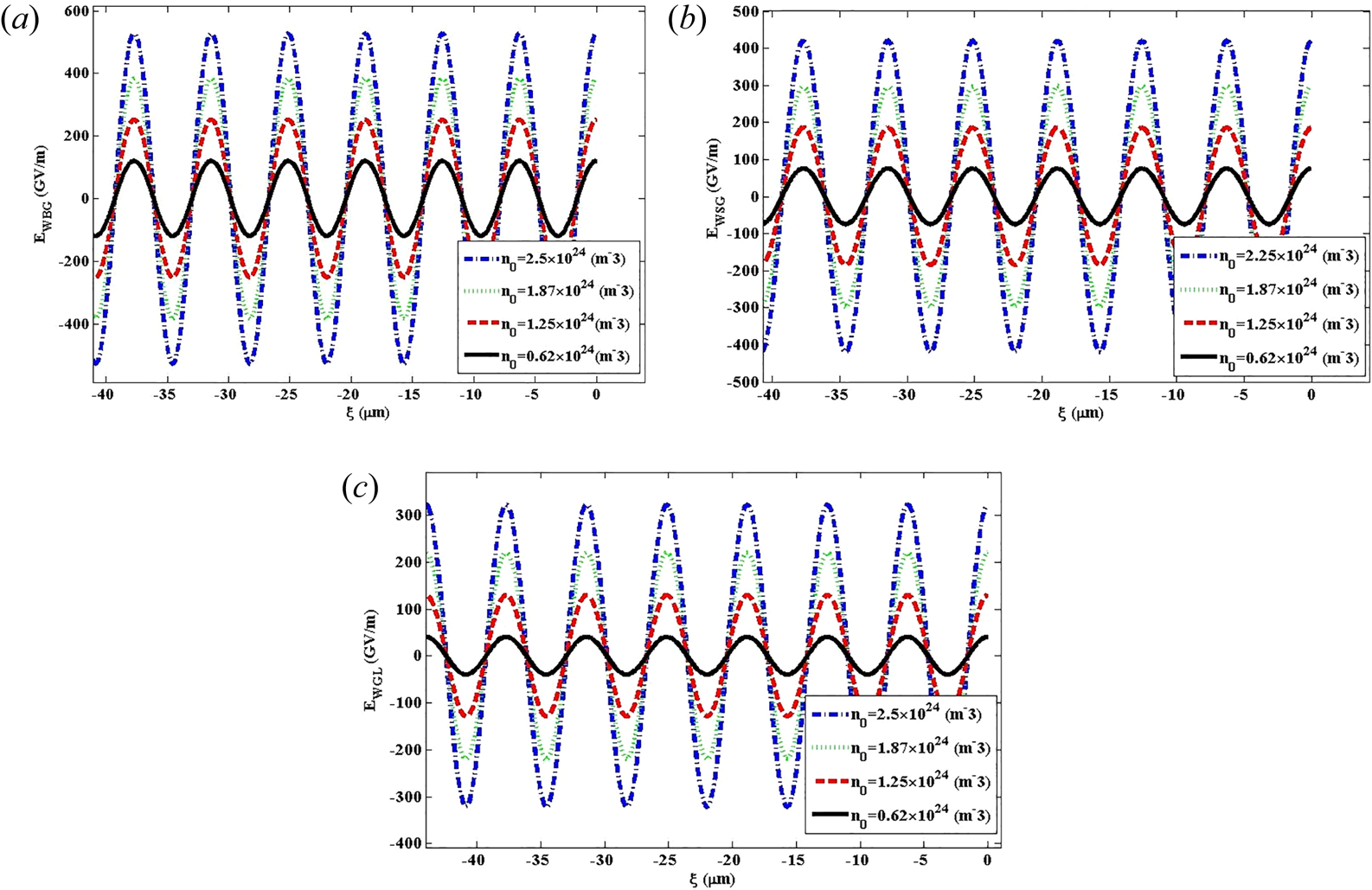
Figure 8. Variation of the wakefield versus the distance for (a) BG, (b) SG and (c) GL laser pulses. The chosen parameters are Bw=50 T, I 0=3 × 1022 W m−2 for different values of n 0=0.62 × 1024 m−3, 1.25 × 1024 m−3, 1.87 × 1024 m−3 and 2.5 × 1024 m−3.
4. Concluding remarks
In this work, considering BG, SG and GL laser pulses propagating in a cold collisionless plasma, the effect of a wiggler magnetic field on wakefield generation and electron acceleration has been. Additionally, using the hydrodynamics fluid equations, Maxwell's equations as well as the perturbation technique for GL, SG and BG laser pulses in the weakly nonlinear regime and in the presence of a planar magnetostatic wiggler, governing equations on the wakefield generation and electron acceleration have been achieved and compared correspondingly. Additionally, the wakefield and the electron energy gain are two important components where their affectability through the wiggler field strengths, laser intensity, pulse length, plasma electron density and laser frequency has been investigated. Numerical results show that increasing the wiggler magnetic field leads to an ascent in the amplitude of the wakefield. Moreover, it has been recognized that in comparison with the wakefield amplitude excited by SG and GL laser pulses, the amplitude of the wakefield excited by a BG laser pulse is larger when the wiggler magnetic field is increased. Furthermore, it is realized that the type of the laser profile, selected laser parameters and wiggler magnetic field are the most decisive and key factors in the wakefield amplitude and shape of the wakefield generation through cold collisionless plasma. Additionally, it has been observed that when the pulse length is enhanced, the impact of the wiggler field on the wakefield amplitude in the presence of the BG, SG, and GL laser pulses is considerable. In addition, it has been observed that as the pulse length declines, the amplitude of the wakefield increases, and correspondingly the resonance positions shift to higher ${({\varOmega _w}/{\varOmega _p})_{max}}$![]() values. Lastly, it is worth mentioning for our ultimate part of the conclusion that the peak of the wakefield can be shifted by adjusting the laser parameters and wiggler field strength, and, correspondingly, a significant change is observed in the wakefield generation and electron acceleration.
values. Lastly, it is worth mentioning for our ultimate part of the conclusion that the peak of the wakefield can be shifted by adjusting the laser parameters and wiggler field strength, and, correspondingly, a significant change is observed in the wakefield generation and electron acceleration.
Acknowledgements
Editor Dmitri Uzdensky thanks the referees for their advice in evaluating this article.
Declaration of interests
The authors report no conflict of interest.
Data availability
The data that supports the findings of this study are available in the paper.