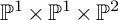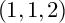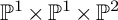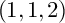1 Introduction
Smooth Fano threefolds have been classified by Iskovskikh, Mori, and Mukai into
![]() $105$
families, which are labeled as
$105$
families, which are labeled as
1.1,
1.2,
1.3,
![]() $\ldots $
,
$\ldots $
,
10.1. See [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3] for the description of these families. Threefolds in each of these
![]() $105$
deformation families can be parametrized by a nonempty rational irreducible variety. It has been proved in [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3], [Reference Fujita11], [Reference Fujita12] that the deformation families
$105$
deformation families can be parametrized by a nonempty rational irreducible variety. It has been proved in [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3], [Reference Fujita11], [Reference Fujita12] that the deformation families

do not have smooth K-polystable members, and general members of the remaining 78 deformation families are K-polystable. In fact, for 54 among these 78 families, we know all K-polystable smooth members [Reference Abban and Zhuang2]–[Reference Cheltsov and Park6], [Reference Denisova9], [Reference Liu14], [Reference Xu and Liu16]. The remaining
![]() $24$
deformation families are
$24$
deformation families are

The goal of this paper is to show that all smooth Fano threefolds in the family
![]() 3.3 are K-stable. Smooth members of this deformation family are smooth divisors in
3.3 are K-stable. Smooth members of this deformation family are smooth divisors in
![]() $\mathbb {P}^1\times \mathbb {P}^1\times \mathbb {P}^2$
of degree
$\mathbb {P}^1\times \mathbb {P}^1\times \mathbb {P}^2$
of degree
![]() $(1,1,2)$
. To be precise, we prove the following result.
$(1,1,2)$
. To be precise, we prove the following result.
Main Theorem. Let X be a smooth divisor in
![]() $\mathbb {P}^1\times \mathbb {P}^1\times \mathbb {P}^2$
of degree
$\mathbb {P}^1\times \mathbb {P}^1\times \mathbb {P}^2$
of degree
![]() $(1,1,2)$
. Then X is K-stable.
$(1,1,2)$
. Then X is K-stable.
2 Smooth Fano threefolds in the deformation family
 3.3
3.3
Let X be a divisor in
![]() $\mathbb {P}^1_{s,t}\times \mathbb {P}^1_{u,v}\times \mathbb {P}^2_{x,y,z}$
of tridegree
$\mathbb {P}^1_{s,t}\times \mathbb {P}^1_{u,v}\times \mathbb {P}^2_{x,y,z}$
of tridegree
![]() $(1,1,2)$
, where
$(1,1,2)$
, where
![]() $([s:t],[u:v],[x:y:z])$
are coordinates on
$([s:t],[u:v],[x:y:z])$
are coordinates on
![]() $\mathbb {P}^1_{s,t}\times \mathbb {P}^1_{u,v}\times \mathbb {P}^2_{x,y,z}$
. Then X is given by the following equation:
$\mathbb {P}^1_{s,t}\times \mathbb {P}^1_{u,v}\times \mathbb {P}^2_{x,y,z}$
. Then X is given by the following equation:
 $$ \begin{align*}\left[ \begin{array}{cc} s & t\\ \end{array} \right] \left[ \begin{array}{cc} a_{11} & a_{12}\\ a_{21} & a_{22}\\ \end{array} \right] \left[ \begin{array}{c} u \\ v \\ \end{array} \right]=0, \end{align*} $$
$$ \begin{align*}\left[ \begin{array}{cc} s & t\\ \end{array} \right] \left[ \begin{array}{cc} a_{11} & a_{12}\\ a_{21} & a_{22}\\ \end{array} \right] \left[ \begin{array}{c} u \\ v \\ \end{array} \right]=0, \end{align*} $$
where each
![]() $a_{ij}=a_{ij}(x,y,z)$
is a homogeneous polynomials of degree
$a_{ij}=a_{ij}(x,y,z)$
is a homogeneous polynomials of degree
![]() $2$
. We can also define X by
$2$
. We can also define X by
 $$ \begin{align*}\left[ \begin{array}{ccc} x & y & z\\ \end{array} \right] \left[ \begin{array}{ccc} b_{11} & b_{12} & b_{13}\\ b_{21} & b_{22} & b_{23}\\ b_{31} & b_{32} & b_{33}\\ \end{array} \right] \left[ \begin{array}{c} x \\ y \\ z \\ \end{array} \right]=0, \end{align*} $$
$$ \begin{align*}\left[ \begin{array}{ccc} x & y & z\\ \end{array} \right] \left[ \begin{array}{ccc} b_{11} & b_{12} & b_{13}\\ b_{21} & b_{22} & b_{23}\\ b_{31} & b_{32} & b_{33}\\ \end{array} \right] \left[ \begin{array}{c} x \\ y \\ z \\ \end{array} \right]=0, \end{align*} $$
where each
![]() $b_{ij}=b_{ij}(s,t;u,v)$
is a bi-homogeneous polynomial of degree
$b_{ij}=b_{ij}(s,t;u,v)$
is a bi-homogeneous polynomial of degree
![]() $(1,1)$
.
$(1,1)$
.
Suppose that X is smooth. Then X is a smooth Fano threefold in the deformation family
3.3. Moreover, every smooth Fano threefold in this deformation family can be obtained in this way. Observe that
![]() $-K_X^3=18$
, and we have the following commutative diagram:
$-K_X^3=18$
, and we have the following commutative diagram:

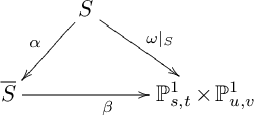
where all maps are induced by natural projections. Note that
![]() $\omega $
is a (standard) conic bundle whose discriminant curve
$\omega $
is a (standard) conic bundle whose discriminant curve
![]() $\Delta _{\mathbb {P}^1\times \mathbb {P}^1}\subset \mathbb {P}^1_{s,t}\times \mathbb {P}^1_{u,v}$
is a (possibly singular) curve of degree
$\Delta _{\mathbb {P}^1\times \mathbb {P}^1}\subset \mathbb {P}^1_{s,t}\times \mathbb {P}^1_{u,v}$
is a (possibly singular) curve of degree
![]() $(3,3)$
given by
$(3,3)$
given by
 $$ \begin{align*}\mathrm{det}\left[\begin{array}{ccc} b_{11} & b_{12} & b_{13}\\ b_{21} & b_{22} & b_{23}\\ b_{31} & b_{32} & b_{33}\\ \end{array} \right]=0. \end{align*} $$
$$ \begin{align*}\mathrm{det}\left[\begin{array}{ccc} b_{11} & b_{12} & b_{13}\\ b_{21} & b_{22} & b_{23}\\ b_{31} & b_{32} & b_{33}\\ \end{array} \right]=0. \end{align*} $$
Similarly, the map
![]() $\pi _3$
is a (nonstandard) conic bundle whose discriminant curve
$\pi _3$
is a (nonstandard) conic bundle whose discriminant curve
![]() $\Delta _{\mathbb {P}^2}$
is a smooth plane quartic curve in
$\Delta _{\mathbb {P}^2}$
is a smooth plane quartic curve in
![]() $\mathbb {P}^2_{x,y,z}$
, which is given by
$\mathbb {P}^2_{x,y,z}$
, which is given by
![]() $a_{11}a_{22}=a_{12}a_{21}$
. Both maps
$a_{11}a_{22}=a_{12}a_{21}$
. Both maps
![]() $\phi _1$
and
$\phi _1$
and
![]() $\phi _2$
are birational morphisms that blow up the following smooth genus
$\phi _2$
are birational morphisms that blow up the following smooth genus
![]() $3$
curves:
$3$
curves:
 $$ \begin{align*} \big\{sa_{11}+ta_{21}=sa_{12}+ta_{22}=0\big\}&\subset\mathbb{P}^1_{s,t}\times\mathbb{P}^2_{x,y,z},\\ \big\{ua_{11}+va_{12}=ua_{21}+va_{22}=0\big\}&\subset\mathbb{P}^1_{u,v}\times\mathbb{P}^2_{x,y,z}. \end{align*} $$
$$ \begin{align*} \big\{sa_{11}+ta_{21}=sa_{12}+ta_{22}=0\big\}&\subset\mathbb{P}^1_{s,t}\times\mathbb{P}^2_{x,y,z},\\ \big\{ua_{11}+va_{12}=ua_{21}+va_{22}=0\big\}&\subset\mathbb{P}^1_{u,v}\times\mathbb{P}^2_{x,y,z}. \end{align*} $$
Finally, both morphisms
![]() $\pi _1$
and
$\pi _1$
and
![]() $\pi _2$
are fibrations into quintic del Pezzo surfaces.
$\pi _2$
are fibrations into quintic del Pezzo surfaces.
Let
![]() $H_1=\pi _1^*(\mathcal {O}_{\mathbb {P}^1}(1))$
, let
$H_1=\pi _1^*(\mathcal {O}_{\mathbb {P}^1}(1))$
, let
![]() $H_2=\pi _2^*(\mathcal {O}_{\mathbb {P}^1}(1))$
, let
$H_2=\pi _2^*(\mathcal {O}_{\mathbb {P}^1}(1))$
, let
![]() $H_3=\pi _3^*(\mathcal {O}_{\mathbb {P}^2}(1))$
, and let
$H_3=\pi _3^*(\mathcal {O}_{\mathbb {P}^2}(1))$
, and let
![]() $E_1$
and
$E_1$
and
![]() $E_2$
be the exceptional divisors of the morphisms
$E_2$
be the exceptional divisors of the morphisms
![]() $\phi _1$
and
$\phi _1$
and
![]() $\phi _2$
, respectively. Then
$\phi _2$
, respectively. Then
 $$ \begin{align*} -K_X&\sim H_1+H_2+H_3,\\ E_1&\sim H_1+2H_3-H_2,\\ E_2&\sim H_2+2H_3-H_1. \end{align*} $$
$$ \begin{align*} -K_X&\sim H_1+H_2+H_3,\\ E_1&\sim H_1+2H_3-H_2,\\ E_2&\sim H_2+2H_3-H_1. \end{align*} $$
This gives
![]() $E_1+E_2\sim 4H_3$
, which also follows from
$E_1+E_2\sim 4H_3$
, which also follows from
![]() $E_1+E_2=\pi _3^*(\Delta _{\mathbb {P}^2})$
. We have
$E_1+E_2=\pi _3^*(\Delta _{\mathbb {P}^2})$
. We have
In particular, we see that
![]() $\alpha (X)\leqslant \frac {2}{3}$
. Note that
$\alpha (X)\leqslant \frac {2}{3}$
. Note that
![]() $E_1\cong E_2\cong \Delta _{\mathbb {P}^2}\times \mathbb {P}^1$
.
$E_1\cong E_2\cong \Delta _{\mathbb {P}^2}\times \mathbb {P}^1$
.
The Mori cone
![]() $\overline {\mathrm {NE}}(X)$
is simplicial and is generated by the curves contracted by
$\overline {\mathrm {NE}}(X)$
is simplicial and is generated by the curves contracted by
![]() $\omega $
,
$\omega $
,
![]() $\phi _1$
, and
$\phi _1$
, and
![]() $\phi _2$
. The cone of effective divisors
$\phi _2$
. The cone of effective divisors
![]() $\mathrm {Eff}(X)$
is generated by the classes of the divisors
$\mathrm {Eff}(X)$
is generated by the classes of the divisors
![]() $E_1$
,
$E_1$
,
![]() $E_2$
,
$E_2$
,
![]() $H_1$
, and
$H_1$
, and
![]() $H_2$
.
$H_2$
.
Lemma 1. Let S be a surface in the pencil
![]() $|H_1|$
. Then S is a normal quintic del Pezzo surface that has at most Du Val singularities, the restriction
$|H_1|$
. Then S is a normal quintic del Pezzo surface that has at most Du Val singularities, the restriction
![]() $\pi _3\vert _{S}\colon S\to \mathbb {P}^2_{x,y,z}$
is a birational morphism, and the restriction
$\pi _3\vert _{S}\colon S\to \mathbb {P}^2_{x,y,z}$
is a birational morphism, and the restriction
![]() $\pi _2\vert _{S}\colon S\to \mathbb {P}^1_{u,v}$
is a conic bundle. Moreover, one of the following cases holds:
$\pi _2\vert _{S}\colon S\to \mathbb {P}^1_{u,v}$
is a conic bundle. Moreover, one of the following cases holds:
 $\bullet $
The surface S is smooth.
$\bullet $
The surface S is smooth.-
(𝔸1) The surface S has one singular point of type
 $\mathbb {A}_1$
.
$\mathbb {A}_1$
. -
(2𝔸1) The surface S has two singular points of type
 $\mathbb {A}_1$
.
$\mathbb {A}_1$
. -
(𝔸2) The surface S has one singular point of type
 $\mathbb {A}_2$
.
$\mathbb {A}_2$
. -
(𝔸3) The surface S has one singular point of type
 $\mathbb {A}_3$
.
$\mathbb {A}_3$
.
Furthermore, in each of these five cases, the del Pezzo surface S is unique up to an isomorphism.
Proof. This is well known [Reference Cheltsov and Prokhorov7], [Reference Coray and Tsfasman8].
Remark 2. In the notations and assumptions of Lemma 1, suppose that the surface S is singular, and let
![]() $\varpi \colon \widetilde {S}\to S$
be its minimal resolution of singularities. Then the dual graph of the
$\varpi \colon \widetilde {S}\to S$
be its minimal resolution of singularities. Then the dual graph of the
![]() $(-1)$
-curves and
$(-1)$
-curves and
![]() $(-2)$
-curves on the surface
$(-2)$
-curves on the surface
![]() $\widetilde {S}$
can be described as follows:
$\widetilde {S}$
can be described as follows:
(
 $\mathbb {A}_1$
) if S has one singular point of type
$\mathbb {A}_1$
) if S has one singular point of type
 $\mathbb {A}_1$
, then the dual graph is
$\mathbb {A}_1$
, then the dual graph is 
(
 $2\mathbb {A}_1$
) if S has two singular points of type
$2\mathbb {A}_1$
) if S has two singular points of type
 $\mathbb {A}_1$
, then the dual graph is
$\mathbb {A}_1$
, then the dual graph is 
(
 $\mathbb {A}_2$
) if S has one singular point of type
$\mathbb {A}_2$
) if S has one singular point of type
 $\mathbb {A}_2$
, then the dual graph is
$\mathbb {A}_2$
, then the dual graph is 
(
 $\mathbb {A}_3$
) if S has one singular point of type
$\mathbb {A}_3$
) if S has one singular point of type
 $\mathbb {A}_3$
, then the dual graph is
$\mathbb {A}_3$
, then the dual graph is 
Here, as in the papers [Reference Cheltsov and Prokhorov7], [Reference Coray and Tsfasman8], we denote a
![]() $(-1)$
-curve by
$(-1)$
-curve by
![]() $\bullet $
, and we denote a
$\bullet $
, and we denote a
![]() $(-2)$
-curve by
$(-2)$
-curve by
![]() $\circ $
.
$\circ $
.
Lemma 3. Let
![]() $S_1$
be a surface in
$S_1$
be a surface in
![]() $|H_1|$
, let
$|H_1|$
, let
![]() $S_2$
be a surface in
$S_2$
be a surface in
![]() $|H_2|$
, and let P be a point in
$|H_2|$
, and let P be a point in
![]() $S_1\cap S_2$
. Then at least one of the surfaces
$S_1\cap S_2$
. Then at least one of the surfaces
![]() $S_1$
or
$S_1$
or
![]() $S_2$
is smooth at P.
$S_2$
is smooth at P.
Proof. Local computations.
Corollary 4. In the notations and assumptions of Lemma 3, suppose that the conic
![]() $S_1\cdot S_2$
is reduced. Then at least one of the surfaces
$S_1\cdot S_2$
is reduced. Then at least one of the surfaces
![]() $S_1$
or
$S_1$
or
![]() $S_2$
is smooth along
$S_2$
is smooth along
![]() $S_1\cap S_2$
.
$S_1\cap S_2$
.
Lemma 5. Let P be a point in X, let C be the scheme fiber of the conic bundle
![]() $\omega $
that contains P, and let Z be the scheme fiber of the conic bundle
$\omega $
that contains P, and let Z be the scheme fiber of the conic bundle
![]() $\pi _3$
that contains P. Then C or Z is smooth at P.
$\pi _3$
that contains P. Then C or Z is smooth at P.
Proof. Local computations.
Lemma 6. Let C be a fiber of the morphism
![]() $\pi _3$
, and let S be a general surface in
$\pi _3$
, and let S be a general surface in
![]() $|H_3|$
that contains C. Then S is smooth,
$|H_3|$
that contains C. Then S is smooth,
![]() $K_S^2=4$
, and
$K_S^2=4$
, and
![]() $-K_S\sim (H_1+H_2)\vert _{S}$
, which implies that
$-K_S\sim (H_1+H_2)\vert _{S}$
, which implies that
![]() $-K_S$
is nef and big. Moreover, one of the following three cases holds:
$-K_S$
is nef and big. Moreover, one of the following three cases holds:
-
(1) The conic C is smooth,
 $-K_S$
is ample, and the restriction
$-K_S$
is ample, and the restriction
 $\omega \vert _{S}\colon S\to \mathbb {P}^1_{s,t}\times \mathbb {P}^1_{u,v}$
is a double cover branched over a smooth curve of degree
$\omega \vert _{S}\colon S\to \mathbb {P}^1_{s,t}\times \mathbb {P}^1_{u,v}$
is a double cover branched over a smooth curve of degree
 $(2,2)$
.
$(2,2)$
. -
(2) The conic C is smooth, the divisor
 $-K_S$
is not ample, the conic
$-K_S$
is not ample, the conic
 $\omega (C)$
is an irreducible component of the discriminant curve
$\omega (C)$
is an irreducible component of the discriminant curve
 $\Delta _{\mathbb {P}^1\times \mathbb {P}^1}$
, the conic C is contained in
$\Delta _{\mathbb {P}^1\times \mathbb {P}^1}$
, the conic C is contained in
 $\mathrm {Sing}(\omega ^{-1}(\Delta _{\mathbb {P}^1\times \mathbb {P}^1}))$
, and the restriction map
$\mathrm {Sing}(\omega ^{-1}(\Delta _{\mathbb {P}^1\times \mathbb {P}^1}))$
, and the restriction map
 $\omega \vert _{S}\colon S\to \mathbb {P}^1_{s,t}\times \mathbb {P}^1_{u,v}$
fits the following commutative diagram: where
$\omega \vert _{S}\colon S\to \mathbb {P}^1_{s,t}\times \mathbb {P}^1_{u,v}$
fits the following commutative diagram: where
 $\alpha $
is a birational morphism that contracts two disjoint
$\alpha $
is a birational morphism that contracts two disjoint
 $(-2)$
-curves, and
$(-2)$
-curves, and
 $\beta $
is a double cover branched over a singular curve of degree
$\beta $
is a double cover branched over a singular curve of degree
 $(2,2)$
, which is a union of the curve
$(2,2)$
, which is a union of the curve
 $\omega (C)$
and another smooth curve of degree
$\omega (C)$
and another smooth curve of degree
 $(1,1)$
, which intersect transversally at two distinct points.
$(1,1)$
, which intersect transversally at two distinct points.
-
(3) The conic C is singular,
 $-K_S$
is ample, and the restriction
$-K_S$
is ample, and the restriction
 $\omega \vert _{S}\colon S\to \mathbb {P}^1_{s,t}\times \mathbb {P}^1_{u,v}$
is a double cover branched over a smooth curve of degree
$\omega \vert _{S}\colon S\to \mathbb {P}^1_{s,t}\times \mathbb {P}^1_{u,v}$
is a double cover branched over a smooth curve of degree
 $(2,2)$
.
$(2,2)$
.
Proof. The smoothness of the surface S easily follows from local computations. If
![]() $-K_S$
is ample, the remaining assertions are obvious. So, to complete the proof, we assume that
$-K_S$
is ample, the remaining assertions are obvious. So, to complete the proof, we assume that
![]() $-K_S$
is not ample. Then the restriction
$-K_S$
is not ample. Then the restriction
![]() $\omega \vert _{S}\colon S\to \mathbb {P}^1_{s,t}\times \mathbb {P}^1_{u,v}$
fits the commutative diagram
$\omega \vert _{S}\colon S\to \mathbb {P}^1_{s,t}\times \mathbb {P}^1_{u,v}$
fits the commutative diagram
where
![]() $\alpha $
is a birational morphism that contracts all
$\alpha $
is a birational morphism that contracts all
![]() $(-2)$
-curves in S, and
$(-2)$
-curves in S, and
![]() $\beta $
is a double cover branched over a singular curve of degree
$\beta $
is a double cover branched over a singular curve of degree
![]() $(2,2)$
. Let
$(2,2)$
. Let
![]() $\ell $
be a
$\ell $
be a
![]() $(-2)$
-curve in S. Then
$(-2)$
-curve in S. Then
so that
![]() $\omega (\ell )$
is a point in
$\omega (\ell )$
is a point in
![]() $\mathbb {P}^1_{s,t}\times \mathbb {P}^1_{u,v}$
. But
$\mathbb {P}^1_{s,t}\times \mathbb {P}^1_{u,v}$
. But
![]() $\pi _3(\ell )$
is a line in
$\pi _3(\ell )$
is a line in
![]() $\mathbb {P}^2_{x,y,z}$
that contains the point
$\mathbb {P}^2_{x,y,z}$
that contains the point
![]() $\pi _3(C)$
. This shows that the curve
$\pi _3(C)$
. This shows that the curve
![]() $\ell $
is an irreducible component of a singular fiber of the conic bundle
$\ell $
is an irreducible component of a singular fiber of the conic bundle
![]() $\omega $
. Therefore, we see that
$\omega $
. Therefore, we see that
![]() $\omega (\ell )\in \Delta _{\mathbb {P}^1\times \mathbb {P}^1}$
. This implies that the conic bundle
$\omega (\ell )\in \Delta _{\mathbb {P}^1\times \mathbb {P}^1}$
. This implies that the conic bundle
![]() $\omega $
maps an irreducible component of the conic C to an irreducible component of the curve
$\omega $
maps an irreducible component of the conic C to an irreducible component of the curve
![]() $\Delta _{\mathbb {P}^1\times \mathbb {P}^1}$
because S is a general surface in the linear system
$\Delta _{\mathbb {P}^1\times \mathbb {P}^1}$
because S is a general surface in the linear system
![]() $|H_3|$
that contains the curve C.
$|H_3|$
that contains the curve C.
If C is singular, an irreducible component of the curve
![]() $\Delta _{\mathbb {P}^1\times \mathbb {P}^1}$
is a curve of degree
$\Delta _{\mathbb {P}^1\times \mathbb {P}^1}$
is a curve of degree
![]() $(1,0)$
or
$(1,0)$
or
![]() $(0,1)$
, which is impossible [Reference Prokhorov15, §3.8]. Therefore, we see that the conic C is smooth and irreducible, and the curve
$(0,1)$
, which is impossible [Reference Prokhorov15, §3.8]. Therefore, we see that the conic C is smooth and irreducible, and the curve
![]() $\omega (C)\cong C$
is an irreducible component of the discriminant curve
$\omega (C)\cong C$
is an irreducible component of the discriminant curve
![]() $\Delta _{\mathbb {P}^1\times \mathbb {P}^1}$
. Since the conic bundle
$\Delta _{\mathbb {P}^1\times \mathbb {P}^1}$
. Since the conic bundle
![]() $\omega $
is standard [Reference Prokhorov15], the surface
$\omega $
is standard [Reference Prokhorov15], the surface
![]() $\omega ^{-1}(\omega (C))$
is irreducible and nonnormal, which easily implies that the conic C is contained in its singular locus.
$\omega ^{-1}(\omega (C))$
is irreducible and nonnormal, which easily implies that the conic C is contained in its singular locus.
Choosing appropriate coordinates on
![]() $\mathbb {P}^1_{s,t}\times \mathbb {P}^1_{u,v}\times \mathbb {P}^2_{x,y,z}$
, we may assume that
$\mathbb {P}^1_{s,t}\times \mathbb {P}^1_{u,v}\times \mathbb {P}^2_{x,y,z}$
, we may assume that
![]() $\pi _3(C)=[0:0:1]$
, the conic C is given by
$\pi _3(C)=[0:0:1]$
, the conic C is given by
![]() $x=y=sv-tu=0$
,
$x=y=sv-tu=0$
,
![]() $([0:1],[0:1])$
is a smooth point of the curve
$([0:1],[0:1])$
is a smooth point of the curve
![]() $\Delta _{\mathbb {P}^1\times \mathbb {P}^1}$
, and the fiber
$\Delta _{\mathbb {P}^1\times \mathbb {P}^1}$
, and the fiber
![]() $\omega ^{-1}([0:1],[0:1])$
is given by
$\omega ^{-1}([0:1],[0:1])$
is given by
![]() $s=u=xy=0$
. Then X is given by
$s=u=xy=0$
. Then X is given by
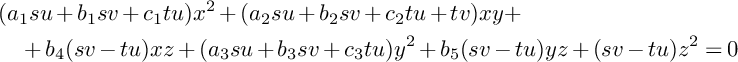 $$ \begin{align*} &(a_1su+b_1sv+c_1 tu)x^2+(a_2su+b_2sv+c_2tu+tv)xy+\\ & \quad +b_4(sv-tu)xz+(a_3su+b_3sv+c_3tu)y^2+b_5(sv-tu)yz+(sv-tu)z^2=0 \end{align*} $$
$$ \begin{align*} &(a_1su+b_1sv+c_1 tu)x^2+(a_2su+b_2sv+c_2tu+tv)xy+\\ & \quad +b_4(sv-tu)xz+(a_3su+b_3sv+c_3tu)y^2+b_5(sv-tu)yz+(sv-tu)z^2=0 \end{align*} $$
for some numbers
![]() $a_1$
,
$a_1$
,
![]() $a_2$
,
$a_2$
,
![]() $a_3$
,
$a_3$
,
![]() $b_1$
,
$b_1$
,
![]() $b_2$
,
$b_2$
,
![]() $b_3$
,
$b_3$
,
![]() $b_4$
,
$b_4$
,
![]() $b_5$
,
$b_5$
,
![]() $c_1$
,
$c_1$
,
![]() $c_2$
,
$c_2$
,
![]() $c_3$
. One can check that
$c_3$
. One can check that
![]() $\Delta _{\mathbb {P}^1\times \mathbb {P}^1}$
indeed splits as a union of the curve
$\Delta _{\mathbb {P}^1\times \mathbb {P}^1}$
indeed splits as a union of the curve
![]() $\omega (C)$
and the curve in
$\omega (C)$
and the curve in
![]() $\mathbb {P}^1_{s,t}\times \mathbb {P}^1_{u,v}$
of degree
$\mathbb {P}^1_{s,t}\times \mathbb {P}^1_{u,v}$
of degree
![]() $(2,2)$
that is given by
$(2,2)$
that is given by
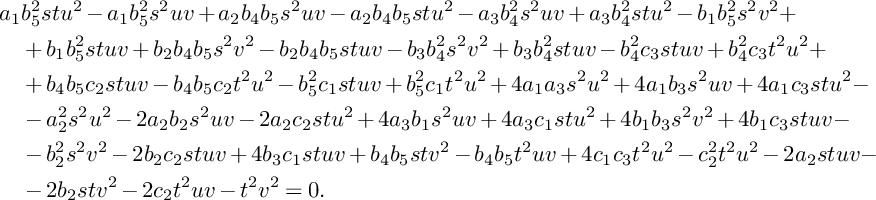 $$ \begin{align*} &a_1b_5^2stu^2-a_1b_5^2s^2uv+a_2b_4b_5s^2uv-a_2b_4b_5stu^2-a_3b_4^2s^2uv+a_3b_4^2stu^2-b_1b_5^2s^2v^2+\\& \quad +b_1b_5^2stuv+b_2b_4b_5s^2v^2-b_2b_4b_5stuv-b_3b_4^2s^2v^2+b_3b_4^2stuv-b_4^2c_3stuv+b_4^2c_3t^2u^2+\\& \quad +b_4b_5c_2stuv-b_4b_5c_2t^2u^2-b_5^2c_1stuv+b_5^2c_1t^2u^2+4a_1a_3s^2u^2+4a_1b_3s^2uv+4a_1c_3stu^2-\\& \quad -a_2^2s^2u^2-2a_2b_2s^2uv-2a_2c_2stu^2+4a_3b_1s^2uv+4a_3c_1stu^2+ 4b_1b_3s^2v^2+4b_1c_3stuv-\\& \quad -b_2^2s^2v^2-2b_2c_2stuv+4b_3c_1stuv+b_4b_5stv^2-b_4b_5t^2uv+4c_1c_3t^2u^2-c_2^2t^2u^2-2a_2stuv-\\& \quad -2b_2stv^2-2c_2t^2uv-t^2v^2=0. \end{align*} $$
$$ \begin{align*} &a_1b_5^2stu^2-a_1b_5^2s^2uv+a_2b_4b_5s^2uv-a_2b_4b_5stu^2-a_3b_4^2s^2uv+a_3b_4^2stu^2-b_1b_5^2s^2v^2+\\& \quad +b_1b_5^2stuv+b_2b_4b_5s^2v^2-b_2b_4b_5stuv-b_3b_4^2s^2v^2+b_3b_4^2stuv-b_4^2c_3stuv+b_4^2c_3t^2u^2+\\& \quad +b_4b_5c_2stuv-b_4b_5c_2t^2u^2-b_5^2c_1stuv+b_5^2c_1t^2u^2+4a_1a_3s^2u^2+4a_1b_3s^2uv+4a_1c_3stu^2-\\& \quad -a_2^2s^2u^2-2a_2b_2s^2uv-2a_2c_2stu^2+4a_3b_1s^2uv+4a_3c_1stu^2+ 4b_1b_3s^2v^2+4b_1c_3stuv-\\& \quad -b_2^2s^2v^2-2b_2c_2stuv+4b_3c_1stuv+b_4b_5stv^2-b_4b_5t^2uv+4c_1c_3t^2u^2-c_2^2t^2u^2-2a_2stuv-\\& \quad -2b_2stv^2-2c_2t^2uv-t^2v^2=0. \end{align*} $$
The surface S is cut out on X by the equation
![]() $y=\lambda x$
, where
$y=\lambda x$
, where
![]() $\lambda $
is a general complex number. Then the double cover
$\lambda $
is a general complex number. Then the double cover
![]() $\beta \colon \overline {S}\to \mathbb {P}^1_{s,t}\times \mathbb {P}^1_{u,v}$
is branched over a singular curve of degree
$\beta \colon \overline {S}\to \mathbb {P}^1_{s,t}\times \mathbb {P}^1_{u,v}$
is branched over a singular curve of degree
![]() $(2,2)$
, which splits as a union of the curve
$(2,2)$
, which splits as a union of the curve
![]() $\omega (C)$
and the curve in
$\omega (C)$
and the curve in
![]() $\mathbb {P}^1_{s,t}\times \mathbb {P}^1_{u,v}$
of degree
$\mathbb {P}^1_{s,t}\times \mathbb {P}^1_{u,v}$
of degree
![]() $(1,1)$
that is given by
$(1,1)$
that is given by
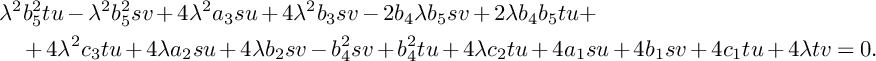 $$ \begin{align*} &\lambda^2 b_5^2tu-\lambda^2b_5^2sv+4\lambda^2a_3su+4\lambda^2b_3sv-2b_4\lambda b_5sv+2\lambda b_4b_5tu+\\& \quad +4\lambda^2c_3tu+4\lambda a_2su+4\lambda b_2sv-b_4^2sv+b_4^2tu+4\lambda c_2tu+4a_1su+4b_1sv+4c_1tu+4\lambda tv=0. \end{align*} $$
$$ \begin{align*} &\lambda^2 b_5^2tu-\lambda^2b_5^2sv+4\lambda^2a_3su+4\lambda^2b_3sv-2b_4\lambda b_5sv+2\lambda b_4b_5tu+\\& \quad +4\lambda^2c_3tu+4\lambda a_2su+4\lambda b_2sv-b_4^2sv+b_4^2tu+4\lambda c_2tu+4a_1su+4b_1sv+4c_1tu+4\lambda tv=0. \end{align*} $$
Since
![]() $\lambda $
is general and X is smooth, these two curves intersect transversally by two points, which implies the remaining assertions of the lemma.
$\lambda $
is general and X is smooth, these two curves intersect transversally by two points, which implies the remaining assertions of the lemma.
Note that the case (
![]() $\mathrm {2}$
) in Lemma 6 indeed can happen. For instance, if X is given by
$\mathrm {2}$
) in Lemma 6 indeed can happen. For instance, if X is given by
then X is smooth, and general surface in
![]() $|H_3|$
that contains the curve
$|H_3|$
that contains the curve
![]() $\pi _3^{-1}([0:0:1])$
is a smooth weak del Pezzo surface, which is not a quartic del Pezzo surface.
$\pi _3^{-1}([0:0:1])$
is a smooth weak del Pezzo surface, which is not a quartic del Pezzo surface.
Lemma 7. Let C be a smooth fiber of the morphism
![]() $\omega $
, and let S be a general surface in
$\omega $
, and let S be a general surface in
![]() $|H_1+H_2|$
that contains the curve C. Then S is a smooth del Pezzo surface of degree
$|H_1+H_2|$
that contains the curve C. Then S is a smooth del Pezzo surface of degree
![]() $2$
, and
$2$
, and
![]() $-K_S\sim H_3\vert _{S}$
.
$-K_S\sim H_3\vert _{S}$
.
Proof. Left to the reader.
3 Applications of Abban–Zhuang theory
Let us use notations and assumptions of §2. Let
![]() $f\colon \widetilde {X}\to X$
be a birational map such that
$f\colon \widetilde {X}\to X$
be a birational map such that
![]() $\widetilde {X}$
is a normal threefold, and let
$\widetilde {X}$
is a normal threefold, and let
![]() $\mathbf {F}$
be a prime divisor in
$\mathbf {F}$
be a prime divisor in
![]() $\widetilde {X}$
. Then, to prove that X is K-stable, it is enough to show that
$\widetilde {X}$
. Then, to prove that X is K-stable, it is enough to show that
![]() $\beta (\mathbf {F})=A_X(\mathbf {F})-S_X(\mathbf {F})>0$
, where
$\beta (\mathbf {F})=A_X(\mathbf {F})-S_X(\mathbf {F})>0$
, where
![]() $A_X(\mathbf {F})=1+\mathrm {ord}_{\mathbf {F}}(K_{\widetilde {X}}/K_X)$
and
$A_X(\mathbf {F})=1+\mathrm {ord}_{\mathbf {F}}(K_{\widetilde {X}}/K_X)$
and
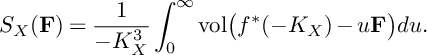 $$ \begin{align*}S_X(\mathbf{F})=\frac{1}{-K_X^3}\int_{0}^{\infty}\mathrm{vol}\big(f^*(-K_X)-u\mathbf{F}\big)du. \end{align*} $$
$$ \begin{align*}S_X(\mathbf{F})=\frac{1}{-K_X^3}\int_{0}^{\infty}\mathrm{vol}\big(f^*(-K_X)-u\mathbf{F}\big)du. \end{align*} $$
This follows from the valuative criterion for K-stability [Reference Fujita11], [Reference Li13].
Let
![]() $\mathfrak {C}$
be the center of the divisor
$\mathfrak {C}$
be the center of the divisor
![]() $\mathbf {F}$
on the threefold X. By [Reference Fujita10, Th. 10.1], we have
$\mathbf {F}$
on the threefold X. By [Reference Fujita10, Th. 10.1], we have
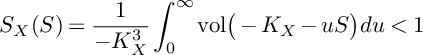 $$ \begin{align*}S_X(S)=\frac{1}{-K_X^3}\int_{0}^{\infty}\mathrm{vol}\big(-K_X-uS\big)du<1 \end{align*} $$
$$ \begin{align*}S_X(S)=\frac{1}{-K_X^3}\int_{0}^{\infty}\mathrm{vol}\big(-K_X-uS\big)du<1 \end{align*} $$
for every surface
![]() $S\subset X$
. Hence, if
$S\subset X$
. Hence, if
![]() $\mathfrak {C}$
is a surface, then
$\mathfrak {C}$
is a surface, then
![]() $\beta (\mathbf {F})>0$
. Thus, to show that X is K-stable, we may assume that
$\beta (\mathbf {F})>0$
. Thus, to show that X is K-stable, we may assume that
![]() $\mathfrak {C}$
is either a curve or a point. If
$\mathfrak {C}$
is either a curve or a point. If
![]() $\mathfrak {C}$
is a curve, then [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Cor. 1.7.26] gives the following corollary.
$\mathfrak {C}$
is a curve, then [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Cor. 1.7.26] gives the following corollary.
Corollary 8. Suppose that
![]() $\beta (\mathbf {F})\leqslant 0$
and that
$\beta (\mathbf {F})\leqslant 0$
and that
![]() $\mathfrak {C}$
is a curve. Let S be an irreducible normal surface in the threefold X that contains
$\mathfrak {C}$
is a curve. Let S be an irreducible normal surface in the threefold X that contains
![]() $\mathfrak {C}$
. Set
$\mathfrak {C}$
. Set
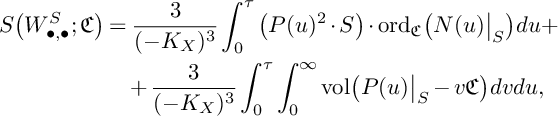 $$ \begin{align*} S\big(W^S_{\bullet,\bullet};\mathfrak{C}\big)&=\frac{3}{(-K_X)^3}\int_0^\tau\big(P(u)^{2}\cdot S\big)\cdot\mathrm{ord}_{\mathfrak{C}}\big(N(u)\big\vert_{S}\big)du+\\ & \quad+\frac{3}{(-K_X)^3}\int_0^\tau\int_0^\infty \mathrm{vol}\big(P(u)\big\vert_{S}-v\mathfrak{C}\big)dvdu, \end{align*} $$
$$ \begin{align*} S\big(W^S_{\bullet,\bullet};\mathfrak{C}\big)&=\frac{3}{(-K_X)^3}\int_0^\tau\big(P(u)^{2}\cdot S\big)\cdot\mathrm{ord}_{\mathfrak{C}}\big(N(u)\big\vert_{S}\big)du+\\ & \quad+\frac{3}{(-K_X)^3}\int_0^\tau\int_0^\infty \mathrm{vol}\big(P(u)\big\vert_{S}-v\mathfrak{C}\big)dvdu, \end{align*} $$
where
![]() $\tau $
is the largest rational number u such that
$\tau $
is the largest rational number u such that
![]() $-K_X-uS$
is pseudoeffective,
$-K_X-uS$
is pseudoeffective,
![]() $P(u)$
is the positive part of the Zariski decomposition of
$P(u)$
is the positive part of the Zariski decomposition of
![]() $-K_X-uS$
, and
$-K_X-uS$
, and
![]() $N(u)$
is its negative part. Then
$N(u)$
is its negative part. Then
![]() $S(W^S_{\bullet ,\bullet };\mathfrak {C})>1$
.
$S(W^S_{\bullet ,\bullet };\mathfrak {C})>1$
.
Let P be a point in
![]() $\mathfrak {C}$
. Then
$\mathfrak {C}$
. Then
 $$ \begin{align*}\frac{A_X(\mathbf{F})}{S_X(\mathbf{F})}\geqslant\delta_P(X)=\inf_{\substack{E/X\\ P\in C_X(E)}}\frac{A_{X}(E)}{S_X(E)}, \end{align*} $$
$$ \begin{align*}\frac{A_X(\mathbf{F})}{S_X(\mathbf{F})}\geqslant\delta_P(X)=\inf_{\substack{E/X\\ P\in C_X(E)}}\frac{A_{X}(E)}{S_X(E)}, \end{align*} $$
where the infimum is taken over all prime divisors E over X whose centers on X that contain P. Therefore, to prove that the Fano threefold X is K-stable, it is enough to show that
![]() $\delta _P(X)>1$
. On the other hand, we can estimate
$\delta _P(X)>1$
. On the other hand, we can estimate
![]() $\delta _P(X)$
by using [Reference Abban and Zhuang1, Th. 3.3] and [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Cor. 1.7.30]. Namely, let S be an irreducible surface in X with Du Val singularities such that
$\delta _P(X)$
by using [Reference Abban and Zhuang1, Th. 3.3] and [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Cor. 1.7.30]. Namely, let S be an irreducible surface in X with Du Val singularities such that
![]() $P\in S$
. Set
$P\in S$
. Set
For
![]() $u\in [0,\tau ]$
, let
$u\in [0,\tau ]$
, let
![]() $P(u)$
be the positive part of the Zariski decomposition of the divisor
$P(u)$
be the positive part of the Zariski decomposition of the divisor
![]() $-K_X-uS$
, and let
$-K_X-uS$
, and let
![]() $N(u)$
be its negative part. Then [Reference Abban and Zhuang1, Th. 3.3] and [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Cor. 1.7.30] give
$N(u)$
be its negative part. Then [Reference Abban and Zhuang1, Th. 3.3] and [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Cor. 1.7.30] give
 $$ \begin{align} \delta_P(X)\geqslant\mathrm{min}\Bigg\{\frac{1}{S_X(S)},\delta_{P}\big(S;W^S_{\bullet,\bullet}\big)\Bigg\} \end{align} $$
$$ \begin{align} \delta_P(X)\geqslant\mathrm{min}\Bigg\{\frac{1}{S_X(S)},\delta_{P}\big(S;W^S_{\bullet,\bullet}\big)\Bigg\} \end{align} $$
for
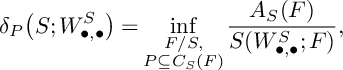 $$ \begin{align*}\delta_{P}\big(S;W^S_{\bullet,\bullet}\big)=\inf_{\substack{F/S,\\ P\subseteq C_S(F)}}\frac{A_S(F)}{S(W^S_{\bullet,\bullet};F)}, \end{align*} $$
$$ \begin{align*}\delta_{P}\big(S;W^S_{\bullet,\bullet}\big)=\inf_{\substack{F/S,\\ P\subseteq C_S(F)}}\frac{A_S(F)}{S(W^S_{\bullet,\bullet};F)}, \end{align*} $$
where
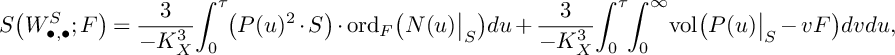 $$ \begin{align*}S\big(W^S_{\bullet,\bullet}; F\big)=\frac{3}{-K_X^3}\kern-1.3pt\int_0^\tau\!\kern-1.2pt\big(P(u)^{2}\cdot S\big)\cdot\mathrm{ord}_{F}\big(N(u)\big\vert_{S}\big)du+\frac{3}{-K_X^3}\!\int_{0}^{\tau}\!\!\int_0^\infty \!\mathrm{vol}\big(P(u)\big\vert_{S}-vF\big)dvdu, \end{align*} $$
$$ \begin{align*}S\big(W^S_{\bullet,\bullet}; F\big)=\frac{3}{-K_X^3}\kern-1.3pt\int_0^\tau\!\kern-1.2pt\big(P(u)^{2}\cdot S\big)\cdot\mathrm{ord}_{F}\big(N(u)\big\vert_{S}\big)du+\frac{3}{-K_X^3}\!\int_{0}^{\tau}\!\!\int_0^\infty \!\mathrm{vol}\big(P(u)\big\vert_{S}-vF\big)dvdu, \end{align*} $$
and now the infimum is taken over all prime divisors F over S whose centers on S that contain P. Let us show how to apply (3.1) in some cases. Recall that
![]() $S_X(S)<1$
by [Reference Fujita10, Th. 10.1].
$S_X(S)<1$
by [Reference Fujita10, Th. 10.1].
Lemma 9. Let C be the fiber of the conic bundle
![]() $\pi _3$
that contains P, and let S be a general surface in
$\pi _3$
that contains P, and let S be a general surface in
![]() $|H_3|$
that contains C. Suppose that S is a smooth del Pezzo of degree
$|H_3|$
that contains C. Suppose that S is a smooth del Pezzo of degree
![]() $4$
and that C is smooth. Then
$4$
and that C is smooth. Then
![]() $\delta _P(X)>1$
.
$\delta _P(X)>1$
.
Proof. One has
![]() $\tau =1$
. Moreover, for
$\tau =1$
. Moreover, for
![]() $u\in [0,1]$
, we have
$u\in [0,1]$
, we have
![]() $N(u)=0$
and
$N(u)=0$
and
![]() $P(u)|_S=-K_S+ (1-u)C$
. Let
$P(u)|_S=-K_S+ (1-u)C$
. Let
![]() $L=-K_S+(1-u)C$
. Using Lemma 24 and arguing as in the proof of Lemma 27, we get
$L=-K_S+(1-u)C$
. Using Lemma 24 and arguing as in the proof of Lemma 27, we get
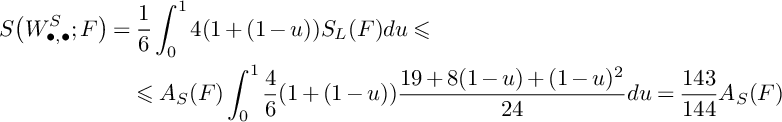 $$ \begin{align*} S\big(W^S_{\bullet,\bullet};F\big)&=\frac{1}{6}\int_0^1 4(1+(1-u))S_L(F)du\leqslant \\ & \quad \leqslant A_S(F)\int_0^1 \frac{4}{6}(1+(1-u)) \frac{19+8(1-u)+(1-u)^2}{24}du=\frac{143}{144}A_S(F) \end{align*} $$
$$ \begin{align*} S\big(W^S_{\bullet,\bullet};F\big)&=\frac{1}{6}\int_0^1 4(1+(1-u))S_L(F)du\leqslant \\ & \quad \leqslant A_S(F)\int_0^1 \frac{4}{6}(1+(1-u)) \frac{19+8(1-u)+(1-u)^2}{24}du=\frac{143}{144}A_S(F) \end{align*} $$
for any prime divisor F over S such that
![]() $P\in C_S(F)$
. Then (3.1) gives
$P\in C_S(F)$
. Then (3.1) gives
![]() $\delta _P(X)>1$
.
$\delta _P(X)>1$
.
Similarly, we obtain the following result.
Lemma 10. Let S be the surface in
![]() $|H_1|$
that contains P. Then
$|H_1|$
that contains P. Then
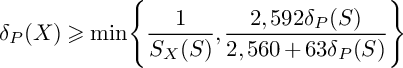 $$ \begin{align*}\delta_P(X)\geqslant\mathrm{min}\Bigg\{\frac{1}{S_X(S)},\frac{2,592\delta_P(S)}{2,560+63\delta_P(S)}\Bigg\} \end{align*} $$
$$ \begin{align*}\delta_P(X)\geqslant\mathrm{min}\Bigg\{\frac{1}{S_X(S)},\frac{2,592\delta_P(S)}{2,560+63\delta_P(S)}\Bigg\} \end{align*} $$
for
![]() $\delta _P(S)=\delta _P(S,-K_S)$
, where
$\delta _P(S)=\delta _P(S,-K_S)$
, where
![]() $\delta _P(S,-K_S)$
is defined in Appendix 1.
$\delta _P(S,-K_S)$
is defined in Appendix 1.
Proof. We have
![]() $\tau =\frac {3}{2}$
. Moreover, we have
$\tau =\frac {3}{2}$
. Moreover, we have
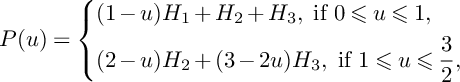 $$ \begin{align*}P(u)=\left\{\begin{aligned} &(1-u)H_1+H_2+H_3,\ \text{if }0\leqslant u\leqslant 1, \\ &(2-u)H_2+(3-2u)H_3,\ \text{if }1\leqslant u\leqslant \frac{3}{2}, \\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}P(u)=\left\{\begin{aligned} &(1-u)H_1+H_2+H_3,\ \text{if }0\leqslant u\leqslant 1, \\ &(2-u)H_2+(3-2u)H_3,\ \text{if }1\leqslant u\leqslant \frac{3}{2}, \\ \end{aligned} \right. \end{align*} $$
and
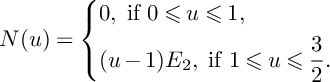 $$ \begin{align*}N(u)=\left\{\begin{aligned} &0,\ \text{if }0\leqslant u\leqslant 1, \\ &(u-1)E_2,\ \text{if }1\leqslant u\leqslant \frac{3}{2}.\\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}N(u)=\left\{\begin{aligned} &0,\ \text{if }0\leqslant u\leqslant 1, \\ &(u-1)E_2,\ \text{if }1\leqslant u\leqslant \frac{3}{2}.\\ \end{aligned} \right. \end{align*} $$
Note also that
![]() $E_2\vert _{S}$
is a smooth genus
$E_2\vert _{S}$
is a smooth genus
![]() $3$
curve contained in the smooth locus of the surface S.
$3$
curve contained in the smooth locus of the surface S.
Recall that S is a quintic del Pezzo surface with at most Du Val singularities and that the restriction morphism
![]() $\pi _2\vert _{S}\colon S\to \mathbb {P}^1_{u,v}$
is a conic bundle. Note that the morphism
$\pi _2\vert _{S}\colon S\to \mathbb {P}^1_{u,v}$
is a conic bundle. Note that the morphism
![]() $\pi _3\vert _{S}\colon S\to \mathbb {P}^2_{x,y,z}$
is birational. Let C be a fiber of the conic bundle
$\pi _3\vert _{S}\colon S\to \mathbb {P}^2_{x,y,z}$
is birational. Let C be a fiber of the conic bundle
![]() $\pi _2\vert _{S}$
, and let L be the preimage in S of a general line in
$\pi _2\vert _{S}$
, and let L be the preimage in S of a general line in
![]() $\mathbb {P}^2_{x,y,z}$
. Then
$\mathbb {P}^2_{x,y,z}$
. Then
![]() $-K_S\sim C+L$
and
$-K_S\sim C+L$
and
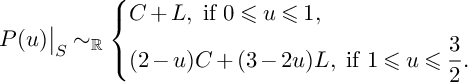 $$ \begin{align*}P(u)\big\vert_{S}\sim_{\mathbb{R}}\left\{\begin{aligned} &C+L,\ \text{if }0\leqslant u\leqslant 1, \\ &(2-u)C+(3-2u)L,\ \text{if }1\leqslant u\leqslant \frac{3}{2}. \\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}P(u)\big\vert_{S}\sim_{\mathbb{R}}\left\{\begin{aligned} &C+L,\ \text{if }0\leqslant u\leqslant 1, \\ &(2-u)C+(3-2u)L,\ \text{if }1\leqslant u\leqslant \frac{3}{2}. \\ \end{aligned} \right. \end{align*} $$
Since
![]() $2L-C$
is pseudoeffective, the divisor
$2L-C$
is pseudoeffective, the divisor
![]() $\frac {7-4u}{3}(-K_S)-(2-u)C-(3-2u)L$
is also pseudoeffective.
$\frac {7-4u}{3}(-K_S)-(2-u)C-(3-2u)L$
is also pseudoeffective.
Let F be a divisor over S such that
![]() $P\in C_S(F)$
. Then it follows from Lemma 27 that
$P\in C_S(F)$
. Then it follows from Lemma 27 that
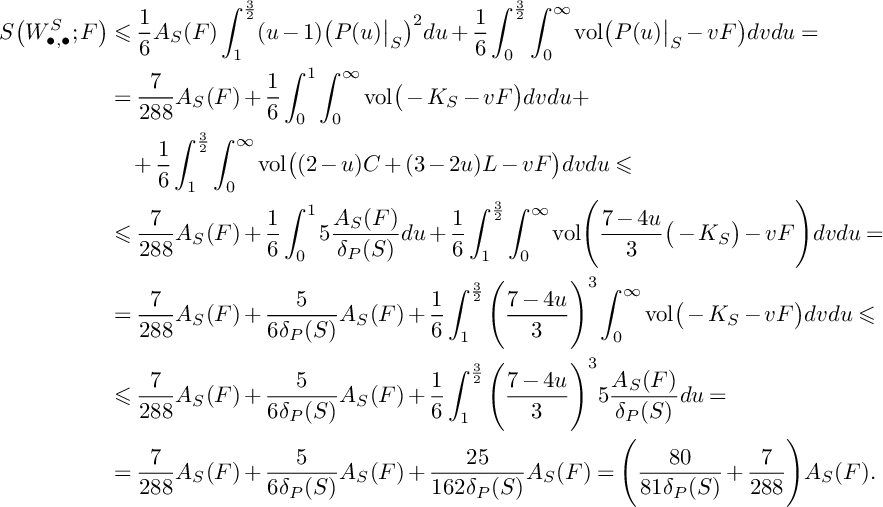 $$ \begin{align*} S\big(W^S_{\bullet,\bullet};F\big)&\leqslant\frac{1}{6}A_S(F)\int_1^{\frac{3}{2}}(u-1)\big(P(u)\big\vert_{S}\big)^2du+\frac{1}{6}\int_{0}^{\frac{3}{2}}\int_0^\infty \mathrm{vol}\big(P(u)\big\vert_{S}-vF\big)dvdu=\\&=\frac{7}{288}A_S(F)+\frac{1}{6}\int_{0}^{1}\int_0^\infty \mathrm{vol}\big(-K_S-vF\big)dvdu+\\&\quad+\frac{1}{6}\int_{1}^{\frac{3}{2}}\int_0^\infty\mathrm{vol}\big((2-u)C+(3-2u)L-vF\big)dvdu\leqslant\\&\leqslant\frac{7}{288}A_S(F)+\frac{1}{6}\int_{0}^{1}5\frac{A_S(F)}{\delta_P(S)}du+\frac{1}{6}\int_{1}^{\frac{3}{2}}\int_0^\infty\mathrm{vol}\Bigg(\frac{7-4u}{3}\big(-K_S\big)-vF\Bigg)dvdu=\\&=\frac{7}{288}A_S(F)+\frac{5}{6\delta_P(S)}A_S(F)+\frac{1}{6}\int_{1}^{\frac{3}{2}}\Bigg(\frac{7-4u}{3}\Bigg)^3\int_0^\infty\mathrm{vol}\big(-K_S-vF\big)dvdu\leqslant\\&\leqslant\frac{7}{288}A_S(F)+\frac{5}{6\delta_P(S)}A_S(F)+\frac{1}{6}\int_{1}^{\frac{3}{2}}\Bigg(\frac{7-4u}{3}\Bigg)^35\frac{A_S(F)}{\delta_P(S)}du=\\&=\frac{7}{288}A_S(F)+\frac{5}{6\delta_P(S)}A_S(F)+\frac{25}{162\delta_P(S)}A_S(F)=\Bigg(\frac{80}{81\delta_P(S)}+\frac{7}{288}\Bigg)A_S(F). \end{align*} $$
$$ \begin{align*} S\big(W^S_{\bullet,\bullet};F\big)&\leqslant\frac{1}{6}A_S(F)\int_1^{\frac{3}{2}}(u-1)\big(P(u)\big\vert_{S}\big)^2du+\frac{1}{6}\int_{0}^{\frac{3}{2}}\int_0^\infty \mathrm{vol}\big(P(u)\big\vert_{S}-vF\big)dvdu=\\&=\frac{7}{288}A_S(F)+\frac{1}{6}\int_{0}^{1}\int_0^\infty \mathrm{vol}\big(-K_S-vF\big)dvdu+\\&\quad+\frac{1}{6}\int_{1}^{\frac{3}{2}}\int_0^\infty\mathrm{vol}\big((2-u)C+(3-2u)L-vF\big)dvdu\leqslant\\&\leqslant\frac{7}{288}A_S(F)+\frac{1}{6}\int_{0}^{1}5\frac{A_S(F)}{\delta_P(S)}du+\frac{1}{6}\int_{1}^{\frac{3}{2}}\int_0^\infty\mathrm{vol}\Bigg(\frac{7-4u}{3}\big(-K_S\big)-vF\Bigg)dvdu=\\&=\frac{7}{288}A_S(F)+\frac{5}{6\delta_P(S)}A_S(F)+\frac{1}{6}\int_{1}^{\frac{3}{2}}\Bigg(\frac{7-4u}{3}\Bigg)^3\int_0^\infty\mathrm{vol}\big(-K_S-vF\big)dvdu\leqslant\\&\leqslant\frac{7}{288}A_S(F)+\frac{5}{6\delta_P(S)}A_S(F)+\frac{1}{6}\int_{1}^{\frac{3}{2}}\Bigg(\frac{7-4u}{3}\Bigg)^35\frac{A_S(F)}{\delta_P(S)}du=\\&=\frac{7}{288}A_S(F)+\frac{5}{6\delta_P(S)}A_S(F)+\frac{25}{162\delta_P(S)}A_S(F)=\Bigg(\frac{80}{81\delta_P(S)}+\frac{7}{288}\Bigg)A_S(F). \end{align*} $$
Then
![]() $\delta _{P}(S;W^S_{\bullet ,\bullet })\geqslant \frac {1}{\frac {80}{81\delta _P(S)}+\frac {7}{288}}=\frac {2,592\delta _P(S)}{2,560+63\delta _P(S)}$
and the required assertion follows from (3.1).
$\delta _{P}(S;W^S_{\bullet ,\bullet })\geqslant \frac {1}{\frac {80}{81\delta _P(S)}+\frac {7}{288}}=\frac {2,592\delta _P(S)}{2,560+63\delta _P(S)}$
and the required assertion follows from (3.1).
Keeping in mind that
![]() $S_X(S)<1$
by [Reference Fujita10, Th. 10.1] and the
$S_X(S)<1$
by [Reference Fujita10, Th. 10.1] and the
![]() $\delta $
-invariant of the smooth quintic del Pezzo surface is
$\delta $
-invariant of the smooth quintic del Pezzo surface is
![]() $\frac {15}{13}$
by [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Lem. 2.11], we obtain the following corollary.
$\frac {15}{13}$
by [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Lem. 2.11], we obtain the following corollary.
Corollary 11. Let S be the surface in
![]() $|H_1|$
that contains P. If S is smooth, then
$|H_1|$
that contains P. If S is smooth, then
![]() $\delta _P(X)>1$
.
$\delta _P(X)>1$
.
Similarly, using Lemmas 25 and 26 from Appendix 1, we obtain the following corollary.
Corollary 12. Let S be the surface in
![]() $|H_1|$
that contains P. Suppose that S has at most singular points of type
$|H_1|$
that contains P. Suppose that S has at most singular points of type
![]() $\mathbb {A}_1$
and that P is not contained in any line in S that passes through a singular point. Then
$\mathbb {A}_1$
and that P is not contained in any line in S that passes through a singular point. Then
![]() $\delta _P(X)>1$
.
$\delta _P(X)>1$
.
Alternatively, we can estimate
![]() $\delta _P(X)$
using [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Th. 1.7.30]. Namely, let C be an irreducible smooth curve in S that contains P. Suppose S is smooth at P. Since
$\delta _P(X)$
using [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Th. 1.7.30]. Namely, let C be an irreducible smooth curve in S that contains P. Suppose S is smooth at P. Since
![]() $S\not \subset \mathrm {Supp}(N(u))$
, we write
$S\not \subset \mathrm {Supp}(N(u))$
, we write
where
![]() $N_S^\prime (u)$
is an effective
$N_S^\prime (u)$
is an effective
![]() $\mathbb {R}$
-divisor on S such that
$\mathbb {R}$
-divisor on S such that
![]() $C\not \subset \mathrm {Supp}(N_S^\prime (u))$
, and
$C\not \subset \mathrm {Supp}(N_S^\prime (u))$
, and
![]() $d(u)=\mathrm {ord}_C(N(u)\vert _S)$
. Now, for every
$d(u)=\mathrm {ord}_C(N(u)\vert _S)$
. Now, for every
![]() $u\in [0,\tau ]$
, we define the pseudoeffective threshold
$u\in [0,\tau ]$
, we define the pseudoeffective threshold
![]() $t(u)\in \mathbb {R}_{\geqslant 0}$
as follows:
$t(u)\in \mathbb {R}_{\geqslant 0}$
as follows:
For
![]() $v\in [0, t(u)]$
, we let
$v\in [0, t(u)]$
, we let
![]() $P(u,v)$
be the positive part of the Zariski decomposition of
$P(u,v)$
be the positive part of the Zariski decomposition of
![]() $P(u)|_S-vC$
, and we let
$P(u)|_S-vC$
, and we let
![]() $N(u,v)$
be its negative part. As in Corollary 8, we let
$N(u,v)$
be its negative part. As in Corollary 8, we let
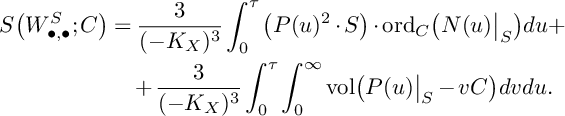 $$ \begin{align*} S\big(W^S_{\bullet,\bullet};C\big)&=\frac{3}{(-K_X)^3}\int_0^\tau\big(P(u)^{2}\cdot S\big)\cdot\mathrm{ord}_{C}\big(N(u)\big\vert_{S}\big)du+\\ & \quad + \frac{3}{(-K_X)^3}\int_0^\tau\int_0^\infty \mathrm{vol}\big(P(u)\big\vert_{S}-vC\big)dvdu. \end{align*} $$
$$ \begin{align*} S\big(W^S_{\bullet,\bullet};C\big)&=\frac{3}{(-K_X)^3}\int_0^\tau\big(P(u)^{2}\cdot S\big)\cdot\mathrm{ord}_{C}\big(N(u)\big\vert_{S}\big)du+\\ & \quad + \frac{3}{(-K_X)^3}\int_0^\tau\int_0^\infty \mathrm{vol}\big(P(u)\big\vert_{S}-vC\big)dvdu. \end{align*} $$
Note that
![]() $C\not \subset \mathrm {Supp}(N(u,v))$
for every
$C\not \subset \mathrm {Supp}(N(u,v))$
for every
![]() $u\in [0, \tau )$
and that
$u\in [0, \tau )$
and that
![]() $v\in (0, t(u))$
. Thus, we can let
$v\in (0, t(u))$
. Thus, we can let
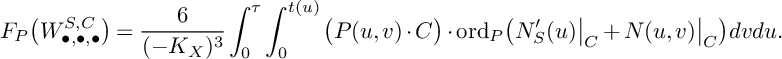 $$ \begin{align*}F_P\big(W_{\bullet,\bullet,\bullet}^{S,C}\big)=\frac{6}{(-K_X)^3} \int_0^\tau\int_0^{t(u)}\big(P(u,v)\cdot C\big)\cdot \mathrm{ord}_P\big(N_S^\prime(u)\big|_C+N(u,v)\big|_C\big)dvdu. \end{align*} $$
$$ \begin{align*}F_P\big(W_{\bullet,\bullet,\bullet}^{S,C}\big)=\frac{6}{(-K_X)^3} \int_0^\tau\int_0^{t(u)}\big(P(u,v)\cdot C\big)\cdot \mathrm{ord}_P\big(N_S^\prime(u)\big|_C+N(u,v)\big|_C\big)dvdu. \end{align*} $$
Finally, we let
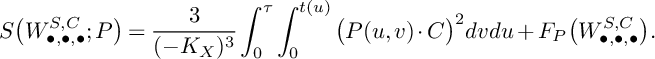 $$ \begin{align*}S\big(W_{\bullet, \bullet,\bullet}^{S,C};P\big)=\frac{3}{(-K_X)^3}\int_0^\tau\int_0^{t(u)}\big(P(u,v)\cdot C\big)^2dvdu+F_P\big(W_{\bullet,\bullet,\bullet}^{S,C}\big). \end{align*} $$
$$ \begin{align*}S\big(W_{\bullet, \bullet,\bullet}^{S,C};P\big)=\frac{3}{(-K_X)^3}\int_0^\tau\int_0^{t(u)}\big(P(u,v)\cdot C\big)^2dvdu+F_P\big(W_{\bullet,\bullet,\bullet}^{S,C}\big). \end{align*} $$
Then [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Th. 1.7.30] gives the following corollary.
Corollary 13. One has
 $$ \begin{align} \frac{A_X(\mathbf{F})}{S_X(\mathbf{F})}\geqslant\delta_P(X)\geqslant \min\left\{\frac{1}{S(W_{\bullet, \bullet,\bullet}^{S,C}; P)}, \frac{1}{S(W_{\bullet,\bullet}^S;C)},\frac{1}{S_X(S)}\right\}. \end{align} $$
$$ \begin{align} \frac{A_X(\mathbf{F})}{S_X(\mathbf{F})}\geqslant\delta_P(X)\geqslant \min\left\{\frac{1}{S(W_{\bullet, \bullet,\bullet}^{S,C}; P)}, \frac{1}{S(W_{\bullet,\bullet}^S;C)},\frac{1}{S_X(S)}\right\}. \end{align} $$
Moreover, if both inequalities in (★) are equalities and
![]() $\mathfrak {C}=P$
, then
$\mathfrak {C}=P$
, then
![]() $\delta _P(X)=\frac {1}{S_X(S)}$
.
$\delta _P(X)=\frac {1}{S_X(S)}$
.
Let us show how to compute
![]() $S(W_{\bullet ,\bullet }^S;C)$
and
$S(W_{\bullet ,\bullet }^S;C)$
and
![]() $S(W_{\bullet , \bullet ,\bullet }^{S,C};P)$
in some cases.
$S(W_{\bullet , \bullet ,\bullet }^{S,C};P)$
in some cases.
Lemma 14. Suppose that
![]() $\omega (P)\not \in \Delta _{\mathbb {P}^1\times \mathbb {P}^1}$
. Let S be a general surface in
$\omega (P)\not \in \Delta _{\mathbb {P}^1\times \mathbb {P}^1}$
. Let S be a general surface in
![]() $|H_1+H_2|$
that contains P, and let C be the fiber of the morphism
$|H_1+H_2|$
that contains P, and let C be the fiber of the morphism
![]() $\omega $
containing P. Then
$\omega $
containing P. Then
![]() $S(W_{\bullet ,\bullet }^S;C)=\frac {31}{36}$
and
$S(W_{\bullet ,\bullet }^S;C)=\frac {31}{36}$
and
![]() $S(W_{\bullet , \bullet ,\bullet }^{S,C};P)=1$
.
$S(W_{\bullet , \bullet ,\bullet }^{S,C};P)=1$
.
Proof. We have
![]() $\tau =1$
. Moreover, for
$\tau =1$
. Moreover, for
![]() $u\in [0,1]$
, we have
$u\in [0,1]$
, we have
![]() $N(u)=0$
and
$N(u)=0$
and
![]() $P(u)|_S=-K_S+2(1-u)C$
. On the other hand, it follows from Lemma 7 that S is a smooth del Pezzo surface of degree
$P(u)|_S=-K_S+2(1-u)C$
. On the other hand, it follows from Lemma 7 that S is a smooth del Pezzo surface of degree
![]() $2$
, and the restriction map
$2$
, and the restriction map
![]() $\pi _3\vert _{S}\colon S\to \mathbb {P}^2_{x,y,z}$
is a double cover that is ramified over a smooth quartic curve. Therefore, applying the Galois involution of this double cover to C, we obtain another smooth irreducible curve
$\pi _3\vert _{S}\colon S\to \mathbb {P}^2_{x,y,z}$
is a double cover that is ramified over a smooth quartic curve. Therefore, applying the Galois involution of this double cover to C, we obtain another smooth irreducible curve
![]() $Z\subset S$
such that
$Z\subset S$
such that
![]() $C+Z\sim -2K_S$
,
$C+Z\sim -2K_S$
,
![]() $C^2=Z^2=0$
and
$C^2=Z^2=0$
and
![]() $C\cdot Z=4$
, which gives
$C\cdot Z=4$
, which gives
Then
![]() $P(u)\vert _{S}-vC$
is pseudoeffective
$P(u)\vert _{S}-vC$
is pseudoeffective
![]() $\iff P(u)\vert _{S}-vC$
is nef
$\iff P(u)\vert _{S}-vC$
is nef
![]() $\iff v\leqslant \frac {5}{2}-2u$
. Thus, we have
$\iff v\leqslant \frac {5}{2}-2u$
. Thus, we have
and
![]() $P(u,v)\cdot C=2$
. Now, integrating, we obtain
$P(u,v)\cdot C=2$
. Now, integrating, we obtain
![]() $S(W_{\bullet ,\bullet }^S;C)=\frac {31}{36}$
and
$S(W_{\bullet ,\bullet }^S;C)=\frac {31}{36}$
and
![]() $S(W_{\bullet ,\bullet ,\bullet }^{S,C};P)=1$
.
$S(W_{\bullet ,\bullet ,\bullet }^{S,C};P)=1$
.
Lemma 15. Suppose that
![]() $P\not \in E_1\cup E_2$
. Let S be a general surface in
$P\not \in E_1\cup E_2$
. Let S be a general surface in
![]() $|H_3|$
that contains P, and let C be the fiber of the morphism
$|H_3|$
that contains P, and let C be the fiber of the morphism
![]() $\pi _3$
containing P. Suppose that S is a smooth del Pezzo surface. Then
$\pi _3$
containing P. Suppose that S is a smooth del Pezzo surface. Then
![]() $S(W_{\bullet ,\bullet }^S;C)=\frac {7}{9}$
and
$S(W_{\bullet ,\bullet }^S;C)=\frac {7}{9}$
and
![]() $S(W_{\bullet , \bullet ,\bullet }^{S,C};P)=1$
.
$S(W_{\bullet , \bullet ,\bullet }^{S,C};P)=1$
.
Proof. We have
![]() $\tau =1$
. Moreover, for
$\tau =1$
. Moreover, for
![]() $u\in [0,1]$
, we have
$u\in [0,1]$
, we have
![]() $N(u)=0$
and
$N(u)=0$
and
![]() $P(u)|_S=-K_S+(1-u)C$
. Since S is a smooth del Pezzo surface, the restriction map
$P(u)|_S=-K_S+(1-u)C$
. Since S is a smooth del Pezzo surface, the restriction map
![]() $\omega \vert _{S}\colon S\to \mathbb {P}^1_{s,t}\times \mathbb {P}^1_{u,v}$
is a double cover ramified over a smooth elliptic curve. Therefore, using the Galois involution of this double cover, we get an irreducible curve
$\omega \vert _{S}\colon S\to \mathbb {P}^1_{s,t}\times \mathbb {P}^1_{u,v}$
is a double cover ramified over a smooth elliptic curve. Therefore, using the Galois involution of this double cover, we get an irreducible curve
![]() $Z\subset S$
such that
$Z\subset S$
such that
![]() $C+Z\sim -K_S$
,
$C+Z\sim -K_S$
,
![]() $C^2=Z^2=0$
, and
$C^2=Z^2=0$
, and
![]() $C\cdot Z=2$
, which gives
$C\cdot Z=2$
, which gives
Then
![]() $P(u)\vert _{S}-vC$
is pseudoeffective
$P(u)\vert _{S}-vC$
is pseudoeffective
![]() $\iff P(u)\vert _{S}-vC$
is nef
$\iff P(u)\vert _{S}-vC$
is nef
![]() $\iff v\leqslant 2-u$
. Thus, we have
$\iff v\leqslant 2-u$
. Thus, we have
and
![]() $P(u,v)\cdot C=2$
. Now, integrating, we obtain
$P(u,v)\cdot C=2$
. Now, integrating, we obtain
![]() $S(W_{\bullet ,\bullet }^S;C)=\frac {7}{9}$
and
$S(W_{\bullet ,\bullet }^S;C)=\frac {7}{9}$
and
![]() $S(W_{\bullet ,\bullet ,\bullet }^{S,C};P)=1$
.
$S(W_{\bullet ,\bullet ,\bullet }^{S,C};P)=1$
.
Lemma 16. Suppose that
![]() $P\not \in E_1\cup E_2$
. Let S be a general surface in
$P\not \in E_1\cup E_2$
. Let S be a general surface in
![]() $|H_3|$
that contains P, and let C be the fiber of the morphism
$|H_3|$
that contains P, and let C be the fiber of the morphism
![]() $\pi _3$
containing P. Suppose S is not a smooth del Pezzo surface. Then
$\pi _3$
containing P. Suppose S is not a smooth del Pezzo surface. Then
![]() $S(W_{\bullet ,\bullet }^S;C)=\frac {8}{9}$
and
$S(W_{\bullet ,\bullet }^S;C)=\frac {8}{9}$
and
![]() $S(W_{\bullet , \bullet ,\bullet }^{S,C};P)=\frac {7}{9}$
.
$S(W_{\bullet , \bullet ,\bullet }^{S,C};P)=\frac {7}{9}$
.
Proof. We have
![]() $\tau =1$
. Moreover, for
$\tau =1$
. Moreover, for
![]() $u\in [0,1]$
, we have
$u\in [0,1]$
, we have
![]() $N(u)=0$
and
$N(u)=0$
and
![]() $P(u)|_S=-K_S+(1-u)C$
. It follows from Lemma 6 that S contains two
$P(u)|_S=-K_S+(1-u)C$
. It follows from Lemma 6 that S contains two
![]() $(-2)$
-curves
$(-2)$
-curves
![]() $\mathbf {e}_1$
and
$\mathbf {e}_1$
and
![]() $\mathbf {e}_2$
such that
$\mathbf {e}_2$
such that
![]() $-K_S\sim 2C+\mathbf {e}_1+\mathbf {e}_2$
. On the surface S, we have
$-K_S\sim 2C+\mathbf {e}_1+\mathbf {e}_2$
. On the surface S, we have
![]() $C^2=0$
,
$C^2=0$
,
![]() $C\cdot \mathbf {e}_1=C\cdot \mathbf {e}_2=1$
,
$C\cdot \mathbf {e}_1=C\cdot \mathbf {e}_2=1$
,
![]() $\mathbf {e}_1^2=\mathbf {e}_2^2=-2$
, and
$\mathbf {e}_1^2=\mathbf {e}_2^2=-2$
, and
Then
![]() $P(u)\vert _{S}-vC$
is pseudoeffective
$P(u)\vert _{S}-vC$
is pseudoeffective
![]() $\iff v\leqslant 3-u$
. Moreover, we have
$\iff v\leqslant 3-u$
. Moreover, we have
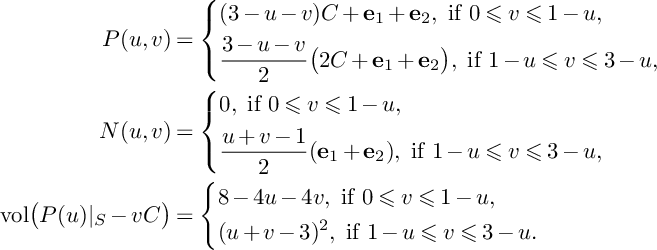 $$ \begin{align*}P(u,v)&=\left\{\begin{aligned} &(3-u-v)C+\mathbf{e}_1+\mathbf{e}_2,\ \text{if }0\leqslant v\leqslant 1-u, \\ &\frac{3-u-v}{2}\big(2C+\mathbf{e}_1+\mathbf{e}_2\big),\ \text{if }1-u\leqslant v\leqslant 3-u, \\ \end{aligned} \right. \\N(u,v)&=\left\{\begin{aligned} &0,\ \text{if }0\leqslant v\leqslant 1-u, \\ &\frac{u+v-1}{2}(\mathbf{e}_1+\mathbf{e}_2),\ \text{if }1-u\leqslant v\leqslant 3-u, \\ \end{aligned} \right. \\\mathrm{vol}\big(P(u)\vert_{S}-vC\big)&= \left\{\begin{aligned} &8-4u-4v,\ \text{if }0\leqslant v\leqslant 1-u, \\ &(u+v-3)^2,\ \text{if }1-u\leqslant v\leqslant 3-u. \\ \end{aligned} \right.\end{align*} $$
$$ \begin{align*}P(u,v)&=\left\{\begin{aligned} &(3-u-v)C+\mathbf{e}_1+\mathbf{e}_2,\ \text{if }0\leqslant v\leqslant 1-u, \\ &\frac{3-u-v}{2}\big(2C+\mathbf{e}_1+\mathbf{e}_2\big),\ \text{if }1-u\leqslant v\leqslant 3-u, \\ \end{aligned} \right. \\N(u,v)&=\left\{\begin{aligned} &0,\ \text{if }0\leqslant v\leqslant 1-u, \\ &\frac{u+v-1}{2}(\mathbf{e}_1+\mathbf{e}_2),\ \text{if }1-u\leqslant v\leqslant 3-u, \\ \end{aligned} \right. \\\mathrm{vol}\big(P(u)\vert_{S}-vC\big)&= \left\{\begin{aligned} &8-4u-4v,\ \text{if }0\leqslant v\leqslant 1-u, \\ &(u+v-3)^2,\ \text{if }1-u\leqslant v\leqslant 3-u. \\ \end{aligned} \right.\end{align*} $$
Now, integrating
![]() $\mathrm {vol}(P(u)\vert _{S}-vC)$
, we obtain
$\mathrm {vol}(P(u)\vert _{S}-vC)$
, we obtain
![]() $S(W_{\bullet ,\bullet }^S;C)=\frac {8}{9}$
.
$S(W_{\bullet ,\bullet }^S;C)=\frac {8}{9}$
.
To compute
![]() $S(W_{\bullet ,\bullet ,\bullet }^{S,C};P)$
, observe that
$S(W_{\bullet ,\bullet ,\bullet }^{S,C};P)$
, observe that
![]() $F_P(W_{\bullet ,\bullet ,\bullet }^{S,C})=0$
, because
$F_P(W_{\bullet ,\bullet ,\bullet }^{S,C})=0$
, because
![]() $P\not \in \mathbf {e}_1\cup \mathbf {e}_2$
, since S is a general surface in
$P\not \in \mathbf {e}_1\cup \mathbf {e}_2$
, since S is a general surface in
![]() $|H_3|$
that contains C. On the other hand, we have
$|H_3|$
that contains C. On the other hand, we have
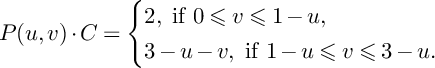 $$ \begin{align*}P(u,v)\cdot C=\left\{\begin{aligned} &2,\ \text{if }0\leqslant v\leqslant 1-u, \\ &3-u-v,\ \text{if }1-u\leqslant v\leqslant 3-u. \\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}P(u,v)\cdot C=\left\{\begin{aligned} &2,\ \text{if }0\leqslant v\leqslant 1-u, \\ &3-u-v,\ \text{if }1-u\leqslant v\leqslant 3-u. \\ \end{aligned} \right. \end{align*} $$
Hence, integrating
![]() $(P(u,v)\cdot C)^2$
, we get
$(P(u,v)\cdot C)^2$
, we get
![]() $S(W_{\bullet ,\bullet ,\bullet }^{S,C};P)=\frac {7}{9}$
as required.
$S(W_{\bullet ,\bullet ,\bullet }^{S,C};P)=\frac {7}{9}$
as required.
Lemma 17. Suppose
![]() $P\in (E_1\cup E_2)\setminus (E_1\cap E_2)$
. Let S be a general surface in
$P\in (E_1\cup E_2)\setminus (E_1\cap E_2)$
. Let S be a general surface in
![]() $|H_3|$
that contains P, and let C be the irreducible component of the fiber of the conic bundle
$|H_3|$
that contains P, and let C be the irreducible component of the fiber of the conic bundle
![]() $\pi _3$
containing P such that
$\pi _3$
containing P such that
![]() $P\in C$
. Then
$P\in C$
. Then
![]() $S(W_{\bullet ,\bullet }^S;C)=1$
and
$S(W_{\bullet ,\bullet }^S;C)=1$
and
![]() $S(W_{\bullet , \bullet ,\bullet }^{S,C};P)\leqslant \frac {31}{36}$
.
$S(W_{\bullet , \bullet ,\bullet }^{S,C};P)\leqslant \frac {31}{36}$
.
Proof. We have
![]() $\tau =1$
. For
$\tau =1$
. For
![]() $u\in [0,1]$
, we have
$u\in [0,1]$
, we have
![]() $N(u)=0$
and
$N(u)=0$
and
![]() $P(u)|_S\sim _{\mathbb {R}}-K_S+(1-u) (C+C^\prime )$
, where
$P(u)|_S\sim _{\mathbb {R}}-K_S+(1-u) (C+C^\prime )$
, where
![]() $C^\prime $
is the irreducible curve in S such that
$C^\prime $
is the irreducible curve in S such that
![]() $C+C^\prime $
is the fiber of the conic bundle
$C+C^\prime $
is the fiber of the conic bundle
![]() $\pi _3$
that passes through the point P. Since
$\pi _3$
that passes through the point P. Since
![]() $P\not \in E_1\cap E_2$
, we see that
$P\not \in E_1\cap E_2$
, we see that
![]() $P\not \in C^\prime $
.
$P\not \in C^\prime $
.
By Lemma 6, the surface S is a smooth del Pezzo surface of degree
![]() $4$
, so we can identify it with a complete intersection of two quadrics in
$4$
, so we can identify it with a complete intersection of two quadrics in
![]() $\mathbb {P}^4$
. Then C and
$\mathbb {P}^4$
. Then C and
![]() $C^\prime $
are lines in S, and S contains four additional lines that intersect C. Denote them by
$C^\prime $
are lines in S, and S contains four additional lines that intersect C. Denote them by
![]() $L_1$
,
$L_1$
,
![]() $L_2$
,
$L_2$
,
![]() $L_3$
, and
$L_3$
, and
![]() $L_4$
, and let
$L_4$
, and let
![]() $Z=L_1+L_2+L_3+L_4$
. Then the intersections of the curves C,
$Z=L_1+L_2+L_3+L_4$
. Then the intersections of the curves C,
![]() $C^\prime $
, and Z on the surface S are given in the table below.
$C^\prime $
, and Z on the surface S are given in the table below.

Observe that
![]() $-K_S\sim _{\mathbb {Q}}\frac {3}{2}C+\frac {1}{2}C^\prime +\frac {1}{2}Z$
. This gives
$-K_S\sim _{\mathbb {Q}}\frac {3}{2}C+\frac {1}{2}C^\prime +\frac {1}{2}Z$
. This gives
![]() $P(u)\vert _{S}-vC\sim _{\mathbb {R}}(\frac {5}{2}-u-v)C+ (\frac {3}{2}-u)C^\prime +\frac {1}{2}Z$
, which implies that
$P(u)\vert _{S}-vC\sim _{\mathbb {R}}(\frac {5}{2}-u-v)C+ (\frac {3}{2}-u)C^\prime +\frac {1}{2}Z$
, which implies that
![]() $P(u)\vert _{S}-vC$
is pseudoeffective
$P(u)\vert _{S}-vC$
is pseudoeffective
![]() $\iff v\leqslant \frac {5}{2}-u$
.
$\iff v\leqslant \frac {5}{2}-u$
.
Moreover, we have
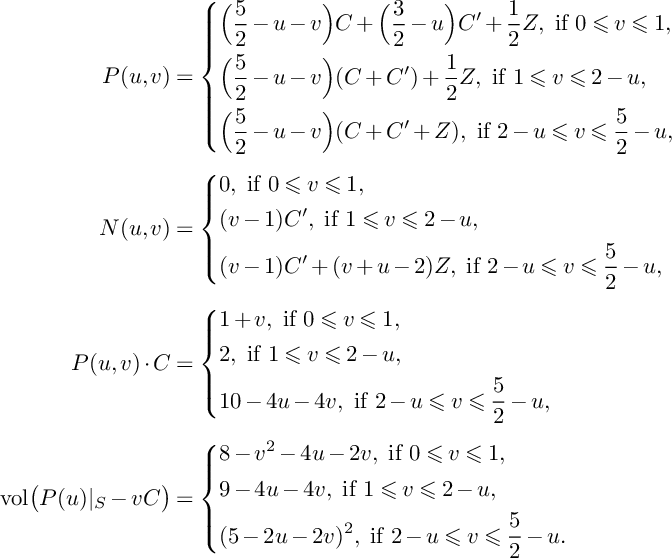 $$ \begin{align*}P(u,v)&=\left\{\begin{aligned} &\Big(\frac{5}{2}-u-v\Big)C+\Big(\frac{3}{2}-u\Big)C^\prime+\frac{1}{2}Z,\ \text{if }0\leqslant v\leqslant 1, \\ &\Big(\frac{5}{2}-u-v\Big)(C+C^\prime)+\frac{1}{2}Z,\ \text{if }1\leqslant v\leqslant 2-u, \\ &\Big(\frac{5}{2}-u-v\Big)(C+C^\prime+Z),\ \text{if }2-u\leqslant v\leqslant \frac{5}{2}-u, \\ \end{aligned} \right.\\[4pt]N(u,v)&=\left\{\begin{aligned} &0,\ \text{if }0\leqslant v\leqslant 1, \\ &(v-1)C^\prime,\ \text{if }1\leqslant v\leqslant 2-u, \\ &(v-1)C^\prime+(v+u-2)Z,\ \text{if }2-u\leqslant v\leqslant \frac{5}{2}-u, \\ \end{aligned} \right.\\[4pt]P(u,v)\cdot C&=\left\{\begin{aligned} &1+v,\ \text{if }0\leqslant v\leqslant 1, \\ &2,\ \text{if }1\leqslant v\leqslant 2-u, \\ &10-4u-4v,\ \text{if }2-u\leqslant v\leqslant \frac{5}{2}-u, \end{aligned} \right.\\[4pt]\mathrm{vol}\big(P(u)\vert_{S}-vC\big)&= \left\{\begin{aligned} &8-v^2-4u-2v,\ \text{if }0\leqslant v\leqslant 1, \\ &9-4u-4v,\ \text{if }1\leqslant v\leqslant 2-u, \\ &(5-2u-2v)^2,\ \text{if }2-u\leqslant v\leqslant \frac{5}{2}-u. \\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}P(u,v)&=\left\{\begin{aligned} &\Big(\frac{5}{2}-u-v\Big)C+\Big(\frac{3}{2}-u\Big)C^\prime+\frac{1}{2}Z,\ \text{if }0\leqslant v\leqslant 1, \\ &\Big(\frac{5}{2}-u-v\Big)(C+C^\prime)+\frac{1}{2}Z,\ \text{if }1\leqslant v\leqslant 2-u, \\ &\Big(\frac{5}{2}-u-v\Big)(C+C^\prime+Z),\ \text{if }2-u\leqslant v\leqslant \frac{5}{2}-u, \\ \end{aligned} \right.\\[4pt]N(u,v)&=\left\{\begin{aligned} &0,\ \text{if }0\leqslant v\leqslant 1, \\ &(v-1)C^\prime,\ \text{if }1\leqslant v\leqslant 2-u, \\ &(v-1)C^\prime+(v+u-2)Z,\ \text{if }2-u\leqslant v\leqslant \frac{5}{2}-u, \\ \end{aligned} \right.\\[4pt]P(u,v)\cdot C&=\left\{\begin{aligned} &1+v,\ \text{if }0\leqslant v\leqslant 1, \\ &2,\ \text{if }1\leqslant v\leqslant 2-u, \\ &10-4u-4v,\ \text{if }2-u\leqslant v\leqslant \frac{5}{2}-u, \end{aligned} \right.\\[4pt]\mathrm{vol}\big(P(u)\vert_{S}-vC\big)&= \left\{\begin{aligned} &8-v^2-4u-2v,\ \text{if }0\leqslant v\leqslant 1, \\ &9-4u-4v,\ \text{if }1\leqslant v\leqslant 2-u, \\ &(5-2u-2v)^2,\ \text{if }2-u\leqslant v\leqslant \frac{5}{2}-u. \\ \end{aligned} \right. \end{align*} $$
Now, integrating
![]() $\mathrm {vol}(P(u)\vert _{S}-vC)$
and
$\mathrm {vol}(P(u)\vert _{S}-vC)$
and
![]() $(P(u,v)\cdot C)^2$
, we get
$(P(u,v)\cdot C)^2$
, we get
![]() $S(W_{\bullet ,\bullet }^S;C)=1$
and
$S(W_{\bullet ,\bullet }^S;C)=1$
and
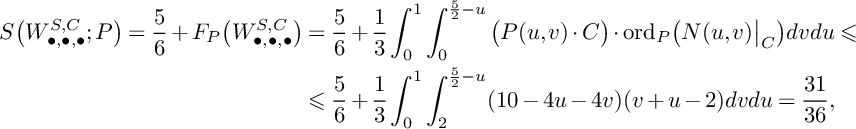 $$ \begin{align*} S\big(W_{\bullet, \bullet,\bullet}^{S,C};P\big)=\frac{5}{6}+F_P\big(W_{\bullet,\bullet,\bullet}^{S,C}\big)&=\frac{5}{6}+\frac{1}{3}\int_0^1\int_0^{\frac{5}{2}-u}\big(P(u,v)\cdot C\big)\cdot \mathrm{ord}_P\big(N(u,v)\big|_C\big)dvdu\leqslant\\ &\leqslant\frac{5}{6}+\frac{1}{3}\int_0^1\int_2^{\frac{5}{2}-u}(10-4u-4v)(v+u-2)dvdu=\frac{31}{36}, \end{align*} $$
$$ \begin{align*} S\big(W_{\bullet, \bullet,\bullet}^{S,C};P\big)=\frac{5}{6}+F_P\big(W_{\bullet,\bullet,\bullet}^{S,C}\big)&=\frac{5}{6}+\frac{1}{3}\int_0^1\int_0^{\frac{5}{2}-u}\big(P(u,v)\cdot C\big)\cdot \mathrm{ord}_P\big(N(u,v)\big|_C\big)dvdu\leqslant\\ &\leqslant\frac{5}{6}+\frac{1}{3}\int_0^1\int_2^{\frac{5}{2}-u}(10-4u-4v)(v+u-2)dvdu=\frac{31}{36}, \end{align*} $$
because
![]() $P\not \in C^\prime $
, and the curves Z and C intersect each other transversally.
$P\not \in C^\prime $
, and the curves Z and C intersect each other transversally.
4 The proof of Main Theorem
Let us use notations and assumptions of §§2 and 3. Recall that
![]() $\mathbf {F}$
is a prime divisor over the threefold X and that
$\mathbf {F}$
is a prime divisor over the threefold X and that
![]() $\mathfrak {C}$
is its center in X. To prove Main Theorem, we must show that
$\mathfrak {C}$
is its center in X. To prove Main Theorem, we must show that
![]() $\beta (\mathbf {F})>0$
.
$\beta (\mathbf {F})>0$
.
Lemma 18. Suppose that
![]() $\mathfrak {C}$
is a curve. Then
$\mathfrak {C}$
is a curve. Then
![]() $\beta (\mathbf {F})>0$
.
$\beta (\mathbf {F})>0$
.
Proof. Suppose that
![]() $\beta (\mathbf {F})\leqslant 0$
. Then
$\beta (\mathbf {F})\leqslant 0$
. Then
![]() $\delta _P(X)\leqslant 1$
for every point
$\delta _P(X)\leqslant 1$
for every point
![]() $P\in \mathfrak {C}$
. Let us seek for a contradiction.
$P\in \mathfrak {C}$
. Let us seek for a contradiction.
Let
![]() $S_1$
be a general surface in the linear system
$S_1$
be a general surface in the linear system
![]() $|H_1|$
. Then
$|H_1|$
. Then
![]() $S_1$
is smooth. Hence, if
$S_1$
is smooth. Hence, if
![]() $S_1\cap \mathfrak {C}\ne \varnothing $
, then
$S_1\cap \mathfrak {C}\ne \varnothing $
, then
![]() $\delta _P(X)\leqslant 1$
for every point
$\delta _P(X)\leqslant 1$
for every point
![]() $P\in S_1\cap \mathfrak {C}$
, which contradicts Corollary 11. We see that
$P\in S_1\cap \mathfrak {C}$
, which contradicts Corollary 11. We see that
![]() $S_1\cdot \mathfrak {C}=0$
. Similarly, we see that
$S_1\cdot \mathfrak {C}=0$
. Similarly, we see that
![]() $S_2\cdot \mathfrak {C}=0$
for a general surface
$S_2\cdot \mathfrak {C}=0$
for a general surface
![]() $S_2\in |H_2|$
. So, we see that
$S_2\in |H_2|$
. So, we see that
![]() $\omega (\mathfrak {C})$
is a point.
$\omega (\mathfrak {C})$
is a point.
Let C be the scheme fiber of the conic bundle
![]() $\omega $
over the point
$\omega $
over the point
![]() $\omega (\mathfrak {C})$
. Then
$\omega (\mathfrak {C})$
. Then
![]() $\mathfrak {C}$
is an irreducible component of the curve C. If the fiber C is smooth, then we
$\mathfrak {C}$
is an irreducible component of the curve C. If the fiber C is smooth, then we
![]() $\mathfrak {C}=C$
.
$\mathfrak {C}=C$
.
Suppose that C is smooth. If S is a general surface in the linear system
![]() $|H_1+H_2|$
that contains
$|H_1+H_2|$
that contains
![]() $\mathfrak {C}$
, then
$\mathfrak {C}$
, then
![]() $S(W_{\bullet ,\bullet }^S;\mathfrak {C})=\frac {31}{36}<1$
by Lemma 14, which contradicts Corollary 8. So, the curve C is singular.
$S(W_{\bullet ,\bullet }^S;\mathfrak {C})=\frac {31}{36}<1$
by Lemma 14, which contradicts Corollary 8. So, the curve C is singular.
Note that
![]() $\pi _3(\mathfrak {C})$
is a line in
$\pi _3(\mathfrak {C})$
is a line in
![]() $\mathbb {P}^2_{x,y,z}$
. On the other hand, the discriminant curve
$\mathbb {P}^2_{x,y,z}$
. On the other hand, the discriminant curve
![]() $\Delta _{\mathbb {P}^2}$
is an irreducible smooth quartic curve in
$\Delta _{\mathbb {P}^2}$
is an irreducible smooth quartic curve in
![]() $\mathbb {P}^2_{x,y,z}$
. Therefore, in particular, the line
$\mathbb {P}^2_{x,y,z}$
. Therefore, in particular, the line
![]() $\pi _3(\mathfrak {C})$
is not contained in
$\pi _3(\mathfrak {C})$
is not contained in
![]() $\Delta _{\mathbb {P}^2}$
. Now, let P be a general point in
$\Delta _{\mathbb {P}^2}$
. Now, let P be a general point in
![]() $\mathfrak {C}$
, let Z be the fiber of the conic bundle
$\mathfrak {C}$
, let Z be the fiber of the conic bundle
![]() $\pi _3$
that passes through P, and let S be a general surface in
$\pi _3$
that passes through P, and let S be a general surface in
![]() $|H_3|$
that contains the curve Z. Then Z and S are both smooth, and it follows from Lemma 6 that S is a del Pezzo of degree
$|H_3|$
that contains the curve Z. Then Z and S are both smooth, and it follows from Lemma 6 that S is a del Pezzo of degree
![]() $4$
, so that
$4$
, so that
![]() $\delta _P(X)>1$
by Lemma 9.
$\delta _P(X)>1$
by Lemma 9.
Hence, to complete the proof of Main Theorem, we may assume that
![]() $\mathfrak {C}$
is a point. Set
$\mathfrak {C}$
is a point. Set
![]() $P=\mathfrak {C}$
. Let
$P=\mathfrak {C}$
. Let
![]() $\mathscr {C}$
be the fiber of the conic bundle
$\mathscr {C}$
be the fiber of the conic bundle
![]() $\omega $
that contains P.
$\omega $
that contains P.
Lemma 19. Suppose that
![]() $P\not \in E_1\cap E_2$
. Then
$P\not \in E_1\cap E_2$
. Then
![]() $\beta (\mathbf {F})>0$
.
$\beta (\mathbf {F})>0$
.
Thus, to complete the proof of Main Theorem, we may assume, in addition, that
![]() $P\in E_1\cap E_2$
. Then the conic
$P\in E_1\cap E_2$
. Then the conic
![]() $\mathscr {C}$
is smooth at P by Lemma 5. In particular, we see that
$\mathscr {C}$
is smooth at P by Lemma 5. In particular, we see that
![]() $\mathscr {C}$
is reduced.
$\mathscr {C}$
is reduced.
Lemma 20. Suppose that
![]() $\mathscr {C}$
is smooth. Then
$\mathscr {C}$
is smooth. Then
![]() $\beta (\mathbf {F})>0$
.
$\beta (\mathbf {F})>0$
.
To complete the proof of Main Theorem, we may assume that
![]() $\mathscr {C}$
is singular. Write
$\mathscr {C}$
is singular. Write
![]() $\mathscr {C}=\ell _1+\ell _2$
, where
$\mathscr {C}=\ell _1+\ell _2$
, where
![]() $\ell _1$
and
$\ell _1$
and
![]() $\ell _2$
are irreducible components of the conic
$\ell _2$
are irreducible components of the conic
![]() $\mathscr {C}$
. Then
$\mathscr {C}$
. Then
![]() $P\ne \ell _1\cap \ell _2$
, since
$P\ne \ell _1\cap \ell _2$
, since
![]() $P\not \in \mathrm {Sing}(\mathscr {C})$
.
$P\not \in \mathrm {Sing}(\mathscr {C})$
.
Let
![]() $S_1$
and
$S_1$
and
![]() $S_2$
be general surfaces in
$S_2$
be general surfaces in
![]() $|H_1|$
and
$|H_1|$
and
![]() $|H_2|$
that pass through the point P, respectively. Then
$|H_2|$
that pass through the point P, respectively. Then
![]() $\mathscr {C}=S_1\cap S_2$
, and it follows from Corollary 4 that
$\mathscr {C}=S_1\cap S_2$
, and it follows from Corollary 4 that
![]() $S_1$
or
$S_1$
or
![]() $S_2$
is smooth along the conic
$S_2$
is smooth along the conic
![]() $\mathscr {C}$
. Without loss of generality, we may assume that
$\mathscr {C}$
. Without loss of generality, we may assume that
![]() $S_1$
is smooth along
$S_1$
is smooth along
![]() $\mathscr {C}$
. We let
$\mathscr {C}$
. We let
![]() $S=S_1$
.
$S=S_1$
.
If S is smooth, then
![]() $\delta _P(X)>1$
by Corollary 11. Thus, we may assume that S is singular.
$\delta _P(X)>1$
by Corollary 11. Thus, we may assume that S is singular.
Recall that S is a quintic del Pezzo surface and that
![]() $\ell _1$
and
$\ell _1$
and
![]() $\ell _2$
are lines in its anticanonical embedding. The preimages of the lines
$\ell _2$
are lines in its anticanonical embedding. The preimages of the lines
![]() $\ell _1$
and
$\ell _1$
and
![]() $\ell _2$
on the minimal resolution of the surface S are
$\ell _2$
on the minimal resolution of the surface S are
![]() $(-1)$
-curves, which do not intersect
$(-1)$
-curves, which do not intersect
![]() $(-2)$
-curves. By Lemma 1 and Remark 2, one of the following cases holds:
$(-2)$
-curves. By Lemma 1 and Remark 2, one of the following cases holds:
(
 $\mathbb {A}_1$
) The surface S has one singular point of type
$\mathbb {A}_1$
) The surface S has one singular point of type
 $\mathbb {A}_1$
.
$\mathbb {A}_1$
.(
 $2\mathbb {A}_1$
) The surface S has two singular points of type
$2\mathbb {A}_1$
) The surface S has two singular points of type
 $\mathbb {A}_1$
.
$\mathbb {A}_1$
.
In both cases, the restriction morphism
![]() $\pi _3\vert _{S}\colon S\to \mathbb {P}^2_{x,y,z}$
is birational. In (
$\pi _3\vert _{S}\colon S\to \mathbb {P}^2_{x,y,z}$
is birational. In (
![]() $\mathbb {A}_1$
)-case, this morphism contracts three disjoint irreducible smooth rational curves
$\mathbb {A}_1$
)-case, this morphism contracts three disjoint irreducible smooth rational curves
![]() $\mathbf {e}_1$
,
$\mathbf {e}_1$
,
![]() $\mathbf {e}_2$
, and
$\mathbf {e}_2$
, and
![]() $\mathbf {e}_3$
such that
$\mathbf {e}_3$
such that
![]() $E_1\vert _{S}=2\mathbf {e}_1+\mathbf {e}_2+\mathbf {e}_3$
, the curves
$E_1\vert _{S}=2\mathbf {e}_1+\mathbf {e}_2+\mathbf {e}_3$
, the curves
![]() $\mathbf {e}_1$
,
$\mathbf {e}_1$
,
![]() $\mathbf {e}_2$
, and
$\mathbf {e}_2$
, and
![]() $\mathbf {e}_3$
are sections of the conic bundle
$\mathbf {e}_3$
are sections of the conic bundle
![]() $\pi _2\vert _{S}\colon S\to \mathbb {P}^1_{u,v}$
, the curve
$\pi _2\vert _{S}\colon S\to \mathbb {P}^1_{u,v}$
, the curve
![]() $\mathbf {e}_1$
passes through the singular point of the surface S, but
$\mathbf {e}_1$
passes through the singular point of the surface S, but
![]() $\mathbf {e}_2$
and
$\mathbf {e}_2$
and
![]() $\mathbf {e}_3$
are contained in the smooth locus of the surface S. In (
$\mathbf {e}_3$
are contained in the smooth locus of the surface S. In (
![]() $2\mathbb {A}_1$
)-case, the morphism
$2\mathbb {A}_1$
)-case, the morphism
![]() $\pi _3\vert _{S}$
contracts two disjoint curves
$\pi _3\vert _{S}$
contracts two disjoint curves
![]() $\mathbf {e}_1$
and
$\mathbf {e}_1$
and
![]() $\mathbf {e}_2$
such that
$\mathbf {e}_2$
such that
![]() $E_1\big \vert _{S}=2\mathbf {e}_1+2\mathbf {e}_2$
, the curves
$E_1\big \vert _{S}=2\mathbf {e}_1+2\mathbf {e}_2$
, the curves
![]() $\mathbf {e}_1$
and
$\mathbf {e}_1$
and
![]() $\mathbf {e}_2$
are sections of the conic bundle
$\mathbf {e}_2$
are sections of the conic bundle
![]() $\pi _2\vert _{S}$
, and each curve among
$\pi _2\vert _{S}$
, and each curve among
![]() $\mathbf {e}_1$
and
$\mathbf {e}_1$
and
![]() $\mathbf {e}_2$
contains one singular point of the surface S. In both cases, we may assume that
$\mathbf {e}_2$
contains one singular point of the surface S. In both cases, we may assume that
![]() $\ell _1\cap \mathbf {e}_1\ne \varnothing $
.
$\ell _1\cap \mathbf {e}_1\ne \varnothing $
.
Let us identify the surface S with its image in
![]() $\mathbb {P}^5$
via the anticanonical embedding
$\mathbb {P}^5$
via the anticanonical embedding
![]() $S\hookrightarrow \mathbb {P}^5$
. Then
$S\hookrightarrow \mathbb {P}^5$
. Then
![]() $\ell _1$
and
$\ell _1$
and
![]() $\ell _2$
and the curves contracted by
$\ell _2$
and the curves contracted by
![]() $\pi _3\vert _{S}$
are lines. In (
$\pi _3\vert _{S}$
are lines. In (
![]() $\mathbb {A}_1$
)-case, the surface S contains two additional lines
$\mathbb {A}_1$
)-case, the surface S contains two additional lines
![]() $\ell _3$
and
$\ell _3$
and
![]() $\ell _4$
such that
$\ell _4$
such that
![]() $\ell _3+\ell _4\sim \ell _1+\ell _2$
, the intersection
$\ell _3+\ell _4\sim \ell _1+\ell _2$
, the intersection
![]() $\ell _3\cap \ell _4$
is the singular point of the surface S, and the intersection graph of the lines
$\ell _3\cap \ell _4$
is the singular point of the surface S, and the intersection graph of the lines
![]() $\ell _1$
,
$\ell _1$
,
![]() $\ell _2$
,
$\ell _2$
,
![]() $\ell _3$
,
$\ell _3$
,
![]() $\ell _4$
,
$\ell _4$
,
![]() $\mathbf {e}_1$
,
$\mathbf {e}_1$
,
![]() $\mathbf {e}_2$
, and
$\mathbf {e}_2$
, and
![]() $\mathbf {e}_3$
is shown here:
$\mathbf {e}_3$
is shown here:

In this picture, we denoted by
![]() $\bullet $
the singular point of the surface S. Moreover, on the surface S, the intersections of the lines
$\bullet $
the singular point of the surface S. Moreover, on the surface S, the intersections of the lines
![]() $\ell _1$
,
$\ell _1$
,
![]() $\ell _2$
,
$\ell _2$
,
![]() $\ell _3$
,
$\ell _3$
,
![]() $\ell _4$
,
$\ell _4$
,
![]() $\mathbf {e}_1$
,
$\mathbf {e}_1$
,
![]() $\mathbf {e}_2$
, and
$\mathbf {e}_2$
, and
![]() $\mathbf {e}_3$
are given in the table below.
$\mathbf {e}_3$
are given in the table below.

Likewise, in (
![]() $2\mathbb {A}_1$
)-case, the surface S contains one additional line
$2\mathbb {A}_1$
)-case, the surface S contains one additional line
![]() $\ell _3$
such that
$\ell _3$
such that
![]() $2\ell _3\sim \ell _1+\ell _2$
, the line
$2\ell _3\sim \ell _1+\ell _2$
, the line
![]() $\ell _3$
passes through both singular points of the del Pezzo surface S, and the intersection graph of the lines on the surface S is shown in the following picture:
$\ell _3$
passes through both singular points of the del Pezzo surface S, and the intersection graph of the lines on the surface S is shown in the following picture:

As above, the singular points of the surface S are denoted by
![]() $\bullet $
. The intersections of the lines
$\bullet $
. The intersections of the lines
![]() $\ell _1$
,
$\ell _1$
,
![]() $\ell _2$
,
$\ell _2$
,
![]() $\ell _3$
,
$\ell _3$
,
![]() $\mathbf {e}_1$
, and
$\mathbf {e}_1$
, and
![]() $\mathbf {e}_2$
on the surface S are given in the table below.
$\mathbf {e}_2$
on the surface S are given in the table below.

Remark 21. By [Reference Cheltsov and Prokhorov7, Lem. 2.9], the lines in S generate the group
![]() $\mathrm {Cl}(S)$
and the cone of effective divisors
$\mathrm {Cl}(S)$
and the cone of effective divisors
![]() $\mathrm {Eff}(S)$
, and every extremal ray of the Mori cone
$\mathrm {Eff}(S)$
, and every extremal ray of the Mori cone
![]() $\overline {\mathrm {NE}}(S)$
is generated by the class of a line.
$\overline {\mathrm {NE}}(S)$
is generated by the class of a line.
In (
![]() $\mathbb {A}_1$
)-case, the point P is one of the points
$\mathbb {A}_1$
)-case, the point P is one of the points
![]() $\mathbf {e}_1\cap \ell _1$
,
$\mathbf {e}_1\cap \ell _1$
,
![]() $\mathbf {e}_2\cap \ell _2$
, or
$\mathbf {e}_2\cap \ell _2$
, or
![]() $\mathbf {e}_3\cap \ell _2$
, because
$\mathbf {e}_3\cap \ell _2$
, because
![]() $P\in E_1\cap E_2$
. On the other hand, if
$P\in E_1\cap E_2$
. On the other hand, if
![]() $P=\mathbf {e}_2\cap \ell _2$
or
$P=\mathbf {e}_2\cap \ell _2$
or
![]() $P=\mathbf {e}_3\cap \ell _2$
, it follows from Corollary 12 that
$P=\mathbf {e}_3\cap \ell _2$
, it follows from Corollary 12 that
![]() $\delta _P(X)>1$
. In (
$\delta _P(X)>1$
. In (
![]() $2\mathbb {A}_1$
)-case, either
$2\mathbb {A}_1$
)-case, either
![]() $P=\mathbf {e}_1\cap \ell _1$
or
$P=\mathbf {e}_1\cap \ell _1$
or
![]() $P=\mathbf {e}_2\cap \ell _2$
. Therefore, to complete the proof of Main Theorem, we may assume that
$P=\mathbf {e}_2\cap \ell _2$
. Therefore, to complete the proof of Main Theorem, we may assume that
![]() $P=\mathbf {e}_1\cap \ell _1$
in both cases.
$P=\mathbf {e}_1\cap \ell _1$
in both cases.
Now, we will apply Corollary 13 to the surface S with
![]() $C=\mathbf {e}_1$
at the point P. We have
$C=\mathbf {e}_1$
at the point P. We have
![]() $\tau =\frac {3}{2}$
. As in the proof of Corollary 10, we see that
$\tau =\frac {3}{2}$
. As in the proof of Corollary 10, we see that
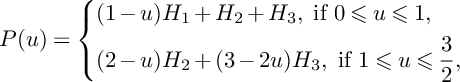 $$ \begin{align*}P(u)=\left\{\begin{aligned} &(1-u)H_1+H_2+H_3,\ \text{if }0\leqslant u\leqslant 1, \\ &(2-u)H_2+(3-2u)H_3,\ \text{if }1\leqslant u\leqslant \frac{3}{2}, \\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}P(u)=\left\{\begin{aligned} &(1-u)H_1+H_2+H_3,\ \text{if }0\leqslant u\leqslant 1, \\ &(2-u)H_2+(3-2u)H_3,\ \text{if }1\leqslant u\leqslant \frac{3}{2}, \\ \end{aligned} \right. \end{align*} $$
and
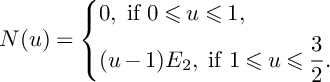 $$ \begin{align*}N(u)=\left\{\begin{aligned} &0,\ \text{if }0\leqslant u\leqslant 1, \\ &(u-1)E_2,\ \text{if }1\leqslant u\leqslant \frac{3}{2}.\\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}N(u)=\left\{\begin{aligned} &0,\ \text{if }0\leqslant u\leqslant 1, \\ &(u-1)E_2,\ \text{if }1\leqslant u\leqslant \frac{3}{2}.\\ \end{aligned} \right. \end{align*} $$
Since
![]() $H_1\vert _{S}\sim 0$
,
$H_1\vert _{S}\sim 0$
,
![]() $H_2\vert _{S}\sim \ell _1+\ell _2$
, and
$H_2\vert _{S}\sim \ell _1+\ell _2$
, and
![]() $H_3\vert _{S}\sim \ell _1+2\mathbf {e}_1$
, we have
$H_3\vert _{S}\sim \ell _1+2\mathbf {e}_1$
, we have
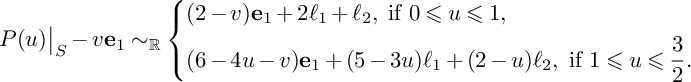 $$ \begin{align*}P(u)\big\vert_{S}-v\mathbf{e}_1\sim_{\mathbb{R}}\left\{\begin{aligned} &(2-v)\mathbf{e}_1+2\ell_1+\ell_2,\ \text{if }0\leqslant u\leqslant 1, \\ &(6-4u-v)\mathbf{e}_1+(5-3u)\ell_1+(2-u)\ell_2,\ \text{if }1\leqslant u\leqslant \frac{3}{2}. \\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}P(u)\big\vert_{S}-v\mathbf{e}_1\sim_{\mathbb{R}}\left\{\begin{aligned} &(2-v)\mathbf{e}_1+2\ell_1+\ell_2,\ \text{if }0\leqslant u\leqslant 1, \\ &(6-4u-v)\mathbf{e}_1+(5-3u)\ell_1+(2-u)\ell_2,\ \text{if }1\leqslant u\leqslant \frac{3}{2}. \\ \end{aligned} \right. \end{align*} $$
Thus, since the intersection form of the curves
![]() $\ell _1$
and
$\ell _1$
and
![]() $\ell _2$
is semi-negative definite, we get
$\ell _2$
is semi-negative definite, we get
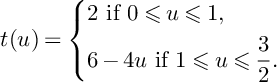 $$ \begin{align*}t(u)=\left\{\begin{aligned} &2\ \text{if }0\leqslant u\leqslant 1, \\ &6-4u\ \text{if }1\leqslant u\leqslant \frac{3}{2}.\\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}t(u)=\left\{\begin{aligned} &2\ \text{if }0\leqslant u\leqslant 1, \\ &6-4u\ \text{if }1\leqslant u\leqslant \frac{3}{2}.\\ \end{aligned} \right. \end{align*} $$
Similarly, if
![]() $0\leqslant u\leqslant 1$
, then
$0\leqslant u\leqslant 1$
, then
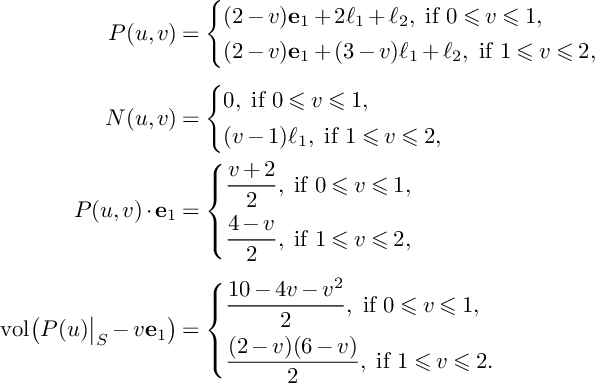 $$ \begin{align*}P(u,v)&=\left\{\begin{aligned} &(2-v)\mathbf{e}_1+2\ell_1+\ell_2,\ \text{if }0\leqslant v\leqslant 1, \\ &(2-v)\mathbf{e}_1+(3-v)\ell_1+\ell_2,\ \text{if }1\leqslant v\leqslant 2, \\ \end{aligned} \right. \\[4pt]N(u,v)&=\left\{\begin{aligned} &0,\ \text{if }0\leqslant v\leqslant 1, \\ &(v-1)\ell_1,\ \text{if }1\leqslant v\leqslant 2,\\ \end{aligned} \right. \\P(u,v)\cdot\mathbf{e}_1&=\left\{\begin{aligned} &\frac{v+2}{2},\ \text{if }0\leqslant v\leqslant 1, \\ &\frac{4-v}{2},\ \text{if }1\leqslant v\leqslant 2, \\ \end{aligned} \right.\\[4pt]\mathrm{vol}\big(P(u)\big\vert_{S}-v\mathbf{e}_1\big)&=\left\{\begin{aligned} &\frac{10-4v-v^2}{2},\ \text{if }0\leqslant v\leqslant 1, \\ &\frac{(2-v)(6-v)}{2},\ \text{if }1\leqslant v\leqslant 2.\\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}P(u,v)&=\left\{\begin{aligned} &(2-v)\mathbf{e}_1+2\ell_1+\ell_2,\ \text{if }0\leqslant v\leqslant 1, \\ &(2-v)\mathbf{e}_1+(3-v)\ell_1+\ell_2,\ \text{if }1\leqslant v\leqslant 2, \\ \end{aligned} \right. \\[4pt]N(u,v)&=\left\{\begin{aligned} &0,\ \text{if }0\leqslant v\leqslant 1, \\ &(v-1)\ell_1,\ \text{if }1\leqslant v\leqslant 2,\\ \end{aligned} \right. \\P(u,v)\cdot\mathbf{e}_1&=\left\{\begin{aligned} &\frac{v+2}{2},\ \text{if }0\leqslant v\leqslant 1, \\ &\frac{4-v}{2},\ \text{if }1\leqslant v\leqslant 2, \\ \end{aligned} \right.\\[4pt]\mathrm{vol}\big(P(u)\big\vert_{S}-v\mathbf{e}_1\big)&=\left\{\begin{aligned} &\frac{10-4v-v^2}{2},\ \text{if }0\leqslant v\leqslant 1, \\ &\frac{(2-v)(6-v)}{2},\ \text{if }1\leqslant v\leqslant 2.\\ \end{aligned} \right. \end{align*} $$
Likewise, if
![]() $1\leqslant u\leqslant \frac {3}{2}$
, then
$1\leqslant u\leqslant \frac {3}{2}$
, then
 $$ \begin{align*}P(u,v)&=\left\{\begin{aligned} &(6-4u-v)\mathbf{e}_1+(5-3u)\ell_1+(2-u)\ell_2,\ \text{if }0\leqslant v\leqslant 3-2u, \\ &(6-4u-v)\mathbf{e}_1+(8-5u-v)\ell_1+(2-u)\ell_2,\ \text{if }3-2u\leqslant v\leqslant 6-4u, \\ \end{aligned} \right. \\[4pt]N(u,v)&=\left\{\begin{aligned} &0,\ \text{if }0\leqslant v\leqslant 3-2u, \\ &(v+2u-3)\ell_1,\ \text{if }3-2u\leqslant v\leqslant 6-4u,\\ \end{aligned} \right.\\[4pt]P(u,v)\cdot\mathbf{e}_1&=\left\{\begin{aligned} &\frac{4+v-2u}{2},\ \text{if }0\leqslant v\leqslant 3-2u, \\ &\frac{10-6u-v}{2},\ \text{if }3-2u\leqslant v\leqslant 6-4u, \\ \end{aligned} \right. \\[4pt]\mathrm{vol}\big(P(u)\big\vert_{S}-v\mathbf{e}_1\big)&=\left\{\begin{aligned} &\frac{66+24u^2+4uv-v^2-80u-8v}{2},\ \text{if }0\leqslant v\leqslant 3-2u, \\ &\frac{(6-4u-v)(14-8u-v)}{2},\ \text{if }3-2u\leqslant v\leqslant 6-4u.\\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}P(u,v)&=\left\{\begin{aligned} &(6-4u-v)\mathbf{e}_1+(5-3u)\ell_1+(2-u)\ell_2,\ \text{if }0\leqslant v\leqslant 3-2u, \\ &(6-4u-v)\mathbf{e}_1+(8-5u-v)\ell_1+(2-u)\ell_2,\ \text{if }3-2u\leqslant v\leqslant 6-4u, \\ \end{aligned} \right. \\[4pt]N(u,v)&=\left\{\begin{aligned} &0,\ \text{if }0\leqslant v\leqslant 3-2u, \\ &(v+2u-3)\ell_1,\ \text{if }3-2u\leqslant v\leqslant 6-4u,\\ \end{aligned} \right.\\[4pt]P(u,v)\cdot\mathbf{e}_1&=\left\{\begin{aligned} &\frac{4+v-2u}{2},\ \text{if }0\leqslant v\leqslant 3-2u, \\ &\frac{10-6u-v}{2},\ \text{if }3-2u\leqslant v\leqslant 6-4u, \\ \end{aligned} \right. \\[4pt]\mathrm{vol}\big(P(u)\big\vert_{S}-v\mathbf{e}_1\big)&=\left\{\begin{aligned} &\frac{66+24u^2+4uv-v^2-80u-8v}{2},\ \text{if }0\leqslant v\leqslant 3-2u, \\ &\frac{(6-4u-v)(14-8u-v)}{2},\ \text{if }3-2u\leqslant v\leqslant 6-4u.\\ \end{aligned} \right. \end{align*} $$
Integrating, we get
![]() $S(W_{\bullet ,\bullet }^S;\mathbf {e}_1)=\frac {137}{144}$
and
$S(W_{\bullet ,\bullet }^S;\mathbf {e}_1)=\frac {137}{144}$
and
![]() $S(W_{\bullet , \bullet ,\bullet }^{S,\mathbf {e}_1};P)=\frac {59}{96}+F_P(W_{\bullet ,\bullet ,\bullet }^{S,\mathbf {e}_1})$
. To compute
$S(W_{\bullet , \bullet ,\bullet }^{S,\mathbf {e}_1};P)=\frac {59}{96}+F_P(W_{\bullet ,\bullet ,\bullet }^{S,\mathbf {e}_1})$
. To compute
![]() $F_P(W_{\bullet ,\bullet ,\bullet }^{S,\mathbf {e}_1})$
, we let
$F_P(W_{\bullet ,\bullet ,\bullet }^{S,\mathbf {e}_1})$
, we let
![]() $Z=E_2\vert _{S}$
. Then Z is a smooth curve of genus
$Z=E_2\vert _{S}$
. Then Z is a smooth curve of genus
![]() $3$
such that
$3$
such that
![]() $\pi (Z)$
is a smooth quartic in
$\pi (Z)$
is a smooth quartic in
![]() $\mathbb {P}^2_{x,y,z}$
. Moreover, the curve Z is contained in the smooth locus of the surface S, and
$\mathbb {P}^2_{x,y,z}$
. Moreover, the curve Z is contained in the smooth locus of the surface S, and
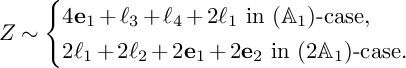 $$ \begin{align*}Z\sim\left\{\begin{aligned} &4\mathbf{e}_1+\ell_3+\ell_4+2\ell_1\ \text{in (}\mathbb{A}_1\text{)-case}, \\ &2\ell_1+2\ell_2+2\mathbf{e}_1+2\mathbf{e}_2\ \text{in (}2\mathbb{A}_1\text{)-case}. \\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}Z\sim\left\{\begin{aligned} &4\mathbf{e}_1+\ell_3+\ell_4+2\ell_1\ \text{in (}\mathbb{A}_1\text{)-case}, \\ &2\ell_1+2\ell_2+2\mathbf{e}_1+2\mathbf{e}_2\ \text{in (}2\mathbb{A}_1\text{)-case}. \\ \end{aligned} \right. \end{align*} $$
In particular, we have
![]() $Z\cdot \mathbf {e}_1=1$
. Since
$Z\cdot \mathbf {e}_1=1$
. Since
![]() $\mathbf {e}_1\not \subset Z$
, we have
$\mathbf {e}_1\not \subset Z$
, we have
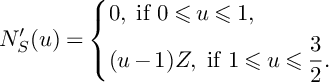 $$ \begin{align*}N_S^\prime(u)=\left\{\begin{aligned} &0,\ \text{if }0\leqslant u\leqslant 1, \\ &(u-1)Z,\ \text{if }1\leqslant u\leqslant \frac{3}{2}.\\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}N_S^\prime(u)=\left\{\begin{aligned} &0,\ \text{if }0\leqslant u\leqslant 1, \\ &(u-1)Z,\ \text{if }1\leqslant u\leqslant \frac{3}{2}.\\ \end{aligned} \right. \end{align*} $$
Note that
![]() $P\in Z$
, because
$P\in Z$
, because
![]() $P\in E_1\cap E_2$
. Thus, since
$P\in E_1\cap E_2$
. Thus, since
![]() $\mathbf {e}_1\cdot Z=1$
and
$\mathbf {e}_1\cdot Z=1$
and
![]() $\mathbf {e}_1\cdot \ell _1=1$
, we have
$\mathbf {e}_1\cdot \ell _1=1$
, we have
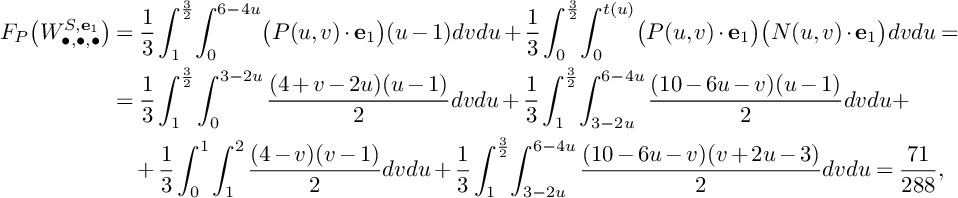 $$ \begin{align*} F_P\big(W_{\bullet,\bullet,\bullet}^{S,\mathbf{e}_1}\big)&=\frac{1}{3}\int_1^{\frac{3}{2}}\!\int_0^{6-4u}\!\big(P(u,v)\cdot \mathbf{e}_1\big)(u-1)dvdu+\frac{1}{3}\int_0^{\frac{3}{2}}\!\int_0^{t(u)}\!\big(P(u,v)\cdot \mathbf{e}_1\big)\big(N(u,v)\cdot \mathbf{e}_1\big)dvdu=\\&=\frac{1}{3}\int_1^{\frac{3}{2}}\int_0^{3-2u}\frac{(4+v-2u)(u-1)}{2}dvdu+\frac{1}{3}\int_1^{\frac{3}{2}}\!\int_{3-2u}^{6-4u}\frac{(10-6u-v)(u-1)}{2}dvdu+\\& \quad +\frac{1}{3}\int_0^{1}\int_1^{2}\frac{(4-v)(v-1)}{2}dvdu+\frac{1}{3}\int_1^{\frac{3}{2}}\!\int_{3-2u}^{6-4u}\frac{(10-6u-v)(v+2u-3)}{2}dvdu=\frac{71}{288}, \end{align*} $$
$$ \begin{align*} F_P\big(W_{\bullet,\bullet,\bullet}^{S,\mathbf{e}_1}\big)&=\frac{1}{3}\int_1^{\frac{3}{2}}\!\int_0^{6-4u}\!\big(P(u,v)\cdot \mathbf{e}_1\big)(u-1)dvdu+\frac{1}{3}\int_0^{\frac{3}{2}}\!\int_0^{t(u)}\!\big(P(u,v)\cdot \mathbf{e}_1\big)\big(N(u,v)\cdot \mathbf{e}_1\big)dvdu=\\&=\frac{1}{3}\int_1^{\frac{3}{2}}\int_0^{3-2u}\frac{(4+v-2u)(u-1)}{2}dvdu+\frac{1}{3}\int_1^{\frac{3}{2}}\!\int_{3-2u}^{6-4u}\frac{(10-6u-v)(u-1)}{2}dvdu+\\& \quad +\frac{1}{3}\int_0^{1}\int_1^{2}\frac{(4-v)(v-1)}{2}dvdu+\frac{1}{3}\int_1^{\frac{3}{2}}\!\int_{3-2u}^{6-4u}\frac{(10-6u-v)(v+2u-3)}{2}dvdu=\frac{71}{288}, \end{align*} $$
so that
![]() $S(W_{\bullet , \bullet ,\bullet }^{S,\mathbf {e}_1};P)=\frac {31}{36}$
. Now, applying Corollary 13, we get
$S(W_{\bullet , \bullet ,\bullet }^{S,\mathbf {e}_1};P)=\frac {31}{36}$
. Now, applying Corollary 13, we get
![]() $\delta _P(X)>1$
, because
$\delta _P(X)>1$
, because
![]() $S_X(S)<1$
. Therefore, we see that
$S_X(S)<1$
. Therefore, we see that
![]() $\beta (\mathbf {F})>0$
. By [Reference Fujita11], [Reference Li13], this completes the proof of Main Theorem.
$\beta (\mathbf {F})>0$
. By [Reference Fujita11], [Reference Li13], this completes the proof of Main Theorem.
Remark 22. Instead of using Corollary 13, we can finish the proof of Main Theorem as follows. Let F be a divisor over S such that
![]() $P\in C_S(F)$
, and let
$P\in C_S(F)$
, and let
![]() $\mathcal {C}$
be a fiber of the conic bundle
$\mathcal {C}$
be a fiber of the conic bundle
![]() $\pi _2\vert _{S}$
. Then, arguing as in the proof of Corollary 10, we get
$\pi _2\vert _{S}$
. Then, arguing as in the proof of Corollary 10, we get
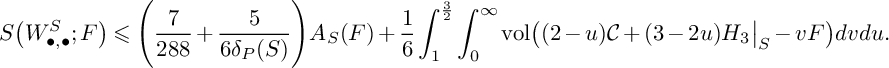 $$ \begin{align*}S\big(W^S_{\bullet,\bullet};F\big)\leqslant \Bigg(\frac{7}{288}+\frac{5}{6\delta_P(S)}\Bigg)A_S(F)+\frac{1}{6}\int_{1}^{\frac{3}{2}}\int_0^\infty\mathrm{vol}\big((2-u)\mathcal{C}+(3-2u)H_3\big\vert_{S}-vF\big)dvdu. \end{align*} $$
$$ \begin{align*}S\big(W^S_{\bullet,\bullet};F\big)\leqslant \Bigg(\frac{7}{288}+\frac{5}{6\delta_P(S)}\Bigg)A_S(F)+\frac{1}{6}\int_{1}^{\frac{3}{2}}\int_0^\infty\mathrm{vol}\big((2-u)\mathcal{C}+(3-2u)H_3\big\vert_{S}-vF\big)dvdu. \end{align*} $$
But
![]() $\delta _P(S)=1$
by Lemmas 25 and 26, since
$\delta _P(S)=1$
by Lemmas 25 and 26, since
![]() $P=\mathbf {e}_1\cap \ell _1$
. Thus, we have
$P=\mathbf {e}_1\cap \ell _1$
. Thus, we have
 $$ \begin{align} S\big(W^S_{\bullet,\bullet};F\big)&\leqslant\frac{247}{288}A_S(F)+\frac{1}{6}\int_{1}^{\frac{3}{2}}\int_0^\infty\mathrm{vol}\big((2-u)\mathcal{C}+(3-2u)H_3\big\vert_{S}-vF\big)dvdu=\\&=\frac{247}{288}A_S(F)+\frac{1}{6}\int_{1}^{\frac{3}{2}}(3-2u)^3\int_0^\infty\mathrm{vol}\Bigg(\frac{2-u}{3-2u}\mathcal{C}+H_3\big\vert_{S}-vF\Bigg)dvdu=\nonumber\\&=\frac{247}{288}A_S(F)+\frac{1}{6}\int_{1}^{\frac{3}{2}}(3-2u)^3\int_0^\infty\mathrm{vol}\Bigg(-K_S+\frac{u-1}{3-2u}\mathcal{C}-vF\Bigg)dvdu.\nonumber \end{align} $$
$$ \begin{align} S\big(W^S_{\bullet,\bullet};F\big)&\leqslant\frac{247}{288}A_S(F)+\frac{1}{6}\int_{1}^{\frac{3}{2}}\int_0^\infty\mathrm{vol}\big((2-u)\mathcal{C}+(3-2u)H_3\big\vert_{S}-vF\big)dvdu=\\&=\frac{247}{288}A_S(F)+\frac{1}{6}\int_{1}^{\frac{3}{2}}(3-2u)^3\int_0^\infty\mathrm{vol}\Bigg(\frac{2-u}{3-2u}\mathcal{C}+H_3\big\vert_{S}-vF\Bigg)dvdu=\nonumber\\&=\frac{247}{288}A_S(F)+\frac{1}{6}\int_{1}^{\frac{3}{2}}(3-2u)^3\int_0^\infty\mathrm{vol}\Bigg(-K_S+\frac{u-1}{3-2u}\mathcal{C}-vF\Bigg)dvdu.\nonumber \end{align} $$
Set
![]() $L=-K_S+t\mathcal {C}$
for
$L=-K_S+t\mathcal {C}$
for
![]() $t\in \mathbb {R}_{\geqslant 0}$
. Then L is ample and
$t\in \mathbb {R}_{\geqslant 0}$
. Then L is ample and
![]() $L^2=5+4t$
. Define
$L^2=5+4t$
. Define
![]() $\delta _P(S,L)$
as in Appendix 1. Then, applying [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Cor. 1.7.24] to the flag
$\delta _P(S,L)$
as in Appendix 1. Then, applying [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Cor. 1.7.24] to the flag
![]() $P\in \mathbf {e}_1\subset S$
, we get
$P\in \mathbf {e}_1\subset S$
, we get
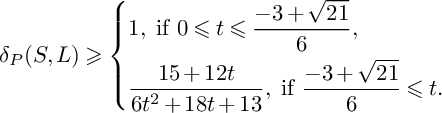 $$ \begin{align*}\delta_P(S,L)\geqslant \left\{\begin{aligned} &1,\ \text{if }0\leqslant t\leqslant \frac{-3+\sqrt{21}}{6}, \\ &\frac{15+12t}{6t^2+18t+13},\ \text{if }\frac{-3+\sqrt{21}}{6}\leqslant t.\\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}\delta_P(S,L)\geqslant \left\{\begin{aligned} &1,\ \text{if }0\leqslant t\leqslant \frac{-3+\sqrt{21}}{6}, \\ &\frac{15+12t}{6t^2+18t+13},\ \text{if }\frac{-3+\sqrt{21}}{6}\leqslant t.\\ \end{aligned} \right. \end{align*} $$
The proof of this inequality is very similar to our computations of
![]() $S(W_{\bullet ,\bullet }^S;\mathbf {e}_1)$
and
$S(W_{\bullet ,\bullet }^S;\mathbf {e}_1)$
and
![]() $S(W_{\bullet , \bullet ,\bullet }^{S,\mathbf {e}_1};P)$
, so that we omit the details. Now, we let
$S(W_{\bullet , \bullet ,\bullet }^{S,\mathbf {e}_1};P)$
, so that we omit the details. Now, we let
![]() $t=\frac {u-1}{3-2u}$
. Then
$t=\frac {u-1}{3-2u}$
. Then
![]() $t\geqslant \frac {-3+\sqrt {21}}{6}\iff u\geqslant \frac {3}{2}(1-\frac {1}{\sqrt {21}})$
, so
$t\geqslant \frac {-3+\sqrt {21}}{6}\iff u\geqslant \frac {3}{2}(1-\frac {1}{\sqrt {21}})$
, so
 $$ \begin{align*} &\frac{1}{6}\int_{1}^{\frac{3}{2}}(3-2u)^3\int_0^\infty\mathrm{vol}\big(-K_S+t\mathcal{C}-vF\big)dvdu=\\& \quad =\frac{1}{6}\int_{1}^{\frac{3}{2}}(3-2u)^3(5+4t)S_{L}(F)du\leqslant \frac{1}{6}\int_{1}^{\frac{3}{2}(1-\frac{1}{\sqrt{21}})}(3-2u)^3(5+4t)A_S(F)du+\\& \qquad +\frac{1}{6}\int_{\frac{3}{2}(1-\frac{1}{\sqrt{21}})}^{\frac{3}{2}}(3-2u)^3(5+4t)\frac{15+12t}{6t^2+18t+13}A_{S}(F)du=\frac{247}{2,016}A_{S}(F). \end{align*} $$
$$ \begin{align*} &\frac{1}{6}\int_{1}^{\frac{3}{2}}(3-2u)^3\int_0^\infty\mathrm{vol}\big(-K_S+t\mathcal{C}-vF\big)dvdu=\\& \quad =\frac{1}{6}\int_{1}^{\frac{3}{2}}(3-2u)^3(5+4t)S_{L}(F)du\leqslant \frac{1}{6}\int_{1}^{\frac{3}{2}(1-\frac{1}{\sqrt{21}})}(3-2u)^3(5+4t)A_S(F)du+\\& \qquad +\frac{1}{6}\int_{\frac{3}{2}(1-\frac{1}{\sqrt{21}})}^{\frac{3}{2}}(3-2u)^3(5+4t)\frac{15+12t}{6t^2+18t+13}A_{S}(F)du=\frac{247}{2,016}A_{S}(F). \end{align*} $$
Now, using (♡), we get
![]() $S(W^S_{\bullet ,\bullet };F)\leqslant \frac {247}{288}A_S(F)+\frac {247}{2,016}A_{S}(F)=\frac {247}{252}A_S(F)$
. Then
$S(W^S_{\bullet ,\bullet };F)\leqslant \frac {247}{288}A_S(F)+\frac {247}{2,016}A_{S}(F)=\frac {247}{252}A_S(F)$
. Then
![]() $\delta _{P}(S;W^S_{\bullet ,\bullet })\geqslant \frac {252}{247}$
, so that
$\delta _{P}(S;W^S_{\bullet ,\bullet })\geqslant \frac {252}{247}$
, so that
![]() $\delta _P(X)>1$
by (3.1), since
$\delta _P(X)>1$
by (3.1), since
![]() $S_X(S)<1$
by [Reference Fujita10, Th. 10.1].
$S_X(S)<1$
by [Reference Fujita10, Th. 10.1].
Appendix A
 $\delta $
-invariants of del Pezzo surfaces
$\delta $
-invariants of del Pezzo surfaces
In this appendix, we present three rather sporadic results about
![]() $\delta $
-invariants of del Pezzo surfaces with at most du Val singularities, which are used in the proof of Main Theorem.
$\delta $
-invariants of del Pezzo surfaces with at most du Val singularities, which are used in the proof of Main Theorem.
Let S be a del Pezzo surface that has at most du Val singularities, let L be an ample
![]() $\mathbb {R}$
-divisor on the surface S, and let P be a point in S. Set
$\mathbb {R}$
-divisor on the surface S, and let P be a point in S. Set
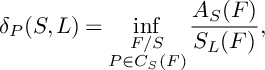 $$ \begin{align*}\delta_P(S,L)=\inf_{\substack{F/S\\ P\in C_S(F)}}\frac{A_{S}(F)}{S_{L}(F)}, \end{align*} $$
$$ \begin{align*}\delta_P(S,L)=\inf_{\substack{F/S\\ P\in C_S(F)}}\frac{A_{S}(F)}{S_{L}(F)}, \end{align*} $$
where infimum is taken over all prime divisors F over S such that
![]() $P\in C_S(F)$
, and
$P\in C_S(F)$
, and
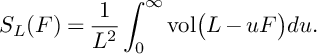 $$ \begin{align*}S_{L}(F)=\frac{1}{L^2}\int_0^\infty \mathrm{vol}\big(L-uF\big)du. \end{align*} $$
$$ \begin{align*}S_{L}(F)=\frac{1}{L^2}\int_0^\infty \mathrm{vol}\big(L-uF\big)du. \end{align*} $$
Example 23. Suppose that S is a smooth cubic surface in
![]() $\mathbb {P}^3$
and that
$\mathbb {P}^3$
and that
![]() $L=-K_S$
. Let T be the hyperplane section of the cubic surface S that is singular at P. Then it follows from [Reference Abban and Zhuang1, Th. 4.6] that
$L=-K_S$
. Let T be the hyperplane section of the cubic surface S that is singular at P. Then it follows from [Reference Abban and Zhuang1, Th. 4.6] that
 $$ \begin{align*}\delta_P(S,L)=\left\{\begin{aligned} &\frac{3}{2},\ \text{if }T\text{ is a union of three lines such that all of them contains }P,\\ &\frac{27}{17},\ \text{if }T\text{ is a~union of a~line and a~conic that are tangent at }P,\\ &\frac{5}{3},\ \text{if }T\text{ is an irreducible cuspidal cubic curve},\\ &\frac{18}{11},\ \text{if }T\text{ is a union of three lines such that only two of them contain }P,\\ &\frac{9}{25-8\sqrt{6}},\ \text{if }T\text{ is a~union of a~line and a~conic that intersect transversally at }P,\\ &\frac{12}{7},\ \text{if }T\text{ is an irreducible nodal cubic curve}. \end{aligned} \right. \end{align*} $$
$$ \begin{align*}\delta_P(S,L)=\left\{\begin{aligned} &\frac{3}{2},\ \text{if }T\text{ is a union of three lines such that all of them contains }P,\\ &\frac{27}{17},\ \text{if }T\text{ is a~union of a~line and a~conic that are tangent at }P,\\ &\frac{5}{3},\ \text{if }T\text{ is an irreducible cuspidal cubic curve},\\ &\frac{18}{11},\ \text{if }T\text{ is a union of three lines such that only two of them contain }P,\\ &\frac{9}{25-8\sqrt{6}},\ \text{if }T\text{ is a~union of a~line and a~conic that intersect transversally at }P,\\ &\frac{12}{7},\ \text{if }T\text{ is an irreducible nodal cubic curve}. \end{aligned} \right. \end{align*} $$
It would be nice to find an explicit formula for
![]() $\delta _P(S,L)$
in all possible cases. But this problem seems to be very difficult. So, we will only estimate
$\delta _P(S,L)$
in all possible cases. But this problem seems to be very difficult. So, we will only estimate
![]() $\delta _P(S,L)$
in three cases when
$\delta _P(S,L)$
in three cases when
![]() $K_S^2\in \{4,5\}$
.
$K_S^2\in \{4,5\}$
.
Suppose that
![]() $4\leqslant K_S^2\leqslant 5$
. Let us identify S with its image in the anticanonical embedding.
$4\leqslant K_S^2\leqslant 5$
. Let us identify S with its image in the anticanonical embedding.
Lemma 24. Suppose that S is smooth and
![]() $K_S^2=4$
. Let C be a possibly reducible conic in S that passes through P, and let
$K_S^2=4$
. Let C be a possibly reducible conic in S that passes through P, and let
![]() $L=-K_S+tC$
for
$L=-K_S+tC$
for
![]() $t\in \mathbb {R}_{\geqslant 0}$
. If the conic C is smooth, then
$t\in \mathbb {R}_{\geqslant 0}$
. If the conic C is smooth, then
 $$ \begin{align} \delta_P(S,L)\geqslant \begin{cases} &\frac{24}{19+8t+t^2},\ \text{if }0\leqslant t\leqslant 1, \\ &\frac{6(1+t)}{5+6t+3t^2},\ \text{if }t\geqslant 1. \end{cases} \end{align} $$
$$ \begin{align} \delta_P(S,L)\geqslant \begin{cases} &\frac{24}{19+8t+t^2},\ \text{if }0\leqslant t\leqslant 1, \\ &\frac{6(1+t)}{5+6t+3t^2},\ \text{if }t\geqslant 1. \end{cases} \end{align} $$
Similarly, if C is a reducible conic, then
 $$ \begin{align} \delta_L(S,L)\geqslant \frac{24(1+t)}{19+30t+12t^2}. \end{align} $$
$$ \begin{align} \delta_L(S,L)\geqslant \frac{24(1+t)}{19+30t+12t^2}. \end{align} $$
Proof. The proof of this lemma is similar to the proof of [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Lem. 2.12]. Namely, as in that proof, we will apply [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Th. 1.7.1], [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Cor. 1.7.12], and [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Cor. 1.7.25] to get (♣) and (♠). Let us use notations introduced in [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Sect. 1] applied to S polarized by the ample divisor L.
First, we suppose that P is not contained in any line in S. In particular, the conic C is smooth. Let
![]() $\sigma \colon \widetilde {S}\to S$
be the blowup of the point P, let E be the exceptional curve of the blowup
$\sigma \colon \widetilde {S}\to S$
be the blowup of the point P, let E be the exceptional curve of the blowup
![]() $\sigma $
, and let
$\sigma $
, and let
![]() $\widetilde {C}$
be the proper transform on
$\widetilde {C}$
be the proper transform on
![]() $\widetilde {S}$
of the conic C. Then
$\widetilde {S}$
of the conic C. Then
![]() $\widetilde {S}$
is a smooth cubic surface in
$\widetilde {S}$
is a smooth cubic surface in
![]() $\mathbb {P}^3$
, and there exists a unique line
$\mathbb {P}^3$
, and there exists a unique line
![]() $\mathbf {l}\subset \widetilde {S}$
such that
$\mathbf {l}\subset \widetilde {S}$
such that
![]() $-K_{\widetilde {S}}\sim \widetilde {C}+E+\mathbf {l}$
. Take
$-K_{\widetilde {S}}\sim \widetilde {C}+E+\mathbf {l}$
. Take
![]() $u\in \mathbb {R}_{\geqslant 0}$
. Then
$u\in \mathbb {R}_{\geqslant 0}$
. Then
which implies that
![]() $\sigma ^*(L)-uE$
is pseudoeffective
$\sigma ^*(L)-uE$
is pseudoeffective
![]() $\iff u\leqslant 2+t$
. Similarly, we see that
$\iff u\leqslant 2+t$
. Similarly, we see that
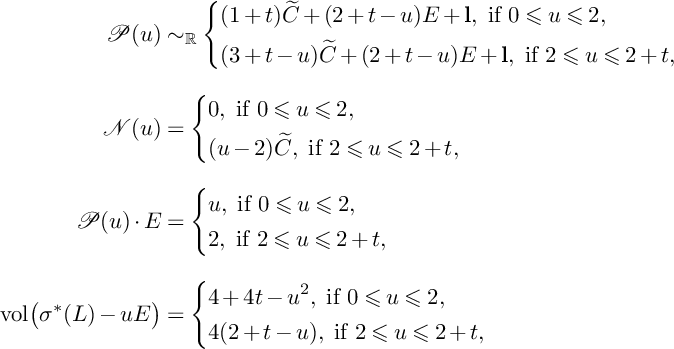 $$ \begin{align*}\mathscr{P}(u)&\sim_{\mathbb{R}}\left\{\begin{aligned} &(1+t)\widetilde{C}+(2+t-u)E+\mathbf{l},\ \text{if }0\leqslant u\leqslant 2, \\ &(3+t-u)\widetilde{C}+(2+t-u)E+\mathbf{l},\ \text{if }2\leqslant u\leqslant2+t, \\ \end{aligned} \right.\\[8pt]\mathscr{N}(u)&=\left\{\begin{aligned} &0,\ \text{if }0\leqslant u\leqslant 2, \\ &(u-2)\widetilde{C},\ \text{if }2\leqslant u\leqslant 2+t,\\ \end{aligned} \right.\\[8pt]\mathscr{P}(u)\cdot E&=\left\{\begin{aligned} &u,\ \text{if }0\leqslant u\leqslant 2, \\ &2,\ \text{if }2\leqslant u\leqslant2+t, \\ \end{aligned} \right.\\[8pt]\mathrm{vol}\big(\sigma^*(L)-uE\big)&=\left\{\begin{aligned} &4+4t-u^2,\ \text{if }0\leqslant u\leqslant 2, \\ &4(2+t-u),\ \text{if }2\leqslant u\leqslant2+t, \\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}\mathscr{P}(u)&\sim_{\mathbb{R}}\left\{\begin{aligned} &(1+t)\widetilde{C}+(2+t-u)E+\mathbf{l},\ \text{if }0\leqslant u\leqslant 2, \\ &(3+t-u)\widetilde{C}+(2+t-u)E+\mathbf{l},\ \text{if }2\leqslant u\leqslant2+t, \\ \end{aligned} \right.\\[8pt]\mathscr{N}(u)&=\left\{\begin{aligned} &0,\ \text{if }0\leqslant u\leqslant 2, \\ &(u-2)\widetilde{C},\ \text{if }2\leqslant u\leqslant 2+t,\\ \end{aligned} \right.\\[8pt]\mathscr{P}(u)\cdot E&=\left\{\begin{aligned} &u,\ \text{if }0\leqslant u\leqslant 2, \\ &2,\ \text{if }2\leqslant u\leqslant2+t, \\ \end{aligned} \right.\\[8pt]\mathrm{vol}\big(\sigma^*(L)-uE\big)&=\left\{\begin{aligned} &4+4t-u^2,\ \text{if }0\leqslant u\leqslant 2, \\ &4(2+t-u),\ \text{if }2\leqslant u\leqslant2+t, \\ \end{aligned} \right. \end{align*} $$
where we denote by
![]() $\mathscr {P}(u)$
the positive part of the Zariski decomposition of the divisor
$\mathscr {P}(u)$
the positive part of the Zariski decomposition of the divisor
![]() $\sigma ^*(L)-uE$
, and we denote by
$\sigma ^*(L)-uE$
, and we denote by
![]() $\mathscr {N}(u)$
its negative part. This gives
$\mathscr {N}(u)$
its negative part. This gives
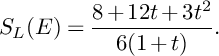 $$ \begin{align*}S_L(E)=\frac{8+12t+3t^2}{6(1+t)}. \end{align*} $$
$$ \begin{align*}S_L(E)=\frac{8+12t+3t^2}{6(1+t)}. \end{align*} $$
Moreover, applying [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Cor. 1.7.25], we obtain
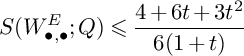 $$ \begin{align*}S(W^E_{\bullet,\bullet};Q)\leqslant\frac{4+6t+3t^2}{6(1+t)} \end{align*} $$
$$ \begin{align*}S(W^E_{\bullet,\bullet};Q)\leqslant\frac{4+6t+3t^2}{6(1+t)} \end{align*} $$
for every point
![]() $Q\in E$
. Note that
$Q\in E$
. Note that
![]() $A_S(E)=2$
. Thus, it follows from [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Cor. 1.7.12] that
$A_S(E)=2$
. Thus, it follows from [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Cor. 1.7.12] that
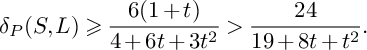 $$ \begin{align*}\delta_P(S,L)\geqslant\frac{6(1+t)}{4+6t+3t^2}>\frac{24}{19+8t+t^2}. \end{align*} $$
$$ \begin{align*}\delta_P(S,L)\geqslant\frac{6(1+t)}{4+6t+3t^2}>\frac{24}{19+8t+t^2}. \end{align*} $$
To complete the proof of the lemma, we may assume that S contains a line
![]() $\ell $
such that
$\ell $
such that
![]() $P\in \ell $
. Then
$P\in \ell $
. Then
![]() $\ell \cdot C=0$
or
$\ell \cdot C=0$
or
![]() $\ell \cdot C=1$
. If
$\ell \cdot C=1$
. If
![]() $\ell \cdot C=0$
, then
$\ell \cdot C=0$
, then
![]() $\ell $
must be an irreducible component of the conic C. Let us apply [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Th. 1.7.1] and [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Cor. 1.7.25] to the flag
$\ell $
must be an irreducible component of the conic C. Let us apply [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Th. 1.7.1] and [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Cor. 1.7.25] to the flag
![]() $P\in \ell $
to estimate
$P\in \ell $
to estimate
![]() $\delta _P(S,L)$
. Take
$\delta _P(S,L)$
. Take
![]() $u\in \mathbb {R}_{\geqslant 0}$
. Let
$u\in \mathbb {R}_{\geqslant 0}$
. Let
![]() $P(u)$
be the positive part of the Zariski decomposition of the divisor
$P(u)$
be the positive part of the Zariski decomposition of the divisor
![]() $L-u\ell $
, and let
$L-u\ell $
, and let
![]() $N(u)$
be its negative part. We must compute
$N(u)$
be its negative part. We must compute
![]() $P(u)$
,
$P(u)$
,
![]() $N(u)$
,
$N(u)$
,
![]() $P(u)\cdot \ell $
, and
$P(u)\cdot \ell $
, and
![]() $\mathrm {vol}(L-u\ell )$
.
$\mathrm {vol}(L-u\ell )$
.
There exists a birational morphism
![]() $\pi \colon S\to \mathbb {P}^2$
that blows up five points
$\pi \colon S\to \mathbb {P}^2$
that blows up five points
![]() $O_1,\dots ,O_5\in \mathbb {P}^2$
such that no three of them are collinear. For every
$O_1,\dots ,O_5\in \mathbb {P}^2$
such that no three of them are collinear. For every
![]() $i\in \{1,\ldots ,5\}$
, let
$i\in \{1,\ldots ,5\}$
, let
![]() $\mathbf {e}_i$
be the
$\mathbf {e}_i$
be the
![]() $\pi $
-exceptional curve such that
$\pi $
-exceptional curve such that
![]() $\pi (\mathbf {e}_i)=O_i$
. Similarly, let
$\pi (\mathbf {e}_i)=O_i$
. Similarly, let
![]() $\mathbf {l}_{ij}$
be the strict transform of the line in
$\mathbf {l}_{ij}$
be the strict transform of the line in
![]() $\mathbb {P}^2$
that contains
$\mathbb {P}^2$
that contains
![]() $O_i$
and
$O_i$
and
![]() $O_j$
, where
$O_j$
, where
![]() $1\leqslant i<j\leqslant 5$
. Finally, let B be the strict transform of the conic on
$1\leqslant i<j\leqslant 5$
. Finally, let B be the strict transform of the conic on
![]() $\mathbb {P}^2$
that passes through the points
$\mathbb {P}^2$
that passes through the points
![]() $O_1,\dots ,O_5$
. Then
$O_1,\dots ,O_5$
. Then
![]() $\mathbf {e}_1,\ldots ,\mathbf {e}_5,\mathbf {l}_{12},\ldots ,\mathbf {l}_{45},B$
are all lines in S, and each extremal ray of the Mori cone
$\mathbf {e}_1,\ldots ,\mathbf {e}_5,\mathbf {l}_{12},\ldots ,\mathbf {l}_{45},B$
are all lines in S, and each extremal ray of the Mori cone
![]() $\overline {\mathrm {NE}}(S)$
is generated by a class of one of these
$\overline {\mathrm {NE}}(S)$
is generated by a class of one of these
![]() $16$
lines.
$16$
lines.
Suppose that the conic C is irreducible. Then
![]() $C\cdot \ell =1$
. In this case, without loss of generality, we may assume that
$C\cdot \ell =1$
. In this case, without loss of generality, we may assume that
![]() $\ell =\mathbf {e}_1$
and
$\ell =\mathbf {e}_1$
and
![]() $C\sim \mathbf {l}_{12}+\mathbf {e}_2$
. If
$C\sim \mathbf {l}_{12}+\mathbf {e}_2$
. If
![]() $0\leqslant t\leqslant 1$
, then
$0\leqslant t\leqslant 1$
, then
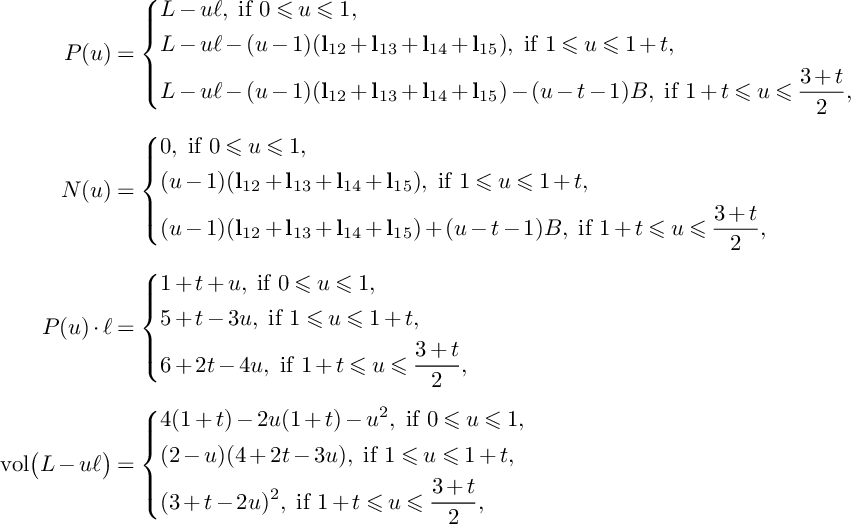 $$ \begin{align*}P(u)&=\left\{\begin{aligned} &L-u\ell,\ \text{if }0\leqslant u\leqslant 1, \\ &L-u\ell-(u-1)(\mathbf{l}_{12}+\mathbf{l}_{13}+\mathbf{l}_{14}+\mathbf{l}_{15}),\ \text{if }1\leqslant u\leqslant 1+t, \\ &L-u\ell-(u-1)(\mathbf{l}_{12}+\mathbf{l}_{13}+\mathbf{l}_{14}+\mathbf{l}_{15})-(u-t-1)B, \ \text{if }1+t\leqslant u\leqslant\frac{3+t}{2}, \\ \end{aligned} \right. \\[5pt]N(u)&=\left\{\begin{aligned} &0, \ \text{if }0\leqslant u\leqslant 1, \\ &(u-1)(\mathbf{l}_{12}+\mathbf{l}_{13}+\mathbf{l}_{14}+\mathbf{l}_{15}),\ \text{if }1\leqslant u\leqslant 1+t, \\ &(u-1)(\mathbf{l}_{12}+\mathbf{l}_{13}+\mathbf{l}_{14}+\mathbf{l}_{15})+(u-t-1)B, \ \text{if }1+t\leqslant u\leqslant\frac{3+t}{2}, \\ \end{aligned} \right.\\[5pt]P(u)\cdot\ell&=\left\{\begin{aligned} &1+t+u,\ \text{if }0\leqslant u\leqslant 1, \\ &5+t-3u,\ \text{if }1\leqslant u\leqslant 1+t, \\ &6+2t-4u,\ \text{if }1+t\leqslant u\leqslant\frac{3+t}{2}, \\ \end{aligned} \right.\\[5pt]\mathrm{vol}\big(L-u\ell\big)&=\left\{\begin{aligned} &4(1+t)-2u(1+t)-u^2, \ \text{if }0\leqslant u\leqslant 1, \\ &(2-u)(4+2t-3u),\ \text{if }1\leqslant u\leqslant 1+t, \\ &(3+t-2u)^2,\ \text{if }1+t\leqslant u\leqslant\frac{3+t}{2}, \\ \end{aligned} \right.\end{align*} $$
$$ \begin{align*}P(u)&=\left\{\begin{aligned} &L-u\ell,\ \text{if }0\leqslant u\leqslant 1, \\ &L-u\ell-(u-1)(\mathbf{l}_{12}+\mathbf{l}_{13}+\mathbf{l}_{14}+\mathbf{l}_{15}),\ \text{if }1\leqslant u\leqslant 1+t, \\ &L-u\ell-(u-1)(\mathbf{l}_{12}+\mathbf{l}_{13}+\mathbf{l}_{14}+\mathbf{l}_{15})-(u-t-1)B, \ \text{if }1+t\leqslant u\leqslant\frac{3+t}{2}, \\ \end{aligned} \right. \\[5pt]N(u)&=\left\{\begin{aligned} &0, \ \text{if }0\leqslant u\leqslant 1, \\ &(u-1)(\mathbf{l}_{12}+\mathbf{l}_{13}+\mathbf{l}_{14}+\mathbf{l}_{15}),\ \text{if }1\leqslant u\leqslant 1+t, \\ &(u-1)(\mathbf{l}_{12}+\mathbf{l}_{13}+\mathbf{l}_{14}+\mathbf{l}_{15})+(u-t-1)B, \ \text{if }1+t\leqslant u\leqslant\frac{3+t}{2}, \\ \end{aligned} \right.\\[5pt]P(u)\cdot\ell&=\left\{\begin{aligned} &1+t+u,\ \text{if }0\leqslant u\leqslant 1, \\ &5+t-3u,\ \text{if }1\leqslant u\leqslant 1+t, \\ &6+2t-4u,\ \text{if }1+t\leqslant u\leqslant\frac{3+t}{2}, \\ \end{aligned} \right.\\[5pt]\mathrm{vol}\big(L-u\ell\big)&=\left\{\begin{aligned} &4(1+t)-2u(1+t)-u^2, \ \text{if }0\leqslant u\leqslant 1, \\ &(2-u)(4+2t-3u),\ \text{if }1\leqslant u\leqslant 1+t, \\ &(3+t-2u)^2,\ \text{if }1+t\leqslant u\leqslant\frac{3+t}{2}, \\ \end{aligned} \right.\end{align*} $$
and
![]() $L-u\ell $
is not pseudoeffective for
$L-u\ell $
is not pseudoeffective for
![]() $u>\frac {3+t}{2}$
. Similarly, if
$u>\frac {3+t}{2}$
. Similarly, if
![]() $t\geqslant 1$
, then
$t\geqslant 1$
, then
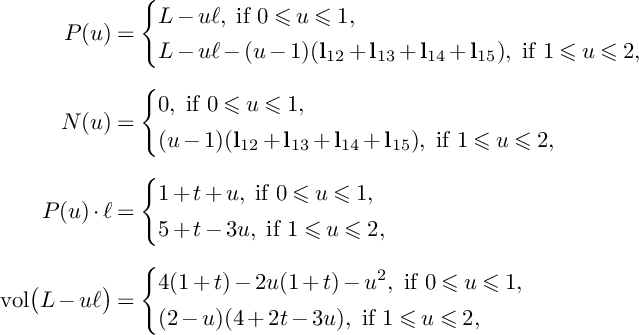 $$ \begin{align*}P(u)&=\left\{\begin{aligned} &L-u\ell,\ \text{if }0\leqslant u\leqslant 1, \\ &L-u\ell-(u-1)(\mathbf{l}_{12}+\mathbf{l}_{13}+\mathbf{l}_{14}+\mathbf{l}_{15}),\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right. \\[6pt]N(u)&=\left\{\begin{aligned} &0, \ \text{if }0\leqslant u\leqslant 1, \\ &(u-1)(\mathbf{l}_{12}+\mathbf{l}_{13}+\mathbf{l}_{14}+\mathbf{l}_{15}), \ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right.\\[6pt]P(u)\cdot\ell&=\left\{\begin{aligned} &1+t+u,\ \text{if }0\leqslant u\leqslant 1, \\ &5+t-3u,\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right.\\[6pt]\mathrm{vol}\big(L-u\ell\big)&=\left\{\begin{aligned} &4(1+t)-2u(1+t)-u^2, \ \text{if }0\leqslant u\leqslant 1, \\ &(2-u)(4+2t-3u),\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}P(u)&=\left\{\begin{aligned} &L-u\ell,\ \text{if }0\leqslant u\leqslant 1, \\ &L-u\ell-(u-1)(\mathbf{l}_{12}+\mathbf{l}_{13}+\mathbf{l}_{14}+\mathbf{l}_{15}),\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right. \\[6pt]N(u)&=\left\{\begin{aligned} &0, \ \text{if }0\leqslant u\leqslant 1, \\ &(u-1)(\mathbf{l}_{12}+\mathbf{l}_{13}+\mathbf{l}_{14}+\mathbf{l}_{15}), \ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right.\\[6pt]P(u)\cdot\ell&=\left\{\begin{aligned} &1+t+u,\ \text{if }0\leqslant u\leqslant 1, \\ &5+t-3u,\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right.\\[6pt]\mathrm{vol}\big(L-u\ell\big)&=\left\{\begin{aligned} &4(1+t)-2u(1+t)-u^2, \ \text{if }0\leqslant u\leqslant 1, \\ &(2-u)(4+2t-3u),\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right. \end{align*} $$
and
![]() $L-u\ell $
is not pseudoeffective for
$L-u\ell $
is not pseudoeffective for
![]() $u>2$
. Then
$u>2$
. Then
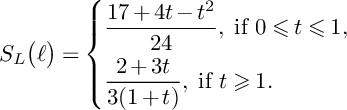 $$ \begin{align*}S_L\big(\ell\big)= \left\{\begin{aligned} &\frac{17+4t-t^2}{24},\ \text{if }0\leqslant t\leqslant 1, \\ &\frac{2+3t}{3(1+t)},\ \text{if }t\geqslant 1. \\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}S_L\big(\ell\big)= \left\{\begin{aligned} &\frac{17+4t-t^2}{24},\ \text{if }0\leqslant t\leqslant 1, \\ &\frac{2+3t}{3(1+t)},\ \text{if }t\geqslant 1. \\ \end{aligned} \right. \end{align*} $$
Observe that
![]() $P\not \in \mathbf {l}_{ij}$
for every
$P\not \in \mathbf {l}_{ij}$
for every
![]() $1\leqslant i<j\leqslant 5$
. Thus, if
$1\leqslant i<j\leqslant 5$
. Thus, if
![]() $t\leqslant 1$
, then [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Cor. 1.7.25] gives
$t\leqslant 1$
, then [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Cor. 1.7.25] gives
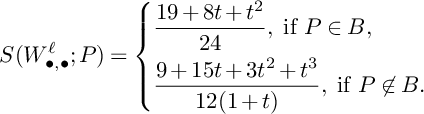 $$ \begin{align*}S(W^{\ell}_{\bullet,\bullet};P)= \left\{\begin{aligned} &\frac{19+8t+t^2}{24},\ \text{if }P\in B, \\ &\frac{9+15t+3t^2+t^3}{12(1+t)},\ \text{if }P\not\in B. \\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}S(W^{\ell}_{\bullet,\bullet};P)= \left\{\begin{aligned} &\frac{19+8t+t^2}{24},\ \text{if }P\in B, \\ &\frac{9+15t+3t^2+t^3}{12(1+t)},\ \text{if }P\not\in B. \\ \end{aligned} \right. \end{align*} $$
Similarly, if
![]() $t\geqslant 1$
, then [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Cor. 1.7.25] gives
$t\geqslant 1$
, then [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Cor. 1.7.25] gives
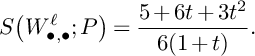 $$ \begin{align*}S\big(W^{\ell}_{\bullet,\bullet};P\big)=\frac{5+6t+3t^2}{6(1+t)}. \end{align*} $$
$$ \begin{align*}S\big(W^{\ell}_{\bullet,\bullet};P\big)=\frac{5+6t+3t^2}{6(1+t)}. \end{align*} $$
Now, using [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Th. 1.7.1], we get (♣).
To complete the proof of the lemma, we may assume that the conic C is reducible. In this case, we let
![]() $\ell $
be an irreducible component of the conic C that contains P. Without loss of generality, we may assume that
$\ell $
be an irreducible component of the conic C that contains P. Without loss of generality, we may assume that
![]() $\ell =\mathbf {e}_1$
and
$\ell =\mathbf {e}_1$
and
![]() $C=\mathbf {e}_1+B$
. Then
$C=\mathbf {e}_1+B$
. Then
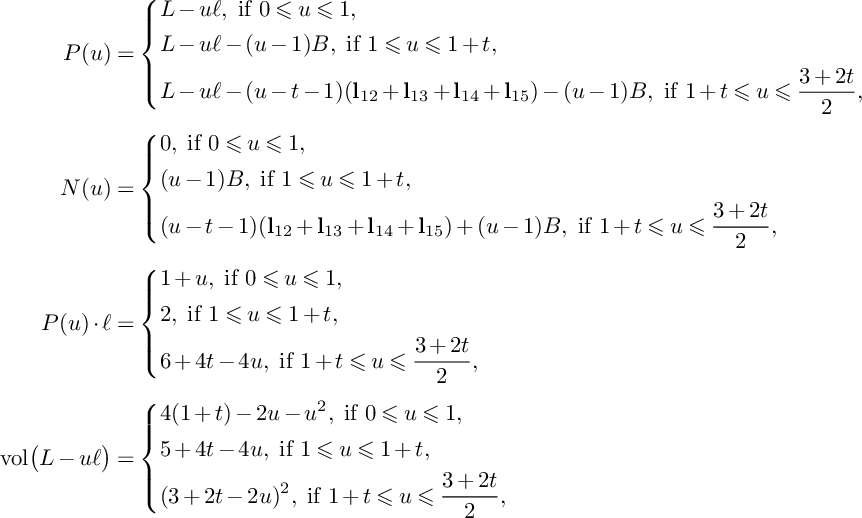 $$ \begin{align*}P(u)&=\left\{\begin{aligned} &L-u\ell,\ \text{if }0\leqslant u\leqslant 1, \\ &L-u\ell-(u-1)B,\ \text{if }1\leqslant u\leqslant 1+t, \\ &L-u\ell-(u-t-1)(\mathbf{l}_{12}+\mathbf{l}_{13}+\mathbf{l}_{14}+\mathbf{l}_{15})-(u-1)B, \ \text{if }1+t\leqslant u\leqslant\frac{3+2t}{2}, \\ \end{aligned} \right. \\[4pt]N(u)&=\left\{\begin{aligned} &0, \ \text{if }0\leqslant u\leqslant 1, \\ &(u-1)B,\ \text{if }1\leqslant u\leqslant 1+t, \\ &(u-t-1)(\mathbf{l}_{12}+\mathbf{l}_{13}+\mathbf{l}_{14}+\mathbf{l}_{15})+(u-1)B, \ \text{if }1+t\leqslant u\leqslant\frac{3+2t}{2}, \\ \end{aligned} \right.\\[4pt]P(u)\cdot\ell&=\left\{\begin{aligned} &1+u,\ \text{if }0\leqslant u\leqslant 1, \\ &2,\ \text{if }1\leqslant u\leqslant 1+t, \\ &6+4t-4u,\ \text{if }1+t\leqslant u\leqslant\frac{3+2t}{2}, \\ \end{aligned} \right. \\[4pt]\mathrm{vol}\big(L-u\ell\big)&=\left\{\begin{aligned} &4(1+t)-2u-u^2,\ \text{if }0\leqslant u\leqslant 1, \\ &5+4t-4u,\ \text{if }1\leqslant u\leqslant 1+t, \\ &(3+2t-2u)^2,\ \text{if }1+t\leqslant u\leqslant\frac{3+2t}{2}, \\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}P(u)&=\left\{\begin{aligned} &L-u\ell,\ \text{if }0\leqslant u\leqslant 1, \\ &L-u\ell-(u-1)B,\ \text{if }1\leqslant u\leqslant 1+t, \\ &L-u\ell-(u-t-1)(\mathbf{l}_{12}+\mathbf{l}_{13}+\mathbf{l}_{14}+\mathbf{l}_{15})-(u-1)B, \ \text{if }1+t\leqslant u\leqslant\frac{3+2t}{2}, \\ \end{aligned} \right. \\[4pt]N(u)&=\left\{\begin{aligned} &0, \ \text{if }0\leqslant u\leqslant 1, \\ &(u-1)B,\ \text{if }1\leqslant u\leqslant 1+t, \\ &(u-t-1)(\mathbf{l}_{12}+\mathbf{l}_{13}+\mathbf{l}_{14}+\mathbf{l}_{15})+(u-1)B, \ \text{if }1+t\leqslant u\leqslant\frac{3+2t}{2}, \\ \end{aligned} \right.\\[4pt]P(u)\cdot\ell&=\left\{\begin{aligned} &1+u,\ \text{if }0\leqslant u\leqslant 1, \\ &2,\ \text{if }1\leqslant u\leqslant 1+t, \\ &6+4t-4u,\ \text{if }1+t\leqslant u\leqslant\frac{3+2t}{2}, \\ \end{aligned} \right. \\[4pt]\mathrm{vol}\big(L-u\ell\big)&=\left\{\begin{aligned} &4(1+t)-2u-u^2,\ \text{if }0\leqslant u\leqslant 1, \\ &5+4t-4u,\ \text{if }1\leqslant u\leqslant 1+t, \\ &(3+2t-2u)^2,\ \text{if }1+t\leqslant u\leqslant\frac{3+2t}{2}, \\ \end{aligned} \right. \end{align*} $$
and the divisor
![]() $L-u\ell $
is not pseudoeffective for
$L-u\ell $
is not pseudoeffective for
![]() $u>\frac {3+2t}{2}$
. This gives
$u>\frac {3+2t}{2}$
. This gives
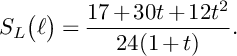 $$ \begin{align*}S_L\big(\ell\big)=\frac{17+30t+12t^2}{24(1+t)}. \end{align*} $$
$$ \begin{align*}S_L\big(\ell\big)=\frac{17+30t+12t^2}{24(1+t)}. \end{align*} $$
Moreover, using [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Cor. 1.7.25], we compute
 $$ \begin{align*}S\big(W^{\ell}_{\bullet,\bullet};P\big)= \left\{\begin{aligned} &\frac{19+30t+12t^2}{24(1+t)},\ \text{if }P\in B, \\ &\frac{19+24t}{24(1+t)},\ \text{if }P\in\mathbf{l}_{12}\cup\mathbf{l}_{13}\cup\mathbf{l}_{14}\cup\mathbf{l}_{15}, \\ &\frac{3+4t}{4(1+t)},\ \text{otherwise}. \\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}S\big(W^{\ell}_{\bullet,\bullet};P\big)= \left\{\begin{aligned} &\frac{19+30t+12t^2}{24(1+t)},\ \text{if }P\in B, \\ &\frac{19+24t}{24(1+t)},\ \text{if }P\in\mathbf{l}_{12}\cup\mathbf{l}_{13}\cup\mathbf{l}_{14}\cup\mathbf{l}_{15}, \\ &\frac{3+4t}{4(1+t)},\ \text{otherwise}. \\ \end{aligned} \right. \end{align*} $$
Now, using [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Th. 1.7.1], we get (♠) as claimed.
In the remaining part of this appendix, we suppose that
![]() $K_S^2=5$
,
$K_S^2=5$
,
![]() $L=-K_S$
, and S has isolated ordinary double points, that is, singular points of type
$L=-K_S$
, and S has isolated ordinary double points, that is, singular points of type
![]() $\mathbb {A}_1$
. As usual, we set
$\mathbb {A}_1$
. As usual, we set
![]() $\delta _P(S)=\delta _P(S,-K_S)$
and
$\delta _P(S)=\delta _P(S,-K_S)$
and
Let
![]() $\eta \colon \widetilde {S}\to S$
be the minimal resolution of the quintic del Pezzo surface S. Since
$\eta \colon \widetilde {S}\to S$
be the minimal resolution of the quintic del Pezzo surface S. Since
![]() $-K_{\widetilde {S}}\sim \eta ^*(-K_S)$
, we can estimate the number
$-K_{\widetilde {S}}\sim \eta ^*(-K_S)$
, we can estimate the number
![]() $\delta _P(S)$
as follows. Let O be a point in the surface
$\delta _P(S)$
as follows. Let O be a point in the surface
![]() $\widetilde {S}$
such that
$\widetilde {S}$
such that
![]() $\eta (O)=P$
, and let C be a smooth irreducible rational curve in
$\eta (O)=P$
, and let C be a smooth irreducible rational curve in
![]() $\widetilde {S}$
such that:
$\widetilde {S}$
such that:
-
• If
 $P\in \mathrm {Sing}(S)$
, then C is the
$P\in \mathrm {Sing}(S)$
, then C is the
 $\eta $
-exceptional curve such that
$\eta $
-exceptional curve such that
 $\eta (C)=P$
.
$\eta (C)=P$
. -
• If
 $P\not \in \mathrm {Sing}(S)$
, then C is appropriately chosen curve that contains O.
$P\not \in \mathrm {Sing}(S)$
, then C is appropriately chosen curve that contains O.
As usual, we set
For
![]() $u\in [0,\tau ]$
, let
$u\in [0,\tau ]$
, let
![]() $P(u)$
be the positive part of the Zariski decomposition of the divisor
$P(u)$
be the positive part of the Zariski decomposition of the divisor
![]() $-K_{\widetilde {S}}-uC$
, and let
$-K_{\widetilde {S}}-uC$
, and let
![]() $N(u)$
be its negative part. Let
$N(u)$
be its negative part. Let
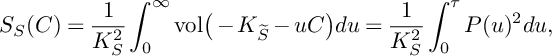 $$ \begin{align*}S_{S}(C)=\frac{1}{K_S^2}\int_{0}^{\infty}\mathrm{vol}\big(-K_{\widetilde{S}}-uC\big)du=\frac{1}{K_S^2}\int_{0}^{\tau}P(u)^2du, \end{align*} $$
$$ \begin{align*}S_{S}(C)=\frac{1}{K_S^2}\int_{0}^{\infty}\mathrm{vol}\big(-K_{\widetilde{S}}-uC\big)du=\frac{1}{K_S^2}\int_{0}^{\tau}P(u)^2du, \end{align*} $$
and let
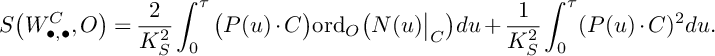 $$ \begin{align*}S\big(W^{C}_{\bullet,\bullet},O\big)= \frac{2}{K_S^2}\int_0^\tau\big(P(u)\cdot C\big)\mathrm{ord}_O\big(N(u)\big\vert_{C}\big)du +\frac{1}{K_S^2}\int_0^\tau(P(u)\cdot C)^2du. \end{align*} $$
$$ \begin{align*}S\big(W^{C}_{\bullet,\bullet},O\big)= \frac{2}{K_S^2}\int_0^\tau\big(P(u)\cdot C\big)\mathrm{ord}_O\big(N(u)\big\vert_{C}\big)du +\frac{1}{K_S^2}\int_0^\tau(P(u)\cdot C)^2du. \end{align*} $$
If
![]() $P\not \in \mathrm {Sing}(S)$
, then [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Th. 1.7.1] and [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Cor. 1.7.25] give
$P\not \in \mathrm {Sing}(S)$
, then [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Th. 1.7.1] and [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Cor. 1.7.25] give
 $$ \begin{align} \frac{1}{S_S(C)}\geqslant\delta_P(S)\geqslant\min\left\{\frac{1}{S_S(C)},\frac{1}{S\big(W^{C}_{\bullet,\bullet},O\big)}\right\}. \end{align} $$
$$ \begin{align} \frac{1}{S_S(C)}\geqslant\delta_P(S)\geqslant\min\left\{\frac{1}{S_S(C)},\frac{1}{S\big(W^{C}_{\bullet,\bullet},O\big)}\right\}. \end{align} $$
Similarly, if
![]() $P\in \mathrm {Sing}(S)$
, then [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Cor. 1.7.12] and [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Cor. 1.7.25] give
$P\in \mathrm {Sing}(S)$
, then [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Cor. 1.7.12] and [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Cor. 1.7.25] give
 $$ \begin{align} \frac{1}{S_S(C)}\geqslant\delta_P(S)\geqslant\min\left\{\frac{1}{S_S(C)},\inf_{O\in C}\frac{1}{S\big(W^{C}_{\bullet,\bullet},O\big)}\right\}. \end{align} $$
$$ \begin{align} \frac{1}{S_S(C)}\geqslant\delta_P(S)\geqslant\min\left\{\frac{1}{S_S(C)},\inf_{O\in C}\frac{1}{S\big(W^{C}_{\bullet,\bullet},O\big)}\right\}. \end{align} $$
Lemma 25. Suppose that S has one singular point. Then
![]() $\delta (S)=\frac {15}{17}$
, and the following assertions hold:
$\delta (S)=\frac {15}{17}$
, and the following assertions hold:
-
• If P is not contained in any line in S that contains the singular point of S, then
 $\delta _P(S)\geqslant \frac {15}{13}$
.
$\delta _P(S)\geqslant \frac {15}{13}$
. -
• If P is not the singular point of the surface S, but P is contained in a line in S that passes through the singular point of the surface S, then
 $\delta _P(S)=1$
.
$\delta _P(S)=1$
. -
• If P is the singular point of the surface S, then
 $\delta _P(S)=\frac {15}{17}$
.
$\delta _P(S)=\frac {15}{17}$
.
Proof. We let
![]() $P_0$
be the singular point of the surface S, and let
$P_0$
be the singular point of the surface S, and let
![]() $\ell _0$
be the
$\ell _0$
be the
![]() $\pi $
-exceptional curve. Then it follows from [Reference Coray and Tsfasman8] that there exists a birational morphism
$\pi $
-exceptional curve. Then it follows from [Reference Coray and Tsfasman8] that there exists a birational morphism
![]() $\pi \colon \widetilde {S}\to \mathbb {P}^2$
such that
$\pi \colon \widetilde {S}\to \mathbb {P}^2$
such that
![]() $\pi (\ell _0)$
is a line, the map
$\pi (\ell _0)$
is a line, the map
![]() $\pi $
blows up three points
$\pi $
blows up three points
![]() $Q_1$
,
$Q_1$
,
![]() $Q_2$
, and
$Q_2$
, and
![]() $Q_3$
contained in
$Q_3$
contained in
![]() $\pi (\ell _0)$
and another point
$\pi (\ell _0)$
and another point
![]() $Q_0\in \mathbb {P}^2\setminus \pi (\ell _0)$
.
$Q_0\in \mathbb {P}^2\setminus \pi (\ell _0)$
.
For
![]() $i\in \{0,1,2,3\}$
, let
$i\in \{0,1,2,3\}$
, let
![]() $\mathbf {e}_i$
be the
$\mathbf {e}_i$
be the
![]() $\pi $
-exceptional curve such that
$\pi $
-exceptional curve such that
![]() $\pi (\mathbf {e}_i)=Q_i$
. For every
$\pi (\mathbf {e}_i)=Q_i$
. For every
![]() $i\in \{1,2,3\}$
, let
$i\in \{1,2,3\}$
, let
![]() $\ell _i$
be the strict transform of the line in
$\ell _i$
be the strict transform of the line in
![]() $\mathbb {P}^2$
that passes through
$\mathbb {P}^2$
that passes through
![]() $Q_0$
and
$Q_0$
and
![]() $Q_i$
. Then
$Q_i$
. Then
![]() $\ell _0$
,
$\ell _0$
,
![]() $\ell _1$
,
$\ell _1$
,
![]() $\ell _2$
,
$\ell _2$
,
![]() $\ell _3$
,
$\ell _3$
,
![]() $\mathbf {e}_0$
,
$\mathbf {e}_0$
,
![]() $\mathbf {e}_1$
,
$\mathbf {e}_1$
,
![]() $\mathbf {e}_2$
, and
$\mathbf {e}_2$
, and
![]() $\mathbf {e}_3$
are the only irreducible curves in the surface
$\mathbf {e}_3$
are the only irreducible curves in the surface
![]() $\widetilde {S}$
that have negative self-intersections. Moreover, the intersections of these curves are given in the following table:
$\widetilde {S}$
that have negative self-intersections. Moreover, the intersections of these curves are given in the following table:

Note that
![]() $\eta (\ell _1)$
,
$\eta (\ell _1)$
,
![]() $\eta (\ell _2)$
,
$\eta (\ell _2)$
,
![]() $\eta (\ell _3)$
,
$\eta (\ell _3)$
,
![]() $\eta (\mathbf {e}_0)$
,
$\eta (\mathbf {e}_0)$
,
![]() $\eta (\mathbf {e}_1)$
,
$\eta (\mathbf {e}_1)$
,
![]() $\eta (\mathbf {e}_2)$
, and
$\eta (\mathbf {e}_2)$
, and
![]() $\eta (\mathbf {e}_3)$
are all lines contained in the surface S. Among them, only the lines
$\eta (\mathbf {e}_3)$
are all lines contained in the surface S. Among them, only the lines
![]() $\eta (\mathbf {e}_1)$
,
$\eta (\mathbf {e}_1)$
,
![]() $\eta (\mathbf {e}_2)$
, and
$\eta (\mathbf {e}_2)$
, and
![]() $\eta (\mathbf {e}_3)$
pass through the singular point
$\eta (\mathbf {e}_3)$
pass through the singular point
![]() $P_0$
.
$P_0$
.
For
![]() $(a_0,a_1,a_2,a_3,b_0,b_1,b_2,b_3)\in \mathbb {R}^8$
, we write
$(a_0,a_1,a_2,a_3,b_0,b_1,b_2,b_3)\in \mathbb {R}^8$
, we write
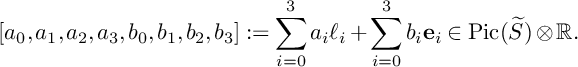 $$ \begin{align*}[a_0,a_1,a_2,a_3,b_0,b_1,b_2,b_3] := \sum_{i=0}^3 a_i \ell_i + \sum_{i=0}^3 b_i \mathbf{e}_i \in \mathrm{Pic} (\widetilde{S}) \otimes \mathbb{R}. \end{align*} $$
$$ \begin{align*}[a_0,a_1,a_2,a_3,b_0,b_1,b_2,b_3] := \sum_{i=0}^3 a_i \ell_i + \sum_{i=0}^3 b_i \mathbf{e}_i \in \mathrm{Pic} (\widetilde{S}) \otimes \mathbb{R}. \end{align*} $$
If
![]() $P=P_0$
, then
$P=P_0$
, then
![]() $C=\ell _0$
, which implies that
$C=\ell _0$
, which implies that
![]() $\tau =2$
and
$\tau =2$
and
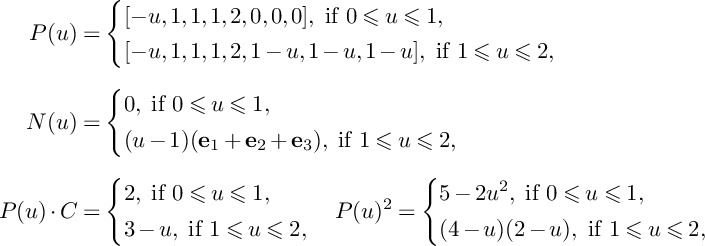 $$ \begin{align*}P(u)&=\left\{\begin{aligned} &[-u, 1, 1, 1, 2, 0, 0, 0],\ \text{if }0\leqslant u\leqslant 1, \\ &[-u, 1, 1, 1, 2, 1-u, 1-u, 1-u],\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right. \\[6pt]N(u)&=\left\{\begin{aligned} &0,\ \text{if }0\leqslant u\leqslant 1, \\ &(u-1)(\mathbf{e}_1+\mathbf{e}_2+\mathbf{e}_3),\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right.\\[6pt]P(u)\cdot C&=\left\{\begin{aligned} &2,\ \text{if }0\leqslant u\leqslant 1, \\ &3 -u,\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right. \quad P(u)^2=\left\{\begin{aligned} &5 - 2 u^2,\ \text{if }0\leqslant u\leqslant 1, \\ &(4-u)(2-u),\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}P(u)&=\left\{\begin{aligned} &[-u, 1, 1, 1, 2, 0, 0, 0],\ \text{if }0\leqslant u\leqslant 1, \\ &[-u, 1, 1, 1, 2, 1-u, 1-u, 1-u],\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right. \\[6pt]N(u)&=\left\{\begin{aligned} &0,\ \text{if }0\leqslant u\leqslant 1, \\ &(u-1)(\mathbf{e}_1+\mathbf{e}_2+\mathbf{e}_3),\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right.\\[6pt]P(u)\cdot C&=\left\{\begin{aligned} &2,\ \text{if }0\leqslant u\leqslant 1, \\ &3 -u,\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right. \quad P(u)^2=\left\{\begin{aligned} &5 - 2 u^2,\ \text{if }0\leqslant u\leqslant 1, \\ &(4-u)(2-u),\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right. \end{align*} $$
which implies that
![]() $S_S(C)=\frac {17}{15}$
and
$S_S(C)=\frac {17}{15}$
and
![]() $S(W^{C}_{\bullet , \bullet };O)=1$
. Therefore, using (♢), we obtain
$S(W^{C}_{\bullet , \bullet };O)=1$
. Therefore, using (♢), we obtain
![]() $\delta _{P_0}(S)=\frac {15}{17}$
.
$\delta _{P_0}(S)=\frac {15}{17}$
.
To proceed, we may assume that
![]() $P\ne P_0$
. If
$P\ne P_0$
. If
![]() $O\in \mathbf {e}_0$
, we let
$O\in \mathbf {e}_0$
, we let
![]() $C=\mathbf {e}_0$
. Then
$C=\mathbf {e}_0$
. Then
![]() $\tau =2$
, and
$\tau =2$
, and
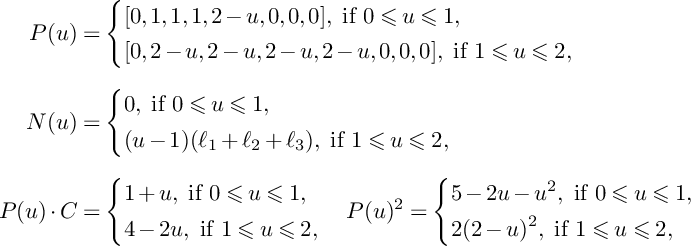 $$ \begin{align*}P(u)&=\left\{\begin{aligned} & [0, 1, 1, 1, 2-u, 0, 0, 0],\ \text{if }0\leqslant u\leqslant 1, \\ &[0, 2-u, 2-u, 2-u, 2-u, 0, 0, 0],\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right. \\[6pt]N(u)&=\left\{\begin{aligned} &0,\ \text{if }0\leqslant u\leqslant 1, \\ &(u-1) (\ell_1 + \ell_2 + \ell_3),\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right. \\[6pt]P(u)\cdot C&=\left\{\begin{aligned} &1+u,\ \text{if }0\leqslant u\leqslant 1, \\ &4-2u,\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right. \quad P(u)^2=\left\{\begin{aligned} &5-2u-u^2,\ \text{if }0\leqslant u\leqslant 1, \\ &2(2-u)^2,\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}P(u)&=\left\{\begin{aligned} & [0, 1, 1, 1, 2-u, 0, 0, 0],\ \text{if }0\leqslant u\leqslant 1, \\ &[0, 2-u, 2-u, 2-u, 2-u, 0, 0, 0],\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right. \\[6pt]N(u)&=\left\{\begin{aligned} &0,\ \text{if }0\leqslant u\leqslant 1, \\ &(u-1) (\ell_1 + \ell_2 + \ell_3),\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right. \\[6pt]P(u)\cdot C&=\left\{\begin{aligned} &1+u,\ \text{if }0\leqslant u\leqslant 1, \\ &4-2u,\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right. \quad P(u)^2=\left\{\begin{aligned} &5-2u-u^2,\ \text{if }0\leqslant u\leqslant 1, \\ &2(2-u)^2,\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right. \end{align*} $$
which implies that
![]() $S_S(C)=\frac {13}{15}$
and
$S_S(C)=\frac {13}{15}$
and
![]() $S(W^{C}_{\bullet , \bullet };O)\leqslant \frac {13}{15}$
, so that
$S(W^{C}_{\bullet , \bullet };O)\leqslant \frac {13}{15}$
, so that
![]() $\delta _P(S)=\frac {15}{13}$
by (⧫).
$\delta _P(S)=\frac {15}{13}$
by (⧫).
If
![]() $O\in \ell _1$
, we let
$O\in \ell _1$
, we let
![]() $C=\ell _1$
. In this case, we have
$C=\ell _1$
. In this case, we have
![]() $\tau =2$
, and
$\tau =2$
, and
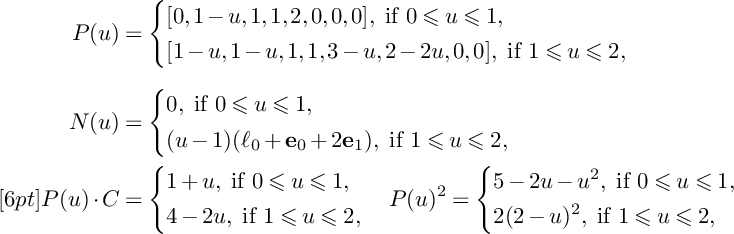 $$ \begin{align*}P(u)&=\left\{\begin{aligned} &[0, 1-u, 1, 1, 2, 0, 0, 0],\ \text{if }0\leqslant u\leqslant 1, \\ &[1-u, 1-u, 1, 1, 3-u, 2-2u, 0, 0],\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right. \\[6pt]N(u)&=\left\{\begin{aligned} &0,\ \text{if }0\leqslant u\leqslant 1, \\ &(u-1)(\ell_0+\mathbf{e}_0+2\mathbf{e}_1),\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right.\\ [6pt]P(u)\cdot C&=\left\{\begin{aligned} &1+u,\ \text{if }0\leqslant u\leqslant 1, \\ &4-2u,\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right. \quad P(u)^2=\left\{\begin{aligned} &5-2u-u^2,\ \text{if }0\leqslant u\leqslant 1, \\ &2(2-u)^2,\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right.\end{align*} $$
$$ \begin{align*}P(u)&=\left\{\begin{aligned} &[0, 1-u, 1, 1, 2, 0, 0, 0],\ \text{if }0\leqslant u\leqslant 1, \\ &[1-u, 1-u, 1, 1, 3-u, 2-2u, 0, 0],\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right. \\[6pt]N(u)&=\left\{\begin{aligned} &0,\ \text{if }0\leqslant u\leqslant 1, \\ &(u-1)(\ell_0+\mathbf{e}_0+2\mathbf{e}_1),\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right.\\ [6pt]P(u)\cdot C&=\left\{\begin{aligned} &1+u,\ \text{if }0\leqslant u\leqslant 1, \\ &4-2u,\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right. \quad P(u)^2=\left\{\begin{aligned} &5-2u-u^2,\ \text{if }0\leqslant u\leqslant 1, \\ &2(2-u)^2,\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right.\end{align*} $$
so that
![]() $S_S(C)=\frac {13}{15}$
. If
$S_S(C)=\frac {13}{15}$
. If
![]() $O\in \ell _1\setminus (\mathbf {e}_0\cup \mathbf {e}_1)$
, then
$O\in \ell _1\setminus (\mathbf {e}_0\cup \mathbf {e}_1)$
, then
![]() $S(W^{C}_{\bullet , \bullet };O)=\frac {11}{15}$
. If
$S(W^{C}_{\bullet , \bullet };O)=\frac {11}{15}$
. If
![]() $O=\ell _1\cap \mathbf {e}_1$
, then
$O=\ell _1\cap \mathbf {e}_1$
, then
![]() $S(W^{C}_{\bullet , \bullet };O)=1$
. Thus, using (⧫), we see that
$S(W^{C}_{\bullet , \bullet };O)=1$
. Thus, using (⧫), we see that
![]() $\delta _P(S)=\frac {15}{13}$
if
$\delta _P(S)=\frac {15}{13}$
if
![]() $O\in \ell _1\setminus \mathbf {e}_1$
, and
$O\in \ell _1\setminus \mathbf {e}_1$
, and
![]() $\delta _P(S)\geqslant 1$
if
$\delta _P(S)\geqslant 1$
if
![]() $O=\ell _1\cap \mathbf {e}_1$
.
$O=\ell _1\cap \mathbf {e}_1$
.
Similarly,
![]() $\delta _P(S)=\frac {15}{13}$
if
$\delta _P(S)=\frac {15}{13}$
if
![]() $O\in \ell _2\setminus \mathbf {e}_2$
or
$O\in \ell _2\setminus \mathbf {e}_2$
or
![]() $O\in \ell _3\setminus \mathbf {e}_3$
, and
$O\in \ell _3\setminus \mathbf {e}_3$
, and
![]() $\delta _P(S)\geqslant 1$
if
$\delta _P(S)\geqslant 1$
if
![]() $O=\ell _2\cap \mathbf {e}_2$
or
$O=\ell _2\cap \mathbf {e}_2$
or
![]() $O=\ell _3\cap \mathbf {e}_3$
.
$O=\ell _3\cap \mathbf {e}_3$
.
If
![]() $O\in \mathbf {e}_1$
, we let
$O\in \mathbf {e}_1$
, we let
![]() $C=\mathbf {e}_1$
. In this case, we have
$C=\mathbf {e}_1$
. In this case, we have
![]() $\tau =2$
, and
$\tau =2$
, and
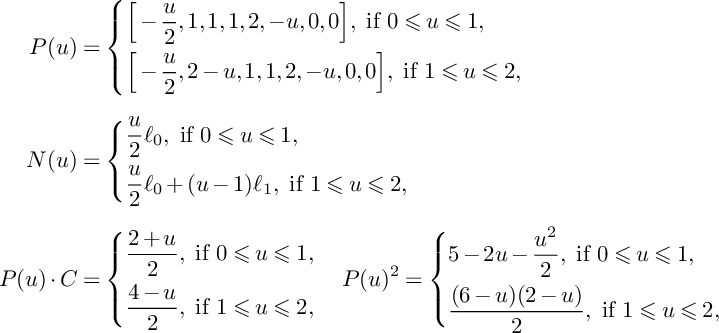 $$ \begin{align*}P(u)&=\left\{\begin{aligned} &\Big[-\frac{u}{2}, 1, 1, 1, 2, -u, 0, 0\Big],\ \text{if }0\leqslant u\leqslant 1, \\ &\Big[-\frac{u}{2}, 2-u, 1, 1, 2, -u, 0, 0\Big],\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right. \\[6pt]N(u)&=\left\{\begin{aligned} &\frac{u}{2} \ell_0,\ \text{if }0\leqslant u\leqslant 1, \\ &\frac{u}{2} \ell_0 + (u-1) \ell_1,\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right.\\[6pt]P(u)\cdot C&=\left\{\begin{aligned} &\frac{2+u}{2},\ \text{if }0\leqslant u\leqslant 1, \\ &\frac{4 - u}{2},\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right. \quad P(u)^2=\left\{\begin{aligned} &5-2u-\frac{u^2}{2},\ \text{if }0\leqslant u\leqslant 1, \\ &\frac{(6-u)(2-u)}{2}, \ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}P(u)&=\left\{\begin{aligned} &\Big[-\frac{u}{2}, 1, 1, 1, 2, -u, 0, 0\Big],\ \text{if }0\leqslant u\leqslant 1, \\ &\Big[-\frac{u}{2}, 2-u, 1, 1, 2, -u, 0, 0\Big],\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right. \\[6pt]N(u)&=\left\{\begin{aligned} &\frac{u}{2} \ell_0,\ \text{if }0\leqslant u\leqslant 1, \\ &\frac{u}{2} \ell_0 + (u-1) \ell_1,\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right.\\[6pt]P(u)\cdot C&=\left\{\begin{aligned} &\frac{2+u}{2},\ \text{if }0\leqslant u\leqslant 1, \\ &\frac{4 - u}{2},\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right. \quad P(u)^2=\left\{\begin{aligned} &5-2u-\frac{u^2}{2},\ \text{if }0\leqslant u\leqslant 1, \\ &\frac{(6-u)(2-u)}{2}, \ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right. \end{align*} $$
which implies that
![]() $S_S(C)=1$
and
$S_S(C)=1$
and
![]() $S(W^{C}_{\bullet , \bullet };O)\leqslant \frac {13}{15}$
if
$S(W^{C}_{\bullet , \bullet };O)\leqslant \frac {13}{15}$
if
![]() $O\in \mathbf {e}_1\setminus \ell _0$
, so that
$O\in \mathbf {e}_1\setminus \ell _0$
, so that
![]() $\delta _P(S)=1$
by (⧫).
$\delta _P(S)=1$
by (⧫).
Likewise, we see that
![]() $\delta _P(S)=1$
in the case when
$\delta _P(S)=1$
in the case when
![]() $O\in \mathbf {e}_2$
or
$O\in \mathbf {e}_2$
or
![]() $O\in \mathbf {e}_3$
. Thus, to complete the proof, we may assume that P is not contained in any line in S.
$O\in \mathbf {e}_3$
. Thus, to complete the proof, we may assume that P is not contained in any line in S.
Now, we let C be the unique curve in the pencil
![]() $|\ell _1+\mathbf {e}_1|$
that contains P. By our assumption, the curve C is smooth and irreducible. Then
$|\ell _1+\mathbf {e}_1|$
that contains P. By our assumption, the curve C is smooth and irreducible. Then
![]() $\tau =2$
, and
$\tau =2$
, and
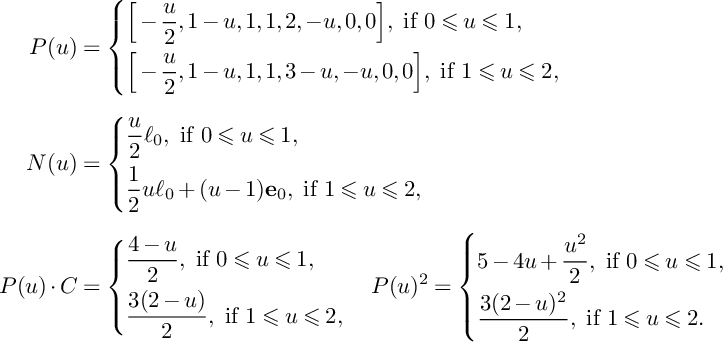 $$ \begin{align*}P(u)&=\left\{\begin{aligned} &\Big[-\frac{u}{2}, 1-u, 1, 1, 2, -u, 0, 0\Big],\ \text{if }0\leqslant u\leqslant 1, \\ &\Big[-\frac{u}{2}, 1-u, 1, 1, 3-u, -u, 0, 0\Big],\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right. \\[6pt]N(u)&=\left\{\begin{aligned} &\frac{u}{2} \ell_0,\ \text{if }0\leqslant u\leqslant 1, \\ &\frac{1}{2} u \ell_0 + (u-1)\mathbf{e}_0,\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right.\\[6pt]P(u)\cdot C&=\left\{\begin{aligned} &\frac{4-u}{2},\ \text{if }0\leqslant u\leqslant 1, \\ &\frac{3(2-u)}{2},\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right. \quad P(u)^2=\left\{\begin{aligned} &5-4u+\frac{u^2}{2},\ \text{if }0\leqslant u\leqslant 1, \\ &\frac{3(2-u)^2}{2},\ \text{if }1\leqslant u\leqslant 2. \\ \end{aligned} \right.\end{align*} $$
$$ \begin{align*}P(u)&=\left\{\begin{aligned} &\Big[-\frac{u}{2}, 1-u, 1, 1, 2, -u, 0, 0\Big],\ \text{if }0\leqslant u\leqslant 1, \\ &\Big[-\frac{u}{2}, 1-u, 1, 1, 3-u, -u, 0, 0\Big],\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right. \\[6pt]N(u)&=\left\{\begin{aligned} &\frac{u}{2} \ell_0,\ \text{if }0\leqslant u\leqslant 1, \\ &\frac{1}{2} u \ell_0 + (u-1)\mathbf{e}_0,\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right.\\[6pt]P(u)\cdot C&=\left\{\begin{aligned} &\frac{4-u}{2},\ \text{if }0\leqslant u\leqslant 1, \\ &\frac{3(2-u)}{2},\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right. \quad P(u)^2=\left\{\begin{aligned} &5-4u+\frac{u^2}{2},\ \text{if }0\leqslant u\leqslant 1, \\ &\frac{3(2-u)^2}{2},\ \text{if }1\leqslant u\leqslant 2. \\ \end{aligned} \right.\end{align*} $$
Then
![]() $S_S(C)=\frac {11}{15}$
and
$S_S(C)=\frac {11}{15}$
and
![]() $S(W^{C}_{\bullet , \bullet };O)=\frac {23}{30}$
. Thus, it follows from (⧫) that
$S(W^{C}_{\bullet , \bullet };O)=\frac {23}{30}$
. Thus, it follows from (⧫) that
![]() $\delta _P (S)\geqslant \frac {30}{23}>\frac {15}{13}$
.
$\delta _P (S)\geqslant \frac {30}{23}>\frac {15}{13}$
.
Finally, let us estimate
![]() $\delta _P(S)$
in the case when the del Pezzo surface S has two singular points. In this case, the surface S contains a line that passes through both its singular points [Reference Coray and Tsfasman8].
$\delta _P(S)$
in the case when the del Pezzo surface S has two singular points. In this case, the surface S contains a line that passes through both its singular points [Reference Coray and Tsfasman8].
Lemma 26. Suppose S has two singular points. Let
![]() $\ell $
be the line in S that passes through both singular points of the surface S. Then
$\ell $
be the line in S that passes through both singular points of the surface S. Then
![]() $\delta (S)=\frac {15}{19}$
. Moreover, the following assertions hold:
$\delta (S)=\frac {15}{19}$
. Moreover, the following assertions hold:
-
• If P is not contained in any line in S that contains a singular point of S, then
 $\delta _P(S)\geqslant \frac {15}{13}$
.
$\delta _P(S)\geqslant \frac {15}{13}$
. -
• If P is not contained in the line
 $\ell $
, but P is contained in a line in S that passes through a singular point of the surface S, then
$\ell $
, but P is contained in a line in S that passes through a singular point of the surface S, then
 $\delta _P(S)=1$
.
$\delta _P(S)=1$
. -
• If
 $P\in \ell $
, then
$P\in \ell $
, then
 $\delta _P(S)=\frac {15}{19}$
.
$\delta _P(S)=\frac {15}{19}$
.
Proof. Let
![]() $\mathbf {e}_1$
and
$\mathbf {e}_1$
and
![]() $\mathbf {e}_2$
be
$\mathbf {e}_2$
be
![]() $\eta $
-exceptional curves. Then
$\eta $
-exceptional curves. Then
![]() $\widetilde {S}$
contains
$\widetilde {S}$
contains
![]() $(-1)$
-curves
$(-1)$
-curves
![]() $\ell _1$
,
$\ell _1$
,
![]() $\ell _2$
,
$\ell _2$
,
![]() $\ell _3$
,
$\ell _3$
,
![]() $\ell _4$
, and
$\ell _4$
, and
![]() $\ell _5$
such that the intersections of the curves
$\ell _5$
such that the intersections of the curves
![]() $\ell _1$
,
$\ell _1$
,
![]() $\ell _2$
,
$\ell _2$
,
![]() $\ell _3$
,
$\ell _3$
,
![]() $\ell _4$
,
$\ell _4$
,
![]() $\ell _5$
,
$\ell _5$
,
![]() $\mathbf {e}_1$
, and
$\mathbf {e}_1$
, and
![]() $\mathbf {e}_2$
on
$\mathbf {e}_2$
on
![]() $\widetilde {S}$
are given in the following table.
$\widetilde {S}$
are given in the following table.

The curves
![]() $\eta (\ell _1)$
,
$\eta (\ell _1)$
,
![]() $\eta (\ell _2)$
,
$\eta (\ell _2)$
,
![]() $\eta (\ell _3)$
,
$\eta (\ell _3)$
,
![]() $\eta (\ell _4)$
, and
$\eta (\ell _4)$
, and
![]() $\eta (\ell _5)$
are the only lines in S. Moreover, we have
$\eta (\ell _5)$
are the only lines in S. Moreover, we have
![]() $\ell =\eta (\ell _1)$
, and
$\ell =\eta (\ell _1)$
, and
![]() $\eta (\ell _1)$
,
$\eta (\ell _1)$
,
![]() $\eta (\ell _2)$
, an
$\eta (\ell _2)$
, an
![]() $\eta (\ell _5)$
are the only lines in S that contain a singular point of the surface S.
$\eta (\ell _5)$
are the only lines in S that contain a singular point of the surface S.
As in the proof of Lemma 25, for
![]() $(a_1,a_2,a_3,a_4,a_5,b_1, b_2)\in \mathbb {R}^7$
, we write
$(a_1,a_2,a_3,a_4,a_5,b_1, b_2)\in \mathbb {R}^7$
, we write
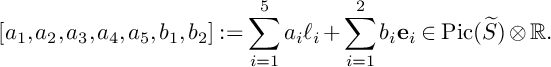 $$ \begin{align*}[a_1,a_2,a_3,a_4,a_5,b_1, b_2] := \sum_{i=1}^5 a_i \ell_i + \sum_{i=1}^2 b_i \mathbf{e}_i \in \mathrm{Pic} (\widetilde{S}) \otimes \mathbb{R}. \end{align*} $$
$$ \begin{align*}[a_1,a_2,a_3,a_4,a_5,b_1, b_2] := \sum_{i=1}^5 a_i \ell_i + \sum_{i=1}^2 b_i \mathbf{e}_i \in \mathrm{Pic} (\widetilde{S}) \otimes \mathbb{R}. \end{align*} $$
If
![]() $O\in \ell _1\setminus (\mathbf {e}_1\cup \mathbf {e}_2)$
, we let
$O\in \ell _1\setminus (\mathbf {e}_1\cup \mathbf {e}_2)$
, we let
![]() $C=\ell _1$
. In this case, we have
$C=\ell _1$
. In this case, we have
![]() $\tau =3$
, and
$\tau =3$
, and
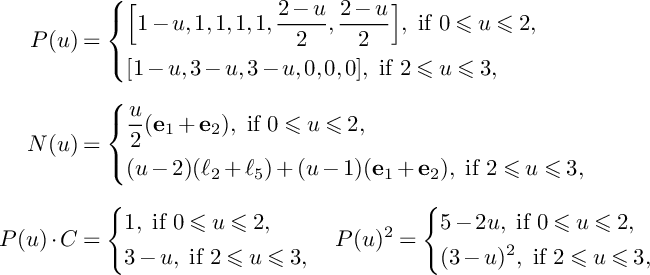 $$ \begin{align*}P(u)&=\left\{\begin{aligned} &\Big[1-u, 1, 1, 1, 1, \frac{2-u}{2}, \frac{2-u}{2}\Big], \ \text{if }0\leqslant u\leqslant 2, \\ &[1-u, 3-u, 3-u, 0, 0, 0],\ \text{if }2\leqslant u\leqslant 3, \\ \end{aligned} \right. \\[6pt]N(u)&=\left\{\begin{aligned} &\frac{u}{2} (\mathbf{e}_1 + \mathbf{e}_2),\ \text{if }0\leqslant u\leqslant 2, \\ &(u-2) (\ell_2 + \ell_5) + (u-1)(\mathbf{e}_1 + \mathbf{e}_2), \ \text{if }2\leqslant u\leqslant 3, \\ \end{aligned} \right. \\[6pt]P(u)\cdot C&=\left\{\begin{aligned} &1, \ \text{if }0\leqslant u\leqslant 2, \\ &3-u, \ \text{if }2\leqslant u\leqslant 3, \\ \end{aligned} \right. \quad P(u)^2=\left\{\begin{aligned} &5 - 2u, \ \text{if }0\leqslant u\leqslant 2, \\ &(3-u)^2, \ \text{if }2\leqslant u\leqslant 3, \\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}P(u)&=\left\{\begin{aligned} &\Big[1-u, 1, 1, 1, 1, \frac{2-u}{2}, \frac{2-u}{2}\Big], \ \text{if }0\leqslant u\leqslant 2, \\ &[1-u, 3-u, 3-u, 0, 0, 0],\ \text{if }2\leqslant u\leqslant 3, \\ \end{aligned} \right. \\[6pt]N(u)&=\left\{\begin{aligned} &\frac{u}{2} (\mathbf{e}_1 + \mathbf{e}_2),\ \text{if }0\leqslant u\leqslant 2, \\ &(u-2) (\ell_2 + \ell_5) + (u-1)(\mathbf{e}_1 + \mathbf{e}_2), \ \text{if }2\leqslant u\leqslant 3, \\ \end{aligned} \right. \\[6pt]P(u)\cdot C&=\left\{\begin{aligned} &1, \ \text{if }0\leqslant u\leqslant 2, \\ &3-u, \ \text{if }2\leqslant u\leqslant 3, \\ \end{aligned} \right. \quad P(u)^2=\left\{\begin{aligned} &5 - 2u, \ \text{if }0\leqslant u\leqslant 2, \\ &(3-u)^2, \ \text{if }2\leqslant u\leqslant 3, \\ \end{aligned} \right. \end{align*} $$
which implies that
![]() $S_S(C)=\frac {19}{15}$
and
$S_S(C)=\frac {19}{15}$
and
![]() $S(W^{C}_{\bullet , \bullet };O)\leqslant \frac {17}{15}$
, so that
$S(W^{C}_{\bullet , \bullet };O)\leqslant \frac {17}{15}$
, so that
![]() $\delta _P(S)=\frac {15}{19}$
by (⧫).
$\delta _P(S)=\frac {15}{19}$
by (⧫).
If
![]() $O\in \mathbf {e}_1$
, then
$O\in \mathbf {e}_1$
, then
![]() $C=\mathbf {e}_1$
. In this case, we have
$C=\mathbf {e}_1$
. In this case, we have
![]() $\tau =2$
, and
$\tau =2$
, and
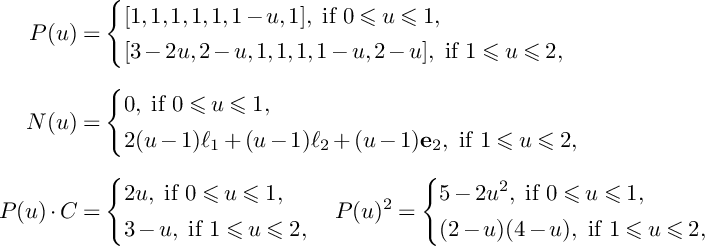 $$ \begin{align*}P(u)&=\left\{\begin{aligned} &[1, 1, 1, 1, 1, 1-u, 1],\ \text{if }0\leqslant u\leqslant 1, \\ &[3-2u, 2-u, 1, 1, 1, 1-u, 2-u],\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right.\\[6pt]N(u)&=\left\{\begin{aligned} &0,\ \text{if }0\leqslant u\leqslant 1, \\ &2(u-1)\ell_1 + (u-1) \ell_2 + (u-1) \mathbf{e}_2,\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right.\\[6pt]P(u)\cdot C&=\left\{\begin{aligned} &2u,\ \text{if }0\leqslant u\leqslant 1, \\ &3-u,\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right. \quad P(u)^2=\left\{\begin{aligned} & 5-2u^2,\ \text{if }0\leqslant u\leqslant 1, \\ &(2-u)(4-u), \ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}P(u)&=\left\{\begin{aligned} &[1, 1, 1, 1, 1, 1-u, 1],\ \text{if }0\leqslant u\leqslant 1, \\ &[3-2u, 2-u, 1, 1, 1, 1-u, 2-u],\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right.\\[6pt]N(u)&=\left\{\begin{aligned} &0,\ \text{if }0\leqslant u\leqslant 1, \\ &2(u-1)\ell_1 + (u-1) \ell_2 + (u-1) \mathbf{e}_2,\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right.\\[6pt]P(u)\cdot C&=\left\{\begin{aligned} &2u,\ \text{if }0\leqslant u\leqslant 1, \\ &3-u,\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right. \quad P(u)^2=\left\{\begin{aligned} & 5-2u^2,\ \text{if }0\leqslant u\leqslant 1, \\ &(2-u)(4-u), \ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right. \end{align*} $$
which implies that
![]() $S_S(C)=\frac {17}{15}$
and
$S_S(C)=\frac {17}{15}$
and
![]() $S(W^{C}_{\bullet , \bullet };O)\leqslant \frac {19}{15}$
, so that
$S(W^{C}_{\bullet , \bullet };O)\leqslant \frac {19}{15}$
, so that
![]() $\delta _P(S)\geqslant \frac {19}{15}$
by (♢).
$\delta _P(S)\geqslant \frac {19}{15}$
by (♢).
On the other hand, we already know that
![]() $S_S(\ell )=\frac {19}{15}$
, which implies that
$S_S(\ell )=\frac {19}{15}$
, which implies that
![]() $\delta _P(S)=\frac {19}{15}$
if
$\delta _P(S)=\frac {19}{15}$
if
![]() $P=\eta (\mathbf {e}_1)$
. Similarly, we see that
$P=\eta (\mathbf {e}_1)$
. Similarly, we see that
![]() $\delta _P(S)=\frac {19}{15}$
if
$\delta _P(S)=\frac {19}{15}$
if
![]() $P=\eta (\mathbf {e}_2)$
. Hence, we may assume that
$P=\eta (\mathbf {e}_2)$
. Hence, we may assume that
![]() $O\not \in \mathbf {e}_1\cup \mathbf {e}_2\cup \ell _1$
.
$O\not \in \mathbf {e}_1\cup \mathbf {e}_2\cup \ell _1$
.
If
![]() $O\in \ell _2$
, we let
$O\in \ell _2$
, we let
![]() $C=\ell _2$
. In this case, we have
$C=\ell _2$
. In this case, we have
![]() $\tau =2$
, and
$\tau =2$
, and
 $$ \begin{align*}P(u)&=\left\{\begin{aligned} &\Big[1, 1-u, 1, 1, 1, \frac{2-u}{2}, 1\Big],\ \text{if }0\leqslant u\leqslant 1, \\ &\Big[1, 1-u, 2-u, 1, 1, \frac{2-u}{2}, 1\Big],\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right. \\[6pt]N(u)&=\left\{\begin{aligned} &\frac{u}{2} \mathbf{e}_1,\ \text{if }0\leqslant u\leqslant 1, \\ &\frac{u}{2} \mathbf{e}_1 + (u-1) \ell_3,\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right.\\[6pt]P(u)\cdot C&=\left\{\begin{aligned} &\frac{2+u}{2},\ \text{if }0\leqslant u\leqslant 1, \\ &\frac{4-u}{2},\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right. \quad P(u)^2=\left\{\begin{aligned} & 5-2u - \frac{u^2}{2},\ \text{if }0\leqslant u\leqslant 1, \\ &\frac{(6-u)(2-u)}{2},\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}P(u)&=\left\{\begin{aligned} &\Big[1, 1-u, 1, 1, 1, \frac{2-u}{2}, 1\Big],\ \text{if }0\leqslant u\leqslant 1, \\ &\Big[1, 1-u, 2-u, 1, 1, \frac{2-u}{2}, 1\Big],\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right. \\[6pt]N(u)&=\left\{\begin{aligned} &\frac{u}{2} \mathbf{e}_1,\ \text{if }0\leqslant u\leqslant 1, \\ &\frac{u}{2} \mathbf{e}_1 + (u-1) \ell_3,\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right.\\[6pt]P(u)\cdot C&=\left\{\begin{aligned} &\frac{2+u}{2},\ \text{if }0\leqslant u\leqslant 1, \\ &\frac{4-u}{2},\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right. \quad P(u)^2=\left\{\begin{aligned} & 5-2u - \frac{u^2}{2},\ \text{if }0\leqslant u\leqslant 1, \\ &\frac{(6-u)(2-u)}{2},\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right. \end{align*} $$
which implies that
![]() $S_S(C)=1$
and
$S_S(C)=1$
and
![]() $S(W^{C}_{\bullet , \bullet };O)\leqslant \frac {13}{15}$
, so that
$S(W^{C}_{\bullet , \bullet };O)\leqslant \frac {13}{15}$
, so that
![]() $\delta _P(S)=1$
by (⧫).
$\delta _P(S)=1$
by (⧫).
Similarly, we see that
![]() $\delta _P(S)=1$
if
$\delta _P(S)=1$
if
![]() $O\in \ell _5$
. Hence, if P is contained in a line in S that passes through a singular point of the surface S, then
$O\in \ell _5$
. Hence, if P is contained in a line in S that passes through a singular point of the surface S, then
![]() $\delta _P(S)=1$
. Thus, we may assume that
$\delta _P(S)=1$
. Thus, we may assume that
![]() $O\not \in \ell _2\cup \ell _2$
.
$O\not \in \ell _2\cup \ell _2$
.
If
![]() $P\in \ell _3$
, we let
$P\in \ell _3$
, we let
![]() $C=\ell _3$
. In this case, we have
$C=\ell _3$
. In this case, we have
![]() $\tau =2$
, and
$\tau =2$
, and
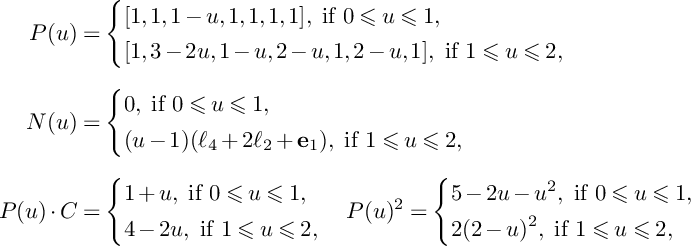 $$ \begin{align*}P(u)&=\left\{\begin{aligned} &[1, 1, 1-u, 1, 1, 1, 1],\ \text{if }0\leqslant u\leqslant 1, \\ & [1, 3-2u, 1-u, 2-u, 1, 2-u, 1],\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right. \\[6pt]N(u)&=\left\{\begin{aligned} &0,\ \text{if }0\leqslant u\leqslant 1, \\ & (u-1) (\ell_4 + 2 \ell_2 + \mathbf{e}_1),\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right.\\[6pt]P(u)\cdot C&=\left\{\begin{aligned} &1+u,\ \text{if }0\leqslant u\leqslant 1, \\ &4-2u,\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right. \quad P(u)^2=\left\{\begin{aligned} &5-2u - u^2,\ \text{if }0\leqslant u\leqslant 1, \\ &2(2-u)^2,\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}P(u)&=\left\{\begin{aligned} &[1, 1, 1-u, 1, 1, 1, 1],\ \text{if }0\leqslant u\leqslant 1, \\ & [1, 3-2u, 1-u, 2-u, 1, 2-u, 1],\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right. \\[6pt]N(u)&=\left\{\begin{aligned} &0,\ \text{if }0\leqslant u\leqslant 1, \\ & (u-1) (\ell_4 + 2 \ell_2 + \mathbf{e}_1),\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right.\\[6pt]P(u)\cdot C&=\left\{\begin{aligned} &1+u,\ \text{if }0\leqslant u\leqslant 1, \\ &4-2u,\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right. \quad P(u)^2=\left\{\begin{aligned} &5-2u - u^2,\ \text{if }0\leqslant u\leqslant 1, \\ &2(2-u)^2,\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right. \end{align*} $$
which implies that
![]() $S_S(C)=\frac {13}{15}$
and
$S_S(C)=\frac {13}{15}$
and
![]() $S(W^{C}_{\bullet , \bullet };O)\leqslant \frac {13}{15}$
, so that
$S(W^{C}_{\bullet , \bullet };O)\leqslant \frac {13}{15}$
, so that
![]() $\delta _P(S)=\frac {15}{13}$
by (⧫).
$\delta _P(S)=\frac {15}{13}$
by (⧫).
Similarly, we see that
![]() $\delta _P(S)=\frac {15}{13}$
if
$\delta _P(S)=\frac {15}{13}$
if
![]() $O\in \ell _4$
. Therefore, we may also assume that
$O\in \ell _4$
. Therefore, we may also assume that
![]() $O\not \in \ell _3\cup \ell _4$
.
$O\not \in \ell _3\cup \ell _4$
.
Let C be the curve in the pencil
![]() $|\ell _2 + \ell _3|$
that contains O. Then C is smooth and irreducible, since O is not contained in the curves
$|\ell _2 + \ell _3|$
that contains O. Then C is smooth and irreducible, since O is not contained in the curves
![]() $\ell _1$
,
$\ell _1$
,
![]() $\ell _2$
,
$\ell _2$
,
![]() $\ell _3$
,
$\ell _3$
,
![]() $\ell _4$
,
$\ell _4$
,
![]() $\ell _5$
,
$\ell _5$
,
![]() $\mathbf {e}_1$
, and
$\mathbf {e}_1$
, and
![]() $\mathbf {e}_2$
by assumption. Then
$\mathbf {e}_2$
by assumption. Then
![]() $\tau =2$
, and
$\tau =2$
, and
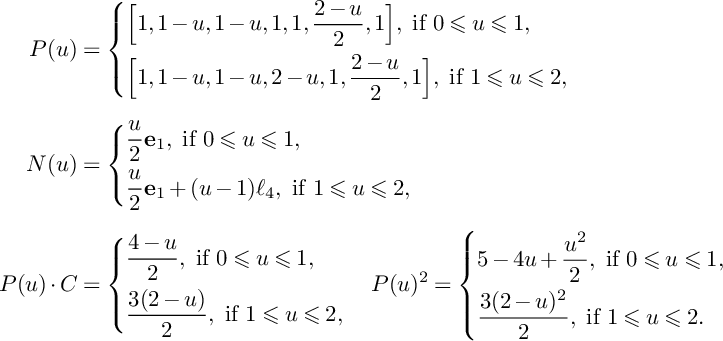 $$ \begin{align*}P(u)&=\left\{\begin{aligned} &\Big[1, 1-u, 1-u, 1, 1, \frac{2-u}{2}, 1\Big],\ \text{if }0\leqslant u\leqslant 1, \\ &\Big[1, 1-u, 1-u, 2-u, 1, \frac{2-u}{2}, 1\Big],\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right. \\[6pt]N(u)&=\left\{\begin{aligned} &\frac{u}{2} \mathbf{e}_1,\ \text{if }0\leqslant u\leqslant 1, \\ &\frac{u}{2} \mathbf{e}_1 + (u-1) \ell_4,\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right.\\[6pt]P(u)\cdot C&=\left\{\begin{aligned} &\frac{4-u}{2},\ \text{if }0\leqslant u\leqslant 1, \\ &\frac{3(2-u)}{2}, \ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right. \quad P(u)^2=\left\{\begin{aligned} &5-4u+\frac{u^2}{2},\ \text{if }0\leqslant u\leqslant 1, \\ &\frac{3(2-u)^2}{2},\ \text{if }1\leqslant u\leqslant 2. \\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}P(u)&=\left\{\begin{aligned} &\Big[1, 1-u, 1-u, 1, 1, \frac{2-u}{2}, 1\Big],\ \text{if }0\leqslant u\leqslant 1, \\ &\Big[1, 1-u, 1-u, 2-u, 1, \frac{2-u}{2}, 1\Big],\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right. \\[6pt]N(u)&=\left\{\begin{aligned} &\frac{u}{2} \mathbf{e}_1,\ \text{if }0\leqslant u\leqslant 1, \\ &\frac{u}{2} \mathbf{e}_1 + (u-1) \ell_4,\ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right.\\[6pt]P(u)\cdot C&=\left\{\begin{aligned} &\frac{4-u}{2},\ \text{if }0\leqslant u\leqslant 1, \\ &\frac{3(2-u)}{2}, \ \text{if }1\leqslant u\leqslant 2, \\ \end{aligned} \right. \quad P(u)^2=\left\{\begin{aligned} &5-4u+\frac{u^2}{2},\ \text{if }0\leqslant u\leqslant 1, \\ &\frac{3(2-u)^2}{2},\ \text{if }1\leqslant u\leqslant 2. \\ \end{aligned} \right. \end{align*} $$
This implies that
![]() $S_S(C)=\frac {11}{15}$
and
$S_S(C)=\frac {11}{15}$
and
![]() $S(W^{C}_{\bullet , \bullet };O)=\frac {23}{30}$
, so that
$S(W^{C}_{\bullet , \bullet };O)=\frac {23}{30}$
, so that
![]() $\delta _P(S)\geqslant \frac {30}{23}>\frac {15}{13}$
by (⧫).
$\delta _P(S)\geqslant \frac {30}{23}>\frac {15}{13}$
by (⧫).
Appendix B Nemuro lemma
Now, let X be any smooth Fano threefold, let
![]() $\pi \colon X\to \mathbb {P}^1$
be a fibration into del Pezzo surfaces, let S be a fiber of the morphism
$\pi \colon X\to \mathbb {P}^1$
be a fibration into del Pezzo surfaces, let S be a fiber of the morphism
![]() $\pi $
such that S is an irreducible reduced normal del Pezzo surface that has at worst du Val singularities, and let P be a point in S. As in §3, set
$\pi $
such that S is an irreducible reduced normal del Pezzo surface that has at worst du Val singularities, and let P be a point in S. As in §3, set
For
![]() $u\in [0,\tau ]$
, let
$u\in [0,\tau ]$
, let
![]() $P(u)$
be the positive part of the Zariski decomposition of the divisor
$P(u)$
be the positive part of the Zariski decomposition of the divisor
![]() $-K_X-uS$
, and let
$-K_X-uS$
, and let
![]() $N(u)$
be its negative part. Suppose, in addition, that
$N(u)$
be its negative part. Suppose, in addition, that
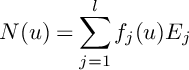 $$ \begin{align*}N(u)=\sum_{j=1}^l f_j(u) E_j \end{align*} $$
$$ \begin{align*}N(u)=\sum_{j=1}^l f_j(u) E_j \end{align*} $$
for some irreducible reduced surfaces
![]() $E_1,\dots ,E_l$
on the Fano threefold X that are different from S, where each
$E_1,\dots ,E_l$
on the Fano threefold X that are different from S, where each
![]() $f_i\colon [0,\tau ]\to \mathbb {R}_{\geqslant 0}$
is some function. For every
$f_i\colon [0,\tau ]\to \mathbb {R}_{\geqslant 0}$
is some function. For every
![]() $j\in \{1,\ldots ,l\}$
, we set
$j\in \{1,\ldots ,l\}$
, we set
![]() $c_j=\mathrm {lct}_{P}(S;E_j|_S)$
. As in Appendix 1, we set
$c_j=\mathrm {lct}_{P}(S;E_j|_S)$
. As in Appendix 1, we set
![]() $\delta _P(S)=\delta _P(S,-K_S)$
. Define
$\delta _P(S)=\delta _P(S,-K_S)$
. Define
![]() $S(W^S_{\bullet ,\bullet };F)$
and
$S(W^S_{\bullet ,\bullet };F)$
and
![]() $\delta _{P}(S;W^S_{\bullet ,\bullet })$
as in [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, §1], or define these numbers using the formulas used in (3.1).
$\delta _{P}(S;W^S_{\bullet ,\bullet })$
as in [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, §1], or define these numbers using the formulas used in (3.1).
Lemma 27. Let F be any prime divisor over S such that
![]() $P\in C_S(F)$
. Then
$P\in C_S(F)$
. Then
 $$ \begin{align} S\big(W^S_{\bullet,\bullet};F\big)&\leqslant A_S(F)\frac{3}{(-K_X)^3}\int_0^\tau\sum_{j=1}^\tau\frac{f_j(u)}{c_j}\big(P(u)\big|_S\big)^2du+\\& \quad +\frac{3}{(-K_X)^3}\int_0^\tau\int_0^\infty\mathrm{vol}\big(P(u)\big|_S-vF\big)dvdu\leqslant \nonumber\\& \leqslant A_S(F)\Biggl(\frac{3}{(-K_X)^3}\sum_{j=1}^l \int_0^\tau \frac{f_j(u)}{c_j}\big(P(u)\big|_S\big)^2 du+\frac{3}{(-K_X)^3}\frac{\tau(-K_S)^2}{\delta_P(S)}\Biggr).\nonumber \end{align} $$
$$ \begin{align} S\big(W^S_{\bullet,\bullet};F\big)&\leqslant A_S(F)\frac{3}{(-K_X)^3}\int_0^\tau\sum_{j=1}^\tau\frac{f_j(u)}{c_j}\big(P(u)\big|_S\big)^2du+\\& \quad +\frac{3}{(-K_X)^3}\int_0^\tau\int_0^\infty\mathrm{vol}\big(P(u)\big|_S-vF\big)dvdu\leqslant \nonumber\\& \leqslant A_S(F)\Biggl(\frac{3}{(-K_X)^3}\sum_{j=1}^l \int_0^\tau \frac{f_j(u)}{c_j}\big(P(u)\big|_S\big)^2 du+\frac{3}{(-K_X)^3}\frac{\tau(-K_S)^2}{\delta_P(S)}\Biggr).\nonumber \end{align} $$
In particular, we have
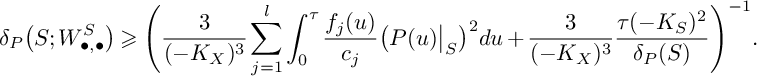 $$ \begin{align*} \delta_{P}\big(S;W^S_{\bullet,\bullet}\big)\geqslant\Biggl(\frac{3}{(-K_X)^3}\sum_{j=1}^l \int_0^\tau \frac{f_j(u)}{c_j}\big(P(u)\big|_S\big)^2 du+\frac{3}{(-K_X)^3}\frac{\tau(-K_S)^2}{\delta_P(S)}\Biggr)^{-1}. \end{align*} $$
$$ \begin{align*} \delta_{P}\big(S;W^S_{\bullet,\bullet}\big)\geqslant\Biggl(\frac{3}{(-K_X)^3}\sum_{j=1}^l \int_0^\tau \frac{f_j(u)}{c_j}\big(P(u)\big|_S\big)^2 du+\frac{3}{(-K_X)^3}\frac{\tau(-K_S)^2}{\delta_P(S)}\Biggr)^{-1}. \end{align*} $$
Proof. Since the log pair
![]() $(S, c_j E_j|_S)$
is log canonical at P, we conclude that
$(S, c_j E_j|_S)$
is log canonical at P, we conclude that
![]() $\mathrm {ord}_F(E_j|_S)\leqslant \frac {A_S(F)}{c_j}$
. Thus, we get the first inequality in (♢). Moreover, since
$\mathrm {ord}_F(E_j|_S)\leqslant \frac {A_S(F)}{c_j}$
. Thus, we get the first inequality in (♢). Moreover, since
![]() $P(u)|_S=-K_S-N(u)|_S$
, we have
$P(u)|_S=-K_S-N(u)|_S$
, we have
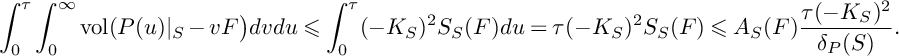 $$ \begin{align*}\int_0^\tau\int_0^\infty\mathrm{vol}(P(u)|_S-vF\big)dvdu\leqslant\int_0^\tau (-K_S)^2 S_S(F)du =\tau (-K_S)^2 S_S(F)\leqslant A_S(F) \frac{\tau (-K_S)^2}{\delta_P(S)}. \end{align*} $$
$$ \begin{align*}\int_0^\tau\int_0^\infty\mathrm{vol}(P(u)|_S-vF\big)dvdu\leqslant\int_0^\tau (-K_S)^2 S_S(F)du =\tau (-K_S)^2 S_S(F)\leqslant A_S(F) \frac{\tau (-K_S)^2}{\delta_P(S)}. \end{align*} $$
Hence, the assertion follows.
Corollary 28. Suppose that
![]() $N(u)=0$
for every
$N(u)=0$
for every
![]() $u\in [0,\tau ]$
, that is, we have
$u\in [0,\tau ]$
, that is, we have
![]() $l=0$
. Then
$l=0$
. Then
 $$ \begin{align*}\delta_P(S,W^S_{\bullet,\bullet})\geqslant\frac{(-K_X)^3\delta_P(S)}{3\tau(-K_S)^2}. \end{align*} $$
$$ \begin{align*}\delta_P(S,W^S_{\bullet,\bullet})\geqslant\frac{(-K_X)^3\delta_P(S)}{3\tau(-K_S)^2}. \end{align*} $$
Corollary 29. Suppose that
![]() $l=1$
,
$l=1$
,
![]() $E_1|_S$
is a smooth curve contained in
$E_1|_S$
is a smooth curve contained in
![]() $S\setminus \mathrm {Sing}(S)$
, and
$S\setminus \mathrm {Sing}(S)$
, and
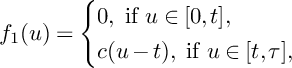 $$ \begin{align*}f_1(u)= \left\{\begin{aligned} &0,\ \text{if }u\in[0,t], \\ &c(u-t),\ \text{if }u\in[t,\tau], \\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}f_1(u)= \left\{\begin{aligned} &0,\ \text{if }u\in[0,t], \\ &c(u-t),\ \text{if }u\in[t,\tau], \\ \end{aligned} \right. \end{align*} $$
for some
![]() $t\in (0,\tau )$
and some
$t\in (0,\tau )$
and some
![]() $c\in \mathbb {R}_{>0}$
. Then
$c\in \mathbb {R}_{>0}$
. Then
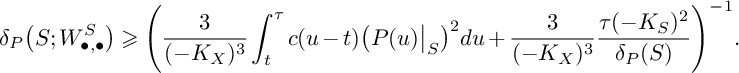 $$ \begin{align*}\delta_{P}\big(S;W^S_{\bullet,\bullet}\big)\geqslant \Biggl( \frac{3}{(-K_X)^3}\int_t^\tau c(u-t)\big(P(u)\big\vert_S\big)^2du +\frac{3}{(-K_X)^3}\frac{\tau(-K_S)^2}{\delta_P(S)}\Biggr)^{-1}. \end{align*} $$
$$ \begin{align*}\delta_{P}\big(S;W^S_{\bullet,\bullet}\big)\geqslant \Biggl( \frac{3}{(-K_X)^3}\int_t^\tau c(u-t)\big(P(u)\big\vert_S\big)^2du +\frac{3}{(-K_X)^3}\frac{\tau(-K_S)^2}{\delta_P(S)}\Biggr)^{-1}. \end{align*} $$
Acknowledgments
We would like to thank the Nemuro city council and Saitama University for excellent working conditions. We would like to thank an anonymous referee for useful comments.