1. Introduction
Current pharmaceutical research and development (R&D) is a high-risk investment that is characterized by a high cost and increasing attrition rate at late-stage drug development (Khanna, Reference Khanna2012). Balancing the risk-reward ratio and improving the productivity of R&D have always been major concerns of the pharmaceutical industry (Paul et al. Reference Paul, Mytelka, Dunwiddie, Persinger, Munos, Lindborg and Schacht2010). To address this issue, several multidisciplinary approaches are required for the process of drug development, including structural biology, computational chemistry, and information technology, which collectively form the basis of rational drug design. Rational drug design refers to the process of finding new pharmaceutical compounds based on the knowledge of a biological target (Liljefors et al. Reference Liljefors, Krogsgaard-Larsen and Madsen2002). Because this process always relies on computer modelling techniques (although not necessarily), it has been considered near-synonymous with the term ‘computer-aided drug design’ (Truhlar et al. Reference Truhlar, Howe, Hopfinger, Blaney and Dammkoehler1999). So far, a wide range of computational approaches have been applied to various aspects of the drug discovery and development process (Durrant & McCammon, Reference Durrant and Mccammon2011; Jorgensen, Reference Jorgensen2004; Xiang et al. Reference Xiang, Cao, Fan, Chen and Mo2012), and it has even been proposed that extensive use of the computational tools could reduce the cost of drug development by up to 50% (Tan et al. Reference Tan, Cong, Hu, Wang, Jia and Liang2010). Rational drug design methods can be divided into two major classes: (1) methods for lead discovery and optimization, which often play an important role in the early state of R&D and help scientists to identify compounds with higher potency and selectivity to one or a few targets; and (2) methods for predicting compounds’ druggability, of which the aim is to prioritize lead molecules for further development by a comprehensive assessment of their therapeutic properties.
The studies to identify leads involve target-to-hit and hit-to-lead processes. Corresponding computational methods include drug target prediction, virtual screening, molecular docking, scaffold hopping, allosteric versus active site modulation, and three-dimensional (3D) quantitative structure-activity relationship (QSAR) analyses (Zheng et al. Reference Zheng, Liu, Xu, Li, Luo and Jiang2013). Several reviews of the development of these methods and their applications have been published (Kalyaanamoorthy & Chen, Reference Kalyaanamoorthy and Chen2011; Ou-Yang et al. Reference Ou-Yang, Lu, Kong, Liang, Luo and Jiang2012; Pei et al. Reference Pei, Yin, Ma and Lai2014; Sliwoski et al. Reference Sliwoski, Kothiwale, Meiler and Lowe2014). The efficiency of these processes and the quality of the generated leads can be significantly improved by the deliberate selection of those computational methods. By contrast, the process to optimize leads into a drug is more challenging. This situation can be easily understood if we roughly compare the number of newly reported active compounds with that of newly approved drugs during the same period. For example, ChEMBL is a database of a large number of bioactive molecules that were extracted from the literature. In 2012, the number of compounds in ChEMBL was 629 943, whereas this number has increased to 1 638 394 by November 2014 (Gaulton et al. Reference Gaulton, Bellis, Bento, Chambers, Davies, Hersey, Light, McGlinchey, Michalovich, Al-Lazikani and Overington2012). Although millions of active compounds have been found, the number of new molecular entities that were approved by the US Food and Drug Administration (FDA) in recent years did not increase. In contrast, there was a slight decline in 2013 compared with 2012 (Mullard, Reference Mullard2014). There are many possible reasons for this decline; except for non-technical (e.g. strategic, commercial) issues, the most relevant are the efficacy and safety deficiencies, which are related in part to absorption, distribution, metabolism and excretion (ADME) properties and various toxicities (T) or adverse side effects. However, the current evaluation methods for ADME/T properties are costly and time consuming and often require a large amount of animal testing, which is often inadequate when managing a large batch of chemicals. Accordingly, in-depth ADME/T scrutiny will not be performed until a limited number of candidate compounds have been identified, meaning that the major chemical scaffolds or preferred core structures have been established at that stage, for which it becomes difficult to make significant structural modifications based on the results of ADME/T evaluation. This disconnect between chemical optimization and ADME/T evaluation has caused many candidate compounds showing excellent in vitro efficacy to be dismissed due to poor ‘druggability’. For example, some compounds could not dissolve in aqueous solution or permeate across the membrane to reach the concentration needed at the required therapeutic level, and some others may exhibit a removal time that is too long or have an excessive number of metabolically unstable sites. In addition, either the compounds or their metabolites may raise toxicity and safety issues, which occasionally cannot be observed by in vitro assays or animal models. Consequently, these issues complicate the assessment of the in vivo efficacy and safety of the drug and hinder the development process. Improving R&D efficiency and productivity will depend heavily on the early assessment of the druggability of compounds. In this sense, the goal of rational drug design is to fully exploit all ADME/T profiling data to prioritise the candidates or, alternatively, to ‘fail early and fail cheap’.
Because it is impractical to perform intricate and costly ADME/T experimental procedures for vast numbers of compounds, in silico ADME/T prediction is becoming the method of choice in early drug discovery. The establishment of high-quality in silico ADME/T models will permit the parallel optimization of compound efficacy and druggability properties, which is expected to not only improve the overall quality of drug candidates and therefore the probability of their success, but also to lower the overall expenses due to a reduced downstream attrition rate. In the last decade, a large number of ADME/T prediction models have been reported, and several reviews regarding the development of these models have been published (Cheng et al. Reference Cheng, Li, Liu and Tang2013; Clark & Pickett, Reference Clark and Pickett2000; Moroy et al. Reference Moroy, Martiny, Vayer, Villoutreix and Miteva2012). Between 2008 and 2012, the Office of Clinical Pharmacology at the FDA received 33 submissions containing physiologically based pharmacokinetic (PBPK) modelling applications for investigational new drugs (INDs) and new drug applications (NDAs) (Huang et al. Reference Huang, Abernethy, Wang, Zhao and Zineh2013). However, compared with the number of newly developed models, reports of the practical applications of these models in medicinal chemistry study or the drug discovery process are rarer. To solve these problems, some solutions have been reported regarding how to develop more effective models and where these models can be used (Gleeson & Montanari, Reference Gleeson and Montanari2012). More importantly, the outcome of ADME/T models can be maximized by intelligently integrating existing in silico, in vitro, and in vivo ADME/T data to guide drug discovery (Wang & Collis, Reference Wang and Collis2011).
In this review, we focused on the development of ADME/T prediction models and their future opportunities and challenges. The first section concerns the influences of physicochemical (PC) parameters on compound druggability and the development of some PC prediction models. The second section introduces the prediction models for some important properties, such as human intestinal absorption, metabolism, membrane transporters, and PBPK models. The third section relates to the prediction models for toxicities, including acute toxicity, genotoxicity, and human ether-a-go-go-related gene (hERG) toxicity. In the last section, we will discuss the future direction of in silico ADME/T modelling.
2. PC parameters
The PC properties of a compound include lipophilicity, solubility, ionization, topology, and molecular mass (Leeson & Oprea, Reference Leeson, Oprea, Livingstone and Davis2011). Consequently, these properties may affect the ADME/T profile of compounds, their potency, selectivity against targets, and the ‘screenability’ in high-throughput screening (HTS) (Leeson & Springthorpe, Reference Leeson and Springthorpe2007). There is substantially increasing interest from both industry and academia in investigating the relationship between bulk PC properties, potency and the ADME/T profile of compounds (Gleeson et al. Reference Gleeson, Hersey, Montanari and Overington2011). Compared with many other ADME/T endpoints, PC parameters are easily available and involve less complex mechanisms, which form the basis for developing reliable and robust in silico methods. Here, we will briefly review the prediction models for three PC properties, namely, lipophilicity, solubility, and ionization constant, and some rule-based models that are closely related to PC properties.
2.1 Lipophilicity
Lipophilicity is an important parameter in drug discovery because it contributes to the solubility, permeability, potency, selectivity, and promiscuity of a compound (Arnott & Planey, Reference Arnott and Planey2012; Waring, Reference Waring2010). The lipophilicity of organic molecules is typically quantified as log P o/w , where P is the ratio of the concentrations of a compound in a mixture of octanol and water phases at equilibrium. The prediction of log P is a prerequisite for the pharmaceutical industry to optimize the pharmacodynamics and pharmacokinetic properties of hits and leads. The current methods for calculating log P fall into three broad classes: ab initio methods based on molecular simulation, substructure-based methods and property-based methods. Ab initio methods for log P prediction were developed based on the absolute solvation Gibbs free energies in different phases at constant temperature (T) and pressure (P), which are estimated with molecular dynamics simulation using the thermodynamic integration approach. According to Eq. (1),
where
![]() $\Delta G_{{\rm solv}}^{{\rm oct}} $
is the solvation Gibbs free energies of compounds in water-saturated octanol,
$\Delta G_{{\rm solv}}^{{\rm oct}} $
is the solvation Gibbs free energies of compounds in water-saturated octanol,
![]() $\Delta G_{{\rm solv}}^w $
is the solvation Gibbs free energies of compounds in water, R is the molar gas constant and T is the temperature (298 K). Therefore, obtaining the solvation free energies of compounds in each phase is the key step in the log P calculation.
$\Delta G_{{\rm solv}}^w $
is the solvation Gibbs free energies of compounds in water, R is the molar gas constant and T is the temperature (298 K). Therefore, obtaining the solvation free energies of compounds in each phase is the key step in the log P calculation.
Solvation remains a challenging calculation problem in molecular simulation. Because treating each solvent molecule as a separate molecule would result in an excessively high computational cost, implicit solvent models have been proposed that represent the solvent as a continuous medium, also called continuum solvent models. The implicit solvation models included accessible surface area (ASA) models and continuum electrostatics models. The first proposed electrostatics models were Poisson–Boltzmann (PB) models that described the electrostatics environment of a solute in solution in the direction that is normal to the charged surface (Fogolari et al. Reference Fogolari, Brigo and Molinari2002). To reduce the computation cost of PB models, generalized Born (GB) models that used an approximation of the exact PB equation were later proposed (Still et al. Reference Still, Tempczyk, Hawley and Hendrickson1990). Subsequently, ASA models and continuum electrostatics models were often combined to develop hybrid models, such as the well-known PB/SA and GB/SA. Many quantum mechanical continuum solvation models have been reported (Cramer & Truhlar, Reference Cramer and Truhlar1999; Tomasi et al. Reference Tomasi, Mennucci and Cammi2005).
For the application of solvation models in the log P calculation, in 1999, Best et al. compared the free energy perturbation (FEP) and continuum of the GB/SA method to calculate log P o/w . Because FEP could not compute the absolute free energies of solvation, the relative free energies of solvation in which solute A is slowly mutated into solute B have been computed, calculating the Gibbs free energy change in solute A mutating into solute B in water-saturated octanol and water and the difference value of log P, Δlog P o/w . The Gibbs free energy changes were also calculated by the continuum GB/SA models. A comparison of the results that were calculated with the FEP and GB/SA models indicated that for the set of 12 solutes in this study, GB/SA actually yielded more accurate estimates of Δlog P o/w at a significantly lower computational cost (Best et al. Reference Best, Merz and Reynolds1999). Garrido et al. computed the Gibbs free energies of solvation for several n-alkanes in 1-octanol and water using three different force fields, namely, Gromos, TraPPE, and OPLS-AA. After a systematic comparison, these authors found that the Gromos force field accurately predicted the solvation Gibbs free energy of n-alkanes up to C8 in the water phase, whereas the OPLS-AA/TraPPE force field was better in the organic phase. The combination of these two models for the log P calculation yielded an absolute average deviation of 0·1 units to the experimental data (Garrido et al. Reference Garrido, Queimada, Jorge, Macedo and Economou2009).
Log P can also be predicted by substructures and molecular properties. Substructure-based methods were also considered fragment-based methods that were generated by decomposing the log P into atomic and fragmental contributions that were determined by a large library of experimentally measured log P values. The correction factors can also be introduced to compensate for intramolecular interactions. Property-based methods were developed based on the quantitative structure-property relationship (QSPR), which can be divided into two types: (1) empirical approaches, which predict log P by a predetermined function and a restricted set of experimental parameters that are related to lipophilicity; and (2) statistical-based models, which are trained with experimental log P values and various descriptors using statistical learning methods. Table 1 summarizes the different types of methods and associated examples.
Table 1. Models for lipophilicity prediction and the methods thereof and examples of their application

All of these methods have been widely used in drug discovery and development processes. Furthermore, there are several reviews comparing the accuracy and application of in silico log P prediction models (Kujawski et al. Reference Kujawski, Popielarska, Myka, Drabińska and Bernard2012; Mannhold et al. Reference Mannhold, Poda, Ostermann and Tetko2009; Tetko et al. Reference Tetko, Poda, Ostermann and Mannhold2009). Mannhold et al. (Reference Mannhold, Poda, Ostermann and Tetko2009) compared the predictive power of representative methods for one public (N = 266) and two in-house datasets from Nycomed (N = 882) and Pfizer (N = 95 809), respectively. The prediction performances of all tested methods were not satisfactory; among these methods, ALOGPS, S + logP, XLOGP3, OsirisP, ALOGP, and ALOGP98 showed a higher accuracy. For the practical use of these models, it is necessary for medicinal chemists to understand their strengths and limitations and their applicability domains, and the use of local models helps to achieve accurate and meaningful in silico predictions (Tetko et al. Reference Tetko, Poda, Ostermann and Mannhold2009).
2.2 Solubility
Aqueous solubility is one of the most important factors affecting drug bioavailability. To be absorbed, a drug must be soluble in water first and then have the opportunity to permeate across biological membranes (Stegemann et al. Reference Stegemann, Leveiller, Franchi, De Jong and Linden2007).
For the methods for solubility prediction from the first principle, a thermodynamic cycle that decomposes the dissolution process into a sublimation of molecules from crystal to vapour and from vapour to solution was proposed, as shown in Scheme 1 (Grant & Higuchi, Reference Grant and Higuchi1990). Then, the relationship between intrinsic solubility (S 0) and the overall change in Gibbs free energy can be expressed as
where
![]() $\Delta G_{{\rm sol}}^{\ast}$
is the Gibbs free energy for solution,
$\Delta G_{{\rm sol}}^{\ast}$
is the Gibbs free energy for solution,
![]() $\Delta G_{{\rm sub}}^{\ast}$
is the Gibbs free energy for sublimation,
$\Delta G_{{\rm sub}}^{\ast}$
is the Gibbs free energy for sublimation,
![]() $\Delta G_{{\rm solv}}^{\ast}$
is the Gibbs free energy for solvation, R is the molar gas constant, T is the temperature (298 K), V
m
is the molar volume of the crystal, and S
0 is the intrinsic solubility in moles per litre.
$\Delta G_{{\rm solv}}^{\ast}$
is the Gibbs free energy for solvation, R is the molar gas constant, T is the temperature (298 K), V
m
is the molar volume of the crystal, and S
0 is the intrinsic solubility in moles per litre.

Scheme 1. Thermodynamic cycle for the transfer from crystal to vapour and then to solution.
Thompson et al. implemented the continuum solvation model SM5·42R into ab initio Hartree–Fock (HF) theory, hybrid density functional theory Becke-3-Lee-Yang-Parr (B3LYP), and the semi-empirical molecular orbital theory Austin Model 1 (AM1) levels to calculate the logarithm of the solubility (log S). Without any data regarding solubility or experimental solute vapour pressures, these models yielded a mean-unsigned error of log S in the range of 0·3–0·45 for a small test set (Thompson et al. Reference Thompson, Cramer and Truhlar2003).
Based on the thermodynamic cycle, Schnieders et al. combined the polarizable Atomic Multipole Optimised Energetics for Biomolecular Applications (AMOEBA) force field with the orthogonal space random walk (OSRW) sampling strategy to predict the structure, thermodynamic stability, and solubility of organic crystal from molecular dynamics simulations. As a polarizable atomic multipole force field, AMOEBA could capture the aspherical atomic electron density and then provide the transferability between different phases and environments with vastly different dielectric constants (Ponder et al. Reference Ponder, Wu, Ren, Pande, Chodera, Schnieders, Haque, Mobley, Lambrecht, Distasio, Head-Gordon, Clark, Johnson and Head-Gordon2010). The OSRW sampling strategy was used to overcome large barriers in the crystalline free energy landscape (Zheng et al. Reference Zheng, Chen and Yang2008). For n-alkylamide compounds, the combinatorial method showed a reasonable prediction with a mean signed error of solubility free energies between the calculated absolute standard state and experimental value of 1·1 kcal mol−1 (Schnieders et al. Reference Schnieders, Baltrusaitis, Shi, Chattree, Zheng, Yang and Ren2012).
Moreover, Palmer et al. tested three different levels of theory for the calculation of sublimation free energy and four different methods for solvation free energy, and the results indicate that the combination of sublimation free energies that were calculated with the B3LYP/6–31G(d,p) level of theory and the solvation free energies with 3D-RISM/UC (reference interaction sites model/universal correction) could yield a root mean square error of 1·45 log S units for 25 drug-like molecules (Palmer et al. Reference Palmer, Mcdonagh, Mitchell, Van Mourik and Fedorov2012). The 3D-RISM is a classical statistical mechanics approach of the molecular integral equation theory for solvation free energy calculation that yields a full molecular picture of the solvation structure and thermodynamics from the first principle, and the 3D-RISM/UC was the extension of 3D-RISM with partial molar volume correction (Kovalenko & Hirata, Reference Kovalenko and Hirata2000; Palmer et al. Reference Palmer, Frolov, Ratkova and Fedorov2010).
Recently, the ab initio methods for solubility prediction have made significant progress with the development of computational power. However, the calculation of the direct computation of solubility via ab initio methods is still not affordable or scalable to the prediction of a large amount of compounds.
The in silico solubility models that have been used for drug design purposes are still mainly based on QSPR based on either simple multiple linear regression methods or complex machine-learning methods, such as neural networks. An example of the first type of model is the general solubility equation (GSE), which was proposed by Jain & Yalkowsky (Reference Jain and Yalkowsky2001). This equation incorporates the log P and experimentally determined melting point (mp) temperature in establishing QSPR equations Eq. (3). In this model, the solubility of a molecule in solid form is governed by the strength of the interaction that is formed between molecules within the solid crystal lattice that was given by the mp and the overall molecular lipophilicity that was determined by log P.
Because the mp is not always available, Wang et al. (Reference Wang, Hou and Xu2009) replaced the mp with an easily calculable molecular polarizability (Pol) (Wang et al. Reference Wang, Xie, Hou and Xu2007) and obtained the model Eq. (4) with a standard error of 0·887 (in log units) and an R 2 of 0·905.
Subsequently, Ali et al. critically assessed the GSE for aqueous solubility prediction by incorporating the effect of the topological polar surface area (TPSA) and developed an alternative simple model Eq. (5). The solubility of 81% of the compounds in the dataset was accurately predicted (Ali et al. Reference Ali, Camilleri, Brown, Hutt and Kirton2012b).
Because the TPSA model yields poor prediction performance for molecules with phenolic and/or phenol-like moieties, Ali et al. modified the TPSA model by incorporating a descriptor pertaining to a simple count of phenol and phenol-like moieties and further improved the predictive ability Eq. (6) (Ali et al. Reference Ali, Camilleri, Brown, Hutt and Kirton2012a). This model highlighted the positive effect of phenolic substituents (aroOHdel) on the solubility of aromatic molecules.
GSE is typically a ‘local’ model that is constructed using a series of chemical analogues and should be used with caution for a chemical outside of its application domain. For example, Moritomo et al. (Reference Moritomo, Yamada, Watanabe, Itahana, Akuzawa, Okada and Ohta2013) exploited the SAR of 5-HT2B and 5-HT7 receptor antagonists and found that their aqueous solubility could be improved by reducing their lipophilicity or increasing their TPSA. However, the TPSA has a negative coefficient for Eqs. (5) and (6), and the contribution of TPSA is unfavourable for increasing solubility. Despite being counterintuitive, TPSA is only one of the molecular properties used that may be inter-correlated (collinear) to each other (TPSA and lipophilicity in this case), and its contribution to different GSEs may vary significantly.
Compared with the GSE, the second type of model was built based on additional descriptors and more sophisticated modelling approaches (Jorgensen & Duffy, Reference Jorgensen and Duffy2002) and was referred to as the ‘black box’ model because the results are often difficult to interpret. In addition, many ‘black box’ solubility prediction models were reported in early years. Recently, Lusci et al. (Reference Lusci, Pollastri and Baldi2013) reported an aqueous solubility prediction model based on undirected graph recursive neural networks (UG-RNNs) with deep architectures and deep learning. The main advantage of the UG-RNN approach is that it can automatically extract the internal representations from the molecular graphs, as suited for solubility prediction. Both types of models have been used in drug-likeness analysis and as efficient filters for compound screening. To assess the quality of these models, Hewitt et al. (Reference Hewitt, Cronin, Enoch, Madden, Roberts and Dearden2009) compared four approaches, including simple linear regression, artificial neural networks (ANNs), category formation, and available in silico models. No one approach could accurately predict the solubility, but the simple regression approach was superior to the more complex modelling methods due to its lower probability of over-fitting. Overall, an insufficient appreciation for the complexity of the solubility phenomenon and the inferior quality of solubility data are the two major reasons for the limited prediction ability of current models (Llinas et al. Reference Llinas, Glen and Goodman2008).
2.3 Ionization constant
The ionization constant, as measured by pK a , is a useful thermodynamic parameter to modulate several key molecular properties (Charifson & Walters, Reference Charifson and Walters2014; Manallack et al. Reference Manallack, Prankerd, Yuriev, Oprea and Chalmers2013). Specifically, drug distribution and diffusion rely heavily on the ionized state of the drugs at a physiological pH because the neutral species of compounds are more lipophilic, whereas ionized ones are polar and water soluble. Additionally, log D, which is an extension of log P by considering all forms of the compound (i.e. ionized and un-ionized), was introduced to consider the influences of ionization on the octanol-water partition coefficient. A previous analysis of known oral drugs showed that 78·6% of compounds contain an invisible group, 4·3% are always ionized, and 5·2% exist in other forms, such as salt (Manallack, Reference Manallack2009). Many methods for high-throughput pK a screening and prediction have been reported to acquire pK a data for a vast amount of compounds in the early stages of R&D (Wan & Ulander, Reference Wan and Ulander2006). Computational methods generally fall into three main categories: (1) ab initio QM calculations; (2) semi-empirical approaches; and (3) statistical and machine-learning approaches.
In ab initio QM calculation, the process of compound ionization is often interpreted as a thermodynamic cycle, as in Scheme 2, and the pK
a
value of a compound is calculated through Eq. (7). In Scheme 2, the deprotonation free energy (i.e. the Gibbs energy change in the process of a compound dissociating a proton into water) was decomposed into three parts and calculated using Eq. (8). As discussed in Section 2.1, various solvation models are available for pK
a
ab initio calculation, and
![]() $\Delta G_g^{\ast}$
is the standard Gibbs energy change for the process in a vacuum and would be computed by the Gibbs Helmholtz equation. In practice, depending on whether a water molecule appears on the reactant or product side of thermodynamic cycle, the correction factor of log[H2O] was subtracted from or added to the pK
a
value, which can reduce a systematic error of 1·74 pK
a
units (Ho & Coote, Reference Ho and Coote2010). In addition to these direct calculation models, there are many more complex models, such as the proton exchange method, hybrid cluster-continuum approaches and implicit explicit approach. A more detailed discussion about the progress of pK
a
calculations from the first principle is provided elsewhere (Ho & Coote, Reference Ho and Coote2010).
$\Delta G_g^{\ast}$
is the standard Gibbs energy change for the process in a vacuum and would be computed by the Gibbs Helmholtz equation. In practice, depending on whether a water molecule appears on the reactant or product side of thermodynamic cycle, the correction factor of log[H2O] was subtracted from or added to the pK
a
value, which can reduce a systematic error of 1·74 pK
a
units (Ho & Coote, Reference Ho and Coote2010). In addition to these direct calculation models, there are many more complex models, such as the proton exchange method, hybrid cluster-continuum approaches and implicit explicit approach. A more detailed discussion about the progress of pK
a
calculations from the first principle is provided elsewhere (Ho & Coote, Reference Ho and Coote2010).
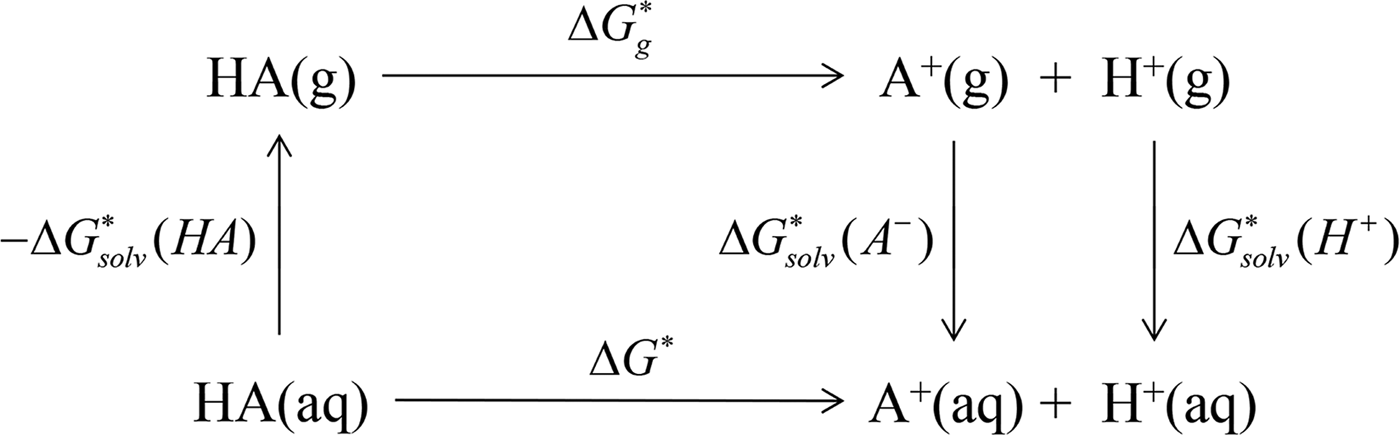
Scheme 2. pK
a
prediction via the thermodynamic cycle. Gas phase (g), aqueous solution (aq), liquid phase (l), solvation (solv).
![]() $\Delta G_{{\rm solv}}^{\ast} ({\rm HA})$
is the solvation free energy of HA,
$\Delta G_{{\rm solv}}^{\ast} ({\rm HA})$
is the solvation free energy of HA,
![]() $\Delta G_g^{\ast}$
is the gas-phase proton affinity of H+, and A−,
$\Delta G_g^{\ast}$
is the gas-phase proton affinity of H+, and A−,
![]() $\Delta G_{{\rm solv}}^{\ast} (A^{-})$
and
$\Delta G_{{\rm solv}}^{\ast} (A^{-})$
and
![]() $\Delta G_{{\rm solv}}^{\ast} (H^{+})$
are the solvation free energies of A− and H+, respectively.
$\Delta G_{{\rm solv}}^{\ast} (H^{+})$
are the solvation free energies of A− and H+, respectively.
Ab initio QM methods have received extensive attention in pK a modelling studies. However, the computation costs are often excessively high for a large set of compounds. In addition, the prediction accuracy depends on the structural optimization, and thus, the conformational flexibility of the compound is a challenge because the optimized structures are not always in their global energy minimum.
With regard to semi-empirical models, a well-known approach is the linear free energy relationship (LFER) (Clark & Perrin, Reference Clark and Perrin1964) based on the Hammett equation, similar to Eq. (9) (Hammett, Reference Hammett1937).
where pK a is the ionization constant for the parent (unsubstituted) molecule; ρ is a reaction constant that depends on the class of molecules, the medium and the temperature; m is the number of substituents; and σ i represents constants expressing the substituent effect on the ionization constant of the parent molecule.
Because the pK
a
values are directly related to the deprotonation energy (as shown in Eq. (7)), adding a substituent to the molecule would change the deprotonation energy of a molecule and its pK
a
values. Thus, the pK
a
values of a molecule could be calculated by adding the contributions of the additive substituents to the
![]() ${\rm p}K_a^0 $
of the reference molecule. The disadvantages of the LFER approach are that the σ
i
constants for all of the involved substituents must be known (Ertl, Reference Ertl1997) and that some non-linear effects cannot be captured. Although the LFER approach was introduced in 1935 (Hammett, Reference Hammett1935), it is still widely used in commercial packages, such as ACD/pK
a
, Epik and Pallas/pKalc.
${\rm p}K_a^0 $
of the reference molecule. The disadvantages of the LFER approach are that the σ
i
constants for all of the involved substituents must be known (Ertl, Reference Ertl1997) and that some non-linear effects cannot be captured. Although the LFER approach was introduced in 1935 (Hammett, Reference Hammett1935), it is still widely used in commercial packages, such as ACD/pK
a
, Epik and Pallas/pKalc.
An increasing number of pK a prediction models have been established by statistic methods involving multi-linear regression (MLR), ANNs, and kernel-based machine learning. Kernel-based machine learning was recently applied to pK a prediction models. For example, Rupp et al. (Reference Rupp, Korner and Tetko2010) used graph kernels and kernel ridge regression to treat molecules based on their graph representation and developed a model showing an accuracy that was comparable with that of the semi-empirical models of Tehan et al. (Reference Tehan, Lloyd, Wong, Pitt, Gancia and Manallack2002a, Reference Tehan, Lloyd, Wong, Pitt, Montana, Manallack and Ganciab). As partial atomic charge is an important descriptor for molecular pK a , Vařeková et al. (Reference Vařeková, Geidl, Ionescu, Skrehota, Bouchal, Sehnal, Abagyan and Koca2013) used an electronegativity equalization method (EEM) to develop QSPR models for pK a prediction (Jirouskova et al. Reference Jirouskova, Varekova, Vanek and Koca2009). The resulted models showed a similar accuracy as that of QM QSPR models but significantly reduced the required computation cost.
Although many prediction approaches have been reported, several benchmarking studies for commercial pK a prediction packages have shown that the prediction of pK a has not been fully solved in the drug discovery setting, and further studies of pK a prediction models are required (Balogh et al. Reference Balogh, Tarcsay and Keserű2012; Liao & Nicklaus, Reference Liao and Nicklaus2009; Manchester et al. Reference Manchester, Walkup, Rivin and You2010). For further method development, high-quality data and meaningful descriptors based on QM are necessary, and the application of new statistical methods, such as kernel-based learning, deep learning, and Gaussian process regression, may be beneficial for the improvement of pK a models (Rupp et al. Reference Rupp, Korner and Tetko2011).
2.4 Rules based on PC properties
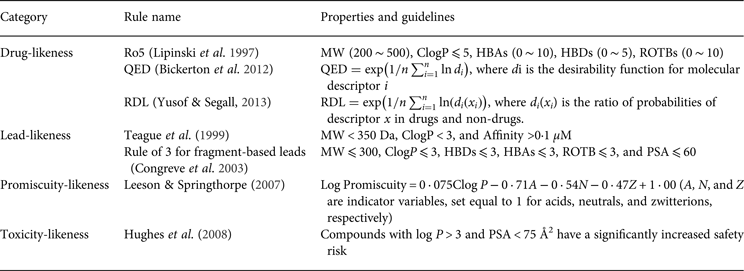
One of the earliest applications of PC properties in drug discovery and development is drug-likeness evaluation. For example, the well-known ‘rule of 5’ (Ro5), which was promulgated by Lipinski et al. (Reference Lipinski, Lombardo, Dominy and Feeney1997), is based on the observation of PC properties of most orally administered drugs. The Ro5 has been used to select compounds that are likely to be orally bioavailable based on five simple rules that are related to molecular properties. Similar to drug-likeness, there are rules for ‘lead-likeness’. For example, a lead-likeness rule that was developed by AstraZeneca can be used to assess the potential of a compound that merits further structural optimization in drug discovery (Teague et al. Reference Teague, Davis, Leeson and Oprea1999). These rules are widely used as filters to prioritize the compounds that are more likely to be drug candidates. However, no discrimination is made beyond a qualitative pass or fail for these filters because all of the compounds that comply with (or violate) the rules are considered equal. Recently, Bickerton et al. reported a quantitative measure of drug-likeness based on a concept of desirability called the quantitative estimate of drug-likeness (QED) (Bickerton et al. Reference Bickerton, Paolini, Besnard, Muresan and Hopkins2012). The QED ranks compounds according to their similarity to marketed drugs by a continuous measure of drug-likeness. Based on this study, Yusof & Segall (Reference Yusof and Segall2013) reported a relative drug likelihood metric (RDL) that employed Bayesian methods to incorporate the distinction between drugs and non-drugs into the desirability function of QED. In addition to the drug-likeness assessment, many studies have highlighted the key role of bulk physical properties in drug promiscuity and drug toxicity (Price et al. Reference Price, Blagg, Jones, Greene and Wager2009; Tarcsay & Keseru, Reference Tarcsay and Keseru2013). Some of the key rule-based PC properties are summarized in Table 2.
Table 2. Summary of the highlighted rules based on the physicochemical properties
3. ADME prediction models
The interaction between drugs and the human body is a bidirectional process: drugs affect the human body, resulting in receptor inhibition, activation, and signal pathway blocking, and the human body disposes of drug by absorption, distribution, metabolism, and excretion. These two processes are interactional and simultaneous and lead to desired pharmacological function or undesirable side effects. Consequently, ADME properties are governing factors for the druggability of chemical compounds. As the in vivo process of a drug is associated with multiple factors and involves complex mechanisms, the prediction of ADME properties is often simplified to the major components or divided into multiple single processes. For example, metabolism prediction may only consider the biotransformation that is mediated by one enzyme in the liver, and the distribution prediction can be further split into the simulations for plasma protein binding (PPB) and the blood-brain barrier. Significant efforts have been devoted to modelling and predicting various ADME-related issues over the past decade. In this section, the models for several important properties are illustrated to explain the development of ADME prediction models.
3.1 Human intestinal absorption (HIA)
The oral administration of drugs is a cost-effective and desired route that is associated with high patient compliance. HIA, as a key procedure of oral absorption, is one of the most influential ADME properties in the early stages of lead discovery and optimization (Artursson & Karlsson, Reference Artursson and Karlsson1991). A large amount of data regarding HIA has been produced rapidly by in vivo and in vitro experimental assays. Many computational classification and correlation models have been developed to predict the HIA based on these data. Several reviews have summarized the previously reported HIA prediction models (Hou et al. Reference Hou, Wang, Zhang, Wang and Xu2006; Stenberg et al. Reference Stenberg, Bergstrom, Luthman and Artursson2002).
For classification models, there are straightforward rule-based models, such as Ro5, and more complex machine learning models. Recently, Shen et al. proposed a substructure pattern recognition approach to build a support vector machine (SVM)-based classification model for HIA prediction, in which each molecule is represented by a set of substructure fingerprints based on a predefined substructure dictionary (Shen et al. Reference Shen, Cheng, Xu, Li and Tang2010). The most influential substructure patterns are recognized by an information gain analysis, which may contribute to an indirect interpretation of the models from a medicinal chemistry perspective. However, because most HIA prediction models were built based on datasets with a highly skewed distribution (i.e. the datasets typically consist of more positive samples (marketed drugs with high HIA absorption) than negative samples), they typically cannot identify poorly absorbed compounds. This problem has restricted the application of these models in the pharmaceutical industry. Recently, based on a dataset of 645 drug and drug-like compounds, Newby et al. under-sampled the class of highly absorbed compounds to establish training sets with a balanced distribution (50:50) and then developed a model using classification and regression tree (Newby et al. Reference Newby, Freitas and Ghafourian2013). These authors also varied the ratio of the costs of false positives to false negatives, aiming to develop a model with lower misclassification rate. These strategies offer some threads regarding how to cope with unbalanced datasets and build classification models with a larger application domain.
QSAR models are also widely used in HIA prediction. Compared with qualitative models, which only classify compounds into high, low or medium absorption classes, quantitative models can rank compounds according to their relative values of HIA. Thomas et al. (Reference Thomas, Brightman, Gill, Lee and Pufong2008) modelled the HIA using Caco-2 permeability in combination with kinetic solubility data. The model was trained and cross-validated with the data for 120 combinations of compounds and Caco-2 permeability and kinetic solubility parameters from different compound doses. The resulting model showed superior results compared with several previously reported models based only on permeability or solubility.
Many studies have aimed to predict the intestinal absorption of chemical compounds, but few attempts have been made to predict the intestinal absorption for peptide information. Because protein therapeutics have gained an increasing amount of attention and the number of peptides entering clinical trials continues to grow, designing oral peptide-based drugs is a future direction for drug discovery (Craik et al. Reference Craik, Fairlie, Liras and Price2013). Recently, Jung et al. used ANNs to develop the first models to predict the intestinal permeability of peptides based on sequence information (Jung et al. Reference Jung, Kim, Kim, Jung, Rhee, Shin, Choi, Kang, Kim and Yun2007). More effort is required to screen the intestinal barrier-permeable peptides from large peptide libraries.
3.2 PPB
Drugs can bind to plasma proteins at constant rates, and this PPB may cause less bioavailability and undesirable drug–drug interactions (DDIs) (Trainor, Reference Trainor2007). Thus, it is critical to predict the binding rate and modify the problematic candidates. A common practice in drug discovery is to use high-performance liquid chromatography (HPLC) screening human serum albumin (HSA) binding affinity. For a given concentration of drug-binding sites and assuming only one binding site per HSA molecule, the binding constant is given by logK HSA = log((t − t 0)/t 0), where t and t 0 are the retention times of the drug and the dead time of the column, respectively (Colmenarejo et al. Reference Colmenarejo, Alvarez-Pedraglio and Lavandera2001). However, this method has several deficiencies. First, as revealed by crystallographic studies, there is in fact more than one potential ligand binding site (Fig. 1). Second, an HSA-immobilized column cannot precisely represent the highly dynamic nature of HSA. These issues can be better addressed by a combination of computational docking, molecular dynamic (MD) analysis and HPLC data mining models. For example, to which PPB site a compound will bind can be predicted by docking studies or can be classified based on its structural characteristics; the binding affinity between the compound and docking site can be predicted by docking or MD simulation methods combined with HPLC data.

Fig. 1. Superimposition of all of the publically available crystal structures of HSA with bound ligands (only one typical protein structure is presented, PDB ID: 1N5U). Six drug-binding sites are shown.
Many in silico models have been proposed regarding two fundamental aspects: (1) binding rate and affinity, which can be directly used to evaluate how tightly a drug binds to HSA; and (2) binding sites and poses, which may provide useful information for structure modification. These models can also be classified as ligand- and receptor-based models, as shown in Fig. 2. The characteristics of small molecules can be directly used for binding site and affinity prediction, forming some ligand-based HSA binding models. Hall et al. (Reference Hall, Jorgensen and Whitehead2013) proposed a Bayesian classifier utilizing a publically available dataset with known binding sites (sites 1 and 2). Li et al. (Reference Li, Chen, Xu, Sui, Guo, Liu and Zhang2011a) developed a multiple linear regression model, in which both intra-molecular descriptors (ligand properties) and inter-molecular interaction descriptors (from docking results) were considered. The obtained plasma protein interaction QSAR (PPI-QSAR) model highlighted five important structural parameters affecting PPB. This PPI-QSAR work also used receptor-based approaches via docking and MD simulation to provide conformation and interaction prediction for HSA and its ligands. To investigate the importance of the protein flexibility of HSA during the ligand-binding process, induced-fit docking was used by Sherman et al. (Reference Sherman, Day, Jacobson, Friesner and Farid2005).

Fig. 2. Schematic of the workflow for the ligand- and receptor-based in silico predicting binding affinity, site, and pose of any user-provided small molecule with HSA.
There are some integrated protocols to predict PPB. A representative example is the web application of Zsila et al. (Reference Zsila, Bikadi, Malik, Hari, Pechan, Berces and Hazai2011) using SVM-aided docking. This platform enables the users to (1) predict whether albumin binds the query ligand, (2) determine the probable ligand binding site, (3) select the albumin X-ray structure in the complex with the ligand that is most similar to the query, and (4) calculate the putative complex using molecular docking calculations. Hall et al. (Reference Hall, Jorgensen and Whitehead2013) implemented a KNIME workflow that is readily accessible to the structure-based drug design community, combined with some established Schrödinger nodes (function components) and QikProp descriptors.
3.3 Blood-brain barrier (BBB)
The BBB is the microvascular endothelial cell layer of the brain and plays a pivotal role in separating the brain from the blood. High penetration is needed for most of the drugs targeting the central nervous system (CNS), whereas BBB penetration should be minimized for non-CNS drugs to avoid undesired side-effects. The BBB penetration of compounds involves complex mechanisms. Compounds may cross the BBB by passive diffusion or via a variety of catalyzed transport systems that carry compounds into the brain (carrier-mediated transport, receptor-mediated transcytosis) or out of the brain (active efflux) (Clark, Reference Clark2003). The highly complex nature of the BBB penetration poses a challenge for its assessment.
Different methodologies have been developed to measure the potential for novel compounds to permeate the BBB. Among these methods, in vivo brain uptake experiments, including non-invasive and invasive techniques, provide the most reliable evaluation of BBB penetration. The key concepts that are used to estimate BBB permeability among in vivo experiments include the rate and extent of brain permeation, which are expressed as log PS (logarithm of the permeable-surface area product) and log BB (logarithm of the brain/blood partitioning ratio at a steady-state), respectively (Bicker et al. Reference Bicker, Alves, Fortuna and Falcao2014). Log BB is by far the most frequently used parameter for evaluating BBB penetration (Lanevskij et al. Reference Lanevskij, Japertas and Didziapetris2013). However, this parameter merely reflects the total drug concentration in the brain rather than providing any insight into the free drug concentration. Log PS is a more appropriate index because it eliminates the effect of PPB or non-specific brain binding and provides a direct measure of BBB apparent permeability (Carpenter et al. Reference Carpenter, Kirshner, Lau, Wong, Nilmeier and Lightstone2014). However, in vivo models are often low-throughput, expensive, and labour-intensive, and there are no in vitro models that can mimic all of the properties of the in vivo BBB. The development of more reliable HTS models remains a challenge (Bicker et al. Reference Bicker, Alves, Fortuna and Falcao2014).
Most in silico models that are devoted to this aim are based on the assumption that compounds are transported across the BBB by passive diffusion. To account for the contribution of transporters, Garg & Verma (Reference Garg and Verma2006) developed an ANN model from the molecular structural parameters, and the P-glycoprotein (P-gp) substrate probability of compounds was used to predict the log BB. The result showed improved prediction performance and indicated that P-gp substrate probability plays an important role in BBB permeability. Lanevskij et al. (Reference Lanevskij, Dapkunas, Juska, Japertas and Didziapetris2011) developed a simple QSAR model based on log P, pK a , and fraction unbound on the plasma for log BB prediction, also considering the influence of brain tissue binding by estimating the negative logarithm of the fraction that is unbound in the brain (−log f u,br ) with a non-linear ionization-specific model that is based on log P and pK a . As a result, the model demonstrated good predictive power for both internal and external validations. Recently, Carpenter et al. (Reference Carpenter, Kirshner, Lau, Wong, Nilmeier and Lightstone2014) predicted the log BB and log PS of 12 small molecules through a simple BBB mimic using MD and binding free energy calculations. After the MD simulations of each compound through a bilayer and free-energy calculation, the effective permeability combining the diffusion coefficient and free energy landscape was calculated, and the values correlated well with both log BB and log PS. Although the model has some limitations, such as the oversimplification of the lipid membrane and the computational cost, it still provides new threads for BBB permeability prediction.
Classification models were also widely explored for predicting whether a compound is BBB permeable (BBB+) or not (BBB−) if its log BB value exceeds a certain threshold (the threshold is typically between 0 and −1) (Lanevskij et al. Reference Lanevskij, Dapkunas, Juska, Japertas and Didziapetris2011). The prediction performances of these models rely on the available BBB data that are presented in the literature. However, most of the BBB datasets that have been reported so far have a distribution of positive/negative samples that is significantly different from that expected in a real-world scenario (e.g. an HTS against an organic chemistry database), where a lower ratio of small molecules may be able to cross the BBB. To address the data biasing issue, Martins et al. (Reference Martins, Teixeira, Pinheiro and Falcao2012) developed a Bayesian approach based on differentially sampling the available data for building training and testing datasets. The obtained model produced an overall capacity of recognizing 83% of BBB positives and 96% of BBB negatives. Another notable issue of the current classification models is that the presented data indicate that a parameter alone (log BB or log PS) is not sufficient for building a reliable classifier, which should account for the cumulative effect of different properties on brain delivery efficiency. Recently, Lanevskij et al. (Reference Lanevskij, Japertas and Didziapetris2012) developed a novel BBB permeation score through the linear combination of two quantitative characteristics, namely, the brain/plasma equilibration rate (log [PS · f u,br ]) and log BB. The resulting prediction model allowed for the classification of drugs by CNS access with 94% accuracy. Furthermore, the devised classification score correlated well with the unbound brain/plasma partitioning coefficient (log K p,uu ), which is an unambiguous determinant of brain exposure.
3.4 Metabolism
Metabolism prediction is a research priority in many areas, including pharmaceutical, food safety, and environmental studies. As a major safety concern to pharmaceutical research, metabolic liability can lead to a number of issues, such as poor bioavailability due to enhanced clearance; toxic effects caused by drug accumulation; and DDIs, including enzyme inhibition, induction, and mechanism-based inactivation (Kell & Goodacre, Reference Kell and Goodacre2014; Kirchmair et al. Reference Kirchmair, Williamson, Tyzack, Tan, Bond, Bender and Glen2012). In addition, metabolic information can offer prospective advice for drug development, for example, to guide the design of a pro-drug for some metabolically unstable drug to enhance bioavailability (Stella et al. Reference Stella, Borchardt, Hageman, Oliyai, Maag and Tilley2007). Drug metabolism can be divided into phases I and II; phase I involves oxidation, reduction, and hydrolysis, whereas phase II only involves conjugation, including methylation, sulphation, glutathione conjugation, and glycine conjugation. Because most enzymes of phases I and II are located in the liver, an in vitro experiment for drug metabolism is often performed on hepatic microsomes or hepatic cells with liquid chromatography-mass spectrometry (LC/MS), which is unable to perform HTS for vast numbers of compounds.
Currently, metabolism-related prediction models have mainly focused on the following studies: (1) the interaction models of enzymes with xenobiotics, which were often used to distinguish whether a xenobiotic is a substrate or inhibitor of Cytochrome P450 monooxygenase system (CYP450s), and then to evaluate DDIs; (2) the clearance models of the liver that could quantitatively predict the metabolic stability of xenobiotics; (3) the site of metabolism (SOM) that can be used to predict the ‘soft spots’ on xenobiotics; and (4) the metabolite prediction models that could predict all of the potential metabolites for xenobiotics. In the following section, we use SOM and metabolite prediction as examples to introduce in silico metabolism modelling.
3.4.1 SOM prediction
The SOMs of compounds, also called soft sites, are the most probable metabolized sites of molecules. The modification of these sites would improve compound metabolic stability. As the major enzymes involved in drug metabolism, the CYP450s accounts for ~75% of drug metabolism; therefore, considerable effort has been dedicated to predicting CYP SOMs. Based on the methods that have been used, reported prediction models can be divided into three classes: reactivity-based, structure-based, and statistical learning models.
According to previous studies, the rate-limiting step of most CYP-related phase I metabolism is the hydrogen atom abstraction, which affects the reactivity of one site most. Thus, hydrogen abstraction energy is a meaningful criterion to distinguish whether one site would be metabolized. Singh et al. performed semi-empirical QM calculations and found that the site with a hydrogen abstraction energy lower than 27 kcal mol−1 and solvent accessible surface area (SASA) greater than 8 Å would be more likely to be metabolized (Singh et al. Reference Singh, Shen, Walker and Sheridan2003). Rydberg et al. developed SMARTCyp, which can predict SOM directly from the 2D structure of a molecule without 3D structure generation, and the prediction speed of this model has increased considerably (Rydberg et al. Reference Rydberg, Gloriam, Zaretzki, Breneman and Olsen2010). In addition, SMARTCyp is based on atom reactivity and accessibility, where the reactivity can be rapidly retrieved from a pool of pre-calculated energies of fragments by SMARTS matching, and the accessibility was evaluated using the relative location of an atom in a molecule. The interpretable descriptors and fast speed make SMARTCyp useful for medicinal researchers.
Structural-based methods can consider the effects of the binding mode more thoroughly than reactivity-based methods. For example, MLlite was developed based on docking methods and quantum chemistry calculations (Oh et al. Reference Oh, Kim, Jung, Cho and No2008). In this model, the catalytic binding mode of xenobiotics was predicted by docking, and the distance between potential atoms to a ferric oxygen atom was measured to evaluate the magnitude of atom exposure to catalysis. If the distance was less than 3·5 Å, the site was considered to be exposed to the haem centre, and a quantum mechanics calculation was performed to obtain the hydrogen abstraction energy. To further consider the effect of protein flexibility during the ligand-binding process, Li et al. reported a CYP-mediated SOM prediction model based on induced-fit docking, where the conformations were refined with the Protein Local Optimization Program (Li et al. Reference Li, Schneebeli, Bylund, Farid and Friesner2011b). The testing of the IDSite on CYP2D6 showed that the IDSite could recover 83% of the experimentally observed SOMs for 56 compounds with a low false positive rate.
Statistical learning models are the most frequently reported methods for SOM prediction. Sheridan et al. used the random forest (RF) method, and their descriptors included structural descriptors, SASA and topological descriptors to develop SOM prediction models for CYP3A4, 2D6, and 2C9. The predictive power of this model is comparable with that of MetaSite (Sheridan et al. Reference Sheridan, Korzekwa, Torres and Walker2007). Zheng et al. calculated quantum chemical descriptors to characterize atom reactivity and used the SVM method to develop six CYP SOM prediction models for major metabolic reaction types. These models could successfully identify 80% of the metabolized sites of Sheridan's dataset (Zheng et al. Reference Zheng, Luo, Shen, Wang, Du, Zhu and Jiang2009). To avoid using quantum chemical descriptors, Rudik et al. (Reference Rudik, Dmitriev, Lagunin, Filimonov and Poroikov2014) reported a statistical-based model for CYP SOM prediction that is based only on the 2D structure of substrates. This model used a modified multilevel neighbourhood of the atom method to describe the SOMs and a Bayesian-like algorithm to train the model. The prediction accuracy of this model was comparable or superior to the reported models based on quantum chemical descriptors. Similarly, Tyzack et al. (Reference Tyzack, Mussa, Williamson, Kirchmair and Glen2014) used 2D topological fingerprints to develop a series of Naive Bayesian (NB) models with various conditional probability estimate methods and then combined these models into a voting system. The top two predictions of the Tyzack et al. model could identify 85, 91, and 88% of the experimentally observed sites for CYP 3A4, 2D6, and 2D9, respectively.
In addition to the CYP SOM prediction models, some statistical learning models have been developed for other enzymes. Sorich et al. (Reference Sorich, Mckinnon, Miners and Smith2006) and Peng et al. (Reference Peng, Lu, Shen, Zheng, Luo, Zhu, Jiang and Chen2014) reported SOM prediction models for UDP-glucuronosyl transferases (UGTs), and the Substrate Product Occurrence Ratio Calculator (Boyer et al. Reference Boyer, Arnby, Carlsson, Smith, Stein and Glen2007), MetaPrint2D (Adams, Reference Adams2010) and Fast Metabolizer (Kirchmair et al. Reference Kirchmair, Williamson, Afzal, Tyzack, Choy, Howlett, Rydberg and Glen2013) were developed for the SOM prediction of global metabolism. The predictive power of the UGTs model appears reasonable, as reported by Peng et al. whereas the predictive power of the SOM prediction model for global metabolism must be improved.
3.4.2 Metabolite prediction
The purpose of metabolite prediction is to identify the primary metabolites for xenobiotics. This type of study can also provide insight into the mechanisms that are involved in metabolite-related toxicity or other pharmacology research. The methods that are available for metabolite prediction can be divided into expert systems and statistical-based methods. Being different from SOM prediction, where a one-step reaction is sufficient, metabolite prediction models are often applied iteratively to yield all of the major metabolites, some of which are products of the metabolites that were generated from previous steps. Consequently, such models can easily suffer from the risk of combinatorial explosion, resulting in a high false-positive rate.
Expert systems were established and maintained by codifying the metabolic reaction rules from the literature, books, and patents, in which expert knowledge plays an important role. Potential metabolites can be identified using the metabolic reaction rules on the query, searching for the candidate substructure present in the query and converting this substructure into the product. All of the expert systems use pre-defined reaction rules as well as their priority or probability. The main difference is the way such priorities are assigned. For example, the priority in META (Klopman et al. Reference Klopman, Dimayuga and Talafous1994, Reference Klopman, Tu and Talafous1997; Talafous et al. Reference Talafous, Sayre, Mieyal and Klopman1994) is an integer between 1 and 9 that was optimized using a genetic algorithm; METEOR (Button et al. Reference Button, Judson, Long and Vessey2003) has absolute and relative reasoning implemented; SyGMa (Ridder & Wagener, Reference Ridder and Wagener2008) calculates a prior probability from a commercial metabolism database as the priority of each type of reaction. As expert systems typically assign the same priority to reactions of the same type without considering the influence of different substrates, additional calculations are often needed to reduce false positives. Taking META as an example, in the case of the oxidation of aromatic molecules, the nucleophilic character of each candidate atom and bond was evaluated by a simple index to determine which will be the most likely target. Moreover, log P was computed for each metabolite to determine whether further biotransformation will be carried out.
Different from a fixed priority for all reactions of the same type in expert systems, statistical learning models can provide a specific probability for different candidate sites by fully considering the influence of other functional groups of the same molecule. For example, MetaPrint2D-React (Adams, Reference Adams2010) is an extension of the SOM-predicting model MetaPrint2D, where sites are represented as circular fingerprints. For a given query molecule, a fingerprint was generated for each candidate atom, followed by searching for similar atoms in the database. Then, a conditional probability was computed as an estimate of the possibility of being metabolized. In this manner, candidate atoms can be analysed in the context of a specific substrate, increasing the probability of identifying metabolites with low probability and thereby reducing the false-positive rate.
The modelling approaches of some representative models for SOM and metabolite prediction are summarized in Fig. 3. These methods have been widely used for drug design. Ahlström et al. (Reference Ahlström, Ridderstr, Zamora and Luthman2007) used MetaSite, a metabolism site prediction program, to optimize the metabolic stability of celecoxib, which is a COX-2 inhibitor that is rapidly metabolized by CYP2C9. MetaSite predicted three ‘soft spots’ of celecoxib that will be metabolized by CYP2C9. To protect or modify these three ‘soft spots’, 13 analogues of celecoxib were designed, synthesized, and evaluated with regard to their metabolic properties and pharmacologic effects. Most analogues may retain their inhibitory activities, and their metabolic stabilities toward CYP2C9 were also improved. Voronkov et al. (Reference Voronkov, Holsworth, Waaler, Wilson, Ekblad, Perdreau-Dahl, Dinh, Drewes, Hopf, Morth and Krauss2013) used a consensus score for metabolism prediction to optimize the tankyrase inhibitor JW74, and the consensus score was developed based on five metabolism prediction methods, including MetaPrint2D, SmartCYP, MetaDrug, MetaSite, and SOME. According to the predictions of the consensus score, hundreds of derivatives were designed by modifying five specific regions of JW74. Finally, the compound G007-LK was found, which showed high potency toward tankyrase and a good pharmacokinetic profile in mice. Metabolite prediction methods can also help identify drug metabolites. For example, Jacobs et al. combined the metabolite prediction method SyGMa with the experimental method LC-HRMS/MS to develop a systematic workflow for identifying human metabolites in plasma or serum (Jacobs et al. Reference Jacobs, Ridder, Ruijken, Rosing, Jager, Beijnen, Bas and Van Dongen2013). The workflow was successfully used to identify tamoxifen metabolites, and the identified metabolites included the known metabolites and several minor metabolites that were not reported before. Taken together, the incorporation of metabolism prediction methods in the R&D process not only could provide information for scientists for drug design but could also help scientists to analyse data from metabolism experiments.

Fig. 3. Modelling approaches of some representative models for SOM and metabolite prediction. Models for SOM prediction are labelled as ‘•’, and models for metabolite prediction are labelled with ‘*’.
3.5 Membrane transporters
Membrane transporters are vital proteins for transmembrane processes that selectively transport endogenous substances and xenobiotics in the intracellular or extracellular directions. Transporters in the human genome belong to two major super families: ATP-binding cassette (ABC) transporters and solute carrier (SLC) transporters. Among all of the membrane transporters, P-gp (MDR1), Multidrug Resistance-Associated Proteins (MRPs), and Breast Cancer Resistance Protein (BCRP) from ABC family and Organic Cation/Anion Transporters (OCTs/OATs), Organic Anion Transporting Polypeptides (OATPs), and Multidrug and Toxin Extrusion Transporters (MATE) from the SLC family are the primary focus of research in drug development. The altered activity of transporters, which are mainly distributed in the polarized cells of the liver, kidney, intestine, and blood–brain barrier, may not only affect the ADME/T characteristics of a drug that will reduce the efficacy but also lead to transporter-mediated DDIs and even severe or lethal adverse effects. To address these issues, many computational efforts have been made to recognize the structural determinants of substances that can interact with transporters.
Because P-gp was the first identified human transporter of clinical importance, extensive experimental studies have been carried out that provide required data for in silico research. In 2002, Ekins et al. developed a series of pharmacophore models of P-gp inhibitors that inhibit digoxin, vinblastine, and verapamil, respectively (Ekins et al. Reference Ekins, Kim, Leake, Dantzig, Schuetz, Lan, Yasuda, Shepard, Winter, Schuetz, Wikel and Wrighton2002a, Reference Ekins, Kim, Leake, Dantzig, Schuetz, Lan, Yasuda, Shepard, Winter, Schuetz, Wikel and Wrightonb). The alignment of these pharmacophore models indicated that important features of P-gp inhibitors include multiple hydrophobic and hydrogen bond acceptor features and that these three-probe substrates are likely to bind to the same or overlapping sites within P-gp. These pharmacophore models yielded a good relationship between the predicted versus observed values in the training set, but the performance in the predicting test set was not stable, partially due to the small amount of training set data. Palmeira et al. used 26 P-gp known inhibitors of the flavonoid family to generate a pharmacophore model that consisted of two aromatic rings and one H-bond acceptor (Palmeira et al. Reference Palmeira, Rodrigues, Sousa, Pinto, Vasconcelos and Fernandes2011). The pharmacophore model was then used to screen the DrugBank database and successfully discover new P-gp inhibitors in old drugs. A relatively large dataset consisting of information of approximately 200 compounds was used to develop pharmacophore models for P-gp substrates (Li et al. Reference Li, Li, Eksterowicz, Ling and Cardozo2007; Penzotti et al. Reference Penzotti, Lamb, Evensen and Grootenhuis2002). The pharmacophore model of Li et al. correctly classified 87·6% of the test set compounds as substrates or non-substrates (Li et al. Reference Li, Li, Eksterowicz, Ling and Cardozo2007). Many QSAR models using linear discriminant analysis or partial least squares discriminant analysis were developed to predict the substrates (Cabrera et al. Reference Cabrera, Gonz Lez, Fern Ndez, Navarro and Bermejo2006; Gombar et al. Reference Gombar, Polli, Humphreys, Wring and Serabjit-Singh2004) or inhibitors (Bakken & Jurs, Reference Bakken and Jurs2000; Crivori et al. Reference Crivori, Reinach, Pezzetta and Poggesi2006) of P-gp. All of these models were based on relatively large datasets containing more than 200 compounds, yielding an averaged predicting accuracy of approximately 80%. In addition to these classical approaches, many statistical learning models have been derived, including SVM, Bayesian classifiers, k-Nearest Neighbour (kNN), and decision trees. Among these models, the SVM model of P-gp substrates that was established by Huang et al. exhibited an average predicting accuracy of >90% (Huang et al. Reference Huang, Ma, Muhammad and Cheng2007). However, the ‘black box’ character of SVMs may limit their application in the process of drug development because they cannot provide direct structural information to understand the interaction between substances and transporters.
Compared with P-gp, only a few studies have been reported for other human transporters, for instance, 3D-QSAR CoMFA and CoMSIA for BCRP inhibitors (Pick et al. Reference Pick, Muller, Mayer, Haenisch, Pajeva, Weigt, Bonisch, Muller and Wiese2011), the SVM model of BCRP substrates (Zhong et al. Reference Zhong, Ma, Zhang, Yang, Wan, Xie, Li and Yang2011), and pharmacophore modelling of stereoselective binding to OCT1 (Moaddel et al. Reference Moaddel, Ravichandran, Bighi, Yamaguchi and Wainer2007). These targets are also of high interest to drug transport but have been studied less extensively due to the lack of sufficient experimental data. Recently, OCT2 has drawn considerable attention because of its significant role in the renal elimination of drugs. Pharmacophore models of OCT2 have recognized the required structural features for the inhibition of different substrate probes (Suhre et al. Reference Suhre, Ekins, Chang, Swaan and Wright2005; Zolk et al. Reference Zolk, Solbach, Konig and Fromm2009). Nevertheless, these models were built based on a small training dataset that could only cover limited chemical space and are therefore of limited use for extrapolating compounds outside of the training data domain. Recently, Giacomini's group screened a drug library of 910 compounds against their inhibitory effects on OCT2 and found 244 OCT2 inhibitors (Kido et al. Reference Kido, Matsson and Giacomini2011). With this relatively larger dataset, Xu et al. developed a combinatorial pharmacophore (CP) model for OCT2 aiming at its multiple inhibitory mechanisms (Xu et al. Reference Xu, Liu, Li, Zhou, Gong, Luo, Luo, Zheng, Jiang and Chen2013). This model performed reasonably well in discriminating inhibitors and non-inhibitors, yielding an overall accuracy of approximately 0·70 for a large test set containing 299 compounds. Additionally, it has been suggested that different pharmacophore hypotheses in the CP model may correspond to different inhibitory mechanisms, which can explain the structural diversity of OCT2 inhibitors. Subsequently, Giacomini's team published their research on another important emerging renal transporter, MATE1, and found 84 inhibitors among 900 prescription drugs (Wittwer et al. Reference Wittwer, Zur, Khuri, Kido, Kosaka, Zhang, Morrissey, Sali, Huang and Giacomini2013). These authors developed an RF model with an average AUC value of 0·78. This RF model was then used to screen the DrugBank, and five compounds were successfully identified as MATE1 inhibitors. The data resource with high quality and clear annotation is still a major obstacle in the computational modelling of transporters. In addition, reasonable integrated strategies should be developed for the modelling of this sophisticated system to improve the predicting accuracy, enabling the application and extraction of valuable information for understanding the transporting process.
3.6 PBPK models
The above sections addressed different properties or parameters that were associated with drug absorption, distribution, metabolism, and excretion processes. However, when a drug enters the body, the four processes always proceed in parallel, each regulated by a wide range of parameters. It is impractical to simulate the complex in vivo pharmacokinetics of the drug based on simplified parameter-based models or their combinations. To gain more general information about the drug intracorporeal process, another type of study tries to model drug kinetics using a realistic physiological description of the animal. PBPK models are built using mathematical techniques, are parameterized with known physiology, and consist of a larger number of compartments, which are typically defined by different organs or tissues in the body and are linked by blood flows into a system. Although a large degree of simplification is still present in those models compared with that of parameter-based models, appropriate physiologically based models could better simulate the in vivo activity of chemicals. There are two well-known physiologically based models, namely, the compartmental absorption and transit (CAT) model and the well-stirred model. The CAT model is a physiologically based mathematical model for drug absorption prediction that assumes the gastrointestinal tract as a series of compartments, each of which has a specific absorption equation (Yu & Amidon, Reference Yu and Amidon1999). Advance compartmental absorption and transit (ACAT) is an extension of CAT that also considers the influences of first-pass metabolism and colon absorption (Agoram et al. Reference Agoram, Woltosz and Bolger2001). The ACAT approach is widely used and implemented in some commercially available software. More physiologically based models to predict oral drug absorption have been summarized by Huang et al. (Reference Huang, Lee and Yu2009). The well-stirred model is a steady-state model for hepatic drug clearance that assumes that the liver is a well-stirred compartment and that the drug is distributed instantly and homogenously throughout the liver and plasma in blood (Wilkinson & Shand, Reference Wilkinson and Shand1975). In addition to the well-stirred model, the parallel tube model and dispersion model are also widely used to model hepatic clearance. Compared with the well-stirred model, the parallel tube model assumes that the liver is a series of parallel tubes and that there is a declining hepatic drug concentration along the length of the tube (Pang & Rowland, Reference Pang and Rowland1977). The dispersion model was developed based on the assumption of both the well-stirred model and tube model. There is a review of other in silico liver microsome models (Gao et al. Reference Gao, Steyn, Chang and Lin2010). Additionally, whole-body physiologically based pharmacokinetic (WB-PBPK) models were generated that treated an organism as a closed circulatory system consisting of compartments that are important for absorption, distribution, metabolism, and elimination. The development and application of WE-PBPK models in drug development are reviewed elsewhere (Edginton et al. Reference Edginton, Theil, Schmitt and Willmann2008; Nestorov, Reference Nestorov2007).
Because PBPK models require not only a large number of system- and drug-specific parameters but also a sound mechanistic basis (Aarons, Reference Aarons2005), the lack of these data and a mechanistic basis in past decades has limited the development and application of these models. Currently, the accumulation of more data, a mechanistic understanding of pharmacokinetic processes and systems biology, and increasingly predictive human in vitro systems have significantly contributed to the development of PBPK models. As mentioned above, from 2008 to 2012, the Office of Clinical Pharmacology of the FDA received 33 submissions using PBPK models (Huang et al. Reference Huang, Abernethy, Wang, Zhao and Zineh2013). The uses of PBPK models in drug development include pharmacokinetic interspecies and inter-individual scaling, extrapolation of indications, dose optimization, and prediction of DDIs. Meanwhile, because drug disposition in vivo can be influenced by various intrinsic and extrinsic factors, such as a patient's organ function, genotype or concomitant medications, PBPK models are also suitable for pharmacodynamic prediction involving both intrinsic and extrinsic factors (Huang & Rowland, Reference Huang and Rowland2012). For instance, Zhao et al. (Reference Zhao, Vieira, Grillo, Song, Wu, Zheng, Arya, Berglund, Atkinson, Sugiyama, Pang, Reynolds, Abernethy, Zhang, Lesko and Huang2012b) used PBPK modelling to evaluate the exposure change of non-renal drug elimination in patients with chronic kidney disease.
To understand how to generate practical PBPK models, Zhao et al. reviewed several submissions for INDs and NDAs between 2008 and 2010 and found that knowledge regarding both the system component (metabolism pathway) and drug-dependent component (PC parameters) is essential to construct an appropriate PBPK model (Zhao et al. Reference Zhao, Zhang, Grillo, Liu, Bullock, Moon, Song, Brar, Madabushi and Wu2011). These authors also summarized the scheme of PBPK modelling and proposal, which involved five steps: (1) identify and quantify the elimination pathways of a drug; (2) incorporate the drug-dependent parameters into the models; (3) compare the simulated profiles with the in vivo data; (4) refine the model with the results from step 3; and (5) predict the unknown clinical settings. Moreover, from the regulatory agencies’ perspective, Zhao et al. (Reference Zhao, Rowland and Huang2012a) suggested that the model should answer the fundamental questions about model adequacy and proposed the essential contents of a valid PBPK model, including an introduction of drug disposition characteristics and the purposes of the model, a detailed description of the modelling procedure, and discussion about the model's biological plausibility, sensitivity, applications, and limitations. Finally, sufficient training and a good understanding of the ADME processes are required to use PBPK modelling effectively in drug development.
4. Toxicity prediction models
Toxicity is the degree to which a substance can damage an organism or substructure of the organism, such as cells and organs, and remains one of the most significant reasons for late-stage drug development failure. A critical priority in drug development is the early identification of severe toxicity before time and resources are expended during late stages. Recently, early-stage high-throughput toxicity prediction methods have emerged and enhanced the yield ratio of subsequent drug development steps. There are some integrated tools providing all-sided prediction for early-stage prediction and decision making. As the first toxicity prediction software, DEREK is a classic knowledge (rule)-based expert system that is based on toxicologists’ experience and information from the literature (Sanderson & Earnshaw, Reference Sanderson and Earnshaw1991). Another structural alert system is ToxAlerts, a web server (http://ochem.eu/alerts) of structural alerts for toxic chemicals with potential adverse effects, whose database is open and expandable (Sushko et al. Reference Sushko, Salmina, Potemkin, Poda and Tetko2012). TOPKAT employs cross-validated QSTR models to assess various measures of toxicity; each module consists of a specific database. MCASE uses a machine-learning approach to identify molecular fragments with a high probability of being associated with observed activity (Klopman, Reference Klopman1992). Although in silico toxicity models are valuable for drug development, more effort is still needed to improve their prediction accuracy and mechanism interpretability. In the following sections, we mainly focus on computational models for three endpoints that are important for preclinical drug toxicity studies: acute toxicity, genotoxicity, and hERG toxicity. As the emerging research field in toxicology, systems toxicology is discussed in the last section.
4.1 Acute toxicity
Acute toxicity describes the adverse effects of a substance that occur within a short period after dose or exposure and is an important indicator of the drug safety assessment. Acute toxicity is typically the first step in toxicological investigations of unknown substances. A common criterion that measures the acute toxicity of a compound is the median lethal dose (LD50), a dose causing 50% death of the treated animals in a given period when administered in an acute toxicity test (Turner, Reference Turner and Turner1965). Currently, most acute toxicity tests are performed using in vivo experiments in rodents, consuming a large amount of tested animals. Due to both economical and ethical reasons, animal experiments on acute toxicity are highly controversial. Thus, it is critical to develop non-animal-based prediction of LD50 using in silico models (Prieto et al. Reference Prieto, Kinsner-Ovaskainen, Stanzel, Albella, Artursson, Campillo, Cecchelli, Cerrato, Diaz, Di Consiglio, Guerra, Gombau, Herrera, Honegger, Landry, O'Connor, Paez, Quintas, Svensson, Turco, Zurich, Zurbano and Kopp-Schneider2013).
Many in silico prediction models have been developed with this aim. A pioneer work was the development of a global QSAR model based on a MLR method and non-congeneric datasets (Enslein et al. Reference Enslein, Lander, Tomb and Craig1989). However, the predictive power of this global model was poor. There are some local models based on congeneric datasets showing some increase in the prediction accuracy, but the application domain of these models is limited (Eldred & Jurs, Reference Eldred and Jurs1999; Guo et al. Reference Guo, Wu, Wright and Lushington2006). Given the complex mechanisms that are involved in acute toxicity, it is challenging to build a single global QSAR model with high prediction accuracy. A consensus model with applicability domain analysis was developed to address this problem. Consisting of five sub-QSAR models using different modelling methods, this model showed improved prediction performance compared with that of individual models (Zhu et al. Reference Zhu, Martin, Ye, Sedykh, Young and Tropsha2009). Recently, Li et al. (Reference Li, Chen, Cheng, Wu, Bian, Xu, Li, Liu, Shen and Tang2014) reported a multi-classification model in which the chemical compounds of the dataset were classified into four categories. Five different types of machine-learning methods (SVMOAO, C4·5, RF, kNN, and NB) and MACCS and FP4 fingerprints were used to construct the classification models. The prediction results of external validation showed that MACCS-SVMOAO is the optimum combination, and the corresponding model yielded the highest predictive accuracy. Using molecular fingerprints, this model highlighted the privileged substructures that were responsible for the acute toxicity of tested compounds. To provide convenience for medicinal chemist users, Drwal et al. (Reference Drwal, Banerjee, Dunkel, Wettig and Preissner2014) reported the web server ProTox (http://tox.charite.de/tox) for rodent oral toxicity prediction. The prediction method was based on chemical similarity and the identification of fragments that were over-represented in toxic compounds. In addition, by collecting protein-ligand-based pharmacophores (‘toxicophores’), this web server can also be used to predict possible toxicity target and shed light on the mechanisms that are involved in toxicity development. Subsequently, Lu et al. (Reference Lu, Peng, Wang, Shen, Bi, Gong, Zheng, Luo, Zhu, Jiang and Chen2014) reported another similarity-based prediction model based on a large reference toxicity dataset and local lazy learning (LLL) scheme. Different from conventional QSAR models, these LLL models were constructed ‘on-the-fly’ by investigating the toxicity profiles of the structural neighbours of a query compound, meaning that there is not pre-established QSAR model until a query compound has been provided. This feature allows for the timely update and expansion of the reference dataset, as the predictive accuracy of these models can be significantly improved by increasing the size and chemical diversity of the reference set. These models would be endowed with more predictive power when the acute toxicity data volume is further expanded.
4.2 Genotoxicity
Genotoxicity is an important factor in the pre-clinical toxicity tests of drug design. Lessons were learned from severe genotoxicity cases, such as the thalidomide crisis and the misuse of oestrogen. Mutagenicity should be tested in the early stages of pharmaceutical research. The Ames test, which was invented by Ames et al. (Reference Ames, Mccann and Yamasaki1975) at the University of California, Berkeley, in the early 1970s, is the standard for assessing mutagenicity in early alerting systems. If a compound induces auxotrophic Salmonella to synthesize histidine again, this compound may be able to cause genetic mutations.
With the development of IT technology and increasing amounts of experimental data, in silico screening and toxicity prediction are attracting an increasing amount of attention. For the Ames test, the estimated inter-laboratory reproducibility is only 85% due to the limitation of the in vitro test itself (Greene, Reference Greene2002). Setting up good computational models to replace the repeating in vitro Ames test is valuable (Xu et al. Reference Xu, Cheng, Chen, Du, Li, Liu, Lee and Tang2012). The mechanism of genotoxicity is complex, including inhibiting DNA synthesis by nucleotide analogues or base pair mismatch caused by macrocyclic organics embedding into the DNA helix (Kazius et al. Reference Kazius, Mcguire and Bursi2005). Current studies focus on ligand-based machine learning QSAR/QSPR, structural genotoxic alerts, and some commercial comprehensive toxicity prediction tools.
The classical QSAR modelling of genotoxicity has been extensively studied. To address the complex situation and gain insight into the hidden mechanism of genotoxicity, additional descriptors, such as physical, quantum chemical, and molecular connectivity descriptors, must be explored, together with advanced statistical analysis tools (e.g. SVMs, k-means clustering, classifiers, and ANNs) (Cheng et al. Reference Cheng, Li, Liu and Tang2013). Reenu (Reference Reenu2014) studied the mutagenicity of nitrified polycyclic aromatic hydrocarbon in the literature, in which a QSAR model was built based on quantum chemistry descriptors, including total energy, the energy of HOMO and LUMO, and commonly employed electron-density based descriptors, such as the electrophilicity index. Another modelling method is to summarize toxicophore/detoxifying groups or other structural alert knowledge. Expert knowledge-based structural alert systems have been developed to highlight the toxicophores by searching substructures in the system. Kazius et al. (Reference Kazius, Mcguire and Bursi2005) analysed an Ames test dataset containing 4337 compounds and identified 8 general toxicophores, 19 specific toxicophores, and some additional toxicophores with detoxicophores. A system based on these toxicophores for mutagenicity prediction was developed, showing an accuracy rate of 85%, which is close to the experimentation error limits of the Ames test. There are also some comprehensive structural alert systems (for example, DEREK) and databases for predicting toxicity. Publicly available genetic toxicity and carcinogenicity datasets include the Chemical Carcinogenesis Research Information System (CCRIS), EPA Gene-tox, the National Toxicology Program (NTP), IARC, Tokyo-Eiken, Mutants, the Carcinogenic Potency project (CPDB), ISSCAN and data from primary publications. Commercial prediction tools together with databases are available, such as Leadscope FDA Model Applier, Derek from Lhasa, toxicity prediction by computer-assisted technology (TOPKAT), MultiCASE, and SciQSAR. In addition, there are freely available tools, such as OncoLogic and lazy structure-activity relationships (LAZAR). One of these tools, the Leadscope system, has been used by FDA and US Environmental Protection Agency researchers for chemical and biological analyses to generate predictive models in the early stages of pharmaceutical development by read-across based on databases, as it provides data-mining and prediction methods considering both biological and chemical data (Benfenati et al. Reference Benfenati, Benigni, Demarini, Helma, Kirkland, Martin, Mazzatorta, Ouedraogo-Arras, Richard, Schilter, Schoonen, Snyder and Yang2009). Progress has been made regarding the in silico Ames test prediction, and many models work well. However, data mining must be more comprehensive and carcinogenicity mechanisms must be further studied to obtain increased predictive ability.
4.3 hERG toxicity
Sudden death induced by a blockade of hERG K+ channels (encoded by the hERG) is widely regarded as the predominant cause of drug-induced QT interval prolongation. Because a diverse range of drug structures can cause hERG toxicity (Table 3), the early regulatory detection of compounds with this undesirable side effect has become another important objective in the pharmaceutical industry (Aronov, Reference Aronov2005). In vitro electrophysiology tests on primary cardiac tissues, such as Purkinje fibres, are performed using the voltage clamp technique (Nobel Prize 1991) and are considered as ‘gold standards’ in hERG toxicity prediction. There are some databases that have collected large amounts of hERG toxicity data, such as WOMBAT-PK and PubChem BioAssay. In silico analysis of hERG toxicity can be performed based on these data to reduce the experimental cost and provide structural optimization guidelines to avoid this effect.
Table 3. Drugs withdrawn since 2000 because of significant hERG toxicity
The detailed X-ray crystallographic structure of the hERG channel is not yet available; therefore, the structural details of the hERG channel are assumed by homology modelling, mutagenesis studies, and computational models. Österberg & Aqvist (Reference Österberg and Aqvist2005) constructed a hERG homology model based on the structures of bacterial KvAP (open) and KcsA (closed) channels. The human hERG potassium channel has a 50% sequence identity to the Drosophila ether-ago-go gene and has six membrane-spanning segments for each of its four subunits. Docking and molecular dynamics results show that known hERG blockers have good affinities to this model. For newly designed compounds, the homology model of the hERG channel can be used to perform docking or MD stimulation and assess their hERG toxicity according to their binding affinity. Seierstad and Agrafiotis developed a QSAR model for hERG toxicity prediction (Seierstad & Agrafiotis, Reference Seierstad and Agrafiotis2006). This model can quantitatively assess the cardiotoxicity of newly designed compounds and provide alerts for compounds with a greater potential to cause toxicity. SciQSAR is a comprehensive QSAR modelling system of good behaviour in hERG toxicity prediction. This system enables researchers to establish reliable QSARs and QSPRs, create new calculators for in silico screening, and generate new compound libraries based on results (Contrera et al. Reference Contrera, Matthews and Benz2003; Muster et al. Reference Muster, Breidenbach, Fischer, Kirchner, Muller and Pahler2008). In practice, it is not typically necessary to know the toxicity of a compound. A binary classification of whether the investigated compound is cardiotoxic or not is sufficient. Although the crystal structure of the hERG potassium channel is still unavailable, a binary classification model for hERG toxicity based on experimental tests may be helpful. In 2006, Sun (Reference Sun2006) developed a NB classifier using a universal, generic molecular descriptor system, which exhibited an ROC accuracy of 0·87 for the identification of hERG blockers. In 2012, Wang et al. (Reference Wang, Li, Wang, Chen, Zhang, Yu and Hou2012) proposed a more thorough analysis on hERG toxicity descriptors and classification methods. These authors built two models using NB classification and recursive partitioning techniques and found that the NB model yielded better prediction results. Recently, Liu et al. (Reference Liu, Lu, Lu, Zheng, Luo, Zhu, Jiang and Chen2014) reported a model that was built by laplacsian-corrected Bayesian classification. Molecular fingerprints (extended-connectivity fingerprints) were used as descriptors, and the established models could identify the substructures as favourable or unfavourable for hERG channel blockage. These models may offer valuable information for designing drugs to avoid hERG toxicity. Many hERG blocker prediction models have been developed, but there is still a need for a ‘gold standard’ dataset to evaluate the performance of these models (Wang et al. Reference Wang, Li, Xu, Li and Hou2013). To date, the major obstacles for the development of hERG blocker models are (1) an unclear mechanism for the hERG blocker and (2) the lack of reliable and extensive experimental data. In the near future, when the crystal structure of the hERG channel becomes available and more quality data are generated, combining molecular modelling and simulating approaches, hERG toxicity prediction will be more accurate.
4.4 Systems toxicology
Systems toxicology is a new discipline that quantitatively studies the toxicological interaction of substances and biological organization at the system level (Waters & Fostel, Reference Waters and Fostel2004). Different from classical toxicology, which evaluates compound toxicity based on one or two toxicity properties, systems toxicology studies the interaction of all of the elements of a given biological system under stress or toxicant perturbation to achieve a comprehensive understanding of the toxicological response. The development of system toxicology is facing formidable challenges because a detailed mechanistic understanding of the toxicity response triggered by substances is required. However, the development of ‘-omics’ technologies, namely, genomics, transcriptomics, proteomics, metabolomics, lipidomics, and toxicogenomics, may help to construct a robust systems toxicology knowledgebase (Sturla et al. Reference Sturla, Boobis, Fitzgerald, Hoeng, Kavlock, Schirmer, Whelan, Wilks and Peitsch2014).
For toxicological assessment, the most relevant ’-omics’ technology is toxicogenomics, which is developed based on all of the other ‘-omics’ technologies. Toxicogenomics analyses the transcript, protein, and metabolite profiling in an integrated manner and combines conventional toxicology to investigate the interaction between genes and the toxicity of substances. Compared with traditional toxicology, toxicogenomics may not only assess the safety profile of chemicals but also help to elucidate the related mechanism and mode of action. In addition, toxicogenomics can also be used to identify toxicity biomarkers and analyse mixture toxicity (Altenburger et al. Reference Altenburger, Scholz, Schmitt-Jansen, Busch and Eschert2012; DeCristofaro & Daniels, Reference Decristofaro, Daniels, Mendrick and Mattes2008). Toxicogenomics has provided valuable mechanistic insight into various adverse drug reactions and has been reviewed with a focus on hepatotoxicity and nephrotoxicity (Kienhuis et al. Reference Kienhuis, Bessems, Pennings, Driessen, Luijten, Van Delft, Peijnenburg and van der Ven2011). With the development of toxicogenomics, many toxicogenomics databases have been created, such as Connectivity map (CMap) (Lamb et al. Reference Lamb, Crawford, Peck, Modell, Blat, Wrobel, Lerner, Brunet, Subramanian, Ross, Reich, Hieronymus, Wei, Armstrong, Haggarty, Clemons, Wei, Carr, Lander and Golub2006), the Genomics-Assisted Toxicity Evaluation System (TGGATEs) (Uehara et al. Reference Uehara, Ono, Maruyama, Kato, Yamada, Ohno and Urushidani2010), and the Comparative Toxicogenomics Database (CTD) (Davis et al. Reference Davis, Murphy, Johnson, Lay, Lennon-Hopkins, Saraceni-Richards, Sciaky, King, Rosenstein, Wiegers and Mattingly2013; Mattingly et al. Reference Mattingly, Rosenstein, Colby, Forrest and Boyer2006). These databases provide insight into complex chemical-gene and protein interaction networks and improve our understanding of the toxicity mechanisms.
In addition to the toxicogenomics database, there are many other databases containing chemical biology, protein-protein interactions, and disease and pathway enrichment information, which have also contributed to the construction of a systems toxicology knowledge base, such as search tool for interacting chemicals (STITCH), ChEMBL, search tool for the retrieval of interacting genes/proteins (STRING), and Kyoto Encyclopedia of Genes and Genomes (KEGG). These databases provide some local and static pathways or biological networks, and systems biology could integrate these pathways or networks into a global network and identify important pathways for toxicological responses. For instance, Kongsbak et al. (Reference Kongsbak, Hadrup, Audouze and Vinggaard2014) used a systems biology approach to predict the human toxic effect of the pesticide prochloraz.
Accurately evaluating the toxicity profile of compounds is always a major challenge in pharmaceutical R&D. Current approaches for toxicology testing mainly rely on toxicity assays in animals, such as rats. The most significant problem is species differences in that the toxic effects of compounds in animals are not necessarily consistent with those in humans, which is also the reason why many drugs fail in clinical trials due to toxicological effects that did not appear in animals in pre-clinical testing. Another relevant issue is animal cost. To solve the above issues, Hartung (Reference Hartung2009) stated that an entirely new toxicology system is needed that should better reflect the use of current tools, integrate various approaches for toxicity evaluation, and employ modern technologies. Systems toxicology, as the integration of current toxicity testing tools, newly developing technologies (such as ’-omics’), and various advanced computational approaches, precisely fits these requirements.
5. Outlook
In silico ADME/T modelling has made significant advances in the past decade. Many novel models have been proposed to address different aspects of pharmacokinetic and safety evaluations of drug-like molecules. However, this situation is still far from the prediction paradise that was expected by van de Waterbeemd & Gifford (Reference Van De Waterbeemd and Gifford2003) 10 years ago, in which in silico methods could support automated decision making in drug discovery. Challenges such as the insufficient prediction reliability, the disconnection between experiments and models, and the lack of systematic perspective on intracorporal processes may be the main reasons why in silico ADME/T modelling has not met this expectation. Making better use of the in silico ADME/T models by medicinal chemists to balance different activities and characteristics within chemical series are also a major challenge in the drug discovery field. To resolve this problem, the communication between synthetic chemists and computational researchers must be strengthened, and the quality of models must be improved. For example, the data source and modelling procedure of a model should be expanded to help users understand the model and predicted property. Delisle et al. (Reference Delisle, Lowrie, Hobbs and Diller2005) suggested some common considerations when building models, including the intended use of the model, data quality, appropriate modelling strategy, and model validation. Regarding model validation, the European Chemicals Agency has proposed the Organization for Economic Co-operation and Development (OECD) principles, which state that a valid model should be associated with the following information: (1) a defined endpoint; (2) an unambiguous algorithm; (3) a defined domain of applicability; (4) appropriate measures of goodness-of-fit, robustness and productivity; and (5) a mechanistic interpretation, if possible (ECHA, 2008). A high-quality model must invest considerable effort. Meanwhile, we will benefit from taking advantage of the development and protocol from other scientific disciplines to establish more reliable and robust models to predict various ADME/T properties.
Currently, how we manage and explore data will be the defining issue of the new era now unfolding. Big data, as one of the largest trends, has brought significant changes to many fields. In drug discovery and design, massive data have accumulated, and more data are being generated at increasing speeds due to the development of various techniques. For example, gene sequencing and HTS technologies have made many conventionally time-consuming tests more efficient and have provided a large amount of data. The emergence of combinatorial chemistry has drastically expanded compound chemical space. Bioinformatics and systems biology studies can illuminate molecular phenomena in biological and chemical systems and integrate conventionally disparate disciplines to form an inter-connected, multi-dimensional continuum (Flower, Reference Flower, Livingstone and Davis2012). The development of these disciplines has already facilitated drug discovery and development, and these changes will also bring brand new vistas for ADME/T in silico modelling.
The data that were generated for drug ADME/T assessment conform to the 3Vs (volume, velocity, and variety) characteristics of big data (defined by Doug Laney in 2001), for example, the rapid accumulation of metabolomics and toxicogenomics data by different institutes or laboratories with high-throughput molecular profiling technologies. These data often have a wide variety of types, such as molecular properties, activity data, and gene expression profile, and typically exhibit high false-positive rates. The big data challenge has undoubtedly made the ADME/T assessment process more complex as a result of an increase in the diversity and scale of information embedded within the process. Many computational solutions have been introduced for big data management and analysis, including cloud computing and heterogeneous computing, providing a bright prospect for exploring ‘new oil’ (Schadt et al. Reference Schadt, Linderman, Sorenson, Lee and Nolan2010). The techniques and technologies that are currently used to address big data problems, together with the underlying methodologies, are reviewed elsewhere (Chen & Zhang, Reference Chen and Zhang2014; Qin, Reference Qin2014). For example, the Hadoop platform enables the large-scale collection and storage of detailed data at a low cost. New software frameworks, such as Kiji and the Cloud era Developer Kit, have made Hadoop data more accessible to analysts for predictive modelling development and deployment. In addition to the technical aspects of big data, there are some recommended strategies. For example, different from our conventional method of addressing small data, in which we often rely on more sophisticated algorithms to achieve a better prediction accuracy, big data problems are better suited to simple algorithms (i.e. to embrace the size of detailed data, rather than the complexity of constructed models). The logic behind the concept is that using more data may help us to make fewer initial assumptions about the underlying model and let the data determine which model is the most appropriate. Regarding the velocity of big data, methods must be real-time- and data-driven and timely updated. An example is the LLL method, which was introduced for acute toxicity, does not require any pre-established model and is constructed ‘on-the-fly’ when a query compound has been provided. These ‘on-the-fly’ models would apply to the expansion of the reference dataset, and the performance of these models can also be significantly improved. Additionally, in the big data era, all researchers, including data providers and model users, must become data scientists to harness big data (Lusher et al. Reference Lusher, Mcguire, Van Schaik, Nicholson and De Vlieg2014).
In addition to big data analysis, another problem is how to integrate a large amount of data into the modelling of endpoints involving complex biochemical, biophysical, and physiological mechanisms. Similar to the mathematical systems theory that states that a complex problem requires a complex solution (Bar-Yam, Reference Bar-Yam2004), the complex problem of ADME/T prediction also requires a complex solution. In this sense, systems biology and systems pharmacology, as the antithesis of the reductionist approaches, may provide complex solutions for ADME/T prediction (Ma'ayan et al. Reference MA'AYAN, Rouillard, Clark, Wang, Duan and Kou2014; Pujol et al. Reference Pujol, Mosca, Farres and Aloy2010). Systems biology is applied in drug discovery to understand physiology and disease at the system level (Butcher et al. Reference Butcher, Berg and Kunkel2004). Based on systems biology, systems pharmacology focuses on complex interactions within biological systems to quantitatively simulate the interaction between a drug and various systems of the body (Vicini & van der Graaf, Reference Vicini and van der Graaf2013). As noted above, the ADME/T of drugs includes complex processes and has a significant impact on the effects of the drug, including transcriptome, proteome, and enzyme activities, as also represented as the ‘sharp end’ of systems biology (Kell & Goodacre, Reference Kell and Goodacre2014). Systems biology and systems pharmacology, which leverage knowledge based on the systematic understanding of the interaction between drugs and the human body, may provide a critically needed blueprint for the ADME/T processes of drugs and help to develop a robust systematic model for drug ADME/T prediction.
To summarize, in the era of big data, a necessary goal is the ability to use rapidly accumulating data to pinpoint potential ADME/T issues before entering late-stage development. However, due to the complex mechanisms and processes that are involved, most in silico ADME/T models are far from perfect, and discovering a more druggable molecule is akin to finding a needle in a haystack. To address this challenge, advanced analytical methods that are developed in computer and informatics science are required to enable ADME/T modelling based on data from a variety of different sources and covering different types of bioassays. Moreover, systems-level studies will be critical in the future, as more reliable ADME/T modelling depends on an understanding of complex mechanisms across different levels and scales, from chemical and molecular interactions to pathways and networks and from cells and tissues to organs and the entire organism. There is much progress to be made to achieve the goal of an ‘automated decision-making engine’ (van de Waterbeemd & Gifford, Reference Van De Waterbeemd and Gifford2003), but with a clear goal and direction, we are confident of a bright future.
Acknowledgements
We gratefully acknowledge the financial support from the National Natural Science Foundation of China (Grants 21210003 and 81230076 to H.J., Grant 81430084 to K.C.), the Hi-Tech Research and Development Program of China (Grant 2012AA020308 to X.L. and 2014AA01A302 to M.Z.), and the National Science and Technology Major Project ‘Key New Drug Creation and Manufacturing Program’ (Grant 2014ZX09507002-005-012 to M.Z.).









