Introduction
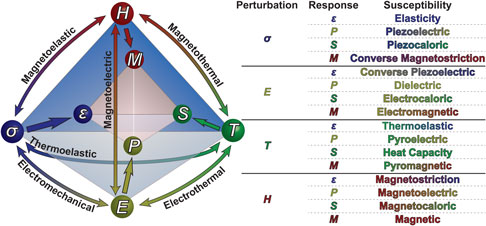
In the last 70 years, there has been a strong focus on designing and engineering materials with “functional” properties—i.e., materials that can convert or transduce energy (e.g., electrical, thermal, mechanical, etc.) for a useful purpose (e.g., sensing, energy production, positioning, etc.).[ Reference Schlom, Chen, Fennie, Gopalan, Muller, Pan, Ramesh and Uecker 1 , Reference Damodaran, Agar, Pandya, Chen, Dedon, Xu, Apgar, Saremi and Martin 2 ] Such materials are critical as they underpin our ability to address a range of salient technological challenges, including how we process and store information, sense and understand the world around us, produce energy, and much more.[ Reference Bowen, Taylor, LeBoulbar, Zabek, Chauhan and Vaish 3 – Reference Muralt and Muralt 6 ] In this regard, ferroic materials, and in particular those which are ferroelectric, magnetic, and/or multiferroic have received considerable interest due to their field switchable stable spontaneous (electric and/or magnetic) polarization which is strongly coupled to the thermal and mechanical responses of the material (represented in an adapted Heckmann diagram, Fig. 1). In particular, some of the most widely studied multifunctional materials are complex oxides which exhibit at least three of these functionalities.

Figure 1. Adapted Heckmann diagram showing ferroelectric susceptibilities in multiferroic materials. Table shows the various susceptibilities that multiferroic materials can exhibit.
The search for, discovery of, and, ultimately, the utilization of these multifunctional materials has been made possible by a number of important advances in theoretical and computational techniques, materials synthesis methodologies, and characterization techniques which collectively have enabled the realization of new materials, control of existing materials, and study of materials across enormous length- and time-scales. In turn, these new materials and the insights gleaned from them have made possible a wide variety of functional devices including: ferroelectric random access memories, mechanical actuators, nano- and micro-electromechanical systems (NEMS or MEMS), infrared detectors, and many more.[ Reference Bowen, Taylor, LeBoulbar, Zabek, Chauhan and Vaish 3 – Reference Muralt and Muralt 6 ] But, the potential impact of these functional materials goes well-beyond these commercial applications and researchers are actively laying the foundation to develop and integrate these materials into next-generation devices in information technology (e.g., spintronic devices, high-density, low-power, multistate logic, integrated non-volatile memories), energy harvesting and conversion (e.g., photovoltaic devices, pyroelectric energy conversion, and catalysis), solid-state cooling (e.g., electrocaloric and multicaloric devices), and more.
In this prospective, we highlight some of the most important recent advances in terms of materials design and discovery, understanding, and characterization for ferroelectric/multiferroic materials while looking to the future for what might lie on the horizon for this community. In particular, we explore potential areas of growth, important techniques, and methodologies gaining traction that could revolutionize our ability to discover, probe, and engineer these materials providing a context for new arenas where these materials might make an impact.
Genome mapping and data mining in ferroics
Advances in high-performance, low-cost computing, high-capacity data storage, and high-speed data transfer have led to an explosion in data generation. It is predicted that worldwide data generation will double every year in the near future.[ Reference Gantz and Reinsel 7 ] Experimental and computational science has followed similar trends, and it is now possible for a single researcher to generate terabytes of data in a single day. Traditionally this data has been sorted and analyzed by “hand”, condensed to a manageable structure, and published as a few thousand words and a few figures. The raw data are, however, rarely curated or published in a systematic way. In turn, most scientific data are only analyzed and interpreted by a select group of researchers with access to the raw data. Such isolated “data nodes” preclude the formation of interconnected, networked segments of scientific knowledge between research groups, significantly limiting the scientific impact extracted from the data. Recently, there has been growing interest in applying data analytics such as unsupervised and supervised neural networks, genetic and evolutionary algorithms, statistics-based methods, and machine learning to rapidly mine data.[ Reference Kalinin, Sumpter and Archibald 8 – Reference Rondinelli, Poeppelmeier and Zunger 16 ] There are considerable challenges, however, due to the significant complexity that has been developed in both the fields of materials science and data analytics. Advances in these approaches will rely heavily on those researchers who can bridge this gap and establish interacting “social networks” between these two communities [Fig. 2(a)]. Here we discuss how the assemblage of these networks could facilitate the discovery of new multifunctional materials and phenomena.

Figure 2. (a) Overview of networked combined computational and experimental approach to discovery of new multifunctional materials (Reprinted from [Reference Jain, Ong, Hautier, Chen, Richards, Dacek, Cholia, Gunter, Skinner, Ceder and Persson32], with the permission of AIP Publishing). (b) Graphical representation of the computed piezoelectric coefficients of 941 materials. A series of concentric circles indicate the maximum value of longitudinal piezoelectric modulus ||e ij ||max. Concentric circles correspond to moduli ||e ij ||max of 1, 2.5, 5,10, and 20 C/m2. The compounds are segmented according to their crystal and point-group symmetry classes (Reprinted with permission from Ref. [Reference de Jong, Chen, Geerlings, Asta and Persson41]).
To date, many of the watershed events in the development of multifunctional ferroic materials have centered on the chance discovery of novel materials or classes of materials. In recent years, however, materials discovery and design has brought to bear an expansive set of theory, modeling, and computational (TMC) approaches including density functional theory (DFT) calculations,[ Reference Resta, Vanderbilt, Ahn, Rabe and Triscone 17 ] atomic-scale simulations (i.e., Monte Carlo,[ Reference Liu, Wang, Chan and Choy 18 ] molecular dynamics,[ Reference Shin, Cooper, Grinberg and Rappe 19 , Reference Sepliarsky, Asthagiri, Phillpot, Stachiotti and Migoni 20 ] and effective Hamiltonians[ Reference Zhong, Vanderbilt and Rabe 21 , Reference Bellaiche, Garcia and Vanderbilt 22 ]), and mesoscale Landau-based thermodynamic models (i.e., numerical phase-field[ Reference Chen 23 , Reference Li, Hu, Liu and Chen 24 ] and Ginzburg–Landau–Devonshire (GLD) models[ Reference Pertsev, Kukhar, Kohlstedt and Waser 25 , Reference Koukhar, Pertsev and Waser 26 ]) that can be used to both predict and understand multifunctional phenomena. These TMC approaches have, however, been relatively limited to a few specific material systems and conditions (i.e., compositional, temperature, strain, etc.) due to both limitations in computing capacity and a lack of availability of phenomenological constants and parameters. In the last decade, and particularly since the launch of the Materials Genome Initiative,[ Reference Ward 27 ] there has been a massive push to utilize predictive high-throughput (HT) electronic-structure calculations based on DFT and the tools of data science to discover new materials with targeted properties, which stands ready to revolutionize how we design and discover new ferroic materials.[ Reference Curtarolo, Hart, Nardelli, Mingo, Sanvito and Levy 9 , Reference Ceder and Persson 28 – Reference Jain, Shin and Persson 30 ] The associated development of curated databases[ Reference Curtarolo, Hart, Nardelli, Mingo, Sanvito and Levy 9 , Reference Saal, Kirklin, Aykol, Meredig and Wolverton 31 – 35 ] and open-source software[ Reference Curtarolo, Setyawan, Wang, Xue, Yang, Taylor, Nelson, Hart, Sanvito, Buongiorno-Nardelli, Mingo and Levy 33 , Reference Pizzi, Cepellotti, Sabatini, Marzari and Kozinsky 34 , Reference Ong, Richards, Jain, Hautier, Kocher, Cholia, Gunter, Chevrier, Persson and Ceder 36 ] for automated property calculations has enabled consideration of tens of thousands of compounds in the search for new materials and property combinations. These efforts have provided a predictive framework for computing a wide range of material properties including: phase stability,[ Reference Chen 23 ] electronic and crystal structure,[ Reference Fischer, Tibbetts, Morgan and Ceder 37 ] elastic moduli,[ Reference De Jong, Chen, Angsten, Jain, Notestine, Gamst, Sluiter, Ande, van der Zwaag and Plata 38 ] thermal conductivity,[ Reference Toher, Plata, Levy, De Jong, Asta, Nardelli and Curtarolo 39 , Reference Yang, Xi, Qiu, Wu, Shi, Chen, Yang, Zhang, Uher and Singh 40 ] dielectric and piezoelectric response,[ Reference de Jong, Chen, Geerlings, Asta and Persson 41 ] polarization, and much more. Furthermore, it is now possible to automate DFT-based computational workflows such that large amounts of data on material properties can be obtained. Similar approaches have already been applied in the search for: improved catalysts,[ Reference Greeley, Stephens, Bondarenko, Johansson, Hansen, Jaramillo, Rossmeisl, Chorkendorff and Norskov 42 ] new electrode materials for batteries,[ Reference Ceder and Persson 28 ] new intermetallic compounds,[ Reference Hart, Blum, Walorski and Zunger 43 ] topological insulators,[ Reference Yang, Setyawan, Wang, Nardelli and Curtarolo 44 ] and thermoelectric materials.[ Reference Xiang 45 ] Despite this progress, relatively little work has focused on HT discovery of new polar/ferroelectric systems,[ Reference Benedek and Fennie 46 ] but such TMC approaches are poised to be implemented in this regard.
In this direction, researchers have demonstrated a database predicting the piezoelectric tensors of 919 different materials [Fig. 2(b)].[ Reference de Jong, Chen, Geerlings, Asta and Persson 41 ] This work suggests a number of novel, Pb-free compounds that are candidates to have high piezoelectric response. Further development of these approaches and screening of multifunctional materials could lead to the discovery of materials with interesting and novel polar phases, strain-induced polar phases, and regions of strain-induced phase instabilities; all of which could provide for enhanced materials performance. These HT TMC approaches can also be adapted to predict phenomenological constants from first principles,[ Reference Jain, Ong, Hautier, Chen, Richards, Dacek, Cholia, Gunter, Skinner, Ceder and Persson 32 ] allowing prediction of temperature- and field-dependent susceptibilities over large length- and time-scales. Computational data collected can also be easily collated to populate online materials databases such as the Materials Project,[ Reference Jain, Ong, Hautier, Chen, Richards, Dacek, Cholia, Gunter, Skinner, Ceder and Persson 32 ] AFLOWlib,[ Reference Curtarolo, Setyawan, Wang, Xue, Yang, Taylor, Nelson, Hart, Sanvito, Buongiorno-Nardelli, Mingo and Levy 33 ] and Open Quantum Materials Database (OQMD).[ Reference Saal, Kirklin, Aykol, Meredig and Wolverton 31 ] Such databases can be combined with experimental data which can then be mined using statistical approaches and predictive machine learning algorithms; providing needed direction for additional (potentially resource intensive) computational exploration and further experimental materials development.
It should be noted, that such data analytics concepts are not limited to computational materials discovery alone and experimental methods are becoming increasingly data intensive, commonly generating large multidimensional datasets (>3 dimensions). Such “big data” experiments are common in (time-resolved) synchrotron- and neutron-based diffraction and imaging,[ Reference Wang, Xu, Yang, Luo, Sun, Zhao, Zheng, Dong, Zhou, Ren, Gao and Cao 47 ] scanning-probe microscopy,[ Reference Jesse, Maksymovych and Kalinin 48 , Reference Jesse, Chi, Belianinov, Beekman, Kalinin, Borisevich and Lupini 49 ] and (scanning) transmission electron microscopy.[ Reference Jesse, Chi, Belianinov, Beekman, Kalinin, Borisevich and Lupini 49 – Reference Ozdol, Gammer, Jin, Ercius, Ophus, Ciston and Minor 51 ] These multidimensional datasets can be particularly powerful as they can provide dynamic spectroscopy of materials enabling the direct observation of material responses under external perturbations (at practically relevant timescales). The large datasets that are produced are generally not suitable for brute force analysis as the pertinent features occur over a dimensionality difficult to comprehend. For example, a relatively simple band-excitation piezoresponse force microscopy (BE-PFM) switching spectroscopy experiment, a scanning-probe-based technique capable of imaging local piezoelectric switching, generates four-dimensional (4D) datasets (space [64 × 64] × frequency [64] × voltage [128]) typically >256 MB in size.[ Reference Jesse, Maksymovych and Kalinin 48 ] Detailed analysis of such multidimensional datasets (beyond 3D) is most effectively analyzed using data analytics such as multivariate statistical analysis to reduce data dimensionality, allowing the visualization and extraction of scientifically relevant information. In this regard, there is an expansive set of statistical tools including principal component analysis, Bayesian de-mixing, independent component analysis (ICA), clustering algorithms, neural networks, etc.[ Reference Kalinin, Sumpter and Archibald 8 , Reference Belianinov, Vasudevan, Strelcov, Steed, Yang, Tselev, Jesse, Biegalski, Shipman and Symons 52 ] that can be adapted to analyze these datasets.
Such approaches have recently been applied to ferroic materials in the study of local relaxation behavior in ferroelectric relaxors (1 − x)Pb(Mg1/3Nb2/3)O3–xPbTiO3 (PMN–xPT).[ Reference Vasudevan, Zhang, Okatan, Jesse, Kalinin and Bassiri-Gharb 53 ] In this example, relaxation in the piezoresponse was measured using BE-PFM as a function of time (in the remanent state) following a DC bias of varying magnitude [Fig. 3(a)]; and thus the final dataset is 4D A = (x, y, V, t). Through the use of ICA the amplitude of the piezoresponse can be represented as the sum of “n” number of independent components (representing a response) multiplied by a mixing coefficient at each point [Figs. 3(b)–3(e)]. ICA of this dataset, assuming two independent components, revealed two primary modes of response whose relative character varies spatially. The first component S 1(t) can be well fit by an exponential function, the expected relaxation response. The second component S 2(t) showed a slower somewhat larger response indicative of mesoscopic disorder. Using these approaches, it was determined that the mesoscopic heterogeneities in PMN–0.28PT are correlated to differing volume fractions of rhombohedral and tetragonal phases under the tip.

Figure 3. (a) Sample-averaged (all 2500 points), off-field piezoresponse relaxation amplitude on PMN-0.28PT. Independent component analysis (b) c1 mixing coefficient map, (c) graph of independent component s 1, (d) c2 mixing coefficient map, (e) graph of component s 2 (Reprinted from [Reference Somnath, Belianinov, Kalinin and Jesse54], with the permission of AIP Publishing).
While there has been a tremendous growth in the implementation of multivariate statistical analysis in the experimental study of multifunctional materials, this is not yet standard practice. Most experimental researchers are unaware of the language, scope, and methodologies of big-data analytics and, in turn, do not effectively mine or even collect all of the data they could. For instance, during data collection most experimental equipment pre-processes data, storing only the data deemed to be of the highest value. As big-data approaches become more integrated into the scientific approach, experimental systems will need to be redesigned or reprogrammed to acquire a fuller set of data (for an example, see g-mode scanning probe studies[ Reference Somnath, Belianinov, Kalinin and Jesse 54 ]). This, as a result, will facilitate the growth of curated experimental databases, which can be rapidly mined using supercomputer-based statistical analyses and machine learning techniques redefining the scope and insight gleaned from experimental characterization. Looking forward, we can expect to see increased collaboration between computational data scientists and experimentalists. As the potential impact of these big-data analysis techniques become more mainstream we can expect the development of complex networks where computational results and raw data from full data-acquisition experiments are fed directly into curated databases accessible to the global research community. These databases will enable the materials genome to be mapped and the data to be mined without constraints of experimental/computational resource availability. This “networked” approach has the potential to reshape the scientific and technological landscape revolutionizing the efficiency of scientific discovery, but will require that researchers establish and implement expectations for participation, data access protocols and rules regarding access, and ownership of intellectual property.
Reshaping ferroic physics—exploring exotic and emergent polarization states
Researchers have explored an enormous phase space of materials by leveraging their ability to manipulate chemistry and elastic boundary conditions (i.e., epitaxial strain, film thickness, geometry, etc.) to engineer the crystal and domain structure, and ultimately, the response and susceptibility of multifunctional materials. Using these conventional strain-based approaches it has been possible to manipulate the properties of multifunctional materials including inducing room temperature ferroelectricity in paraelectric SrTiO3,[ Reference Biegalski, Jia, Schlom, Trolier-McKinstry, Streiffer, Sherman, Uecker and Reiche 55 , Reference Haeni, Irvin, Chang, Uecker, Reiche, Li, Choudhury, Tian, Hawley, Craigo, Tagantsev, Pan, Streiffer, Chen, Kirchoefer, Levy and Schlom 56 ] enhancing ferroelectric transition temperatures and remnant polarization in BaTiO3,[ Reference Choi, Biegalski, Li, Sharan, Schubert, Uecker, Reiche, Chen, Pan, Gopalan, Chen, Schlom and Eom 57 ] and creating the novel multiferroic EuTiO3 which is neither ferroelectric nor ferromagnetic in the bulk.[ Reference Lee, Fang, Vlahos, Ke, Jung, Kourkoutis, Kim, Ryan, Heeg, Roeckerath, Goian, Bernhagen, Uecker, Hammel, Rabe, Kamba, Schubert, Freeland, Muller, Fennie, Schiffer, Gopalan, Johnston-Halperin and Schlom 58 ] Recently advances in control of interface chemistry and in situ monitoring/control of growth processes has enabled the manipulation of these materials at the sub-unit-cell level.[ Reference Martin, Chu and Ramesh 59 ] In turn, it is possible to create tailored interfaces and superlattices that are nearly “atomically sharp” (minimal chemical intermixing) as well as designer chemical gradients. This ability to manipulate the chemistry, strain and strain gradients, and the electrostatic boundary conditions of multifunctional material allows for the design of nano-/meso-scale polar structures with unique susceptibilities and response.
For example, there has been growing interest in generating inhomogeneous polarization states (or polarization gradients) in multifunctional materials. Such inhomogeneous polarization states are interesting as they provide a way to break symmetry, generate a preferred poling direction,[ Reference Agar, Damodaran, Velarde, Pandya, Mangalam and Martin 60 , Reference Mangalam, Agar, Damodaran, Karthik and Martin 61 ] broaden ferroelectric transition temperatures,[ Reference El-Naggar, Dayal, Goodwin and Bhattacharya 62 , Reference Cole, Ngo, Hirsch, Demaree, Zhong and Alpay 63 ] decouple typically coupled order parameters,[ Reference Mangalam, Agar, Damodaran, Karthik and Martin 61 , Reference Catalan, Sinnamon and Gregg 64 ] give rise to exotic space charge arrangements,[ Reference Cross 65 , Reference Chu, Jang, Sung, Shin, Lee, Song, Lee, Woo, Kim, Choi, Koo, Kim, Oh, Jo and Yang 66 ] among other effects, enabling the optimization of materials responses[ Reference Mangalam, Agar, Damodaran, Karthik and Martin 61 , Reference Majdoub, Sharma and Cagin 67 ] and even giving rise to novel functionalities.[ Reference Bhaskar, Banerjee, Abdollahi, Solanas, Rijnders and Catalan 68 ] While there are many routes to achieve inhomogeneous polarization gradients, the most common approach leverages the flexoelectric effect [Fig. 4(a)], the linear coupling of a strain gradient ∂ε ij /∂x k to the polarization (P i ), an interaction mediated by a fourth-rank flexoelectric tensor (μ ijkl ).[ Reference Indenbom, Loginov and Osipov 69 ] From a materials engineering standpoint there are now many effective routes to generate large strain gradients (on the order of 105–106 m−1), including: controlled strain relaxation,[ Reference Lee, Jeon, Yoon, Shin, Lee, Song, Bu, Kim, Chung, Yoon and Noh 70 ] ferroelastic domain walls,[ Reference Catalan, Lubk, Vlooswijk, Snoeck, Magen, Janssens, Rispens, Rijnders, Blank and Noheda 71 , Reference Jia, Urban, Alexe, Hesse and Vrejoiu 72 ] through compositional grading,[ Reference Agar, Damodaran, Velarde, Pandya, Mangalam and Martin 60 , Reference Mangalam, Agar, Damodaran, Karthik and Martin 61 , Reference Agar, Damodaran, Okatan, Kacher, Gammer, Vasudevan, Pandya, Dedon, Mangalam, Velarde, Jesse, Balke, Minor, Kalinin and Martin 73 , Reference Mangalam, Karthik, Damodaran, Agar and Martin 74 ] and by creating nanoscale free-standing structures.[ Reference Bhaskar, Banerjee, Abdollahi, Wang, Schlom, Rijnders and Catalan 75 ] For example, to achieve strain gradients using compositional gradients, an epitaxially strained film is grown wherein the chemistry is changed such that the bulk lattice parameter(s) of the film evolves with the thickness [Fig. 4(b)]. Using this approach large strain gradients of the order of 105 m−1 have been achieved in compositionally-graded PbZr1−x Ti x O3 resulting in shifted ferroelectric hysteresis loops (i.e., built-in potentials), highly suppressed dielectric susceptibilities, and enhanced pyroelectric figures of merit.[ Reference Agar, Damodaran, Velarde, Pandya, Mangalam and Martin 60 , Reference Mangalam, Agar, Damodaran, Karthik and Martin 61 , Reference Mangalam, Karthik, Damodaran, Agar and Martin 74 ] Additionally, it has been found that these chemical and strain gradients can modify the morphology and response of ferroelastic domains; making them appear more needle-like rather than parallelepiped-like [Fig. 4(c)].[ Reference Agar, Damodaran, Okatan, Kacher, Gammer, Vasudevan, Pandya, Dedon, Mangalam, Velarde, Jesse, Balke, Minor, Kalinin and Martin 73 ] Subsequent studies of electric-field induced switching identified that these needle-like ferroelastic domains are highly mobile expanding (or contracting) from the free surface depending on the direction of the applied bias.[ Reference Agar, Damodaran, Okatan, Kacher, Gammer, Vasudevan, Pandya, Dedon, Mangalam, Velarde, Jesse, Balke, Minor, Kalinin and Martin 73 ] This unusual field-dependent response renders these domains highly mobile in the out-of-plane direction yet spatially localized in the plane; prompting them to be called “springy” in nature.[ Reference Dörr 76 ] Such work highlights the ability to utilize strain gradients to finely control the structure, response, and properties of ferroelastic domains. These new modalities of domain engineering provide a nearly limitless space to engineer domain wall functionalities facilitating the fabrication of a range of proposed domain wall-based devices.

Figure 4. (a) Schematic illustration indicating the fundamental principles of flexoelectricity. (b) Phase diagram and lattice parameter evolution in PbZr1−x Ti x O3 system showing how compositional gradients with large strain gradients can be fabricated (Reprinted with permission from Ref. [Reference Agar, Damodaran, Velarde, Pandya, Mangalam and Martin60]. Copyright 2015 American Chemical Society). (c) Cross-sectional nanobeam diffraction strain mapping out-of-plane strain image of needle-like ferroelastic domains in compositionally-graded heterostructures. Strain values indicated are in reference to the GdScO3 pseudocubic lattice parameter (Reprinted with permission from Ref. [Reference Agar, Damodaran, Okatan, Kacher, Gammer, Vasudevan, Pandya, Dedon, Mangalam, Velarde, Jesse, Balke, Minor, Kalinin and Martin73], Copyright 2016 Nature Publishing Group). (d) Top, schematic drawing of flexoelectric actuator consisting of SrTiO3 sandwiched between to SrRuO3 electrodes. Bottom left, optical image of an array of fabricated nanocantilevers. Bottom Right, image of nanocantilever colored to indicate the out-of-plane deflection (Reprinted with permission from Ref. [Reference Bhaskar, Banerjee, Abdollahi, Wang, Schlom, Rijnders and Catalan75], Copyright 2016 Nature Publishing Group).
To provide greater flexibility in the design of strain/polarization gradients, researchers have created free-standing heterostructures wherein the strain/polarization gradients can be tuned “on-demand”.[ Reference Bhaskar, Banerjee, Abdollahi, Wang, Schlom, Rijnders and Catalan 75 , Reference Baek, Park, Kim, Aksyuk, Das, Bu, Felker, Lettieri, Vaithyanathan, Bharadwaja, Bassiri-Gharb, Chen, Sun, Folkman, Jang, Kreft, Streiffer, Ramesh, Pan, Trolier-McKinstry, Schlom, Rzchowski, Blick and Eom 77 ] Such, NEMS/MEMS permit the generation of large dynamic strain gradients wherein flexoelectricity is a dominant feature. One recent example using this concept was the fabrication of all-oxide nanocantilevers composed of SrTiO3 sandwiched between two SrRuO3 electrodes on SrTiO3-buffered Si [Fig. 4(d)].[ Reference Bhaskar, Banerjee, Abdollahi, Wang, Schlom, Rijnders and Catalan 75 ] This study demonstrated that SrTiO3-based free-standing devices fabricated using state-of-the-art techniques with large flexoelectric effects can outperform the best piezoelectric electromechanical actuators.[ Reference Bhaskar, Banerjee, Abdollahi, Wang, Schlom, Rijnders and Catalan 75 ] These foundational studies are just the tip of the iceberg. It will be exciting to see these concepts become mature technologies.
Despite these recent successes there are still many open questions regarding the understanding and utilization of strain/polarization gradients and flexoelectricity. The principal area of contention relates to the magnitude of the flexoelectric coefficient which experiments find to be orders of magnitude larger than theoretical predictions.[ Reference Biancoli, Fancher, Jones and Damjanovic 78 ] The recent implementation of advanced nanoscale transmission electron microscopy techniques coupled with “big data” analytics are on the brink of being able to reconcile this discrepancy[ Reference Agar, Damodaran, Okatan, Kacher, Gammer, Vasudevan, Pandya, Dedon, Mangalam, Velarde, Jesse, Balke, Minor, Kalinin and Martin 73 , Reference Cao, Li, Chen and Kalinin 79 ] as they can now directly measure strain gradients in materials and this new understanding will, in turn, likely usher in a new era of strain gradient-based polarization engineering.
Leveraging the ability to generate inhomogeneous strain and polarization gradients, researchers have also sought routes to generate topological structures in polar materials. While simple planar topological defects, such as those formed by domains have been utilized to stabilize new phases and structures[ Reference Farokhipoor, Magén, Venkatesan, Íñiguez, Daumont, Rubi, Snoeck, Mostovoy, De Graaf, Müller, Döblinger, Scheu and Noheda 80 ] that can act as nanoscale functional elements,[ Reference Seidel 81 , Reference Seidel, Vasudevan and Valanoor 82 ] there is both fundamental[ Reference Choudhury, Walizer, Lisenkov and Bellaiche 83 , Reference Nahas, Prokhorenko and Bellaiche 84 ] and technological[ Reference Seidel, Vasudevan and Valanoor 82 ] interest in designing more complex topological states in multifunctional materials such as vortices, waves, merons, skyrmions, etc. [Figs. 5(a)–5(e)][ Reference Hong, Catalan, Fang, Artacho and Scott 85 , Reference Nahas, Prokhorenko, Louis, Gui, Kornev and Bellaiche 86 ] and exploring their formation, susceptibilities, and phase transition characteristics.[ Reference Prosandeev, Ponomareva, Kornev, Naumov and Bellaiche 87 ] Using computational approaches, a wide range of novel orders, structures, and effects have been predicted including axial peizotoroidic, electric toroidal susceptibility, pyrotoroidic, etc.[ Reference Prosandeev, Ponomareva, Naumov, Kornev and Bellaiche 88 ] The highly coupled order parameters in these topological structures could facilitate new device concepts for random access memory (RAM), nanoscale transducers, sensors, switches, motors, etc.[ Reference Prosandeev, Ponomareva, Kornev, Naumov and Bellaiche 87 ] In particular, it has been proposed that vortex structures could give rise to a multifold increase in storage capacity for non-volatile ferroelectric RAM.[ Reference Naumov, Bellaiche and Fu 89 ] Despite considerable theoretical and modeling work,[ Reference Chen, Zheng, Wang and Liu 90 – Reference Baudry, Sene, Luk'yanchuk, Lahoche and Scott 92 ] it was only in the last year that such novel topologies of polarization were experimentally realized. For example, smoothly varying polar vortices, were created and observed in superlattices of paraelectric SrTiO3 and ferroelectric PbTiO3 [Figs. 5(f)–5(i)].[ Reference Yadav, Nelson, Hsu, Hong, Clarkson, Schlepüetz, Damodaran, Shafer, Arenholz, Dedon, Chen, Vishwanath, Minor, Chen, Scott, Martin and Ramesh 93 ] These vortex structures are thought to be stabilized by a competition of gradient, electrostatic, and elastic energies. Initial studies have suggested that these vortex states can be transformed into a uniform polarization state providing a potential pathway for controllability and, ultimately, functionality.[ Reference Naumov and Fu 94 ]

Figure 5. 2D projections of proposed/realized topological structures based on ferroelectric polarization wherein the order parameter is represented by the direction of the arrows for (a) a radial skyrmion, (b–c) vortex structures, (d) a chiral skyrmion, and (e) a four-quadrant closure structure (Reprinted with permission from Ref. [Reference Seidel, Vasudevan and Valanoor82]). (f) Observation of vortex/anti-vortex structures in intermediate periodicity (PbTiO3)10/(SrTiO3)10 superlattices realized using cross-sectional, atomic-scale imaging via scanning transmission electron microscopy (the overlaid polarization vector maps represent the local polar distortion). (g) A magnified image of a single vortex/anti-vortex pair where the polarization state within such vortex pairs can be visualized. (h) Phase-field simulations of the same superlattice structure also predicting the vortex pairs. (i) The curl of polarization (∇ × P) for a vortex pair, extracted from the data in (g). The data is plotted with a red/blue color scale where no-vorticity (curl = 0) is white, clockwise (negative) is blue and anticlockwise (positive) is red. (Reprinted with permission from Ref. [Reference Yadav, Nelson, Hsu, Hong, Clarkson, Schlepüetz, Damodaran, Shafer, Arenholz, Dedon, Chen, Vishwanath, Minor, Chen, Scott, Martin and Ramesh93], Copyright 2016 Nature Publishing Group).
With experiments now catching-up with theoretical and modeling approaches, there are expansive opportunities to explore new systems and create new topologies; and it will be exciting to see how future studies can control, manipulate, and utilize these topological states. Future work will likely leverage multi-scale modeling approaches to deterministically control polarization field textures (i.e., type, scaling, winding number, etc.).[ Reference Hong, Catalan, Fang, Artacho and Scott 85 , Reference Nahas, Prokhorenko, Louis, Gui, Kornev and Bellaiche 86 ] Furthermore, it is possible that topological polarization states can be induced in intrinsically multiferroic materials (such as BiFeO3), such that the ferroelectric polarization which is coupled to antiferromagnetic and canted moments[ Reference Heron, Bosse, He, Gao, Trassin, Ye, Clarkson, Wang, Liu, Salahuddin, Ralph, Schlom, Iniguez, Huey and Ramesh 95 ] can induce topological states in the magnetic sublattice. Such multiferroic topological states could provide a powerful and versatile pathway to achieve large susceptibilities and novel functionalities. Finally, due to the complexity of these topological polarization states an extension of common characterization protocols will be required to understand their structure and response under applied fields. This will motivate the development and implementation of advanced electron microscopy, resonant x-ray scattering, spatially-resolved optical techniques, as well as polarized light temperature-dependent studies of susceptibilities in exotic structures (e.g., electric toroidic and pyrotorodic).
All told, the community stands poised to reshape ferroelectric physics or order by manipulating chemistry and electrical and elastic boundary conditions at the nanoscale. The combination of detailed computational simulation, advances in growth and fabrication techniques, and deeper understanding of polarization physics are now enabling researchers to directly mold polarization states “on demand,” making the design of novel and technologically relevant nanoscale functional elements possible.
Addressing global challenges—ferroics in energy and the environment
Little needs to be said to emphasize the growing importance and immediate impact that cutting-edge research and development needs to have on matters of extreme societal import including energy and the environment. In this section, we highlight the potential role for ferroic materials in this regard.
One area of interest that is poised for major impact in the coming years is the study of ferroelectric photovoltaics.[ Reference Yuan, Xiao, Yang and Huang 96 – Reference Butler, Frost and Walsh 98 ] The bulk photovoltaic effect (or photogalvanic effect) is observed in non-centrosymmetric materials exhibiting a polarization without the need for junction-based structures. Recent years have seen marked advances in our understanding of these effects wherein theoretical approaches have highlighted how excitation of quantum wave packets in non-centrosymmetric materials can lead to the formation of “shift currents” or the excitation of carriers from one band to another while moving from the initial real space location.[ Reference Young, Zheng and Rappe 99 – Reference Young and Rappe 101 ] A second effect, the anomalous or ballistic photovoltaic effect, describes how, unlike in conventional photovoltaics where the photovoltage is limited by the band gap of the material, in systems with a spontaneous polarization, photovoltages can be orders of magnitude higher than the band gap. The ballistic contribution to the bulk photovoltaic effect is now thought to arise from asymmetric scattering from phonons and lattice defects. In polydomain ferroelectrics, an additional opportunity arises wherein the domain walls can act as charge separators. In ferroelectric and multiferroic materials, a high density of domain walls can amplify the anomalous photovoltaic effect.[ Reference Yang, Martin, Byrnes, Conry, Basu, Paran, Reichertz, Ihlefeld, Adamo, Melville, Chu, Yang, Musfeldt, Schlom, Ager and Ramesh 102 – Reference Seidel, Fu, Yang, Alarcón-Lladó, Wu, Ramesh and Ager 106 ] Subsequent research has worked to better understand these bulk photovoltaic and domain-wall-based mechanisms.[ Reference Yan, Chen, Lu and Spanier 107 , Reference Bhatnagar, Chaudhuri, Kim, Hesse and Alexe 108 ] This area is primed for future development as researchers determine how to create devices with the optimum geometries required to extract useful function from these systems. Particularly there is interest in how to enhance photoexcited carrier concentrations and motilities as well as determining the role of electron correlations in photo transport. In turn, efficiencies and applicability will be improved. In this regard, one of the most promising developments in recent years has been the design of a new class of low band gap polar materials, including [KNbO3]1−x [BaNi1/2Nb1/2O3−δ ] x which can be tuned to have a band gap from 1.1 to 3.8 eV and (with x = 0.1 and a band gap of 1.39 eV) have produced photocurrent densities ~50 times larger than classic ferroelectric photovoltaics![ Reference Grinberg, West, Torres, Gou, Stein, Wu, Chen, Gallo, Akbashev, Davies, Spanier and Rappe 109 ]
Another area of impact for ferroic materials is in the development of cooling technologies. Refrigeration accounts for nearly 10% of commercial energy use[ Reference Michaels 110 ]; however, within the past few decades, refrigeration technologies have remained essentially unchanged. Multifunctional materials which allow the mutual convertibility of work from an external perturbation (i.e., mechanical, magnetic, and/or elastic) and heat (or entropy) represent a potentially important class of materials to realize solid state refrigeration without the need for gaseous refrigerants.[ Reference Lang 111 ] For instance, if one was to take an expanded spring and release the tension, move a piece of nickel away from a magnet, or remove an electric field from a paraelectric crystal these materials would absorb heat (entropy) from the environment thereby cooling it. In turn, there is significant interest in cooling via application of magnetic fields (magnetocaloric), electric fields (electrocaloric), and/or mechanical stress (elastocaloric). While most of the caloric effects (elastocaloric and magnetocaloric) have predominantly been studied in polymers, intermetallics, and alloys, electrocaloric effects which require a material with a spontaneous polarization are limited to pyroelectric, ferroelectric, or multiferroic materials.
The recent reemergence of interest in the electrocaloric effect, in particular, has been driven by demonstrations in thin-film devices wherein small voltages (<5 V) can drive potentially large electrocaloric responses [Fig. 6(a)]. Large effects generally occur when designing materials in the vicinity of phases transition,[ Reference Moya, Kar-Narayan and Mathur 112 ] typically achieved using strain or variations in chemical composition. Using this approach, large electrocaloric effects (comparable with the thermoelectric effect) have been reported in PbZr0.95Ti0.05O3 (ΔT = 12 K, ΔE = 481 kV/cm),[ Reference Mischenko, Zhang, Scott, Whatmore and Mathur 113 ] relaxor ferroelectrics such as (1 − x)PbMg y Nb1−y O3–(x)PbTiO3 (PMN–PT) (ΔT = 5–9 K, ΔE = 720–985 kV/cm),[ Reference Mischenko, Zhang, Whatmore, Scott and Mathur 114 ] and SrBi2Ta2O9 (ΔT = 4.93 K, ΔE = 600 kV/cm).[ Reference Chen, Ren, Wu, Yang and Liu 115 ] Concern remains, however, as to how to accurately measure these effects, particularly in films where the temperature changes and thermal mass is small. Generally, indirect routes where the polarization is measured as a function of temperature is used to estimate the electrocaloric temperature change via a Maxwell relation (which allows for estimation of an adiabatic temperature or isothermal entropy change) are preferred because of their simplicity. Despite their widespread utilization, these indirect approaches neglect secondary effects such as elastocaloric effects that can be large in thin films, and thus tend to overestimate the electrocaloric temperature change. In recent years, efforts have led to the development of techniques capable of measuring the electrocaloric response directly via infrared imaging,[ Reference Guo, Gao, Yu, Santhanam, Fedder, McGaughey and Yao 116 ] microfabricated device structures [Fig. 6(b)],[ Reference Bhatia, Damodaran, Cho, Martin and King 117 ] laser thermoreflectance-based measurements,[ Reference Tong, Karthik, Mangalam, Martin and Cahill 118 , Reference Tong, Karthik, Martin and Cahill 119 ] and differential scanning calorimetry.[ Reference Goupil, Berenov, Axelsson, Valant and Alford 120 ]

Figure 6. (a) Schematic diagram indicating the change in polarization that gives rise to electrocaloric and pyroelectric effects (Ref. [Reference Lang111]). (b) Schematic drawing of microfabricated device capable of measuring pyroelectric/electrocaloric response at high frequency. The device consists of a BaTiO3 thin-film capacitor with electrical access to top and bottom electrodes. A gold strip placed above the pyroelectric capacitor serves as the resistive heater. A high resistivity SiO2 layer, sandwiched between the top electrode and heater strip, electrically insulates the pyroelectric film and minimizes interference from the heating voltage (Reprinted from Ref. [Reference Bhatia, Damodaran, Cho, Martin and King117], with the permission of AIP Publishing.). (c) Intrinsic and extrinsic magnetocaloric effect of La0.7Ca0.3MnO3/BaTiO3 heterostructures. Graph shows film entropy change ΔS(T) at selected fields. There is evidence of a strong extrinsic magnetocaloric response near the BaTiO3 rhombohedral to orthorhombic transition. A small magnetocaloric effect is observed at the Tc of La0.7Ca0.3MnO3 (Reprinted with permission from Ref. [Reference Moya, Hueso, Maccherozzi, Tovstolytkin, Podyalovskii, Ducati, Phillips, Ghidini, Hovorka, Berger, Vickers, Defay, Dhesi and Mathur124], Copyright 2016 Nature Publishing Group).
Leveraging such measurements, new insights into the physics of these systems are being unraveled. Of particular interest are coupled terms and resulting multicaloric responses (e.g., piezoelectrocaloric, elastocaloric, magnetoelectrocaloric, etc.). For example, in PbZr0.2Ti0.8O3 thin films, direct electrocaloric measurements revealed a ~50% reduction in the electrocaloric entropy change due to elastocaloric effects arising from substrate clamping.[ Reference Tong, Karthik, Mangalam, Martin and Cahill 118 , Reference Karthik and Martin 121 ] Based on first principles studies of PbTiO3, it was predicted that the multicaloric effect could far exceed either the electrocaloric or elastocaloric effects.[ Reference Lisenkov, Mani, Chang, Almand and Ponomareva 122 ] In turn, future heterostructure design concepts must be chosen to leverage (or at least consider) these secondary effects. In a similar vein, researchers have sought routes to engineering multicaloric responses using magnetoelectric coupling in multiferroic materials/heterostructures where application of either electric or magnetic fields can couple to both ferroic order parameters (ferroelectric and ferromagnetic). Initial work in this regard has focused on magnetoelectric heterostructures designed to exhibit strongly coupled ferroic order. For example, indirect estimates of such effects have been reported for Ni44Co5.2Mn36.7In14.1 ribbon and PMN–PT composites[ Reference Gong, Wang, Cao, Liu, Liu and Du 123 ]. Recently this concept was exploited in an all-oxide heterostructure of La0.7Ca0.3MnO3 on BaTiO3 substrates wherein it was shown that giant reversible magnetocaloric effects can be driven by interfacial strain resulting from the rhombohedral-to-tetragonal phase transition in BaTiO3 at ~200 K. It was determined that the giant entropic change observed (|ΔS/μ 0ΔH|~9 J/K/kg/T) was due to strain induced changes in ferromagnetic/paramagnetic volume fractions [Fig. 6(c)].[ Reference Moya, Hueso, Maccherozzi, Tovstolytkin, Podyalovskii, Ducati, Phillips, Ghidini, Hovorka, Berger, Vickers, Defay, Dhesi and Mathur 124 ] With a similar directive, recently it was demonstrated that the irreversible nature of the giant magnetocaloric effect in FeRh can be overcome by a dual-stimulus magnetic–electric refrigeration cycle enabling large electrocaloric effects to be achieved over ~100 K temperature range inclusive of room temperature.[ Reference Liu, Phillips, Mattana, Bibes, Barthélémy and Dkhil 125 ] These exciting results motivate the exploration of new composite geometries and material, which could be used to optimize the magnitude and operational range (i.e., temperature, magnetic field, etc.) where large magnetoelectrocaloric effects can be achieved.
Looking forward, work on calorics has a rather clear, but not straightforward goal: create the biggest temperature changes with the least applied fields across the widest temperature range possible. To achieve these goals, novel heterostructure concepts are needed. For example, work on compositionally-graded ferroelectrics has already shown that the presence of a built-in field can suppress the dielectric permittivity while having minimal effect on the pyroelectric response, in turn, enhancing the pyroelectric and the electrocaloric figures of merit.[ Reference Mangalam, Agar, Damodaran, Karthik and Martin 61 ] Likewise, such compositionally-graded ferroelectrics may also exhibit large responses over wider temperature ranges than homogeneous materials. Alternatively, exotic highly-ordered ferroelectric phases such as polar vortices in oxide superlattices[ Reference Yadav, Nelson, Hsu, Hong, Clarkson, Schlepüetz, Damodaran, Shafer, Arenholz, Dedon, Chen, Vishwanath, Minor, Chen, Scott, Martin and Ramesh 93 ] could give rise to novel caloric effects, namely the toroidocaloric effect,[ Reference Castán, Planes and Saxena 126 ] analogous to those observed in magnetic-vortex structures such as LiCo(PO4)3 and Ba2CoGe2O7. While the jury is still out on what the most effective material and/or device structure is to maximize caloric responses in multifunctional materials these exciting recent developments hold promise that these effects previously deemed just a scientific curiosity will be developed into integrated and functional devices.
A low-power future—ferroics for novel energy efficient devices
Driven by the already large and growing market for mobile, battery-powered devices and the rapidly emerging “Internet-of-Things (IOT),” a new bottleneck in terms of speed and power consumption now dominates. As electronics approach the critical lengthscale of sub-10 nm, Moore's Law,[ Reference Moore 127 ] which so far has set the pace for transistor scaling, is nearing its “demise.”[ Reference Markoff 128 ] As a consequence, there is quite a bit of interest in alternative approaches to information processing, such as quantum or neuromorphic computing. The possibility for multiple analog states in a ferroelectric hysteresis loop makes it likely that ferroelectrics will play a key role in neuromorphic computing.[ Reference Mead 129 ] In parallel, ferroics are already playing a critical role in enhancing conventional digital electronics. A particularly emergent example is the use of the negative capacitance time domain regime of ferroelectric switching[ Reference Khan, Chatterjee, Wang, Drapcho, You, Serrao, Bakaul, Ramesh and Salahuddin 130 ] and the potential to leverage nanodomain structures to produce negative capacitance over a large temperature range.[ Reference Zubko, Wojdeł, Hadjimichael, Fernandez-Pena, Sené, Luk'yanchuk, Triscone and Íñiguez 131 ] Such approaches will enable us to, at least temporarily, overcome the 60 mV/decade limit that is current in CMOS transistors.
On the memory front, it would be extremely desirable to significantly lower the energy consumption/bit of information stored. Current memory technologies operate approximately in the few picoJoule/bit regime of energy consumption.[ Reference Dean 132 ] Approaching the fundamental “Landauer limit” (kT[ln 2]) poses several fundamental and materials challenges.[ Reference Landauer 133 ] As an intermediate step, the goal is to create logic and memory that can operate with an energy consumption of the order of attojoules per logic or memory operation. This requires a reinvention of the materials and architectures of logic and memory. Multifunctional materials with their multiple susceptibilities represent a versatile platform to design future microelectronic devices with the potential of attojoule operation.
Toward this objective, there is considerable interest in designing composite structures which couple multifunctional materials such that they manipulate the functional properties of one another. Coupling of functionalities can be mediated by the lattice (which is typically the case as in piezoelectrics), or through coupling of spin (exchange coupling), charge (field effects), and/or orbital effects. Within this framework, there has been a significant amount of interest in electric-field control of both the direction and state of magnetism.[ Reference Chu, Martin, Holcomb, Gajek, Han, He, Balke, Yang, Lee, Hu, Zhan, Yang, Fraile-Rodríguez, Scholl, Wang and Ramesh 134 ] Typically, these device concepts rely on generating an acoustic pulse or strain in one component of the composite structure which is elastically coupled in such a way that it can generate a measureable change in response in another material. In this regard, many device concepts have been explored including piezoelectronic transistors which operate by using a piezoelectric layer to drive a metal-insulator transition in a piezoresistive material [Fig. 7(a)],[ Reference Newns, Elmegreen, Liu and Martyna 135 , Reference Solomon, Bryce, Kuroda, Keech, Shetty, Shaw, Copel, Hung, Schrott, Armstrong, Gordon, Reuter, Theis, Haensch, Rossnagel, Miyazoe, Elmegreen, Liu, Trolier-McKinstry, Martyna and Newns 136 ] magnetic or ferroelectric tunnel junctions where the polarization direction alters the tunneling electroresistance enabling the formation of non-volatile memories with large on/off ratios [Fig. 7(b)],[ Reference Tsymbal and Kohlstedt 137 – Reference Garcia and Bibes 140 ] (potentially) field effect transistors with negative capacitance that could allow for ultra-low-power electronic devices,[ Reference Khan, Chatterjee, Wang, Drapcho, You, Serrao, Bakaul, Ramesh and Salahuddin 130 , Reference Khan, Bhowmik, Yu, Kim, Pan, Ramesh and Salahuddin 141 ] and others. In an alternative approach, the presence of a ferroelectric polarization can manipulate the carrier density, and in turn, the electronic properties of 2D materials (e.g., graphene) enabling the design of robust field-effect transistors.[ Reference Baeumer, Rogers, Xu, Martin and Shim 142 – Reference Baeumer, Saldana-Greco, Martirez, Rappe, Shim and Martin 145 ] The considerable excitement about these device concepts has recently lead to the study of ferroelectric/FeRh heterostructures as a new way to harness these effects [Fig. 7(c)].[ Reference Cherifi, Ivanovskaya, Phillips, Zobelli, Infante, Jacquet, Garcia, Fusil, Briddon, Guiblin, Mougin, Ünal, Kronast, Valencia, Dkhil, Barthélémy and Bibes 146 – Reference Phillips, Cherifi, Ivanovskaya, Zobelli, Infante, Jacquet, Guiblin, Ãœnal, Kronast, Dkhil, Barthélémy, Bibes and Valencia 149 ] Heterostructures based on FeRh are particularly promising compared with strongly correlated complex oxides (e.g., cuprates and doped maganites) due to the giant electroresistance which can be achieved at near ambient temperatures. FeRh exhibits a temperature-dependent, first-order phase transition from antiferromagnetic (low temperature) to ferromagnetic (high temperature) at ~100 °C which is characterized by a ~1% volumetric expansion.[ Reference Marti, Fina, Frontera, Liu, Wadley, He, Paull, Clarkson, Kudrnovsky, Turek, Kunes, Yi, Chu, Nelson, You, Arenholz, Salahuddin, Fontcuberta, Jungwirth and Ramesh 150 ] By growing epitaxial films of FeRh on single crystals of BaTiO3 it was shown that magnetoelectric coupling coefficients of the order of ~10−5 s/m can be achieved; the largest reported for any multiferroic heterostructure and providing potential for use in electric-field-driven magnetic and resistive memory devices [Fig. 7(d)].[ Reference Cherifi, Ivanovskaya, Phillips, Zobelli, Infante, Jacquet, Garcia, Fusil, Briddon, Guiblin, Mougin, Ünal, Kronast, Valencia, Dkhil, Barthélémy and Bibes 146 ] Direct evidence of this strain-induced magnetic phase transition was observed using magnetic force microscopy [Figs. 7(e) and 7(f)].[ Reference Liu, Li, Gai, Clarkson, Hsu, Wong, Fan, Lin, Rouleau, Ward, Lee, Sefat, Christen and Ramesh 147 ] Ultimately, to achieve low-power device operation requires low-voltage operation. Future studies will likely focus on how to create similar devices with thin film piezoelectric/ferroelectric layers capable of significantly reducing the operational voltage.

Figure 7. (a) Piezoelectronic resistor concept with fulling intergraded transductive stack consisting of a piezoresistive element on top of a piezoelectric element confined by a high Young's modulus (HYM) yoke. The three metal contacts (gray) are called gate, common, and sense. The large piezoelectric/piezoresistive cross-sectional area ~25:1 serves to amplify the stress in the piezoresistive layer relative to the piezoelectric layer (Reprinted with permission from Ref. [Reference Solomon, Bryce, Kuroda, Keech, Shetty, Shaw, Copel, Hung, Schrott, Armstrong, Gordon, Reuter, Theis, Haensch, Rossnagel, Miyazoe, Elmegreen, Liu, Trolier-McKinstry, Martyna and Newns136]. Copyright 2015 American Chemical Society). (b) Schematic of a ferroelectric tunnel junction consisting of an ultra-thin ferroelectric layer sandwiched between two metal layers. Readout is performed by passing a small current across the ferroelectric layer, which does not change the polarization state. Due to the tunneling electroresistance effect the current depends of the direction of the polarization (Reprinted with permission from Ref. [Reference Tsymbal and Gruverman139], Copyright 2016 Nature Publishing Group). (c) Schematic of electric-field-induced magnetic phase transition in multiferroic heterostructures consisting of an epitaxial FeRh layer and a perovskite ferroelectric substrate (such as BaTiO3 and PMN-PT, image courtesy of Dr. X. Renshaw Wang, NTU, Singapore). (d) Variation of the magnetization in FeRh/BaTiO3 heterostructure with the applied voltage at 385 K, after heating under an external voltage of +21 V. The symmetric dependence of magnetization indicates that the voltage-induced strain effect from the ferroelectric BaTiO3 dominates the magnetoeletric response. The inset shows the voltage dependence of the out-of-plane parameter of FeRh at 390 K (Reprinted with permission from Ref. [Reference Cherifi, Ivanovskaya, Phillips, Zobelli, Infante, Jacquet, Garcia, Fusil, Briddon, Guiblin, Mougin, Ünal, Kronast, Valencia, Dkhil, Barthélémy and Bibes146], Copyright 2016 Nature Publishing Group). (e) MFM phase images (8 × 8 μm2) of an FeRh/BTO heterostructure collected after heating up to 376 K with zero E. (f) MFM image of the same region after application of E = −1 kV/cm to the BTO substrate (at 376 K). The false color stands for the phase shift Δφ, which reflects the strength and orientation of out-of-plane magnetic moment (orange color represents up moment and blue color down). Green color Δφ ~ 0 corresponds to negligible moment (Reprinted with permission from Ref. [Reference Liu, Li, Gai, Clarkson, Hsu, Wong, Fan, Lin, Rouleau, Ward, Lee, Sefat, Christen and Ramesh147]).
While these proof-of-concept studies are exciting there are many scientific and engineering challenges that need to be addressed. From a materials physics perspective, perhaps the top priority is to identify the fundamental limits of cross-coupling. Additionally, and equally important, is determining the limitations on dynamics of various coupling phenomena (i.e., switching speed). From a materials synthesis perspective, one of the most difficult challenges in creating these heterostructure devices is finding ways to strongly couple (at the atomic level) dissimilar materials which could have incompatible chemical structure and reactivity, large lattice mismatch, incompatible surface energies, and/or deposition conditions.[ Reference Liu, Biegalski, Hsu, Shang, Marker, Liu, Li, Fan, Meyer, Wong, Nichols, Chen, You, Chen, Wang, Wang, Ward, Gai, Lee, Sefat, Lauter, Liu and Christen 151 ] Future studies will surely explore how to tailor the interfaces to increase coupling between these layers. Furthermore, creating heterostructure devices generally requires the patterning of multifunctional oxide materials. Currently the most common routes involve multistep processes using focused ion beam,[ Reference Solomon, Bryce, Kuroda, Keech, Shetty, Shaw, Copel, Hung, Schrott, Armstrong, Gordon, Reuter, Theis, Haensch, Rossnagel, Miyazoe, Elmegreen, Liu, Trolier-McKinstry, Martyna and Newns 136 , Reference Ganpule, Stanishevsky, Su, Aggarwal, Melngailis, Williams and Ramesh 152 ] or sacrificial oxide hardmask processes[ Reference Karthik, Damodaran and Martin 153 ]; however, selective wet-chemical etching would be preferable. One potential route to achieve increased selectivity in wet-chemical etching processes could involve the adaption of metal-assisted chemical etching to complex oxides.[ Reference Li 154 ] Regardless of the route, the gargantuan impact of composite structures of multifunctional materials will drive a significant research effort and advancement within the next decade.
Beyond just using ferroic materials as elements in a composite structure, there is also growing interest in utilizing the innate potential for collective, long-range interactions in ferroic materials to enable novel low-energy devices. The idea here is that controllable excitation of low-energy perturbations of the elementary building blocks of these materials could enable long-range and deterministic changes in the ensemble system. Such collective behavior is pervasive in nature, and has been observed in biological (e.g., clustering of migratory animals),[ Reference Cavagna, Cimarelli, Giardina, Parisi, Santagati, Stefanini and Viale 155 ] chemical (e.g., self-assembly of colloidal Janus particles),[ Reference Yan, Chaudhary, Bae, Lewis and Granick 156 ] and physical (e.g., superconductivity, magnetism, and martensitic transformations) systems. In ferroics, collective behavior has been observed in magnets which result in novel spin states such as skyrmions[ Reference Mochizuki 157 ] and artificial spin ice structures.[ Reference Nisoli, Moessner and Schiffer 158 ] As an example, recent work has revealed the collective dynamics of magnetic moment reversal in artificial spin ice systems that give rise to avalanches with the appearance of 1D Dirac strings as a natural degree of freedom [Figs. 8(a)–8(c)].[ Reference Mengotti, Heyderman, Rodriguez, Nolting, Huegli and Braun 159 , Reference Ladak, Read, Perkins, Cohen and Branford 160 ]

Figure 8. XMCD images showing direct observation of field reversal in a fully polarized honeycomb lattice. This processes proceeds by creation and propagation of avalanches of pairs of opposite magnetic charges separated by a Dirac string. Evolution shown as a function of applied field (a) <82%, (b) 92% and (c) 99% of the coercive field Hc (Reprinted with permission from Ref. [Reference Mengotti, Heyderman, Rodriguez, Nolting, Huegli and Braun159], Copyright 2016 Nature Publishing Group). (d–f) Maps of the piezoelectric nonlinearity in PZT films of different thickness (Reprinted with permission from Ref. [Reference Vasudevan, Marincel, Jesse, Kim, Kumar, Kalinin and Trolier-McKinstry163]). (g) The highly ordered nanotwinned domain structure with high density ferroelastic domain walls in (111)-oriented PbZr0.2Ti0.8O3 thin films (Reprinted with permission from Ref. [Reference Xu, Liu, Grinberg, Karthik, Damodaran, Rappe and Martin169], Copyright 2016 Nature Publishing Group).
While collective phenomena are clearly at play on the atomic scale in magnetic systems there has been budding interest in exploiting mesoscale collective phenomena in ferroelectrics. In ferroelectrics, collective phenomenon can occur when domain walls move in a correlated manner. Such collective domain wall motion reduces the travel distance of the domain walls enabling fast switching and, potentially, low-power operation for devices. Recent studies have observed the alignment of ferroelastic and ferroelectric domains across multiple grain boundaries as a result of both long-range substrate clamping and short-range inter-granular coupling.[ Reference Ivry, Chu, Scott and Durkan 161 ] Due to the collective nature of these domain walls, avalanche-like correlated domain wall motion can occur upon application of an external electric field impacting both the nonlinear dielectric properties in low-field, sub-switching Rayleigh regimes and switching properties in high-field regimes [Figs. 8(d)–8(g)].[ Reference Gruverman, Auciello and Tokumoto 162 – Reference Ivry, Scott, Salje and Durkan 167 ] While the length scale of collective phenomena in polycrystalline ferroelectrics is rather small (as compared with magnetic systems) due to the presence of grain boundaries, these limitations can be skirted in ferroelectric single crystals or epitaxial thin films. In turn, there has been a dedicated effort to generate highly ordered ferroelastic domain structures to exploit collective phenomenon. One particularly promising example was demonstrated in (111)-oriented PbZr1−x Ti x O3 films which exhibit a highly ordered, nanotwinned domain structure with dense ferroelastic domain walls, wherein the strong elastic coupling between nanotwinned domains should result in collective motion of domain wall twins [Fig. 7(h)].[ Reference Xu, Karthik, Damodaran and Martin 168 , Reference Xu, Liu, Grinberg, Karthik, Damodaran, Rappe and Martin 169 ] Alternatively, dense ordered ferroelastic domain structures capable of exhibiting collective phenomenon can be obtained by manipulating the geometry, dimension, and elastic boundary conditions of ferroelectric structures.[ Reference Schilling, Bowman, Catalan, Scott and Gregg 170 ] This approach has been successfully demonstrated in magnetic comb structures where domain walls can be driven at high velocities,[ Reference Lewis, Petit, O'Brien, Fernandez-Pacheco, Sampaio, Jausovec, Zeng, Read and Cowburn 171 ] but has only been minimally exploited in ferroelectrics.
All told, while ferroic-based, low-powered devices are in the infancy of their development they hold significant promise due to the large number of highly coupled susceptibilities which can be exploited. By carefully interweaving the interactions between dissimilar materials with differing responses and susceptibilities there are near limitless bounds on the device architectures. There are many important questions, however, that need to be addressed including exploring the potential physical limitations of device relevant parameters such as stable minimum feature size, minimum coercive field, energy dissipation, switching speed, etc. Nevertheless, with the correct design schemes one could envision creating ferroic-based, low-power “beyond binary” logic and memory devices that could truly revolutionize our computational and data storage capabilities.
Conclusions
In the end, ferroic and multiferroic materials offer a veritable playground for physicists, material scientists, and engineers alike. The advances in understanding in the prediction, production, and study of these materials in the last few decades have been astounding, but with each passing year the complexity and depth of detail that these materials present has also opened up new questions and paths forward. Today we stand at a crossroads for many applications as we look for new materials and functions to satisfy the needs of the next-generation logic and memory, sensing, energy conversion, and much more. Ferroic materials—and their strong physical responses to applied stimuli and cross-coupled function—stand poised to impact on these fields. With continued research our ability to tune and control these materials in a deterministic fashion will improve to a point that it becomes viable to consider them in real consumer applications. As such, the research of today is laying the groundwork for a new generation of uses for this versatile class of materials.
Acknowledgments
The J. C. A., S. P., R. X., S. S., and L. W. M. acknowledge support from the Air Force Office of Scientific Research under grant FA9550-12-1-0471, the Army Research Office under grant W911NF-14-1-0104, the Director, Office of Science, Office of Basic Energy Sciences, Materials Science and Engineering Division of the Department of Energy under grant No. DE-SC0012375, and the National Science Foundation under grants DMR-1451219, CMMI-1434147, and OISE-1545907. R. R. and L. W. M. acknowledge support from the Gordon and Betty Moore Foundation's EPiQS Initiative, Grant GBMF5307. A. K. Y. and R. R. acknowledge support from the Director, Office of Science, Office of Basic Energy Sciences, Materials Sciences and Engineering Division, of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231 through the Thermoelectrics Materials FWP. T.A. acknowledges support from a National Science Foundation Graduate Research Fellowship. M. A. acknowledges support from the Materials Project. R. R. also acknowledges was supported by FAME, one of six centers of STARnet, a Semiconductor Research Corporation program sponsored by MARCO and DARPA.