1. Introduction
Understanding the interactions between legislators and external agents is important in the scholarship of lobbying and interbranch relations. In particular, studying communication between legislators and unelected outside agents, such as lobbyists, experts, and agency officials, sheds light on a legislature’s capacity to seek external policy-relevant information and helps to identify the external actors that influence the policymaking process. In most theories of political communication and information search, the interaction between lobbyist and legislator depends on the proximity of their preferences regarding policies (e.g. Austen-Smith Reference Austen-Smith1992; Bauer, de Sola Pool, and Dexter Reference Bauer, de Sola Pool and Dexter1963; Calvert Reference Calvert1985; Hall and Deardorff Reference Hall and Deardorff2006; MacKuen et al. Reference MacKuen, Wolak, Keele and Marcus2010; Peterson and Iyengar Reference Peterson and Iyengar2021).
An empirical test of preference dependence in communication requires a strategy for measuring the preferences of each type of actor. Recently, several studies have developed measurement strategies that place the preferences of legislators and outside agents on a one-dimensional common space (Abi-Hassan et al. Reference Abi-Hassan, Box-Steffensmeier, Christenson, Kaufman and Libgober2023; Barberá Reference Barberá2015; Battista, Peress, and Richman Reference Battista, Peress and Richman2022; Bonica Reference Bonica2013; Crosson, Furnas, and Lornez Reference Crosson, Furnas and Lornez2020; McKay Reference McKay2008; Shor, Berry, and McCarty Reference Shor, Berry and McCarty2010). Legislators’ preferences tend to be defined over the implications of a legislative action on their reelection prospects, and hence legislator preference measures inferred from roll calls are informed by partisanship or left–right ideology (Tausanovitch and Warshaw Reference Tausanovitch and Warshaw2017).
Nonelected agents are not pressured by constituents, party officials, or donors, however. Instead, policy experts often have their own goals and incentives and tend to evaluate policies in terms of analytical considerations regarding the placement of a trade-off along a possibility frontier, rather than relying on ideology as a heuristic (Tetlock Reference Tetlock1986). This in turn defines a second, expert-informed preference dimension. In that case, an a priori assumption that reduces preferences of different groups of political actors to a single dimension will be inappropriate (Jessee Reference Jessee2016).
We argue that it is necessary to allow flexibility in measuring the policy preferences of both elected and nonelected agents when testing hypotheses about the interactions between legislators and outside agents using observational data.Footnote 1 Focusing on communication patterns in legislative hearings, we present a new measurement method to place policy preferences on a two-dimensional common space, one dimension for legislators and the other for the witnesses who are invited to testify. This flexibility allows us to let the witness policy preferences to take a different slope, which we call a “rotation,” and a different intercept, which we call a “shift,” from those of the legislators, which renders the conventional one-dimensional common space measurements a special case of our model.
The primary advantages of our proposed measurement method are twofold. First, statistically, our method helps to reduce measurement error that can occur when a two-dimensional space is artificially reduced to a single dimension. For example, in an extreme case where the preference dimensions of the outside agents and legislators are orthogonal, the one-dimensional measurement strategy would erroneously measure agent preferences with what are essentially random numbers, while our measurement conveys meaningful variations across agents reflected in the two-dimensional space. Second, substantively, our method extracts additional information about the nature of the dimension that structures policy preferences among the outside agents, which is often of interest in itself.
The scholarship on ideology and preferences has certainly benefited from the methodological advances in single-dimensional measurements of political agents’ latent preferences, given their simplicity and wide applicability. The trade-off in informational loss and potential measurement errors has received relatively less attention, however (Jessee Reference Jessee2016). Our study highlights this understudied aspect of preference measurement strategies by relaxing the single-dimensional constraint and showcases what we might have missed under these simpler representations of the empirical world.
In our application that examines Medicare hearings, we recover a preference dimension for witnesses that is orthogonal to legislators’ roll-call preference dimension. Medicare policy is an example of a complex policy where expert preferences are unlikely to be rigidly constrained by a single underlying, fixed left–right ideology dimension. Instead, policy experts understand that changes to Medicare, as a health coverage plan, generally imply moves along a cost–quality possibility frontier. These external experts will evaluate the merits of policy proposals and form their preferences over proposals based on their analytical understanding of the proposal given their specific policy-relevant commitments. Using text analysis of witnesses’ testimony, we demonstrate that the expert witnesses’ preferences at Medicare hearings map onto a health care “cost–quality” dimension that is orthogonal to legislator preferences as measured by legislative roll-call votes.
At the same time, the policy views of experts can matter for legislators. Even though legislators’ roll-call preferences and witnesses’ expert policy preferences are orthogonal in our hearings, one direction of the expert policy preference space is by design closer in distance to liberals and the other to conservatives. For example, we find that witnesses’ emphasis on health care costs is more relevant to conservative legislators and quality is more relevant to liberals. Thus, even though witnesses have expert-informed views, expert preferences have liberal and conservative positions, and interactions in hearings remain political in this fundamental sense.
We show that the witness preference estimates that we recover in our flexible model have better construct validity than preference estimates that constrain all actors’ preferences to a single dimension in that only our unconstrained preference estimates have a clear correspondence with institutional theories predicting preference dependence in political communication. This empirical test demonstrates a use case and the validity of our measurement method, and it contributes to research on lobbying as it presents the first evidence using observational data to support established theories that legislators tend to seek information from agents whose preference is closer to theirs than those with preferences distant from theirs (e.g., Austen-Smith Reference Austen-Smith1992; Bauer et al. Reference Bauer, de Sola Pool and Dexter1963).
2. Preferences and Information-Seeking Questions in Committee Hearings
To substantively validate our new measurement strategy and demonstrate a use case of our measurement, we test hypotheses from theoretical lobbying models in the context of U.S. congressional committee hearings. In committee hearings, legislators publicly pose statements and questions regarding the hearing topic to outside agents such as lobbyists and policy specialists, who in this context are referred to as “witnesses,” and who typically have both preferences and expertise on the given policy topic (Esterling Reference Esterling2004). In general, legislators must rely on outside experts and lobbyists to subsidize their limited capacity to understand the complexities of legislation (Ban, Park, and You Reference Ban, Park and You2023; Hall and Deardorff Reference Hall and Deardorff2006).Footnote 2
Committee hearings are an excellent venue to understand communication between legislators and outside agents, for at least three reasons. First, committee hearings are a core component of the legislative process where we can observe communication patterns of legislators. Second, U.S. congressional committee hearings are fully transcribed while there is no written record of behind the scenes lobbying. Third, in hearings we can observe with which witnesses members choose to engage when given the opportunity to choose among witnesses with diverging preferences,Footnote 3 while in behind the scenes lobbying members only interact with groups to which they choose to give access.
Many theoretical frameworks of political communication suggest that communication patterns between actors tend to be shaped by the distribution of their preferences on an issue under consideration, and we expect that these theories apply to legislator–witness communication in committee hearings. For example, economic models of strategic information transmission suggest that when communication is costless, messages should be more informative to a receiver, and hence more valuable for updating beliefs if the preferences of the receiver (the legislator) and sender (the witness) are closer to each other (see Austen-Smith Reference Austen-Smith1992; Crawford and Sobel Reference Crawford and Sobel1982); in other strategic situations, such as some costly signaling or lobbying with verification game structures, witnesses with more distant preferences are more informative (e.g., Calvert Reference Calvert1985; Diermeier and Feddersen Reference Diermeier and Feddersen2000). Alternatively, an extensive psychological literature documents that individuals often engage in motivated reasoning where they search for information that is compatible with their existing views and preferences (Peterson and Iyengar Reference Peterson and Iyengar2021). Noninformational mechanisms may be at work as well. For example, an established sociological framework relies on the concept of homophily indicating legislators might be attracted to communicate with witnesses who are sociologically similar irrespective of any informational considerations (Bauer et al. Reference Bauer, de Sola Pool and Dexter1963).
While these frameworks lay out different mechanisms to explain patterns of communication in committee hearings, what is common is they all highlight that preference distance has a role in governing the interactions between legislators and witnesses. As we explain below, the weak, generic assumption that communication in hearings depends in any way on preferences is the only assumption that we need to motivate the method we propose to measure preference distance in the naturalistic setting of committee hearings. The identification of our model does not depend on the underlying mechanism that drives preference dependence in communication, although the revealed (estimated) direction of dependence can help adjudicate which of the mechanisms is at work.
As our primary outcome, we examine whether members of Congress condition their information-seeking behavior on preference distance in hearing communications. To capture members’ information-seeking behavior, we count the number of falsifiable sentences that each member directs to each witness, which is a measure of the extent to which the member engages the witnesses in informational, epistemic discourse (Esterling Reference Esterling2011). As secondary measures, we evaluate whether preference-distance matters even when legislators express non-falsifiable opinion or ask anecdotal questions, which indicate a non-epistemic discourse (Esterling Reference Esterling2007), such as when members engage in messaging behavior through grandstanding (Park Reference Park2021).
Comparing the preference-distance test across these different question types enables us to further analyze whether any observed preference dependence is primarily informational or noninformational. If preferences matter for all three types of sentences, that implies that the underlying mechanism is a sociological one because more frequent communications out of homophily would not necessarily apply only to falsifiable questions; if they matter only for falsifiable sentences, that implies that the legislators’ information-seeking incentives are motivating the observed communication pattern.
Finally, if committee members are motivated by economic incentives for learning information, we expect that the dependence of falsifiable questions on preference distance should be especially apparent among witnesses that have research-based expertise, when there is stronger policy information asymmetry between members and witnesses (Austen-Smith Reference Austen-Smith1993), but should be less apparent for nonexperts who provide less of an opportunity to update beliefs. Conversely, if committee members are primarily motivated by psychological desires to confirm their existing beliefs, the degree of expertise should not matter for information-seeking behavior.
3. Statistical Model
We propose a flexible model that measures witnesses’ policy preferences in order to test for preference dependence using data from hearings. Our model requires two types of data: (1) DW-Nominate scores to measure legislator preferences and (2) the count of legislators’ questions or statements directed to each witnesses within a committee hearing. Optionally, our model can exploit (3) data that construct a common space ideology measure such as survey responses or CF scores from Bonica (Reference Bonica2013). The common space measure can aid in describing the geometric relationship between legislator and witness preferences.
We use these data in a statistical model to measure witnesses’ latent preferences over policy topics for use in hypothesis tests regarding communication patterns in hearings. In our notation, Latin letters indicate observed data and Greek letters indicate parameters. Label legislators’ policy-relevant preferences regarding legislation as
![]() $L_j$
and agents’ policy-relevant preferences regarding the same legislation as
$L_j$
and agents’ policy-relevant preferences regarding the same legislation as
![]() $\zeta _i$
. Within a given hearing, each legislator (indexed by j) directs some number of each type of question to each witness as an outside agent (indexed by i). In this context, the outcome
$\zeta _i$
. Within a given hearing, each legislator (indexed by j) directs some number of each type of question to each witness as an outside agent (indexed by i). In this context, the outcome
![]() $O^m_{ij}$
is the count of sentences of type
$O^m_{ij}$
is the count of sentences of type
![]() $m \in \{falsifiable, opinion, anecdotal\}$
within the
$m \in \{falsifiable, opinion, anecdotal\}$
within the
![]() $ij$
th member–witness dyad. We model the dyadic count outcomes as a function of the preference distance between legislator and agent using the equation set,
$ij$
th member–witness dyad. We model the dyadic count outcomes as a function of the preference distance between legislator and agent using the equation set,
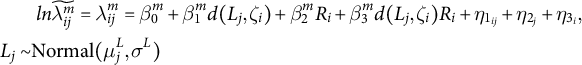 $$ \begin{align} &\ ln\widetilde{\lambda^m_{ij}} = \lambda^m_{ij} = \beta^m_{0} + \beta^m_{1}d(L_{j}, \zeta_{i}) + \beta^m_{2}R_i + \beta^m_{3}d(L_{j},\zeta_{i})R_i + \eta_{1_{ij}} + \eta_{2_j} + \eta_{3_i}, \nonumber \\ L_{j} \sim & \mbox{Normal}(\mu^L_{j}, \sigma^{L}) \end{align} $$
$$ \begin{align} &\ ln\widetilde{\lambda^m_{ij}} = \lambda^m_{ij} = \beta^m_{0} + \beta^m_{1}d(L_{j}, \zeta_{i}) + \beta^m_{2}R_i + \beta^m_{3}d(L_{j},\zeta_{i})R_i + \eta_{1_{ij}} + \eta_{2_j} + \eta_{3_i}, \nonumber \\ L_{j} \sim & \mbox{Normal}(\mu^L_{j}, \sigma^{L}) \end{align} $$
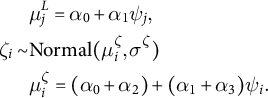 $$ \begin{align} & \mu^L_{j} = \alpha_0 + \alpha_1\psi_{j},\qquad\qquad\qquad\qquad\qquad \nonumber \\ \zeta_{i} \sim & \mbox{Normal}(\mu^{\zeta}_{i}, \sigma^{\zeta})\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad \\ & \mu^{\zeta}_{i} = (\alpha_0 + \alpha_2) + (\alpha_1 + \alpha_3)\psi_{i}.\qquad\qquad\qquad\qquad \qquad\qquad\qquad\quad\nonumber \end{align} $$
$$ \begin{align} & \mu^L_{j} = \alpha_0 + \alpha_1\psi_{j},\qquad\qquad\qquad\qquad\qquad \nonumber \\ \zeta_{i} \sim & \mbox{Normal}(\mu^{\zeta}_{i}, \sigma^{\zeta})\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad \\ & \mu^{\zeta}_{i} = (\alpha_0 + \alpha_2) + (\alpha_1 + \alpha_3)\psi_{i}.\qquad\qquad\qquad\qquad \qquad\qquad\qquad\quad\nonumber \end{align} $$
Here, each count outcome is modeled in Equation (1a) using a Poisson stochastic process with parameter
![]() $\widetilde {\lambda ^m_{ij}}$
conditional on the data and normally distributed random effects to accommodate overdispersion.Footnote 4 The term
$\widetilde {\lambda ^m_{ij}}$
conditional on the data and normally distributed random effects to accommodate overdispersion.Footnote 4 The term
![]() $d(L_{j}, \zeta _{i})$
is a preference-distance function that measures the distance in preferences between the
$d(L_{j}, \zeta _{i})$
is a preference-distance function that measures the distance in preferences between the
![]() $j^{\mathrm {th}}$
committee member and the ith witness; we implement the distance function using a quadratic distance,
$j^{\mathrm {th}}$
committee member and the ith witness; we implement the distance function using a quadratic distance,
![]() $d(L_{j}, \zeta _{i}) = (L_{j} - \zeta _{i})^2$
. To complete the outcome model,
$d(L_{j}, \zeta _{i}) = (L_{j} - \zeta _{i})^2$
. To complete the outcome model,
![]() $R_i$
is an observed indicator variable that equals one if the witness, i, comes from an organization that specializes in policy research, and equals zero otherwise. The parameter
$R_i$
is an observed indicator variable that equals one if the witness, i, comes from an organization that specializes in policy research, and equals zero otherwise. The parameter
![]() $\beta ^m_{1}$
tests the preference-distance hypothesis among witnesses that are not from research-based organizations and
$\beta ^m_{1}$
tests the preference-distance hypothesis among witnesses that are not from research-based organizations and
![]() $\beta ^m_{3}$
tests whether preference distance matters differently for witnesses from research-based organizations.
$\beta ^m_{3}$
tests whether preference distance matters differently for witnesses from research-based organizations.
![]() $\beta ^m_{0}$
and
$\beta ^m_{0}$
and
![]() $\beta ^m_{2}$
are constants. Finally, the model includes one random effect at the witness level (
$\beta ^m_{2}$
are constants. Finally, the model includes one random effect at the witness level (
![]() $\eta _3)$
, one at the legislator level (
$\eta _3)$
, one at the legislator level (
![]() $\eta _2$
), and one at the dyad level (
$\eta _2$
), and one at the dyad level (
![]() $\eta _1$
).Footnote 5
$\eta _1$
).Footnote 5
Equations (1b) and (1c) are the optional bridging equations that establish the functional relationship between legislator preferences L and agent preferences
![]() $\zeta $
;
$\zeta $
;
![]() $\psi $
is a bridging variable used only for identification. Consider each of L and
$\psi $
is a bridging variable used only for identification. Consider each of L and
![]() $\zeta $
in turn.
$\zeta $
in turn.
Congress scholars routinely take legislators’ preferences, L, as indicated by their observed roll-call votes, and hence recovered correctly through well-established scaling procedures such as IDEAL (Clinton, Jackman, and Rivers Reference Clinton, Jackman and Rivers2004) or DW-NOMINATE (Poole and Rosenthal Reference Poole and Rosenthal1991). Roll-call votes indicate legislators’ office-induced or operational preferences (Burden, Caldeira, and Groseclose Reference Burden, Caldeira and Groseclose2000; Rhode Reference Rhode1991), preferences which summarize the full vector of relevant influences on each legislator including party, constituency, interest group, and donor pressure along with her personal beliefs. Therefore, it is legislators’ operational preferences measured in roll-call vote scaling that are relevant to most institutional tests (Burden et al. Reference Burden, Caldeira and Groseclose2000).
The next statistical task is to measure outside agents’ preferences in a comparable legislative policy preference space
![]() $\zeta $
in order to establish the distance
$\zeta $
in order to establish the distance
![]() $d(L_{j}, \zeta _{i})$
between legislator and agent. Since agents are not legislators, their occupation neither requires nor enables them to vote on legislation, and so roll-call preferences do not and indeed cannot exist for them. In addition, while legislators vote on many bills, we typically only observe individual agents take a position on a single bill before the committee, if they take any position at all, and often witnesses’ support or opposition is to technical provisions in the legislation. As a result, the legislatively relevant preferences,
$d(L_{j}, \zeta _{i})$
between legislator and agent. Since agents are not legislators, their occupation neither requires nor enables them to vote on legislation, and so roll-call preferences do not and indeed cannot exist for them. In addition, while legislators vote on many bills, we typically only observe individual agents take a position on a single bill before the committee, if they take any position at all, and often witnesses’ support or opposition is to technical provisions in the legislation. As a result, the legislatively relevant preferences,
![]() $\zeta $
, that govern interaction in a hearing are missing data for all outside agents.
$\zeta $
, that govern interaction in a hearing are missing data for all outside agents.
3.1. Bridging Using Constrained Regression
To impute the missing agent preferences, one can attempt to exploit a data source that establishes a common space
![]() $\psi $
for legislator and agent preferences, such as their left–right ideology, and then use the bridging functions (1b) and (1c) to map the common preference space
$\psi $
for legislator and agent preferences, such as their left–right ideology, and then use the bridging functions (1b) and (1c) to map the common preference space
![]() $\psi $
to both legislator preferences L and agent preferences
$\psi $
to both legislator preferences L and agent preferences
![]() $\zeta $
(Shor et al. Reference Shor, Berry and McCarty2010). In the application, we use survey items and an IRT model to measure
$\zeta $
(Shor et al. Reference Shor, Berry and McCarty2010). In the application, we use survey items and an IRT model to measure
![]() $\psi $
. Other possible common space scores include Bonica (Reference Bonica2013) estimates from contribution-giving patterns and Barberá (Reference Barberá2015) estimates from Twitter follower data.Footnote 6 If the parameters of both bridging functions are identified, the analyst can then use the estimated parameters in the bridging function (1c) and the common space measure
$\psi $
. Other possible common space scores include Bonica (Reference Bonica2013) estimates from contribution-giving patterns and Barberá (Reference Barberá2015) estimates from Twitter follower data.Footnote 6 If the parameters of both bridging functions are identified, the analyst can then use the estimated parameters in the bridging function (1c) and the common space measure
![]() $\widehat {\psi _{i}}$
to impute the missing agent preferences—that is, to measure each
$\widehat {\psi _{i}}$
to impute the missing agent preferences—that is, to measure each
![]() $\zeta _{i}$
.
$\zeta _{i}$
.
Since we take L as observed via roll-call scaling and take
![]() $\psi $
as estimated using the survey items that measure legislators’ left–right ideology, the parameters
$\psi $
as estimated using the survey items that measure legislators’ left–right ideology, the parameters
![]() $\alpha _0$
and
$\alpha _0$
and
![]() $\alpha _1$
in Equation (1b) are identified as in ordinary regression and provide a mapping from the common space ideology scale
$\alpha _1$
in Equation (1b) are identified as in ordinary regression and provide a mapping from the common space ideology scale
![]() $\psi $
to the legislators’ roll-call preference space L. We follow convention and use DW-NOMINATE scores to measure L, and hence the relationship between
$\psi $
to the legislators’ roll-call preference space L. We follow convention and use DW-NOMINATE scores to measure L, and hence the relationship between
![]() $\psi $
and L is a simple linear regression.
$\psi $
and L is a simple linear regression.
Next, consider the bridge from the common space to agent preferences in Equation (1c). The parameter
![]() $\alpha _2$
allows the agent preference dimension to have a different intercept, which we call a “shift,” relative to the legislator mapping recovered in Equation (1b). Likewise, the parameter
$\alpha _2$
allows the agent preference dimension to have a different intercept, which we call a “shift,” relative to the legislator mapping recovered in Equation (1b). Likewise, the parameter
![]() $\alpha _3$
allows the agent preference dimension to have a different slope, which we call a “rotation.” These parameters flexibly accommodate the preferences of legislators and agents in a two-dimensional space. In the special case where
$\alpha _3$
allows the agent preference dimension to have a different slope, which we call a “rotation.” These parameters flexibly accommodate the preferences of legislators and agents in a two-dimensional space. In the special case where
![]() $\alpha _2$
and
$\alpha _2$
and
![]() $\alpha _3$
are both equal to zero, then
$\alpha _3$
are both equal to zero, then
![]() $\zeta $
and L describe the same line, leaving only a single dimension to describe both legislator and agent preferences as a special case. In the case where
$\zeta $
and L describe the same line, leaving only a single dimension to describe both legislator and agent preferences as a special case. In the case where
![]() $\alpha _3 = -\alpha _1$
(and if the error terms in Equations (1b) and (1c) are independent), then
$\alpha _3 = -\alpha _1$
(and if the error terms in Equations (1b) and (1c) are independent), then
![]() $\zeta $
is orthogonal to both L and to
$\zeta $
is orthogonal to both L and to
![]() $\psi $
; in any other case,
$\psi $
; in any other case,
![]() $\zeta $
and L are correlated in two dimensions by their common relationship with
$\zeta $
and L are correlated in two dimensions by their common relationship with
![]() $\psi $
. Since
$\psi $
. Since
![]() $\zeta $
is missing for all agents, however, the
$\zeta $
is missing for all agents, however, the
![]() $\boldsymbol {\alpha }_{\mathbf {a}} = [\alpha _2, \alpha _3]'$
parameters are not identified in Equation (1c).
$\boldsymbol {\alpha }_{\mathbf {a}} = [\alpha _2, \alpha _3]'$
parameters are not identified in Equation (1c).
To solve this identification problem, the traditional bridging approach recommends using a regression-based mapping that assumes the agents and legislators share identical parameters in the bridging functions (e.g., as in Crosson et al. Reference Crosson, Furnas and Lornez2020). Under this approach, one imputes the missing agent preferences by setting the unidentified parameters in Equation (1c) to zero (
![]() $[\alpha _2, \alpha _3]' \equiv {\mathbf {0}}$
), and setting
$[\alpha _2, \alpha _3]' \equiv {\mathbf {0}}$
), and setting
![]() $\sigma ^{\zeta }=\sigma ^{L}$
and the implied covariance
$\sigma ^{\zeta }=\sigma ^{L}$
and the implied covariance
![]() $\sigma ^{{\zeta },{L}} = 0$
.
$\sigma ^{{\zeta },{L}} = 0$
.
![]() $\widehat {\zeta _{i}}$
can then be imputed using the point estimates from the legislator bridging Equation (1b) (
$\widehat {\zeta _{i}}$
can then be imputed using the point estimates from the legislator bridging Equation (1b) (
![]() $[\widehat {\alpha _0}, \widehat {\alpha _1}]'$
) along with the estimates for agents’ common space preferences (
$[\widehat {\alpha _0}, \widehat {\alpha _1}]'$
) along with the estimates for agents’ common space preferences (
![]() $\widehat {\psi _{i}}$
) and the linearity assumption for the mapping from Equation (1c).
$\widehat {\psi _{i}}$
) and the linearity assumption for the mapping from Equation (1c).
The constrained-regression procedure thus involves three steps. First, the analyst uses legislator data to estimate the bridging equation (1b) to infer the mapping from the common space to the roll-call preference space. Second, the analyst uses the results of this estimation and witnesses’ common space scores to place witnesses into the roll-call preference space. Third, the analyst uses the distance in estimated preferences within each dyad in a hearing as a right-hand side variable in the outcome equation.
This solution imposes the unidimensional assumption that legislator and agent preferences have an identical functional relationship to
![]() $\psi $
, which is the special case of identical lines. Conceptually, since this identification strategy relies exclusively on the mapping from
$\psi $
, which is the special case of identical lines. Conceptually, since this identification strategy relies exclusively on the mapping from
![]() $\psi $
to legislator preferences, L, the imputation under this constraint is the counterfactual of what agents’ preferences would have been, if they instead had been legislators.
$\psi $
to legislator preferences, L, the imputation under this constraint is the counterfactual of what agents’ preferences would have been, if they instead had been legislators.
3.2. Unconstrained Flexible Model
Of course, witnesses are not legislators, and so it is better to measure witness preferences in a separate dimension. We offer a flexible solution to this identification problem by estimating a distance function, which includes a random effect (
![]() $\zeta _i$
), on the right-hand side of a regression. We rely on that distance function to estimate the parameter testing the relationship between the distance and the question rate.
$\zeta _i$
), on the right-hand side of a regression. We rely on that distance function to estimate the parameter testing the relationship between the distance and the question rate.
Identification of the flexible model is straightforward and relies only on the nested structure of the dyadic data that naturally occurs in the context of committee hearings.Footnote 7 To see the identification, first note that we include witness-level (
![]() $\eta _3$
), member-level (
$\eta _3$
), member-level (
![]() $\eta _2$
), and dyad-level (
$\eta _2$
), and dyad-level (
![]() $\eta _1$
) random effects, each of which is identified by nesting in the data.Footnote 8 Second, note that the witness preference parameter
$\eta _1$
) random effects, each of which is identified by nesting in the data.Footnote 8 Second, note that the witness preference parameter
![]() $\zeta _i$
is also a random effect at the witness level, and it is identified separately from
$\zeta _i$
is also a random effect at the witness level, and it is identified separately from
![]() $\eta _3$
because it is embedded inside of a nonlinear function.Footnote 9 Finally, we set the variance of
$\eta _3$
because it is embedded inside of a nonlinear function.Footnote 9 Finally, we set the variance of
![]() $\zeta $
in the bridging equations to equal the variance of our observed DW-NOMINATE scores, and as a result,
$\zeta $
in the bridging equations to equal the variance of our observed DW-NOMINATE scores, and as a result,
![]() $\zeta $
behaves as a covariate in the outcome equation to estimate the preference-distance parameter
$\zeta $
behaves as a covariate in the outcome equation to estimate the preference-distance parameter
![]() $\beta _1$
.
$\beta _1$
.
Unlike the constrained-regression approach, the bridging equations are not necessary for inferring witness preferences in our flexible model. Instead, the bridging equation (1c) hierarchically models
![]() $\zeta $
as a witness-level random effect using witness-level covariates, and so each of the parameters is identified via hierarchical random effect regression, including the “shift” (
$\zeta $
as a witness-level random effect using witness-level covariates, and so each of the parameters is identified via hierarchical random effect regression, including the “shift” (
![]() $\alpha _2$
) and “rotation” (
$\alpha _2$
) and “rotation” (
![]() $\alpha _3$
) parameters. Empirically, in both our simulations and in the application, including this witness-level equation has virtually no effect on the estimates for witness preferences beyond increasing their precision. As a result, the analyst can choose to estimate the model with or without the bridging equations; they are fully optional. Substantively, estimating the shift and rotation parameters shows the geometric relationship between the witness preference space and the common space ideology score.
$\alpha _3$
) parameters. Empirically, in both our simulations and in the application, including this witness-level equation has virtually no effect on the estimates for witness preferences beyond increasing their precision. As a result, the analyst can choose to estimate the model with or without the bridging equations; they are fully optional. Substantively, estimating the shift and rotation parameters shows the geometric relationship between the witness preference space and the common space ideology score.
While the model is theoretically identified, there are two core empirical requirements for identification. First, because we recover witness preferences as a random effect, witnesses must be nested in repeated dyads—that is, each witness must testify before a committee with more than one member, which is virtually always the case, for example, in the U.S. Congress. Second, preference distance must in fact be relevant to the pattern of communication observed in committee hearings. If this condition is not met, then the patterns of communication in committee hearings will not reveal witnesses’ preferences.
Geometrically, our approach allows the agent preference dimension
![]() $\zeta $
to rotate away from L. We define
$\zeta $
to rotate away from L. We define
![]() $\zeta ^0$
as constrained-regression agent preferences that are imputed from the unidimensional constraint which sets
$\zeta ^0$
as constrained-regression agent preferences that are imputed from the unidimensional constraint which sets
![]() $\alpha _2=\alpha _3=0$
and so forces
$\alpha _2=\alpha _3=0$
and so forces
![]() $\zeta $
and L to be the same dimension, and the flexible, unconstrained preferences
$\zeta $
and L to be the same dimension, and the flexible, unconstrained preferences
![]() $\zeta ^1$
are imputed from the flexible model. The rotation indicated by
$\zeta ^1$
are imputed from the flexible model. The rotation indicated by
![]() $\alpha _3$
can be converted to the angle
$\alpha _3$
can be converted to the angle
![]() $\theta $
(measured in radians) governing the direction of the relationship through a Cartesian coordinate space, and one can retrieve
$\theta $
(measured in radians) governing the direction of the relationship through a Cartesian coordinate space, and one can retrieve
![]() $\theta $
post-estimation via the cosine rule and the vectors of constrained and unconstrained preferences (Binmore and Davies Reference Binmore and Davies2001, 18),
$\theta $
post-estimation via the cosine rule and the vectors of constrained and unconstrained preferences (Binmore and Davies Reference Binmore and Davies2001, 18),
 $$ \begin{align} \theta = \cos^{-1}{\frac{\langle \boldsymbol{\zeta}^{\mathbf{0}}, \boldsymbol{\zeta}^{\mathbf{1}} \rangle}{\| \boldsymbol{\zeta}^{\mathbf{0}} \|\| \boldsymbol{\zeta}^{\mathbf{1}} \|}}. \end{align} $$
$$ \begin{align} \theta = \cos^{-1}{\frac{\langle \boldsymbol{\zeta}^{\mathbf{0}}, \boldsymbol{\zeta}^{\mathbf{1}} \rangle}{\| \boldsymbol{\zeta}^{\mathbf{0}} \|\| \boldsymbol{\zeta}^{\mathbf{1}} \|}}. \end{align} $$
Setting aside any shift between the two lines, the angle
![]() $\theta =0$
is the parallel case;
$\theta =0$
is the parallel case;
![]() $\theta =\pi /2$
is orthogonal; and
$\theta =\pi /2$
is orthogonal; and
![]() $0<\theta <\pi /2$
is oblique.Footnote 10 The constrained-regression method forces the rotation to always and often implausibly equal the parallel case with
$0<\theta <\pi /2$
is oblique.Footnote 10 The constrained-regression method forces the rotation to always and often implausibly equal the parallel case with
![]() $\theta \equiv 0$
.
$\theta \equiv 0$
.
4. Application to Medicare Hearings
We use our flexible model to test for the relationship between preference distance and questioning in congressional committee hearings on the Medicare program. To select the sample, we randomly drew 29 hearings from the universe of all hearings on the Medicare program that were held between 2000 and 2003 across 12 different congressional committees and subcommittees. In all, across all of the 29 hearings, there are 67 witnesses, 87 committee members, and 669 dyads. The replication package is Esterling and Park (Reference Esterling and Park2024).
To capture legislators’ speaking patterns
![]() $(O_{ij}^m)$
, we construct three dependent variables. We follow Esterling’s (Reference Esterling2007) coding rules for classifying member statements in committee hearing transcripts into the three mutually exclusive sentence types: falsifiable, opinion, and anecdotal.Footnote 11 We count the number of each of these three types of sentences that legislators make within each legislator–witness dyad. That is, we concatenated each legislator’s statements directed to each witness, and then counted the number of occurrences of each type of sentence. Table 1 shows the descriptives for the 669 dyads in the sample.
$(O_{ij}^m)$
, we construct three dependent variables. We follow Esterling’s (Reference Esterling2007) coding rules for classifying member statements in committee hearing transcripts into the three mutually exclusive sentence types: falsifiable, opinion, and anecdotal.Footnote 11 We count the number of each of these three types of sentences that legislators make within each legislator–witness dyad. That is, we concatenated each legislator’s statements directed to each witness, and then counted the number of occurrences of each type of sentence. Table 1 shows the descriptives for the 669 dyads in the sample.
Table 1 Member–lobbyist dyadic outcome data.
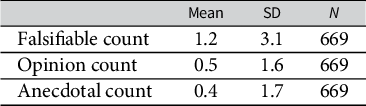
Note in Table 1 that under our coding, at these hearings, members are most likely to make falsifiable inquiries. Most members ask zero questions to most witnesses, and so these counts have low means and high standard deviations. We accommodate this over dispersion in the count variables in the statistical model by including dyad-level random effects (Harrison Reference Harrison2014; Skrondal and Rabe-Hesketh Reference Skrondal and Rabe-Hesketh2007).
We have two key independent variables. First, to measure legislator preferences
![]() $(L)$
, we use first dimension DW-NOMINATE scores (Lewis et al. Reference Lewis, Poole, Rosenthal, Boche, Rudkin and Sonnet2018; Poole and Rosenthal Reference Poole and Rosenthal1991) from the
$(L)$
, we use first dimension DW-NOMINATE scores (Lewis et al. Reference Lewis, Poole, Rosenthal, Boche, Rudkin and Sonnet2018; Poole and Rosenthal Reference Poole and Rosenthal1991) from the
![]() $108$
th Congress to measure legislators’ roll-call preferences L.Footnote 12 Second, we construct an indicator for witnesses from research-based organizations
$108$
th Congress to measure legislators’ roll-call preferences L.Footnote 12 Second, we construct an indicator for witnesses from research-based organizations
![]() $(R)$
which is coded as 1 for witnesses from universities, foundations, and think tanks, and 0 otherwise.Footnote 13 Under this coding, 37% of the sample is research-based.
$(R)$
which is coded as 1 for witnesses from universities, foundations, and think tanks, and 0 otherwise.Footnote 13 Under this coding, 37% of the sample is research-based.
Optionally, in case a researcher wants to use the bridging function, the common space ideology measure for a personal ideology scale
![]() $(\psi )$
, which is the core component of the bridging equation, needs to be estimated. For this, we administered a survey containing a battery of ideology items to the witnesses who appeared at the hearings in the data set, and to former members of Congress, who are not in the hearings sample. That is, we use survey responses from former members of Congress who did not attend the sampled hearings rather than the committee members from the sampled hearings, most of whom at the time of the data collection were current incumbents. Since former members’ DW-NOMINATE scores are in the same roll-call preference space L as the committee members in the sample, it is not necessary to use the same legislators in the bridging component as in the outcome component of the model; it is the same preference dimension for both. We estimate
$(\psi )$
, which is the core component of the bridging equation, needs to be estimated. For this, we administered a survey containing a battery of ideology items to the witnesses who appeared at the hearings in the data set, and to former members of Congress, who are not in the hearings sample. That is, we use survey responses from former members of Congress who did not attend the sampled hearings rather than the committee members from the sampled hearings, most of whom at the time of the data collection were current incumbents. Since former members’ DW-NOMINATE scores are in the same roll-call preference space L as the committee members in the sample, it is not necessary to use the same legislators in the bridging component as in the outcome component of the model; it is the same preference dimension for both. We estimate
![]() $\psi $
via an IRT model.
$\psi $
via an IRT model.
Administering the survey to former members rather than current members is preferable for two reasons. First, while in office, many members have a policy not to respond to academic surveys, and even those who respond would likely assign staff to complete and return the survey which would introduce measurement error in the measure of personal ideology
![]() $\psi $
. Former members are either retirees or they are employed where it is unlikely that staff support would fill out surveys relevant to their past legislative work. Second, like the witnesses, former members are typically private citizens, not elected officials, and so former members are more likely to fill out the responses based on their own, personal ideology rather than on an office-induced preference that is conditioned by pressure from constituents, party, donors, or groups. Measuring office-induced preferences would undermine bridging equation (1b), which is a mapping from legislators’ personal ideology
$\psi $
. Former members are either retirees or they are employed where it is unlikely that staff support would fill out surveys relevant to their past legislative work. Second, like the witnesses, former members are typically private citizens, not elected officials, and so former members are more likely to fill out the responses based on their own, personal ideology rather than on an office-induced preference that is conditioned by pressure from constituents, party, donors, or groups. Measuring office-induced preferences would undermine bridging equation (1b), which is a mapping from legislators’ personal ideology
![]() $\psi $
to their office-induced preference L. However, here we assume that individuals’ ideology is constant over time so that their personal ideology is the same once they are former members as it was when they were members.
$\psi $
to their office-induced preference L. However, here we assume that individuals’ ideology is constant over time so that their personal ideology is the same once they are former members as it was when they were members.
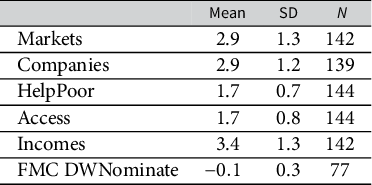
To measure the common space scale
![]() $\psi $
, we administered the following survey items to both a set of former members of Congress (FMC)Footnote 14 and to the witnesses in the sample. These questions are validated to measure each individual’s left–right ideology.Footnote 15
$\psi $
, we administered the following survey items to both a set of former members of Congress (FMC)Footnote 14 and to the witnesses in the sample. These questions are validated to measure each individual’s left–right ideology.Footnote 15
-
• [Markets] The protection of consumer interests is best insured by a vigorous competition among sellers rather than by federal government regulation on behalf of consumers.
-
• [Companies] There is too much power concentrated in the hands of a few large companies for the good of the country.
-
• [HelpPoor] One of the most important roles of government is to help those who cannot help themselves, such as the poor, the disadvantaged, and the unemployed.
-
• [Access] All Americans should have access to quality medical care regardless of ability to pay.
-
• [Incomes] The differences in income among occupations should be reduced.
The labels in square brackets were not included in the survey question wording.
To complete the bridging data set, we merged in the most recent DW-NOMINATE scores for each former member, that is, the score from the Congress just prior to the member separating from the institution.Footnote 16 The descriptives of the survey responses and DW-NOMINATE scores are in Table 2. In this rectangular dataset, we have responses to the ideology survey questions from both former members and the witnesses, but the first-dimension DW-NOMINATE scores are missing for every witness. We estimate
![]() $\psi $
via an IRT model; SM Section A.4 shows the full model and we suppress the IRT model in Equations (1b) and (1c) to simplify the presentation.
$\psi $
via an IRT model; SM Section A.4 shows the full model and we suppress the IRT model in Equations (1b) and (1c) to simplify the presentation.
Table 2 Ideology indicator descriptives for former members and witnesses.
In the outcome model, we include legislator-, witness-, and dyad-specific random effects to address any omitted covariates at each level. The legislator-specific random effect,
![]() $\eta _2$
, captures the committee member’s propensity to ask questions and make statements of all types to witnesses; a witness-specific random effect,
$\eta _2$
, captures the committee member’s propensity to ask questions and make statements of all types to witnesses; a witness-specific random effect,
![]() $\eta _3$
, captures the witness’s propensity to attract questions and comments from legislators; and a dyad-specific random effect,
$\eta _3$
, captures the witness’s propensity to attract questions and comments from legislators; and a dyad-specific random effect,
![]() $\eta _1$
, captures latent causes for the extent of the interaction between a legislator and a witness, such as if something a witness says leads to additional questions from a member. Furthermore,
$\eta _1$
, captures latent causes for the extent of the interaction between a legislator and a witness, such as if something a witness says leads to additional questions from a member. Furthermore,
![]() $\eta _1$
also accounts for overdispersion that comes from added variance in the count data (Skrondal and Rabe-Hesketh Reference Skrondal and Rabe-Hesketh2007).
$\eta _1$
also accounts for overdispersion that comes from added variance in the count data (Skrondal and Rabe-Hesketh Reference Skrondal and Rabe-Hesketh2007).
We estimate both the single equation “constrained-regression” model and our flexible model using Bayesian MCMC estimation with uninformative priors.Footnote 17 The constrained-regression approach estimates the bridging model and the outcomes model separately and so the outcome equations do not update the preferences of agents, yielding agent preference estimates
![]() $\zeta ^0$
that are derived under the assumption that legislator and agent preferences are constrained to a single dimension. The flexible model estimates both models simultaneously so that they jointly inform the posterior distribution over each
$\zeta ^0$
that are derived under the assumption that legislator and agent preferences are constrained to a single dimension. The flexible model estimates both models simultaneously so that they jointly inform the posterior distribution over each
![]() $\zeta ^1$
. More details about our statistical model and estimation are in SM Section A.4.
$\zeta ^1$
. More details about our statistical model and estimation are in SM Section A.4.
5. Results
Here, we summarize the main findings. We first discuss the results that use the constrained-regression approach that restricts agent and legislator preferences to a single dimension, that is, relying on the point estimates of
![]() $\widehat {\zeta ^0}$
to test the preference-distance hypothesis. We then discuss results from our proposed flexible model that relaxes this constraint and uses instead the posterior distribution preference estimates
$\widehat {\zeta ^0}$
to test the preference-distance hypothesis. We then discuss results from our proposed flexible model that relaxes this constraint and uses instead the posterior distribution preference estimates
![]() $\widehat {\zeta ^1}$
from the flexible model. In SM Section A.5, we report results across all model specifications, and Widely Applicable Information Criterion (WAIC) values, which is a measure of the ability of the model to make out of sample predictions (Vehtari, Gelman, and Gabry Reference Vehtari, Gelman and Gabry2017), and several posterior predictive checks.
$\widehat {\zeta ^1}$
from the flexible model. In SM Section A.5, we report results across all model specifications, and Widely Applicable Information Criterion (WAIC) values, which is a measure of the ability of the model to make out of sample predictions (Vehtari, Gelman, and Gabry Reference Vehtari, Gelman and Gabry2017), and several posterior predictive checks.
5.1. Results from the Constrained-Regression Model
In the constrained-regression measurement strategy, agent preferences on the left-hand side of Equation (1c) are imputed using
![]() $\psi $
and the bridging parameters estimated in Equation (1b), and by setting
$\psi $
and the bridging parameters estimated in Equation (1b), and by setting
![]() $\alpha _{2}=\alpha _{3}=0$
. Overall, the results across the specifications show that under this measurement strategy, communication patterns in hearings do not seem to depend on preferences, for all three types of questions. This seems to imply that committee members do not condition their interactions on distance in the preference space, where “distance” is with respect to the constrained-regression estimates for agent preferences
$\alpha _{2}=\alpha _{3}=0$
. Overall, the results across the specifications show that under this measurement strategy, communication patterns in hearings do not seem to depend on preferences, for all three types of questions. This seems to imply that committee members do not condition their interactions on distance in the preference space, where “distance” is with respect to the constrained-regression estimates for agent preferences
![]() $\widehat {\zeta ^0}$
.
$\widehat {\zeta ^0}$
.
We present the results of the constrained-regression strategy in Figure 1 (setting the random effects to their sample means). In this figure, the columns correspond to falsifiable, opinion, and anecdotal questions, respectively, and the rows correspond to witnesses who represent research-focused (top) and nonresearch (bottom) organizations. The dark line in each frame indicates the conditional point estimate for each subgroup and each outcome, and the light shaded areas indicate 95% conditional credibility intervals. Note that when placing the unidimensional constraint on preferences, the analyst would need to conclude that expectations of preference dependence under each of the economic, psychological, and sociological frameworks for political communication are false—that is, using this method, there appears to be no significant relationship between preference distance and the count of any of the three types of sentences, for each type of witness.
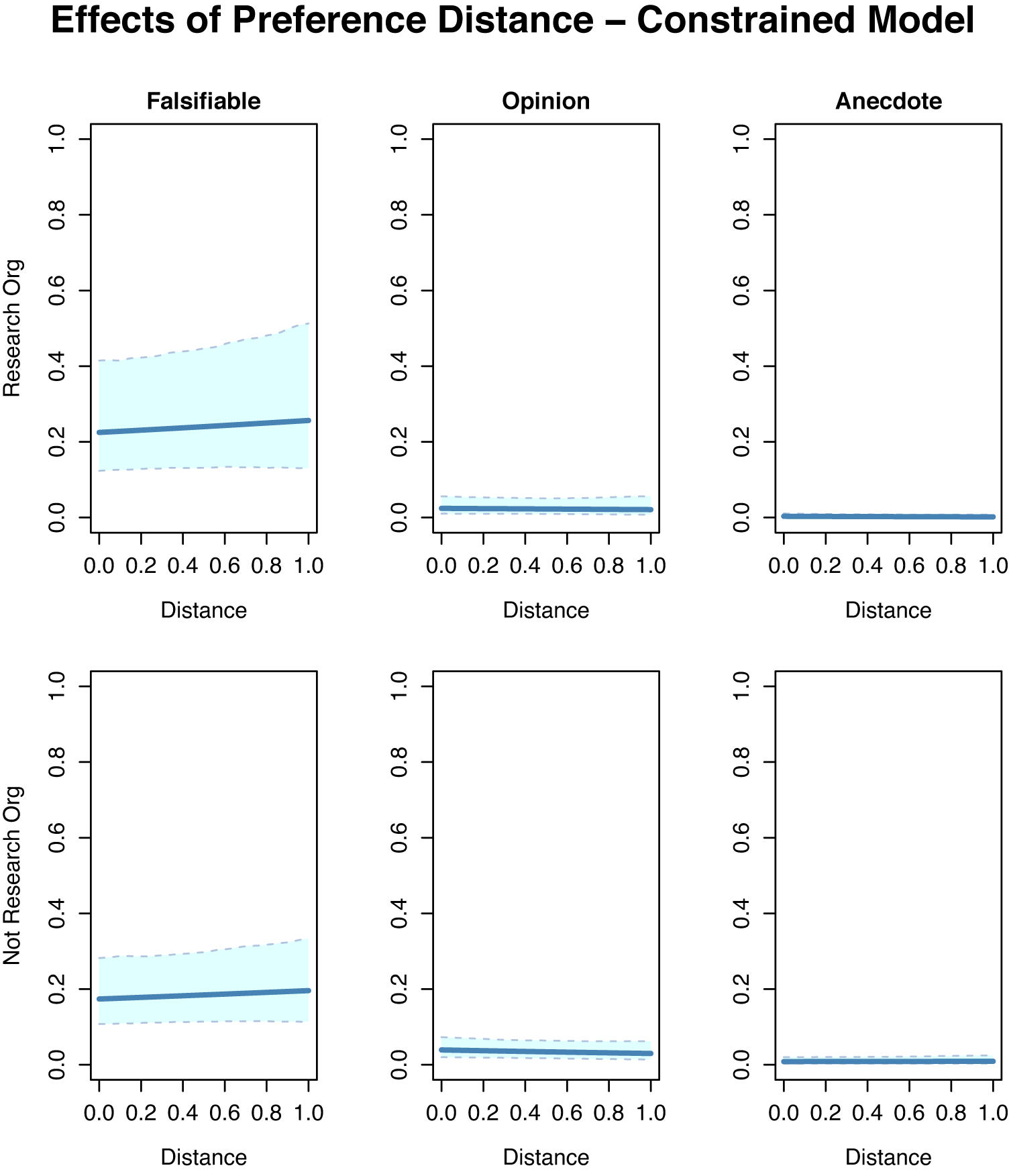
Figure 1 Relationship between preference distance and count outcomes, using the constrained-regression approach, indicating a lack of construct validity under the unidimensional assumption. Confidence bands indicate 95% conditional credible intervals.
![]() $N_{dyads}=669, N_{witnesses}=67, N_{members}=87$
.
$N_{dyads}=669, N_{witnesses}=67, N_{members}=87$
.
5.2. Results from the Flexible Model
The flexible model permits a shift and rotation of the witness preference space
![]() $\zeta ^1$
away from the legislator roll-call preference space L. In this model, the coefficients testing the preference-distance hypotheses are large and statistically significant. In addition, the WAIC statistics show lower values compared to the constrained-regression models, indicating the added complexity from the unconstrained parameters improves expected out of sample prediction (Vehtari et al. Reference Vehtari, Gelman and Gabry2017).
$\zeta ^1$
away from the legislator roll-call preference space L. In this model, the coefficients testing the preference-distance hypotheses are large and statistically significant. In addition, the WAIC statistics show lower values compared to the constrained-regression models, indicating the added complexity from the unconstrained parameters improves expected out of sample prediction (Vehtari et al. Reference Vehtari, Gelman and Gabry2017).
First, consider the relationship between the estimated witness preferences from the flexible model, which yields unconstrained estimates for the preferences
![]() $\zeta ^1$
, and those estimated for the constrained-regression case
$\zeta ^1$
, and those estimated for the constrained-regression case
![]() $\zeta ^0$
. Figure 2 plots the relationship. In this figure, each circle represents a witness; the blue dots indicate witnesses who come from Democrat constituency groups, the red from Republican (see SM Section A.5 for coding rules). The size of the circle is proportional to the variance of the posterior preference estimate. As Figure 2 demonstrates, the rotation is virtually orthogonal (
$\zeta ^0$
. Figure 2 plots the relationship. In this figure, each circle represents a witness; the blue dots indicate witnesses who come from Democrat constituency groups, the red from Republican (see SM Section A.5 for coding rules). The size of the circle is proportional to the variance of the posterior preference estimate. As Figure 2 demonstrates, the rotation is virtually orthogonal (
![]() $\theta = \frac {\pi }{2.47}$
), in direct contrast to the assumption motivating the constrained-regression approach that the two preference spaces are unidimensional. If the true agent preference space is orthogonal to legislators’ roll-call preference space, then imposing the unidimensional constraint is clearly inappropriate, and the result is similar to “measuring” agents’ preferences using the equivalent of a random number generator. Note as well, though, that the (red dot) agents we coded as in the Republican constituency tend to locate in the top-right quadrant, that is, on the conservative sides of both dimensions, which shows the relative orientation of both scales is correct.
$\theta = \frac {\pi }{2.47}$
), in direct contrast to the assumption motivating the constrained-regression approach that the two preference spaces are unidimensional. If the true agent preference space is orthogonal to legislators’ roll-call preference space, then imposing the unidimensional constraint is clearly inappropriate, and the result is similar to “measuring” agents’ preferences using the equivalent of a random number generator. Note as well, though, that the (red dot) agents we coded as in the Republican constituency tend to locate in the top-right quadrant, that is, on the conservative sides of both dimensions, which shows the relative orientation of both scales is correct.
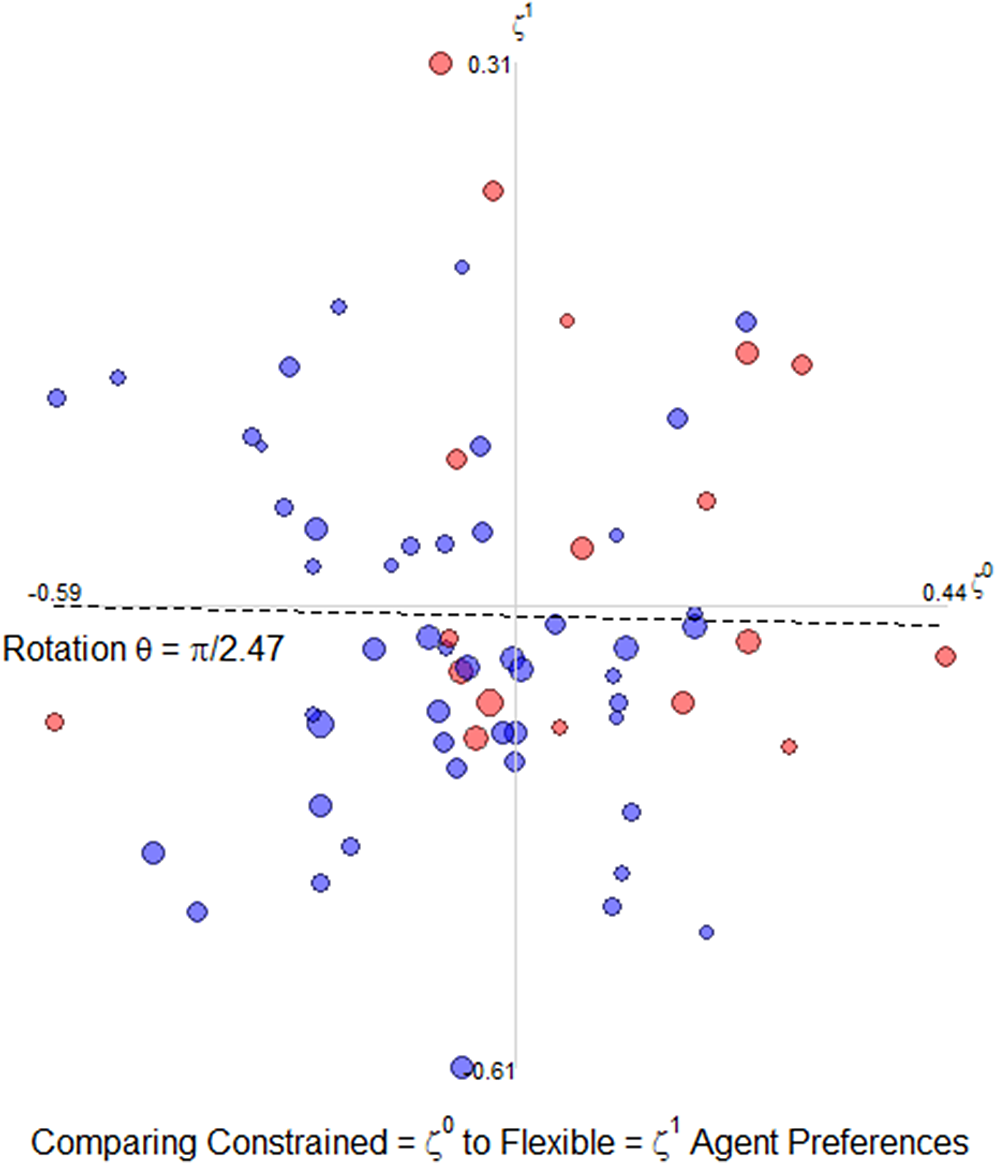
Figure 2 The relationship between agents’ constrained-regression preference estimates
![]() $\zeta ^0$
and unconstrained, flexible model preference estimates
$\zeta ^0$
and unconstrained, flexible model preference estimates
![]() $\zeta ^1$
. Blue dots indicate that witness is classified as in the Democratic party constituency, and red dots Republican. Note that the estimated rotation is almost fully orthogonal.
$\zeta ^1$
. Blue dots indicate that witness is classified as in the Democratic party constituency, and red dots Republican. Note that the estimated rotation is almost fully orthogonal.
SM Section A.5 shows that the precision of the imputed agent preferences are higher in the flexible model relative to the constrained model, and posterior predictive checks of the outcome data lend strong support to the flexible model. Further, the SM results show that the flexible model has better goodness of fit to the outcomes as well as lower WAIC scores for each of the three count outcomes compared to the constrained model.
To contrast the two estimation approaches, Figure 3 shows the results of the outcome equation parameter estimates for the flexible model, and is the same setup as Figure 1. Here, one can see that, in contrast to the results in Figure 1, there is a clear negative relationship between preference distance and the number of sentences a witness attracts in the committee hearings.Footnote 18 The most obvious and striking result is that committee members condition falsifiable and opinion questions on preference distance, although especially so for falsifiable statements.
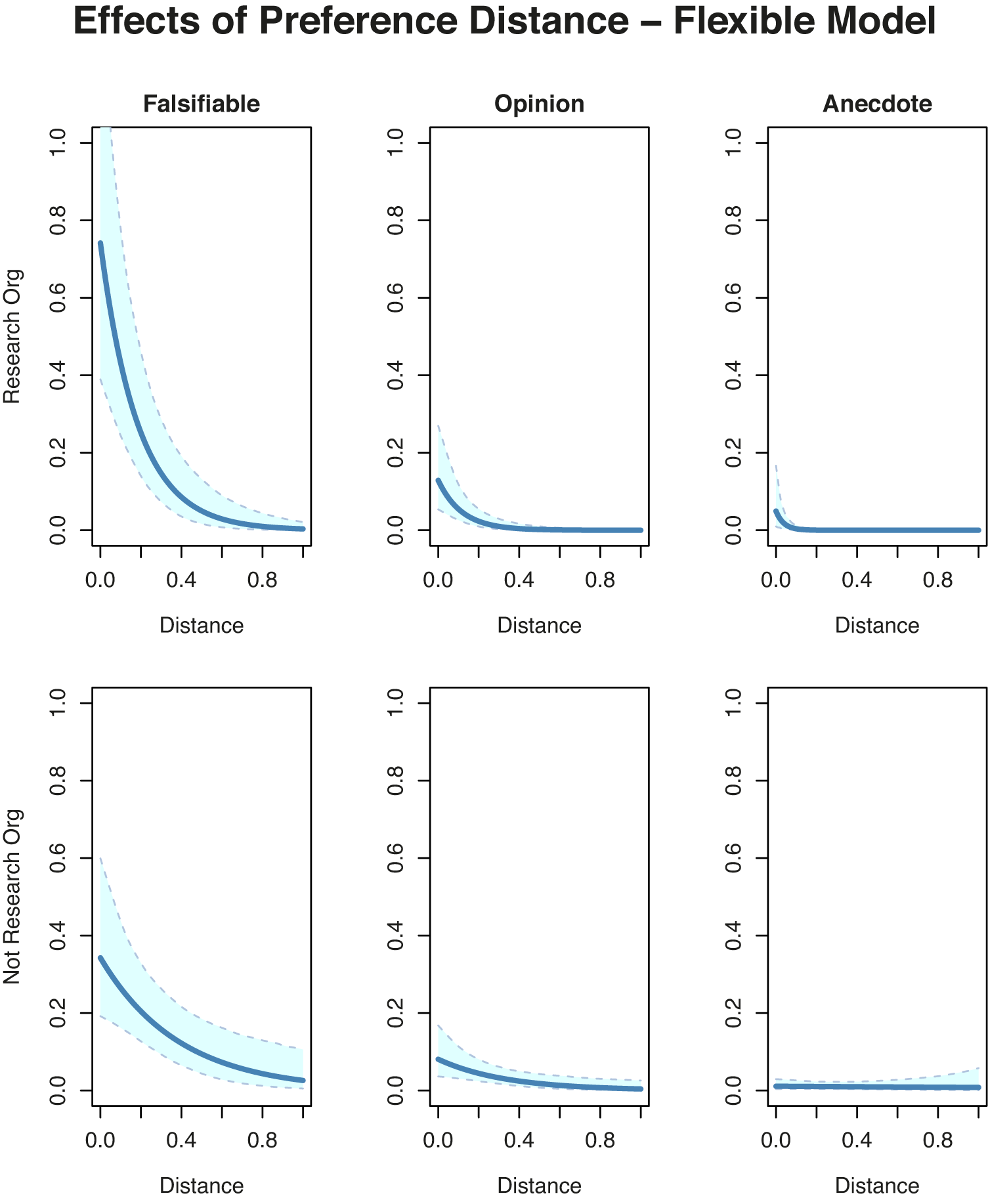
Figure 3 Relationship between preference distance and count outcomes, using the flexible model estimates, indicating good construct validity in contrast to the constrained results of the previous figure. Confidence bands indicate 95% conditional credible intervals.
![]() $N_{dyads}=669, N_{witnesses}=67, N_{members}=87$
.
$N_{dyads}=669, N_{witnesses}=67, N_{members}=87$
.
Recall that there are competing reasons that preferences might matter within the hearing. First, members might simply have a sociological aversion to interacting with witnesses who are dissimilar (Bauer et al. Reference Bauer, de Sola Pool and Dexter1963). This is a common phenomenon in social interactions since people are typically more comfortable interacting with those who share similar attitudes and traits. Second, members might tend to direct questions to witnesses whose statements are most informative in sense of economic models of strategic information transmission or psychological information search. There is some suggestive evidence from comparisons across the frames of Figure 3 that the members are engaging in information-seeking in the hearings.Footnote 19 First, note that members are more responsive to preference distance for falsifiable sentences than they are for opinion sentences, and that is true for both types of groups. This pattern is consistent with information search, but not with homophily. These latter contrasts serve as a type of placebo test of information theory, showing the preferences matter most for falsifiable and epistemic discourse at the hearings.
Second, note that members condition their falsifiable sentences on the type of organization, which is consistent with economic information-seeking behavior for updating beliefs rather than the psychological perspective of information confirmation. There is a greater informational asymmetry between legislators and witnesses from research organizations who have relatively high policy expertise, and this asymmetry should not matter if members are only seeking confirmation of their prior beliefs.
5.3. Shift and Rotation Parameters
Optionally, the analyst can use common space preference measures to recover the shift and rotation parameters in Equation (1c), estimating the single model to learn the geometric relationship between the roll-call space and the witness preference space. SM Section A.5 shows that the estimates for
![]() $\alpha _1$
and
$\alpha _1$
and
![]() $\alpha _3$
are of nearly identical magnitude but of opposite signs, showing that the rotation is nearly orthogonal, matching the post-estimation procedure results we report in Figure 2 comparing the constrained and flexible estimates using the cosine rule.
$\alpha _3$
are of nearly identical magnitude but of opposite signs, showing that the rotation is nearly orthogonal, matching the post-estimation procedure results we report in Figure 2 comparing the constrained and flexible estimates using the cosine rule.
Note that the common space measure
![]() $\psi $
only serves to identify the bridging equation. We use a scale based on an IRT model and validated survey items, but one can use any common space score for this purpose. In SM Section A.5, we report the results of a replication for Figures 1 and 3, but using the CF scores of Bonica (Reference Bonica2013) in place of our survey items to measure the ideological common space
$\psi $
only serves to identify the bridging equation. We use a scale based on an IRT model and validated survey items, but one can use any common space score for this purpose. In SM Section A.5, we report the results of a replication for Figures 1 and 3, but using the CF scores of Bonica (Reference Bonica2013) in place of our survey items to measure the ideological common space
![]() $\psi $
. The results replicate exactly, except with slightly higher uncertainty estimates given that we use Bonica’s point estimates to substitute for the IRT-derived common space scores that we use in the main model, and the point estimates include added measurement error. This shows one can use off-the-shelf CF scores in place of a survey to recover the rotation and shift in witness preferences using our approach. The SM also demonstrates, however, that using the CF scores directly as preference measures leads to null results identical to Figure 1, which is also no surprise given these are unidimensional preference measures.
$\psi $
. The results replicate exactly, except with slightly higher uncertainty estimates given that we use Bonica’s point estimates to substitute for the IRT-derived common space scores that we use in the main model, and the point estimates include added measurement error. This shows one can use off-the-shelf CF scores in place of a survey to recover the rotation and shift in witness preferences using our approach. The SM also demonstrates, however, that using the CF scores directly as preference measures leads to null results identical to Figure 1, which is also no surprise given these are unidimensional preference measures.
5.4. Describing the Posterior Preference Dimension
Since the witness preference dimension that we recover is orthogonal to their personal ideology, it is important to understand the scale and why it makes substantive sense for the witnesses’ policy preferences to be structured in this way.Footnote 20 In general, as Tetlock (Reference Tetlock1986) notes, policy experts tend to view policies through an analytical lens, rather than through ideology as a heurisitic; policy experts are more likely to understand the real-world impacts of policy interventions as well as the trade-offs involved and so condition their preferences on this knowledge. To give an example, on the topic of managed care, the witnesses that were the most extreme on each side of the estimated witness preference dimension
![]() $\widehat {\zeta ^1}$
were both academics. The witness closest to liberals was a professor of public health who testified about the importance of providing better coverage through the Medicare+Choice program. The one closest to conservatives was a professor of health economics who testified about the need to harness market incentives in managed care to promote cost savings.
$\widehat {\zeta ^1}$
were both academics. The witness closest to liberals was a professor of public health who testified about the importance of providing better coverage through the Medicare+Choice program. The one closest to conservatives was a professor of health economics who testified about the need to harness market incentives in managed care to promote cost savings.
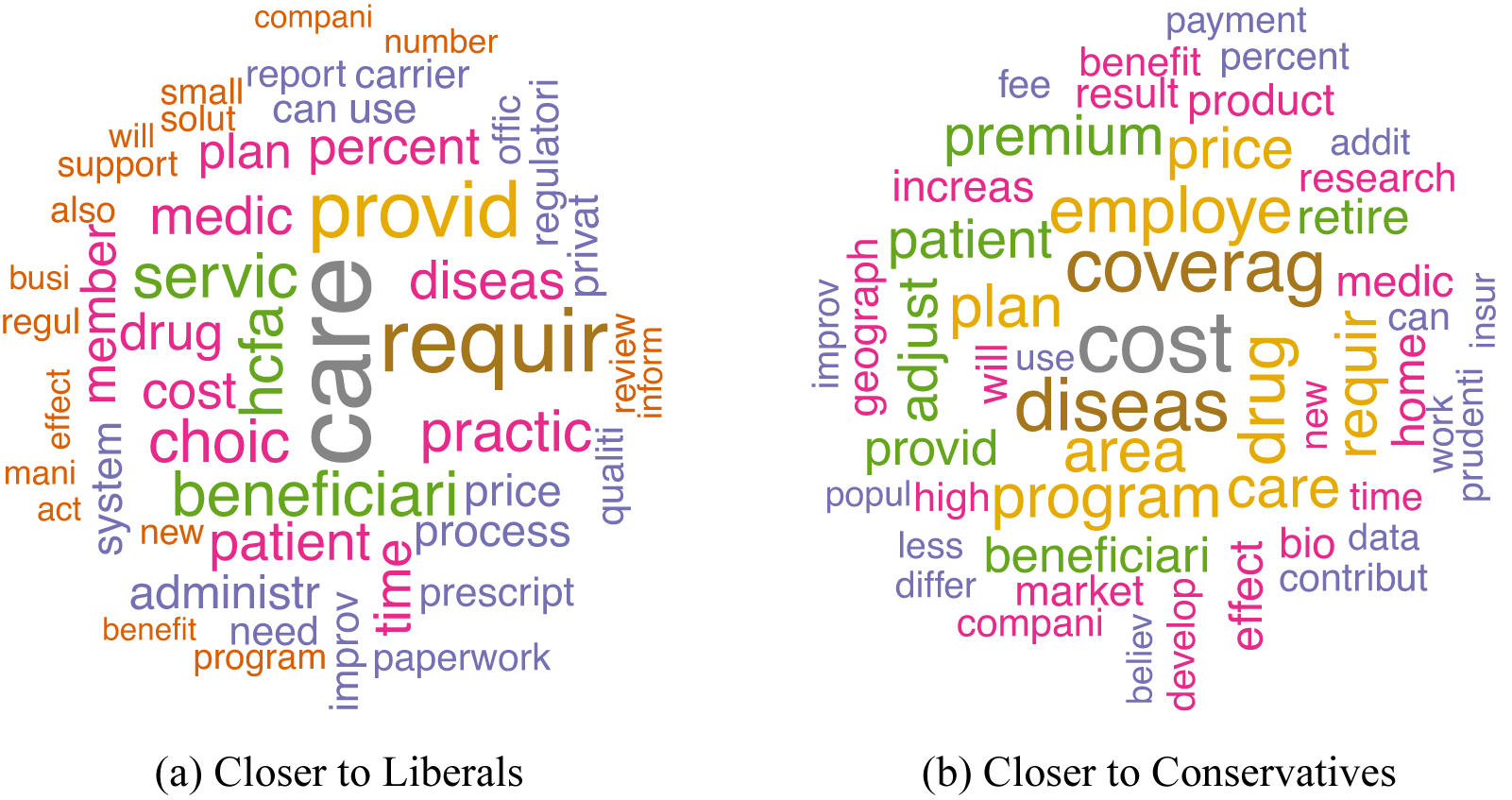
Figure 4 Content of the Witness Preference Dimension. Word clouds for agents spatially closer to liberal legislators are on the left, and closer to conservative legislators on the right. Text analysis procedures described in SM Section A.6.
That left–right ideology does not structure witnesses’ preferences over a complex policy such as Medicare should therefore be no surprise. The nature of the dimension that underlies witnesses’ policy preferences over Medicare policy is of substantive interest, and our approach is able to identify this preference dimension. We use text analysis to systematically understand the content of the witness preference dimension. To do this, we conduct a word frequency analysis of the written testimonyFootnote 21 separately for witnesses who have a high preference score
![]() $\zeta ^1$
and those with a low preference score, stratified by topic.Footnote 22 The resulting word clouds are in Figure 4. Notice that the witnesses that are in closer proximity to conservatives focus more on costs, premiums, and coverage, and those closer to liberals focus more on care, plan requirements, and beneficiaries.
$\zeta ^1$
and those with a low preference score, stratified by topic.Footnote 22 The resulting word clouds are in Figure 4. Notice that the witnesses that are in closer proximity to conservatives focus more on costs, premiums, and coverage, and those closer to liberals focus more on care, plan requirements, and beneficiaries.
6. Discussion and Conclusion
Much of the institutions literature posits that “preferences” matter for political communication. However, this literature has not sufficiently conceptualized the kinds of preferences that matter in a given political context. Here, we proposed that while legislators’ policy preferences are driven by their personal left–right ideology and office-specific incentives, witnesses’ policy preferences may reflect their expert-informed policy commitments based on an analytical understanding of policy tradeoffs, such as the quality/cost tradeoff in health care, and are not informed by an ideology heuristic. Thus, when the political interaction of statistical interest is between elected legislators and nonelected outside agents, in the general case, the analyst must construct and measure two separate preference dimensions, and must then identify the functional correspondence between these two dimensions that reflects the actual relationship that occurred between agent and legislator.
Our solution to recover agent preferences makes use of information revealed by legislators’ behavior within the contextually situated interaction of a committee hearing. We demonstrate how to estimate agents’ preferences using a flexible model that takes witnesses’ preferences as a random effect. Our flexible model allows the recovered witness preference dimension to shift and rotate relative to the legislative roll-call preference space. Our application shows, for the first time using observational data, that committee members in the U.S. Congress communicate more frequently with witnesses who are closer in preference space in a manner that is consistent with economic models of uncertainty reduction and belief updating. We note, however, that it remains an open question if committee members use these interactions in committee hearings to update beliefs, or alternatively these interactions reflect staff preparation prior to the meeting.
We find that legislators’ roll-call preferences and witnesses’ policy preferences are orthogonal, but this does not necessarily mean that experts are somehow apolitical when they testify before committees. Instead, witnesses have substantive commitments to the technical aspects of policies, such as their relative priorities over underlying policy trade-offs. For example, in health care, quality and costs are trade-offs—increased quality leads to higher costs, and vice versa. In our application, we found that witnesses who emphasize quality of care were closer to liberal committee members, and those who emphasize costs were closer to conservative members. But witnesses’ preferences over quality and costs does not correspond to their personal left–right ideology—indeed, both liberals and conservatives would prefer higher quality at lower cost. Bridging methods that ignore this contrast in the nature of the preferences that witnesses and legislators hold over policies will not be able to explain their interactions well.
The fundamental problem of recovering the preferences of outside agents applies to nearly all legislatures, and indeed much cross-institutional research, in any application where the researcher seeks to model the interaction between actors that come from different institutions (Jessee Reference Jessee2016). We show that outside agent preferences can be recovered from text data publicly available at hearings. The flexible simultaneous equation method thus should generalize to other institutional interactions and can be used to explore hypotheses about communication in other settings in future research.
Acknowledgements
Presented at the Society for Political Methodology, July 2018; at the Annual Meeting of the American Political Science Association, September 2016 and August 2018; at the UCR Department of Statistics colloquium, at the UCR Data Science Center seminar series, and at the UC Institute for Prediction Technology in Fall 2017. Thanks to Tim Feddersen, Constanza Schibber, Chris Tausanovich, Teppei Yamamoto, and Hye Young You for very helpful comments; Jessica Ungard and Michael Wessels for excellent research assistance; and Ben Treves and Diogo Ferrari for Linux testing of the repository.
Funding Statement
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Competing Interests
The authors have no competing interest to declare.
Ethical Standards
The human subjects protocol for this study was approved by the UCR IRB (HS-03-091).
Data Availability Statement
Replication code and data for this article are available online in Esterling and Park (Reference Esterling and Park2024) at https://doi.org/10.7910/DVN/ZU5QTG.
Supplementary Material
For supplementary material accompanying this paper, please visit https://doi.org/10.1017/pan.2024.6.











