Introduction
Most of the rivers in Nepal are glacier-fed and provide sustained flow during dry seasons to fulfil the water requirements for irrigation, domestic use, hydropower and industrial use (Reference Immerzeel, Van Beeke and BierkensImmerzeel and others, 2010; Reference Nepal, Krause, Flügel, Fink and FischerNepal and others, 2014). The hydrology of mountainous regions is largely dependent on the climatic conditions of the region as they usually receive large amounts of precipitation, which may be stored in the form of snow and glaciers (Reference Nepal, Krause, Flügel, Fink and FischerNepal and others, 2014). Climate change is expected to contribute to increased variability of river runoff due to changes in the timing and intensity of precipitation, as well as the melting of glaciers. Runoff will initially increase as glaciers melt and will then decrease as deglaciation progresses (Reference SolomonSolomon and others, 2007).
Accurate modelling of the hydrological response to climate change in mountain catchments is complicated due to the large climatic heterogeneity, lack of data, resolution and accuracy of general circulation model (GCM) outputs, and uncertainty about the response of glacier and snow dynamics (Reference BenistonBeniston, 2003). Most hydrological impact studies deploy simple degree-day methods (Reference HockHock, 2005) and assume hypothetical reduction in future glacier areas (Reference Singh and BengtssonSingh and Bengtsson, 2004; Reference HockHock, 2005; Reference Rees and CollinsRees and Collins, 2006; Immerzel and others, 2009).
In this study, a positive degree-day model (PDDM) is used to estimate discharge from different elevation bands, and the total discharge is calculated as the sum of the discharge from all the elevation bands. The PDDM requires limited data so it is appropriate to use it in the Langtang River basin where there are no adequate data. This model estimates snow and ice melt and its relative contribution to the basin runoff from mean monthly air temperature and precipitation (Reference Kayastha, Ageta, Fujita, Jong, Collins and RanziKayastha and others, 2005). The model runs on a monthly basis so time lag is not incorporated, which is one of the limitations of the model. The main aim of this study is to simulate the monthly discharge from the glacierized Langtang River basin by applying the concept of degree-day factor using the PDDM. The model is first calibrated by using different parameters, after which it is validated to check the model performance. Projected temperature and precipitation from the Weather Research and Forecasting (WRF) model are then used to generate the future water scenarios in the basin.
Study Area
Langtang River basin lies in the Langtang Valley, Rasuwa district, Nepal, and is - 6 0 km north of Kathmandu. It is the headwater area of the Trisuli River in the Narayani River system. ArcMap 9.3 is used to calculate the area and land types. Landsat Thematic Mapper 5 (TM5) images from 23 January 2009 and an Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) digital elevation model (DEM) of 30 m resolution from 2009 are used. Glacier area in the catchment is delineated manually. The total area of Langtang River basin is 353.59 km2, with elevation ranging from 3652 to 7215m a.s.l. The average altitude is 5169 m a.s.l. with a mean slope of 26.78. Of the total basin area, 39% (137 km2) is covered by glaciers (debris-covered and clean-ice) and the remaining 6 1% (216 km2) is covered by rock and vegetation (Fig. 1). Meteorological and hydrological data from Kyangjing station were obtained from the Department of Hydrology and Meteorology (DHM), Government of Nepal. Annual mean temperature over the basin is 3.5°C (1988–2010) and the annual mean precipitation is 655.7 mm (1988–2012). The discharge regime can be classified as glacial, with maximum discharges in July and August and minimum discharges during winter. Winter discharge is characterized by a constant base flow with negligible inflows of rainwater and meltwater as the air temperature is generally below melting point (Reference Immerzeel, Van Beek, Konz, Shrestha and BierkensImmerzeel and others, 2012).
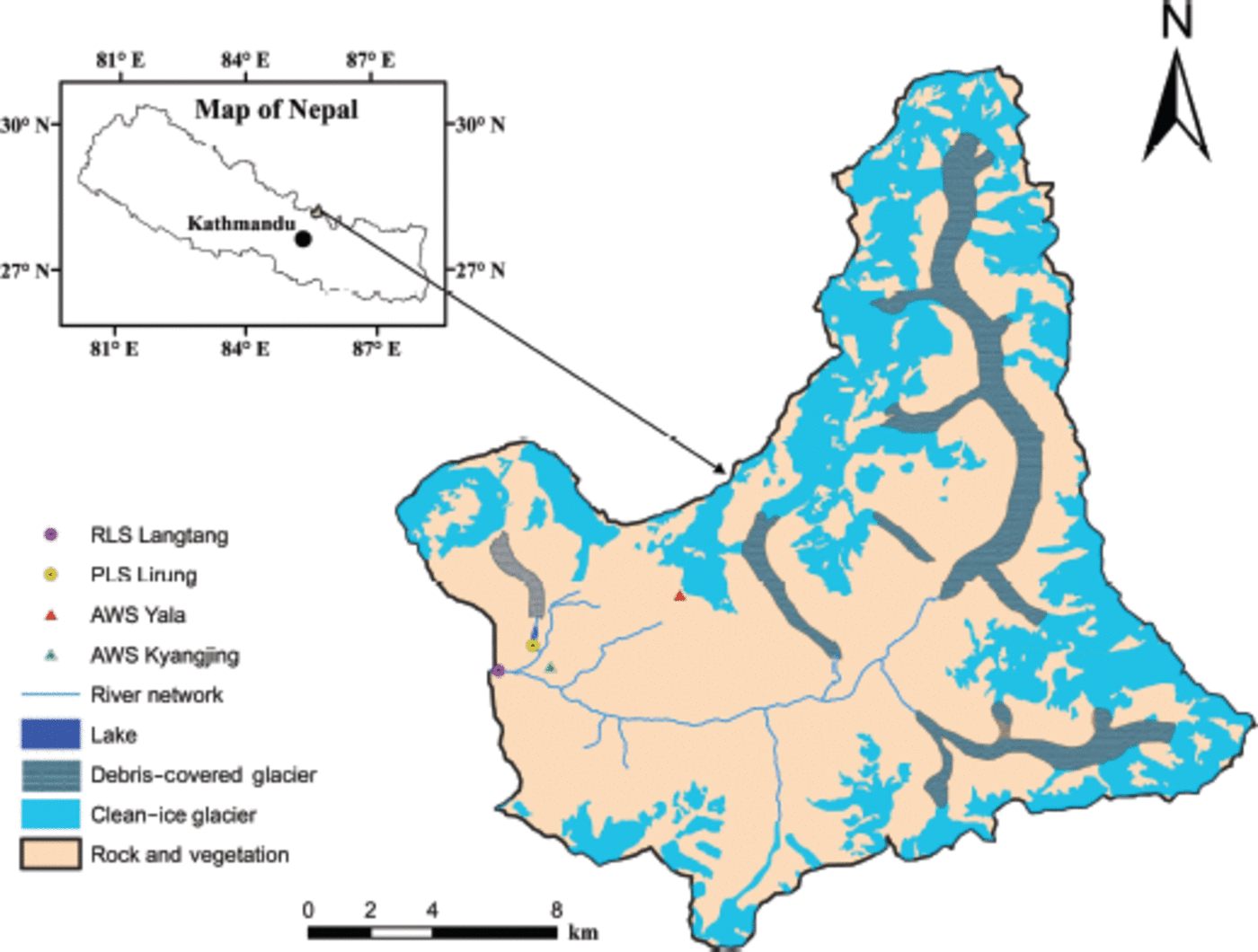
Fig. 1. Location map of Langtang River basin including radar level sensor (RLS and pressure level sensor (PLS).
Modelling Description and Set-Up
The PDDM is a simple but useful model with minimum field data requirements for precise calculation of melting in the Himalaya. The model estimates the river discharge from major hydrological processes such as precipitation, snow/ice melt, evaporation, infiltration and base flow. Similarly, the model considers basin characteristics and snow and ice melt from glaciers and rocky areas, and ice melt under a debris layer is also taken into consideration.
Positive degree-day model
The PDDM is based on positive degree-days (PDDs) calculated from monthly mean air temperature (Reference BraithwaiteBraithwaite, 1985). In this study, the entire basin is divided into 18 elevation zones and discharge from each zone is calculated. The hypsometry of Langtang River basin is shown in Figure 2.
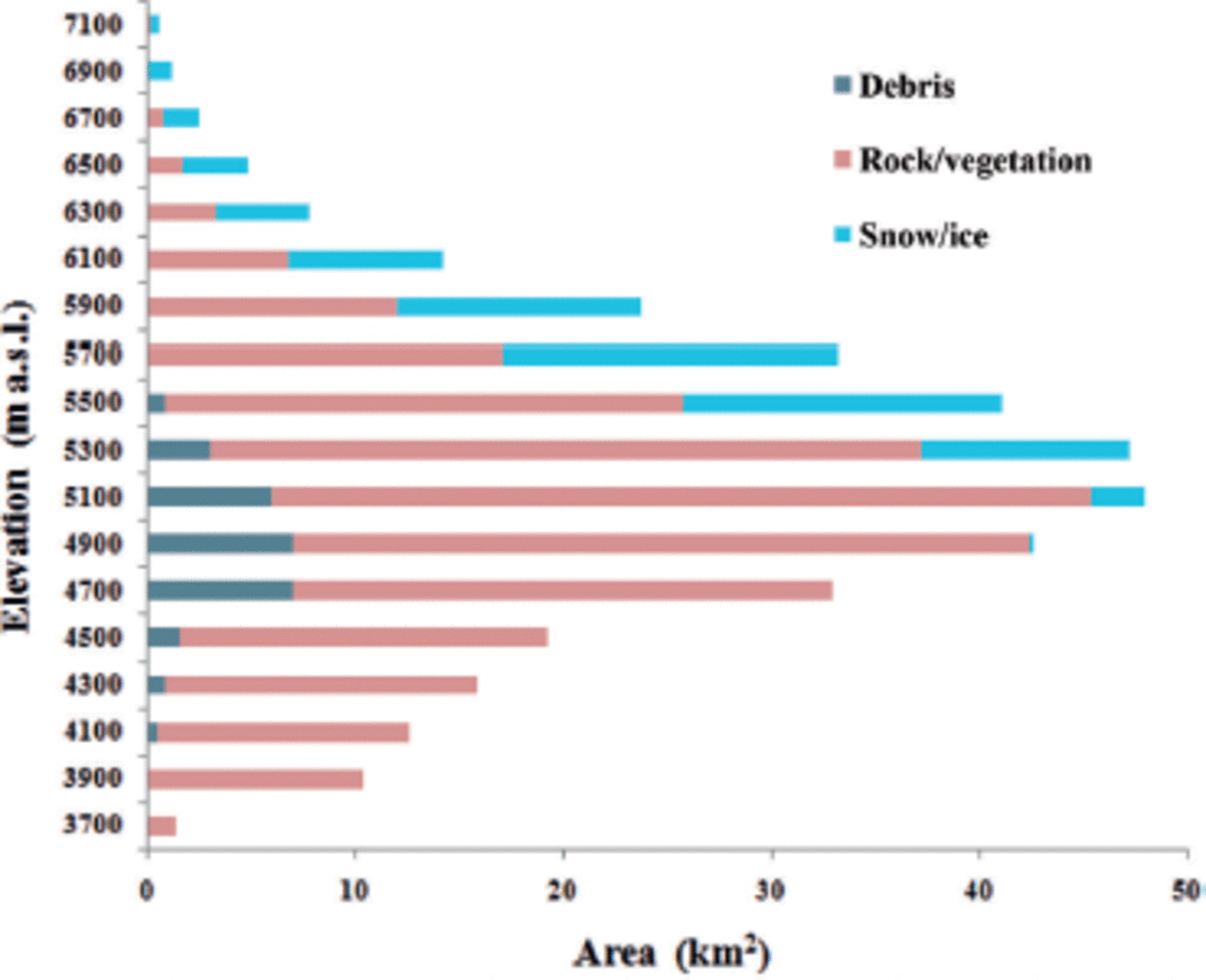
Fig. 2. Hypsometry of Langtang River basin.
The total discharge from the basin is calculated as the sum of discharges from every zone:
where q 1 is the discharge from elevation zone 1, q 2 is the discharge from elevation zone 2, etc.
Temperature and precipitation gradients were applied to obtain the temperature and precipitation at each elevation zone (z) from the base house (BH) at Kyangjing automatic weather station (AWS) (Table 1).
Table 1. Calculation of temperature and precipitation gradient

For temperature and precipitation gradients, data from Kyangjing AWS (3920m a.s.l.) and Yala AWS (5050 ma.s.l.) were used.
In this model, precipitation is separated into snow and rain by taking 3.6°C as the threshold temperature (Reference Kayastha, Ageta, Fujita, Jong, Collins and RanziKayastha and others, 2005). Beyond this temperature, snow goes to the snowmelt module and rain is passed into the rain module. Only representative concentration pathway 4.5 (RCP4.5) of the WRF model was used for future projection of temperature and precipitation, and time lag is not applied in the discharge calculation. These are the main limitations of this model.
Snowmelt module
In this module, we have melt from snow, and ice from glaciers, rocks and vegetation (Q1), and ice melt under debris (Q2). The snow and ice ablation from glaciers and rocky areas (Q1) is calculated by multiplying the monthly PDDs and the PDD factor (k s for snow or kb for ice):
The PDD factor used in this study is derived from the summer values obtained on glacier AX010, east Nepal, and Yala Glacier in the Langtang Valley (Reference Kayastha, Ageta and NakawoKayastha and others, 2000a, Reference Kayastha, Ageta, Nakawo, Fujita, Sakai and Matsuda2003). The number of PDDs left after melting the snow above the debris is used to melt the ice under it, which is computed as explained by Kayastha and others (2000b) as
The method requires the PDD factor for ice ablation and a relation between degree-day factor and debris properties, namely the relation between the ratio of degree-day factor for a given debris thickness (k d) to the factor for ice ablation (k b) and the ratio of thermal resistance of debris (R) to thermal resistance for critical debris thickness (R c) (Reference Kayastha, Takeuchi, Nakawo and AgetaKayastha and others, 2000b):
A list of parameters and factors used in the current study is shown in Table 2.
Table 2. List of parameters and factors used in the present model

The base flow of 1.94 m3 s–1 is estimated by plotting a hydrograph from the observed monthly discharge data (1993–2006) and separating the base flow by applying the base flow separation method II/concave method (Reference SubramanyaSubramanya, 1994). Furthermore, potential evapotranspiration (PET) is calculated using an equation taken from the Blaney and Criddle formula in Reference SubramanyaSubramanya (1994), which is given by
and
where PET is in cm, K is an empirical coefficient, which depends on the type of crop, F is the sum of monthly consumptive use factors for the period, Ph is the monthly percentage of annual daytime hours, which depends on the latitude of the location, and Tf is the mean monthly temperature (8F). Values of K depend on the month and location; 0.8 is used for natural vegetation in the basins studied. The number of monthly sunshine hours at 30° latitude is used in the present study.
Infiltration of 90 mm month–1 was taken from the field observations carried out in the Langtang Valley in 1996 (Reference Sakai, Fujita and KubotaSakai and others, 2004). Figure 3 shows the flow chart of the PDDM used in this study.

Fig. 3. Flow chart of the PDDM.
Effective rainfall (Q3) is calculated as:
Total monthly discharge (Q) from the different elevation zones is calculated as the sum of Q1, Q2 and Q3.
Hydrometeorological input data
Hydrometeorological data from the Langtang River basin, which were required for the PDDM, were acquired from the DHM. For future climate projection, regional climate model (RCM) data for the RCP4.5 scenario are used. The projected precipitation and temperature data from 2010 to 2050 were obtained from the Bjerknes Centre for Climate Research (BCCR) Norwegian Earth System Model (NorESM) GCM. For this study we used the WRF RCM output computed at 12 km x 12 km horizontal resolution. The WRF output from 1996 to 2009 is used for model comparison and bias correction.
Future climate data analysis
The RCM output is bias-corrected using the equation of Reference Cheng and SteenburghCheng and Steenburgh (2007) for temperature (T) and the equation of Reference NazrulNazrul (2009) for precipitation (P):
where T* is the value obtained after calibration, T obs and T mod are the observed and model monthly temperatures, respectively, T is the mean value and SD is the standard deviation:
where α is the slope and β is the intercept of regression line, which are obtained from a scatter plot of precipitation from both model estimation and observation for the period under consideration. The bias-corrected model data are then compared with the observational data.
Hydrometeorological analysis
Trend analysis was carried out using the non-parametric Mann-Kendall test (Reference MannMann, 1945). This is a statistical method used for studying the spatial variation and temporal trends of hydro-climatic series. Data from Kyangjing station, which is the permanent station of the DHM, are used. For the temperature trend analysis, available data from 1988 to 2010 are used. This data analysis revealed that temperature shows an increasing trend of 0.133°Ca–1, which is statistically significant at the 95% confidence level. The available precipitation data from 1988 to 2012 showed an increasing trend of 6.96 mm a–1, which is also significant. Average annual temperature and total annual precipitation trends are shown in Figure 4.

Fig. 4. Average annual temperature trend (1988–2010) and total annual precipitation trend (1988–2012) at Kyangjing station, Langtang Valley.
Figure 5 shows the observed precipitation at Kyangjing station and discharge of the Langtang River gauging site (28.209° N, 85.548° E) of the Langtang River basin between 1993 and 2006. The streamflows begin to increase in June and reach their peak in July and August. During the monsoon period (June-September), precipitation in the accumulation area falls as snow, and when the temperature starts to increase, the snow and glacier melt also contribute to the streamflow. In the post-monsoon period and in winter, snowmelt contribution to the total discharge is large.

Fig. 5. Average monthly observed precipitation and discharge for the Langtang River basin from 1993 to 2006.
Future climatic trend analysis
The projected temperature data from 2010 to 2050 for Langtang show an increase of 0.015°C a–1, whereas the projected precipitation for the same period shows a negative trend of –1.905mma– 1. However, the future precipitation and temperature projected by the WRF model are not consistent with the observed trends. In particular the future precipitation trend is negative while the observed trend is positive. A similar study in Langtang Valley by Reference Immerzeel, Van Beek, Konz, Shrestha and BierkensImmerzeel and others (2012) reported that the temperature is projected to increase by 0.06°C a–1 and precipitation by 1.9 mm a–1. This is because Reference MannImmerzeel and others (2012) used downscaled data of five GCMs, but in this study we used only the RCP4.5 scenario for a single NorESM GCM using the WRF model, which is also one of the limitations of this study. Statistical analysis shows that both trends are significant. Figure 6 shows the projected average annual temperature and total annual precipitation trends.

Fig. 6. Projected average annual temperature and total annual precipitation for the Langtang River basin (2010–50).
Results and Discussion
Model calibration and validation
The calibration period for this study was 1993–98. Model quality assessments were carried out using the Nash–Sutcliffe value and volume difference, which were found to be 0.85 and 7.5%, respectively, for the calibration period. Since PDD is less, the PDDM has underestimated the discharge. The PDD factor is the main calibrating parameter in the PDDM. After calibration, validation was carried out for 1999–2006. The quality of the hydrological and meteorological data was not good in 2001 and 2005, so we have not used these periods for validation. For the validation period, the Nash–Sutcliffe value and volume difference were found to be 0.80 and –7.3%, respectively. As PDD is high in the validation period, the PDDM has overestimated the discharge. Figure 7 shows the calibration and validation of the PDDM.

Fig. 7. Calibration and validation of the PDDM.
Future discharge projection
After the model calibration and validation, future discharge was estimated for 2010–50 by using projected temperature and precipitation data from the WRF model. Figure 8 shows the projected discharge and projected precipitation in the Langtang River basin. Projected discharge shows no significant trend from 2010 to 2050. However, decadal hydrographs for 2010–20, 2021–30, 2031–40 and 2041–50 (Fig. 9) show that in the pre-monsoon period the discharge will increase due to the increase in temperature. A change in the timing of streamflow can be seen in the hydrographs: peak discharge is in July, due to the high temperature and precipitation data.

Fig. 8. The projected discharge simulated from the PDDM and projected precipitation.

Fig. 9. Comparison of projected decadal hydrographs with the observed hydrograph (1993–2006).
Snow/ice contribution
From the model output, the relative contribution of snow/ice melt from glaciers, snowmelt from rocks and vegetation, rain and base flow to total discharge is analyzed. From the WRF model, the contribution of snow and ice melt from glaciers and snowmelt from rocks and vegetation is 54.3% in the period 1993–2006, whereas it is slightly higher in 2010–20 (55%) and then decreases again in the periods 2021–30 (52%), 2031–40 (51%) and 2041–50 (50%). In the period 2041–50, due to increased temperature, more rain than snow is observed in precipitation, and melting of snow and ice from glaciers also increases. In the other periods, more precipitation is in the form of snow, and melting of snow and ice is high in the monsoon season mainly in July, August and September. Figure 10 shows the contributions of snow/ice melt from glaciers, snowmelt from rocks, rain and base flow to the total discharge in the periods 1993–2006, 2010–20, 2021–30, 2031–40 and 2041–50.

Fig. 10. Contribution of snow, ice, rain and base flow in different periods.
Sensitivity analysis
Three parameters (temperature, precipitation and glacier area) were chosen for the sensitivity analysis. Temperature (2°C increase and decrease), precipitation (20% increase and decrease), different combinations of temperature and precipitation (+2°C temperature and +20% precipitation, +2°C temperature and –20% precipitation, –2°C temperature and +20% precipitation , and –2°C temperature and –20% precipitation) and clean-type glacier area (reduced in such a way that the area that lies in each zone is reduced by 25% and 50%) were used to test the sensitivity of the model. Figure 11 shows the result of the sensitivity analysis. The analysis reveals that the model is more sensitive to temperature than precipitation and glacier area. The combination of increased temperature and precipitation shows the highest change in discharge (+43.9%), and the combination of decreased temperature and precipitation shows the lowest change (–20.1%). A temperature decrease of 2°C shows a change in the timing of the peak hydrograph. This is because of precipitation falling in the form of snow, which will melt after some time interval. In this context we did not consider change in mass balance. Changes in percentage discharge from different sensitivity analyses are given in Table 3.
Table 3. Change in discharge from different sensitivity analyses

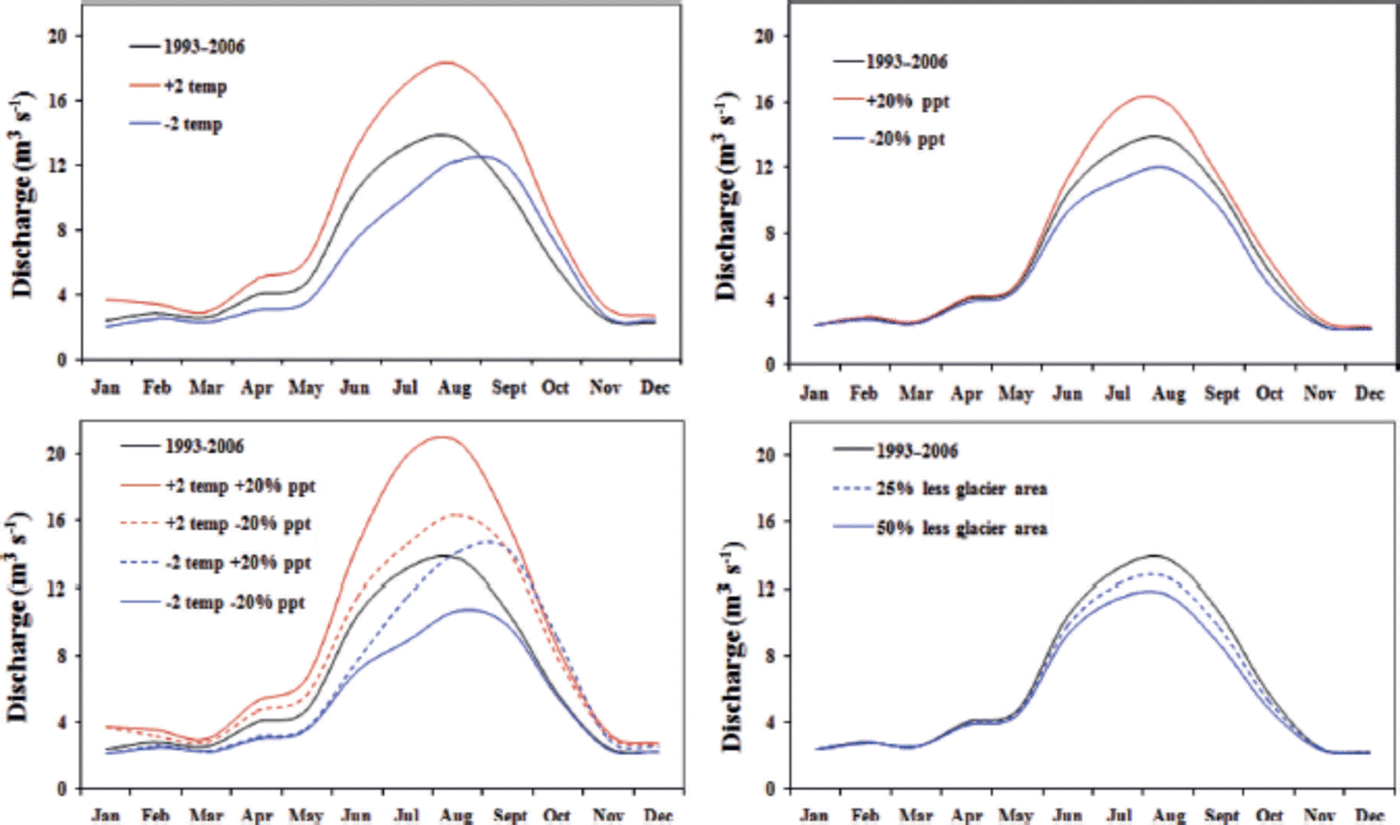
Fig. 11. Sensitivity analysis of the PDDM.
Conclusions
The PDDM was used to estimate discharge from the Langtang River basin. As the model provides information on snow/ice melt from glaciers, snowmelt from rocks and vegetation, ice melt from debris-covered glaciers, rain and base flow, it gives insights into the hydrological system dynamics of the basin.
Projected annual average temperature from 2010 to 2050 shows an increasing trend of 0.015°C a–1, and total annual precipitation shows a negative trend of 1.905 mma–1.
Although the model is simple, it was able to simulate the discharge in the calibration as well as in the validation period. For the calibration and validation period, Nash–Sutcliffe values were found to be 0.85 and 0.80, respectively.
Future water scenarios from this model suggest that the discharge will increase in the pre-monsoon period and the peak discharge will be in July. However, only WRF model output from a single GCM (i.e. NorESM) is used for projected temperature and precipitation. Further comparison of the WRF model with other RCMs is required in the future.
The highest contribution of snow and ice to the total discharge is 55% in 2010–20, whereas in 2041–50 it is reduced to 50%.
From the sensitivity analysis, the PDDM is more sensitive to temperature than other parameters. However, increases in both temperature and precipitation show the highest increase in discharge.
From the overall analysis with the PDDM, the impact of climate change in the Himalayan catchment is pronounced, along with increasing temperature and changing precipitation. These results will help the water resource management planners in the Himalayan region to develop sustainable policies and plans for irrigation, hydropower, drinking water supply and flood forecasting. Similar studies should be carried out in the other parts of the Himalayan region to increase understanding of the hydrological system dynamics and potential impact of climate change.
Acknowledgements
We acknowledge support from the HKH (Hindu Kush Himalayan) Cryosphere Monitoring Project implemented by the International Centre for Integrated Mountain Development (ICIMOD) and supported by the Norwegian Ministry of Foreign Affairs, and from the Himalayan Climate Change Adaption Program (HICAP) implemented jointly by ICIMOD and other agencies. We thank the project partners for their help in carrying out this study, including: the Himalayan Cryosphere, Climate and Disaster Research Center, Kathmandu University; the Department of Hydrology and Meteorology, Government of Nepal; the Department of National Park and Wild Life Conservation, Government of Nepal; the Central Department of Hydrology and Meteorology, Tribhuvan University; and the Water and Energy Commission Secretariat, Government of Nepal. We also thank Ahuti Shrestha, Achut Parajuli and Sunil Kumar Pariyar for providing valuable input during this study.















