Introduction
A shape query in computer-aided design (CAD) systems is enabled by a database query requesting the retrieval of instances of shapes from a CAD database. The list of the commands available to a designer to perform a query for a particular shape is impressive and involves multiple ways of interfacing with the CAD software including typing, pointing, and pictorially interacting with the model in a variety of ways including clockwise and counterclockwise window-selecting, cross-selecting shapes, drop-down menus, listboxes, checkboxes, toggles, steppers, and so on, all with ready-made or ad hoc lists of shapes, combinations of shapes, and properties of shapes; and yet, regrettably, all are ultimately useless when it comes to enabling the designers retrieve shapes that cannot be derived from the ones inserted in the database.
Surprisingly, shape query under a given Euclidean, affine, or linear transformation (shape embedding) is entirely absent from current CAD systems: This might come at a surprise when CAD geometry is intimately related to computational geometry – an ever-growing field of algorithms dealing with geometric problems involving operations on points, lines, planes, and solids (see, e.g., Preparata and Shamos, Reference Preparata and Shamos1990; Goodman and O'Rourke, Reference Goodman and O'Rourke1997). An impressive list of formal approaches on comparison of shapes (shape matching) in computational geometry include diverse matching techniques such as tree pruning, pose clustering, geometric hashing, deformable templates, Fourier descriptors, wavelet transforms, and neural networks (Besl and Jain, Reference Besl and Jain1985; Foley et al., Reference Foley, Van Dam, Feiner and Hughes1997; Loncaric, Reference Loncaric1998; Campbell and Flynn, Reference Campbell and Flynn2001; Cardone et al., Reference Cardone, Gupta and Karnik2003); and an expanding universe of classes of shapes to be compared including sketch-based shapes, non-rigid shapes, relief surface patches, multi-domain protein shapes, gesture sequence shapes, watertight models, and so forth (Tangelder and Vetlkamp, Reference Tangelder and Veltkamp2008). And yet, the single most important characteristic in all these approaches, the measurement of how similar or dissimilar a shape is with another shape, using some appropriately constructed similarity or dissimilarity measure (Veltkamp and Hagedoorn, Reference Veltkamp and Hagedoorn2001), is an indifferent measure when it comes to the notion of shape embedding under a given Euclidean, affine, or linear transformation (Stiny, Reference Stiny2006).
The only systems that have attempted to implement shape embedding are the shape grammar interpreters – computer applications that process shape rules encoded in shape grammars (Krishnamurti, Reference Krishnamurti1981, Reference Krishnamurti1982, Reference Krishnamurti1992; Krishnamurti and Giraud, Reference Krishnamurti and Giraud1986; Stouffs, Reference Stouffs1994; Tapia, Reference Tapia1999; Trescak et al., Reference Trescak, Rodriguez and Esteva2009; Jowers et al., Reference Jowers, Hogg, McKay, Chau and Pennington2010; Jowers and Earl, Reference Jowers and Earl2011; Grasl and Economou, Reference Grasl and Economou2013; Ruiz-Montiel et al., Reference Ruiz-Montiel, Belmonte, Boned, Mandow, Millán, Badillo and Pérez2014; Stouffs and Li, Reference Stouffs and Li2020). A shape grammar consists of shape-rewriting rules cast in the form u → v, for a shape u is rewritten as a shape v (Stiny, Reference Stiny1975). A shape rule u → v is applied to a shape W, when there is a geometric transformation f that makes the shape f(u) part of the shape W – or alternatively, when there is a transformation f that embeds the shape f(u) in W. The resulting computation identifies the instance of the shape f(u) in the shape W and replaces it with the corresponding instance of the shape f(v) to generate a new shape W′ = W − f(u) − f(v). Clearly, any application of a shape rule requires that the shape u can be embedded in a design. And if there is no need for the specification of a design action (shape v), these the shape rewrite rules are modeled after the identity shape rule u → u (Stiny, Reference Stiny1996; Economou et al., Reference Economou, Hong, Ligler, Park and Lee2021). Shape grammars do offer a generous formalism for design supporting ambiguity, redescription, and variability – and since their introduction in the mid-seventies have always offered a radical counterpart to mainstream research in CAD (McCullough, Reference McCullough2006; Knight, Reference Knight2015).
All shape grammar interpreters approach the problem of implementing shape embedding in two ways, namely, by (a) the database query of the maximal elements that the shapes are made of, see for example, GRAPE (Grasl and Economou, Reference Grasl and Economou2013, Reference Grasl and Economou2018) and Sortal (Stouffs, Reference Stouffs2018; Stouffs and Li, Reference Stouffs and Li2020) and (b) the derivation of the transformation matrix that embeds one shape into another, see for example, SGI (Krishnamurti, Reference Krishnamurti1982; Krishnamurti and Giraud, Reference Krishnamurti and Giraud1986); SGS (Chase, Reference Chase1989); GRAIL (Krishnamurti, Reference Krishnamurti1992); and GEdit (Tapia, Reference Tapia1999). Both approaches rely on the formal descriptions of the maximal representation of shape and its registration marks or points (Stiny, Reference Stiny1975, Reference Stiny2006; Krishnamurti, Reference Krishnamurti1981). The implementation of shape embedding through database query, despite its success in well-structured cases and design workflows, fails to provide a general solution to the subshape problem (McKay et al., Reference McKay, Chase, Shea and Chau2012). The implementation of shape embedding through the derivation of the transformation matrices is still the most promising method, but it is plagued by a series of problems across several fronts (Stouffs, Reference Stouffs2019; Hong and Economou, Reference Hong, Economou and Gero2021).
The work here focuses on the systematic exposition of the challenges underlying the implementation of the derivation of the transformation matrices for shape embedding, and the opportunities residing in the reworking of the problem. More specifically, 14 cases of shape embedding are identified with respect to the number of available registration points, four for determinate cases and ten for indeterminate ones, and an approach is sketched to take on the complexities underlying the indeterminate cases. All shape calculations are done with shapes consisting of straight lines in the Euclidean plane, that is, the algebra U ij for i = 1 the dimension of lines, and j = 2 the dimension of space in which the lines are defined, transformed, and combined (Stiny, Reference Stiny1991, Reference Stiny2006; Krstic, Reference Krstic and Gero2014). Aspects of interface design and integration to current work design workflows are deliberately left aside.
Calculating embedding
Shape embedding is the process of embedding a shape u into a shape W under a transformation f. The two main parts of the visual match to consider are (a) the relation between the shape u and its instance f(u) and (b) the relation between the shape f(u) and W. In the first case, we are interested in the transformation f that relates the shapes u and f(u): Do we want to search for congruent shapes with the exact size and shape with the shape u? Or similar shapes differing in size? Or affine congruent ones? Or projective congruent ones? The invariance of particular characteristics between the shapes u and f(u) for Euclidean, affine, and linear transformations f require radically different geometrical constructions (Veblen and Young, Reference Veblen and Young2007). In the second case, we are interested in the part relation between the shapes f(u) and W, that is, the case that f(u) ≤ W holds true. Does a particular transformation f make the shape f(u) part of W? Are there more instances f(u) of the shape u that can be embedded in W under a particular group of transformations? Are there none? It might be that a visual search or embedding for a congruent instance f(u) of a shape u gives null results but a more relaxed search for an affine congruent shape f(u) does; or it might be that the visual match is indeterminate, that is, additional instructions and calculations have to be performed. A brief account of both steps of the visual match is given below confined for shapes made of lines in the algebra U 12.
The first step for a visual embedding of a shape u into a shape W is the appropriate specification of the geometric relation between the shape u and the shape f(u) to be matched in W: More broadly, for a shape u, the shape f(u) can be modeled by four types of transformations: (a) isometric transformations (or isometries) including translations, reflections, and rotations; (b) similarity transformations (or similarities) including isometric transformations, scale transformations and their combinations; (c) affine transformations (or affinities) including similarities, stretch, compress, and shear transformations and their combinations; and (d) linear transformations (or linearities) including affine transformations, one-point and two-point perspective transformations and their combinations. Each of these types of transformations vary some aspects of the shape and leave other aspects invariant: The isometric transformations preserve lengths and angles and vary position; the similarity transformations preserve angles and vary length and position; the affine transformations preserve parallelism and vary angles, lengths, and position; and the linear transformations preserve cross ratio and vary parallelism, angles, lengths, and position (March and Steadman, Reference March and Steadman1974). Any finite sequence of the above transformations specify the type of geometric congruence between the two shapes u and f(u): two shapes are congruent if there is a finite sequence of isometric transformations mapping one shape to another; two shapes are similar if there is a finite sequence of similarity transformations mapping one shape to another; two shapes are affine congruent if there is a finite sequence of affine transformations mapping one shape to another; and two shapes are projective congruent if there is a finite sequence of linear transformations mapping one shape to another. The rising hierarchy of the transformations f is given in Figure 1 for a shape u in the form of a lowercase k. The initial instance of the shape u is taken here as the identity transformation f(u).

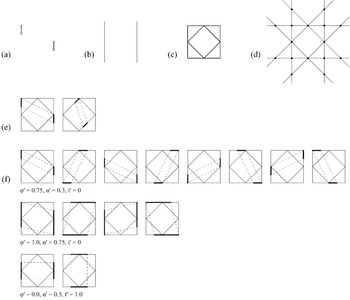
Fig. 1. Types of linear transformations. (a) Identity; (b) reflection; (c) direct transformations (from left to right): translation; rotation; scale; shear; stretch; one-point perspective; two-point perspective; (d) indirect or handed versions of the transformations in (c).
The second step for a visual embedding of a shape u into a shape W is the specification of the appropriate registration mechanism to capture the geometric congruence of the shape f(u) with parts of the shape W including the complete shape W. The selection of these registration points has been somewhat of a moving target in the literature and various approaches have been proposed (see, e.g., Stiny, Reference Stiny1975, Reference Stiny2006; Krishnamurti, Reference Krishnamurti1981; Krishnamurti and Giraud, Reference Krishnamurti and Giraud1986; Krishnamurti and Earl, Reference Krishnamurti and Earl1992; Stouffs, Reference Stouffs1994; Earl, Reference Earl1997; Tapia, Reference Tapia1999). Here, the registration points are solely defined as the intersections of the hyperplanes (see, e.g., Alexanderson and Wetzel, Reference Alexanderson and Wetzel1978) that the maximal lines are embedded in Stouffs and Krishnamurti (Reference Stouffs and Krishnamurti2019). More specifically, a registration point can be incident with (a) two maximal lines; (b) a maximal line and a boundary of maximal line; (c) two boundaries of maximal lines; (d) a maximal line and a hyperplane upon which a maximal line is embedded; (e) a boundary of a maximal line and a hyperplane upon which a maximal line is embedded; and (f) two hyperplanes upon which two maximal lines are embedded. A visual illustration of the six types of registration points and an instance of a shape u featuring all types of registration points are both given in Figure 2.
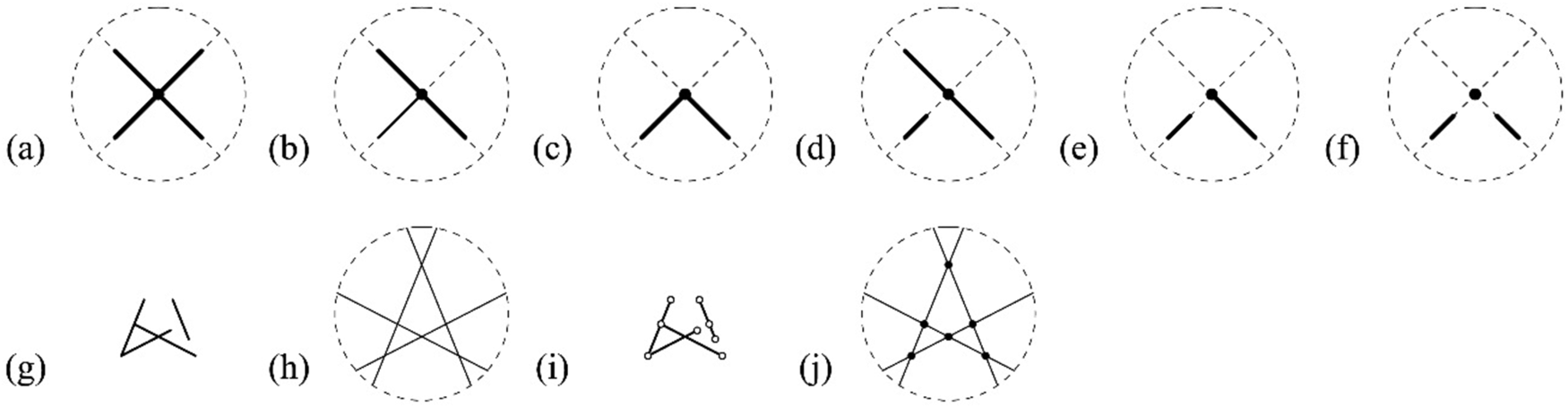
Fig. 2. Congruence of shapes and registration points. (a–-(f) Six types of registration points; (g) a shape exhibiting all six types of registration points; (h) four construction lines (hyperplanes) of shape u; (i) seven endpoints of shape u; and (j) six registration points of shape u.
The selection of the particular type of geometric congruence between the shape u and f(u) – namely, the choice whether the shape f(u) is a congruent, similar, affine congruent or projective congruent instance of u – and the available registration points R u of the shape u and the points R w of the shape W determine (a) whether there is indeed an embedding of the shape f(u) in W, and if there is one, (b) whether this embedding can be done in a determinate or indeterminate way. A comprehensive overview for all possible cases of determinate and indeterminate embeddings under Euclidean and affine transformations for all algebras U ij, 0 ≤ i ≤ j ≤ 3 has been given by Krishnamurti and Stouffs (Reference Krishnamurti and Stouffs1997). Interestingly, shapes made up of lines can be embedded in a determinate way under a particular kind of transformation and in an indeterminate way under some other. Most of the current shape grammar implementations use algorithms that can calculate determinate embeddings under isometric and similarity transformations (Euclidean transformations), and there is no general way to treat indeterminate embeddings. The goal of this work is to trace these cases and identify the conditions that need to be resolved for a general implementation of embedding. The work focuses on the outstanding issues associated with this method and illustrates them through a series of iterative visual calculations against a single shape W to make them as manifest as possible. The shape W pays homage to the familiar shape of the two nested squares (or four triangles, four pentagons, two hexagons, and so forth) that has characterized the field of the shape grammars since its first appearance in Stiny (Reference Stiny1975) and Gips (Reference Gips1975) and afterwards (see, e.g., Stiny, Reference Stiny1980; Knight and Stiny, Reference Knight and Stiny2001; Mitchell, Reference Mitchell, Antonsson and Kagan2001; Stouffs and Krishnamurti, Reference Stouffs and Krishnamurti2019).
Implementation of determinate embedding using transformation matrices
The general algorithm to the derivation of the transformation f for shape embedding by calculating transformation matrices has been given in Krishnamurti (Reference Krishnamurti1981, Reference Krishnamurti1982) and Krishnamurti and Giraud (Reference Krishnamurti and Giraud1986): A 3 × 3 matrix is used to represent all linear transformations, including isometries, similarities, affinities, and linearities. The calculation of the transformation between two shapes in 2D space is done by the derivation of the 3 × 3 matrix by plugging in the coordinates of the required number of registration points between the two shapes. This method is based on the fact that any point on the Cartesian plane is assigned with a coordinate with three real numbers x, y, and z to represent an absolute location in the space. For the four types of linear transformations and Num(R u) the number of registration points of the shape u, there are four cases of determinate embedding to consider: (a) Num(R u) = 1 under isometric transformations; (b) Num(R u) = 2 under similarity transformations; (c) Num(R u) = 3 under affine transformations; and (d) Num(R u) = 4 under linear transformations. Clearly, any embedding with a larger set of available registration points should be determined, calculable, and otherwise straightforward – but see some further notes on this topic in the end of this work.
Determinate embedding under isometric transformations
An embedding of a congruent instance of a shape u in a shape W is determinate when the shape u has one or more registration points. An example of a determinate congruent embedding of a shape u having one registration point is shown in Figure 3. Note that the limiting case that the shape u has only one registration point – that is, one point coincident with the intersection of its hyperplanes cannot be calculated by the current algorithm of the derivation of the isometry matrix because the algorithm requires two points from each shape to resolve the three unknown variables of the isometric matrix, namely, the rotation angle θ, the translation in the x-direction t x, and the translation in the y-direction t y. In this sense, the embedding is visually possible but operationally impossible in terms of the given algorithm. The manual addition of “distinguishable” points in the set of registration points of the shape u is not readily deployable in automated applications of the algorithm, and the automated sampling of endpoints of maximal lines, regrettably, brings more problems than actual solutions – a pictorial example is offered in the final part of this work along with a series of cases that need to be considered for the automated implementation of visual matching. The eight possible congruent embeddings of the shape f i(u) are all determined by the interactions of the symmetry elements of the symmetry groups of the shapes u and W (Stiny, Reference Stiny1991) – here, the cyclic group C 1 of order 1 and the dihedral group D 4 of order 8, respectively (Armstrong, Reference Armstrong1997).
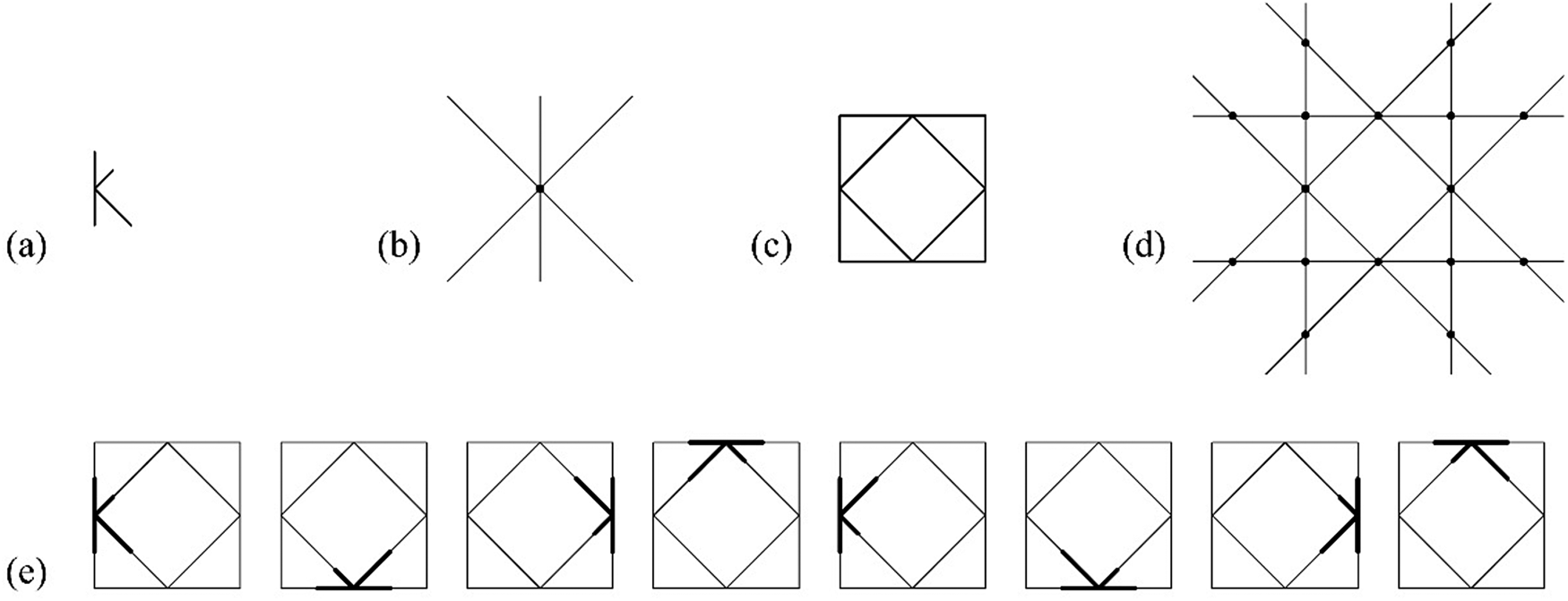
Fig. 3. An example of determinate congruent embedding with one registration point that cannot be implemented by the derivation of the isometry matrix. (a) Shape u; (b) registration points R u; (c) shape W; (d) registration points R W; and (e) eight results of determinate embedding under isometric transformations.
Determinate embedding under similarity transformations
An embedding of a similar instance of a shape u in a shape W is determinate when the shape u has two or more registration points. An example of a determinate embedding under similarity transformations of a shape u having two registration points that is successfully implemented by the derivation of the similarity matrix is shown in Figure 4. The automated derivation of the similarity matrix is successful because all possible pairs of points sampled from the sets of registration points of the shapes u and W can be used to resolve the four unknown variables of the similarity matrix, that is, translation in the x-direction t x, translation in the y-direction t y, rotation angle θ, and scaling factor s. More specifically, the shape u has two registration points, both coincident with the intersections of two pairs of hyperplanes, and the shape W has 16 registration points, all coincident with the intersections of the hyperplanes of its maximal lines. The automated sampling of two points out of the set of two registration points in the shape u and the set of 16 registration points in the shape W yields ![]() $C_2^{16} = 120$ pairs. The algorithm of the derivation of the similarity matrix checks whether any of the 120 pairs of pairs of points resolves the four unknown variables and the calculation yields eight pairs that lead to eight pictorially nonequivalent matches. Note that the derivation of the similarity matrix for a shape u having two or more registration points is the only one that currently works well among all possible cases of embedding, see, for example, SGI (Krishnamurti, Reference Krishnamurti1982; Krishnamurti and Giraud, Reference Krishnamurti and Giraud1986); SGS (Chase, Reference Chase1989); GRAIL (Krishnamurti, Reference Krishnamurti1992); GEdit (Tapia, Reference Tapia1999); and SGI-RF (Trescak et al., Reference Trescak, Rodriguez and Esteva2009).
$C_2^{16} = 120$ pairs. The algorithm of the derivation of the similarity matrix checks whether any of the 120 pairs of pairs of points resolves the four unknown variables and the calculation yields eight pairs that lead to eight pictorially nonequivalent matches. Note that the derivation of the similarity matrix for a shape u having two or more registration points is the only one that currently works well among all possible cases of embedding, see, for example, SGI (Krishnamurti, Reference Krishnamurti1982; Krishnamurti and Giraud, Reference Krishnamurti and Giraud1986); SGS (Chase, Reference Chase1989); GRAIL (Krishnamurti, Reference Krishnamurti1992); GEdit (Tapia, Reference Tapia1999); and SGI-RF (Trescak et al., Reference Trescak, Rodriguez and Esteva2009).

Fig. 4. An example of determinate similar embedding with two registration points that is successfully implemented by the automated derivation of the similarity matrix. (a) Shape u; (b) registration points R u; (c) shape W; (d) registration points R W; and (e) eight results of unrestricted embedding under similarity transformations.
Determinate embedding under affine transformations
An embedding of an affine instance of a shape u in a shape W is determinate when the shape u has three or more registration points – provided that at least three registration points in the shapes u and W are not collinear. The three noncollinear registration points provide sufficient information to resolve six unknown variables of affine matrix including translation in the x-direction t x, translation in the y-direction t y, rotation angle θ, and stretching factor in the x-direction α x, stretching factor in the y-direction α x, and a shearing angle φ. An example of a determinate embedding under affinity transformations of a shape u having three registration points that is successfully – albeit partially – implemented by the derivation of the affine matrix is shown in Figure 5. The shape u has three registration points, all coincident with the intersections of three pairs of hyperplanes, and the shape W has 16 registration points arranged as discussed above. The automated derivation of the affine matrix is partially successful here because some triples sampled from the set of registration points of the shapes W are collinear and in these cases the computation fails to resolve the six unknown variables. The automated sampling of three points out of the set of 16 registration points in the shape W should limit itself in the set comprised by the complete set of registration points minus the triples of points incident in the four pairs of hyperplanes above, that is, ![]() $C_3^{16} -( {4 \times C_3^5 {\rm \;} + 4 \times C_3^4 } ) = $
$C_3^{16} -( {4 \times C_3^5 {\rm \;} + 4 \times C_3^4 } ) = $ ![]() $560-54 = 504$ triples of registration points. The algorithm of the automated derivation of the affine matrix should check whether any of the 504 pairs of triples of points resolves the six unknown variables and the calculation should yield eight pairs of triples that lead to eight pictorially nonequivalent matches.
$560-54 = 504$ triples of registration points. The algorithm of the automated derivation of the affine matrix should check whether any of the 504 pairs of triples of points resolves the six unknown variables and the calculation should yield eight pairs of triples that lead to eight pictorially nonequivalent matches.
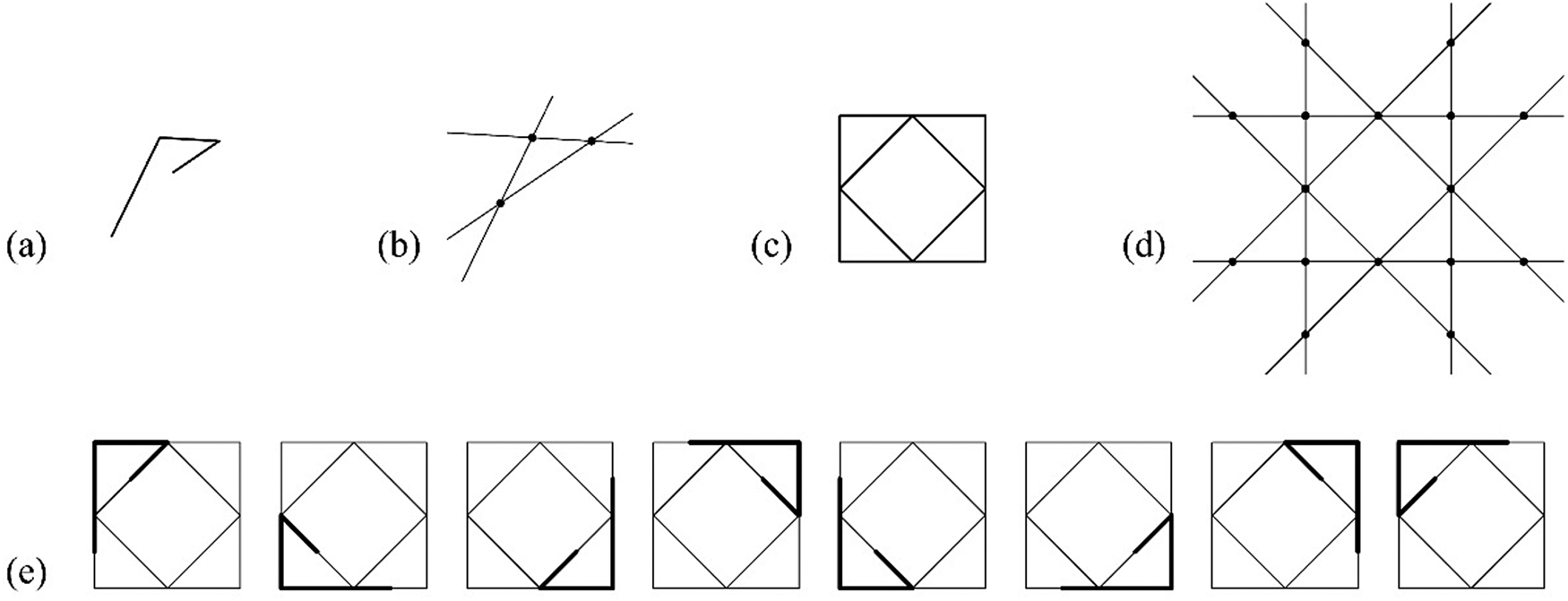
Fig. 5. An example of determinate affine embedding using three registration points that is partially implemented by the automated derivation of the affine matrix. (a) Shape u; (b) registration points R u; (c) shape W; (d) registration points R W; and (e) eight results of determinate embedding under affinity transformations.
Determinate embedding under linear transformations
An embedding of a projective instance of a shape u in a shape W is determinate when the shape u has four or more registration points – provided that at least three registration points in the shapes u and W are not collinear. An example of a determinate embedding under linearity transformations of a shape u having four registration points that is successfully – albeit partially – implemented by the derivation of the homography matrix (Hartley and Zisserman, Reference Hartley and Zisserman2004) is shown in Figure 6. The four noncollinear registration points provide sufficient information to resolve the nine unknown variables of a homography matrix h 0 to h 8, including the combinations of the rotation angles θ x, θ y, and θ z; translation in the x-direction t x, translation in the y-direction t y, translation in the z-direction t z, and a projection parameter p. Note that the rotation and the translation parameters represent the transformation of the camera (viewer), that is, the transformation of the world coordinates. With the projection parameter p, the two-dimensional perspective transformation can be represented as a homography matrix with nine variables. The shape u has six registration points, two coincident with the intersections of two pairs of maximal lines and four more coincident with the intersections of four pairs of hyperplanes; and the shape W has 16 registration points arranged as discussed above. The automated derivation of the homography matrix is partially successful because some quadruples and triples of points sampled from the set of registration points of the shape W are collinear, and thusly, the computation fails to resolve the nine unknown variables for these particular subsets. The problem here is that the computation of the derivation of the homography matrix needs to exclude: (a) the four sets of collinear triples of registration points in the shape u and (b) the eight sets of collinear triples in the shape W. The automated sampling of four points out of the set of six registration points in the shape u should limit itself to a pair of registration points for each hyperplane, that is, ![]() $C_4^6 -4 \times C_3^3 \times 3 = 3$ quadruples (as opposed to
$C_4^6 -4 \times C_3^3 \times 3 = 3$ quadruples (as opposed to ![]() $C_4^6 = 15) , \;$ and the corresponding automated sampling of four points out of the set of 16 registration points in the shape W should limit itself to a pair of registration points for each hyperplane too, that is,
$C_4^6 = 15) , \;$ and the corresponding automated sampling of four points out of the set of 16 registration points in the shape W should limit itself to a pair of registration points for each hyperplane too, that is, ![]() $C_4^{16} -4 \times C_3^5 {\rm \;} \times 13-4 \times C_3^4 \times 13 = 1092$ quadruples as opposed to
$C_4^{16} -4 \times C_3^5 {\rm \;} \times 13-4 \times C_3^4 \times 13 = 1092$ quadruples as opposed to ![]() $C_4^{16} = 1820$. The algorithm of the automated derivation of the homography matrix should check whether any of the 1092 pairs of quadruples of points resolves the nine unknown variables and the calculation should yield 32 pairs of quadruples that lead to 32 pictorially nonequivalent matches.
$C_4^{16} = 1820$. The algorithm of the automated derivation of the homography matrix should check whether any of the 1092 pairs of quadruples of points resolves the nine unknown variables and the calculation should yield 32 pairs of quadruples that lead to 32 pictorially nonequivalent matches.
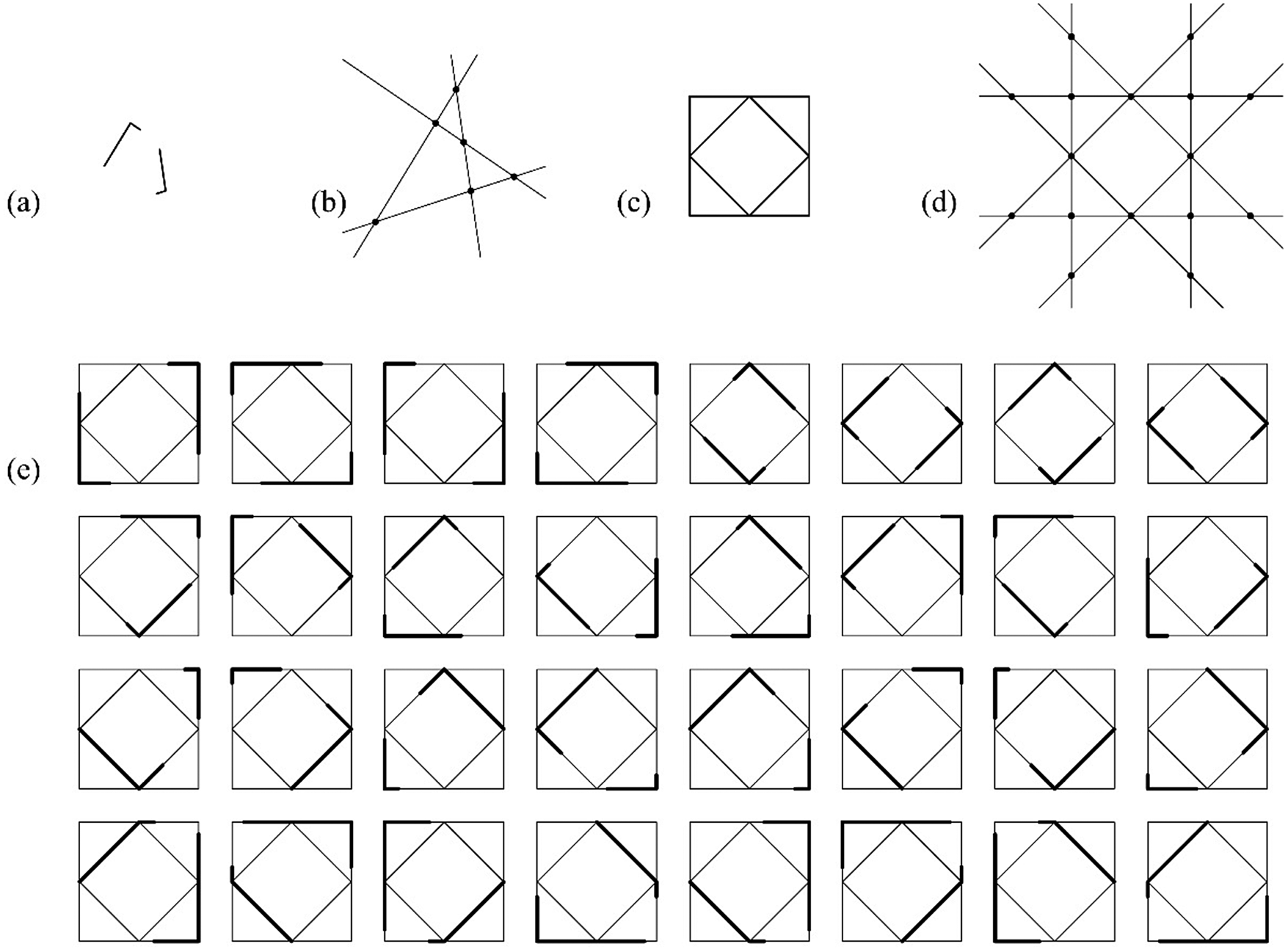
Fig. 6. An example of a determinate projective embedding using four registration points that is partially implemented by the automated derivation of the homography matrix. (a) Shape u; (b) registration points R u; (c) shape W; (d) registration points R W; and (e) 32 results of determinate embedding under linearity transformations.
Implementation of indeterminate embedding using transformation matrices
The review of the implementation of the derivation of the transformation matrices for determinate embeddings foregrounded several problems with the implementation of the current algorithm and its ability to provide robust calculations for visual embeddings. Intuitively, the review of the implementation of the derivation of the transformation matrices for indeterminate embeddings will foreground even more challenges that will need to be properly addressed. In general, the embedding is indeterminate when the shape u has less registration points than required to derive the transformation matrices. For the four types of linear transformations and Num(R u) the number of registration points of the shape u, there are ten cases of indeterminate embedding to consider: (a) Num(R u) = 0 under isometric transformations; (b) Num(R u) = 1 or 0 under similarity transformations; (c) Num(R u) = 2, 1, or 0 under affine transformations; and (d) Num(R u) = 3, 2, 1, or 0 under linear transformations. Clearly, none of these cases can be resolved by current implementations of automated derivations of transformation matrices, and yet, the fundamental problem remains the same as the one already encountered in the problems discussed on determinate embeddings: the selection of the right kind of families of registration points for the automated sampling to derive the transformation matrices. A possible way to address this issue is to identify ways to pick up “distinguishable” points (Krishnamurti, Reference Krishnamurti1981) in the shape u, test their spatial relations to other points in the shape u as well as to corresponding pairs of points in the shape W, and then determine gradually the transformation and the derivation of the matrix. Put differently, a possible way to address the issue is to view the shape u as an instance of a parameterized shape U comprised by variables x – typically, the lines and the angles between the lines of the shape u and their associated midpoints and endpoints (intersections are already collected in the set of registration points) – assign real values determined by a function g to satisfy explicit conditions and constraints to produce the shape g(U) (Stiny, Reference Stiny, Newsome, Spillers and Finger1989) and check whether there is a transformation f of the shape g(U), such that the shape f(g(U)) is part of the design W. For every match of one of the variables of the shape f(g(U)) in W, there is an emergent set of distinguishable registration points that may be selected to determine the visual match. This multi-stepped process can indeed address all possible cases of indeterminate embedding and it always involves a number of steps equal to Num(required registration points) − Num(R g(U)) + 1. Even more, the spatial relation between the shape f(g(U)) and the shape W partitions the symmetry group of the shape f(g(U)) into q classes in terms of W, and in congruence with the determinate matchings, it specifies how the shape rule can be used in q distinct ways (Stiny, Reference Stiny1991).
Significantly, the sequence of transformations for the resolution of the indeterminate does matter and may involve loops too. For example, the sequence for a shape embedding under isometric transformations consists of a translation, rotation, and a reflection, if required. Any transformation f derived in this manner is the product (multiplication) of the sequence of the applicable transformations, that is, t 1t 2…t n. Note that not every transformation t i is effective. A trivial example is when the shape g(U) is equal to shape W where shape embedding is processed without applying any transformation, regardless shape embedding is processed under isometric, similar, affine or linear transformation. More importantly though, not all transformations t 1, t 2,…, t n, within the sequence of transformations can be determined. In the same example of, say, a shape embedding under isometric transformations, if the translation cannot be determined, then the next transformation in the sequence, rotation, is determined by calculating the angle between the hyperplanes of g(U) and W – even at the absence of a registration point found in g(U) – and the translation is determined afterwards based on some value selected through a user response from an admissible range or some predefined criterion. The section below provides an overview of the ten possible cases of indeterminate embedding that feature less registration points than the ones required for the derivation of the transformation matrices and fills with some detail the sketch outlined above.
Indeterminate embedding under isometric transformations
An example of an indeterminate embedding under isometric transformations of a shape u having no registration points is shown in Figure 7. The shape u does not have the required registration points for the derivation of the isometric matrix and the computation fails. To resolve the three unknown variables of the isometric matrix including the translation in the x-direction t x, the translation in the y-direction t y, and the rotation angle θ, a multi-stepped process can be adopted to address this problem. In this case, a two-stepped process is used to determine the embedding results. The first step is processed automatically by taking two endpoints of the shape g(U) to determine the rotation θ and confine the translation range to a one-dimensional space, that is, any maximal line of W that has a larger length than g(U). After the first step, the indeterminacy of embedding occurs in translation within any maximal line which is longer than g(U). The second step requires an additional input (manual visual inspection or an automated optimization calculation) for a translational parameter t with a range lower bound ≤ t ≤ upper bound, here, the lower bound = 0 and upper bound = (l i − a)/2, where l i is the lengths of the sides of the two squares and a is the length of the line of g(U) – the two parametric values are different for each square. Once the value of t is provided, in some absolute or relative sense, the system can determine the final embedding results. Note that the calculation of the range of translations for each embedding uses the midpoint of the shape f(g(U)) as a distinguishable point so that it can calculate specifically the nonequivalent matchings that will be then permuted by the actions of the symmetry group of each line in the shape W. In this particular case, the translation of the shape g(U) in any of the two types of embedding schemas in the shape W produces eight matchings but when the midpoint of the shape f(g(U)) coincides with the midpoint of any of the edges of the shape W, one symmetry element of the shape g(U) coincides with one of the symmetry elements of the shape W and the shape matches reduce to four per square.
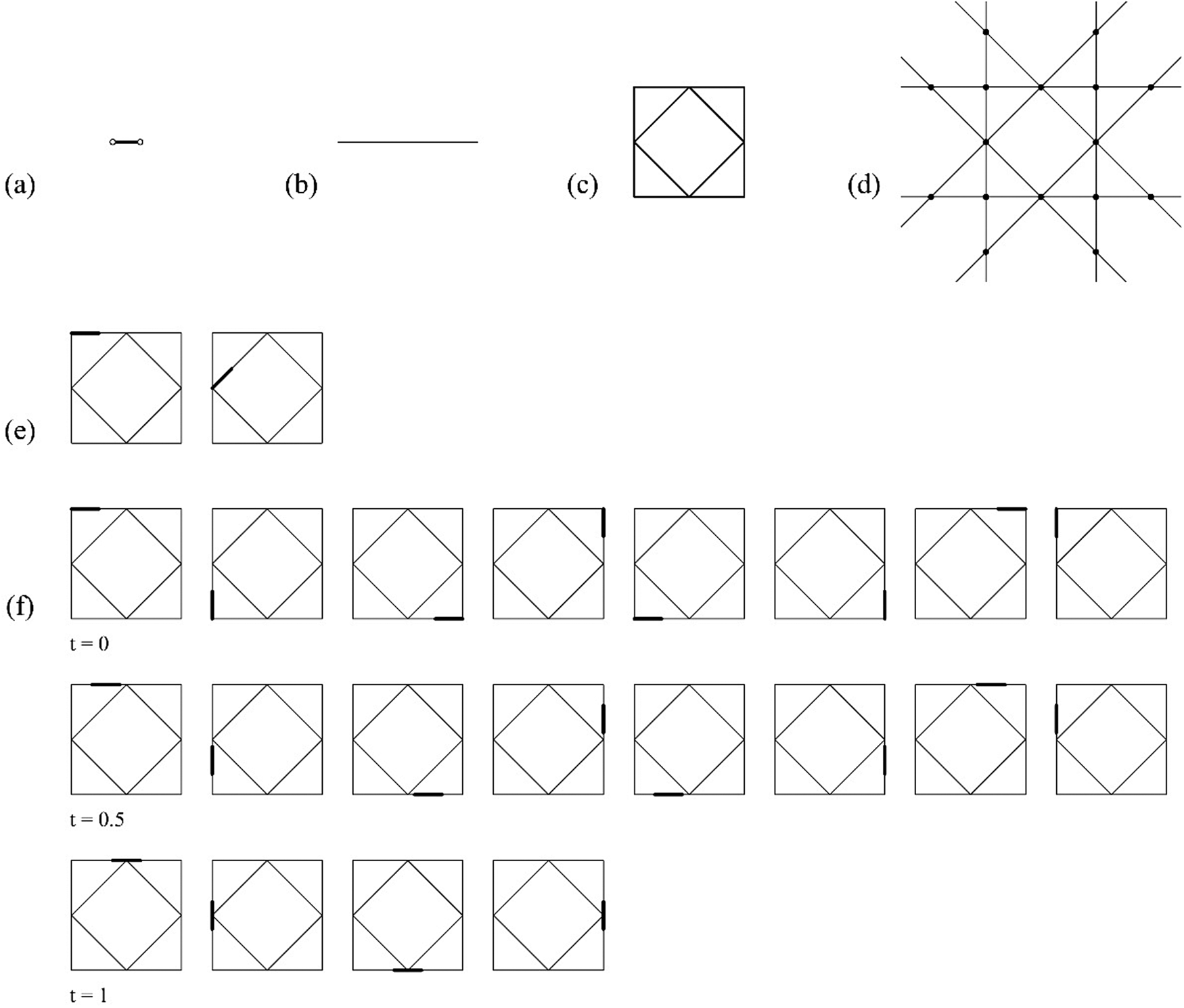
Fig. 7. An example of indeterminate congruent embedding using no registration points. (a) An instance of a parameterized shape g(U); (b) registration points R g(U); (c) shape W; (d) registration points R W; (e) two embedding schemas, one per set of lines of equal lengths; (f) three instances of one of the two embedding schemas with assignments t: 0, 0.25, and 0.5, one per row, and their equivalent embeddings by the actions of the symmetry group of the shape W.
Indeterminate embedding under similarity transformation
An example of an indeterminate embedding under similarity transformations of a shape u having one registration point is given in Figure 8. In this example, two registration points are required to resolve the four unknown variables of a similarity matrix including the rotation angle θ, the translation in the x-direction t x, the translation in the y-direction t y, and the scaling factor s. The shape u does not have the required registration points for the derivation of the similarity matrix and the computation fails. To address this problem, a two-stepped process is used to determine the embedding results. The first step is processed automatically by taking one registration point and one endpoint of g(U) to derive θ, t x, and t y. The second step requires an additional input for the scaling factor s because the indeterminacy occurs in scaling. The process of dealing with indeterminate embedding in scaling is similar to the indeterminate embedding in translation and it can be similarly resolved by manual visual inspection or an automated optimization calculation. The shape embedding can be parameterized with a scaling parameter s that has a scaling range lower bound ≤ s ≤ upper bound, in this example, the lower bound = 0 and the upper bound = 1. The calculation of the lower bound and upper bound is context-sensitive, and the indeterminacy might show up as multiple parameters. In this example, there is a single embedding schema of the shape f(g(U)) in the shape W, eight matches under the symmetry group of the shape W, and for each one of them there is an assignment g parameterized with a scaling factor s with a range 0 ≤ s ≤ 1.
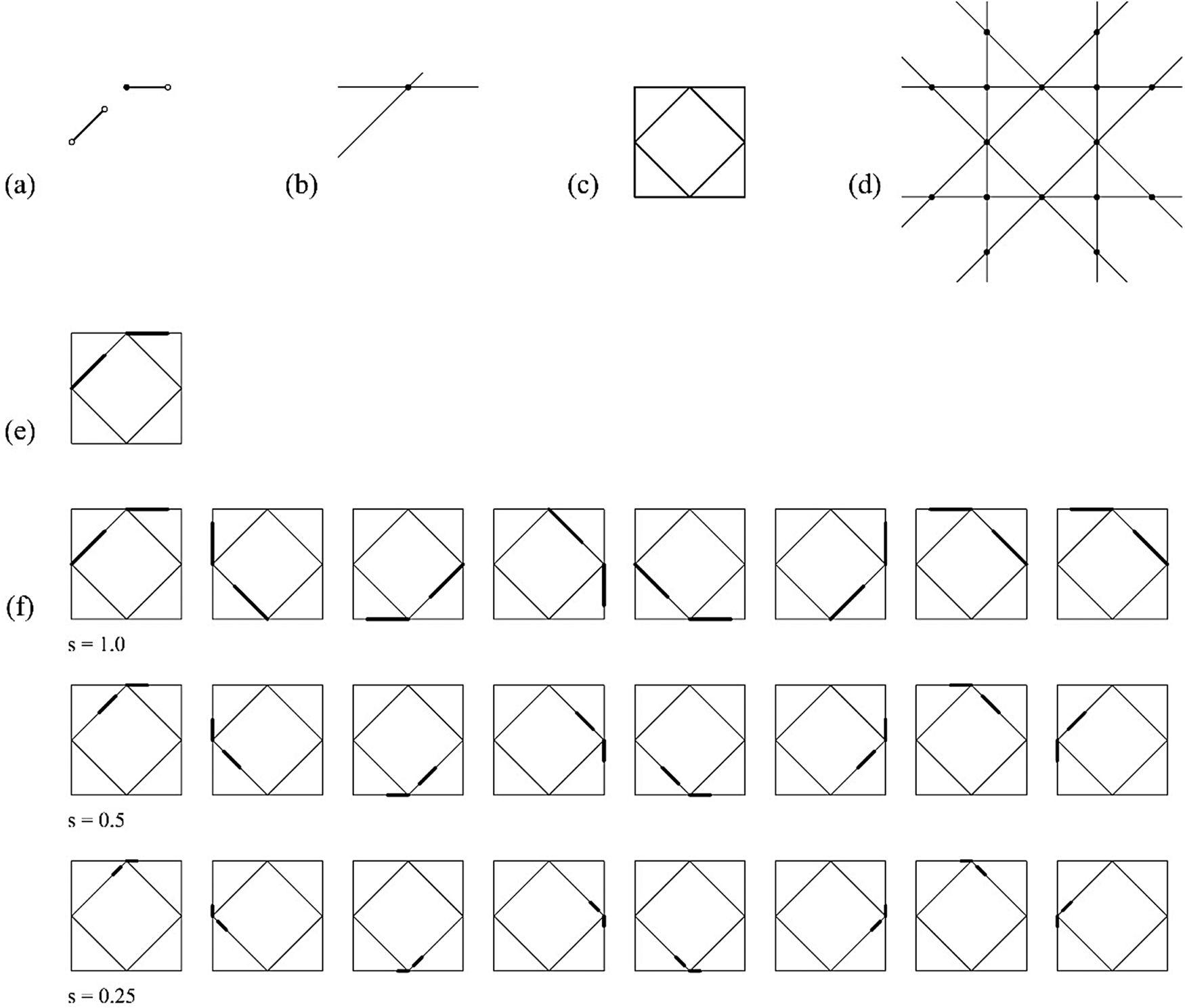
Fig. 8. An example of indeterminate similar embedding using one registration point. An instance of a parameterized shape g(U); (b) registration points R g(U); (c) shape W; (d) registration points R W; (e) the single embedding schema; (d) three instances of the single embedding schema with assignments s: 1, 0.5, and 0.25, one per row, and their equivalent embeddings by the actions of the symmetry group of the shape W.
An example of an indeterminate embedding under similarity transformations of a shape u having no registration points is given in Figure 9. In this example, two registration points are required to resolve the four unknown variables of the similarity matrix including the rotation angle θ, the translation in the x-direction t x, the translation in the y-direction t y, and the scaling factor s. The shape u does not have the required registration points for the derivation of the similarity matrix and the computation fails. To address this problem, a three-stepped process is used to determine the embedding results. The first step is processed automatically by taking two endpoints of g(U) to derive θ, and confine the translation range in one-dimensional space, that is, any maximal line of W. The second step requires an additional input for the scaling parameter s as the indeterminacy occurs in both scaling and translation. The third step requires an input for the translation parameter t. In this case, the scaling parameter s has a range lower bounds ≤ s ≤ upper bounds, here, the lower bounds = 0 and upper bounds = l i/a, where l i is the lengths of the sides of the two squares and a is the length of the line of g(U). The translational parameter t has a range lower bound ≤ t ≤ upper bound, here, the lower bond = 0 and upper bound = (l i − s × a)/2, where l i the lengths of the sides of the two squares and a is the length of the line of g(U). To simplify the notation, the translation parameter can be normalized as a parameter t′ with a normalized range 0 ≤ t′ ≤ 1. In this example, there are two embedding schemas of the shape f(g(U)) in the shape W, eight matches for each shape under the symmetry group of the shape W, four matches when the midpoint of the shape f(g(U)) coincides with the midpoint of any of the edges of the shape W, and for each one of them, there is an assignment g parameterized with a translation factor t with a range 0 ≤ t′ ≤ 1.
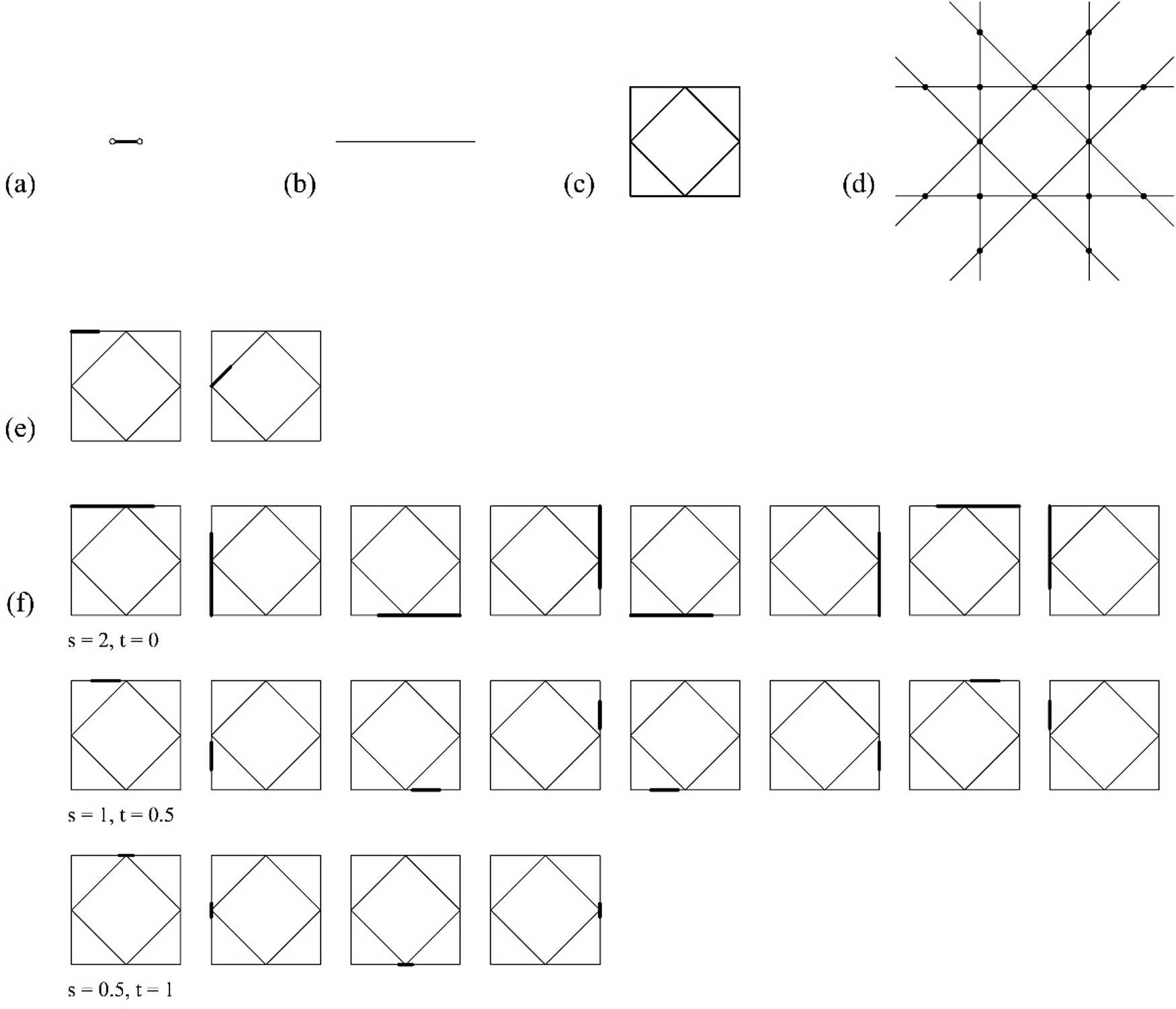
Fig. 9. An example of indeterminate similar embedding using no registration points. (a) An instance of a parameterized shape g(U); (b) registration points R g(U); (c) shape W; (d) registration points R W; (e) two embedding schemas, one per set of lines of equal lengths; (f) three instances of one of the two embedding schemas with assignments s, t: (2, 0), (1, 0.5), and (0.5, 1), one per row, and their equivalent embeddings by the actions of the symmetry group of the shape W.
Indeterminate embedding under affine transformations
An example of an indeterminate embedding under affine transformations of a shape u having two registration points is given in Figure 10. In this example, three registration points are required to resolve the six unknown variables of an affine matrix including a rotation angle θ, translation in the x-direction t x, translation in the y-direction t y, stretching in the x-direction α x, stretching in the y-direction α y, and a shearing angle φ. The shape u does not have the required registration points for the derivation of the affine matrix and the computation fails. To determine the embeddings, a two-stepped process is used to determine the embedding results. The first step is processed automatically by taking two registration points and two endpoints of g(U) to derive θ, t x, t y, α y, and φ. The second step requires an input for the stretching parameter in the x-direction α x as the indeterminacy occurs in stretching in the x-direction in this particular instance (see Fig. 10f, first column). Note that the stretching direction varies from instance to instance, and the system should automatically detect the stretching direction and provide a valid range of stretching. Furthermore, the stretching parameters α x and α y are one-dimensional scaling parameters, that is, the uniform scaling is presented when α x = α y. In this case, in total, there are ![]() $C_2^{16} = 120$ pairs of registration points, and among these 120 pairs, there are eight pairs in the configuration where two lines are in parallel and one line is intersecting with the other two, in which the shape u can be embedded under an affine transformation. These eight pairs of embeddings represent two families and each family is parameterized by a stretching parameter α i with two ranges lower bond ≤ α i ≤ upper bond, for α i representing the stretching factor l i/a of two squares, where l i is the length of the side of the two squares and a is the length of the open-ended line of g(U). One of the embedding schemas has a range 0 ≤ α 1 ≤ 4, and the other a range
$C_2^{16} = 120$ pairs of registration points, and among these 120 pairs, there are eight pairs in the configuration where two lines are in parallel and one line is intersecting with the other two, in which the shape u can be embedded under an affine transformation. These eight pairs of embeddings represent two families and each family is parameterized by a stretching parameter α i with two ranges lower bond ≤ α i ≤ upper bond, for α i representing the stretching factor l i/a of two squares, where l i is the length of the side of the two squares and a is the length of the open-ended line of g(U). One of the embedding schemas has a range 0 ≤ α 1 ≤ 4, and the other a range ![]() $0 \le \alpha _2 \le 2\sqrt 2$. To simplify the notation of parameters, the parameter α i can be normalized with a range
$0 \le \alpha _2 \le 2\sqrt 2$. To simplify the notation of parameters, the parameter α i can be normalized with a range ![]() $0 \le \alpha _i^{\prime} \le 1$ for each family.
$0 \le \alpha _i^{\prime} \le 1$ for each family.
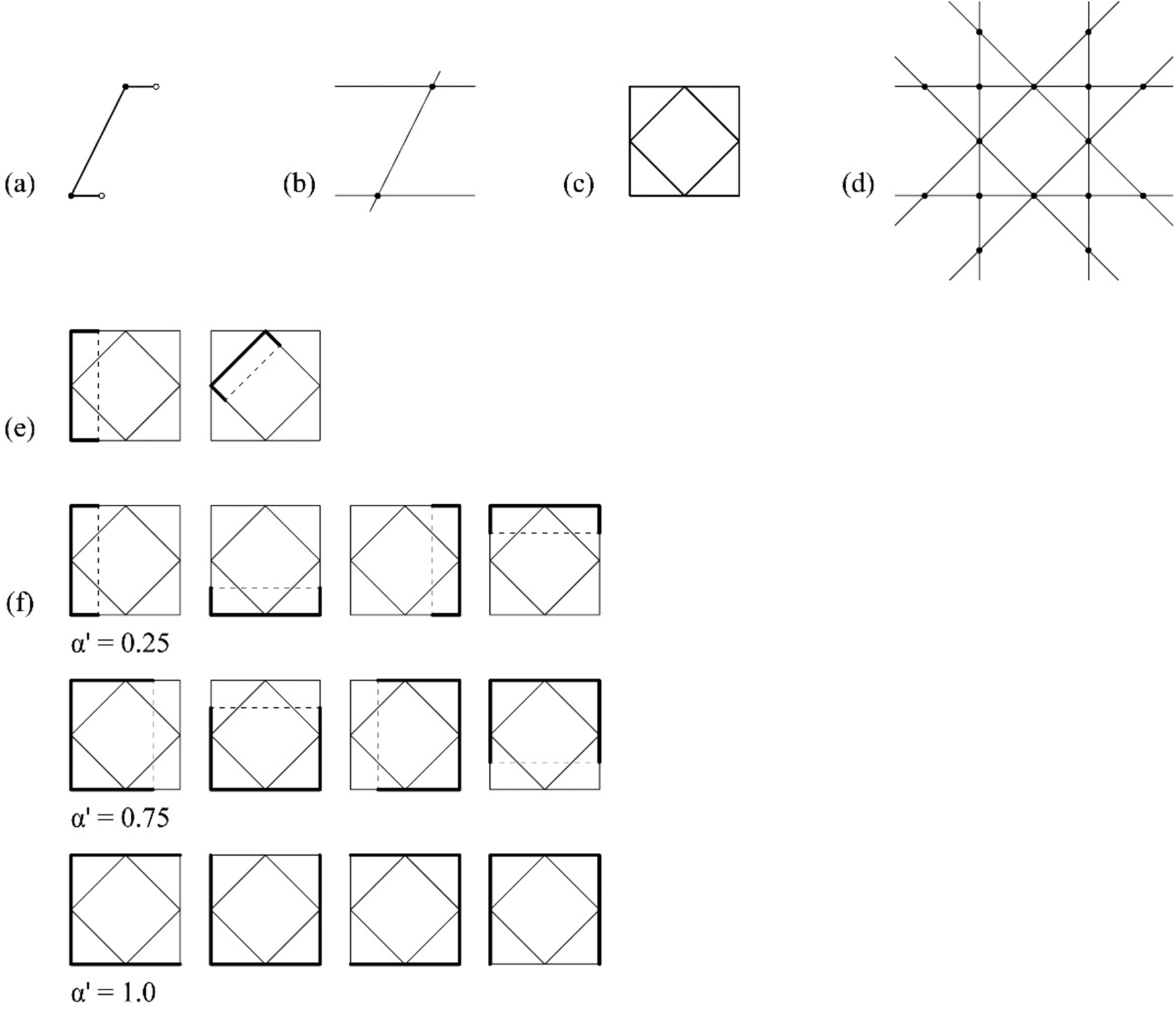
Fig. 10. An example of indeterminate affine embedding using no registration points. (a) An instance of a parameterized shape g(U); (b) registration points R g(U); (c) shape W; (d) registration points R W; (e) two embedding schemas, one per two pairs of parallel lines; (f) three instances of one of the two embedding schemas with assignments α′: 0.25, 0.75, and 1.0, one per row, and their equivalent embeddings by the actions of the symmetry group of the shape W.
An example of an indeterminate embedding under affine transformations of a shape u having one registration point is given in Figure 11. In this example, three registration points are required to resolve the six unknown variables of an affine matrix including a rotation angle θ, translation in the x-direction t x, translation in the y-direction t y, stretching in the x-direction α x, stretching in the y-direction α y, and a shearing angle φ. The shape u does not have the required registration points for the derivation of the affine matrix and the computation fails. To determine the embeddings, a three-stepped process is used to determine the embedding results. The first step is processed automatically by taking one registration point and two endpoints of g(U) to derive θ, t x, t y, and φ. Since the indeterminacy occurs in stretching both in the x-direction and y-direction, the second step requires an input for the stretching parameter in the x-direction α x and the third step requires an input for the stretching parameter in the y-direction α y for this particular instance (see Fig. 11f, first column). In this example, two ranges of stretching are provided: 0 ≤ α x ≤ 2 in the x-direction and 0 ≤ α y ≤ 2 in the y-direction. Among these 16 registration points in the shape W, there are four registration points where two maximal lines meet, four registration points where three maximal lines meet, and eight registration points where no maximal lines meet. Among those, the first two sets represent registration points in which the shape f(g(U) can be embedded, and therefore, there are 24 pairs of embedding classified into four schemas. Each schema is parameterized with two parameters α x and α y representing the stretching factors in the x-direction and y-direction, with ranges 0 ≤ α x ≤ l i/a x and 0 ≤ α y ≤ l i/a y, and l i representing the length of the sides for each square, a x is the length of the horizontal line of g(u), and a y is the length of the other line of g(u). To avoid double counting the results of embedding, a constraint of α x and α y is applied: a x ≤ a y.

Fig. 11. An example of indeterminate affine embedding using one registration points. (a) An instance of a parameterized shape g(U); (b) registration points R g(U); (c) shape W; (d) registration points R W; (e) four embedding schemas, one per two pairs of converging lines; (f) three instances of one of the four embedding schemas with assignments α x, α y: 1, 1, (1, 2), and (0.5, 3), one per row, and their equivalent embeddings by the actions of the symmetry group of the shape W.
An example of an indeterminate embedding under affine transformations of a shape u having no registration point is given in Figure 12. In this example, three registration points are required to resolve the six unknown variables of an affine matrix including a rotation angle θ, translation in the x-direction t x, translation in the y-direction t y, stretching in the x-direction α x, stretching in the y-direction α y, and a shearing angle φ. The shape u does not have the required registration points for the derivation of the affine matrix and the computation fails. To determine the embeddings, a four-stepped process is used to determine the embedding results. The first step is processed automatically by taking four endpoints of g(U) to derive θ. Since the indeterminacy occurs in shear, stretch, and translation, the four endpoints can be used to confine the shear range, stretch range, and translation range to one-dimensional space in the y-direction for this particular instance (see Fig. 12f, first column). Here, the indeterminacy of the embedding occurs in three parameters so their ranges are correlated in a complex parametric function. More specifically, the shear transformation is parameterized with an angle parameter φ with a range ![]() $-\cos ^{{-}1}( 2\sqrt 5 /5) \le $
$-\cos ^{{-}1}( 2\sqrt 5 /5) \le $ ![]() $\varphi \le \cos ^{{-}1}( 4/5) -\cos ^{{-}1}\left({2\sqrt 5 /5} \right)$, which can be normalized as 0 ≤ φ′ ≤ 1; the stretch transformation, where l i is the length of sides of the two squares and a is the length of the lines of g(U), is parameterized with a range
$\varphi \le \cos ^{{-}1}( 4/5) -\cos ^{{-}1}\left({2\sqrt 5 /5} \right)$, which can be normalized as 0 ≤ φ′ ≤ 1; the stretch transformation, where l i is the length of sides of the two squares and a is the length of the lines of g(U), is parameterized with a range
 $$0 \le \alpha \le \left({\displaystyle{{l_i} \over a}\cdot \left({\displaystyle{{\tan \left({( {\cos }^{{-}1}\displaystyle{{\sqrt 5 } \over 5}} \right)-\varphi ) -1} \over {\tan \left({( {\cos }^{{-}1}\displaystyle{{\sqrt 5 } \over 5}} \right)-\varphi ) }}} \right)-1} \right), \;$$
$$0 \le \alpha \le \left({\displaystyle{{l_i} \over a}\cdot \left({\displaystyle{{\tan \left({( {\cos }^{{-}1}\displaystyle{{\sqrt 5 } \over 5}} \right)-\varphi ) -1} \over {\tan \left({( {\cos }^{{-}1}\displaystyle{{\sqrt 5 } \over 5}} \right)-\varphi ) }}} \right)-1} \right), \;$$which can be normalized as 0 ≤ α′ ≤ 1; and the translation parameter has a range
 $$0 \le t \le \displaystyle{{l_i} \over 2}\cdot \left({\displaystyle{{\tan \left({( {\cos }^{{-}1}\displaystyle{{\sqrt 5 } \over 5}} \right)-\varphi ) -1} \over {\tan \left({( {\cos }^{{-}1}\displaystyle{{\sqrt 5 } \over 5}} \right)-\varphi ) }}} \right)-\alpha \cdot a, \;$$
$$0 \le t \le \displaystyle{{l_i} \over 2}\cdot \left({\displaystyle{{\tan \left({( {\cos }^{{-}1}\displaystyle{{\sqrt 5 } \over 5}} \right)-\varphi ) -1} \over {\tan \left({( {\cos }^{{-}1}\displaystyle{{\sqrt 5 } \over 5}} \right)-\varphi ) }}} \right)-\alpha \cdot a, \;$$which can be normalized as 0 ≤ t′ ≤ 1. Note that the range of translation is constrained to avoid double counting. In this case, there are two embedding schemas and each schema is parameterized with three normalized parameters φ′, α′, and t′.
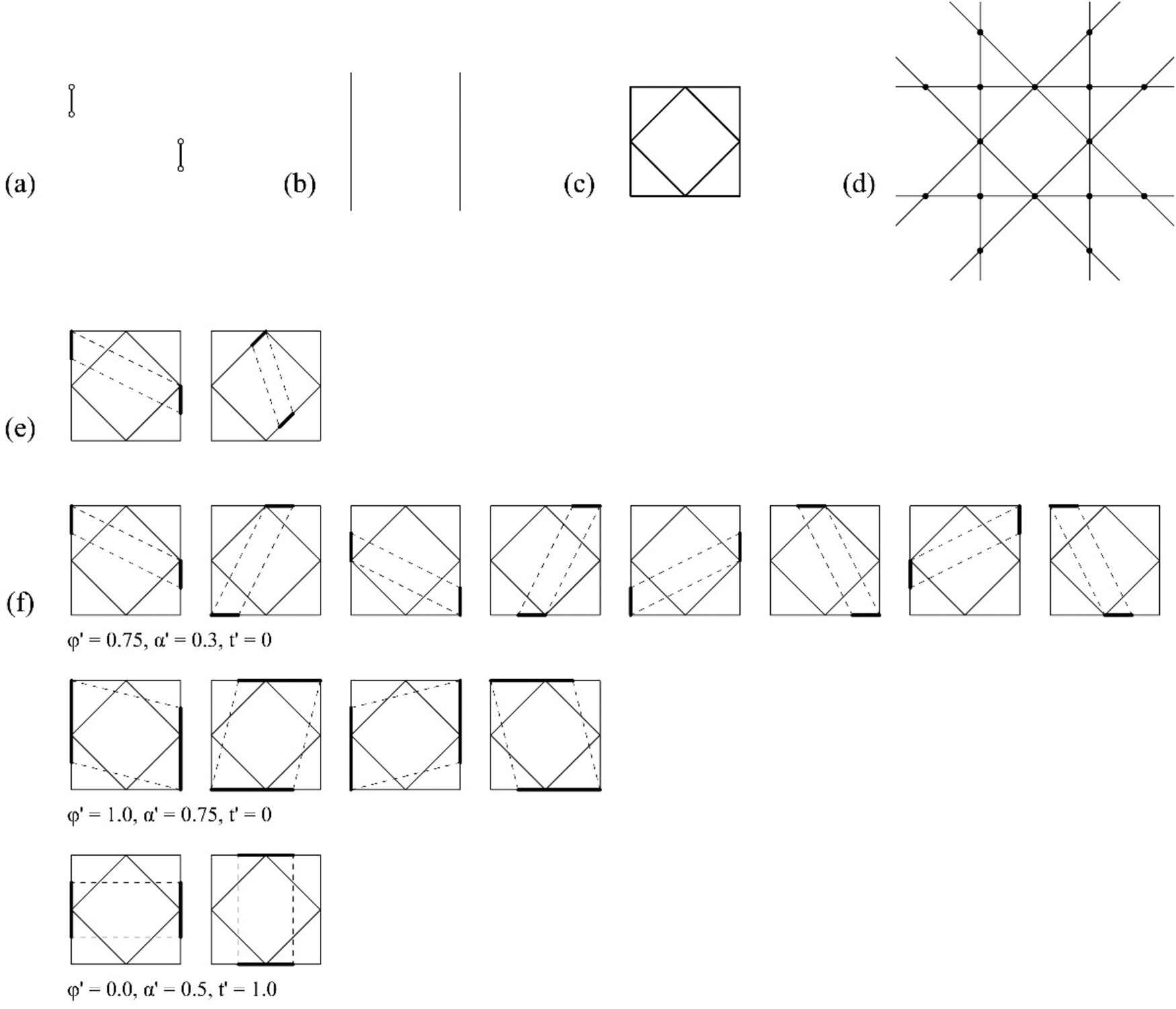
Fig. 12. An example of indeterminate affine embedding using no registration points. (a) An instance of a parameterized shape g(U); (b) registration points R g(U); (c) shape W; (d) registration points R W; (e) two embedding schemas, one per two pairs of parallel lines; (f) three instances with assignments φ′, α′, t′: (0.75, 0.3, 0), (1, 0.75, 0), and 0, 0.5, 1, one per row, and their equivalent embeddings by the actions of the symmetry group of the shape W.
Indeterminate embedding under linear transformation
An example of an indeterminate embedding under linear transformations of a shape u having three registration points is shown in Figure 13. For linear transformation, four registration points are required to resolve the nine unknown variables of a homography matrix. The shape u does not have the required registration points for the derivation of the homography matrix and the computation fails. To determine the embeddings, a two-stepped process is used. The first step is processed automatically by taking three registration points which can be viewed as the process that the shape g(U) is translated and rotated so that the three registration points are aligned with any three registration points of W. Once the three registration points are embedded into W, the second step requires an input for the fourth point to determine the final embeddings. In this case, the valid range of the additional point lies in a convex quadrilateral bounding box added on the shape g(U). In this case, there are eight registration points of W, where two or more lines meet, in which the shape g(U) can possibly be embedded. The single embedding schema is parameterized by the additional registration point represented with a pair of normalized parameters (p x, p y) with two normalized ranges 0 < p x < ∞ and 0 < p y < ∞. Note that p x and p y is constrained by a relation p x + p y > l i/2 to keep the bounding box as a convex quadrilateral and constrained by a relation p x ≥ p y to avoid double counting.
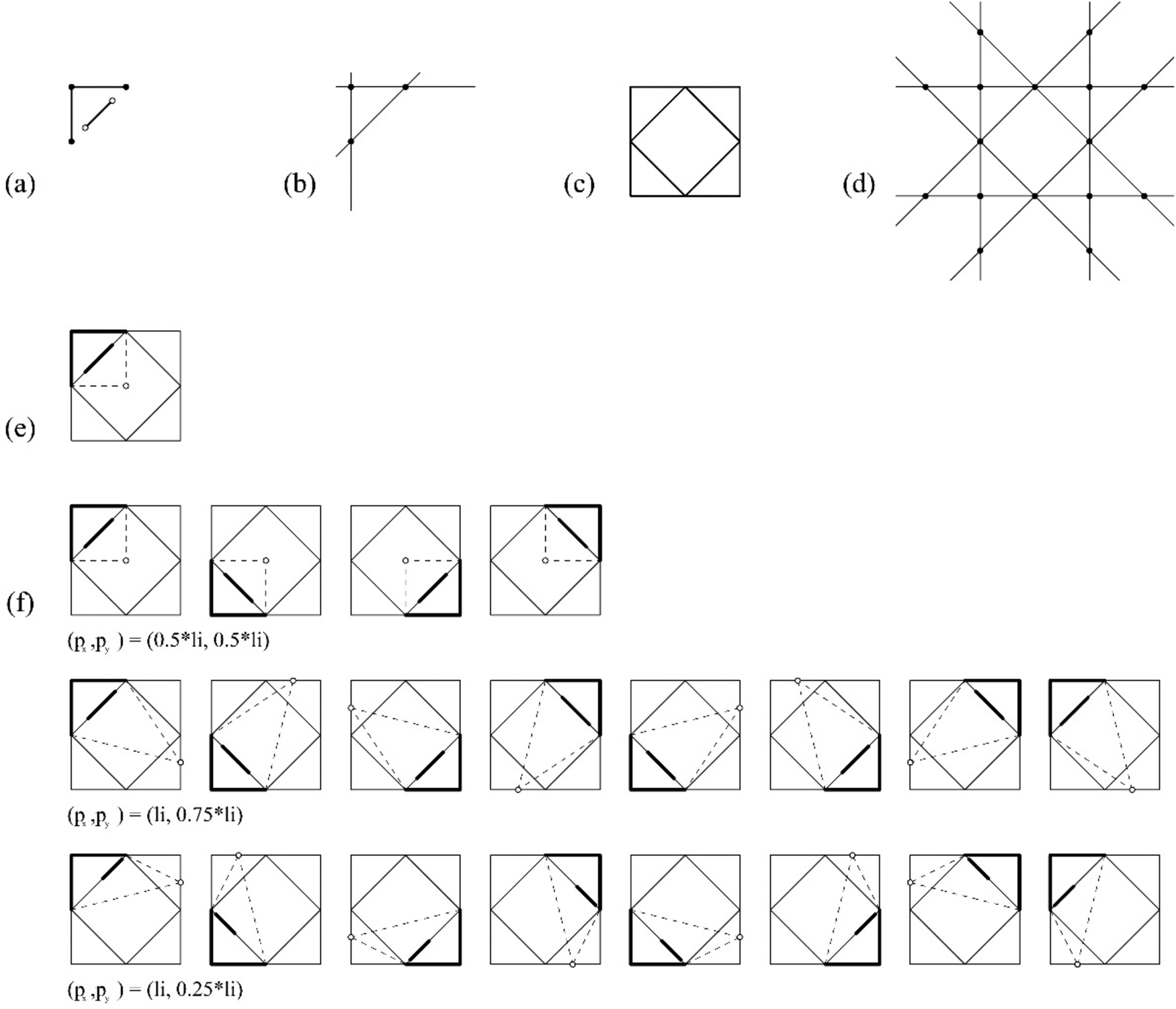
Fig. 13. An example of indeterminate projective embedding using three registration points. An instance of a parameterized shape g(U); (b) registration points R g(U); (c) shape W; (d) registration points R W; (e) one embedding schema; (f) three instances of the single embedding schema with assignments of ![]() $p_x^{\prime} , \;p_y^{\prime}$: 0.5l i, 0.5l i, (l i, 0.75l i), and l i, 0.25l i one per row, and their equivalent embeddings by the actions of the symmetry group of the shape W.
$p_x^{\prime} , \;p_y^{\prime}$: 0.5l i, 0.5l i, (l i, 0.75l i), and l i, 0.25l i one per row, and their equivalent embeddings by the actions of the symmetry group of the shape W.
An example of an indeterminate embedding under linearity transformations of a shape u having two registration points is shown in Figure 14. Similar to the previous case, four registration points are required to resolve the nine unknown variables of a homography matrix h 0 to h 8. The shape u does not have the required registration points for the derivation of the homography matrix and the computation fails. To determine the embeddings, a three-stepped process is used. The first step is processed automatically by taking two registration points of the shape g(U), map them with any two registration points of W, and have the two short lines of g(U) rotated to align with two maximal lines of W. Once the two registration points are embedded into W and the two short lines are embedded in the two maximal lines of W, the second step requires an input for the third point. In general, the third point can be any point on the world plane, however, the selection of the third point can be confined in a certain range, in this example, as the translation of the endpoint of the upper short line of the shape g(U) within the maximal line of W. Similarly, the third step requires an input for the fourth point, and the endpoint of the lower short line of g(U) as the fourth point. In total, there are ![]() $C_3^8 = 56$ triplets of lines in triangular configurations and the configurations where two lines are in parallel and the other line is nonparallel to another two. Among these 56 triplets, there are 40 triplets where f(g(U)) can be embedded for the bonding boxes of the triplets are convex quadrilaterals. There 40 triplets are classified into seven embedding schemas, and each schema is parameterized by two additional registration points represented as two normalized parameters
$C_3^8 = 56$ triplets of lines in triangular configurations and the configurations where two lines are in parallel and the other line is nonparallel to another two. Among these 56 triplets, there are 40 triplets where f(g(U)) can be embedded for the bonding boxes of the triplets are convex quadrilaterals. There 40 triplets are classified into seven embedding schemas, and each schema is parameterized by two additional registration points represented as two normalized parameters ![]() $p_1^{\prime}$ and
$p_1^{\prime}$ and ![]() $p_2^{\prime}$ with the normalized ranges
$p_2^{\prime}$ with the normalized ranges ![]() $0 < p_1^{\prime} < 1$ and
$0 < p_1^{\prime} < 1$ and ![]() $0 < p_2^{\prime} < 1$. Note that a constraint
$0 < p_2^{\prime} < 1$. Note that a constraint ![]() $p_1^{\prime} < p_2^{\prime}$ is applied to avoid double counting. This case shows a strategy of inputting additional points to avoid infinite possibilities. Note that the indeterminacy theoretically occurs in one-point perspective transformation, but the indeterminacy can be mapped to the translation of the two endpoints because the bounding box of g(U) is a parallelogram which is defined by the two registration points and two endpoints. Hence, the perspective transformation can be viewed as the transformation from a parallelogram to a trapezoid and the two endpoints must occur on the two maximal lines of W. In the cases later in this section, the selection of the additional points follows this strategy demonstrated in this example.
$p_1^{\prime} < p_2^{\prime}$ is applied to avoid double counting. This case shows a strategy of inputting additional points to avoid infinite possibilities. Note that the indeterminacy theoretically occurs in one-point perspective transformation, but the indeterminacy can be mapped to the translation of the two endpoints because the bounding box of g(U) is a parallelogram which is defined by the two registration points and two endpoints. Hence, the perspective transformation can be viewed as the transformation from a parallelogram to a trapezoid and the two endpoints must occur on the two maximal lines of W. In the cases later in this section, the selection of the additional points follows this strategy demonstrated in this example.
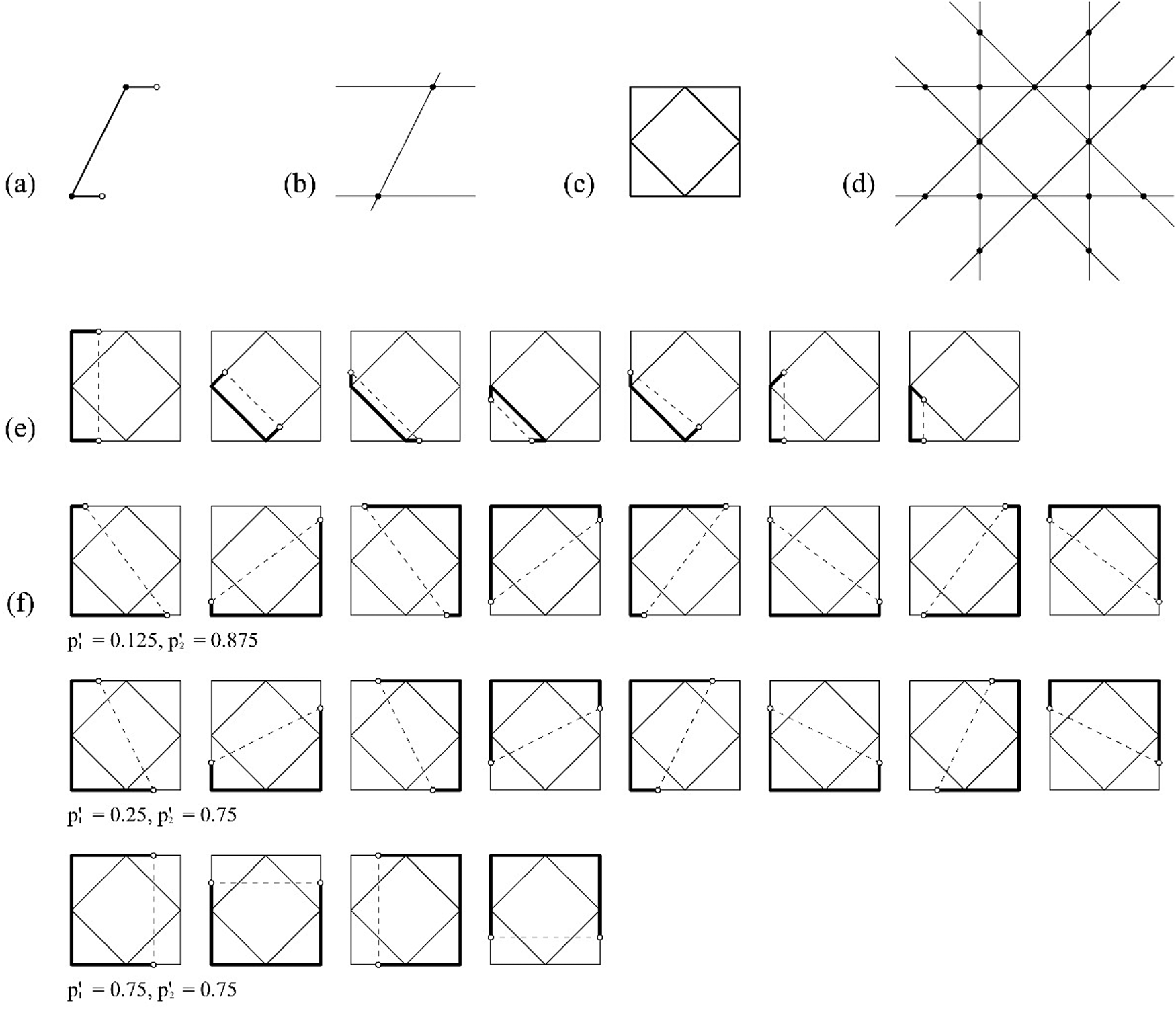
Fig. 14. An example of indeterminate projective embedding using two registration points. (a) An instance of a parameterized shape g(U); (b) registration points R g(U); (c) shape W; (d) registration points R W; (e) seven embedding schemas, one per a U-shape configuration of lines; (f) three instances of one of the seven embedding schemas with assignments ![]() $p_1^{\prime} , \;p_2^{\prime}$:
$p_1^{\prime} , \;p_2^{\prime}$: ![]() $( {0.125, \;0.875} )$, (0.25, 0.75), and 0.75, 0.75, one per row, and their equivalent embeddings by the actions of the symmetry group of the shape W.
$( {0.125, \;0.875} )$, (0.25, 0.75), and 0.75, 0.75, one per row, and their equivalent embeddings by the actions of the symmetry group of the shape W.
An example of an indeterminate embedding under linearity transformations of a shape u having one registration point is shown in Figure 15. Similar to the previous cases, four registration points are required to resolve the nine unknown variables of a homography matrix h 0 to h 8. The shape u does not have the required registration points for the derivation of the homography matrix and the computation fails. To determine the embeddings, a four-stepped process is used. The first step is processed automatically by taking one registration point and two endpoints of g(U), and this step can be viewed as the process that the shape g(U) is translated and rotated so that the registration point is aligned with a registration point of W, and the two lines of g(U) are rotated to align with the two maximal lines of W. Once the registration point is embedded into W and the two lines are embedded in the two maximal lines of W, the second step requires an input for the second point. In this case, the second point is suggested by the system as the endpoint of the longer line because this endpoint must be embedded in the maximal line of W (in this particular instance, the upper line of the large square of W) and can only translate along the maximal line if f(g(U)) ≤ W holds true. Thusly, the required input for this step is the position of this endpoint along the maximal line in which this endpoint is embedded. Similarly to the previous step, the third step requires an input for the third point which is suggested by the system as the farther endpoint (from the registration point) of the shorter line for the same reason. Thusly, the required input for this step is the position of this endpoint along the maximal line (in this particular instance, the left line of the large square of W) in which this endpoint is embedded. The fourth step requires an input for the fourth point, in this case, any point on the world plane with the constraint, that is, its selection should keep the bonding box of the shape g(U) as a convex quadrilateral. The valid ranges of the three registration points are all open-ended and can be calculated by manual visual inspection or some automated optimization. Among the 16 registration points in W, there are four registration points where two maximal lines meet and four registration points where three maximal lines meet and therefore, there are six embedding schemas for the shape g(U). Each schema is parameterized with three additional registration points represented as two normalized parameters ![]() $p_1^{\prime}$ and
$p_1^{\prime}$ and ![]() $p_2^{\prime}$ with normalized ranges
$p_2^{\prime}$ with normalized ranges ![]() $0 < p_1^{\prime} < 1$ and
$0 < p_1^{\prime} < 1$ and ![]() $0 < p_2^{\prime} < 1$, and one pair of normalized parameters
$0 < p_2^{\prime} < 1$, and one pair of normalized parameters ![]() $p_{3x}^{\prime} \;{\rm and\;}p_{3y}^{\prime}$ with a normalized range
$p_{3x}^{\prime} \;{\rm and\;}p_{3y}^{\prime}$ with a normalized range ![]() $0 < p_{3x}^{\prime} < \infty$ and
$0 < p_{3x}^{\prime} < \infty$ and ![]() $0 < p_{3y}^{\prime} < \infty$. Note that the parameters
$0 < p_{3y}^{\prime} < \infty$. Note that the parameters ![]() $p_{3x}^{\prime}$ and
$p_{3x}^{\prime}$ and ![]() $p_{3y}^{\prime}$ are constrained by a relation
$p_{3y}^{\prime}$ are constrained by a relation ![]() $p_{3x}^{\prime} + ( p_2^{\prime} /p_1^{\prime} ) p_{3y}^{\prime} -p_2^{\prime} > 0$.
$p_{3x}^{\prime} + ( p_2^{\prime} /p_1^{\prime} ) p_{3y}^{\prime} -p_2^{\prime} > 0$.
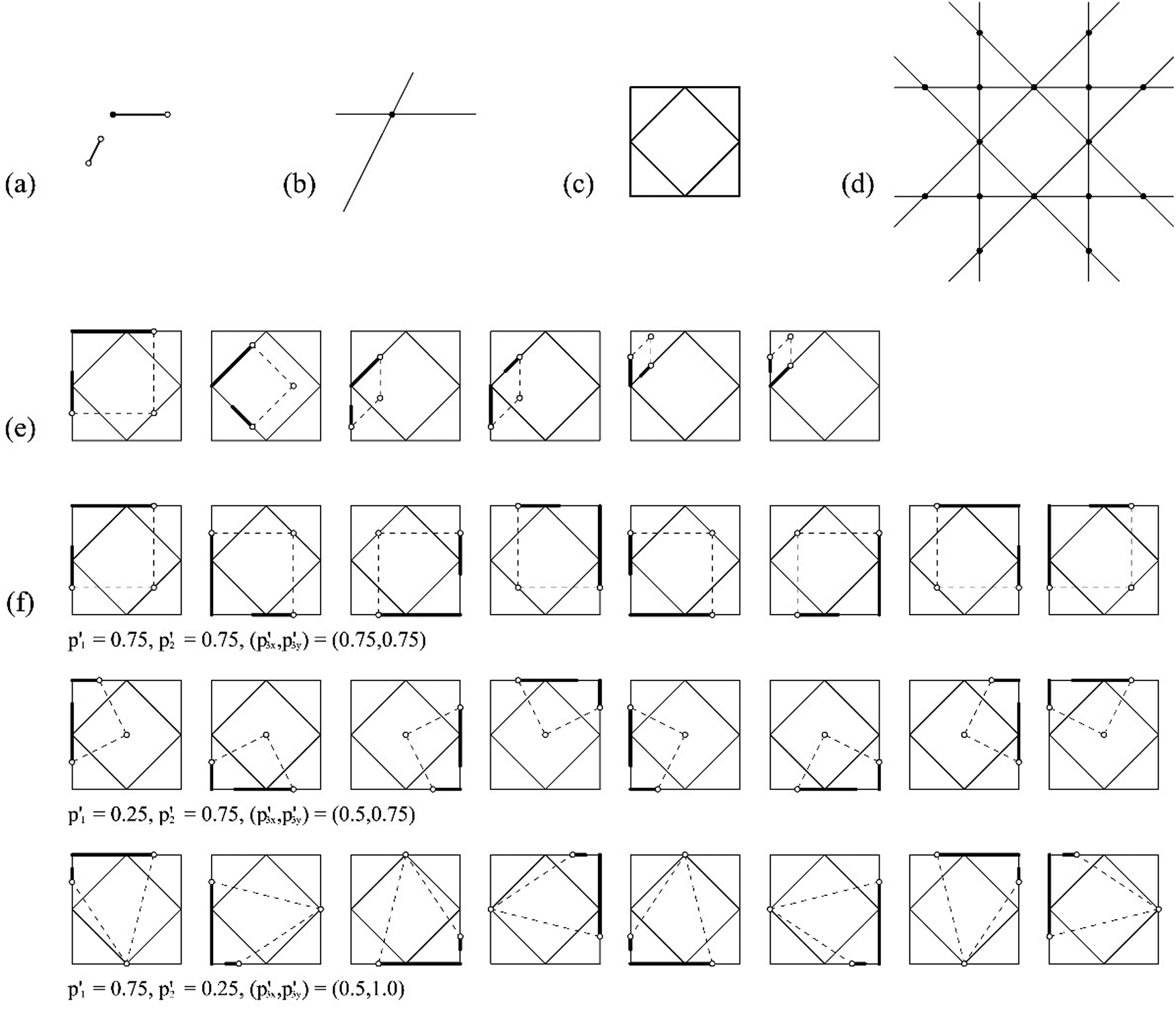
Fig. 15. An example of indeterminate projective embedding using one registration points. (a) An instance of a parameterized shape g(U); (b) registration points R g(U); (c) shape W; (d) registration points R W; (e) six embedding schemas one per pair of converging lines; (f) three instances of one of the six embedding schemas with assignments ![]() $p_1^{\prime} , \;p_2^{\prime} , \;p_{3x}^{\prime} , \;p_{3y}^{\prime}$: (0.75, 0.75, 0.75, 0.75), (0.25, 0.75, 0.5, 0.75), and (0.75, 0.25, 0.5, 1.0), one per row, and their equivalent embeddings by the actions of the symmetry group of the shape W.
$p_1^{\prime} , \;p_2^{\prime} , \;p_{3x}^{\prime} , \;p_{3y}^{\prime}$: (0.75, 0.75, 0.75, 0.75), (0.25, 0.75, 0.5, 0.75), and (0.75, 0.25, 0.5, 1.0), one per row, and their equivalent embeddings by the actions of the symmetry group of the shape W.
An example of an indeterminate embedding under linear transformations of a shape u having no registration points is shown in Figure 16. Similarly to the previous cases, four registration points are required to resolve the nine unknown variables of a homography matrix h 0 to h 8. The shape u does not have the required registration points for the derivation of the homography matrix and the computation fails. To determine the embeddings, a five-stepped process is used. The first step is processed automatically by taking all the four endpoints of g(U), and this step can be viewed as the process that the two lines of g(U) are translated and rotated so that the two lines are embedded in any two maximal lines of W. Once the two lines are embedded into W, the second step requires an input for the first point. Similar to the previous cases the selection of the first point is the left endpoint of the upper line of g(U) and it can be translated within the maximal line of W on which it occurs. The third step requires an input for the second point, which is the right endpoint of the upper line of g(U) and it can be translated within the maximal line of W on which it occurs. The fourth step requires an input for the third point, which is the left endpoint of the lower line of g(U) and it can be translated within the maximal line of W on which it occurs. The last step requires an input for the fourth point which is the right endpoint of the lower line of g(U) and it can be translated within the maximal line of W on which it occurs. Theoretically, any four points on the world plane can be used to calculate the linear transformation, nevertheless, the selection of endpoint helps system to reduce the sampling space. Note that the four points form the bonding box of g(U) so that the input coordinates of the four points should keep the bonding box a convex quadrilateral. In total, there are ![]() $C_2^8 = 28$ parallel and convergent pairs of lines in the shape W, in which the shape f(g((U)) can be embedded and seven embedding schemas, each parameterized with four registration points
$C_2^8 = 28$ parallel and convergent pairs of lines in the shape W, in which the shape f(g((U)) can be embedded and seven embedding schemas, each parameterized with four registration points ![]() $p_1^{\prime}$,
$p_1^{\prime}$, ![]() $p_2^{\prime}$,
$p_2^{\prime}$, ![]() $p_3^{\prime}$, and
$p_3^{\prime}$, and ![]() $p_4^{\prime}$ with normalized ranges
$p_4^{\prime}$ with normalized ranges ![]() $0 < p_1^{\prime} < p_2^{\prime}$,
$0 < p_1^{\prime} < p_2^{\prime}$, ![]() $p_1^{\prime} < p_2^{\prime} < 1$,
$p_1^{\prime} < p_2^{\prime} < 1$, ![]() $0 < p_3^{\prime} < p_4^{\prime}$, and
$0 < p_3^{\prime} < p_4^{\prime}$, and ![]() $p_3^{\prime} < p_4^{\prime} < 1$. To avoid double counting, a constraint
$p_3^{\prime} < p_4^{\prime} < 1$. To avoid double counting, a constraint ![]() $p_2^{\prime} -p_1^{\prime} \le p_4^{\prime} -p_3^{\prime}$ is applied. Note that the indeterminacy is also involved with translation when the four registration points are all determined. The range of t is
$p_2^{\prime} -p_1^{\prime} \le p_4^{\prime} -p_3^{\prime}$ is applied. Note that the indeterminacy is also involved with translation when the four registration points are all determined. The range of t is
which can be normalized as 0 ≤ t′ ≤ 1.
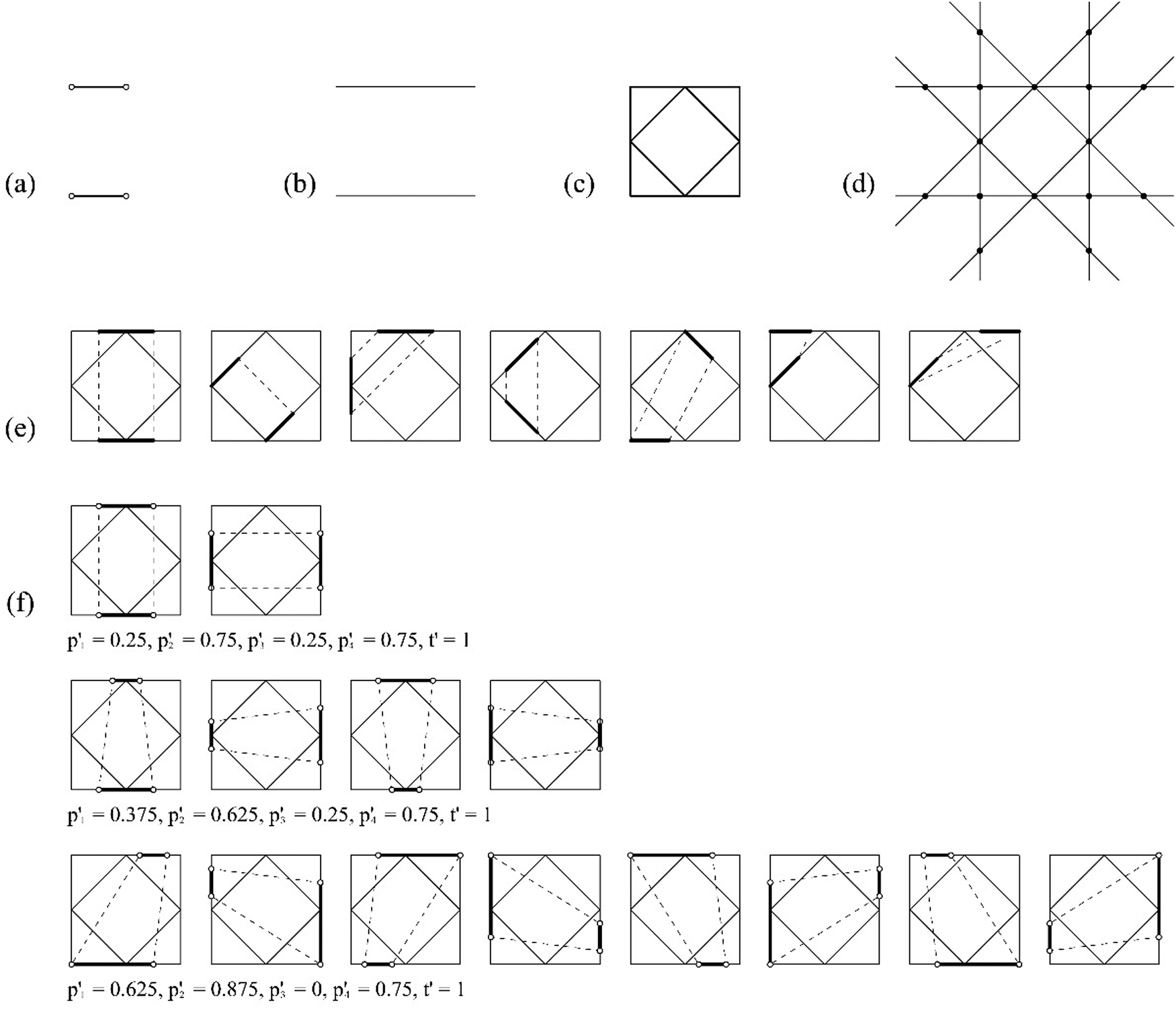
Fig. 16. An example of indeterminate projective embedding using no registration points. (a) An instance of a parameterized shape g(U); (b) registration points R g(U); (c) shape W; (d) registration points R W; (e) seven embedding schemas one per pair of parallel or converging lines; (f) three instances of one of the seven embedding schemas with assignments ![]() $p_1^{\prime} , \;p_2^{\prime} , \;p_3^{\prime} , \;p_4^{\prime} , \;{t}^{\prime}$: 0.25, 0.75, 0.25, 0.75, 1 (0.375, 0.625, 0.25, 0.75, 1), and (0.625, 0.875, 0, 0.75, 1), one per row, and their equivalent embeddings by the actions of the symmetry group of the shape W.
$p_1^{\prime} , \;p_2^{\prime} , \;p_3^{\prime} , \;p_4^{\prime} , \;{t}^{\prime}$: 0.25, 0.75, 0.25, 0.75, 1 (0.375, 0.625, 0.25, 0.75, 1), and (0.625, 0.875, 0, 0.75, 1), one per row, and their equivalent embeddings by the actions of the symmetry group of the shape W.
Discussion
Shape embedding continues to be one of the most difficult tasks for a shape grammar interpreter and a tabula incognita for CAD systems. The title of the paper playfully underscores this state by using a pan on George Stiny's “What Designers Do That Computers Should” a paper written in the late 1980s foregrounding the need for computation to support ambiguity and variability in design (Stiny, Reference Stiny, McCullough, Mitchell and Purcell1990). In the years that have passed since, work on variability has produced an impressive array of tools and processes all in support of design, parametric representations, optimizations, building information modeling, and so forth (see, e.g., Eastman et al., Reference Eastman, Teicolz, Sacks and Liston2018; Woodbury, Reference Woodburry2010; Woodbury et al., Reference Woodbury, Mohiuddin, Cichy and Mueller2017). Work on ambiguity (embedding) not so much. The opening lines in this work reaffirmed just that shape embedding under a given Euclidean, affine, or linear transformation is entirely absent from current CAD systems. Be it as it may, the problem is tractable and it is strongly suggested that the work here provides a firm step toward the solution.
The review of the implementation of the derivation of the transformation matrices algorithm for determinate and indeterminate embeddings revealed a complex problem in shape embedding that does not lend itself easily to a unified solution. A series of the specific challenges that the algorithm faces for the successful derivation of particular transformation matrices includes the calculation of the numbers of registration points incident in each hyperplane per shape, for each shape u and W separately, and one against the other.
Clearly, the greatest challenge in the automated implementation of the derivation of the transformation matrix is the appropriate selection of the required registration points to resolve the variables. The automated sampling of missing registration points to include the endpoints of maximal lines of the two shapes (Stiny, Reference Stiny1975; Krishnamurti, Reference Krishnamurti1981) produces several failed computations. An example of a failed sampling of endpoints to derive the isometric matrix for an isometry embedding of a shape u with one registration point is given in Figure 17. The algorithm requires two points to resolve all three unknown variables and the endpoint sampling leads to an incorrect derivation of the isometry matrix.
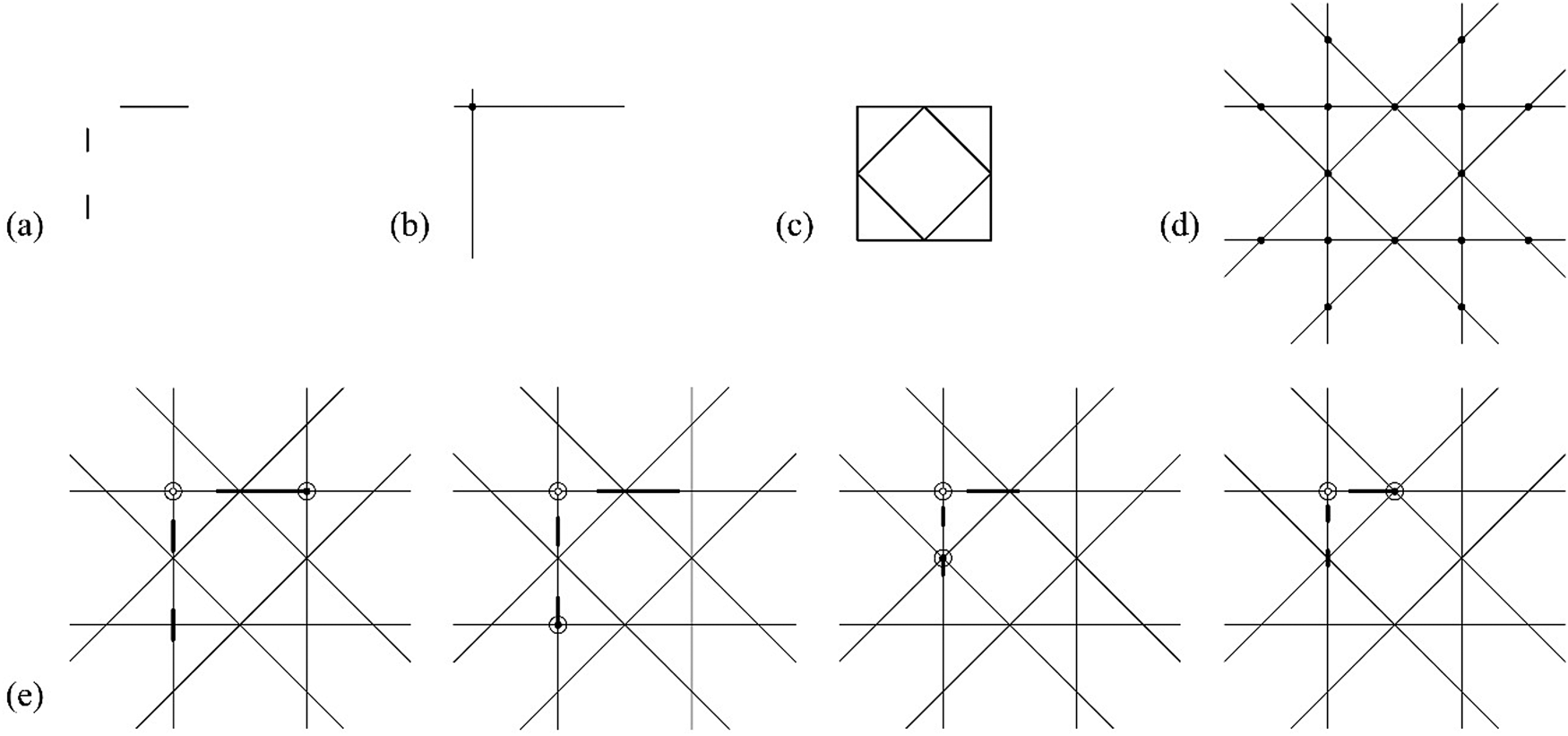
Fig. 17. Automated point sampling for the derivation of an isometric matrix. (a) failed and (b–-(d) correct.
A second challenge in the automated implementation of the derivation of the affine and homography matrices is the appropriate exclusion of the all triples of collinear registration points to resolve the variables. An example of a problematic automated selection of collinear triples of registration points from the shape W has already been given earlier in this work. An example of a failed sampling of registration points from the shape u to derive the affine matrix is briefly discussed here and illustrated in Figure 18. In this case, the shape u has seven registration points and five hyperplanes, and there are ![]() $C_3^7 = 35$ ways to sample three registration points from it, however, five of them are collinear and provide failed calculations when they are fed in the derivation algorithm, that is, there is a chance of 5/35 ≈ 14.28% to have an invalid triplet if the system blindly processes the sampling. Hence, the collinear triples should be filtered out before processing the embedding. It has already been discussed above that there are 504 applicable triples of registration points in the shape W to be compared to derive the affine matrix with an extra computational load filtering out the collinear triples.
$C_3^7 = 35$ ways to sample three registration points from it, however, five of them are collinear and provide failed calculations when they are fed in the derivation algorithm, that is, there is a chance of 5/35 ≈ 14.28% to have an invalid triplet if the system blindly processes the sampling. Hence, the collinear triples should be filtered out before processing the embedding. It has already been discussed above that there are 504 applicable triples of registration points in the shape W to be compared to derive the affine matrix with an extra computational load filtering out the collinear triples.
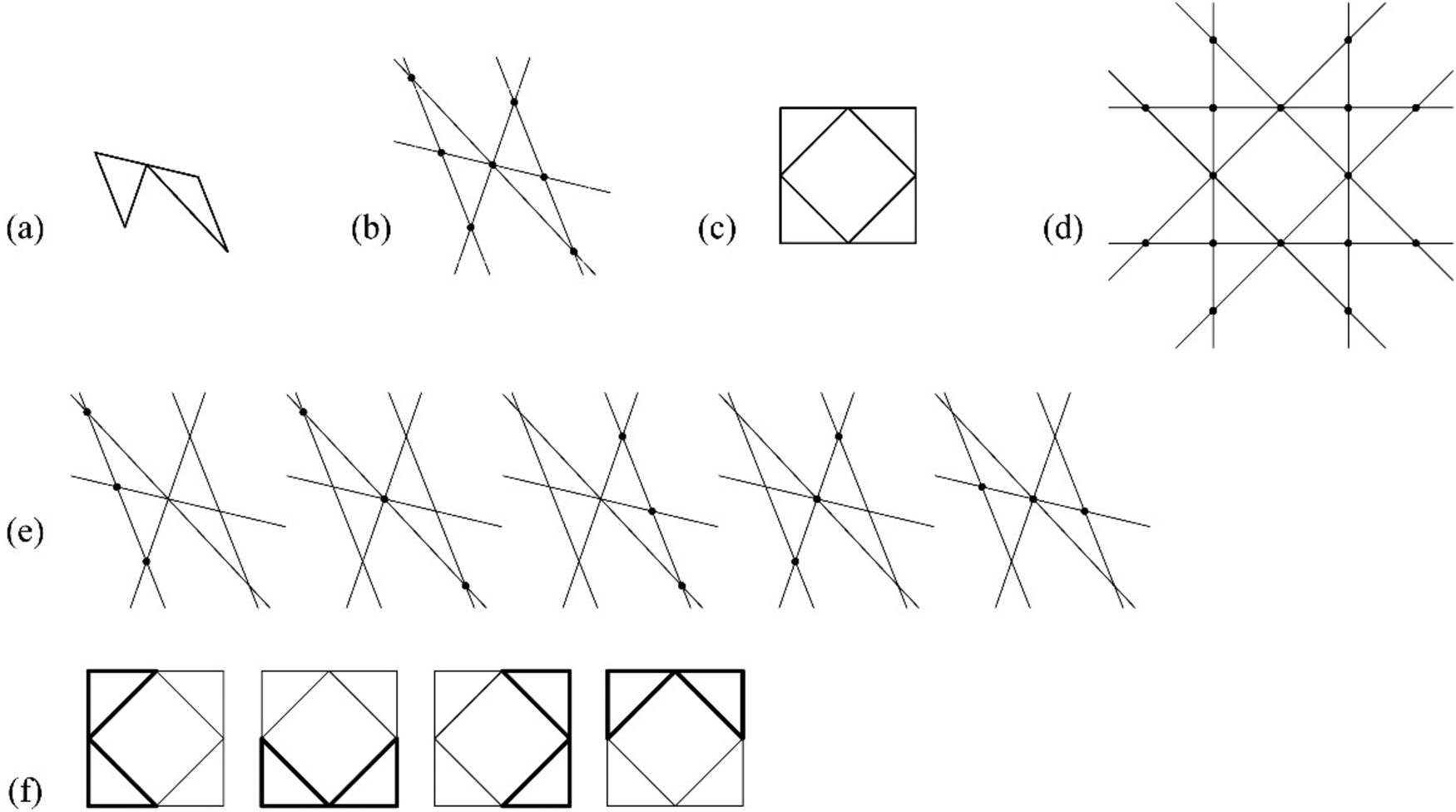
Fig. 18. An example of determinate embedding under affine transformation that cannot be completely determined by the affine matrix. (a) Shape u and the registration points R u; (b) shape W and the registration points R W; (c) five failed intersection samplings from the shape u; and (e) four results of determinate embedding under affinity transformation.
A third challenge in the automated implementation of the derivation of the transformation matrices appears in special cases of geometrical constraints of the shape W that condition whether an embedding will be determinate or indeterminate, irrelevant of the number of required registration points in the shape u. This problem is significant to the extent that current implementations of the derivation of the transformation matrices miss determinate embeddings that an experienced designer can see. A case of determinate embedding under a similarity transformation where the shape u has no registration point is shown in Figure 19. Typically, the embedding of a shape u under similarity and no registration point is indeterminate, and yet, in this particular example, one of the four pairs of the endpoints of the two maximal lines of the shape u is incident with eight pairs of registration points in the shape W under similarity, and thusly, the shape u can be embedded in W in eight determinate ways.
Fig. 19. An example of determinate similar embedding using no registration points. (a) Shape u and the registration points R u; (b) shape W and the registration points R W; and (c) eight results of determinate embedding under similarity transformations.
A fourth challenge in the automated implementation of the derivation of the transformation matrices is the seamless integration of determinate and indeterminate embeddings in one unified modeling workflow. In determinate cases of embedding, the registration points are appropriately selected from a given set of points; in indeterminate cases, the registration points have to be defined in some other alternative way. It is suggested here that transformation f that maps a shape onto another shape can be decomposed into a finite sequence of applicable transformations, that is, f 1f 2…f n. Among these applicable transformations, some of them can be first derived with the given registration points. For the rest of the transformations, they are indeterminate. As the following step, the ranges of the indeterminate transformations are calculated (as shown in previous sections) one by one, and the requests are sent to users to input the values of the transformation factors step by step to determine the transformations so that the embedding can be processed.
Lastly, and certainly not least, a major challenge in the automated implementation of the derivation of the transformation matrices is related with aspects of performance in shape recognition and with the calculations involved in the various procedures of embedding outlined in this work: The complexity of embedding follows the number of the registration points available in the current design W. The method of the 3 × 3 matrix allows the system to use two registration points to achieve a Euclidean transformation, thus, the complexity of the embedding under Euclidean transformations is O(n 2) for n the number of the registration points of W. For affine transformations, the complexity increases to O(n 3), and for linear transformations, the complexity increases to O(n 4). For more on algorithmic complexity and the Big-O notation, see, for example, Cormen et al. (Reference Cormen, Leiserson, Rivest and Stein2009).
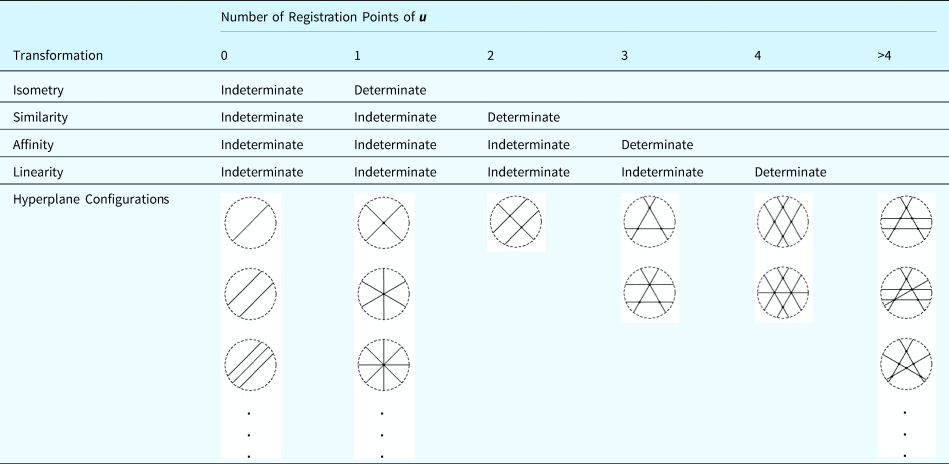
The results of all possible 14 cases of shape embedding, including four determinate ones and ten indeterminate ones, are tabulated in Table 1 according to the number of intersection of hyperplanes and illustrated by the corresponding hyperplane arrangements upon which maximal lines are embedded: solid lines denote the hyperplanes and a dashed circle denotes the Euclidean plane that the hyperplanes are embedded in. There is an infinite number of hyperplane arrangements that have zero or one intersection point, namely, those consisting of parallel hyperplanes or hyperplanes that pass through a point, respectively. There is only one hyperplane arrangement with two registration points produced by three hyperplanes; two hyperplane arrangements with three registration points produced by the intersection of three and four hyperplanes, respectively; two hyperplane arrangements of four registration points produced by the intersection of three and four hyperplanes, respectively; and an infinite number of hyperplane arrangements with more than four registration points produced by the intersection of four or more hyperplanes (Economou et al., Reference Economou, Yu and Park2019).
Table 1. 14 cases of shape embedding
The goal of this study is to rework the problem of shape embedding in the algebra U 12 and explore a general solution for a shape grammar interpreter implementation for any number of registration points and for all linear transformations, including isometries, similarities, affinities, and projectivities. An initial effort to put some of the 14 calculations outlined above in practice is evidenced in the making of the Shape Machine, a new shape grammar interpreter designed from scratch (Hong and Economou, Reference Hong and Economou2019). An initial set of shape calculations in Shape Machine pertaining to shapes consisting of lines, arcs and their combinations in the plane, has successfully met the requirements for all determinate cases as well as for two cases of indeterminate embedding under isometric and similarity transformations of shapes having one registration point (Economou et al., Reference Economou, Hong, Ligler, Park and Lee2021). Interestingly, the structured sequence of the steps required to resolve the indeterminate cases reported in the work, and the guided choices made by the designer through the process – suggest a different way to tackle ambiguity in shape embedding. This process requires additional information typically given in the form of written instructions or numerical values to generate the candidate shape to be embedded. These decisions along the steps generate different instances of shapes, different embeddings into the design, and ultimately a different understanding of the design in terms of the shapes that become parts of it. It is hoped that the extension of these findings for all indeterminate cases for shapes made up of lines in the plane will make a coherent and unified framework for queries based on shape embedding, and a visual tool to provide insight in highly unstructured visual searches and design actions (shape replacements).
Clearly, there is lots of ground that needs to be covered including the expansion of the range of geometry descriptors for various types of shapes in different dimensions, implementation of corresponding maximal representations of shapes embedded in these descriptors, Boolean operations for these kinds of geometries, resolution of indeterminant visual embeddings for all such types, and of course, extensions to parametric definitions and rule schemata. Additional directions pertaining to the design of the interfaces of these systems and their seamless integration with current modes of practice provide indeed a bright future for their development.
Tzu-Chieh Kurt Hong is a lecturer in the School of Architecture at the Georgia Institute of Technology teaching courses in media modeling, parametric modeling and design scripting. His research focuses on the areas of shape grammars, generative modeling, parametric design, and CAD software development. Kurt is a research scientist at the Shape Computation Lab working with Dr. Athanassios Economou on the Shape Machine, a new shape-rewrite computational technology, designing and implementing its geometry kernel, data representation and system architecture. Before entering the Shape Computation Lab, Kurt was a research assistant at the Digital Building Lab working with Dr. Dennis Shelden, and his main contribution to Digital Building Lab included the implementation of an automatic routing system in architecture and an interactive web-based data visualization platform, Smart 3D Atlanta. Kurt holds a BSEE, MSEE, and an M.Arch from the National Chiao Tung University (Taiwan), an MS.Arch from the University of Michigan, and a PhD in Architecture from Georgia Institute of Technology.
Athanassios Economou is Professor at the School of Architecture in the College of Design, and Adjunct Professor at the School of Interactive Computing at Georgia Institute of Technology. Dr. Economou's teaching and research are in the areas of shape grammars, computational design, computer-aided design and design theory, with over sixty published papers in these areas. He is the Director of the Shape Computation Lab, a research group that explores how the visual nature of shape can be formally implemented with new technologies to enable new paradigms in visual computation, design automation, and creative design. Recent projects include the Shape Machine, a new computational technology that successfully implements direct shape rewriting algorithms in CAD systems, and CourtsWeb, the most significant visual database on Federal Courthouses, sponsored by GSA and US.Courts. Design projects from his studios at Georgia Tech have received prestigious awards in international and national architectural competitions. He has been invited to give talks, seminars, and workshops at several universities including MIT, Harvard, TU Vienna, U. Michigan, KAIST, Chiao Tung U Taiwan, Emory, Seoul National U, Cambridge U, Tsinghua U, UCLA, NTUA, U.Thessaly, U.Aegean, among others. Dr. Economou holds a Diploma in Architecture from NTUA, Athens, Greece, an M.Arch from USC, and a PhD in Architecture from UCLA.