1. INTRODUCTION
A wide range of Continuous Operating Reference Stations (CORS) have been established, and are now part of an important infrastructure that supports high-precision positioning applications. Real-Time Kinematics (RTK) users can easily obtain centimetre-accurate user positions in real-time.
In current Network RTK (NRTK) implementations, we must guarantee correct integer Double-Differenced (DD) carrier phase ambiguities, so that the network corrections of systematic errors can be calculated and interpolated (Vollath et al., Reference Vollath, Buecherl, Landau, Pagels and Wagner2000; Landau et al., Reference Landau, Vollath and Chen2003). The most common errors can be eliminated or reduced using a DD scheme (Zhang and Lachapelle, Reference Zhang and Lachapelle2001). Hence the DD baseline solution is used in most CORS systems as a network Ambiguity Resolution (AR) solution (e.g., Leica Spider (Brown et al., Reference Brown, Geisler and Troyer2006) and Trimble GPSNet (Herbert et al., Reference Herbert, Ulrich and Xiaoming2009)). However, the differential baseline solution is limited by the baseline length, because the DD AR becomes increasingly unreliable when the baselines exceed 50 km owing to tropospheric and ionospheric errors. Researchers have developed many data processing strategies that consider atmospheric delays to expand the station separation beyond 100 km (Wielgosz et al., Reference Wielgosz, Kashani and Grejner-Brzezinska2005; Takasu and Yasuda, Reference Takasu and Yasuda2010; Li et al., Reference Li, Shen, Feng, Gao and Yang2014b). Furthermore, with independent baseline selection, efficient data use is also restricted by the common tracking satellites (Wübbena et al., Reference Wübbena, Schmitz and Bagge2005). The computational workload of the DD baseline solution increases sharply with the number of stations, so the DD baseline solution cannot benefit from a distributed system architecture, and the extensive CORS software is difficult to implement for practical use.
To overcome the above problems, Precise Point Positioning (PPP) has been studied by many researchers (Zumberge et al., Reference Zumberge, Heflin, Jefferson, Watkins and Webb1997; Kouba and Héroux, Reference Kouba and Héroux2001). As a very pragmatic tool for achieving millimetre positioning accuracy in static mode, the co-variances among the parameters of different stations are not of interest. The main disadvantage of PPP, when compared to differential processing, is that the integer property of the UD ambiguities deteriorates because of phase bias absorption. The solutions generally take longer to converge than ambiguity-resolved differential solutions, and it requires precise satellite orbits and corresponding clock products. PPP-RTK extends the PPP concept by providing single-receiver users information about the satellite phase biases, and the “integerness” of a user's single-receiver ambiguities could be recovered (Ge et al., Reference Ge, Gendt, Rothacher, Shi and Liu2008; Collins, Reference Collins2008; Laurichesse et al., Reference Laurichesse, Mercier, Berthias, Broca and Cerri2008). The goal of this contribution is to present the principles of PPP-RTK, together with our view of the different mechanisations. However, these ambiguity resolution approaches based on ionosphere-free observations also need a long convergence time to separate the Un-calibrated Phase Delay (UPD) and integer ambiguities (Geng et al., Reference Geng, Teferle, Meng and Dodson2011; Li and Zhang, Reference Li and Zhang2012). Teunissen et al. (Reference Teunissen, Odijk and Zhang2010) described the PPP-RTK concept by re-parameterising the un-differenced GNSS observation equations, and proved that the integer ambiguity resolution at the PPP-RTK user side is always that of double-differenced ambiguities (Teunissen and Khodabandeh, Reference Teunissen and Khodabandeh2014). Based on fixed DD ambiguities, Un-differenced RTK (URTK) was proposed by Ge et al. (Reference Ge, Gendt, Rothacher, Shi and Liu2008). The key idea of URTK is to transform fixed DD ambiguities of the reference network into UD ambiguities, thus achieving position solutions equivalent to the current NRTK method (Zou et al., Reference Zou, Ge, Tang, Shi and Liu2013). In contrast, there have been few studies of DD ambiguities for the UD model. The following challenges also arise when applying the UD model in CORS systems.
1.1. Application of the real-time PPP product
The satellite clock offsets are highly correlated with other GNSS biases if they are estimated in the model. In DD data processing, the satellite clock offsets can be cancelled. In UD data processing, there are too many parameters compared to observations for the estimation process, if the satellite clock offsets must be estimated. With the support of the Real-Time Pilot Project (RTPP) launched by the International GNSS Service (IGS), the vigorously promoted real-time Global Navigation Satellite System (GNSS) products have been provided to ensure real-time applications of the PPP technology (Dow et al., Reference Dow, Neilan and Rizos2009). To weaken the high correlations between satellite clock offsets and other GNSS biases, the real-time satellite clock products can be used as quasi observations. Their uncertainties should be considered in the data processing steps.
1.2. Robustness of AR
As mentioned by Li et al. (Reference Li, Verhagen and Teunissen2014a), the accuracy of ambiguities may be affected by the underlying model strength and inadequately modelled biases. Most unknown parameters can be eliminated in the DD method, but correlations among the ambiguities and Zenith tropospheric Wet Delays (ZWD) of two stations are inevitably introduced (Hofmann-Wellenhof et al., Reference Hofmann-Wellenhof, Lichtenegger and Collins2001). With the UD model in network RTK, we only estimate one ZWD. The correlation between ambiguities and ZWD is smaller than the DD method.
1.3. Unification of UD and DD model
UD and DD data processing methods are logically equivalent. They use the network data to recover the integer property of the DD ambiguities (Xu, Reference Xu2003). Any combination of the DD observation equations can be obtained from the UD original equations using the relevant linear transformation matrix. De Jonge (Reference De Jonge1998) introduced the advantages and disadvantages of the un-differenced and differenced methods. More research efforts are needed to explore the advantages of the UD and DD models.
Considering these three challenges, we propose a modified method that extracts UD ambiguities and improves the performance of the network AR. In the data processing steps, we estimate the unknown parameters (receiver and satellite clock offsets, ionospheric slant delay, ZWD, and basic UD ambiguities) epoch by epoch at each reference station. Because of the uncertainties of IGS real-time clock products, we use real-time clock products as quasi-observations. According to the user location, several adjacent stations are selected to recover the DD integer ambiguities. The ambiguities remain in DD form and the covariance matrix retains fewer correlations. Meanwhile, the method effectively helps to establish distributed structures in the extensive CORS system.
The remainder of this paper is organised as follows. Section 2 introduces the generation method for UD ambiguities. We also discuss the ill-posedness of the proposed model. In Section 3, we describe details of the network solution for the UD ambiguities. Section 4 presents our results, including a comparison of the Wide-Lane (WL) and L1 ambiguity bias results for the DD and proposed methods. The final section contains a summary of our findings.
2. THE OBSERVATION EQUATIONS
The un-combined model was proposed by Keshin et al. (Reference Keshin, Le and Marel2006). Four types of UD GNSS measurements are used to reflect the influence of atmospheric changes. The code and phase observations from satellite s to receiver k at frequency j are
where P denotes a raw code observation, Φ is a raw phase observation, ![]() $\rho_k^s $ is the geometric range between the satellite and receiver antenna phase centres (m). δt k and
$\rho_k^s $ is the geometric range between the satellite and receiver antenna phase centres (m). δt k and ![]() $\delta t_{}^s $ are the receiver and satellite clock offsets, respectively.
$\delta t_{}^s $ are the receiver and satellite clock offsets, respectively. ![]() $T_k^s $ is the troposphere delay.
$T_k^s $ is the troposphere delay. ![]() $I_k^s$ represents the ionospheric delays, which are related to the signal frequency. α i is the frequency scaling, set to
$I_k^s$ represents the ionospheric delays, which are related to the signal frequency. α i is the frequency scaling, set to ![]() ${\alpha _j} = {{f_1^2} / {f_j^2}} $.
${\alpha _j} = {{f_1^2} / {f_j^2}} $. ![]() $d_{k,{P_j}}^{} $ and
$d_{k,{P_j}}^{} $ and ![]() $d_{{P_j}}^s $ are receiver and satellite code hardware biases. It is important to note that the bias is related to the frequency.
$d_{{P_j}}^s $ are receiver and satellite code hardware biases. It is important to note that the bias is related to the frequency. ![]() $\varepsilon _{k,others}^s $ is the remaining error that can be modelled (and combines tidal corrections, plate motions, etc.).
$\varepsilon _{k,others}^s $ is the remaining error that can be modelled (and combines tidal corrections, plate motions, etc.). ![]() $b_{{\Phi _j}}^s $ is the receiver and satellite carrier phase fractional bias at a set frequency. λ j is the carrier wavelength and N j is the carrier-phase ambiguity (cycle).
$b_{{\Phi _j}}^s $ is the receiver and satellite carrier phase fractional bias at a set frequency. λ j is the carrier wavelength and N j is the carrier-phase ambiguity (cycle). ![]() $\varepsilon _{k,{P_j}}^s $ and
$\varepsilon _{k,{P_j}}^s $ and ![]() $\varepsilon _{k,{\Phi _j}}^s $ are the phase multipath and phase noise. The multipath effect has less influence on the carrier phase compared with the code observation. Theoretically, the maximum multipath effect on carrier phase observables is about 4·8 cm for the GPS L1 carrier and can be accomplished by averaging over a sufficiently long period of observation (Lau et al., Reference Lau and Cross2007).
$\varepsilon _{k,{\Phi _j}}^s $ are the phase multipath and phase noise. The multipath effect has less influence on the carrier phase compared with the code observation. Theoretically, the maximum multipath effect on carrier phase observables is about 4·8 cm for the GPS L1 carrier and can be accomplished by averaging over a sufficiently long period of observation (Lau et al., Reference Lau and Cross2007).
Overall, the code's hardware bias can be divided into three parts. First, the satellite ionosphere-free Differential Code Biases (DCB) can be eliminated by the satellite clock bias released by IGS. Second, the receiver ionosphere-free DCB is absorbed into the receiver clock bias. Third, the remaining part of the hardware delay is related to the frequency of the data processing, and is absorbed by each satellite ionospheric delay (Zhang et al., Reference Zhang, Teunissen and Odijk2011a). That is,
 $$c\delta {t_k}^{\prime} = c\delta t_k+ d_{k,{P_{if}}}, c\delta t_{IGS}^s = c\delta t^s + d_{{P_{if}}}^s, I_k^{s{\prime}} = I_k^s + \displaystyle{{\,f_2^2} \over {\,f_1^2 - f_2^2}} ({B_k} - {B^s})$$
$$c\delta {t_k}^{\prime} = c\delta t_k+ d_{k,{P_{if}}}, c\delta t_{IGS}^s = c\delta t^s + d_{{P_{if}}}^s, I_k^{s{\prime}} = I_k^s + \displaystyle{{\,f_2^2} \over {\,f_1^2 - f_2^2}} ({B_k} - {B^s})$$
where ![]() $c\delta t_{IGS}^s $ is the satellite clock offset obtained from IGS data, and
$c\delta t_{IGS}^s $ is the satellite clock offset obtained from IGS data, and ![]() $I_k^s $ is the true ionospheric delay between the satellite and receiver.
$I_k^s $ is the true ionospheric delay between the satellite and receiver. ![]() $I_k^s{^{\prime}}$ is the ionospheric delay that contains a code bias.
$I_k^s{^{\prime}}$ is the ionospheric delay that contains a code bias. ![]() $B_k^{} $ and
$B_k^{} $ and ![]() $B_{}^s $ are the receiver and satellite differential code biases between P1and P2.
$B_{}^s $ are the receiver and satellite differential code biases between P1and P2. ![]() ${B_k} = d_{k,{P_2}}^{} - d_{k,{P_1}}^{} $ and
${B_k} = d_{k,{P_2}}^{} - d_{k,{P_1}}^{} $ and ![]() ${B^s} = d_{{P_2}}^s - d_{{P_1}}^s $.
${B^s} = d_{{P_2}}^s - d_{{P_1}}^s $. ![]() $d_{k,{P_{if}}}^{} $ and
$d_{k,{P_{if}}}^{} $ and ![]() $d_{{P_{if}}}^s $ are the receiver and satellite differential code ionosphere-free biases (Zhang et al., Reference Zhang, Gao, Ge, Niu, Huang, Tu and Li2013).
$d_{{P_{if}}}^s $ are the receiver and satellite differential code ionosphere-free biases (Zhang et al., Reference Zhang, Gao, Ge, Niu, Huang, Tu and Li2013).
Note that the receiver clock offset and slant ionospheric delay is not decoupled for code and phase observations, and the code and phase biases from the receiver and satellites are absorbed into the ambiguities (Geng et al., Reference Geng, Meng, Dodson and Teferle2010). The estimated N 1 and N 2 ambiguities are defined as
 $${\lambda _j}{N_j}^{\prime} = {\lambda _j}{N_j} - {\alpha _j}\displaystyle{{\,f_2^2} \over {\,f_1^2 - f_2^2}} ({B_k} - {B^s}) - b_{{\Phi _j}}^s + d_{{P_{IF}}}^s + {b_{k,{\Phi _j}}} - {d_{k,{P_{IF}}}}$$
$${\lambda _j}{N_j}^{\prime} = {\lambda _j}{N_j} - {\alpha _j}\displaystyle{{\,f_2^2} \over {\,f_1^2 - f_2^2}} ({B_k} - {B^s}) - b_{{\Phi _j}}^s + d_{{P_{IF}}}^s + {b_{k,{\Phi _j}}} - {d_{k,{P_{IF}}}}$$The observation and dynamic models use Kalman filters. Using the known coordinates of the reference stations, the estimatable state vector (which includes receiver and satellite clock offsets, ionospheric slant delay, ZWD, and UD basic ambiguities) is estimated epoch by epoch at each station. If the receiver collects phase and code observations from n satellites at epoch i, the Kalman filter is
The unknown parameter vector is divided into temporal and non-temporal parts. The temporal part includes the ZWD, receiver clock offset, n-dimensional state vector of ionospheric slant delay (STEC), and an n-dimensional state vector of satellite clock offsets. The non-temporal part is composed of the original UD ambiguities:
The observation vector L i is composed of four UD measurements and the constraints of satellite clock. The real-time clock products could be interpreted as fictitious observations or quasi-observations in the observation vector. This leads to the total observation equations L i and the design matrix B i:
 $${L_i} = \left[ {\matrix{ {P_{1,k}^s} \cr {P_{2,k}^s} \cr {\Phi _{1,k}^s} \cr {\Phi _{2,k}^s} \cr {\delta t_{IGS}^s} \cr}} \right],{B_i} = \left[ {\matrix{ {{B_{M{F_w}}}} & {{B_{\delta {t_k}^{\prime}}}} & {{B_I}} & { - {B_{\delta {t^{s \prime}}}}} & 0 & 0 \cr {{B_{M{F_w}}}} & {{B_{\delta {t_k}^{\prime}}}} & {\displaystyle{{\,f_1^2} \over {\,f_2^2}} {B_I}} & { - {B_{\delta {t^{s \prime}}}}} & 0 & 0 \cr {{B_{M{F_w}}}} & {{B_{\delta {t_k}^{\prime}}}} & { - {B_I}} & { - {B_{\delta {t^{s \prime}}}}} & {{B_{{N_1}}}} & 0 \cr {{B_{M{F_w}}}} & {{B_{\delta {t_k}^{\prime}}}} & { - \displaystyle{{\,f_1^2} \over {\,f_2^2}} {B_I}} & { - {B_{\delta {t^{s \prime}}}}} & 0 & {{B_{{N_2}}}} \cr 0 & 0 & 0 & {{B_{\delta {t^{s \prime}}}}} & 0 & 0 \cr}} \right]$$
$${L_i} = \left[ {\matrix{ {P_{1,k}^s} \cr {P_{2,k}^s} \cr {\Phi _{1,k}^s} \cr {\Phi _{2,k}^s} \cr {\delta t_{IGS}^s} \cr}} \right],{B_i} = \left[ {\matrix{ {{B_{M{F_w}}}} & {{B_{\delta {t_k}^{\prime}}}} & {{B_I}} & { - {B_{\delta {t^{s \prime}}}}} & 0 & 0 \cr {{B_{M{F_w}}}} & {{B_{\delta {t_k}^{\prime}}}} & {\displaystyle{{\,f_1^2} \over {\,f_2^2}} {B_I}} & { - {B_{\delta {t^{s \prime}}}}} & 0 & 0 \cr {{B_{M{F_w}}}} & {{B_{\delta {t_k}^{\prime}}}} & { - {B_I}} & { - {B_{\delta {t^{s \prime}}}}} & {{B_{{N_1}}}} & 0 \cr {{B_{M{F_w}}}} & {{B_{\delta {t_k}^{\prime}}}} & { - \displaystyle{{\,f_1^2} \over {\,f_2^2}} {B_I}} & { - {B_{\delta {t^{s \prime}}}}} & 0 & {{B_{{N_2}}}} \cr 0 & 0 & 0 & {{B_{\delta {t^{s \prime}}}}} & 0 & 0 \cr}} \right]$$where
 $$\eqalign{& {B_{M{F_w}}} = \overbrace {{{\left[ {\matrix{ {M{F_w}({\theta ^1})} & \cdots & {M{F_w}({\theta ^n})} \cr}} \right]}^T}}^{n \times 1},{B_{\delta {t_k}^{\prime}}} = {[\overbrace {\matrix{ c & \cdots & c \cr}} ^{n \times 1}]^T},{B_{\delta {t^{s \prime}}}} = diag{[\overbrace {\matrix{ c & \cdots & c \cr}} ^{n \times n}]^T} \cr & {B_I} = diag(\overbrace {\matrix{ 1 & \cdots & 1 \cr}} ^{n \times n}),{B_{{N_1}}} = diag(\overbrace {\matrix{ {{\lambda _1}} & \cdots & {{\lambda _1}} \cr}} ^{n \times n}),{B_{{N_2}}} = diag(\overbrace {\matrix{ {{\lambda _2}} & \cdots & {{\lambda _2}} \cr}} ^{n \times n})} $$
$$\eqalign{& {B_{M{F_w}}} = \overbrace {{{\left[ {\matrix{ {M{F_w}({\theta ^1})} & \cdots & {M{F_w}({\theta ^n})} \cr}} \right]}^T}}^{n \times 1},{B_{\delta {t_k}^{\prime}}} = {[\overbrace {\matrix{ c & \cdots & c \cr}} ^{n \times 1}]^T},{B_{\delta {t^{s \prime}}}} = diag{[\overbrace {\matrix{ c & \cdots & c \cr}} ^{n \times n}]^T} \cr & {B_I} = diag(\overbrace {\matrix{ 1 & \cdots & 1 \cr}} ^{n \times n}),{B_{{N_1}}} = diag(\overbrace {\matrix{ {{\lambda _1}} & \cdots & {{\lambda _1}} \cr}} ^{n \times n}),{B_{{N_2}}} = diag(\overbrace {\matrix{ {{\lambda _2}} & \cdots & {{\lambda _2}} \cr}} ^{n \times n})} $$Here, MF w(θ) is the mapping function of ZWD with satellite elevation θ.
Φi,i−1 is the (4n + 2) × (4n + 2) state transition matrix corresponding to two consecutive epochs, defined as
where ![]() ${\Phi _{ZT{D_{w,k}}}} = \exp ( - \displaystyle{{\Delta t} \over {{\tau _{ZT{D_{w,k}}}}}})$,
${\Phi _{ZT{D_{w,k}}}} = \exp ( - \displaystyle{{\Delta t} \over {{\tau _{ZT{D_{w,k}}}}}})$,![]() ${\Phi _{\delta {t_k}^{\prime}}} = 0$,
${\Phi _{\delta {t_k}^{\prime}}} = 0$,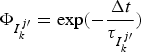 ${\Phi _{I_k^ {j\prime}}} = \exp ( - \displaystyle{{\Delta t} \over {{\tau _{I_k^ {j\prime}}}}})$,
${\Phi _{I_k^ {j\prime}}} = \exp ( - \displaystyle{{\Delta t} \over {{\tau _{I_k^ {j\prime}}}}})$, ![]() ${\Phi _{\delta {t^{s \prime}}}} = \exp ( - \displaystyle{{\Delta t} \over {{\tau _{\delta {t^{s \prime}}}}}})$, and
${\Phi _{\delta {t^{s \prime}}}} = \exp ( - \displaystyle{{\Delta t} \over {{\tau _{\delta {t^{s \prime}}}}}})$, and ![]() ${\Phi _{N_1^j}} = {\Phi _{N_2^j}} = {E_n}$.
${\Phi _{N_1^j}} = {\Phi _{N_2^j}} = {E_n}$.
Q i is the (4n + 2) × (4n + 2) dynamic noise correlation matrix, set to
The ZWD parameter is considered a first-order Gauss-Markov process, and ![]() ${Q_{ZW{D_k}}} = {q_{ZWD}}\Delta t$. Δt is the time interval between epochs. The white noise process can simply and effectively describe the random process of the receiver and the satellite clock offsets. The ionospheric slant delay parameters are also considered as a random walk related to the satellite zenith angle (z′) of the position of the ionospheric puncture, that is,
${Q_{ZW{D_k}}} = {q_{ZWD}}\Delta t$. Δt is the time interval between epochs. The white noise process can simply and effectively describe the random process of the receiver and the satellite clock offsets. The ionospheric slant delay parameters are also considered as a random walk related to the satellite zenith angle (z′) of the position of the ionospheric puncture, that is, ![]() ${Q_{I_k^{s {\prime}}}} = {q_{Ion}}\Delta t/\cos (z^{\prime})$. The ambiguity is regarded as an invariant parameter,
${Q_{I_k^{s {\prime}}}} = {q_{Ion}}\Delta t/\cos (z^{\prime})$. The ambiguity is regarded as an invariant parameter, ![]() ${Q_{N_1^s}} = {Q_{N_2^s}} = {E_n} \otimes {10^{ - 16}}\Delta t$.
${Q_{N_1^s}} = {Q_{N_2^s}} = {E_n} \otimes {10^{ - 16}}\Delta t$.
Compared to the short baseline RTK model, the PPP model has a slower convergence speed. This is because of the obvious influence of the model error (which is weakened using the DD-RTK model), and because of the ill-posedness of the entire model.
In the DD model, the DD operator is introduced to reduce the number of unknown parameters. We ignore the effects of the atmospheric delay and orbital errors. This may lead to a lower success rate for the fixed ambiguities over long inter-station baselines if we do not consider atmospheric biases. In the UD model, there are more unknown parameters that must be considered, and we rely on the rapid movements of satellites to mitigate the ill-posedness.
As a common indicator for measuring or diagnosing ill-conditioned systems, the condition number is a reflection of the internal relationships between ambiguities in GNSS high-precision carrier positioning. A smaller condition number corresponds to a more robust solution. The ratio of code to carrier-phase noise and the precision of the quasi-observation also affect the condition number. Because of the symmetry and positivity of the normal matrix of the ambiguity, the condition number can be written as (Steward, Reference Steward1973)
where ![]() ${Q_{\hat N\hat N}}$ is the covariance matrix of the float ambiguities;
${Q_{\hat N\hat N}}$ is the covariance matrix of the float ambiguities; ![]() $\left\vert \cdot \right\vert$ represents the norm; and λ max and λ min are the maximum and minimum Eigenvalues.
$\left\vert \cdot \right\vert$ represents the norm; and λ max and λ min are the maximum and minimum Eigenvalues.
3. NETWORK SOLUTION
DD L1 and L2 ambiguities are not only used to generate the users’ local simulated error corrections in the Virtual Reference Station (VRS) technique. They are also used to estimate the satellite UPD. Typically, we first fix the DD WL ambiguities, and then determine basic integer ambiguities based on the ionosphere-free model (Teunissen, Reference Teunissen1995). The zenith tropospheric wet delay parameters of two stations must also be estimated for the long-distance baseline (Zhang and Lachapelle, Reference Zhang and Lachapelle2001). However, there are several PPP integer AR methods that recover the integer property of the ambiguity based on regional CORS. Methods include the decoupled clock model (Laurichesse et al., Reference Laurichesse, Mercier, Berthias, Broca and Cerri2008), integer phase clock model (Collins, Reference Collins2008), and Single-Difference (SD) between-satellites method (Ge et al., Reference Ge, Gendt, Rothacher, Shi and Liu2008; Geng et al., Reference Geng, Teferle, Meng and Dodson2011). The datum is included to solve the rank deficient problem using these methods.
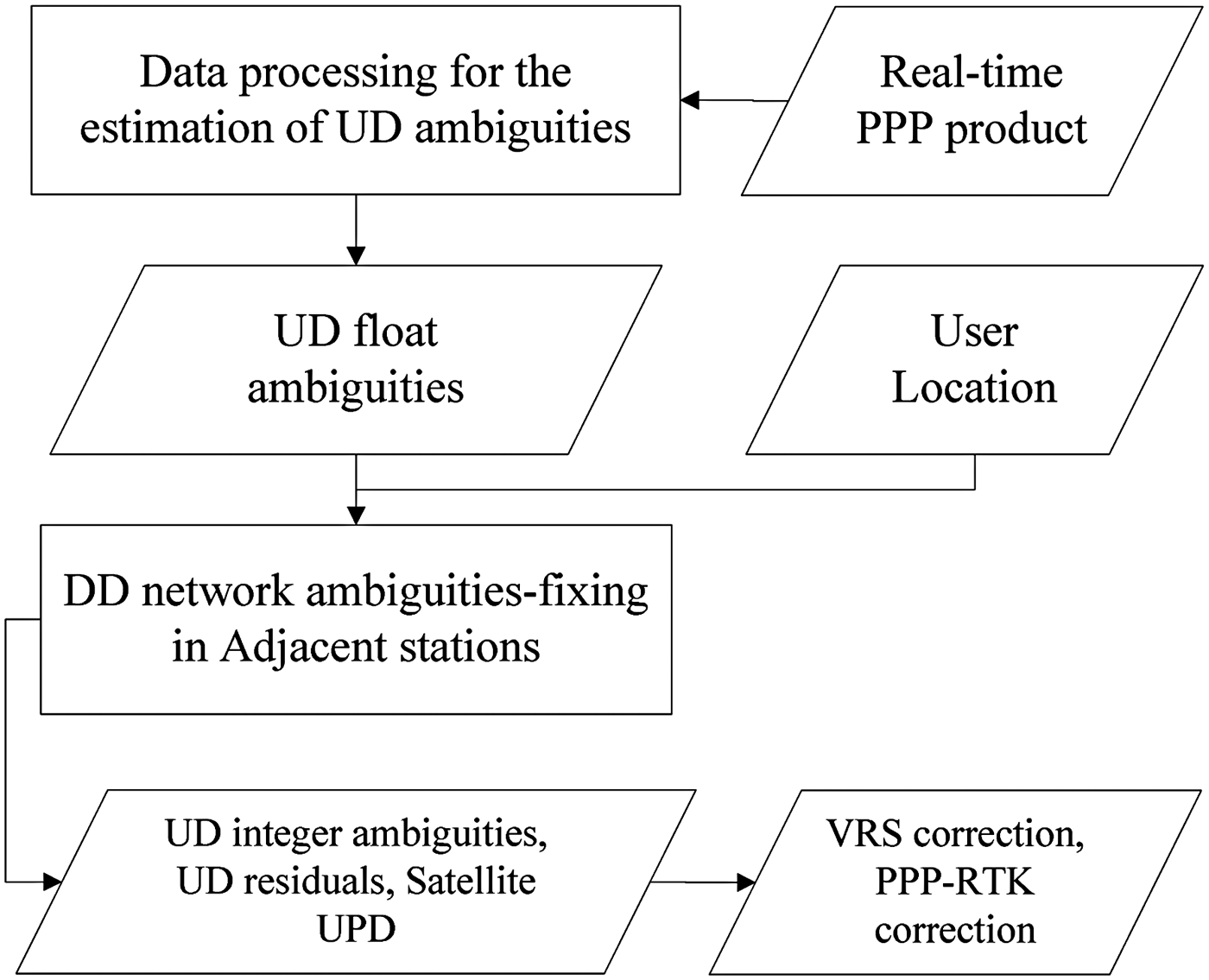
In this paper, we selected several adjacent stations to recover the DD integer ambiguities based on the user location. The UD basic ambiguities determine the entire net adjustment, which is beneficial when overcoming the baseline length limit in the CORS network. The covariance matrix of the DD ambiguity is equivalent to the combined UD ambiguity, which avoids the correlations between the ambiguities and two tropospheric parameters. Figure 1 shows the concept of the proposed method in terms of a block diagram.

Figure 1. Data processing scheme.
Using the UD ambiguity estimated for adjacent stations, DD ambiguities of the entire network can be recovered in a single epoch. We use the different accuracies of UD ambiguities with the LAMBDA method (Least-squares AMBiguity Decorrelation Adjustment) (Teunissen, Reference Teunissen1995) to determine the integer ambiguity. The ratio and success rate of the LAMBDA method are used to evaluate the quality.
The closest station is selected as the pivot differenced station. First, we determine the SD ambiguities between the remaining stations and the pivot station. The code and phase biases of satellites in the UD ambiguity are eliminated by the between-station differences. Second, the code and phase biases related to the receiver are eliminated to recover the integer property using the between-satellite difference. By specifying an appropriate difference matrix, we can determine the DD ambiguity epoch by epoch. The between-station differences matrix (C kd) and between-satellite differences matrix (C sd) are defined as
 $$\eqalign{& \matrix{ {\mathop {X_{k1}^s} \limits_{2n \times 1} = {{[\matrix{ {N_{1,k1}^1} & \cdots & {N_{1,k1}^n} & {N_{2,k1}^1} & \cdots & {N_{2,k1}^n} \cr} ]}^T},} & {Q_{k1}^s = \left[ {\matrix{ {{Q_{{{\hat N}_1}{{\hat N}_1}}}} & {{Q_{{{\hat N}_1}{{\hat N}_2}}}} \cr {{Q_{{{\hat N}_2}{{\hat N}_1}}}} & {{Q_{{{\hat N}_2}{{\hat N}_2}}}} \cr}} \right]} \cr} \cr & \matrix{ {\mathop {{C^{sd}}}\limits_{2(n - 1) \times 2n} = \left[ {\matrix{ {C_1^{sd}} & {} \cr {} & {C_2^{sd}} \cr}} \right],} & {\mathop {C_1^{sd}} \limits_{(n - 1) \times n} = \mathop {C_2^{sd}} \limits_{(n - 1) \times n} = \left[ {\matrix{ { - 1} & 1 & {} & {} \cr { - 1} & {} & 1 & {} \cr { - 1} & {} & {} & 1 \cr}} \right],} \ {\mathop {{C_{kd}}}\limits_{2(n - 1) \times 4(n - 1)} \!=\! \left[ {\matrix{ I \, { - I} \cr}} \right]} \cr}} $$
$$\eqalign{& \matrix{ {\mathop {X_{k1}^s} \limits_{2n \times 1} = {{[\matrix{ {N_{1,k1}^1} & \cdots & {N_{1,k1}^n} & {N_{2,k1}^1} & \cdots & {N_{2,k1}^n} \cr} ]}^T},} & {Q_{k1}^s = \left[ {\matrix{ {{Q_{{{\hat N}_1}{{\hat N}_1}}}} & {{Q_{{{\hat N}_1}{{\hat N}_2}}}} \cr {{Q_{{{\hat N}_2}{{\hat N}_1}}}} & {{Q_{{{\hat N}_2}{{\hat N}_2}}}} \cr}} \right]} \cr} \cr & \matrix{ {\mathop {{C^{sd}}}\limits_{2(n - 1) \times 2n} = \left[ {\matrix{ {C_1^{sd}} & {} \cr {} & {C_2^{sd}} \cr}} \right],} & {\mathop {C_1^{sd}} \limits_{(n - 1) \times n} = \mathop {C_2^{sd}} \limits_{(n - 1) \times n} = \left[ {\matrix{ { - 1} & 1 & {} & {} \cr { - 1} & {} & 1 & {} \cr { - 1} & {} & {} & 1 \cr}} \right],} \ {\mathop {{C_{kd}}}\limits_{2(n - 1) \times 4(n - 1)} \!=\! \left[ {\matrix{ I \, { - I} \cr}} \right]} \cr}} $$ $$\mathop {X_{k1,k2}^{s,r}} \limits_{2(n - 1) \times 1} = {C^{sd}} \cdot {C_{kd}} \cdot \left[ {\matrix{ {X_{k1}^s} \cr {X_{k2}^s} \cr}} \right] = {\left[ {\matrix{ {N_{1,k1,k2}^{s,r}} & {N_{2,k1,k2}^{s,r}} \cr}} \right]^T}$$
$$\mathop {X_{k1,k2}^{s,r}} \limits_{2(n - 1) \times 1} = {C^{sd}} \cdot {C_{kd}} \cdot \left[ {\matrix{ {X_{k1}^s} \cr {X_{k2}^s} \cr}} \right] = {\left[ {\matrix{ {N_{1,k1,k2}^{s,r}} & {N_{2,k1,k2}^{s,r}} \cr}} \right]^T}$$ $$\mathop {Q_{k1,k2}^{s,r}} \limits_{2(n - 1) \times 2(n - 1)} = {C^{sd}} \cdot {C_{kd}} \cdot \left[ {\matrix{ {Q_{k1}^s} & {} \cr {} & {Q_{k2}^s} \cr}} \right] \cdot {\left( {{C_{kd}}} \right)^T}{\left( {{C^{sd}}} \right)^T}$$
$$\mathop {Q_{k1,k2}^{s,r}} \limits_{2(n - 1) \times 2(n - 1)} = {C^{sd}} \cdot {C_{kd}} \cdot \left[ {\matrix{ {Q_{k1}^s} & {} \cr {} & {Q_{k2}^s} \cr}} \right] \cdot {\left( {{C_{kd}}} \right)^T}{\left( {{C^{sd}}} \right)^T}$$
Here, k1 and k2 represent two different receivers; ![]() $Q_{k1}^s $ denotes the covariance matrix of UD ambiguities (as shown in Section 2); and r refers to the reference satellite. The “−1” column is determined according to the position of the reference satellite in transfer matrices
$Q_{k1}^s $ denotes the covariance matrix of UD ambiguities (as shown in Section 2); and r refers to the reference satellite. The “−1” column is determined according to the position of the reference satellite in transfer matrices ![]() $C_1^{sd} $ and
$C_1^{sd} $ and ![]() $C_2^{sd} $.
$C_2^{sd} $.
To improve the searching efficiency of the LAMBDA method for the entire network, we use a step-by-step strategy to reduce the number of ambiguities. The WL ambiguities are less affected by errors and can be easily fixed. The linear transformation matrix is applied to the observation matrix ![]() $X_{k1,k2}^{s,r} $ and covariance matrix
$X_{k1,k2}^{s,r} $ and covariance matrix ![]() $Q_{k1,k2}^{s,r} $. The transformation matrix is defined as
$Q_{k1,k2}^{s,r} $. The transformation matrix is defined as
 $$\eqalign{& \matrix{ {\mathop {{C_{linear}}}\limits_{2(n - 1) \times 2(n - 1)} = \left[ {\matrix{ I & { - I} \cr I & 0 \cr}} \right],} & {{X_{nw,n1}} = {C_{linear}} \times X_{k1,k2}^{s,r} = \left[ {\matrix{ {{{\hat a}_{{N_w}}}} \cr {{{\hat a}_{{N_1}}}} \cr}} \right]} \cr} \cr & {Q_{nw,n1}} = {C_{linear}}Q_{k1,k2}^{s,r} {C_{linear}}^T = \left[ {\matrix{ {{Q_{{{\hat a}_{{N_w}}}{{\hat a}_{{N_w}}}}}} & {{Q_{{{\hat a}_{{N_w}}}{{\hat a}_{{N_1}}}}}} \cr {{Q_{{{\hat a}_{{N_1}}}{{\hat a}_{{N_w}}}}}} & {{Q_{{{\hat a}_{{N_1}}}{{\hat a}_{{N_1}}}}}} \cr}} \right]} $$
$$\eqalign{& \matrix{ {\mathop {{C_{linear}}}\limits_{2(n - 1) \times 2(n - 1)} = \left[ {\matrix{ I & { - I} \cr I & 0 \cr}} \right],} & {{X_{nw,n1}} = {C_{linear}} \times X_{k1,k2}^{s,r} = \left[ {\matrix{ {{{\hat a}_{{N_w}}}} \cr {{{\hat a}_{{N_1}}}} \cr}} \right]} \cr} \cr & {Q_{nw,n1}} = {C_{linear}}Q_{k1,k2}^{s,r} {C_{linear}}^T = \left[ {\matrix{ {{Q_{{{\hat a}_{{N_w}}}{{\hat a}_{{N_w}}}}}} & {{Q_{{{\hat a}_{{N_w}}}{{\hat a}_{{N_1}}}}}} \cr {{Q_{{{\hat a}_{{N_1}}}{{\hat a}_{{N_w}}}}}} & {{Q_{{{\hat a}_{{N_1}}}{{\hat a}_{{N_1}}}}}} \cr}} \right]} $$Using the WL ambiguities as known quantities, we determine the N1 ambiguity integers using
 $$\eqalign{& {{{\breve a}}_{{N_1}}} = {{\hat a}_{{N_1}}} - {Q_{{{\hat a}_{{N_1}}}{{\hat a}_{{N_w}}}}}Q_{{{\hat a}_{{N_w}}}{{\hat a}_{{N_w}}}}^{ - 1} ({{\hat a}_{{N_w}}} - {{{\breve a}}_{{N_w}}}) \cr & {Q_{{{{\breve a}}_{{N_1}}}{{{\breve a}}_{{N_1}}}}} = {Q_{{{\hat a}_{{N_1}}}{{\hat a}_{{N_1}}}}} - {Q_{{{\hat a}_{{N_1}}}{{\hat a}_{{N_w}}}}}Q_{{{\hat a}_{{N_w}}}{{\hat a}_{{N_w}}}}^{ - 1} {Q_{{{\hat a}_{{N_w}}}{{\hat a}_{{N_1}}\!.}}}} $$
$$\eqalign{& {{{\breve a}}_{{N_1}}} = {{\hat a}_{{N_1}}} - {Q_{{{\hat a}_{{N_1}}}{{\hat a}_{{N_w}}}}}Q_{{{\hat a}_{{N_w}}}{{\hat a}_{{N_w}}}}^{ - 1} ({{\hat a}_{{N_w}}} - {{{\breve a}}_{{N_w}}}) \cr & {Q_{{{{\breve a}}_{{N_1}}}{{{\breve a}}_{{N_1}}}}} = {Q_{{{\hat a}_{{N_1}}}{{\hat a}_{{N_1}}}}} - {Q_{{{\hat a}_{{N_1}}}{{\hat a}_{{N_w}}}}}Q_{{{\hat a}_{{N_w}}}{{\hat a}_{{N_w}}}}^{ - 1} {Q_{{{\hat a}_{{N_w}}}{{\hat a}_{{N_1}}\!.}}}} $$Unlike the DD and conventional UD-PPP methods, we only use the parameters of the time-invariant ambiguities to adjust the entire network. The length of the baseline and the effect of the atmospheric delay are less vulnerable to the adjusted result. The improved computational efficiency of the proposed method means that it can be used to design and implement large-scale software systems.
4. TEST RESULTS AND ANALYSIS
We used a 24-hour observed data set to investigate the performance of the UD strategy. We gathered the Receiver Independent Exchange Format (RINEX) observation data and navigation data, which was received from the Plate Boundary Observatory (PBO) by University Navstar Consortium (UNAVCO). The test case consisted of nine reference stations, as shown in Figure 2. The data sampling rate was 15 s.

Figure 2. Network distribution for the experiment. The observation data of nine CORS stations on 29 August 2014 were used to analyse the performance of the proposed method.
To simulate sparse network RTK, we considered PBO site p332 as the pivot station, and formed eight independent baselines with an average length of approximately 150 km, as shown in Table 1.
Table 1. Eight baselines formed by nine stations from PBO.

We used the UC and UD model, and estimated the satellite clock offsets. Detailed option settings for the test are given in Table 2.
Table 2. Settings for the offline test to evaluate the proposed strategy.

4.1. Precision analysis of a real-time satellite clock product
The IGS real-time data were received on 29 August 2014 and included European Space Operations Centre (ESOC) clock product (CLK50), IGS integrated single epoch product (IGS01), and IGS integrated filter product (IGS02). We restored the real-time precise clock offset to analyse its continuity and stability. We used the second-difference comparison method (Zhang et al., Reference Zhang, Li and Guo2011b) to calculate the RMS (Root Mean Squared error) of the IGS rapid satellite clock product and evaluate the accuracy. The strategy can be summarised as follows.
(1) First, the IGS final clocks are processed into satellite differenced form based on the same reference satellite using the IGS rapid satellite clocks. This step eliminates the difference between two benchmarks.
(2) Second, the difference between the IGS rapid satellite differenced clocks and IGS final satellite-differenced clock is calculated (Δi). Then, the average value of the differences from all epochs is calculated (![]() $\bar \Delta $). The average difference can be considered as the systematic bias caused by noise in the pseudo-range observations from the starting epoch. As described previously, this average difference does not influence the positioning results.
$\bar \Delta $). The average difference can be considered as the systematic bias caused by noise in the pseudo-range observations from the starting epoch. As described previously, this average difference does not influence the positioning results.
(3) Third, we calculate the RMS of the quadratic differential results using
 $$RMS = \sqrt {\displaystyle{{\sum\limits_{i = 1}^n {{{({\Delta _i} - \bar \Delta )}^2}}} \over {n - 1}}},$$
$$RMS = \sqrt {\displaystyle{{\sum\limits_{i = 1}^n {{{({\Delta _i} - \bar \Delta )}^2}}} \over {n - 1}}},$$
where Δi represents the quadratic differential results; ![]() $\bar \Delta $ is the mean of the results; and n is the number of epochs. The RMS of each satellite clock error is shown in Figure 3.
$\bar \Delta $ is the mean of the results; and n is the number of epochs. The RMS of each satellite clock error is shown in Figure 3.

Figure 3. Sigma clock differences (ns) compared to the IGS rapid product on 29 August 2014. The blue bar indicates the ESOC clock product (CLK50), the green bar indicates the IGS integrated single epoch product (IGS01), and the red bar indicates the IGS integrated filter product (IGS02).
In Figure 3, PRN01 was chosen as the reference satellite. In the navigation ephemeris, there were no ephemeris files for PRN03 and the ephemeris of PRN09 was not healthy. Thus, a precise ephemeris of the two satellites was not available during the observation period. The RMS of most satellites can be guaranteed within 0·25 ns for real-time data, but there are still large errors for some satellites (0·3 ns for PRN04 and 0·4 ns for PRN08). The time delay for the IGS real-time products was approximately 25 to 30 seconds, and we should consider the extrapolation in real-time applications.
To clearly describe the precision of the real-time satellite clock products, we used PRN8 (which had the largest RMS) and PRN32 (which has the smallest RMS), as shown in Figure 4.

Figure 4. The clock differences (ns) of PRN08 (left) and PRN32 (right) compared to the IGS rapid product (IGS01).
In Figure 4, PRN08 follows Δ ~ N(0·320, 0·434) and PRN32 follows Δ ~ N(0·067, 0·052). These show that there are systematic deviations for different satellites, which affect the stability of the ambiguities and the positioning result. At the same time, the missing real-time satellite data flow would affect the application of the real-time clock, for example, the missing 2·5 hours for PRN 8 (between 19:00 and 22:00). These uncertain product biases affect the estimates of UD ambiguities, and the phase biases become time-varying between adjacent epochs. As a result, we must estimate the satellite clock to ensure the time-invariant nature of ambiguities in real-time applications.
The accuracy of the real-time clock product can found on the IGS website (ftp://cddis.gsfc.nasa.gov/gps/products/rtpp/).
4.2. Application of the real-time satellite clock product
Based on the above unstable satellite clock analysis, the UD and UC observation model can be used with the estimates of the satellite clock offsets. The real-time satellite clock products are used as the constraints. The prior variance of real-time satellite clock products about each satellite should be appropriately set according to the accuracy of the real-time clock product. We used Equation (9) to compare the condition numbers for various precisions of quasi-observations. The results are shown in Figure 5.

Figure 5. The condition number of the UD model for varying precisions of quasi-observations. The blue line represents the model that did not estimate the satellite clock offsets (CondN-NT), the green line represents the model with the prior precision of real-time satellite products set to 0·1 ns (CondN-0·1 ns), the black line represents the model with a prior precision of 0·2 ns (CondN-0·2 ns), and the red line represents the model with a prior precision of 0·3 ns (CondN-0·3 ns).
In Figure 5, the 0·3 ns numerical clock precision was obtained with the smallest condition number, that is, the most robust model. However, lowering the weight of quasi-observations can enhance the stability. Note that the blue line had the most unstable state, which cannot be controlled by changing the observation time span.
Although the quasi-observations can enhance the model stability, they can also affect the Ambiguity Dilution of the Precision (ADOP). Figure 6 shows the ADOP values of the four comparative models mentioned above.

Figure 6. ADOPs of the UD model for varying precisions of quasi-observations. The blue line represents the model that did not estimate the satellite clock offsets (ADOP-NT), the green line represents the model with a prior precision of 0·1 ns (ADOP-0·1 ns), the black line represents the model with a prior precision of 0·2 ns (ADOP-0·2 ns), and the red line represents the model with a prior precision of 0·3 ns (ADOP-0·3 ns). The purple dotted line indicates the 0·12 cycle corresponding to an ambiguity success rate of 0·999.
ADOP was introduced by Teunissen (Reference Teunissen1997) as an easy-to-compute scalar diagnostic. Instead of Position Dilution of Precision (PDOP) (which is commonly used to describe the impact of receiver-satellite geometry on the positioning precision), ADOP was used to measure the intrinsic precision characteristics of ambiguities in the filter. It is invariant for the class of admissible ambiguity transformations (Teunissen et al., Reference Teunissen, Odijk and Jong2000) and is defined as
 $$ADOP = {\sqrt {\left \vert {{Q_{\hat N\hat N}}} \right \vert} ^{\displaystyle{1 \over n}}}$$
$$ADOP = {\sqrt {\left \vert {{Q_{\hat N\hat N}}} \right \vert} ^{\displaystyle{1 \over n}}}$$In Figure 6, more time was needed to ensure 99·9% credibility for the AR when the accuracies of the real-time satellite clock products decreased. Generally, higher precision satellite clock products correspond to higher confidence intervals for the ambiguities.
In the single-station process, the filter residuals of the observation equations from three different models were compared to validate the performances of the proposed model with estimated satellite clocks.
In Figure 7, the residual error was bigger for low satellite elevations. This is because the accuracy of the tropospheric mapping function is related to the satellite elevation. Overall, the un-combined model reduced the observation noise, and the satellite clock estimates mean that the model is better adapted to unstable real-time satellite clock data.

Figure 7. Filter residuals of the observation equations in PBO site p345 (left) and p332 (right). In each figure, the horizontal axis represents the elevation of the satellites and the vertical axis represents the residuals. The top figure is the ionosphere-free model, the middle is the un-combined model without the satellite clock estimates, and the bottom is the un-combined model with the satellite clock estimates.
4.3. Fixed success ratio of the DD ambiguity
To verify the performance of the proposed UD network RTK strategy, we ran some experiments regarding the DD ambiguities, using the post-processing mode with various lengths.
The Melbourne-Wübbena (MW) (Wübbena, Reference Wübbena1985) linear combination is typically used to calculate the DD WL ambiguities. The results of the MW and UD-UC methods were obtained within an observation time span of 15 minutes. There were 4254 groups of WL float ambiguity biases in this set of test data.
The statistical results are shown in Figure 8. Both methods resulted in normally distributed WL ambiguities, but the UD-UC method performed slightly better. This is because the UD-UC method uses a geometry-based model and takes full advantage of the observations from all satellites. The DD-MW method uses a geometry-free model and relies on the quality of observations from a single satellite, especially the quality of the pseudo range observations. A decrease in the satellite elevation increased the code errors and multipath effect, resulting in a worse performance in terms of the WL AR.

Figure 8. The WL float ambiguity biases for the DD-MW (left) and UD-UC (right) methods. The successful fixed rate for the DD-MW method was 99·95% (for two sets of ambiguity deviations of 0·6 and 0·65 cycles), and was 100% for UD-UC method.
After the WL ambiguities are fixed, we can calculate the N1 ambiguity. In the UD-UC method, the N1 ambiguities are derived using Equations (10)–(12).
Based on an accurate WL AR, we used two options for the DD AR: the conventional DD method (where ZWD parameters for each reference station are estimated for the long-distance baseline), and the UD and UC method proposed in this paper. Two baselines were used to verify and evaluate the performance of the different long baselines (82·6 km and 204·5 km).
Figure 9 shows the results of the conventional DD method with AR (ZWD parameters for each reference station). During the initialisation phase, the float ambiguities of all satellites had larger fluctuations. The satellites only receive double difference ambiguities after 60 epochs (15 minutes). However, the UD and UC method is insensitive to the baseline length and can obtain the float ambiguities of all the satellites within a short time period. This is mainly because the ambiguity correlations were reduced using the proposed UD model.

Figure 9. Float ambiguity bias comparison for different baseline distances and AR methods. The upper figure represents the experiment with an 82·6 km baseline and the bottom used a 204·5 km baseline. The top of each sub-figure contains the results for the UD-UC method and the bottom is the conventional DD method.
To verify the ambiguity correlation problem of different methods, the condition numbers of the ambiguity covariance matrices are shown in Figure 10.

Figure 10. The condition numbers of the model for the UD method (CondN-UD, green) and the DD method (CondN-DD, blue). The left figure represents the experiment with an 82·6 km baseline and the right used a 204·5 km baseline.
In Figure 10, it is obvious that the condition number increases at the beginning of the filter. The condition numbers for the UD method suggest that there are significantly lower correlations than in the DD method.
We gathered the results for the eight baselines to generate 4254 groups of N1 float ambiguity biases. The results are shown in Figure 11.

Figure 11. The DD N1 float ambiguity biases for the DD-Ionfree (left) and UD-UC (right) methods. The successful fixed rate for the DD method using the LAMBDA technique was 96·41%, whereas the UD-UC method was 98·40%.
Figure 11 shows that the DD N1 ambiguities using the UD-UC method are more concentrated around the N1 float ambiguity bias. The UD and UC method performed better for L1 AR than the DD baseline method.
5. CONCLUSIONS
We proposed an alternative method for applying the UD and UC model to the network RTK. Based on the UD model, the proposed method does not need common satellites, thus avoiding the loss of observation information. Additionally, the UD-UC model is suitable for the distributed architecture of extensive CORS systems that result from an increasing number of stations.
We analysed the enhanced UD and UC model with the satellite clocks as parameters, which are properly constrained by real-time satellite clock products. The basic UD ambiguities were used to restore the DD ambiguities. We also reduced the effect of the correlations between ambiguities by the UD methods. The performance of the WL ambiguities and basic (N1 or N2) AR was quantitatively evaluated for NRTK, and compared with the conventional long-distance baseline mode. The UD and UC method performed slightly better for WL AR than the MW baseline method. The MW method was 99·95% accurate and the UD and UC method was 100% accurate. Furthermore, the DD N1 ambiguities determined by the UD and UC method were more concentrated around the float ambiguity biases. The successful fixed rate was 96·4% for the DD method and 98·4% for the UD-UC method.
The following conclusions can be made based on the results. (1) To apply real-time PPP, it is better to consider the biases of the satellite clock products; (2) the quasi-observations can improve the method's robustness to errors; (3) with the support of IGS real-time satellite products, the UD-UC method better estimates the WL ambiguity and basic ambiguity for network RTK. To improve the PPP-RTK performance, we will investigate the UD regional atmospheric model in the future.
ACKNOWLEDGEMENTS
This work is supported by the Key Projects in the National Science & Technology Pillar Program during the Twelfth Five-year Plan Period (No. 2012BAJ23B01). The authors are very grateful to the anonymous reviewers for their constructive comments and suggestions. We would like to express our thanks to Dr. Zhang Baocheng of Curtin University of Technology for his help and suggestions in data processing and writing process of the paper. All RINEX files used in this study are freely available from PBO (Plate Boundary Observatory) by UNAVCO. We thank PBO for providing the valuable data for scientific research.