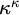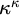1. Introduction
Definition 1. Let
$\kappa \leq \lambda $
be regular cardinals. We call a sequence
$\langle a_\xi : \xi \in \lambda \rangle $
, where
$a_\xi $
is a subset of
$\kappa $
of cardinality
$\kappa $
, i.e.,
$a_\xi \in [\kappa ]^{\kappa }$
, a
$\kappa $
-tower of length
$\lambda $
iff
-
(i) For all
$\xi < \xi ' < \lambda : a_\xi \supseteq ^{*} a_{\xi '}$
, i.e.,
$|a_{\xi '} \setminus a_{\xi }|< \kappa $
, -
(ii) There does not exist an
$a \in [\kappa ]^{\kappa }$
with
$\forall \xi < \lambda : a_\xi \supseteq ^{*}a$
(no pseudo-intersection).
Let
$\mathfrak {sp}(\mathfrak {t}(\kappa )):=\{\lambda : \text {there exists a }\kappa \text {-tower of length }\lambda \}$
be the
$\kappa $
-tower spectrum and
$\mathfrak {t}(\kappa ):=\min (\mathfrak {sp}(\mathfrak {t}(\kappa )))$
the
$\kappa $
-tower number.
Note that this definition excludes towers of non-regular length and of length
${<}\kappa $
, i.e.,
$\mathfrak {sp}(\mathfrak {t}(\kappa ))$
is a set of regular cardinals above
$\kappa $
. This is of course no real restriction, since we can always extract a cofinal subsequence from any ordinal-length tower. Conversely, we can always artificially extend a tower as in the definition to an ordinal-length tower by repeating elements. The requirement that
$\lambda \geq \kappa $
is a consequence of the following pathology that arises in the generalized Baire spaces:
Fact 1. Let
$\kappa $
be regular and uncountable. Decompose
$\kappa $
as
$\kappa :=\bigcup _{n\in \omega }X_n$
, where each
$X_n$
has cardinality
$\kappa $
. Then the family
$\{\bigcup _{m \geq n} X_m: n \in \omega \}$
is well-ordered by
$\supseteq ^{*}$
and has no pseudo-intersection.
The
$\omega $
-tower spectrum has been well-studied for many decades, for example by Hechler in [Reference Hechler7], by Baumgartner and Dordal in [Reference Baumgartner and Dordal2] or by Dordal in [Reference Dordal4]. In particular, Hechler [Reference Hechler7] showed that consistently, there exists an
$\omega $
-tower of length
$\lambda $
for each regular
$\lambda \in [\omega _1,\,2^\omega ]$
. Dordal [Reference Dordal4, Corollary 2.6] showed that for any set A of regular cardinals containing all of its regular limit points and the successors of its singular limit points (A is an Easton set), it is consistent that
$\mathfrak {sp}(\mathfrak {t}(\omega ))=A$
.
The present paper is motivated by the more recent interest in studying generalizations of classical cardinal invariants to the generalized Baire space
$\kappa ^\kappa $
. In particular, we are interested in controlling invariants globally, i.e., for all regular
$\kappa $
simultaneously. This line of inquiry specifically can be seen as building upon Easton’s famous Theorem [Reference Easton5], which establishes global control over the class function
$\kappa \to 2^\kappa $
. In particular, we follow recent work by Bağ, the first author and Friedman [Reference Bağ, Fischer and Friedman1], who analysed the spectrum of the generalized maximal almost-disjointness number globally.
In addition to
$\mathfrak {t}(\kappa )$
, we need the following generalized cardinal invariants:
Definition 2. Let
$\kappa $
be a regular cardinal.
-
(i) A subset
$\mathcal {B}\subseteq \kappa ^\kappa $
is unbounded iff
$\forall f \in \kappa ^\kappa \;\exists g \in \mathcal {B}: g \nleq ^{*}f$
, where
$g \leq ^{*} f :\iff |\{\eta \in \kappa : g(\eta )>f(\eta )\}|< \kappa $
. Let
$\mathfrak {b}(\kappa ):=\min \{|\mathcal {B}|: \mathcal {B} \subseteq \kappa ^\kappa \;\text {is unbounded}\}$
be the
$\kappa $
-bounding number. -
(ii) A subset
$\mathcal {D}\subseteq \kappa ^\kappa $
is dominating iff
$\forall f\in \kappa ^\kappa \;\exists g \in \mathcal {D}: f \leq ^{*}g$
. Let
$\mathfrak {d}(\kappa ):=\min \{|\mathcal {D}|: \mathcal {D} \subseteq \kappa ^\kappa \;\text {is dominating}\}$
be the
$\kappa $
-dominating number. -
(iii) A family
$\mathcal {A} \subseteq [\kappa ]^\kappa $
is almost disjoint iff
$\forall a \neq b \in \mathcal {A}: |a \cap b|< \kappa $
. Furthermore,
$\mathcal {A}$
is maximal almost disjoint (
$\kappa $
-mad) if
$\mathcal {A}$
is not properly contained in a different almost disjoint family. Let
$\mathfrak {sp}(\mathfrak {a}(\kappa )):=\{\delta : \text {there exists a}\;\kappa \text {-mad family}\; \mathcal {A} \text { with } \kappa \leq |\mathcal {A}|=\delta \leq 2^\kappa \}$
be the
$\kappa $
-mad spectrum and
$\mathfrak {a}(\kappa ):=\min (\mathfrak {sp}(\mathfrak {a}(\kappa )))$
the
$\kappa $
-maximal almost disjointness number. -
(iv) Let
$\mathfrak {sp}(\mathfrak {t}_{\text {cl}}(\kappa )){\kern1pt}:={\kern1pt}\{\lambda : {\kern1pt}\text{there }{\kern1pt}\text{exists }{\kern1pt}\text{a }{\kern1pt}\kappa {\kern1pt}\text{-tower }{\kern1pt}\text{of }{\kern1pt}\text{length }{\kern1pt}\lambda {\kern1pt}\text{ consisting }{\kern1pt}\text{of }{\kern1pt}\text{club } \text{sets}\}$
and
$\mathfrak {t}_{\text {cl}}(\kappa ):=\min (\mathfrak {sp}(\mathfrak {t}_{\text {cl}}(\kappa )))$
.
The following basic fact, due to Schilhan [Reference Schilhan10], establishes that
$\mathfrak {b}(\kappa )\in \mathfrak {sp}(\mathfrak {t}(\kappa ))$
for uncountable
$\kappa $
. It essentially follows by transforming
$f\in \kappa ^\kappa $
into the club
$c_f:= \{\alpha \in \kappa : \forall \beta \in \alpha : f(\beta ) \in \alpha \}$
, and, vice versa, a club
$c\in [\kappa ]^\kappa $
into the function
$f_c(\alpha ):=\min (c\setminus (\alpha +1))$
.
Lemma 1 [Reference Schilhan10, Theorem 2.9]
Let
$\kappa $
be regular uncountable. Then
$\mathfrak {b}(\kappa )=\mathfrak {t}_{\text {cl}}(\kappa )$
.
In the case
$\kappa =\omega $
, we have the following:
Lemma 2 (Folklore)
Assume
$\mathfrak {b}(\omega )< \mathfrak {d}(\omega )$
. Then
$\mathfrak {b}(\omega ) \in \mathfrak {sp}(\mathfrak {t}(\omega ))$
.
Proof. Let
$\mathcal {B} =\{g_\xi : \xi \in \mathfrak {b}(\omega )\}\subseteq \omega ^\omega $
be unbounded and such that
$\xi < \xi ' \implies g_\xi \leq ^{*} g_{\xi '}$
. Assume further that every
$g_\xi \in \mathcal {B}$
is strictly increasing. Since
$\mathfrak {b}(\omega )< \mathfrak {d}(\omega )$
, there exists
$f\in \omega ^\omega $
that is not dominated by
$\mathcal {B}$
. For each
$\xi \in \mathfrak {b}(\omega )$
, let
$a_\xi :=\{n \in \omega : f(n)> g_\xi (n)\}$
. Clearly, the sequence
$\langle a_\xi : \xi \in \mathfrak {b}(\omega )\rangle $
is well-ordered by
$\supseteq ^{*}$
. If it were pseudo-intersected by
$p \in [\omega ]^\omega $
, the function
$f_p \in \omega ^\omega $
given by
$f_p(n):=f(\min (p\setminus (n+1)))$
would dominate
$\mathcal {B}$
.
Note that if
$\mathfrak {b}(\omega )=\mathfrak {d}(\omega )$
, the above conclusion consistently fails: After a
$\lambda $
-stage finite-support iteration of Hechler forcing over a ground model satisfying
$\mathsf {CH}$
, we obtain a model in which
$\mathfrak {b}(\omega )=\mathfrak {d}(\omega )=2^\omega =\lambda $
, but which contains no
$\omega $
-towers of length
$\lambda $
. This was shown by Baumgartner and Dordal [Reference Baumgartner and Dordal2, Theorem 4.1].
The following well-known fact essentially follows from Lemma 1. For uncountable
$\kappa $
, it is originally due to Shelah and Spasojević [Reference Shelah and Spasojević11].
Fact 2 [Reference Shelah and Spasojević11, Fact 1.4]
For all regular
$\kappa $
:
$\mathfrak {t}(\kappa ) \leq \mathfrak {b}(\kappa )$
.
1.1. Structure of the paper
In Section 2, we begin by observing that in the Easton model, the
$\kappa $
-tower spectrum is
$\{\kappa ^{+}\}$
, globally. More specifically,
Theorem (Theorem 1)
For any Easton function E, it is consistent that
$$\begin{align*}\forall \kappa \in \text{dom}(E): \mathfrak{sp}(\mathfrak{t}(\kappa))=\{\kappa^{+}\} \text{ and } 2^\kappa=E(\kappa).\end{align*}$$
This will follow from a straightforward isomorphism-of-names argument. We then show that by a very similar argument, a small tower spectrum is consistent globally with an arbitrarily large
$\kappa $
-mad spectrum:
Theorem (Theorem 2)
Let E be an index function such that for every
$\kappa \in \text {dom}(E)$
,
$E(\kappa )$
is a closed set of cardinals with
$\min E(\kappa )\geq \kappa ^{+}$
,
$\text {cf}(\max E(\kappa ))> \kappa $
and such that
$\kappa < \kappa ' \implies \max E(\kappa ) \leq \max E(\kappa ')$
. Then, consistently,
$$\begin{align*}\forall \kappa \in \text{dom}(E):\mathfrak{sp}(\mathfrak{t}(\kappa))=\{\kappa^{+}\},\; E(\kappa) \subseteq \mathfrak{sp}(\mathfrak{a}(\kappa)) \text{ and } 2^\kappa=\max E(\kappa).\end{align*}$$
Furthermore, by only controlling these spectra at successors of regular cardinals together with
$\aleph _0$
, and restricting the range of E to so-called
$\kappa $
-Blass spectra, we have
Corollary (Corollary 1)
Let E be an index function defined on successors of regular cardinals together with
$\aleph _0$
, and such that
$E(\kappa )$
is a
$\kappa $
-Blass spectrum for every
$\kappa \in \text {dom}(E)$
. Then, consistently,
$$\begin{align*}\forall \kappa \in \text{dom}(E): \mathfrak{sp}(\mathfrak{t}(\kappa))=\{\kappa^{+}\} \text{ and } \mathfrak{sp}(\mathfrak{a}(\kappa))=E(\kappa).\end{align*}$$
This is based on previous work by Bağ, the first author and Friedman [Reference Bağ, Fischer and Friedman1]. While the high-level argument is again an isomorphism of names, constructing the appropriate isomorphism turns out to be surprisingly convoluted. In Section 3, we show that arbitrarily large
$\kappa $
-tower spectra are consistent globally. In fact, we show the following.
Theorem (Theorem 3 and Corollary 3)
Let E be an Easton function. Then, consistently,
$$\begin{align*}\forall \kappa \in \text{dom}(E): \mathfrak{sp}(\mathfrak{t}(\kappa))=\mathfrak{sp}(\mathfrak{t}_{\text{cl}}(\kappa)) =[\kappa^{+}, 2^\kappa], \text{ where } 2^\kappa=E(\kappa) \text{ and } \mathfrak{b}(\kappa)=\kappa^{+}.\end{align*}$$
Here,
$[\kappa ^{+}, 2^\kappa ]$
denotes the set of regular cardinals between
$\kappa ^{+}$
and
$2^\kappa $
. Finally, in Section 4, we prove that any non-trivial upper bound on the
$\kappa $
-tower spectrum is consistent. More precisely,
Theorem (Theorem 4)
For any regular
$\beta> \kappa $
and
$\mu $
with
$\text {cf}(\mu )\geq \beta $
, it is consistent that
$$\begin{align*}\mathfrak{sp}(\mathfrak{t}(\kappa))\subseteq [\kappa^{+}, \mathfrak{b}(\kappa)], \text{ where } \mathfrak{b}(\kappa)=\beta \text{ and } 2^\kappa=\mu.\end{align*}$$
Tightness of this upper bound for uncountable
$\kappa $
or for
$\beta <\mu $
follows from Lemmas 1 and 2 above. Furthermore, Lemma 1 implies the following.
Corollary (Corollary 5)
For any regular uncountable
$\kappa $
and
$\beta , \mu $
as above, it is consistent that
$$\begin{align*}\mathfrak{sp}(\mathfrak{t}_{\text{cl}}(\kappa)) =\{\beta\} \text{ and } 2^\kappa=\mu.\end{align*}$$
1.2. Convention
We say that a forcing notion
$\mathbb {P}$
is
$\kappa $
-closed if every decreasing sequence of
$\mathbb {P}$
-conditions of length
$\lambda < \kappa $
has a lower bound. Furthermore, we say that
$\mathbb {P}$
satisfies the
$\kappa $
-chain condition (
$\kappa $
-c.c.) if antichains have size
${<}\kappa $
. For cardinals
$\delta $
and
$\gamma $
, we denote by
$[\delta , \gamma ]$
the set of regular cardinals between
$\delta $
and
$\gamma $
.
2. Globally small tower spectra
It is folklore that there are no towers of length
${>}\omega _1$
in the Cohen Model. We observe that this can be generalized to a global result.
Definition 3.
-
(i) A function E is an index function if
$\text {dom}(E)$
is a class of regular cardinals. -
(ii) An index function E is an Easton function if for every
$\kappa \in \text {dom}(E)$
,
$ E(\kappa )$
is a cardinal with
$\text {cf}(E(\kappa ))>\kappa $
and such that
$\kappa < \kappa ' \implies E(\kappa ) \leq E(\kappa ')$
.
If E is an index function and
$\kappa \in \text {dom}(E)$
, we let
$E^{\leq \kappa }:=E|_{\kappa +1}$
and
$E^{{>}\kappa }:=E|_{\text {dom}(E)\setminus (\kappa +1)}$
. Furthermore, if there is a forcing notion
$\mathbb {P}_\kappa $
for each
$\kappa \in \text {dom}(E)$
, the Easton-product
$\mathbb {P}(E)$
of the
$\mathbb {P}_\kappa $
consists of conditions of the form
$p=\langle p(\kappa ): \kappa \in \text {dom}(E)\rangle $
, where for each regular cardinal 
. The set 
is called the support of p and denoted by
$\text {supp}(p)$
. It is clear that
$\mathbb {P}(E)$
is isomorphic to
$\mathbb {P}(E^{\leq \kappa })\times \mathbb {P}(E^{>\kappa })$
.
Definition 4. Let E be an Easton function. Easton forcing relative to E is the Easton-product of the forcing notions
$\text {Fn}_{<\kappa }(E(\kappa ) \times \kappa , 2)$
over all
$\kappa \in \text {dom}(E)$
.
It is well-known that for each
$\kappa \in \text {dom}(E): \mathbb {P}(E^{\leq \kappa })$
satisfies the
$\kappa ^{+}$
-c.c. and
$\mathbb {P}(E^{{>} \kappa })$
is
$\kappa ^{+}$
-closed, provided that
$2^{<\kappa }=\kappa $
.
Theorem 1. Let
$\mathbf {V}\models \mathsf {GCH}$
, let E be an Easton function and denote Easton forcing relative to E by
$\mathbb {P}(E)$
. Then, in any
$\mathbb {P}(E)$
-generic extension of
$\mathbf {V}$
:
$$\begin{align*}\forall \kappa \in \text{dom}(E): \mathfrak{sp}(\mathfrak{t(\kappa)})=\{\kappa^{+}\} \text{ and } 2^\kappa=E(\kappa).\end{align*}$$
Proof. The second equality is well-known. Fix
$\kappa \in \text {dom}(E)$
and let G be
$\mathbb {P}({E})$
generic over
$\mathbf {V}$
. Assume by contradiction that there exists a
$\kappa $
-tower
$\langle a_\xi : \xi \in \lambda \rangle $
of length
$\lambda \geq \kappa ^{++}$
in
$\mathbf {V}[G]$
. We can assume that
$\langle a_\xi : \xi \in \lambda \rangle $
is strictly
$\supseteq ^{*}$
-descending, by extracting such a subsequence. Decompose
$\mathbb {P}(E)$
as
$\mathbb {P}(E^{\leq \kappa }) \times \mathbb {P}(E^{> \kappa })$
and
${G= G^{\leq \kappa } \times G ^{> \kappa }} $
accordingly. Since
$\mathbb {P}(E^{> \kappa })$
is
$\kappa ^{+}$
-closed, the
$\mathsf {GCH}$
at
$\delta \leq \kappa $
still holds in
$\mathbf {V}[G ^{> \kappa }]$
and
$(\mathbb {P}(E^{\leq \kappa }))^{\mathbf {V}[G^{{>} \kappa }]}=(\mathbb {P}(E^{\leq \kappa }))^{\mathbf {V}}$
. We designate
$\mathbf {V}[G^{>\kappa }]$
as the new ground model.
For each
$\xi \in \kappa ^{++}$
, let
$\dot a_\xi $
be a nice
$\mathbb {P}(E^{\leq \kappa })$
-name for
$a_\xi $
and let
$p_0 \in G^{\leq \kappa }$
be a
$ \mathbb {P}(E^{\leq \kappa })$
-condition such that
$\forall \xi < \xi ' < \kappa ^{++}: p_0 \Vdash _{\mathbb {P}(E^{\leq \kappa })} {"}\dot a_\xi \supsetneq ^{*} \dot a_{\xi '}"$
.
Any nice
$\mathbb {P}(E^{\leq \kappa })$
-name
$\dot x$
is of the form
$\dot x= \bigcup _{\alpha \in \kappa }\{\check \alpha \}\times A_\alpha (\dot x)$
, where
$A_\alpha (\dot x)$
is an antichain in
$\mathbb {P}(E^{\leq \kappa })$
. Since
$\mathbb {P}(E^{\leq \kappa })$
satisfies the
$\kappa ^{+}$
-c.c., the set
$$\begin{align*}S^\delta(\dot x):=\bigcup_{\substack{{\alpha \in \kappa}\\{p \in A_\alpha(\dot x)}}}\text{dom}(p(\delta)) \cup \text{dom}(p_0(\delta))\end{align*}$$
has cardinality at most
$\kappa $
for every
$\delta \in \text {dom}(E^{\leq \kappa })$
, and thus the same holds for the set
$S(\dot x):=\bigcup _{\delta \in \text {dom}(E^{\leq \kappa })}S^\delta (\dot x)$
.
By applying the
$\Delta $
-system Lemma, which requires the
$\mathsf {GCH}$
at
$\kappa $
, to the family
$\{S(\dot a_\xi ): \xi \in \kappa ^{++}\}$
, we find some
$X \subseteq \kappa ^{++}$
of cardinality
$\kappa ^{++}$
and a sequence
$\langle R^\delta : \delta \in \text {dom}(E^{\leq \kappa })\rangle $
such that for all
$\xi \neq \xi ' \in X$
and all
$\delta \in \text {dom}(E^{\leq \kappa }): S^\delta (\dot a_\xi ) \cap S^\delta (\dot a_{\xi '})=R^\delta $
. Note that
$\text {dom}(p_0(\delta )) \subseteq R^\delta $
. Since
$S^\delta (\dot a_\xi )$
has cardinality
${\leq }\kappa $
and since
$\kappa ^\kappa =\kappa ^{+}$
, we find by the pigeonhole principle some
$X'\subseteq X$
of cardinality
$\kappa ^{++}$
such that
$|S^\delta (\dot a_\xi )\setminus R^{\delta }|=|S^\delta (\dot a_{\xi '})\setminus R^{\delta }|$
for all
$\xi \neq \xi ' \in X'$
and
$\delta \in \text {dom}(E^{\leq \kappa })$
.
Fix some
$\xi _0\in X'$
and choose for each
$\xi \in X'$
and each
$\delta \in \text {dom}(E^{\leq \kappa })$
a permutation of
$E(\delta ) \times \delta $
of order 2 that maps
$S^\delta (\dot a_\xi )$
to
$S^\delta (\dot a_{\xi _0})$
and fixes everything besides
$S^\delta (\dot a_\xi ) \cup S^\delta (\dot a_{\xi _0}) \setminus R^\delta $
. Denote by
$\varphi ^\delta _{\xi }$
the automorphism of
$\text {Fn}_{<\delta }(E(\delta ) \times \delta , 2)$
that this permutation induces. By applying these automorphisms coordinate-wise, we obtain automorphisms of
$\mathbb {P}(E^{\leq \kappa })$
, which we denote by
$\varphi _{\xi }$
. Since we chose permutations fixing the
$R^\delta $
, we have
$\varphi _\xi (p_0)=p_0$
. The automorphisms
$\varphi _\xi $
extend to
$\mathbb {P}(E^{\leq \kappa })$
-names in the obvious way.
Note that
$\varphi _{\xi }(\dot a_\xi )$
is a nice name with
$S(\varphi _{\xi }(\dot a_\xi )) \subseteq S(\dot a_{\xi _0})$
. By counting, we see that there are at most
$\kappa ^{+}$
many nice names
$\dot x$
with
$S(\dot x) \subseteq S(\dot a_{\xi _0})$
. Therefore, there exists
$X" \subseteq X'$
of cardinality
$\kappa ^{++}$
and a nice name
$\dot x$
such that
$\varphi _{\xi }(\dot a_\xi )=\dot x$
for every
$\xi \in X"$
.
Now, fix
$\xi < \xi ' \in X"\setminus \{\xi _0\}$
and define the following automorphism of
$\mathbb {P}(E^{\leq \kappa })$
:
$$\begin{align*}\chi:= \varphi_{\xi} \circ \varphi_{\xi'} \circ \varphi_{\xi}.\end{align*}$$
Note that
$\chi (\dot a_\xi )=\dot a_{\xi '}$
, that
$\chi (\dot a_{\xi '})=\dot a_{\xi }$
and that
$\chi (p_0)=p_0$
. By assumption,
$p_0 \Vdash _{\mathbb {P}(E^{\leq \kappa })} \dot a_\xi \supsetneq ^{*} \dot a_{\xi '}$
. Thus,
$ \chi (p_0)\Vdash _{\chi (\mathbb {P}(E^{\leq \kappa }))} \chi (\dot a_\xi ) \supsetneq ^{*} \chi (\dot a_{\xi '})$
, which implies that
$$\begin{align*}p_0\Vdash \dot a_{\xi'} \supsetneq^{*} \dot a_{\xi} \;\text{and}\; \dot a_{\xi} \supsetneq^{*} \dot a_{\xi'},\end{align*}$$
a contradiction.
The above result can be generalized to show that consistently, the
$\kappa $
-tower spectrum equals
$\{\kappa ^{+}\}$
for all regular
$\kappa $
, while the
$\kappa $
-mad spectrum is arbitrarily large. More precisely, we prove the following:
Theorem 2. Let
$\mathbf {V}\models \mathsf {GCH}$
and let E be an index function such that for every
$\kappa \in \text {dom}(E)$
,
$E(\kappa )$
is a closed set of cardinals with
$\min E(\kappa )\geq \kappa ^{+}$
,
$\text {cf}(\max E(\kappa ))> \kappa $
and such that
$\kappa < \kappa ' \implies \max E(\kappa ) \leq \max E(\kappa ')$
. There is a forcing extension of
$\mathbf {V}$
in which
$$\begin{align*}\forall \kappa \in \text{dom}(E):\mathfrak{sp}(\mathfrak{t}(\kappa))=\{\kappa^{+}\},\; E(\kappa) \subseteq \mathfrak{sp}(\mathfrak{a}(\kappa)) \text{ and } 2^\kappa=\max E(\kappa).\end{align*}$$
This is based on a construction by Bağ, the first author and Friedman [Reference Bağ, Fischer and Friedman1]. As is shown in that paper, the same construction allows for more accurate control of
$\mathfrak {sp}(\mathfrak {a}(\kappa ))$
by restricting the domain of E to successors of regular cardinals together with
$\aleph _0$
, and the range of E to so-called
$\kappa $
-Blass spectra. While the definition of a
$\kappa $
-Blass spectrum is not necessary for our purposes, we give it for the sake of completeness.
Definition 5 [Reference Bağ, Fischer and Friedman1, Definition 2.1]
A
$\kappa $
-Blass spectrum is a set A of cardinals satisfying
$\min A=\kappa ^{+}$
,
$\forall \mu \in A: [\text {cf}(\mu )\leq \kappa \implies \mu ^{+}\in A]$
and
$\gamma \in A$
for every cardinal
$\kappa ^{+} \leq \gamma \leq |A|$
.
Corollary 1 (GCH)
If E is defined on successors of regular cardinals together with
$\aleph _0$
, and
$E(\kappa )$
is a
$\kappa $
-Blass spectrum for every
$\kappa \in \text {dom}(E)$
, we consistently have
$$\begin{align*}\forall \kappa \in \text{dom}(E):\mathfrak{sp}(\mathfrak{t}(\kappa))=\{\kappa^{+}\} \text{ and } \mathfrak{sp}(\mathfrak{a}(\kappa))=E(\kappa).\end{align*}$$
Proof of Theorem 2
We begin by defining the relevant forcing notions.
Definition 6 [Reference Bağ, Fischer and Friedman1, Definition 4.2]
Define for each
$\kappa \in \text {dom}(E)$
and each
$\lambda \in E(\kappa )$
the following forcing notion
$\mathbb {A}^{\kappa , \lambda }$
: An
$\mathbb {A}^{\kappa ,\lambda }$
-condition is a function
$p: \Delta ^{p} \to [\kappa ]^{{<}\kappa }$
, where
$\Delta ^p \in [\lambda ]^{{<}\kappa }$
. We define
$p' \leq p$
iff:
-
(i)
$\Delta ^{p}\subseteq \Delta ^{p'}$
, -
(ii)
$\forall x \in \Delta ^{p}: p(x)\subseteq p'(x)$
, -
(iii)
$\forall \eta _1 \neq \eta _2 \in \Delta ^{p}: p'(\eta _1)\cap p'(\eta _2)\subseteq p(\eta _1)\cap p(\eta _2)$
.
For each
$\kappa \in \text {dom}(E)$
, let
$\mathbb {A}^\kappa $
be the
${<}\kappa $
-support product of the
$\mathbb {A}^{\kappa ,\lambda }$
over all
$\lambda \in E(\kappa )$
. Then, let
$\mathbb {A}$
be the Easton-product of the
$\mathbb {A}^\kappa $
.
Let G be
$\mathbb {A}$
-generic over
$\mathbf {V}$
. It is shown in [Reference Bağ, Fischer and Friedman1, Theorem 4.6 and Remark 4.7] that for all
$\kappa \in \text {dom}(E): E(\kappa )\subseteq \mathfrak {sp}(\mathfrak {a}(\kappa ))$
and
$2^\kappa =\max E(\kappa )$
holds in
$\mathbf {V}[G]$
. To show the other equality, let
$\kappa \in \text {dom}(E)$
and decompose
$\mathbb {A}$
as
$\mathbb {A}^{{>}\kappa }\times \mathbb {A}^{\leq \kappa }$
and
$G=G^{{>}\kappa }\times G^{\leq \kappa }$
accordingly. As is shown in [Reference Bağ, Fischer and Friedman1, Lemma 4.3],
$\mathbb {A}^{{>}\kappa }$
is
$\kappa ^{+}$
-closed and
$\mathbb {A}^{\leq \kappa }$
satisfies the
$\kappa ^{+}$
-c.c., which implies that the
$\mathsf {GCH}$
at
$\delta \leq \kappa $
still holds in
$\mathbf {V}[G^{{>}\kappa }]$
and that
$(\mathbb {A}^{\leq \kappa })^{\mathbf {V}[G^{{>}\kappa }]}=(\mathbb {A}^{\leq \kappa })^{\mathbf {V}}$
. Let
$\mathbf {W}:=\mathbf {V}[G^{{>}\kappa }]$
be the new ground model.
Assume by contradiction that
$\langle a_\xi : \xi < \kappa ^{++}\rangle $
is a strictly
$\supseteq ^{*}$
-descending sequence of cofinal subsets of
$\kappa $
in
$\mathbf {W}[G^{\leq \kappa }]$
. Let
$\dot a_\xi $
be a nice
$\mathbb {A}^{\leq \kappa }$
-name for
$a_\xi $
and let
$p_0$
be such that for all
$\xi < \xi ' < \kappa ^{++}: p_0\Vdash \dot a_\xi \supsetneq ^{*} \dot a_{\xi '}$
.
In order to find the required isomorphisms, we must first extend the forcing notion
$\mathbb {A}^{\leq \kappa }$
to a larger forcing notion
$\mathbb {Q}^{\leq \kappa }$
into which
$\mathbb {A}^{\leq \kappa }$
completely embeds.
Definition 7. For every
$\delta \in \text {dom}(E^{\leq \kappa })$
, let
$b^\delta :=|E(\delta )|$
and
$J^\delta :=\max E(\delta )$
, and for every
$\beta \in b^\delta $
, let
$\mathbb {Q}^{\delta ,\beta }$
be the forcing notion
$\mathbb {A}^{\delta , J_\delta }$
. Let
$\mathbb {Q}^{\delta }$
be the
${<}\kappa $
-support product of the
$\mathbb {Q}^{\delta , \beta }$
and
$\mathbb {Q}^{\leq \kappa }$
the Easton-product over all
$\delta \in \text {dom}(E^{\leq \kappa })$
of the
$\mathbb {Q}^{\delta }$
.
It is easy to verify that
$\mathbb {A}^{\leq \kappa }$
completely embeds into
$\mathbb {Q}^{\leq \kappa }$
(see [Reference Bağ, Fischer and Friedman1, Lemma 4.8]). Thus,
$\forall \xi < \xi ' < \kappa ^{++}:p_0 \Vdash _{\mathbb {Q}^{\leq \kappa }} \dot a_\xi \supsetneq ^{*} \dot a_{\xi '}$
.
Definition 8. Let
$\dot x$
be a nice
$\mathbb {Q}^{\leq \kappa }$
-name for a subset of
$\kappa $
, i.e.,
$\dot x = \bigcup _{\alpha \in \kappa }\{\check \alpha \} \times A_\alpha (\dot x)$
. For each
$\delta \in \text {dom}(E^{\leq \kappa })$
and
$\beta \in b^\delta $
, define the following sets:
$$\begin{align*}\begin{aligned} \text{supp}^{\delta}(\dot x) &:= \bigcup_{\substack{{\alpha \in \kappa}\\p \in A_\alpha(\dot x)}}\text{supp}(p(\delta)) \cup \text{supp}(p_0(\delta)) \in [b^\delta]^{\leq \kappa}\\ \Delta^{\delta, \beta}(\dot x)&:= \bigcup_{\substack{{\alpha \in \kappa}\\p \in A_\alpha(\dot x)}}\Delta^{p(\delta)(\beta)} \cup \Delta^{p_0(\delta)(\beta)}\in [J^{\delta}]^{\leq \kappa.} \end{aligned} \end{align*}$$
By applying the
$\Delta $
-system Lemma, we obtain some
$X \subseteq \kappa ^{++}$
of cardinality
$\kappa ^{++}$
and for each
$\delta \in \text {dom}(E^{\leq \kappa })$
a root
$R^\delta $
such that for all
$\xi \neq \xi ' \in X: \text {supp}^{\delta }(\dot a_\xi )\cap \text {supp}^{\delta }(\dot a_{\xi '})=R^\delta $
. Since
$\kappa ^\kappa =\kappa ^{+}< \kappa ^{++}$
, we can assume without loss of generality that for every
$\delta \in \text {dom}(E^{\leq \kappa })$
, the value
$|\text {supp}^{\delta }(\dot a_\xi )\setminus R^\delta |$
does not depend on
$\xi \in X$
.
Fix some
$\xi _0\in X$
and let
$\psi ^\delta _\xi $
be a permutation of
$b^\delta $
of order 2 that maps
$\text {supp}^{\delta }(\dot a_\xi )$
to
$\text {supp}^{\delta }(\dot a_{\xi _0})$
and fixes everything outside of
$(\text {supp}^{\delta }(\dot a_\xi )\cup \text {supp}^{\delta }(\dot a_{\xi _0})) \setminus R^\delta $
. This permutation naturally induces an automorphisms of
$\mathbb {Q^\delta }$
. By applying these automorphisms coordinate-wise, we obtain for each
$\xi \in X$
an automorphism of the entire
$\mathbb {Q}^{\leq \kappa }$
, which we call
$\psi _\xi $
. It recursively extends to
$\mathbb {Q}^{\leq \kappa }$
-names. Note that
$\forall \delta \in \text {dom}(E^{\leq \kappa }): \text {supp}^{\delta }(\psi _\xi (\dot a_\xi ))=\text {supp}^{\delta }(\dot a_{\xi _0})$
,
$\psi _\xi (p_0)=p_0$
and for every
${\xi '\in X\setminus \{\xi , \xi _0\}: \psi _\xi (\dot a_{\xi '})=\dot a_{\xi '}}$
.
In an abuse of notation, we assume that the sets
$J^\delta $
underlying the forcing notions
$\mathbb {Q}^{\delta ,\beta }$
are disjoint for different
$(\delta , \beta )$
and apply the
$\Delta $
-system Lemma to the family
$$\begin{align*}\left\{\bigcup \{\Delta^{\delta, \beta}(\psi_\xi(\dot a_\xi)): \;\delta \in \text{dom}(E^{\leq \kappa}), \; \beta \in b^\delta\}: \xi \in X\right\}.\end{align*}$$
We obtain some
$X'\subseteq X$
of cardinality
$\kappa ^{++}$
and for each
$\delta \in \text {dom}(E^{\leq \kappa })$
and each
$\beta \in b^\delta $
a root
$R^{\delta , \beta }$
, i.e., we have for all
$\xi \neq \xi ' \in X'$
, every
$\delta \in \text {dom}(E^{\leq \kappa })$
and every
$\beta \in b^\delta $
:
$\Delta ^{\delta , \beta }(\psi _\xi (\dot a_\xi ))\cap \Delta ^{\delta , \beta }(\psi _{\xi '}(\dot a_{\xi '}))=R^{\delta , \beta }$
.
Since
$\text {supp}^{\delta }(\psi _\xi (\dot a_\xi ))=\text {supp}^{\delta }(\dot a_{\xi _0})$
, and since
$\kappa ^\kappa < \kappa ^{++}$
, we can again assume without loss of generality that the value
$|\Delta ^{\delta , \beta }(\psi _\xi (\dot a_\xi ))\setminus R^{\delta , \beta }|$
does not depend on
$\xi \in X'$
. We may therefore fix
$\xi _1 \in X'$
and choose for each
$\delta \in \text {dom}(E^{\leq \kappa })$
and
$\beta \in b^\delta $
some permutation
$\varphi ^{\delta , \beta }_\xi $
of order 2 of
$J^{\delta }$
that maps
$\Delta ^{\delta , \beta }(\psi _\xi (\dot a _\xi ))$
to
$\Delta ^{\delta , \beta }(\psi _{\xi _1}(\dot a _{\xi _1}))$
, and fixes everything except for
$(\Delta ^{\delta , \beta }(\psi _\xi (\dot a _\xi )) \cup \Delta ^{\delta , \beta }(\psi _{\xi _1}(\dot a _{\xi _1})))\setminus R^{\delta , \beta }$
. This map induces an automorphism of
$\mathbb {Q}^{\delta , \beta }$
, and by applying the maps coordinate-wise, we again obtain an automorphism of the entire
$\mathbb {Q}^{\leq \kappa }$
, which we denote by
$\varphi _\xi $
. Note that
$\varphi _\xi (p_0)=p_0$
and for every
$\xi ' \in X'\setminus \{\xi ,\xi _1\}: \varphi _\xi (\dot a_{\xi '})= \dot a_{\xi '}.$
By definition of the maps,
$\varphi _\xi \circ \psi _\xi (\dot a_\xi )$
is a nice name satisfying for every
${\delta \in \text {dom}(E^{\leq \kappa })}$
and
$\beta \in b^\delta $
:
$$\begin{align*}\text{supp}^{\delta}(\varphi_\xi \circ \psi_\xi(\dot a_\xi))=\text{supp}^{\delta}(\dot a_{\xi_0}) \text{ and } \Delta^{\delta, \beta}(\varphi_\xi \circ \psi_\xi(\dot a_\xi))=\Delta^{\delta, \beta}(\psi_{\xi_1}(\dot a_{\xi_1})).\end{align*}$$
By an easy counting argument, there are at most
$\kappa ^{+}$
many nice names with this property, which implies that there exist fixed
$\xi \neq \xi ' \in X'\setminus \{\xi _0, \xi _1\}$
and a nice name
$\dot z$
such that
$\varphi _\xi \circ \psi _\xi (\dot a_\xi ) = \varphi _{\xi '} \circ \psi _{\xi '}(\dot a_{\xi '})=\dot z$
.
Since we have fixed
$\xi $
and
$\xi '$
, we will from now on use the shorthands
${\psi :=\psi _\xi ,\; \psi ':=\psi _{\xi '},\; \varphi :=\varphi _\xi , \;\varphi ':=\varphi _{\xi '}}$
. The rest of the proof consists in showing that the automorphism
$$\begin{align*}\chi:=\psi' \circ \varphi' \circ \psi \circ \varphi \circ \varphi' \circ \psi' \circ \varphi \circ \psi \circ \varphi \circ \psi \end{align*}$$
satisfies
$\chi (\dot a_\xi )=\dot a_{\xi '}$
and
$\chi (\dot a_{\xi '})=\dot a_{\xi }$
. Unfortunately, there does not seem to be a shorter one that works. Since
$\chi (p_0)=p_0$
, we obtain the contradiction
$$\begin{align*}p_0 \Vdash_{\mathbb{Q}^{\leq \kappa}}\dot a_\xi \subsetneq^{*} \dot a_{\xi'} \land \dot a_{\xi'} \subsetneq^{*} \dot a_{\xi},\end{align*}$$
just as in the proof of Theorem 1.
Definition 9. Let
$U^{\delta }:=\text {supp}^{\delta }(\dot a_{\xi _0}), \;U^{\delta , \beta }:=\Delta ^{\delta , \beta }(\psi _{\xi _1}(\dot a_{\xi _1}))$
and define the following subsets of
$\mathbb {Q^{\leq \kappa }}$
:
-
(i)
$\mathbb {R}^{\mathsf {R}}:=\{p \in \mathbb {Q}^{\leq \kappa }: \forall \delta \in \text {dom}(E^{\leq \kappa })\;\forall \beta \in b^\delta : \text {supp}(p(\delta ))\subseteq R^{\delta } \land \Delta ^{p(\delta )(\beta )}\subseteq R^{\delta , \beta }\}.$
-
(ii)
$\mathbb {R}^{\mathsf {U}}:=\{p \in \mathbb {Q}^{\leq \kappa }: \forall \delta \in \text {dom}(E^{\leq \kappa })\,\forall \beta \in b^\delta : \text {supp}(p(\delta ))\subseteq R^{\delta } \land \Delta ^{p(\delta )(\beta )}\subseteq U^{\delta , \beta } \setminus R^{\delta , \beta }\}.$
-
(iii)
$\mathbb {R}^{\xi }:=\{p \in \mathbb {Q}^{\leq \kappa }: \forall \delta \in \text {dom}(E^{\leq \kappa })\,\forall \beta \in b^\delta : \text {supp}(p(\delta ))\subseteq R^{\delta } \land \Delta ^{p(\delta )(\beta )}\subseteq \Delta ^{\delta , \beta }(\dot a_\xi )\setminus R^{\delta , \beta } \}$
, and define
$\mathbb {R}^{\xi '}$
analogously. -
(iv)
$\mathbb {U}:= \{p \in \mathbb {Q}^{\leq \kappa }: \forall \delta \in \text {dom}(E^{\leq \kappa }): \text {supp}(p(\delta ))\subseteq U^{\delta }\setminus R^{\delta }\}.$
-
(v)
$\mathbb {P}^\xi :=\{p \in \mathbb {Q}^{\leq \kappa }: \forall \delta \in \text {dom}(E^{\leq \kappa }): \text {supp}(p(\delta ))\subseteq \text {supp}^{\delta }(\dot a_\xi )\setminus R^\delta \}$
, and define
$\mathbb {P}^{\xi '}$
analogously. -
(vi))
$\mathbb {S}^\xi :=\{p \in \mathbb {Q}^{\leq \kappa }: \forall \delta \in \text {dom}(E^{\leq \kappa })\,\forall \beta \in R^{\delta }: \text {supp}(p(\delta ))\subseteq \text {supp}^{\delta }(\dot a_\xi ) \land \Delta ^{p(\delta )(\beta )} \subseteq \Delta ^{\delta , \beta }(\dot a_\xi )\}$
, and define
$\mathbb {S}^{\xi '}$
analogously.Figure 1 The supports at coordinate
$\delta \in \text {dom}(E^{\leq \kappa })$
of conditions in the sets defined in Definition 9, and how the maps
$\varphi , \psi , \varphi '$
and
$\psi '$
act on these sets. Note that conditions in
$\mathbb {S}^\xi $
live in the union of the regions labeled
$\mathbb {P}^\xi , \mathbb {R}^\xi ,$
and
$\mathbb {R}^{\mathsf {R}}$
(and analogously for
$\mathbb {S}^{\xi '}$
).
These sets, as well as the actions of
$\varphi , \psi , \varphi '$
and
$\psi '$
on them, are depicted in Figure 1. Note that
$\mathbb {R}^{\mathsf {R}} \cup \mathbb {R}^\xi \cup \mathbb {P}^\xi \subseteq \mathbb {S}^\xi $
.
Fact 3. The following properties are very easy to verify.
-
(i)
$\psi |_{\mathbb {R}^{\mathsf {R}}}=\psi |_{\mathbb {R}^{\mathsf {U}}}=\psi |_{\mathbb {R}^\xi }=\text {id}$
, and the same for
$\psi '$
in place of
$\psi $
. -
(ii)
$\psi [\mathbb {U}] = \mathbb {P}^\xi $
, and analogously
$\psi '[\mathbb {U}] = \mathbb {P}^{\xi '}$
. -
(iii)
$\varphi |_{\mathbb {R}^{\mathsf {R}}}=\text {id}$
, and the same for
$\varphi '$
in place of
$\varphi $
. -
(iv)
$\varphi [\mathbb {R}^{\mathsf {U}}] = \mathbb {R}^\xi $
, and analogously
$\varphi '[\mathbb {R}^{\mathsf {U}}] = \mathbb {R}^{\xi '}$
. -
(v)
$\psi |_{\mathbb {S}^{\xi '}}=\text {id}$
, and analogously
$\psi '|_{\mathbb {S}^{\xi }}=\text {id}$
. -
(vi)
$\varphi |_{\mathbb {S}^{\xi '}}=\text {id}$
, and analogously
$\varphi '|_{\mathbb {S}^{\xi }}=\text {id}$
. -
(vii)
$\varphi |_{\mathbb {P}^\xi }=\text {id}$
, and analogously
$\varphi '|_{\mathbb {P}^{\xi '}}=\text {id}$
.
Definition 10. Let
$\delta \in \text {dom}(E^{\leq \kappa })$
and let q and
$q'$
be
$\mathbb {Q}^{\delta }$
-conditions such that for all
$\beta \in b^\delta : \Delta ^{q(\delta )(\beta )}\cap \Delta ^{q'(\delta )(\beta )} = \emptyset $
. We define the condition
$q + q' := \langle q(\delta )(\beta )\cup q'(\delta )(\beta ): \beta \in b^\delta \rangle $
.
Furthermore, if p and
$p'$
are
$\mathbb {Q}^{\leq \kappa }$
conditions such that for all
$\delta \in \text {dom}(E^{\leq \kappa })$
and all
$\beta \in b^\delta : \Delta ^{q(\delta )(\beta )}\cap \Delta ^{q'(\delta )(\beta )} = \emptyset $
, we define
$$\begin{align*}p \oplus p':=\langle p(\delta)+ p'(\delta): \delta \in \text{dom}(E^{\leq \kappa})\rangle.\end{align*}$$
Fact 4. For every
$\theta \in \{\psi , \varphi , \psi ', \varphi '\}: \theta (p \oplus p')= \theta (p)\oplus \theta (p')$
.
Recall that the nice name
$\dot z$
is of the form
$\dot z=\bigcup _{\alpha \in \kappa }\{\check \alpha \}\times A_\alpha (\dot z)$
. Let
$\alpha \in \kappa $
and
$q \in A_\alpha (\dot z)$
. By construction, for every
$\delta \in \text {dom}(E^{\leq \kappa }): \text {supp}(q(\delta ))\subseteq U^{\delta }$
. We can therefore decompose q as
$q=\bar q \oplus u$
, where for every
$\delta \in \text {dom}(E^{\leq \kappa }): \text {supp}(\bar q(\delta ))\subseteq R^\delta $
and
$\text {supp}(u(\delta ))\subseteq U^\delta \setminus R^\delta $
. Again by construction, we have for every
$\beta \in b^\delta : \Delta ^{q(\delta )(\beta )} \subseteq U^{\delta , \beta }$
. We can thus further decompose
$\bar q$
as
$q^{\mathsf {R}} \oplus q^{\mathsf {U}}$
, where
$\Delta ^{q^{\mathsf {R}}(\delta )(\beta )}\subseteq R^{\delta , \beta }$
and
$\Delta ^{q^{\mathsf {U}}(\delta )(\beta )} \subseteq U^{\delta , \beta }\setminus R^{\delta , \beta }$
.
This gives us a decomposition
$q=q^{\mathsf {R}} \oplus q^{\mathsf {U}} \oplus u$
, where
$q^{\mathsf {R}} \in \mathbb {R}^{\mathsf {R}}$
,
$q^{\mathsf {U}} \in \mathbb {R}^{\mathsf {U}}$
and
$u \in \mathbb {U}$
.
Lemma 3. Define the automorphism
$$\begin{align*}\bar \chi:= \psi \circ \varphi \circ \varphi' \circ \psi' \circ \varphi \circ \psi,\end{align*}$$
i.e., we have
$\chi = \psi ' \circ \varphi ' \circ \bar \chi \circ \varphi \circ \psi $
. Then,
$\bar \chi |_{A_\alpha (\dot z)}=\text {id}$
for every
$\alpha \in \kappa $
.
Proof. Let
$\alpha \in \kappa $
and
$q \in A_\alpha (\dot z)$
. We decompose
$q=q^{\mathsf {R}} \oplus q^{\mathsf {U}} \oplus u$
as described above. From Fact 4 it follows that
$\bar \chi (q)=\bar \chi (q^{\mathsf {R}}) \oplus \bar \chi (q^{\mathsf {U}}) \oplus \bar \chi (u)$
, and it therefore suffices to show that
$q^{\mathsf {R}}$
,
$q^{\mathsf {U}}$
and u are fixed by
$\bar \chi $
. We use Fact 3.
Claim 1.
$\bar \chi (q^{\mathsf {R}})=q^{\mathsf {R}}$
.
Proof. This is clear, since all of
$\psi , \varphi , \psi '$
and
$\varphi '$
are the identity on
$\mathbb {R}^{\mathsf {R}}$
, by (i).
Claim 2.
$\bar \chi (q^{\mathsf {U}})=q^{\mathsf {U}}$
.
Proof. Firstly,
$\psi (q^{\mathsf {U}})= q^{\mathsf {U}} $
by (i). Next,
$\varphi (q^{\mathsf {U}}) \in \mathbb {R}^\xi $
by (iv). Thus,
$\varphi (q^{\mathsf {U}})$
is fixed by the next two automorphisms
$\psi '$
and then
$\varphi '$
, by (i) and (vi), respectively. Then we again apply
$\varphi $
to get
$\varphi (\varphi (q^{\mathsf {U}}))= q^{\mathsf {U}} $
. Finally,
$q^{\mathsf {U}} $
is fixed by
$\psi $
by (i).
Claim 3.
$\bar \chi (u)=u$
.
Proof. Firstly,
$\psi (u) \in \mathbb {P}^\xi $
by (ii). Thus,
$\psi (u)$
is fixed by
$\varphi $
by (vii), by
$\psi '$
by (v), by
$\varphi '$
by (vi) and then again by
$\varphi $
by (vii). The final application of
$\psi $
gives
$\psi (\psi (u))=u$
.
This finishes the proof of Lemma 3.
We are now ready to prove that
$\chi $
does what we want it to do.
Lemma 4. The automorphism
$$\begin{align*}\chi:=\psi' \circ \varphi' \circ \psi \circ \varphi \circ \varphi' \circ \psi' \circ \varphi \circ \psi \circ \varphi \circ \psi\end{align*}$$
satisfies
$\chi (\dot a_\xi )=\dot a_{\xi '}$
and
$\chi (\dot a_{\xi '})=\dot a_{\xi }$
.
Proof. We begin with the first equality. We have
$\dot a_{\xi }=\bigcup _{\alpha \in \kappa } \{\check \alpha \}\times A_\alpha (\dot a_\xi )$
and thus,
$\chi (\dot a_\xi )= \bigcup _{\alpha \in \kappa } \{\check \alpha \}\times \chi [A_\alpha (\dot a_\xi )]$
. Therefore, we must show that for every
$\alpha \in \kappa : \chi [A_\alpha (\dot a_\xi )]=A_\alpha (\dot a_{\xi '})$
.
Let
$\alpha \in \kappa $
. First, we deal with
$\chi [A_\alpha (\dot a_\xi )] \subseteq A_\alpha (\dot a_{\xi '})$
. Thus, let
$p\in A_\alpha (\dot a_\xi )$
. We know that
$\varphi \circ \psi (\dot a_\xi )= \dot z$
, which implies that
$q:=\varphi \circ \psi (p)\in A_\alpha (\dot z)$
. We also know that
$\psi ' \circ \varphi ' (\dot z)=\dot a_{\xi '}$
, and therefore
$\psi ' \circ \varphi ' (q) \in A_\alpha (\dot a_{\xi '})$
. Since
$\bar \chi (q)=q$
by Lemma 3, we indeed obtain
$$\begin{align*}\chi(p)=\psi' \circ \varphi' \circ \bar \chi \circ \varphi \circ \psi (p)\in A_\alpha(\dot a_{\xi'}).\end{align*}$$
The reverse inclusion
$A_\alpha (\dot a_\xi ) \supseteq \chi ^{-1}[A_\alpha (\dot a_{\xi '})]$
follows from essentially the same proof: Note that
$\chi ^{-1}=\psi \circ \varphi \circ \bar \chi ^{-1} \circ \varphi ' \circ \psi '$
, and by Lemma 3,
$\bar \chi ^{-1}$
is the identity on
$A_\alpha (\dot z)$
as well.
To show the second equality, i.e.,
$\chi (\dot a_{\xi '})=\dot a_\xi $
, we again fix
$\alpha \in \kappa $
and show
$\chi [A_\alpha (\dot a_{\xi '})]=A_\alpha (\dot a_\xi )$
. Here, we have to deal with the entire
$\chi $
at once, we again use Fact 3. To verify the direction “
$\subseteq $
”, let
$p' \in A_\alpha (\dot a_{\xi '})$
. Since
$p' \in \mathbb {S}^{\xi '}$
, we have
$\psi (p')=p'$
by (v) and
$\varphi (p')=p'$
by (vi). The next two automorphisms map
$p'$
to
$\varphi '(\psi '(p'))$
, which is equal to a condition
$q \in A_\alpha (\dot z)$
, since
$\varphi '(\psi '(\dot a_{\xi '}))=\dot z$
. Then, q is mapped to
$\psi (\varphi (q))$
, which is some
$p \in A_\alpha (\dot a_{\xi })$
, because
$\psi (\varphi (\dot z))=\dot a_\xi $
. The last two automorphisms
$\varphi '$
and
$\psi '$
fix p, again by (v) and (vi).
Finally, the proof of the reverse inclusion
$\chi [A_\alpha (\dot a_{\xi '})] \supseteq A_\alpha (\dot a_\xi )$
is analogous and left as an exercise to the reader.
3. Globally large tower spectra
Next, we show that arbitrarily large tower spectra at all regular cardinals simultaneously are consistent. In fact, we show that
$\mathfrak {sp}(\mathfrak {t}_{\text {cl}}(\kappa ))$
can be arbitrarily large globally. The forcing notion we use is similar to a part of the forcing notion developed by Hechler in [Reference Hechler7], designed to force the existence of many
$\omega $
-towers.
Theorem 3. Let
$\mathbf {V}\models \mathsf {GCH}$
and let E be an Easton function. There is a forcing extension of
$\mathbf {V}$
in which
$$\begin{align*}\forall \kappa \in \text{dom}(E): \mathfrak{sp}(\mathfrak{t}(\kappa))=\mathfrak{sp}(\mathfrak{t}_{\text{cl}}(\kappa)) =[\kappa^{+}, 2^\kappa], \text{ where } 2^\kappa=E(\kappa).\end{align*}$$
Proof. We begin by defining the relevant forcing notion.
Definition 11. Define for each
$\kappa \in \text {dom}(E)$
the set
$\mathcal {I}^{\kappa }:=\{\langle \kappa , \xi \rangle : \xi \in E(\kappa )\}$
, which serves as an index set. The purpose of the entry
$\kappa $
is to ensure that the different
$\mathcal {I}^{\kappa }$
are disjoint.
For each
$\kappa \in \text {dom}(E)$
, let
$\mathbb {T}^{\kappa }$
consist of conditions
$q: \Delta ^{q} \times \eta ^{q} \to 2$
, where
${\Delta ^{q} \in [\mathcal {I}^{\kappa }]^{{<}\kappa }}$
and
$\eta ^{q} \in \kappa \setminus \{0\}$
. Let
$q' \leq q$
iff
-
(i)
$q \subseteq q' $
, -
(ii) For all
$\xi < \xi ' \text { with } \langle \kappa , \xi \rangle , \langle \kappa , \xi '\rangle \in \Delta ^{q}$
and for all
$\eta ^{q}\leq \mu < \eta ^{q'}: q'(\langle \kappa , \xi \rangle , \mu )=0 \implies q'(\langle \kappa , \xi ' \rangle , \mu )=0$
.
Let
$\mathbb {T}$
be the Easton-product of the
$\mathbb {T}^\kappa $
.
Lemma 5. Let
$\kappa \in \text {dom}(E)$
and decompose
$\mathbb {T}$
as
$\mathbb {T}^{\leq \kappa } \times \mathbb {T}^{{>}\kappa }$
. Then,
$\mathbb {T}^{{>}\kappa } $
is
$\kappa ^{+}$
-closed and
$\mathbb {T}^{\leq \kappa }$
satisfies the
$\kappa ^{+}$
-c.c.
Proof. The first statement is easy to verify. To show the second statement, let A be a
$\kappa ^{+}$
-sized set of
$\mathbb {T}^{\leq \kappa }$
-conditions. For each
$p\in A$
, let
$S_p:=\bigcup \{\Delta ^{p(\delta )}\times \eta ^{p(\delta )}: \delta \in \text {supp}(p)\}$
. Note that
$S_p$
has cardinality
${<}\kappa $
. By the
$\Delta $
-system Lemma, we obtain some
$A'\subseteq A$
of cardinality
$\kappa ^{+}$
and for each
$\delta \in \text {dom}(E^{\leq \kappa })$
some
$R^{\delta }\in [\mathcal {I}^{\delta }]^{{<}\delta }$
and some
$r^{\delta } \in \delta $
, such that for all these
$\delta $
and all
$p \neq p' \in A': (\Delta ^{p(\delta )}\times \eta ^{p(\delta )}) \cap (\Delta ^{p'(\delta )}\times \eta ^{p'(\delta )})= R^{\delta } \times r^{\delta } $
. Note that the set
$C:=\{\delta : R^{\delta } \times r^{\delta } \neq \emptyset \}$
has cardinality
${<}\kappa $
. For each
$\delta \in C$
, there is at most one
$p\in A'$
with
$\eta ^{p(\delta )}\neq r^{\delta }$
. By removing these
${<}\kappa $
many conditions, we can assume that no such p exist in
$A'$
.
The set
$\bigcup \{R^{\delta } \times r^{\delta }: \delta \in C \}$
has cardinality
${<}\kappa $
. By the
$\mathsf {GCH}$
, we have
$2^{{<}\kappa }=\kappa $
, and we can therefore assume that for all
$p,p' \in A'$
and all
$\delta \in \text {dom}(E^{\leq \kappa })$
, the functions
$p(\delta )$
and
$p'(\delta )$
agree on the intersection of their domains. It is now easy to verify that the conditions in
$A'$
are pairwise compatible.
It follows by standard methods that
Corollary 2.
$\mathbb {T}$
preserves cofinalities and hence cardinals.
See, for example, the proof of Easton’s Theorem in [Reference Kunen9, Chapter VIII and Lemma 4.6].
Proposition 1. Let
$\mathbf {V}\models \textrm {GCH}$
and let G be
$\mathbb {T}$
-generic over
$\mathbf {V}$
. Then, for any
${\kappa \in \text {dom}(E)}$
and any regular
$\lambda \in [\kappa ^{+}, E(\kappa )]$
, there is a
$\kappa $
-tower of length
$\lambda $
consisting of clubs in
$\mathbf {V}[G]$
.
Proof. Let
$\kappa \in \text {dom}(E)$
and
$\lambda \in [\kappa ^{+}, E(\kappa )]$
. As before, decompose
$\mathbb {T}$
as
$\mathbb {T}^{\leq \kappa } \times \mathbb {T}^{{>}\kappa }$
and
$G=G^{\leq \kappa }\times G^{{>}\kappa }$
accordingly. Since
$\mathbb {T}^{{>}\kappa }$
is
$\kappa ^{+}$
-closed, the
$\mathsf {GCH}$
at
$\delta \leq \kappa $
still holds in
$\mathbf {V}[G ^{> \kappa }]$
and
$(\mathbb {T}^{\leq \kappa })^{\mathbf {V}[G ^{> \kappa }]}=(\mathbb {T}^{\leq \kappa })^{\mathbf {V}}$
. We work in
$\mathbf {W}:=\mathbf {V}[G ^{> \kappa }]$
.
Since
$\kappa $
and
$\lambda $
are fixed and since we are only interested in the
$\kappa $
-th coordinate of each
$\mathbb {T}^{\leq \kappa }$
-condition p, define for notational simplicity for each
$p \in \mathbb {T}^{\leq \kappa } $
the following abbreviation
$q_p$
:
-
(i)
$\forall \xi \in E(\kappa )\;\forall \alpha \in \kappa : q_p(\xi , \alpha ):=p(\kappa )(\langle \kappa , \xi \rangle , \alpha ).$
-
(ii)
$\Delta ^{q_p}:= \Delta ^{p(\kappa )}.$
-
(iii)
$\eta ^{q_p}:=\eta ^{p(\kappa )}$
.
In
$\mathbf {W}[G^{\leq \kappa }]$
, define for each
$\xi \in E(\kappa )$
the
$\kappa $
-real
$g_\xi := \{\alpha \in \kappa : \exists p \in G^{\leq \kappa }: q_p(\xi , \alpha ) =1\}$
. We assume that
$\lambda < E(\kappa )$
and define
$a_\xi :=\text {cl}(g_\xi \setminus g_\lambda )$
for all
$\xi < \lambda $
. We show that the sequence
$\langle a_{\xi }: \xi \in \lambda \rangle $
is a
$\kappa $
-tower of length
$\lambda $
in
$\mathbf {W}[G^{\leq \kappa }]$
. If
$\lambda = E(\kappa )$
, it follows by a very similar but simplified argument that setting
$a_\xi := \text {cl}(g_\xi )$
yields a
$\kappa $
-tower of length
$E(\kappa )$
.
It is easy to see that
$\langle g_{\xi }: \xi \in E(\kappa )\rangle $
is well-ordered by
$\supseteq ^{*}$
, and therefore,
$\langle a_{\xi }: \xi \in \lambda \rangle $
is as well. In order to show that
$\langle a_{\xi }: \xi \in \lambda \rangle $
does not have a pseudo-intersection in
$\mathbf {W}[G^{\leq \kappa }]$
, let
$\dot x$
be a
$\mathbb {T}^{\leq \kappa }$
-name for a subset of
$\kappa $
and
$p_0 \in G^{\leq \kappa }$
a condition such that
$p_0 \Vdash {"}|\dot x|=\kappa "$
. For each
$\alpha \in \kappa $
, let
$A_{\alpha }$
be a maximal antichain deciding
$"\alpha \in \dot x"$
. By the
$\kappa ^{+}$
-c.c. of
$\mathbb {T}^{\leq \kappa }$
, the set
$\Delta := \bigcup \{\Delta ^{q_p}: p \in A_\alpha ,\;\alpha \in \kappa \}$
has cardinality at most
$\kappa $
. Thus, by regularity of
$\lambda $
, there exists
$\langle \kappa , \xi _0\rangle \in \mathcal {I}^{\kappa }$
such that
$\xi < \xi _0 < \lambda $
for every
$\xi < \lambda $
with
$\langle \kappa , \xi \rangle \in \Delta $
. We show that for every
$\nu \in \kappa $
, the set of conditions forcing
$"\dot x \setminus \nu \nsubseteq \dot {a}_{\xi _0}"$
is dense below
$p_0$
.
Let
$p \leq p_0$
. By extending p, we can assume that
$\langle \kappa , \lambda \rangle \in \Delta ^{q_p}$
. Since
$p \Vdash {"}|\dot x|=\kappa " $
, there exists
$\alpha _0> \max \{\eta ^{q_p}, \nu \}$
and
$\bar p \leq p$
with
$\bar p \Vdash \check \alpha _0 \in \dot x$
. Therefore
$\bar p$
is compatible with some
$r \in A_{\alpha _0}$
via some common extension s. In particular, p and r are compatible via s. Without loss of generality, we can assume that
$\langle \xi _0, \alpha _0 \rangle , \langle \lambda , \alpha _0\rangle \in \text {dom}(q_s)$
.
Note that for all
$\xi _0 \leq \xi < \lambda $
and all
$\max \{\eta ^{q_p}, \nu \}\leq \alpha \leq \alpha _0$
with
$\langle \xi , \alpha \rangle \in \text {dom}(q_{s}):\langle \xi , \alpha \rangle \notin \text {dom}(q_p) \cup \text {dom}(q_r)$
, since
$\alpha \geq \eta ^{q_p}$
and by the choice of
$\xi _0$
. Therefore, we can set
$\bar s$
equal to s except that for all such
$\xi $
and
$\alpha : q_{\bar s}(\xi , \alpha ):=\min \{q_s(\xi , \alpha ),\,q_s(\lambda , \alpha )\}$
. It follows that
$\bar s$
is a common extension of p and r, and for every
$\max \{\eta ^{q_p}, \nu \}\leq \alpha \leq \alpha _0: \;\bar s \Vdash {"}\check \alpha \in \dot g_{\xi _0} \implies \check \alpha \in \dot g_{\lambda }"$
. Thus,
$\bar s \Vdash {"}\check \alpha _0 \in \dot x \setminus \text {cl}(\dot g_{\xi _0}\setminus \dot g_{\lambda })"$
, finishing the proof of the proposition.
Lastly, it can be checked easily, by counting nice
$\mathbb {T}^{\leq \kappa }$
-names for subsets of
$\kappa $
, that
$\forall \kappa \in \text {dom}(E): 2^\kappa =E(\kappa )$
in every
$\mathbb {T}$
-generic extension of
$\mathbf {V}\models \mathsf {GCH}$
.
Corollary 3. In the above extension,
$\mathfrak {b}(\kappa )=\kappa ^{+}$
for every
$\kappa \in \text {dom}(E)$
.
Proof. For uncountable
$\kappa $
, this follows from Lemma 1. In the case
$\kappa =\omega $
, it can easily be seen that the forcing notion
$\mathbb {T}^{\omega }$
densely embeds into the part of the forcing notion introduced by Hechler [Reference Hechler7] that deals with towers. The first author, Koelbing and Wohofsky [Reference Fischer, Koelbing and Wohofsky6, Corollary 5.1] have shown that the latter forces
$\mathfrak {b}(\omega )=\omega _1$
, by showing that it decomposes as a finite support iteration of Mathias forcings that preserve the unboundedness of ground model scales.
4. A locally bounded tower spectrum
Our final result establishes that the
$\kappa $
-tower spectrum may consistently have any upper bound below
$2^\kappa $
, where this upper bound is given by
$\mathfrak {b}(\kappa )$
.
Theorem 4. Assume
$\mathbf {V}\models \mathsf {GCH}$
. Let
$\kappa < \beta $
be regular and let
$\mu $
be such that
${\text {cf}(\mu )\geq \beta }$
. There is a generic extension of
$\mathbf {V}$
in which
$$\begin{align*}\mathfrak{sp}(\mathfrak{t}(\kappa))\subseteq [\kappa^{+}, \mathfrak{b}(\kappa)], \text{ where } \mathfrak{b}(\kappa)=\beta \text{ and } 2^\kappa=\mu.\end{align*}$$
Proof. We begin by briefly sketching the idea of the proof. We force
$\mathfrak {b}(\kappa )=\beta $
and
$2^\kappa =\mu $
using a non-linear iteration of
$\kappa $
-Hechler forcing. Non-linear iterations of Hechler forcing at
$\omega $
were introduced by Hechler in [Reference Hechler8] and generalized to the uncountable by Cummings and Shelah in [Reference Cummings and Shelah3]. The strategy is to force the existence of a cofinal embedding from some partial order
$\mathbb {Q}$
into the partial order
$(\kappa ^\kappa , \leq ^{*})$
, where an order-preserving embedding
$f: \mathbb {Q} \to \mathbb {Q}'$
is cofinal iff
$\forall p \in \mathbb {Q}'\; \exists q \in \mathbb {Q}: p \leq _{\mathbb {Q}'}f(q)$
. By choosing a
$\mathbb {Q}$
with appropriate bounding and dominating properties, one obtains the desired values of
$\mathfrak {b}(\kappa )$
and
$\mathfrak {d}(\kappa )$
in the extension. These properties are formalized by the following definition.
Definition 12. Let
$\mathbb {Q}$
be a partially ordered set. We say that
$B \subseteq \mathbb {Q}$
is unbounded iff
$\forall q \in \mathbb {Q}\;\exists p \in B: p \nleq _{\mathbb {Q}}q$
. Let
$\mathfrak {b}(\mathbb {Q})$
be the minimal cardinality of an unbounded subset of
$\mathbb {Q}$
and let
$\mathfrak {d}(\mathbb {Q})$
be the minimal cardinality of a cofinal (or dominating) subset of
$\mathbb {Q}$
. Thus,
$\mathfrak {b}(\kappa )=\mathfrak {b}((\kappa ^\kappa , \leq ^{*}))$
and
$\mathfrak {d}(\kappa )=\mathfrak {d}((\kappa ^\kappa , \leq ^{*}))$
.
The following fact is easy to check.
Fact 5. If
$f: \mathbb {Q} \to \mathbb {Q}'$
is a cofinal embedding, then
$\mathfrak {b}(\mathbb {Q}')=\mathfrak {b}(\mathbb {Q})$
and
$\mathfrak {d}(\mathbb {Q}')=\mathfrak {d}(\mathbb {Q})$
.
Therefore, by choosing a
$\mathbb {Q}$
satisfying
$\mathfrak {b}(\mathbb {Q})=\beta $
and
$\mathfrak {d}(\mathbb {Q})=\mu $
in the forcing extension, we will obtain
$\mathfrak {b}(\kappa )=\beta $
and
$2^\kappa \geq \mathfrak {d}(\kappa )=\mu $
. The reverse inequality
${2^\kappa \leq \mu }$
will follow by counting nice names.
We then show that there are no
$\kappa $
-towers of length greater than
$\beta $
in the forcing extension, again due to an isomorphism of names. For this argument to succeed, we first use a preparatory forcing to obtain a particular partial order, one in which every element only lies above few others. This complication stems from the fact that we need to iterate along a well-founded partial order, where
$\mathbb {Q}$
is well-founded if every
$C \subseteq \mathbb {Q}$
contains a minimal element. While it is folklore that every partial order contains a cofinal, well-founded subset, choosing any such subset in our proof will not yield the upper bound we aim for. Note however that the preparatory forcing step could be skipped if we were to start with an inaccessible
$\beta $
.
Lemma 6. Assume
$\beta $
is regular,
$\beta ^{{<}\beta }=\beta $
and
$\mu $
is such that
$\text {cf}(\mu )\geq \beta $
. Consider the partial order
$([\mu ]^{<\beta }, \subseteq )$
. There is a
$\beta $
-closed,
$\beta ^{+}$
-c.c. forcing notion
$\mathbb {P}$
that adds a cofinal subset
$\mathbb {Q}^{*}\subseteq [\mu ]^{{<}\beta }$
, satisfying:
-
(i)
$\mathbb {Q}^{*}$
is well-founded, -
(ii) For all
$x \in \mathbb {Q}^{*}: |\{y \in \mathbb {Q}^{*}: y \subseteq x\}| < \beta $
, -
(iii)
$\mathfrak {b}(\mathbb {Q}^{*})=\beta $
, -
(iv)
$\mathfrak {d}(\mathbb {Q}^{*})=|\mathbb {Q}^{*}|=\mu $
.
Proof. Let p be a
$\mathbb {P}$
-condition iff p is a well-founded subset of
$[\mu ]^{{<}\beta }$
of cardinality
${<}\beta $
. The order is given by
$$\begin{align*}q \leq p:\iff p \subseteq q \;\,\text{and}\,\; \forall x \in p \;\forall y \in q \setminus p: y \nsubseteq x.\end{align*}$$
Claim 4.
$\mathbb {P}$
is
$\beta $
-closed and satisfies the
$\beta ^{+}$
-c.c.
Proof. Checking the first part is routine. For the second part, let
$A\in [\mathbb {P}]^{\beta ^{+}}$
. Applying the
$\Delta $
-system Lemma to the family
$\{\bigcup p: p \in A\}$
yields some
$A' \subseteq A$
of cardinality
$\beta ^{+}$
and a root
$R \in [\mu ]^{{<}\beta }$
. There are at most
$2^{{<}\beta }=\beta $
many subsets of R, and since
$\beta ^{{<}\beta }=\beta $
, we can assume that
$p \cap \mathcal {P}(R)$
does not depend on
$p \in A'$
. It follows that the
$p \in A'$
are pairwise compatible.
Now, let H be
$\mathbb {P}$
-generic over
$\mathbf {V}$
and define
$\mathbb {Q}^{*}:=\bigcup H$
. By the above claim, cardinalities and cofinalities are preserved in
$\mathbf {V}[H]$
and we have
$([\mu ]^{<\beta })^{\mathbf {V}[H]}=([\mu ]^{<\beta })^{\mathbf {V}}$
.
It is easy to see that for every
$x \in [\mu ]^{{<}\beta }$
, the set
$\mathcal {D}_x:=\{p \in \mathbb {P}: \exists y \in p: y \supseteq x\}$
is open dense in
$\mathbb {P}$
, by adding
$\bigcup p \cup x$
to the p in question. Thus,
$\mathbb {Q}^{*}$
is indeed cofinal in
$[\mu ]^{{<}\beta }$
. Well-foundedness of
$\mathbb {Q}^{*}$
follows from H being directed. By the same reason, we have that for every
$x \in \mathbb {Q}^{*}: \{y \in \mathbb {Q}^{*}: y \subseteq x\} \subseteq p$
, where
$p \in H$
is any condition containing x. Thus
$|\{y \in \mathbb {Q}^{*}: y \subseteq x\}| < \beta $
.
It remains to show (iii) and (iv). In order to verify
$\mathfrak {b}(\mathbb {Q}^{*})=\beta $
and
$\mathfrak {d}(\mathbb {Q}^{*})=\mu $
, it suffices, by Fact 5, to verify
$\mathfrak {b}(([\mu ]^{<\beta }, \subseteq ))= \beta $
and
$\mathfrak {d}(([\mu ]^{<\beta }, \subseteq ))=\mu $
in
$\mathbf {V}[H]$
. To check the first statement, note that by regularity of
$\beta $
, every
$B \subseteq [\mu ]^{<\beta }$
of cardinality
${<}\beta $
is bounded. On the other hand, for any
$X \in [\mu ]^{\beta }$
, the set
$\{\{\eta \}: \eta \in X\}$
is unbounded, which yields
$\mathfrak {b}(([\mu ]^{<\beta }, \subseteq ))= \beta $
.
Similarly, any
$D \subseteq [\mu ]^{<\beta }$
of cardinality
${<}\mu $
cannot be dominating, since
$\bigcup D \neq \mu $
. This gives us
$\mathfrak {d}([\mu ]^{<\beta })\geq \mu $
. The reverse inequality holds because
$|[\mu ]^{<\beta }|=\mu $
, which follows by the assumption
$\text {cf}(\mu )\geq \beta $
and by the
$\mathsf {GCH}$
in
$\mathbf {V}$
. Since
$\mathbb {Q}^{*}$
is itself cofinal, this also yields
$|\mathbb {Q}^{*}|=\mu $
.
We now fix some
$\mathbb {P}$
-generic H and designate
$\mathbf {W}:=\mathbf {V}[H]$
as the new ground model. Note that since
$\mathbb {P}$
is
$\beta $
-closed, the
$\mathsf {GCH}$
still holds at all cardinals below
$\beta $
and
$\rho ^{\kappa }=\rho $
for all
$\rho $
with
$\text {cf}(\rho )>\kappa $
.
Definition 13 (see [Reference Cummings and Shelah3, Theorem 1])
Let
$\mathbb {Q}$
be any well-founded partially ordered set. Extend
$\mathbb {Q}$
to
$\mathbb {Q}\cup \{\text {top}\}$
, where
$\forall a \in \mathbb {Q}:\text {top}> a$
. Denote by
$\mathbb {Q}_a$
the partial order
$\mathbb {Q}_{a}:=\{b \in \mathbb {Q}: b < a\}$
, so that
$\mathbb {Q}=\mathbb {Q}_{\text {top}}$
. By induction, we define for each
$a \in \mathbb {Q} \cup \{\text {top}\}$
the forcing notion
$\mathbb {D}(\mathbb {Q}_a)$
. Assume
$\mathbb {D}(\mathbb {Q}_b)$
is already defined for all
$b < a$
. We let p be a
$\mathbb {D}(\mathbb {Q}_a)$
-condition iff:
-
(i) p is a function with
$\text {dom}(p)\in [\mathbb {Q}_{a}]^{{<}\kappa }$
. -
(ii) For each
$b \in \text {dom}(p): p(b)=\langle s,\dot {f}\rangle $
, where
$s\in {^{{<}\kappa }}\kappa $
and
$\dot {f}$
is a nice
$\mathbb {D}(\mathbb {Q}_b)$
-name for an element of
$\kappa ^\kappa $
. That is,
$\dot f$
is of the form
${\dot f=\bigcup _{\langle \alpha _1, \alpha _2\rangle \in \kappa \times \kappa }\{\text {op}(\check {\alpha }_1, \check {\alpha }_2)\} \times A_{\langle \alpha _1, \alpha _2 \rangle }}$
, where
$A_{\langle \alpha _1, \alpha _2 \rangle }$
is an antichain in
$\mathbb {D}(\mathbb {Q}_b)$
and
$\Vdash _{\mathbb {D}(\mathbb {Q}_b)} \dot f \in {\check {\kappa }^\kappa }$
.
Let
$q \leq p$
iff
-
(a)
$\text {dom}(p) \subseteq \text {dom}(q)$
, -
(b) For all
$b \in \text {dom}(p)$
, if
$p(b)=\langle s, \dot {f}\rangle $
and
$q(b)=\langle t, \dot {g}\rangle $
, then
$s\subseteq t$
and
$$\begin{align*}q|_{\mathbb{Q}_b}\Vdash_{\mathbb{D}(\mathbb{Q}_b)} \begin{cases} \forall \eta \in \kappa: \dot{f}(\eta) \leq \dot{g}(\eta) \;\;\text{and}\\ \forall \eta \in \text{dom}(t)\setminus \text{dom}(s): t(\eta)> \dot{f}(\eta). \end{cases} \end{align*}$$
Finally,
$\mathbb {D}(\mathbb {Q})=\mathbb {D}(\mathbb {Q}_{\text {top}})$
.
Lemma 7. Let
$\mathbb {Q}$
be any well-founded partial order. Then the following holds.
-
(i)
$\mathbb {D}(\mathbb {Q})$
is
$\kappa $
-closed. -
(ii)
$\mathbb {D}(\mathbb {Q})$
satisfies the
$\kappa ^{+}$
-c.c. -
(iii) Let
$\mathbb {A}\subseteq \mathbb {Q}$
be downward-closed, i.e., for all
$p \in \mathbb {A}$
and
$q \in \mathbb {Q} : q \leq _{\mathbb {Q}}p \implies q \in \mathbb {A}$
. Then
$\mathbb {D}(\mathbb {A})$
is a complete suborder of
$\mathbb {D}(\mathbb {Q})$
. -
(iv) Assume
$|\mathbb {Q}|^{\kappa } = |\mathbb {Q}| $
. There are at most
$|\mathbb {Q}|$
many nice
$\mathbb {D}(\mathbb {Q})$
-names for subsets of
$\kappa $
.
Proof. Parts (i) and (ii) are proved in [Reference Cummings and Shelah3, Claims 1 and 2]. Part (iii) is straightfoward to check. For part (iv), let
$|\mathbb {Q}|= \rho $
with
$\rho ^\kappa =\rho $
and let
$a \in \mathbb {Q}\cup \{\text {top}\}$
. Assume by induction that for all
$b < a$
there are at most
$\rho $
many nice
$\mathbb {D}(\mathbb {Q}_b)$
-names for subsets of
$\kappa $
. In particular, there are at most
$\rho $
many nice
$\mathbb {D}(\mathbb {Q}_b)$
-names for elements of
$\kappa ^\kappa $
. Since
$\mathbb {D}(\mathbb {Q}_a)$
satisfies the
$\kappa ^{+}$
-c.c., the number of nice
$\mathbb {D}(\mathbb {Q}_a)$
-names for subsets of
$\kappa $
is bounded by
$|\mathbb {D}(\mathbb {Q}_a)|^{\kappa }$
. Note that
$|\mathbb {D}(\mathbb {Q}_a)| \leq |\mathbb {Q}_a|^{{<}\kappa } \cdot \kappa ^{<\kappa } \cdot \rho ^{{<}\kappa }$
by the induction hypothesis. This is at most
$\rho $
, because
$\mathbb {Q}_a\subseteq \mathbb {Q}$
and
$\rho ^{{<}\kappa }=\rho $
, which finally yields that there are at most
$\rho ^\kappa =\rho $
nice
$\mathbb {D}(\mathbb {Q}_a)$
-names for subsets of
$\kappa $
.
Lemma 8. [Reference Cummings and Shelah3, Theorem 1]
Let
$\mathbb {Q}$
be any well-founded partial order with
$\mathfrak {b}(\mathbb {Q})\geq \kappa ^{+}$
. In any
$\mathbb {D}(\mathbb {Q})$
-generic extension,
$\mathbb {Q}$
can be cofinally embedded into
$(\kappa ^\kappa , \leq ^{*})$
.
Corollary 4. Let G be
$\mathbb {D}(\mathbb {Q}^{*})$
-generic over
$\mathbf {W}$
, where
$\mathbb {Q}^{*}$
is from Lemma 6. Then,
$$\begin{align*}\mathbf{W}[G]\models \mathfrak{b}(\kappa)=\beta \;\,\text{and}\;\, 2^\kappa=\mathfrak{d}(\kappa)=\mu.\end{align*}$$
Proof. We have
$|\mathbb {Q}^{*}|=\mu $
by Lemma 6 (iv), which implies by Lemma 7 (iv) that there are at most
$\mu $
many nice
$\mathbb {D}(\mathbb {Q}^{*})$
-names for subsets of
$\kappa $
. Thus,
$\mathbf {W}[G]\models 2^\kappa \leq \mu $
. In order to verify the remaining claims, it suffices by the above Lemma 8 and by Fact 5 to check that
$\mathfrak {b}(\mathbb {Q}^{*})=\beta $
and
$\mathfrak {d}(\mathbb {Q}^{*})=\mu $
still holds in
$\mathbf {W}[G]$
. However, this very easily follows from
$\mathbb {D}(\mathbb {Q}^{*})$
satisfying the
$\kappa ^{+}$
-c.c.
Proposition 2. Let G be
$\mathbb {D}(\mathbb {Q}^{*})$
-generic over
$\mathbf {W}$
. Then
$\mathbf {W}[G]\models \mathfrak {sp}(\mathfrak {t}(\kappa )) \subseteq [\kappa ^{+}, \beta ]$
.
Proof. Assume towards a contradiction that
$\langle a_\xi : \xi \in \beta ^{+}\rangle $
is a strictly
$\supseteq ^{*}$
-descending sequence in
$\mathbf {W}[G]$
. For each
$\xi \in \beta ^{+}$
, let
$\dot {a}_\xi =\bigcup _{\alpha \in \kappa }\{\check {\alpha }\}\times A_\alpha ^\xi $
be a nice
$\mathbb {D}(\mathbb {Q}^{*})$
-name for
$a_\xi $
. Assume
$p_0\in \mathbb {D}(\mathbb {Q}^{*})$
is such that for all
$\xi < \xi ' < \beta ^{+}: p_0 \Vdash _{\mathbb {D}(\mathbb {Q}^{*})} \dot {a}_\xi \supsetneq ^{*} \dot {a}_{\xi '}$
.
Define for every
$\xi \in \beta ^{+}$
the set
$$\begin{align*}d_\xi:=\bigcup \{x: x \in \text{dom}(p), \;p \in A_\alpha^\xi,\;\alpha \in \kappa\} \;\cup\; \bigcup \{x: x \in \text{dom}(p_0)\},\end{align*}$$
which is a subset of
$\mu $
of size
${<}\beta $
. Since
$\mathbb {Q}^{*}$
is cofinal in
$[\mu ]^{<\beta }$
, we find for each
$\xi \in \beta ^{+}$
some
$D_\xi \supseteq d_\xi $
in
$\mathbb {Q}^{*}$
. As noted before, the
$\mathsf {GCH}$
holds in
$\mathbf {W}$
below
$\beta $
and we may therefore apply the
$\Delta $
-system Lemma to the family
$\{D_\xi : \xi \in \beta ^{+}\}$
to obtain some
$X \subseteq \beta ^{+}$
of cardinality
$\beta ^{+}$
and a root R. Set
$\mathbb {Q}^{*}_\xi :=\{y \in \mathbb {Q}^{*}: y \subseteq D_\xi \}$
and
$\mathbb {R}:=\{y \in \mathbb {Q}^{*}: y \subseteq R\}$
. Note that
$\mathbb {R}$
is the root of the
$\mathbb {Q}^{*}_\xi $
. By Lemma 6 (ii), we have
$| \mathbb {Q}^{*}_\xi |<\beta $
, and we may therefore assume by the pigeonhole principle that
$\forall \xi \in X: |\mathbb {Q}^{*}_\xi |=\theta < \beta $
.
Claim 5. There exists
$X'\subseteq X$
of cardinality
$\beta ^{+}$
such that for all
$\xi , \xi '\in X'$
, there is an order-preserving isomorphism
$\psi _{\xi , \xi '}: \mathbb {Q}^{*}_\xi \to \mathbb {Q}^{*}_{\xi '}$
with
$\psi _{\xi , \xi '}|_{\mathbb {R}}=\text {id}$
.
Proof. To see this, let L be some set of cardinality
$|\mathbb {Q}^{*}_\xi \setminus \mathbb {R}|$
disjoint from
$\mathbb {R}$
. For each
$\xi \in X$
, we can map
$\mathbb {Q}^{*}_\xi $
bijectively to
$L \cup \mathbb {R}$
, such that this bijection restricted to
$\mathbb {R}$
is the identity. This bijection induces a partial order on
$L \cup \mathbb {R}$
. Since there are at most
$2^\theta \leq \beta $
many partial orders on
$L \cup \mathbb {R}$
, we find the desired
$X'$
as well as the isomorphisms
$\psi _{\xi , \xi '}$
by the pigeonhole principle.
Define the downward-closed partially ordered set
$\mathbb {A}:=\bigcup _{\xi \in X'}\mathbb {Q}^{*}_{\xi }$
. Note that by definition of
$D_\xi $
,
$\dot a_\xi $
is a nice
$\mathbb {D}(\mathbb {Q}^{*}_\xi )$
-name and thus a nice
$\mathbb {D}(\mathbb {A})$
-name. Furthermore,
$p_0$
is a
$\mathbb {D}(\mathbb {R})$
-condition. For a fixed
$\xi _0 \in X'$
, the isomorphism
$\psi _{\xi , \xi _0}$
extends to an automorphism of order 2 of
$\mathbb {A}$
, which we denote by
$\psi _{\xi }$
. This automorphism
$\psi _{\xi }$
naturally induces an automorphism
$\varphi _{\xi }$
of
$\mathbb {D}(\mathbb {A})$
in the obvious way: Let
${a \in \mathbb {A}\cup \{\text {top}\}}$
and assume by induction that for every
$b< a$
, the isomorphism
$$\begin{align*}\varphi_{\xi}|_{\mathbb{D}(\mathbb{A}_b)}: \mathbb{D}(\mathbb{A}_b) \to \mathbb{D}(\mathbb{A}_{\psi_{\xi}(b)})\end{align*}$$
has been defined (note the abuse of notation). In particular, this isomorphism extends to
$\mathbb {D}(\mathbb {A}_b)$
-names. Now let p be any
$\mathbb {D}(\mathbb {A}_a)$
-condition. We write for every
$b \in \text {dom}(p): p(b)=\langle s(b), \dot f(b)\rangle $
, and define
$$\begin{align*}\varphi_{\xi}|_{\mathbb{D}(\mathbb{A}_a)}(p):=q, \;\text{where}\; \begin{cases} \text{dom}(q):=\psi_{\xi}[\text{dom}(p)] \;\;\text{and}\\ \forall \psi_{\xi}(b) \in \text{dom}(q): q(\psi_{\xi}(b)):= \langle s(b), \varphi_{\xi}|_{\mathbb{D}(\mathbb{A}_b)}(\dot f)\rangle \end{cases} \end{align*}$$
It follows by induction that
$\varphi _{\xi }$
is an automorphism and that
$\varphi _{\xi }|_{\mathbb {D}(\mathbb {R})}=\text {id}$
.
Note that
$\varphi _{\xi }(\dot a_\xi )$
is a nice
$\mathbb {D}(\mathbb {Q}^{*}_{\xi _0})$
-name and that by Lemma 7 (iv), there are at most
$|\mathbb {Q}^{*}_{\xi _0}|<\beta $
many nice
$\mathbb {D}(\mathbb {Q}^{*}_{\xi _0})$
-names for subsets of
$\kappa $
. Thus, we can extract
$X" \subseteq X'$
of cardinality
$\beta ^{+}$
such that
$\varphi _{\xi }(\dot a_\xi )$
is the same nice
$\mathbb {D}(\mathbb {Q}^{*}_{\xi _0})$
-name for all
$\xi \in X"$
.
Fix
$\xi < \xi ' \in X"\setminus \{\xi _0\}$
and define the automorphism
$\chi _{\xi , \xi '}:=\varphi _{\xi '} \circ \varphi _{\xi } \circ \varphi _{\xi '}$
of
$\mathbb {A}$
. By construction,
$\chi _{\xi , \xi '}(\dot a_\xi )=\dot a_{\xi '}$
,
$\chi _{\xi , \xi '}(\dot a_{\xi '})=\dot a_{\xi }$
and
$\chi _{\xi , \xi '}(p_0)=p_0$
. Since
$\mathbb {D}(\mathbb {A})$
is a complete suborder of
$\mathbb {D}(\mathbb {Q}^{*})$
by Lemma 7 (iii), we have
$p_0 \Vdash _{\mathbb {D}(\mathbb {A})} \dot a_\xi \supsetneq ^{*} \dot a_{\xi '} $
, which yields the contradiction
$p_0 \Vdash _{\mathbb {D}(\mathbb {A})} \dot a_{\xi '} \supsetneq ^{*} \dot a_{\xi } \land \dot a_{\xi } \supsetneq ^{*} \dot a_{\xi '}$
, just as in the proof of Theorem 1.
Together with Lemma 1, the above Theorem yields the following corollary.
Corollary 5. Let
$\kappa < \beta $
be regular uncountable and let
$\mu $
be such that
$\text {cf}(\mu )\geq \beta $
. Then, consistently,
$$\begin{align*}\mathfrak{sp}(\mathfrak{t}_{\text{cl}}(\kappa)) =\{\beta\} \text{ and } 2^\kappa=\mu.\end{align*}$$
As a final remark, note that by Lemma 1 and Lemma 2, the upper bound given by Theorem 4 is tight, in the sense that there always exists a
$\kappa $
-tower of length
$\mathfrak {b}(\kappa )$
, if
$\kappa $
is uncountable or if
$\mathfrak {b}(\omega )<\mathfrak {d}(\omega )$
. If both
$\kappa =\omega $
and
$\beta =\mu $
however, a well-founded cofinal subset of the partial order
$([\beta ]^{<\beta }, \subseteq )$
as in Lemma 6 is given by the well-ordered set
$\beta $
, in which case we have a simple finite-support,
$\beta $
-stage linear iteration of Hechler forcing, and thus no
$\omega $
-tower of length
$\beta =\mathfrak {b}(\omega )$
in the extension, as was shown by Baumgartner and Dordal [Reference Baumgartner and Dordal2, Theorem 4.1]
5. Open problems
Our first question is whether a global version of the result in Section 4 is consistent. More concretely:
Question 1. Let E be an index function attaining values
$E(\kappa )=\langle \beta (\kappa ), \mu (\kappa )\rangle $
, such that
$\kappa ^{+} \leq \text {cf}(\beta (\kappa ))=\beta (\kappa ) \leq \text {cf}(\mu (\kappa ))$
for every
$\kappa \in \text {dom}(E)$
and such that
$\kappa < \kappa ' \implies \mu (\kappa )\leq \mu (\kappa ')$
. Is it consistent that for every
$\kappa \in \text {dom}(E): \mathfrak {sp}(\mathfrak {t}(\kappa )) \subseteq [\kappa ^{+}, \mathfrak {b}(\kappa )]$
, where
$\mathfrak {b}(\kappa )=\beta (\kappa )$
and
$2^\kappa =\mu (\kappa )$
?
Cummings and Shelah [Reference Cummings and Shelah3, Theorem 4] have shown that the global separation of
$\mathfrak {b}(\kappa )$
and
$2^\kappa $
as above is consistent. The issue is whether the bound on the tower spectrum carries over to their construction, which uses an Easton-tail iteration (i.e., a hybrid between Easton-iteration and Easton-product). An analogous question is whether a global non-trivial lower bound on the tower spectrum is consistent, i.e.,
Question 2. To what extent can the characteristic
$\mathfrak {t}(\kappa )$
be controlled globally?
Here, the complication lies in the fact that the generalized continuum function and the class function
$\kappa \to \mathfrak {t}(\kappa )$
are strongly correlated: If
$\kappa \leq \delta < \mathfrak {t}(\kappa )$
, then
$2^\delta =2^\kappa $
, as was shown by Shelah and Spasojević [Reference Shelah and Spasojević11, Main Lemma 2.1].
Finally, strengthening both of the above questions:
Question 3. Let E be an index function such that
$E(\kappa )$
is a set of regular cardinals for all
$\kappa \in \text {dom}(E)$
. Is it consistent that
$$\begin{align*}\forall \kappa \in \text{dom}(E): \mathfrak{sp}(\mathfrak{t}(\kappa))=E(\kappa)?\end{align*}$$
Acknowledgments
We thank the anonymous referee for their very helpful corrections and suggestions.
Funding
This research was funded in whole or in part by the Austrian Science Fund (FWF) through project START Y1012 [10.55776/Y1012]. The second author would additionally like to thank the Swiss European Mobility Programme (SEMP) for financially supporting his stay at the University of Vienna.
Open access
