No CrossRef data available.
Article contents
Angular momentum and energy transport in disc–jet systems: Unravelling the contribution of saturated thermal conduction
Published online by Cambridge University Press: 21 March 2024
Abstract
This study builds upon our prior work to further explore and unravel the effects of saturated thermal conduction within a viscous resistive MHD framework on the intricate transport mechanisms of angular momentum and energy in disc-jet systems. We conducted a series of 2.5-dimensional non-relativistic time-dependent numerical simulations using the PLUTO code. Employing a saturation parameter spanning [0.002-0.01], our results are consistent with previous investigations that omitted consideration of thermal conduction, affirming the established understanding that kinetic torque plays a predominant role in governing the total accretion angular momentum, surpassing the magnetic contribution within the disc. At the initial time steps of our calculations, we find that thermal conduction enhances this kinetic contribution, while concurrently diminishing the effect of magnetic contribution. In contrast to the prevailing influence of kinetic torque within the disc, we also assert the magnetic torque as the primary contributor to the total ejection angular momentum. We further unveil that doubling the saturation parameter leads to bolstering of approximately 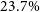 $23.7\%$ in the integral dominance of magnetic torque compared to kinetic torque within the jet. Our findings reveal that doubling the effect of thermal conduction improves the integral total accretion power by approximately 2%, thereby slightly amplifying the energy content within the system and increasing overall energy output. We underscore that as the local energy dissipation within the disc intensifies, the significance of the enthalpy accretion flux increases at the expense of the jet power. We reveal that increasing the saturation parameter mitigates enthalpy accumulation within the disc, and further restricts the jet’s energy extraction from the disc. This limitation is determined in our analysis through the decrease in the integral ratio between the bipolar jet and liberated power of approximately
$23.7\%$ in the integral dominance of magnetic torque compared to kinetic torque within the jet. Our findings reveal that doubling the effect of thermal conduction improves the integral total accretion power by approximately 2%, thereby slightly amplifying the energy content within the system and increasing overall energy output. We underscore that as the local energy dissipation within the disc intensifies, the significance of the enthalpy accretion flux increases at the expense of the jet power. We reveal that increasing the saturation parameter mitigates enthalpy accumulation within the disc, and further restricts the jet’s energy extraction from the disc. This limitation is determined in our analysis through the decrease in the integral ratio between the bipolar jet and liberated power of approximately 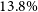 $13.8\%$, for twice the strength of the saturation parameter. We identify the Poynting flux as the primary contributor to total jet power, with thermal conduction exerting minimal influence on magnetic contributions. Additionally, we emphasise the integration of jet enthalpy as another significant factor in determining overall jet power, highlighting a distinct correlation between the rise in saturation parameter and heightened enthalpy contribution. Moreover, we observe the promotion of Poynting flux over kinetic flux at advanced time steps of our simulations, a trend supported by the presence of thermal conduction, which demonstrates an integral increase of approximately
$13.8\%$, for twice the strength of the saturation parameter. We identify the Poynting flux as the primary contributor to total jet power, with thermal conduction exerting minimal influence on magnetic contributions. Additionally, we emphasise the integration of jet enthalpy as another significant factor in determining overall jet power, highlighting a distinct correlation between the rise in saturation parameter and heightened enthalpy contribution. Moreover, we observe the promotion of Poynting flux over kinetic flux at advanced time steps of our simulations, a trend supported by the presence of thermal conduction, which demonstrates an integral increase of approximately 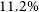 $11.2\%$ when considering a doubling of the saturation parameter.
$11.2\%$ when considering a doubling of the saturation parameter.
Keywords
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press on behalf of Astronomical Society of Australia



