Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Kahkeshani, Soroush
and
Di Carlo, Dino
2016.
Drop formation using ferrofluids driven magnetically in a step emulsification device.
Lab on a Chip,
Vol. 16,
Issue. 13,
p.
2474.
Morris, Jeffrey F.
2016.
High-speed trains: in microchannels?.
Journal of Fluid Mechanics,
Vol. 792,
Issue. ,
p.
1.
Gao, Yanfeng
Magaud, Pascale
Baldas, Lucien
Lafforgue, Christine
Abbas, Micheline
and
Colin, Stéphane
2017.
Self-ordered particle trains in inertial microchannel flows.
Microfluidics and Nanofluidics,
Vol. 21,
Issue. 10,
Haddadi, Hamed
and
Di Carlo, Dino
2017.
Inertial flow of a dilute suspension over cavities in a microchannel.
Journal of Fluid Mechanics,
Vol. 811,
Issue. ,
p.
436.
Martel-Foley, Joseph M.
2017.
Microtechnology for Cell Manipulation and Sorting.
p.
193.
Gupta, Anupam
Magaud, Pascale
Lafforgue, Christine
and
Abbas, Micheline
2018.
Conditional stability of particle alignment in finite-Reynolds-number channel flow.
Physical Review Fluids,
Vol. 3,
Issue. 11,
Yuan, Dan
Zhao, Qianbin
Yan, Sheng
Tang, Shi-Yang
Alici, Gursel
Zhang, Jun
and
Li, Weihua
2018.
Recent progress of particle migration in viscoelastic fluids.
Lab on a Chip,
Vol. 18,
Issue. 4,
p.
551.
Hood, Kaitlyn
and
Roper, Marcus
2018.
Pairwise interactions in inertially driven one-dimensional microfluidic crystals.
Physical Review Fluids,
Vol. 3,
Issue. 9,
Del Giudice, Francesco
D’Avino, Gaetano
Greco, Francesco
Maffettone, Pier Luca
and
Shen, Amy Q.
2018.
Fluid Viscoelasticity Drives Self-Assembly of Particle Trains in a Straight Microfluidic Channel.
Physical Review Applied,
Vol. 10,
Issue. 6,
Fan, Liang-Liang
Yan, Qing
Zhe, Jiang
and
Zhao, Liang
2018.
Single particle train ordering in microchannel based on inertial and vortex effects.
Journal of Micromechanics and Microengineering,
Vol. 28,
Issue. 6,
p.
065011.
Yuan, Chen
Pan, Zhenhai
and
Wu, Huiying
2018.
Inertial migration of single particle in a square microchannel over wide ranges of Re and particle sizes.
Microfluidics and Nanofluidics,
Vol. 22,
Issue. 9,
Pan, Zhenhai
Zhang, Runlin
Yuan, Chen
and
Wu, Huiying
2018.
Direct measurement of microscale flow structures induced by inertial focusing of single particle and particle trains in a confined microchannel.
Physics of Fluids,
Vol. 30,
Issue. 10,
Tatsumi, Kazuya
Kawano, Koki
Shintani, Hiromichi
and
Nakabe, Kazuyoshi
2019.
Particle Timing Control and Alignment in Microchannel Flow by Applying Periodic Force Control Using Dielectrophoretic Force.
Analytical Chemistry,
Vol. 91,
Issue. 10,
p.
6462.
Chung, Aram J.
2019.
A Minireview on Inertial Microfluidics Fundamentals: Inertial Particle Focusing and Secondary Flow.
BioChip Journal,
Vol. 13,
Issue. 1,
p.
53.
Pedrol, Eric
Massons, Jaume
Díaz, Francesc
and
Aguiló, Magdalena
2019.
Study of Local Inertial Focusing Conditions for Spherical Particles in Asymmetric Serpentines.
Fluids,
Vol. 5,
Issue. 1,
p.
1.
Gao, Yanfeng
Magaud, Pascale
Lafforgue, Christine
Colin, Stéphane
and
Baldas, Lucien
2019.
Inertial lateral migration and self-assembly of particles in bidisperse suspensions in microchannel flows.
Microfluidics and Nanofluidics,
Vol. 23,
Issue. 7,
Belotti, Yuri
Tolomeo, Serenella
Conneely, Michael J.
Huang, Tianjun
McKenna, Stephen J.
Nabi, Ghulam
and
McGloin, David
2019.
High-Throughput, Time-Resolved Mechanical Phenotyping of Prostate Cancer Cells.
Scientific Reports,
Vol. 9,
Issue. 1,
Dietsche, Claudius
Mutlu, Baris R.
Edd, Jon F.
Koumoutsakos, Petros
and
Toner, Mehmet
2019.
Dynamic particle ordering in oscillatory inertial microfluidics.
Microfluidics and Nanofluidics,
Vol. 23,
Issue. 6,
Asghari, Mohammad
Serhatlioglu, Murat
Saritas, Resul
Guler, Mustafa Tahsin
and
Elbuken, Caglar
2019.
Tape’n roll inertial microfluidics.
Sensors and Actuators A: Physical,
Vol. 299,
Issue. ,
p.
111630.
Schaaf, Christian
Rühle, Felix
and
Stark, Holger
2019.
A flowing pair of particles in inertial microfluidics.
Soft Matter,
Vol. 15,
Issue. 9,
p.
1988.
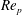 $\mathit{Re}_{p}$ ), is a key parameter, where
$\mathit{Re}_{p}$ ), is a key parameter, where 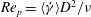 $\mathit{Re}_{p}=\langle \dot{\unicode[STIX]{x1D6FE}}\rangle D^{2}/\unicode[STIX]{x1D708}$ depends on the mean shear rate
$\mathit{Re}_{p}=\langle \dot{\unicode[STIX]{x1D6FE}}\rangle D^{2}/\unicode[STIX]{x1D708}$ depends on the mean shear rate  $\langle \dot{\unicode[STIX]{x1D6FE}}\rangle$ , particle diameter
$\langle \dot{\unicode[STIX]{x1D6FE}}\rangle$ , particle diameter 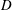 $D$ and fluid kinematic viscosity
$D$ and fluid kinematic viscosity  $\unicode[STIX]{x1D708}$ . Controlling the location of inertial focusing positions and the interparticle distance is critical in applications such as flow cytometry, imaging and cell entrapment in droplets. By using experimental observations in rectangular microchannels and lattice Boltzmann numerical simulations of dilute suspension flow, the spacing between particles aligned in trains is measured. From the modes of the probability density function of interparticle spacing, preferred spacings at
$\unicode[STIX]{x1D708}$ . Controlling the location of inertial focusing positions and the interparticle distance is critical in applications such as flow cytometry, imaging and cell entrapment in droplets. By using experimental observations in rectangular microchannels and lattice Boltzmann numerical simulations of dilute suspension flow, the spacing between particles aligned in trains is measured. From the modes of the probability density function of interparticle spacing, preferred spacings at 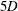 $5D$ and
$5D$ and 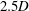 $2.5D$ are observed. At lower
$2.5D$ are observed. At lower 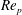 $\mathit{Re}_{p}$ , the preferred spacing forms around
$\mathit{Re}_{p}$ , the preferred spacing forms around 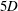 $5D$ , and with increasing
$5D$ , and with increasing 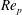 $\mathit{Re}_{p}$ the spacing at
$\mathit{Re}_{p}$ the spacing at 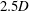 $2.5D$ becomes more pronounced. With increasing concentration of the suspension the spacing is influenced by particle crowding effects until stable trains are no longer observed.
$2.5D$ becomes more pronounced. With increasing concentration of the suspension the spacing is influenced by particle crowding effects until stable trains are no longer observed.

